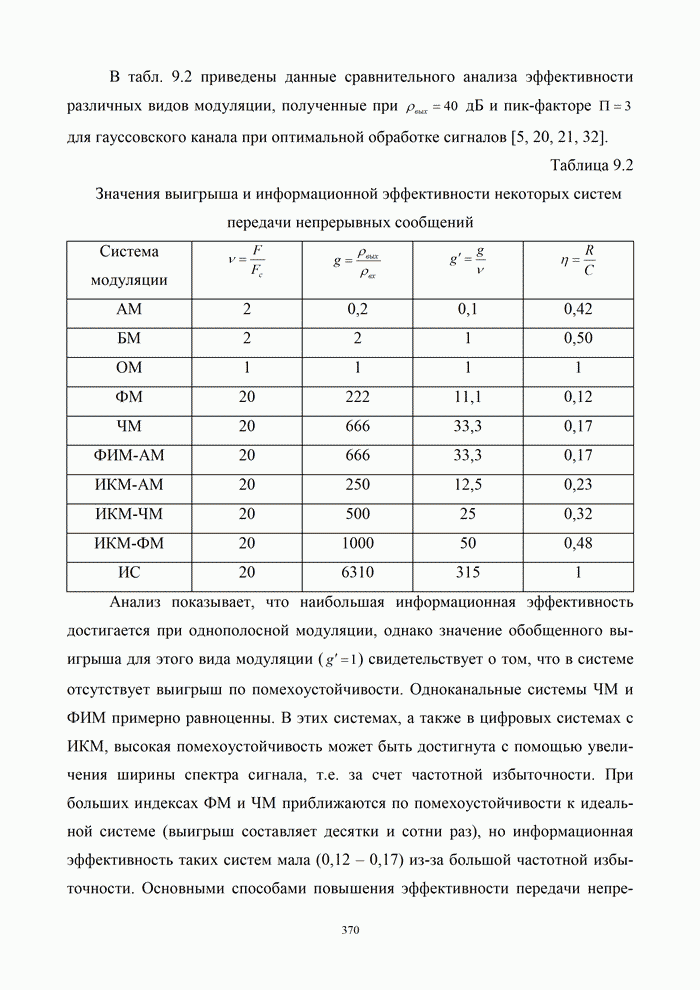
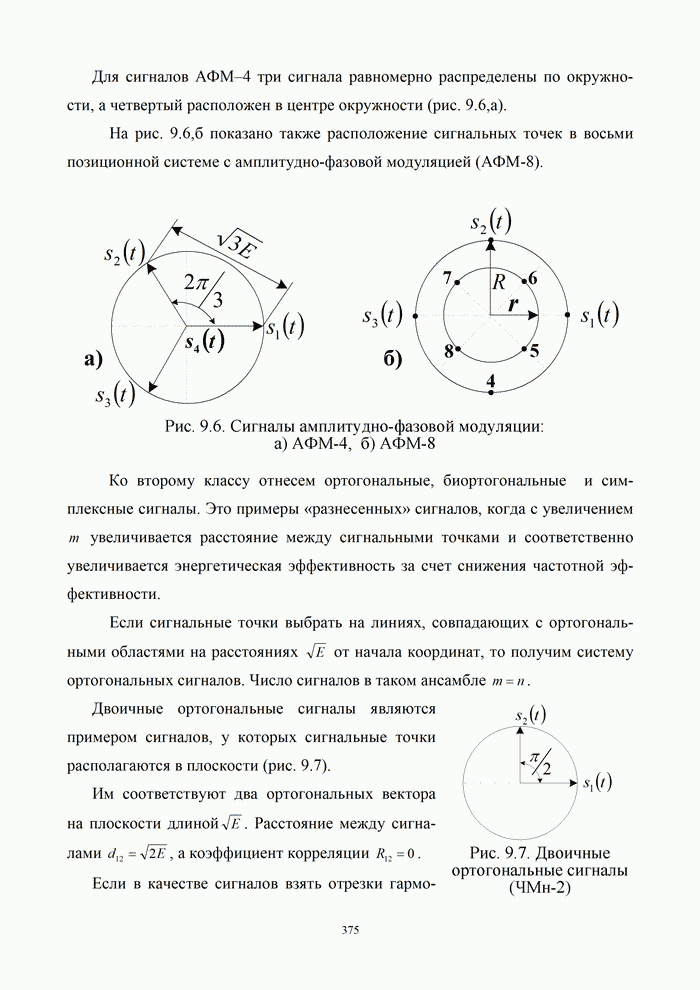
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
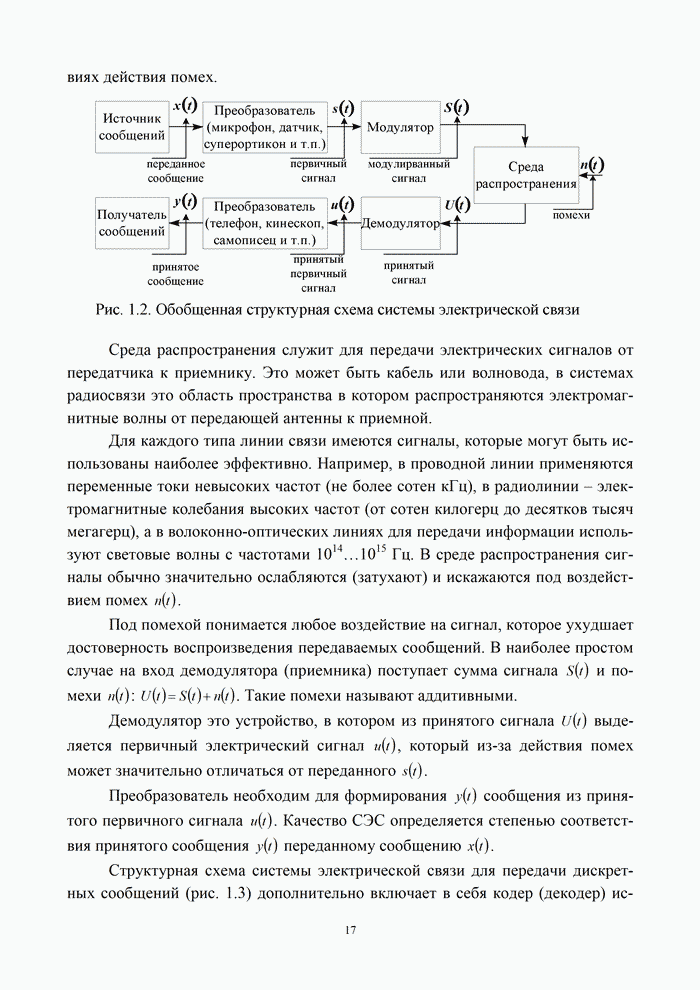
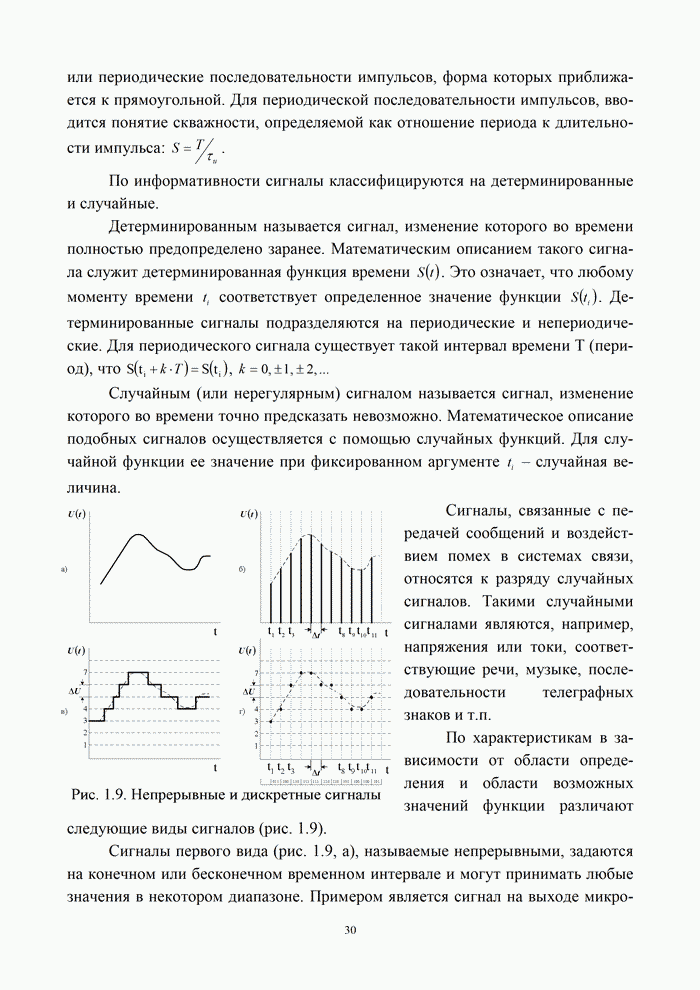
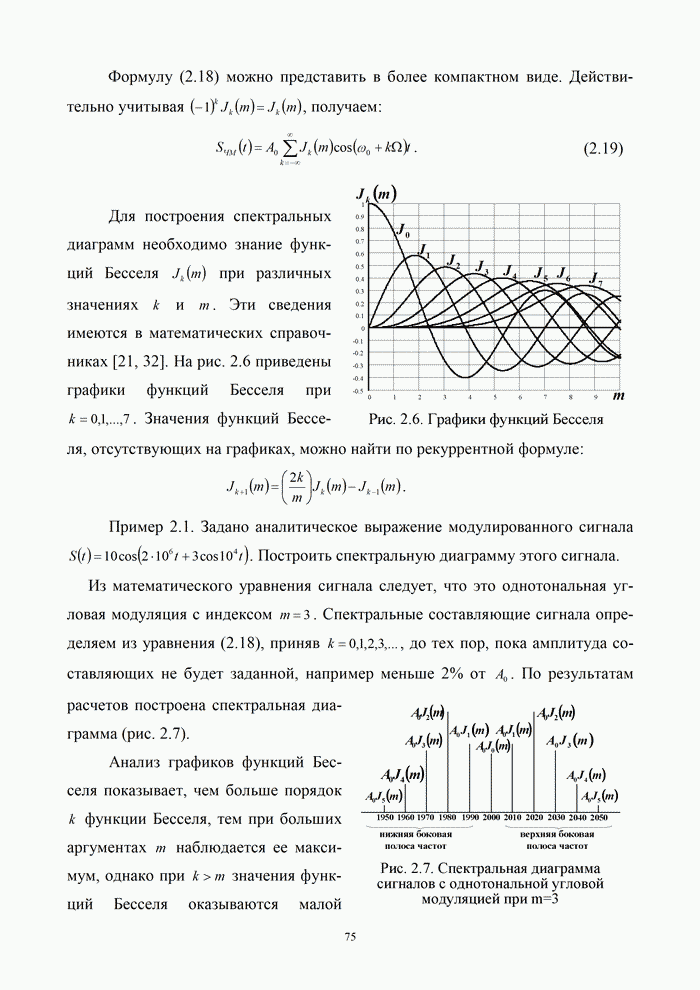
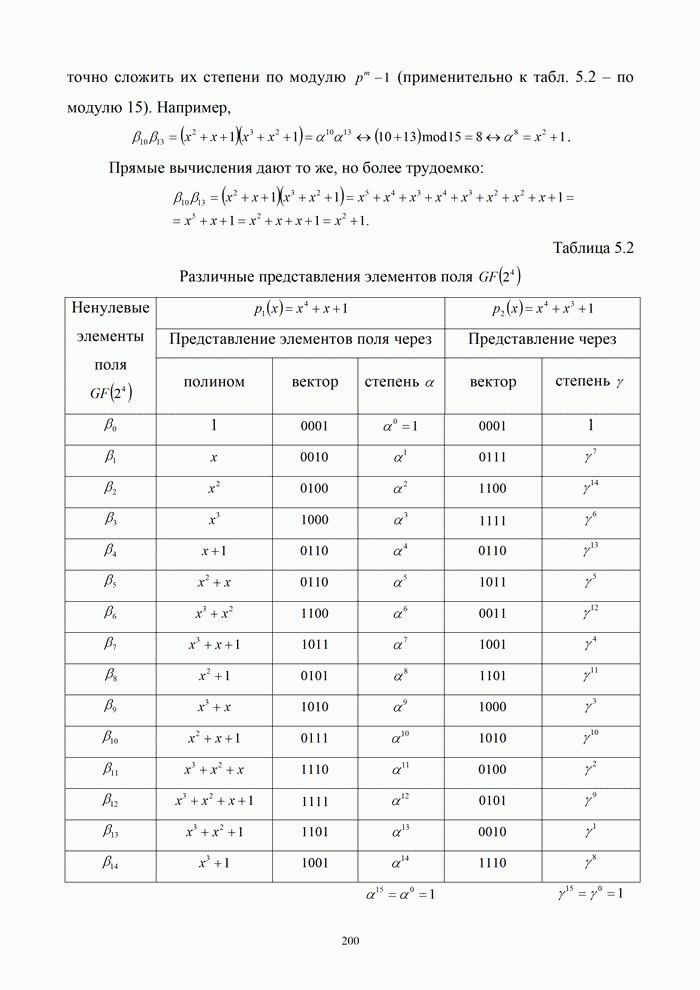
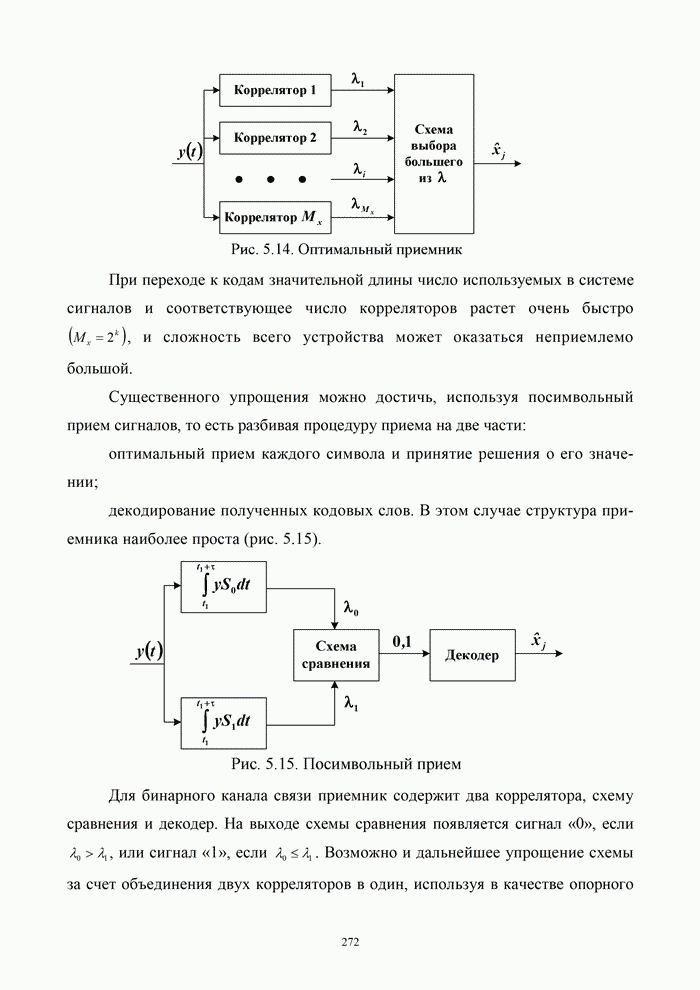
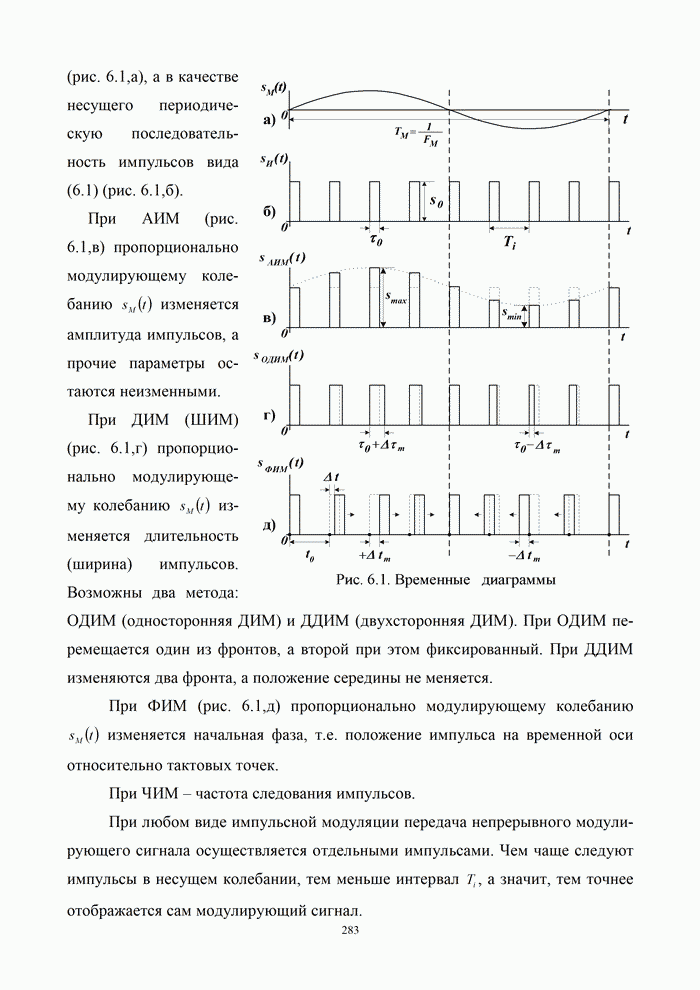
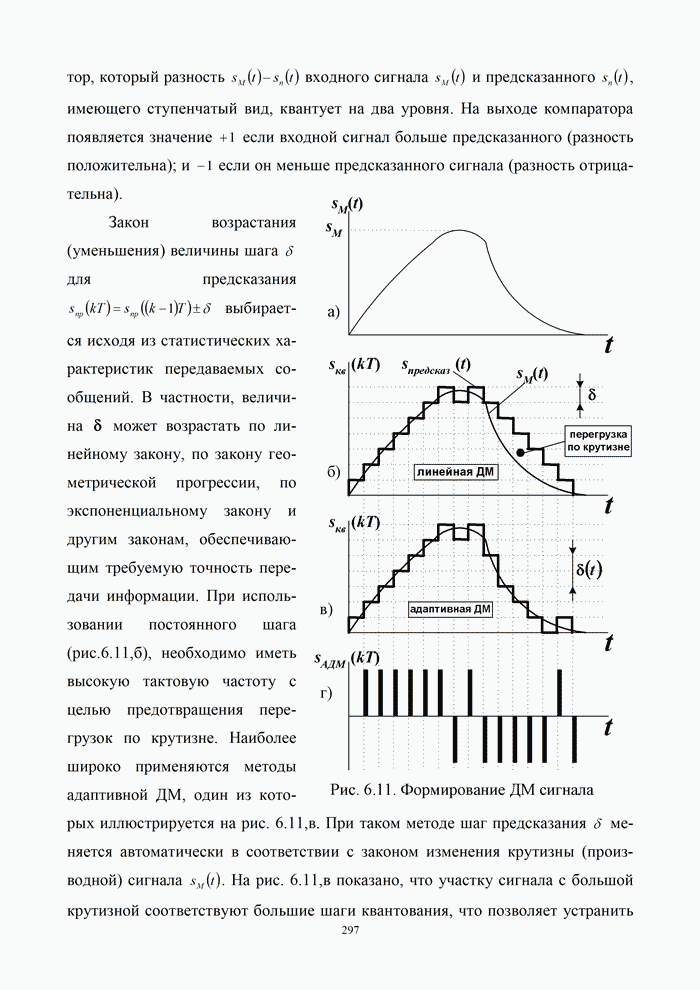
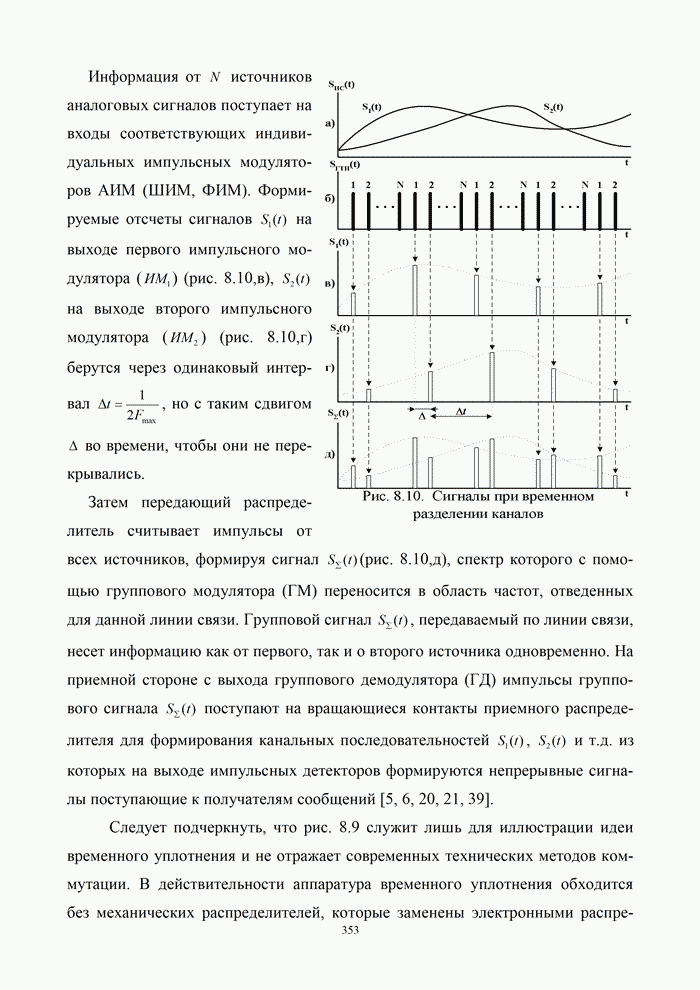
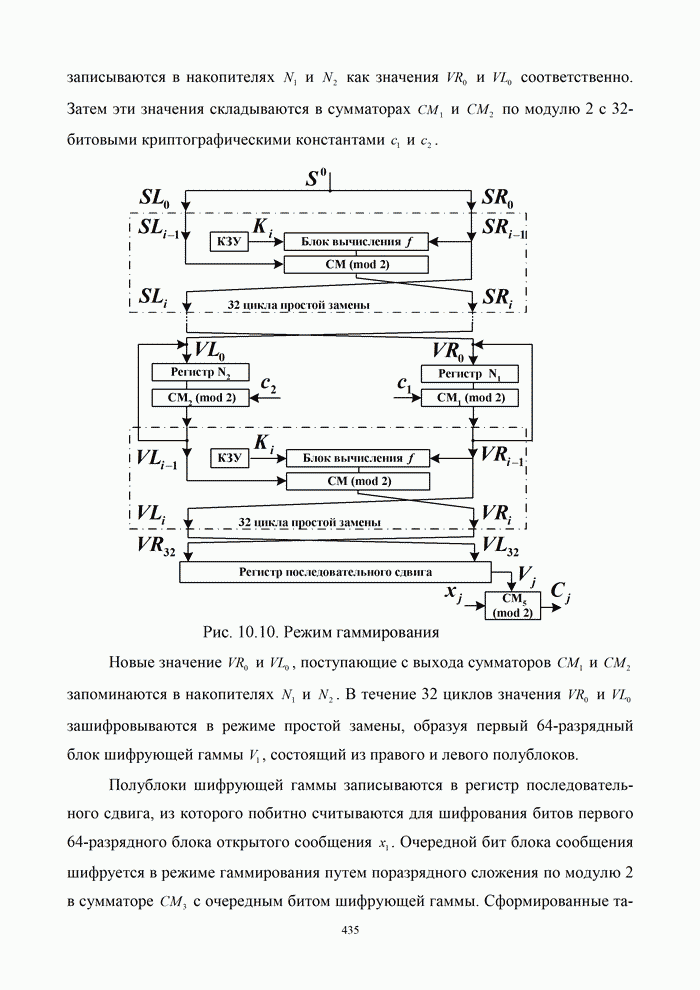
9.5. Алгоритмы цифровой обработки сигналов
9.5.1. Дискретные сигналы и их спектры
Дискретизация
непрерывного сигнала. С аналитической точки зрения процедуру получения дискретизированного
(дискретного) сигнала ![]() удобно рассматривать как
непосредственное умножение непрерывного сигнала
удобно рассматривать как
непосредственное умножение непрерывного сигнала ![]() на вспомогательную последовательность
на вспомогательную последовательность ![]() дискретизирующих
прямоугольных импульсов единичной амплитуды
дискретизирующих
прямоугольных импульсов единичной амплитуды
|
|
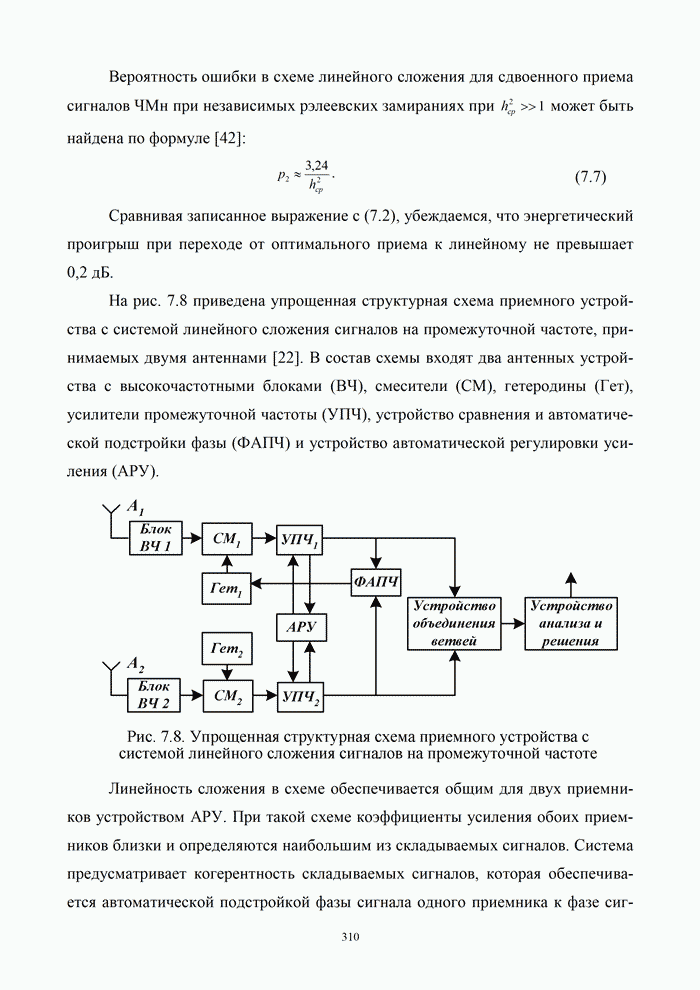
(9.24) |
Длительность
дискретизирующих импульсов ![]() должна быть много меньше интервала
дискретизации
должна быть много меньше интервала
дискретизации ![]() .
.
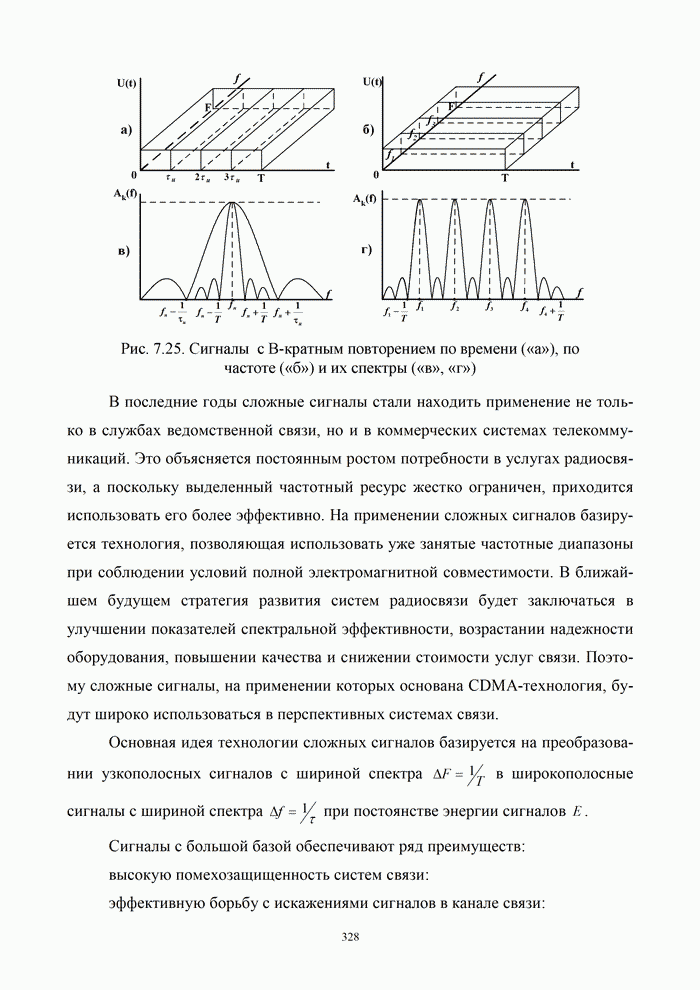
Принцип формирования
дискретного сигнала показан на рис. 7.7, б…в, где изображены графики функций ![]()
![]()
![]() . При этом реальный дискретный сигнал
. При этом реальный дискретный сигнал ![]() имеет вид
импульсно-модулированного колебания, т. е. АИМ-сигнала.
имеет вид
импульсно-модулированного колебания, т. е. АИМ-сигнала.

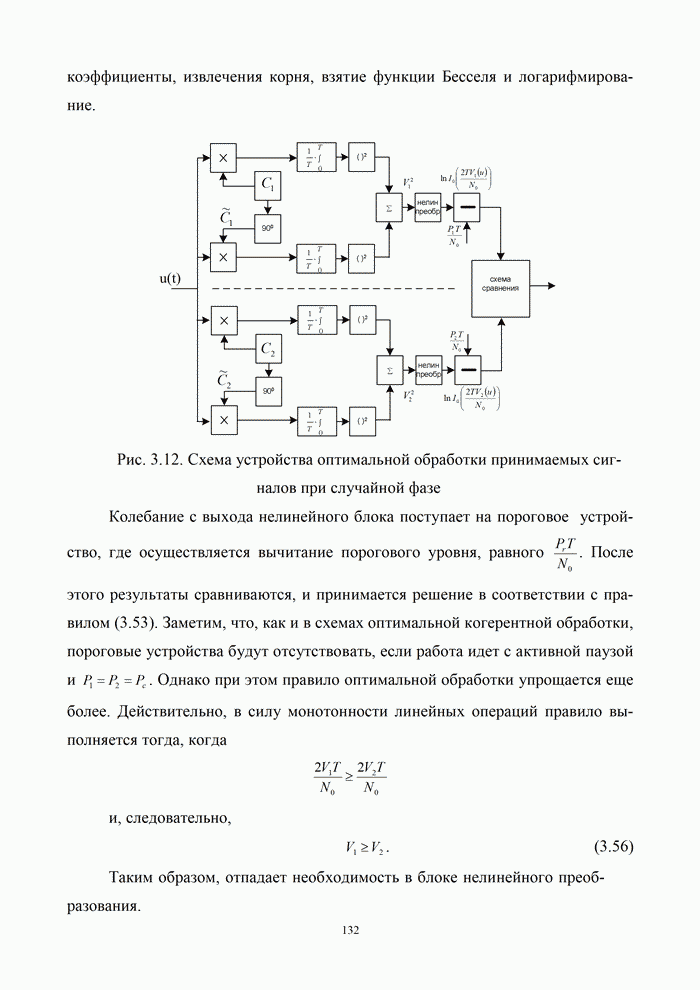
Рис.9.14. Дискретизация сигналов
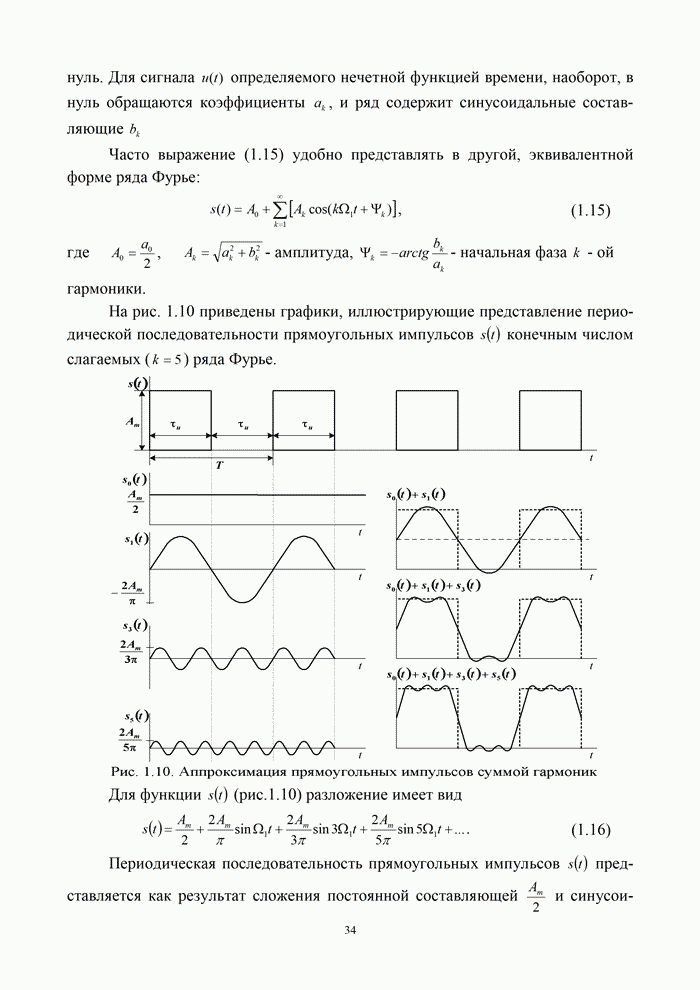
Спектр дискретного
сигнала. Чтобы дать оценку требованиям к длительности дискретизирующих
импульсов, определим спектральный состав дискретного сигнала ![]() . Пусть некоторый
непрерывный сигнал
. Пусть некоторый
непрерывный сигнал ![]() имеет
спектральную плотность
имеет
спектральную плотность ![]() . Представим последовательность
дискретизирующих прямоугольных импульсов
. Представим последовательность
дискретизирующих прямоугольных импульсов ![]() рядом Фурье, в котором частота
рядом Фурье, в котором частота ![]() :
:
|
|
(9.25) |
где
|
|
(9.26) |
Подставив формулу (9.25) в (9.24), получим
|
|
(9.27) |
Проанализируем первое и
второе слагаемые этого выражения отдельно. Первому слагаемому соответствует
спектральная плотность ![]() исходного сигнала
исходного сигнала ![]() . К произведению
. К произведению ![]() второго слагаемого
применим прямое преобразование Фурье. Используя формулу Эйлера и проведя
несложные математические выкладки, запишем
второго слагаемого
применим прямое преобразование Фурье. Используя формулу Эйлера и проведя
несложные математические выкладки, запишем
![]()
В этом выражении первый
интеграл представляет собой спектральную плотность сигнала ![]() на частотах
на частотах![]() а второй - ту же
спектральную плотность, но на частотах
а второй - ту же
спектральную плотность, но на частотах ![]() . Поэтому
. Поэтому
|
|
(9.28) |
Следовательно, дискретному сигналу вида (9.27) соответствует спектральная плотность
|
|
(9.29) |
Поскольку при ![]() коэффициент
коэффициент ![]() , запишем
, запишем
|
|
(9.30) |

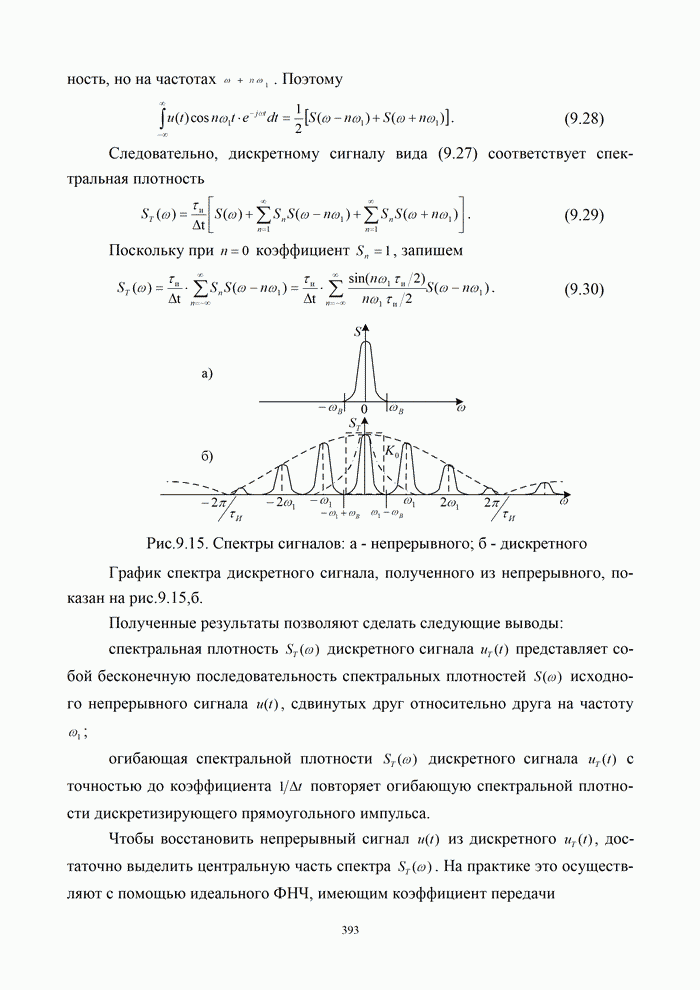
График спектра дискретного сигнала, полученного из непрерывного, показан на рис.9.15,б.
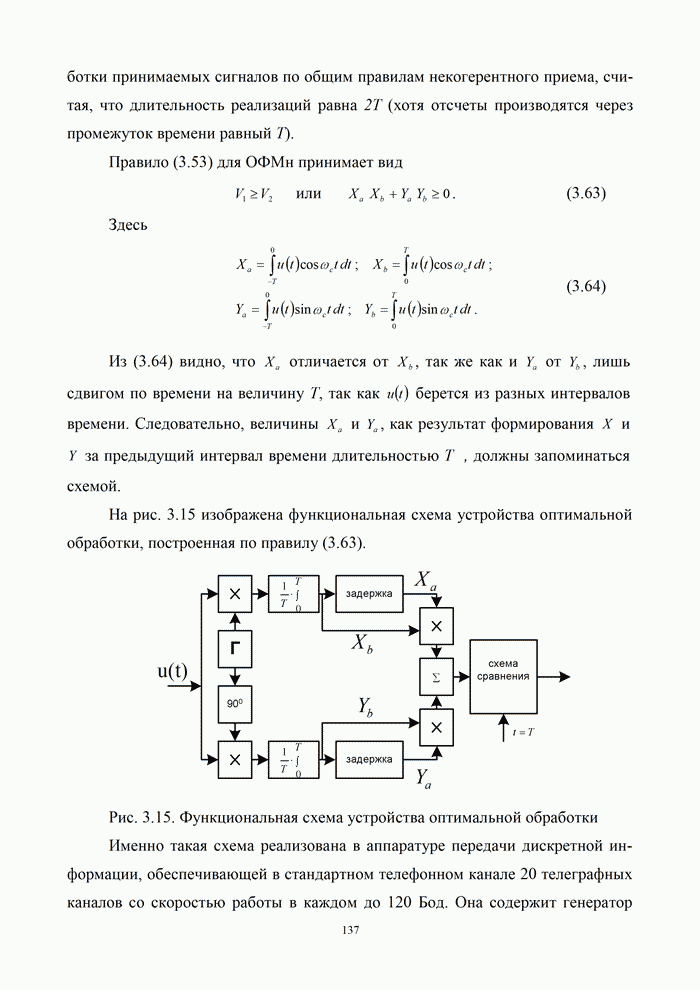
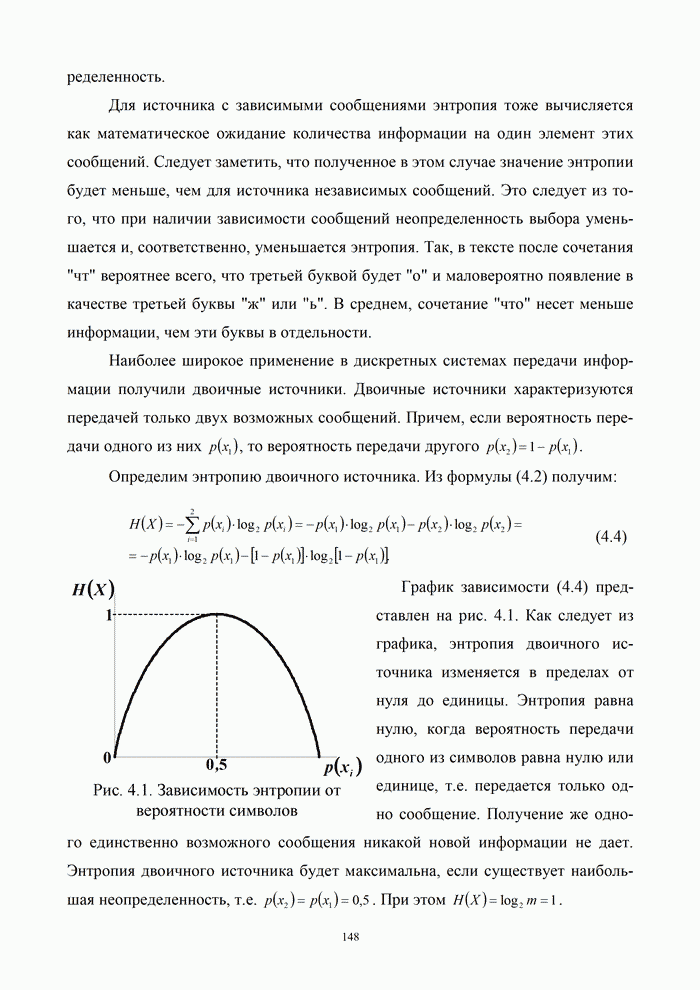
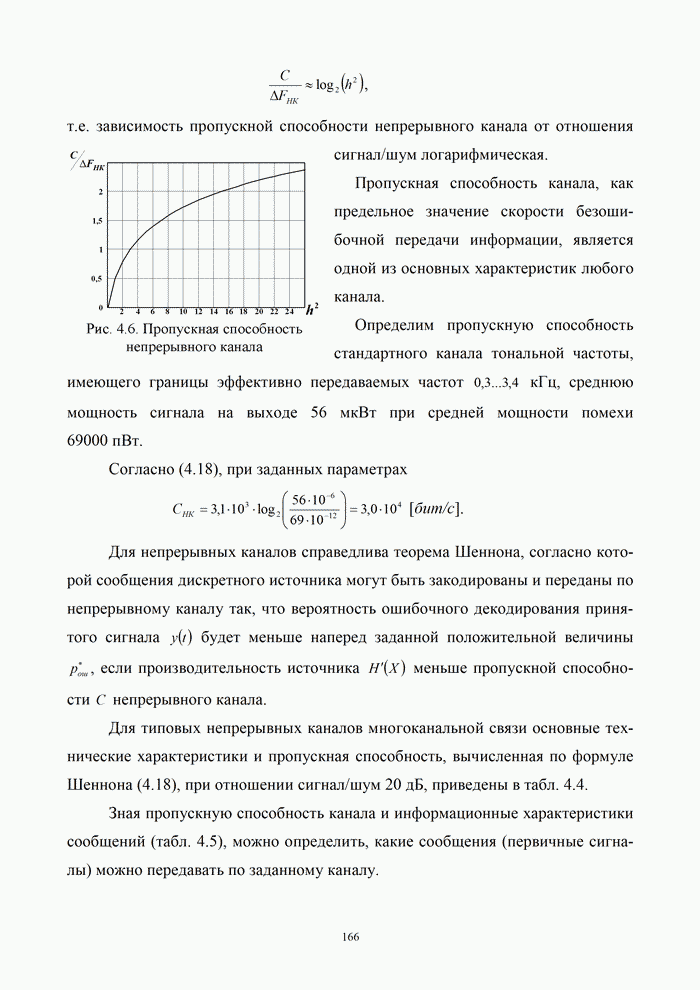
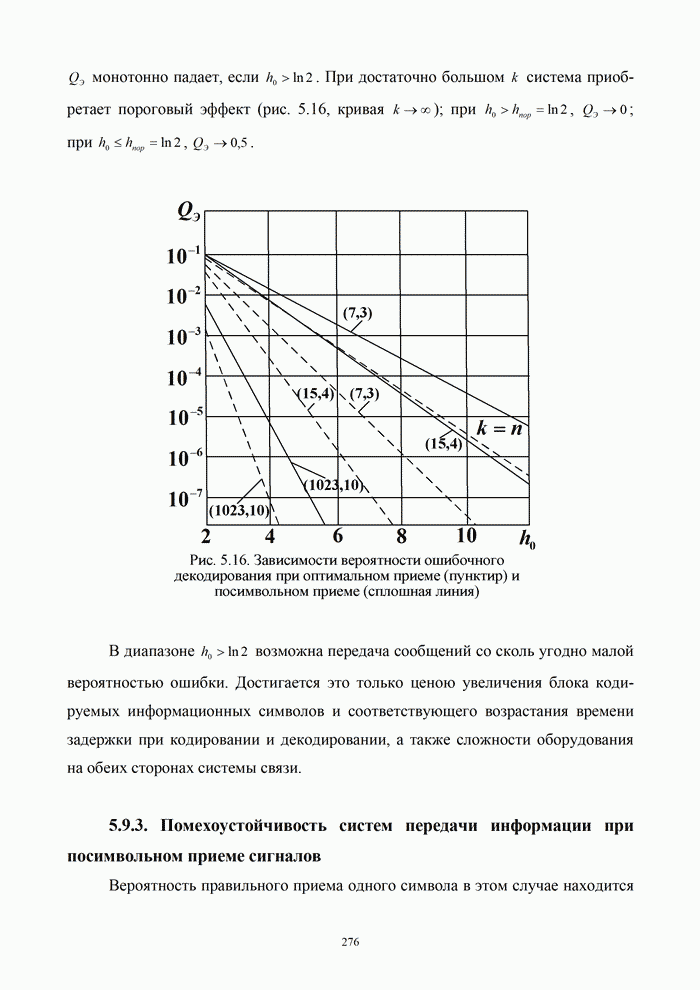
Полученные результаты позволяют сделать следующие выводы:
- спектральная плотность
 дискретного сигнала
дискретного сигнала  представляет собой
бесконечную последовательность спектральных плотностей
представляет собой
бесконечную последовательность спектральных плотностей  исходного непрерывного
сигнала
исходного непрерывного
сигнала  ,
сдвинутых друг относительно друга на частоту
,
сдвинутых друг относительно друга на частоту  ;
;
- огибающая спектральной
плотности
 дискретного
сигнала
дискретного
сигнала  с
точностью до коэффициента
с
точностью до коэффициента  повторяет огибающую спектральной плотности
дискретизирующего прямоугольного импульса.
повторяет огибающую спектральной плотности
дискретизирующего прямоугольного импульса.
Чтобы восстановить
непрерывный сигнал ![]() из
дискретного
из
дискретного ![]() ,
достаточно выделить центральную часть спектра
,
достаточно выделить центральную часть спектра ![]() . На практике это осуществляют с помощью
идеального ФНЧ, имеющим коэффициент передачи
. На практике это осуществляют с помощью
идеального ФНЧ, имеющим коэффициент передачи
|
|
(9.31) |
Вместе с тем известно,
что идеальный ФНЧ физически нереализуем и может служить лишь теоретической
моделью для пояснения принципа восстановления непрерывного сигнала на основе
теоремы Котельникова. Реальный ФНЧ имеет частотную характеристику, которая либо
охватывает несколько лепестков спектра (штрих - пунктирная линия на рис. 9.15,б),
либо имеет конечную крутизну ската характеристики и не полностью охватывает
центральный лепесток. В практических схемах интервал дискретизации,
определяемый формулой ![]() , уменьшают в 2...5 раз. В этом случае
отдельные составляющие спектра дискретного сигнала не перекрываются, как это и
показано на рис. 9.15, б, и могут быть разделены фильтрами.
, уменьшают в 2...5 раз. В этом случае
отдельные составляющие спектра дискретного сигнала не перекрываются, как это и
показано на рис. 9.15, б, и могут быть разделены фильтрами.
При уменьшении
длительности дискретизирующего импульса ![]() , амплитуды спектральных составляющих с
ростом частоты убывают медленнее. В предельном случае, при
, амплитуды спектральных составляющих с
ростом частоты убывают медленнее. В предельном случае, при ![]() спектр дискретного сигнала
будет представлять собой бесконечную последовательность «копий» спектров
исходного сигнала, имеющих равную амплитуду. Если одновременно с уменьшением
длительности увеличивать амплитуду импульса так, чтобы его площадь оставалась
неизменной и равной единице, то дискретизирующие сигналы преобразуются в последовательность
дельта-функций:
спектр дискретного сигнала
будет представлять собой бесконечную последовательность «копий» спектров
исходного сигнала, имеющих равную амплитуду. Если одновременно с уменьшением
длительности увеличивать амплитуду импульса так, чтобы его площадь оставалась
неизменной и равной единице, то дискретизирующие сигналы преобразуются в последовательность
дельта-функций:
![]() .
.
В этом случае формула (9.24) запишется следующим образом:
|
|
(9.32) |
Спектральная плотность дискретного сигнала в этом случае примет вид:
|
|
(9.33) |
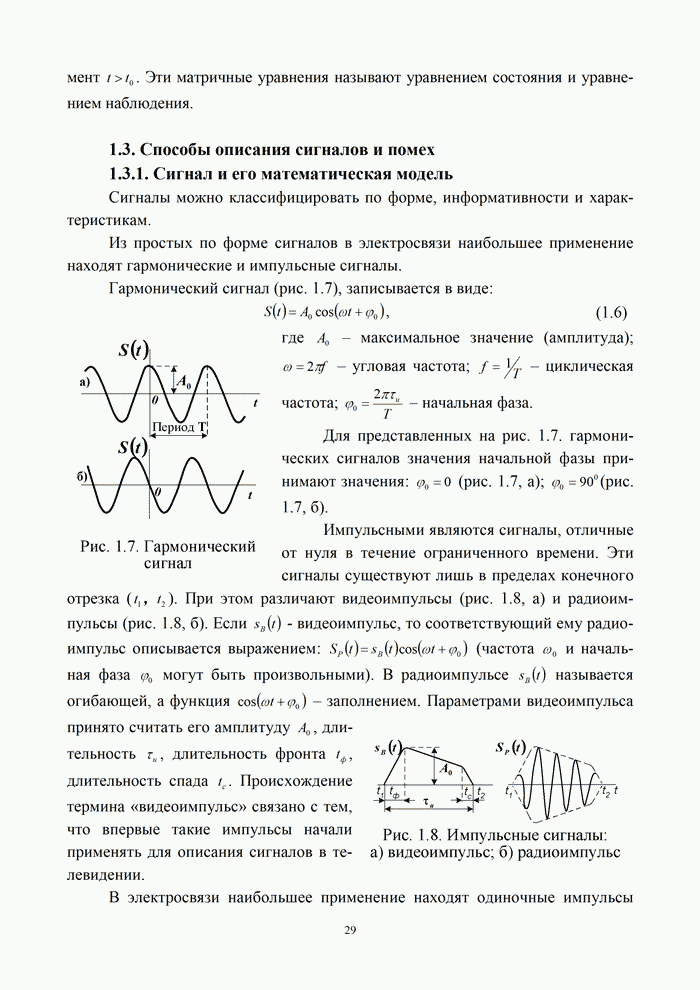
Пример 9.1. Непрерывный
сигнал, имеющий форму прямоугольного импульса напряжения с единичной амплитудой
и длительностью ![]() ,
дискретизирован 10 отсчетами. Определить спектр дискретного сигнала.
,
дискретизирован 10 отсчетами. Определить спектр дискретного сигнала.
Решение. Для
нахождения спектра воспользуемся формулой (9.33). В ней частота ![]() , а интервал
дискретизации
, а интервал
дискретизации ![]() .
Тогда
.
Тогда
 .
.
Возможность представления
дискретных сигналов ![]() в форме (9.32) существенно упрощает их
анализ. В частности, спектральную плотность
в форме (9.32) существенно упрощает их
анализ. В частности, спектральную плотность ![]() можно вычислить непосредственно по
совокупности временных отсчетов
можно вычислить непосредственно по
совокупности временных отсчетов ![]() . Действительно, применив прямое
преобразование Фурье
. Действительно, применив прямое
преобразование Фурье ![]() к соотношению (9.32) для отсчетов
только с положительными номерами
к соотношению (9.32) для отсчетов
только с положительными номерами ![]() , со, получим с учетом фильтрующего
свойства дельта-функции:
, со, получим с учетом фильтрующего
свойства дельта-функции:
|
|
(9.34) |
При этом существенно сокращается время обработки реальных непрерывных сигналов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
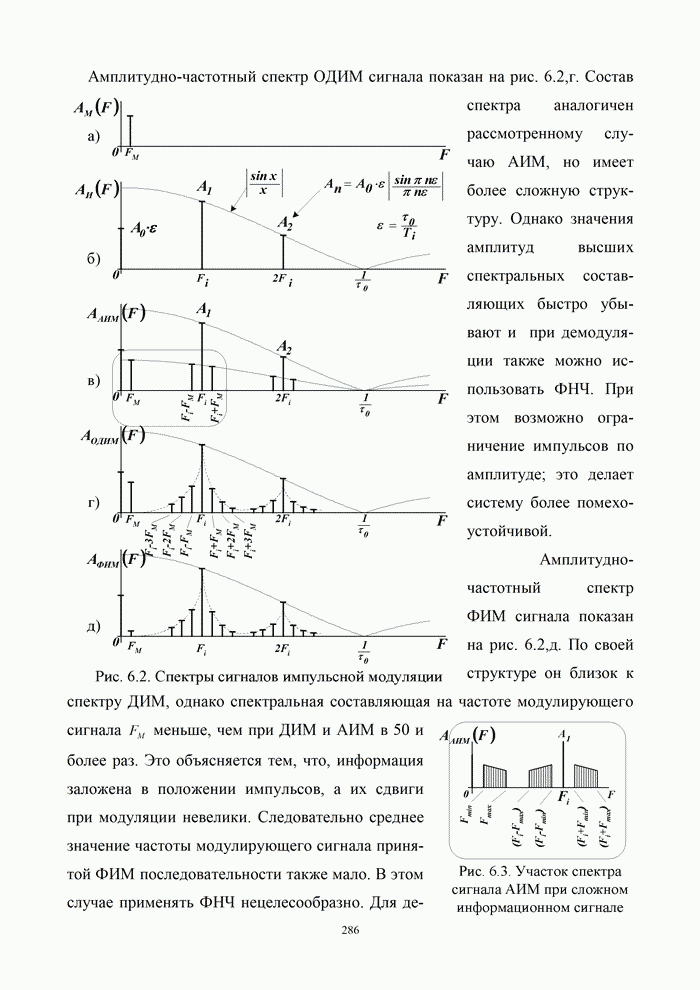
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
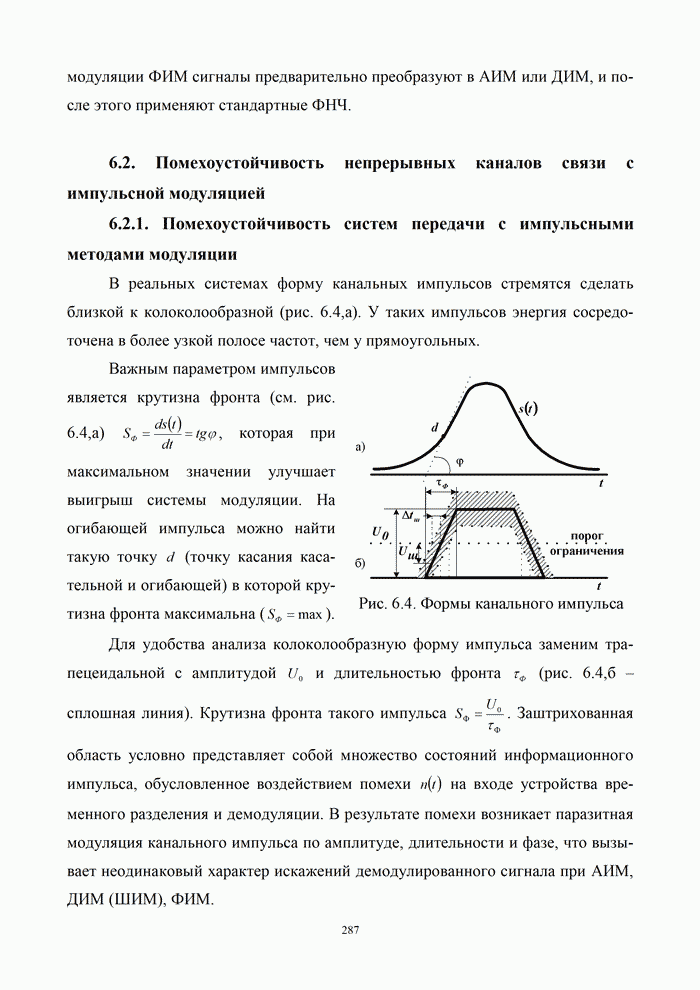
- 6.3. Цифровые методы передачи непрерывных сообщений
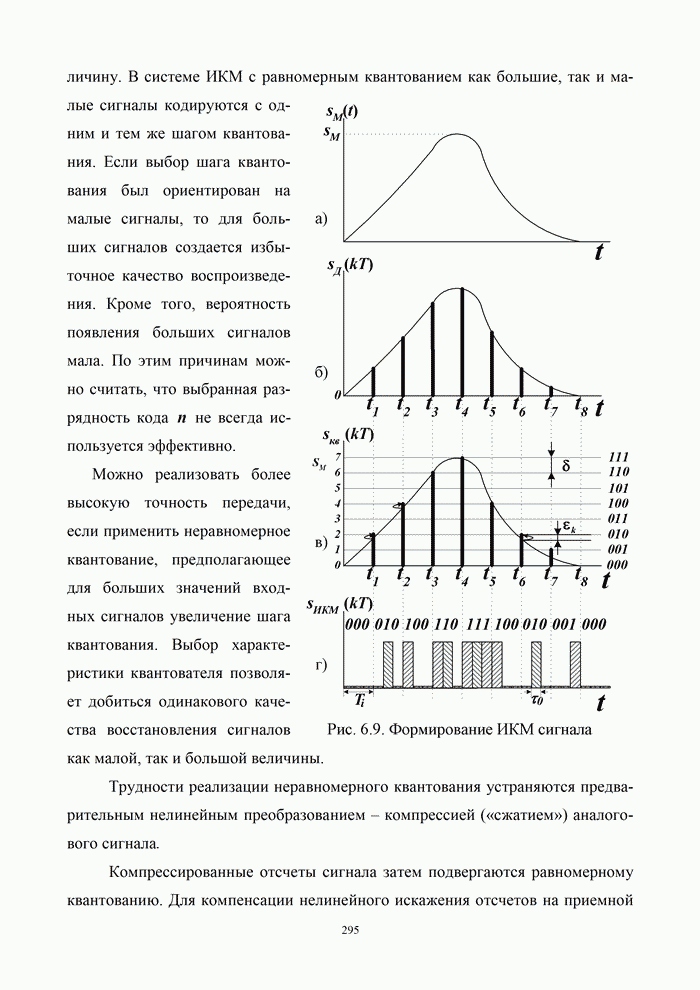
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
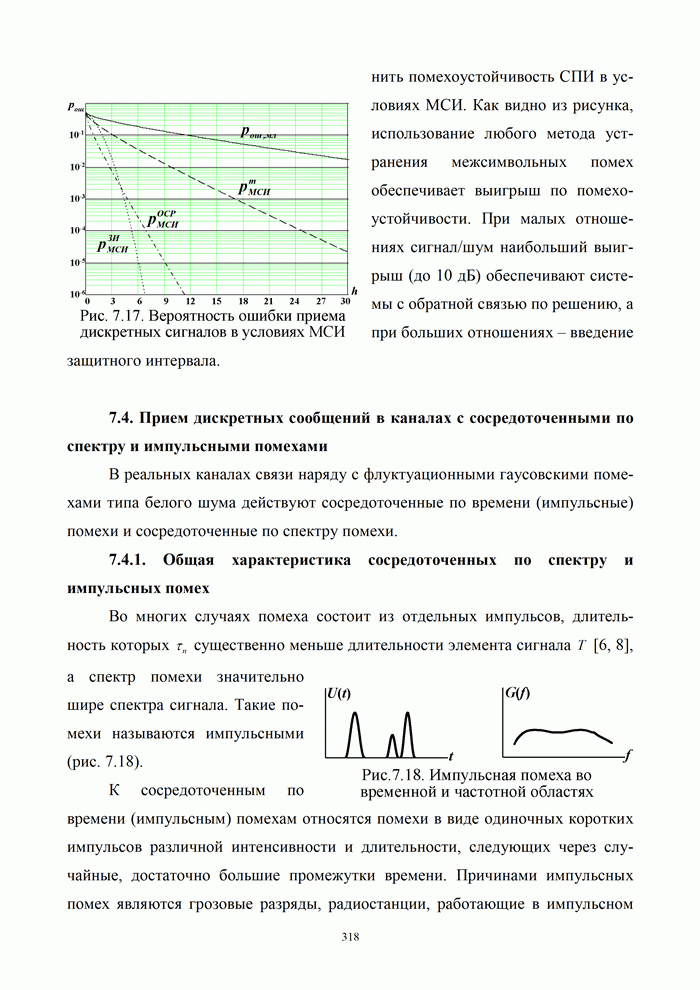
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
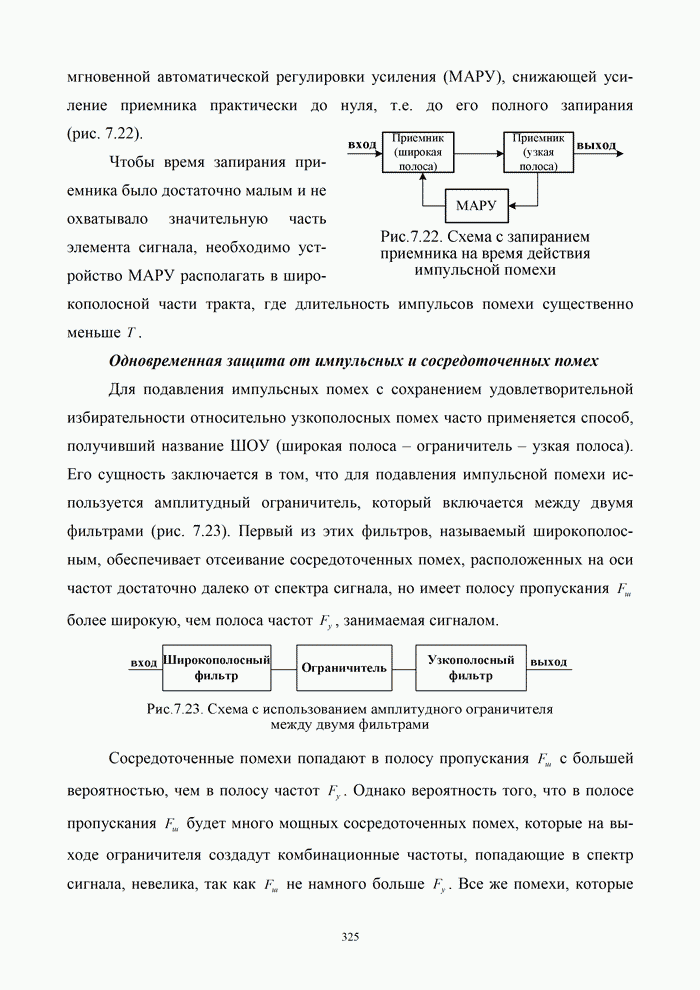
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
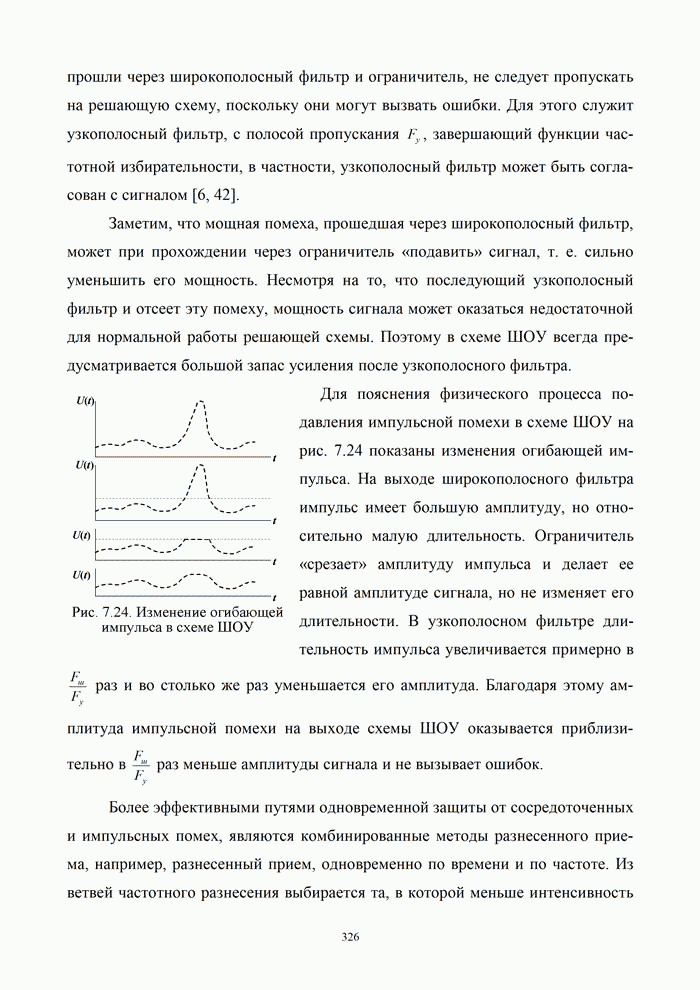
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
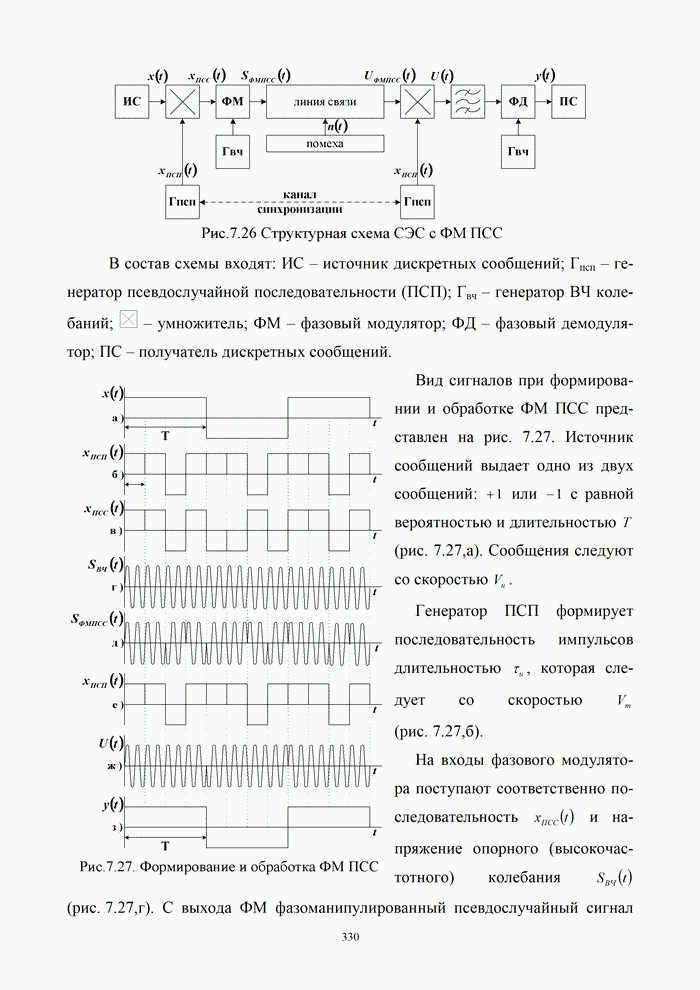
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
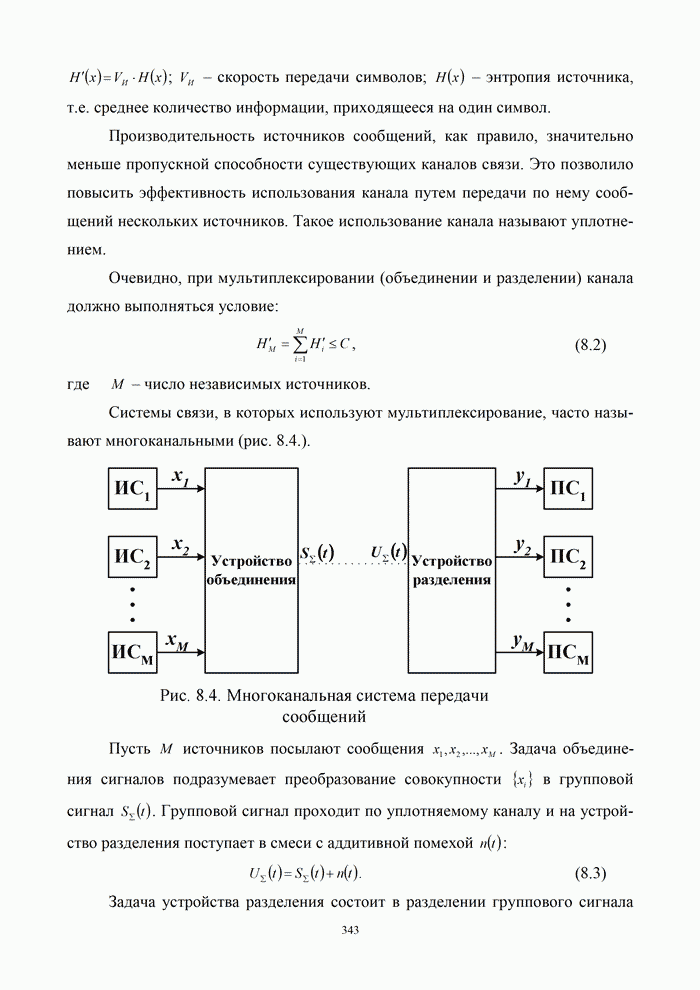
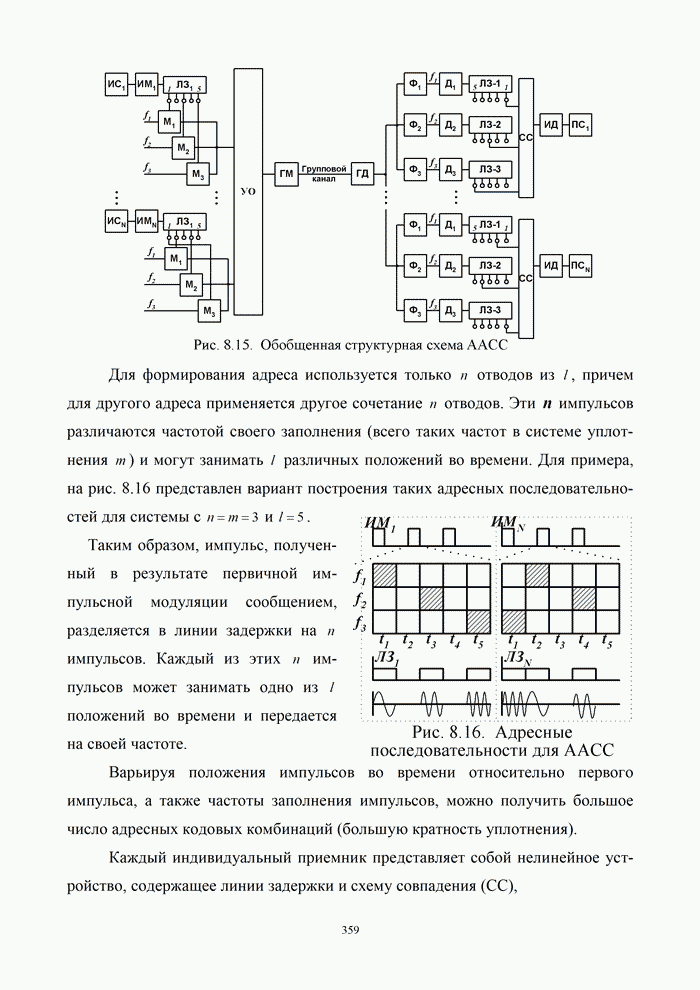
- Глава 8. Многоканальная связь и распределение информации
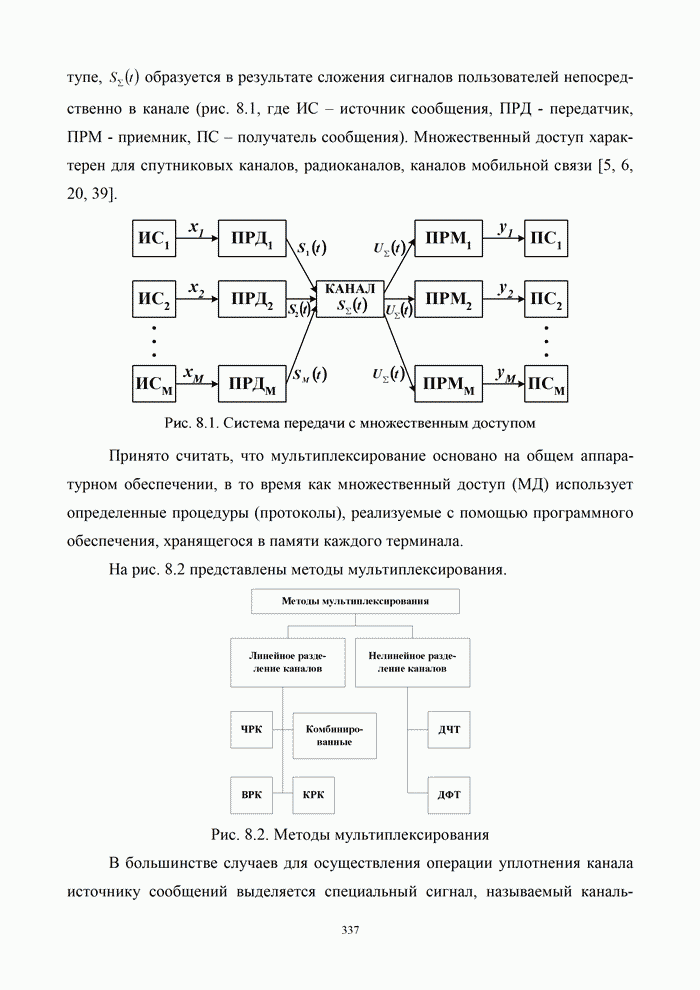
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
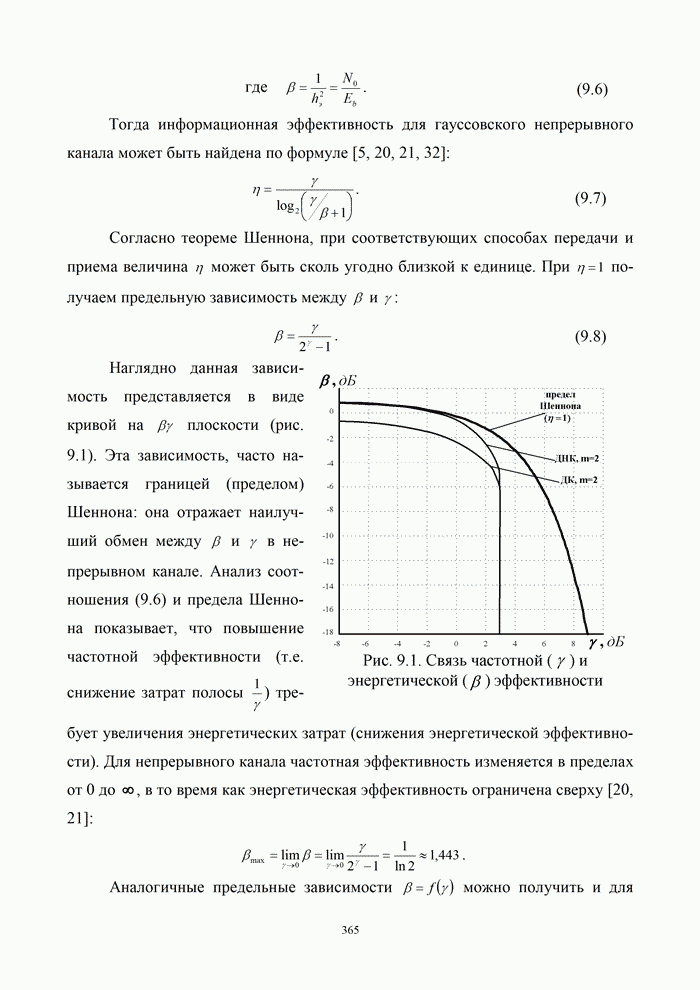
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
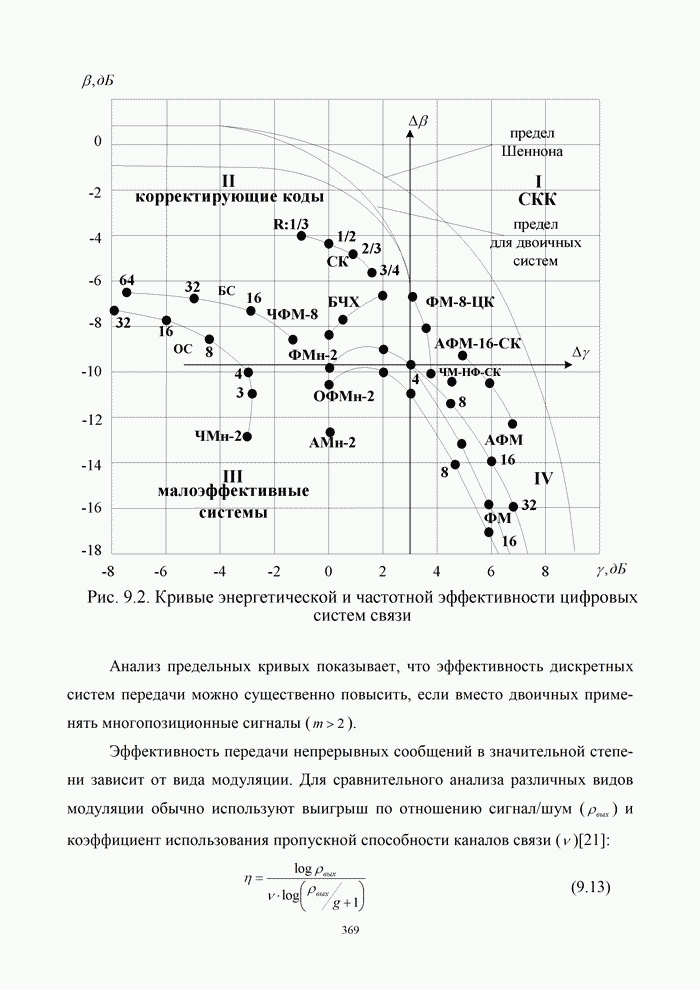
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
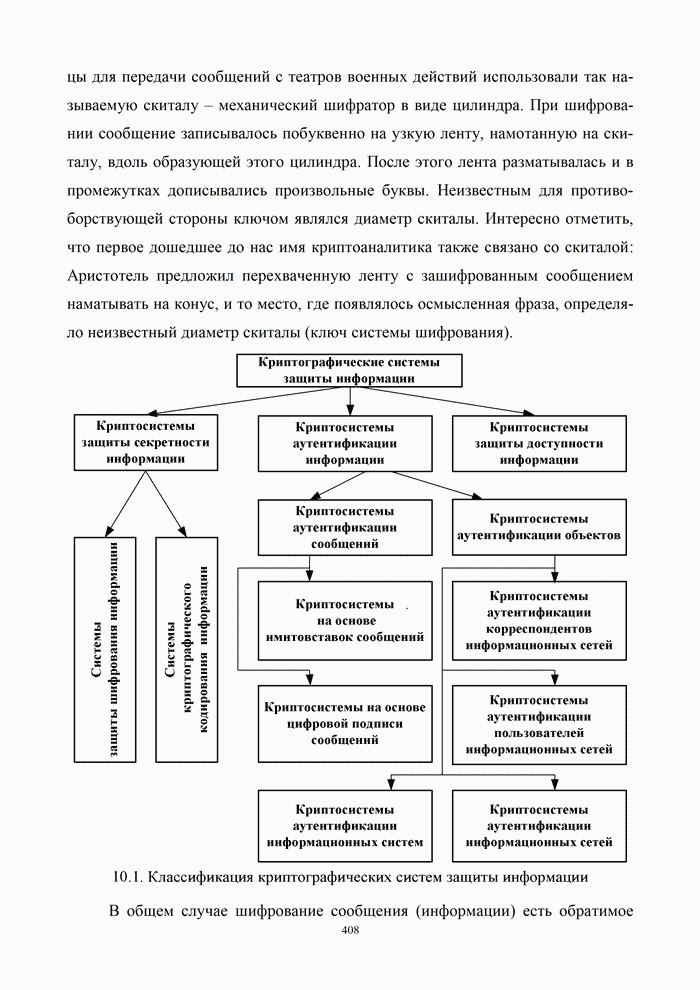
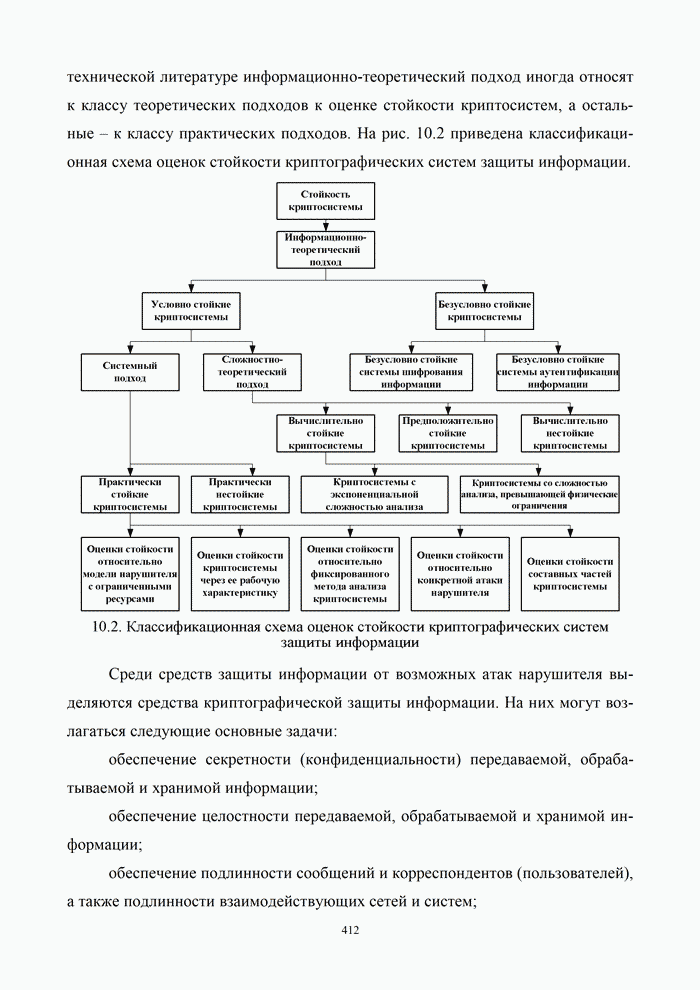
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
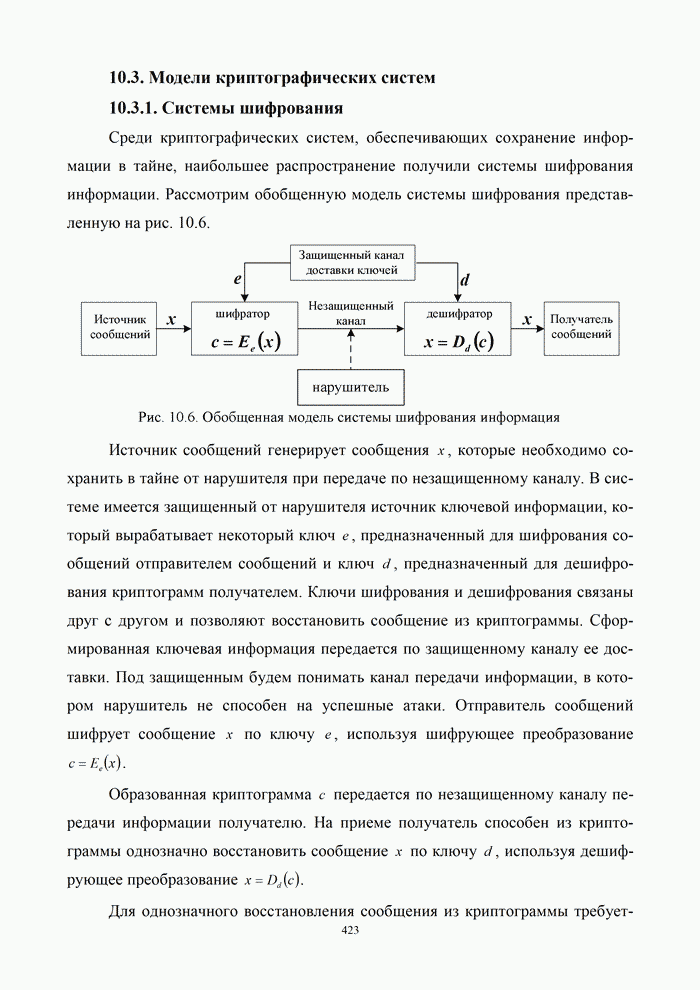
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
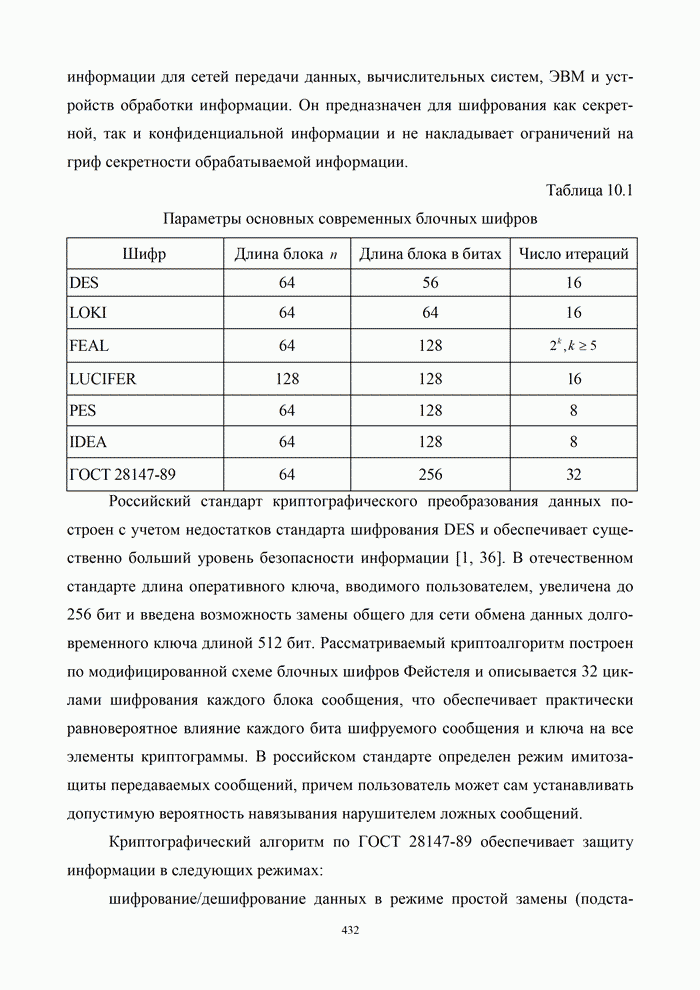
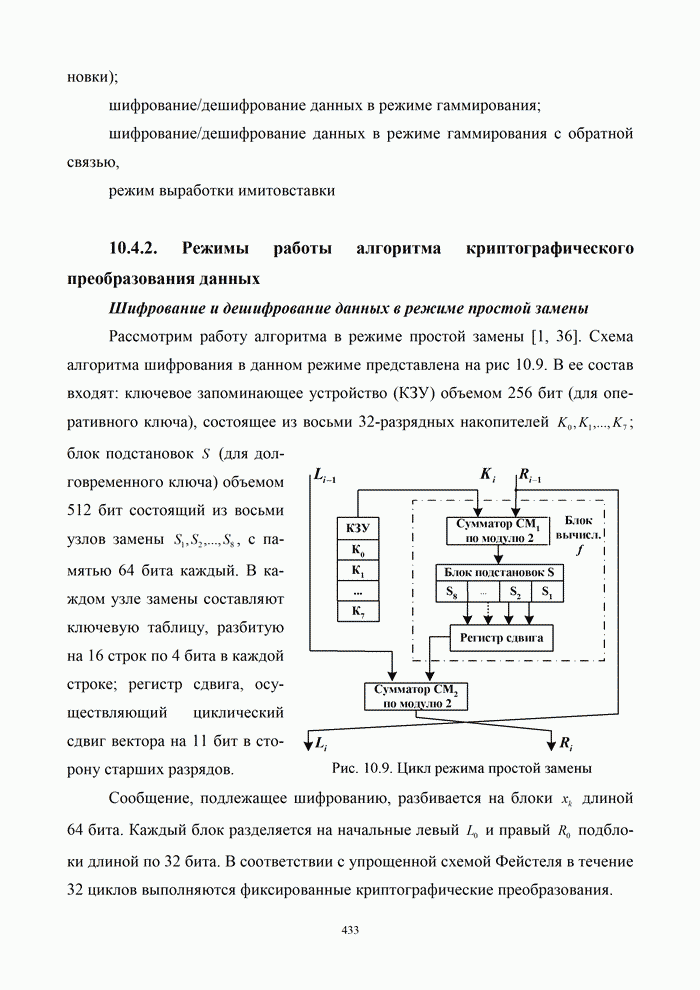
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 .
.
