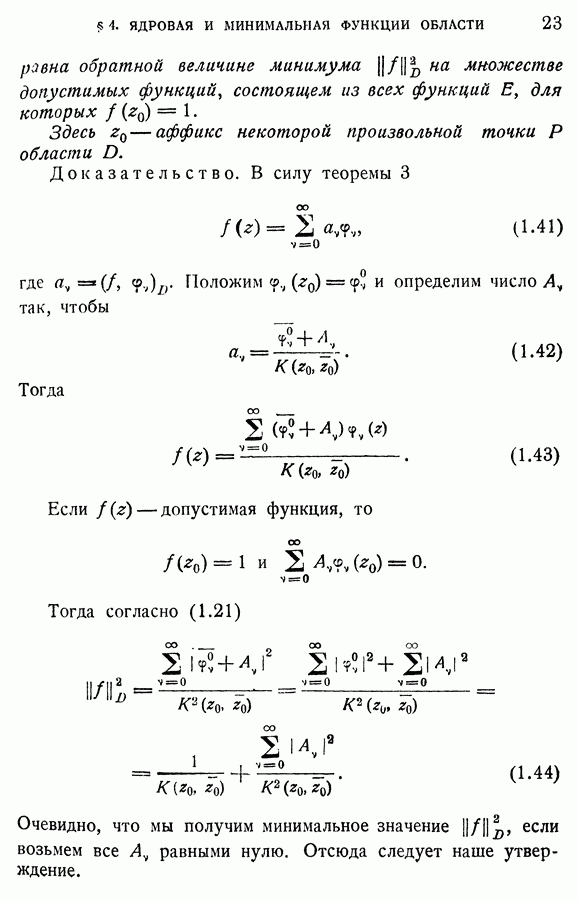| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Треугольники Лобачевского
Мы обратимся, прежде всего, к вычислению площади  -треугольника в инвариантной метрике. Площадь некоторой области
-треугольника в инвариантной метрике. Площадь некоторой области  в метрике
в метрике

как известно, находится по формуле

Поэтому в случае метрики (2.3) для верхней полуплоскости

Здесь предполагается, что в точках  всегда
всегда  (если при
(если при  то интеграл (2.46) следует понимать как несобственный). Величину 5 мы будем далее называть площадью Лобачевского, кратко
то интеграл (2.46) следует понимать как несобственный). Величину 5 мы будем далее называть площадью Лобачевского, кратко  -площадью области
-площадью области  Очевидно, что величина 5 может иметь только положительные значения.
Очевидно, что величина 5 может иметь только положительные значения.

Рис. 13.
Каков бы ни был данный  -треугольник
-треугольник  мы можем соответствующим
мы можем соответствующим  -движением совместить одну из его сторон с положительной полуосью у. Предположим для определенности, что после этого
-движением совместить одну из его сторон с положительной полуосью у. Предположим для определенности, что после этого  -движения рассматриваемый
-движения рассматриваемый  -треугольник расположится так, как это показано на рис. 13. Пусть
-треугольник расположится так, как это показано на рис. 13. Пусть  аффиксы его вершин (у нас
аффиксы его вершин (у нас  соответствующие внутренние углы.
соответствующие внутренние углы.
Допустим далее, что

— уравнение  -прямой
-прямой  проходящей через точки
проходящей через точки  а
а

— уравнение  -прямой
-прямой  проходящей через точки
проходящей через точки  Здесь
Здесь  абсциссы центров окружностей, часть которых составляют и
абсциссы центров окружностей, часть которых составляют и  их радиусы.
их радиусы.
Подсчет интеграла (2.46) дает, что

Из чертежа непосредственно видно (см. рис. 13), что в рассматриваемом случае

Итак,

Тот же самый результат получается и при других расположениях вершин  -треугольника
-треугольника  Мы оставляем читателю вывод формулы (2.51) для этих случаев.
Мы оставляем читателю вывод формулы (2.51) для этих случаев.
Таким образом, нами доказана следующая теорема: Теорема 8. Если  внутренние углы
внутренние углы  -треугольника, то его
-треугольника, то его  -площадъ равна
-площадъ равна

Отметим важное следствие из этой теоремы. Так как Л-пло-щадь  — заведомо положительная величина (мы исключаем из рассмотрения случаи вырождения), то
— заведомо положительная величина (мы исключаем из рассмотрения случаи вырождения), то

т. е. во всяком  -треугольнике сумма внутренних углов меньше
-треугольнике сумма внутренних углов меньше  Отсюда далее следует, что у нас
Отсюда далее следует, что у нас  сумма двух внутренних углов
сумма двух внутренних углов  -треугольника (и тем более каждый из них) меньше внешнего угла
-треугольника (и тем более каждый из них) меньше внешнего угла  -треугольника, не смежного с ним.
-треугольника, не смежного с ним.
Величина  называется угловым дефектом
называется угловым дефектом  -треугольника
-треугольника  (иногда ради краткости просто «дефектом
(иногда ради краткости просто «дефектом  -треугольника А»). Как видно из теоремы 8, с увеличением углового дефекта
-треугольника А»). Как видно из теоремы 8, с увеличением углового дефекта  -площадь Л-треугольника возрастает. Когда
-площадь Л-треугольника возрастает. Когда  стремятся к нулю, угловой дефект
стремятся к нулю, угловой дефект  -треугольника стремится к
-треугольника стремится к  а
а  -площадь — к у. Все
-площадь — к у. Все  -треугольники имеют площадь, меньшую чем
-треугольники имеют площадь, меньшую чем  .
.
Легко видеть, что при приближении углов  к нулю
к нулю  -прямые, являющиеся сторонами
-прямые, являющиеся сторонами  -треугольника, стремятся стать
-треугольника, стремятся стать  -параллельными друг другу; вершины Л-тре-угольника в пределе обращаются в их концевые точки. Возникающую таким образом фигуру мы будем называть предельным
-параллельными друг другу; вершины Л-тре-угольника в пределе обращаются в их концевые точки. Возникающую таким образом фигуру мы будем называть предельным  -треугольником.
-треугольником.

Рис. 14.

Рис. 15.
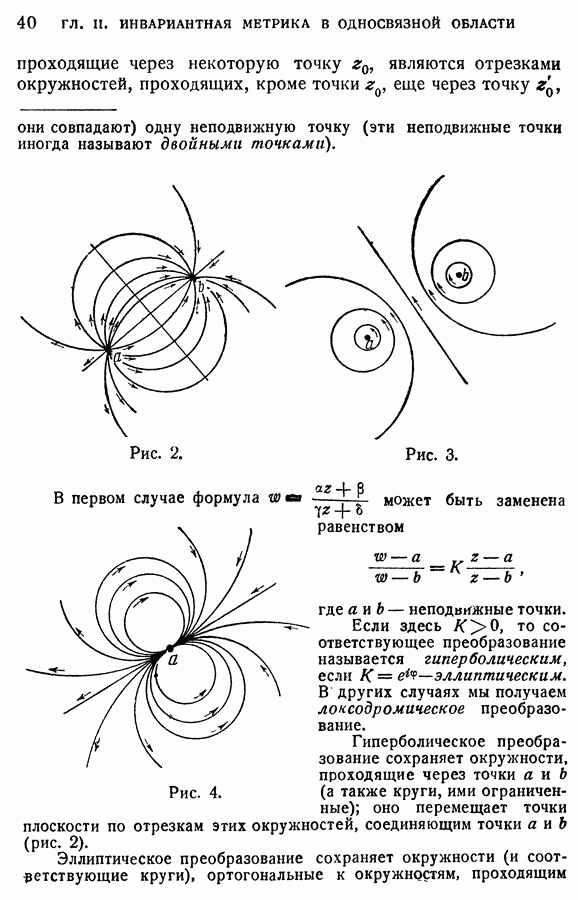
Предельный  -треугольник для верхней полуплоскости изображен на рис. 14, а для круга
-треугольник для верхней полуплоскости изображен на рис. 14, а для круга  на рис. 15. Из предыдущего следует, что
на рис. 15. Из предыдущего следует, что  -площади всех предельных
-площади всех предельных  -треугольников (в метрике, построенной для соответствующей области) равны
-треугольников (в метрике, построенной для соответствующей области) равны 
В качестве следствия теоремы 8 можно получись еще следующее интересное предложение:
Теорема 9.  -треугольники, имеющие равные углы,
-треугольники, имеющие равные углы,  -конгруентны.
-конгруентны.
Доказательство этой теоремы удобнее вести для случай круга  Пусть
Пусть  углы данных
углы данных  -треуголь ников. Прежде всего мы переместим данные нам
-треуголь ников. Прежде всего мы переместим данные нам  -треугольники соответствующими
-треугольники соответствующими  -движениями так, чтобы их вершины, соответствующие углу
-движениями так, чтобы их вершины, соответствующие углу  попали в точку
попали в точку  а вершины, отвечающие углу
а вершины, отвечающие углу  на положительную действительную полуось. Тогда стороны этих
на положительную действительную полуось. Тогда стороны этих  -треугольников, выходящие из точки
-треугольников, выходящие из точки  все совместятся с какими-то радиусами круга
все совместятся с какими-то радиусами круга  Если после этого наши
Если после этого наши  -треугольники окажутся лежащими по разные стороны от действительной оси, мы заменим один из них симметричным (относительно действительной оси)
-треугольники окажутся лежащими по разные стороны от действительной оси, мы заменим один из них симметричным (относительно действительной оси)  -треугольни-ком. Таким образом, данные
-треугольни-ком. Таким образом, данные  -треугольники займут положения
-треугольники займут положения  указанные на рис. 16. Благодаря тому, что
указанные на рис. 16. Благодаря тому, что  имеют в силу теоремы 8 одинаковую
имеют в силу теоремы 8 одинаковую  -площадь (которая является аддитивной функцией области и всегда положительна), стороны
-площадь (которая является аддитивной функцией области и всегда положительна), стороны  и
и  должны пересечься внутри угла
должны пересечься внутри угла  (как это и указано на рис. 16). Пусть
(как это и указано на рис. 16). Пусть  точка пересечения этих сторон. Тогда внутренний угол треугольника
точка пересечения этих сторон. Тогда внутренний угол треугольника  в вершине В и его внешний угол в вершине В должны равняться друг другу (так же, как внутренний угол треугольника
в вершине В и его внешний угол в вершине В должны равняться друг другу (так же, как внутренний угол треугольника  в вершине С и его внешний угол в вершине С). Это невозможно, и поэтому точка В должна совпасть с точкой В точка С — с точкой С. Наша теорема доказана.
в вершине С и его внешний угол в вершине С). Это невозможно, и поэтому точка В должна совпасть с точкой В точка С — с точкой С. Наша теорема доказана.

Рис. 16.
Таким образом, подобные  -треугольники (т. е. имеющие одинаковые углы) всегда конгруентны.
-треугольники (т. е. имеющие одинаковые углы) всегда конгруентны.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКЦИИ
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ ИНВАРИАНТНОЙ МЕТРИКИ
- § 1. Ортонормированные системы функций
- § 2. Замкнутые системы функций
- § 3. Существование замкнутых систем
- § 4. Ядровая и минимальная функции области
- § 6. Изменение ядровой функции области при конформных отображениях. Метрика, инвариантная при конформных отображениях
- ГЛАВА II. ИНВАРИАНТНАЯ МЕТРИКА В ОДНОСВЯЗНОЙ ОБЛАСТИ
- § 1. Гауссова кривизна
- § 2. Геодезические линии
- § 3. Группа движений Лобачевского
- § 4. Расстояние Лобачевского между двумя точками
- § 5. Аксиомы конгруентности и непрерывности
- § 6. Параллельность Лобачевского
- § 7. Треугольники Лобачевского
- § 8. Линии постоянной кривизны Лобачевского
- § 9. Пучки гиперциклов и орициклов
- § 10. Окружности Лобачевского
- § 11. Некоторые общие предложения
- ГЛАВА III. ГРУППА ДВИЖЕНИЙ ИНВАРИАНТНОЙ ГЕОМЕТРИИ В ОДНОСВЯЗНОЙ ОБЛАСТИ
- § 1. Классификация движений Лобачевского
- § 2. Собственно разрывные подгруппы группы движений Лобачевского
- § 3. Приведенные области собственно разрывных подгрупп
- § 4. Стороны 1-го рода приведенной области
- § 5. Вершины приведенной области
- ГЛАВА IV. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНВАРИАНТНОЙ МЕТРИКИ К ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 1. Лемма Шварца и ее обобщения
- § 2. Распространение леммы Шварца на орициклы и гиперциклы
- § 3. Оценки при приближении к границе области
- ГЛАВА V. МЕТРИКА, ИНВАРИАНТНАЯ ПРИ ПСЕВДОКОНФОРМНЫХ ОТОБРАЖЕНИЯХ
- § 1. Введение инвариантной метрики
- § 2. Кривизна инвариантной геометрии
- § 3. Группа движений инвариантной геометрии
- § 4. Случаи бицилиндра и шара