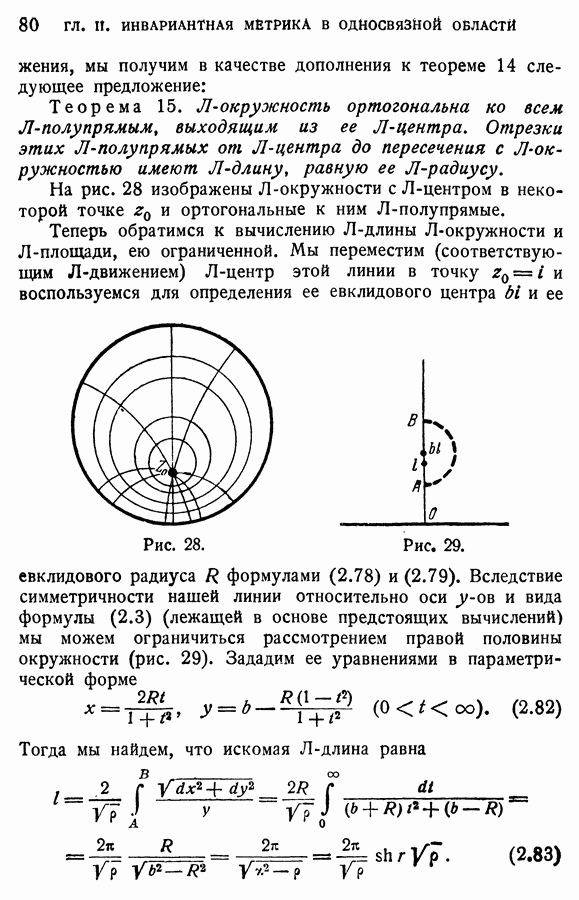
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Вершины приведенной области
Мы рассмотрим сейчас вершины 1-го рода  -многоуголь-ников
-многоуголь-ников  (иначе — вершины 1-й категории). Прежде всего следует отметить, что к числу этих вершин принадлежат все неподвижные точки
(иначе — вершины 1-й категории). Прежде всего следует отметить, что к числу этих вершин принадлежат все неподвижные точки  -вращений, входящих в состав подгруппы
-вращений, входящих в состав подгруппы  Действительно, в любой окрестности неподвижной точки а
Действительно, в любой окрестности неподвижной точки а  -вращения
-вращения  имеются пары гомологичных точек. Поэтому такая точка не может лежать внутри какого-либо многоугольника Она не может быть и внутренней точкой какой-либо стороны этого
имеются пары гомологичных точек. Поэтому такая точка не может лежать внутри какого-либо многоугольника Она не может быть и внутренней точкой какой-либо стороны этого  -многоугольника. Если для Л-по-ворота
-многоугольника. Если для Л-по-ворота  то все точки
то все точки  (их число в этом случае заведомо больше двух) находятся на одинаковом
(их число в этом случае заведомо больше двух) находятся на одинаковом  -расстоянии от точки а, которая поэтому оказывается вершиной
-расстоянии от точки а, которая поэтому оказывается вершиной  если
если  то точка а (как мы условились выше) тоже рассматривается как вершина
то точка а (как мы условились выше) тоже рассматривается как вершина  -многоугольника Положение остальных вершин
-многоугольника Положение остальных вершин  -многоугольников
-многоугольников  зависит от выбора точки
зависит от выбора точки  Благодаря этому последние вершины называются случайными в отличие от первых, которые называются эллиптическими, иногда — необходимыми.
Благодаря этому последние вершины называются случайными в отличие от первых, которые называются эллиптическими, иногда — необходимыми.
Пусть а — некоторая случайная вершина 1-го рода  -много-угольника
-много-угольника  Рассмотрим все другие вершины этого
Рассмотрим все другие вершины этого  -многоугольника, гомологичные вершине а относительно подгруппы
-многоугольника, гомологичные вершине а относительно подгруппы  Пусть
Пусть  одна из таких вершин,
одна из таких вершин,  -движение, переводящее вершину
-движение, переводящее вершину  в вершину а. Тогда
в вершину а. Тогда  -движение А переводит
-движение А переводит  -многоугольник
-многоугольник  в другой
в другой  -многоугольник имеющий точку а своей вершиной. Рассмотрим все
-многоугольник имеющий точку а своей вершиной. Рассмотрим все  -много-угольники имеющие точку а своей вершиной. Заметим, что число их обязательно конечно, так как конечно количество точек
-много-угольники имеющие точку а своей вершиной. Заметим, что число их обязательно конечно, так как конечно количество точек  лежащих на одной
лежащих на одной  -окружности с
-окружности с  -центром в точке
-центром в точке  Обозначим эти
Обозначим эти  -многоугольники символами
-многоугольники символами  в том порядке, как они встречаются при обходе точки а в направлении, противоположном направлению вращения часовой стрелки. Пусть
в том порядке, как они встречаются при обходе точки а в направлении, противоположном направлению вращения часовой стрелки. Пусть  есть
есть  -движение, переводящее
-движение, переводящее  -многоугольник где
-многоугольник где  в
в  -многоугольник
-многоугольник  Это
Это  -движение переводит вершину а в другую вершину
-движение переводит вершину а в другую вершину  -многоугольника
-многоугольника  которую мы назовем а. Вершины а очевидно, гомологичны вершине а
которую мы назовем а. Вершины а очевидно, гомологичны вершине а
относительно подгруппы  Таким образом, нами установлено соответствие между вершинами
Таким образом, нами установлено соответствие между вершинами  -многоугольника
-многоугольника  гомологичными вершине
гомологичными вершине  -многоугольниками имеющими точку а своей вершиной. В нашем случае благодаря тому, что а — случайная вершина, это соответствие взаимно однозначно (проверка этого факта предоставляется читателю). Отсюда следует, что число вершин равно
-многоугольниками имеющими точку а своей вершиной. В нашем случае благодаря тому, что а — случайная вершина, это соответствие взаимно однозначно (проверка этого факта предоставляется читателю). Отсюда следует, что число вершин равно  что все они различны между собой и отличаются от вершины а. Далее, так как
что все они различны между собой и отличаются от вершины а. Далее, так как  -движения
-движения  сохраняют углы, то сумма внутренних углов
сохраняют углы, то сумма внутренних углов  -многоугольника
-многоугольника  при гомологичных случайных вершинах
при гомологичных случайных вершинах  оказывается равной
оказывается равной 
Легко установить связь между  -движениями
-движениями  и производящими
и производящими  -движейиями подгруппы
-движейиями подгруппы  Так как
Так как  -много-угольник граничит с
-много-угольник граничит с  -многоугольником то
-многоугольником то  одно из производящих
одно из производящих  -движений подгруппы
-движений подгруппы  Оно переводит вершину
Оно переводит вершину  в вершину
в вершину  -движение
-движение  (оно тоже производящее) переводит вершину а в вершину
(оно тоже производящее) переводит вершину а в вершину  Затем мы составим
Затем мы составим  -движение
-движение  Это — производящее Л-движение, так как оно переводит
Это — производящее Л-движение, так как оно переводит  -многоугольник
-многоугольник  соседний с ним
соседний с ним  -многоугольник Под его воздействием вершина
-многоугольник Под его воздействием вершина  переходит в вершину
переходит в вершину  Действуя таким образом далее, мы найдем, что вообще для любого
Действуя таким образом далее, мы найдем, что вообще для любого  -движе-ние
-движе-ние  является производящим и переводит вершину
является производящим и переводит вершину  Наконец, мы возьмем
Наконец, мы возьмем  -движение
-движение  Это — производящее
Это — производящее  -движение, переводящее вершину в исходную вершину а. Таким образом, мы построили серию производящих
-движение, переводящее вершину в исходную вершину а. Таким образом, мы построили серию производящих  -движений, последовательно переводящих вершину а в затем вершину в вершину
-движений, последовательно переводящих вершину а в затем вершину в вершину  и, наконец, вершину
и, наконец, вершину  в вершину а.
в вершину а.
Указанные обстоятельства служат поводом для следующего определения:
Определение 4. Совокупность вершин  -многоуголь-ника
-многоуголь-ника  гомологичных случайной вершине 1-го рода а этого
гомологичных случайной вершине 1-го рода а этого  -многоугольника, называется простым циклом.
-многоугольника, называется простым циклом.
Наши предыдущие рассуждения позволяют нам высказать следующую теорему:
Теорема 8. Число случайных вершин 1-го рода  -многоугольника
-многоугольника  составляющих простой цикл, всегда
составляющих простой цикл, всегда
конечно. Сумма внутренних углов  -многоугольника
-многоугольника  при его случайных вершинах, составляющих простой циклу равна
при его случайных вершинах, составляющих простой циклу равна 
Сюда еще можно добавить, что из сказанного вытекает наличие соотношения

между производящими  -движениями
-движениями  Здесь «1» означает тождественное преобразование.
Здесь «1» означает тождественное преобразование.
Теперь обратимся к рассмотрению эллиптических вершин. Сначала мы рассмотрим случай, когда у эллиптической вершины  -многоугольника
-многоугольника  нет гомологов среди других вершин этого
нет гомологов среди других вершин этого  -многоугольника. Тогда единственными
-многоугольника. Тогда единственными  -движениями подгруппы
-движениями подгруппы  преобразующими точку а снова в вершину
преобразующими точку а снова в вершину  -многоугольника
-многоугольника  будут
будут  -вращения, имеющие а своей неподвижной точкой. Легко видеть, что, поскольку эти
-вращения, имеющие а своей неподвижной точкой. Легко видеть, что, поскольку эти  -вращения входят в состав собственно разрывной подгруппы группы
-вращения входят в состав собственно разрывной подгруппы группы  -движений, они должны являться степенями некоторого
-движений, они должны являться степенями некоторого  -поворота
-поворота  вида
вида

где  некоторое целое число, большее единицы.
некоторое целое число, большее единицы.
Во всех других случаях, если в состав подгруппы  входят
входят  -вращения (3.31) с
-вращения (3.31) с  целое число, большее единицы), она должна содержать бесконечное множество
целое число, большее единицы), она должна содержать бесконечное множество  -движений (3.31); среди них должны иметься как угодно близкие друг другу. Тогда подгруппа
-движений (3.31); среди них должны иметься как угодно близкие друг другу. Тогда подгруппа  неизбежно должна была бы содержать бесконечно малые
неизбежно должна была бы содержать бесконечно малые  -движения, что противоречит нашим предположениям. Очевидно, что в этом случае
-движения, что противоречит нашим предположениям. Очевидно, что в этом случае  -повороты
-повороты  поворачивают
поворачивают  -многоугольник
-многоугольник  на углы, кратные
на углы, кратные  вокруг точки а, совмещая его с одним из
вокруг точки а, совмещая его с одним из  -многоугольников
-многоугольников  имеющих точку а своей вершиной. Углы всех этих
имеющих точку а своей вершиной. Углы всех этих  -многоугольников при вершине а равны
-многоугольников при вершине а равны  -движение
-движение  удовлетворяет соотношению
удовлетворяет соотношению

Теперь рассмотрим общий случай. Пусть а — неподвижная точка  -вращения (3.31) с
-вращения (3.31) с  целое число, большее единицы), входящего в состав подгруппы
целое число, большее единицы), входящего в состав подгруппы  Сверх того предполагается, что
Сверх того предполагается, что  -многоугольник
-многоугольник  имеет еще
имеет еще  вершин
вершин  гомологичных вершине а. Если
гомологичных вершине а. Если  -движение, переводящее вершину
-движение, переводящее вершину  в вершину а, то оно переведет
в вершину а, то оно переведет  -многоугольник
-многоугольник  в другой
в другой  -многоугольник
-многоугольник  тоже имеющий точку а своей вершиной. Очевидно, что тогда все
тоже имеющий точку а своей вершиной. Очевидно, что тогда все  -движения
-движения

тоже будут переводить вершину  в а, совмещая
в а, совмещая  -многоугольник
-многоугольник  -многоугольником
-многоугольником  имеющим точку а своей вершиной. Все эти
имеющим точку а своей вершиной. Все эти  -многоугольники будут иметь при вершине а внутренний угол, равный внутреннему углу
-многоугольники будут иметь при вершине а внутренний угол, равный внутреннему углу  -многоугольника
-многоугольника  при вершине а Сумма углов
при вершине а Сумма углов  -многоугольников
-многоугольников  при вершине а, таким образом, оказывается равной
при вершине а, таким образом, оказывается равной  Рассуждая таким же образом для всех вершин
Рассуждая таким же образом для всех вершин  и обозначая еще угол
и обозначая еще угол  -многоугольника
-многоугольника  при вершине а через мы найдем, что
при вершине а через мы найдем, что

или

Мы будем говорить, что вершины  образуют эллиптический цикл порядка
образуют эллиптический цикл порядка  Каждая из этих вершин является неподвижной точкой
Каждая из этих вершин является неподвижной точкой  -поворота с параметром
-поворота с параметром  принадлежащего к подгруппе
принадлежащего к подгруппе  в каждой из этих вершин сходятся две сопряженные стороны
в каждой из этих вершин сходятся две сопряженные стороны  -много-угольника
-много-угольника  сторон
сторон  -многоугольников
-многоугольников  (считая и
(считая и  -многоугольник
-многоугольник 
Нами доказана следующая теорема:
Теорема 9. Число эллиптических вершин 1-го рода  -многоугольника
-многоугольника  составляющих эллиптический цикл любого порядка
составляющих эллиптический цикл любого порядка  всегда конечно. Сумма внутренних углов
всегда конечно. Сумма внутренних углов  -многоугольника
-многоугольника  при этих вершинах равна
при этих вершинах равна 
Кроме вершин 1-го рода (1-й категории)  -многоуголь-ник
-многоуголь-ник  может иметь вершины 2-го рода, лежащие на абсолюте. Здесь надо различать две возможности. В первом случае в точке абсолюта сходятся две стороны 1-го рода; они составляют здесь угол, равный нулю, касаются друг друга (иначе говоря, стороны 1-го рода, встречающиеся в этой вершине,
может иметь вершины 2-го рода, лежащие на абсолюте. Здесь надо различать две возможности. В первом случае в точке абсолюта сходятся две стороны 1-го рода; они составляют здесь угол, равный нулю, касаются друг друга (иначе говоря, стороны 1-го рода, встречающиеся в этой вершине,  -параллельны). Подобная вершина называется вершиной 2-й категории. Во втором случае в точке абсолюта встречаются сторона
-параллельны). Подобная вершина называется вершиной 2-й категории. Во втором случае в точке абсолюта встречаются сторона  -многоугольника
-многоугольника  -го рода (отрезок
-го рода (отрезок  -прямой) и сторона этого
-прямой) и сторона этого  -многоугольника 2-го рода (отрезок абсолюта). Они всегда взаимно перпендикулярны. Подобная вершина называется вершиной 3-й категории.
-многоугольника 2-го рода (отрезок абсолюта). Они всегда взаимно перпендикулярны. Подобная вершина называется вершиной 3-й категории.
Мы не будем рассматривать здесь свойства этих вершин. Некоторые сведения о них читатель может найти в книге  Адамара [8]. Систематическое изложение относящихся сюда фактов следует искать в специальных руководствах.
Адамара [8]. Систематическое изложение относящихся сюда фактов следует искать в специальных руководствах.
Теоремы 7, 8 и 9 устанавливают ряд свойств  -многоугольника
-многоугольника  являющегося приведенной областью собственно разрывной подгруппы
являющегося приведенной областью собственно разрывной подгруппы  группы
группы  -движений. Является ли наличие этих свойств у некоторого
-движений. Является ли наличие этих свойств у некоторого  -многоугольника достаточным для того, чтобы он был приведенной областью некоторой собственно разрывной подгруппы
-многоугольника достаточным для того, чтобы он был приведенной областью некоторой собственно разрывной подгруппы  группы
группы  -движений?
-движений?
Оказывается, что на поставленный вопрос следует дать положительный ответ. Это обстоятельство играет важную роль во всей теории, так как открывает геометрический способ образования собственно разрывных подгрупп группы  -движений (с помощью производящих
-движений (с помощью производящих  -движений, связанных с соответствующими
-движений, связанных с соответствующими  -многоугольниками).
-многоугольниками).
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКЦИИ
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ВВЕДЕНИЕ ИНВАРИАНТНОЙ МЕТРИКИ
- § 1. Ортонормированные системы функций
- § 2. Замкнутые системы функций
- § 3. Существование замкнутых систем
- § 4. Ядровая и минимальная функции области
- § 6. Изменение ядровой функции области при конформных отображениях. Метрика, инвариантная при конформных отображениях
- ГЛАВА II. ИНВАРИАНТНАЯ МЕТРИКА В ОДНОСВЯЗНОЙ ОБЛАСТИ
- § 1. Гауссова кривизна
- § 2. Геодезические линии
- § 3. Группа движений Лобачевского
- § 4. Расстояние Лобачевского между двумя точками
- § 5. Аксиомы конгруентности и непрерывности
- § 6. Параллельность Лобачевского
- § 7. Треугольники Лобачевского
- § 8. Линии постоянной кривизны Лобачевского
- § 9. Пучки гиперциклов и орициклов
- § 10. Окружности Лобачевского
- § 11. Некоторые общие предложения
- ГЛАВА III. ГРУППА ДВИЖЕНИЙ ИНВАРИАНТНОЙ ГЕОМЕТРИИ В ОДНОСВЯЗНОЙ ОБЛАСТИ
- § 1. Классификация движений Лобачевского
- § 2. Собственно разрывные подгруппы группы движений Лобачевского
- § 3. Приведенные области собственно разрывных подгрупп
- § 4. Стороны 1-го рода приведенной области
- § 5. Вершины приведенной области
- ГЛАВА IV. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНВАРИАНТНОЙ МЕТРИКИ К ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ
- § 1. Лемма Шварца и ее обобщения
- § 2. Распространение леммы Шварца на орициклы и гиперциклы
- § 3. Оценки при приближении к границе области
- ГЛАВА V. МЕТРИКА, ИНВАРИАНТНАЯ ПРИ ПСЕВДОКОНФОРМНЫХ ОТОБРАЖЕНИЯХ
- § 1. Введение инвариантной метрики
- § 2. Кривизна инвариантной геометрии
- § 3. Группа движений инвариантной геометрии
- § 4. Случаи бицилиндра и шара