| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
Уравнение Ван-дер-Ваальса
В 1873 г. Ван-дер-Ваальс на основе молекулярной модели несжимаемых шаров диаметра а, притягивающих друг друга с силой, изменяющейся обратно пропорционально четвертой степени расстояния, вывел свое удивительно простое и замечательное уравнение.
В реальном газе в результате межмолекулярного притяжения увеличивается кинетическое давление по сравнению с давлением в идеальном газе. Так как сила межмолекулярного притяжения пропорциональна  то им обусловлено дополнительное давление обратно пропорциональное шестой степени расстояния или квадрату концентрации
то им обусловлено дополнительное давление обратно пропорциональное шестой степени расстояния или квадрату концентрации 
В результате межмолекулярного отталкивания свободный объем в реальном газе меньше, чем объем сосуда, занимаемого газом. Запрещенный объем вокруг каждой молекулы, в который не может попасть центр другой молекулы из-за взаимного отталкивания, Ван-дер-Ваальс оценил как объем сферы —  где а — расстояние между центрами двух несжимаемых шаров диаметра а. Следовательно, полный запрещенный объем моля газа будет равен
где а — расстояние между центрами двух несжимаемых шаров диаметра а. Следовательно, полный запрещенный объем моля газа будет равен  т. е. равен учетверенному объему
т. е. равен учетверенному объему  несжимаемых шаров — молекул.
несжимаемых шаров — молекул.
Уравнение Клайперона для идеального газа 
Уравнение Ван-дер-Ваальса представляет собой уравнение Клайперона, в которое введены перечисленные выше поправки на возросшее вследствие межмолекулярного взаимодействия кинетическое давление и уменьшенный реальный свободный объем:

 постоянная,
постоянная,  где
где  объем молекулы.
объем молекулы.
Если в качестве переменных  использовать их относительные значения:
использовать их относительные значения:  (где
(где  критические значения), то закон Ван-дер-Ваальса приобретает вид универсального закона соответственных состояний:
критические значения), то закон Ван-дер-Ваальса приобретает вид универсального закона соответственных состояний:

Следствие из этого закона может быть сформулировано следующим образом: все вещества кипят при одних и тех же относительных давлениях и температурах. Или еще — относительные объемы всех веществ одинаковы при одних и тех же относительных давлениях и температурах.
Уравнение Ван-дер-Ваальса можно записать в виде

т. e. представить в виде разложения потенциала притяжения по обратным степеням температуры, в котором учтен только первый член. Оправданием такого приближения служит предположение о малой величине и дальнодействующем характере сил притяжения. Так как в случае дальнодействия можно считать, что при переходе от одной конфигурации молекул к другой их потенциальная энергия не изменится, т. е.  вследствие того, что они находятся в среднем поле соседей с постоянной плотностью энергии. Это было показано Уленбеком в 1963 г.
вследствие того, что они находятся в среднем поле соседей с постоянной плотностью энергии. Это было показано Уленбеком в 1963 г.
Математическое и экспериментальное исследование этого уравнения показали, что поправки Ван-дер-Ваальса обладают глубоким физическим смыслом. Они не только качественно описывают изменения свойств системы, определяющих фазовый переход газ-жидкость, но и форму критической области. Кроме того, если силы притяжения нельзя рассматривать постоянными из-за близкодействия, обусловленного спецификой строения молекул, то уравнение Ван-дер-Ваальса допускает следующее приближение с учетом члена 
Справедливость модели Ван-дер-Ваальса в приближении 1/7 можно установить на основании проверки ряда ее выводов. Так, Олдер и Хувер в 1971 г. показали, что:
1. График зависимости  от
от  оказывается линейным от критической температуры до какой-то большой температуры, при которой эта линия пересекает ось ординат, определяя значение
оказывается линейным от критической температуры до какой-то большой температуры, при которой эта линия пересекает ось ординат, определяя значение  если потенциал имеет вид прямоугольной ямы, и искривляется для реальной системы (аргон) при высоких температурах.
если потенциал имеет вид прямоугольной ямы, и искривляется для реальной системы (аргон) при высоких температурах.
2. Величина  строго постоянна только с точностью до второго вириального коэффициента (т. е. в области малых плотностей).
строго постоянна только с точностью до второго вириального коэффициента (т. е. в области малых плотностей).
3. Последующие члены в разложении потенциала притяжения по обратной температуре малы только в области малых плотностей. В суперпозиционном приближении были
вычислены коэффициенты при  для ряда приведенных объемов
для ряда приведенных объемов

где  объем цлотной упаковки, а
объем цлотной упаковки, а  где
где  глубина потенциальной ямы.
глубина потенциальной ямы.
Таким образом, уравнение Ван-дер-Ваальса не описывает свойства жидкостей при нормальных условиях даже в первом приближении из-за того, что в жидкости при  первые два члена практически полностью взаимно уничтожаются и давление определяется последующими членами разложения
первые два члена практически полностью взаимно уничтожаются и давление определяется последующими членами разложения 
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
- Теплоемкость льда I
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
- Диэлектрические свойства
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
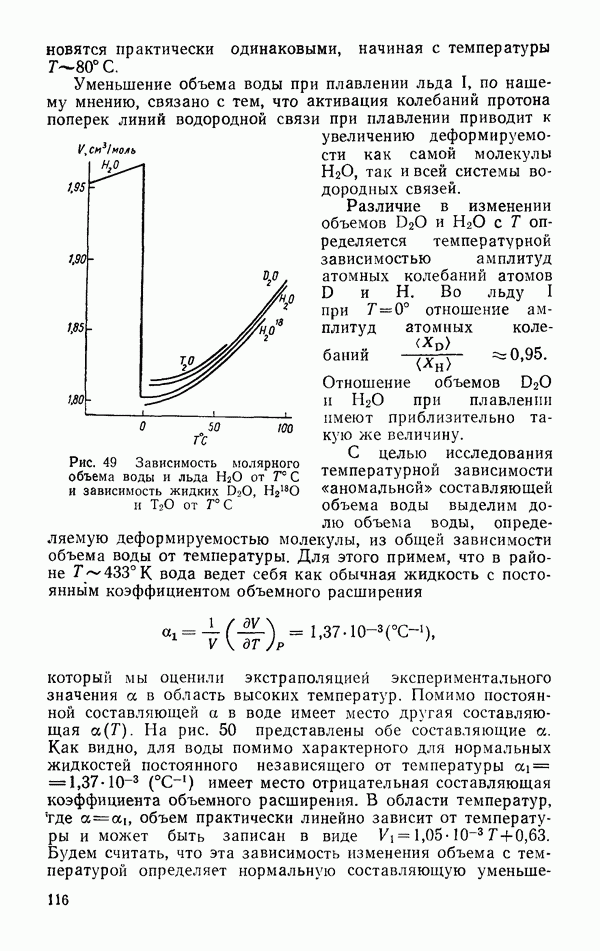
- Зависимость объема и его производных от температуры
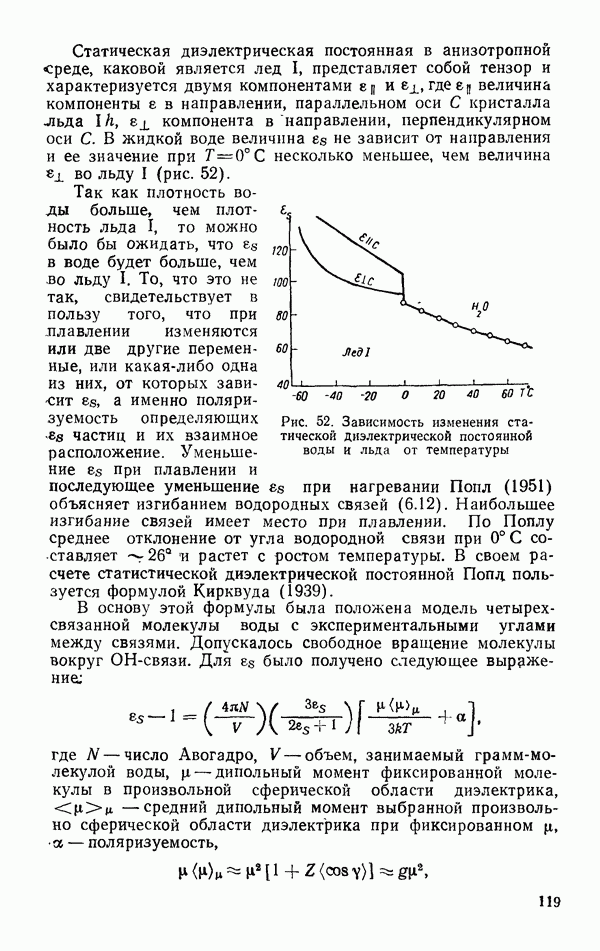
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
- Вязкость
- Теплопроводность
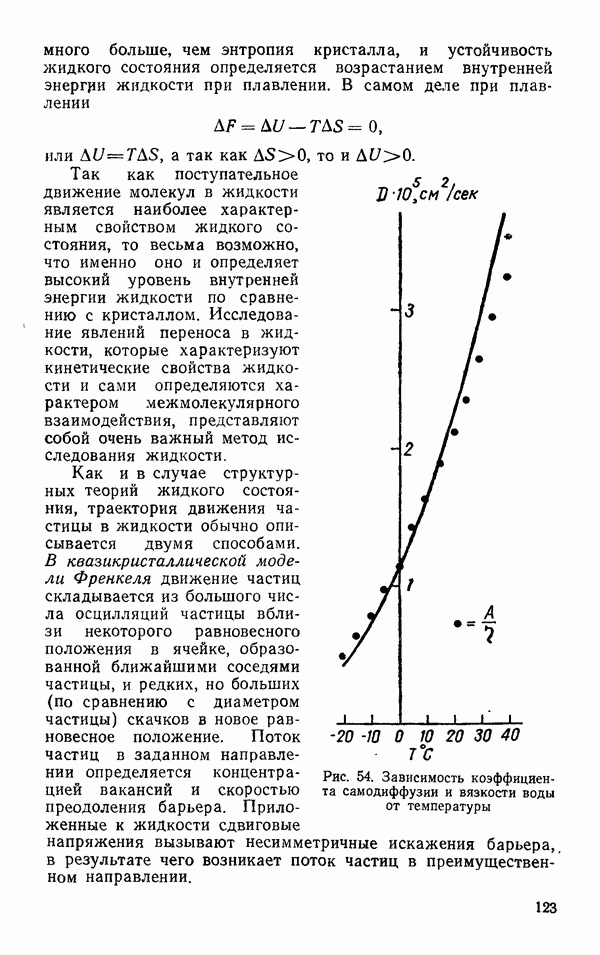
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА