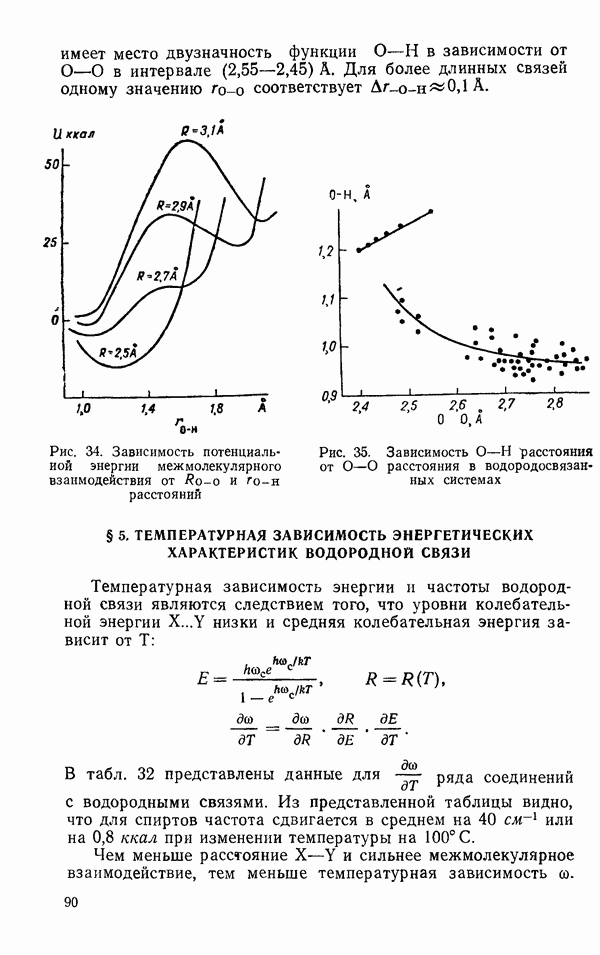
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
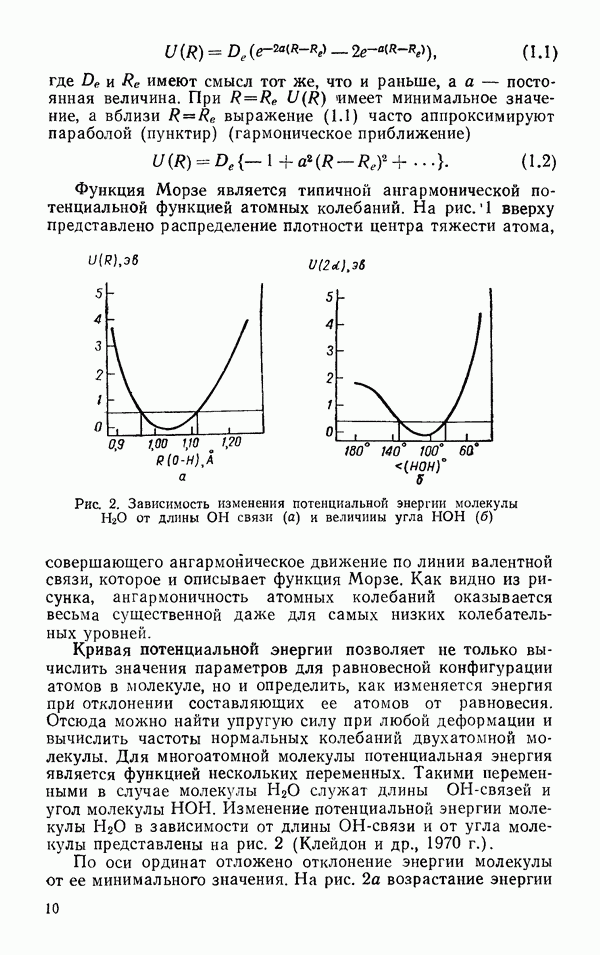
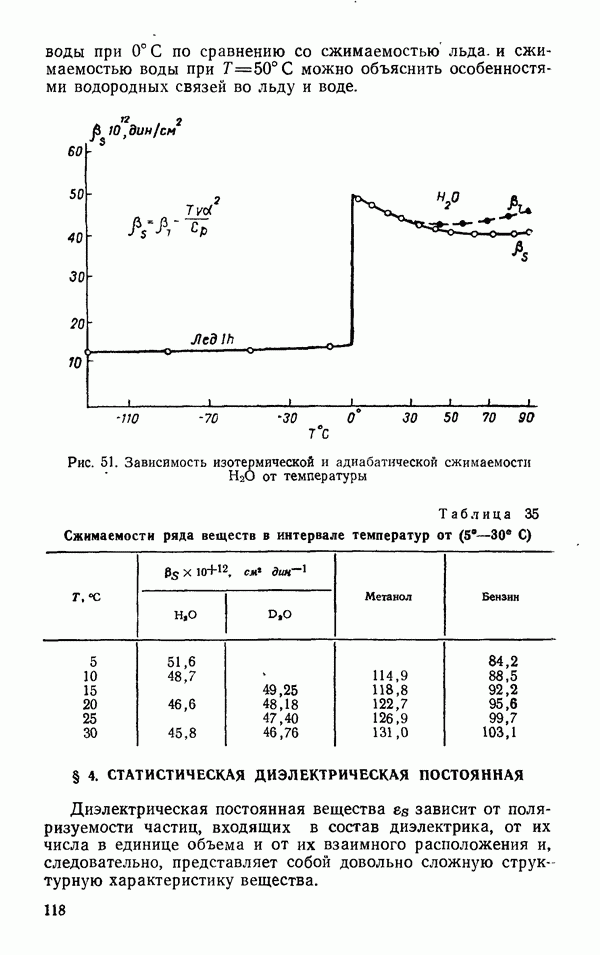
§ 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
Диэлектрическая постоянная вещества  зависит от поляризуемости частиц, входящих в состав диэлектрика, от их числа в единице объема и от их взаимного расположения и, следовательно, представляет собой довольно сложную структурную характеристику вещества.
зависит от поляризуемости частиц, входящих в состав диэлектрика, от их числа в единице объема и от их взаимного расположения и, следовательно, представляет собой довольно сложную структурную характеристику вещества.
Статическая диэлектрическая постоянная в анизотропной среде, каковой является лед I, представляет собой тензор и характеризуется двумя компонентами  гдебц величина компоненты
гдебц величина компоненты  в направлении, параллельном оси С кристалла льда
в направлении, параллельном оси С кристалла льда  компонента в направлении, перпендикулярном оси С. В жидкой воде величина
компонента в направлении, перпендикулярном оси С. В жидкой воде величина  не зависит от направления и ее значение при
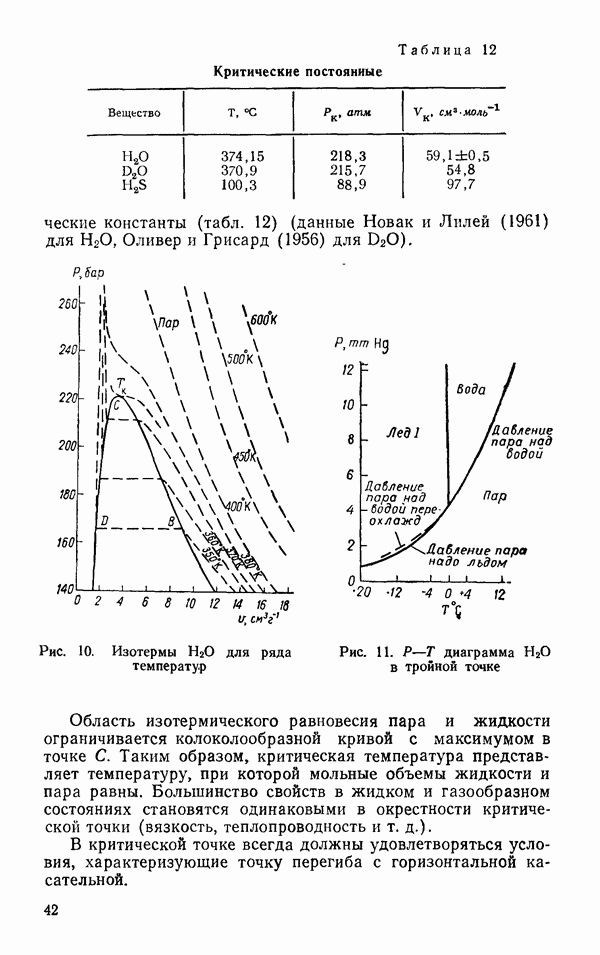
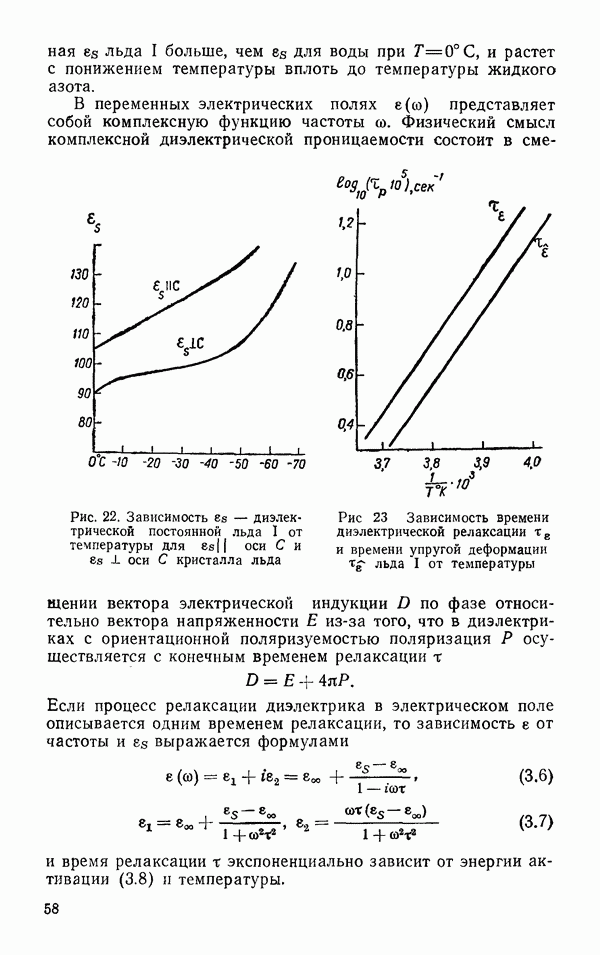
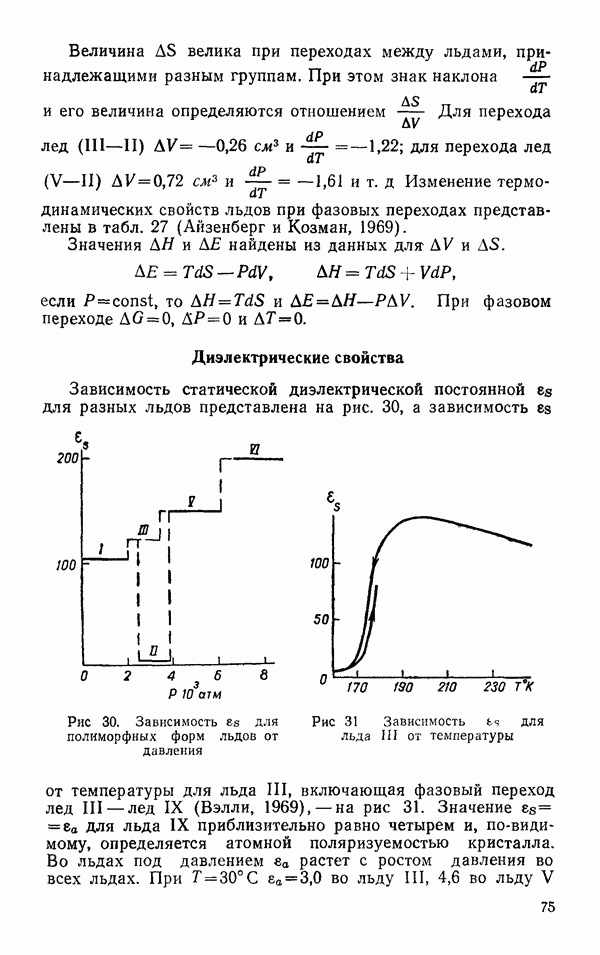
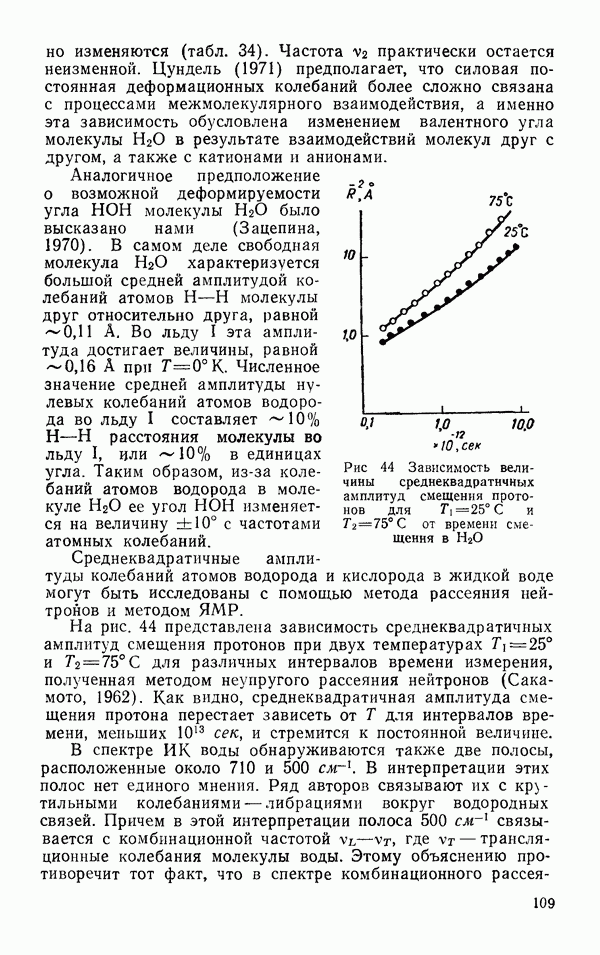
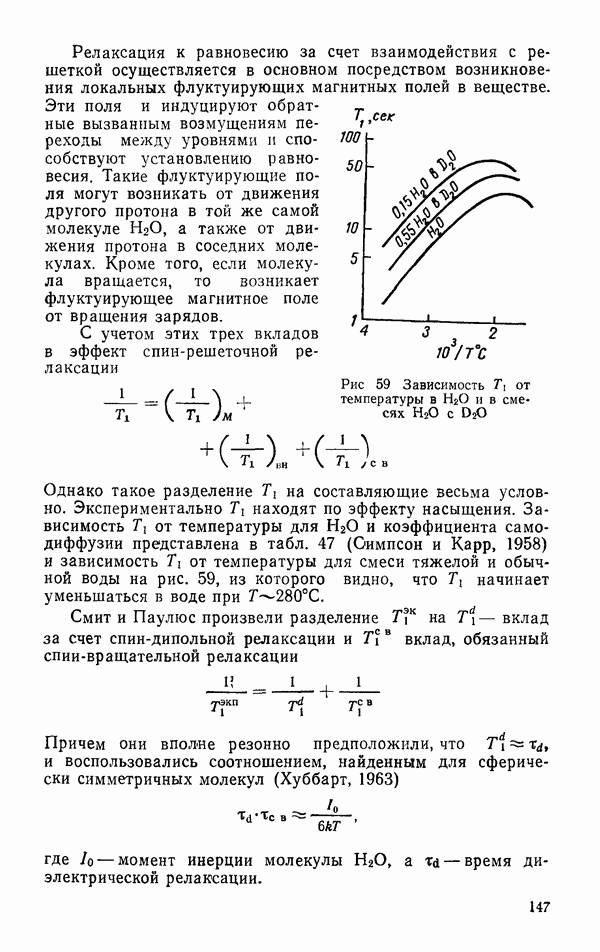
не зависит от направления и ее значение при  несколько меньшее, чем величина во льду I (рис. 52).
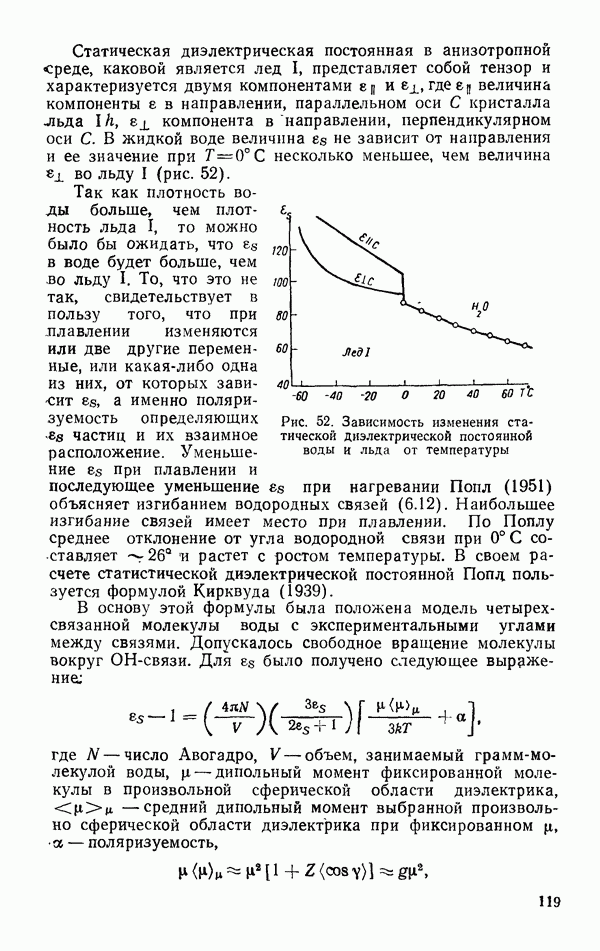
несколько меньшее, чем величина во льду I (рис. 52).

Рис. 52. Зависимость изменения статической диэлектрической постоянной воды и льда от температуры
Так как плотность воды больше, чем плотность льда I, то можно было бы ожидать, что  в воде будет больше, чем во льду
в воде будет больше, чем во льду  То, что это не так, свидетельствует в пользу того, что при плавлении изменяются или две другие переменные, или какая-либо одна из них, от которых зависит
То, что это не так, свидетельствует в пользу того, что при плавлении изменяются или две другие переменные, или какая-либо одна из них, от которых зависит  а именно поляризуемость определяющих
а именно поляризуемость определяющих  частиц и их взаимное расположение. Уменьшение
частиц и их взаимное расположение. Уменьшение  при плавлении и последующее уменьшение
при плавлении и последующее уменьшение  при нагревании Попл (1951) объясняет изгибанием водородных связей (6.12). Наибольшее изгибание связей имеет место при плавлении. По Поплу среднее отклонение от угла водородной связи при 0° С составляет
при нагревании Попл (1951) объясняет изгибанием водородных связей (6.12). Наибольшее изгибание связей имеет место при плавлении. По Поплу среднее отклонение от угла водородной связи при 0° С составляет  и растет с ростом температуры. В своем расчете статистической диэлектрической постоянной Попд пользуется формулой Кирквуда (1939).
и растет с ростом температуры. В своем расчете статистической диэлектрической постоянной Попд пользуется формулой Кирквуда (1939).
В основу этой формулы была положена модель четырехсвязанной молекулы воды с экспериментальными углами между связями. Допускалось свободное вращение молекулы вокруг ОН-связи. Для  было получено следующее выражение;
было получено следующее выражение;

где  число Авогадро, V — объем, занимаемый грамм-молекулой воды,
число Авогадро, V — объем, занимаемый грамм-молекулой воды,  дипольный момент фиксированной молекулы в произвольной сферической области диэлектрика,
дипольный момент фиксированной молекулы в произвольной сферической области диэлектрика,  — средний дипольный момент выбранной произвольно сферической области диэлектрика при фиксированном
— средний дипольный момент выбранной произвольно сферической области диэлектрика при фиксированном  а — поляризуемость,
а — поляризуемость,

где  число ближайших соседей,
число ближайших соседей,  характеризует средний угол между молекулами-диполями
характеризует средний угол между молекулами-диполями

 относительные ориентации при вращении ближайших соседей. Согласно Фрелиху (1960),
относительные ориентации при вращении ближайших соседей. Согласно Фрелиху (1960),

где  дипольный момент молекулы воды в вакууме, а
дипольный момент молекулы воды в вакууме, а 
Оценку Попл провел в предположении изгибания водородных связей. Его оценка показала, что в его модели всеми соседями, кроме четырех первых, можно пренебречь. Значение  учитывающее взаимодействие только с четырьмя первыми соседями, у него имеет следующий вид:
учитывающее взаимодействие только с четырьмя первыми соседями, у него имеет следующий вид:

где  постоянная изгибания водородных связей
постоянная изгибания водородных связей

 энергия изгибания водородных связей, определяемая как
энергия изгибания водородных связей, определяемая как  где
где  углы изгибания водородных связей (рис. 53).
углы изгибания водородных связей (рис. 53).  Попл оценивает из радиальной функции распределения
Попл оценивает из радиальной функции распределения  .
.

Рис. 53. Схема изгибания водородных связей в воде
Величина  уменьшается как с ростом Т, так и с ростом давления. Так, при
уменьшается как с ростом Т, так и с ростом давления. Так, при  а при
а при 
Проведенный расчет  привел автора к правильной температурной зависимости для
привел автора к правильной температурной зависимости для  которую определил рост угла изгибания водородных связей с ростом температуры. Однако абсолютные значения
которую определил рост угла изгибания водородных связей с ростом температуры. Однако абсолютные значения  разошлись с экспериментальными данными, они оказались на 20% меньше.
разошлись с экспериментальными данными, они оказались на 20% меньше.
Харрис и Олдрер (1953) в своем расчете диэлектрической постоянной воды и других полярных жидкостей воспользовались методом Кирквуда. Однако они исключили из
рассмотрения искажения поляризуемости молекул в процессе взаимодействия и предположили, что действие внешнего поля на сферический образец диэлектрика в вакууме не сопровождается изменением поляризуемости, как это получилось у Кирквуда, а состоит лишь в изменении ориентации постоянных диполей. При этом, если положить постоянный дипольный момент молекулы диэлектрика равным нулю, то поляризация должна удовлетворять уравнению Клаузиуса-Моссоти. Их соотношение для  имеет вид
имеет вид

Если  то получаем
то получаем

- соотношение Клаузиуса — Моссоти.
У Кирквуда же, если  то из его соотношения получается
то из его соотношения получается

или

Таблица 36 (см. скан) Данные для  экспериментальные и вычисленные рядом авторов
экспериментальные и вычисленные рядом авторов
Оценку  Харрис и Олдер заимствовали у Попла и получили для воды замечательное в пределах 3% согласие абсолютных значений с экспериментом и правильную температурную зависимость (табл. 36). Они произвели расчет
Харрис и Олдер заимствовали у Попла и получили для воды замечательное в пределах 3% согласие абсолютных значений с экспериментом и правильную температурную зависимость (табл. 36). Они произвели расчет  и для тяжелой воды
и для тяжелой воды  с той же константой изгибания водородных связей
с той же константой изгибания водородных связей  тем же числом соседей и тем же молярным объемом, как в обычной воде. Они учли только различную поляризуемость свободных молекул
тем же числом соседей и тем же молярным объемом, как в обычной воде. Они учли только различную поляризуемость свободных молекул  Согласие при этих предположениях эксперимента и расчета оказалось весьма хорошим.
Согласие при этих предположениях эксперимента и расчета оказалось весьма хорошим.
Таким образом, результаты анализа данных относительно величины и температурной зависимости  в жидкой воде показывают, что основную роль в межмолекулярном взаимодействии в воде играет деформация водородных связей в жидкой воде по сравнению со льдом
в жидкой воде показывают, что основную роль в межмолекулярном взаимодействии в воде играет деформация водородных связей в жидкой воде по сравнению со льдом 
Выводы
1. Структурные и спектральные данные свидетельствуют в пользу того, что вода не представляет собой смеси льда и пара, а представляет собой полностью водородосвязанную систему с широким распределением энергий водородной связи и  расстояний.
расстояний.
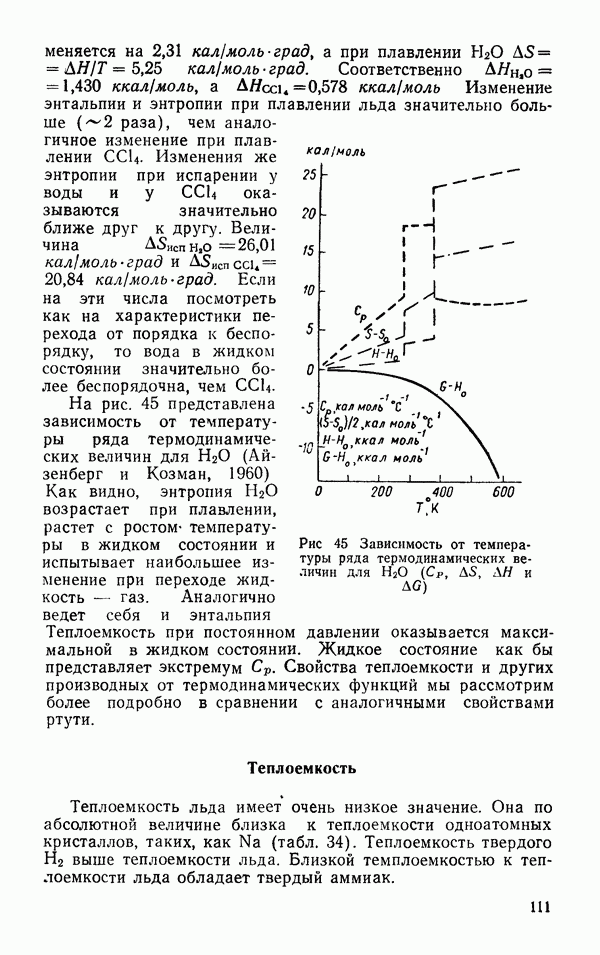
2. Молярная теплоемкость воды  в отличие от
в отличие от  ртути велика по абсолютной величине, что в первом приближении хорошо объясняется большой свободой атомов молекулы
ртути велика по абсолютной величине, что в первом приближении хорошо объясняется большой свободой атомов молекулы  в воде, определяемой большими амплитудами атомных колебаний.
в воде, определяемой большими амплитудами атомных колебаний.
Теплоемкость воды  отличается от
отличается от  ртути более резкой и нелинейной зависимостью от
ртути более резкой и нелинейной зависимостью от  Уменьшение
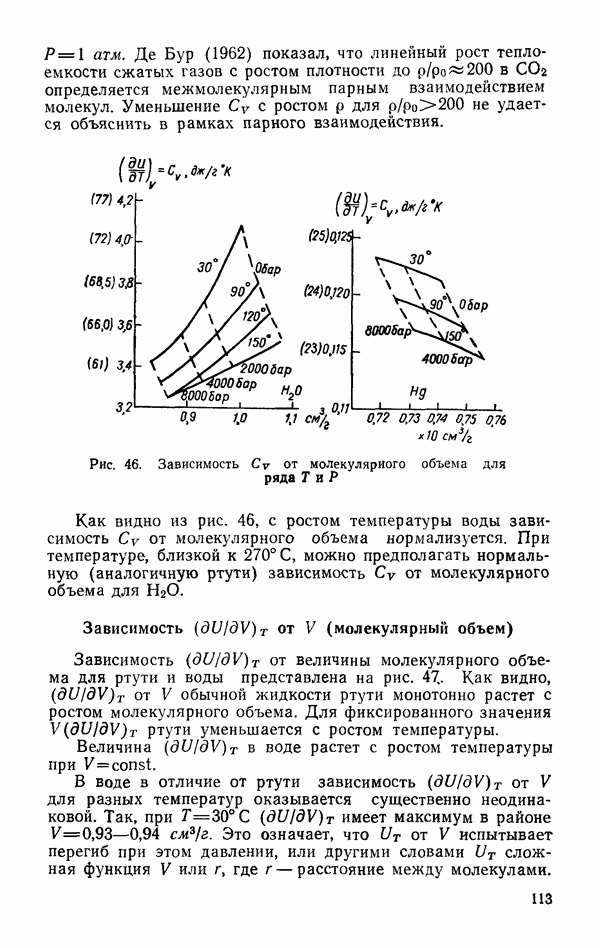
Уменьшение  при
при  с ростом плотности в воде аналогично уменьшению
с ростом плотности в воде аналогично уменьшению  в сильно сжатых газах, для которых
в сильно сжатых газах, для которых  и, как и в случае газов, не может быть объяснено без учета много частичного взаимодействия.
и, как и в случае газов, не может быть объяснено без учета много частичного взаимодействия.
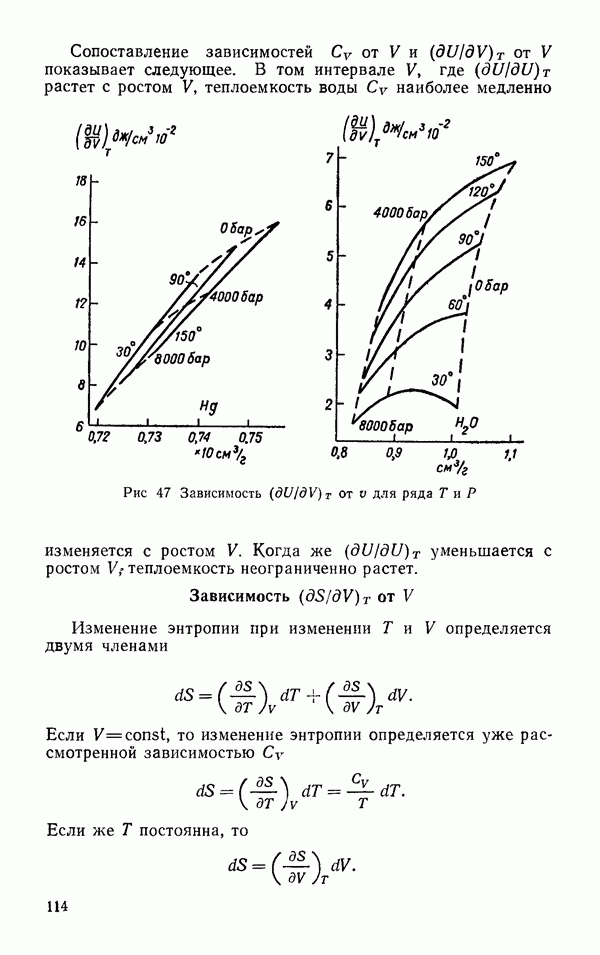
3. Зависимость  от
от  при
при  имеет максимум при
имеет максимум при  Экстремальный характер зависимости (от
Экстремальный характер зависимости (от  свидетельствует в пользу того, что наивысшая степень
свидетельствует в пользу того, что наивысшая степень  в зависимости
в зависимости  в воде не является второй, как в случае ртути.
в воде не является второй, как в случае ртути.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
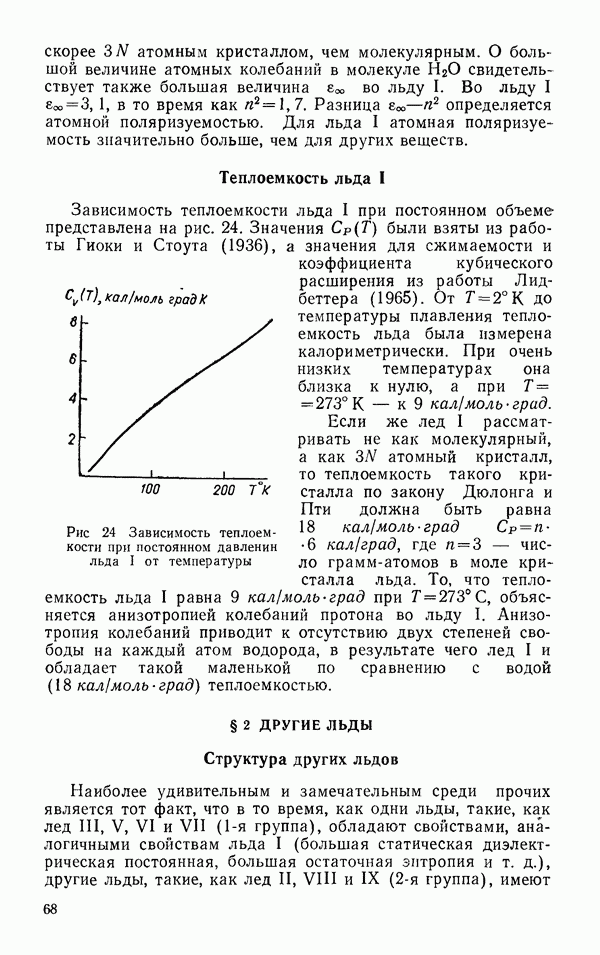
- Теплоемкость льда I
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
- Диэлектрические свойства
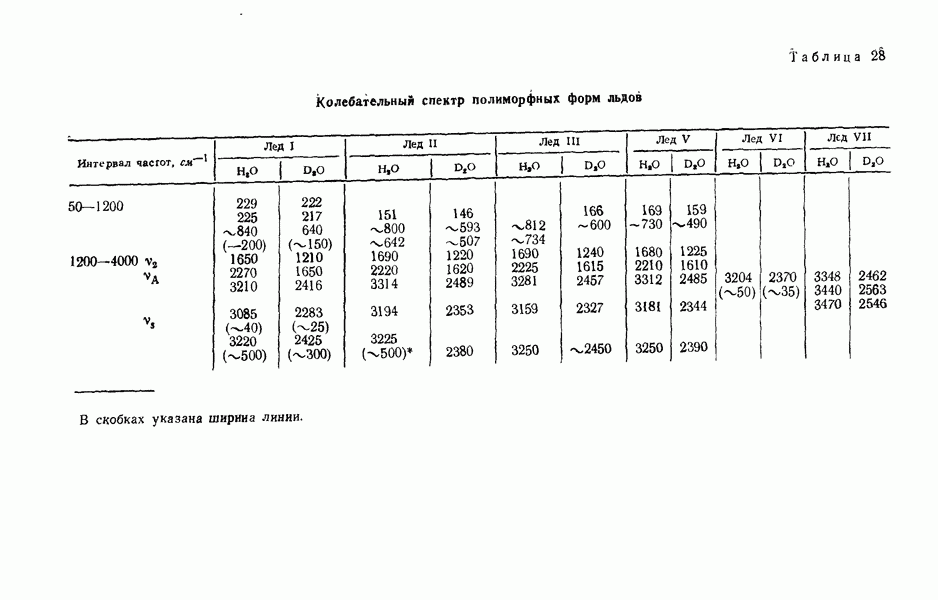
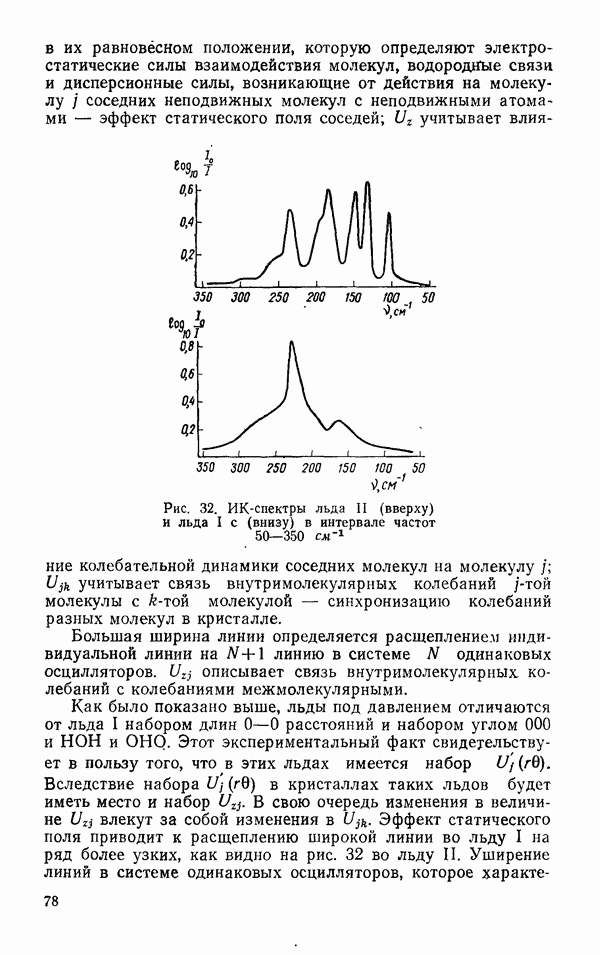
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
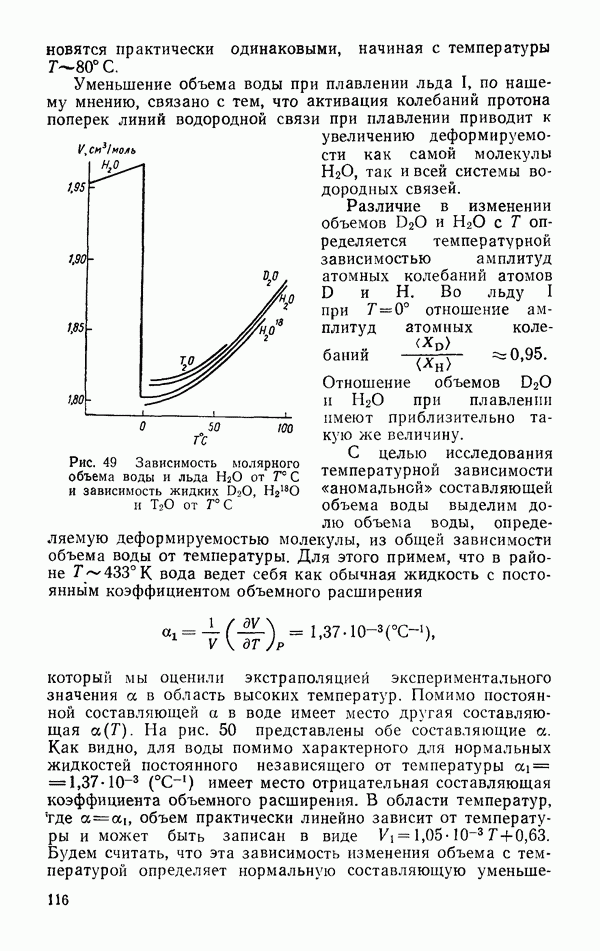
- Зависимость объема и его производных от температуры
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
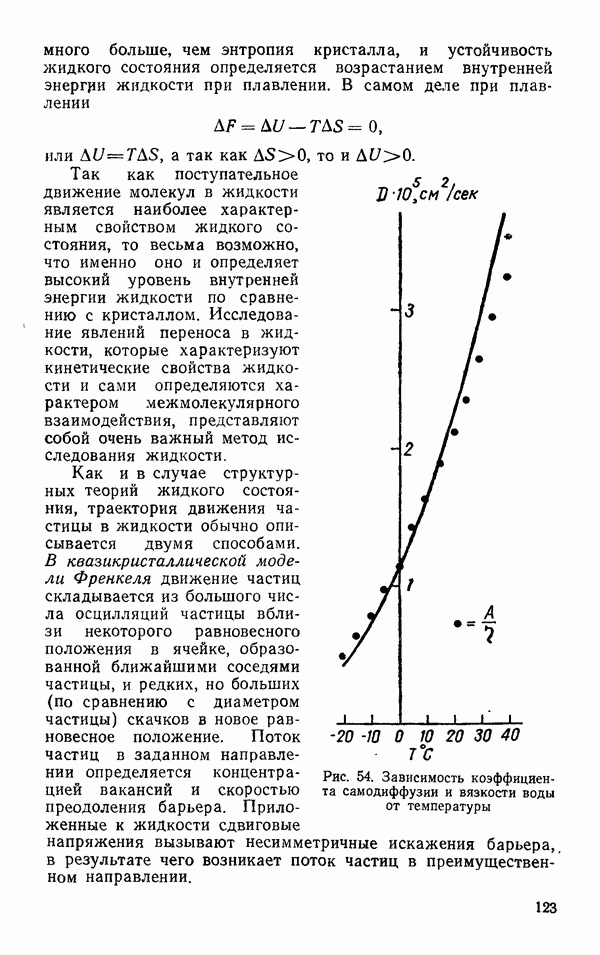
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
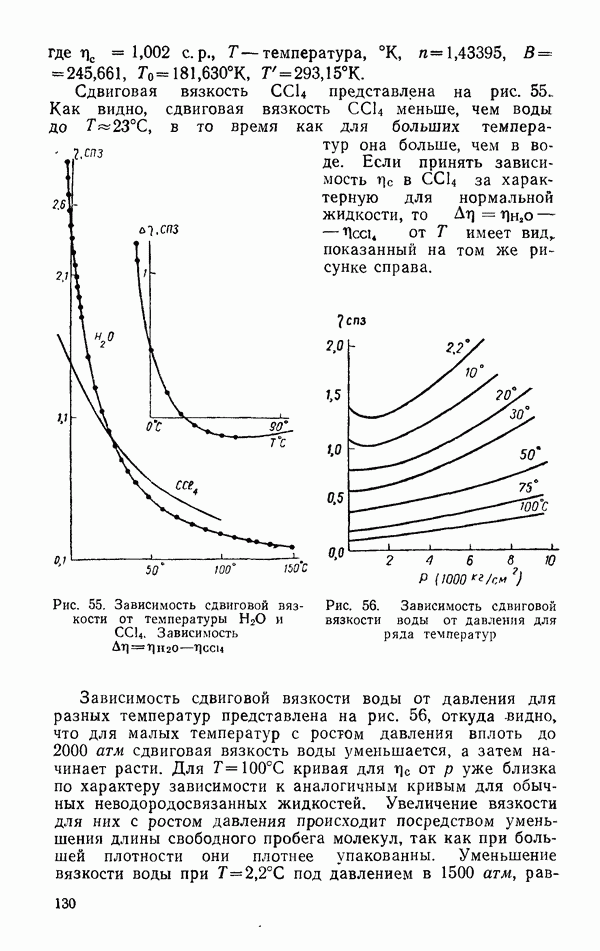
- Вязкость
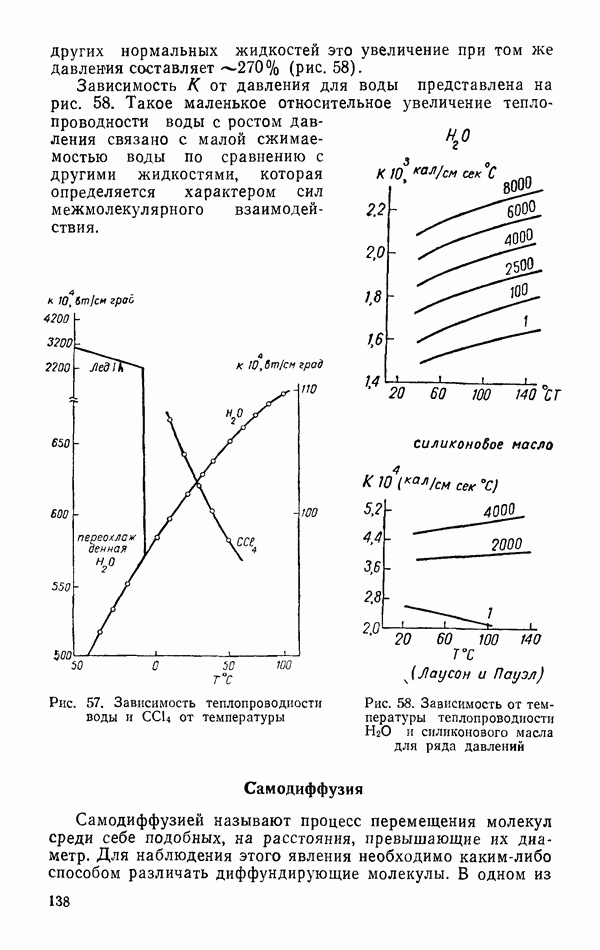
- Теплопроводность
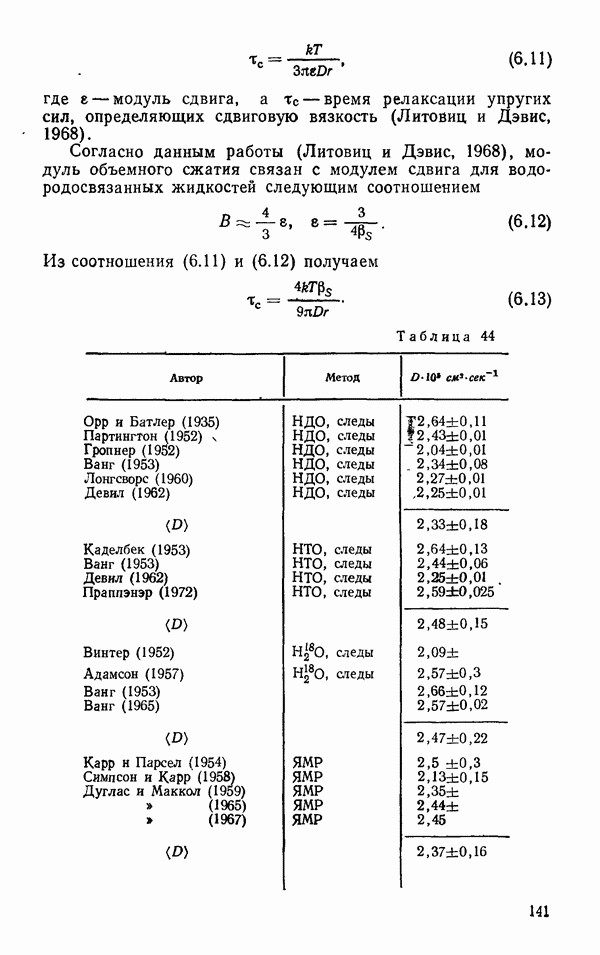
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА