| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. ЖИДКОЕ СОСТОЯНИЕ
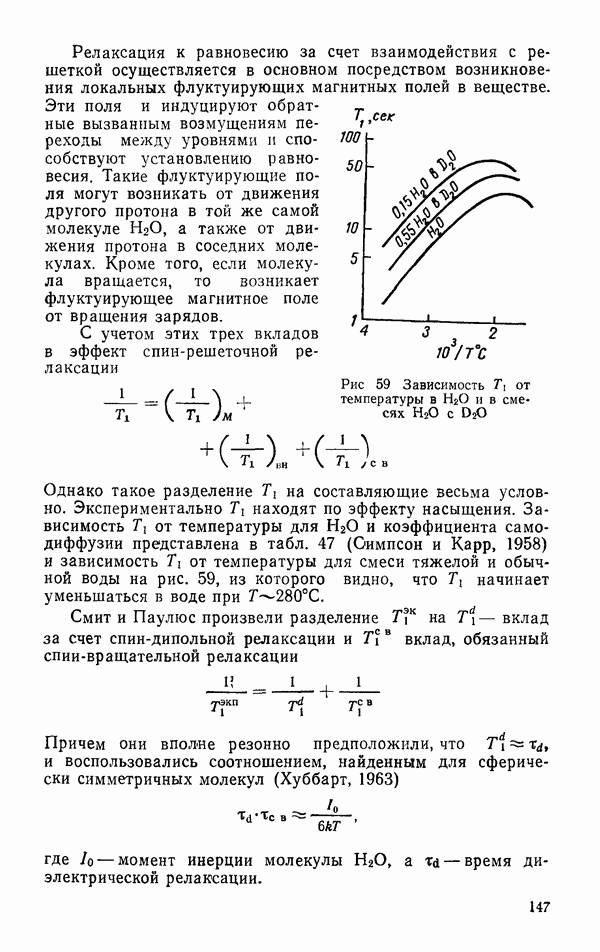
Основная проблема жидкости может быть сформулирована в виде вопроса: почему имеют место две формы конденсированного состояния, близкие по энергии межмолекулярного взаимодействия и колоссально отличающиеся по кинетике межмолекулярного взаимодействия?
§ 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
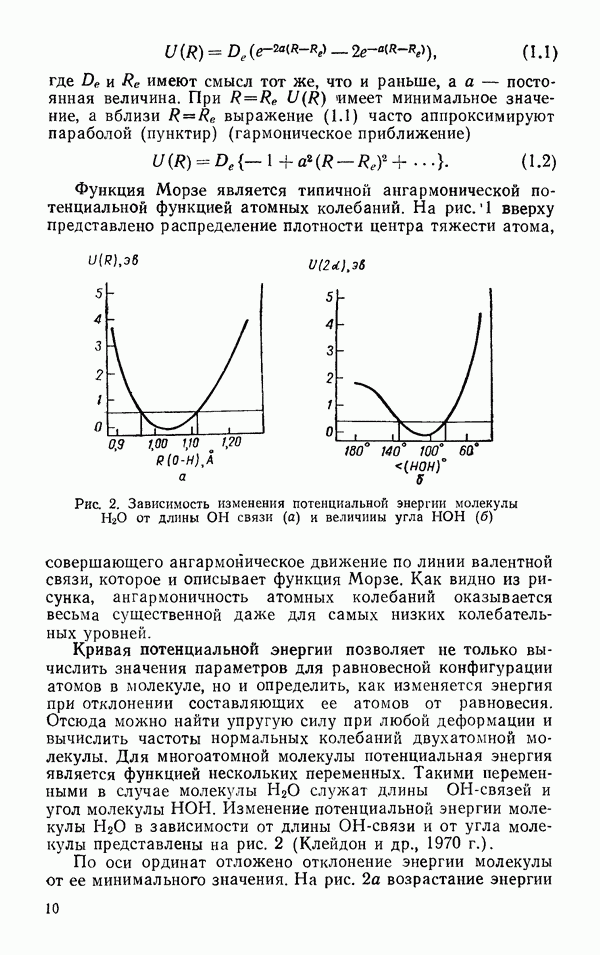
До Лапласа на жидкость смотрели как на сплошную среду и пытались решить проблему жидкого состояния методами гидродинамики и теории упругости. Пьер Симон Лаплас в конце XVIII в. предположил, что все свойства жидкости определяются короткодействующими силами между молекулами, которые практически исчезают, когда расстояние между молекулами превышает некоторое значение  Он получил для скрытой теплоты испарения и поверхностного натяжения выражения в форме интегралов от потенциалов межмолекулярного взаимодействия. Сравнив численные значения полученных интегралов с экспериментальными данными, он грубо оценил величину
Он получил для скрытой теплоты испарения и поверхностного натяжения выражения в форме интегралов от потенциалов межмолекулярного взаимодействия. Сравнив численные значения полученных интегралов с экспериментальными данными, он грубо оценил величину  эффективный радиус молекулы, обосновав тем самым молекулярный подход к проблеме жидкости.
эффективный радиус молекулы, обосновав тем самым молекулярный подход к проблеме жидкости.
Молекулярные теории жидкого состояния в качестве нулевых приближений используют теорию плотных газов — теории межмолекулярного поля, или теорию твердого тела — квазикристаллические теории жидкости.
Теории межмолекулярного поля
В 1873 г. Ван-дер-Ваальс написал свое классическое уравнение. Введенные им поправки в уравнение для идеальных газов, учитывающие внутреннее давление (силы притяжения) и объем молекул (силы отталкивания), предсказали
конденсацию молекул в жидкость при определенной плотности вещества. Как сейчас ясно из работ Уленбека (1963 г.) величина  в уравнении Ван-дер-Ваальса строго определяет притяжение, только если радиус действия межмолекулярных сил велик по сравнению с диаметром молекул. В этом случае можно считать, что каждая молекула находится в потенциальном поле соседей, причем величина этого поля пропорциональна
в уравнении Ван-дер-Ваальса строго определяет притяжение, только если радиус действия межмолекулярных сил велик по сравнению с диаметром молекул. В этом случае можно считать, что каждая молекула находится в потенциальном поле соседей, причем величина этого поля пропорциональна  где
где  число частиц,
число частиц,  объем. Теории, основанные на предположении дальнодействия межмолекулярных сил, известны под названием «теорий межмолекулярного поля».
объем. Теории, основанные на предположении дальнодействия межмолекулярных сил, известны под названием «теорий межмолекулярного поля».
Подход к проблеме жидкости со стороны твердого тела
Плотная упаковка молекул в жидкости, близкая к упаковке молекул в твердом теле, давала основания подойти к проблеме жидкости со стороны другого ее граничного состояния — твердого тела. Следствием плотной упаковки молекул в жидкости и в твердом теле является близость потенциальных энергий межмолекулярного взаимодействия в этих состояниях. Эти соображения послужили основой создания квазикристаллических теорий жидкого состояния, в чем большая заслуга принадлежит Я. И. Френкелю, который в 1945 г. создал теорию, рассматривающую твердое и газообразное состояние как предельные формы жидкого состояния. Он объединил «кочевое» движение, свойственное идеальному газу, с колебательным движением около положения равновесия, характерным для кристалла. Подобно молекуле в твердом теле молекула в жидкости какое-то время колеблется около какого-то положения равновесия, но в жидкости это состояние временное, и силовое поле представляет собой потенциальный рельеф из последовательных максимумов и минимумов (как это показано на рис. 37 в одномерном случае). Частица переходит из одного положения с минимумом потенциальной энергии в другое.

Рис. 37. Одномерный потенциальный рельеф квазистационарных положений равновесия молекулы в жидкости по Френкелю
Время перехода то имеет порядок времени, необходимого для перехода из одного квазистационарного положения в другое со средней скоростью, характерной для колебательного
движения частицы в твердом теле (так как средняя скорость движения частицы в газе не зависит от ее положения в произвольном силовом поле), то  сек.
сек.
Время  много больше, чем время то, так как оно связано со средней длительностью пребывания частицы в одной из ям, т. е. со временем, которое необходимо для приобретения молекулой кинетической энергии, равной глубине потенциальной ямы. Если глубина потенциальной ямы
много больше, чем время то, так как оно связано со средней длительностью пребывания частицы в одной из ям, т. е. со временем, которое необходимо для приобретения молекулой кинетической энергии, равной глубине потенциальной ямы. Если глубина потенциальной ямы  то согласно формуле Больцмана, связывающей вероятность состояния с его длительностью, может быть записано простое соотношение
то согласно формуле Больцмана, связывающей вероятность состояния с его длительностью, может быть записано простое соотношение

Можно легко найти среднюю скорость перемещения атома в жидкости. Если  расстояние между ямами,
расстояние между ямами, 

но так как

то

и если  где
где  скорость перехода из ямы в яму, и ширина ямы и расстояния между ямами одинаковы и равны
скорость перехода из ямы в яму, и ширина ямы и расстояния между ямами одинаковы и равны  то
то  т. е. средняя скорость движения в жидкости в
т. е. средняя скорость движения в жидкости в  раз меньше, чем скорость теплового дижения молекулы в газе при соответствующей температуре.
раз меньше, чем скорость теплового дижения молекулы в газе при соответствующей температуре.
Таким образом, с ростом  стремится к
стремится к  и при понижении температуры значению, характерному для твердого тела, т. е. зависимость от Т таких свойств, как средняя скорость, а следовательно, и коэффициент диффузии и коэффициенты подвижности определяются одинаковым множителем
и при понижении температуры значению, характерному для твердого тела, т. е. зависимость от Т таких свойств, как средняя скорость, а следовательно, и коэффициент диффузии и коэффициенты подвижности определяются одинаковым множителем  с едином для всех этих процессов энергией активации
с едином для всех этих процессов энергией активации 
Эти рассуждения непосредственно приложимы к простым жидкостям. Если жидкость образована сложными молекулами, тогда наряду с перемещениями молекул как целых надо учитывать парциальные перемещения, которые связаны со структурой сложных молекул и определяют процессы
колебаний отдельных атомов молекулы друг относительно друга и процессы диссоциации. Именно эти свойства жидкостей и кристаллов из многоатомных молекул выделяют их в особый класс сложных веществ.
Подход Бернала
Д. Бернал (1959—1960) рассматривает жидкость как однородное, связанное силами сцепления (и следовательно, занимающее близкий объем к объему твердого тела, другого связанного состояния вещества) существенно нерегулярное построение молекул, не содержащих никаких кристаллических участков или дырок, достаточно больших, чтобы позволить другим молекулам внедриться в них (рочь идет о простых жидкостях).
Бернал построил много моделей жидкости как плоских, так и трехмерных. При их построении он руководствовался законом  при размещении молекул в пространстве и допускал возможность варьирования трех параметров:
при размещении молекул в пространстве и допускал возможность варьирования трех параметров:  числа ближайших соседей в координационной сфере; — среднего расстояния между координационными сферами и
числа ближайших соседей в координационной сфере; — среднего расстояния между координационными сферами и  расстояния между соседями в координационной сфере. Его задача состояла в построении системы связанных частиц, для которых характерен закон
расстояния между соседями в координационной сфере. Его задача состояла в построении системы связанных частиц, для которых характерен закон  и которые имеют меньшую
и которые имеют меньшую  плотность, чем плотность твердого тела. Одной из его моделей была модель, выполненная из пластилиновых шаров, которые были нерегулярно упакованы тем способом, как это было уже рассказано, и затем равномерно сжаты. Этот метод использовал ботаник Марвин для исследования формы клеток растений. Как эта модель, так и другие (шар и стержень и т. д.) показали, что в нерегулярной системе, близкой по плотности к плотности простой жидкости, преимущественно имеет место пятиугольная симметрия. Из исследуемых 65 пластилиновых шаров после всестороннего сжатия было найдено в получившихся после такой процедуры многоугольниках абсолютное преобладание пятиугольных граней. Такой тип симметрии отсутствует в регулярной кристаллической структуре и встречается только в нерегулярных сложных структурах сплавов, классифицированных Френком.
плотность, чем плотность твердого тела. Одной из его моделей была модель, выполненная из пластилиновых шаров, которые были нерегулярно упакованы тем способом, как это было уже рассказано, и затем равномерно сжаты. Этот метод использовал ботаник Марвин для исследования формы клеток растений. Как эта модель, так и другие (шар и стержень и т. д.) показали, что в нерегулярной системе, близкой по плотности к плотности простой жидкости, преимущественно имеет место пятиугольная симметрия. Из исследуемых 65 пластилиновых шаров после всестороннего сжатия было найдено в получившихся после такой процедуры многоугольниках абсолютное преобладание пятиугольных граней. Такой тип симметрии отсутствует в регулярной кристаллической структуре и встречается только в нерегулярных сложных структурах сплавов, классифицированных Френком.
Пятиугольная симметрия, не имеющая места в кристалле, позволила Берналу объяснить способность простых жидкостей к переохлаждению, большую энтропию жидкости по сравнению с кристаллом и текучесть.
Д. Бернал на основании своих экспериментов пришел к выводу, что при переходе к расстояниям между частицами в
трехмерной структуре, соответствующим 0,95 V от объема плотной упаковки, никакой беспорядок невозможен.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
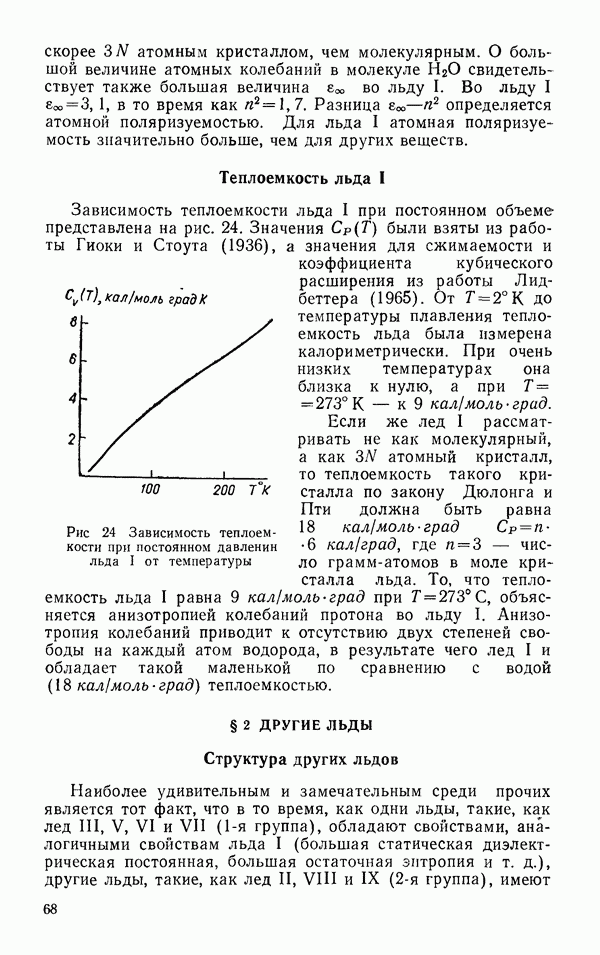
- Теплоемкость льда I
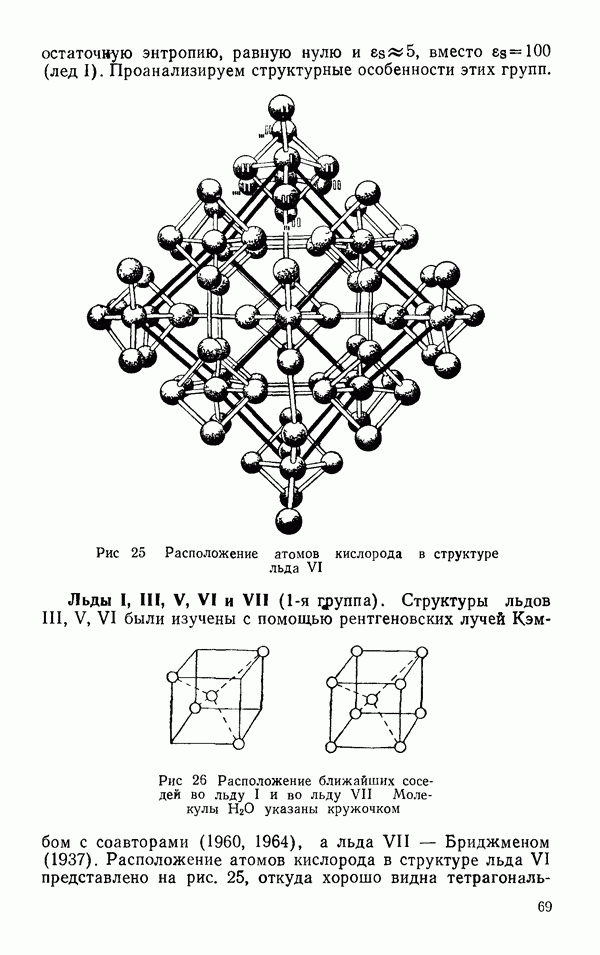
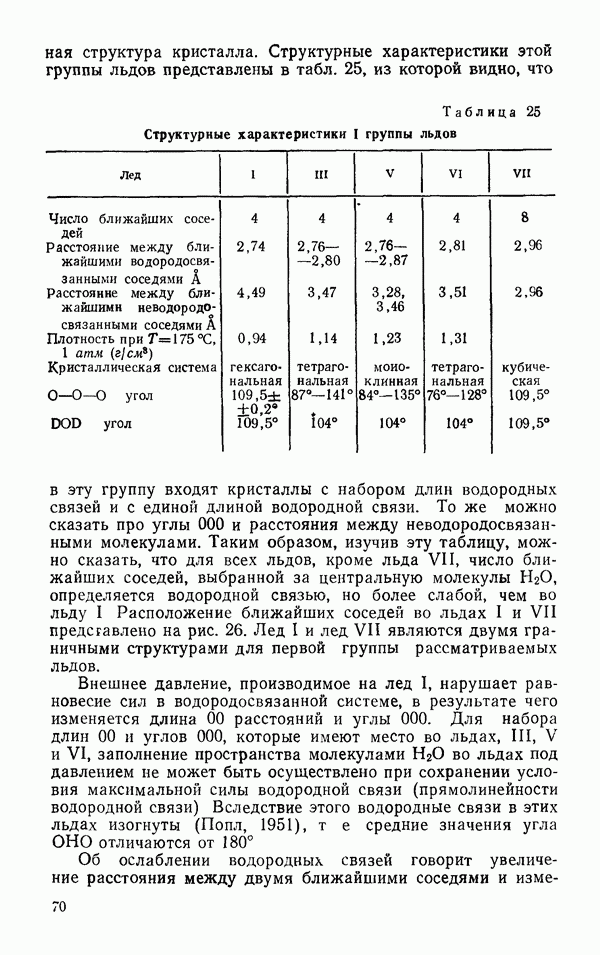
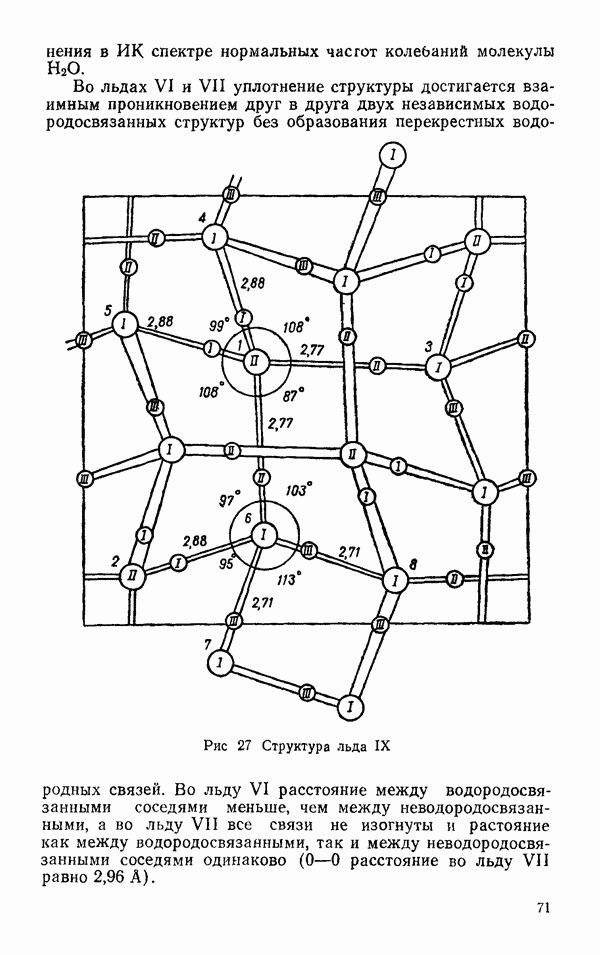
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
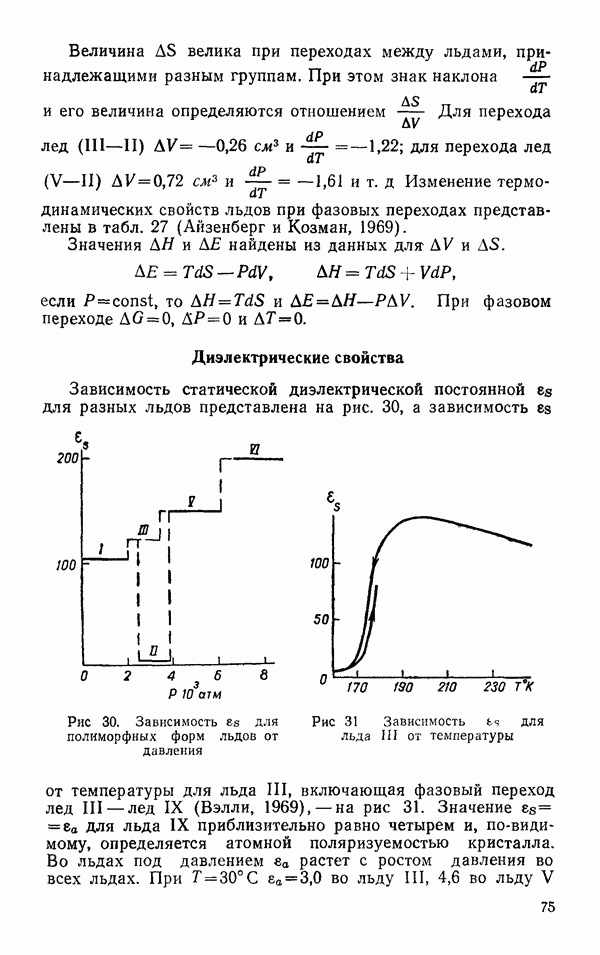
- Диэлектрические свойства
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
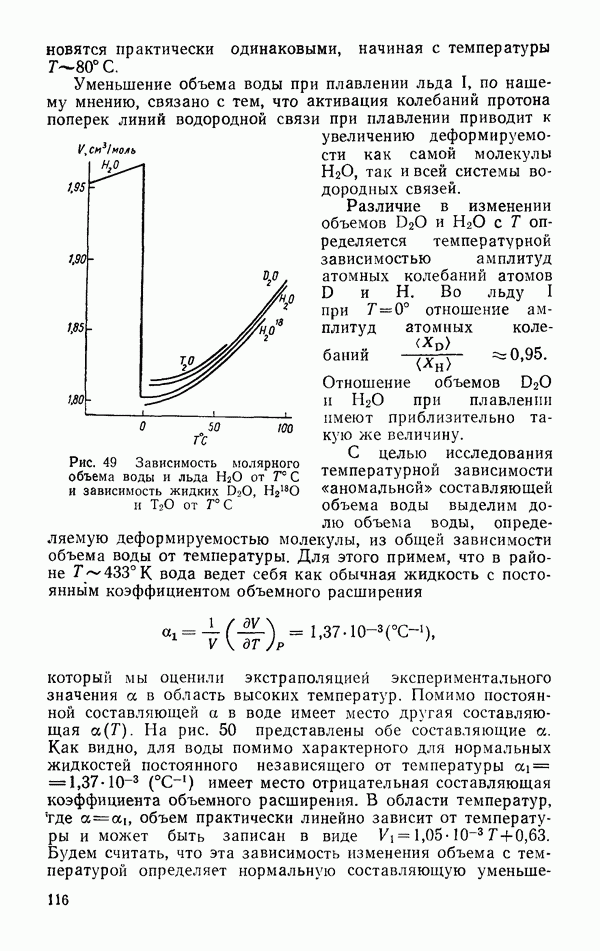
- Зависимость объема и его производных от температуры
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
- Вязкость
- Теплопроводность
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА