| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Вязкость
Если один слой жидкости равномерно движется относительно другого, то на него действует тангенциальная сила  которая, как показал впервые Ньютон, пропорциональна площади слоя и градиенту скорости
которая, как показал впервые Ньютон, пропорциональна площади слоя и градиенту скорости  в перпендикулярном движению направлении. Коэффициент пропорциональности
в перпендикулярном движению направлении. Коэффициент пропорциональности

 представляет сдвиговую вязкость или внутреннее трение, величина
представляет сдвиговую вязкость или внутреннее трение, величина  кинематическая вязкость. Величина
кинематическая вязкость. Величина  носит название текучести.
носит название текучести.
При деформации типа объемного сжатия, которая имеет место в звуковой волне, вязкие потери помимо сдвиговой вязкости определяются также объемной вязкостью

где а — измеренный коэффициент поглощения звука, а  коэффициент поглощения звука, рассчитанный по классической формуле
коэффициент поглощения звука, рассчитанный по классической формуле

 скорость звука,
скорость звука,  плотность,
плотность,  коэффициент теплопроводности,
коэффициент теплопроводности,  теплоемкость при постоянном давлении,
теплоемкость при постоянном давлении,  — отношение удельных теплоемкостей
— отношение удельных теплоемкостей 
Вязкость жидкости зависит от Т и Р.
Экспериментальная зависимость сдвиговой вязкости воды  температуры впервые была выражена Пуазейлем следующей формулой:
температуры впервые была выражена Пуазейлем следующей формулой:

где  сдвиговая вязкость воды при
сдвиговая вязкость воды при  и
и  — эмпирические постоянные.
— эмпирические постоянные.
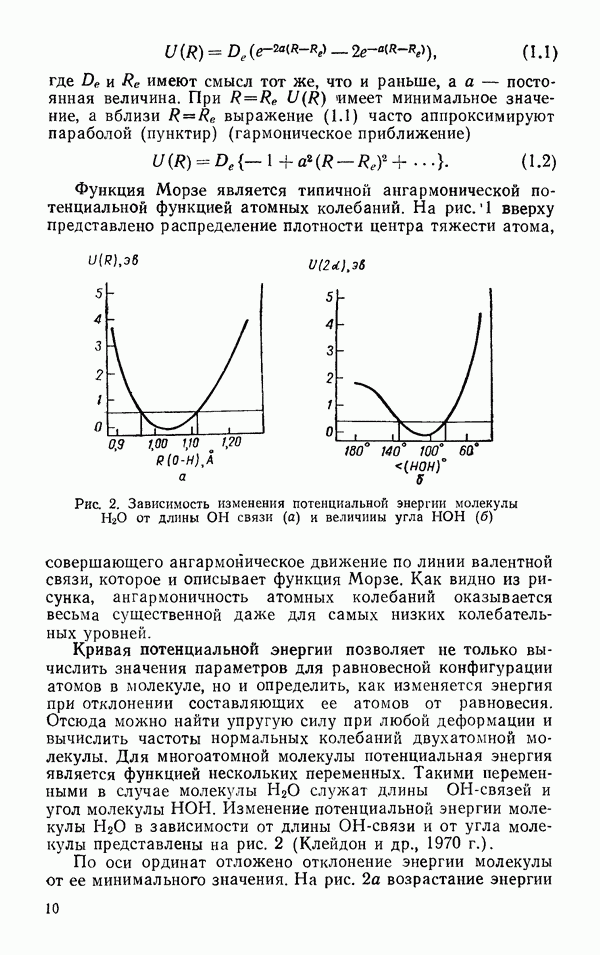
Экспериментальные данные относительно сдвиговой вязкости воды при разных температурах, включая и область переохлажденной воды, представлены на рис. 55. Зависимость  была записана в виде двух соотношений. (Лауренс и др., 1971). В области от —10° до 40 °С справедливо соотношение
была записана в виде двух соотношений. (Лауренс и др., 1971). В области от —10° до 40 °С справедливо соотношение

где  — вязкость воды при
— вязкость воды при  где
где  температура в градусах Цельсия.
температура в градусах Цельсия.
В области температур от  справедливо соотношение
справедливо соотношение

где  — температура,
— температура, 
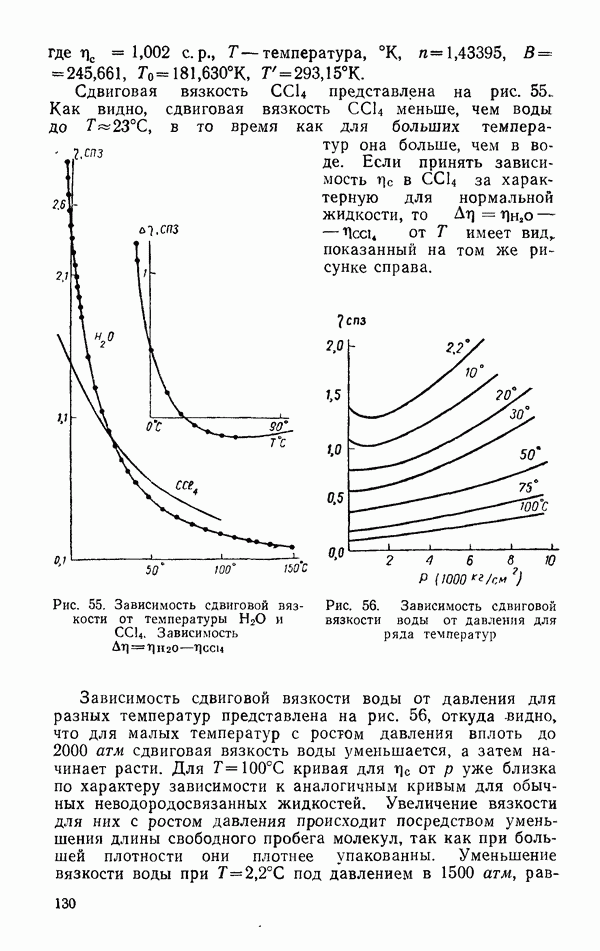
Сдвиговая вязкость  представлена на рис. 55. Как видно, сдвиговая вязкость
представлена на рис. 55. Как видно, сдвиговая вязкость  меньше, чем воды до
меньше, чем воды до  в то время как для больших температур она больше, чем в воде. Если принять зависимость
в то время как для больших температур она больше, чем в воде. Если принять зависимость  за характерную для нормальной жидкости, то
за характерную для нормальной жидкости, то  от Т имеет вид, показанный на том же рисунке справа.
от Т имеет вид, показанный на том же рисунке справа.

Рис. 55. Зависимость сдвиговой вязкости от температуры  Зависимость
Зависимость 

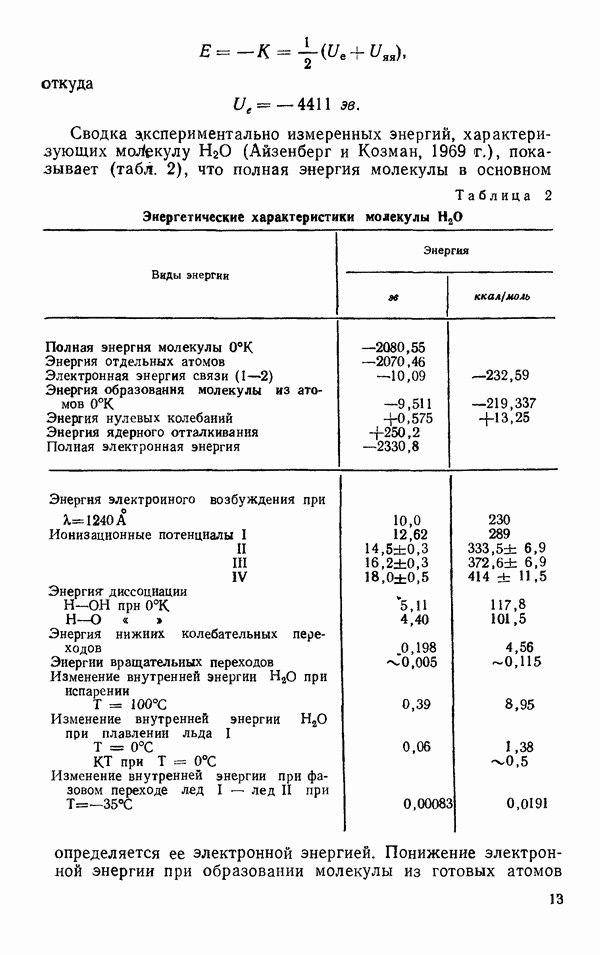
Рис. 56. Зависимость сдвиговой вязкости воды от давления для ряда температур
Зависимость сдвиговой вязкости воды от давления для разных температур представлена на рис. 56, откуда видно, что для малых температур с ростом давления вплоть до 2000 атм сдвиговая вязкость воды уменьшается, а затем начинает расти. Для  кривая для
кривая для  от
от  уже близка по характеру зависимости к аналогичным кривым для обычных неводородосвязанных жидкостей. Увеличение вязкости для них с ростом давления происходит посредством уменьшения длины свободного пробега молекул, так как при большей плотности они плотнее упакованны. Уменьшение вязкости воды при
уже близка по характеру зависимости к аналогичным кривым для обычных неводородосвязанных жидкостей. Увеличение вязкости для них с ростом давления происходит посредством уменьшения длины свободного пробега молекул, так как при большей плотности они плотнее упакованны. Уменьшение вязкости воды при  под давлением в 1500 атм,
под давлением в 1500 атм,
равное  оказывается практически равным избыточной вязкости воды по сравнению с вязкостью
оказывается практически равным избыточной вязкости воды по сравнению с вязкостью  при той же температуре (рис. 55). Избыточная вязкость воды по сравнению с вязкостью
при той же температуре (рис. 55). Избыточная вязкость воды по сравнению с вязкостью  при той же температуре, по нашему мнению, определяется процессами атомных колебаний протонов в системе водородных связей в воде. В результате действия сил давления водородные связи дополнительно изгибаются и ослабляются.
при той же температуре, по нашему мнению, определяется процессами атомных колебаний протонов в системе водородных связей в воде. В результате действия сил давления водородные связи дополнительно изгибаются и ослабляются.
Очень интересен подход к проблеме вязкости Максвелла (1868), который определил явление вязкости как отклонение от равновесия системы, вызванное возбуждением системы, обусловленным напряжением или упругой силой  Как известно, упругая сила связана с деформацией
Как известно, упругая сила связана с деформацией

где А — деформация, которая представляет собой относительное изменение какой-либо величины, например при деформации объема  модуль упругости.
модуль упругости.
Если нет вязкости, то деформация и сила проявляются одновремейно

Если же среда вязкая, то упругая сила будет изменяться в зависимости от величины силы и от природы тела. Первым естественным предположением у Максвелла было предположение пропорциональности деформации величине приложенной силы

если  постоянная величина, то
постоянная величина, то  Если
Если  т. е. имеет место равномерное движение, которое все время увеличивает смещение, то
т. е. имеет место равномерное движение, которое все время увеличивает смещение, то

Коэффициент при скорости деформации  представляет собой вязкость. Таким образом, вязкость по Максвеллу определяется произведением модуля упругости на время релаксации упругих сил:
представляет собой вязкость. Таким образом, вязкость по Максвеллу определяется произведением модуля упругости на время релаксации упругих сил:

Модуль сдвига  полностью определяет сдвиговую вязкость
полностью определяет сдвиговую вязкость

В случае объемной вязкости процесс деформации будет определяться модулем объемной упругости 
Как  так и В, могут быть как адиабатическими, так и изотермическими, в зависимости от условий эксперимента.
так и В, могут быть как адиабатическими, так и изотермическими, в зависимости от условий эксперимента.
Если прилагаемое синусоидальное напряжение создается звуковой волной, то изменение объема жидкости происходит адиабатически.
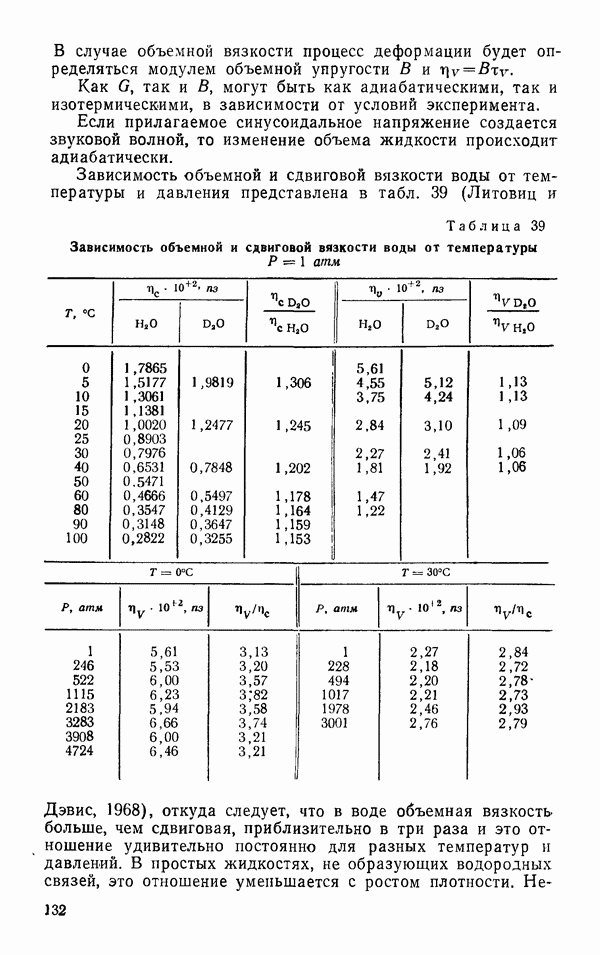
Таблица 39 (см. скан) Зависимость объемной и сдвиговой вязкости воды от температуры 
Зависимость объемной и сдвиговой вязкости воды от температуры и давления представлена в табл. 39 (Литовиц и Дэвис, 1968), откуда следует, что в воде объемная вязкость больше, чем сдвиговая, приблизительно в три раза и это отношение удивительно постоянно для разных температур и давлений. В простых жидкостях, не образующих водородных связей, это отношение уменьшается с ростом плотности.
Некоторые авторы рассматривают постоянство отношения объемной вязкости к сдвиговой в воде при разных  как еще одну «аномалию» воды.
как еще одну «аномалию» воды.
Как сдвиговая, так и объемная вязкость определяют поглощение энергии в звуковой волне. Причина поглощения звука состоит в том, что деформация смещена по фазе по отношению к изменению давления, как это было предположено Максвеллом.
Таблица 40 Зависимость коэффициентов поглощения звука в  от
от 

В табл. 40 представлены данные относительно скорости звука, сдвиговой вязкости и поглощения звука в зависимости от давления в воде для двух температур  и
и  Как видно из табл. 40 (данные Литовца, 1955), коэффициент поглощения звука уменьшается как с ростом давления, так и с ростом температуры. Процессы поглощения звука при малых давлениях и малых температурах определяются динамикой водородных связей.
Как видно из табл. 40 (данные Литовца, 1955), коэффициент поглощения звука уменьшается как с ростом давления, так и с ростом температуры. Процессы поглощения звука при малых давлениях и малых температурах определяются динамикой водородных связей.
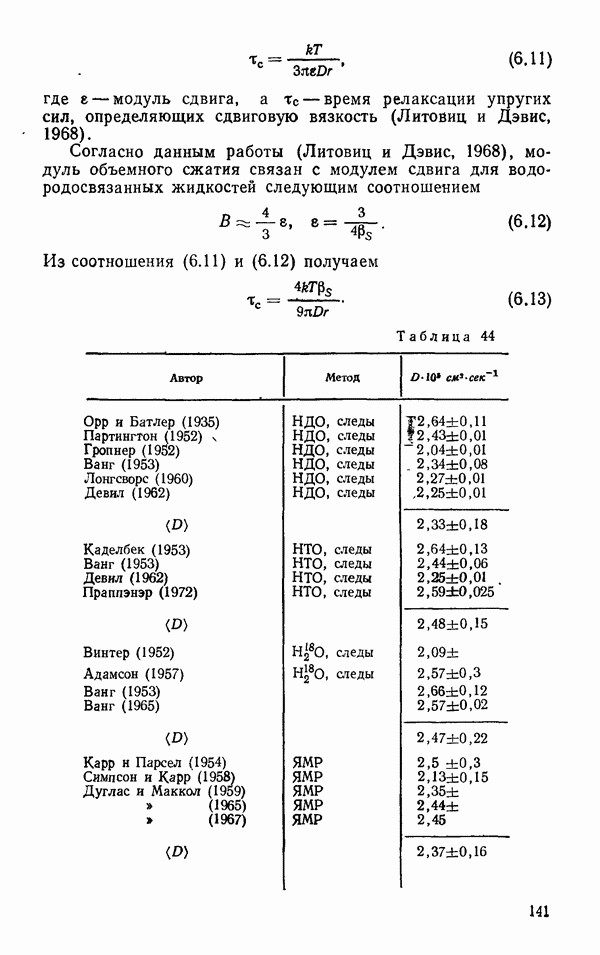
Так как коэффициент объемной вязкости согласно Максвеллу зависит от времени релаксации  то, зная
то, зная  можно вычислить время релаксации объемной вязкости. Температурная зависимость высокочастотного модуля упругости в воде была получена
можно вычислить время релаксации объемной вязкости. Температурная зависимость высокочастотного модуля упругости в воде была получена  и др. в 1966 г. на основании данных по скорости ультразвука в смесях вода — глицерол, линейной экстраполяцией данных для смеси к 100% воде. Эти данные представлены в табл. 41. Как видно из таблицы, при
и др. в 1966 г. на основании данных по скорости ультразвука в смесях вода — глицерол, линейной экстраполяцией данных для смеси к 100% воде. Эти данные представлены в табл. 41. Как видно из таблицы, при 
Таким образом, высокочастотная сжимаемость воды существенно меньше, чем низкочастотная сжимаемость при той же температуре, и близка по абсолютной величине к сжимаемости льда.
Таблица 41 Температурная зависимость высокочастотного модуля сдвига и модуля сжимаемости воды 

Таблица 42 Соотношение между временами релаксации объемной вязкости и диэлектрической релаксации в зависимости от температуры в 

В габл. 42 представлены данные времени объемной релаксации по Масквеллу и времени диэлектрической релаксации (Колли и др., 1948). Время диэлектрической релаксации характеризует восстановление равновесной поляризации в диэлектрике после отключения внешнего поля. Как видно из табл. 42, время объемной релаксации в воде на порядок меньше времени диэлектрической релаксации.
Выше представленные данные показывают, что в настоящий момент мы располагаем достаточно точными результатами зависимости вязкости от давления и температуры «Аномалии» вязкости воды состоят в существовании отрицательного коэффициента в зависимости вязкость — давление и в наличии минимума в изотермах вязкости при низких температурах. Теория вязкости, которая описывала бы эти аномалии, исходя из одной какой-либо модели воды, не существует. Оценка времени релаксации вязкости показывает, что оно имеет порядок времени молекулярных колебаний
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
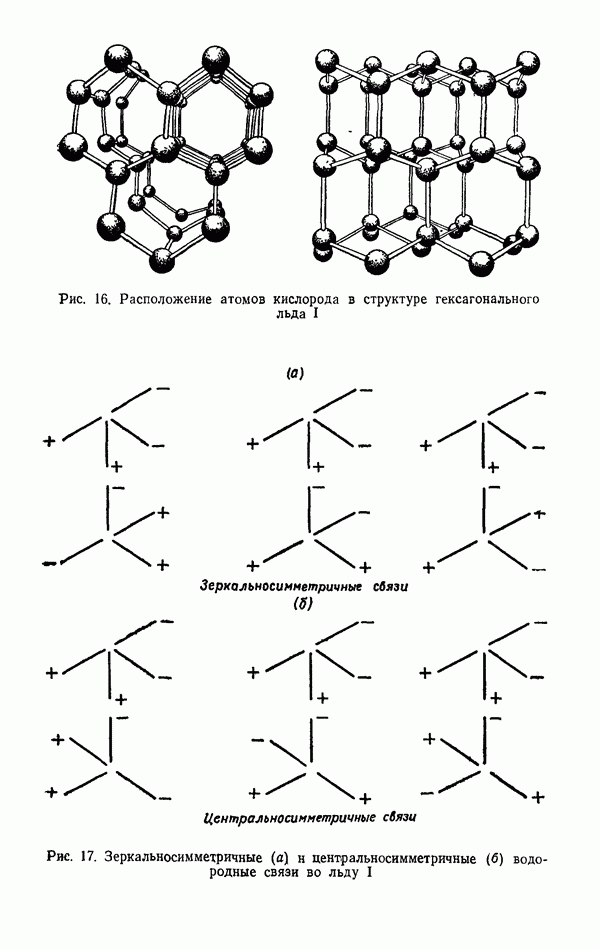
- § 1. ЛЕД
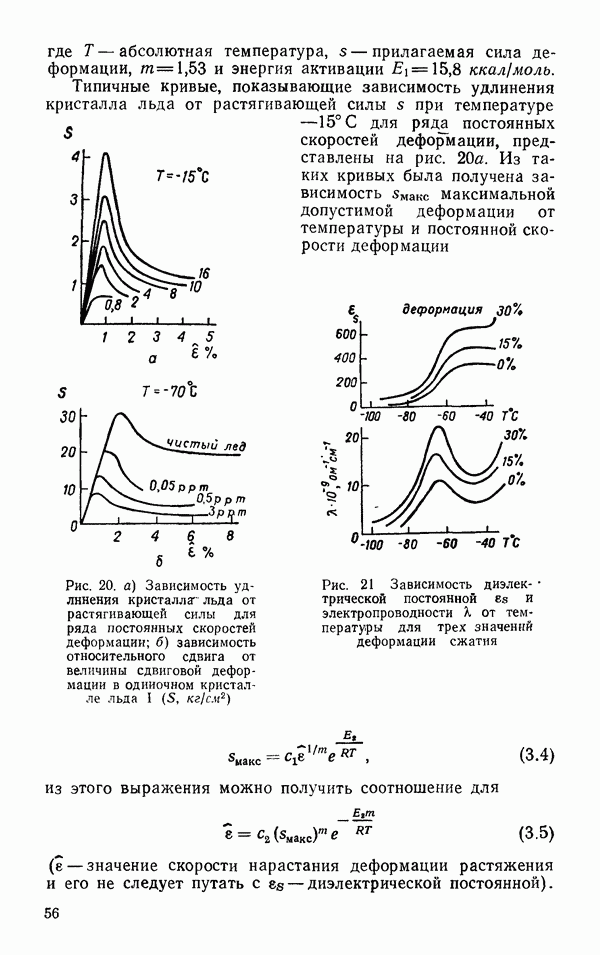
- Пластическая деформация монокристалла льда I
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
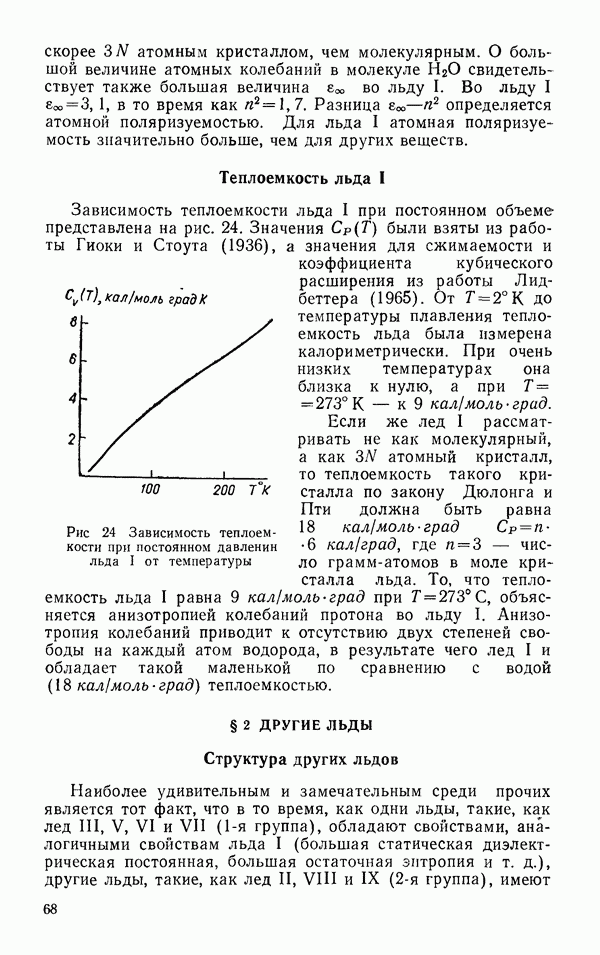
- Теплоемкость льда I
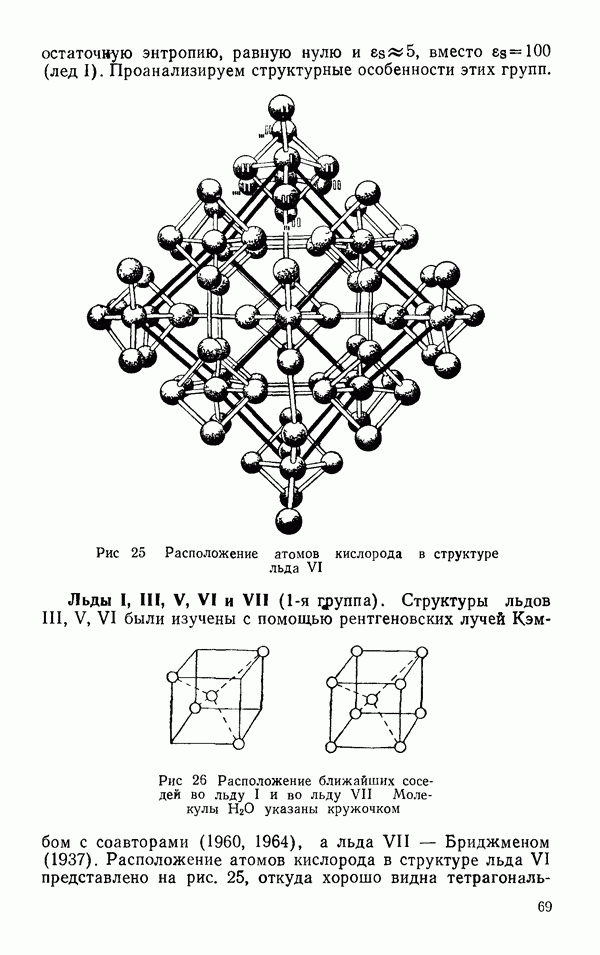
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
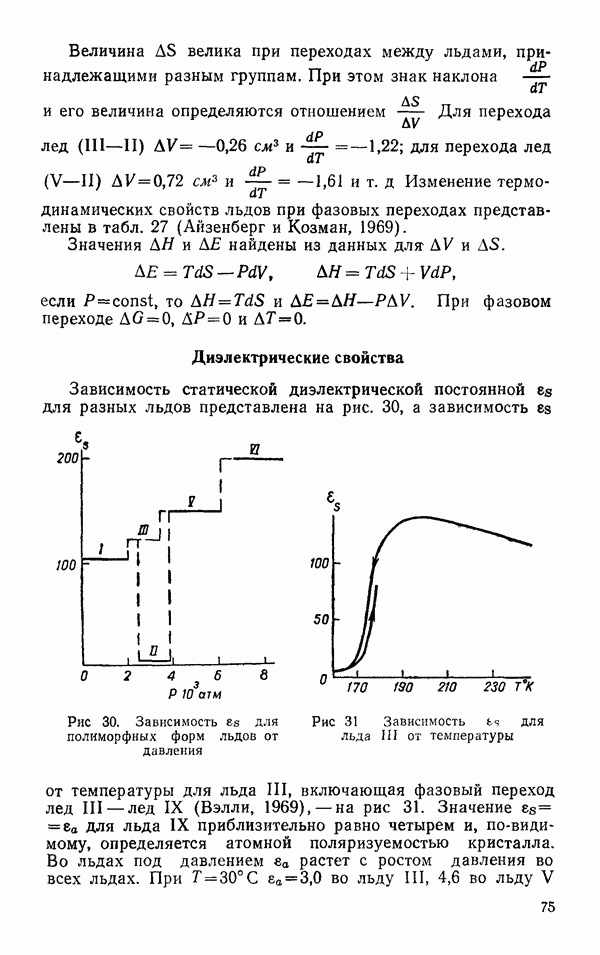
- Диэлектрические свойства
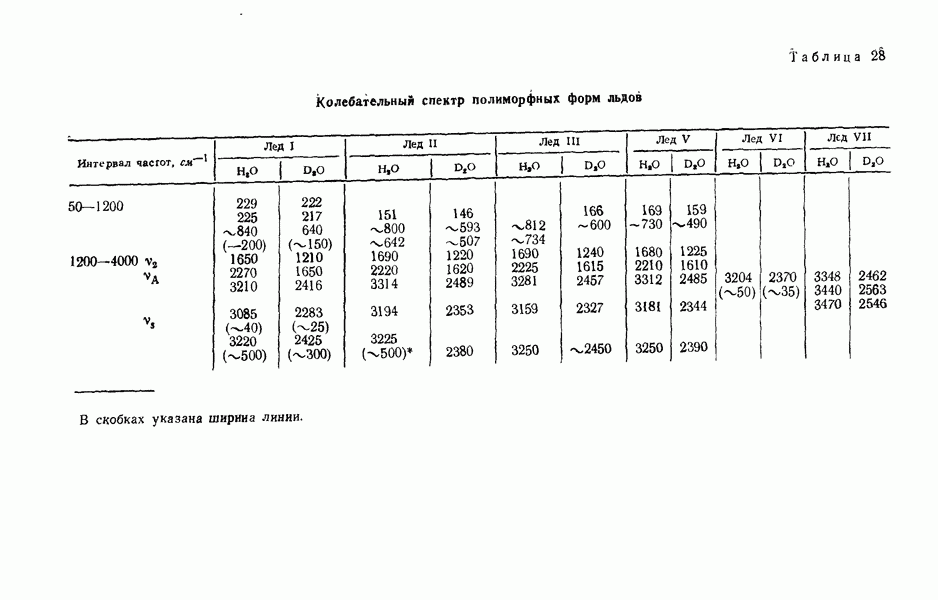
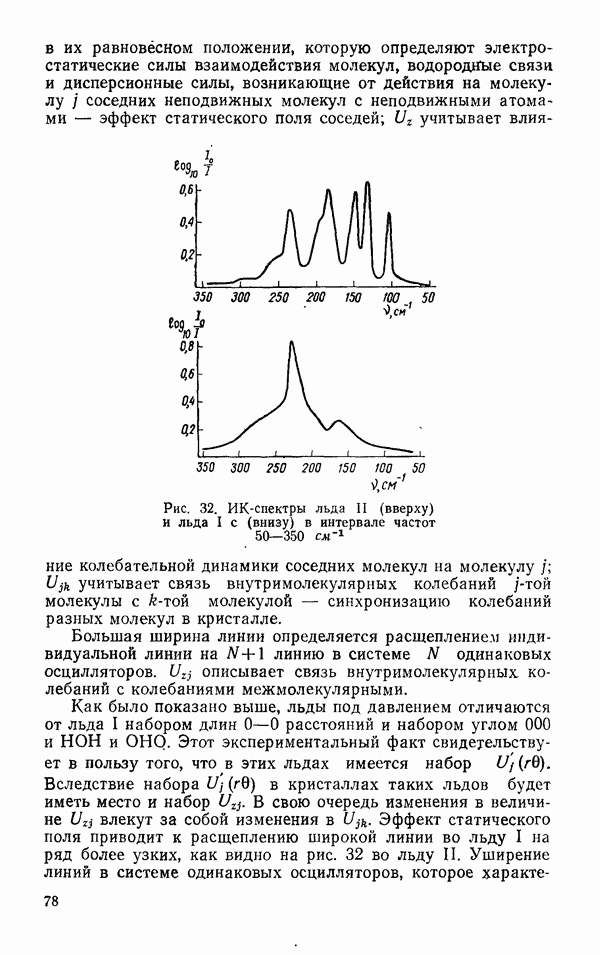
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
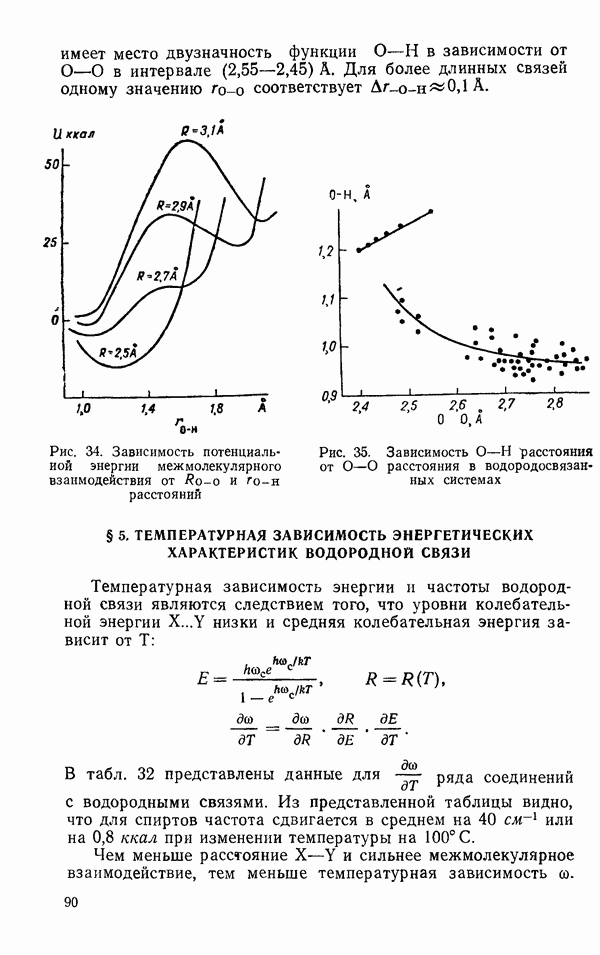
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
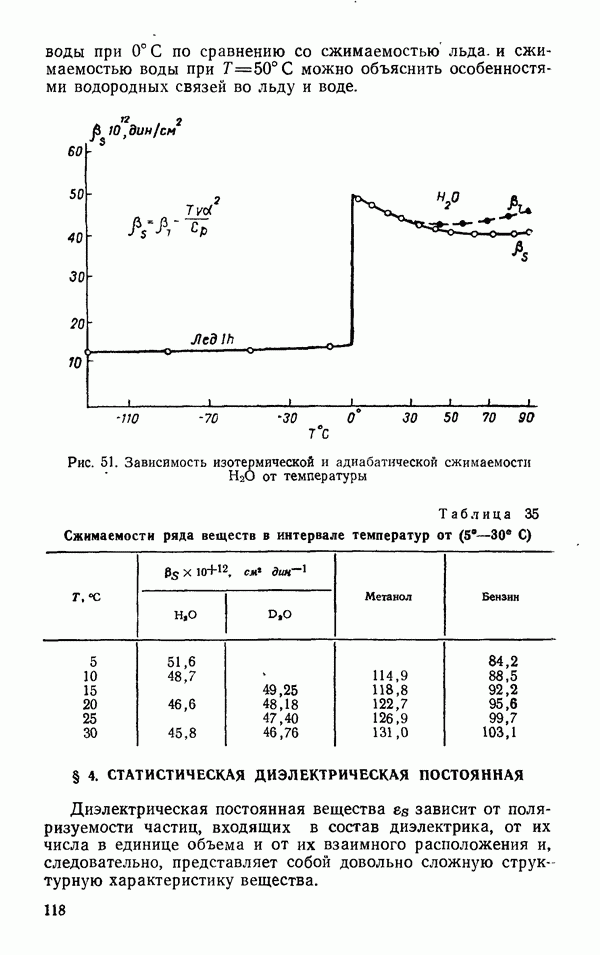
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
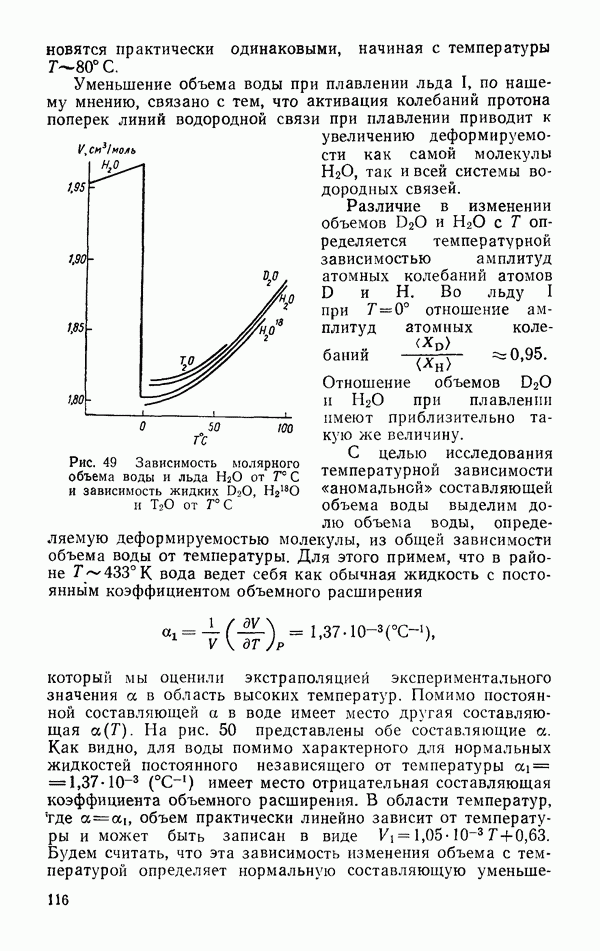
- Зависимость … от V (молекулярный объем)
- Зависимость объема и его производных от температуры
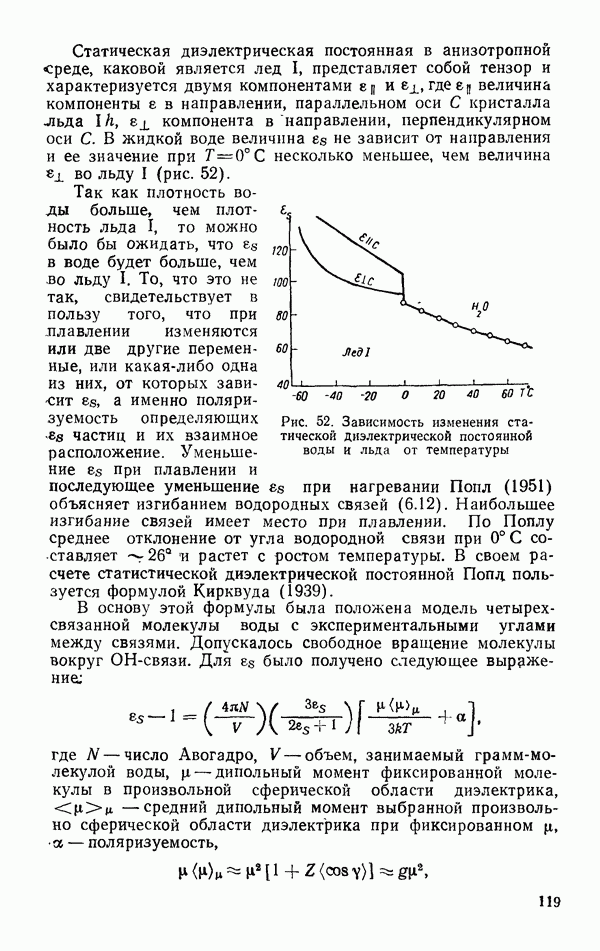
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
- Вязкость
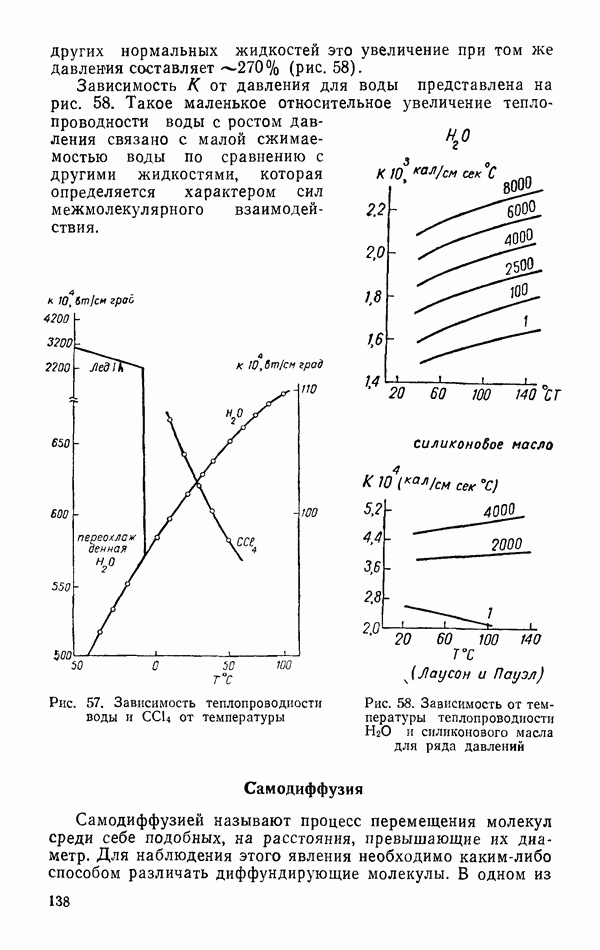
- Теплопроводность
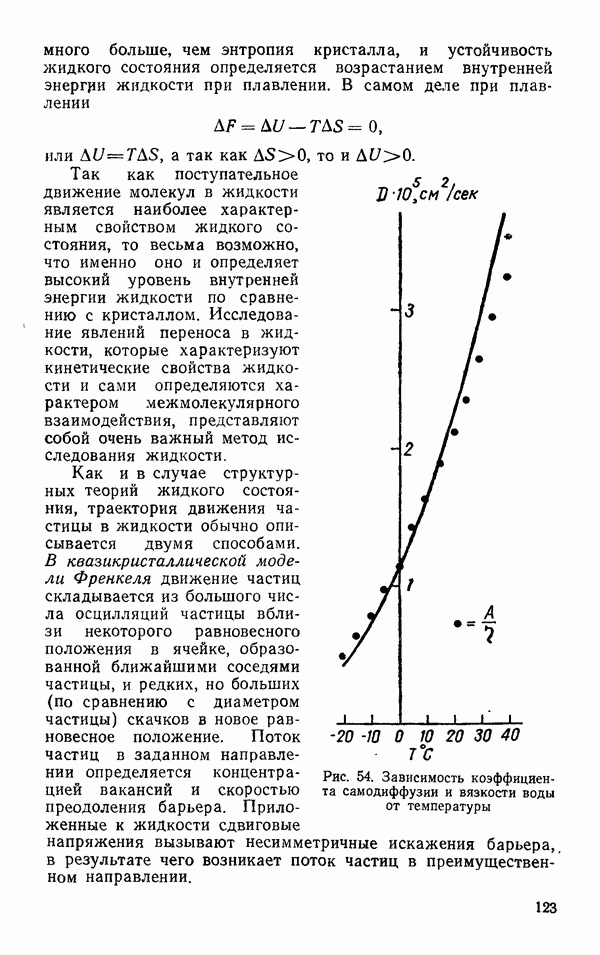
- Самодиффузия
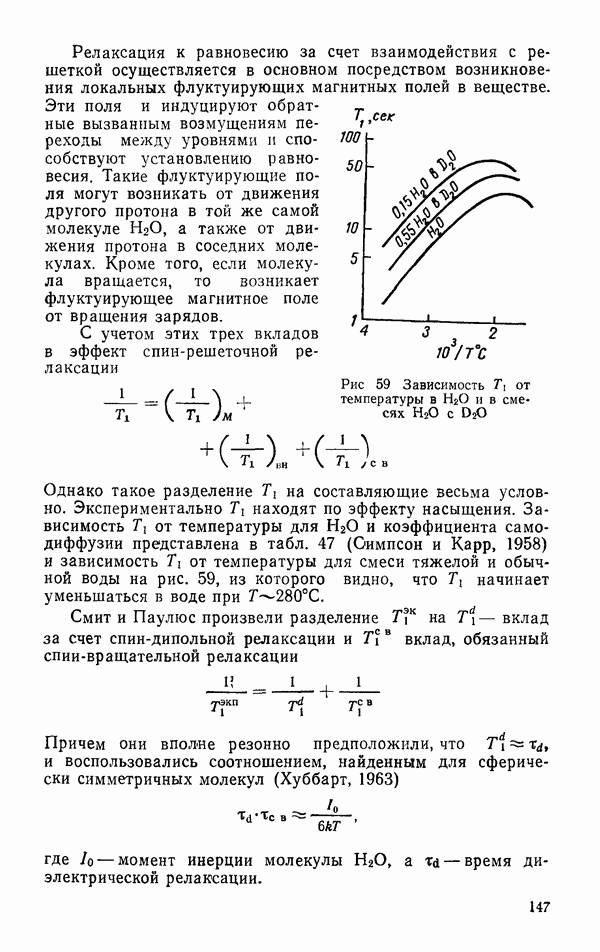
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
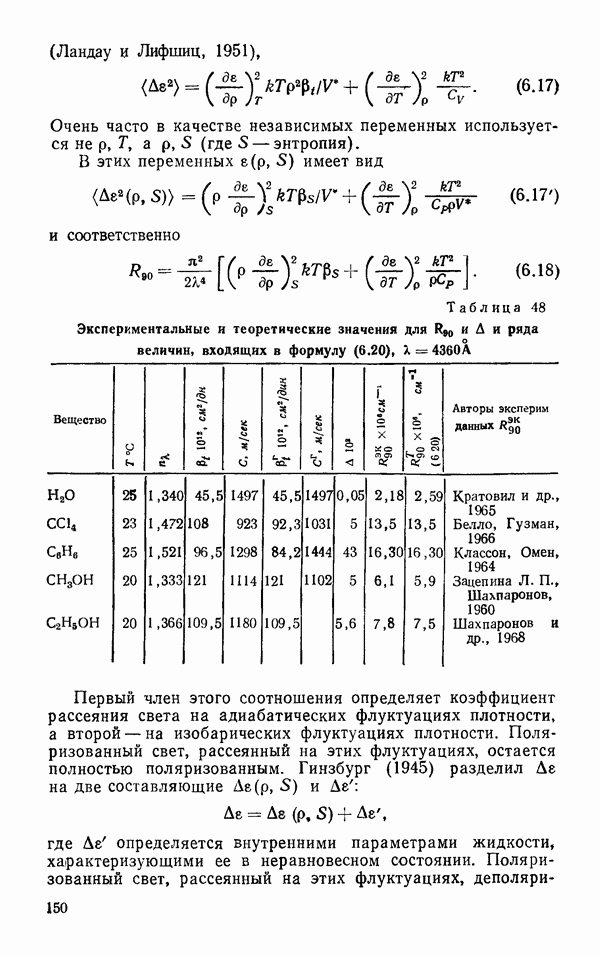
- Молекулярное рассеяние света
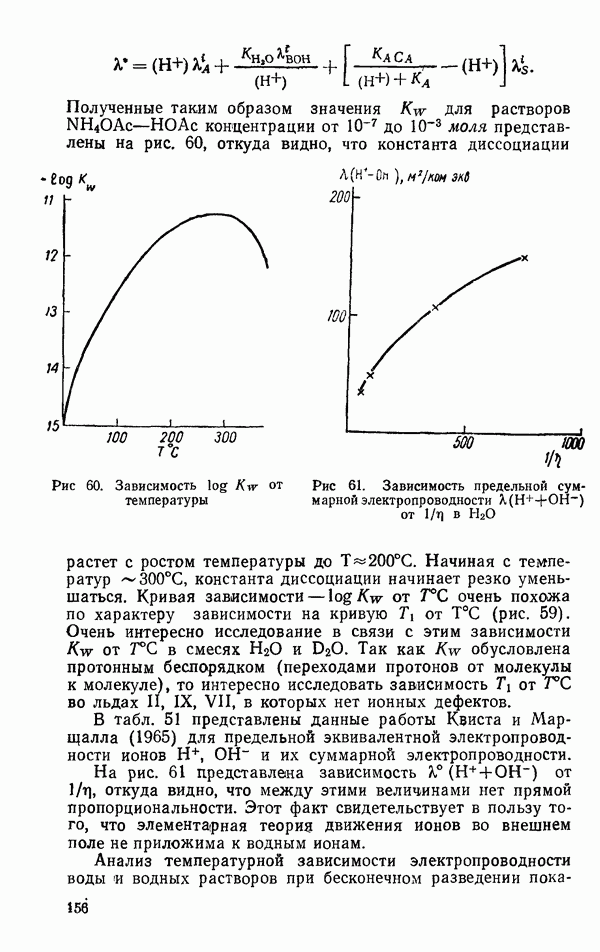
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА