| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. СТРУКТУРА ЖИДКОСТИ
Термин «структура жидкости» весьма распространен. В отличие от кристаллической структуры твердого тела под структурой жидкости следует понимать статистическую закономерность межмолекулярных расстояний и ориентаций, характерную для любой плотноупакованной системы. Благодаря конечному размеру молекул силам межмолекулярного взаимодействия любой жидкости свойствен ближний порядок в расположении частиц и отсутствие дальнего порядка. Отсутствие дальнего порядка означает, что порядок в одном месте никак не действует на порядок в другом.
Удобным методом описания структуры простой жидкости является функция радиального распределения, которая может быть рассчитана на основании данных по расстоянию рентгеновских лучей и нейтронов. Вероятность того, что элемент объема  в жидкости объема V содержит заданную молекулу, пропорциональна
в жидкости объема V содержит заданную молекулу, пропорциональна  Вероятность, что данная пара молекул занимает два таких объема
Вероятность, что данная пара молекул занимает два таких объема  (при этом предполагается, что расстояние
(при этом предполагается, что расстояние  между частицами достаточно велико и их межмолекулярный потенциал мал).
между частицами достаточно велико и их межмолекулярный потенциал мал).
Если же расстояние между молекулами приближается к диаметру молекулы  то объем молекулы и силы межмолекулярного взаимодействия жестко определяют расстояние между молекулами. В этом случае вероятность того, что данная пара занимает два определенных элемента объема, будет равна
то объем молекулы и силы межмолекулярного взаимодействия жестко определяют расстояние между молекулами. В этом случае вероятность того, что данная пара занимает два определенных элемента объема, будет равна

где  радиальная функция распределения, или поправка к фактору свободного распределения. Вероятность найти какую-либо молекулу в объеме
радиальная функция распределения, или поправка к фактору свободного распределения. Вероятность найти какую-либо молекулу в объеме  на расстоянии
на расстоянии  от центра фиксированной молекулы будет равна
от центра фиксированной молекулы будет равна

Число молекул в сферической области толщины  (рис. 38) будет равно
(рис. 38) будет равно

где  число молекул в объеме
число молекул в объеме 


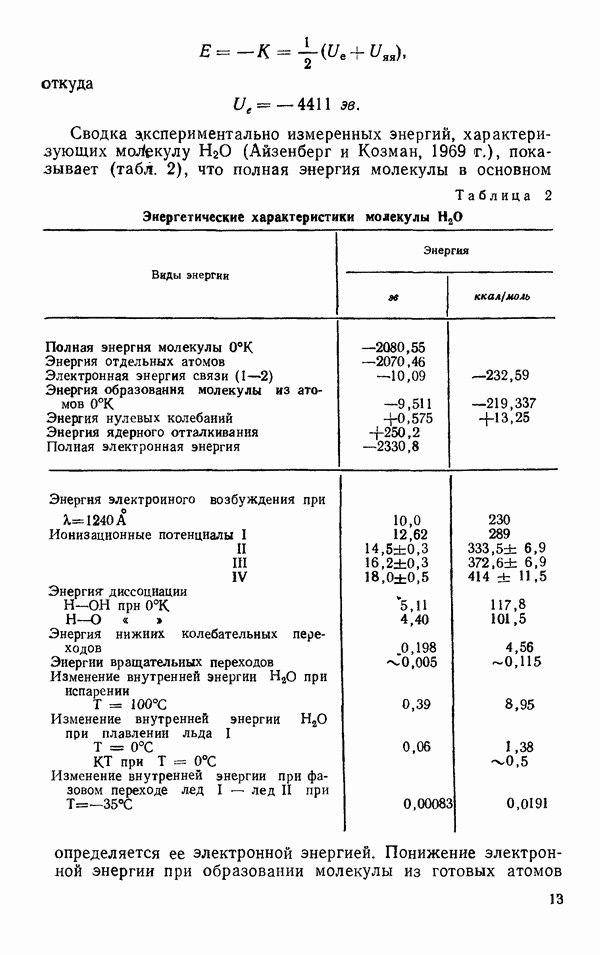
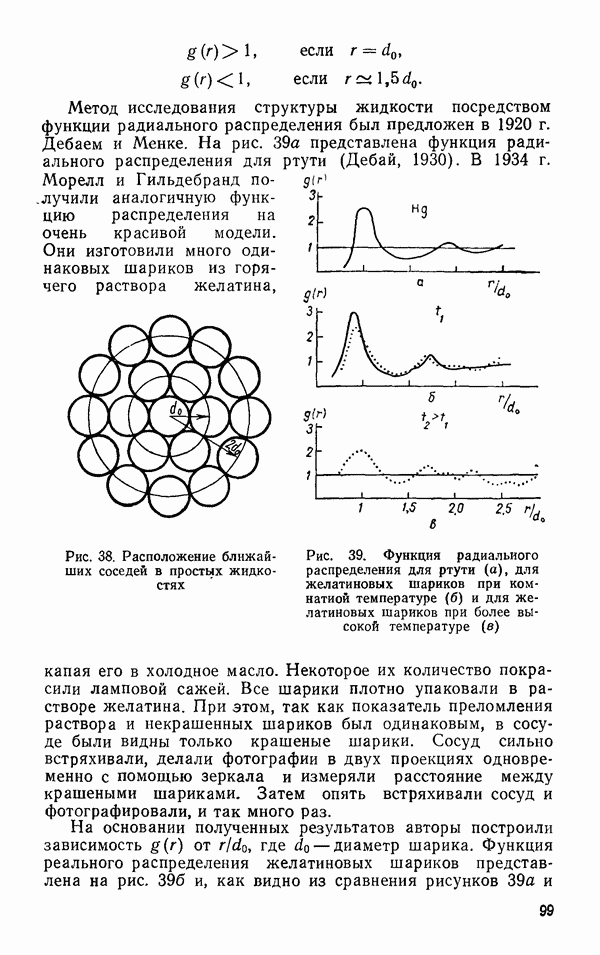
Метод исследования структуры жидкости посредством функции радиального распределения был предложен в 1920 г. Дебаем и Менке. На рис. 39а представлена функция радиального распределения для ртути (Дебай, 1930). В 1934 г. Морелл и Гильдебранд получили аналогичную функцию распределения на очень красивой модели.
Они изготовили много одинаковых шариков из горячего раствора желатина, капая его в холодное масло.

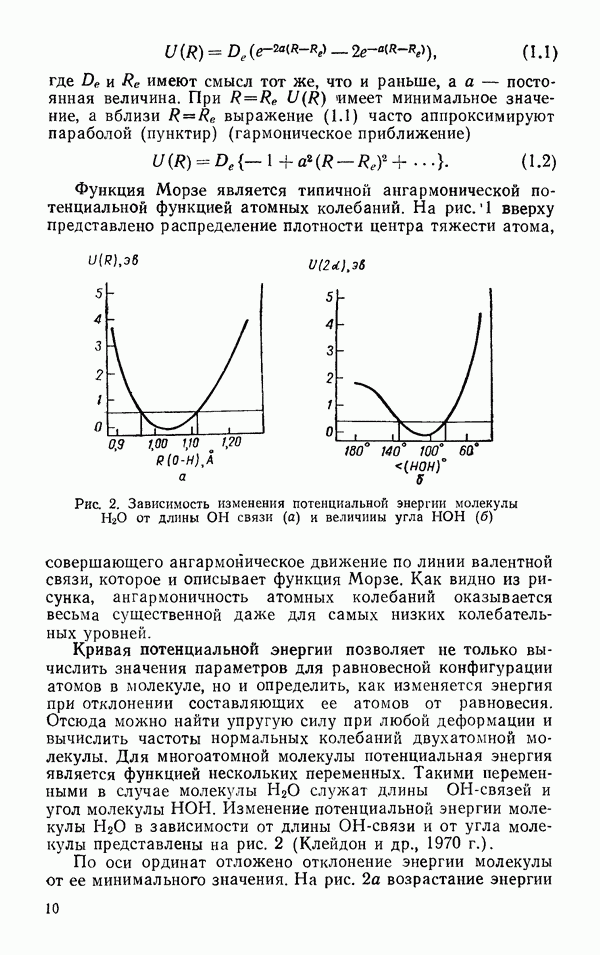
Рис. 38. Расположение ближайших соседей в простых жидкостях

Рис. 39. Функция радиального распределения для ртути (а), для желатиновых шариков при комнатной температуре (б) и для желатиновых шариков при более высокой температуре (в)
Некоторое их количество покрасили ламповой сажей. Все шарики плотно упаковали в растворе желатина. При этом, так как показатель преломления раствора и некрашенных шариков был одинаковым, в сосуде были видны только крашеные шарики. Сосуд сильно встряхивали, делали фотографии в двух проекциях одновременно с помощью зеркала и измеряли расстояние между крашеными шариками. Затем опять встряхивали сосуд и фотографировали, и так много раз.
На основании полученных результатов авторы построили зависимость  от
от  где
где  диаметр шарика. Функция реального распределения желатиновых шариков представлена на рис. 39б и, как видно из сравнения рисунков 39а и
диаметр шарика. Функция реального распределения желатиновых шариков представлена на рис. 39б и, как видно из сравнения рисунков 39а и
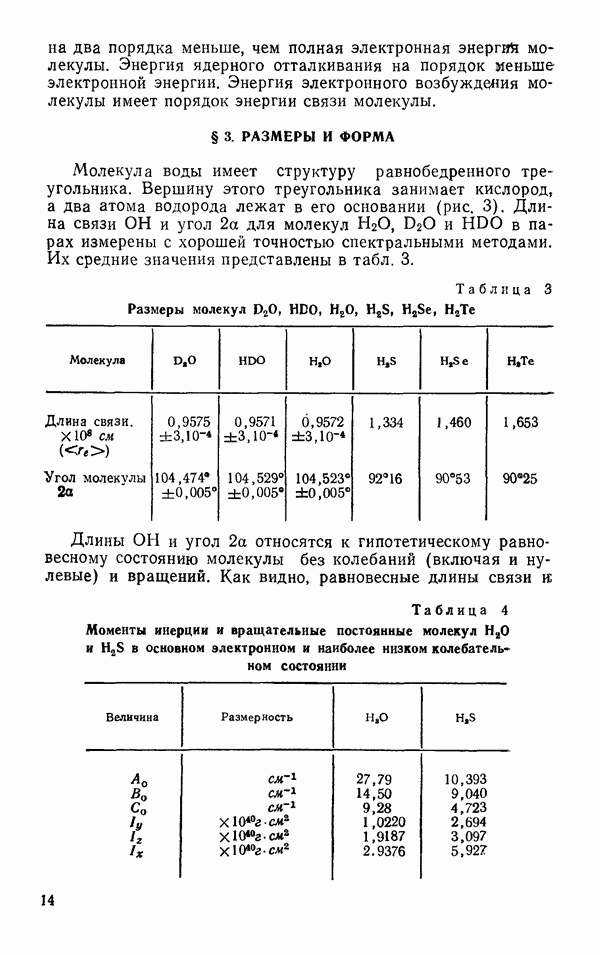
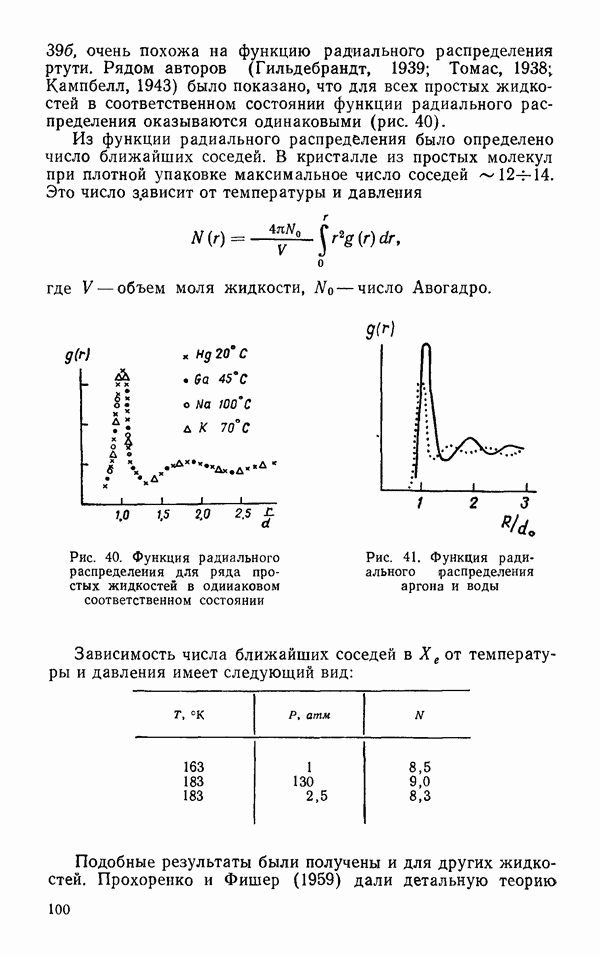
39б, очень похожа на функцию радиального распределения ртути. Рядом авторов (Гильдебрандт, 1939; Томас, 1938; Кампбелл, 1943) было показано, что для всех простых жидкостей в соответственном состоянии функции радиального распределения оказываются одинаковыми (рис. 40).
Из функции радиального распределения было определено число ближайших соседей. В кристалле из простых молекул при плотной упаковке максимальное число соседей —  Это число зависит от температуры и давления
Это число зависит от температуры и давления

где V — объем моля жидкости,  число Авогадро.
число Авогадро.

Рис. 40. Функция радиального распределения для ряда простых жидкостей в одинаковом соответственном состоянии

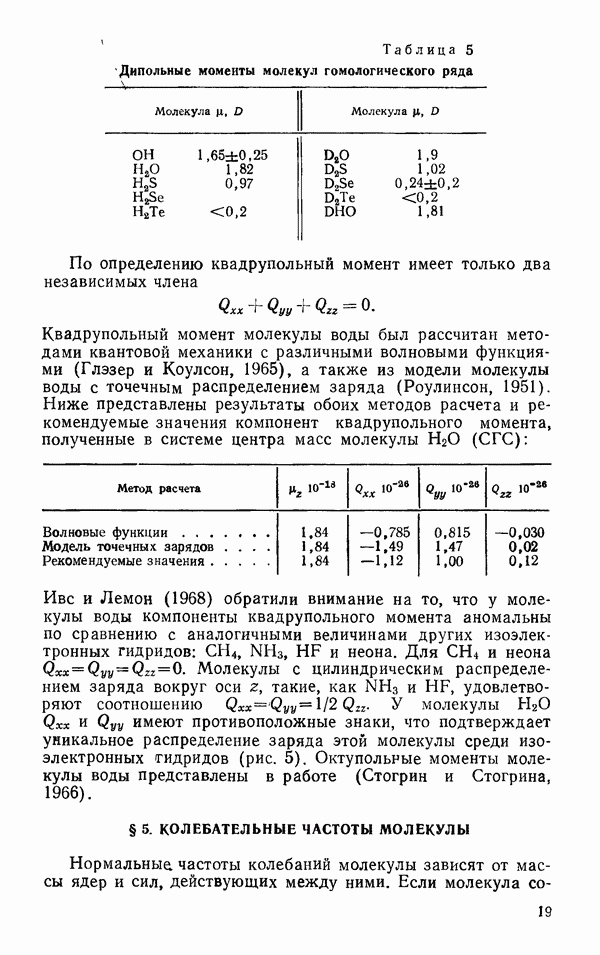
Рис. 41, Функция радиального распределения аргона и воды
Зависимость числа ближайших соседей в Xе от температуры и давления имеет следующий вид:

Подобные результаты были получены и для других жидкостей. Прохоренко и Фишер (1959) дали детальную теорию
флуктуаций координационного числа простых жидкостей. Они заключили, что полученные ими результаты противоречат квазикристаллическим моделям простых жидкостей и свидетельствуют в пользу статистического распределения молекул в жидкости.
В 1953 г. Гильдебрандт опубликовал рядом два графика, представляющие функцию радиального распределения рассеяния рентгеновских лучей галлием при одной и той же температуре. В одном случае исследовалось рассеяние рентгеновских лучей мелким порошком  а в другом случае расплавом галлия при
а в другом случае расплавом галлия при  . В расплаве не было обнаружено никаких следов хорошо определенной структуры порошка. Эта работа была направлена на опровержение широко распространенных квазикристаллических теорий жидкости и, в частности, теории сиботаксических состояний Стюарта (1927).
. В расплаве не было обнаружено никаких следов хорошо определенной структуры порошка. Эта работа была направлена на опровержение широко распространенных квазикристаллических теорий жидкости и, в частности, теории сиботаксических состояний Стюарта (1927).
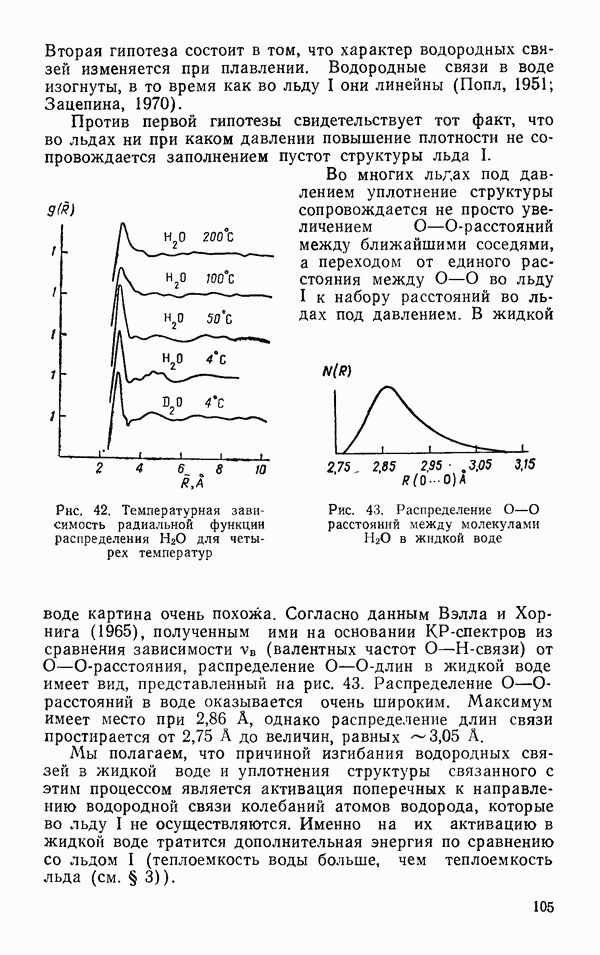
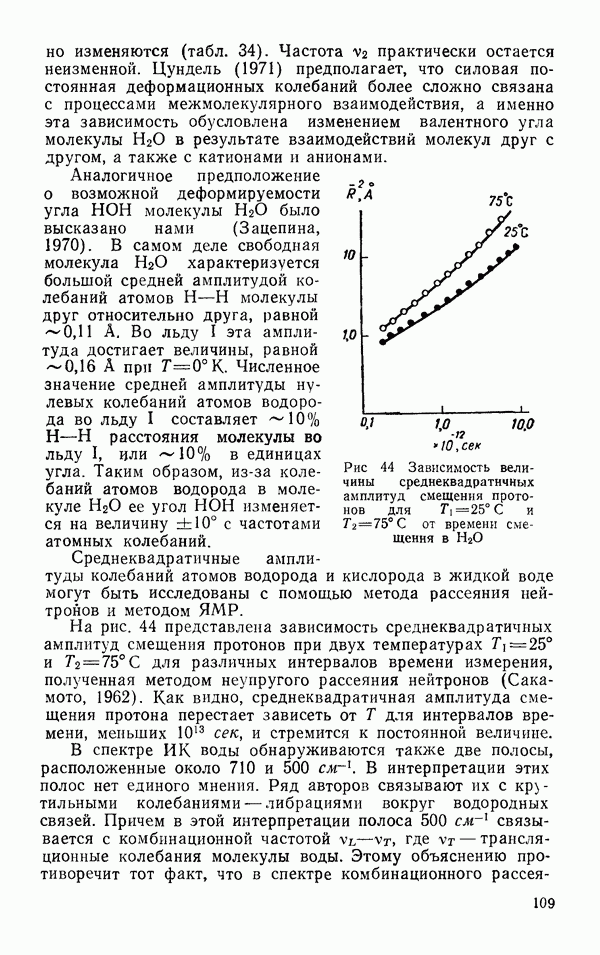
Функция радиального распределения для сложных многоатомных молекул естественно не совпадает с радиальной функцией распределения сферически симметричных простых молекул. Прежде всего это связано с тем, что для несимметричных молекул функция распределения является функцией не только расстояния, но и углов. На рис. 41 представлена функция радиального распределения аргона (сплошная кривая) и воды (Бен-Нейм, 1969).
Большое теоретическое значение функции радиального распределения состоит в следующем. Во-первых, она непосредственно экспериментально связана с функцией рассеяния рентгеновских лучей и нейтронов. Во-вторых, если известна температурная зависимость  зависимость ее от числа частиц в объеме и потенциал межмолекулярного взаимодействия
зависимость ее от числа частиц в объеме и потенциал межмолекулярного взаимодействия  то определены все свойства жидкости, так как потенциальная энергия системы, пропорциональна интегралу
то определены все свойства жидкости, так как потенциальная энергия системы, пропорциональна интегралу

Причем Кирквуд (1935) показал, что  в принципе могут быть связаны интегральными уравнениями. Для этого он ввел «эффективное двухчастичное взаимодействие», которое согласно его определению не теряет смысла даже тогда, когда в системе действуют многочастичные силы.
в принципе могут быть связаны интегральными уравнениями. Для этого он ввел «эффективное двухчастичное взаимодействие», которое согласно его определению не теряет смысла даже тогда, когда в системе действуют многочастичные силы.
Однако до сих пор
1) точный вид функции  известен с очень малой точностью,
известен с очень малой точностью,
2) точной связи  нет,
нет,
3) роль многочастичных взаимодействии остается не выясненной, и проблема жидкого состояния ждет разрешения.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
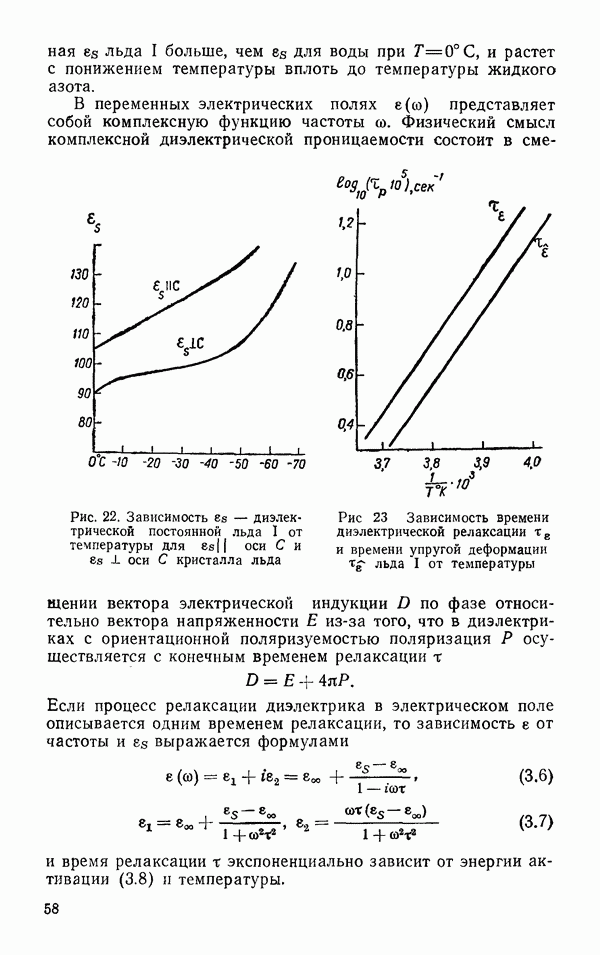
- Диэлектрические свойства льда 1
- Электропроводность льда
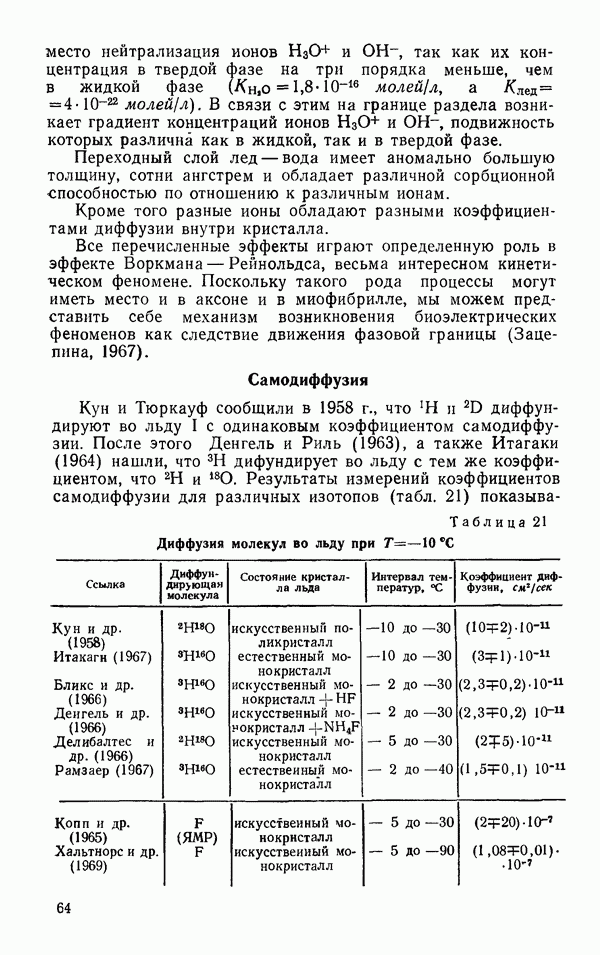
- Самодиффузия
- Спектральные свойства льда I
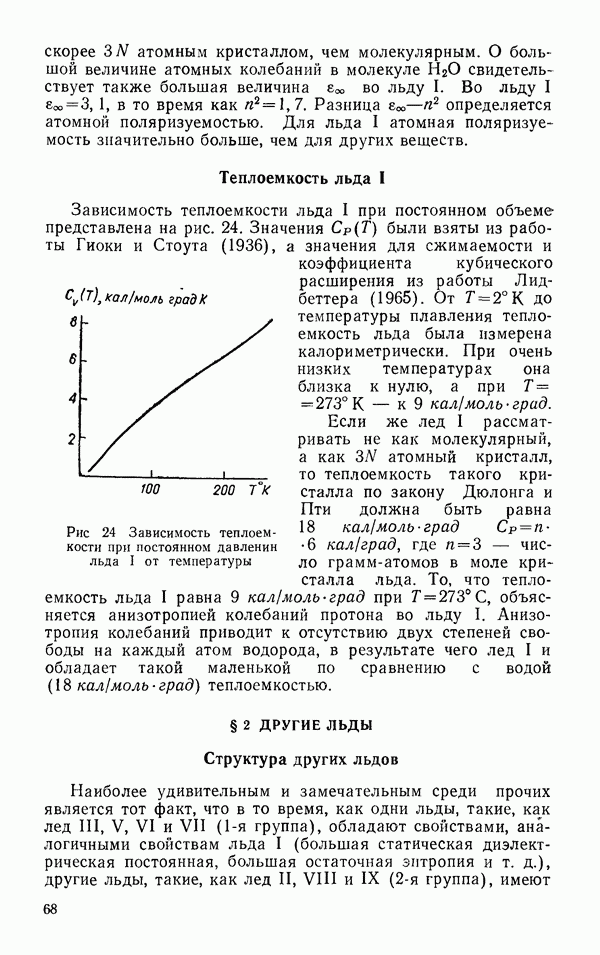
- Теплоемкость льда I
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
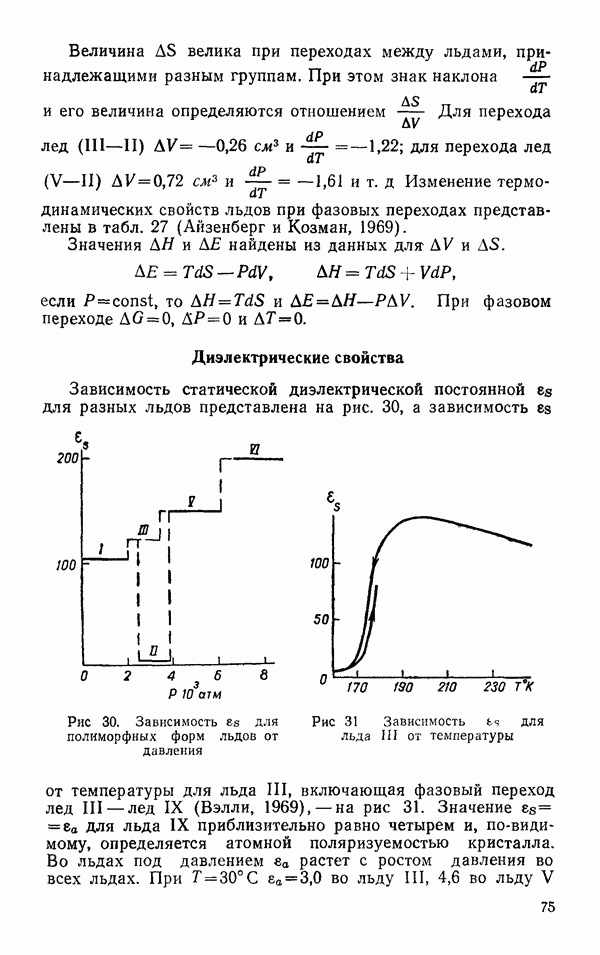
- Диэлектрические свойства
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
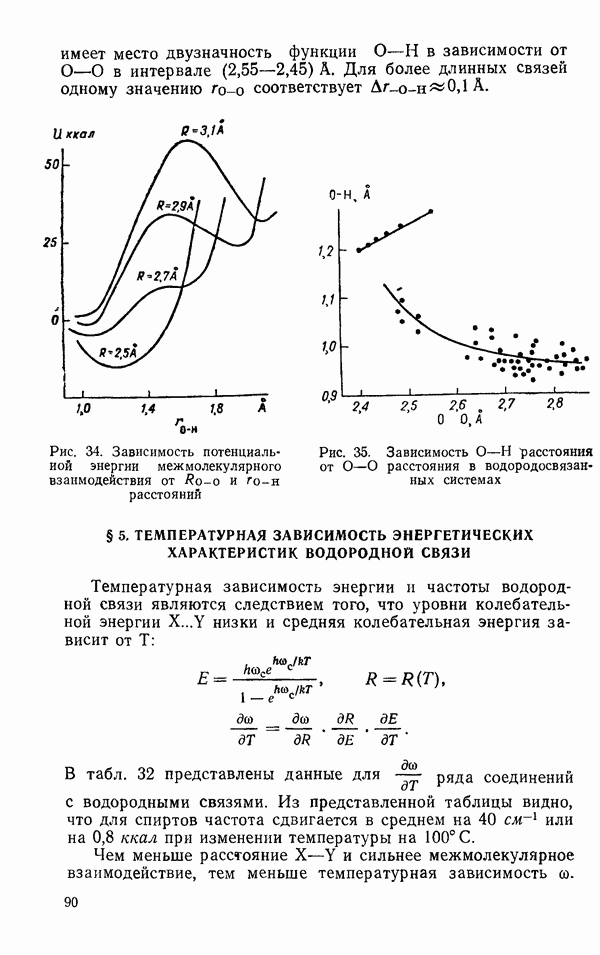
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
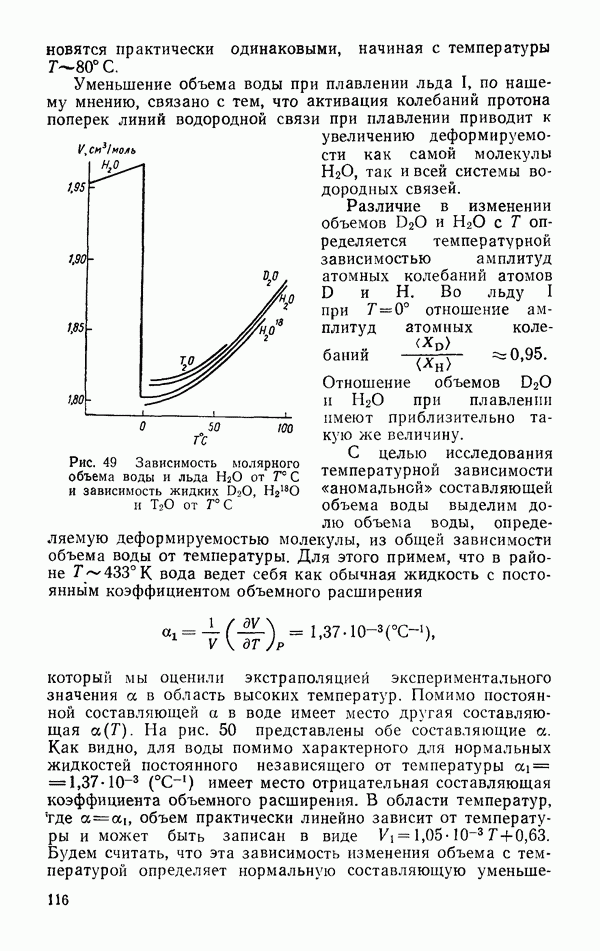
- Зависимость объема и его производных от температуры
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
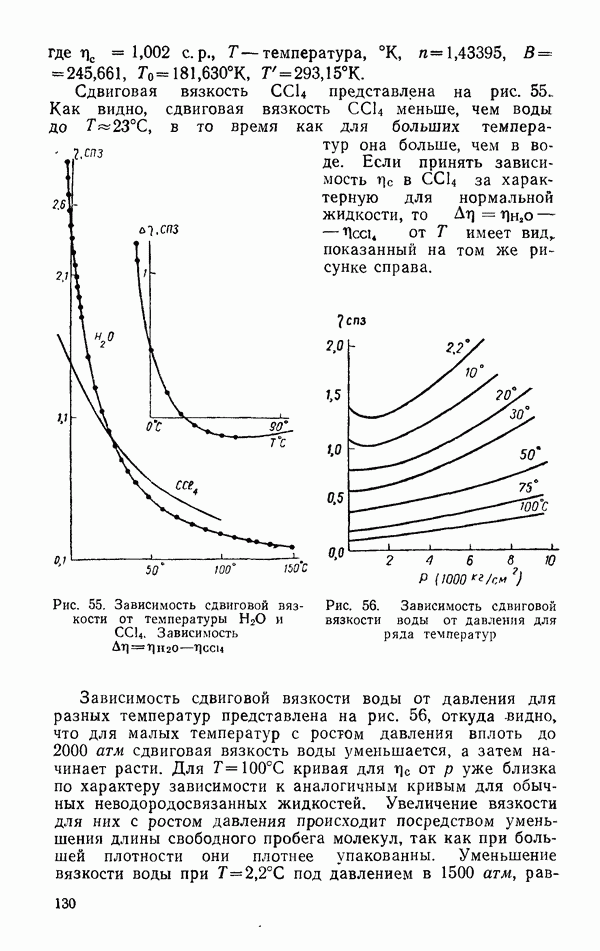
- Вязкость
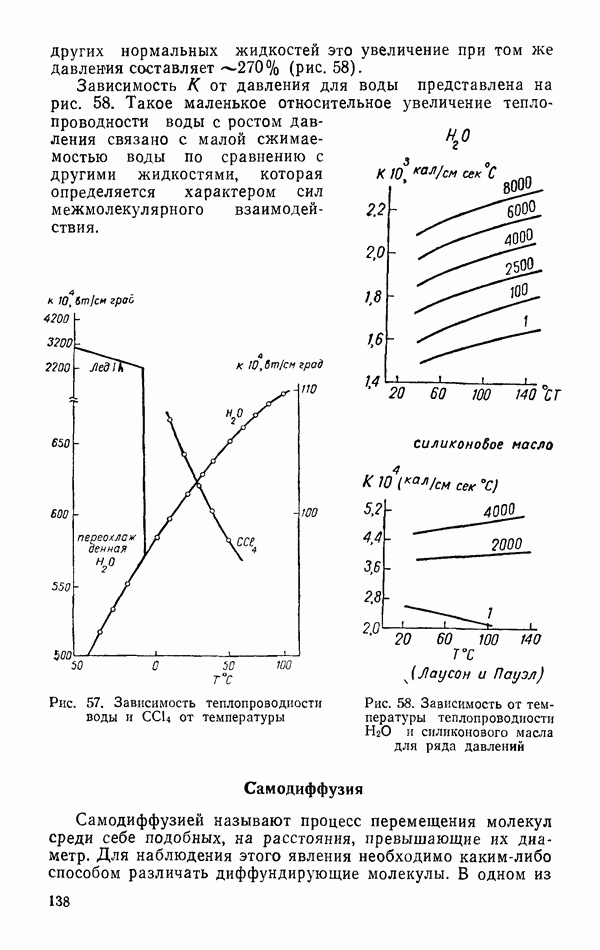
- Теплопроводность
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
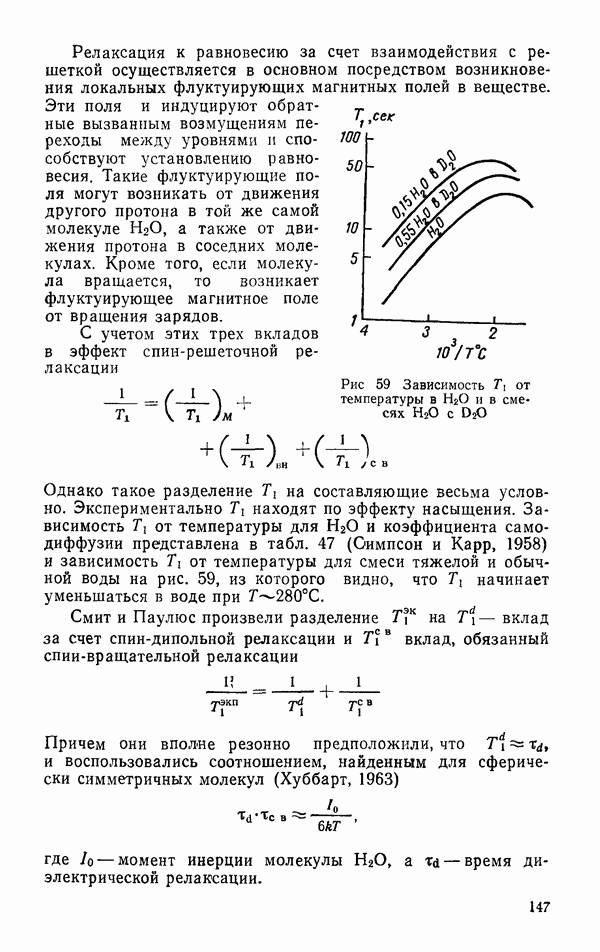
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
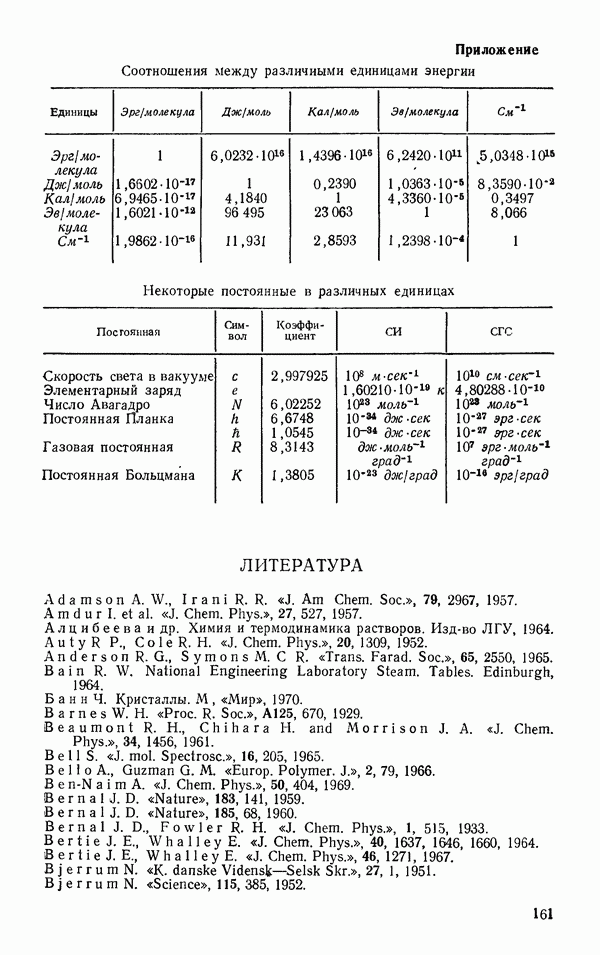
- ЛИТЕРАТУРА