| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
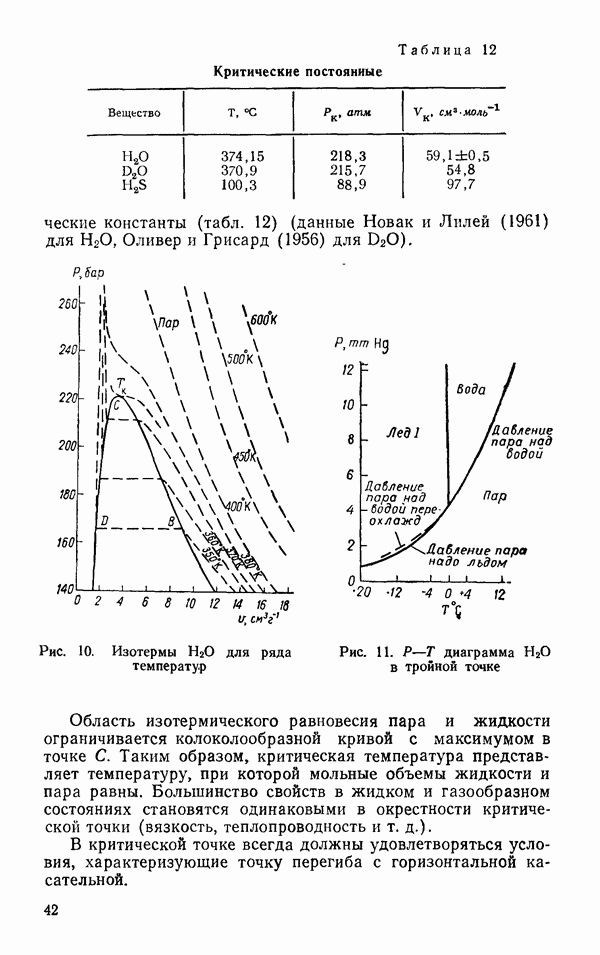
Глава 2. СВОЙСТВА ПАРА
В этой главе в приближении разделения межмолекулярного потенциала на потенциал притяжения и отталкивания рассматриваются отдельные
«оставляющие потенциала взаимодействия двух молекул воды. Приводятся температурные зависимости второго и третьего вариальных коэффициентов для  Термодинамические свойства пара и вязкость пара сравниваются с аналогичными свойствами
Термодинамические свойства пара и вязкость пара сравниваются с аналогичными свойствами  так же как в гл. 1. На основании представленных данных делается вывод о диполь-дипольном характере взаимодействия двух молекул воды в пару, свойственном молекулам, обладающим постоянным дипольным моментом
так же как в гл. 1. На основании представленных данных делается вывод о диполь-дипольном характере взаимодействия двух молекул воды в пару, свойственном молекулам, обладающим постоянным дипольным моментом
§ 1 СИЛЫ МЕЖМОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
Типы сил межмолекулярного взаимодействия
То, что две молекулы притягиваются друг к другу на больших расстояниях и отталкиваются на малых расстояниях, лослужило основанием разделения межмолекулярного потенциала взаимодействия на два независимых члена, один из которых соответствует притяжению и сравнительно медленно убывает с ростом расстояния между молекулами  а другой соответствует отталкиванию и более резко меняется с
а другой соответствует отталкиванию и более резко меняется с  Приближение независимости сил притяжения и отталкивания совместно с приближением аддитивности сил (что означает возможность представления потенциала группы молекул
Приближение независимости сил притяжения и отталкивания совместно с приближением аддитивности сил (что означает возможность представления потенциала группы молекул  суммой парных потенциалов из
суммой парных потенциалов из  возможных пар) лежит в основе большинства современных теорий межмолекулярного взаимодействия.
возможных пар) лежит в основе большинства современных теорий межмолекулярного взаимодействия.
В этом приближении отрицательный член потенциала межмолекулярного взаимодействия, соответствующий притяжению, обычно разделяется на три составляющие.
К первой составляющей относится притяжение между осциллирующими облаками электронов в молекулах. Это наиболее важный для понимания природы конденсированных фаз тип межмолекулярного потенциала. Он был разработан Лондоном, который в 1930 г. дал теорию сил притяжения
неполярных молекул. Он писал, что механизм этих сил нельзя представить в рамках классической механики, одйако его можно проиллюстрировать квазиклассическим языком. Нулевые колебания электронов молекул представляют собой очень быстрые колебания диполей, которые индуцируют дипольные моменты в соседних молекулах в фазе с колебаниями, их вызвавшими. Таким образом, нулевые колебания сопровождаются электрическим, синхронно изменяющимся полем, но не полем излучения, так как энергия нулевых колебаний не растрачивается. Как показал Лондон, потенциальная энергия притяжения двух разных неполярных молекул в этом случае имеет вид

где  частоты нулевых колебаний дисперсионных электронов, внешних электронов атома, ответственных за дисперсию света; а — поляризуемость и
частоты нулевых колебаний дисперсионных электронов, внешних электронов атома, ответственных за дисперсию света; а — поляризуемость и  расстояние между центрами атомов. Величина
расстояние между центрами атомов. Величина  практически равна ионизационному потенциалу, и энергия межмолекулярного взаимодействия двух разных неполярных молекул имеет вид
практически равна ионизационному потенциалу, и энергия межмолекулярного взаимодействия двух разных неполярных молекул имеет вид

для одинаковых молекул

Если атом имеет только один дисперсионный электрон, как, например, натрий или водород, то расчет по формуле (2.3) приводит к значению для  и к
и к  . Такая большая разница значений К для натрия и водорода обусловлена тем, что натрий поляризуется существенно сильнее, чем водород.
. Такая большая разница значений К для натрия и водорода обусловлена тем, что натрий поляризуется существенно сильнее, чем водород.
Для многоэлектронных атомов энергия дисперсионного взаимодействия равна сумме членов типа (2.2), причем на каждую пару электронов приходится один член.
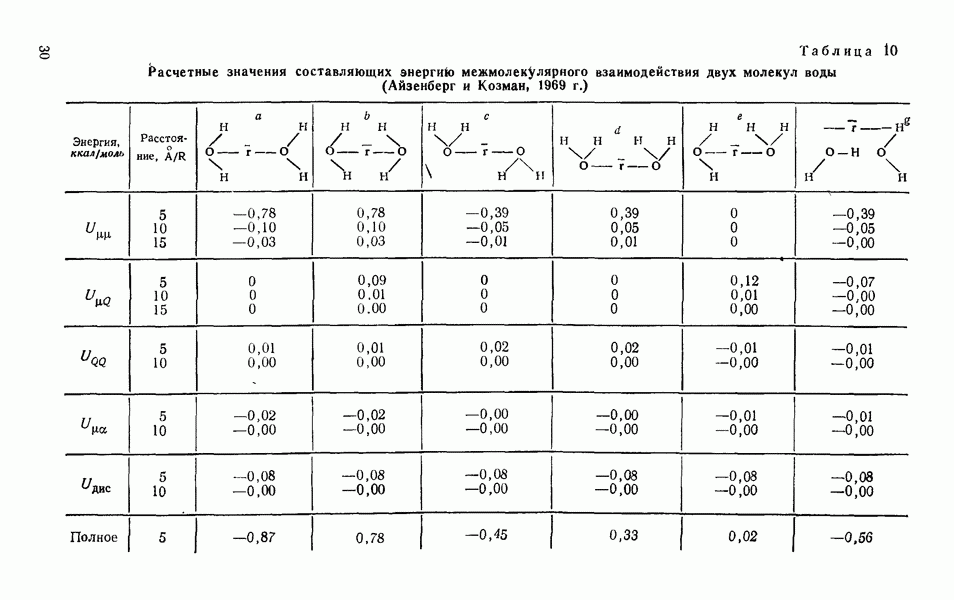
Расчетные значения энергии дисперсионного взаимодействия двух молекул воды на расстоянии 5 и 10 А представлены в табл. 10. Как видно из таблицы, на расстоянии, равном 5 А, энергия дисперсионного взаимодействия составляет  от энергии диполь-дипольного взаимодействия, когда диполи ориентированы самым выгодным способом (голова— хвост). На расстоянии, равном 10 А, энергия диполь-дипольного взаимодействия все еще велика, в то время как энергия дисперсионного взаимодействия равна нулю.
от энергии диполь-дипольного взаимодействия, когда диполи ориентированы самым выгодным способом (голова— хвост). На расстоянии, равном 10 А, энергия диполь-дипольного взаимодействия все еще велика, в то время как энергия дисперсионного взаимодействия равна нулю.
Каковы основные черты этих сил?
Во-первых, они действуют между сферически симметричными молекулами (инертные газы).
Во-вторых, они аддитивны и их можно выражать через парный потенциал.
В-третьих, их роль велика в межмолекулярном взаимодействии любых молекул, т. е. они неспецифичны.
В-четвертых, эти силы практически не зависят от температуры, т. е. от агрегатного состояния вещества.
Как и в случае сил отталкивания, мало что известно относительно зависимости этих сил от ориентации несферических, молекул (анизотропии поляризуемости). Де Бур (1942) рассмотрел две крайние ориентации вытянутых молекул.

Рис. 7. Система координат, в которой рассматривается взаимодействие двух молекул 
Первая — это когда они расположены в линию, вторая — когда они параллельны друг другу. Оказалось, что дисперсионная энергия в первом случае больше в 1,4 раза, чем во втором, для одинакового расстояния между центрами молекул. Однако при этом потенциал отталкивания в 10 раз больше в первом случае, чем во втором, а так как силы отталкивания более короткодействующие, то полная энергия проходит через более глубокий минимум, если оси длинных молекул параллельны, по сравнению с тем случаем, когда они колинеарны.
Взаимодействие вытянутых молекул более сложно зависит от распределения заряда по молекуле, чем сферически симметричных. Несимметричное стационарное распределение заряда по молекуле сказывается в наличии постоянного дипольного, квадрупольного и т. д. моментов. Силы притяжения между молекулами, обладающими постоянными моментами, относятся ко второму типу сил притяжения и зависят от этих моментов.
Рядом авторов было показано (Роулинсон, 1959), что при аксиальной симметрии в распределении заряда энергию межмолекулярного взаимодействия можно представить в виде:

где  четыре угла, которые определяют ориентацию двух аксиально симметричных молекул по отношению к линии, соединяющей их центры (рис. 7);
четыре угла, которые определяют ориентацию двух аксиально симметричных молекул по отношению к линии, соединяющей их центры (рис. 7);
X — функция только расстояния между молекулами 

(кликните для просмотра скана)
Молекулы в газе вращаются и электростатические силы между вращающимися молекулами меньше, чем между жестко ориентированными молекулами, так как притяжение при одних ориентациях сменяется электростатическим отталкиванием при других. Если принять, что величина  почти постоянна при молекулярном вращении, то можно найти статистические средние значения для вращающихся молекул
почти постоянна при молекулярном вращении, то можно найти статистические средние значения для вращающихся молекул

где

для температур, при которых 

Третья компонента сил притяжения в выражении для энергии межмолекулярного взаимодействия пердставляет индукционное взаимодействие постоянного диполя со сферически симметричной молекулой с поляризуемостью а. Эти силы более слабые, они пропорциональны  и практически не зависят от температуры.
и практически не зависят от температуры.
Таким образом, все три составляющие межмолекулярного потенциала, определяющего притяжение молекул, зависят от шестой степени расстояния. Учет эффектов запаздывания повышает степень до 8—7. При взаимодействии двух молекул воды в зависимости от их обоюдной ориентации различные составляющие  в ккал/моль, определяющие притяжение молекул, представлены в табл. 10 (Айзенберг и Козман, 1969).
в ккал/моль, определяющие притяжение молекул, представлены в табл. 10 (Айзенберг и Козман, 1969).
Среднее значение потенциала отталкивания для всех ориентаций  если расстояние между молекулами
если расстояние между молекулами  ккал/моль. Для трех конфигураций
ккал/моль. Для трех конфигураций  и с средние значения потенциала отталкивания
и с средние значения потенциала отталкивания  взяты из экспериментов по рассеянию атомов
взяты из экспериментов по рассеянию атомов  из данных по рассеянию атомов неона представлены в табл.
из данных по рассеянию атомов неона представлены в табл. 
Дисперсионное взаимодействие в табл. 10 оценивалось из соотношения Кирквуда — Мюллера


(кликните для просмотра скана)
Таблица 11 Значения потенциала отталкивания для трех конфигураций молекул (табл. 10)

где  , с — скорость света,
, с — скорость света,  масса электрона,
масса электрона,  число Авогадро,
число Авогадро,  диамагнитная восприимчивость
диамагнитная восприимчивость

 — среднеквадратичное расстояние электронов от центра масс молекулы
— среднеквадратичное расстояние электронов от центра масс молекулы

Из представленных оценок потенциальной энергии взаимодействия двух молекул (табл. 10, 11) следует, что наиболее выгодной конфигурацией в смысле притяжения является конфигурация а, а не  которая представляет водородную связь.
которая представляет водородную связь.
Межмолекулярный потенциал взаимодействия двух молекул  обусловленный только дисперсионными силами и отталкиванием, имеет следующий вид
обусловленный только дисперсионными силами и отталкиванием, имеет следующий вид

где  — усредненный по углам потенциал межмолекулярного отталкивания двух молекул. Постоянная К по данным разных авторов (Стокмайре, 1941 и Роулинсон, 1951) имеет значение
— усредненный по углам потенциал межмолекулярного отталкивания двух молекул. Постоянная К по данным разных авторов (Стокмайре, 1941 и Роулинсон, 1951) имеет значение  . Величина
. Величина  ккал/моль и
ккал/моль и  см.
см.
Зависимость потенциальной энергии взаимодействия двух молекул  от расстояния между ними при фиксированных обоюдных ориентациях представлена на рис. 8. Кривая
от расстояния между ними при фиксированных обоюдных ориентациях представлена на рис. 8. Кривая  показывает теоретическую зависимость Стокмайера.
показывает теоретическую зависимость Стокмайера.
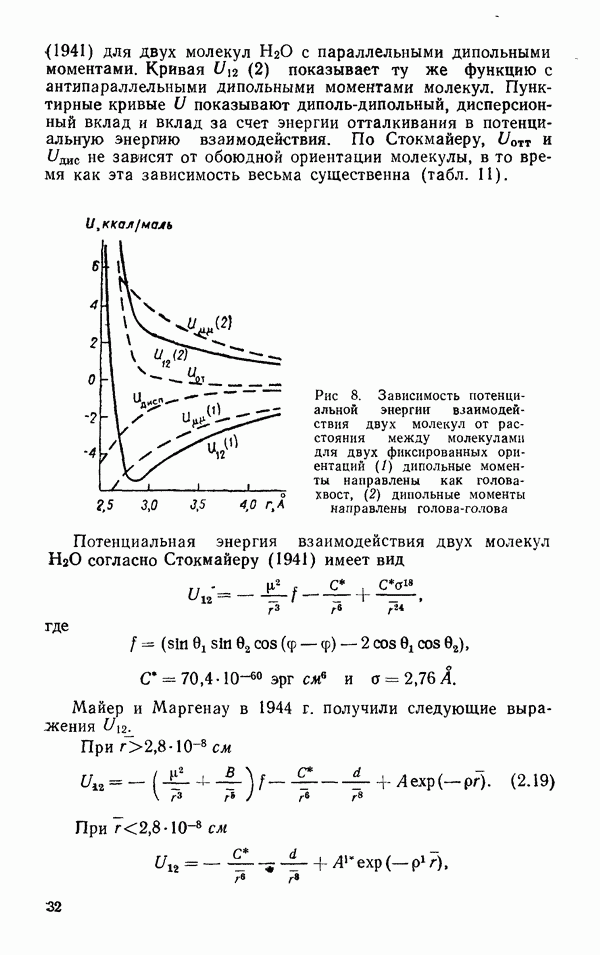
(1941) для двух молекул  с параллельными дипольными моментами. Кривая
с параллельными дипольными моментами. Кривая  показывает ту же функцию с антипараллельными дипольными моментами молекул. Пунктирные кривые
показывает ту же функцию с антипараллельными дипольными моментами молекул. Пунктирные кривые  показывают диполь-дипольный, дисперсионный вклад и вклад за счет энергии отталкивания в потенциальную энергию взаимодействия. По Стокмайеру,
показывают диполь-дипольный, дисперсионный вклад и вклад за счет энергии отталкивания в потенциальную энергию взаимодействия. По Стокмайеру,  не зависят от обоюдной ориентации молекулы, в то время как эта зависимость весьма существенна (табл. 11).
не зависят от обоюдной ориентации молекулы, в то время как эта зависимость весьма существенна (табл. 11).

Рис. 8. Зависимость потенциальной энергии взаимодействия двух молекул от расстояния между молекулами для двух фиксированных ориентаций  дипольные моменты направлены как голова-хвост, (2) дипольные моменты направлены голова-голова
дипольные моменты направлены как голова-хвост, (2) дипольные моменты направлены голова-голова
Потенциальная энергия взаимодействия двух молекул  согласно Стокмайеру (1941) имеет вид
согласно Стокмайеру (1941) имеет вид

где

Майер и Маргенау в 1944 г. получили следующие выражения 
При 

При 

Здесь

Силы отталкивания в этом выражении описывают экспоненциальные члены; диполь-дипольные члены  квадруполь-квадрупольное взаимодействие
квадруполь-квадрупольное взаимодействие  и дисперсионное
и дисперсионное  Это выражение получено при предположении, что электростатическая энергия взаимодействия двух молекул существенна только тогда, когда они находятся в конфигурации наиболее выгодной в смысле притяжения (конфигурация а и
Это выражение получено при предположении, что электростатическая энергия взаимодействия двух молекул существенна только тогда, когда они находятся в конфигурации наиболее выгодной в смысле притяжения (конфигурация а и  в табл. 2.1), остальные конфигурации молекул описаны с помощью общего выражения (2.18).
в табл. 2.1), остальные конфигурации молекул описаны с помощью общего выражения (2.18).
Положительный член в выражении (2.19) описывает силы межмолекулярного отталкивания и главным образом обусловлен перекрыванием электронных облаков взаимодействующих молекул. При концентрации электронов в малой области понижается ассоциированная с ними волна де Бройля, а так как  то при понижении К возрастает
то при понижении К возрастает  (импульс), а следовательно, увеличивается кинетическая энергия электронов, что и приводит к отталкиванию. Для двух взаимодействующих молекул
(импульс), а следовательно, увеличивается кинетическая энергия электронов, что и приводит к отталкиванию. Для двух взаимодействующих молекул  если расстояние между ними 3 А, доминирует отталкивание. Гиршфельдер и Букингем (1956) показали, что силы межмолекулярного отталкивания описывает член вида
если расстояние между ними 3 А, доминирует отталкивание. Гиршфельдер и Букингем (1956) показали, что силы межмолекулярного отталкивания описывает член вида  где
где  полином от
полином от  положительный параметр. Однако из-за своей сложности в таком виде потенциал отталкивания практически не используется при расчетах, а заменяется модельным потенциалом или
положительный параметр. Однако из-за своей сложности в таком виде потенциал отталкивания практически не используется при расчетах, а заменяется модельным потенциалом или  или
или 
Исследования, посвященные изучению сил отталкивания, весьма ограниченны; так, до сих пор очень мало известно о зависимости этих сил от обоюдной ориентации молекул. Обычно предполагают, что симметрия электронов повторяет симметрию ядерного скелета (гл. 1).
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
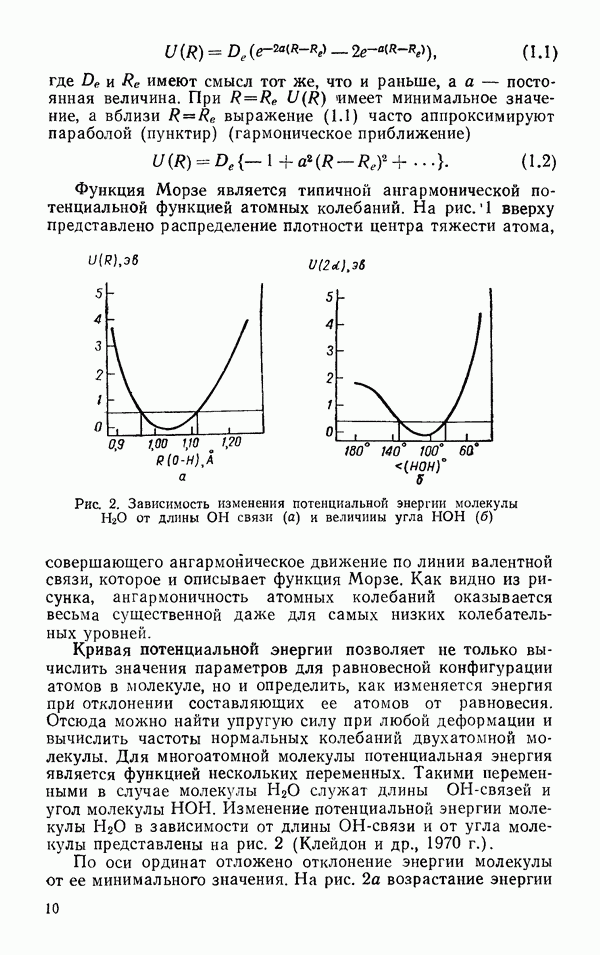
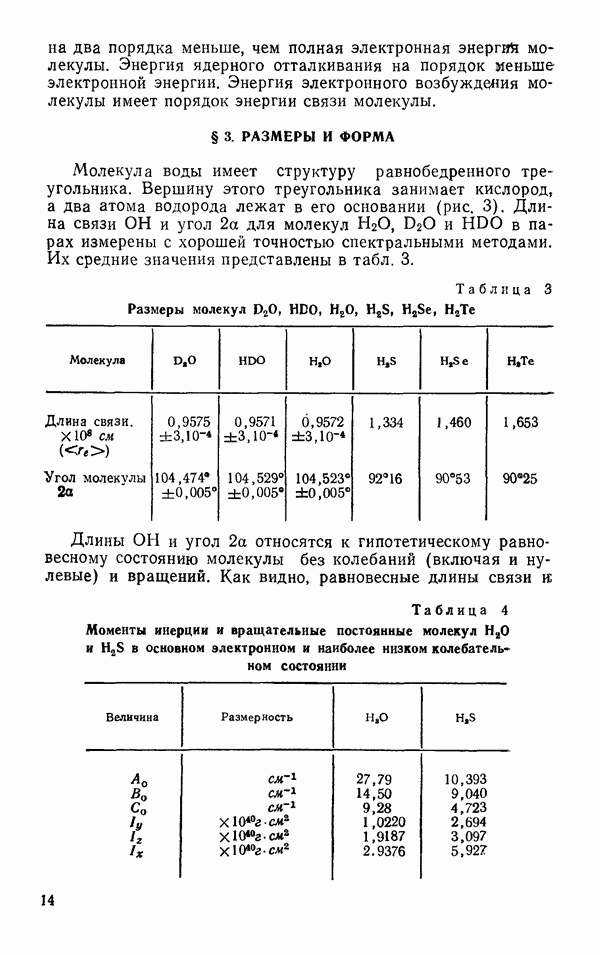
- § 3. РАЗМЕРЫ И ФОРМА
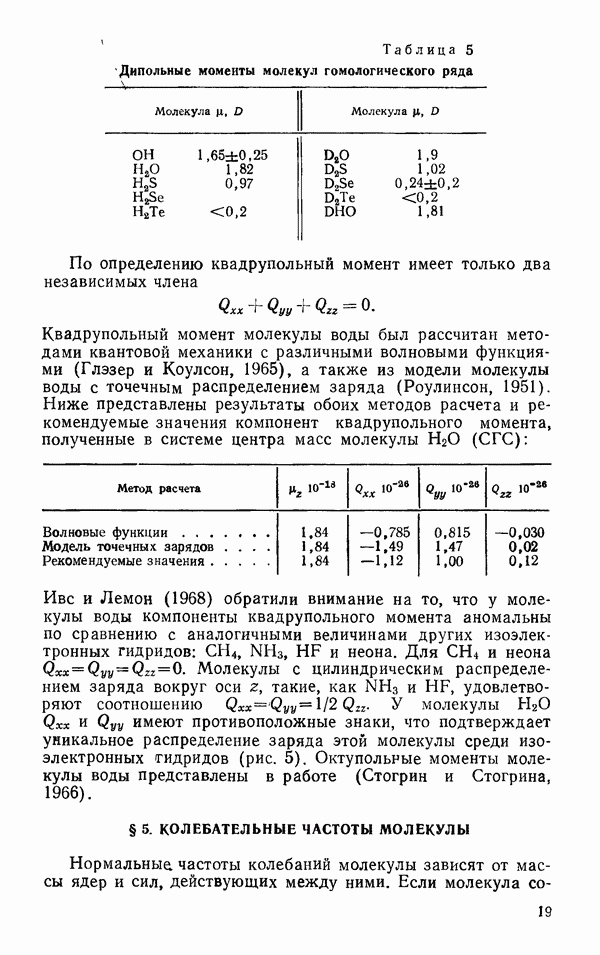
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
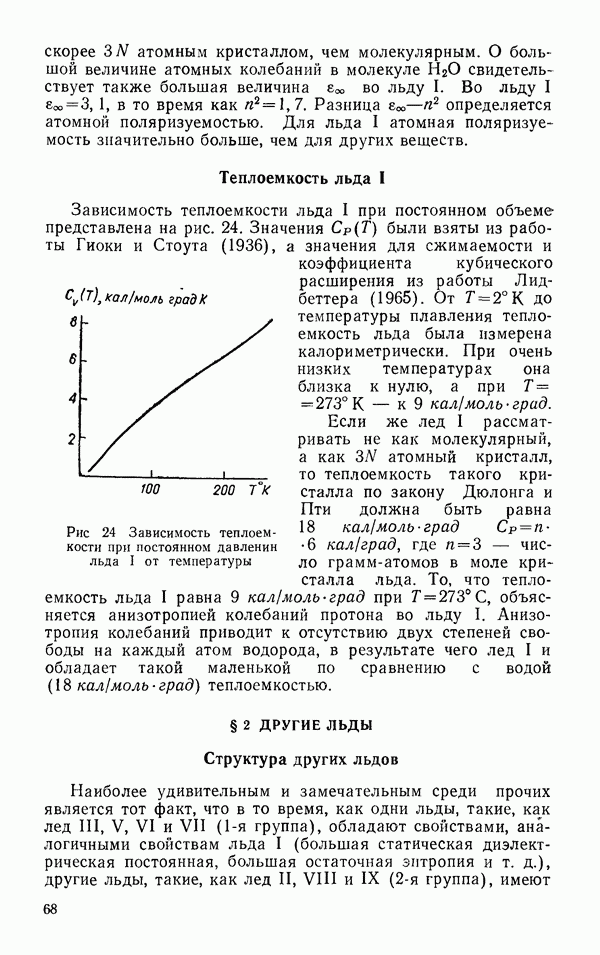
- Теплоемкость льда I
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
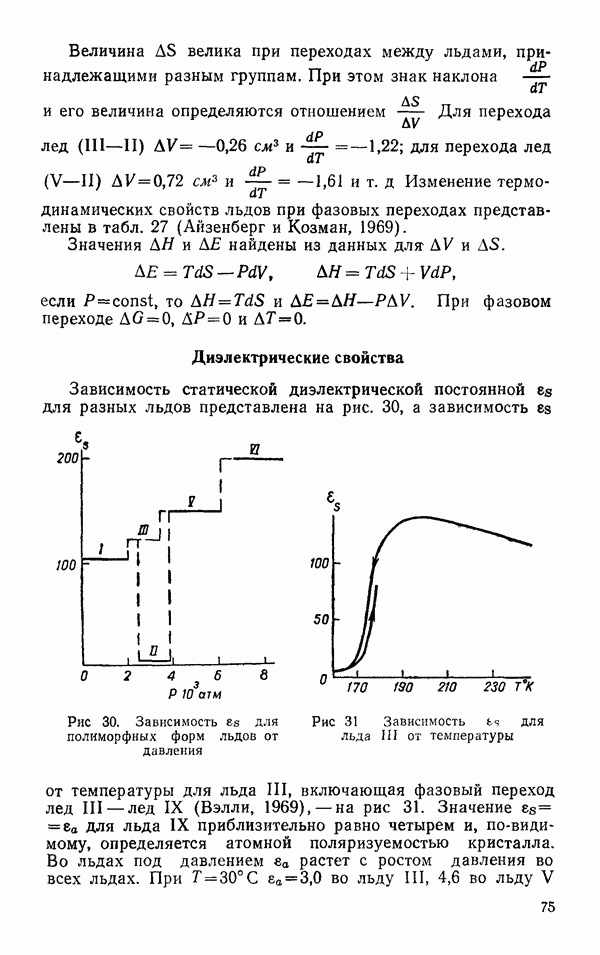
- Диэлектрические свойства
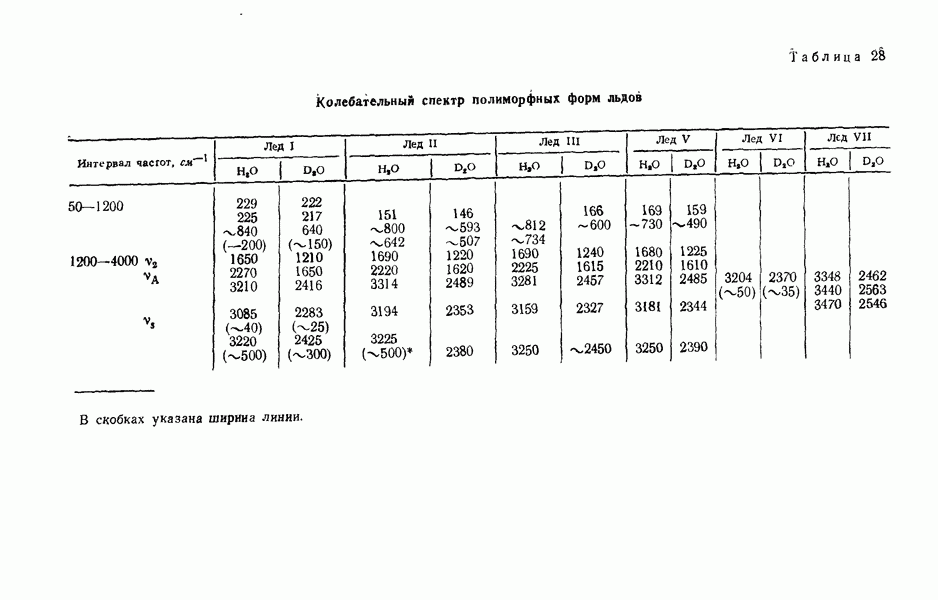
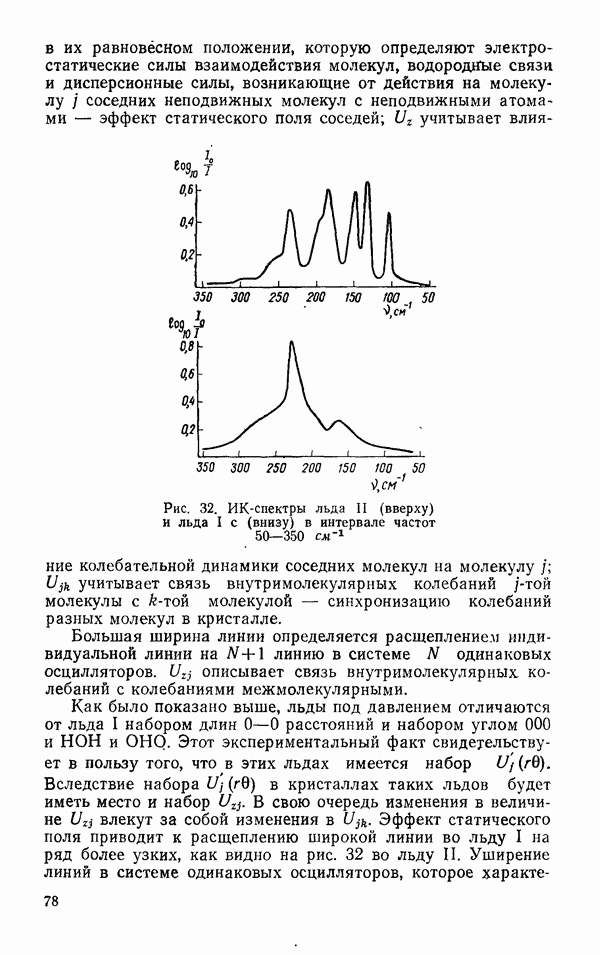
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
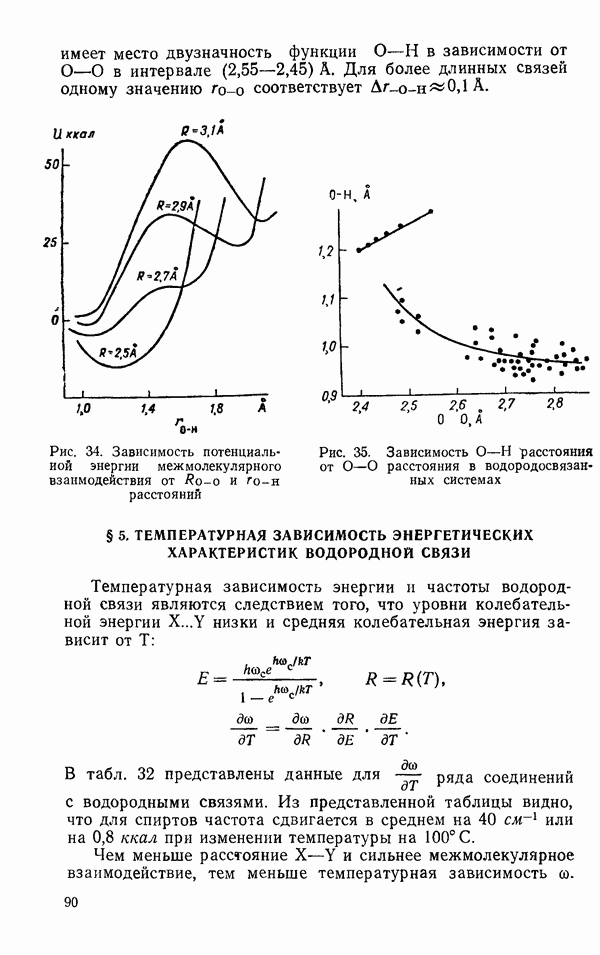
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
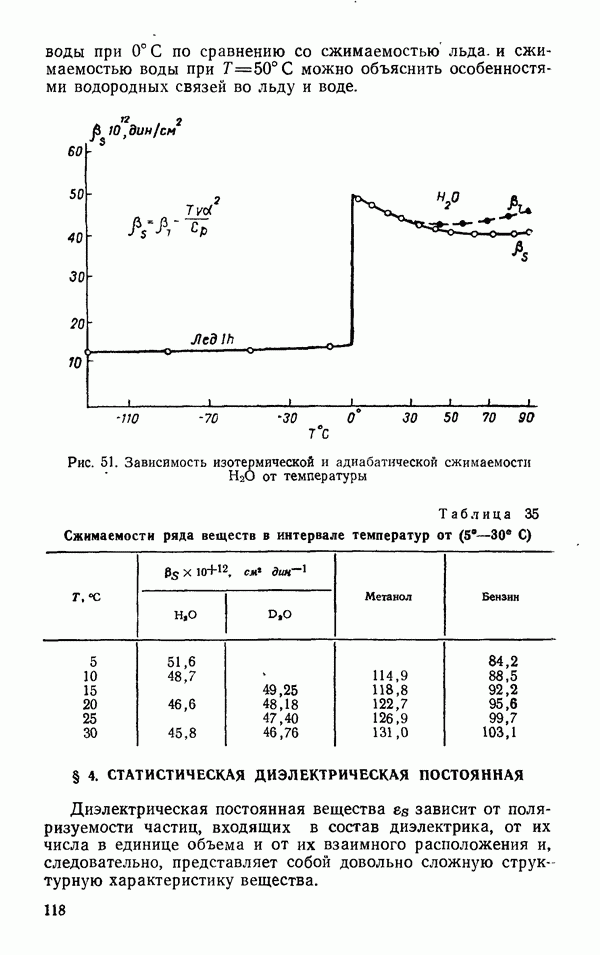
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
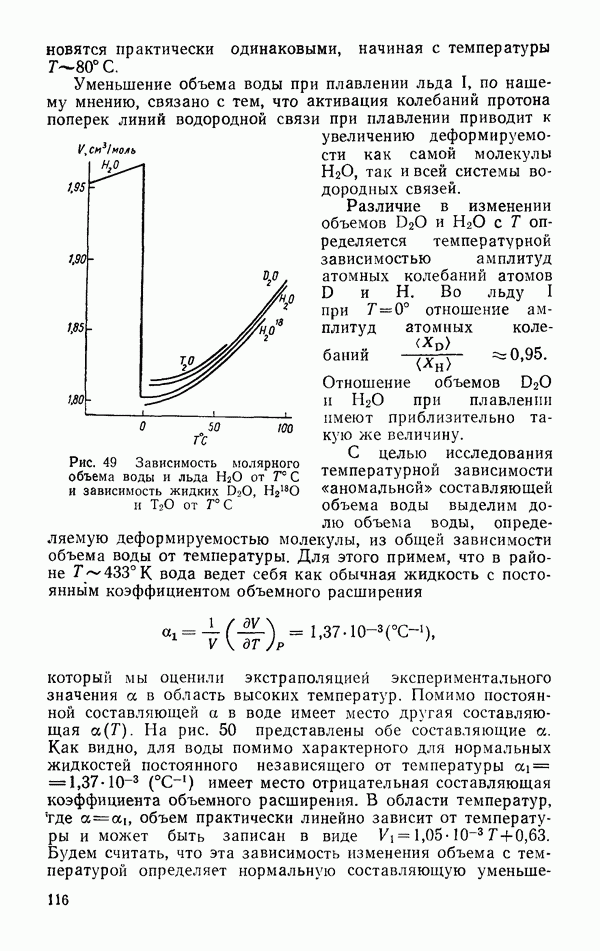
- Зависимость объема и его производных от температуры
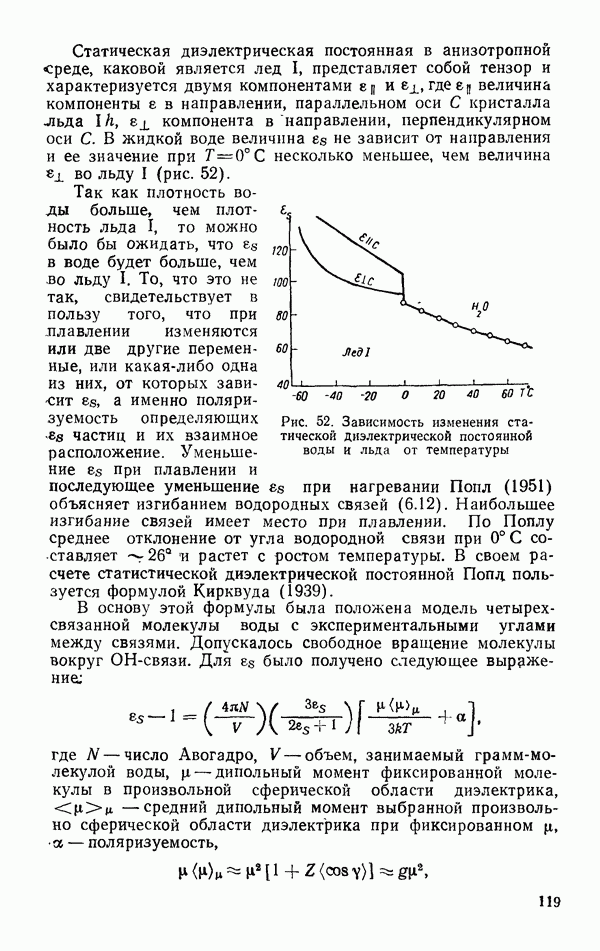
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
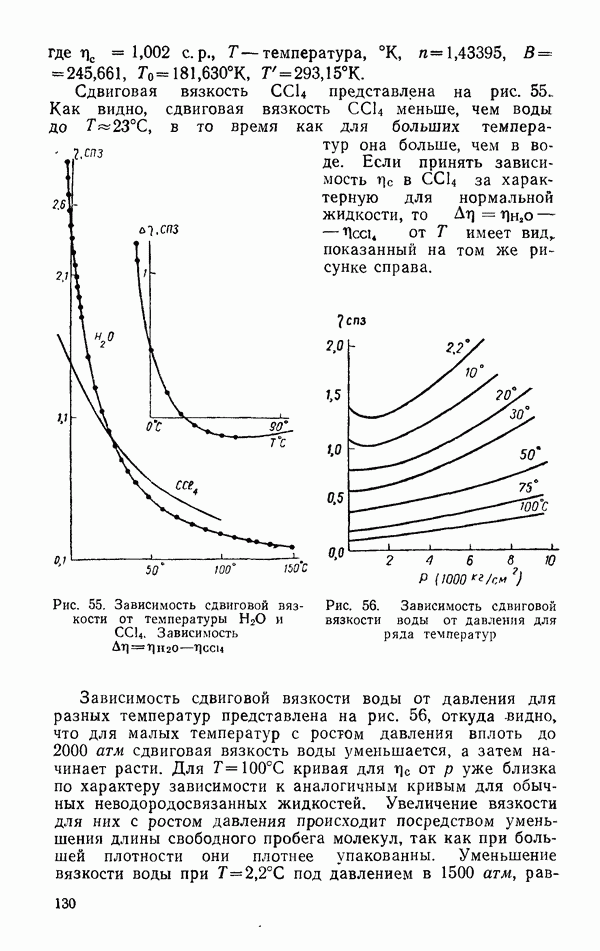
- Вязкость
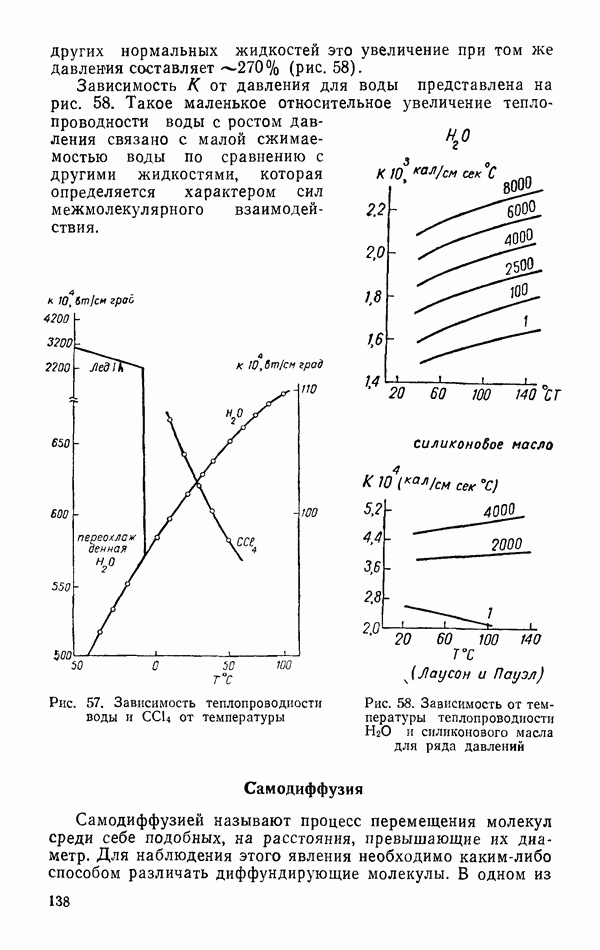
- Теплопроводность
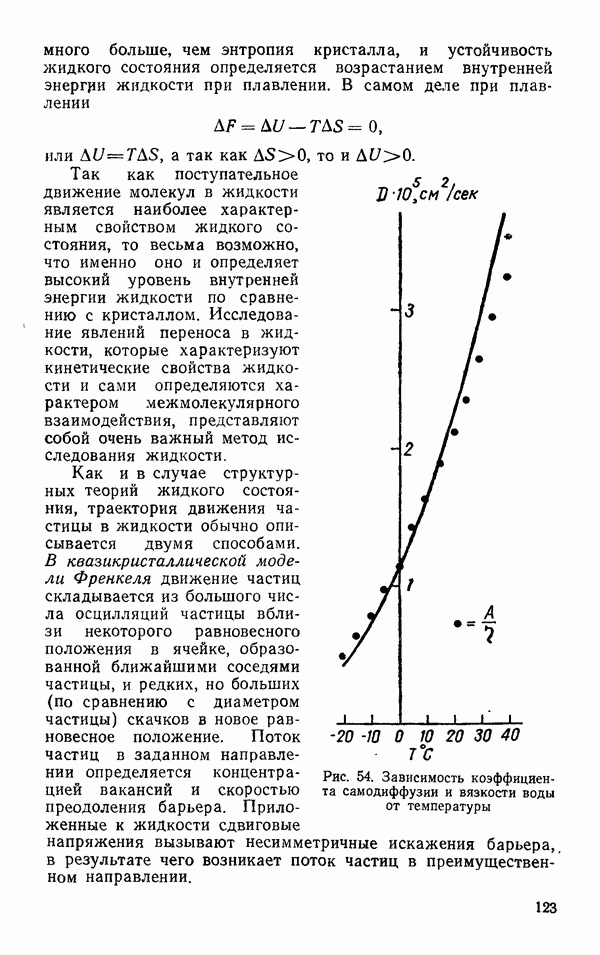
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
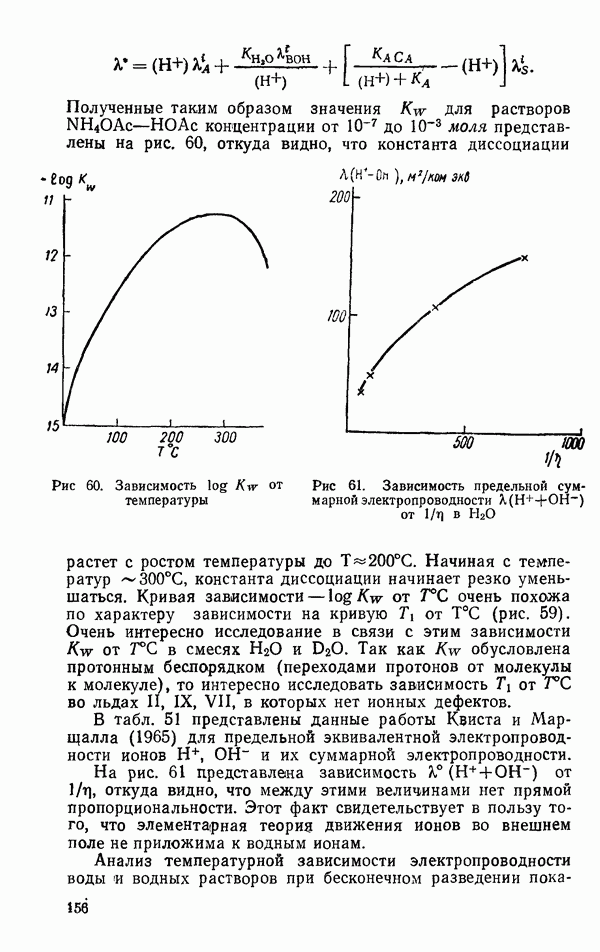
- Молекулярное рассеяние света
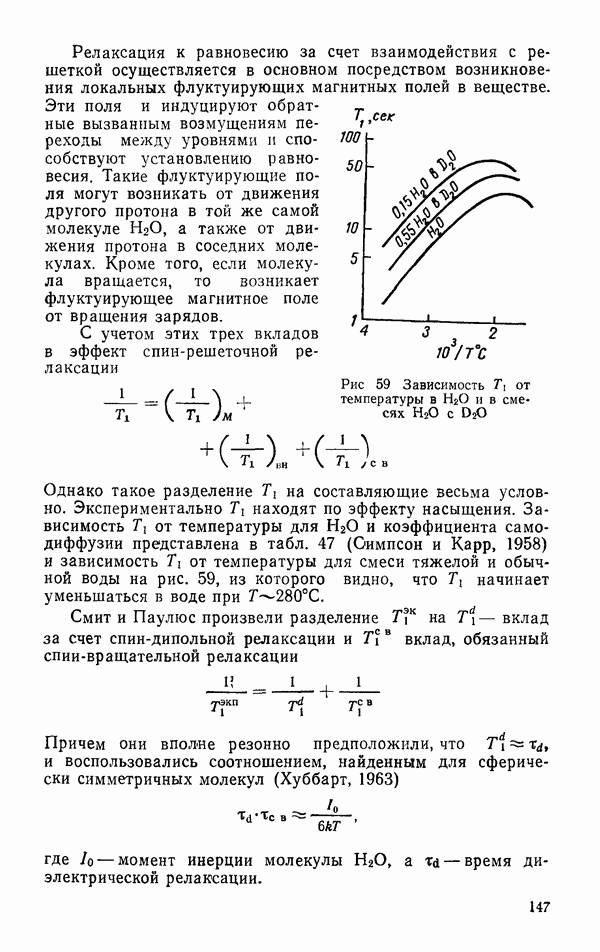
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА