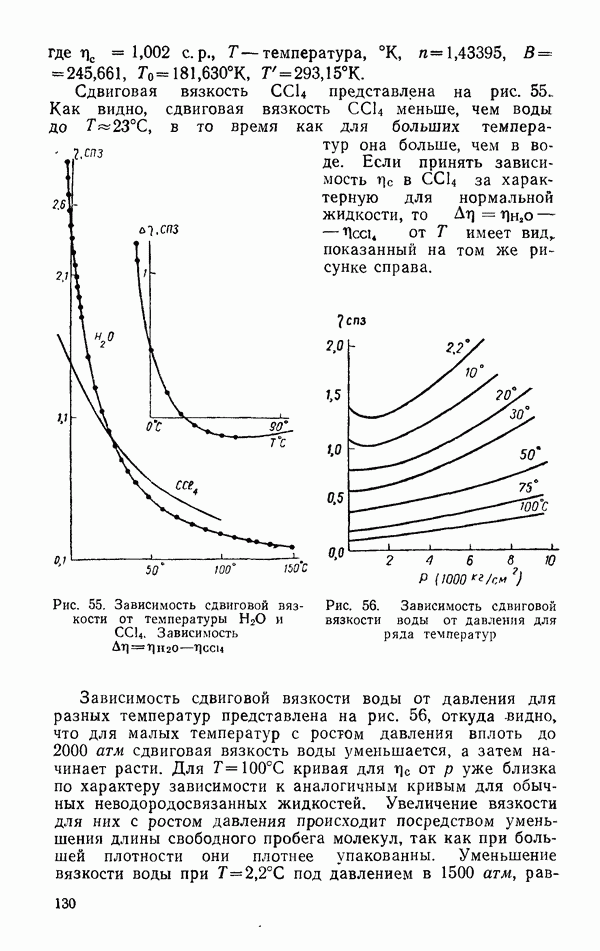
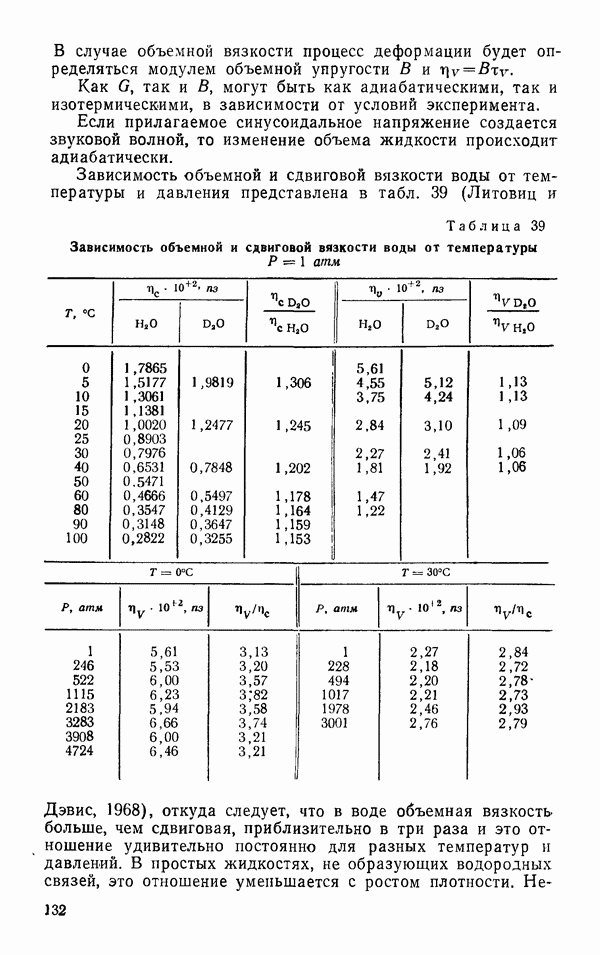
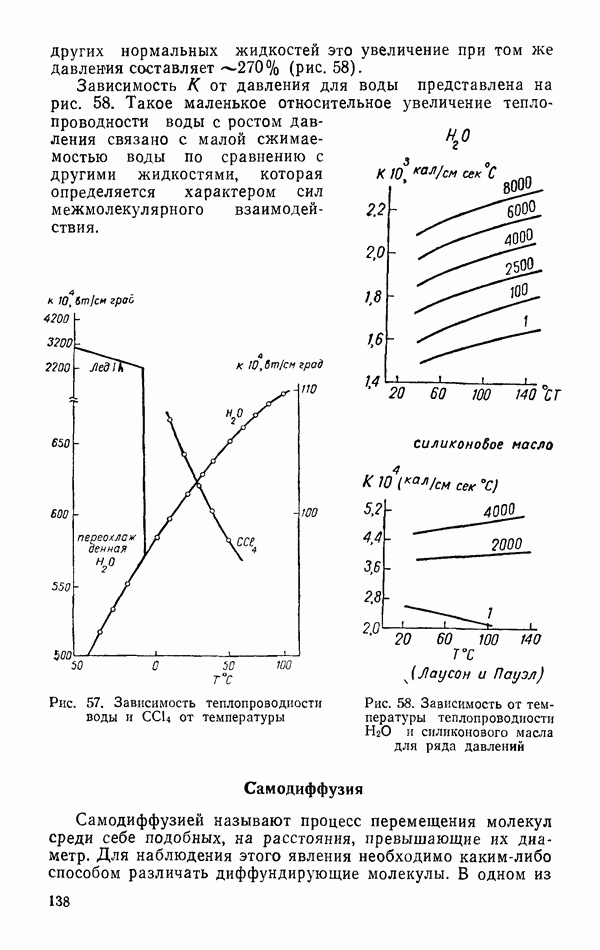
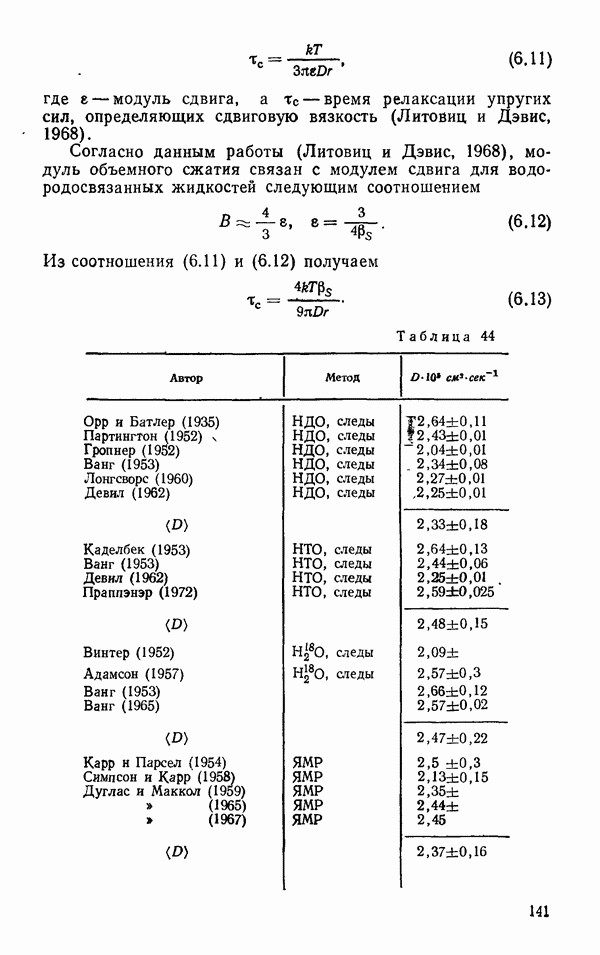
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
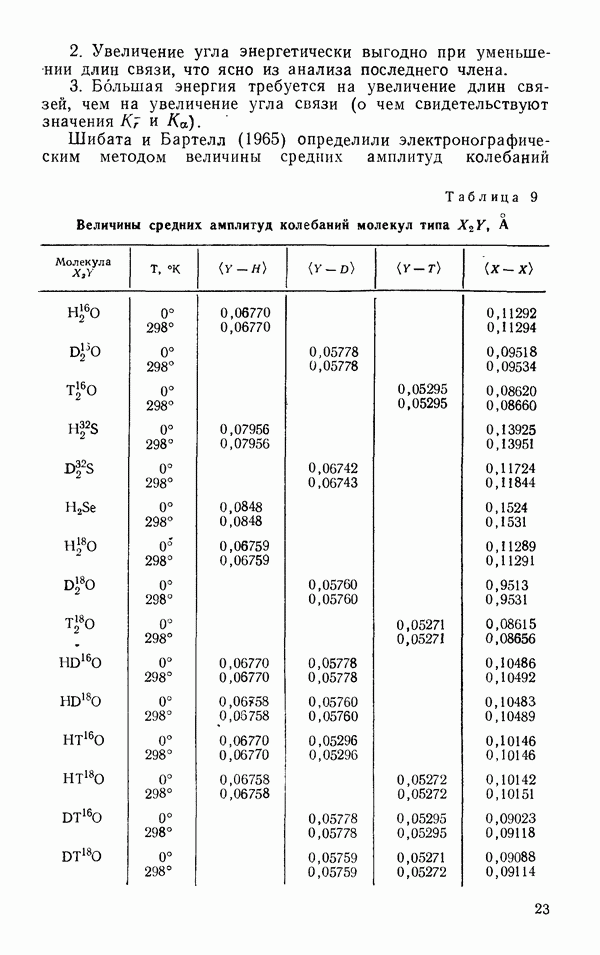
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Молекулярное рассеяние света
Исследование термодинамических флуктуаций ведет свое начало с работ Смолуховского (1908) и Эйнштейна (1910), посвященных теории рассеяния света на тепловых флуктуациях плотности. К возникновению флуктуаций плотности в жидкости приводит статистический характер теплового движения молекул. Релеевское светорассеяние вызывают флуктуации плотности и ориентаций в объемах, малых по сравнению с длиной световой волны.
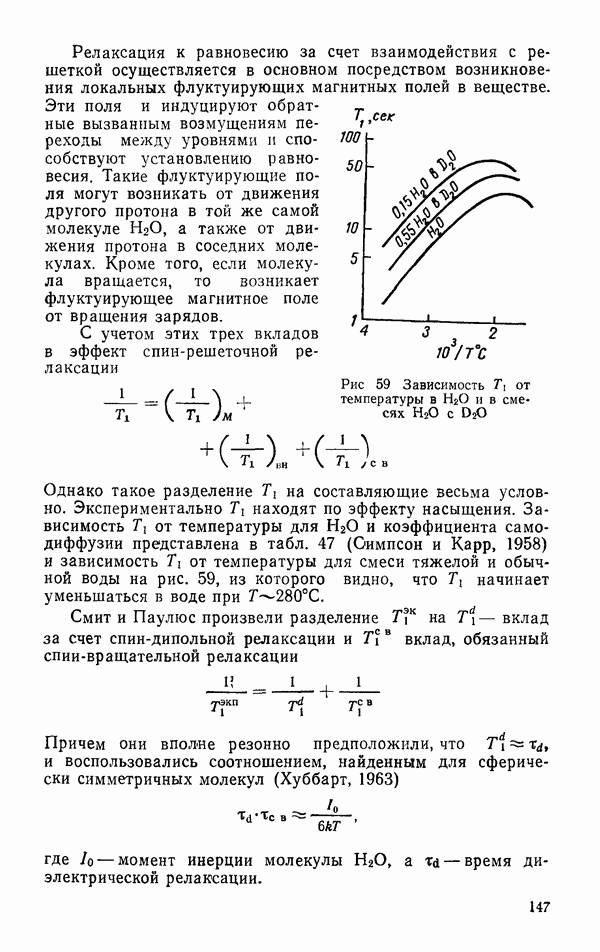
Таблица 47 (см. скан) Зависимость коэффициента диффузии и времени спин-решеточной релаксации от температуры
Объем флуктуаций  Если
Если  см, то V много меньше,
см, то V много меньше, 
Согласно теории Смолуховского — Эйнштейна экспериментально измеряемый коэффициент рассеяния — коэффициент Релея  определяется соотношением
определяется соотношением

где  интенсивность света рассеянного под углом 90°,
интенсивность света рассеянного под углом 90°,  интенсивность падающего света,
интенсивность падающего света,  расстояние от центра рассеивающего объема до точки наблюдения и V — объем рассеивающей системы. Величина
расстояние от центра рассеивающего объема до точки наблюдения и V — объем рассеивающей системы. Величина  средний квадрат флуктуаций диэлектрической проницаемости жидкости в оптическом диапазоне, где
средний квадрат флуктуаций диэлектрической проницаемости жидкости в оптическом диапазоне, где  Зависимость
Зависимость  определяется формулами Клаузиуса — Мосотти и Лоренц — Лорентца.
определяется формулами Клаузиуса — Мосотти и Лоренц — Лорентца.
Макроскопическая формула Лоренц — Лорентца

Если предположить, что короткодействующее взаимодействие молекул не влияет на поляризуемость, то

где  число молекул в грамм-моле,
число молекул в грамм-моле,  молекулярная поляризуемость.
молекулярная поляризуемость.
Тогда

где В — постоянная.
Это уравнение представляет собой молекулярное уравнение Лоренц-Лорентца, в основе которого лежит предположение, что  функции только термодинамических параметров. В этом случае
функции только термодинамических параметров. В этом случае

где

(Ландау и Лифшиц, 1951),

Очень часто в качестве независимых переменных используется не  (где
(где  энтропия).
энтропия).
В этих переменных  имеет вид
имеет вид

и соответственно
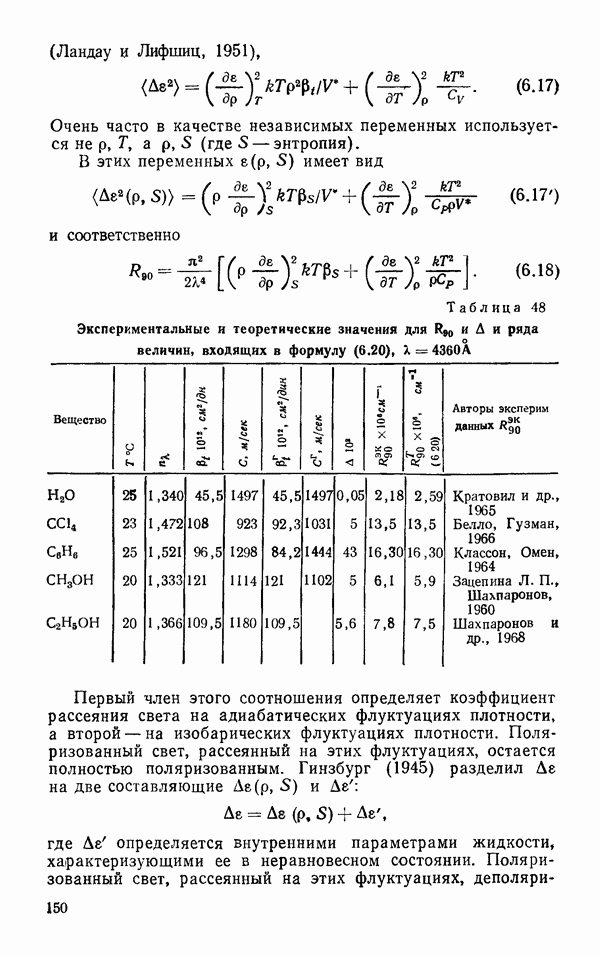
Таблица 48 Экспериментальные и теоретические значения для  и А и ряда
и А и ряда


величин, входящих в формулу (6.20), 
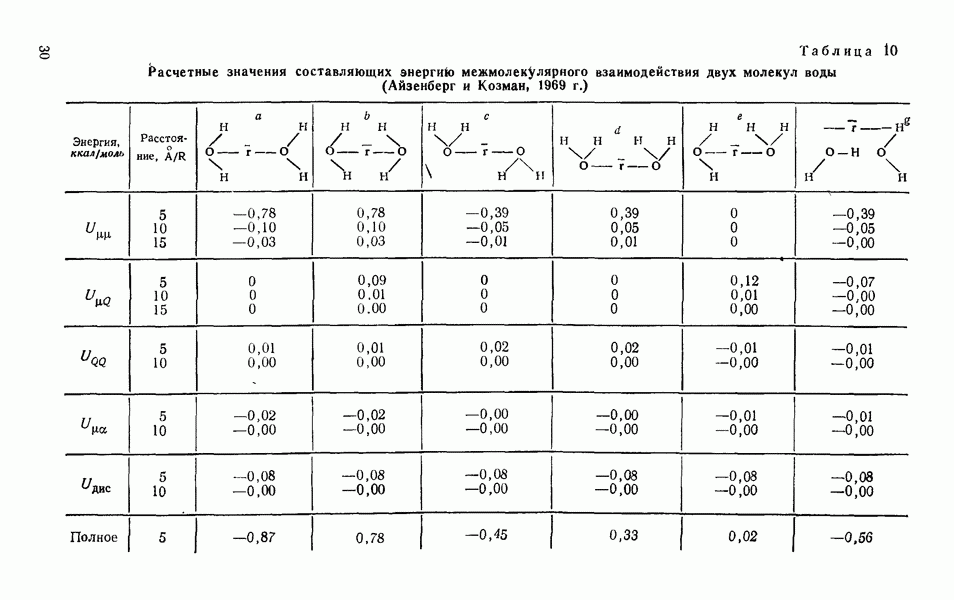
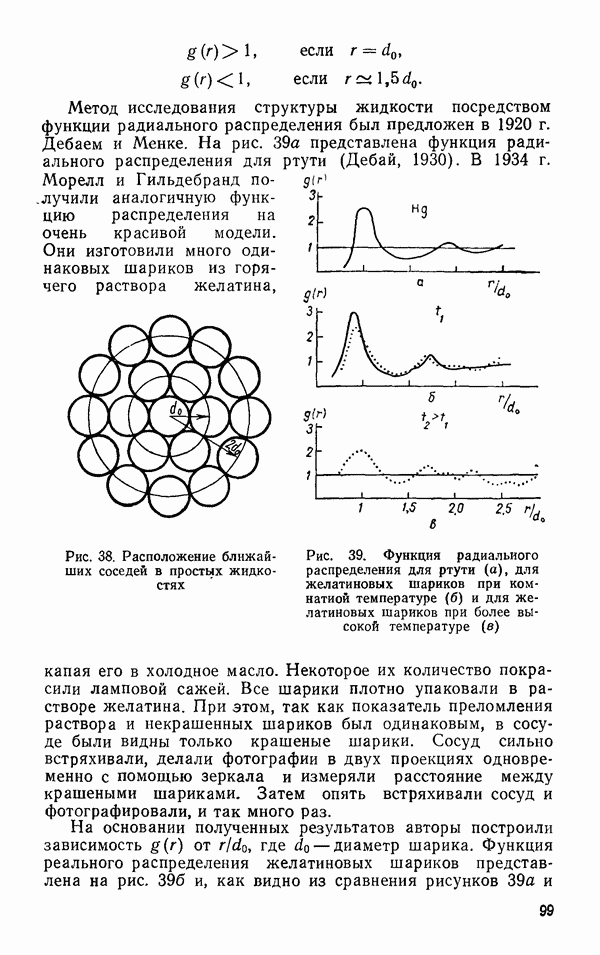
Первый член этого соотношения определяет коэффициент рассеяния света на адиабатических флуктуациях плотности, а второй — на изобарических флуктуациях плотности. Поляризованный свет, рассеянный на этих флуктуациях, остается полностью поляризованным. Гинзбург (1945) разделил  на две составляющие
на две составляющие 

где  определяется внутренними параметрами жидкости, характеризующими ее в неравновесном состоянии. Поляризованный свет, рассеянный на этих флуктуациях,
определяется внутренними параметрами жидкости, характеризующими ее в неравновесном состоянии. Поляризованный свет, рассеянный на этих флуктуациях,
деполяризуется. Учет деполяризащии приводит к следующему соотношению

где  коэффициент Релея с учетом деполяризации, А — коэффициент деполяризации.
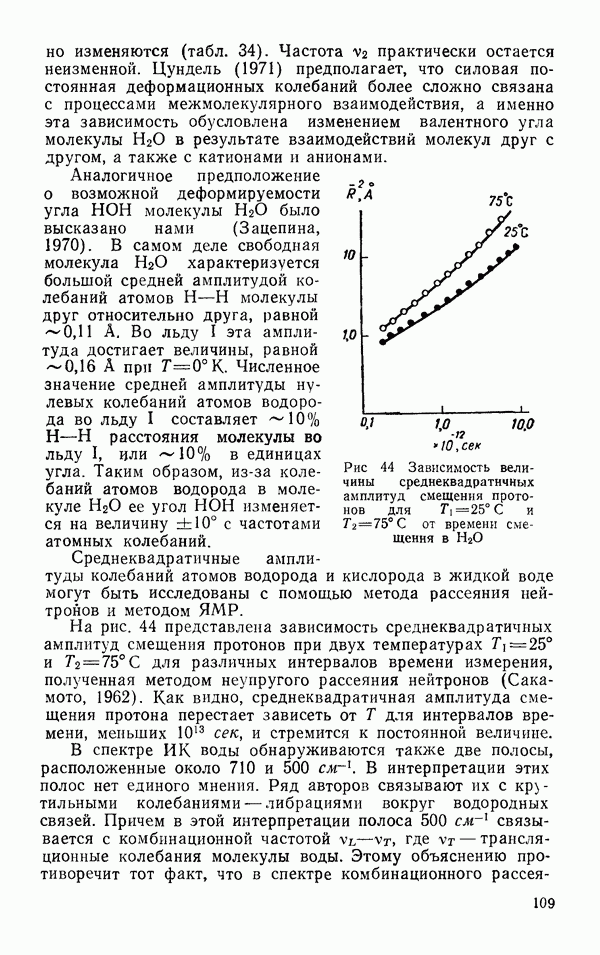
коэффициент Релея с учетом деполяризации, А — коэффициент деполяризации.
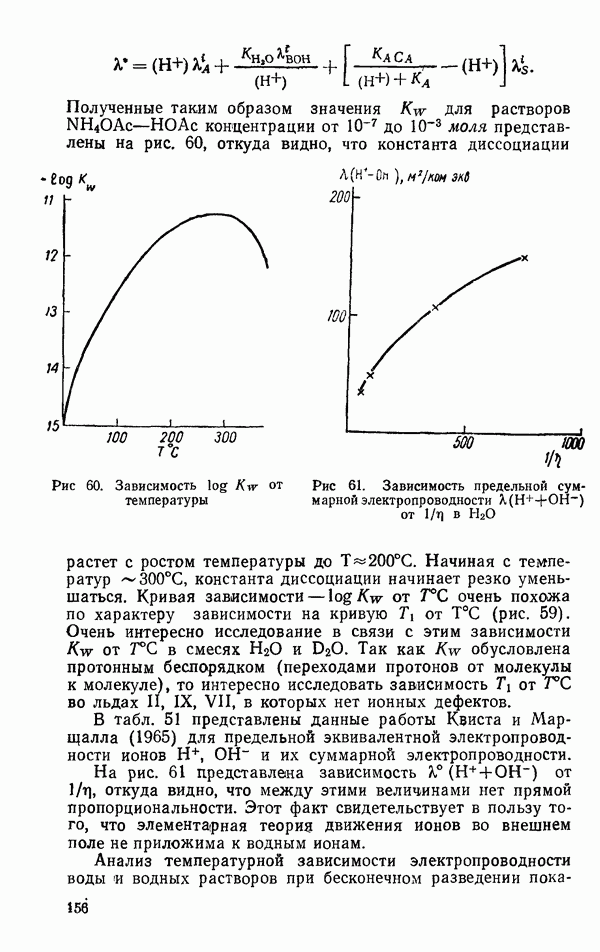
Как было показано Фабелинским (1957, 1965), второй член (6.18), зависящий от  составляет 2% от величины первого члена, т. е. рассеяние света на изобарических флуктуациях плотности много меньше, чем на адиабатических флуктуациях плотности.
составляет 2% от величины первого члена, т. е. рассеяние света на изобарических флуктуациях плотности много меньше, чем на адиабатических флуктуациях плотности.
Таким образом, уравнение Смолуховского — Эйнштейна может быть записано в виде

Основные трудности расчета  из этого соотношения связаны с тем, что экспериментальные данные относительно
из этого соотношения связаны с тем, что экспериментальные данные относительно  как правило, отсутствуют. Эйнштейн и Смолуховский для определения
как правило, отсутствуют. Эйнштейн и Смолуховский для определения  воспользовались формулой Лоренц — Лорентца и нашли, что
воспользовались формулой Лоренц — Лорентца и нашли, что

В этом случае формула (6.19) приобретает вид

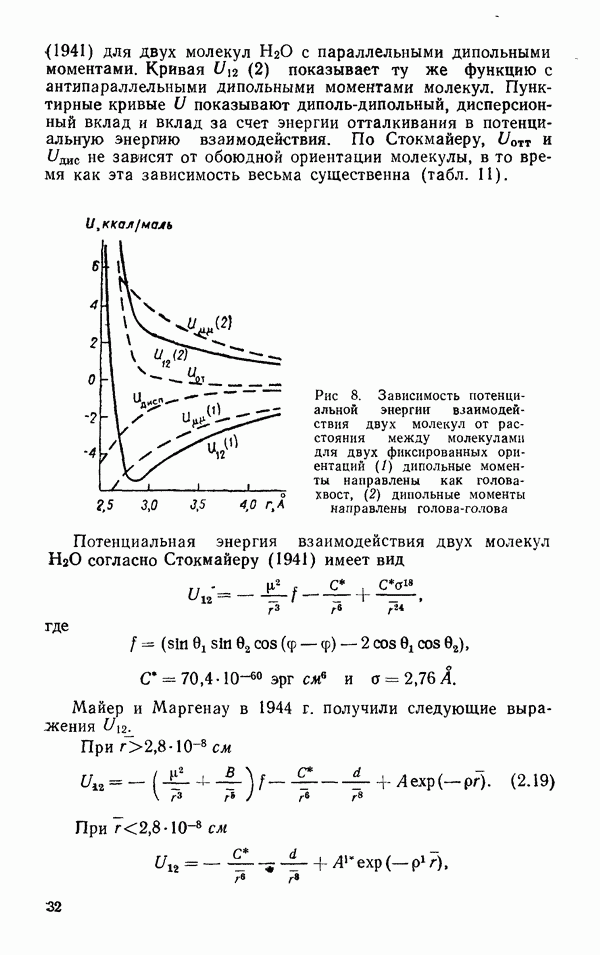
Фабелинский (1965) предложил метод учета дисперсии  в гиперакустическом районе частот.
в гиперакустическом районе частот.
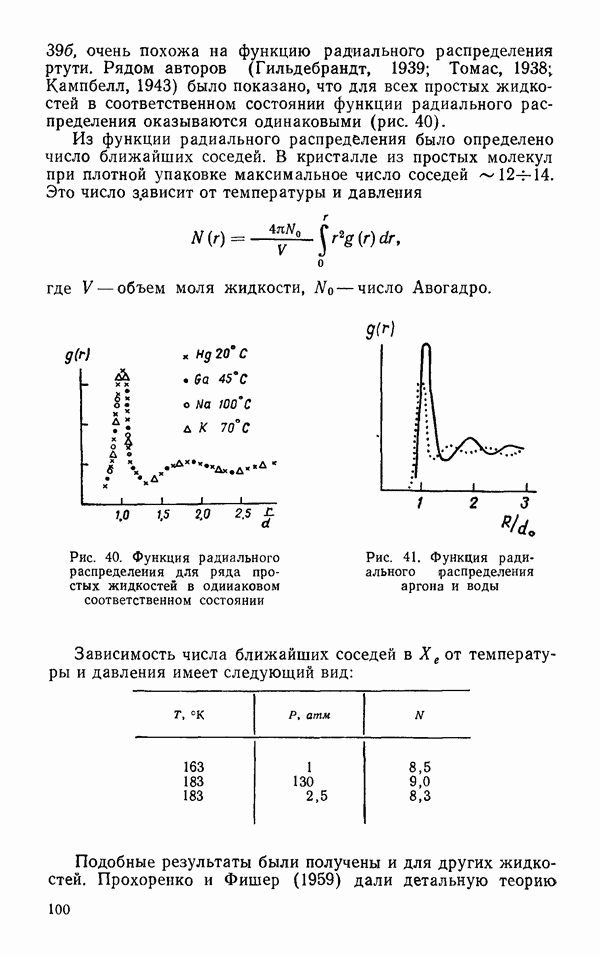
В табл. 48 представлены экспериментальные данные относительно  и А для ряда веществ и расчетные данные, полученные по формуле Эйнштейна — Смолуховского — Кабана, с учетом коэффициента сжимаемости по Фабелинскому. Как видно, вода обладает наименьшим значением коэффициента Релея и коэффициента деполяризации среди других веществ. Анализ данных табл. 48 показывает, что формула (6.20) оказывается очень точной для
и А для ряда веществ и расчетные данные, полученные по формуле Эйнштейна — Смолуховского — Кабана, с учетом коэффициента сжимаемости по Фабелинскому. Как видно, вода обладает наименьшим значением коэффициента Релея и коэффициента деполяризации среди других веществ. Анализ данных табл. 48 показывает, что формула (6.20) оказывается очень точной для  и
и  в то время как отклонения от нее оказываются большими для спиртов и воды, соединений, образующих водородные связи. Причем в воде
в то время как отклонения от нее оказываются большими для спиртов и воды, соединений, образующих водородные связи. Причем в воде  а в спиртах
а в спиртах  По-видимому, расхождение экспериментальных и теоретических значений
По-видимому, расхождение экспериментальных и теоретических значений
обусловлено тем, что в теории предполагается равенство поляризуемости молекулы в жидкости и в газе, что ,45 жидкостях с водородными связями маловероятно. Очень маленькая величина  по абсолютному значению в воде определяется малой сжимаемостью воды, обусловленной ее структурой.
по абсолютному значению в воде определяется малой сжимаемостью воды, обусловленной ее структурой.
При использовании в качестве источников света лазеров был обнаружен целый ряд новых явлений, в основе которых лежит релеевское рассеяние света. Эти явления получили название вынужденного комбинационного рассеяния и основали новую область науки — нелинейную оптику. Нелинейная оптика затрагивает эффекты, определяемые изменениями во времени нелинейной части коэффициента поглощения света. Напряженность поля в световой волне при изучении эффектов вынужденного рассеяния света составляет  в/см. Такая световая волна изменяет состояние среды. Эксперименты показали, что и вынужденное молекулярное рассеяние света в воде также очень мало по сравнению с рассеянием света другими жидкостями (Фабелинский, 1969).
в/см. Такая световая волна изменяет состояние среды. Эксперименты показали, что и вынужденное молекулярное рассеяние света в воде также очень мало по сравнению с рассеянием света другими жидкостями (Фабелинский, 1969).
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
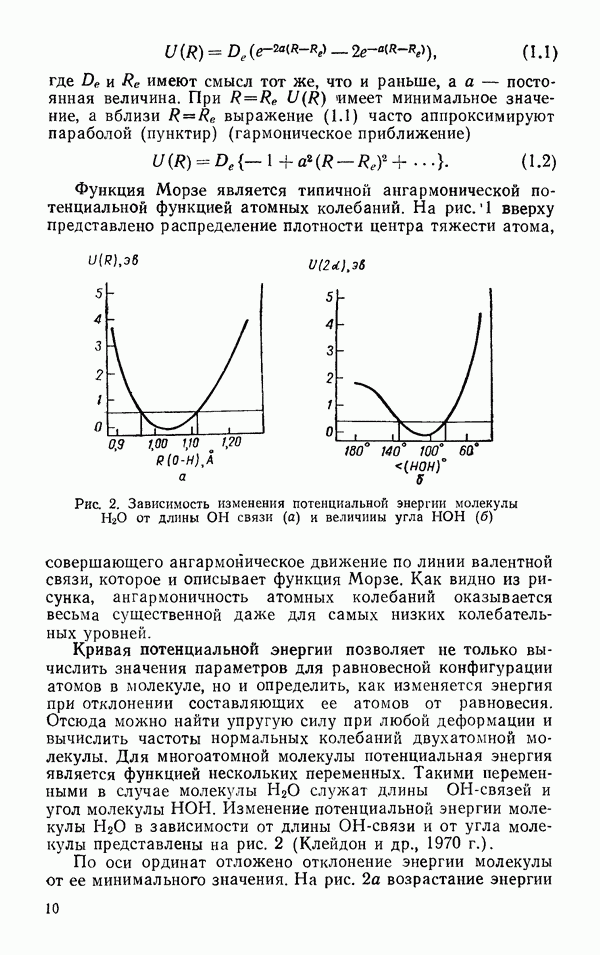
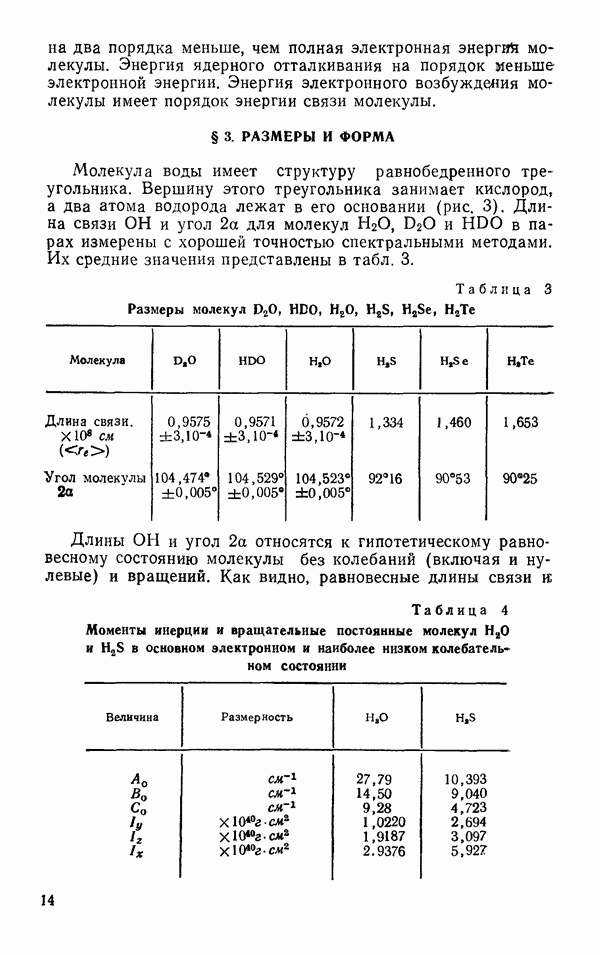
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
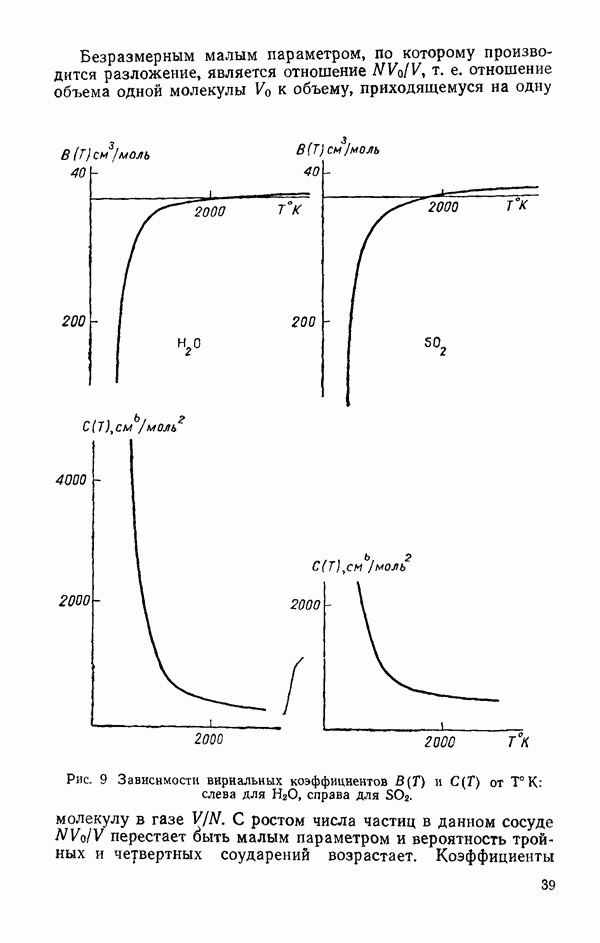
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
- § 1. ЛЕД
- Пластическая деформация монокристалла льда I
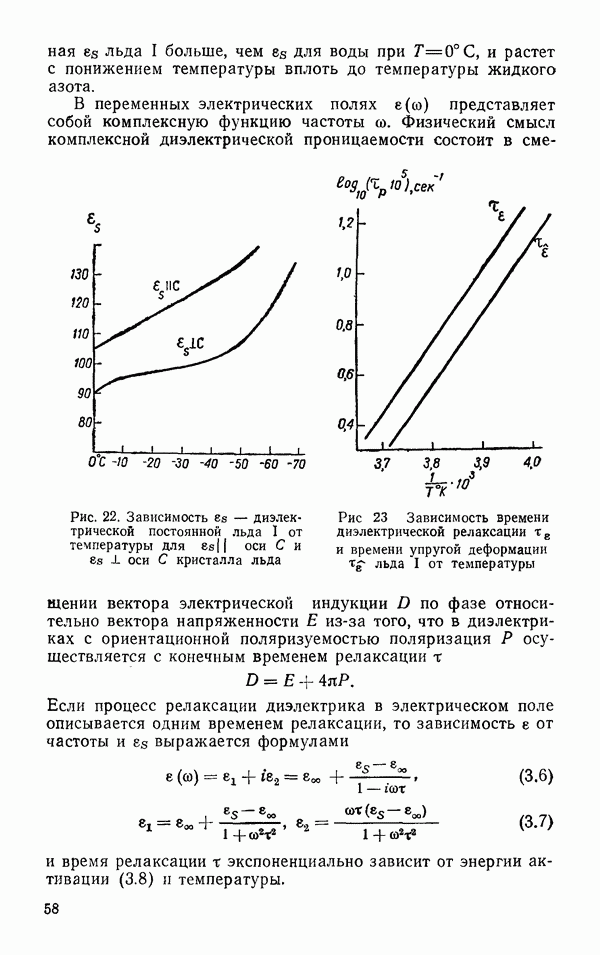
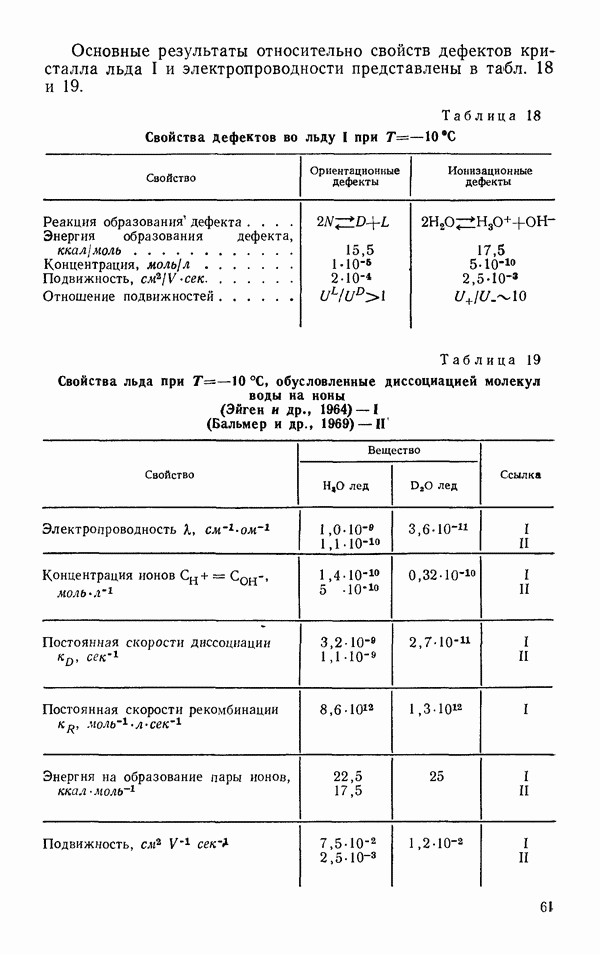
- Диэлектрические свойства льда 1
- Электропроводность льда
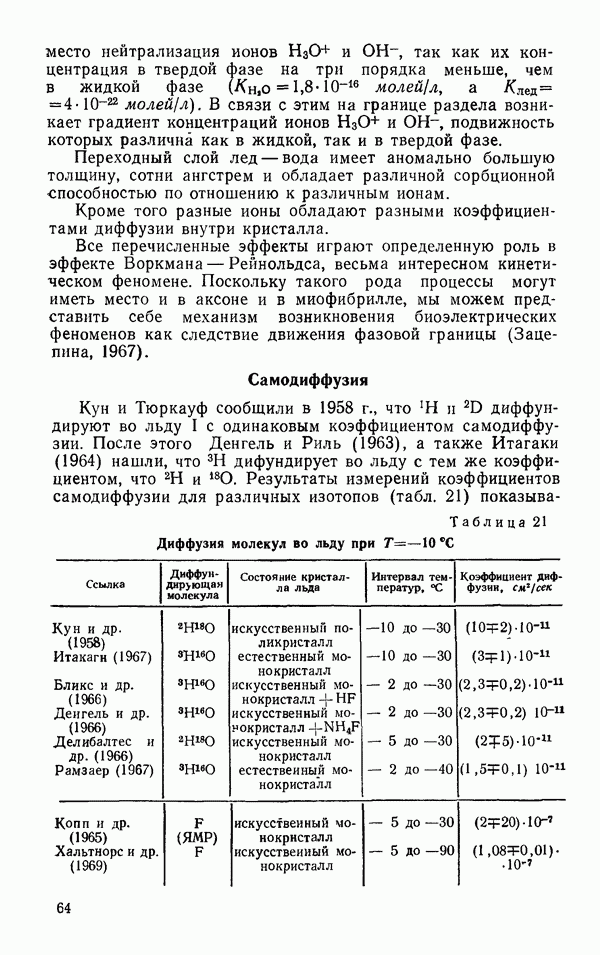
- Самодиффузия
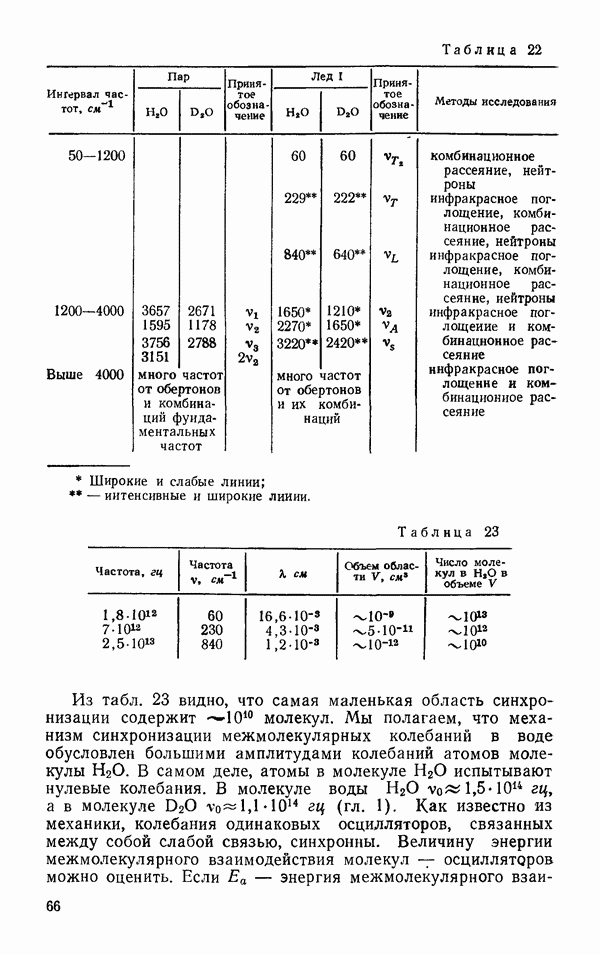
- Спектральные свойства льда I
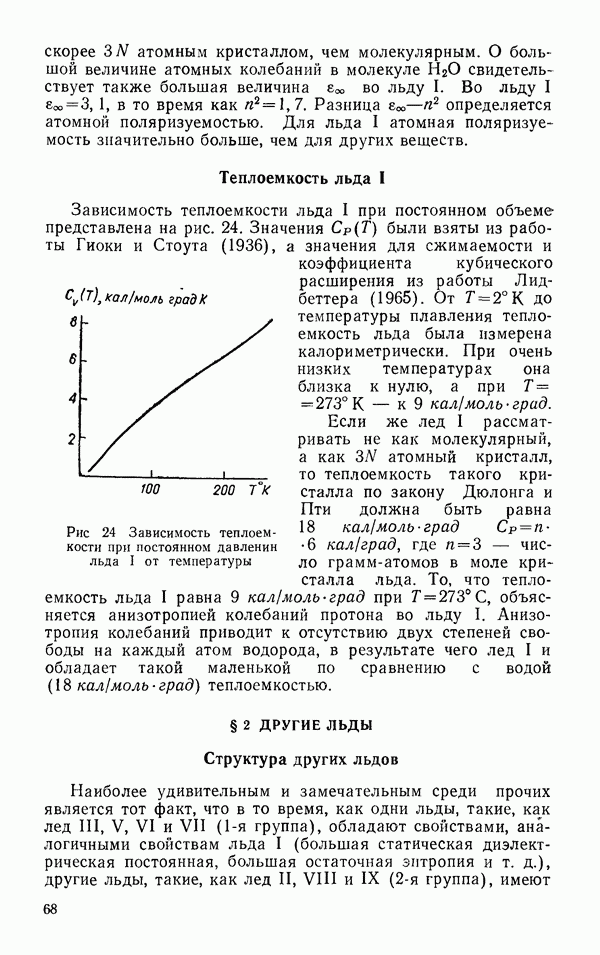
- Теплоемкость льда I
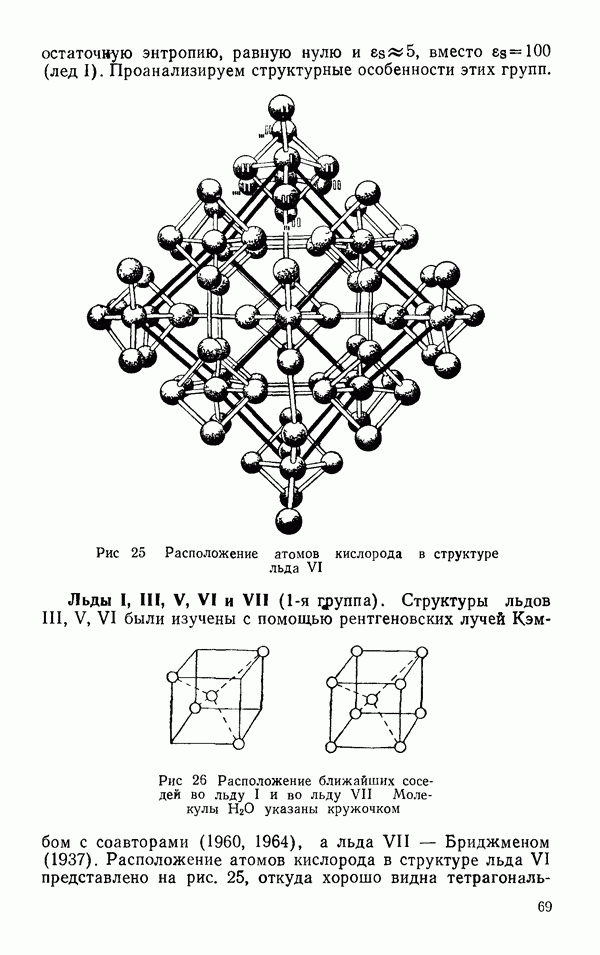
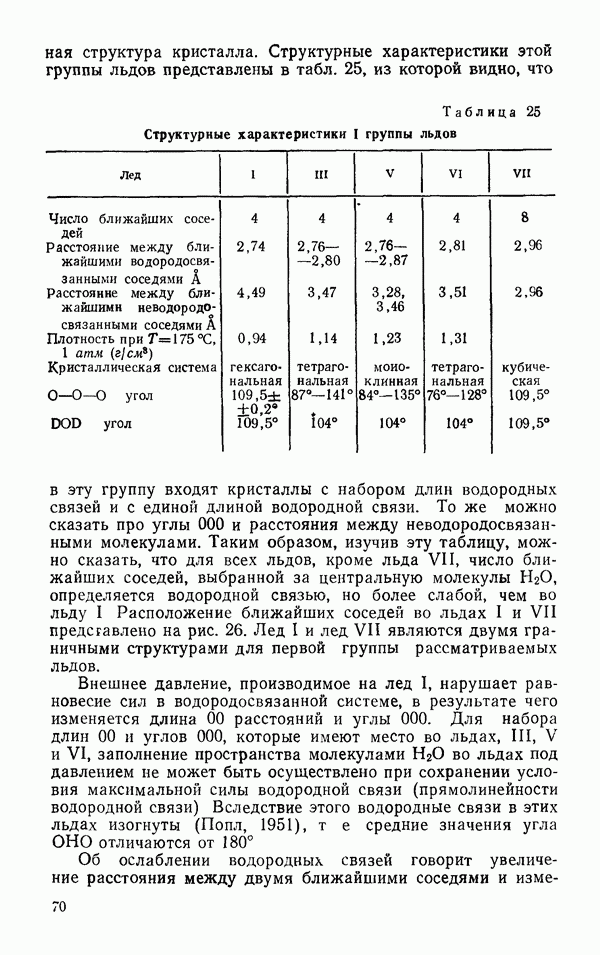
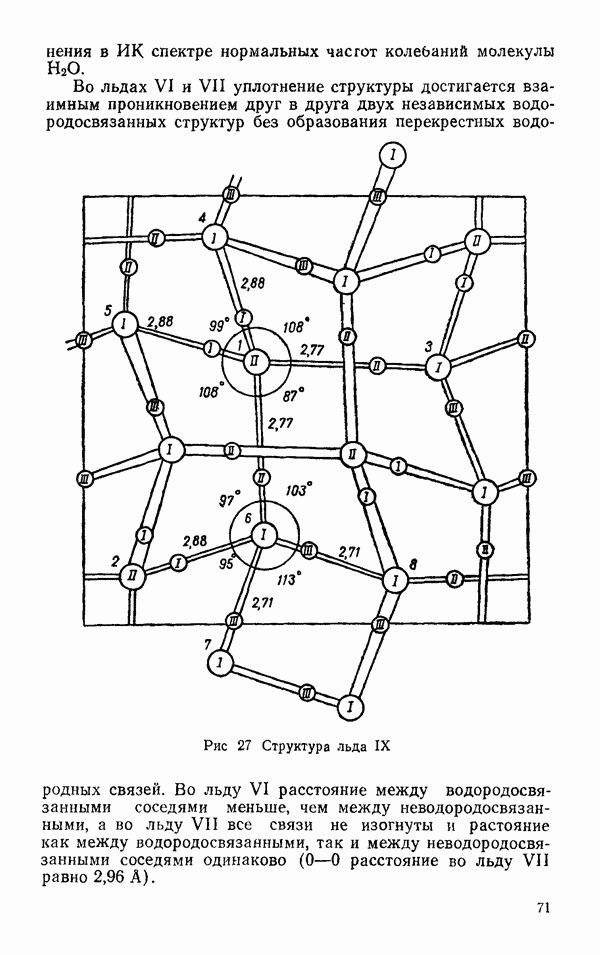
- § 2 ДРУГИЕ ЛЬДЫ
- Термодинамические свойства льдов
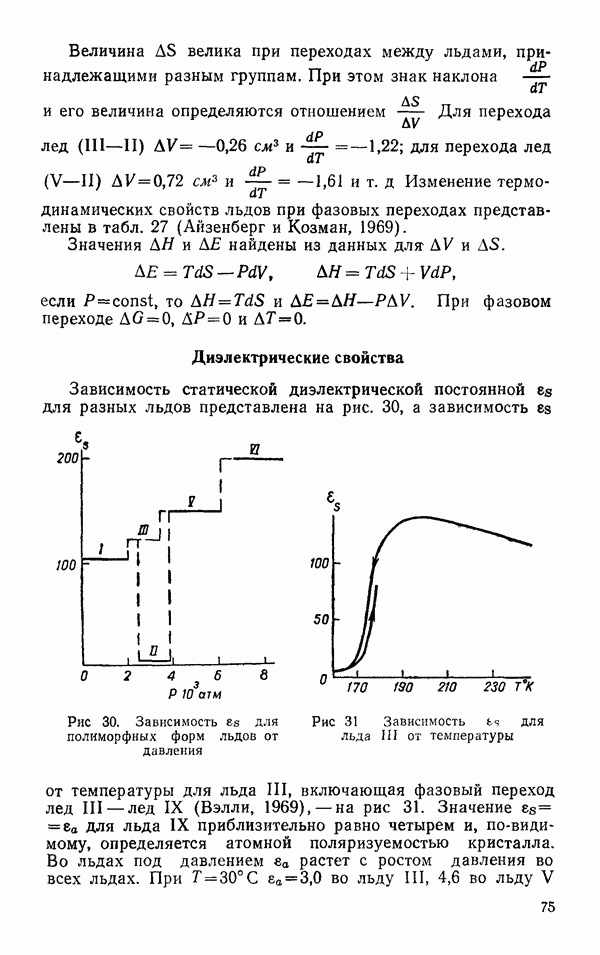
- Диэлектрические свойства
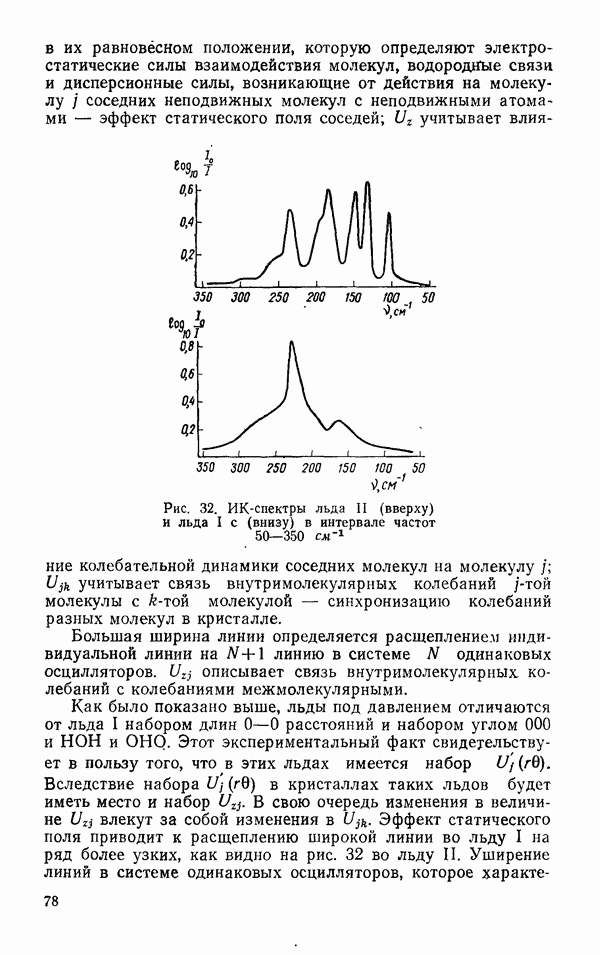
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
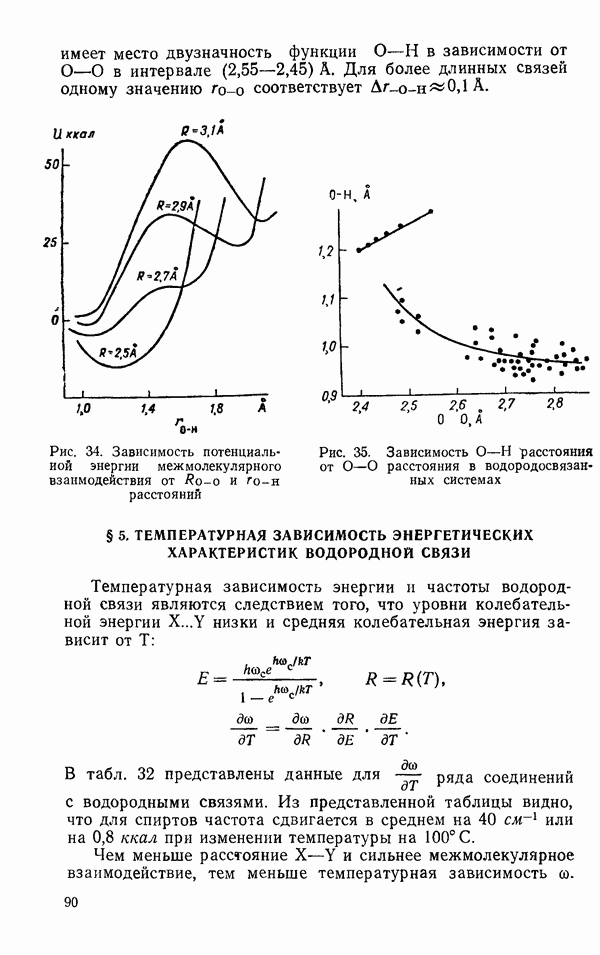
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
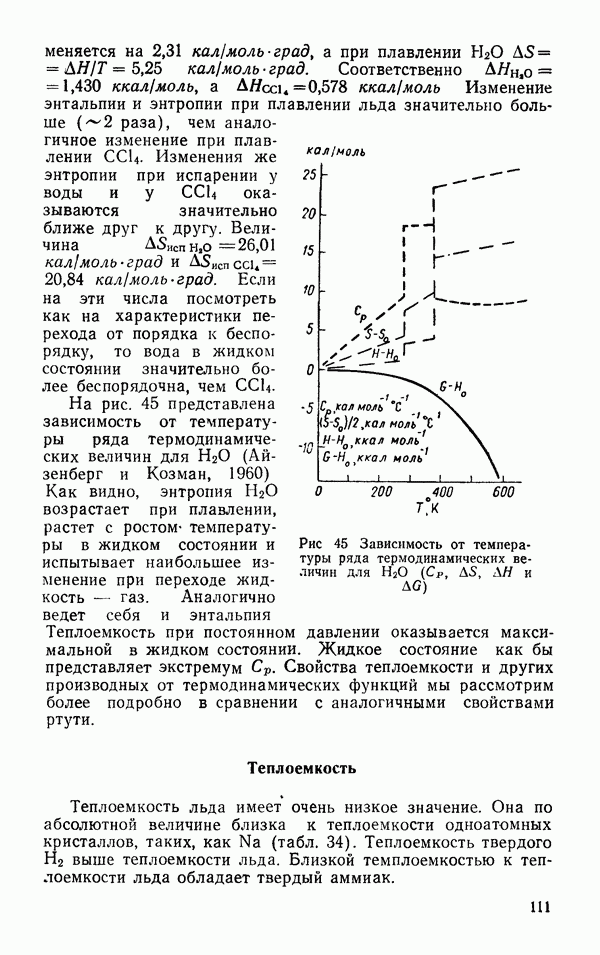
- Теплоемкость
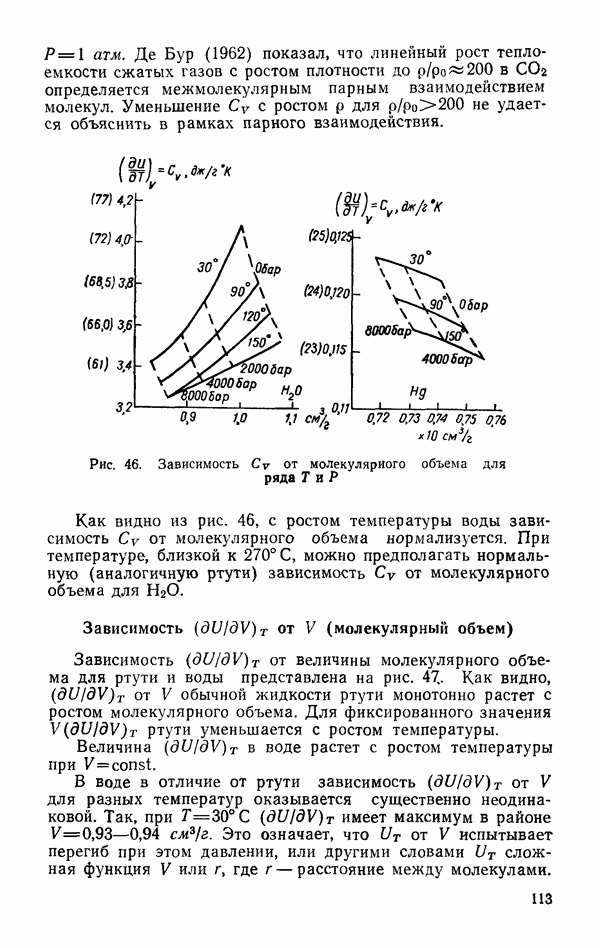
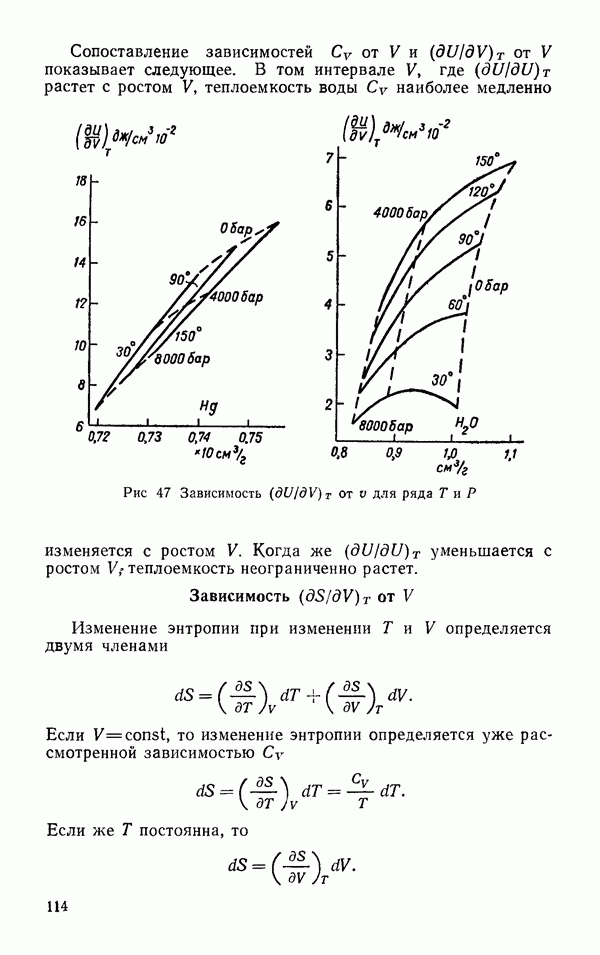
- Зависимость … от V (молекулярный объем)
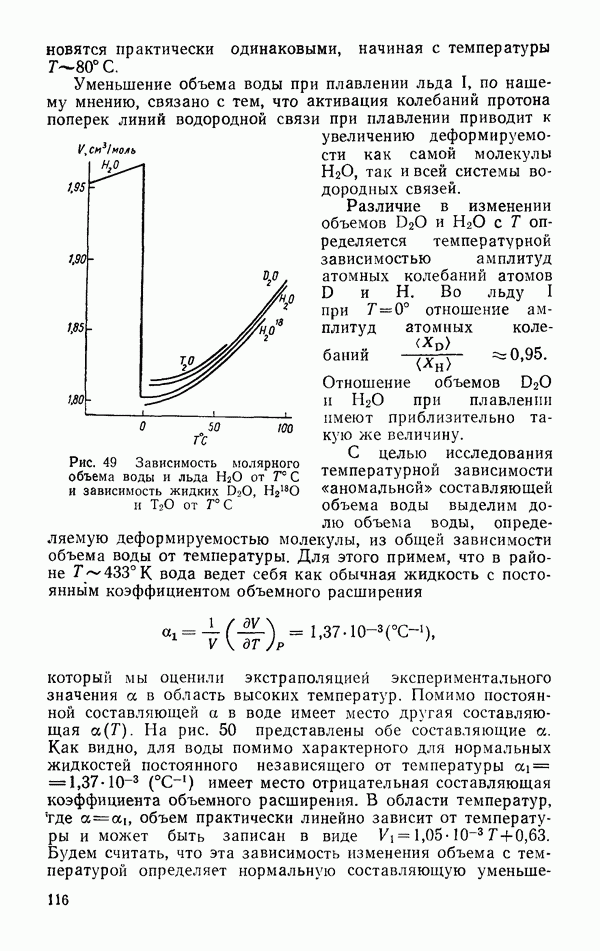
- Зависимость объема и его производных от температуры
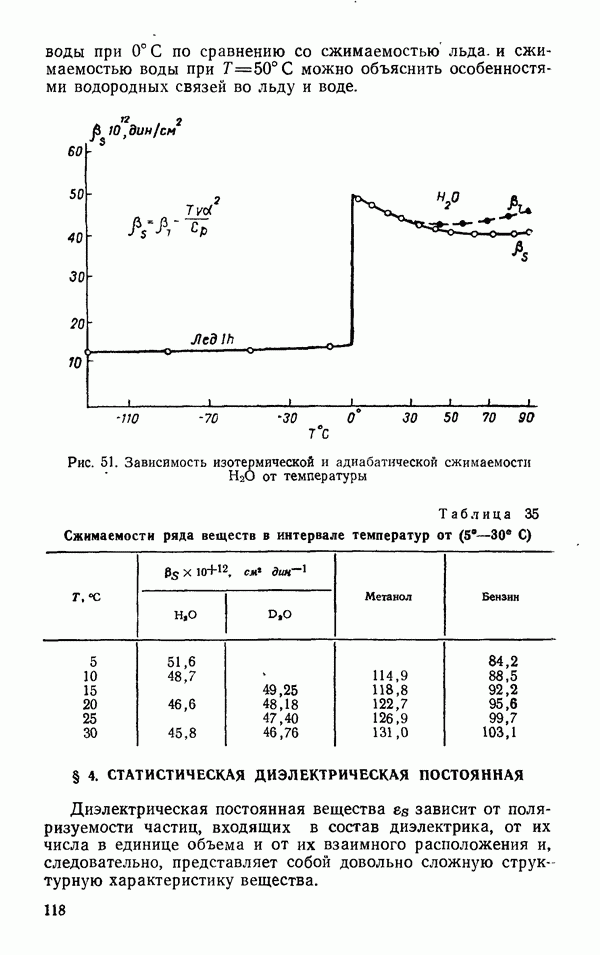
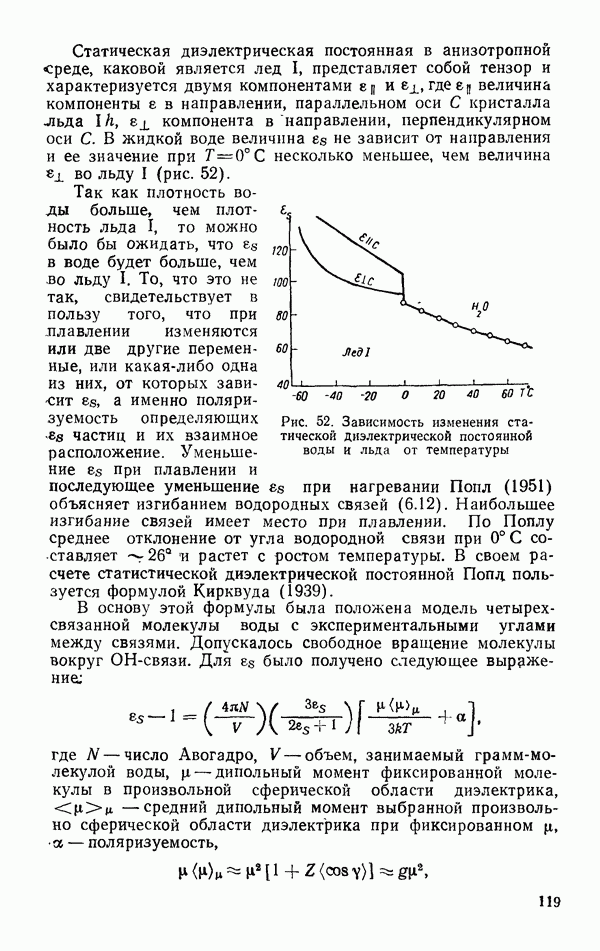
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
- Вязкость
- Теплопроводность
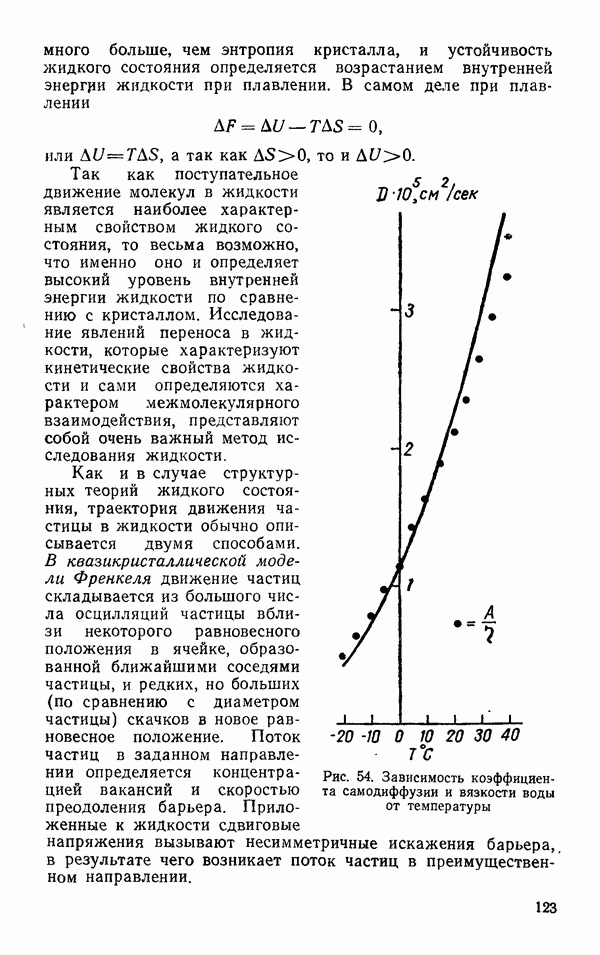
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА