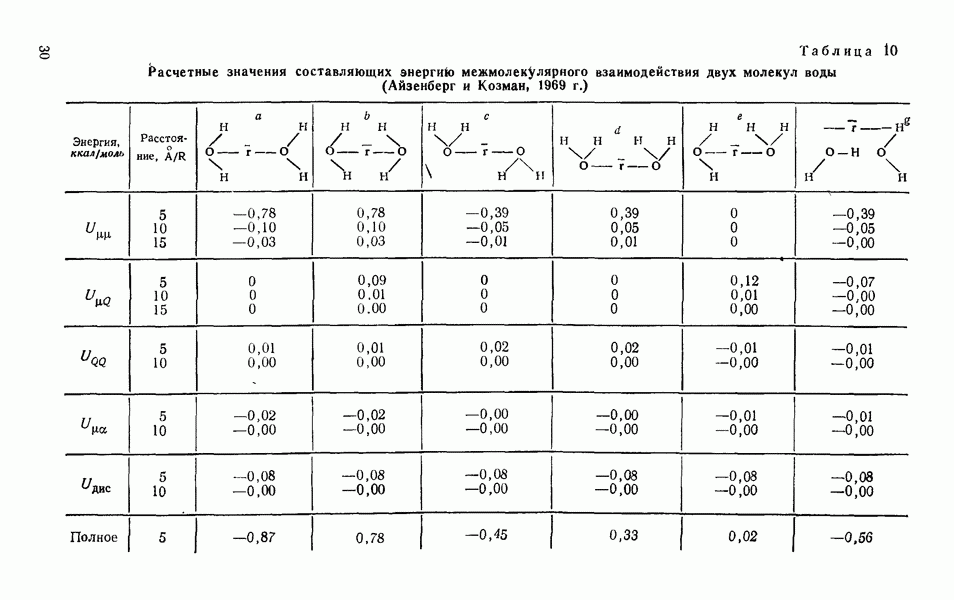
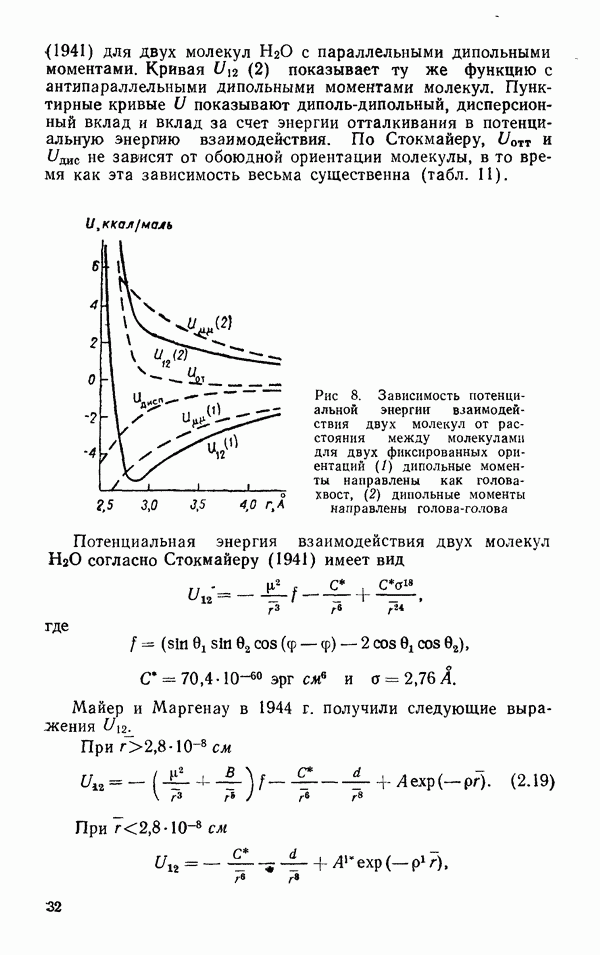
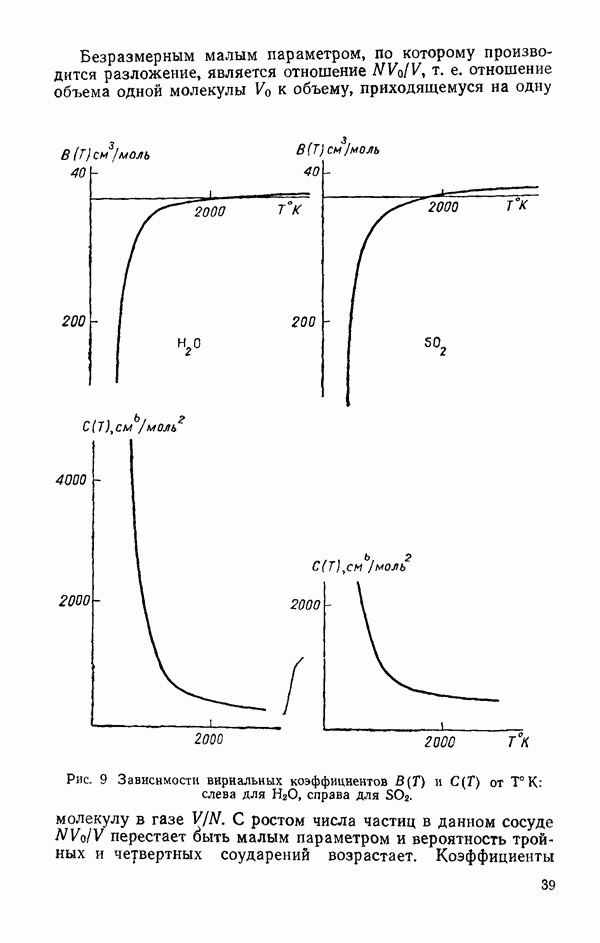
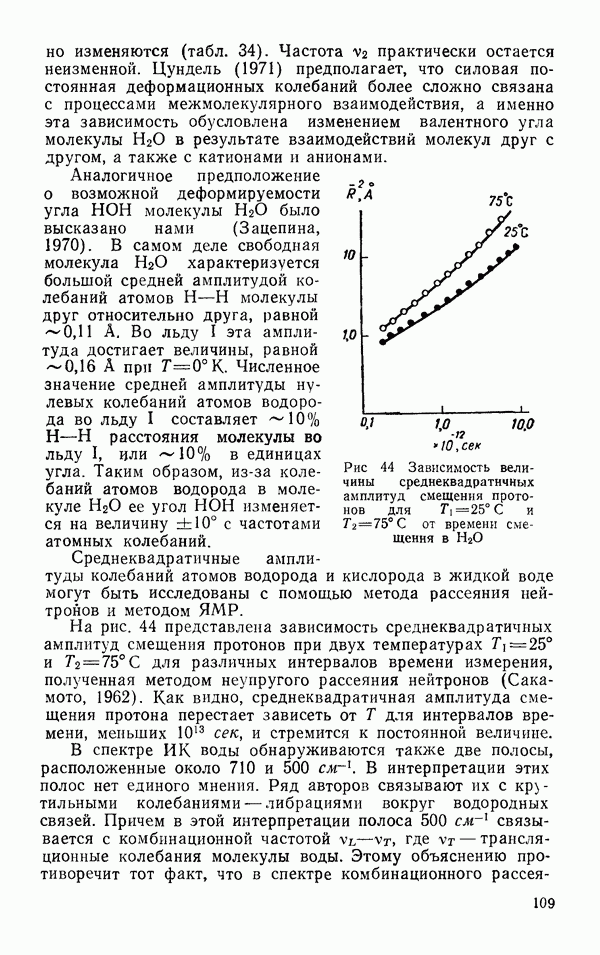
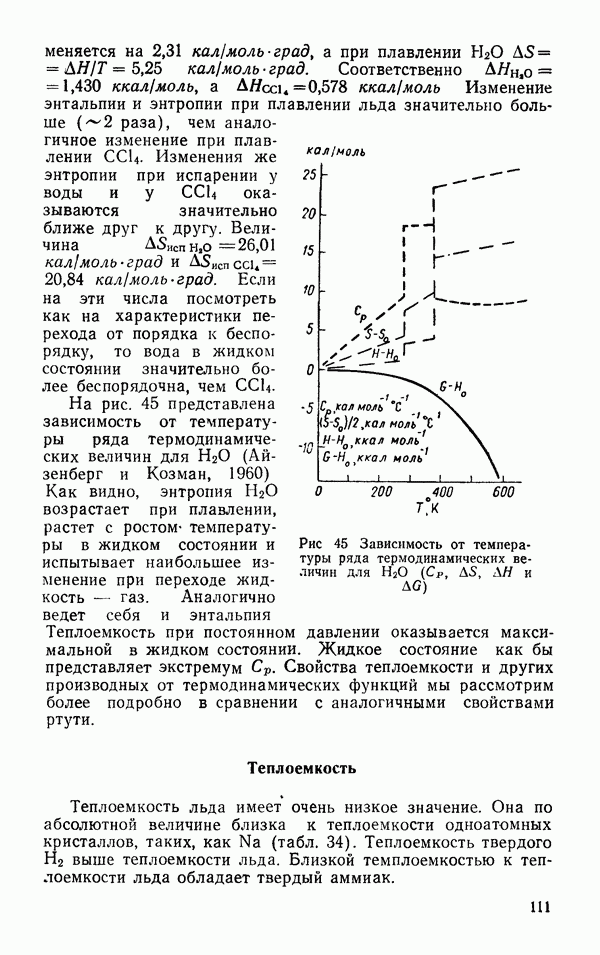
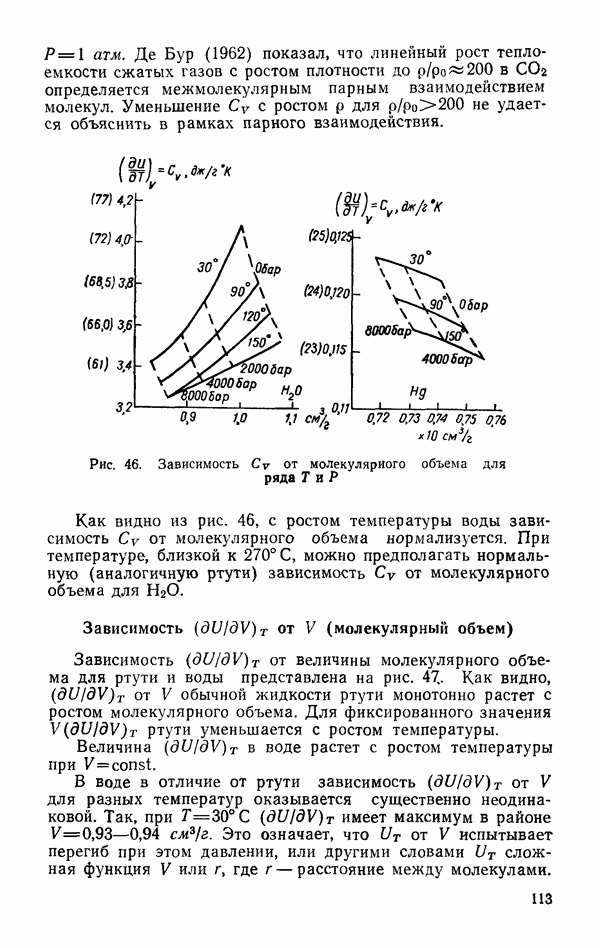
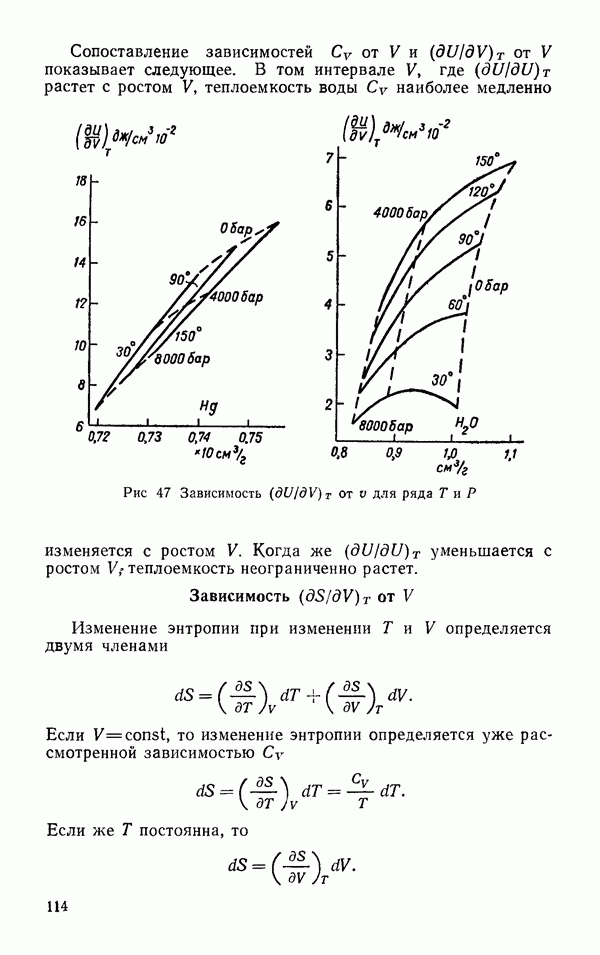
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
Нормальные, частоты колебаний молекулы зависят от массы ядер и сил, действующих между ними. Если молекула
состоит из  атомов, то она представляет собой систему, обладающую
атомов, то она представляет собой систему, обладающую  степенями свободы. Три степени свободы соответствуют перемещению молекулы, три степени свободы соответствуют вращению молекулы и
степенями свободы. Три степени свободы соответствуют перемещению молекулы, три степени свободы соответствуют вращению молекулы и  соответствуют деформации — движению атомов друг относительно друга. Молекула воды состоит из трех атомов и для нее имеет место
соответствуют деформации — движению атомов друг относительно друга. Молекула воды состоит из трех атомов и для нее имеет место  колебательные степени свободы.
колебательные степени свободы.

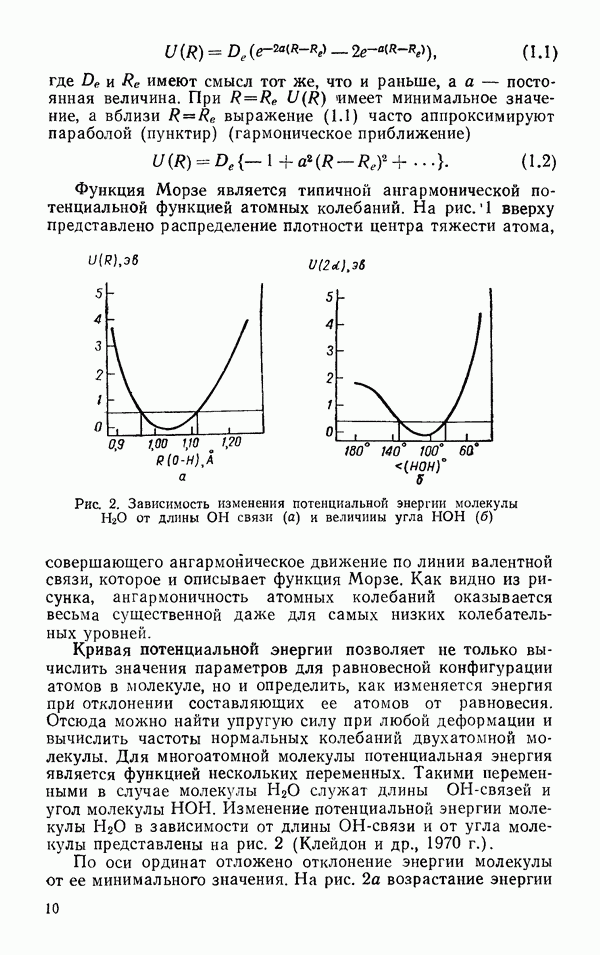
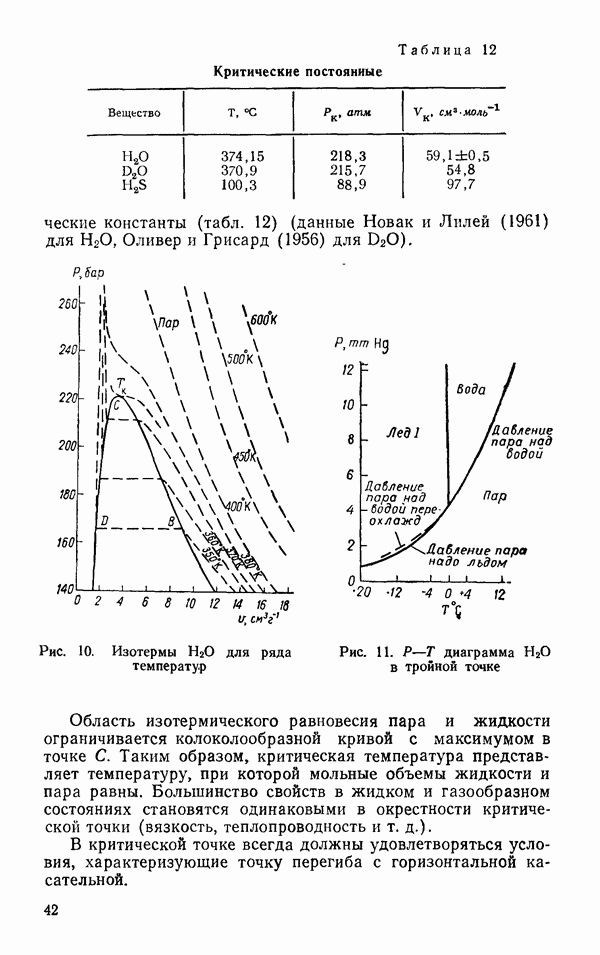
Рис. 6. Характеристические моды колебаний молекулы 
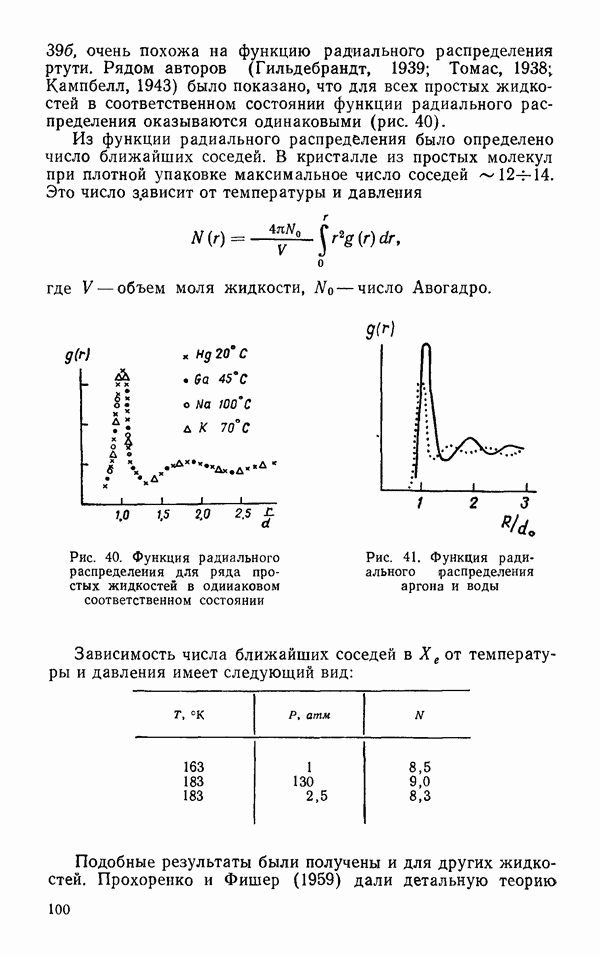
Характеристические типы колебаний можно вывести из наглядных соображений. Для этого сначала сопоставляются все элементы симметрии молекулы и подбираются такие типы колебаний, во время которых молекула сохраняет полную симметрию. Такие колебания называются полностью симметричными. В молекуле  к таким колебаниям относятся
к таким колебаниям относятся  (рис. 6). В колебании
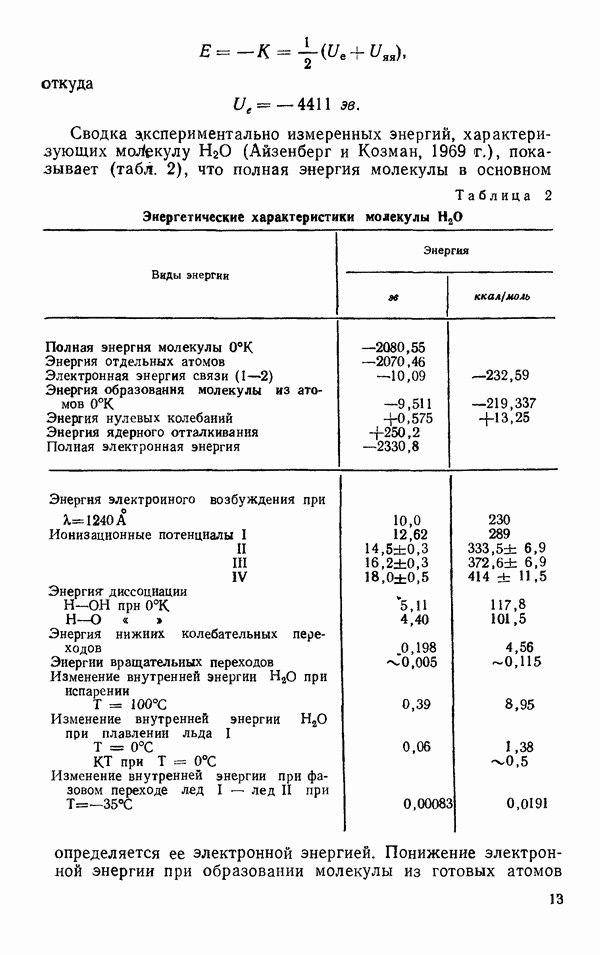
(рис. 6). В колебании  сохраняется только одна из плоскостей симметрии. В табл. 6 (Краснов и др., 1968) представлены значения наблюдаемых колебательных частот для ряда молекул изотопов
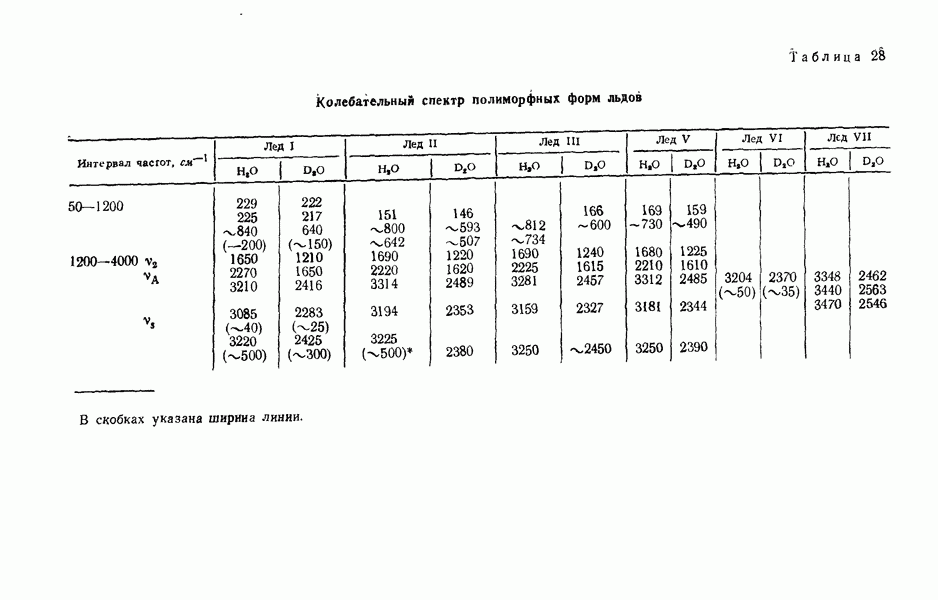
сохраняется только одна из плоскостей симметрии. В табл. 6 (Краснов и др., 1968) представлены значения наблюдаемых колебательных частот для ряда молекул изотопов  и молекул
и молекул  мологического ряда в их основном состоянии. Как видно из представленной таблицы, молекула
мологического ряда в их основном состоянии. Как видно из представленной таблицы, молекула  имеет самые высокие частоты
имеет самые высокие частоты
Таблица 6 Частоты нормальных колебаний свободных молекул в основном состоянии

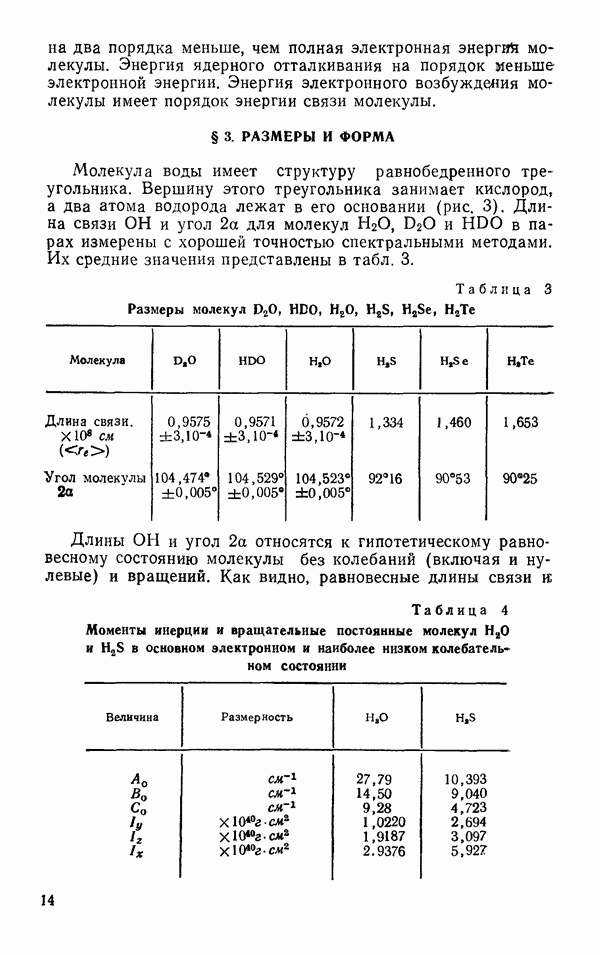
характеристических колебаний среди гомологов. Характеристические частоты колебаний молекул  в возбужденных состояниях представлены в табл. 7 (Айзенберг и Козман, 1969).
в возбужденных состояниях представлены в табл. 7 (Айзенберг и Козман, 1969).
Таблица 7 Наблюдаемые колебательные уровни свободных молекул

При колебательном возбуждении квантовые числа  характеризующие
характеризующие  изменяются на целое число единиц. Так, переход от основного состояния молекулы к состоянию, в котором возбуждено только одно нормальное колебание
изменяются на целое число единиц. Так, переход от основного состояния молекулы к состоянию, в котором возбуждено только одно нормальное колебание  описывается следующими квантовыми числами
описывается следующими квантовыми числами  При этом поглощается энергия
При этом поглощается энергия  где
где 
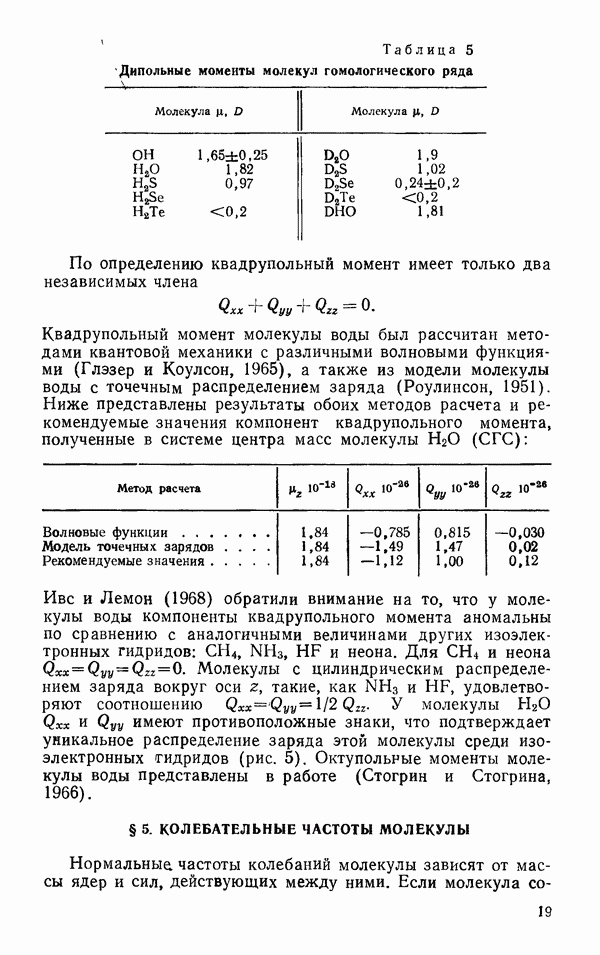
Частоты колебательных переходов во втором приближении (с учетом ангармоничности) описывает сравнительно простое выражение, включающее девять постоянных

где  энергия возбужденного состояния,
энергия возбужденного состояния,  гармоническая частота, которая соответствует полностью гармоническому колебанию молекулы,
гармоническая частота, которая соответствует полностью гармоническому колебанию молекулы,  константы ангармоничности. Эти постоянные представлены в табл. 8.
константы ангармоничности. Эти постоянные представлены в табл. 8.
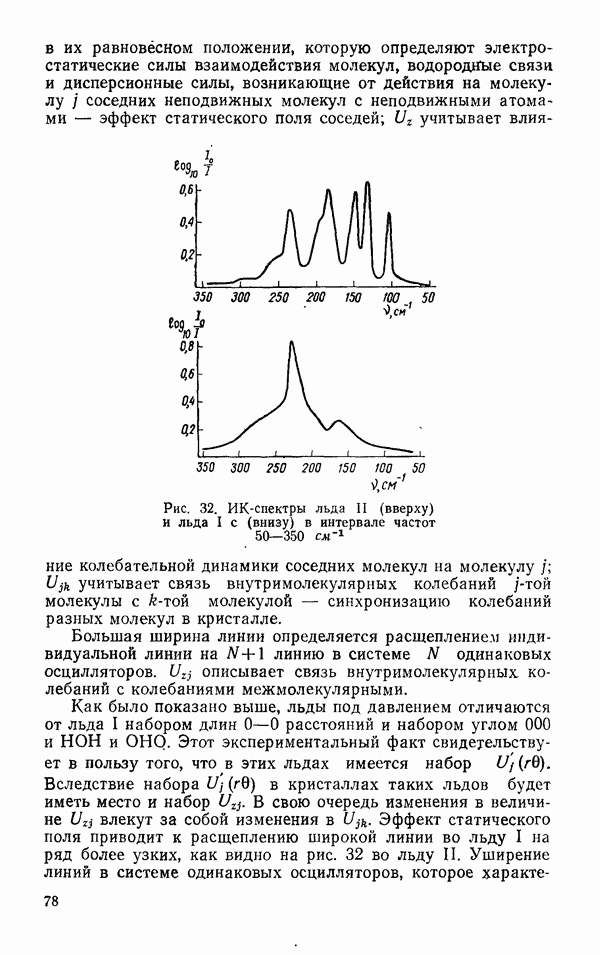
То, что константы ангармоничности отрицательны, свидетельствует о том, что колебательные уровни реальной молекулы расположены более плотно, чем уровни в гипотетической молекуле с гармоническими колебаниями.
Таблица 8 Значение гармонических частот и констант ангармоничности для молекулы воды

Пользуясь формулой (1.5) для  можно определить энергию нулевых колебаний молекулы
можно определить энергию нулевых колебаний молекулы

Для молекулы  она составляет
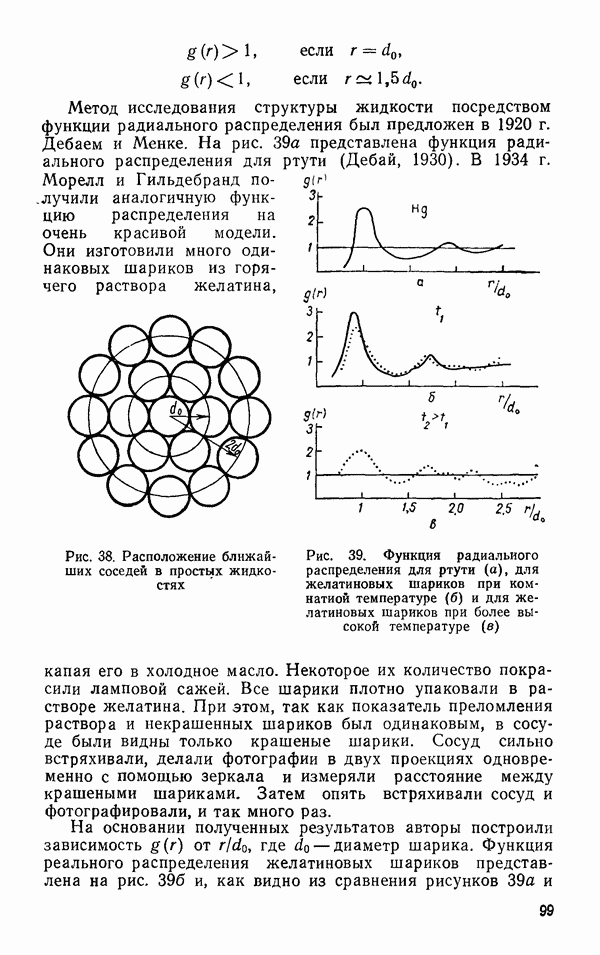
она составляет  или 13,25 ккал/моль. Для
или 13,25 ккал/моль. Для 
В результате возбуждения деформационных колебаний изменяется потенциальная энергия молекулы. В гармоничном приближении зависимость  от изменения длины первой
от изменения длины первой  связи
связи  длины второй
длины второй  связи
связи  и угла
и угла  имеет вид (Айзенберг и Козман, 1969 г.)
имеет вид (Айзенберг и Козман, 1969 г.)

где  равновесное расстояние
равновесное расстояние  (все
(все  измерены в см;
измерены в см;  — в рад; силовые постоянные К выражены в
— в рад; силовые постоянные К выражены в 
Из анализа соотношения для  ясно следующее:
ясно следующее:
1. Отрицательный знак  показывает, что если длина одной связи возросла, то увеличение второй связи энергетически выгодно.
показывает, что если длина одной связи возросла, то увеличение второй связи энергетически выгодно.
2. Увеличение угла энергетически выгодно при уменьшении длин связи, что ясно из анализа последнего члена.
3. Большая энергия требуется на увеличение длин связей, чем на увеличение угла связи (о чем свидетельствуют значения 
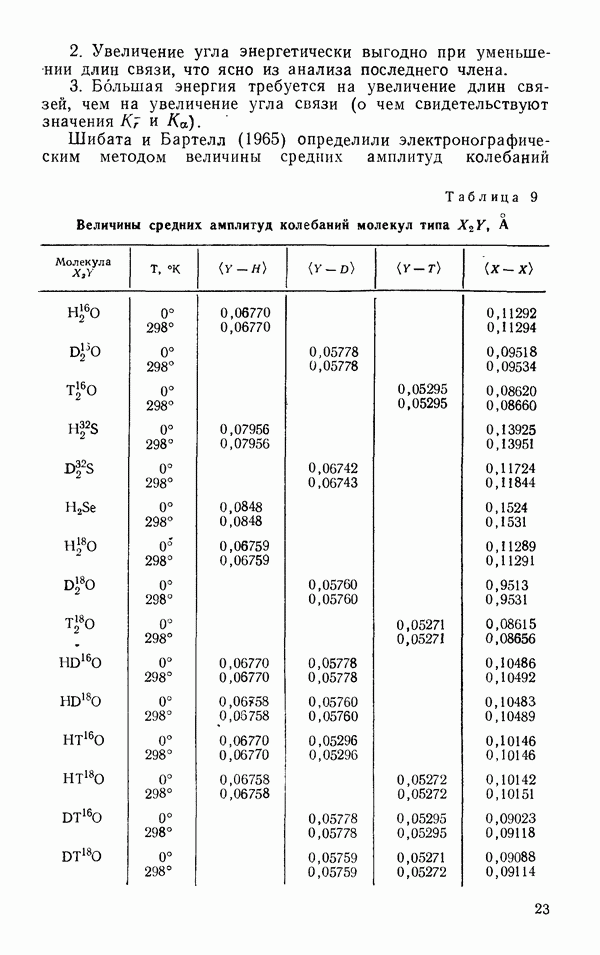
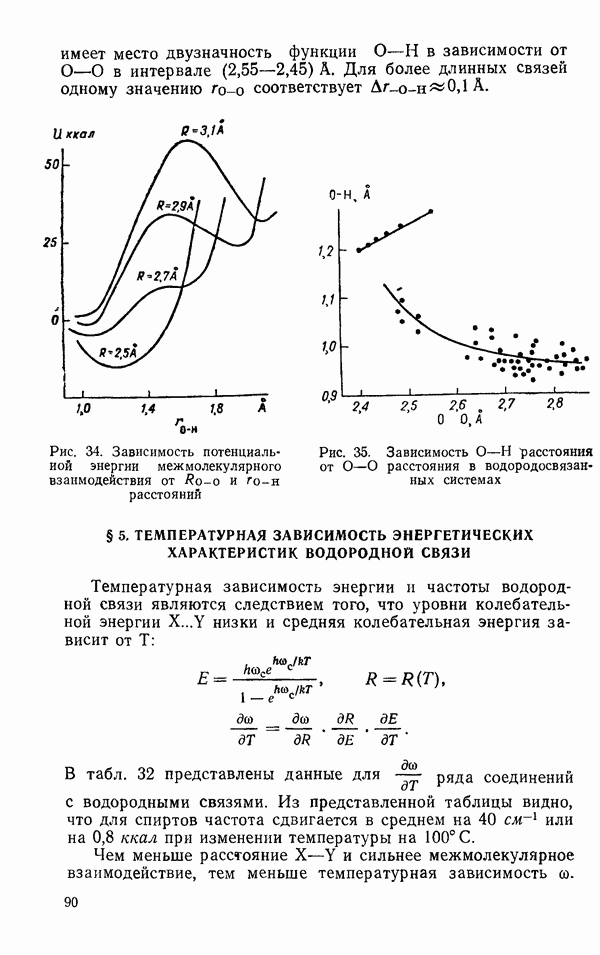
Шибата и Бартелл (1965) определили электронографическим методом величины средних амплитуд колебаний
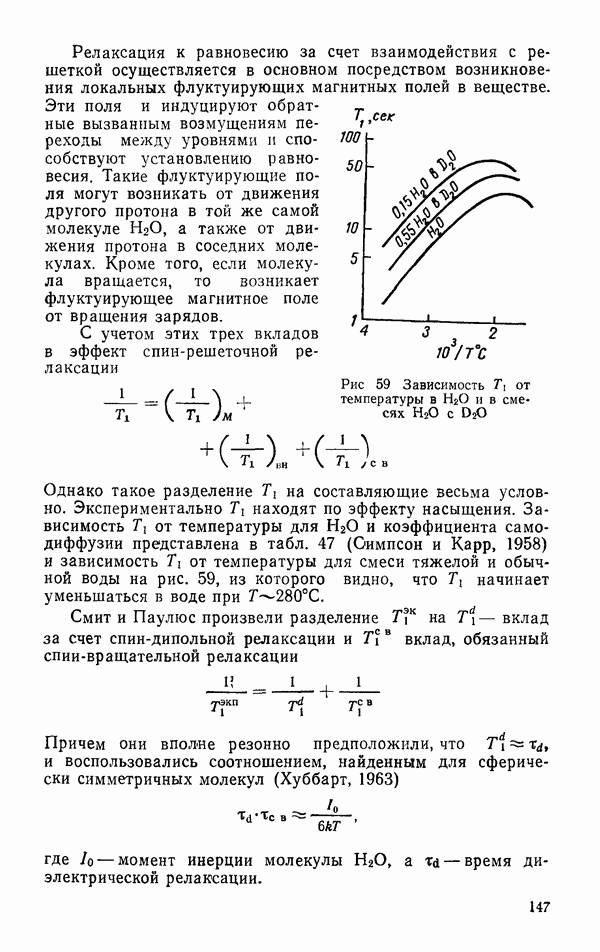
Таблица 9 (см. скан) Величины средних амплитуд колебаний молекул типа 
связанных пар атомов в молекулах  Для пары
Для пары  они получили значение 0,0666 А, а для пары
они получили значение 0,0666 А, а для пары  значение 0,0564 А.
значение 0,0564 А.
Молекула воды также была объектом расчетов на основе спектроскопических данных с учетом ангармоничности  Сивин, 1971). Как видно из табл. 9, средние амплитуды колебаний как
Сивин, 1971). Как видно из табл. 9, средние амплитуды колебаний как  так и
так и  для молекулы типа
для молекулы типа  практически не зависят от температуры, т. е. они нацело определяются нулевыми колебаниями. Амплитуды колебаний несвязанных пар атомов
практически не зависят от температуры, т. е. они нацело определяются нулевыми колебаниями. Амплитуды колебаний несвязанных пар атомов  значительно больше, чем амплитуды колебаний связанных пар
значительно больше, чем амплитуды колебаний связанных пар  Для гомологического ряда молекул амплитуды колебаний растут с ростом массы тяжелого атома и уменьшаются с ростом массы легкого атома. У молекулы
Для гомологического ряда молекул амплитуды колебаний растут с ростом массы тяжелого атома и уменьшаются с ростом массы легкого атома. У молекулы  самые маленькие значения средних амплитуд колебаний атомов среди молекул гомологического ряда, но тем не менее они велики по абсолютной величине
самые маленькие значения средних амплитуд колебаний атомов среди молекул гомологического ряда, но тем не менее они велики по абсолютной величине  от длины связи).
от длины связи).
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Глава 1. МОЛЕКУЛА H2O
- Энергия образования молекулы
- Полная энергия молекулы
- § 3. РАЗМЕРЫ И ФОРМА
- § 4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА
- § 5. КОЛЕБАТЕЛЬНЫЕ ЧАСТОТЫ МОЛЕКУЛЫ
- ЗАКЛЮЧЕНИЕ
- Глава 2. СВОЙСТВА ПАРА
- Исследования межмолекулярных сил отталкивания
- § 2. УРАВНЕНИЯ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА
- Вириальная форма уравнения состояния
- Эмпирическое уравнение состояния
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Термодинамические функции
- Зависимость термодинамических функций от P и T
- § 4. ВЯЗКОСТЬ
- Глава 3. СВОЙСТВА ЛЬДОВ
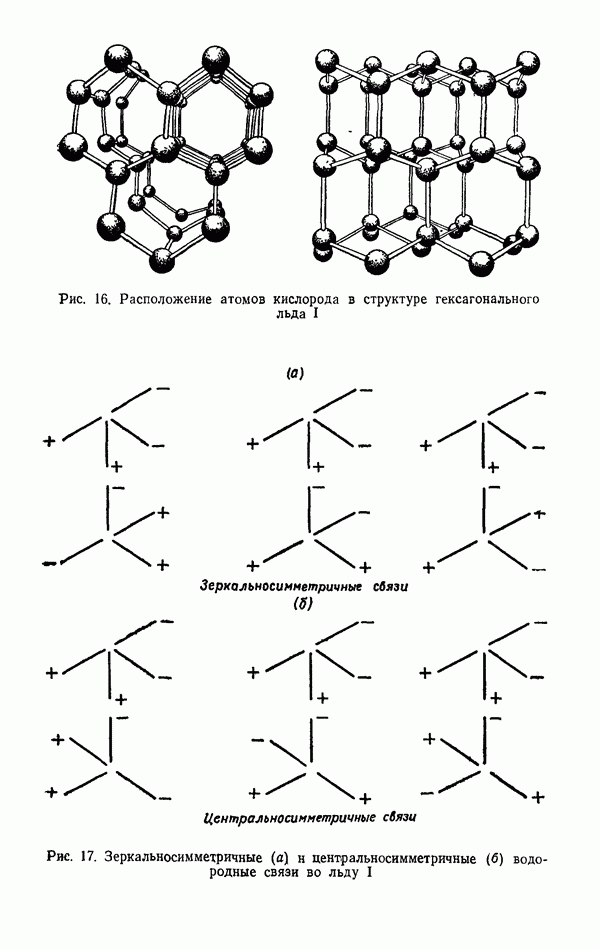
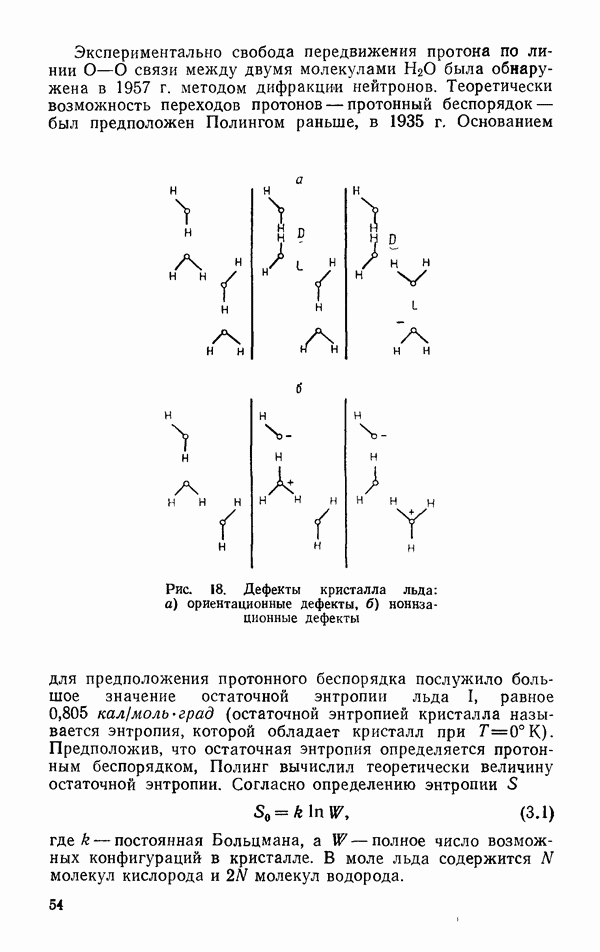
- § 1. ЛЕД
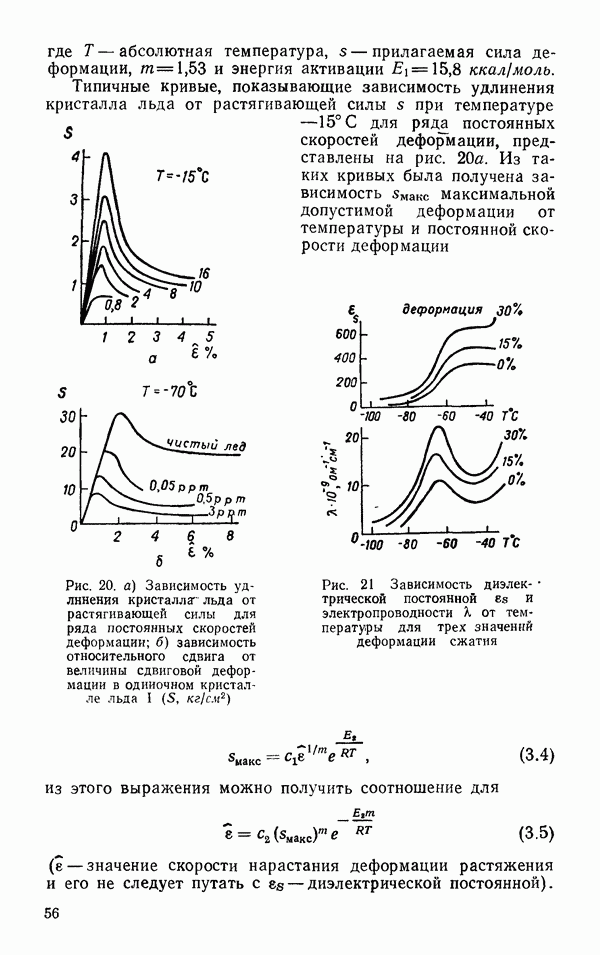
- Пластическая деформация монокристалла льда I
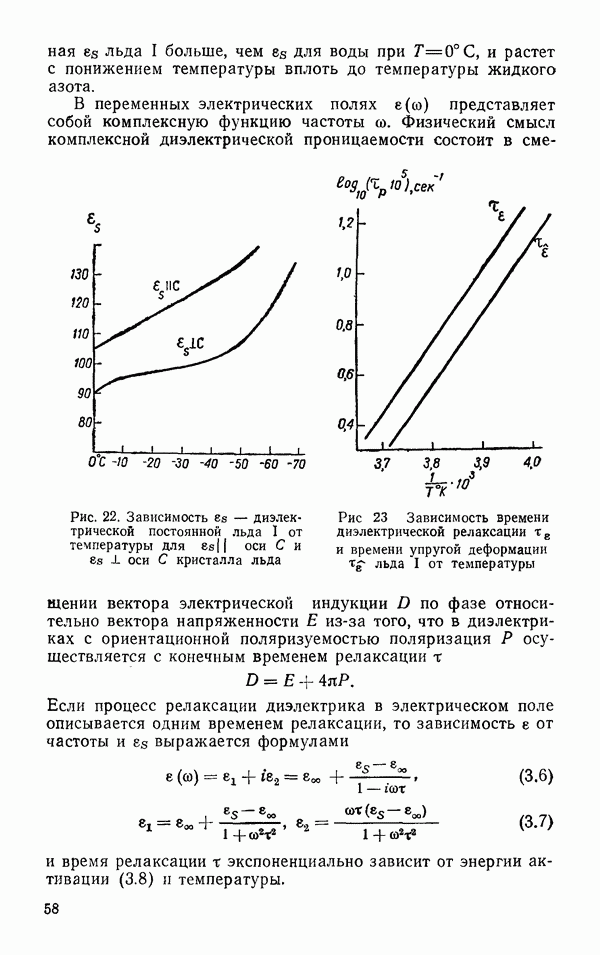
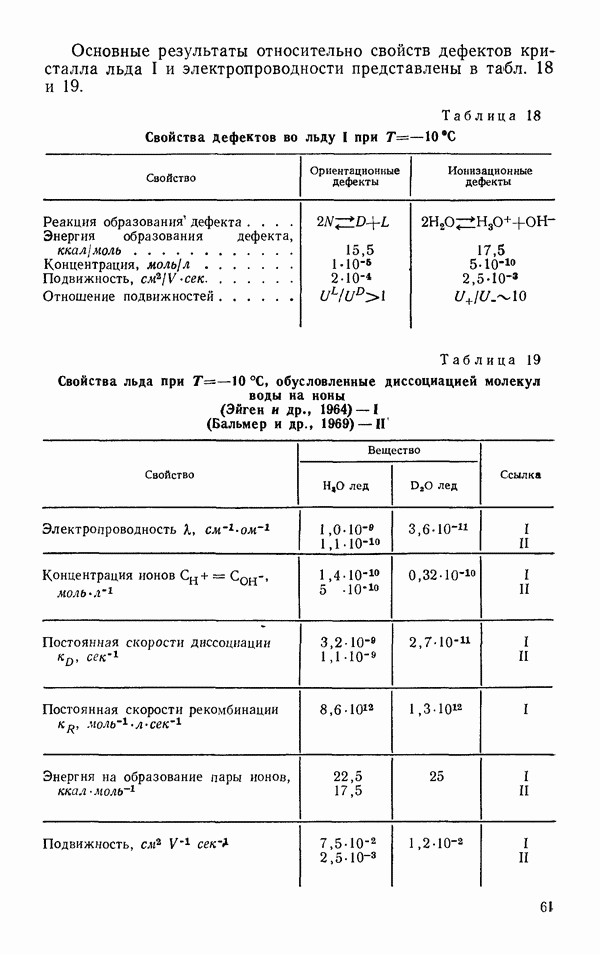
- Диэлектрические свойства льда 1
- Электропроводность льда
- Самодиффузия
- Спектральные свойства льда I
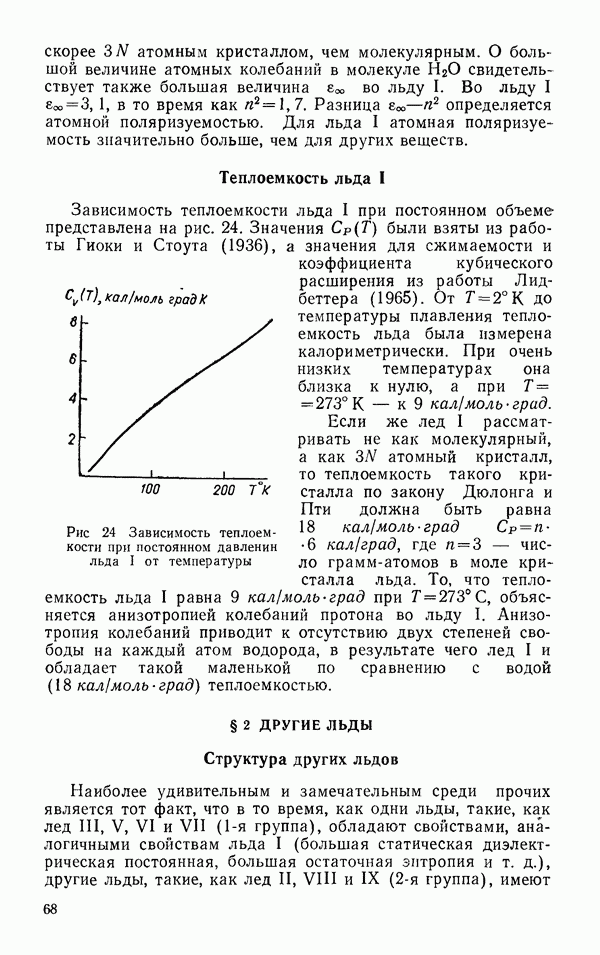
- Теплоемкость льда I
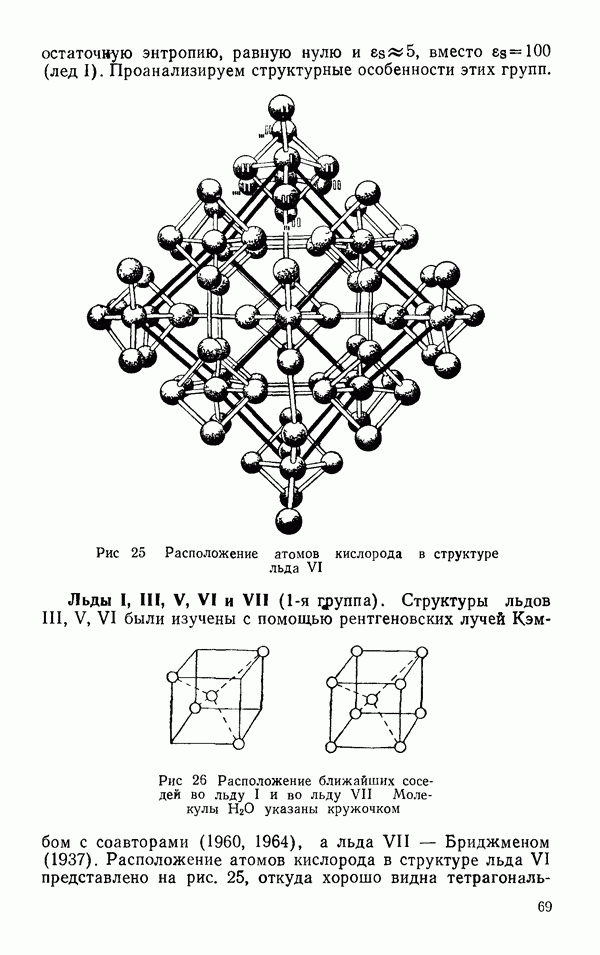
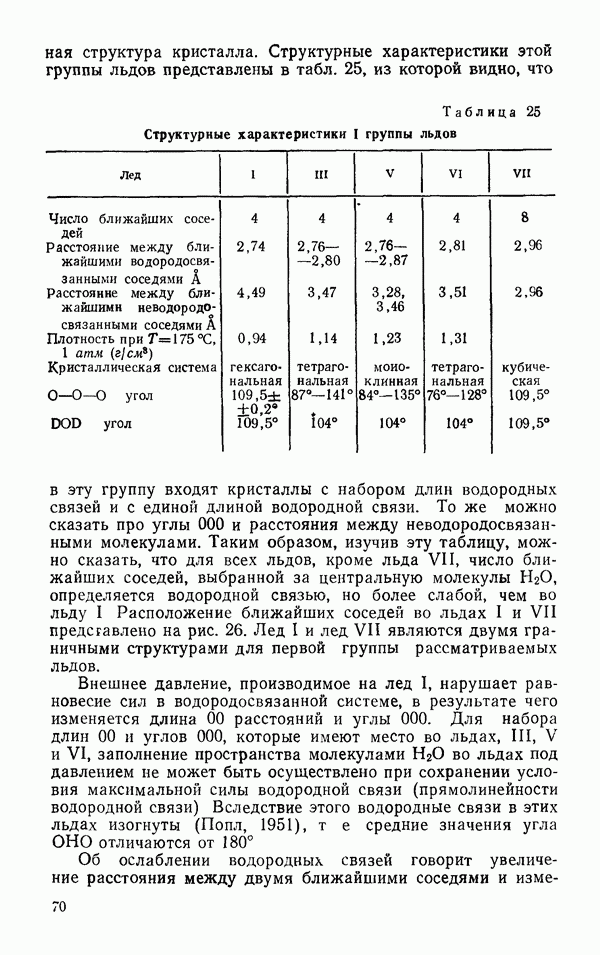
- § 2 ДРУГИЕ ЛЬДЫ
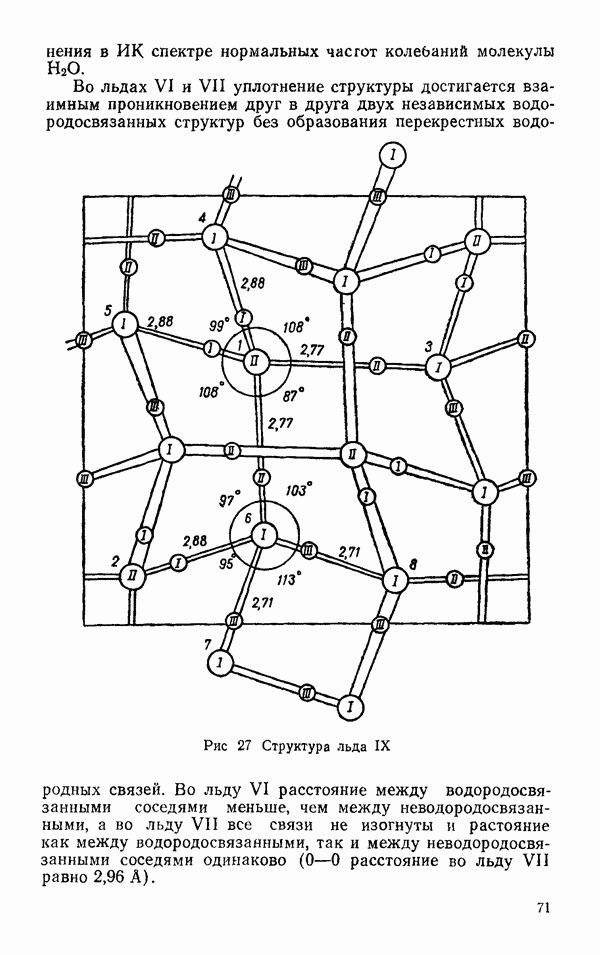
- Термодинамические свойства льдов
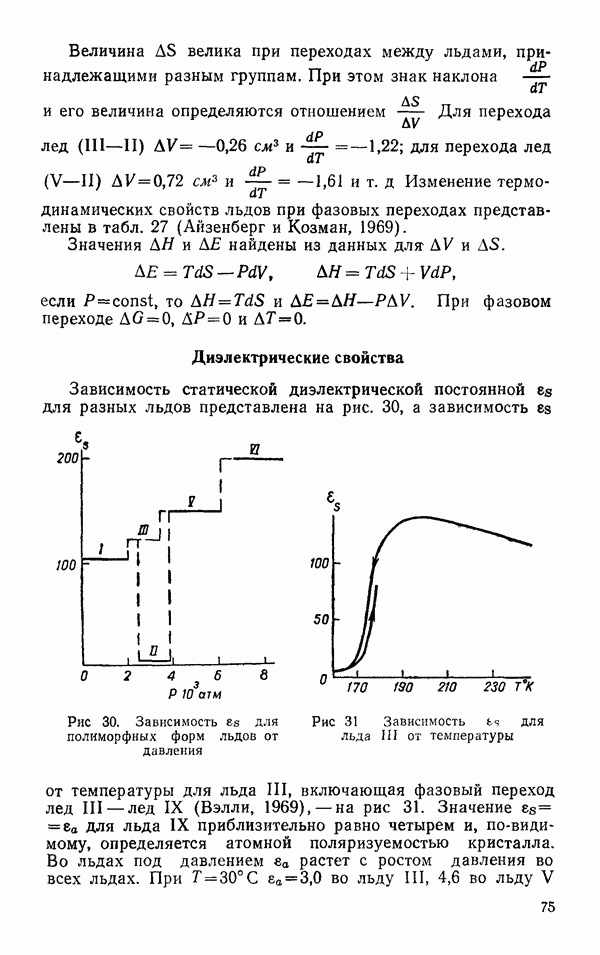
- Диэлектрические свойства
- Спектральные свойства
- ЗАКЛЮЧЕНИЕ
- Глава 4. ВОДОРОДНАЯ СВЯЗЬ
- § 2. СВОЙСТВА АТОМОВ, ОБРАЗУЮЩИХ ВОДОРОДНУЮ СВЯЗЬ
- § 3. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭНЕРГИИ
- § 4. ПОЛУЭМПИРИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
- § 5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ВОДОРОДНОЙ СВЯЗИ
- ЗАКЛЮЧЕНИЕ
- Глава 5. ЖИДКОЕ СОСТОЯНИЕ
- § 1. РАЗЛИЧНЫЕ ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ ЖИДКОГО СОСТОЯНИЯ
- § 2. СТРУКТУРА ЖИДКОСТИ
- § 3. ПЛАВЛЕНИЕ
- Глава 6. СВОЙСТВА ЖИДКОЙ ВОДЫ
- § 2. СПЕКТРАЛЬНЫЕ ДАННЫЕ
- § 3. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА
- Теплоемкость
- Зависимость … от V (молекулярный объем)
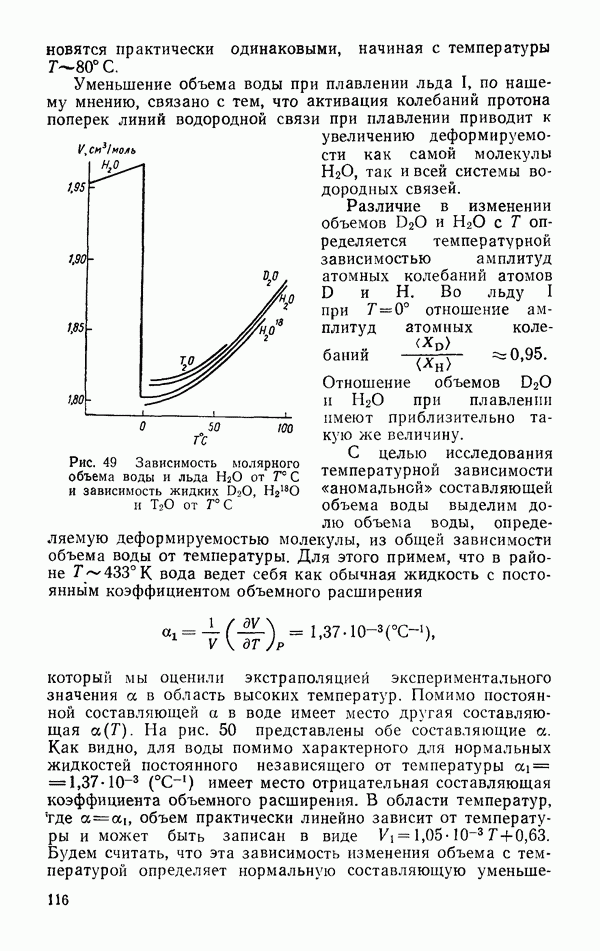
- Зависимость объема и его производных от температуры
- § 4. СТАТИСТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- § 5. ЯВЛЕНИЕ ПЕРЕНОСА
- Вязкость
- Теплопроводность
- Самодиффузия
- § 6. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ МОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ
- Молекулярное рассеяние света
- Вода как самодиссоциирующая среда
- § 7. ВОДА D2O
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА