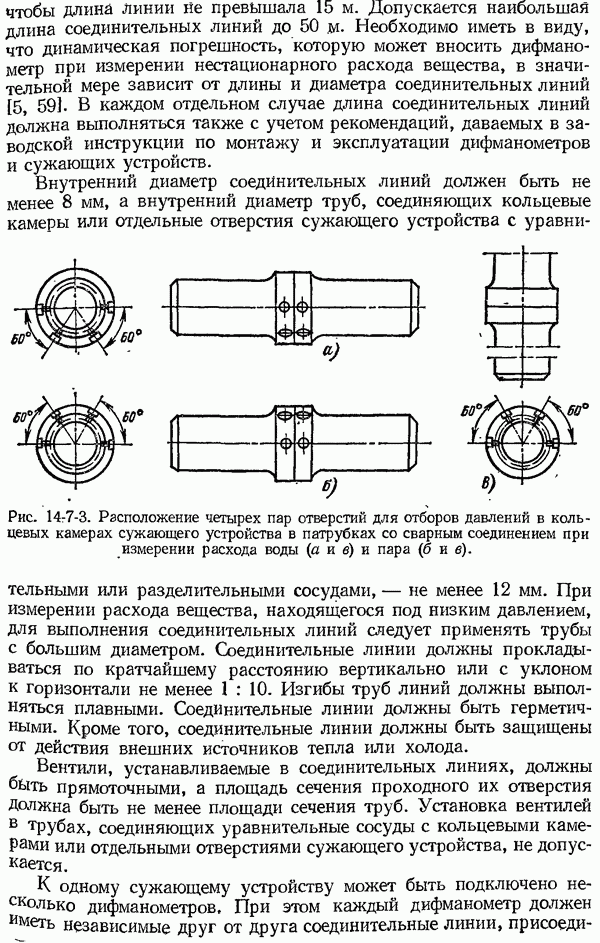
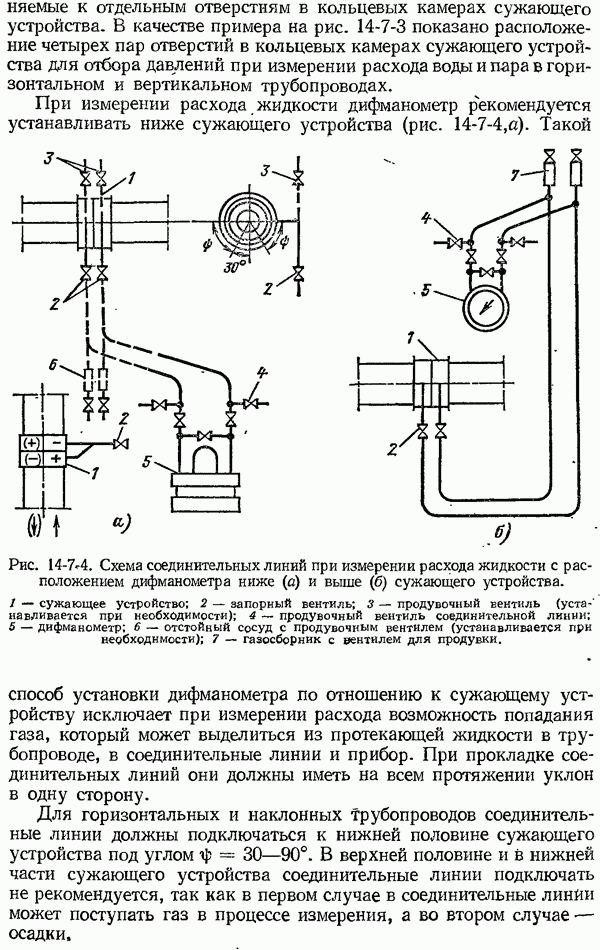
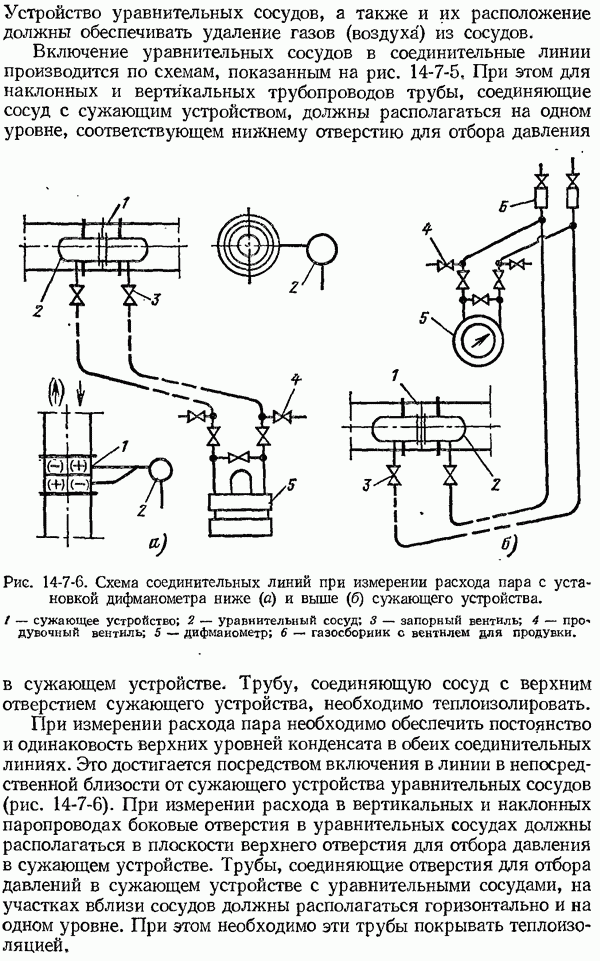
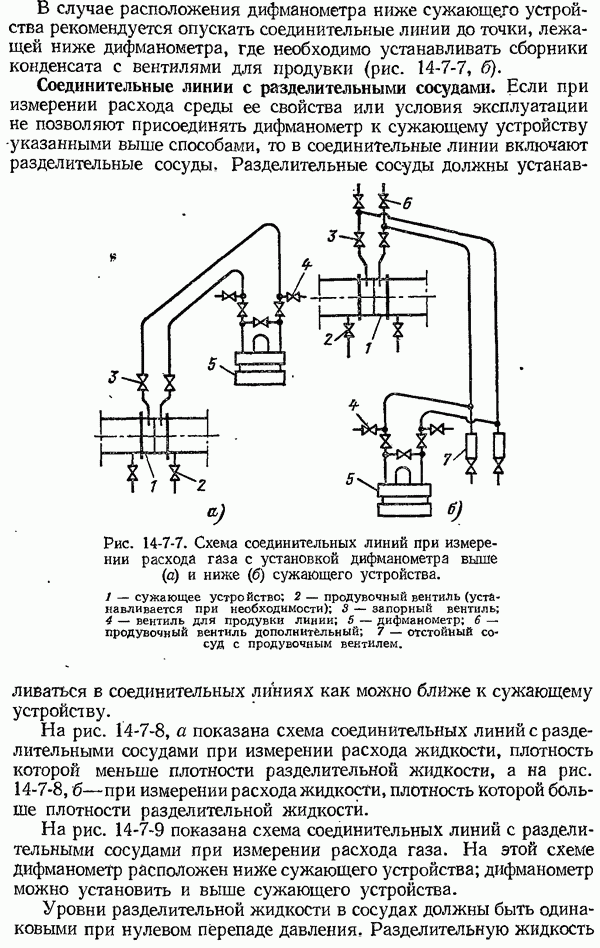
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
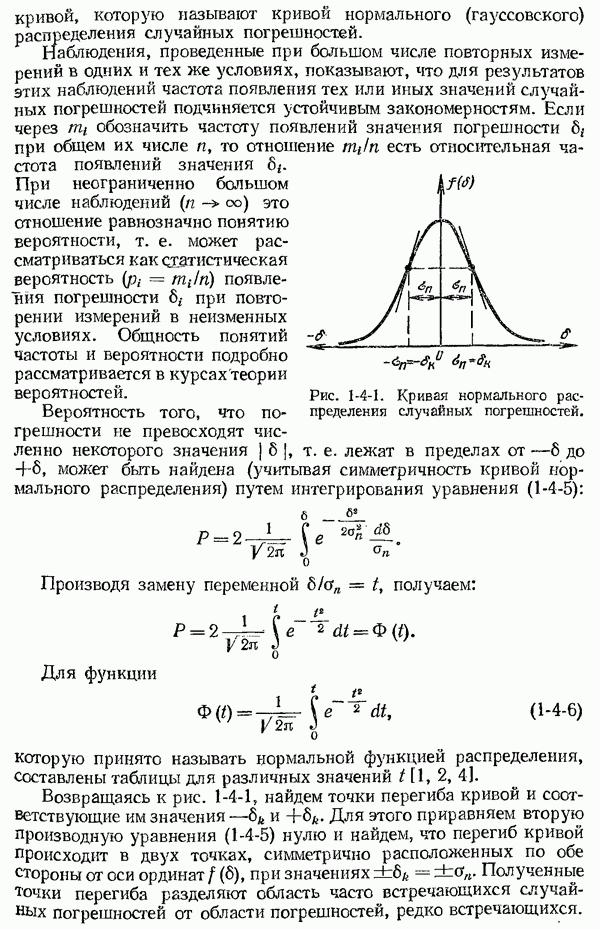
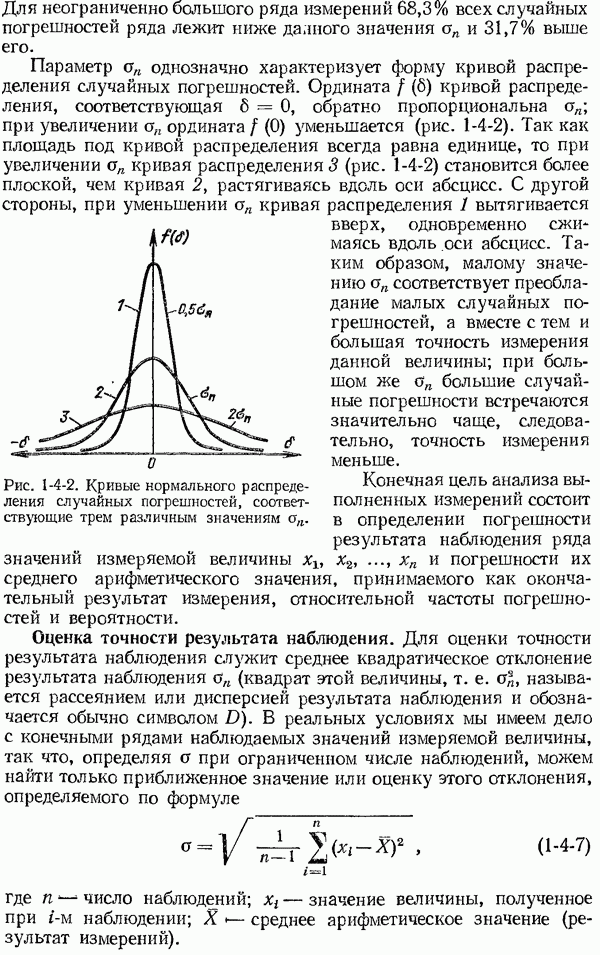
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
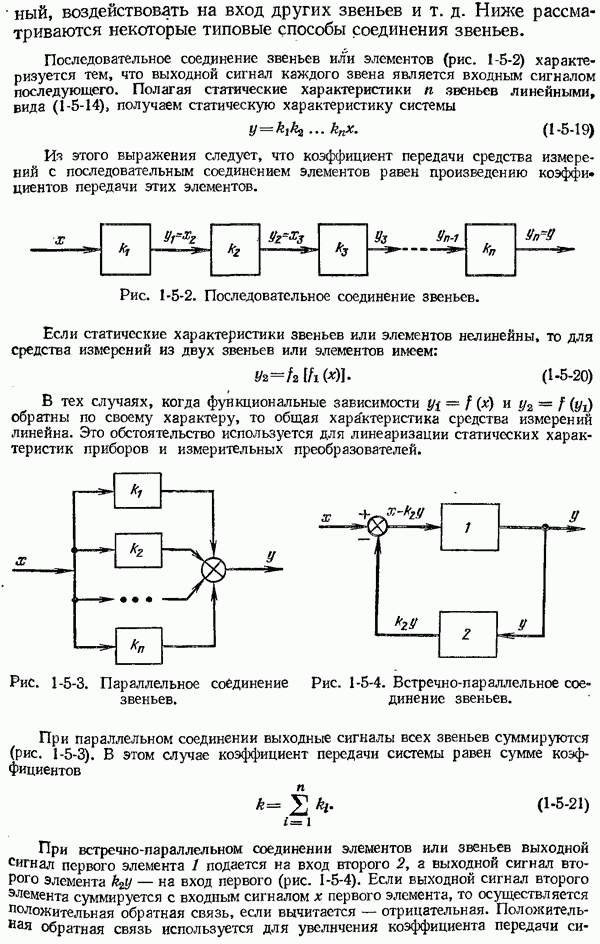
Средства измерений, а во многих случаях и их преобразовательные элементы выполняются так, что происходящие в них преобразования сигналов обладают свойством необратимости или направленности. Это значит, что изменение сигнала на входе средства измерения (или его элемента) приводит к соответствующему изменению сигнала на выходе, но обратное влияние выходного сигнала на входной отсутствует. Сигнал, вызывающий изменение другой величины, называют входной величиной (сигналом), а сигнал на выходе — выходной величиной (сигналом). Статической характеристикой средства измерений (измерительного прибора или преобразователя) называют функциональную зависимость между выходной величиной у (перемещением указателя прибора или выходным сигналом преобразователя) и входной величиной х в установившемся режиме:

Функциональную зависимость (1-5-12) называют также уравнением шкалы прибора, градуировочной характеристикой прибора или преобразователя. Статическая характеристика может быть задана аналитически, графически (рис. 1-5-1) или в виде таблицы.
В общем случае линейная или линеаризованная статическая характеристика средства измерения описывается уравнением вида

где а — постоянная, имеющая размерность  — коэффициент, имеющий размерность
— коэффициент, имеющий размерность 
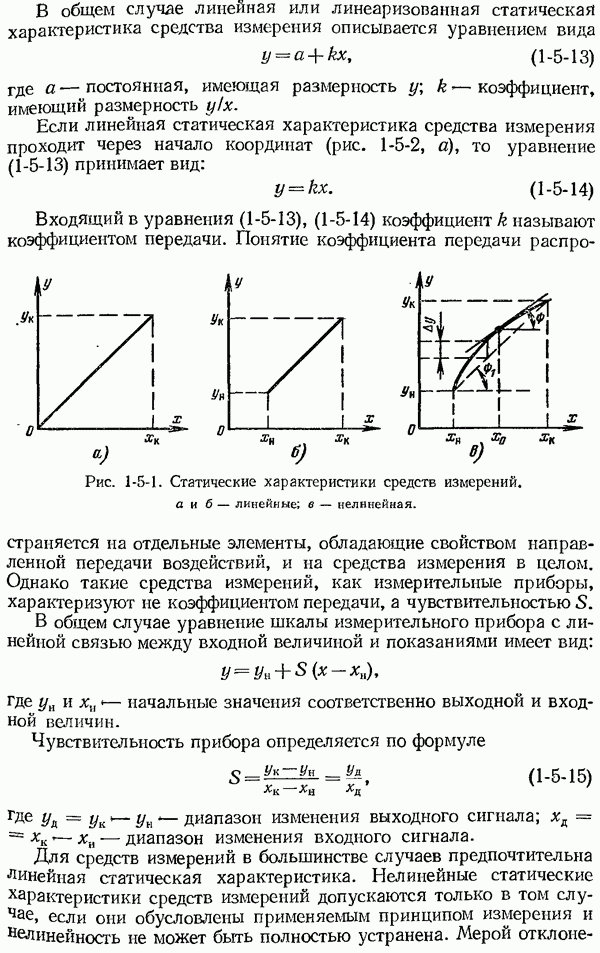
Если линейная статическая характеристика средства измерения проходит через начало координат (рис. 1-5-2, а), то уравнение (1-5-13) принимает вид:

Входящий в уравнения (1-5-13), (1-5-14) коэффициент  называют коэффициентом передачи.
называют коэффициентом передачи.

Рис. 1-5-1. Статические характеристики средств измерений. а и б - линейные; в — нелинейная.
Понятие коэффициента передачи распространяется на отдельные элементы, обладающие свойством направленной передачи воздействий, и на средства измерения в целом. Однако такие средства измерений, как измерительные приборы, характеризуют не коэффициентом передачи, а чувствительностью 
В общем случае уравнение шкалы измерительного прибора с линейной связью между входной величиной и показаниями имеет вид:

где  начальные значения соответственно выходной и входной величин.
начальные значения соответственно выходной и входной величин.
Чувствительность прибора определяется по формуле

Где  диапазон изменения выходного сигнала;
диапазон изменения выходного сигнала;  диапазон изменения входного сигнала.
диапазон изменения входного сигнала.
Для средств измерений в большинстве случаев предпочтительна линейная статическая характеристика. Нелинейные статические характеристики средств измерений допускаются только в том случае если они обусловлены применяемым принципом измерения и нелинейность не может быть полностью устранена. Мерой
отклонения нелинейной характеристики от линейной служит относительная нелинейность статической характеристики, определяемая отношением  где
где  максимальный отрезок выходной координаты между статической характеристикой и прямой, соединяющей начало
максимальный отрезок выходной координаты между статической характеристикой и прямой, соединяющей начало  и конец
и конец  нелинейной характеристики (рис. 1-5-1, в), a
нелинейной характеристики (рис. 1-5-1, в), a  - нормирующее значение (см. выше).
- нормирующее значение (см. выше).
Под чувствительностью измерительного прибора с нелинейной статической характеристикой понимают предел отношения приращения выходного сигнала А у к приращению входной величины 

Очевидно, что в случае линейной статической характеристики (рис. 1-5-1, а) чувствительность остается постоянной для любой точки шкалы. Если статическая характеристика задана в виде уравнения  то для определения чувствительности необходимо продифференцировать это уравнение по х. При нелинейной зависимости у от х чувствительность зависит от значения входного сигнала.
то для определения чувствительности необходимо продифференцировать это уравнение по х. При нелинейной зависимости у от х чувствительность зависит от значения входного сигнала.
Если относительная нелинейность статической характеристики невелика или диапазон изменения х ограничен, то можно линеаризовать характеристику, т. е. заменить реальную нелинейную зависимость у от х приближенной линейной. Линеаризацию заданной графически характеристики осуществляют методом касательной или секущей. При линеаризации касательной (рис. 1-5-1, в) коэффициент передачи (или чувствительность) определяют тангенсом угла наклона касательной в данной точке:

где  — масштабы графика
— масштабы графика 
Линеаризация секущей позволяет, например, определить среднее значение коэффициента передачи (чувствительности), равное тангенсу угла наклона прямой, соединяющей начальную и конечную точки характеристики (рис. 1-5-1, в):

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
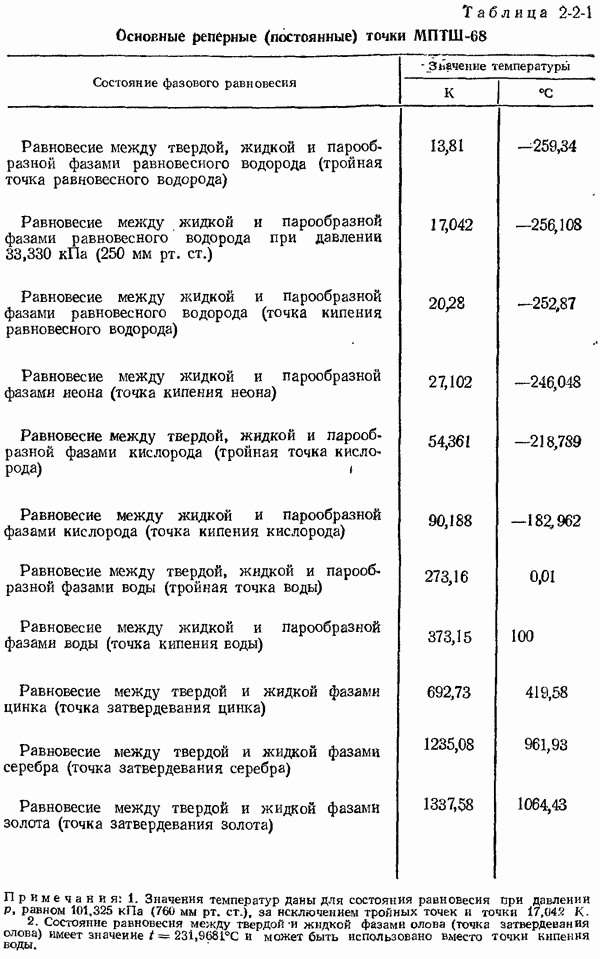
- 2-1. Основные сведения о температуре и температурных шкалах
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
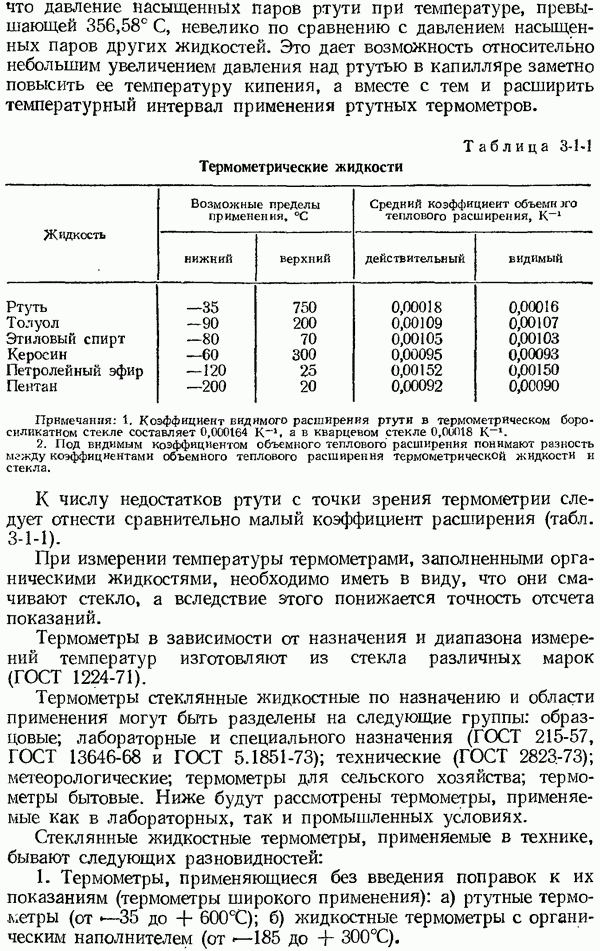
- 3-1. Термометры стеклянные жидкостные
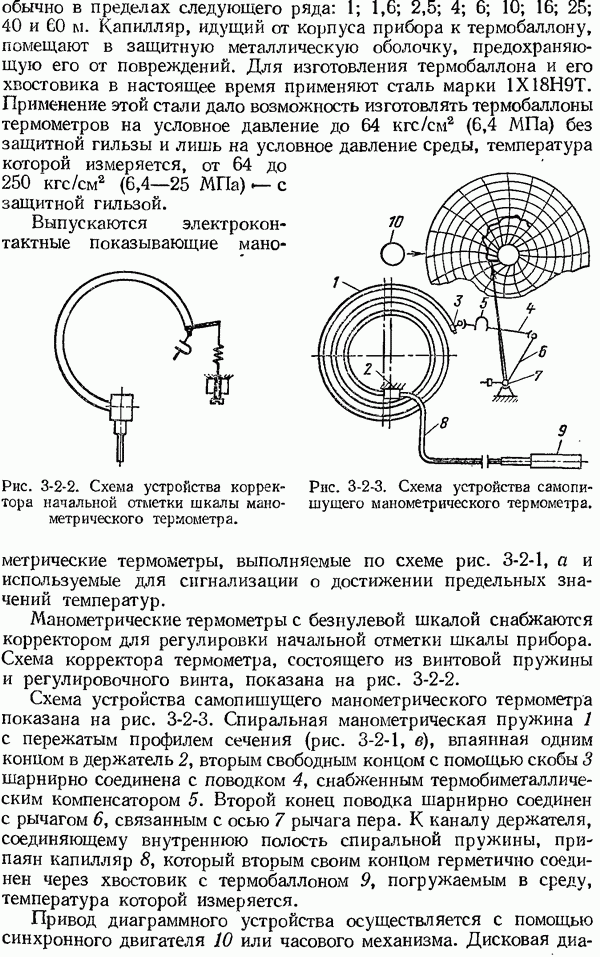
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
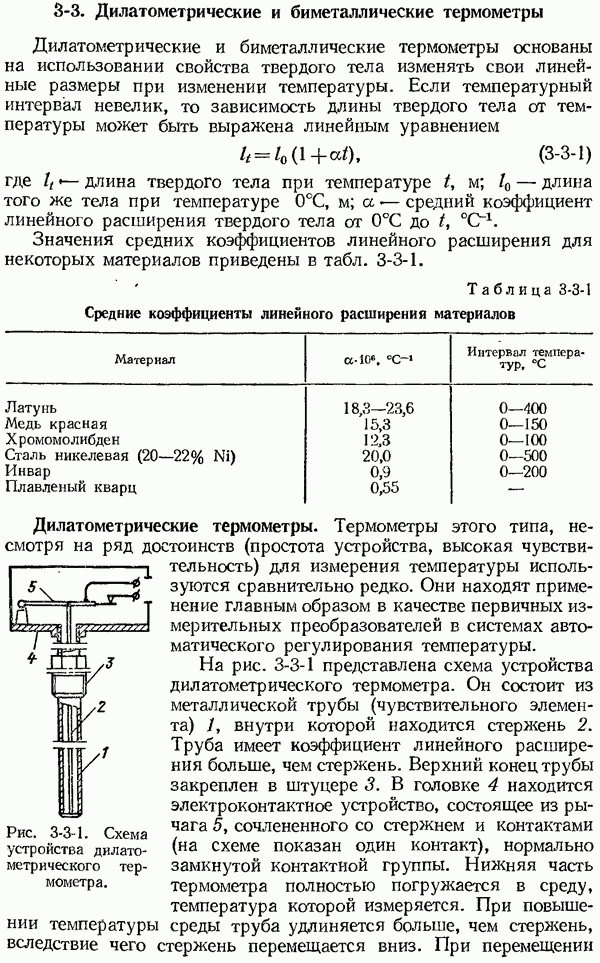
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
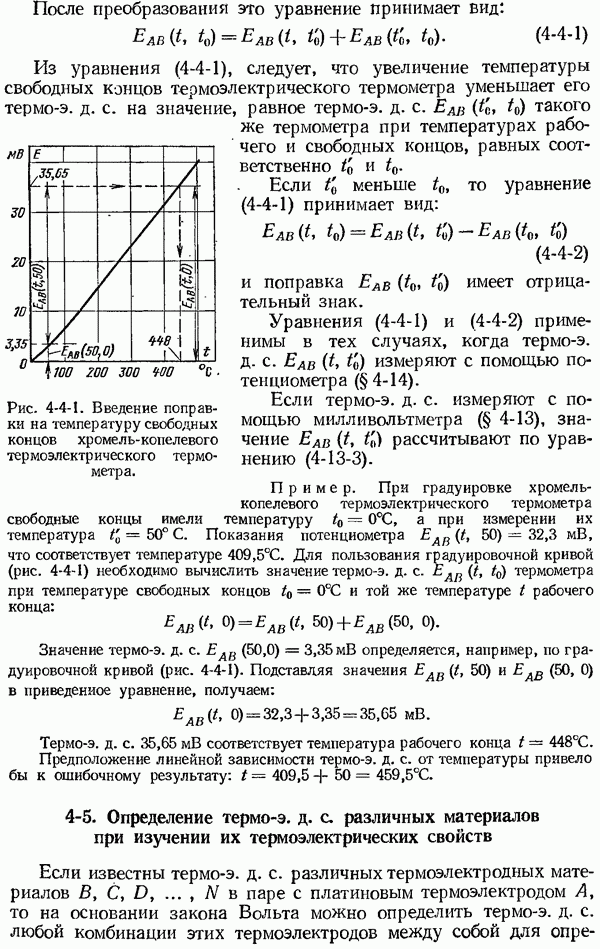
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
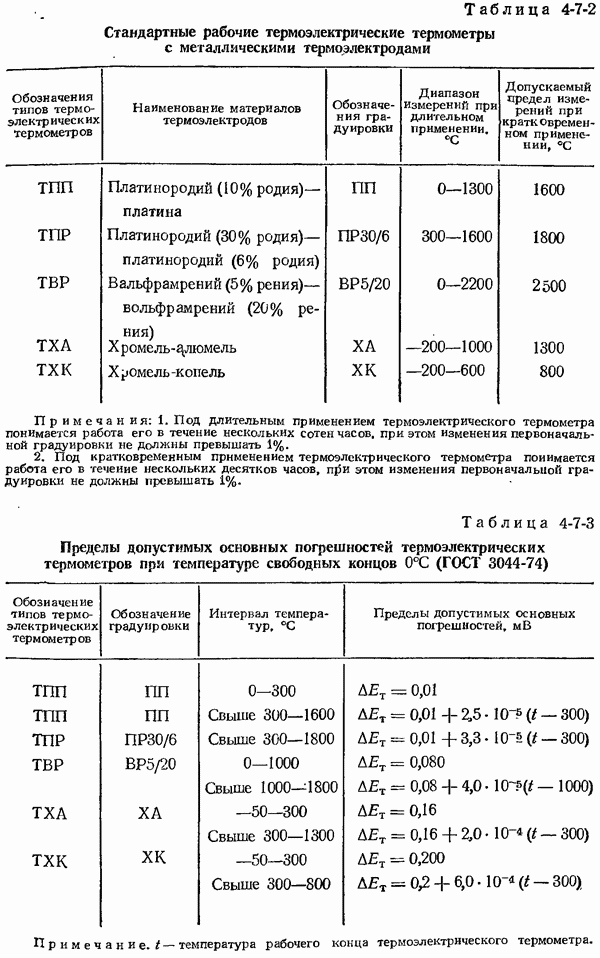
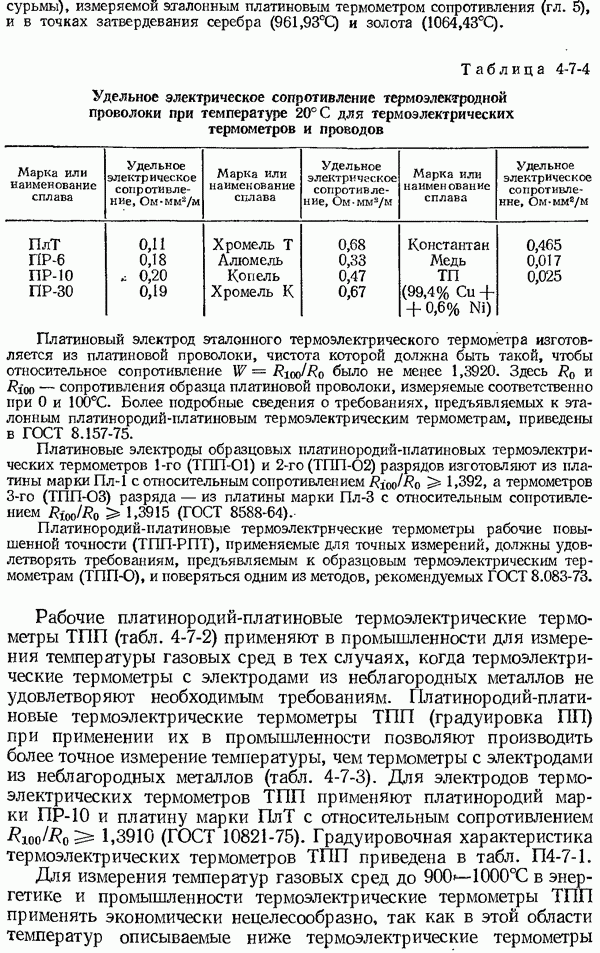
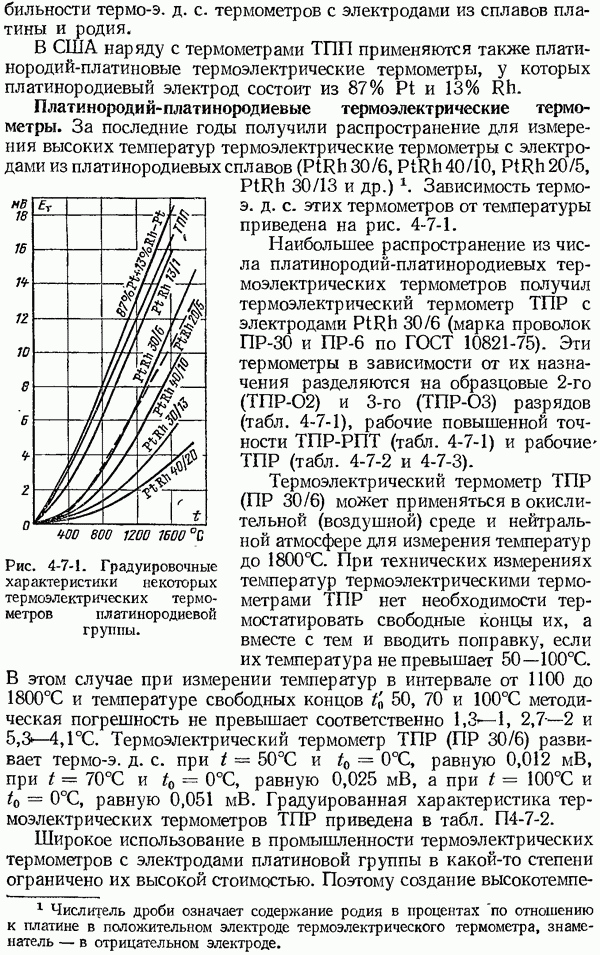
- 4-7. Общие сведения о термоэлектрических термометрах
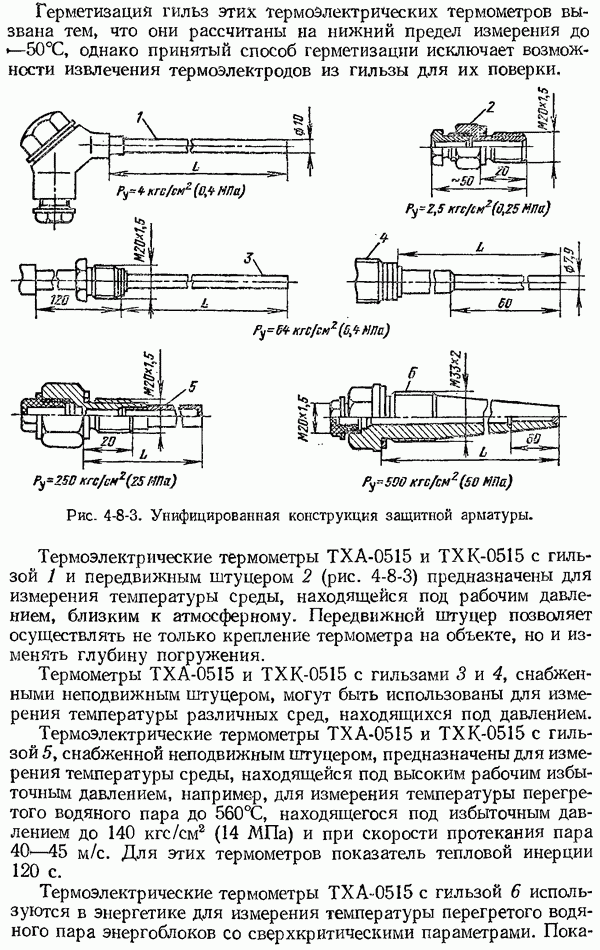
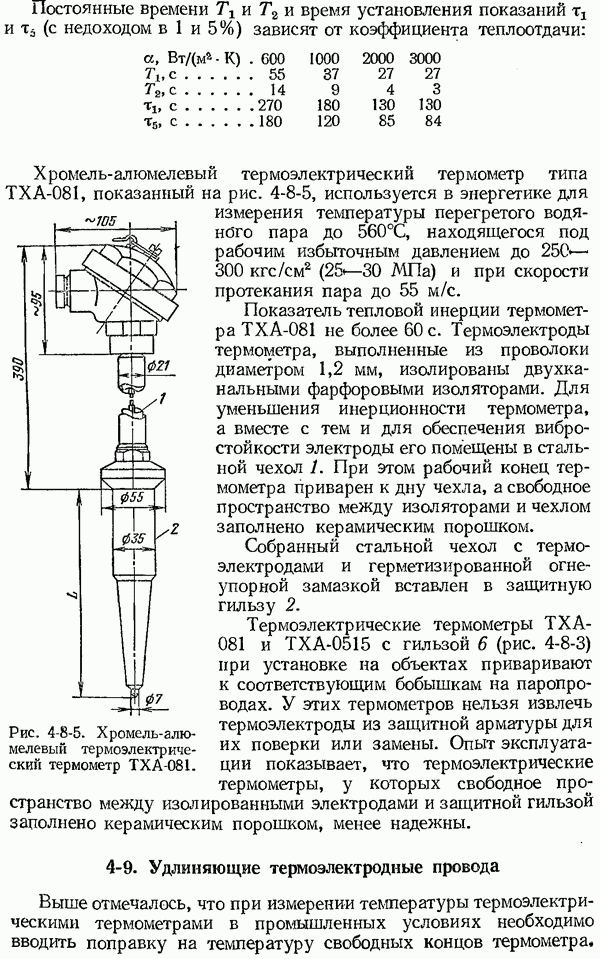
- 4-8. Устройство термоэлектрических термометров
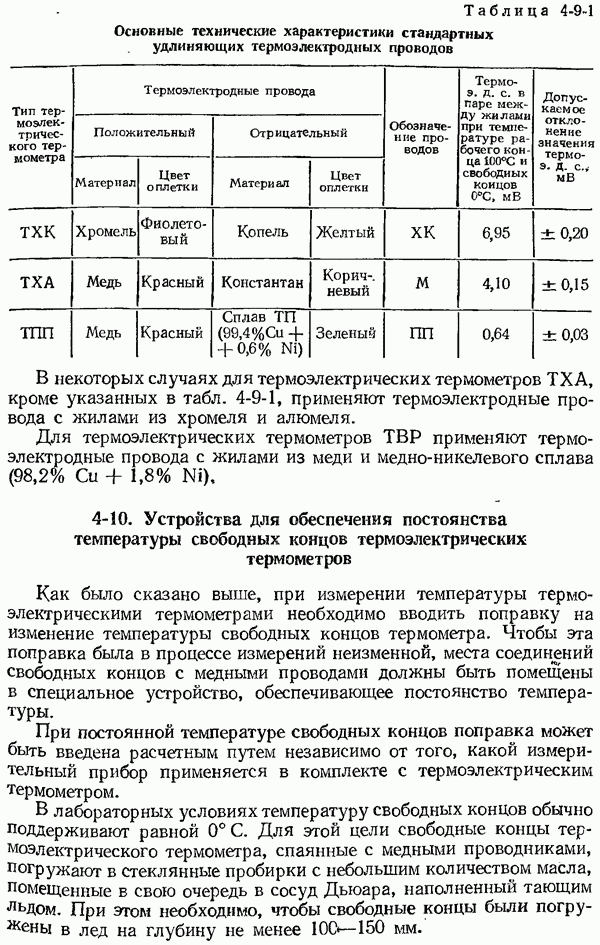
- 4-9. Удлиняющие термоэлектродные провода
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
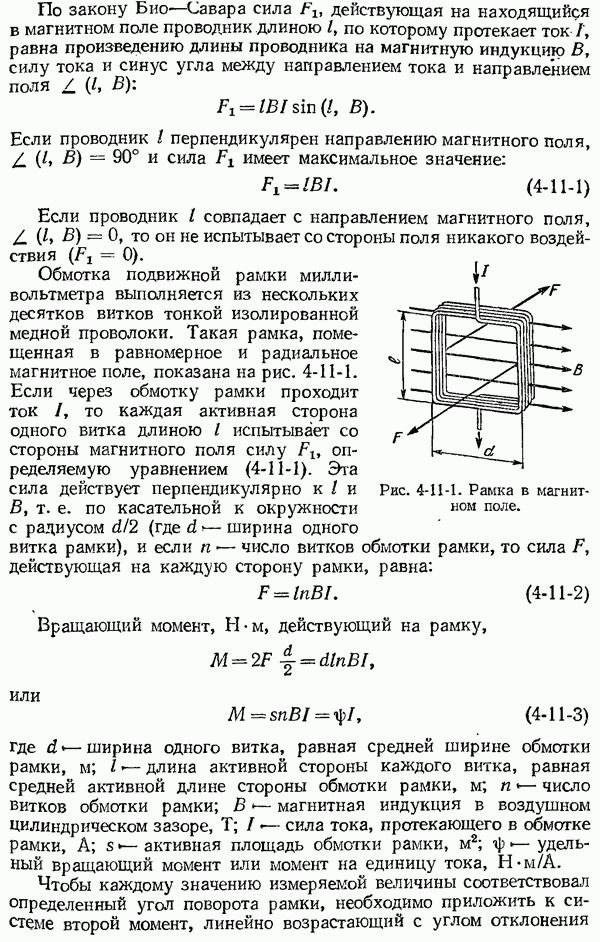
- 4-11. Милливольтметры
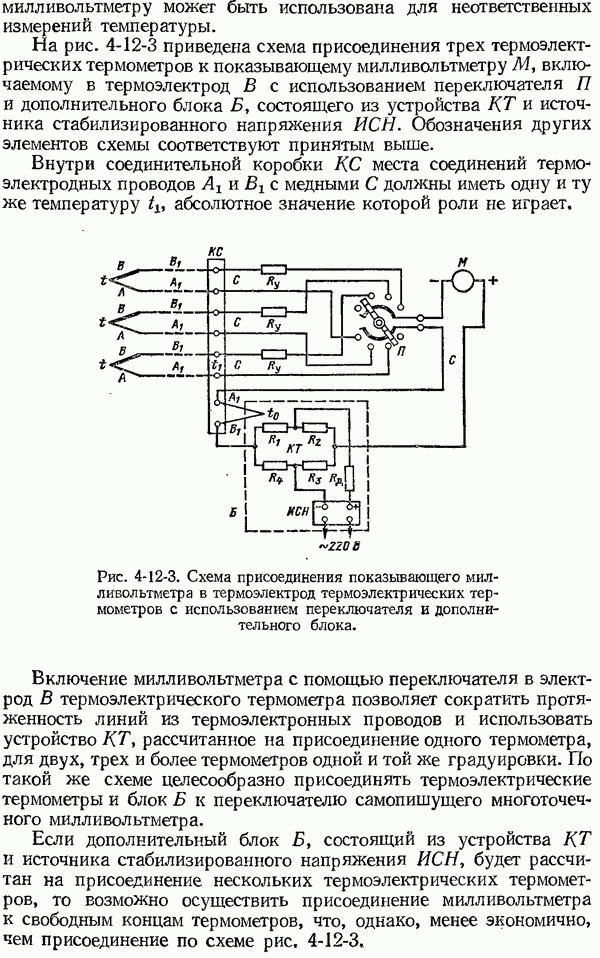
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
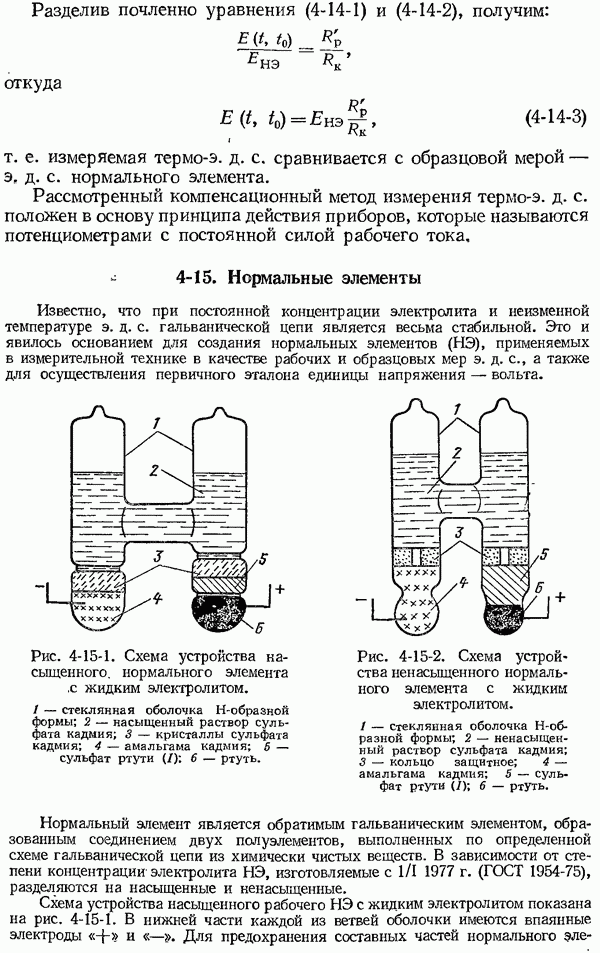
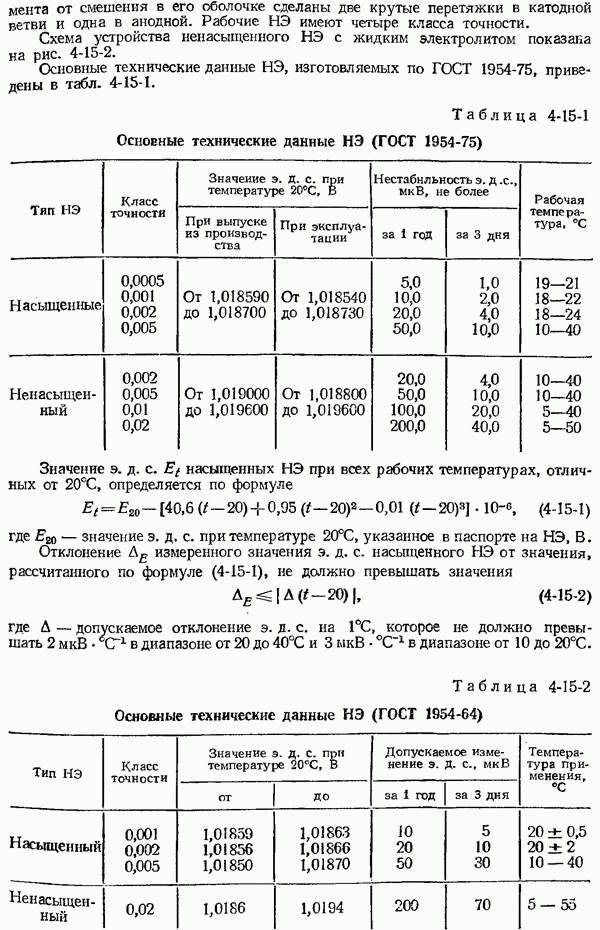
- 4-15. Нормальные элементы
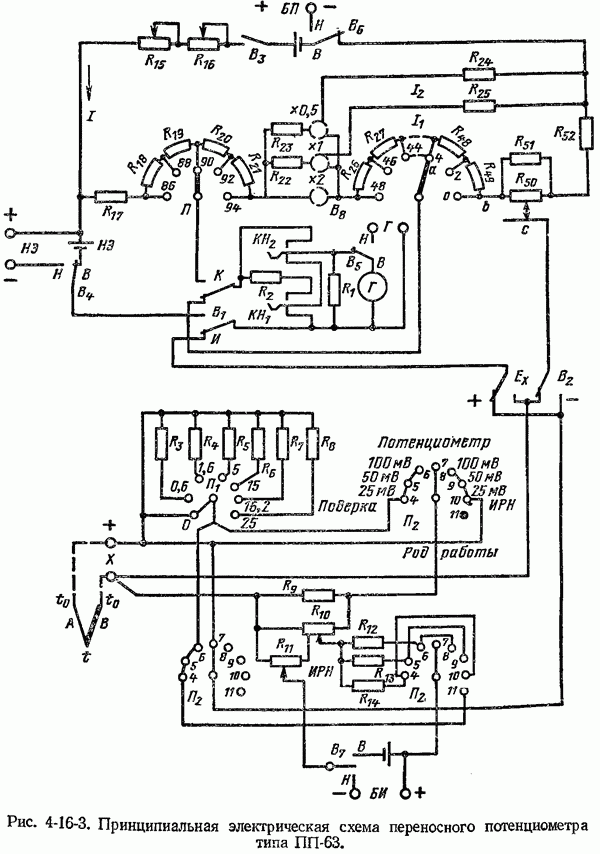
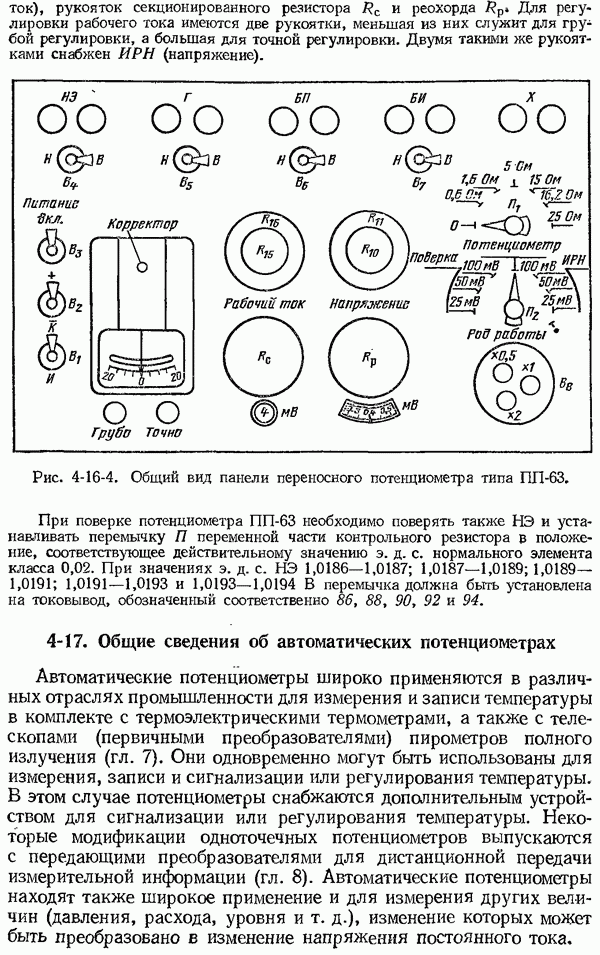
- 4-16. Потенциометры переносные и лабораторные
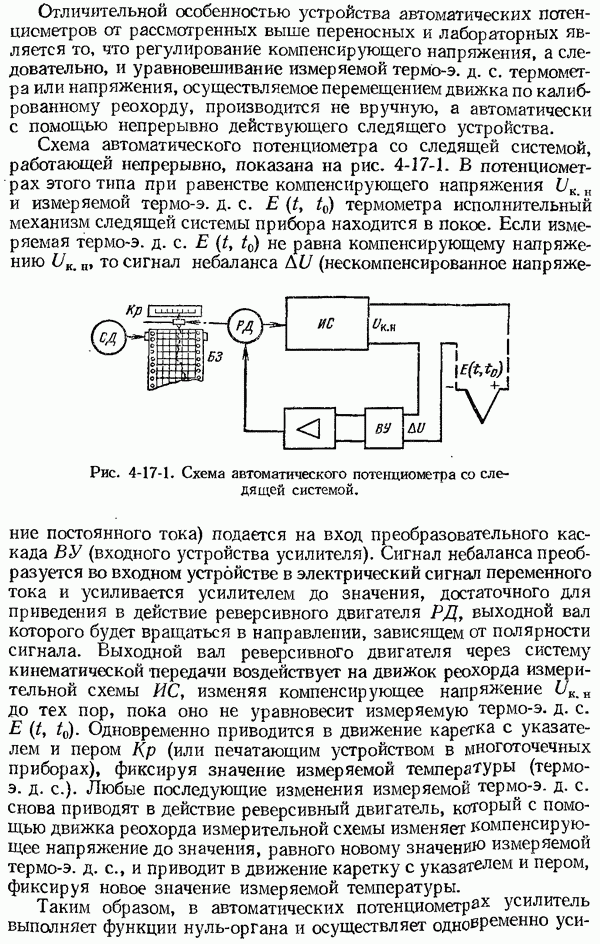
- 4-17. Общие сведения об автоматических потенциометрах
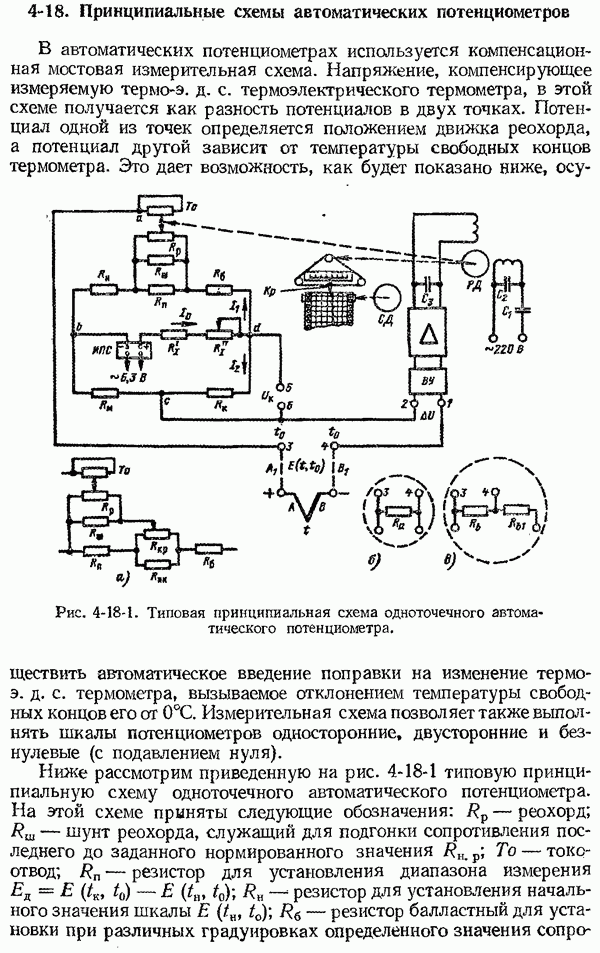
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
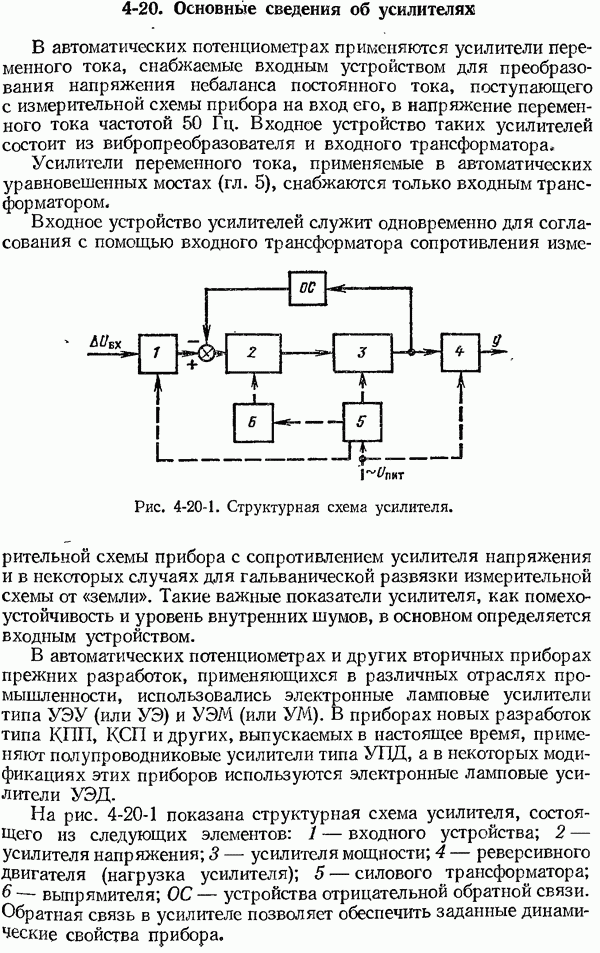
- 4-20. Основные сведения об усилителях
- 4-21. Основные сведения об источниках стабилизированного питания
- 4-22. Устройство автоматических потенциометров
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
- 5-3. Устройство платиновых и медных термометров сопротивления
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
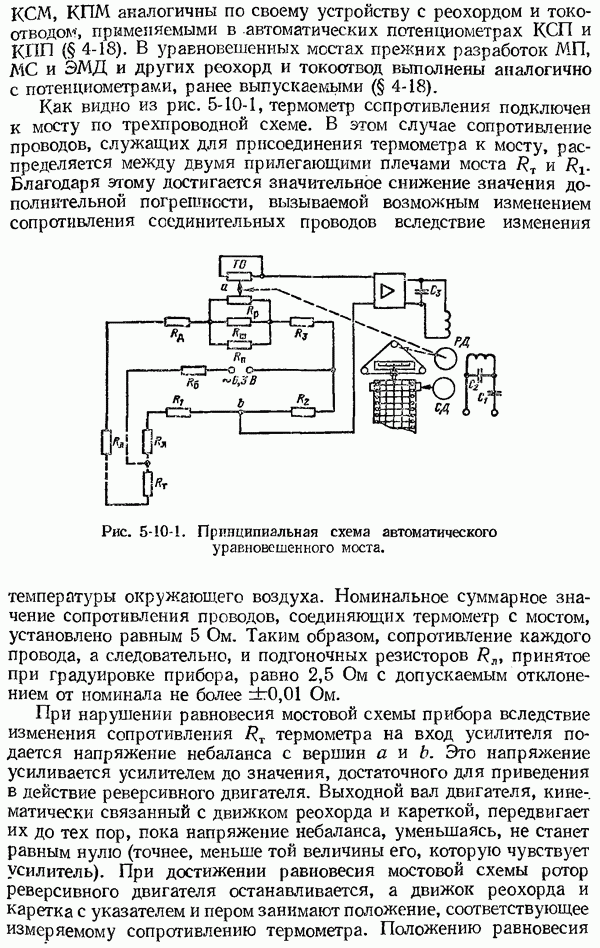
- 5-10. Принципиальная схема автоматического уравновешенного моста
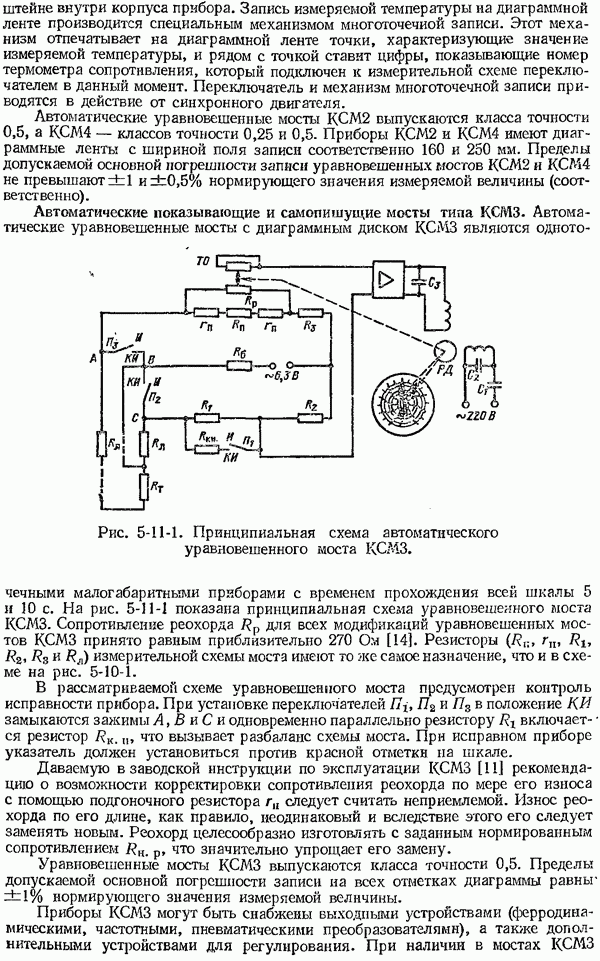
- 5-11. Устройство автоматических уравновешенных мостов
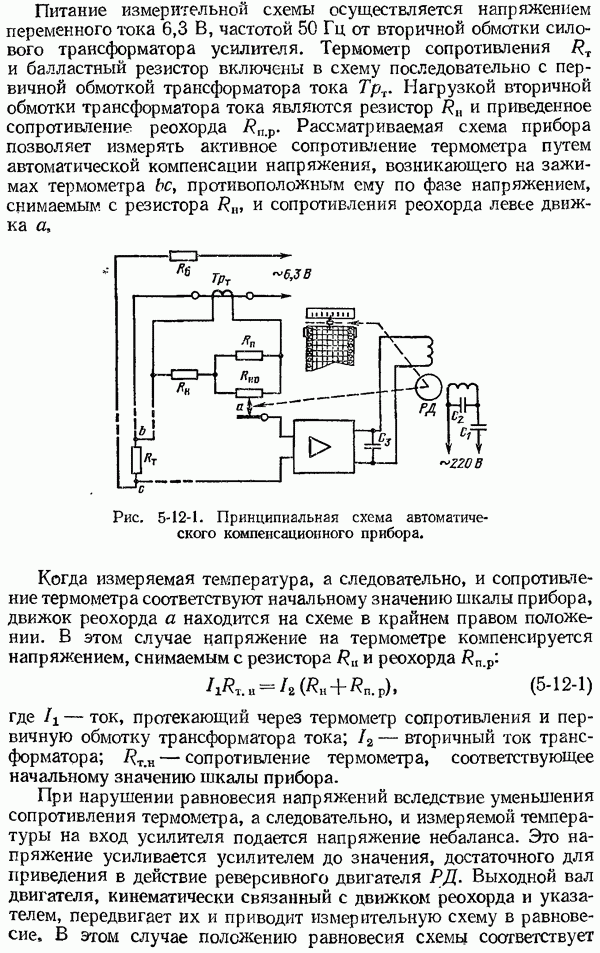
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
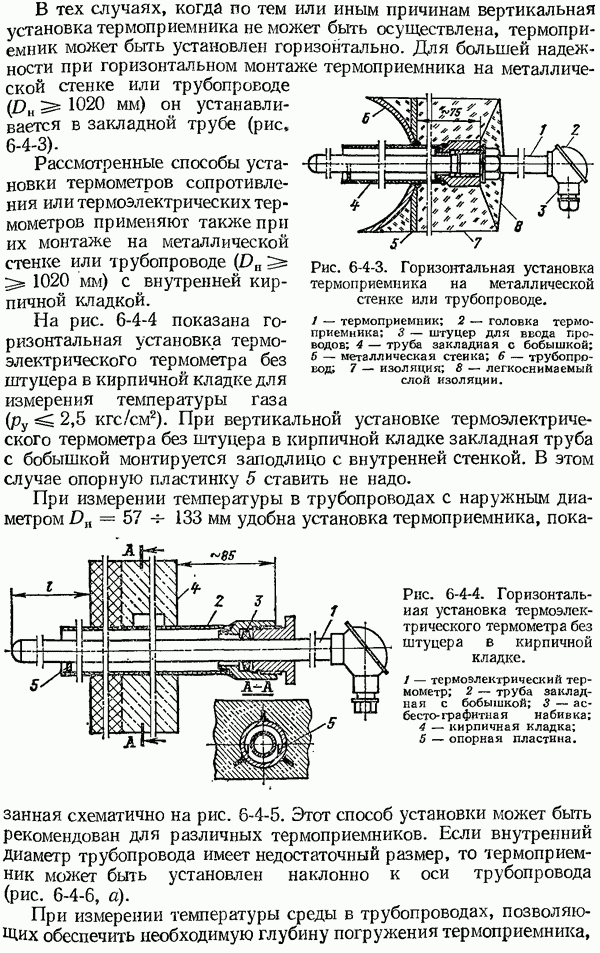
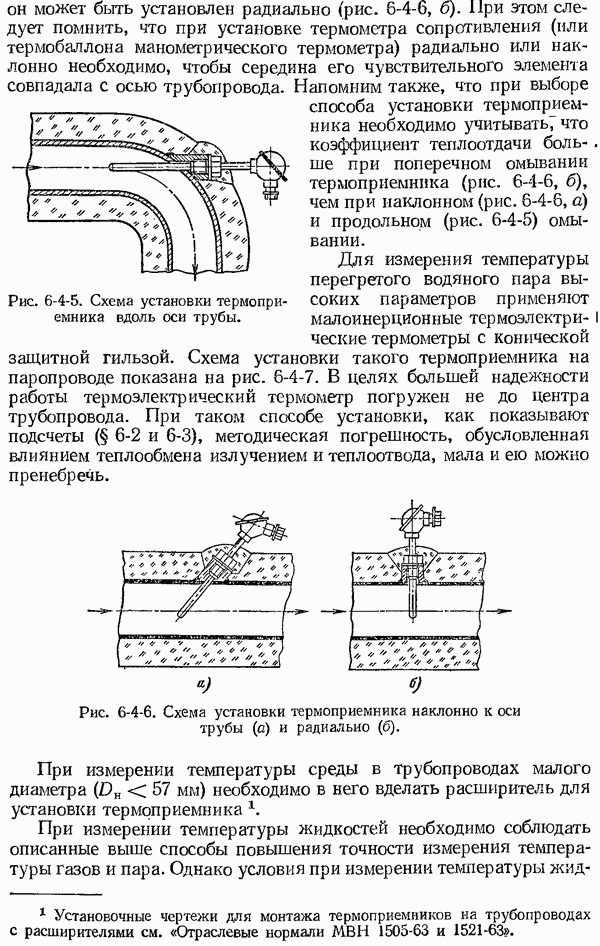
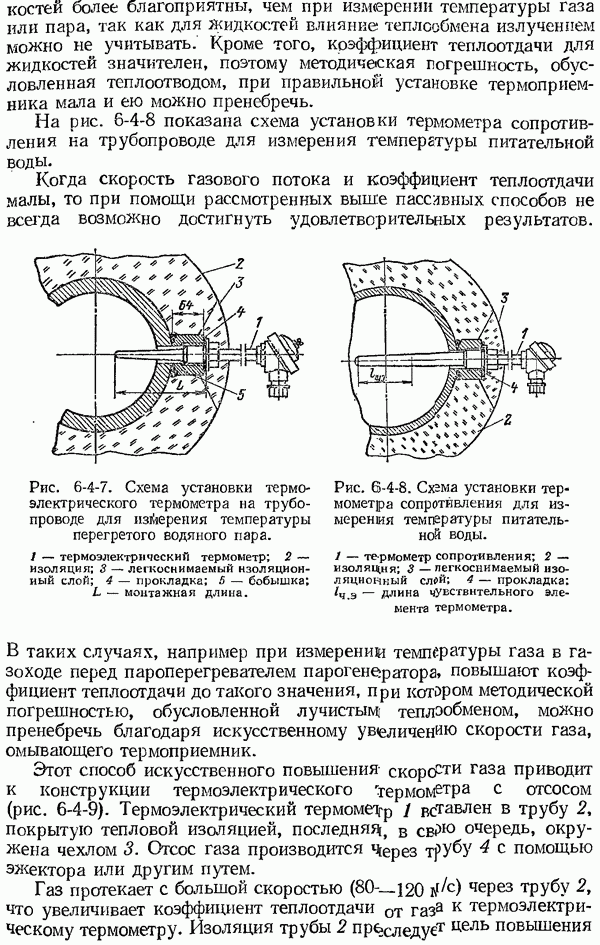
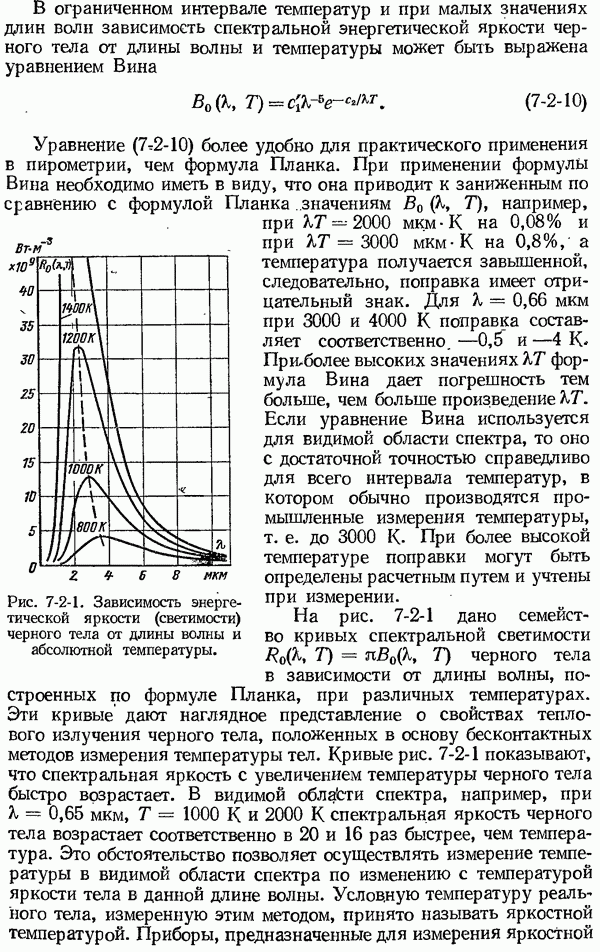
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
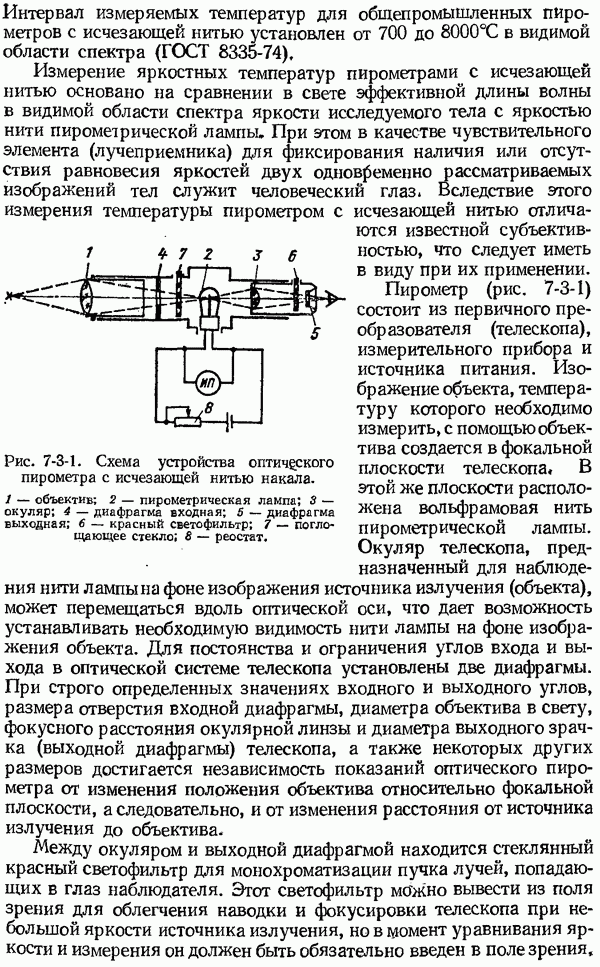
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
- 7-3. Оптические пирометры
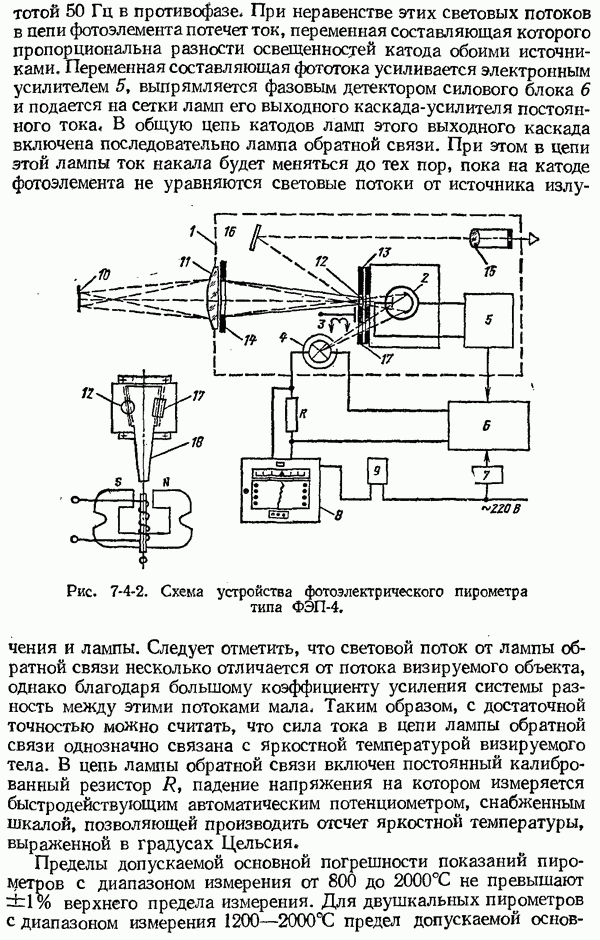
- 7-4. Фотоэлектрические пирометры
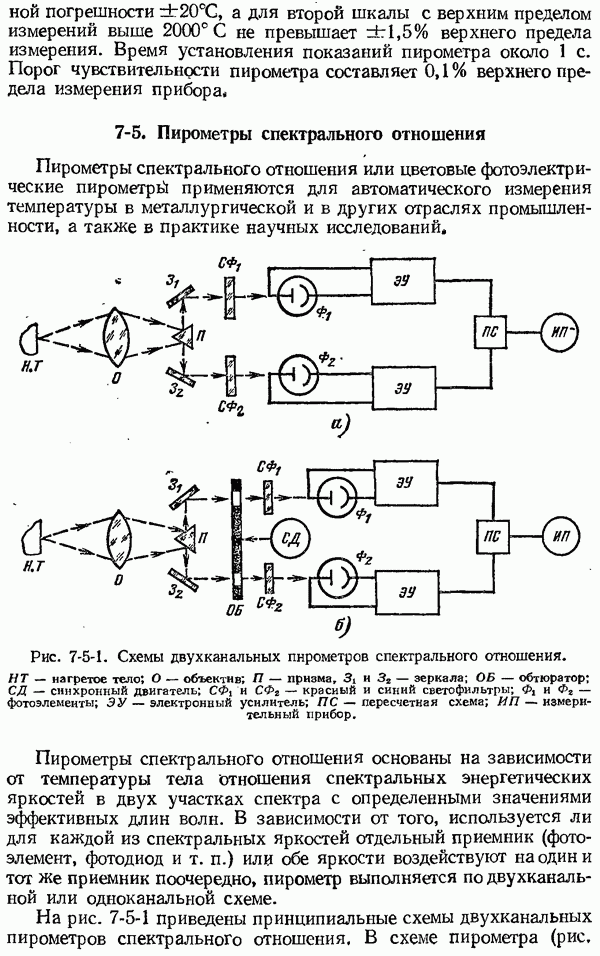
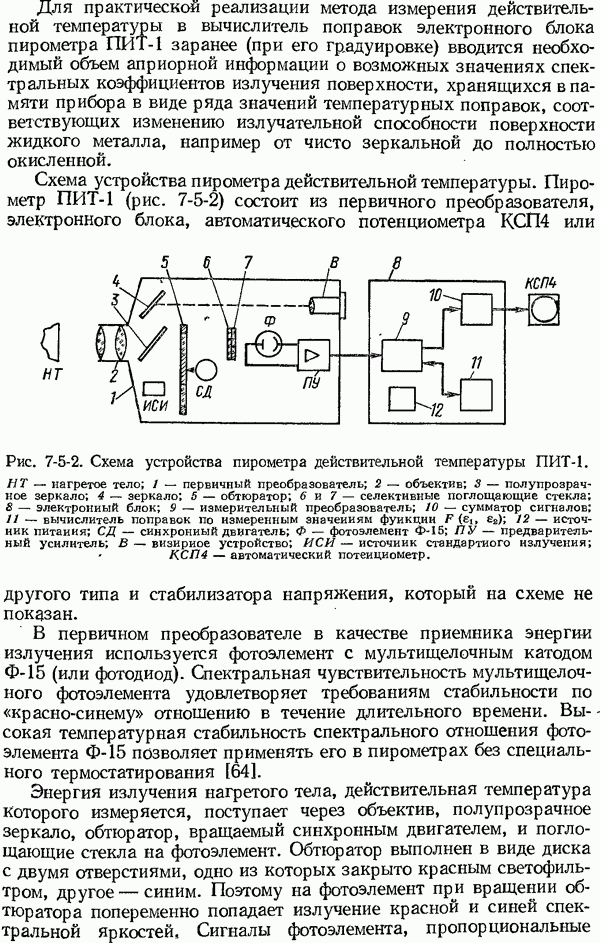
- 7-5. Пирометры спектрального отношения
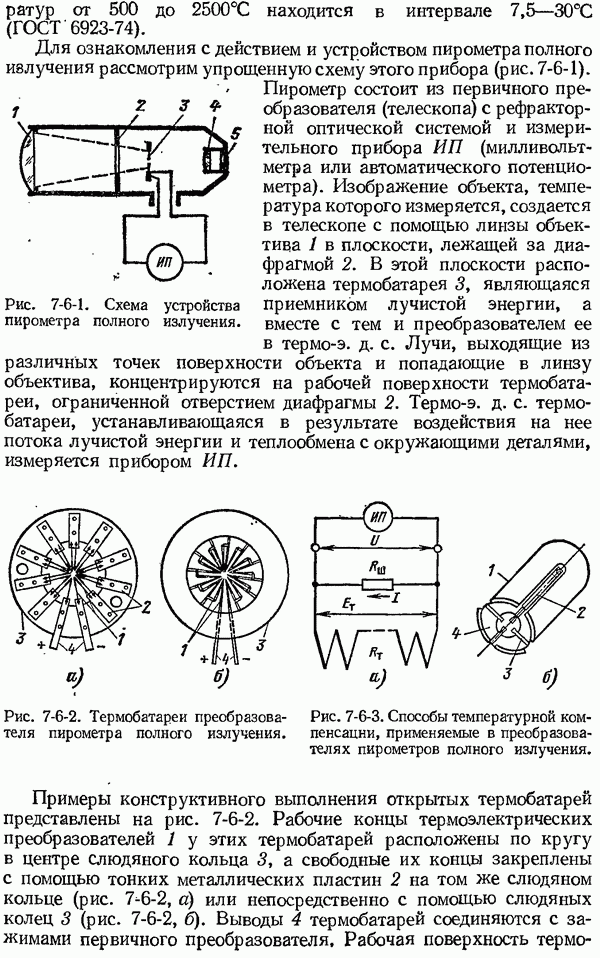
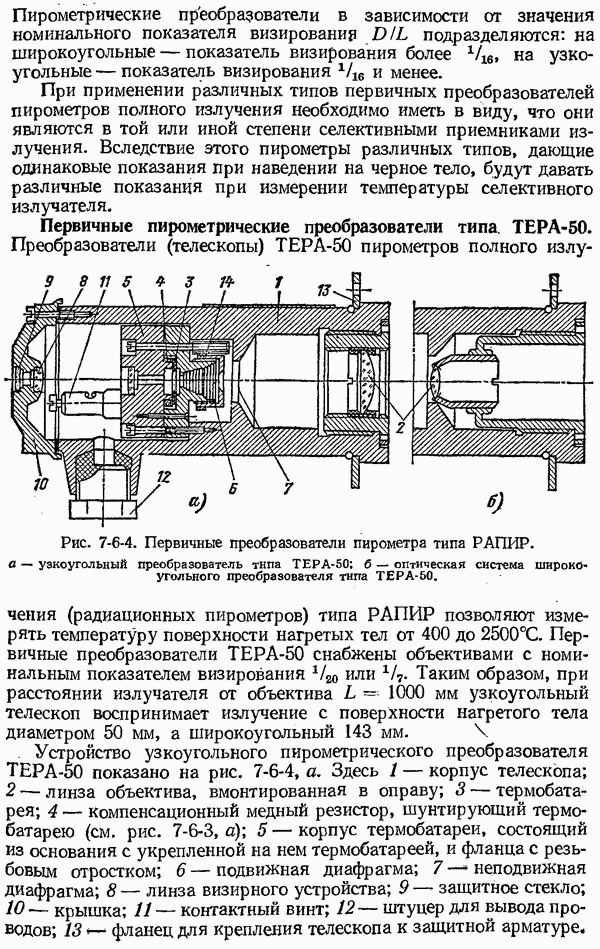
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
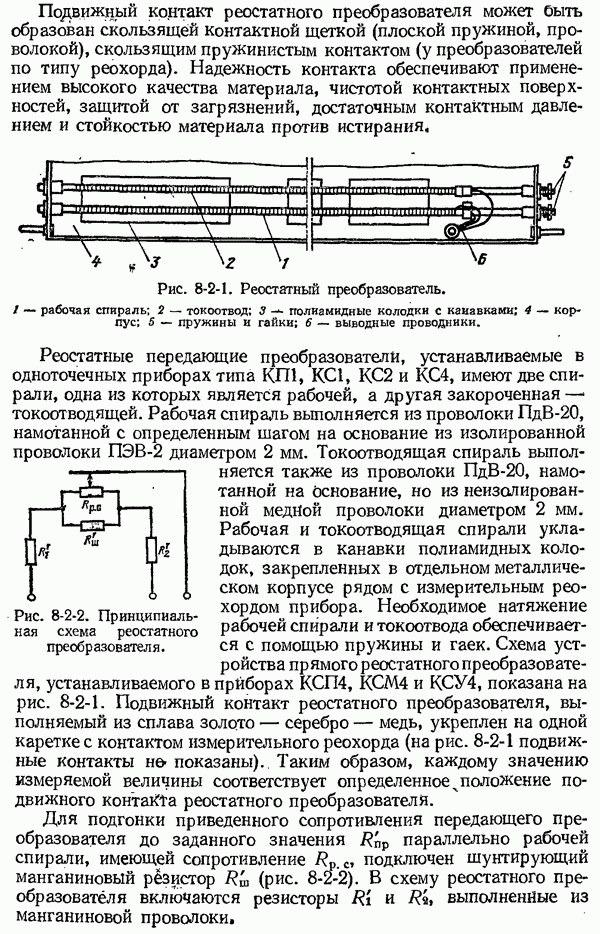
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
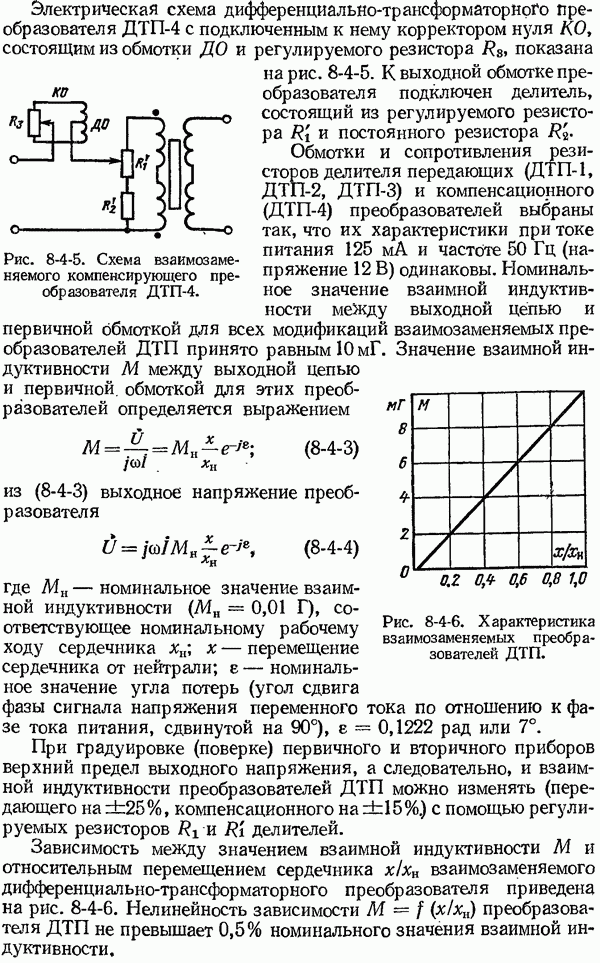
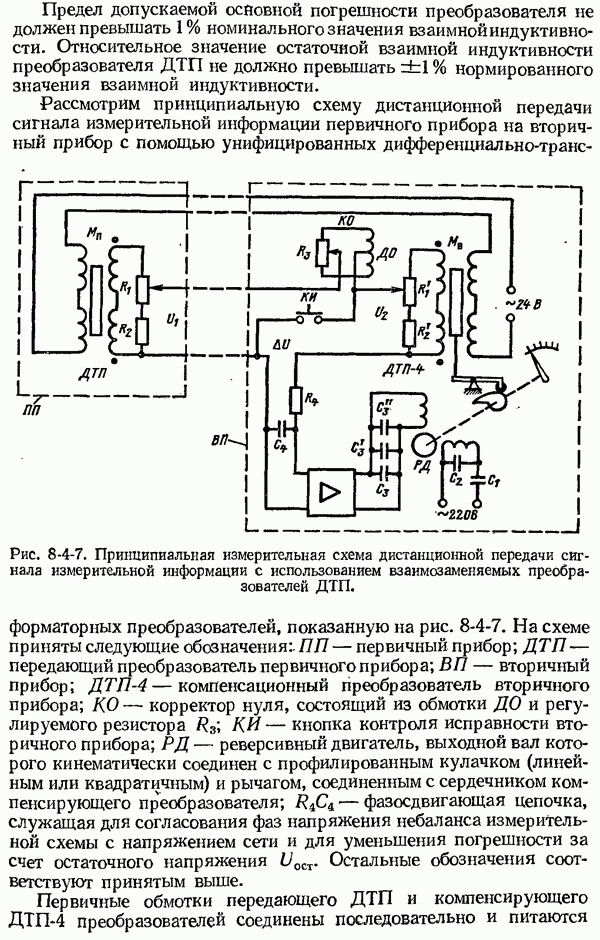
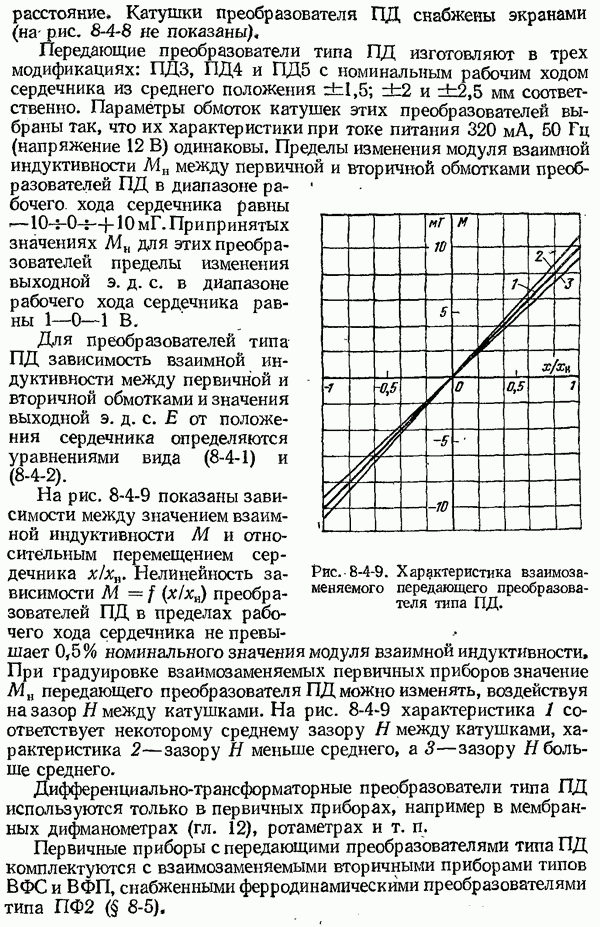
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
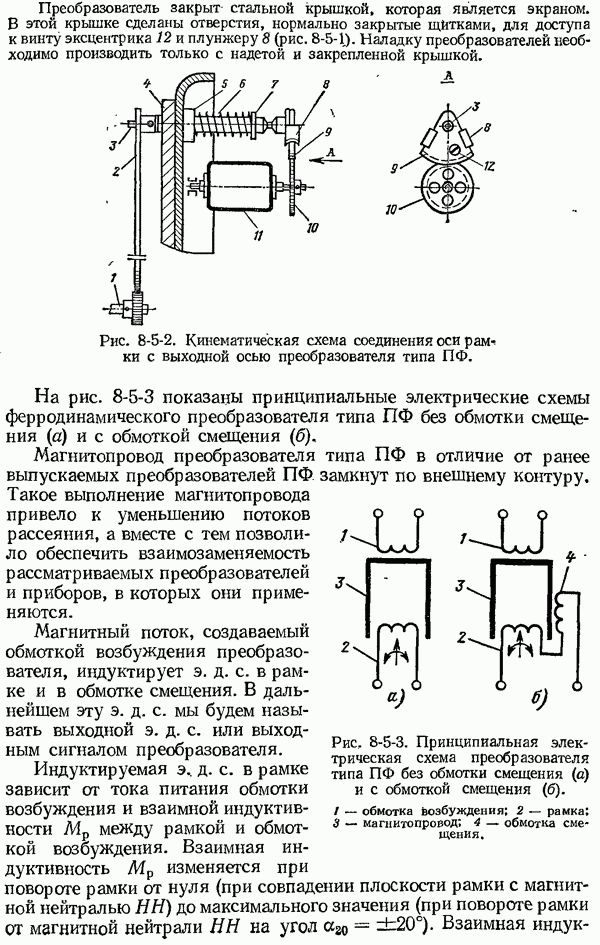
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
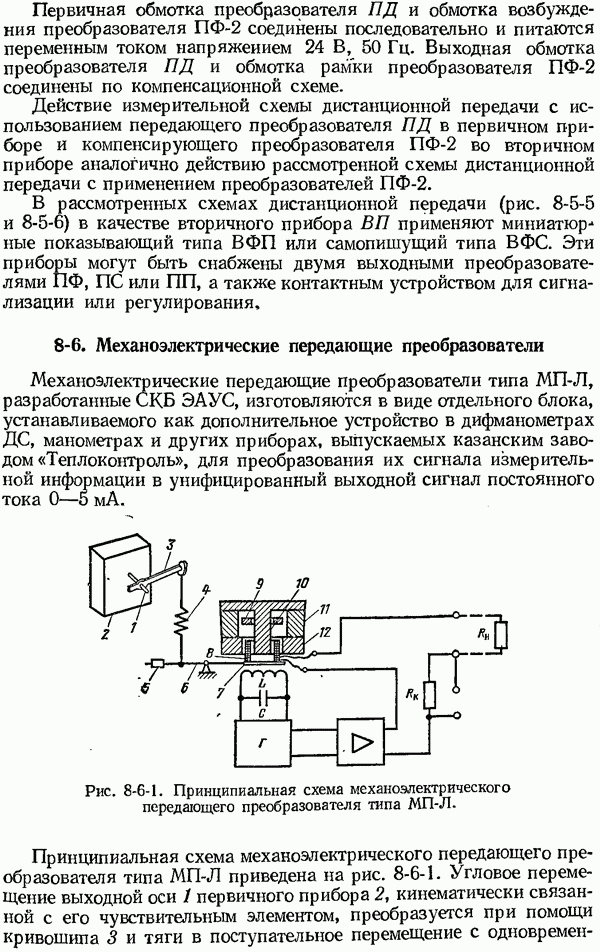
- 8-6. Механоэлектрические передающие преобразователи
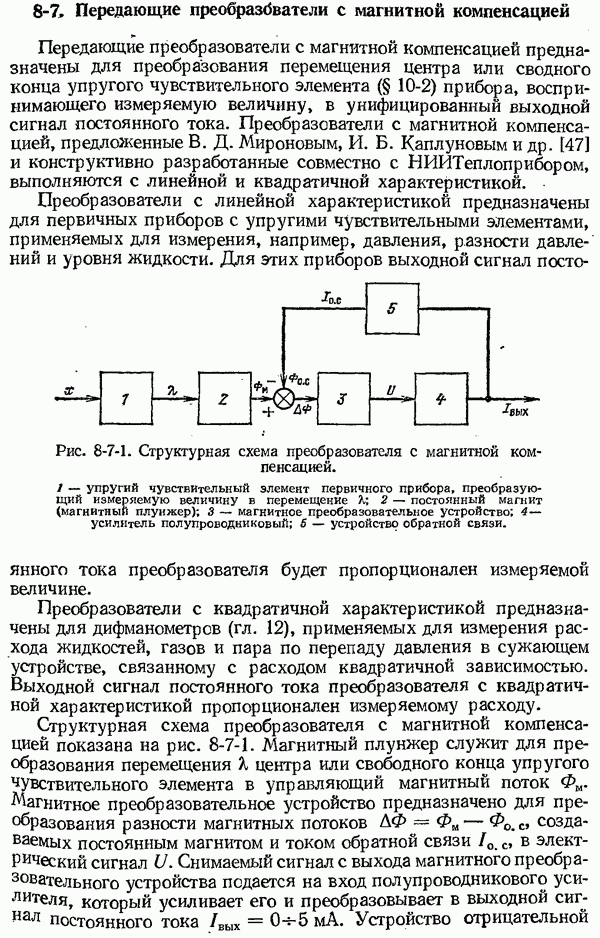
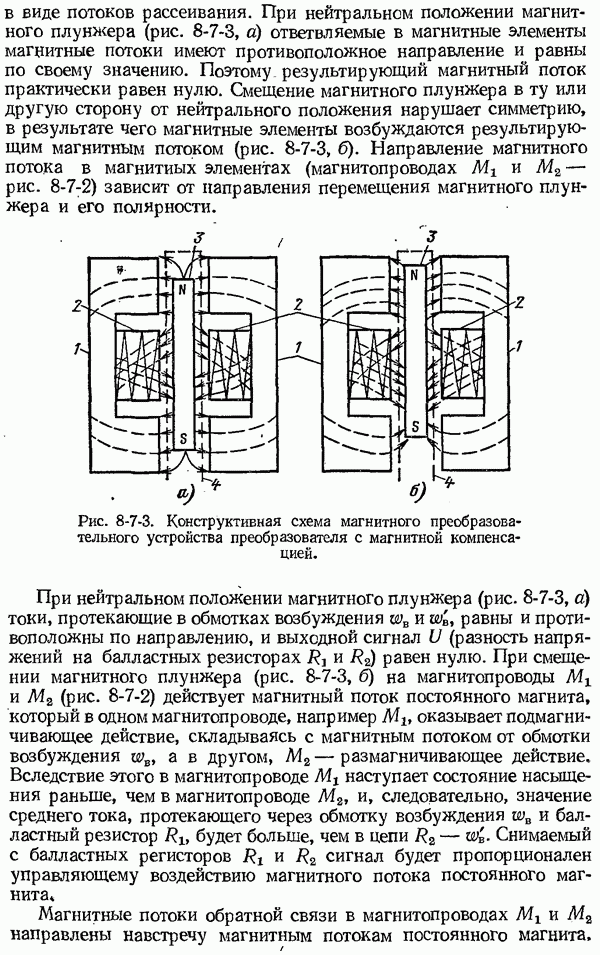
- 8-7. Передающие преобразователи с магнитной компенсацией
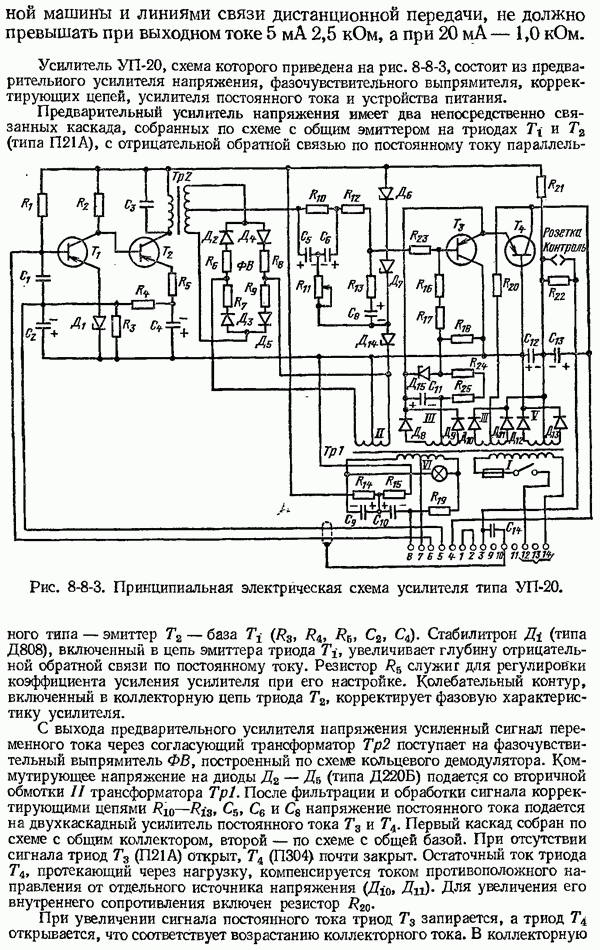
- 8-8. Электросиловые преобразователи
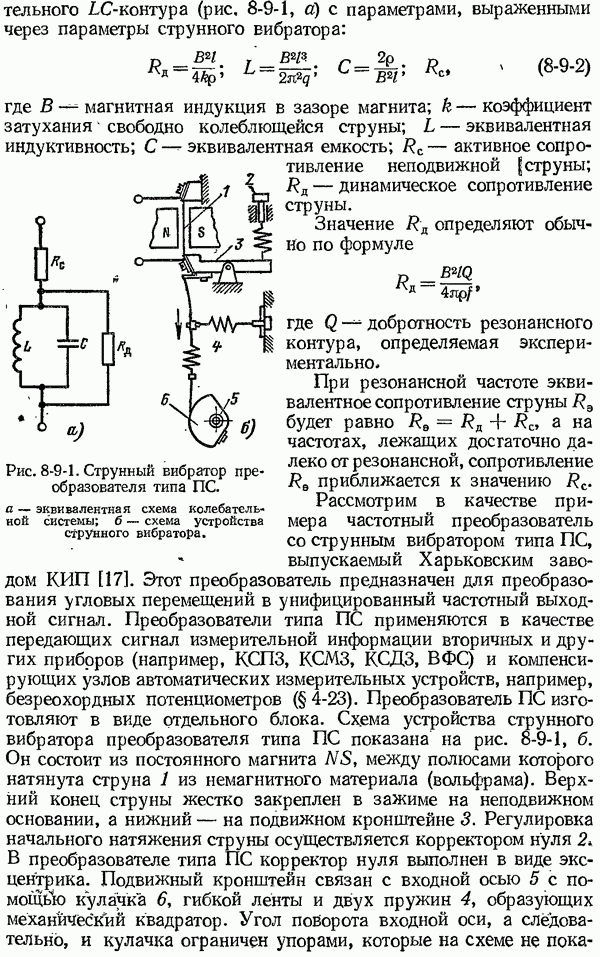
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
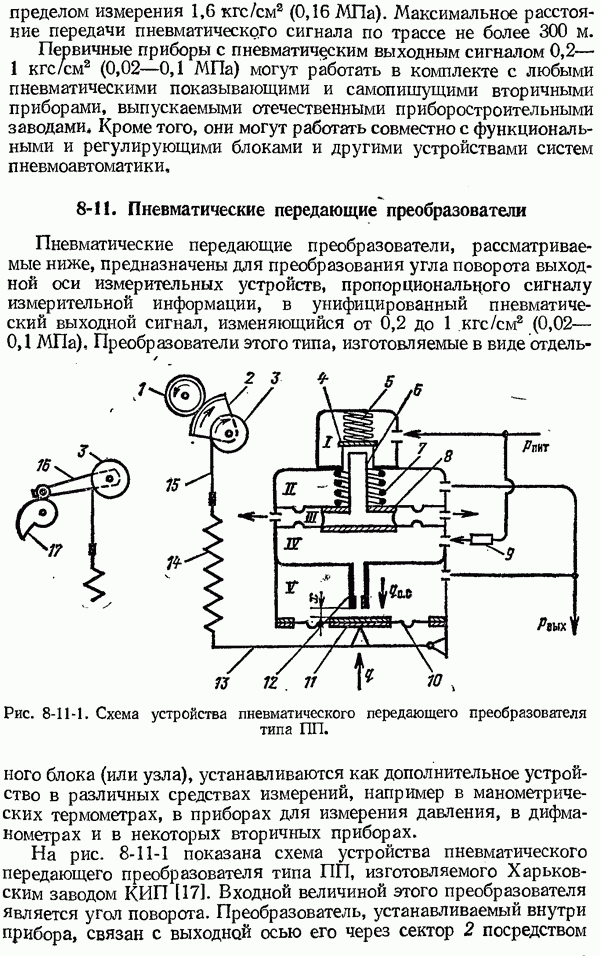
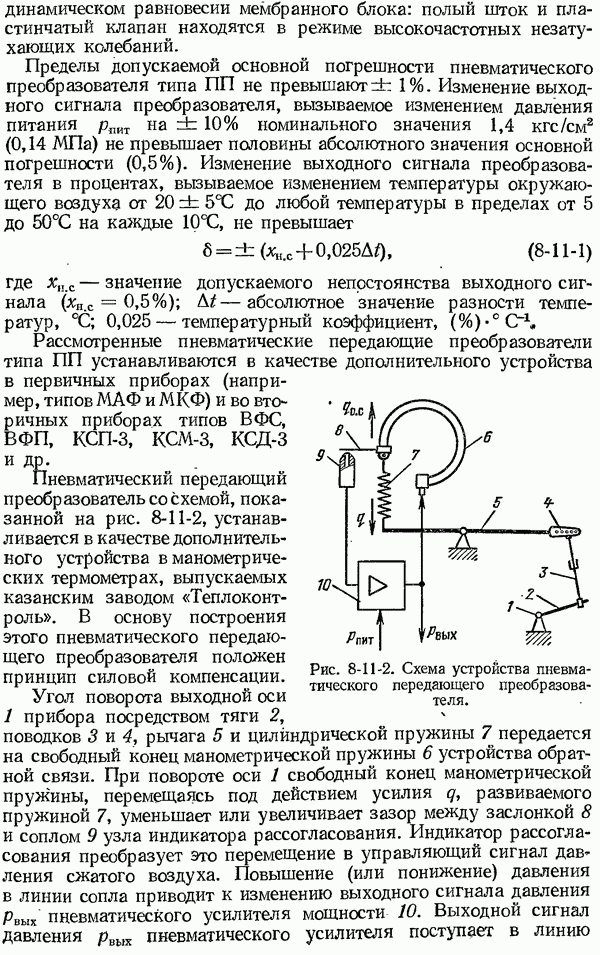
- 8-11. Пневматические передающие преобразователи
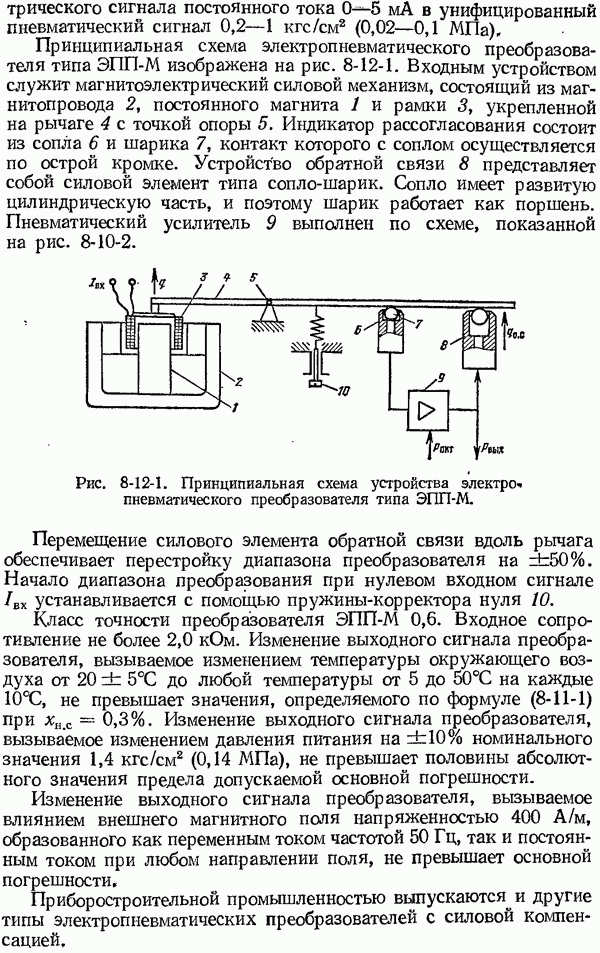
- 8-12. Электропневматические и пневмоэлектрические преобразователи
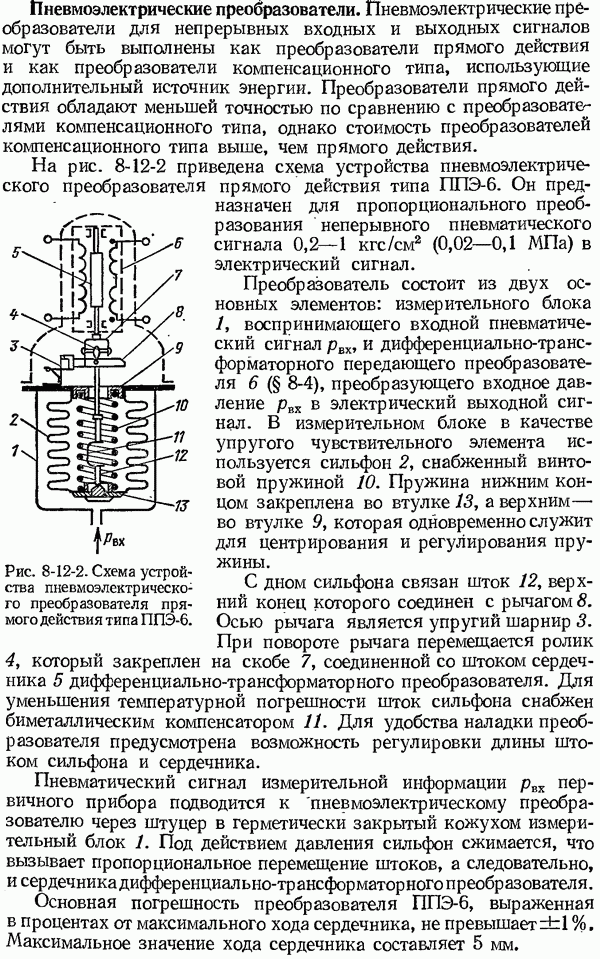
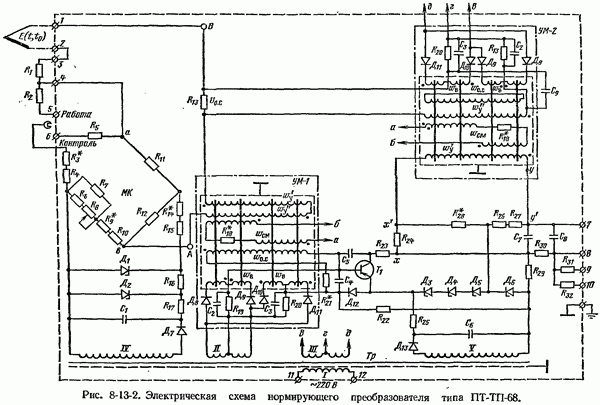
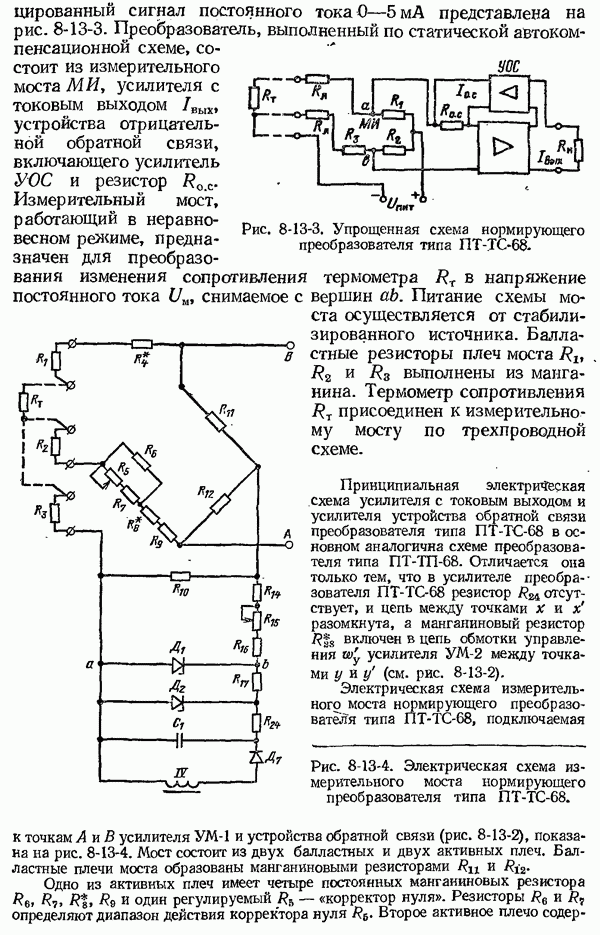
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
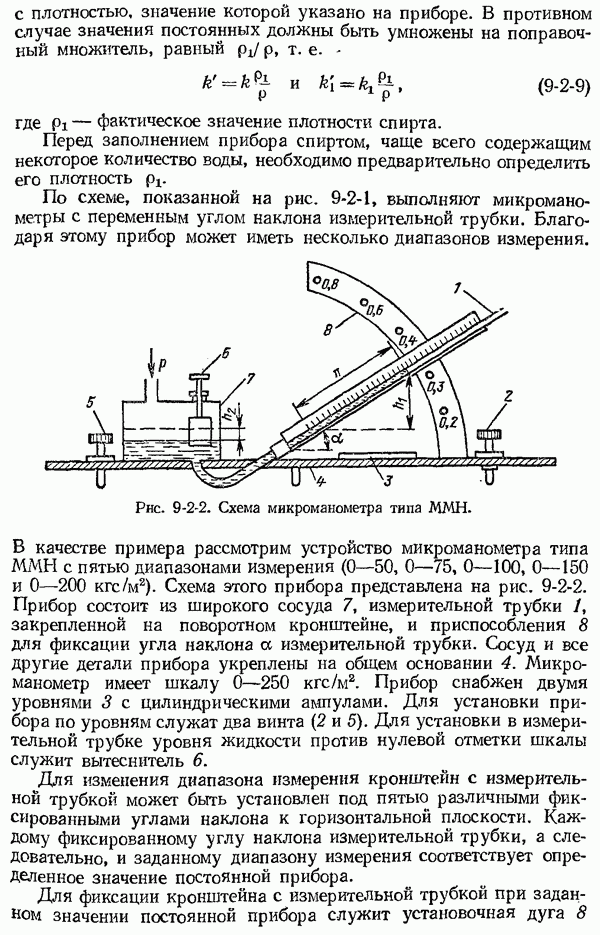
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
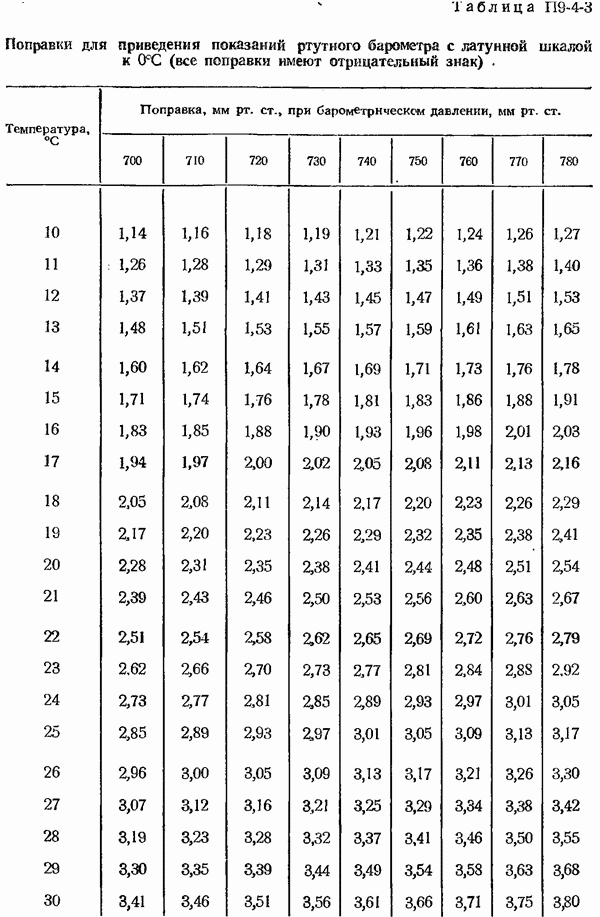
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
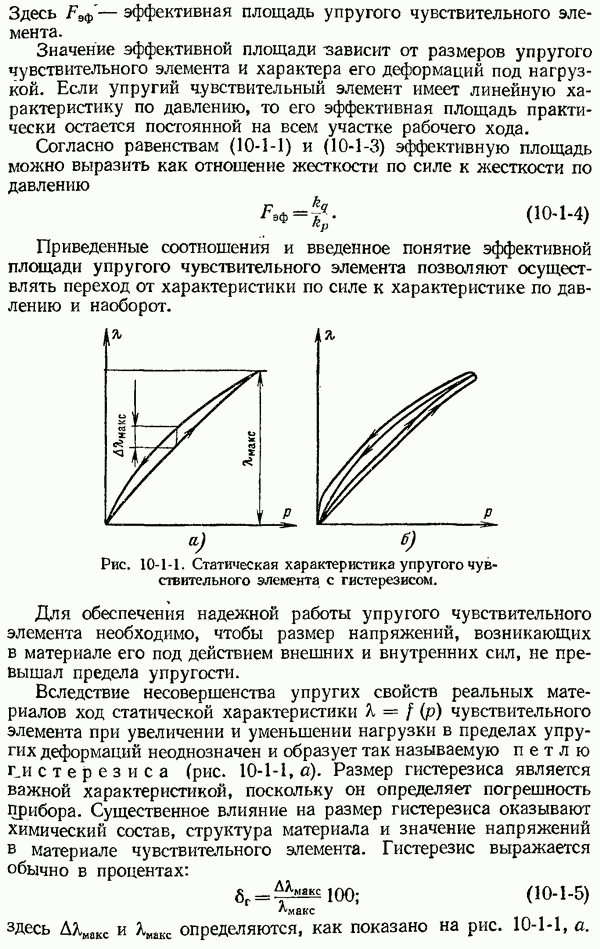
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
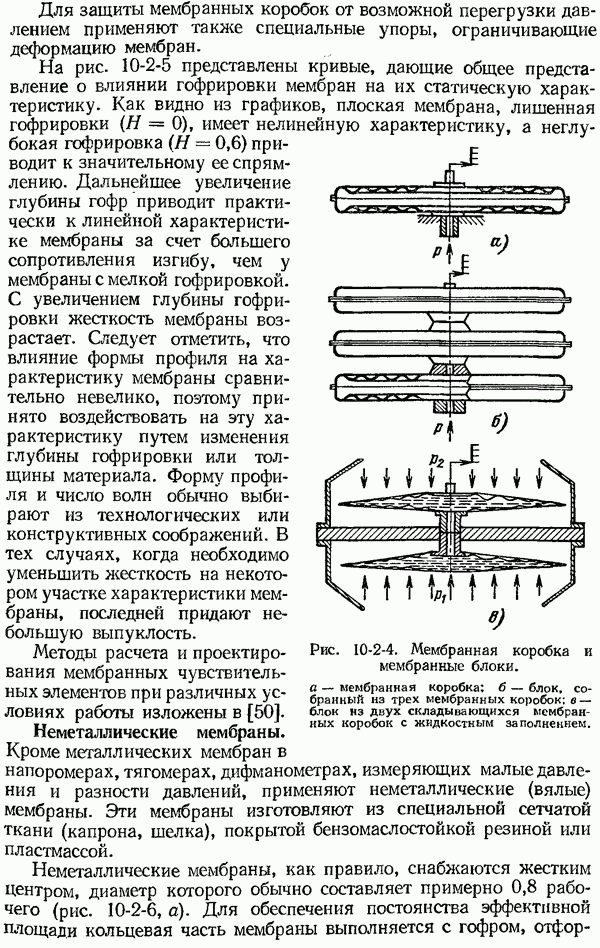
- 10-2. Упругие чувствительные элементы
- 10-3. Приборы давления прямого действия
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
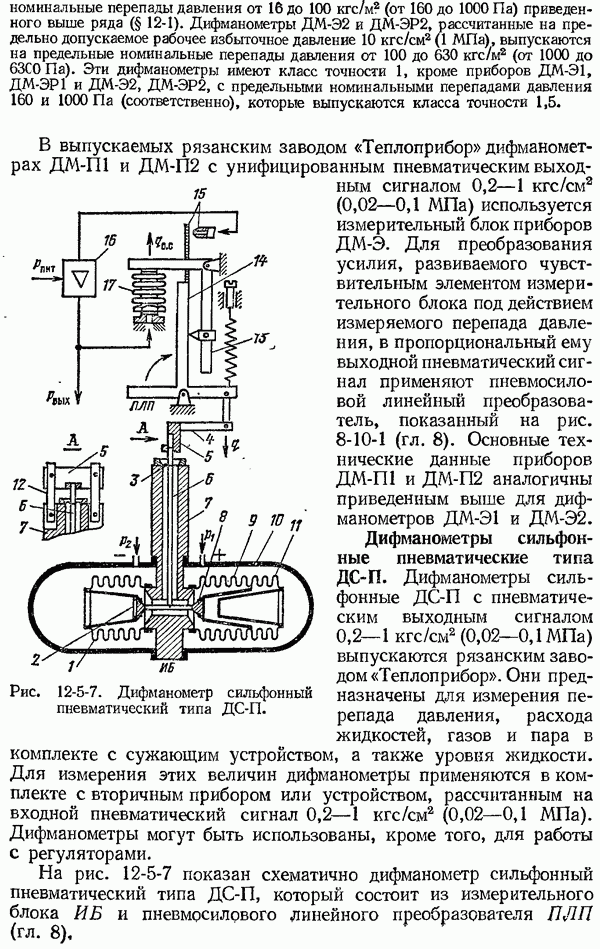
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
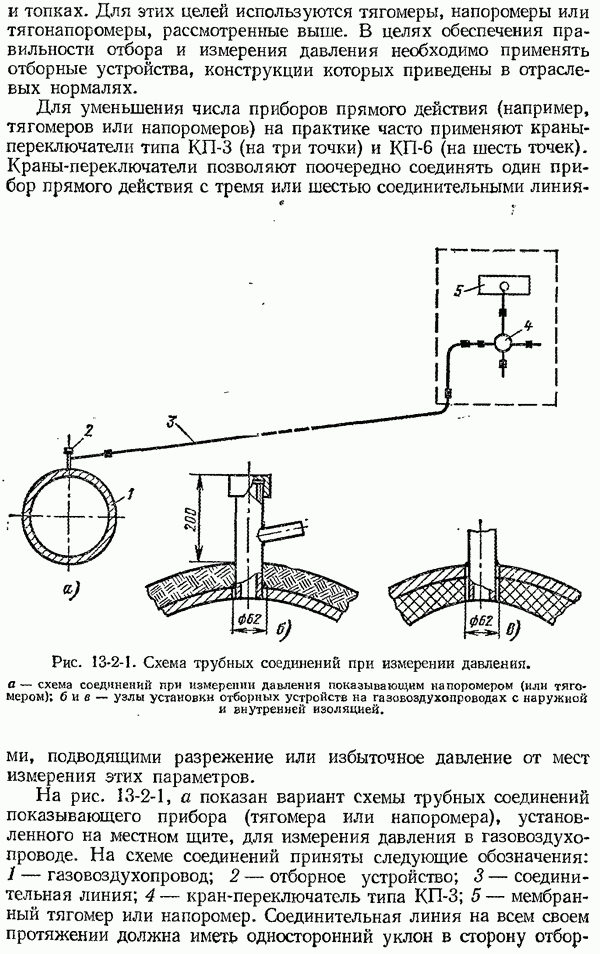
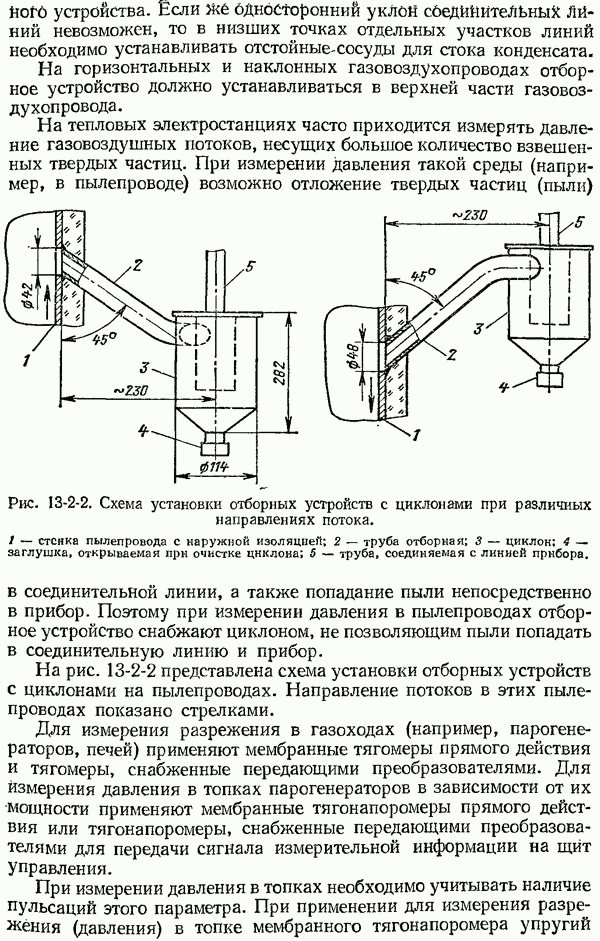
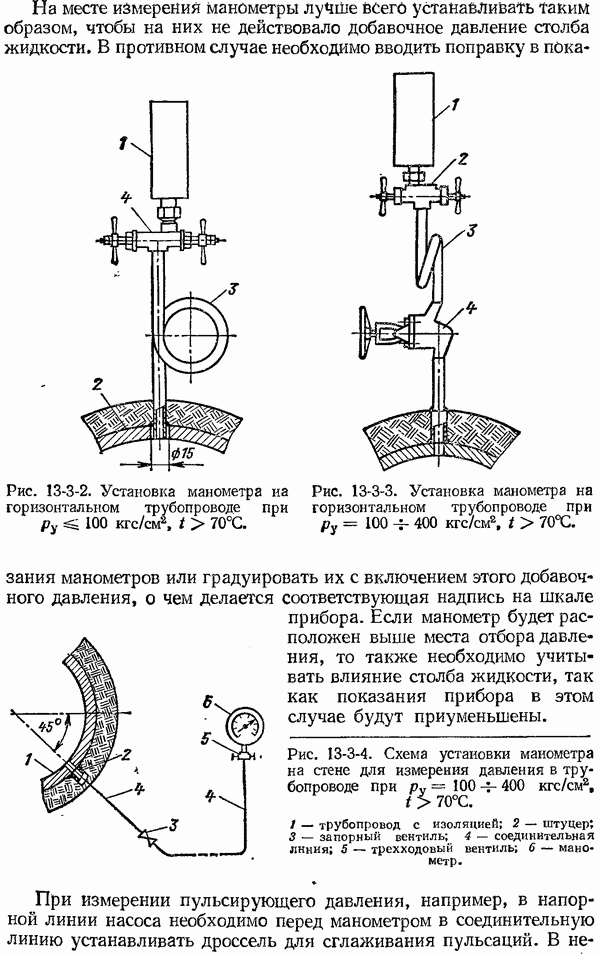
- 13-2. Измерение близкого к атмосферному давления газовых сред
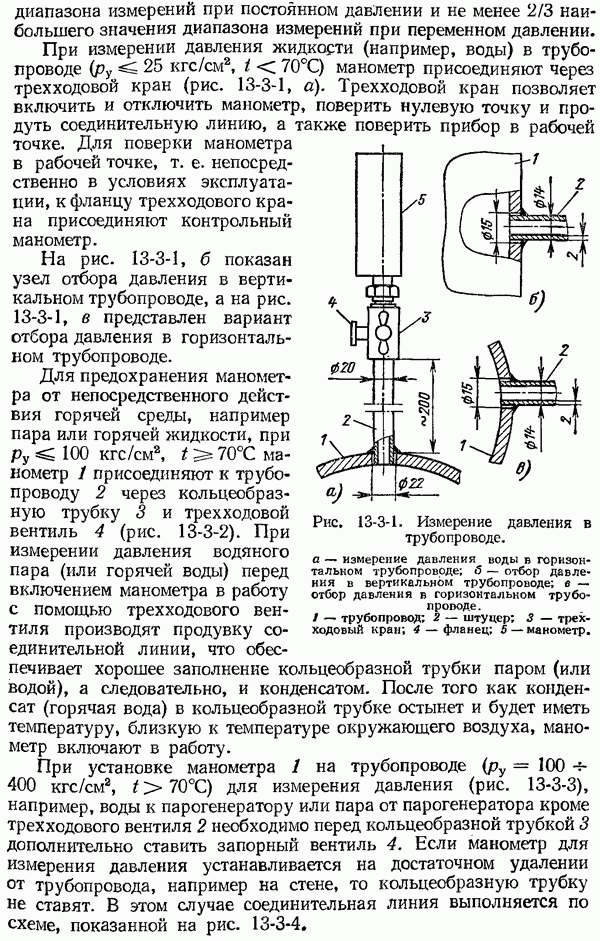
- 13-3. Измерение давления газов, жидкостей и пара
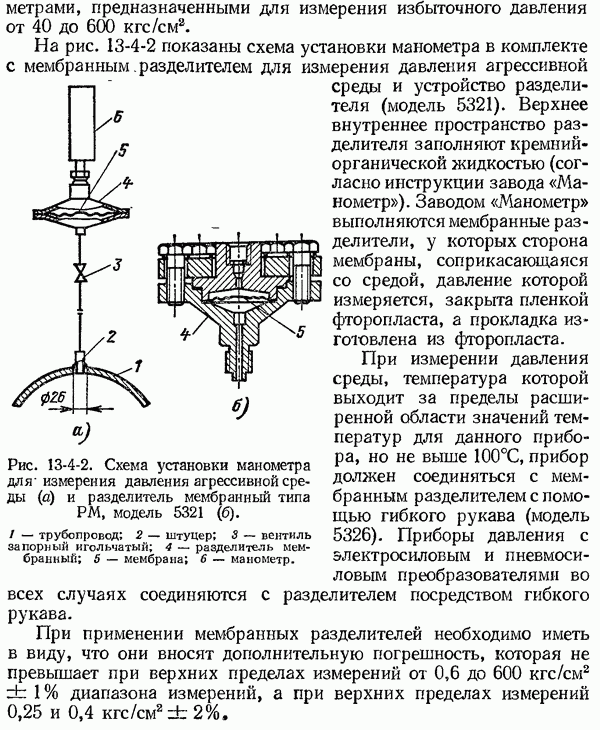
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
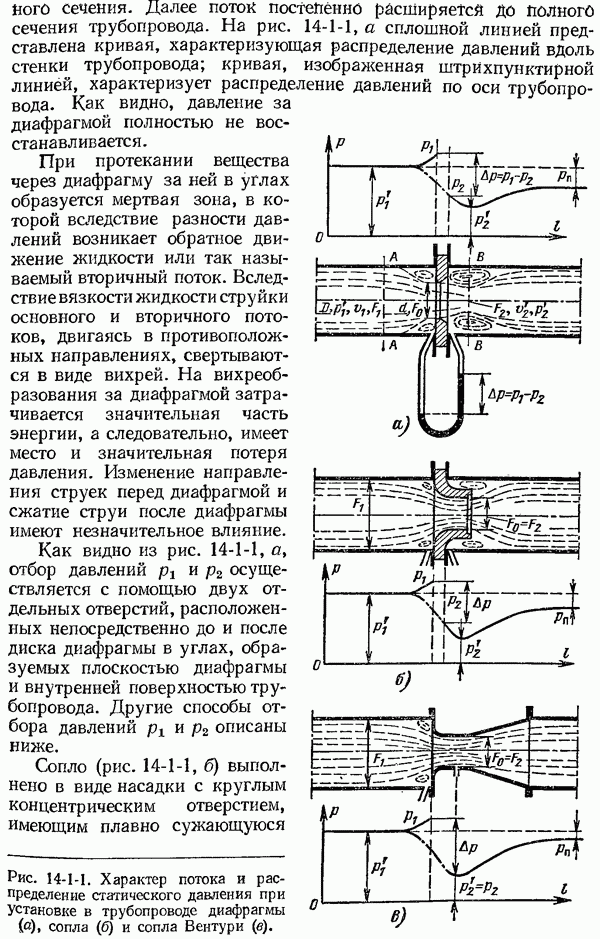
- 14-1. Основы теории и уравнения расхода
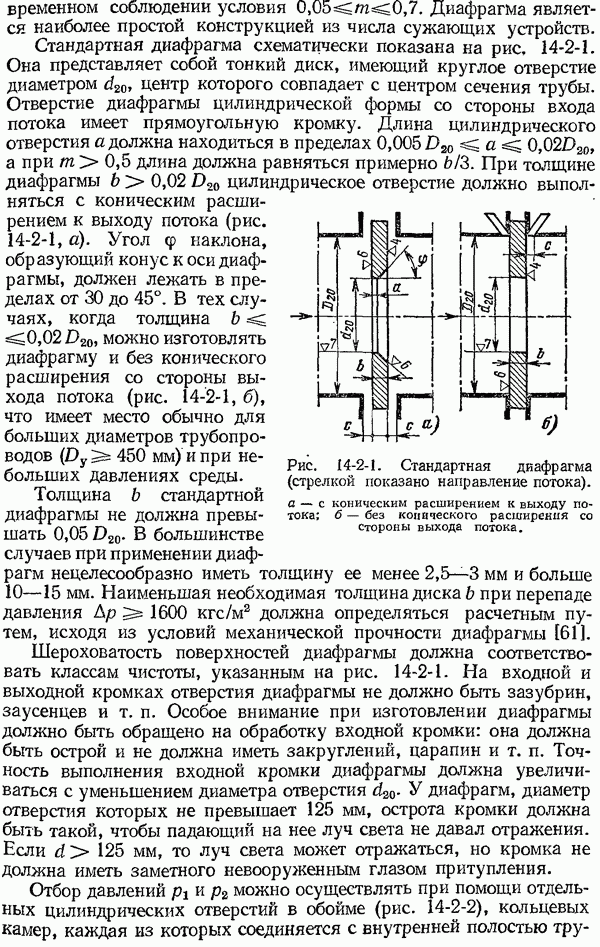
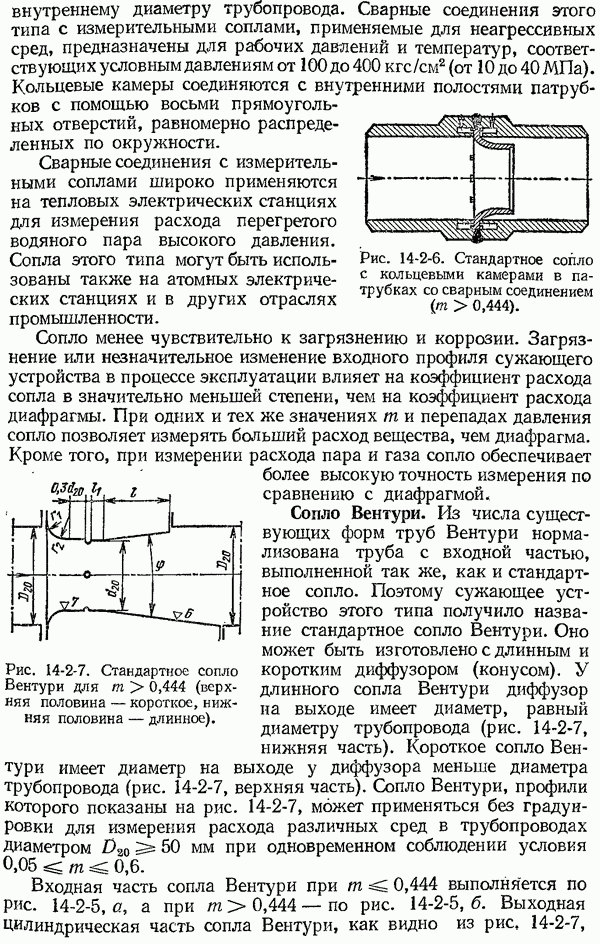
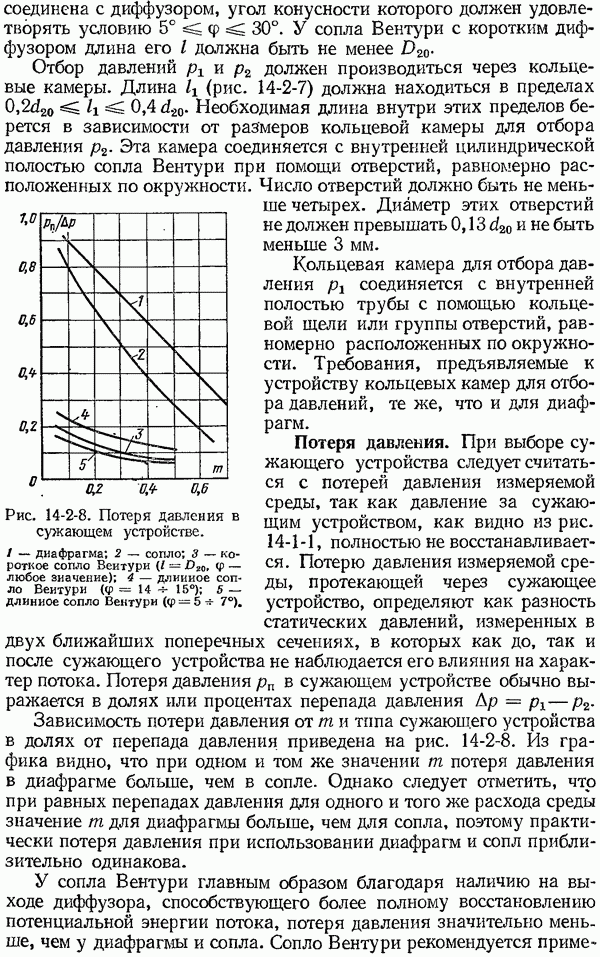
- 14-2. Стандартные сужающие устройства
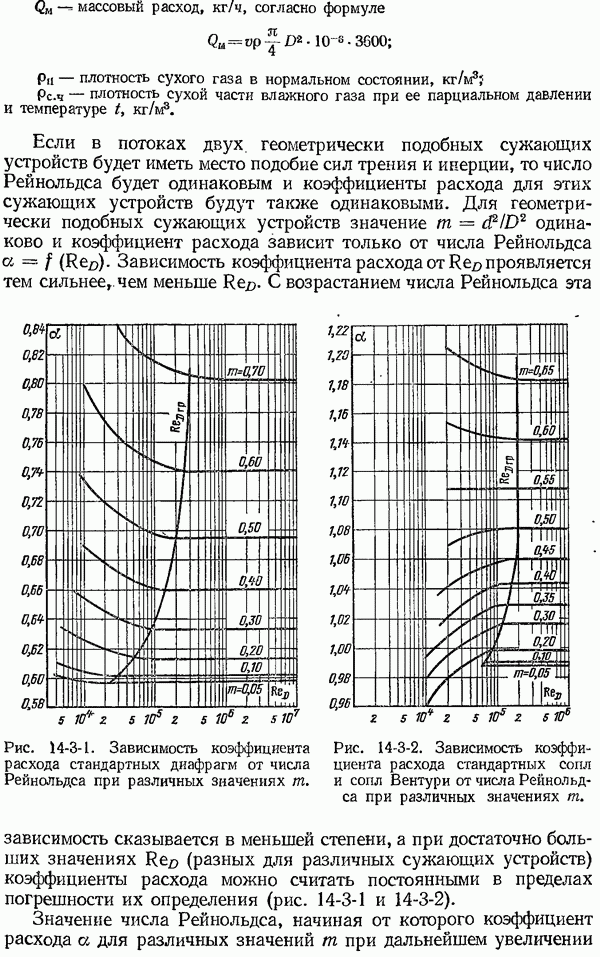
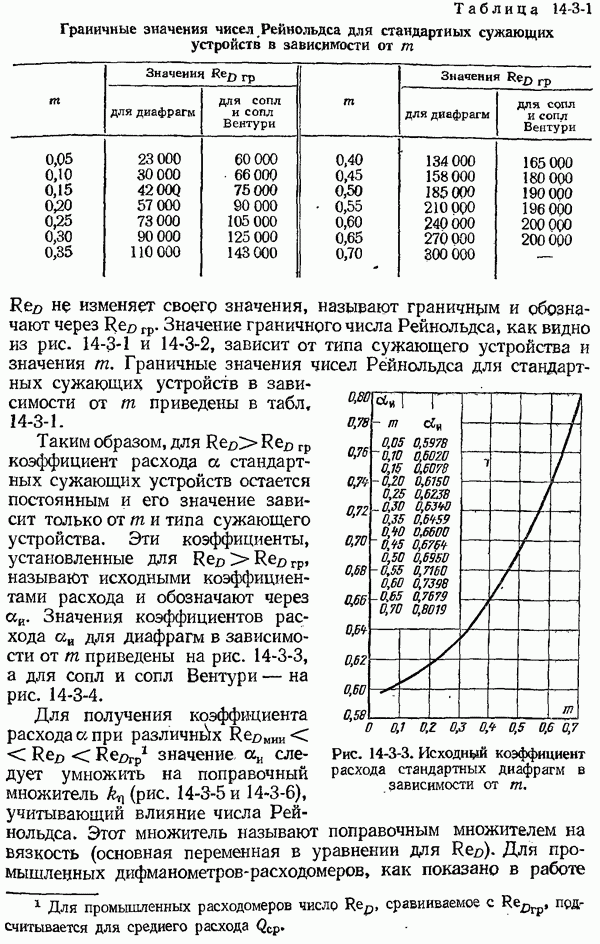
- 14-3. Коэффициенты расхода и поправочные множители к ним
- 14-4. Поправочный множитель на расширение измеряемой среды
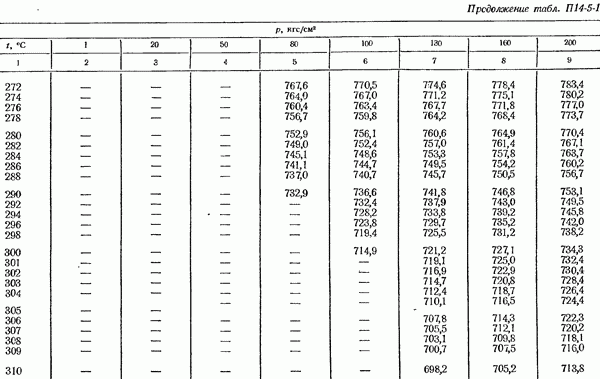
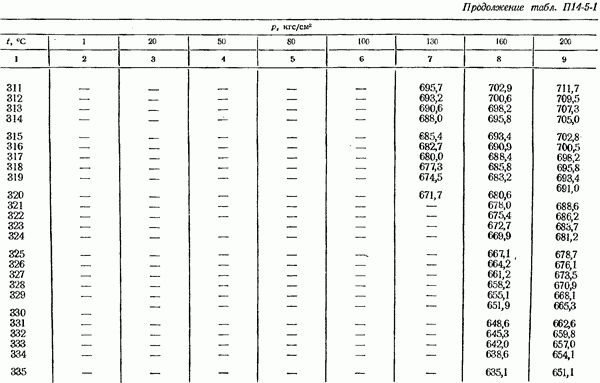
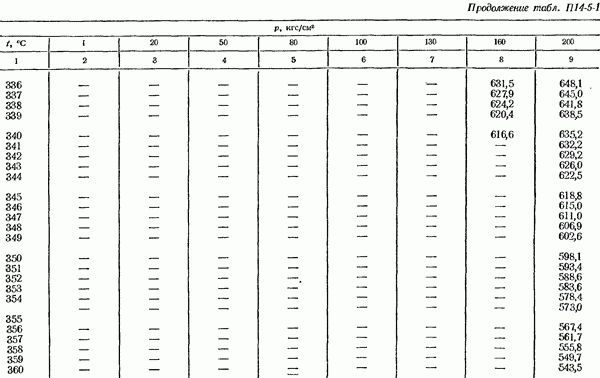
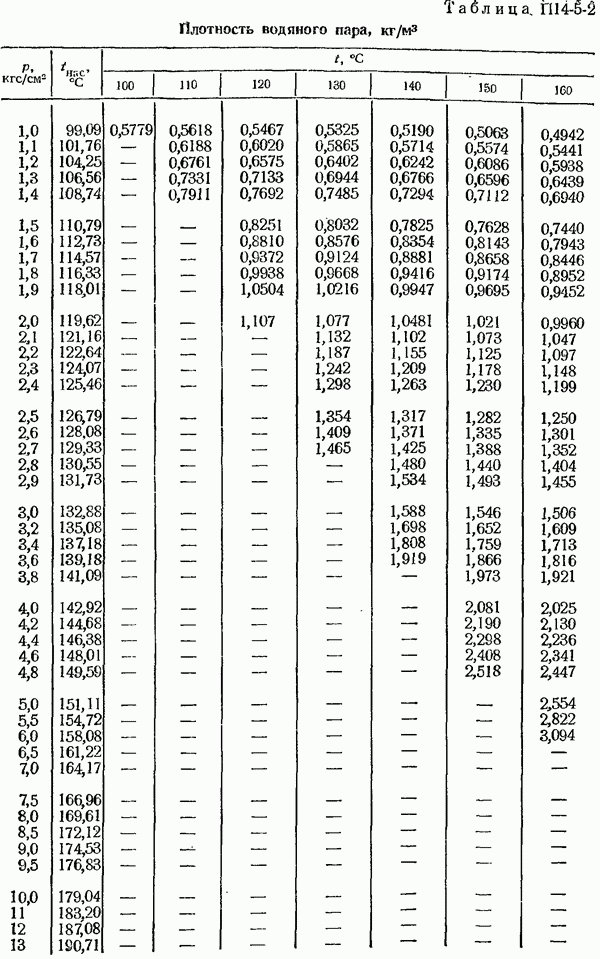
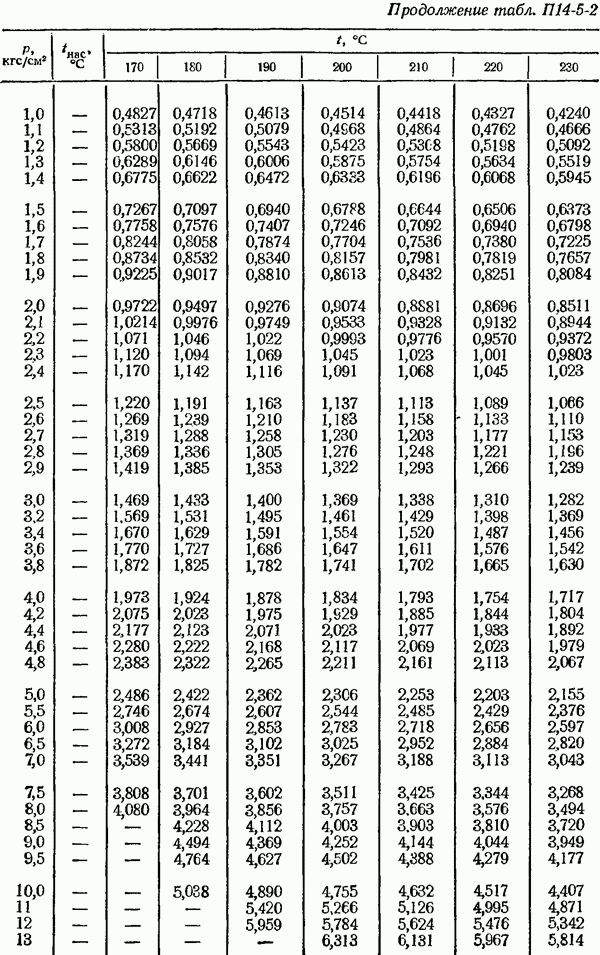
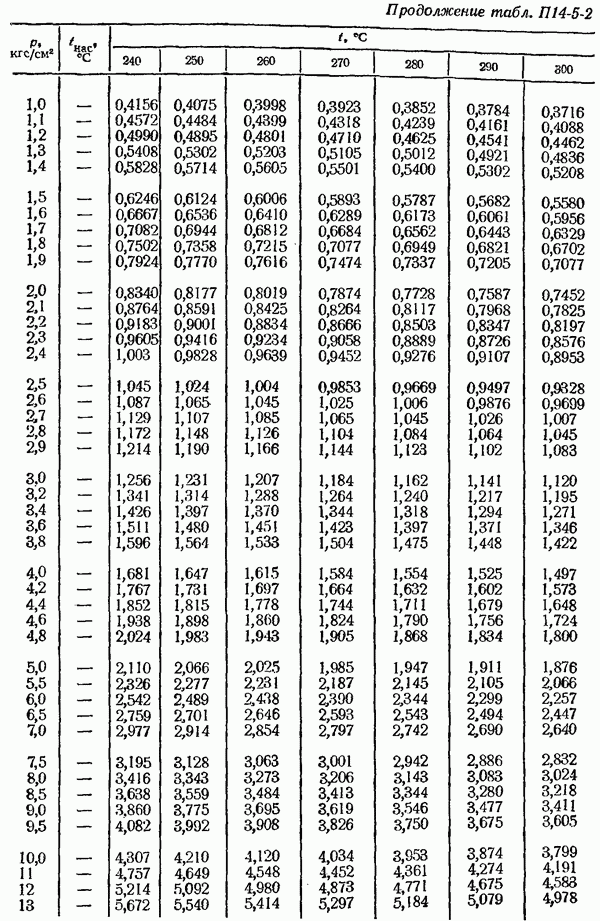
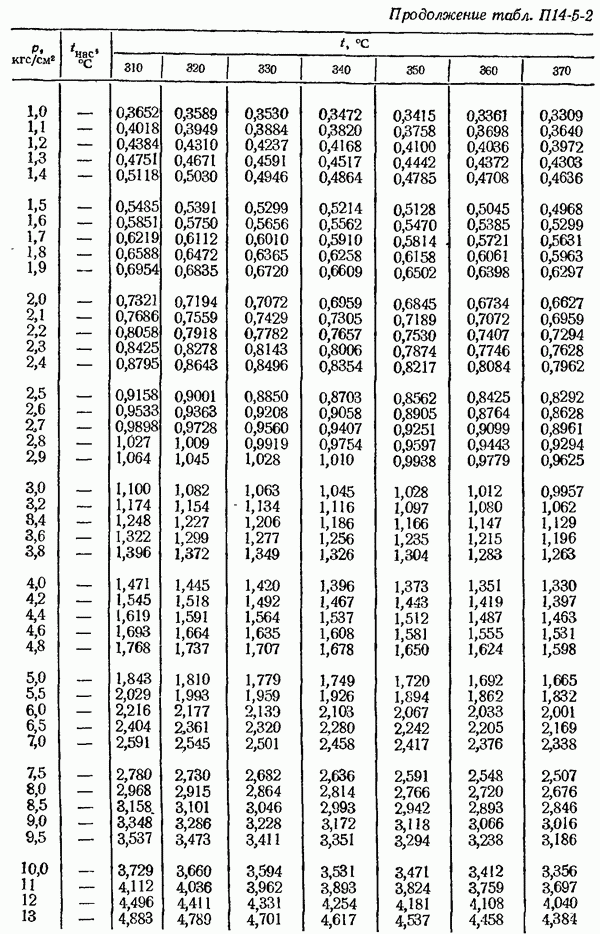
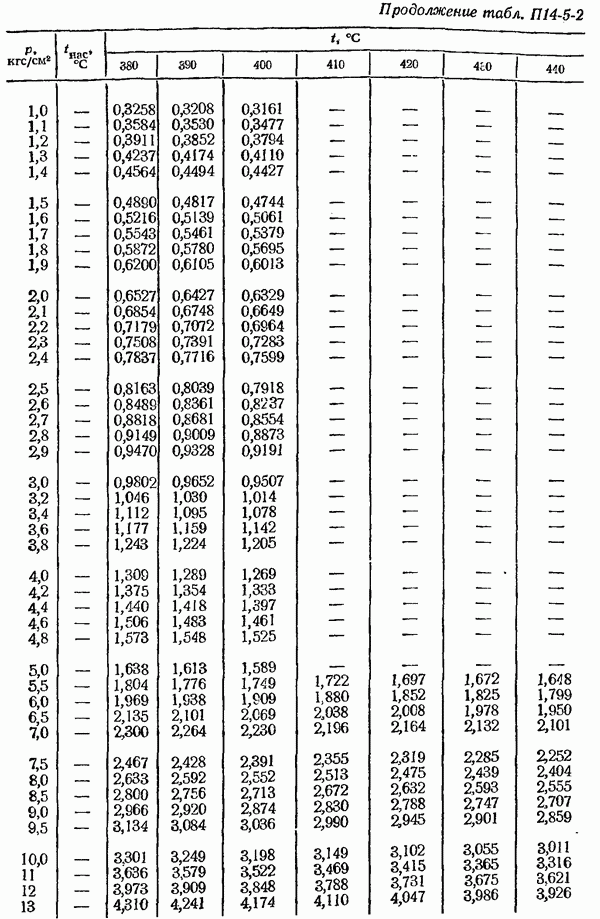
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
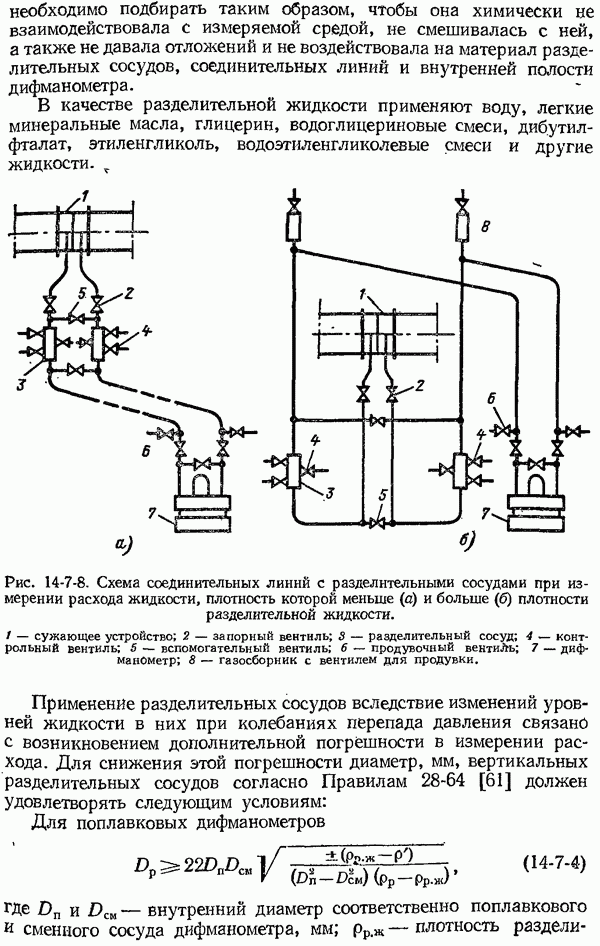
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
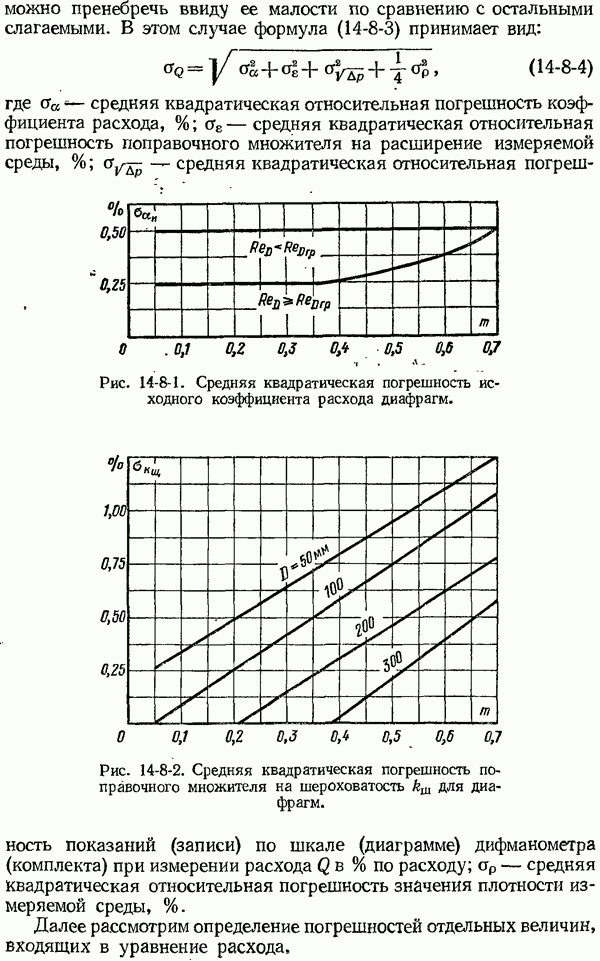
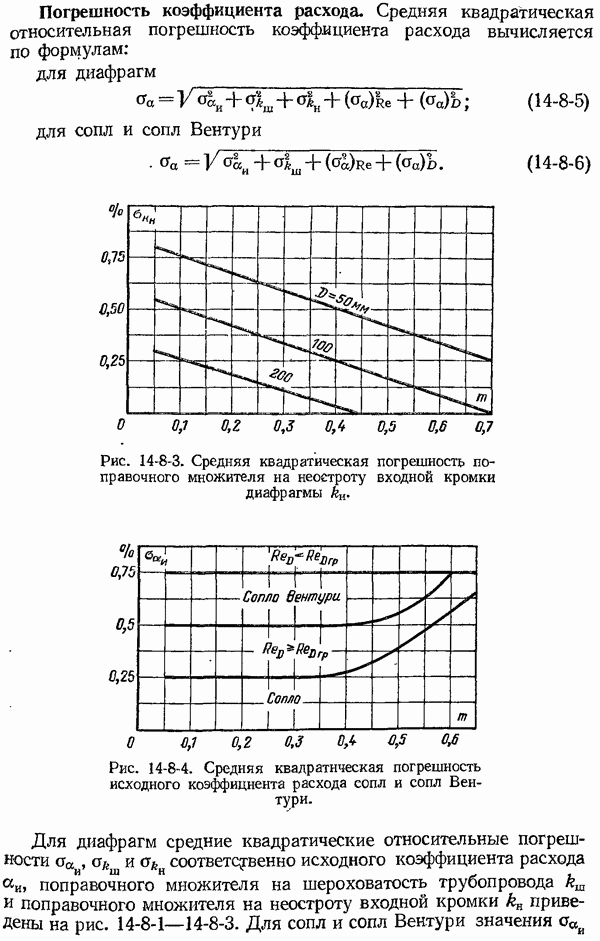
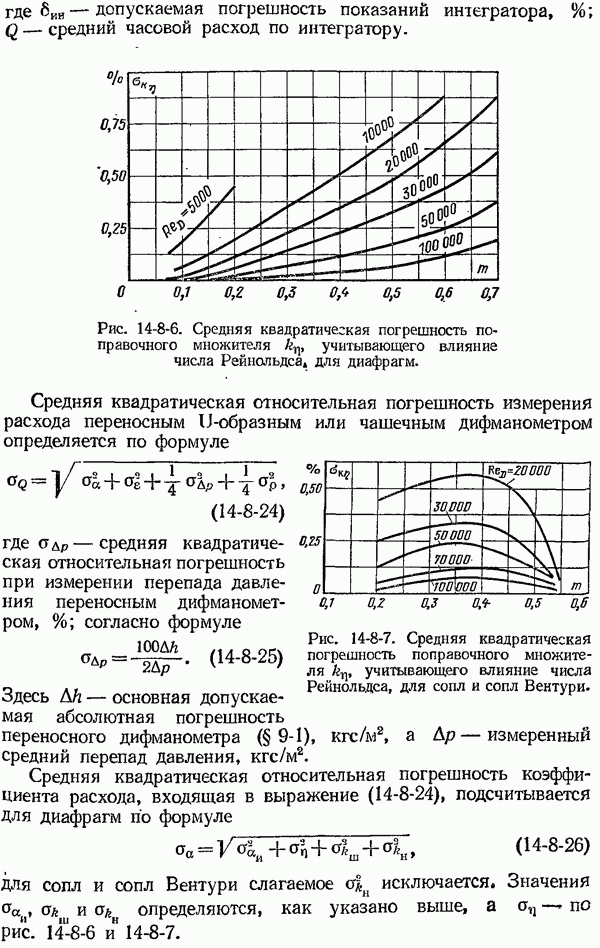
- 14-8. Погрешности измерения расхода
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
- 14-11. Измерение расхода при малых числах Рейнольдса
- 14-12. Измерение расхода загрязненных жидкостей и газов
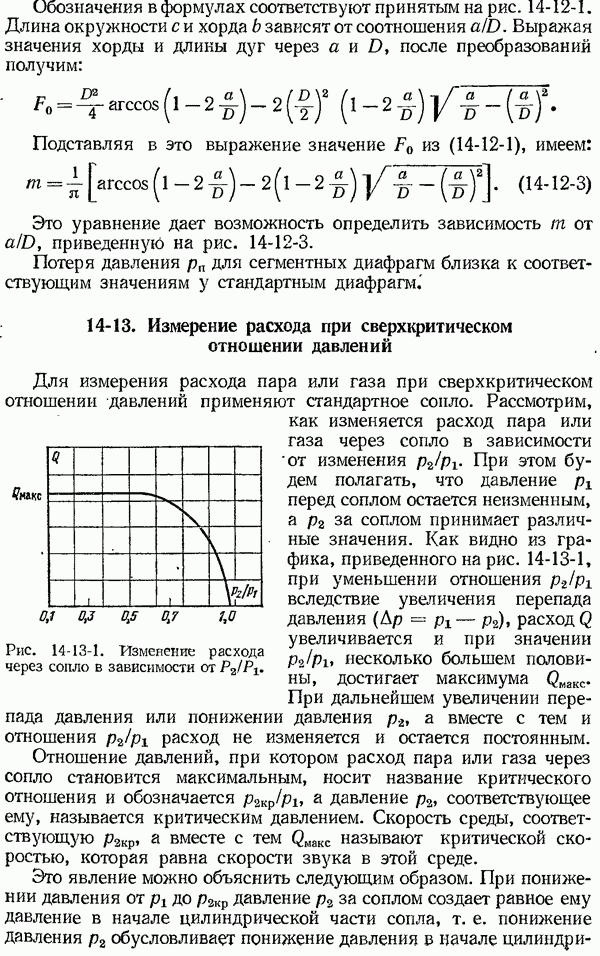
- 14-13. Измерение расхода при сверхкритическом отношении давлений
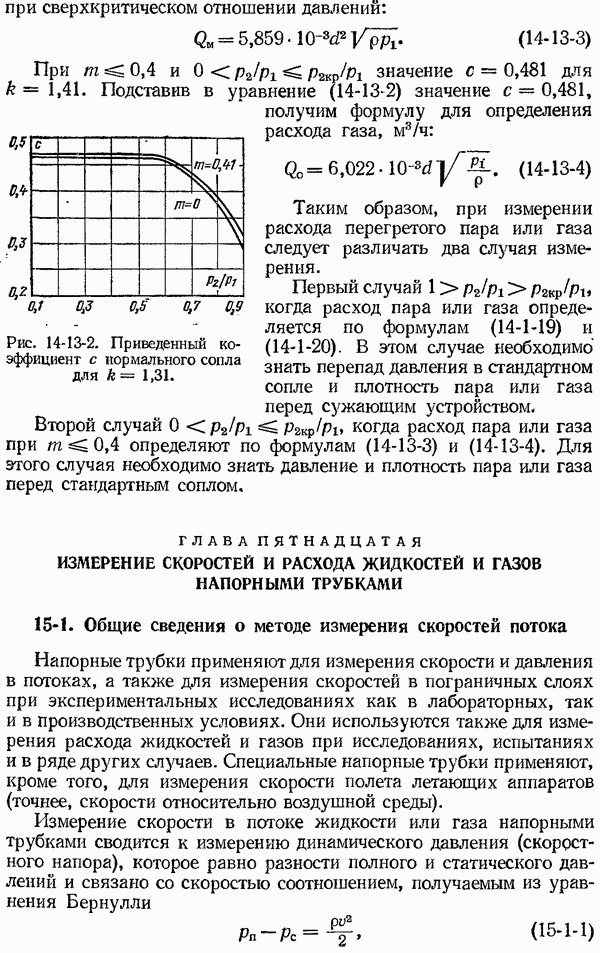
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
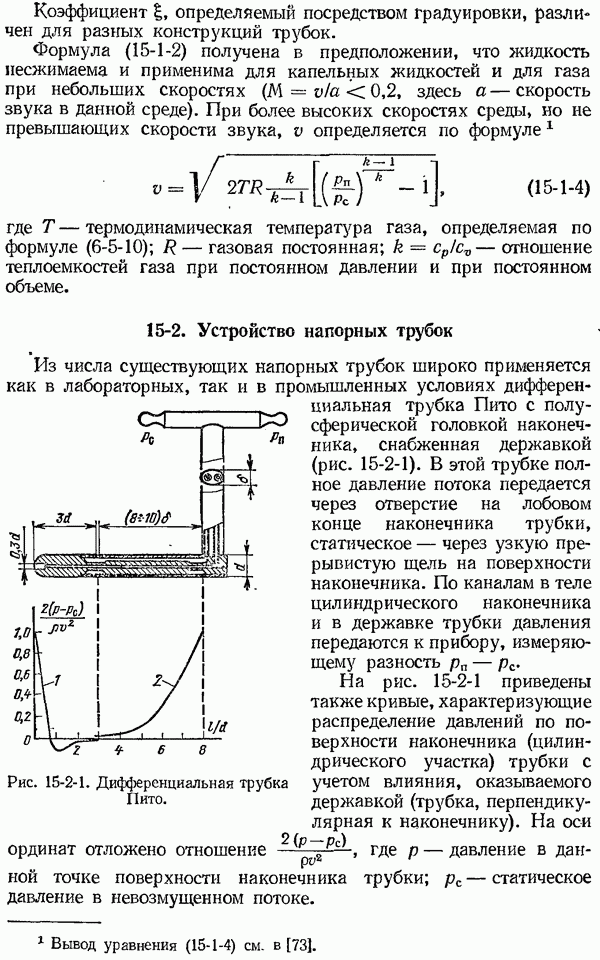
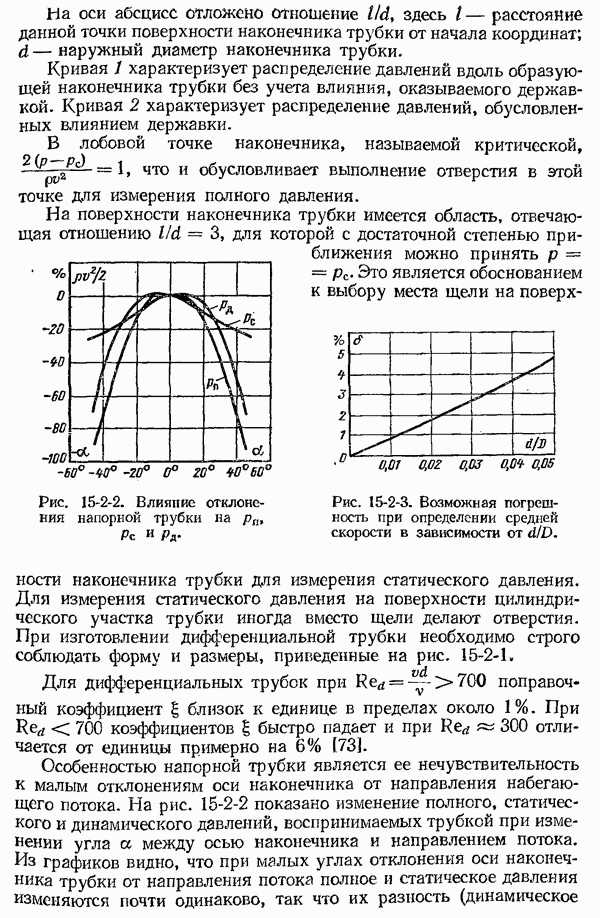
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
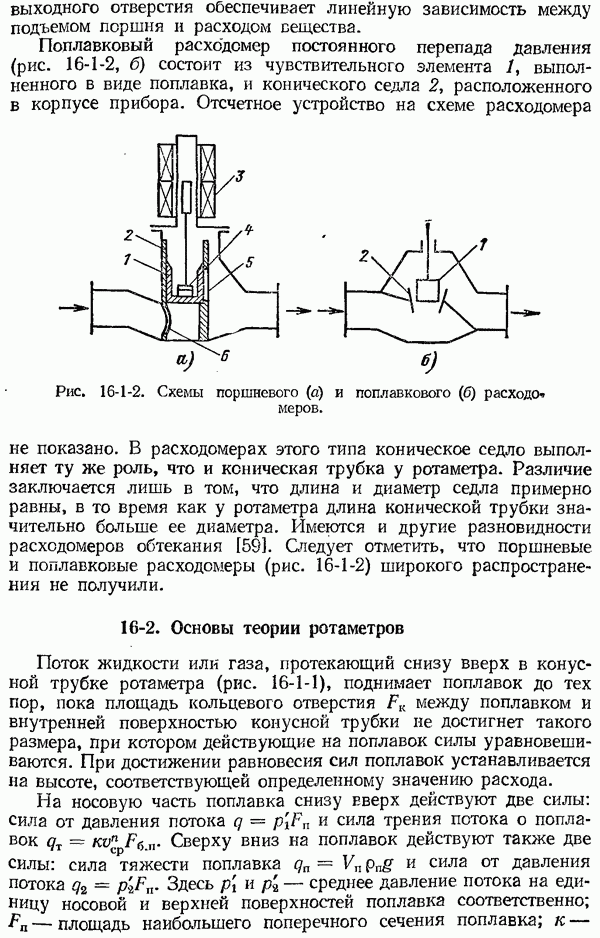
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
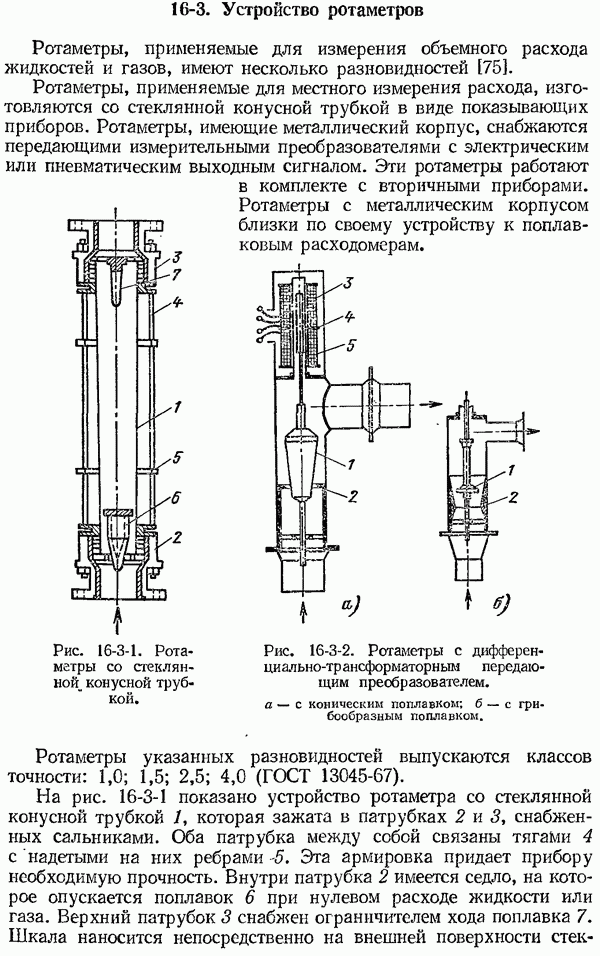
- 16-2. Основы теории ротаметров
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
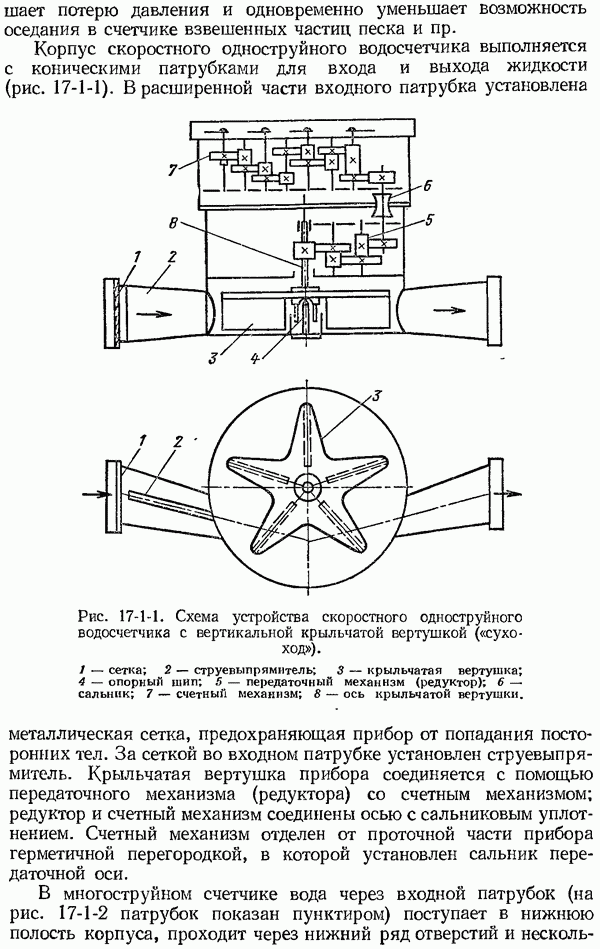
- 17-1. Тахометрические счетчики количества жидкостей
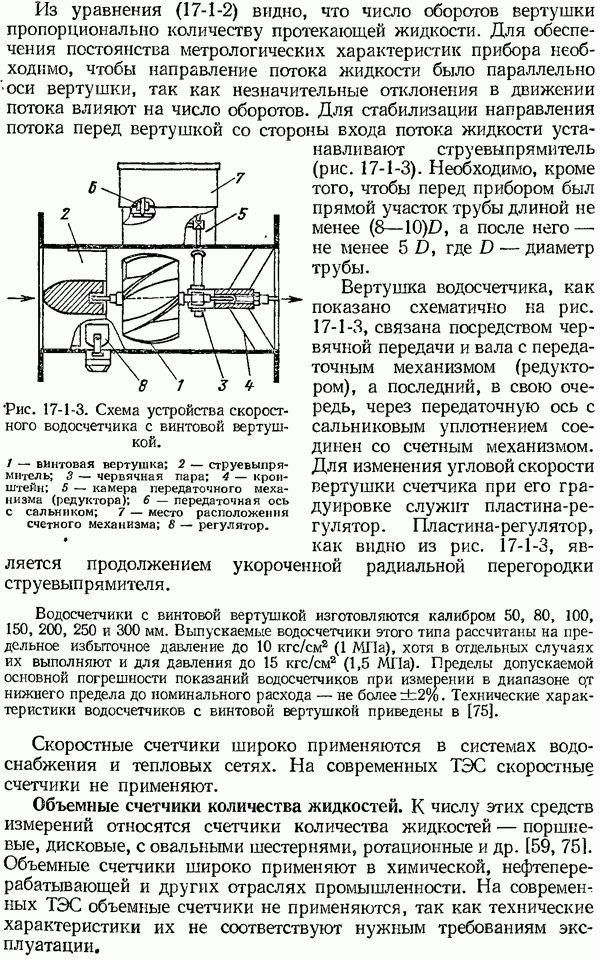
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
- 19-2. Измерение уровня воды в барабане парогенераторов
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
- 19-5. Емкостные уровнемеры
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
- 20-2. Сигнализаторы уровня сыпучих тел
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- 21-2. Газоанализаторы химические
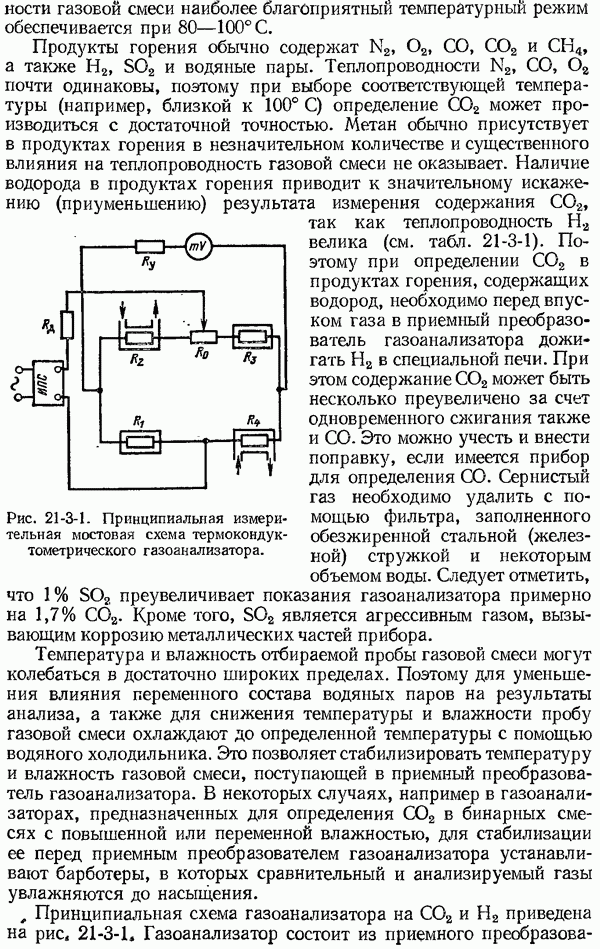
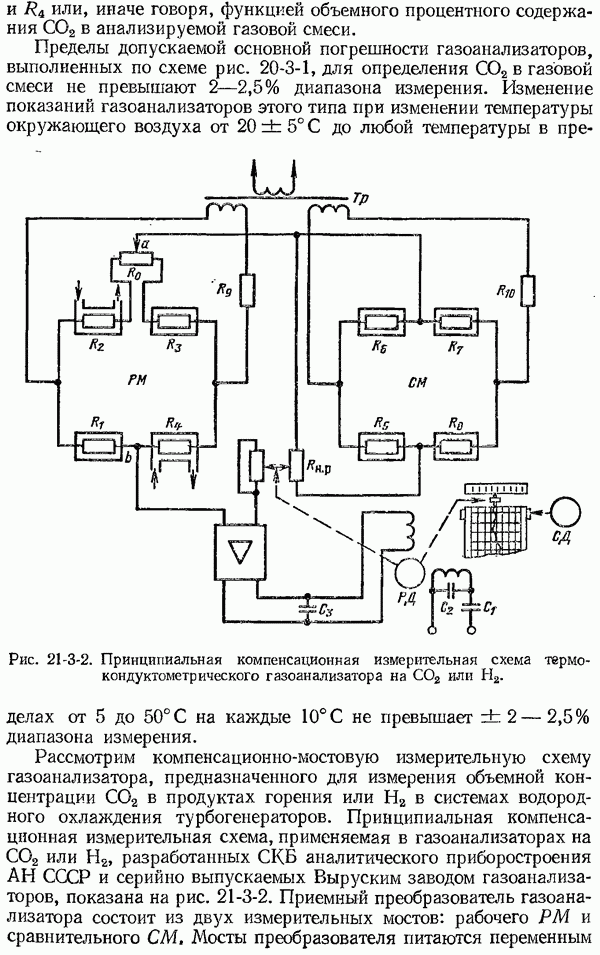
- 21-3. Тепловые газоанализаторы
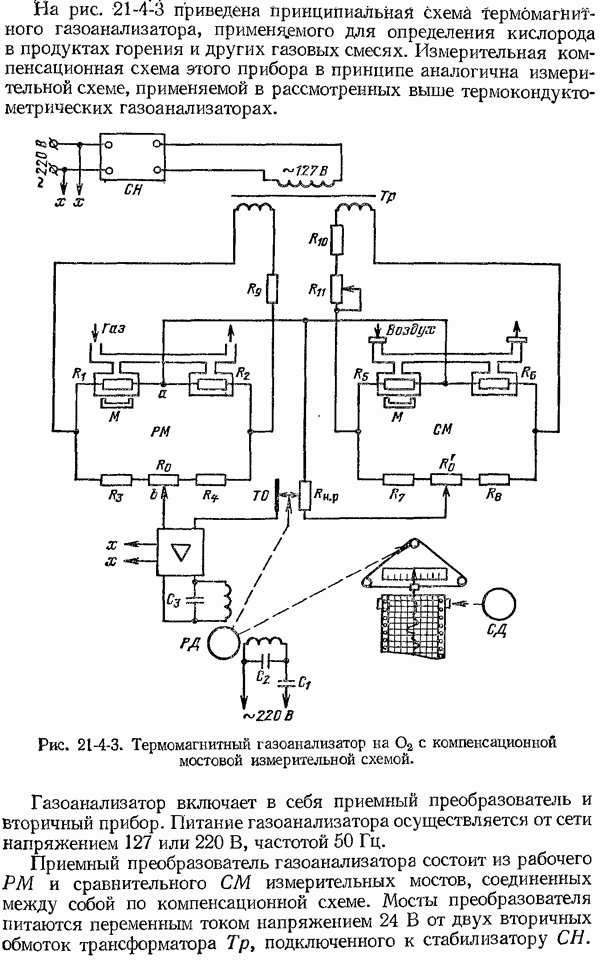
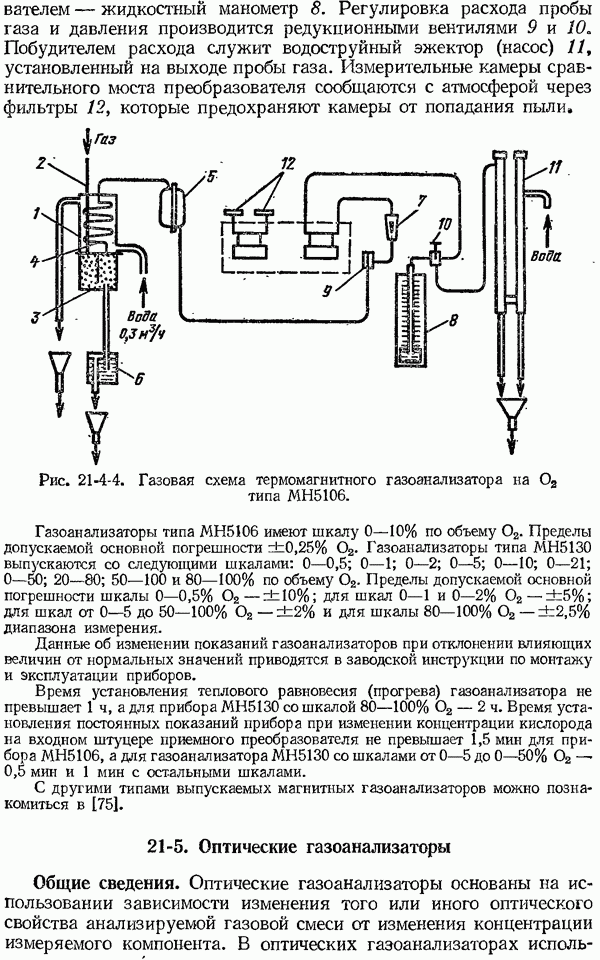
- 21-4. Магнитные газоанализаторы
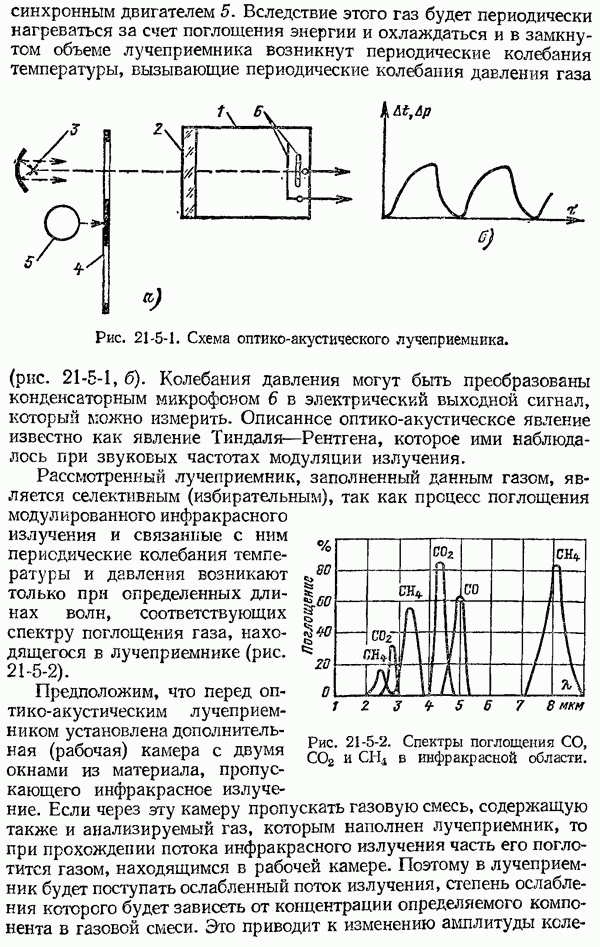
- 21-5. Оптические газоанализаторы
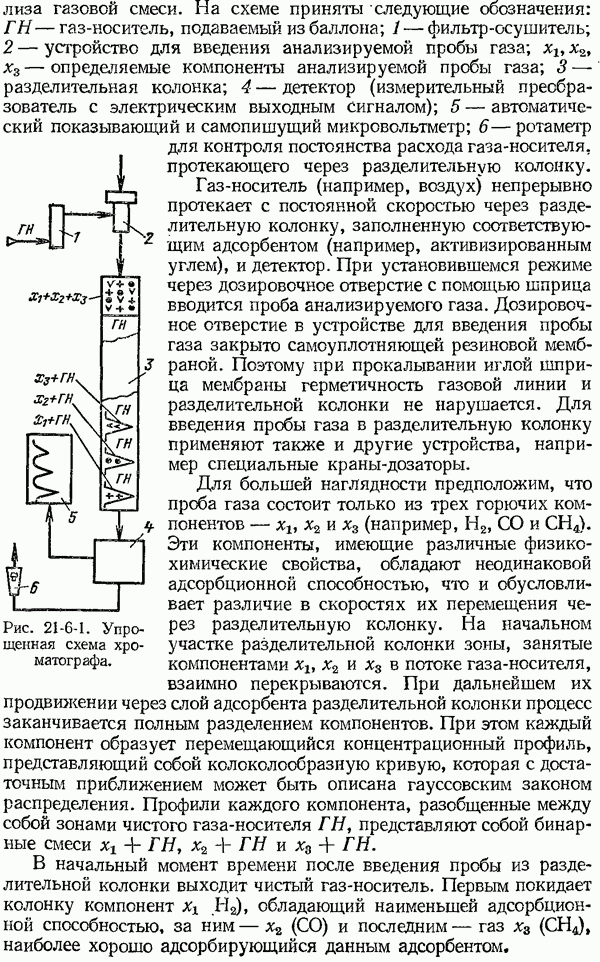
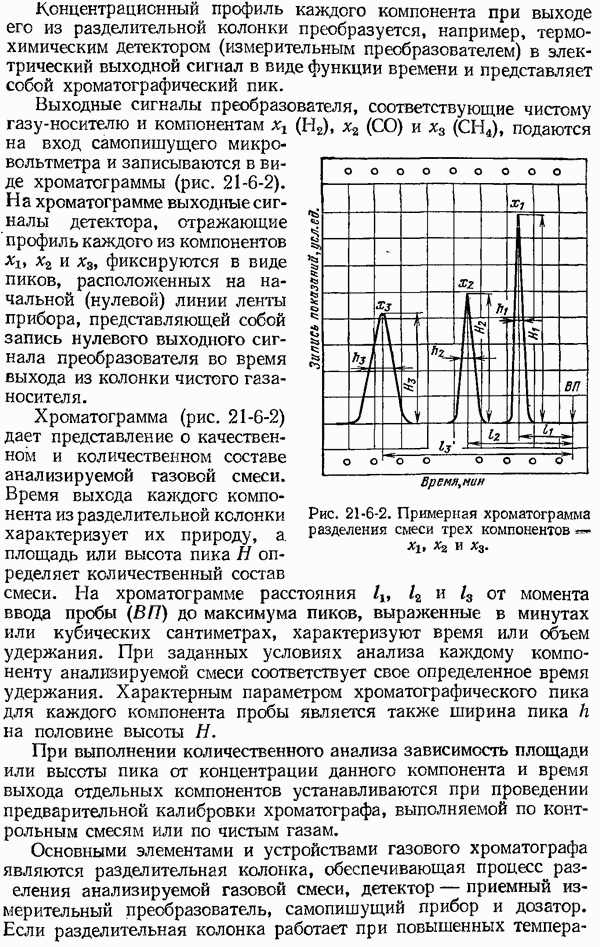
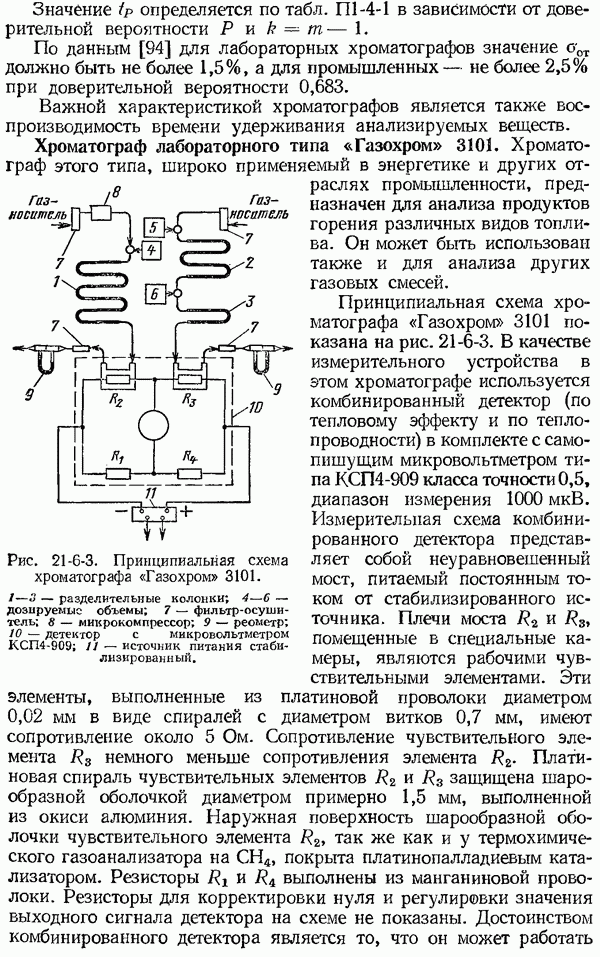
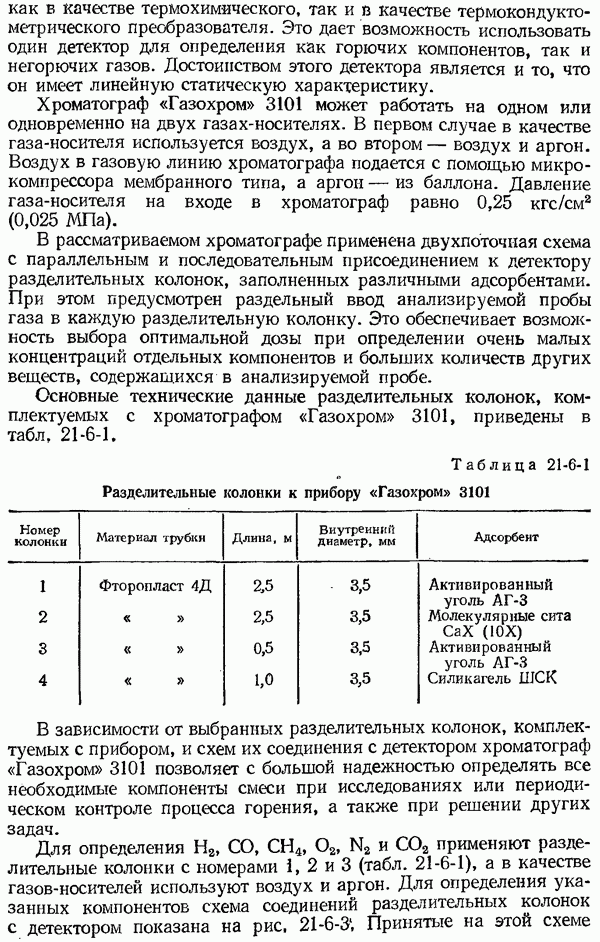
- 21-6. Газовые хроматографы
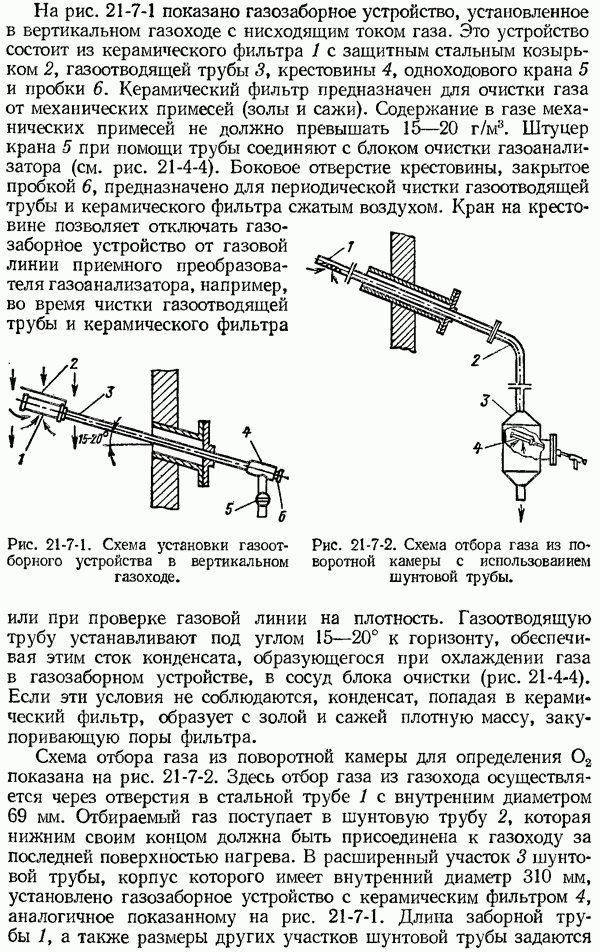
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
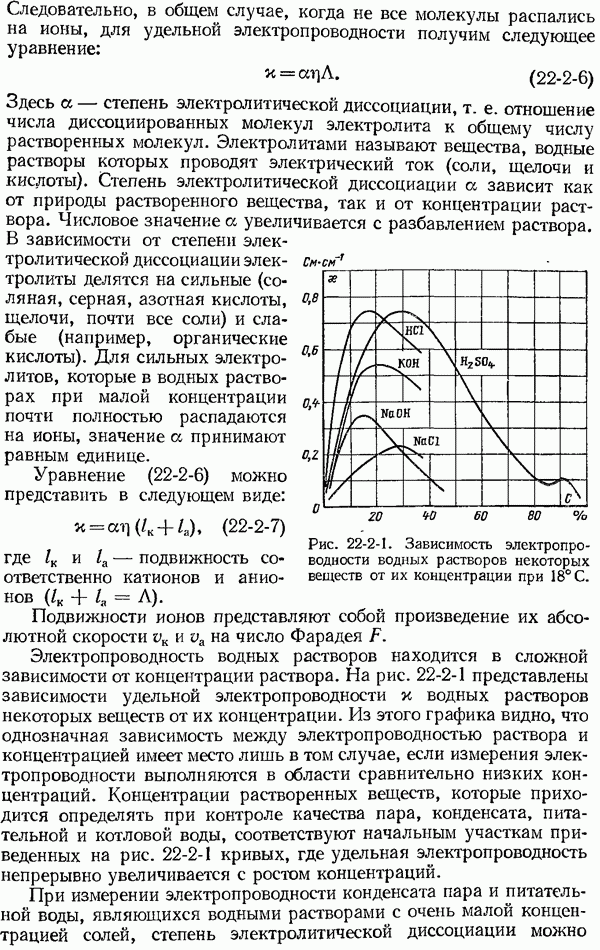
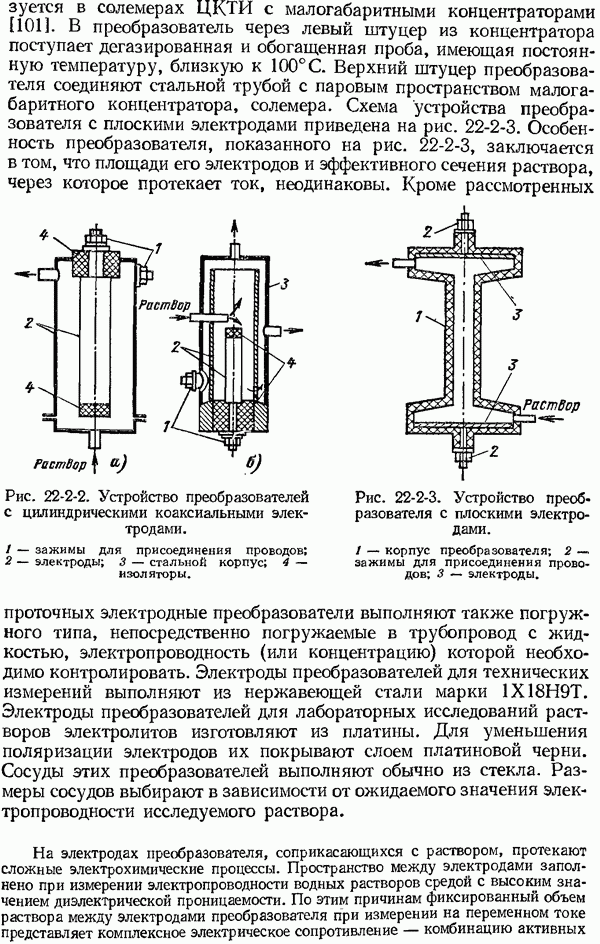
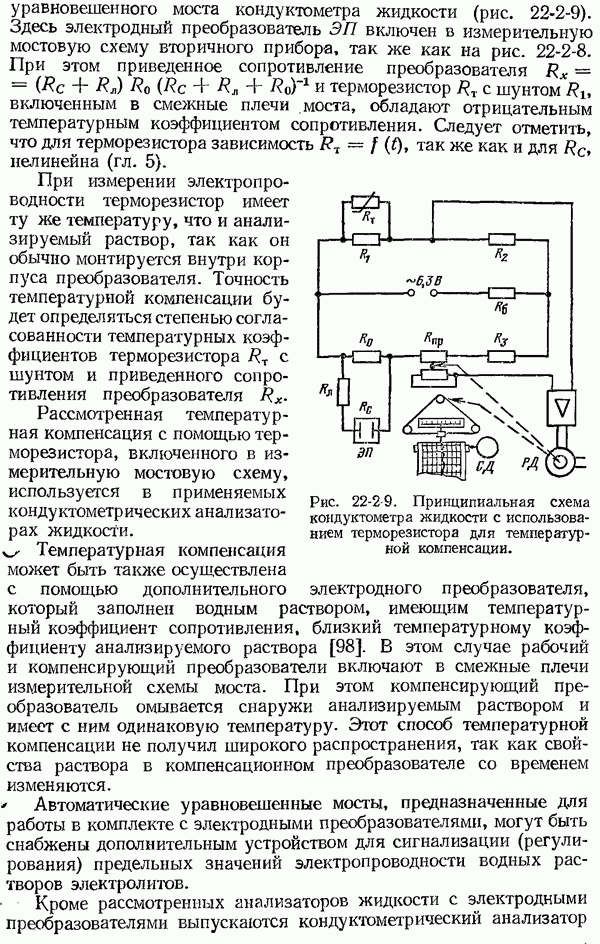
- 22-2. Измерение удельной электропроводности водных растворов
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
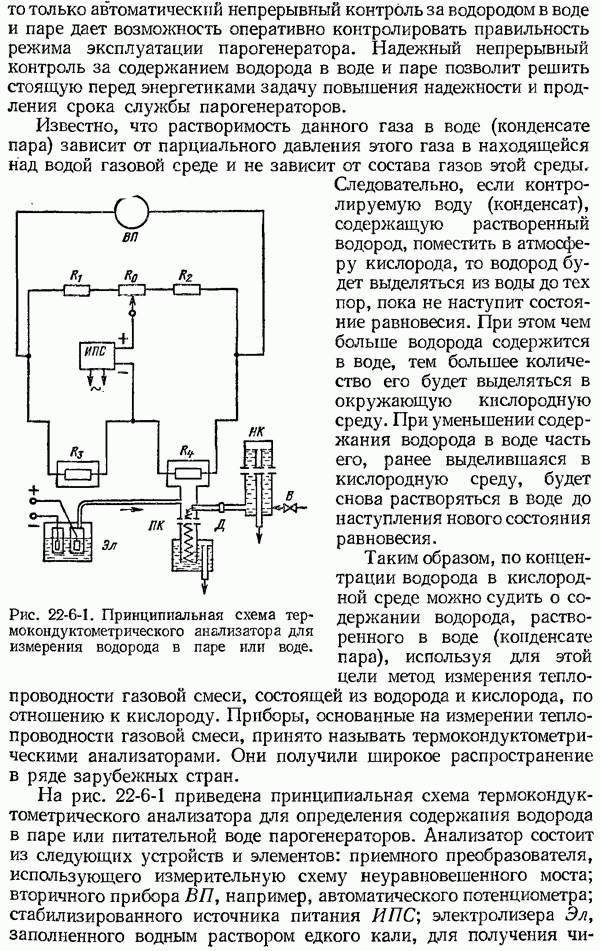
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ