| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1-4. Оценка и учет погрешностей при точных измерениях
При выполнении точных измерений пользуются средствами измерений повышенной точности, а вместе с тем применяют и более совершенные методы измерения. Однако, несмотря на это, вследствие неизбежного наличия во всяком измерении случайных погрешностей истинное значение измеряемой величины остается неизвестным и вместо него мы принимаем некоторое среднее арифметическое значение, относительно которого при большом числе измерений, как показывает теория вероятностей и математическая статистика, у нас есть обоснованная уверенность считать, что оно является наилучшим приближением к истинному значению.
Обычно, кроме случайных погрешностей, на точность измерения могут влиять систематические погрешности. Измерения должны проводиться так, чтобы систематических погрешностей не было. В дальнейшем при применении предложений и выводов, вытекающих из теории погрешностей, и обработке результатов наблюдения будем полагать, что ряды измерений не содержат систематических погрешностей, а также из них исключены грубые погрешности.
Теория случайных погрешностей, а вместе с тем и суждение о закономерностях, которым подчиняются случайные погрешности, основывается на двух аксиомах, базирующихся на опытных данных [2].
Аксиома случайности. При очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто, т. е. число отрицательных погрешностей равно числу положительных.
Аксиома распределения. Малые погрешности случаются чаще, чем большие. Очень большие погрешности не встречаются.
Пусть неизвестное истинное значение некоторой неизменной величины есть  При измерении этой величины получено
При измерении этой величины получено  независимых друг от друга результатов наблюдений
независимых друг от друга результатов наблюдений  Измерения выполнены одним и тем же прибором и с одинаковой тщательностью, т. е. одинаково точными и свободными от систематической погрешности. Предположим, что каждому измерению сопутствует случайная погрешность
Измерения выполнены одним и тем же прибором и с одинаковой тщательностью, т. е. одинаково точными и свободными от систематической погрешности. Предположим, что каждому измерению сопутствует случайная погрешность  — различная по значению и по знаку. Следовательно, для каждого результата наблюдений можно написать выражение вида
— различная по значению и по знаку. Следовательно, для каждого результата наблюдений можно написать выражение вида  и затем получить совокупность уравнений для ряда измерений:
и затем получить совокупность уравнений для ряда измерений:

Предположим, что в выполненных измерениях число, сумма и числовые значения положительных случайных погрешностей приблизительно равны числу, сумме и значениям отрицательных погрешностей. Другими словами, распределение случайных погрешностей — равностороннее по отношению к среднему значению измерений 
Таким образом, по предположению,

и потому

Это равенство позволяет считать, что среднее арифметическое значение X (или математическое ожидание  является наиболее близким к истинному значению измеряемой величины X, какое только можно получить из имеющихся опытных данных. Сделанное допущение о справедливости
является наиболее близким к истинному значению измеряемой величины X, какое только можно получить из имеющихся опытных данных. Сделанное допущение о справедливости  и приводит к справедливости выражения (1-4-3).
и приводит к справедливости выражения (1-4-3).
После того как найдено среднее значение X (1-4-3) для ряда наблюдений  для изучения погрешностей необходимо найти случайные отклонения
для изучения погрешностей необходимо найти случайные отклонения  каждого результата наблюдения от среднего значения X:
каждого результата наблюдения от среднего значения X:

В соответствии с аксиомой случайности

Выше отмечалось, что отклонения в измерениях или погрешности являются случайными, т. е. значение (размер) их для каждого отдельного измерения нельзя предвидеть. Поэтому представляется естественным применять к ним те общие законы для случайных явлений (или величин), которые рассматриваются в теории вероятностей и математической статистике.
Закон нормального распределения случайных погрешностей выражается следующим уравнением:

где  — плотность распределения вероятностей;
— плотность распределения вероятностей;  среднее квадратическое отклонение результата наблюдения при большом числе измерений
среднее квадратическое отклонение результата наблюдения при большом числе измерений  основание натуральных логарифмов;
основание натуральных логарифмов; 
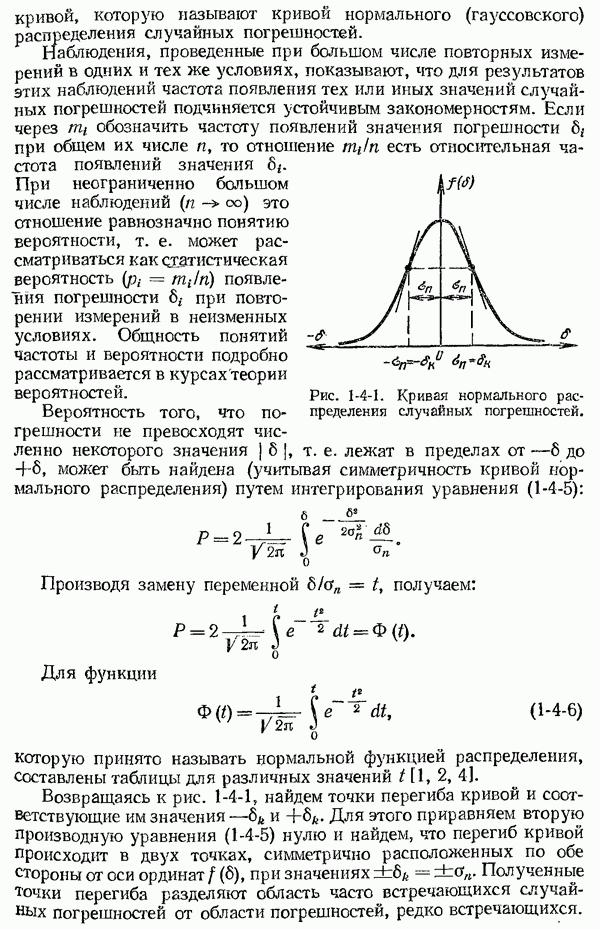
На рис. 1-4-1 закон распределения случайных погрешностей, выражаемый уравнением (1-4-5), представлен в виде симметричной
кривой, которую называют кривой нормального (гауссовского) распределения случайных погрешностей.
Наблюдения, проведенные при большом числе повторных измерений в одних и тех же условиях, показывают, что для результатов этих наблюдений частота появления тех или иных значений случайных погрешностей подчиняется устойчивым закономерностям. Если через  обозначить частоту появлений значения погрешности
обозначить частоту появлений значения погрешности  ; при общем их числе
; при общем их числе  то отношение
то отношение  есть относительная частота появлений значения
есть относительная частота появлений значения 

Рис. 1-4-1. Кривая нормального распределения случайных погрешностей.
При неограниченно большом числе наблюдений  это отношение равнозначно понятию вероятности, т. е. может рассматриваться как статистическая вероятность
это отношение равнозначно понятию вероятности, т. е. может рассматриваться как статистическая вероятность  появления погрешности
появления погрешности  при повторении измерений в неизменных условиях. Общность понятий частоты и вероятности подробно рассматривается в курсахтеории вероятностей.
при повторении измерений в неизменных условиях. Общность понятий частоты и вероятности подробно рассматривается в курсахтеории вероятностей.
Вероятность того, что погрешности не превосходят численно некоторого значения  т. е. лежат в пределах от
т. е. лежат в пределах от  до
до  может быть найдена (учитывая симметричность кривой нормального распределения) путем интегрирования уравнения (1-4-5):
может быть найдена (учитывая симметричность кривой нормального распределения) путем интегрирования уравнения (1-4-5):

Производя замену переменной  получаем:
получаем:

Для функции

которую принято называть нормальной функцией распределения, составлены таблицы для различных значений  [1, 2, 4].
[1, 2, 4].
Возвращаясь к рис. 1-4-1, найдем точки перегиба кривой и соответствующие им значения  Для этого приравняем вторую производную уравнения (1-4-5) нулю и найдем, что перегиб кривой происходит в двух точках, симметрично расположенных по обе стороны от оси ординат
Для этого приравняем вторую производную уравнения (1-4-5) нулю и найдем, что перегиб кривой происходит в двух точках, симметрично расположенных по обе стороны от оси ординат  при значениях
при значениях  Полученные Точки перегиба разделяют область часто встречающихся случайных погрешностей от области погреашостей, редко встречающихся.
Полученные Точки перегиба разделяют область часто встречающихся случайных погрешностей от области погреашостей, редко встречающихся.
Для неограниченно большого ряда измерений 68,3% всех случайных погрешностей ряда лежит ниже далного значения  и 31,7% выше его.
и 31,7% выше его.
Параметр  однозначно характеризует форму кривой распределения случайных погрешностей. Ордината
однозначно характеризует форму кривой распределения случайных погрешностей. Ордината  кривой распределения, соответствующая
кривой распределения, соответствующая  обратно пропорциональна
обратно пропорциональна  при увеличении
при увеличении  ордината
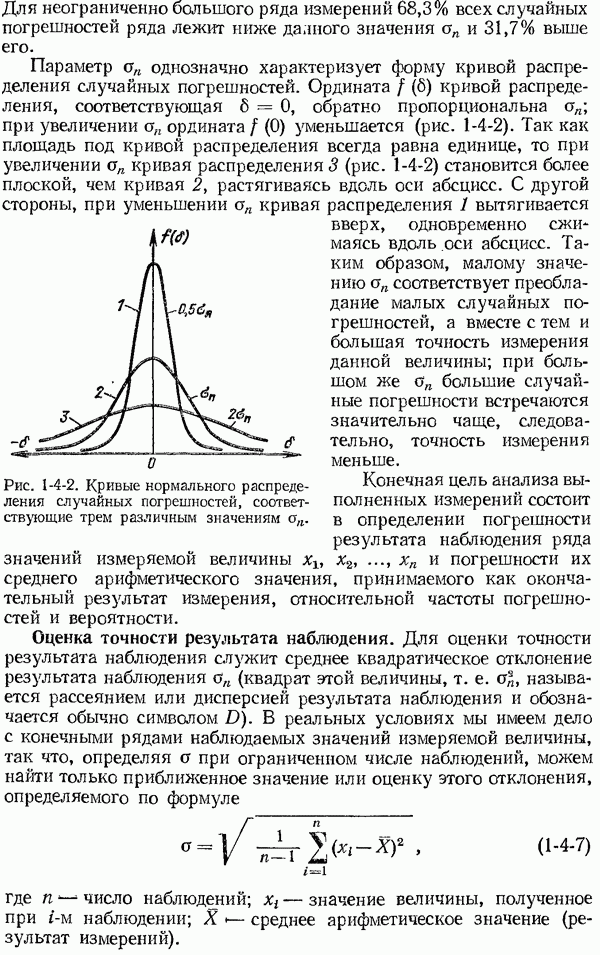
ордината  уменьшается (рис. 1-4-2). Так как площадь под кривой распределения всегда равна единице, то при увеличении
уменьшается (рис. 1-4-2). Так как площадь под кривой распределения всегда равна единице, то при увеличении  кривая распределения 3 (рис. 1-4-2) становится более плоской, чем кривая 2, растягиваясь вдоль оси абсцисс. С другой стороны, при уменьшении
кривая распределения 3 (рис. 1-4-2) становится более плоской, чем кривая 2, растягиваясь вдоль оси абсцисс. С другой стороны, при уменьшении  кривая распределения 1 вытягивается вверх, одновременно сжимаясь вдоль оси абсцисс. Таким образом, малому значению
кривая распределения 1 вытягивается вверх, одновременно сжимаясь вдоль оси абсцисс. Таким образом, малому значению  соответствует преобладание малых случайных погрешностей, а вместе с тем и большая точность измерения данной величины; при большом же
соответствует преобладание малых случайных погрешностей, а вместе с тем и большая точность измерения данной величины; при большом же  большие случайные погрешности встречаются значительно чаще, следовательно, точность измерения меньше.
большие случайные погрешности встречаются значительно чаще, следовательно, точность измерения меньше.

Рис. 1-4-2. Кривые нормального распределения случайных погрешностей, соответствующие трем различным значениям 
Конечная цель анализа выполненных измерений состоит в определении погрешности результата наблюдения ряда значений измеряемой величины  и погрешности их среднего арифметического значения, принимаемого как окончательный результат измерения, относительной частоты погрешностей и вероятности.
и погрешности их среднего арифметического значения, принимаемого как окончательный результат измерения, относительной частоты погрешностей и вероятности.
Оценка точности результата наблюдения. Для оценки точности результата наблюдения служит среднее квадратическое отклонение результата наблюдения  (квадрат этой величины, т. е.
(квадрат этой величины, т. е.  называется рассеянием или дисперсией результата наблюдения и обозначается обычно символом
называется рассеянием или дисперсией результата наблюдения и обозначается обычно символом  . В реальных условиях мы имеем дело с конечными рядами наблюдаемых значений измеряемой величины, так что, определяя а при ограниченном числе наблюдений, можем найти только приближенное значение или оценку этого отклонения, определяемого по формуле
. В реальных условиях мы имеем дело с конечными рядами наблюдаемых значений измеряемой величины, так что, определяя а при ограниченном числе наблюдений, можем найти только приближенное значение или оценку этого отклонения, определяемого по формуле

где  число наблюдений;
число наблюдений;  значение величины, полученное при
значение величины, полученное при  наблюдении; X — среднее арифметическое значение (результат измерений).
наблюдении; X — среднее арифметическое значение (результат измерений).
Выражение (1-4-7). при ограниченном числе наблюдений дает несмещенную оценку среднего квадратического отклонения результата наблюдений [1].
Для получения полного представления о точности и надежности оценки случайного отклонения результата наблюдения должны быть указаны доверительные границы, доверительный интервал и доверительная вероятность. При известном а доверительные границы указываются следующим образом: нижняя граница —  или
или  верхняя граница
верхняя граница  или
или  а (сокращенно
а (сокращенно  или
или  за пределы которых с вероятностью
за пределы которых с вероятностью  (или 68,3%) не выйдут значения случайных отклонений
(или 68,3%) не выйдут значения случайных отклонений  или результатов отдельных наблюдений
или результатов отдельных наблюдений  ряда измерений. Доверительный интервал выражается в виде
ряда измерений. Доверительный интервал выражается в виде

В зависимости от целей измерения могут задаваться и другие доверительные границы:  или
или  или
или  Чтобы избежать при определении значения величины
Чтобы избежать при определении значения величины

обратного интерполирования табличной функции  (1-4-6), пользуются специально составленной таблицей [1]. Значения
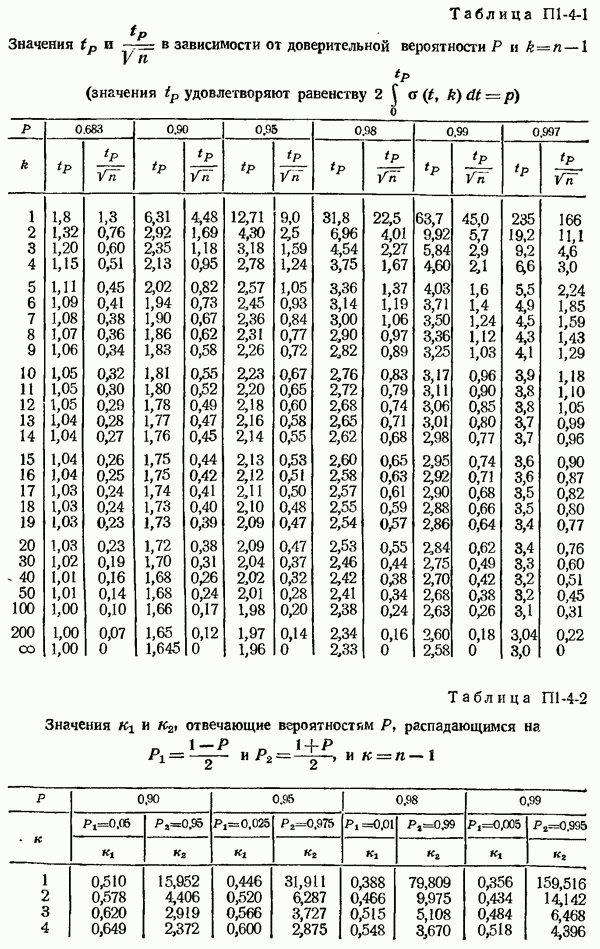
(1-4-6), пользуются специально составленной таблицей [1]. Значения  для наиболее употребительных доверительных вероятностей при
для наиболее употребительных доверительных вероятностей при  приведены в табл. 1-4-1. В инженерной практике предпочтение отдается вероятности 0,95 и 0,997,
приведены в табл. 1-4-1. В инженерной практике предпочтение отдается вероятности 0,95 и 0,997,
Таблица 1-4-1 (см. скан) Значения  для наиболее употребительных вероятностей при
для наиболее употребительных вероятностей при 
Оценка точности результата измерения. Для оценки достоверности результата измерения, принимаемого равным среднему значению X, применяют показатель точности, аналогичный показателю точности результата наблюдения. При этом согласно теории погрешностей оценка среднего квадратического отклонения результата измерения в  раз меньше оценки среднего квадратического отклонения результата наблюдения (1-4-7). Таким образом, при числе измерений
раз меньше оценки среднего квадратического отклонения результата наблюдения (1-4-7). Таким образом, при числе измерений  оценка среднего квадратического отклонения результата измерения
оценка среднего квадратического отклонения результата измерения

Доверительные границы погрешности результата измерения указываются следующим образом: нижняя граница  или
или  , верхняя граница
, верхняя граница  или
или  за пределы которых с вероятностью 0,683 не выйдут погрешности результата измерения или среднее арифметическое значение
за пределы которых с вероятностью 0,683 не выйдут погрешности результата измерения или среднее арифметическое значение  Доверительный интервал представляют в виде
Доверительный интервал представляют в виде

В зависимости от назначения измерений может быть задана и другая доверительная вероятность. В этом случае доверительные границы записываются как  или
или  или
или  а доверительный интервал
а доверительный интервал

Оценка точности результата измерения при малом числе наблюдений. На практике, как правило, число измерений конечно и в большинстве случаев не превышает  отдельных наблюдений, а при ответственных измерениях
отдельных наблюдений, а при ответственных измерениях  — нескольких десятков. При малом числе наблюдений
— нескольких десятков. При малом числе наблюдений  и условии, что распределение погрешностей отдельных измерений следует нормальному, пользуются для определения
и условии, что распределение погрешностей отдельных измерений следует нормальному, пользуются для определения  таблицей, основанной на распределении Стьюдента.
таблицей, основанной на распределении Стьюдента.
Измерения при малом числе наблюдений чаще дают преуменьшенное значение средней квадратической погрешности по сравнению с погрешностью для достаточно большего ряда тех же измерений. Распределение Стьюдента, упрошенно говоря, учитывает это обстоятельство, и при одинаковой доверительной вероятности значе ние  больше в распределении Стьюдента, чем в нормальном. Иными словами, вероятность появления, например, одинаково больших погрешностей в распределении Стьюдента, т. е. при малом числе измерений, — больше.
больше в распределении Стьюдента, чем в нормальном. Иными словами, вероятность появления, например, одинаково больших погрешностей в распределении Стьюдента, т. е. при малом числе измерений, — больше.
В табл. 1-4-2 приведены вычисленные по распределению Стьюдента, вероятности  появления погрешностей, превышающих
появления погрешностей, превышающих  в зависимости от числа измерений
в зависимости от числа измерений 
Таблица 1-4-2 (см. скан) Вероятности  появления погрешностей, превышающих
появления погрешностей, превышающих 
Распределение Стьюдента с к степенями свободы определяется следующим выражением:

где  — гамма-функция:
— гамма-функция:

Выражение (1-4-9) позволяет решить вопрос о вероятности неравенств  для любого значения
для любого значения  Вероятность
Вероятность  того, что
того, что  определяется так:
определяется так:

Из (1-4-10) следует равносильная вероятность

Если задана вероятность, то, пользуясь выражением для  можно найти положительное число
можно найти положительное число  которое будет зависеть только от
которое будет зависеть только от 
Полагая

получаем из уравнения (1-4-11)

при этом 8 будет зависеть от  и значений
и значений  которые входят в 8 через
которые входят в 8 через  Выражение (1-4-13) позволяет достаточно точно произвести оценку приближенного равенства
Выражение (1-4-13) позволяет достаточно точно произвести оценку приближенного равенства 
При практическом применении распределения Стьюдента погрешность 8 среднего арифметического значения (результата измерения) при малом числе наблюдений  и заданной доверительной вероятности
и заданной доверительной вероятности  определяется из значений 0 или
определяется из значений 0 или  вычисленных по формулам (1-4-7) или (1-4-8), с помощью выражения
вычисленных по формулам (1-4-7) или (1-4-8), с помощью выражения

Значения  для наиболее употребительных доверительных вероятностей
для наиболее употребительных доверительных вероятностей  и различных
и различных  приведены в табл,
приведены в табл,  .
.
При  распределение Стьюдента сходится с нормальным.
распределение Стьюдента сходится с нормальным.
Для оценки среднего арифметического значения X, принимаемого как окончательный результат измерения, указываются доверительные границы и доверительный интервал при выбранной доверительной вероятности. Доверительные границы указываются следующим образом: нижняя граница  верхняя граница
верхняя граница  или сокращенно
или сокращенно  Доверительный интервал выражается в виде
Доверительный интервал выражается в виде

где  определяется формулой (1-4-14) и выражается в единицах измеряемой величины.
определяется формулой (1-4-14) и выражается в единицах измеряемой величины.
Если  выражается в долях среднего арифметического значения измеряемой величины, то доверительные границы указываются следующим образом:
выражается в долях среднего арифметического значения измеряемой величины, то доверительные границы указываются следующим образом:

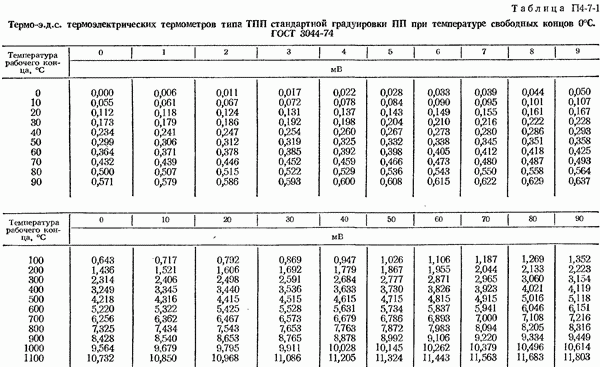
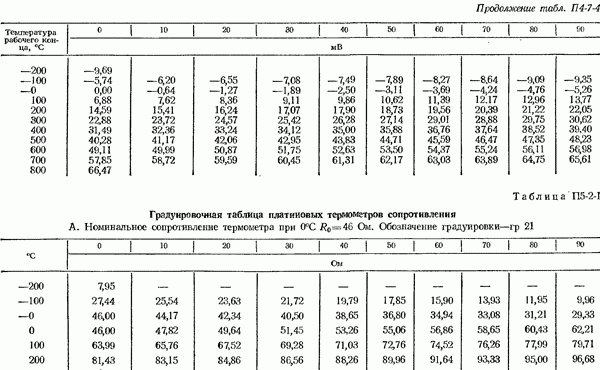
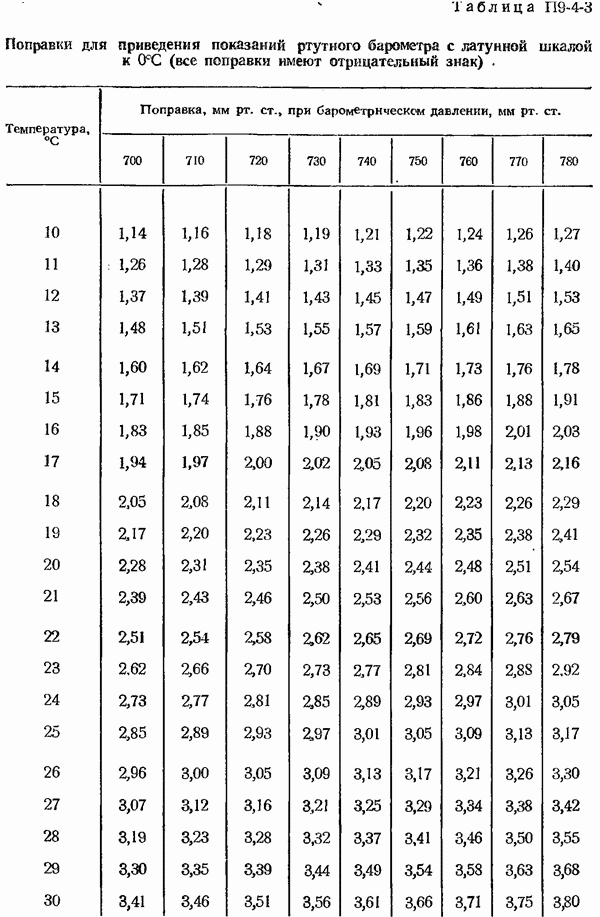
Пример 1. В табл. 1-4-3 приведены данные 12 измерений термо-э. д. с. платинородий-платинового термоэлектрического термометра при температуре рабочего конца 419, 58°С и свободных концов  Результаты измерений не содержат систематических погрешностей.
Результаты измерений не содержат систематических погрешностей.
Используя формулу (1-4-3), получаем среднее арифметическое значение

Случайные отклонения результатов наблюдений  и их квадраты
и их квадраты  приведены в табл. 1-4-3.
приведены в табл. 1-4-3.
Таблица 1-4-3 (см. скан) Данные измерения термо-э.д.с. платинородий-платинового термоэлектрического термометра при температуре рабочего конца 419,58°С и свободных концов 0°С
Средние квадратические отклонения результатов наблюдения и измерения определяются соответственно по формулам (1-4-7) и (1-4-8):

Истинное значение термо-э. д. с. X термоэлектрического термометра можно приближенно положить равным найденному среднему арифметическому значению X, т. е.  Для оценки достоверности этого равенства зададим доверительную вероятность
Для оценки достоверности этого равенства зададим доверительную вероятность  и найдем доверительные границы, соответствующие этой вероятности. По табл. П1-4-1 для
и найдем доверительные границы, соответствующие этой вероятности. По табл. П1-4-1 для  и
и  находим
находим  Согласно выражению (1-4-14) получим:
Согласно выражению (1-4-14) получим:

В соответствии с принятым условием, т. е. с вероятностью 0,95, мы можем утверждать, что истинное значение термо-э. д. с. заключено между доверительными границами:

Неточность оценки среднего квадратического отклонения и необходимое число наблюдений. Как было сказано выше, среднее квадратическое отклонение а (или дисперсия  при ограниченном числе наблюдений может быть определено только приближенно. При этом оценка о будет отличаться от среднего квадратического отклонения
при ограниченном числе наблюдений может быть определено только приближенно. При этом оценка о будет отличаться от среднего квадратического отклонения  неограниченно большого ряда тех же измерений тем больше, чем меньше произведено наблюдений.
неограниченно большого ряда тех же измерений тем больше, чем меньше произведено наблюдений.
В математической статистике доказывается, что оценка среднего квадратического отклонения а (или  найденная при малом числе наблюдений в предположении нормального распределения, позволяет судить о среднем квадратическом отклонении
найденная при малом числе наблюдений в предположении нормального распределения, позволяет судить о среднем квадратическом отклонении  (или
(или  ) неограниченно большого ряда тех же наблюдений и найти доверительный интервал для
) неограниченно большого ряда тех же наблюдений и найти доверительный интервал для  с заданной вероятностью Р:
с заданной вероятностью Р:

Коэффициенты  для вероятности
для вероятности  находят из условий
находят из условий

Значения  определяются из выражений
определяются из выражений

при  отвечающем вероятности
отвечающем вероятности 

при  .
.
Для определения значений  отвечающих соответственно вероятностям
отвечающих соответственно вероятностям  и числу степеней свободы
и числу степеней свободы  пользуются таблицами распределения
пользуются таблицами распределения  которые обычно составляются только до
которые обычно составляются только до  так как при степенях свободы более 30 распределение может быть выражено через нормальное.
так как при степенях свободы более 30 распределение может быть выражено через нормальное.
Доверительный интервал  для среднего квадратического отклонения
для среднего квадратического отклонения  находят по выражению
находят по выражению

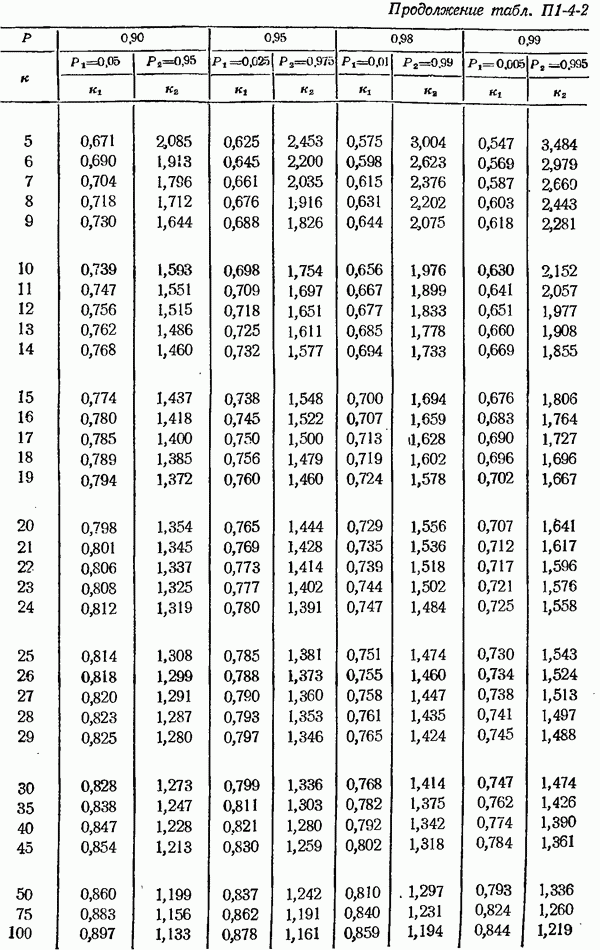
Коэффициенты  для наиболее часто выбираемых вероятностей
для наиболее часто выбираемых вероятностей  которым соответствуют вероятности
которым соответствуют вероятности  со степенями свободы
со степенями свободы  даны в табл. П1-4-2.
даны в табл. П1-4-2.
Следует отметить, что при малом числе измерений границы доверительного интервала, заключающие внутри себя  не расположены равносторонне по отношению к вычисленному значению среднего квадратического отклонения. При достаточно большом числе измерений можно ожидать, что
не расположены равносторонне по отношению к вычисленному значению среднего квадратического отклонения. При достаточно большом числе измерений можно ожидать, что  лежит в равносторонних границах.
лежит в равносторонних границах.
Пример 2. Определить доверительный интервал для  характеризующий неточность определения приближенного значения а, по данным примера 1, если известно, что распределение близко к нормальному.
характеризующий неточность определения приближенного значения а, по данным примера 1, если известно, что распределение близко к нормальному.
Выбираем вероятность  По табл.
По табл.  находим при
находим при  для
для  значение
значение  ; для
; для  значение
значение 
Доверительный интервал для о при выбранной вероятности  и значении
и значении  найдем по формуле (1-4-20):
найдем по формуле (1-4-20):

При точных измерениях важно знать, сколько нужно сделать наблюдений измеряемой величины X, чтобы в результате независимых равноточных измерений получить приближенное равенство  с требуемой точностью и надежностью. Определение числа измерений для заданной точности среднего квадратического отклонения производится соответственно соображениям, изложенным ниже. Задаются вероятностью того, что среднее квадратическое отклонение
с требуемой точностью и надежностью. Определение числа измерений для заданной точности среднего квадратического отклонения производится соответственно соображениям, изложенным ниже. Задаются вероятностью того, что среднее квадратическое отклонение  для большого числа наблюдений находится в некоторых границах, опирающихся на оценку среднего квадратического отклонения а при малом числе наблюдений.
для большого числа наблюдений находится в некоторых границах, опирающихся на оценку среднего квадратического отклонения а при малом числе наблюдений.
Пусть, например, ставится вопрос о наименьшем числе измерений для определения среднего квадратического отклонения  по небольшому ряду наблюдений с дисперсией
по небольшому ряду наблюдений с дисперсией  при вероятности 0,95 для отношения верхней границы к нижней
при вероятности 0,95 для отношения верхней границы к нижней  Учитывая выражения
Учитывая выражения  и (14-19), имеем:
и (14-19), имеем:

По табл. П1-4-2 для вероятностей  находим для заданного отношения
находим для заданного отношения  и наименьшее число наблюдений
и наименьшее число наблюдений 
Если взять не столь широкие границы, то число наблюдений оказывается более значительным. Пусть при вероятности 0,95 границы установлены в ± 0,1. Определим число измерений для заданных условий, пользуясь формулой [4]:

Для  отвечающего вероятности 0,95, имеем:
отвечающего вероятности 0,95, имеем:

откуда 
С уменьшением ширины доверительной границы значительно растет число наблюдений. Поэтому для достижения желательной точности измерений необходимо заботиться не только о числе, но и о точности измерений отдельных наблюдений, отражающейся на значении оценки среднего квадратического отклонения а.
Наблюдения, не заслуживающие доверия. Выше было сказано, что наблюдения, содержащие грубые погрешности, должны быть отброшены как не заслуживающие доверия. Поэтому необходимо уточнить, в каких же случаях сильно отклоняющиеся результаты измерения должны быть отброшены. На практике часто пользуются простым предложением отбрасывать результаты наблюдения, содержащие большие погрешности, т. е. превышающие 3а или 4а. Однако этот прием нельзя считать достаточно строгим, так как погрешности являются случайными и потому появление большой погрешности само по себе не зависит от числа наблюдений.
При малом числе наблюдений для определения, какие наблюдения из ряда подлежат отбрасыванию, применяют критерий В. И. Романовского, основанный на распределении Стьюдента. Пусть при измерении некоторой постоянной величины получено  результатов наблюдения
результатов наблюдения  При этом
При этом  значений результатов наблюдения измеряемой величины не вызывают сомнений в отношении соответствия их закономерному ряду, а одно наблюдение
значений результатов наблюдения измеряемой величины не вызывают сомнений в отношении соответствия их закономерному ряду, а одно наблюдение  кажется сомнительным в этом ряду. Определим для ряда наблюдений от
кажется сомнительным в этом ряду. Определим для ряда наблюдений от  до
до  среднее арифметическое значение
среднее арифметическое значение

и оценку среднего квадратического отклонения

Далее, исходя из степени достоверности, которая должна быть обеспечена, зададимся вероятностью  того, что разность
того, что разность  не превышает некоторое допускаемое значение ей, определяемое по формуле
не превышает некоторое допускаемое значение ей, определяемое по формуле

Значения  для различных
для различных  приведены в табл. 1-4-4.
приведены в табл. 1-4-4.
Таблица 14-4 (см. скан) Значения  для различных
для различных 
Если  наблюдение
наблюдение  подлежит исключению из ряда, как не заслуживающее доверия.
подлежит исключению из ряда, как не заслуживающее доверия.
Пример 3. В дополнение к наблюдениям, данные которых приведены в табл. 1-4-3, было проведено тринадцатое наблюдение, значение которого  а отклонение от среднего
а отклонение от среднего  Оценка среднего квадратического отклонения по результатам 12 наблюдений (табл. 1-4-3)
Оценка среднего квадратического отклонения по результатам 12 наблюдений (табл. 1-4-3)

Задаваясь  по табл. 1-4-4, для
по табл. 1-4-4, для  находим
находим  и определяем:
и определяем:

Тринадцатое наблюдение, для которого  подлежит исключению из ряда, так как
подлежит исключению из ряда, так как 
Оценка погрешности среднего взвешенного. В некоторых случаях при определении значения измеряемой величины приходится иметь дело с обработкой рядов прямых измерений различной достоверности, т. е. измерений, производимых с различной степенью точности или с различным числом наблюдений в каждом ряду и т. п. Вследствие этого не представляется возможным принять за наиболее
достоверное значение измеряемом величины среднее арифметическое из всех полученных результатов измерения. В этом случае необходимо ввести понятие о весе измерения как о числе, служащем мерой степени доверия к результату измерения. При этом, чем больше вес измерения (степень доверия к результату), тем большее число ему приписывается.
Учет различной достоверности результатов измерений отдельных рядов приводит к определению так называемого «среднего взвешенного»  по формуле
по формуле

где  средние значения для отдельных групп наблюдений
средние значения для отдельных групп наблюдений  соответствующие им веса измерений
соответствующие им веса измерений 
Веса измерений, произведенных с различной степенью точности чаще всего устанавливают обратно пропорциональными дисперсии  .
.
В некоторых случаях (например, при равноточных измерениях с различным числом наблюдений в каждом ряду) веса устанавливаются пропорционально числу наблюдений в каждом ряду, взятых для вычисления среднего арифметического каждого ряда измерений. Вес ряда с наименьшим количеством наблюдений для удобства принимают за единицу, а веса остальных рядов находят как частное от деления числа наблюдений в данном ряду на число наблюдений ряда, Бес которого принят за единицу.
Для оценки точности среднего взвешенного пользуются средним квадратическим отклонением, вычисляемым по формуле

где  — число рядов измерений.
— число рядов измерений.
Доверительные границы и доверительный интервал среднего взвешенного при заданной доверительной вероятности определяют аналогично рассмотренному выше.
Оценка точности косвенных измерений. В косвенных измерениях определение значения искомой величины у производится на основании прямых измерений других величин, связанных с у функциональной зависимостью

где  — средние арифметические значения прямых измерений с одинаковым числом отдельных наблюдений
— средние арифметические значения прямых измерений с одинаковым числом отдельных наблюдений 
При определении искомой величины у полагаем, что результаты измерения величин  свободны от систематических погрешностей.
свободны от систематических погрешностей.
Погрешность результата косвенного измерения величины у зависит от погрешности результатов прямых измерений независимых друг от друга величин 
Для оценки точности результата косвенного измерения величины у применяют среднее квадратическое отклонение, вычисляемое по формуле

где  - средние квадратические отклонения результатов измерения величин
- средние квадратические отклонения результатов измерения величин 
В зависимости от требований к измерениям может быть задана различная доверительная вероятность. Обозначая для выбранной доверительной вероятности  через
через  погрешности величин
погрешности величин  связанные с
связанные с  или
или  равенством
равенством

и подставляя  в формулу (1-4-24), получаем:
в формулу (1-4-24), получаем:

Погрешности  в формулах (1-4-24) и (1-4-25) выражаются в тех же единицах, что и искомая величина у.
в формулах (1-4-24) и (1-4-25) выражаются в тех же единицах, что и искомая величина у.
Если непосредственно измеряемые величины являются по своей природе разнородными, то пользуются относительными погрешностями этих величин.
При использовании оценок средних квадратических отклонений  значение погрешности результата косвенного измерения также будет приближенно.
значение погрешности результата косвенного измерения также будет приближенно.
Приведенные выше формулы для определения погрешности результата косвенного измерения у могут быть использованы и в том случае, если у находится по отдельным значениям прямых измерений, т. е.

В этом случае должно быть известно значение среднего квадратического отклонения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
- 2-1. Основные сведения о температуре и температурных шкалах
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
- 3-1. Термометры стеклянные жидкостные
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
- 4-7. Общие сведения о термоэлектрических термометрах
- 4-8. Устройство термоэлектрических термометров
- 4-9. Удлиняющие термоэлектродные провода
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
- 4-11. Милливольтметры
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
- 4-15. Нормальные элементы
- 4-16. Потенциометры переносные и лабораторные
- 4-17. Общие сведения об автоматических потенциометрах
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
- 4-20. Основные сведения об усилителях
- 4-21. Основные сведения об источниках стабилизированного питания
- 4-22. Устройство автоматических потенциометров
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
- 5-3. Устройство платиновых и медных термометров сопротивления
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
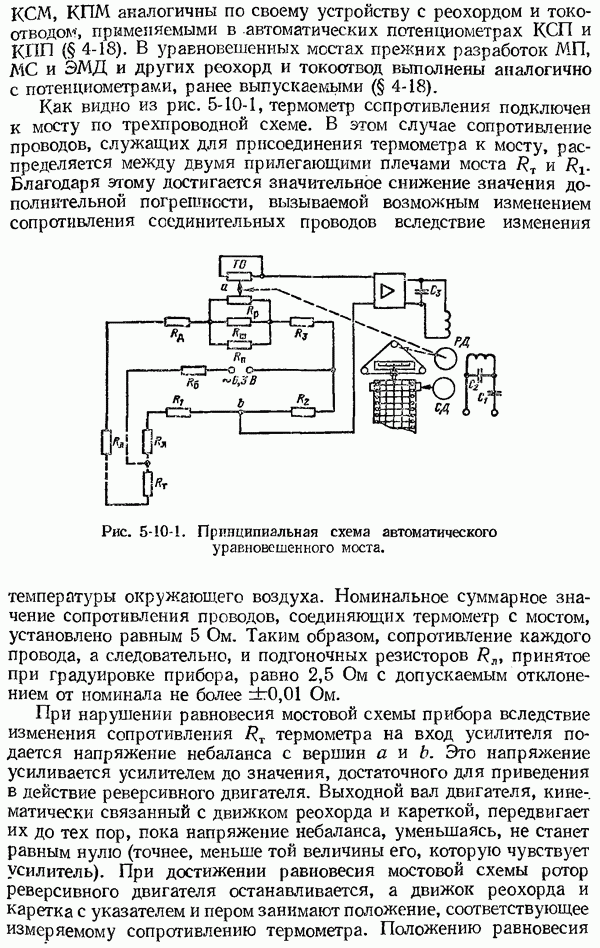
- 5-10. Принципиальная схема автоматического уравновешенного моста
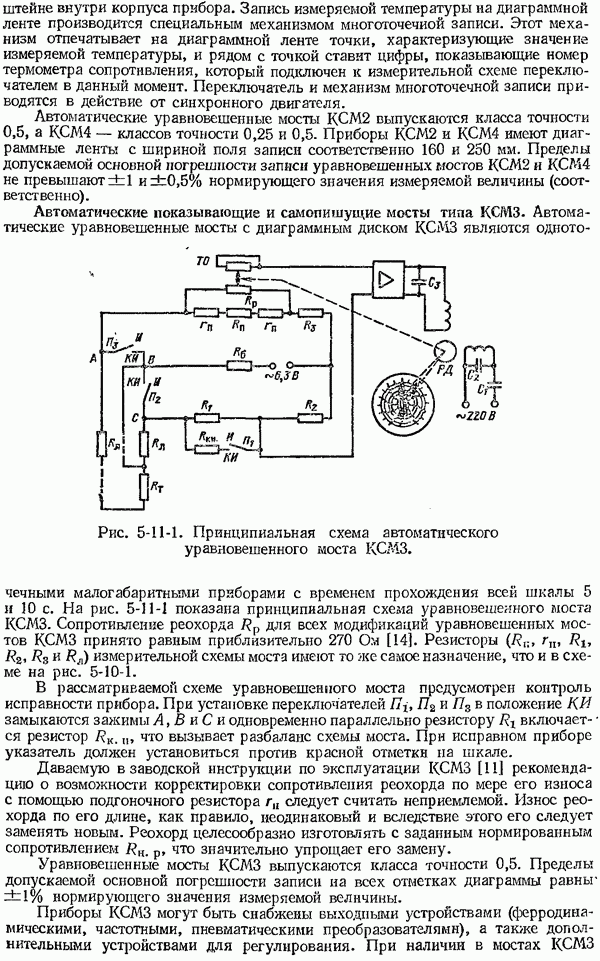
- 5-11. Устройство автоматических уравновешенных мостов
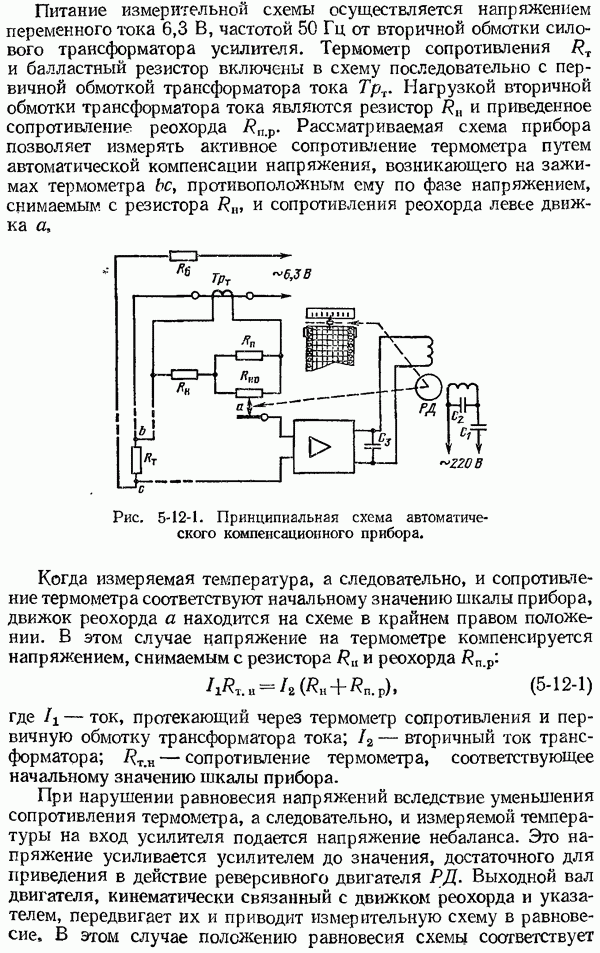
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
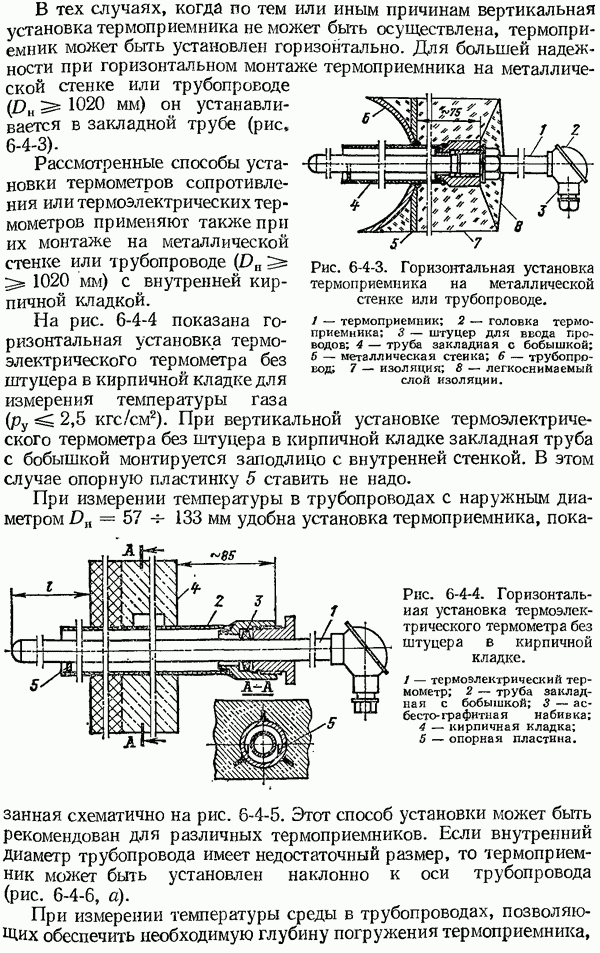
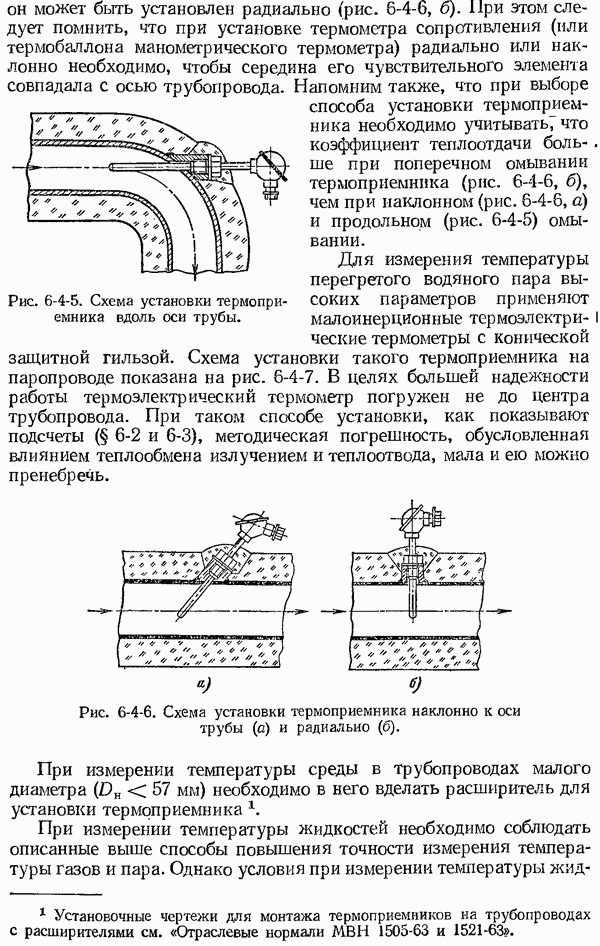
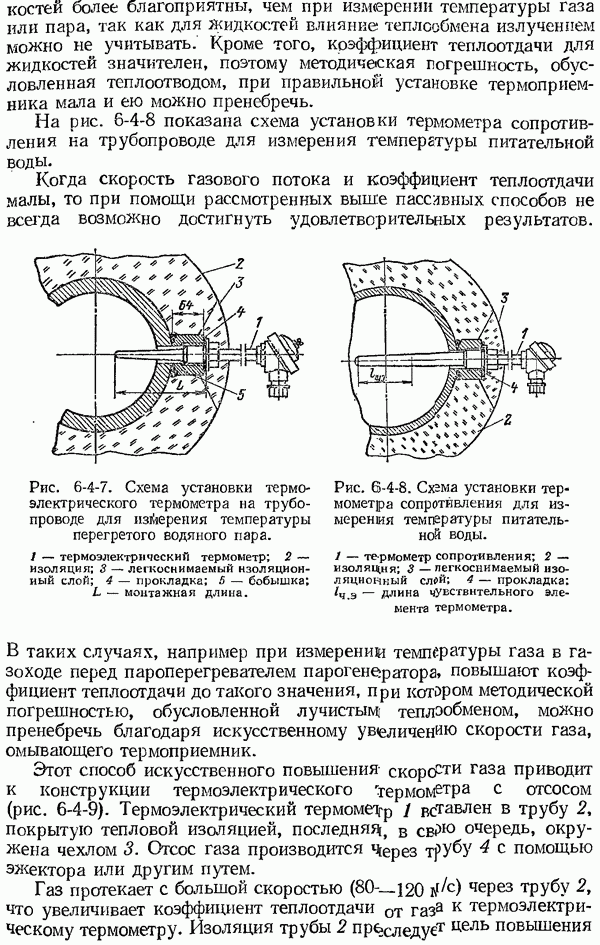
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
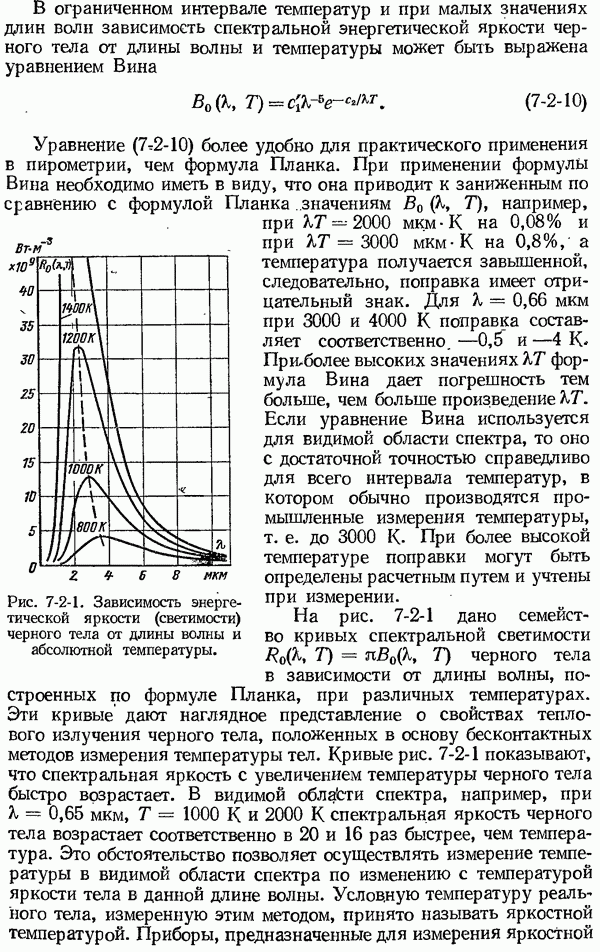
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
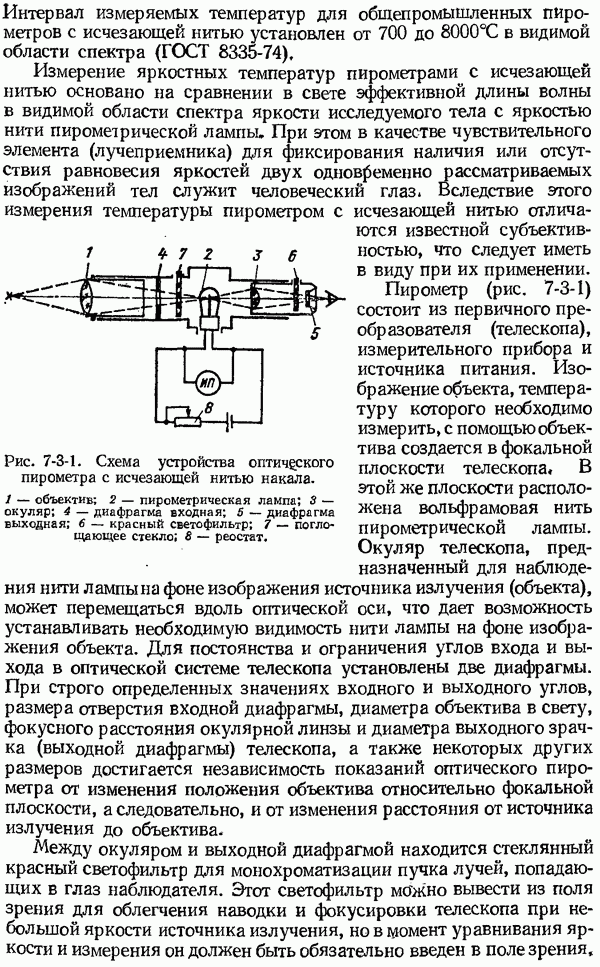
- 7-3. Оптические пирометры
- 7-4. Фотоэлектрические пирометры
- 7-5. Пирометры спектрального отношения
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
- 8-6. Механоэлектрические передающие преобразователи
- 8-7. Передающие преобразователи с магнитной компенсацией
- 8-8. Электросиловые преобразователи
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
- 8-11. Пневматические передающие преобразователи
- 8-12. Электропневматические и пневмоэлектрические преобразователи
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
- 10-2. Упругие чувствительные элементы
- 10-3. Приборы давления прямого действия
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 13-2. Измерение близкого к атмосферному давления газовых сред
- 13-3. Измерение давления газов, жидкостей и пара
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
- 14-1. Основы теории и уравнения расхода
- 14-2. Стандартные сужающие устройства
- 14-3. Коэффициенты расхода и поправочные множители к ним
- 14-4. Поправочный множитель на расширение измеряемой среды
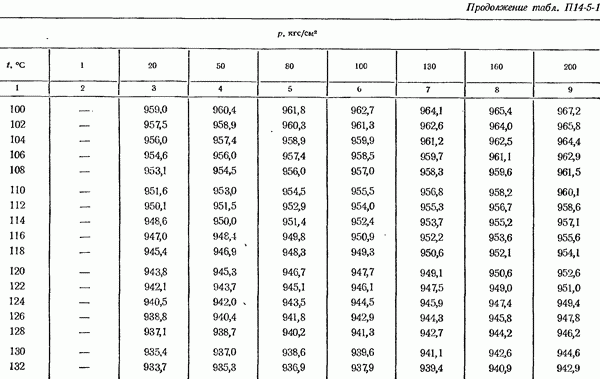
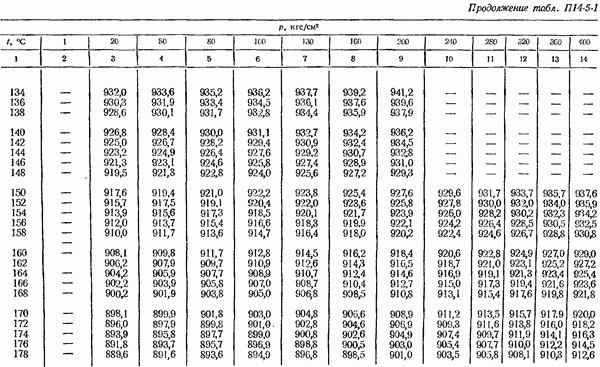
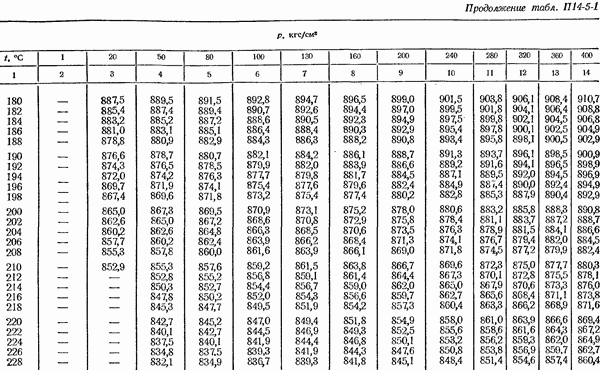
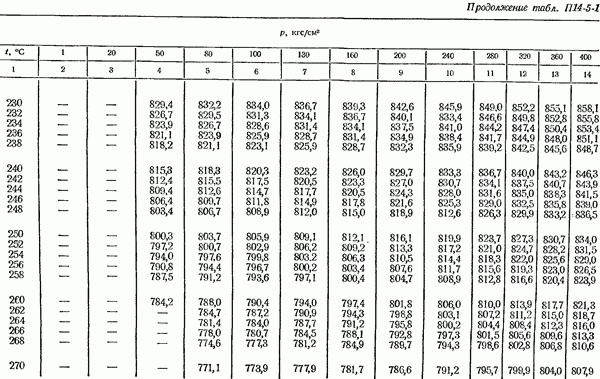
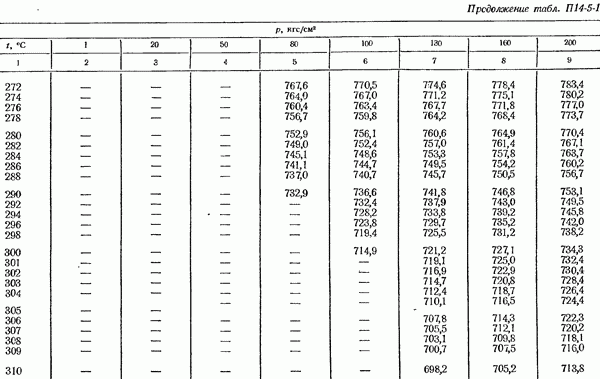
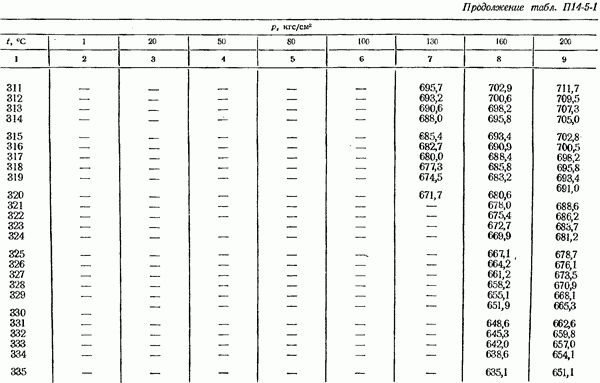
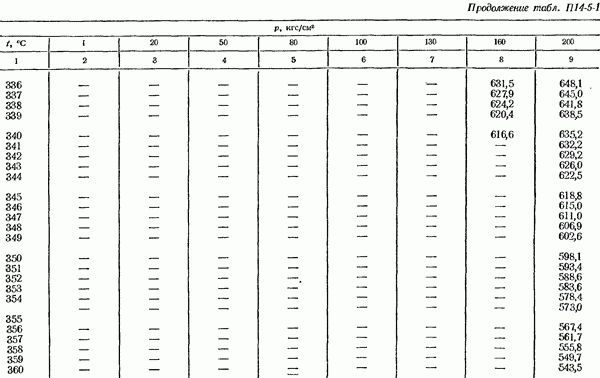
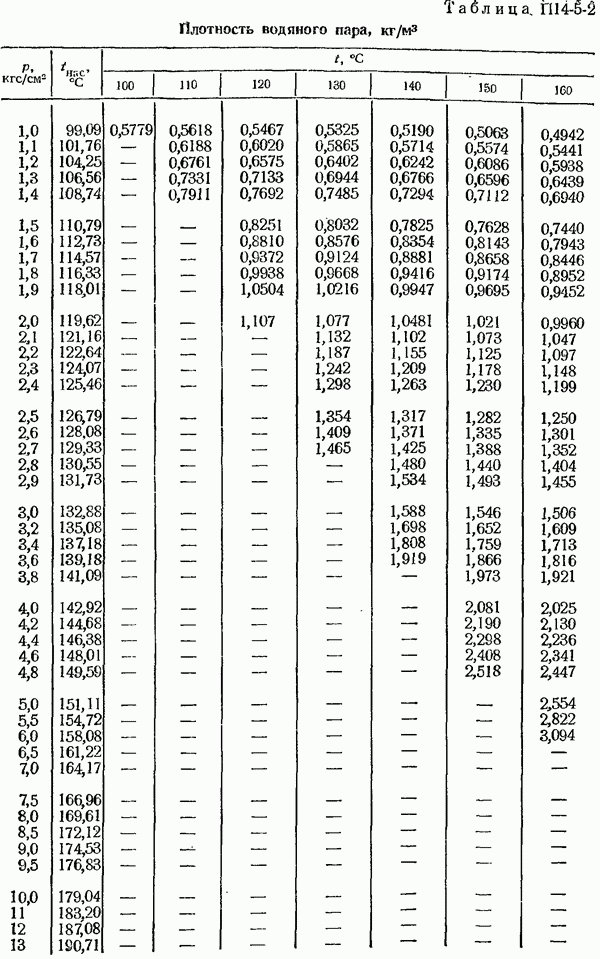
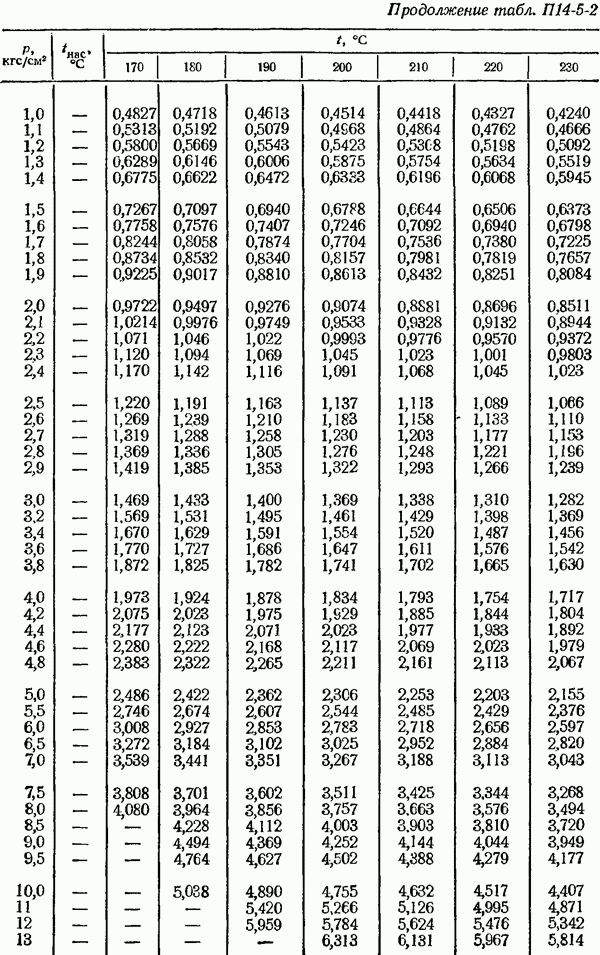
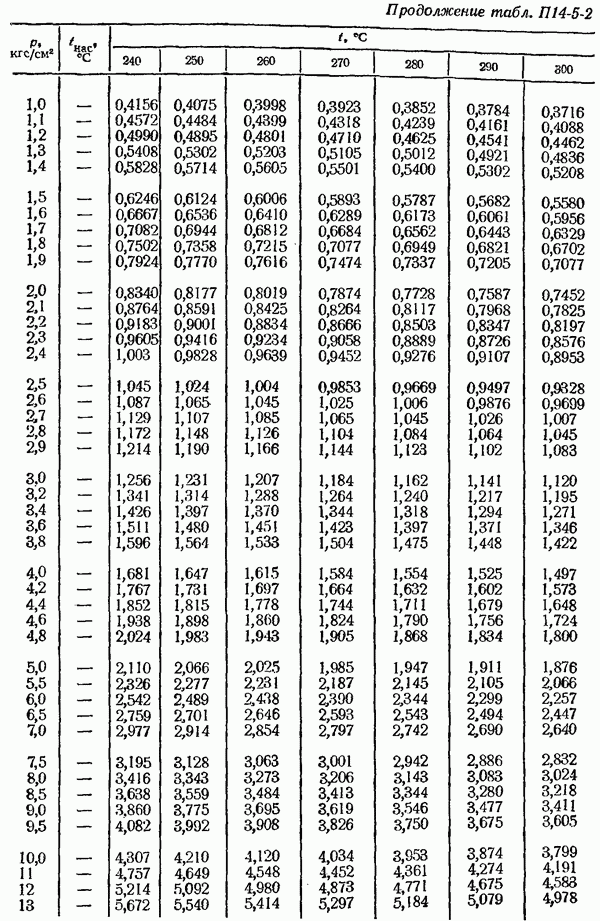
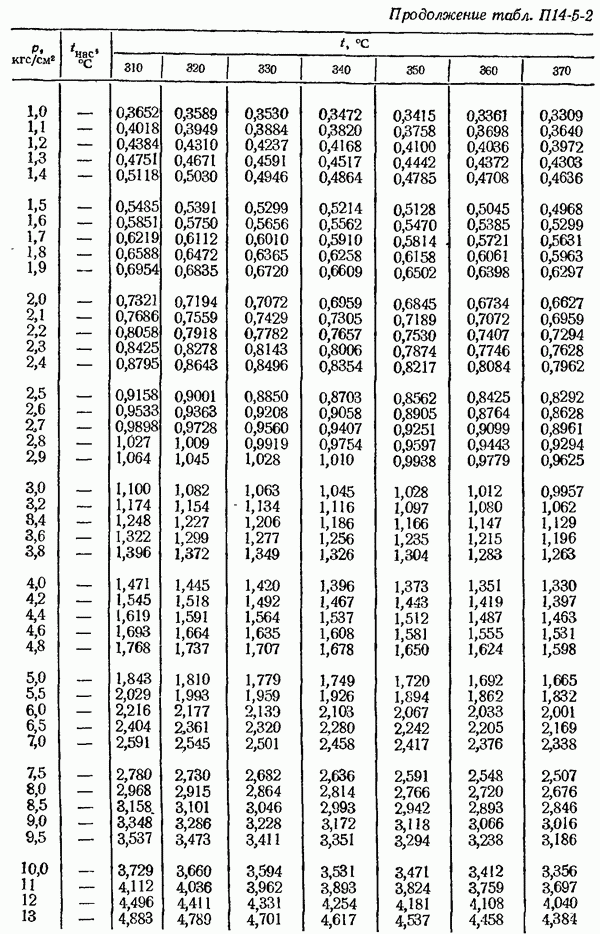
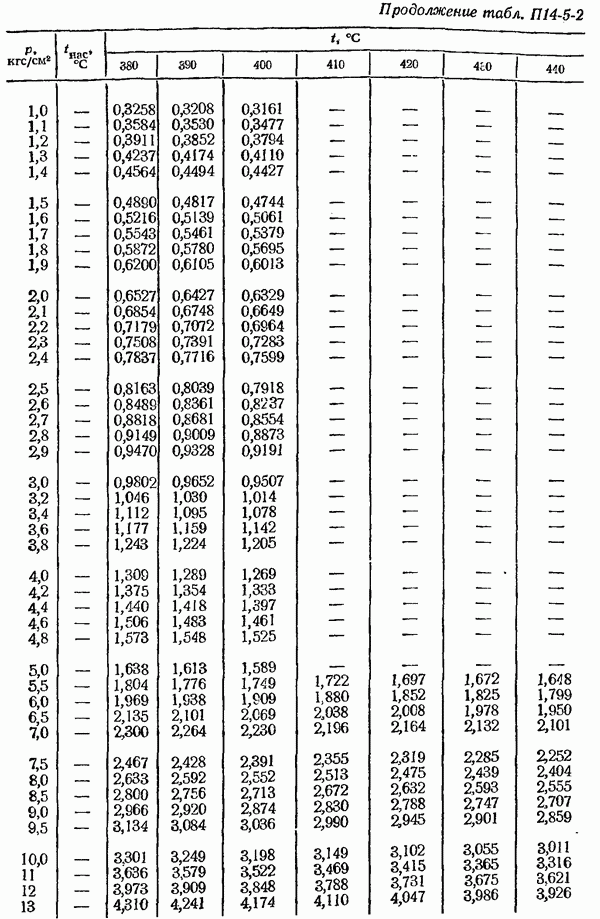
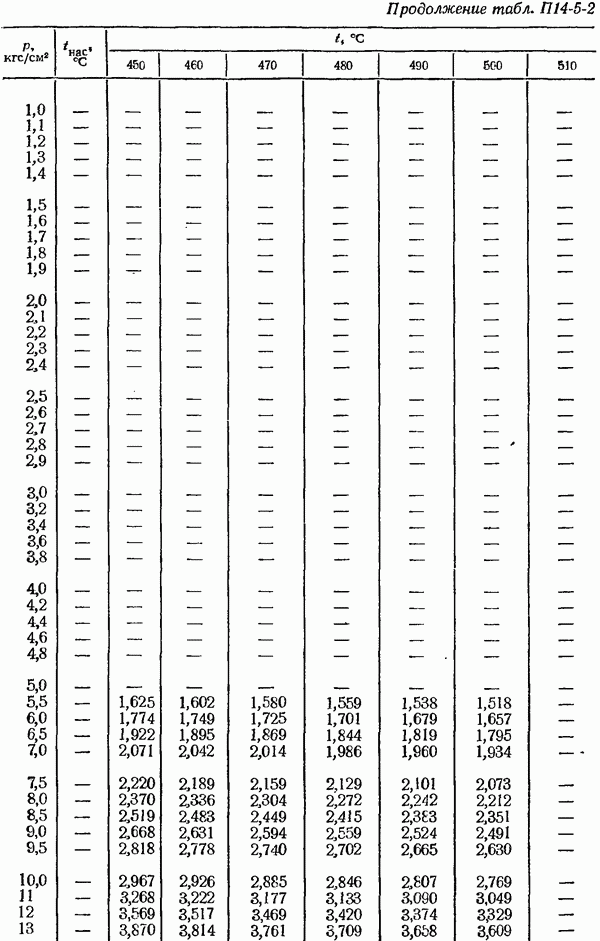
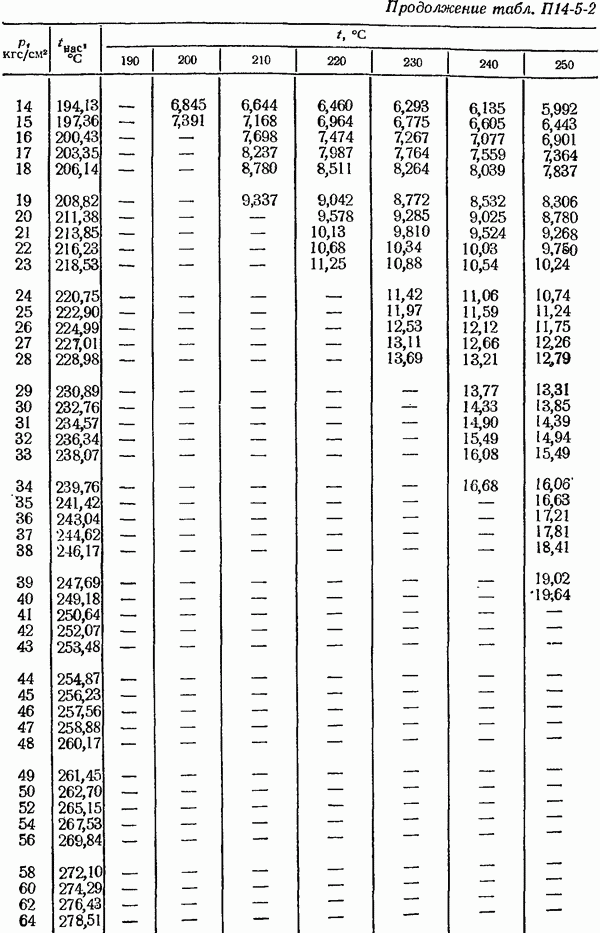
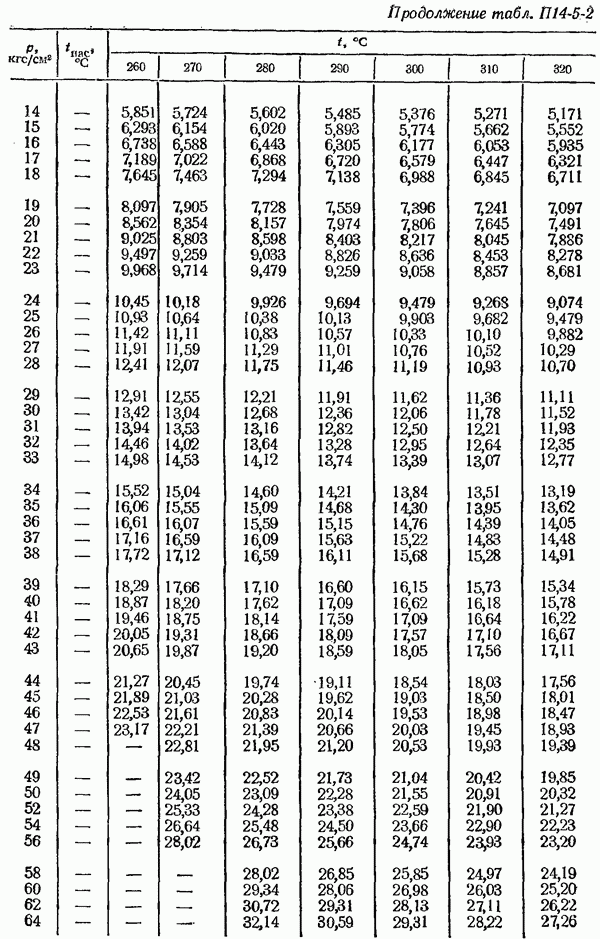
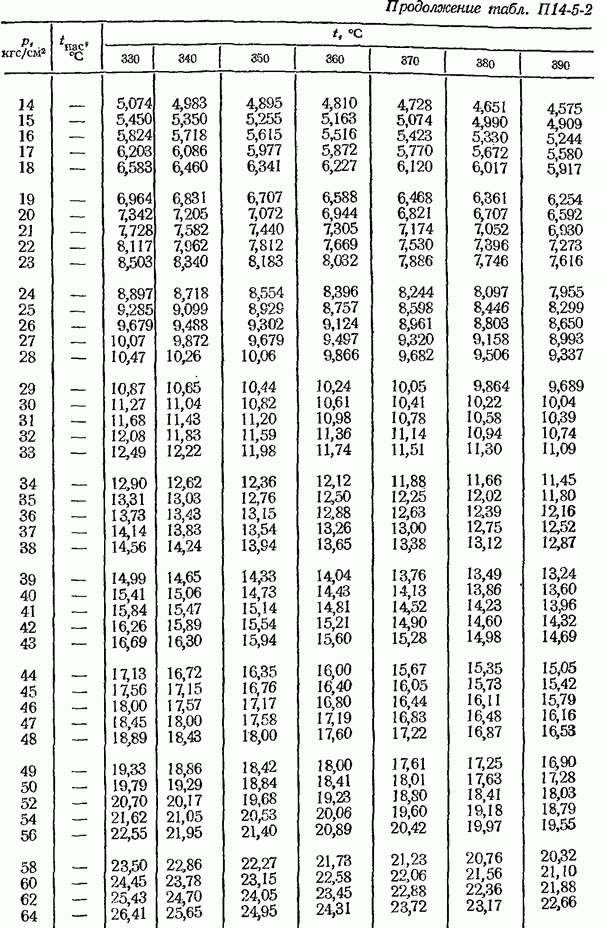
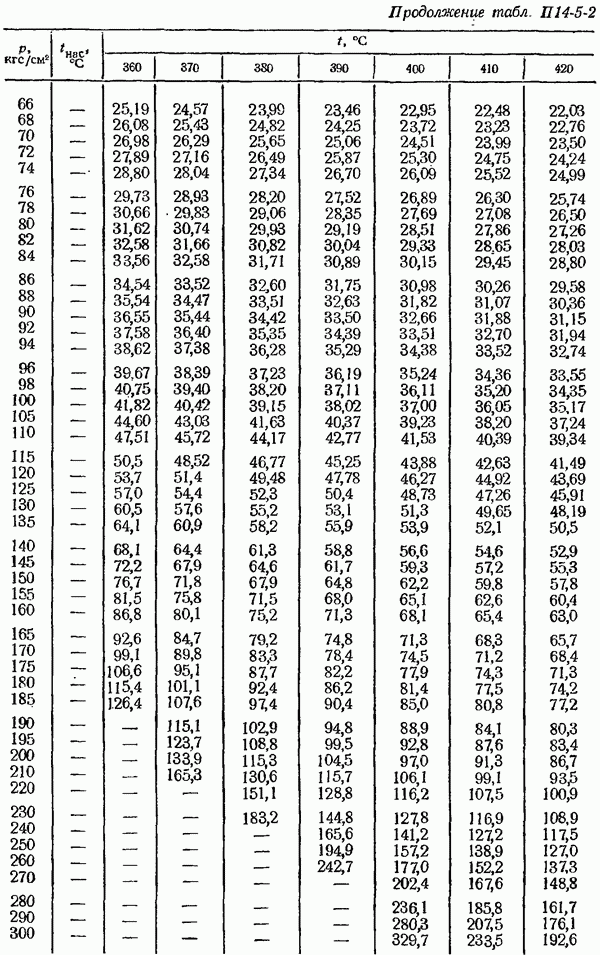
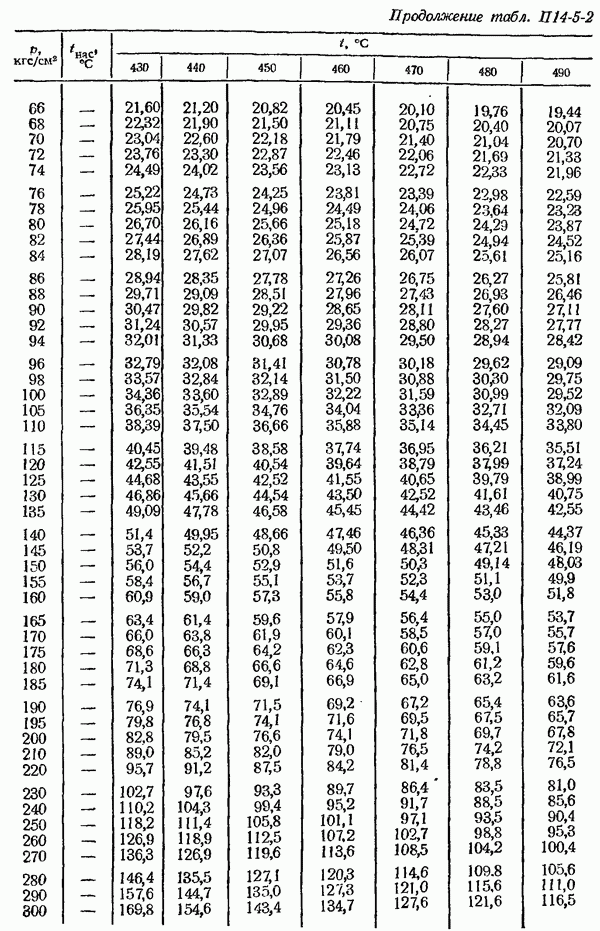
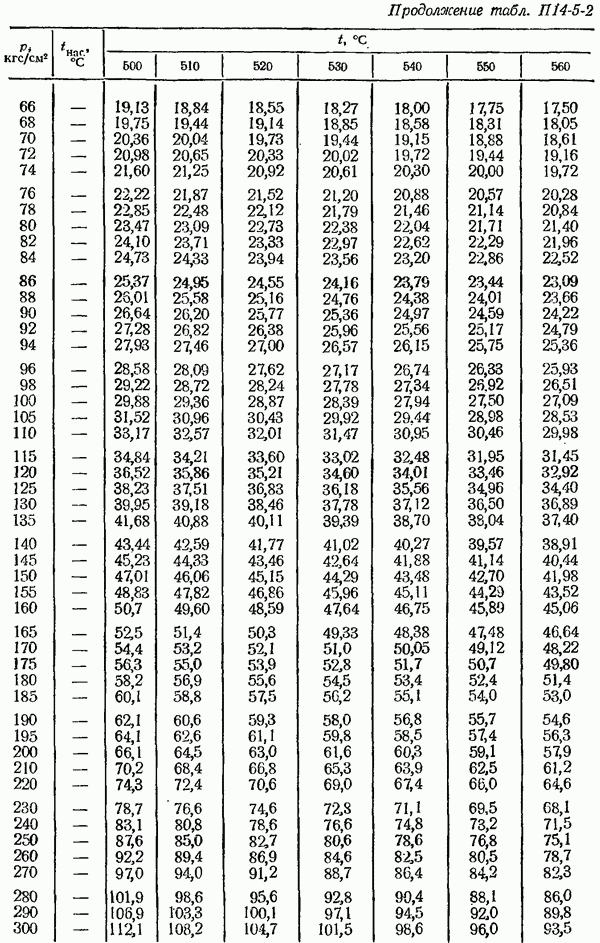
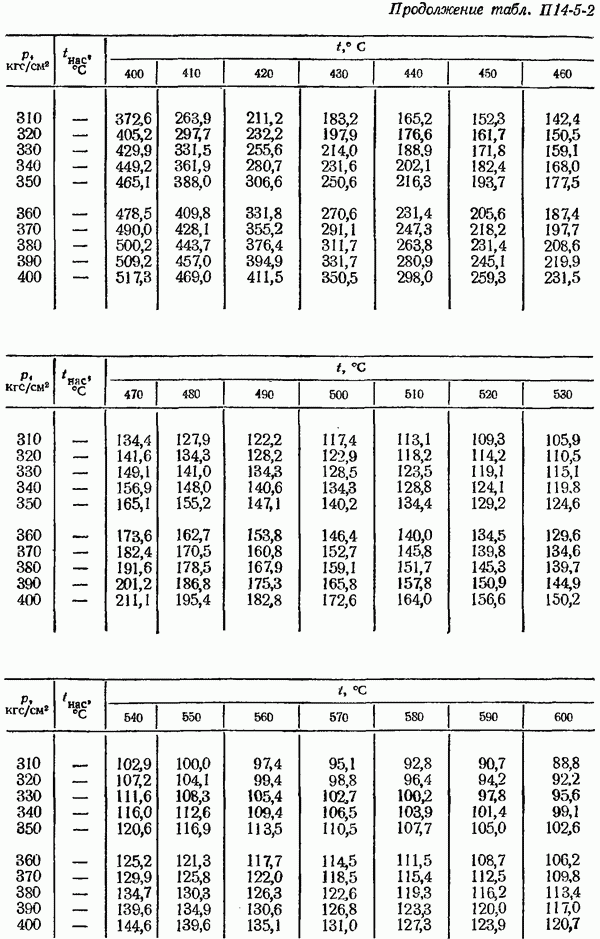
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
- 14-8. Погрешности измерения расхода
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
- 14-11. Измерение расхода при малых числах Рейнольдса
- 14-12. Измерение расхода загрязненных жидкостей и газов
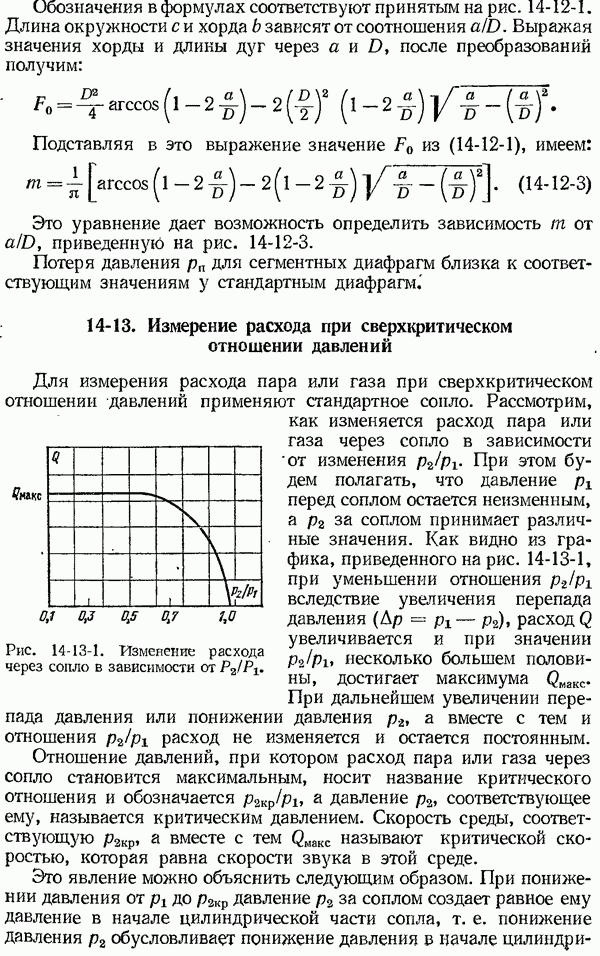
- 14-13. Измерение расхода при сверхкритическом отношении давлений
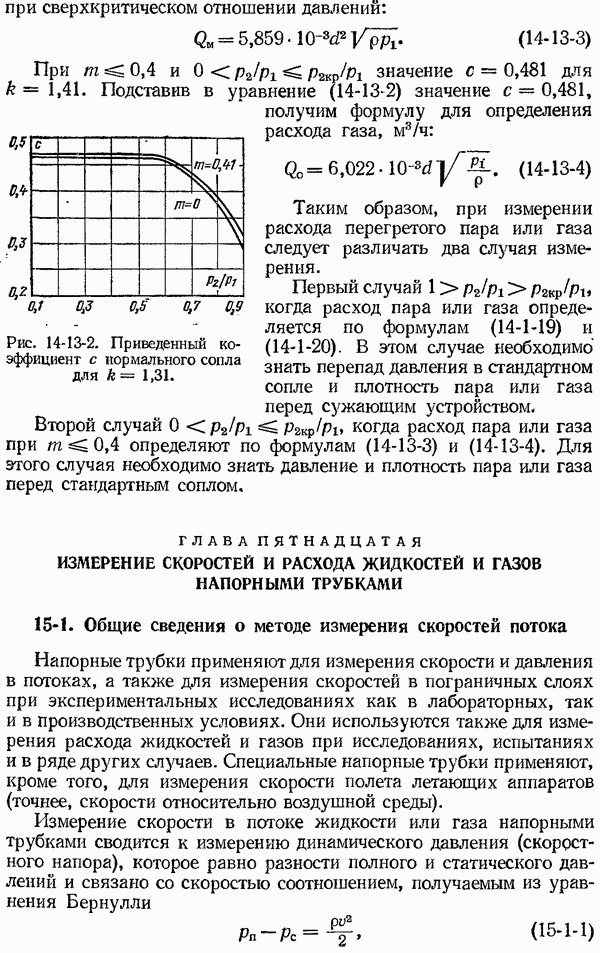
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
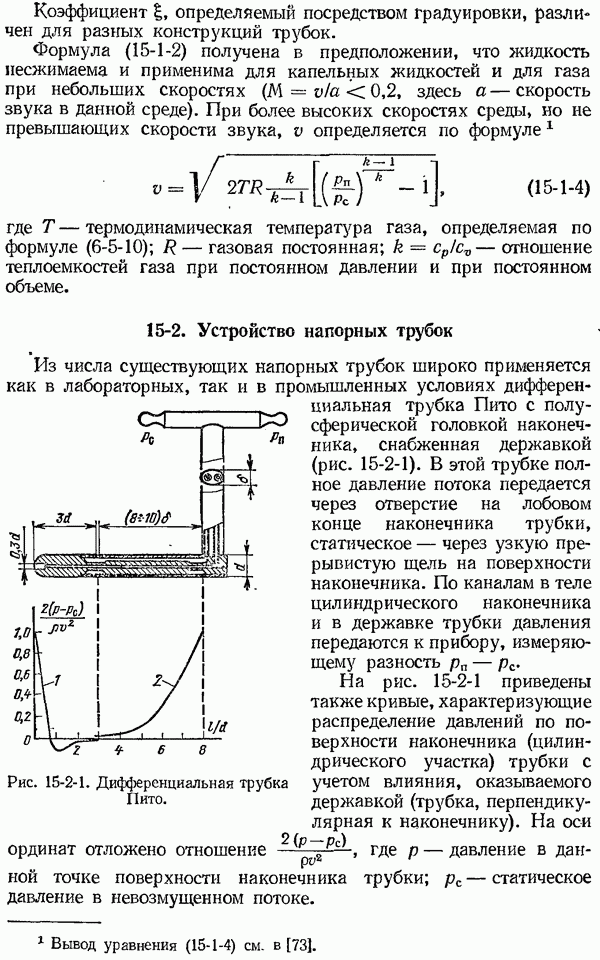
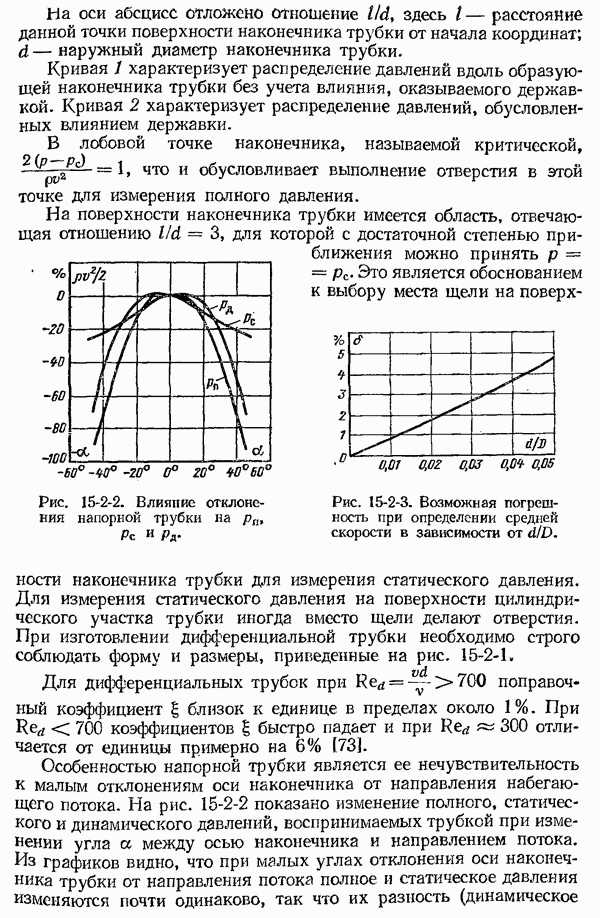
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
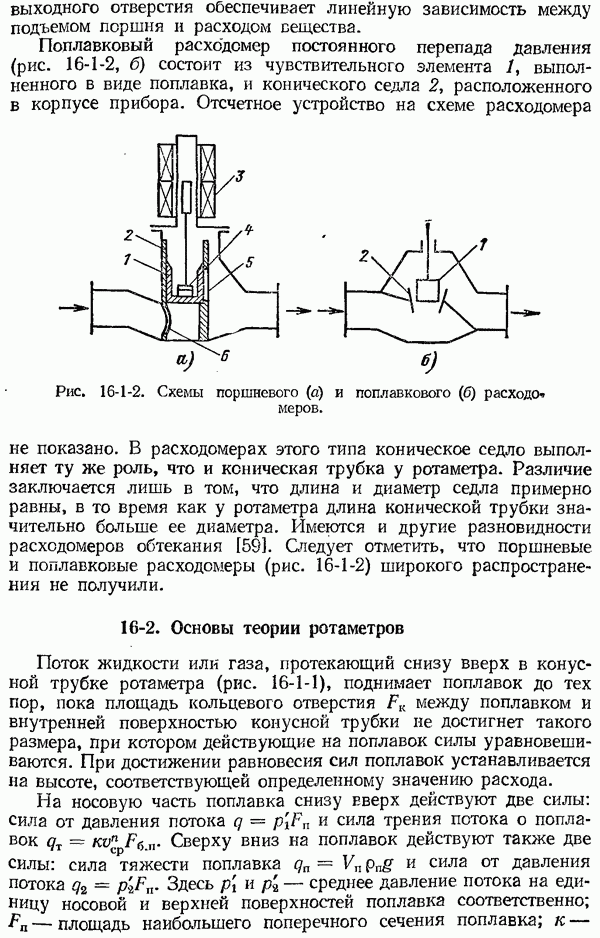
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
- 16-2. Основы теории ротаметров
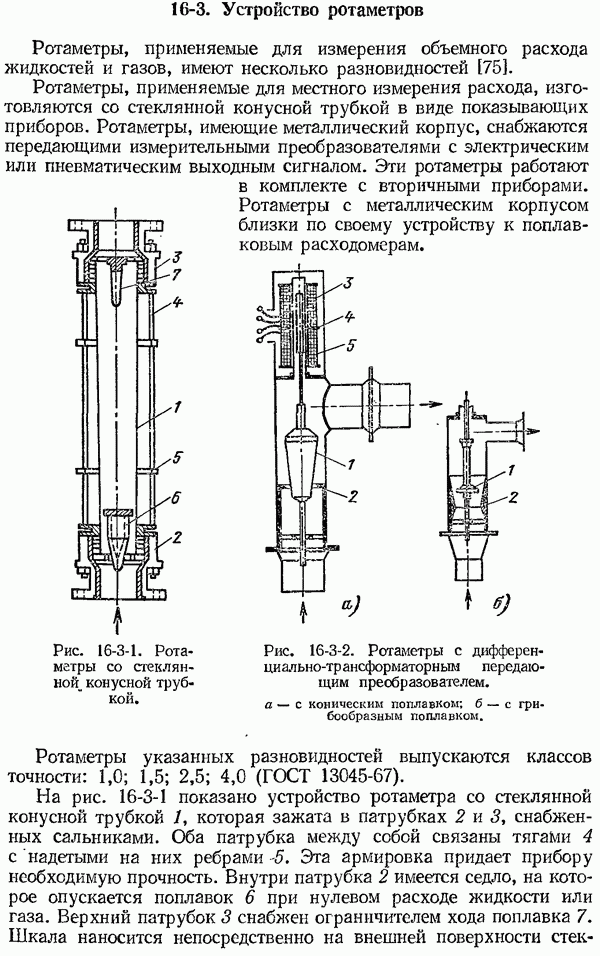
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
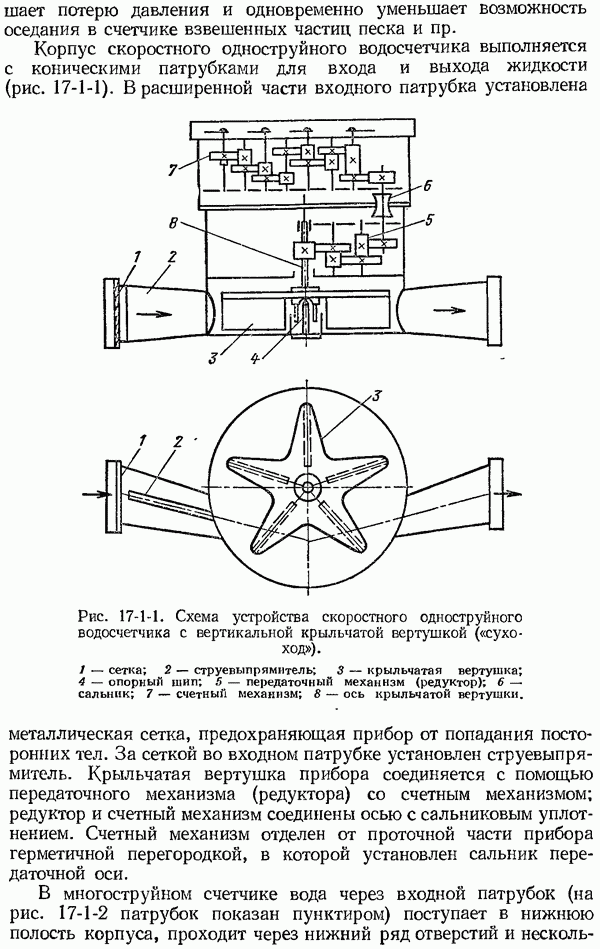
- 17-1. Тахометрические счетчики количества жидкостей
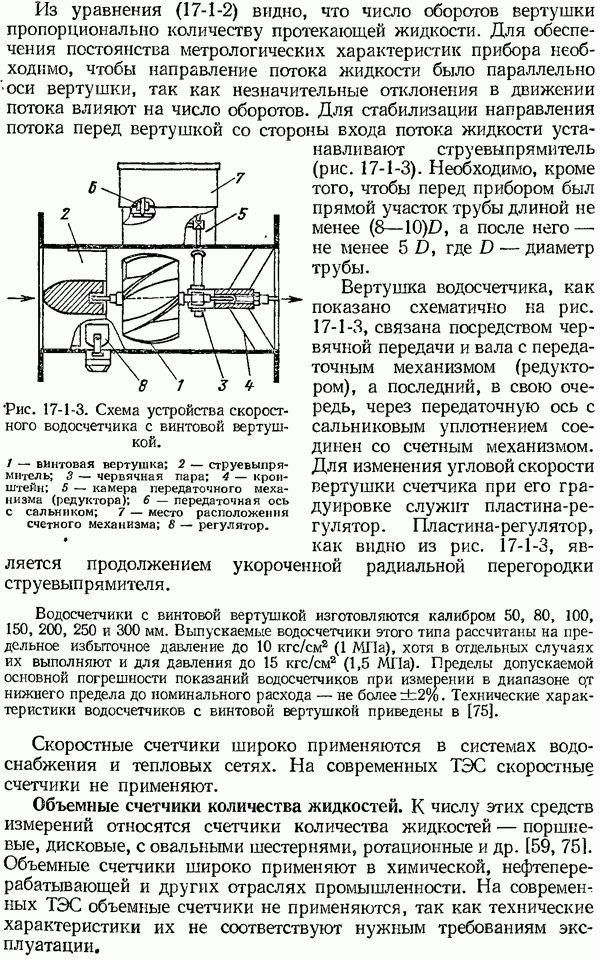
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
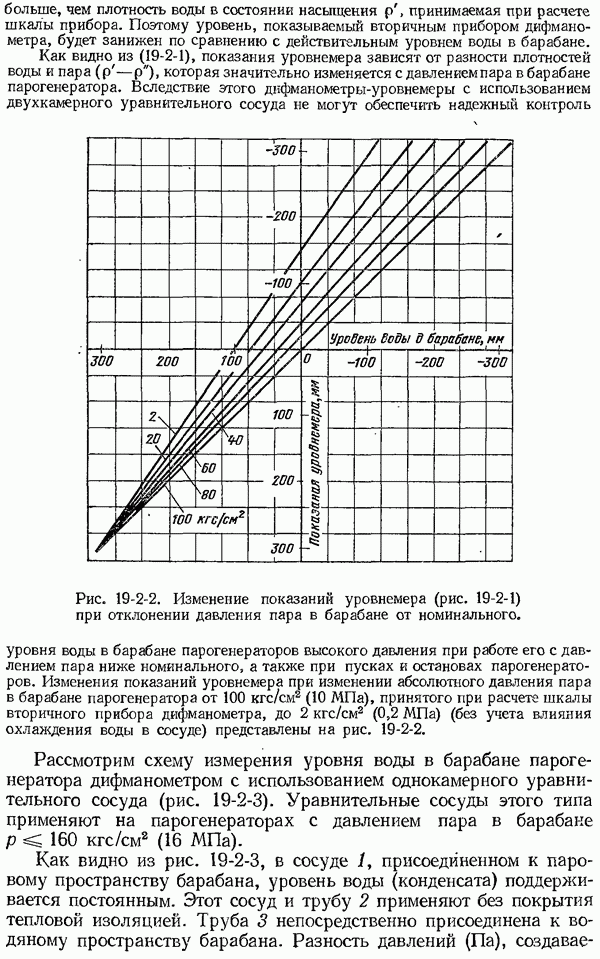
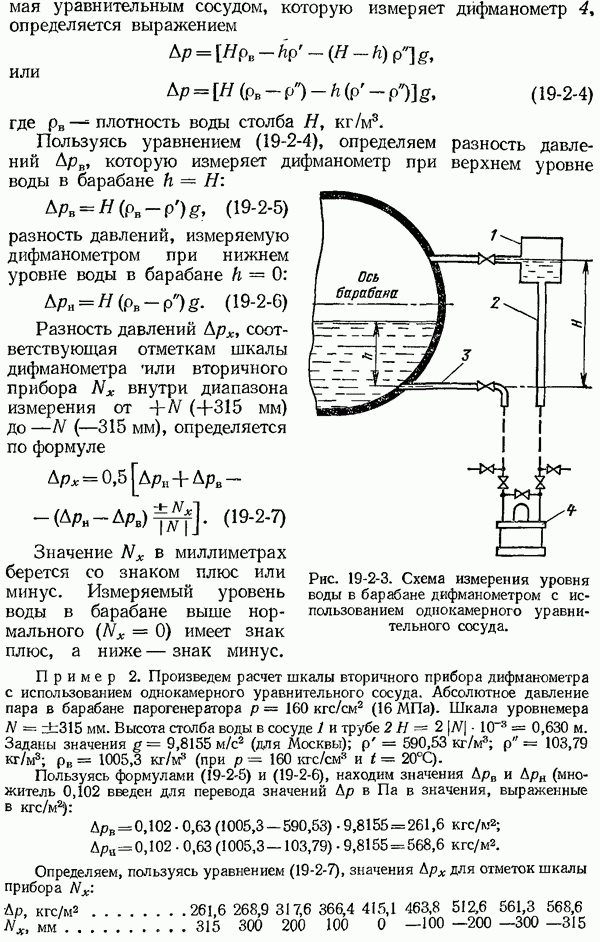
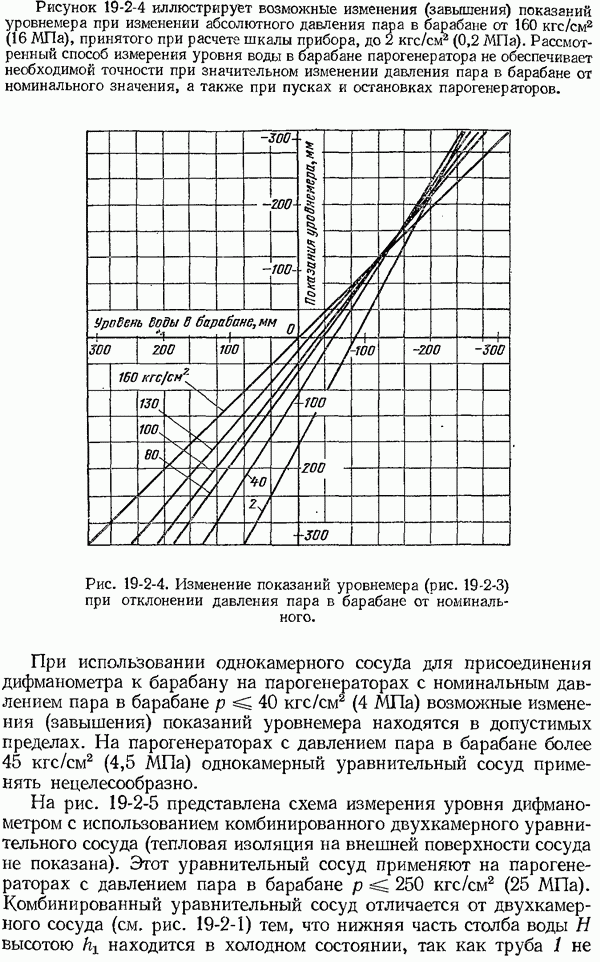
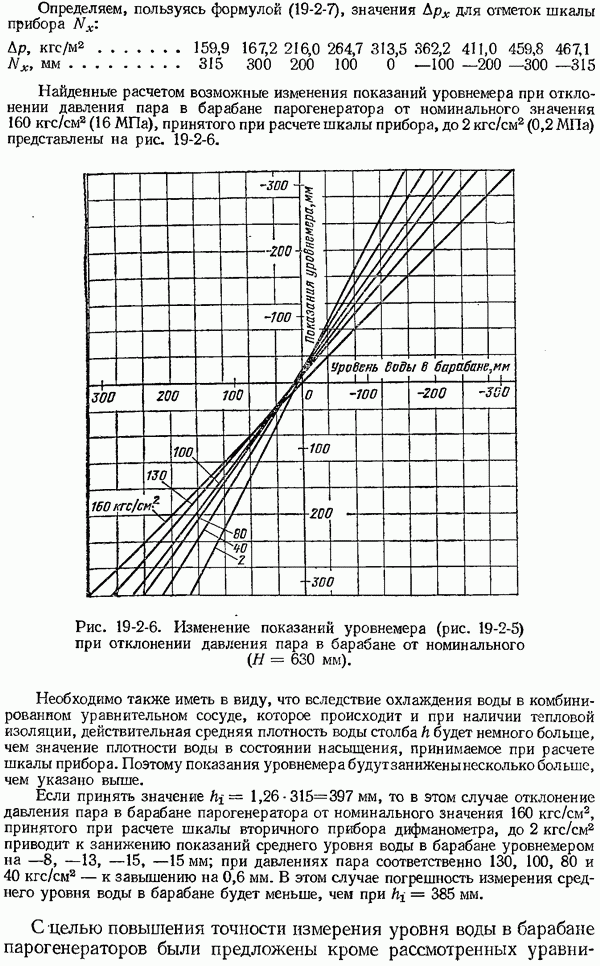
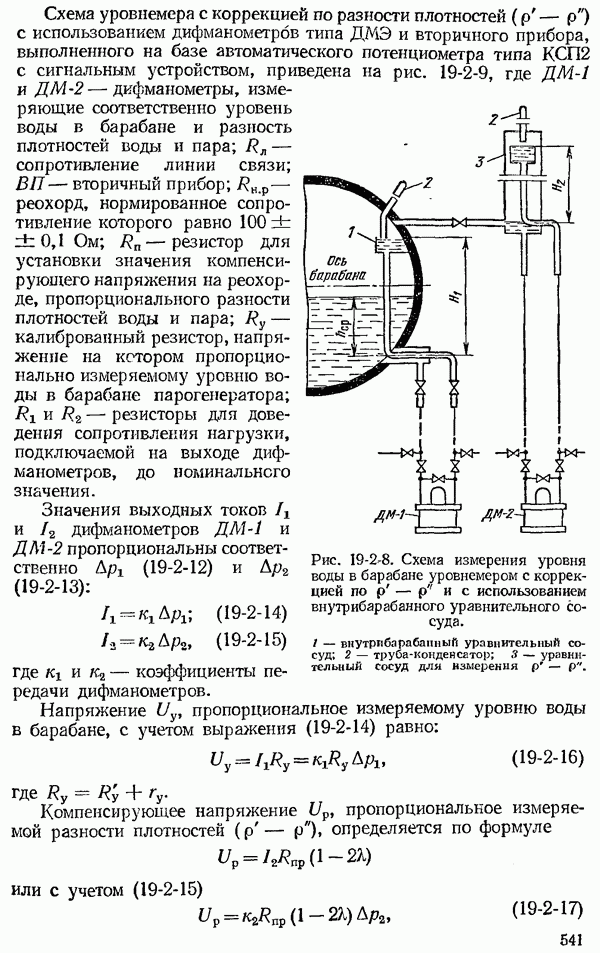
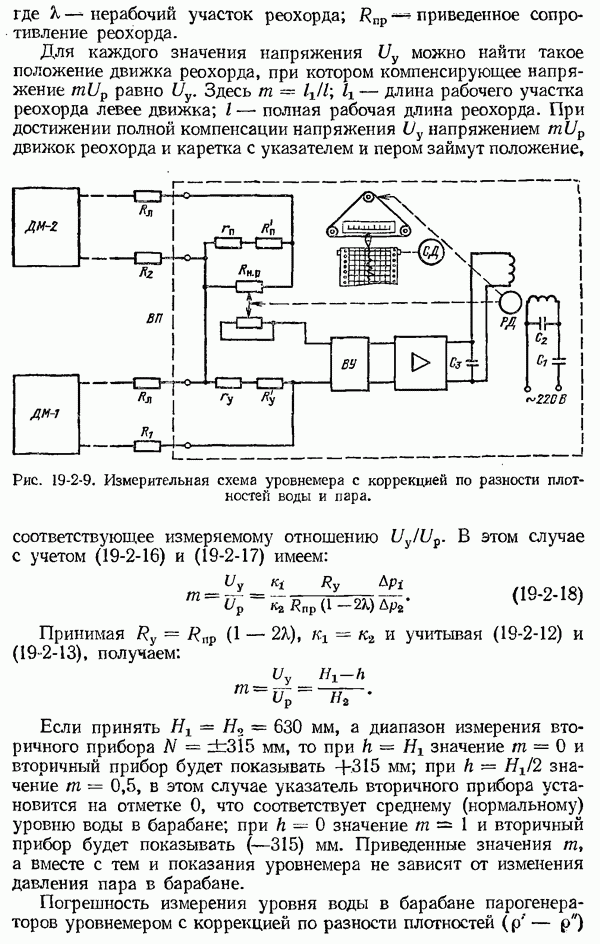
- 19-2. Измерение уровня воды в барабане парогенераторов
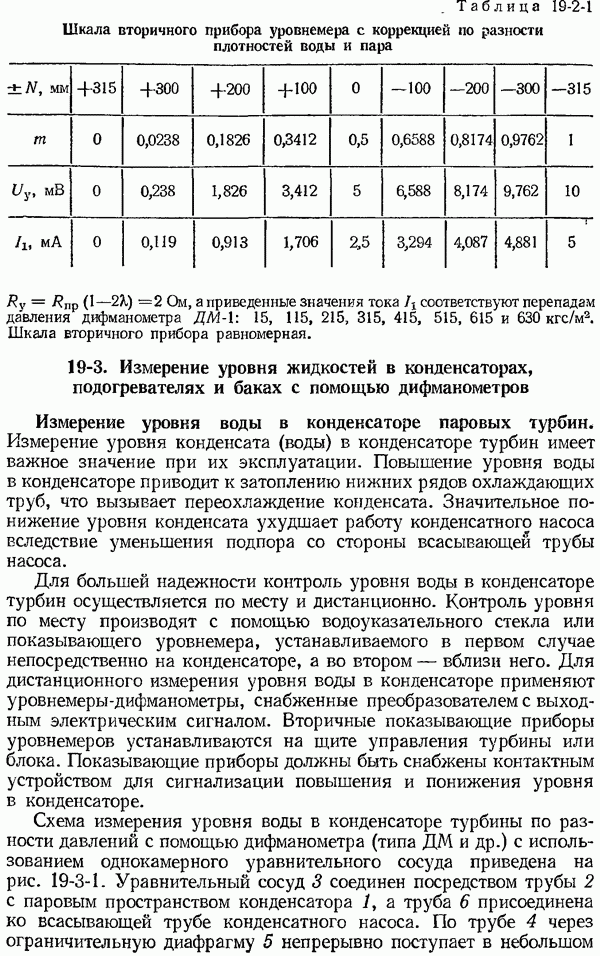
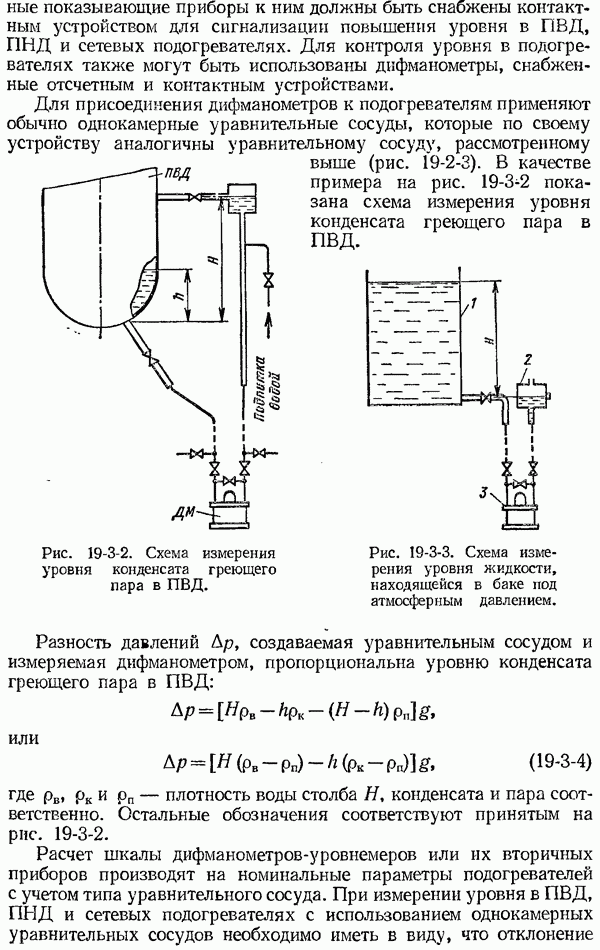
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
- 19-5. Емкостные уровнемеры
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
- 20-2. Сигнализаторы уровня сыпучих тел
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- 21-2. Газоанализаторы химические
- 21-3. Тепловые газоанализаторы
- 21-4. Магнитные газоанализаторы
- 21-5. Оптические газоанализаторы
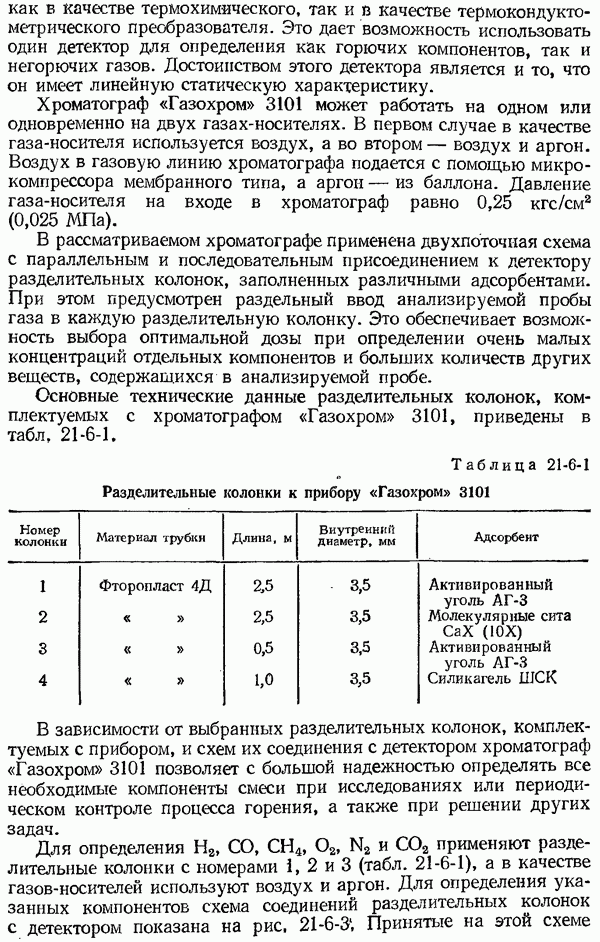
- 21-6. Газовые хроматографы
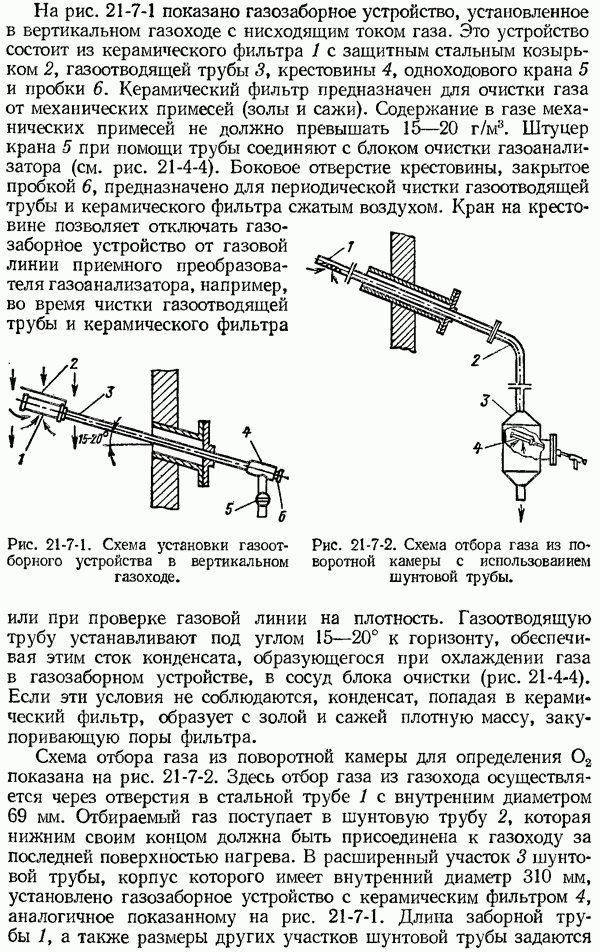
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
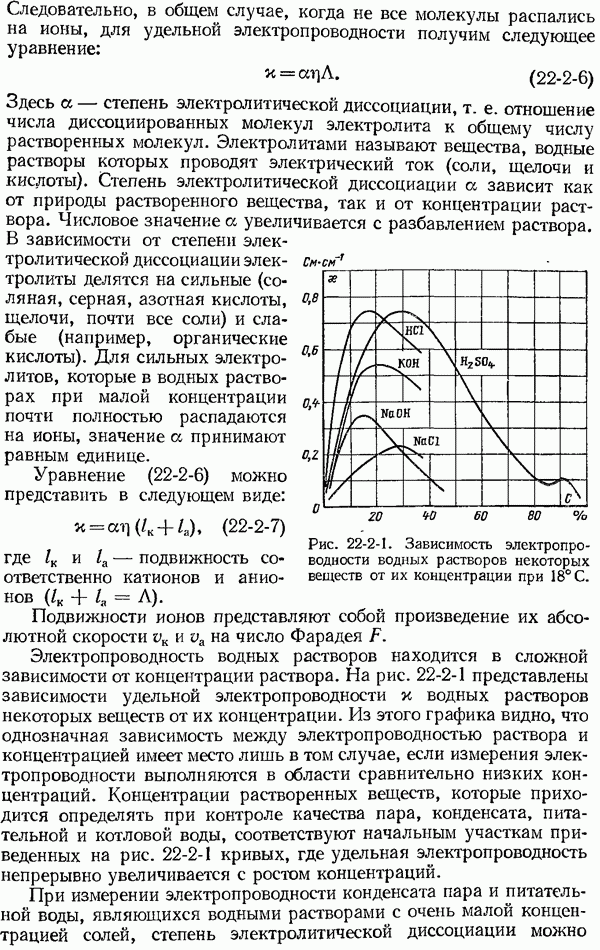
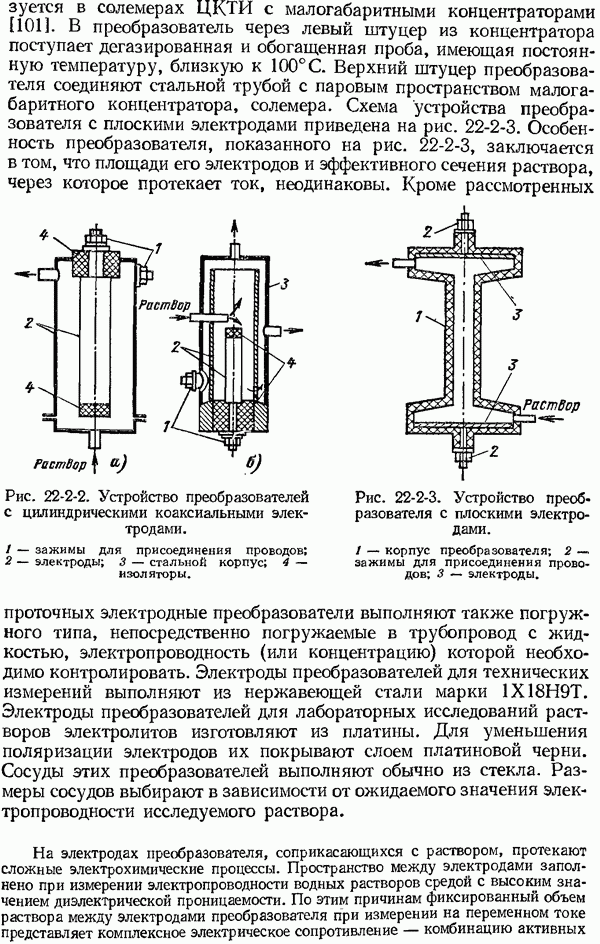
- 22-2. Измерение удельной электропроводности водных растворов
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ