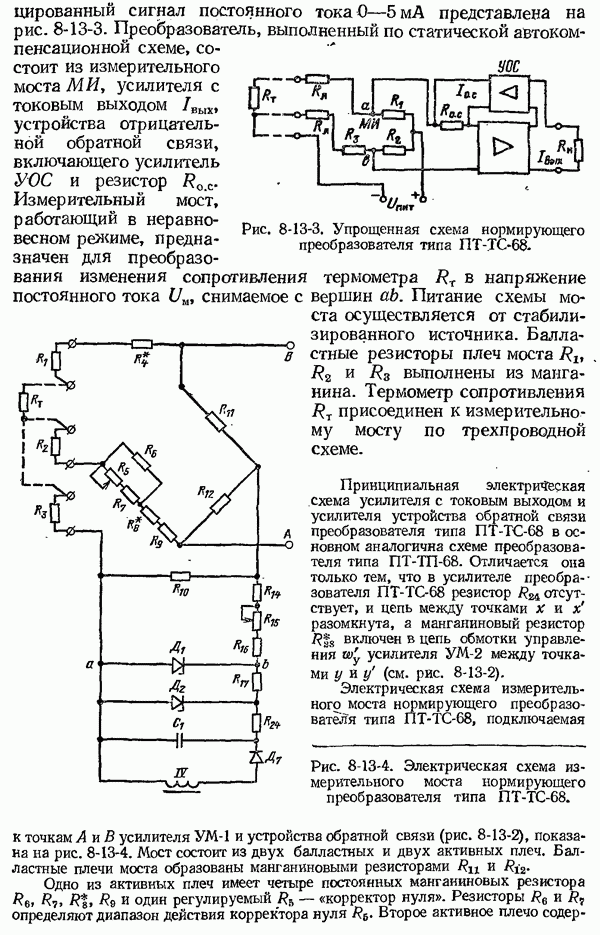
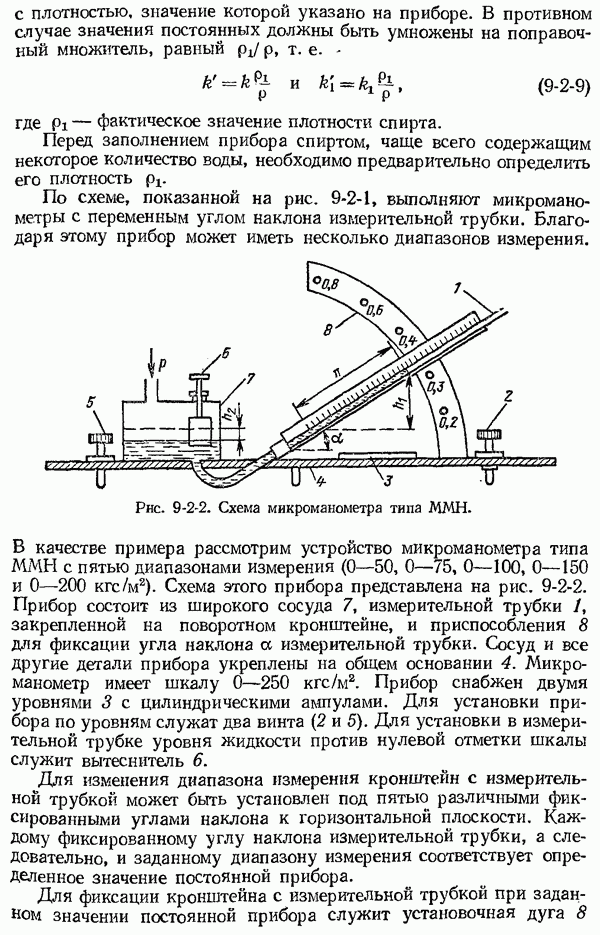
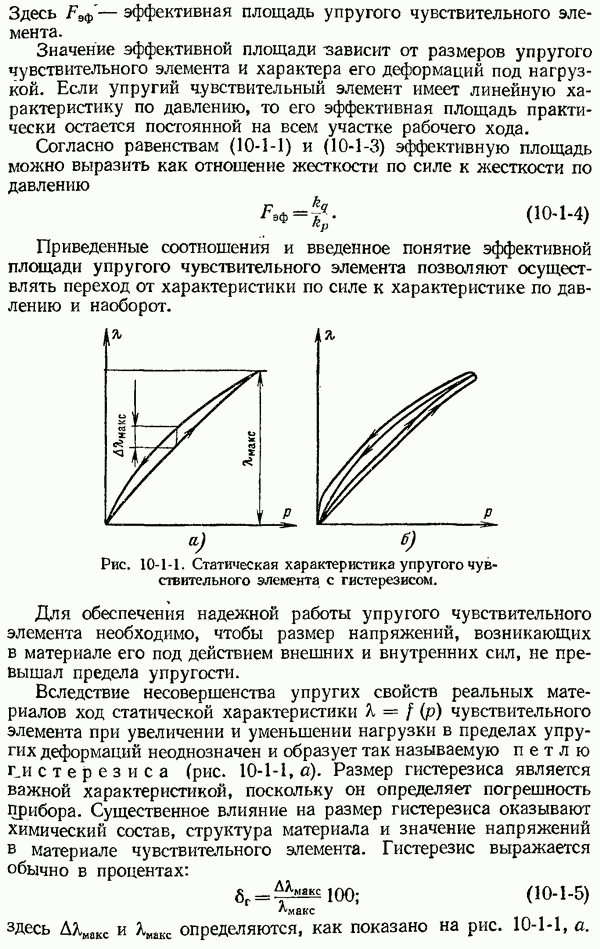
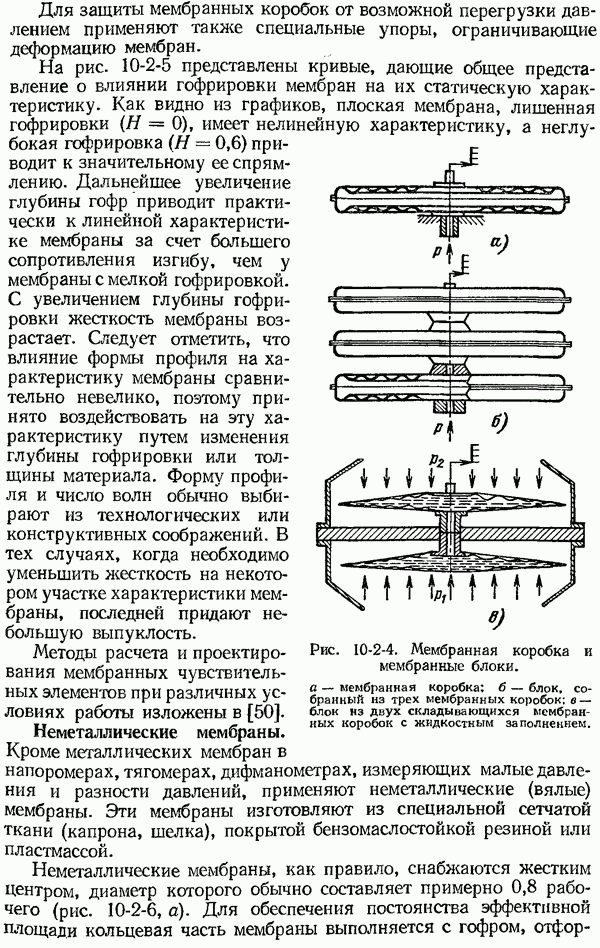
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
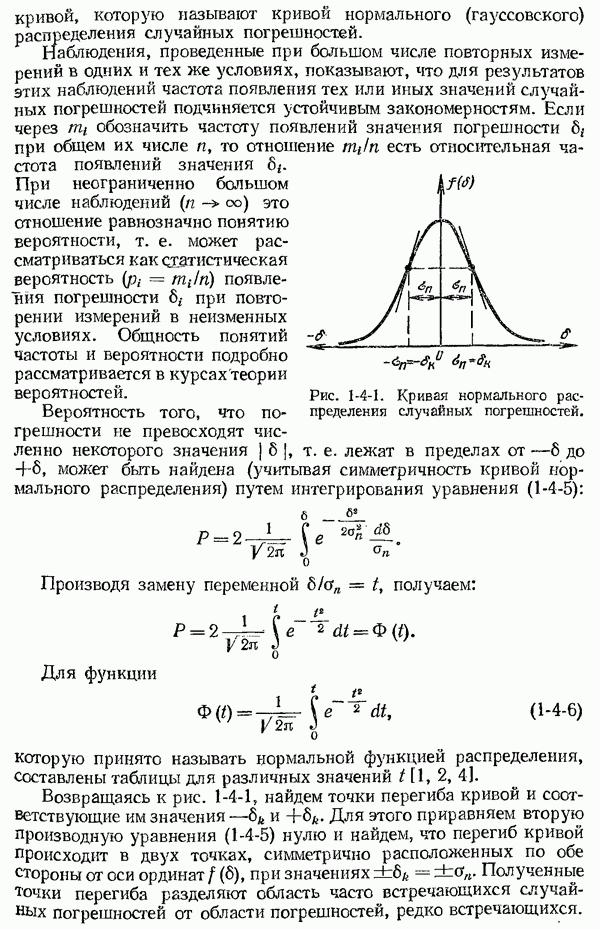
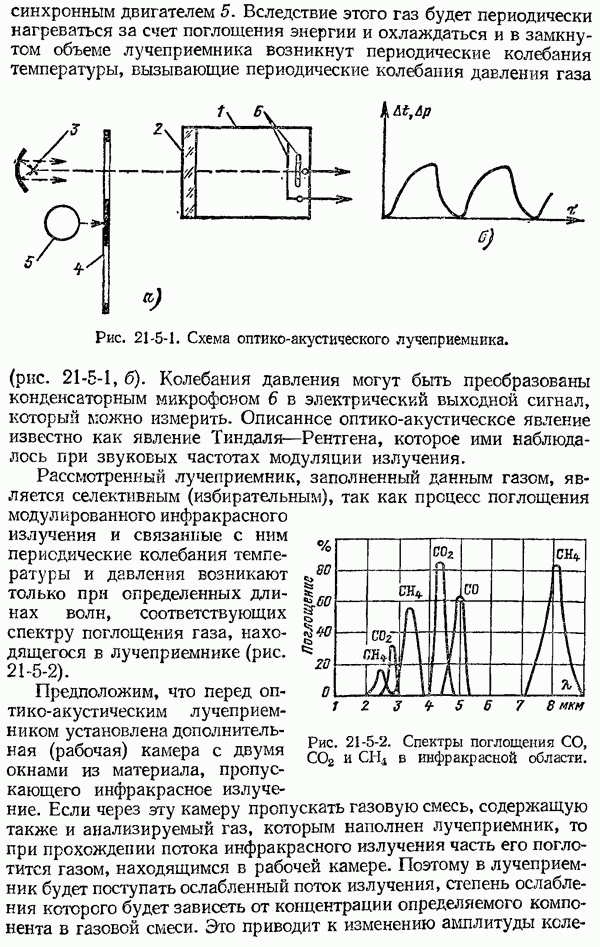
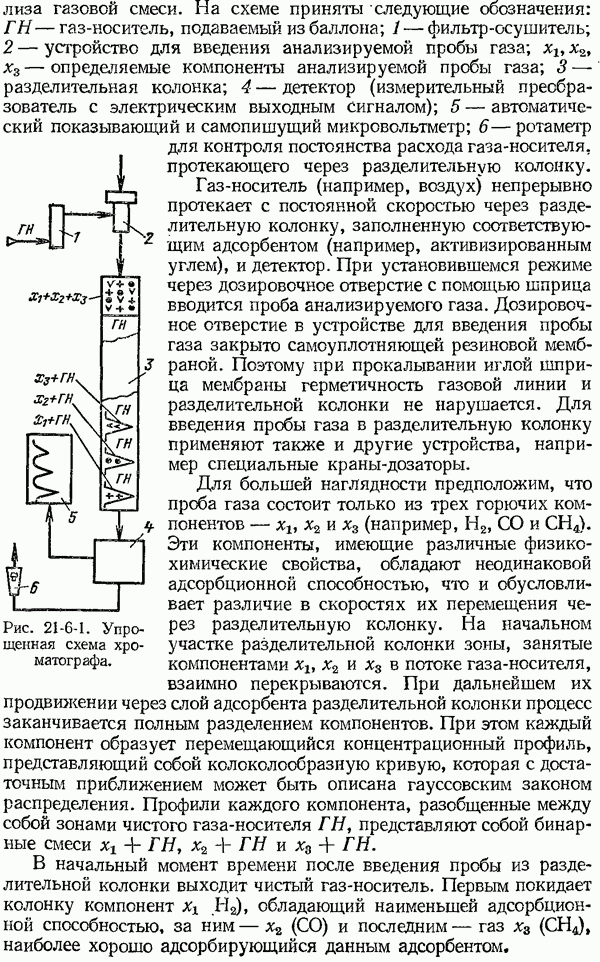
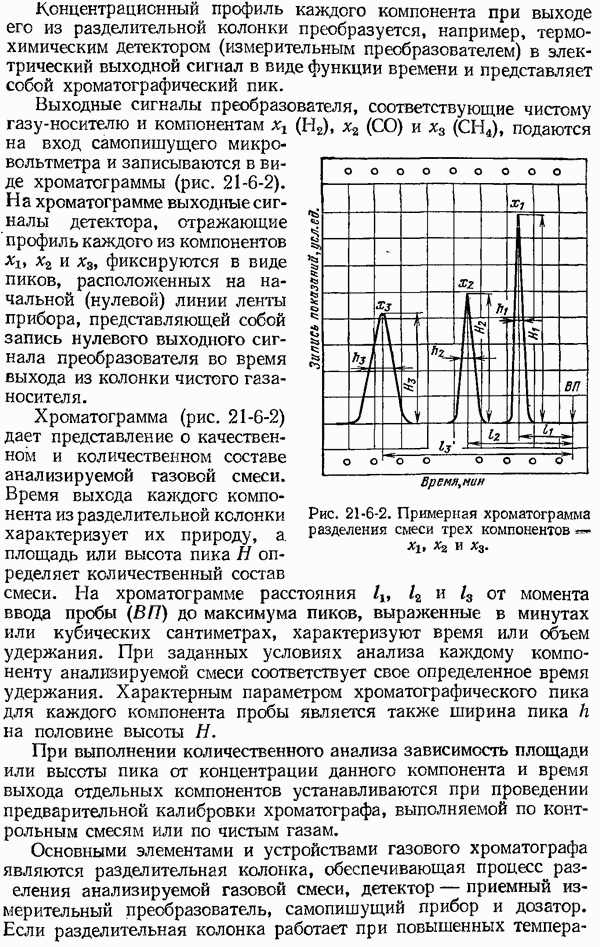
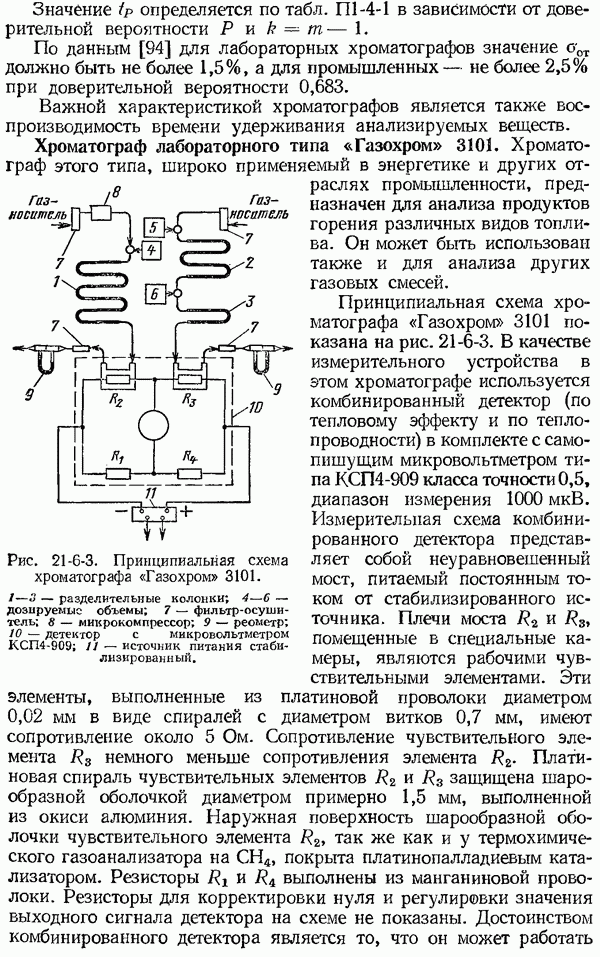
1-6. Общие сведения о динамических характеристиках средств измерений
Рассмотренные выше основные метрологические свойства средств измерений характеризуют их только при статическом преобразовании измеряемой величины. При измерении (преобразовании) величины, меняющейся во времени, результаты измерения могут оказаться искаженными помимо допускаемых (статических) погрешностей и погрешностей, обусловленных условиями измерения, погрешностью еще одного вида, возникающей только в динамическом режиме и получившей вследствие этого наименование динамической погрешности.
В дальнейшем под динамической погрешностью средства измерений будем понимать разность между погрешностью средства измерений в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени. При этом Полагаем, что погрешности, обусловленные условиями измерения, отсутствуют.
Если входная величина выражается функцией  а выходная величина — функцией
а выходная величина — функцией  то в каждый момент времени при отсутствии статических погрешностей абсолютная динамическая
то в каждый момент времени при отсутствии статических погрешностей абсолютная динамическая
погрешность

где  - выходная величина «идеального» в динамическом отношении прибора, равная
- выходная величина «идеального» в динамическом отношении прибора, равная  здесь
здесь 
 — коэффициент передачи (или чувствительность) «идеального» прибора.
— коэффициент передачи (или чувствительность) «идеального» прибора.
В дальнейшем будут рассматриваться методы описания линейных динамических измерительных устройств, под которыми понимают устройства, подчиняющиеся принципу наложения (суперпозиции). Согласно этому принципу эффект нескольких приложенных к измерительному устройству воздействий равен сумме эффектов каждого из этих воздействий в отдельности.

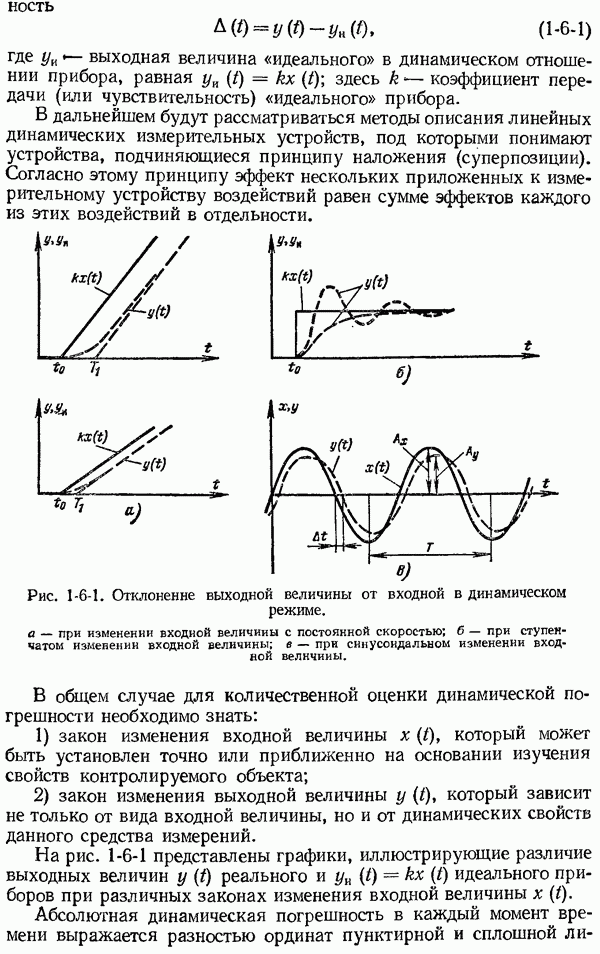
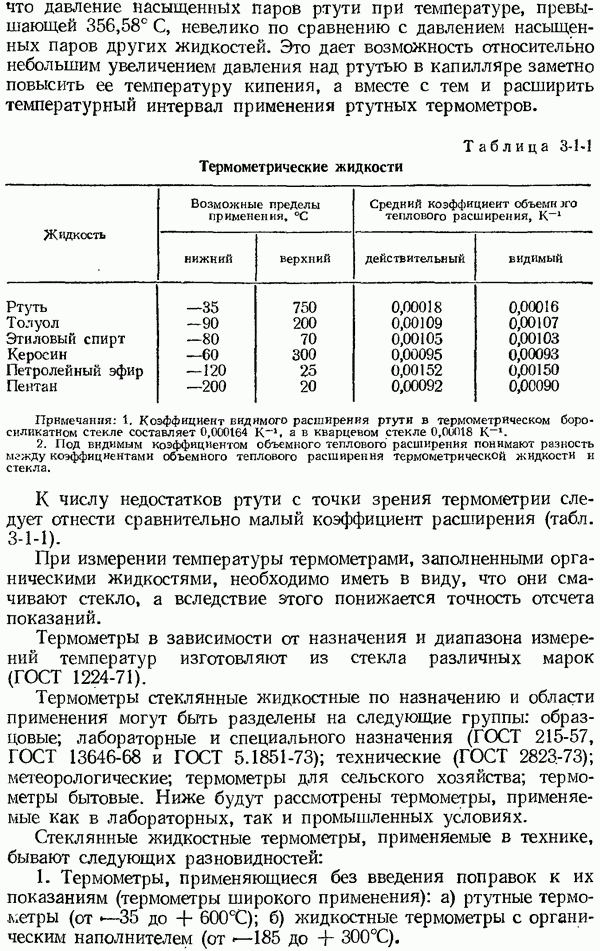
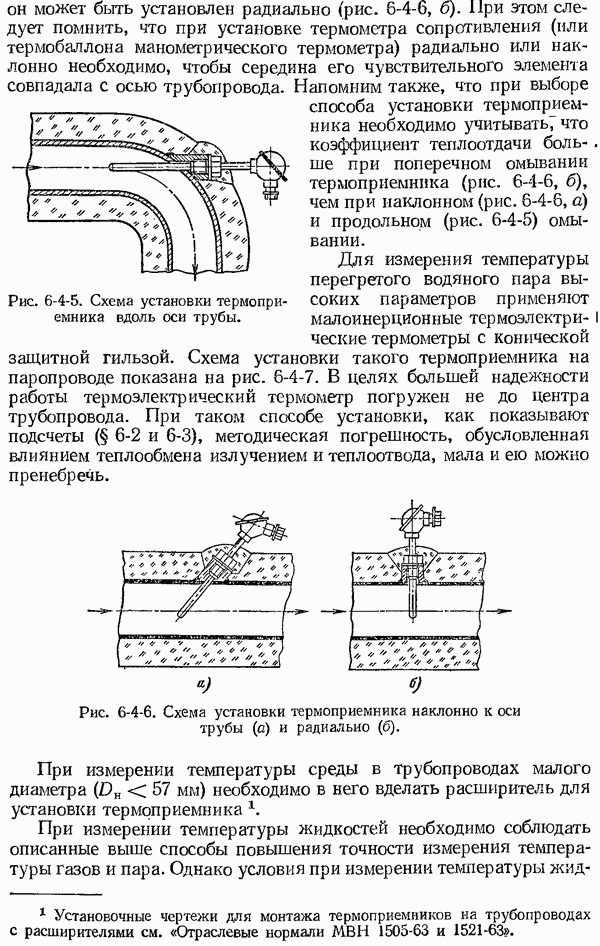
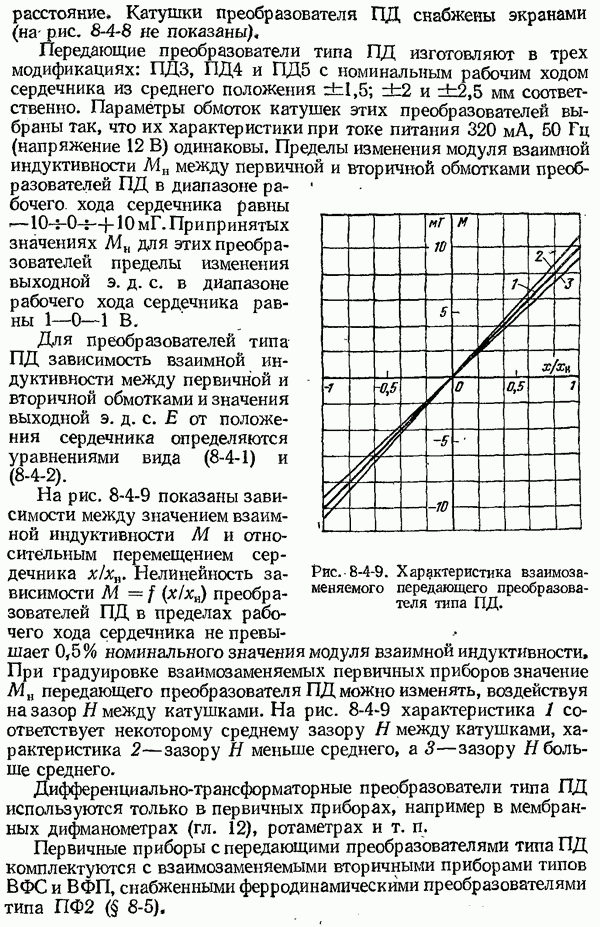
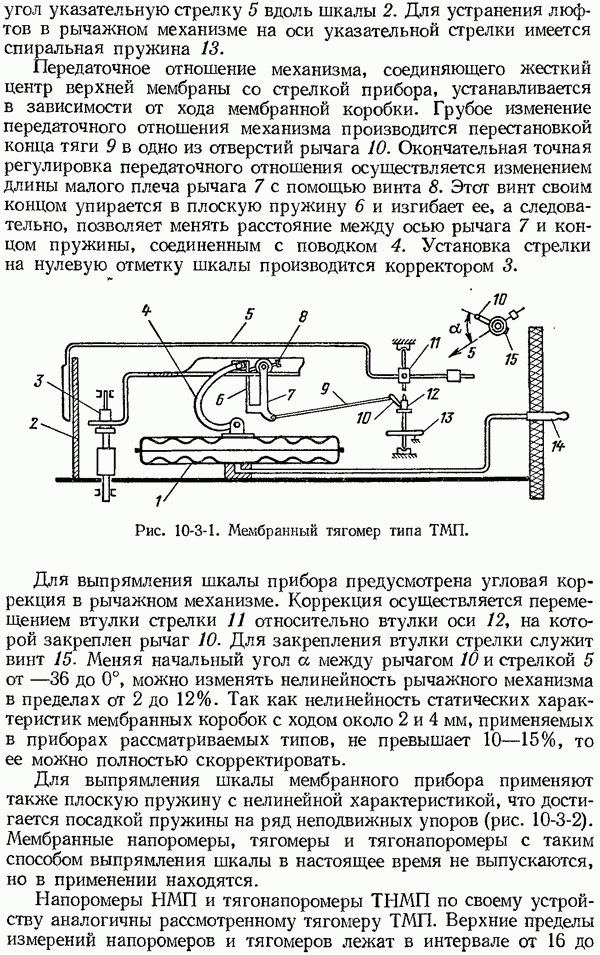
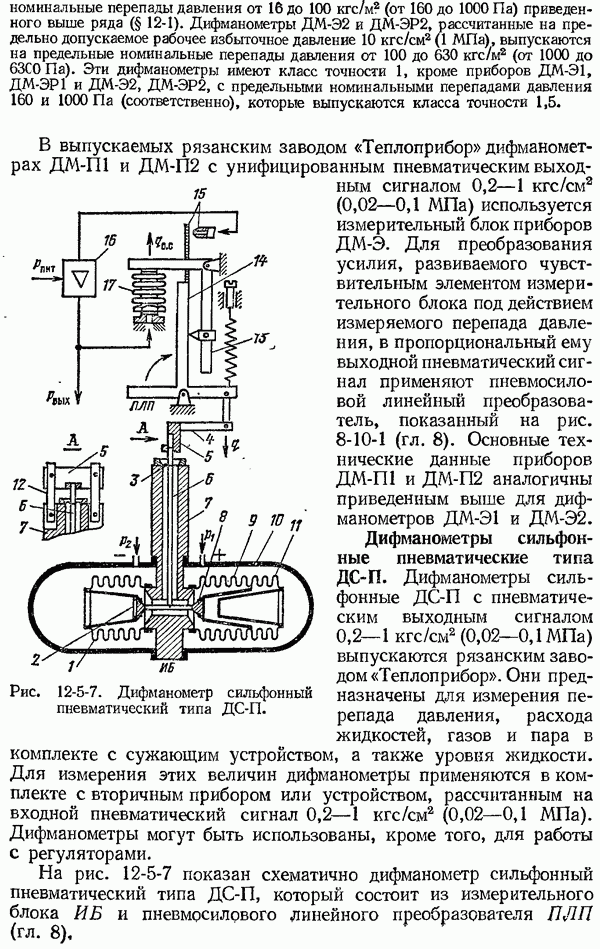
Рис. 1-6-1. Отклонение выходной величины от входной в динамическом режиме. а - при изменении входной величины с постоянной скоростью; б - при ступенчатом изменении входной величины; в — при синусоидальном изменении входной величины.
В общем случае для количественной оценки динамической погрешности необходимо знать:
1) закон изменения входной величины  который может быть установлен точно или приближенно на основании изучения свойств контролируемого объекта;
который может быть установлен точно или приближенно на основании изучения свойств контролируемого объекта;
2) закон изменения выходной величины  который зависит не только от вида входной величины, но и от динамических свойств данного средства измерений.
который зависит не только от вида входной величины, но и от динамических свойств данного средства измерений.
На рис. 1-6-1 представлены графики, иллюстрирующие различие выходных величин  реального и
реального и  идеального приборов при различных законах изменения входной величины
идеального приборов при различных законах изменения входной величины 
Абсолютная динамическая погрешность в каждый момент времени выражается разностью ординат пунктирной и сплошной
линий и, как видно из графиков, зависит от характера изменения  Например, при изменении входной величины с постоянной скоростью динамическая погрешность увеличивается с возрастанием скорости изменения входной величины и при достаточно больших значениях
Например, при изменении входной величины с постоянной скоростью динамическая погрешность увеличивается с возрастанием скорости изменения входной величины и при достаточно больших значениях  выходная величина
выходная величина  запаздывает относительно
запаздывает относительно  на время Т (рис. 1-6-1, а).
на время Т (рис. 1-6-1, а).
Ступенчатому изменению входной величины в зависимости от свойств средства измерений соответствует апериодическое изменение или затухающие колебания выходной величины (рис. 1-6-1, б). В последнем случае динамическая погрешность периодически, с определенной частотой, изменяет свой знак, уменьшаясь по мере затухания колебаний. При синусоидальном изменении входной величины с амплитудой  и некоторой постоянной частотой выходная величина в установившемся режиме представляет собою также синусоидальные колебания с амплитудой
и некоторой постоянной частотой выходная величина в установившемся режиме представляет собою также синусоидальные колебания с амплитудой  той же частоты (рис. 1-6-1, в). Как видно из графика, амплитуда и фаза выходной величины не совпадают с амплитудой и фазой входной величины. Изменение амплитуды и фазовый временной сдвиг выходной величины зависят от свойств средств измерений и частоты входных колебаний.
той же частоты (рис. 1-6-1, в). Как видно из графика, амплитуда и фаза выходной величины не совпадают с амплитудой и фазой входной величины. Изменение амплитуды и фазовый временной сдвиг выходной величины зависят от свойств средств измерений и частоты входных колебаний.
Динамические свойства средств измерений зависят от внутренней структуры средства измерений и его элементов. Следует иметь в виду, что измерительные устройства (манометры, дифманометры), предназначенные для измерения давления, разности давлений, расхода Еещества по перепаду давления в сужающем устройстве и других величин, в эксплуатационных условиях работают при наличии соединительных импульсных линий. В этом случае необходимо учитывать влияние соединительных линий на динамику манометров и дифманометров [5].
Динамические свойства первичных преобразователей, например термоэлектрических термометров или термометров сопротивления зависят от размеров, положения чувствительного элемента в системе термометра, теплофизических свойств его отдельных элементов, а также от условий теплообмена между термометром и средой, температура которой измеряется.
Для аналитического описания динамики линейных измерительных устройств применяют линейные дифференциальные уравнения. Однако средства измерений, применяемые на теплоэнергетических установках, во многих случаях являются физическими устройствами, содержащими нелинейные элементы [14, 15]. Поэтому в инженерной практике идут на упрощение, которое обычно сводится к линеаризации характеристик средств измерений. Это позволяет использовать для описания характера динамического преобразования сигнала средством измерений линейные дифференциальные уравнения вида

где  постоянные коэффициенты
постоянные коэффициенты 
Если в результате аналитического изучения исследуемого средства измерений получено дифференциальное уравнение, которое путем упрощений оказалось возможным привести к виду (1-6-2), то для оценки допустимости сделанных упрощений необходимо иметь для сравнения экспериментальные данные при некотором заданном виде испытательного воздействия. При этом для линеаризованных уравнений должны быть указаны исходный режим и границы допускаемого изменения входной величины, в которых принятые допущения позволяют использовать уравнение вида (1-6-2).
Наряду с дифференциальными уравнениями для описания динамических систем используют передаточные функции.
Для нулевых начальных условий уравнение (1-6-2) в изображениях по Лапласу записывают в следующем виде:

где

Отношение изображения выходной величины  к изображению входной величины
к изображению входной величины  при нулевых начальных условиях называется передаточной функцией. Согласно (1-6-3) передаточная функция имеет вид:
при нулевых начальных условиях называется передаточной функцией. Согласно (1-6-3) передаточная функция имеет вид:

Другими словами, передаточная функция определяется отношением полинома правой части  к полиному левой части
к полиному левой части  уравнения (1-6-3).
уравнения (1-6-3).
Как отмечалось выше, в большинстве случаев средства измерений или измерительные системы (например, первичный преобразователь — вторичный прибор) являются системой из последовательно соединенных элементов направленного действия (см. рис. 1-5-2). В этом случае передаточная функция измерительной системы равна произведению передаточных функций каждого элемента

Если измерительная система состоит из первичного прибора (манометра или дифманометра) с импульсными линиями и вторичного прибора, то передаточная функция такой измерительной системы имеет вид (1-6-5), но  является передаточной функцией первичного прибора с импульсными линиями [5].
является передаточной функцией первичного прибора с импульсными линиями [5].
Передаточная функция полностью характеризует динамические свойства линейной системы и позволяет производить оценку свойств средств измерений. Для измерительных целей описание динамических свойств средств измерений передаточной функцией удобно
использовать в тех случаях, когда коэффициенты дифференциального уравнения зависят от условий применения средств измерений, а вид аппроксимирующей функции  изменяется. Характерным примером средств измерений такого типа являются термоэлектрические термометры, термометры сопротивления, манометрические термометры.
изменяется. Характерным примером средств измерений такого типа являются термоэлектрические термометры, термометры сопротивления, манометрические термометры.
Динамические характеристики средств измерений, характеризующие реакцию средств измерений на гармонические воздействия в широком диапазоне частот, принято называть частотными характеристиками, которые включают в себя амплитудно-частотную и фазо-частотную характеристики. Частотные характеристики имеют наглядный физический смысл и могут быть получены экспериментальным и расчетным путем.
При экспериментальном определении частотных характеристик на вход средства измерений с помощью генератора подаются гармонические, например, синусоидальные колебания

Если исследуемое средство измерений является линейной динамической системой, то колебания выходной величины в установившемся режиме будут также синусоидальными (см. рис. 1-6-1, в)

где  начальная фаза, рад;
начальная фаза, рад;  — угловая скорость,
— угловая скорость, 
Амплитуда выходных колебаний и их фазовый (временной) сдвиг зависят от свойств средств измерений и частоты входных колебаний.
Зависимость  показывающая, как изменяется с частотой отношение амплитуды выходных колебаний
показывающая, как изменяется с частотой отношение амплитуды выходных колебаний  линейной динамической системы к амплитуде входных колебаний
линейной динамической системы к амплитуде входных колебаний  называется амплитудно-частотной характеристикой (АЧХ) этой системы.
называется амплитудно-частотной характеристикой (АЧХ) этой системы.

Зависимость от частоты сдвига по фазе между входными и выходными колебаниями называется фазо-частотной характеристикой (ФЧХ) системы

Значение амплитудно-частотной характеристики исследуемого средства измерений для данной частоты колебаний 

Сдвиг по фазе  между колебаниями
между колебаниями  и
и  для значения определяется по формуле
для значения определяется по формуле

где  время, соответствующее сдвигу (отставанию) по фазе между входными и выходными колебаниями (см. рис. 1-6-1, в),
время, соответствующее сдвигу (отставанию) по фазе между входными и выходными колебаниями (см. рис. 1-6-1, в),  период колебаний, с.
период колебаний, с.
Эксперимент по определению частотных характеристик проводится для нескольких значений  входных колебаний с фиксированной амплитудой. Следует отметить, что у реальных средств измерений с возрастанием частоты обычно уменьшается амплитуда выходных колебаний и увеличивается временной сдвиг
входных колебаний с фиксированной амплитудой. Следует отметить, что у реальных средств измерений с возрастанием частоты обычно уменьшается амплитуда выходных колебаний и увеличивается временной сдвиг  выходной величины относительно входной, в результате чего растет и динамическая погрешность.
выходной величины относительно входной, в результате чего растет и динамическая погрешность.
Экспериментальное определение частотных характеристик средств измерений следует проводить во всем рабочем диапазоне частот от 0 до  при котором
при котором  отличается от 0.
отличается от 0.

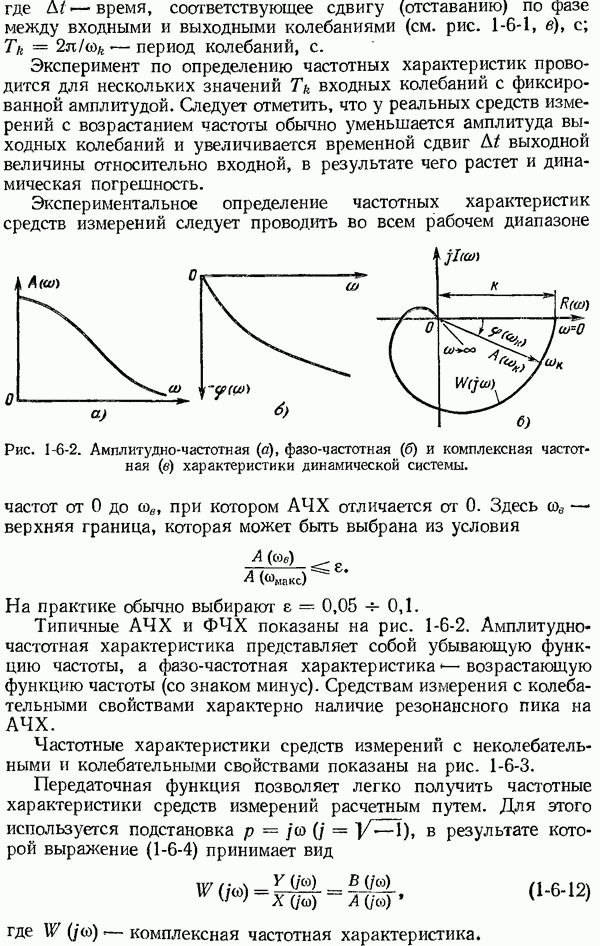
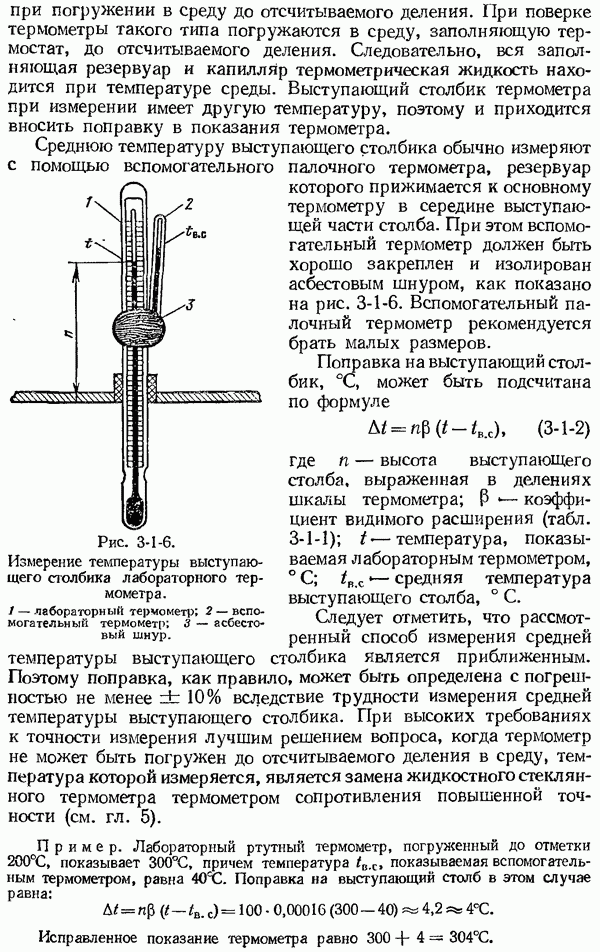
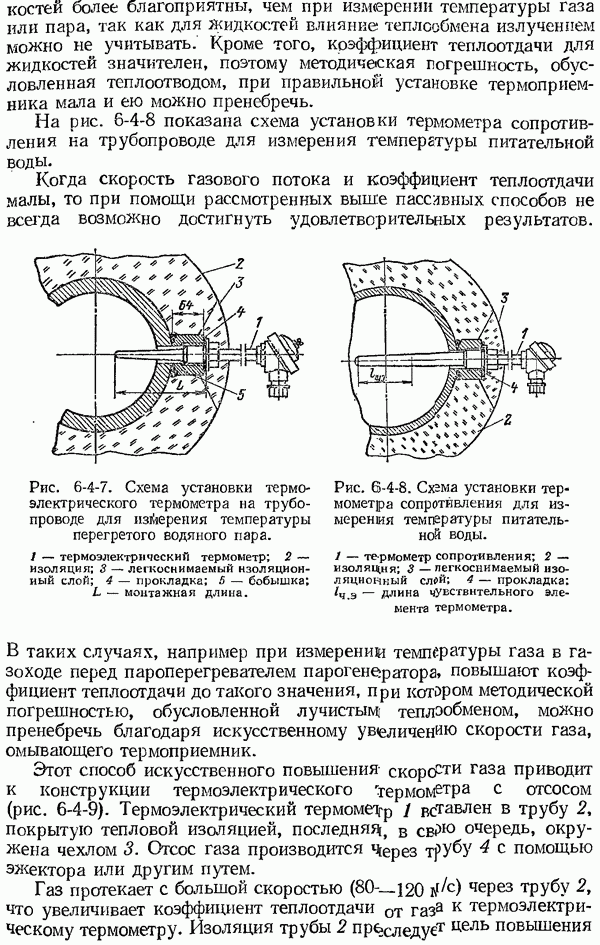
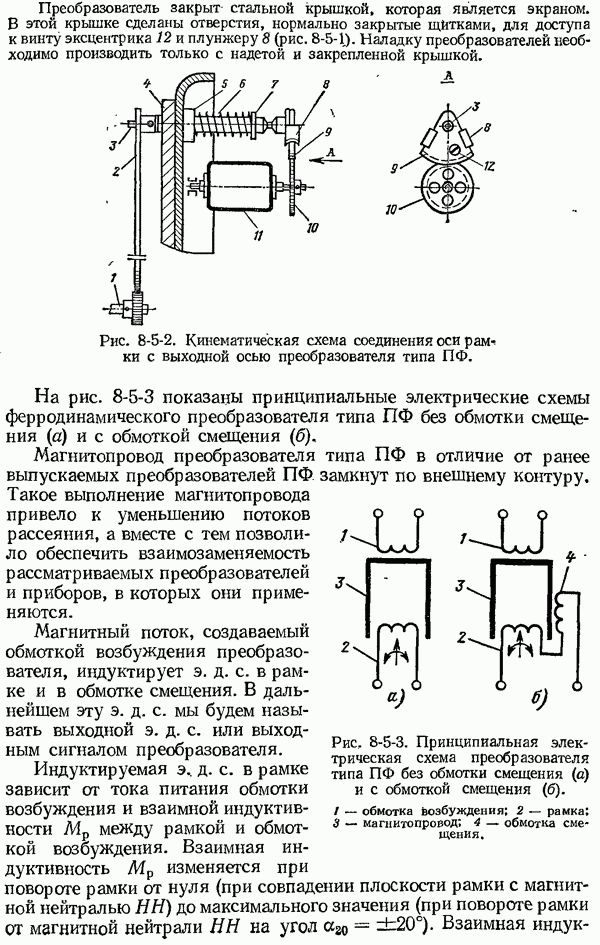
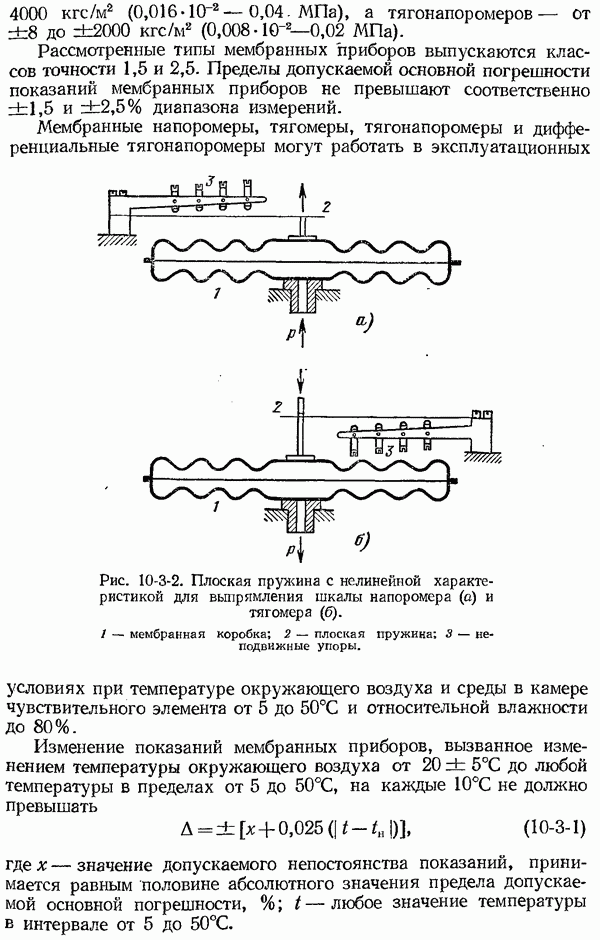
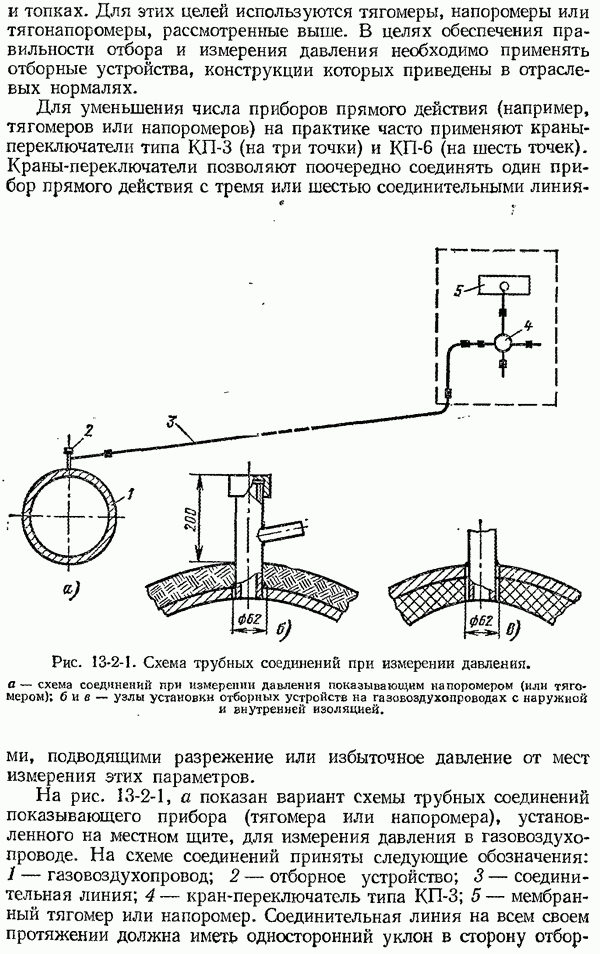
Рис. 1-6-2. Амплитудно-частотная (а), фазо-частотная (б) и комплексная частотная  характеристики динамической системы.
характеристики динамической системы.
Здесь  верхняя граница, которая может быть выбрана из условия
верхняя граница, которая может быть выбрана из условия

На практике обычно выбирают 
Типичные  и
и  показаны на рис. 1-6-2. Амплитудно-частотная характеристика представляет собой убывающую функцию частоты, а фазо-частотная характеристика
показаны на рис. 1-6-2. Амплитудно-частотная характеристика представляет собой убывающую функцию частоты, а фазо-частотная характеристика  возрастающую функцию частоты (со знаком минус). Средствам измерения с колебательными свойствами характерно наличие резонансного пика на
возрастающую функцию частоты (со знаком минус). Средствам измерения с колебательными свойствами характерно наличие резонансного пика на 
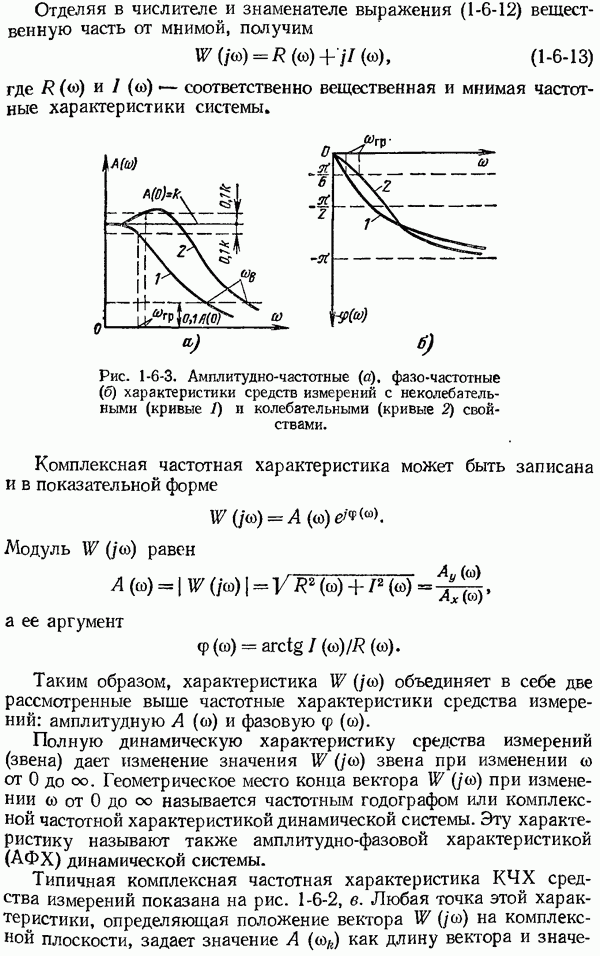
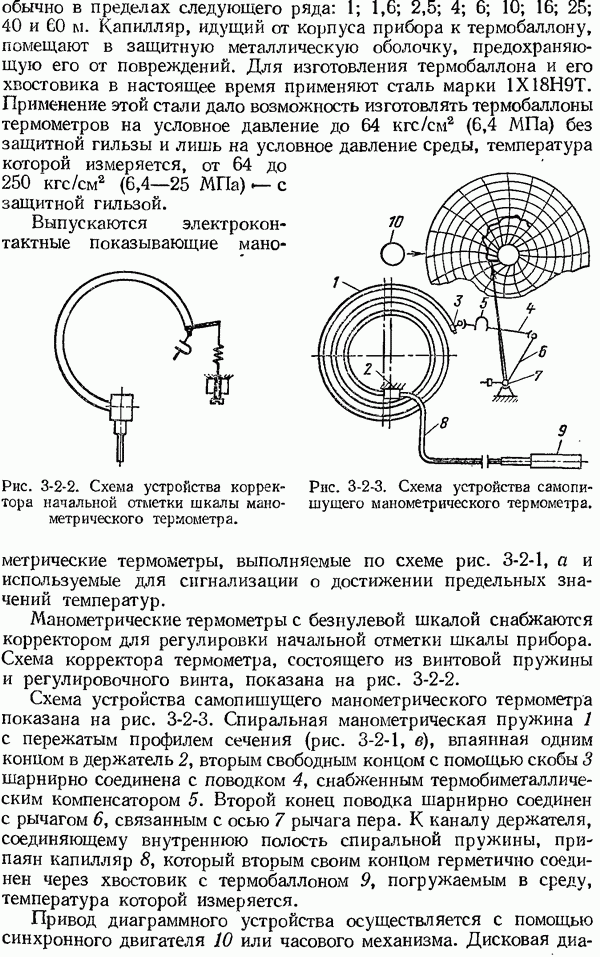
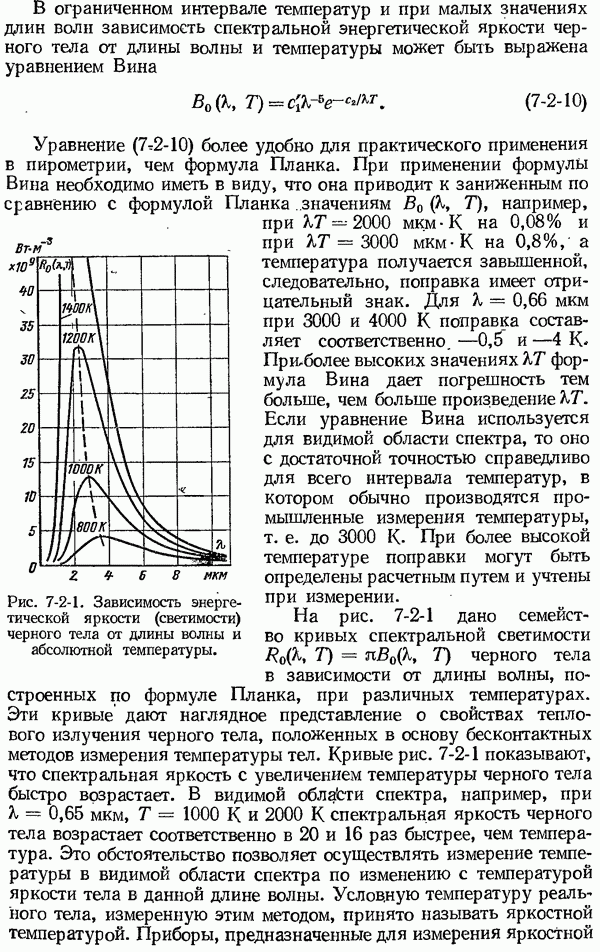
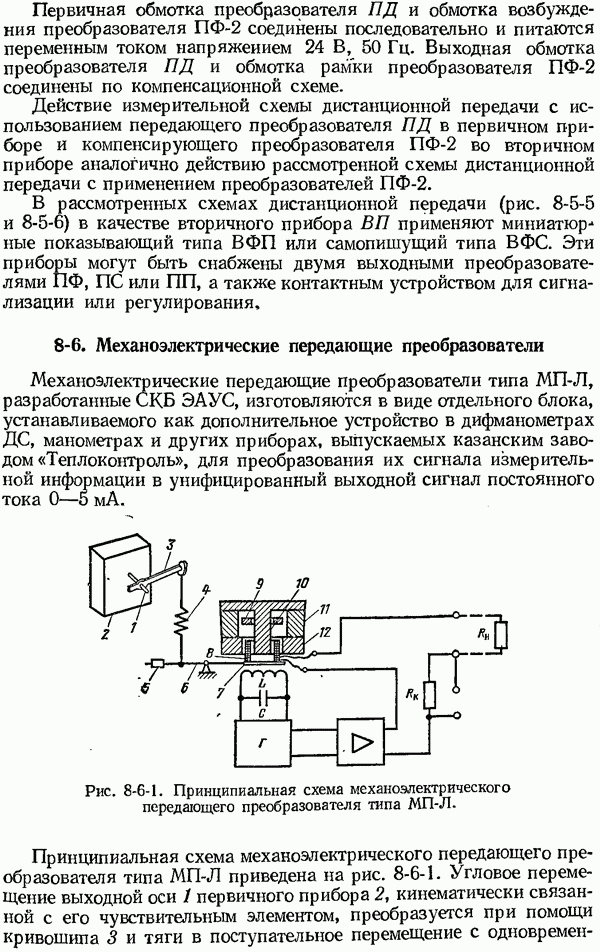
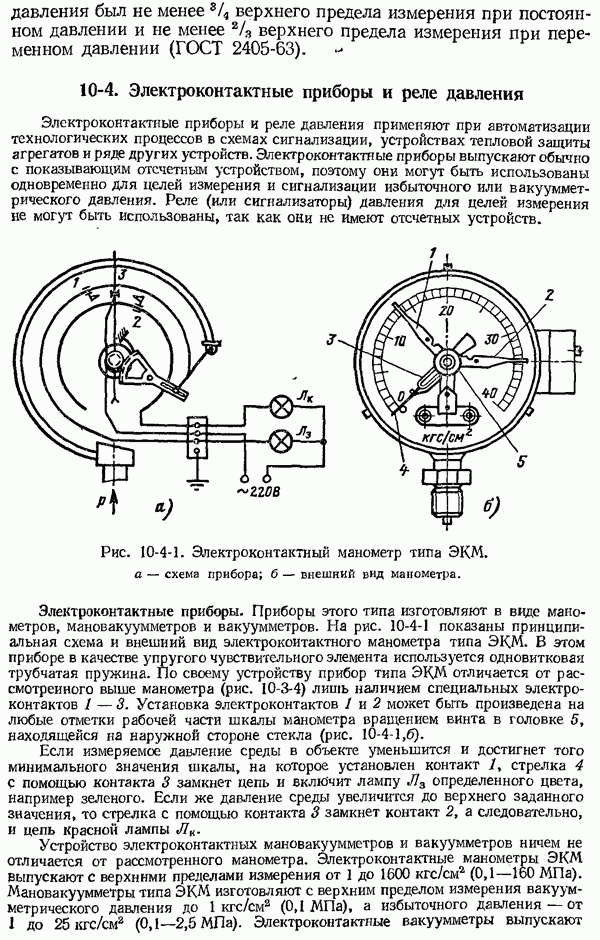
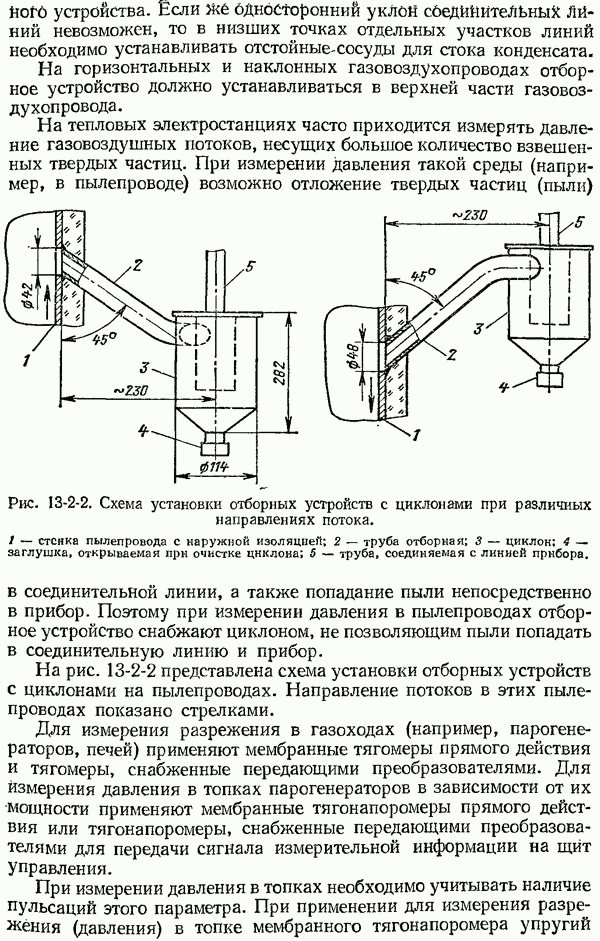
Частотные характеристики средств измерений с неколебательными и колебательными свойствами показаны на рис. 1-6-3.
Передаточная функция позволяет легко получить частотные характеристики средств измерений расчетным путем. Для этого используется подстановка  в результате которой выражение (1-6-4) принимает вид
в результате которой выражение (1-6-4) принимает вид

где  комплексная частотная характеристика»
комплексная частотная характеристика»
Отделяя в числителе и знаменателе выражения (1-6- 2) вещественную часть от мнимой, получим

где  соответственно вещественная и мнимая частотные характеристики системы.
соответственно вещественная и мнимая частотные характеристики системы.

Рис. 1-6-3. Амплитудно-частотные (а), фазо-частотные (б) характеристики средств измерений с неколебательными (кривые 1) и колебательными (кривые 2) свойствами.
Комплексная частотная характеристика может быть записана и в показательной форме

Модуль  равен
равен

а ее аргумент

Таким образом, характеристика  объединяет в себе две рассмотренные выше частотные характеристики средства измерений: амплитудную
объединяет в себе две рассмотренные выше частотные характеристики средства измерений: амплитудную  и фазовую
и фазовую 
Полную динамическую характеристику средства измерений (звена) дает изменение значения  звена при изменении со от 0 до
звена при изменении со от 0 до  Геометрическое место конца вектора
Геометрическое место конца вектора  при изменении со от 0 до
при изменении со от 0 до  называется частотным годографом или комплексной частотной характеристикой динамической системы. Эту характеристику называют также амплитудно-фазовой характеристикой
называется частотным годографом или комплексной частотной характеристикой динамической системы. Эту характеристику называют также амплитудно-фазовой характеристикой  динамической системы.
динамической системы.
Типичная комплексная частотная характеристика  средства измерений показана на рис. 1-6-2, в. Любая точка этой характеристики, определяющая положение вектора
средства измерений показана на рис. 1-6-2, в. Любая точка этой характеристики, определяющая положение вектора  на комплексной плоскости, задает значение
на комплексной плоскости, задает значение  как длину вектора и
как длину вектора и
значение  как угол, о разованныи этим вектором с положительной вещественной полуосью
как угол, о разованныи этим вектором с положительной вещественной полуосью  Направление поворота по часовой стрелке принято считать отрицательным. При стремлении со к нулю
Направление поворота по часовой стрелке принято считать отрицательным. При стремлении со к нулю  стремится к значению коэффициента передачи
стремится к значению коэффициента передачи  Мнимая часть
Мнимая часть  при этом обращается в нуль. По
при этом обращается в нуль. По  можно осуществить оценку динамической точности линейной динамической системы.
можно осуществить оценку динамической точности линейной динамической системы.
Амплитудно-частотная и фазо-частотная характеристики полностью описывают динамические свойства линейных средств измерений и позволяют, в частности, установить область частот нормальной их работы или рабочую полосу пропускания частот.
Рабочей полосой пропускания частот средств измерений называют область частот, в которой отклонение  от значения
от значения  при
при  не превышает ±10% (или
не превышает ±10% (или  а сдвиг по фазе
а сдвиг по фазе  не превышает
не превышает  рад). Верхнее значение частоты рабочей полосы пропускания называется граничной частотой согр (рис. 1-6-3).
рад). Верхнее значение частоты рабочей полосы пропускания называется граничной частотой согр (рис. 1-6-3).
Для характеристики динамических свойств средств измерений используют ряд параметров, определяемых по переходным характеристикам (функциям). Переходная характеристика представляет собой реакцию динамической системы на единичное ступенчатое воздействие

На практике используют ступенчатые воздействия произвольного значения. Переходная характеристика  связана с реакцией линейной динамической системы
связана с реакцией линейной динамической системы  на реальное (неединичное) ступенчатое воздействие
на реальное (неединичное) ступенчатое воздействие

простым соотношением

где  значение произвольного ступенчатого воздействия.
значение произвольного ступенчатого воздействия.
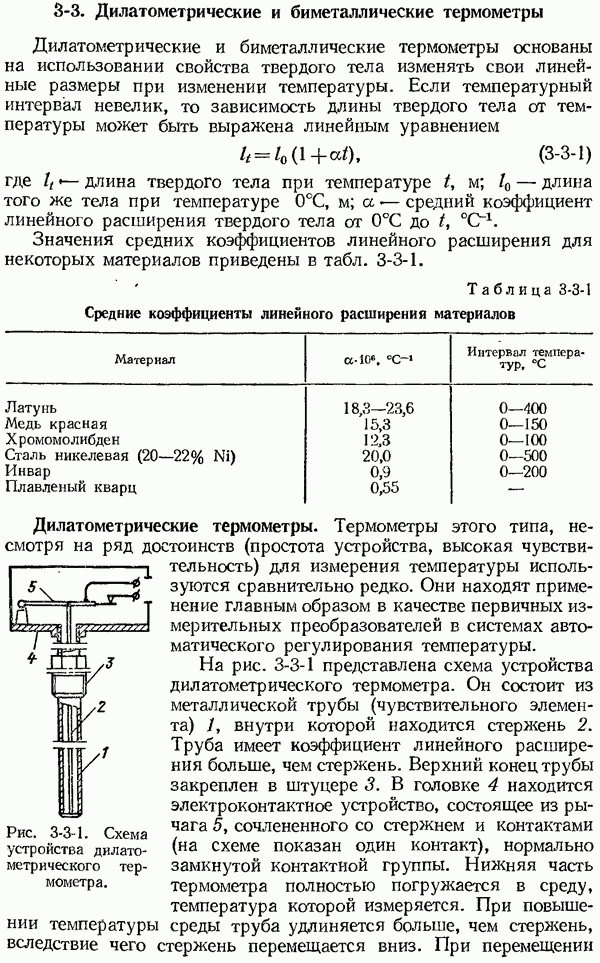
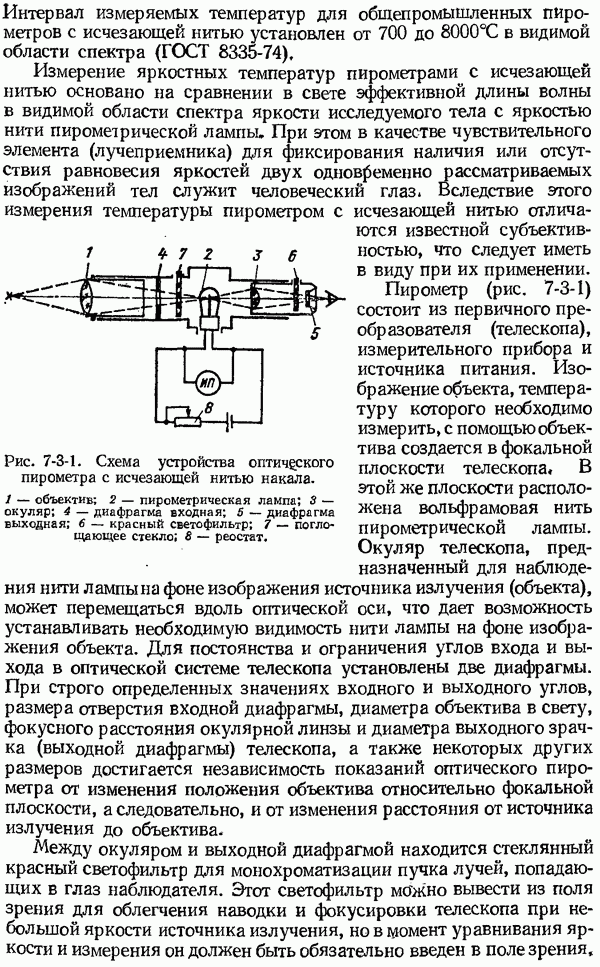
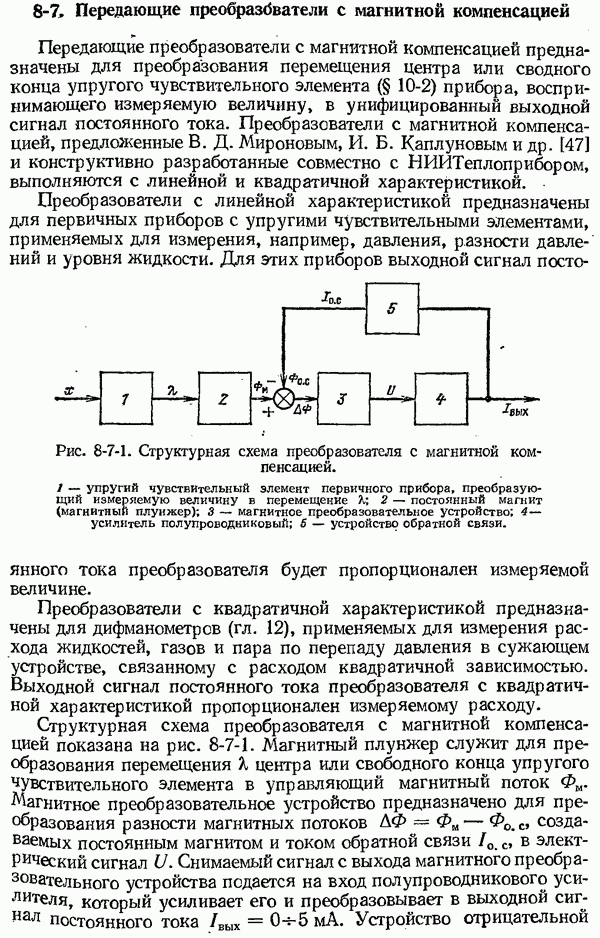
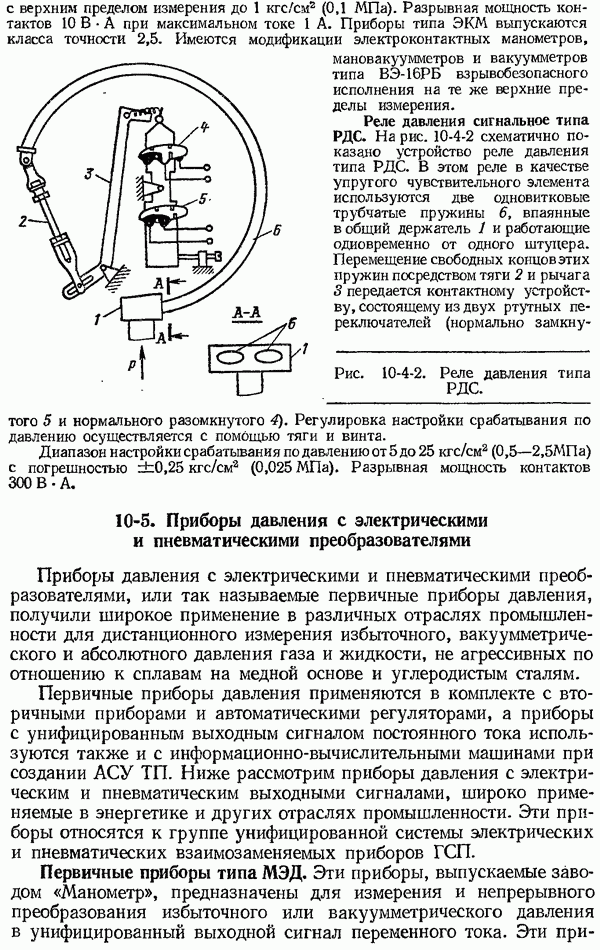
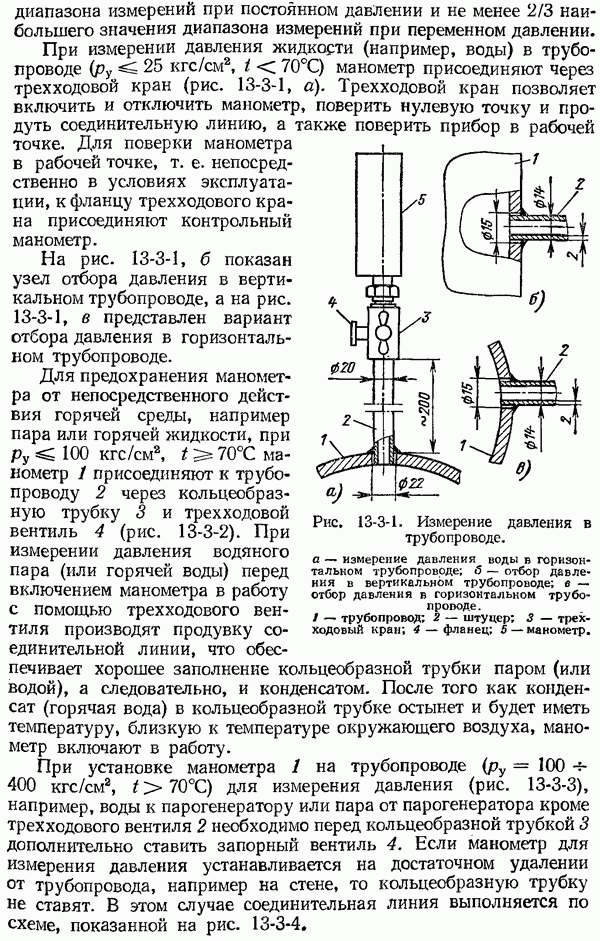
Переходная характеристика  может иметь апериодическую (рис. 1-6-4, а) или колебательную (рис. 1-6-4, б) формы.
может иметь апериодическую (рис. 1-6-4, а) или колебательную (рис. 1-6-4, б) формы.
Динамические характеристики линейного средства измерений не зависят от значения и знака ступенчатого возмущения, и переходные характеристики, снятые экспериментально при различных значениях ступенчатых возмущений, должны практически совпадать. Если опыты при различных по значению и знаку ступенчатых возмущениях приводят к неодинаковым количественным и качественным результатам, то это свидетельствует о нелинейности исследуемого средства измерения.
По переходным характеристикам, представленным на рис. 1-6-4, можно определить ряд используемых на практике параметров,
Характеризующих динамические свойства данного Средства Измерений. К ним относятся:
1) время установления показаний (переходного процесса)  время, по истечении которого выходная величина не выходит из заданной зоны, например ±5% или 1% (на рис. 1-6-4 показана пунктиром) от нового установившегося значения выходной величины
время, по истечении которого выходная величина не выходит из заданной зоны, например ±5% или 1% (на рис. 1-6-4 показана пунктиром) от нового установившегося значения выходной величины  (момент нанесения ступенчатого возмущения отмечен буквой
(момент нанесения ступенчатого возмущения отмечен буквой 
2) длительность периода колебаний Тк (рис. 1-6-4, б);
3) первый выброс выходной величины (рис. 1-6-4, б), определяемый отношением первой амплитуды  колебаний входной величины к нормирующему значению
колебаний входной величины к нормирующему значению  пли диапазону измерения;
пли диапазону измерения;
4) степень затухания 
5) постоянная времени  определяемая как отрезок под касательной, проведенной в точке перегиба
определяемая как отрезок под касательной, проведенной в точке перегиба  (рис. 1-6-4, а)
(рис. 1-6-4, а)
6) время запаздывания 
7) время успокоения.

Рис. 1-6-4. Переходные функции средств измерений с апериодической (а) и колебательной (б) формой переходного процесса.
По переходной характеристике, снятой экспериментально, можно определить передаточную функцию, амплитудно- и фазо-частотные характеристики, представляющие собою аппроксимацию действительных характеристик средств измерений [8—10].
При выборе тех или иных динамических параметров, которыми должны характеризоваться динамические свойства средств измерений, необходимо исходить из назначения средств измерений и условий их применения.
Часто используемыми динамическими параметрами средств измерений являются время установления показаний и рабочая полоса пропускания частот с нормированной амплитудой. В некоторых случаях необходимо дополнительно иметь передаточную функцию, например, для средств измерений, используемых в автоматических системах регулирования. Для средств измерений, используемых в схемах защиты и сигнализации, важным динамическим параметром является первый выброс, так как при его большом значении возможно ложное срабатывание защиты. Важной характеристикой для вторичных приборов является характер их успокоения.
Динамические параметры (время установления показаний, рабочая полоса пропускания частот, первый выброс и др.), вводимые в стандарты (например, ГОСТ 7164-71, ГОСТ 14763-69,
ГОСТ 14764-69) и технические условия на средства измерений, позволяют более правильно производить выбор приборов как для технологического контроля, сигнализации и защиты, так и для регулирования.
Следует отметить, что в некоторых случаях динамические свойства средств измерений характеризуются только временем установления показаний (например, пирометров полного излучения).
Динамические свойства термоэлектрических термометров и термометров сопротивления по ГОСТ 6616-74 и ГОСТ 6651-59 характеризуют показателем тепловой инерции ею, который часто называют постоянной времени термометра. Этот показатель фактически представляет собой постоянную времени экспоненциальной переходной характеристики термометра. Определение показателя тепловой инерции ем производится по методике, приведенной в ГОСТ 6616-74 и ГОСТ 6651-59.
Следует учитывать, что эти динамические параметры дают весьма ограниченную информацию о динамических свойствах средств измерений и каждый из них в отдельности не является достаточным критерием нормирования их динамических свойств.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
- 2-1. Основные сведения о температуре и температурных шкалах
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
- 3-1. Термометры стеклянные жидкостные
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
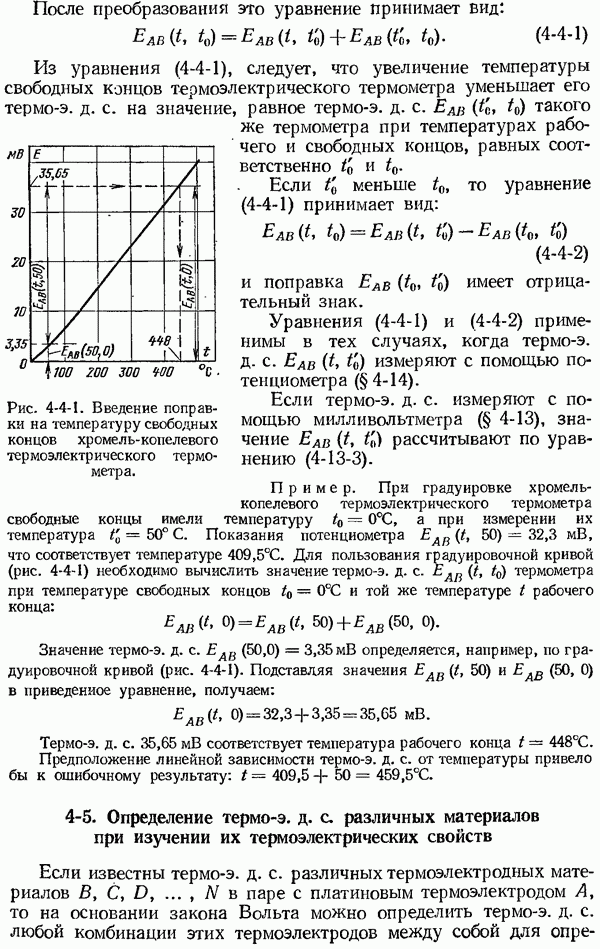
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
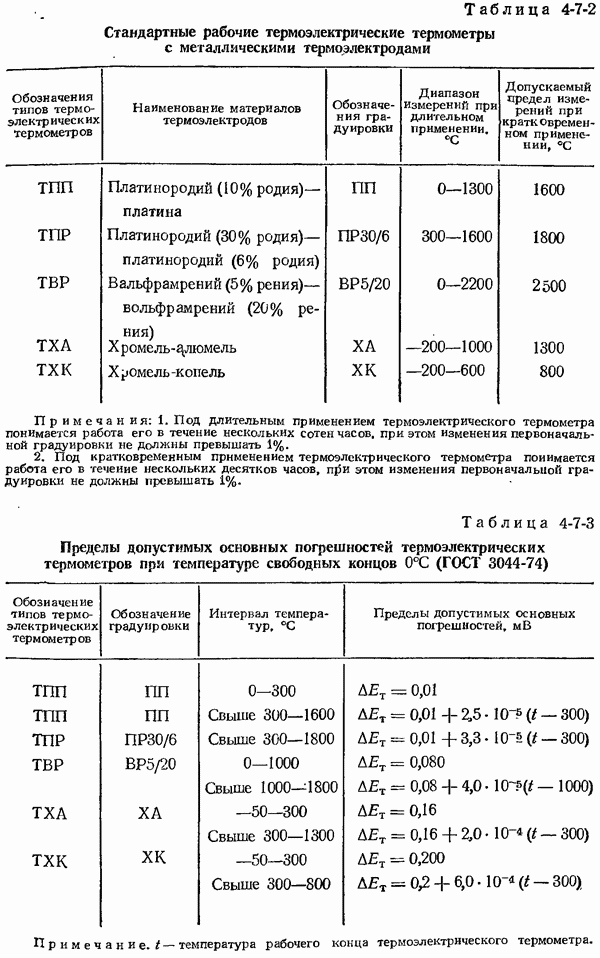
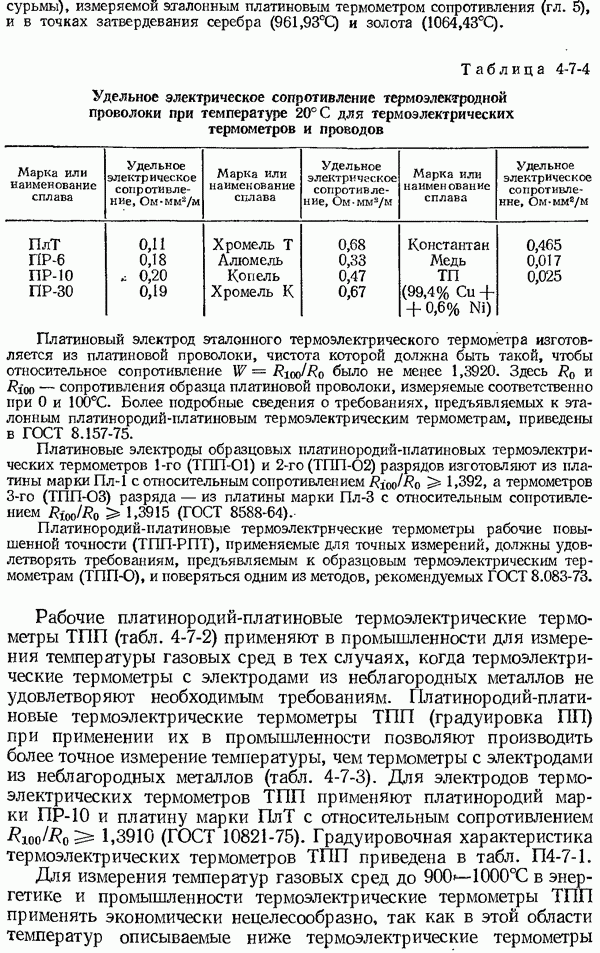
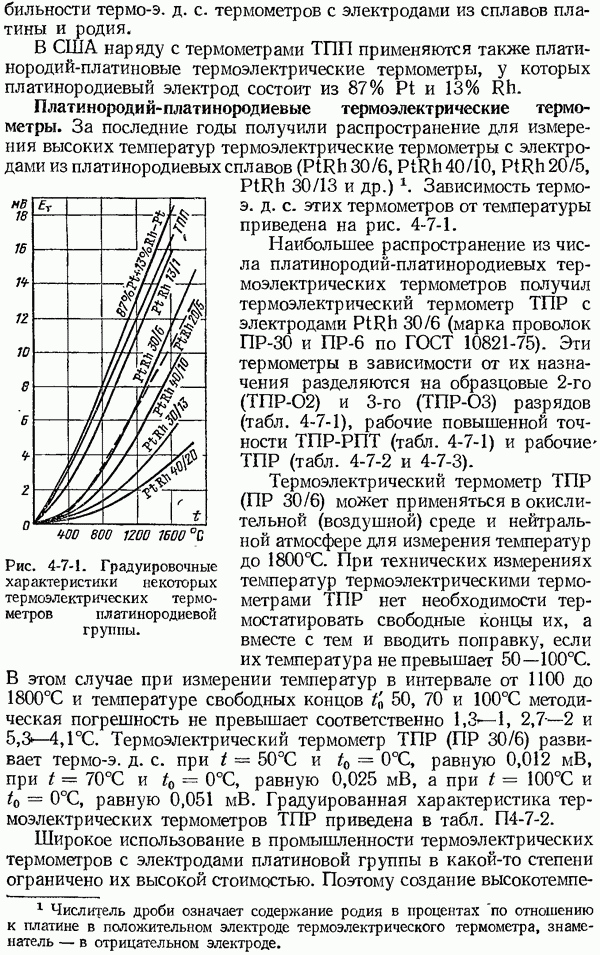
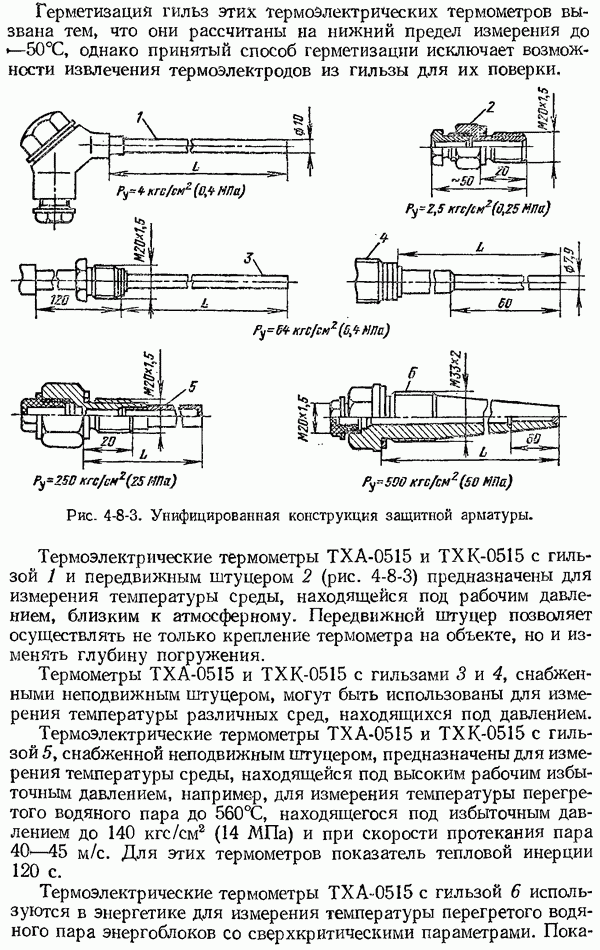
- 4-7. Общие сведения о термоэлектрических термометрах
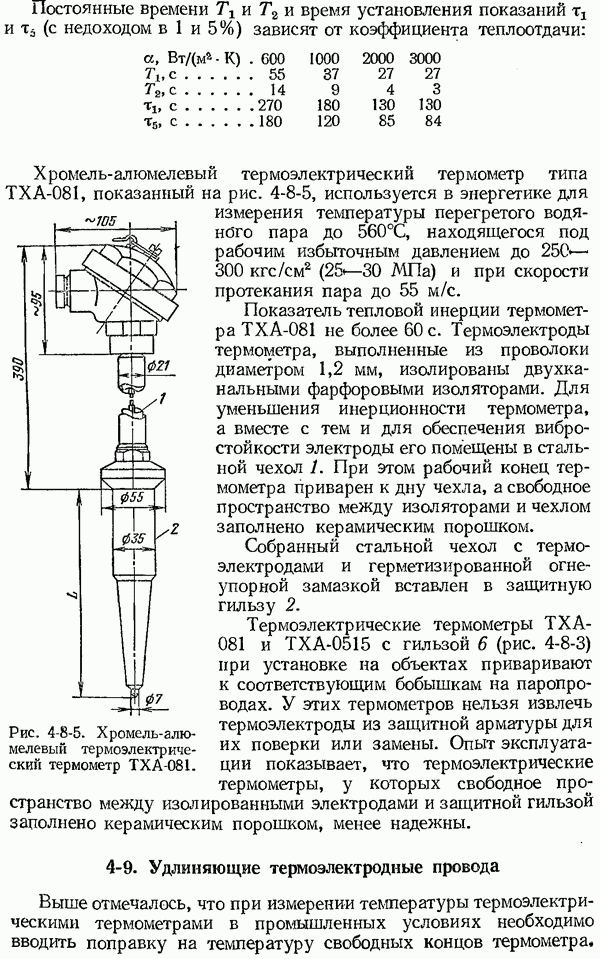
- 4-8. Устройство термоэлектрических термометров
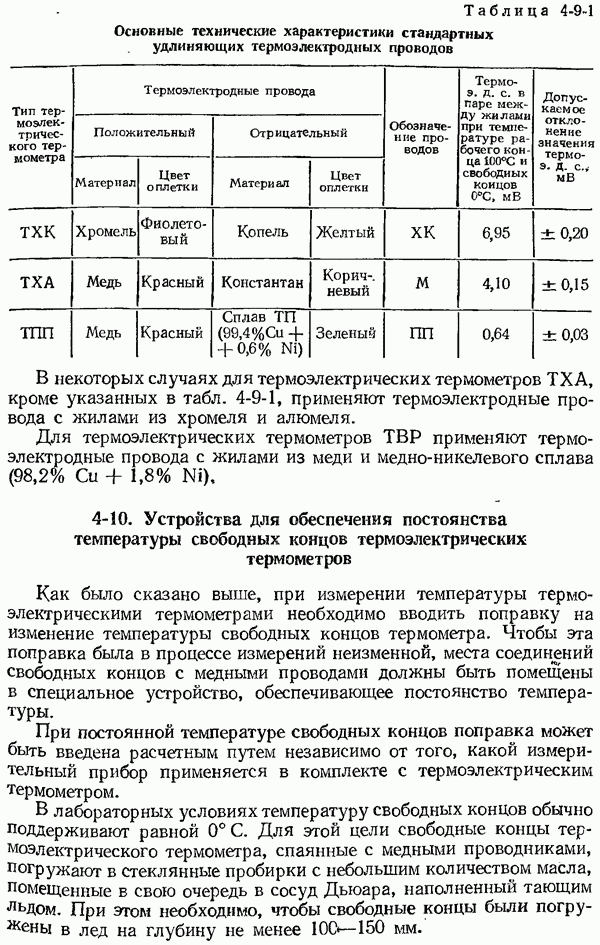
- 4-9. Удлиняющие термоэлектродные провода
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
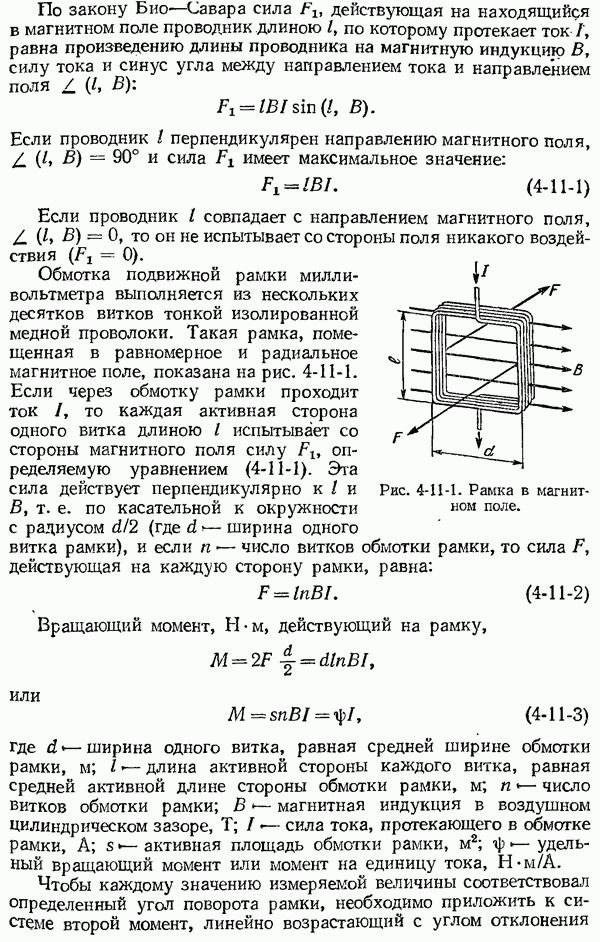
- 4-11. Милливольтметры
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
- 4-15. Нормальные элементы
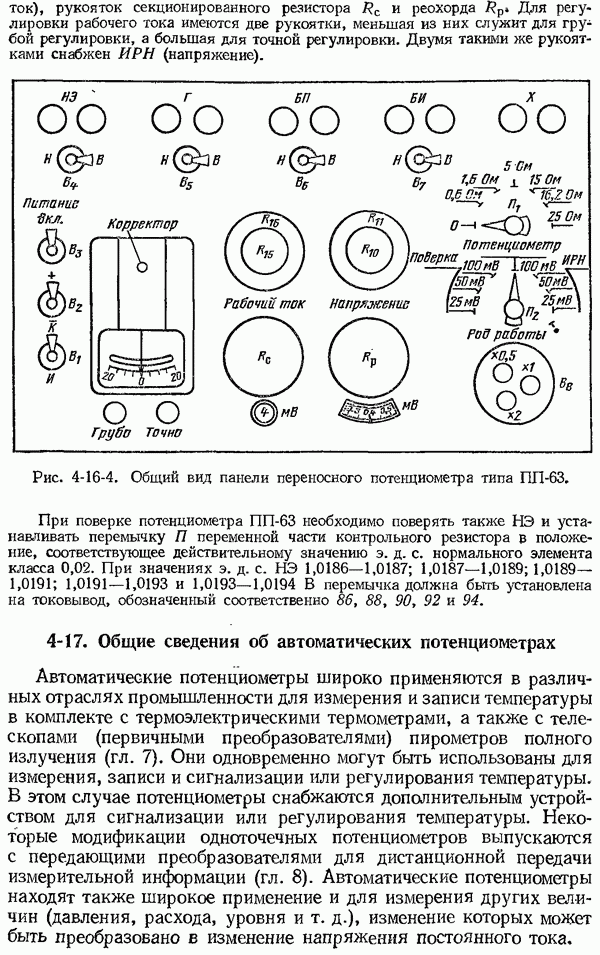
- 4-16. Потенциометры переносные и лабораторные
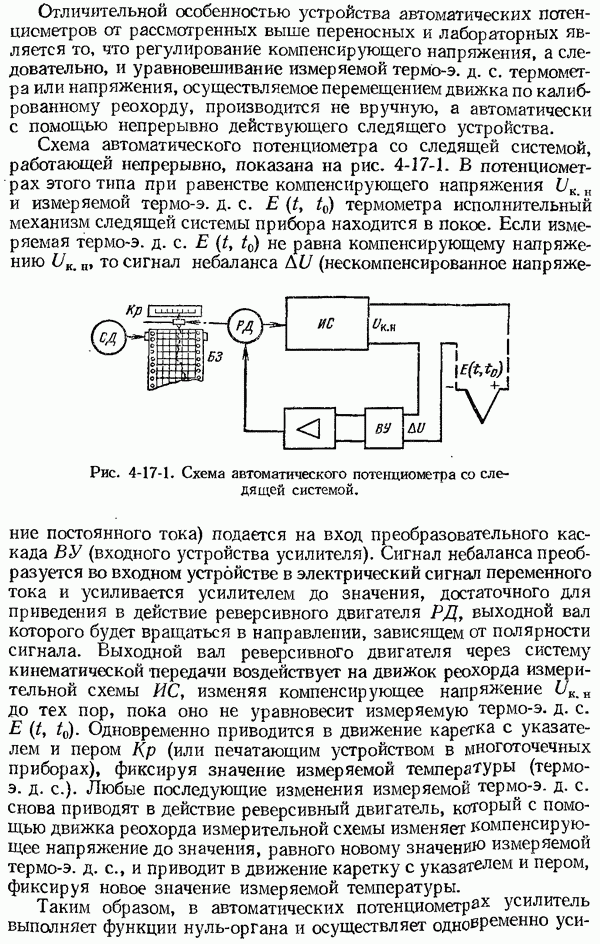
- 4-17. Общие сведения об автоматических потенциометрах
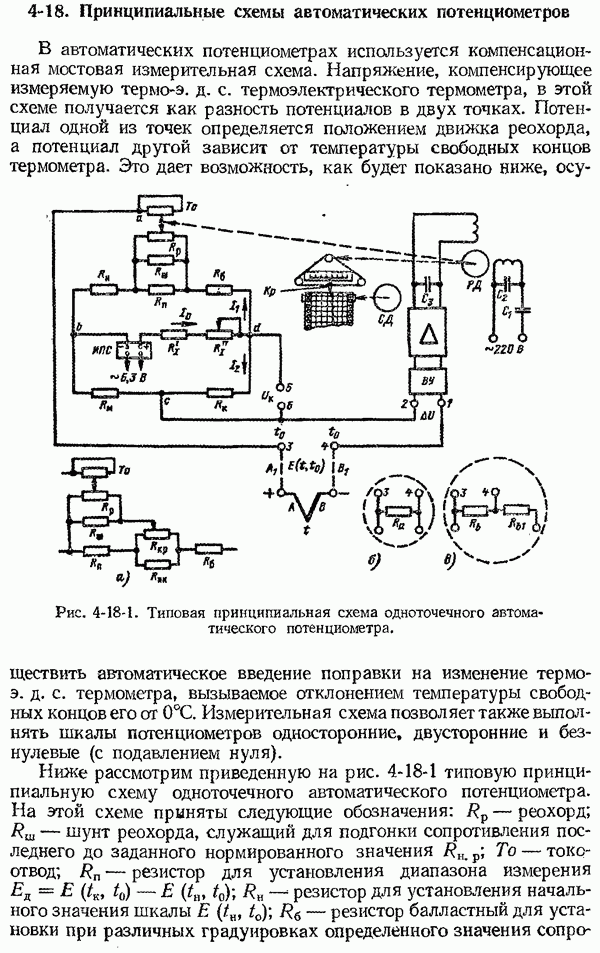
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
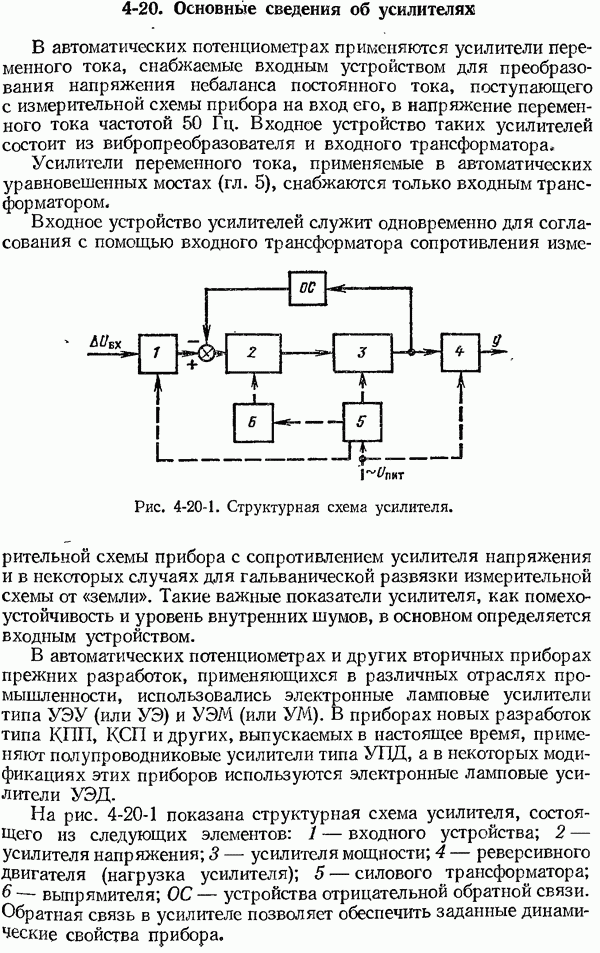
- 4-20. Основные сведения об усилителях
- 4-21. Основные сведения об источниках стабилизированного питания
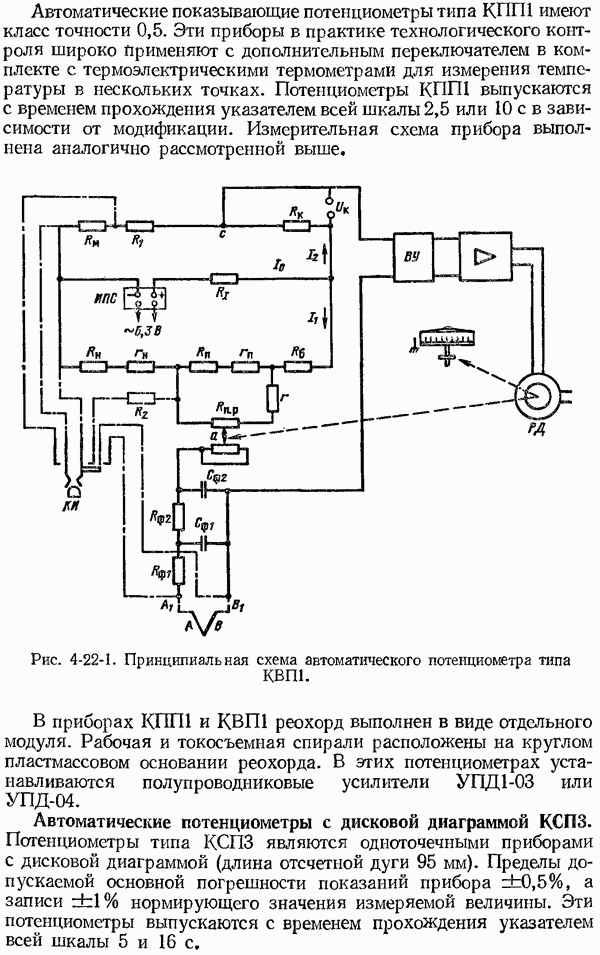
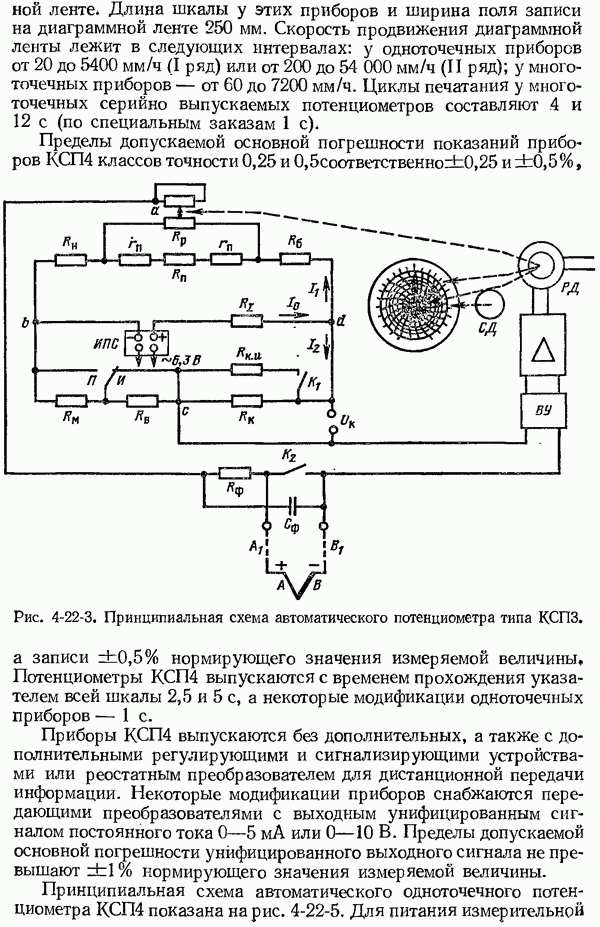
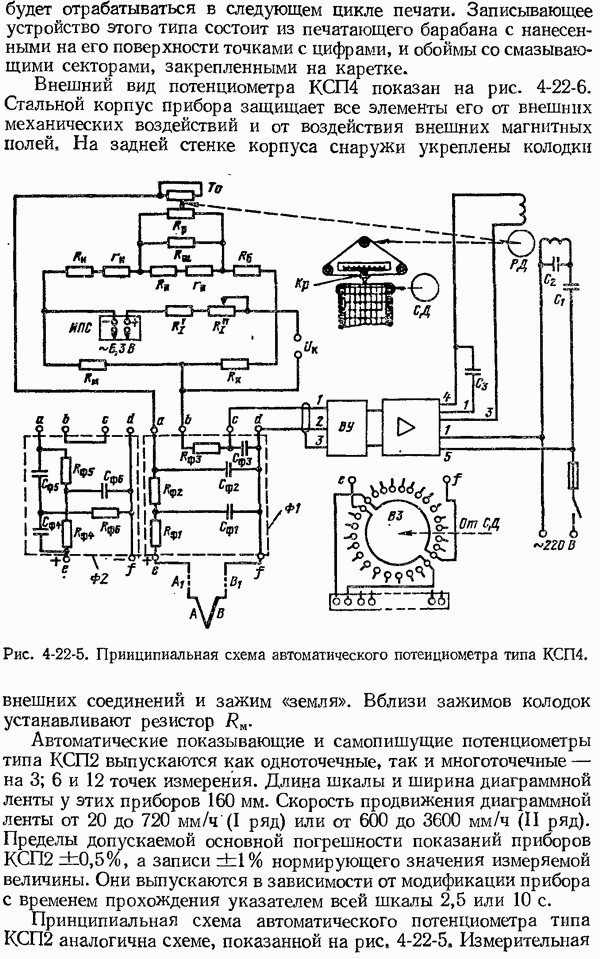
- 4-22. Устройство автоматических потенциометров
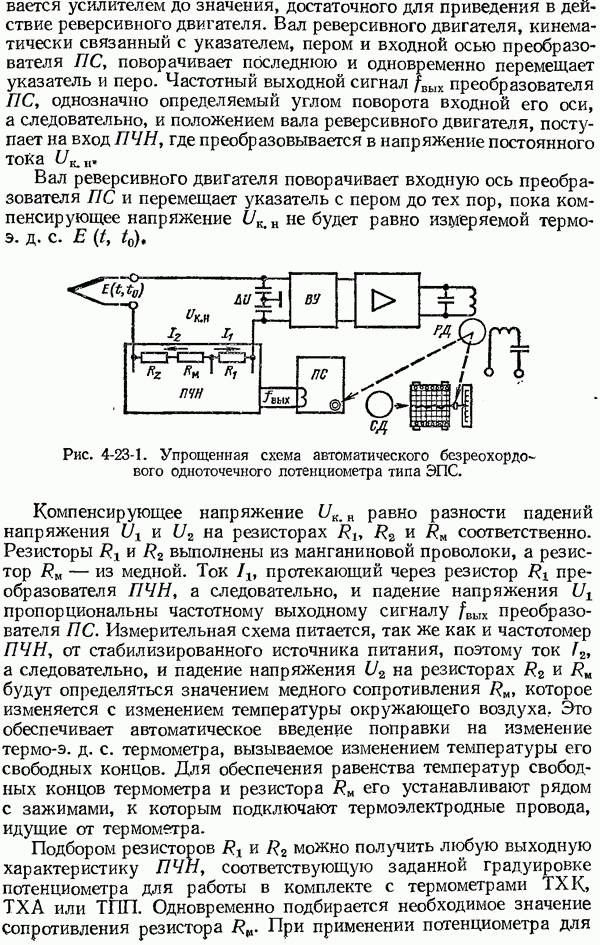
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
- 5-3. Устройство платиновых и медных термометров сопротивления
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
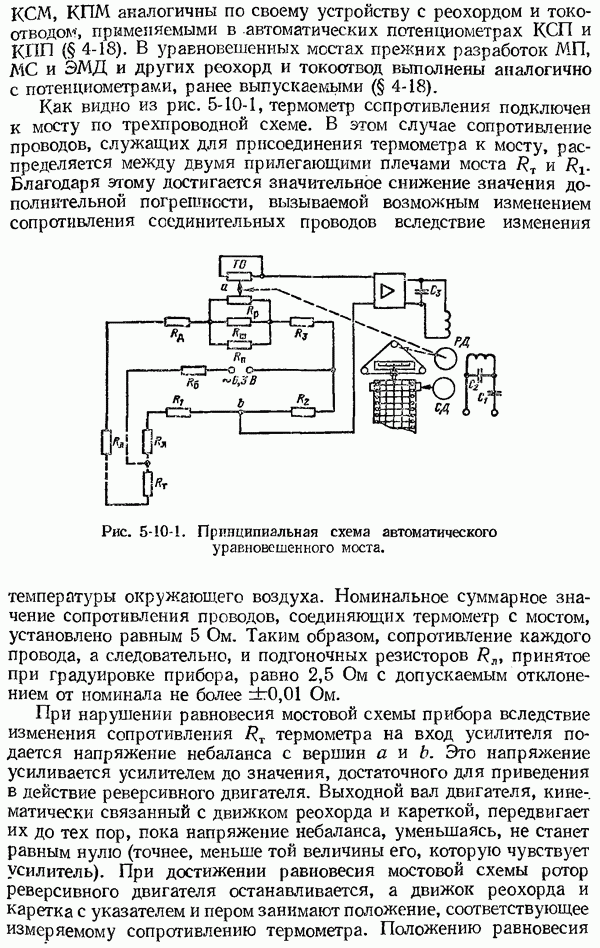
- 5-10. Принципиальная схема автоматического уравновешенного моста
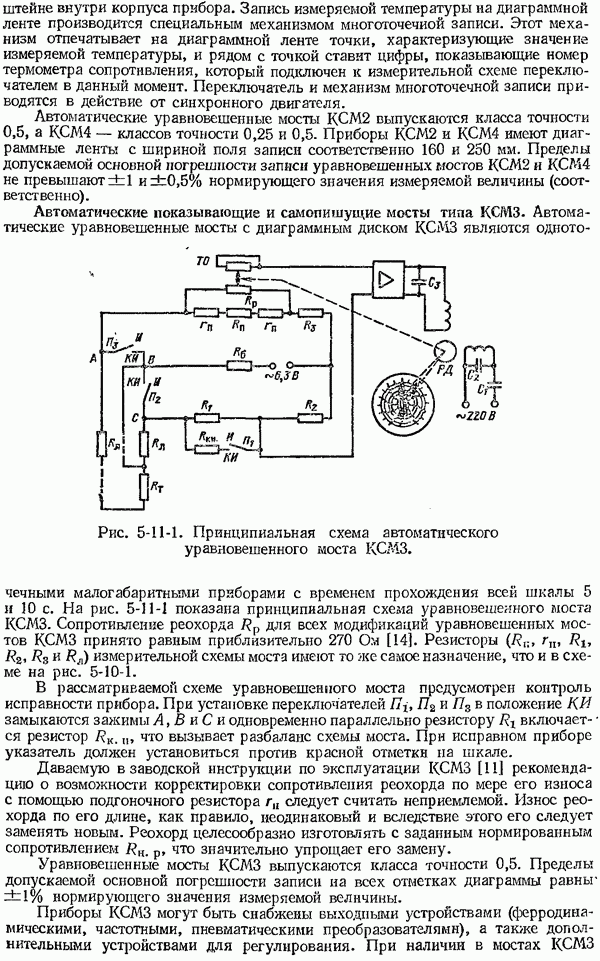
- 5-11. Устройство автоматических уравновешенных мостов
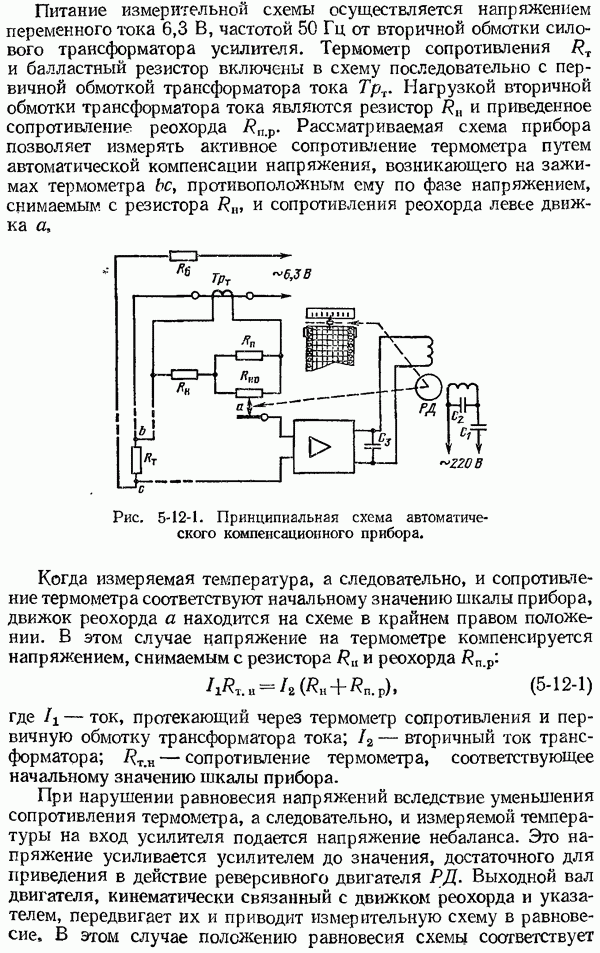
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
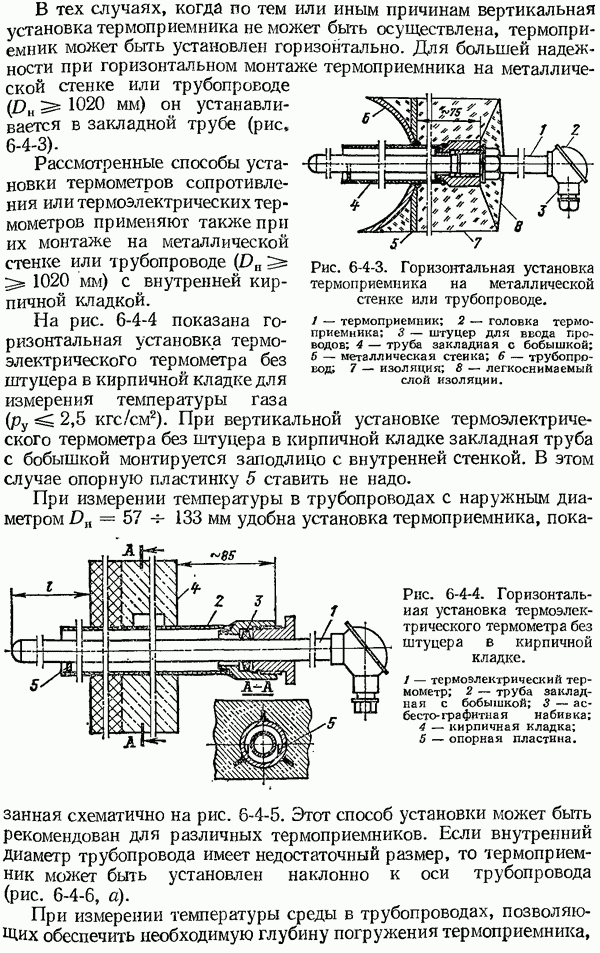
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
- 7-3. Оптические пирометры
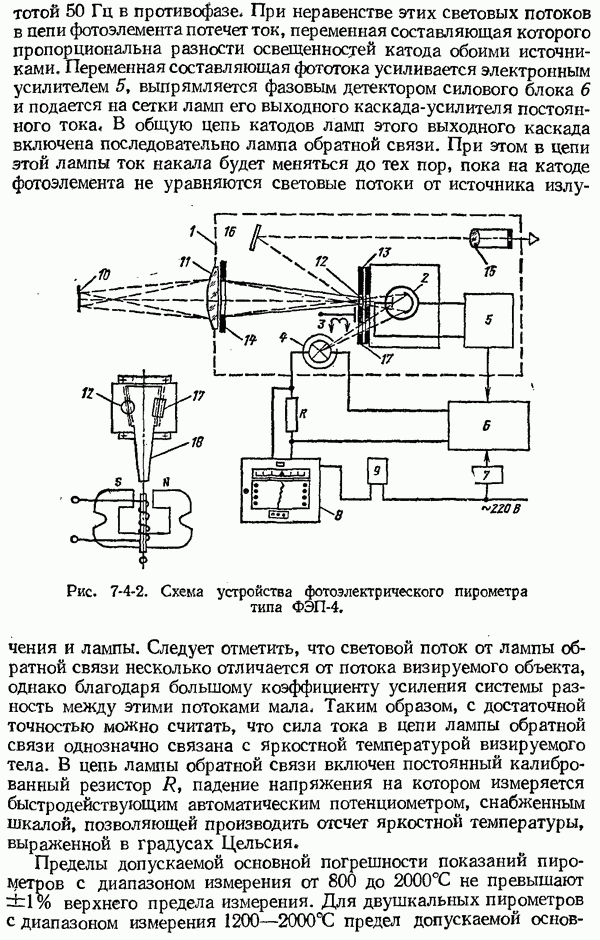
- 7-4. Фотоэлектрические пирометры
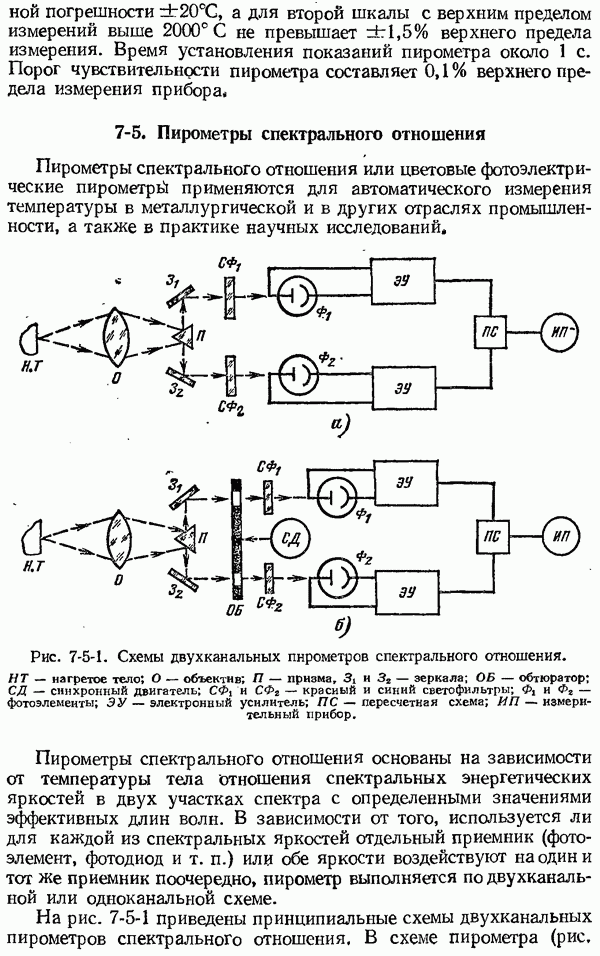
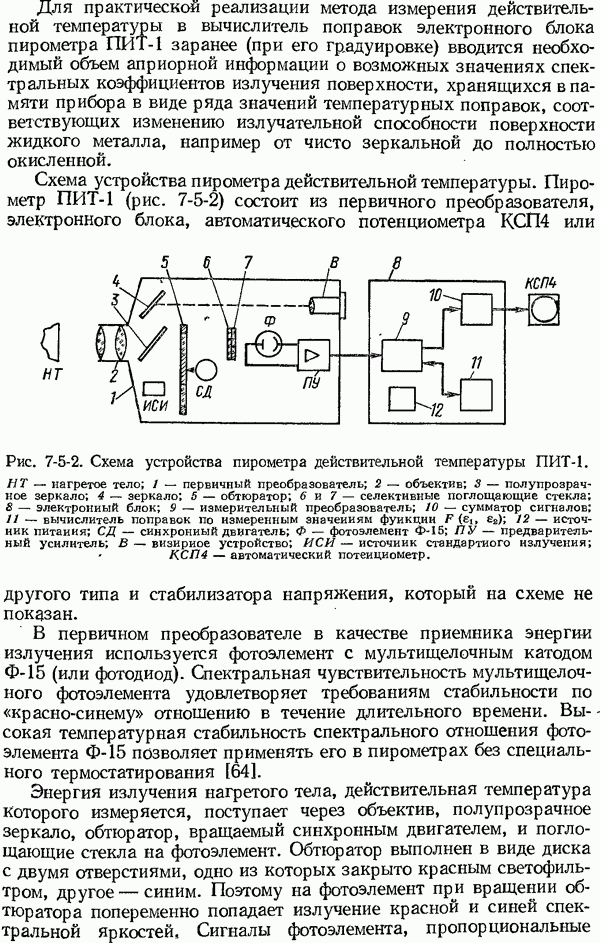
- 7-5. Пирометры спектрального отношения
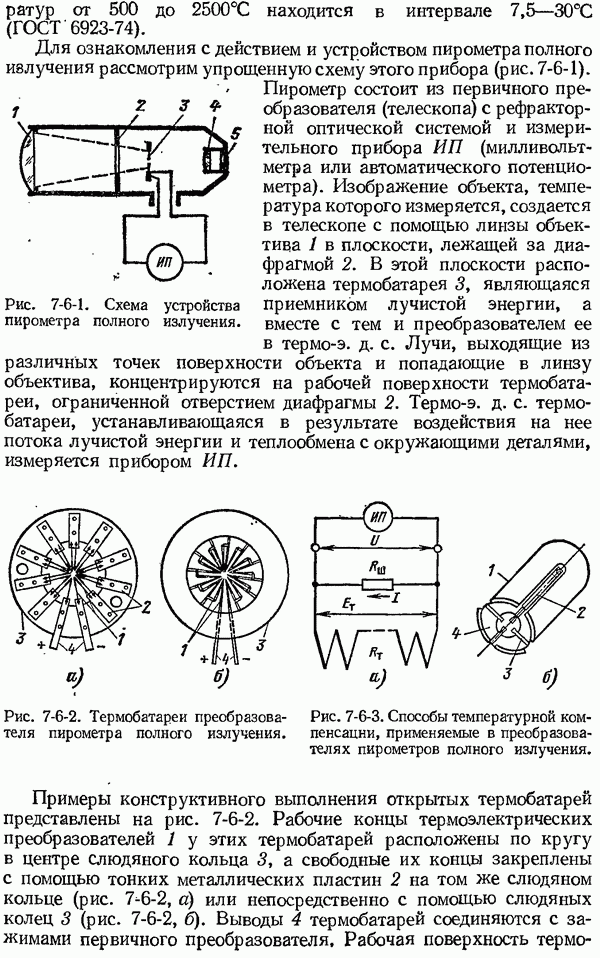
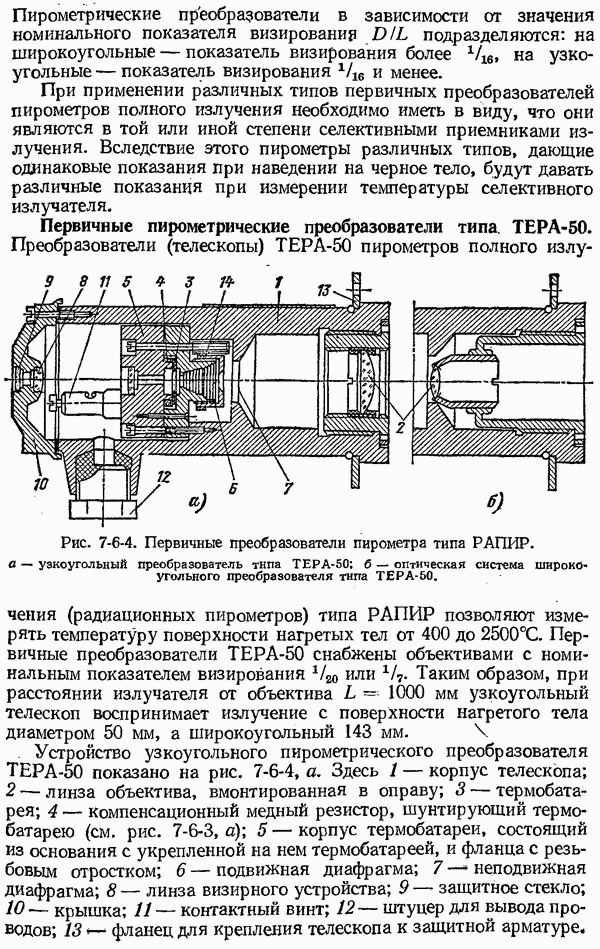
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
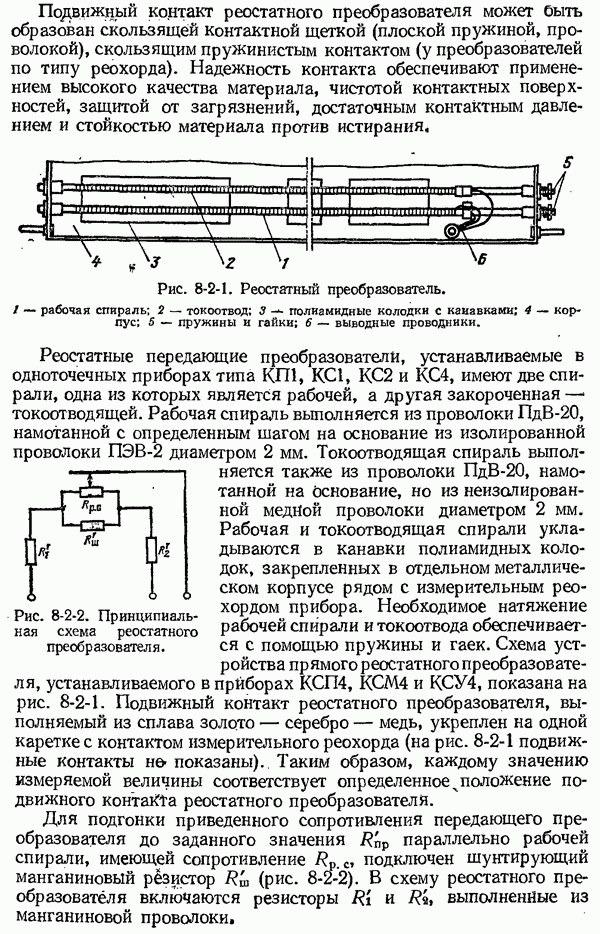
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
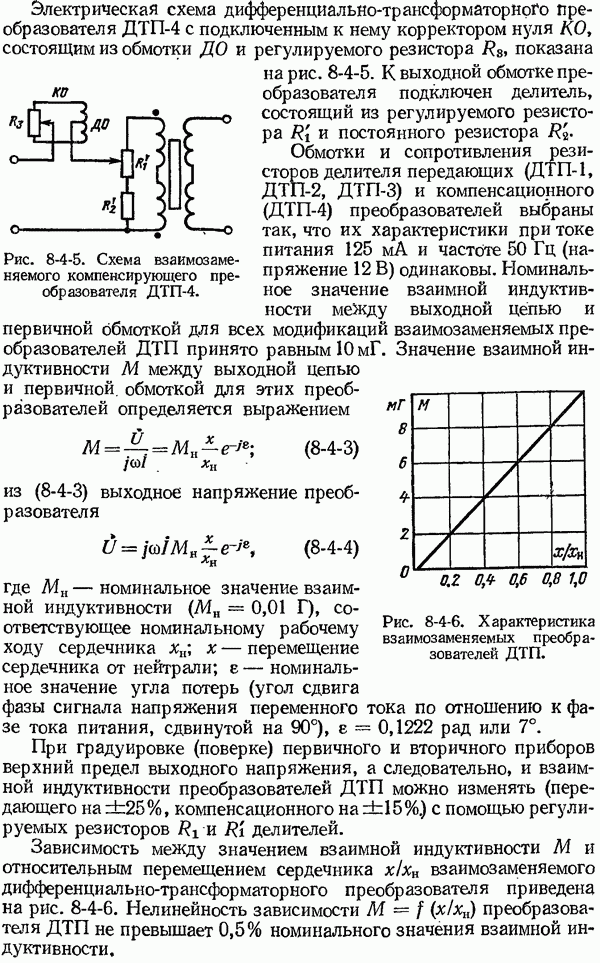
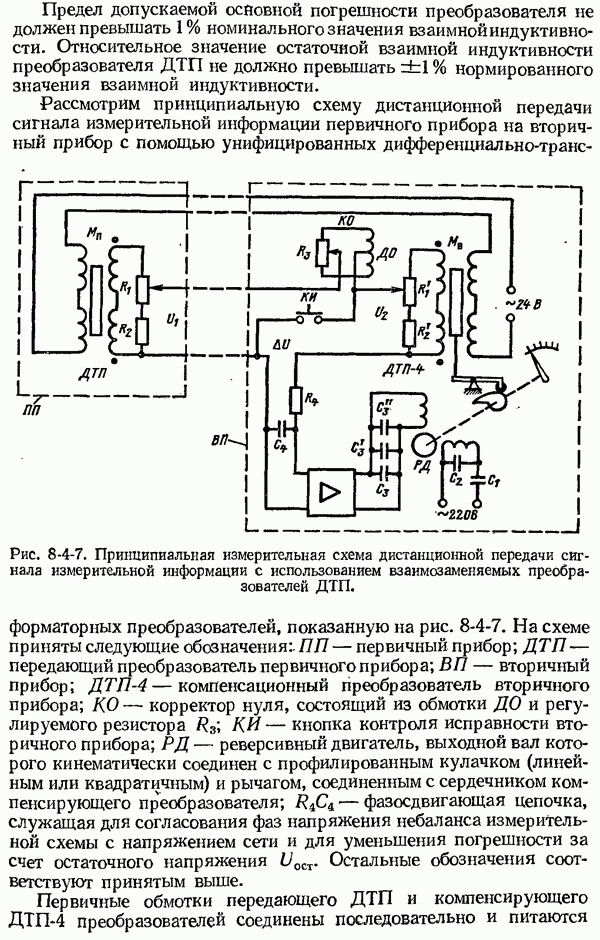
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
- 8-6. Механоэлектрические передающие преобразователи
- 8-7. Передающие преобразователи с магнитной компенсацией
- 8-8. Электросиловые преобразователи
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
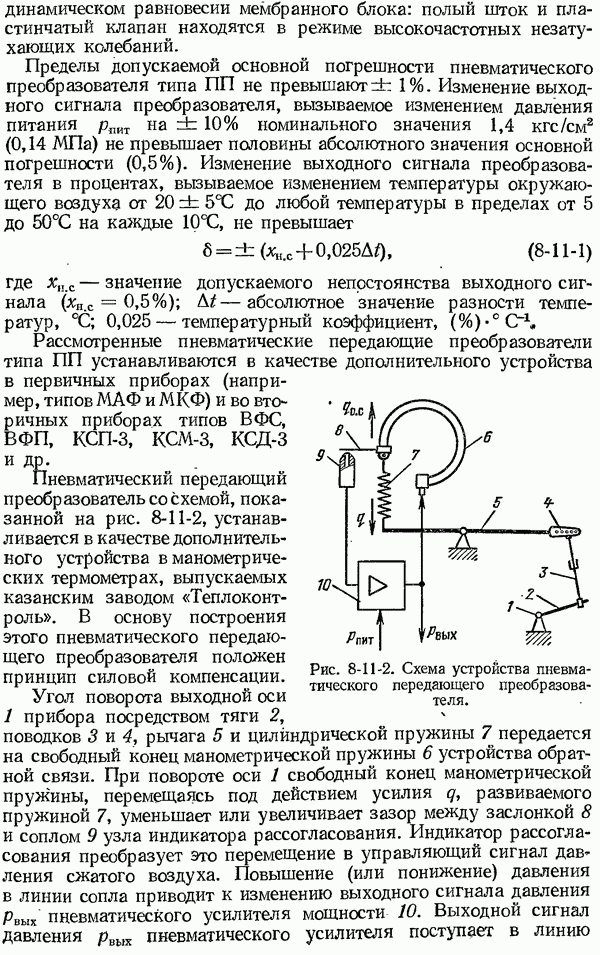
- 8-11. Пневматические передающие преобразователи
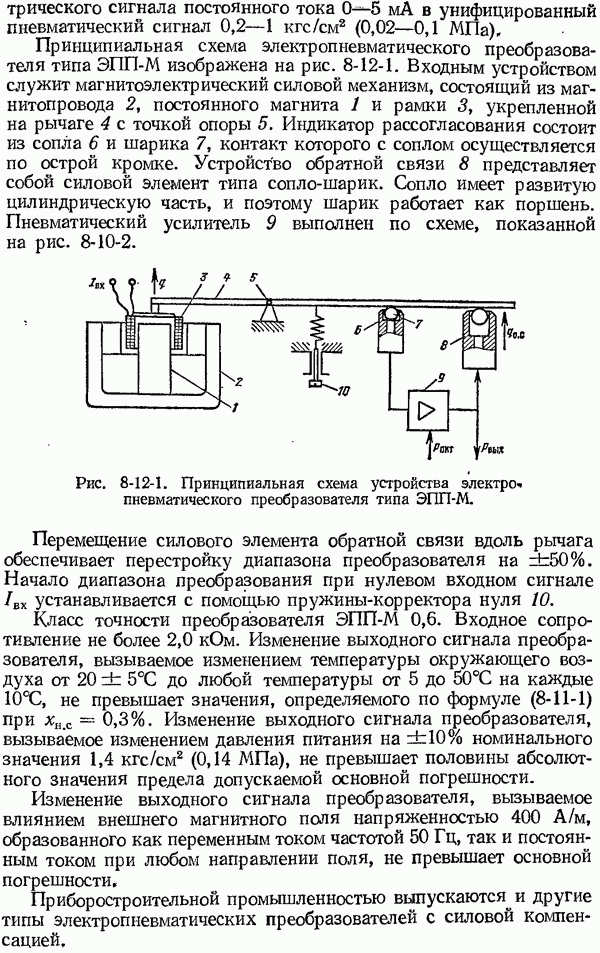
- 8-12. Электропневматические и пневмоэлектрические преобразователи
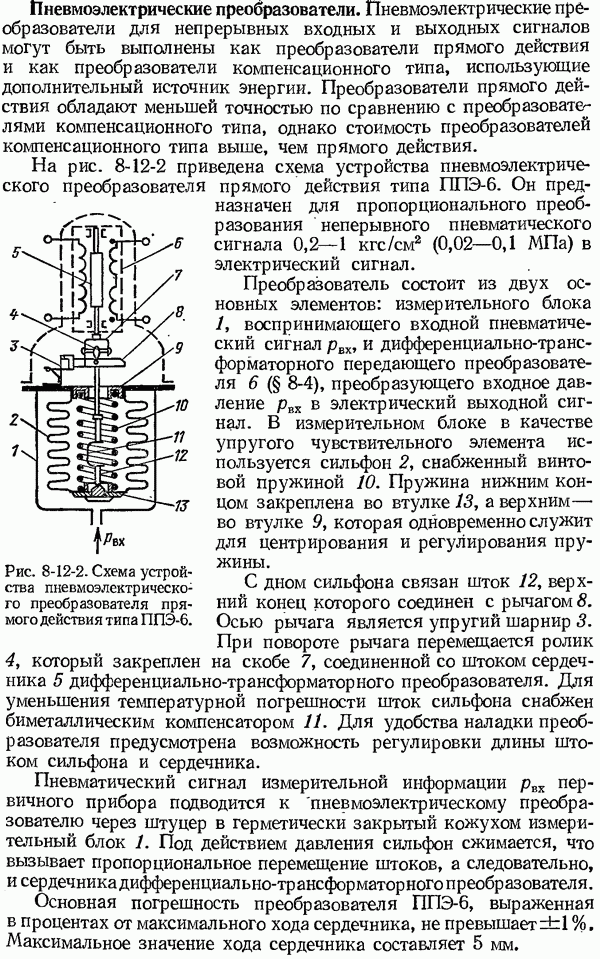
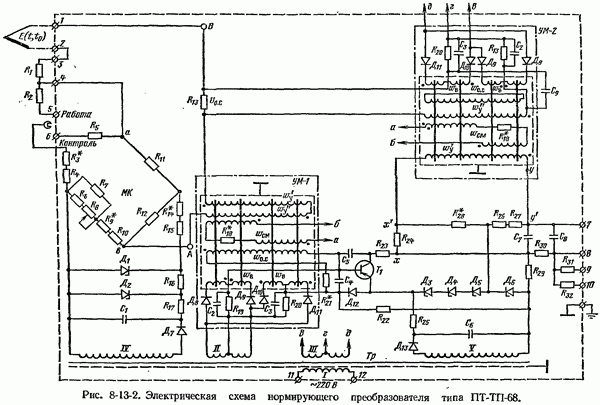
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
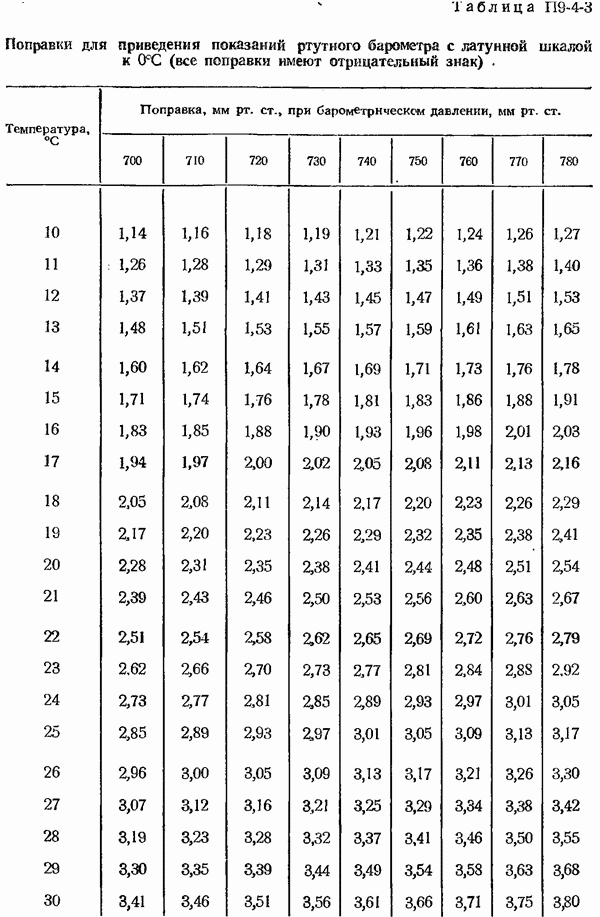
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
- 10-2. Упругие чувствительные элементы
- 10-3. Приборы давления прямого действия
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 13-2. Измерение близкого к атмосферному давления газовых сред
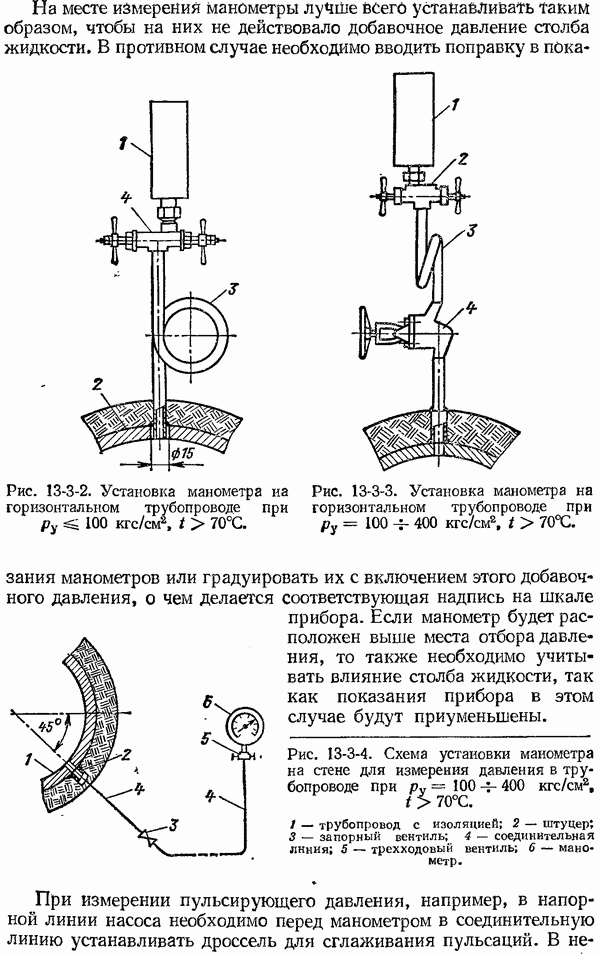
- 13-3. Измерение давления газов, жидкостей и пара
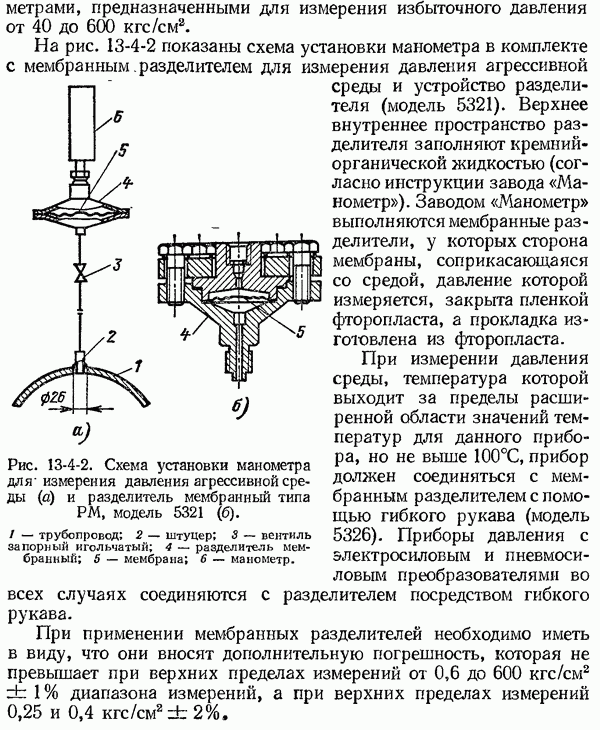
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
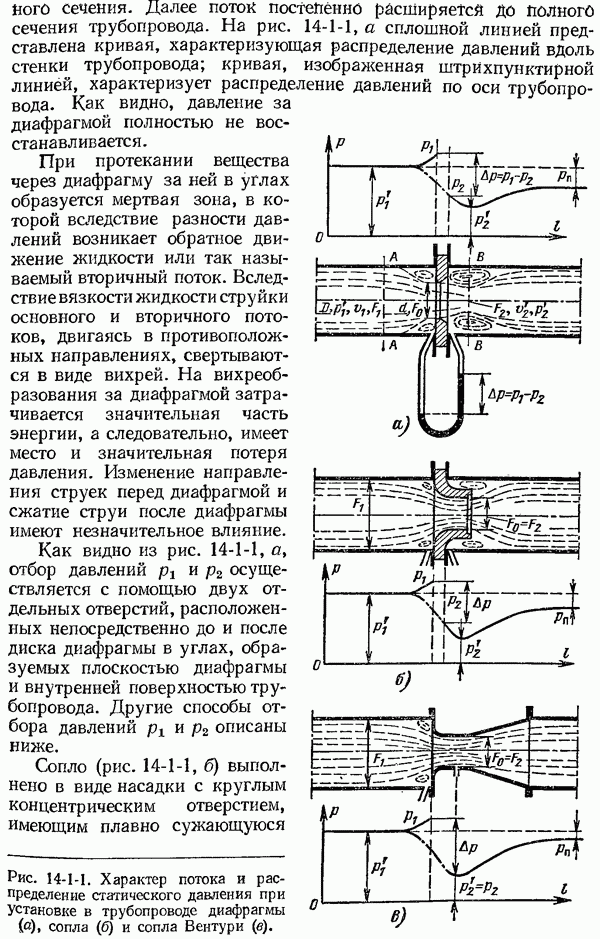
- 14-1. Основы теории и уравнения расхода
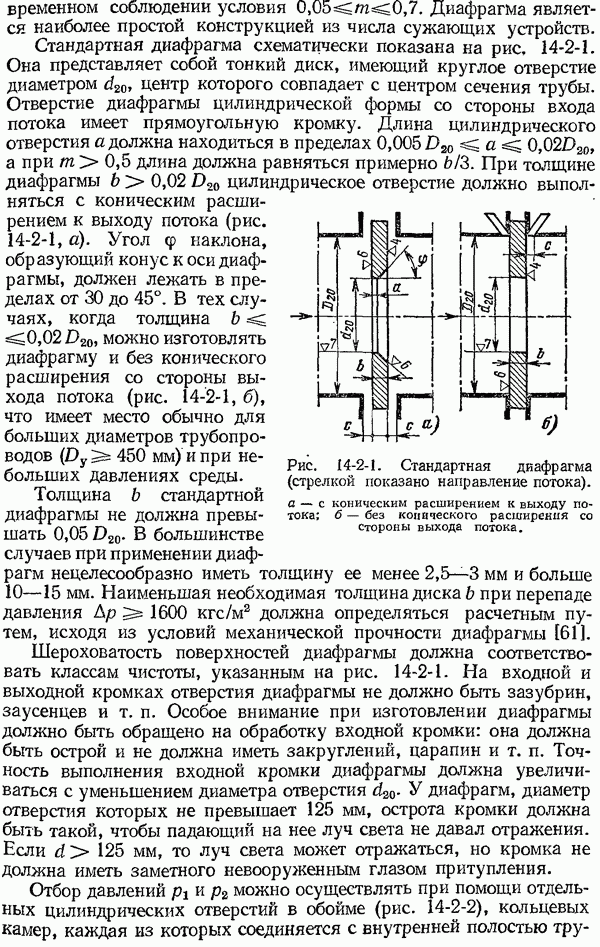
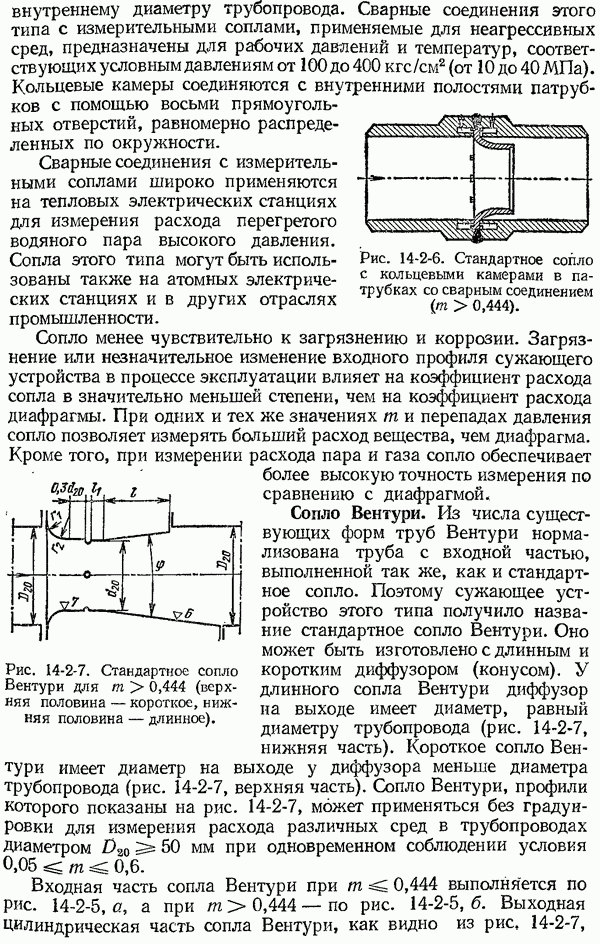
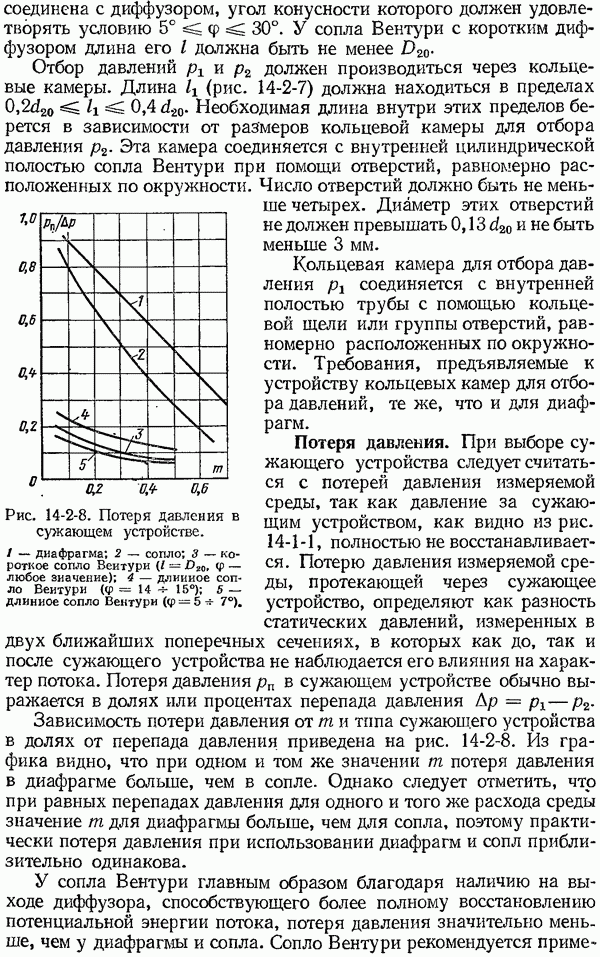
- 14-2. Стандартные сужающие устройства
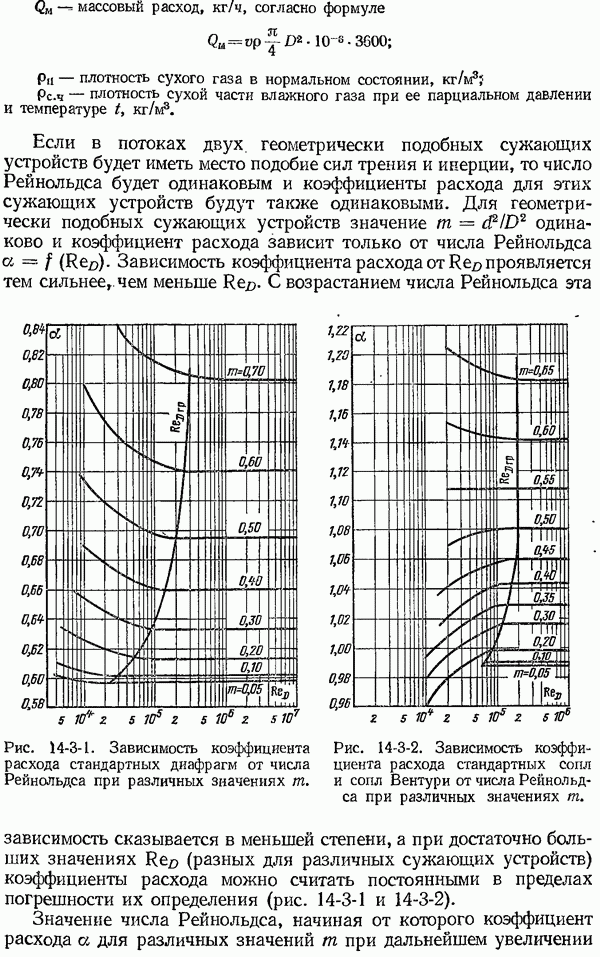
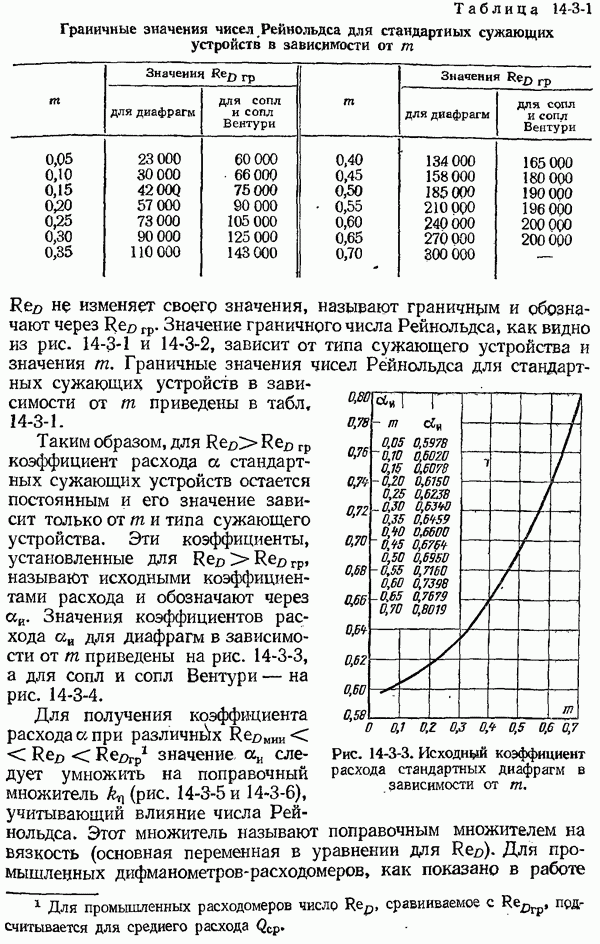
- 14-3. Коэффициенты расхода и поправочные множители к ним
- 14-4. Поправочный множитель на расширение измеряемой среды
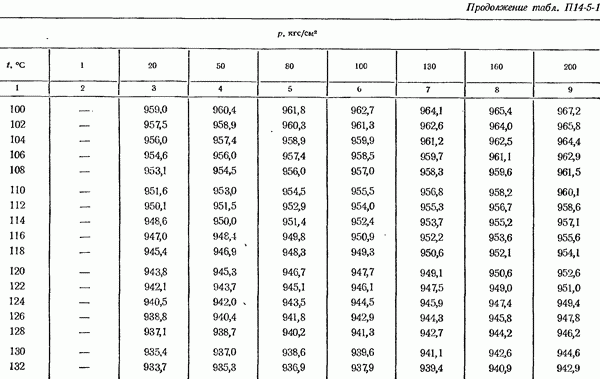
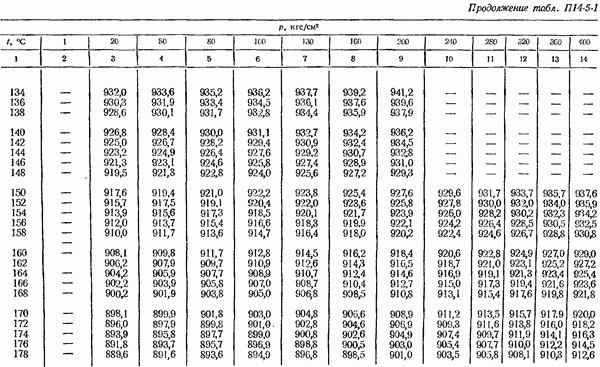
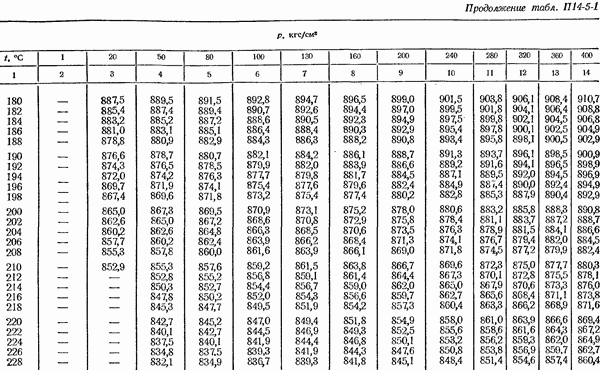
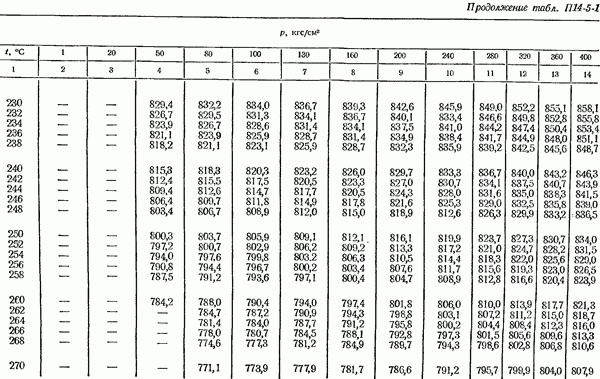
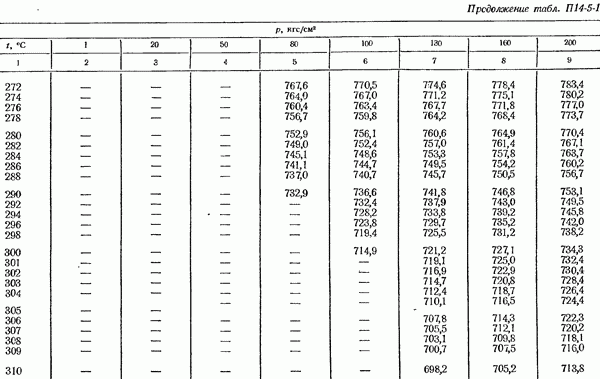
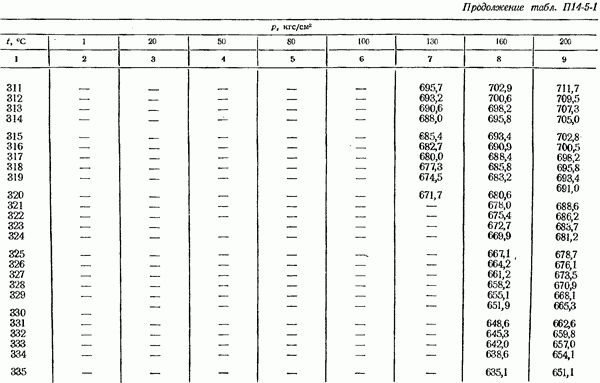
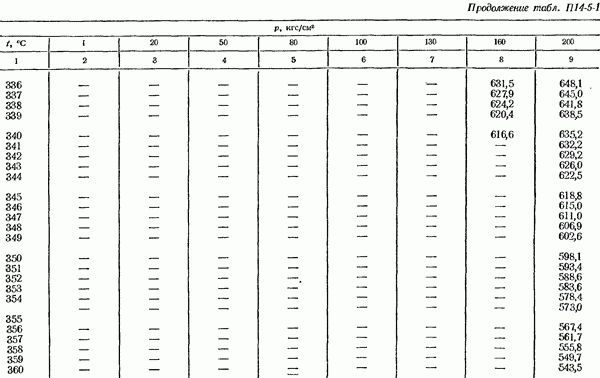
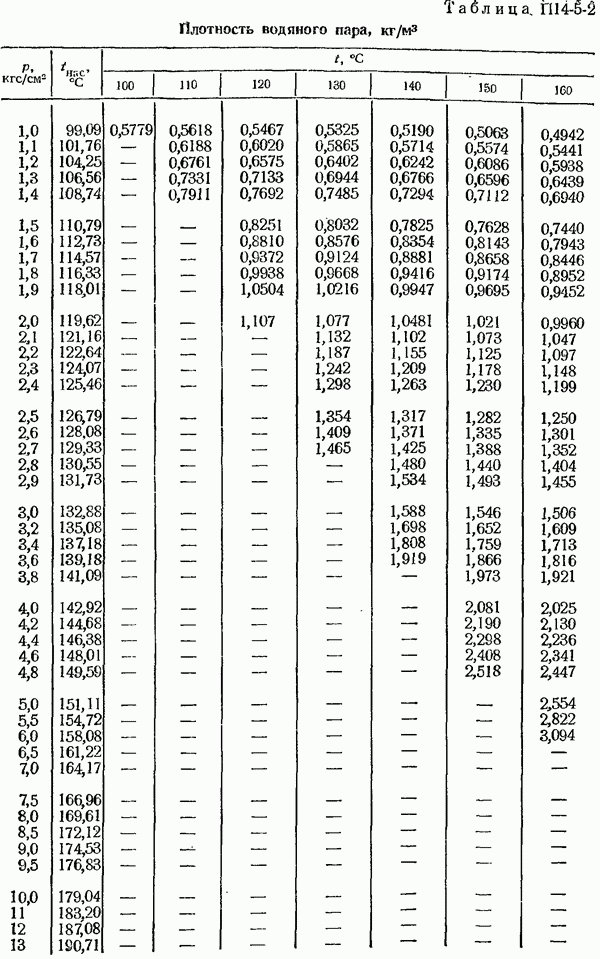
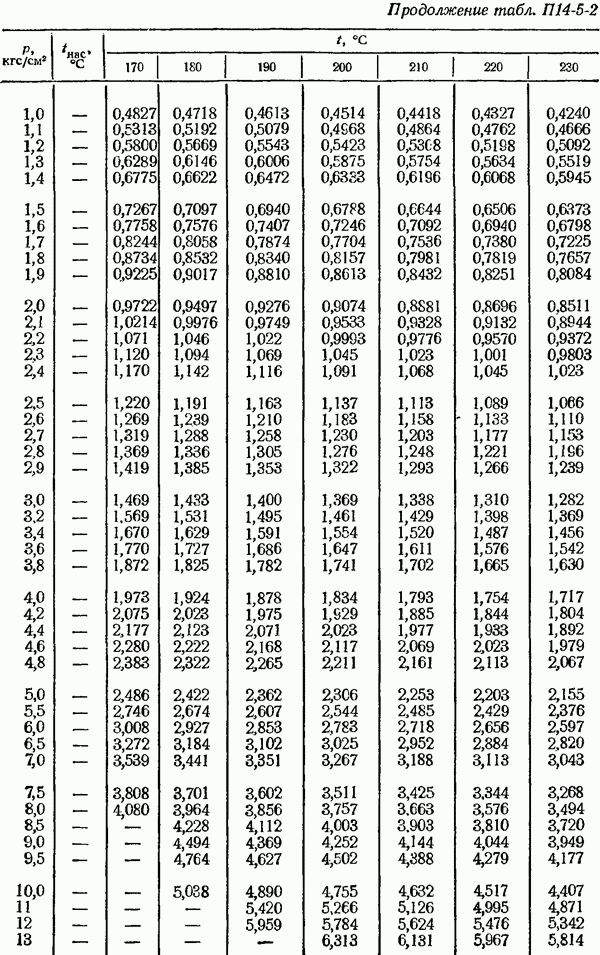
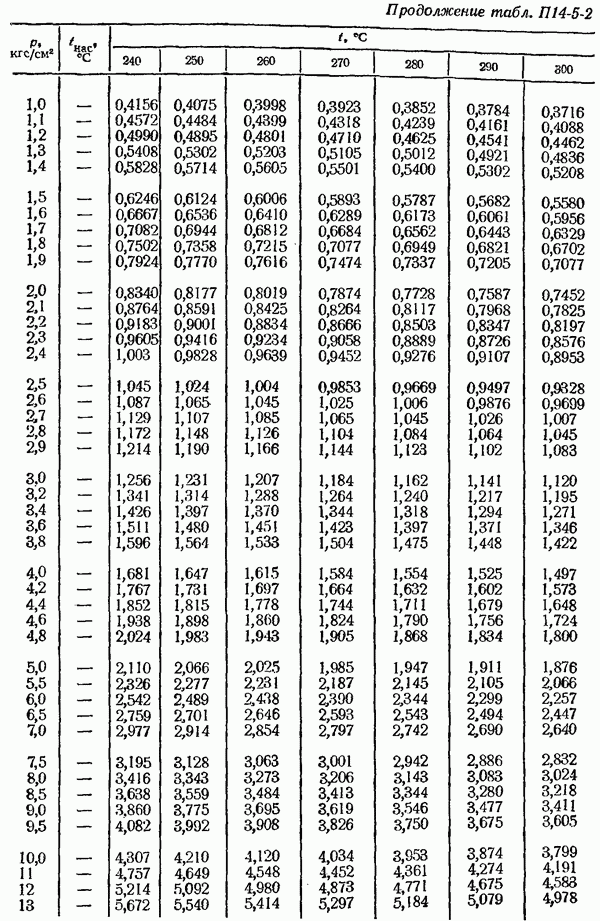
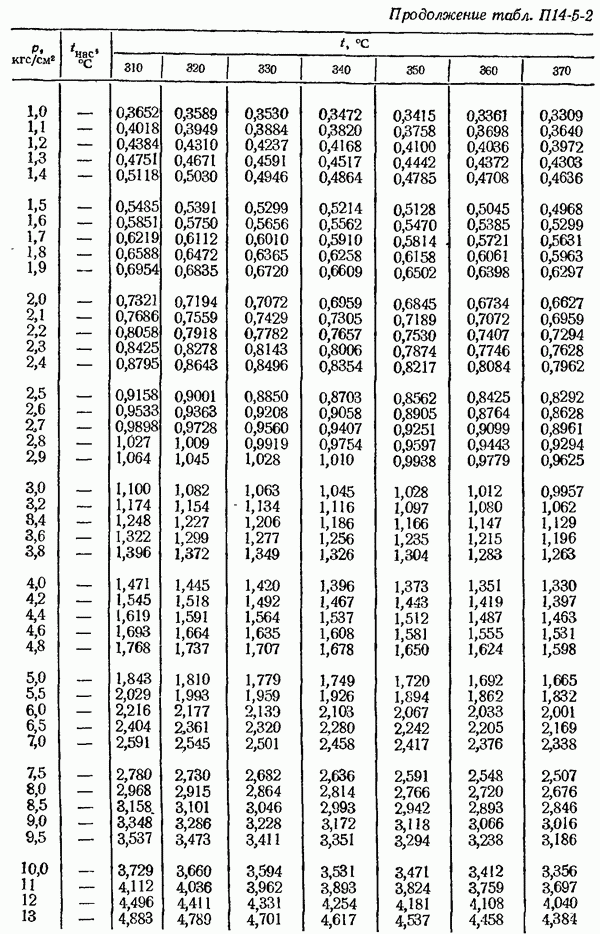
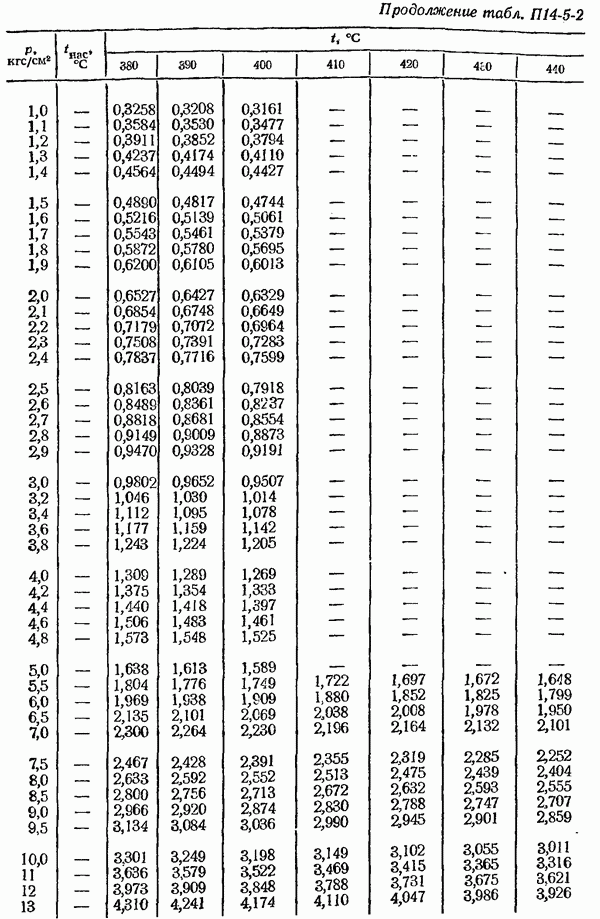
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
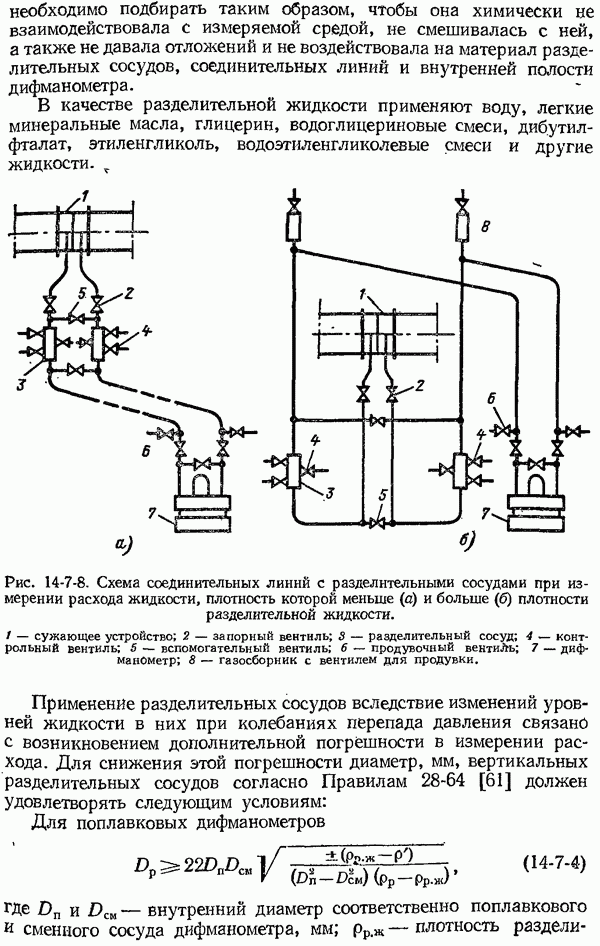
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
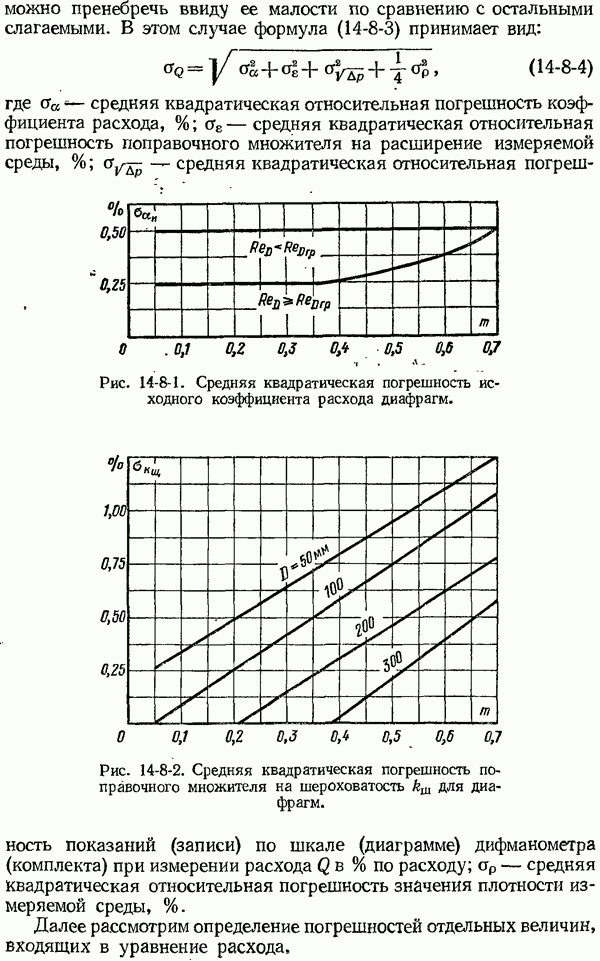
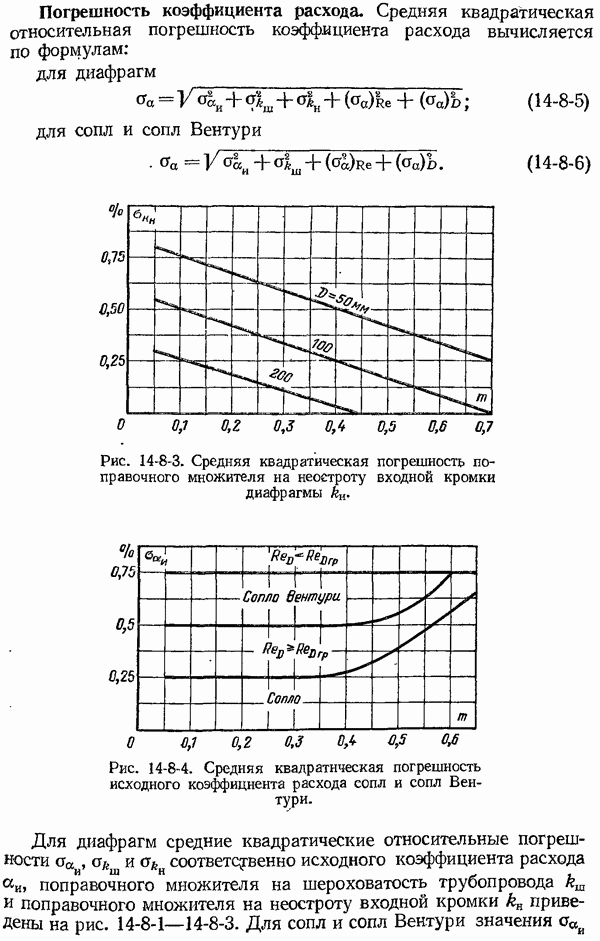
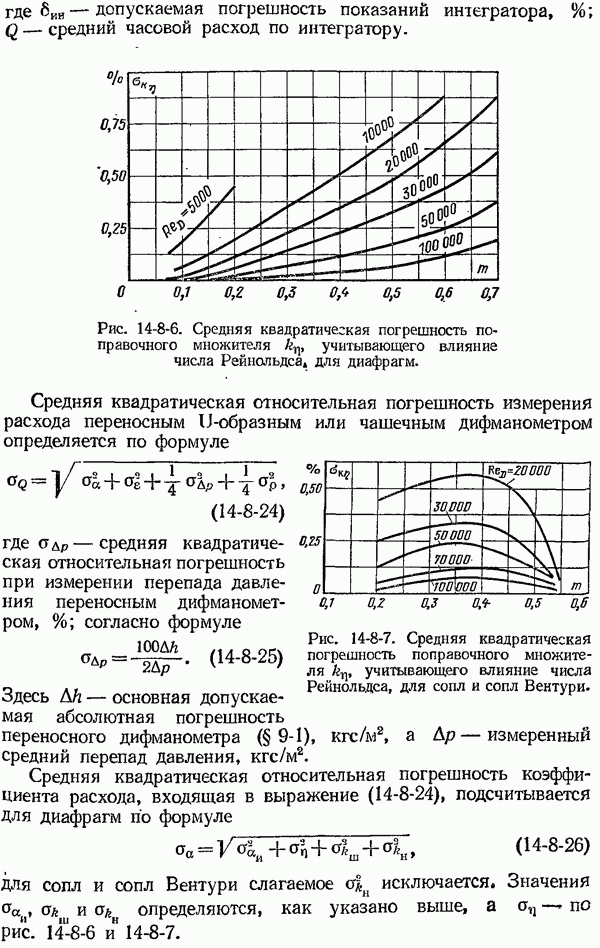
- 14-8. Погрешности измерения расхода
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
- 14-11. Измерение расхода при малых числах Рейнольдса
- 14-12. Измерение расхода загрязненных жидкостей и газов
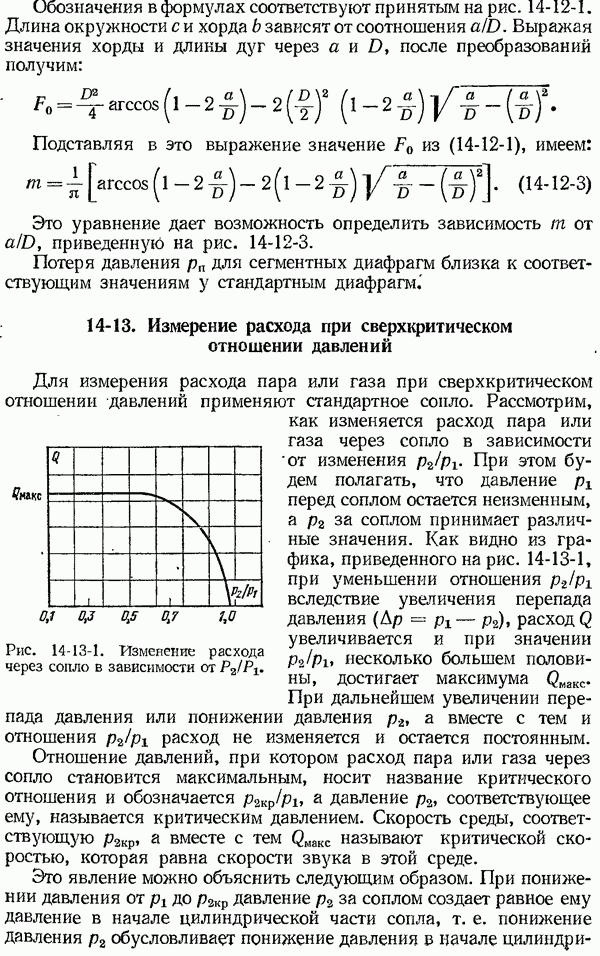
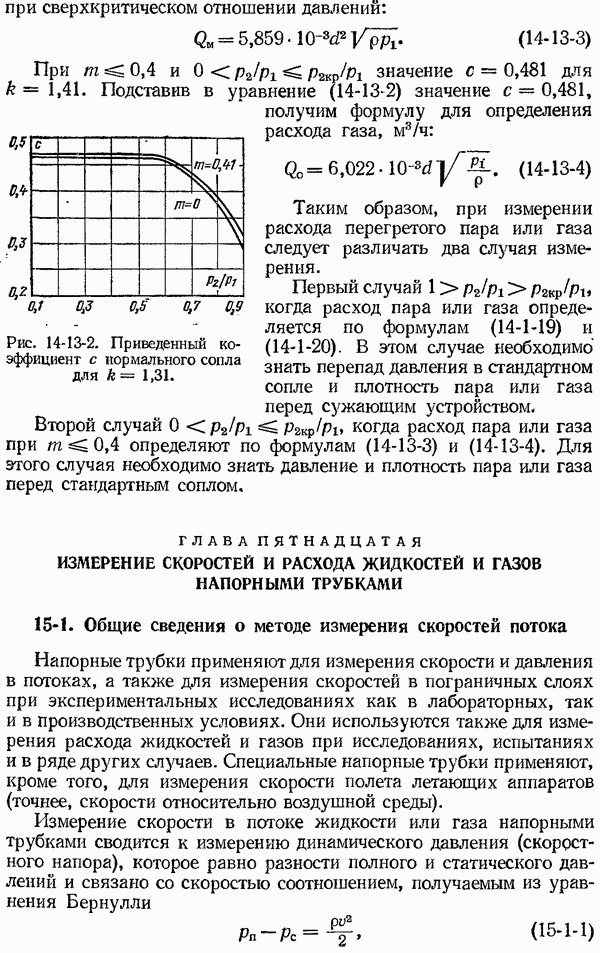
- 14-13. Измерение расхода при сверхкритическом отношении давлений
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
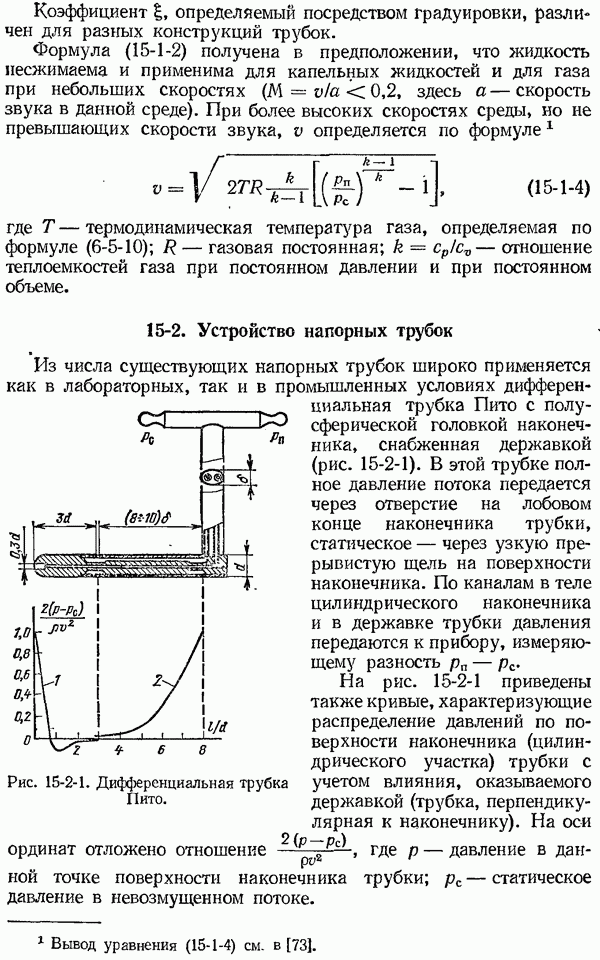
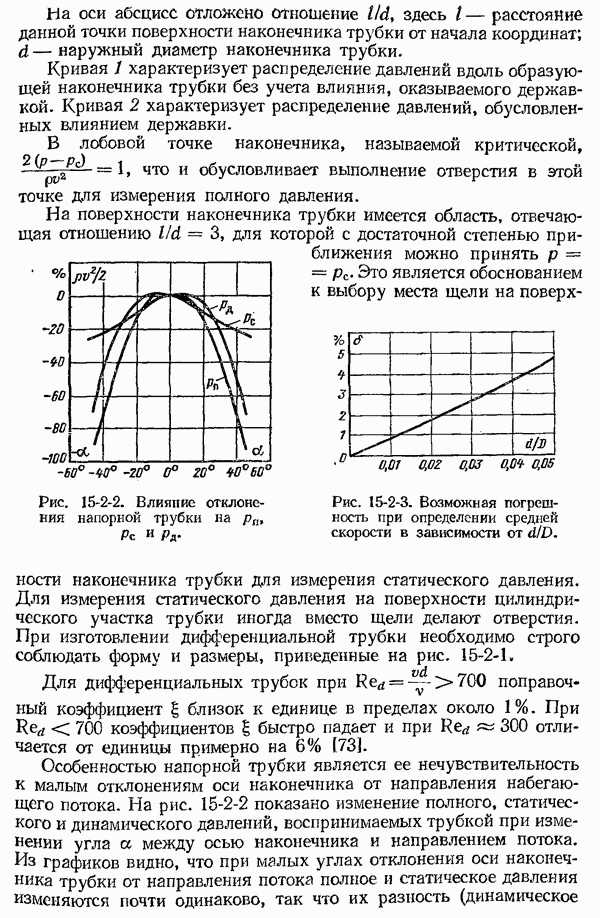
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
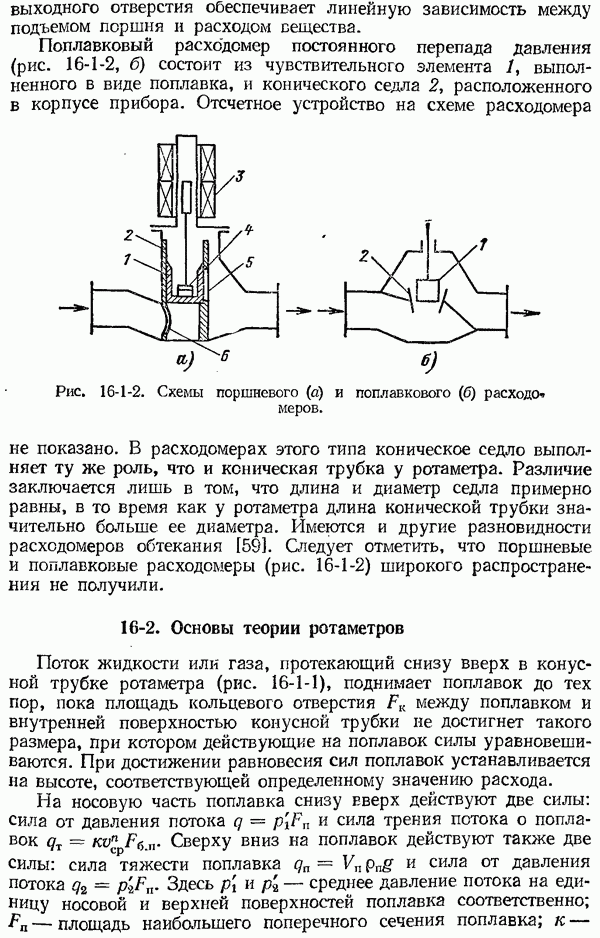
- 16-2. Основы теории ротаметров
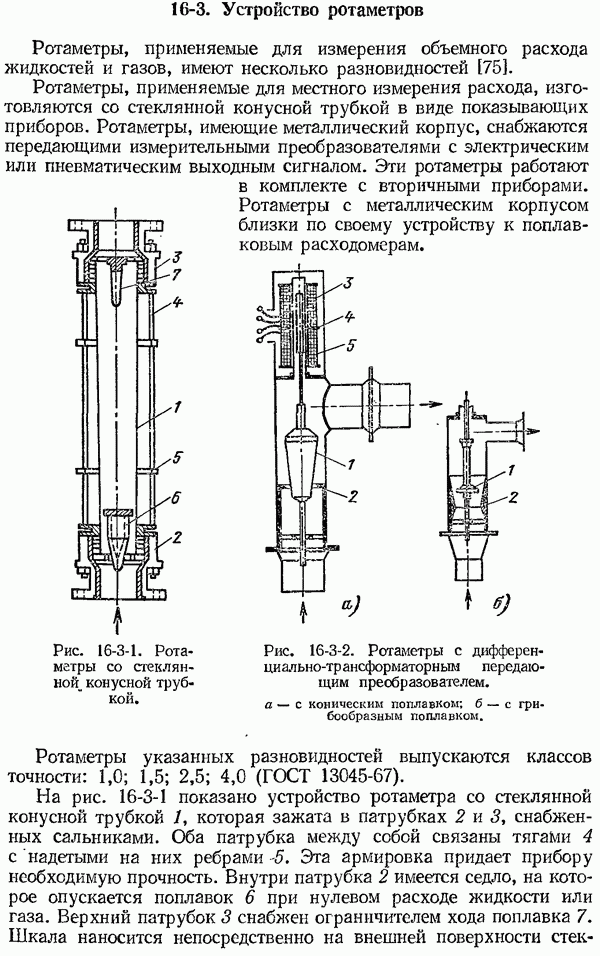
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
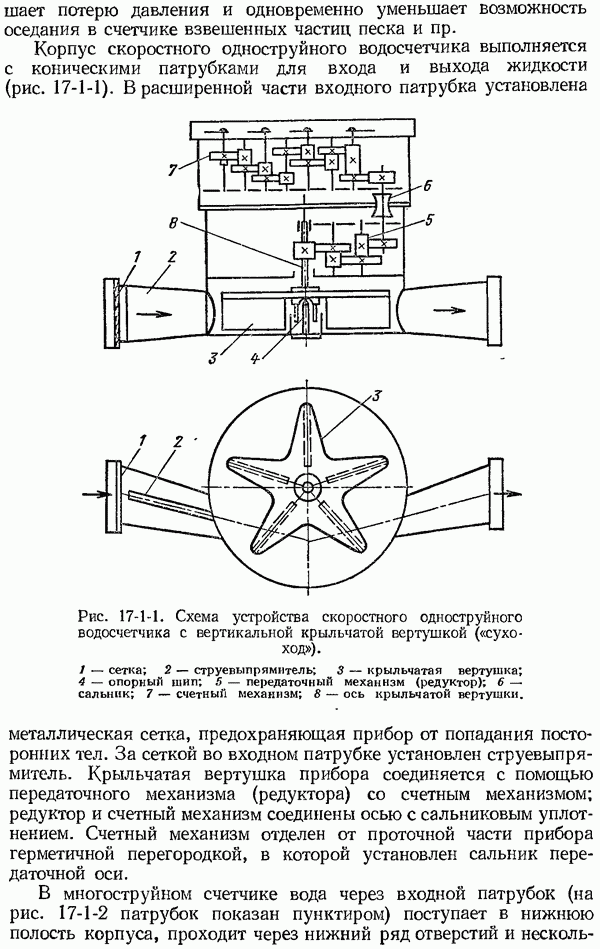
- 17-1. Тахометрические счетчики количества жидкостей
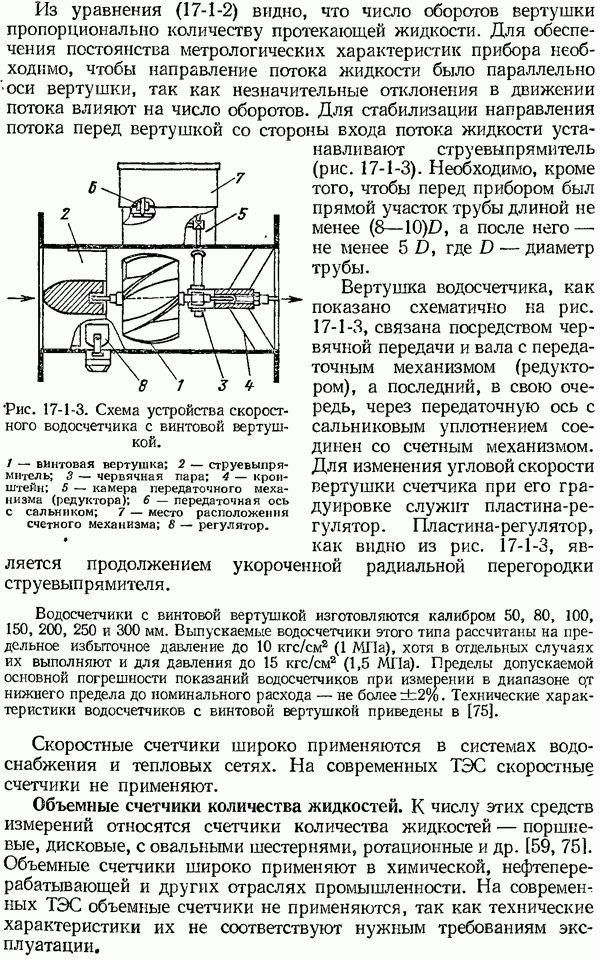
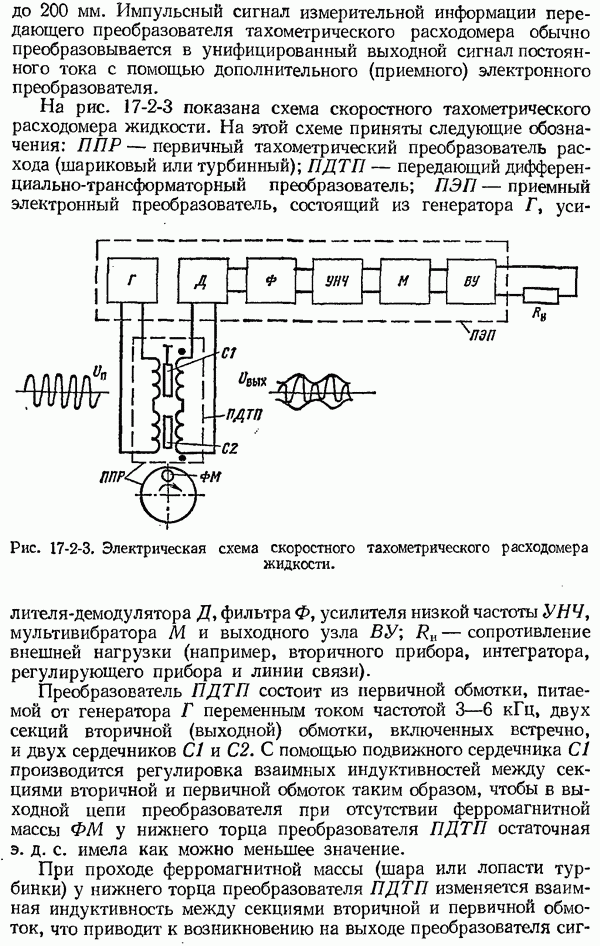
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
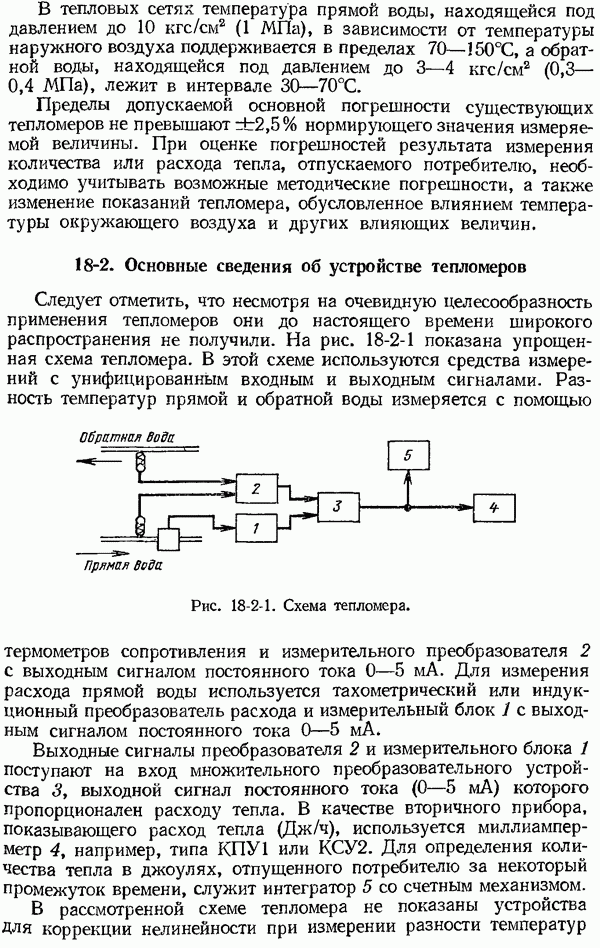
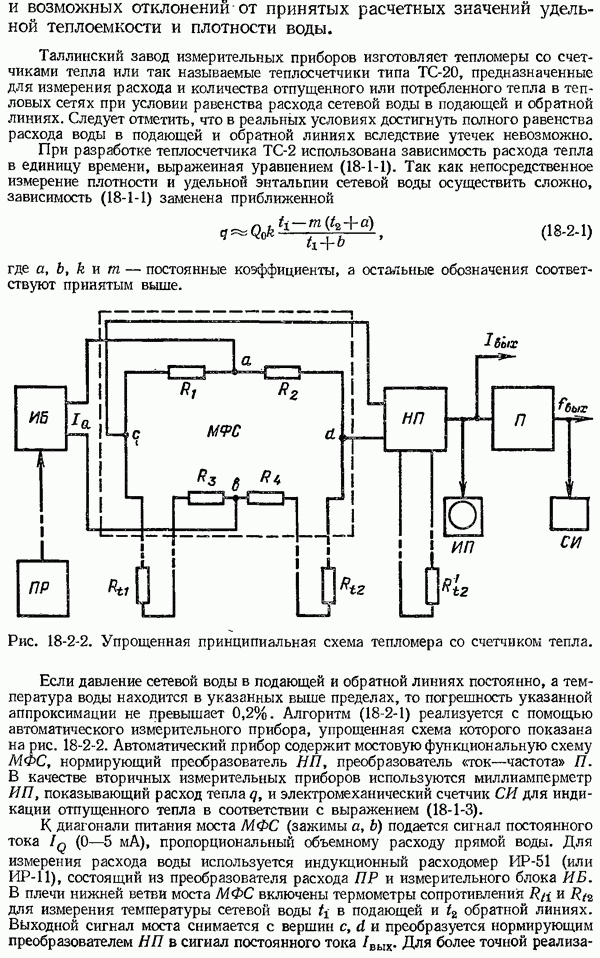
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
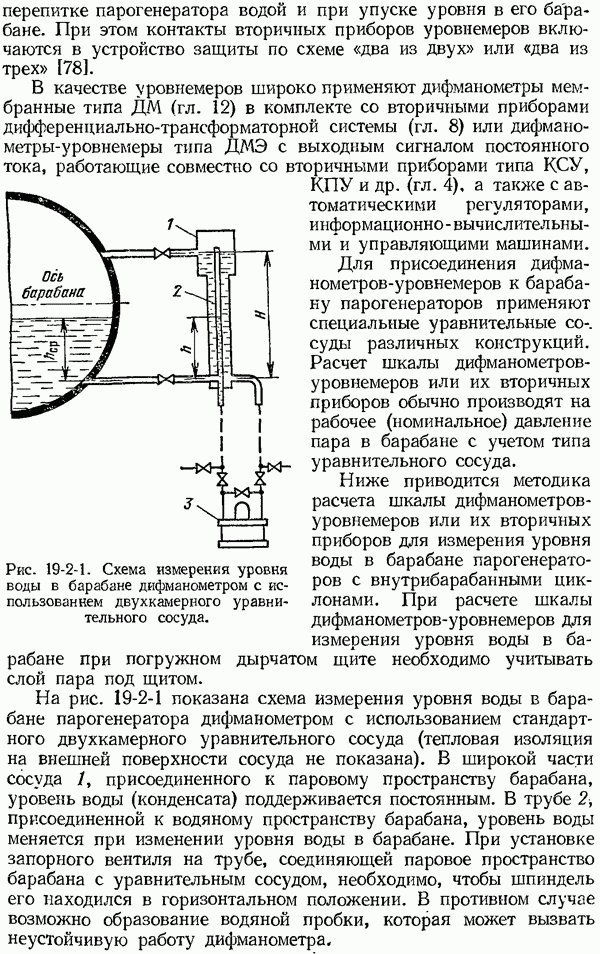
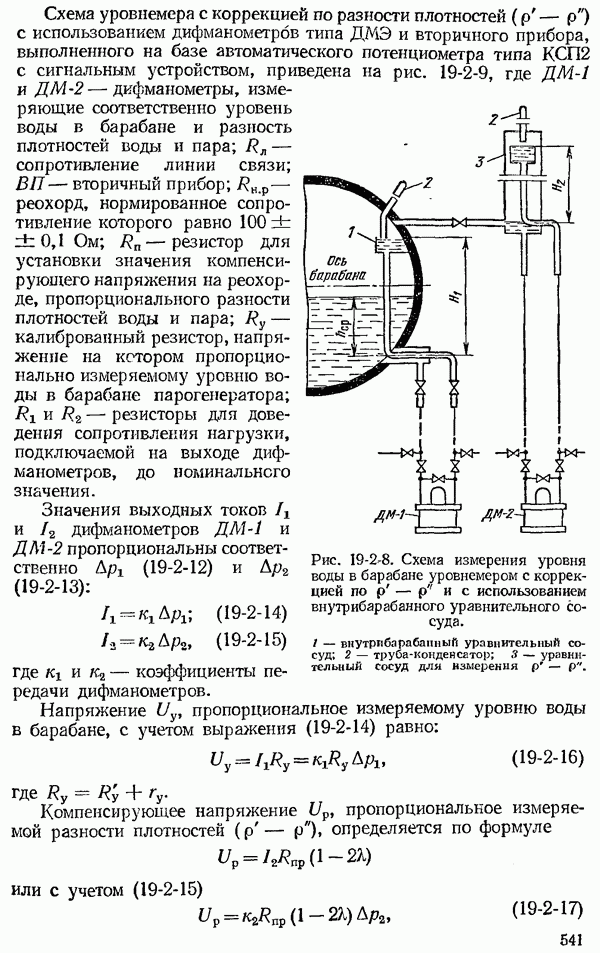
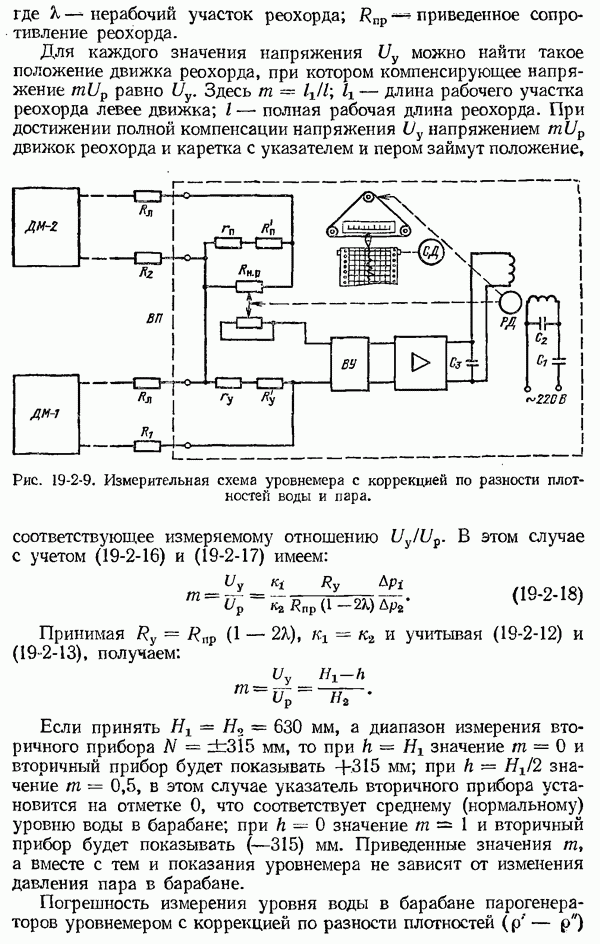
- 19-2. Измерение уровня воды в барабане парогенераторов
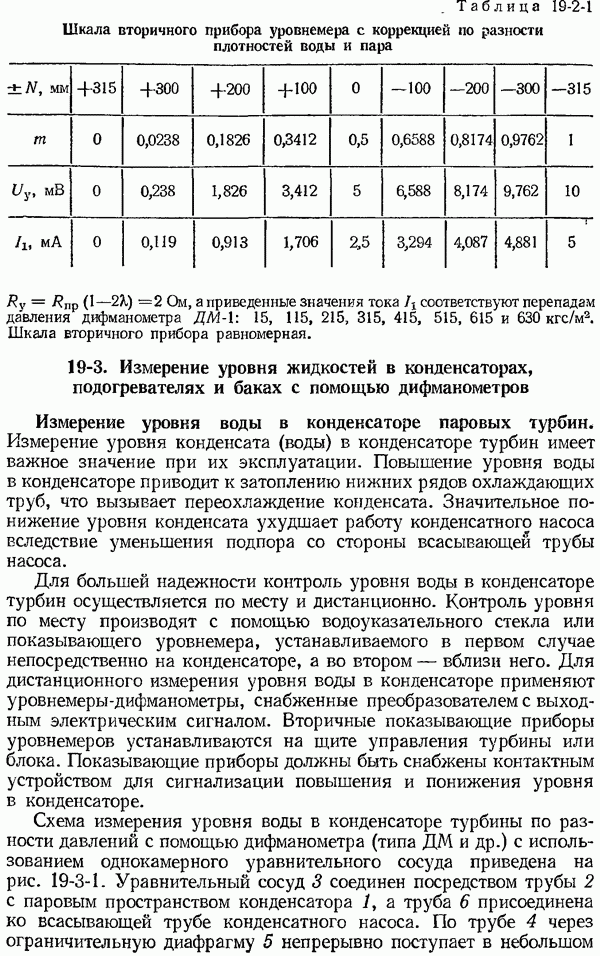
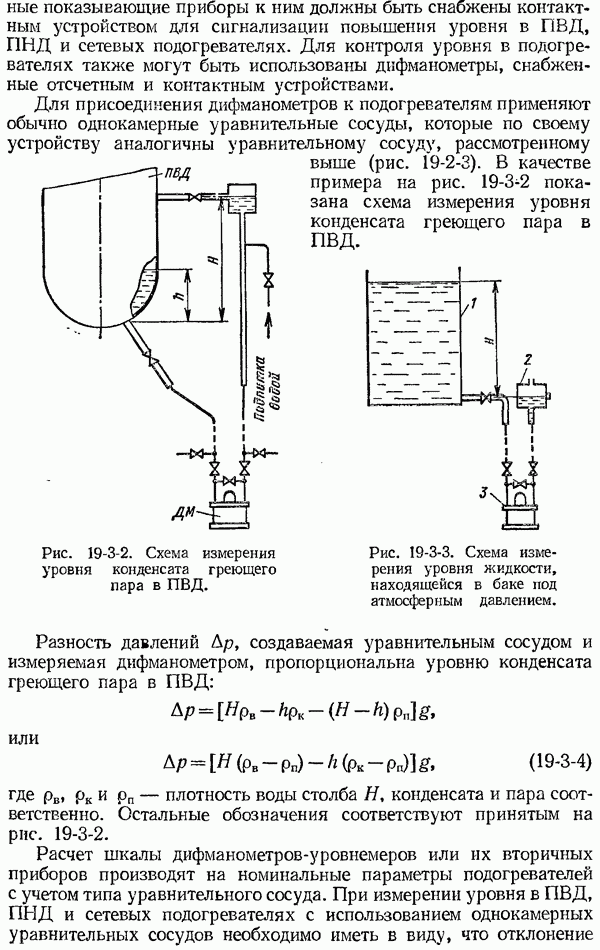
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
- 19-5. Емкостные уровнемеры
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
- 20-2. Сигнализаторы уровня сыпучих тел
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- 21-2. Газоанализаторы химические
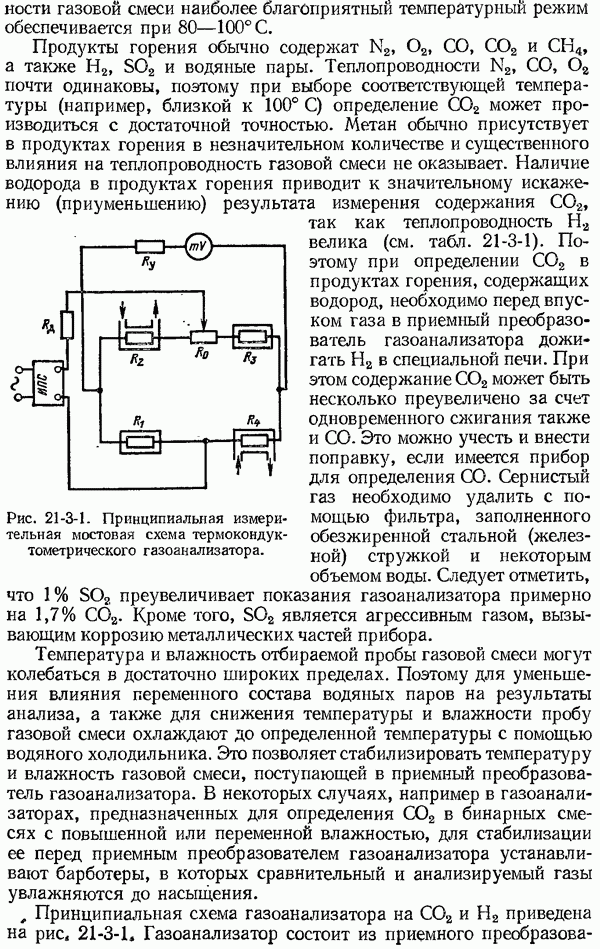
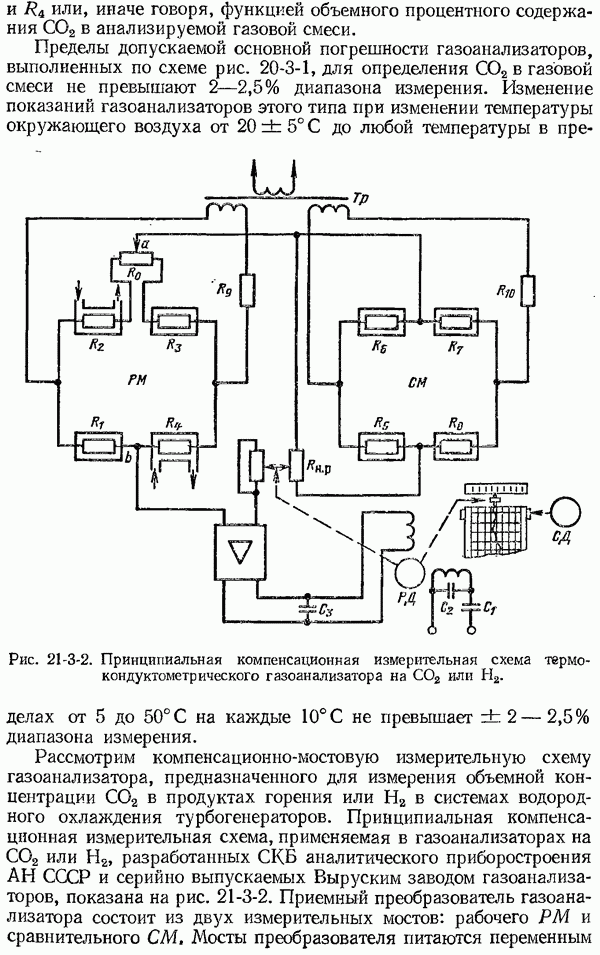
- 21-3. Тепловые газоанализаторы
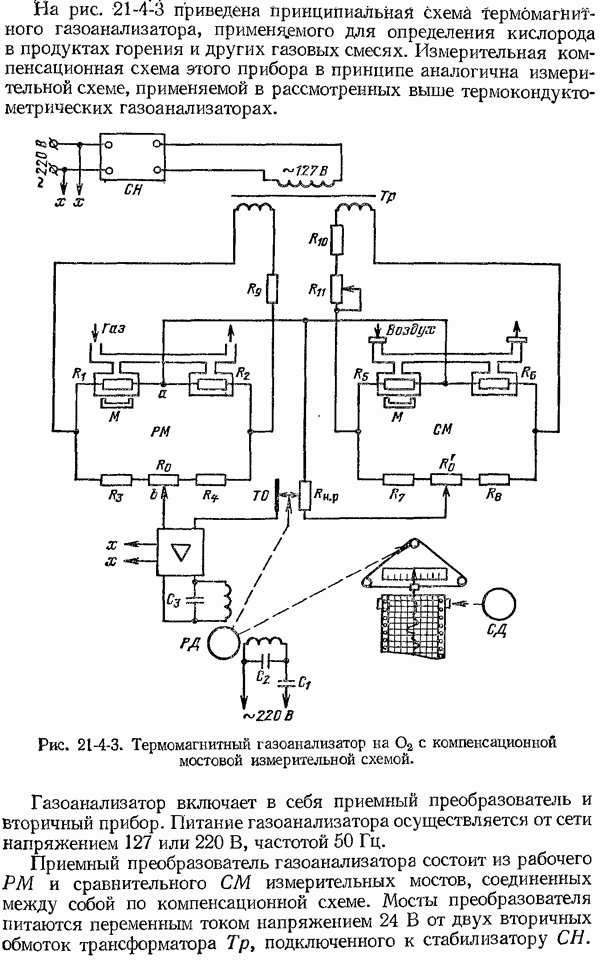
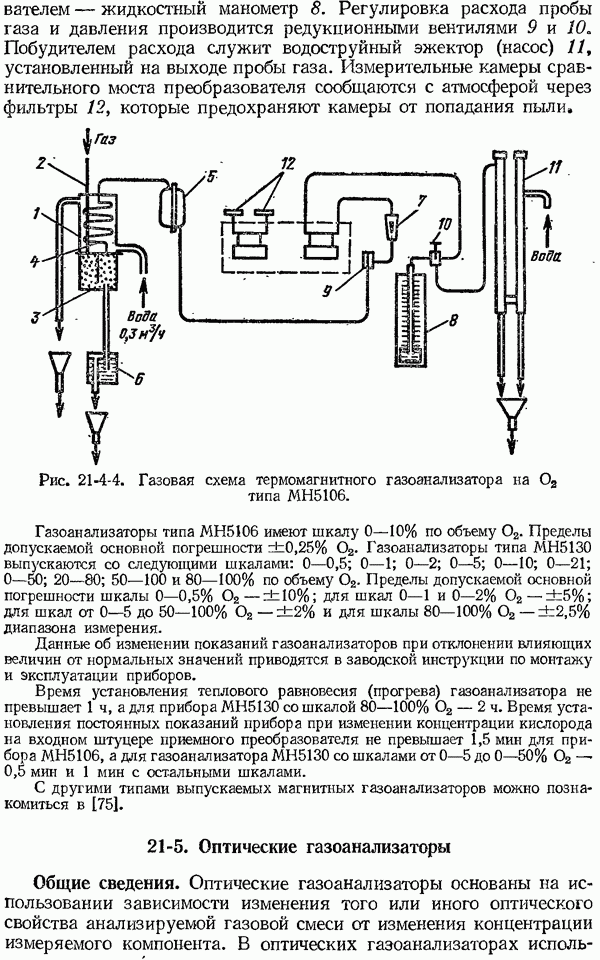
- 21-4. Магнитные газоанализаторы
- 21-5. Оптические газоанализаторы
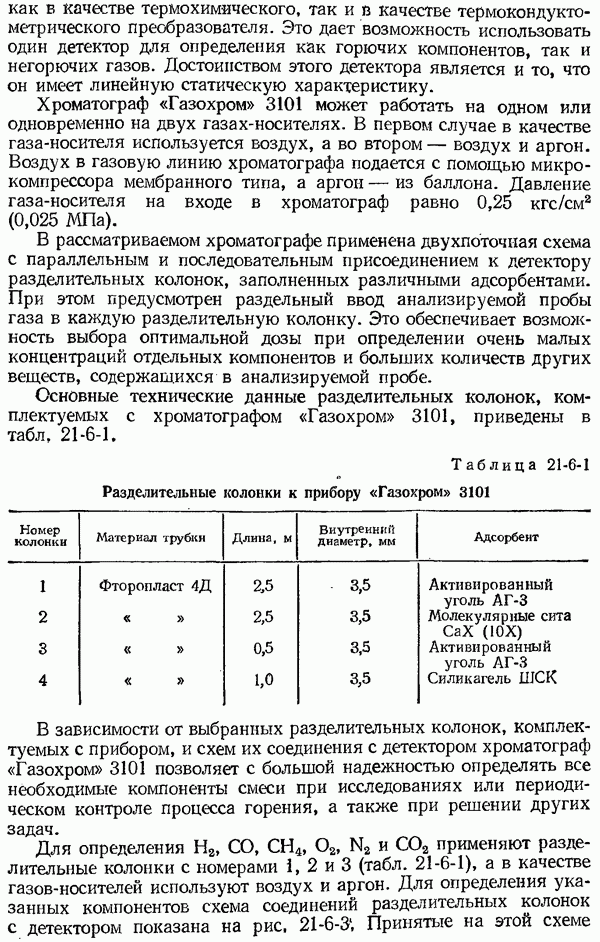
- 21-6. Газовые хроматографы
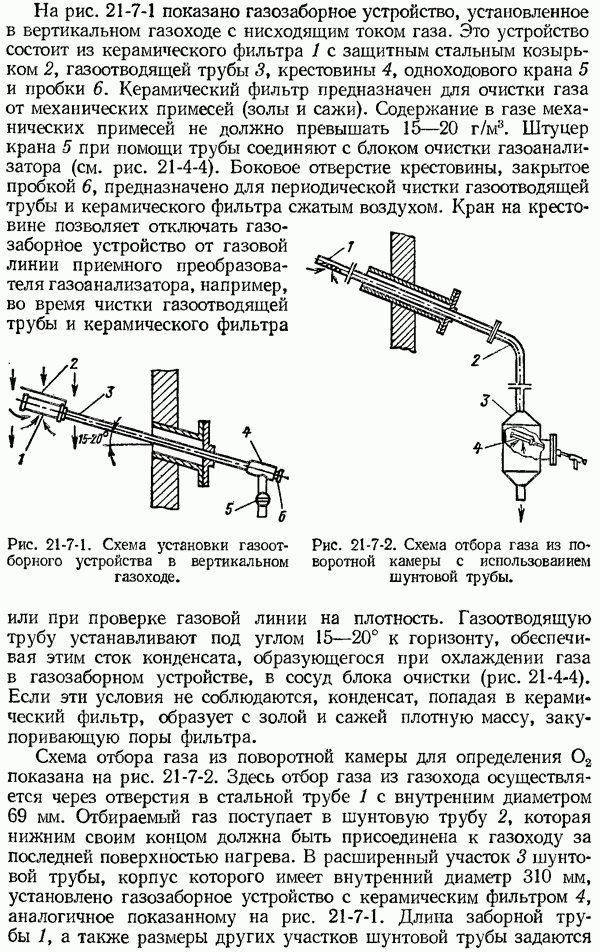
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
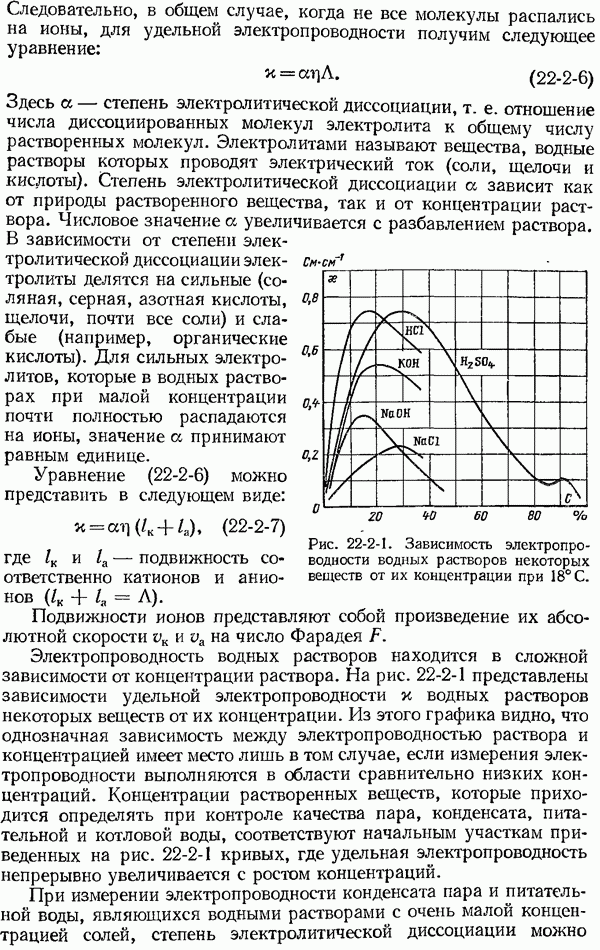
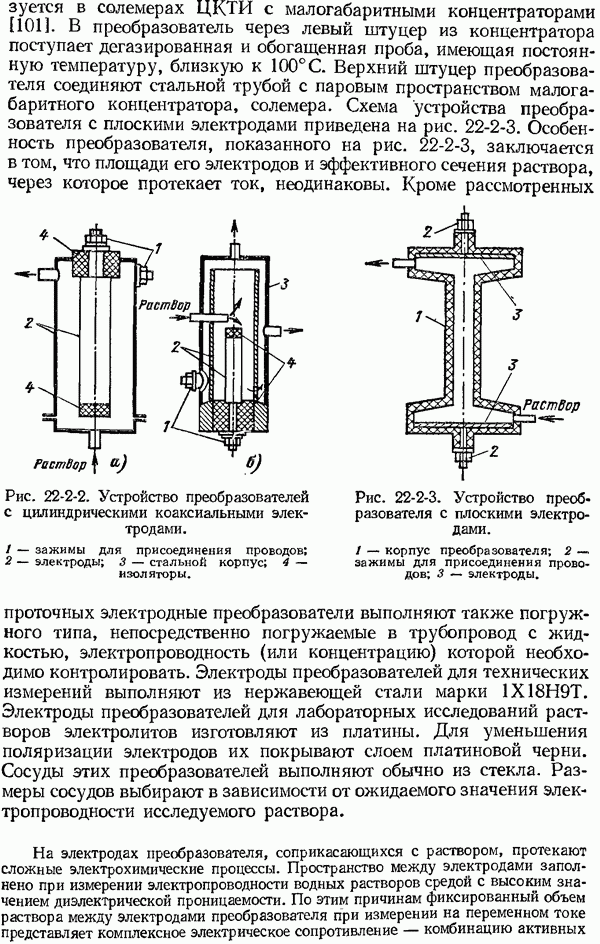
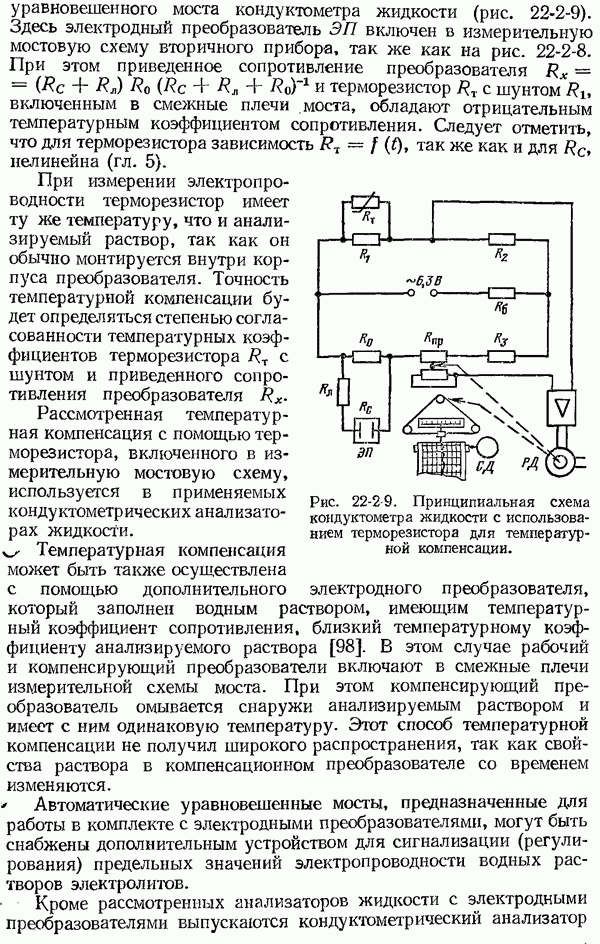
- 22-2. Измерение удельной электропроводности водных растворов
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
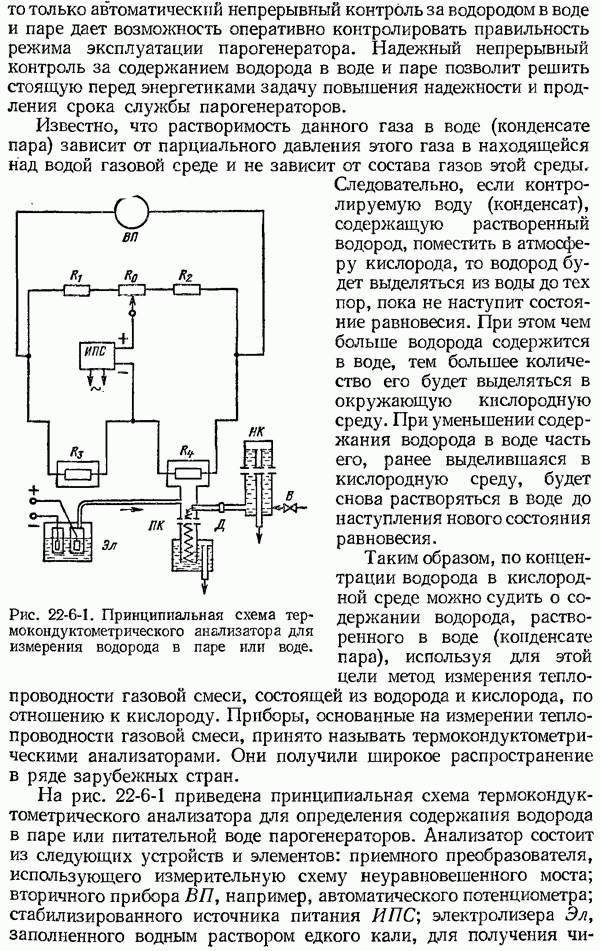
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ