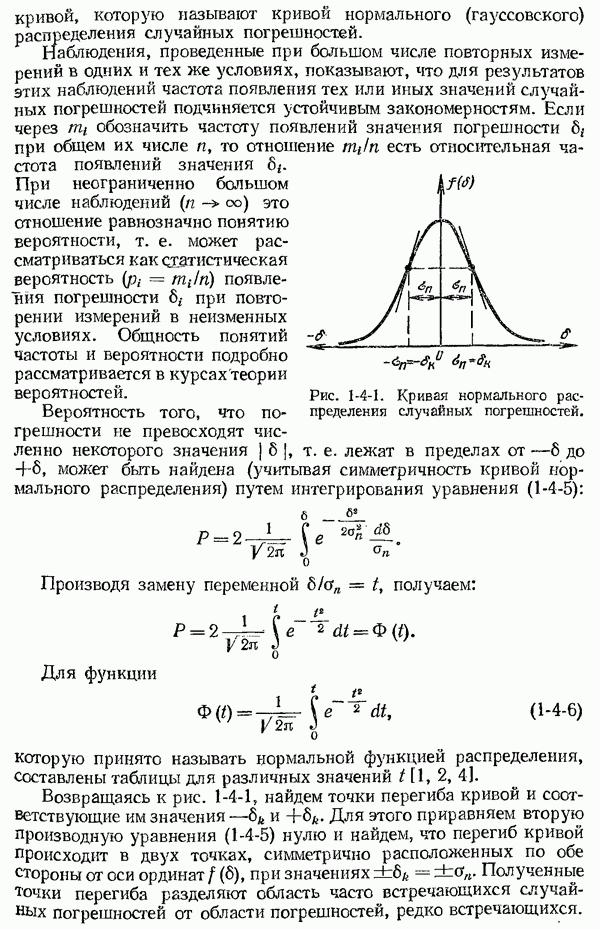
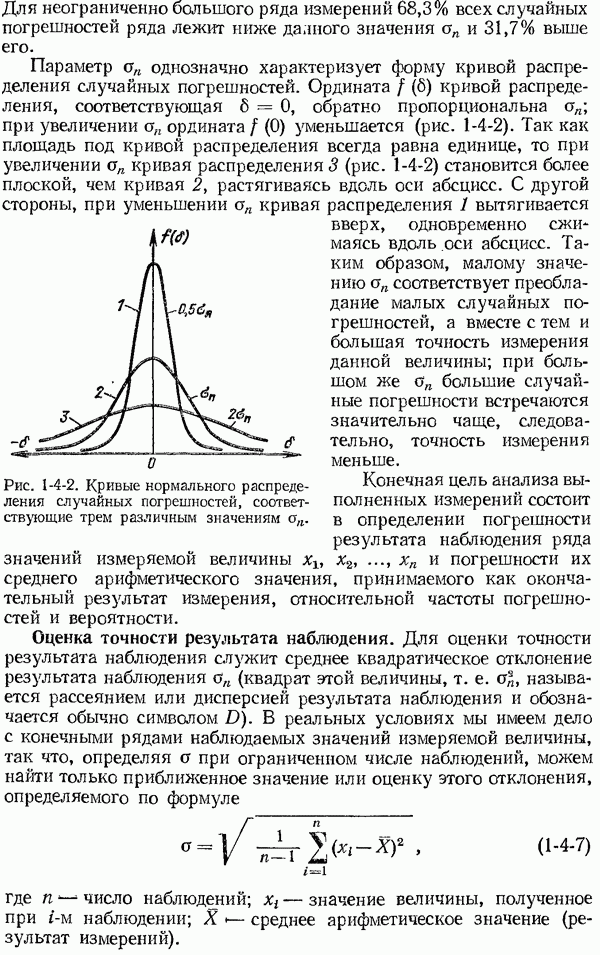
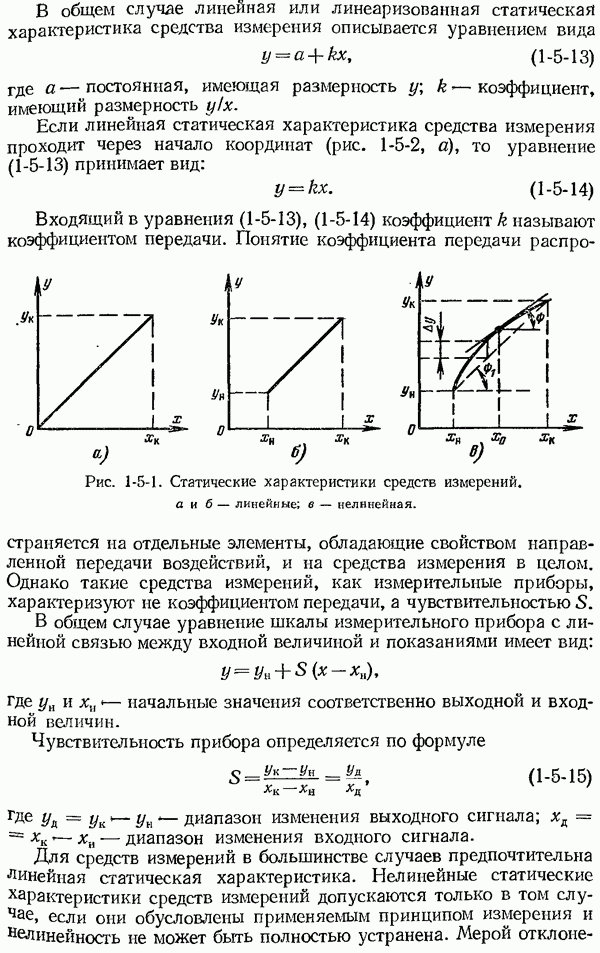
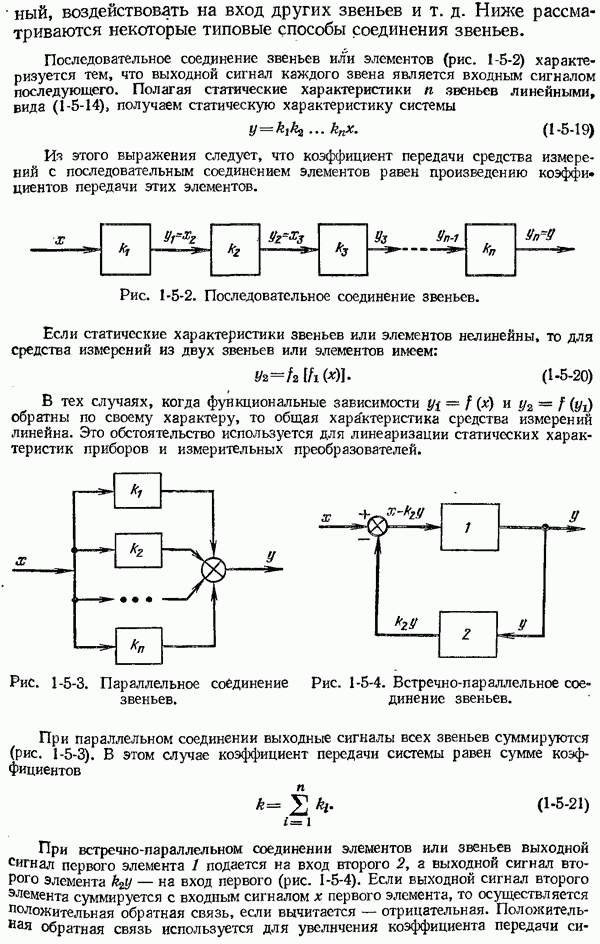
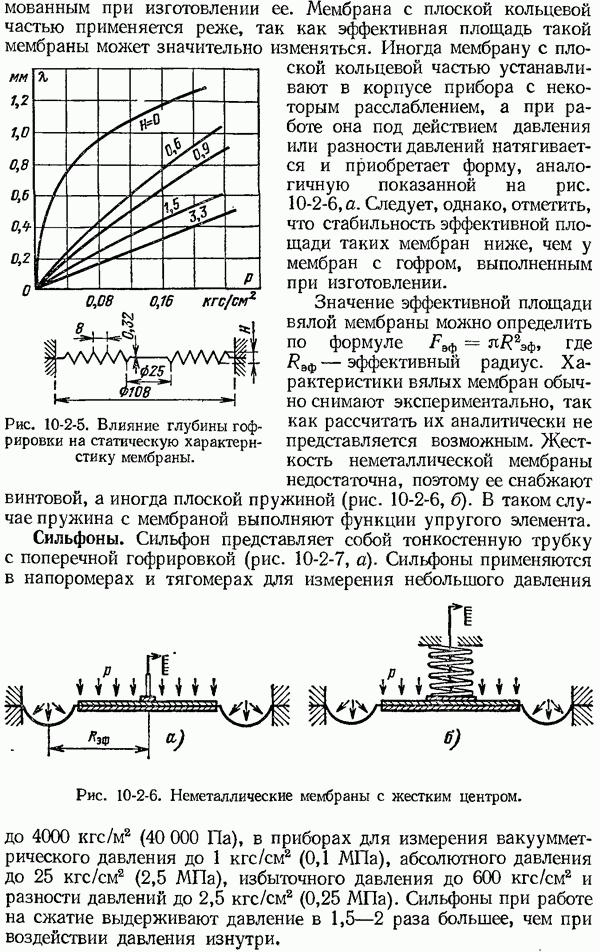
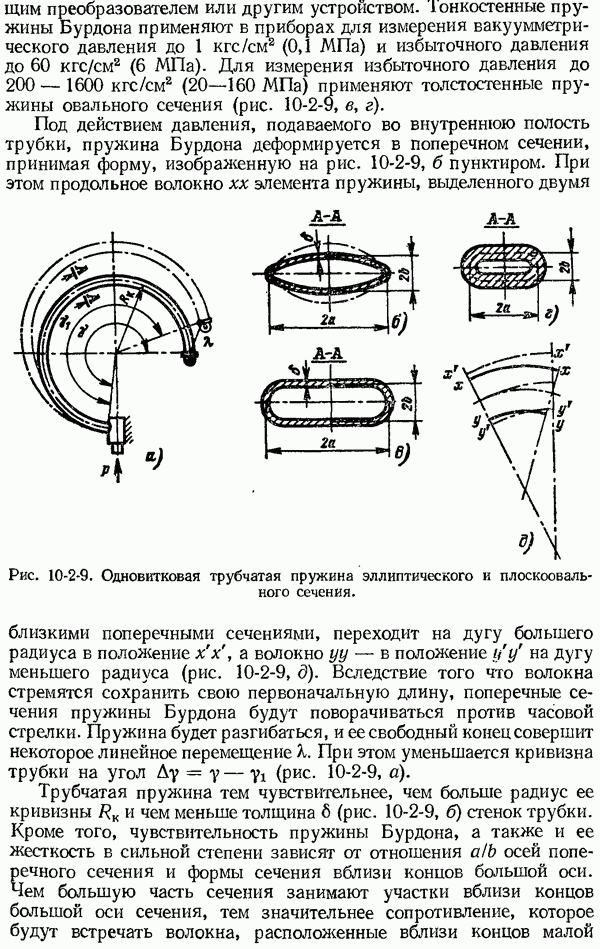
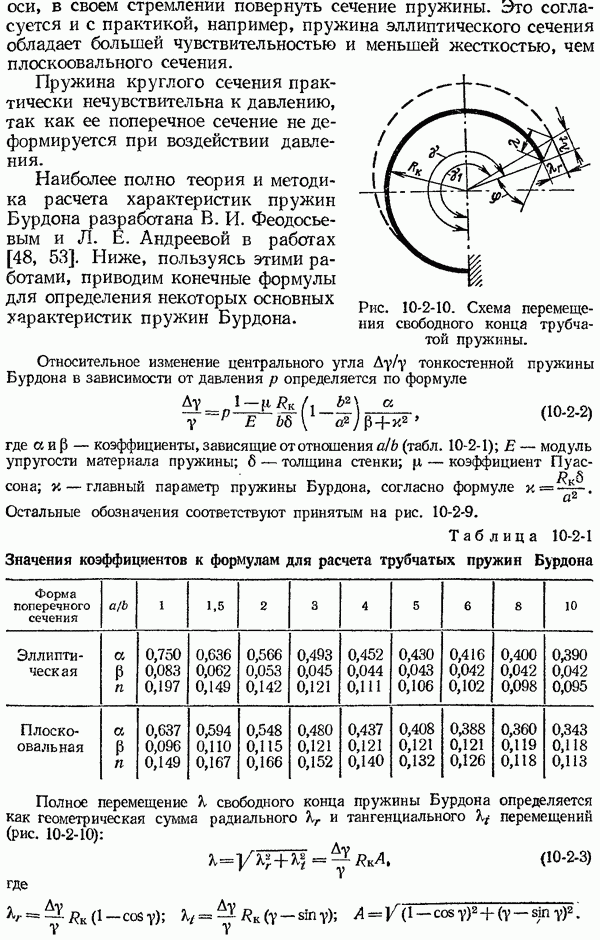
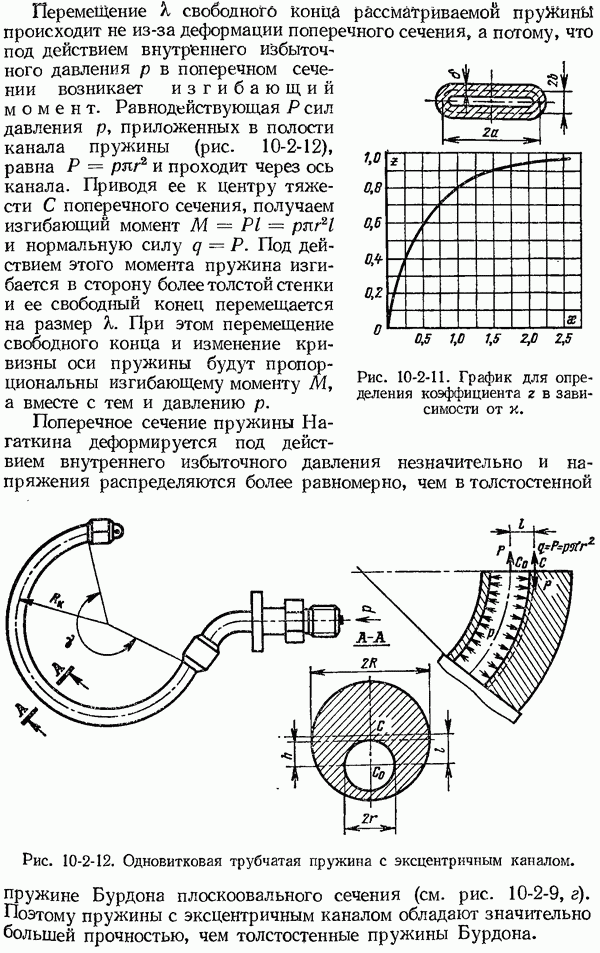
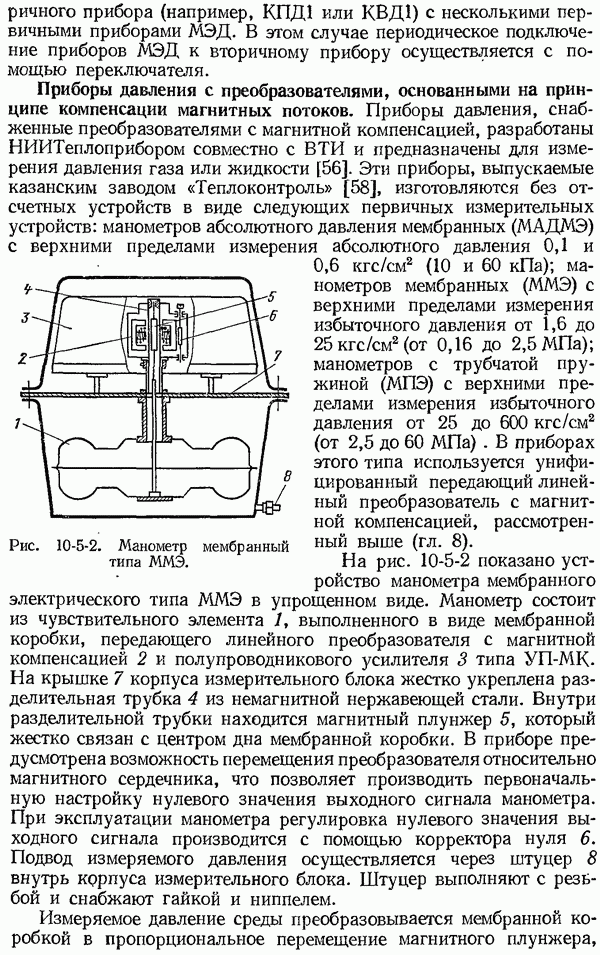
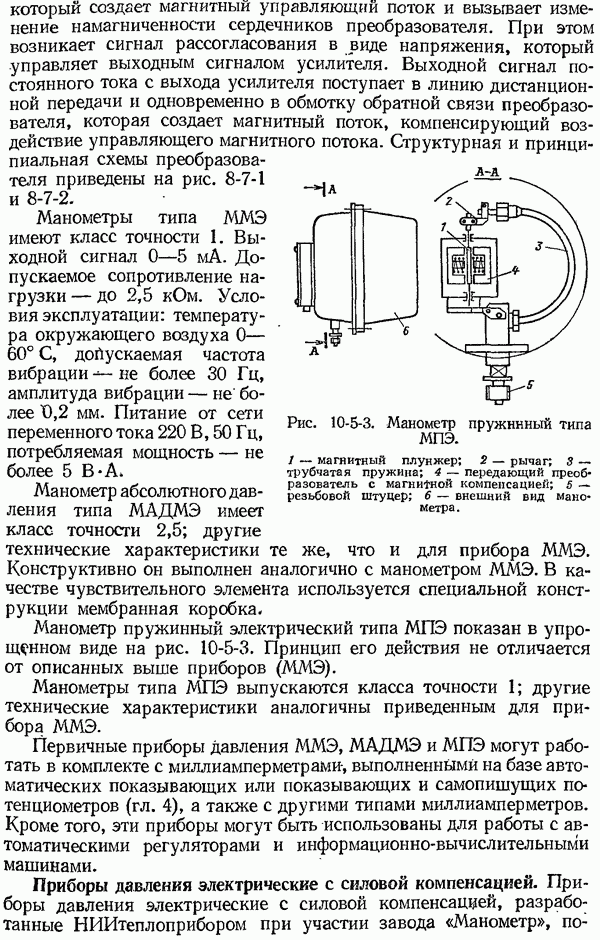
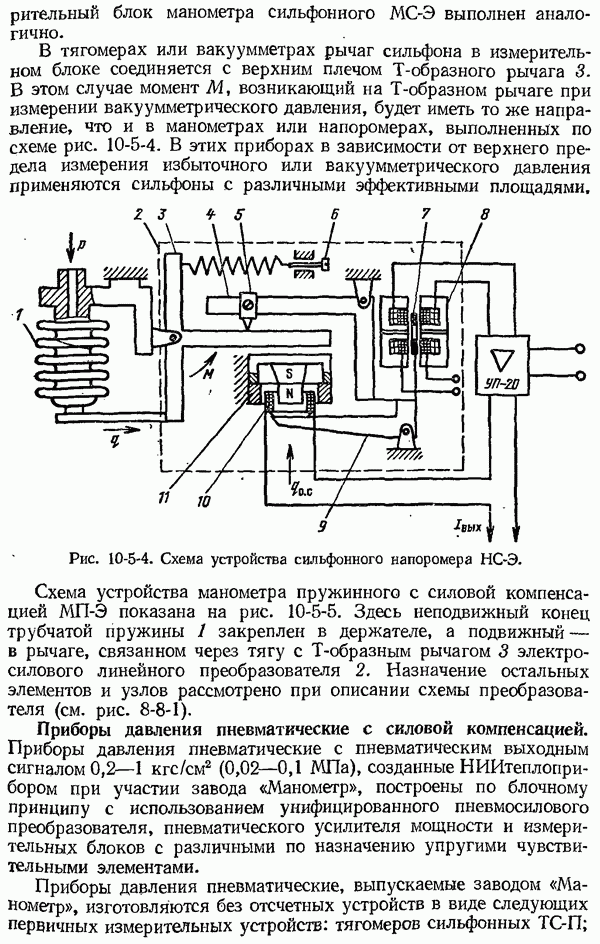
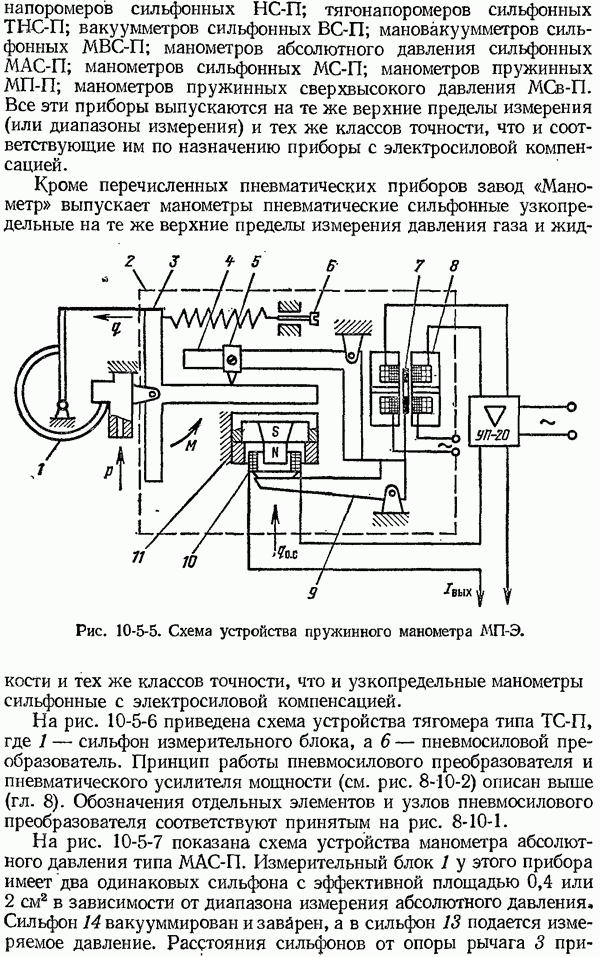
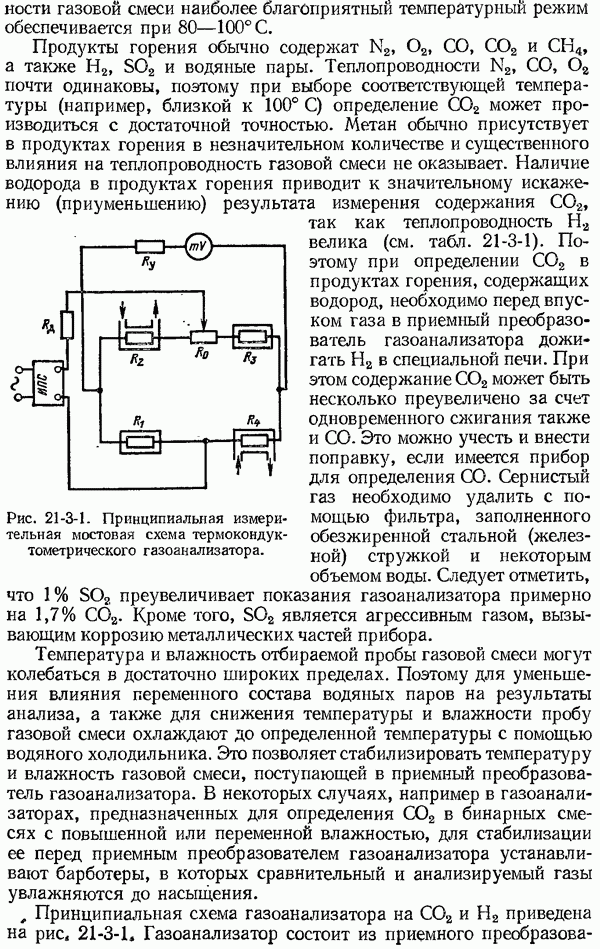
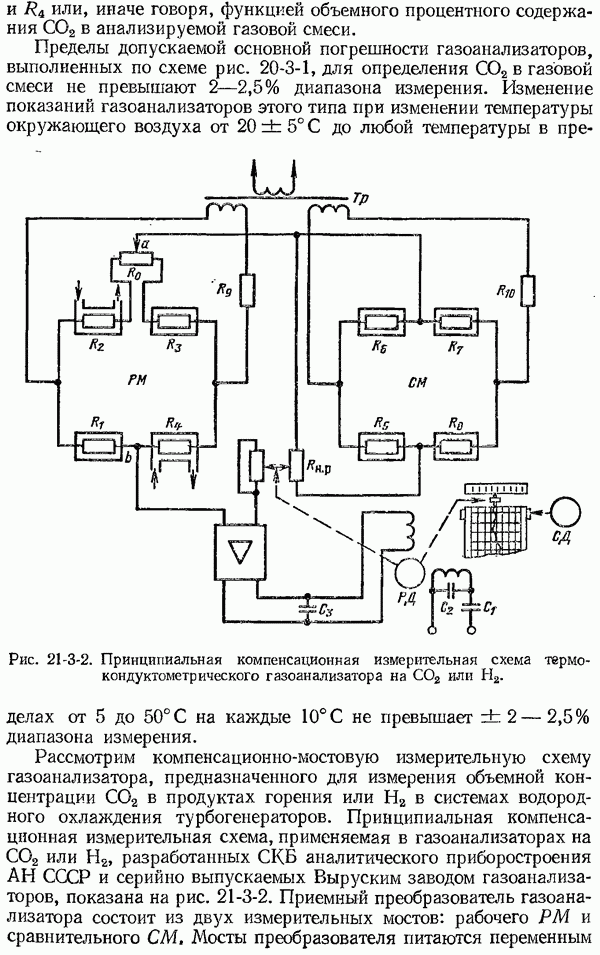
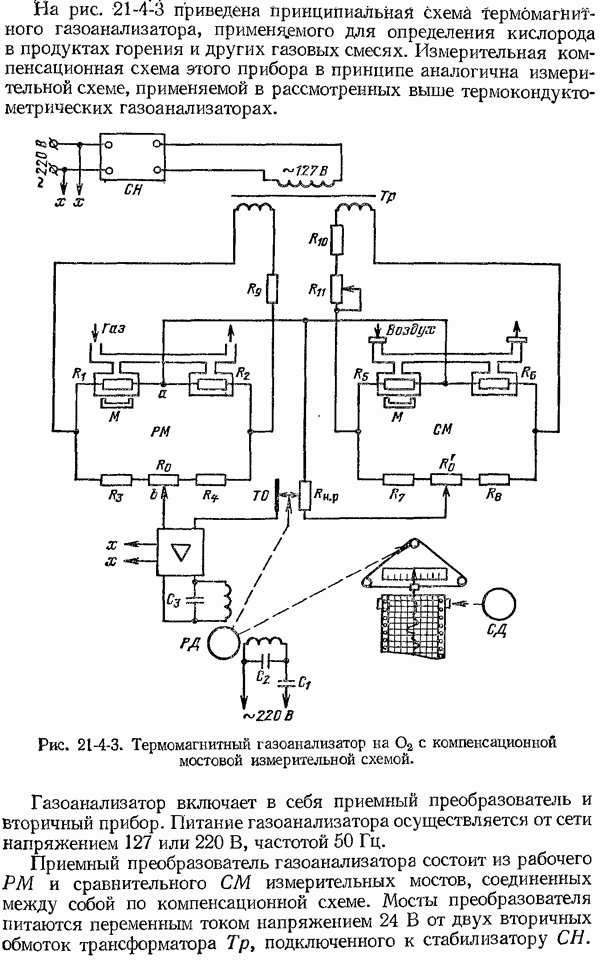
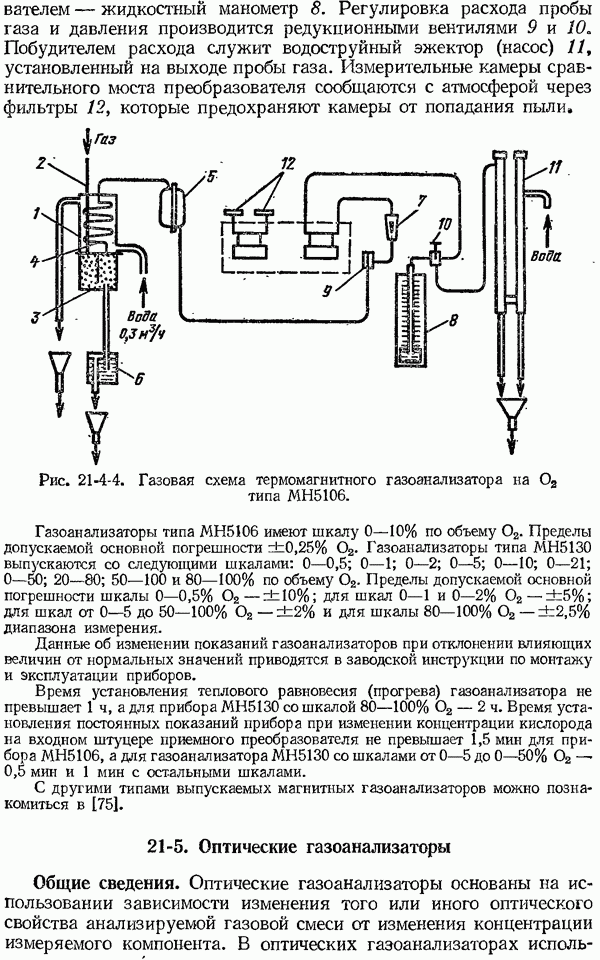
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
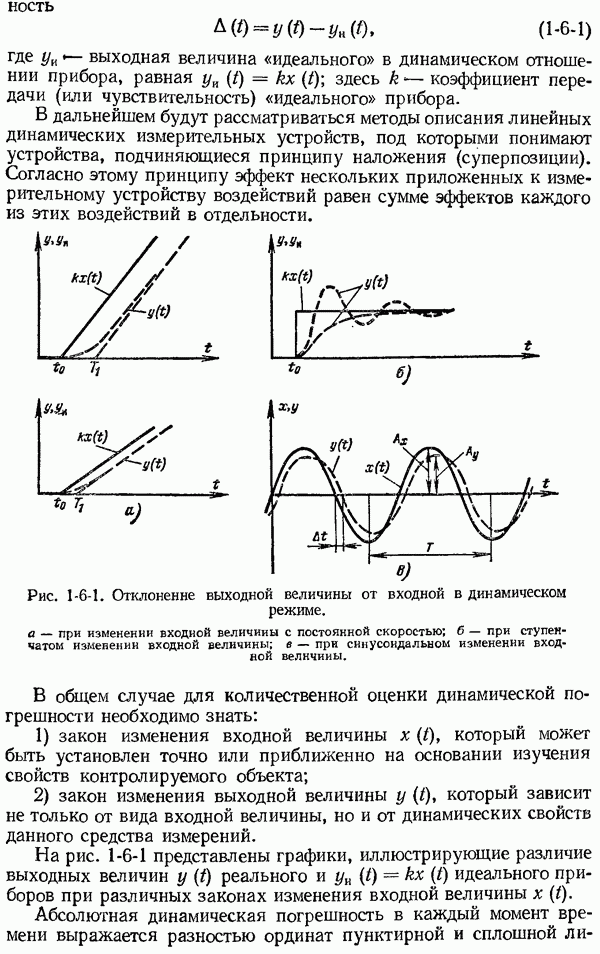
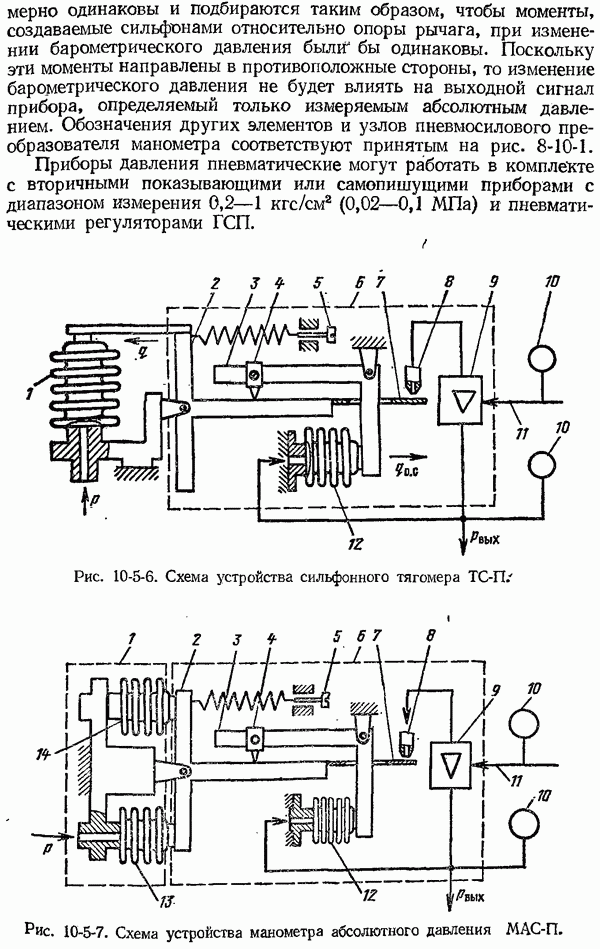
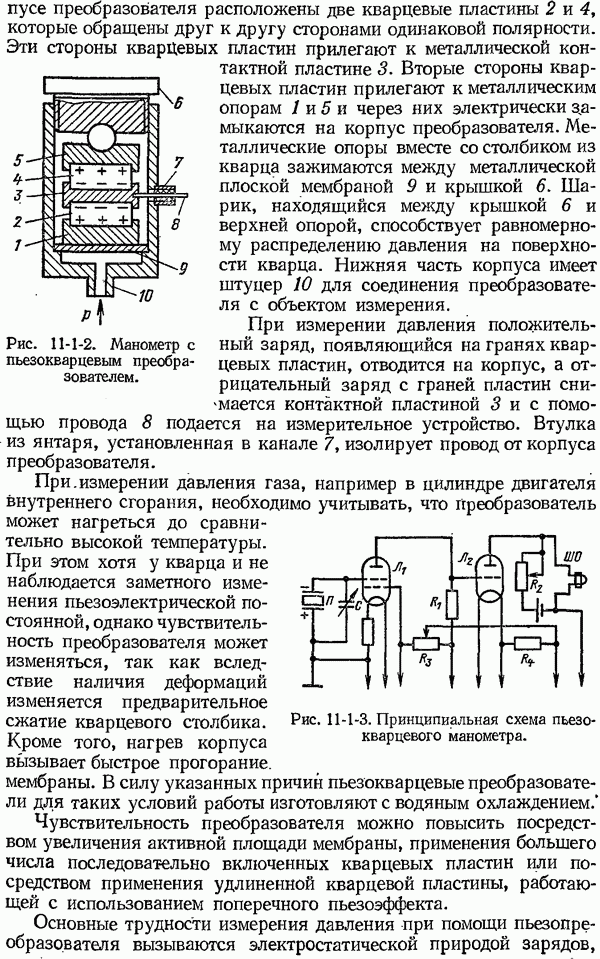
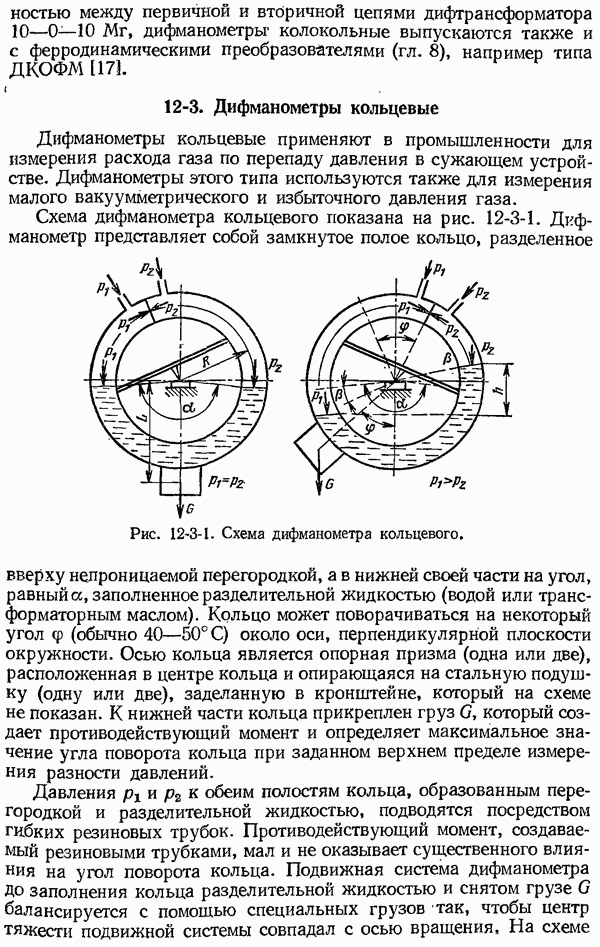
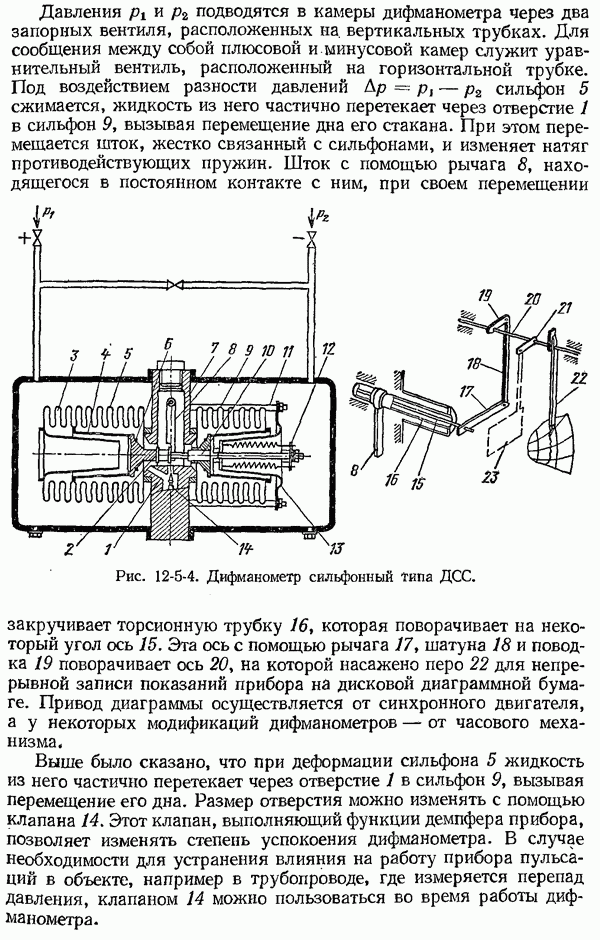
Оценка точности результата косвенных технических измерений.
До настоящего времени нет математически обоснованного правила для оценки достоверности результата косвенных технических измерений, когда прямые однократные измерения величин  оцениваются не средними квадратическими погрешностями, а допускаемыми погрешностями средств измерения и погрешностями, обусловленными условиями измерения.
оцениваются не средними квадратическими погрешностями, а допускаемыми погрешностями средств измерения и погрешностями, обусловленными условиями измерения.
Если косвенно измеряемая величина у связана с независимыми друг от друга величинами  измеряемыми прямым однократным способом, функциональной зависимостью
измеряемыми прямым однократным способом, функциональной зависимостью

то очевидно, что предельная погрешность результата косвенного измерения будет слагаться из допускаемых погрешностей и погрешностей, зависящих от условий измерения каждого прямого однократного измерения величин 
При оценке результата косвенного измерения часто исходят из положения, что при наименее благоприятном случае максимальная абсолютная погрешность результата измерения

где  абсолютная предельная погрешность прямого однократного измерения величины
абсолютная предельная погрешность прямого однократного измерения величины 
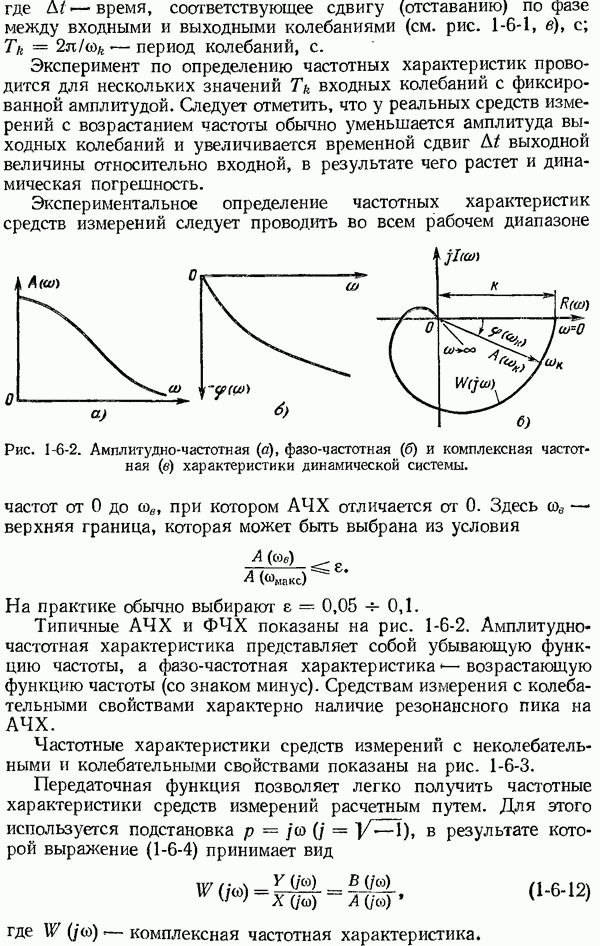
После несложных преобразований выражения (1-7-4) получим уравнение, выражающее относительную максимальную
погрешность результата косвенного измерения, 

Такой способ определения максимальной погрешности результата измерения у, когда у является функцией более чем двух величии  дает завышенное значение
дает завышенное значение  или
или  Вероятность того, что все суммируемые погрешности величин
Вероятность того, что все суммируемые погрешности величин  будут одного знака, например, равна 0,062 при
будут одного знака, например, равна 0,062 при  и 0,002 при
и 0,002 при 
Вероятность же того, что погрешности прямых однократных измерений величин  будут одного знака и одновременно будут иметь максимальные значения, практически равна нулю.
будут одного знака и одновременно будут иметь максимальные значения, практически равна нулю.
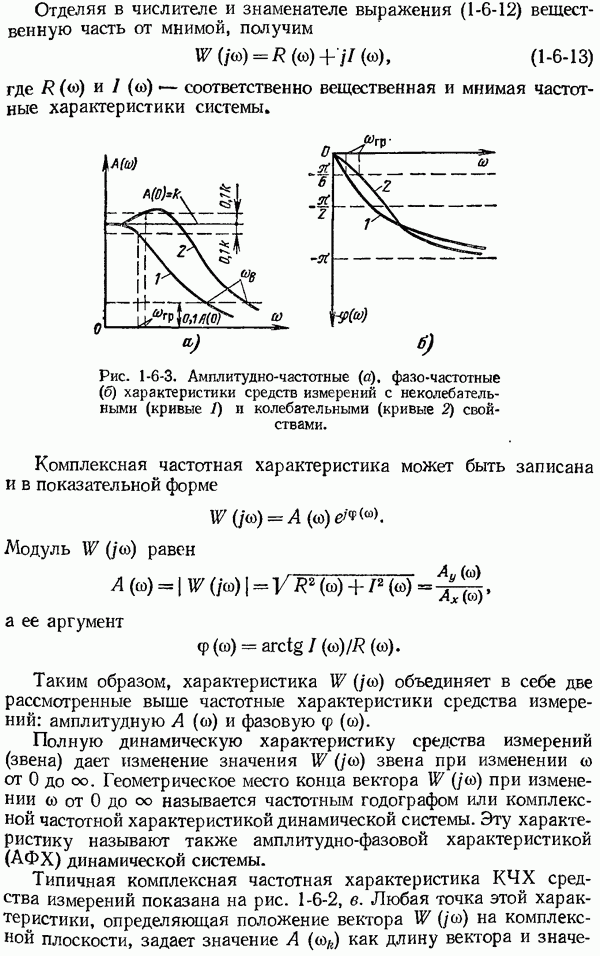
Так как нельзя ожидать, что указанный выше неблагоприятный случай будет часто встречаться, при оценке точности результата измерения целесообразно производить квадратичное суммирование по формуле

Если непосредственно измеряемые величины являются по своей природе разнородными, то пользуются уравнением

Следует отметить, что вероятность максимальных или предельных погрешностей  и результата косвенного измерения не может быть оценена с достаточной достоверностью.
и результата косвенного измерения не может быть оценена с достаточной достоверностью.
Необходимо отметить, что при действующем способе нормирования метрологических характеристик средств измерений не представляется возможным теоретически обосновано производить оценку погрешности измерений физических величин в реальных условиях эксплуатации. Математическое описание погрешностей средств измерений в соответствии с основными положениями ГОСТ 8.009-72 позволяет теоретически обосновано и с необходимой достоверностью производить оценку погрешности сложных измерительных систем [57].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
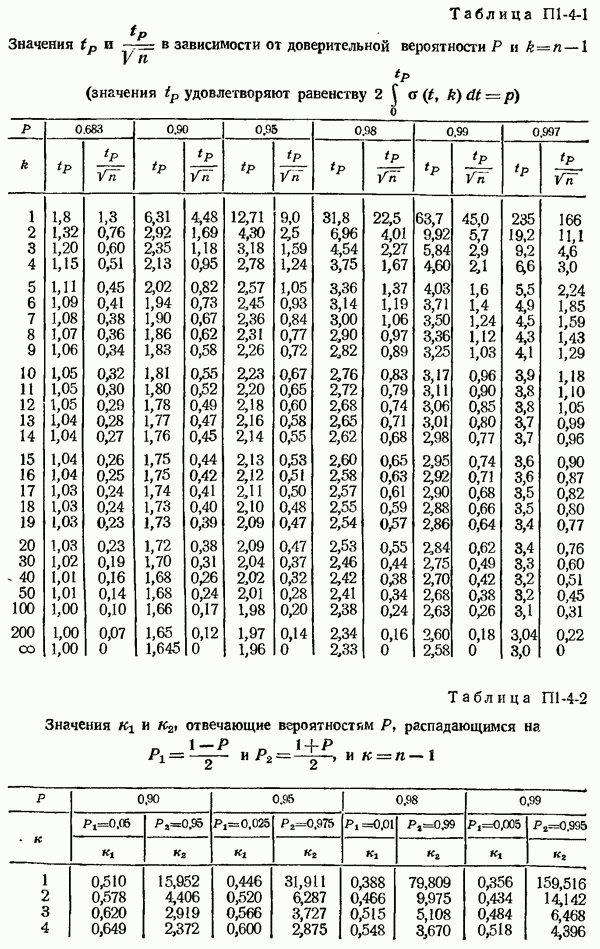
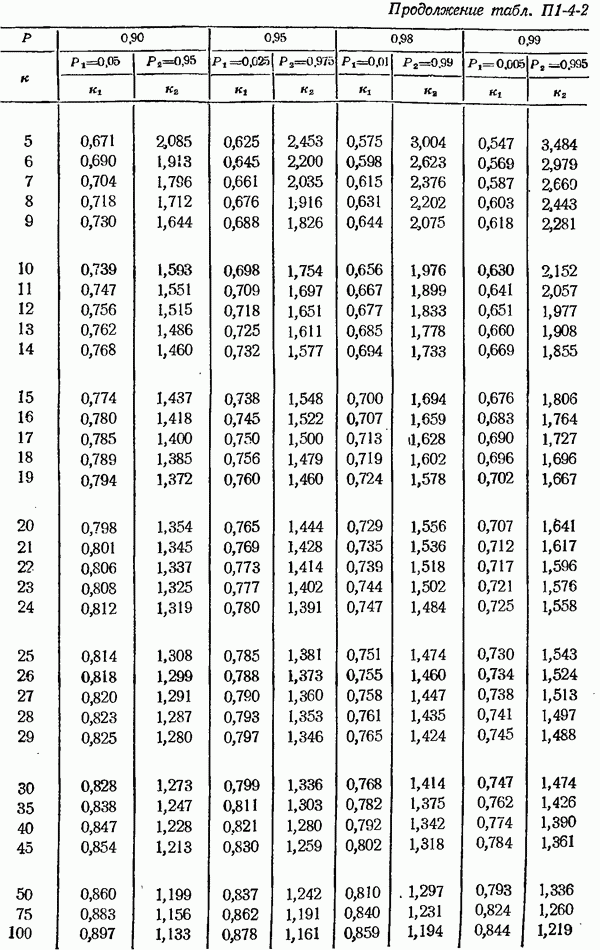
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
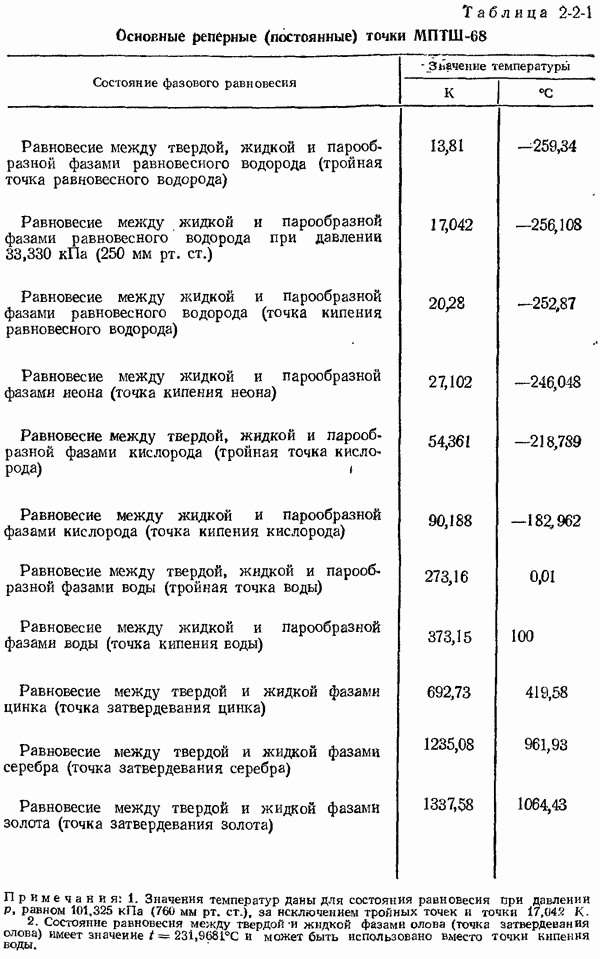
- 2-1. Основные сведения о температуре и температурных шкалах
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
- 3-1. Термометры стеклянные жидкостные
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
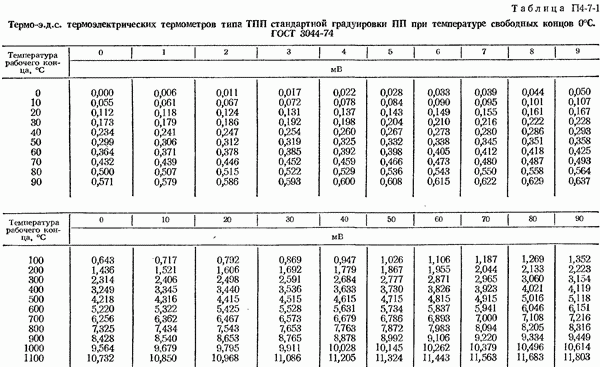
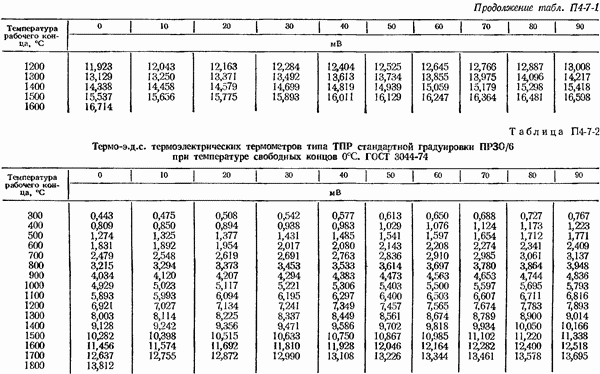
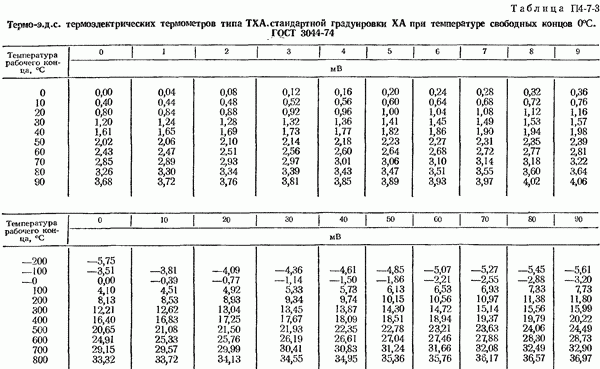
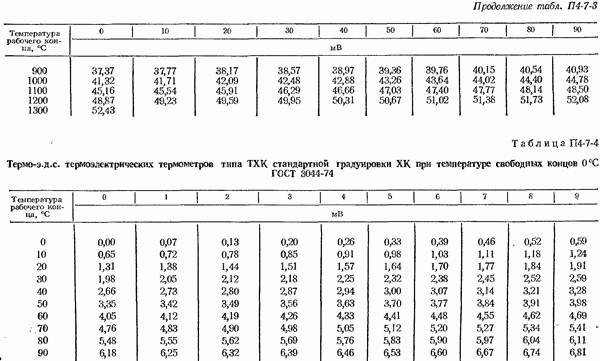
- 4-7. Общие сведения о термоэлектрических термометрах
- 4-8. Устройство термоэлектрических термометров
- 4-9. Удлиняющие термоэлектродные провода
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
- 4-11. Милливольтметры
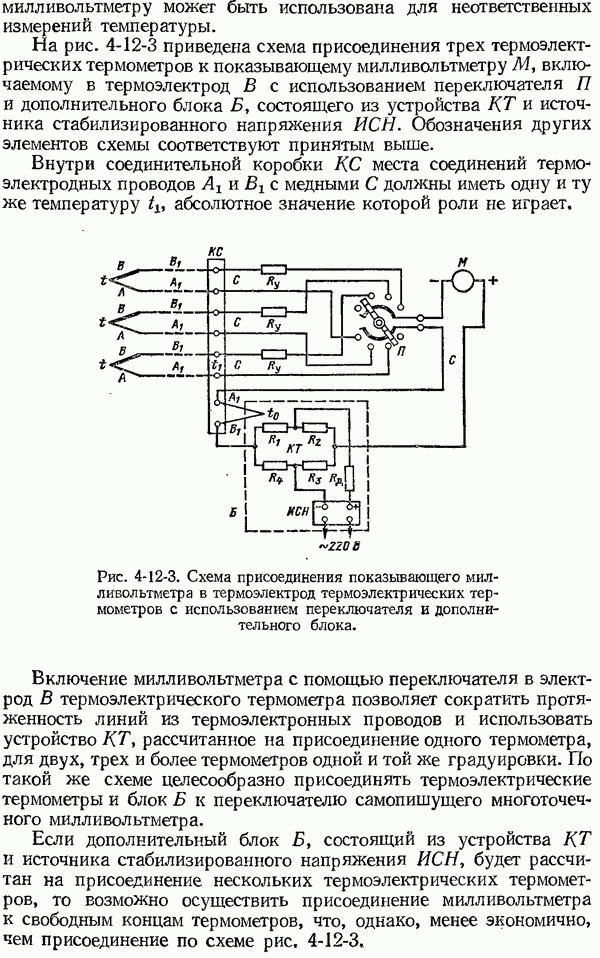
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
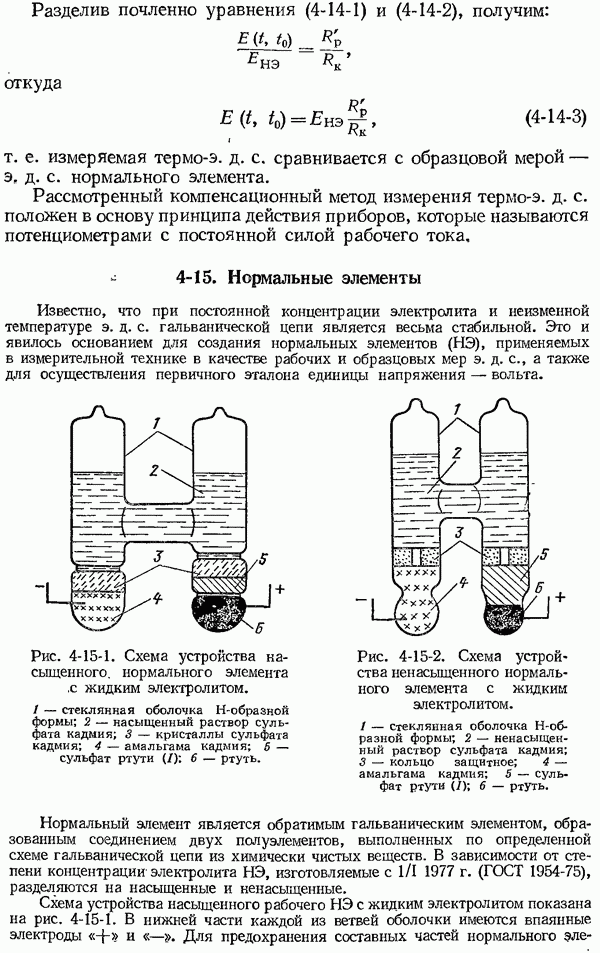
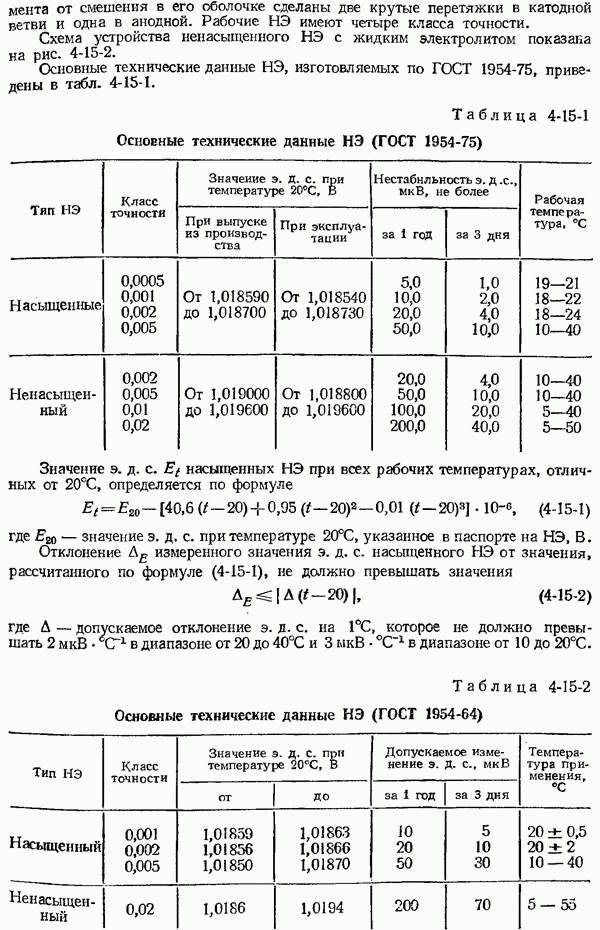
- 4-15. Нормальные элементы
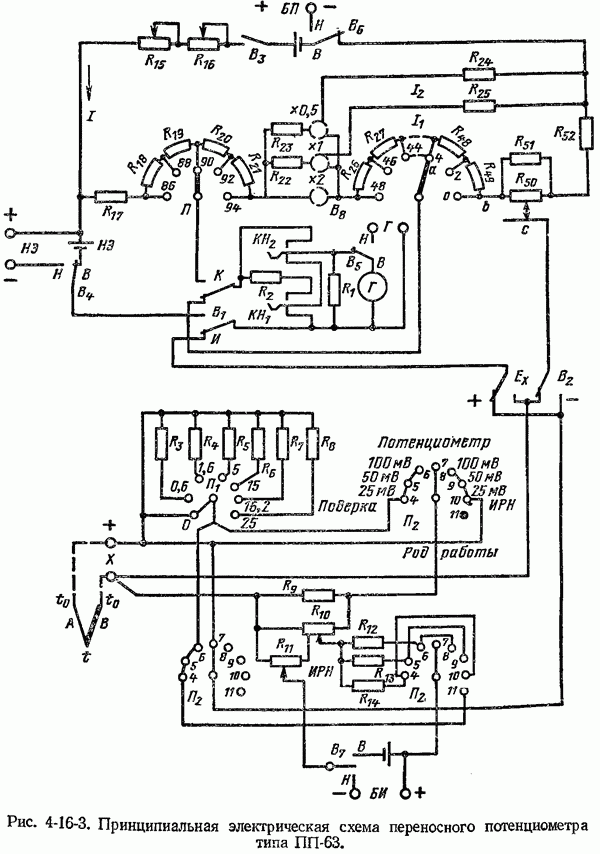
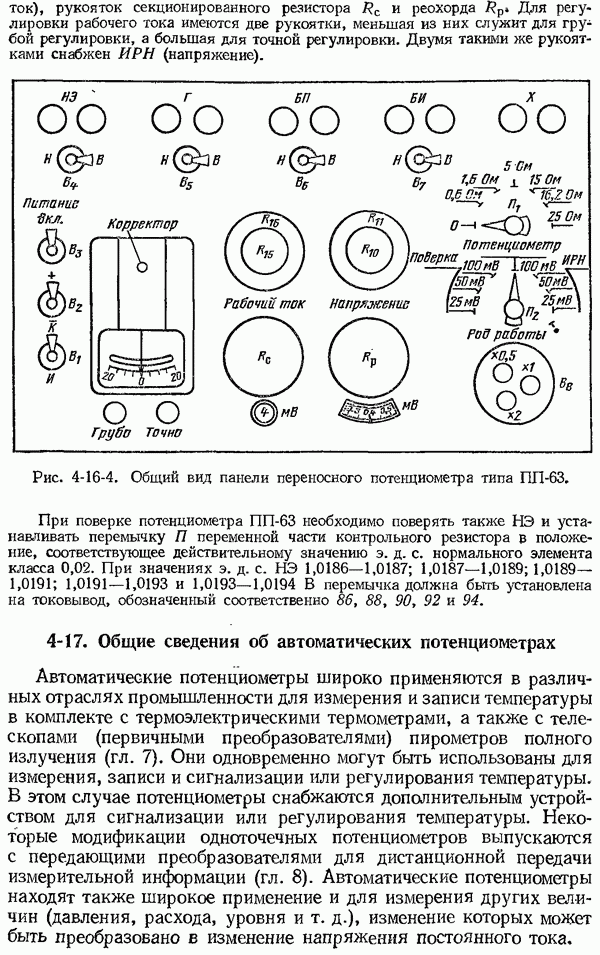
- 4-16. Потенциометры переносные и лабораторные
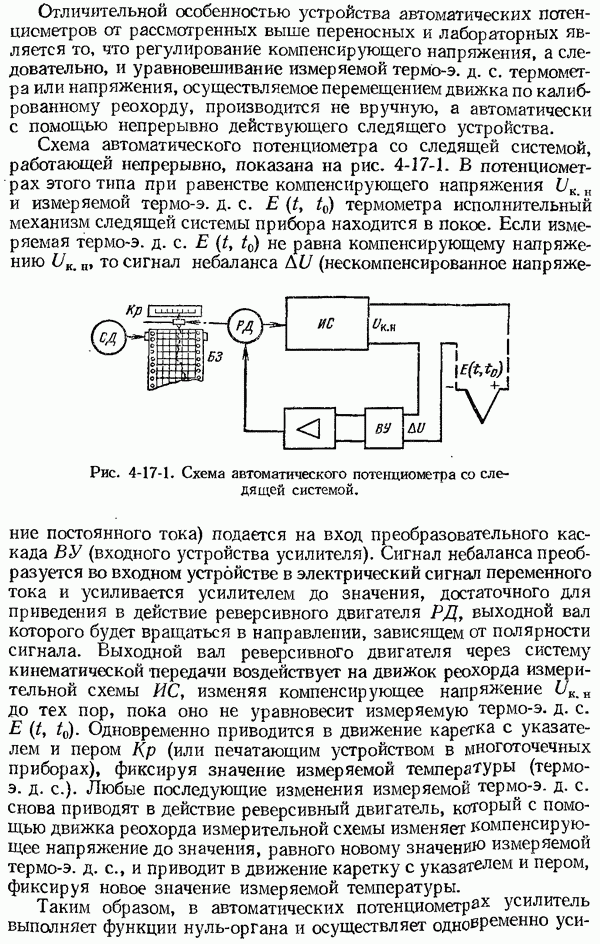
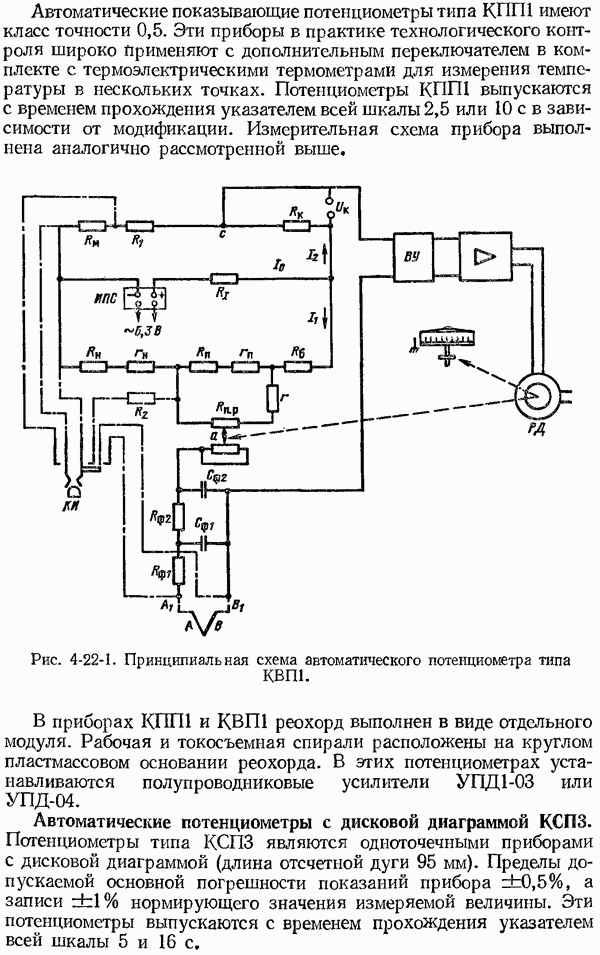
- 4-17. Общие сведения об автоматических потенциометрах
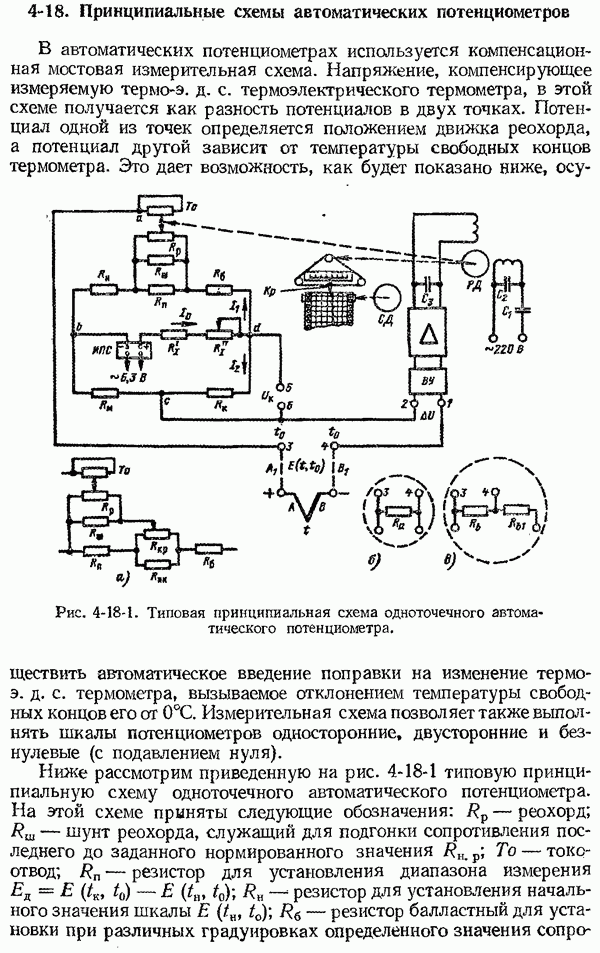
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
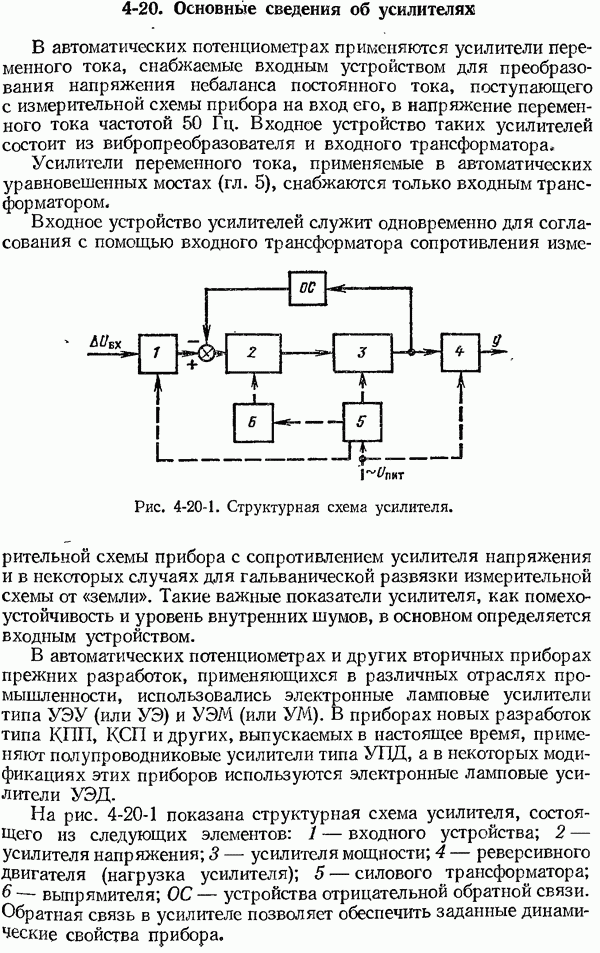
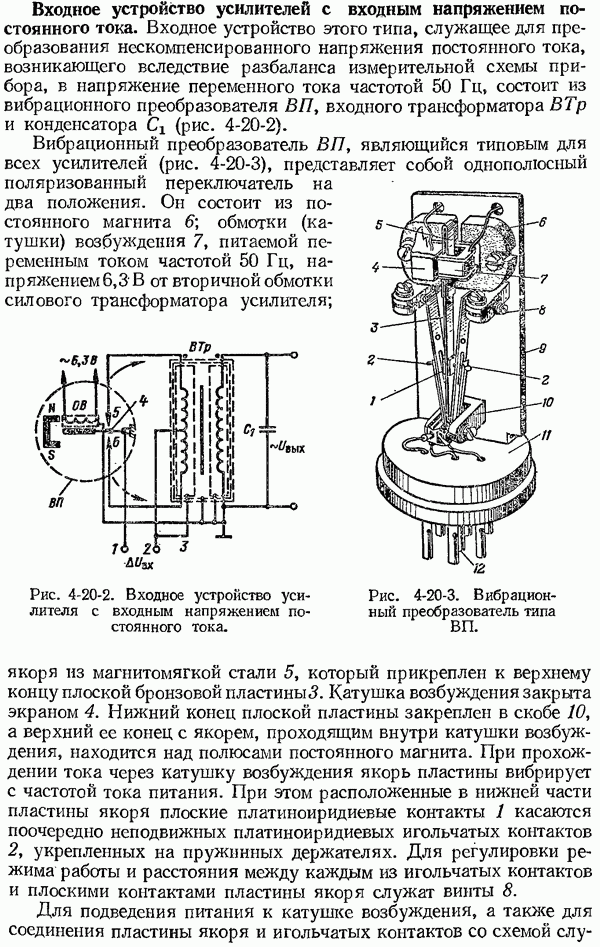
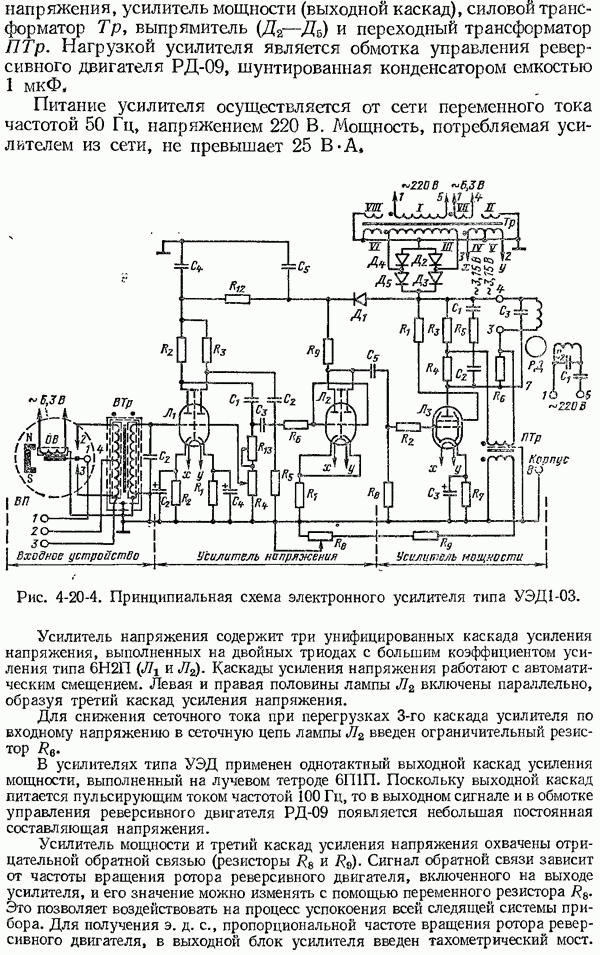
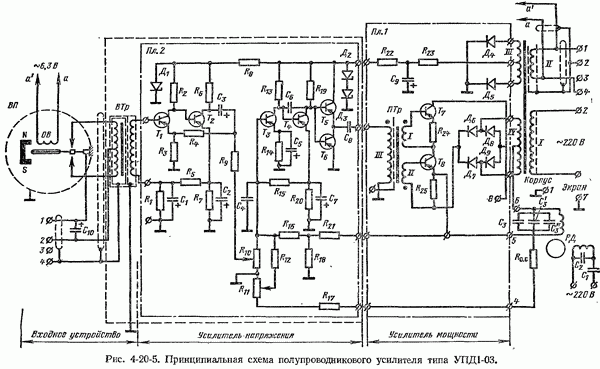
- 4-20. Основные сведения об усилителях
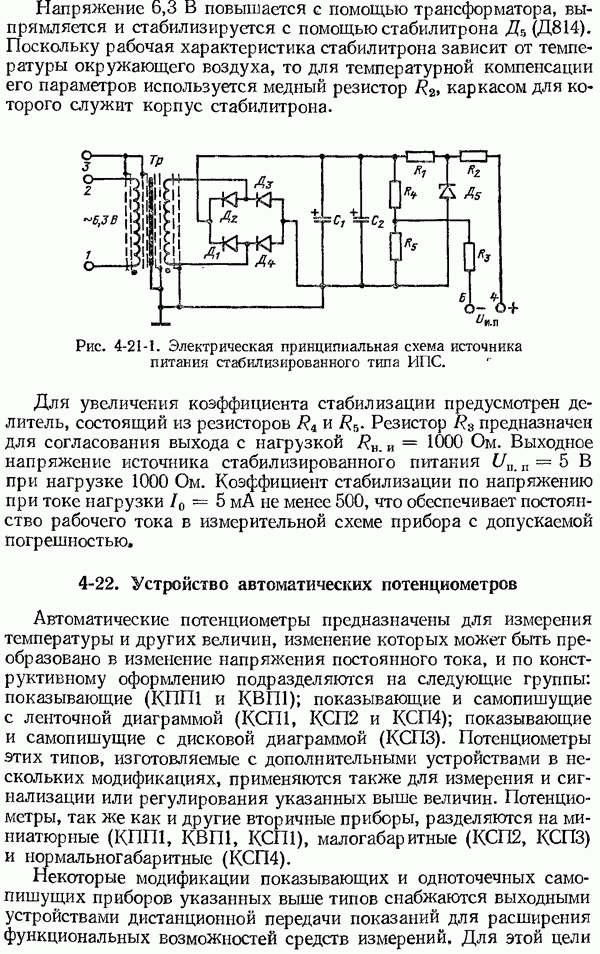
- 4-21. Основные сведения об источниках стабилизированного питания
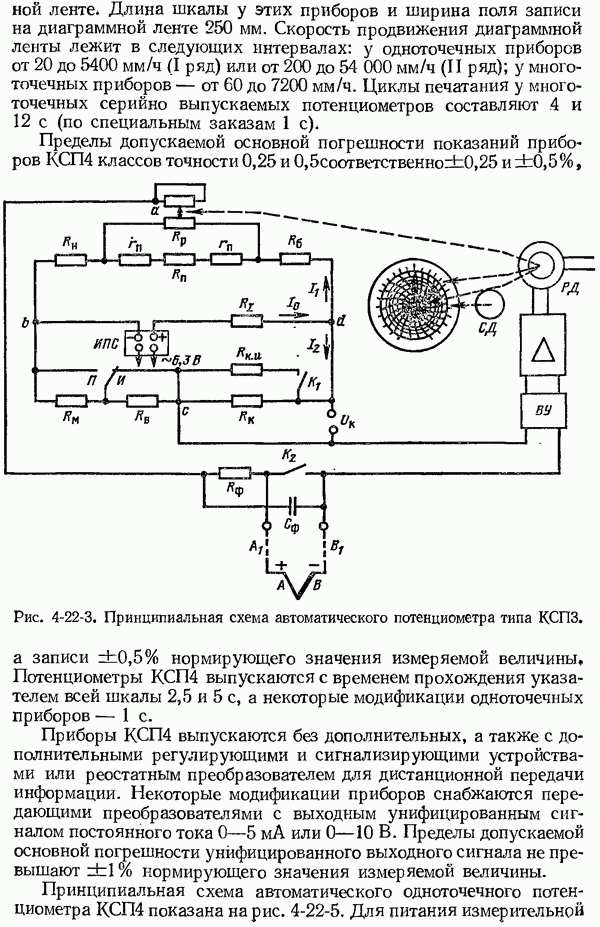
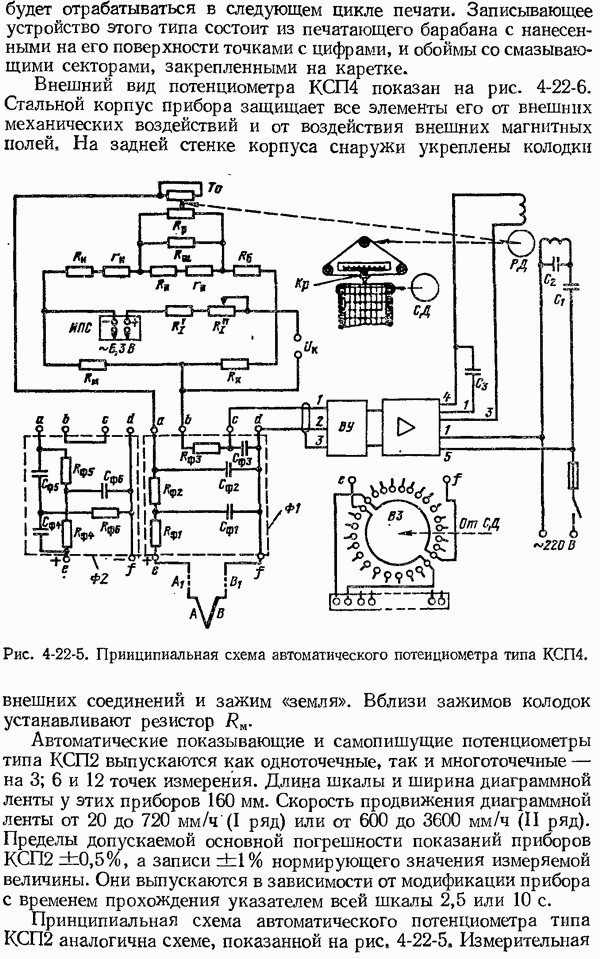
- 4-22. Устройство автоматических потенциометров
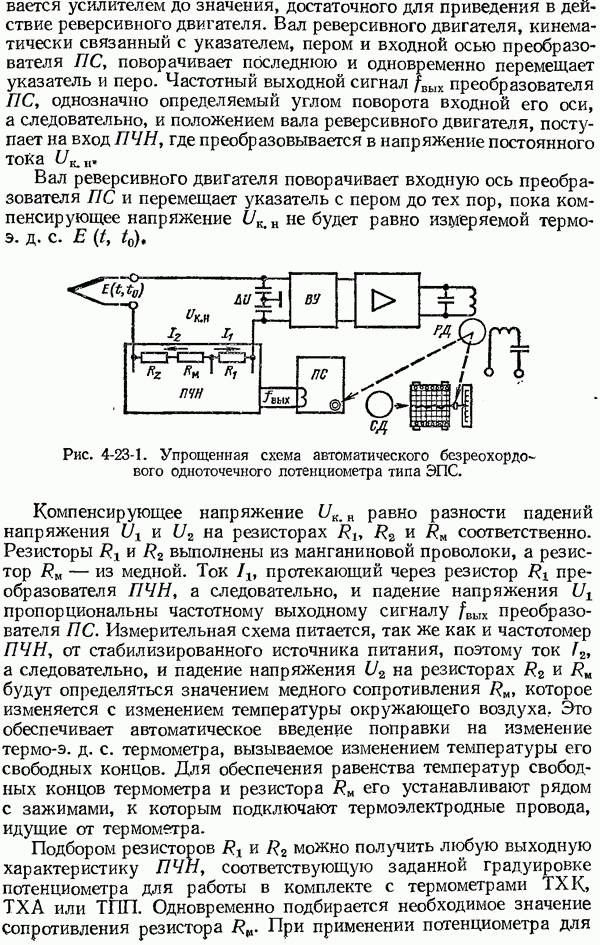
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
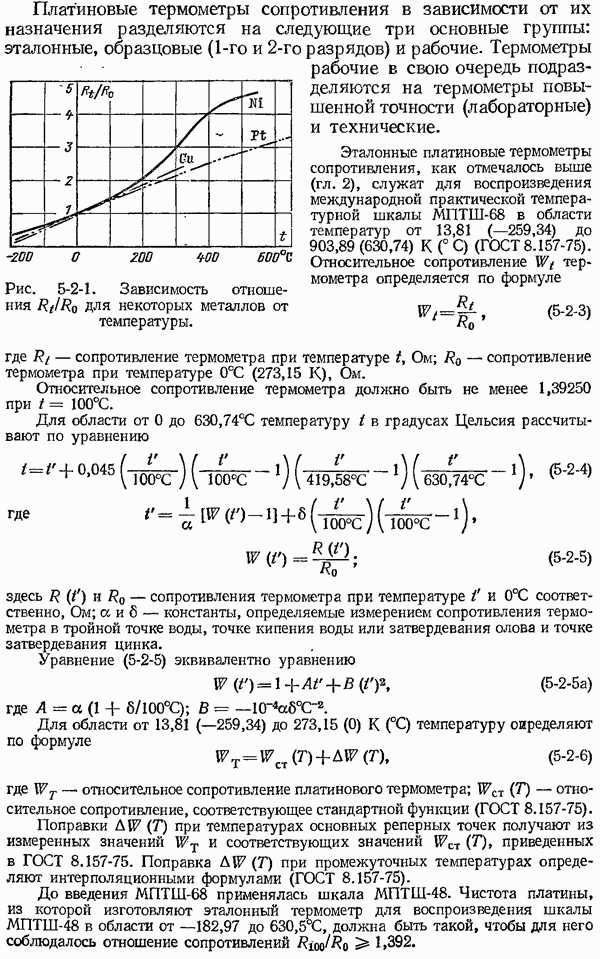
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
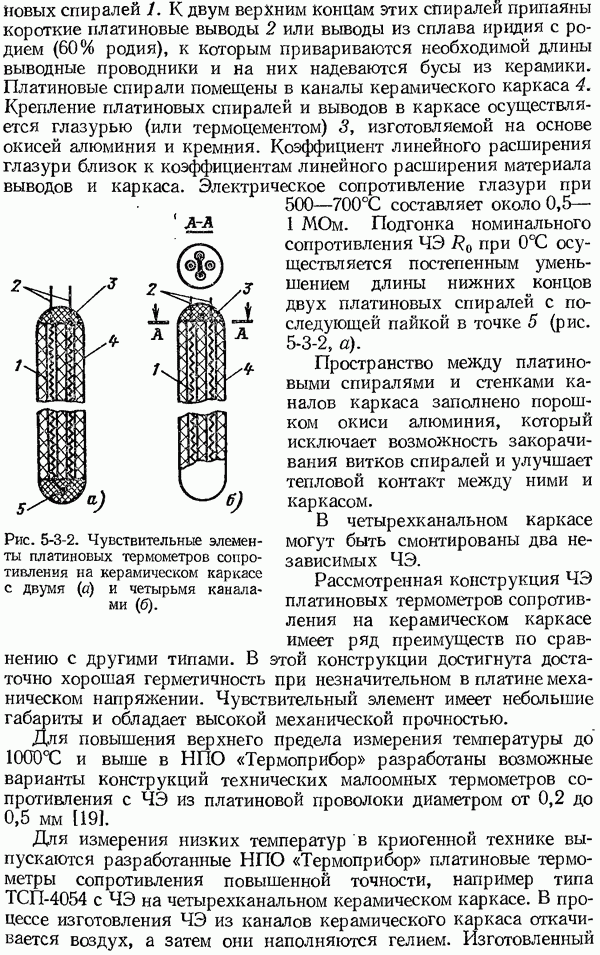
- 5-3. Устройство платиновых и медных термометров сопротивления
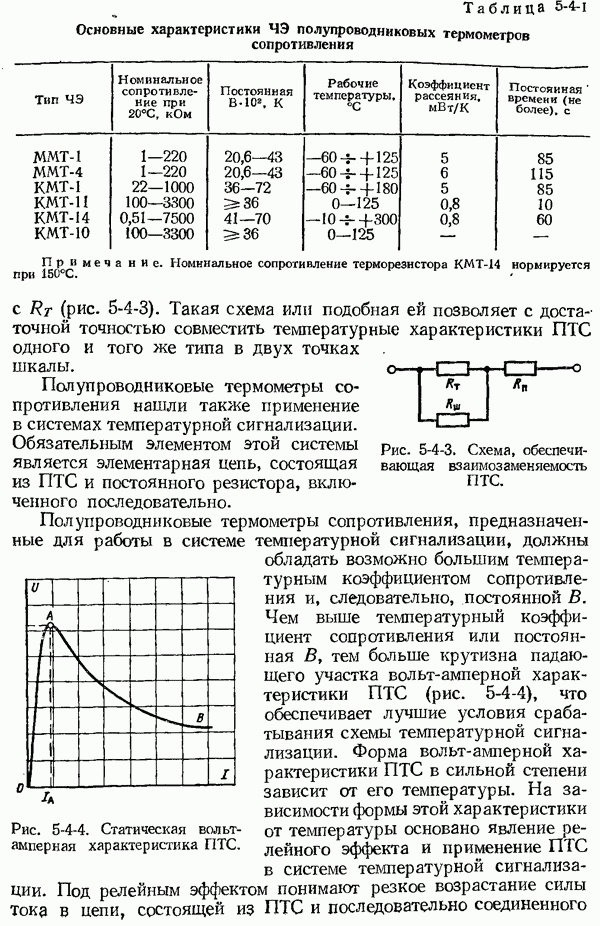
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
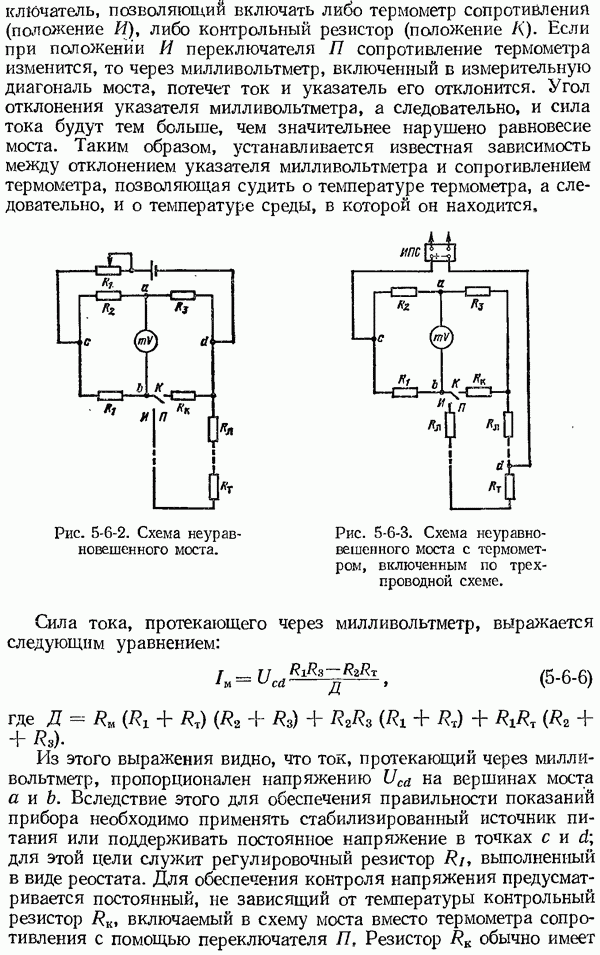
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
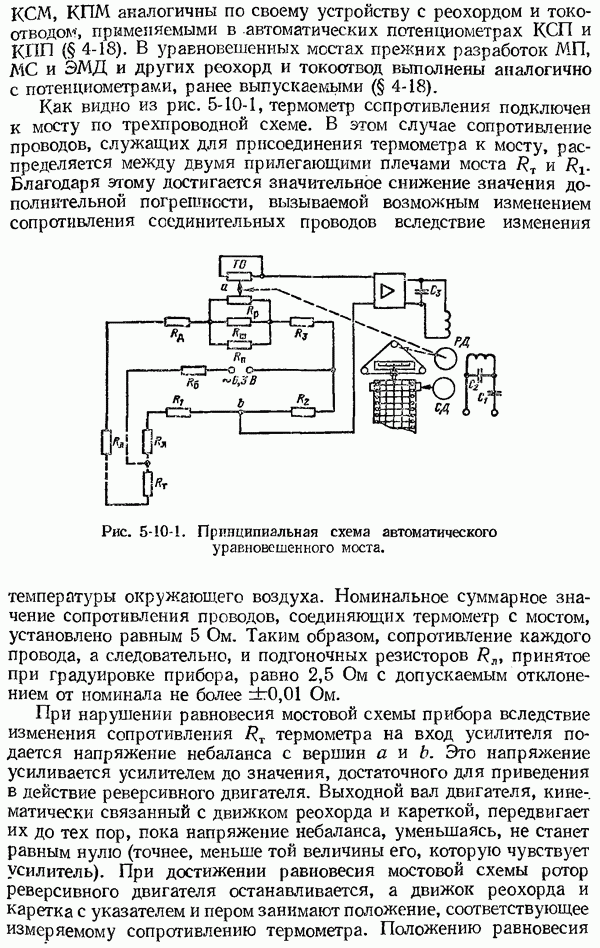
- 5-10. Принципиальная схема автоматического уравновешенного моста
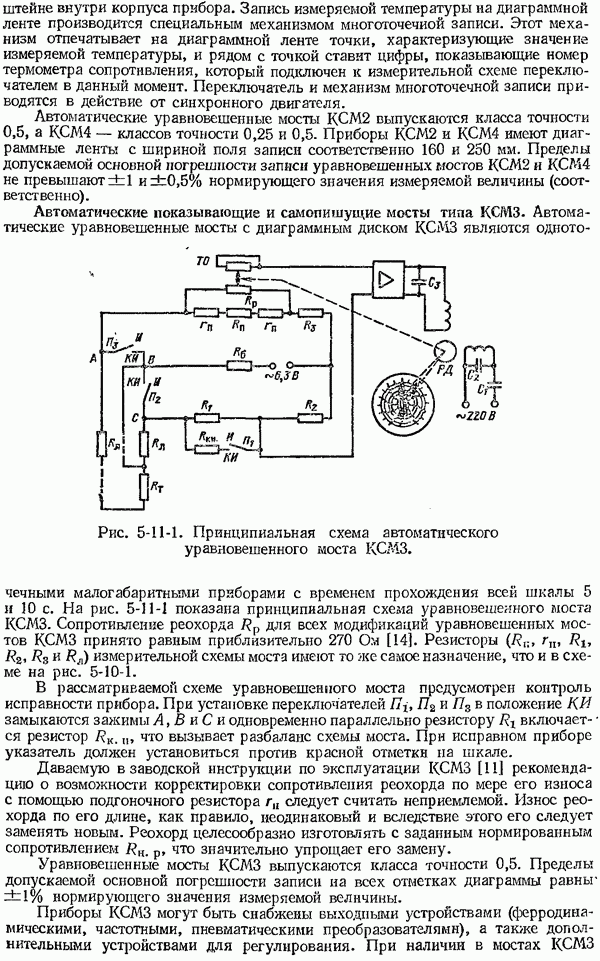
- 5-11. Устройство автоматических уравновешенных мостов
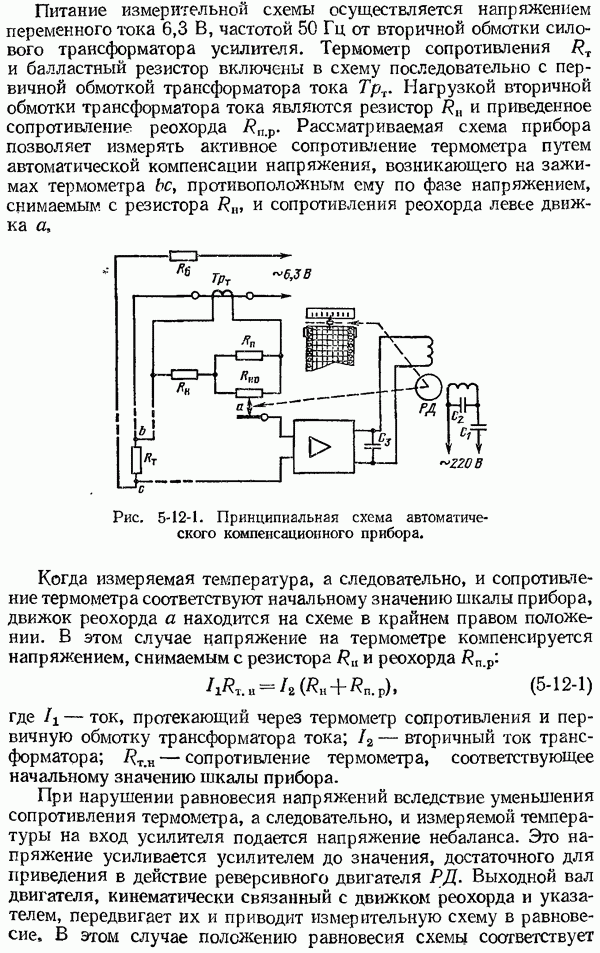
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
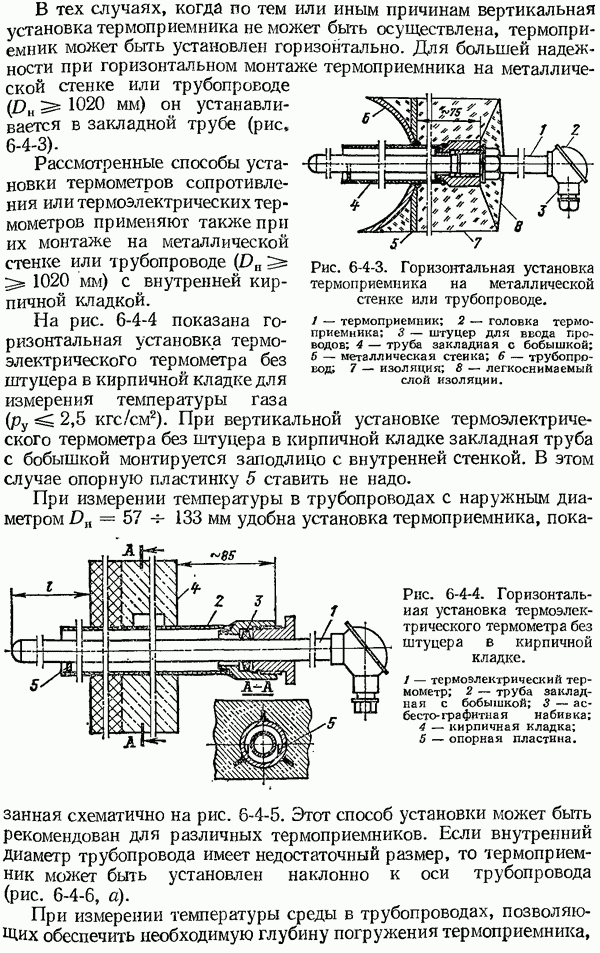
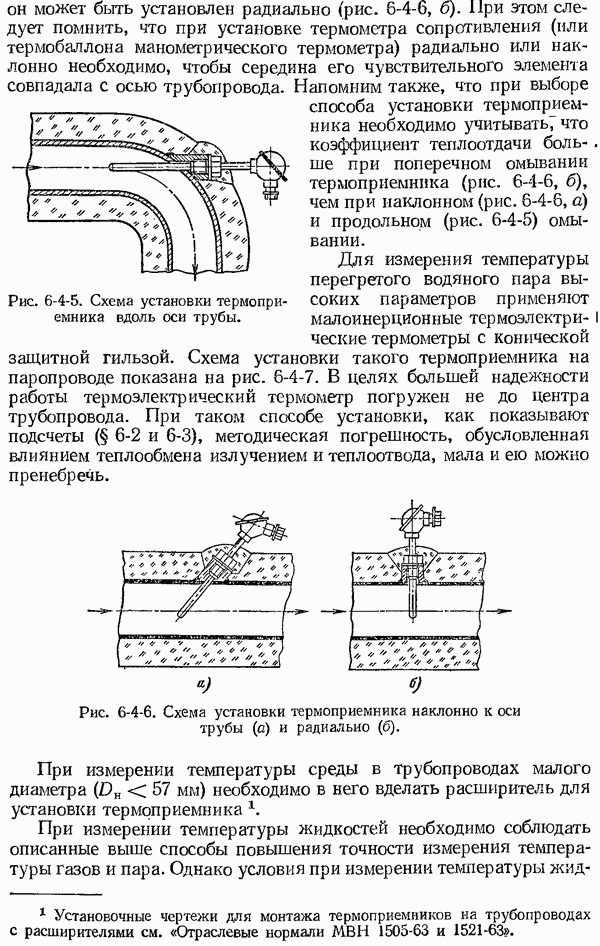
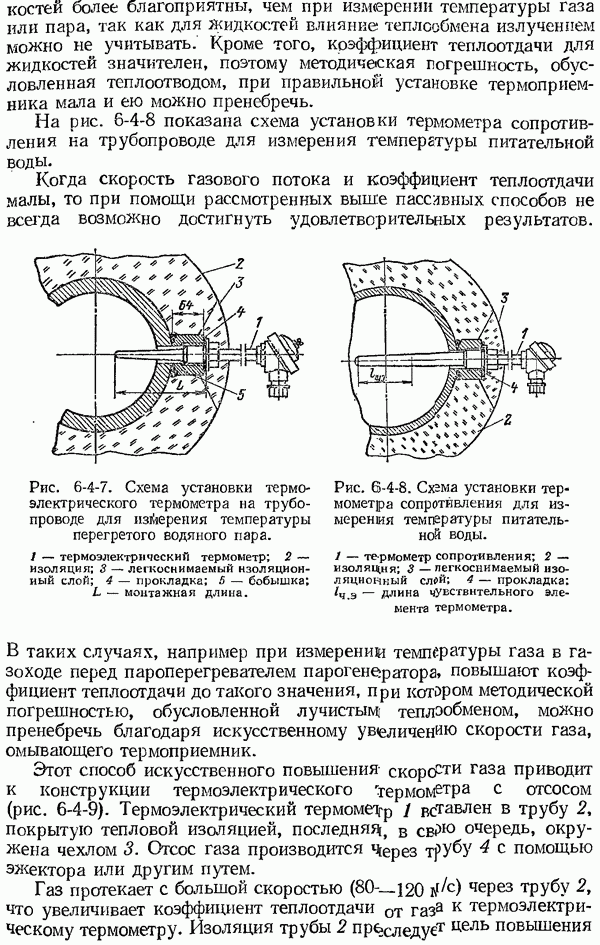
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
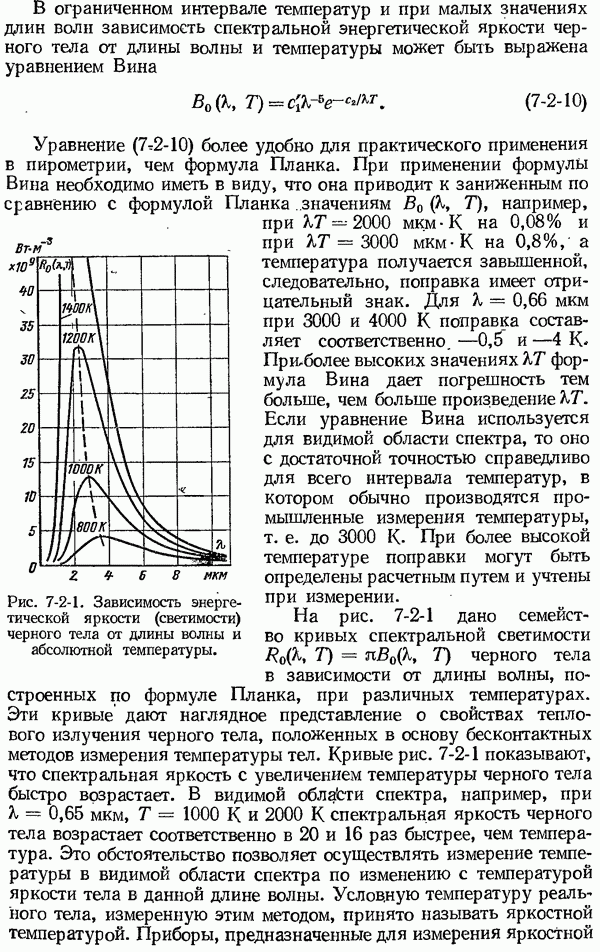
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
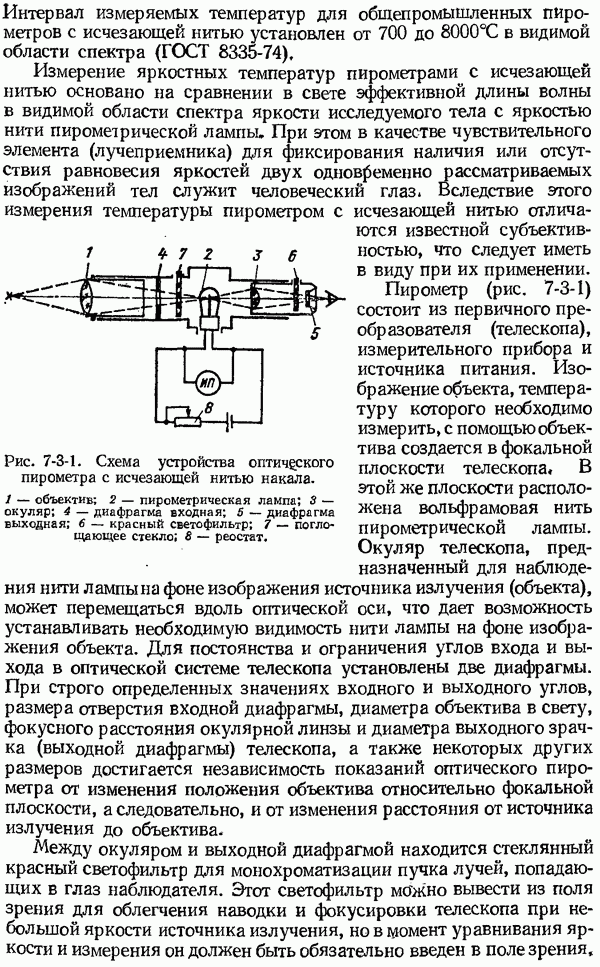
- 7-3. Оптические пирометры
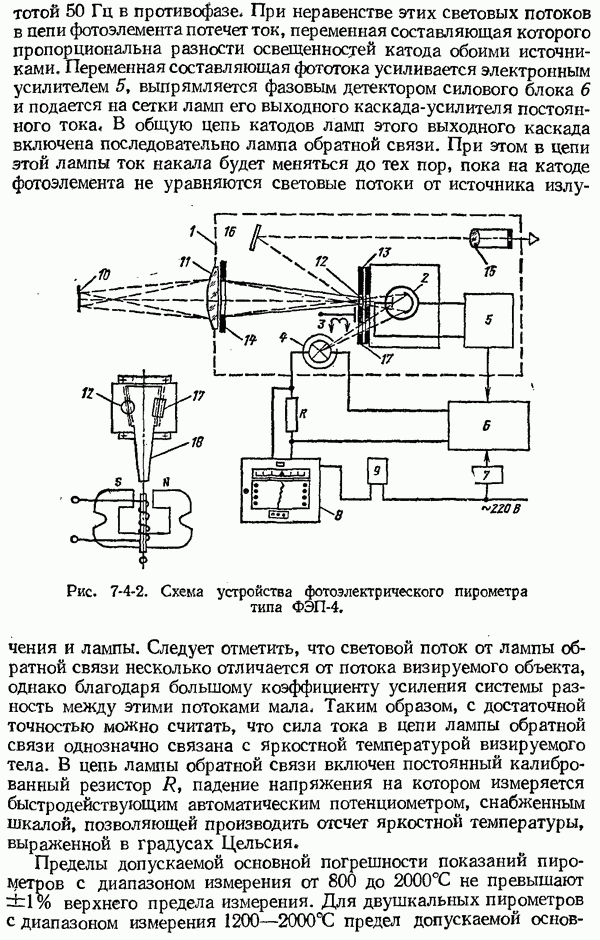
- 7-4. Фотоэлектрические пирометры
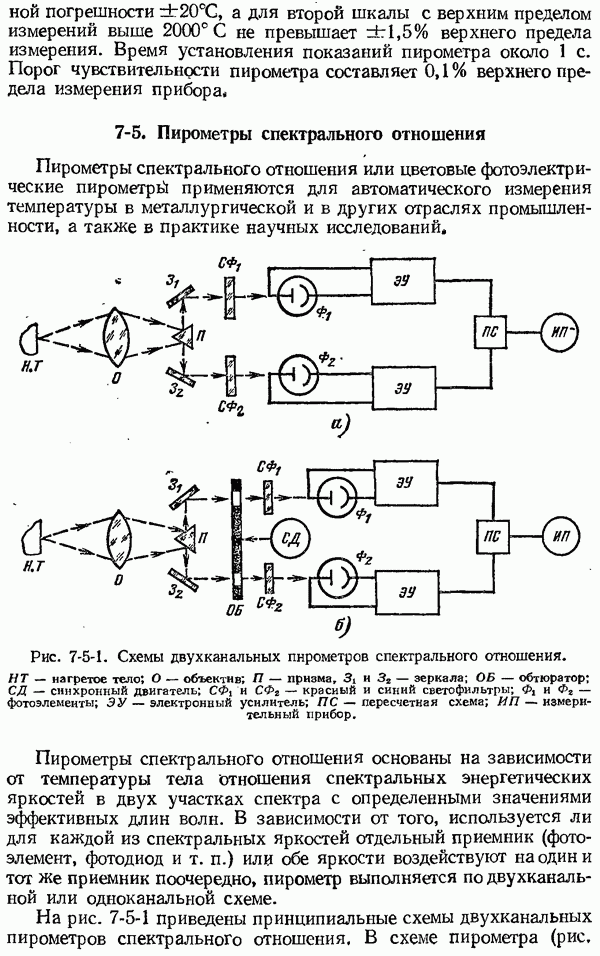
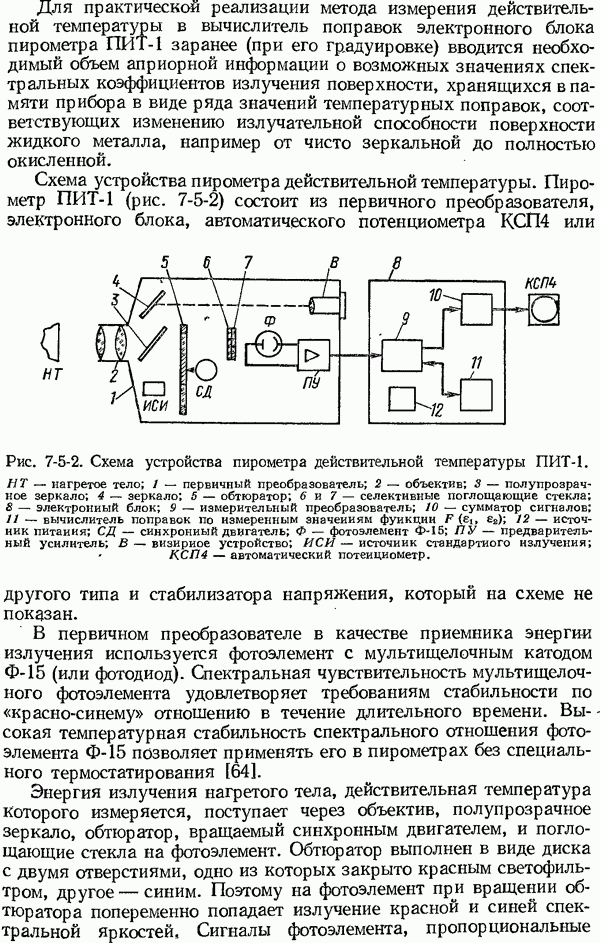
- 7-5. Пирометры спектрального отношения
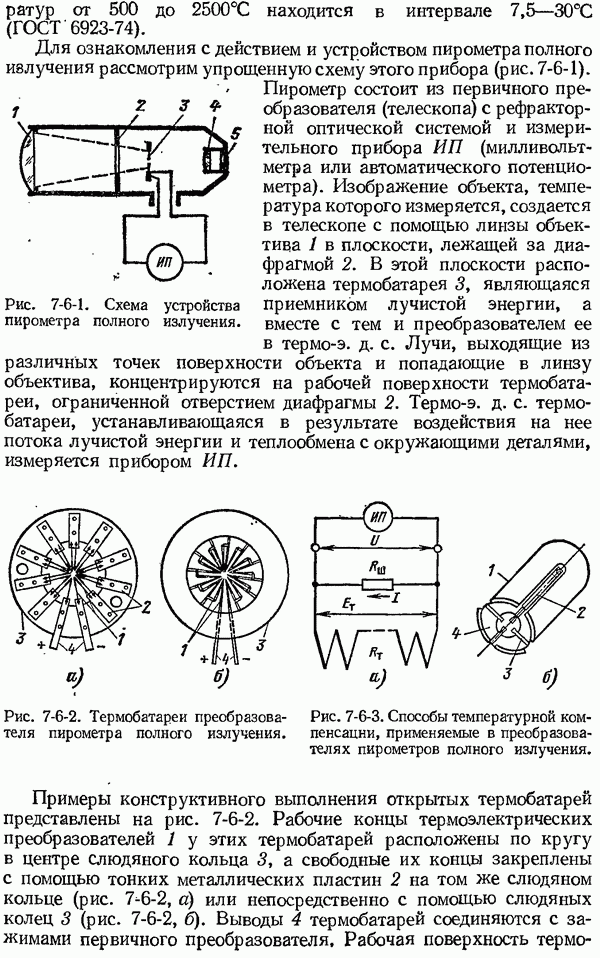
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
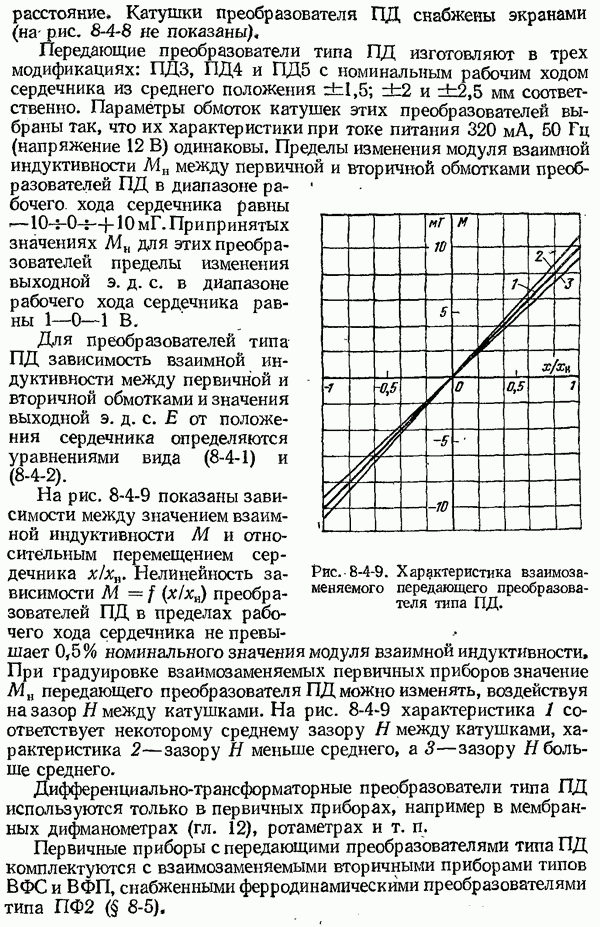
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
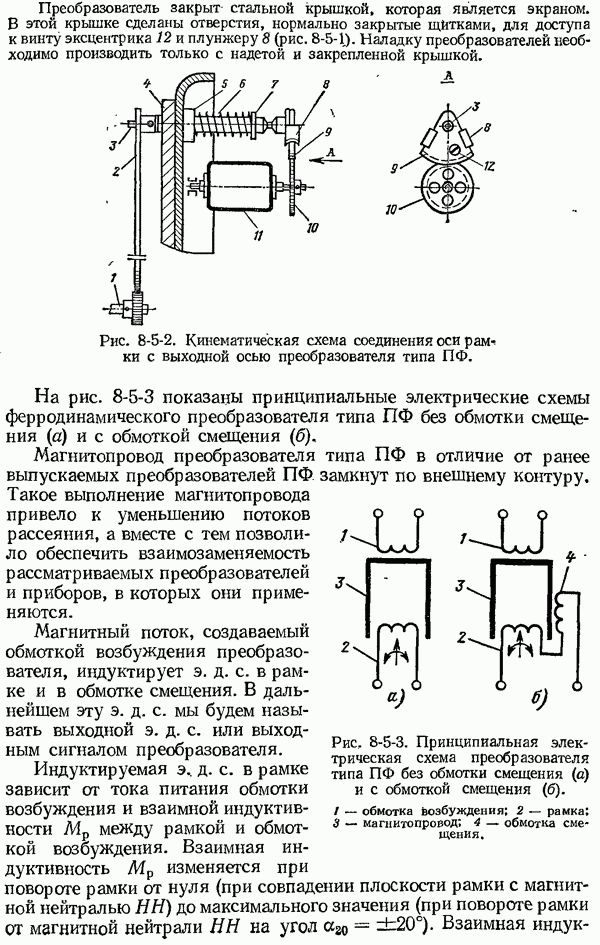
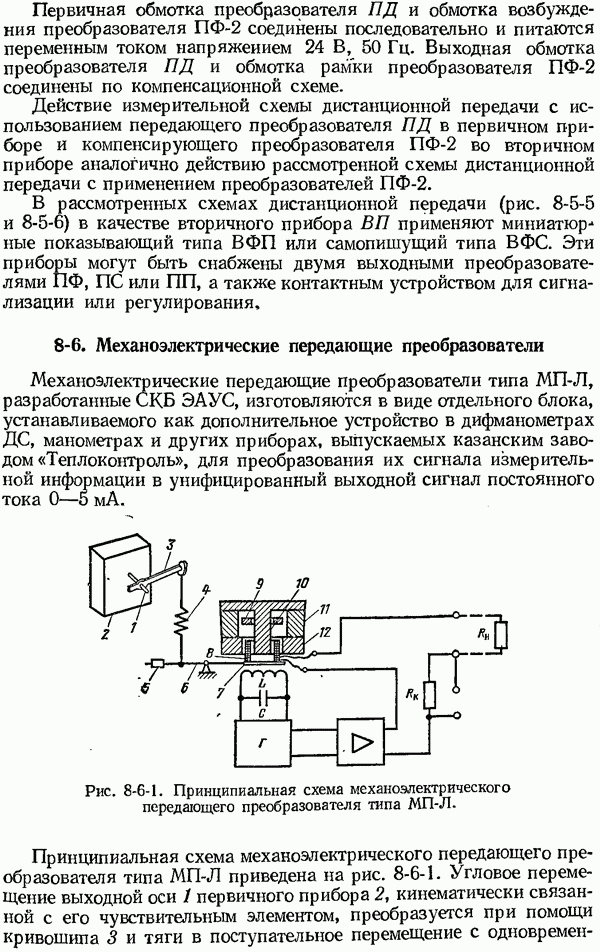
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
- 8-6. Механоэлектрические передающие преобразователи
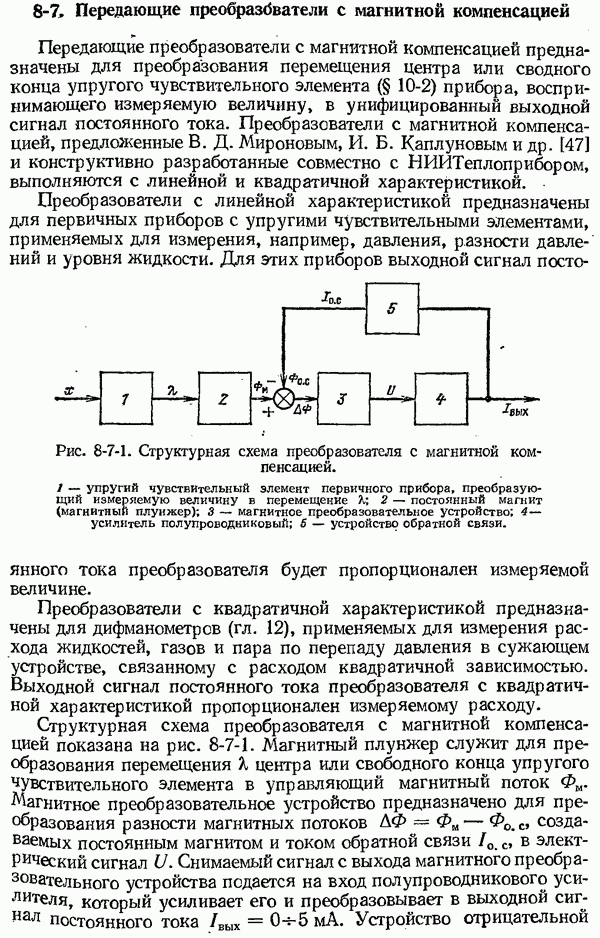
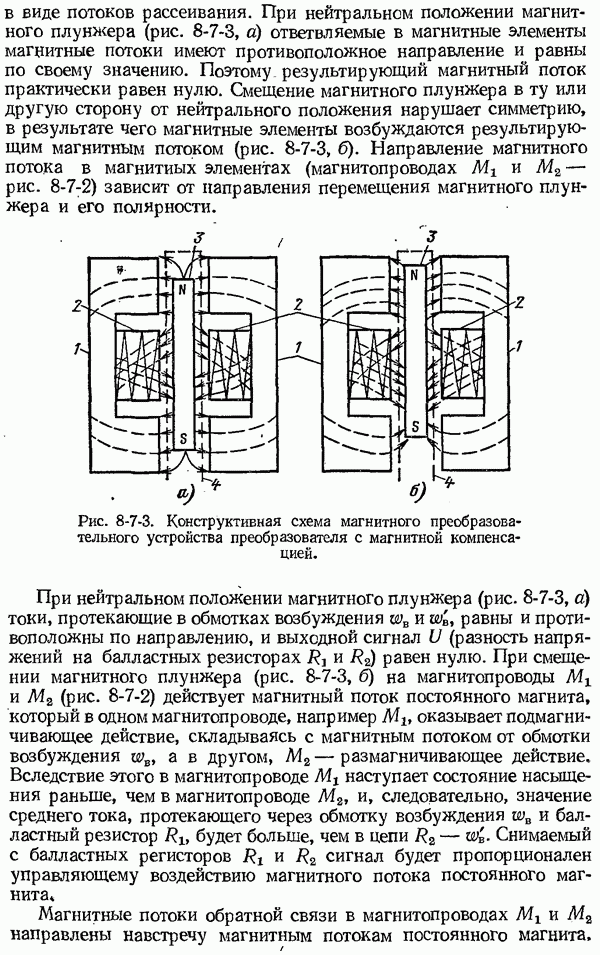
- 8-7. Передающие преобразователи с магнитной компенсацией
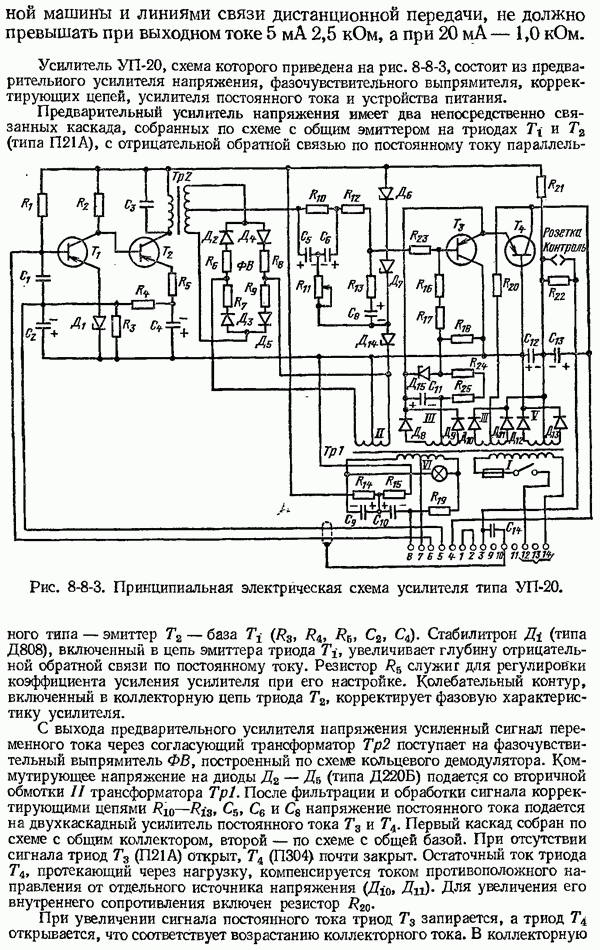
- 8-8. Электросиловые преобразователи
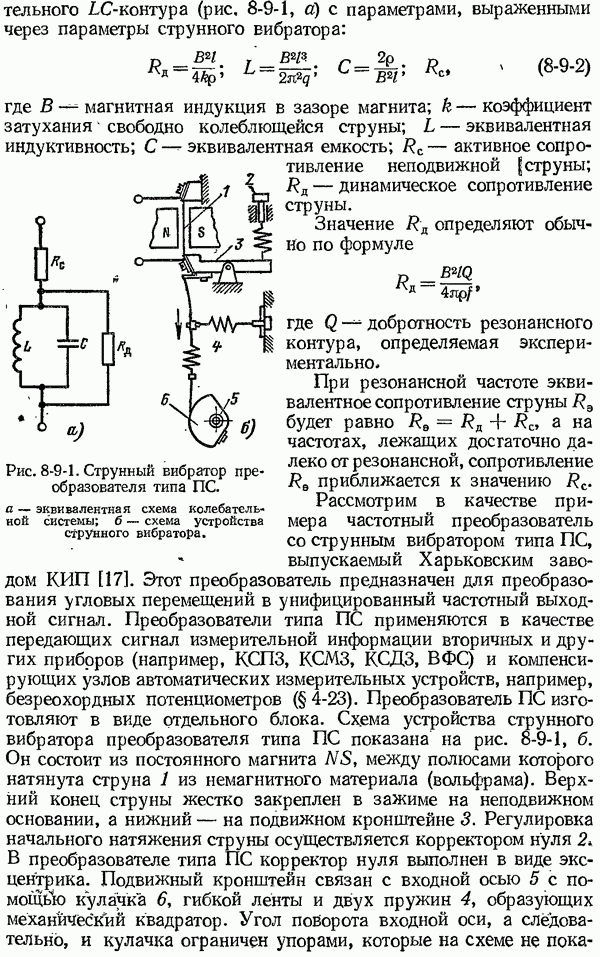
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
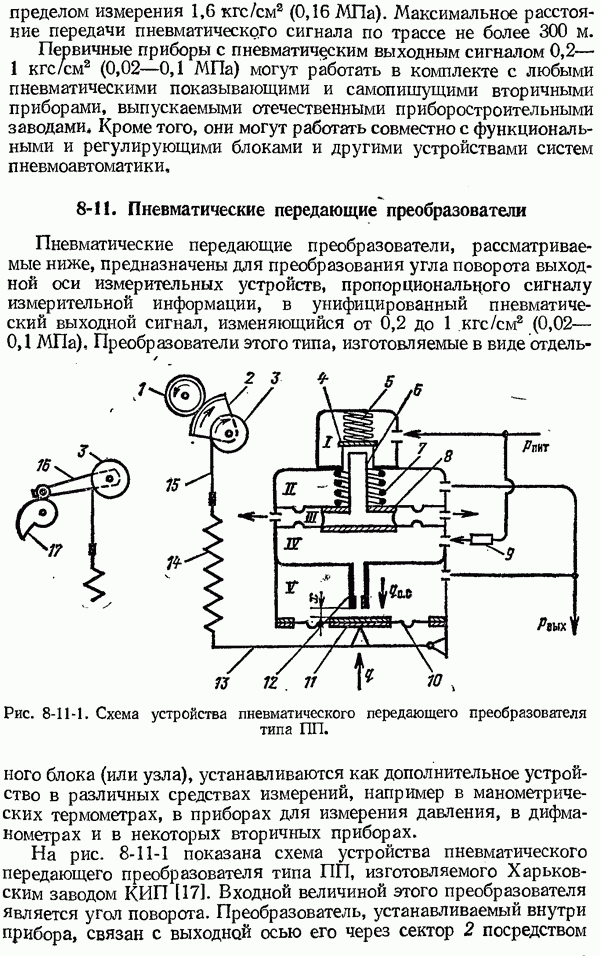
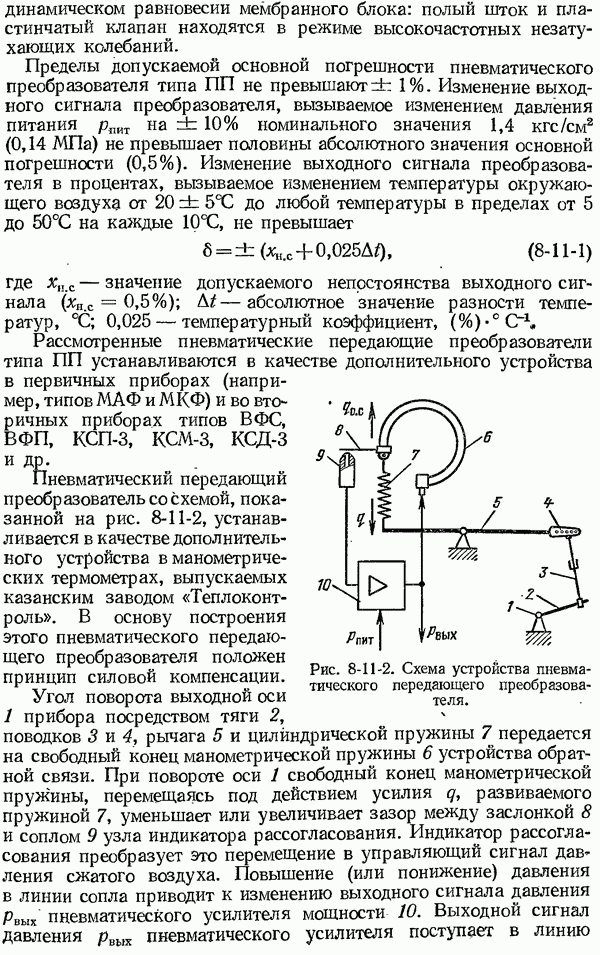
- 8-11. Пневматические передающие преобразователи
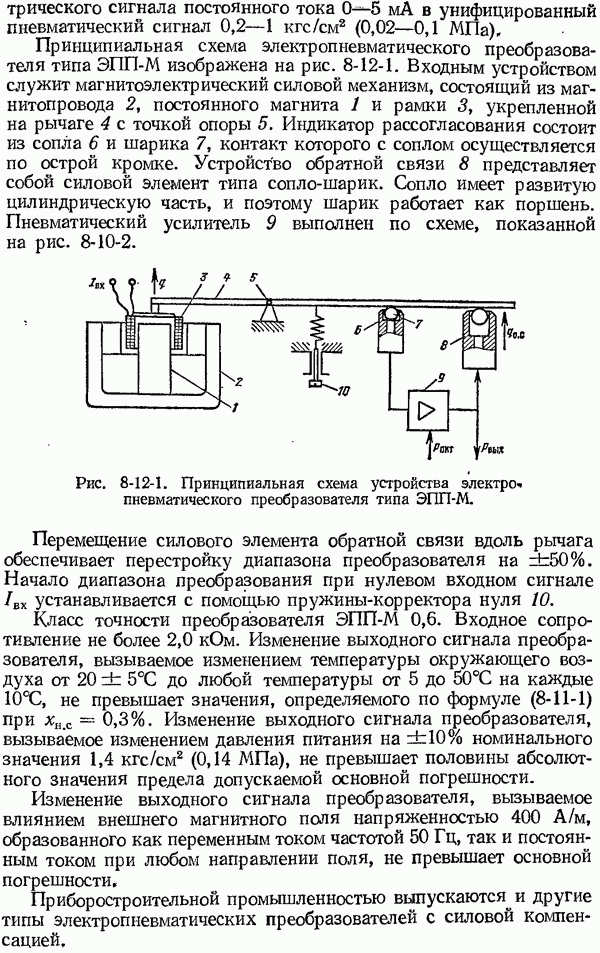
- 8-12. Электропневматические и пневмоэлектрические преобразователи
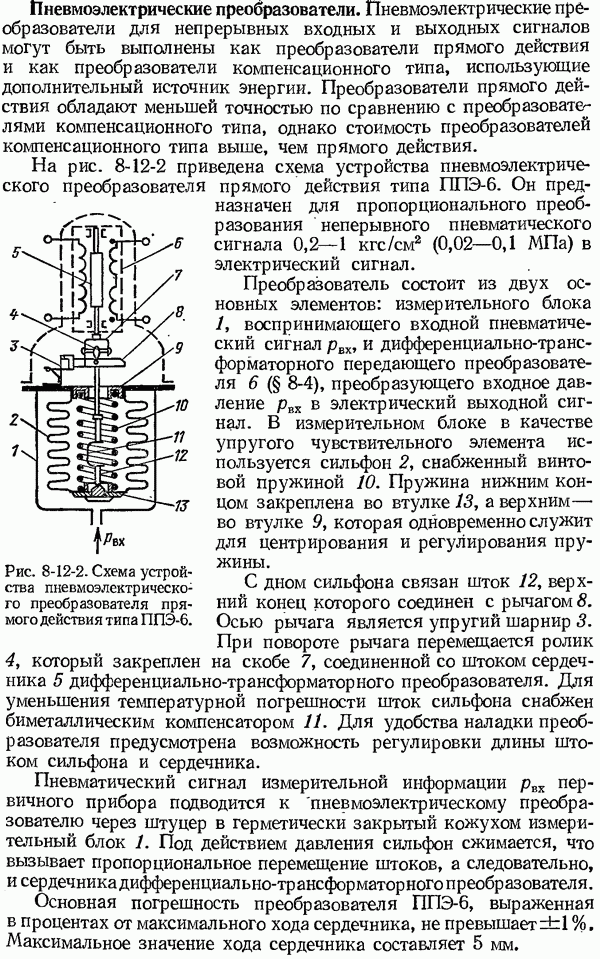
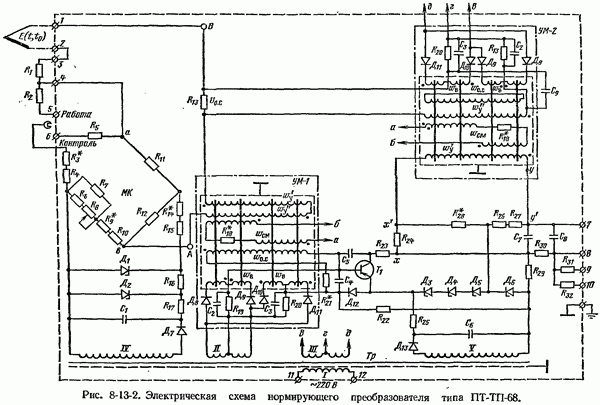
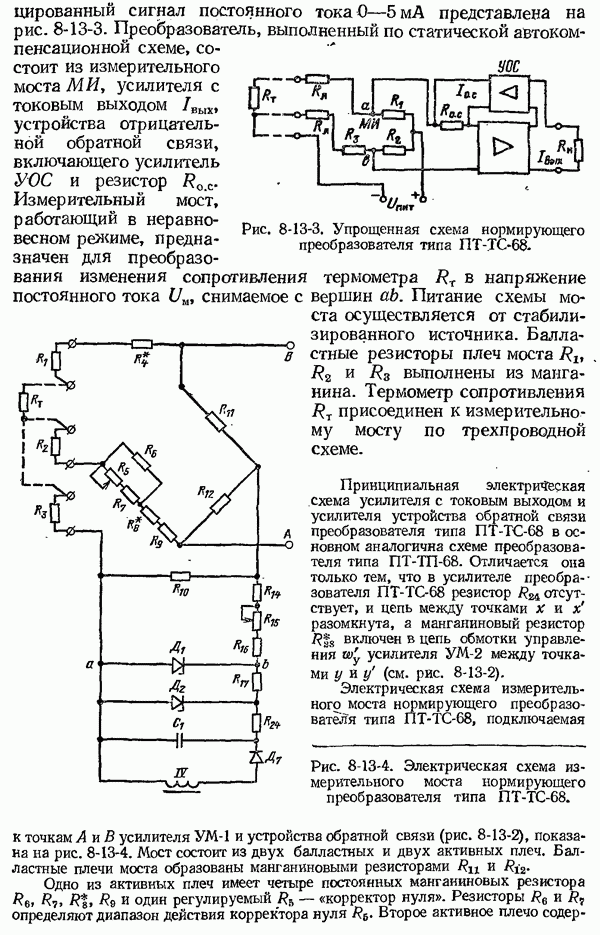
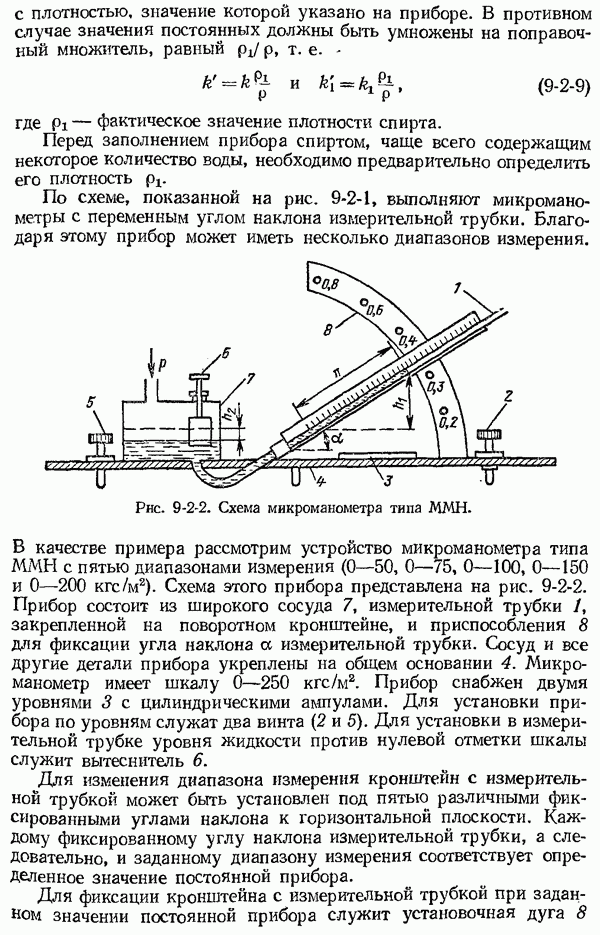
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
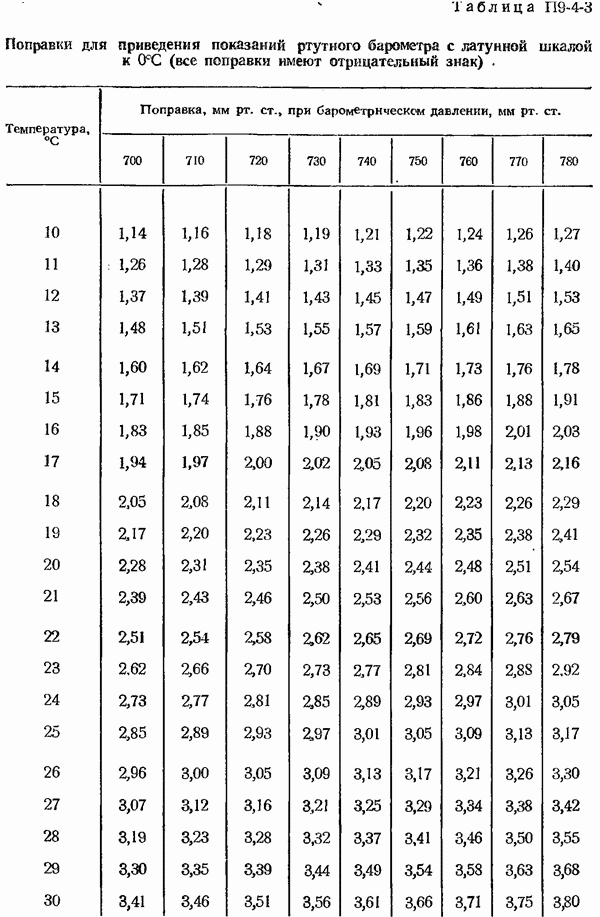
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
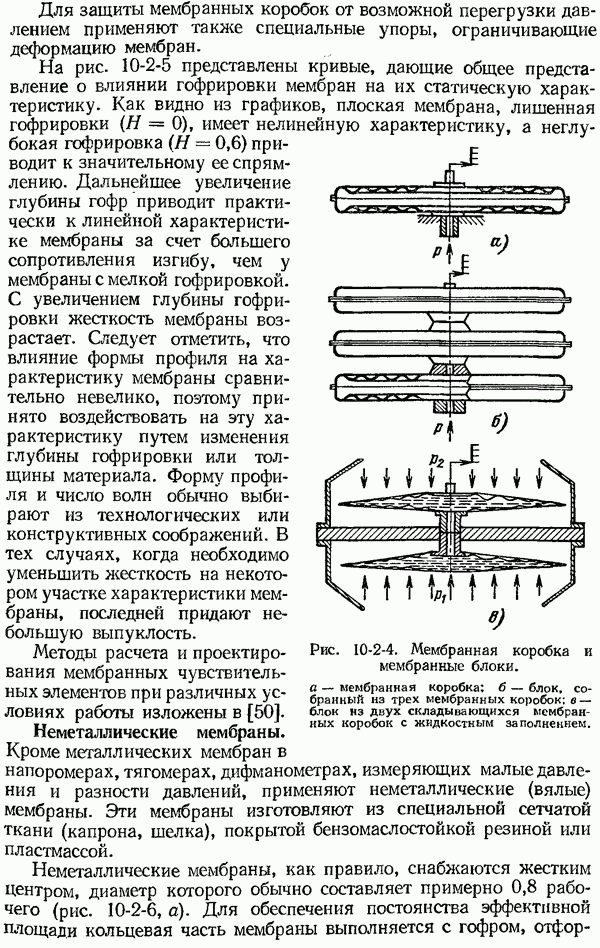
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
- 10-2. Упругие чувствительные элементы
- 10-3. Приборы давления прямого действия
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
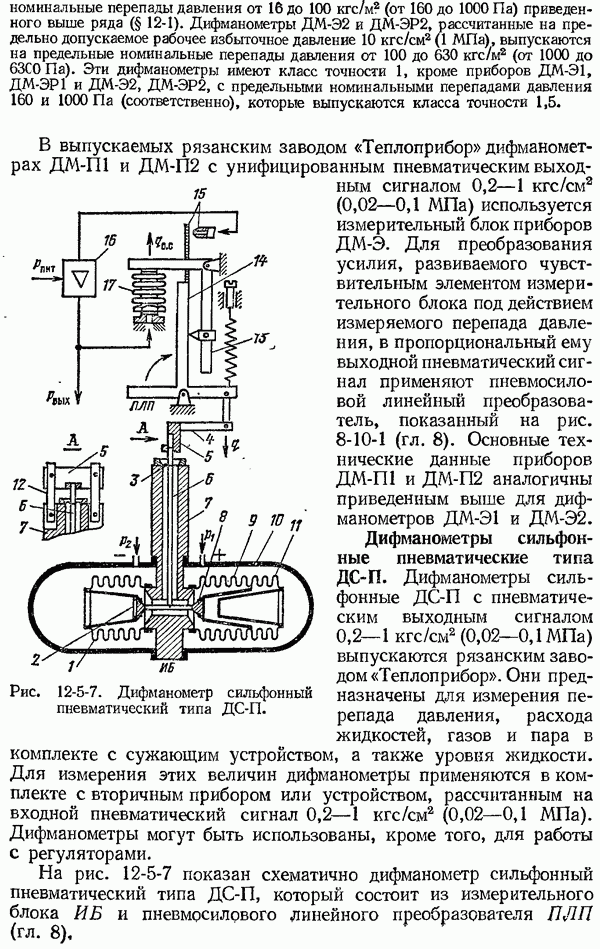
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
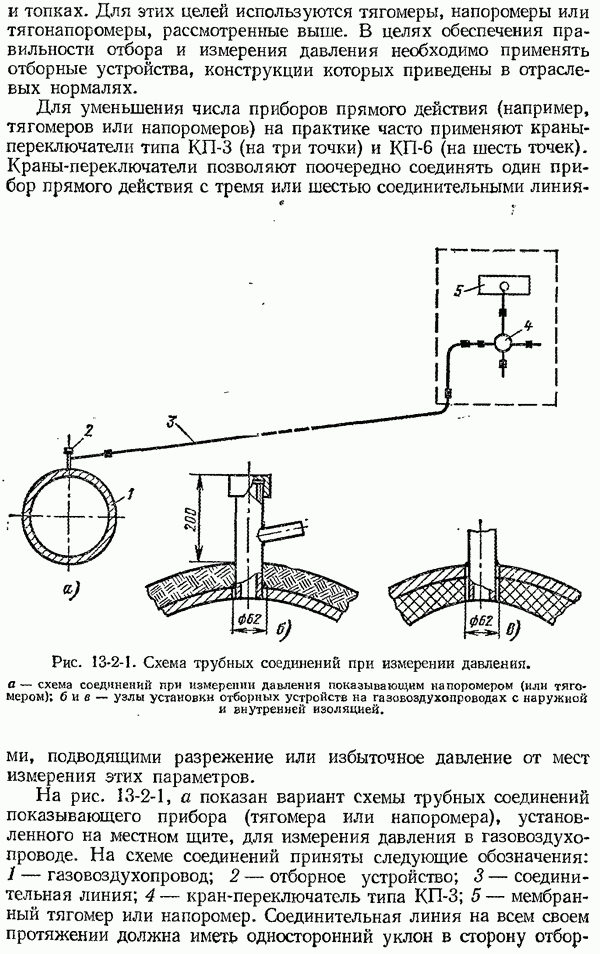
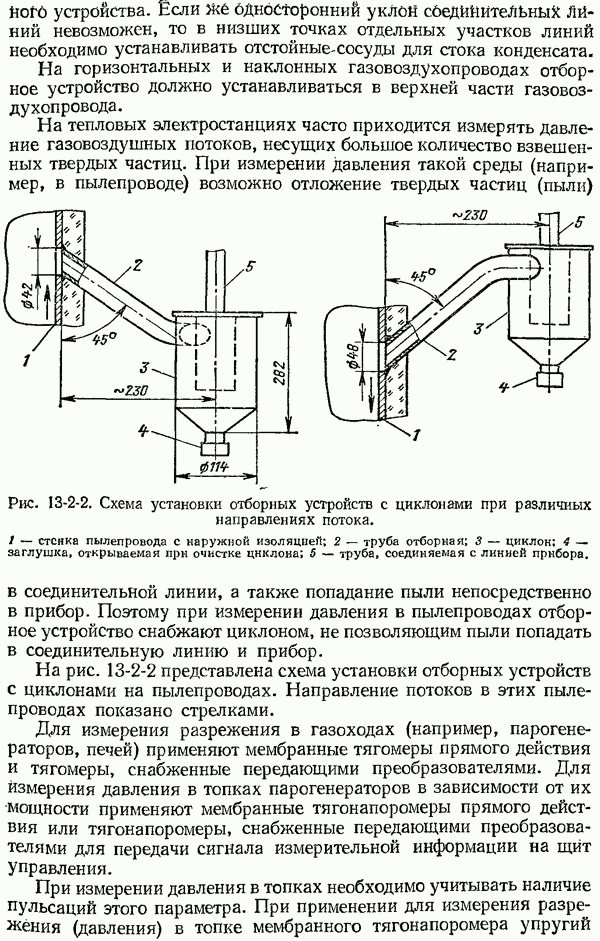
- 13-2. Измерение близкого к атмосферному давления газовых сред
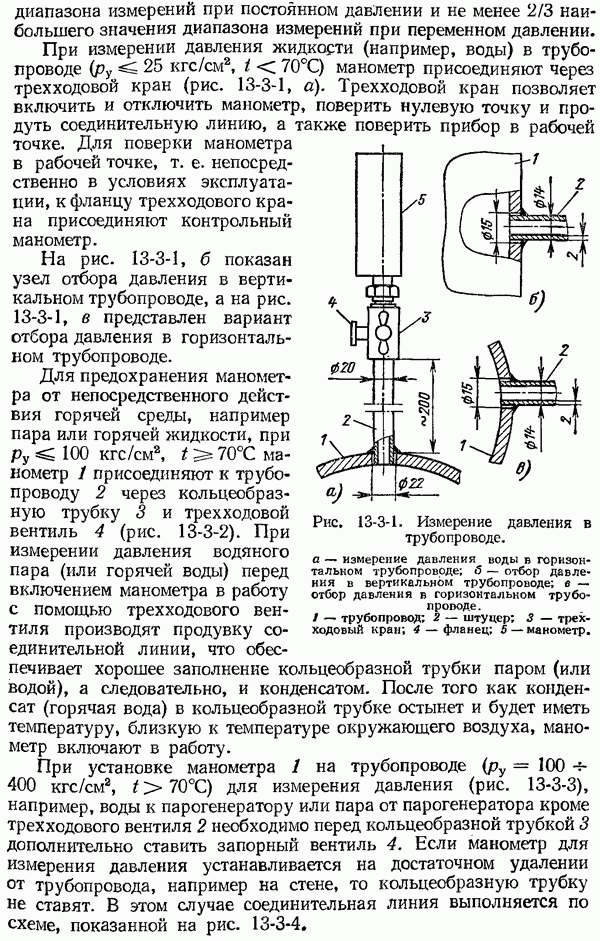
- 13-3. Измерение давления газов, жидкостей и пара
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
- 14-1. Основы теории и уравнения расхода
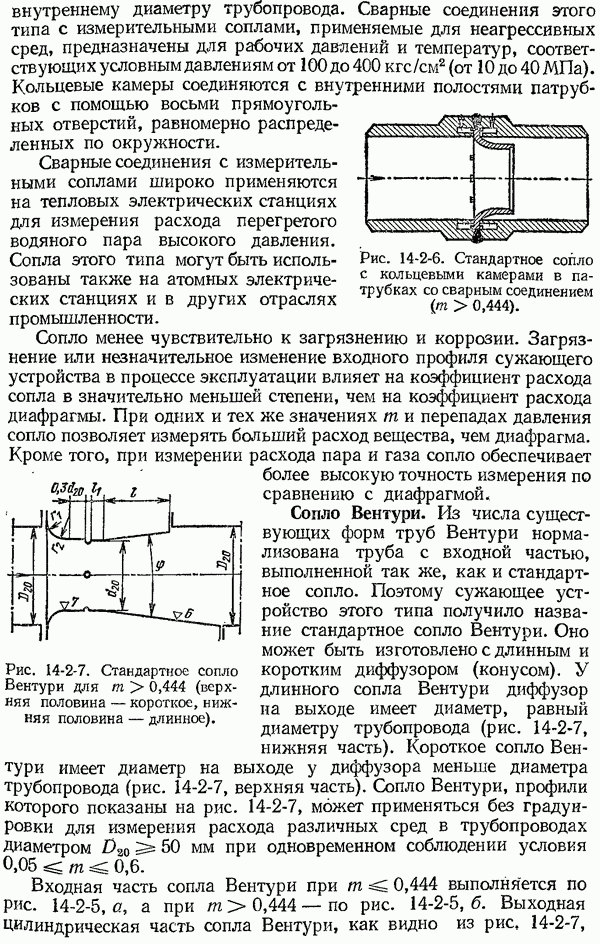
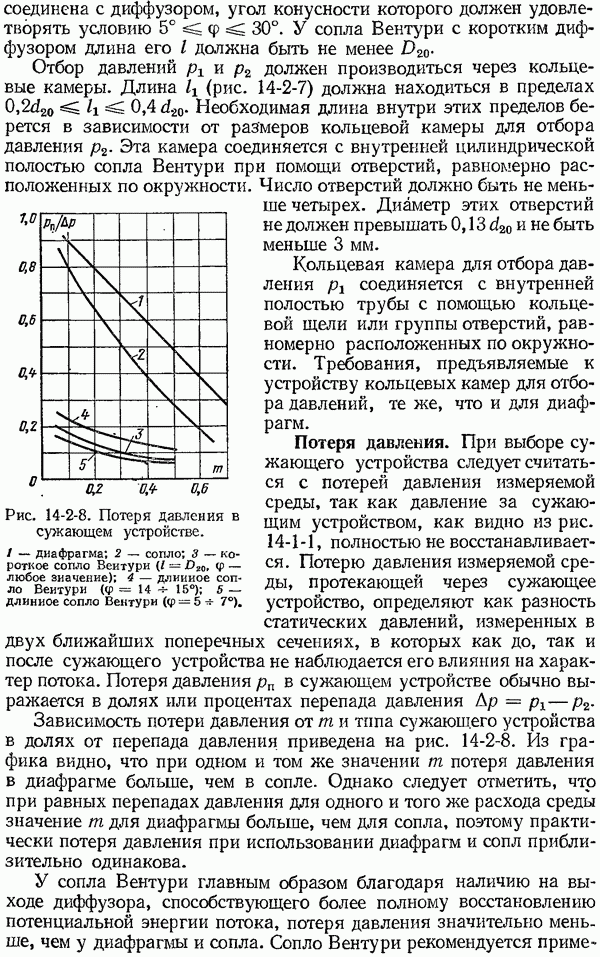
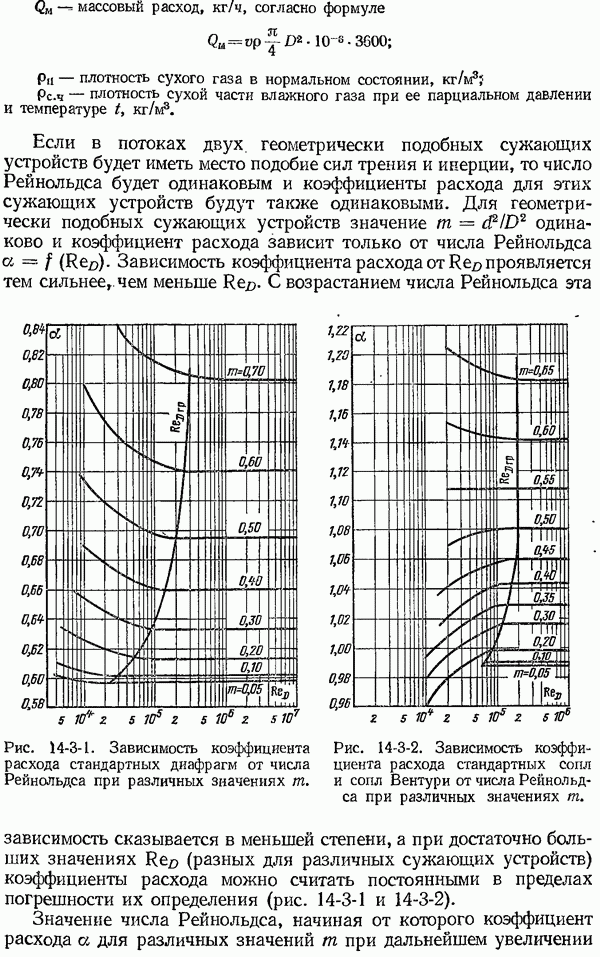
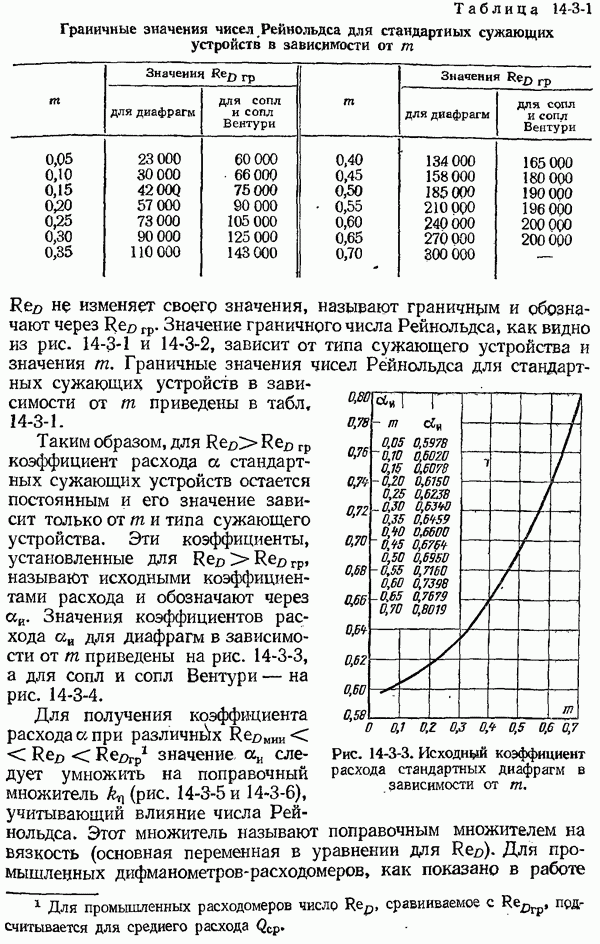
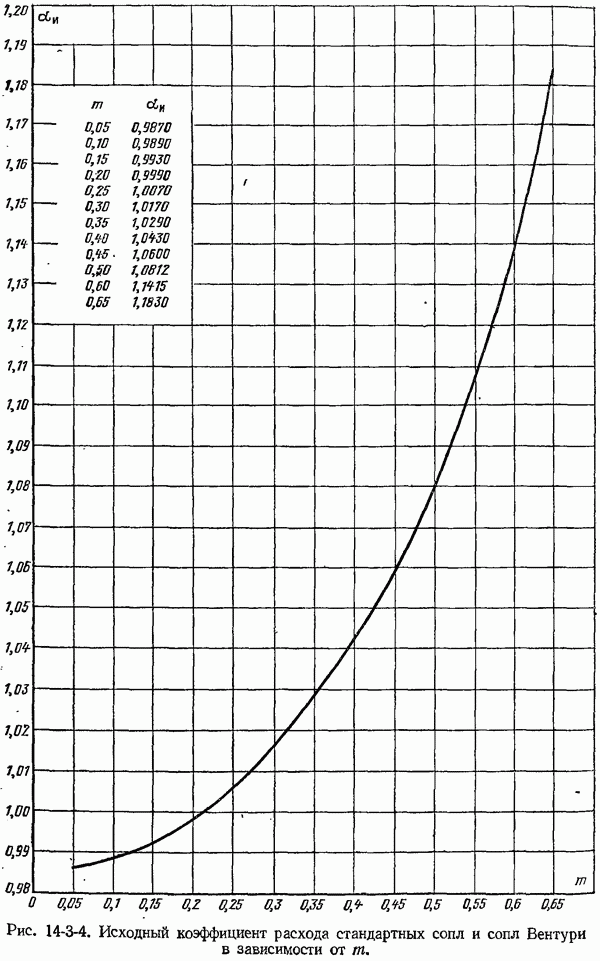
- 14-2. Стандартные сужающие устройства
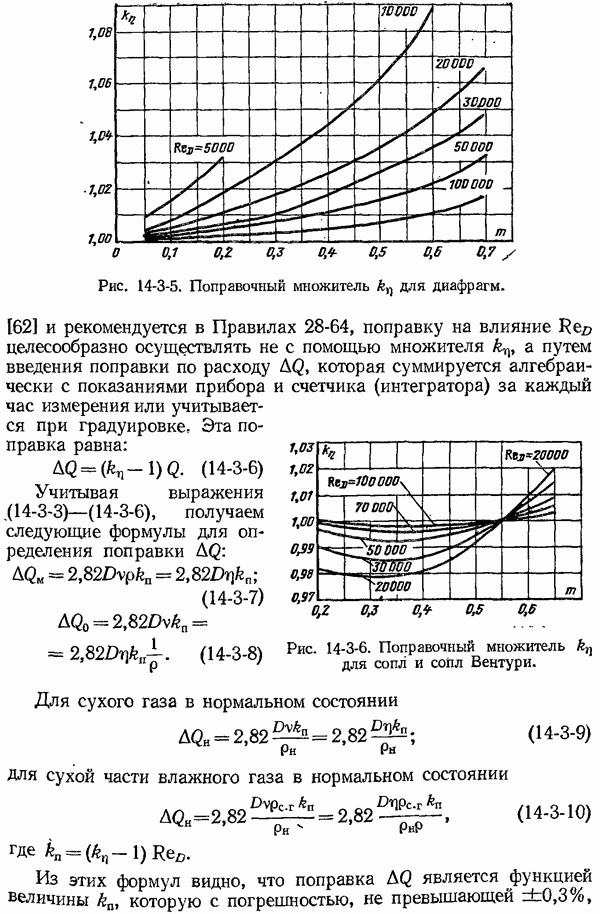
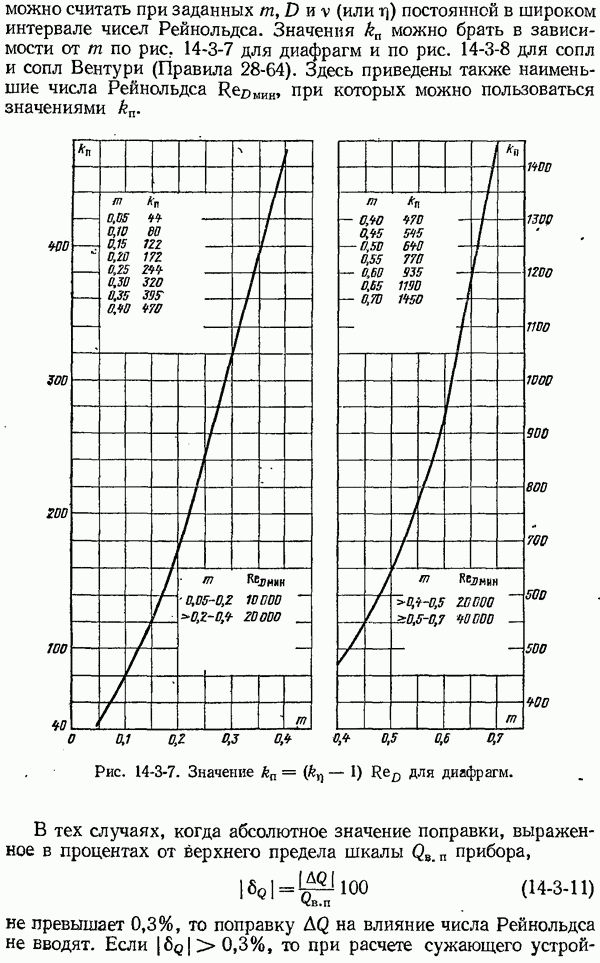
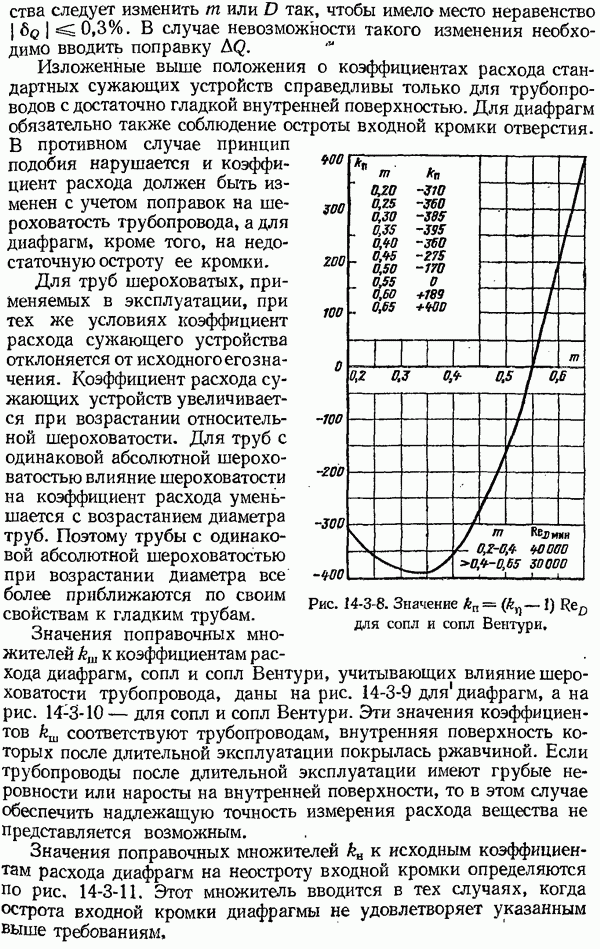
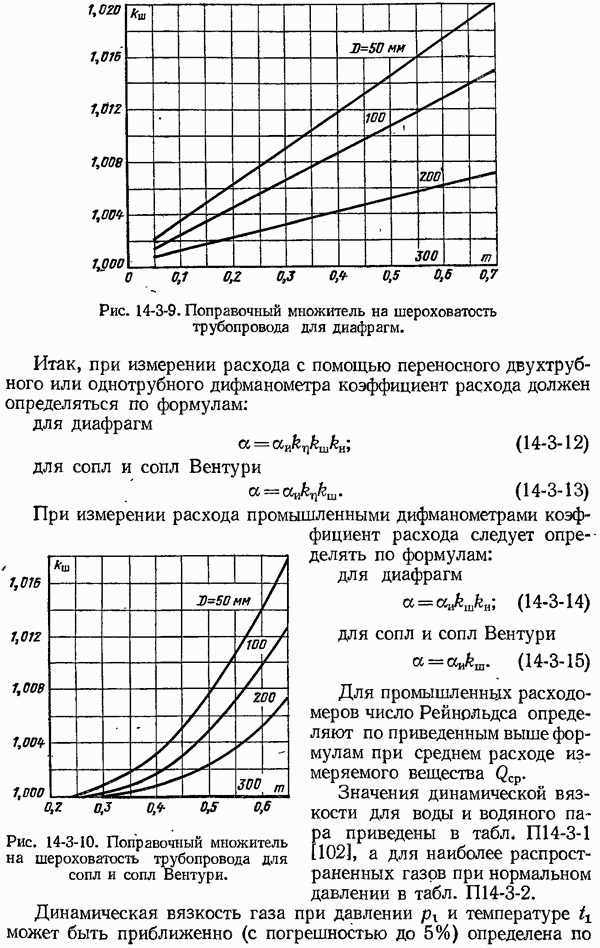
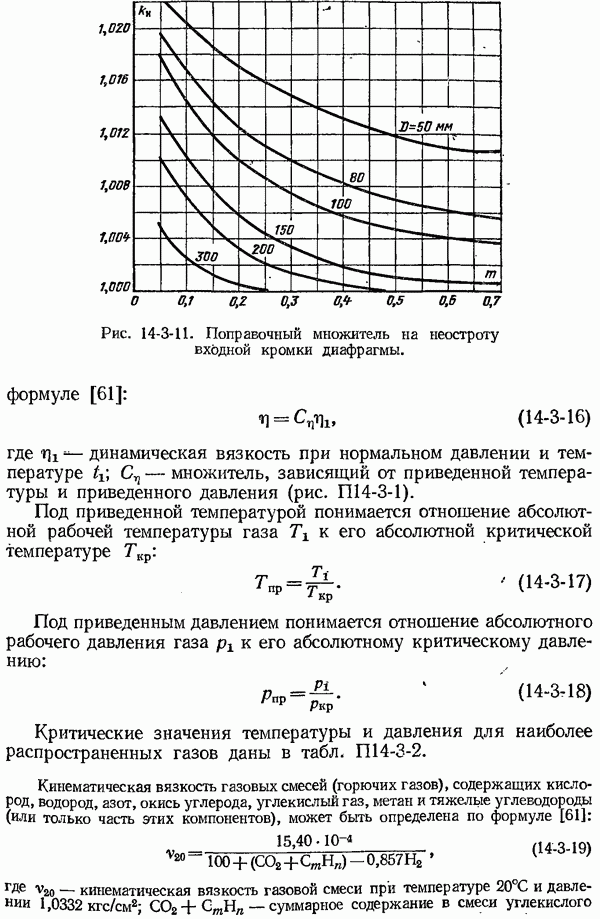
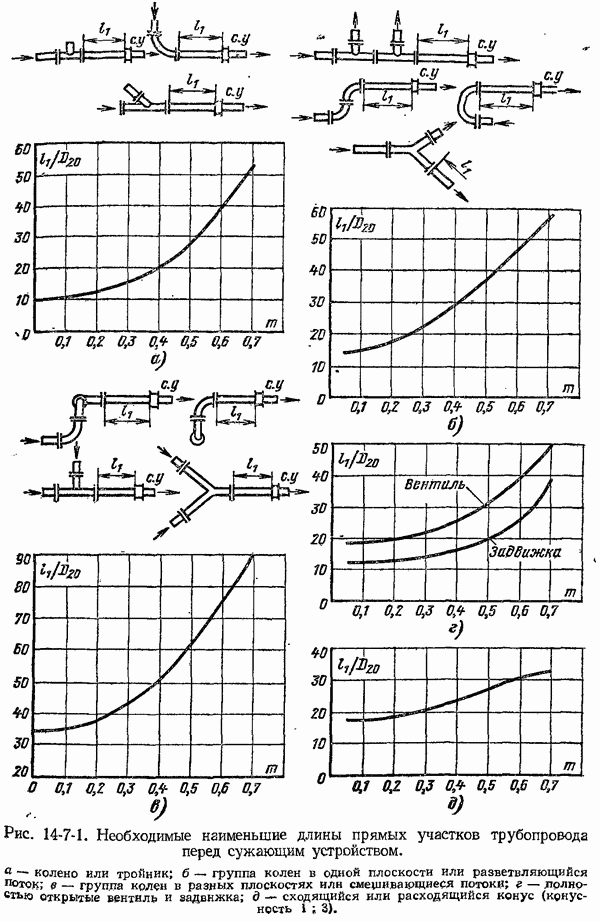
- 14-3. Коэффициенты расхода и поправочные множители к ним
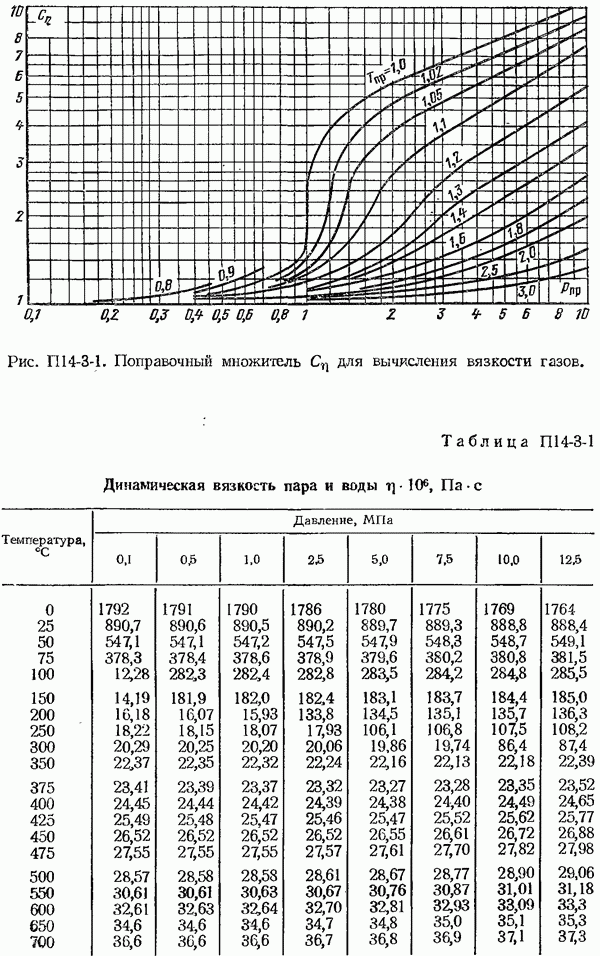
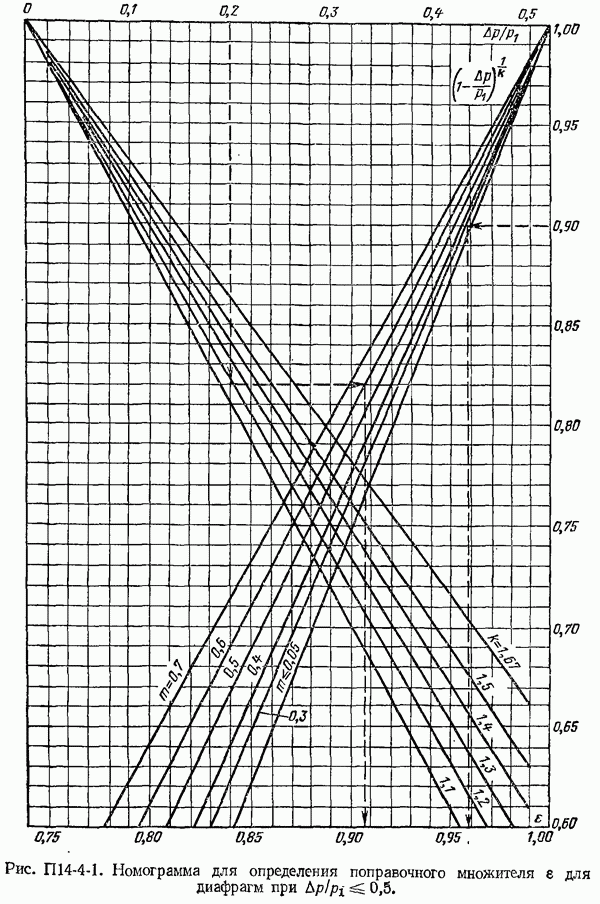
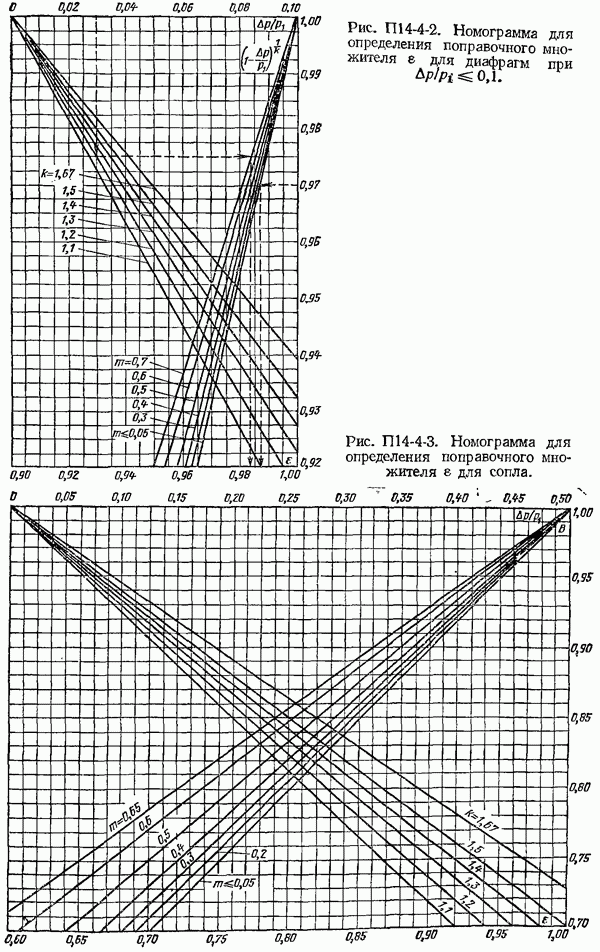
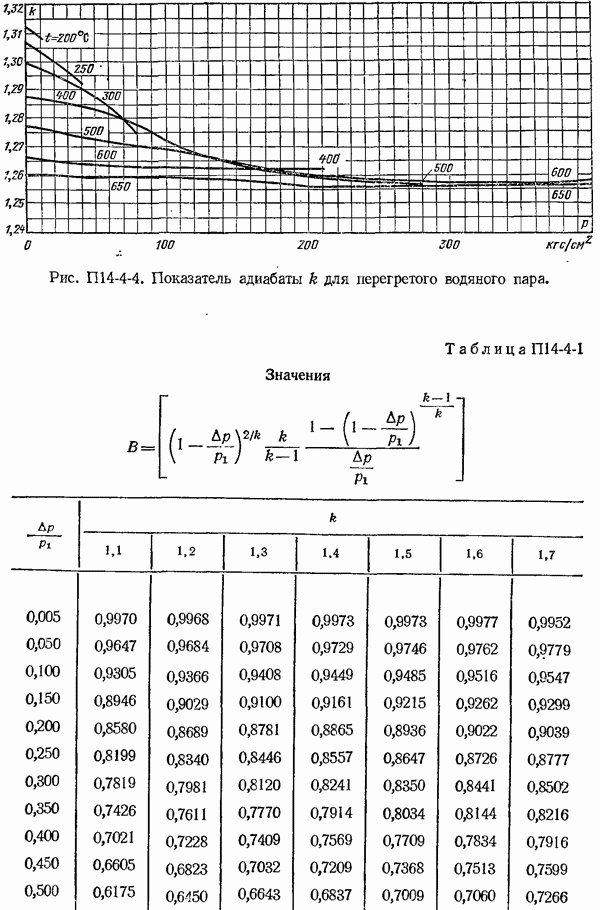
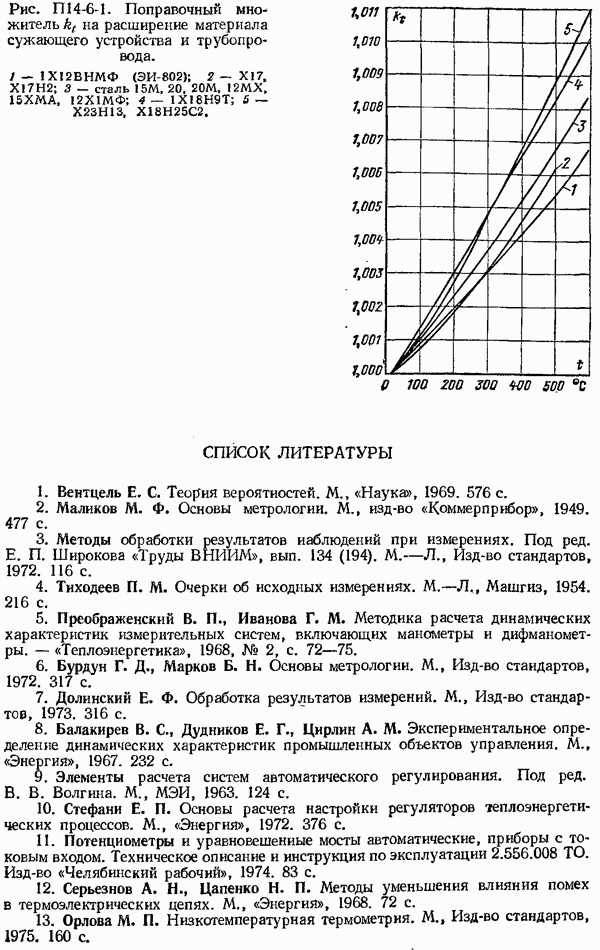
- 14-4. Поправочный множитель на расширение измеряемой среды
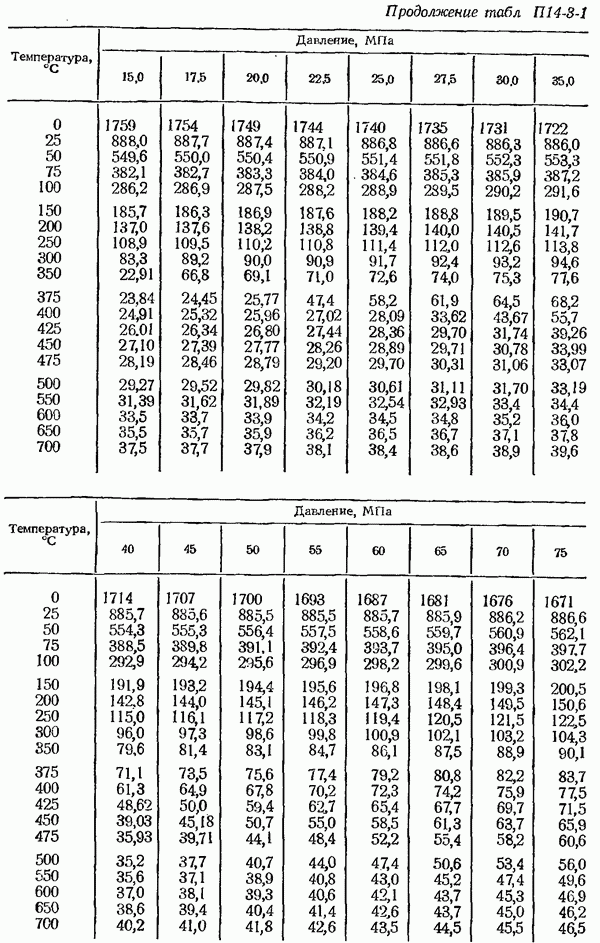
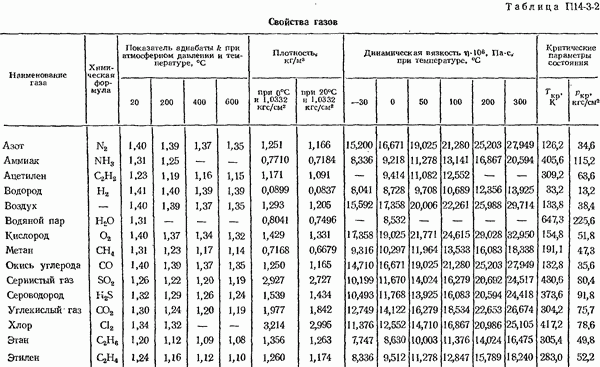
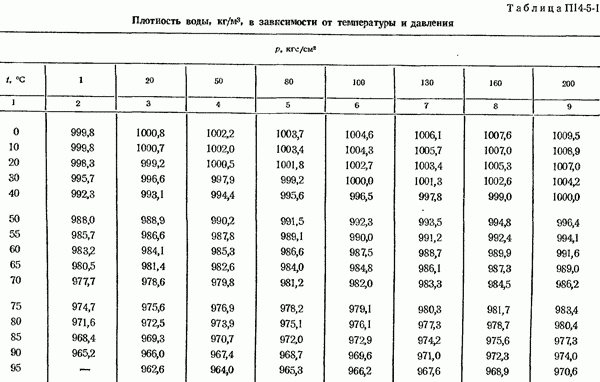
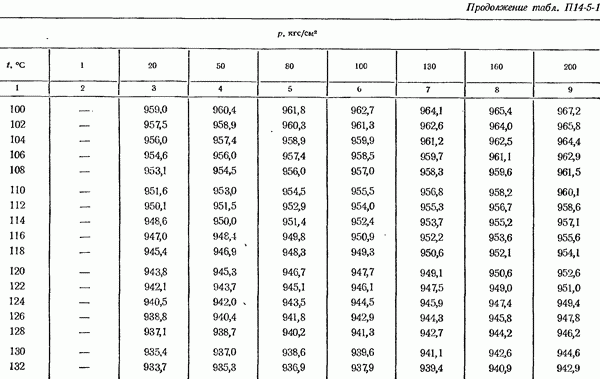
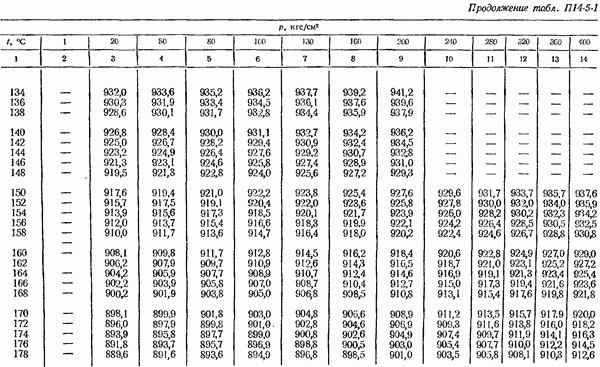
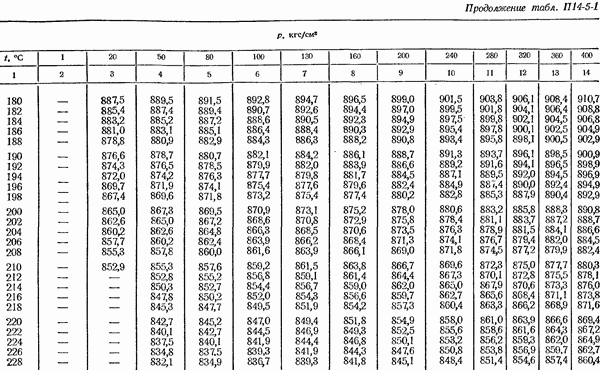
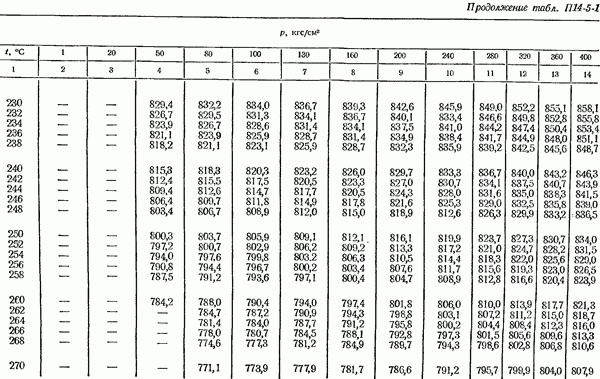
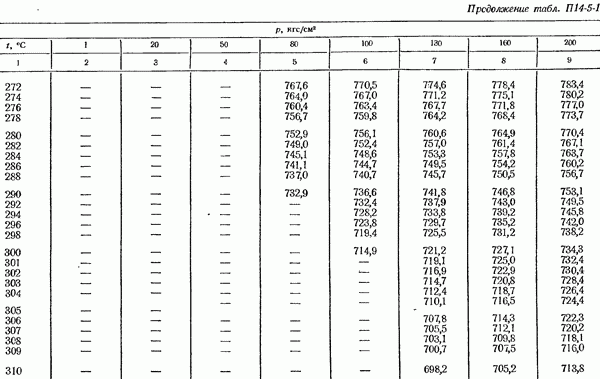
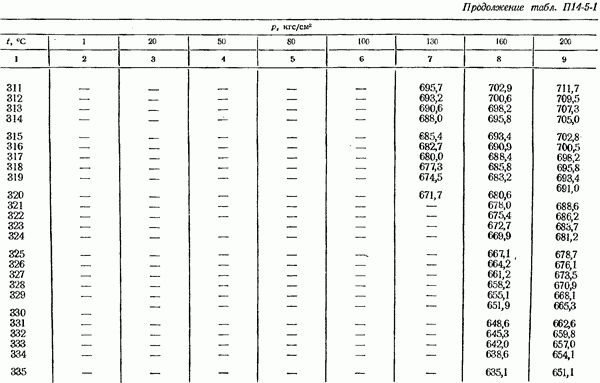
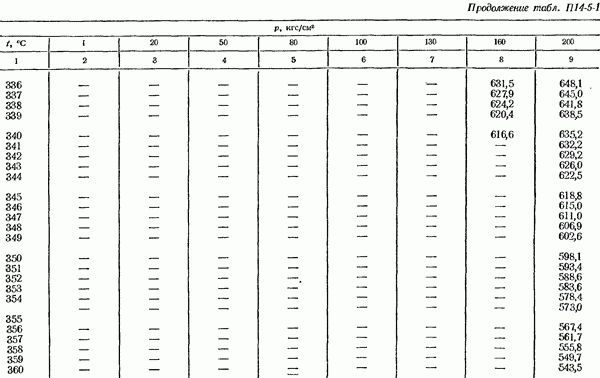
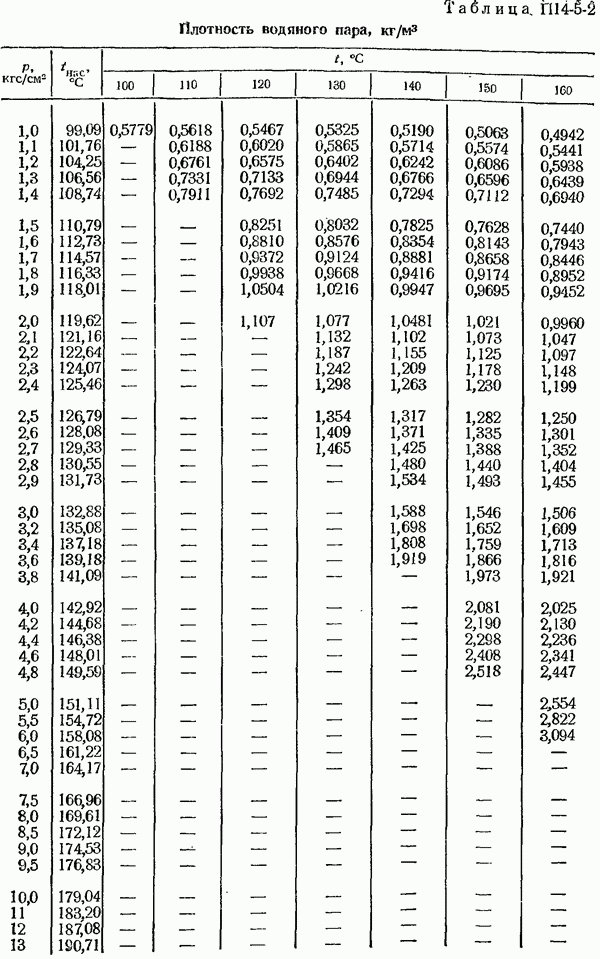
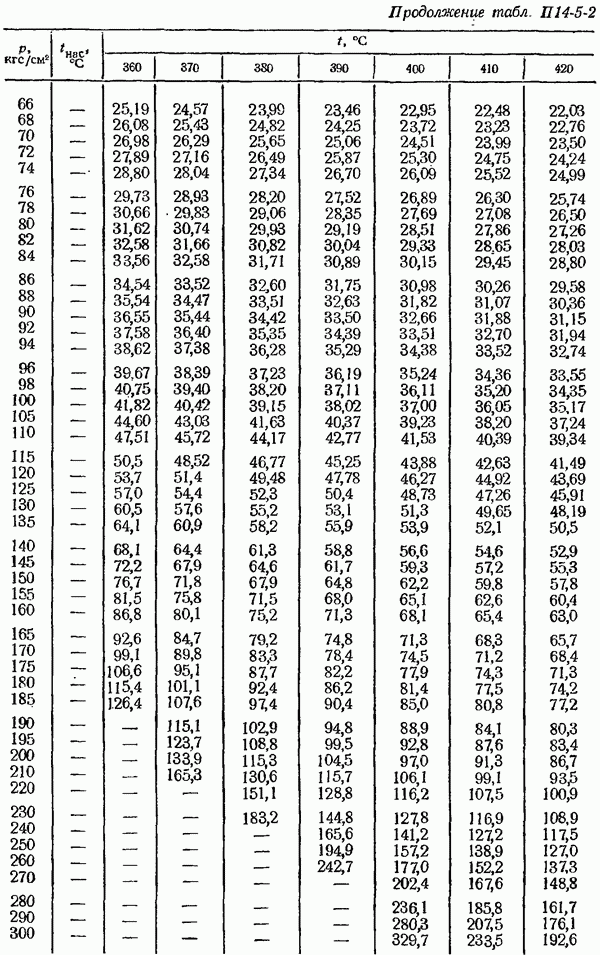
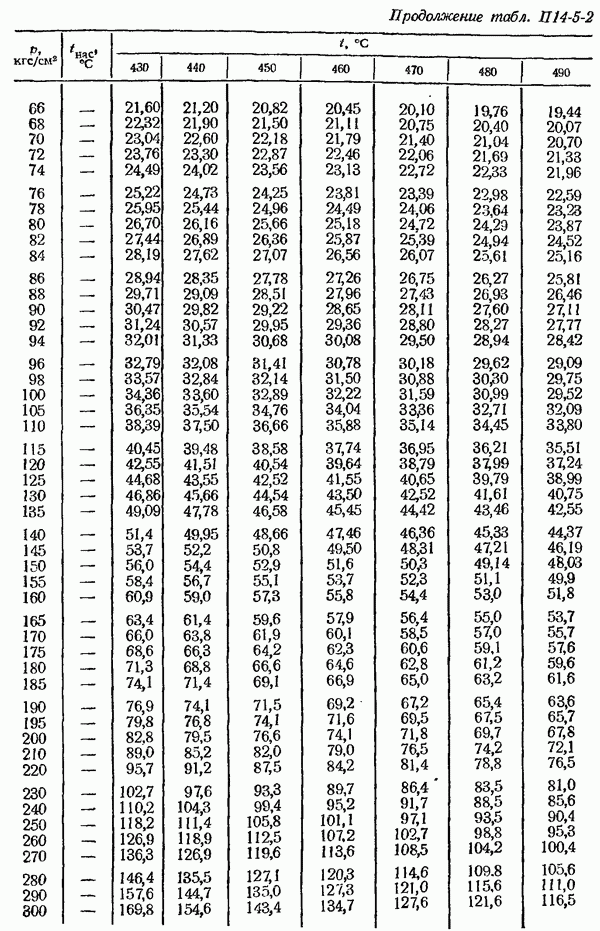
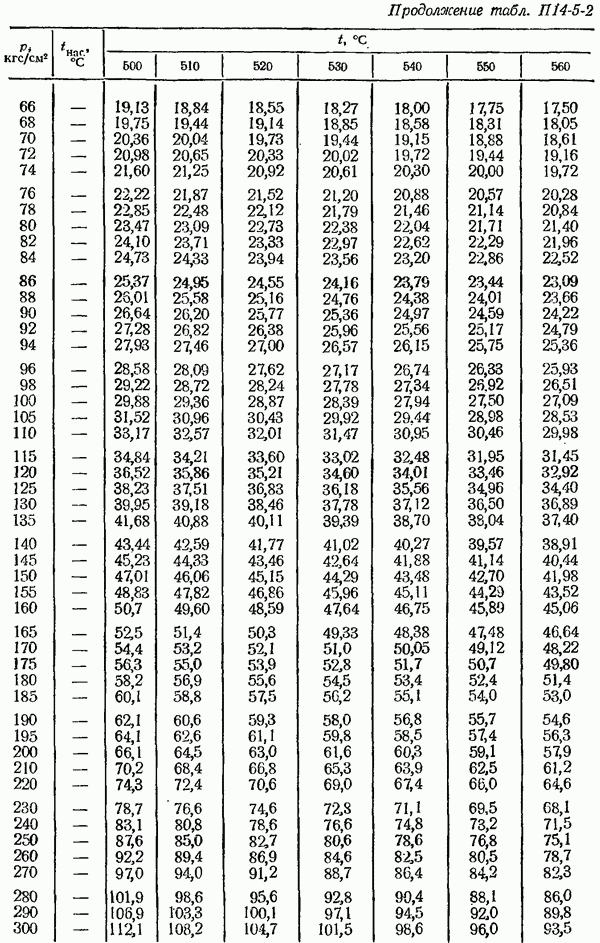
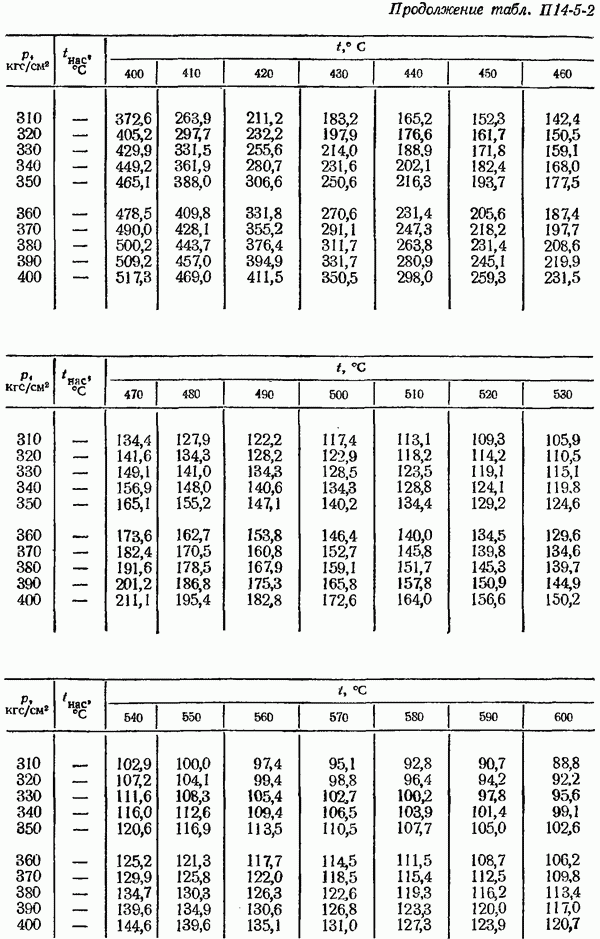
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
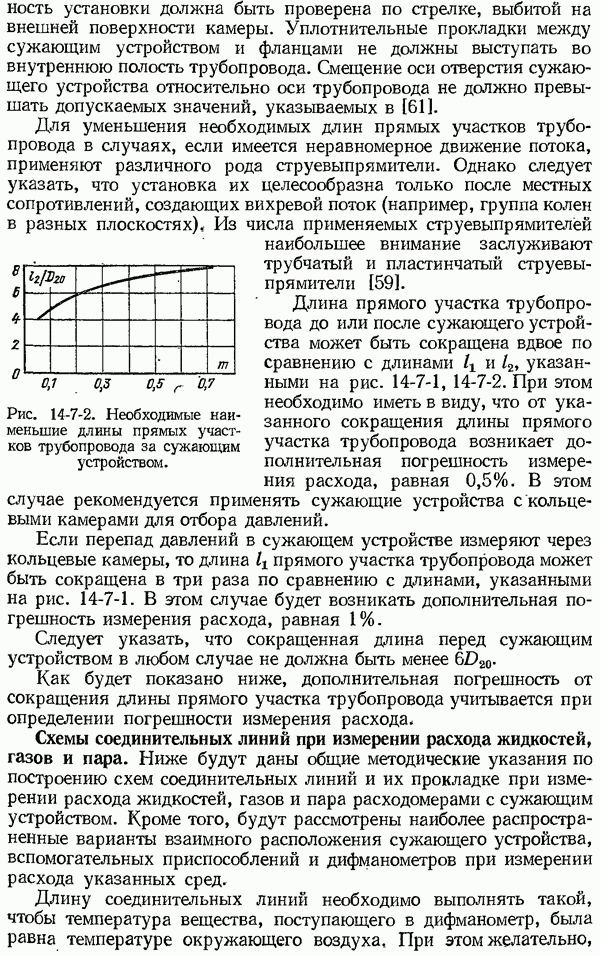
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
- 14-8. Погрешности измерения расхода
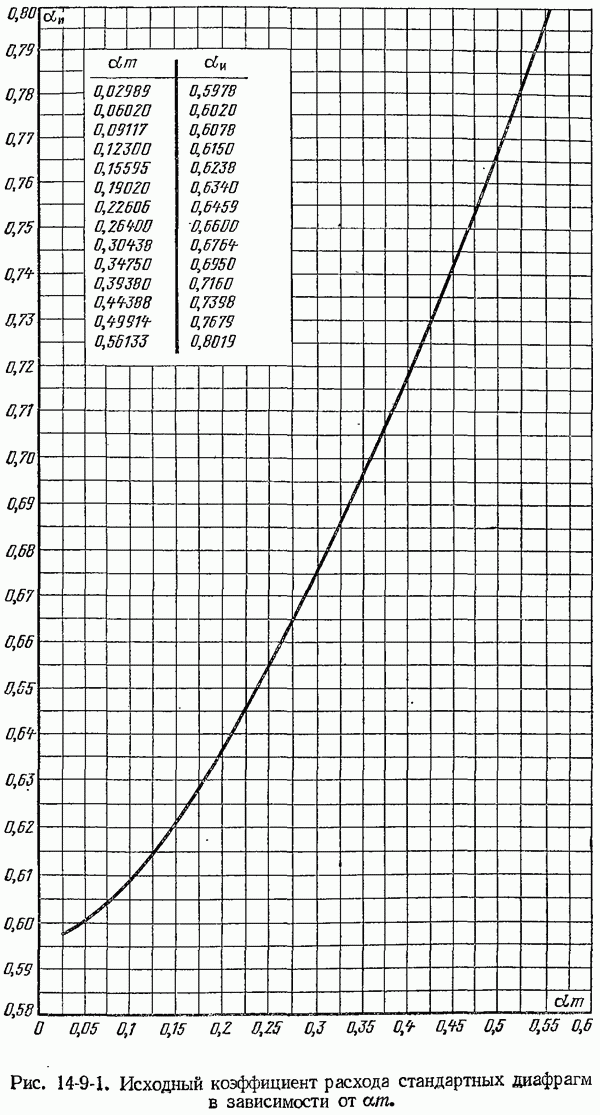
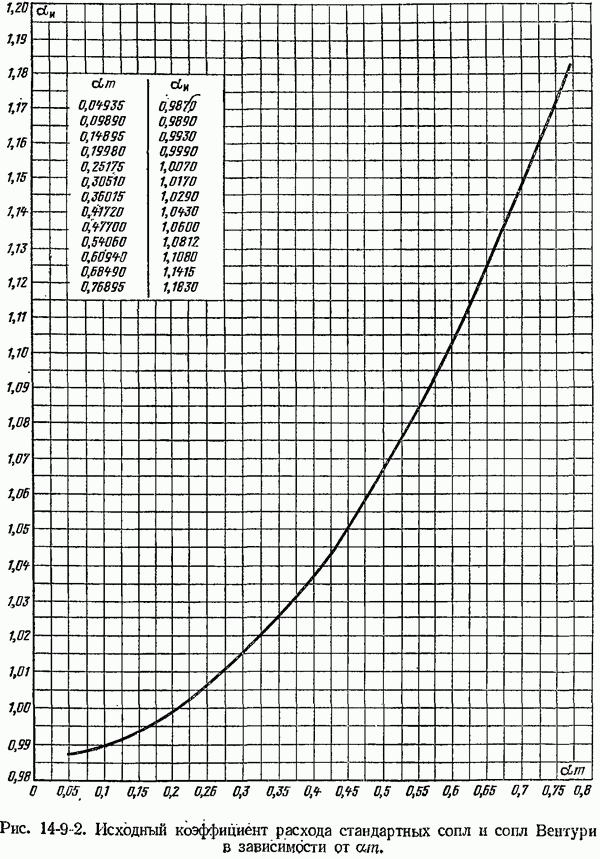
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
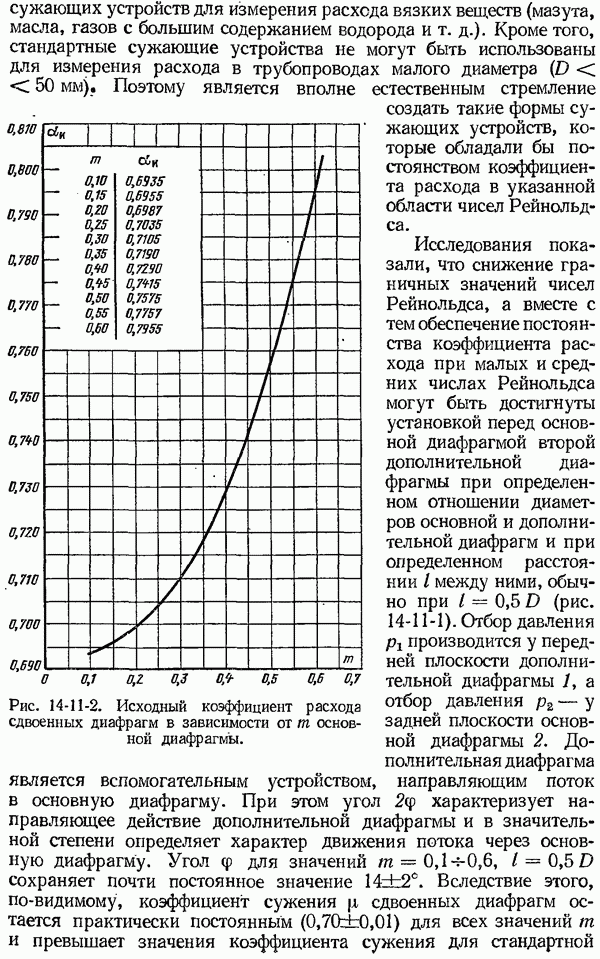
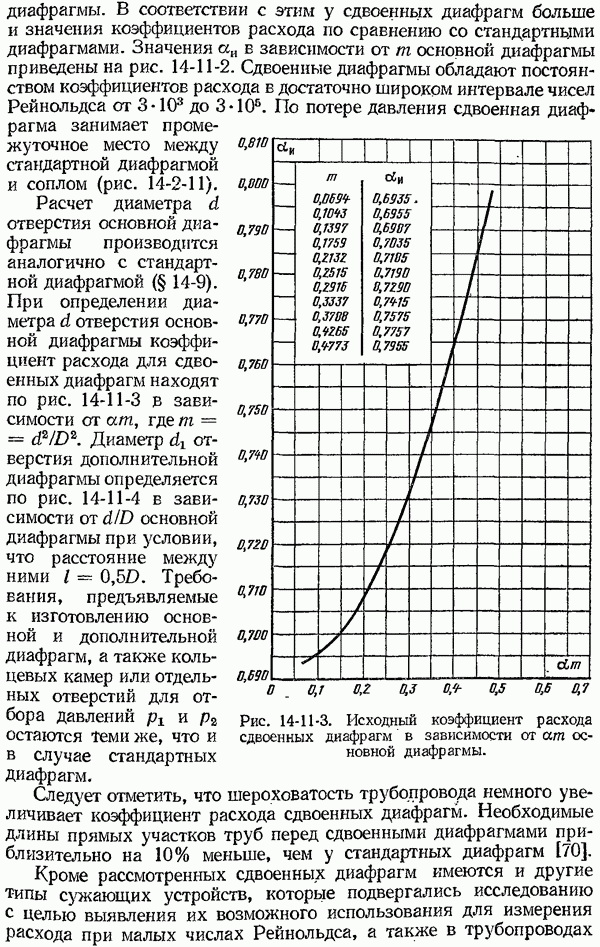
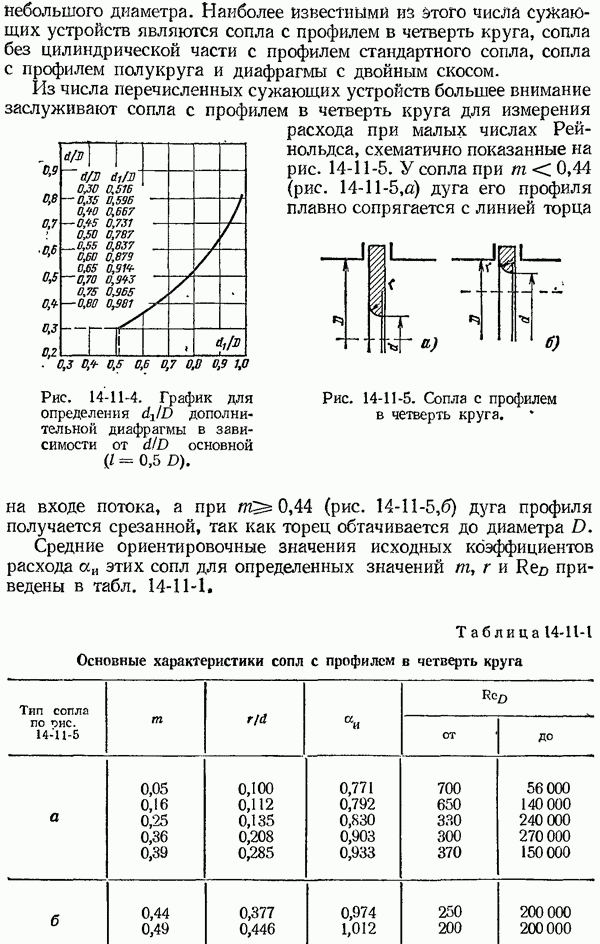
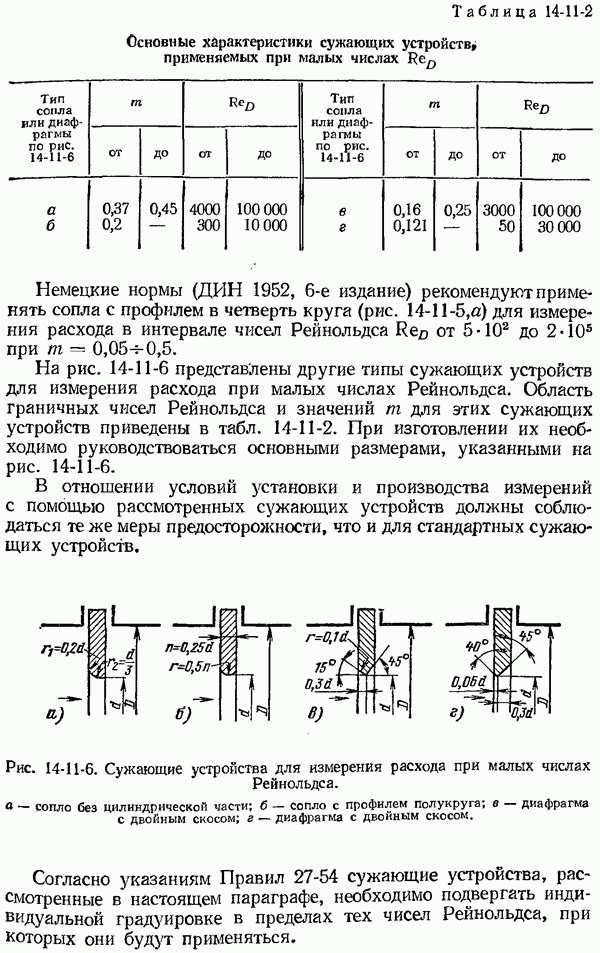
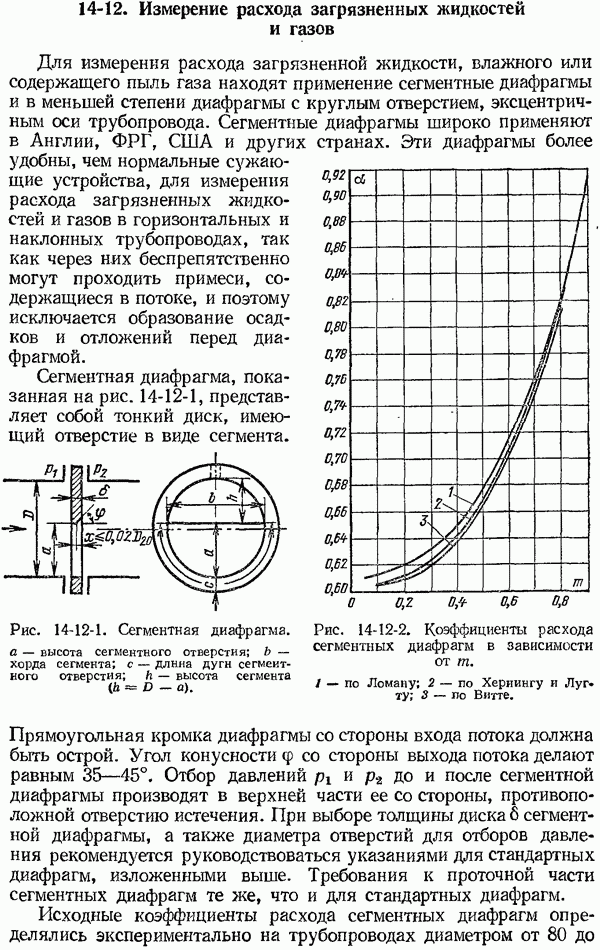
- 14-11. Измерение расхода при малых числах Рейнольдса
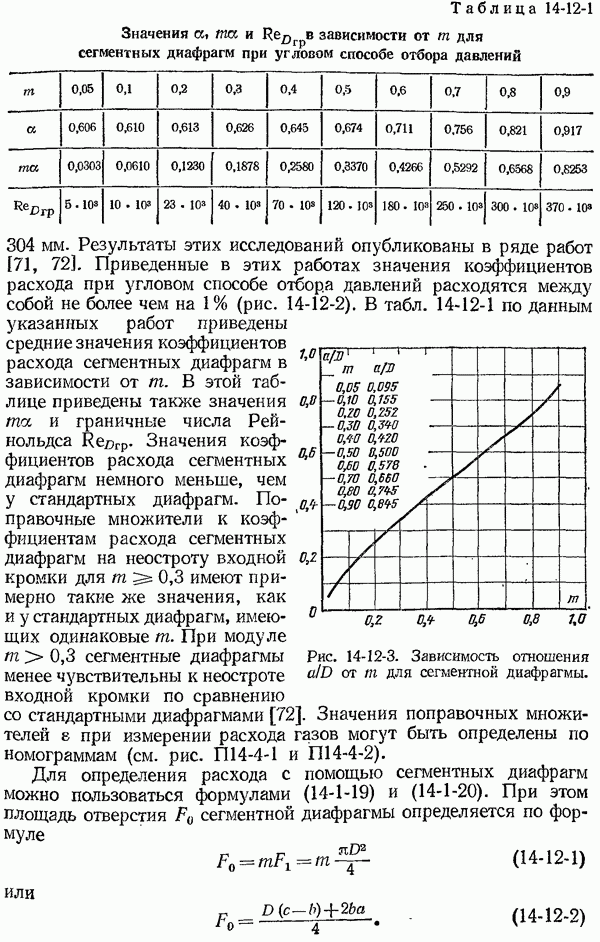
- 14-12. Измерение расхода загрязненных жидкостей и газов
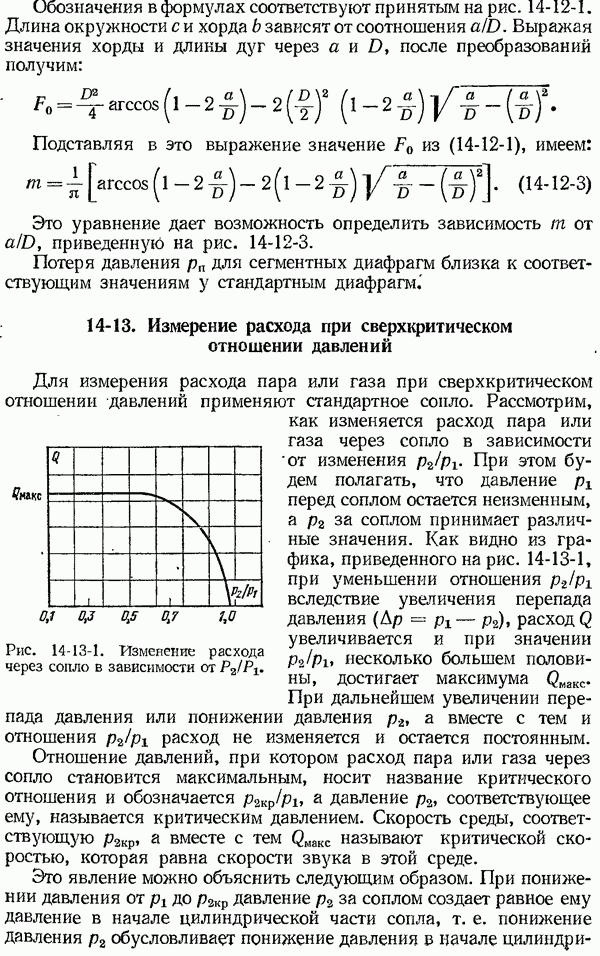
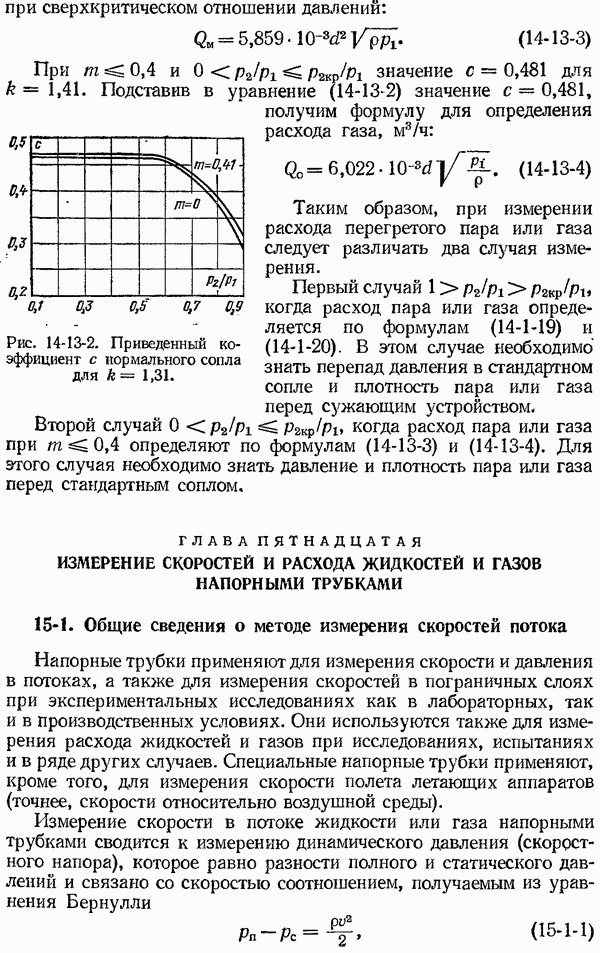
- 14-13. Измерение расхода при сверхкритическом отношении давлений
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
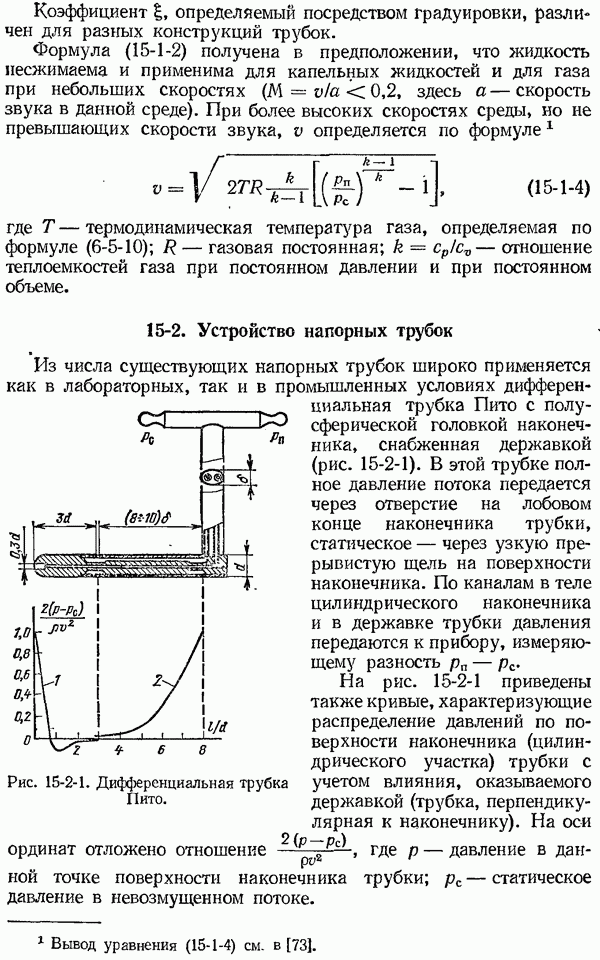
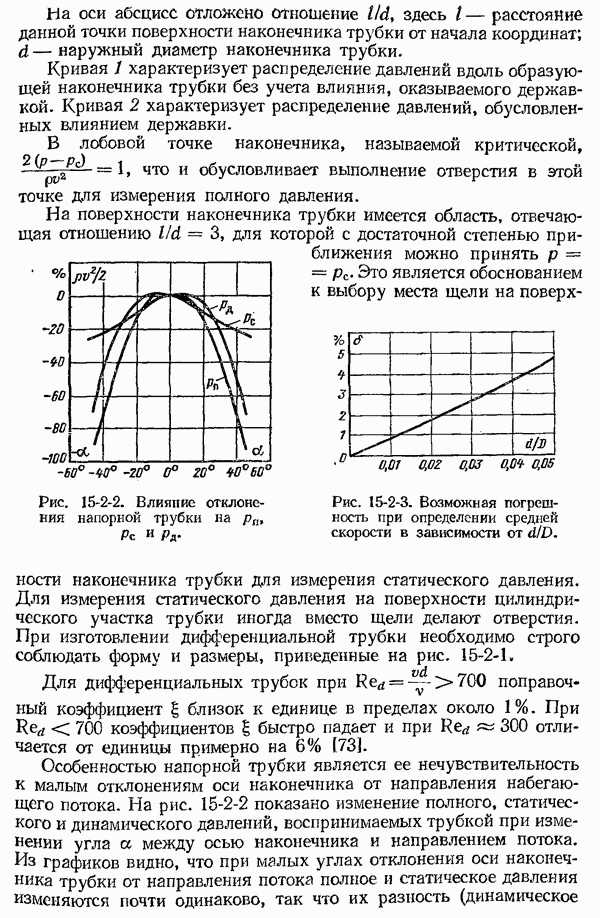
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
- 16-2. Основы теории ротаметров
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
- 17-1. Тахометрические счетчики количества жидкостей
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
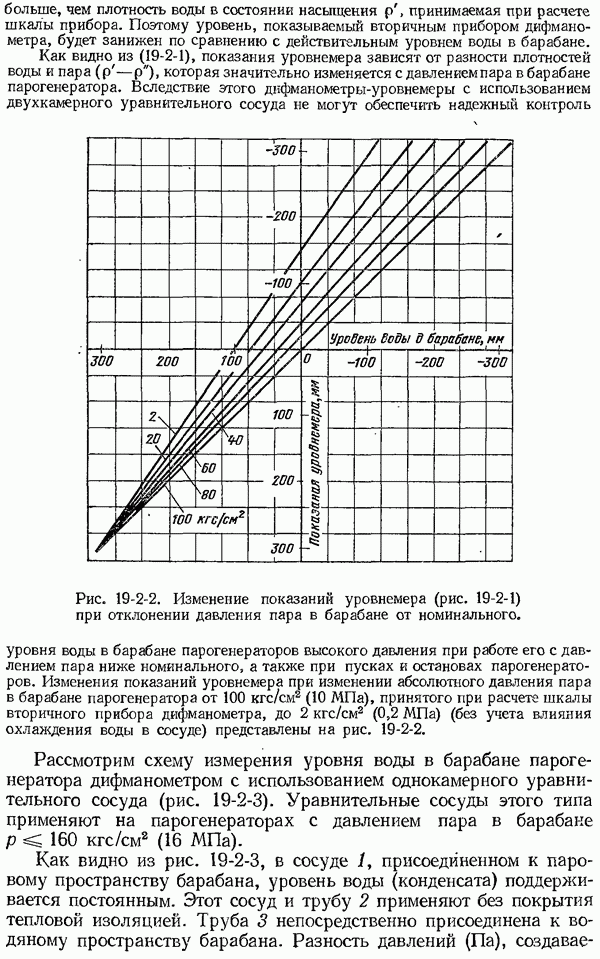
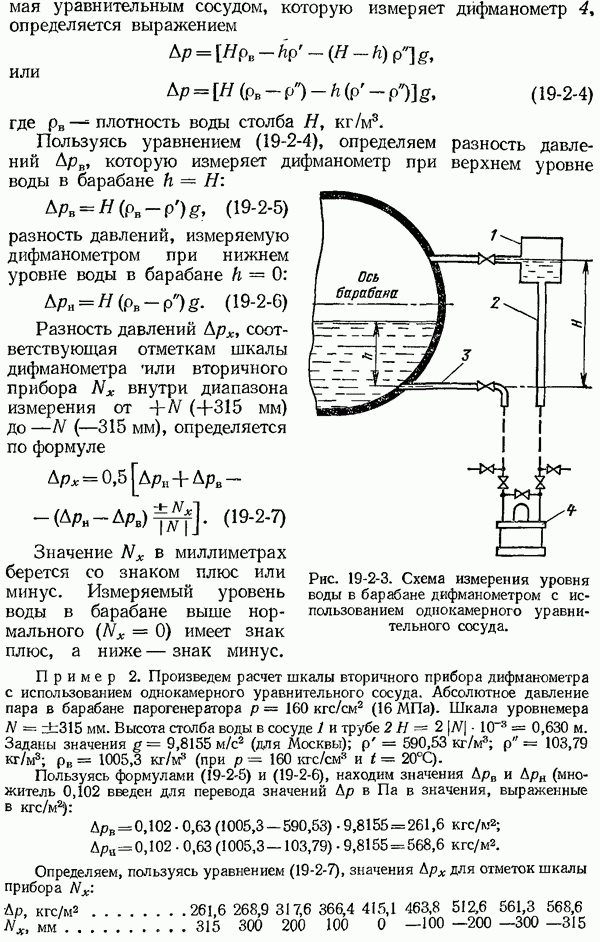
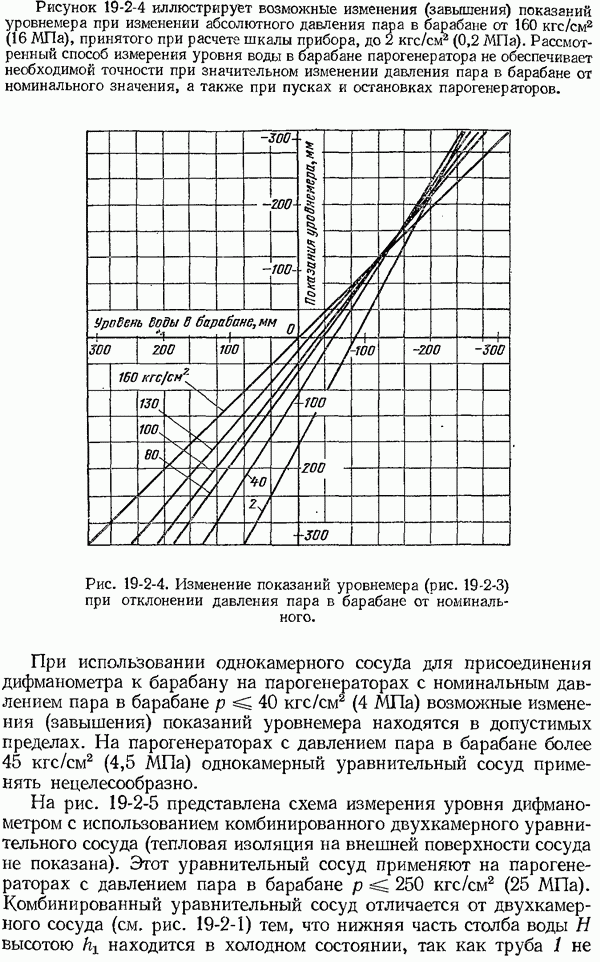
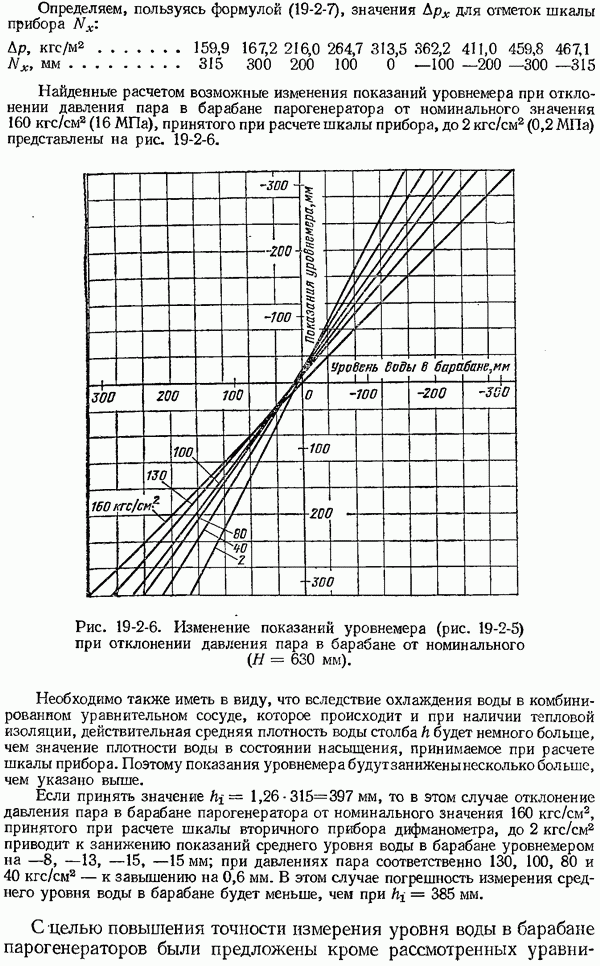
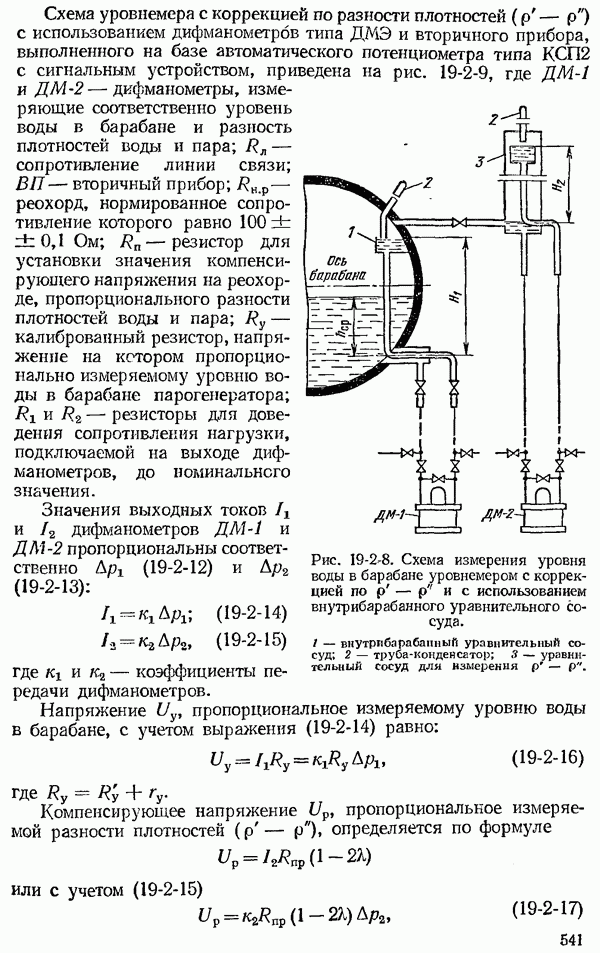
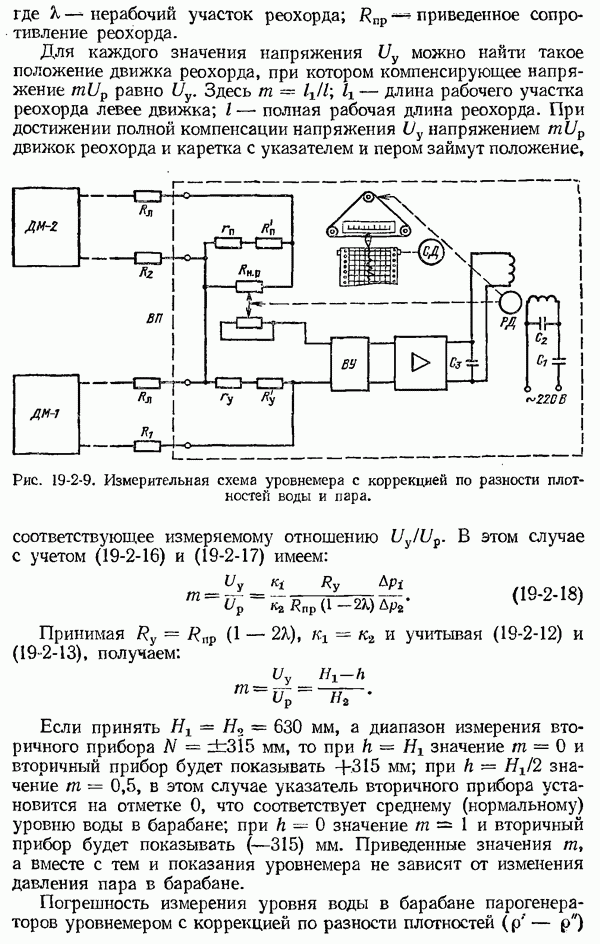
- 19-2. Измерение уровня воды в барабане парогенераторов
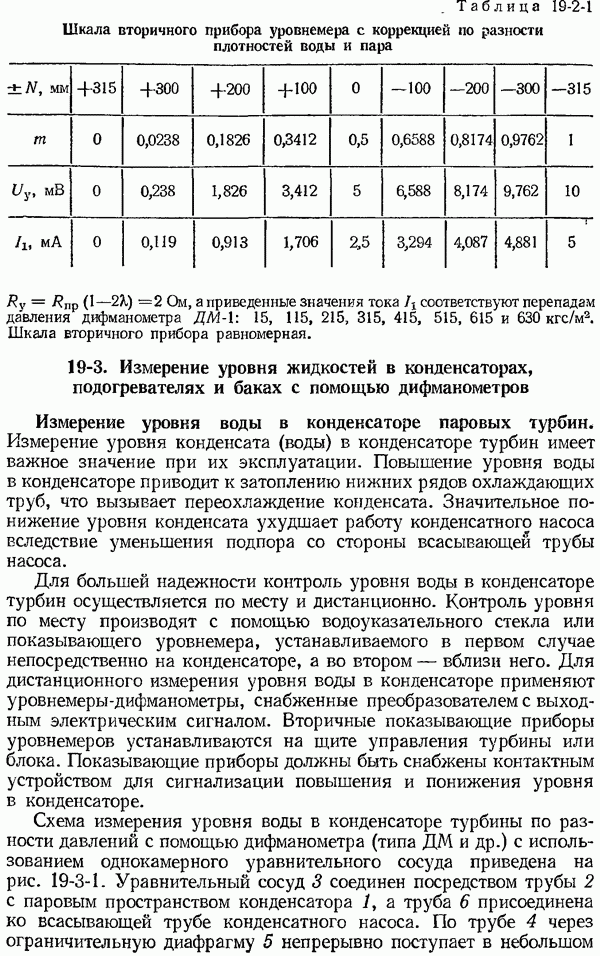
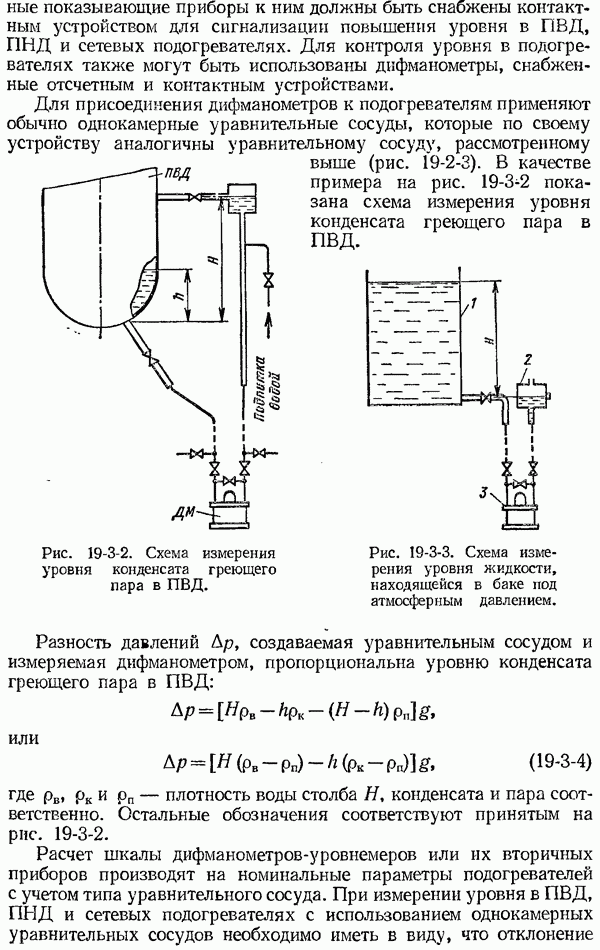
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
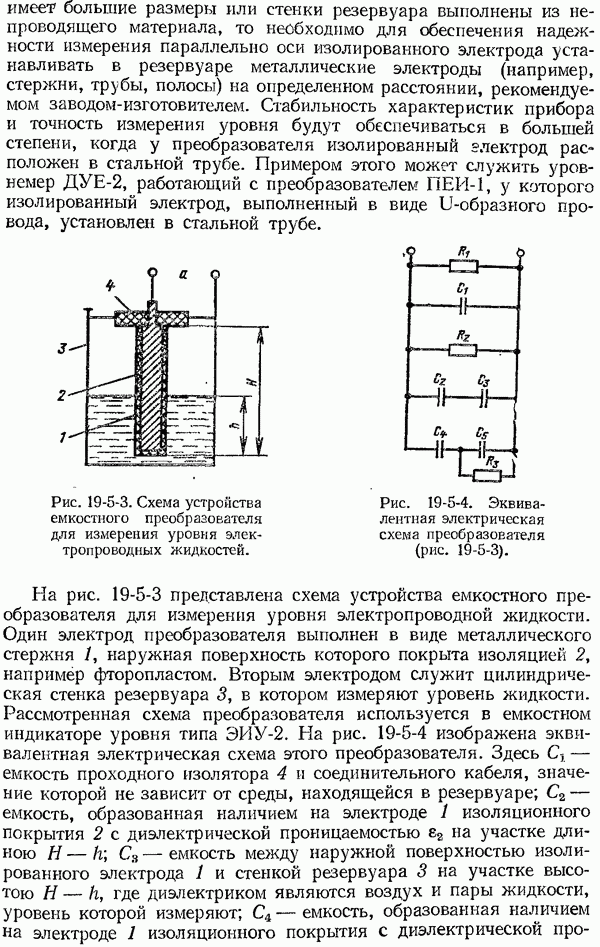
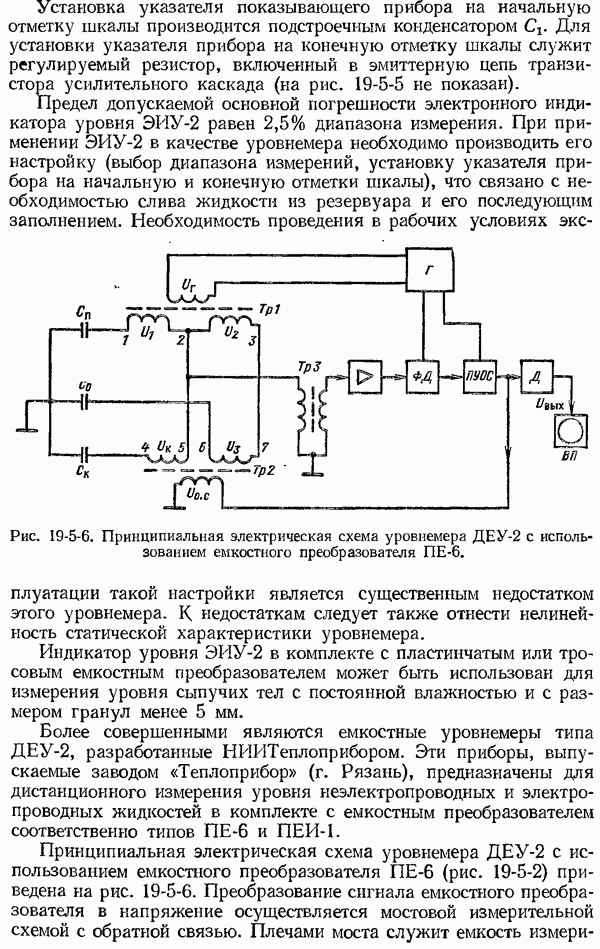
- 19-5. Емкостные уровнемеры
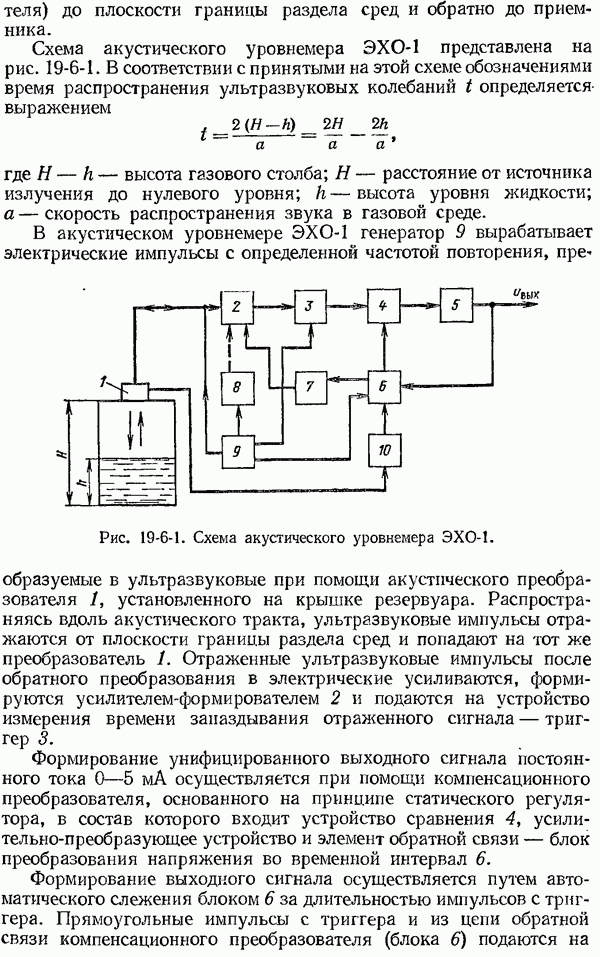
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
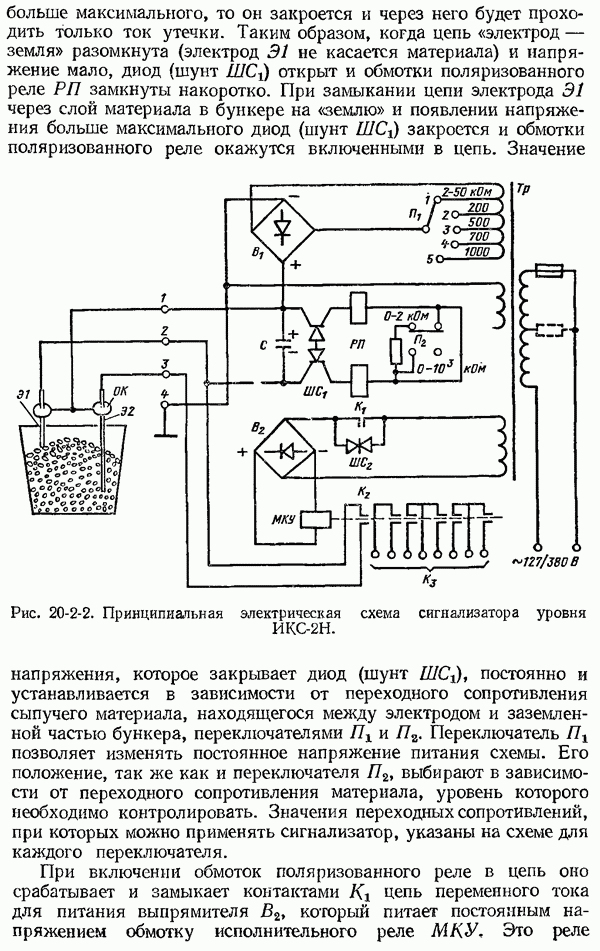
- 20-2. Сигнализаторы уровня сыпучих тел
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- 21-2. Газоанализаторы химические
- 21-3. Тепловые газоанализаторы
- 21-4. Магнитные газоанализаторы
- 21-5. Оптические газоанализаторы
- 21-6. Газовые хроматографы
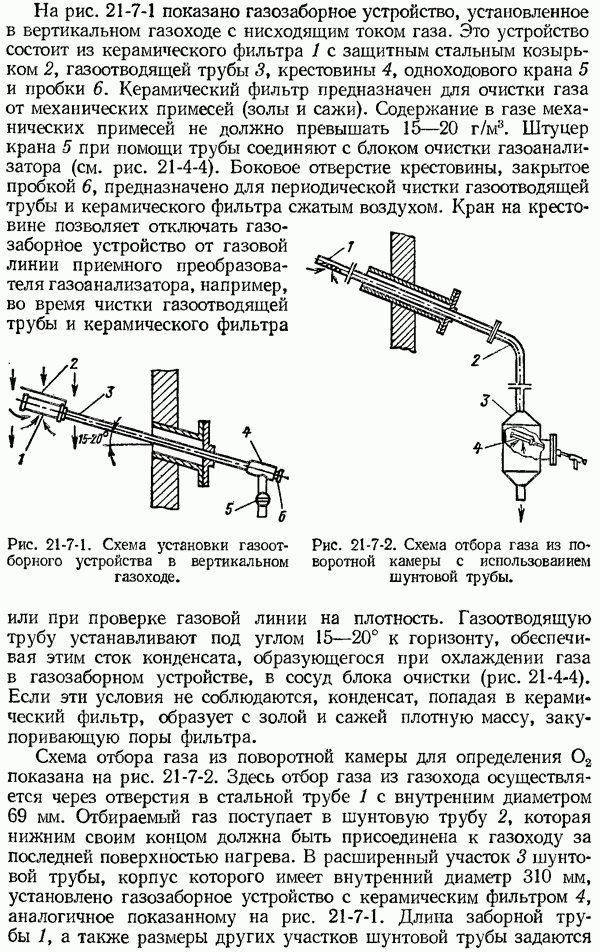
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
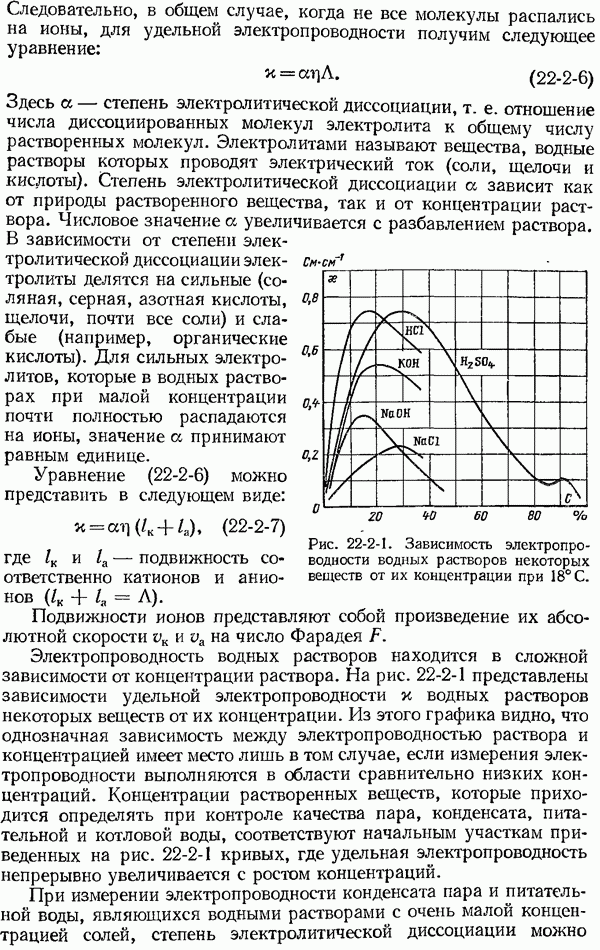
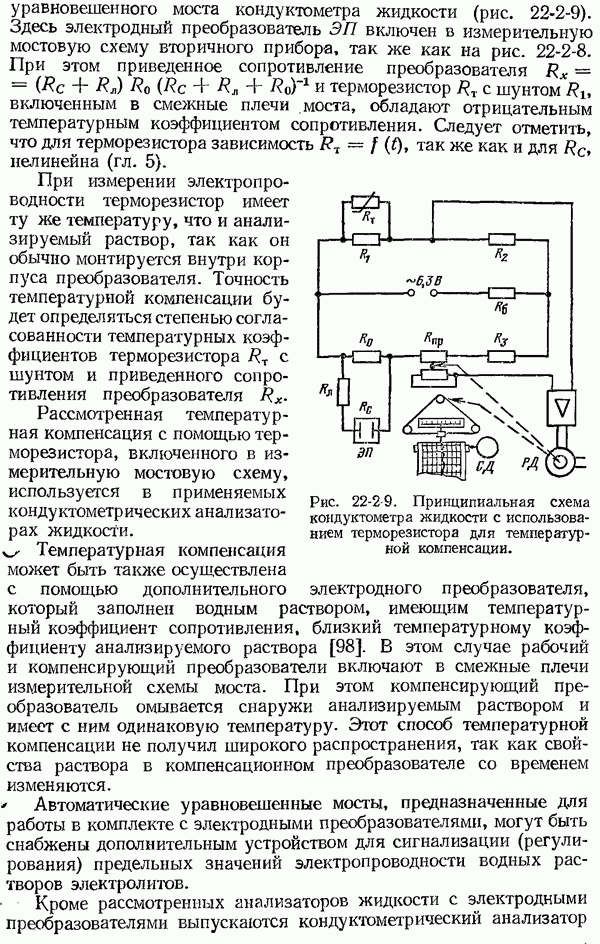
- 22-2. Измерение удельной электропроводности водных растворов
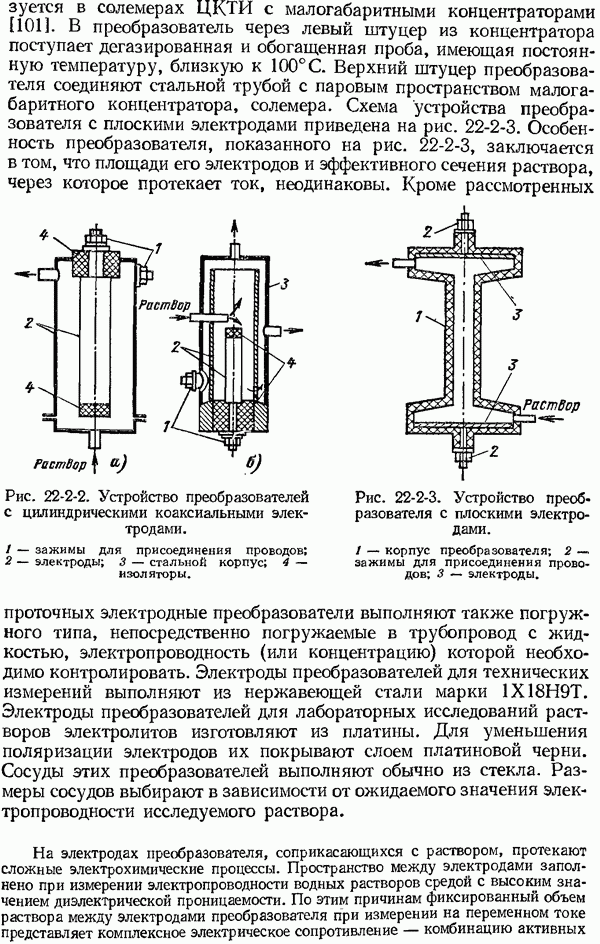
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
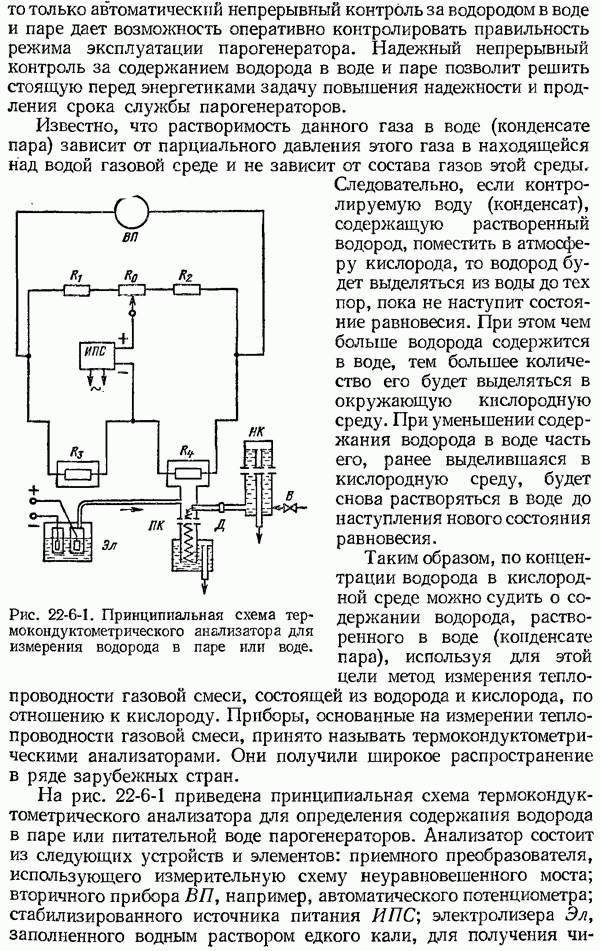
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
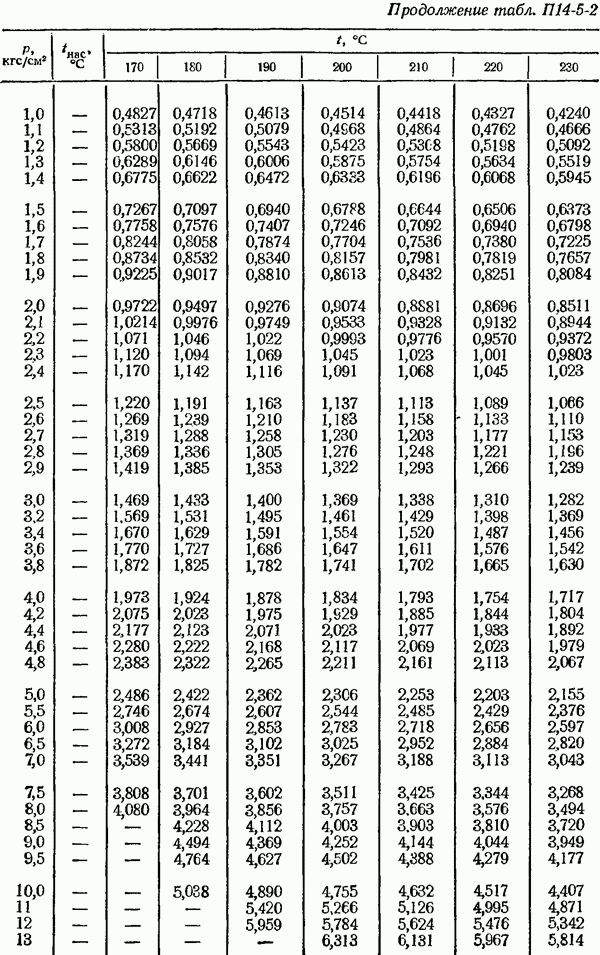
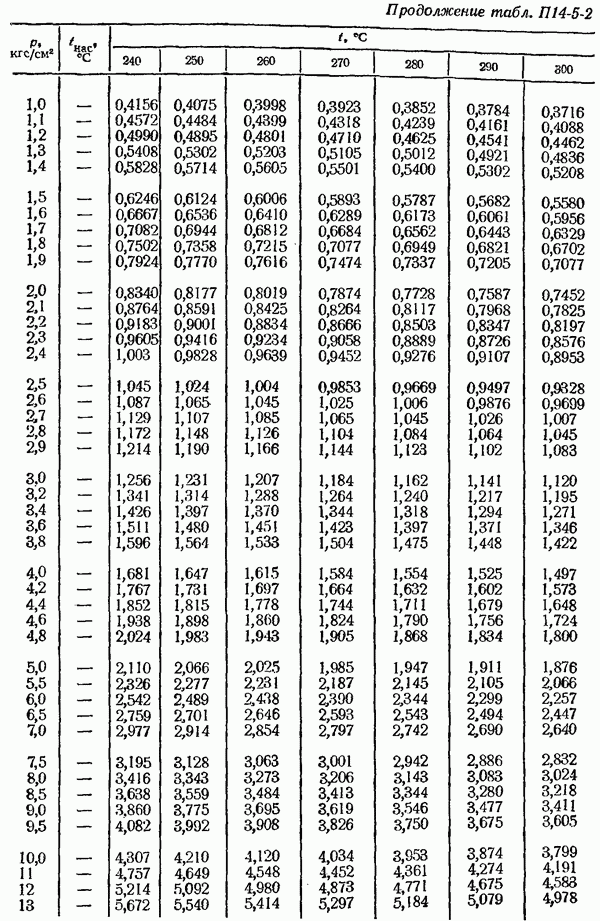
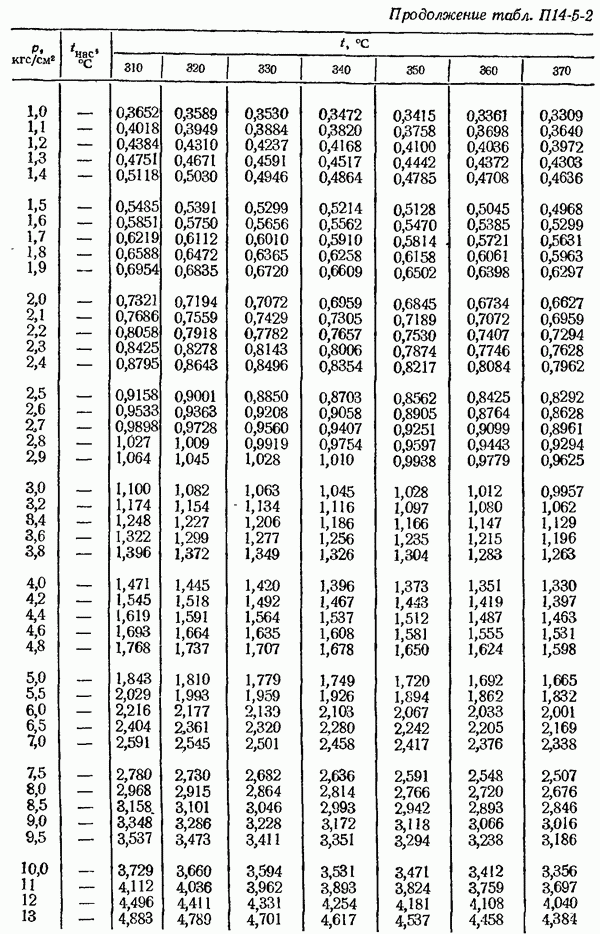
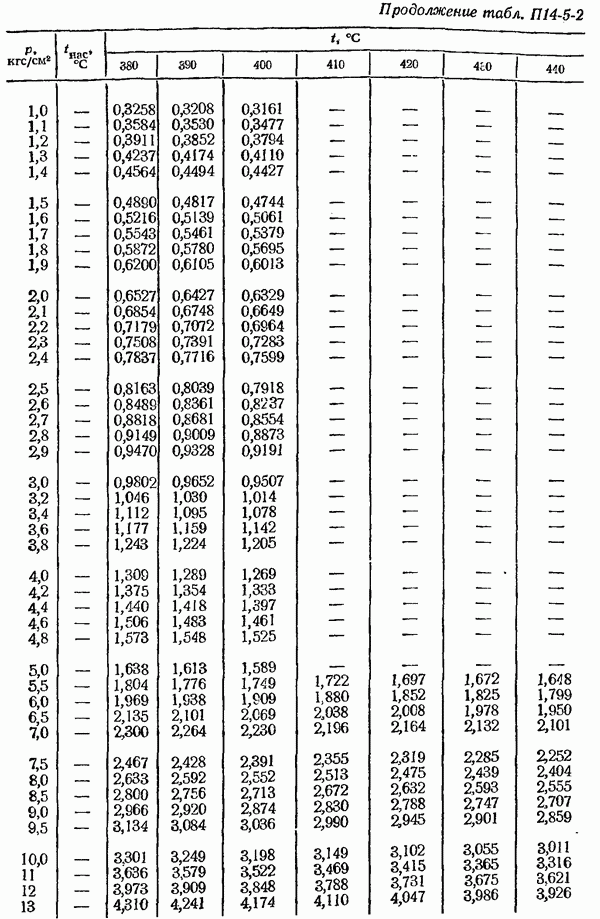
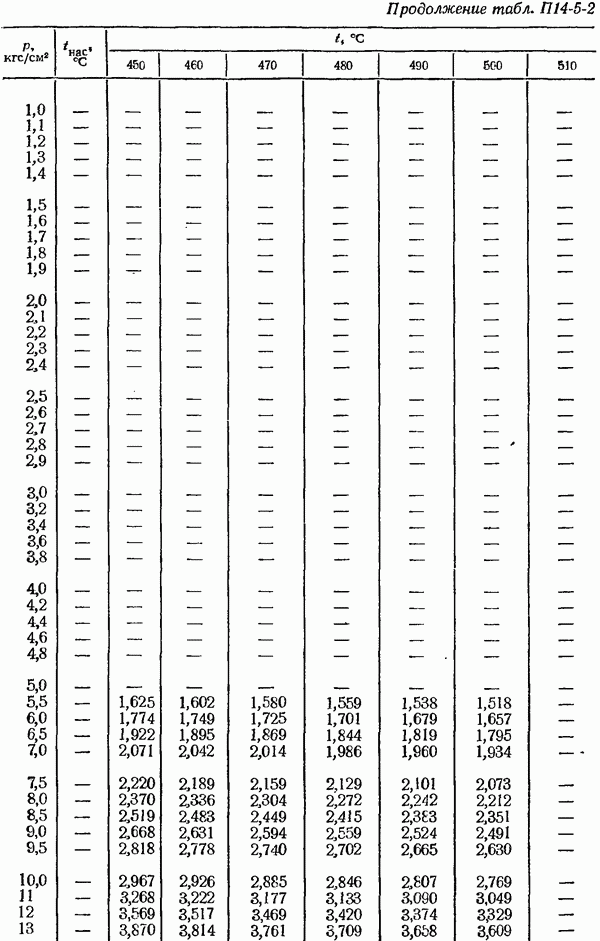
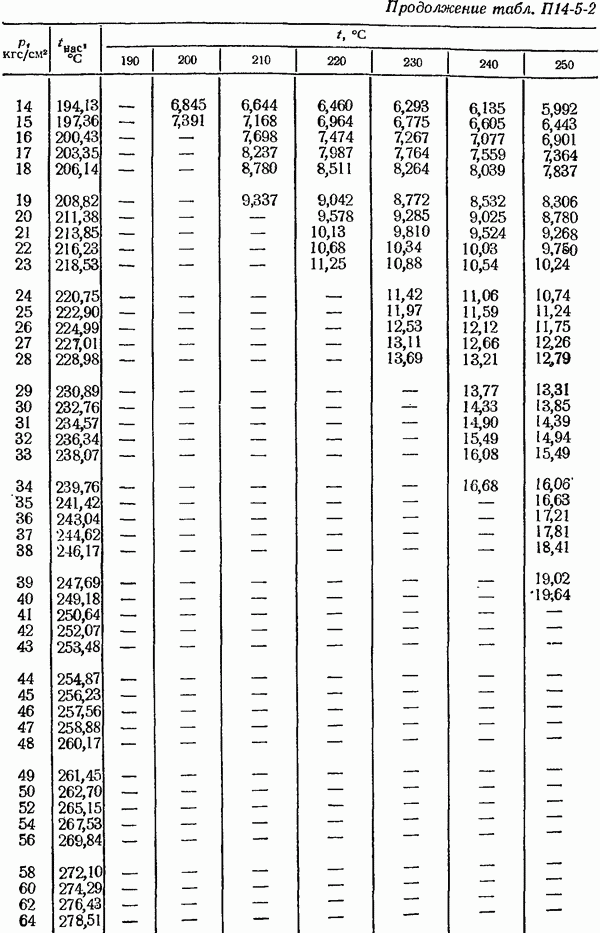
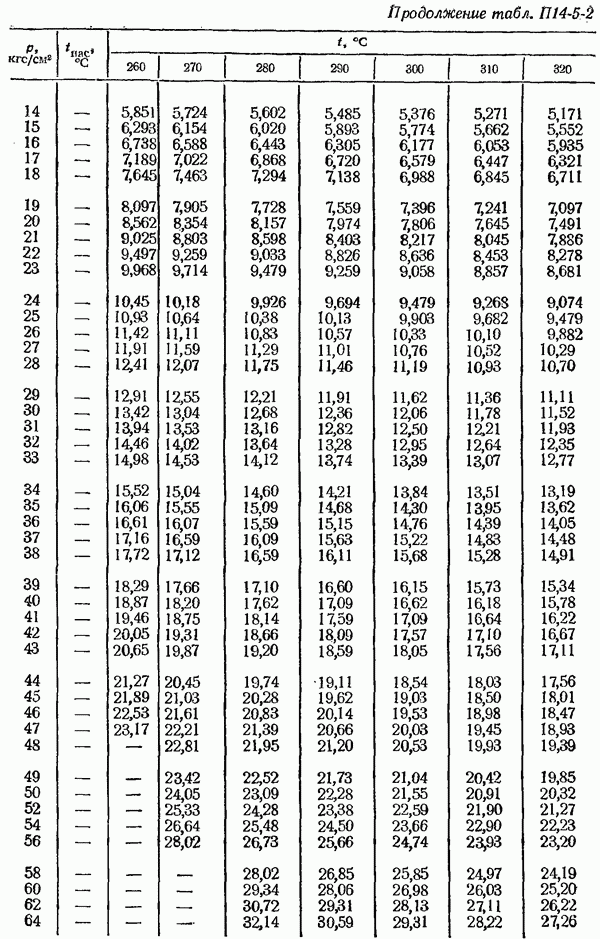
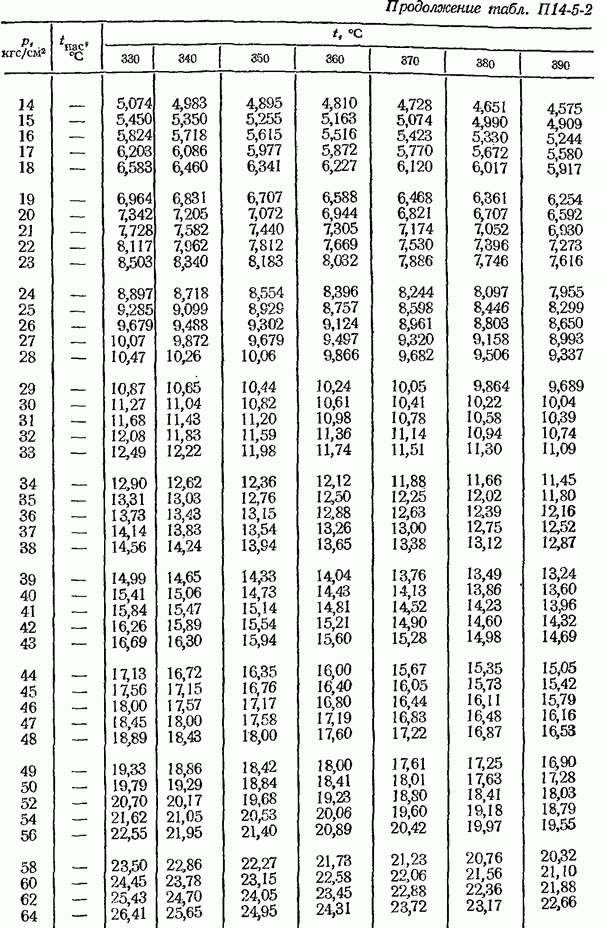
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ