| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
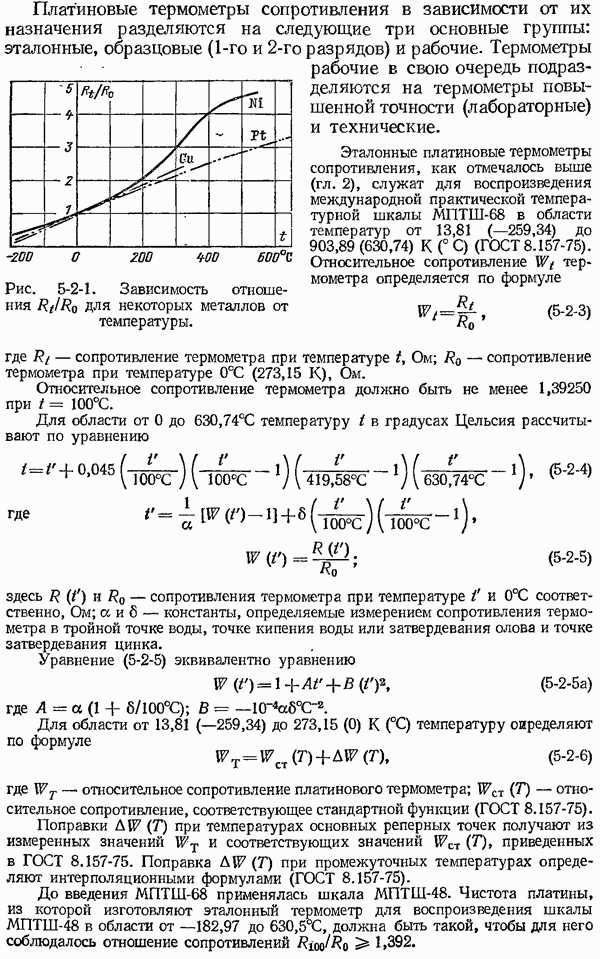
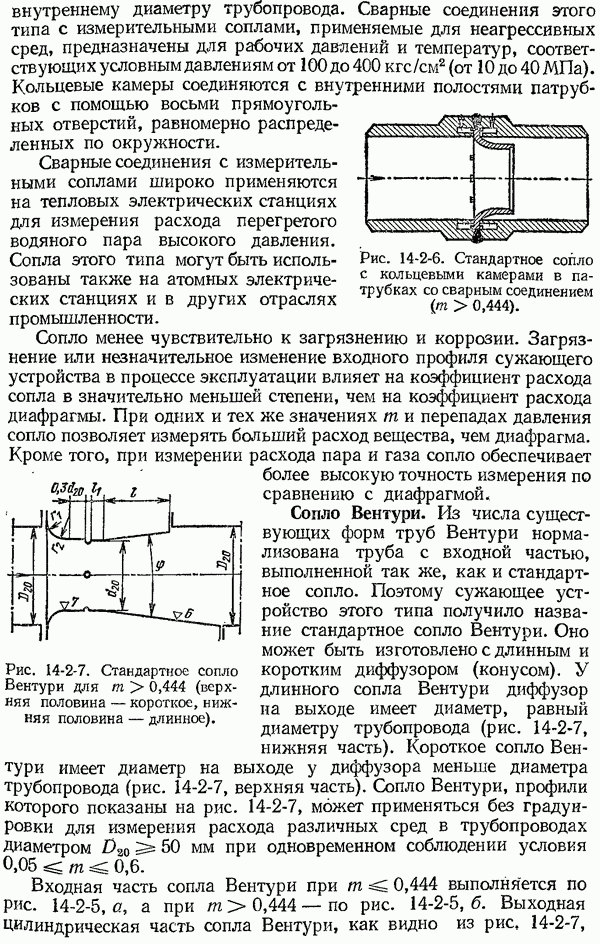
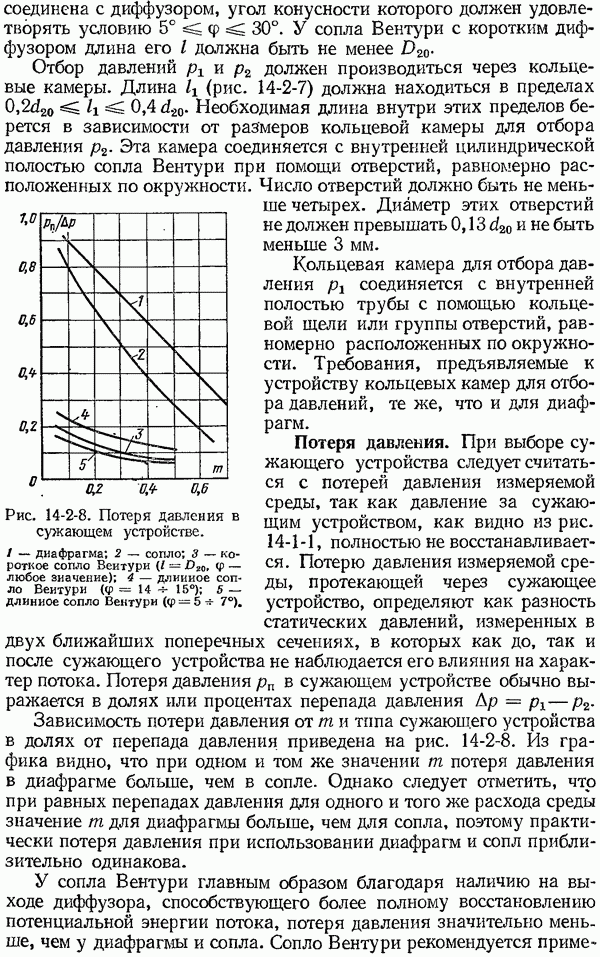
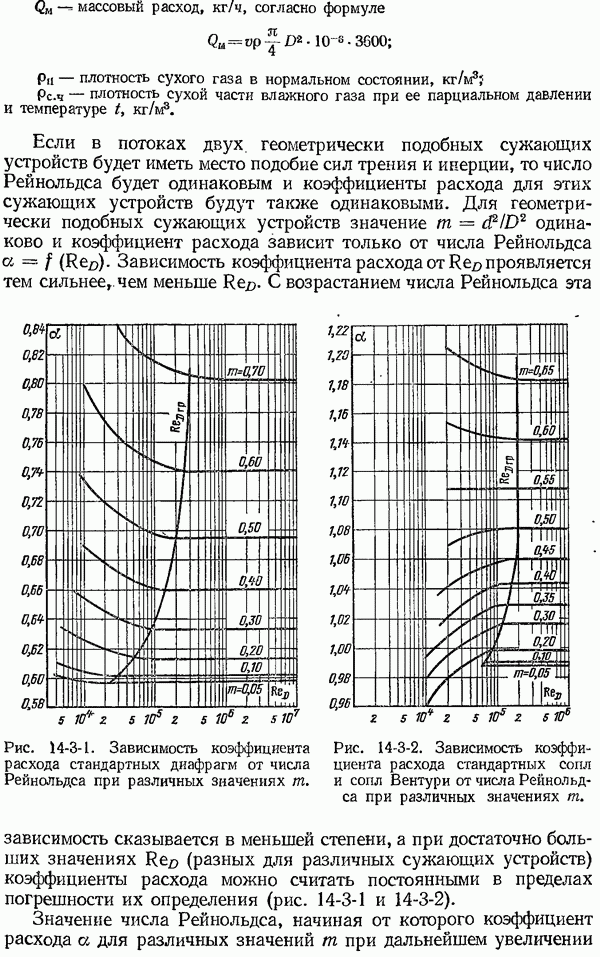
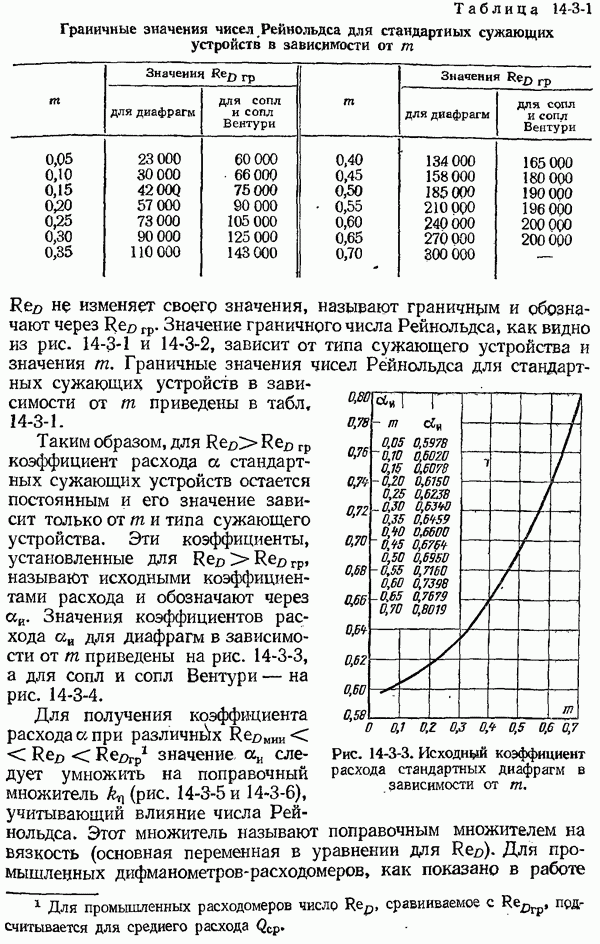
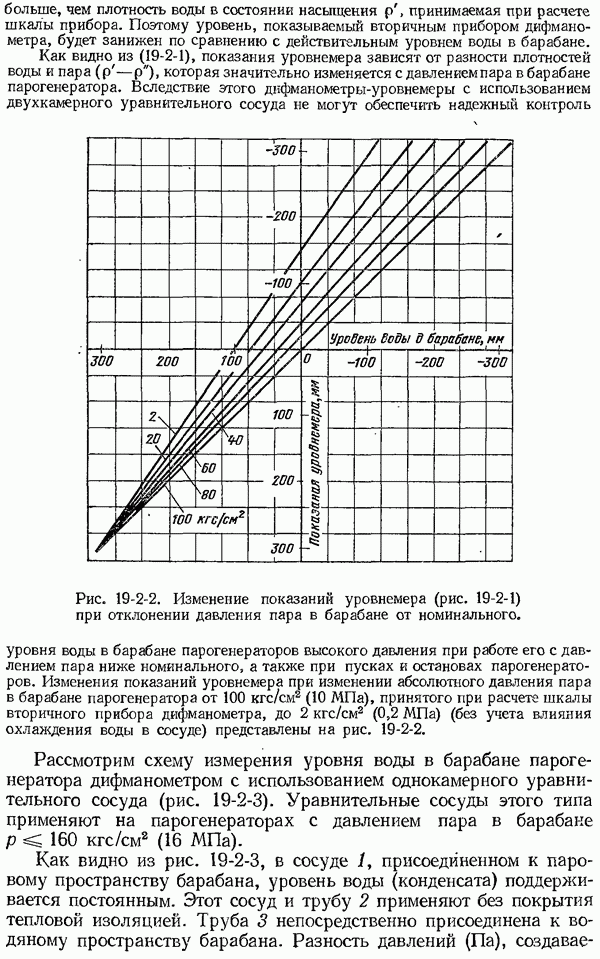
7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
Методы измерения температур, использующие различные свойства теплового излучения тел, вытекающие из законов излучения абсолютно черного тела, нашли широкое практическое применение. Под абсолютно черным телом понимают тело, которое поглощает всю падающую на него лучистую энергию. Такие тела в природе отсутствуют, но модель черного тела можно осуществить с достаточной степенью приближения.
Моделью, наиболее приближающейся по своим свойствам к абсолютно черному телу, является полое непрозрачное тело с малым отверстием, все участки поверхности которого имеют одну и ту же температуру. Для такой модели черного тела коэффициент поглощения можно принять равным единице, так как энергия луча, попадающего в малое отверстие полого тела, практически полностью поглощается внутри последнего вследствие многократных отражений от внутренней поверхности. В дальнейшем все величины, относящиеся к абсолютно черному телу, мы будем отмечать индексом 
В пирометрии излучения в качестве величин, характеризующих тепловое излучение тел, применяют энергетическую светимость (излучательность) и энергетическую яркость (лучистость). При этом следует различать полную и спектральную светимость и яркость.
Под полной энергетической светимостью тела понимают полную (интегральную) поверхностную плотность излучаемой мощности, т. е.

где  полная энергетическая светимость при температуре
полная энергетическая светимость при температуре  длина волны излучения,
длина волны излучения,  спектральная энергетическая светимость, отнесенная к очень узкой области спектра
спектральная энергетическая светимость, отнесенная к очень узкой области спектра  (от А, до
(от А, до  ).
).
Очевидно, что в соответствии с (7-2-1)

где  доля полной светимости в спектральном интервале
доля полной светимости в спектральном интервале  при температуре
при температуре 
Энергетической яркостью тела в данном направлении называется мощность излучения в единичный телесный угол с единицы площади проекции поверхности тела на плоскость, перпендикулярную данному направлению. Полная энергетическая яркость тела определяется, аналогично предыдущему, выражением

где  — полная энергетическая яркость при температуре
— полная энергетическая яркость при температуре  спектральная энергетическая яркость,
спектральная энергетическая яркость,
отнесенная к очень узкой области спектра  Согласно формуле (7-2-3)
Согласно формуле (7-2-3)

где  доля полной яркости в спектральном интервале
доля полной яркости в спектральном интервале  при температуре
при температуре 
Источники излучения, яркость которых от направления не зависит, подчиняются закону Ламберта, и энергетическая светимость и яркость таких источников связаны между собой соотношением

строго говоря, таким излучателем является только черное тело.
Энергетическая яркость (лучистость) является основной величиной, непосредственно воспринимаемой человеческим глазом, а также всеми пирометрами, основанными на измерении температуры по тепловому излучению
Все реальные тела по степени поглощения ими лучистой энергии отличаются от черного тела и имеют коэффициент поглощения меньше единицы, Излучательная способность реальных тел также отличается от лучеиспускательной способности черного тела и может быть характеризована коэффициентом излучения полным или спектральным.
Полный коэффициент излучения  является мерой, определяющей ту часть полной энергии, которую составляет излучение данного тела от полного излучения черного тела при той же температуре,
является мерой, определяющей ту часть полной энергии, которую составляет излучение данного тела от полного излучения черного тела при той же температуре, 

где  и
и  полная энергетическая яркость соответственно реального и черного тела при температуре
полная энергетическая яркость соответственно реального и черного тела при температуре 
Обозначая через спектральный коэффициент излучения, характеризующий относительную лучеиспускательную способность тела при данных  и
и  аналогично предыдущему можем написать:
аналогично предыдущему можем написать:

где  спектральная энергетическая яркость соответственно реального и черного тела,
спектральная энергетическая яркость соответственно реального и черного тела, 
Следует отметить, что на основании закона Кирхгофа спектральный коэффициент излучения любого тела равен его спектральному коэффициенту поглощения, 
Для всех реальных тел  Коэффициенты излучения
Коэффициенты излучения  зависят от вещества тела, состояния его поверхности и температуры. Спектральный коэффициент зависит также от
зависят от вещества тела, состояния его поверхности и температуры. Спектральный коэффициент зависит также от  от спектрального состава излучения,
от спектрального состава излучения,
Так как излучательная способность зависит от индивидуальных особенностей реальных тел, то возникает необходимость градуировать пирометры по излучению черного тела. Применяя эти пирометры для измерения температуры реальных тел, излучающих сплошной
спектр, мы в большинстве случаев получаем значения температур, отличающиеся от действительных температур данных тел, поскольку их излучение не соответствует излучению черного тела. Эти температуры реальных тел, измеренные по их тепловому излучению, называют обычно условными.
Условные температуры находятся в определенном соотношении с действительными температурами реальных тел, причем эти соотношения между условными и действительными температурами устанавливаются теоретически с помощью законов излучения. При этом для определения значения действительной температуры с помощью полученных соотношений необходимо знать также коэффициент излучения реальных тел в тех лучах, которыми предложено оперировать при измерении их условной температуры.
Следует также иметь в виду, что условные температуры данного тела получаются при одной и той же его действительной температуре различными, в зависимости от того, какое свойство излучения положено в основу метода измерения условной температуры. Поэтому при установлении соотношения между условной и действительной температурой необходимо руководствоваться методом измерения условной температуры реальных тел. Условные температуры тел, измеренные пирометрами, тем больше отличаются от действительных, чем значительнее характер излучения этих тел отличается от характера излучения черного тела. Это является принципиальным недостатком методов измерения температуры тел по тепловому излучению. Применяемые неавтоматические способы введения соответствующих методических поправок в показания пирометров, позволяющие перейти от измеренных условных температур к действительным температурам тел, мало надежны. Рассматриваемый ниже метод автоматического введения поправок, позволивший создать пирометр для измерения действительной температуры тел (см, § 7-5), является перспективным.
Ниже ознакомимся с различными свойствами теплового излучения черного тела, вытекающими из законов излучения, положенными в основу наиболее распространенных бесконтактных методов измерения температур реальных тел.
Зависимость спектральной энергетической светимости черного тела от длины волны и температуры описывается уравнением Планка

где  и
и  - постоянные коэффициенты
- постоянные коэффициенты  длина волны,
длина волны,  температура,
температура,  основание натуральных логарифмов.
основание натуральных логарифмов.
Учитывая соотношение (7-2-5), получаем формулу Планка для спектральной энергетической яркости черного тела:

где 
В ограниченном интервале температур и при малых значениях длин волн зависимость спектральной энергетической яркости черного тела от длины волны и температуры может быть выражена уравнением Вина

Уравнение (72-10) более удобно для практического применения в пирометрии, чем формула Планка. При применении формулы Вина необходимо иметь в виду, что она приводит к заниженным по сравнению с формулой Планка значениям  , например, при
, например, при  на 0,08% и при
на 0,08% и при  на 0,8%, а температура получается завышенной, следовательно, поправка имеет отрицательный знак. Для
на 0,8%, а температура получается завышенной, следовательно, поправка имеет отрицательный знак. Для  при 3000 и 4000 К поправка составляет соответственно —0,5 и —4 К.
при 3000 и 4000 К поправка составляет соответственно —0,5 и —4 К.

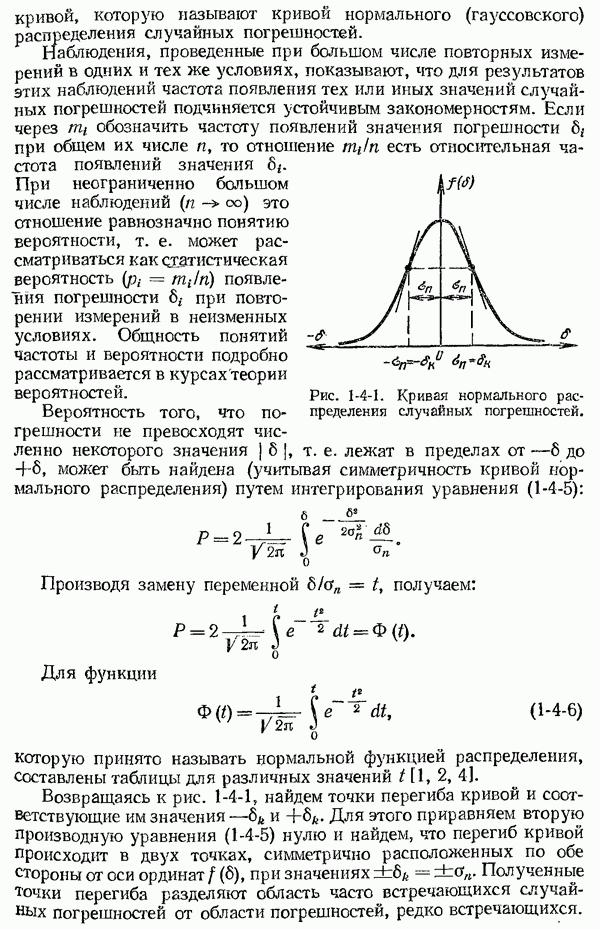
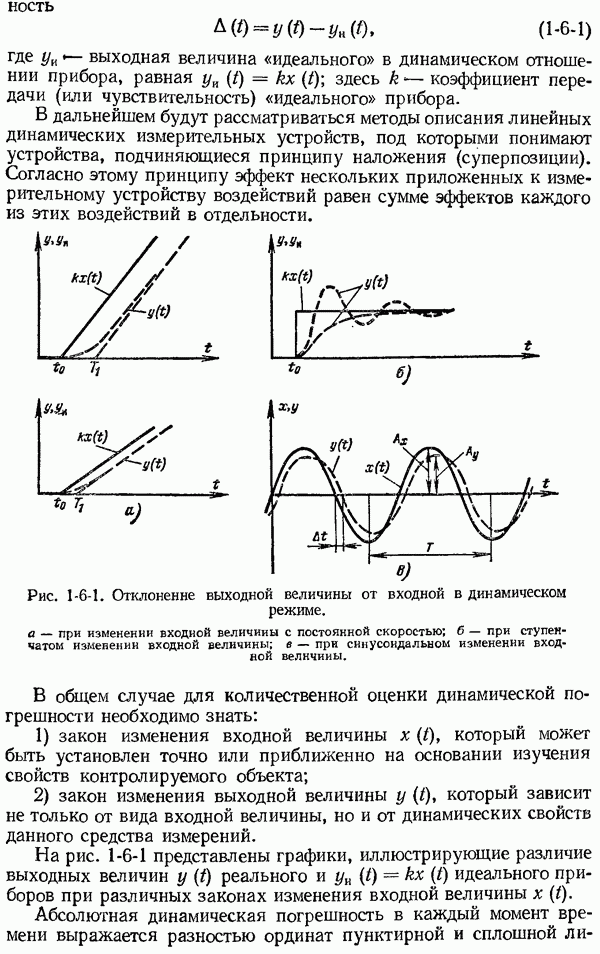
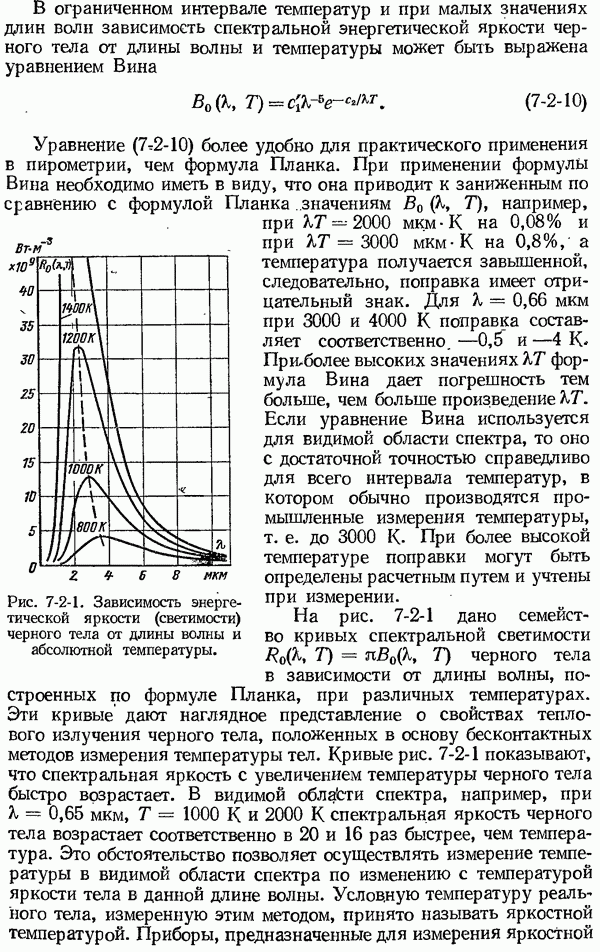
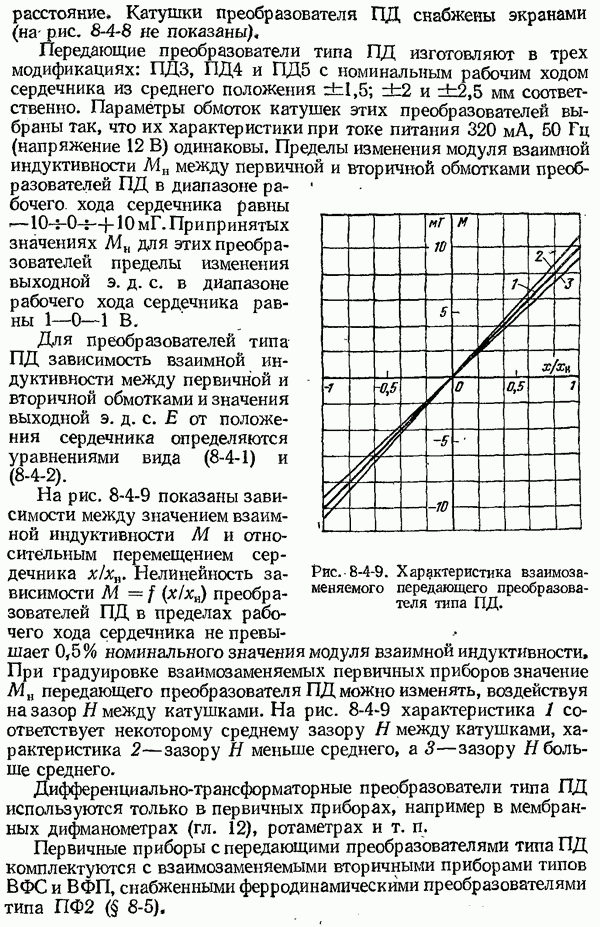
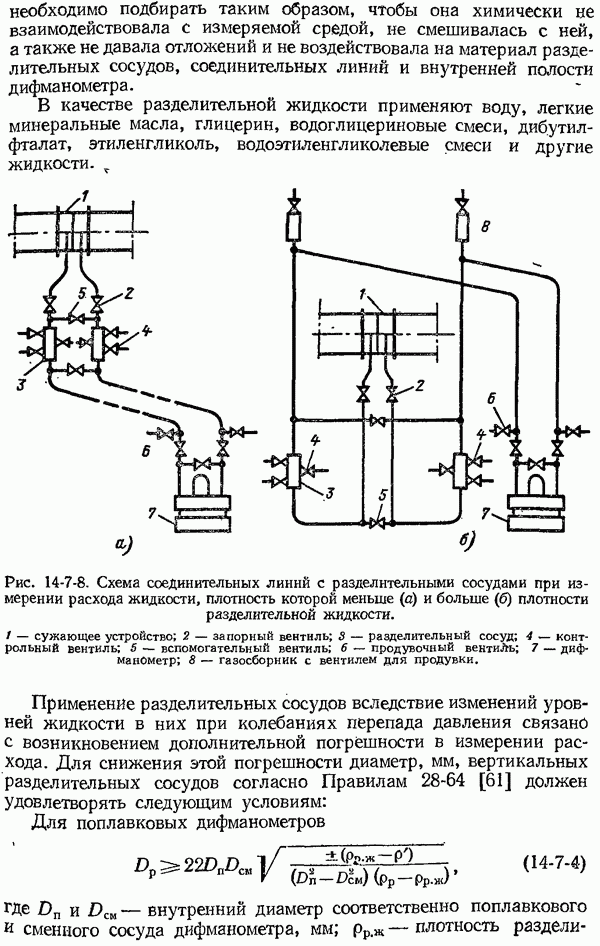
Рис. 7-2-1. Зависимость энергетической яркости (светимости) черного тела от длины волны и абсолютной температуры.
При-более высоких значениях  формула Вина дает погрешность тем больше, чем больше произведение
формула Вина дает погрешность тем больше, чем больше произведение  Если уравнение Вина используется для видимой области спектра, то оно с достаточной точностью справедливо для всего интервала температур, в котором обычно производятся промышленные измерения температуры, т. е. до 3000 К. При более высокой температуре поправки могут быть определены расчетным путем и учтены при измерении.
Если уравнение Вина используется для видимой области спектра, то оно с достаточной точностью справедливо для всего интервала температур, в котором обычно производятся промышленные измерения температуры, т. е. до 3000 К. При более высокой температуре поправки могут быть определены расчетным путем и учтены при измерении.
На рис. 7-2-1 дано семейство кривых спектральной светимости  черного тела в зависимости от длины волны, построенных по формуле Планка, при различных температурах. Эти кривые дают наглядное представление о свойствах теплового излучения черного тела, положенных в основу бесконтактных методов измерения температуры тел. Кривые рис. 7-2-1 показывают, что спектральная яркость с увеличением температуры черного тела быстро возрастает. В видимой области спектра, например, при
черного тела в зависимости от длины волны, построенных по формуле Планка, при различных температурах. Эти кривые дают наглядное представление о свойствах теплового излучения черного тела, положенных в основу бесконтактных методов измерения температуры тел. Кривые рис. 7-2-1 показывают, что спектральная яркость с увеличением температуры черного тела быстро возрастает. В видимой области спектра, например, при  К и 2000 К спектральная яркость черного тела возрастает соответственно в 20 и 16 раз быстрее, чем температура. Это обстоятельство позволяет осуществлять измерение температуры в видимой области спектра по изменению с температурой яркости тела в данной длине волны. Условную температуру реального тела, измеренную этим методом, принято называть яркостной температурой. Приборы, предназначенные для измерения яркостной
К и 2000 К спектральная яркость черного тела возрастает соответственно в 20 и 16 раз быстрее, чем температура. Это обстоятельство позволяет осуществлять измерение температуры в видимой области спектра по изменению с температурой яркости тела в данной длине волны. Условную температуру реального тела, измеренную этим методом, принято называть яркостной температурой. Приборы, предназначенные для измерения яркостной
температуры в видимои области спектра, обычно называют оптическими и фотоэлектрическими пирометрами.
Из кривых, представленных на рис. 7-2-1, видно, что по мере уменьшения температуры черного тела максимум распределения энергии его излучения смещается в сторону длинноволновой области спектра. Это и явилось основанием использовать для измерения яркостной температуры тел инфракрасную область спектра, выделяя из нее сравнительно неширокий рабочий спектральный участок. Используя инфракрасную область спектра, представляется возможность обеспечить измерение яркостных температур тел более низких, чем в видимой области спектра.
При выборе спектрального участка необходимо учитывать, что по мере возрастания длин волн и понижения температуры коэффициент излучения для большинства металлов снижается. Кроме того, при выборе рабочего интервала в инфракрасной области спектра необходимо также учитывать, что некоторые участки спектра претерпевают в воздушном слое между прибором и излучателем замег-ное поглощение. Основными компонентами в воздухе, создающими заметное поглощение лучистой энергии в некоторых участках инфракрасной области спектра, являются водяные пары и углекислый газ.
Как видно из рис. 7-2-1, с повышением температуры максимум кривой распределения энергии излучения по спектру смещается в сторону коротких волн. Длина волны Ямакс, соответствующая максимуму кривой распределения энергии в спектре излучения черного тела, связана с абсолютной температурой  соотношением
соотношением

где  постоянная, равная
постоянная, равная 
Соотношение (7-2-11) носит название закона смещения Вина. Пунктирная линия (рис. 7-2-1), проходящая через максимумы всех кривых, - соответствует закону смещения Вина.
В видимой части спектра смещение  следовательно, перераспределение энергии, вызываемое изменением температуры тела, приводит к изменению его цвета. Это и послужило основанием существующие методы измерения температур тел, основанные на изменении с температурой распределения энергии внутри данного участка спектра излучения, называть цветовыми методами. Условная температура тела, измеренная этими методами, называется цветовой температурой.
следовательно, перераспределение энергии, вызываемое изменением температуры тела, приводит к изменению его цвета. Это и послужило основанием существующие методы измерения температур тел, основанные на изменении с температурой распределения энергии внутри данного участка спектра излучения, называть цветовыми методами. Условная температура тела, измеренная этими методами, называется цветовой температурой.
Наибольшее распространение из существующих получил метод измерения цветовой температуры в видимой области спектра по отношению энергетических яркостей в двух спектральных интервалах. Этот метод измерения цветовой температуры реальных тел может быть перенесен и на инфракрасную область спектра. В этом случае термин «цветовая температура» будет иметь чисто условный смысл, указывающий на метод измерения этой величины. Приборы, предназначенные для измерения цветовой температуры по
отношению спектральных энергетических яркостей, прин то называть Пирометрами спектрального отношения или цветовыми пирометрами.
Цветовая температура может быть измерена путём сравнения цвета реального тела с цветом черного тела, или сравнением в данной области спектра распределения энергии излучения рассматриваемого реального и черного тела. Последние два метода измерения цветовой температуры не получили широкого применения и поэтому ниже рассматриваться не будут.
Возвращаясь к кривым рис. 7-2-1, легко заметить, что полная мощность излучения черного тела по всему спектру от  до
до  при температуре
при температуре  может быть определена по формуле Планка (7-2-8)
может быть определена по формуле Планка (7-2-8)

Интегрируя, приходим к выражению

где  постоянная, равная
постоянная, равная 
Выражение (7-2-12) широко применяется и называется законом Стефана-Больцмана для полной энергетической светимости. Пользуясь формулой Планка (7-2-9), аналогично предыдущему получим выражение закона Стефана—Больцмана для интегральной энергетической яркости

Постоянная об связана с постоянной  соотношением
соотношением 
Закон Стефана-Больцмана положен в основу метода измерения температур тел по их полному тепловому излучению. Условную температуру реального тела, измеренную этим методом, принято называть радиационной температурой или температурой полного излучения. Пирометры, предназначенные для измерения радиационной температуры, обычно называют пирометрами полного излучения или радиационными.
Как уже отмечалось, зависимость от температуры спектральной энергетической яркости излучения черного тела определяется формулой Планка или Вина в виде (7-2-9) и (7-2-10), справедливом для монохроматического излучения. При использовании этих формул для установления соотношения между условными (яркостной и цветовой) температурами необходимо иметь в виду, что строго монохроматических излучений в природе не существует. Любое измеряемое излучение с помощью точных спектральных приборов, как бы мал ни был спектральный интервал, имеющий конечную ширину, является квазимонохроматическим. Это излучение в ряде случаев можно рассматривать как эквивалентное монохроматическое с определенным значением длины волны  находящимся внутри выбранного конечного спектрального интервала и остающимся
находящимся внутри выбранного конечного спектрального интервала и остающимся
постоянным в диапазоне температур от  до 2 с заданной погрешностью, Длина волны
до 2 с заданной погрешностью, Длина волны  эквивалентного монохроматического излучения называется в пирометрии эффективной длиной волны. Методика расчета или определения эффективных длин волн монохроматизирующих устройств подробно излагается в монографиях, посвященных пирометрии.
эквивалентного монохроматического излучения называется в пирометрии эффективной длиной волны. Методика расчета или определения эффективных длин волн монохроматизирующих устройств подробно излагается в монографиях, посвященных пирометрии.
Далее уточним понятия условных (яркосгной, цветовой, радиационной) температур и выведем уравнения, позволяющие осуществить переход от условных температур реальных тел к их действительной температуре.
Яркостная температура. Яркосгной температурой реального тела  в свете длины волны
в свете длины волны  называется такая температура черного тела, при которой спектральные энергетические яркости реального тела, имеющего температуру
называется такая температура черного тела, при которой спектральные энергетические яркости реального тела, имеющего температуру  и черного тела в лучах той же длины волны равны между собой. Согласно этому определению яркостной температуры с учетом выражения (7-2-7) имеем:
и черного тела в лучах той же длины волны равны между собой. Согласно этому определению яркостной температуры с учетом выражения (7-2-7) имеем:

Подставив в это уравнение значения спектральных яркостей по формуле (7-2-10), получим:

После сокращения подобных членов и логарифмирования последнее выражение принимает вид:

Это уравнение при условии  позволяет вычислить действительную температуру физического тела
позволяет вычислить действительную температуру физического тела  зная его спектральный коэффициент излучения
зная его спектральный коэффициент излучения  и яркостную температуру 6, измеренную пирометром. Яркостная температура 6 тем больше отличается от действительной
и яркостную температуру 6, измеренную пирометром. Яркостная температура 6 тем больше отличается от действительной  чем меньше спектральный коэффициент излучения
чем меньше спектральный коэффициент излучения  Так как
Так как  то правая часть уравнения (7-2-14) всегда положительна и яркостная температура физических тел всегда меньше их действительной температуры.
то правая часть уравнения (7-2-14) всегда положительна и яркостная температура физических тел всегда меньше их действительной температуры.
Если измерение температур тел производится в области значений  в которой формула (7-2-14) не обеспечивает необходимую точность определения
в которой формула (7-2-14) не обеспечивает необходимую точность определения  то для получения соотношения между действительной температурой реального тела и его яркостной температурой используют формулу, следующую из уравнения Планка
то для получения соотношения между действительной температурой реального тела и его яркостной температурой используют формулу, следующую из уравнения Планка

Цветовая температура. Цветовой температурой реального тела  называется такая температура черного тела, при которой отношение энергетических яркостей его при двух эффективных длинах волн и равно отношению энергетических яркостей реального тела, обладающего температурой
называется такая температура черного тела, при которой отношение энергетических яркостей его при двух эффективных длинах волн и равно отношению энергетических яркостей реального тела, обладающего температурой  при тех же длинах волн.
при тех же длинах волн.
Согласно этому определению цветовой температуры с учетом выражения (7-2-7) имеем:

Учитывая уравнение (7-2-10), на основании (7-2-16) получим:

После сокращения подобных членов и логарифмирования последнее соотношение принимает вид:

Эта формула позволяет вычислить действительную температуру реального тела  зная значение отношения его спектральных коэффициентов излучения и
зная значение отношения его спектральных коэффициентов излучения и  и цветовую температуру
и цветовую температуру  намеренную пирометром.
намеренную пирометром.
Для серых тел, у которых значение спектрального коэффициента излучения в данном участке спектра не меняется с длиной волны  правая часть формулы (7-2-17) обращается в нуль и поэтому цветовая температура
правая часть формулы (7-2-17) обращается в нуль и поэтому цветовая температура  таких тел равна их действительной температуре.
таких тел равна их действительной температуре.
Следует отметить, что при температурах выше 1000°С излучение большого количества окислов и карбидов металлов практически серое. В частности, серый характер обычно имеет излучение окисных пленок (ванадия, хрома, кремния и т. п.) на поверхности стальной ванны. Это подтверждает преимущество цветового метода, так как яркостная и радиационная температура всегда, в отличие от цветовой, ниже действительной.
Для тел, у которых спектральный коэффициент черноты излучения убывает с ростом длины волны  (большинство металлов), цветовая температура больше действительной температуры. Для тел, у которых спектральный коэффициент черноты излучения возрастает по мере роста длины волны
(большинство металлов), цветовая температура больше действительной температуры. Для тел, у которых спектральный коэффициент черноты излучения возрастает по мере роста длины волны  (многие неметаллические тела), цветовая температура меньше действительной.
(многие неметаллические тела), цветовая температура меньше действительной.
Следует отметить, что уравнение (7-2-17) может быть использовано, для перехода от измеренной цветовой температуры реального тела к его действительной температуре только в пределах применимости формулы Вина. Для получения уравнения, свободного от ограничений при переходе от цветовой температуры тела к его действительной температуре, необходимо в выражение (7-2-16) подставлять значения спектральных яркостей по формуле Планка,
Цветовую температуру тела  можно выразить через яркостные температуры и
можно выразить через яркостные температуры и  того же тела, измеренные в лучах эффективных длин волн
того же тела, измеренные в лучах эффективных длин волн  Для нахождения связи яркостных температур тела
Для нахождения связи яркостных температур тела  и
и  в лучах длин волн и
в лучах длин волн и  с цветовой температурой того же тела
с цветовой температурой того же тела  измеренной при тех же длинах волн, представим выражение (7-2-16) в следующем виде:
измеренной при тех же длинах волн, представим выражение (7-2-16) в следующем виде:

Подставив в правую часть этого уравнения значения спектральных яркостей по формуле Вина, после сокращения и логарифмирования получим:

Формулу (7-2-18) используют в метрологической практике при градуировке на цветовые температуры образцовых излучателей, применяемых для градуировки цветовых пирометров.
Радиационная температура. Радиационной температурой реального тела  называется такая температура черного тела, при которой его полная мощность излучения равна полной энергии, излучаемой реальным телом при температуре
называется такая температура черного тела, при которой его полная мощность излучения равна полной энергии, излучаемой реальным телом при температуре  Согласно этому определению радиационной температуры с учетом выражения (7-2-6) имеем:
Согласно этому определению радиационной температуры с учетом выражения (7-2-6) имеем:

Учитывая формулу Стефана-Больцмана (7-2-12), получим:

откуда

Эта формула позволяет осуществлять переход к действительной температуре тела  зная коэффициент излучения и радиационную температуру
зная коэффициент излучения и радиационную температуру  измеренную пирометром. При определении
измеренную пирометром. При определении  по таблицам, приводимым в литературе, необходимо иметь в виду, что применяемые пирометры полного излучения (радиационные пирометры) не используют весь спектр от нуля до бесконечности. Поэтому выбранное значение
по таблицам, приводимым в литературе, необходимо иметь в виду, что применяемые пирометры полного излучения (радиационные пирометры) не используют весь спектр от нуля до бесконечности. Поэтому выбранное значение  должно соответствовать спектральной характеристике применяемого пирометра полного излучения. Так как для всех реальных тел
должно соответствовать спектральной характеристике применяемого пирометра полного излучения. Так как для всех реальных тел  то, как видно из формулы (7-2-19), радиационная температура тела всегда будет меньше его действительной температуры.
то, как видно из формулы (7-2-19), радиационная температура тела всегда будет меньше его действительной температуры.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
- 2-1. Основные сведения о температуре и температурных шкалах
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
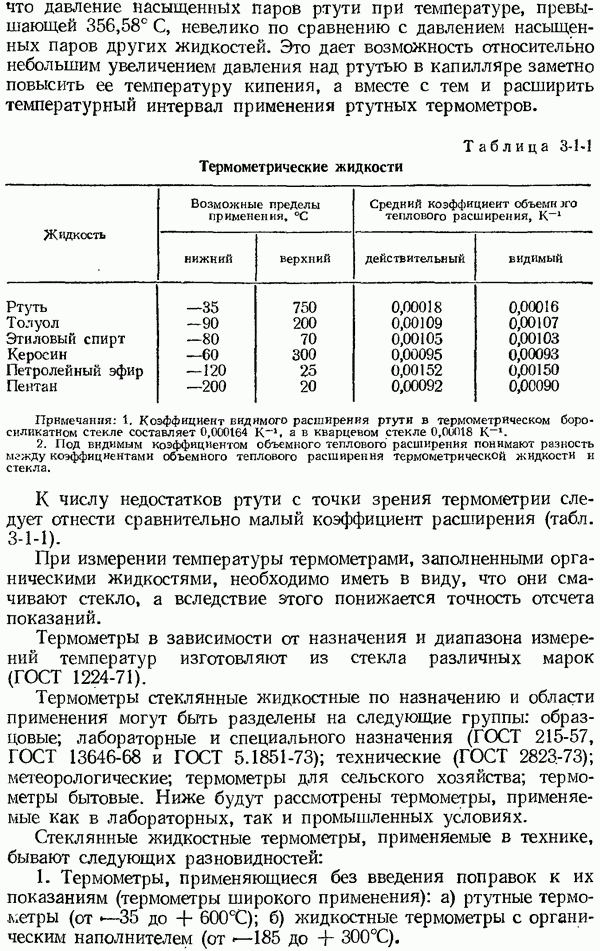
- 3-1. Термометры стеклянные жидкостные
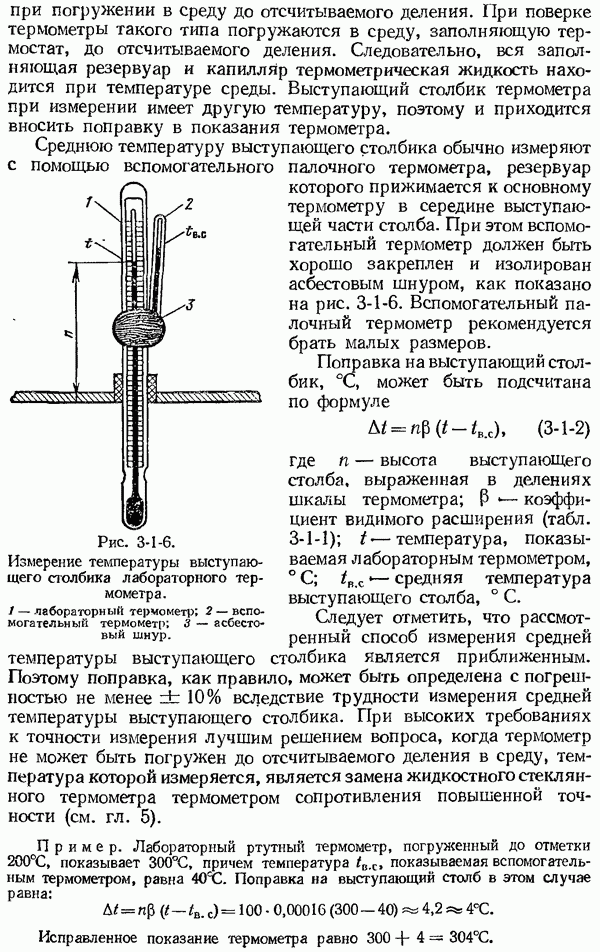
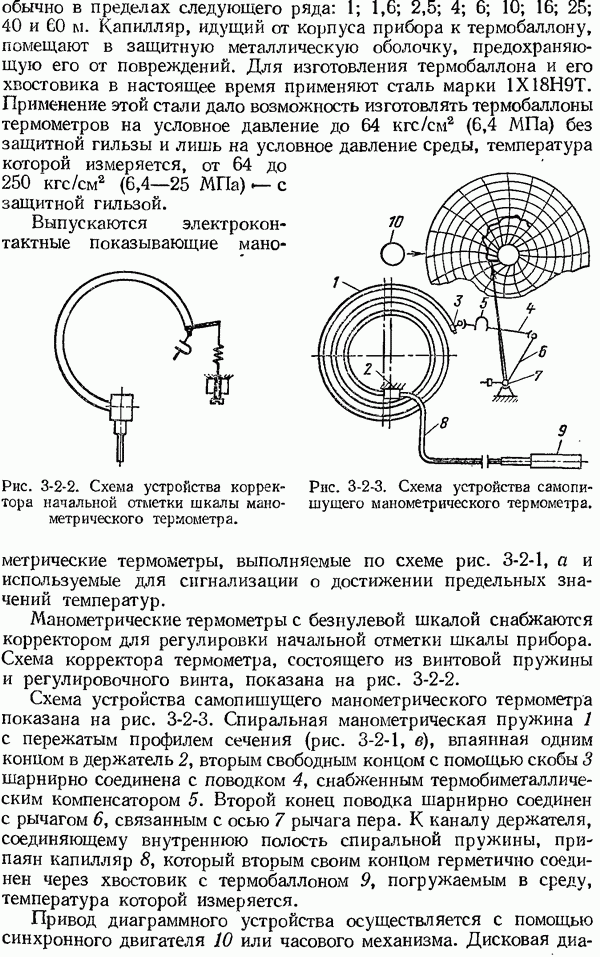
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
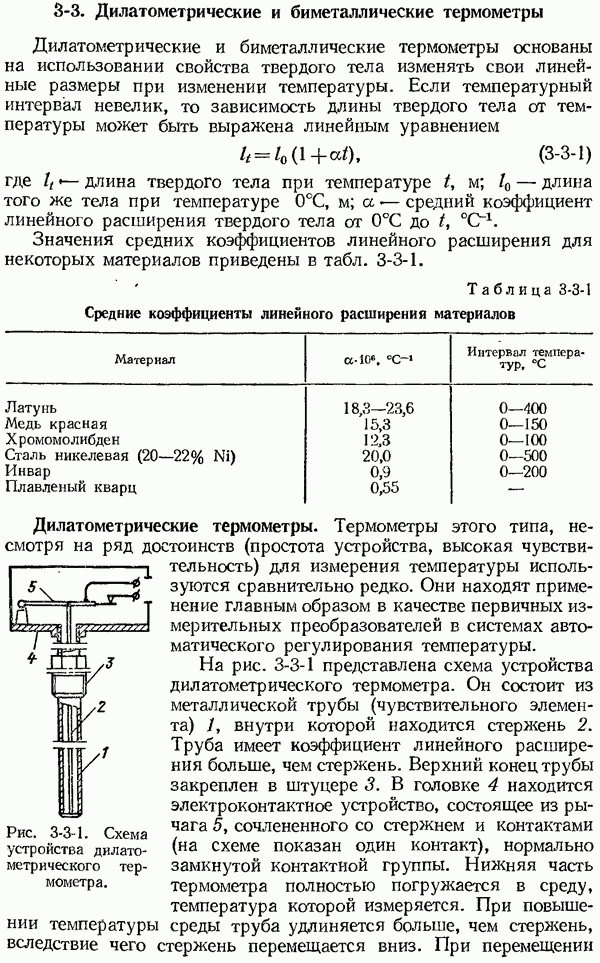
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
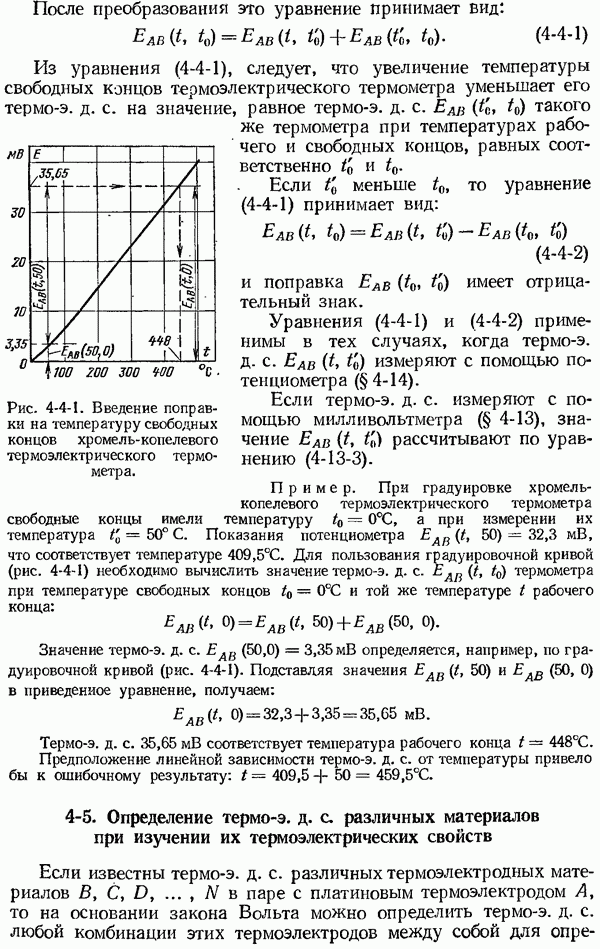
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
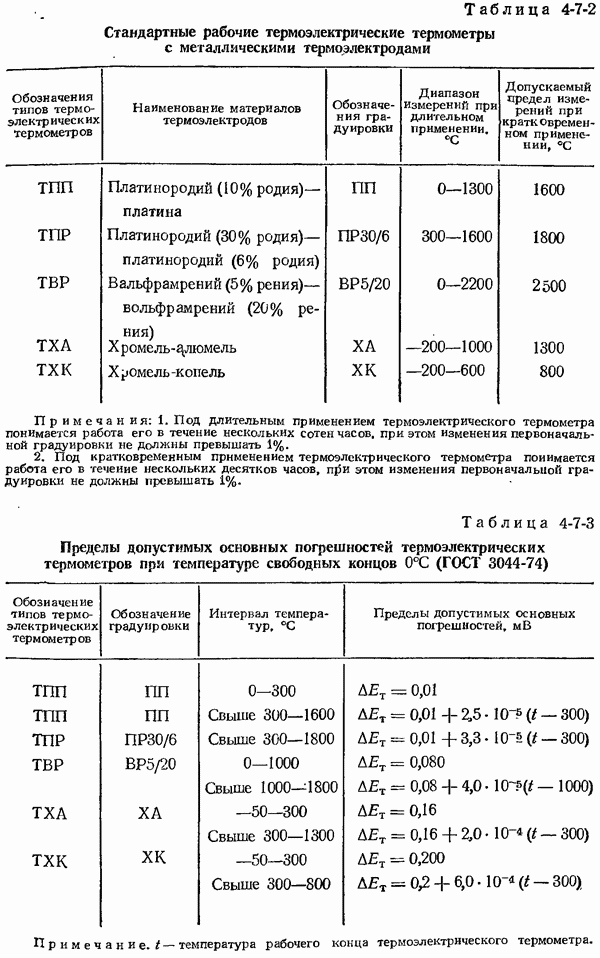
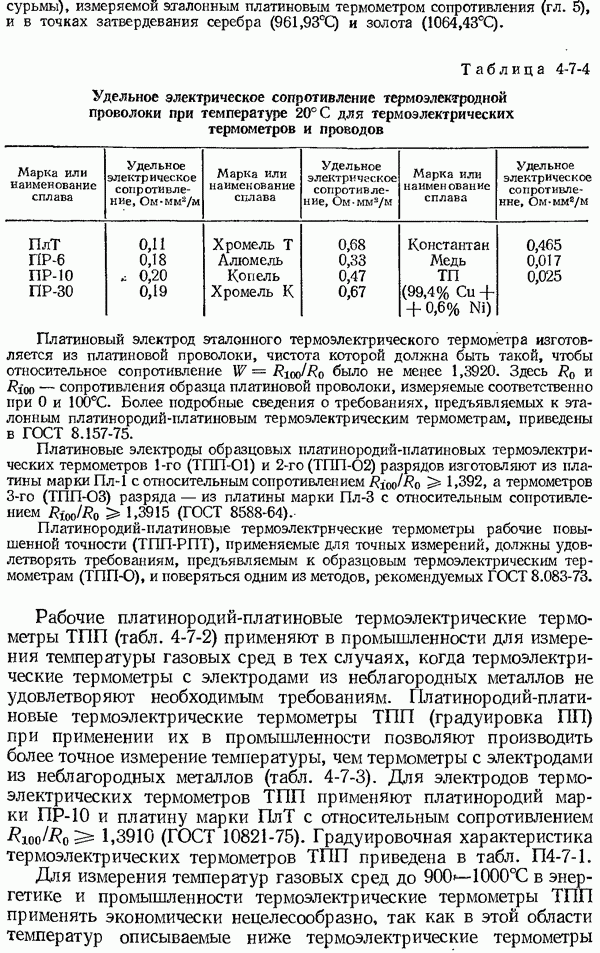
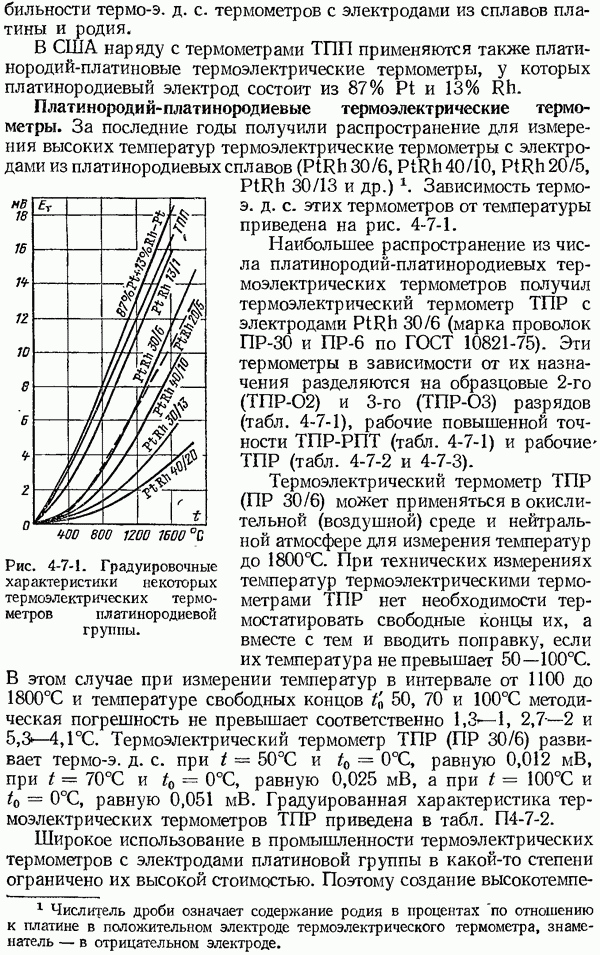
- 4-7. Общие сведения о термоэлектрических термометрах
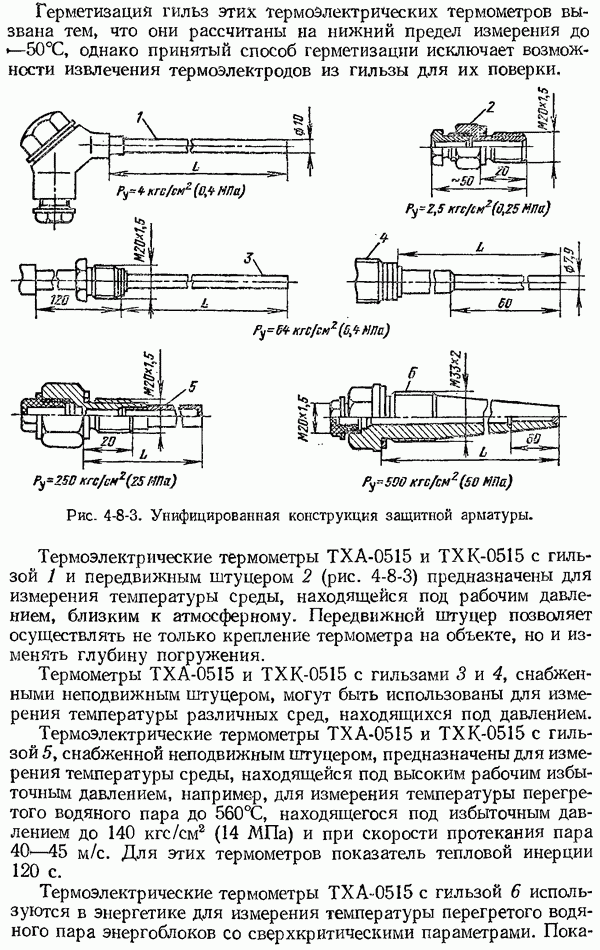
- 4-8. Устройство термоэлектрических термометров
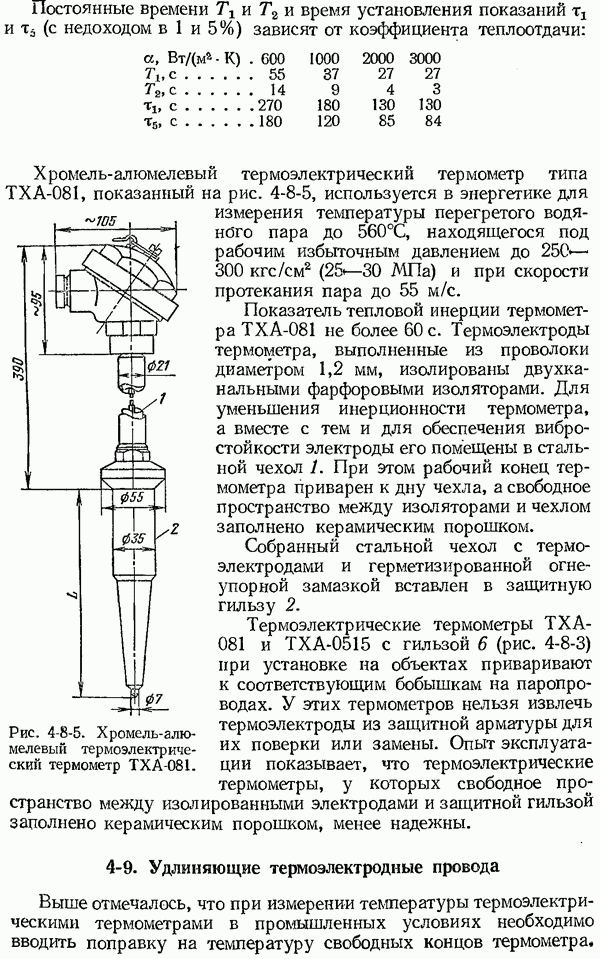
- 4-9. Удлиняющие термоэлектродные провода
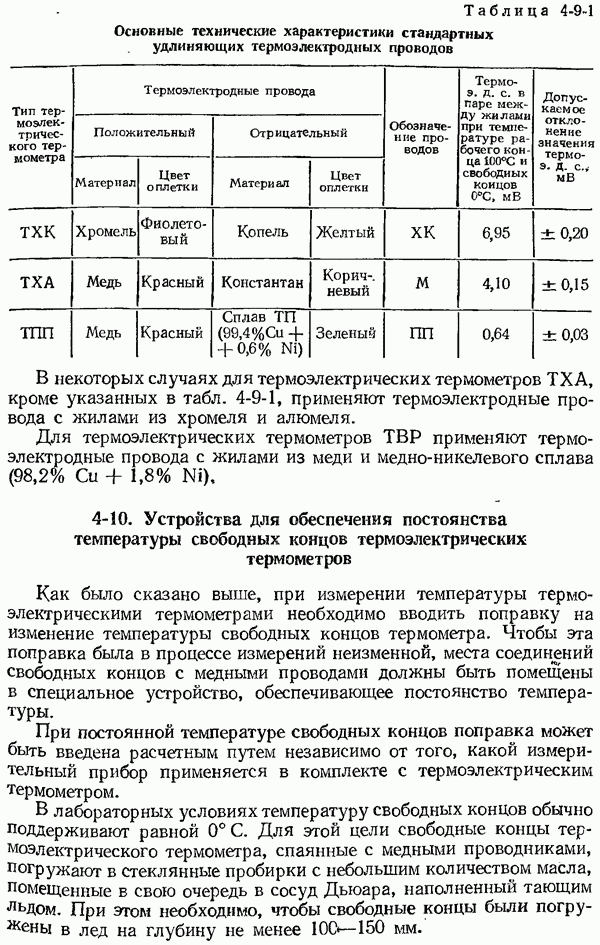
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
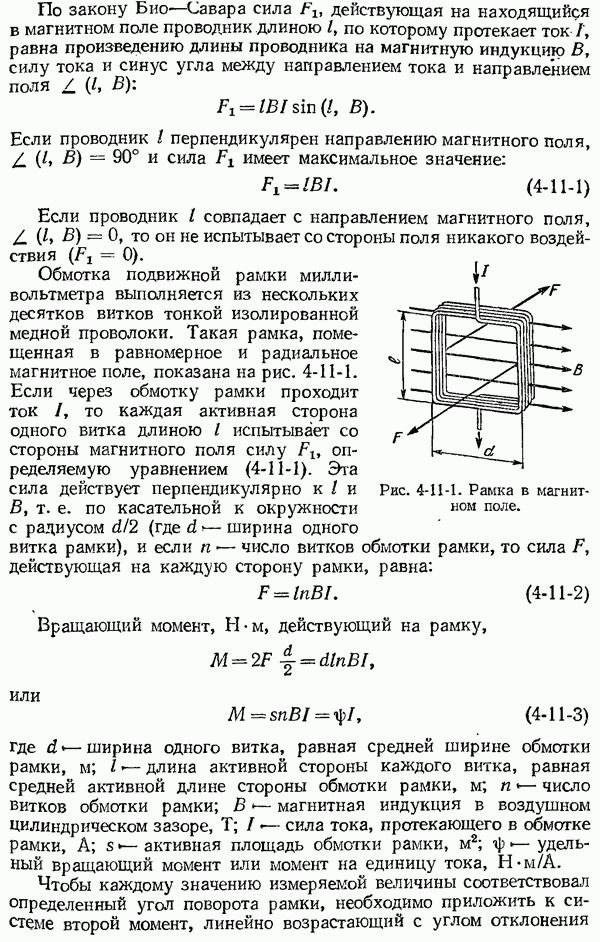
- 4-11. Милливольтметры
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
- 4-15. Нормальные элементы
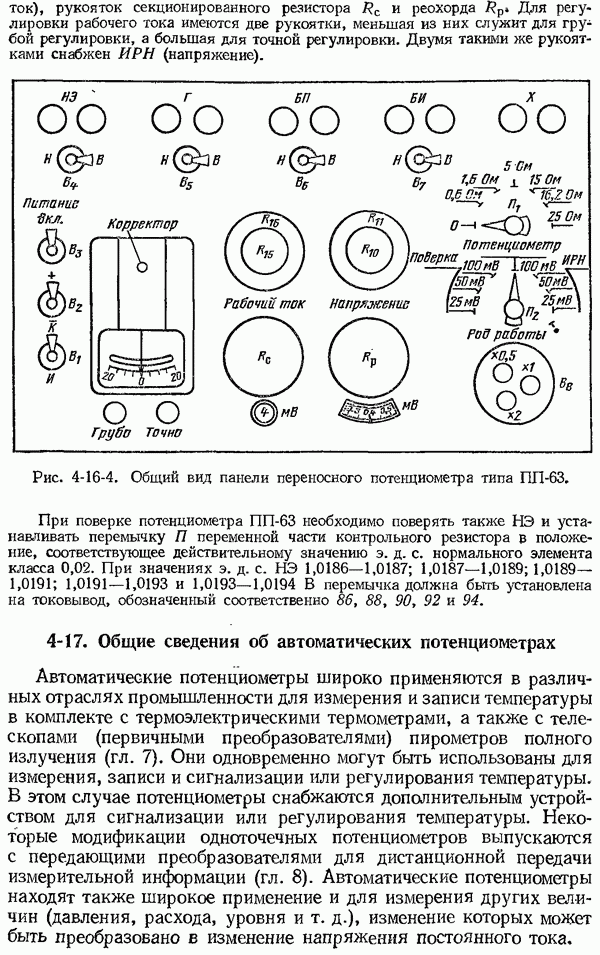
- 4-16. Потенциометры переносные и лабораторные
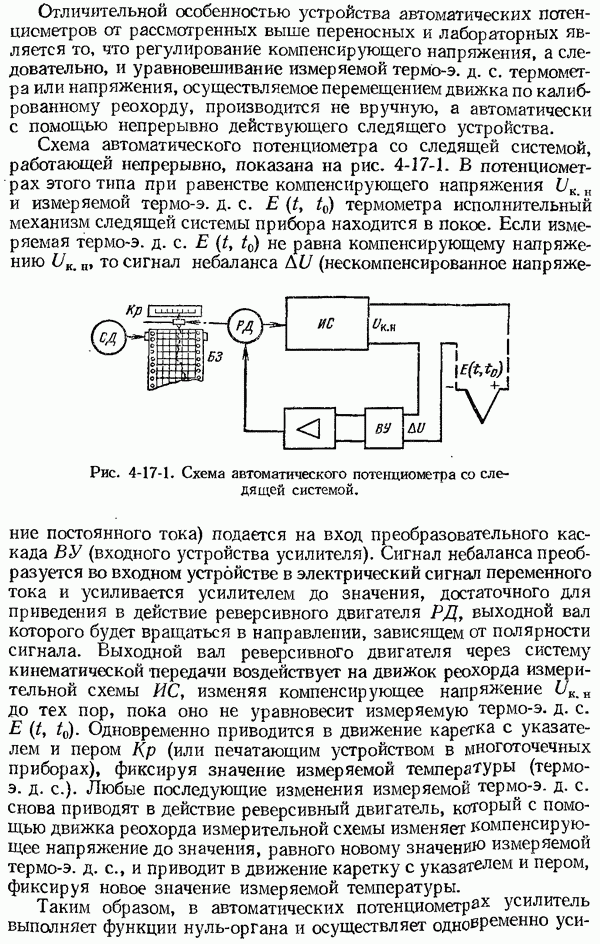
- 4-17. Общие сведения об автоматических потенциометрах
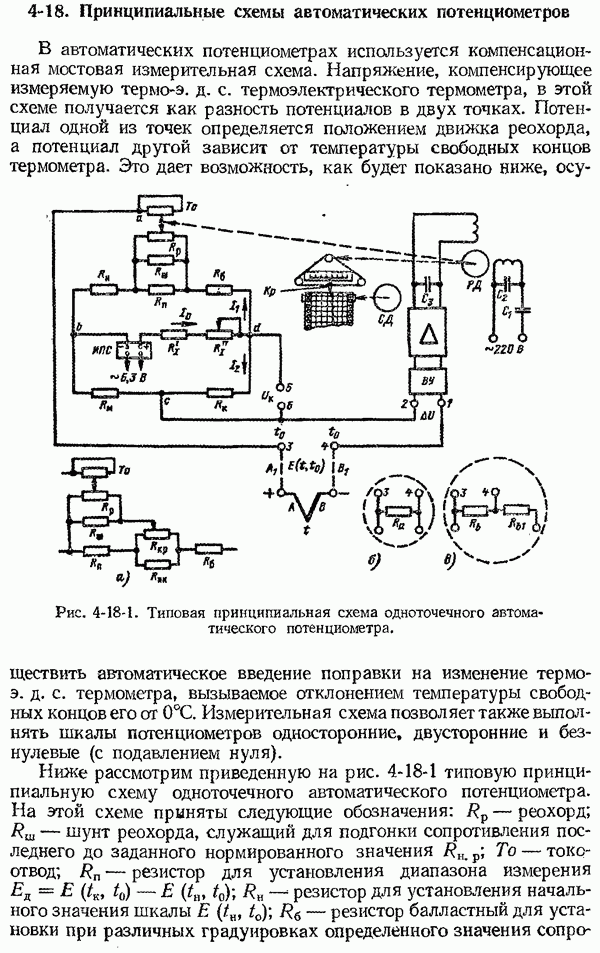
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
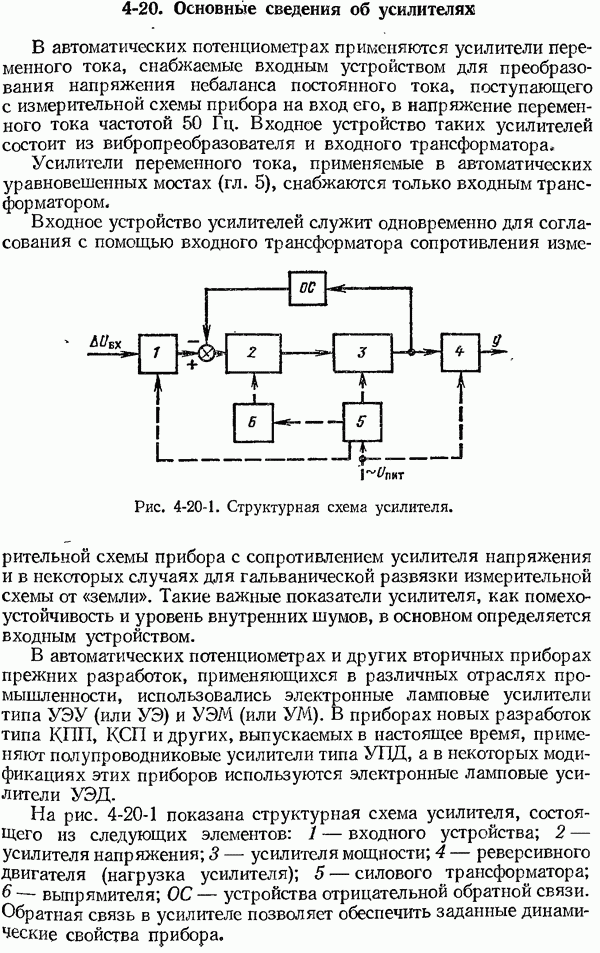
- 4-20. Основные сведения об усилителях
- 4-21. Основные сведения об источниках стабилизированного питания
- 4-22. Устройство автоматических потенциометров
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
- 5-3. Устройство платиновых и медных термометров сопротивления
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
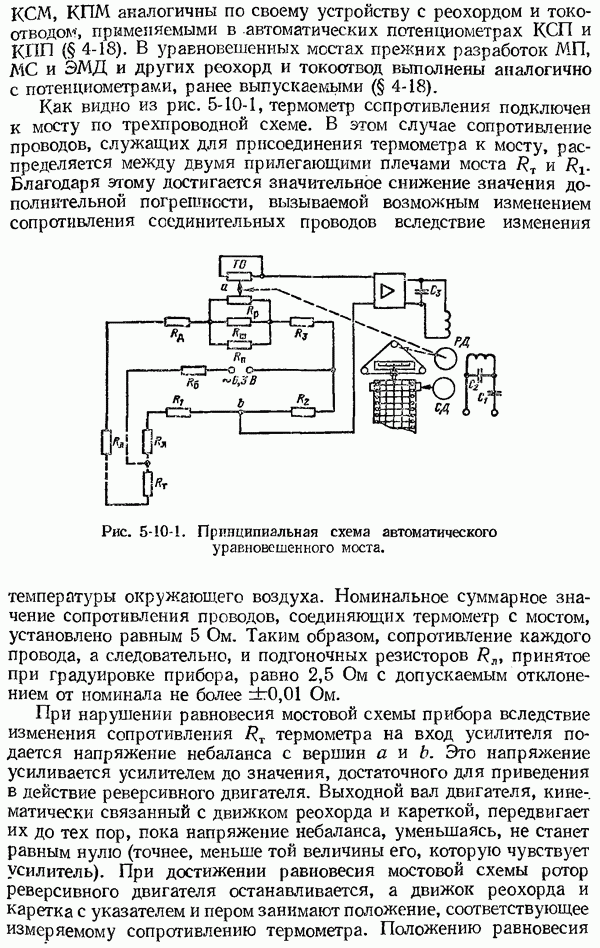
- 5-10. Принципиальная схема автоматического уравновешенного моста
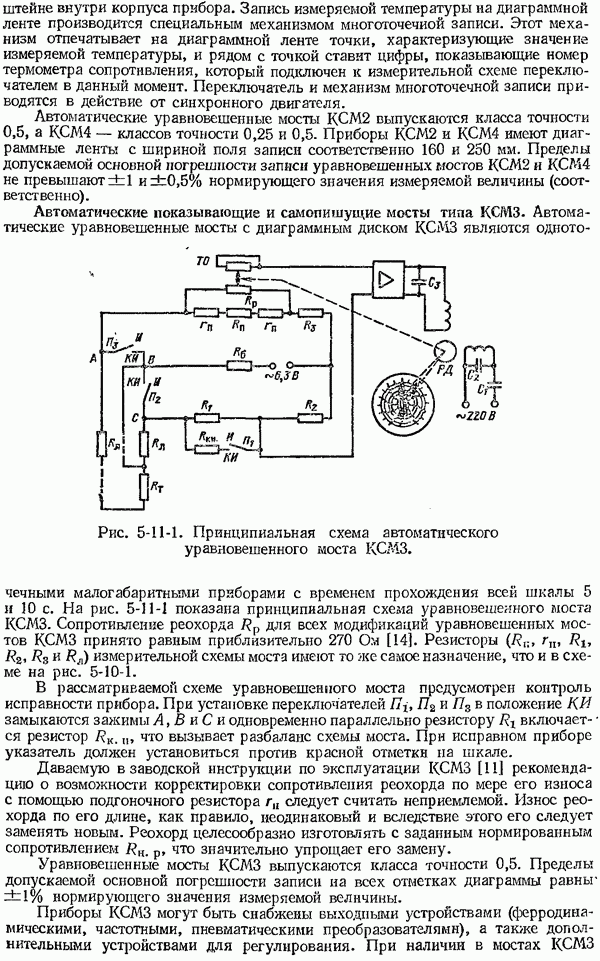
- 5-11. Устройство автоматических уравновешенных мостов
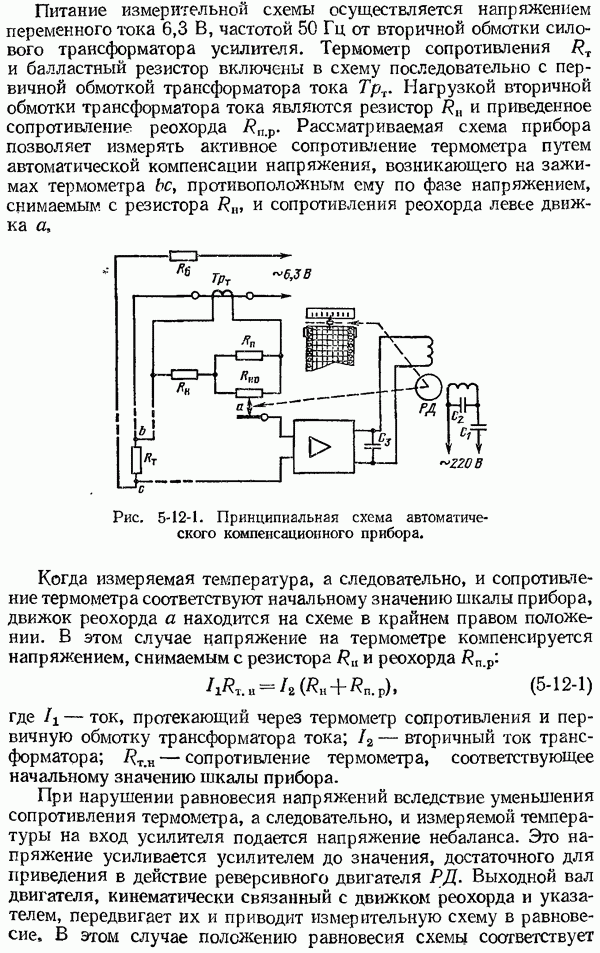
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
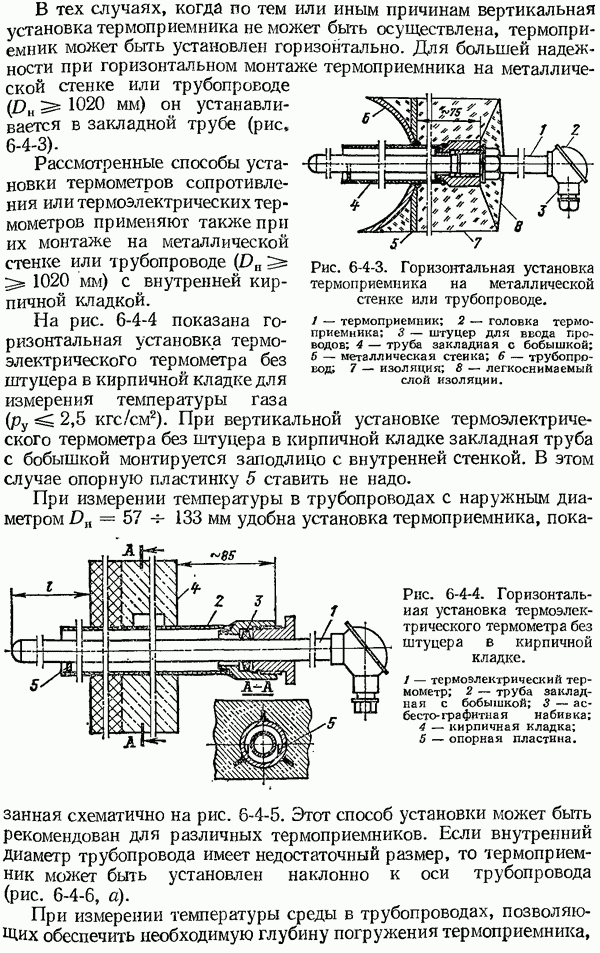
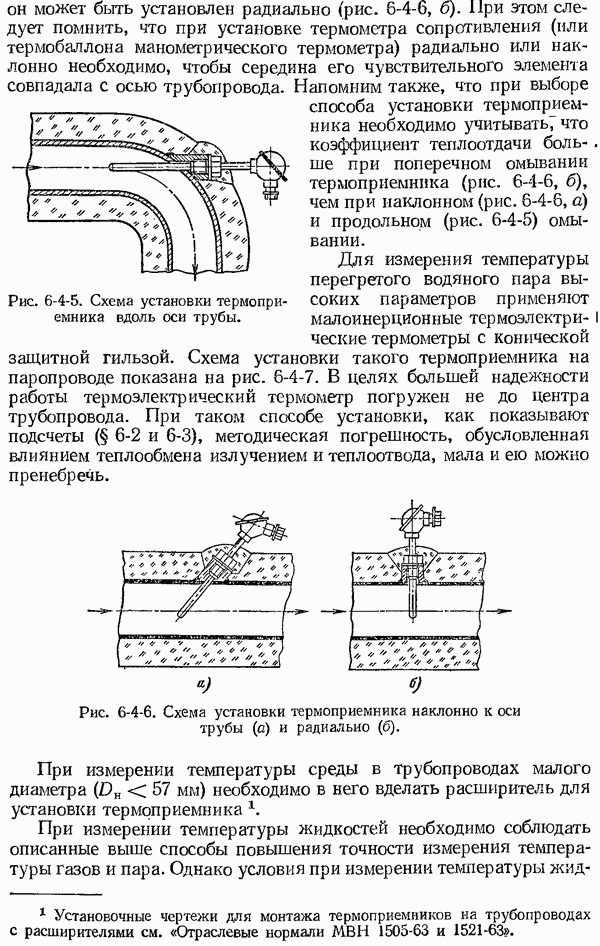
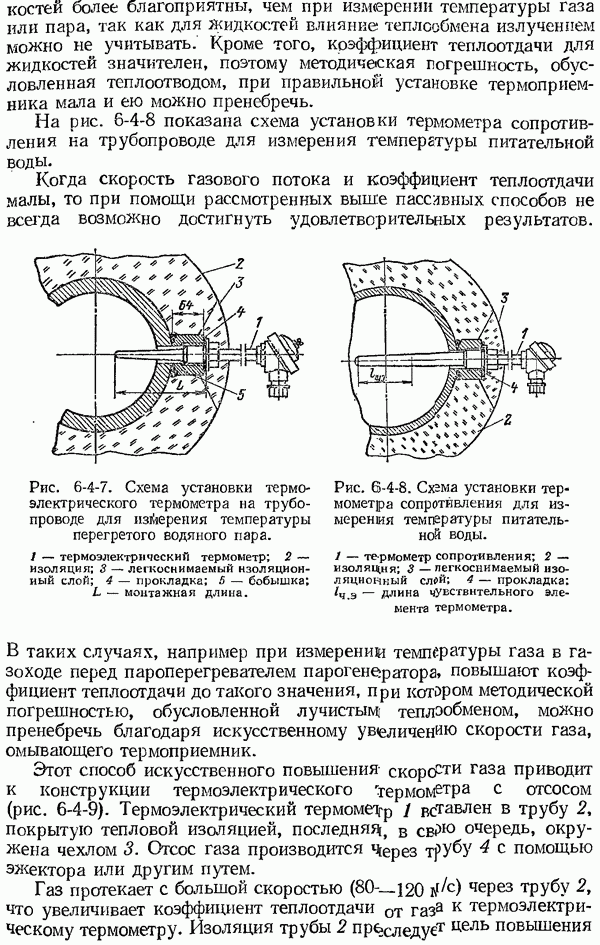
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
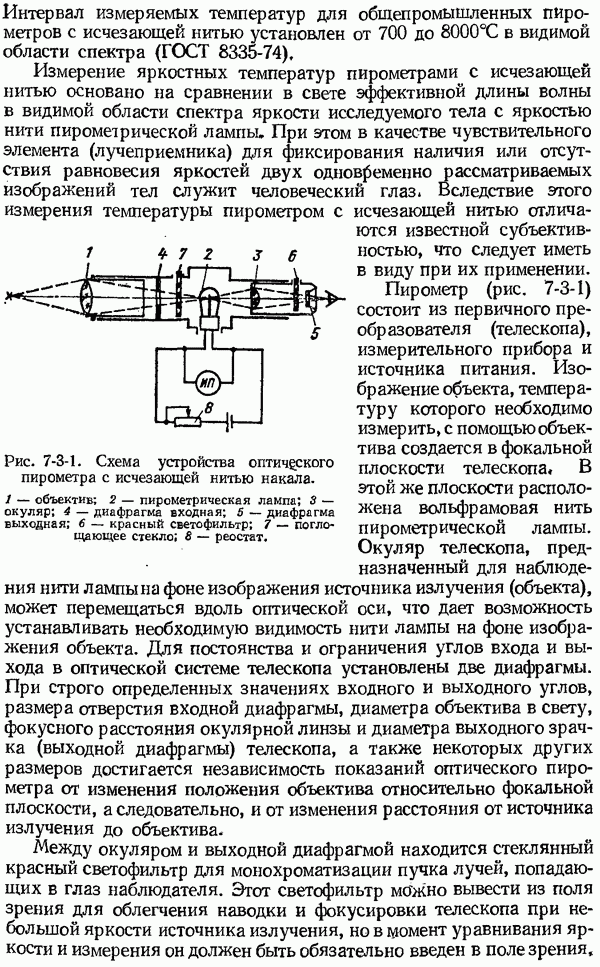
- 7-3. Оптические пирометры
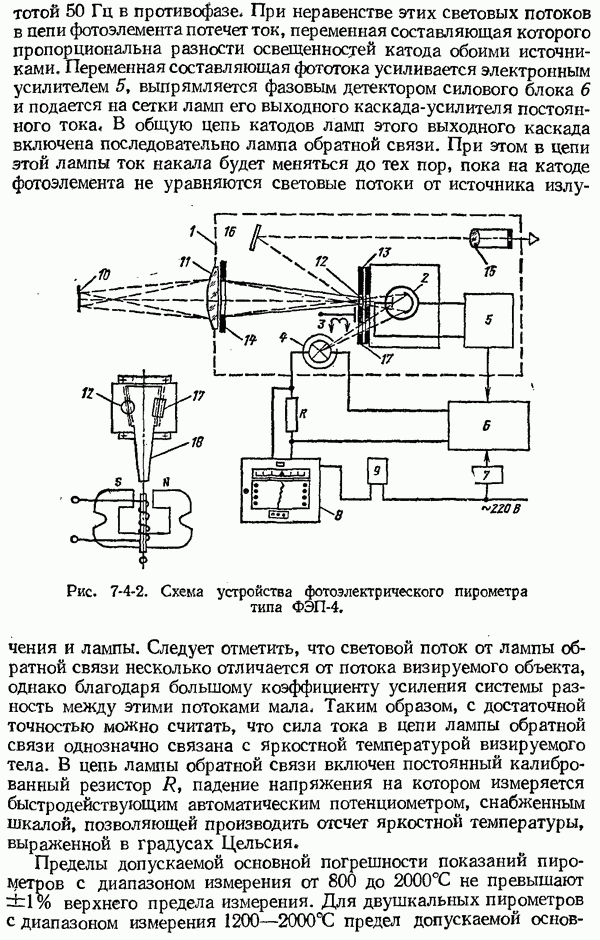
- 7-4. Фотоэлектрические пирометры
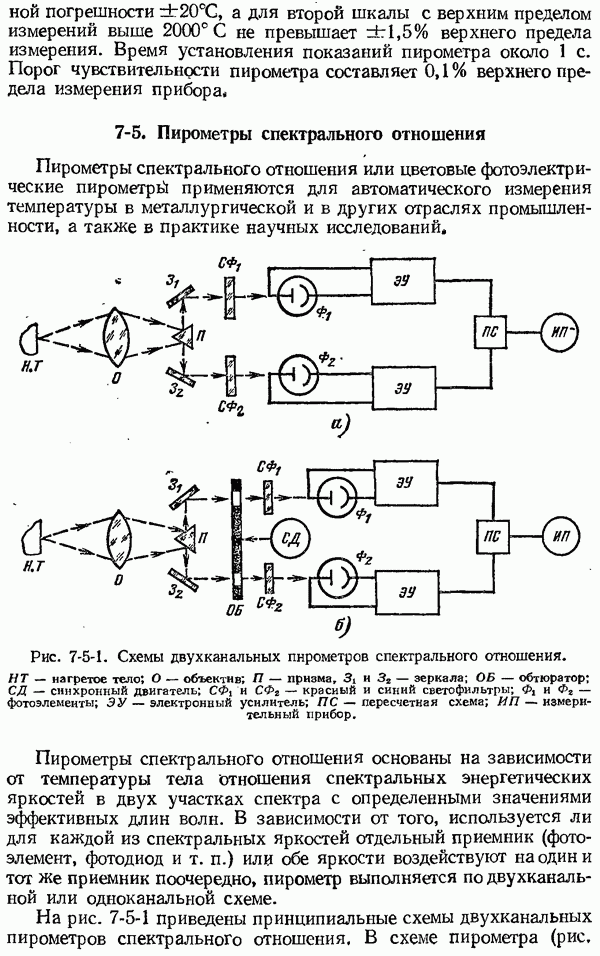
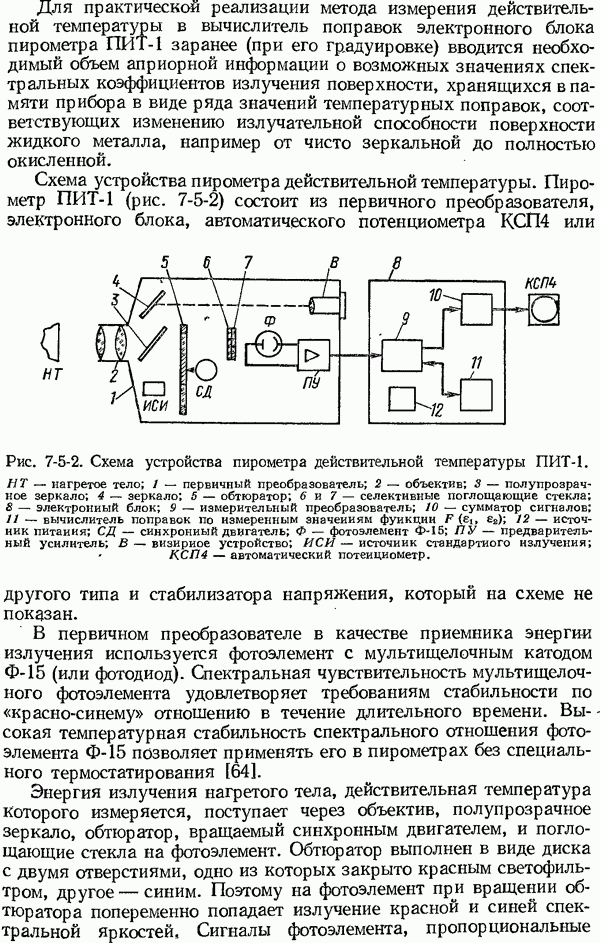
- 7-5. Пирометры спектрального отношения
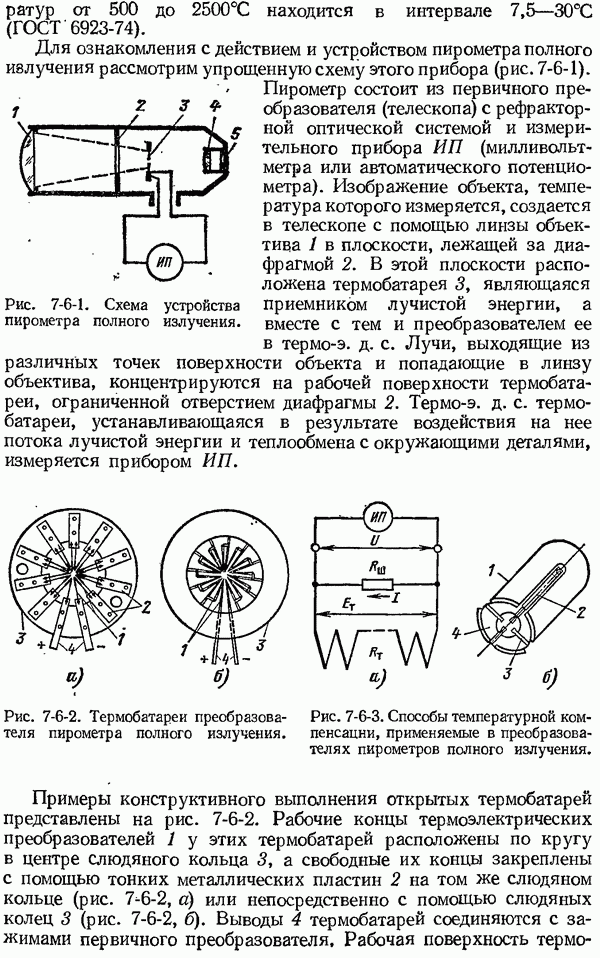
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
- 8-6. Механоэлектрические передающие преобразователи
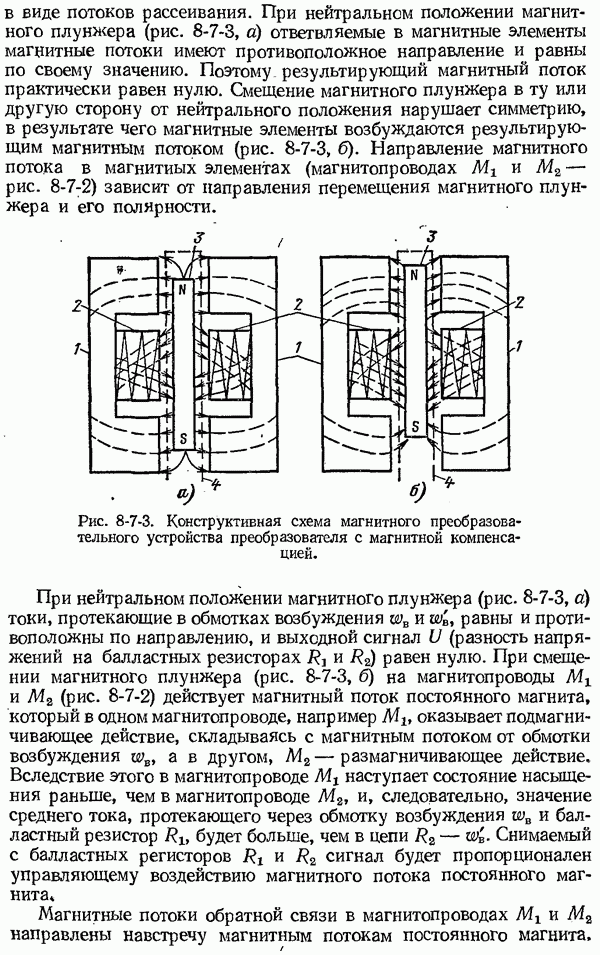
- 8-7. Передающие преобразователи с магнитной компенсацией
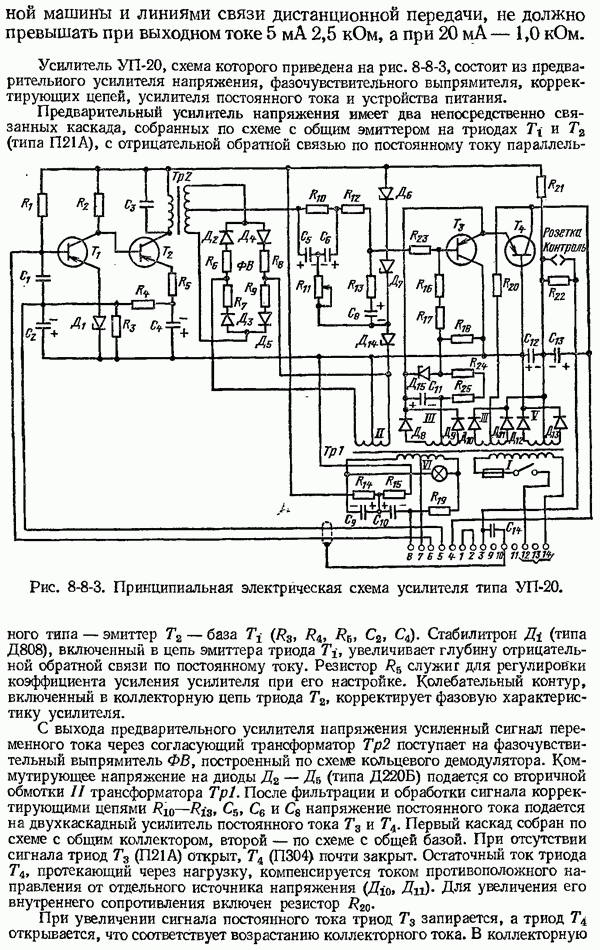
- 8-8. Электросиловые преобразователи
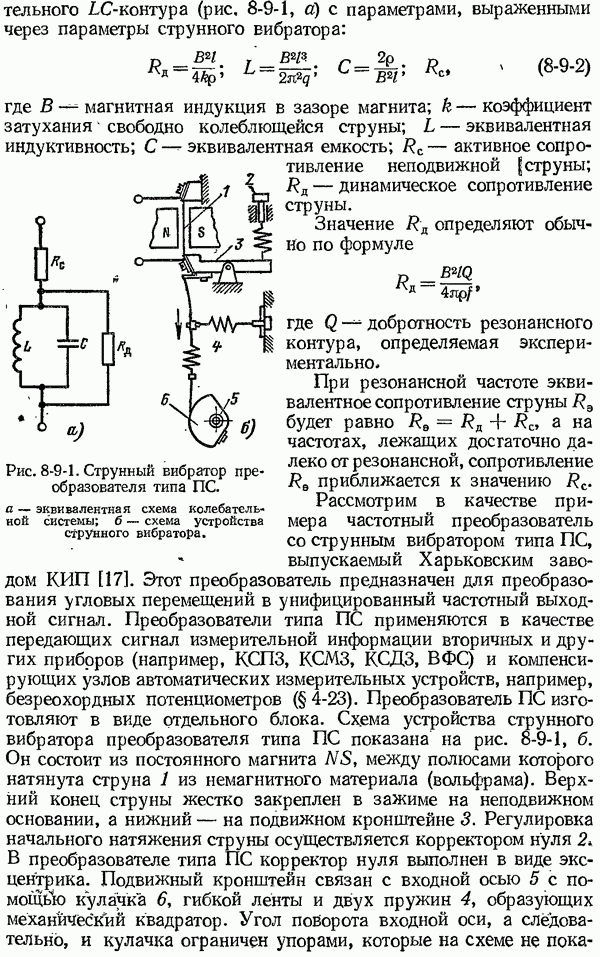
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
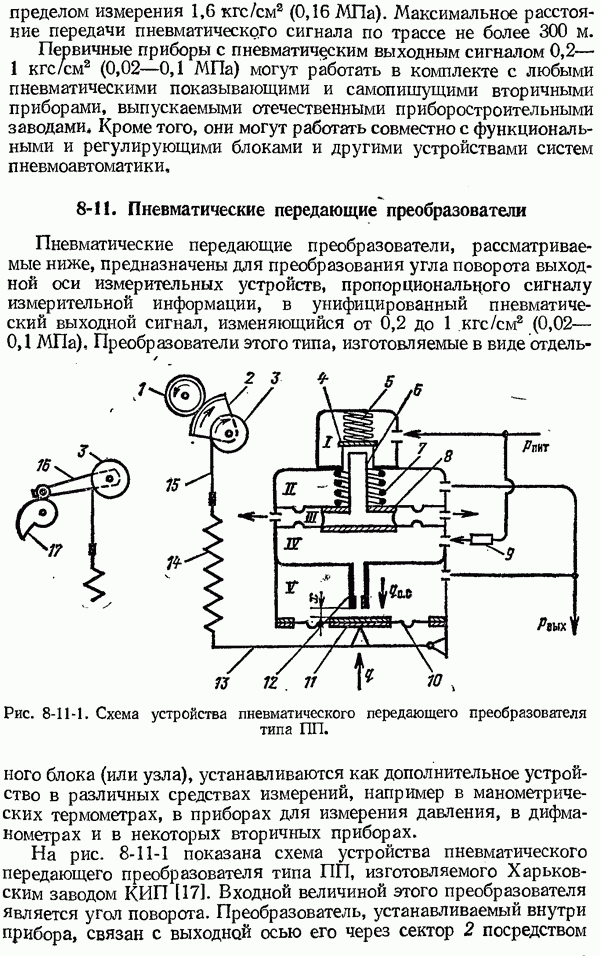
- 8-11. Пневматические передающие преобразователи
- 8-12. Электропневматические и пневмоэлектрические преобразователи
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
- 10-2. Упругие чувствительные элементы
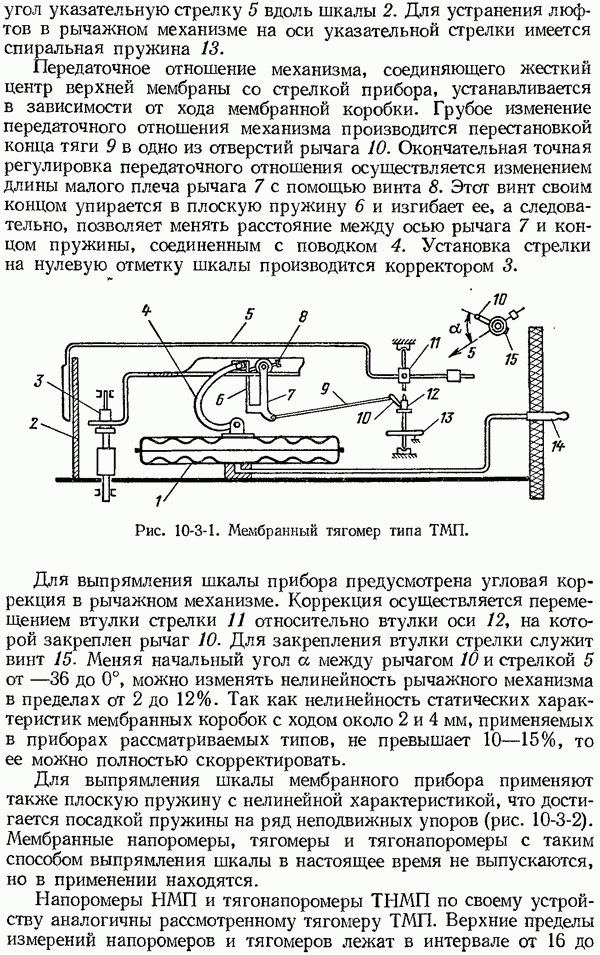
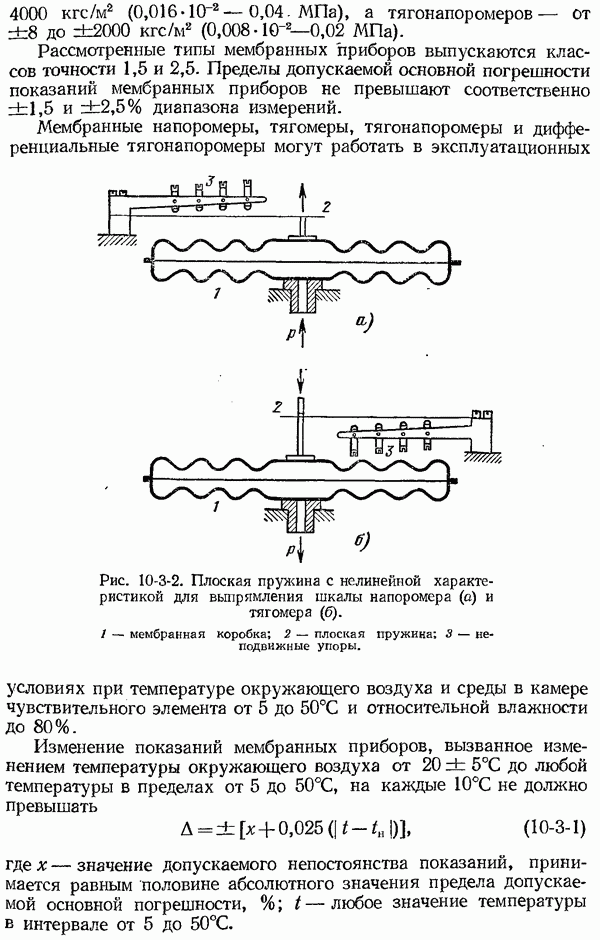
- 10-3. Приборы давления прямого действия
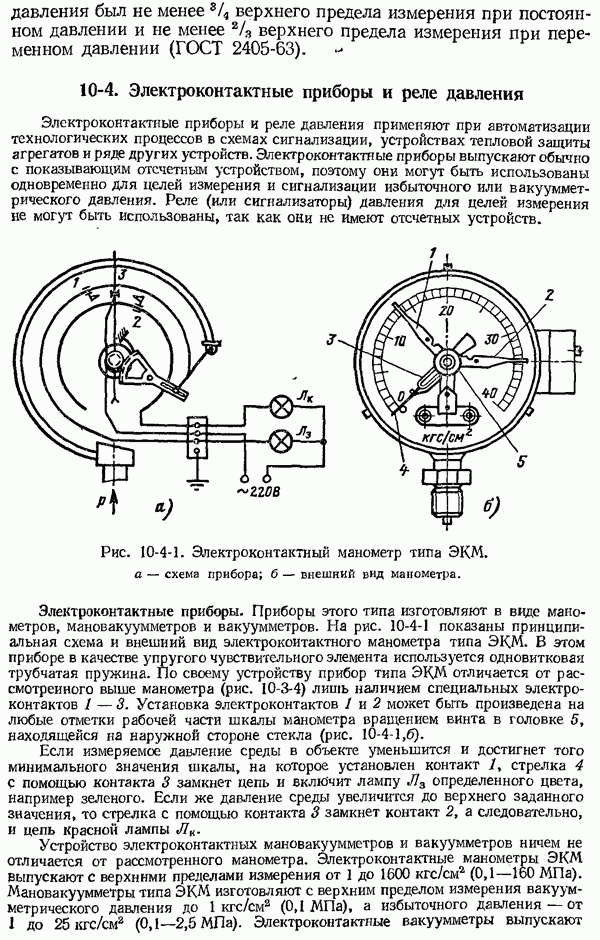
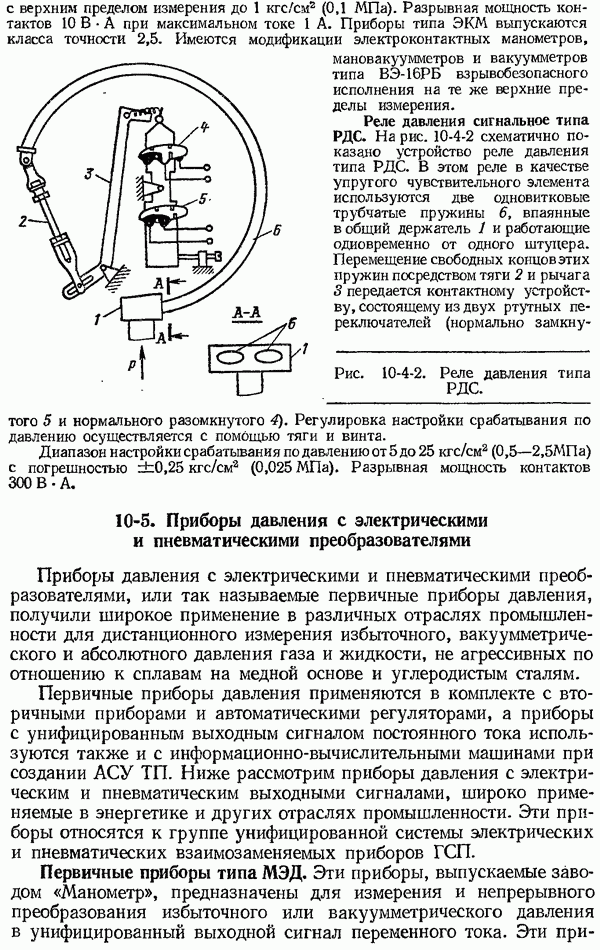
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 13-2. Измерение близкого к атмосферному давления газовых сред
- 13-3. Измерение давления газов, жидкостей и пара
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
- 14-1. Основы теории и уравнения расхода
- 14-2. Стандартные сужающие устройства
- 14-3. Коэффициенты расхода и поправочные множители к ним
- 14-4. Поправочный множитель на расширение измеряемой среды
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
- 14-8. Погрешности измерения расхода
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
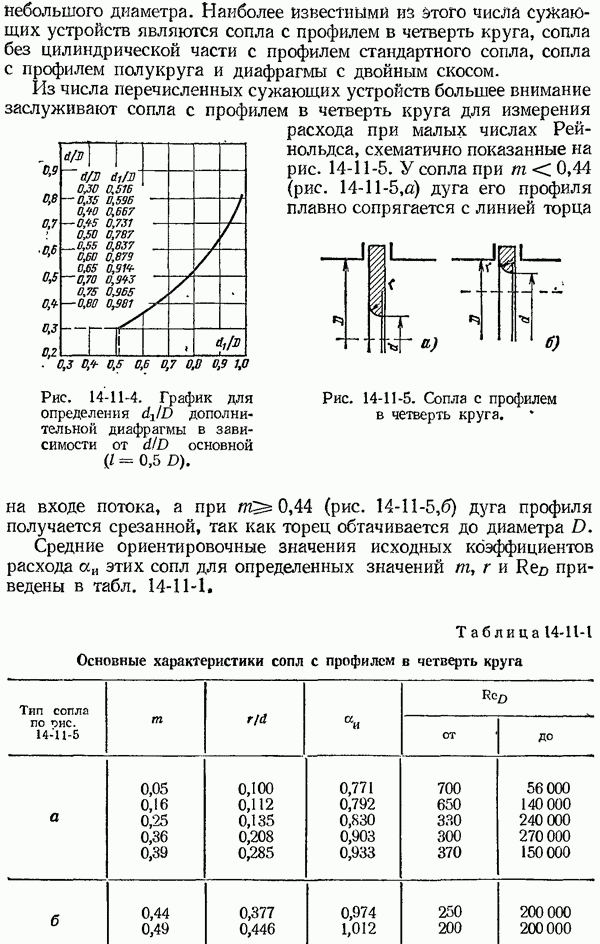
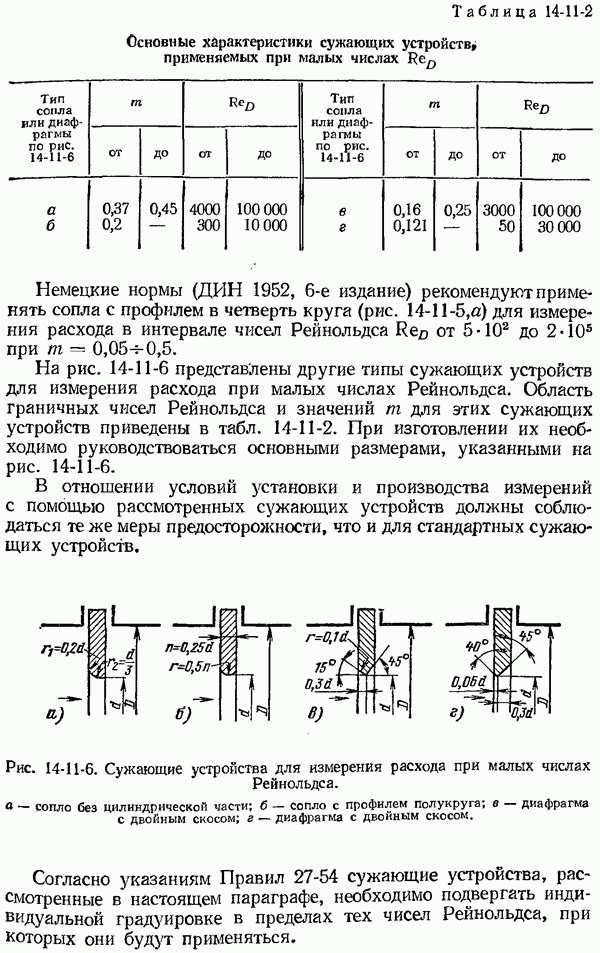
- 14-11. Измерение расхода при малых числах Рейнольдса
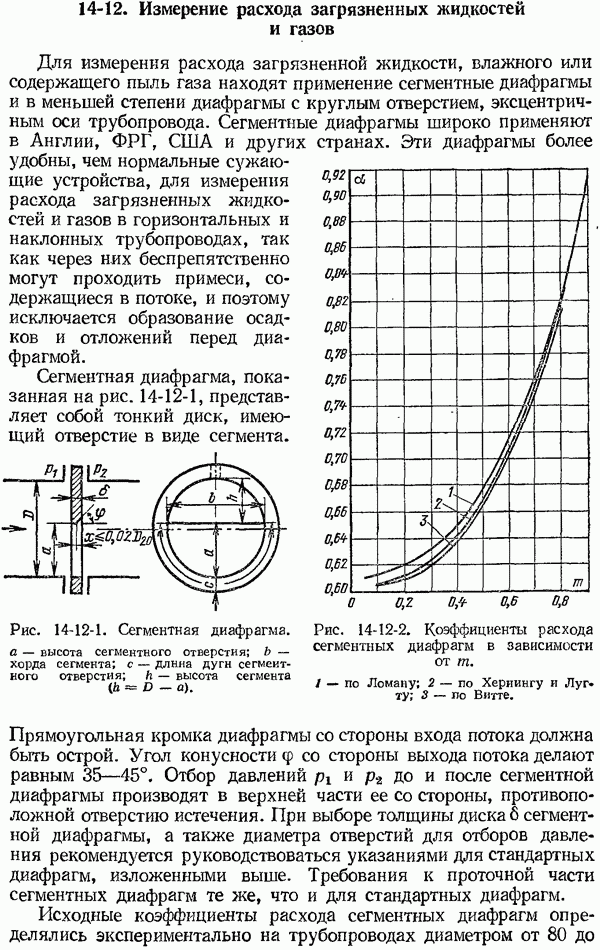
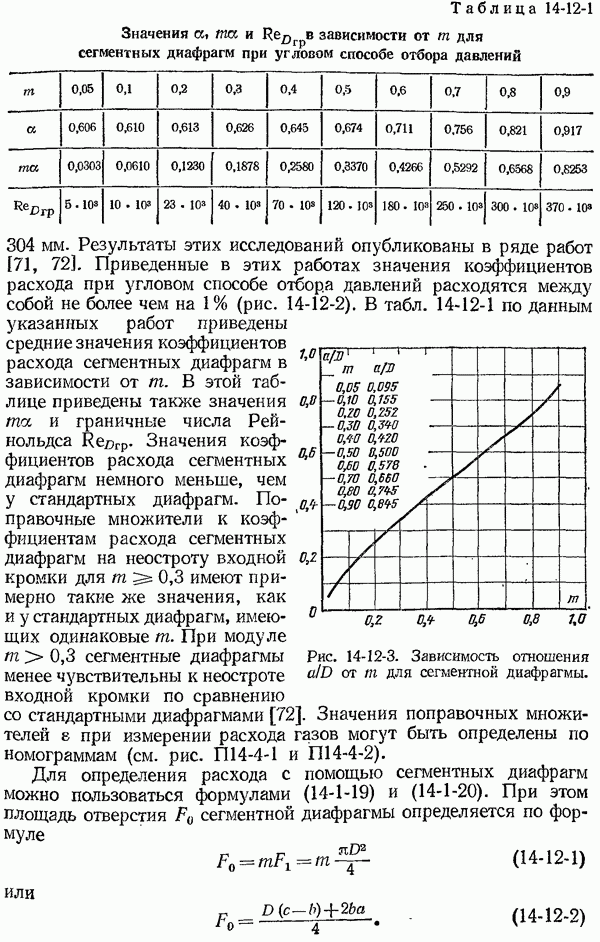
- 14-12. Измерение расхода загрязненных жидкостей и газов
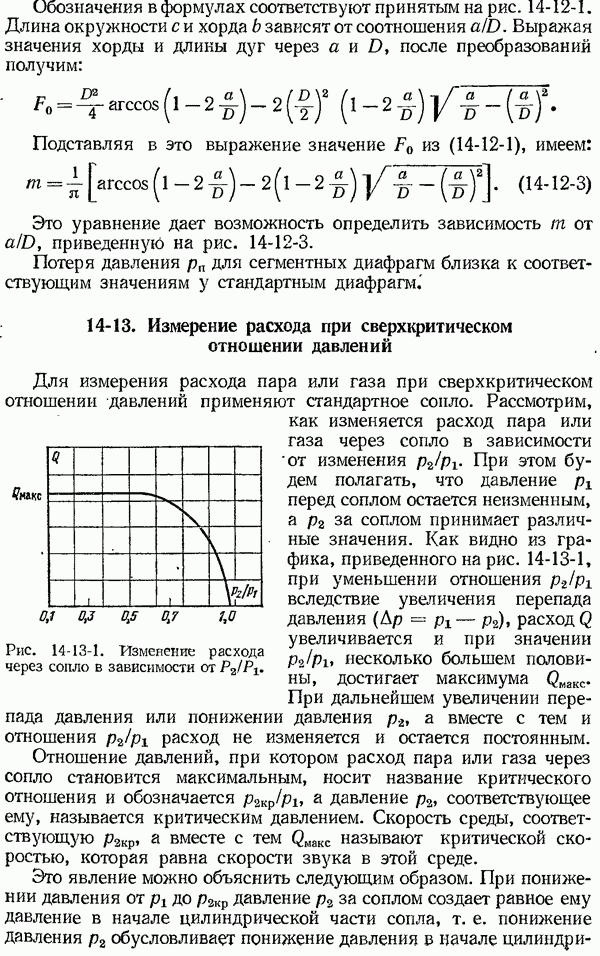
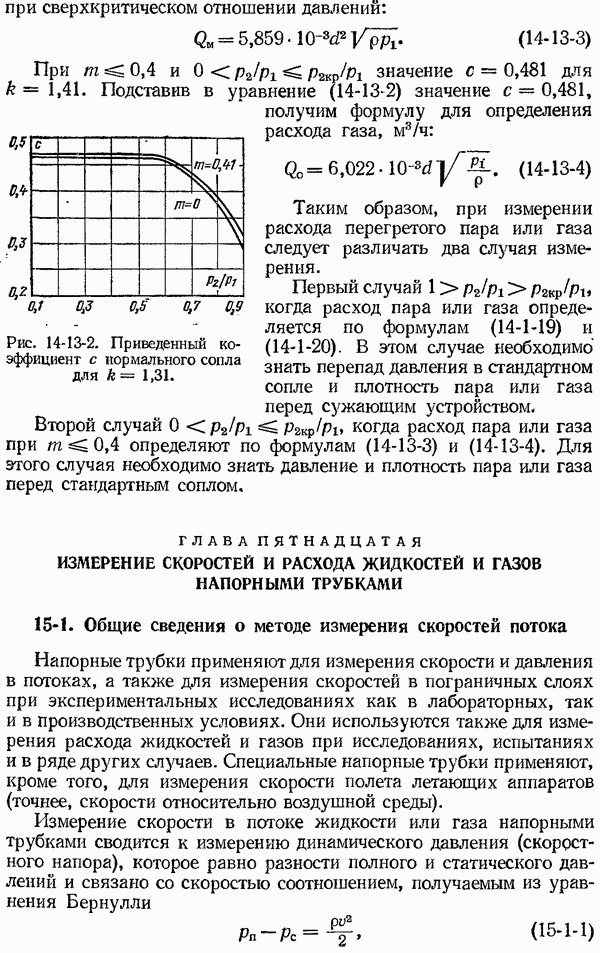
- 14-13. Измерение расхода при сверхкритическом отношении давлений
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
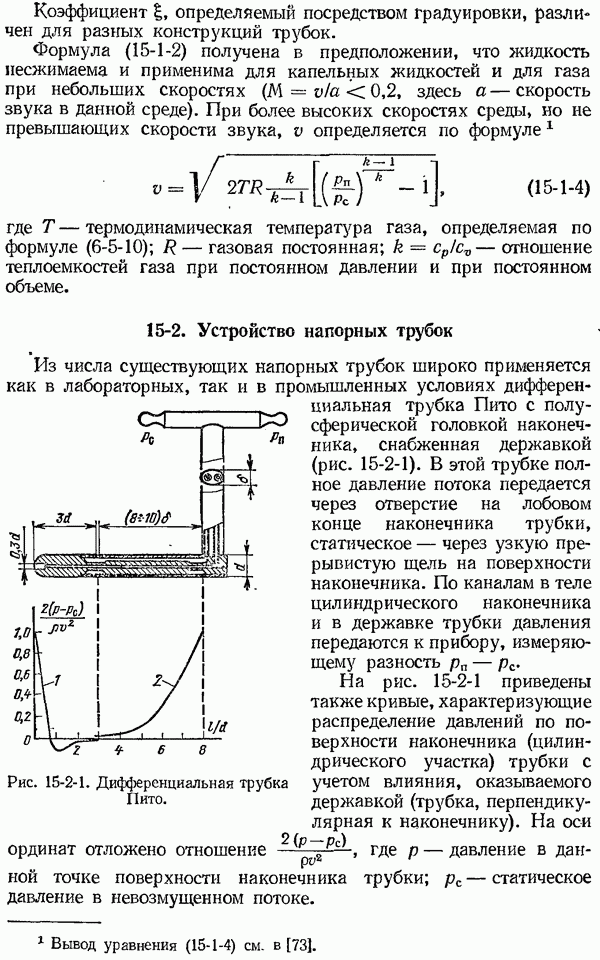
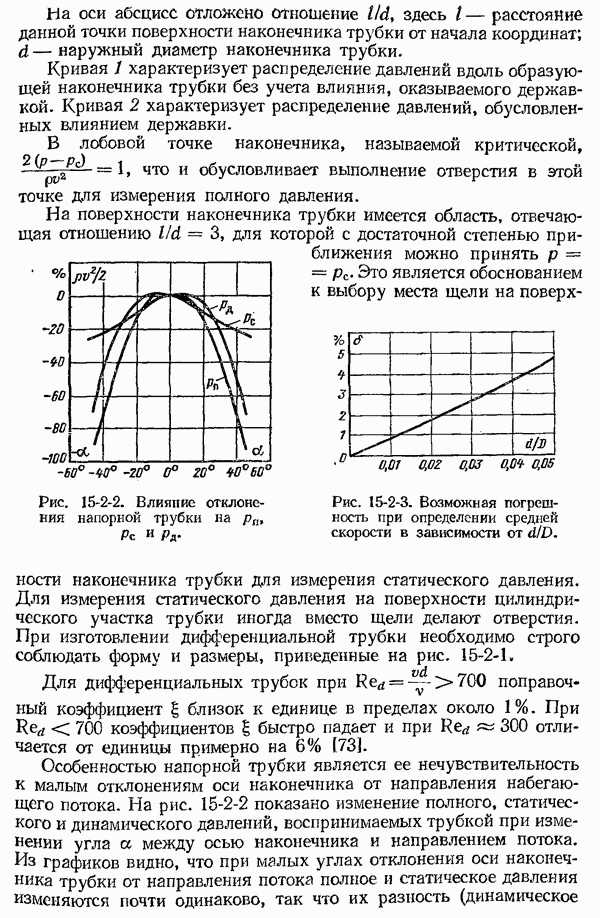
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
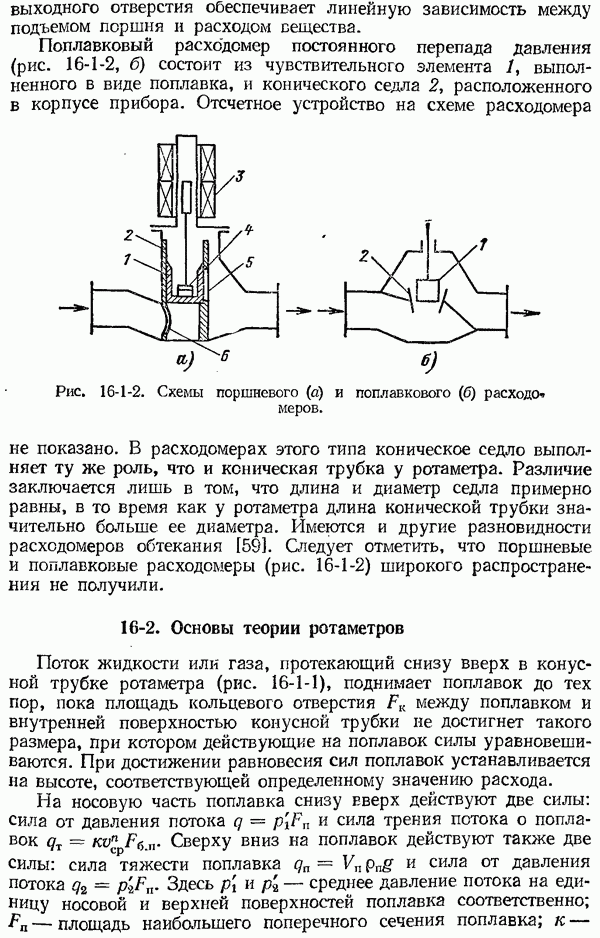
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
- 16-2. Основы теории ротаметров
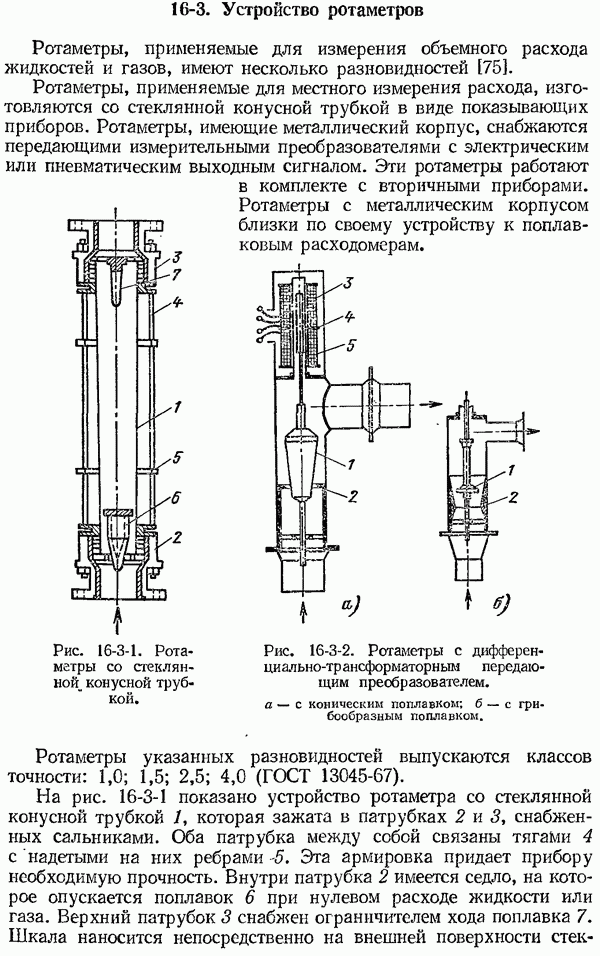
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
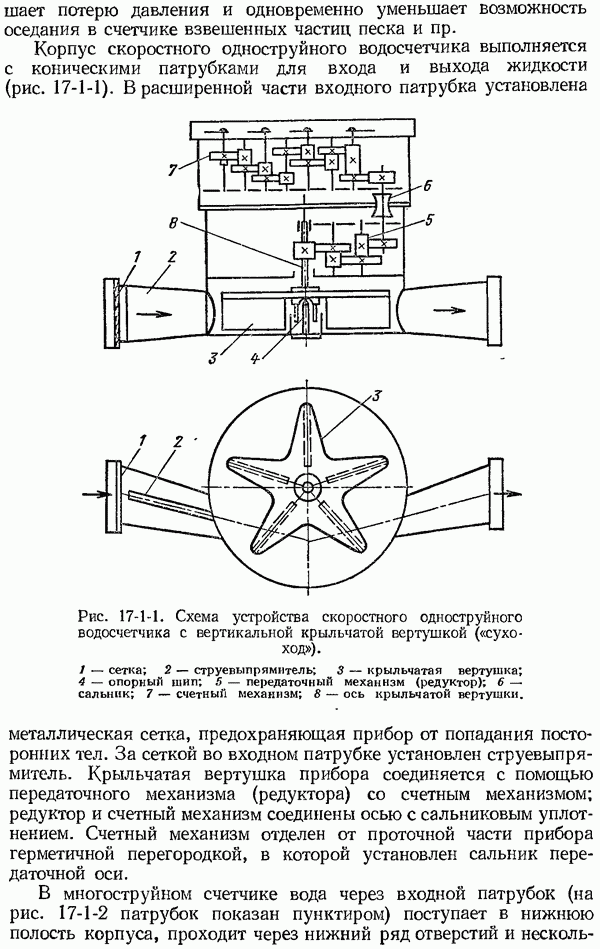
- 17-1. Тахометрические счетчики количества жидкостей
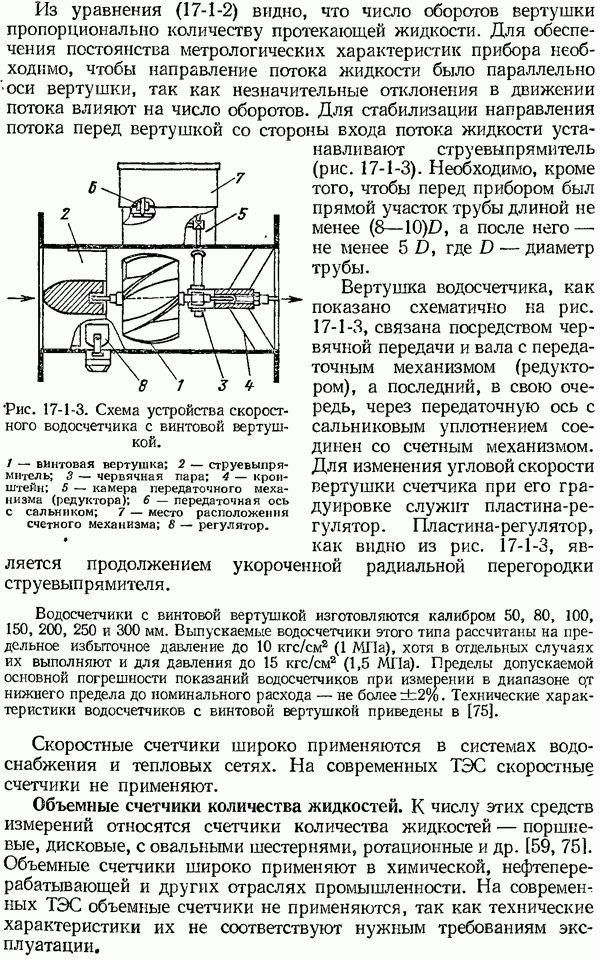
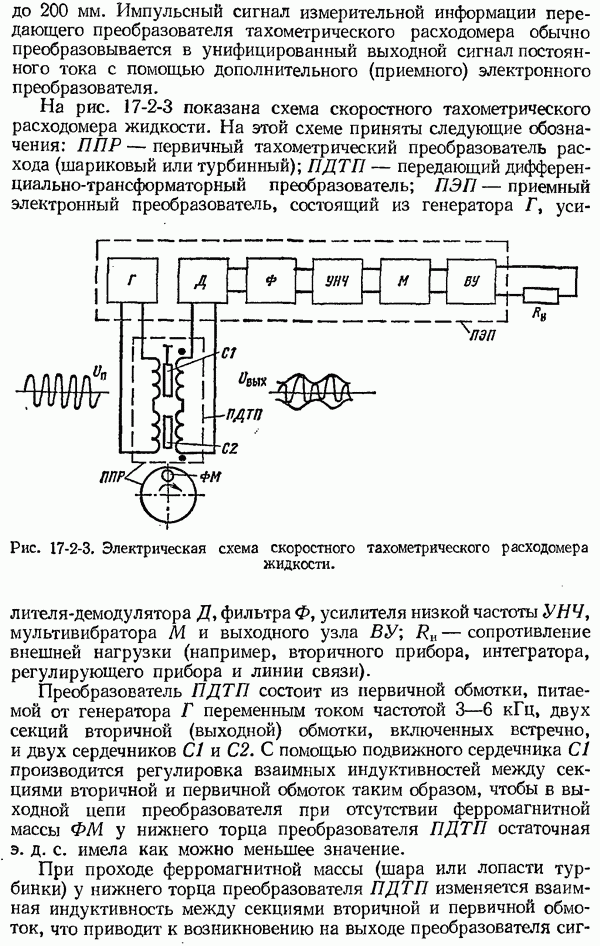
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
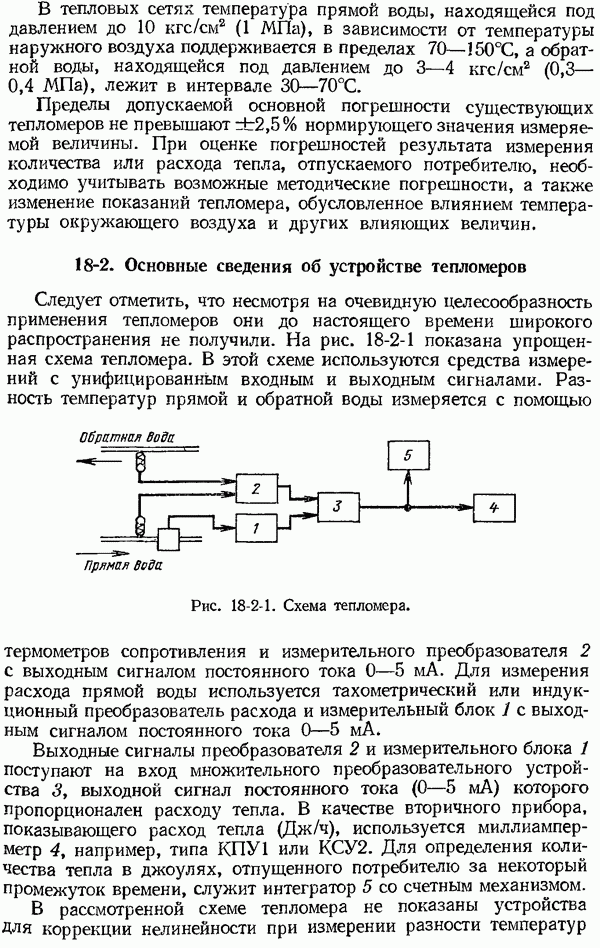
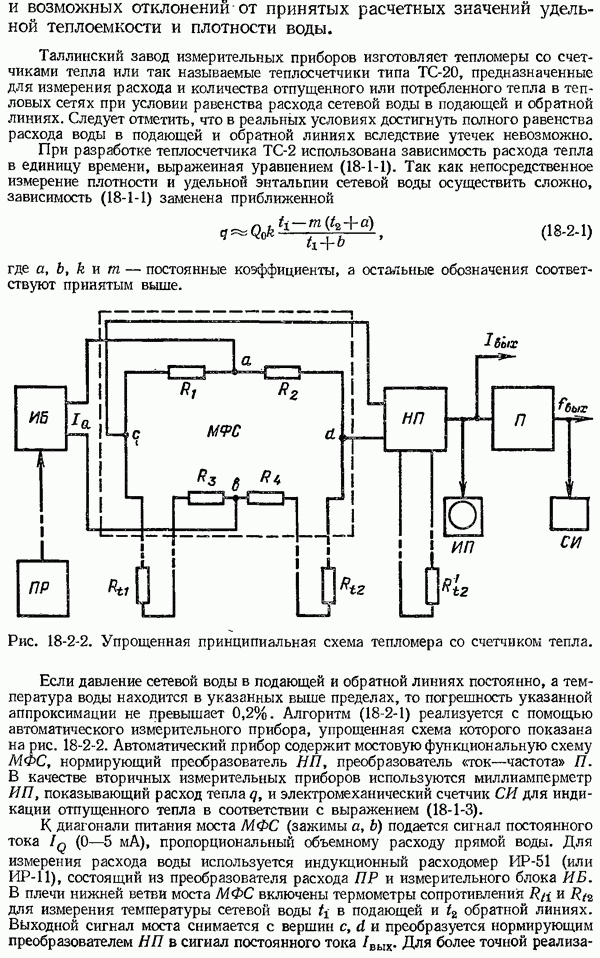
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
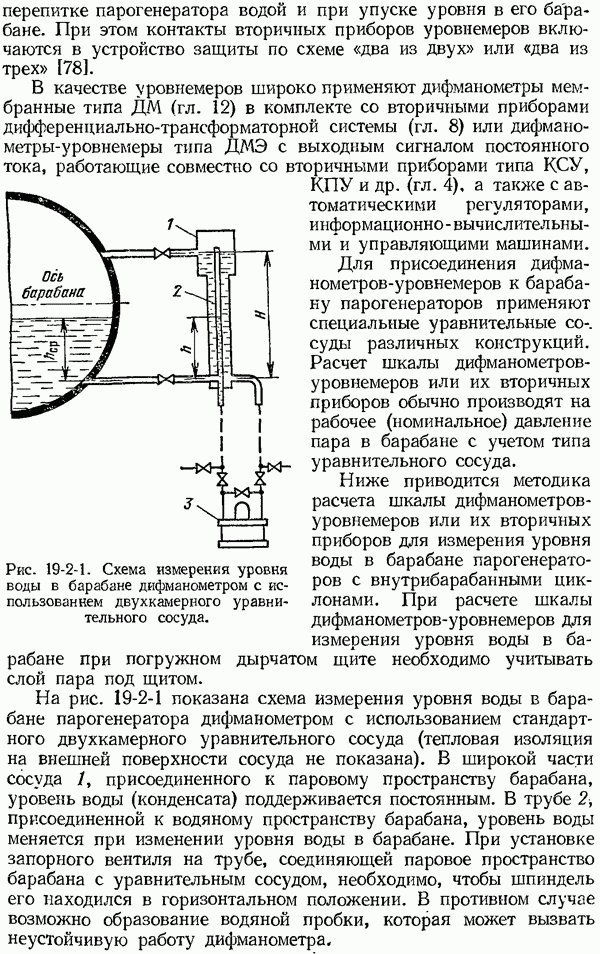
- 19-2. Измерение уровня воды в барабане парогенераторов
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
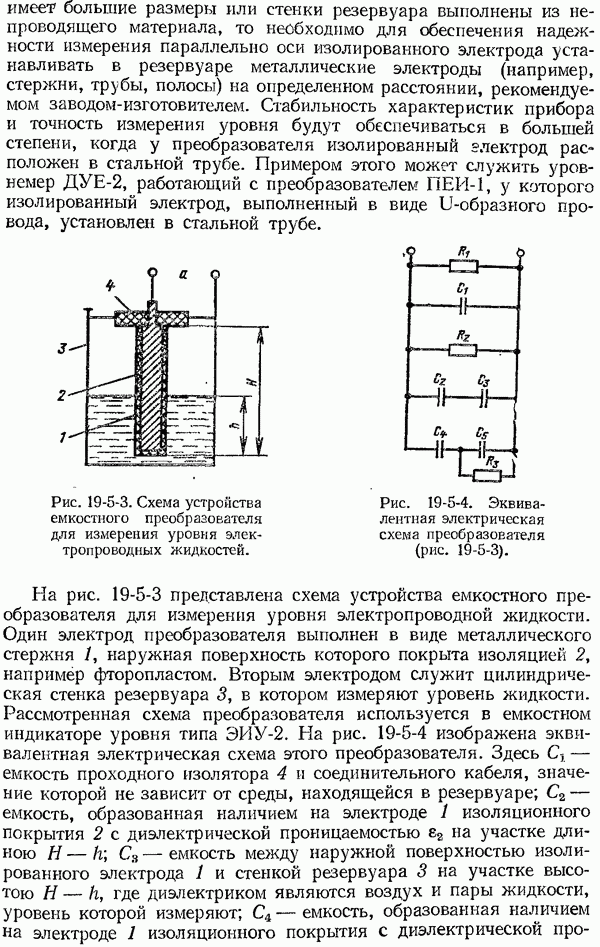
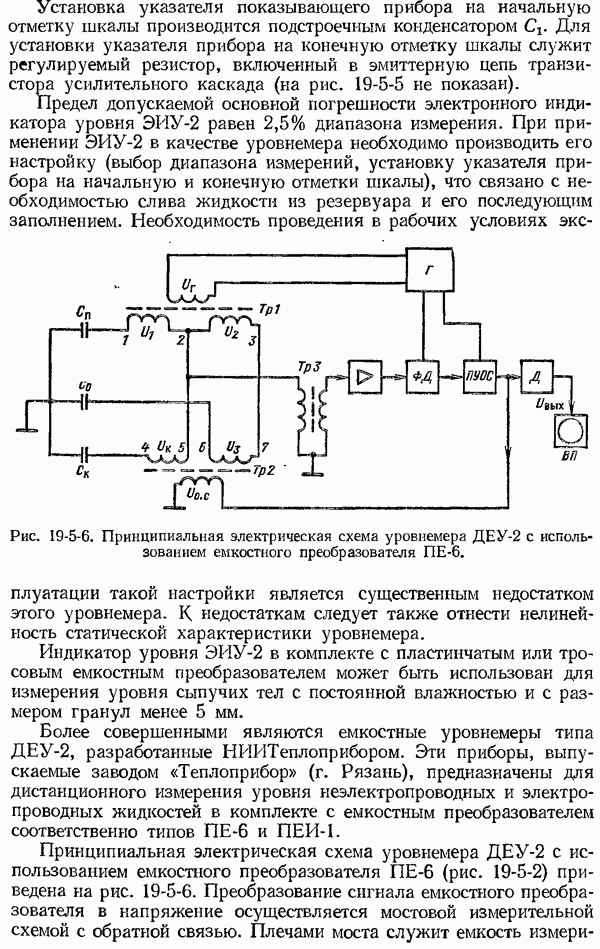
- 19-5. Емкостные уровнемеры
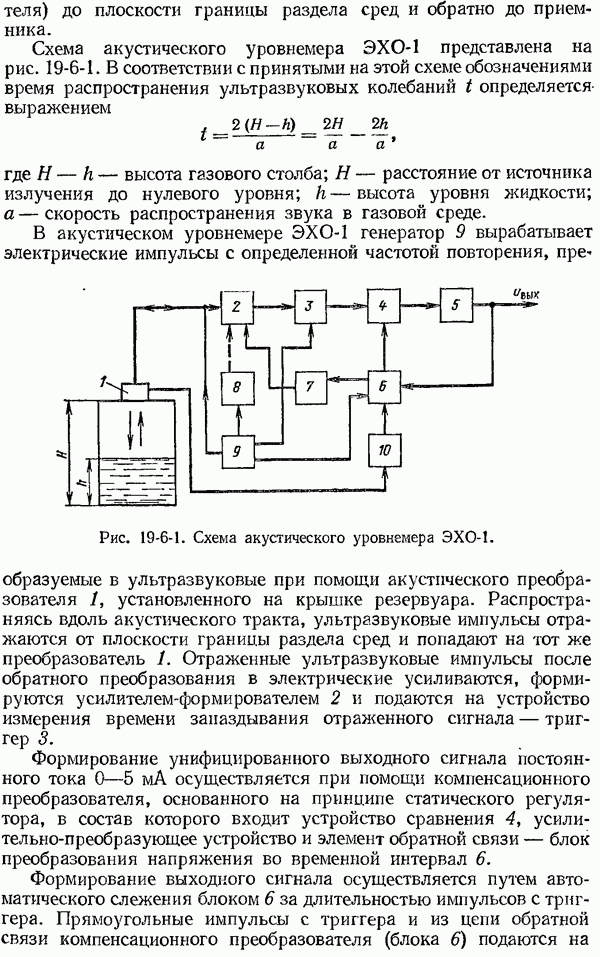
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
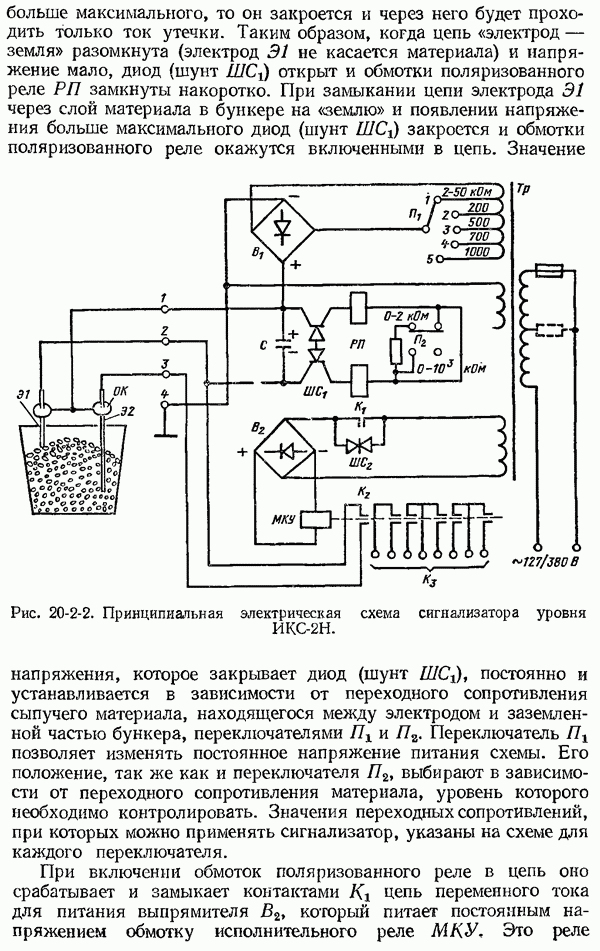
- 20-2. Сигнализаторы уровня сыпучих тел
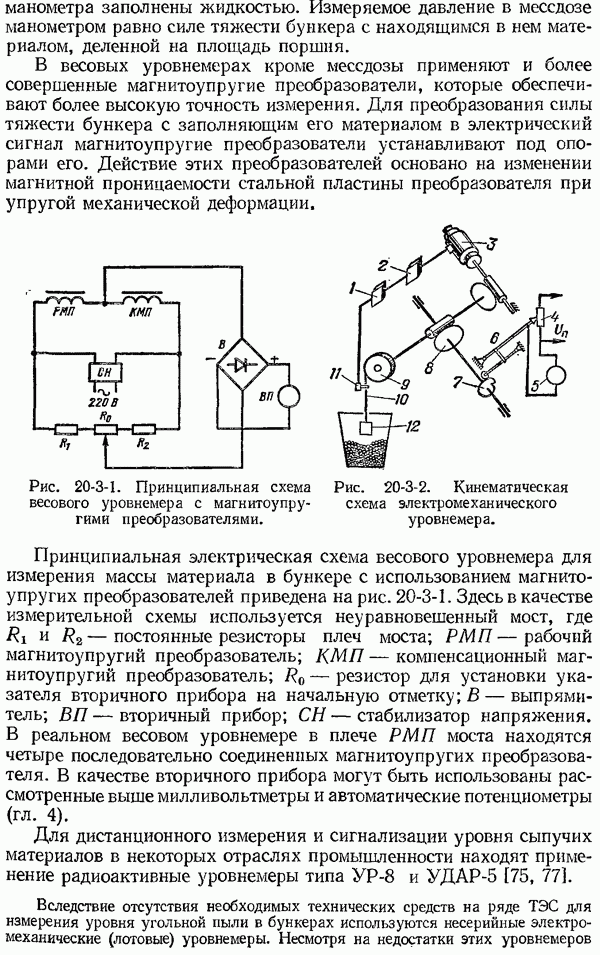
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
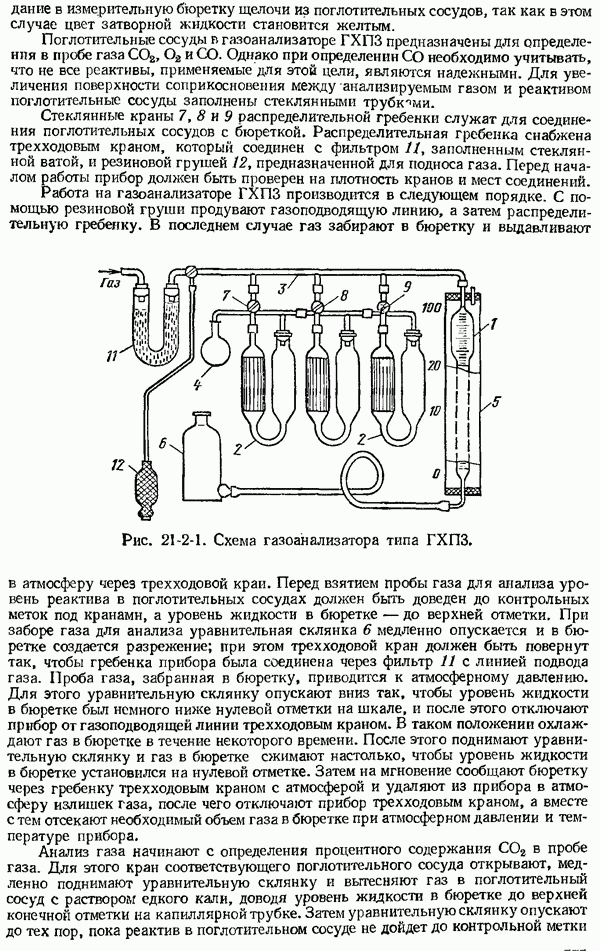
- 21-2. Газоанализаторы химические
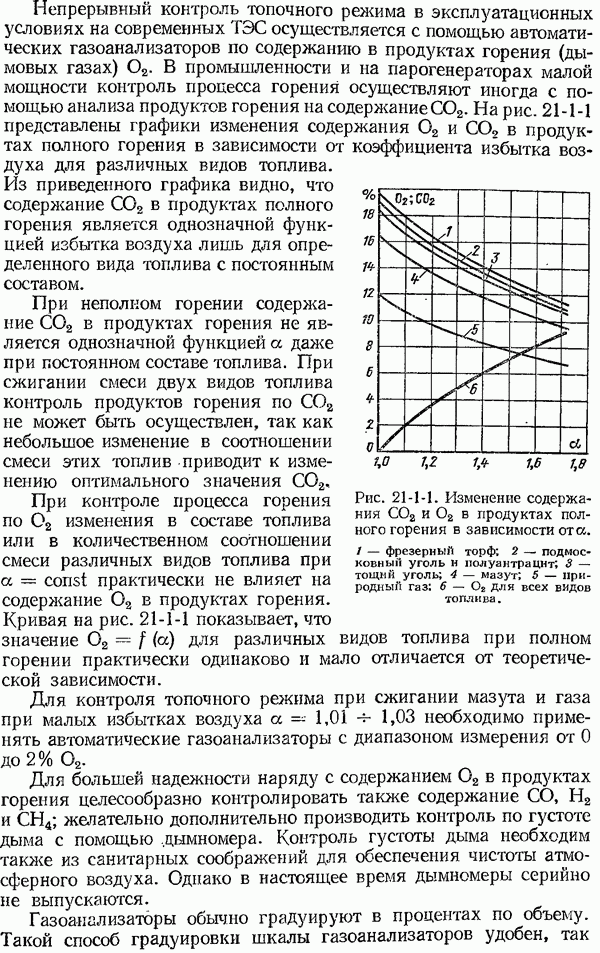
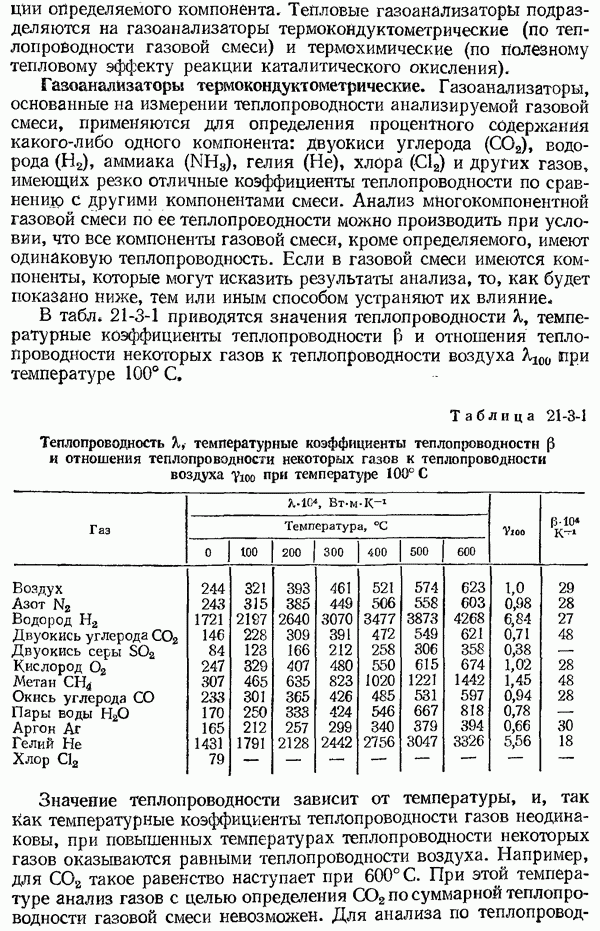
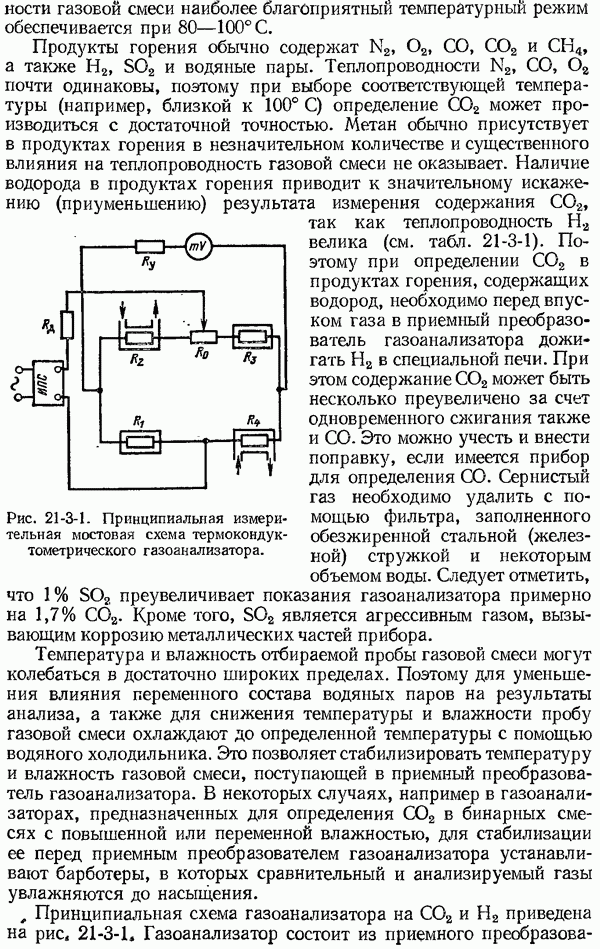
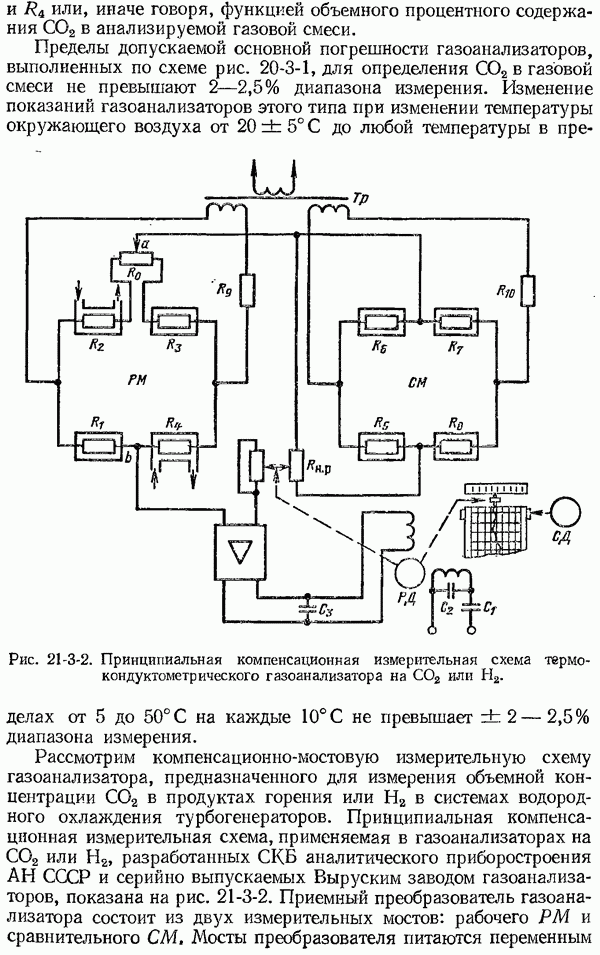
- 21-3. Тепловые газоанализаторы
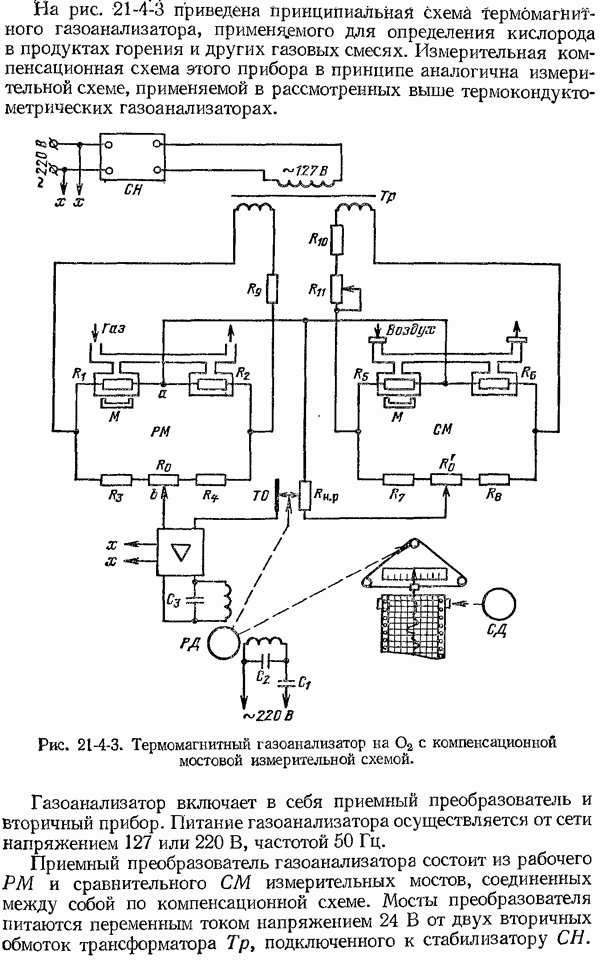
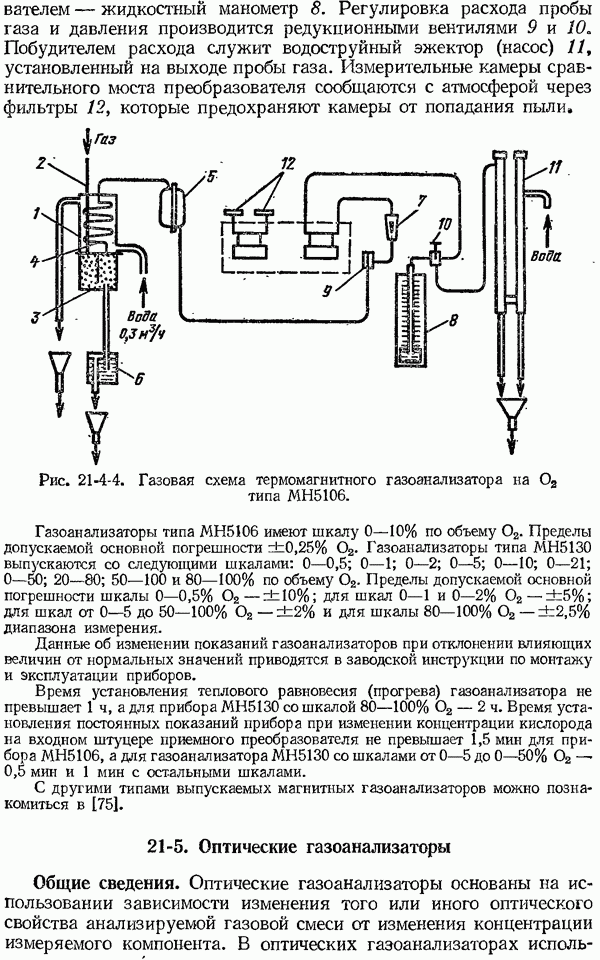
- 21-4. Магнитные газоанализаторы
- 21-5. Оптические газоанализаторы
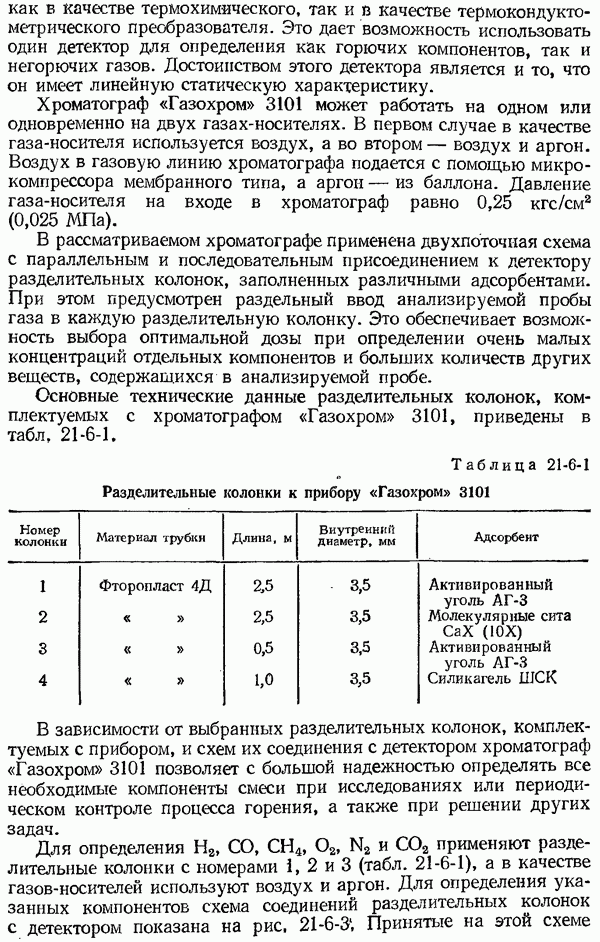
- 21-6. Газовые хроматографы
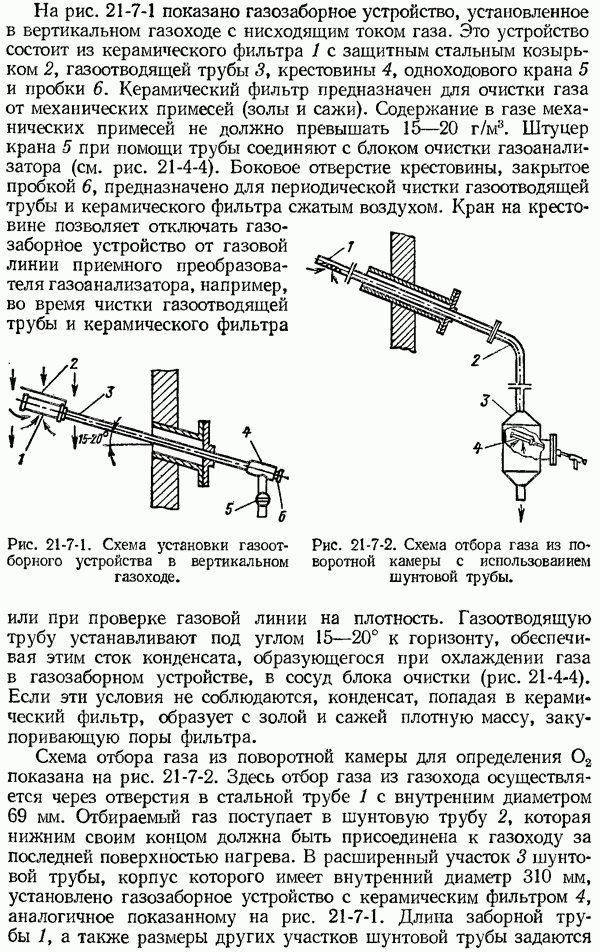
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
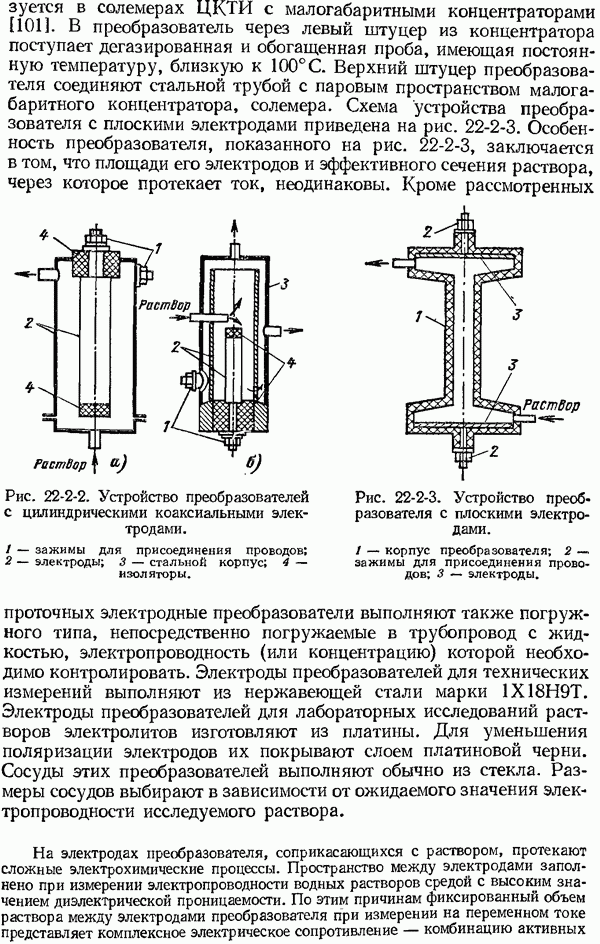
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
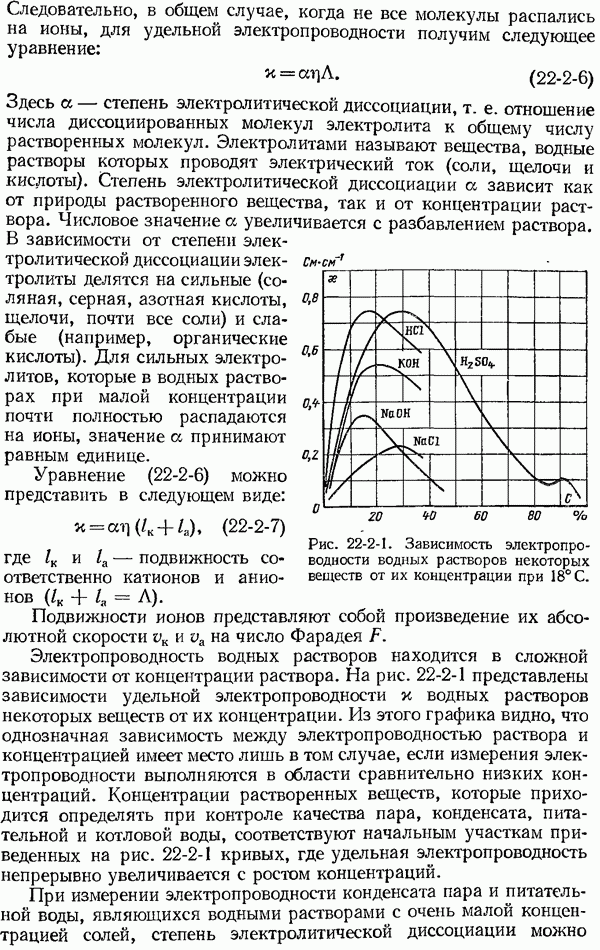
- 22-2. Измерение удельной электропроводности водных растворов
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ