| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4-2. Основы теории термоэлектрических термометров
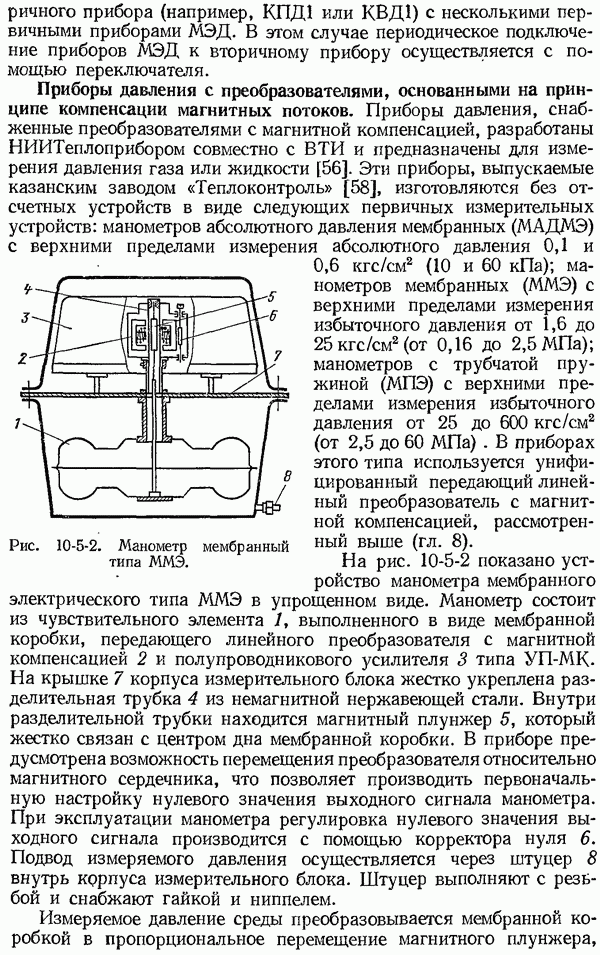
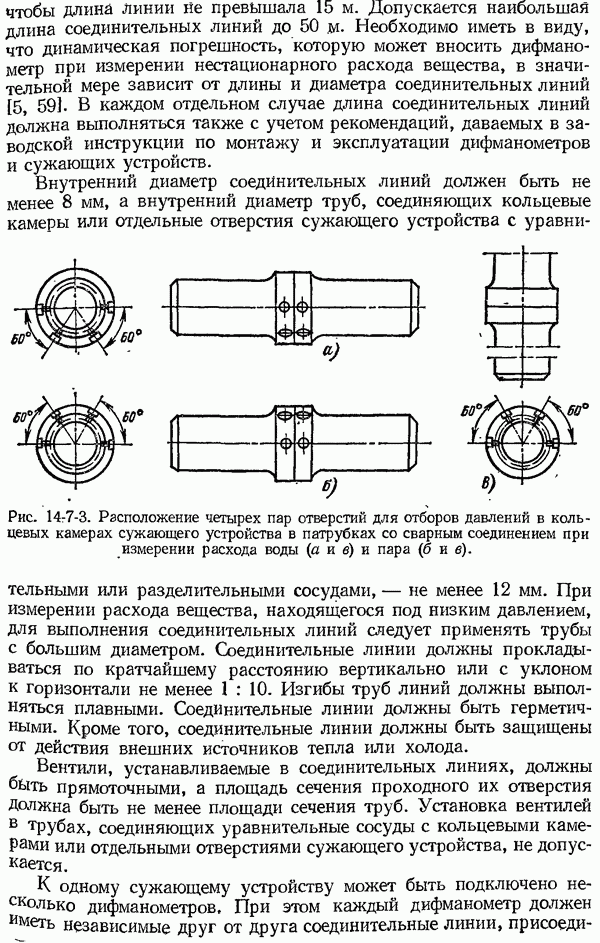
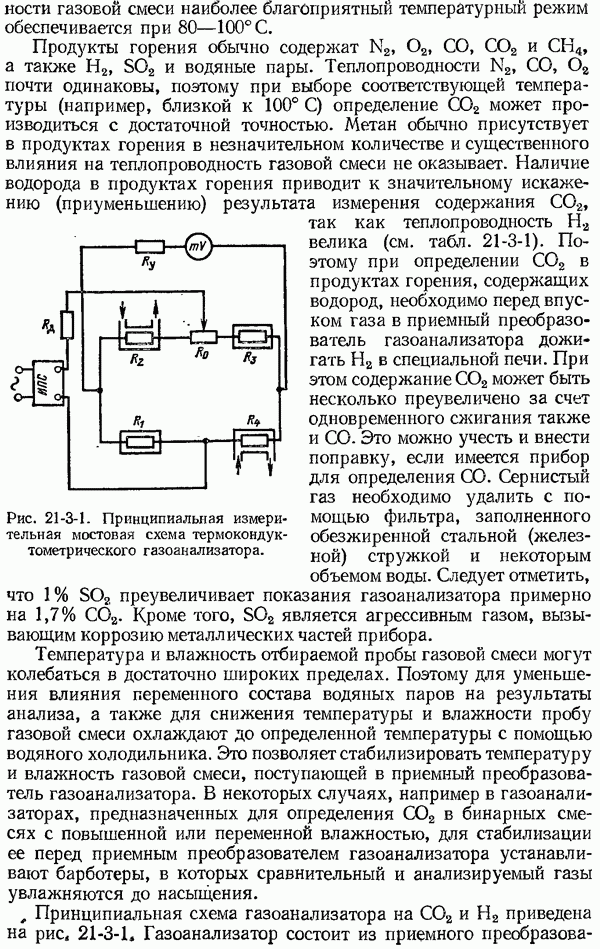
В основу измерения температур с помощью термоэлектрических термометров положены термоэлектрические явления, открытые Зеебеком в 1821 г. Применение этих явлений к измерению температур основано на существовании определенной зависимости между термо-э. д. с., устанавливающейся в цепи, составленной из разнородных проводников, и температурами мест их соединения. Если взять цепь (рис. 4-2-1), составленную из двух различных термоэлектрически однородных по длине проводников  (например, меди и платины), то при подогреве спая 1 в цепи появляется электрический ток, который в более нагретом спае 1 направлен от платины В к меди А, а в холодном спае
(например, меди и платины), то при подогреве спая 1 в цепи появляется электрический ток, который в более нагретом спае 1 направлен от платины В к меди А, а в холодном спае  от меди к платине. При подогреве спая 2 ток получает обратное направление. Такие токи называются термоэлектрическими. Электродвижущая сила, обусловленная неодинаковыми температурами мест соединения 1 и 2, называются термоэлектродвижущей силой, а создающий ее преобразователь — термоэлектрическим первичным преобразователем или термометром (употреблявшееся название — термопара).
от меди к платине. При подогреве спая 2 ток получает обратное направление. Такие токи называются термоэлектрическими. Электродвижущая сила, обусловленная неодинаковыми температурами мест соединения 1 и 2, называются термоэлектродвижущей силой, а создающий ее преобразователь — термоэлектрическим первичным преобразователем или термометром (употреблявшееся название — термопара).
Для объяснения механизма возникновения термо-э. д. с. воспользуемся электронной теорией, которая основывается на представлении о наличии в металлах свободных электронов. В различных металлах плотность свободных электронов (число электронов в

Рис. 4-2-1. Термоэлектрическая цепь из двух различных однородных проводников 
единице о ъема) неодинакова. Вследствие этого в местах соприкосновения двух разнородных металлов, например, в спае 1 (рис. 4-2-1), электроны будут диффундировать из металла А в металл В с меньшей плотностью свободных электронов в большем количестве, чем обратно из металла В в металл А. Возникающее при этом в месте соединения электрическое поле будет препятствовать этой диффузии, и когда скорость диффузионного перехода электронов станет равна скорости их обратного перехода под влиянием установившегося определенного поля, наступит состояние подвижного равновесия. При таком состоянии между металлами  возникает некоторая контактная разность потенциалов. Так как плотность свободных электронов зависит также и от температуры места соединения металлов
возникает некоторая контактная разность потенциалов. Так как плотность свободных электронов зависит также и от температуры места соединения металлов  то в месте соприкосновения этих проводников при любых температурах возникает э. д. с.
то в месте соприкосновения этих проводников при любых температурах возникает э. д. с.

называемая контактной термо-э. д. с., значение и знак которой зависят от природы металлов  и температуры
и температуры  места их соприкосновения.
места их соприкосновения.
В замкнутой цепи (рис. 4-2-1) из двух разнородных проводников  (например, меди и платины), когда
(например, меди и платины), когда  появляется, как было сказано выше, термоток. Направление этого тока в спае 2 определяет знак как самого проводника, так и термо-э. д. с. Положительным называют тот термоэлектрод, от которого ток идет в спае, имеющем температуру
появляется, как было сказано выше, термоток. Направление этого тока в спае 2 определяет знак как самого проводника, так и термо-э. д. с. Положительным называют тот термоэлектрод, от которого ток идет в спае, имеющем температуру  отрицательным — к которому ток идет в том же спае. Так как в рассматриваемой цепи ток направлен в спае 2 от А к В (от меди к платине), то термоэлектрод А — термоположительный,
отрицательным — к которому ток идет в том же спае. Так как в рассматриваемой цепи ток направлен в спае 2 от А к В (от меди к платине), то термоэлектрод А — термоположительный,  термоотрицательный. Порядок написания термоэлектродов
термоотрицательный. Порядок написания термоэлектродов  в индексе символа контактной термо-э. д. с.
в индексе символа контактной термо-э. д. с.  указывает на направление тока в спае 2 и поэтому термоэлектрод, написанный в индексе первым — положительный, а вторым — отрицательный.
указывает на направление тока в спае 2 и поэтому термоэлектрод, написанный в индексе первым — положительный, а вторым — отрицательный.
При изменении температуры спаев 1 и 2 (рис. 4-2-1)  направление термотока в спаях этой цепи изменяется, но знак термоэлектрода А при этом остается прежним, так как в спае 1 ток, как и раньше, направлен от
направление термотока в спаях этой цепи изменяется, но знак термоэлектрода А при этом остается прежним, так как в спае 1 ток, как и раньше, направлен от  к В.
к В.
На основании закона Вольта в замкнутой цепи, состоящей из двух разнородных проводников А и В, когда температуры мест их соединения одинаковы  и отсутствуют посторонние э. д. с., термотока не возникает. Вследствие этого необходимо принять, что возникающие при этом контактные термо-э. д. с. в местах соединения 1 и 2 равны между собой, но различны по знаку, и поэтому суммарная термо-э. д. с. Е цепи равна нулю:
и отсутствуют посторонние э. д. с., термотока не возникает. Вследствие этого необходимо принять, что возникающие при этом контактные термо-э. д. с. в местах соединения 1 и 2 равны между собой, но различны по знаку, и поэтому суммарная термо-э. д. с. Е цепи равна нулю:

или

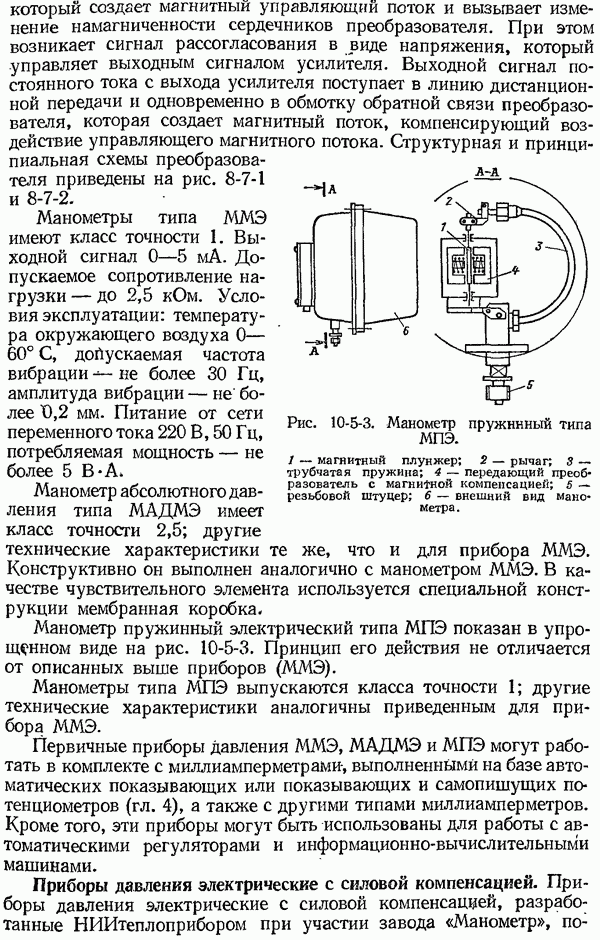
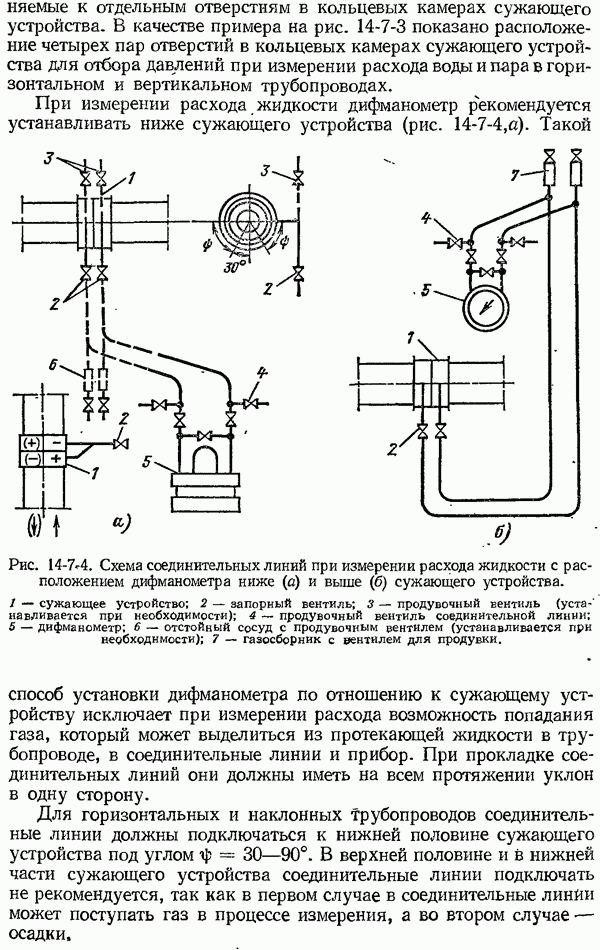
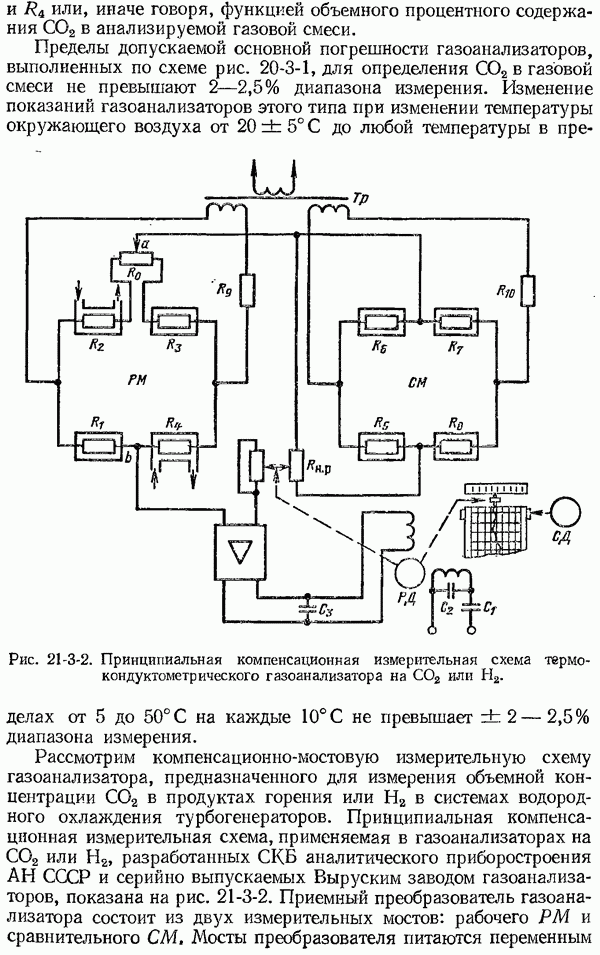
Для цепи из трех различных однородных проводников  (рис. 4-2-2), места соединений которых имеют одну и ту же температуру
(рис. 4-2-2), места соединений которых имеют одну и ту же температуру  будем иметь:
будем иметь:

т. е. сумма контактных термо-э. д. с. в замкнутой цепи из трех различных однородных проводников при одной и той же температуре мест их соединения равна нулю.
Из этого также следует, что

т. е. если известна контактная термо-э. д. с. двух проводников по отношению к третьему, то этим самым определяется и контактная термо-э. д. с. между первыми двумя.

Рис. 4-2-2. Термоэлектрическая цепь из трех различных однородных проводников.
Закон Вольта можно распространить также и на замкнутую цепь, состоящую из любого числа различных однородных проводников  Тогда при одинаковой температуре
Тогда при одинаковой температуре  мест их соединения сумма контактных термо-э. д. с. равна нулю:
мест их соединения сумма контактных термо-э. д. с. равна нулю:

Следует отметить, что этот закон является прямым следствием второго закона термодинамики, так как если бы сумма контактных термо-э. д. с. в подобной цепи не равнялась нулю, то в цепи был бы термоток. Если бы в цепи имелся термоток, то часть цепи стала бы нагреваться, а другая  охлаждаться, это означало бы, что отвод и подвод тепла осуществляется без затраты работы. Это противоречит второму закону термодинамики и приводит к выводу, что сумма контактных термо-э. д. с. в такой цепи равна нулю.
охлаждаться, это означало бы, что отвод и подвод тепла осуществляется без затраты работы. Это противоречит второму закону термодинамики и приводит к выводу, что сумма контактных термо-э. д. с. в такой цепи равна нулю.
В замкнутом термоэлектрически однородном по всей длине проводнике независимо от размеров и формы его при неодинаковом нагреве его частей не возникает термотока. Однако из этого не следует, что в нем не возникает термо-э. д. с. На основании общего представления о возникновении этих сил вполне возможно допустить появление разности потенциалов в двух поперечных сечениях однородного проводника, когда температура этих сечений отличается на  Учитывая уравнение (4-2-1), имеем:
Учитывая уравнение (4-2-1), имеем:

отсюда для замкнутого однородного проводника, неодинаково нагретого, получаем:

так как места замыкания имеют равную температуру 
В незамкнутом однородном проводнике, если он неравномерно нагрет, на его концах может возникнуть разность потенциалов Де:

которая зависит только от температур концов проводника и не зависит от распределения температуры по его длине.
Сказанное выше приводит к выводу, что термо-э. д. с., возни-, кающая в термоэлектрической цепи (рис. 4-2-1), зависит лишь от температуры мест соединения 1 и 2 различных термоэлектрически однородных по всей длине проводников  и от их природы и не может зависеть от распределения температур в каждом ее отдельном термоэлектрически однородном проводнике. Однако получить на практике термоэлектрически однородные по всей длине проводники, особенно из сплавов неблагородных металлов, не легко. Необходимо также иметь в виду, что и химически однородный проводник становится источником паразитных термо-э. д. с., когда его части отличаются друг от друга физическим состоянием. Например, термо-э. д. с. термоэлектрического термометра может измениться, если термоэлектроды подвергаются действию магнитного поля или механическим воздействиям (сжатию, растяжению, кручению). Следует обратить внимание и на то, что металлы в отпущенном состоянии обычно имеют иное значение термо-э. д. с., чем в закаленном. Это особенно проявляется у сплавов. Местные загрязнения термоэлектрода также изменяют его термоэлектрические свойства. Если термоэлектрический термометр будет изготовлен из электродов с некоторой степенью термоэлектрической неоднородности, то при погружении в среду с неравномерным температурным полем образующиеся в нем паразитные термо-э. д. с. будут искажать его суммарную термо-э. д. с. тем больше, чем больше степень их неоднородности. Значение паразитной термо-э. д. с. зависит также и от степени неравномерности температурного поля среды.
и от их природы и не может зависеть от распределения температур в каждом ее отдельном термоэлектрически однородном проводнике. Однако получить на практике термоэлектрически однородные по всей длине проводники, особенно из сплавов неблагородных металлов, не легко. Необходимо также иметь в виду, что и химически однородный проводник становится источником паразитных термо-э. д. с., когда его части отличаются друг от друга физическим состоянием. Например, термо-э. д. с. термоэлектрического термометра может измениться, если термоэлектроды подвергаются действию магнитного поля или механическим воздействиям (сжатию, растяжению, кручению). Следует обратить внимание и на то, что металлы в отпущенном состоянии обычно имеют иное значение термо-э. д. с., чем в закаленном. Это особенно проявляется у сплавов. Местные загрязнения термоэлектрода также изменяют его термоэлектрические свойства. Если термоэлектрический термометр будет изготовлен из электродов с некоторой степенью термоэлектрической неоднородности, то при погружении в среду с неравномерным температурным полем образующиеся в нем паразитные термо-э. д. с. будут искажать его суммарную термо-э. д. с. тем больше, чем больше степень их неоднородности. Значение паразитной термо-э. д. с. зависит также и от степени неравномерности температурного поля среды.
На основании вышеизложенного мы можем написать основное уравнение термоэлектрического термометра, выражающее в общем виде зависимость суммарной термо-э. д. с., возникающей в цепи из двух разнородных термоэлектродов  от температуры мест их соединения:
от температуры мест их соединения:

или

т. е. термо-э. д. с. термоэлектрического термометра (цепи из двух разнородных; проводников), места соединений которых имеют разные температуры, равна разности контактных термо-э. д. с.
Принимая во внимание уравнение (4-2-1), представим уравнение (4-2-9) в следующем виде:

Вид функциональной зависимости  от температур
от температур  определяется видом функции
определяется видом функции  Однако при современном уровне наших знаний определить вид этой функции теоретически не представляется возможным, а потому его устанавливают опытным путем.
Однако при современном уровне наших знаний определить вид этой функции теоретически не представляется возможным, а потому его устанавливают опытным путем.
При измерении температуры термоэлектрическим термометром  поддерживают постоянной,
поддерживают постоянной,  в этом случае является переменной температурой. Полагая в уравнении (4-2-10)
в этом случае является переменной температурой. Полагая в уравнении (4-2-10)  и вводя обозначение
и вводя обозначение  приходим к зависимости
приходим к зависимости

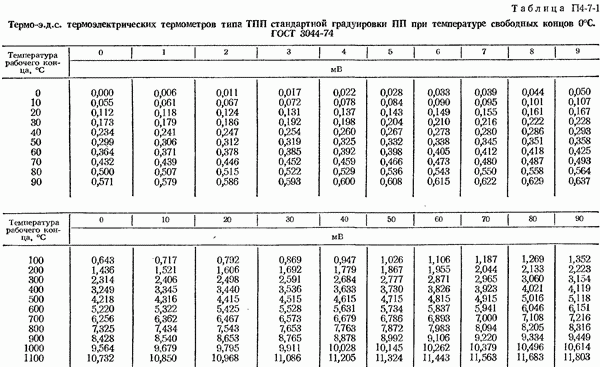
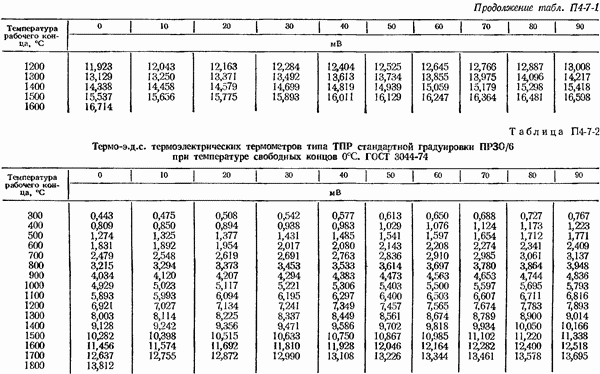
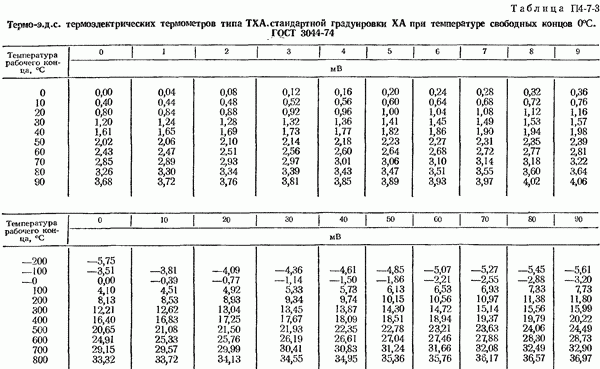
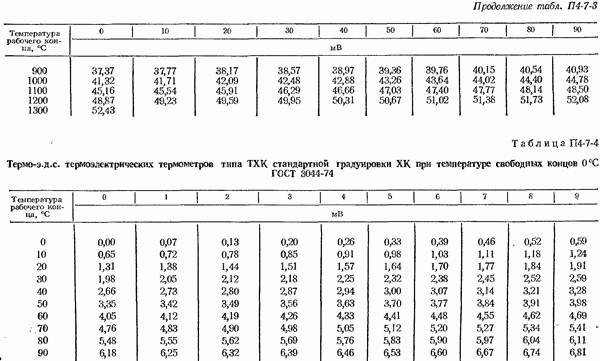
Если зависимость, выраженная уравнением (4-2-11), известна из кривой или таблицы, составленной на основании эксперимента, т. е. путем градуировки термоэлектрического термометра, например, методом сравнения с образцовым термометром, то измерение неизвестной температуры  сводится к измерению
сводится к измерению  При этом предполагается, что температура
При этом предполагается, что температура  остается неизменной, так как нарушение постоянства этой температуры влечет за собой изменение термо-э. д. с. термоэлектрического термометра. Обычно градуировку термоэлектрических первичных преобразователей или термометров производят при температуре
остается неизменной, так как нарушение постоянства этой температуры влечет за собой изменение термо-э. д. с. термоэлектрического термометра. Обычно градуировку термоэлектрических первичных преобразователей или термометров производят при температуре 
При пользовании градуировочными таблицами производится интерполирование (обычно линейное) между табличными значениями термо-э. д. с. Если табличные точки слишком редки, то линейная интерполяция приводит к большим погрешностям. В этом случае для целей интерполяции рекомендуется пользоваться специальными градуировочными таблицами  или графиками, а также эмпирическими формулами, которые для некоторых термоэлектрических термометров приведены ниже.
или графиками, а также эмпирическими формулами, которые для некоторых термоэлектрических термометров приведены ниже.
Из уравнения (4-2-11) непосредственно вытекает, что термо-э. д. с.  термоэлектрического термометра можно рассматривать как непрерывную функцию от
термоэлектрического термометра можно рассматривать как непрерывную функцию от  производная которой
производная которой

значение  зависит от температуры
зависит от температуры  и от природы термоэлектродов, образующих термоэлектрический термометр и характеризует его чувствительность.
и от природы термоэлектродов, образующих термоэлектрический термометр и характеризует его чувствительность.
При небольшой нелинейности зависимости  на отдельных ее участках можно считать эту зависимость линейной. Тогда
на отдельных ее участках можно считать эту зависимость линейной. Тогда  и
и  в выражении (4-2-12) могут быть заменены конечными приращениями
в выражении (4-2-12) могут быть заменены конечными приращениями 

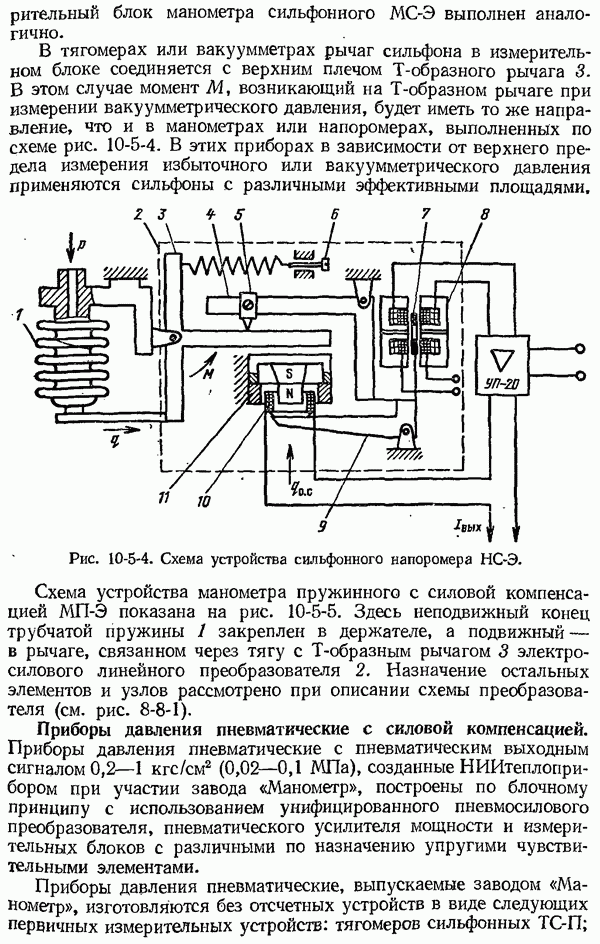
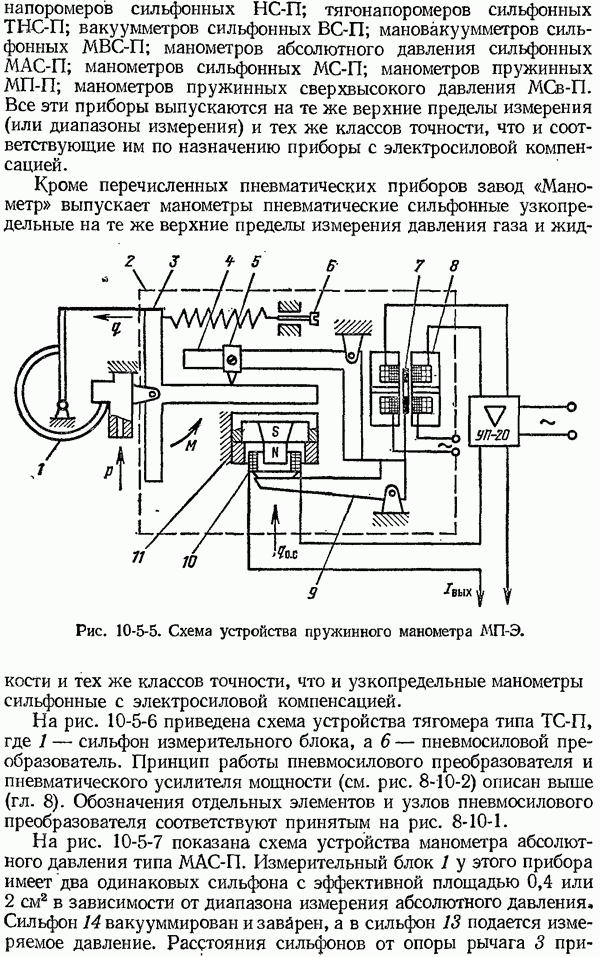
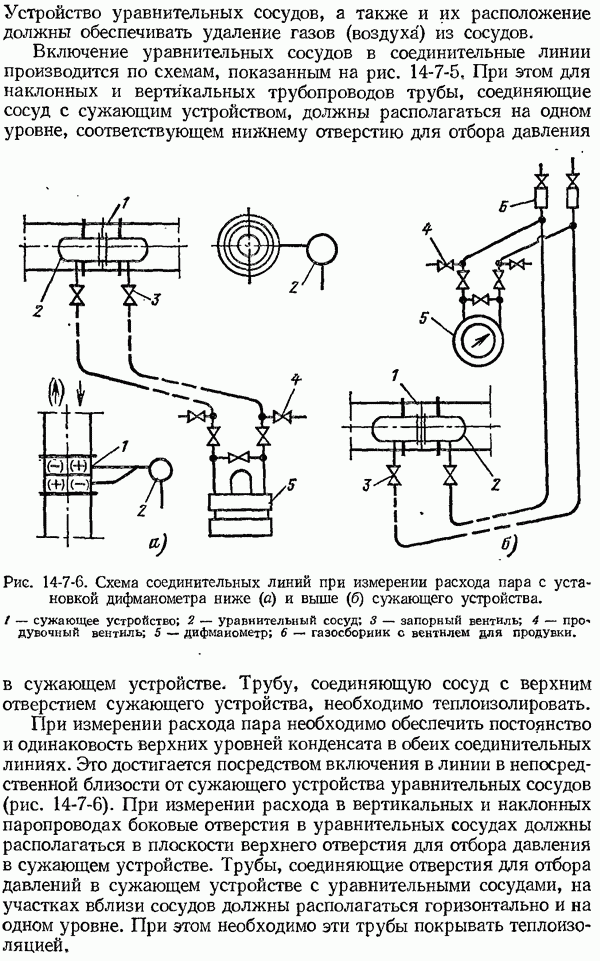
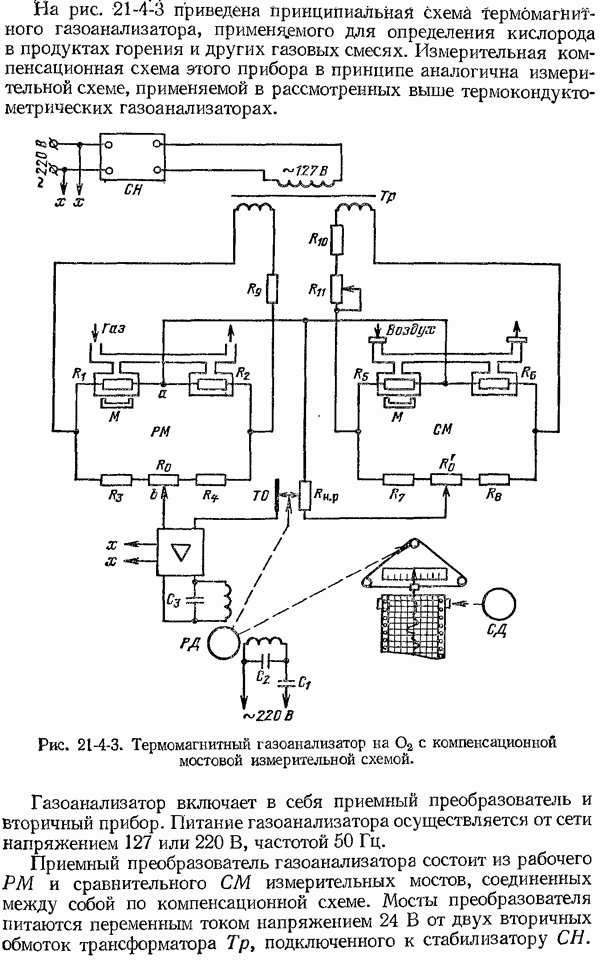
ыясним, как влияет на значение термо-э. д. с. термоэлектрического термометра третий проводник, включенный в его цепь. Для этой цели рассмотрим термоэлектрический термометр, состоящий из термоэлектродов  в цепь которого включен проводник С (рис. 4-2-3, а). При этом температура спая 1 равна
в цепь которого включен проводник С (рис. 4-2-3, а). При этом температура спая 1 равна  а температура мест соединения
а температура мест соединения  Определим термо-э. д. с. Е для этой цепи. В соответствии с принятыми условиями
Определим термо-э. д. с. Е для этой цепи. В соответствии с принятыми условиями

Принимая во внимание уравнение (4-2-3), получаем из (4-2-13):

Это уравнение полностью совпадает с (4-2-9).
Рассмотрим теперь термоэлектрическую цепь, изображенную на рис. 4-2-3, б. Полагая, что температуры мест соединений 3 и 4 равны между собой, будем иметь:

Полученное уравнение легко приводится к виду (4-2-9), если учесть, что 
Из этого следует, что термо-э. д. с. термоэлектрического термометра не изменяется от введения в его цепь третьего проводника, если температуры концов этого проводника одинаковы. Данное положение легко распространить на цепь, состоящую из любого числа проводников, т. е. включение одного, двух или более проводников в цепь термоэлектрического термометра не оказывает влияния на значение его термо-э. д. с., если концы этих проводников будут иметь одинаковую температуру.

Рис. 4-2-3. Схема термоэлектрического термометра. а. — с включенным в его свободные концы проводником С; б - с включенным в термоэлектрод В проводником С.
Из сказанного выше также следует, что способ изготовления рабочего конца (сваркой, пайкой) на значение термо-э. д. с. термоэлектрического термометра не влияет, если только размеры спая таковы, что температура его во всех точках одинакова. Положение это верно также и для всех соединений термоэлектрической цепи. Нарушение же равенства температур концов третьего проводника, включенного в цепь термоэлектрического термометра, вызывает появление паразитной термо-э. д. с., которая будет зависеть от природы третьего проводника и от температуры мест его присоединения.
Предположим, что (рис. 4-2-3, а) температура спая 3 проводника С с проводником В не равна температуре  и имеет отличное от
и имеет отличное от  значение
значение  причем
причем  . В этом случае
. В этом случае
термо-э. д. с. цепи оудет равна:

Вычитая из уравнения (4-2-9) уравнение (4-2-16), получаем:

воспользовавшись уравнением (4-2-3), выразим разность термо-э. д. с. в форме

В этом уравнении правая часть представляет собой термо-э. д. с.  , развиваемую термоэлектрической цепью
, развиваемую термоэлектрической цепью  с температурой спаев, равной температуре концов проводника С, т. е.
с температурой спаев, равной температуре концов проводника С, т. е. 
Аналогично предыдущему предположим, что в схеме рис. 4-2-3, б температура места соединения 4 проводника С с проводником В не равна температуре места соединения 3 и имеет значение  В этом случае термо-э. д. с. цепи будет равна:
В этом случае термо-э. д. с. цепи будет равна:

Вычитая из уравнения (4-2-9) уравнение (4-2-19), получаем:

Из уравнений (4-2-18) и (4-2-20) видно, что при неравенстве температур спаев 2 и 3 (рис. 4-2-3, а) или мест соединений 3 и 4 (рис. 4-2-3, б) термо-э. д. с. термоэлектрического термометра изменяется соответственно на значение термо-э. д. с.  термоэлектрической цепи, составленной из проводника С в паре с термоэлектродом В.
термоэлектрической цепи, составленной из проводника С в паре с термоэлектродом В.
Из сказанного следует, что нежелательно употреблять материалы для изготовления отдельных элементов термоэлектрического комплекта, значительно различающиеся термоэлектрически, даже там, где постоянство температур относительно обеспечено. Например, для изготовления добавочных или регулировочных резисторов следует избегать применения константана, дающего высокую термо-э. д. с. в паре с медью, и рекомендуется применять манганин.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ
- 1-1. Понятие об измерении, виды и методы измерений
- 1-2. Общие сведения о средствах измерений
- 1-3. Общие сведения о точности измерений и погрешности измерений
- 1-4. Оценка и учет погрешностей при точных измерениях
- 1-5. Основные сведения о метрологических характеристиках средств измерений
- Способы числового выражения погрешностей средств измерений.
- Поправка.
- Статическая характеристика, коэффициент передачи и чувствительность средств измерений.
- Структурные схемы.
- Порог чувствительности измерительного прибора или преобразователя.
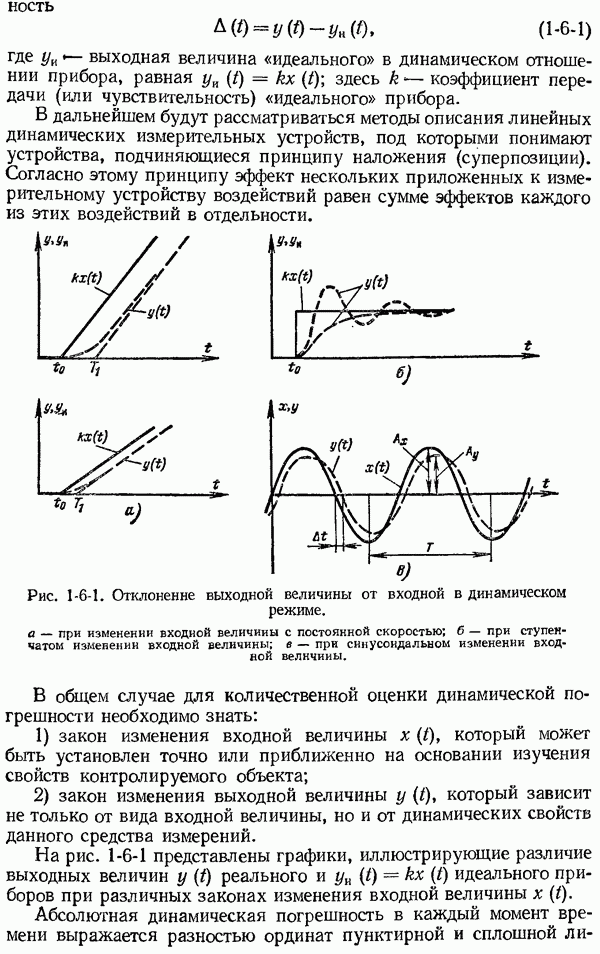
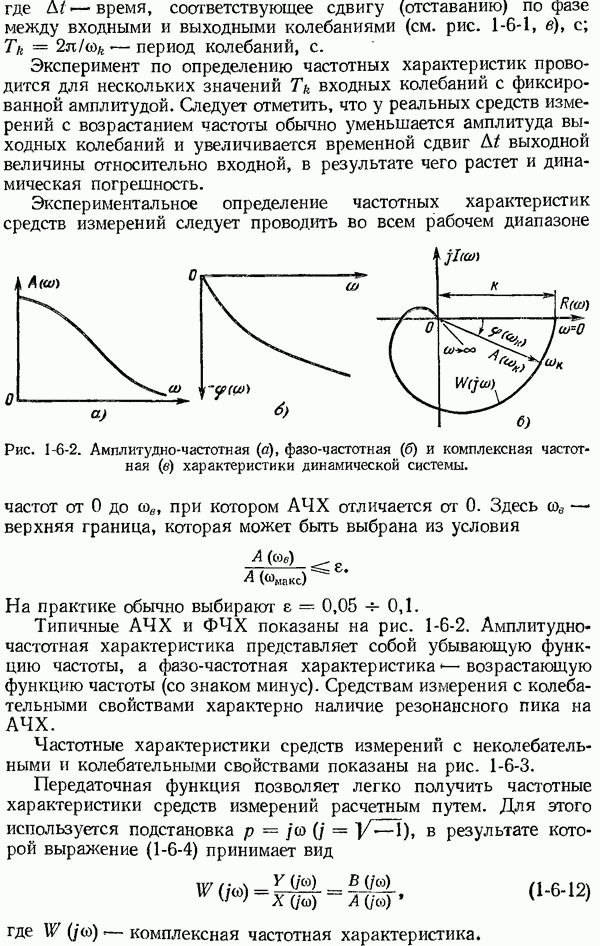
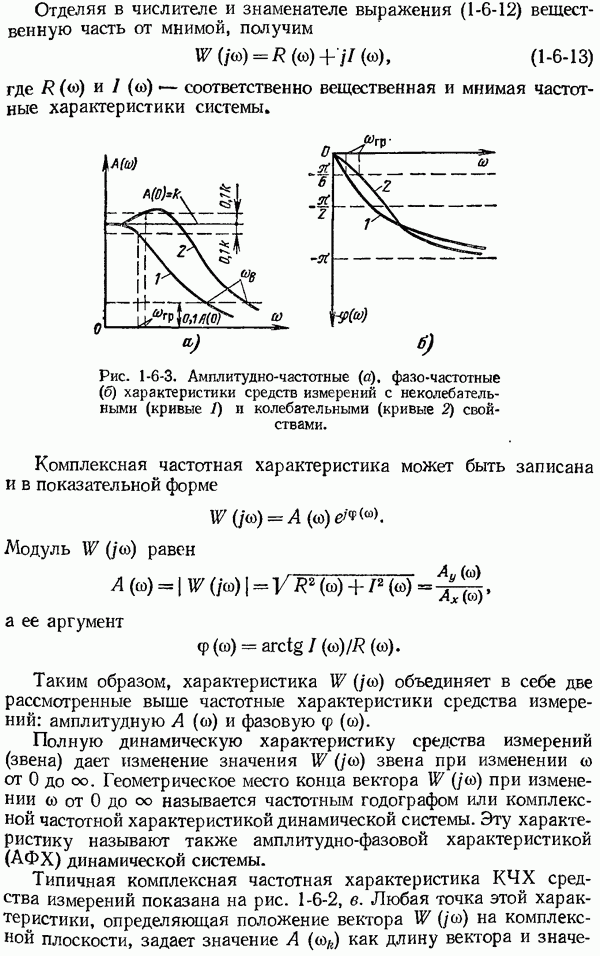
- 1-6. Общие сведения о динамических характеристиках средств измерений
- 1-7. Оценка и учет погрешностей при технических измерениях
- Оценка точности результата косвенных технических измерений.
- РАЗДЕЛ ВТОРОЙ. ИЗМЕРЕНИЕ ТЕМПЕРАТУР
- 2-1. Основные сведения о температуре и температурных шкалах
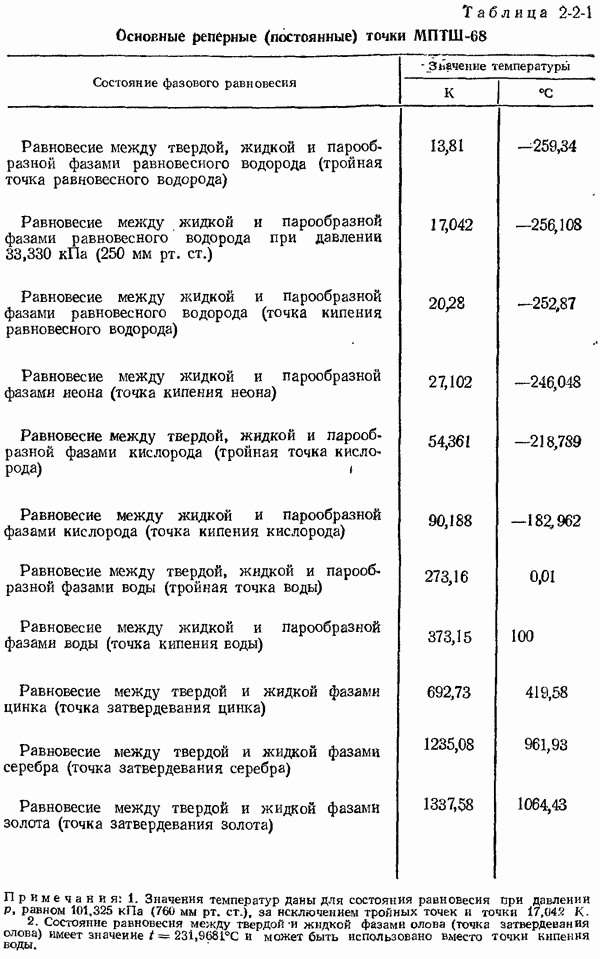
- 2-2. Практические температурные шкалы
- Глава третья. ТЕРМОМЕТРЫ, ОСНОВАННЫЕ НА РАСШИРЕНИИ И ИЗМЕНЕНИИ ДАВЛЕНИЯ РАБОЧЕГО ВЕЩЕСТВА
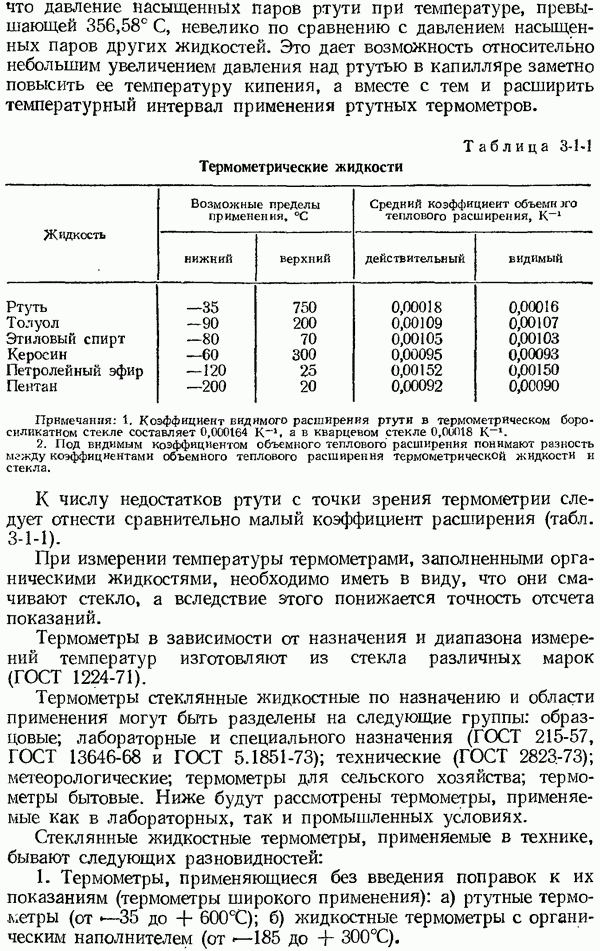
- 3-1. Термометры стеклянные жидкостные
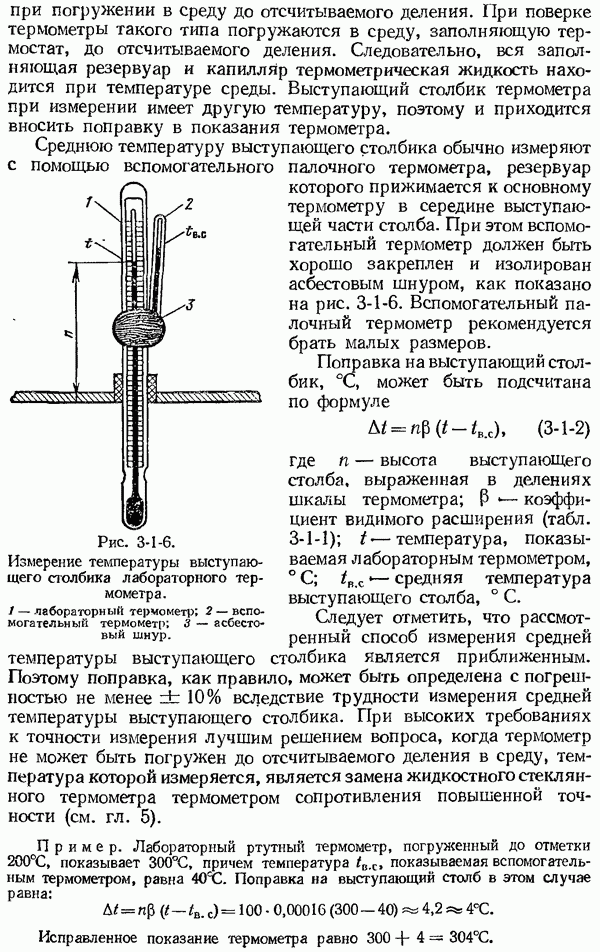
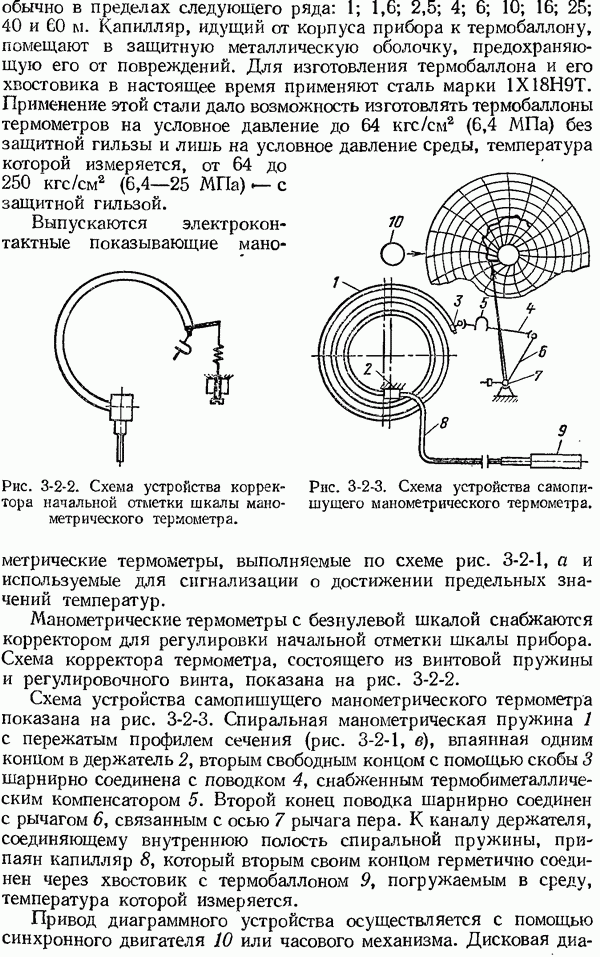
- 3-2. Термометры манометрические
- Термометры газовые.
- Конденсационные термометры.
- Термометры жидкостные.
- Основные метрологические характеристики манометрических термометров.
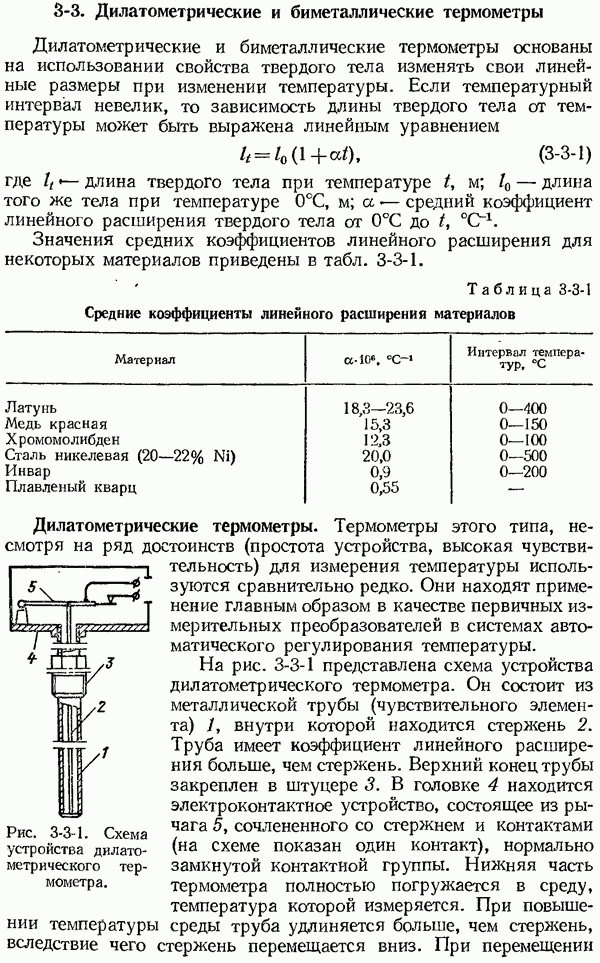
- 3-3. Дилатометрические и биметаллические термометры
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОЭЛЕКТРИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ ТЕМПЕРАТУР
- 4-2. Основы теории термоэлектрических термометров
- 4-3. Включение измерительного прибора в цепь термоэлектрического термометра
- 4-4. Поправка на температуру свободных концов термоэлектрического термометра
- 4-5. Определение термо-э. д. с. различных материалов при изучении их термоэлектрических свойств
- 4-6. Основные требования, предъявляемые к термоэлектродным материалам
- 4-7. Общие сведения о термоэлектрических термометрах
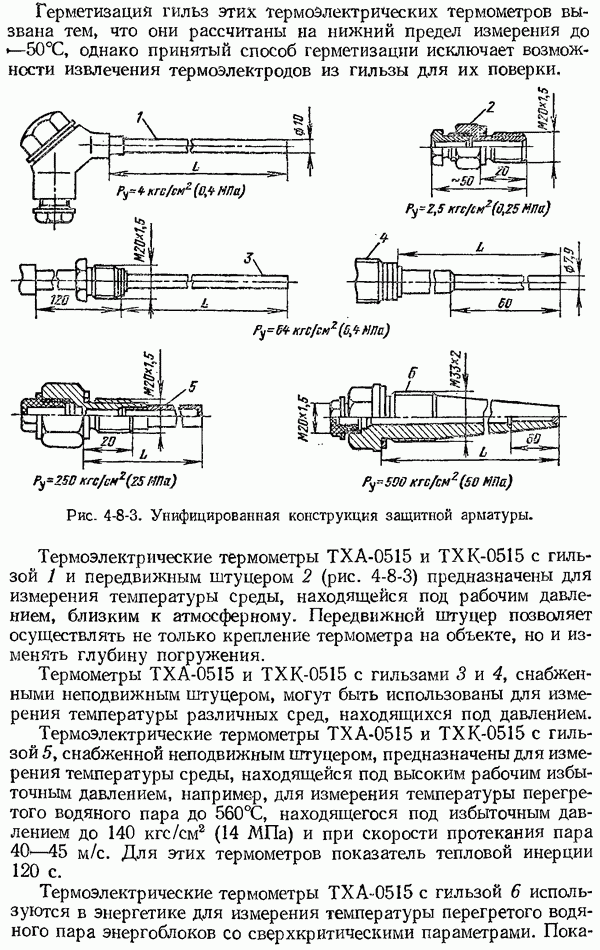
- 4-8. Устройство термоэлектрических термометров
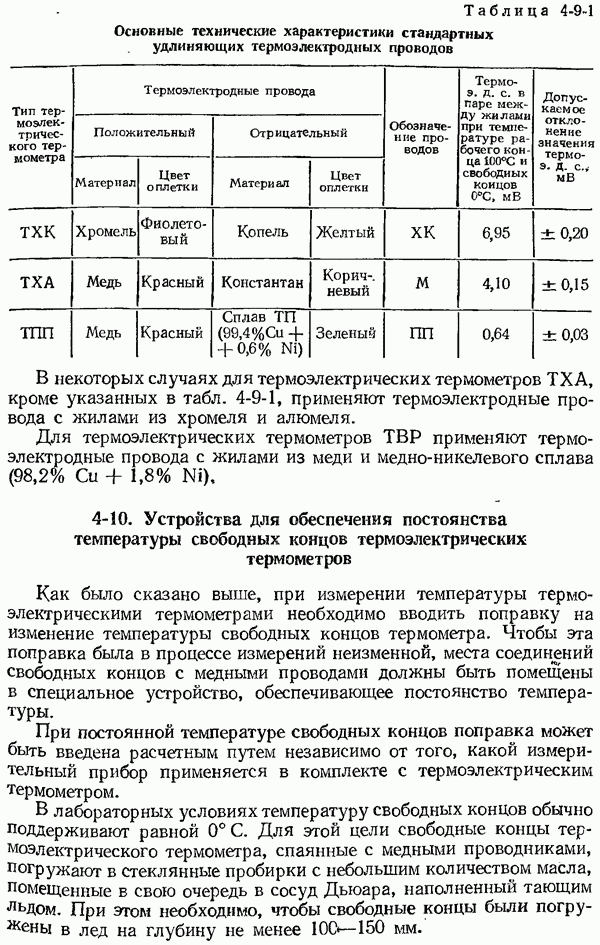
- 4-9. Удлиняющие термоэлектродные провода
- 4-10. Устройства для обеспечения постоянства температуры свободных концов термоэлектрических термометров
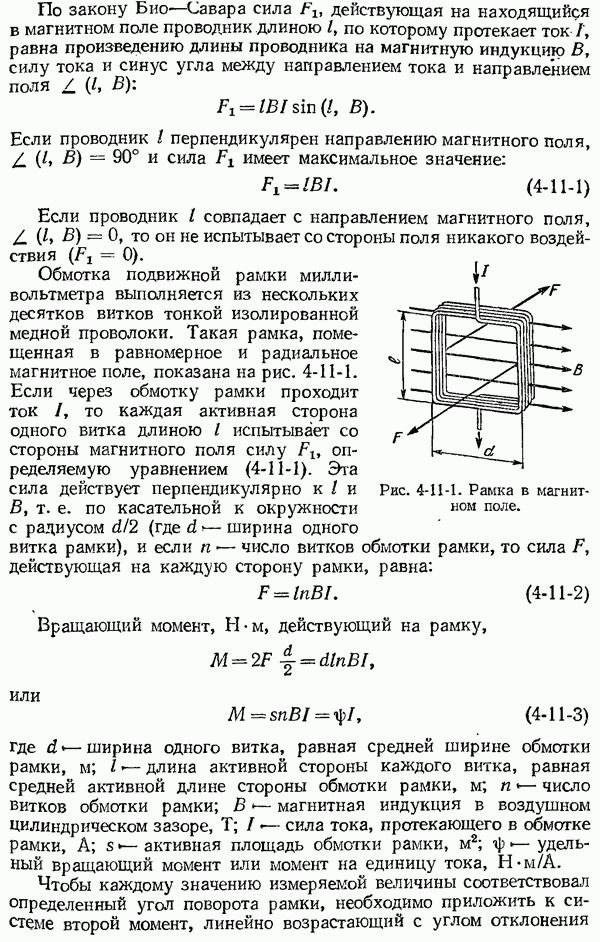
- 4-11. Милливольтметры
- 4-12. Устройство КТ и схемы присоединения нескольких термоэлектрических термометров к одному милливольтметру
- 4-13. Измерение термо-э. д. с. милливольтметром
- 4-14. Компенсационный метод измерения термо-э. д. с.
- 4-15. Нормальные элементы
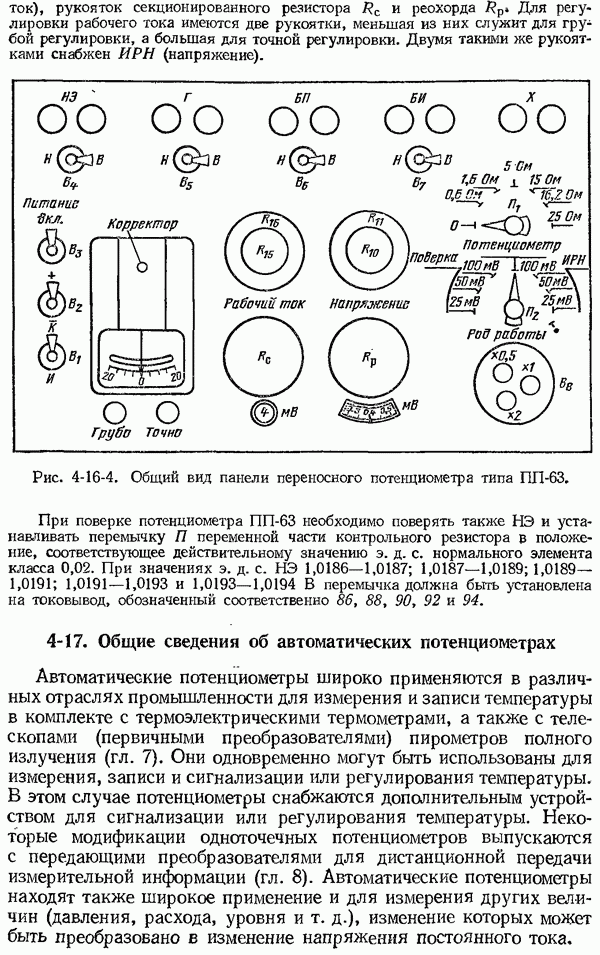
- 4-16. Потенциометры переносные и лабораторные
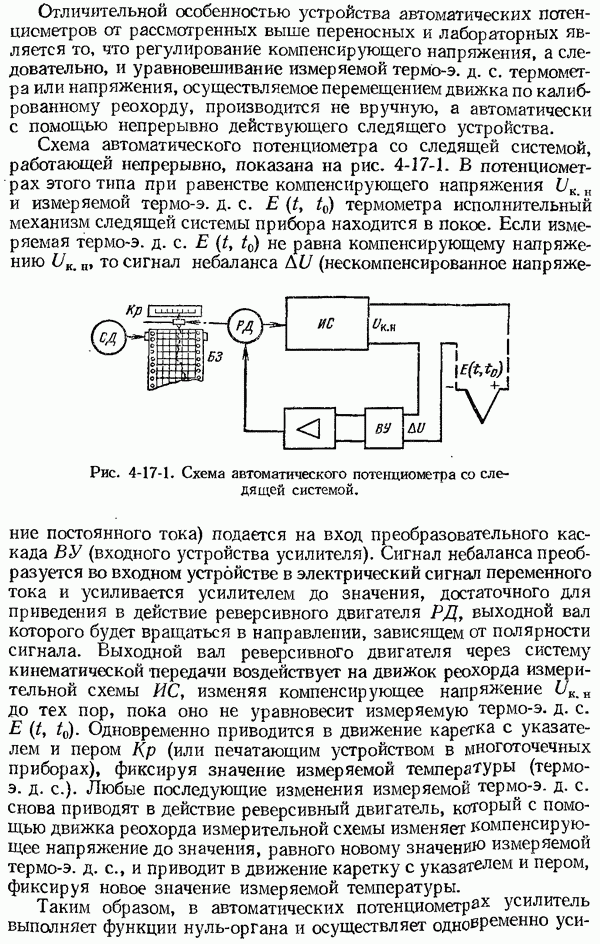
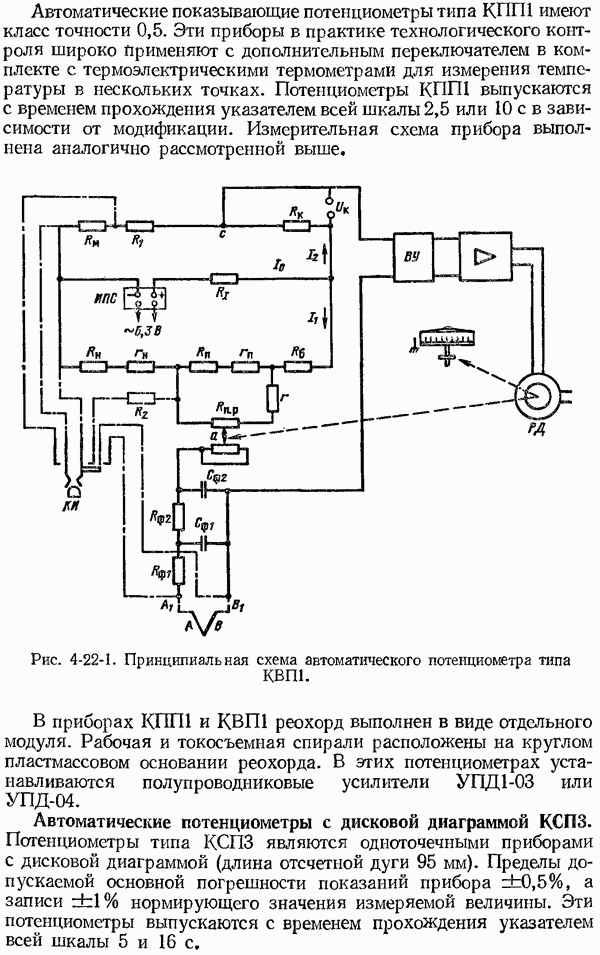
- 4-17. Общие сведения об автоматических потенциометрах
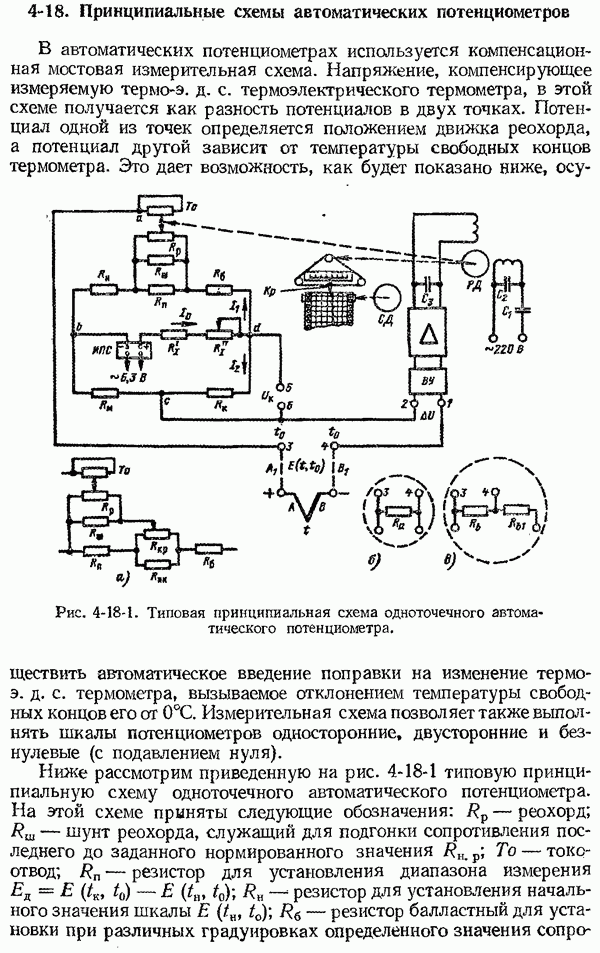
- 4-18 Принципиальные схемы автоматических потенциометров
- 4-19. Методика расчета сопротивлений резисторов измерительной схемы автоматических потенциометров
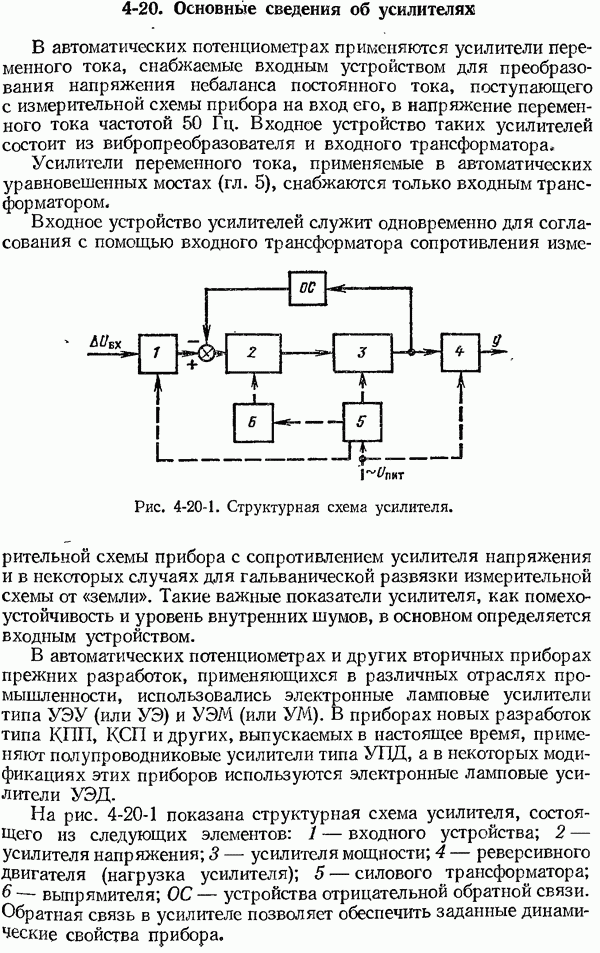
- 4-20. Основные сведения об усилителях
- 4-21. Основные сведения об источниках стабилизированного питания
- 4-22. Устройство автоматических потенциометров
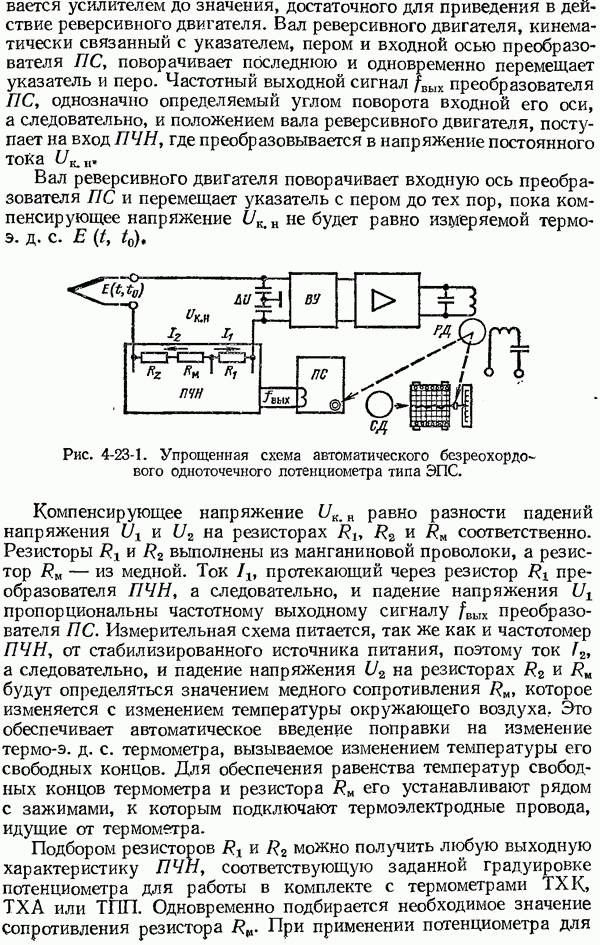
- 4-23. Автоматические безреохордные потенциометры
- ГЛАВА ПЯТАЯ. ТЕРМОМЕТРЫ СОПРОТИВЛЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ К НИМ
- 5-2. Основные сведения о термометрах сопротивления и металлах, применяемых для их изготовления
- 5-3. Устройство платиновых и медных термометров сопротивления
- 5-4. Полупроводниковые термометры сопротивления
- 5-5. Компенсационный метод измерения сопротивления термометра
- 5-6. Измерение сопротивления термометра мостом
- 5-7. Логометры
- 5-8. Общие сведения об автоматических уравновешенных мостах
- 5-9. Принципиальные измерительные схемы автоматических уравновешенных мостов
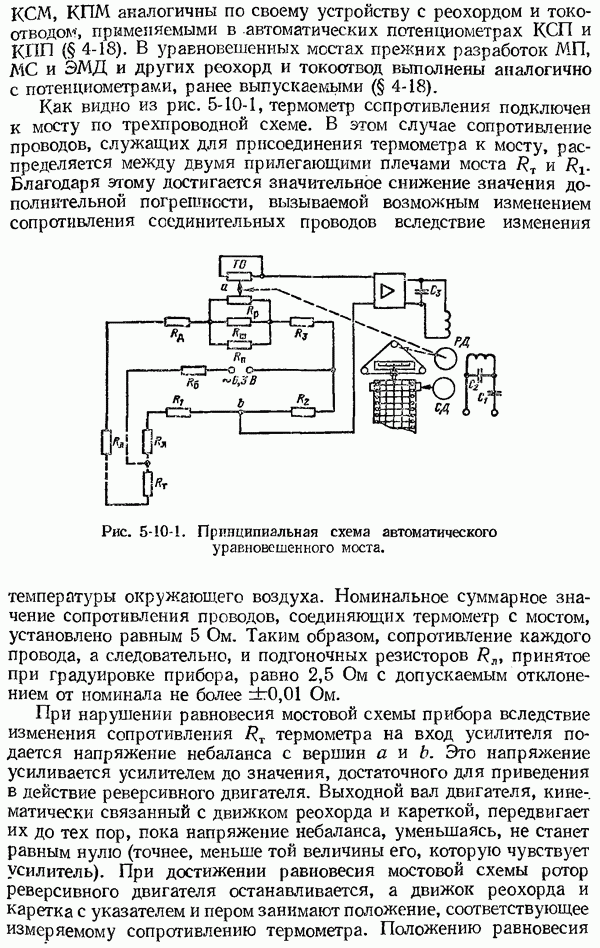
- 5-10. Принципиальная схема автоматического уравновешенного моста
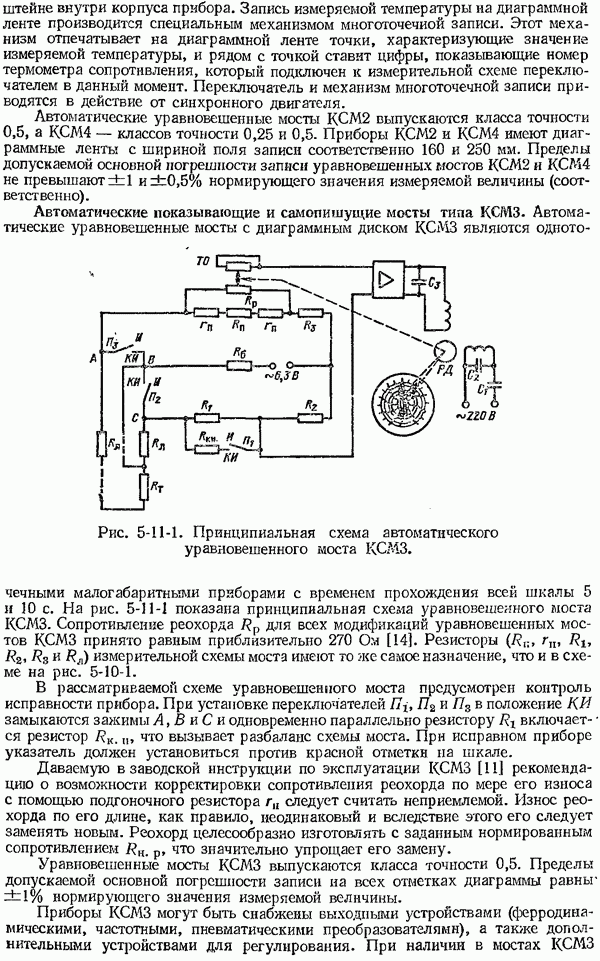
- 5-11. Устройство автоматических уравновешенных мостов
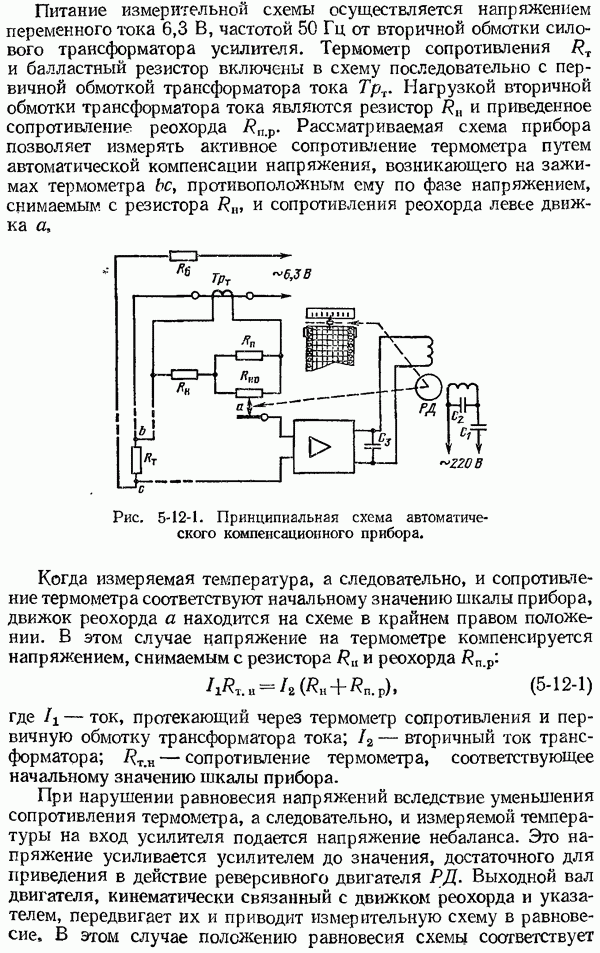
- 5-12. Автоматические компенсационные приборы для работы с малоомными термометрами сопротивления
- ГЛАВА ШЕСТАЯ. МЕТОДИКА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ КОНТАКТНЫМИ МЕТОДАМИ, ПОГРЕШНОСТИ ПРИ ИЗМЕРЕНИИ И СПОСОБЫ ИХ УЧЕТА И УМЕНЬШЕНИЯ
- 6-2. Методические погрешности при измерении температур газа, обусловленные влиянием теплообмена излучением
- 6-3. Методические погрешности при измерении температуры среды, обусловленные отводом или подводом тепла по термоприемнику
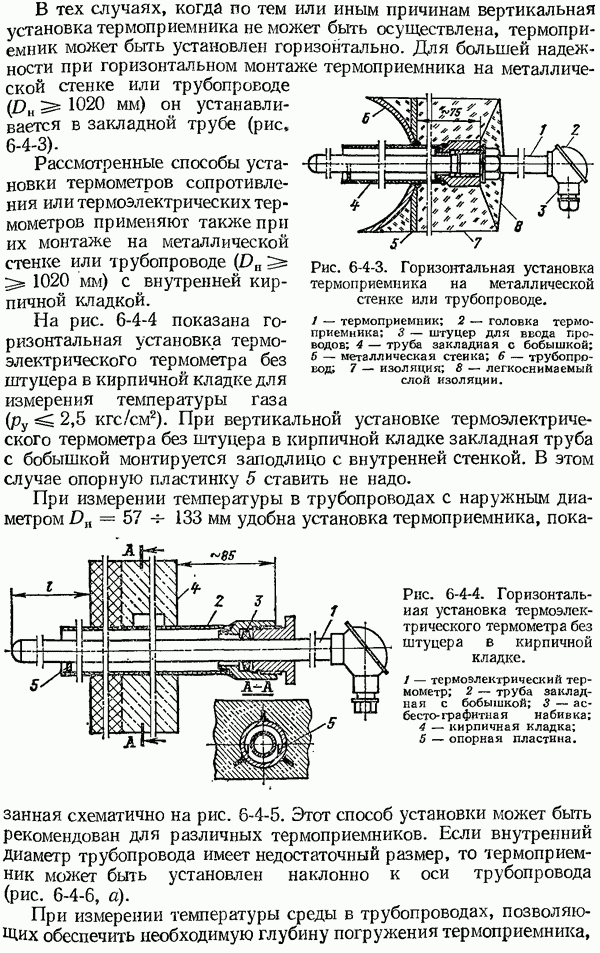
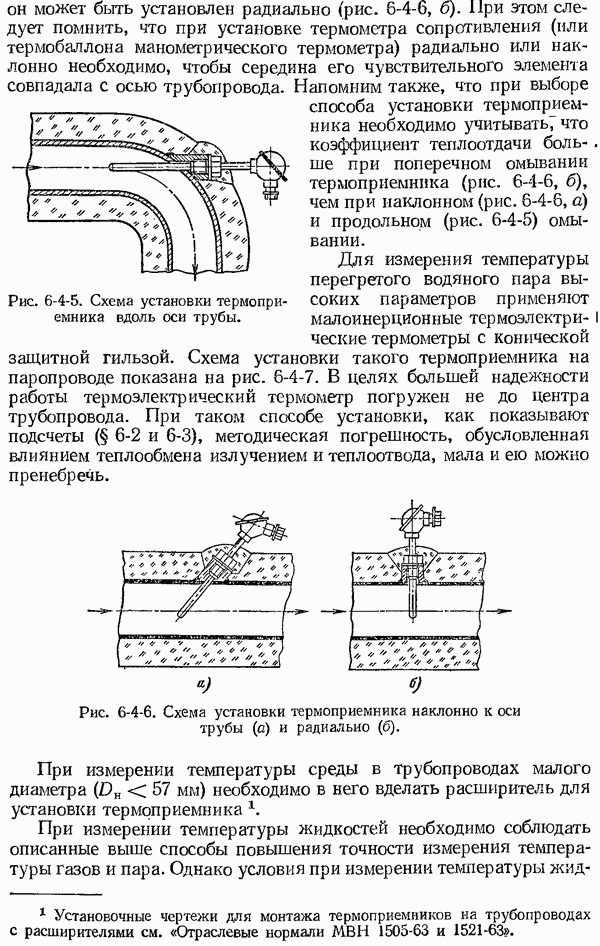
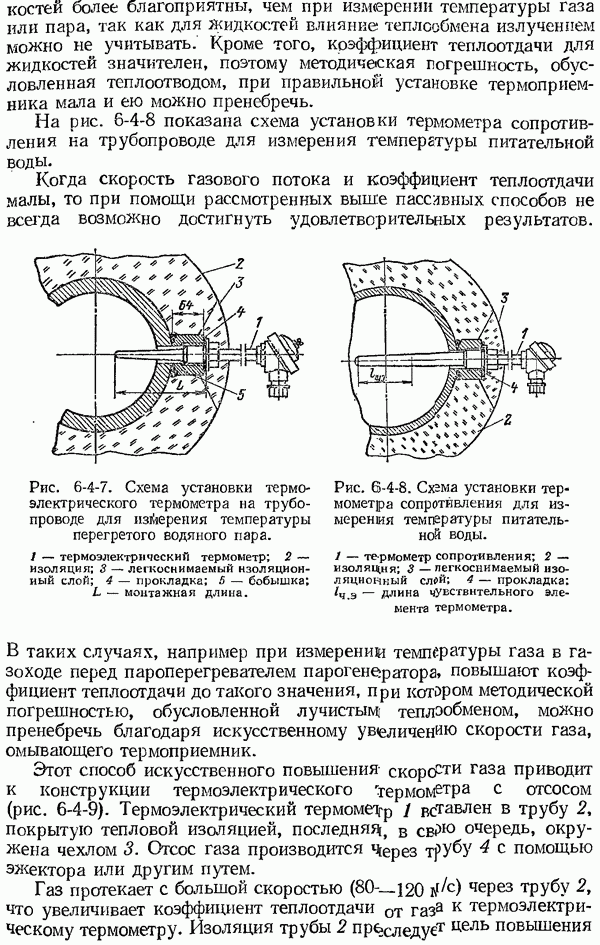
- 6-4. Установка термоприемников при измерении температуры газов, пара и жидкостей
- 6-5. Измерение температуры газовых потоков большой скорости
- 6-6. Измерение температуры поверхности и внутри тела
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ТЕЛ ПО ИХ ТЕПЛОВОМУ ИЗЛУЧЕНИЮ
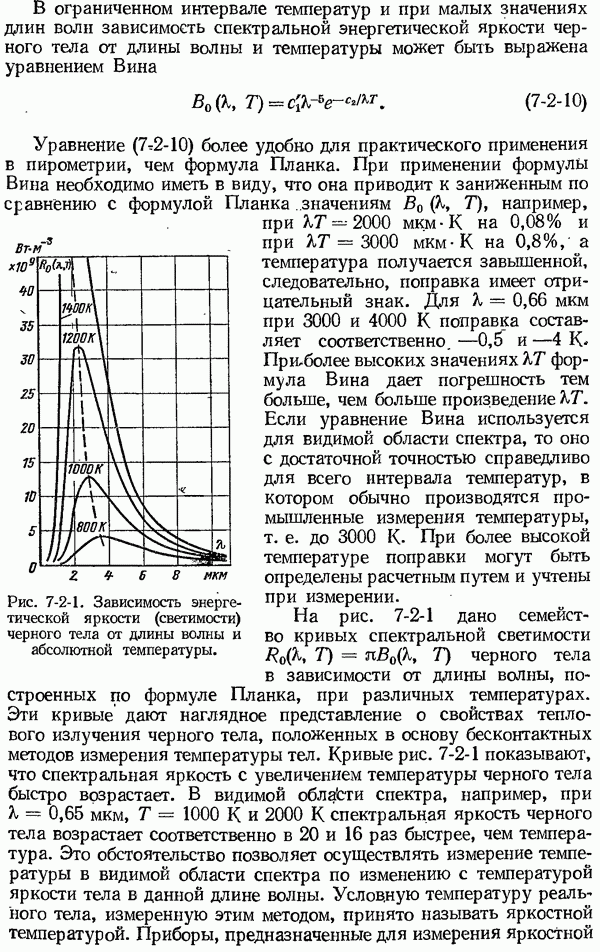
- 7-2. Теоретические основы методов измерения температуры тел по их тепловому излучению
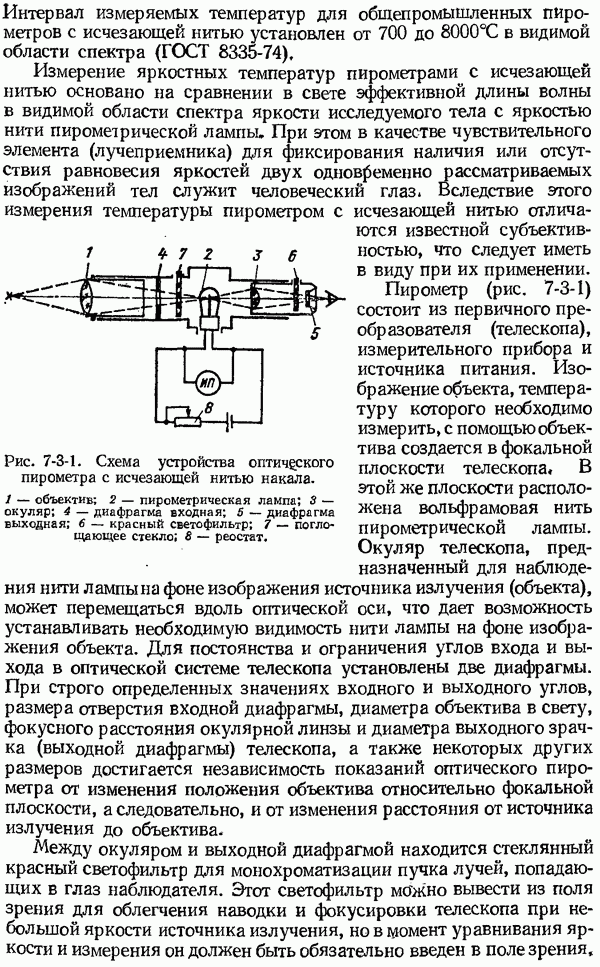
- 7-3. Оптические пирометры
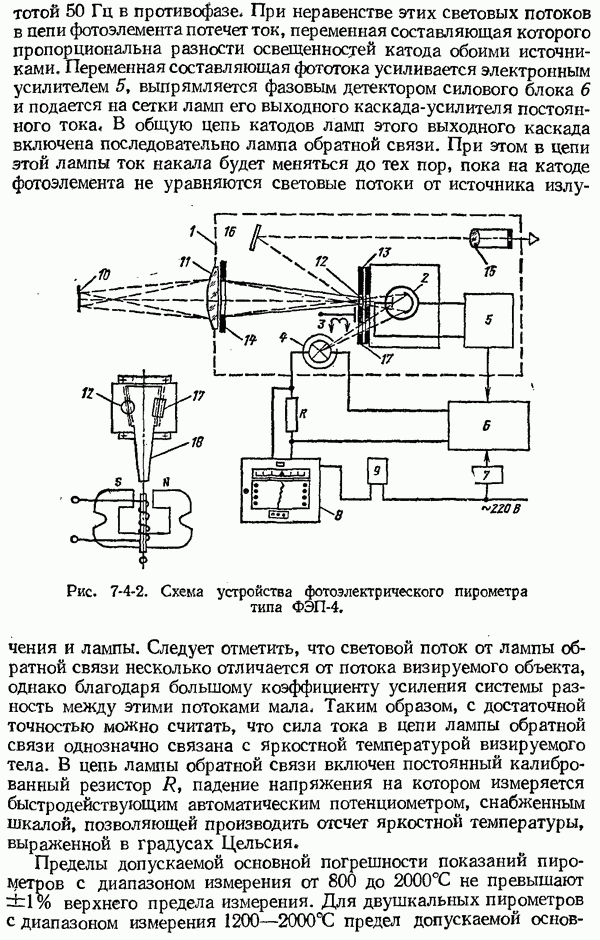
- 7-4. Фотоэлектрические пирометры
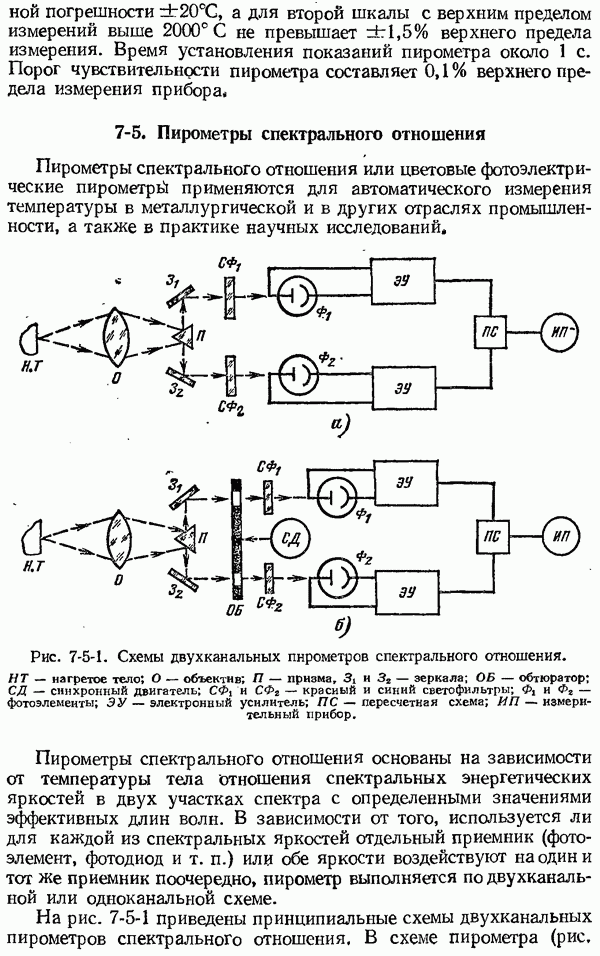
- 7-5. Пирометры спектрального отношения
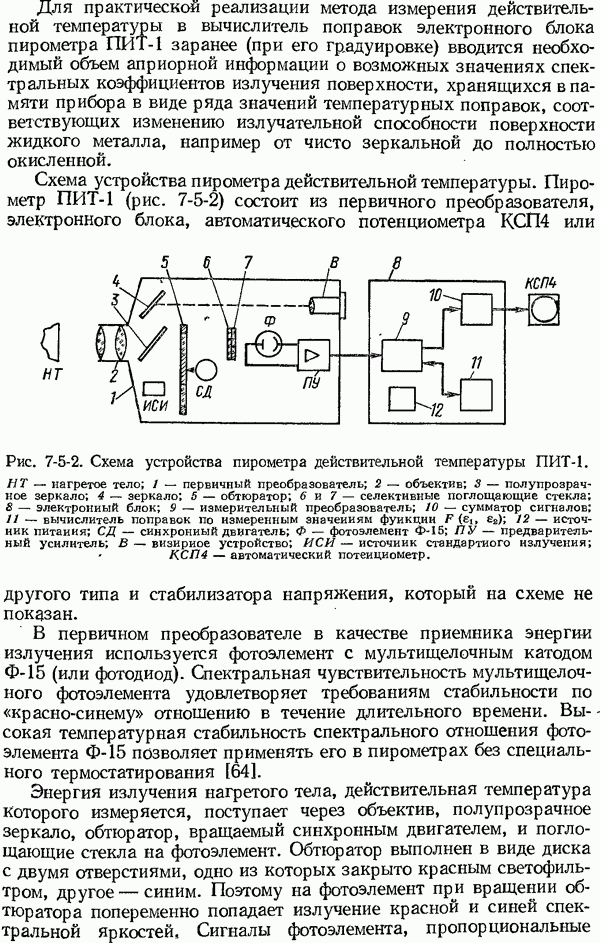
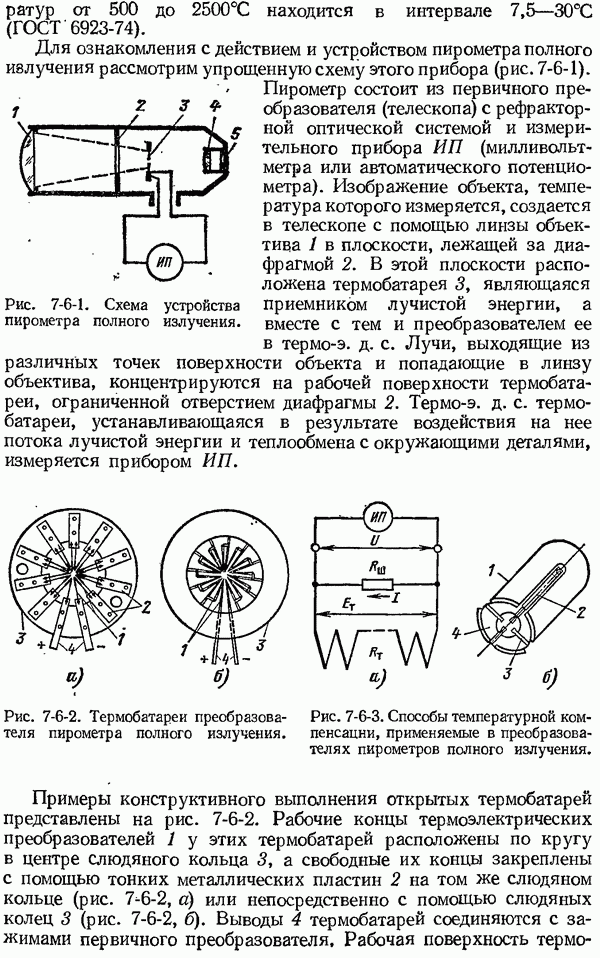
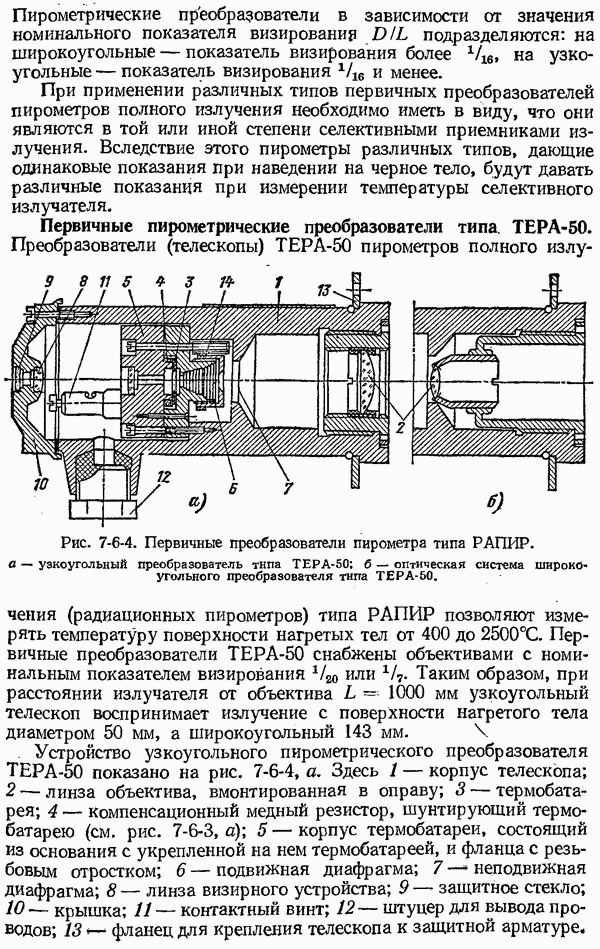
- 7-6. Пирометры полного излучения
- РАЗДЕЛ ТРЕТИЙ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
- ГЛАВА ВОСЬМАЯ. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И СХЕМЫ ДИСТАНЦИОННОЙ ПЕРЕДАЧИ ПОКАЗАНИЙ
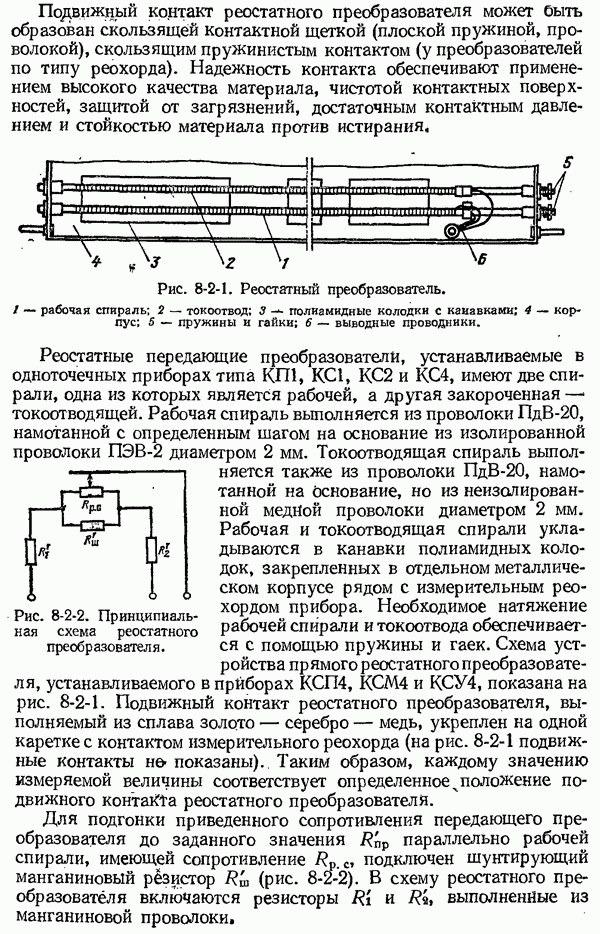
- 8-2. Реостатные измерительные преобразователи и схемы дистанционной передачи
- 8-3. Измерительные тензопреобразователи
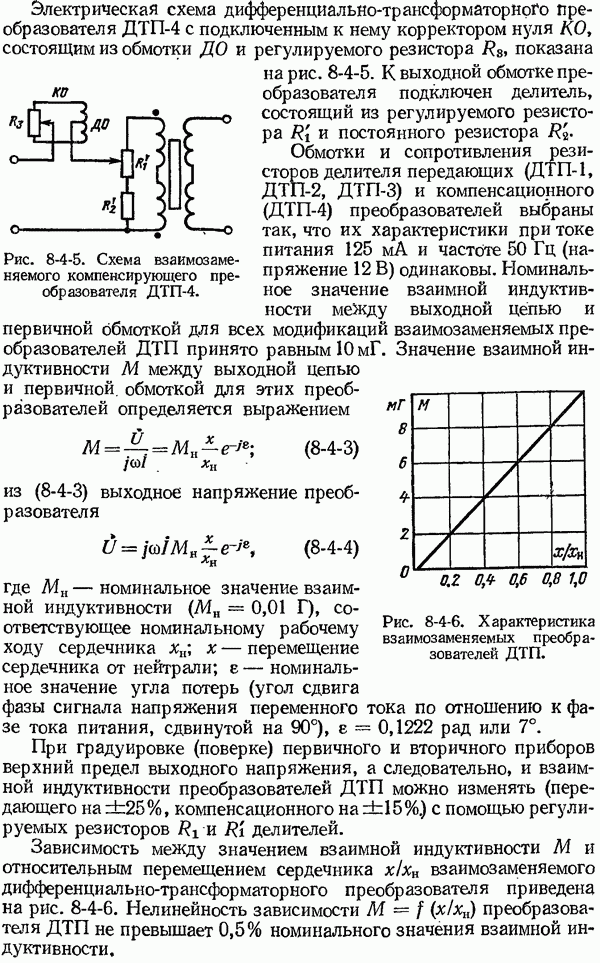
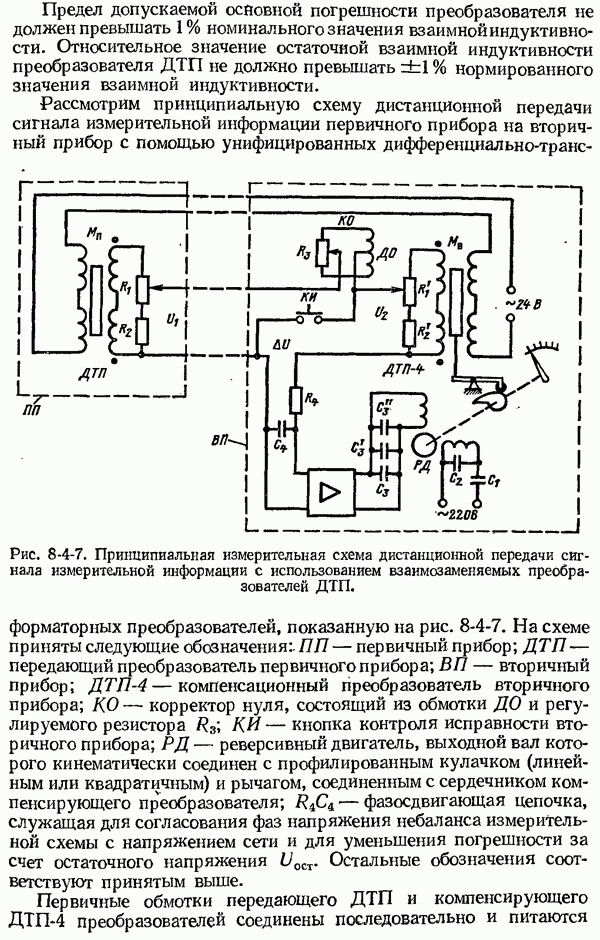
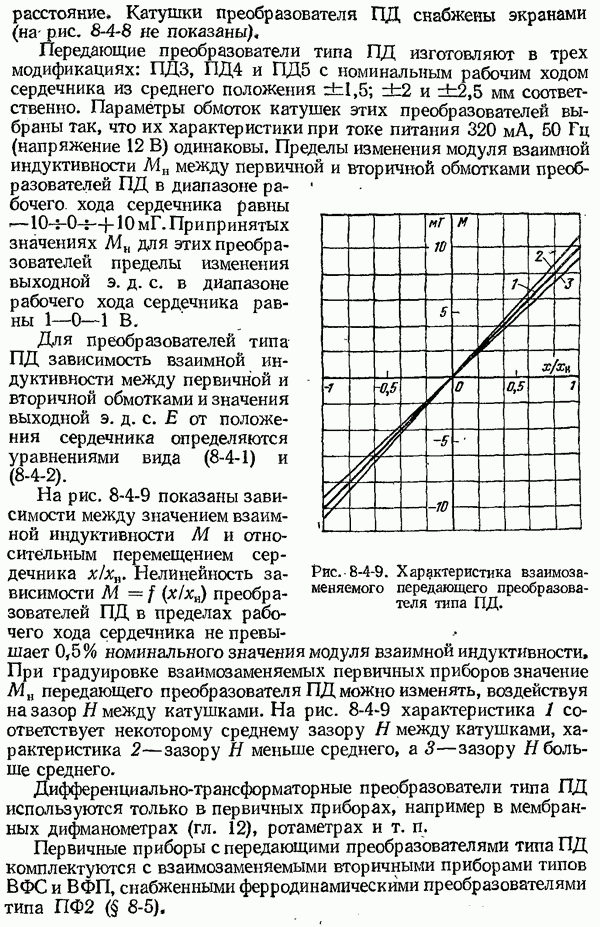
- 8-4. Дифференциально-трансформаторные преобразователи и схемы дистанционной передачи
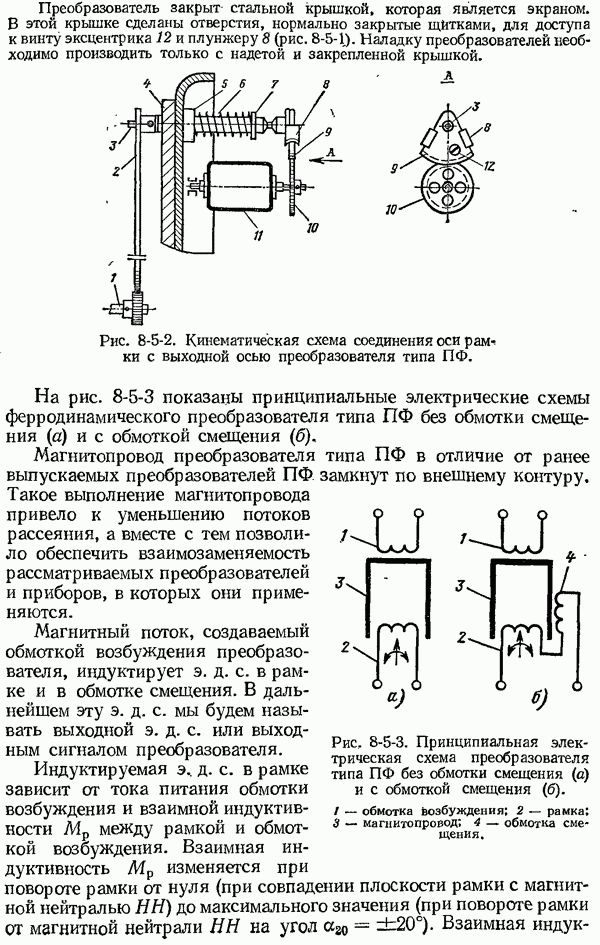
- 8-5. Ферродинамические преобразователи и схемы дистанционной передачи
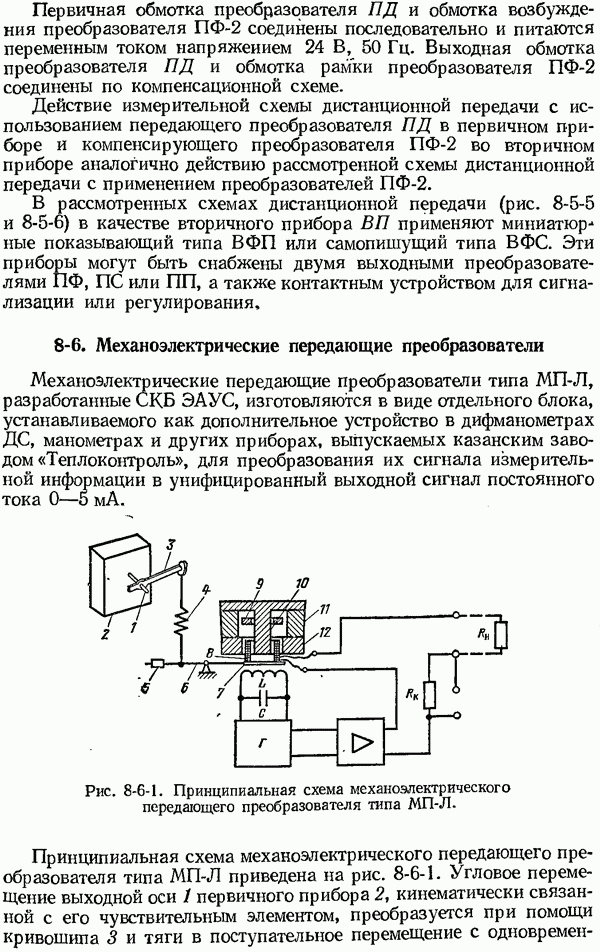
- 8-6. Механоэлектрические передающие преобразователи
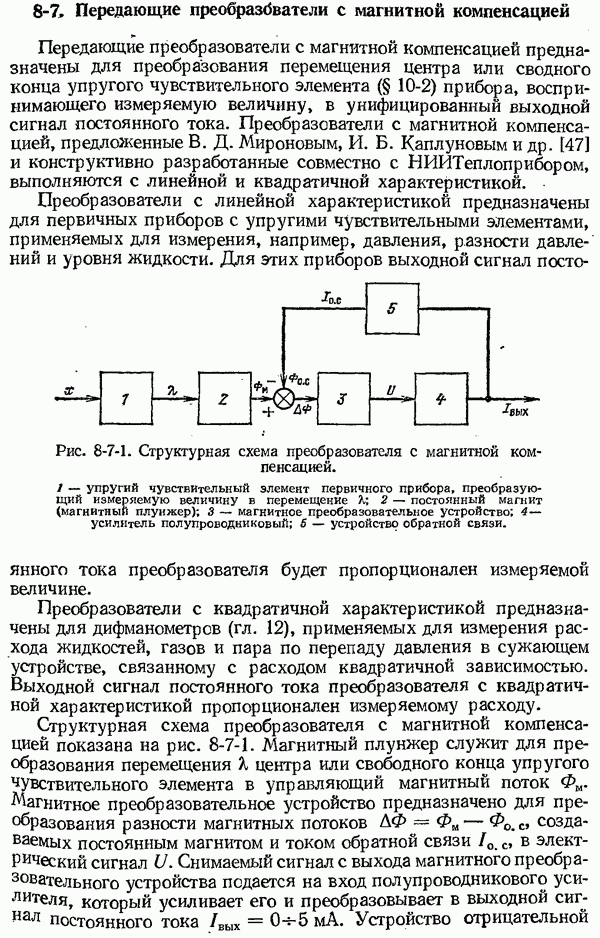
- 8-7. Передающие преобразователи с магнитной компенсацией
- 8-8. Электросиловые преобразователи
- 8-9. Частотные преобразователи со струнным вибратором
- 8-10. Пневмосиловые преобразователи
- 8-11. Пневматические передающие преобразователи
- 8-12. Электропневматические и пневмоэлектрические преобразователи
- 8-13. Нормирующие измерительные преобразователи
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ И РАЗНОСТИ ДАВЛЕНИЙ
- ГЛАВА ДЕВЯТАЯ. ЖИДКОСТНЫЕ ПРИБОРЫ ДАВЛЕНИЯ С ВИДИМЫМ УРОВНЕМ
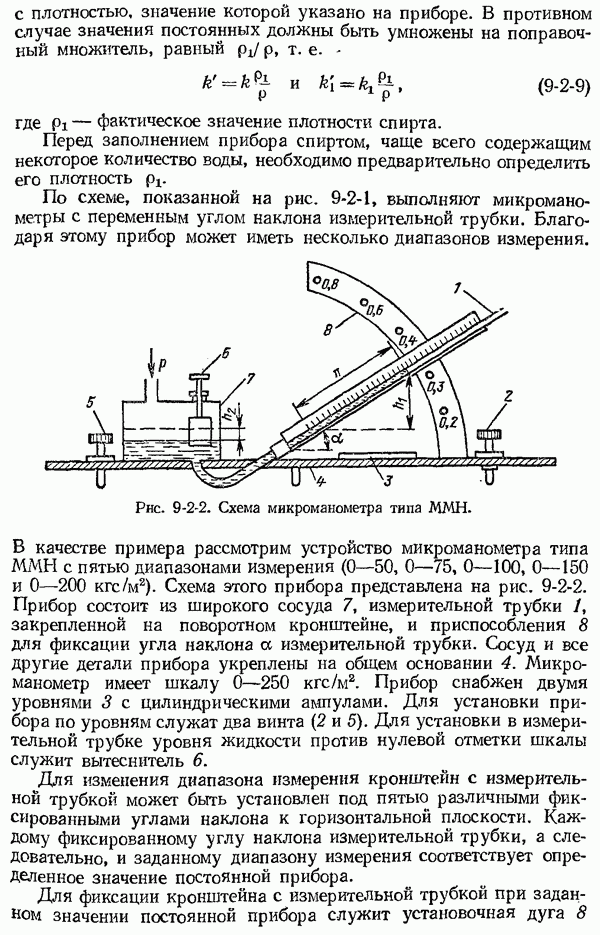
- 9-2. Микроманометры
- 9-3. Поправки к показаниям жидкостных приборов
- 9-4. Барометры ртутные
- ГЛАВА ДЕСЯТАЯ. ПРИБОРЫ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
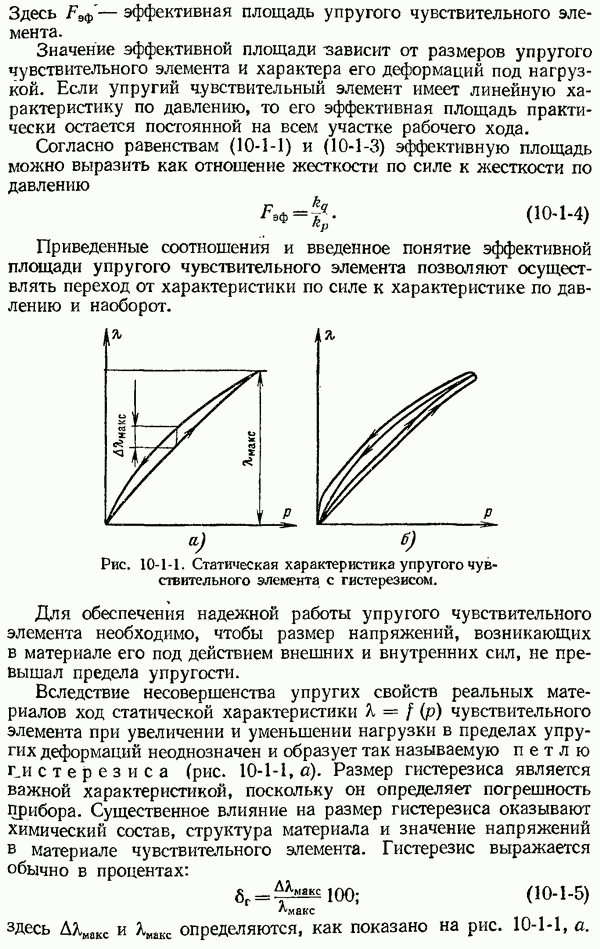
- 10-1. Общие сведения и основные свойства упругих чувствительных элементов
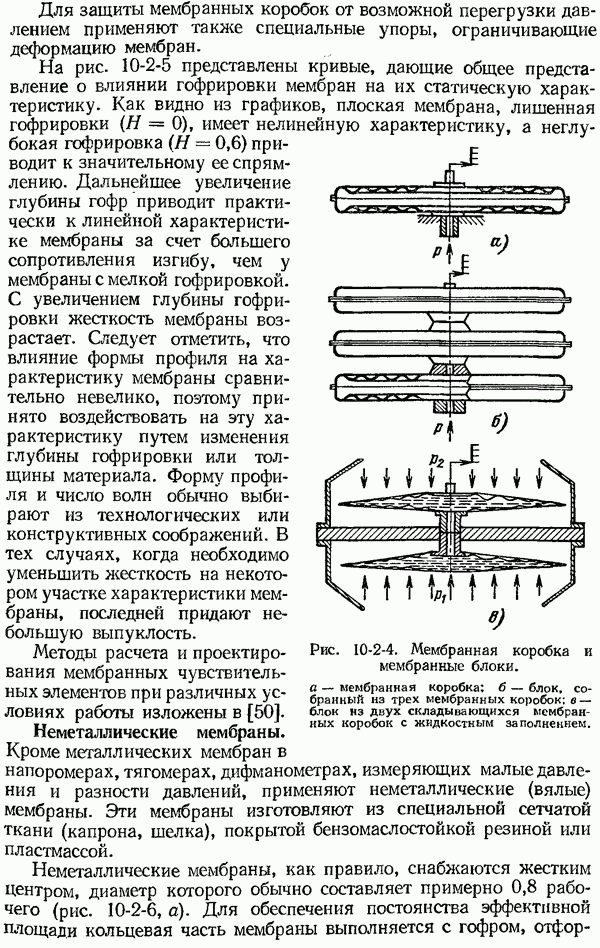
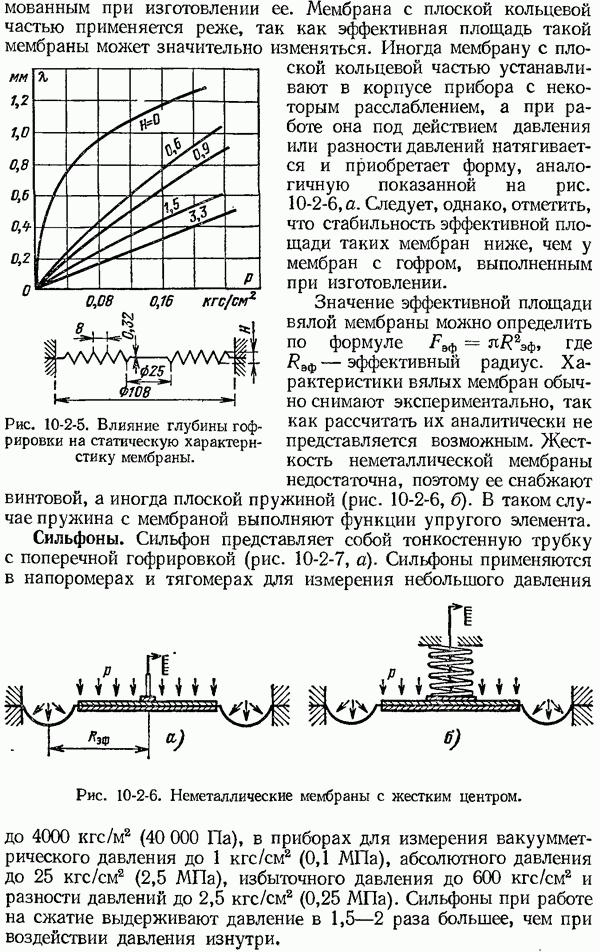
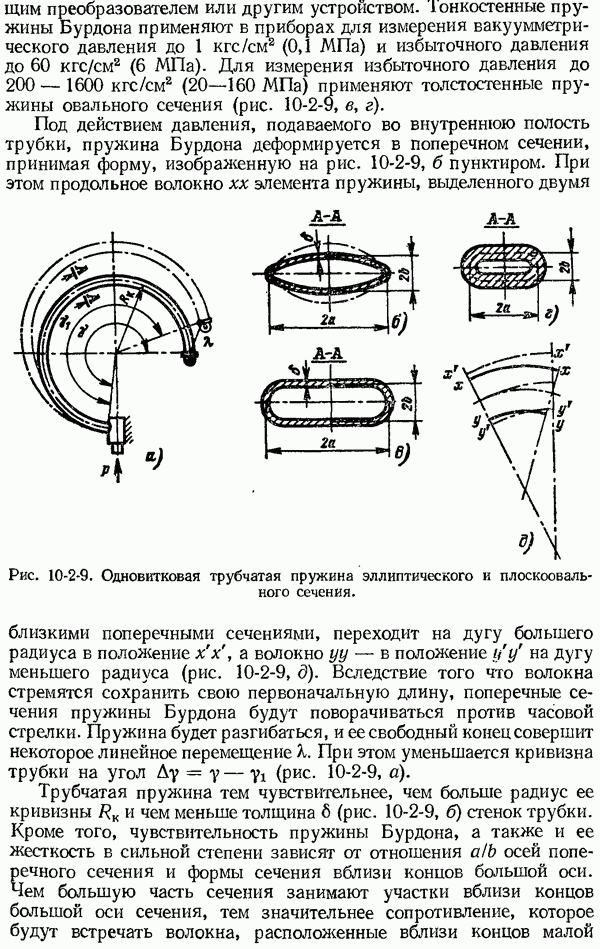
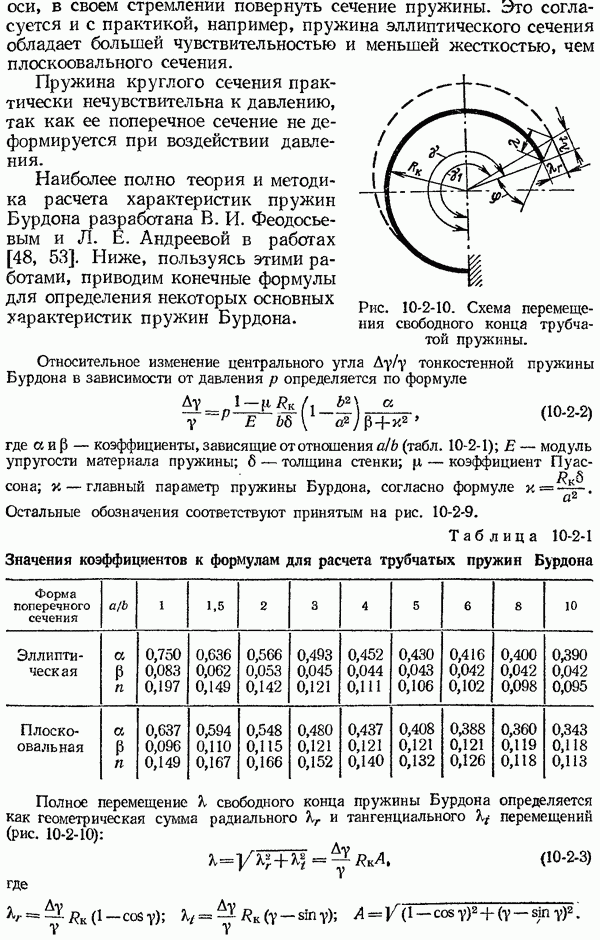
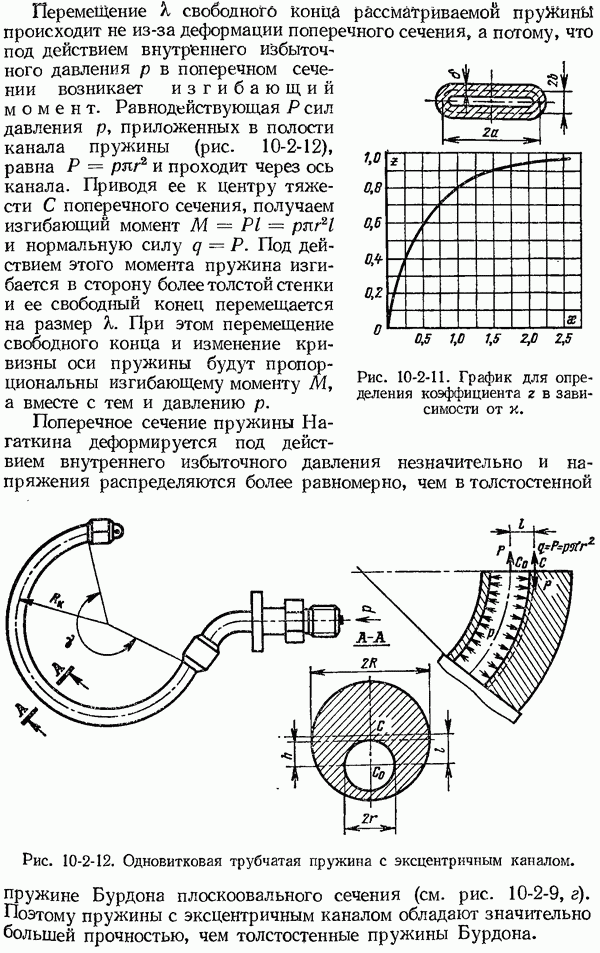
- 10-2. Упругие чувствительные элементы
- 10-3. Приборы давления прямого действия
- 10-4. Электроконтактные приборы и реле давления
- 10-5. Приборы давления с электрическими и пневматическими преобразователями
- ГЛАВА ОДИННАДЦАТАЯ. ПРИБОРЫ ДАВЛЕНИЯ ЭЛЕКТРИЧЕСКИЕ
- 11-1. Пьезоэлектрические манометры
- 11-2. Манометры сопротивления
- ГЛАВА ДВЕНАДЦАТАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ МАНОМЕТРЫ
- 12-2. Дифманометры колокольные
- 12-3. Дифманометры кольцевые
- 12-4. Дифманометры поплавковые
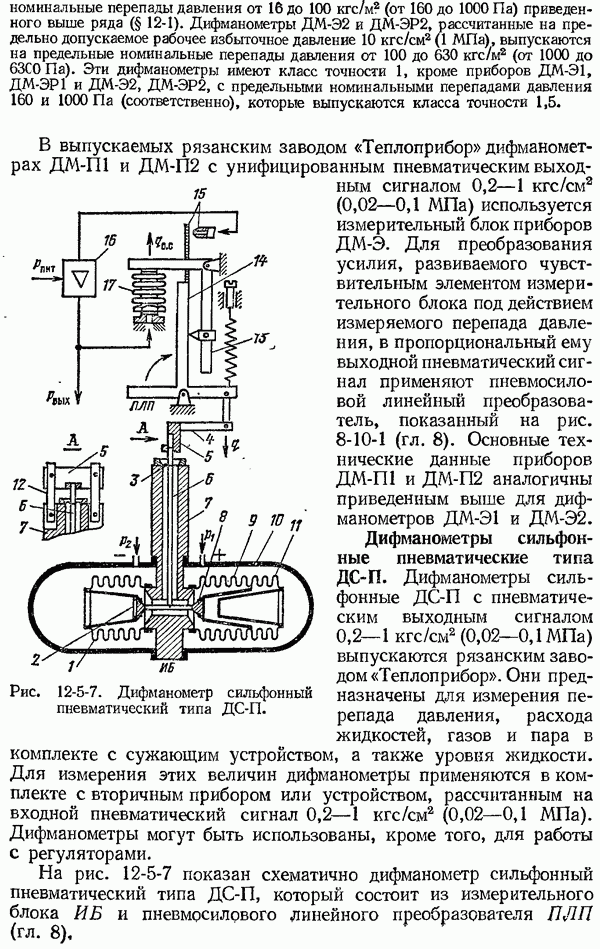
- 12-5. Дифманометры с упругими чувствительными элементами
- ГЛАВА ТРИНАДЦАТАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О МЕТОДИКЕ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
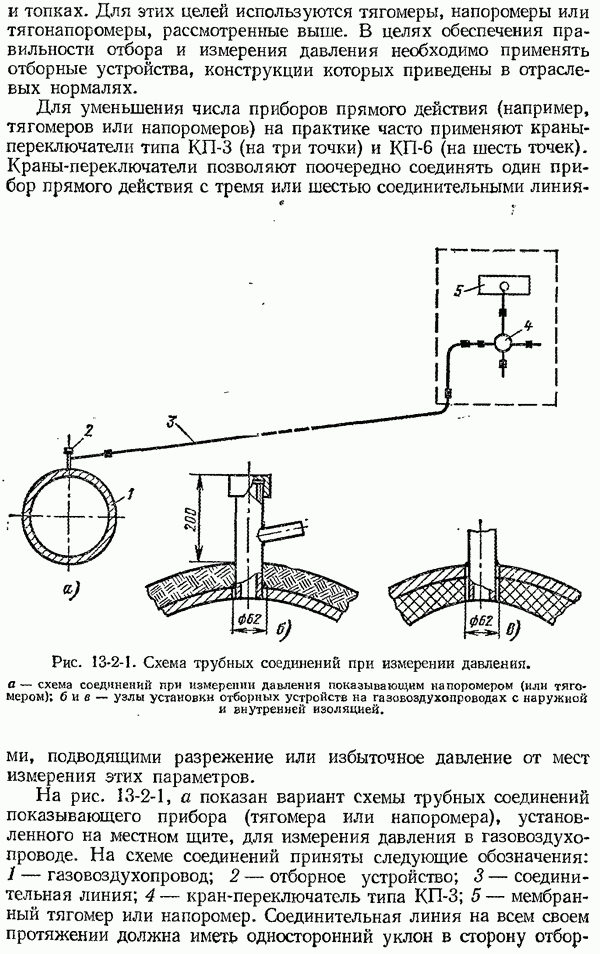
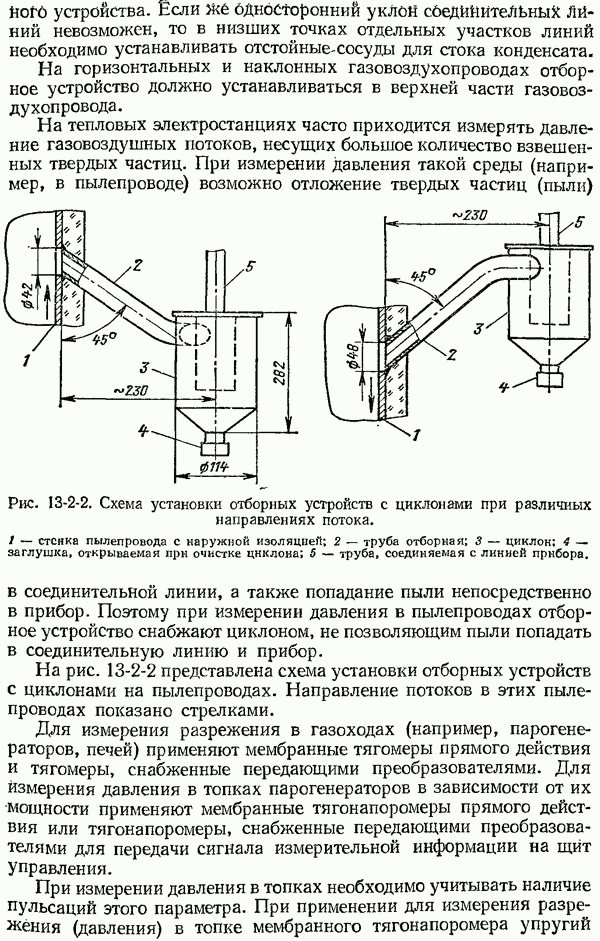
- 13-2. Измерение близкого к атмосферному давления газовых сред
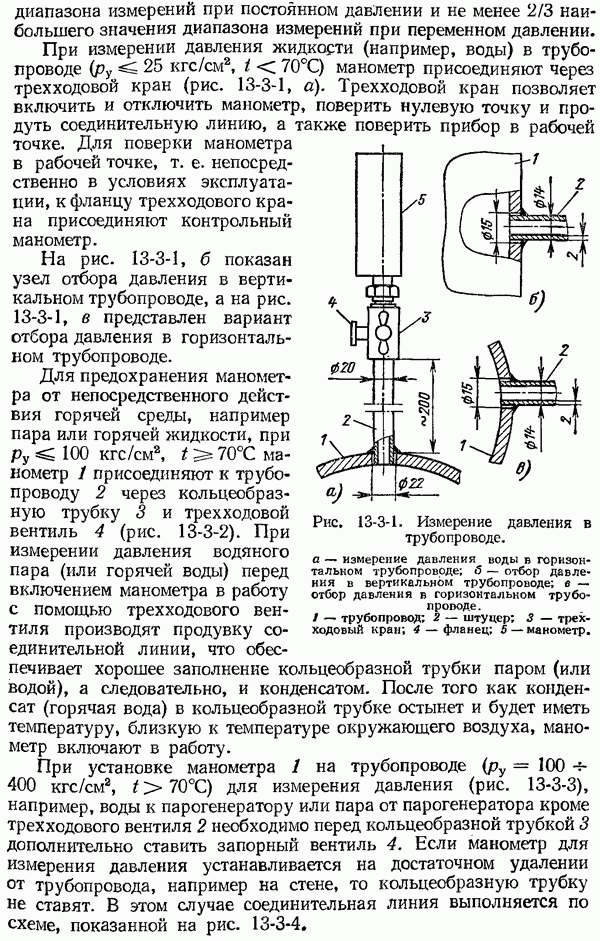
- 13-3. Измерение давления газов, жидкостей и пара
- 13-4. Разделители жидкостные и мембранные
- РАЗДЕЛ ПЯТЫЙ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА, ПАРА И ТЕПЛА
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИЗМЕРЕНИЕ РАСХОДА И КОЛИЧЕСТВА ЖИДКОСТЕЙ, ГАЗА И ПАРА ПО ПЕРЕПАДУ ДАВЛЕНИЯ В СУЖАЮЩЕМ УСТРОЙСТВЕ
- 14-1. Основы теории и уравнения расхода
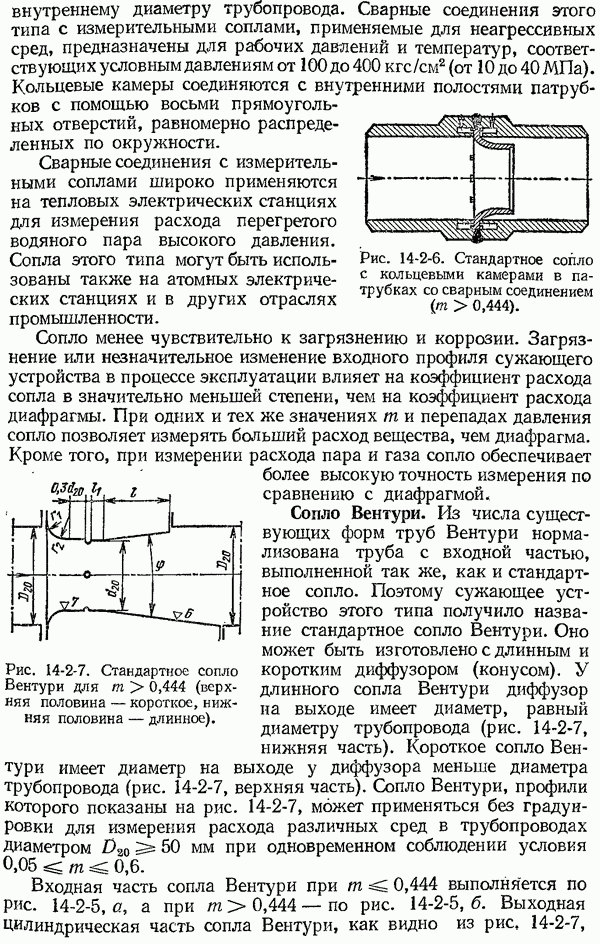
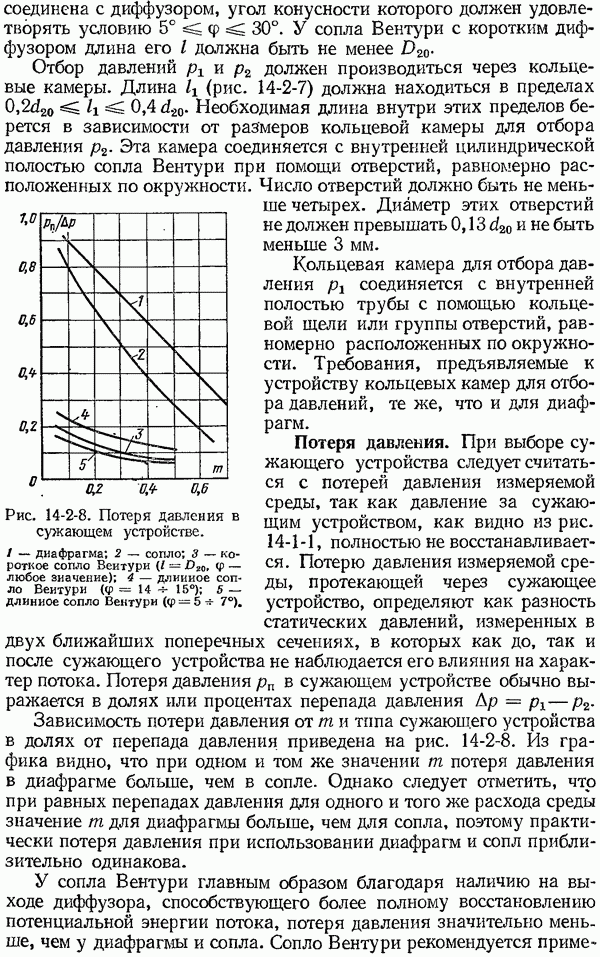
- 14-2. Стандартные сужающие устройства
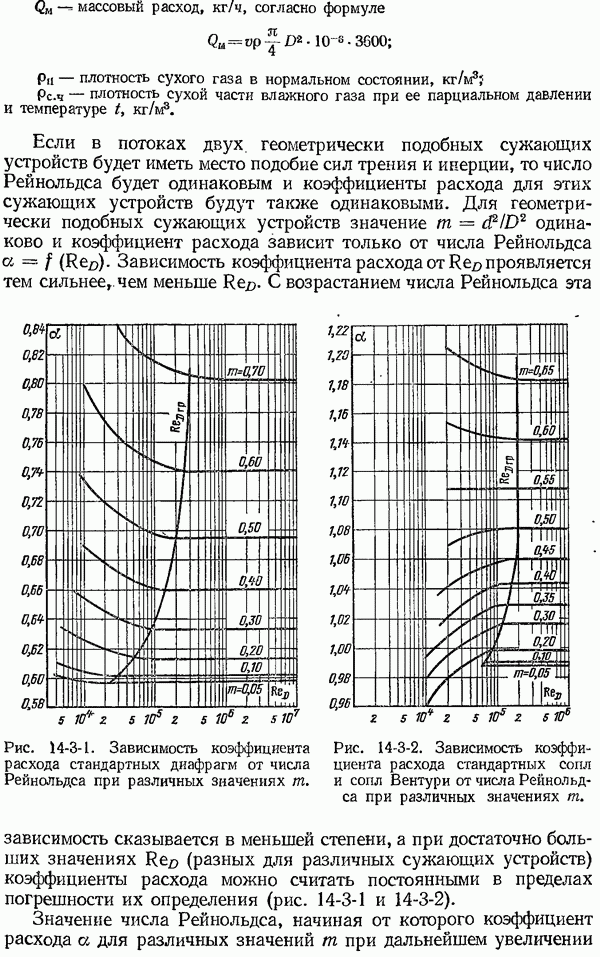
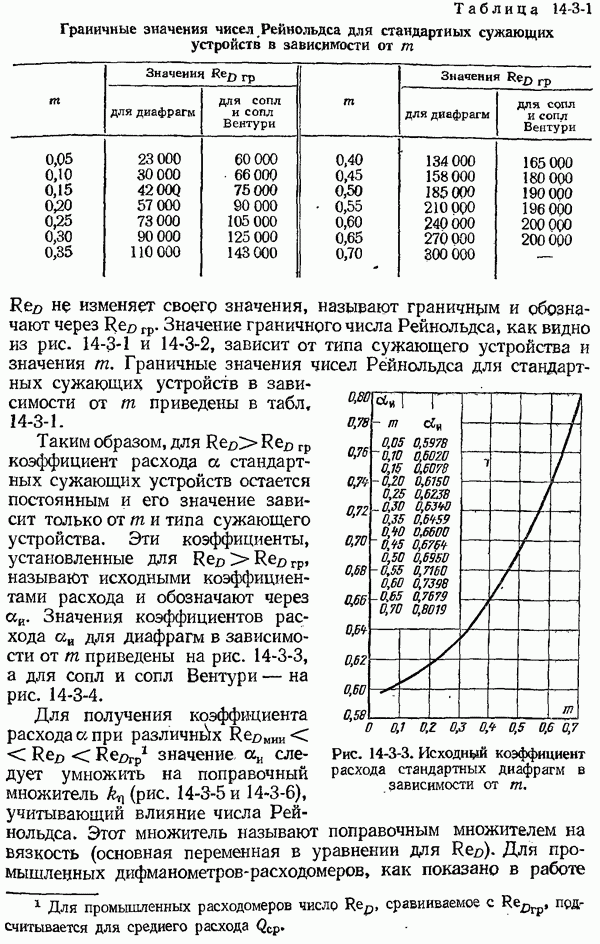
- 14-3. Коэффициенты расхода и поправочные множители к ним
- 14-4. Поправочный множитель на расширение измеряемой среды
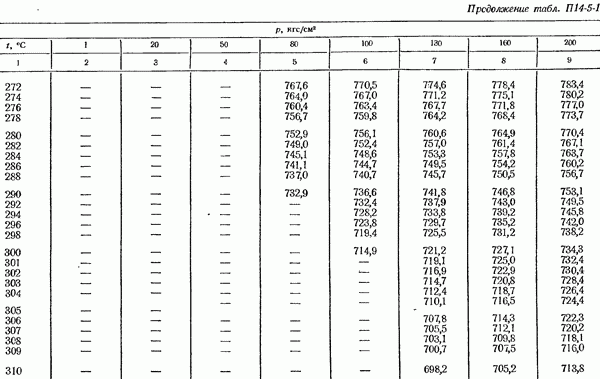
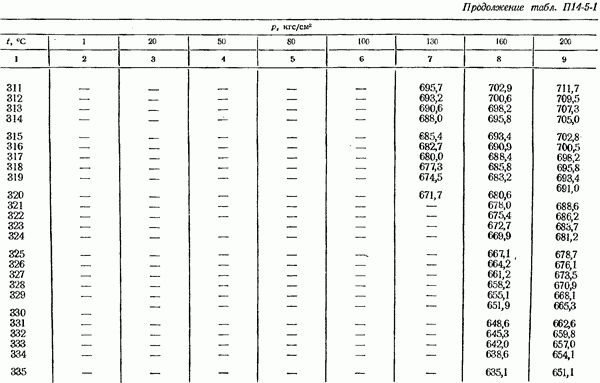
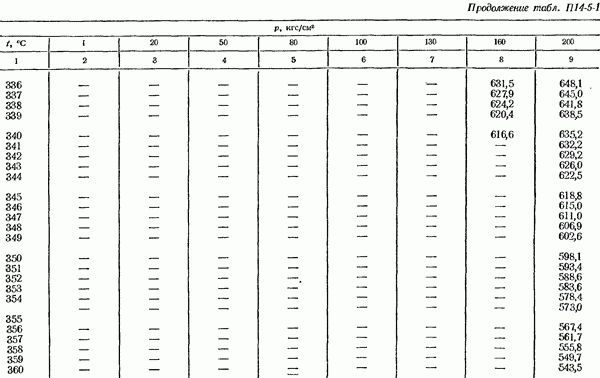
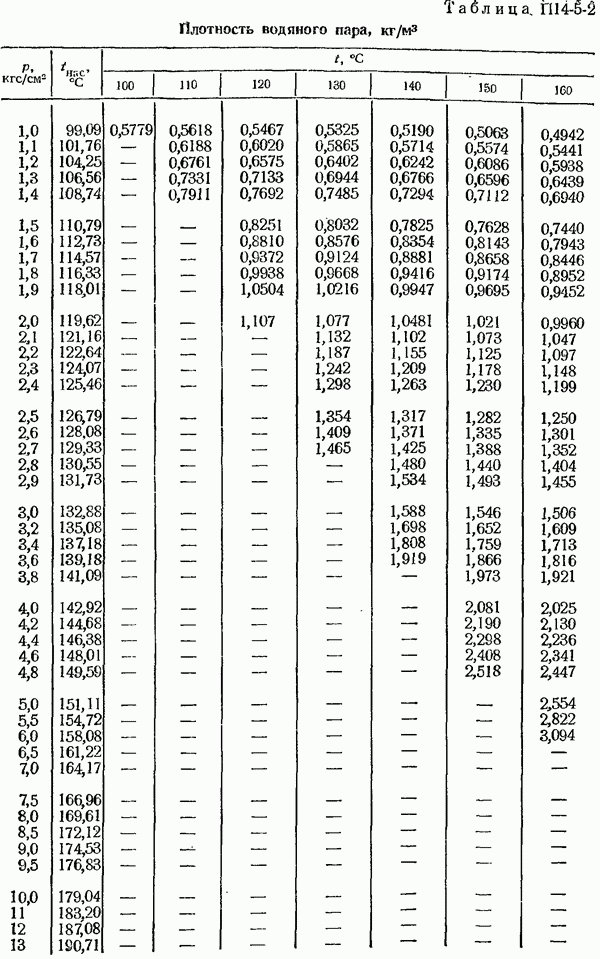
- 14-5. Определение плотности измеряемом среды
- 14-6. Основные расчетные формулы расхода
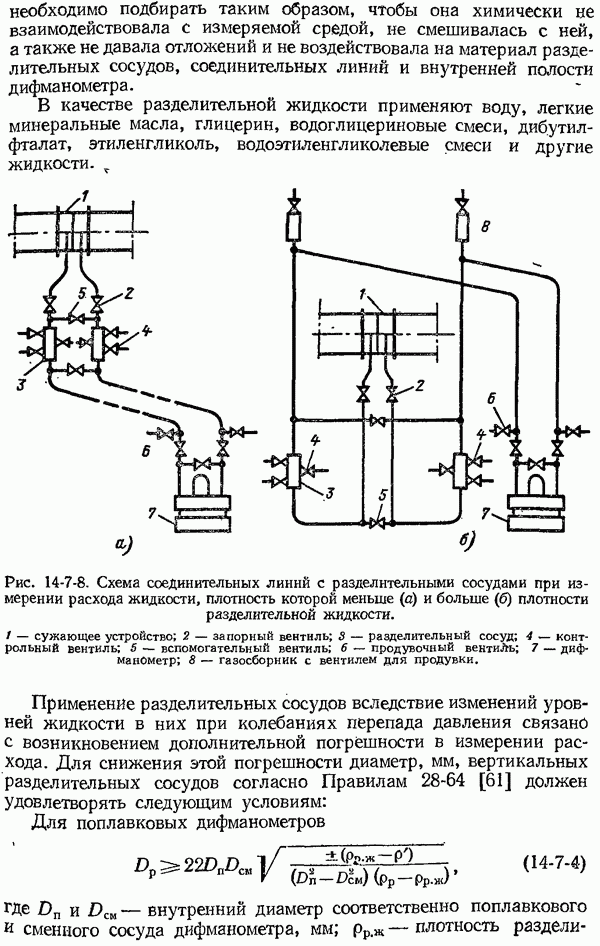
- 14-7. Методические указания по измерению расхода жидкостей, газов и пара расходомерами с сужающим устройством
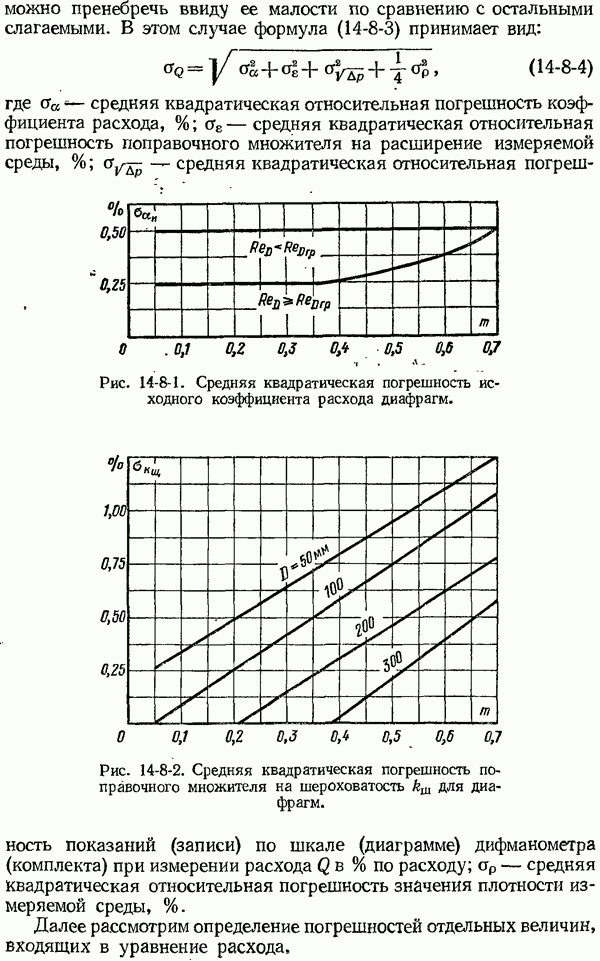
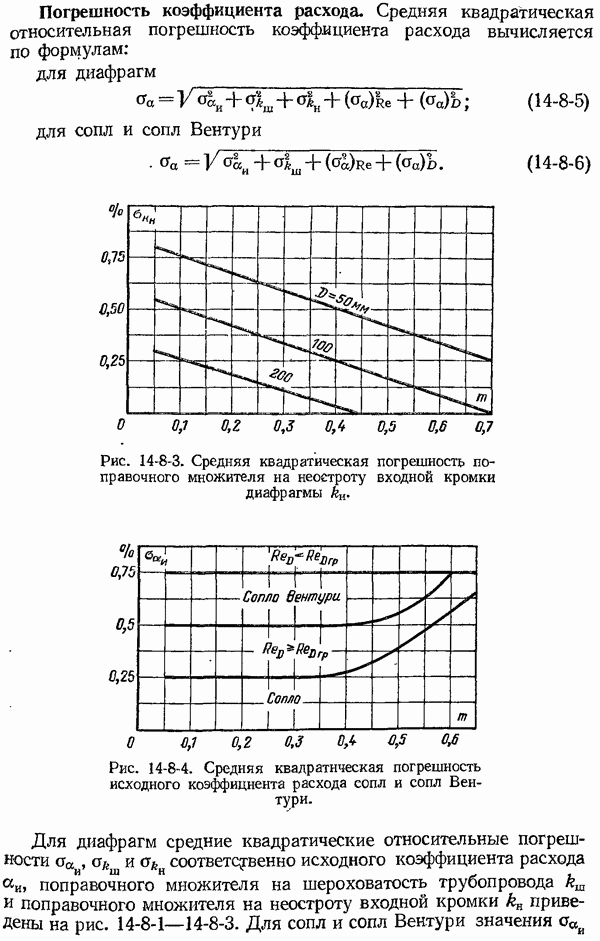
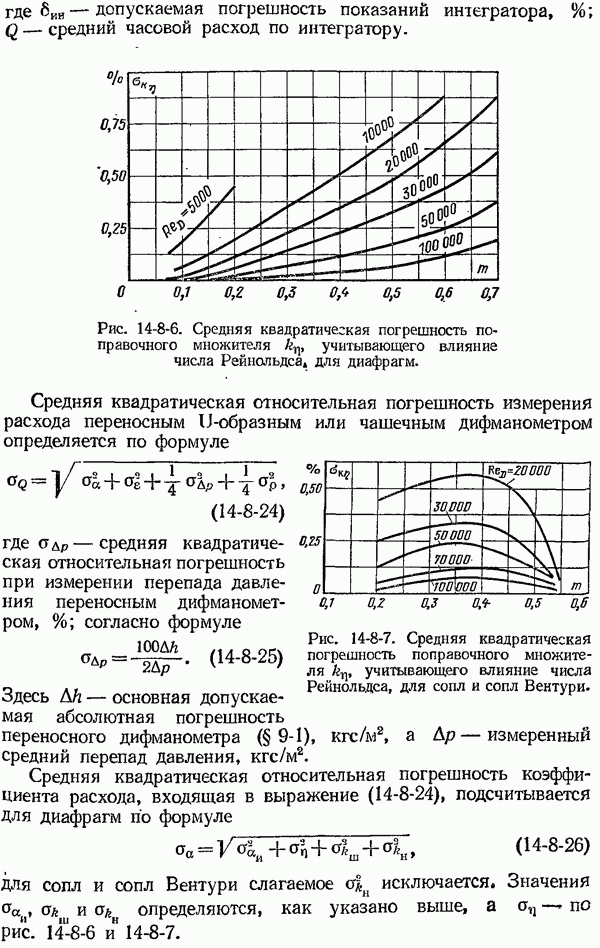
- 14-8. Погрешности измерения расхода
- 14-9. Основные сведения о методике расчета сужающих устройств
- 14-10. Измерение расхода на входе в трубопровод или на выходе из него
- 14-11. Измерение расхода при малых числах Рейнольдса
- 14-12. Измерение расхода загрязненных жидкостей и газов
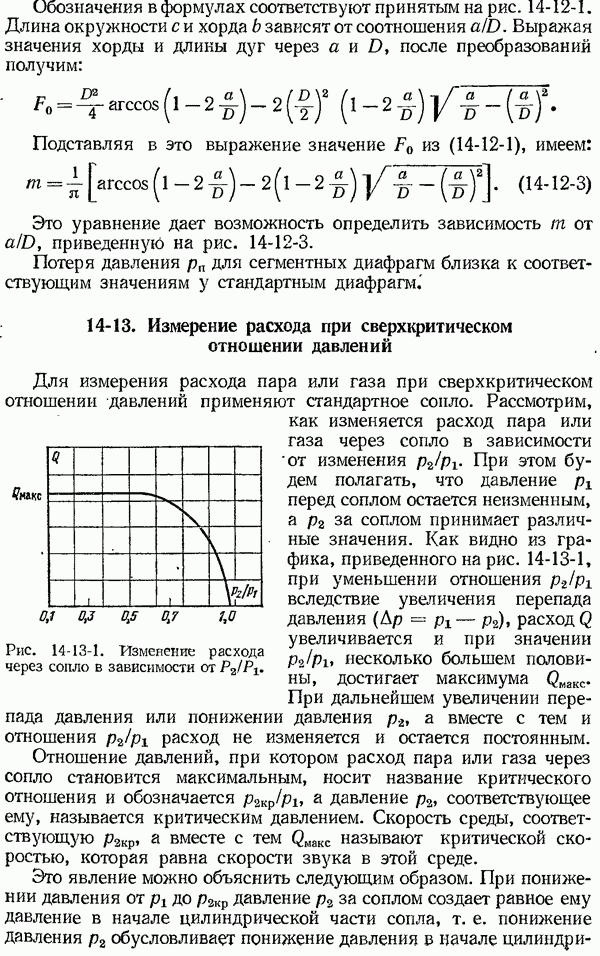
- 14-13. Измерение расхода при сверхкритическом отношении давлений
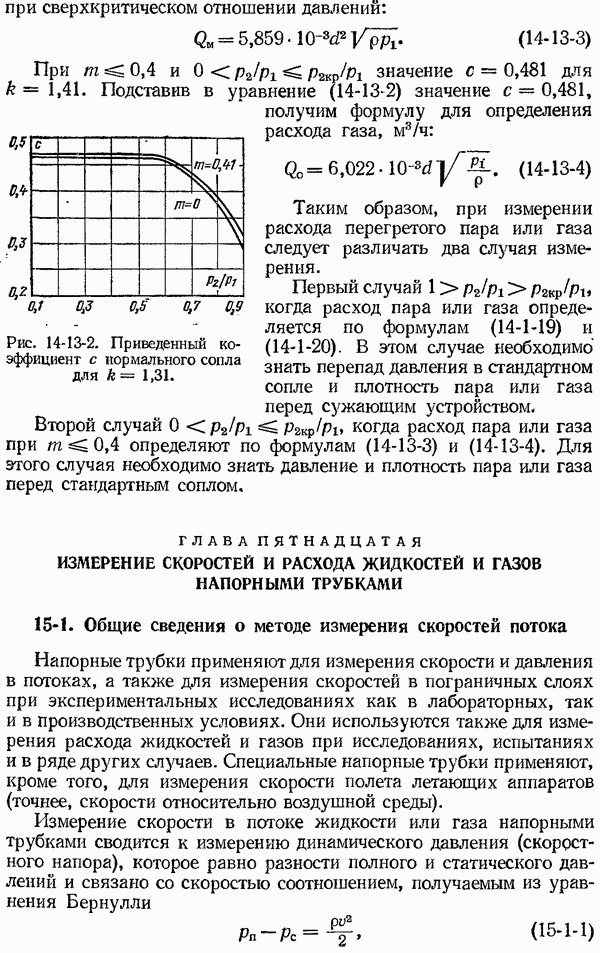
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ СКОРОСТЕЙ И РАСХОДА ЖИДКОСТЕЙ И ГАЗОВ НАПОРНЫМИ ТРУБКАМИ
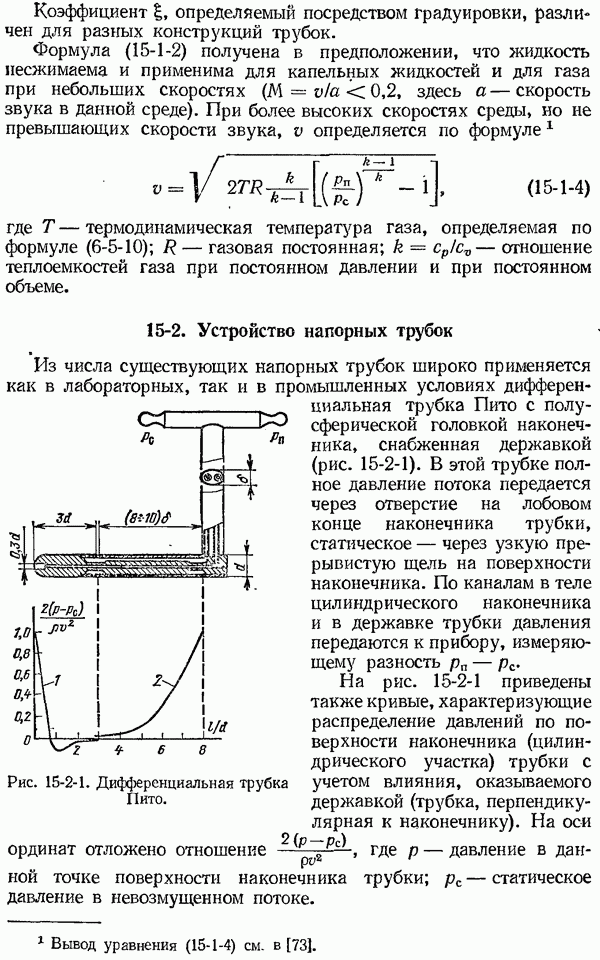
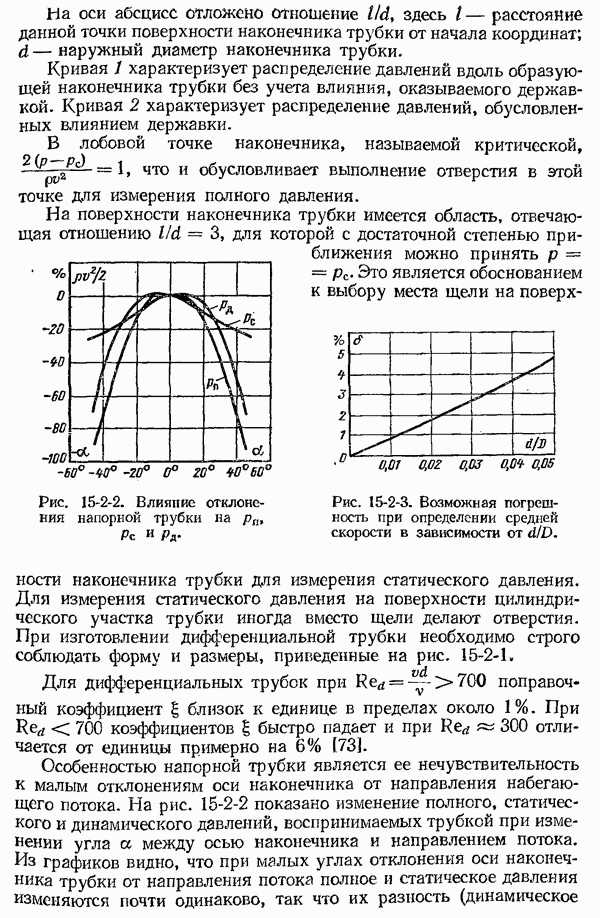
- 15-2. Устройство напорных трубок
- 15-3. Определение средней скорости потока и расхода
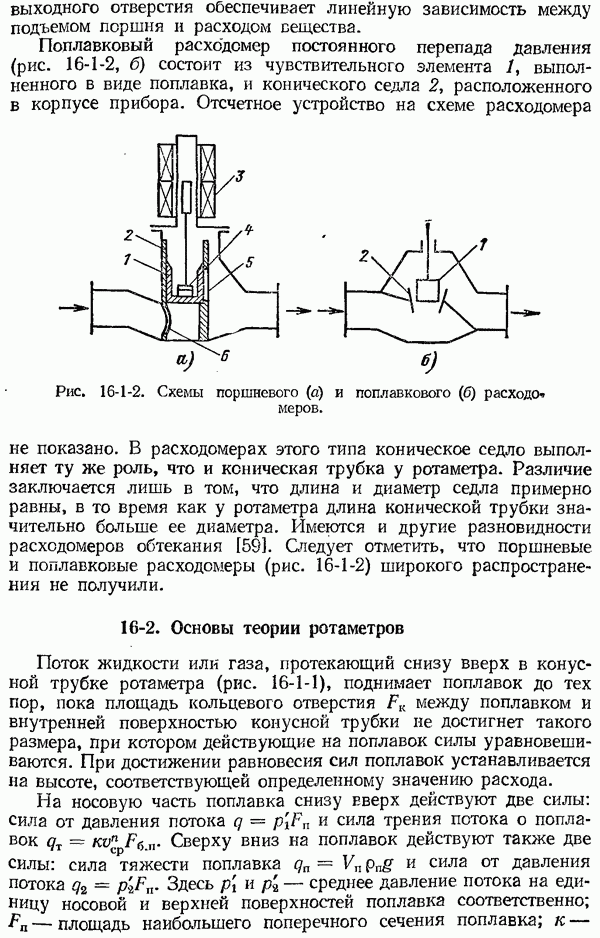
- ГЛАВА ШЕСТНАДЦАТАЯ. РАСХОДОМЕРЫ ПОСТОЯННОГО ПЕРЕПАДА ДАВЛЕНИЯ
- 16-2. Основы теории ротаметров
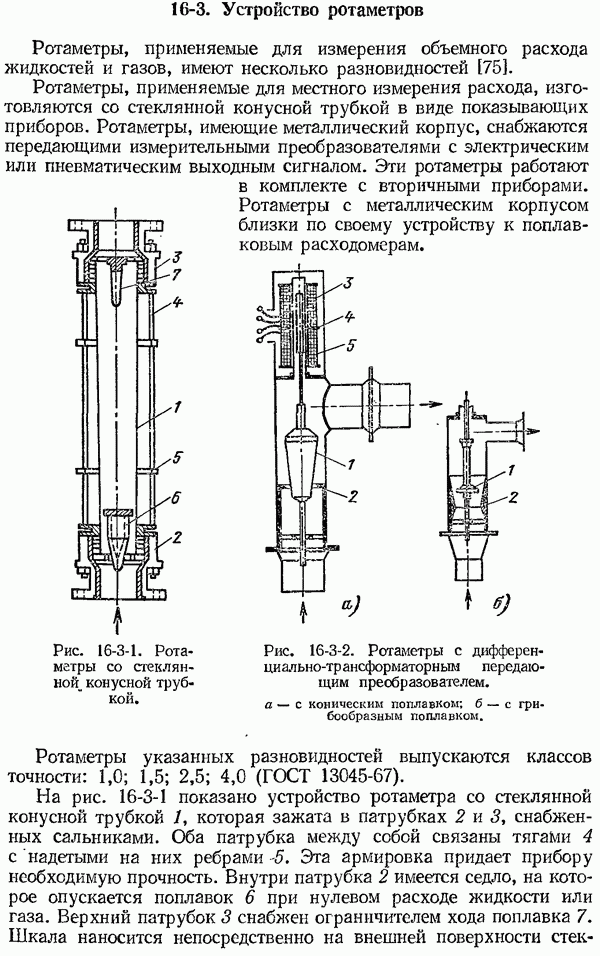
- 16-3. Устройство ротаметров
- ГЛАВА СЕМНАДЦАТАЯ. ТАХОМЕТРИЧЕСКИЕ РАСХОДОМЕРЫ И СЧЕТЧИКИ КОЛИЧЕСТВА И ЭЛЕКТРОМАГНИТНЫЕ РАСХОДОМЕРЫ
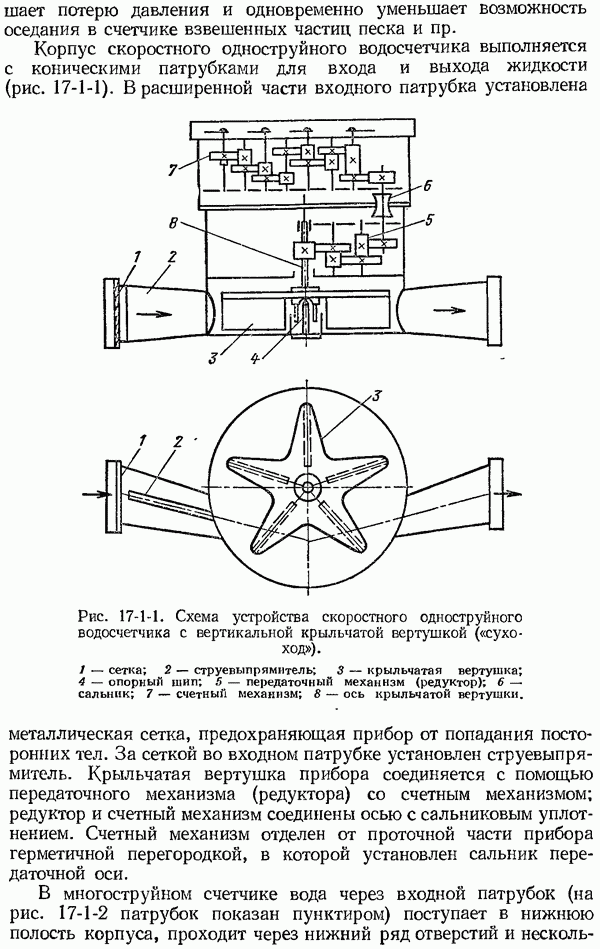
- 17-1. Тахометрические счетчики количества жидкостей
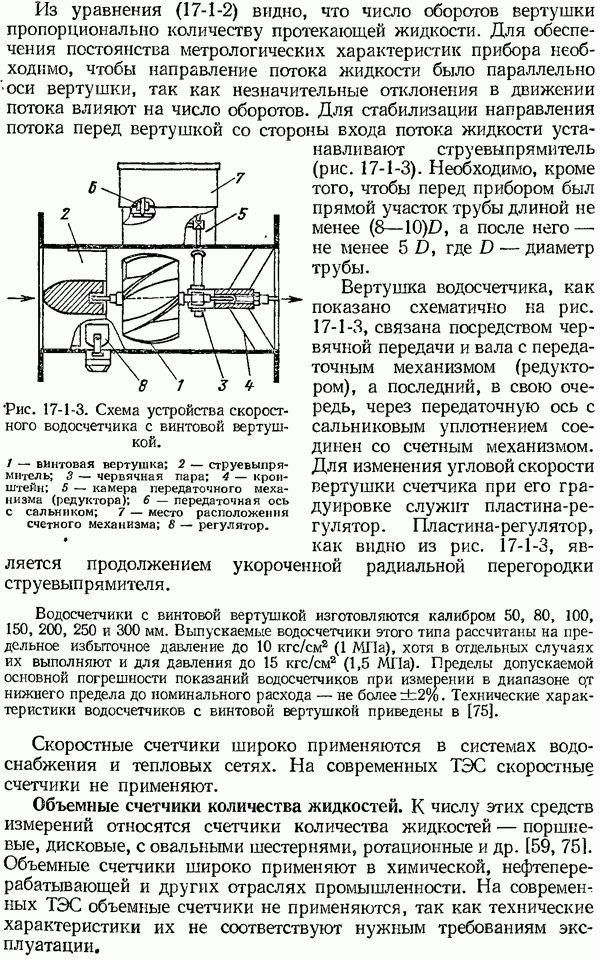
- 17-2. Тахометрические расходомеры жидкостей
- 17-3. Электромагнитные расходомеры
- ГЛАВА ВОСЕМНАДЦАТАЯ. ИЗМЕРЕНИЕ КОЛИЧЕСТВА И РАСХОДА ТЕПЛА В ТЕПЛОФИКАЦИОННЫХ СИСТЕМАХ
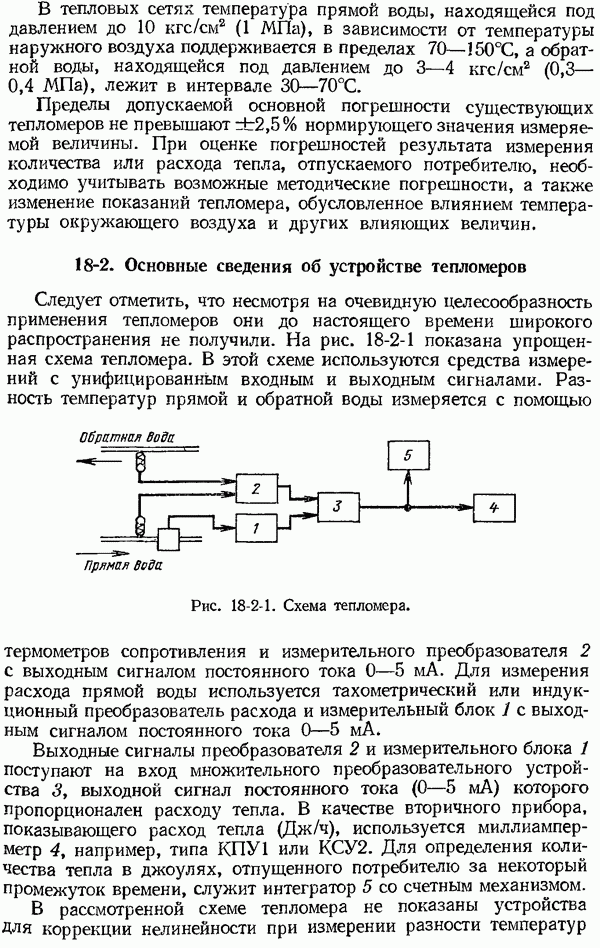
- 18-2. Основные сведения об устройстве тепломеров
- РАЗДЕЛ ШЕСТОЙ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ И СЫПУЧИХ ТЕЛ
- ГЛАВА ДЕВЯТНАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ ЖИДКОСТЕЙ
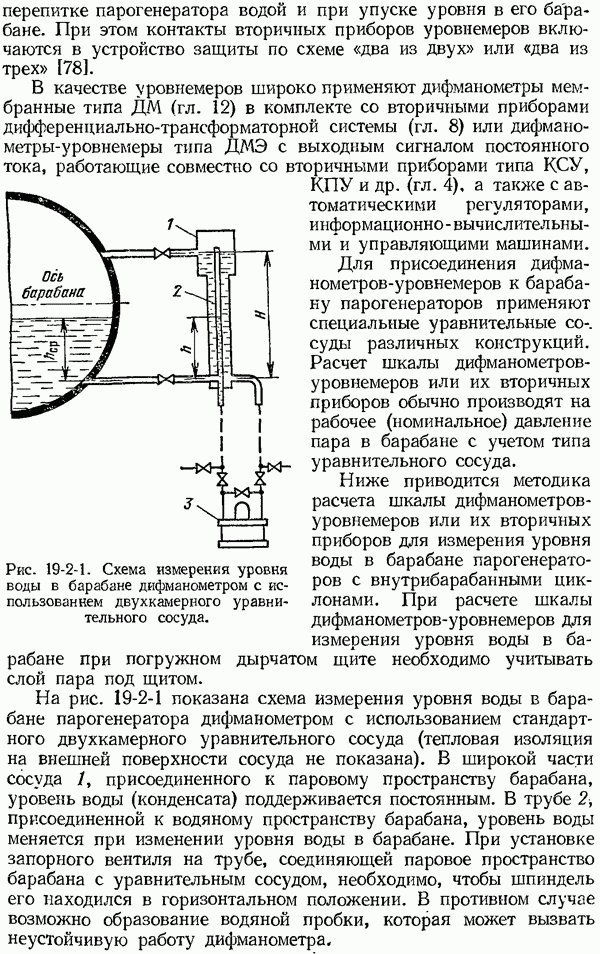
- 19-2. Измерение уровня воды в барабане парогенераторов
- 19-3. Измерение уровня жидкостей в конденсаторах, подогревателях и баках с помощью дифманометров
- 19-4. Измерение уровня жидкостей с помощью поплавковых и буйковых уровнемеров
- 19-5. Емкостные уровнемеры
- 19-6. Акустические и ультразвуковые уровнемеры
- ГЛАВА ДВАДЦАТАЯ. ИЗМЕРЕНИЕ УРОВНЯ СЫПУЧИХ ТЕЛ
- 20-2. Сигнализаторы уровня сыпучих тел
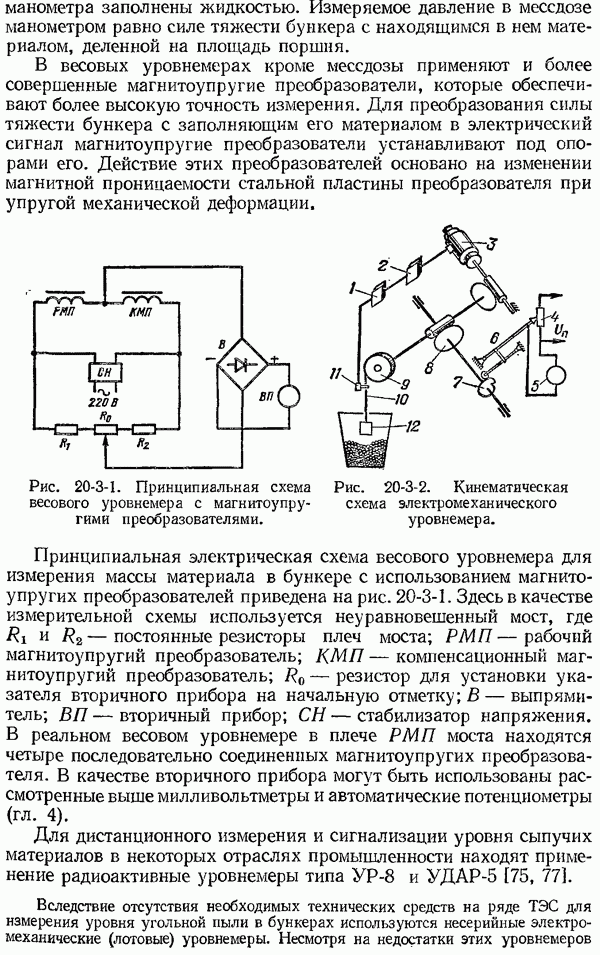
- 20-3. Приборы для измерения уровня сыпучих тел
- РАЗДЕЛ СЕДЬМОЙ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
- ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ СОСТАВА ГАЗОВ
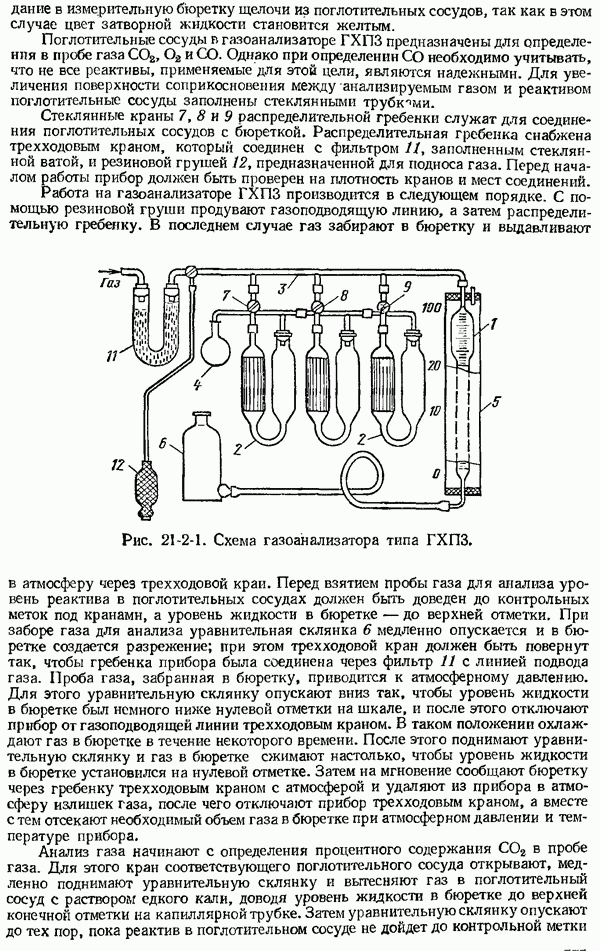
- 21-2. Газоанализаторы химические
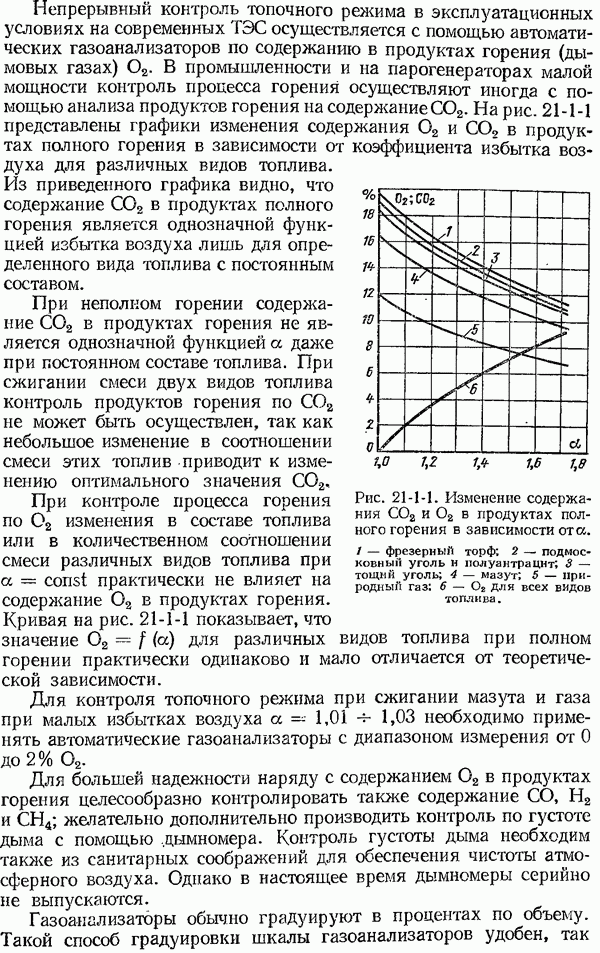
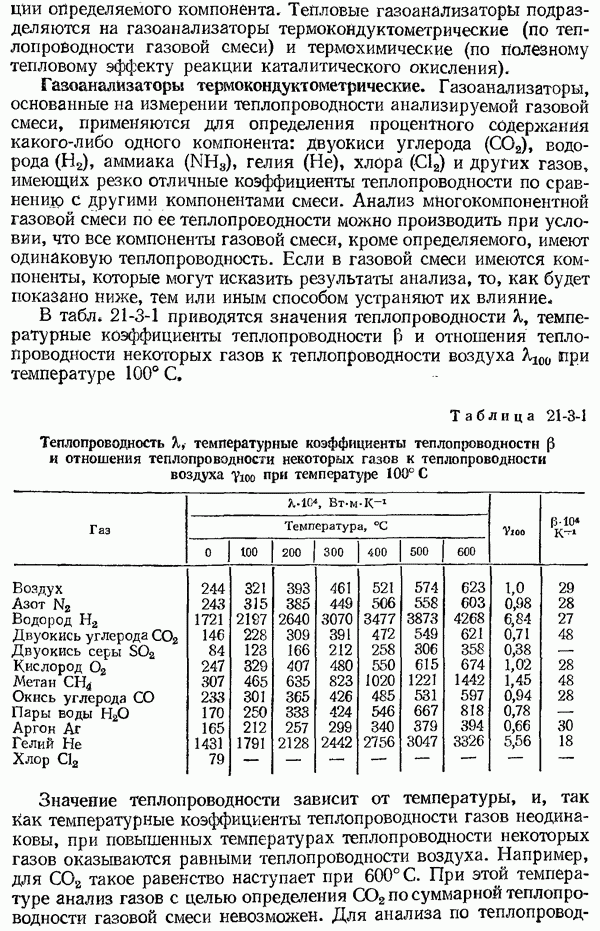
- 21-3. Тепловые газоанализаторы
- 21-4. Магнитные газоанализаторы
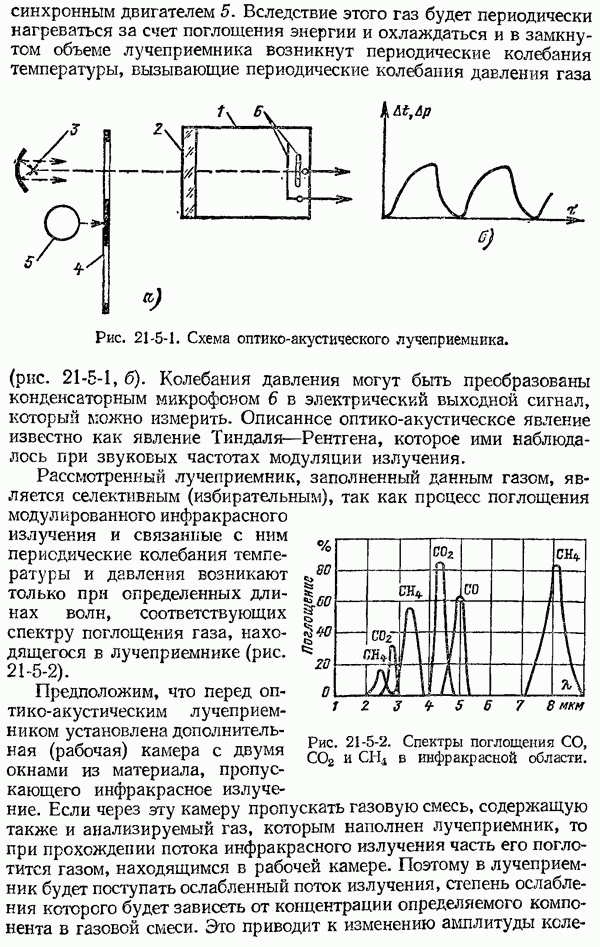
- 21-5. Оптические газоанализаторы
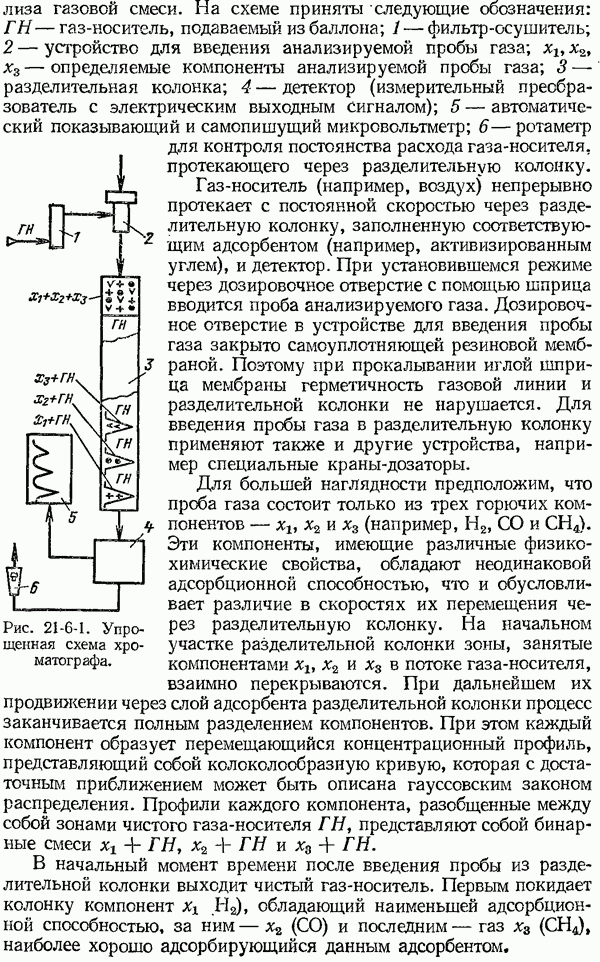
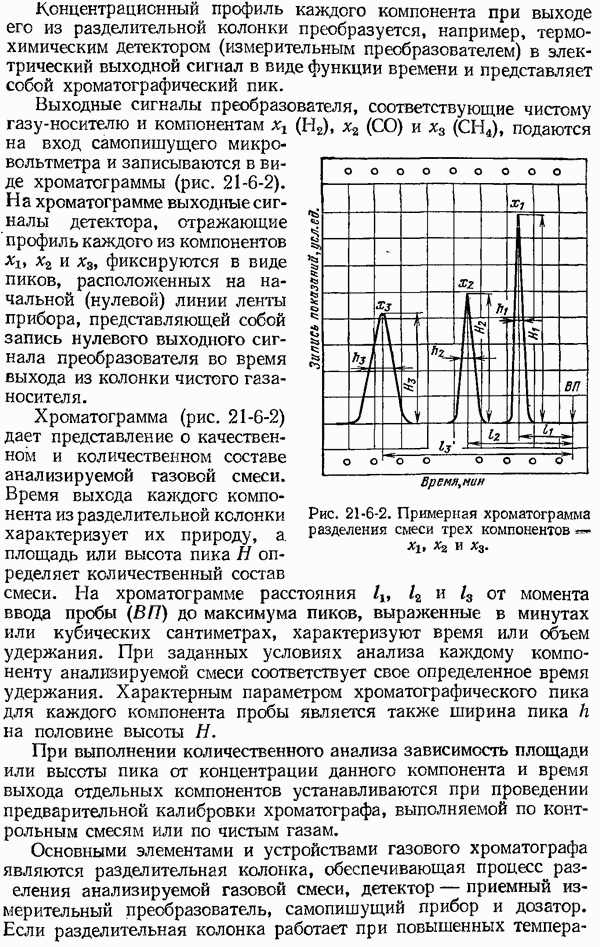
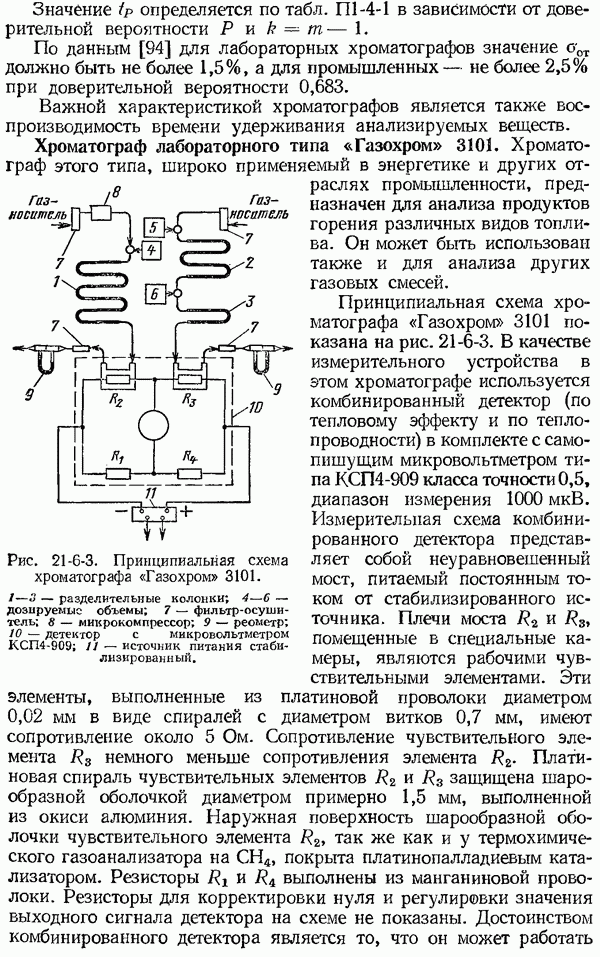
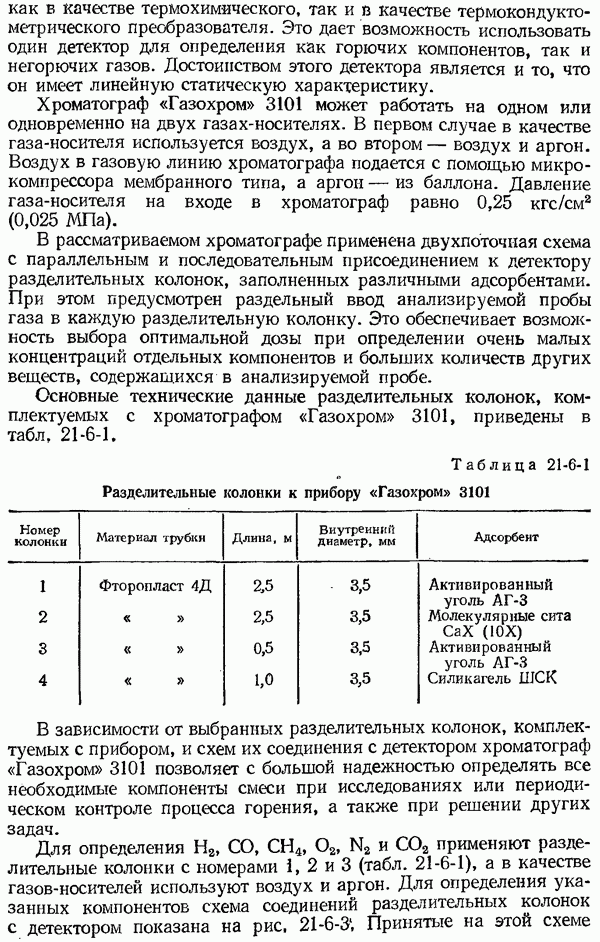
- 21-6. Газовые хроматографы
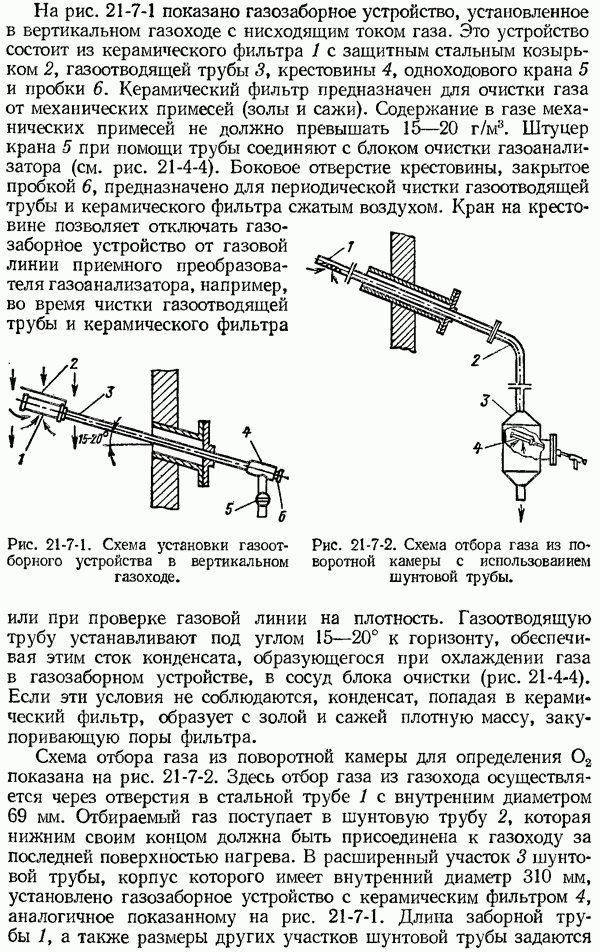
- 21-7. Методические указания по отбору проб газа для анализа
- РАЗДЕЛ ВОСЬМОЙ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
- ГЛАВА ДВАДЦАТЬ ВТОРАЯ. МЕТОДЫ И ТЕХНИЧЕСКИЕ СРЕДСТВА КОНТРОЛЯ КАЧЕСТВА ВОДЫ, ПАРА, КОНДЕНСАТА И КОНЦЕНТРАЦИИ РАСТВОРОВ
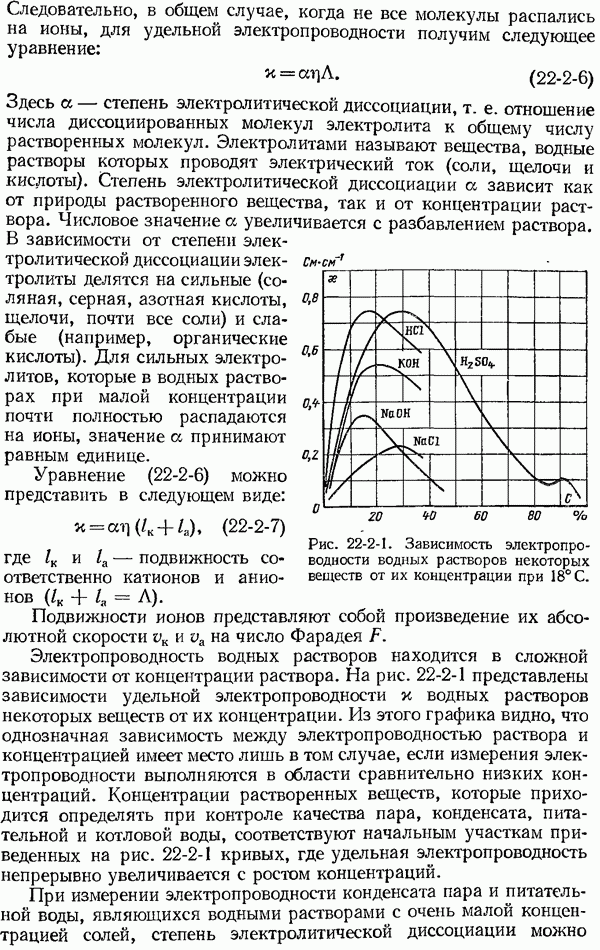
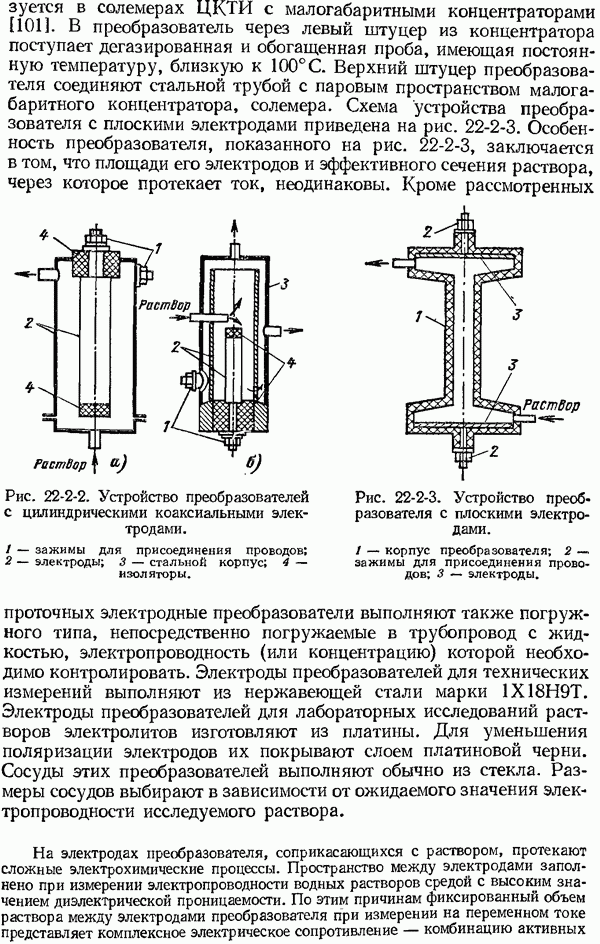
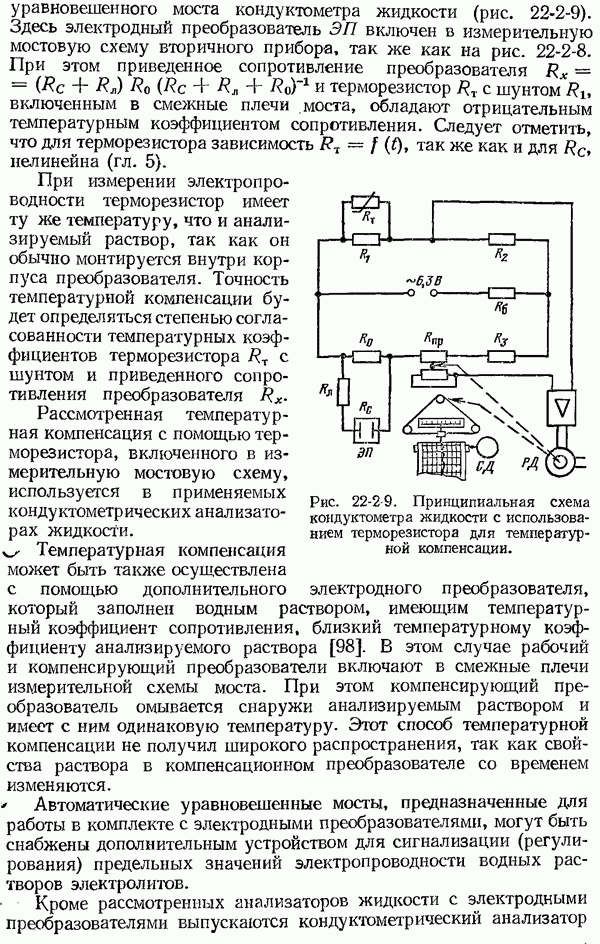
- 22-2. Измерение удельной электропроводности водных растворов
- 22-3. Кондуктометры жидкости с дегазацией и обогащением пробы
- 22-4. Безэлектродные кондуктометрические анализаторы жидкости
- 22-5. Анализаторы для определения растворенного в воде кислорода
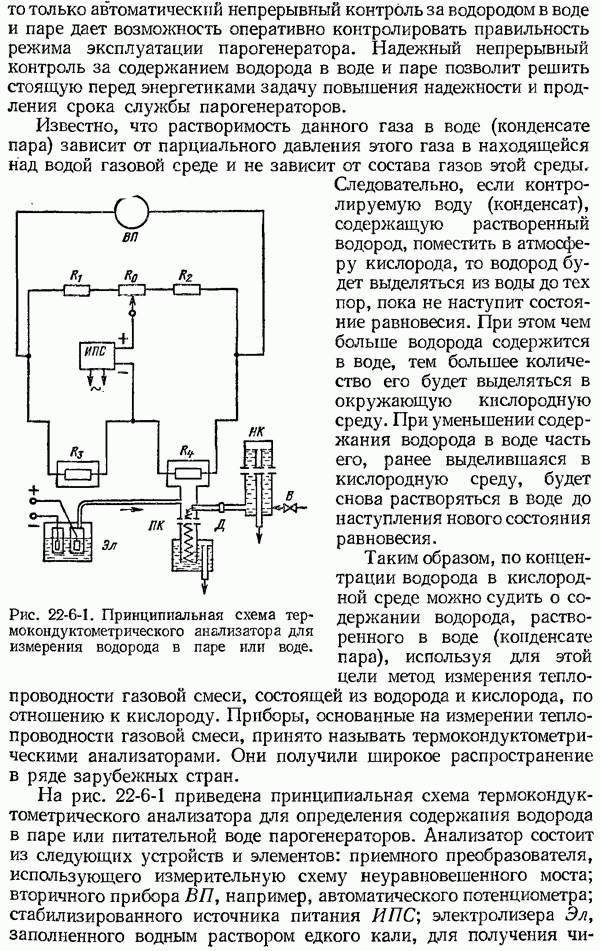
- 22-6. Анализаторы для определения растворенного в воде и паре водорода
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ