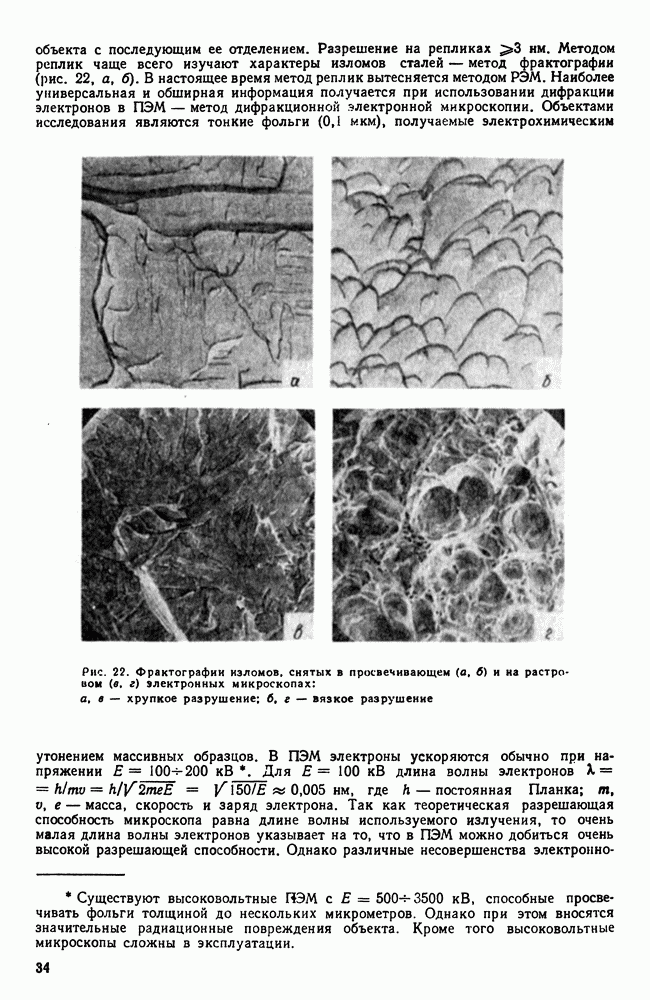
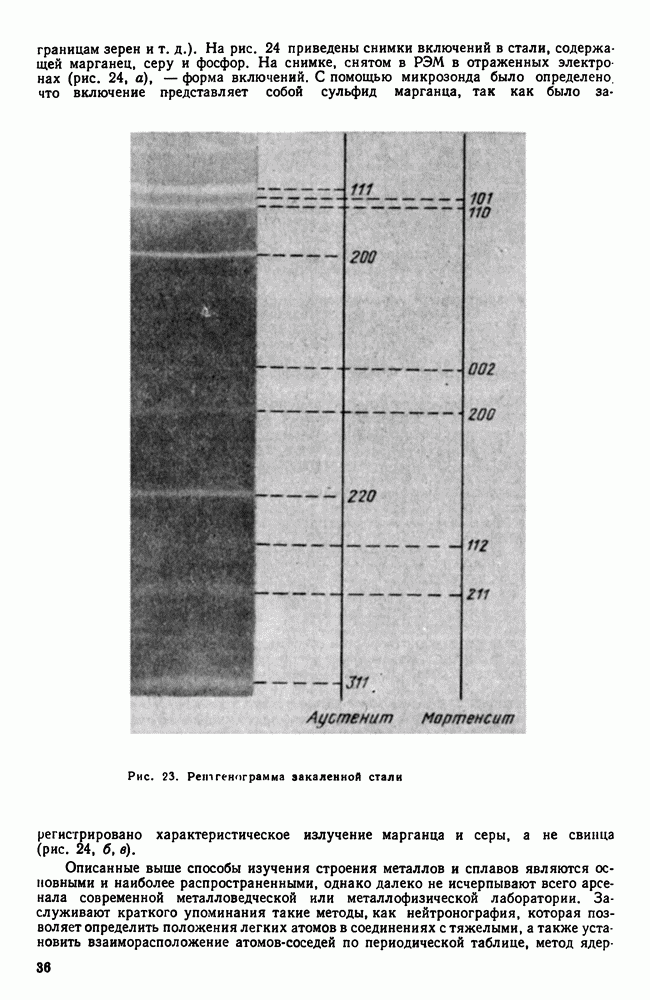
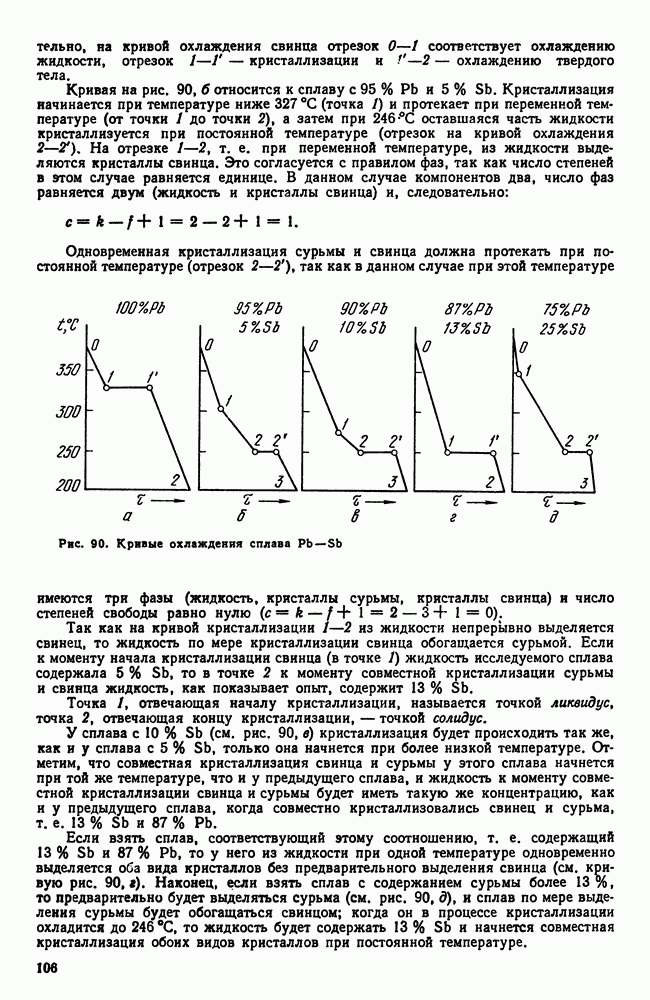
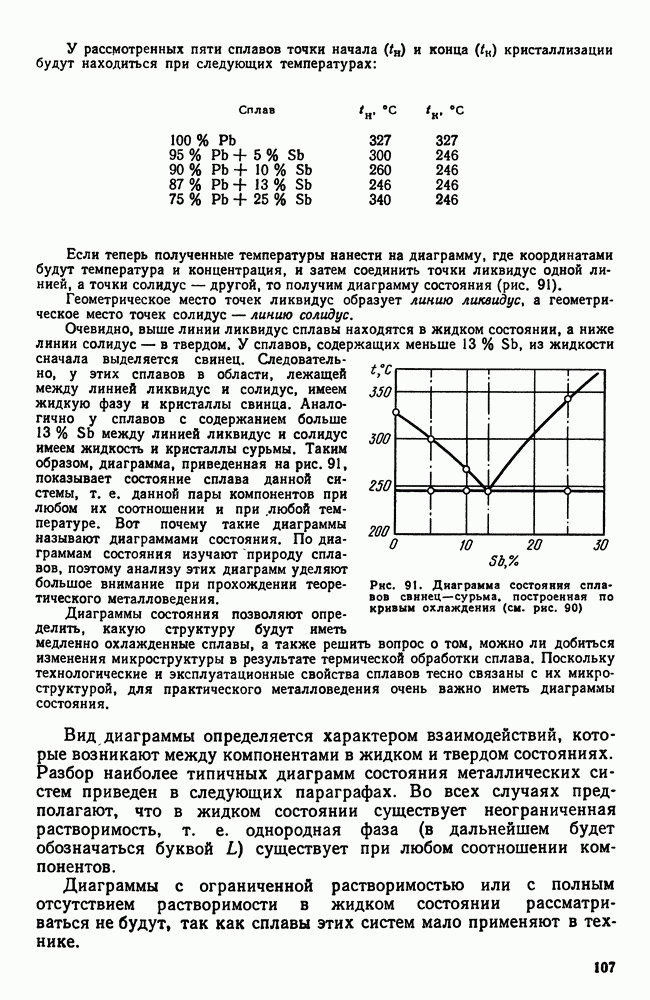
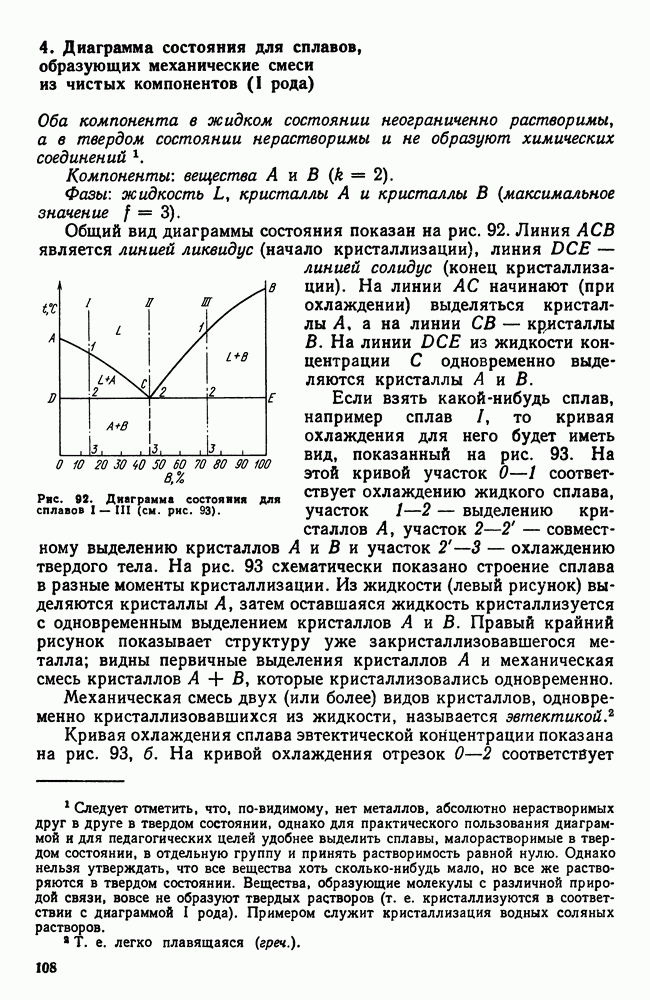
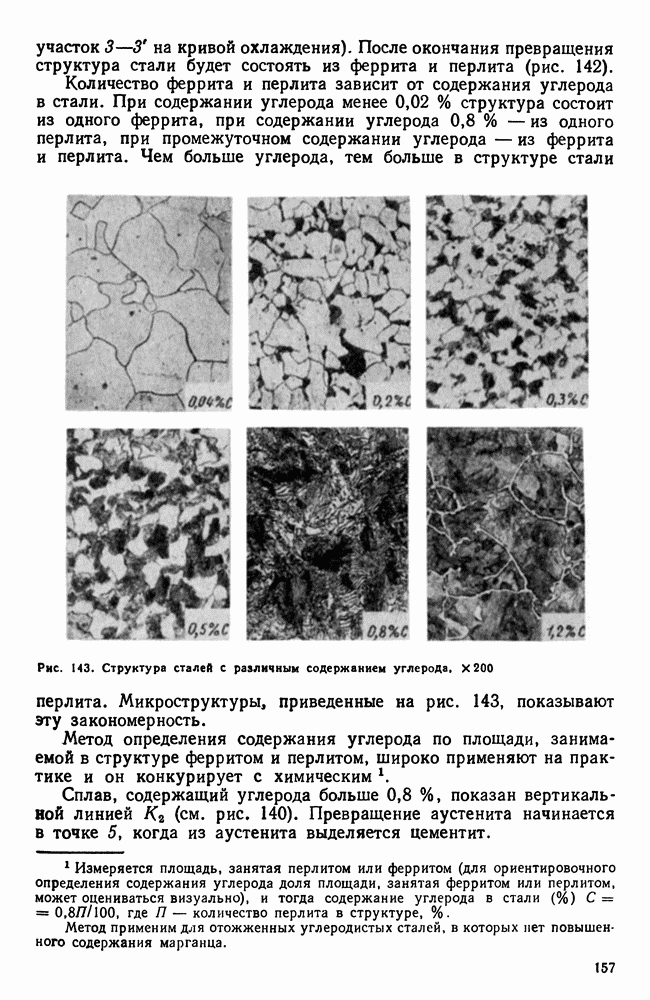
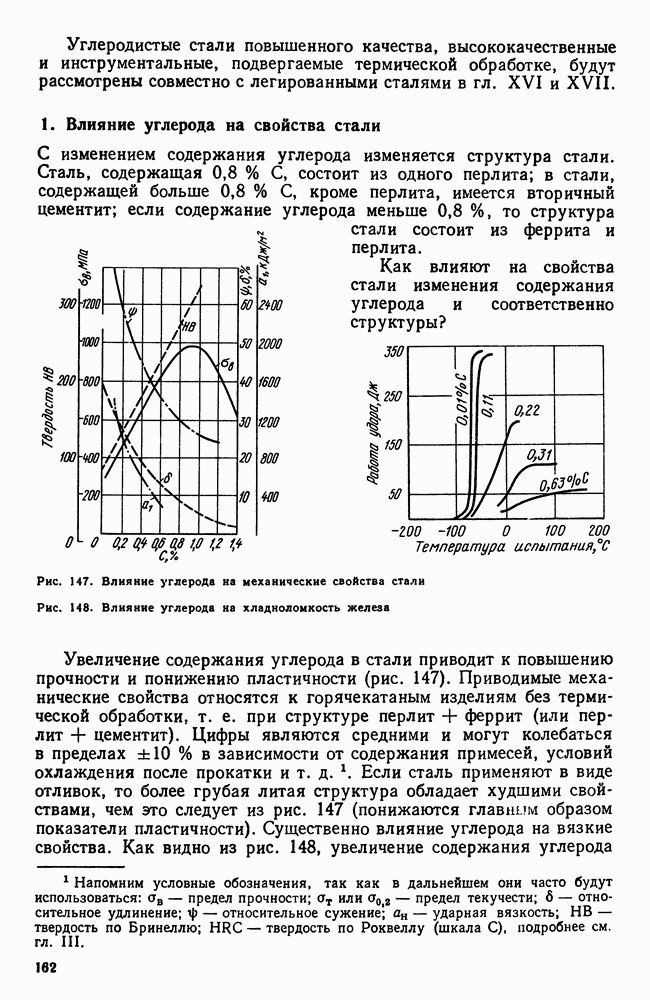
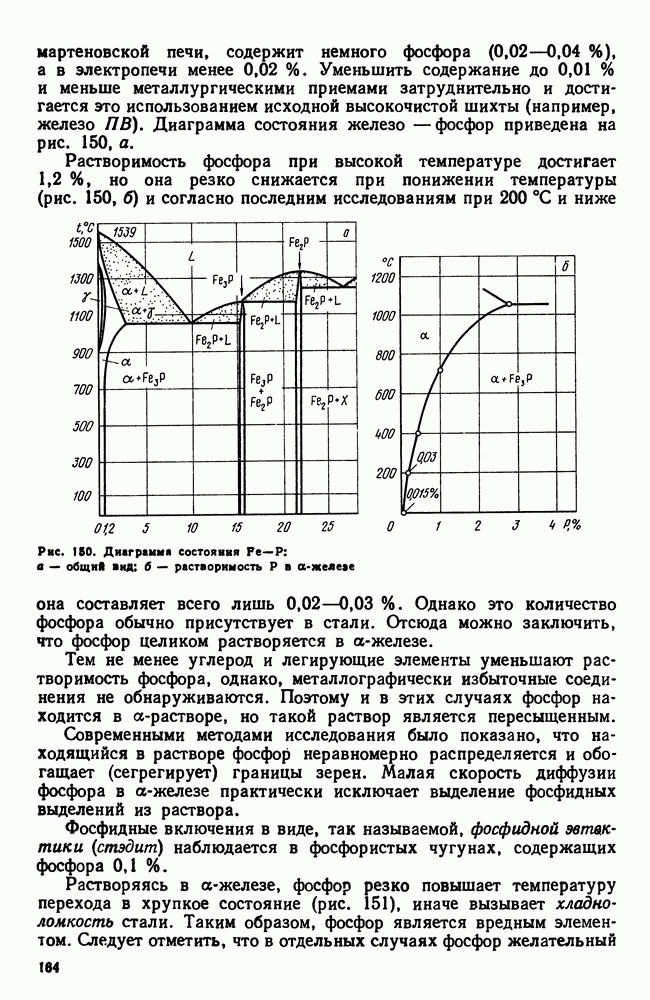
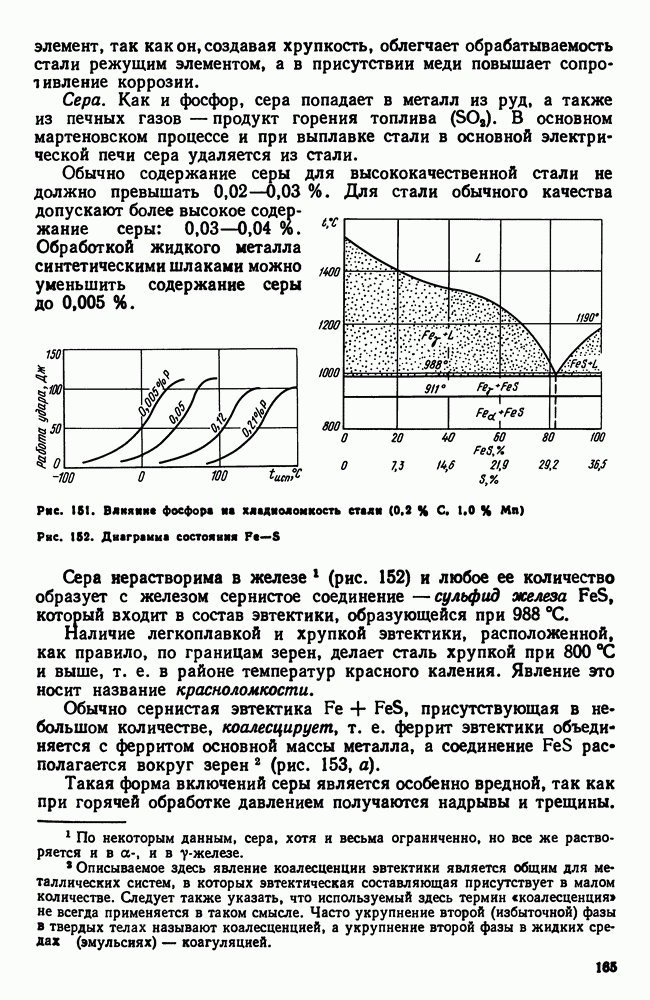
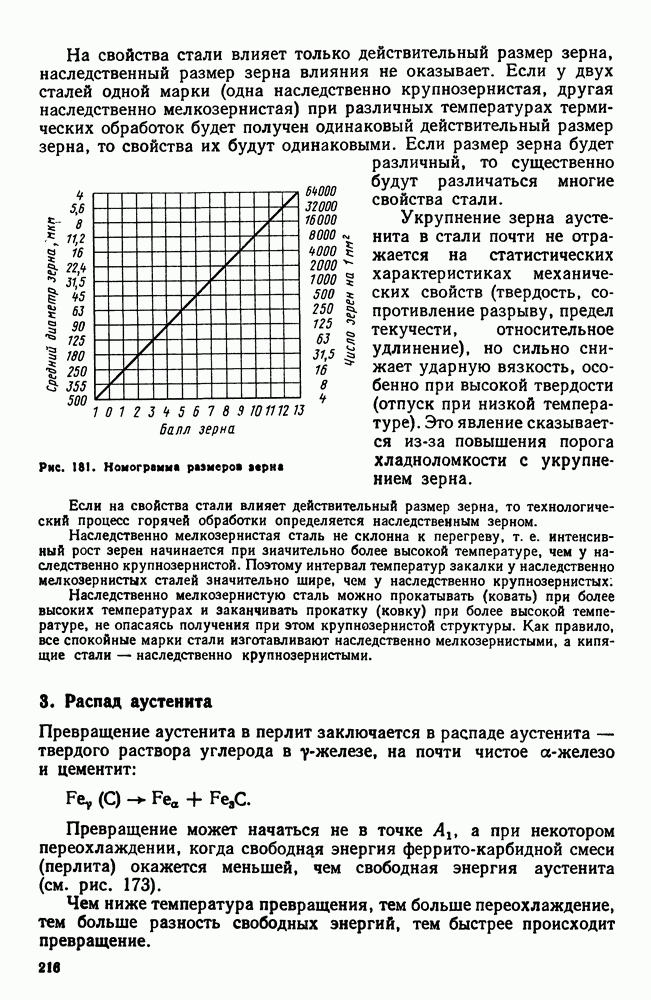
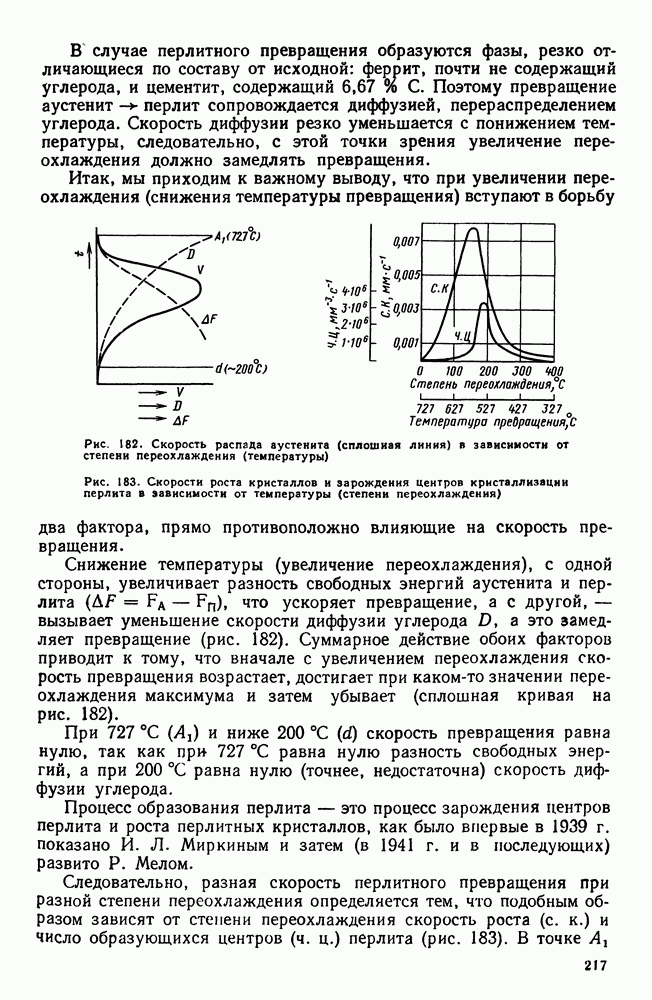
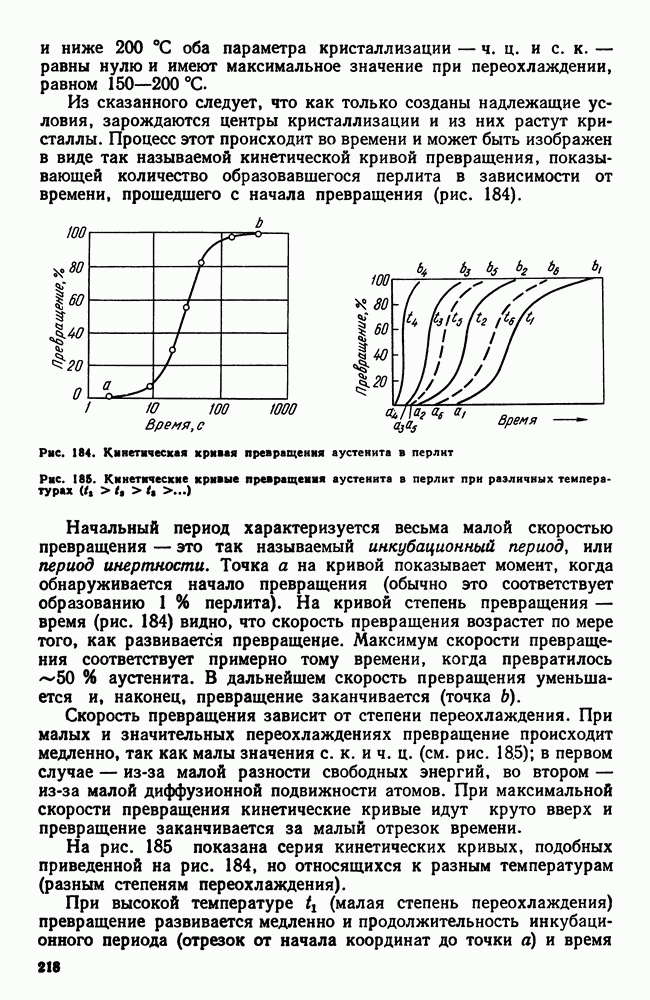
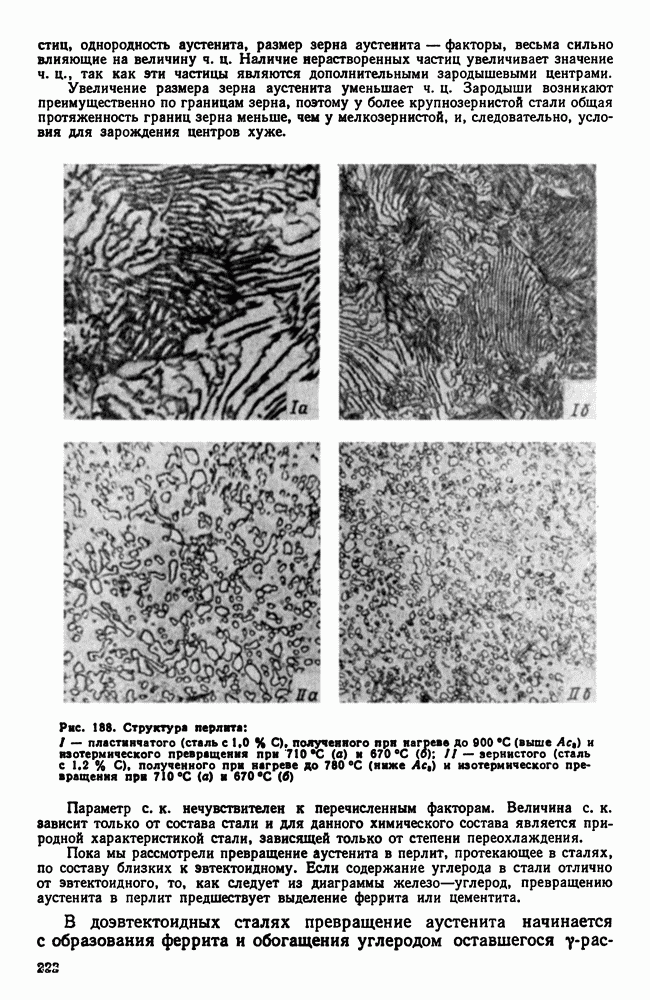
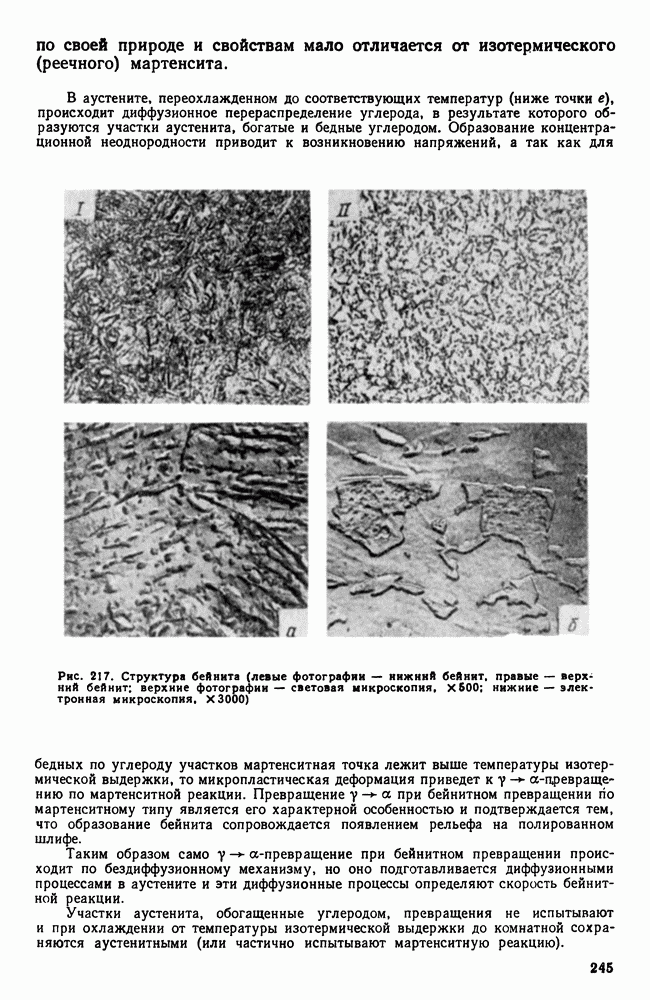
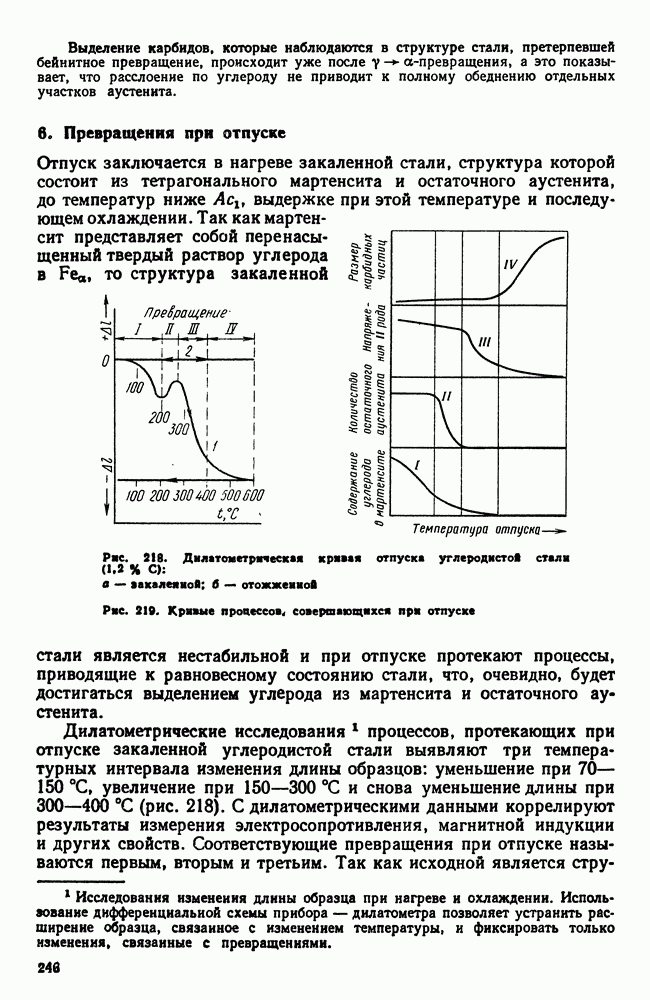
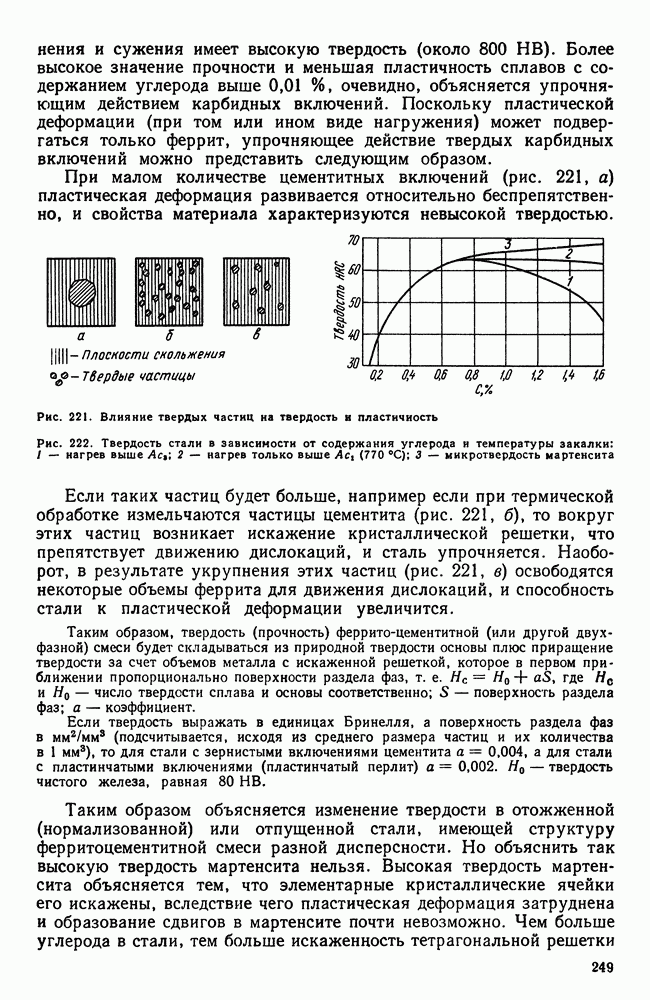
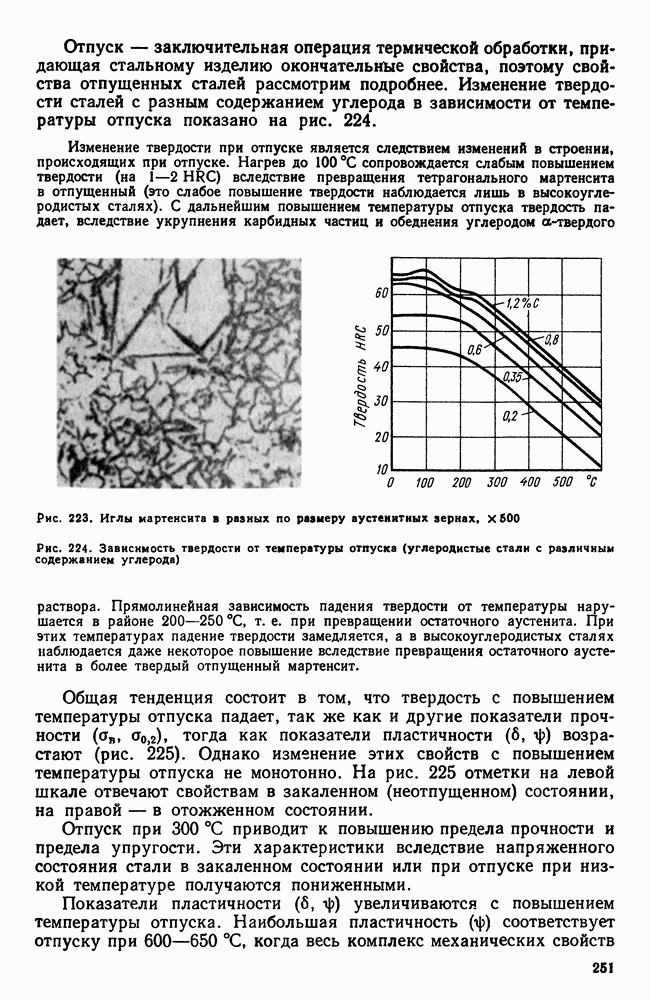
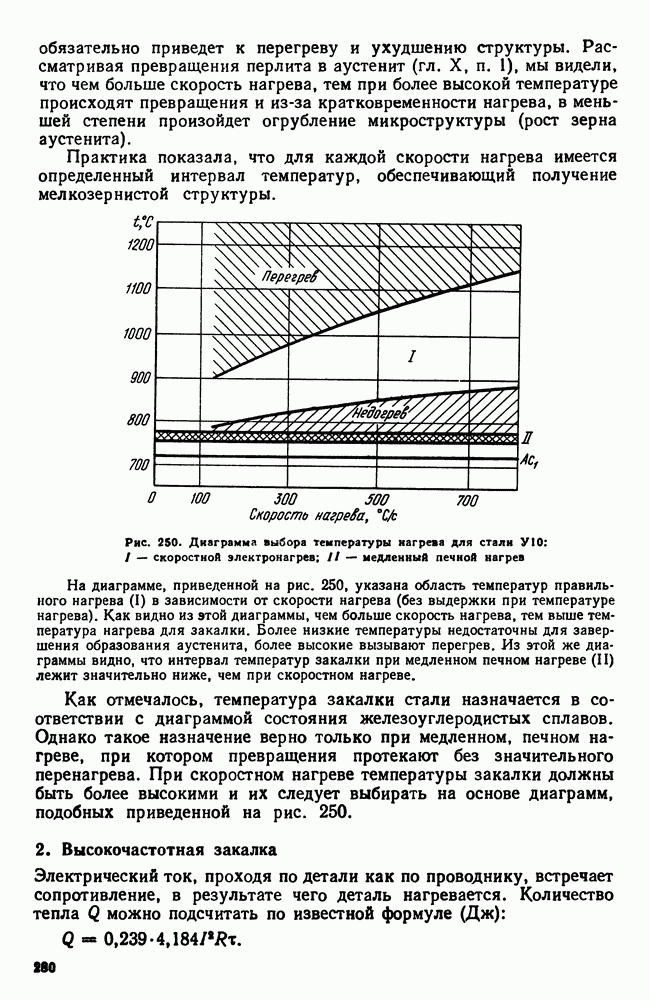
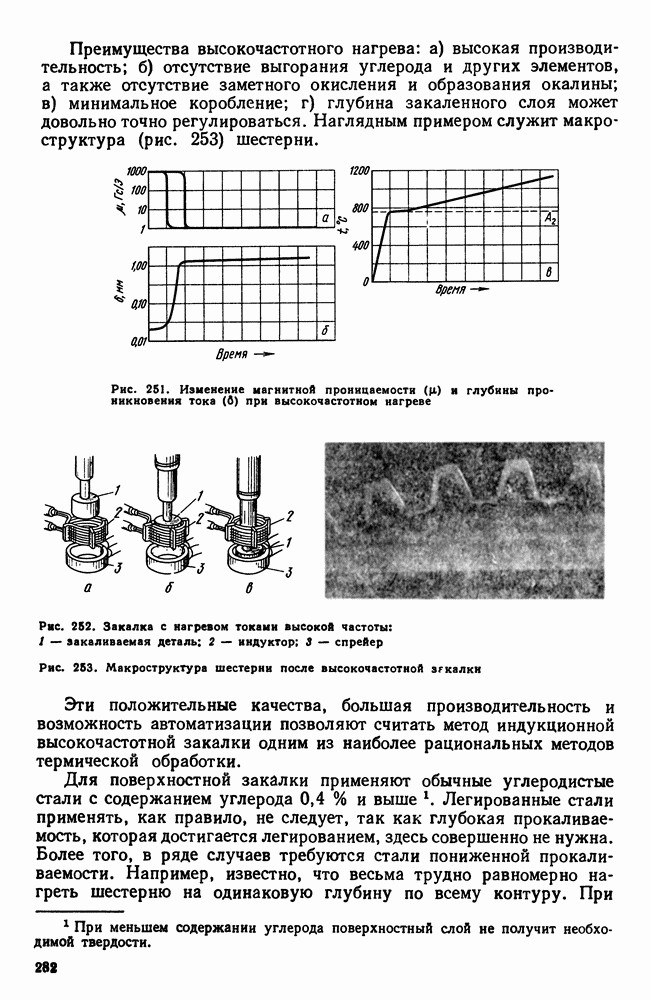
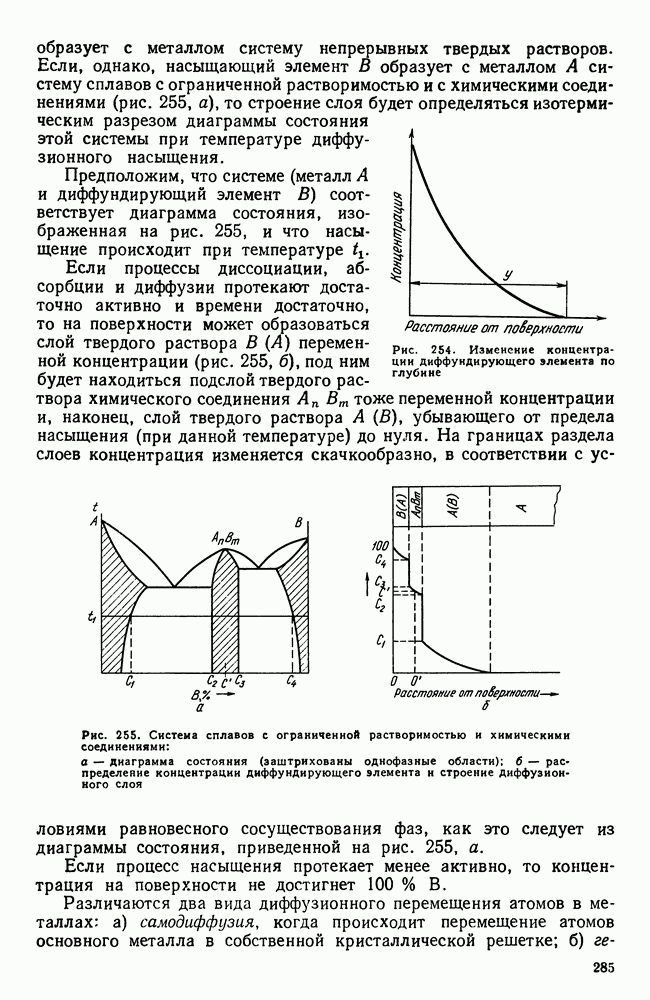
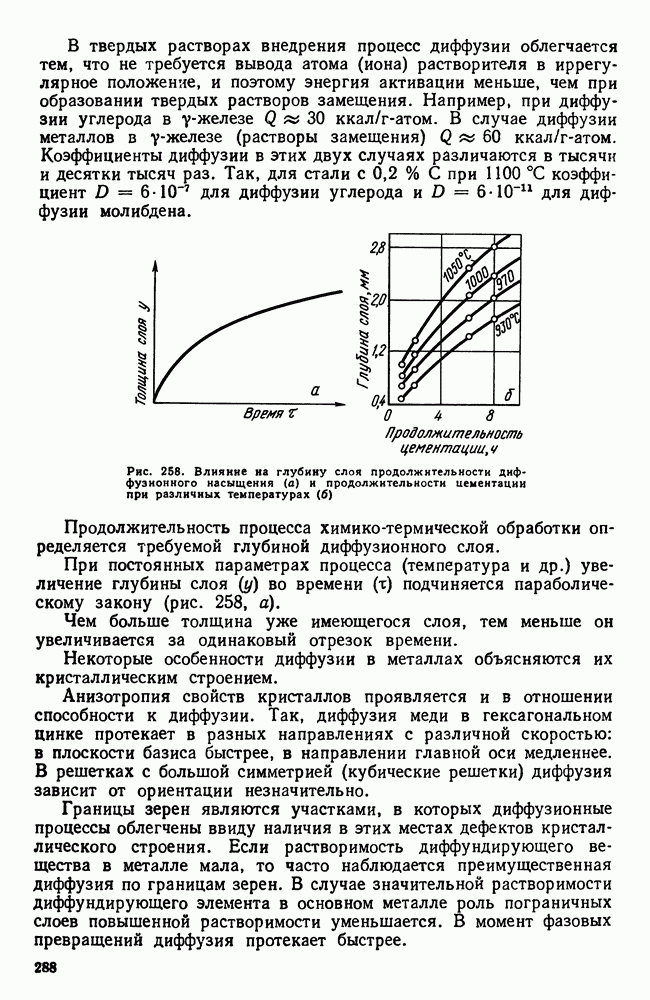
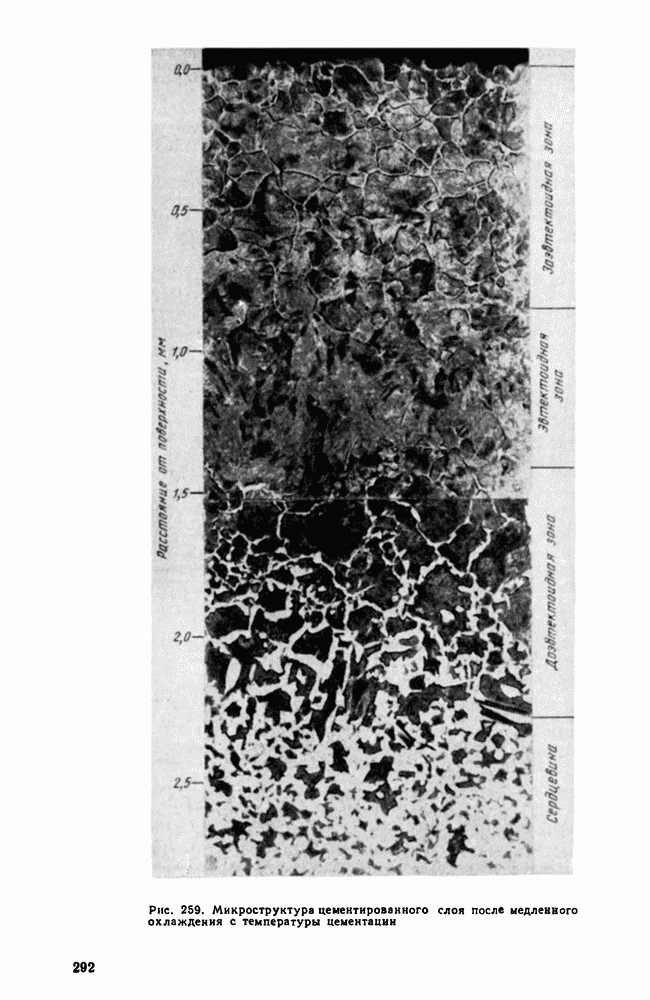
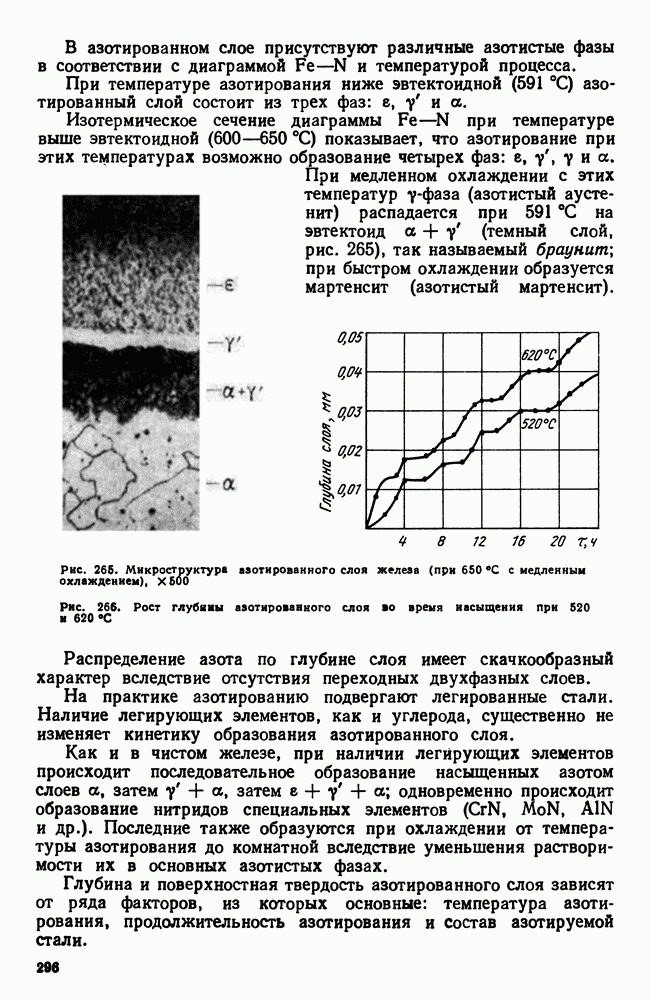
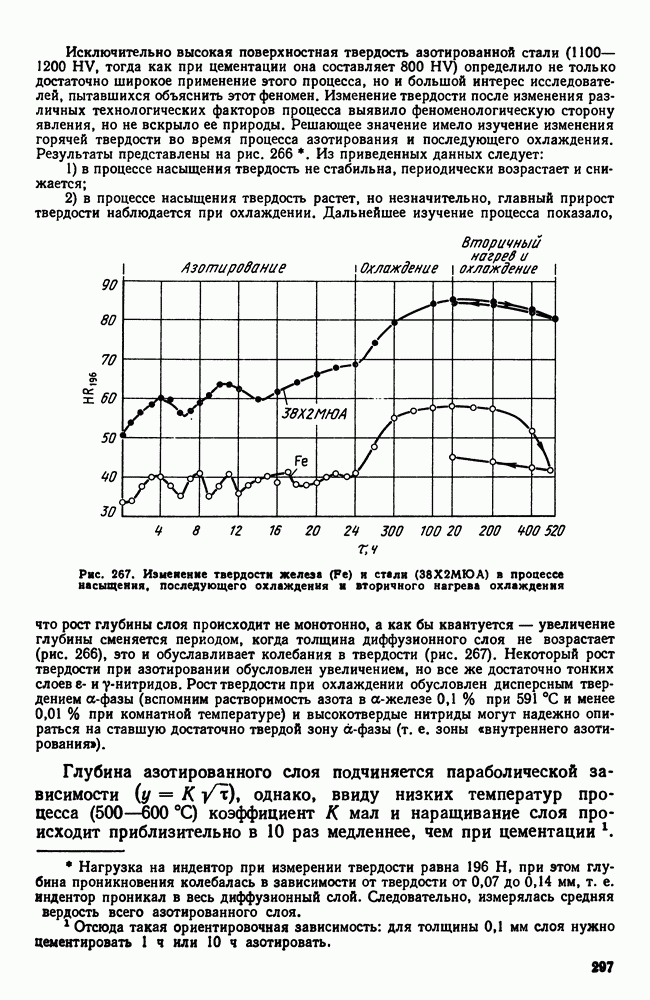
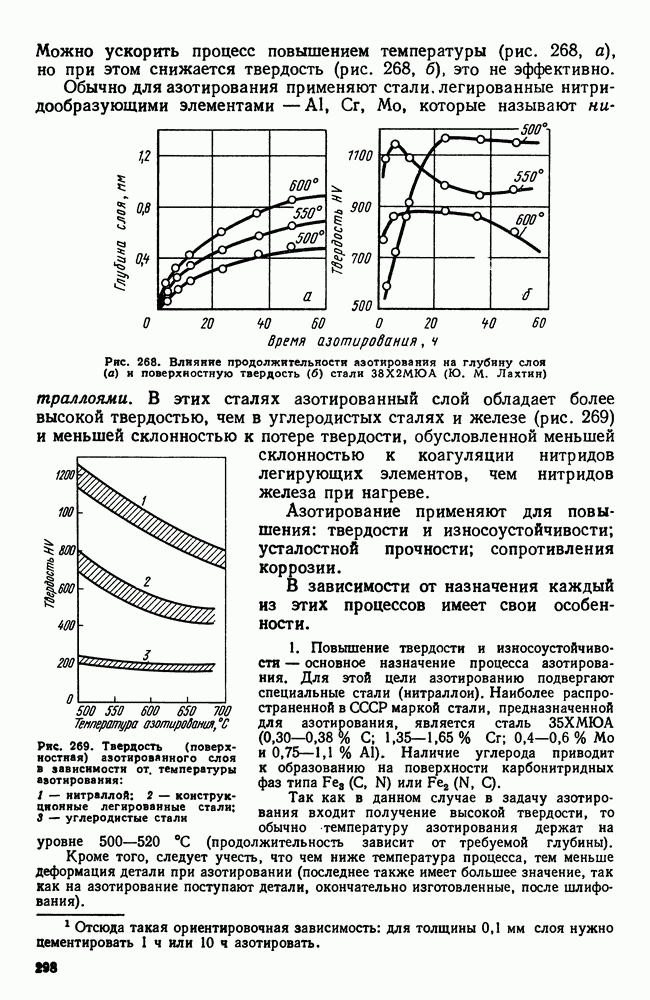
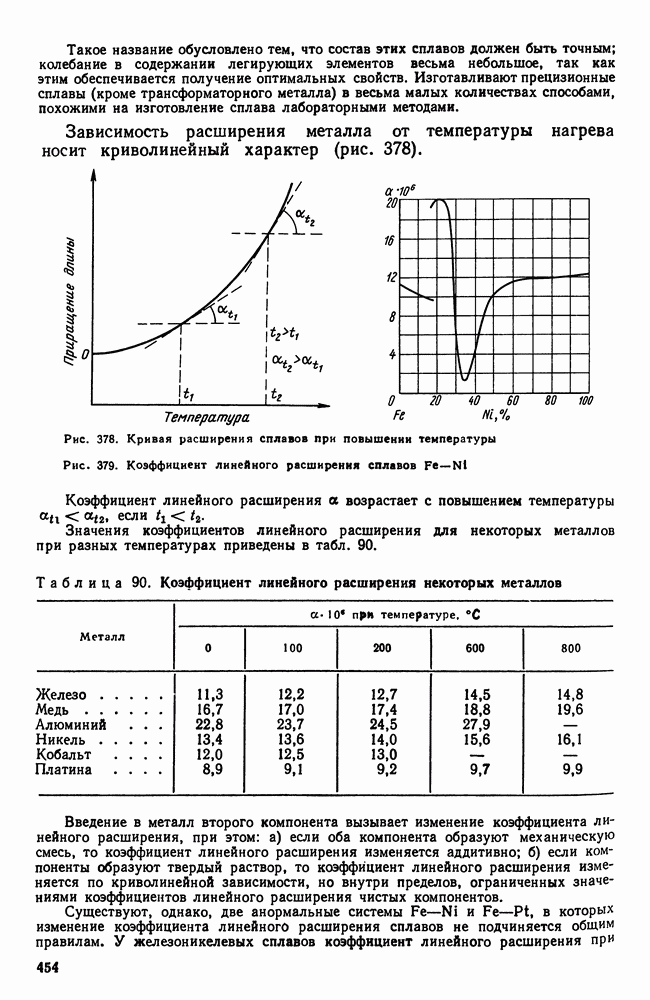
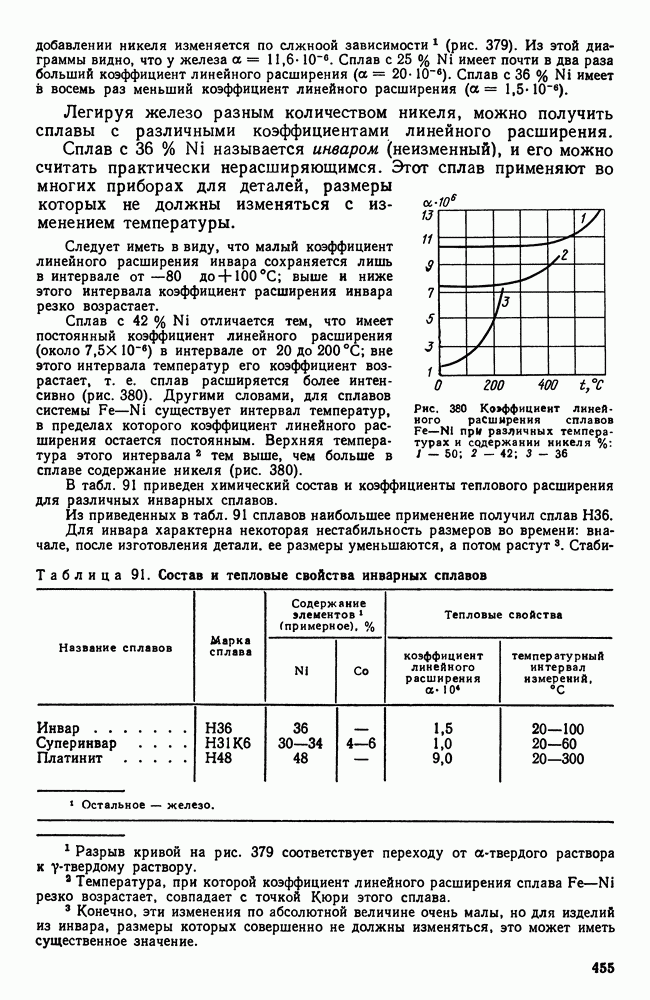
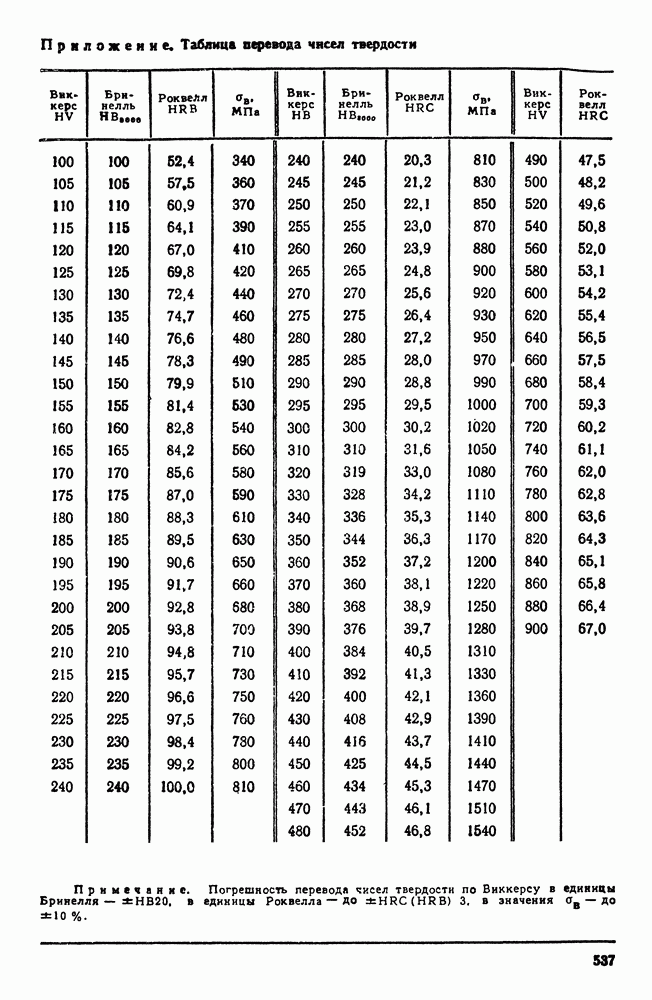
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
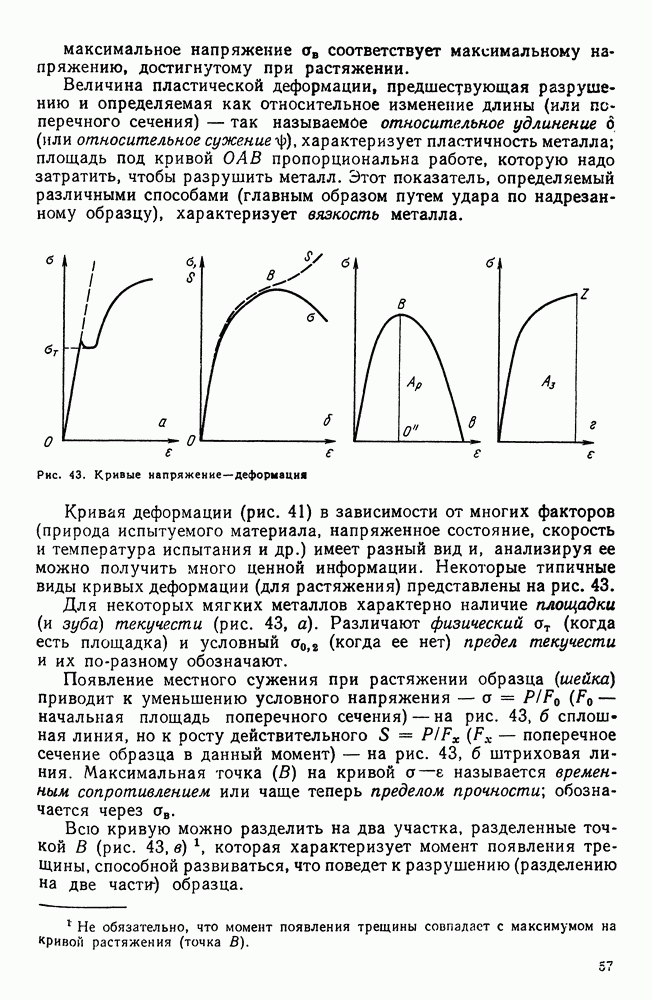
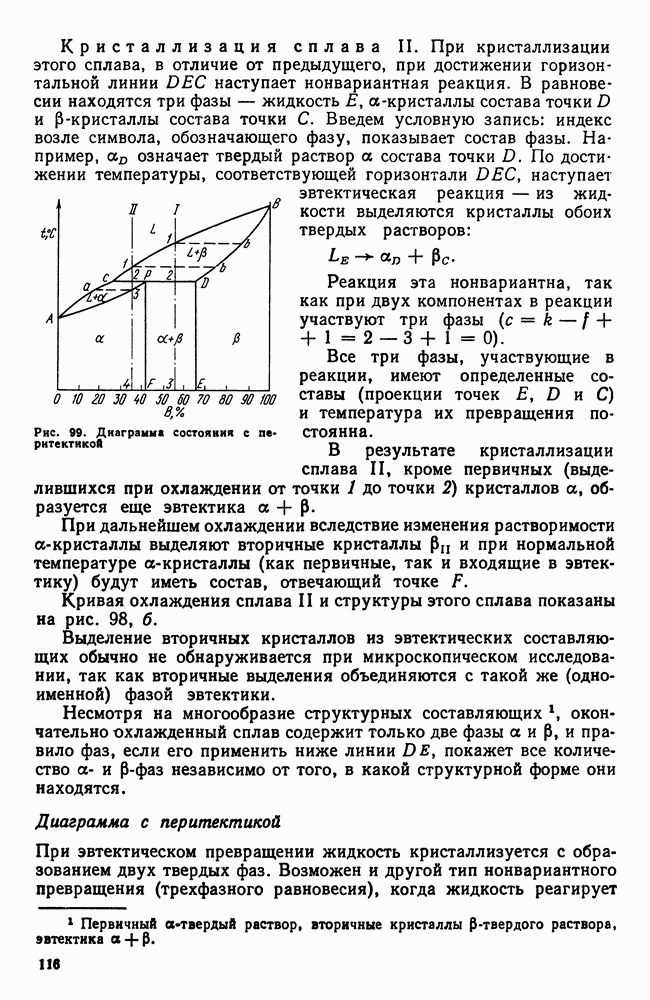
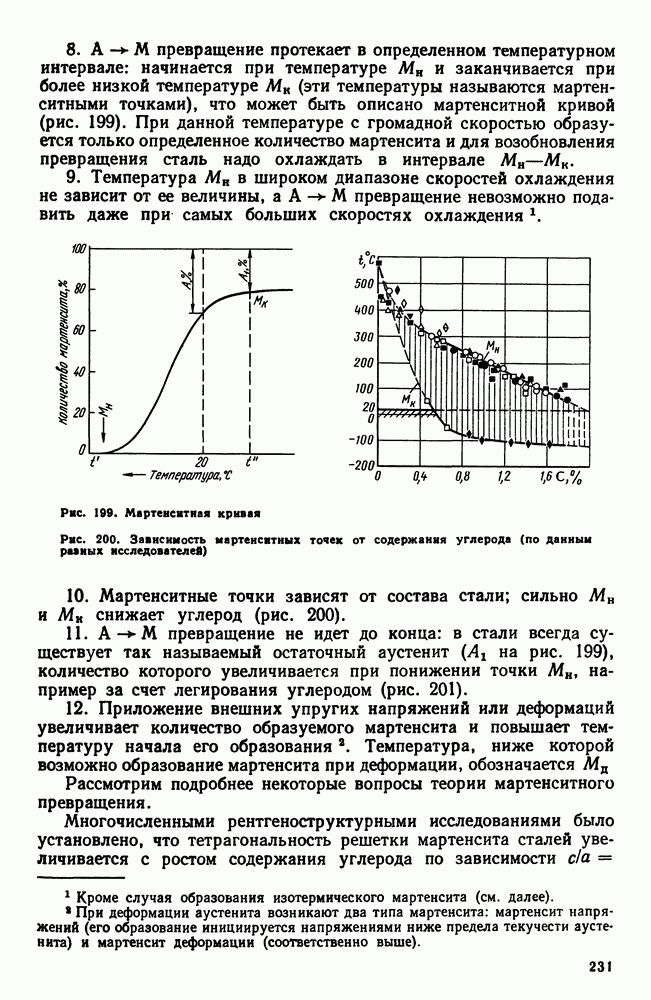
2. Общие замечания о построении диаграмм состояния
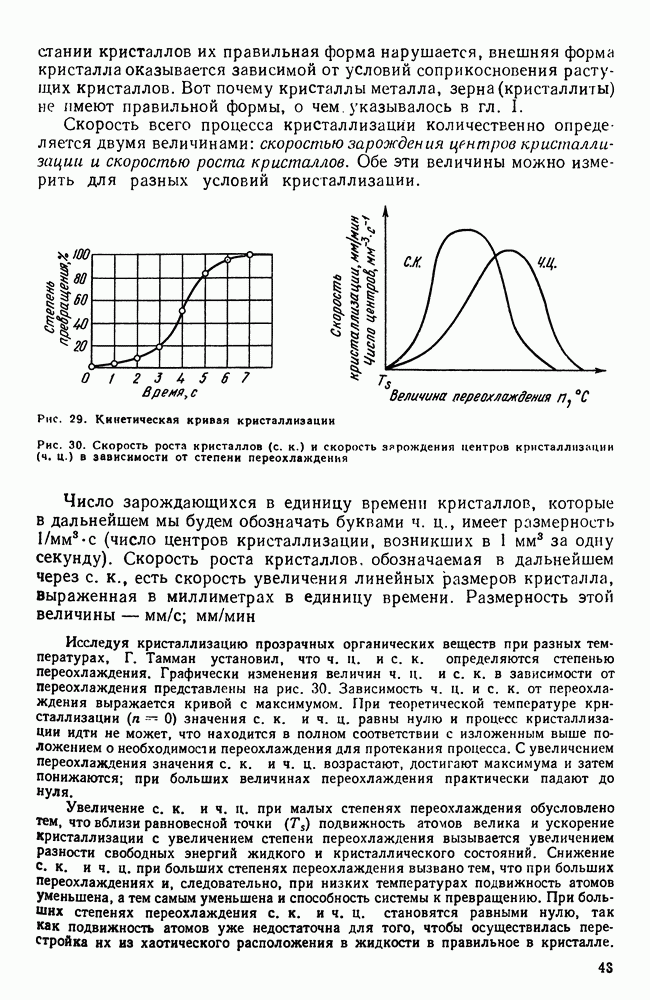
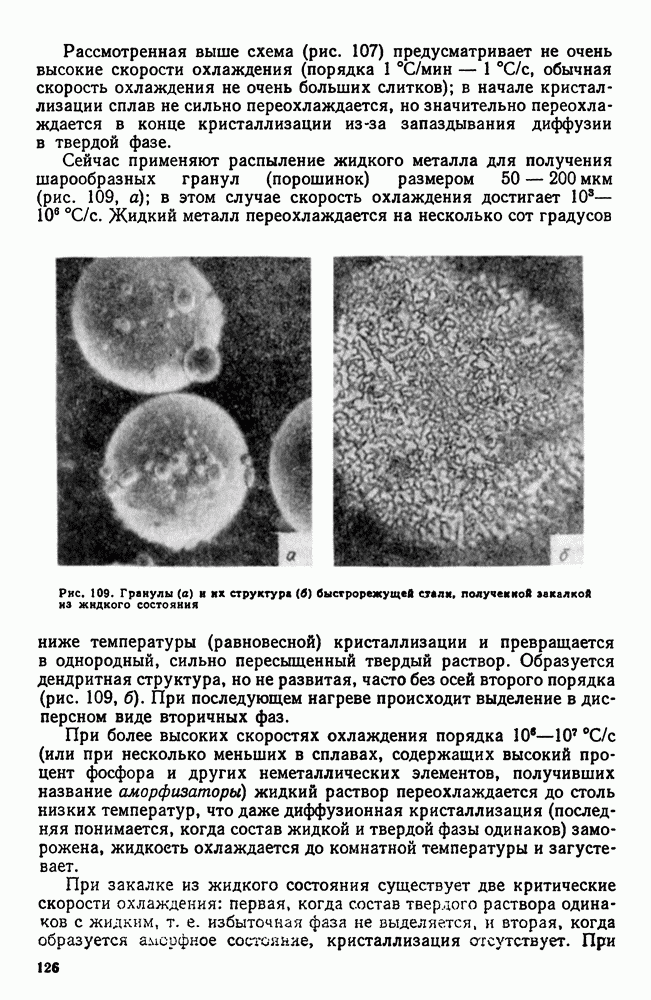
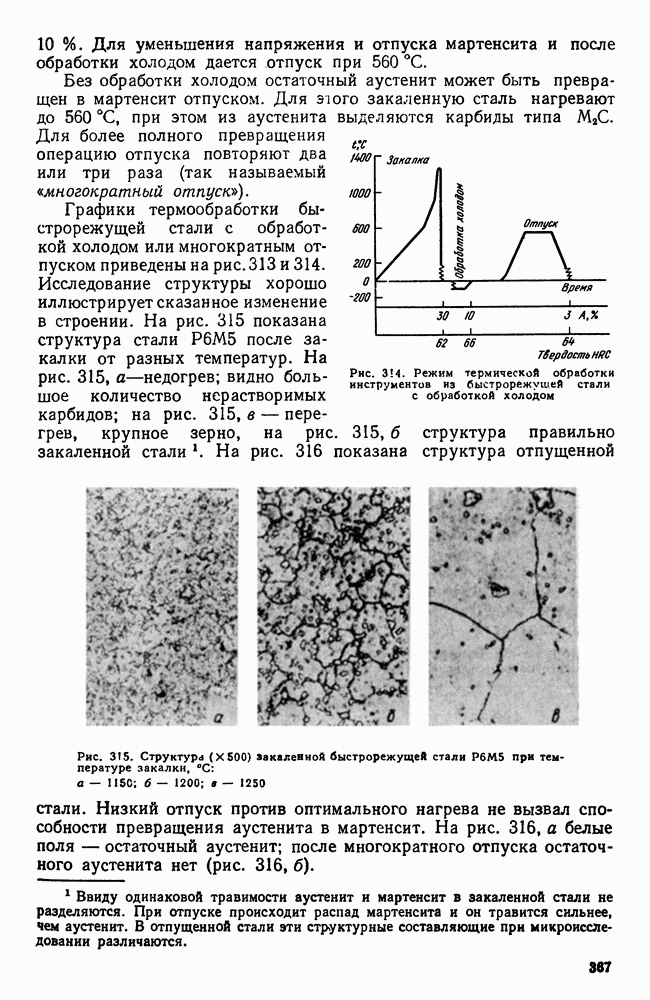
Диаграмма состояния показывает изменение состояния в зависимости от температуры (давление постоянно для всех рассматриваемых случаев) и концентрации.
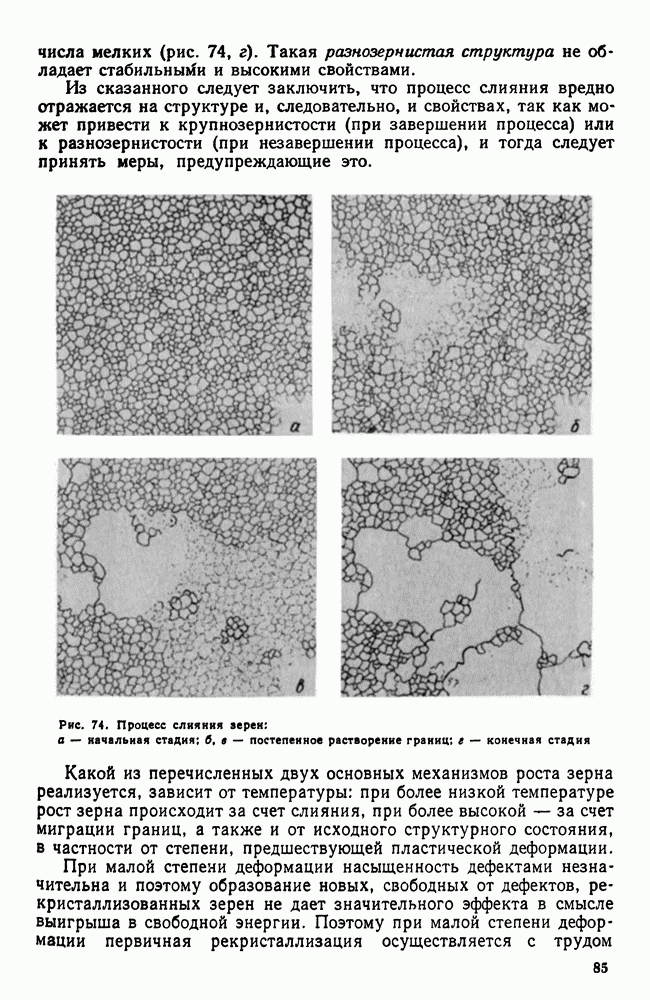
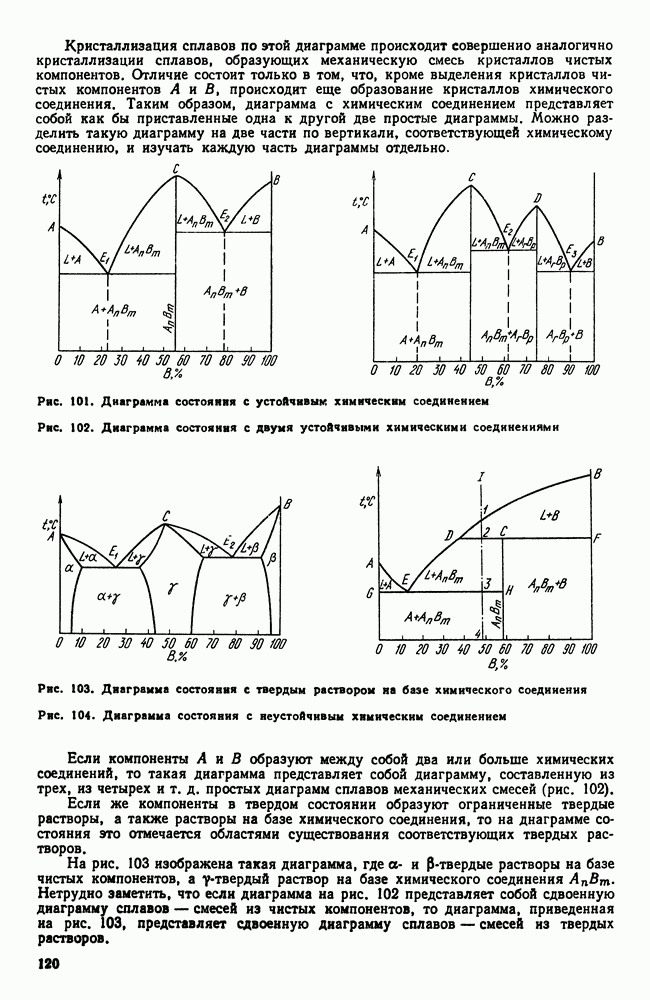
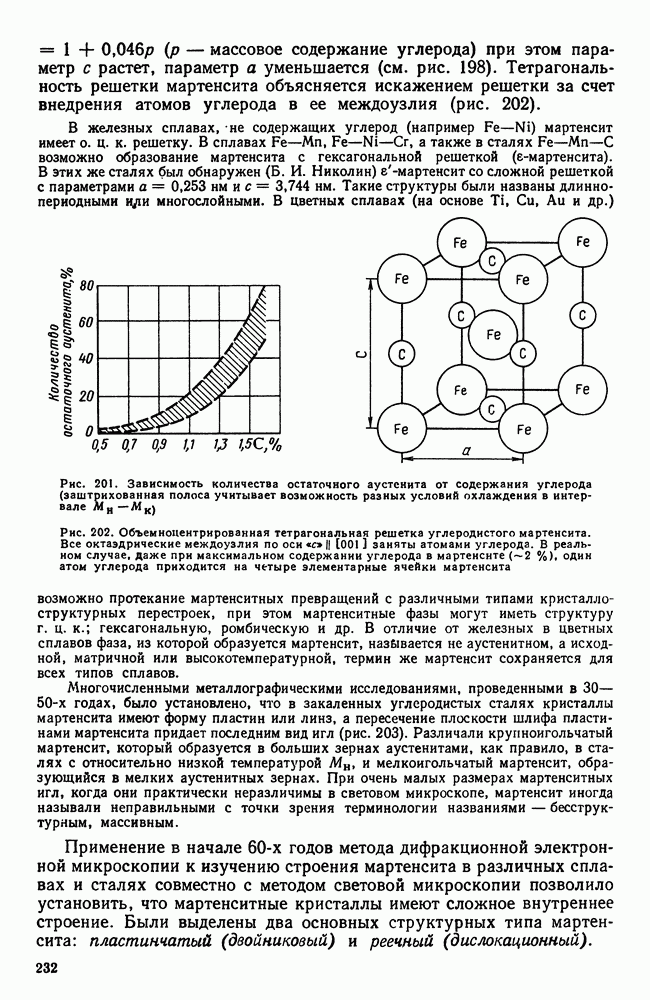
Если система однокомпонентна, то диаграмма состояния будет иметь одно измерение (шкала температур) и соответствующие точки на прямой покажут равновесную температуру изменения агрегатного состояния (рис. 86).

Рис. 86. Изменение агрегатного состояния однокомпонентной системы в зависимости от температуры

Рис. 87. Координаты для изображения состояний двухкомпонентной системы
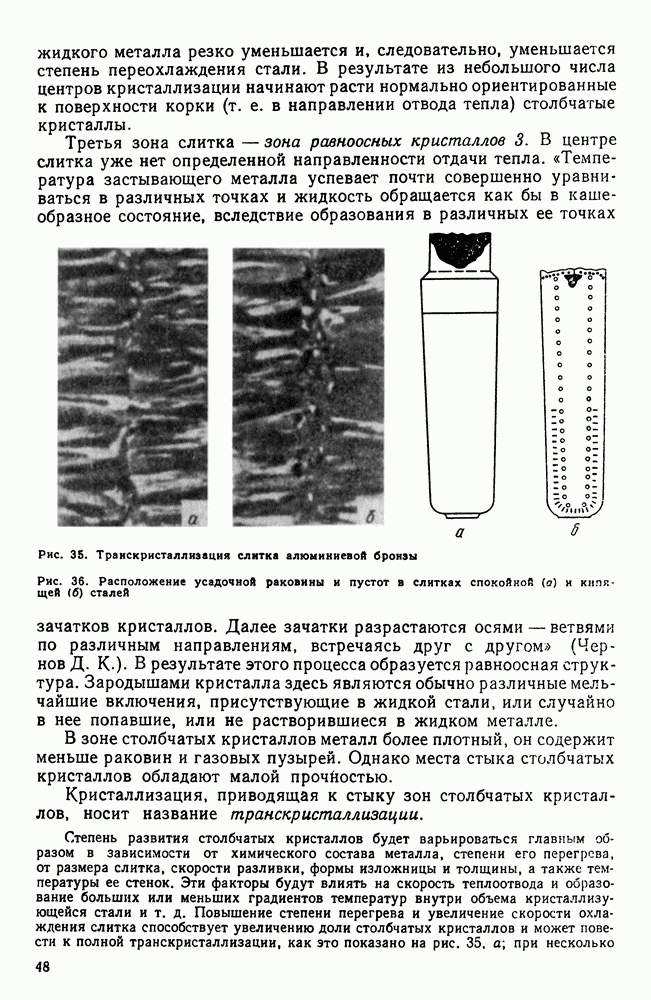
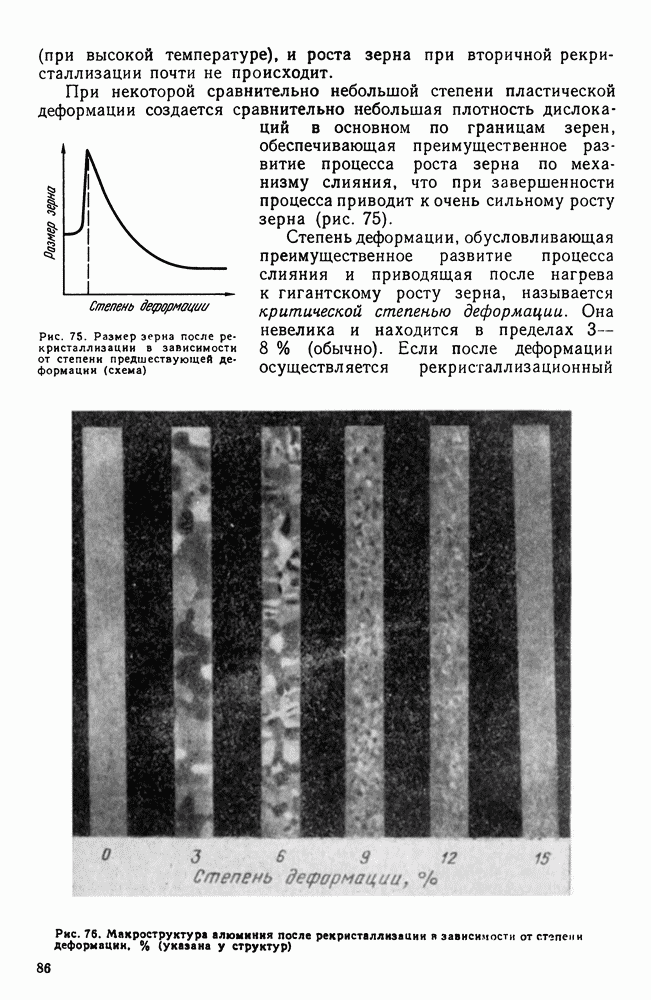
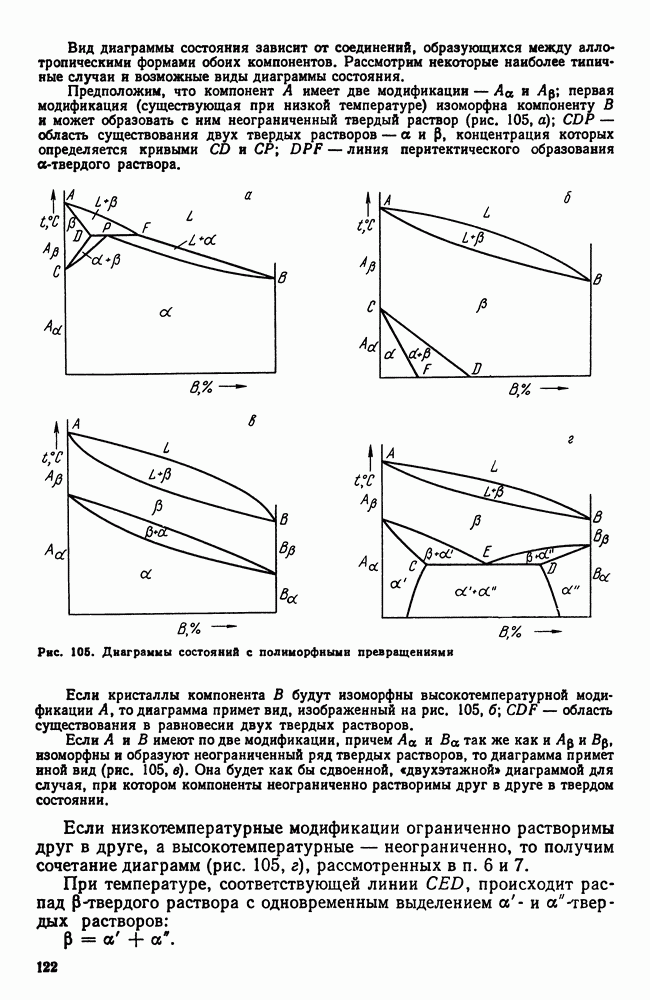
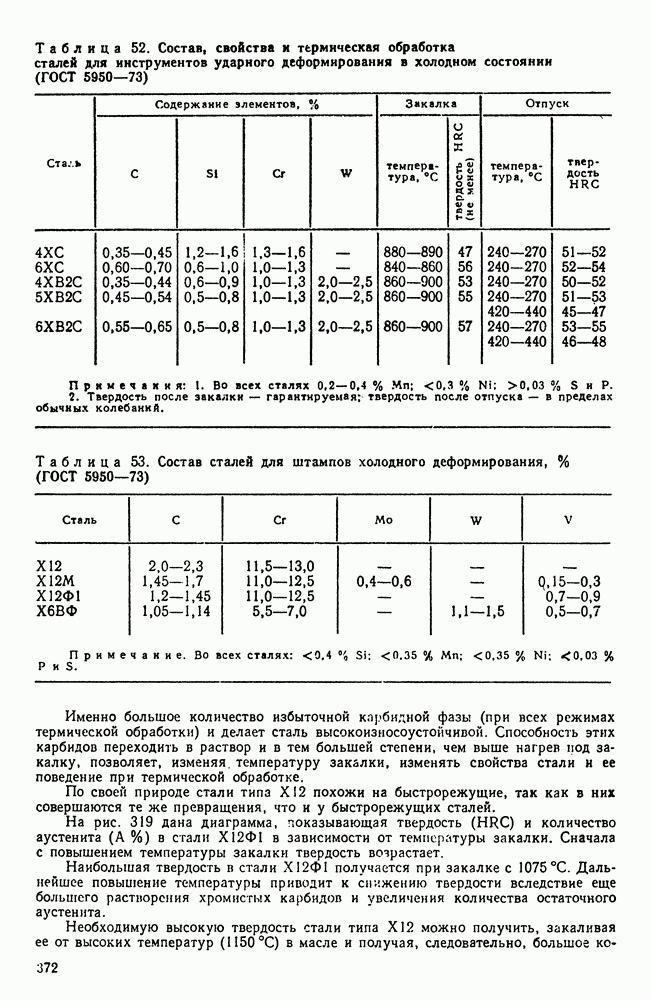
Если в системе два компонента, то второе измерение покажет концентрацию сплава: диаграмму строят в двух измерениях (температура — концентрация) (рис. 87).
По оси ординат откладывают температуру по оси абсцисс—концентрацию.
Общее содержание обоих компонентов в сплаве равно  и каждая точка на оси абсцисс соответствует определенному содержанию каждого компонента. В точке
и каждая точка на оси абсцисс соответствует определенному содержанию каждого компонента. В точке  ; в точке
; в точке  По мере удаления от точки А увеличивается количество компонента
По мере удаления от точки А увеличивается количество компонента  точке В его будет 100 %. Следовательно, крайние ординаты на диаграмме соответствуют чистым компонентам, а ординаты между ними — двойным сплавам.
точке В его будет 100 %. Следовательно, крайние ординаты на диаграмме соответствуют чистым компонентам, а ординаты между ними — двойным сплавам.
Диаграмма состояния сплавов с тремя компонентами имеет пространственный вид (две оси концентрационные и одна температурная). Четырехкомпонентную систему и системы с большим числом
компонентов также изображают в виде пространственных диаграмм, но с некоторыми упрощениями, так как они имеют больше трех независимых переменных.
Каждая точка на диаграмме состояния показывает состояние сплава данной концентрации при данной температуре. Каждая вертикаль соответствует изменению температуры определенного сплава. Изменение фазового состояния сплава отмечается на диаграмме точкой. Линии, соединяющие точки аналогичных превращений, разграничивают на диаграмме области аналогичных фазовых состояний.

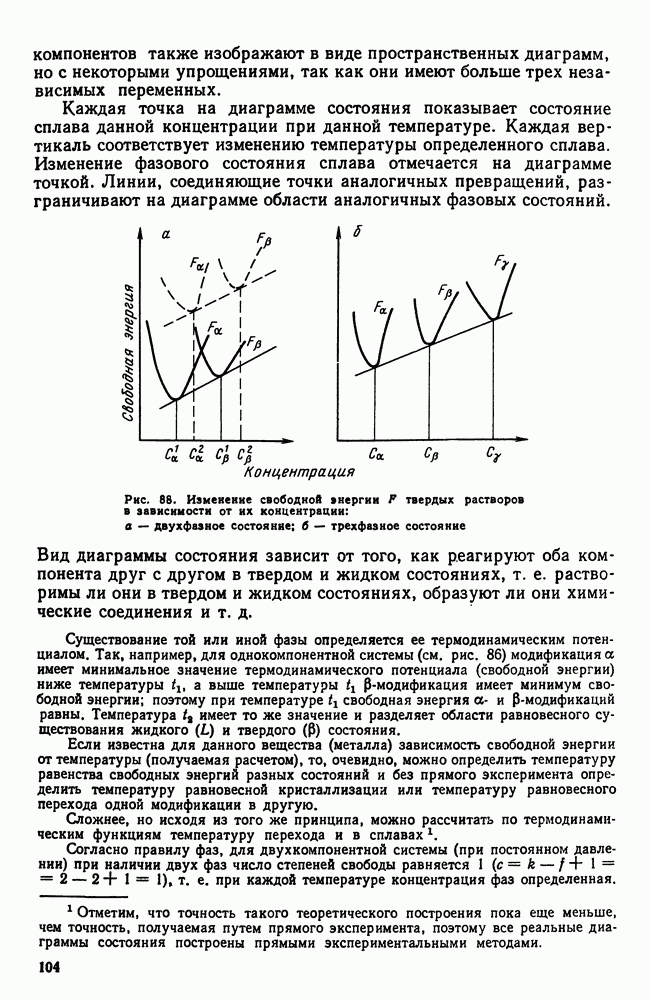
Рис. 88. Измекекие свободной энергии  твердых растворов в зависимости от их концентрации: а — двухфазное состояние;
твердых растворов в зависимости от их концентрации: а — двухфазное состояние;  — трехфазное состояние
— трехфазное состояние
Вид диаграммы состояния зависит от того, как реагируют оба компонента друг с другом в твердом и жидком состояниях, т. е. растворимы ли они в твердом и жидком состояниях, образуют ли они химические соединения и т. д.
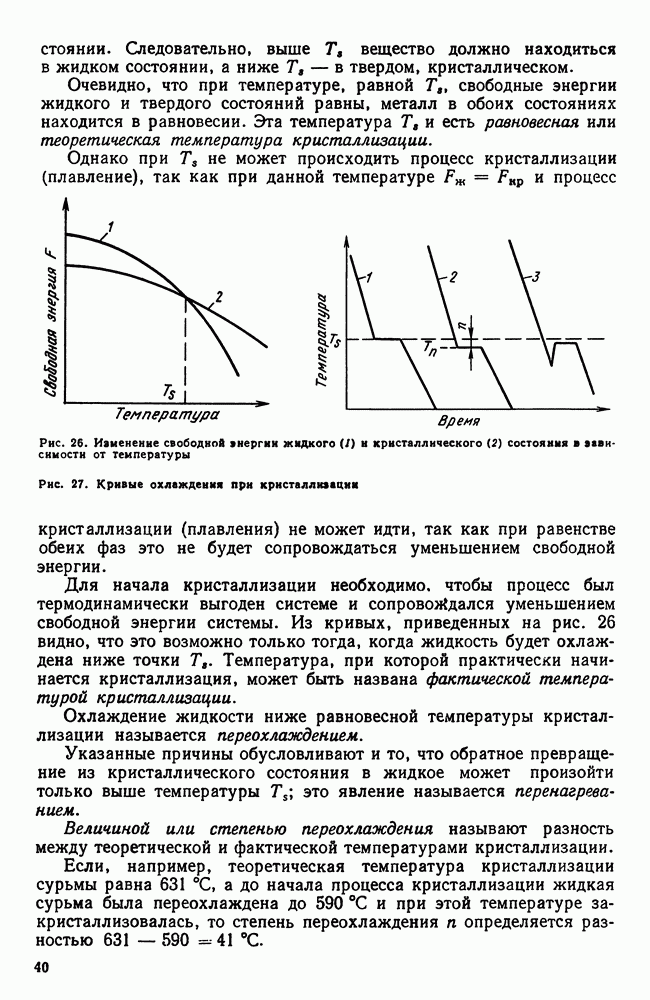
Существование той или иной фазы определяется ее термодинамическим потенциалом. Так, например, для однокомпонентной системы (см. рис. 86) модификация а имеет минимальное значение термодинамического потенциала (свободной энергии) ниже температуры  а выше температуры
а выше температуры  -модификация имеет минимум свободной энергии; поэтому при температуре
-модификация имеет минимум свободной энергии; поэтому при температуре  свободная энергия а- и
свободная энергия а- и  -модификаций равны. Температура
-модификаций равны. Температура  имеет то же значение и разделяет области равновесного существования жидкого
имеет то же значение и разделяет области равновесного существования жидкого  и твердого
и твердого  состояния.
состояния.
Если известна для данного вещества (металла) зависимость свободной энергии от температуры (получаемая расчетом), то, очевидно, можно определить температуру равенства свободных энергий разных состояний и без прямого эксперимента определить температуру равновесной кристаллизации или температуру равновесного перехода одной модификации в другую.
Сложнее, но исходя из того же принципа, можно рассчитать по термодинамическим функциям температуру перехода и в сплавах
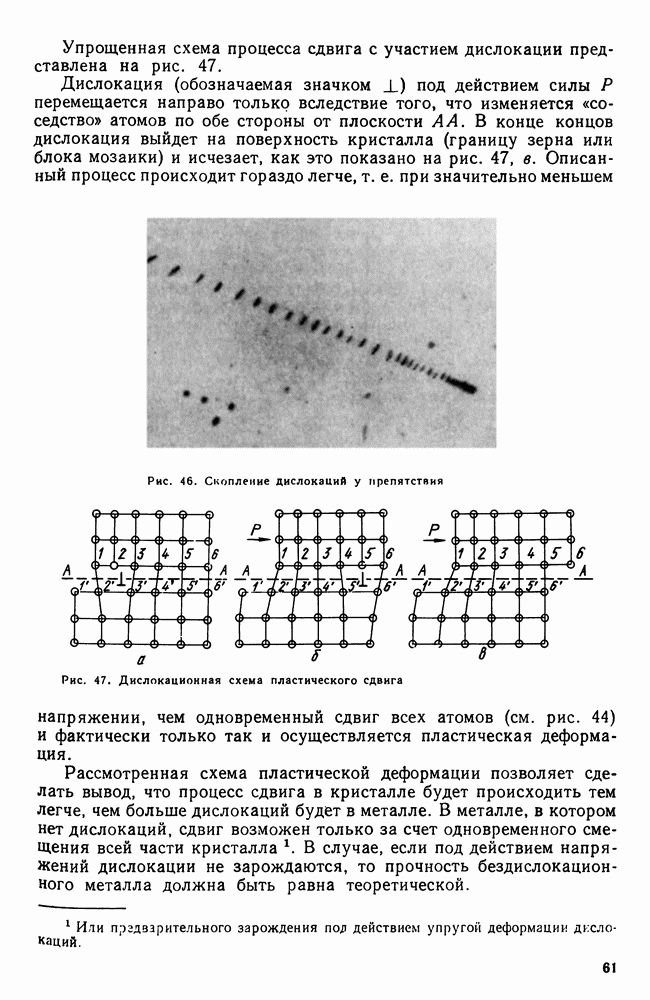
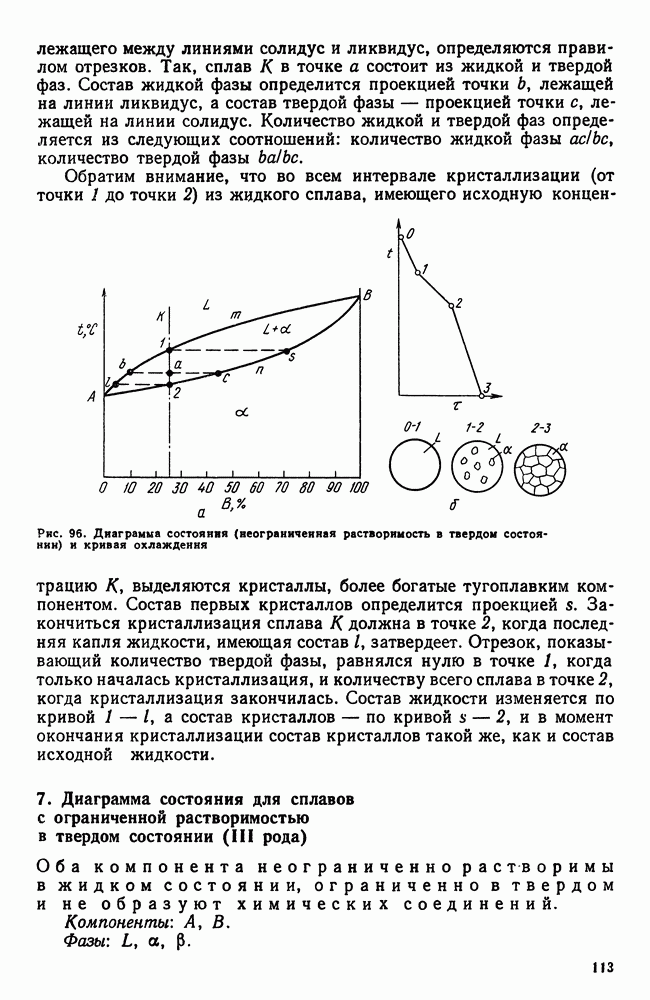
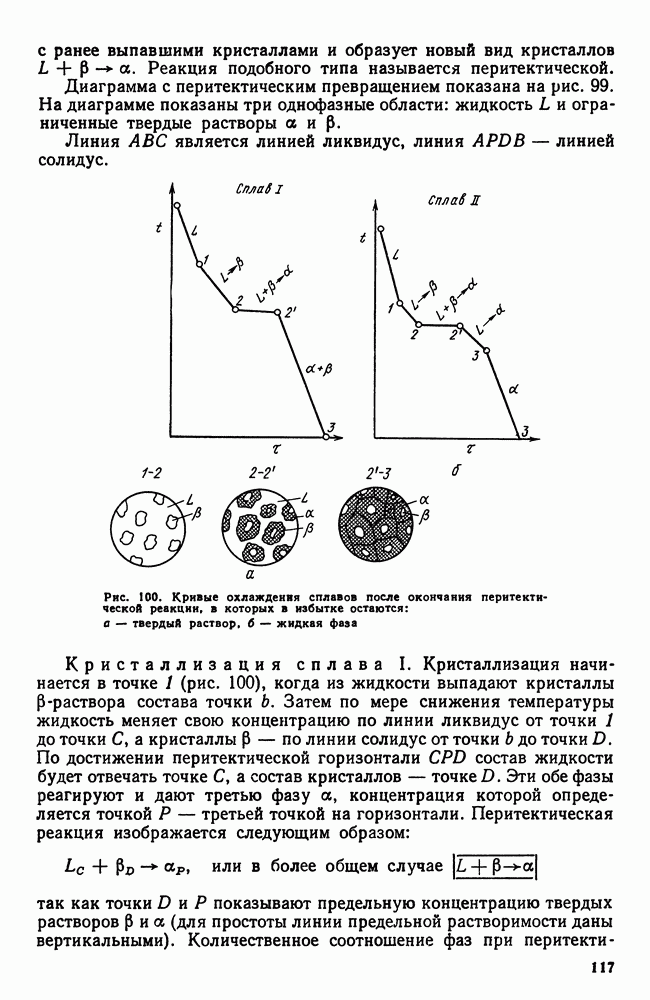
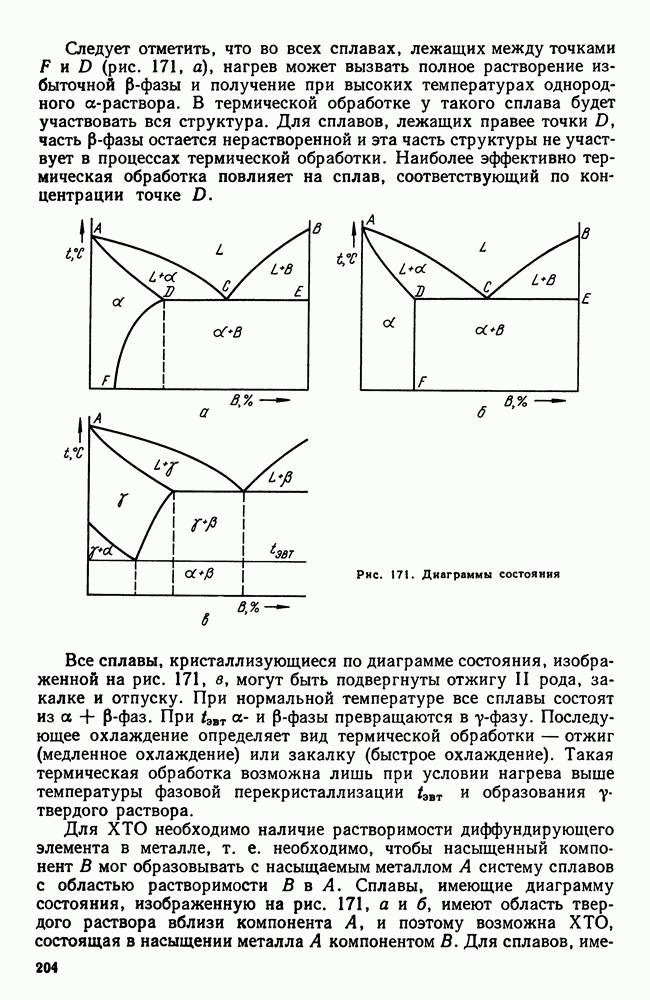
Согласно правилу фаз, для двухкомпонентной системы (при постоянном давлении) при наличии двух фаз число степеней свободы равняется  т. е. при каждой температуре концентрация фаз определенная.
т. е. при каждой температуре концентрация фаз определенная.
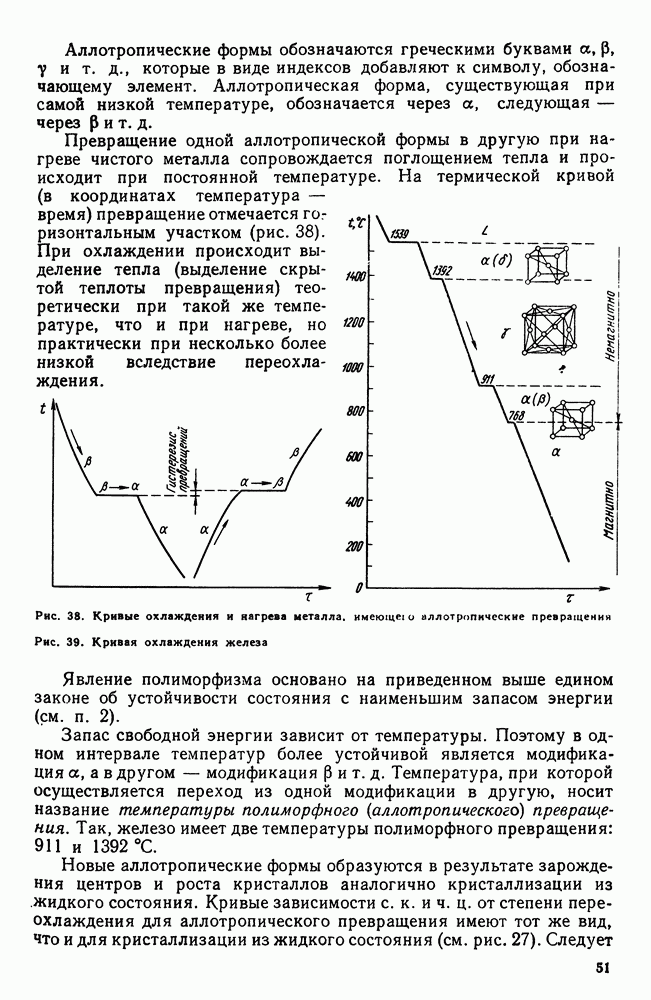
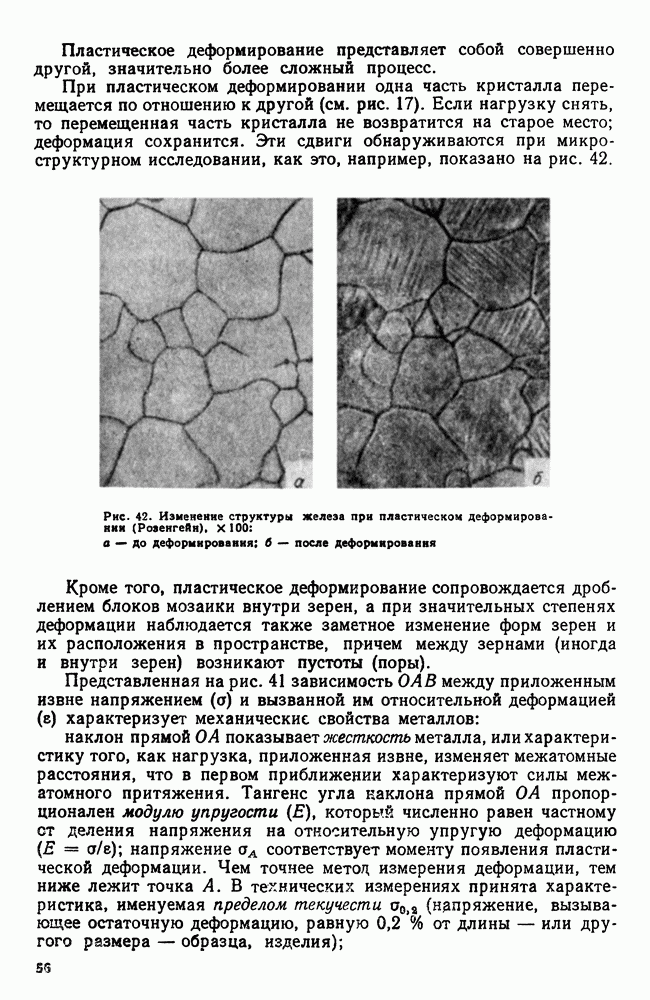
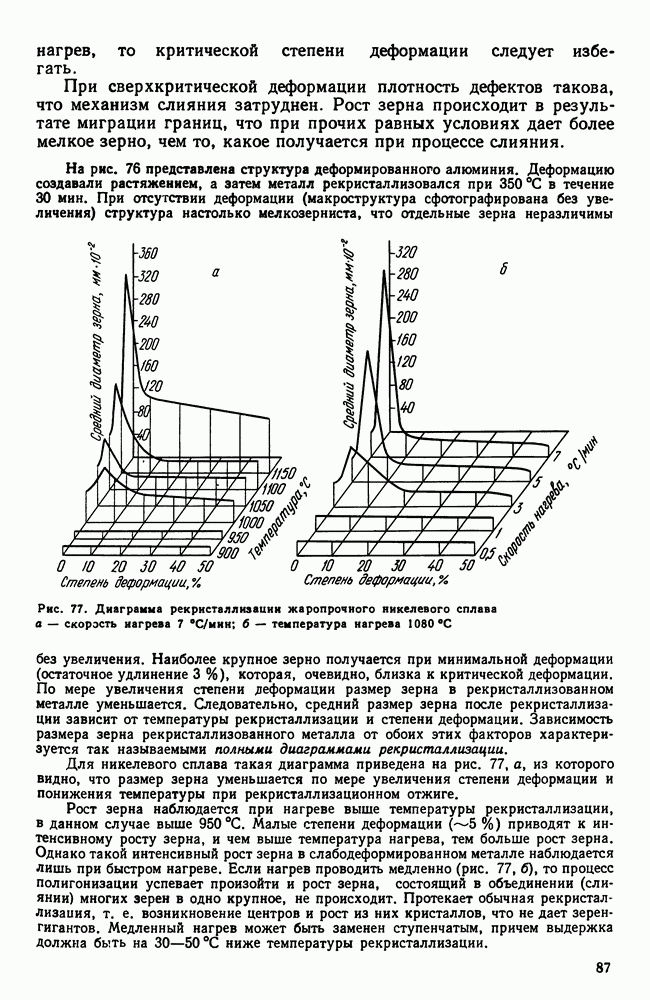
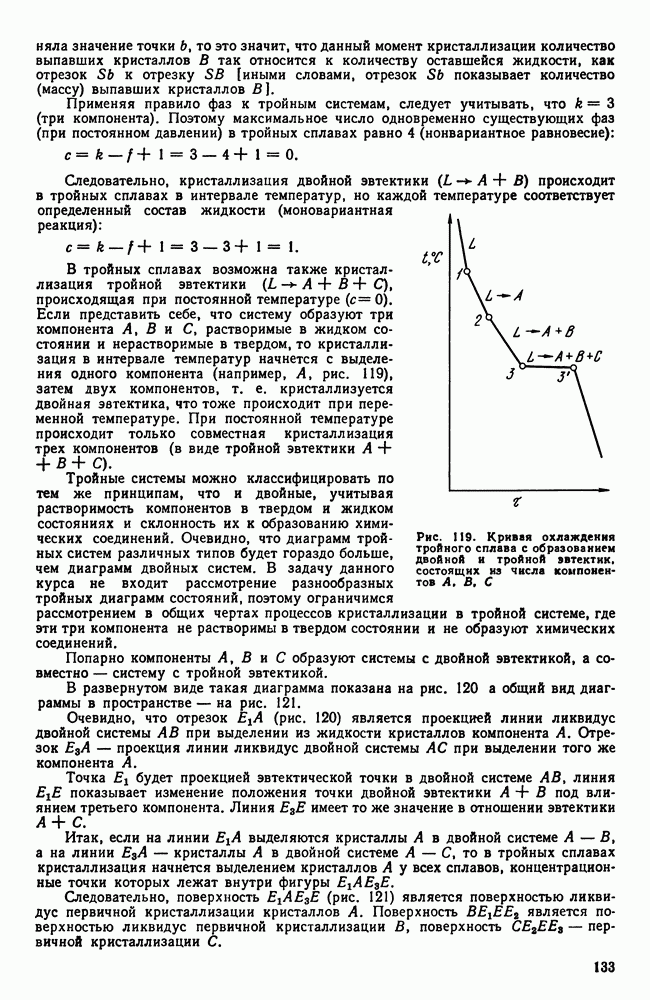
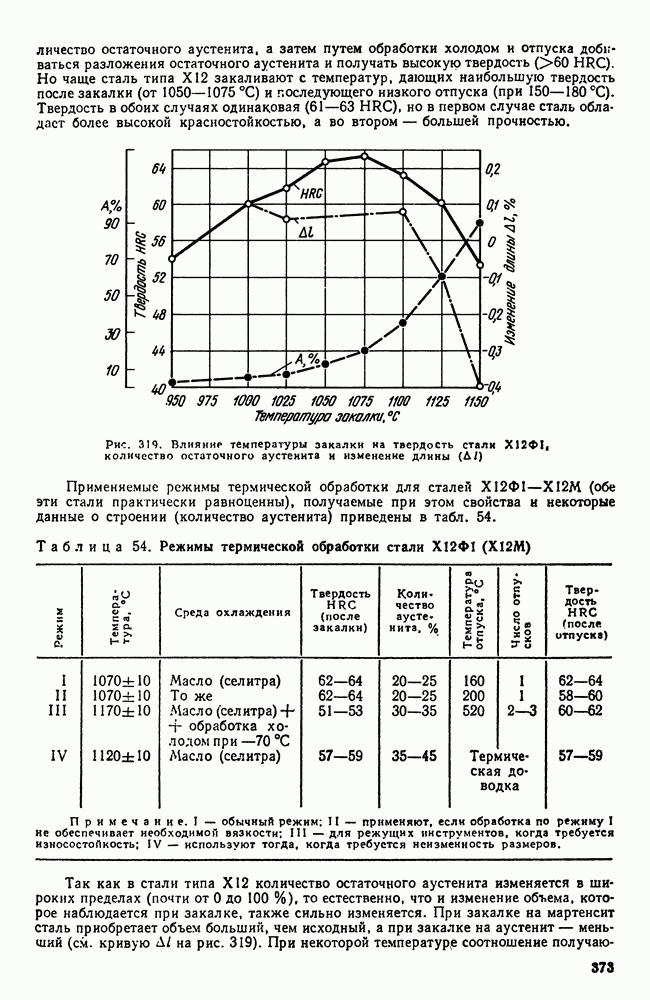
Если рассматривать свободную энергию двух твердых растворов а и Р в зависимости от концентрации, то для данной температуры минимум свободной энергии каждой фазы будет отвечать определенной концентрации (рис. 88). Другими словами, для температуры  (сплошные линии на рис. 88, а) это будет
(сплошные линии на рис. 88, а) это будет  и а для
и а для  (штриховые линии на том же рисунке) это будет и
(штриховые линии на том же рисунке) это будет и  Для многофазных систем (две фазы и более) по точкам, соответствующим минимальным значениям для данной фазы свободных энергий, можно провести касательную.
Для многофазных систем (две фазы и более) по точкам, соответствующим минимальным значениям для данной фазы свободных энергий, можно провести касательную.
В случае трехфазного равновесия  т. е. такое равновесие может быть лишь при определенной температуре и составе фаз. Поскольку под влиянием температуры свободные энергии фаз а, Р, у изменяются с разной интенсивностью, имеется лишь одна температура, при которой можно провести одну касательную ко всем трем точкам — минимумам (рис. 88, б). Это состояние и отвечает условиям нонвариантного равновесия
т. е. такое равновесие может быть лишь при определенной температуре и составе фаз. Поскольку под влиянием температуры свободные энергии фаз а, Р, у изменяются с разной интенсивностью, имеется лишь одна температура, при которой можно провести одну касательную ко всем трем точкам — минимумам (рис. 88, б). Это состояние и отвечает условиям нонвариантного равновесия 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть первая. ТЕОРИЯ СПЛАВОВ
- Глава I. КРИСТАЛЛИЧЕСКОЕ СТРОЕНИЕ МЕТАЛЛОВ
- 2. Классификация металлов
- 3. Кристаллическое строение металлов
- 4. Кристаллические решетки металлов
- 5. Реальное строение металлических кристаллов
- 6. Анизотропия свойств кристаллов
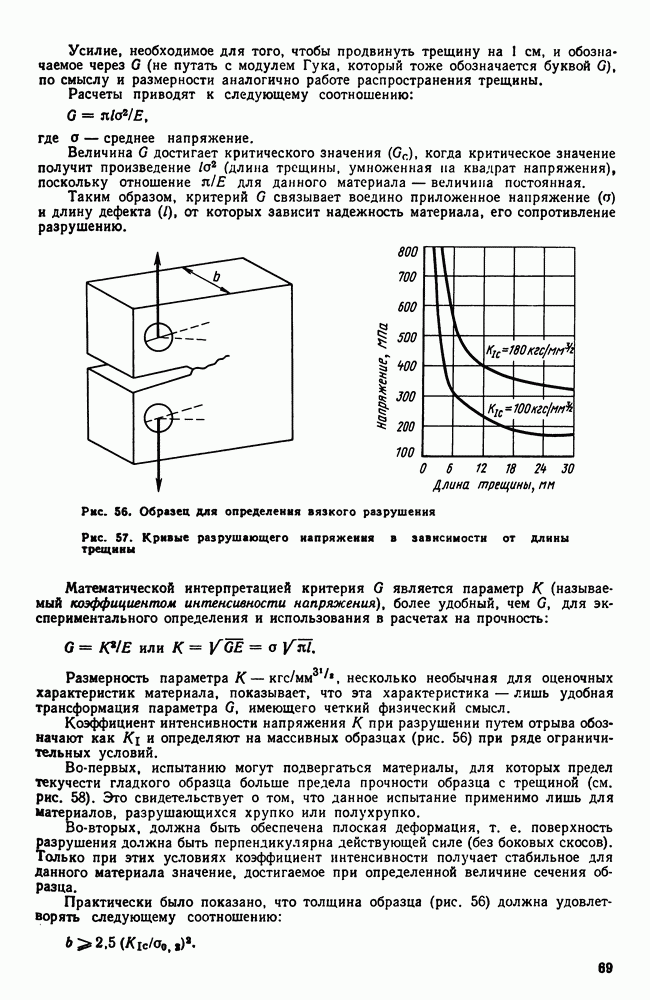
- 7. Методы изучения строения металлов
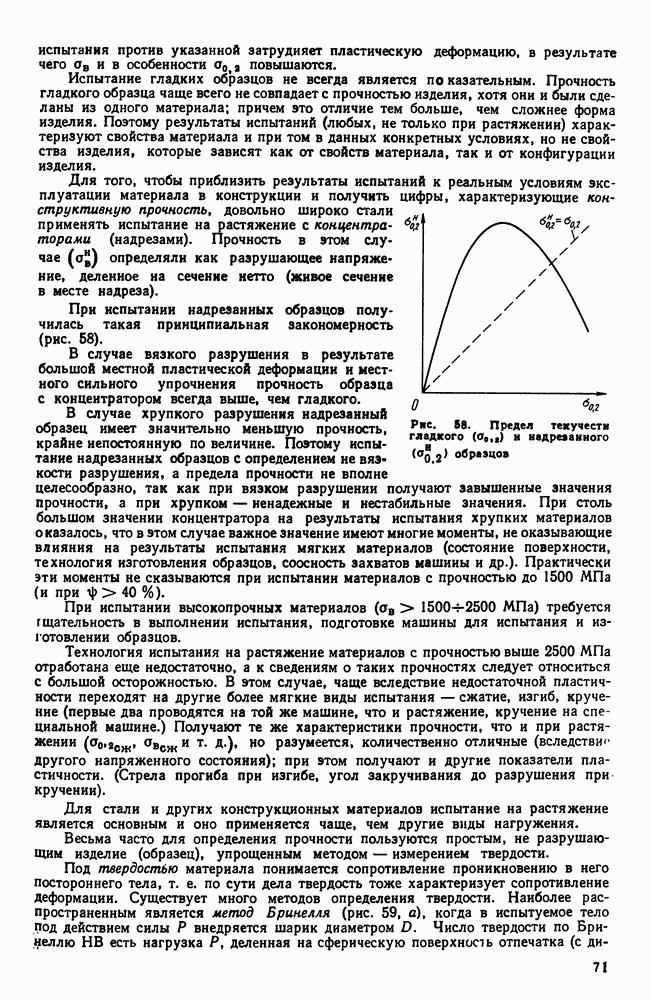
- Глава II. КРИСТАЛЛИЗАЦИЯ
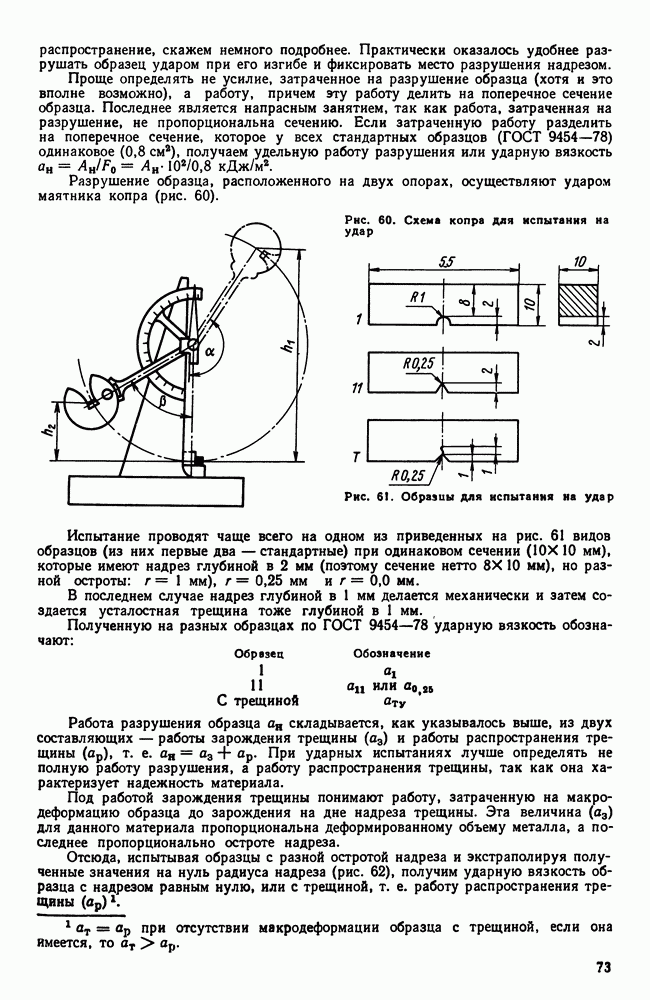
- 1. Три состояния вещества
- 2. Энергетические условия процесса кристаллизации
- 3. Механизм процесса кристаллизации
- 4. Форма кристаллических образований
- 5. Строение слитка
- 6. Превращения в твердом состояние. Полиморфизм
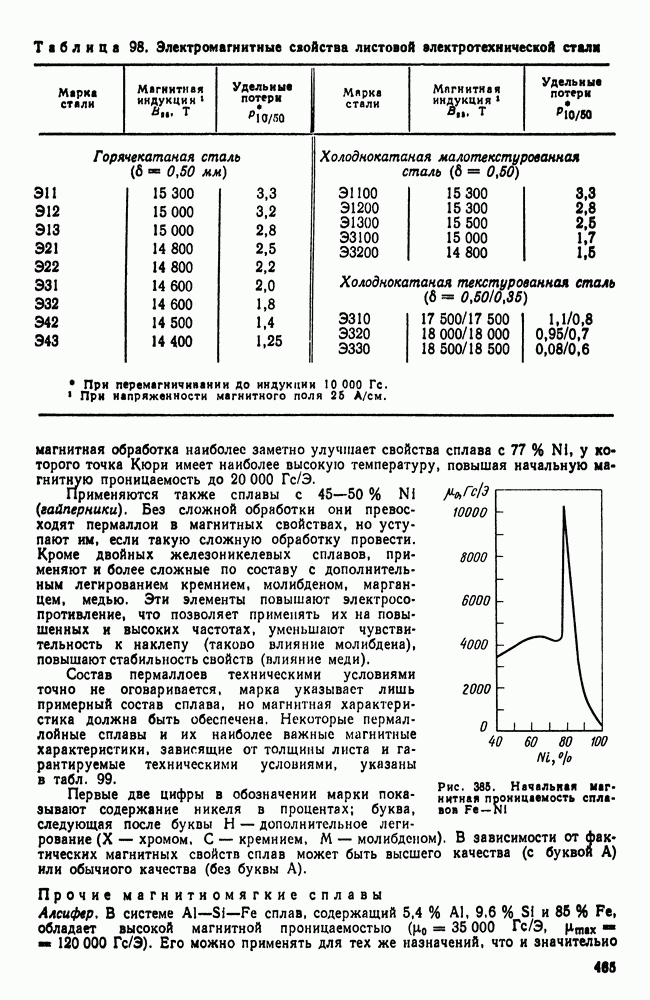
- 7. Магнитные превращения
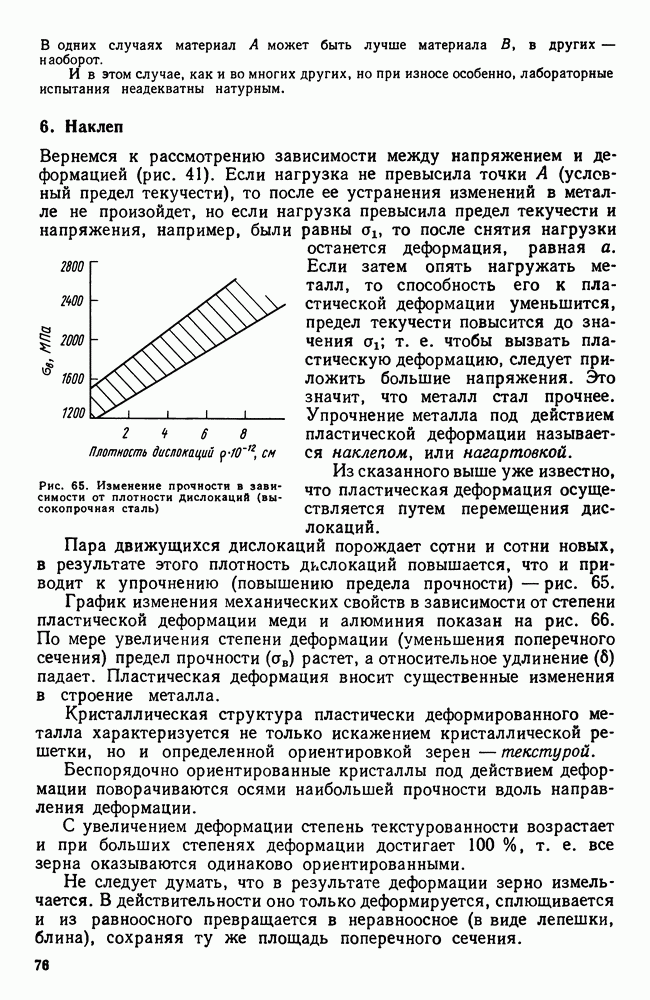
- 8. Закалка из жидкого состояния. Аморфное состояние
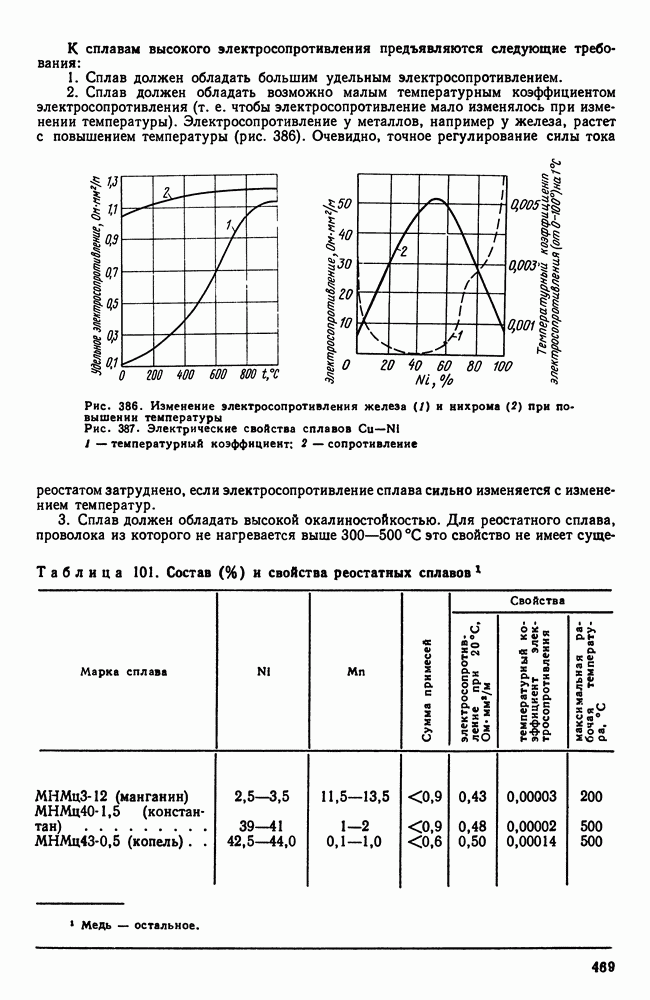
- Глава III. МЕХАНИЧЕСКИЕ СВОЙСТВА. НАКЛЕП И РЕКРИСТАЛЛИЗАЦИЯ
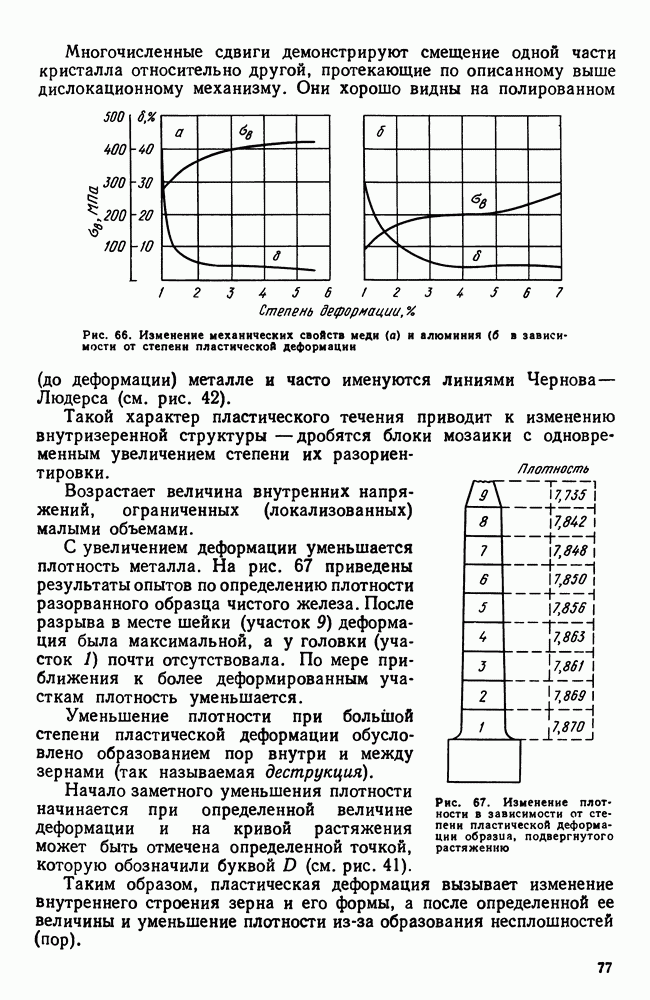
- 2. Упругая и пластическая деформация. Несовершенства решетки и прочность металлов
- 3. Сверхпластичность
- 4. Разрушение
- 5. Методы определения механических свойств
- 6. Наклеп
- 7. Влияние нагрева на строение и свойства деформированного металла (рекристаллизационные процессы)
- Глава IV. СТРОЕНИЕ СПЛАВОВ
- 2. Химическое соединение
- 3. Твердый раствор на основе одного из компонентов сплава
- 4. Твердый раствор на основе химического соединения
- 5. Упорядоченные твердые растворы
- 6. Электронные соединения (фазы Юм-Розери)
- 7. Фазы Лавеса
- 8. Фазы внедрения
- Глава V. ДИАГРАММА СОСТОЯНИЯ
- 2. Общие замечания о построении диаграмм состояния
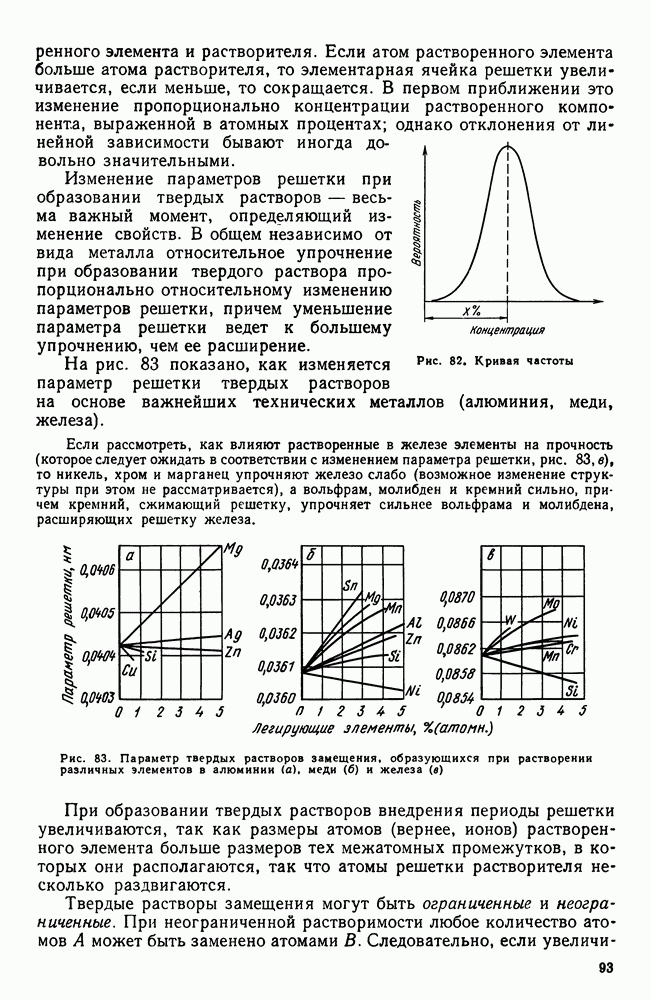
- 3. Экспериментальное построение диаграмм
- 4. Диаграмма состояния для сплавов, образующих механические смеси из чистых компонентов (I рода)
- 5. Правило отрезков
- 6. Диаграмма состояния для сплавов с неограниченной растворимостью в твердом состоянии (II рода)
- 7. Диаграмма состояния для сплавов с ограниченной растворимостью в твердом состоянии (III рода)
- 8. Диаграмма состояния для сплавов, образующих химические соединения (IV рода)
- 9. Диаграмма состояния для сплавов, испытывающих полиморфные превращения
- 10. Кристаллизация сплавов в неравновесных условиях
- 11. Системы с тремя компонентами
- 12. Упрощенные методы изучения многокомпонентных систем
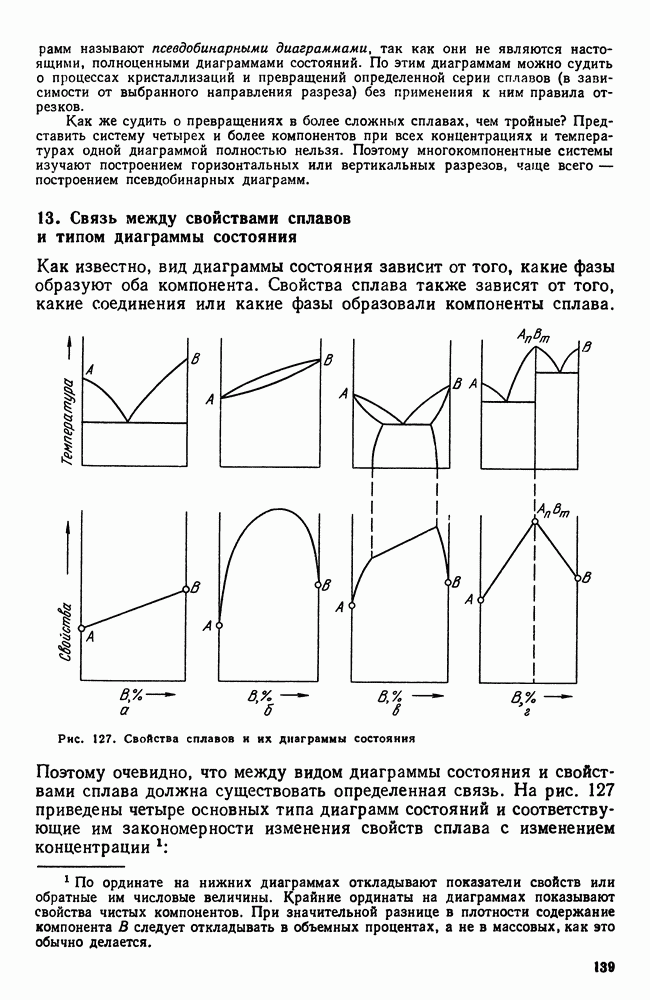
- 13. Связь между свойствами сплавов и типом диаграммы состояния
- Часть вторая. ЖЕЛЕЗОУГЛЕРОДИСТЫЕ СПЛАВЫ
- Глава VI. ДИАГРАММА ЖЕЛЕЗО—УГЛЕРОД
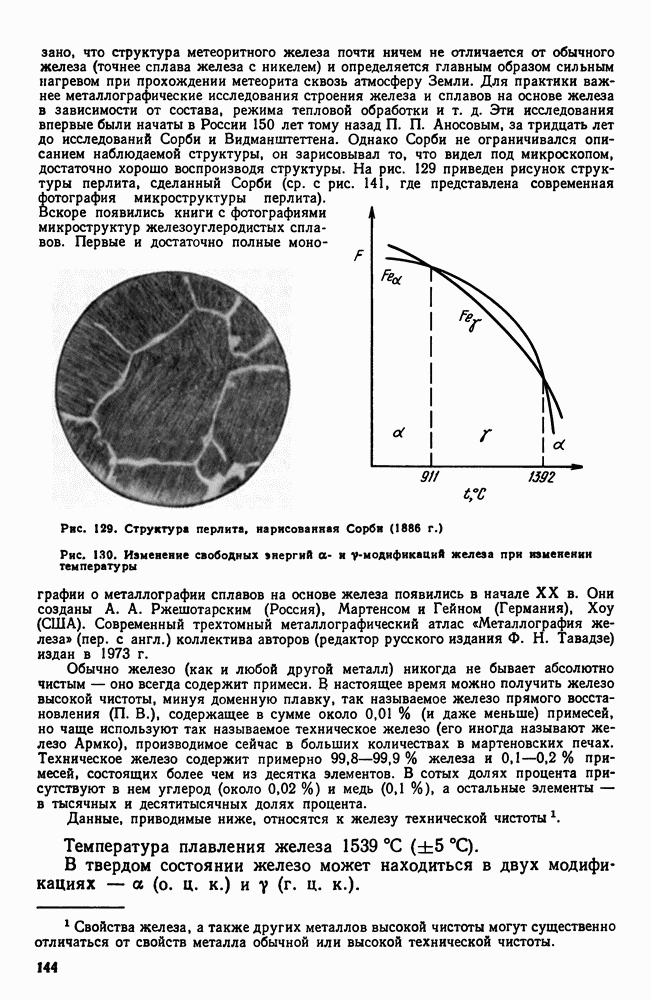
- 2. Железо
- 3. Цементит
- 4. Диаграмма состояния
- Глава VII. УГЛЕРОДИСТЫЕ СТАЛИ
- 1. Влияние углерода на свойства стали
- 2. Влияние постоянных примесей на свойства стали
- 3. Сталь различных способов производства. Чистая сталь
- 4. Углеродистая сталь общего назначения
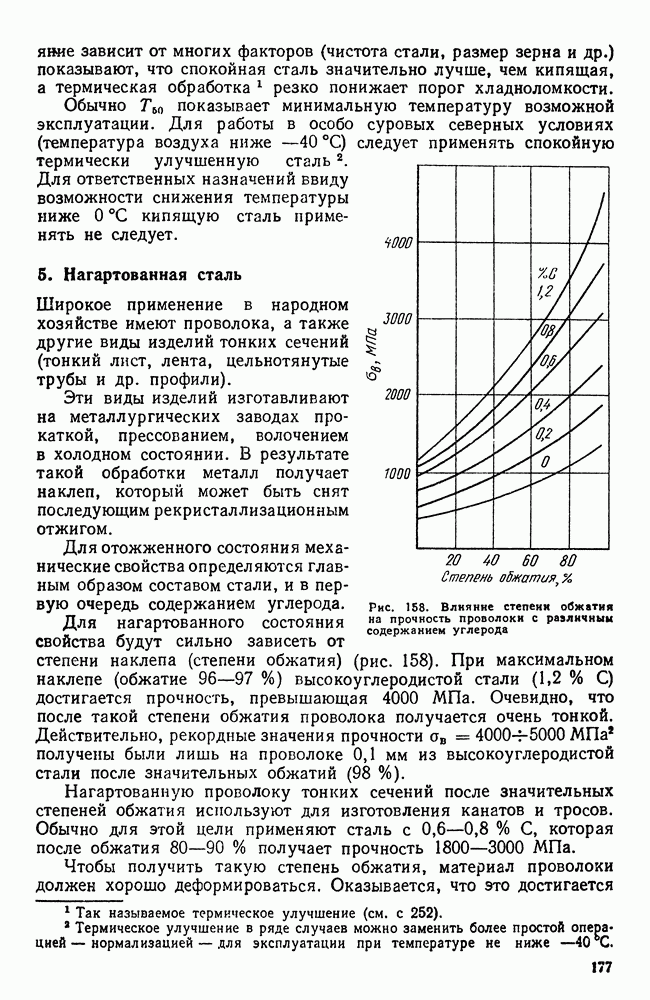
- 5. Нагартованная сталь
- 6. Листовая сталь для холодной штамповки
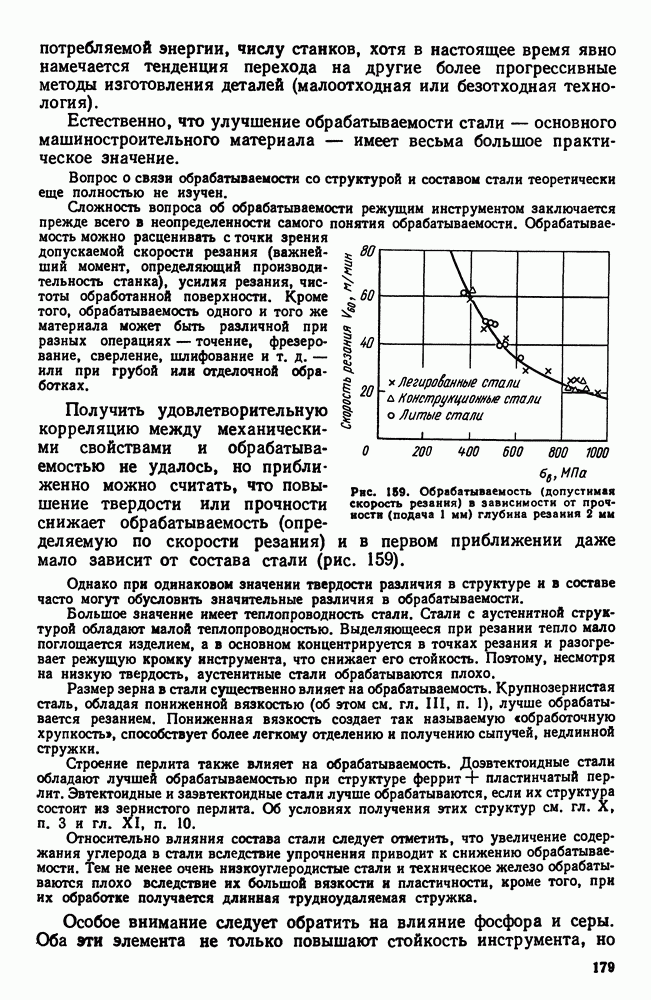
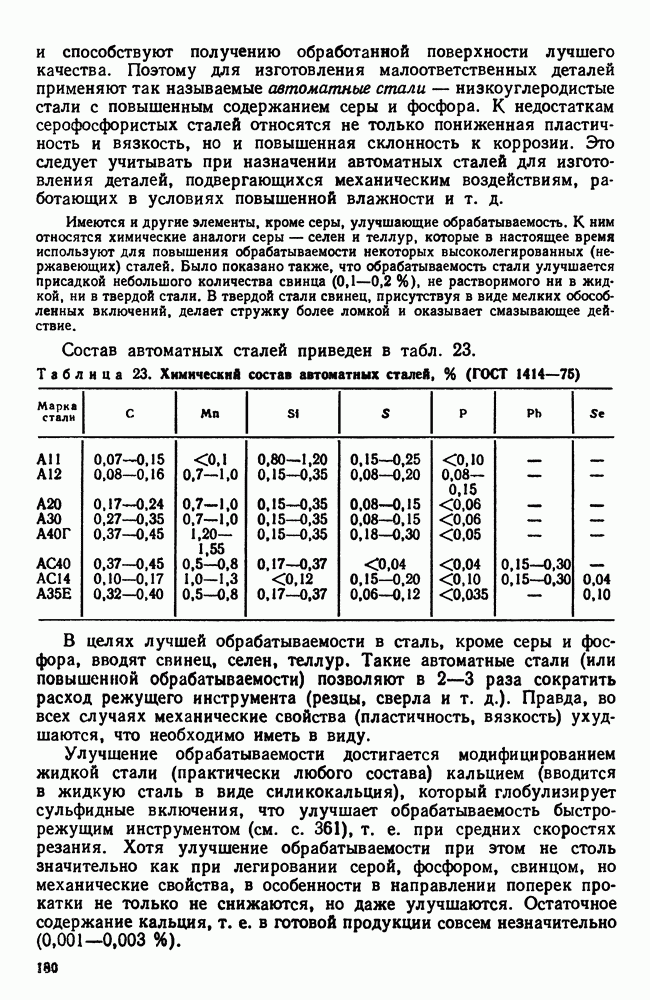
- 7. Обрабатываемость резанием. Автоматные стали
- Глава VIII. ЧУГУН
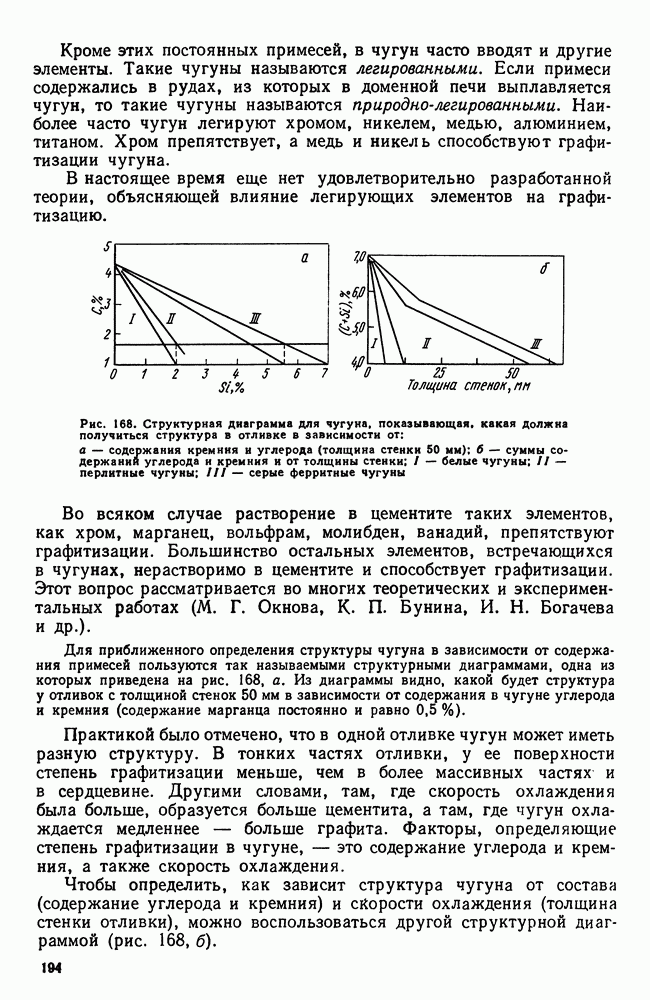
- 2. Структура чугуна. Формы графита
- 3. Структура и свойства чугуна
- 4. Примеси в чугуне
- 5. Марки серых и высокопрочных чугунов
- 6. Ковкий чугун
- Часть третья. ТЕРМИЧЕСКАЯ ОБРАБОТКА
- Глава IX. ОБЩИЕ ПОЛОЖЕНИЯ ТЕРМИЧЕСКОЙ ОБРАБОТКИ
- 2. Классификация видов термической обработки
- 3. Термическая обработка и диаграмма состояния
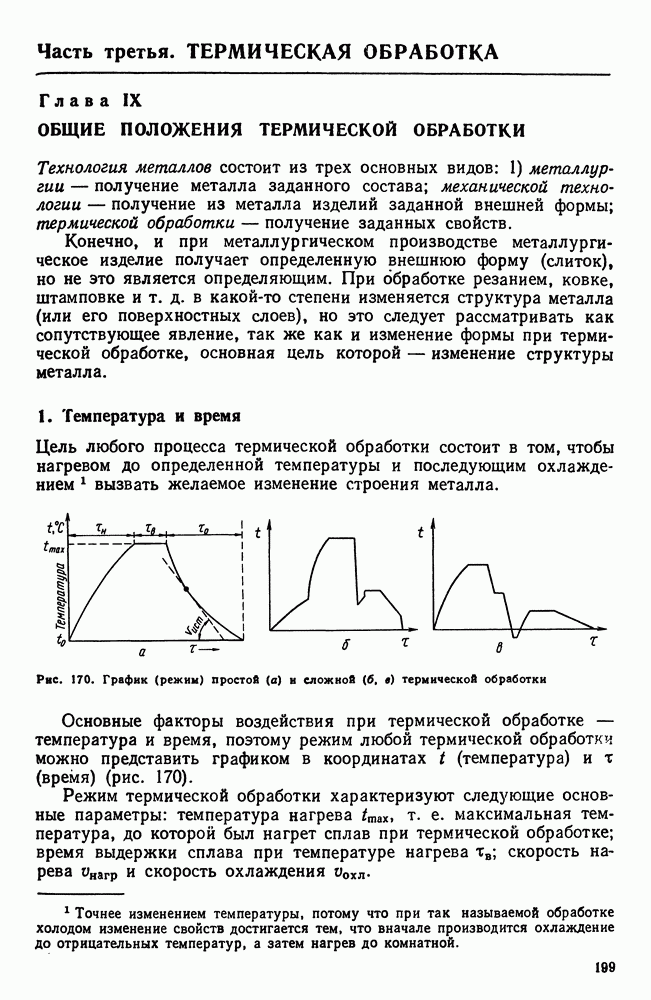
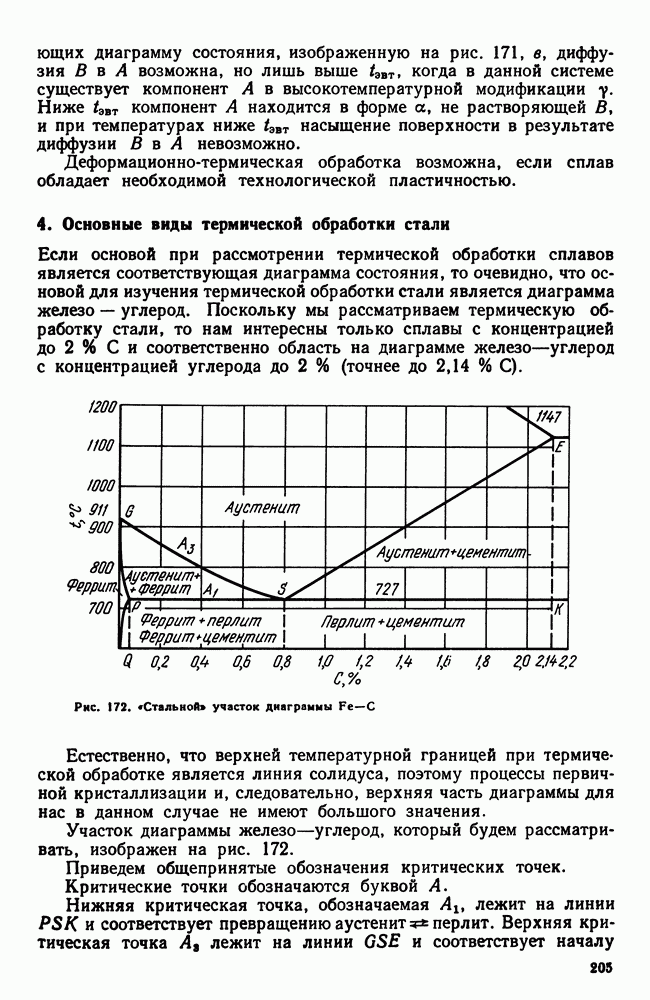
- 4 Основные виды термической обработки стали
- 5. Четыре основных превращения в стали
- Глава X. ТЕОРИЯ ТЕРМИЧЕСКОЙ ОБРАБОТКИ СТАЛИ
- 2. Рост аустенитного зерна
- 3. Распад аустенита
- 4. Мартенситное превращение
- 5. Бейнитное превращение
- 6. Превращения при отпуске
- 7. Влияние термической обработки на свойства стали
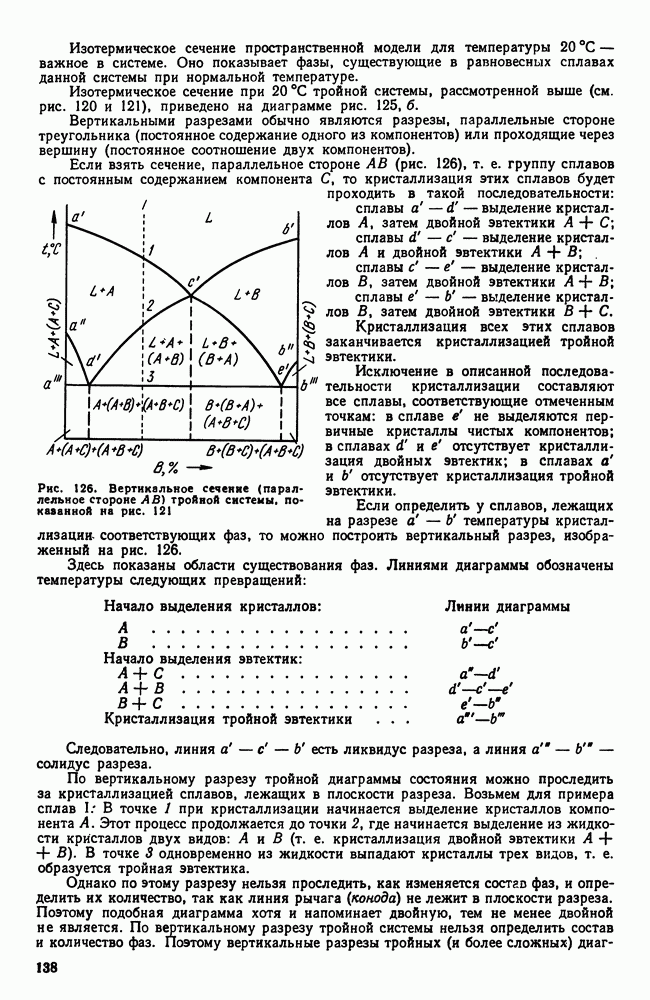
- 8. Термомеханическая обработка
- Глава XI. ПРАКТИКА ТЕРМИЧЕСКОЙ ОБРАБОТКИ СТАЛИ
- 2. Время нагрева
- 3. Химическое воздействие нагревающей среды
- 4. Закалочные среды
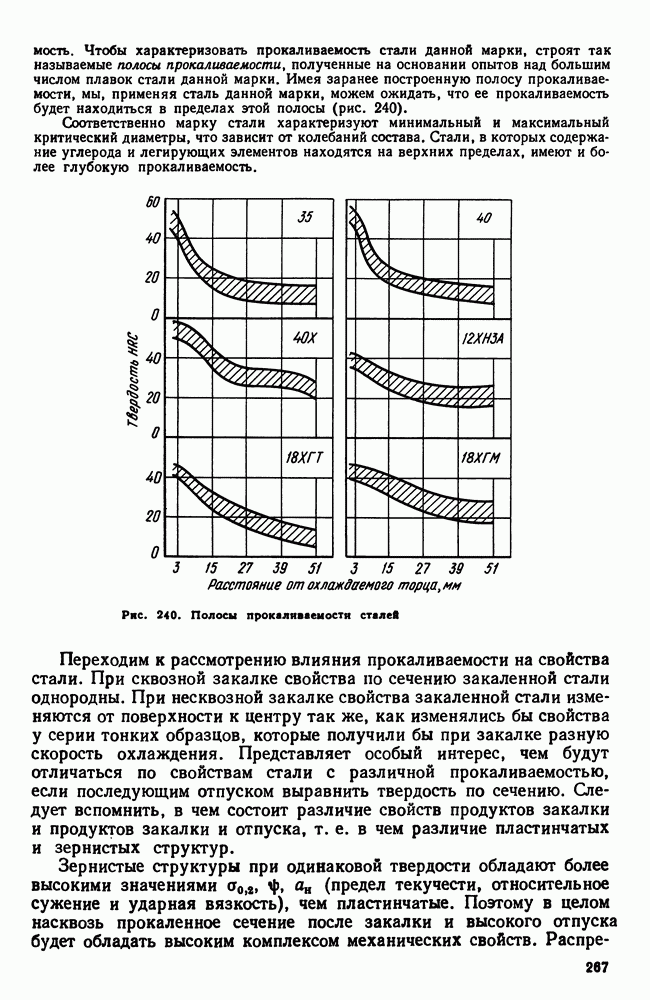
- 5. Прокаливаемость
- 6. Внутренние напряжения
- 7. Способы закалки
- 8. Обработка стали холодом
- 9. Дефекты, возникающие при закалке
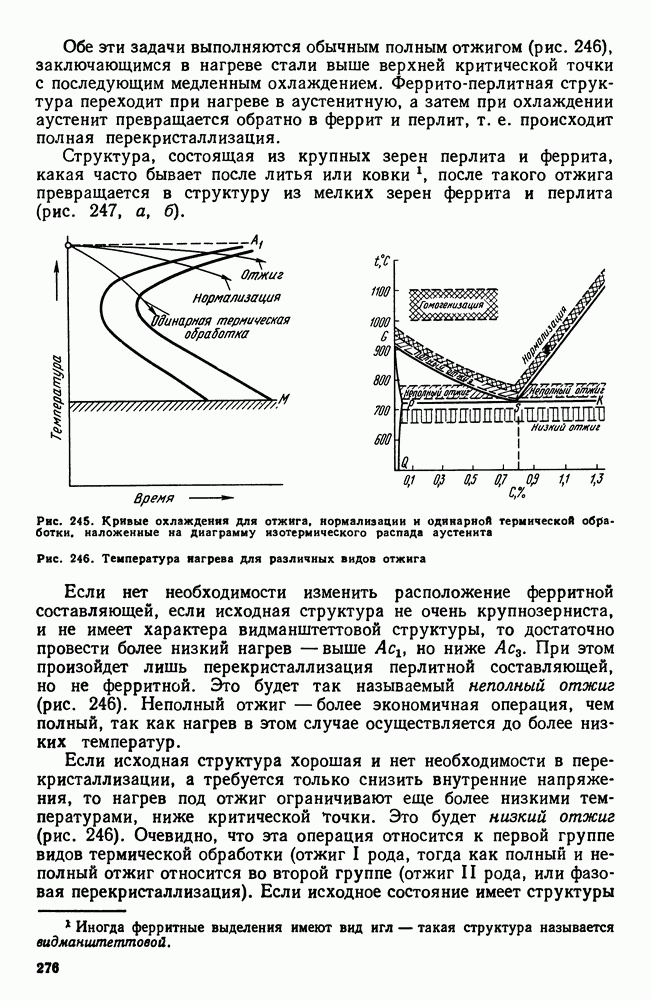
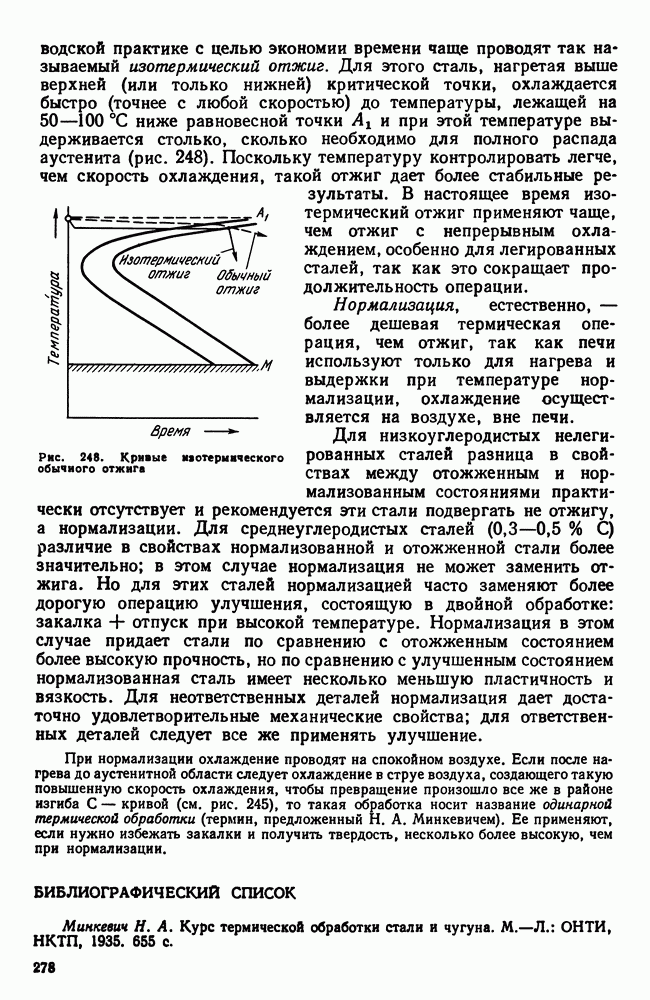
- 10. Отжиг и нормализация
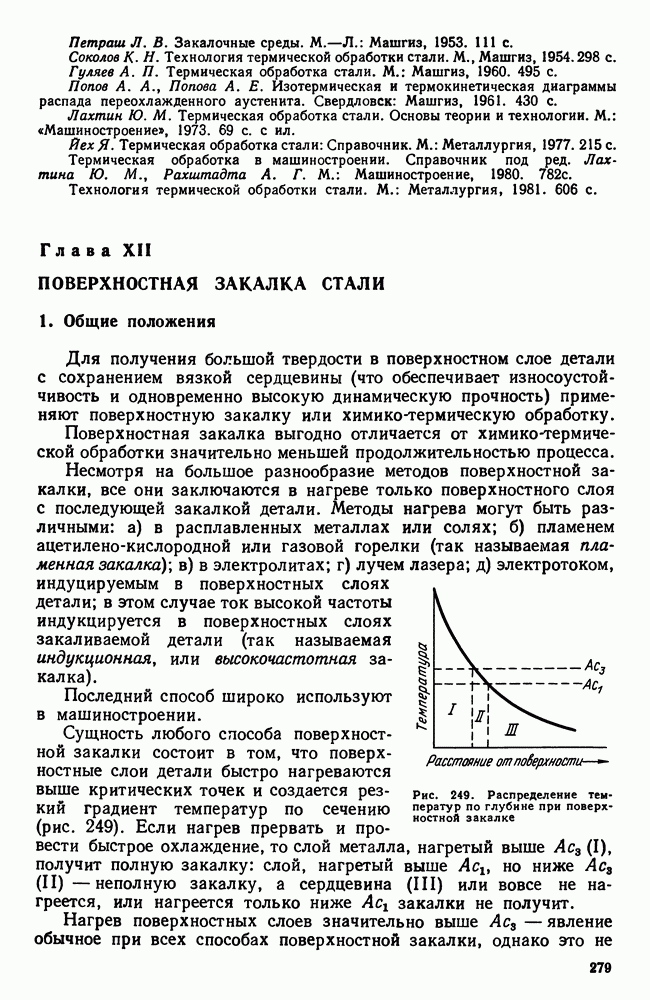
- Глава XII. ПОВЕРХНОСТНАЯ ЗАКАЛКА СТАЛИ
- 2. Высокочастотная закалка
- Глава XIII. ХИМИКО-ТЕРМИЧЕСКАЯ ОБРАБОТКА СТАЛИ
- 2. Цементация стали
- 3. Азотирование стали
- 4. Цианирование стали
- 5. Диффузионная металлизация
- Часть четвертая. ЛЕГИРОВАННЫЕ СТАЛИ И СПЛАВЫ
- Глава XIV. ВЛИЯНИЕ ЛЕГИРУЮЩИХ ЭЛЕМЕНТОВ
- 2. Влияние элементов на полиморфизм железа
- 3. Распределение легирующих элементов в стали
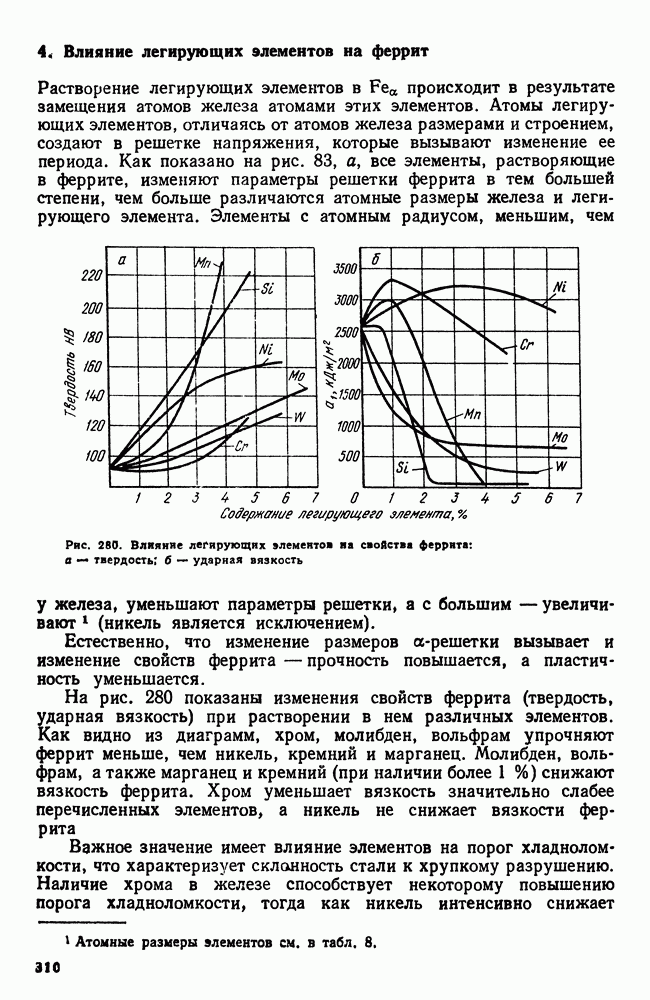
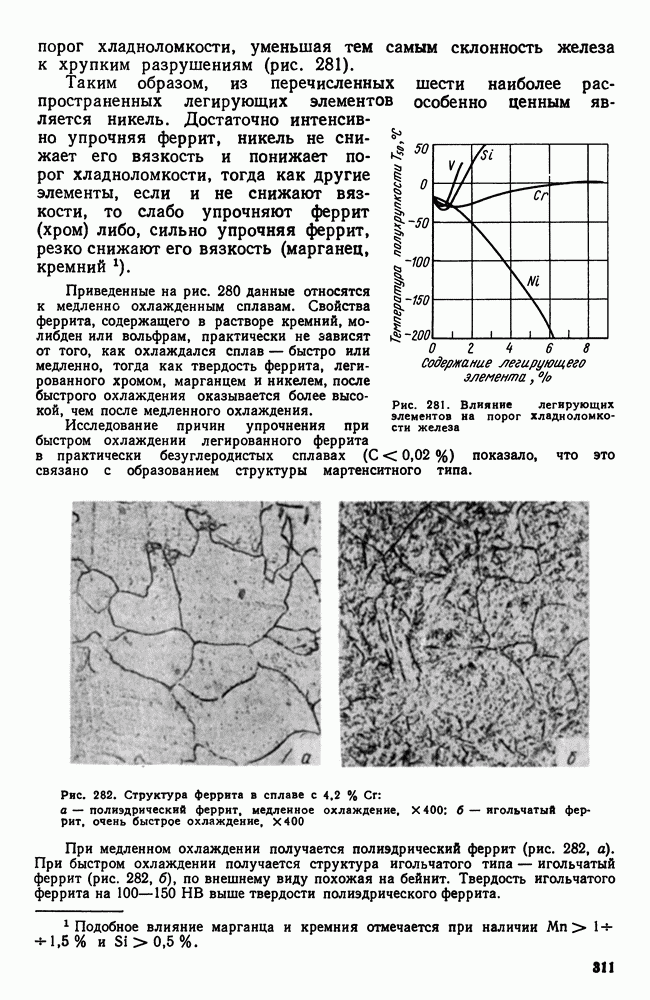
- 4. Влияние легирующих элементов на феррит
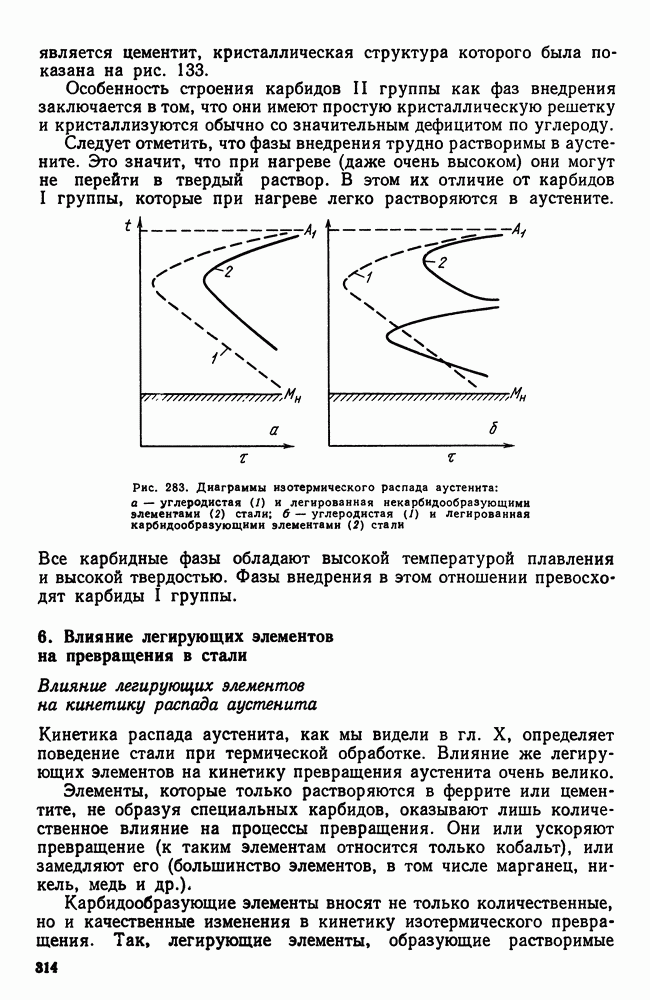
- 5. Карбидная фаза в легированных сталях
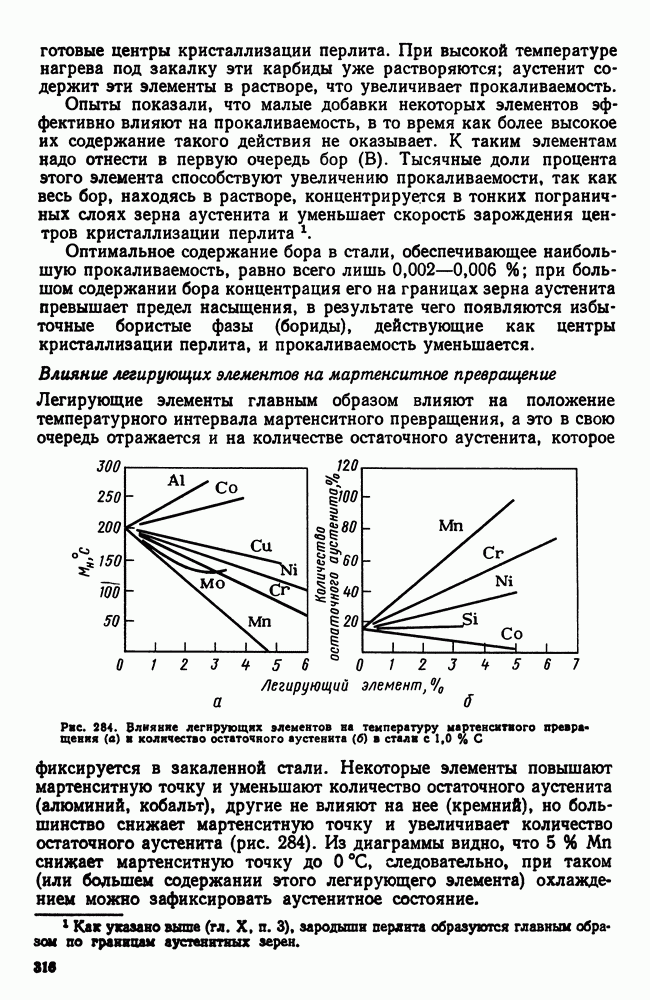
- 6. Влияние легирующих элементов на превращения в стали
- Глава XV. КЛАССИФИКАЦИЯ И МАРКИРОВКА ЛЕГИРОВАННЫХ СТАЛЕЙ
- 2. Маркировка легированных сталей
- Глава XVI. КОНСТРУКЦИОННЫЕ СТАЛИ
- 1. Механические свойства стали, влияние структуры и легирующих элементов
- 2. Термическая обработка конструкционных сталей
- 3. Цементуемые (низкоуглеродистые) стали
- 4. Улучшаемые (среднеуглеродистые) стали
- 5. Высокопрочные стали
- 6. Свариваемость стали
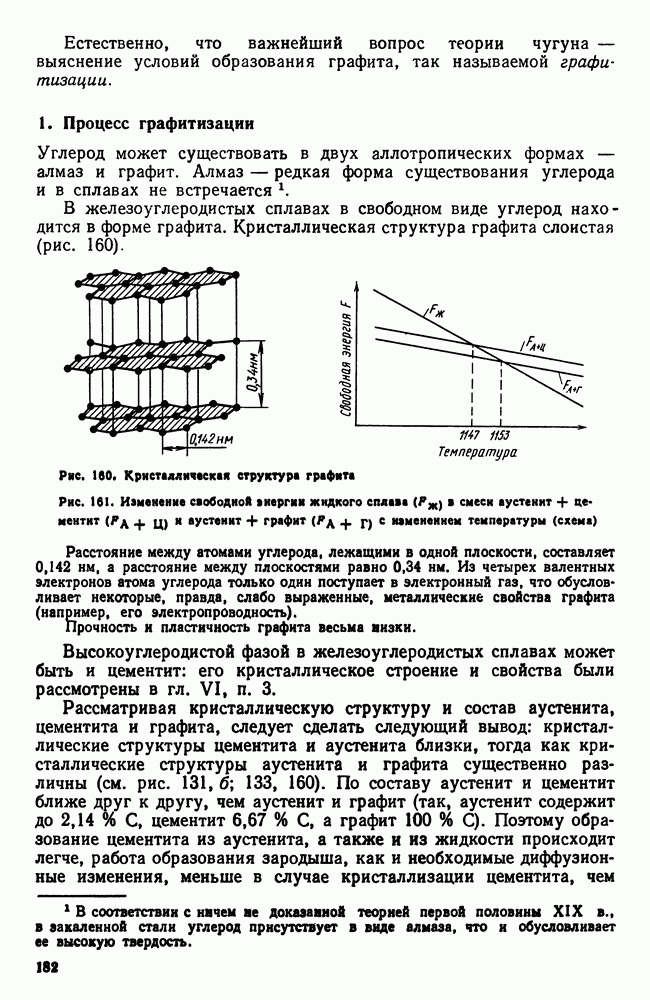
- 7. Строительная сталь
- 8. Арматурная сталь
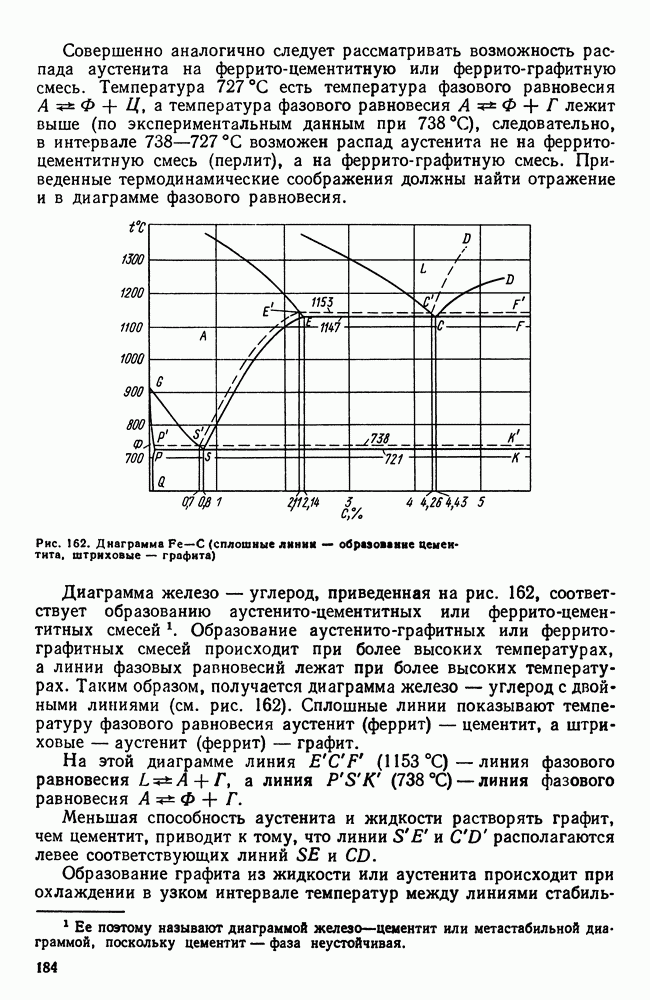
- 9. Пружинная сталь
- 10. Шарикоподшипниковая сталь
- 11. Дефекты легированных сталей
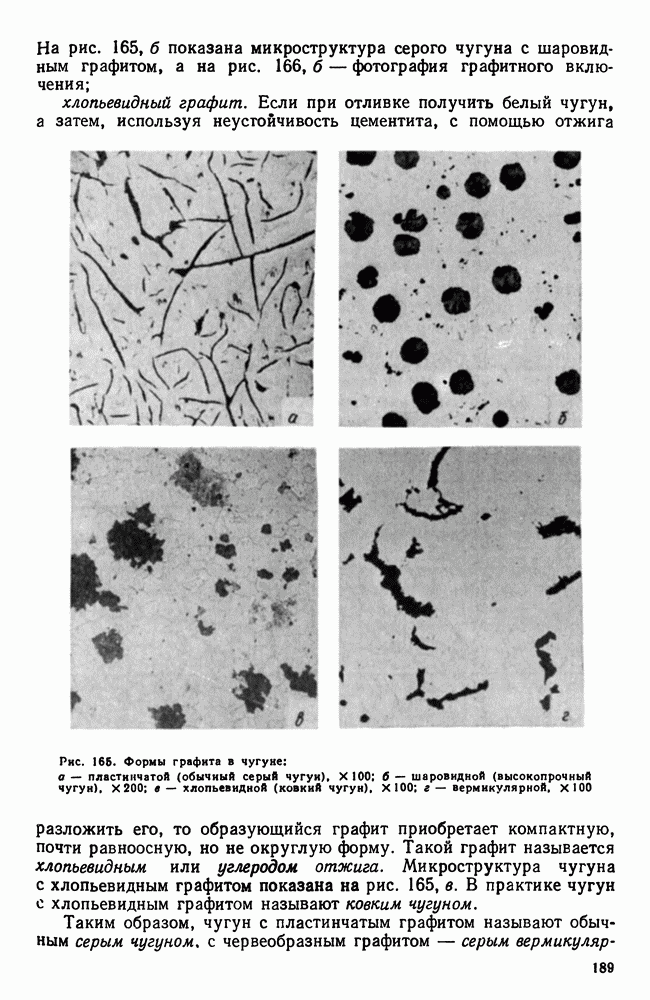
- Глава XVII. ИНСТРУМЕНТАЛЬНЫЕ СТАЛИ
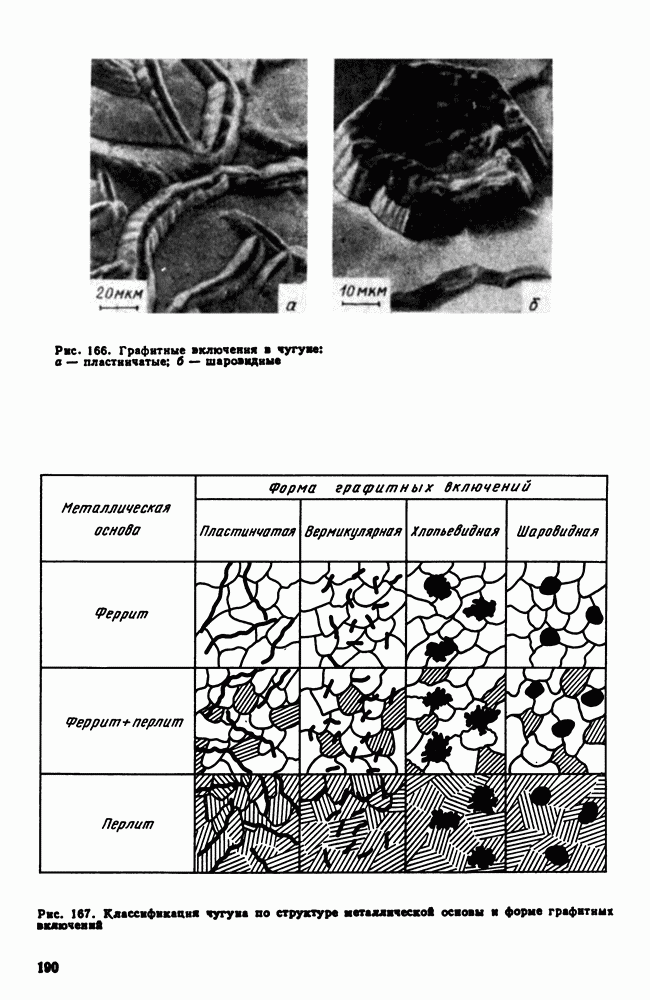
- 2. Инструментальные стали пониженной прокаливаемости
- 3. Инструментальные стали повышенной прокаливаемости (легированные инструментальные стали)
- 4. Быстрорежущие стали
- 5. Штамповые стали
- 6. Твердые сплавы
- Глава XVIII. ЖАРОСТОЙКИЕ И ЖАРОПРОЧНЫЕ СТАЛИ И СПЛАВЫ
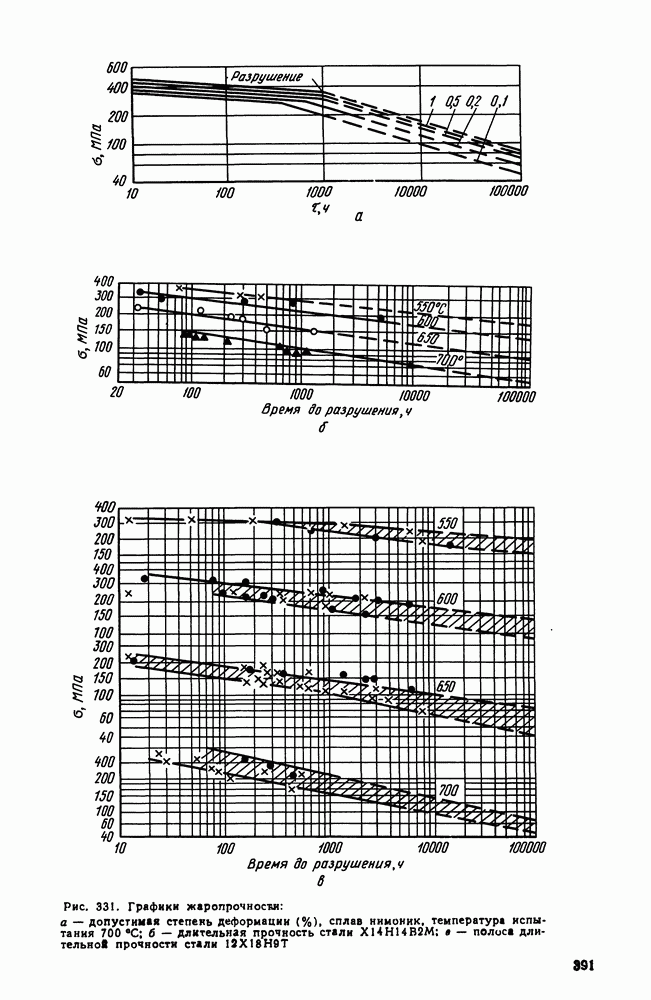
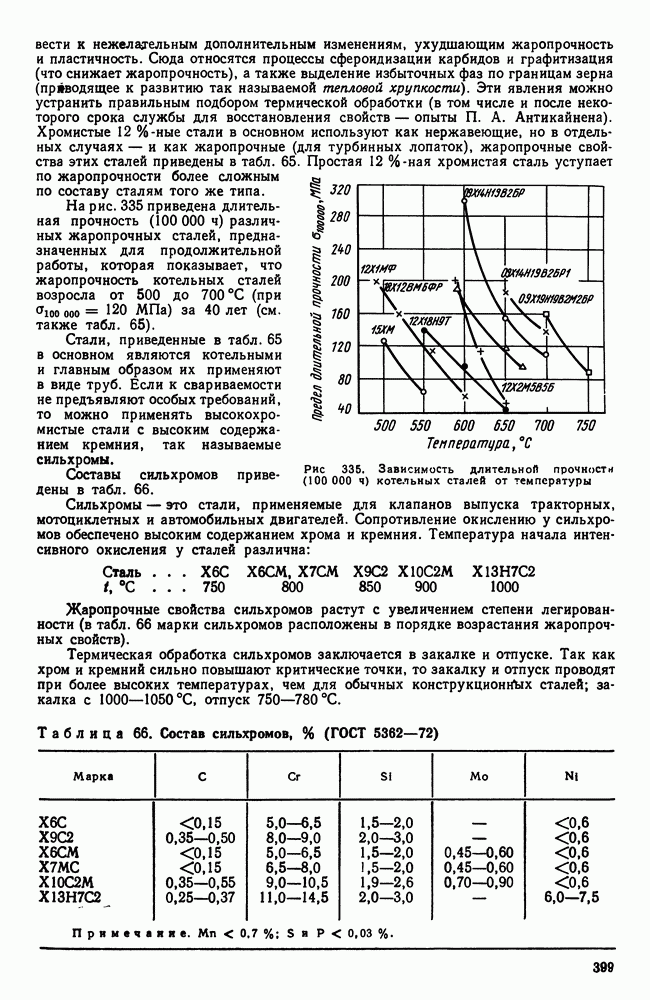
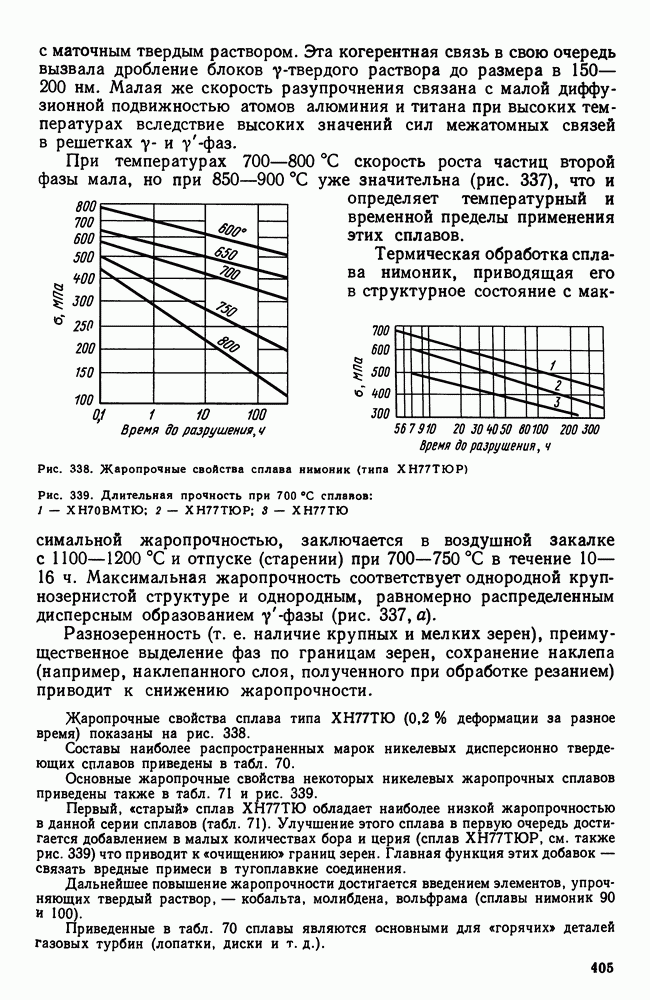
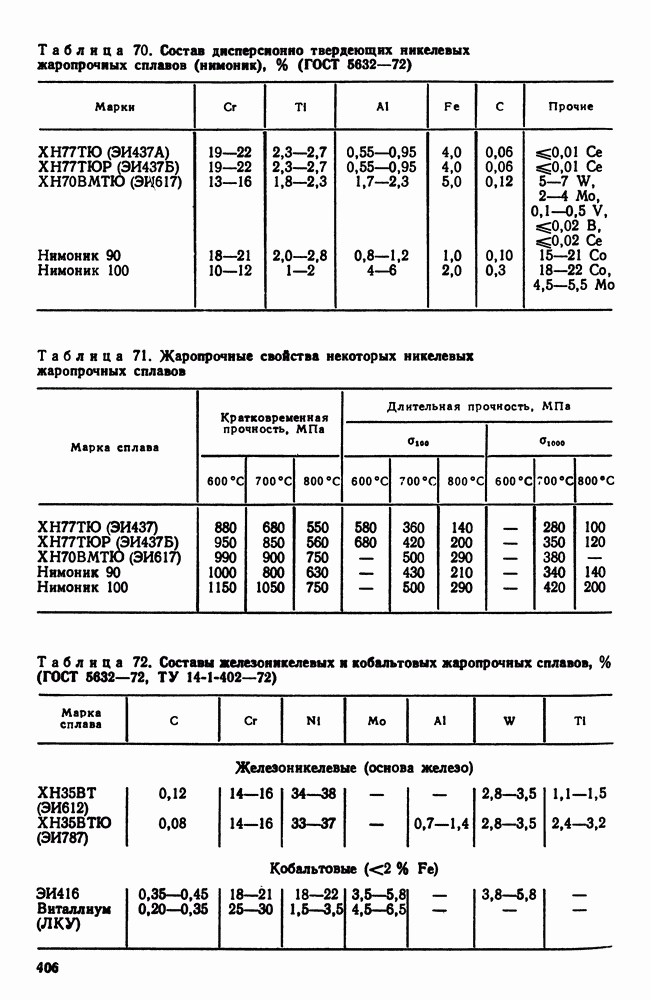
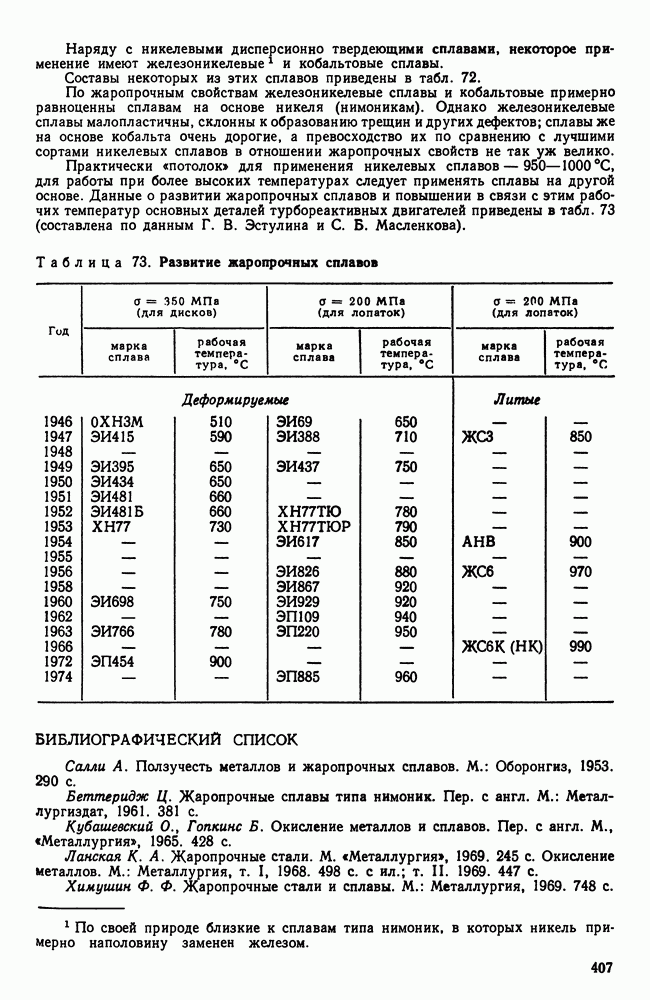
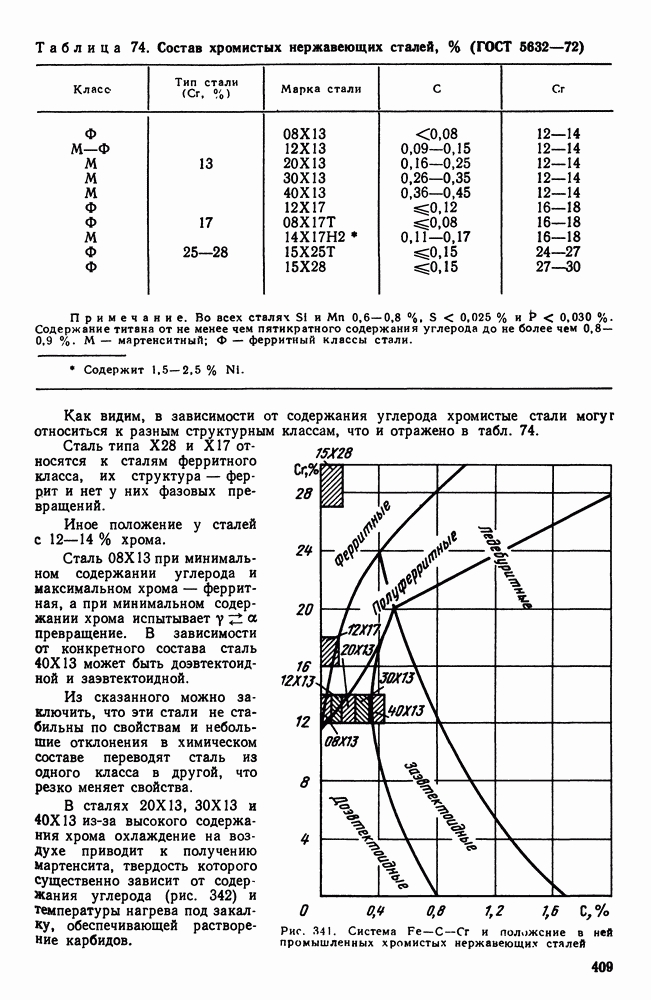
- 2. Жаропрочность
- 3. Оценка жаропрочных свойств
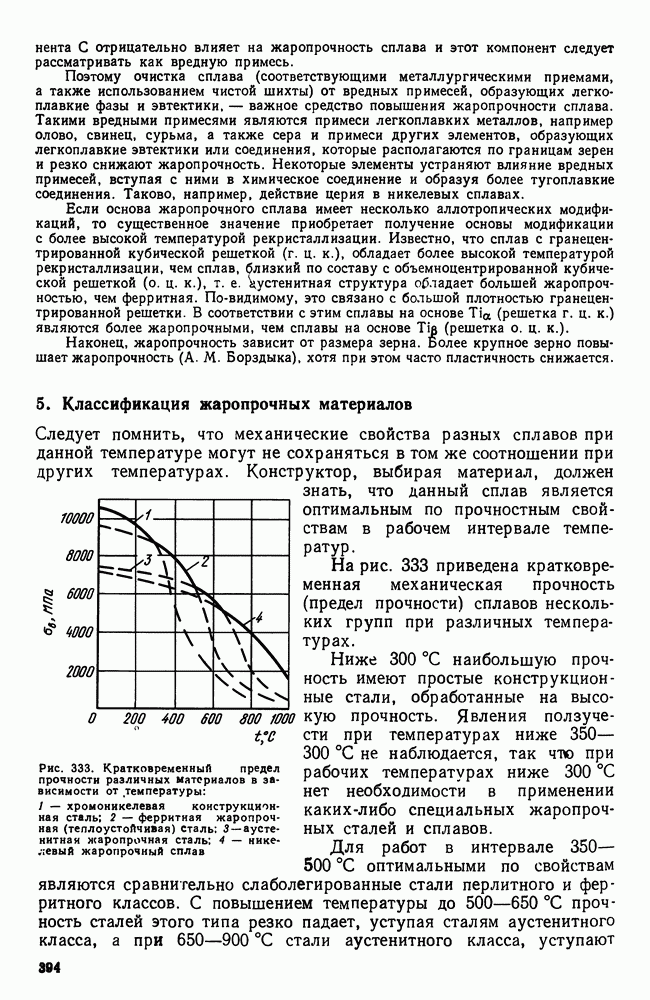
- 4. Влияние структуры и состава на жаропрочность
- 5. Классификация жаропрочных материалов
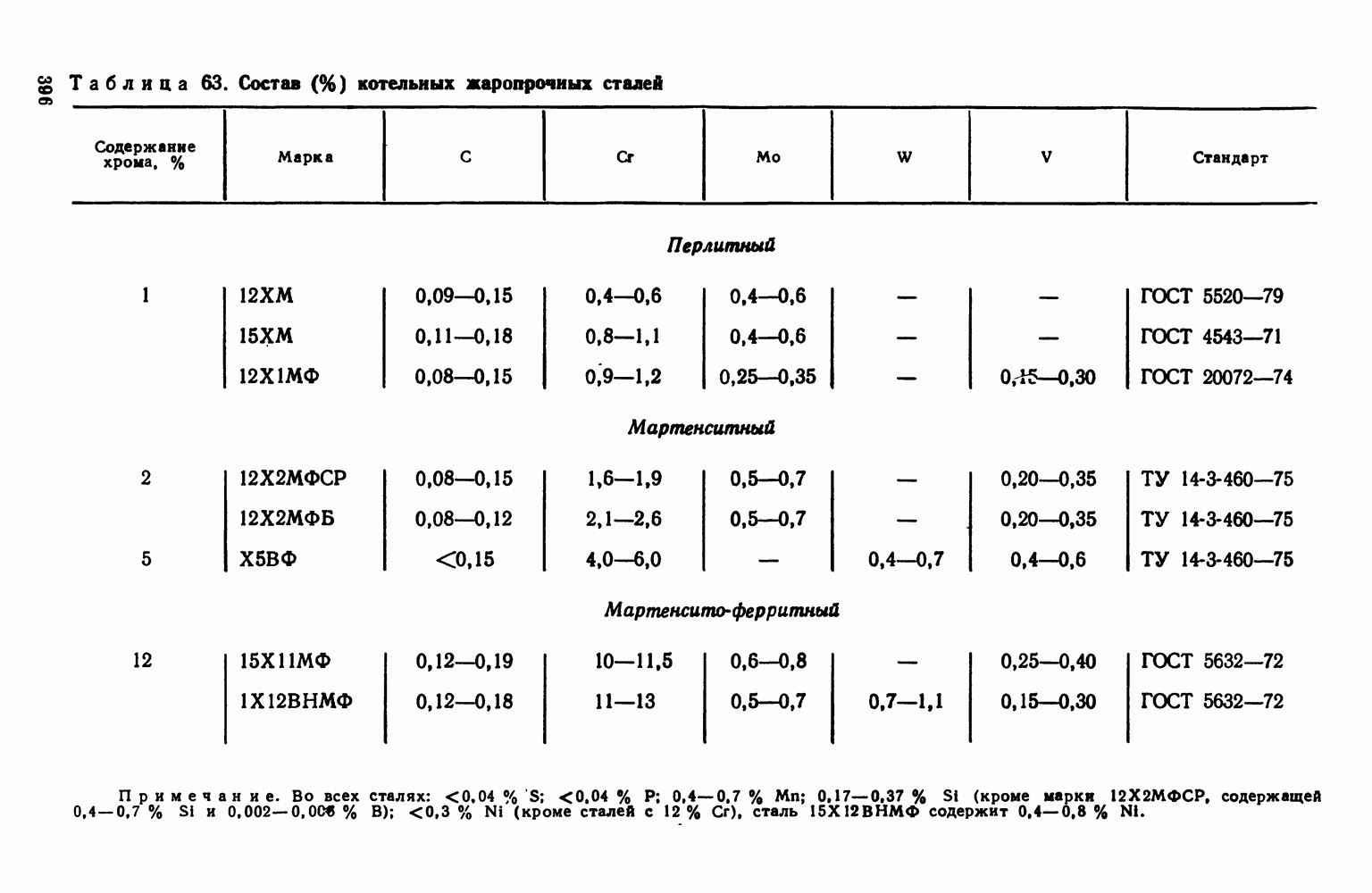
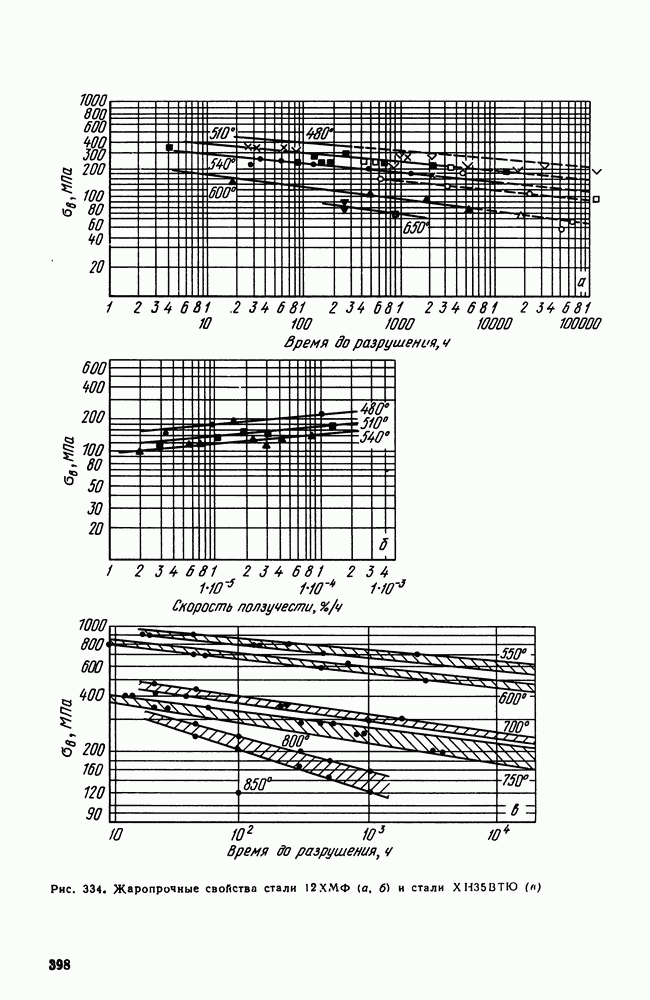
- 6. Перлитные и мартенситные жаропрочные стали
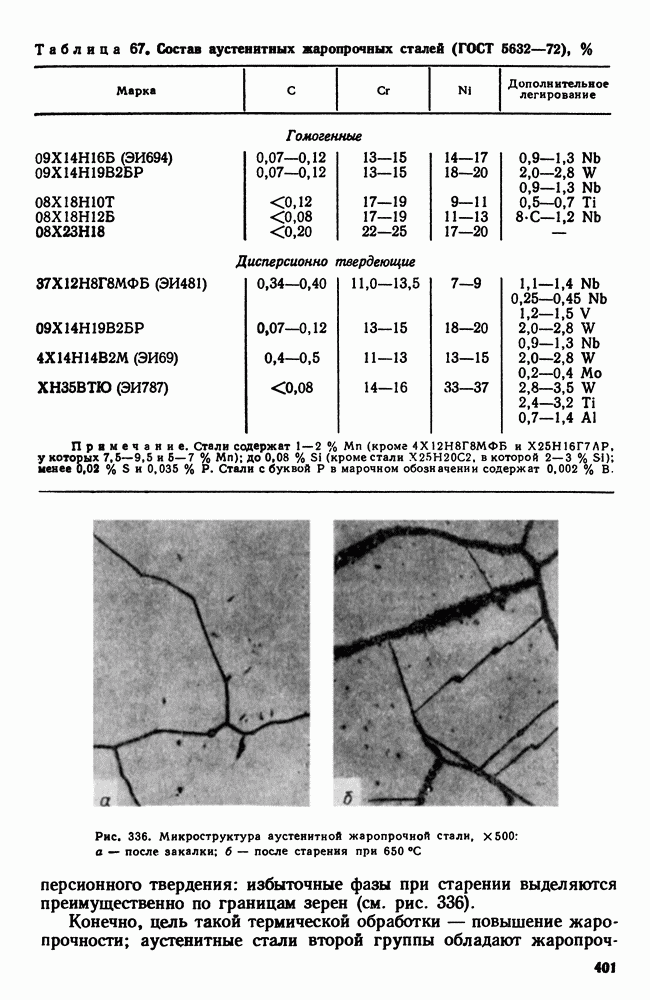
- 7. Аустенитные жаропрочные стали
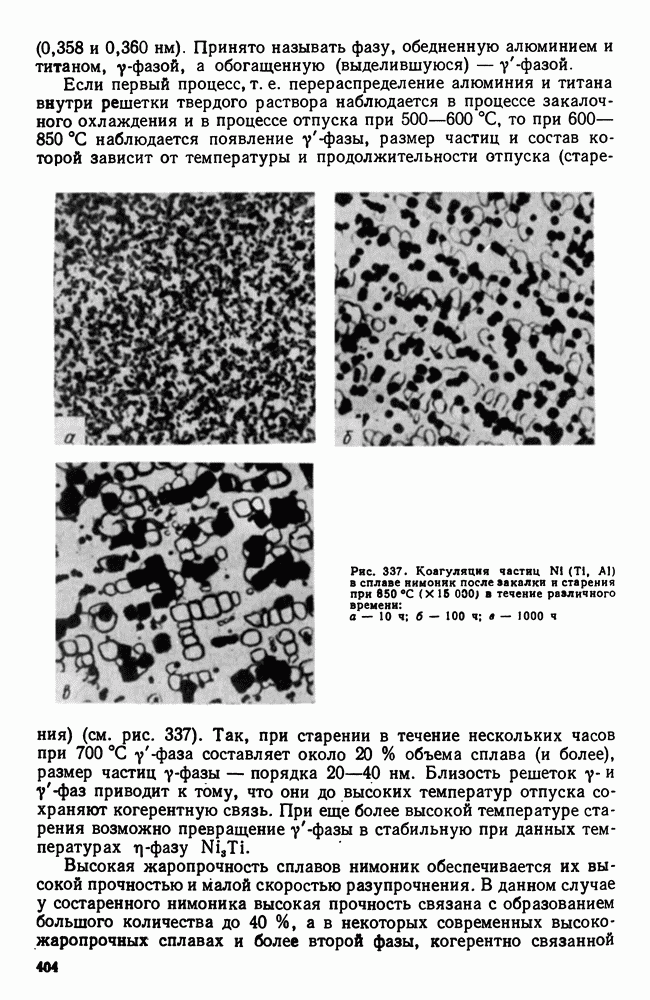
- 8. Никелевые и кобальтовые жаропрочные сплавы
- Глава XIX. КОРРОЗИОННОСТОЙКИЕ (НЕРЖАВЕЮЩИЕ) СТАЛИ И СПЛАВЫ
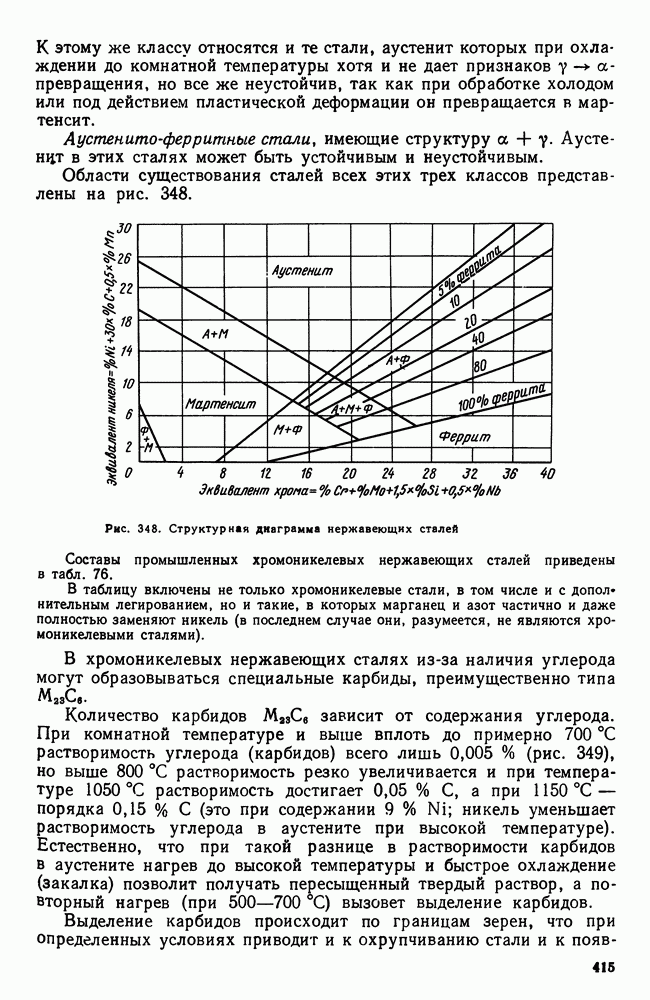
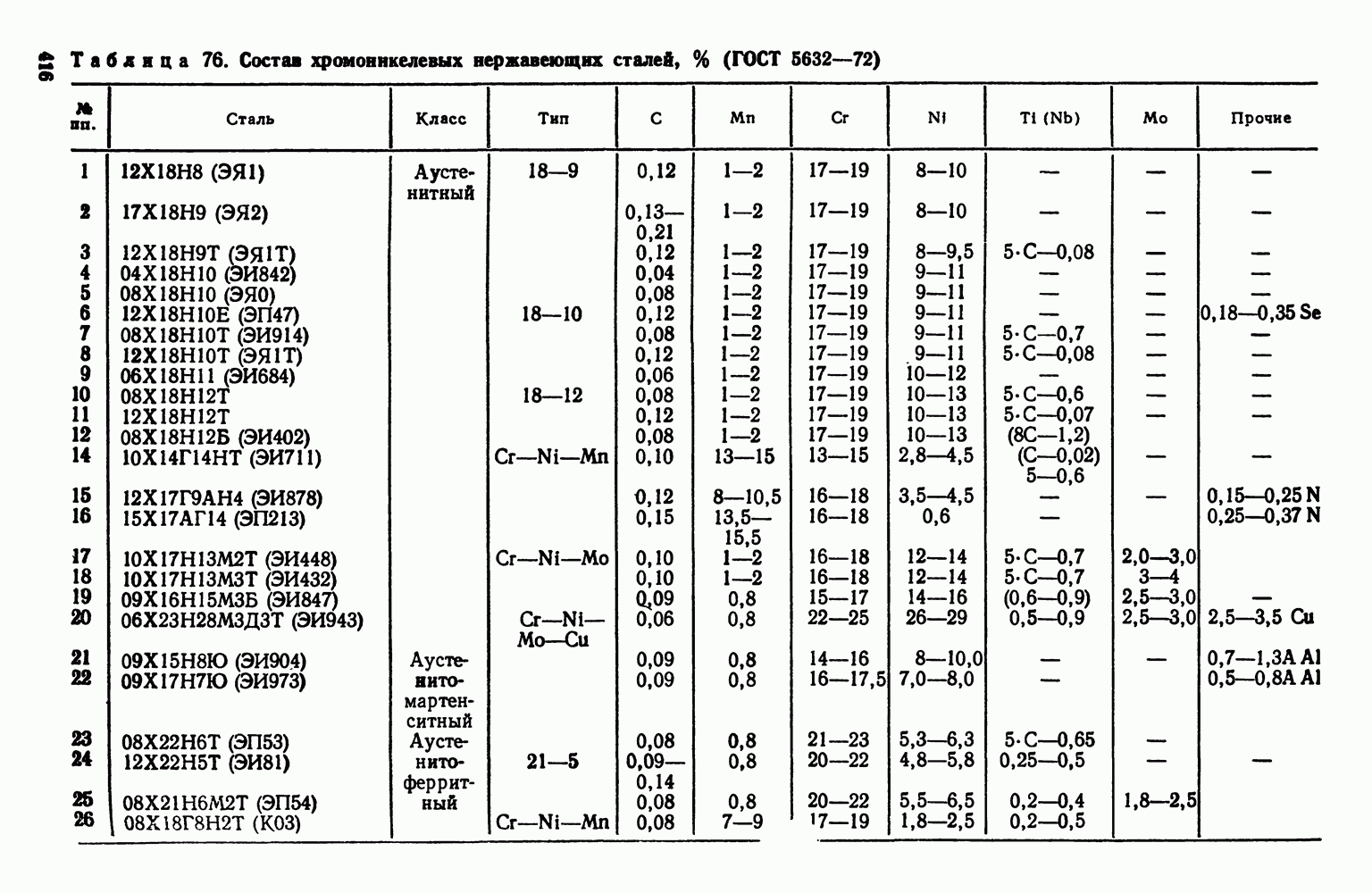
- 2. Хромоникелевые нержавеющие стали
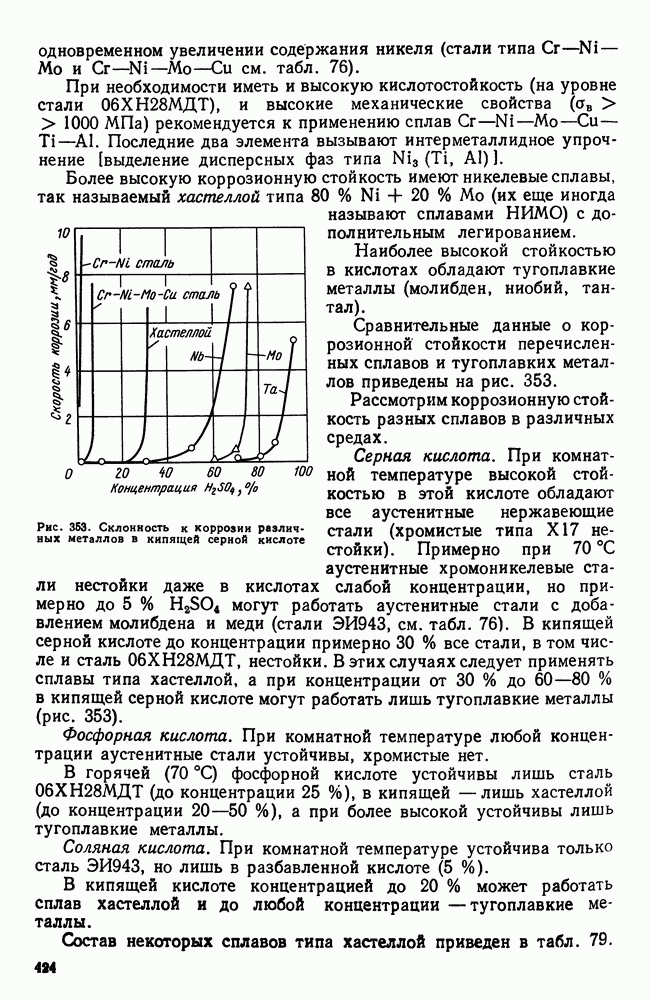
- 3. Кислотостойкие стали и сплавы
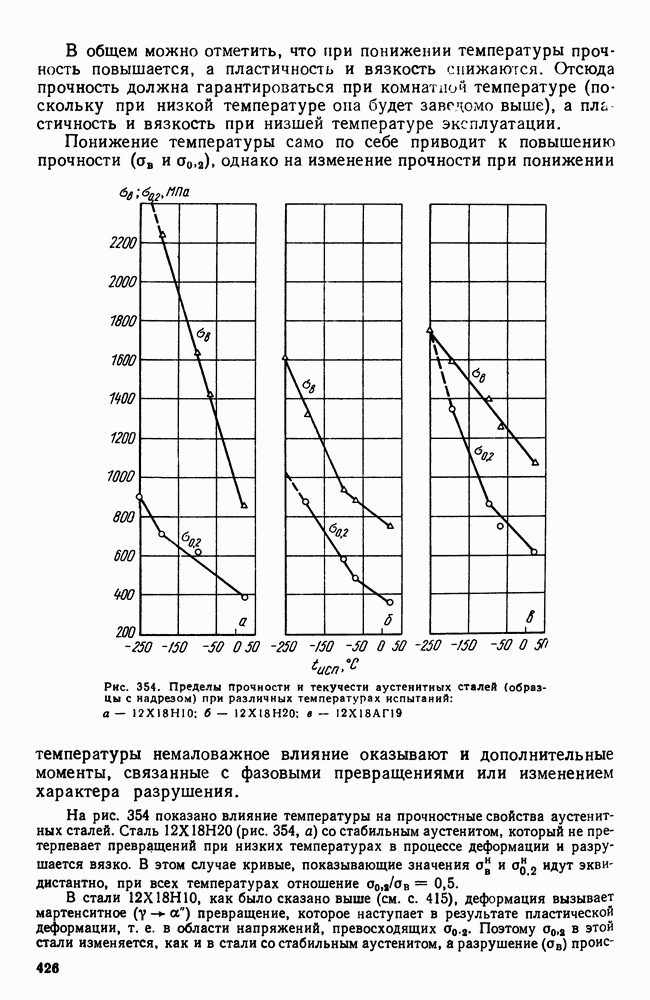
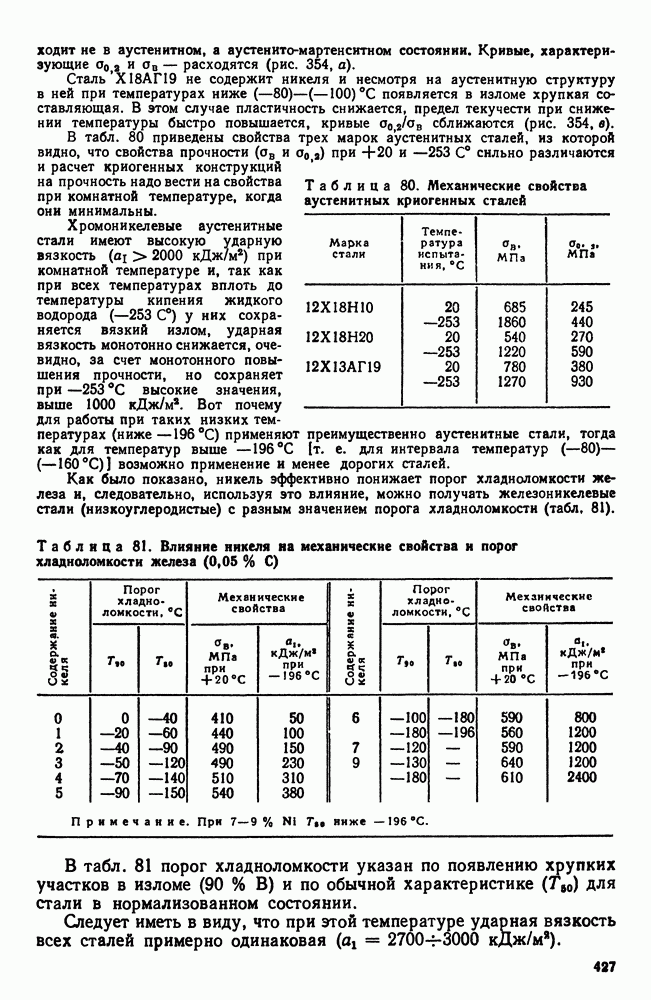
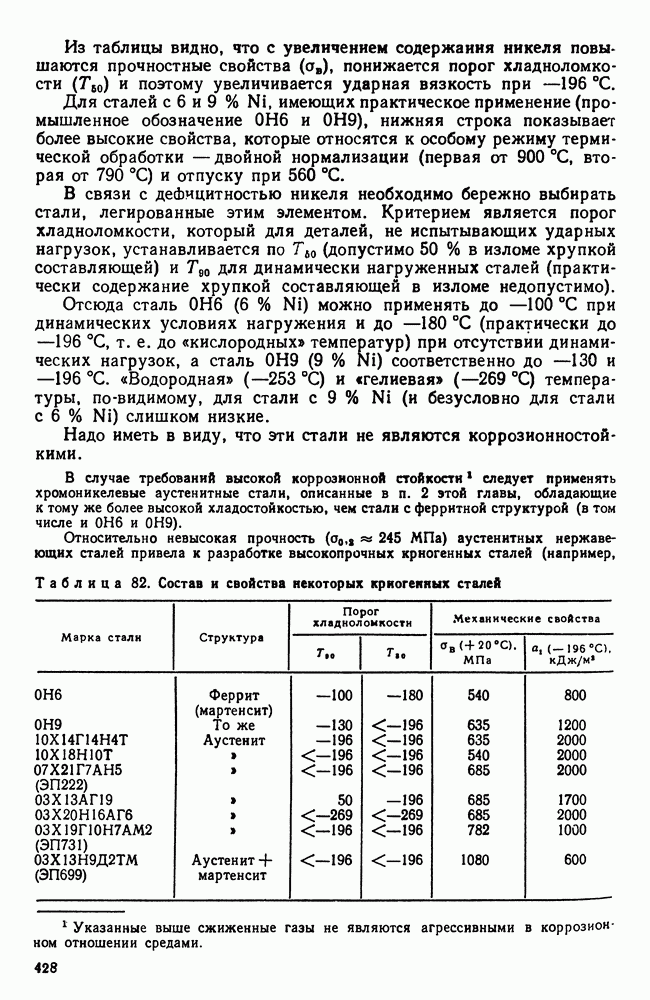
- 4. Криогенные стали и сплавы
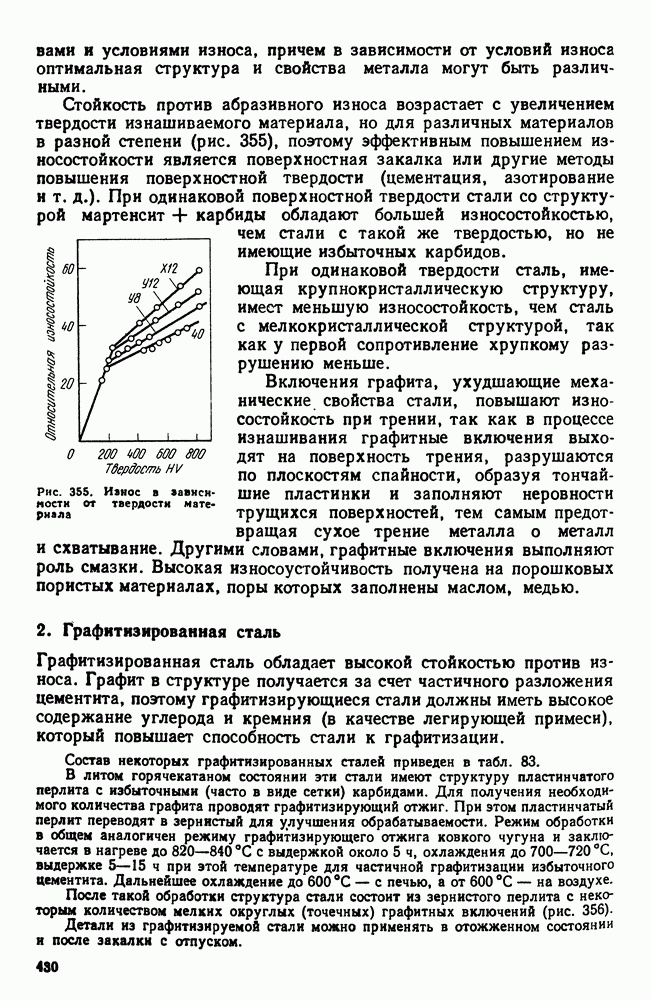
- Глава XX. ИЗНОСОСТОЙКИЕ СТАЛИ И СПЛАВЫ
- 2. Графитизированная сталь
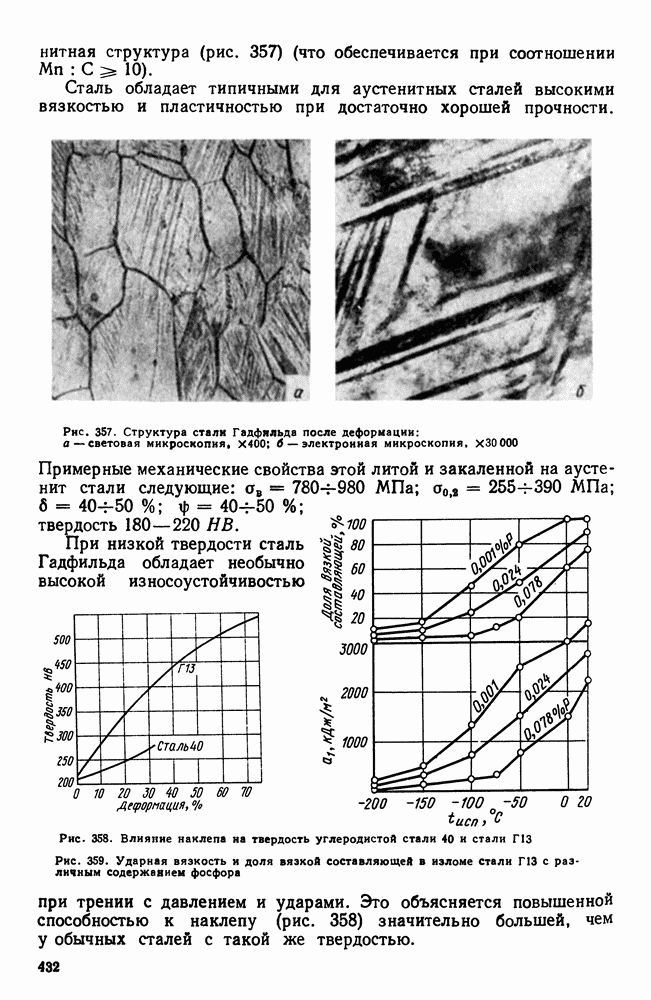
- 3. Высокомарганцовистая сталь
- 4. Наплавочные материалы
- Глава XXI. ТИТАН И ЕГО СПЛАВЫ
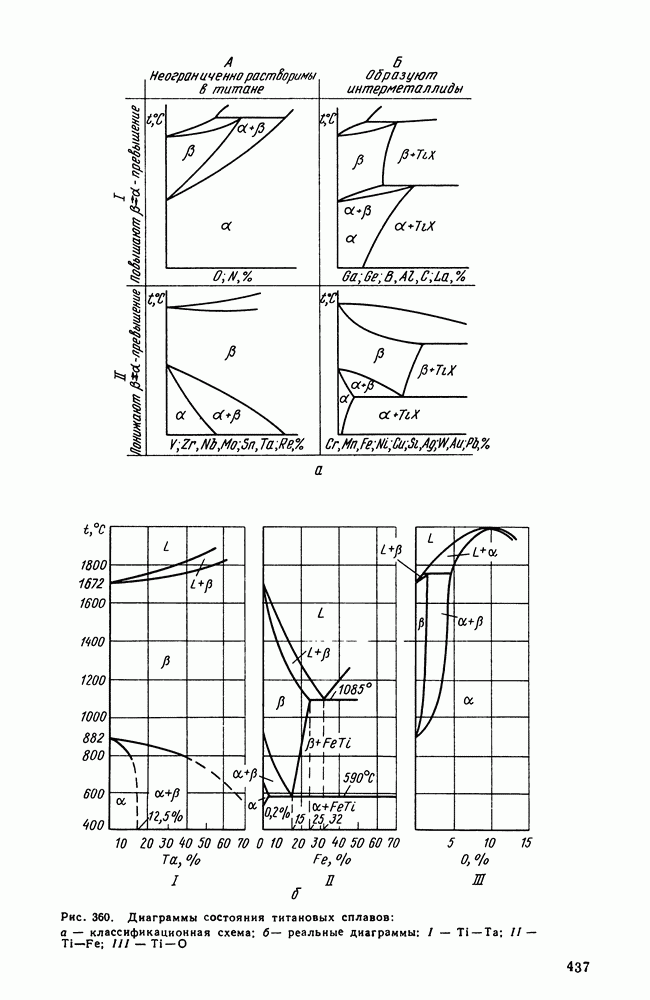
- 2. Легирование титана
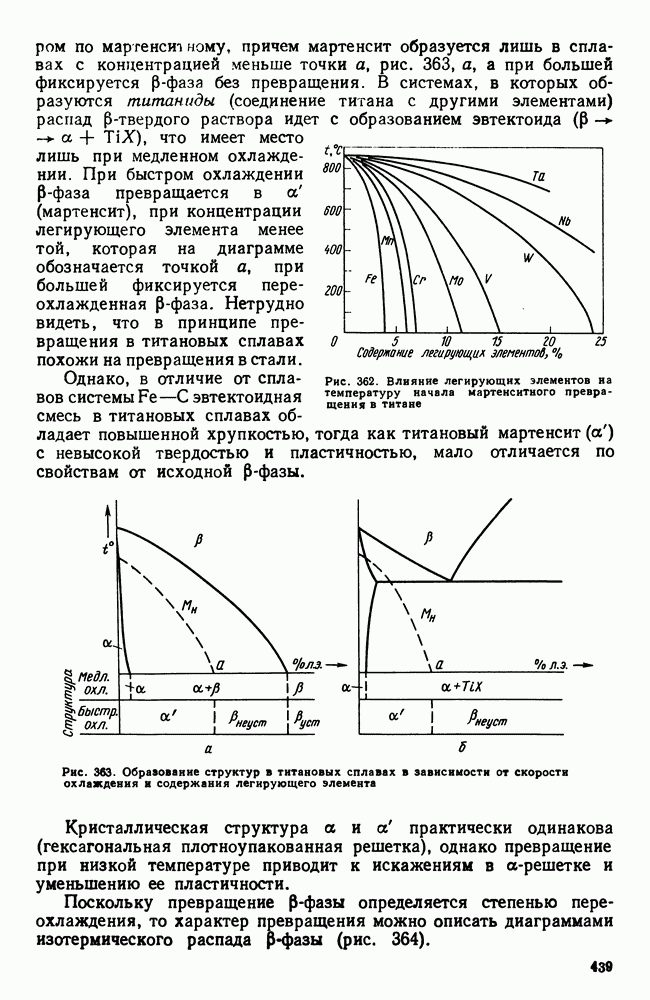
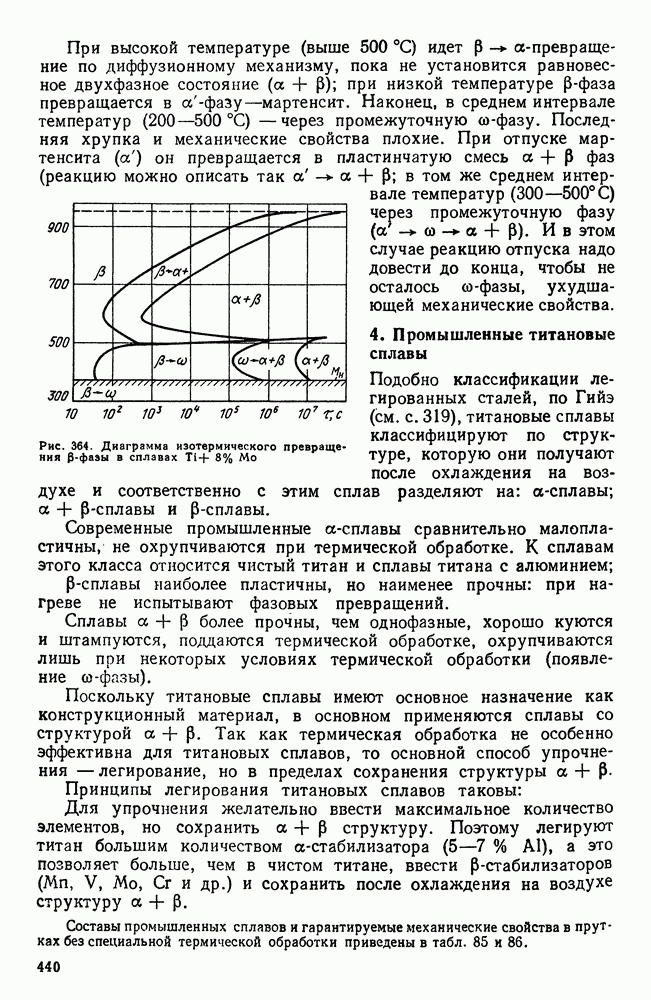
- 3. Фазовые превращения в титановых сплавах
- 5. Термическая обработка титановых сплавов
- 6. Примеси в титановых сплавах
- 7. Коррозионная стойкость титана
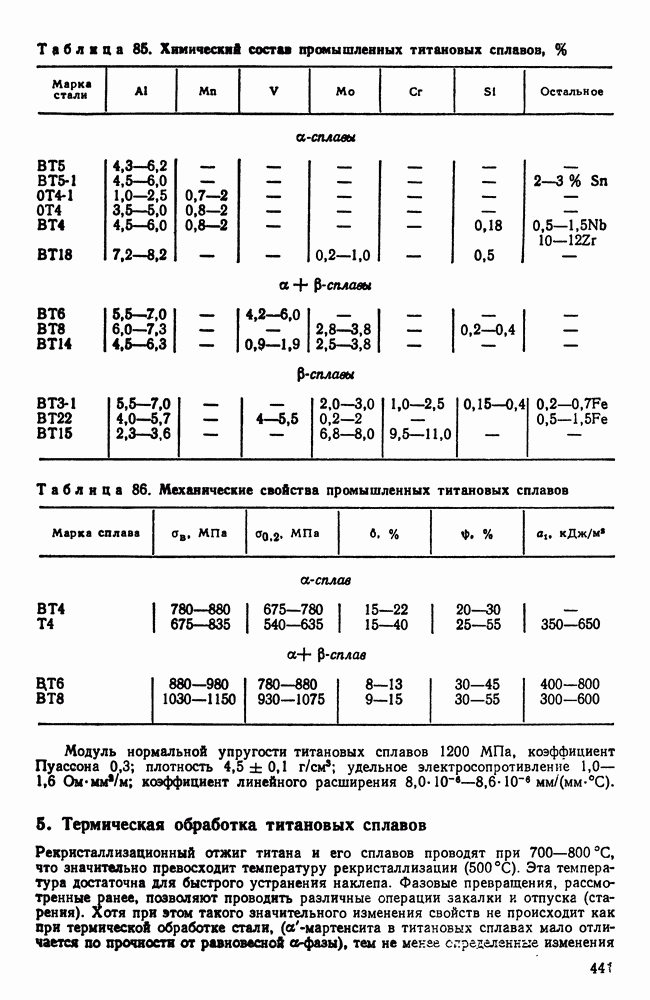
- Глава XXII. ТУГОПЛАВКИЕ МЕТАЛЛЫ
- 2. Взаимодействие тугоплавких металлов с другими элементами и между собой
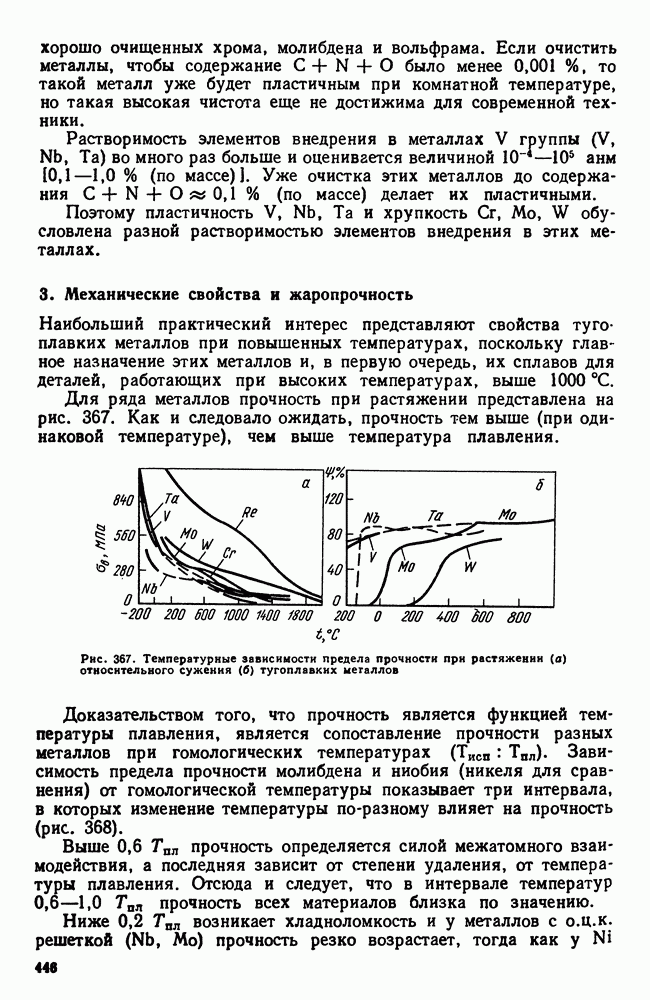
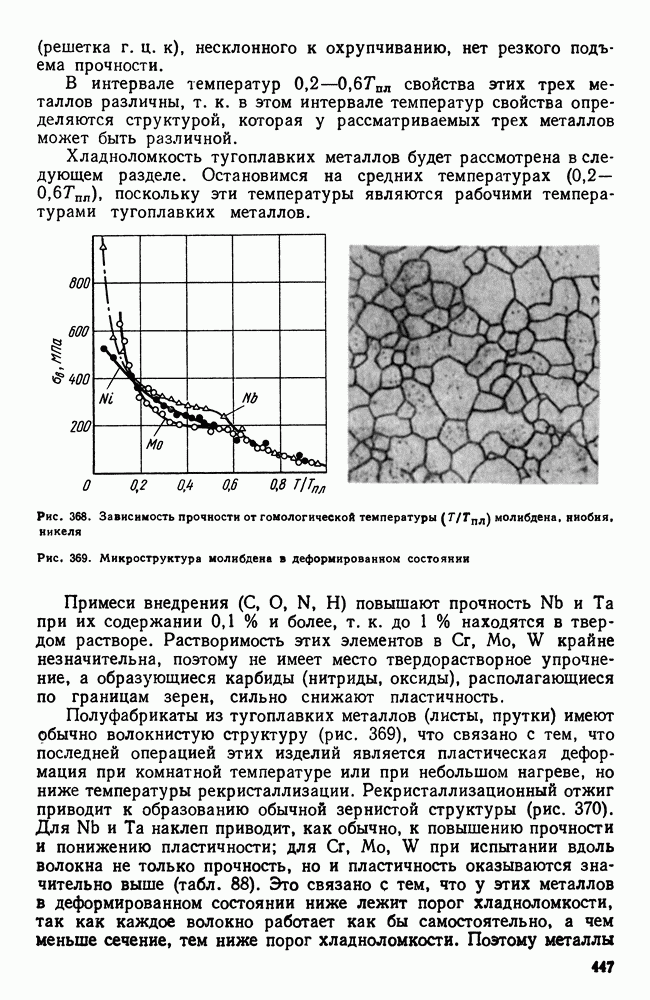
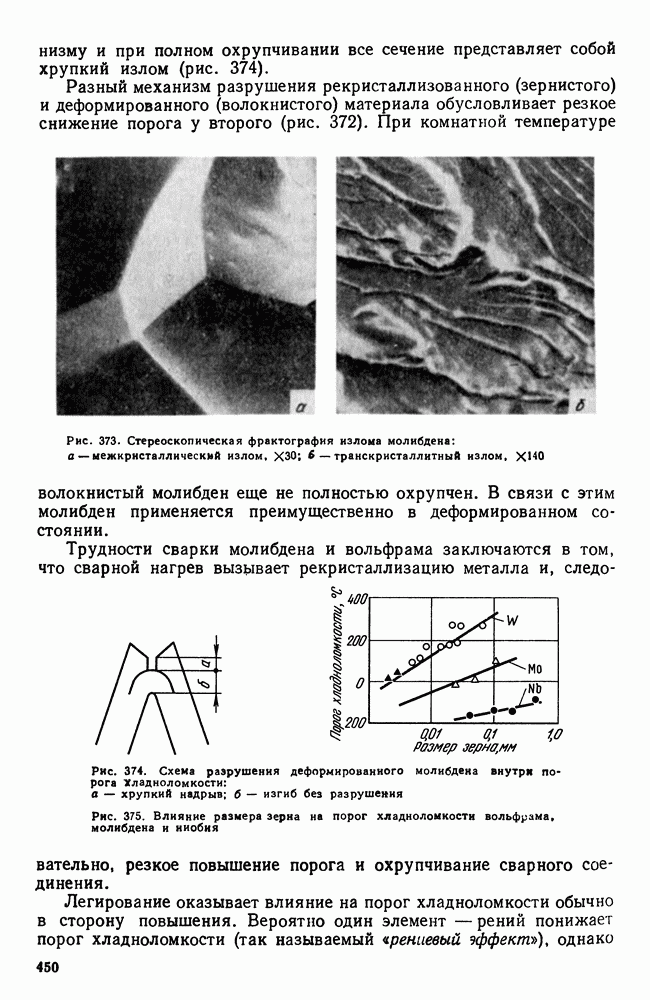
- 3. Механические свойства и жаропрочность
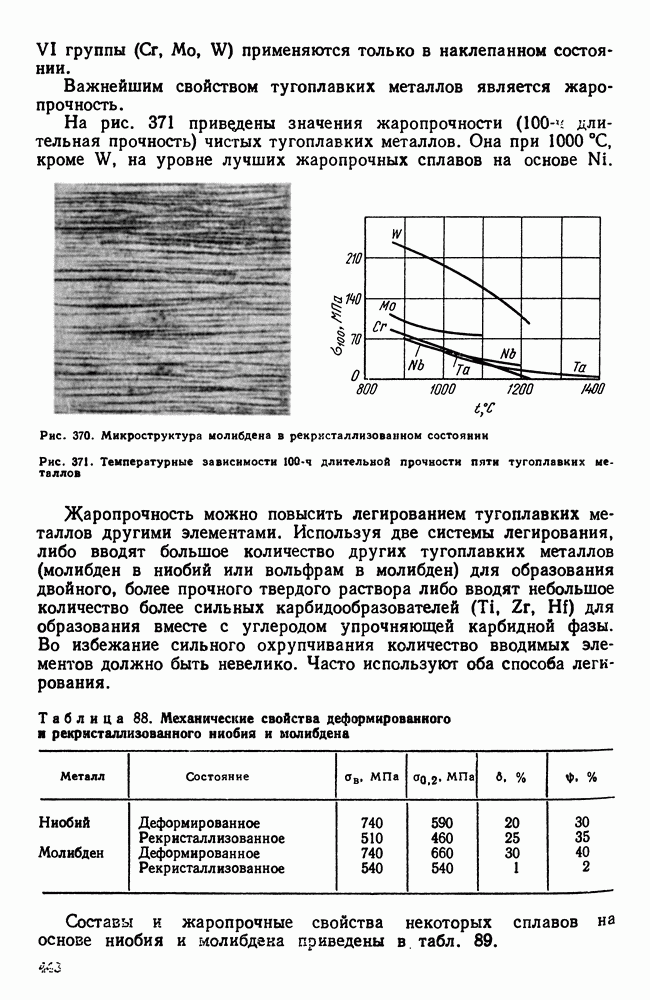
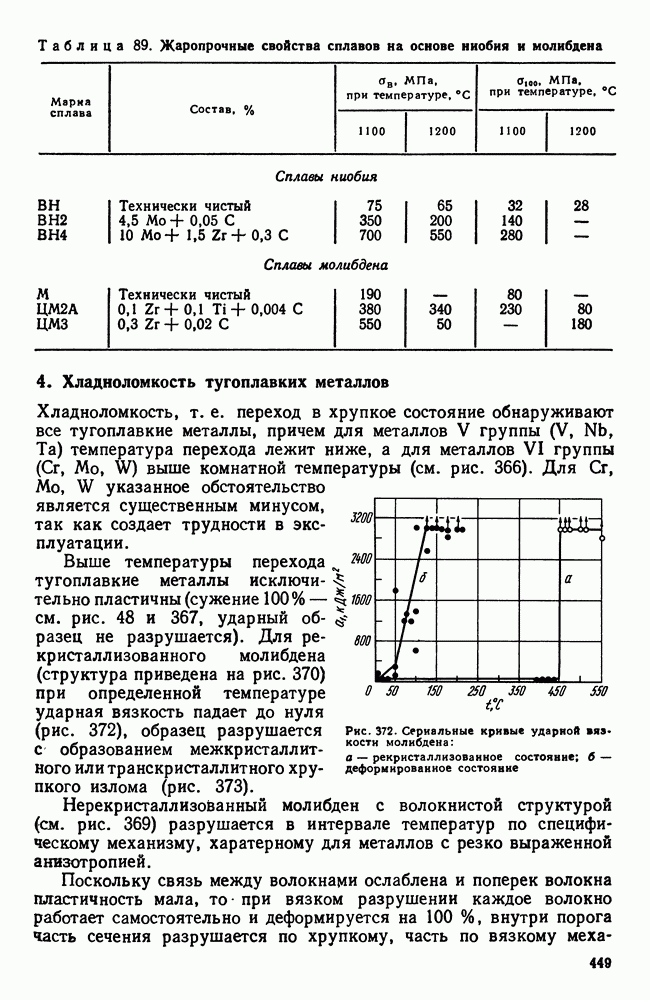
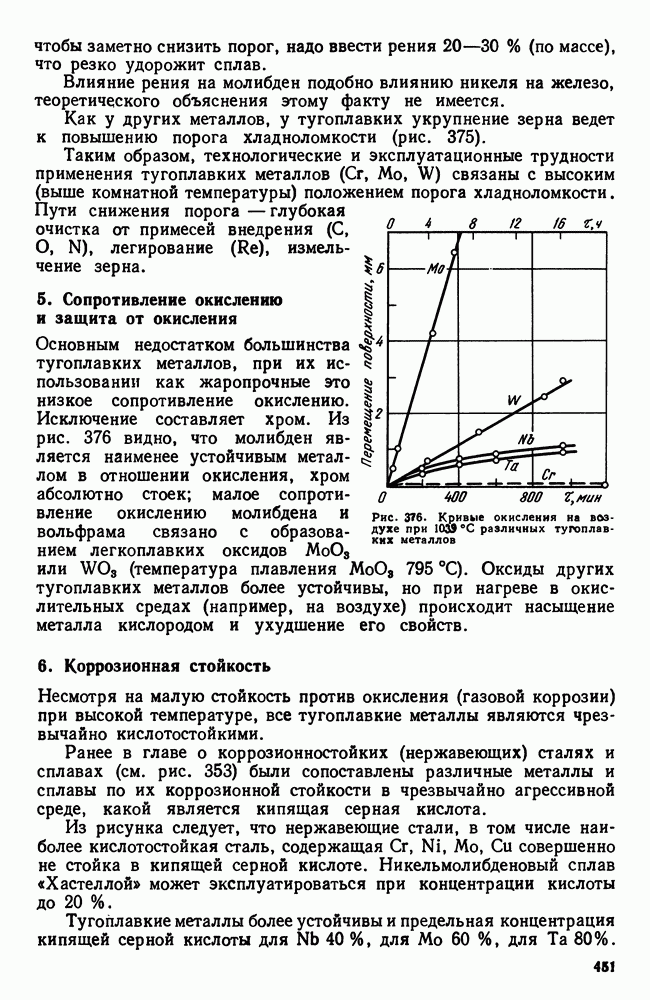
- 4. Хладноломкость тугоплавких металлов
- 5. Сопротивление окислению и защита от окисления
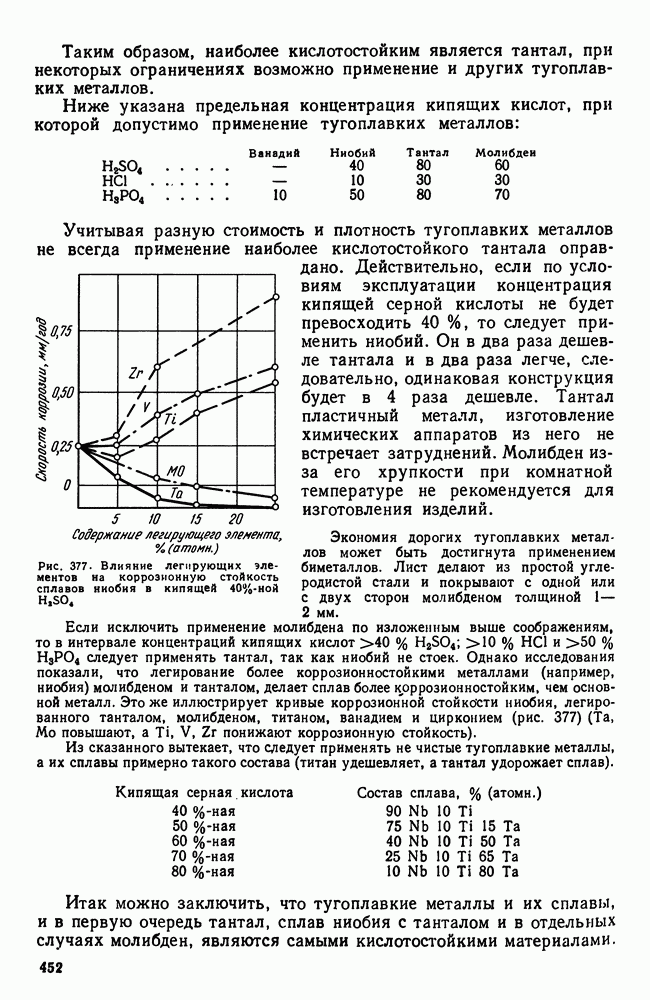
- 6. Коррозионная стойкость
- Глава XXIII. СПЛАВЫ С ОСОБЫМИ ТЕПЛОВЫМИ И УПРУГИМИ СВОЙСТВАМИ
- 2. Сплавы с постоянным модулем упругости
- Глава XXIV. МАГНИТНЫЕ СТАЛИ И СПЛАВЫ
- 2. Стали и сплавы для постоянных магнитов (магнитнотвердые сплавы)
- 3. Магнитномягкие сплавы
- 4. Немагнитные стали
- 5. Электротехнические сплавы
- Глава XXV. СПЛАВЫ АТОМНОЙ ЭНЕРГЕТИКИ
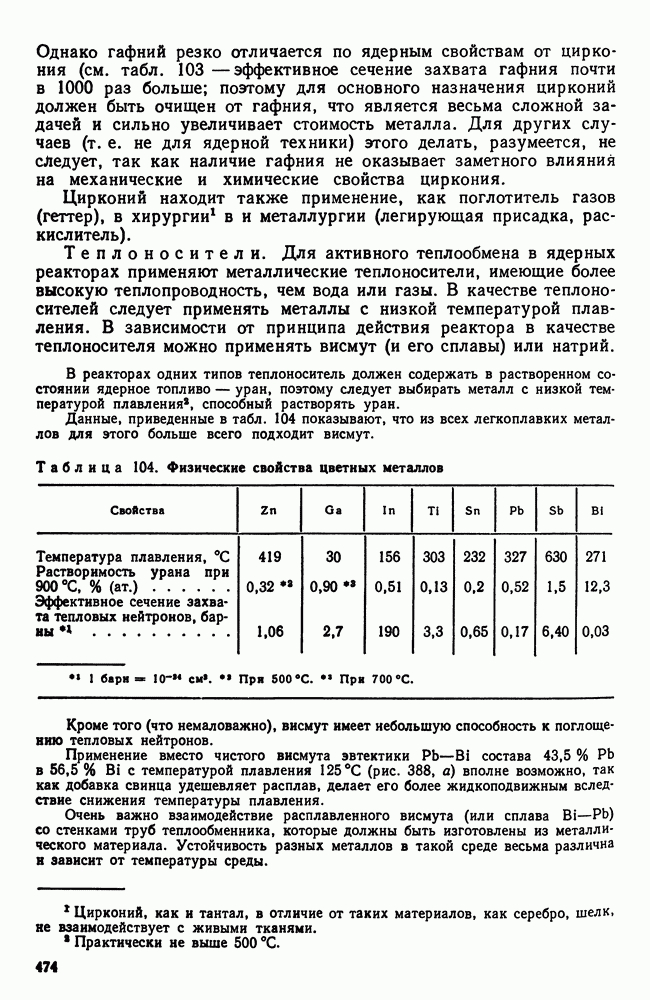
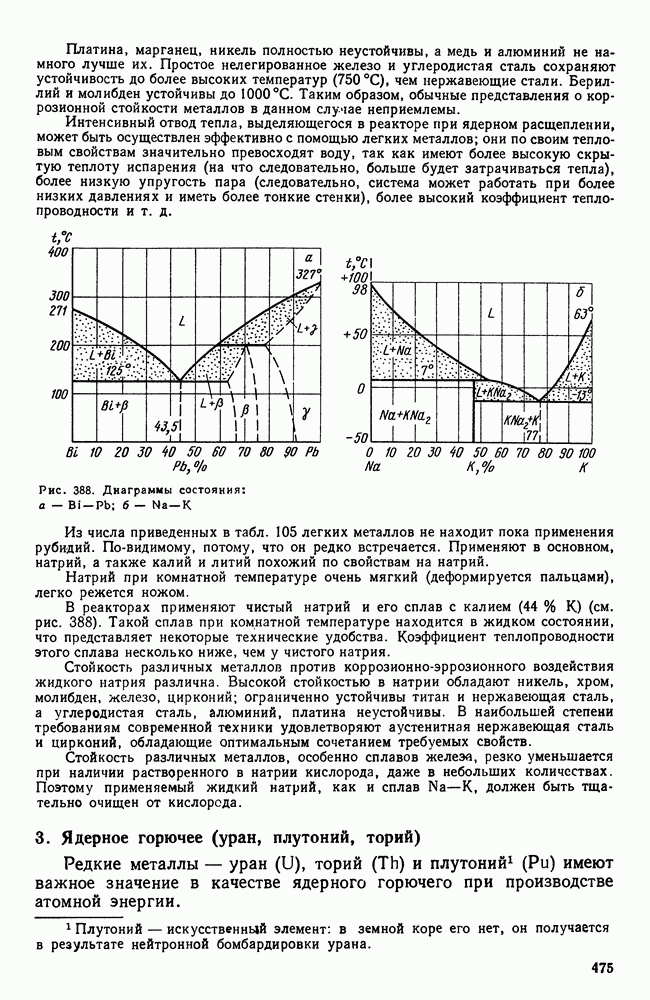
- 2. Конструкционные материалы. Теплоносители
- 3. Ядерное горючее (уран, плутоний, торий)
- Часть пятая. Цветные металлы и сплавы
- Глава XXVI. ЛЕГКИЕ МЕТАЛЛЫ И ИХ СПЛАВЫ
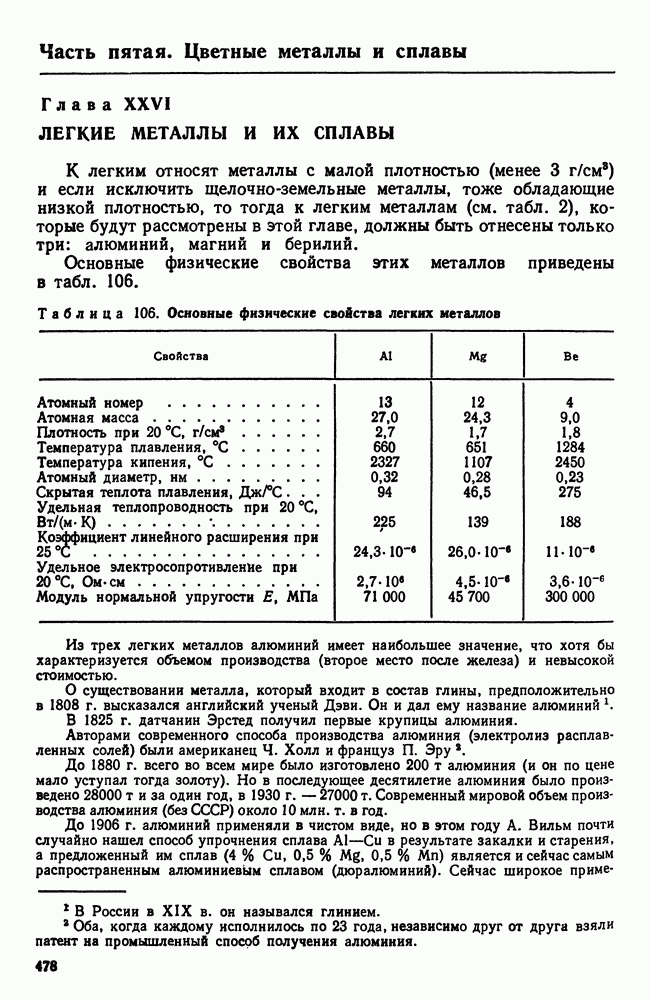
- 1. Свойства алюминия
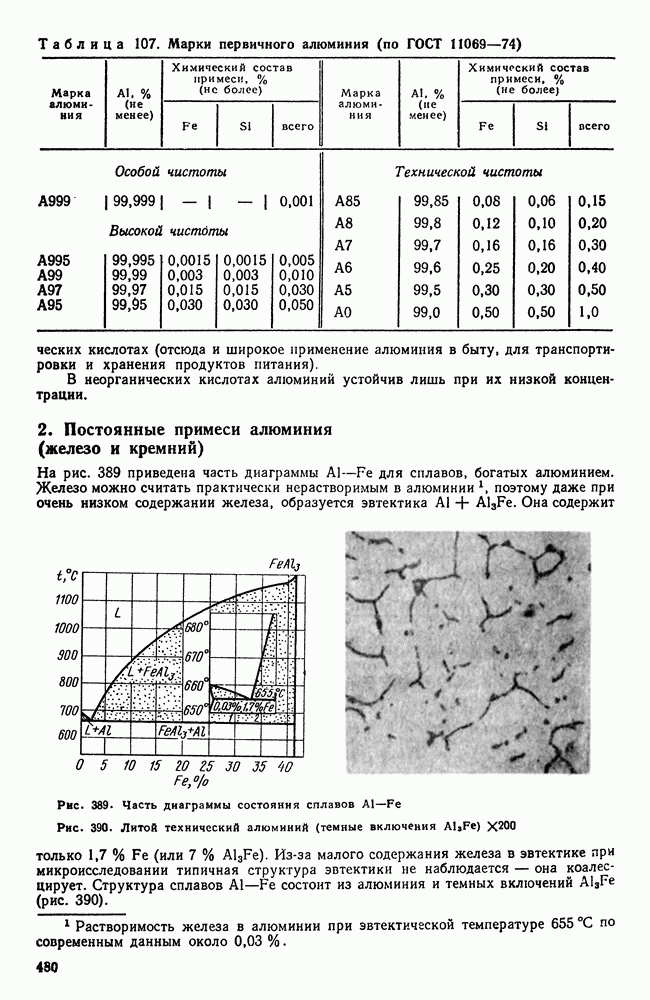
- 2. Постоянные примеси алюминия (железо и кремний)
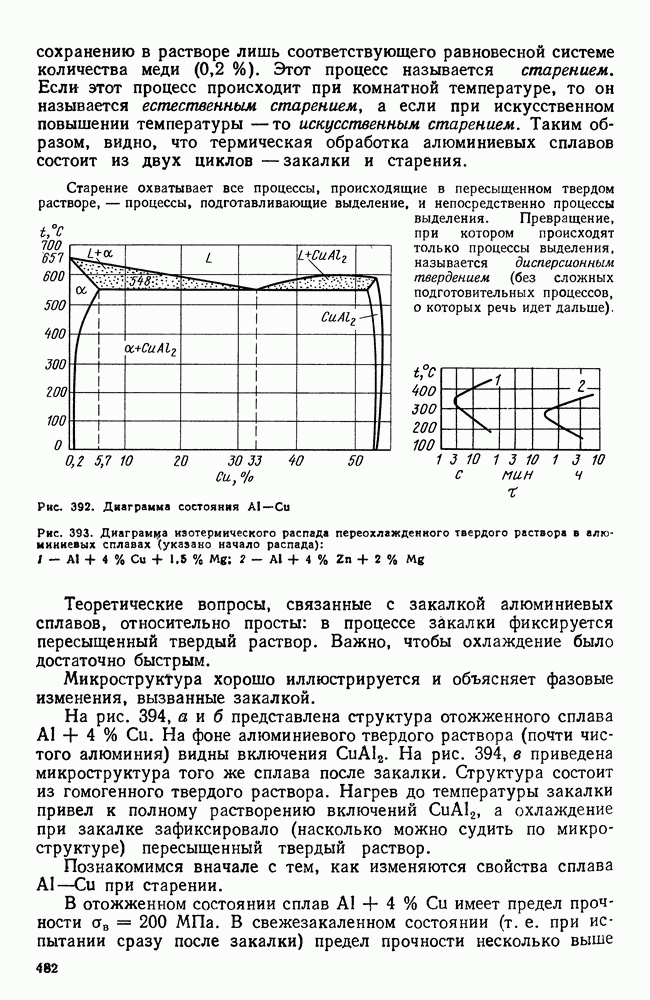
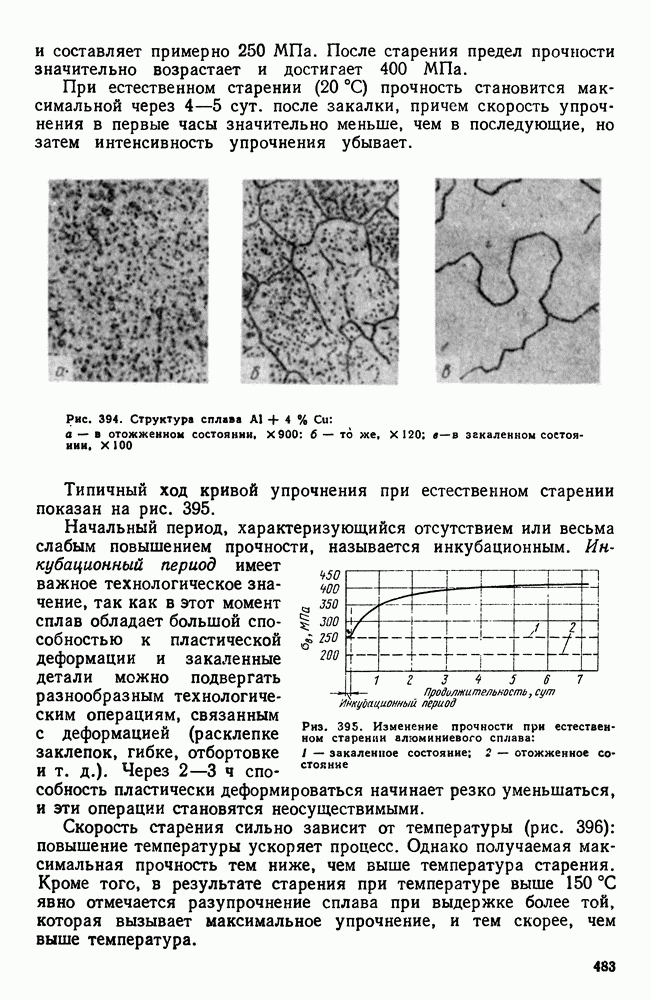
- 3. Термическая обработка сплавов Al-Cu
- 4. Влияние состава алюминиевых сплавов на процессы, происходящие при термической обработке
- 5. Классификация алюминиевых сплавов
- 6. Деформируемые сплавы, не упрочняемые термической обработкой
- 7. Дюралюминий и другие деформируемые сплавы, упрочняемые термической обработкой
- 8. Алюминиевые сплавы для поковок и штамповок
- 9. Силумины и другие алюминиевые сплавы для фасонного литья
- 10. Жаропрочные алюминиевые сплавы
- 11. Магний
- 12. Сплавы магния
- 13. Бериллий
- 14. Сплавы бериллия
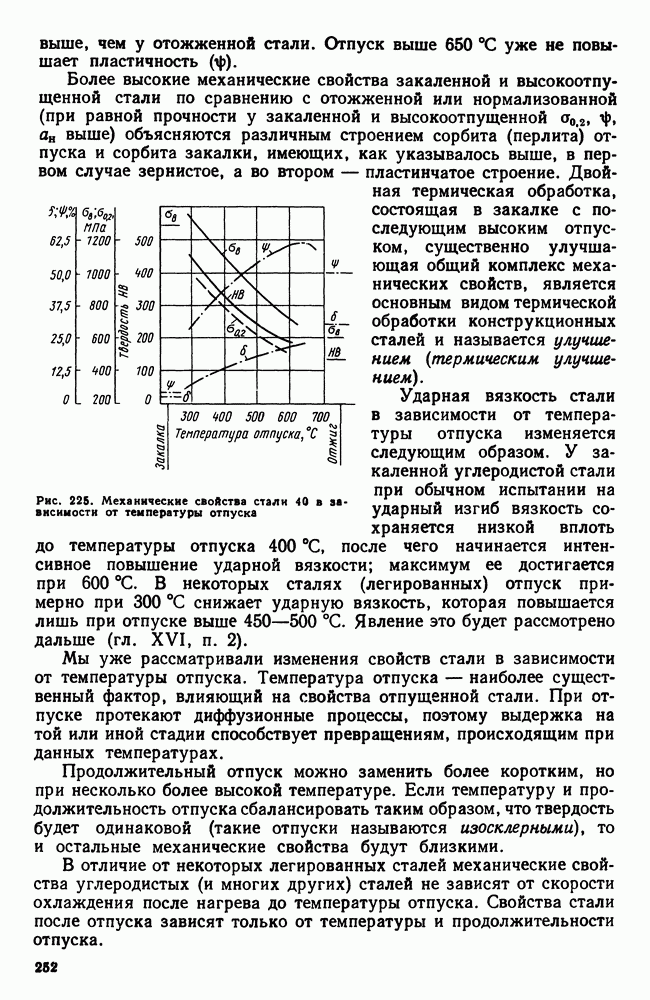
- Глава XXVII. МЕДЬ И ЕЕ СПЛАВЫ
- 2. Сплавы меди с цинком (латуни)
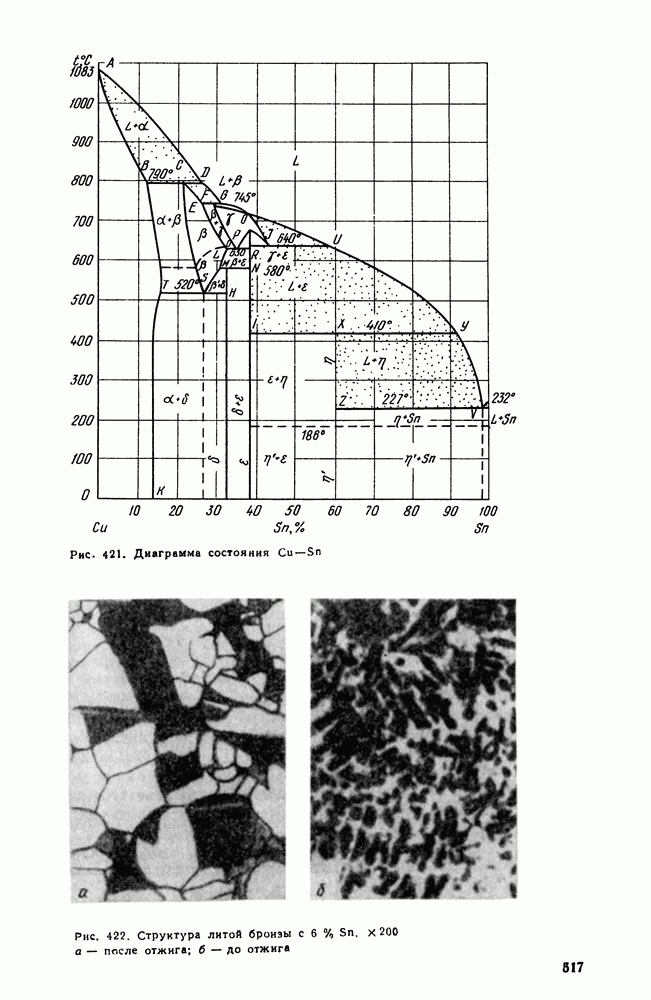
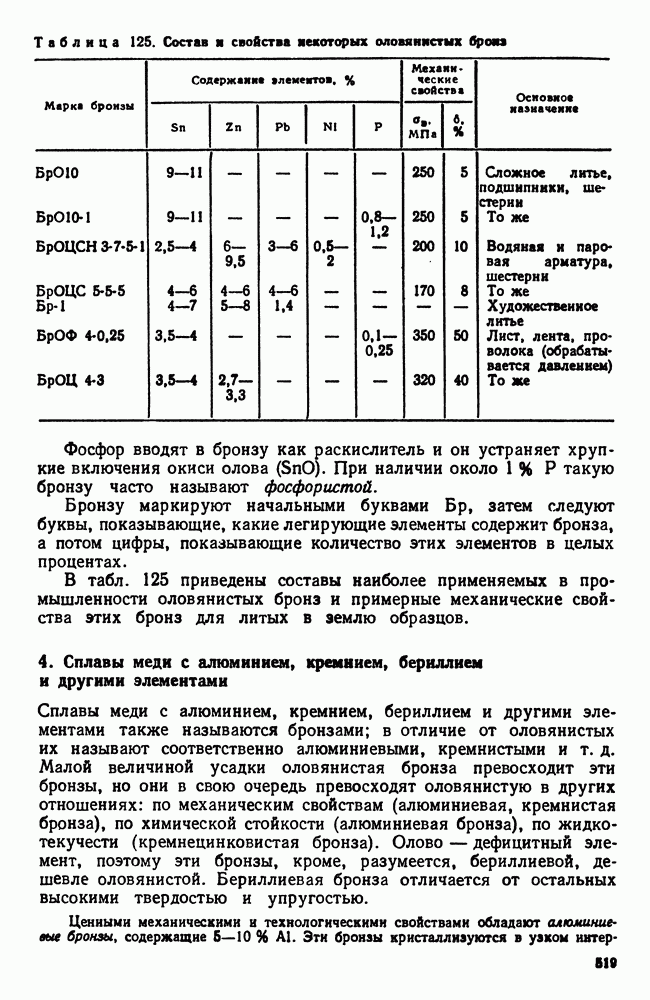
- 3. Сплавы меди с оловом (оловянистые бронзы)
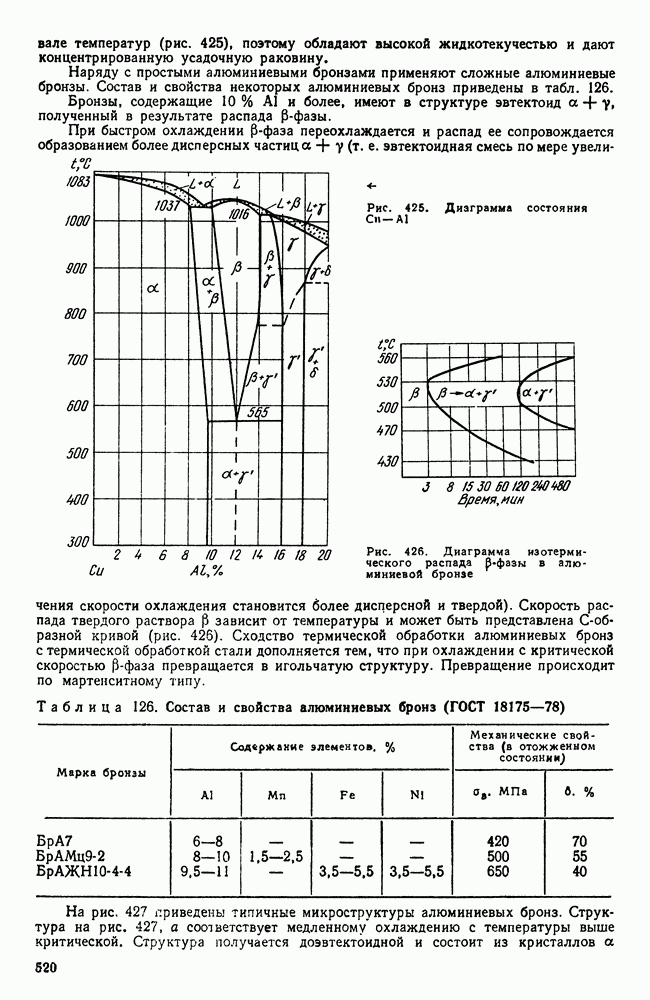
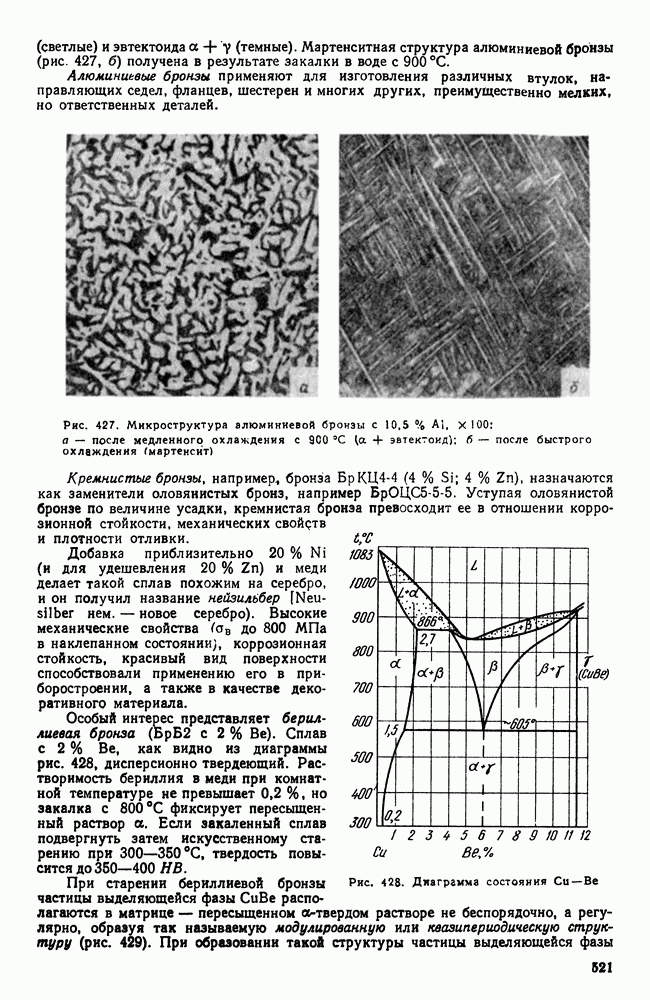
- 4. Сплавы меди с алюминием, кремнием, бериллием и другими элементами
- ГЛАВА XXVIII. ПОДШИПНИКОВЫЕ СПЛАВЫ И ПРИПОИ
- 2. Легкоплавкие подшипниковые сплавы (баббиты)
- 3. Припои
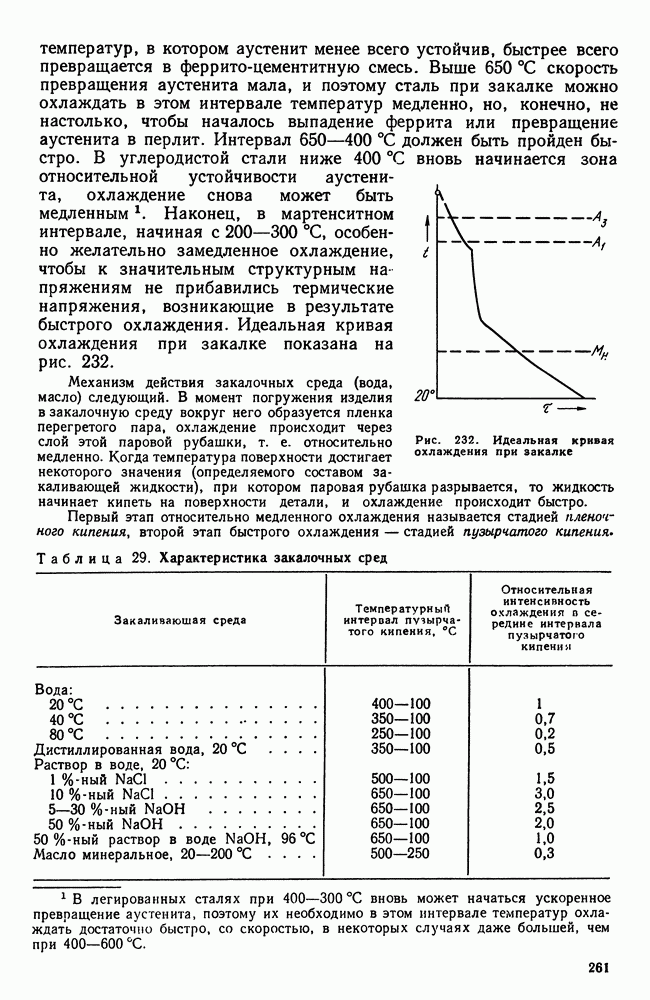
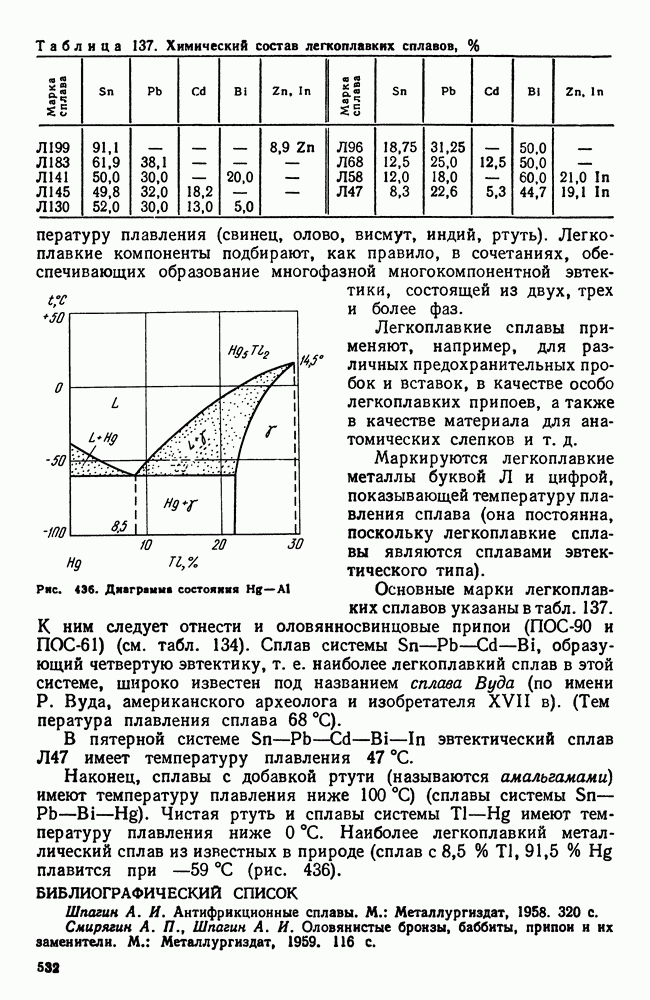
- 4. Легкоплавкие сплавы
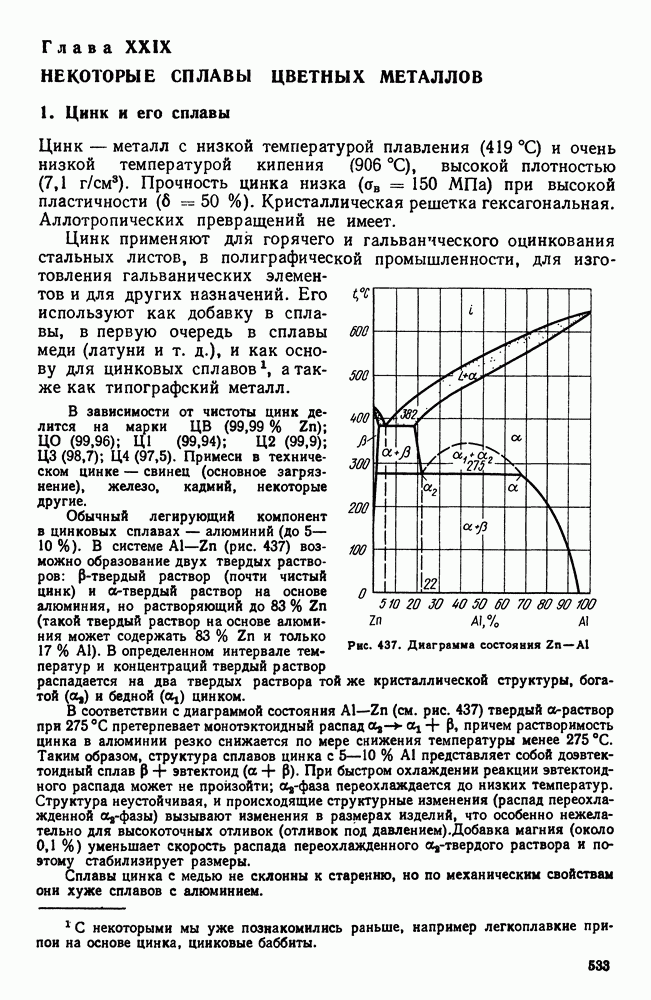
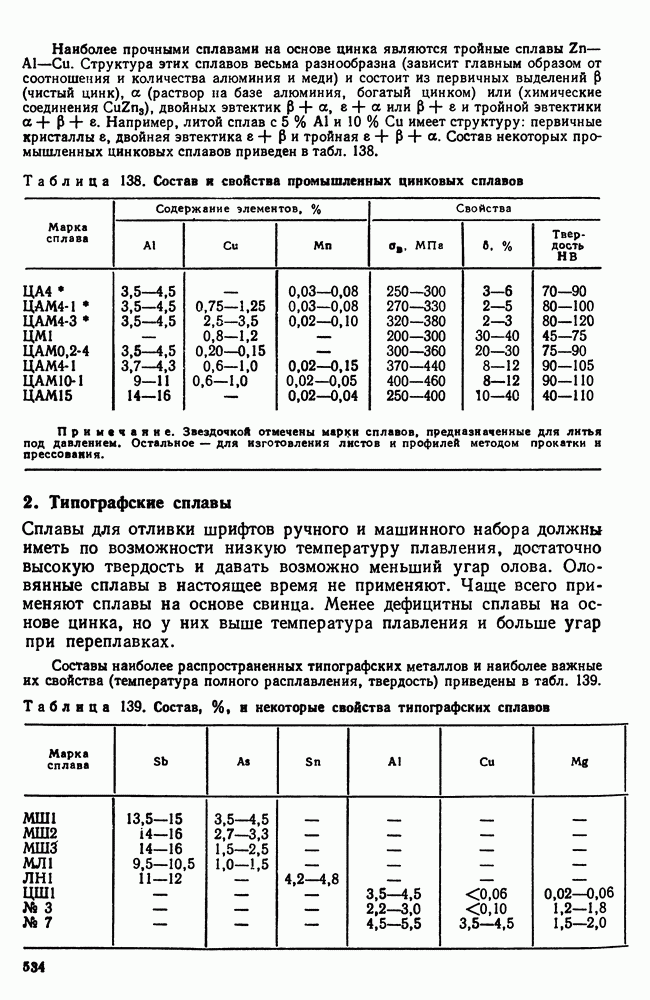
- Глава XXIX. НЕКОТОРЫЕ СПЛАВЫ ЦВЕТНЫХ МЕТАЛЛОВ
- 2. Типографские сплавы
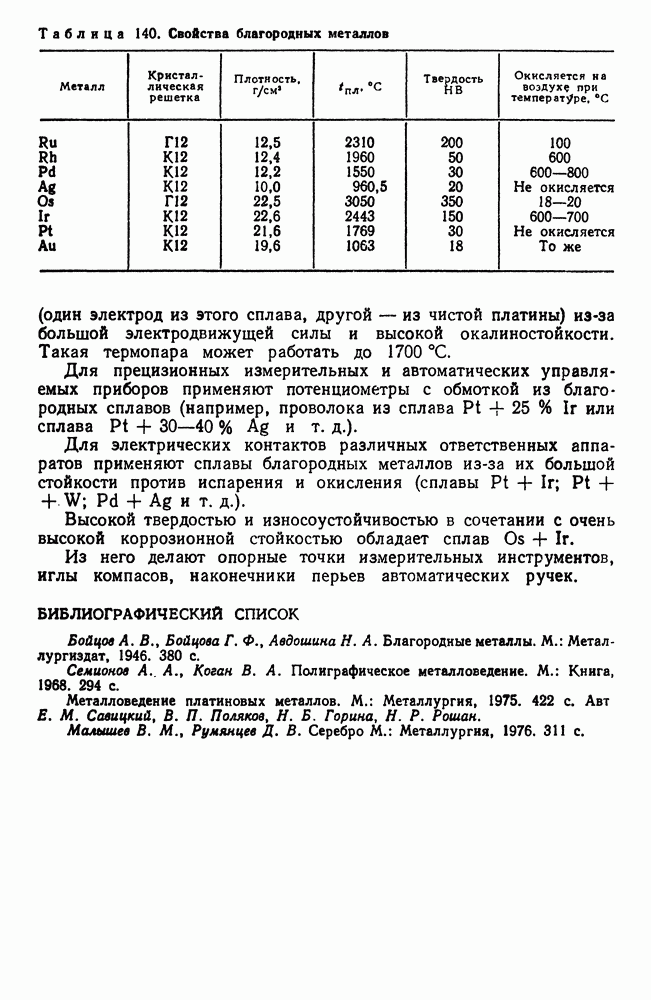
- 3. Благородные металлы