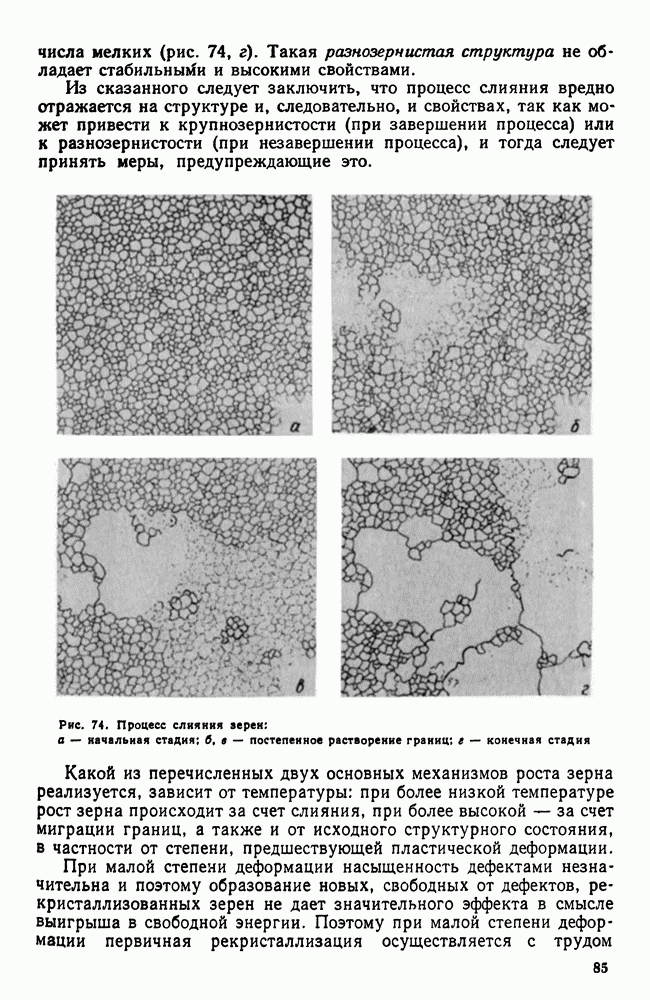
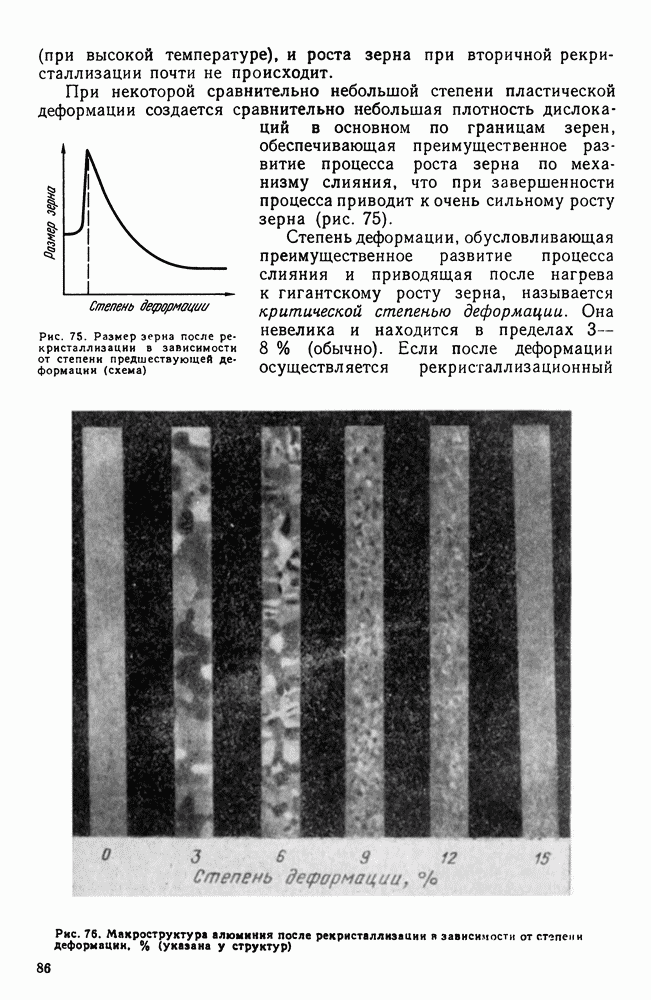
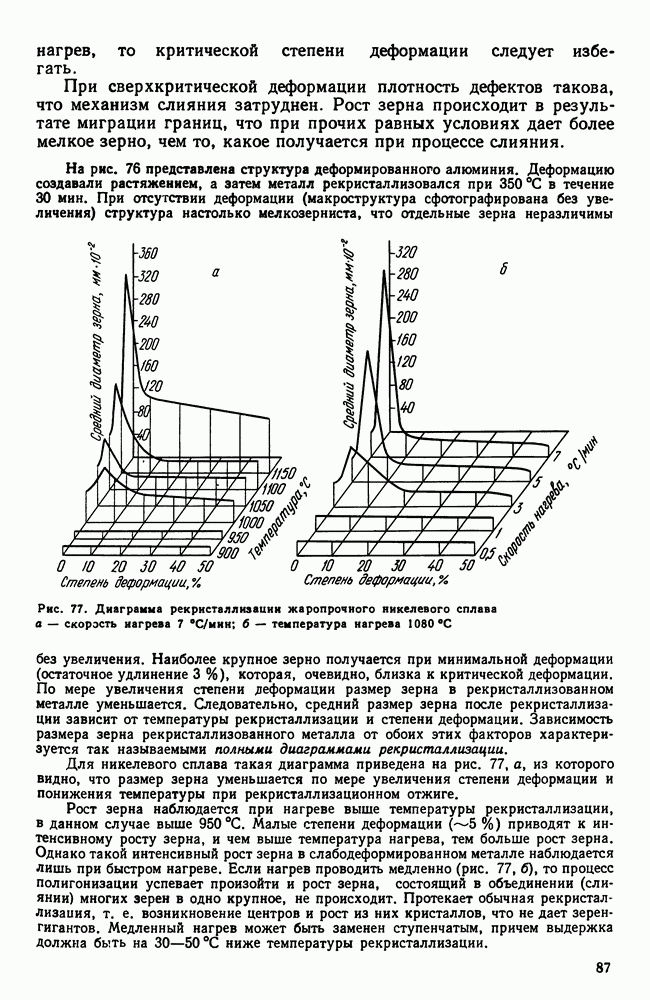
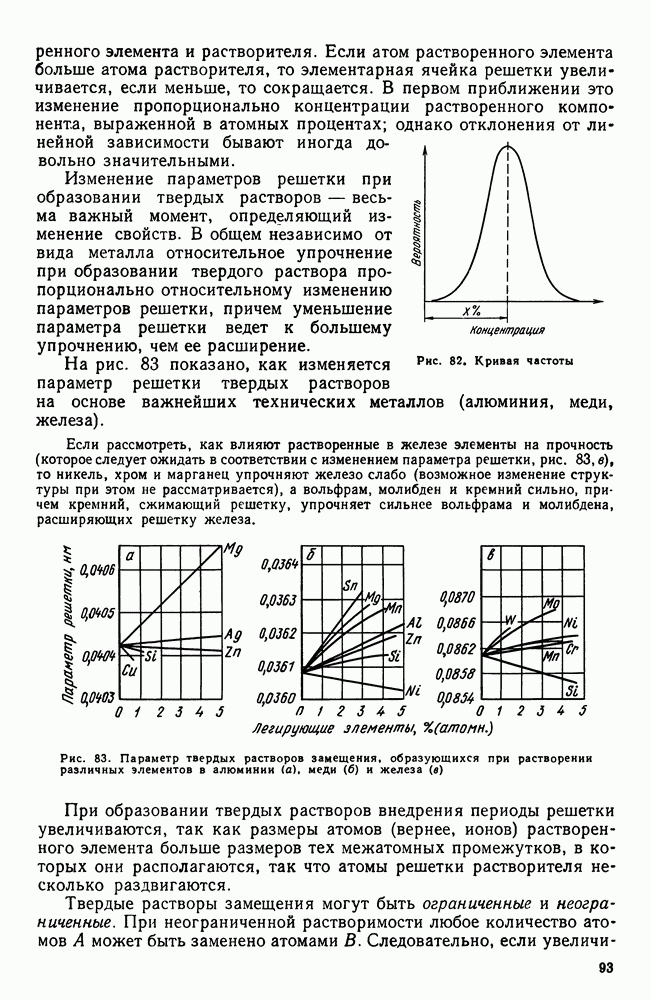
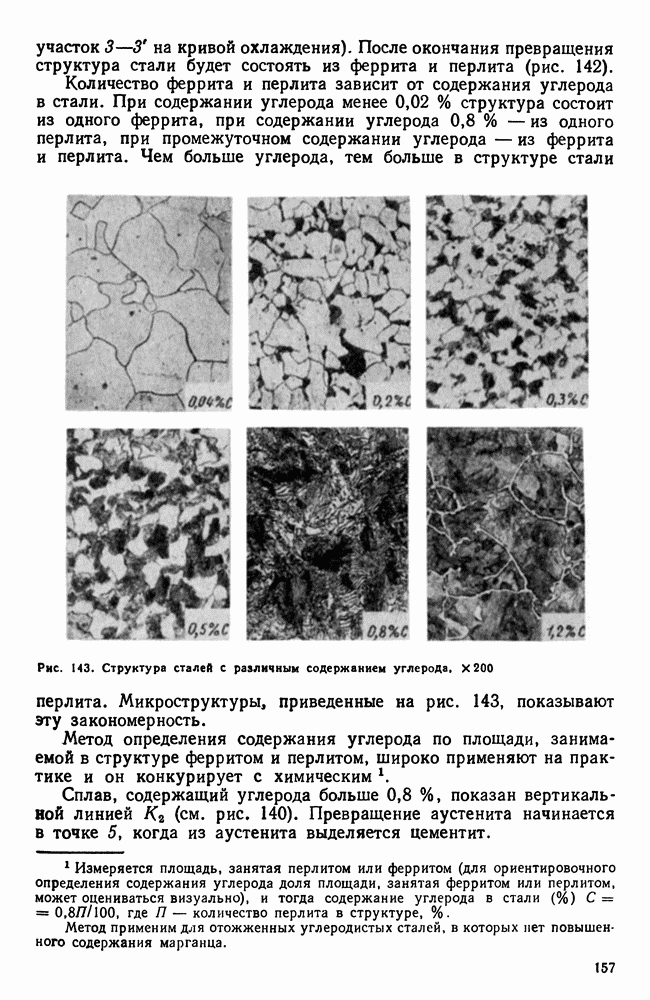
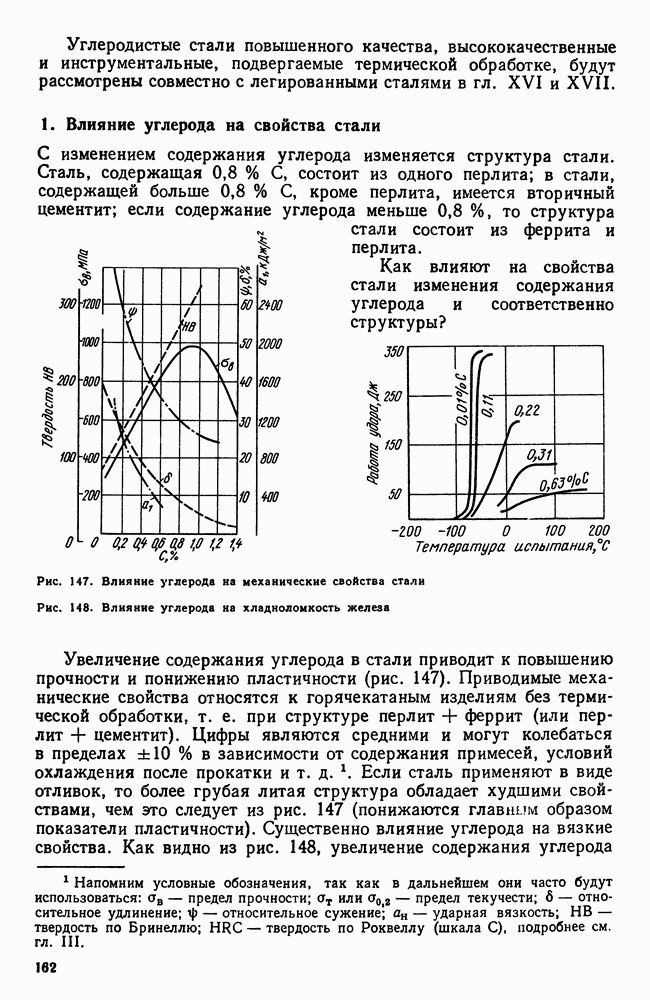
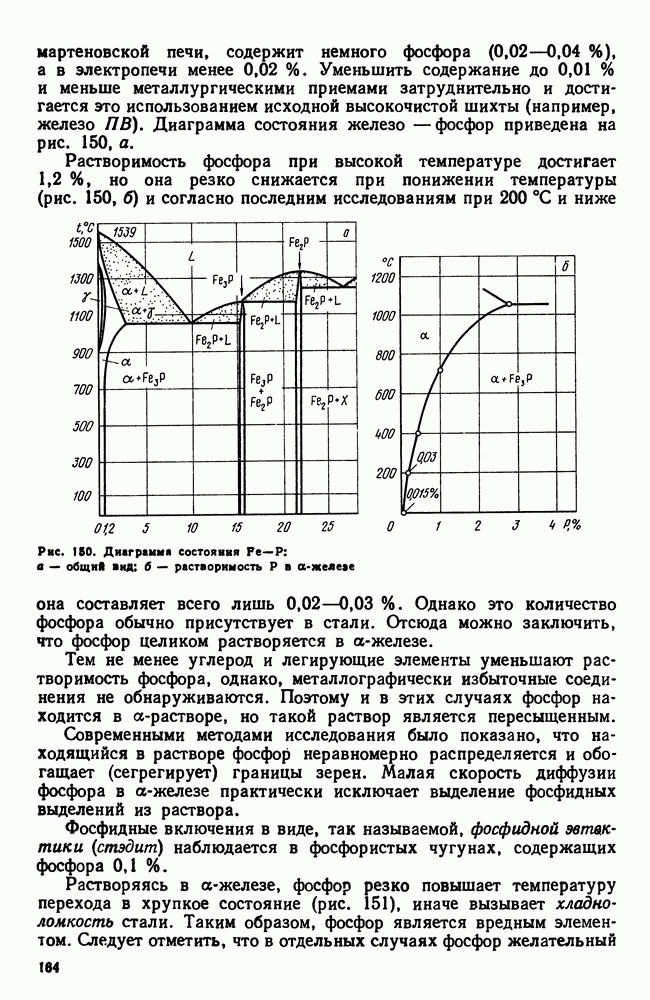
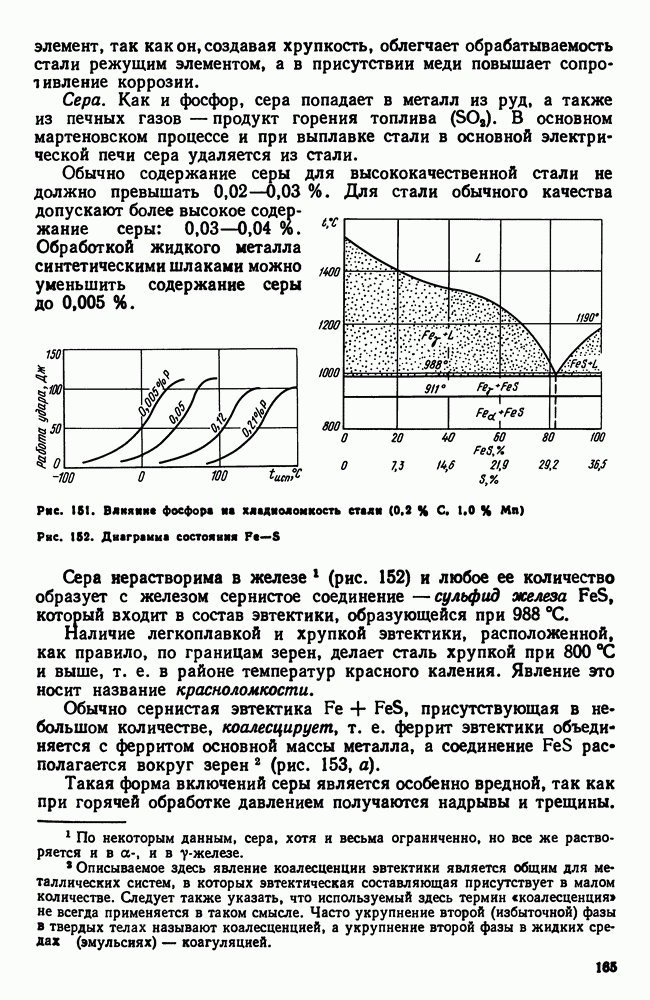
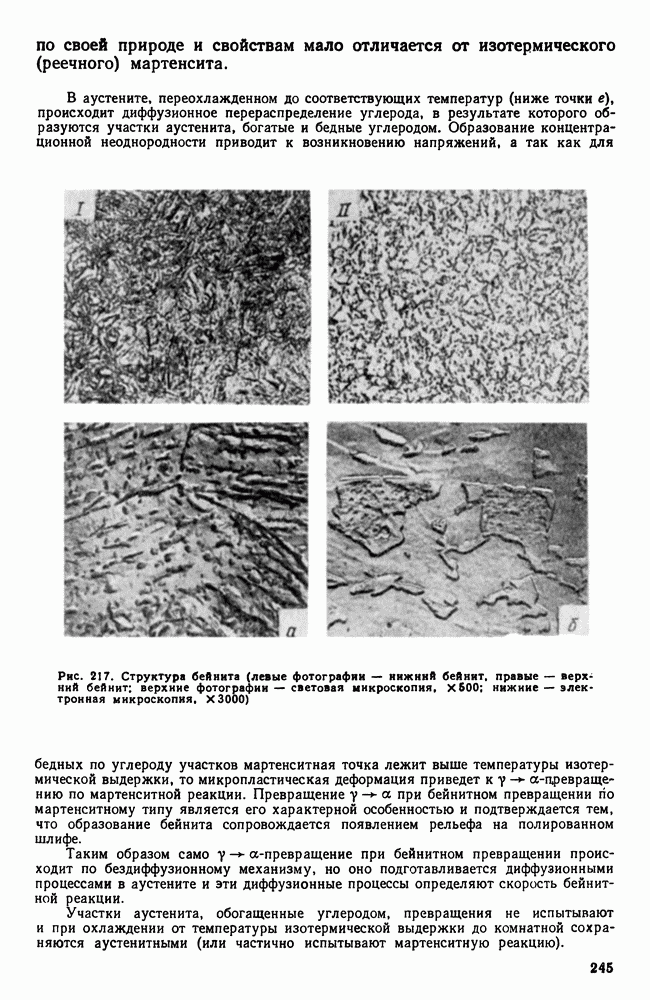
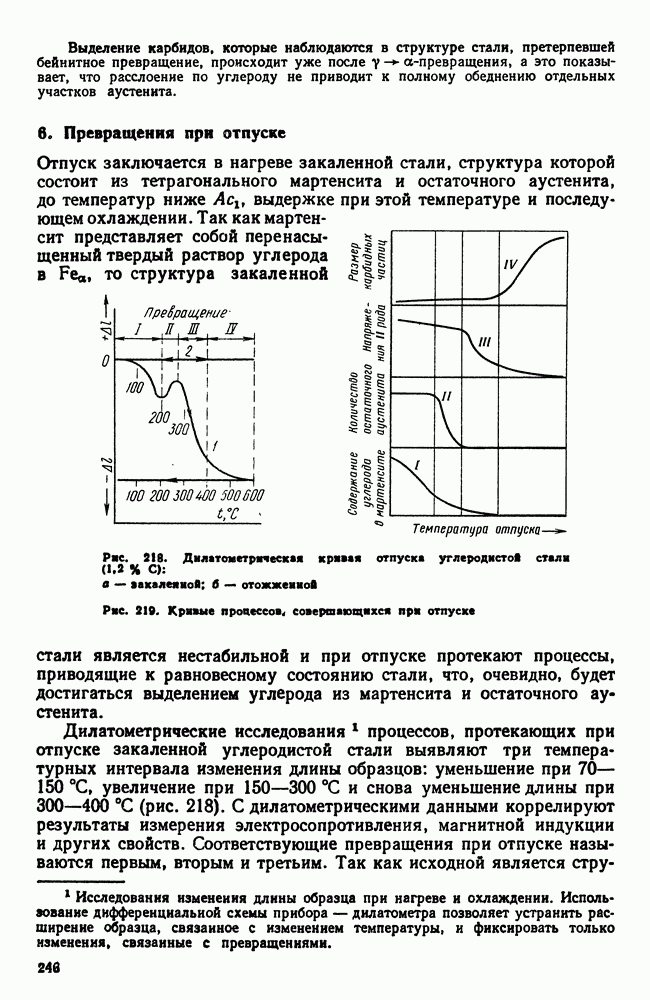
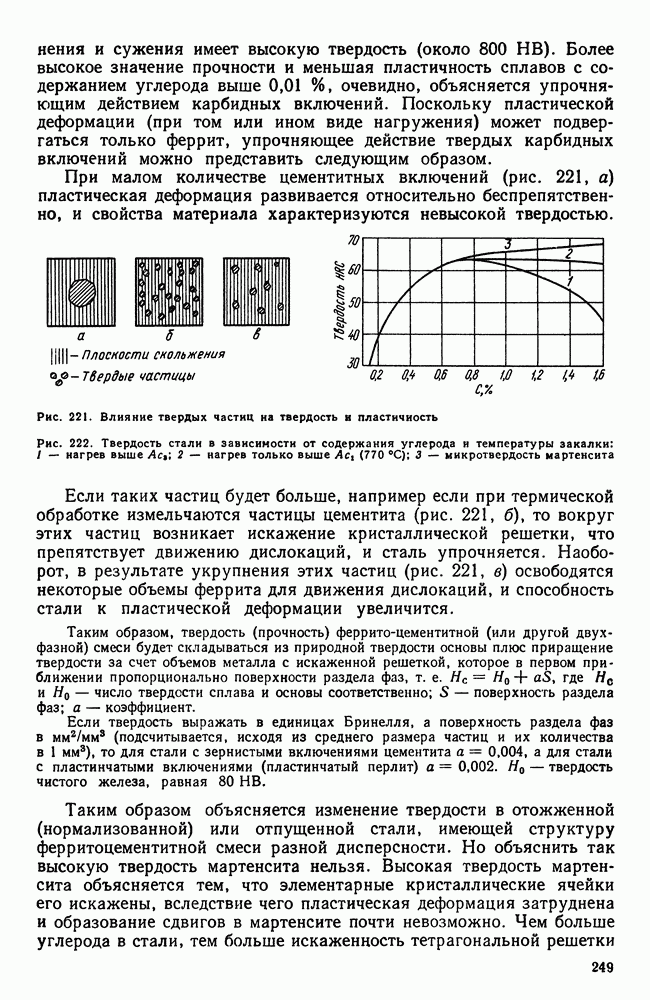
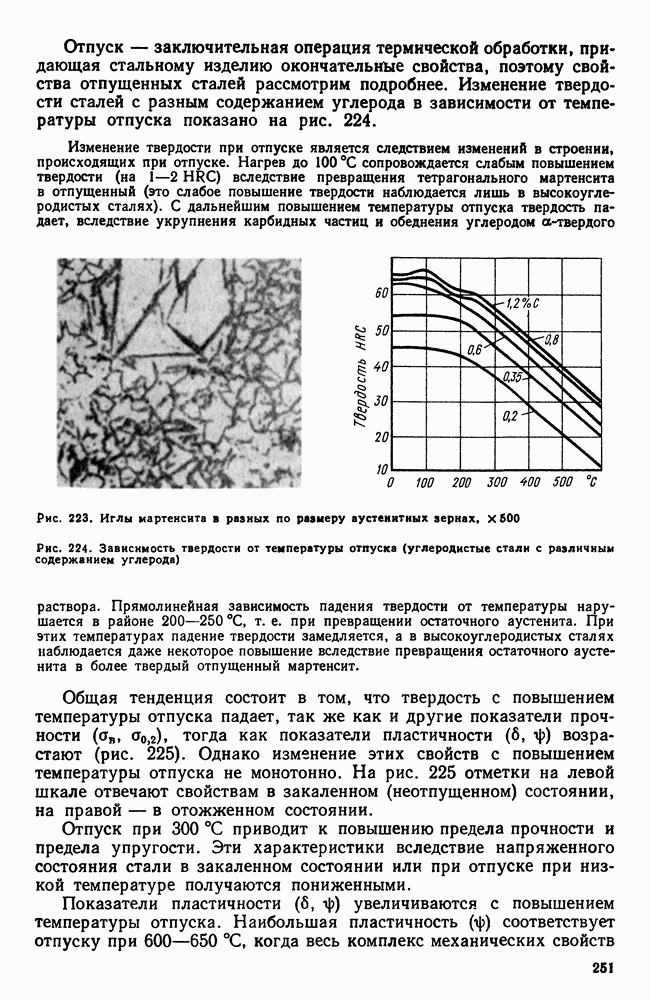
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
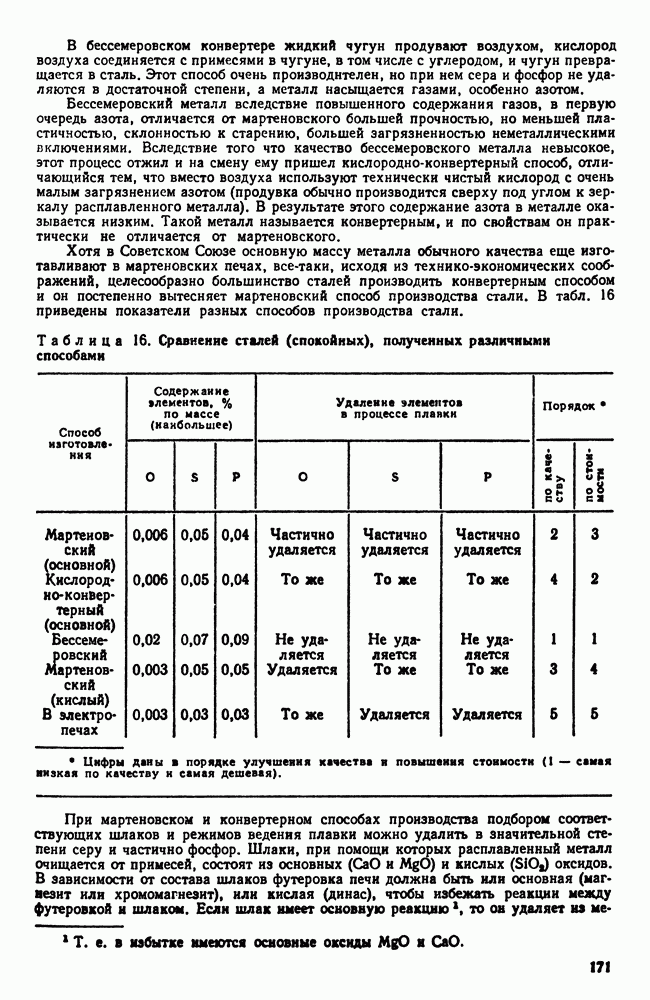
11. Системы с тремя компонентами
Современная техника не ограничивается применением чистых металлов и двойных сплавов. В большинстве случаев практически применяемые сплавы являются сплавами многих компонентов. Поэтому,
естественно, возникает необходимость изучения тройных и более сложных систем.
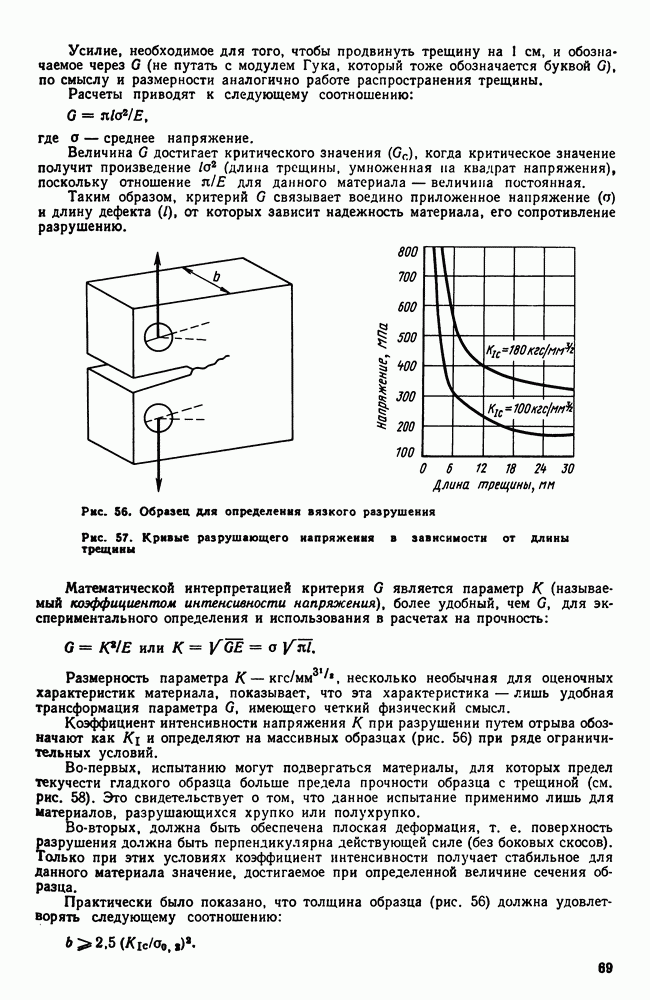
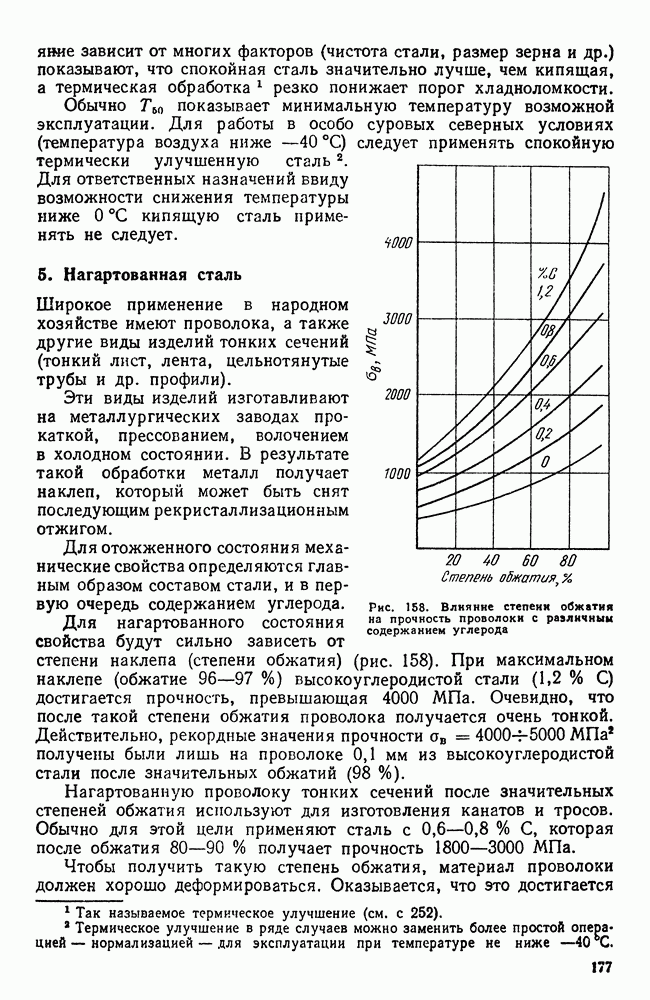
Как видели раньше, для изображения однокомпонентной системы достаточно нанести точки на прямую линию (см. рис. 86), диаграмму состояния двухкомпонентной системы изображают в виде плоского графика (см. рис. 87). Диаграмма состояния сплавов с тремя компонентами изображается в пространстве; при этом одна ось будет показывать изменение содержания одного компонента, другая — другого, а третья ось — температурная (рис. 112). Если содержание двух компонентов задано, то содержание третьего определяется равенством  .
.

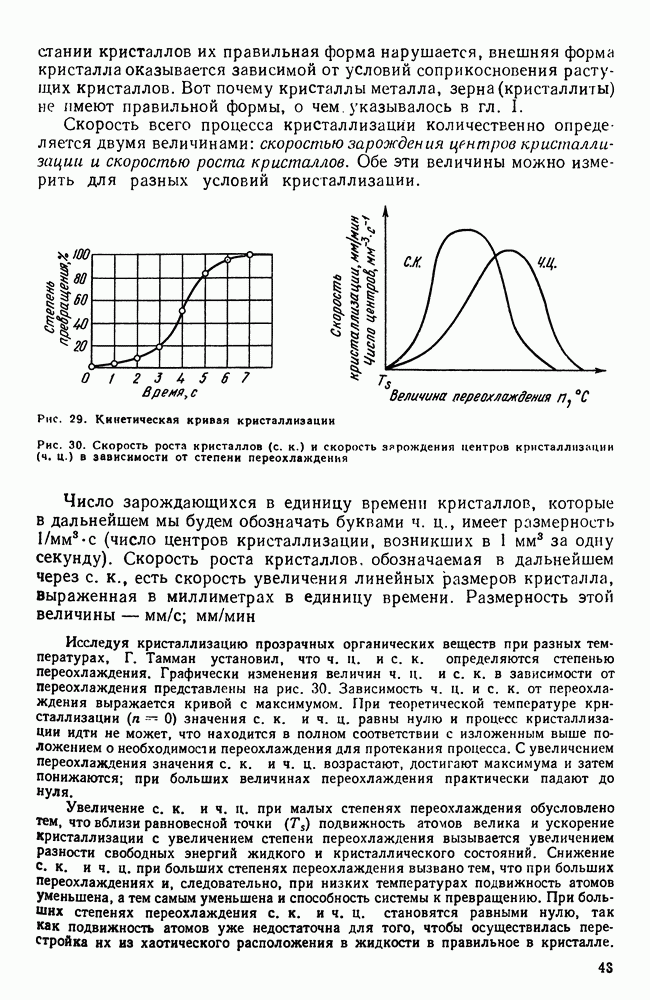
Рис. 112. Координаты для трехкомпонентной системы

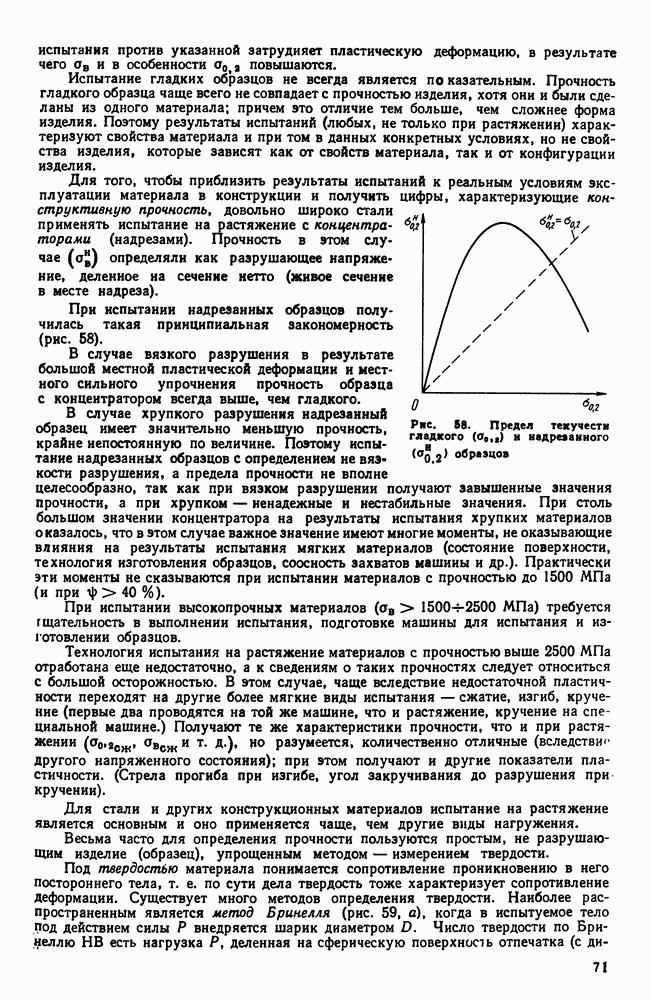
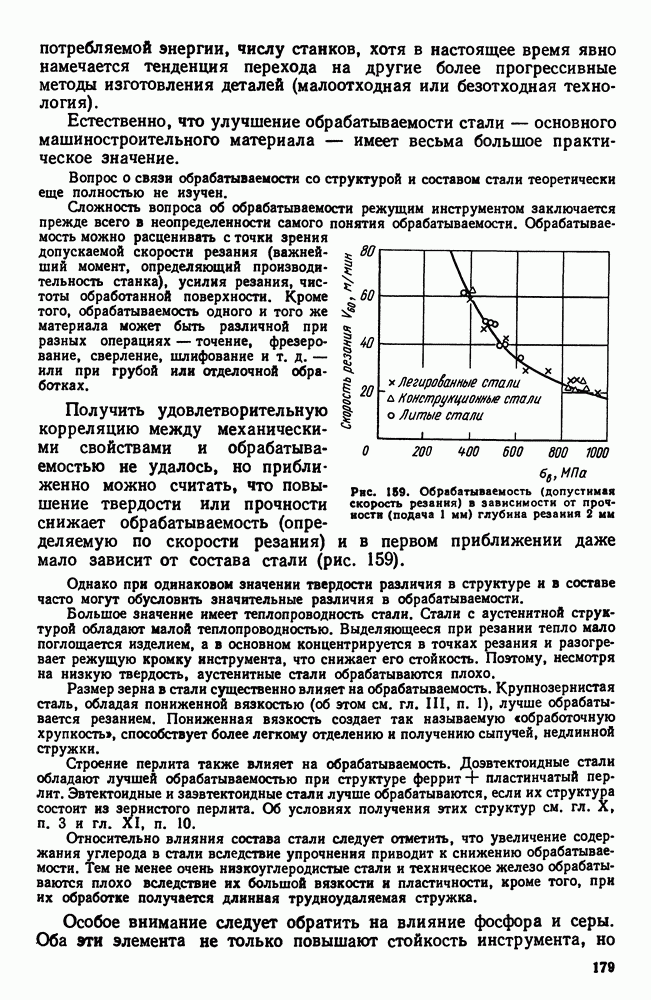
Рис. 113. Концентрационный треугольник (прямоугольный)
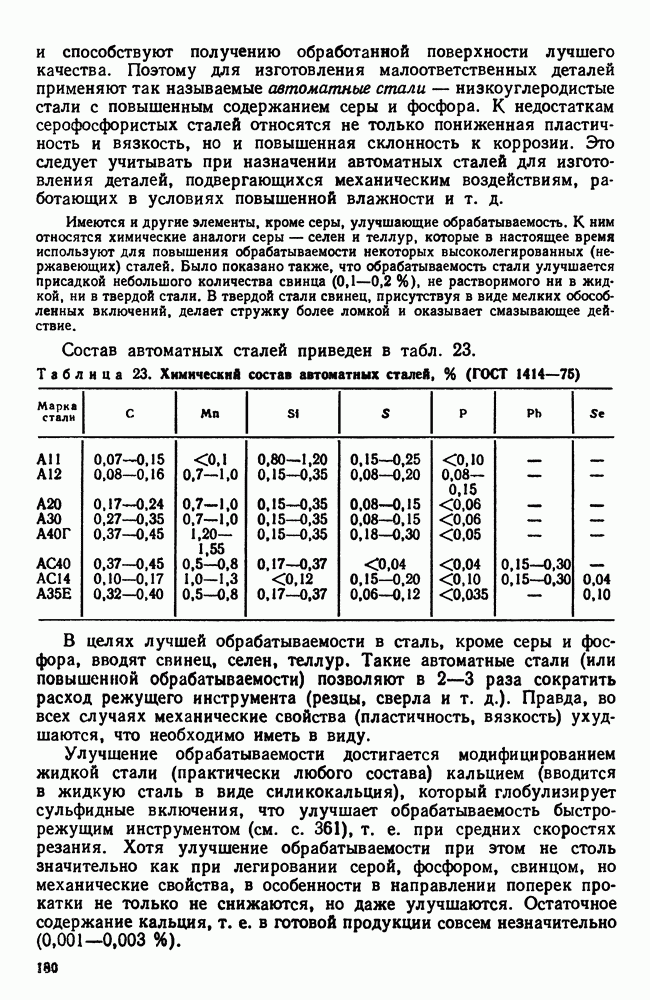
На вертикальные линии (рис. 112) наносят точки фазовых превращений сплавов. Изучив достаточное количество сплавов, точки одинаковых превращений можно объединить в поверхности. Таким образом, пространственная модель диаграммы состоит из различных поверхностей, между которыми заключены объемы одинаковых фазовых состояний. На диаграмме, следовательно, будет пространственная область, соответствующая жидкому состоянию, которая от об: ласти равновесия жидкого состояния с кристаллическим отделяется поверхностью ликвидус. Область сосуществования жидкости и кристаллических фаз отделяется от области существования одного только кристаллического вещества поверхностью солидус.
Изучение тройных систем начнем со способов изображения концентрации. Можно воспользоваться прямоугольной системой координат. Вершина координат соответствует чистому компоненту А. По осям откладывают концентрации В и С (рис. 113) так же, как это делали применительно к двойным системам (см. рис. 87). Крайние точки на обеих осях соответствуют чистым компонентам В и С. Если масштаб на обеих осях одинаков, то точки В и С одинаково удалены от начала координат.
Двойные сплавы  и
и  лежат на осях координат и могут иметь одинаковый масштаб; двойной же сплав
лежат на осях координат и могут иметь одинаковый масштаб; двойной же сплав  должен расположиться на гипотенузе прямоугольного треугольника.
должен расположиться на гипотенузе прямоугольного треугольника.
Недостатком такого метода изображения является различие масштабов для концентраций отдельных компонентов. Этот метод применяют главным образом при изображении не всей диаграммы состояния, а только части ее, для сплавов, богатых компонентом А.
Для полного изображения всей тройной системы, так чтобы изменение концентрации каждого компонента измерялось в одинаковом масштабе, используются косоугольные координаты с углом 60°. В этом случае вместо прямоугольного треугольника основанием пространственной модели будет равносторонний треугольник, на который наносят сетку концентраций и который называется концентрационным треугольником (рис. 114).
При определении концентраций компонентов тройного сплава следует предположить, что вершины равностороннего треугольника соответствуют чистым компонентам А, В и С. Линия  изображает двойные сплавы
изображает двойные сплавы  Аналогично стороны
Аналогично стороны  и
и  изображают двойные сплавы
изображают двойные сплавы  . Внутри треугольника расположены точки, отвечающие тройным сплавам.
. Внутри треугольника расположены точки, отвечающие тройным сплавам.

Рис. 114. Концентрированный треугольник (равносторонний)
В каждом тройном сплаве сумма концентраций трех компонентов является постоянной величиной, т. е.  (так же, как и для двойных сплавов
(так же, как и для двойных сплавов  и равна оси концентрации
и равна оси концентрации 
Следовательно, за  принимают сторону треугольника
принимают сторону треугольника  .
.
Если через заданную точку О, лежащую внутри треугольника, провести линии, параллельные его сторонам (рис. 115), то из элементарного геометрического построения видно, что расходящиеся из точки О под углом в 120° отрезки  в сумме равны стороне треугольника, т. е. а
в сумме равны стороне треугольника, т. е. а 
Так как сторона треугольника показывает нам количество всего сплава, то сумма а  с также показывает количество всего сплава, а каждый член в этой сумме показывает количество (концентрацию в сплаве) одного из компонентов.
с также показывает количество всего сплава, а каждый член в этой сумме показывает количество (концентрацию в сплаве) одного из компонентов.
В двойной системе по мере приближения концентрационной точки к началу координат, например к точке Л, лежащей на стороне  содержание компонента А увеличивается, а В уменьшается. В тройной системе по мере приближения точки, расположенной внутри треугольника, к вершине А отрезок а увеличивается, а отрезок
содержание компонента А увеличивается, а В уменьшается. В тройной системе по мере приближения точки, расположенной внутри треугольника, к вершине А отрезок а увеличивается, а отрезок  и с уменьшаются. Когда такая точка окажется на стороне
и с уменьшаются. Когда такая точка окажется на стороне  сплав будет бинарным
сплав будет бинарным  , отрезок с станет равным нулю. Когда точка сольется с вершиной треугольника, имеем чистый компонент
, отрезок с станет равным нулю. Когда точка сольется с вершиной треугольника, имеем чистый компонент  , отрезки бис будут равны нулю, а отрезок а будет равен стороне АС, или 100 %.
, отрезки бис будут равны нулю, а отрезок а будет равен стороне АС, или 100 %.
Следовательно, отрезок а показывает содержание (концентрацию) в тройном сплаве компонента А. Соответственно отрезок  показывает содержание компонента В, а отрезок с — содержание компонента С.
показывает содержание компонента В, а отрезок с — содержание компонента С.
Чтобы определить концентрацию компонентов в тройном сплаве, через данную точку проводят линии, параллельные сторонам треугольника. Длина отрезка какой-либо линии, доведенной до одной из сторон треугольника, определяет концентрацию того компонента, который отвечает вершине треугольника, противолежащей этой стороне 1.
Для удобства на сторонах треугольника (по вращению часовой стрелки или против нее) откладывают содержание компонентов  .
.

Рис. 115. Определение коицеитрации сплавов в равностороннем концентрационном треугольнике

Рис. 116. Определение концентрации в равностороннем концентрационном треугольнике
Концентрационные отрезки  и с проектируются на стороны, показывающие изменение соответствующего компонента. Отрезки
и с проектируются на стороны, показывающие изменение соответствующего компонента. Отрезки  и
и  лежащие на сторонах треугольника, соответственно равны концентрационным отрезкам
лежащие на сторонах треугольника, соответственно равны концентрационным отрезкам  и показывают состав сплава (отрезок а — концентрацию компонента
и показывают состав сплава (отрезок а — концентрацию компонента  — компонента Вне — компонента С).
— компонента Вне — компонента С).
Во многих случаях удобно откладывать концентрации С и В по сторонам исходящим из вершины компонента А.
Для сплава О концентрация компонента В выражается отрезком  компонента С — отрезком
компонента С — отрезком  так как очевидно, что отрезок
так как очевидно, что отрезок  (рис. 116).
(рис. 116).
Концентрацию компонента А определяют по разности  .
.
Если рассмотрим серию сплавов, лежащих на прямой, параллельной одной из сторон треугольника, например стороне  (рис. 117), то нетрудно видеть, что во всех этих сплавах концентрационные отрезки, опущенные на сторону
(рис. 117), то нетрудно видеть, что во всех этих сплавах концентрационные отрезки, опущенные на сторону  , т. е. отрезки, показывающие содержание компонента В, равны. Следовательно, сплавы, лежащие на линии, параллельной стороне
, т. е. отрезки, показывающие содержание компонента В, равны. Следовательно, сплавы, лежащие на линии, параллельной стороне  имеют постоянное содержание компонента В.
имеют постоянное содержание компонента В.
Если взять серию сплавов, лежащих на линии, проходящей через вершину треугольника, например через вершину В, то из закона подобия треугольников получим для всех сплавов, лежащих на этой линии, постоянное отношение отрезков:

т. е. для всех сплавов, лежащих на прямой, проходящей через вершину В, соотношение компонентов А и С будет постоянным.
Итак, анализ концентрационного треугольника показывает, что:
1) вершины треугольника изображают чистые компоненты Л, В и С;
2) на сторонах треугольника лежат точки, отвечающие двойным сплавам;
3) точки внутри треугольника изображают тройные сплавы;
4) сплавы, которые изображаются точками, лежащими на линии, параллельной стороне треугольника, имеют постоянную концентрацию того компонента, который соответствует противолежащей вершине треугольника;
5) сплавы, которые находятся на линии, проходящей через какую-либо вершину треугольника, характеризуются постоянным отношением концентраций двух компонентов.

Рис. 117. Сечение концентрационного треугольника

Рис. 118. Правило отрезков в тройной системе
Процесс кристаллизации тройных сплавов подчиняется тем же основным правилам, что и кристаллизация двойных сплавов, т. е. правилу фаз и правилу отрезков, только применение последнего несколько затрудняется более сложным изображением системы (в пространстве).
Приведем пример для объяснения правила отрезков (которое в отношении к тройным системам, может быть, удобнее именовать правилом прямой линии).
Если даны два двойных сплава с 60 и  , то сплавляя их, получим третий двойной сплав, для которого концентрация В лежит между 40 и 60 % В (в нем не может быть В меньше
, то сплавляя их, получим третий двойной сплав, для которого концентрация В лежит между 40 и 60 % В (в нем не может быть В меньше  и больше
и больше  т. е. если имеем два сплава
т. е. если имеем два сплава  (см. рис. 87), то концентрация третьего сплава, полученного путем сплавления этих двух, будет отвечать точке, лежащей между точками
(см. рис. 87), то концентрация третьего сплава, полученного путем сплавления этих двух, будет отвечать точке, лежащей между точками 
Если даны два тройных сплава —  , то точка, изображающая третий сплав, полученный их сплавлением, будет лежать на линии, соединяющей точки
, то точка, изображающая третий сплав, полученный их сплавлением, будет лежать на линии, соединяющей точки  и Е (рис. 118).
и Е (рис. 118).
Чем больше взято сплава  , тем ближе будет лежать точка О, характеризующая состав полученного сплава, к точке Е.
, тем ближе будет лежать точка О, характеризующая состав полученного сплава, к точке Е.
Если взять  сплава
сплава  сплава
сплава  то положение точки О определится из соотношения:
то положение точки О определится из соотношения:

которое является уже известным нам уравнением правила отрезков (см. 
Если предположить обратный процесс (например, сплав в точке О распадается на две фазы —  ), то концентрационные точки этих сплавов будут лежать на одной прямой
), то концентрационные точки этих сплавов будут лежать на одной прямой  и количество фазы
и количество фазы  определится отрезком
определится отрезком  , а фазы Е отрезком
, а фазы Е отрезком  если отрезок
если отрезок  показывает все количество сплава.
показывает все количество сплава.
Если из жидкости  (рис. 118) выделяются кристаллы чистого компонента В, то состав оставшейся жидкости изменяется по прямой, являющейся продолжением линии
(рис. 118) выделяются кристаллы чистого компонента В, то состав оставшейся жидкости изменяется по прямой, являющейся продолжением линии  Если в какой-то момент кристаллизации концентрация жидкости
Если в какой-то момент кристаллизации концентрация жидкости
приняла значение точки 6, то это значит, что данный момент кристаллизации количество выпавших кристаллов В так относится к количеству оставшейся жидкости, как отрезок  к отрезку
к отрезку  [иными словами, отрезок
[иными словами, отрезок  показывает количество (массу) выпавших кристаллов В].
показывает количество (массу) выпавших кристаллов В].
Применяя правило фаз к тройным системам, следует учитывать, что  (три компонента). Поэтому максимальное число одновременно существующих фаз (при постоянном давлении) в тройных сплавах равно 4 (нонвариантное равновесие):
(три компонента). Поэтому максимальное число одновременно существующих фаз (при постоянном давлении) в тройных сплавах равно 4 (нонвариантное равновесие):

Следовательно, кристаллизация двойной эвтектики  происходит в тройных сплавах в интервале температур, но каждой температуре соответствует определенный состав жидкости (моновариантная реакция):
происходит в тройных сплавах в интервале температур, но каждой температуре соответствует определенный состав жидкости (моновариантная реакция):

В тройных сплавах возможна также кристаллизация тройной эвтектики  , происходящая при постоянной температуре
, происходящая при постоянной температуре 
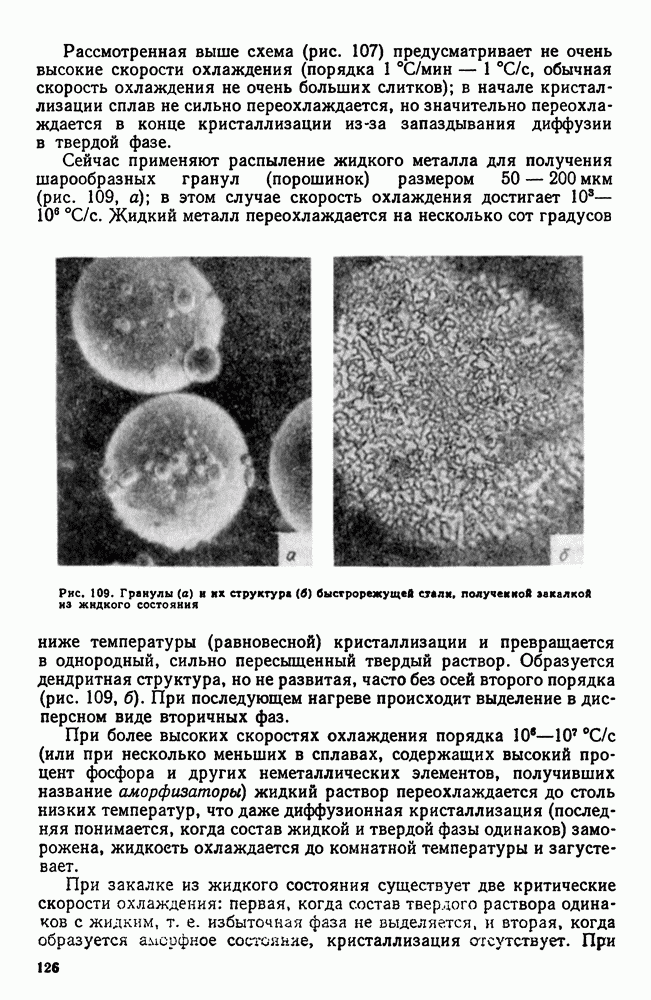
Если представить себе, что систему образуют три компонента А, В и С, растворимые в жидком состоянии и нерастворимые в твердом, то кристаллизация в интервале температур начнется с выделения одного компонента (например, А, рис. 119), затем двух компонентов, т. е. кристаллизуется двойная эвтектика, что тоже происходит при переменной температуре. При постоянной температуре происходит только совместная кристаллизация трех компонентов (в виде тройной эвтектики 

Рис. 119. Кривая охлаждения тройного сплава с образованием двойной и тройной эвтектик. состоящих из числа компонентов А. В, С
Тройные системы можно классифицировать по тем же принципам, что и двойные, учитывая растворимость компонентов в твердом и жидком состояниях и склонность их к образованию химических соединений. Очевидно, что диаграмм тройных систем различных типов будет гораздо больше, чем диаграмм двойных систем. В задачу данного курса не входит рассмотрение разнообразных тройных диаграмм состояний, поэтому ограничимся рассмотрением в общих чертах процессов кристаллизации в тройной системе, где эти три компонента не растворимы в твердом состоянии и не образуют химических соединений.
Попарно компоненты А, В и С образуют системы с двойной эвтектикой, а совместно — систему с тройной эвтектикой.
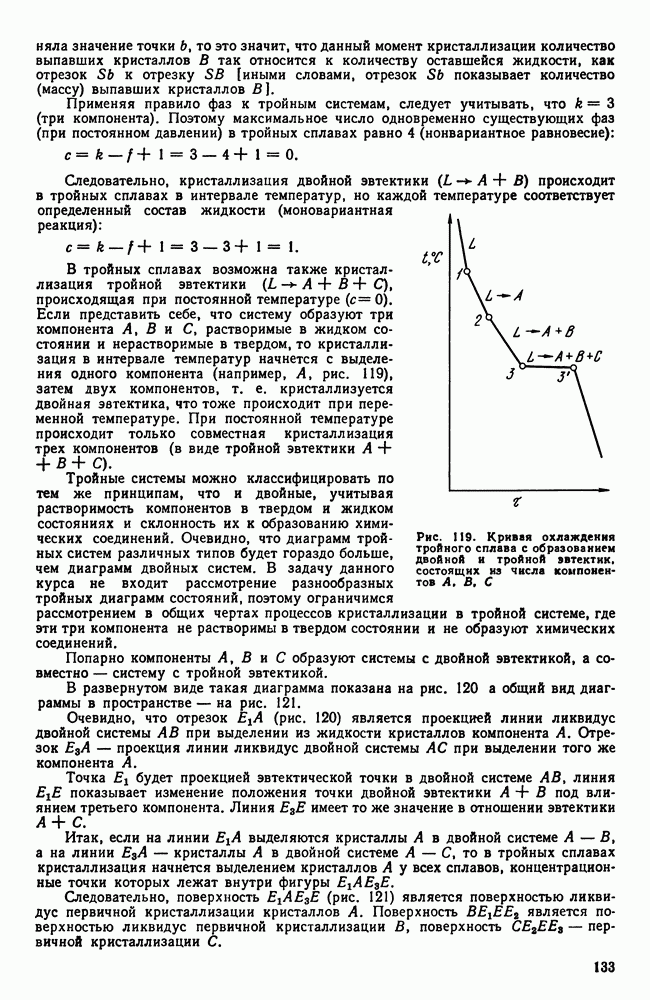
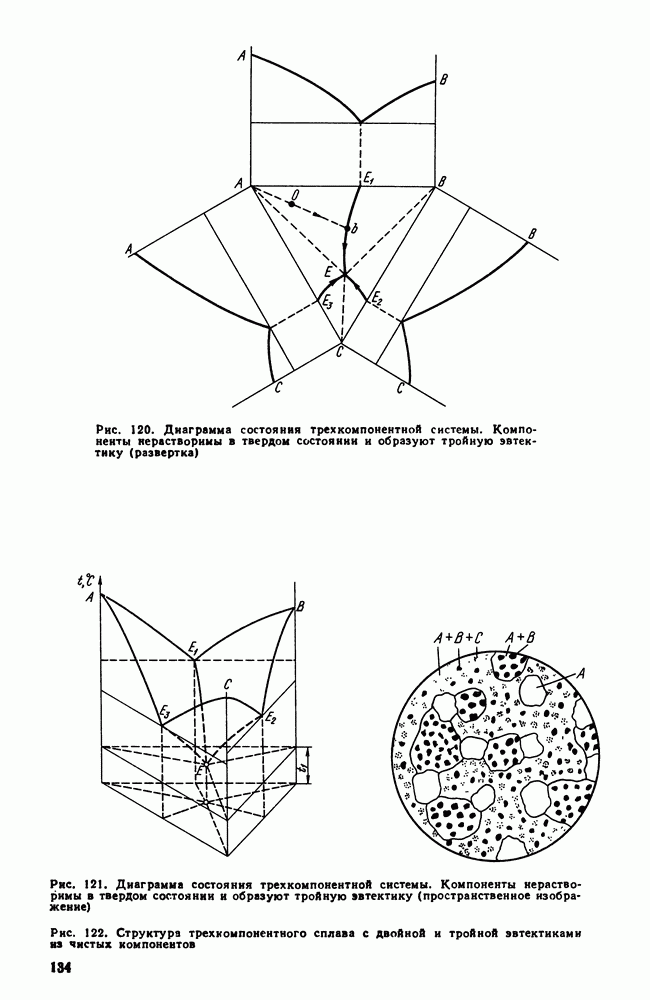
В развернутом виде такая диаграмма показана на рис. 120 а общий вид диаграммы в пространстве — на рис. 121.
Очевидно, что отрезок  (рис. 120) является проекцией линии ликвидус двойной системы
(рис. 120) является проекцией линии ликвидус двойной системы  при выделении из жидкости кристаллов компонента А. Отрезок
при выделении из жидкости кристаллов компонента А. Отрезок  — проекция линии ликвидус двойной системы
— проекция линии ликвидус двойной системы  при выделении того же компонента А.
при выделении того же компонента А.
Точка  будет проекцией эвтектической точки в двойной системе АВ, линия
будет проекцией эвтектической точки в двойной системе АВ, линия  показывает изменение положения точки двойной эвтектики
показывает изменение положения точки двойной эвтектики  под влиянием третьего компонента. Линия
под влиянием третьего компонента. Линия  имеет то же значение в отношении эвтектики
имеет то же значение в отношении эвтектики  .
.
Итак, если на линии  выделяются кристаллы
выделяются кристаллы  в двойной системе А — В, а на линии
в двойной системе А — В, а на линии  — кристаллы
— кристаллы  в двойной системе А — С, то в тройных сплавах кристаллизация начнется выделением кристаллов
в двойной системе А — С, то в тройных сплавах кристаллизация начнется выделением кристаллов  у всех сплавов, концентрационные точки которых лежат внутри фигуры
у всех сплавов, концентрационные точки которых лежат внутри фигуры 
Следовательно, поверхность  (рис. 121) является поверхностью ликвидус первичной кристаллизации кристаллов А. Поверхность
(рис. 121) является поверхностью ликвидус первичной кристаллизации кристаллов А. Поверхность  является поверхностью ликвидус первичной кристаллизации В, поверхность
является поверхностью ликвидус первичной кристаллизации В, поверхность  — первичной кристаллизации С.
— первичной кристаллизации С.

(кликните для просмотра скана)
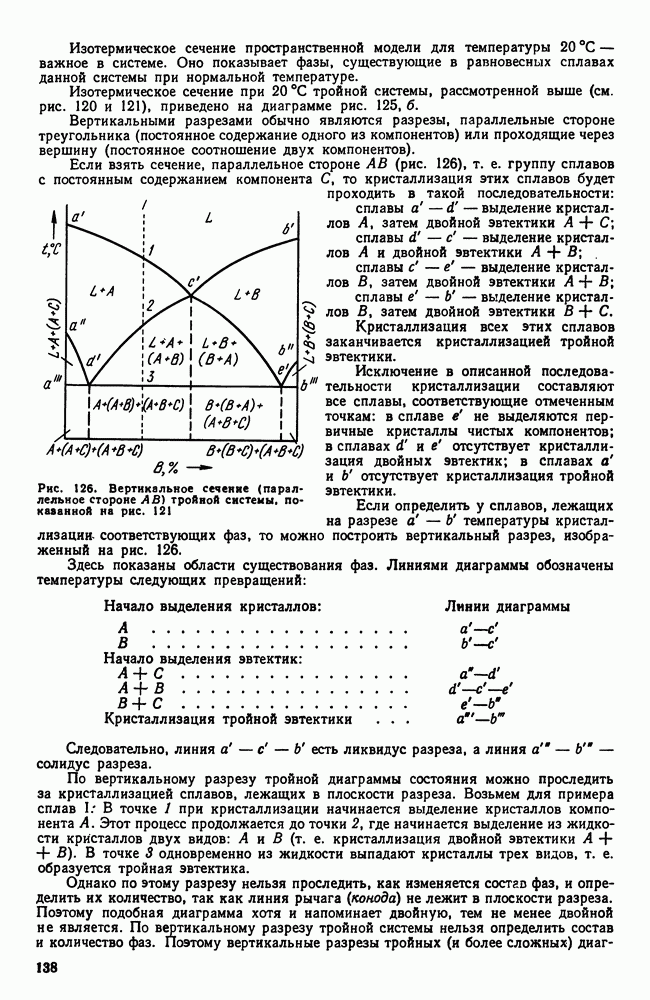
Рассмотрим сплав О (см. рис. 120) из него при охлаждении будут выпадать кристаллы  в соответствии с правилом прямой линии состав жидкой фазы будет меняться по продолжению прямой
в соответствии с правилом прямой линии состав жидкой фазы будет меняться по продолжению прямой  до тех пор, пока точка, показывающая концентрации жидкой фазы, не попадет в точку
до тех пор, пока точка, показывающая концентрации жидкой фазы, не попадет в точку  лежащую на эвтектической линии
лежащую на эвтектической линии  является линией кристаллизации двойной эвтектики
является линией кристаллизации двойной эвтектики  . Когда кристаллизация компонентов в жидкости будет отвечать точке 6, начнет кристаллизоваться двойная эвтектика
. Когда кристаллизация компонентов в жидкости будет отвечать точке 6, начнет кристаллизоваться двойная эвтектика  и состав жидкости будет изменяться в сторону увеличения в ней компонента С до тех пор, пока не станет характеризоваться точкой Е. Жидкость состава Е при температуре
и состав жидкости будет изменяться в сторону увеличения в ней компонента С до тех пор, пока не станет характеризоваться точкой Е. Жидкость состава Е при температуре  рис. 121) кристаллизуется, образуя тройную эвтектику
рис. 121) кристаллизуется, образуя тройную эвтектику  , т. е. при охлаждении идет реакция:
, т. е. при охлаждении идет реакция:

Соединим прямой линией точки Е и А. Концентрационная точка сплава О будет лежать внутри фигуры  . Продолжение прямой, соединяющей вершину А с точкой любого сплава, лежащего внутри этой фигуры, достигнет (пересечет) линию
. Продолжение прямой, соединяющей вершину А с точкой любого сплава, лежащего внутри этой фигуры, достигнет (пересечет) линию  т. е. по выделении кристаллов А начнется выделение двойной эвтектики
т. е. по выделении кристаллов А начнется выделение двойной эвтектики  и затем тройной эвтектики
и затем тройной эвтектики  . Если концентрационная точка лежит внутри фигуры
. Если концентрационная точка лежит внутри фигуры  то после выделения кристаллов А будет выделяться эвтектика
то после выделения кристаллов А будет выделяться эвтектика  .
.
Таким образом, можно установить три этапа кристаллизации нашего сплава: выделение первичных кристаллов (отрезок 1—2, см. рис. 119), выделение двойной эвтектики (отрезок 2—3) и выделение тройной эвтектики (отрезок 3—3).
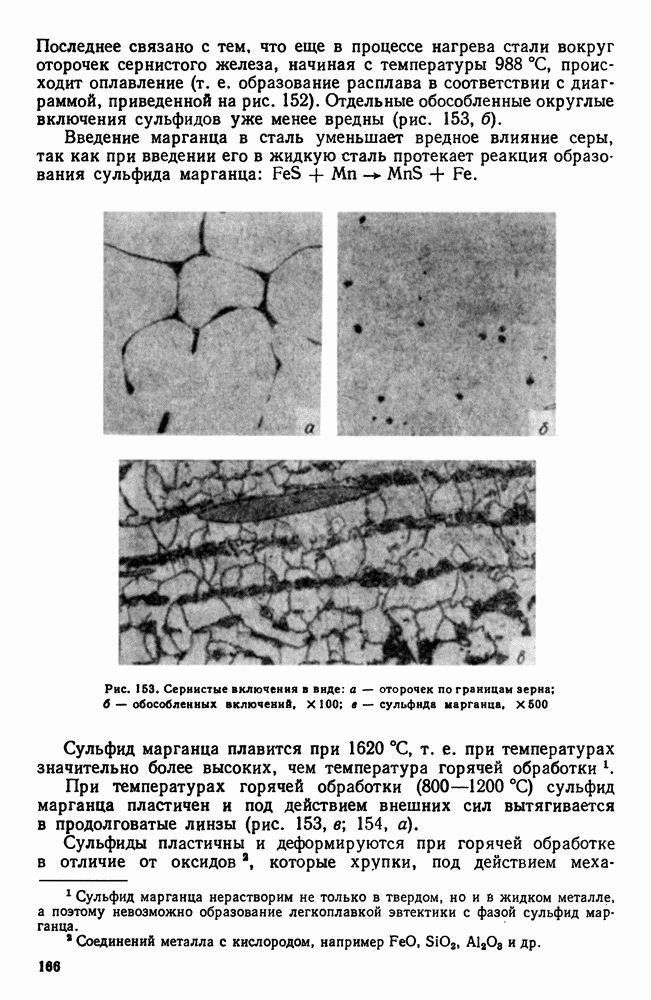
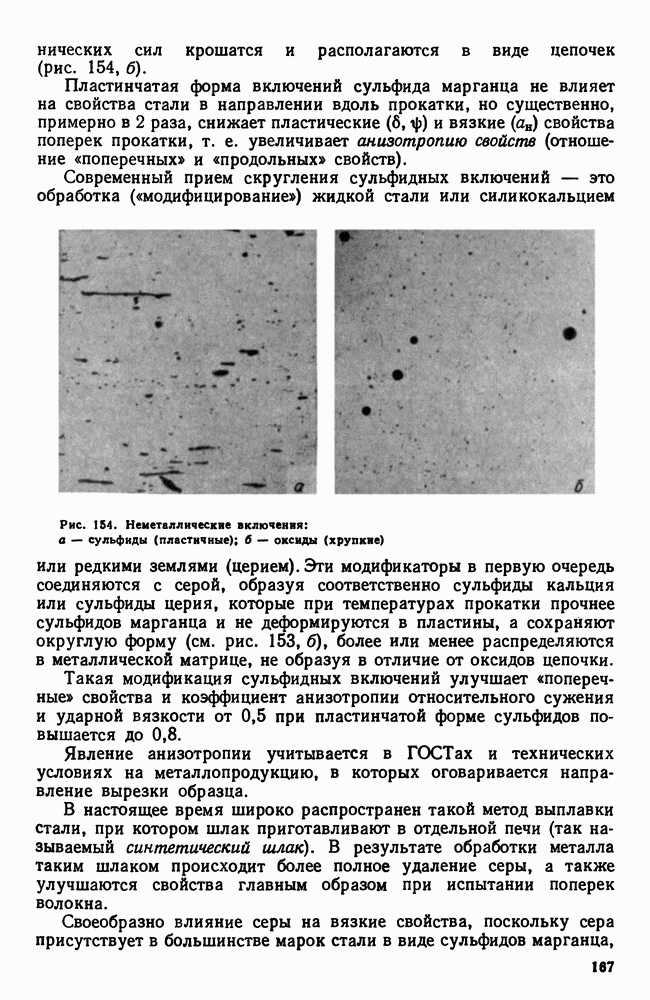
Структура тройного сплава (рис. 122) будет состоять из первичных кристаллов (кристаллы  ), двойной (кристаллы
), двойной (кристаллы  и тройной
и тройной  эвтектик.
эвтектик.
Тройная эвтектика образуется во всех тройных сплавах, кристаллизующихся по типу, изображенному на диаграммах рис. 120 и 121. Природа первичных кристаллов и двойной эвтектики зависит от того, в какой области диаграммы будет находиться концентрационная точка сплава (табл. 13).
Таблица 13. (см. скан) Область на тройной диаграмме и соответствующая ей структура
Конечно, в структуре двойных сплавов  не будет тройной эвтектики. В сплавах, лежащих на линиях двойных эвтектик
не будет тройной эвтектики. В сплавах, лежащих на линиях двойных эвтектик  не будет первичных кристаллов чистых компонентов; в этих сплавах кристаллизаций начнется выделением сразу двойной эвтектики. Сплавы, лежащие на линиях, соединяющих точку тройной эвтектики и вершины треугольника, также не будут иметь в структуре двойной эвтектики. Применяя правило прямой линии, приходим к выводу, что в таких сплавах после выделения чистого компонента жидкость примет концентрацию точки Е и тогда начнется кристаллизация тройной эвтектики.
не будет первичных кристаллов чистых компонентов; в этих сплавах кристаллизаций начнется выделением сразу двойной эвтектики. Сплавы, лежащие на линиях, соединяющих точку тройной эвтектики и вершины треугольника, также не будут иметь в структуре двойной эвтектики. Применяя правило прямой линии, приходим к выводу, что в таких сплавах после выделения чистого компонента жидкость примет концентрацию точки Е и тогда начнется кристаллизация тройной эвтектики.
Наконец, сплав, отвечающий точке Е, состоит из тройной эвтектики. В данной системе это самый легкоплавкий сплав. Процесс кристаллизации начнется при температуре  с одновременным выделением кристаллов всех трех компонентов.
с одновременным выделением кристаллов всех трех компонентов.
На плоскостном изображении диаграммы (см. рис. 120) температурной оси нет. Можно проследить последовательно за процессом кристаллизации, не отмечая, при какой температуре какая фаза начинает кристаллизоваться. Если на диаграмму нанести линии, соответствующие одинаковым температурам (изотермы), т. е. линии,
которые представляют собой пересечения горизонтальных изотермических) плоскостей с поверхностями диаграммы, то можно будет с некоторым приближением судить о температурах превращения.
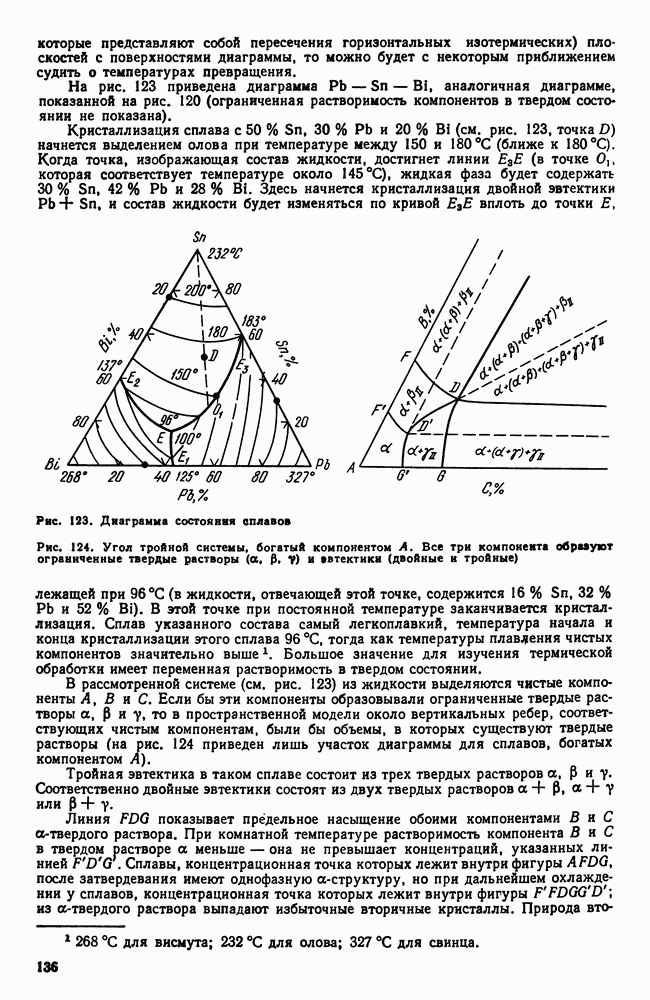
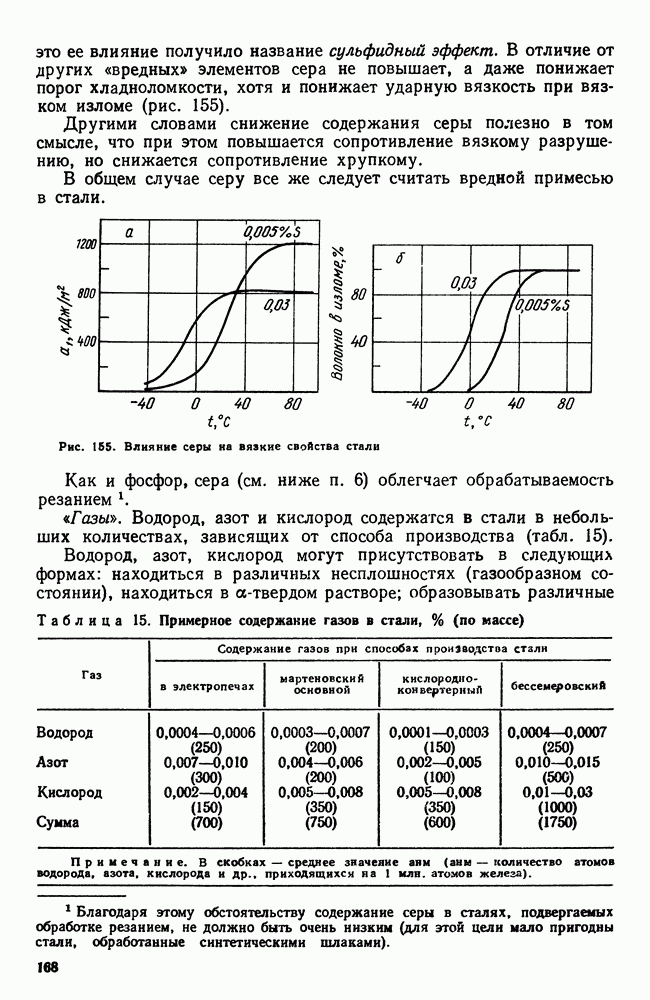
На рис. 123 приведена диаграмма  аналогичная диаграмме, показанной на рис. 120 (ограниченная растворимость компонентов в твердом состоянии не показана).
аналогичная диаграмме, показанной на рис. 120 (ограниченная растворимость компонентов в твердом состоянии не показана).
Кристаллизация сплава с  и
и  (см. рис. 123, точка
(см. рис. 123, точка  начнется выделением олова при температуре между 150 и 180°С (ближе к
начнется выделением олова при температуре между 150 и 180°С (ближе к  Когда точка, изображающая состав жидкости, достигнет линии
Когда точка, изображающая состав жидкости, достигнет линии  (в точке
(в точке  которая соответствует температуре около
которая соответствует температуре около  жидкая фаза будет содержать
жидкая фаза будет содержать  и
и  Здесь начнется кристаллизация двойной эвтектики
Здесь начнется кристаллизация двойной эвтектики  и состав жидкости будет изменяться по кривой
и состав жидкости будет изменяться по кривой  вплоть до точки Е, лежащей при
вплоть до точки Е, лежащей при  (в жидкости, отвечающей этой точке, содержится
(в жидкости, отвечающей этой точке, содержится  и
и 

Рис. 123. Диаграмма состояния сплавов

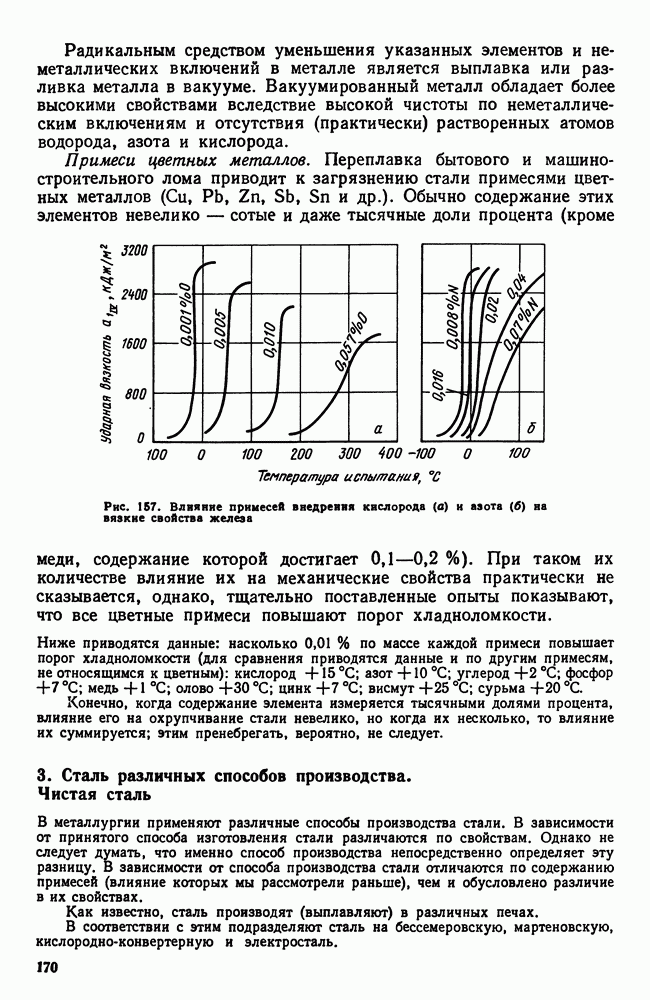
Рис. 124. Угол тройной системы, богатый компонентом А. Все три компонента образуют ограниченные твердые растворы  и «втектики (двойные и тройные)
и «втектики (двойные и тройные)
В этой точке при постоянной температуре заканчивается кристаллизация. Сплав указанного состава самый легкоплавкий, температура начала и конца кристаллизации этого сплава  тогда как температуры плавления чистых компонентов значительно выше. Большое значение для изучения термической обработки имеет переменная растворимость в твердом состоянии.
тогда как температуры плавления чистых компонентов значительно выше. Большое значение для изучения термической обработки имеет переменная растворимость в твердом состоянии.
В рассмотренной системе (см. рис. 123) из жидкости выделяются чистые компоненты А, В и С, Если бы эти компоненты образовывали ограниченные твердые растворы а, Р и 7, то в пространственной модели около вертикальных ребер, соответствующих чистым компонентам, были бы объемы, в которых существуют твердые растворы (на рис. 124 приведен лишь участок диаграммы для сплавов, богатых компонентом А).
Тройная эвтектика в таком сплаве состоит из трех твердых растворов  . Соответственно двойные эвтектики состоят из двух твердых растворов а
. Соответственно двойные эвтектики состоят из двух твердых растворов а  или
или  .
.
Линия  показывает предельное насыщение обоими компонентами
показывает предельное насыщение обоими компонентами  -твердого раствора. При комнатной температуре растворимость компонента
-твердого раствора. При комнатной температуре растворимость компонента  в твердом растворе а меньше — она не превышает концентраций, указанных линией
в твердом растворе а меньше — она не превышает концентраций, указанных линией  Сплавы, концентрационная точка которых лежит внутри фигуры
Сплавы, концентрационная точка которых лежит внутри фигуры  после затвердевания имеют однофазную
после затвердевания имеют однофазную  -структуру, но при дальнейшем охлаждении у сплавов, концентрационная точка которых лежит внутри фигуры
-структуру, но при дальнейшем охлаждении у сплавов, концентрационная точка которых лежит внутри фигуры  из
из  -твердого раствора выпадают избыточные вторичные кристаллы. Природа
-твердого раствора выпадают избыточные вторичные кристаллы. Природа
вторичных фаз указана на рис. 124 и определяется составом сплава (на линии  избыточные
избыточные  и у-фазы выделяются одновременно, что характеризует процесс эвтектоидного превращения).
и у-фазы выделяются одновременно, что характеризует процесс эвтектоидного превращения).
Сплавы, лежащие внутри фигуры  являются однофазными (а-твердый раствор) при всех температурах существования сплава в твердом состоянии.
являются однофазными (а-твердый раствор) при всех температурах существования сплава в твердом состоянии.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ТЕОРИЯ СПЛАВОВ
- Глава I. КРИСТАЛЛИЧЕСКОЕ СТРОЕНИЕ МЕТАЛЛОВ
- 2. Классификация металлов
- 3. Кристаллическое строение металлов
- 4. Кристаллические решетки металлов
- 5. Реальное строение металлических кристаллов
- 6. Анизотропия свойств кристаллов
- 7. Методы изучения строения металлов
- Глава II. КРИСТАЛЛИЗАЦИЯ
- 1. Три состояния вещества
- 2. Энергетические условия процесса кристаллизации
- 3. Механизм процесса кристаллизации
- 4. Форма кристаллических образований
- 5. Строение слитка
- 6. Превращения в твердом состояние. Полиморфизм
- 7. Магнитные превращения
- 8. Закалка из жидкого состояния. Аморфное состояние
- Глава III. МЕХАНИЧЕСКИЕ СВОЙСТВА. НАКЛЕП И РЕКРИСТАЛЛИЗАЦИЯ
- 2. Упругая и пластическая деформация. Несовершенства решетки и прочность металлов
- 3. Сверхпластичность
- 4. Разрушение
- 5. Методы определения механических свойств
- 6. Наклеп
- 7. Влияние нагрева на строение и свойства деформированного металла (рекристаллизационные процессы)
- Глава IV. СТРОЕНИЕ СПЛАВОВ
- 2. Химическое соединение
- 3. Твердый раствор на основе одного из компонентов сплава
- 4. Твердый раствор на основе химического соединения
- 5. Упорядоченные твердые растворы
- 6. Электронные соединения (фазы Юм-Розери)
- 7. Фазы Лавеса
- 8. Фазы внедрения
- Глава V. ДИАГРАММА СОСТОЯНИЯ
- 2. Общие замечания о построении диаграмм состояния
- 3. Экспериментальное построение диаграмм
- 4. Диаграмма состояния для сплавов, образующих механические смеси из чистых компонентов (I рода)
- 5. Правило отрезков
- 6. Диаграмма состояния для сплавов с неограниченной растворимостью в твердом состоянии (II рода)
- 7. Диаграмма состояния для сплавов с ограниченной растворимостью в твердом состоянии (III рода)
- 8. Диаграмма состояния для сплавов, образующих химические соединения (IV рода)
- 9. Диаграмма состояния для сплавов, испытывающих полиморфные превращения
- 10. Кристаллизация сплавов в неравновесных условиях
- 11. Системы с тремя компонентами
- 12. Упрощенные методы изучения многокомпонентных систем
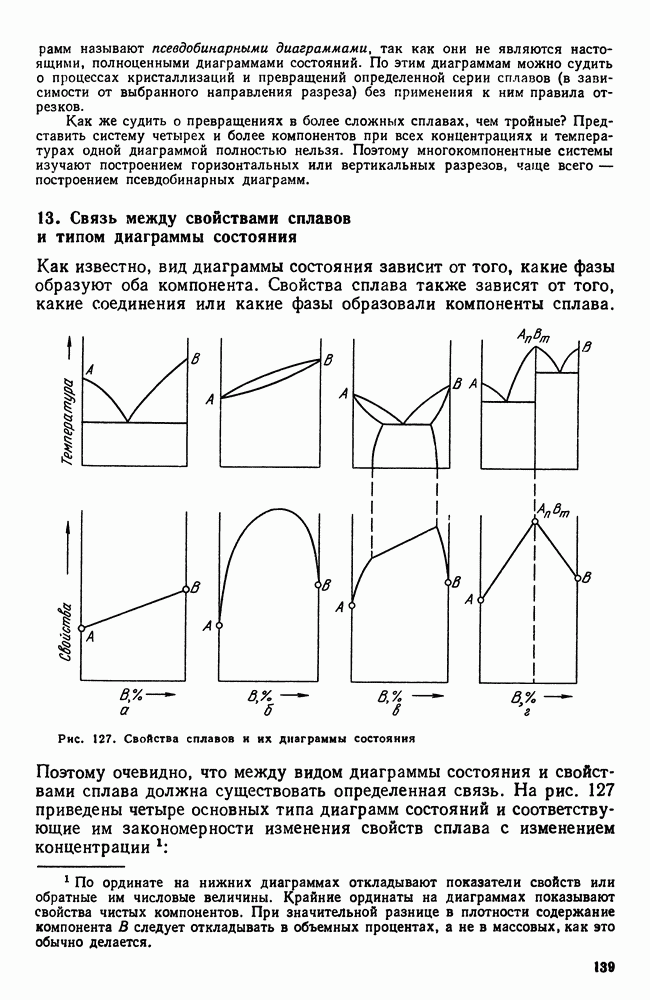
- 13. Связь между свойствами сплавов и типом диаграммы состояния
- Часть вторая. ЖЕЛЕЗОУГЛЕРОДИСТЫЕ СПЛАВЫ
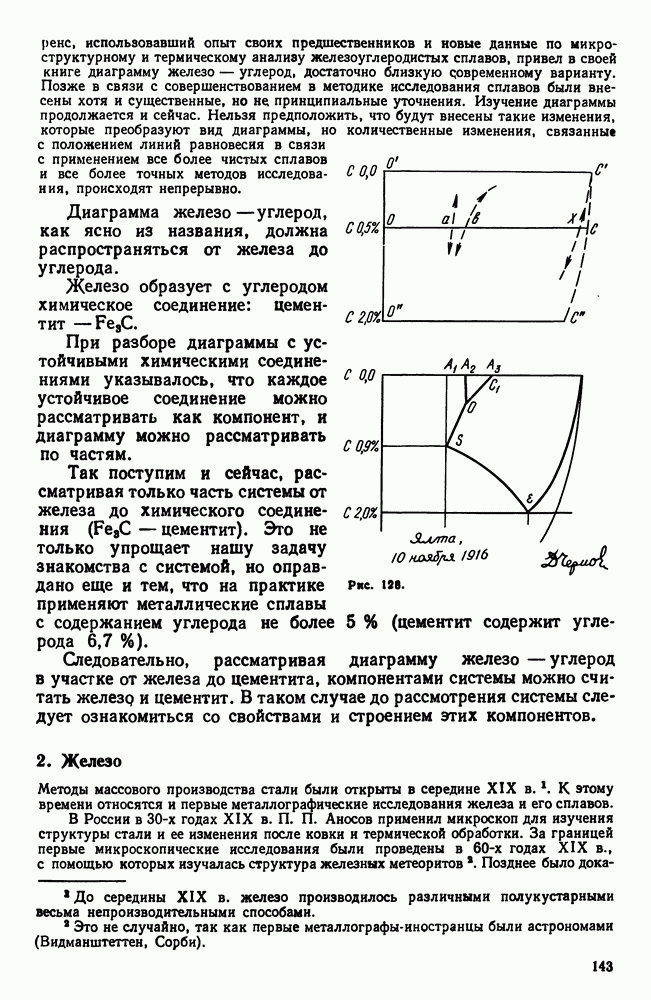
- Глава VI. ДИАГРАММА ЖЕЛЕЗО—УГЛЕРОД
- 2. Железо
- 3. Цементит
- 4. Диаграмма состояния
- Глава VII. УГЛЕРОДИСТЫЕ СТАЛИ
- 1. Влияние углерода на свойства стали
- 2. Влияние постоянных примесей на свойства стали
- 3. Сталь различных способов производства. Чистая сталь
- 4. Углеродистая сталь общего назначения
- 5. Нагартованная сталь
- 6. Листовая сталь для холодной штамповки
- 7. Обрабатываемость резанием. Автоматные стали
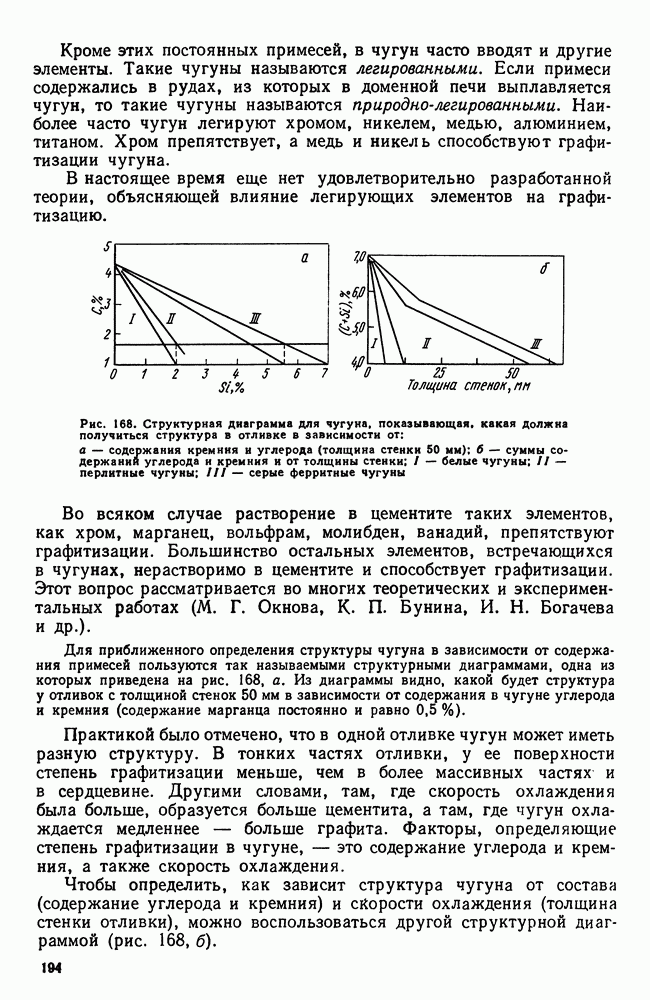
- Глава VIII. ЧУГУН
- 2. Структура чугуна. Формы графита
- 3. Структура и свойства чугуна
- 4. Примеси в чугуне
- 5. Марки серых и высокопрочных чугунов
- 6. Ковкий чугун
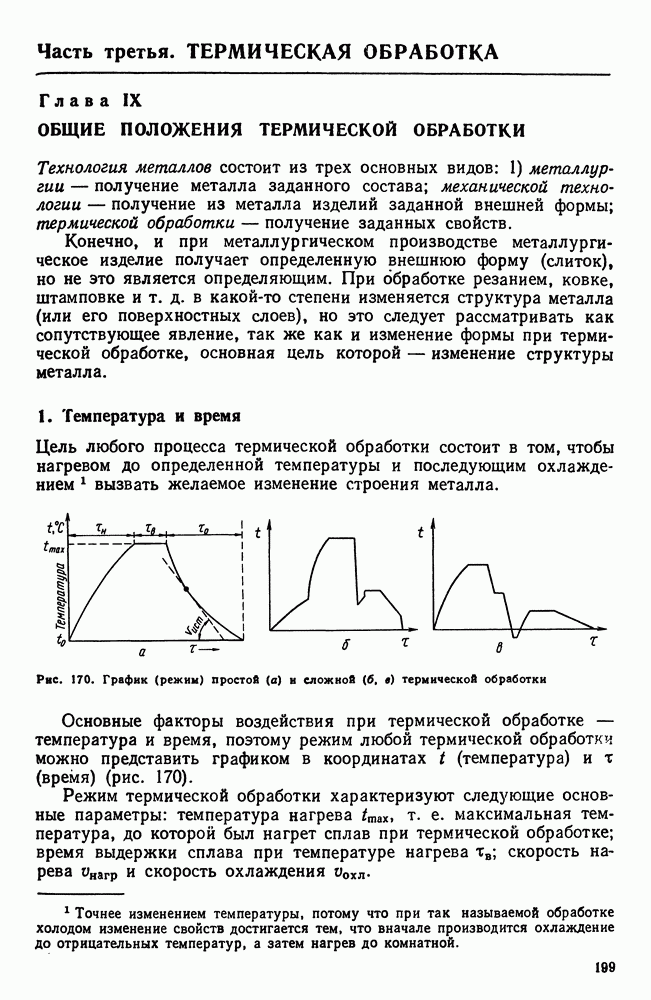
- Часть третья. ТЕРМИЧЕСКАЯ ОБРАБОТКА
- Глава IX. ОБЩИЕ ПОЛОЖЕНИЯ ТЕРМИЧЕСКОЙ ОБРАБОТКИ
- 2. Классификация видов термической обработки
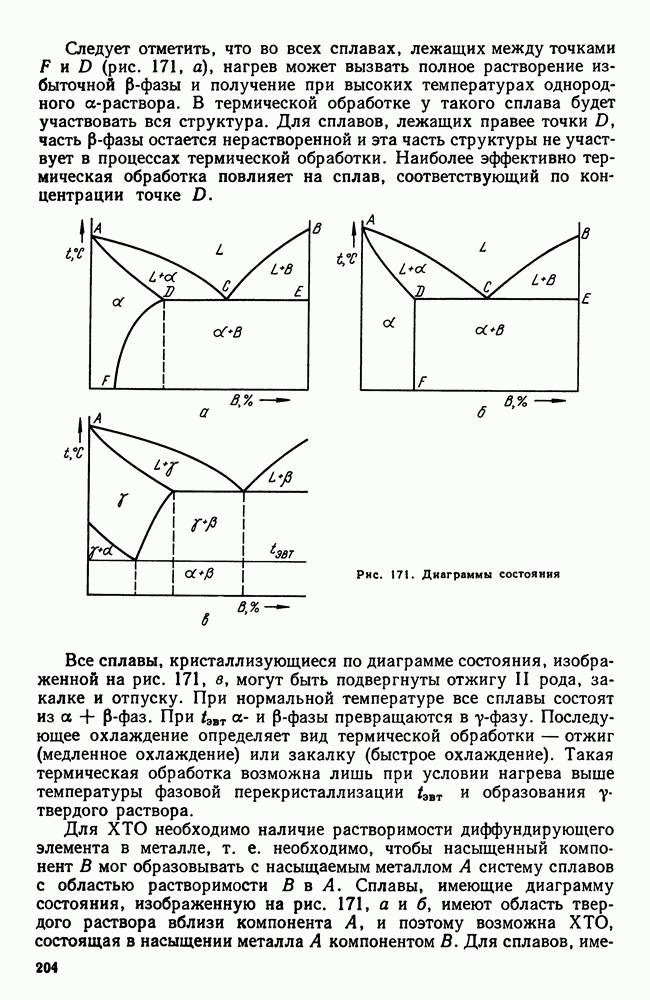
- 3. Термическая обработка и диаграмма состояния
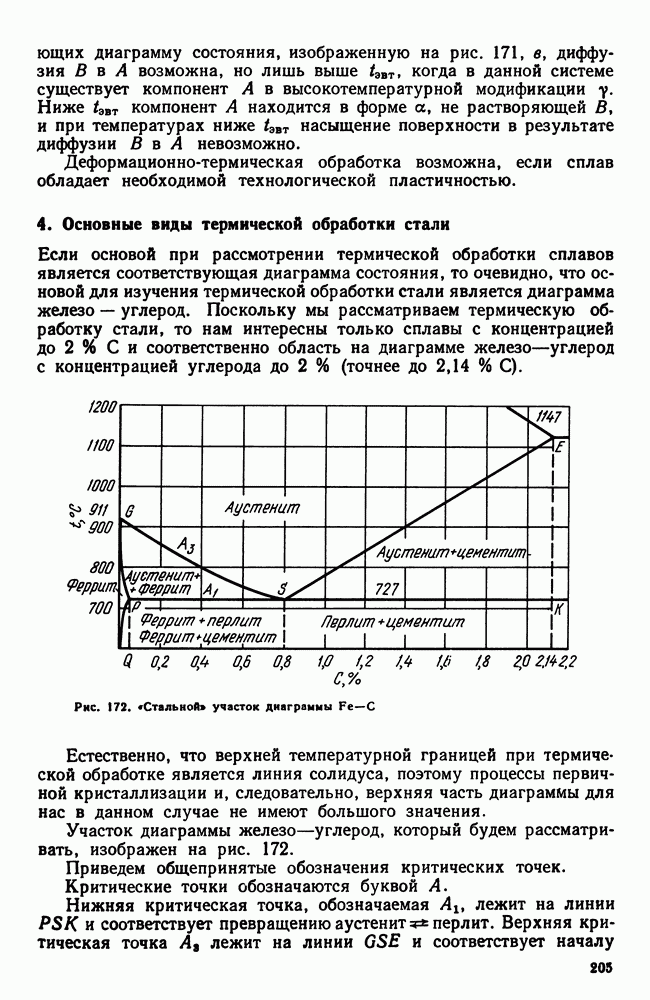
- 4 Основные виды термической обработки стали
- 5. Четыре основных превращения в стали
- Глава X. ТЕОРИЯ ТЕРМИЧЕСКОЙ ОБРАБОТКИ СТАЛИ
- 2. Рост аустенитного зерна
- 3. Распад аустенита
- 4. Мартенситное превращение
- 5. Бейнитное превращение
- 6. Превращения при отпуске
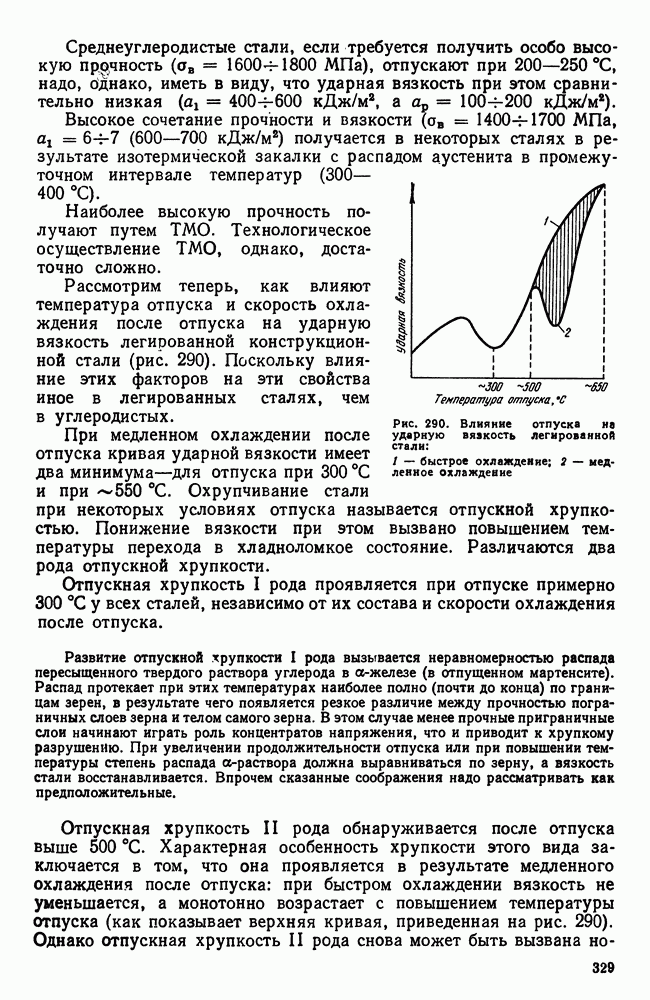
- 7. Влияние термической обработки на свойства стали
- 8. Термомеханическая обработка
- Глава XI. ПРАКТИКА ТЕРМИЧЕСКОЙ ОБРАБОТКИ СТАЛИ
- 2. Время нагрева
- 3. Химическое воздействие нагревающей среды
- 4. Закалочные среды
- 5. Прокаливаемость
- 6. Внутренние напряжения
- 7. Способы закалки
- 8. Обработка стали холодом
- 9. Дефекты, возникающие при закалке
- 10. Отжиг и нормализация
- Глава XII. ПОВЕРХНОСТНАЯ ЗАКАЛКА СТАЛИ
- 2. Высокочастотная закалка
- Глава XIII. ХИМИКО-ТЕРМИЧЕСКАЯ ОБРАБОТКА СТАЛИ
- 2. Цементация стали
- 3. Азотирование стали
- 4. Цианирование стали
- 5. Диффузионная металлизация
- Часть четвертая. ЛЕГИРОВАННЫЕ СТАЛИ И СПЛАВЫ
- Глава XIV. ВЛИЯНИЕ ЛЕГИРУЮЩИХ ЭЛЕМЕНТОВ
- 2. Влияние элементов на полиморфизм железа
- 3. Распределение легирующих элементов в стали
- 4. Влияние легирующих элементов на феррит
- 5. Карбидная фаза в легированных сталях
- 6. Влияние легирующих элементов на превращения в стали
- Глава XV. КЛАССИФИКАЦИЯ И МАРКИРОВКА ЛЕГИРОВАННЫХ СТАЛЕЙ
- 2. Маркировка легированных сталей
- Глава XVI. КОНСТРУКЦИОННЫЕ СТАЛИ
- 1. Механические свойства стали, влияние структуры и легирующих элементов
- 2. Термическая обработка конструкционных сталей
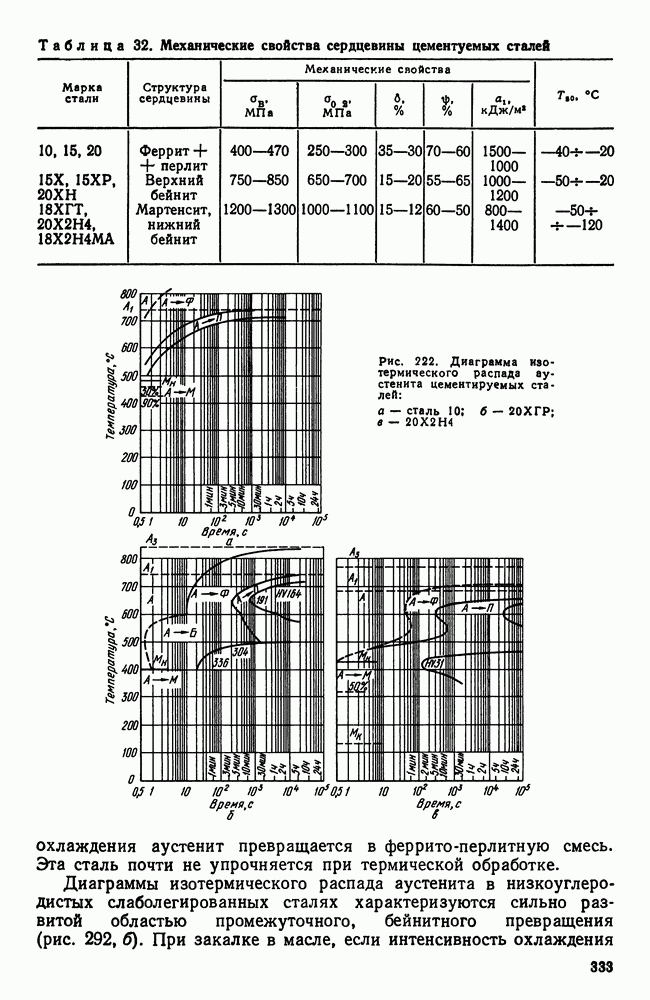
- 3. Цементуемые (низкоуглеродистые) стали
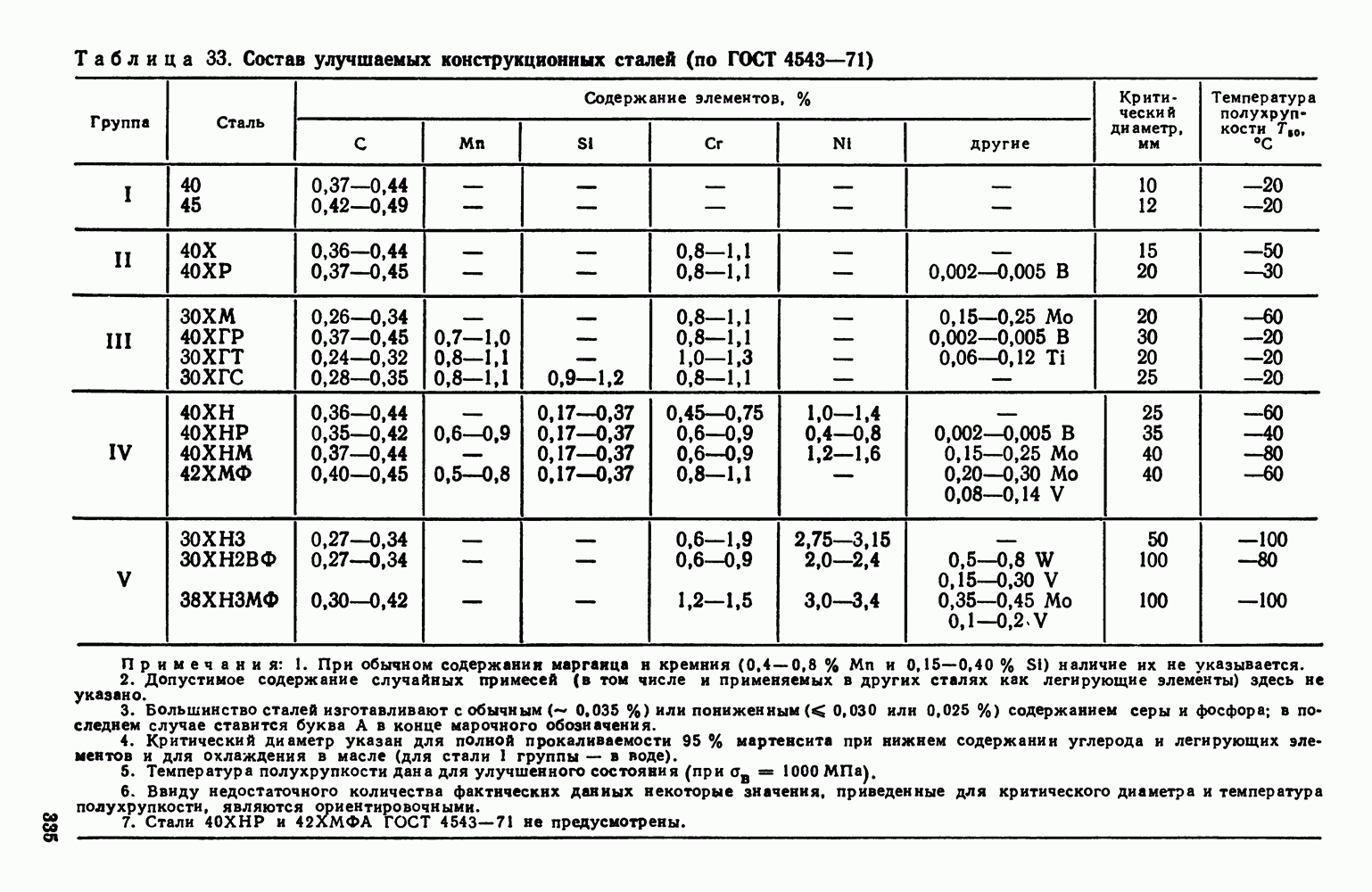
- 4. Улучшаемые (среднеуглеродистые) стали
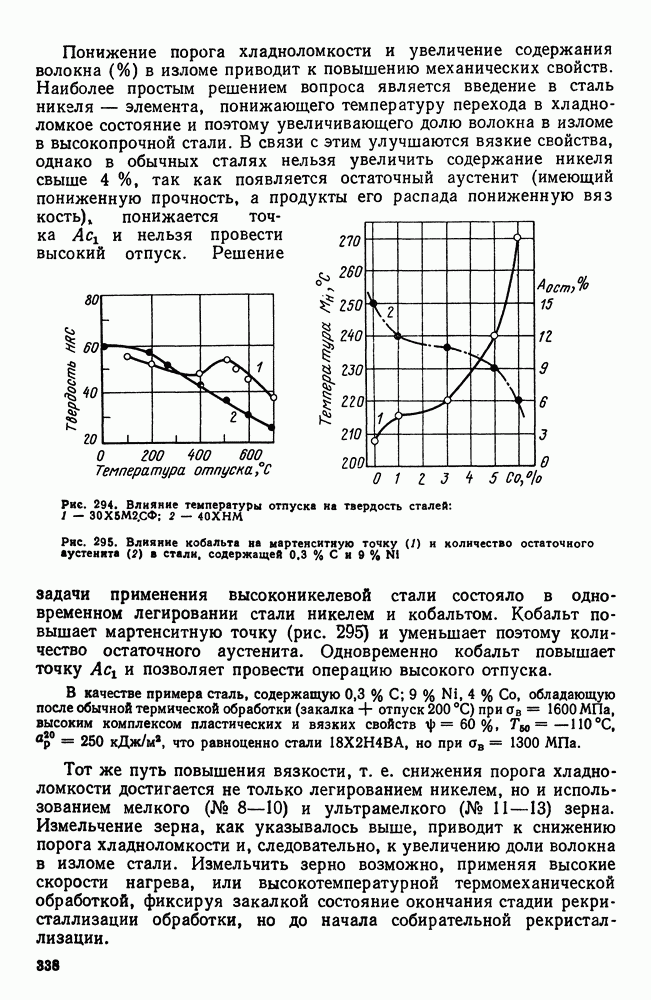
- 5. Высокопрочные стали
- 6. Свариваемость стали
- 7. Строительная сталь
- 8. Арматурная сталь
- 9. Пружинная сталь
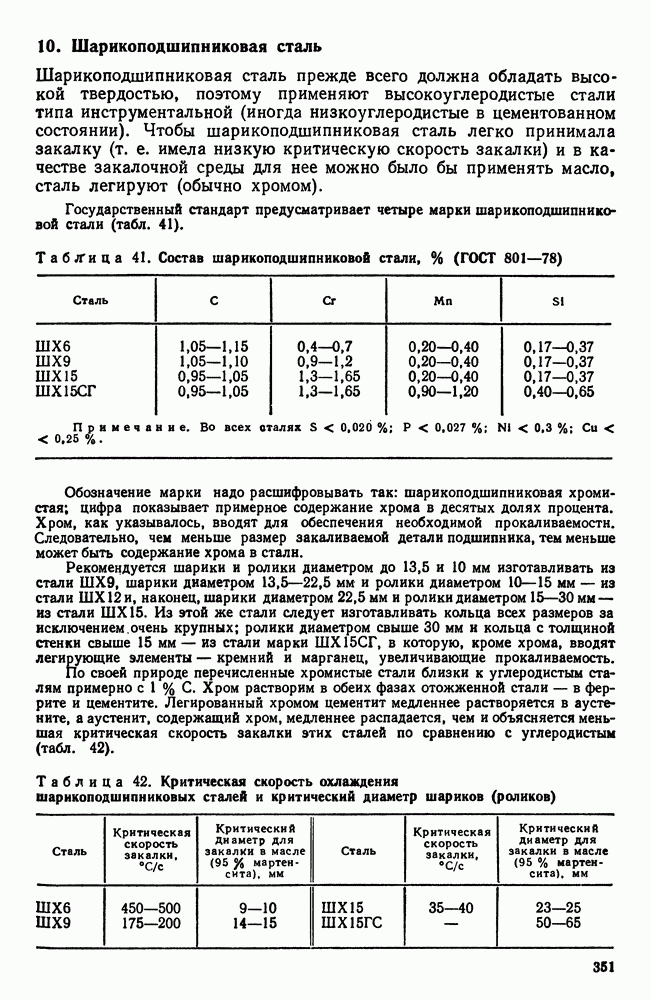
- 10. Шарикоподшипниковая сталь
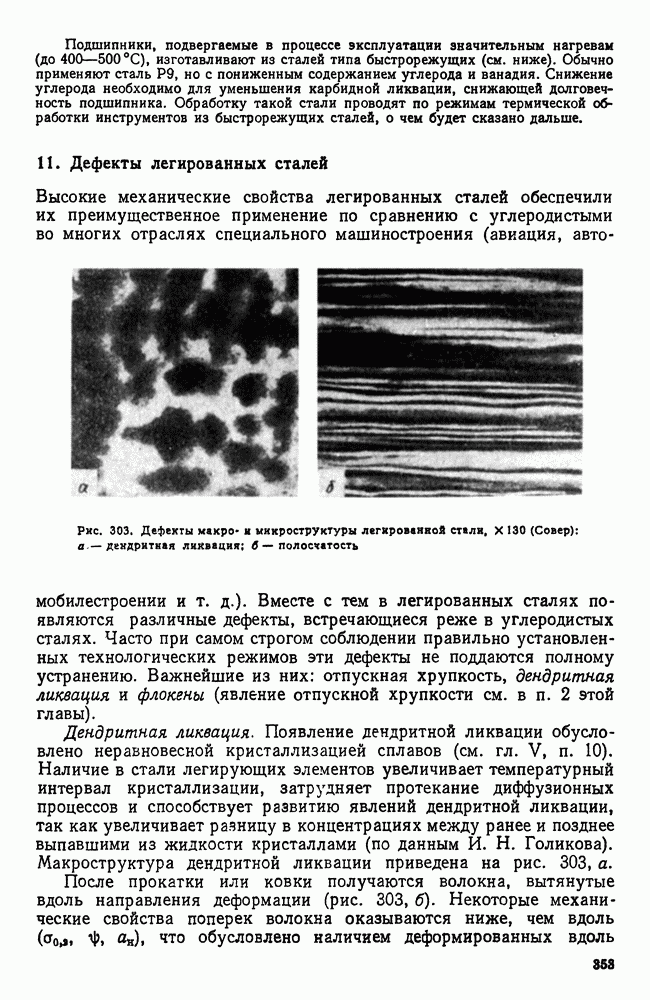
- 11. Дефекты легированных сталей
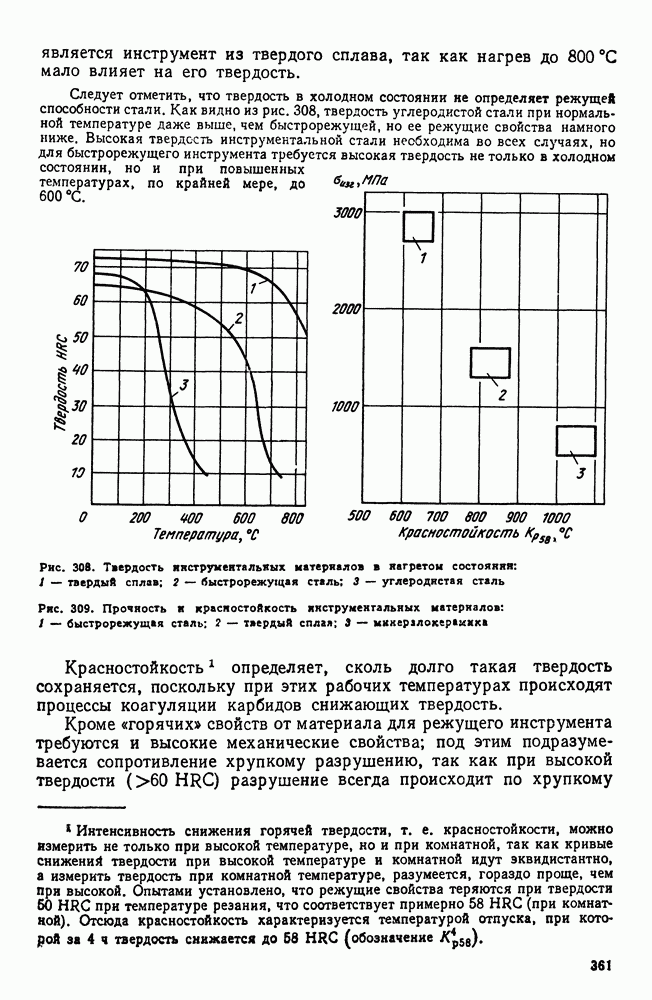
- Глава XVII. ИНСТРУМЕНТАЛЬНЫЕ СТАЛИ
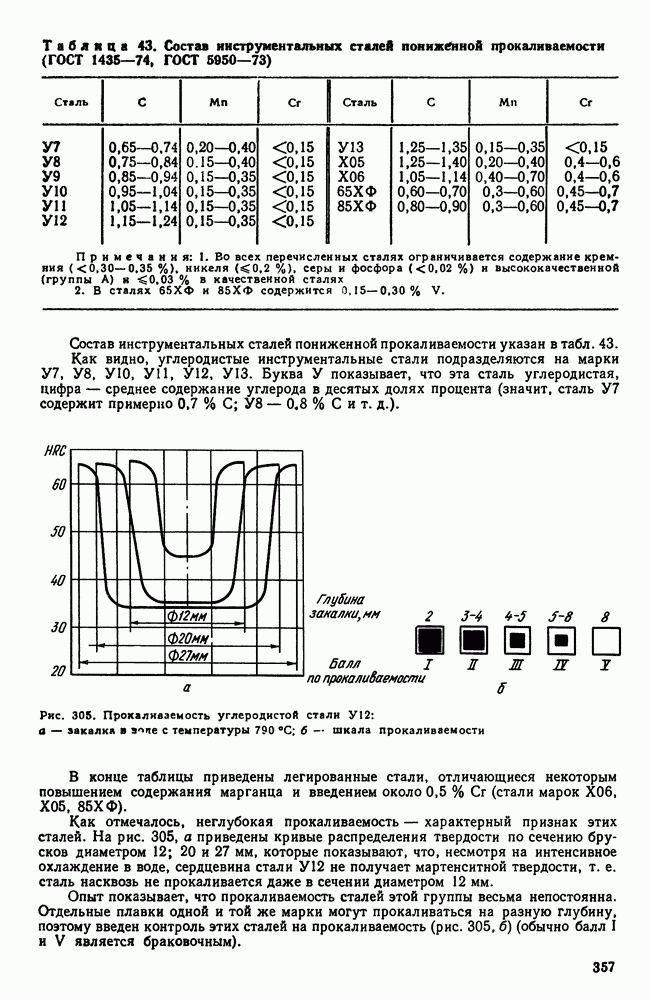
- 2. Инструментальные стали пониженной прокаливаемости
- 3. Инструментальные стали повышенной прокаливаемости (легированные инструментальные стали)
- 4. Быстрорежущие стали
- 5. Штамповые стали
- 6. Твердые сплавы
- Глава XVIII. ЖАРОСТОЙКИЕ И ЖАРОПРОЧНЫЕ СТАЛИ И СПЛАВЫ
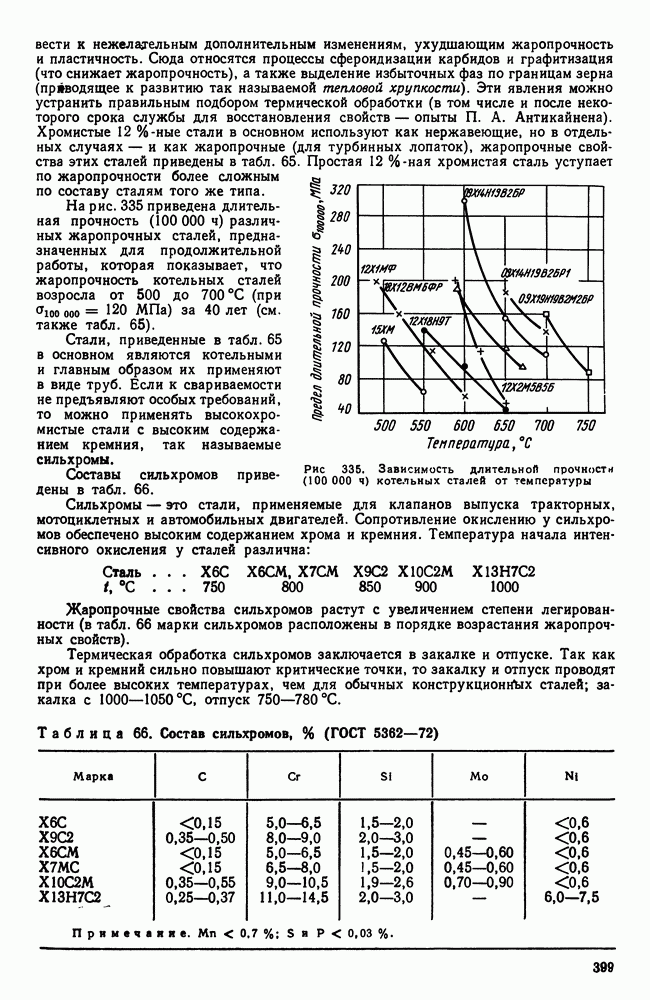
- 2. Жаропрочность
- 3. Оценка жаропрочных свойств
- 4. Влияние структуры и состава на жаропрочность
- 5. Классификация жаропрочных материалов
- 6. Перлитные и мартенситные жаропрочные стали
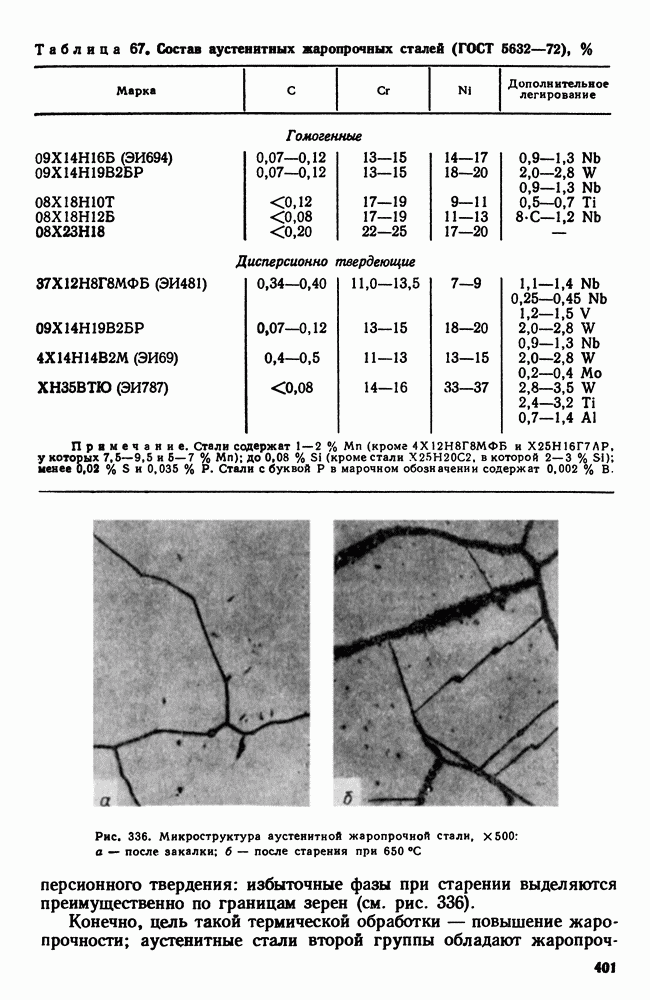
- 7. Аустенитные жаропрочные стали
- 8. Никелевые и кобальтовые жаропрочные сплавы
- Глава XIX. КОРРОЗИОННОСТОЙКИЕ (НЕРЖАВЕЮЩИЕ) СТАЛИ И СПЛАВЫ
- 2. Хромоникелевые нержавеющие стали
- 3. Кислотостойкие стали и сплавы
- 4. Криогенные стали и сплавы
- Глава XX. ИЗНОСОСТОЙКИЕ СТАЛИ И СПЛАВЫ
- 2. Графитизированная сталь
- 3. Высокомарганцовистая сталь
- 4. Наплавочные материалы
- Глава XXI. ТИТАН И ЕГО СПЛАВЫ
- 2. Легирование титана
- 3. Фазовые превращения в титановых сплавах
- 5. Термическая обработка титановых сплавов
- 6. Примеси в титановых сплавах
- 7. Коррозионная стойкость титана
- Глава XXII. ТУГОПЛАВКИЕ МЕТАЛЛЫ
- 2. Взаимодействие тугоплавких металлов с другими элементами и между собой
- 3. Механические свойства и жаропрочность
- 4. Хладноломкость тугоплавких металлов
- 5. Сопротивление окислению и защита от окисления
- 6. Коррозионная стойкость
- Глава XXIII. СПЛАВЫ С ОСОБЫМИ ТЕПЛОВЫМИ И УПРУГИМИ СВОЙСТВАМИ
- 2. Сплавы с постоянным модулем упругости
- Глава XXIV. МАГНИТНЫЕ СТАЛИ И СПЛАВЫ
- 2. Стали и сплавы для постоянных магнитов (магнитнотвердые сплавы)
- 3. Магнитномягкие сплавы
- 4. Немагнитные стали
- 5. Электротехнические сплавы
- Глава XXV. СПЛАВЫ АТОМНОЙ ЭНЕРГЕТИКИ
- 2. Конструкционные материалы. Теплоносители
- 3. Ядерное горючее (уран, плутоний, торий)
- Часть пятая. Цветные металлы и сплавы
- Глава XXVI. ЛЕГКИЕ МЕТАЛЛЫ И ИХ СПЛАВЫ
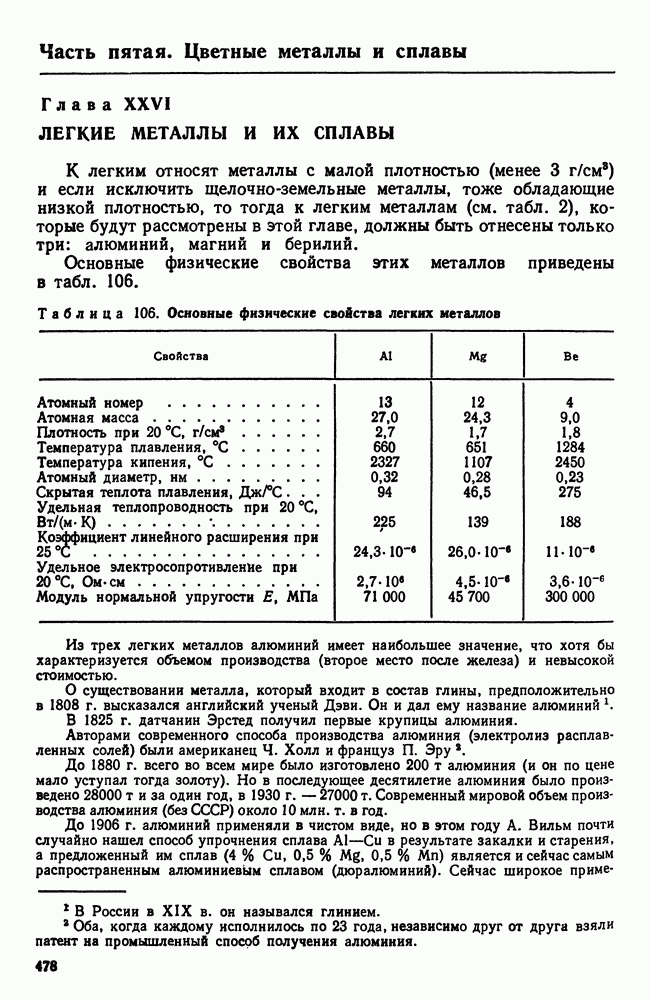
- 1. Свойства алюминия
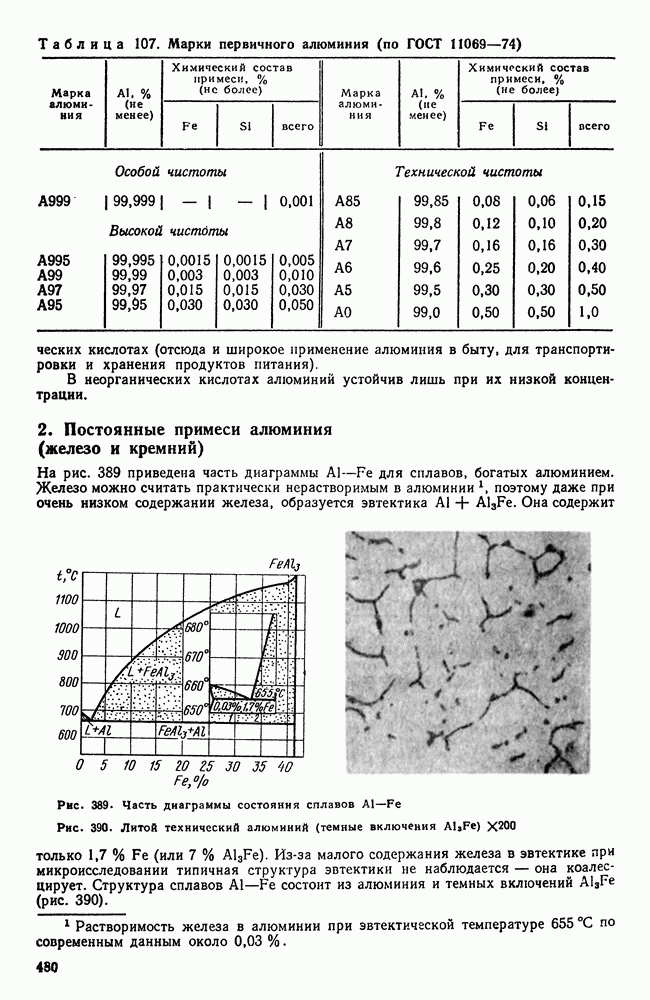
- 2. Постоянные примеси алюминия (железо и кремний)
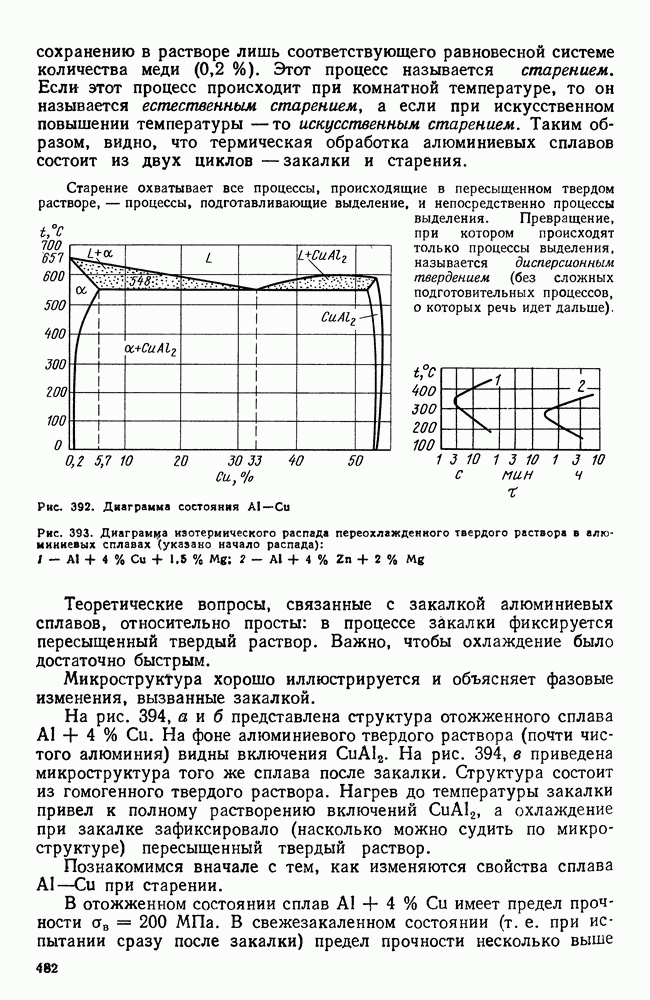
- 3. Термическая обработка сплавов Al-Cu
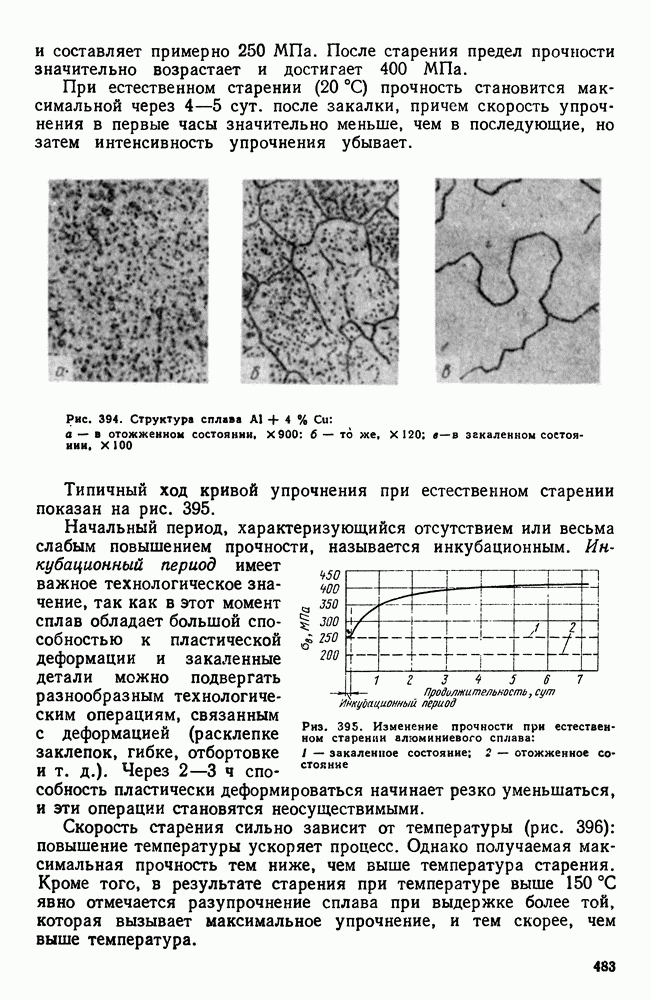
- 4. Влияние состава алюминиевых сплавов на процессы, происходящие при термической обработке
- 5. Классификация алюминиевых сплавов
- 6. Деформируемые сплавы, не упрочняемые термической обработкой
- 7. Дюралюминий и другие деформируемые сплавы, упрочняемые термической обработкой
- 8. Алюминиевые сплавы для поковок и штамповок
- 9. Силумины и другие алюминиевые сплавы для фасонного литья
- 10. Жаропрочные алюминиевые сплавы
- 11. Магний
- 12. Сплавы магния
- 13. Бериллий
- 14. Сплавы бериллия
- Глава XXVII. МЕДЬ И ЕЕ СПЛАВЫ
- 2. Сплавы меди с цинком (латуни)
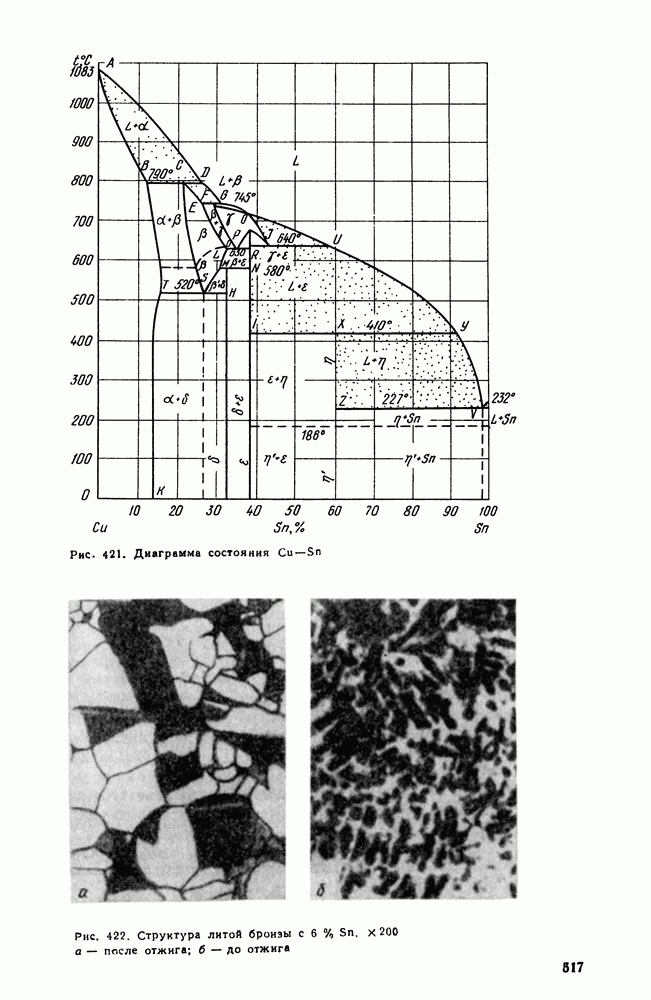
- 3. Сплавы меди с оловом (оловянистые бронзы)
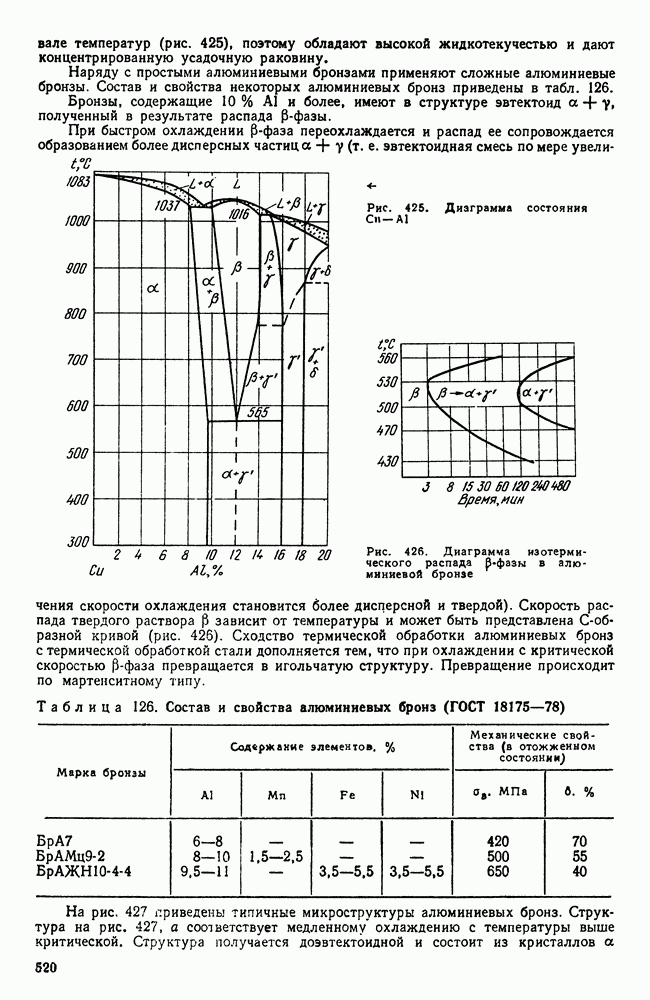
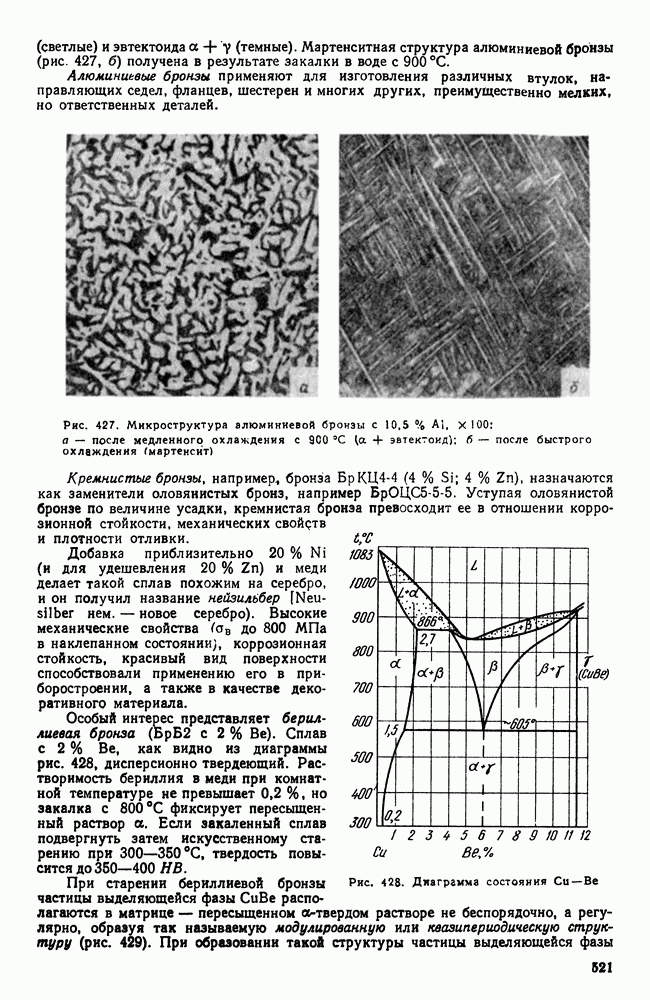
- 4. Сплавы меди с алюминием, кремнием, бериллием и другими элементами
- ГЛАВА XXVIII. ПОДШИПНИКОВЫЕ СПЛАВЫ И ПРИПОИ
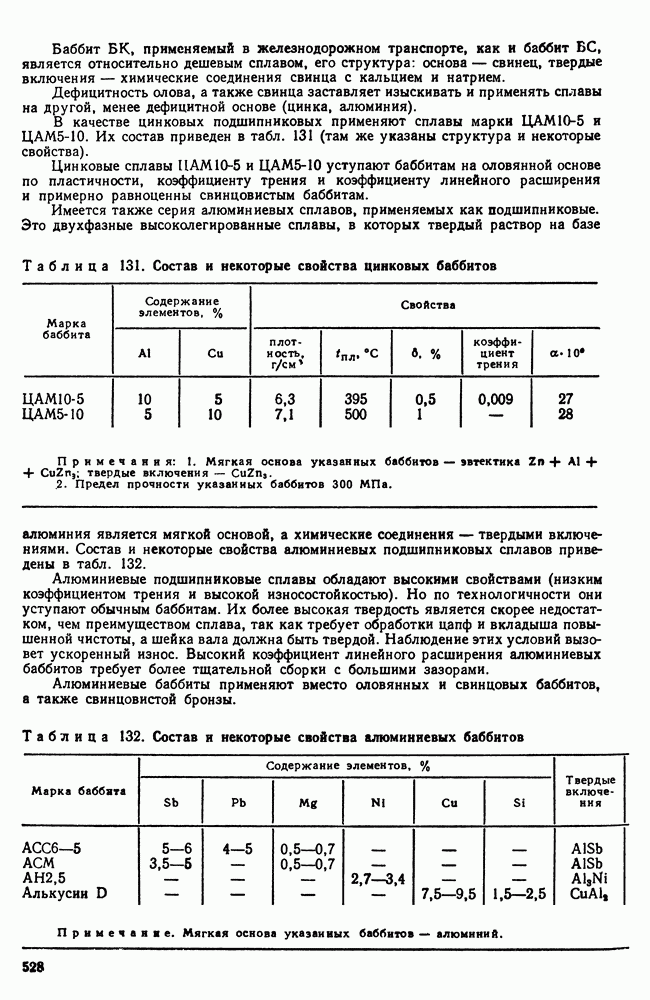
- 2. Легкоплавкие подшипниковые сплавы (баббиты)
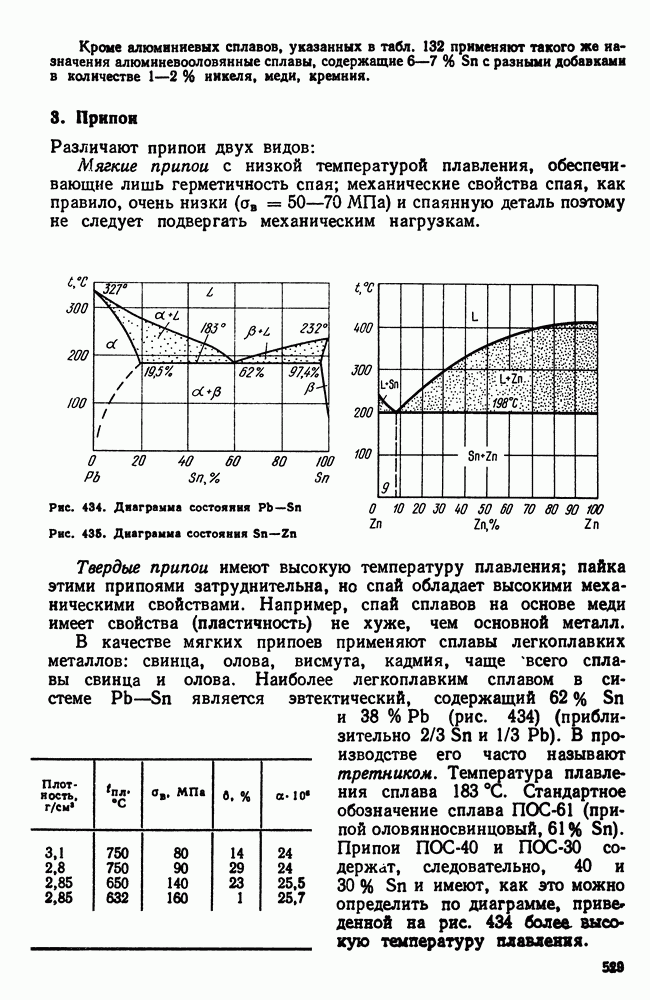
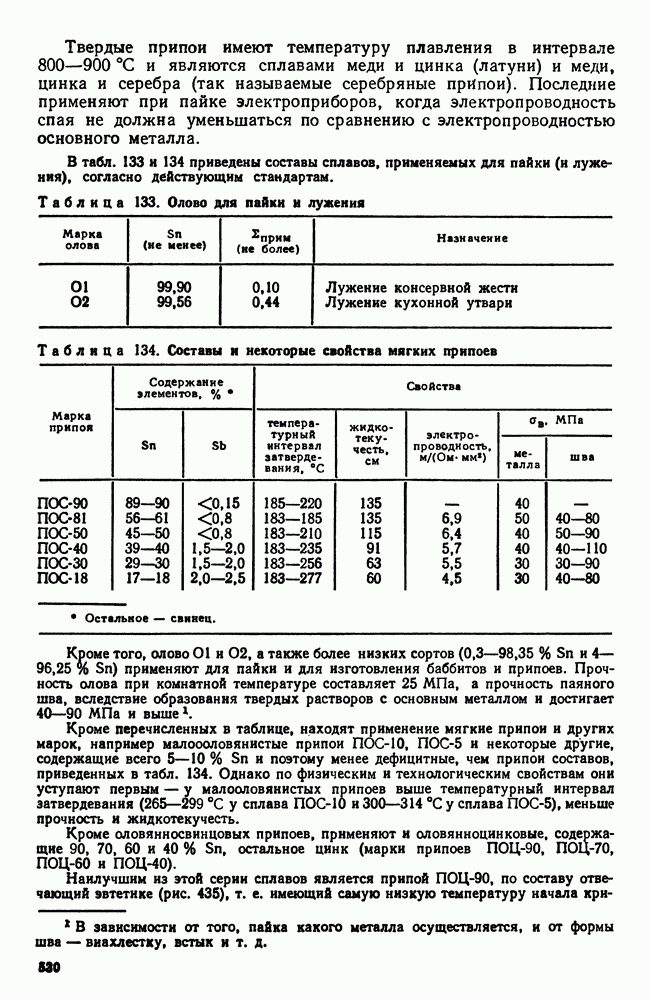
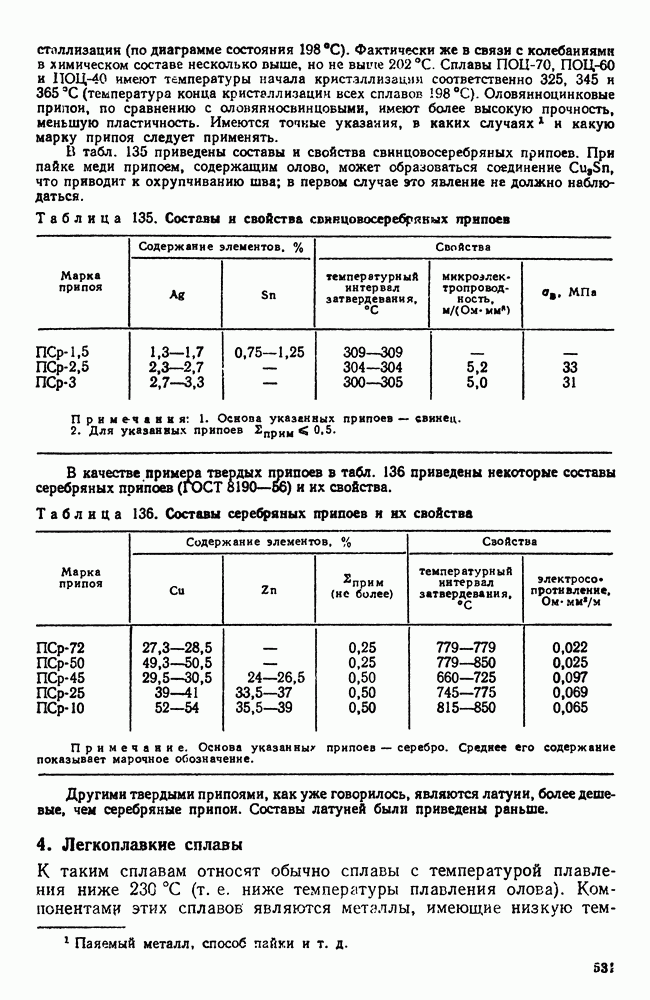
- 3. Припои
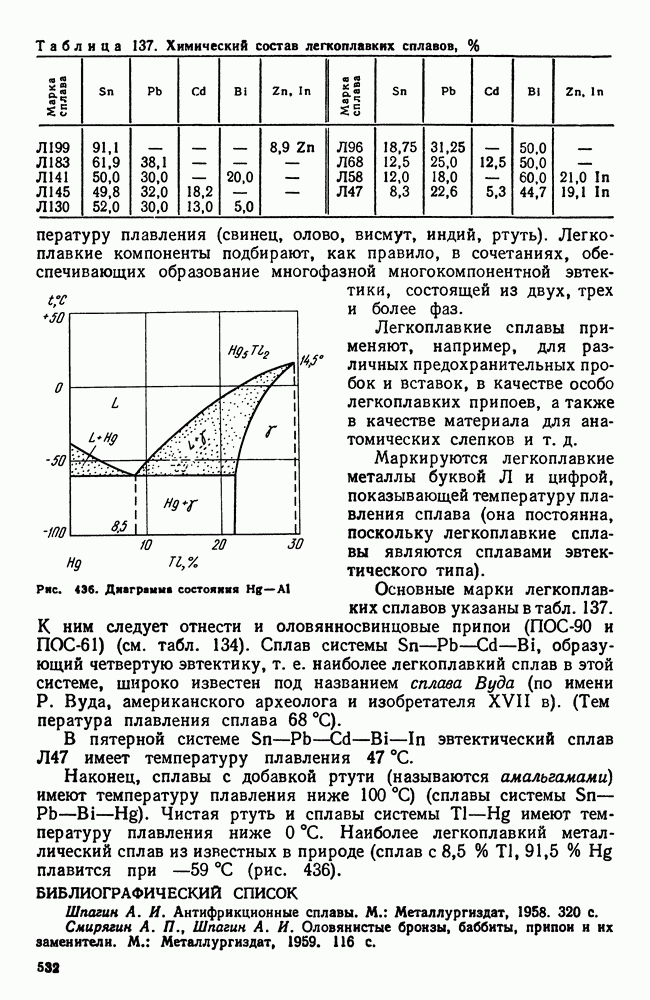
- 4. Легкоплавкие сплавы
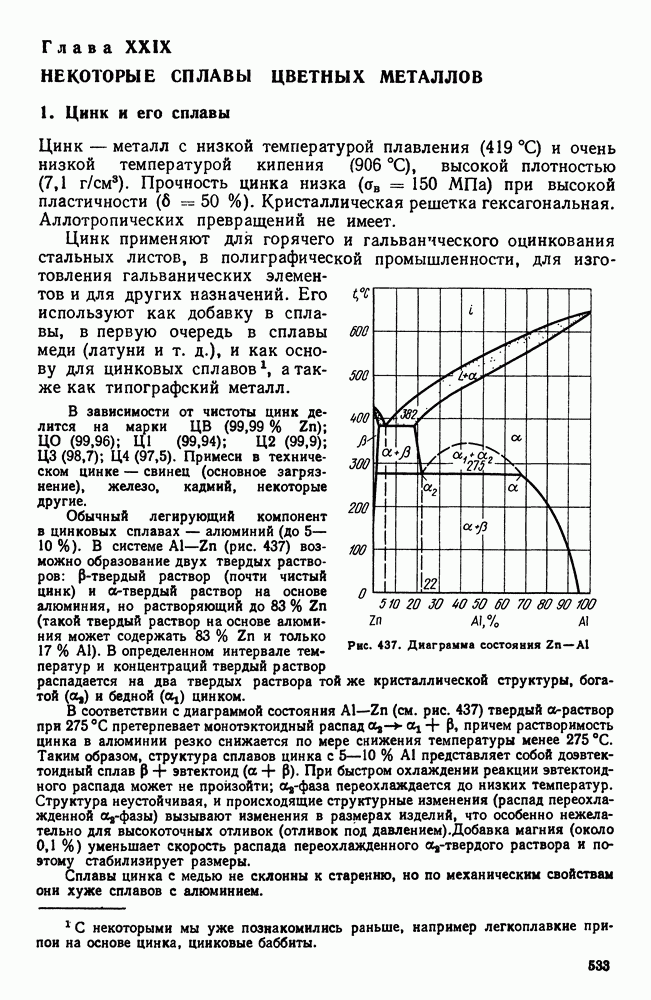
- Глава XXIX. НЕКОТОРЫЕ СПЛАВЫ ЦВЕТНЫХ МЕТАЛЛОВ
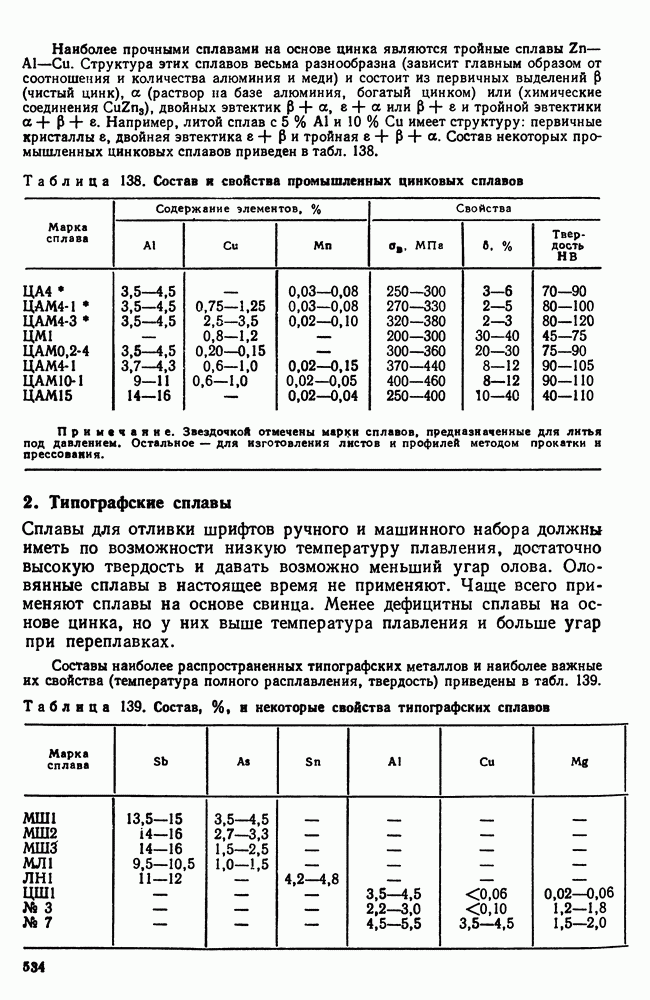
- 2. Типографские сплавы
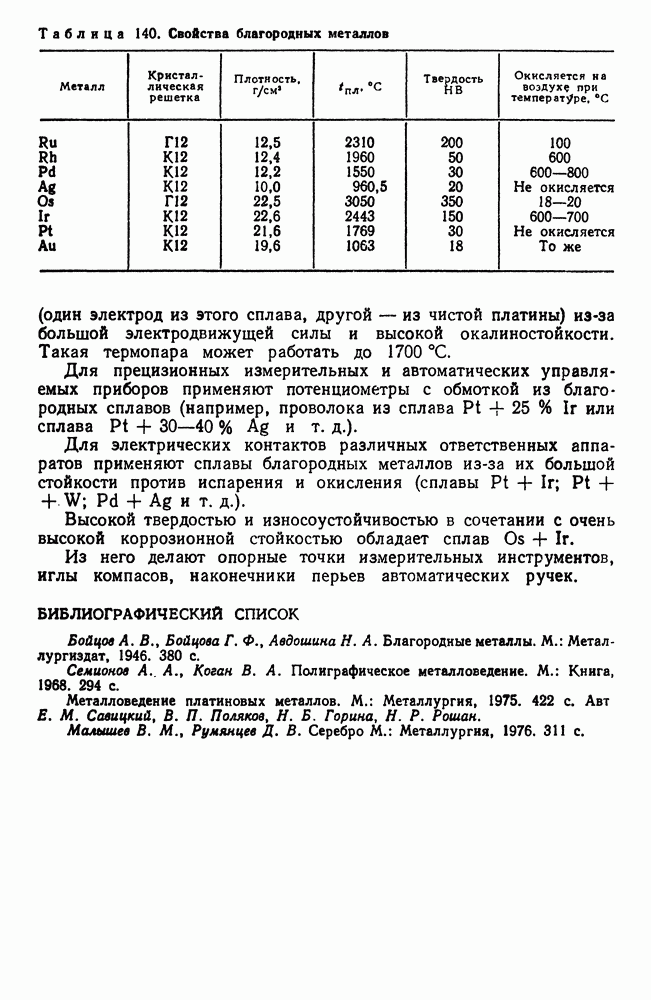
- 3. Благородные металлы