| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
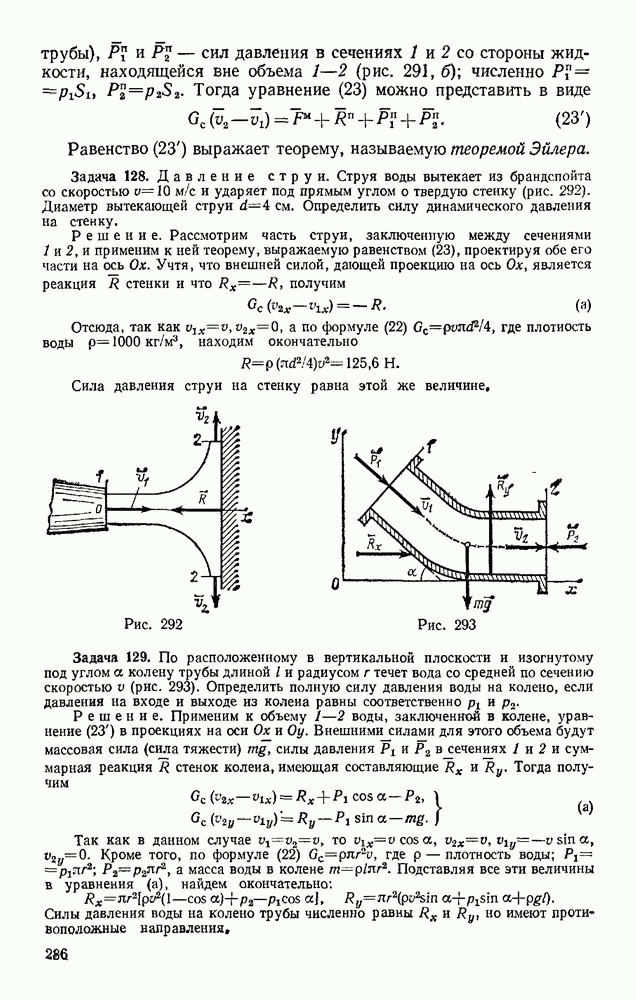
§ 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
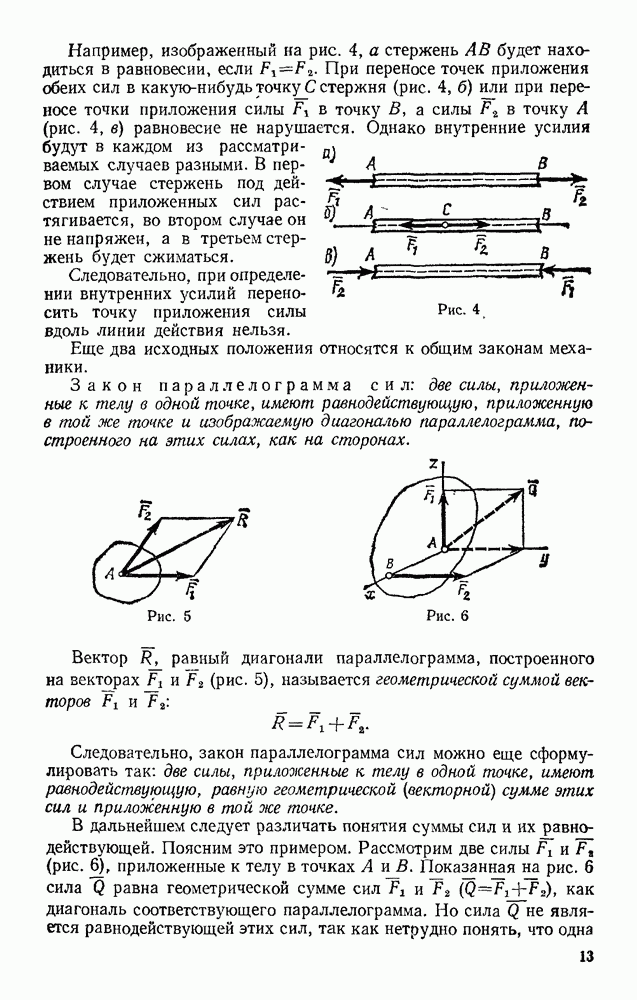
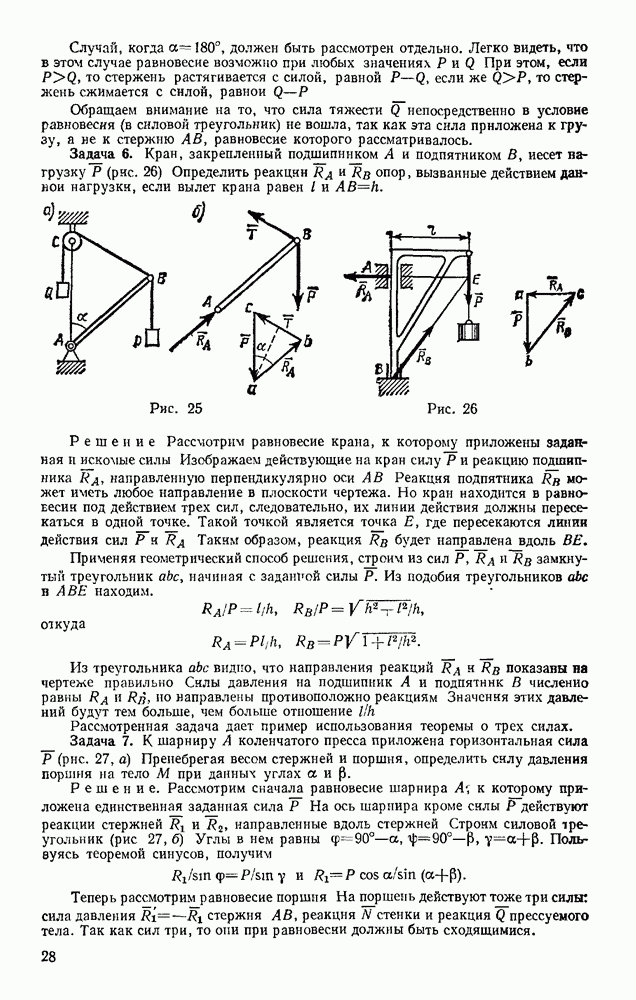
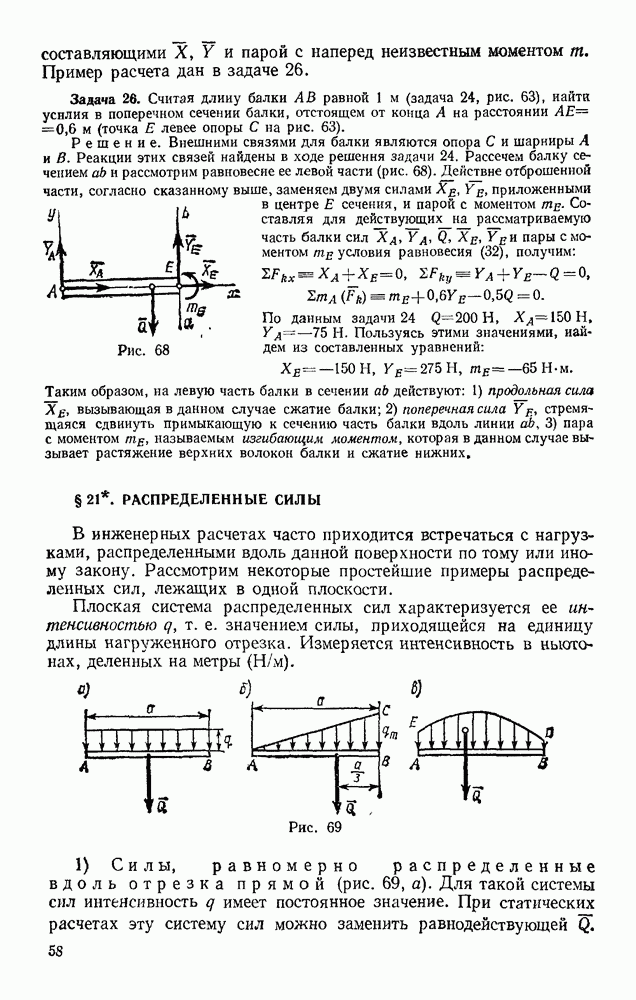
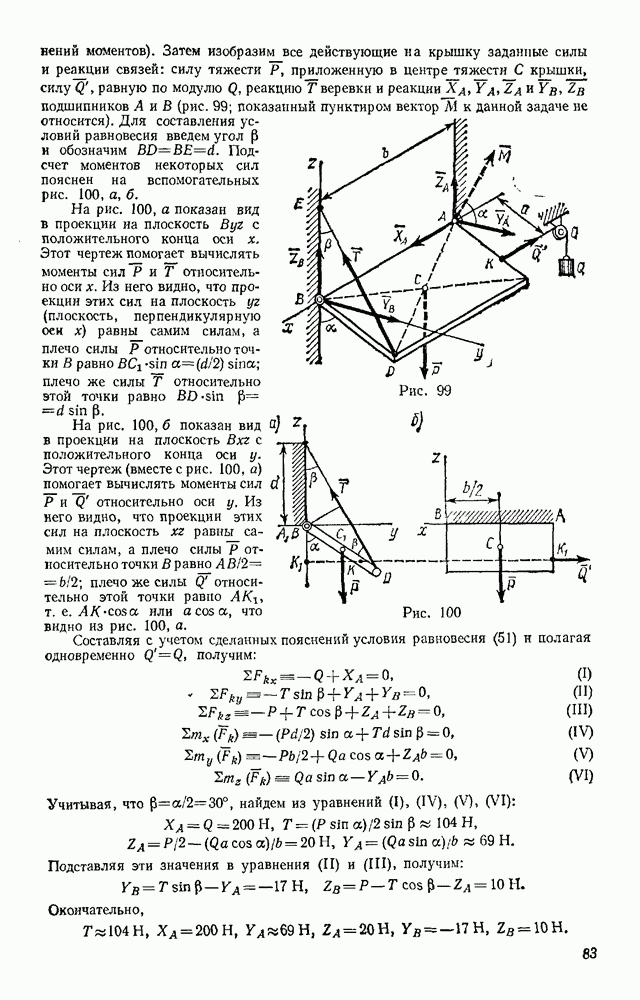
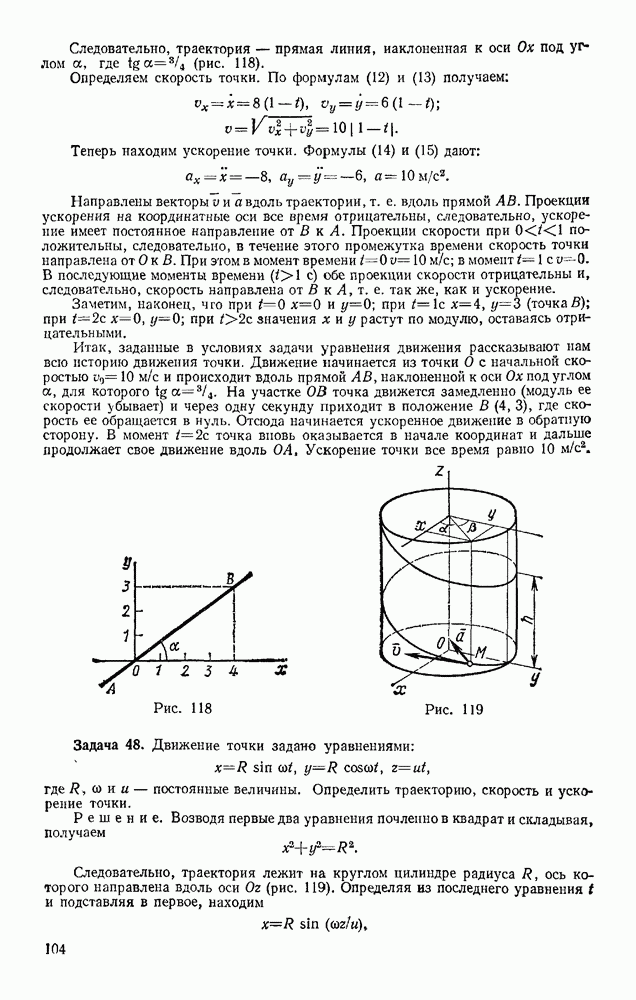
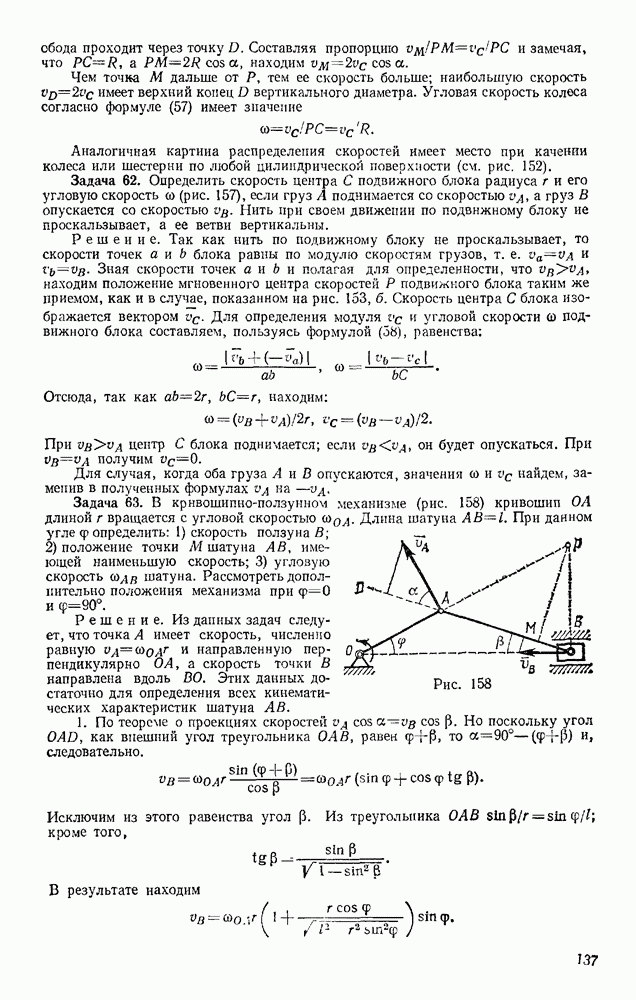
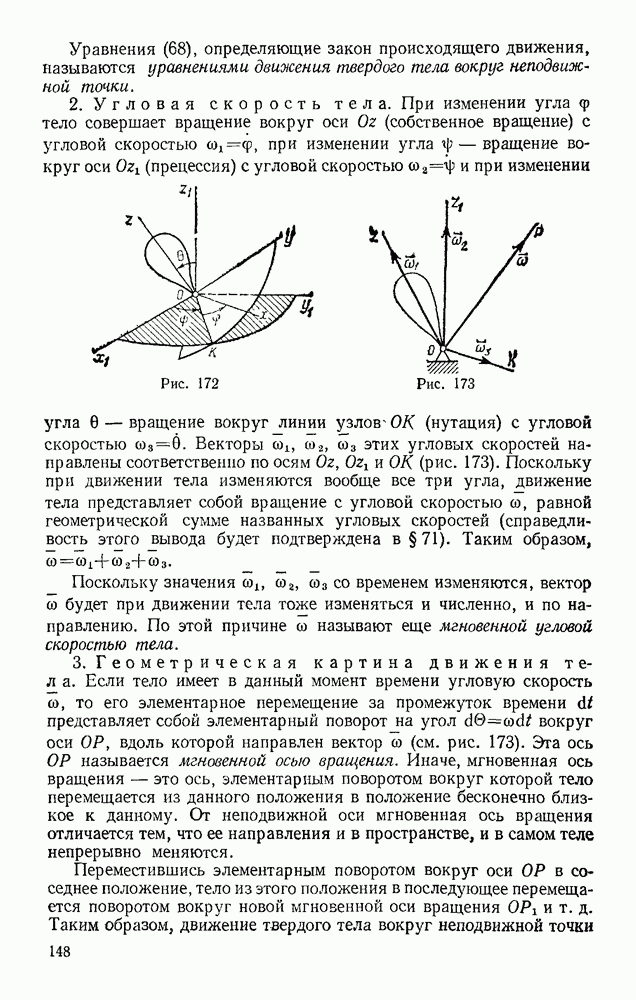
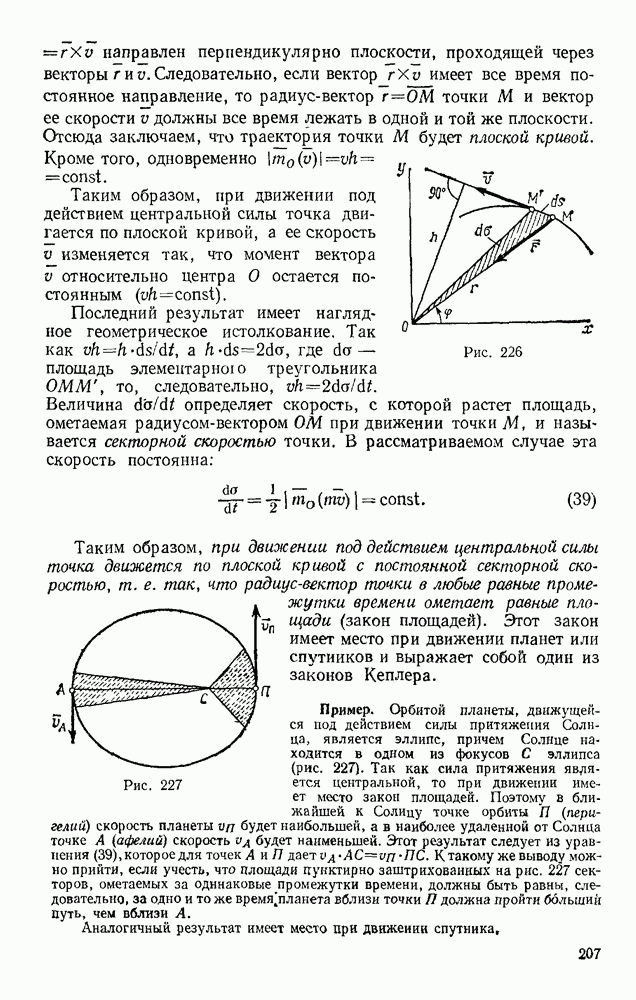
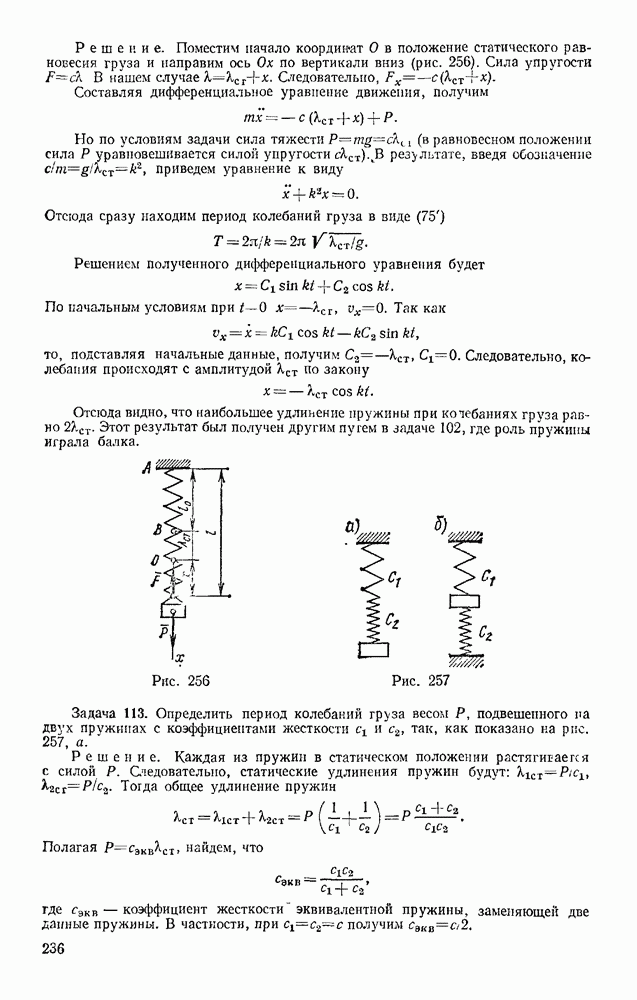
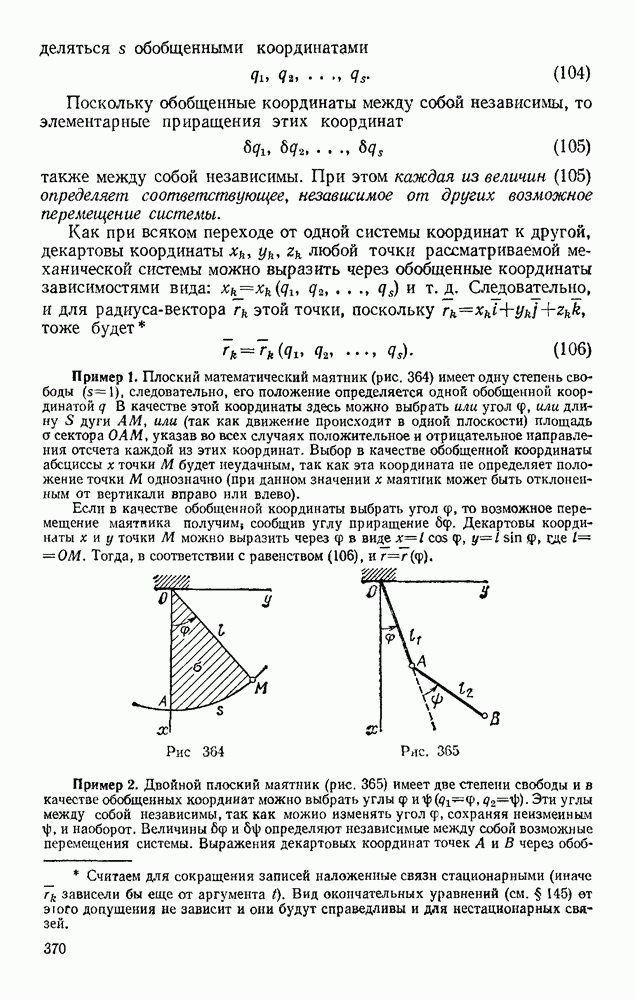
Положение тела, совершающего плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота вокруг полюса (см. § 52). Задачи динамики будут решаться проще всего, если за полюс принять центр масс С тела (рис. 327) и определять положение тела координатами  и углом
и углом 
На рис. 327 изображено сечение тела плоскостью, параллельной плоскости движения и проходящей через центр масс С. Пусть на тело действуют внешние силы  лежащие в плоскости этого сечения. Тогда уравнения движения точки С найдем по теореме о движении центра масс
лежащие в плоскости этого сечения. Тогда уравнения движения точки С найдем по теореме о движении центра масс

а вращательное движение вокруг центра С будет определяться уравнением (66), так как теорема, из которой получено это уравнение, справедлива и для движения системы вокруг центра масс. В результате, проектируя обе части равенства (70) на координатные оси, получим:

или

Уравнения (71) представляют собой дифференциальные уравнения плоскопараллельного движения твердого тела. С их помощью можно по заданным силам определить закон движения тела или, зная закон движения тела, найти главный вектор и главный момент действующих сил.
При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобнее составлять в проекциях на касательную  и главную нормаль
и главную нормаль  к этой траектории. Тогда вместо системы (71) получим:
к этой траектории. Тогда вместо системы (71) получим:

где  — радиус кривизны траектории центра масс.
— радиус кривизны траектории центра масс.

Рис. 327
Заметим, что если движение является несвободным, то в правые части уравнений (71) или (72) войдут еще неизвестные реакции связей. Для их определения надо будет составить дополнительные уравнения, отражающие те условия, которые налагаются на движение тела связями (см. задачу 151 и др.). Часто уравнения несвободного движения будут составляться проще с помощью теоремы об изменении кинетической энергии, которой можно воспользоваться вместо одного из уравнений (71) или (72).
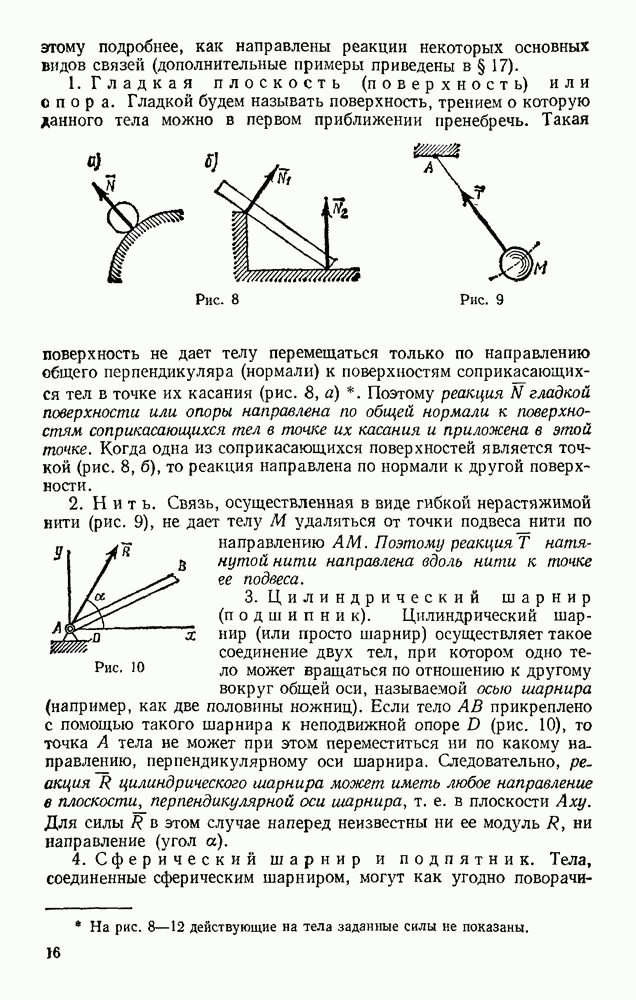
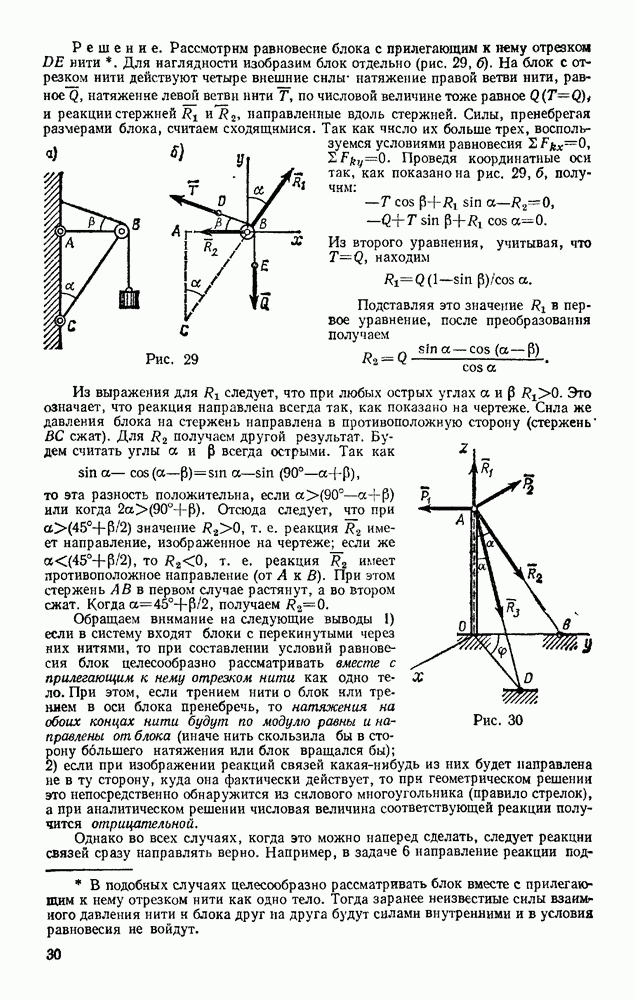
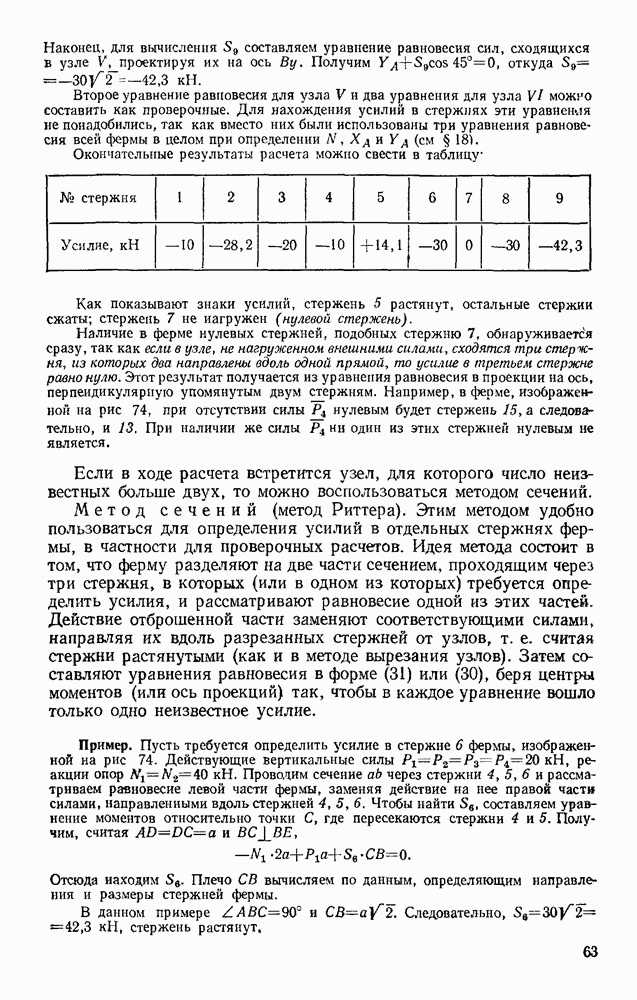
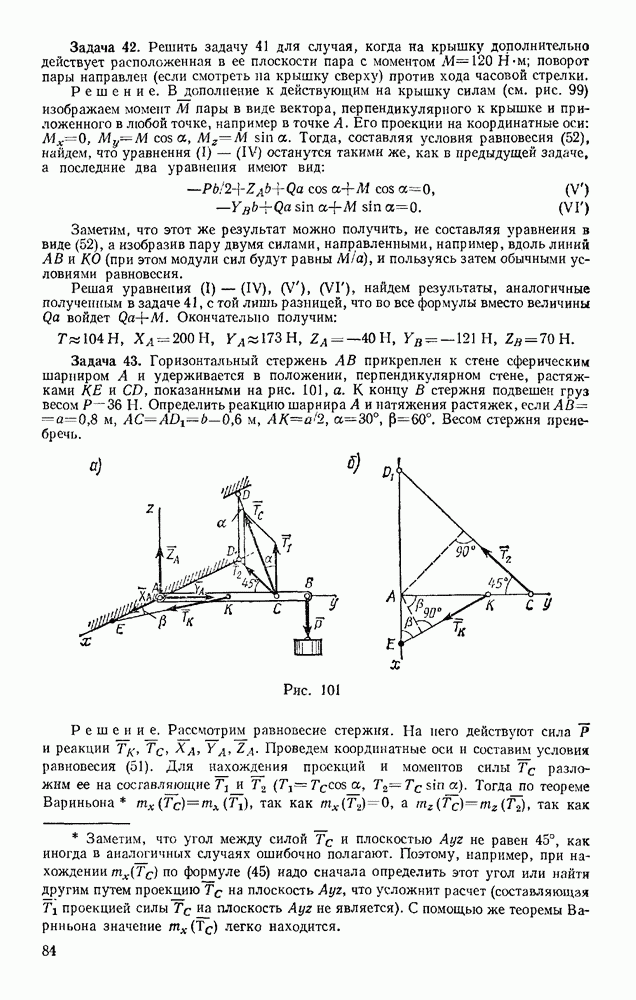
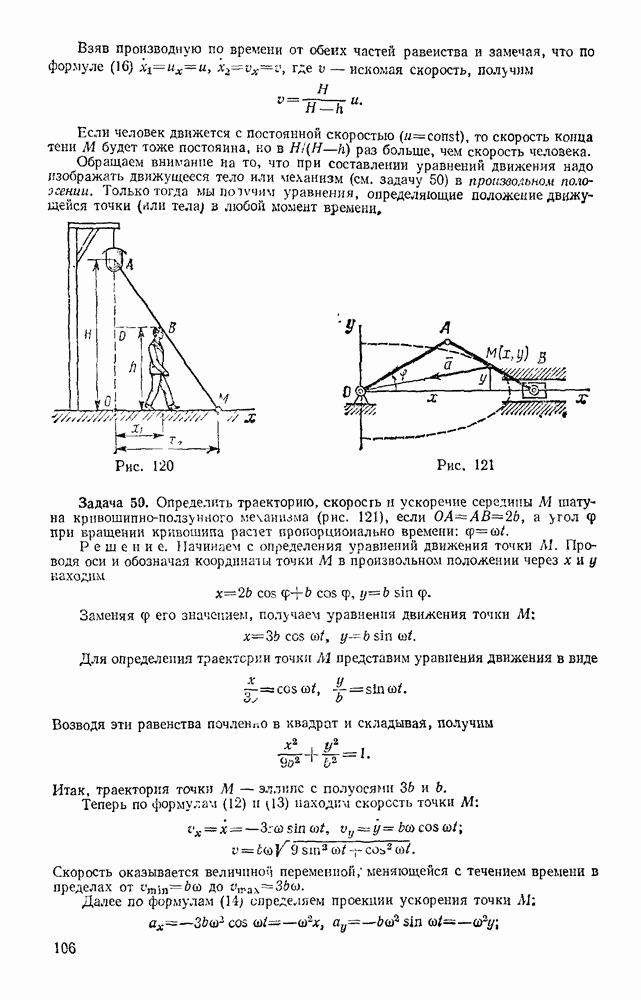
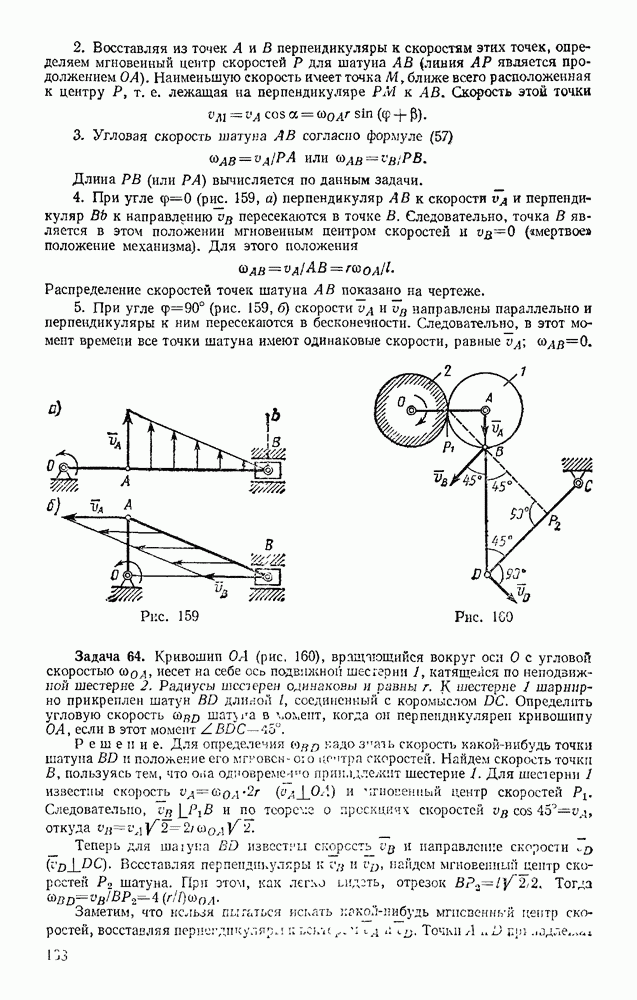
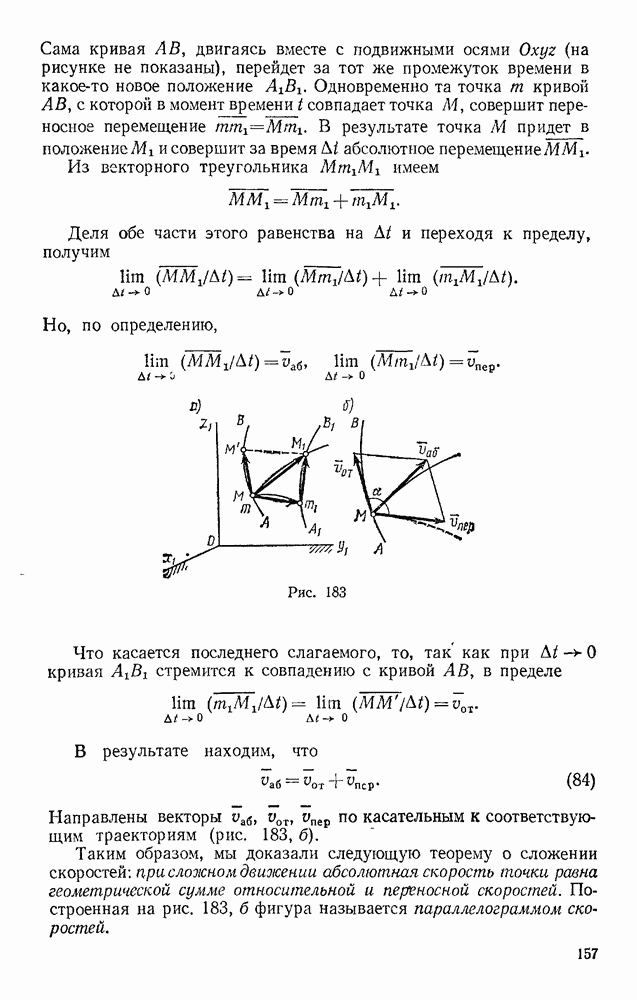
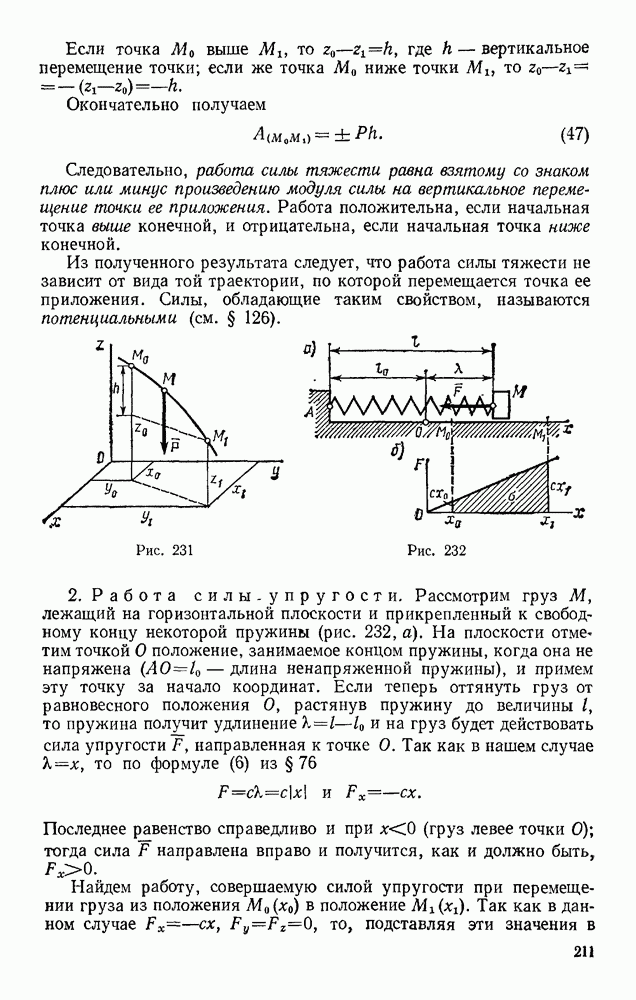
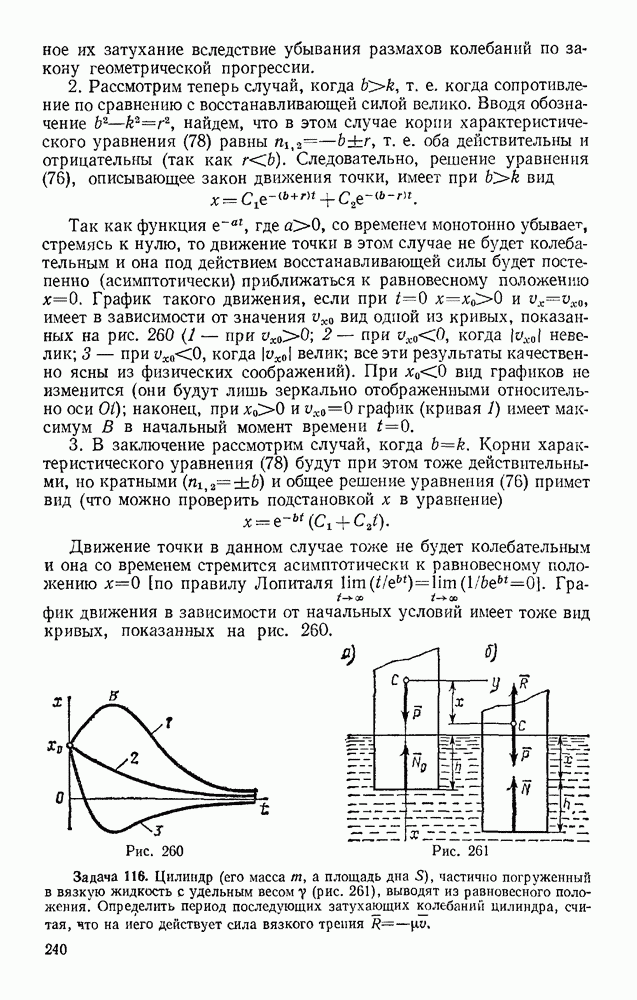
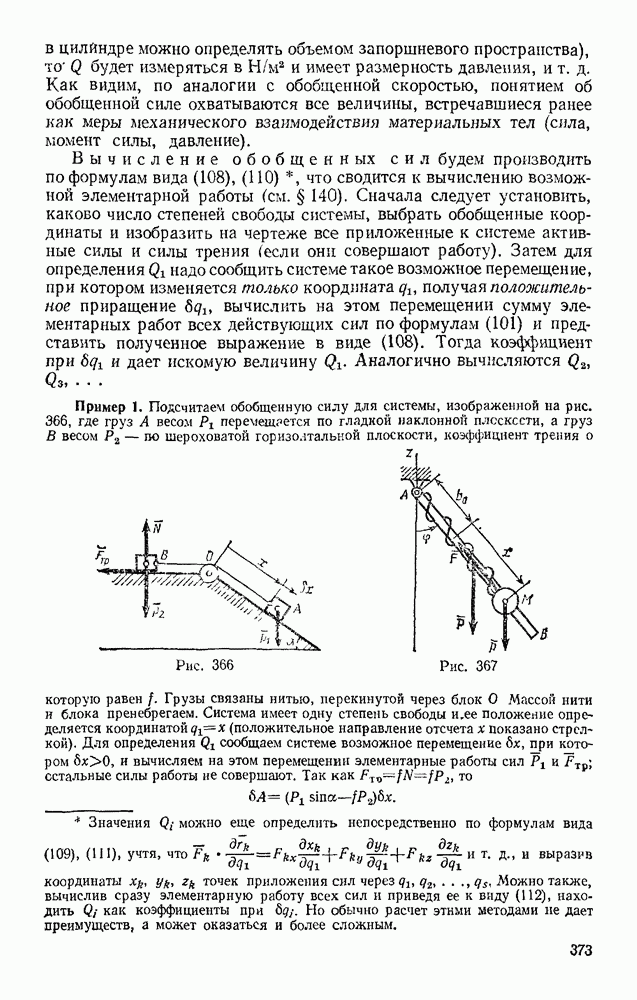
Задача 151. Сплошной однородный круговой цилиндр скатывается по наклонной плоскости с углом наклона а (рис. 328). Определить ускорение центра цилиндра и наименьший коэффициент трения  цилиндра о плоскость, при котором возможно качение без скольжения, в двух случаях: 1) пренебрегая сопротивлением качению; 2 учитывая сопротивление качению (коэффициент трения качения k и радиус цилиндра R известны).
цилиндра о плоскость, при котором возможно качение без скольжения, в двух случаях: 1) пренебрегая сопротивлением качению; 2 учитывая сопротивление качению (коэффициент трения качения k и радиус цилиндра R известны).
Решение. 1. Изображаем действующие на цилиндр силы; силу тяжести  наименьшую силу трения F, при которой возможно качение без скольжения, реакцию N плоскости, приложенную, когда сопротивление качению не учитывается, в точке касания.
наименьшую силу трения F, при которой возможно качение без скольжения, реакцию N плоскости, приложенную, когда сопротивление качению не учитывается, в точке касания.
Направим ось  вдоль наклонной плоскости, а ось Оу — перпендикулярно ей.
вдоль наклонной плоскости, а ось Оу — перпендикулярно ей.
Так как вдоль оси  центр масс цилиндра не перемещается, то
центр масс цилиндра не перемещается, то  и первое из уравнений (71) дает
и первое из уравнений (71) дает

Составляя другие два уравнения системы (71), учтем, что  и будем считать момент положительным, когда он направлен в сторону вращения цилиндра. Получим:
и будем считать момент положительным, когда он направлен в сторону вращения цилиндра. Получим:

Уравнения (а) содержат три неизвестные величины  ей F (здесь нельзя считать
ей F (здесь нельзя считать  так как это равенство имеет место, когда точка касания скользит вдоль плоскости, а при отсутствии скольжения может быть
так как это равенство имеет место, когда точка касания скользит вдоль плоскости, а при отсутствии скольжения может быть  см. § 23). Дополнительную зависимость между нризвестными величинами найдем, учитывая, что при
см. § 23). Дополнительную зависимость между нризвестными величинами найдем, учитывая, что при  качении
качении  откуда, дифференцируя, получим
откуда, дифференцируя, получим  Тогда второе из равенств (а), если учесть, что для сплошного цилиндра
Тогда второе из равенств (а), если учесть, что для сплошного цилиндра  примет вид
примет вид


Рис. 328
Подставляя это значение F в первое из равенств (а), получим

Теперь находим из выражения (б)

Такая сила трения должна действовать на катящийся цилиндр, чтобы он катился без скольжения. Выше было указано, что  Следовательно, чистое качение будет происходить, когда
Следовательно, чистое качение будет происходить, когда

Если коэффициент треиия будет меньше этой величины, то сила F не может принять значения, определяемого равенством ( ), и цилиндр будет катиться с проскальзыванием. В этом случае
), и цилиндр будет катиться с проскальзыванием. В этом случае  не связаны зависимостью
не связаны зависимостью  (точка касания не является мгновенным центром скоростей), но зато величина F имеет предельное значение, т. е.
(точка касания не является мгновенным центром скоростей), но зато величина F имеет предельное значение, т. е.  а, и уравнения (а) принимают вид:
а, и уравнения (а) принимают вид:

откуда

Центр цилиндра в этом случае движется с ускорением  а сам цилиндр вращается с угловым ускорением
а сам цилиндр вращается с угловым ускорением  , значения которых определяются равенствами
, значения которых определяются равенствами 
2. При учете сопротивления качению реакция N будет смещена в сторону движения на величину k (расположена так, как на рис. 308, б) и ее момент относительно центра С будет равен  Тогда второе из уравнений (а) примет вид
Тогда второе из уравнений (а) примет вид

Остальные уравнения сохраняют свой вид, т. е. будет по-прежнему

Из уравнений  учитывая, что и в данном случае
учитывая, что и в данном случае  наймем окончательно:
наймем окончательно:

После этого из неравенства  получим, что f должно иметь для обеспечения качения без скольжения значение
получим, что f должно иметь для обеспечения качения без скольжения значение 
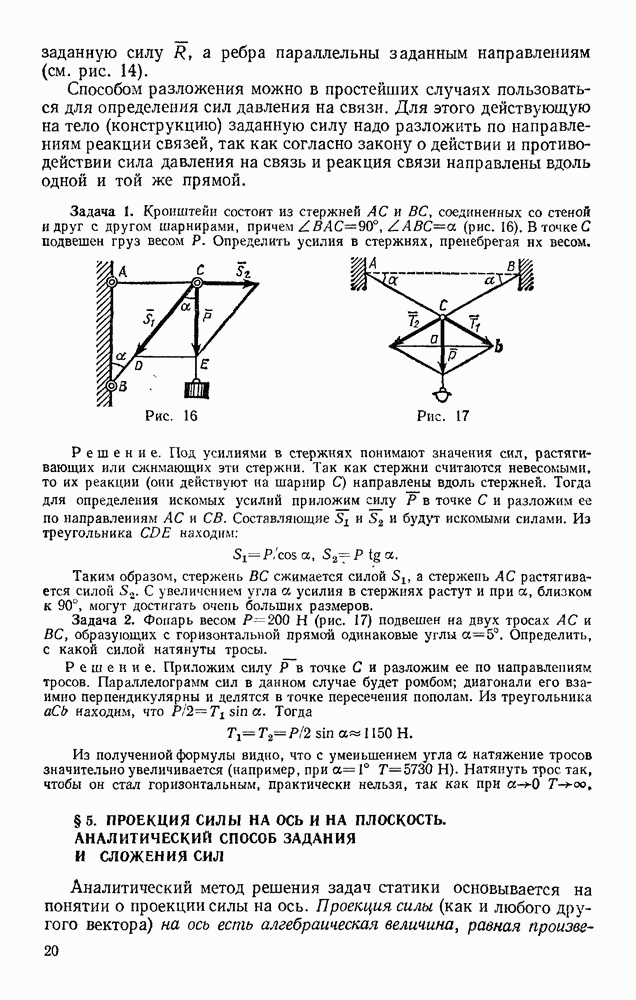
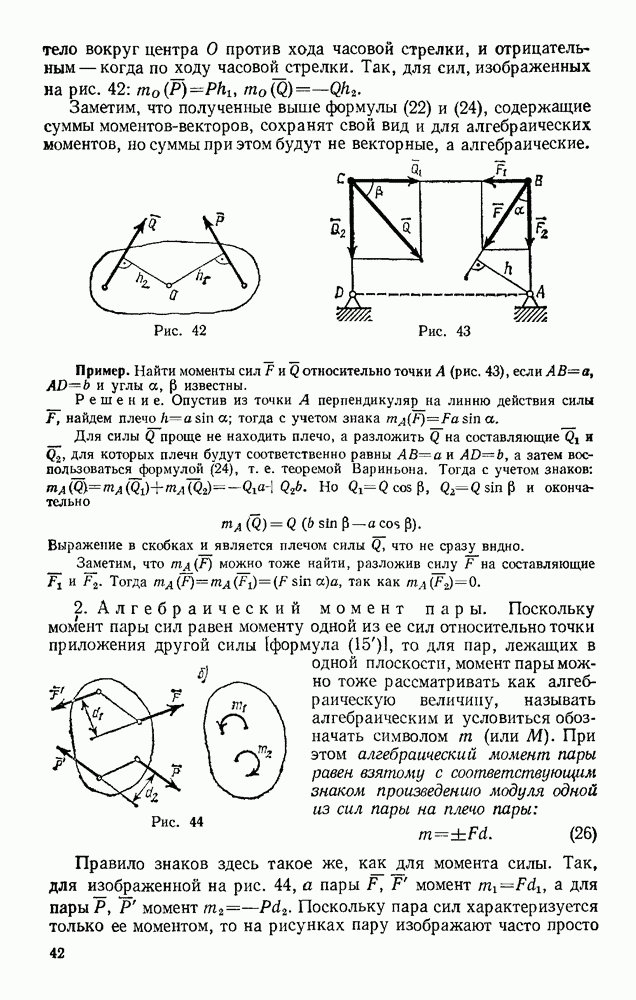
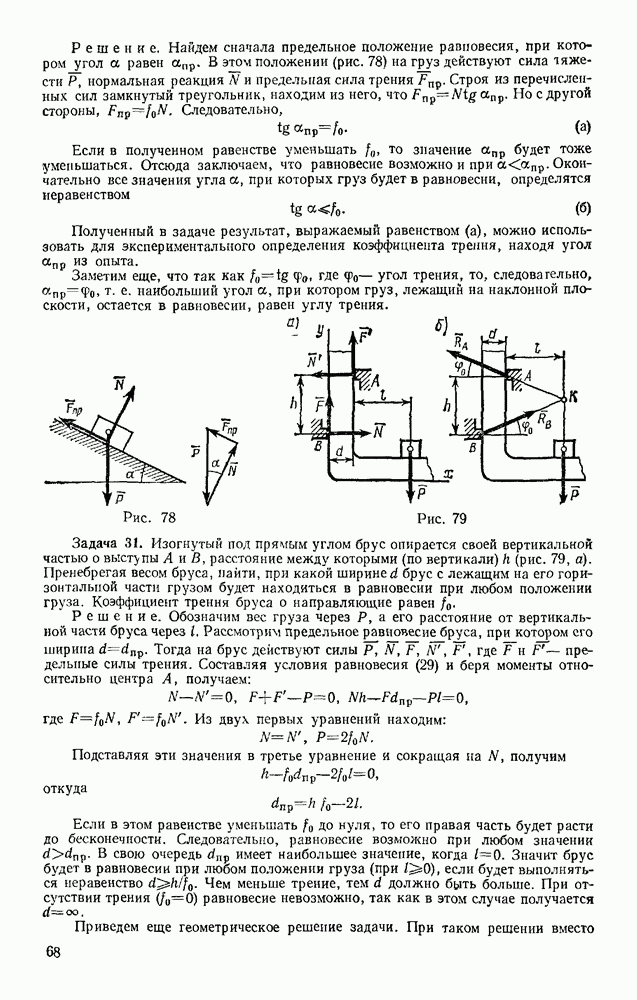
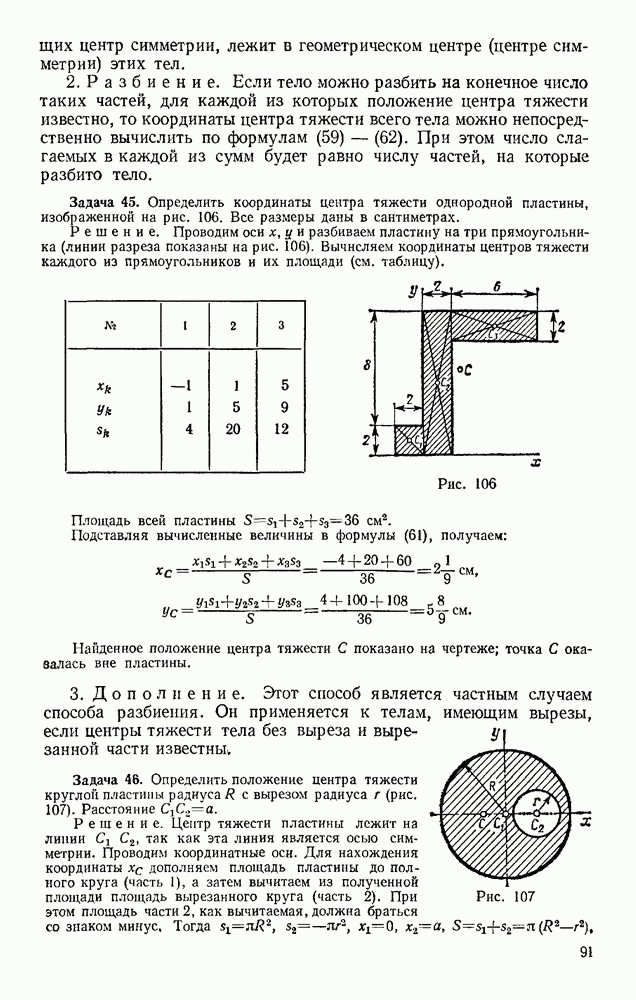
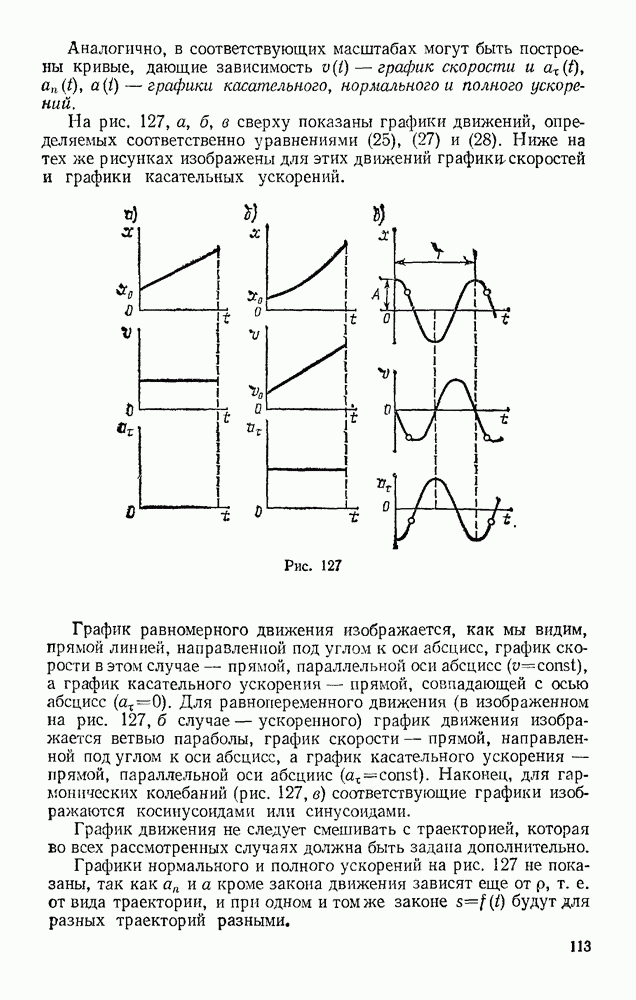
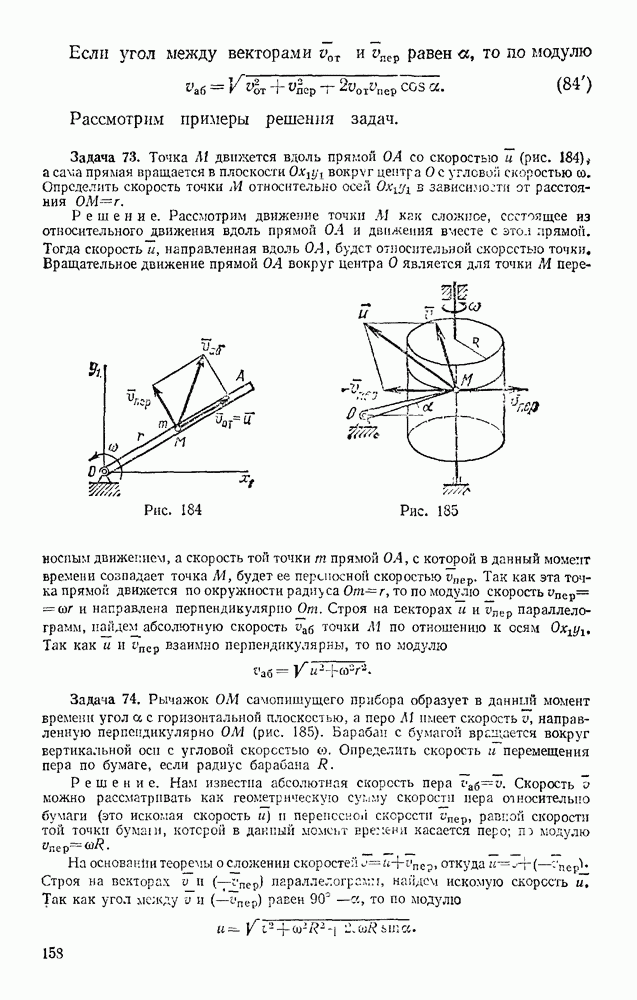
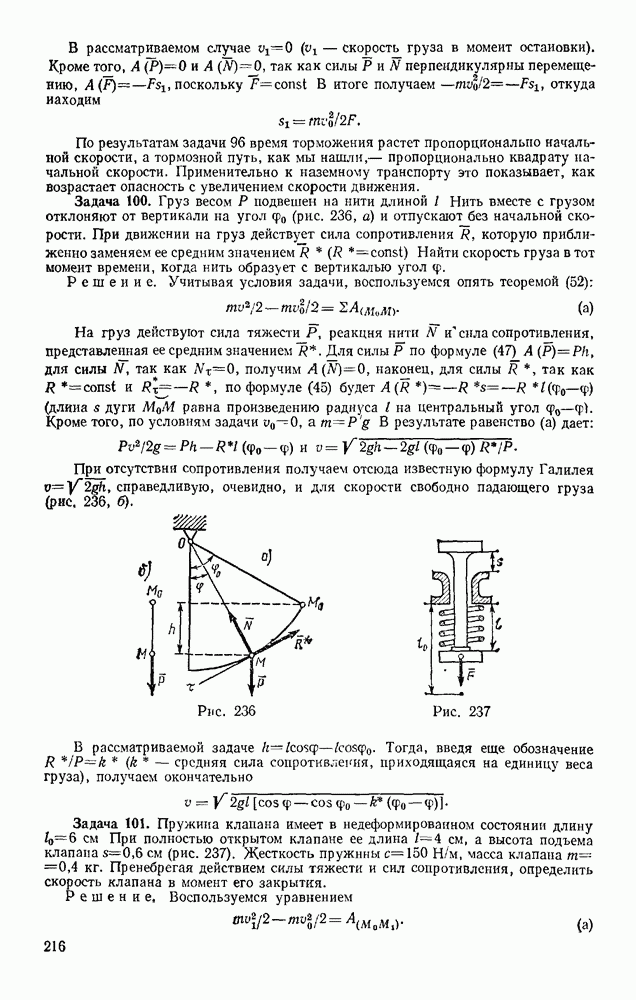
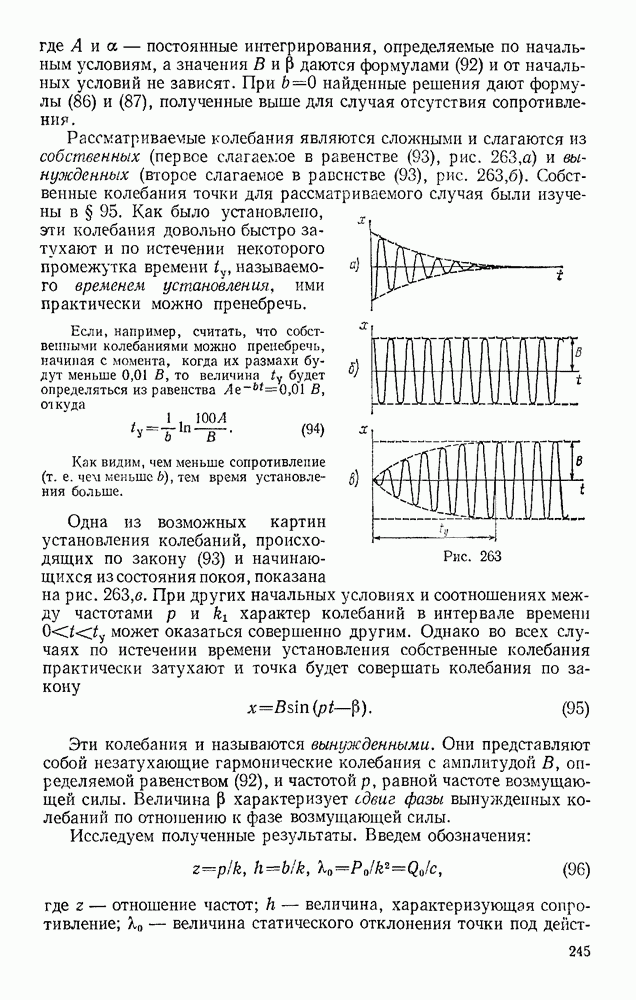
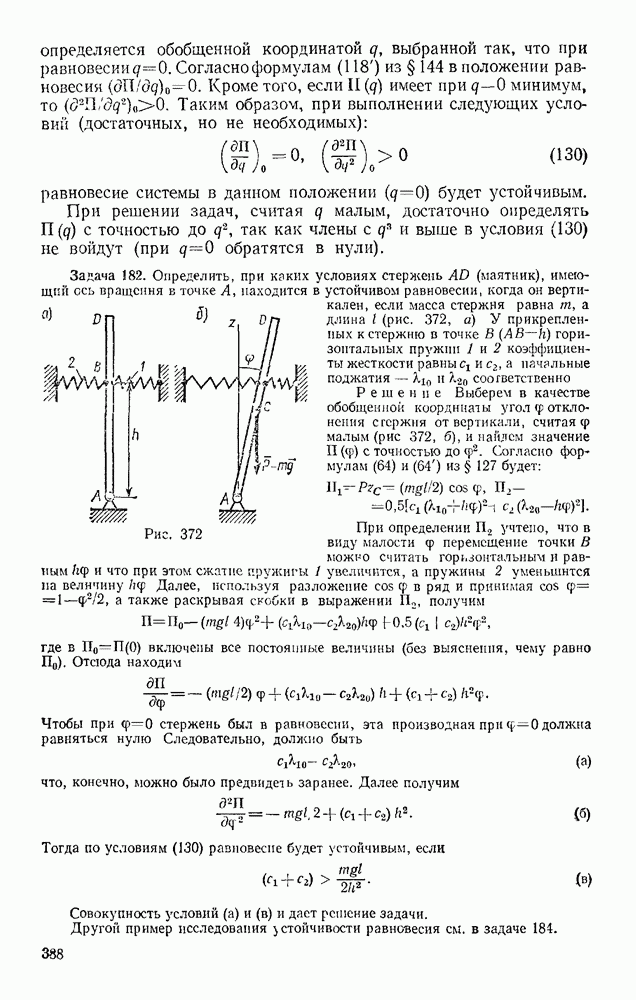
Задача 152. По шероховатой цилиндрической поверхности радиуса R (рис. 329) из положения, определяемого углом  начинает катиться без скольжения сплошной однородный цилиндр радиусом
начинает катиться без скольжения сплошной однородный цилиндр радиусом  . Пренебрегая сопротивлением качению, определить закон движения центра цилиндра, когда угол
. Пренебрегая сопротивлением качению, определить закон движения центра цилиндра, когда угол  мал. Найти также, при каких значениях
мал. Найти также, при каких значениях  возможно качение без скольжения, если коэффициент трения цилиндра о поверхность
возможно качение без скольжения, если коэффициент трения цилиндра о поверхность 

Рис. 329
Решение. Рассмотрим цилиндр при его качении вниз (движение происходит в вертикальной плоскости). В положении, определяемом углом  на цилиндр действуют сила тяжести
на цилиндр действуют сила тяжести  сила трения скольжения F и реакция
сила трения скольжения F и реакция 
Проведя касательную  к траектории центра С (в сторону движения этого центра) и учтя, что для цилиндра
к траектории центра С (в сторону движения этого центра) и учтя, что для цилиндра  составим первое и третье из уравнений
составим первое и третье из уравнений  в виде:
в виде:

где  — угловая скорость цилиндра.
— угловая скорость цилиндра.
Выразим все скорости через  . Одновременно учтем, что в точке К. находится мгновенный центр скоростей. Тогда, поскольку при качении цилиндра вниз
. Одновременно учтем, что в точке К. находится мгновенный центр скоростей. Тогда, поскольку при качении цилиндра вниз  убывает и
убывает и  будет:
будет:

При этих значениях  и
и  уравнения (а) примут вид:
уравнения (а) примут вид:

Исключая из равенств (б) силу F, найдем окончательно следующее дифференциальное уравнение, определяющее движение центра С:

Поскольку очевидно, что при движении цилиндра  то, когда угол
то, когда угол  мал, можно приближенно принять
мал, можно приближенно принять  . Тогда получим известное дифференциальное уравнение гармонических колебаний
. Тогда получим известное дифференциальное уравнение гармонических колебаний

В данной задаче при  Интегрируя уравнения (в) при этих: начальных условиях, найдем следующий закон малых колебаний цилиндра:
Интегрируя уравнения (в) при этих: начальных условиях, найдем следующий закон малых колебаний цилиндра:

Период этих колебаний

В заключение найдем условие качения без скольжения, учитывая, что  (см. § 23). Значение F дает второе из равенств (б):
(см. § 23). Значение F дает второе из равенств (б):

Но согласно уравнению (в)  и так как
и так как  то окончательно
то окончательно

Теперь заметим, что при малом  часть цилиндрической поверхности, по которой катается цилиндр, можно рассматривать как часть горизонтальной плоскости и считать приближенно
часть цилиндрической поверхности, по которой катается цилиндр, можно рассматривать как часть горизонтальной плоскости и считать приближенно  Тогда неравенство
Тогда неравенство  дает
дает  Так как наибольшее значение
Так как наибольшее значение  равно
равно  то при рассматриваемых малых колебаниях качение цилиндра будет происходить без скольжения, когда
то при рассматриваемых малых колебаниях качение цилиндра будет происходить без скольжения, когда 
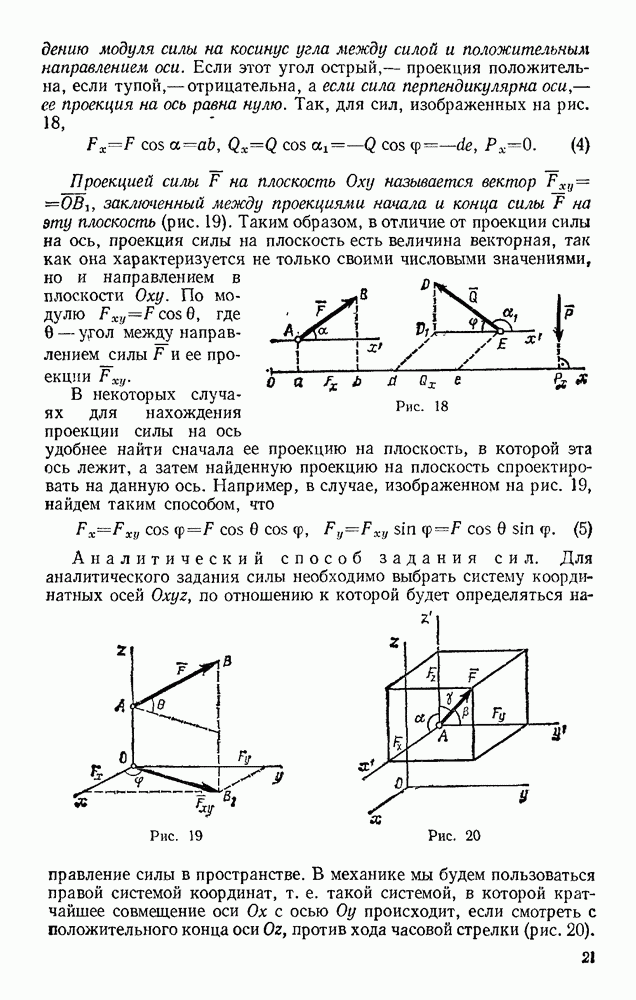
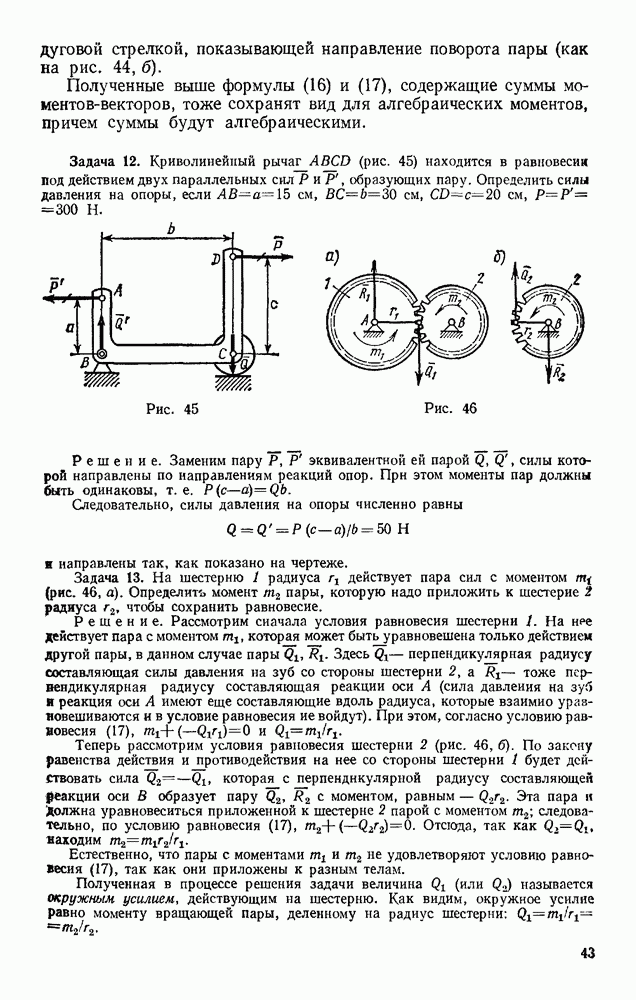
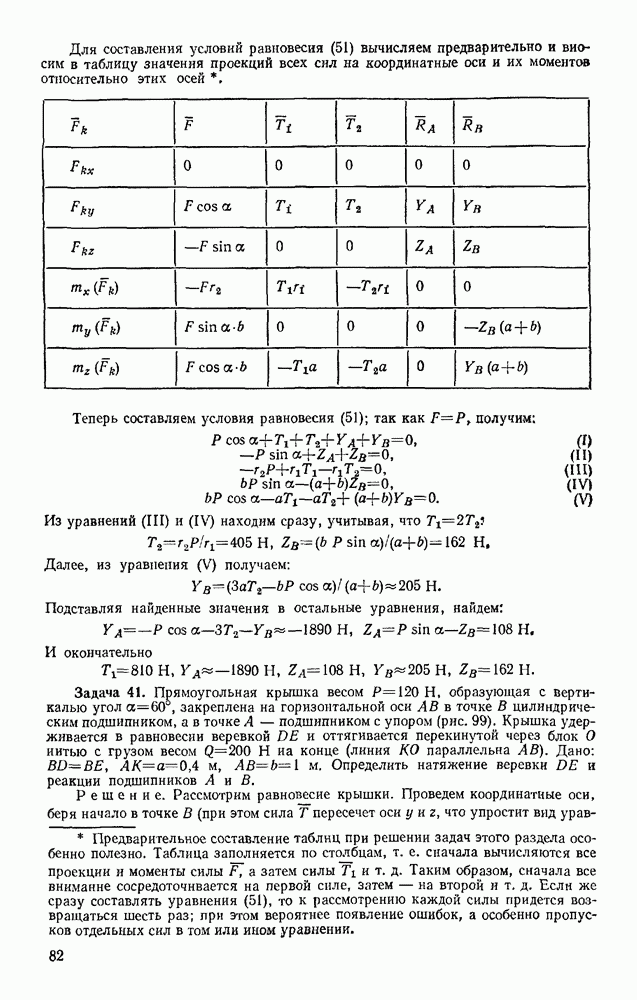
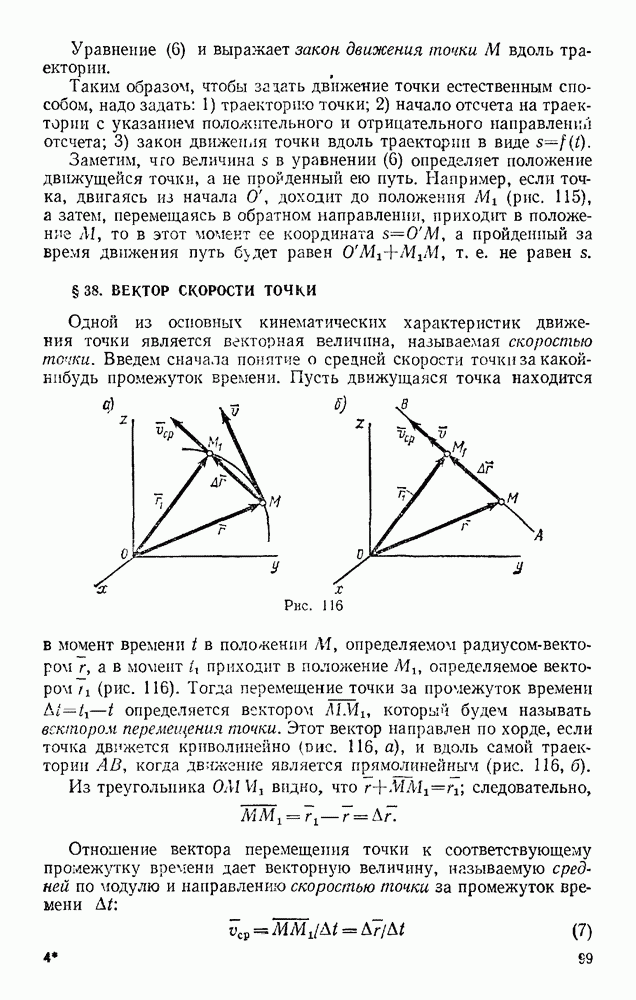
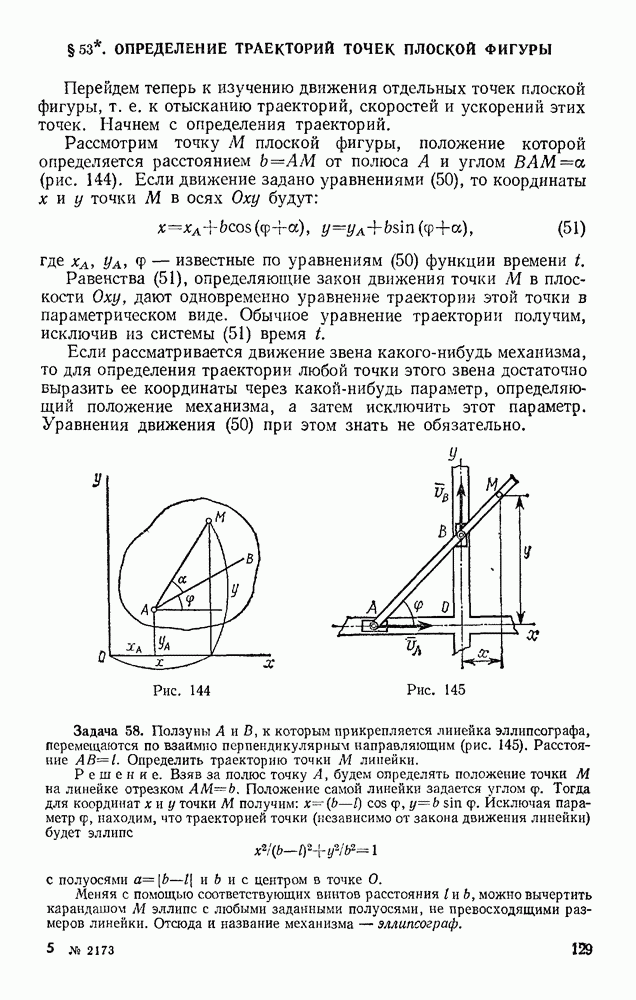
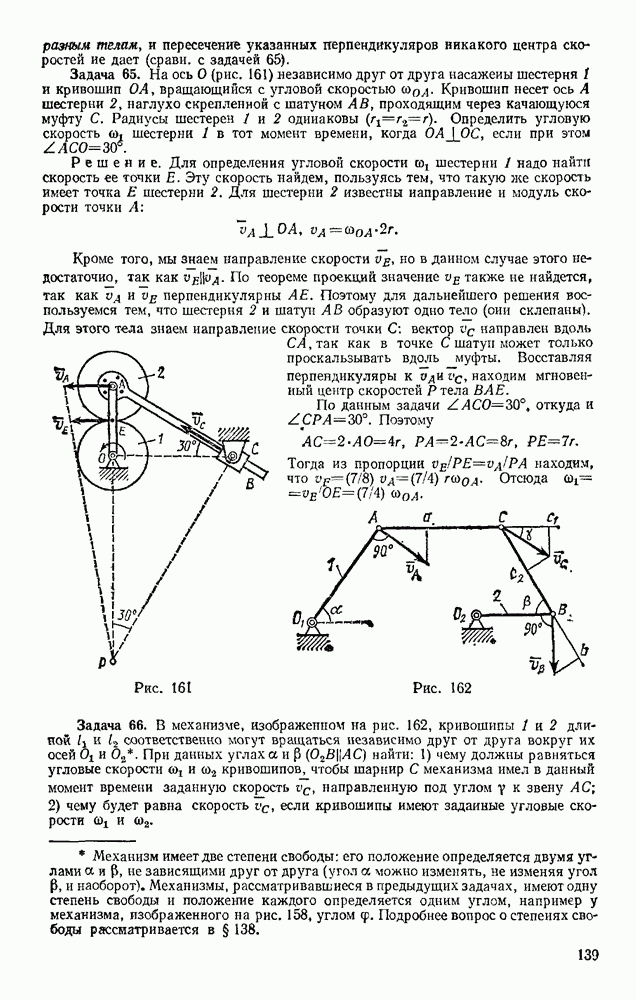
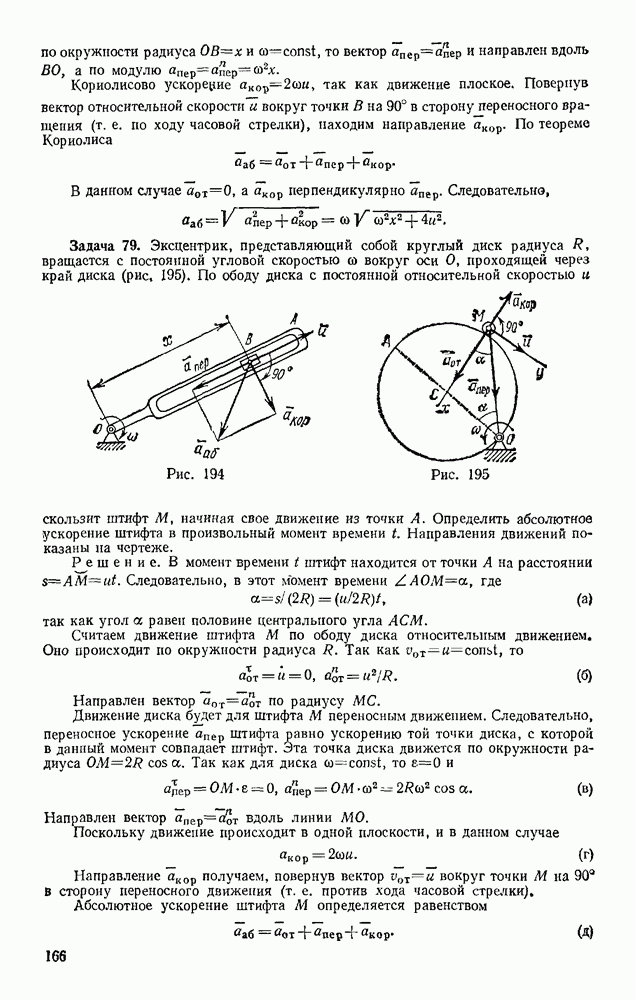
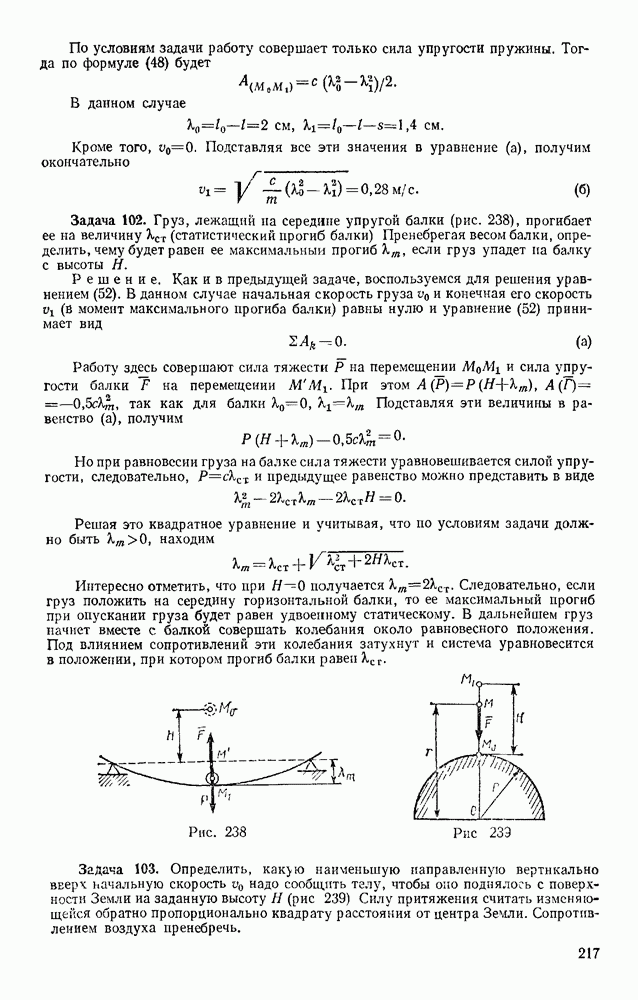
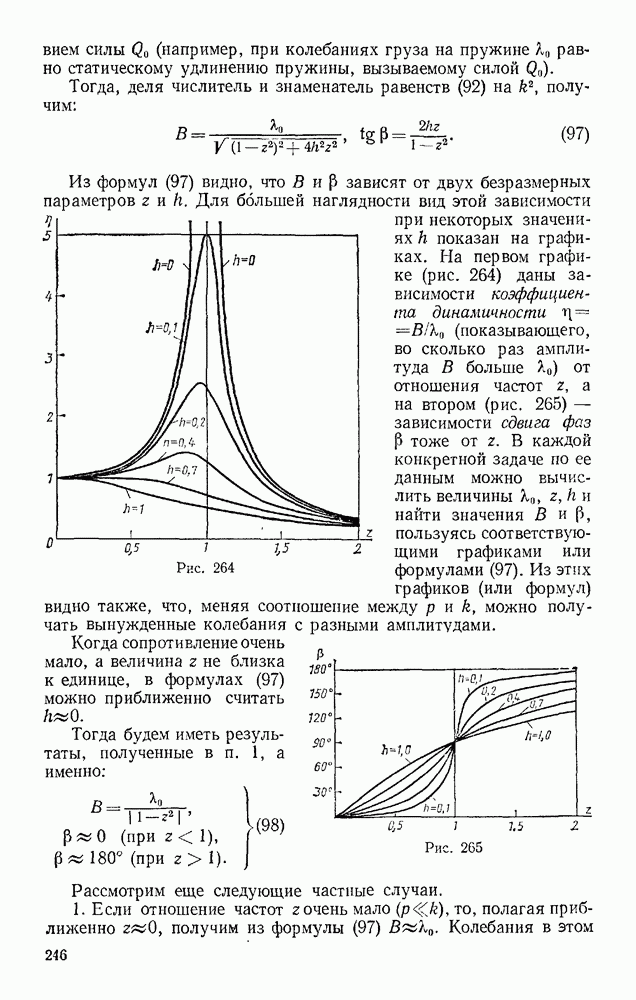
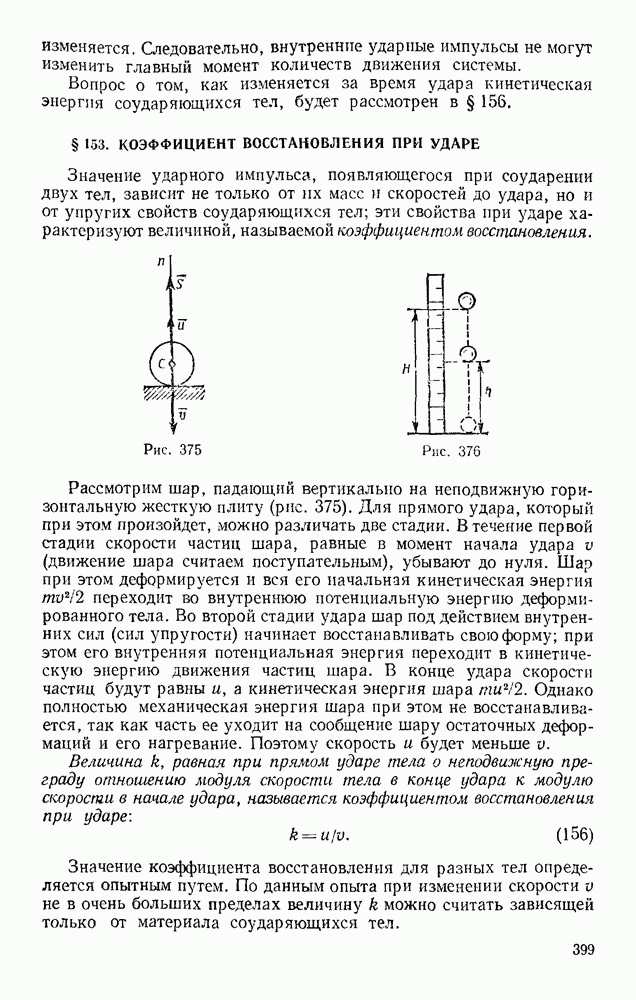
Задача 153. Тело весом Р опирается в точке В на пьезоэлектрический датчик прибора, измеряющего силу давления, а в точке А поддерживается нитью AD (рис. 330). При равновесии линия АС горизонтальна, а давление в точке В равно  Вычислить, чему равен момент инерции
Вычислить, чему равен момент инерции  тела относительно оси, проходящей через его центр масс С, если в момент, когда нить пережигают, давление в точке В становится равным
тела относительно оси, проходящей через его центр масс С, если в момент, когда нить пережигают, давление в точке В становится равным  Расстояние l известно.
Расстояние l известно.
Решение. 1. В положении равновесия  Отсюда находим
Отсюда находим 
2. Когда нить пережигают, тело начинает двигаться плоскопараллельно. Для начального элементарного промежутка времени изменением положения тела можно пренебречь. Тогда уравнения (71), справедливые только для этого промежутка времени, будут иметь вид:

Так как  то точка С начинает перемещаться по вертикали вниз, а точка В скользит горизонтально (трение в опоре считаем малым). Восставляя перпендикуляры к направлениям этих перемещений, находим, что мгновенный центр скоростей будет в точке К? Следовательно,
то точка С начинает перемещаться по вертикали вниз, а точка В скользит горизонтально (трение в опоре считаем малым). Восставляя перпендикуляры к направлениям этих перемещений, находим, что мгновенный центр скоростей будет в точке К? Следовательно,  Дифференцируя это равенство и считая в течение рассматриваемого элементарного промежутка времени
Дифференцируя это равенство и считая в течение рассматриваемого элементарного промежутка времени  , получим
, получим  Тогда первое из уравнений (а) дает
Тогда первое из уравнений (а) дает

Определяя отсюда  , найдем окончательно
, найдем окончательно

Полученный результат можно использовать для экспериментального определения моментов инерции.

Рис. 330

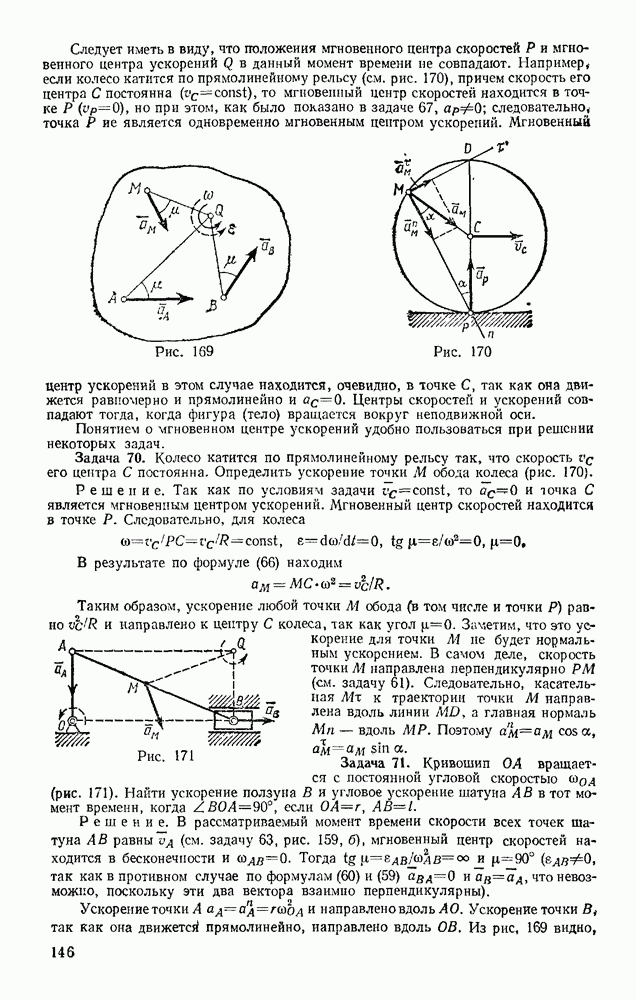
Рис. 331
Задача 154. Вес автомобиля с колесами равен Р (рис. 331); вес каждого из четырех его колес равен  , радиус
, радиус  , радиус инерции относительно оси
, радиус инерции относительно оси 
К задним (ведущим) колесам приложен вращающийся момент  . Автомобиль, начиная движение из состояния покоя, испытывает сопротивление воздуха, пропорциональное квадрату его поступательной скорости:
. Автомобиль, начиная движение из состояния покоя, испытывает сопротивление воздуха, пропорциональное квадрату его поступательной скорости:  . Момент трепня в оси каждого колеса
. Момент трепня в оси каждого колеса  . Пренебрегая сопротивлением качению, определить: 1) предельную скорость автомобиля; 2) силу трения скольжения, действующую на ведущие и ведомые колеса при движении.
. Пренебрегая сопротивлением качению, определить: 1) предельную скорость автомобиля; 2) силу трения скольжения, действующую на ведущие и ведомые колеса при движении.
Решение. 1. Для определения предельной скорости составим дифференциальное уравнение движения автомобиля, пользуясь равенством (49)

Кинетическая энергия автомобиля равна энергии кузова и колес. Учитывая, что Р — вес всего автомобиля,  (так как скорость
(так как скорость  центра С колеса равна скорости у кузова), получим
центра С колеса равна скорости у кузова), получим

где полагалось, что  — угловая скорость колеса.
— угловая скорость колеса.
Из внешних сил работу совершает только сила сопротивления воздуха, так как сопротивлением качению мы пренебрегаем, а работа сил трения  колес о грунт равна в этом случае нулю (см. § 122).
колес о грунт равна в этом случае нулю (см. § 122).
Следовательно,

где  — элементарное перемещение кузова.
— элементарное перемещение кузова.
Работа внутренних сил (вращающего момента и сил трения в осях), если учесть, что  , где
, где  — угол поворота колеса, будет
— угол поворота колеса, будет

Подставим все эти значения в равенство (а) и одновременно разделим обе его части на  Тогда, учтя еще, что
Тогда, учтя еще, что  получим
получим

Отсюда, сокращая на V, находим

Когда скорость автомобиля стремиться к ее предельному значению, его ускорение а стремится к нулю. Следовательно,  найдется из уравнения
найдется из уравнения

откуда 

Этот результат можно получить сразу, приравняв нулю сумму работ всех сил. Цель предыдущих выкладок — показать, как составляется уравнение движения (б).
2. Для определения сил трения, действующих на каждое колесо, составим уравнения вращательного движения колес относительно их осей. Для двух ведущих колес, учитывая, что действующая на каждое из них сила трения направлена вперед (см. § 108, рис. 284), получим

Так как при качении  то окончательно найдем
то окончательно найдем

Действующая на каждое из ведомых колес сила трения  направлена назад. Следовательно, для ведомого колеса будет
направлена назад. Следовательно, для ведомого колеса будет

откуда

Из равенства (б) видно, что с увеличением скорости ускорение а убывает, стремясь к нулю, когда v стремится к  . Таким образом, сила трения, действующая на ведущие колеса, при разгоне несколько возрастает и достигает наибольшего значения, когда движение установится
. Таким образом, сила трения, действующая на ведущие колеса, при разгоне несколько возрастает и достигает наибольшего значения, когда движение установится  . Если подставить значение а из равенства (б), то легко видеть, что последнее слагаемое в формуле (в) будет много меньше первого, так как
. Если подставить значение а из равенства (б), то легко видеть, что последнее слагаемое в формуле (в) будет много меньше первого, так как  Поэтому практически величина
Поэтому практически величина  изменяется незначительно.
изменяется незначительно.
На ведомых колесах сила трения имеет наибольшее значение в момент начала движения, а затем убывает и при равномерном движении  равна наименьшему значению
равна наименьшему значению 
Если коэффициент трения колес о грунт не будет достаточен для того, чтобы снла трения могла принять значение  или
или  , то соответствующие колеса будут буксовать. Так как
, то соответствующие колеса будут буксовать. Так как  много больше
много больше  то в первую очередь буксование угрожает ведущим колесам.
то в первую очередь буксование угрожает ведущим колесам.
При выключенном двигателе все колеса являются ведомыми и на них вначале будет действовать сила трения  Действие тормозных колодок эквивалентно увеличению момента
Действие тормозных колодок эквивалентно увеличению момента  в осях, а следовательно, и силы трения, действующей на каждое из колес, чем и ускоряется торможение автомобиля (см. § 108).
в осях, а следовательно, и силы трения, действующей на каждое из колес, чем и ускоряется торможение автомобиля (см. § 108).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА