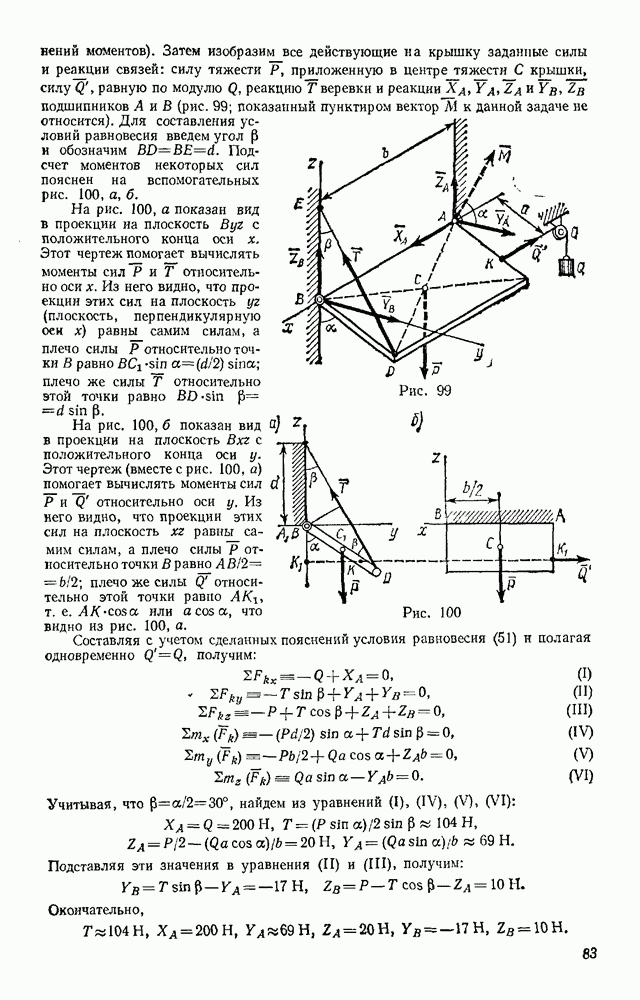
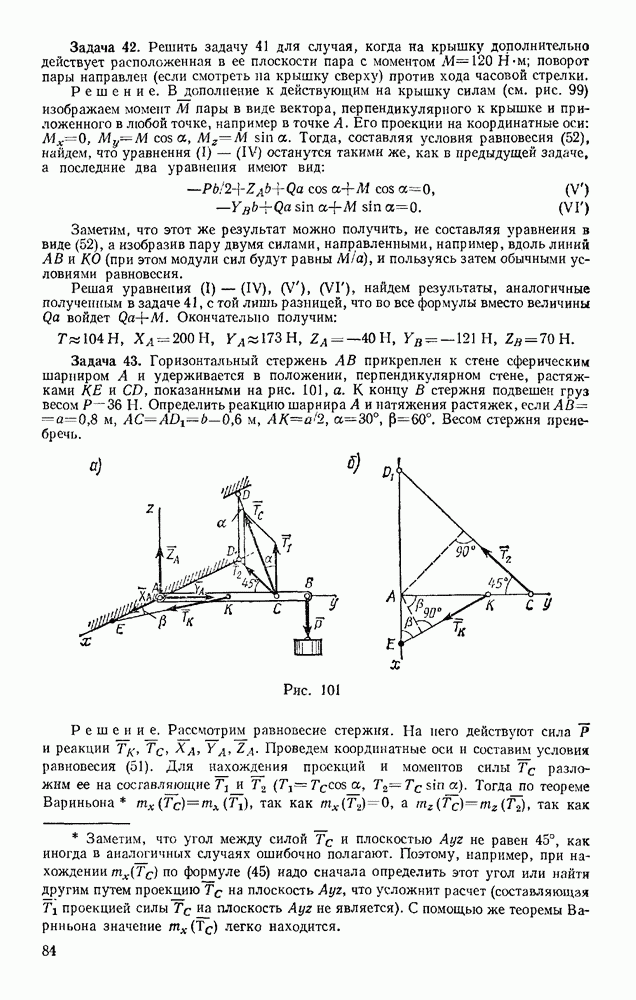
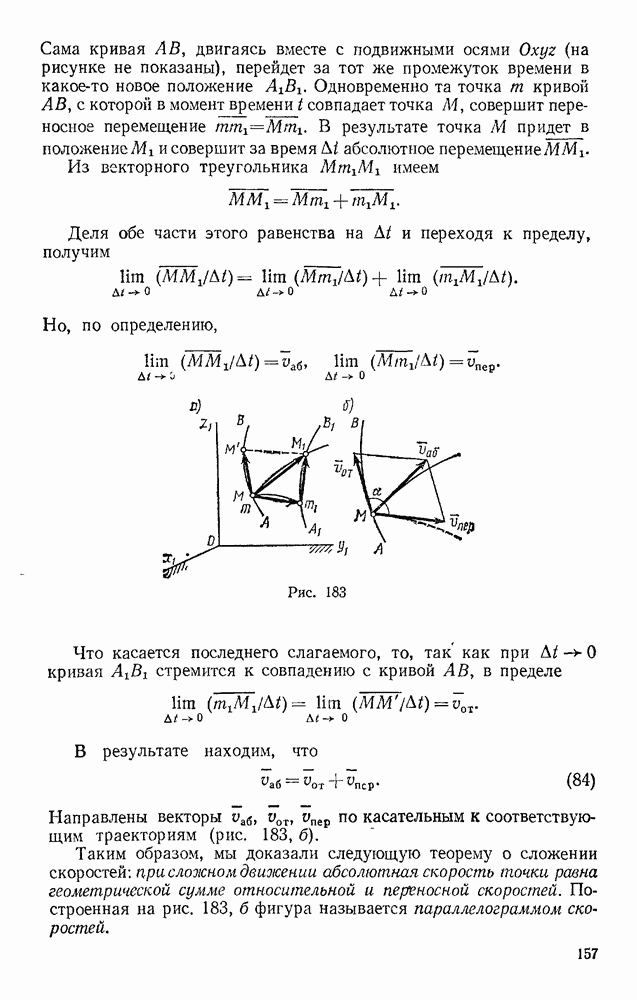
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
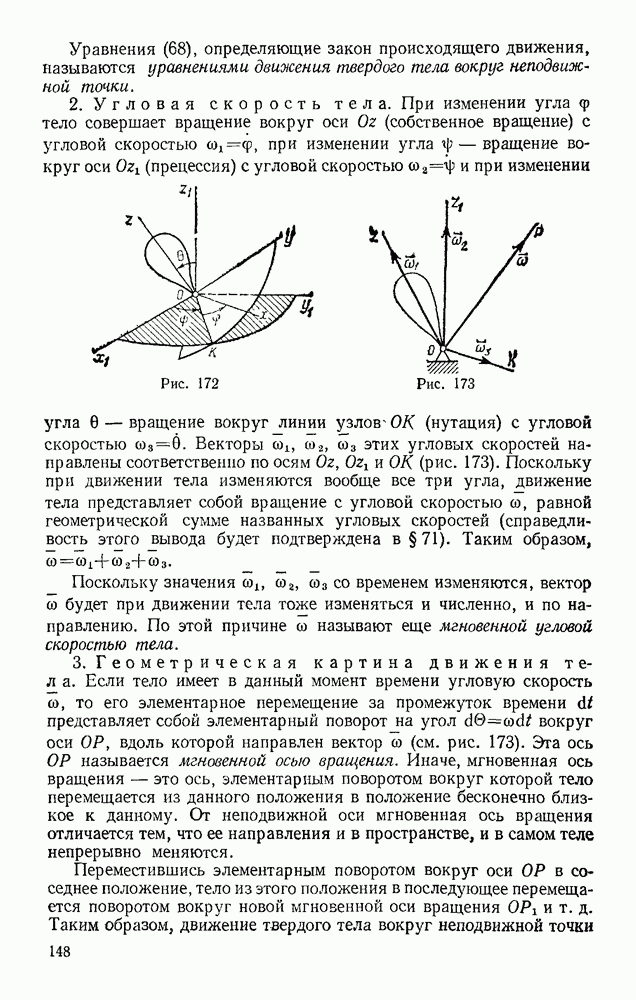
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
Введем понятие еще об одной основной динамической характеристике движения  о кинетической энергии. Кинетической энергией материальной точки называется скалярная величина
о кинетической энергии. Кинетической энергией материальной точки называется скалярная величина  равная половине произведения массы точки на квадрат ее скорости.
равная половине произведения массы точки на квадрат ее скорости.
Единица измерения кинетической энергии та же, что и работы (в СИ — 1 Дж). Найдем зависимость, которой связаны эти две величины.
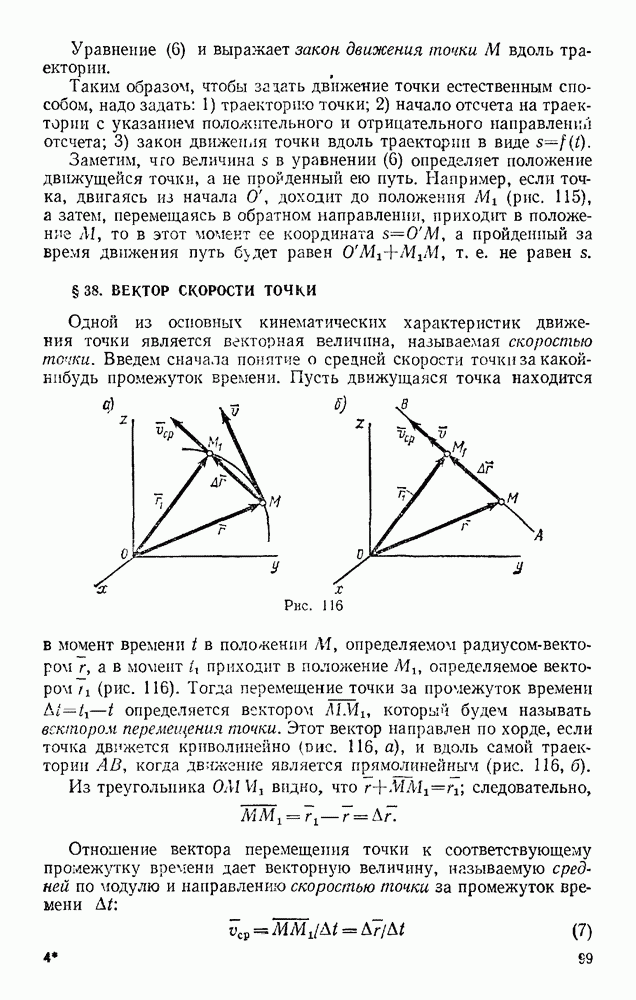
Рассмотрим материальную точку с массой  , перемещающуюся из положения
, перемещающуюся из положения  , где она имеет скорость
, где она имеет скорость  в положение
в положение  , где ее скорость
, где ее скорость 
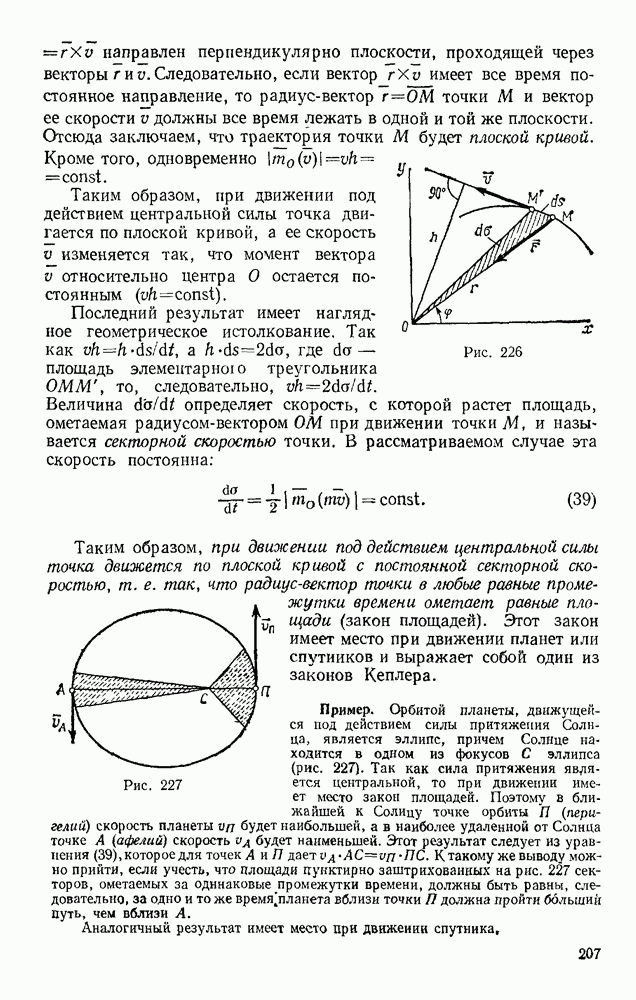
Для получения искомой зависимости обратимся к выражающему основной закон динамики уравнению  Проектируя обе его части на касательную
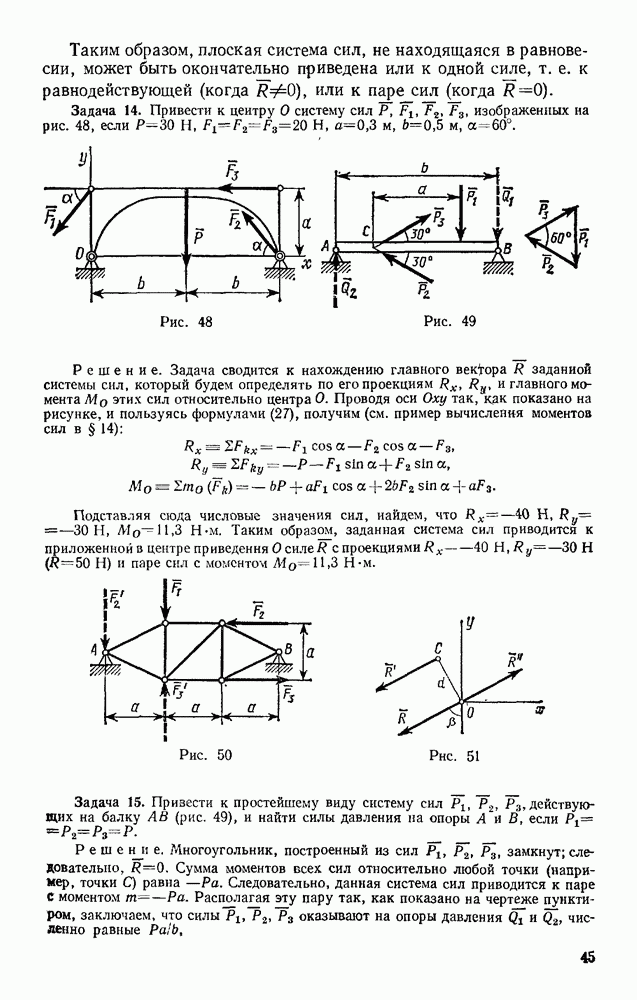
Проектируя обе его части на касательную  к траектории точки М, направленную в сторону движения, получим
к траектории точки М, направленную в сторону движения, получим

Входящее сюда касательное ускорение точки представим в виде

В результате найдем, что

Умножим обе части этого равенства на  и внесем
и внесем  под знак дифференциала. Тогда, замечая, что
под знак дифференциала. Тогда, замечая, что  где
где  — элементарная работа силы
— элементарная работа силы  получим выражение теоремы об изменении кинетической энергии точки в дифференциальной форме:
получим выражение теоремы об изменении кинетической энергии точки в дифференциальной форме:

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках  найдем окончательно
найдем окончательно

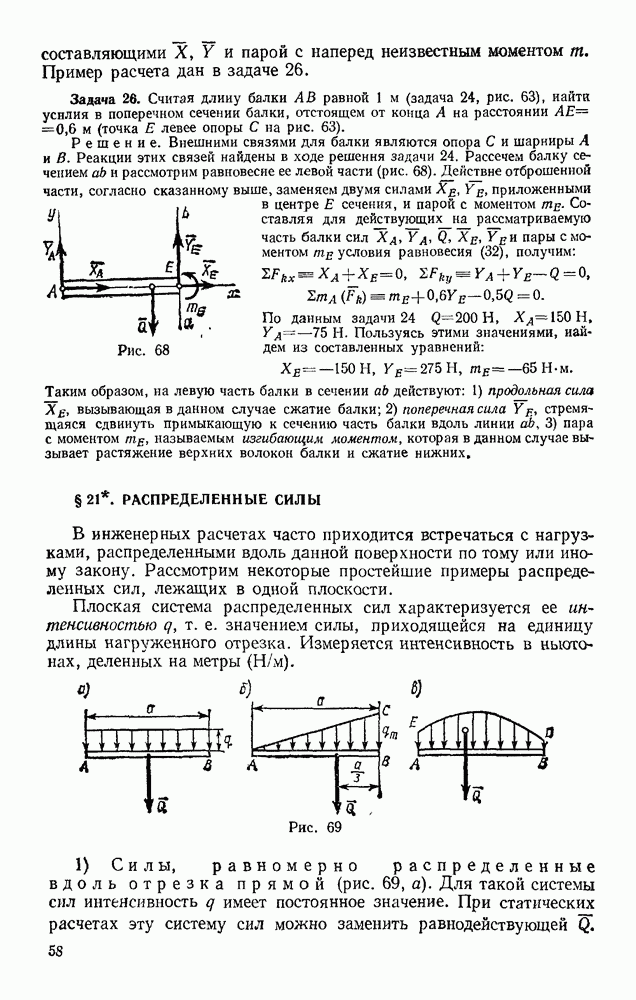
Уравнение (52) выражает теорему об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
Случай несвободного движения. При несвободном движении точки в правую часть равенства (52) войдет работа заданных (активных) сил  и работа реакции связи. Ограничимся рассмотрением движения точки по неподвижной гладкой (лишенной трения) поверхности или кривой. В этом случае реакция N (см. рис. 233) будет направлена по нормали к траектории точки и
и работа реакции связи. Ограничимся рассмотрением движения точки по неподвижной гладкой (лишенной трения) поверхности или кривой. В этом случае реакция N (см. рис. 233) будет направлена по нормали к траектории точки и  . Тогда, согласно формуле (44), работа реакции неподвижной гладкой поверхности (или кривой) при любом перемещении точки будет равна нулю, и из уравнения (52) получим
. Тогда, согласно формуле (44), работа реакции неподвижной гладкой поверхности (или кривой) при любом перемещении точки будет равна нулю, и из уравнения (52) получим 

Следовательно, при перемещении по неподвижной гладкой поверхности (или кривой) изменение кинетической энергии точки равно сумме работ на этом перемещении приложенных к точке активных сил.
Если поверхность (кривая) не является гладкой, то к работе активных сил прибавится работа силы трения (см. § 88). Если же поверхность (кривая) движется, то абсолютное перемещение точки М может не быть перпендикулярно N и тогда работа реакции N не будет равна нулю (например, работа реакции платформы лифта).
Решение задач. Теорема об изменении кинетической энергии [формула (52)] позволяет, зная как при движении точки изменяется ее скорость, определить работу действующих сил (первая задача динамики) или, зная работу действующих сил, определить, как изменяется при движении скорость точки (вторая задача динамики). При решении второй задачи, когда заданы силы, надо вычислить их работу. Как видно из формул (44), (44), это можно сделать лишь тогда, когда силы постоянны или зависят только от положения (координат) движущейся точки, как, например, силы упругости или тяготения (см. § 88).
Таким образом, формулу (52) можно непосредственно использовать для решения второй задачи динамики, когда в задаче в число данных и искомых величин входят: действующие силы, перемещение точки и ее начальная и конечная скорости (т. е. величины  ), причем силы должны быть постоянными или зависящими только от положения (координат) точки.
), причем силы должны быть постоянными или зависящими только от положения (координат) точки.
Теорему в дифференциальной форме [формула (51)] можно, конечно, применять при любых действующих силах.

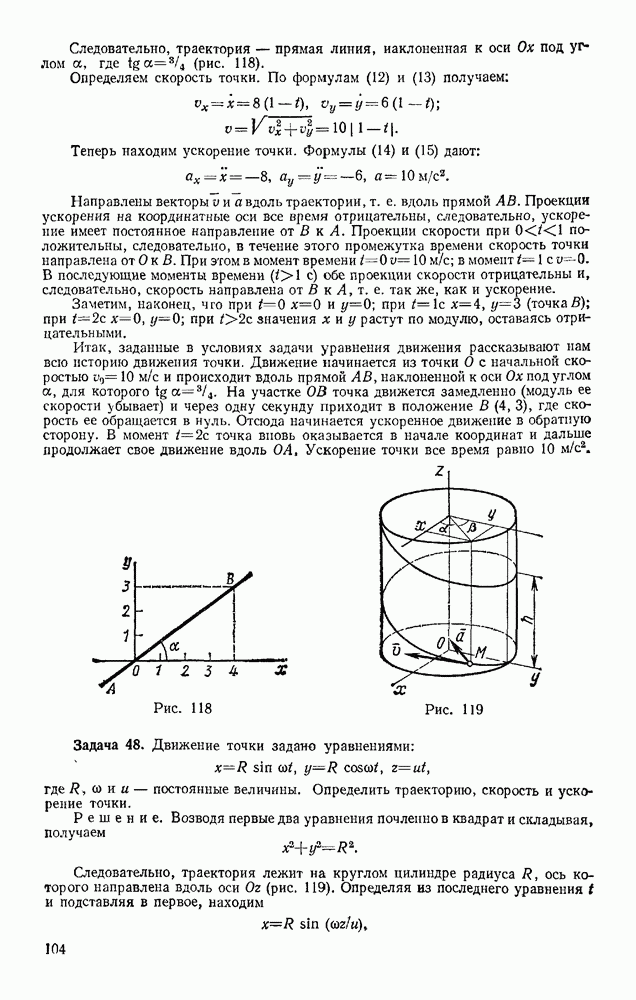
Рис. 235
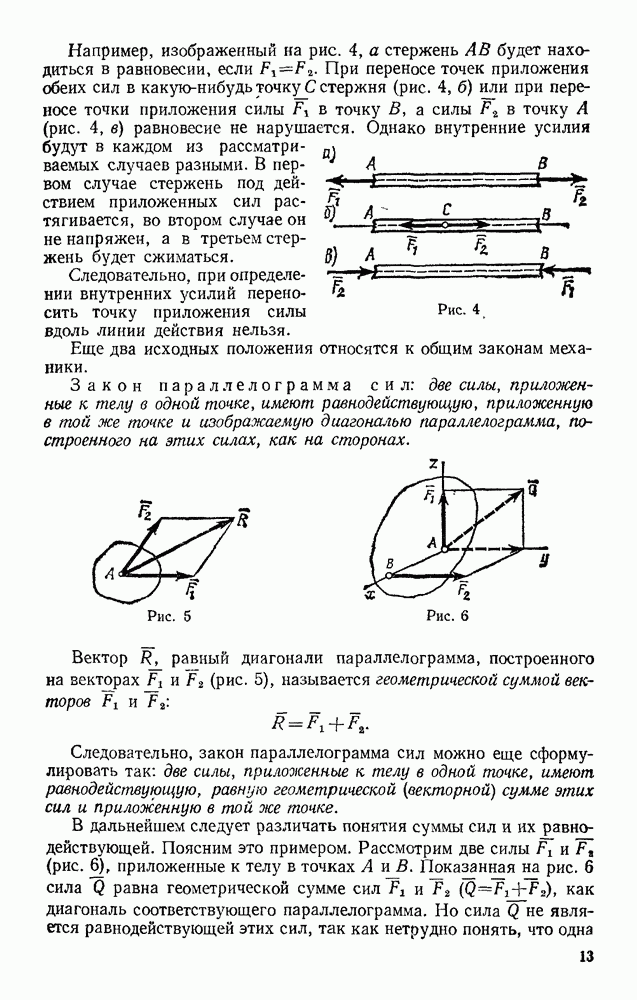
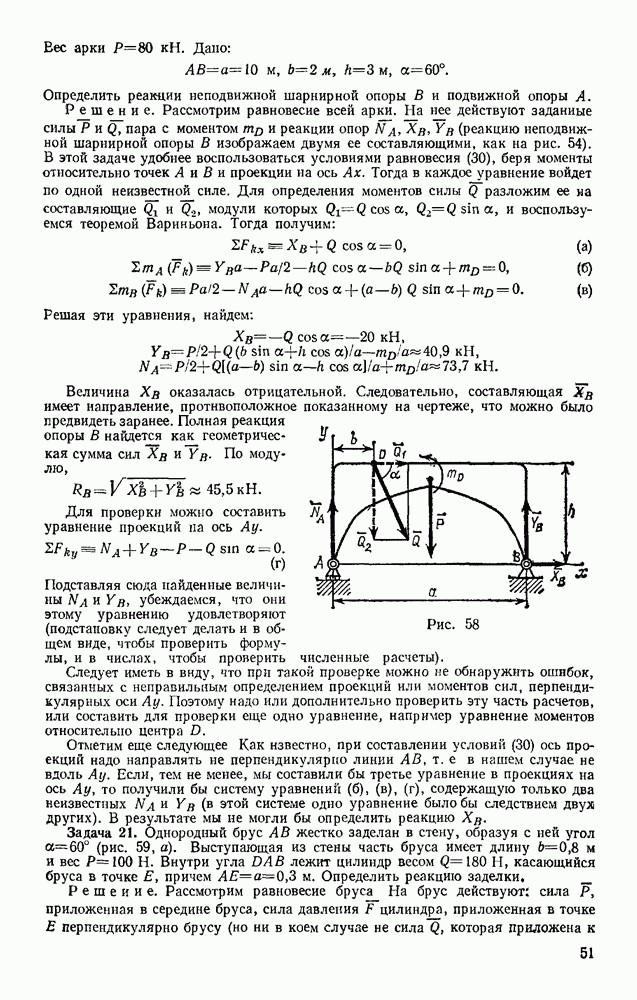
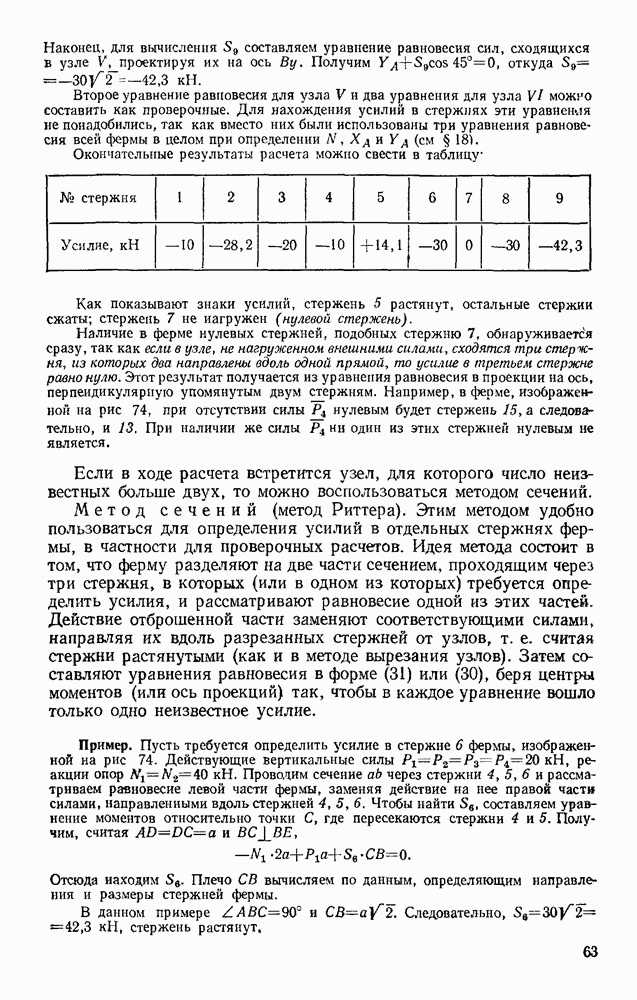
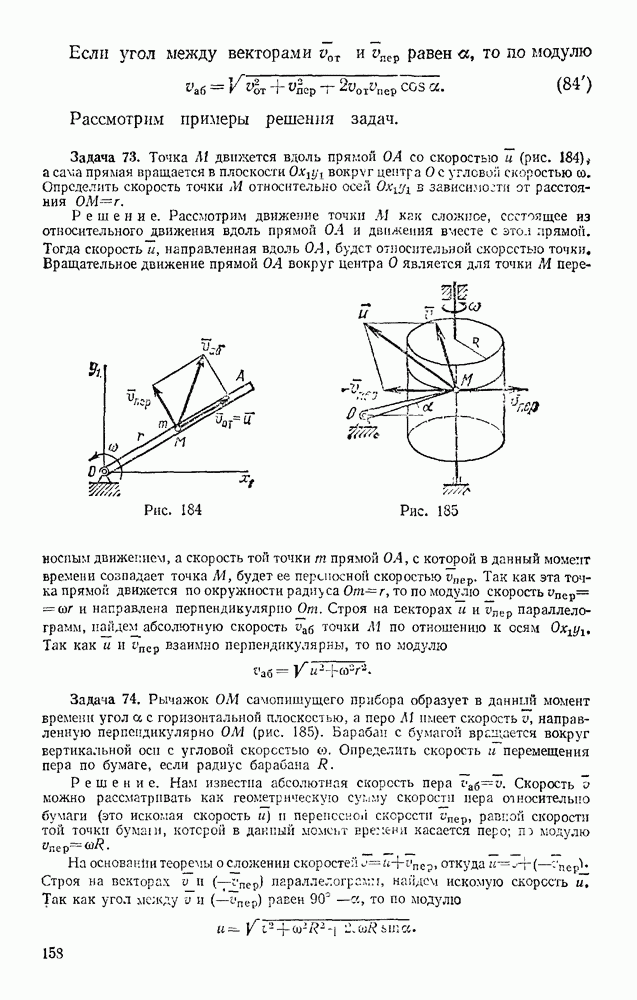
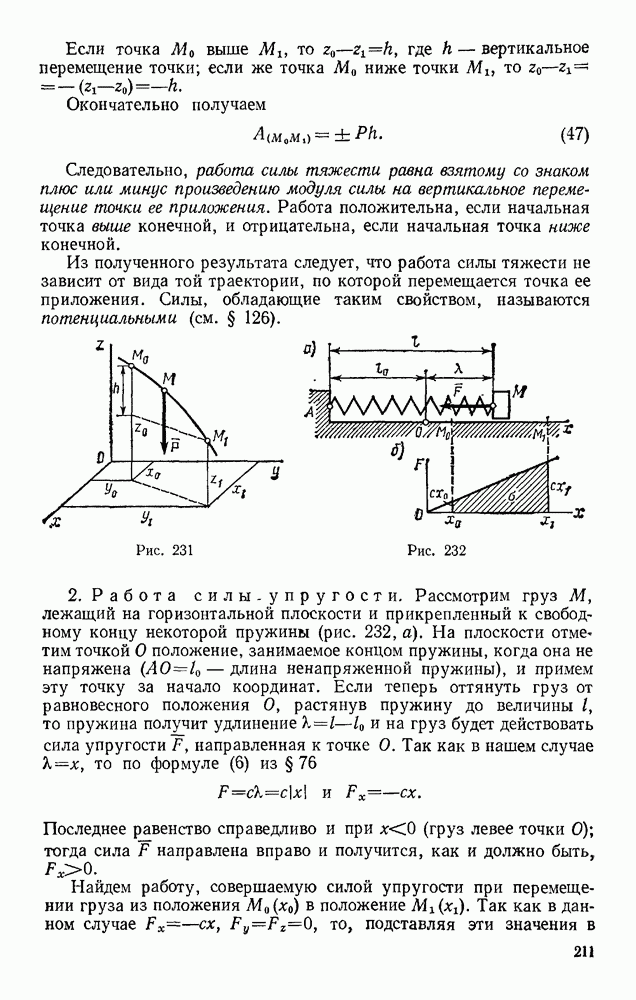
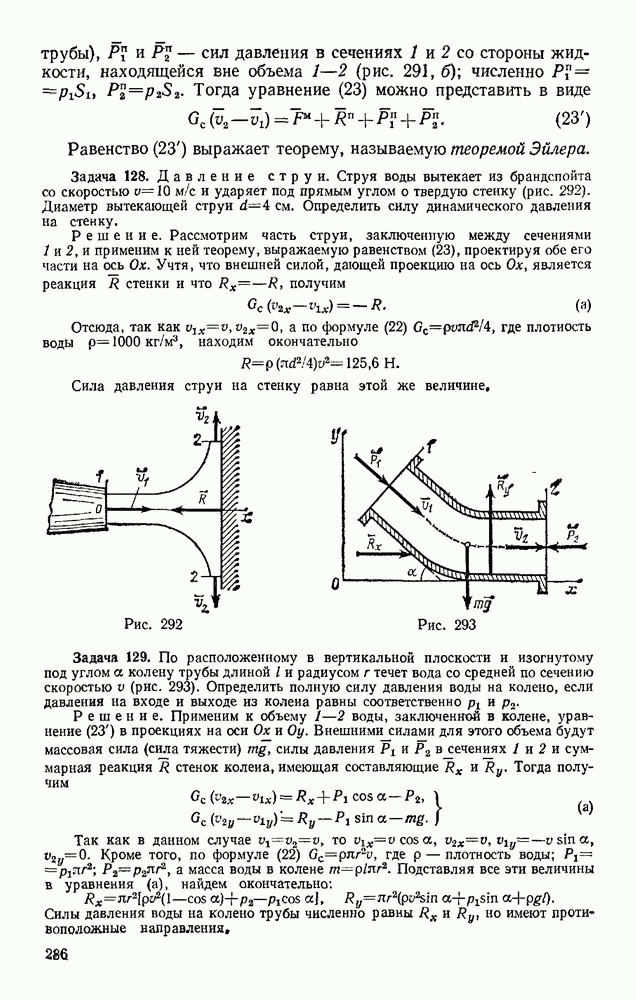
Задача 98. Груз массой  кг, брошенный со скоростью
кг, брошенный со скоростью  из пункта А, находящегося на высоте
из пункта А, находящегося на высоте  (рис. 235), имеет в точке падения С скорость
(рис. 235), имеет в точке падения С скорость  Определить, чему равна работа действующей на груз при его движении силы сопротивления воздуха
Определить, чему равна работа действующей на груз при его движении силы сопротивления воздуха 
Решение. На груз при его движении действуют сила тяжести Р и сила сопротивления воздуха R. По теореме об изменении кинетической энергии, считая груз материальной точкой, имеем

Из этого равенства, так как согласно формуле  находим
находим

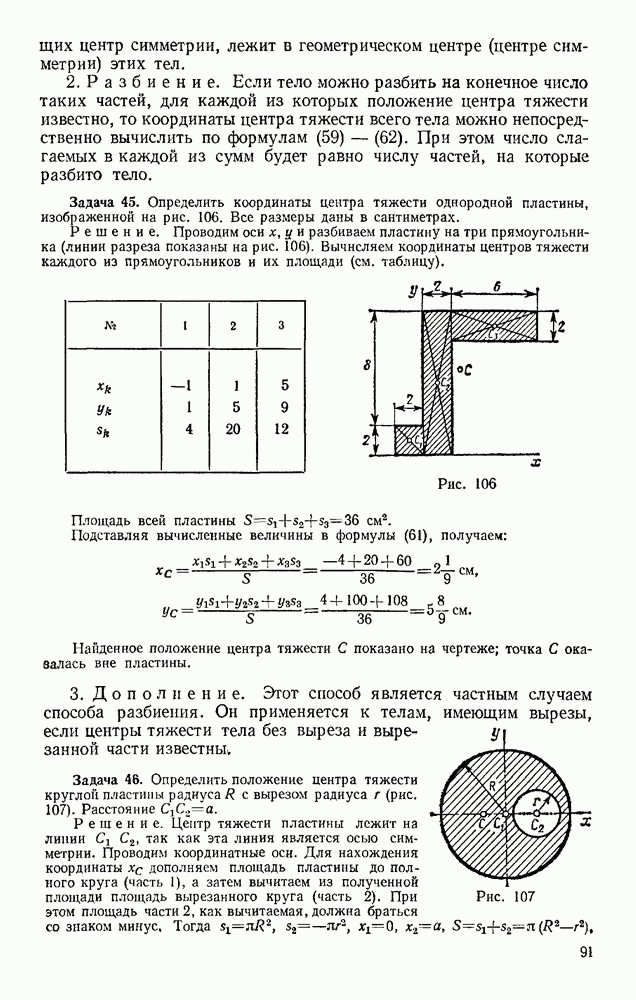
Задача 99. При условиях задачи 96 (см.[§ 84) определить, какой путь пройдет груз до остановки (см. рис, 223, где  — начальное положение груза, а
— начальное положение груза, а  — конечное).
— конечное). 
Решение. На груз, как и в задаче 96, действуют силы Р, N, F. Для определения тормозного пути  учитывая, что в условия данной задачи входят
учитывая, что в условия данной задачи входят  и постоянная сила F, воспользуемся теоремой об изменении кинетической энергии
и постоянная сила F, воспользуемся теоремой об изменении кинетической энергии

В рассматриваемом случае  — скорость груза в момент остановки). Кроме того,
— скорость груза в момент остановки). Кроме того,  так как силы Р и N перпендикулярны перемещению,
так как силы Р и N перпендикулярны перемещению,  В итоге получаем
В итоге получаем  откуда находим
откуда находим

По результатам задачи 96 время торможения растет пропорционально начальной скорости, а тормозной путь, как мы нашли, — пропорционально квадрату начальной скорости. Применительно к наземному транспорту это показывает, как возрастает опасность с увеличением скорости движения.
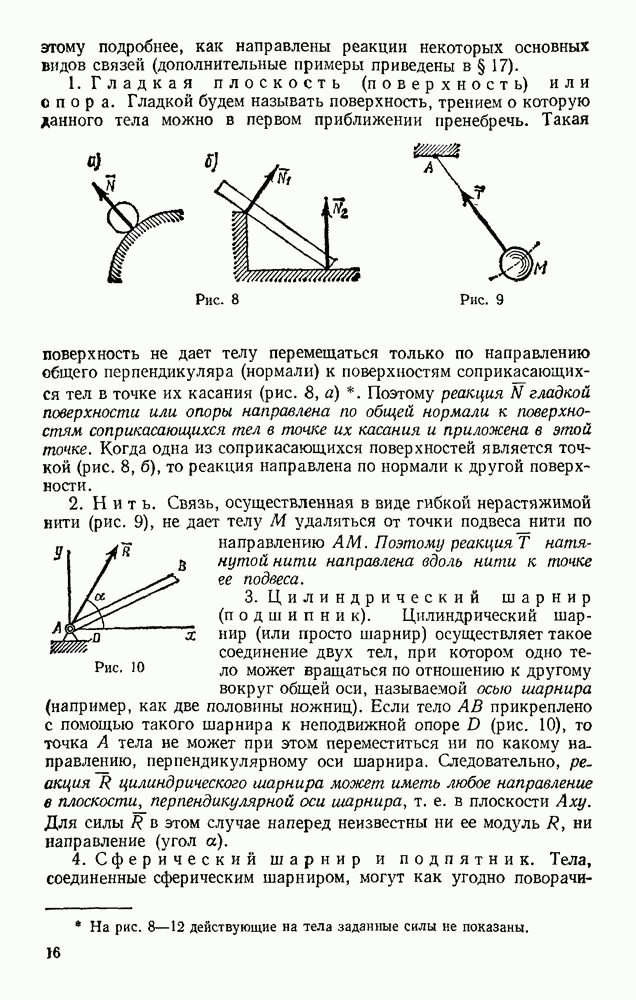
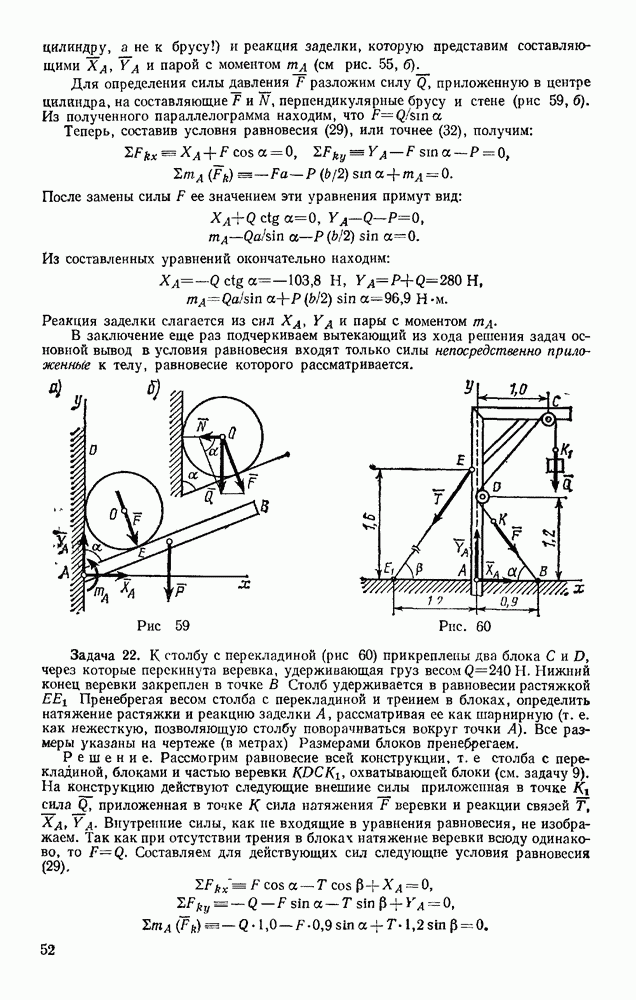
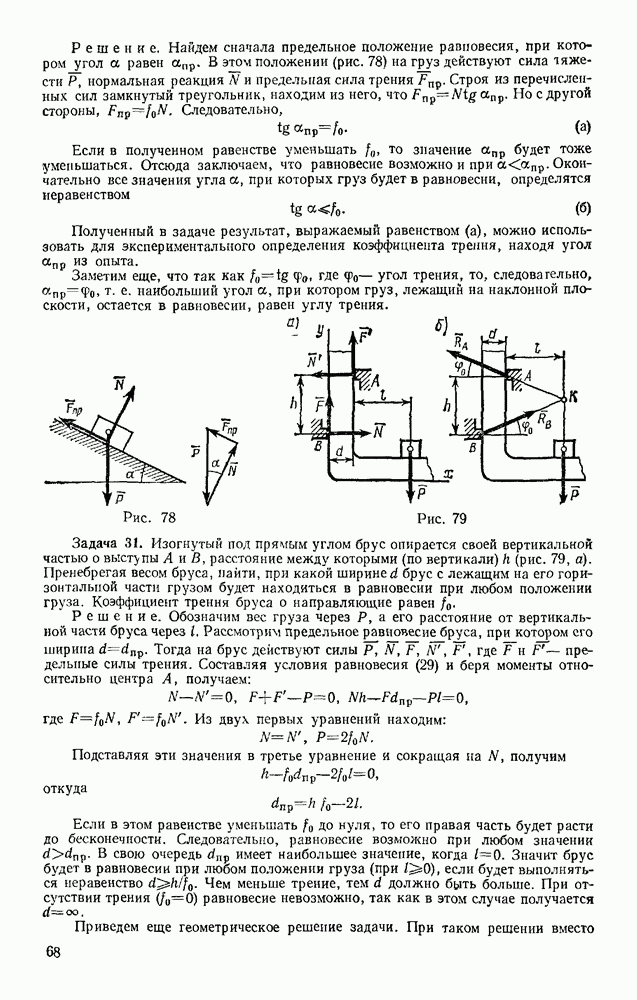
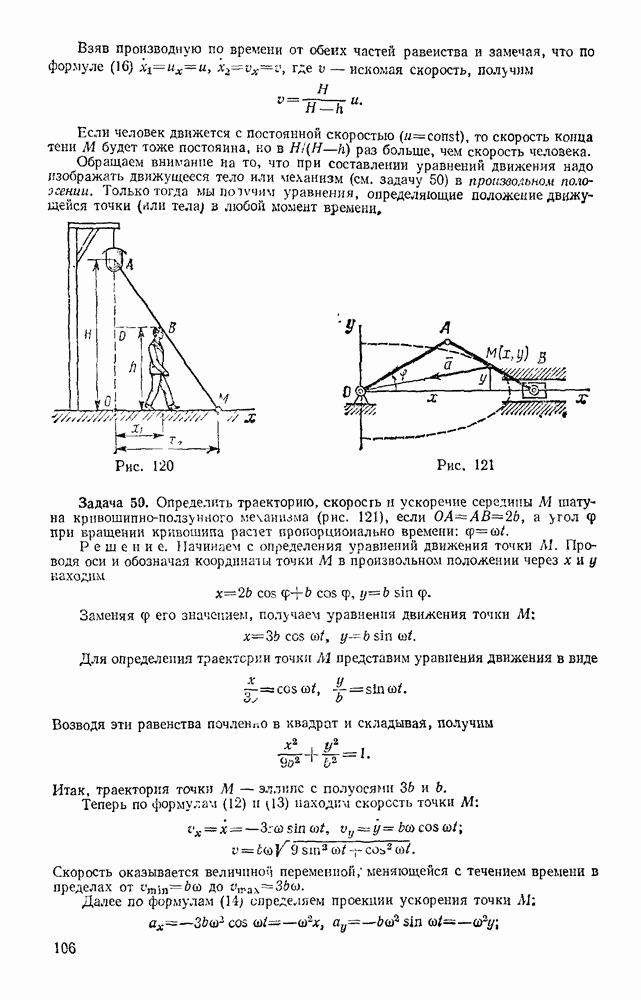
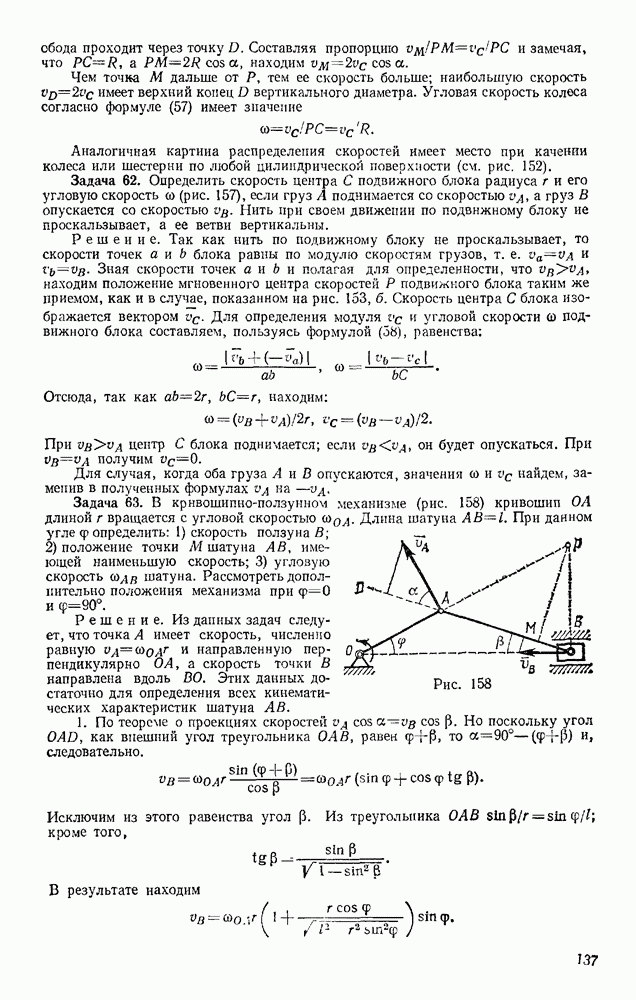
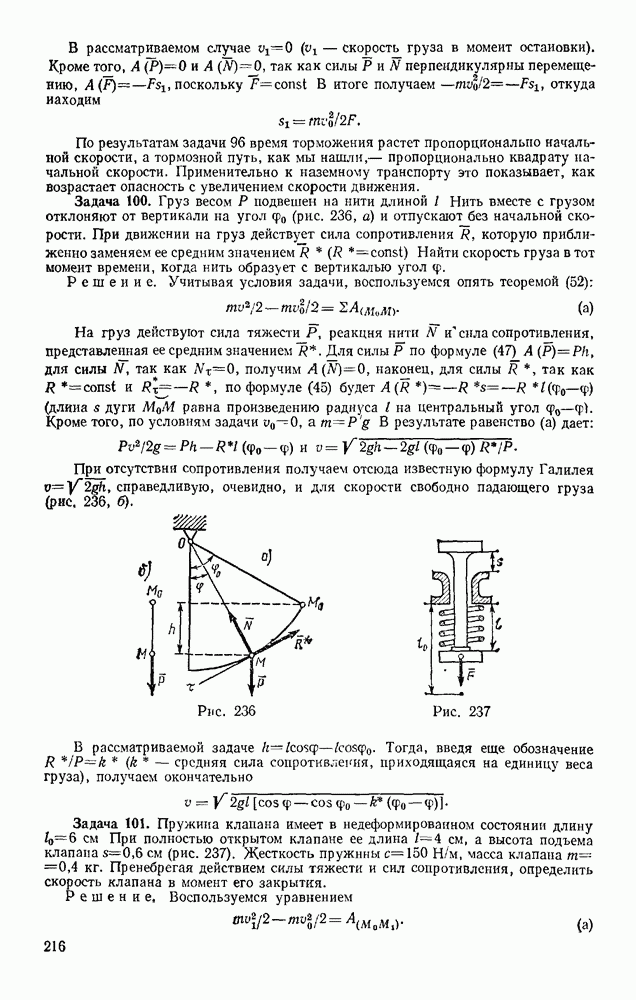
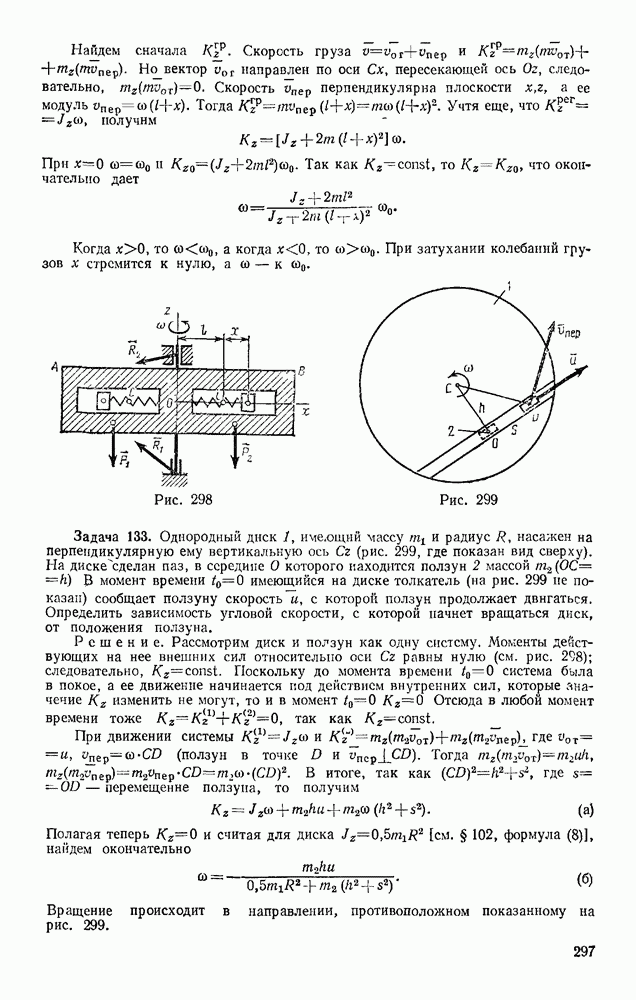
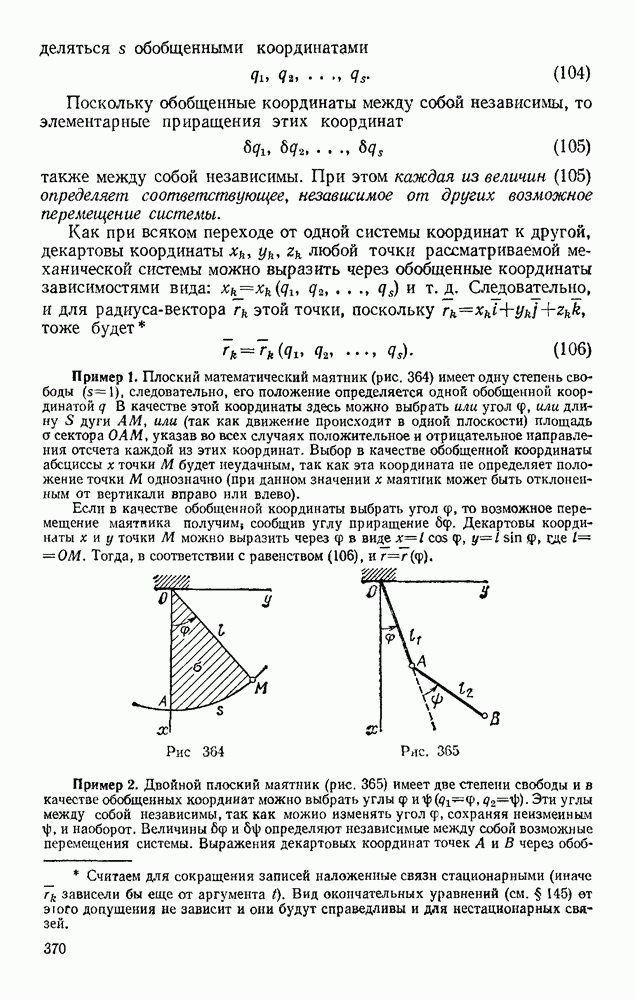
Задача 100. Груз весом Р подвешен на нити длиной l Нить вместе с грузом отклоняют от вертикали на угол  (рис. 236, а) и отпускают без начальной скорости. При движении на груз действует сила сопротивления R, которую приближенно заменяем ее средним значением
(рис. 236, а) и отпускают без начальной скорости. При движении на груз действует сила сопротивления R, которую приближенно заменяем ее средним значением  Найти скорость груза в тот момент времени, когда нить образует с вертикалью угол
Найти скорость груза в тот момент времени, когда нить образует с вертикалью угол 
Решение. Учитывая условия задачи, воспользуемся опять теоремой (52):

На груз действуют сила тяжести Р, реакция нити  сопротивления, представленная ее средним значением R. Для силы Р по формуле (47)
сопротивления, представленная ее средним значением R. Для силы Р по формуле (47)  для силы N, так как
для силы N, так как  получим
получим  наконец, для силы
наконец, для силы  так как
так как  по формуле (45) будет
по формуле (45) будет  (длина s дуги
(длина s дуги  равна произведению радиуса l на центральный угол
равна произведению радиуса l на центральный угол  ). Кроме того, по условиям задачи
). Кроме того, по условиям задачи  В результате равенство (а) дает:
В результате равенство (а) дает:

При отсутствии сопротивления получаем отсюда известную формулу Галилея  справедливую, очевидно, и для скорости свободно падающего груза (рис, 236, б).
справедливую, очевидно, и для скорости свободно падающего груза (рис, 236, б).

Рис. 236

Рис. 237
В рассматриваемой задаче  Тогда, введя еще обозначение
Тогда, введя еще обозначение  — средняя сила сопротивления, приходящаяся на единицу веса груза), получаем окончательно
— средняя сила сопротивления, приходящаяся на единицу веса груза), получаем окончательно

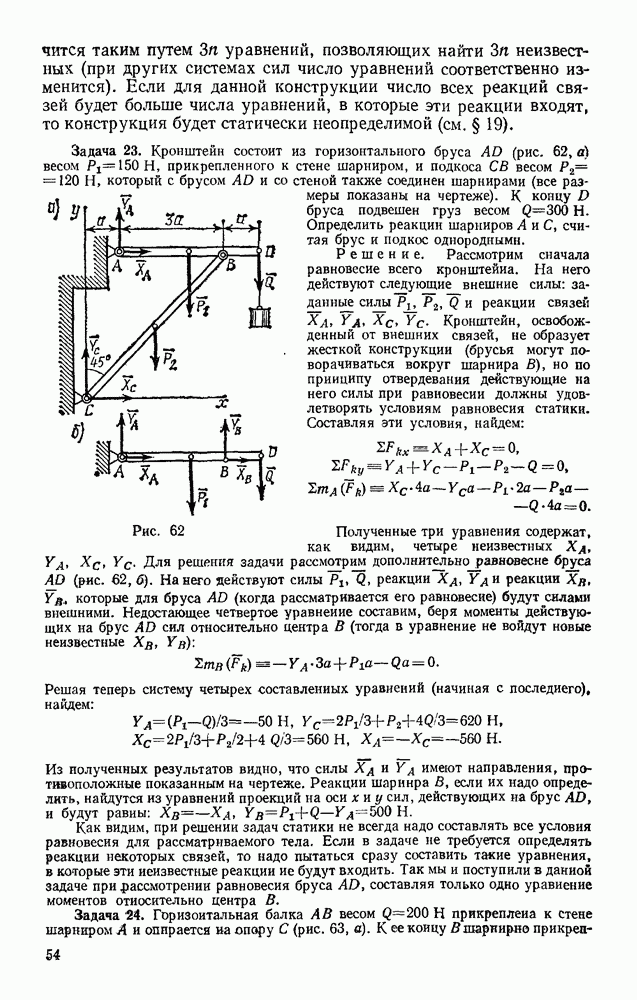
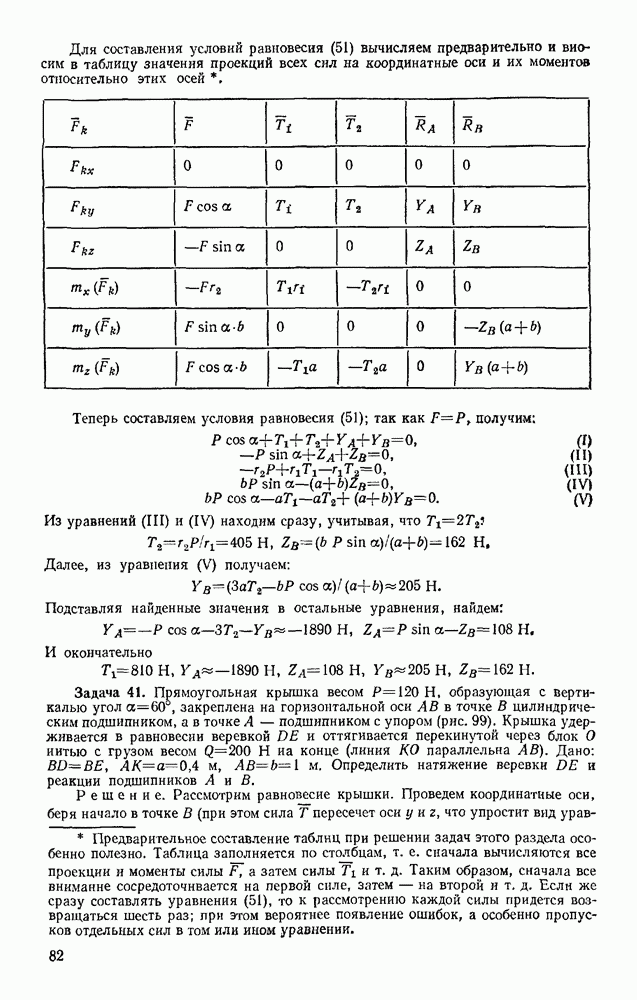
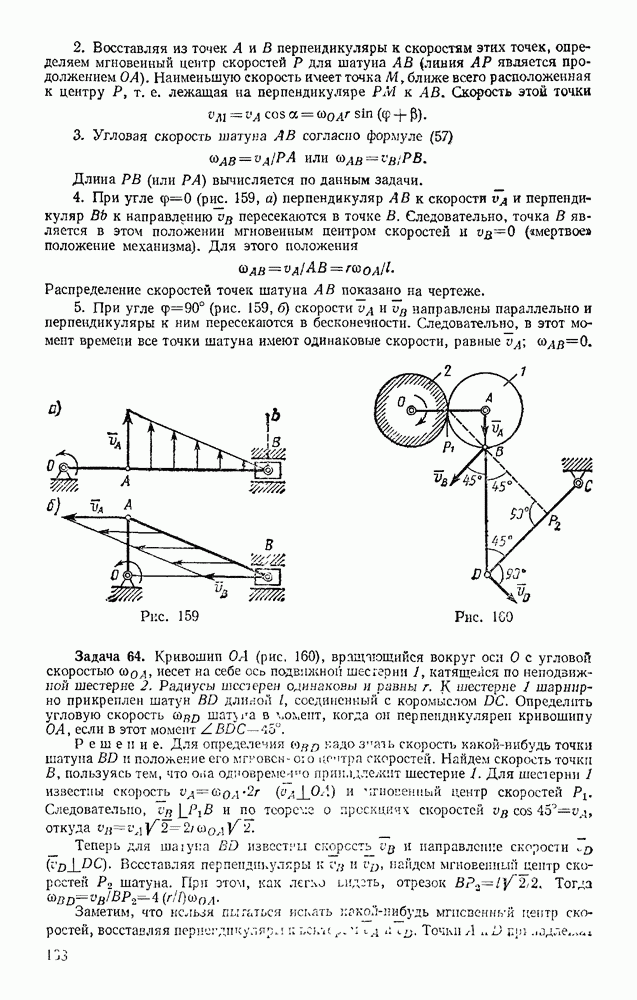
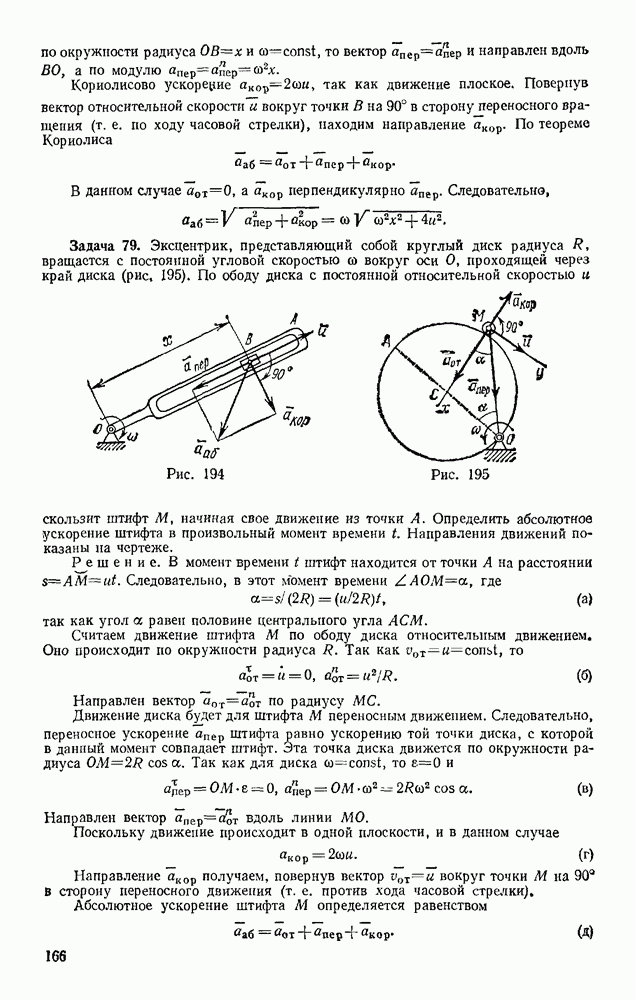
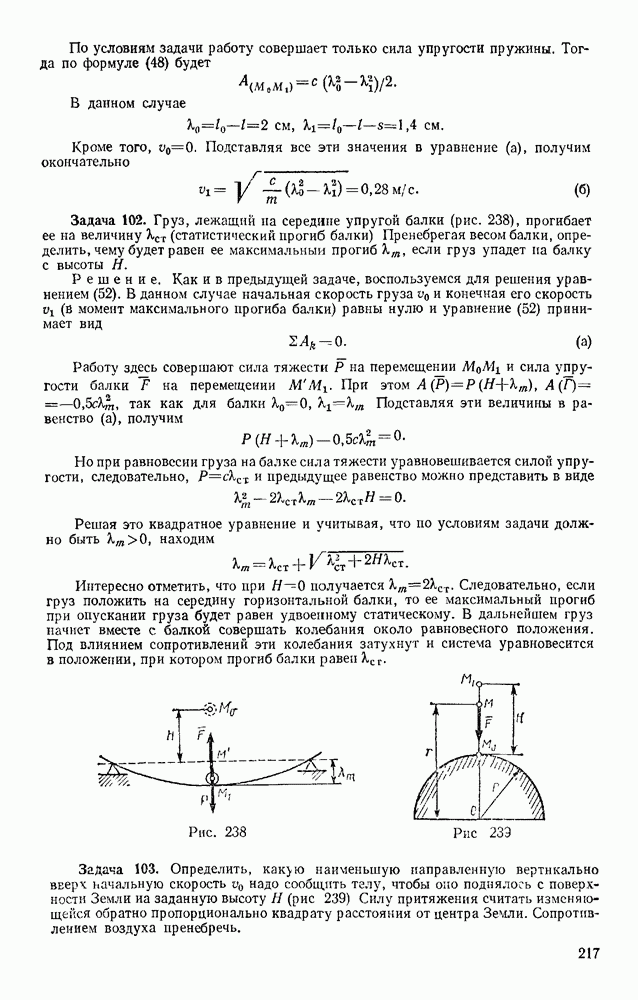
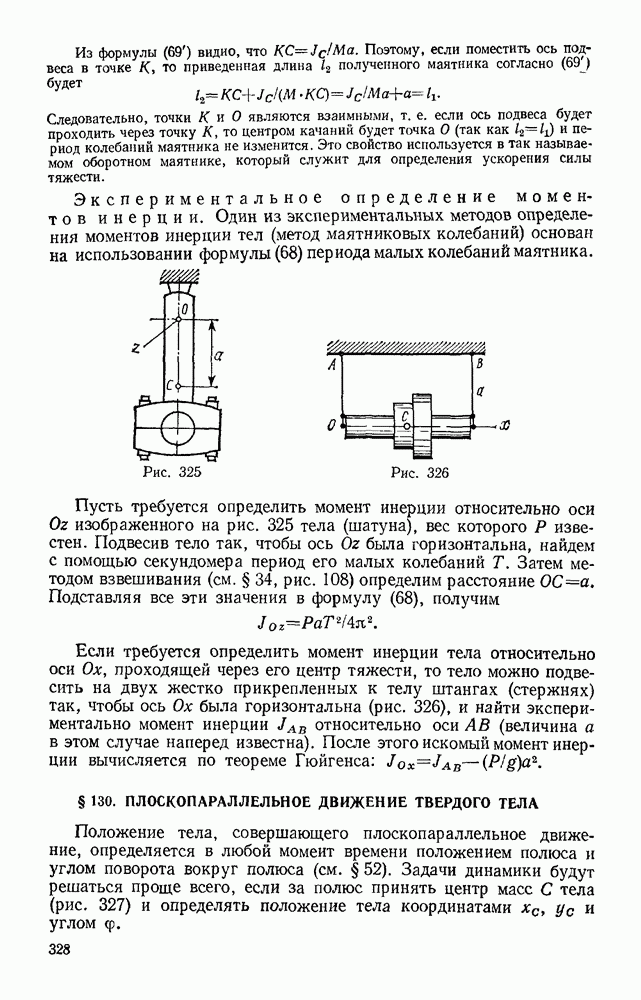
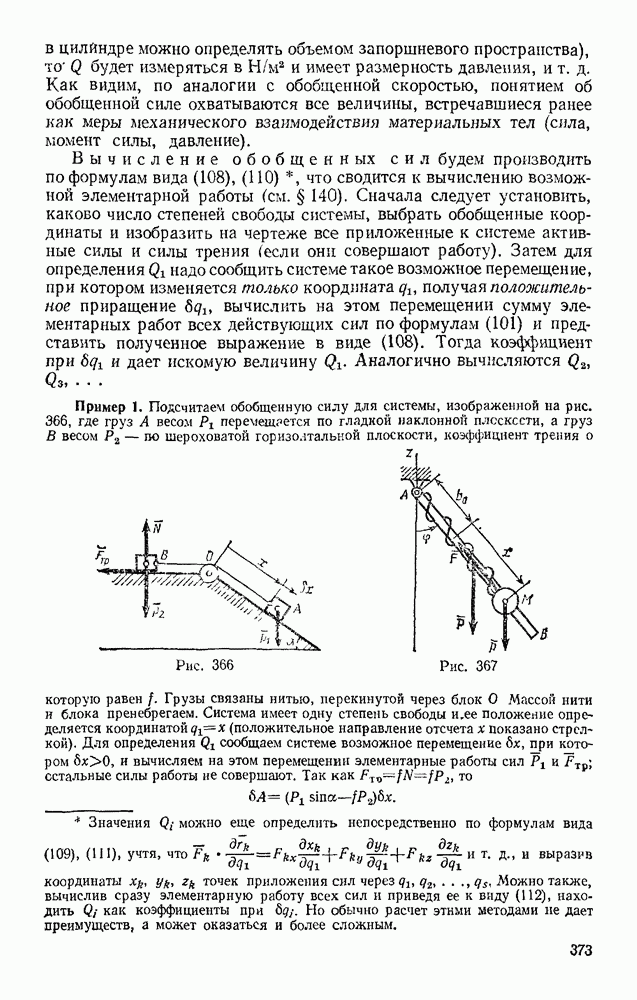
Задача 101. Пружина клапана имеет в недеформироваином состоянии длину  см. При полностью открытом клапане ее длина
см. При полностью открытом клапане ее длина  см, а высота подъема клапана
см, а высота подъема клапана  см (рис. 237). Жесткость пружины
см (рис. 237). Жесткость пружины  масса клапана
масса клапана  кг. Пренебрегая действием силы тяжести и сил сопротивления, определить скорость клапана в момент его закрытая.
кг. Пренебрегая действием силы тяжести и сил сопротивления, определить скорость клапана в момент его закрытая.
Решение, Воспользуемся уравнением

По условиям задачи работу совершает только сила упругости пружины. Тогда по формуле (48) будет

В данном случае

Кроме того,  Подставляя все эти значения в уравнение (а), получим окончательно
Подставляя все эти значения в уравнение (а), получим окончательно

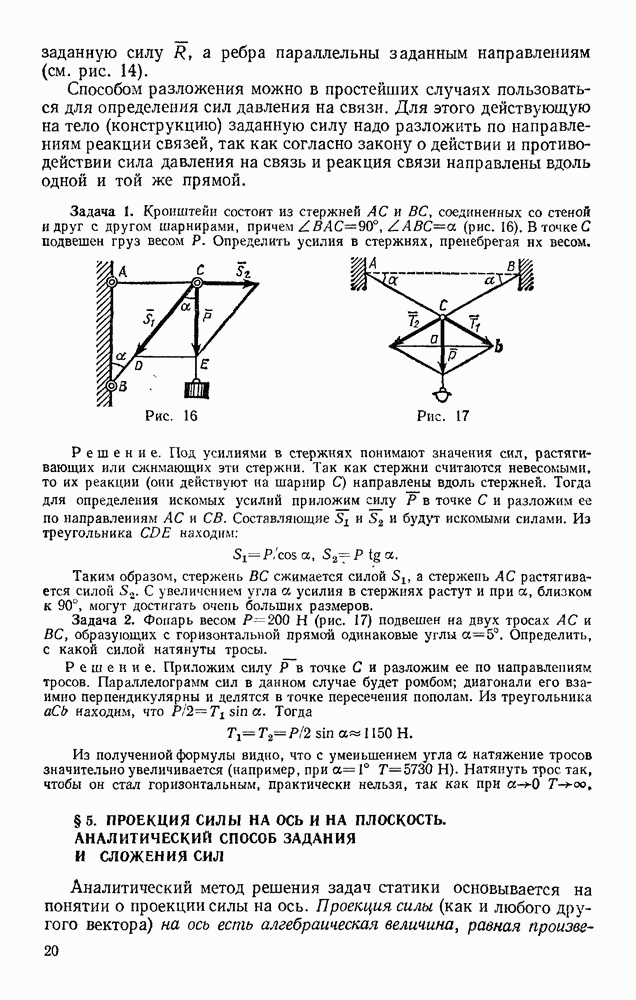
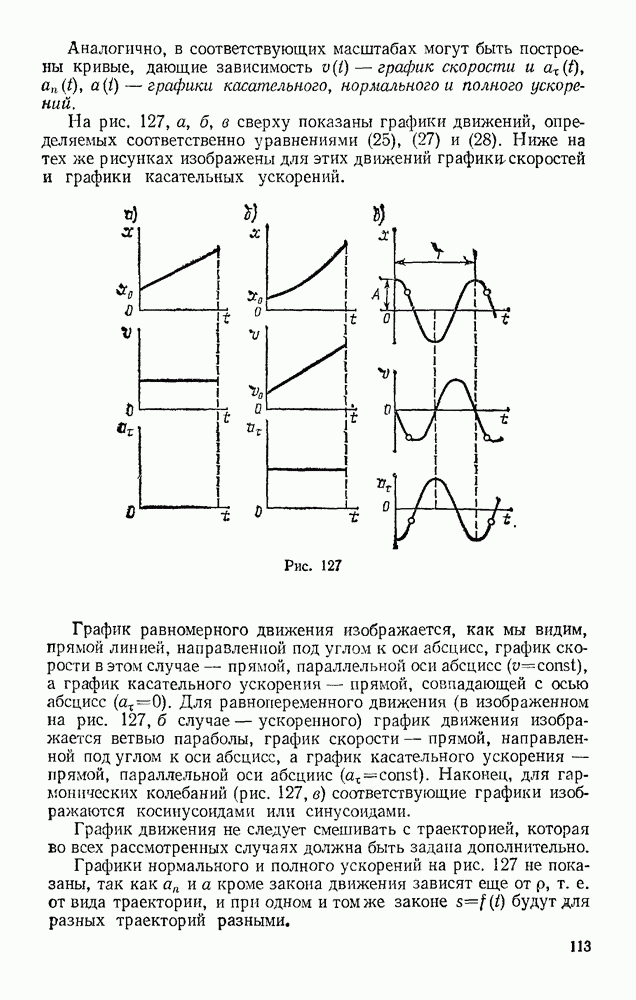
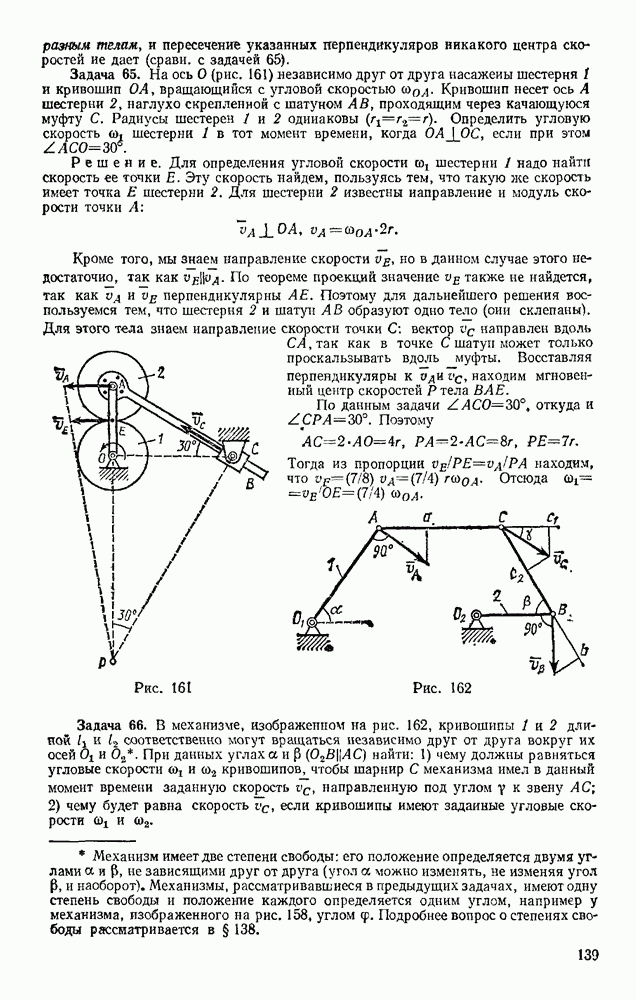
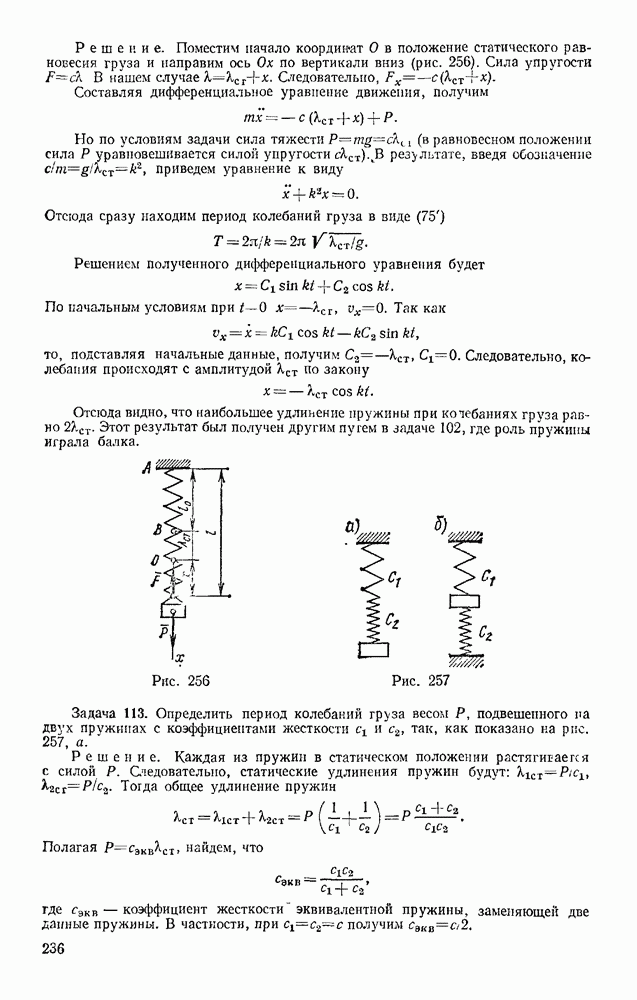
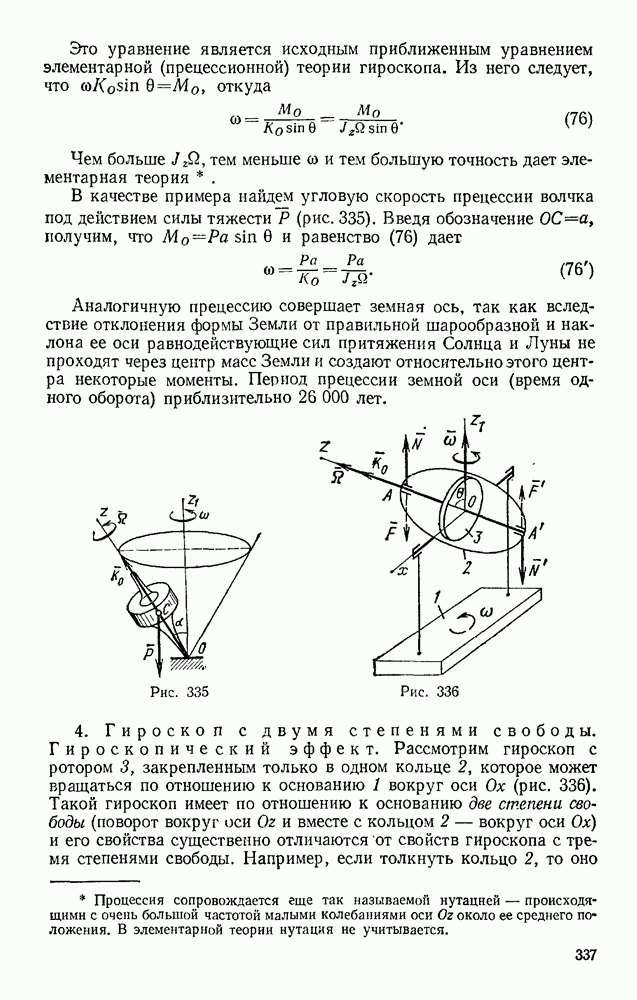
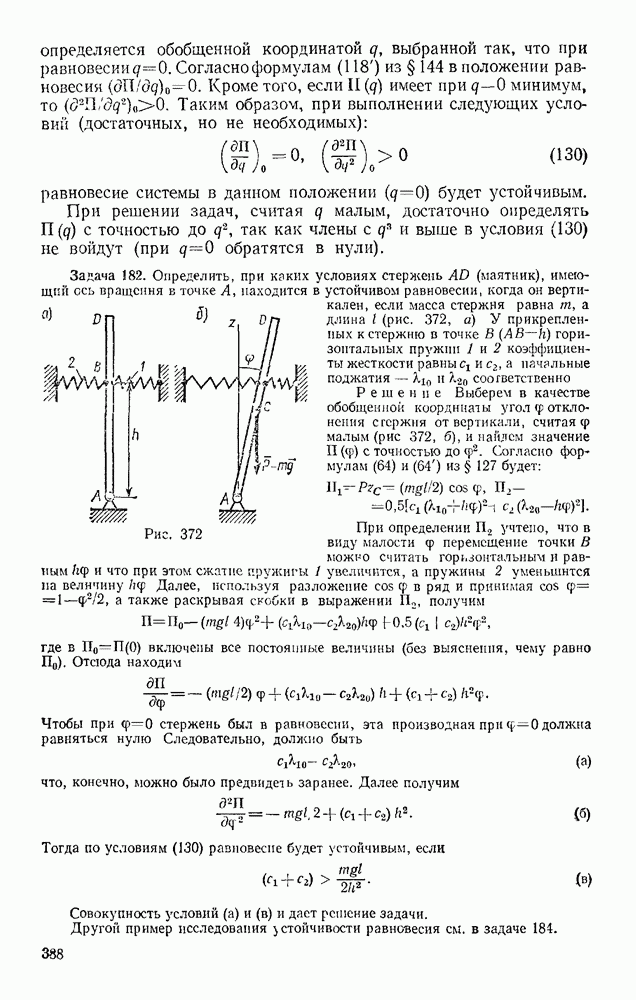
Задача 102. Груз, лежащий на середине упругой балки (рис. 238), прогибает ее на величину  (статистический прогиб балки) Пренебрегая весом балки, определить, чему будет равен ее максимальный прогиб
(статистический прогиб балки) Пренебрегая весом балки, определить, чему будет равен ее максимальный прогиб  если груз упадет на балку с высоты Н.
если груз упадет на балку с высоты Н.
Решение. Как и в предыдущей задаче, воспользуемся для решения уравнением (52). В данном случае начальная скорость груза  и конечная его скорость
и конечная его скорость  (В момент максимального прогиба балки) равны нулю и уравнение (52) принимает вид
(В момент максимального прогиба балки) равны нулю и уравнение (52) принимает вид

Работу здесь совершают сила тяжести Р на перемещении  и сила упругости балки F на перемещении
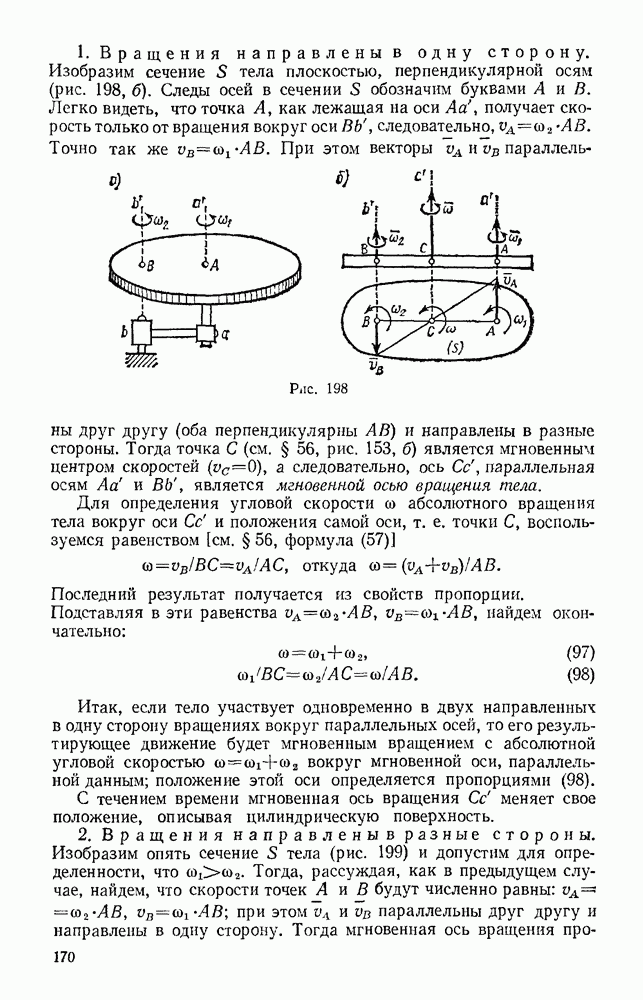
и сила упругости балки F на перемещении  При этом
При этом  так как для балкн
так как для балкн  Подставляя эти величины в равенство (а), получим
Подставляя эти величины в равенство (а), получим

Но при равновесии груза на балке сила тяжести уравновешивается силой упругости, следовательно,  и предыдущее равенство можно представить в виде
и предыдущее равенство можно представить в виде

Решая это квадратное уравнение и учитывая, что по условиям задачи должно быть  находим
находим

Интересно отметить, что при  получается
получается  Следовательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб при опускании груза будет равен удвоенному статическому. В дальнейшем груз начнет вместе с балкой совершать колебания около равновесного положения. Под влиянием сопротивлений эти колебания затухнут и система уравновесится в положении, при котором прогиб балки равен
Следовательно, если груз положить на середину горизонтальной балки, то ее максимальный прогиб при опускании груза будет равен удвоенному статическому. В дальнейшем груз начнет вместе с балкой совершать колебания около равновесного положения. Под влиянием сопротивлений эти колебания затухнут и система уравновесится в положении, при котором прогиб балки равен 

Рис. 238

Рис. 239
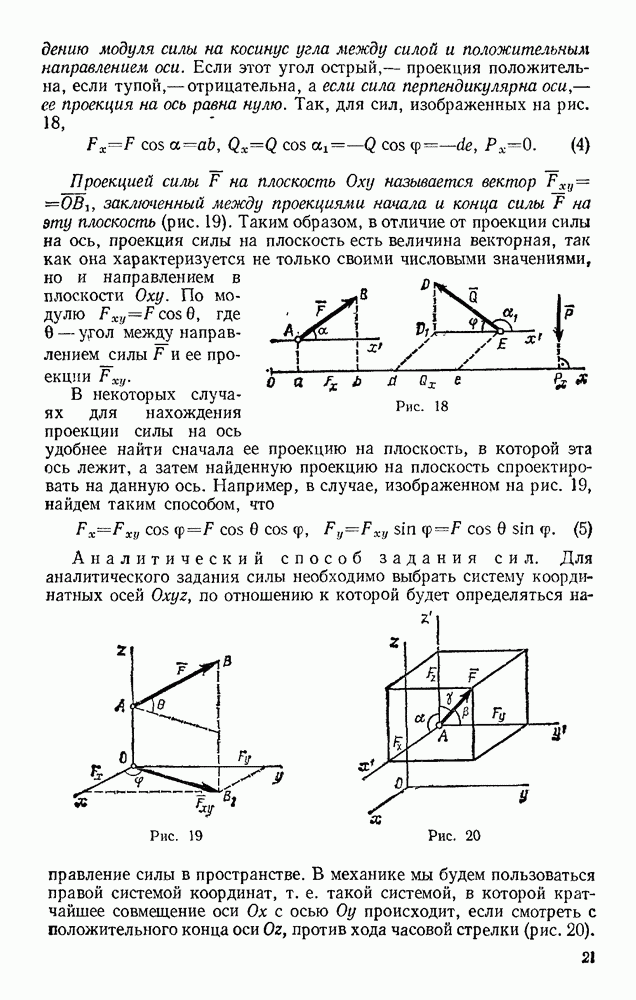
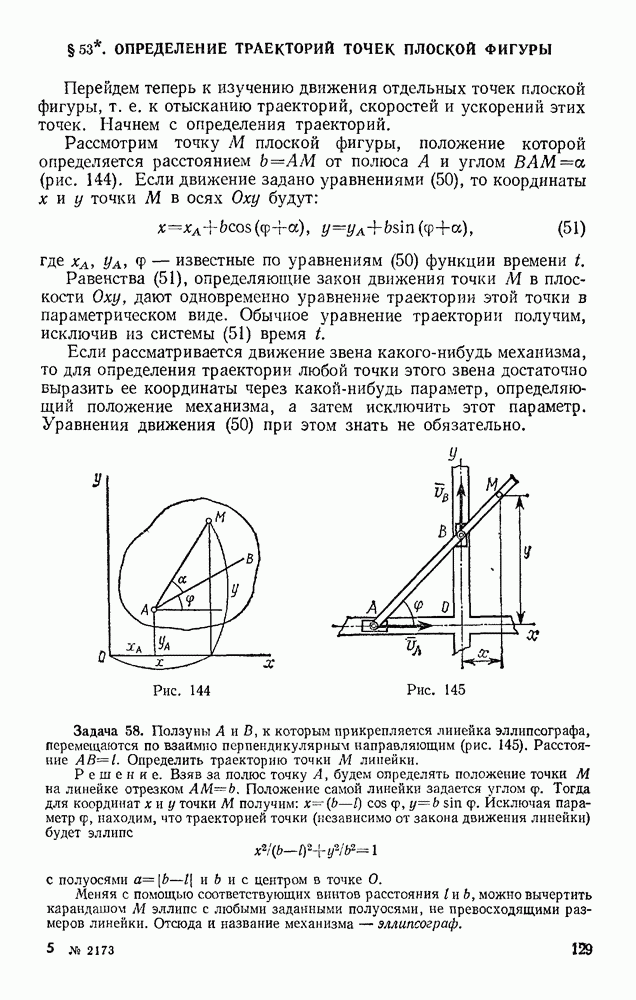
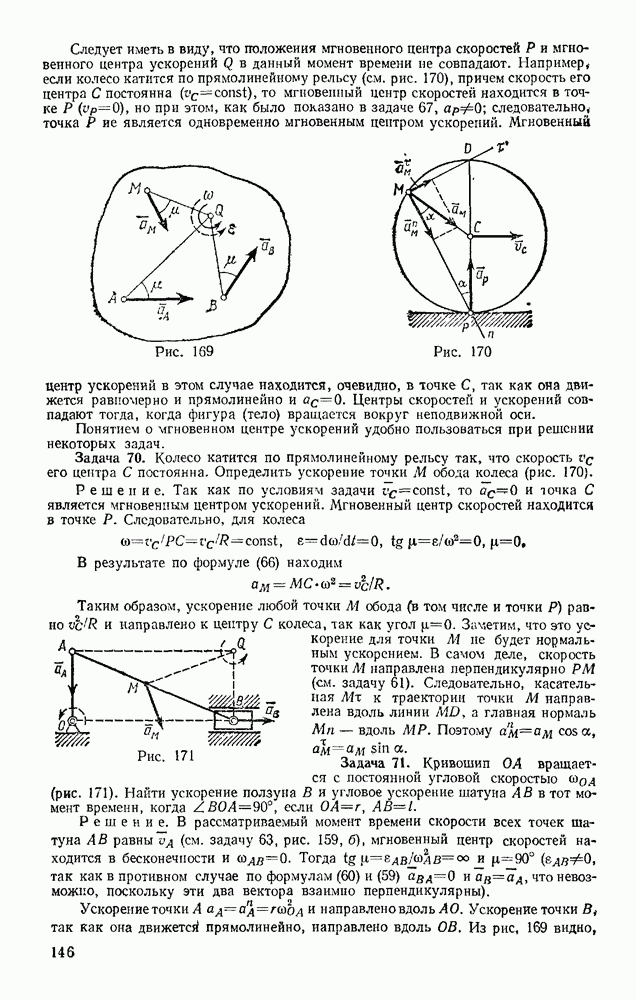
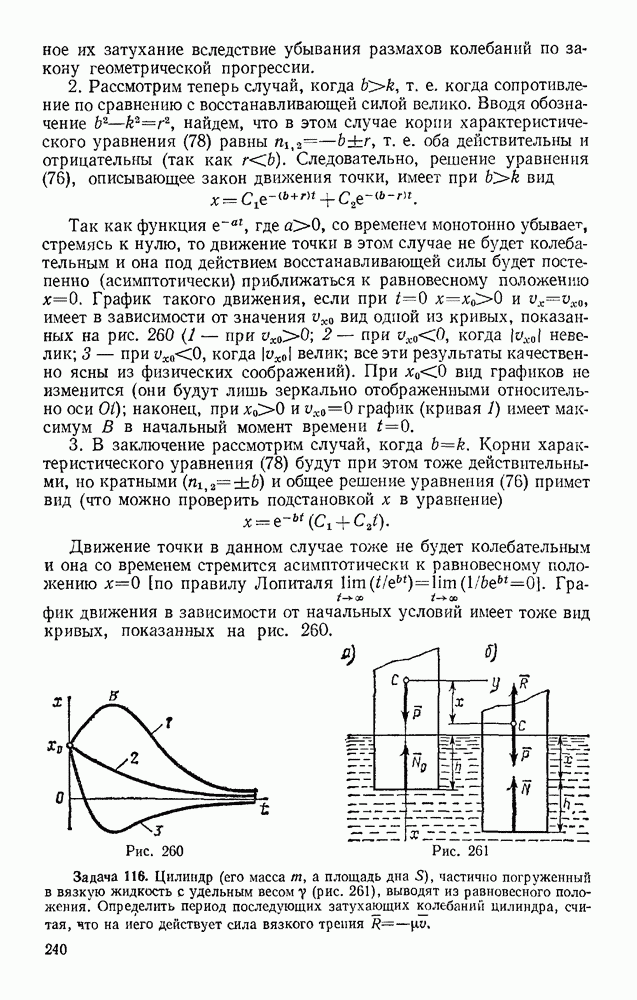
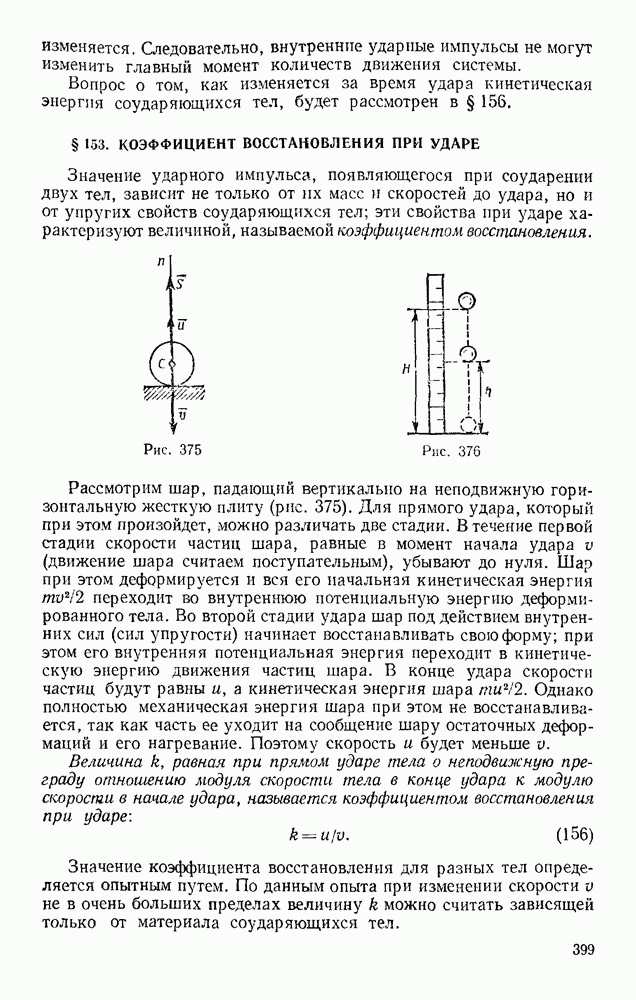
Задача 103. Определить,  наименьшую направленную вертикально виерх начальную скорость
наименьшую направленную вертикально виерх начальную скорость  надо сообщить телу, чтобы оно поднялось с поверхности Земли на заданную высоту Н (рис 239) Силу притяжения считать изменяющейся обратно пропорционально квадрату расстояния от центра Земли. Сопротивлением воздуха пренебречь.
надо сообщить телу, чтобы оно поднялось с поверхности Земли на заданную высоту Н (рис 239) Силу притяжения считать изменяющейся обратно пропорционально квадрату расстояния от центра Земли. Сопротивлением воздуха пренебречь.
Решение. Рассматривая тело как материальную точку с массой  , воспользуемся уравнением
, воспользуемся уравнением

Работу здесь совершает сила тяготения F. Тогда по формуле (50), учитывая, что в данном случае  где R — радиус Земли, получим
где R — радиус Земли, получим

Так как в наивысшей точке  то при найденном значении работы уравнение (а) дает
то при найденном значении работы уравнение (а) дает

Рассмотрим частные случай:
а) пусть Н очень мало по сравнению с R. Тогда  — величина, близкая к нулю. Деля числитель и знаменатель
— величина, близкая к нулю. Деля числитель и знаменатель  получим
получим

Таким образом, при малых Н приходим к формуле Галилея;
б) найдем, при какой начальной скорости брошенное тело уйдет в бесконечность, Деля числитель и знаменатель на А, получим

При  считая средний радиус Зели
считая средний радиус Зели  км, находим
км, находим

Следовательно, тело, брошенное с поверхности Земли со скоростью  навсегда покинет поле земного тяготения. Скорость, определяемая равенством (б), называется второй космической скоростью.
навсегда покинет поле земного тяготения. Скорость, определяемая равенством (б), называется второй космической скоростью.
Можно доказать (см. гл. XX), что при начальных скоростях, лежащих приблизительно в пределах  тело, брошенное по направлению касательной к земной поверхности, не упадет обратно на Землю, а превратится в земного спутника. При начальных скоростях, меньших
тело, брошенное по направлению касательной к земной поверхности, не упадет обратно на Землю, а превратится в земного спутника. При начальных скоростях, меньших  или при негоризонтальном бросании тело, описав эллиптическую траекторию, упадет обратно на Землю. Все эти результаты относятся к движению в безвоздушном пространстве.
или при негоризонтальном бросании тело, описав эллиптическую траекторию, упадет обратно на Землю. Все эти результаты относятся к движению в безвоздушном пространстве.

Рис. 240
Задача 104. Определить, пренебрегая трением, какую постоянную силу Q надо приложить к поршню 1 (площадь поршня S, начальная скорость  ), чтобы сжать газ, находящийся в цилиндре 2, до давления
), чтобы сжать газ, находящийся в цилиндре 2, до давления  если начальное давление равно
если начальное давление равно  (рис. 240). Считать, что при сжатии давление газа
(рис. 240). Считать, что при сжатии давление газа  растет обратно пропорционально его объему V (сжатие происходит медленно, процесс изотермический).
растет обратно пропорционально его объему V (сжатие происходит медленно, процесс изотермический).
Решение. На поршень действуют сила Q и сила давления газа Р. Так как у поршня  то по теореме об изменении кинетической энергии
то по теореме об изменении кинетической энергии

Направим ось  в сторону движения поршня, считая, что при
в сторону движения поршня, считая, что при  давление
давление  Обозначим через
Обозначим через  начальное расстояние поршня от дна цилиндра, а через
начальное расстояние поршня от дна цилиндра, а через  — перемещение поршия до положения, при котором
— перемещение поршия до положения, при котором  и давление
и давление 
Так как численно  то по формуле (44)
то по формуле (44)

Зависимость  от
от  найдем из условия, что давление обратно пропорционально объему, т. е.
найдем из условия, что давление обратно пропорционально объему, т. е.  где начальный объем
где начальный объем  а объем в произвольном положении
а объем в произвольном положении  Тогда для
Тогда для  , а талсже для координаты
, а талсже для координаты  при которой
при которой  получим выражения:
получим выражения:

Учтя эти зависимости, найдем из равенства (б)

Далее, так как  , получим с учетом соотношений (в)
, получим с учетом соотношений (в)

При иайдеиных значениях работ равенстве (а) дает окончательно

Если  полагая приближенно
полагая приближенно  получим
получим

Сила Q с увеличением  растет на логарифмическому закону, т. е. довольно медленно. Например, при
растет на логарифмическому закону, т. е. довольно медленно. Например, при  а при
а при 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
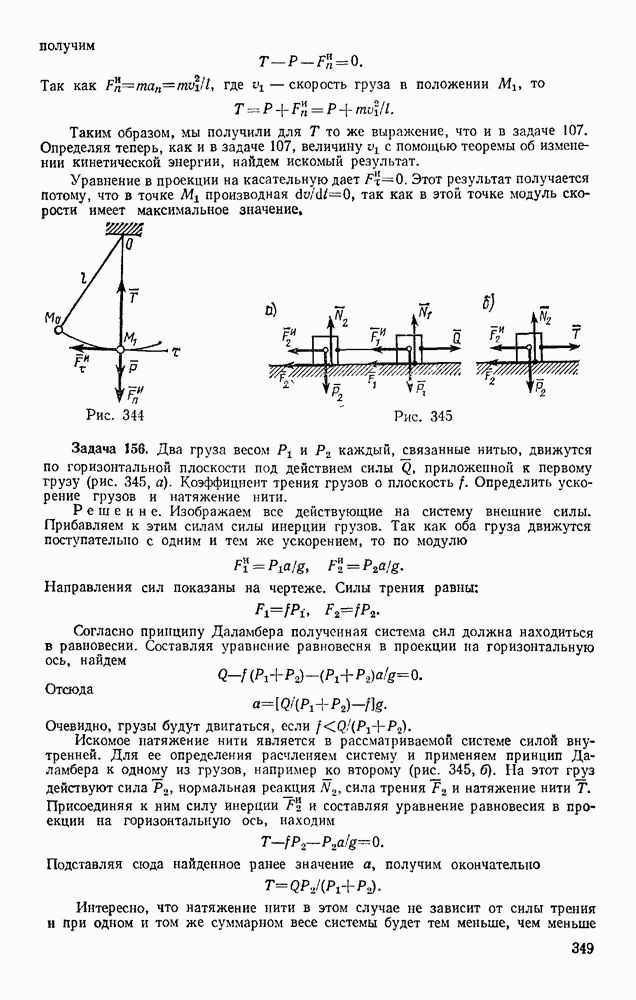
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
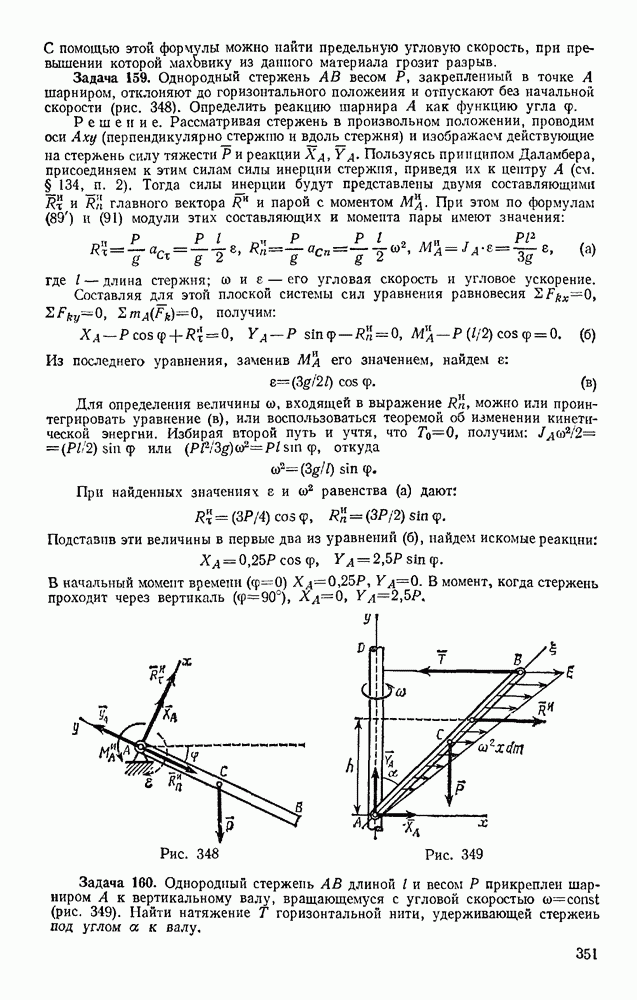
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА