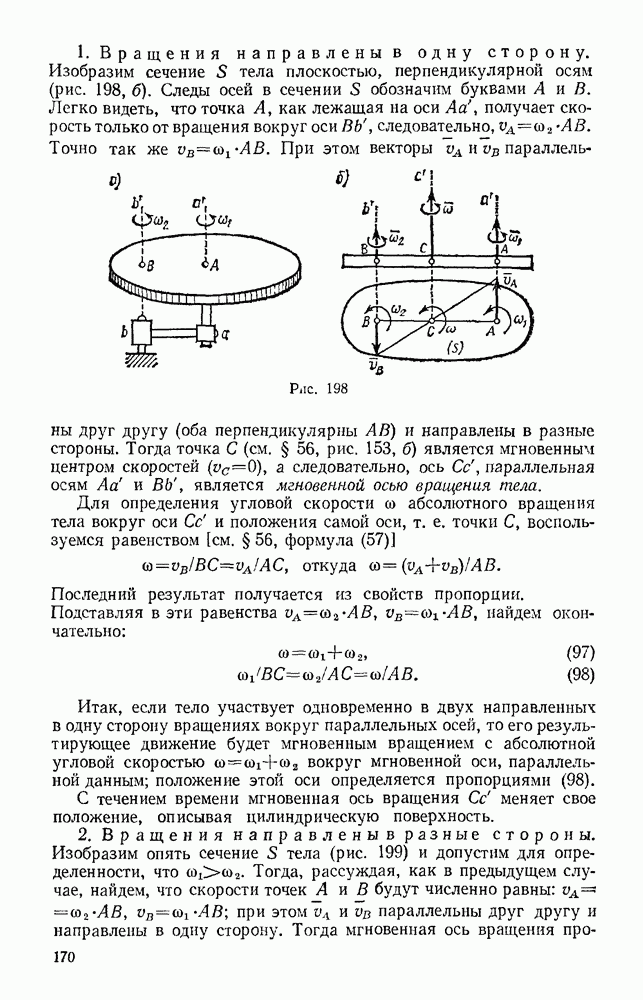
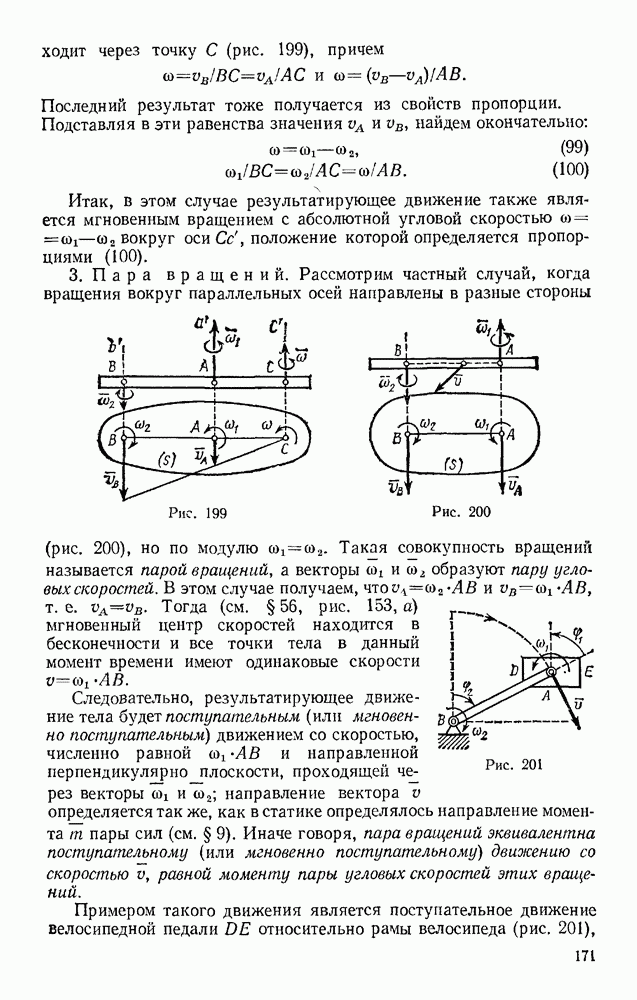
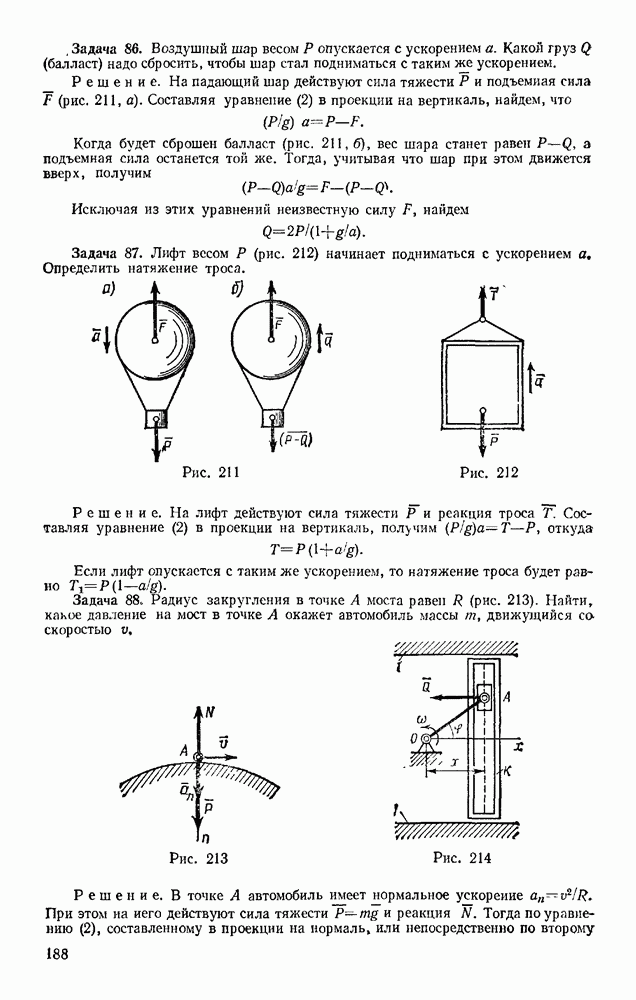
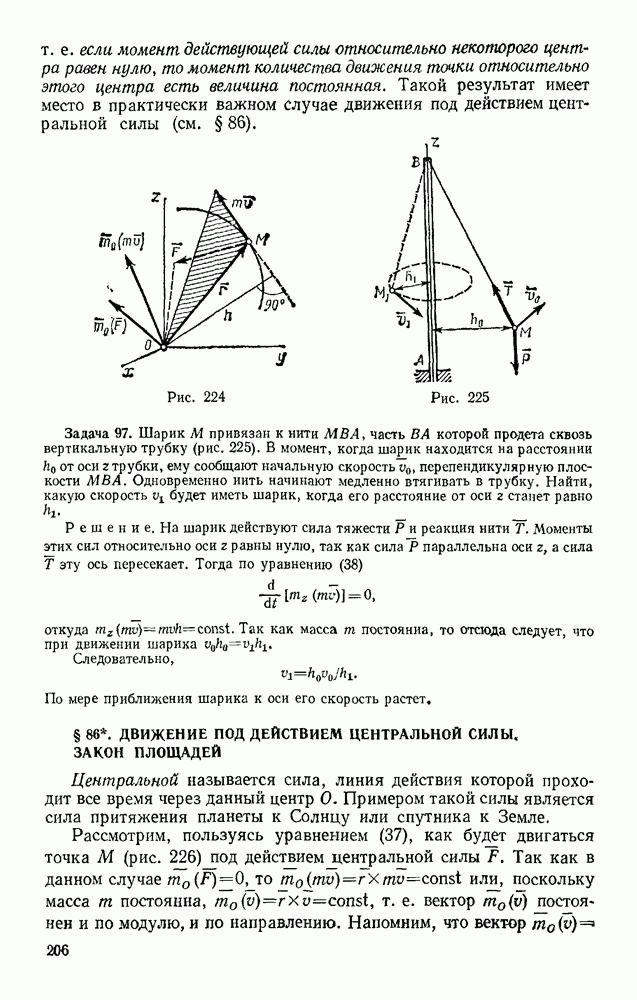
| << Предыдущий параграф | Следующий параграф >> |
Пред.
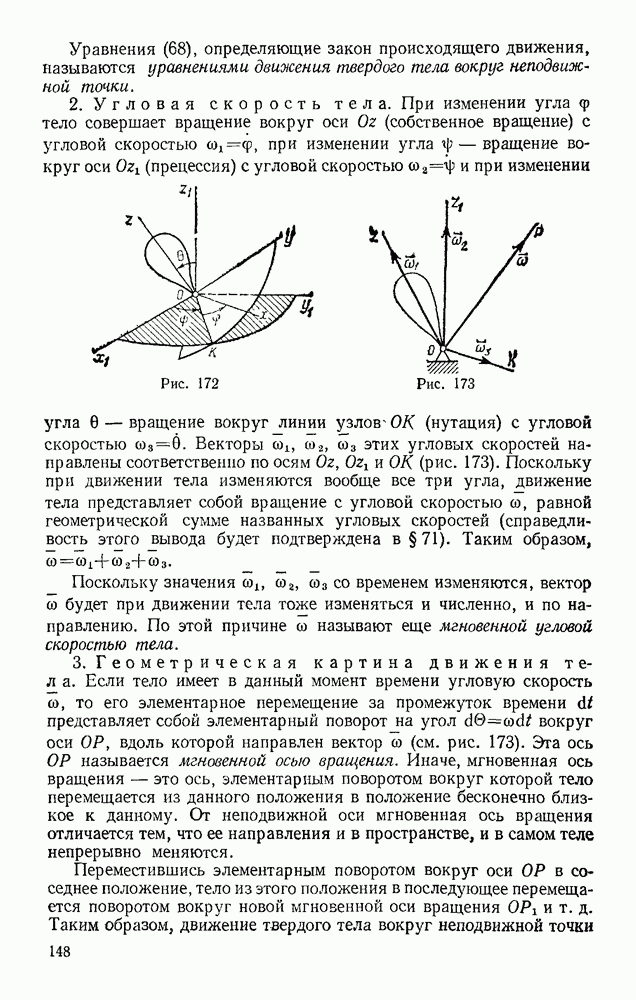
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
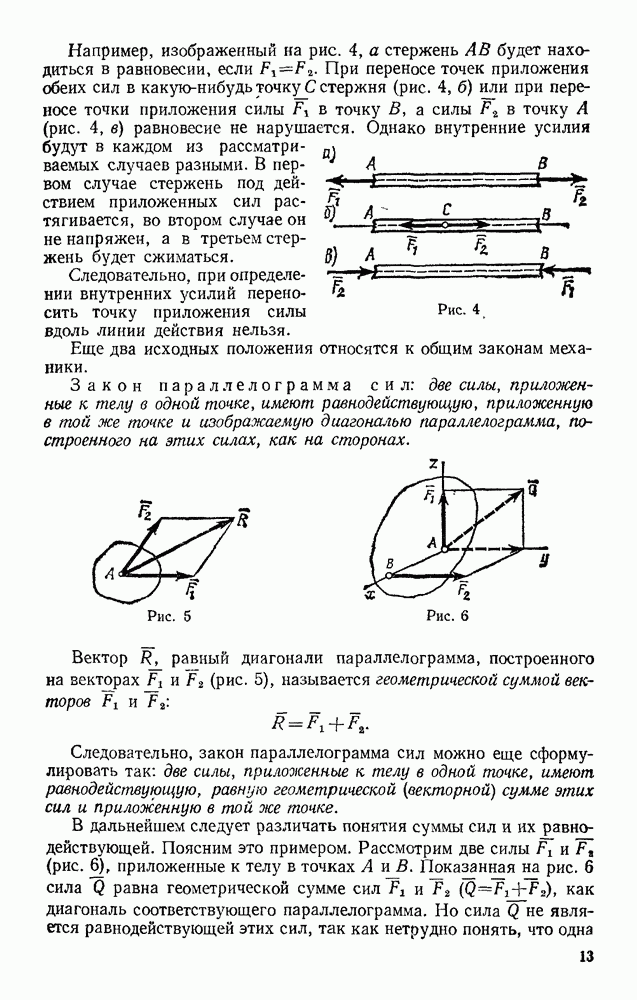
§ 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Следовательно, применяя эти два принципа одновременно, мы можем получить общий метод решения задач динамики.
Рассмотрим систему материальных точек, на которую наложены идеальные связи. Если ко всем точкам системы кроме действующих на них активных сил  и реакций связей
и реакций связей  прибавить соответствующие силы инерции
прибавить соответствующие силы инерции  то согласно принципу Даламбера полученная система сил будет находиться в равновесии. Тогда, применяя к этим силам принцип возможных перемещений, получим
то согласно принципу Даламбера полученная система сил будет находиться в равновесии. Тогда, применяя к этим силам принцип возможных перемещений, получим

Но последняя сумма по условию (98) равна нулю и окончательно будет:

Из полученного результата вытекает следующий принцип Даламбера — Лагранжа: при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.
Уравнение (102), выражающее этот принцип, называют общим уравнением динамики. В аналитической форме уравнение (102) имеет вид

Уравнения (102) или (103) позволяют составить дифференциальные уравнения движения механической системы.
Если при этом система представляет собой совокупность каких-нибудь твердых тел, то для составления уравнений нужно к действующим на каждое тело активным еилам прибавить приложенную в любом центре силу, равную главному вектору сил инерции, и пару с моментом, равным главному моменту сил инерции относительно этого центра (или одну из этих величин, см. § 134), а затем применить принцип возможных перемещений.
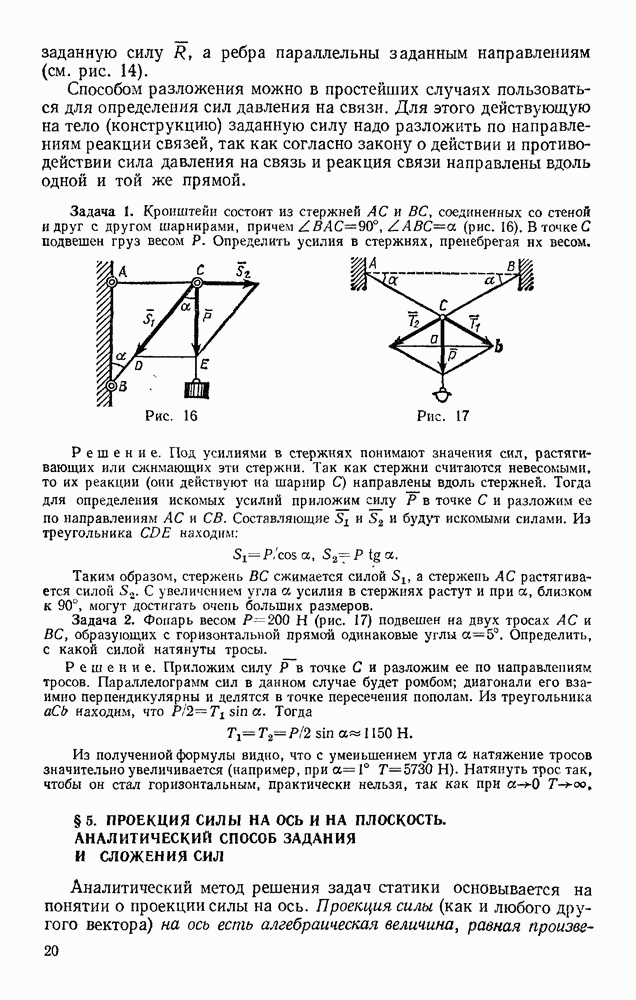
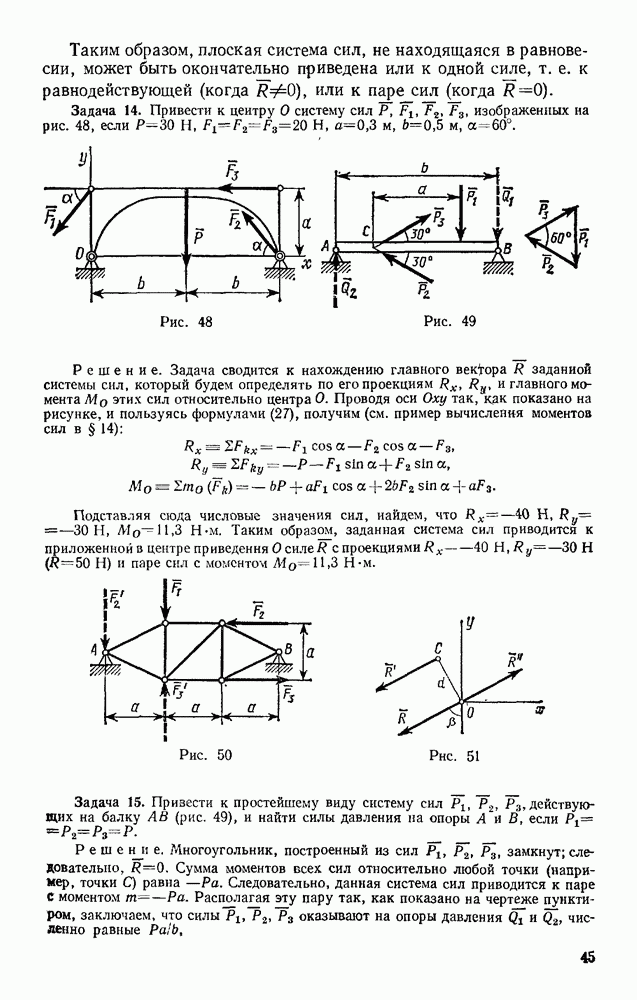
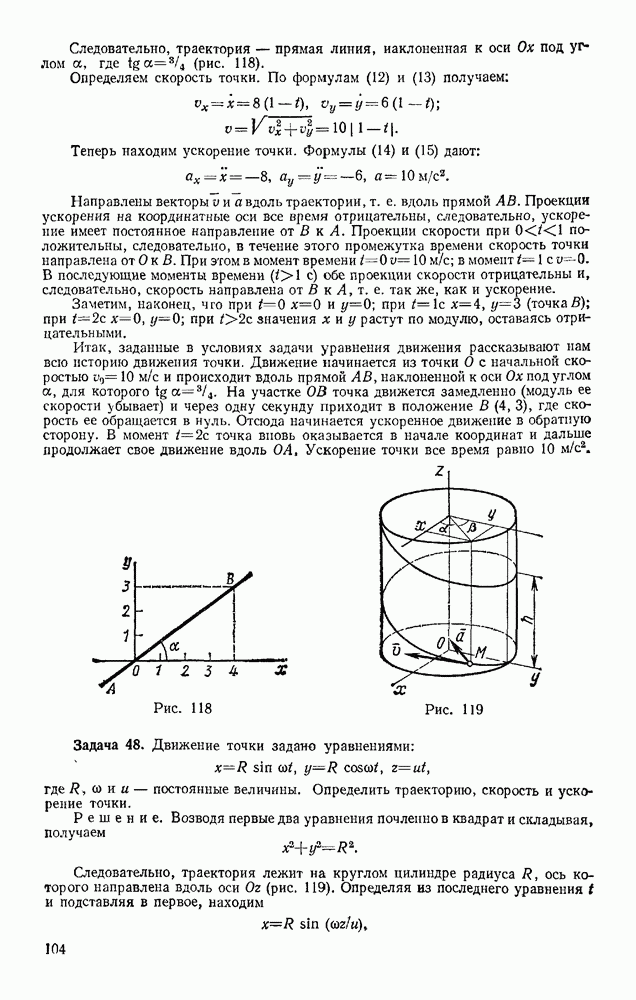
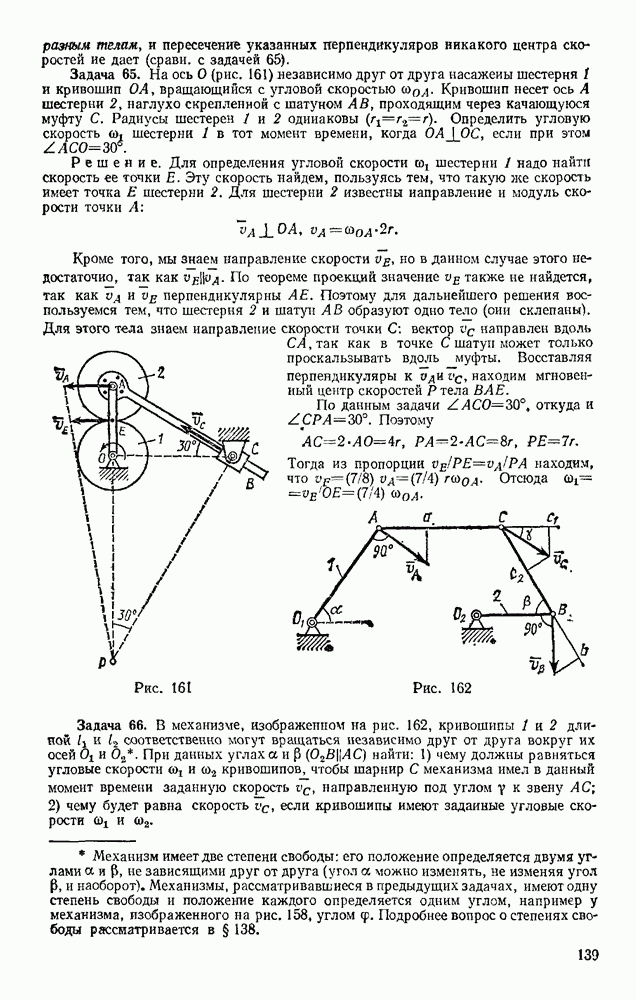
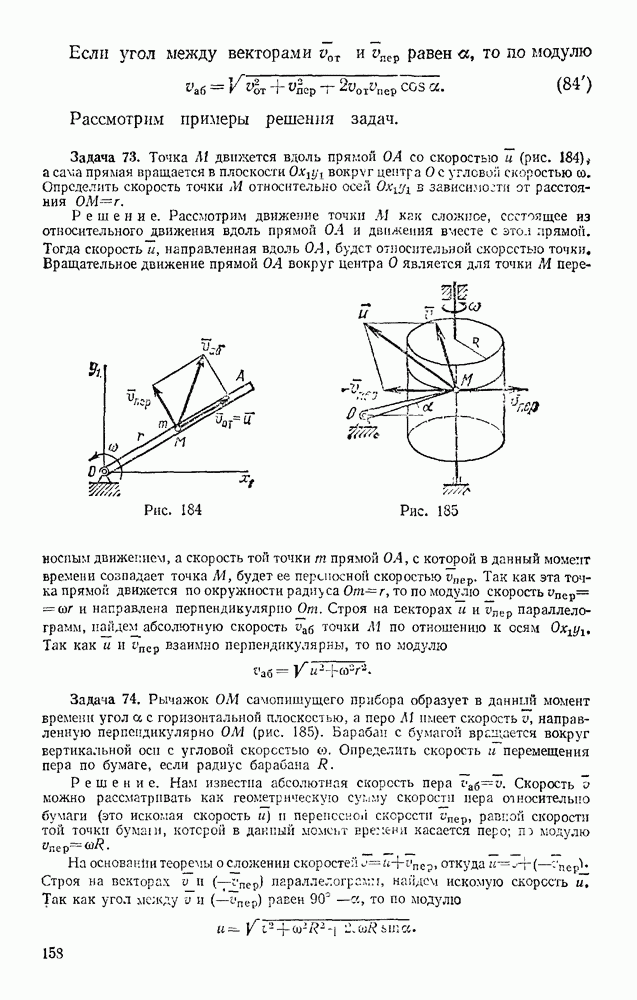
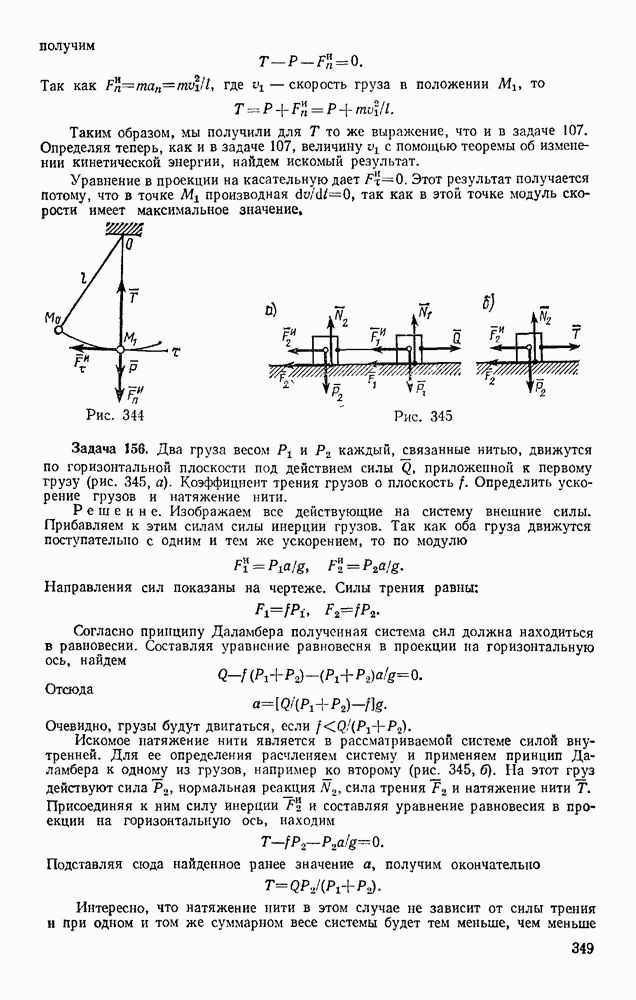
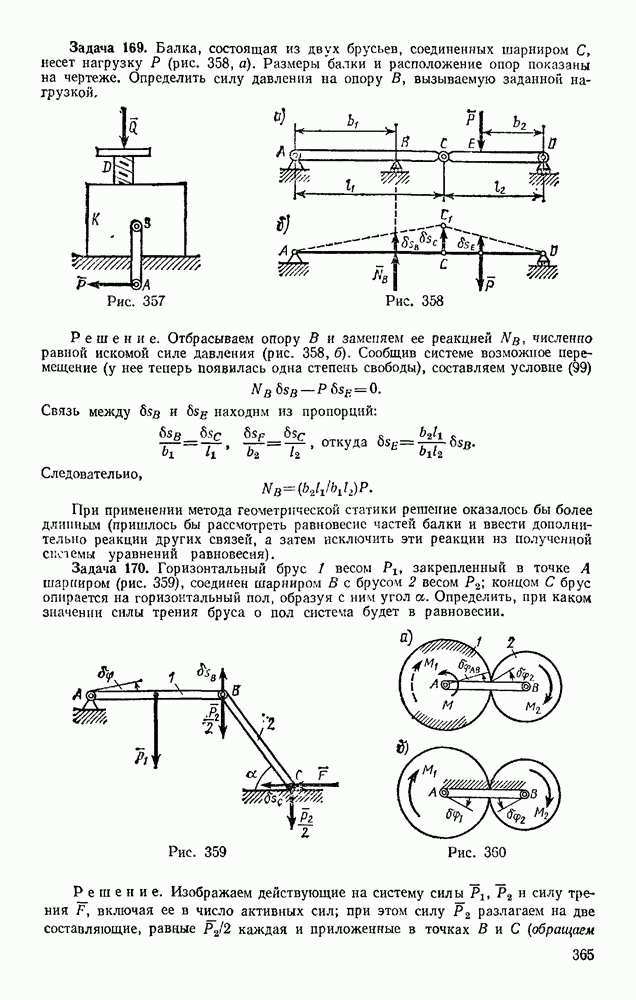
Задача 173. В центробежном регуляторе, равномерно вращающемся вокруг вертикальной оси с угловой скоростью со (рис. 362), вес каждого из шаров и  равен
равен  вес муфты
вес муфты  равен Q. Пренебрегая весом стержней, определить угол а, если
равен Q. Пренебрегая весом стержней, определить угол а, если 
Решение. Присоединяем к активным силам  центробежные силы инерции
центробежные силы инерции  (сила инерцни муфты, очевидно, будет равна нулю) и составляем общее уравнение динамики в виде (103). Тогда, вычисляя проекции всех сил на координатные оси, получим
(сила инерцни муфты, очевидно, будет равна нулю) и составляем общее уравнение динамики в виде (103). Тогда, вычисляя проекции всех сил на координатные оси, получим

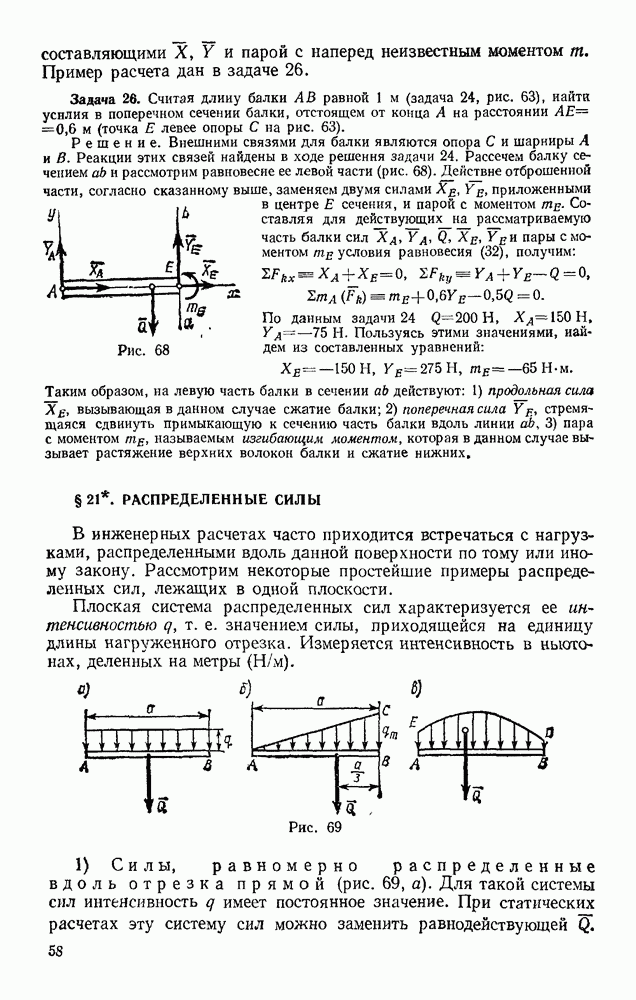
Координаты точек приложения сил равны:

Дифференцируя эти выражения, находим:

Подставляя все найденные значения в уравнение (а), получаем

Отсюда окончательно

Так как  то шары будут отклоняться, когда
то шары будут отклоняться, когда  . С увеличением
. С увеличением  угол а растет, стремясь к 90° при
угол а растет, стремясь к 90° при 

Рис. 362

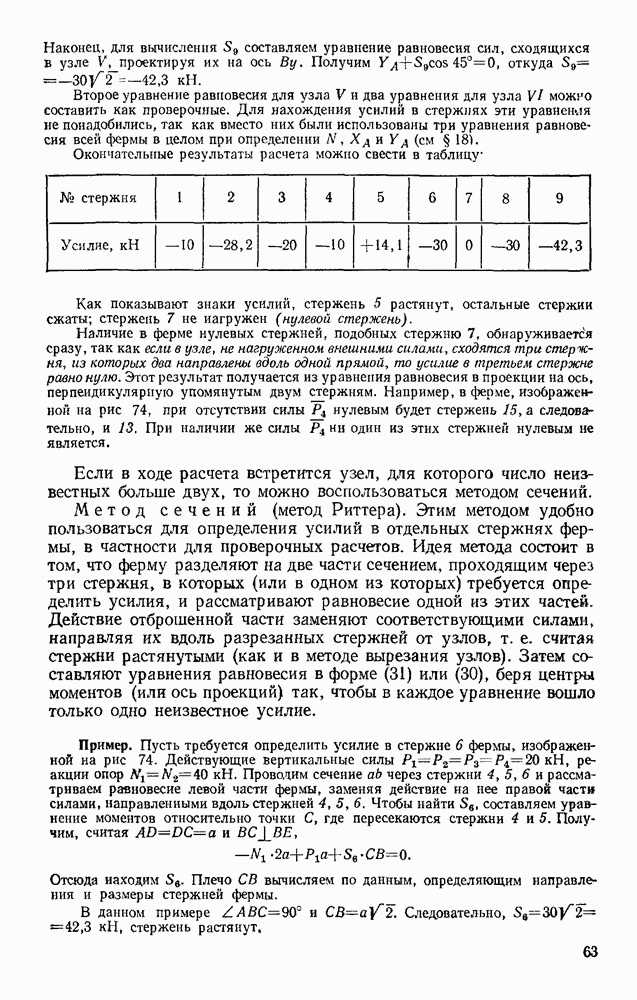
Рис. 363
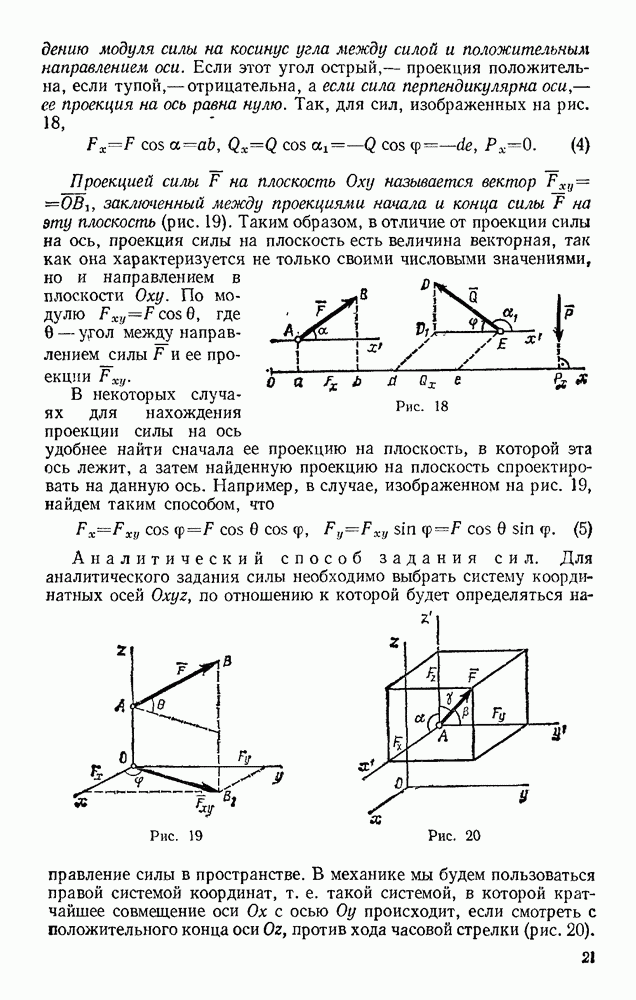
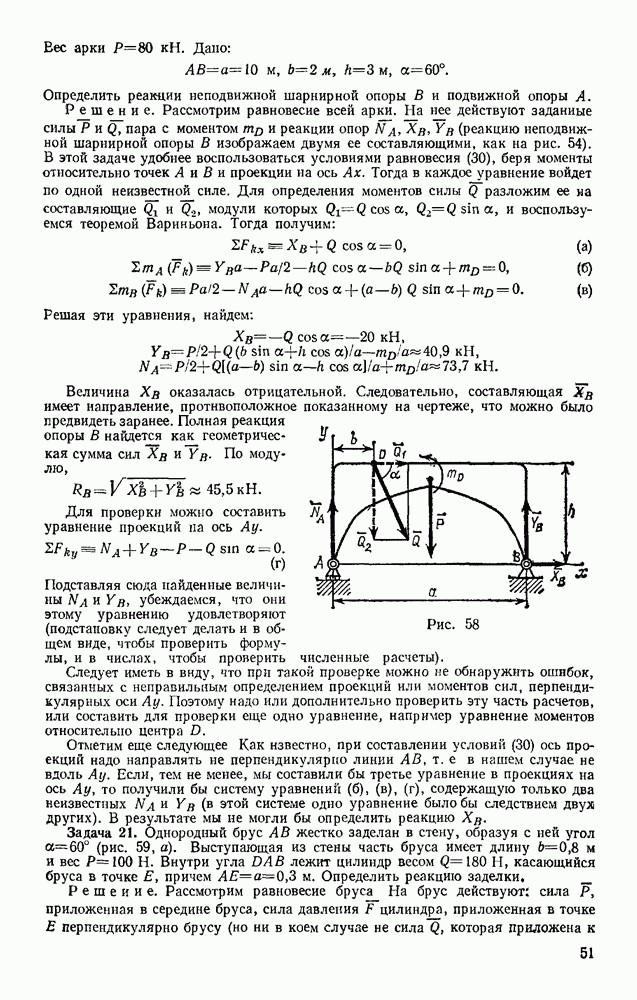
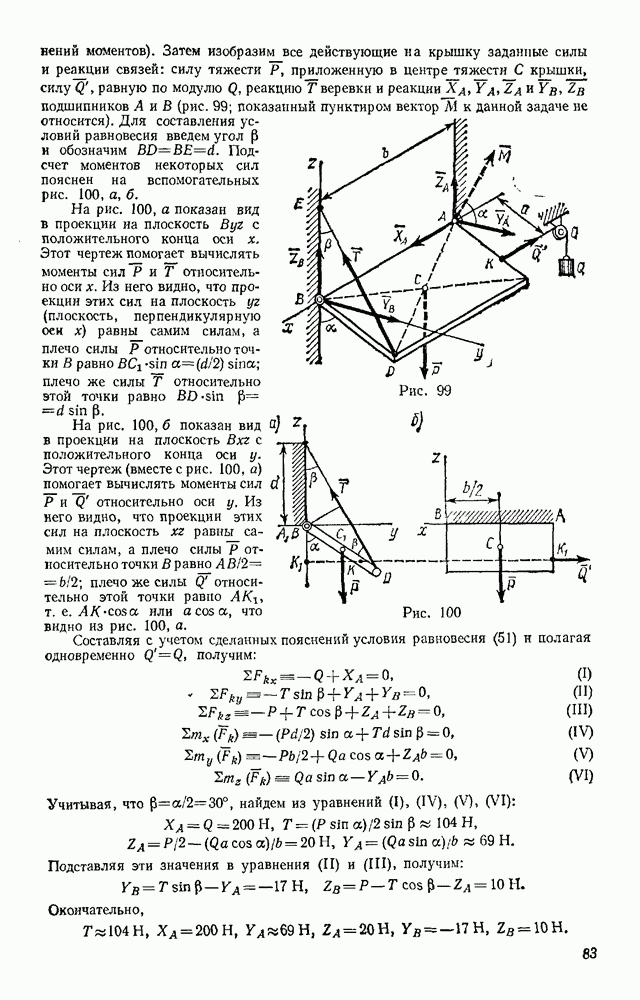
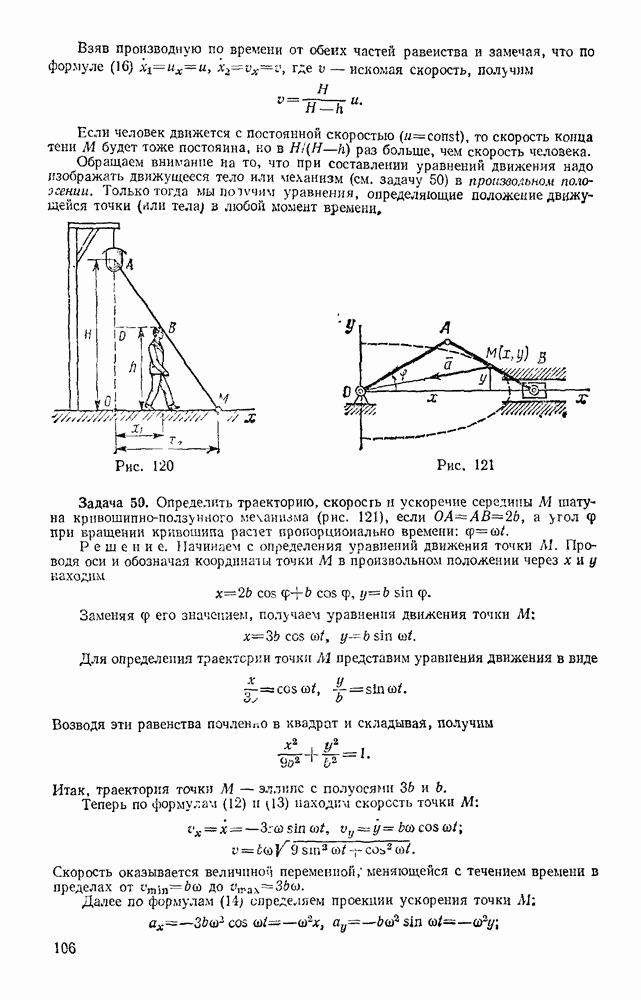
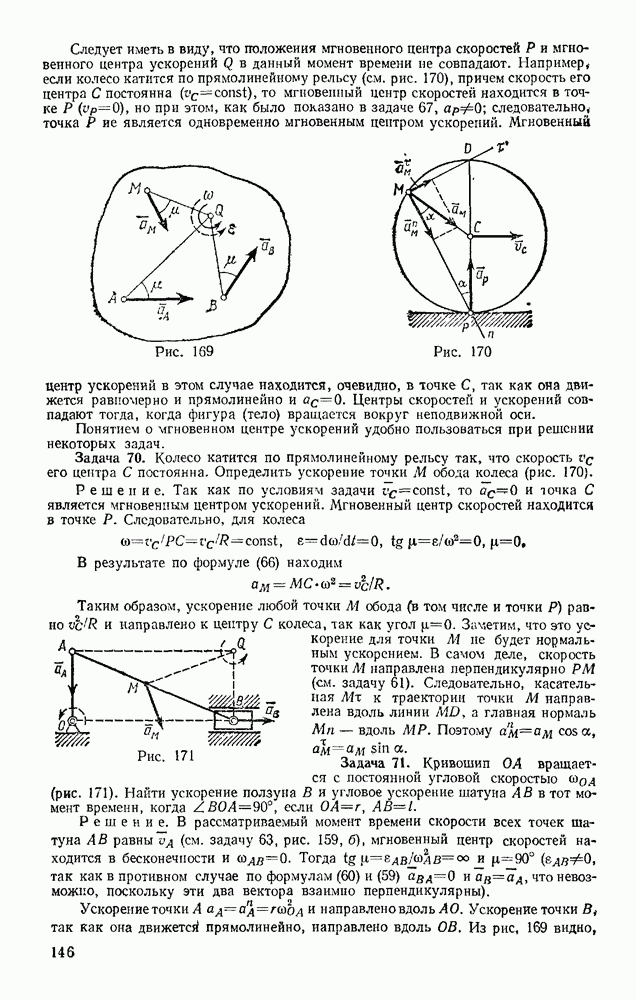
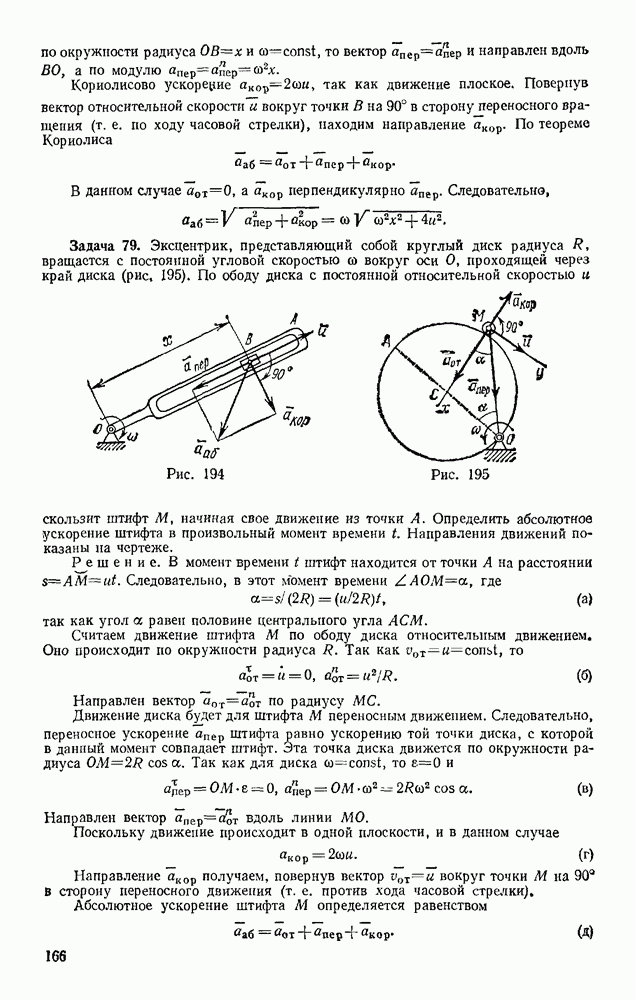
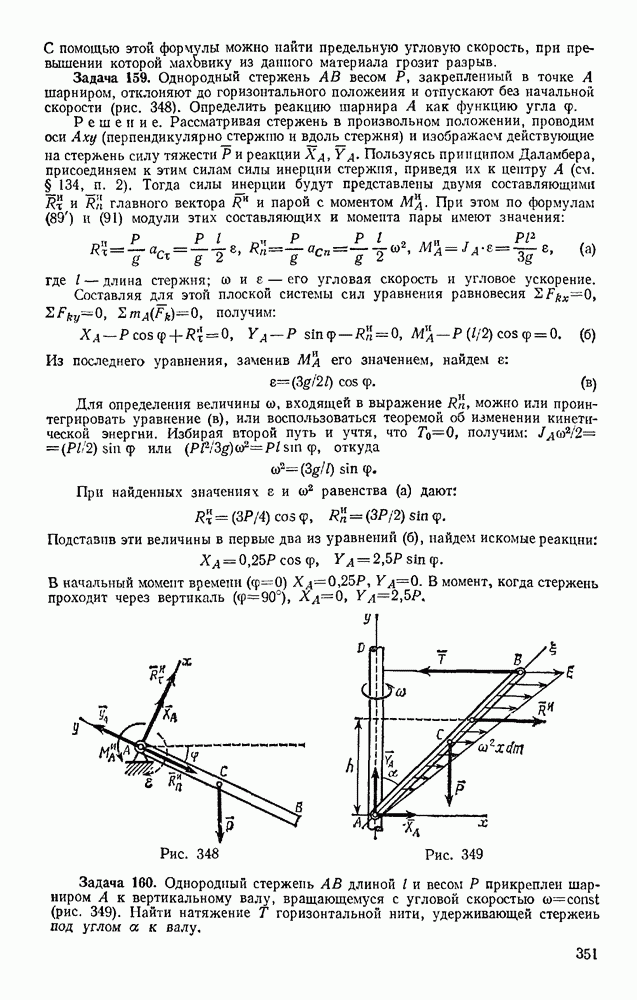
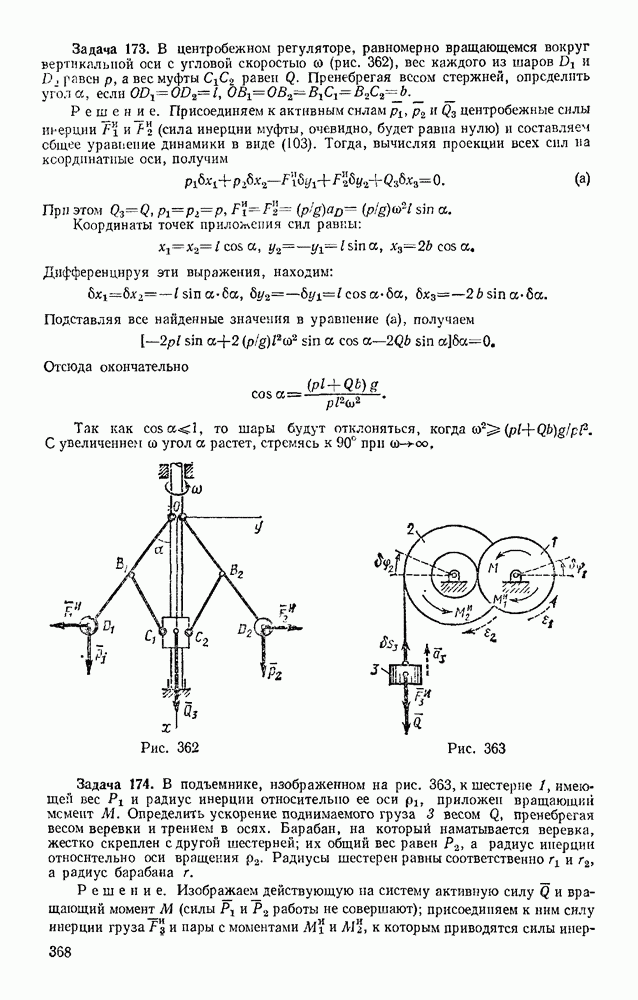
Задача 174. В подъемнике, изображенном на рис. 363, к шестерне  имеющей вес
имеющей вес  и радиус инерции относительно ее оси
и радиус инерции относительно ее оси  приложен вращающий мемент М. Определить ускорение поднимаемого груза 3 весом Q, пренебрегая весом веревки и трением в осях. Барабан, на который наматывается веревка, жестко скреплен с другой шестерней; их общий вес равен
приложен вращающий мемент М. Определить ускорение поднимаемого груза 3 весом Q, пренебрегая весом веревки и трением в осях. Барабан, на который наматывается веревка, жестко скреплен с другой шестерней; их общий вес равен  , а радиус инерции относительно оси вращения
, а радиус инерции относительно оси вращения  Радиусы шестерен равны соответственно
Радиусы шестерен равны соответственно  а радиус барабана
а радиус барабана  .
.
Решение. Изображаем действующую на систему активную силу Q и вращающий момент М (силы  работы не совершают); присоединяем к ним силу инерции груза
работы не совершают); присоединяем к ним силу инерции груза  и пары с моментами
и пары с моментами  и
и  к которым приводятся силы инерции вращающихся тел (см. § 134).
к которым приводятся силы инерции вращающихся тел (см. § 134).
Эти величины по модулю равны:

Направления всех величин показаны на чертеже. Сообщая системе возможное перемещение и составляя уравнение (102), получим

Выражая все перемещения через  найдем, что
найдем, что

Окончательно уравнение движения примет вид

Входящие сюда величины  выразим через искомое ускорение
выразим через искомое ускорение  . Учитывая, что
. Учитывая, что  связаны между собой так же, как и
связаны между собой так же, как и  получим:
получим:

В результате найдем окончательно

Задачу можно было бы решить и с помощью теоремы об изменении кинетической энергии (см. § 124),
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
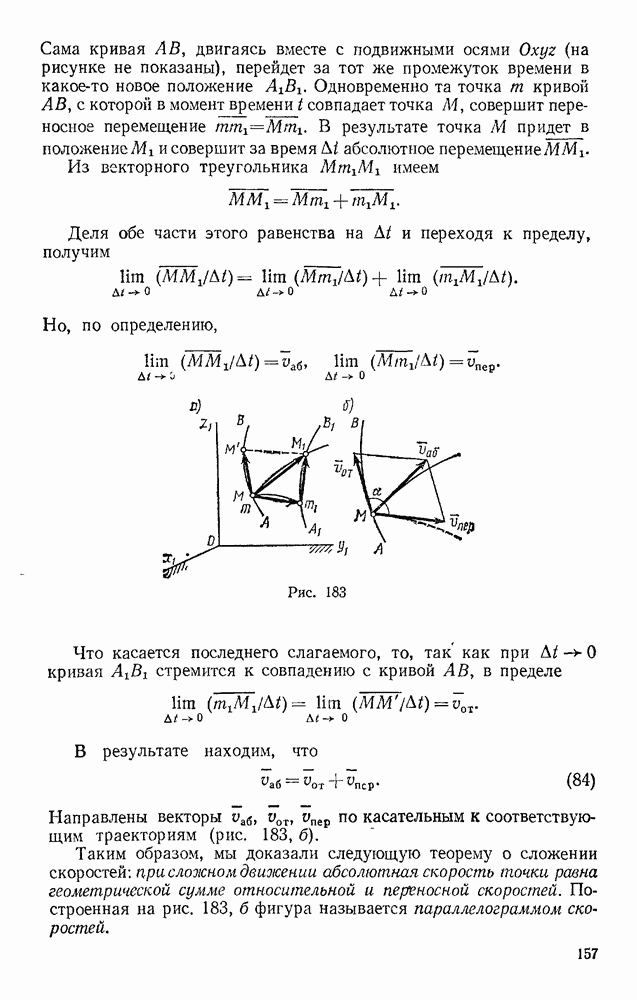
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
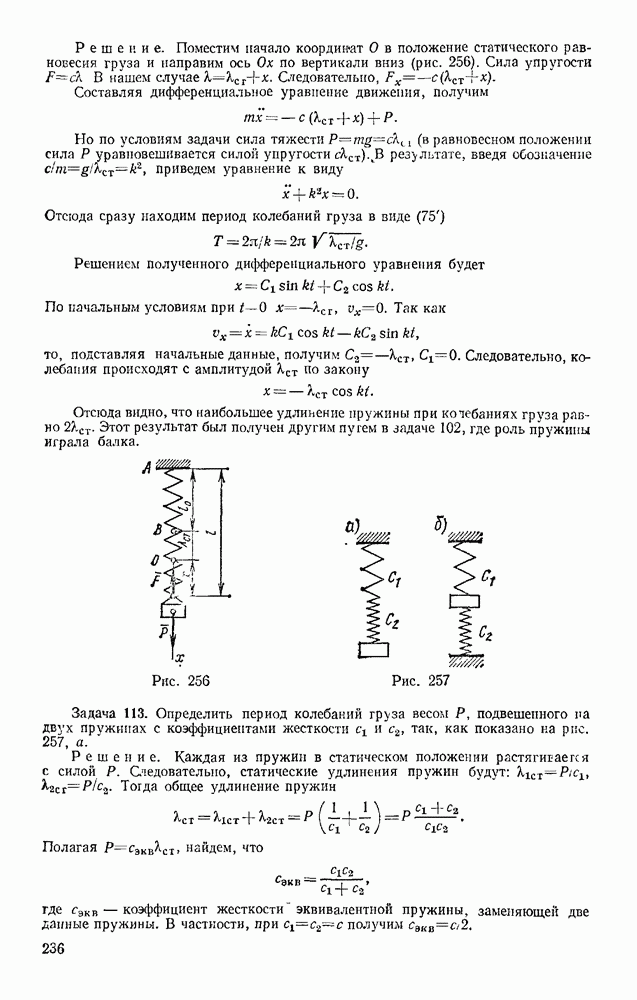
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
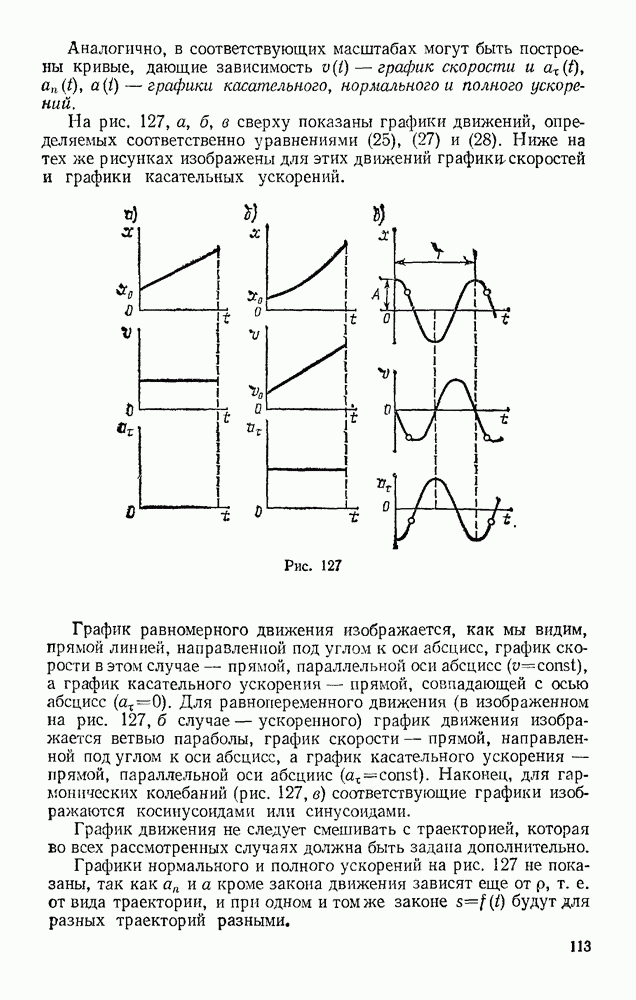
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
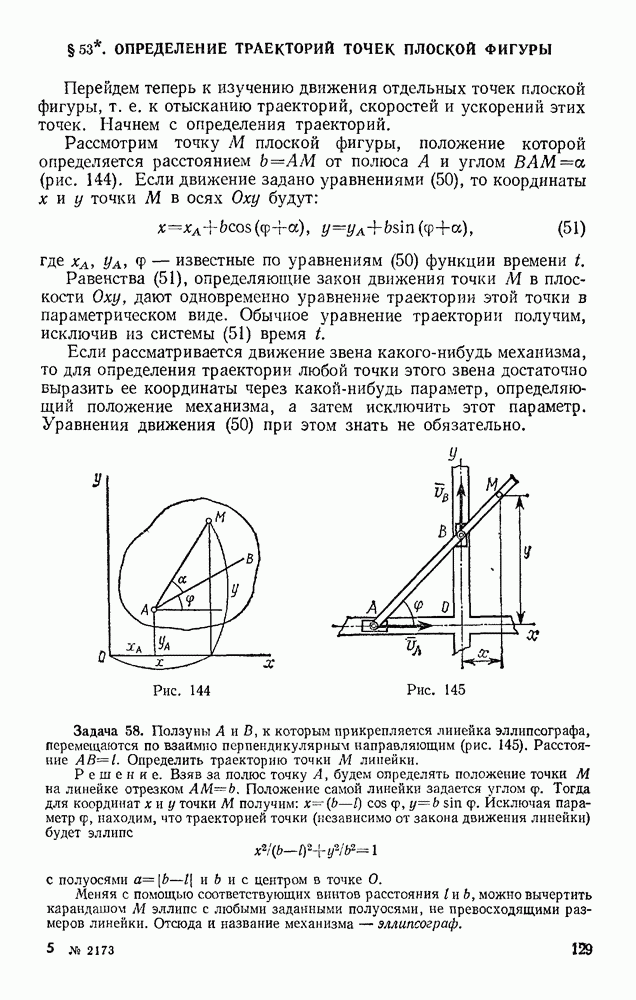
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
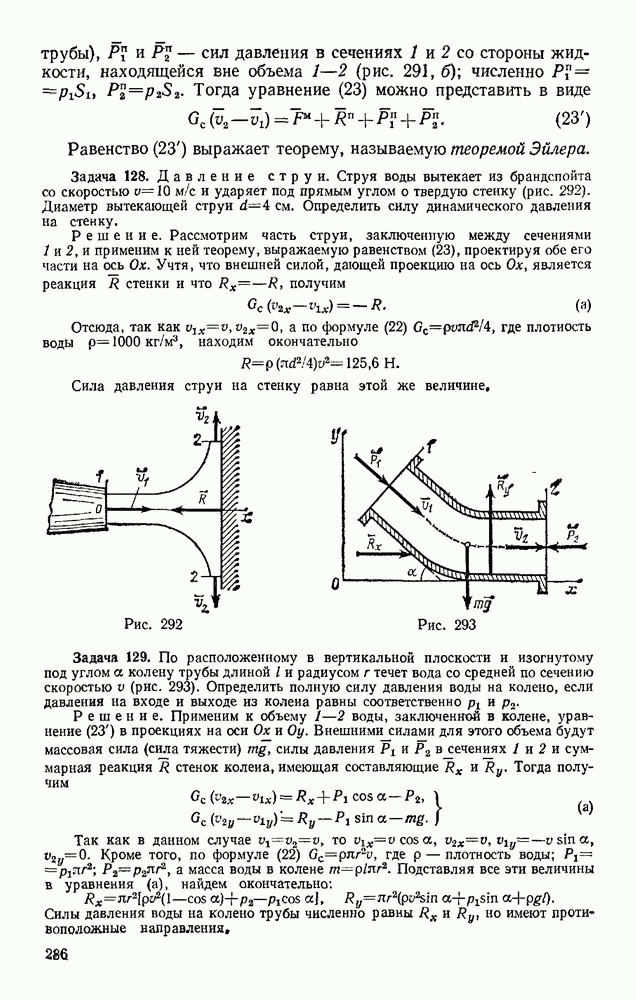
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
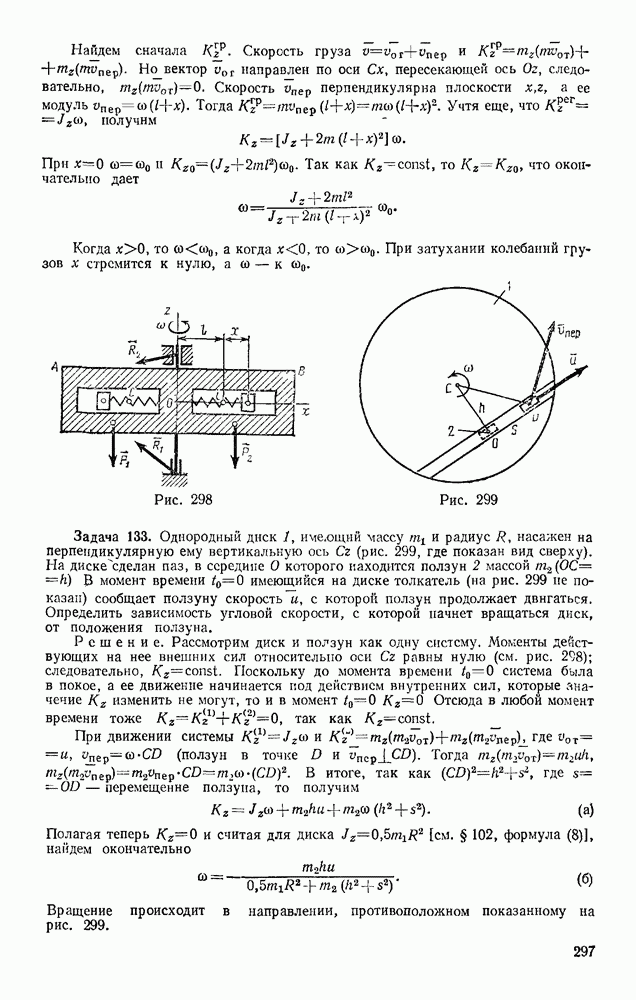
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
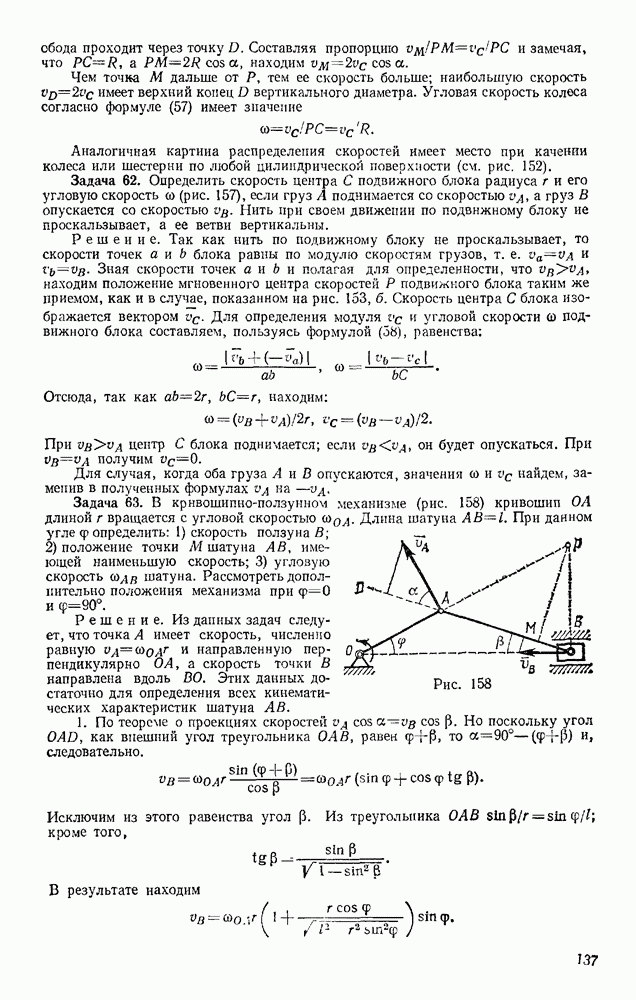
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
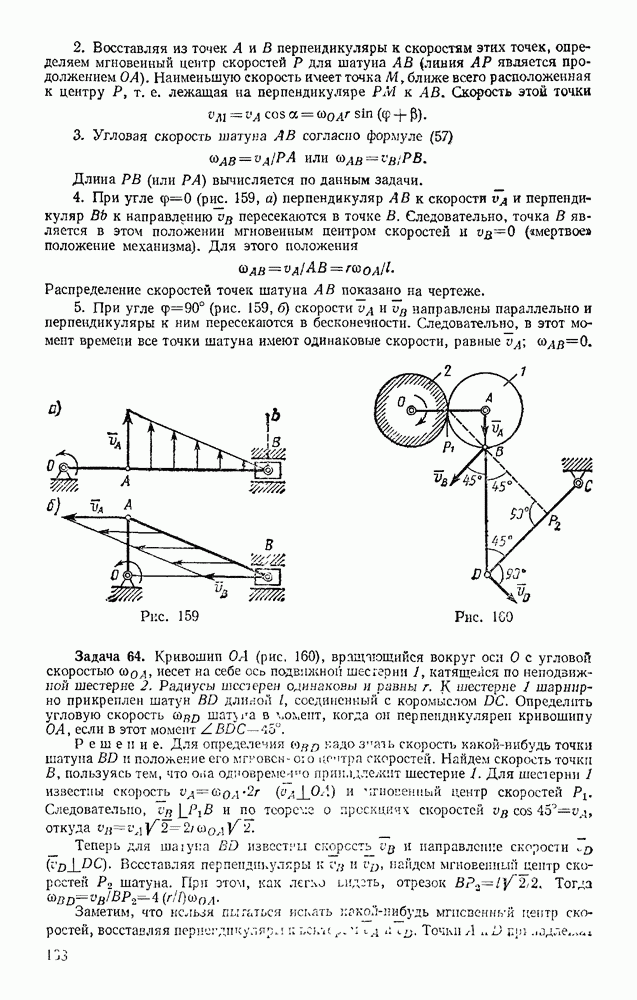
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
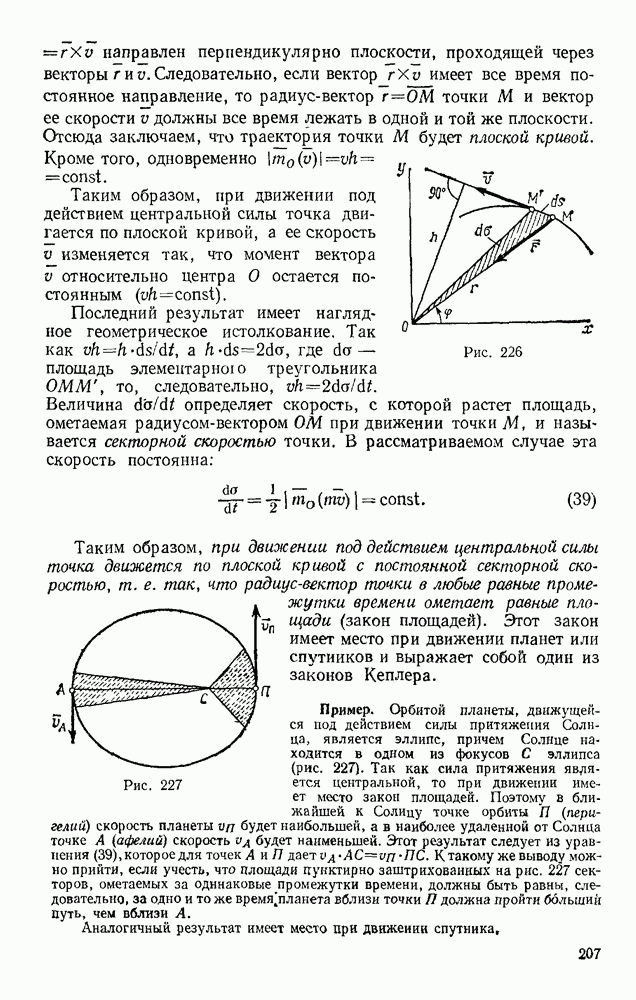
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
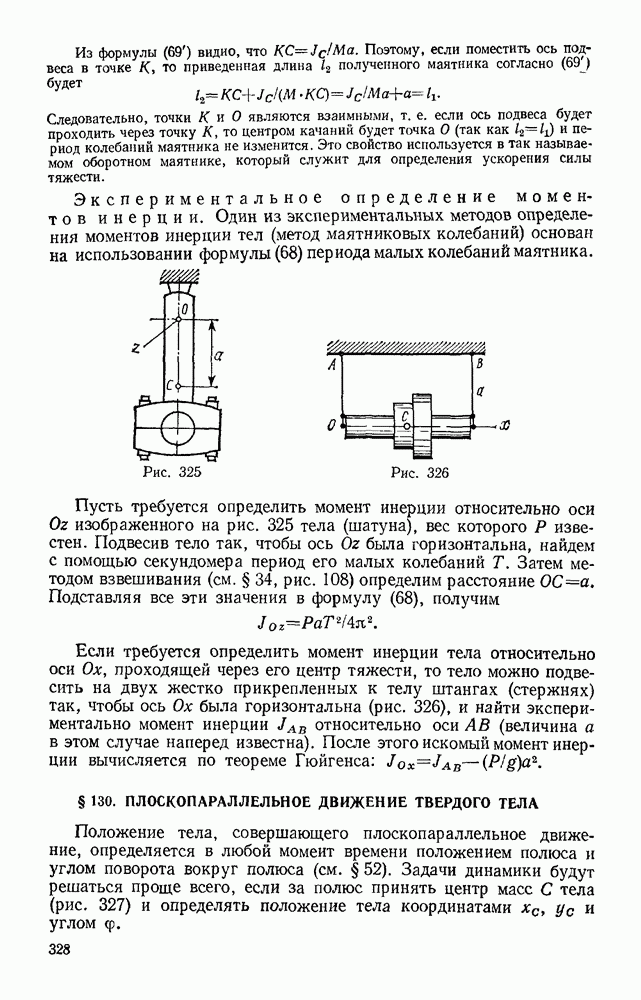
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
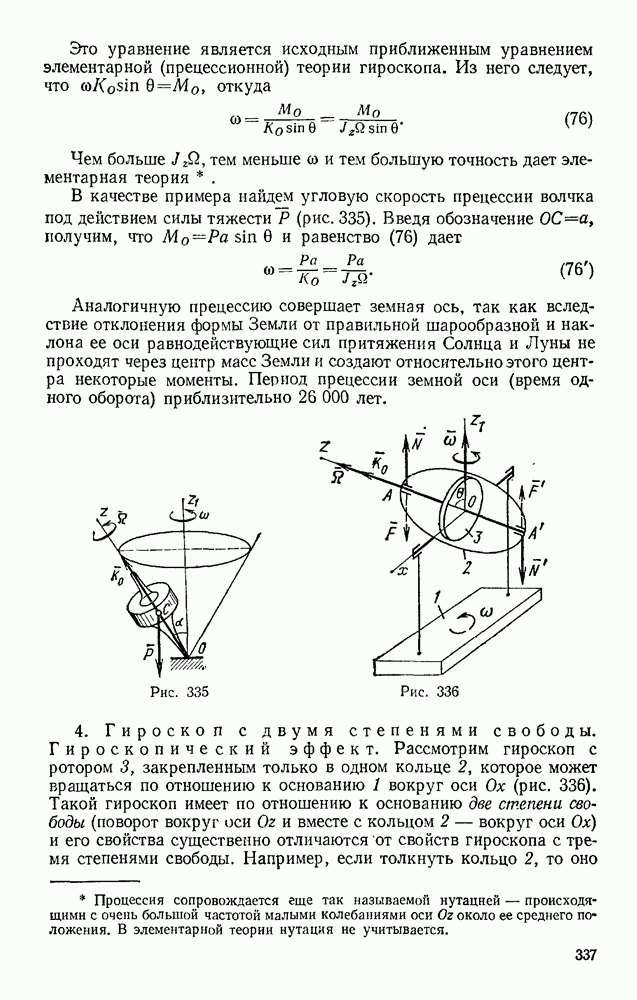
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
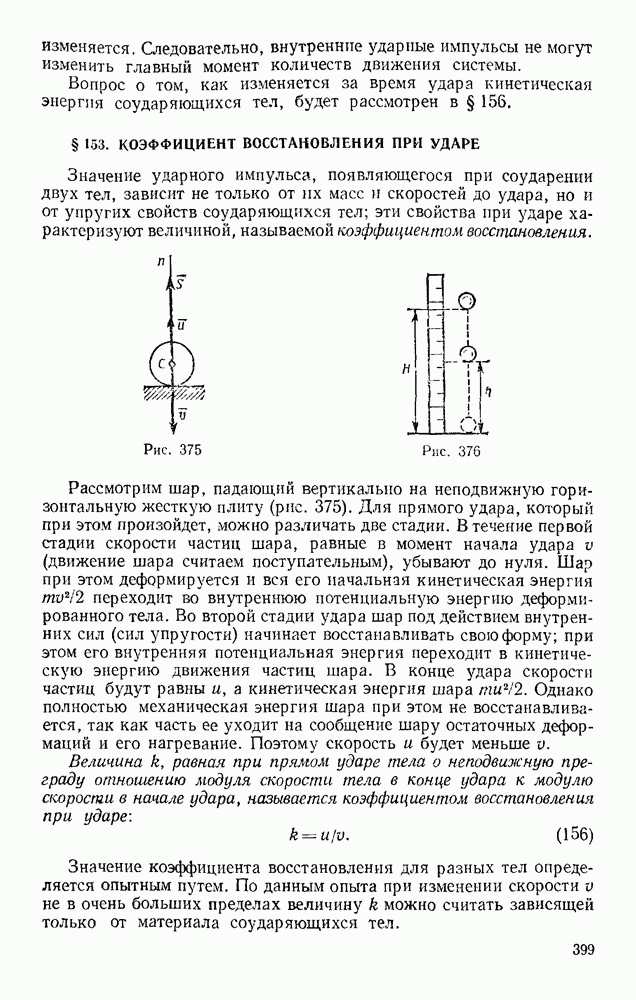
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА