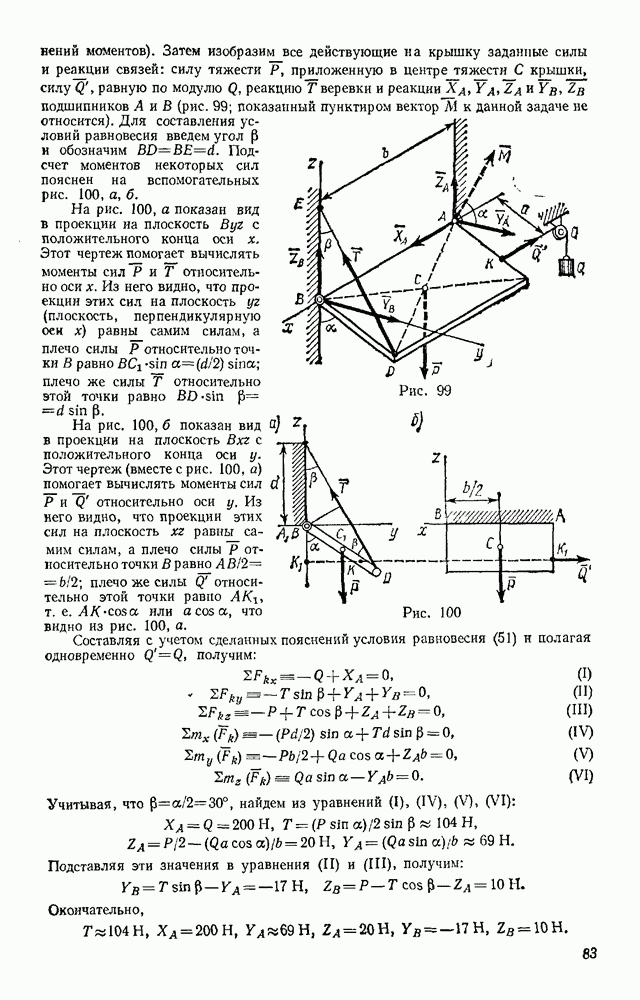
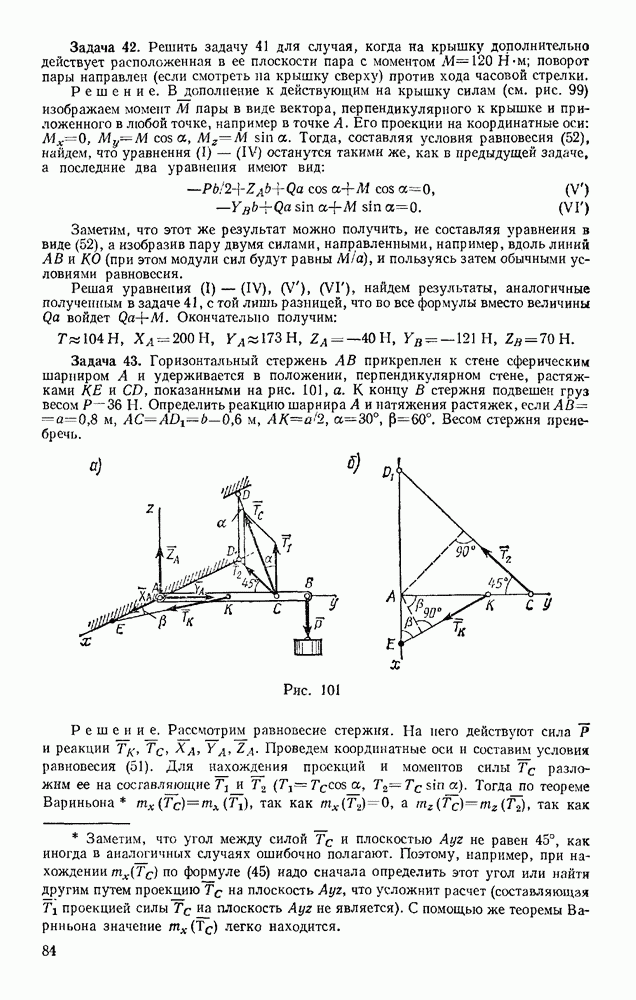
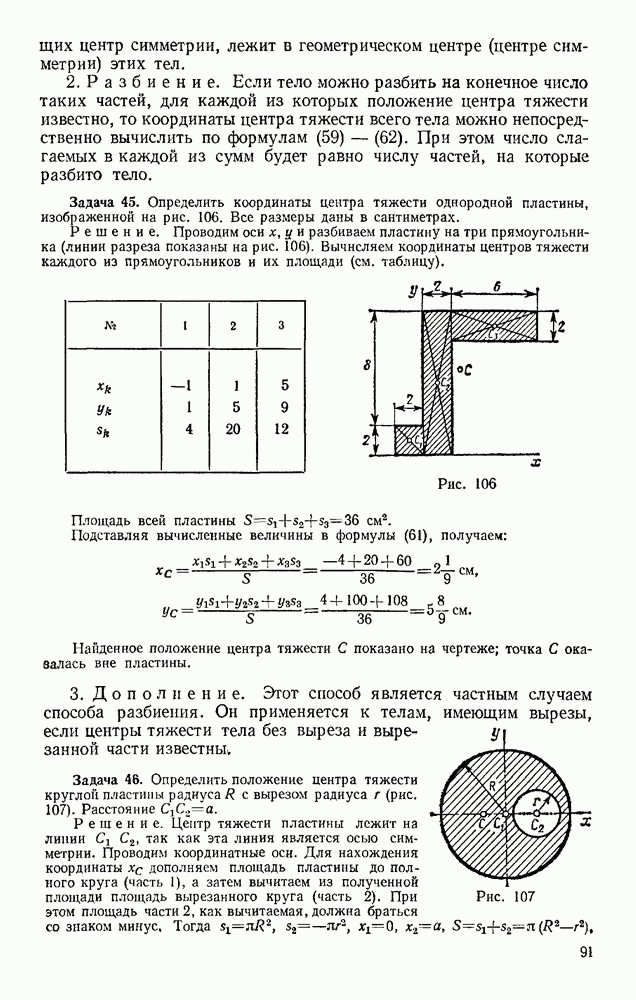
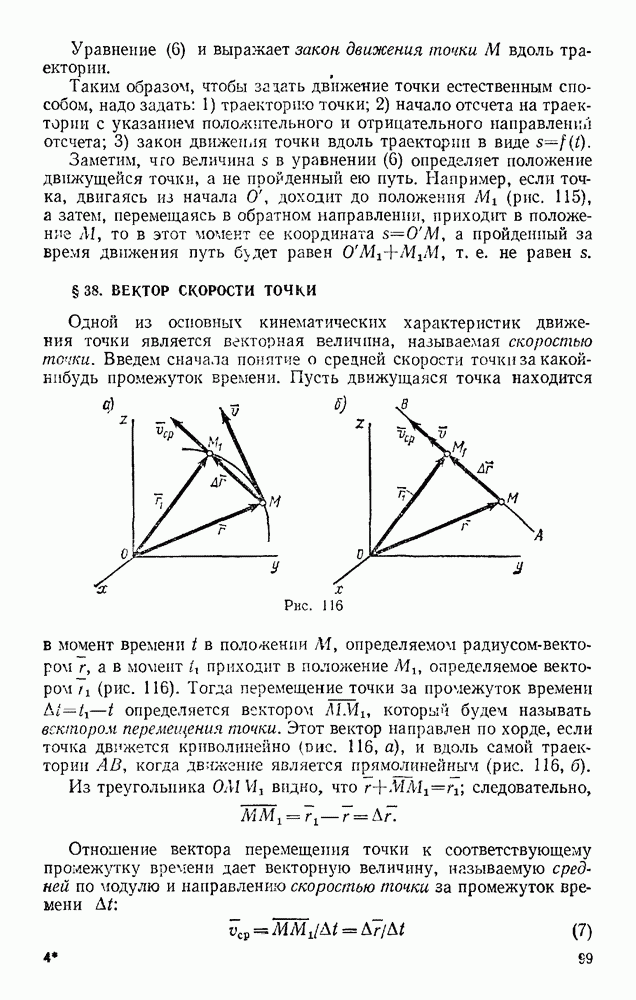
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
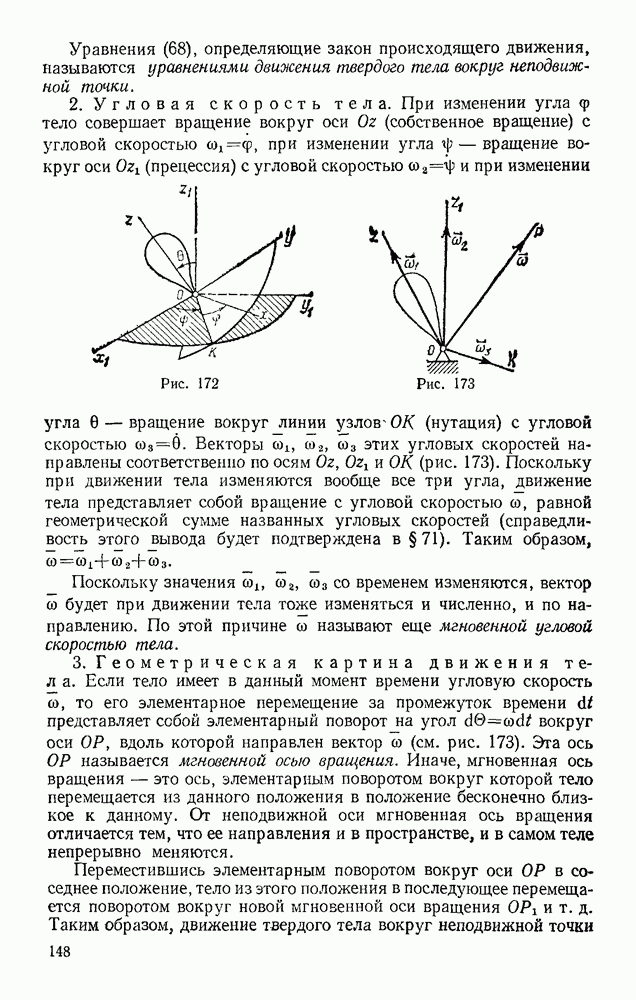
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Решение задач динамики точки путем интегрирования соответствующих дифференциальных уравнений движения сводится к следующим операциям.
1. Составление дифференциального уравнения движения. Для его составления в случае прямолинейного движения надо:
а) выбрать начало отсчета (как правило, совмещая его с начальным положением точки) и провести координатную ось, направляя ее вдоль траектории и, как правило, в сторону движения; если под действием приложенных сил точка может находиться в каком-нибудь положении в равновесии, то начало отсчета удобно помещать в положении статического равновесия;
б) изобразить двужущуюся точку в произвольном положении (но так, чтобы было  последнее существенно, когда среди сил есть силы, зависящие от скорости) и показать все действующие на точку силы;
последнее существенно, когда среди сил есть силы, зависящие от скорости) и показать все действующие на точку силы;
в) подсчитать сумму проекций всех сил на координатную ось и подставить эту сумму в правую часть дифференциального уравнения движения; при этом надо обязательно все переменные силы выразить через те величины (t, х или v), от которых эти силы зависят.
2. Интегрирование дифференциального уравнения движения. Интегрирование производится методами, известными из курса высшей математики и зависящими от вида полученного уравнения, т. е. от вида его правой части.
В тех случаях, когда на точку кроме постоянных сил действует одна переменная сила, зависящая только от времени t или только от расстояния  или же только от скорости v, уравнение прямолинейного движения можно проинтегрировать методом разделения переменных (см. задачи 91—93). Если при этом в задаче требуется определить только скорость, то часто можно при решении ограничиться интегрированием одного из уравнений (13) или (14).
или же только от скорости v, уравнение прямолинейного движения можно проинтегрировать методом разделения переменных (см. задачи 91—93). Если при этом в задаче требуется определить только скорость, то часто можно при решении ограничиться интегрированием одного из уравнений (13) или (14).
3. Определение постоянных интегрирования. Для определения постоянных интегрирования надо по данным задачи установить начальные условия в виде (16). Значения постоянных по начальным условиям находятся так, как это было показано в задаче 90. При этом постоянные можно определять непосредственно после каждого интегрирования.
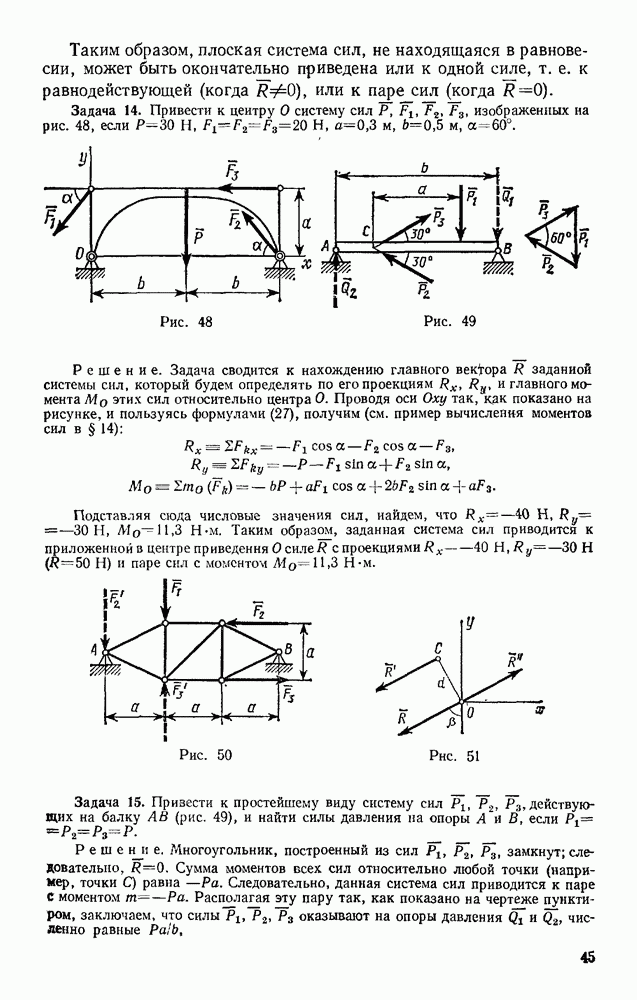
Если дифференциальное уравнение движения является уравнением с разделяющимися переменными, то вместо введения постоянных интегрирования можно брать сразу от обеих частей равенства определенные интегралы в соответствующих пределах; пример такого расчета дан в задаче 93.
4. Нахождение искомых в задаче величин и исследование полученных результатов. Чтобы иметь возможность исследовать решение, а также произвести косвенную проверку результата подсчетом размерностей, надо все решение проводить до конца в общем виде (в буквах), подставляя числовые данные только в окончательные результаты.
Сделанные здесь указания относятся и к случаю криволинейного движения.
Рассмотрим три конкретные задачи, в которых сила зависит от времени, от расстояния и от скорости точки.
1. Сила зависит от времени
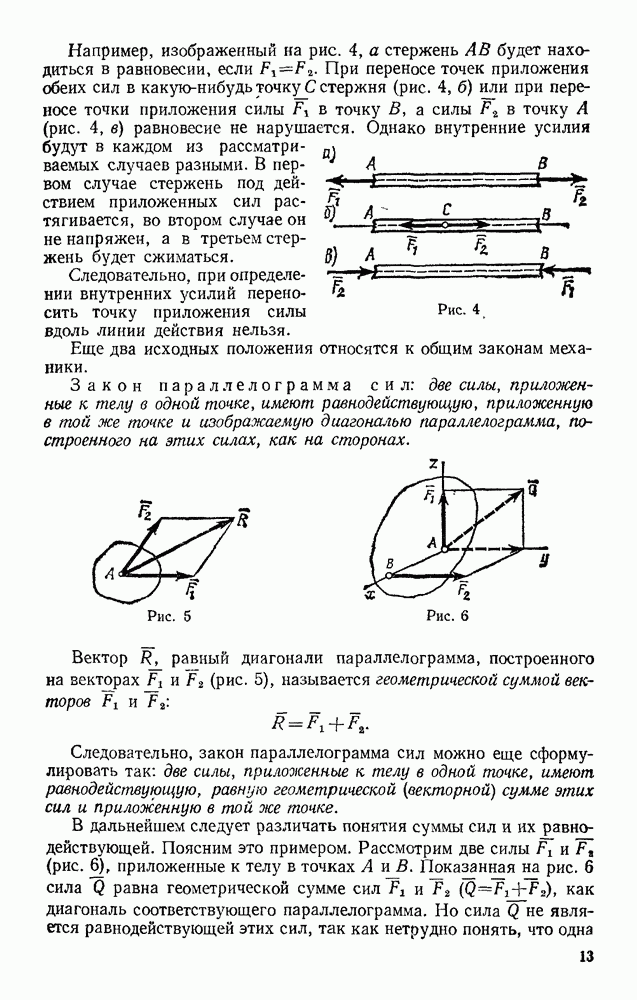
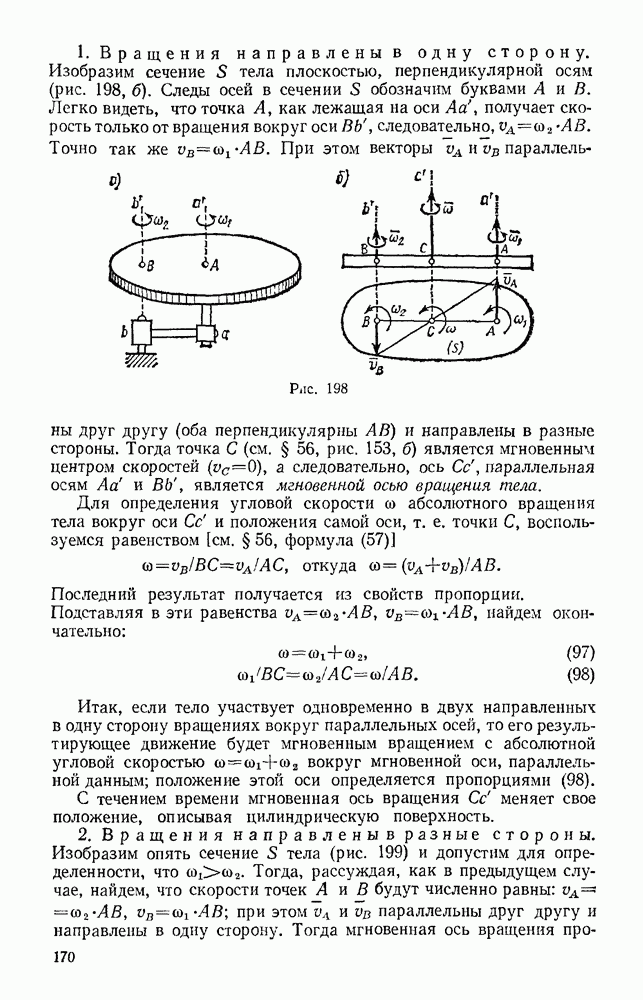
Задача 91. Груз весом Р начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F, значение которой растет пропорционально времени по закону  . Найти закон движения груза.
. Найти закон движения груза.
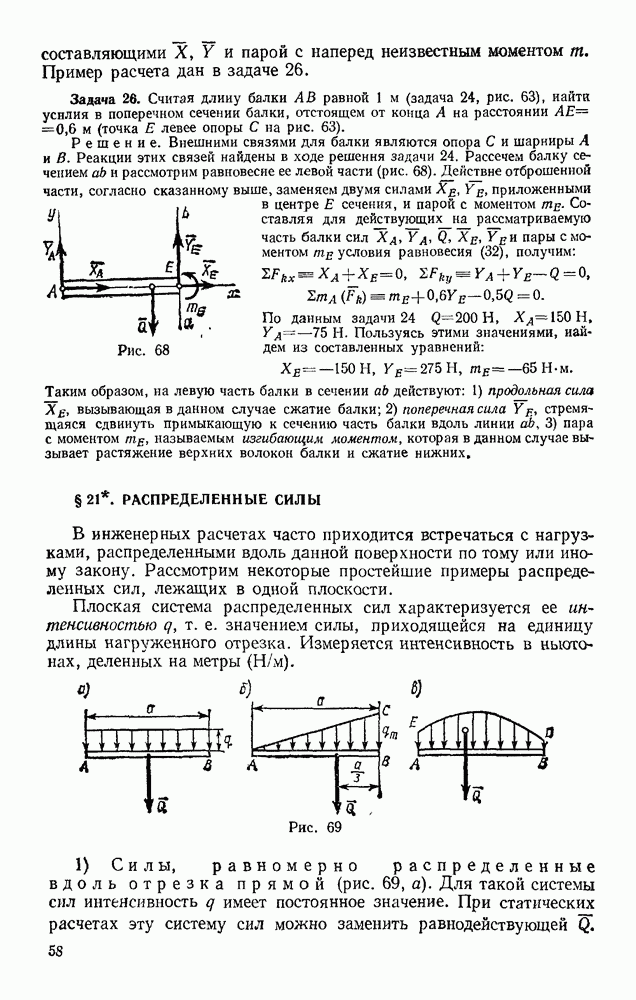
Решение. Выберем начало отсчета О в начальном положении груза и направим ось  в сторону движения (рис. 216). Тогда начальные условия будут: при
в сторону движения (рис. 216). Тогда начальные условия будут: при  Изображаем в произвольном положении груз и действующие на него силы F, Р (сила тяжести) и N (реакция плоскости). Проекции этих сил на ось
Изображаем в произвольном положении груз и действующие на него силы F, Р (сила тяжести) и N (реакция плоскости). Проекции этих сил на ось  имеют значения
имеют значения  и уравнение (13) примет вид
и уравнение (13) примет вид


Рис. 216
Умножив обе части этого равенства на  мы сразу разделим переменные и, интегрируя, получим
мы сразу разделим переменные и, интегрируя, получим

Подставляя сюда начальные данные, найдем, что  Тогда, заменяя в полученном результате
Тогда, заменяя в полученном результате  на
на  представим его в виде
представим его в виде

Умножая обе части этого равенства на  опять разделим переменные и, интегрируя, найдем
опять разделим переменные и, интегрируя, найдем

Подстановка начальных данных дает  и окончательно получаем закон движения груза в виде
и окончательно получаем закон движения груза в виде

Таким образом, проходимый грузом путь будет расти пропорционально кубу времени.
2. Сила зависит от расстояния
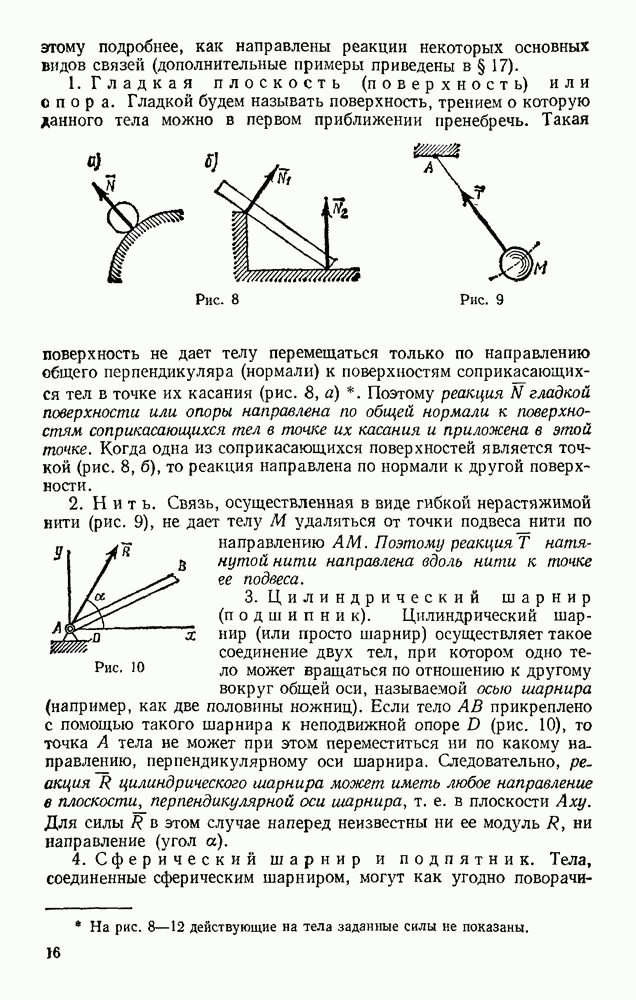
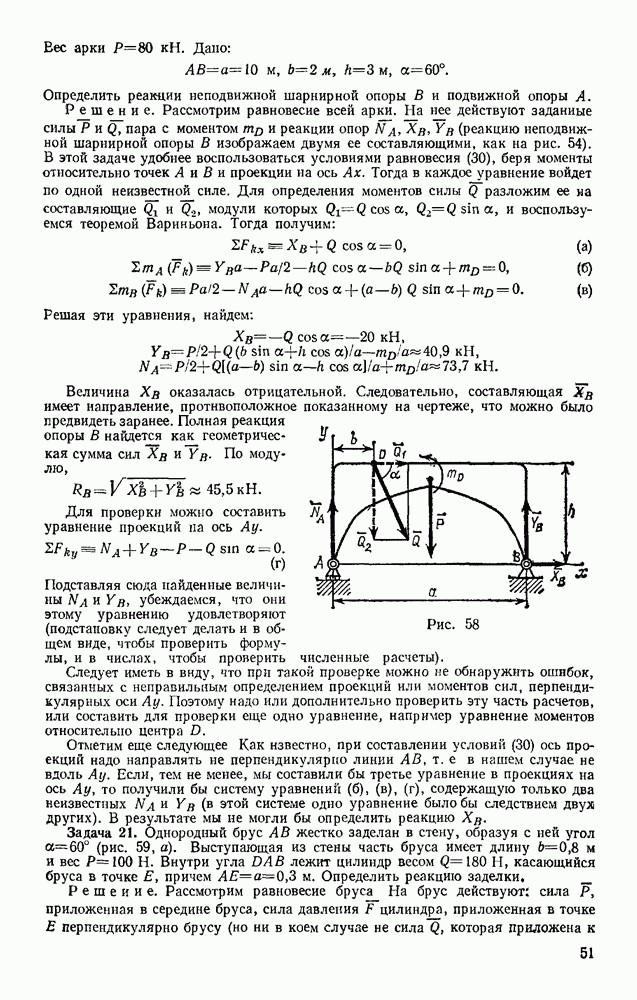
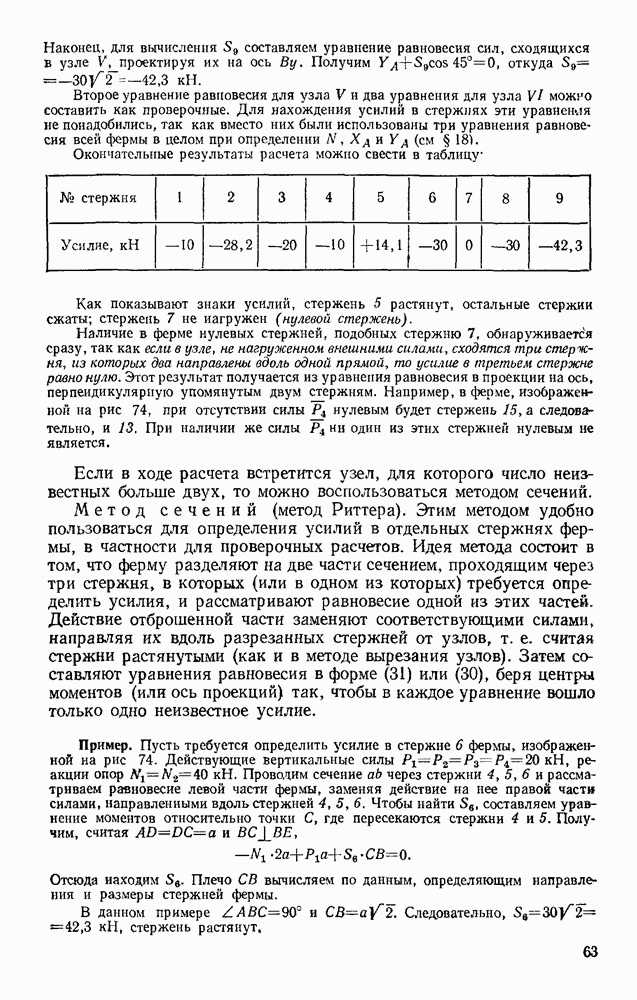
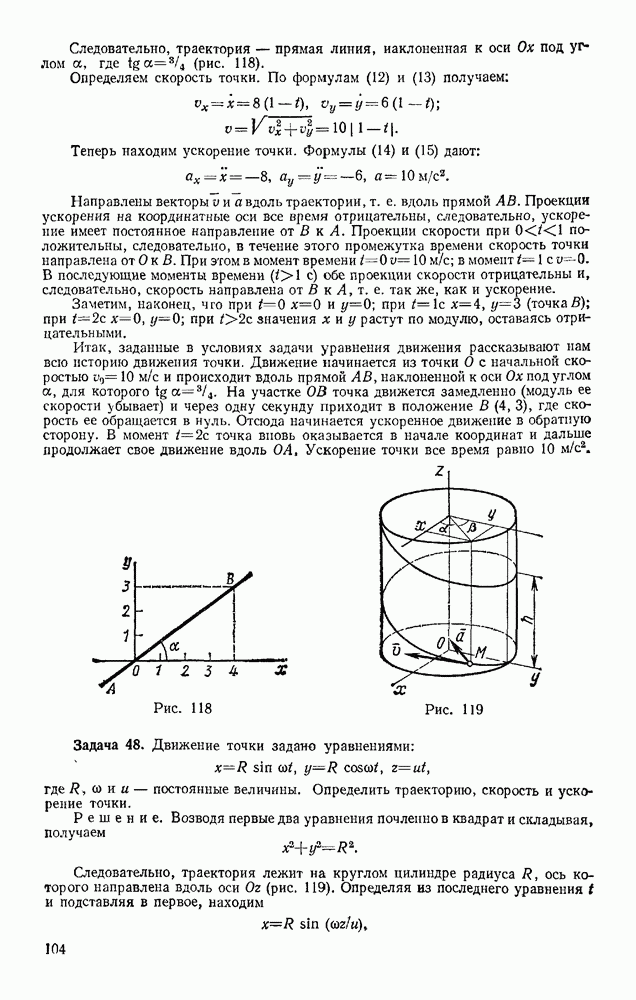
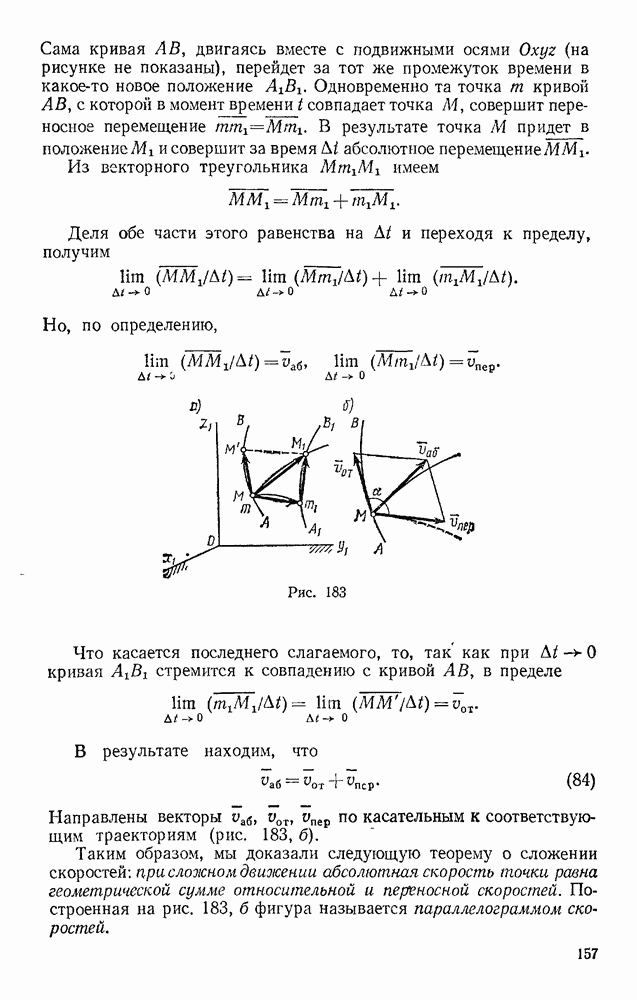
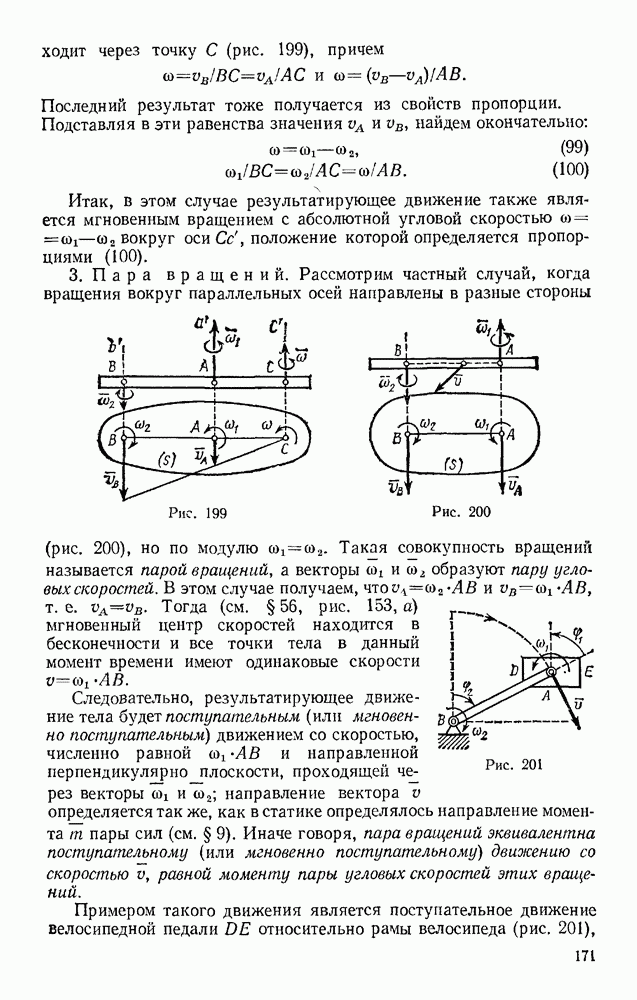
Задача 92. Пренебрегая трением и сопротивлением воздуха, определить, в течение какого промежутка времени тело пройдет по прорытому сквозь Землю вдоль хорды АВ каналу от его начала А до конца В (рис. 217). При подсчете считать радиус Земли  км.
км.

Рис. 217
Указани е. В теории притяжения доказывается, что тело, находящееся внутри Земли, притягивается к ее центру с силой F, прямо пропорциональной расстоянию  до этого центра.
до этого центра.
Принимая во внимание, что при  (т. е. на поверхности Земли) сила F равна силе тяжести
(т. е. на поверхности Земли) сила F равна силе тяжести  получим, что внутри Земли
получим, что внутри Земли

где  — расстояние от точки М до центра Земли.
— расстояние от точки М до центра Земли.
Решение. Поместим начало отсчета О в середине хорды АВ (в этой точке тело, находящееся в канале, было бы в равновесии) и направим ось  вдоль линии ОА. Если обозначить длину хорды АВ через
вдоль линии ОА. Если обозначить длину хорды АВ через  , то начальные условия задачи будут: при
, то начальные условия задачи будут: при 
В произвольном положении на тело действуют силы F и N. Следовательно,

так как из чертежа видно, что  .
.
Действующая сила оказалась зависящей от координаты  точки М. Чтобы в этом случае в дифференциальном уравнении движения разделились переменные, составим его в виде (14). Тогда сокращая на
точки М. Чтобы в этом случае в дифференциальном уравнении движения разделились переменные, составим его в виде (14). Тогда сокращая на  и вводя обозначение
и вводя обозначение

получим

Умножая обе части этого равенства на  сразу разделяем переменные и, интегрируя, находим
сразу разделяем переменные и, интегрируя, находим

По начальным условиям при  . Следовательно,
. Следовательно,  Подставляя это значение
Подставляя это значение  получаем
получаем

Считая, что в рассматриваемом положении скорость направлена от М к О, т. е. что  берем перед корнем знак минус (легко, однако, проверить, что тот же окончательный результат получится и при знаке плюс). Тогда, заменяя vx на dx/dt, найдем, что
берем перед корнем знак минус (легко, однако, проверить, что тот же окончательный результат получится и при знаке плюс). Тогда, заменяя vx на dx/dt, найдем, что

Разделяя переменные, приведем это уравнение к виду

и, интегрируя, получим

Подставляя сюда начальные данные (при  ), находим, что
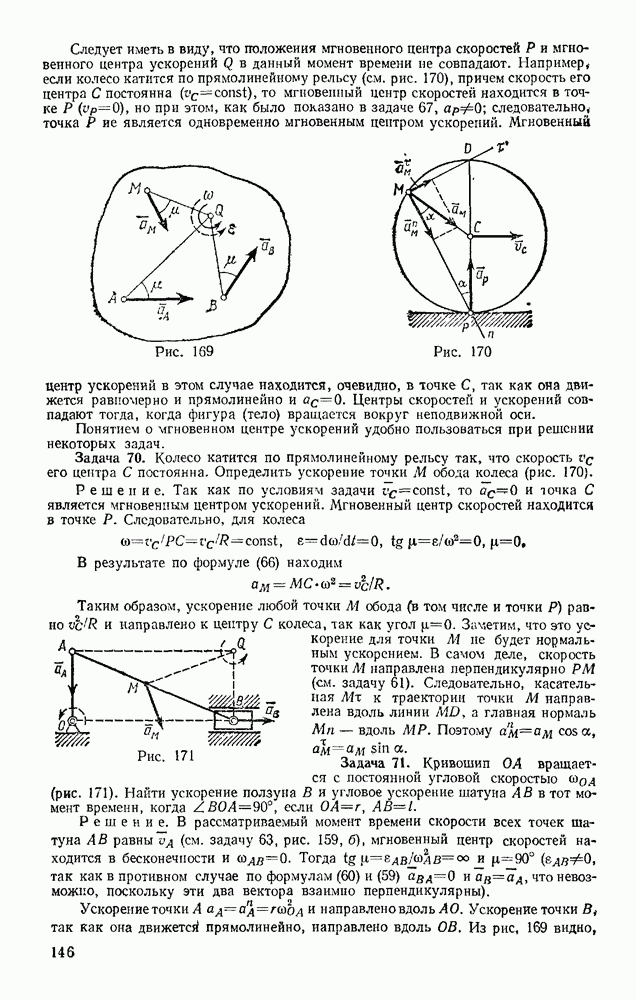
), находим, что  Окончательно закон движения тела в канале будет иметь вид
Окончательно закон движения тела в канале будет иметь вид

Следовательно, тело будет совершать в канале АВ гармонические колебания с амплитудой а.
Найдем теперь время движения тела до конца В канала. В точке В координата  . Подставляя это значение в уравнение движения, получим
. Подставляя это значение в уравнение движения, получим  , откуда
, откуда  Но по введенному обозначению
Но по введенному обозначению  . Отсюда, произведя подсчет, находим, что время движения по каналу АВ при условиях задачи не зависит от его длины и всегда равно
. Отсюда, произведя подсчет, находим, что время движения по каналу АВ при условиях задачи не зависит от его длины и всегда равно

Этот очень интересный результат породил ряд (пока еще фантастических) проектов прорытия такого канала.
Найдем дополнительно, чему будет равна при движении максимальная скорость тела. Из выражения для  видно, что
видно, что  при
при  , т. е. в точке О. Следовательно,
, т. е. в точке О. Следовательно,

Если, например,  (приблизительно расстояние от Москвы до Ленинграда), то
(приблизительно расстояние от Москвы до Ленинграда), то 
Колебания, совершаемые материальной точкой под действием силы, пропорциональной расстоянию, будут подробнее изучены в гл. XIX. Там будет рассмотрен другой метод интегрирования получающихся в этом случае дифференциальных уравнений движения.
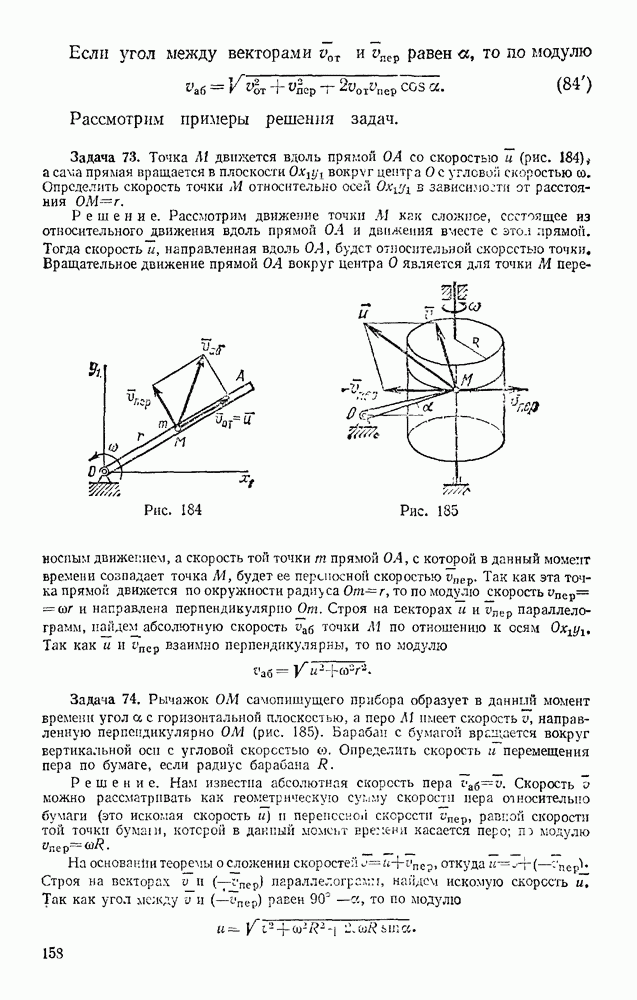
3. Сила зависит от скорости
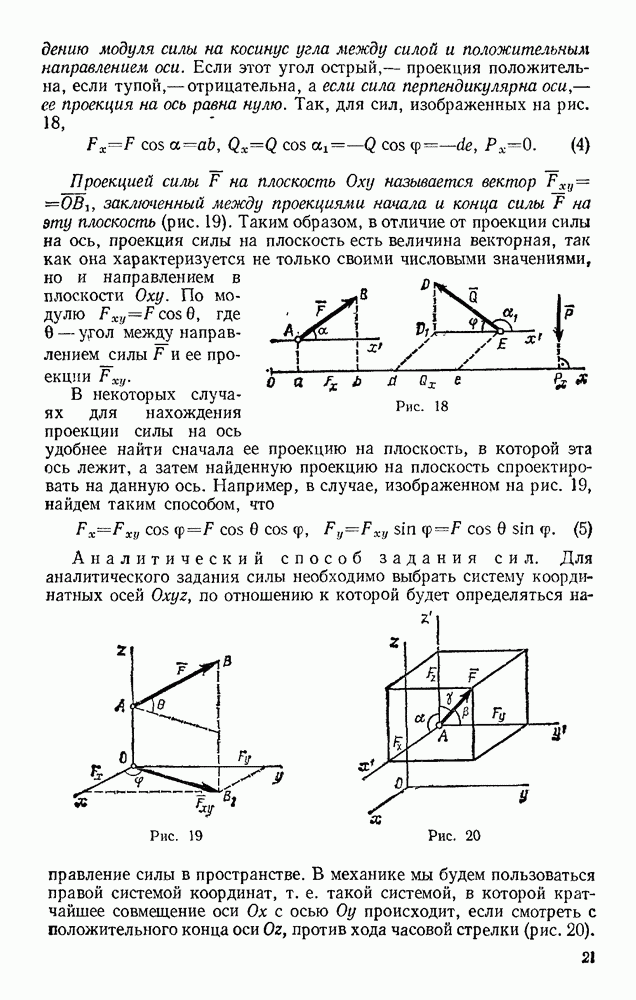
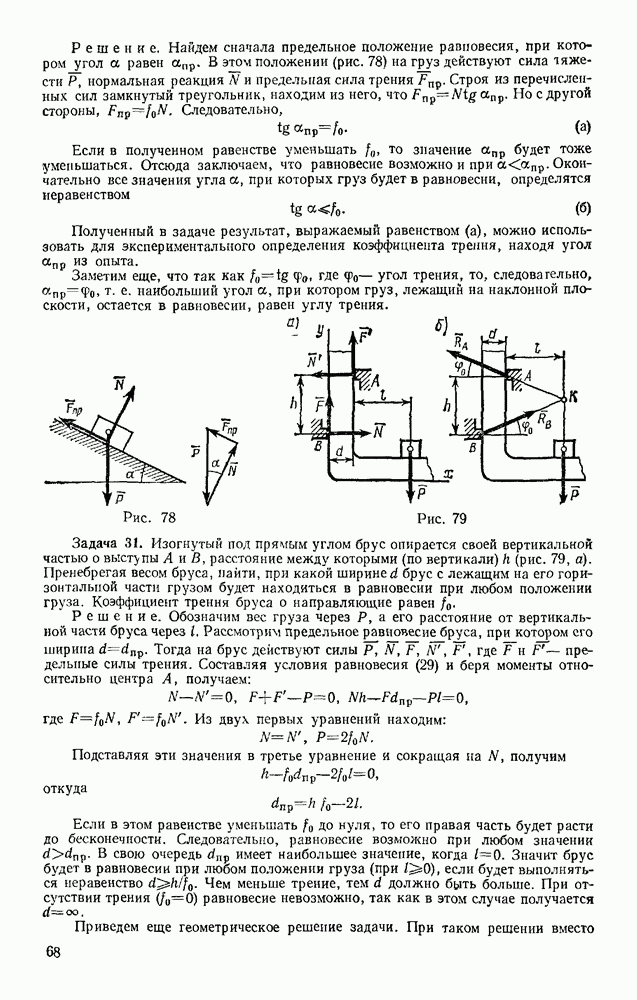
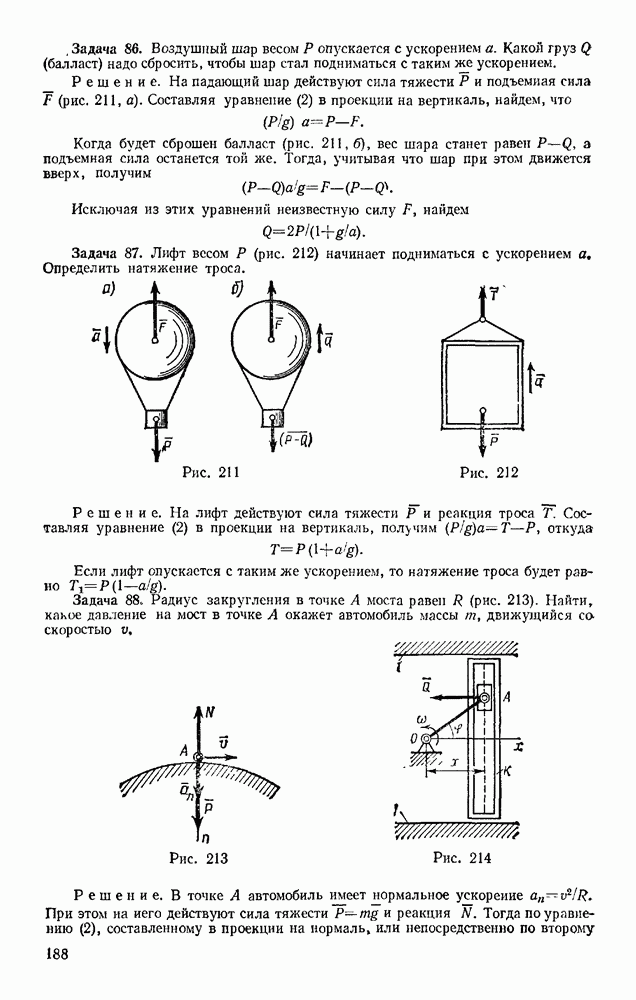
Задача 93. Лодку, масса которой  , толкают, сообщая ей начальную скорость
, толкают, сообщая ей начальную скорость  Считая, силу сопротивления: веяв» при малых скоростях изменяющейся по закону (7), т. а. считая
Считая, силу сопротивления: веяв» при малых скоростях изменяющейся по закону (7), т. а. считая  , где коэффициент
, где коэффициент  определить, через сколько времени скорость лодки уменьшится вдвое и какой она за это время пройдет путь. Найти также, какой путь пройдет лодка до полной остановки.
определить, через сколько времени скорость лодки уменьшится вдвое и какой она за это время пройдет путь. Найти также, какой путь пройдет лодка до полной остановки.

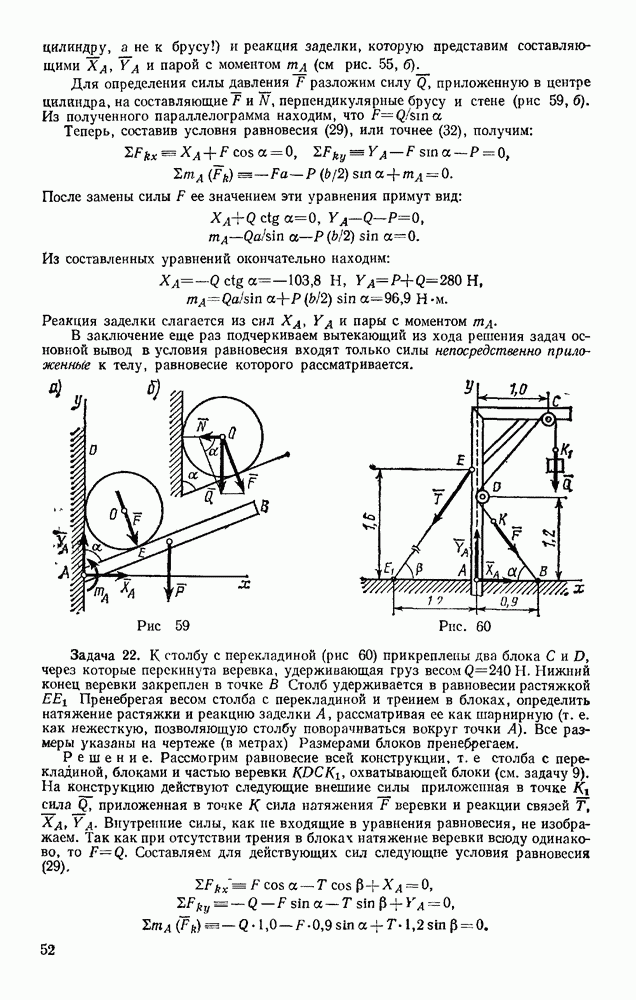
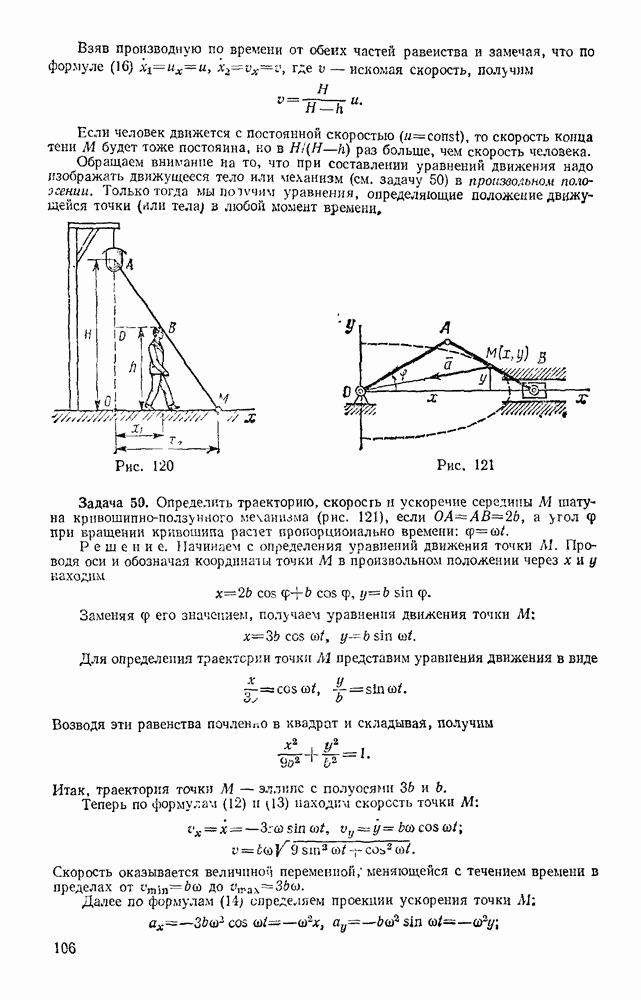
Рис. 218
Решение. Совместим начало отсчета О с начальным положением лодки и направим ось Ох в сторону движения (рис. 218). Тогда начальные условия будут: при  Изображаем в произвольном положении лодку и действующие на нее силы R.
Изображаем в произвольном положении лодку и действующие на нее силы R.
Примечание. Никакие другие силы на лодку не действуют. Сила, сообщившая лодке толчок, действовала на лодку до момента  . Результат этого действия учитывается заданием начальной скорости
. Результат этого действия учитывается заданием начальной скорости  , которую сила за время толчка сообщила лодке (см. § 79.) Чтобы правильно определить, какие силы действительно действуют на тело при его движении, надо помнить, что сила есть результат взаимодействия данного тела с другими телами. В данном случае сила тяжести Р является результатом действия на лодку Земли, а силы N и R — результат действия на лодку воды Никакие другие материальные тела с лодкой при ее движении не взаимодействуют, значит, никаких других действующих сил нет. Обращаем внимание на этот вопрос, так как он часто является источником ошибок при решении задач.
, которую сила за время толчка сообщила лодке (см. § 79.) Чтобы правильно определить, какие силы действительно действуют на тело при его движении, надо помнить, что сила есть результат взаимодействия данного тела с другими телами. В данном случае сила тяжести Р является результатом действия на лодку Земли, а силы N и R — результат действия на лодку воды Никакие другие материальные тела с лодкой при ее движении не взаимодействуют, значит, никаких других действующих сил нет. Обращаем внимание на этот вопрос, так как он часто является источником ошибок при решении задач.
Вычисляя проекции действующих сил, находим, что

Для определения времени движения составляем дифференциальное уравнение (13), Замечая, что в данном случае  получим
получим

Проинтегрируем это уравнение, беря от обеих его частей после разделения переменных соответствующие определенные интегралы. При этом нижним пределом каждого из интегралов будет значение переменного интегрирования в начальный момент, а верхним — значение того же переменного в произвольный момент времени.
По условиям данной задачи при  и, следовательно,
и, следовательно,

Отсюда окончательно

Искомое время  определим, полагая
определим, полагая  . Это время, как видим, не зависит в данном случае от величины
. Это время, как видим, не зависит в данном случае от величины  Так как
Так как  то
то

Для определения пройденного пути целесообразно вновь составить дифференциальное уравнение движения в виде (14), так как это уравнение позволяет сразу установить зависимость между х и v, Тогда получим

Отсюда, сокращая на v, разделяя переменные и учитывая, что при  получим
получим

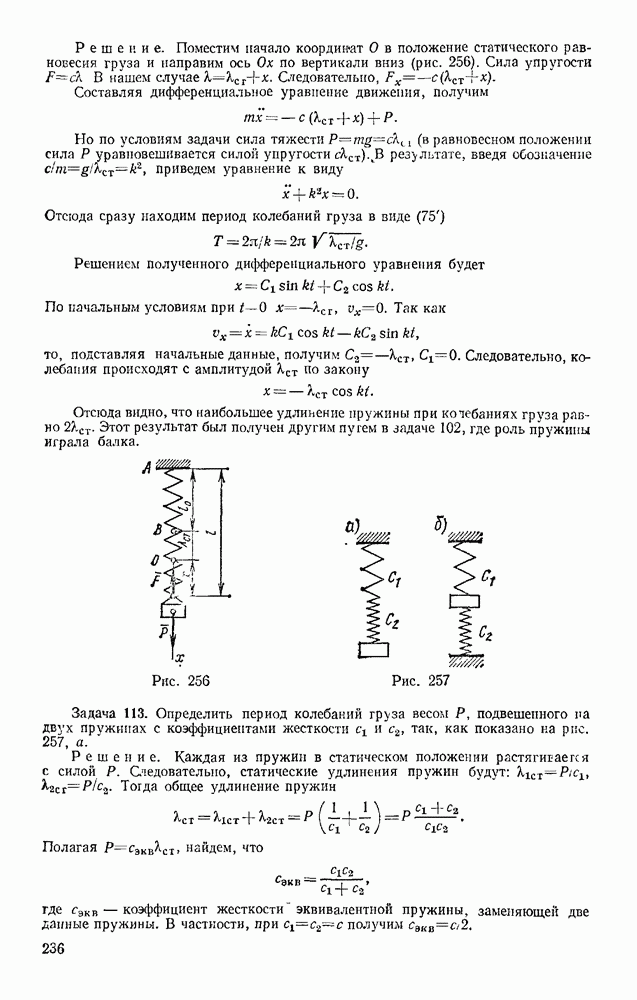
Следовательно,

Полагая  найдем искомый путь:
найдем искомый путь:  .
.
Чтобы найти путь, пройденный лодкой до остановки, следует в равенстве (б) положить  Тогда получим, что
Тогда получим, что 
Определяя время движения до остановки, мы из равенства (а) найдем, что при  время
время  Это означает, что при принятом законе сопротивления
Это означает, что при принятом законе сопротивления  лодка будет к своему конечному положению (определяемому координатой
лодка будет к своему конечному положению (определяемому координатой  ) приближаться асимптотически. Фактически же время движения лодки до остановки будет конечным, так как с уменьшением скорости закон сопротивления становится другим и соответственно изменяется вид зависимости v от t (см, например, задачу 105 в § 90).
) приближаться асимптотически. Фактически же время движения лодки до остановки будет конечным, так как с уменьшением скорости закон сопротивления становится другим и соответственно изменяется вид зависимости v от t (см, например, задачу 105 в § 90).
Другой интересный пример движения под действием силы, зависящей от скорости, рассмотрен в следующем параграфе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
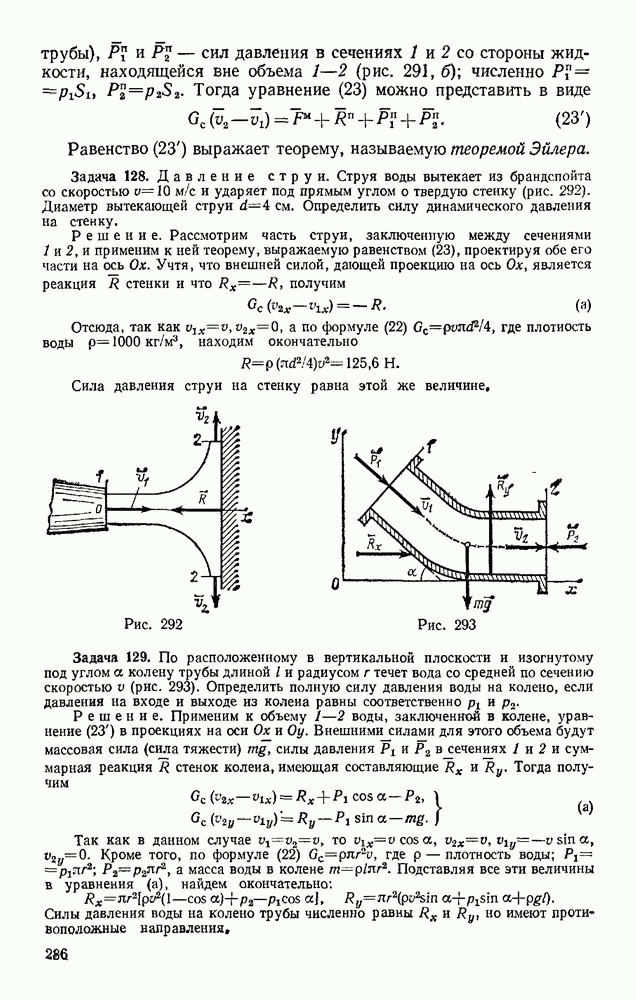
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
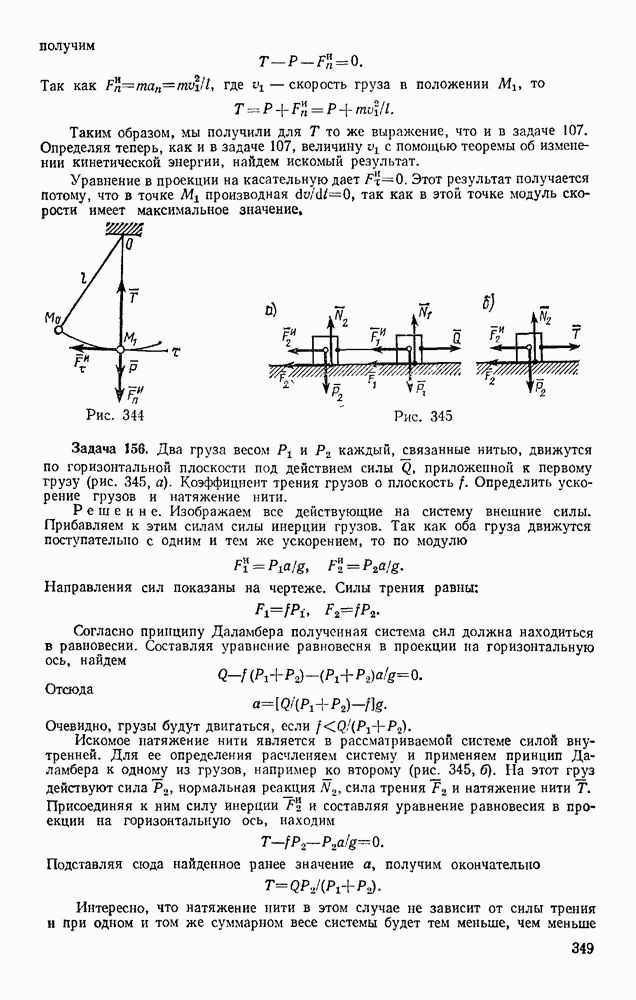
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
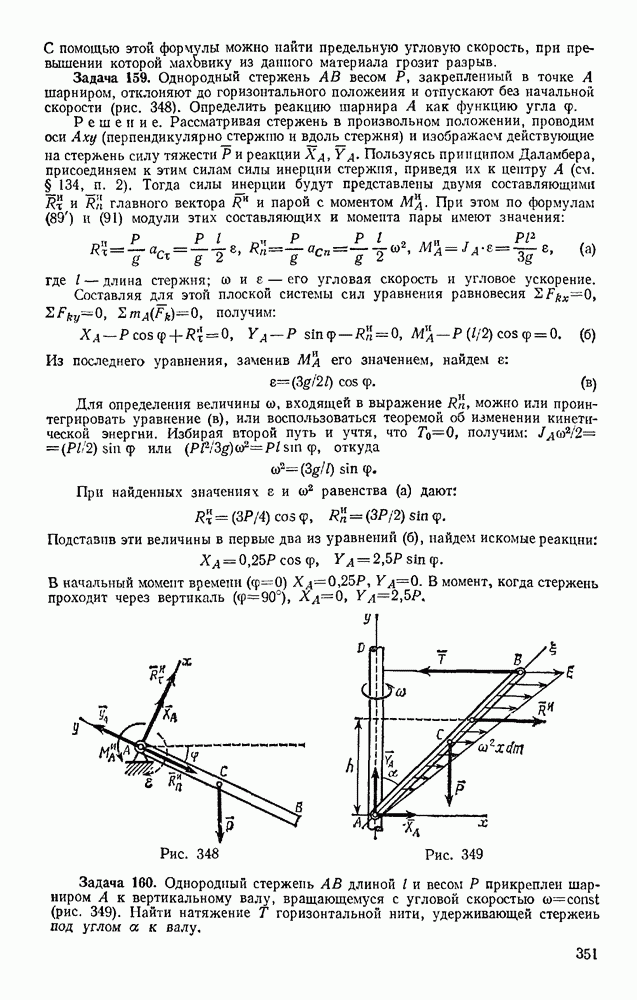
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
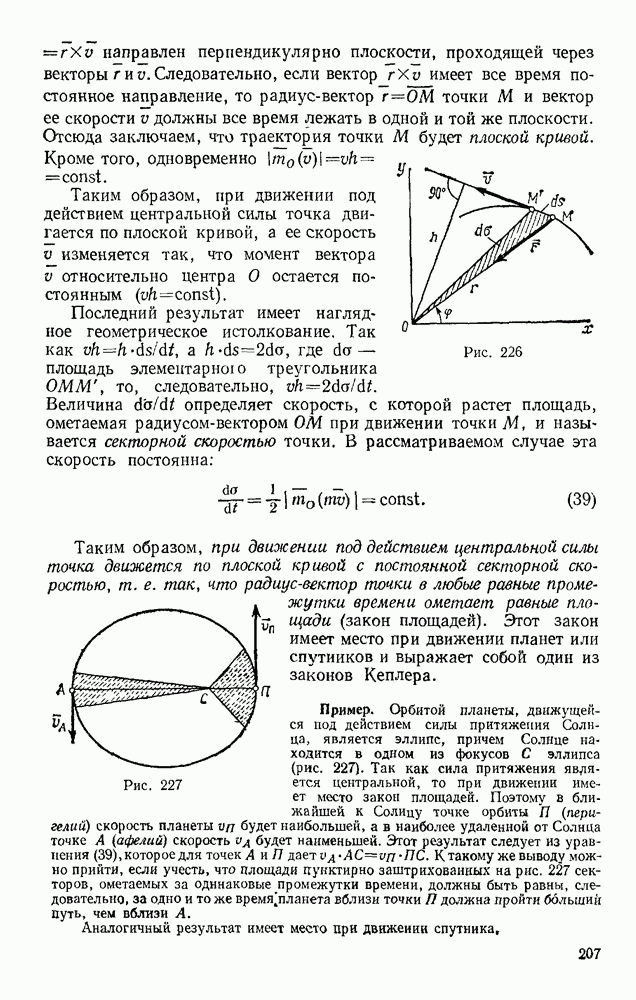
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
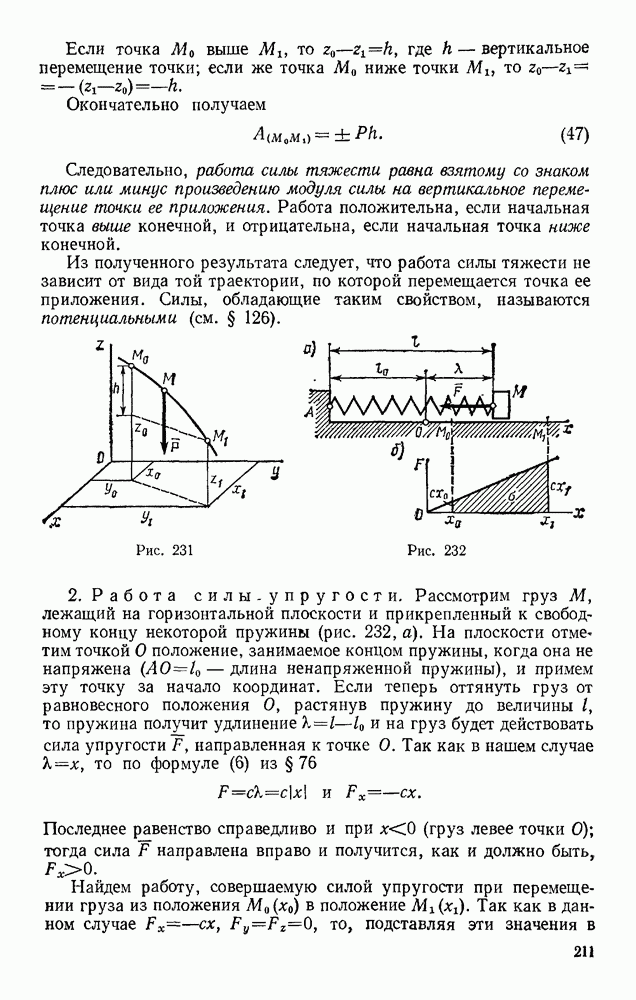
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
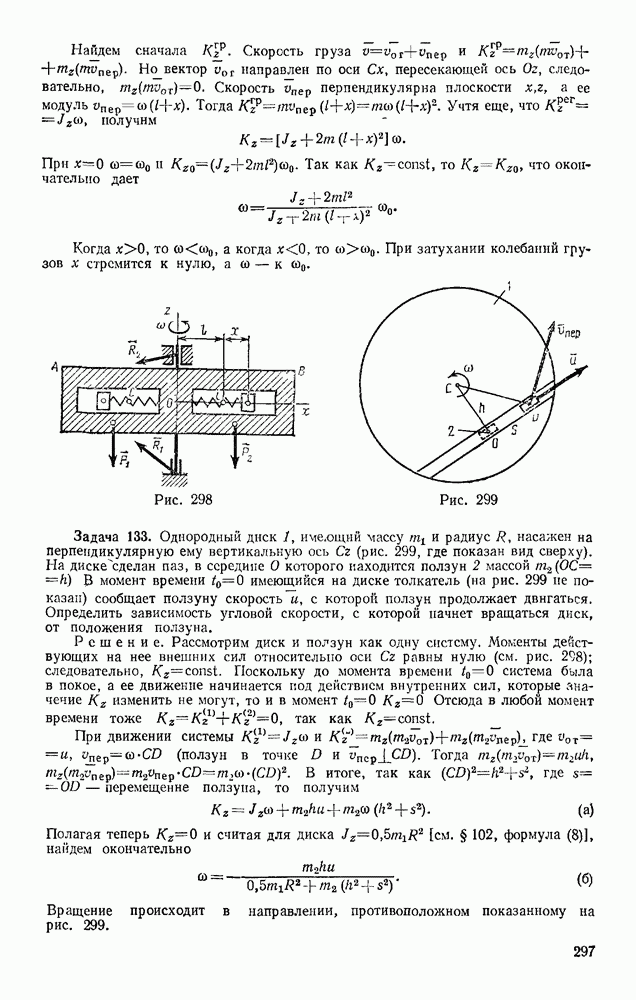
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
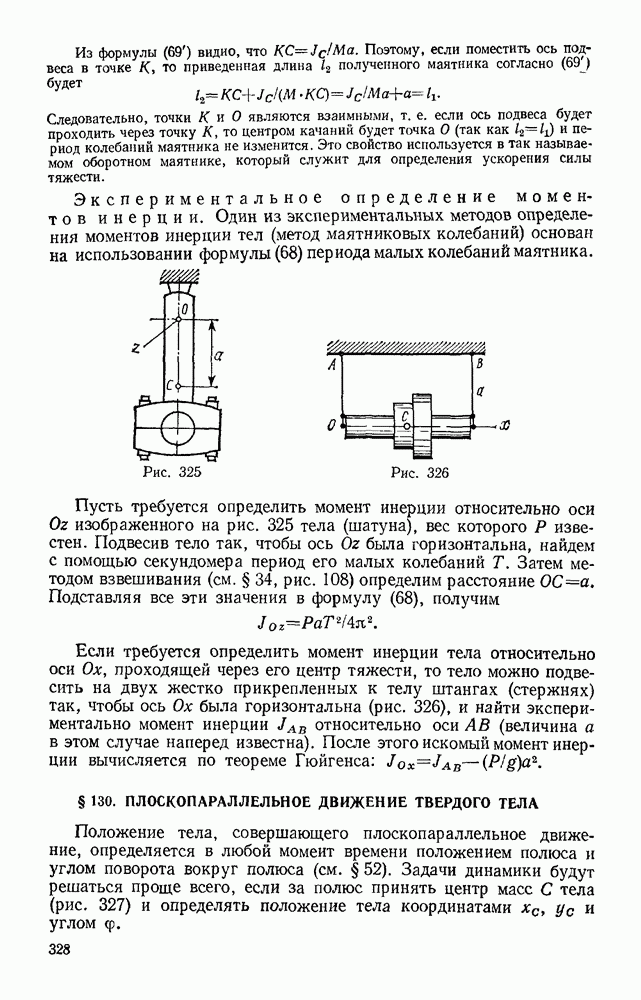
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
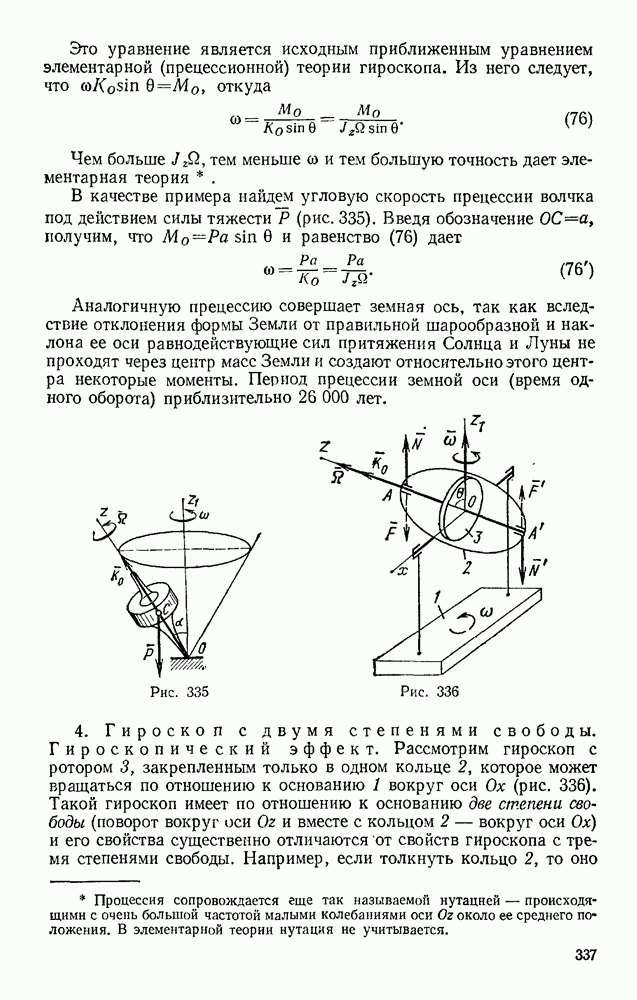
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА