| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
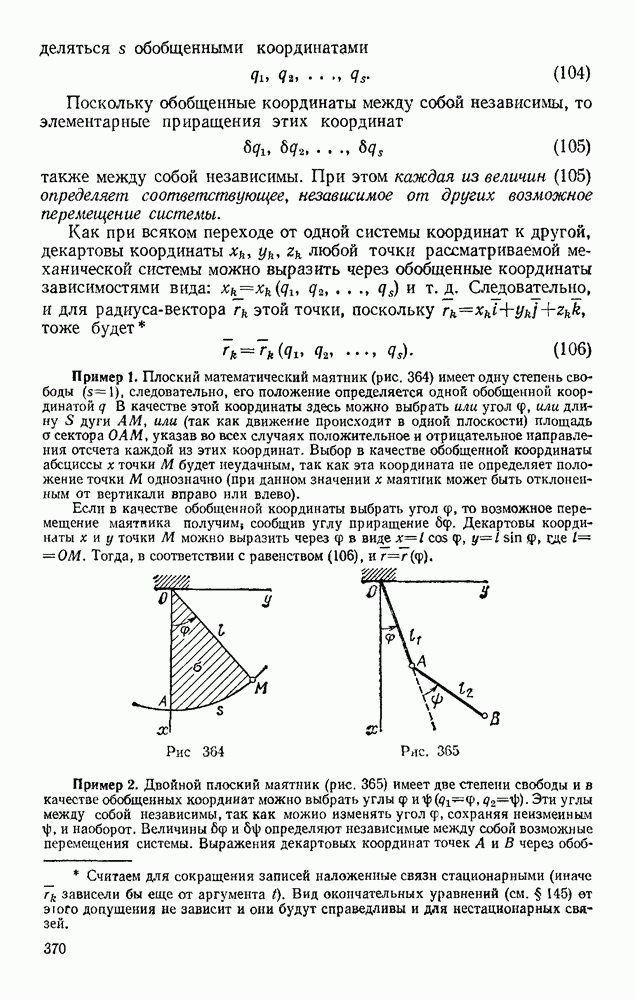
§ 140. РЕШЕНИЕ ЗАДАЧ
Приступая к решению задачи, следут вначале определить число степеней свободы рассматриваемой системы (в частности, механизма), по числу независимых возможных перемещений или координат системы.
В плоских механизмах число степеней свободы можно практически определять так. Представим себе, что механизм движется. Если, остановив поступательное или вращательное движение какого-нибудь одного звена, мы одновременно останавливаем весь механизм, то он имеет одну степень свободы. Если после этого часть механизма может продолжать движение, но, когда затем будет остановлено перемещение какого-нибудь другого звена, механизм остановится, то он имеет две степени свободы и т. д. Аналогично, если определить положение механизма какой-нибудь координатой и когда она постоянна, механизм не может двигаться — у него одна степень свободы. Если же после этого часть механизма может двигаться, то выбирается вторая координата и т. д.
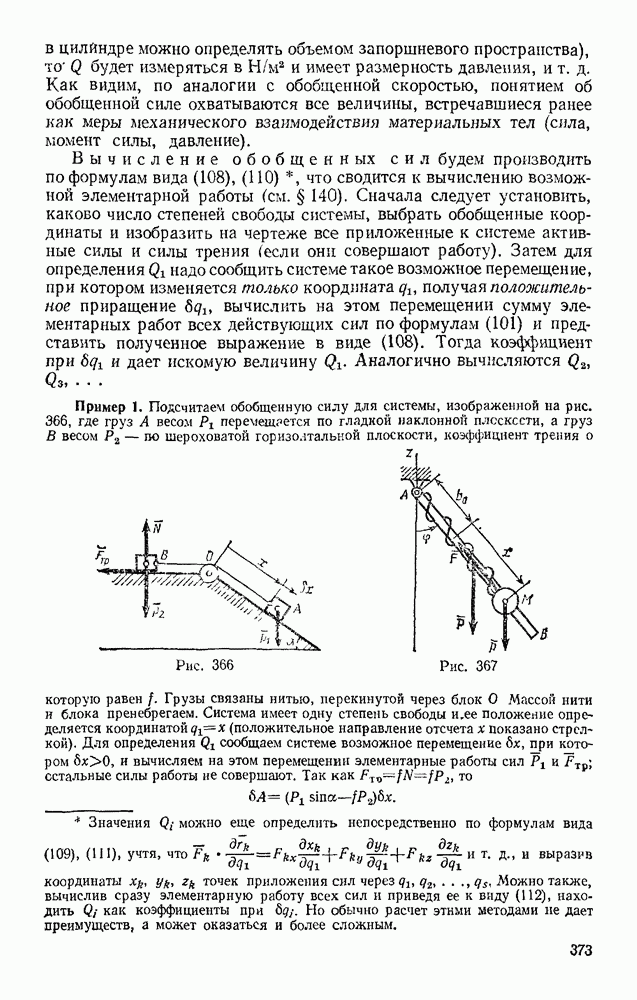
Для решения задачи геометрическим методом, когда система имеет одну степень свободы, надо: 1) изобразить все действующие на систему активные силы; 2) сообщить системе возможное перемещение и показать на чертеже элементарные перемещения  точек приложения сил или углы 69,, элементарных поворотов тел, на которые действуют силы (у элементарных перемещений будем на чертеже указывать их модули
точек приложения сил или углы 69,, элементарных поворотов тел, на которые действуют силы (у элементарных перемещений будем на чертеже указывать их модули  , которые непосредственно входят в условия равновесия); 3) подсчитать элементарные работы всех активных сил на данном перемещении по формулам:
, которые непосредственно входят в условия равновесия); 3) подсчитать элементарные работы всех активных сил на данном перемещении по формулам:

и составить условие (99); 4) установить зависимость между величинами  вошедшими в равенство (99), и выразить эти величины через какую-нибудь одну, что для системы с одной степенью свободы всегда можно сделать.
вошедшими в равенство (99), и выразить эти величины через какую-нибудь одну, что для системы с одной степенью свободы всегда можно сделать.
После замены в равенстве (99) всех величн  через одну получим уравнение, из которого и найдется искомая в задаче величина или зависимость.
через одну получим уравнение, из которого и найдется искомая в задаче величина или зависимость.
Зависимости между  можно находить: а) из соответствующих геометрических соотношений (задачи 164, 169); б) из кинематических соотношений, считая, что система движется, и определяя при данном положении системы зависимости между линейными
можно находить: а) из соответствующих геометрических соотношений (задачи 164, 169); б) из кинематических соотношений, считая, что система движется, и определяя при данном положении системы зависимости между линейными  или угловыми скоростями соответствующих точек или тел системы, а затем полагая
или угловыми скоростями соответствующих точек или тел системы, а затем полагая  , что справедливо, так как получаемые точками или телами за время dt действительные перемещения будут при стационарных связях одними из возможных (иначе, здесь можно сразу считать зависимости между возможными перемещениями такими же, как между соответствующими скоростями, см. задачи 165, 166 и др.).
, что справедливо, так как получаемые точками или телами за время dt действительные перемещения будут при стационарных связях одними из возможных (иначе, здесь можно сразу считать зависимости между возможными перемещениями такими же, как между соответствующими скоростями, см. задачи 165, 166 и др.).
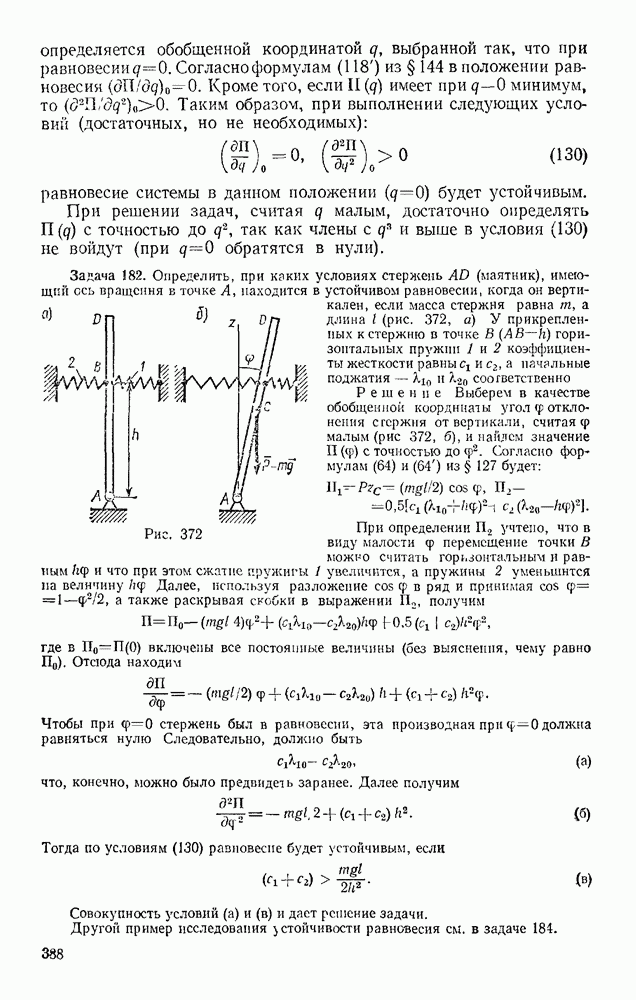
Для системы с несколькими степенями свободы задачу можно решать, составляя условие (99) для каждого из независимых возможных перемещений системы и преобразуя его тем же путем. В результате для системы получится столько условий равновесия, сколько она имеет степеней свободы. Другой метод решения, приводящий к тем же результатам, изложен в § 144.
При аналитическом методе расчета условие равновесия составляют в виде (100). Для этого выбирают координатные оси, связанные с телом, которое при возможных перемещениях системы остается неподвижным. Затем вычисляют проекции всех активных сил на выбранные оси и координаты  точек приложения этих сил, выражая все координаты через какой-нибудь параметр (например, угол). После этого величины
точек приложения этих сил, выражая все координаты через какой-нибудь параметр (например, угол). После этого величины  находятся дифференцированием координат
находятся дифференцированием координат  по этому параметру.
по этому параметру.
Если все координаты  выразить через один параметр сразу не удается, то надо ввести несколько параметров, а затем установить зависимость между ними.
выразить через один параметр сразу не удается, то надо ввести несколько параметров, а затем установить зависимость между ними.
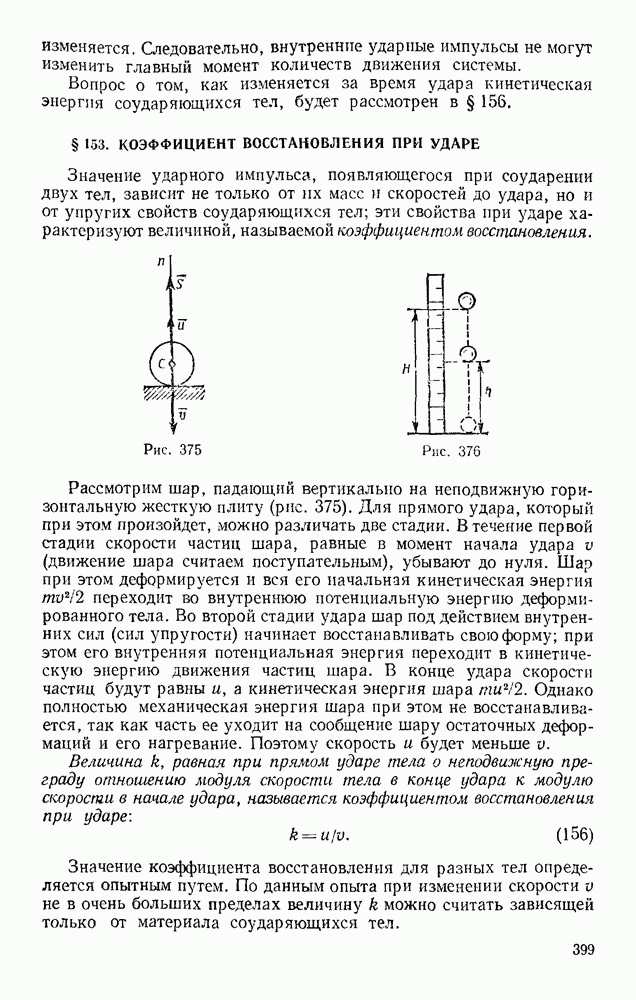
Отметим в заключение, что условиями (99) или (100) можно пользоваться для решения задач и при наличии трения, включая силу трения в число активных сил. Этим же путем можно находить реакции связей, если, отбросив связь, заменить ее соответствующей реакцией, включить последнюю в число активных сил и учесть, что после отбрасывания связи у системы появляется новая степень свободы.
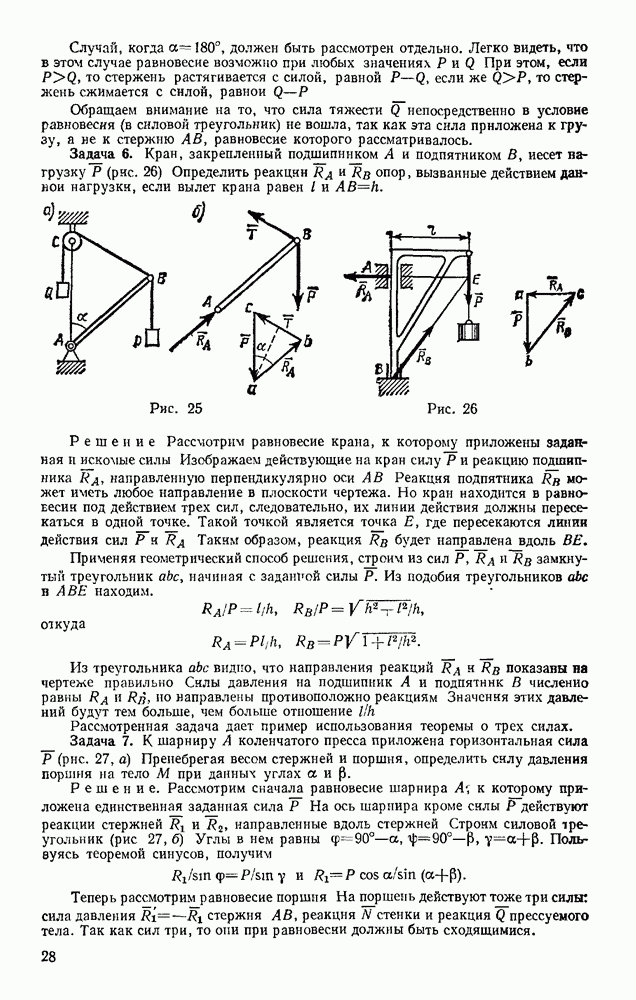
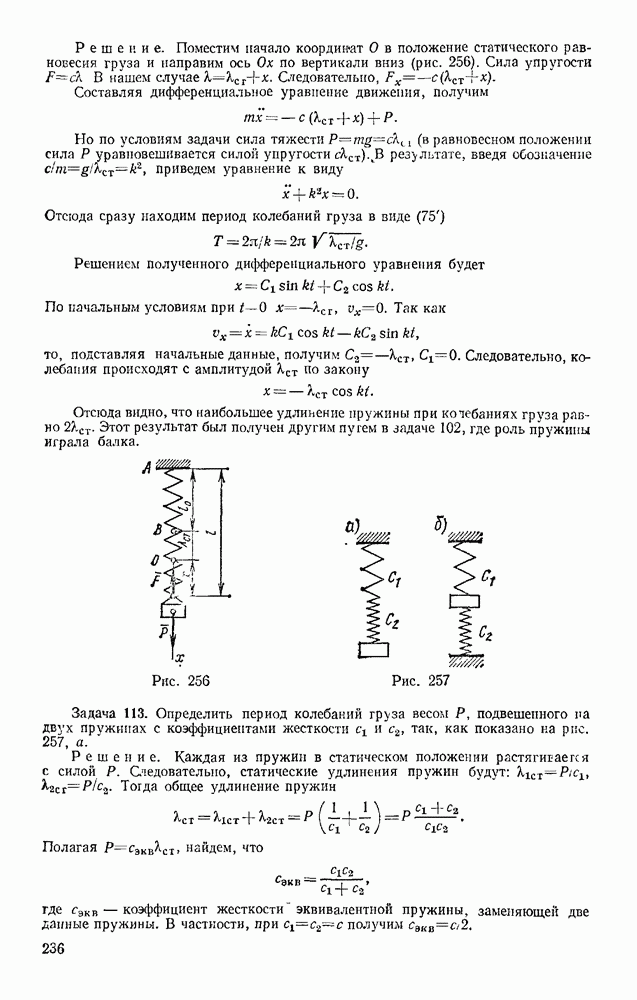
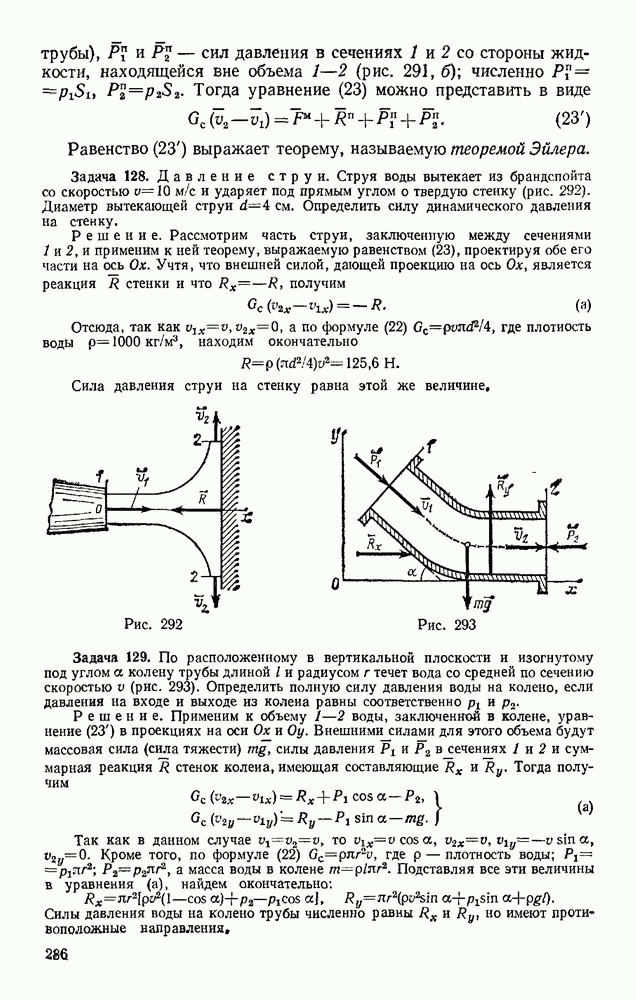
Задача 164. В механизме, изображенном на рис. 354, найти зависимость между силами Р и Q при равновесии.
Решение, У системы одна степень свободы. Если сообщить системе возможное перемещение, то все диагонали параллелограммов, образованных стержнями, удлинятся на одну и ту же величину  . Тогда
. Тогда  .
.
Составляя уравнение (99), получим:

откуда  . Результат получается очень просто.
. Результат получается очень просто.

Рис. 354
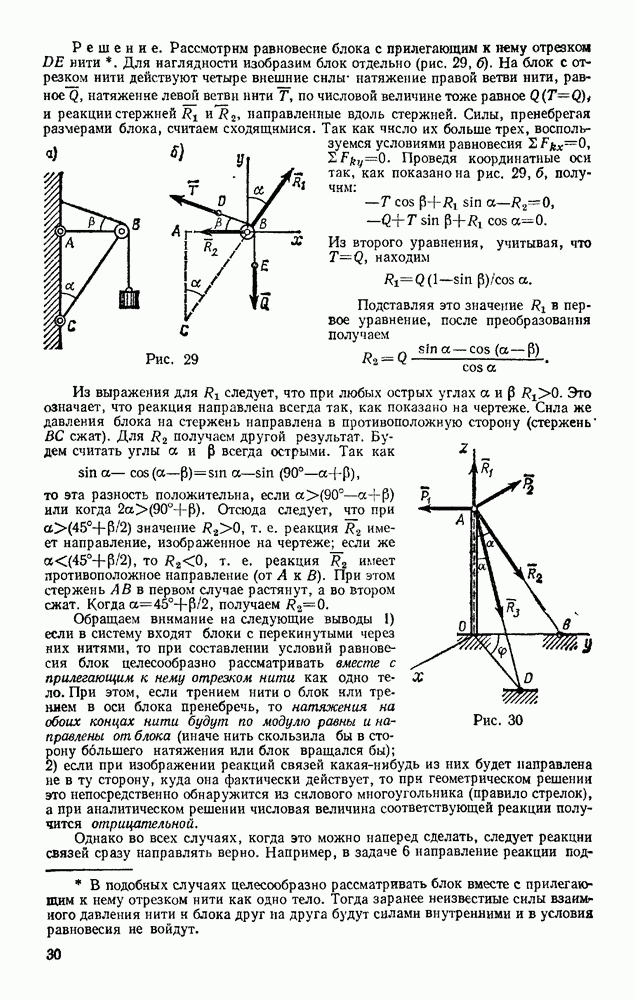
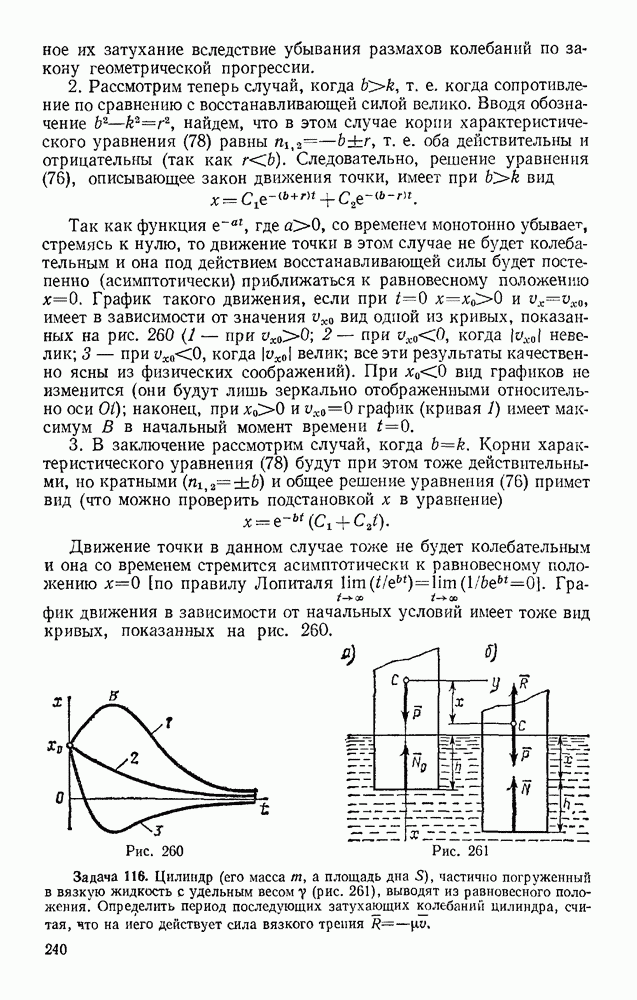
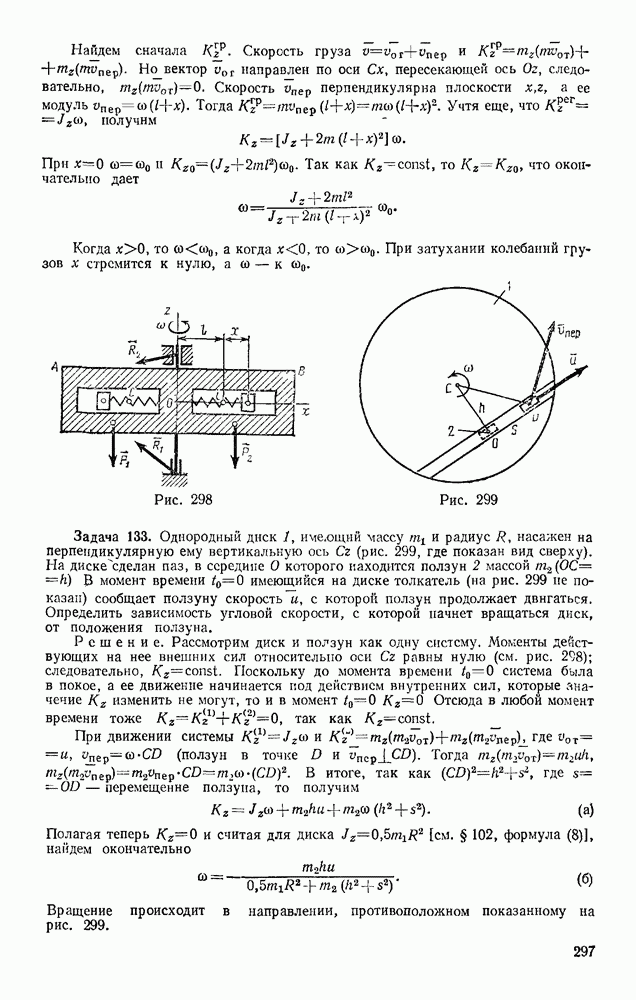
Задача 165. Вес бревна Q, вес каждого из двух цилиндрических катков, на которые оно положено, Р. Определить, какую силу F надо приложить к бревну, чтобы удержать его в равновесии на наклонной плоскости при данном угле наклона а (рис. 355). Трение катков о плоскость и бревно обеспечивает отсутствие скольжения.
Решение. Если пренебречь сопротивлением качению, то плоскость для катков будет идеальной связью. При качении без скольжения у системы одна степень свободы. Сообщая системе возможное перемещение, получаем по условию (99)

где  — возможное перемещение бревна, совпадающее с перемещением точки В.
— возможное перемещение бревна, совпадающее с перемещением точки В.
Точка касания К является мгновенным центром скоростей катка. Следовательно,  , если считать
, если считать  , Подставляя это значение
, Подставляя это значение  в предыдущее уравнение, найдем окончательно
в предыдущее уравнение, найдем окончательно

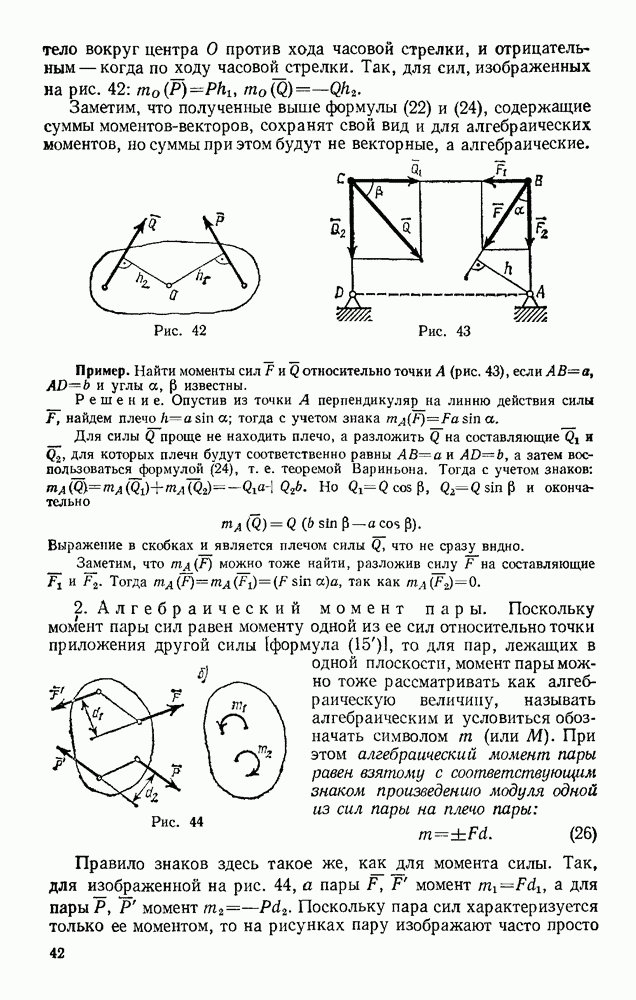
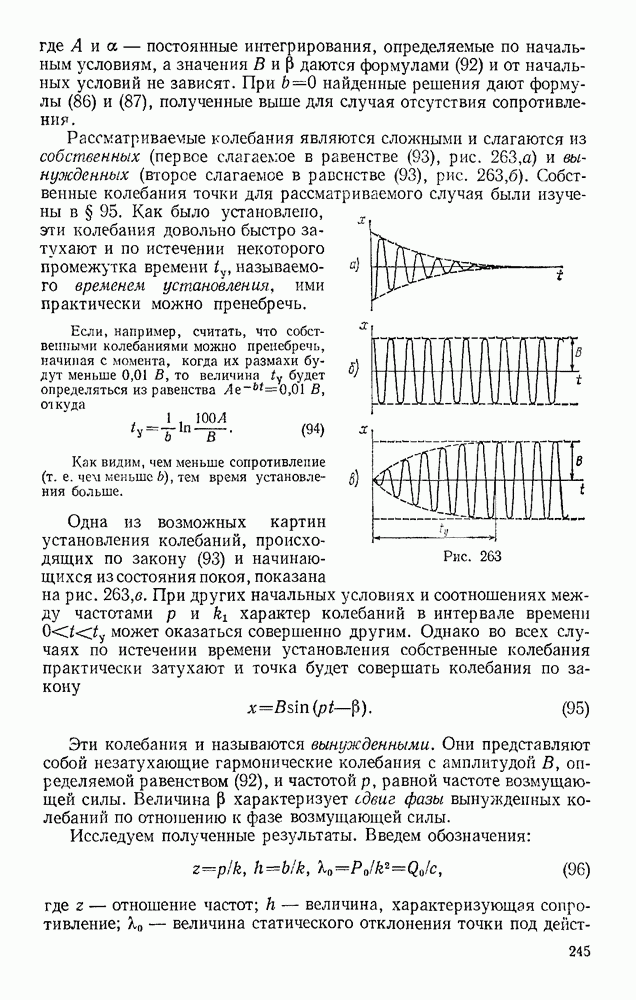
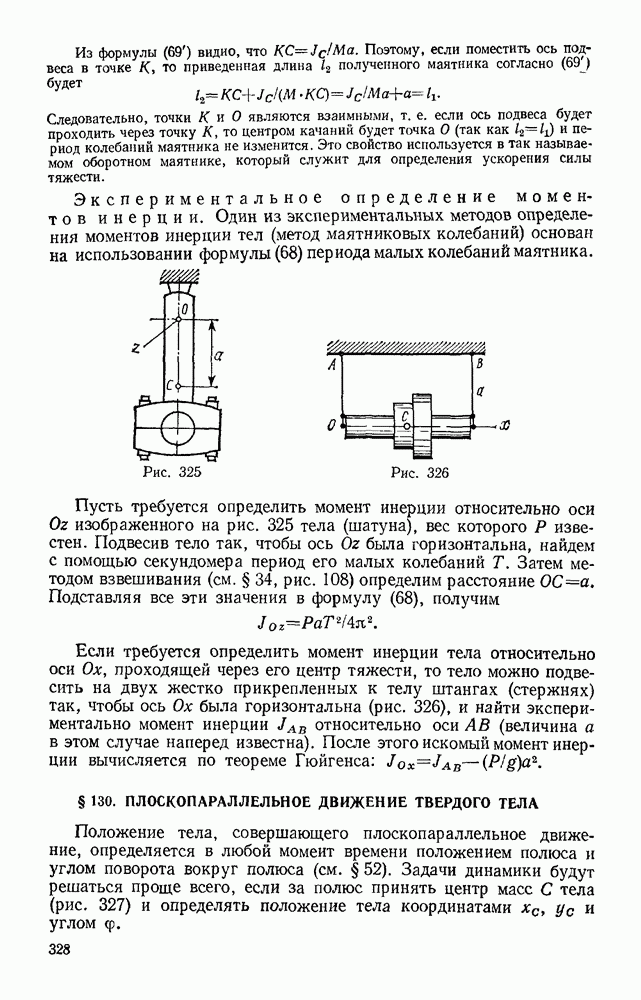
Задача 166. Найти зависимость между моментом М пары, действующей на кривошип кривошипно-ползунного механизма (рис, 356), и силой давления Р на поршень при равновесии, если 

Рис. 355

Рис. 356
Решение. У механизма одна степепь свободы. Из условия равновесия (99), если положить  получим:
получим:

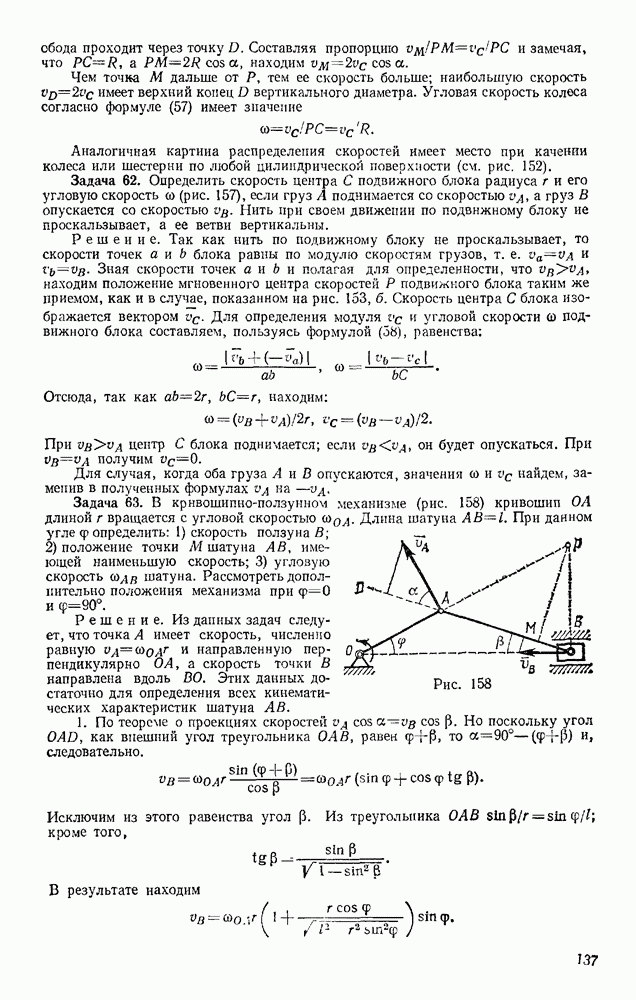
Решение сводится к нахождению зависимости между  Эта кинематическая задача была решена ранее (см. § 57, задача 63). Пользуясь полученным там результатом, находим
Эта кинематическая задача была решена ранее (см. § 57, задача 63). Пользуясь полученным там результатом, находим

Задача 167. Для редуктора, рассмотренного в задаче 83 (см. § 70), найти зависимость между вращающим моментом  приложенным к ведущему валу А, и моментом сопротивлений
приложенным к ведущему валу А, и моментом сопротивлений  приложенным к ведомому валу В, когда оба вала вращаются равномерно.
приложенным к ведомому валу В, когда оба вала вращаются равномерно.
Решение. При равномерном вращении соотношение между  будет таким же, как при равновесии. Следовательно, по условию (99), если положить
будет таким же, как при равновесии. Следовательно, по условию (99), если положить  будет:
будет:

Отсюда, пользуясь результатом, полученным в задаче 83, находим

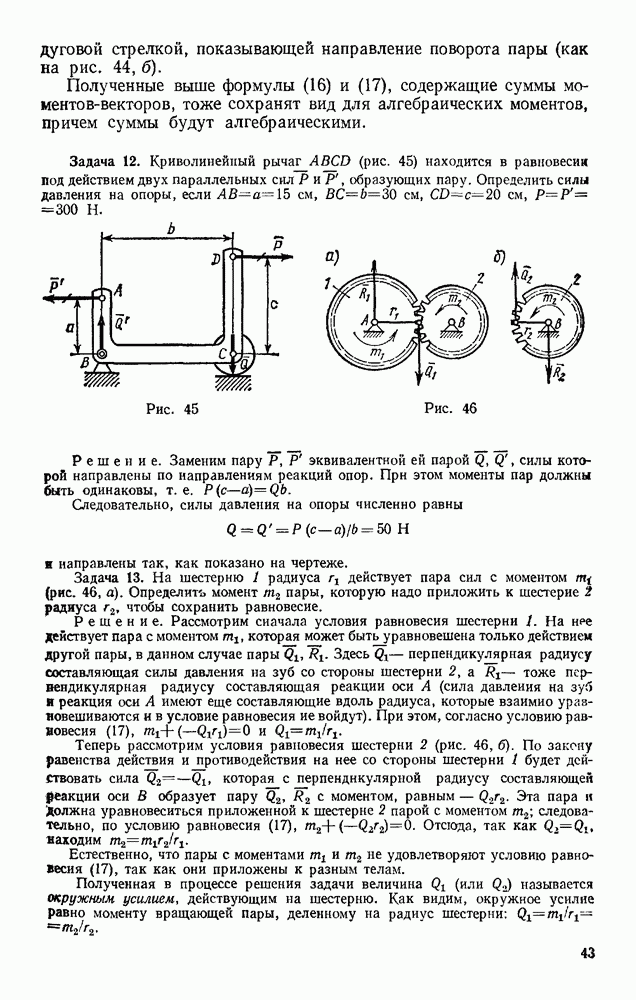
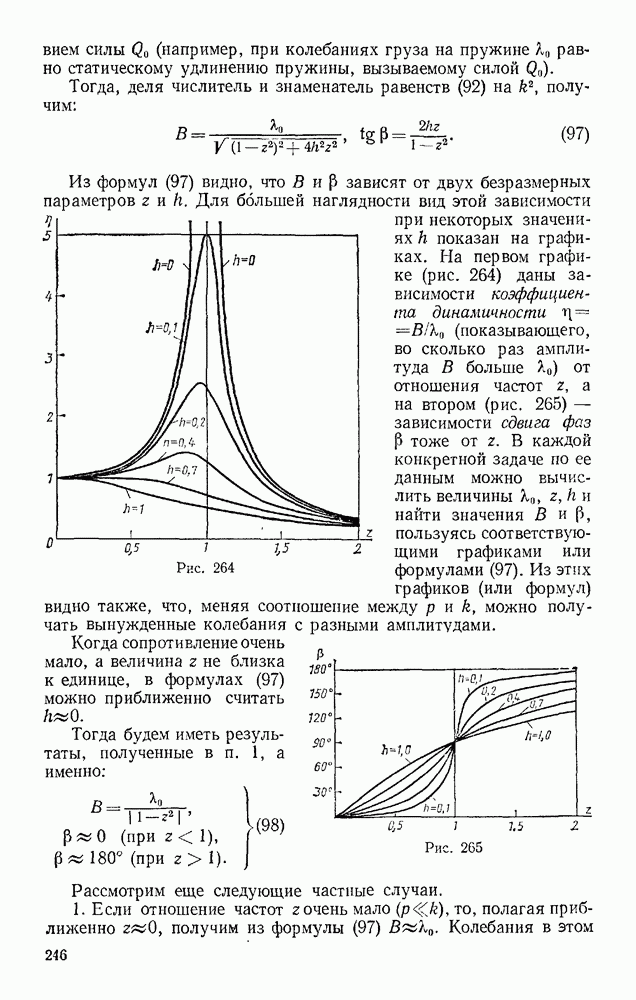
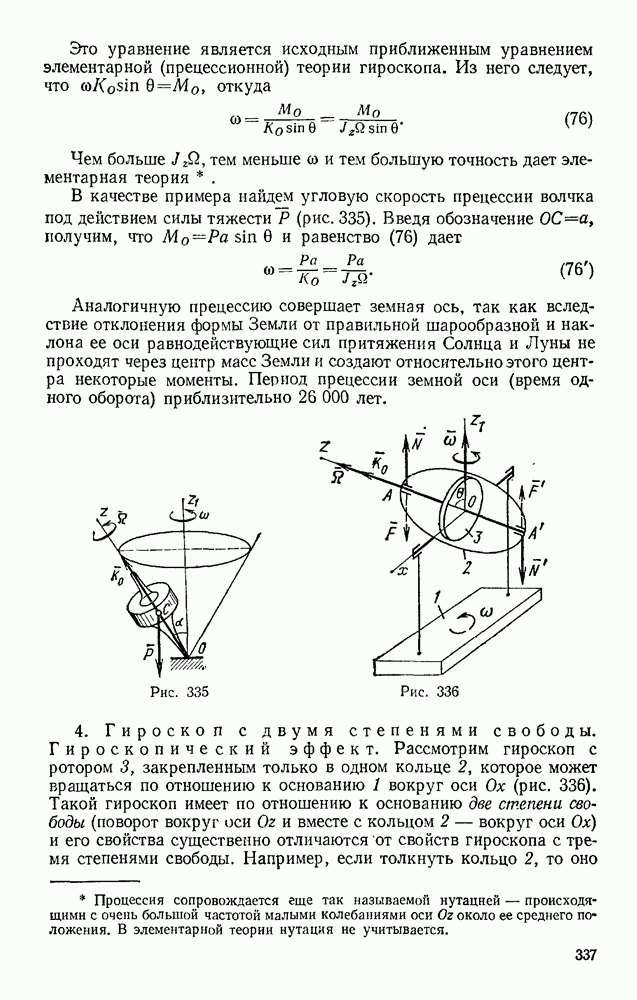
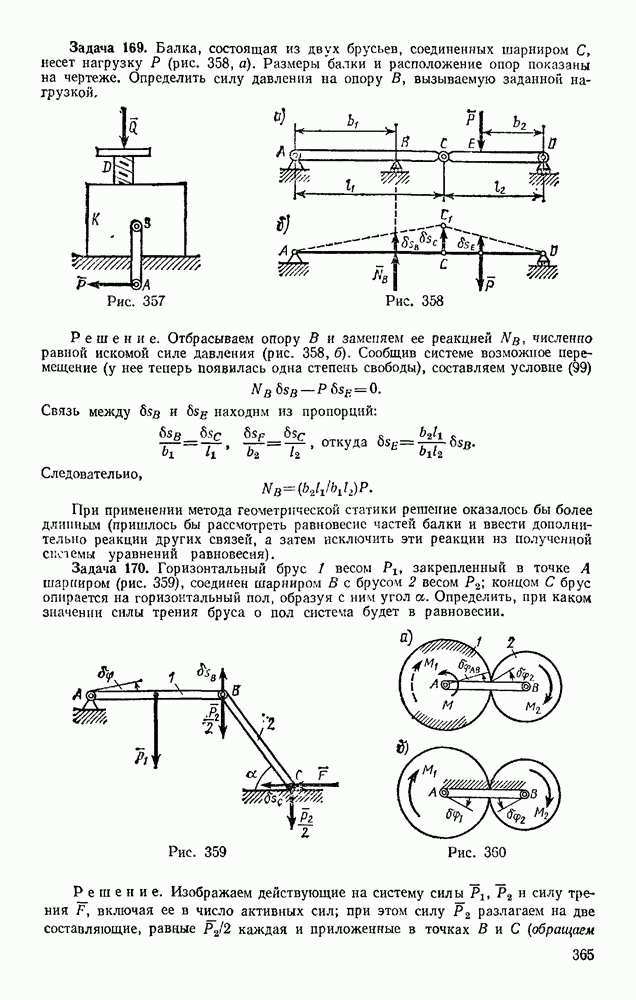
Задача 168. Пайтн зависимость между силами Р и Q в подъемном механизме детали которого скрыты в коробке К (рис. 357), если известно, что при каждом повороте рукоятки  винт D выдвигается на величину
винт D выдвигается на величину 
Решение. Составляя условие равновесия (99), получаем

Предполагается, что при равномерном вращении рукоятки виит вывинчивается также равномерно, тогда

Подставляя это значение  в предыдущее равенство, находим
в предыдущее равенство, находим

Заметим, что методами геометрической статики эту несложную задачу вообще нельзя было бы решить, так как детали механизма не известны.
Решенная задача показывает, каковы (принципиально) возможности примененного метода. Но при конкретном инженерном расчёте подобного механизма необходимо будет, конечно, учесть трение между его деталями, для чего понадобится знать, каков механизм.
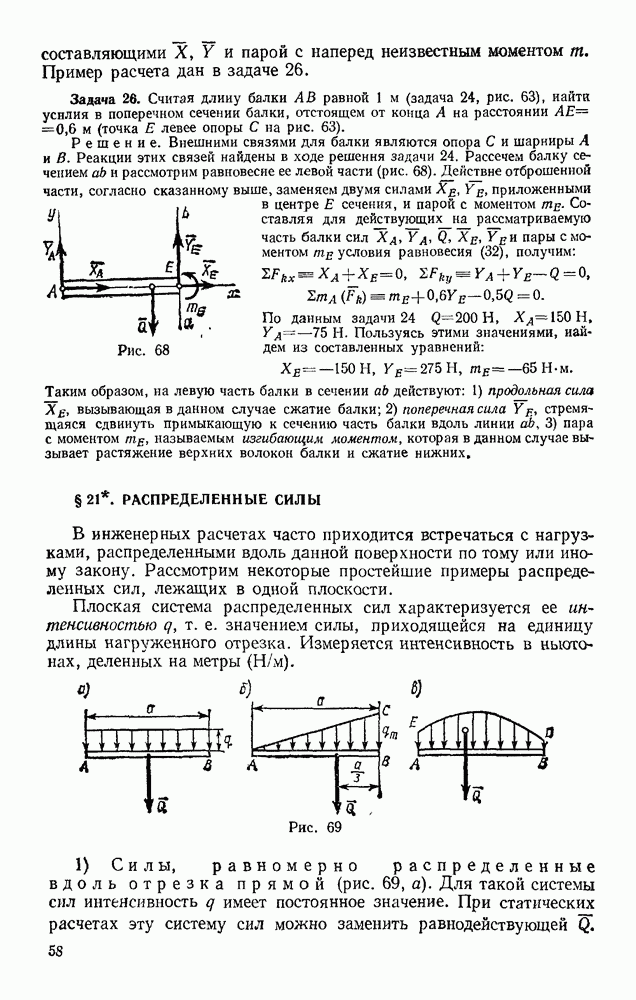
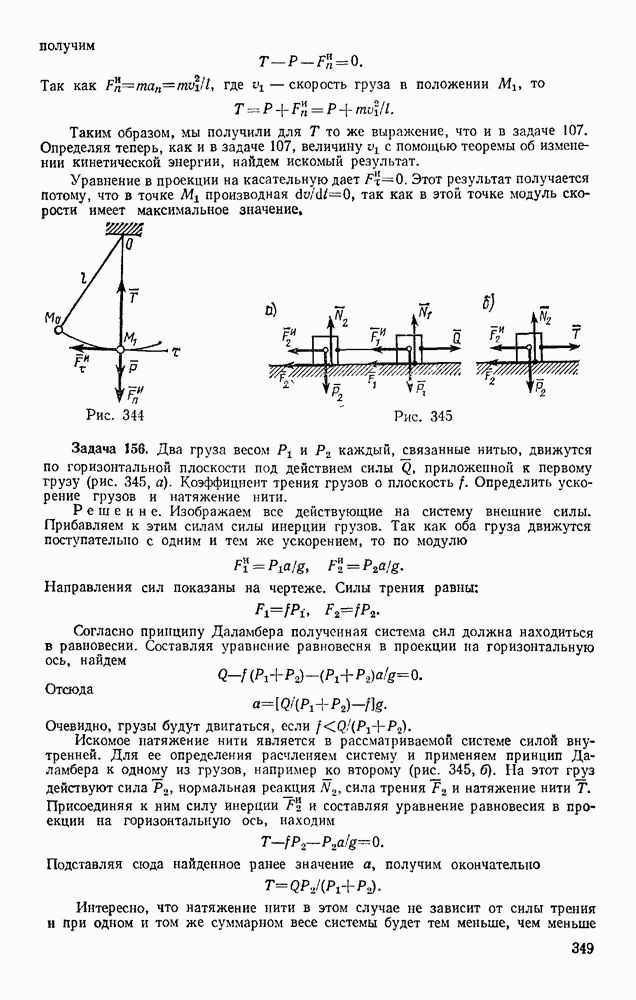
Задача 169. Балка, состоящая из двух брусьев, соединенных шарниром С, несет нагрузку Р (рис. 358, а). Размеры балки и расположение опор показаны на чертеже. Определить силу давления на опору В, вызываемую заданной нагрузкой.

Рис. 357

Рис. 358
Решение. Отбрасываем опору В и заменяем ее реакцией N в, численно равной искомой силе давления (рис. 358, б). Сообщив системе возможное перемещение (у нее теперь появилась одна степень свободы), составляем условие (99)

Связь между  находим из пропорций:
находим из пропорций:

откуда 
Следовательно,

При применении метода геометрической статики решение оказалось бы более длинным (пришлось бы рассмотреть равновесие частей балки и ввести дополнительно реакции других связей, а затем исключить эти реакции из полученной системы уравнений равновесия).
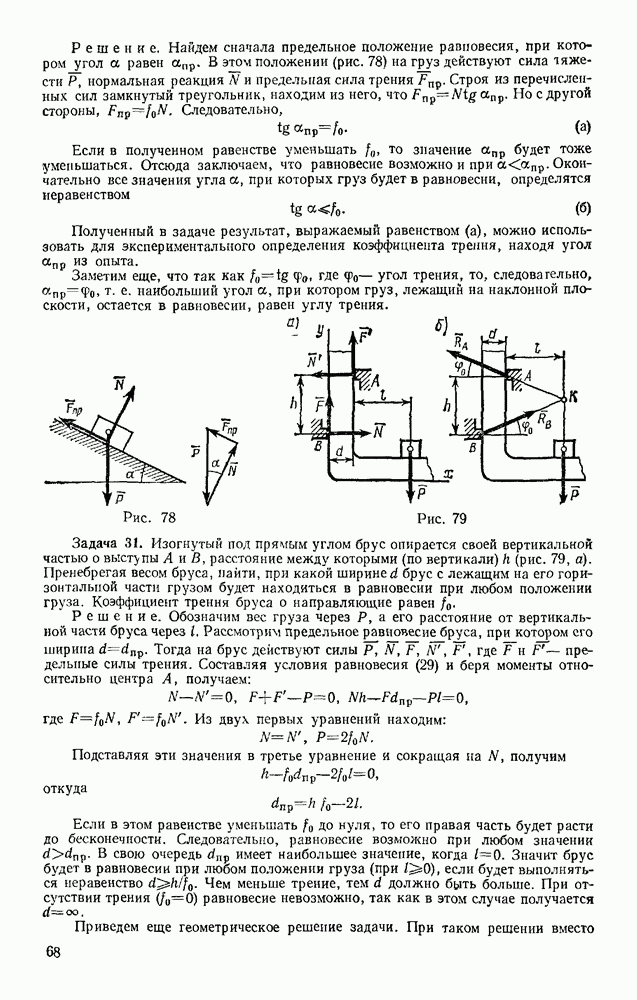
Задача 170. Горизонтальный брус 1 весом  закрепленный в точке А шарниром (рис. 359), соединен шарниром В с брусом 2 весом
закрепленный в точке А шарниром (рис. 359), соединен шарниром В с брусом 2 весом  концом С брус опирается на горизонтальный пол, образуя с ним угол а. Определить, при каком значении силы трения бруса о пол система будет в равновесии.
концом С брус опирается на горизонтальный пол, образуя с ним угол а. Определить, при каком значении силы трения бруса о пол система будет в равновесии.

Рис. 359

Рис. 360
Решение. Изображаем действующие на систему силы  и силу трения F, включая ее в число активных сил; при этом силу
и силу трения F, включая ее в число активных сил; при этом силу  разлагаем на две составляющие, равные
разлагаем на две составляющие, равные  каждая и приложенные в точках В и С (обращаем внимание на этот прием, существенно облегчающий вычисление возможной работы).
каждая и приложенные в точках В и С (обращаем внимание на этот прием, существенно облегчающий вычисление возможной работы).
Составляя условие равновесия (99) и учитывая формулы (101), получим обозначив 

Но, по аналогии с теоремой о проекциях скоростей двух точек тела,  , где
, где  . Тогда
. Тогда  и окончательно
и окончательно

Заметим, что методами геометрической статики в этой задаче составить только одно уравнение, из которого сразу найдется F, нельзя.
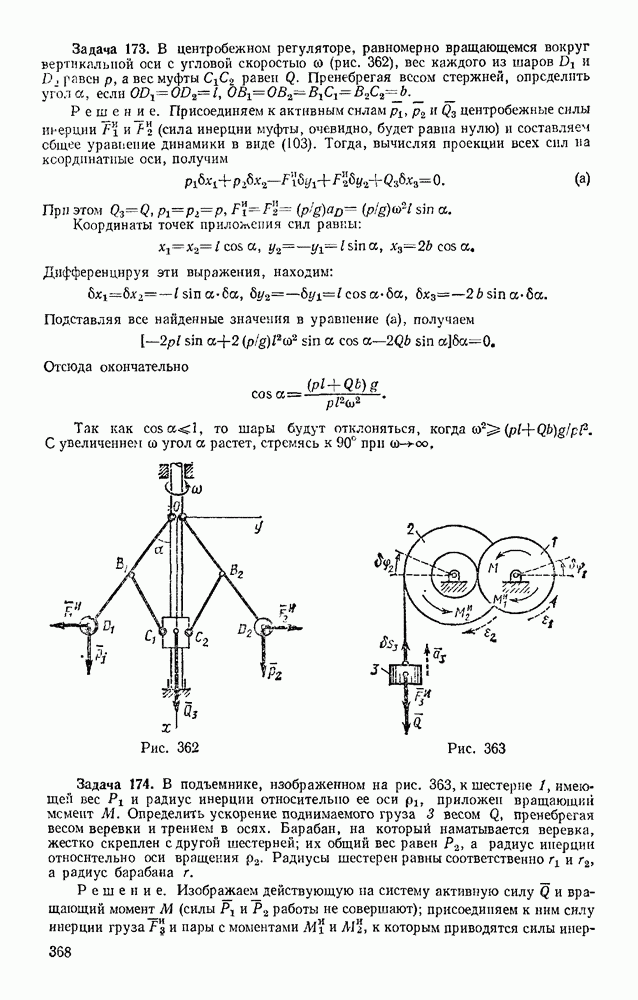
Задача 171. В планетарном механизме с дифференциальной передачей (см. § 70) на ось А независимо друг от друга насажены шестерня 1 радиусом  и кривошип АВ, несущий на себе ось В шестерни 2 радиусом
и кривошип АВ, несущий на себе ось В шестерни 2 радиусом  (рис. 360). На кривошип действует вращающий момент М, а на шестерни 1 и 2 — моменты сопротивлений
(рис. 360). На кривошип действует вращающий момент М, а на шестерни 1 и 2 — моменты сопротивлений  Найти значения
Найти значения  при равновесии механизма.
при равновесии механизма.
Решение. Механизм имеет две степени свободы, так как в нем возможны два независимых перемещения: а) поворот кривошипа АВ при неподвижной шестерне  и б) поворот шестерни 1 при неподвижном кривошипе АВ. Сообщим сйачала системе возможное перемещение, при котором шестерня 1 остается неподвижной (рис, 360, а), Для этого перемещения уравнение (99) дает
и б) поворот шестерни 1 при неподвижном кривошипе АВ. Сообщим сйачала системе возможное перемещение, при котором шестерня 1 остается неподвижной (рис, 360, а), Для этого перемещения уравнение (99) дает

Но когда шестерня 1 неподвижна, точка касания шестерен будет мгновенным центром скоростей для шестерни 2. Следовательно,  . В то же время
. В то же время  . Отсюда
. Отсюда  или
или  и мы получаем
и мы получаем 
Теперь сообщим системе другое, независимое от первого возможное перемещение, при котором кривошип АВ неподвижен (рис. 360, б). Для этого перемещения по условию (99) будет  . Но при неподвижном кривошипе
. Но при неподвижном кривошипе


Рис. 361
Окончательно находим:

Задача 172. В прессе, изображенном на рис. 361, найти зависимость между силами  при равновесии
при равновесии  Углы
Углы  известны. Весом стержней пренебречь.
известны. Весом стержней пренебречь.
Решение. Чтобы дать пример аналитического расчета, воспользуемся условием равновесия (100). Беря начало в неподвижной точке А и проводя оси ли у, получим

так как остальные проекции сил обращаются в нули.
Для нахождения  определим значения координат
определим значения координат  точен приложения сил, выразив их через углы а и
точен приложения сил, выразив их через углы а и  Получим, обозначая длины стержней через а и b:
Получим, обозначая длины стержней через а и b:

Дифференцируя эти выражения, найдем:

Подстановка полученных величин в равенство (а) дает (с учетом того, что  )
)

Для нахождения зависимости между  воспользуемся тем, что в данном случае расстояние
воспользуемся тем, что в данном случае расстояние  . Следовательно,
. Следовательно,  Дифференцируя это равенство, получим:
Дифференцируя это равенство, получим:

Подставляя это значение  в равенство (б) найдем
в равенство (б) найдем

откуда

При угле P, близком к a, сила давления Р получается очень большой,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА