| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
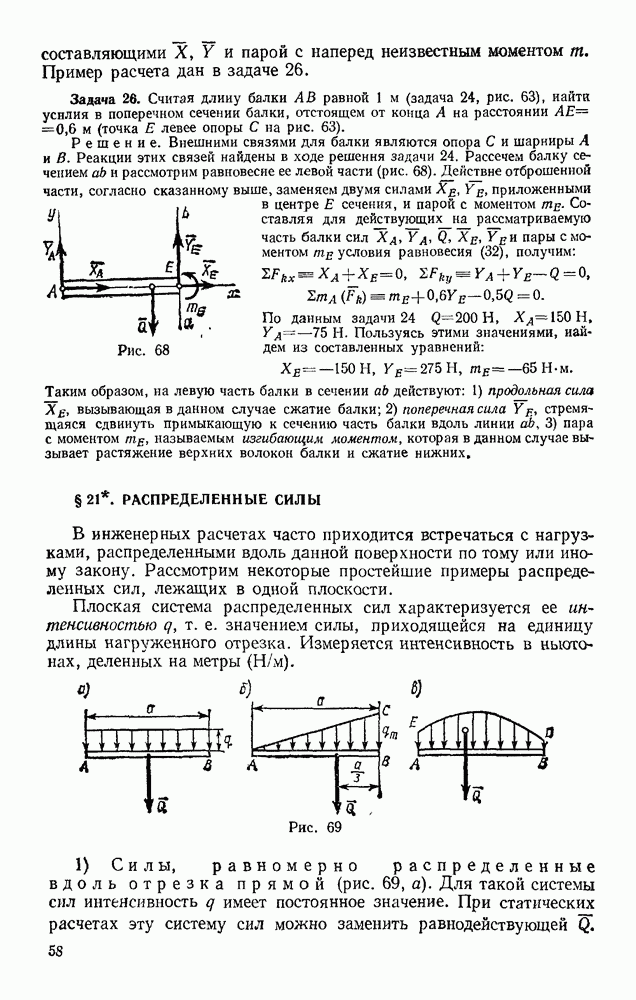
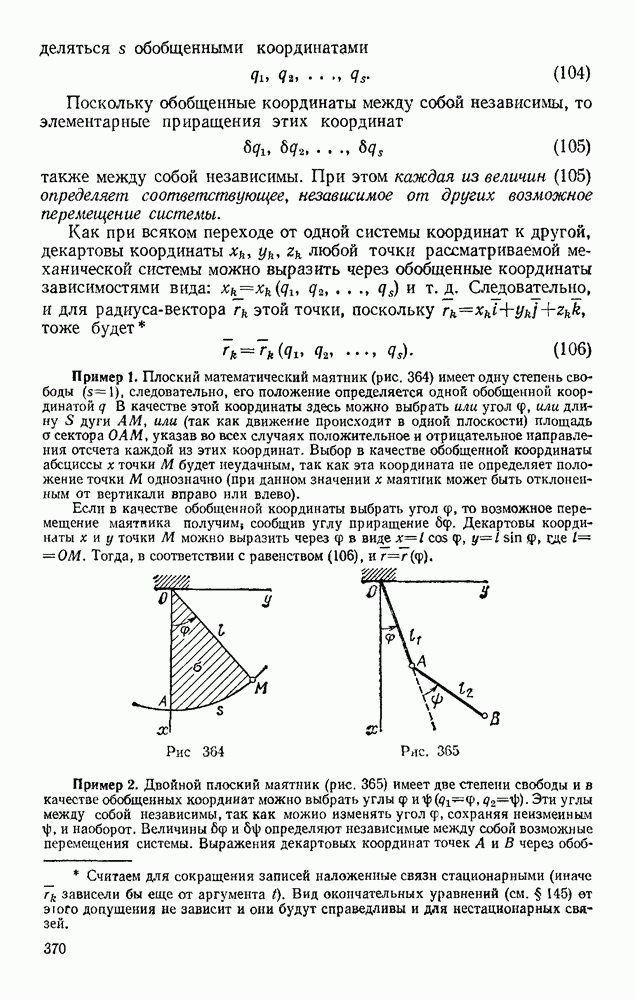
В § 8 было введено понятие о моменте силы относительно центра О. Это вектор  направленный перпендикулярно плоскости ОАВ (рис. 85), модуль которого согласно формуле (13) имеет значение
направленный перпендикулярно плоскости ОАВ (рис. 85), модуль которого согласно формуле (13) имеет значение


Рис. 85
Как это было и для силы, в дальнейшем окажется необходимым рассматривать проекции вектора  на разные оси. Проекция вектора
на разные оси. Проекция вектора  т. е. момента силы F относительно центра О, на какую-нибудь ось
т. е. момента силы F относительно центра О, на какую-нибудь ось  , проходящую через этот центр, называется моментом силы F относительно оси
, проходящую через этот центр, называется моментом силы F относительно оси  , т. е.
, т. е.

где  — момент силы F относительно оси z; у — угол между вектором
— момент силы F относительно оси z; у — угол между вектором  и осью z.
и осью z.
Из определения следует, что  как проекция вектора на ось, является величиной алгебраической (знак
как проекция вектора на ось, является величиной алгебраической (знак  ) определяется так же, как знак проекции любого вектора, например, на рис.
) определяется так же, как знак проекции любого вектора, например, на рис. 
Найдем другое выражение для  позволяющее непосредственно вычислять эту величину. Для этого проведем через произвольную точку
позволяющее непосредственно вычислять эту величину. Для этого проведем через произвольную точку  оси
оси  (рис. 85) плоскость
(рис. 85) плоскость  перпендикулярную этой оси, и спроектируем АОАВ на эту плоскость. Так как вектор
перпендикулярную этой оси, и спроектируем АОАВ на эту плоскость. Так как вектор  перпендикулярен плоскости ОАВ, а ось
перпендикулярен плоскости ОАВ, а ось  перпендикулярна плоскости
перпендикулярна плоскости  то угол у, как угол между нормалями к названным плоскостям, является углом между этими плоскостями. Следовательно, если одновременно учесть равенство (44), то
то угол у, как угол между нормалями к названным плоскостям, является углом между этими плоскостями. Следовательно, если одновременно учесть равенство (44), то

Но, как видно из рис. 85, в треугольнике ОАВ сторона  представляет собой одновременно проекцию
представляет собой одновременно проекцию  силы F на плоскость
силы F на плоскость  (см.§ 5). Тогда
(см.§ 5). Тогда  где
где  алгебраический момент силы
алгебраический момент силы  относительно центра
относительно центра  Из этого и предыдущего равенств следует (с учетом знаков), что
Из этого и предыдущего равенств следует (с учетом знаков), что

Таким образом, момент силы F относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси  , взятому относительно точки
, взятому относительно точки  пересечения оси с этой плоскостью Этот результат может служить другим определением понятия момента силы относительно оси.
пересечения оси с этой плоскостью Этот результат может служить другим определением понятия момента силы относительно оси.
Замечая как направлен поворот, который стремится совершить сила  когда
когда  (см. рис. 85; случай, когда
(см. рис. 85; случай, когда  получится, если изменить направление силы F на прямо противоположное), приходим к следующему выводу, момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила
получится, если изменить направление силы F на прямо противоположное), приходим к следующему выводу, момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила  виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.
виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.
Из рис. 85 видно еще, что если менять положение точки О на оси z, то и модуль и направление вектора  будут при этом изменяться, но
будут при этом изменяться, но  а с ним и значение
а с ним и значение  изменяться не будут.
изменяться не будут. 
Механический смысл величины  состоит в том, что она характеризует вращательный эффект силы F, когда эта сила стремится повернуть тело вокруг оси
состоит в том, что она характеризует вращательный эффект силы F, когда эта сила стремится повернуть тело вокруг оси  . В самом деле, если разложить силу F на составляющие
. В самом деле, если разложить силу F на составляющие  где
где  (рис. 86), то поворот вокруг оси
(рис. 86), то поворот вокруг оси  будет совершать только составляющая
будет совершать только составляющая  и вращательный эффект всей силы F будет, согласно формуле (45), определяться величиной
и вращательный эффект всей силы F будет, согласно формуле (45), определяться величиной  Составляющая же
Составляющая же  повернуть тело вокруг оси
повернуть тело вокруг оси  не может (она лишь может сдвинуть тело вдоль оси
не может (она лишь может сдвинуть тело вдоль оси  ).
).
В заключение рассмотрим подробнее, как вычисляется момент силы относительно оси  по формуле (45). Для этого надо (рис. 87):
по формуле (45). Для этого надо (рис. 87):
1) провести плоскость  перпендикулярную оси
перпендикулярную оси  (в любом месте);
(в любом месте);
2) спроектировать силу F на эту плоскость и найти величину 

Рис. 86

Рис. 87

Рис. 88
3) опустить из точки пересечения оси с плоскостью (на рис. 87 это точка О) перпендикуляр на линию действия  и найти его длину
и найти его длину 
4) вычислить произведение  определить знак момента.
определить знак момента.
При вычислении моментов надо иметь в виду следующие частные случаи:
1) если сила параллельна оси, то ее момент относительно оси равен нулю (так как  );
);
2) если линия действия силы пересекает ось, то ее момент относительно оси также равен нулю (так как  ).
).
Объединяя оба случая вместе, заключаем, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости-,
3) если сила перпендикулярна оси (лежит в плоскости, перпендикулярной этой оси), то ее момент относительно оси равен взятому с соответствующим знаком произведению модуля силы на расстояние между линией действия силы и осью, т. е. вычисляется по формуле (45), в которую вместо  войдет модуль силы
войдет модуль силы 
Задача 35. Найти моменты относительно осей  сил Р и Q, которые действуют на горизонтальную плиту, изображенную на рис. 88.
сил Р и Q, которые действуют на горизонтальную плиту, изображенную на рис. 88.
Решение. 1. Сила Р параллельна оси  ; она перпендикулярна осям
; она перпендикулярна осям  и у и проходит от них на расстояниях
и у и проходит от них на расстояниях  Следовательно, с учетом знаков:
Следовательно, с учетом знаков:

2. Для вычисления  проектируем силу Q на плоскость
проектируем силу Q на плоскость  получаем
получаем 
Плечо силы  относительно точки О равно b, а поворот ее с конца оси
относительно точки О равно b, а поворот ее с конца оси  виден происходящим против хода часовой стрелки; следовательно,
виден происходящим против хода часовой стрелки; следовательно,

Теперь вычисляем  Сила Q лежит в плоскости ABD, перпендикулярной оси у и пересекающейся с нею в точке В. Следовательно,
Сила Q лежит в плоскости ABD, перпендикулярной оси у и пересекающейся с нею в точке В. Следовательно,  Опуская из точки В перпендикуляр на линию действия силы Q (см. вспомогательный чертеж справа), находим, что его длина
Опуская из точки В перпендикуляр на линию действия силы Q (см. вспомогательный чертеж справа), находим, что его длина  . Окончательно, учитывая направление поворота, получаем
. Окончательно, учитывая направление поворота, получаем

Наконец, для вычисления  проектируем силу Q на плоскость
проектируем силу Q на плоскость  и находим, что
и находим, что  , а плечо этой проекции относительно точки О равно
, а плечо этой проекции относительно точки О равно  Поэтому с учетом знака
Поэтому с учетом знака

Теорема Вариньона для моментов силы относительно оси. Если обе части векторного равенства  спроектировать на какую-нибудь ось
спроектировать на какую-нибудь ось  , проходящую через центр О, то согласно формулам (44) получим
, проходящую через центр О, то согласно формулам (44) получим

Следовательно, теорема Вариньона о моменте равнодействующей справедлива и для моментов относительно любой оси. Теоремой особенно удобно пользоваться для нахождения моментов силы относительно координатных осей, разлагая силу на составляющие, параллельные осям или их пересекающие.
Задача 36. Найти моменты относительно осей  силы Q, приложенной к плите в точке D (рис. 89), если
силы Q, приложенной к плите в точке D (рис. 89), если  и толщина плиты h; угол а задан.
и толщина плиты h; угол а задан.

Рис. 89
Решение. Разлагая силу Q на составляющие  параллельные соответственно осям х и z, где по модулю
параллельные соответственно осям х и z, где по модулю  , и применяя теорему Вариньона, получим:
, и применяя теорему Вариньона, получим:

так как 
Как видим, с помощью теоремы Вариньона моменты силы вычисляются довольно просто (с ее помощью легко найти моменты силы Q и в задаче 35). Поэтому рекомендуется во всех подобных случаях пользоваться данной теоремой. При некотором навыке все подсчеты легко проделать, опуская промежуточные выкладки; например, сразу видно, что  и т. д.
и т. д.
Аналитические формулы для моментов силы относительно координатных осей. Разложим силу F, приложенную в точке А с координатами  , на составляющие
, на составляющие  параллельные координатным осям (рис. 90, а).
параллельные координатным осям (рис. 90, а).
Тогда по теореме Вариньона

Но так как составляющая  параллельна оси
параллельна оси  а составляющие
а составляющие  и перпендикулярны, то с учетом знаков будет:
и перпендикулярны, то с учетом знаков будет:  и в результате
и в результате  Аналогично находятся моменты относительно осей у и z. Окончательно получим:
Аналогично находятся моменты относительно осей у и z. Окончательно получим:

Формулы (47) дают аналитические выражения для моментов силы относительно координатных осей. С их помощью моменты можно вычислять, зная проекции силы и координаты точки ее приложения. Заметим, что каждая следующая формула в равенствах (47) получается из предыдущей так называемой круговой перестановки букв и индексов, т. е. последовательной заменой  на
на  на
на  на
на  (рис. 90, б).
(рис. 90, б).

Рис. 90
Отметим еще один результат: поскольку левые части равенств (47) являются одновременно проекциями вектора  на координатные оси (где О — начало координат), то с помощью этих равенств можно найти модуль момента
на координатные оси (где О — начало координат), то с помощью этих равенств можно найти модуль момента  по формуле
по формуле

Задача 37. Вычислить по аналитическим формулам моменты силы Q, изображенной на рис 89, относительно осей  и центра О
и центра О
Решение Сила Q приложена в точке D с координатами  Ее проекции на координатные оси
Ее проекции на координатные оси

Подставляя эти значения в формулы (47), получим тот же результат, что и в задаче 36 Для  по формуле (48) найдем
по формуле (48) найдем

Вычисление главного вектора и главного момента системы сил. Согласно формулам (21) и (22), полученным в § 12, значения главного вектора R и главного момента  системы сил определяются равенствами:
системы сил определяются равенствами: 
Покажем, как значения R и  вычисляются аналитически, т. е. по их проекциям на координатные оси, что нам в дальнейшем понадобится.
вычисляются аналитически, т. е. по их проекциям на координатные оси, что нам в дальнейшем понадобится.
Выражения для  уже известны (§ 5). Проекции вектора
уже известны (§ 5). Проекции вектора  на координатные оси будем обозначать
на координатные оси будем обозначать  По теореме о проекциях суммы векторов на ось
По теореме о проекциях суммы векторов на ось  или, согласно равенству (44),
или, согласно равенству (44),  . Аналогично находятся
. Аналогично находятся 
Окончательно  проекций главного вектора R и главного момента
проекций главного вектора R и главного момента  получим формулы:
получим формулы:

В § 12 было отмечено, что две системы сил, у которых величины R и  совпадают, эквивалентны. Отсюда следует, что для задания (или определения) любой системы сил, действующих на твердое тело, достаточно задать (определить) ее главный вектор и главный момент относительно некоторого центра, т. е. шесть величин, входящих в левые части равенств (49) и (50) [в случае рассмотренной в § 15 плоской системы сил — три величины, входящие в равенства (27)]. Этим нередко пользуются на практике, например, при задании (определении) аэродинамических сил, действующих на самолет, ракету, автомобиль, или при определении внутренних усилий в частях конструкции (см. задачу 26 в § 20).
совпадают, эквивалентны. Отсюда следует, что для задания (или определения) любой системы сил, действующих на твердое тело, достаточно задать (определить) ее главный вектор и главный момент относительно некоторого центра, т. е. шесть величин, входящих в левые части равенств (49) и (50) [в случае рассмотренной в § 15 плоской системы сил — три величины, входящие в равенства (27)]. Этим нередко пользуются на практике, например, при задании (определении) аэродинамических сил, действующих на самолет, ракету, автомобиль, или при определении внутренних усилий в частях конструкции (см. задачу 26 в § 20).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА