| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
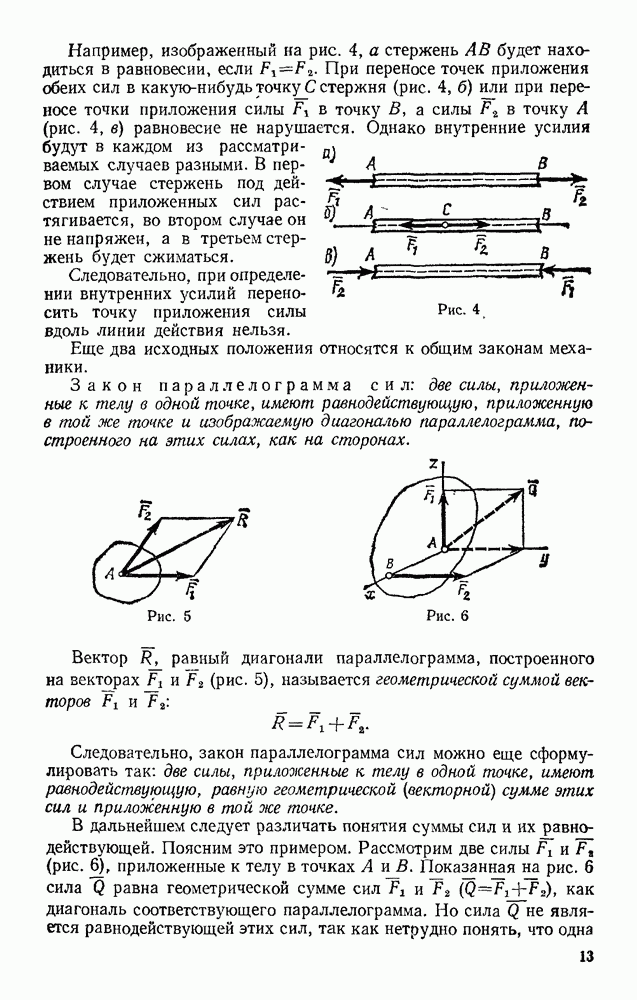
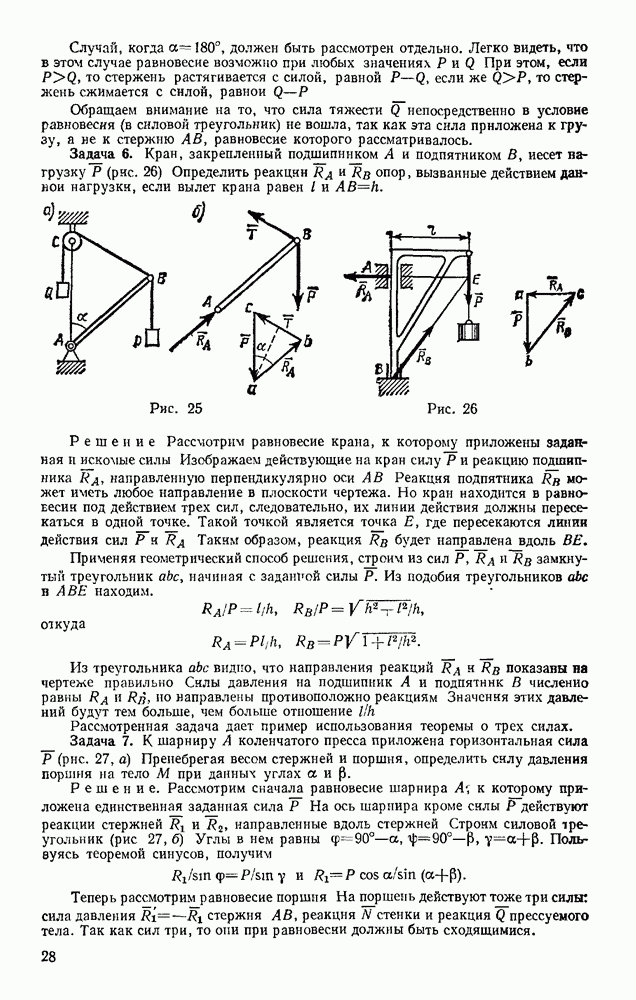
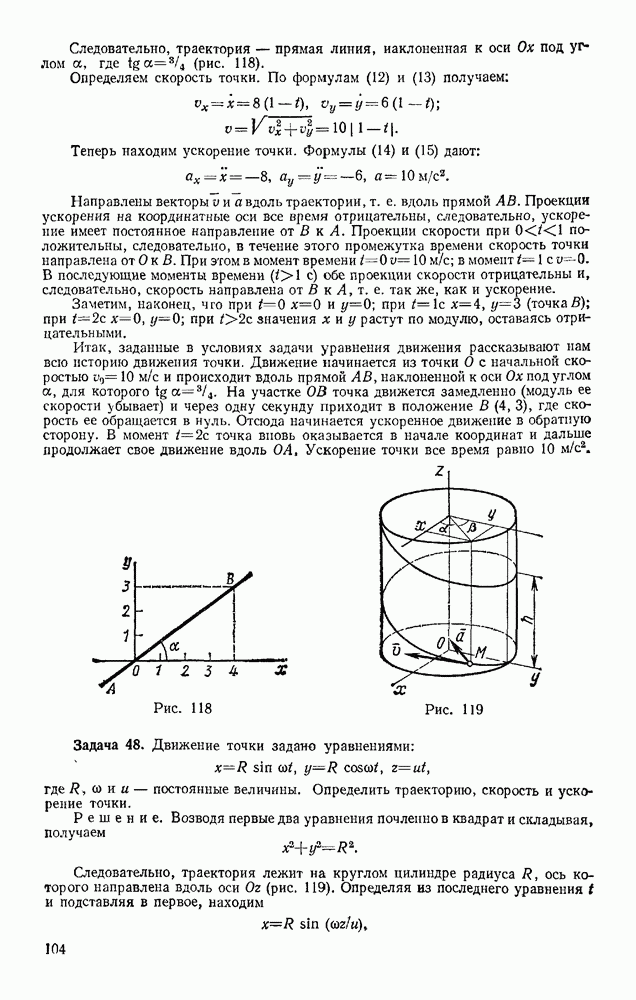
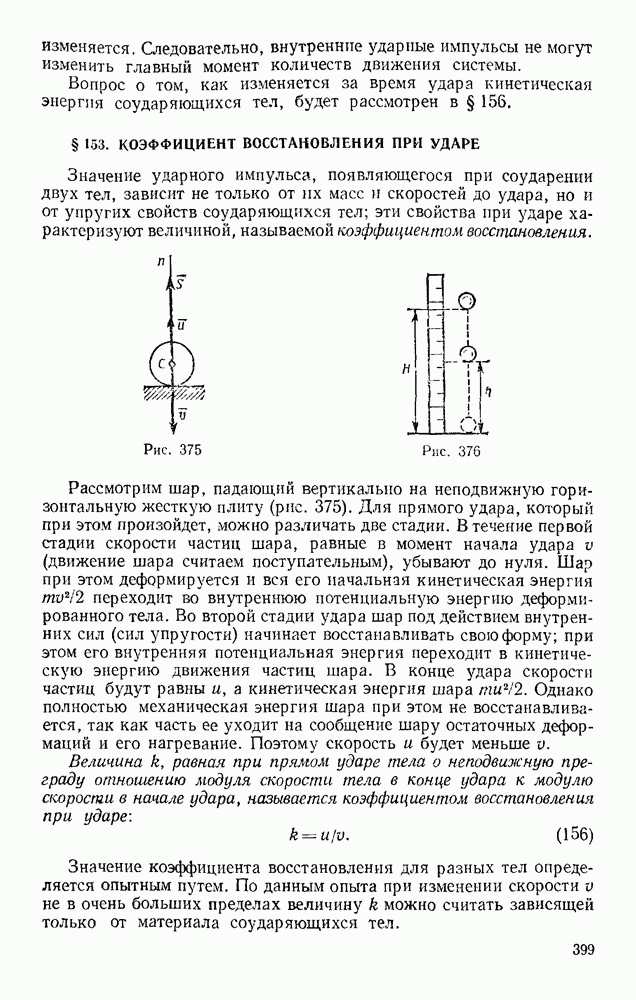
Рассмотрим материальную точку, падающую с не очень большой (по сравнению с радиусом Земли) высоты Н на поверхность Земли. Силу тяжести Р при падении будем считать постоянной; сопротивлением воздуха пренебрегаем. Направим ось  вертикально вверх, а ось Ох — на восток (рис. 252, а). Чтобы учесть вращение Земли, к точке кроме силы Р надо приложить силу
вертикально вверх, а ось Ох — на восток (рис. 252, а). Чтобы учесть вращение Земли, к точке кроме силы Р надо приложить силу  направленную, как было установлено в первом приближении, на восток. Тогда дифференциальные уравнения относительного движения точки примут вид:
направленную, как было установлено в первом приближении, на восток. Тогда дифференциальные уравнения относительного движения точки примут вид:

а начальные условия будут: при 

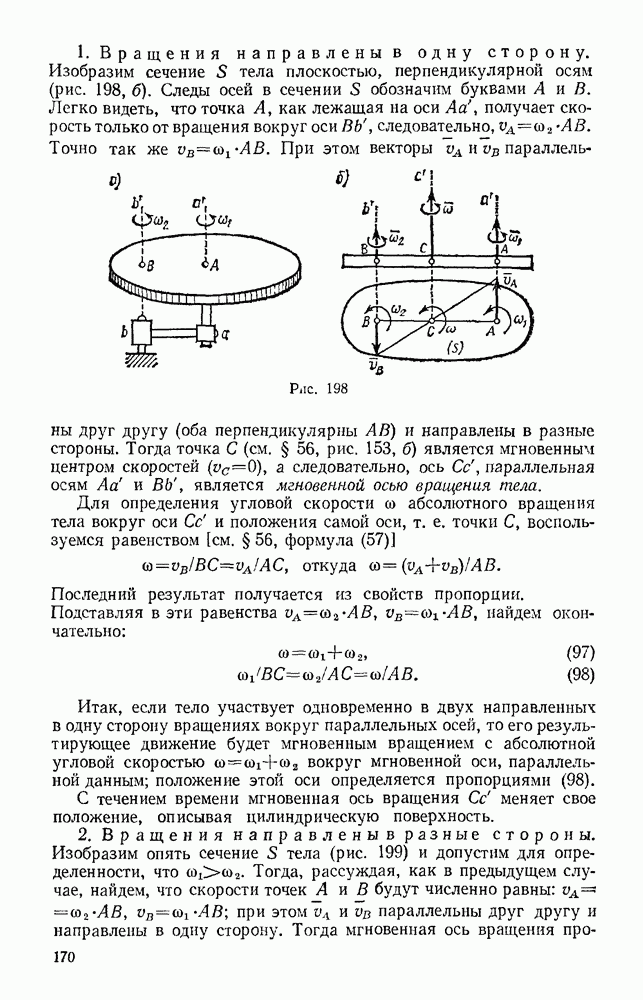
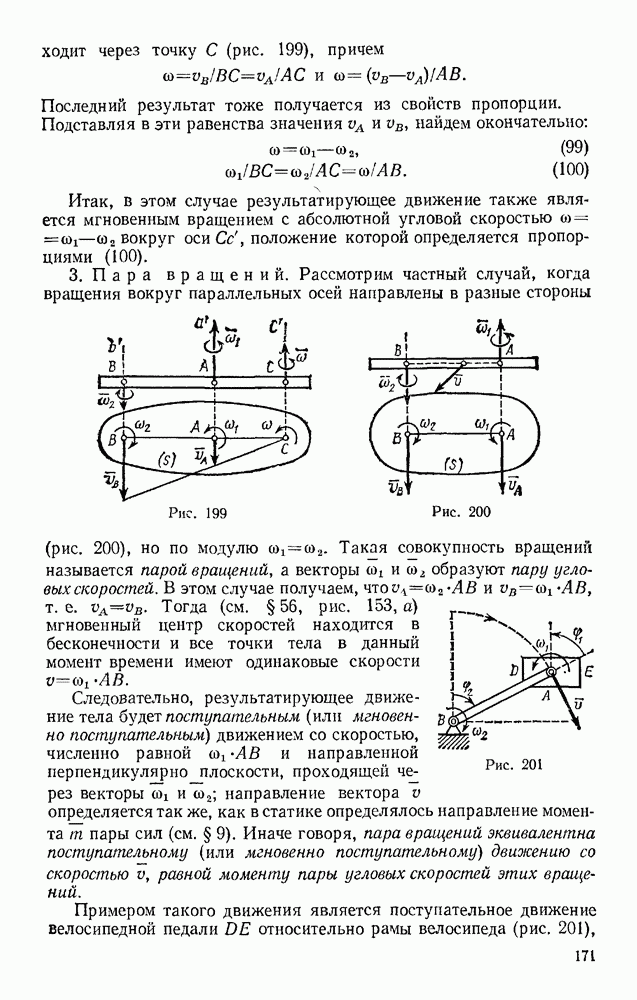
Рис. 252
Интегрируя второе из уравнений  определяя постоянные интегрирования по начальным условиям, найдем:
определяя постоянные интегрирования по начальным условиям, найдем:

При вычислении модуля  пренебрежем, как мы уже делали, определяя направление
пренебрежем, как мы уже делали, определяя направление  составляющей скорости
составляющей скорости  по сравнению с
по сравнению с  (так как сила
(так как сила  много меньше Р) и, отыскивая приближенное решение, будем считать
много меньше Р) и, отыскивая приближенное решение, будем считать  При этом скорость v будет направлена по вертикали вниз (по линии МО на рис. 251) и образует с осью вращения Земли угол
При этом скорость v будет направлена по вертикали вниз (по линии МО на рис. 251) и образует с осью вращения Земли угол  где А — широта.
где А — широта.
Следовательно,  и первое из уравнений (60) примет вид
и первое из уравнений (60) примет вид

Так как величина, стоящая в скобках, постоянная, то, интегрируя это уравнение, получим:

Подстановка начальных данных дает  Таким образом, уравнения, приближенно определяющие закон относительного движения точки, будут:
Таким образом, уравнения, приближенно определяющие закон относительного движения точки, будут:

Движение оказывается непрямолинейным и падающая точка действительно отклоняется к востоку. Исключив из предыдущих равенств время t, получим в первом приближении уравнение траектории точки (полукубическая парабола):

Полагая здесь  найдем восточное отклонение
найдем восточное отклонение  которое точка будет иметь в момент падения на Землю:
которое точка будет иметь в момент падения на Землю:

Как видим, отклонение  пропорционально угловой скорости Земли
пропорционально угловой скорости Земли  и является величиной малой. Например, на широте Москвы
и является величиной малой. Например, на широте Москвы  при падении с высоты
при падении с высоты  величина
величина  см.
см.
Ряд опытов, проведенных во многих пунктах Земли разными исследователями, подтверждает правильность результата, который дает формула (61).
Рассмотрим движение точки, брошенной из пункта О вертикально вверх с начальной скоростью  Сила
Сила  при подъеме будет в первом приближении направлена на запад. Тогда, если направить ось
при подъеме будет в первом приближении направлена на запад. Тогда, если направить ось  также на запад (рис. 252, б), то дифференциальные уравнения движения сохраняют вид (60), а начальные условия будут: при
также на запад (рис. 252, б), то дифференциальные уравнения движения сохраняют вид (60), а начальные условия будут: при 
При этих условиях второе из уравнений (60) дает:
 (62)
(62)
Тогда, считая, как и в предыдущей задаче, приближенно  получим
получим  и первое из уравнений (60) примет вид
и первое из уравнений (60) примет вид

Это уравнение будет описывать движение точки и при ее падении вниз, так как происходящее при этом изменение направления вектора  учтется изменением знака множителя
учтется изменением знака множителя 
Интегрируя полученное уравнение при начальных условиях задачи, найдем окончательно

Полагая в равенстве  найдем время движения точки до момента ее падения на Землю:
найдем время движения точки до момента ее падения на Землю: 
Учитывая одновременно, что  где
где  — высота подъема, определим из уравнения (63) западное отклонение точки в момент падения:
— высота подъема, определим из уравнения (63) западное отклонение точки в момент падения:

Из формул (61) и (64) видно, что при  отклонение
отклонение 
Если движение точки может продолжаться дальше (точка бросания О не на поверхности Земли), то траектория точки, начиная от пункта В, будет все время отклоняться на восток.
Все эти расчеты относятся, как было указано, к движению в безвоздушном пространстве и учитывают влияние вращения Земли только в первом приближении,
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА