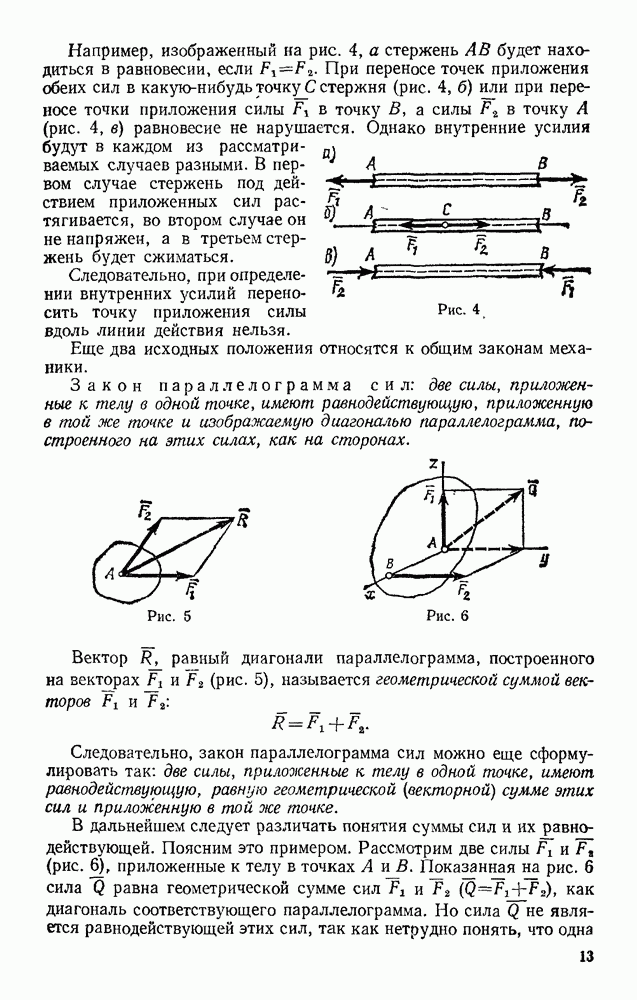
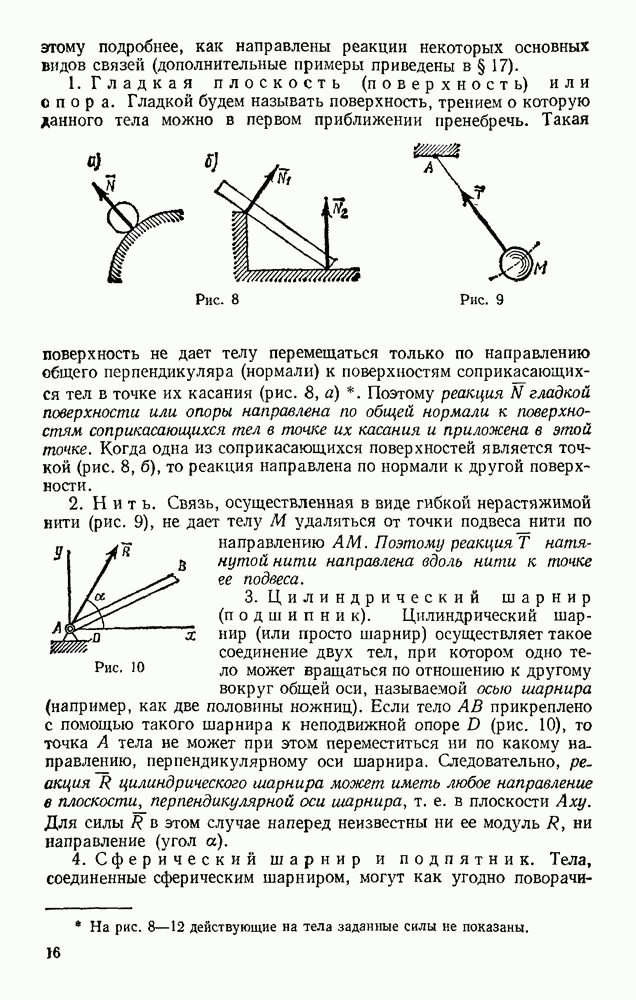
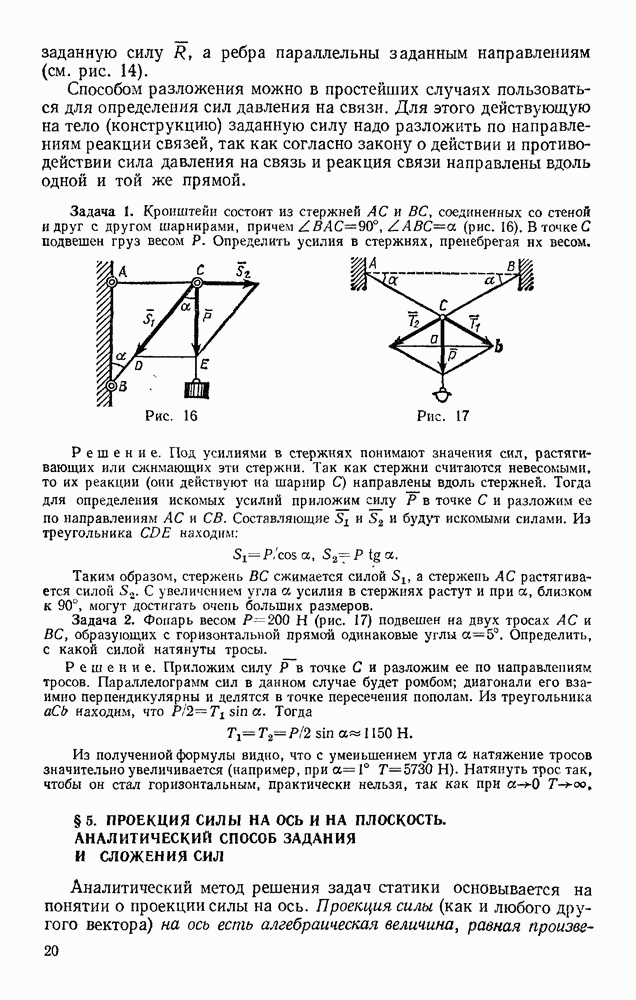
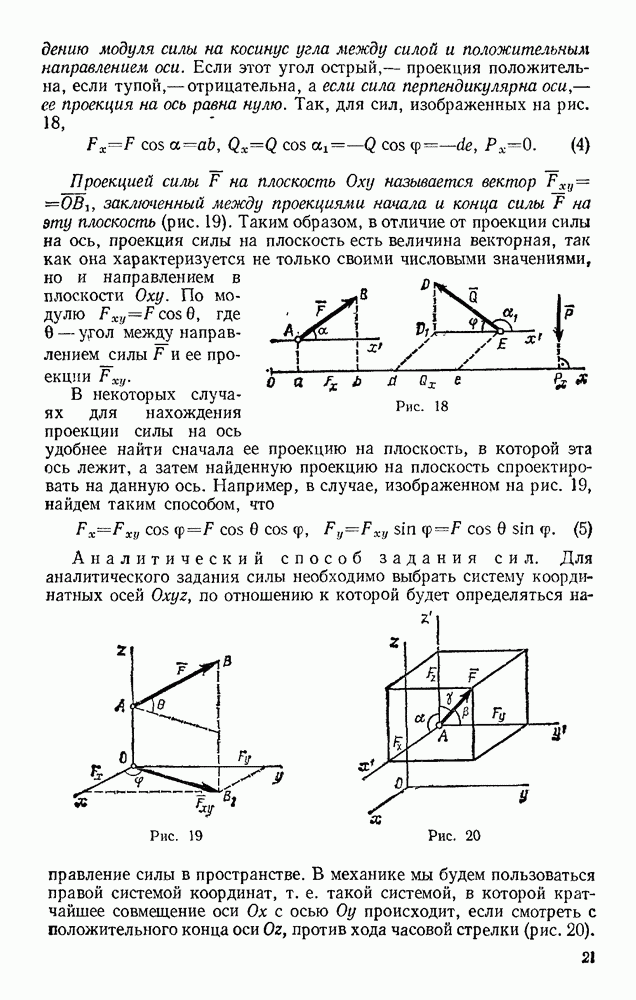
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
Решаемые методами статики задачи могут быть одного из следующих двух типов: 1) задачи, в которых известны (полностью или частично) действующие на тело силы и требуется найти, в каком положении или при каких соотношениях между действующими силами тело будет находиться в равновесии (задачи 4, 5); 2) задачи, в которых известно, что тело заведомо находится в равновесии и требуется найти, чему равны при этом все или некоторые из действующих на тело сил (задачи 6, 7, 8 и др.). Реакции связей являются величинами, наперед неизвестными во всех задачах статики.
Приступая к решению любой задачи, следует прежде всего установить, равновесие какого тела (или каких тел) надо рассмотреть, чтобы найти искомые величины. Процесс решения сводится к следующим операциям.
1. Выбор тела (или тел), равновесие которого должно быть рассмотрено. Для решения задачи надо рассмотреть равновесие тела, к которому приложены заданные и искомые силы или силы, равные искомым (например, если надо найти давление на опору, то можно рассмотреть равновесие тела, к которому приложена численно равная этой силе реакция опоры и т. п.).
Когда заданные силы действуют на одно тело, а искомые на другое или когда те и другие силы действуют одновременно на несколько тел, может оказаться необходимым рассмотреть равновесие системы этих тел или последовательно равновесие каждого тела в отдельности.
2. Изображение действующих сил. Установив, равновесие какого тела или тел рассматривается (и только после этого), следует на чертеже изобразить все действующие на это тело (или тела) внешние силы, включая как заданные, так и искомые силы, в том числе реакции всех связей. При изображении реакций учесть все сказанное о них в § 3.
3. Составление условий равновесия. Условия равновесия составляют для сил, действующих на тело (или тела), равновесие которых рассматривается. Об особенностях составления условий равновесия для различных систем сил будет сказано в соответствующих местах курса.
4. Определение искомых величин, проверка правильности решения и исследование полученных результатов. Важное значение в процессе решения имеет аккуратный чертеж (он помогает быстрее найти правильный путь решения и избежать ошибок при составлении условий равновесия) и последовательное проведение всех выкладок.
Все расчеты при решении задач рекомендуется, как правило, производить в общем виде (алгебраически). Тогда для искомых величин будут получаться формулы, дающие возможность проанализировать найденные результаты. Кроме того, решение в общем виде позволяет иногда обнаружить сделанные ошибки путем проверки размерностей (размерности каждого из слагаемых в обеих частях равенства должны быть одинаковыми).
Числа, если решение производится в общем виде, подставляются только в окончательные результаты.
В этом параграфе рассмотрим задачи на равновесие тела под действием сходящихся сил. Для их решения можно пользоваться геометрическим или аналитическим методом.
Геометрический метод. Им удобно пользоваться, когда общее число действующих на тело сил (и заданных, и искомых) равно трем. При равновесии треугольник, построенный из этих сил, должен быть замкнутым (построение следует начинать с заданной силы). Решая этот треугольник, найдем искомые величины.
Аналитический метод. Им можно пользоваться при любом числе приложенных сил. Для составления условий равновесия, которых в случае плоской системы сходящихся сил будет два [формулы (12)], а в случае пространственной системы три [формулы(11)], надо сначала выбрать координатные оси. Этот выбор можно производить произвольно, но полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно какой-либо неизвестной силе.
Для составления условий равновесия полезно на первых порах предварительно вычислить проекции всех сил на выбранные оси, внося их в отдельную таблицу (см. задачу 4).
Ряд дополнительных указаний дается в ходе решения рассматриваемых ниже задач.
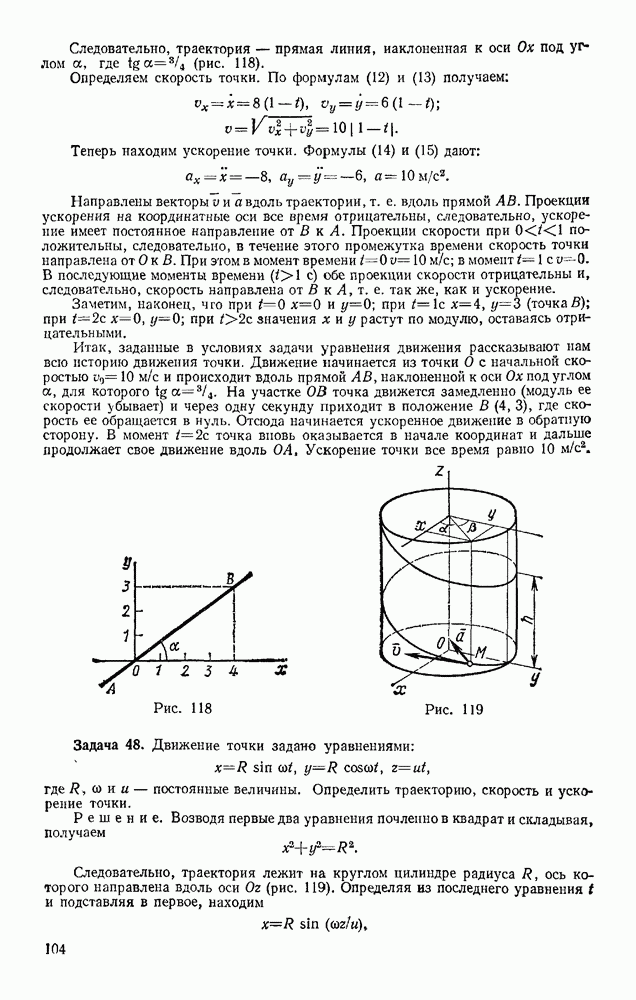
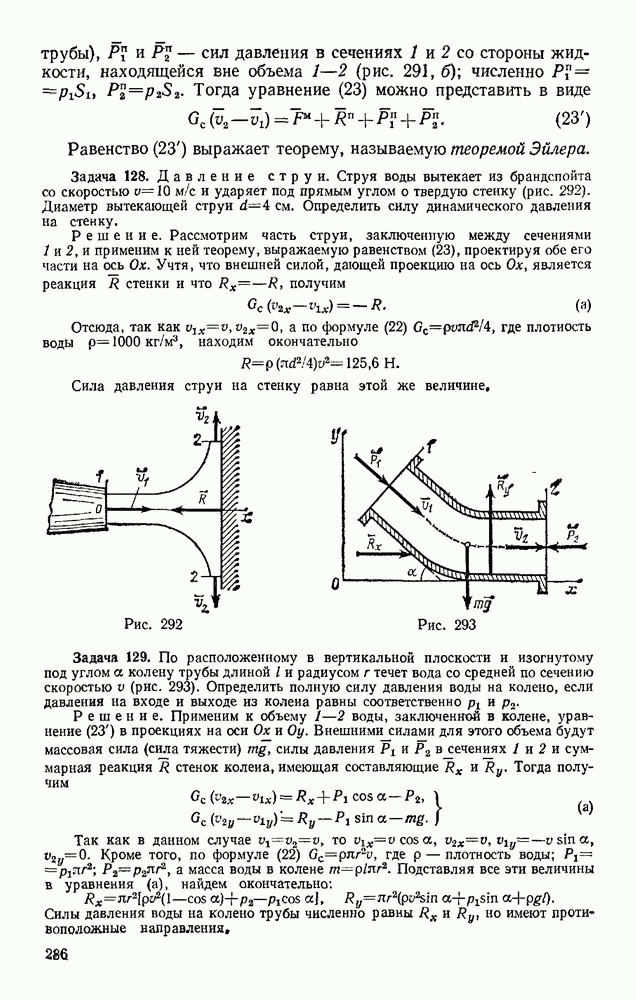
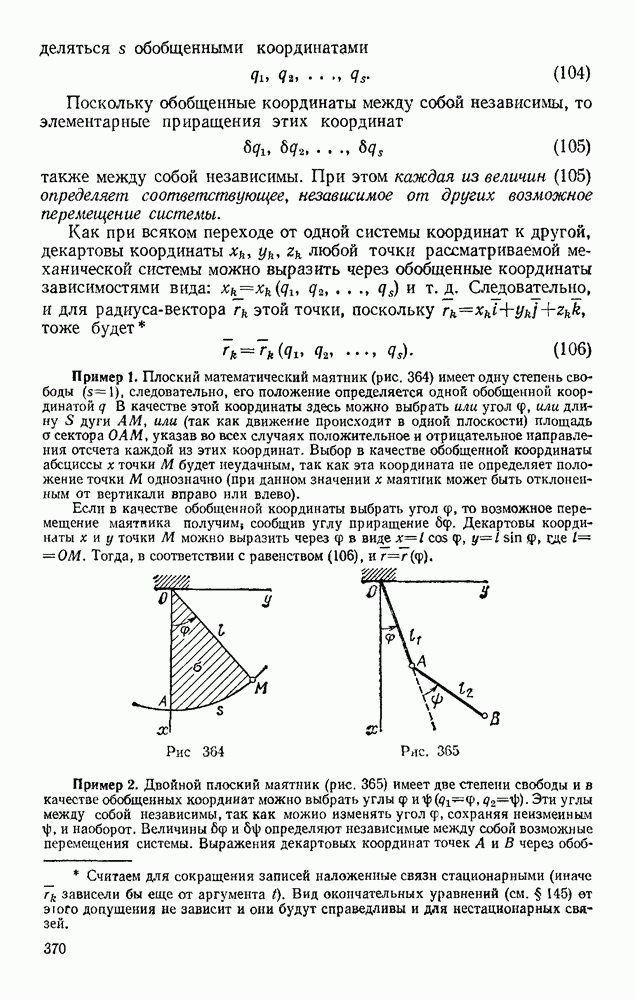
Задача 4. Груз весом Р лежит на гладкой наклонной плоскости с углом наклона а (рис. 24, о). Определить значение горизонтальной силы F, которую надо приложить к грузу, чтобы удержать его в равновесии, и найти, чему при этом равна сила давления Q груза на плоскость.
Решение. Искомые силы действуют на разные тела: сила F на груз, сила Q — на плоскость. Для решения задачи вместо силы Q будем искать равную ей по модулю, но противоположно направленную реакцию плоскости N. Тогда заданная сила Р и искомые силы F и N будут действовать на груз, т. е. на одиои то же тело. Рассмотрим равновесие груза и изобразим действующие на этот груз силы Р и F и реакцию связи N. Для определения искомых сил можно воспользоваться или геометрическим, или аналитическим условиями равновесия. Рассмотрим оба способа решения.

Рис. 24
Геометрический способ. При равновесии треугольник, построенный из сил Р, F к  должен быть замкнутым. Построение треугольника начинаем с заданной силы. От произвольной точки а в выбранном масштабе откладываем силу Р (рис. 24, б). Через начало и конец этой силы проводим прямые, параллельные направлениям сил F и Ж Точка пересечения этнх прямых дает третью вершину с замкнутого силового треугольника
должен быть замкнутым. Построение треугольника начинаем с заданной силы. От произвольной точки а в выбранном масштабе откладываем силу Р (рис. 24, б). Через начало и конец этой силы проводим прямые, параллельные направлениям сил F и Ж Точка пересечения этнх прямых дает третью вершину с замкнутого силового треугольника  в котором стороны
в котором стороны  равны в выбранном масштабе искомым силам. Направление сил определяется правилом стрелок: так как здесь равнодействующая равна нулю, то при обходе треугольника острия стрелок нигде не должны встречаться в одной точке.
равны в выбранном масштабе искомым силам. Направление сил определяется правилом стрелок: так как здесь равнодействующая равна нулю, то при обходе треугольника острия стрелок нигде не должны встречаться в одной точке.
Модули искомых сил можно из треугольника  иайти и путем численного расчета (в этом случае соблюдать масштаб при изображении сил не надо). Замечая, что
иайти и путем численного расчета (в этом случае соблюдать масштаб при изображении сил не надо). Замечая, что  получим:
получим:

Аналитический способ. Так как система действующих сходящихся сил является плоской,  нее надо составить два условия равновесия (12). Сначала проводим координатные оси; при этом для получения более простых уравнений ось
нее надо составить два условия равновесия (12). Сначала проводим координатные оси; при этом для получения более простых уравнений ось  направляем перпендикулярно неизвестной силе N. Далее вычисляем проекции сил
направляем перпендикулярно неизвестной силе N. Далее вычисляем проекции сил  на оси
на оси  и у, внося их в таблицу
и у, внося их в таблицу

Теперь составляем уравнения  Получим:
Получим:

Решая эти уравнения, найдем:

Геометрическое решение в подобных простых задачах (когда действующи СИЛ три) оказывается более компактным, чем аналитическое. Как видно, при  а при
а при  при любом
при любом 
Искомая сила давления груза на плоскость численно равна N, но направлена В противоположную сторону 
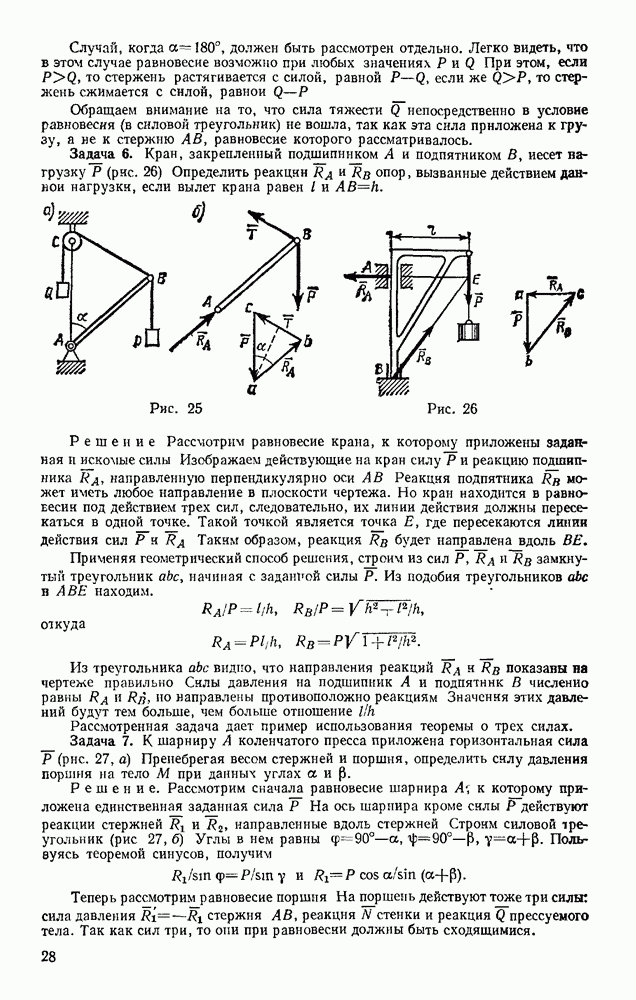
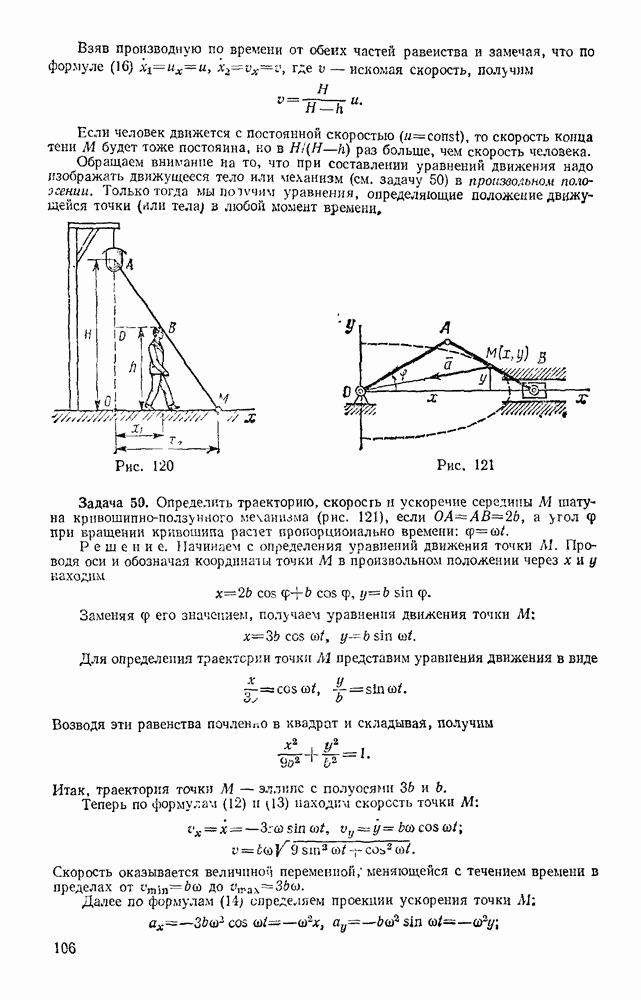
Задача 5. Стержень АВ прикреплен к неподвижной опоре шарниром А (рис. 25, а). К концу В стержня подвешен груз весом Р и прикреплена ннть. Нить перекинута через блок С и к ней подвешен груз весом Q. Оси блока С и шарнира А расположены на одной вертикали, причем  Найти, при каком угле а система будет в равновесии и чему при этом равно усилие в стержне А В; весом стержня и размером блока пренебречь.
Найти, при каком угле а система будет в равновесии и чему при этом равно усилие в стержне А В; весом стержня и размером блока пренебречь.
Решение. Рассмотрим равновесие стержня АВ, к которому приложены все данные и искомые силы. Изобразим для наглядности стержень отдельно (рис, 25, б) и покажем действующие на него силы: снлу  численно равную весу Груза, натяжение Т нити и реакцию
численно равную весу Груза, натяжение Т нити и реакцию  направленную вдоль стержня, так как стержень считается невесомым. Если трением в оси блока пренебречь, то натяжение нити, перекинутой через блок, при равновесии всюду одинаково, следовательно,
направленную вдоль стержня, так как стержень считается невесомым. Если трением в оси блока пренебречь, то натяжение нити, перекинутой через блок, при равновесии всюду одинаково, следовательно, 
Применяя геометрический способ решения, строим из сил Р, Т и замкнутый силовой треугольник  (рис. 25, в), начиная с силы Р. Из подобия треугольников
(рис. 25, в), начиная с силы Р. Из подобия треугольников  и ABC находим, что
и ABC находим, что  . Следовательно,
. Следовательно,

Из полученных результатов следует, что при  равновесие возможно только, если
равновесие возможно только, если  Стержень при этом будет сжат с силой, равной Р, независимо от значений груза Q и угла а.
Стержень при этом будет сжат с силой, равной Р, независимо от значений груза Q и угла а.
Случай, когда  , должен быть рассмотрен отдельно. Легко видеть, что в этом случае равновесие возможно при любых значениях Р и Q При этом, если
, должен быть рассмотрен отдельно. Легко видеть, что в этом случае равновесие возможно при любых значениях Р и Q При этом, если  то стержень растягивается с силой, равной
то стержень растягивается с силой, равной  если же
если же  то стержень сжимается с силой, равной
то стержень сжимается с силой, равной 
Обращаем внимание на то, что сила тяжести Q непосредственно в условие равновесия (в силовой треугольник) не вошла, так как эта сила приложена к грузу, а не к стержню АВ, равновесие которого рассматривалось.
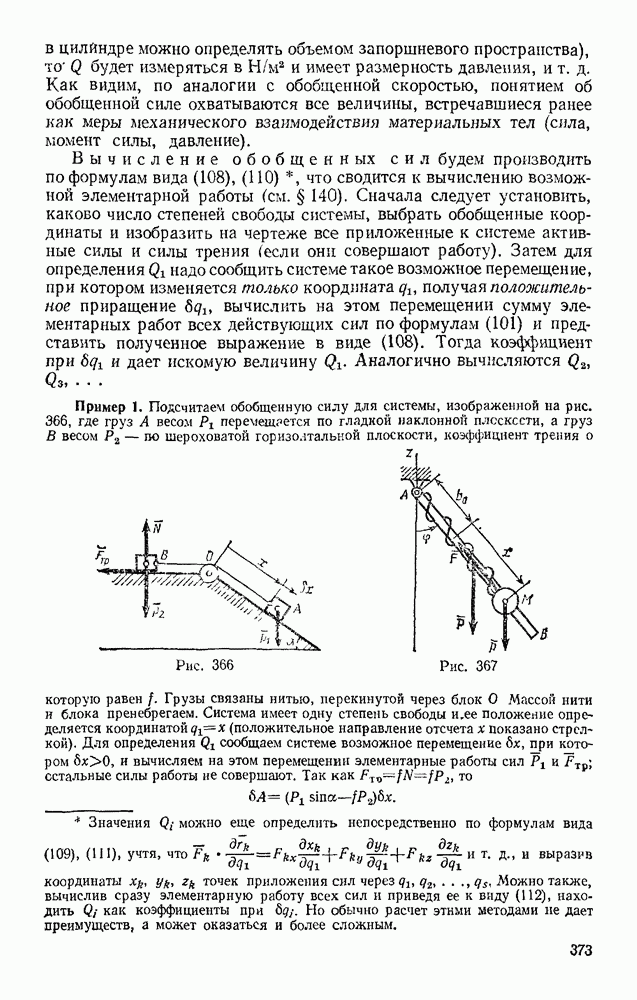
Задача 6. Кран, закрепленный подшипником А и подпятником В, иесет нагрузку Р (рис. 26) Определить реакции RA и RB опор, вызванные действием данной нагрузки, если вылет крана равен 

Рис. 25

Рис. 26
Решение Рассмотрим равновесие крана, к которому приложены заданная и искомые силы Изображаем действующие на кран силу Р и реакцию подшипника RA, направленную перпендикулярно оси АВ Реакция подпятника  может иметь любое направление в плоскости чертежа. Но кран находится в равновесии под действием трех сил, следовательно, их линии действия должны пересекаться в одной точке. Такой точкой является точка Е, где пересекаются линии действия сил Р и RA Таким образом, реакция
может иметь любое направление в плоскости чертежа. Но кран находится в равновесии под действием трех сил, следовательно, их линии действия должны пересекаться в одной точке. Такой точкой является точка Е, где пересекаются линии действия сил Р и RA Таким образом, реакция  будет направлена вдоль
будет направлена вдоль 
Применяя геометрический способ решения, строим из сил Р, RA и  замкнутый треугольник
замкнутый треугольник  начиная с заданной силы Р. Из подобия треугольников
начиная с заданной силы Р. Из подобия треугольников  в А BE находим.
в А BE находим.

откуда

Из треугольника  видно, что направления реакций RA и
видно, что направления реакций RA и  показаны
показаны  чертеже правильно
чертеже правильно  . Силы давления на подшипник А и подпятник В численно равны
. Силы давления на подшипник А и подпятник В численно равны  но направлены противоположно реакциям Значения этих давлений будут тем больше, чем больше отношение
но направлены противоположно реакциям Значения этих давлений будут тем больше, чем больше отношение 
Рассмотренная задача дает пример использования теоремы о трех силах.
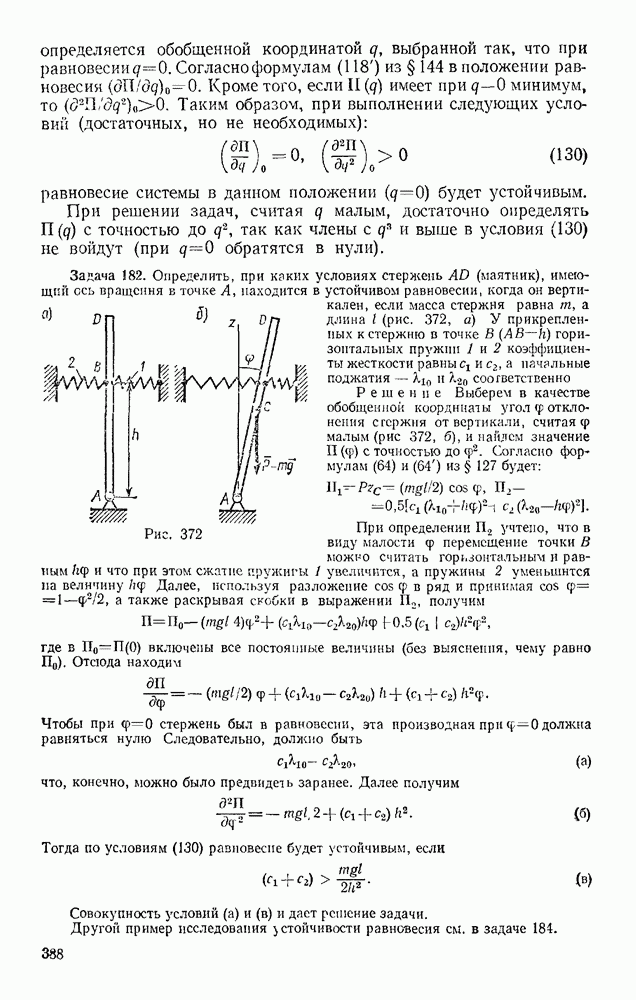
Задача 7. К шарниру А коленчатого пресса приложена горизонтальная сила Р (рис. 27, а) Пренебрегая весом стержней и поршня, определить силу давления поршня на тело М при данных углах 
Решение. Рассмотрим сначала равновесие шарнира  к которому приложена единственная заданная сила Р На ось шарнира кроме силы Р действуют реакции стержней и
к которому приложена единственная заданная сила Р На ось шарнира кроме силы Р действуют реакции стержней и  направленные вдоль стержней Строим силовой треугольник (рис 27, б) Углы в нем равны
направленные вдоль стержней Строим силовой треугольник (рис 27, б) Углы в нем равны  Пользуясь теоремой синусов, получим
Пользуясь теоремой синусов, получим

Теперь рассмотрим равновесие поршня. На поршень действуют тоже три силы: сила давления  стержня АВ, реакция N стенки и реакция Q прессуемого тела. Так как сил три, то они при равновесии должны быть сходящимися.
стержня АВ, реакция N стенки и реакция Q прессуемого тела. Так как сил три, то они при равновесии должны быть сходящимися.
Строя из этих сил силовой треугольник (рис. 27, в), находим из него

Подставляя вместо  равную ей
равную ей  получаем окончательно
получаем окончательно

Сила давления поршня на тело М равна по модулю Q и направлена в противоположную сторону Из последней формулы видно, что при одной и той же силе Р сила Q возрастает с уменьшением углов 
Если длины стержней ОА и АВ одинаковы, то  а.
а.

Рис. 27

Рис. 28
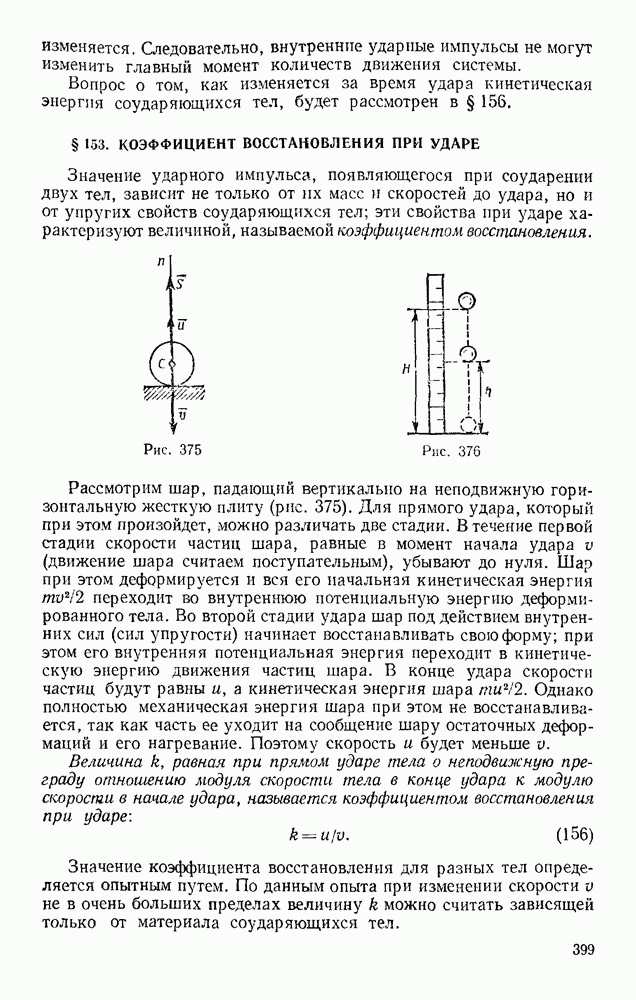
Задача 8. На цилиндр весом Р, лежащий на гладкой горизонтальной плоскости, действует горизонтальная сила Q, прижимающая его к выступу В (рис. 28). Определить реакции в точках А и В, если  — раднус цилиндра).
— раднус цилиндра).
Решение Рассмотрим равновесие цилиндра, на который действуют заданные силы Р, Q и реакции связей  и
и  (реакция
(реакция  направлена по нормали к коверхности цилиндра, т. е. вдоль радиуса ВС). Все силы лежат в одной плоскости и сходятся в точке С Так как сил четыре, то удобнее воспользоваться аналитическими условиями равновесия
направлена по нормали к коверхности цилиндра, т. е. вдоль радиуса ВС). Все силы лежат в одной плоскости и сходятся в точке С Так как сил четыре, то удобнее воспользоваться аналитическими условиями равновесия  . Проведя координатные оси так, как показано на рис 28, получим
. Проведя координатные оси так, как показано на рис 28, получим

При  Тогда из первого уравнения находим
Тогда из первого уравнения находим

Подставляя это значение  во второе уравнение, получим
во второе уравнение, получим

При  реакция
реакция  обращается в нуль, а если
обращается в нуль, а если  то цилиндр оторвется от плоскости и под действием силы Q начнет поворачиваться вокруг Выступа В.
то цилиндр оторвется от плоскости и под действием силы Q начнет поворачиваться вокруг Выступа В.
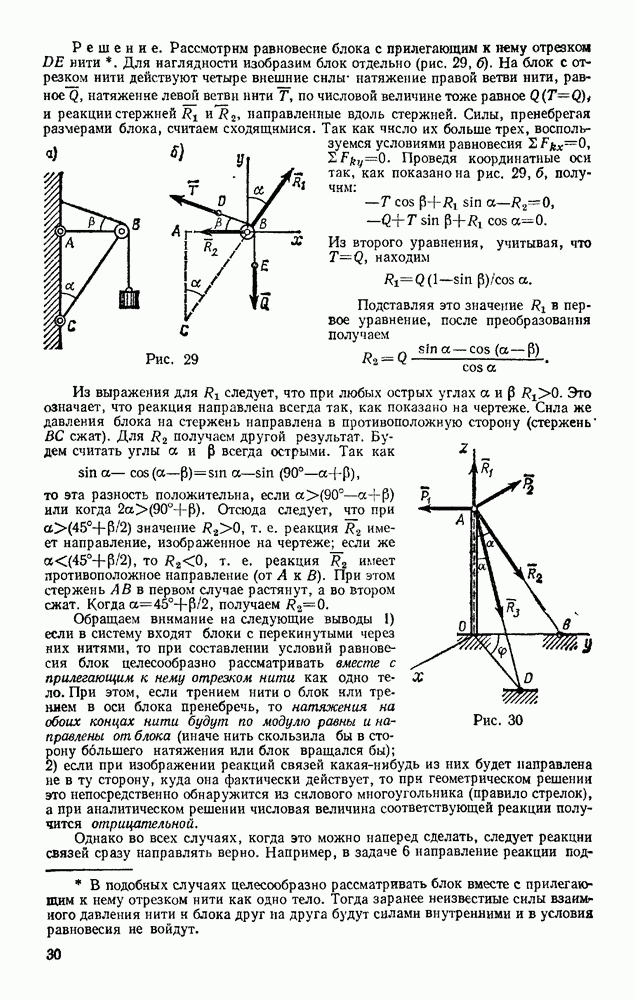
Задача 9. На кронштейне, состоящем из стержней АВ и ВС, скрепленных друг с другом и со стекой шарнирами, укреплен в точке В блок (рис 29, а). Через блок перекинута нить, один конец которой привязан к стене, а на другом подвешен груз весом Q. Определить реакции стержней, пренебрегая их весом и размерами блока. Углы  заданы.
заданы.
Решение. Рассмотрим равновесие блока с прилегающим к нему отрезком DE нити  Для наглядности изобразим блок отдельно (рис, 29, б). На блок с отрезком нити действуют четыре внешние снльг натяжение правой ветви нити, равное Q, натяжение левой ветви нити Т, по числовой величине тоже равное
Для наглядности изобразим блок отдельно (рис, 29, б). На блок с отрезком нити действуют четыре внешние снльг натяжение правой ветви нити, равное Q, натяжение левой ветви нити Т, по числовой величине тоже равное  и реакции стержней
и реакции стержней  направленные вдоль стержней. Силы, пренебрегая размерами блока, считаем сходящимися. Так как число их больше трех, воспользуемся условиями равновесия
направленные вдоль стержней. Силы, пренебрегая размерами блока, считаем сходящимися. Так как число их больше трех, воспользуемся условиями равновесия  Проведя координатные оси так, как показано на рис. 29, б, получим:
Проведя координатные оси так, как показано на рис. 29, б, получим:

Из второго уравнения, учитывая, что  находим
находим

Подставляя это значение  в первое уравнение, после преобразования получаем
в первое уравнение, после преобразования получаем


Рис. 29

Рис. 30
Из выражения для  следует, что при любых острых углах а и
следует, что при любых острых углах а и  Это означает, что реакция направлена всегда так, как показано на чертеже. Снла же давления блока на стержень направлена в противоположную сторону (стержень ВС сжат). Для
Это означает, что реакция направлена всегда так, как показано на чертеже. Снла же давления блока на стержень направлена в противоположную сторону (стержень ВС сжат). Для  получаем другой результат. Будем считать углы а и (3 всегда острыми. Так как
получаем другой результат. Будем считать углы а и (3 всегда острыми. Так как

то эта разность положительна, если  или когда
или когда  Отсюда следует, что при
Отсюда следует, что при  значение
значение  т. е. реакция
т. е. реакция  имеет направление, изображенное на чертеже; если же
имеет направление, изображенное на чертеже; если же  то
то  т. е. реакция
т. е. реакция  имеет противоположное направление (от А к В). При этом стержень А В в первом случае растянут, а во втором сжат. Когда
имеет противоположное направление (от А к В). При этом стержень А В в первом случае растянут, а во втором сжат. Когда  получаем
получаем 
Обращаем внимание на следующие выводы 1) если в систему входят блоки с перекинутыми через них нитями, то при составлении условий равновесия блок целесообразно рассматривать вместе с прилегающим к нему отрезком нити как одно тело. При этом, если трением нити о блок или трением в оси блока пренебречь, то натяжения на обоих концах нити будут по модулю равны и направлены от блока (иначе нить скользила бы в сторону большего натяжения или блок вращался бы);
2) если при изображении реакций связей какая-нибудь из них будет направлена не в ту сторону, куда она фактически действует, то при геометрическом решении это непосредственно обнаружится из силового многоугольника (правило стрелок), а при аналитическом решении числовая величина соответствующей реакции получится отрицательной.
Однако во всех случаях, когда это можно наперед сделать, следует реакции связей сразу направлять верно.
Например, в задаче 6 направление реакции подшипника А устанавливается следующими рассуждениями: если убрать подшипник, то кран под действием силы Р начнет падать вправо; следовательно, сила  чтобы удержать кран в равновесии, должна быть направлена влево.
чтобы удержать кран в равновесии, должна быть направлена влево.
Задача 10. Стоящий на земле вертикальный столб ОА удерживается растяжками АВ и AD, образующими со столбом равные углы а; угол между плоскостями АОВ и  равен
равен  (рис. 30). К столбу подвешены два горизонтальных провода; один, параллельный оси
(рис. 30). К столбу подвешены два горизонтальных провода; один, параллельный оси  натянут с силой
натянут с силой  а другой, параллельный оси
а другой, параллельный оси  — с силой
— с силой  Найти силу вертикального давления на столб и усилия в тросах, пренебрегая их весами.
Найти силу вертикального давления на столб и усилия в тросах, пренебрегая их весами.
Решение. Рассмотрим равновесие узла А, к которому прикреплены провода и тросы. На него действуют силы натяжения проводов  реакции растяжек
реакции растяжек  и реакция столба
и реакция столба  Система сил оказалась пространственной. В этом случае будем пользоваться только аналитическим способом решения. Для составления условий равновесия (11) проводим координатные оси (см. рис. 30) и вычисляем предварительно проекции всех сил на эти оси, внося их в таблицу:
Система сил оказалась пространственной. В этом случае будем пользоваться только аналитическим способом решения. Для составления условий равновесия (11) проводим координатные оси (см. рис. 30) и вычисляем предварительно проекции всех сил на эти оси, внося их в таблицу:

Проекции силы  на оси
на оси  и у определяем так, как это было указано в начале § 5 (см. рис, 19).
и у определяем так, как это было указано в начале § 5 (см. рис, 19).
Теперь, составляя уравнения  получим:
получим:

Решая эти уравнения, найдем:

Из полученных результатов видно, что при  получается
получается  и реакция
и реакция  должна иметь направление, противоположное показанному на рисунке, что невозможно, так как трос не может работать на сжатие. Следовательно, растяжку AD надо располагать так, чтобы угол
должна иметь направление, противоположное показанному на рисунке, что невозможно, так как трос не может работать на сжатие. Следовательно, растяжку AD надо располагать так, чтобы угол  удовлетворял неравенству
удовлетворял неравенству 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА
- § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ
- § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ
- § 3. СВЯЗИ И ИХ РЕАКЦИИ
- Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ
- § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ
- § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ
- Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ
- § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ)
- § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ
- § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР
- Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ
- § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
- § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ
- Глава V. ПЛОСКАЯ СИСТЕМА СИЛ
- § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ
- § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- § 17. РЕШЕНИЕ ЗАДАЧ
- § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ)
- § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ
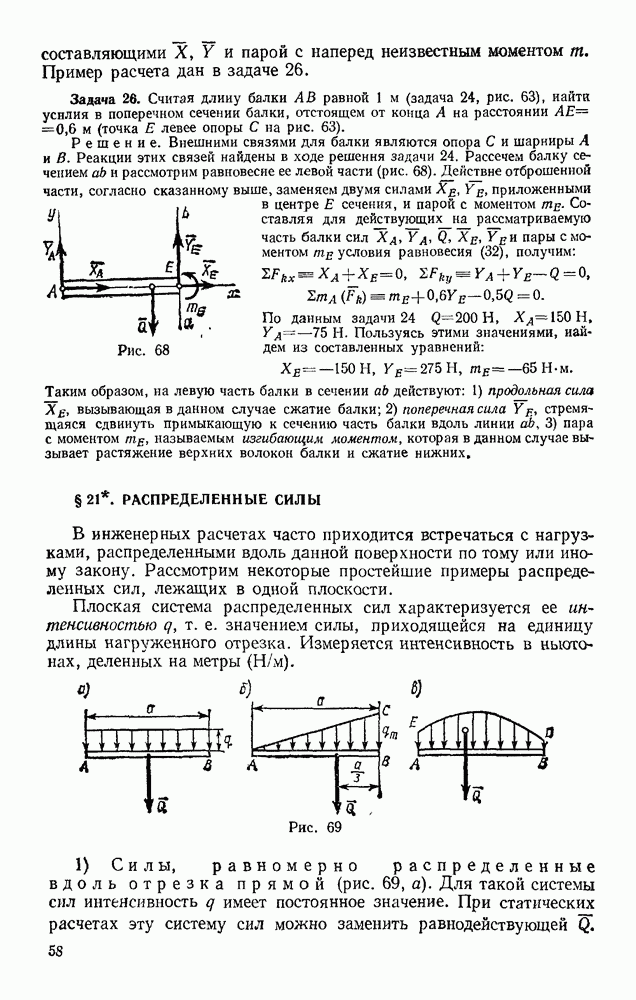
- § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ
- § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ
- Глава VI. ТРЕНИЕ
- § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ
- § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ
- § 27. ТРЕНИЕ КАЧЕНИЯ
- Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ
- § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ
- Глава VIII. ЦЕНТР ТЯЖЕСТИ
- § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
- § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ
- § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ
- § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ
- Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ
- § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 38. ВЕКТОР СКОРОСТИ ТОЧКИ
- § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ
- § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ
- § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ
- § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ
- § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ
- § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ
- § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
- § 46. РЕШЕНИЕ ЗАДАЧ
- § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ
- Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
- § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ
- § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА
- Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
- § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА
- § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ
- § 57. РЕШЕНИЕ ЗАДАЧ
- § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ
- ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА
- § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ
- § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
- § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА)
- § 67. РЕШЕНИЕ ЗАДАЧ
- Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ
- § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ
- § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ
- Раздел третий. ДИНАМИКА ТОЧКИ
- Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ
- § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 75. СИСТЕМЫ ЕДИНИЦ
- § 76. ОСНОВНЫЕ ВИДЫ СИЛ
- Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ
- § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)
- § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ)
- § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ
- Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ
- § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ
- § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)
- § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ
- § 87. РАБОТА СИЛЫ. МОЩНОСТЬ
- § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ
- Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ
- § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ
- § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ
- Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
- § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ
- § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ)
- § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС
- Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ
- § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА
- Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА
- § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
- § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС
- § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ
- § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА
- § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА
- § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ
- Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
- § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
- § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
- § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 109. РЕШЕНИЕ ЗАДАЧ
- Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ
- § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ
- § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ
- Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ
- § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ)
- § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ
- § 118. РЕШЕНИЕ ЗАДАЧ
- § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА)
- § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
- § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ
- § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- § 124. РЕШЕНИЕ ЗАДАЧ
- § 125. СМЕШАННЫЕ ЗАДАЧИ
- § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ
- § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА
- § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
- § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА
- § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- Глава XXVII. ПРИНЦИП ДАЛАМБЕРА
- § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
- § 135. РЕШЕНИЕ ЗАДАЧ
- § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ
- Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ
- § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
- § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 140. РЕШЕНИЕ ЗАДАЧ
- § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ
- § 143. ОБОБЩЕННЫЕ СИЛЫ
- § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ
- § 145. УРАВНЕНИЯ ЛАГРАНЖА
- § 146. РЕШЕНИЕ ЗАДАЧ
- Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
- § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ
- § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
- § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
- Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА
- § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА
- § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА
- § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ
- § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ
- § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ)
- § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО
- § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА