| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
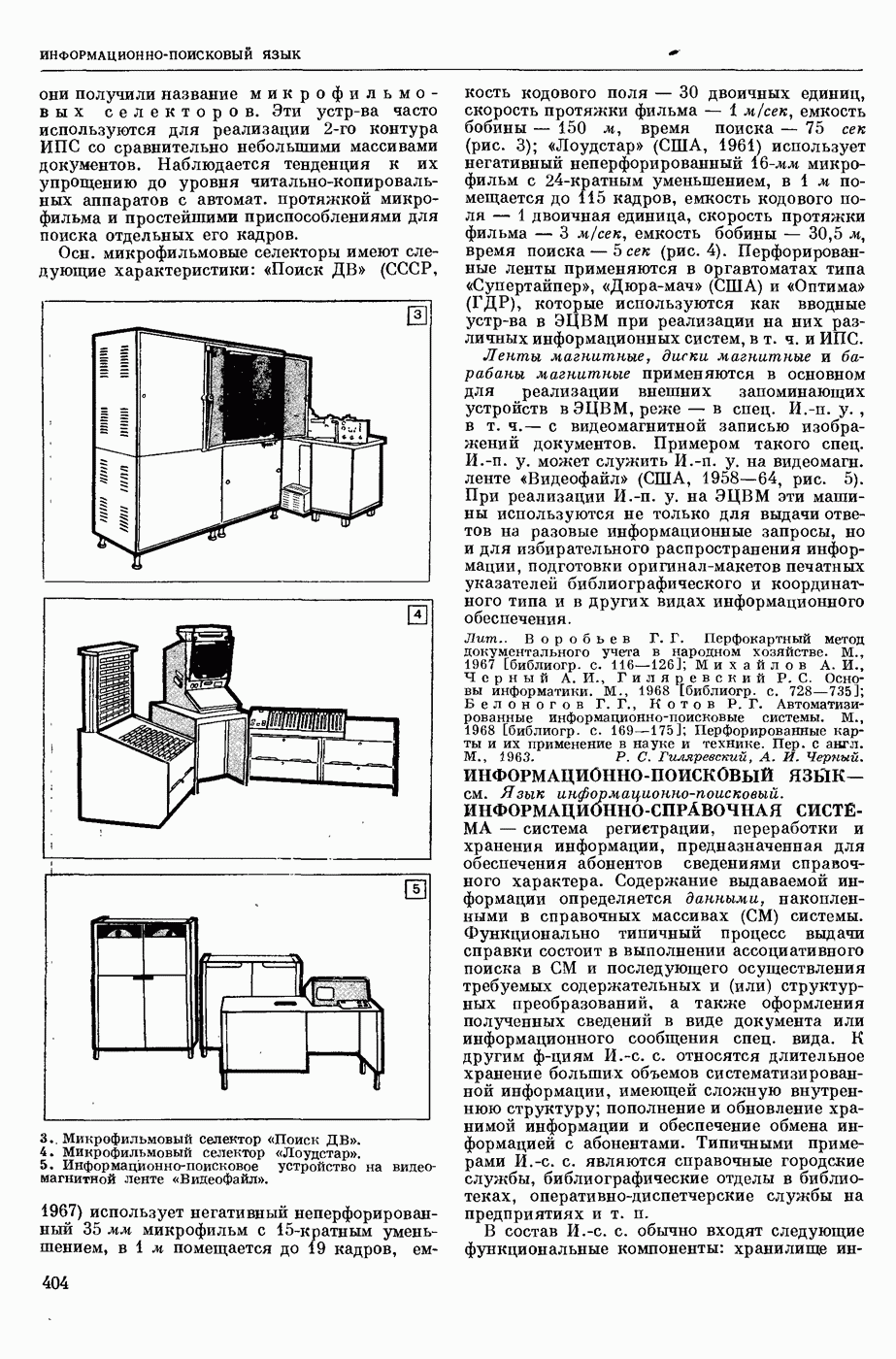
Макеты страниц
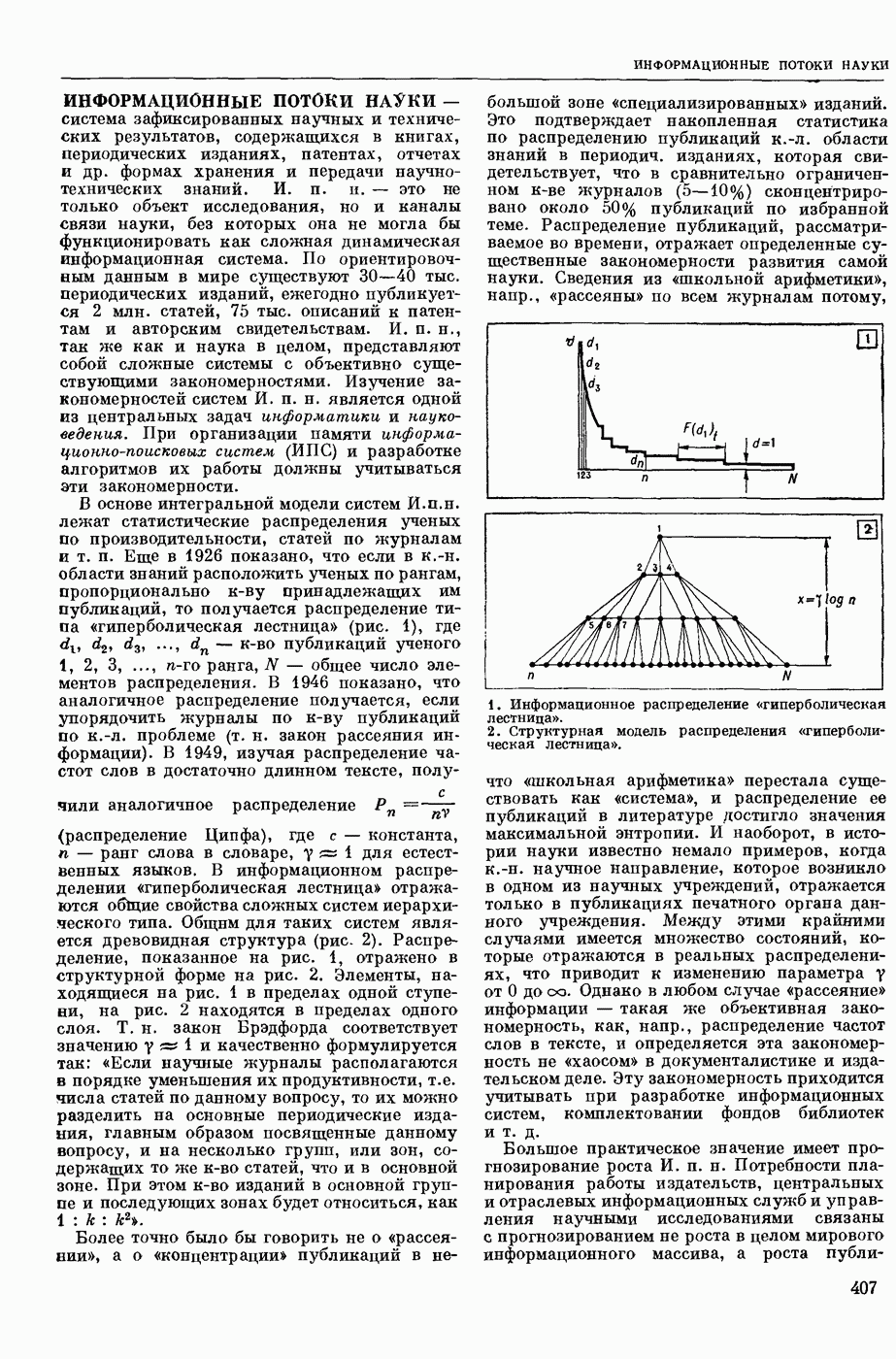
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
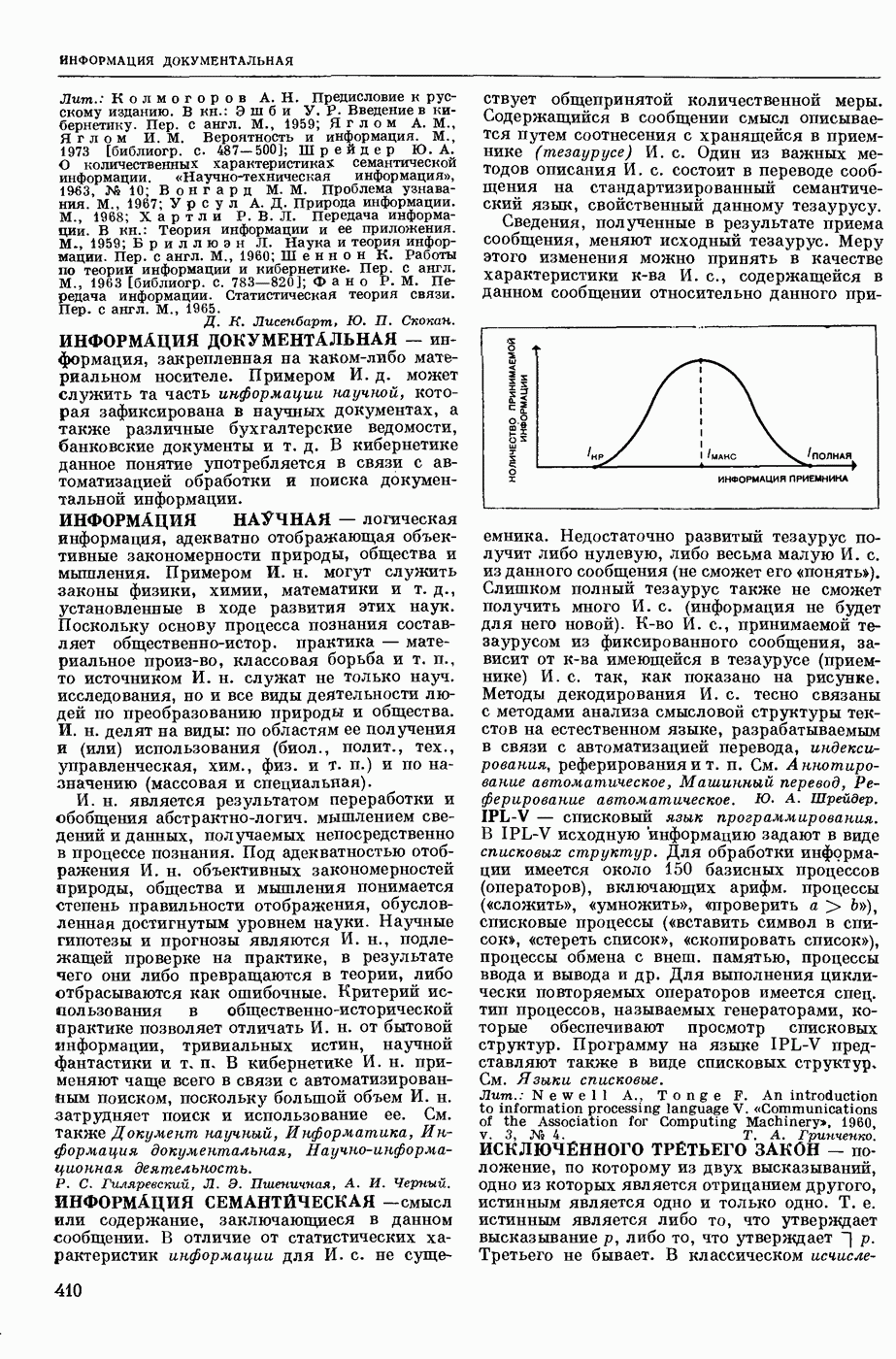
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
КОРНЕЙ АЛГЕБРАИЧЕСКИХ МНОГОЧЛЕНОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
Нахождение всех корней алгебр, многочлена является одной из наиболее часто встречающихся вспомогательных задач, возникающих неоднократно при решении таких важных задач, как устойчивость движения, и др. Рассмотрим детально лишь два наиболее эффективных способа нахождения корней на цифровых и гибридных вычисл. машинах.
Для больших ЦВМ необходимы такие методы нахождения корней многочлена, которые, с одной стороны, были бы универсальными, т. е. пригодными для любых коэфф. (комплексных или действительных), не зависели от входных данных (начального приближения и т. п.), требовали при своей реализации только наличия коэфф. многочлена (минимум информации); с другой стороны, являлись бы быстросходящимися. Построить такие методы возможно путем создания «гибридов» между методами спуска и методом Ньютона; это связано с отсутствием у поверхности  где
где  многочлен
многочлен  экстремумов локальных, отличных от корней.
экстремумов локальных, отличных от корней.
Пусть  и для некоторого х
и для некоторого х

Тогда, используя разложение в ряд Тейлора, получим:

Перемножив эти равенства, получим

где  . При достаточно малом
. При достаточно малом  знак левой части равенства (1) определяется знаком
знак левой части равенства (1) определяется знаком  Он отрицательный при
Он отрицательный при  т. е. для каждой фиксированной точки z есть I секторов убывания и I секторов возрастания ф-ции
т. е. для каждой фиксированной точки z есть I секторов убывания и I секторов возрастания ф-ции  где I — порядок первой отличной от нуля производной ф-ции
где I — порядок первой отличной от нуля производной ф-ции  в точке z. Наискорейшее убывание
в точке z. Наискорейшее убывание  (наискорейший спуск) будет при
(наискорейший спуск) будет при

Следовательно,

где  . Из (1) ясно, что при t достаточно малом и h, выбранном согласно равенству (2), будет выполняться неравенство
. Из (1) ясно, что при t достаточно малом и h, выбранном согласно равенству (2), будет выполняться неравенство 
Заменив z на  на и h на
на и h на  получим
получим

где  порядок первой отличной от нуля производной ф-ции
порядок первой отличной от нуля производной ф-ции  в точке
в точке 
При  имеем (метод Воеводина)
имеем (метод Воеводина)

Т. о., взяв в ур-нии (3) одно из значений корня степени  из комплексного числа, получим единую итеративную схему как для стационарной, так и для нестационарной точек.
из комплексного числа, получим единую итеративную схему как для стационарной, так и для нестационарной точек.
Т. к. в ур-нии  заранее неизвестно, то используют следующий итеративный процесс:
заранее неизвестно, то используют следующий итеративный процесс:

если  Ясно, что найдется такой номер 7, для которого будет справедливо неравенство
Ясно, что найдется такой номер 7, для которого будет справедливо неравенство  В этом случае полагаем
В этом случае полагаем  Итеративный процесс (3) и (5) сходится с любого начального приближения к одному из корней алгебр, многочлена. В связи с тем, что
Итеративный процесс (3) и (5) сходится с любого начального приближения к одному из корней алгебр, многочлена. В связи с тем, что  вблизи искомого корня находится окрестность этого корня, в которой сходится метод Ньютона. Поэтому процесс (3) и (5) после конечного числа итераций К перейдет в метод Ньютона
вблизи искомого корня находится окрестность этого корня, в которой сходится метод Ньютона. Поэтому процесс (3) и (5) после конечного числа итераций К перейдет в метод Ньютона

т. е. будет сходиться с квадратичной скоростью (для некратных корней). После отыскания одного из корней  определяют
определяют  и находят корень многочлена
и находят корень многочлена  степени
степени  и т. д. до тех пор, пока не будут определены все
и т. д. до тех пор, пока не будут определены все  корней алгебр, многочлена.
корней алгебр, многочлена.
Указанный способ может быть обобщен на решение след, задачи: определить  в данной области D, где
в данной области D, где  многочлен. Для этой задачи также всякий локальный экстремум является экстремумом глобальным.. При отыскании направления убывания
многочлен. Для этой задачи также всякий локальный экстремум является экстремумом глобальным.. При отыскании направления убывания  в D, необходимо из всех возможных
в D, необходимо из всех возможных
направлений убывания  вытекающих из
вытекающих из  определить направление, вдоль которого возможно конечное движение в пределах D. Шаг
определить направление, вдоль которого возможно конечное движение в пределах D. Шаг  необходимо также подчинить требованию, чтобы точки
необходимо также подчинить требованию, чтобы точки  оставались в D (более подробно о такого типа алгоритмах см. Возможных направлений метод).
оставались в D (более подробно о такого типа алгоритмах см. Возможных направлений метод).
Эффективная реализация К. а. м. с. в. на ЦВМ невозможна без учета всех видов погрешностей, связанных с данной задачей.  погрешность
погрешность  за счет неточности задания коэфф. многочлена в окрестности корня
за счет неточности задания коэфф. многочлена в окрестности корня  оценивается выражением
оценивается выражением

где  погрешности коэфф. Если все
погрешности коэфф. Если все  не превосходят
не превосходят  то
то

Абс. погрешность метода  может быть (для некратных корней) оценена по ф-ле
может быть (для некратных корней) оценена по ф-ле

Абс. погрешность округлений при вычислении многочлена  по схеме Горнера оценивается как
по схеме Горнера оценивается как

при представлении чисел в форме с фиксированной запятой и

при  при представлении чисел в форме с плавающей запятой, где
при представлении чисел в форме с плавающей запятой, где  число двоичных разрядов мантиссы маш. представления числа. Один из целесообразных планов отыскания корней с учетом указанных погрешностей может состоять в следующем. После того, как ориентировочно найдена величина одного из корней, следует вычислить погрешность
число двоичных разрядов мантиссы маш. представления числа. Один из целесообразных планов отыскания корней с учетом указанных погрешностей может состоять в следующем. После того, как ориентировочно найдена величина одного из корней, следует вычислить погрешность  Соответственно, задаются некоторой величиной
Соответственно, задаются некоторой величиной  положив для определенности, что она не превосходит
положив для определенности, что она не превосходит  Ориентируясь на требуемую величину
Ориентируясь на требуемую величину  можно определить точность, с которой следует вести вычисления, напр., число разрядов
можно определить точность, с которой следует вести вычисления, напр., число разрядов  для машин с переменной разрядностью. Если машина имеет постоянную разрядность и метод решения фиксирован, то погрешность округления играет ту же роль, что и погрешность
для машин с переменной разрядностью. Если машина имеет постоянную разрядность и метод решения фиксирован, то погрешность округления играет ту же роль, что и погрешность 
Наиболее распространенным К. а. м. с. в. на гибридных вычислительных машинах является метод сведения к задаче отыскания минимумов ф-ции  где
где  положительно определенная, непрерывная вместе со своими производными ф-ция вида
положительно определенная, непрерывная вместе со своими производными ф-ция вида  действительные ф-ции,
действительные ф-ции,  — достаточно малая постоянная величина. Ф-ция
— достаточно малая постоянная величина. Ф-ция  имеет в каждой точке столько секторов убывания и возрастания, каков наименьший порядок производной многочлена
имеет в каждой точке столько секторов убывания и возрастания, каков наименьший порядок производной многочлена  отличной от нуля.
отличной от нуля.  не имеет локальных минимумов, отличных от глобального. Для отыскания корней на гибридных вычисл. машинах применяются методы быстрого спуска, в частности, методы покоординатного спуска из различных точек пространства искомых переменных, что обусловлено быстрым отысканием корней из различных точек (время поиска равно 0,5 сек) и хорошей наглядностью поиска корней. На внешних устр-вах гибридных вычисл. машин удобно наблюдать траектории поиска корней из различных точек пространства искомых переменных, сечения ф-ции Ф плоскостями
не имеет локальных минимумов, отличных от глобального. Для отыскания корней на гибридных вычисл. машинах применяются методы быстрого спуска, в частности, методы покоординатного спуска из различных точек пространства искомых переменных, что обусловлено быстрым отысканием корней из различных точек (время поиска равно 0,5 сек) и хорошей наглядностью поиска корней. На внешних устр-вах гибридных вычисл. машин удобно наблюдать траектории поиска корней из различных точек пространства искомых переменных, сечения ф-ции Ф плоскостями  и т. д. Для вычисления любого многочлена здесь можно ограничиться такими операциями, как линейная комбинация и перемножение ф-ций, а также суперпозиция ф-ций. Для конструирования ф-лы многочлена с помощью таких операций вводятся дополнительные ур-ния, напр., для многочлена 4-й степени
и т. д. Для вычисления любого многочлена здесь можно ограничиться такими операциями, как линейная комбинация и перемножение ф-ций, а также суперпозиция ф-ций. Для конструирования ф-лы многочлена с помощью таких операций вводятся дополнительные ур-ния, напр., для многочлена 4-й степени  с помощью дополнительных ур-ний находятся элементы комплексного числа
с помощью дополнительных ур-ний находятся элементы комплексного числа  после чего
после чего

Лит.: Загускин В. Л. Справочник по численным методам решения алгебраических и трансцендентных уравнений. М., 1960 [библиогр. с. 210—213]; Воеводин В. В. Применение метода спуска для определения всех корней алгебраического многочлена. «Журнал вычислительной математики и математической физики», 1961, т. 1, № 2; Кац И. С., Маергойз М. Д. Решение нелинейных алгебраических и трансцендентных уравнений в комплексной области. «Журнал вычислительной математики и математической физики», 1967, т. 7, 1963.
Г. И. Грездов, В. В. Иванов, М. Д. Маергойз.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- КАК ПОЛЬЗОВАТЬСЯ ЭНЦИКЛОПЕДИЕЙ КИБЕРНЕТИКИ
- ОСНОВНЫЕ СОКРАЩЕНИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
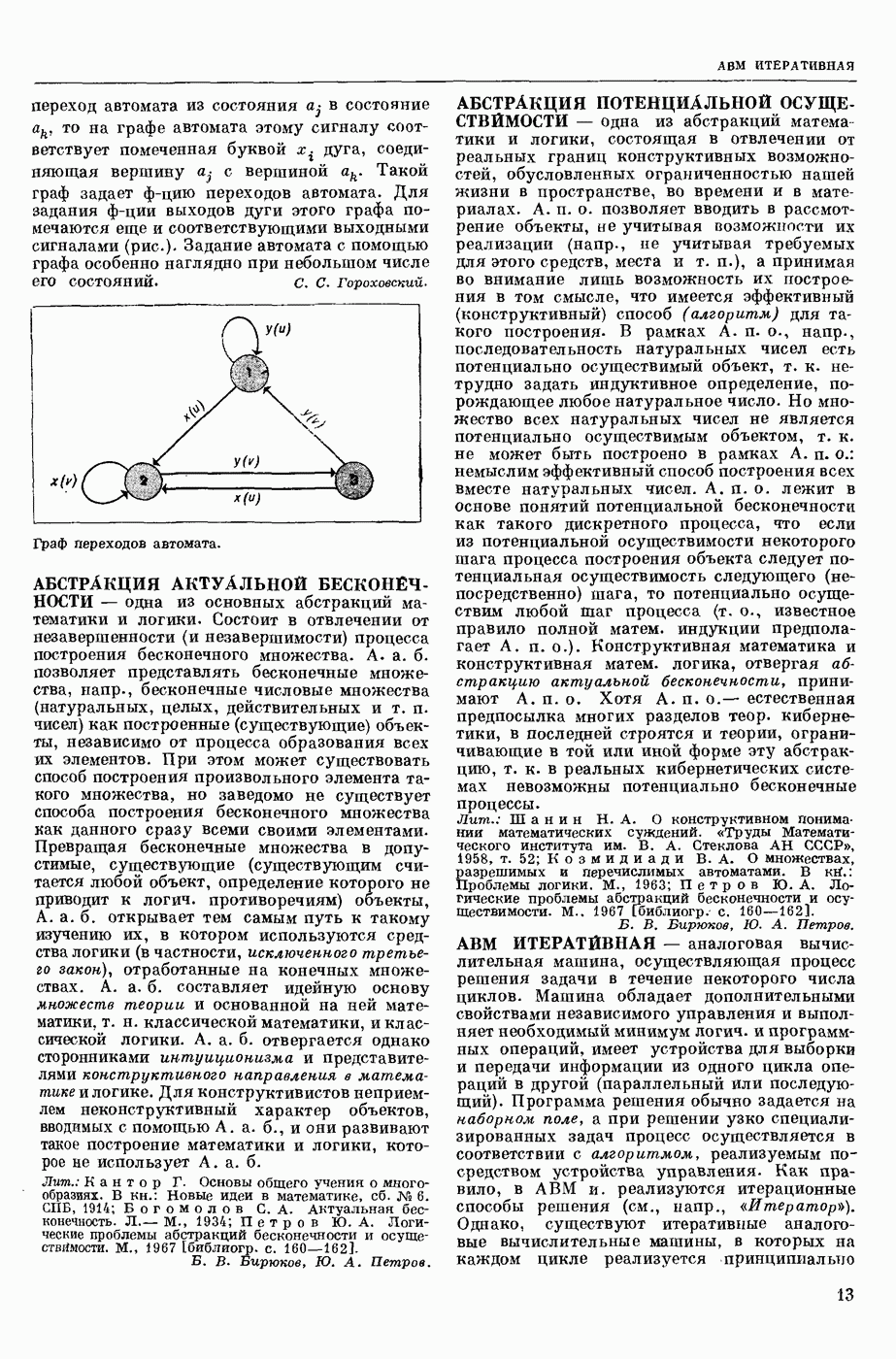
- АБСТРАКТНАЯ ТЕОРИЯ АВТОМАТОВ
- АБСТРАКТНОГО АВТОМАТА ГРАФ
- АБСТРАКЦИЯ АКТУАЛЬНОЙ БЕСКОНЕЧНОСТИ
- АБСТРАКЦИЯ ПОТЕНЦИАЛЬНОЙ ОСУЩЕСТВИМОСТИ
- АВМ ИТЕРАТИВНАЯ
- АВМ МЕХАНИЧЕСКАЯ
- АВМ ПНЕВМАТИЧЕСКАЯ
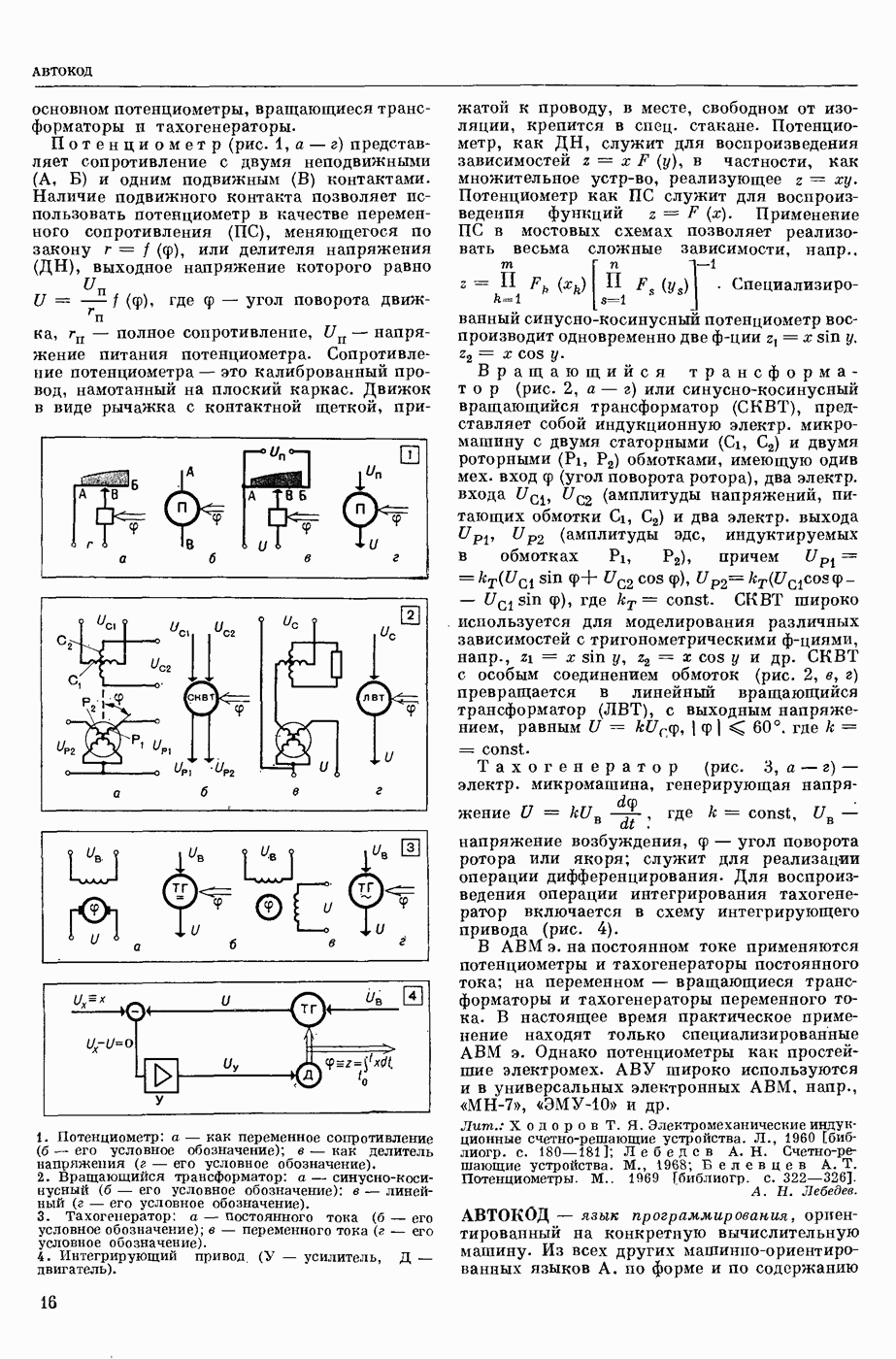
- АВМ ЭЛЕКТРОМЕХАНИЧЕСКАЯ
- АВТОКОД
- АВТОКОЛЕБАНИЯ
- АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- АВТОМАТ
- АВТОМАТ АВТОНОМНЫЙ
- АВТОМАТ АСИНХРОННЫЙ
- АВТОМАТ БЕЗ ПАМЯТИ
- АВТОМАТ ВЕРОЯТНОСТНЫЙ
- АВТОМАТ ДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ДЕФИНИТНЫЙ
- АВТОМАТ ИНИЦИАЛЬНЫЙ
- АВТОМАТ КОНЕЧНЫЙ
- АВТОМАТ ЛИНЕЙНЫЙ
- АВТОМАТ МАГАЗИННЫЙ
- АВТОМАТ МИКРОПРОГРАММНЫЙ
- АВТОМАТ МИНИМАЛЬНЫЙ
- АВТОМАТ НЕДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ОПЕРАЦИОННЫЙ
- АВТОМАТ ПРИВЕДЁННЫЙ
- АВТОМАТ ПУШ-ДАУН
- АВТОМАТ РЕГИСТРОВЫЙ
- АВТОМАТ С МАГАЗИННОЙ ПАМЯТЬЮ
- АВТОМАТ САМОВОСПРОИЗВОДЯЩИЙСЯ
- АВТОМАТ СВОБОДНЫЙ.
- АВТОМАТ СВЯЗНЫЙ
- АВТОМАТ УПРАВЛЯЮЩИЙ
- АВТОМАТ ЧАСТИЧНЫЙ
- АВТОМАТА ДИАГРАММА
- АВТОМАТА МАТРИЦА ПЕРЕХОДОВ
- АВТОМАТА ПАМЯТЬ
- АВТОМАТА ТАБЛИЦА
- АВТОМАТА ФУНКЦИЯ
- АВТОМАТИЗАЦИЯ КОМПЛЕКСНАЯ
- АВТОМАТИЗАЦИЯ ЛИНГВИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
- АВТОМАТИЗАЦИЯ МЕДИЦИНСКОЙ ДИАГНОСТИКИ
- АВТОМАТИЗАЦИЯ ПРОГРАММИРОВАНИЯ
- АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНИЯ ПРОИЗВОДСТВЕННЫМ ПРОЦЕССОМ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНЧЕСКОГО ТРУДА
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
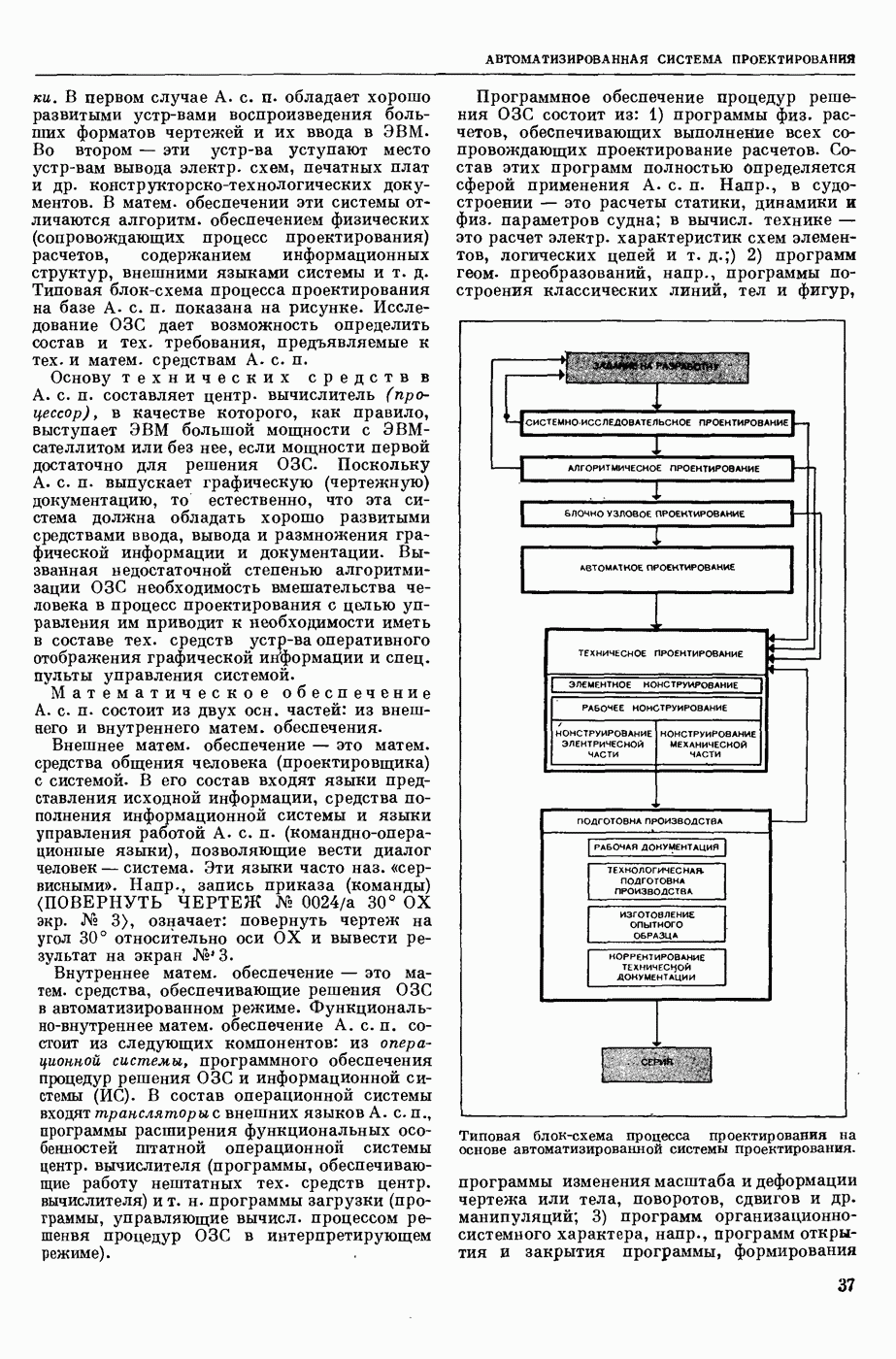
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ПРОЕКТИРОВАНИЯ
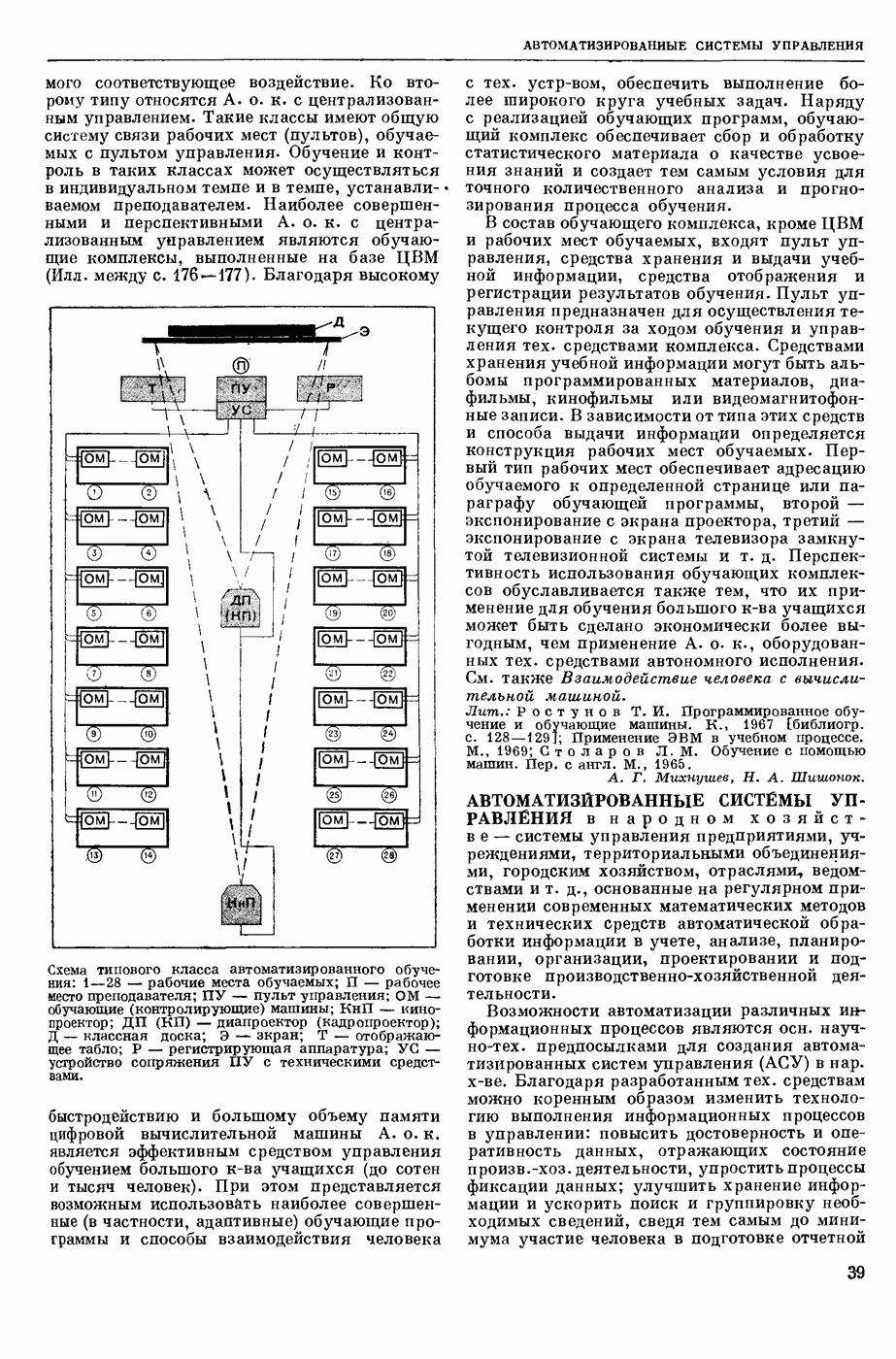
- АВТОМАТИЗИРОВАННОГО ОБУЧЕНИЯ КЛАСС
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ (АСУП)
- АВТОМАТИЗИРОВАННЫЙ ПОИСК ДОКАЗАТЕЛЬСТВ ТЕОРЕМ
- «АВТОМАТИКА»
- «АВТОМАТИКА И ТЕЛЕМЕХАНИКА»
- АВТОМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- АВТОМАТИЧЕСКИЙ АНАЛИЗ МЕДИКО-БИОЛОГИЧЕСКИХ ПРОЦЕССОВ
- АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- АВТОМАТИЧЕСКОЕ ЦИФРО-ПЕЧАТАЮЩЕЕ УСТРОЙСТВО
- АВТОМАТНОЕ ОТОБРАЖЕНИЕ
- АВТОМАТОВ АБСТРАКТНАЯ ТЕОРИЯ
- АВТОМАТОВ АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ
- АВТОМАТОВ АНАЛИЗ
- АВТОМАТОВ ГОМОМОРФИЗМ.
- АВТОМАТОВ ДЕКОМПОЗИЦИЯ
- АВТОМАТОВ ИГРЫ
- АВТОМАТОВ ИЗОМОРФИЗМ
- АВТОМАТОВ КОМПОЗИЦИИ
- АВТОМАТОВ МИНИМИЗАЦИЯ
- АВТОМАТОВ ПОВЕДЕНИЕ
- АВТОМАТОВ ПРОИЗВЕДЕНИЕ
- АВТОМАТОВ ПРЯМАЯ СУММА
- АВТОМАТОВ СИНТЕЗ
- АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ
- АВТОМАТОВ СТРУКТУРНАЯ ТЕОРИЯ
- АВТОМАТОВ СУПЕРПОЗИЦИЯ
- АВТОМАТОВ ТЕОРИЯ
- АВТОМАТОВ ЭКВИВАЛЕНТНОСТЬ
- АВТОМАТЫ БЕСКОНЕЧНЫЕ
- АВТОМАТЫ ИТЕРАТИВНЫЕ
- АВТОМАТЫ РАСТУЩИЕ
- АВТОНОМНОСТЬ
- АВТОПИЛОТИРОВАНИЕ
- АГРЕГАТНАЯ УНИФИЦИРОВАННАЯ СИСТЕМА (АУС)
- АГРЕГАТНО-БЛОЧНОЕ ПОСТРОЕНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- АДАМСА МЕТОД
- АДАПТАЦИЯ В КИБЕРНЕТИКЕ
- АДАПТИВНАЯ СИСТЕМА
- АДРЕС В ПРОГРАММИРОВАНИИ
- АДРЕС МАТЕМАТИЧЕСКИЙ
- АДРЕСНЫЙ ЯЗЫК
- АДРЕСОВ МОДИФИКАЦИЯ
- АИКА
- АЛГЕБРА АЛГОРИТМОВ
- АЛГЕБРА ЛИНЕЙНАЯ
- АЛГЕБРА ЛОГИКИ
- АЛГЕБРА МАТРИЦ
- АЛГЕБРА МНОЖЕСТВ
- АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ АВТОМАТОВ
- АЛГЕБРАИЧЕСКАЯ ТОПОЛОГИЯ
- АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
- АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
- АЛГЕБРЫ СОБЫТИЙ
- АЛГЕБРЫ УНИВЕРСАЛЬНЫЕ.
- АЛГОЛ-60
- АЛГОЛ-68
- АЛГОРИТМ, АЛГОРИФМ
- АЛГОРИТМ ЛОКАЛЬНЫЙ
- АЛГОРИТМ РАСПОЗНАВАНИЯ
- АЛГОРИТМИЗАЦИЯ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ
- АЛГОРИТМИЗАЦИЯ ТВОРЧЕСКИХ ПРОЦЕССОВ
- АЛГОРИТМИЧЕСКАЯ СТРУКТУРА ЦВМ
- АЛГОРИТМИЧЕСКИЙ СИНТЕЗ ЦВМ
- АЛГОРИТМИЧЕСКИЙ ЯЗЫК
- АЛГОРИТМИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- АЛГОРИТМОВ ГРАФ-СХЕМЫ, ГРАФ-СХЕМЫ АЛГОРИТМОВ
- АЛГОРИТМОВ РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- АЛГОРИТМОВ СЛОЖНОСТЬ
- АЛГОРИТМОВ СХЕМА
- АЛГОРИТМОВ ТЕОРИЯ
- АЛГОРИТМОВ ЭКВИВАЛЕНТНОСТЬ
- АЛГЭК
- АЛГЭМ
- АЛМО
- АЛФАВИТНО-ЦИФРОВОЕ ПЕЧАТАЮЩЕЕ УСТРОЙСТВО (АЦПУ)
- АЛФАВИТНЫЙ ОПЕРАТОР
- АЛЬГИБР
- АЛЬФА-СИСТЕМА
- АЛЬФА-ЯЗЫК
- АМПЛИТУДНО-ИМПУЛЬСНАЯ МОДЕЛЬ
- АНАЛИЗАТОРНЫЕ СИСТЕМЫ
- АНАЛИТИК
- АНАЛИТИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ НА ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ.
- АНАЛОГ ЦИФРОВОЙ, ЦИФРОВАЯ МОДЕЛЬ
- АНАЛОГИИ
- АНАЛОГОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ABM)
- АНАЛОГО-ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- АНАЛОГО-ЦИФРОВАЯ СИСТЕМА
- АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ, ПРЕОБРАЗОВАТЕЛЬ АНАЛОГ-КОД
- АННОТИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- АНСАМБЛЬ СООБЩЕНИЙ
- АНТИГРАДИЕНТ ФУНКЦИИ
- АППРОКСИМАЦИЯ ФУНКЦИИ СРЕДНЕКВАДРАТИЧНАЯ
- АППРОКСИМАЦИЯ ФУНКЦИЙ
- АППРОКСИМАЦИЯ ФУНКЦИЙ РАВНОМЕРНАЯ (чебышевская)
- АРИФМЕТИЗАЦИЯ МАТЕМАТИКИ
- АРИФМЕТИКА С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
- АРИФМЕТИКА С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- АРИФМЕТИКА ФОРМАЛЬНАЯ
- АРИФМЕТИЧЕСКАЯ И АНАЛИТИЧЕСКАЯ ИЕРАРХИИ
- АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ ЦВМ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО (АУ)
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРХИВ в автоматизированных системах управления или системах обработки данных
- АСИНХРОННЫХ АВТОМАТОВ ТЕОРИЯ
- «АСОР», автоматизированная система организации работ
- АССЕМБЛЕР
- АССОЦИАТИВНЫЙ ЭЛЕМЕНТ
- АСТАТИЗМ n-ПОРЯДКА
- БАЗА ДАННЫХ
- БАЙЕСА ФОРМУЛА, формула вероятностей гипотез
- БАЙЕСОВСКИЙ МЕТОД
- БАЙЕСОВСКОЕ ОБУЧЕНИЕ
- БАЙЕСОВСКОЕ РЕШАЮЩЕЕ ПРАВИЛО
- БАЙТ (англ. byte)
- БАЛАНС МЕЖОТРАСЛЕВОЙ
- БАЛАНСОВЫЕ МОДЕЛИ
- БАНК ДАННЫХ
- БАРАБАН МАГНИТНЫЙ
- ВЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ
- ВЕЛЛМАНА УРАВНЕНИЕ
- БЕЛЫЙ ШУМ
- БЕРЖА ГРАФ
- БЕРНУЛЛИ РАСПРЕДЕЛЕНИЕ
- «БЕРРАУЗ КОРПОРЕЙШЕН» (Burroughs Corporation)
- БИАКС
- БИБЛИОГРАФИЧЕСКИЙ ПОИСК
- БИБЛИОТЕКА СТАНДАРТНЫХ ПОДПРОГРАММ
- БИБЛИОТЕЧНЫХ ПОДПРОГРАММ МЕТОД
- БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ.
- БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- БИОЛОГИЧЕСКИЕ СИСТЕМЫ
- БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- БИОЛОГИЧЕСКИХ СИСТЕМ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- БИОЛОГИЧЕСКИХ СИСТЕМ ОРГАНИЗАЦИЯ
- БИОМЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- БИОНИКА
- БИОЭЛЕКТРИЧЕСКОЕ УПРАВЛЕНИЕ
- БИТ
- БЛЕЙКА АЛГОРИТМ
- БЛОК в программировании
- БЛОК ПЕРЕМЕННЫХ КОЭФФИЦИЕНТОВ
- БЛОК ХРАНЕНИЯ ИНФОРМАЦИИ
- БЛОКИ ЦВМ ТИПОВЫЕ
- БЛОКИРОВКА ОБСЛУЖИВАНИЯ
- БЛОК-СХЕМА ПРОГРАММЫ
- БЛОЧНЫЙ СИНТЕЗ ЦВМ
- БОЛЬЦА ЗАДАЧА
- БОЛЬШАЯ ИНТЕГРАЛЬНАЯ СХЕМА (БИС)
- БОЛЬШИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- БОЛЬШИХ ЧИСЕЛ ЗАКОН
- БУБНОВА — ГАЛЕРКИНА МЕТОД
- БУЛЕВА АЛГЕБРА
- БУЛЕВЫ ФУНКЦИИ
- БУХГАЛТЕРСКОГО УЧЁТА АВТОМАТИЗАЦИЯ
- БЫСТРОДЕЙСТВИЕ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- БЫСТРОДЕЙСТВИЕ ЦВМ
- БЭКУСА НОРМАЛЬНАЯ ФОРМА
- «БЭСМ»
- ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
- ВАРИАЦИОННЫЕ МЕТОДЫ
- ВАРИАЦИОННЫЙ РЯД
- ВВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЕЙЧА ДИАГРАММА
- ВЕКТОР ОБОБЩЕННОГО ГРАДИЕНТА
- ВЕНГЕРСКИЙ МЕТОД
- ВЕРОЯТНОСТЕЙ РАСПРЕДЕЛЕНИЕ
- ВЕРОЯТНОСТЕЙ ТЕОРИЯ
- ВЕРОЯТНОСТНАЯ МАШИНА
- ВЕРОЯТНОСТНЫЙ ПРОЦЕСС
- ВЕРОЯТНОСТЬ
- ВЕРОЯТНОСТЬ УСЛОВНАЯ
- «ВЕСНА»
- ВЕСОВАЯ ФУНКЦИЯ
- ВЕТВЕЙ И ГРАНИЦ МЕТОД
- ВЕТВЯЩИЙСЯ ПРОЦЕСС
- ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- ВЗАИМОДЕЙСТВИЕ ЧЕЛОВЕКА С ВЫЧИСЛИТЕЛЬНОЙ МАШИНОЙ
- ВИНЕРА—ХОПФА УРАВНЕНИЕ первого рода
- ВНЕШНЕЕ ОБОРУДОВАНИЕ
- ВНЕШНИЕ УСТРОЙСТВА
- «ВНИИЭМ»
- ВОЗБУЖДЕНИЯ КЛЕТКИ ТЕОРИЯ
- ВОЗМОЖНЫХ НАПРАВЛЕНИЙ МЕТОД
- ВОЗМУЩАЮЩЕЕ ВОЗДЕЙСТВИЕ,
- ВОЛЬТЕРРЫ УРАВНЕНИЕ
- ВОССТАНОВЛЕНИЯ ТЕОРИЯ
- ВРЕМЕННОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ
- ВРЕМЕННЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ВРЕМЯ ВОССТАНОВЛЕНИЯ после отказа
- ВРЕМЯ ВЫБОРКИ ИНФОРМАЦИИ
- ВРЕМЯ МОДЕЛИРОВАНИЯ ДЕЙСТВИТЕЛЬНОЕ
- ВРЕМЯ ОБРАЩЕНИЯ К ЗАПОМИНАЮЩЕМУ УСТРОЙСТВУ
- ВРЕМЯ ОЖИДАНИЯ
- ВРЕМЯ РАБОТЫ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ПОЛЕЗНОЕ
- ВСЕСОЮЗНЫЙ ИНСТИТУТ НАУЧНОЙ И ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ (ВИНИТИ)
- ВСПОМОГАТЕЛЬНОГО ОПЕРАТОРА МЕТОД
- ВХОДНОЕ УСТРОЙСТВО
- ВЫБОРКА ТРЕНИРОВОЧНАЯ
- ВЫВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЫДЕЛЕНИЕ СИГНАЛОВ НА ФОНЕ ПОМЕХ
- ВЫИГРЫША ФУНКЦИЯ
- ВЫИГРЫШЕЙ МАТРИЦА
- ВЫПУКЛАЯ ОБОЛОЧКА
- ВЫПУКЛАЯ ФУНКЦИЯ
- ВЫПУКЛОЕ МНОГОГРАННОЕ МНОЖЕСТВО
- ВЫПУКЛОЕ МНОЖЕСТВО
- ВЫПУКЛЫЙ КОНУС
- ВЫПУКЛЫЙ МНОГОГРАННИК
- ВЫПУКЛЫЙ МНОГОГРАННЫЙ КОНУС
- ВЫСКАЗЫВАНИЙ ИСЧИСЛЕНИЕ
- ВЫСКАЗЫВАНИЯ ЛОГИЧЕСКИ ИСТИННЫЕ, высказывания тождественно истинные
- ВЫСКАЗЫВАНИЯ ЭКЗИСТЕНЦИАЛЬНЫЕ
- ВЫХОДНОЕ УСТРОЙСТВО
- ВЫЧИСЛЕНИЯ В РЕАЛЬНОЕ ВРЕМЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА КЛАВИШНАЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА ОБЩЕГО НАЗНАЧЕНИЯ
- ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА
- ВЫЧИСЛИТЕЛЬНАЯ СХЕМА
- ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА ПОГРЕШНОСТЬ
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА СХОДИМОСТЬ
- ВЫЧИСЛИТЕЛЬНЫЕ СРЕДЫ
- ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК АРМЯНСКОЙ ССР И ЕРЕВАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР СИБИРСКОГО ОТДЕЛЕНИЯ АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ ХАРАКТЕРИСТИКИ
- ВЫЧИСЛИТЕЛЬНЫХ МАШИН И СИСТЁМ КОМПЛЕКСЫ
- ВЫЧИСЛИТЕЛЬНЫХ РАБОТ МЕТОДЫ ОРГАНИЗАЦИИ
- ВЫЧИСЛИТЕЛЬНЫХ ЦЕНТРОВ СЕТИ
- ГАМИЛЬТОНОВ ПУТЬ (контур)
- ГАМИЛЬТОНОВА ЦЕПЬ
- ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- ГАУССА МЕТОД
- ГАУССА РАСПРЕДЕЛЕНИЕ
- ГАУССОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ГЕДЕЛЯ ТЕОРЕМЫ О НЕПОЛНОТЕ
- ГЕНЕРАТОР ПРОГРАММ
- ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ
- ГЕНЦЕНА ФОРМАЛЬНЫЕ СИСТЕМЫ
- ГИБРИДНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ГИДРОБИОНИКА
- ГИПЕРБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ГИПЕРГРАФ
- ГИПЕРПЛОСКОСТИ ОТСЕКАЮЩЕЙ МЕТОД
- ГИПОТЕЗА КОМПАКТНОСТИ
- ГИСТОГРАММА
- ГЛОБАЛЬНОГО ПОИСКА МЕТОДЫ
- ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
- ГНЕЗДОВОЙ СПИСОК
- ГНОСЕОЛОГИЧЕСКИЕ ОСНОВЫ КИБЕРНЕТИКИ
- ГОЛОГРАФИЯ
- ГОМЕОСТАЗИС
- ГОМЕОСТАТИЧЕСКАЯ СИСТЕМА
- ГОМОРИ МЕТОД
- ГОНОК ПРОБЛЕМА
- ГОРНЕРА СХЕМА
- ГОСУДАРСТВЕННЫЙ ФОНД АЛГОРИТМОВ И ПРОГРАММ (ГФАП)
- ГРАДИЕНТ
- ГРАДИЕНТНЫЙ МЕТОД
- ГРАММАТИКА АВТОМАТНАЯ, грамматика с конечным числом состояний
- ГРАММАТИКА БЕСКОНТЕКСТНАЯ, грамматика контекстно-свободная
- ГРАММАТИКА ЗАВИСИМОСТЕЙ, грамматика управлений
- ГРАММАТИКА КАТЕГОРИАЛЬНАЯ
- ГРАММАТИКА ЛИНЕЙНАЯ
- ГРАММАТИКА ПОРОЖДАЮЩАЯ
- ГРАММАТИКА РАСПОЗНАЮЩАЯ
- ГРАММАТИКА СОСТАВЛЯЮЩИХ, грамматика непосредственно составляющих
- ГРАММАТИКА ТРАНСФОРМАЦИОННАЯ
- ГРАММАТИКА ФОРМАЛЬНАЯ
- ГРАНИЧНАЯ ЗАДАЧА
- ГРАФ
- ГРАФ ВЗВЕШЕННЫЙ
- ГРАФ РАСКРАШЕННЫЙ
- ГРАФИЧЕСКОЕ РЕГИСТРИРУЮЩЕЕ УСТРОЙСТВО
- ГРАФОВ СВЯЗНОСТЬ
- ГРАФОВ ТЕОРИЯ
- ГРАФОПОСТРОИТЕЛЬ
- ГРУПП ТЕОРИЯ
- ГРУППА в алгебре
- ГРУППОВОЙ ИСТОЧНИК НАПРЯЖЕНИЯ
- ГРУППЫ НЕПРЕРЫВНЫЕ.
- ГУРВИЦА КРИТЕРИЙ
- ГУРВИЦА ТЕОРЕМА
- ДАННЫЕ
- ДАТЧИК ВРЕМЕНИ,
- ДАТЧИК ОДИНОЧНЫХ ИМПУЛЬСОВ
- ДАТЧИК РАБОЧЕГО ЦИКЛА
- ДАТЧИК СЛУЧАЙНЫХ ЧИСЕЛ
- ДВИГАТЕЛЬ ПОЛИМЕРНЫЙ
- ДВОЙСТВЕННАЯ ЗАДАЧА ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ.
- ДВОЙСТВЕННАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- ДВОЙСТВЕННОСТИ ЗАКОН, принцип двойственности
- ДВОЙСТВЕННОСТИ ТЕОРИЯ в программировании линейном
- ДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ДВОЙСТВЕННЫЙ ГРАДИЕНТНЫЙ МЕТОД
- ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД, метод последовательного уточнения оценок
- ДВОЙСТВЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ДВУПОЛЮСНИК КОНТАКТНЫЙ
- ДВУХТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ДЕЙСТВИТЕЛЬНОЕ ВРЕМЯ МОДЕЛИРОВАНИЯ
- ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО
- ДЕКОМПОЗИЦИИ МЕТОД, блочный метод
- ДЕЛЕЖ в теории игр
- ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
- ДЕЛЬТА-ФУНКЦИЯ
- ДЕМОДУЛЯТОР, детектор
- ДЕМПФИРОВАНИЕ
- «ДЕРЕВО» в теории графов
- «ДЕРЕВО» КОНТАКТНОЕ с n реле
- ДЕСКРИПТОР
- ДЕТЕРМИНИРОВАННЫЕ СИСТЕМЫ
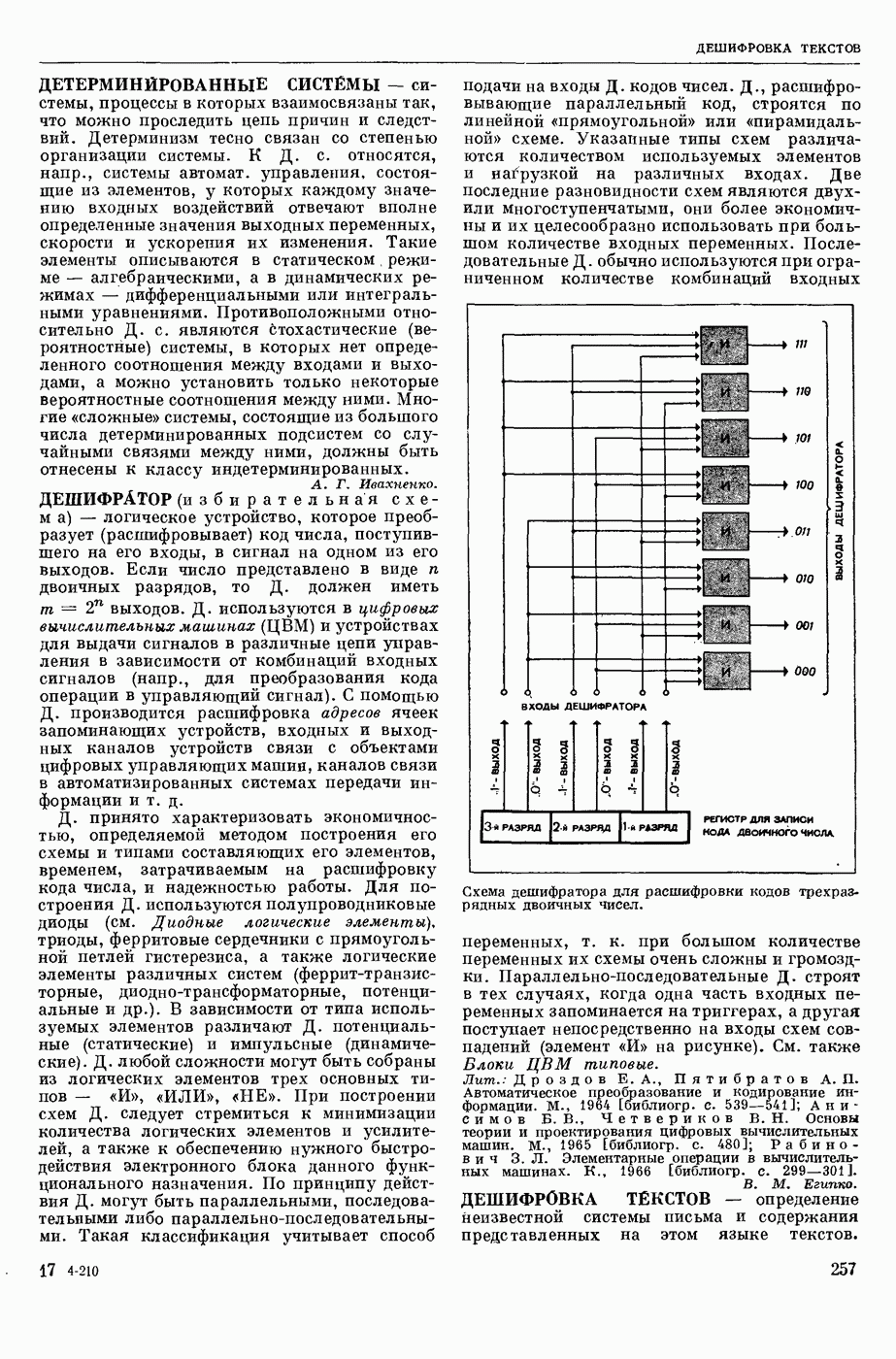
- ДЕШИФРАТОР
- ДЕШИФРОВКА ТЕКСТОВ
- ДИАГНОСТИКА АВТОМАТИЧЕСКАЯ
- ДИАГНОСТИКА НЕИСПРАВНОСТЕЙ ЦВМ
- ДИАГНОСТИРОВАНИЕ СЛОЖНЫХ ТЕХНИЧЕСКИХ КОМПЛЕКСОВ, техническая диагностика
- ДИАЛОГА РЕЖИМ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (ДНФ)
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА ТУПИКОВАЯ.
- ДИЗЪЮНКЦИЯ
- ДИЗЪЮНКЦИЯ СЛАБАЯ
- ДИЗЪЮНКЦИЯ СТРОГАЯ, антиэквивалентность, сложение по модулю 2
- ДИНАМИЧЕСКИХ СИСТЕМ ТЕОРИЯ ЧУВСТВИТЕЛЬНОСТИ
- ДИНАМИЧЕСКИХ СИСТЕМ УСЛОВИЯ ГРУБОСТИ
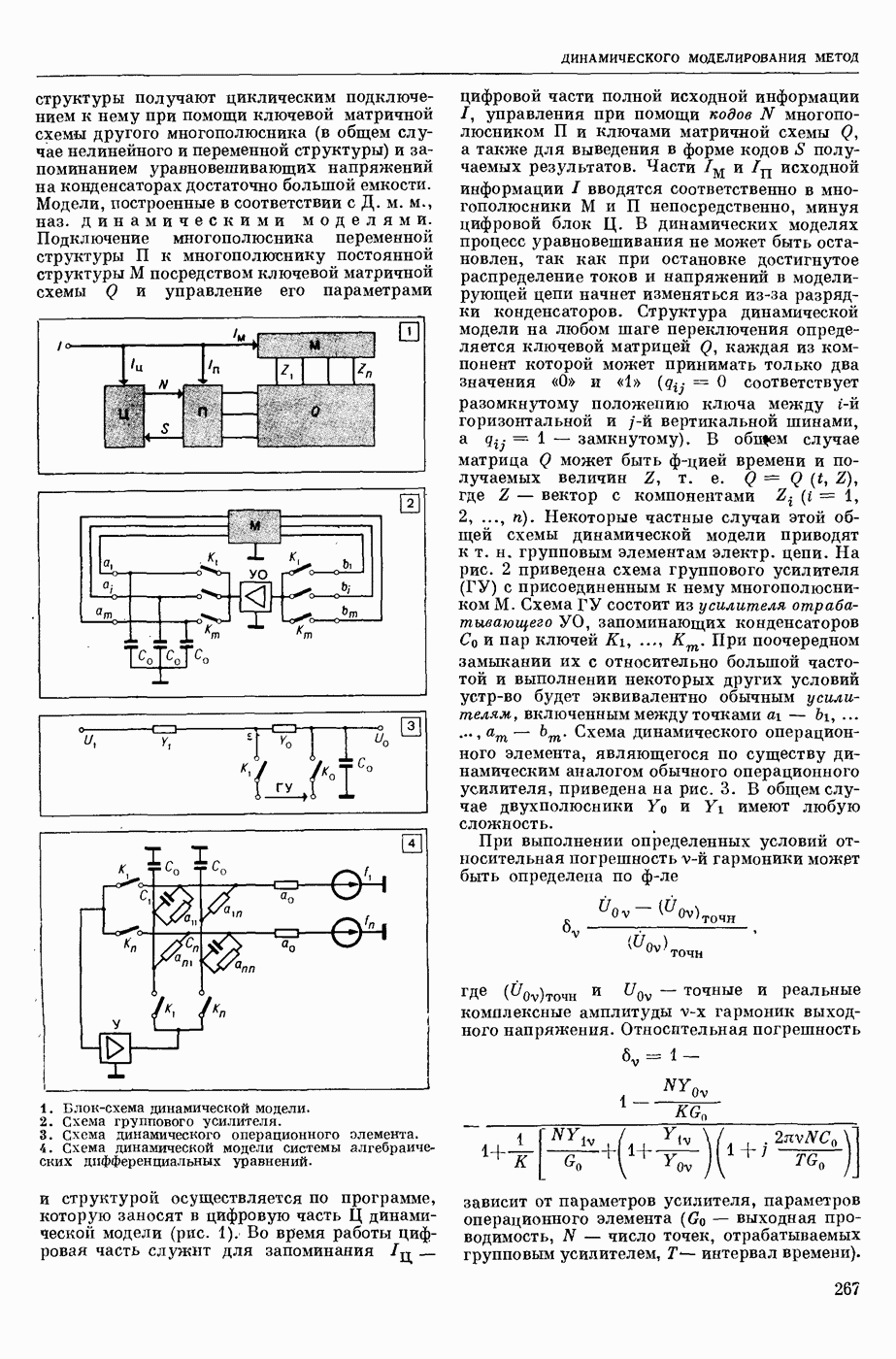
- ДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ МЕТОД
- ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ
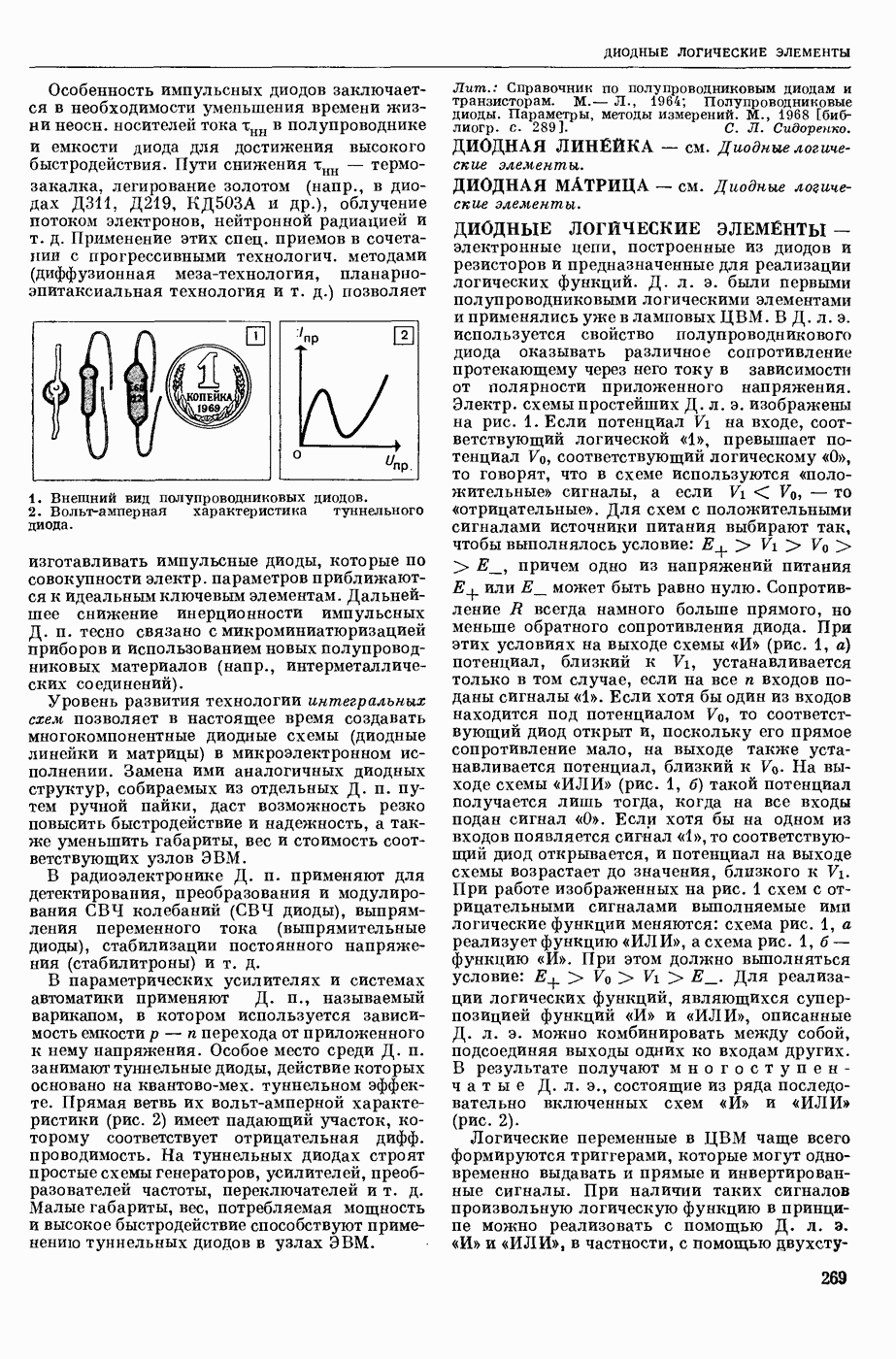
- ДИОД ПОЛУПРОВОДНИКОВЫЙ
- ДИОДНАЯ ЛИНЕЙКА
- ДИОДНАЯ МАТРИЦА
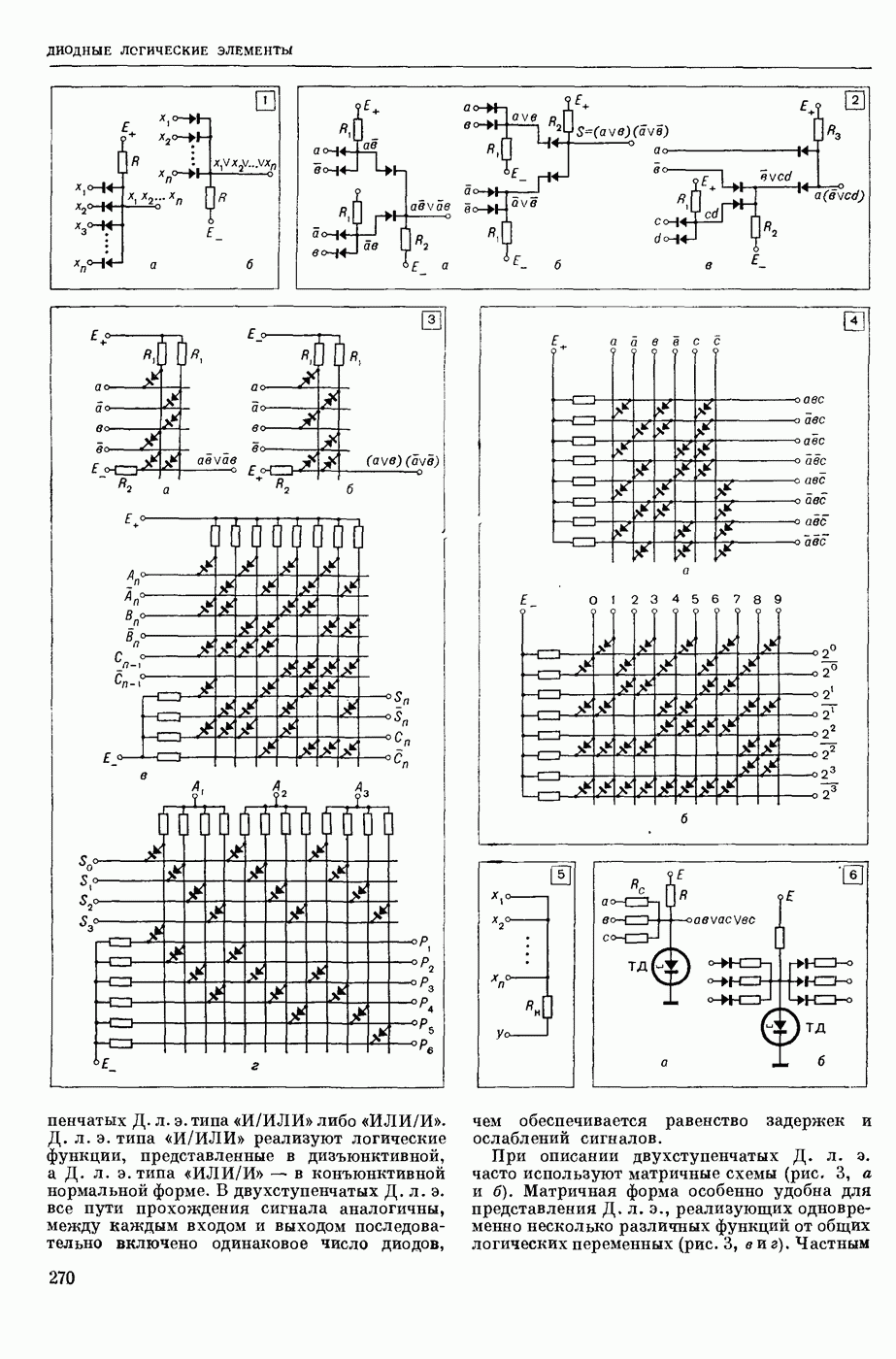
- ДИОДНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ДИРАКА ФУНКЦИЯ
- ДИСК МАГНИТНЫЙ
- ДИСКРЕТИЗАЦИЯ ИЗОБРАЖЕНИЙ
- ДИСКРЕТНАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- ДИСКРЕТНАЯ СИСТЕМА
- ДИСКРЕТНАЯ СИСТЕМА УПРАВЛЕНИЯ, импульсная система управления
- ДИСКРЕТНЫЙ АНАЛИЗ
- ДИСКРЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ ТЕОРИЯ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- ДИСКРЕТНЫХ ЭЛЕМЕНТОВ СИСТЕМА
- ДИСПЕРСИОННЫЙ АНАЛИЗ
- ДИСПЕРСИЯ
- ДИСПЕТЧЕР в программировании
- ДИСПЕТЧЕРСКОГО УПРАВЛЕНИЯ АВТОМАТИЗАЦИЯ
- ДИСТАНЦИОННОЕ УПРАВЛЕНИЕ
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
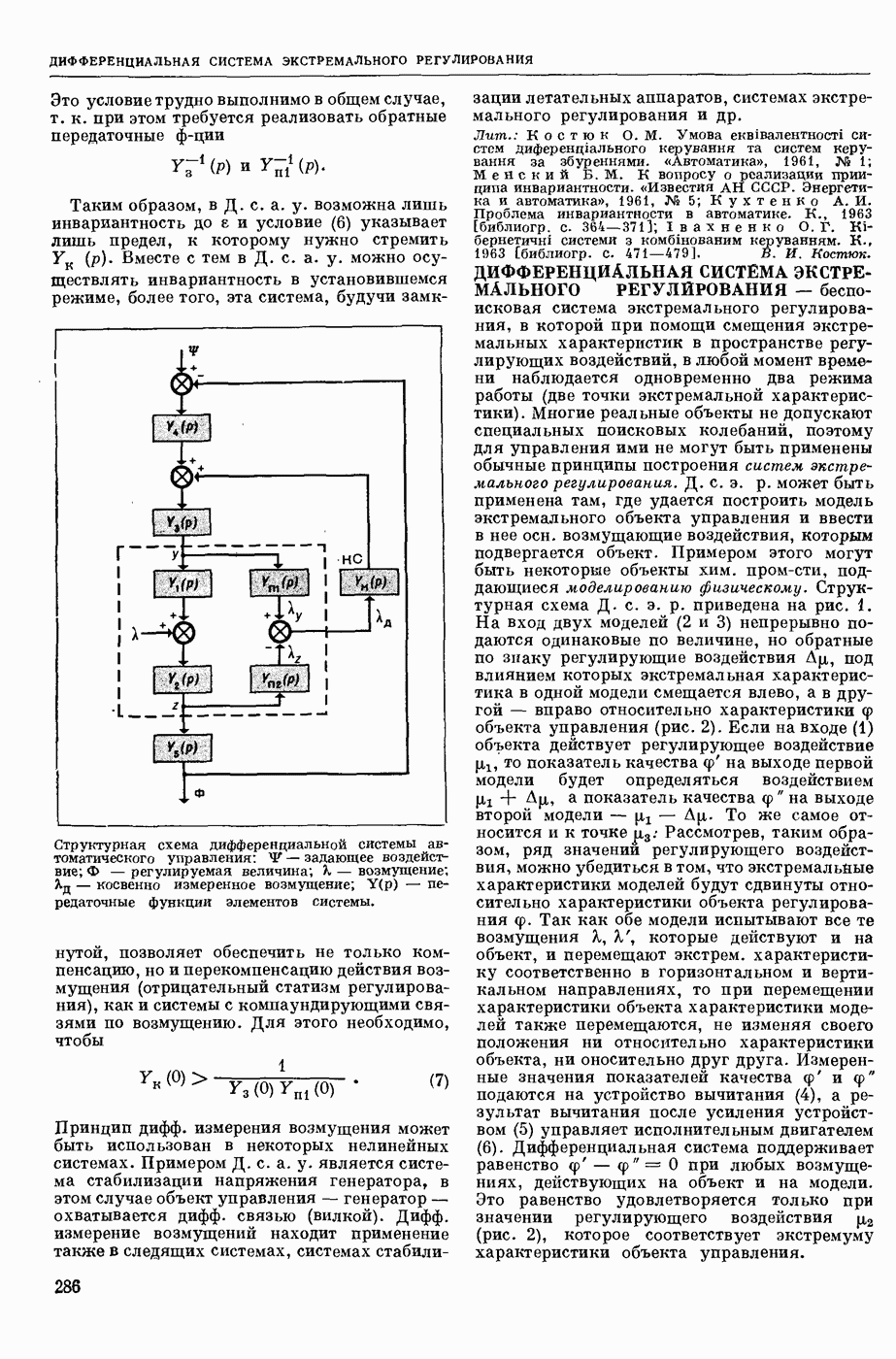
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
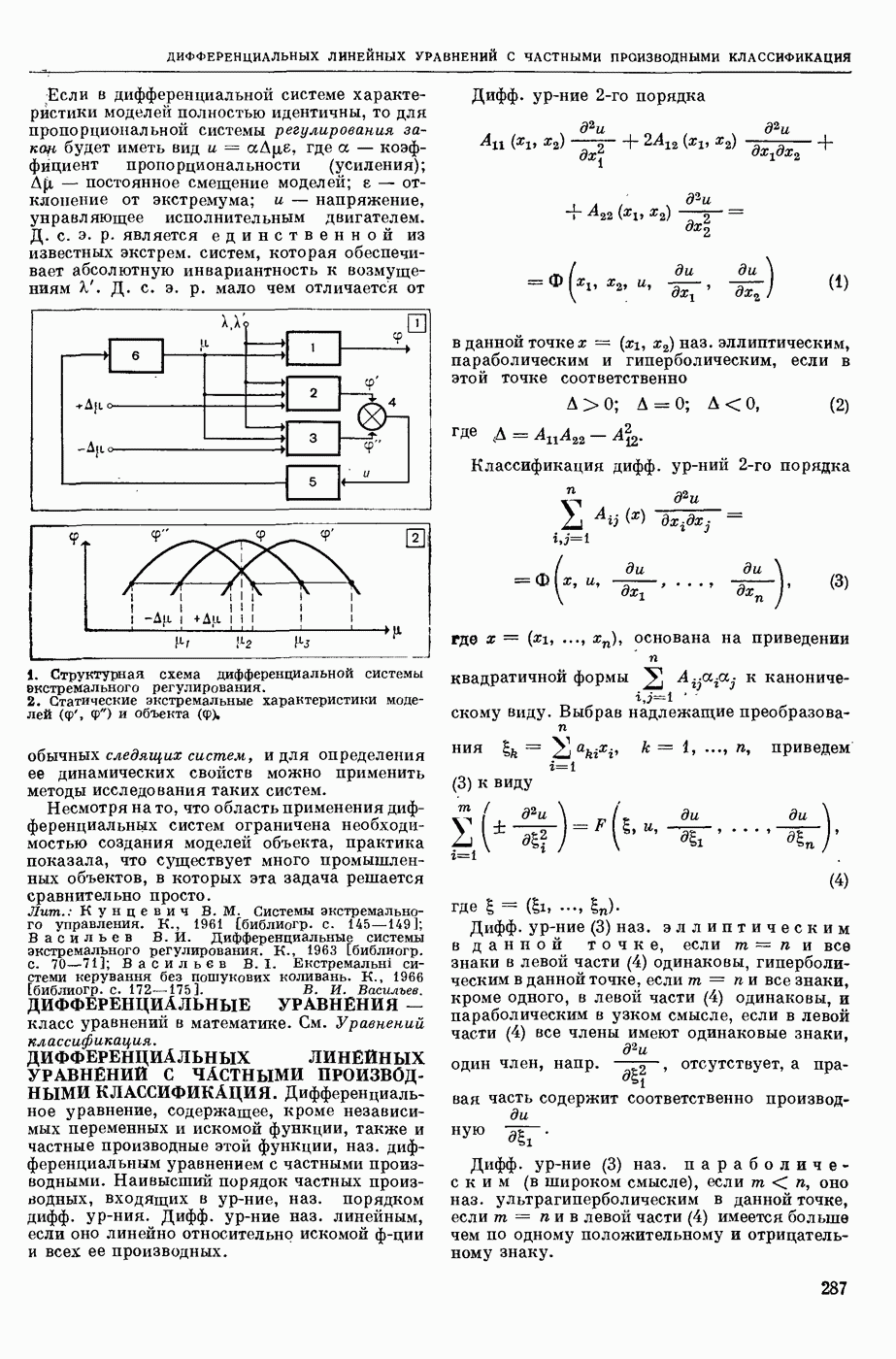
- ДИФФЕРЕНЦИАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ КЛАССИФИКАЦИЯ.
- ДИФФЕРЕНЦИАЛЬНЫХ РЕНТ МЕТОД
- ДИФФЕРЕНЦИАТОР
- ДИФФЕРЕНЦИРОВАНИЕ СИГНАЛОВ
- ДИФФЕРЕНЦИРОВАНИЕ СИМВОЛЬНОЕ, дифференцирование аналитическое
- ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ
- ДИФФУЗИОННЫЙ ПРОЦЕСС
- ДЛИНА ОЧЕРЕДИ
- ДЛИТЕЛЬНОСТЬ ОЖИДАНИЯ
- «ДНЕПР»
- ДОВЕРИТЕЛЬНАЯ ОБЛАСТЬ
- ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
- ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
- ДОВЕРИТЕЛЬНЫЙ УРОВЕНЬ
- ДОКАЗАТЕЛЬСТВ ТЕОРИЯ, метаматематика
- ДОКАЗАТЕЛЬСТВО ТЕОРЕМ НА ЭВМ, машинный поиск логического вывода
- ДОКУМЕНТ НАУЧНЫЙ
- ДОКУМЕНТАЛЬНАЯ ИНФОРМАЦИОННОПОИСКОВАЯ СИСТЕМА
- ДОКУМЕНТАЛЬНО-ФАКТОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
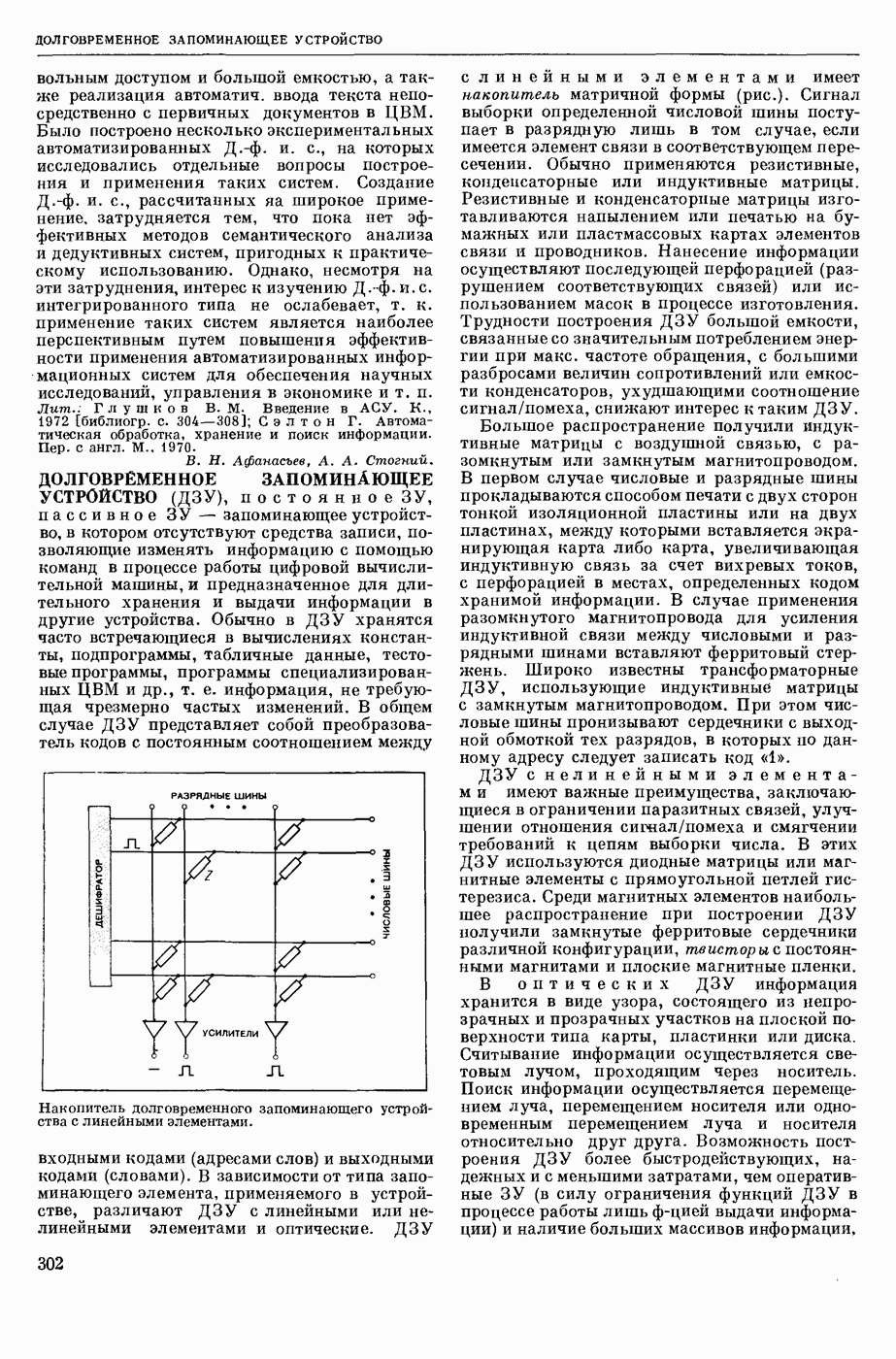
- ДОЛГОВРЕМЕННОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ДЗУ)
- ДОМИНИРОВАНИЕ в теории игр.
- ДОПУСТИМАЯ ОБЛАСТЬ
- ДОПУСТИМАЯ ТОЧКА
- ДОПУСТИМОЕ МНОЖЕСТВО
- ДОПУСТИМОЕ УПРАВЛЕНИЕ
- ДОПУСТИМЫЙ ВЕКТОР
- ДОПУСТИМЫЙ ПУТЬ в теории графов
- ДОПУСТИМЫХ НАПРАВЛЕНИЙ МЕТОД
- ДОСТАТОЧНОСТЬ ПРИЗНАКОВ.
- ДОСТАТОЧНЫЕ СТАТИСТИКИ
- ДОСТУП ПОСЛЕДОВАТЕЛЬНЫЙ
- ДОСТУП ПРОИЗВОЛЬНЫЙ
- ДРЕЙФ НУЛЕВОГО УРОВНЯ операционного усилителя
- ДРОБНО-ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ЗАДАЧА
- ДРОБНЫХ ШАГОВ МЕТОД
- ДУАЛЬНОЕ УПРАВЛЕНИЕ
- ДУГА графа
- ДУЭЛЬ в теории игр
- ЕДИНАЯ СИСТЕМА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН (ЕС ЭВМ)
- ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ
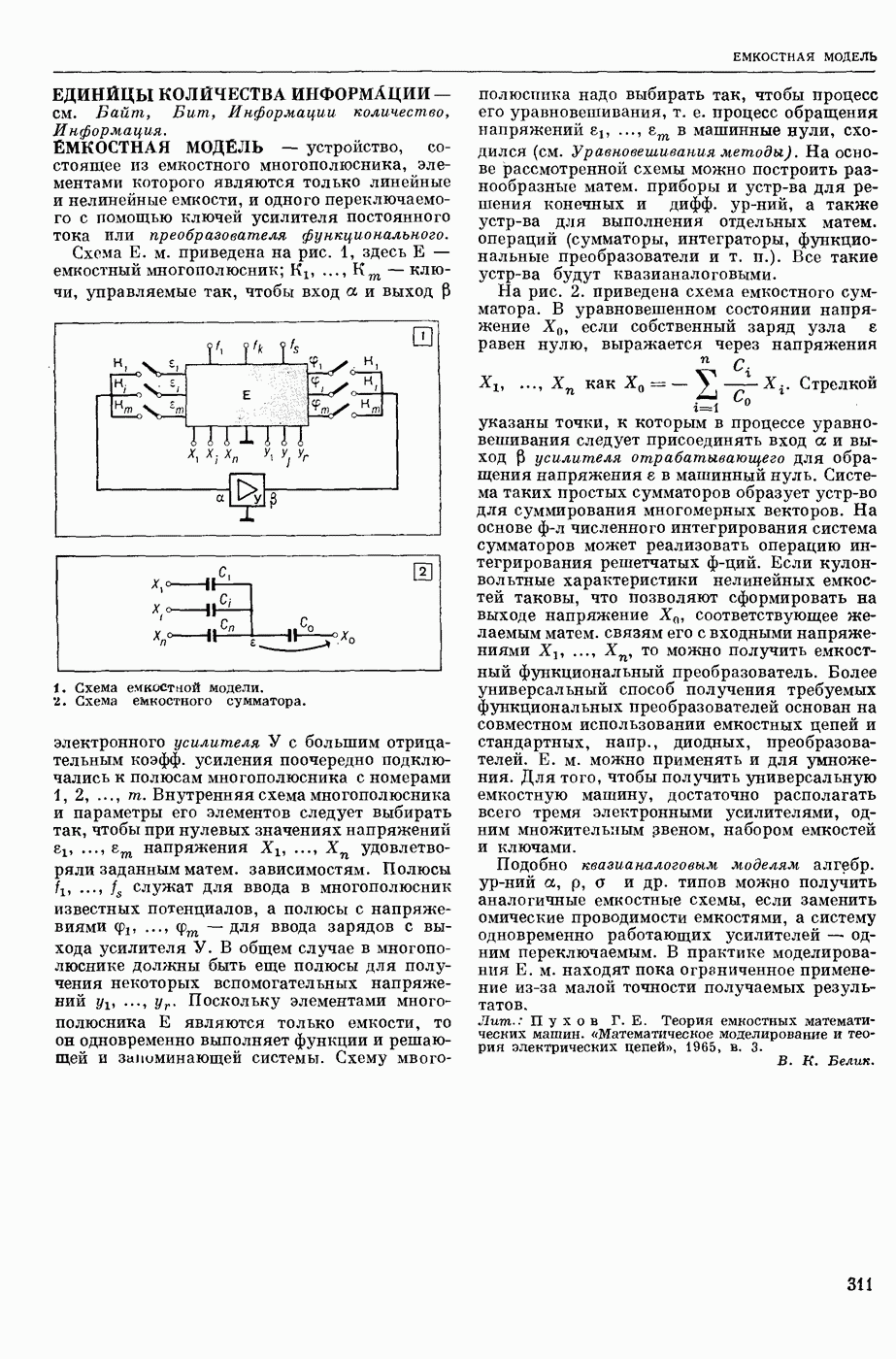
- ЕМКОСТНАЯ МОДЕЛЬ
- ЖЕГАЛКИНА АЛГЕБРА
- ЗАГРУЗЧИК в программировании
- ЗАДАЧА О КОММИВОЯЖЕРЕ
- ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ
- ЗАДАЧА О НАЗНАЧЕНИЯХ
- ЗАДАЧА О ПЕРЕВОЗКАХ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
- ЗАДАЧА О РАСПРЕДЕЛЕНИИ ПОСТАВОК
- ЗАДАЧА О РЮКЗАКЕ
- ЗАДАЧА О СКЛАДЕ
- ЗАДАЧА ОБ ОПТИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
- ЗАДАЧА ОБ УЗКИХ МЕСТАХ
- ЗАДАЧА С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
- ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
- ЗАМЫКАНИЕ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА
- ЗАПАЗДЫВАНИЯ БЛОК
- ЗАПАСОВ ТЕОРИЯ, теория управления запасами
- ЗАПИСЬ
- ЗАПИСЬ БЕССКОБОЧНАЯ, польская запись
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЕМКОСТЬ
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЗОНА
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ЗУ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АВМ (ЗУ АВМ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АДРЕСНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АССОЦИАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО БУФЕРНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ВНЕШНЕЕ, внешний накопитель
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ДОЛГОВРЕМЕННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО МАГАЗИННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО НА ЛИНИЯХ ЗАДЕРЖКИ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ОПЕРАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПОСЛЕДОВАТЕЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПРОИЗВОЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩИЙ ЭЛЕМЕНТ
- ЗАЦИКЛИВАНИЕ
- ЗАЩИТА ПАМЯТИ
- ЗНАКОВЫЙ РАЗРЯД
- ЗНАЧАЩИЕ ЦИФРЫ приближенного числа
- ИБМ (International Business Machines)
- ИГР ТЕОРИЯ
- ИГРА АЗАРТНАЯ
- ИГРА БЕЗ ПОБОЧНЫХ ПЛАТЕЖЕЙ
- ИГРА БЕСКОАЛИЦИОННАЯ
- ИГРА ВЫПУКЛАЯ
- ИГРА ВЫРОЖДЕННАЯ
- ИГРА ДИНАМИЧЕСКАЯ
- ИГРА КООПЕРАТИВНАЯ
- ИГРА НА ГРАФЕ
- ИГРА НА ЕДИНИЧНОМ КВАДРАТЕ
- ИГРА ПОЗИЦИОННАЯ
- ИГРА ПРОСТАЯ
- ИГРА РЕКУРСИВНАЯ
- ИГРА С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ
- ИГРА СТОХАСТИЧЕСКАЯ
- ИГРУШКИ КИБЕРНЕТИЧЕСКИЕ
- ИГРЫ АНТАГОНИСТИЧЕСКИЕ
- ИГРЫ ДИФФЕРЕНЦИАЛЬНЫЕ
- ИГРЫ ЗНАЧЕНИЕ
- ИГРЫ МАТРИЧНЫЕ
- ИГРЫ НА ВЫЖИВАНИЕ
- ИГРЫ РЕФЛЕКСИВНЫЕ
- ИДЕНТИФИКАТОР
- ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ
- ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (ИСУ)
- ИЕРАРХИЧНОСТЬ УПРАВЛЕНИЯ
- ИЗБЫТОЧНОСТЬ СИСТЕМЫ
- ИЗБЫТОЧНОСТЬ СООБЩЕНИЙ
- ИМПЛИКАЦИЯ в алгебре логики
- ИМПЛИКАЦИЯ СТРОГАЯ
- ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ
- ИМПУЛЬСНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ИНВАРИАНТНОСТЬ ПРИЗНАКОВ
- ИНВАРИАНТНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ИНВЕРТОР
- ИНГВЕ ГИПОТЕЗА, гипотеза глубины
- ИНДЕКСИРОВАНИЕ
- ИНДИКАТОРЫ ИНФОРМАЦИИ
- ИНЖЕНЕРНЫЕ МЕТОДЫ СИНТЕЗА ДИСКРЕТНЫХ АВТОМАТОВ
- ИНЖЕНЕРНЫХ РАСЧЕТОВ АВТОМАТИЗАЦИЯ
- ИНСТИТУТ АВТОМАТИКИ АКАДЕМИИ НАУК КИРГИЗСКОЙ ССР
- ИНСТИТУТ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ (ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ) АКАДЕМИИ НАУК СССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК АЗЕРБАЙДЖАНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ЭСТОНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ С ВЫЧИСЛИТЕЛЬНЫМ ЦЕНТРОМ АКАДЕМИИ НАУК УЗБЕКСКОЙ ССР
- ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ И МЕХАНИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ СИСТЕМ УПРАВЛЕНИЯ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ АКАДЕМИИ НАУК БЕЛОРУССКОЙ ССР
- ИНСТИТУТ ТОЧНОЙ МЕХАНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК СССР
- ИНСТИТУТ ЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК ЛАТВИЙСКОЙ ССР
- ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ, приборная погрешность
- ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ИНТЕГРАЛЬНАЯ СХЁМА
- ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ СИНГУЛЯРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАТОР
- ИНТЕГРИРОВАНИЕ СИМВОЛЬНОЕ, интегр ирование аналитическое
- ИНТЕГРИРОВАНИЕ ЧИСЛЕННОЕ
- ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕНСИВНОСТЬ ПОТОКА в теории массового обслуживания
- «ИНТЕРНЕЙШЕНАЛ БИЗНЕС МАШЙНЗ КОРПОРЕЙШЕН», ИБМ (International Business Machines Corporation, IBM)
- «ИНТЕРНЕЙШЕНАЛ КОМПЬЮТЕРЗ ЛЙМИТЕД» (International Computers Limited, I. С. L.)
- ИНТЕРПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
- ИНТЕРПОЛЯТОР
- ИНТЕРПРЕТАЦИЯ ЯЗЫКА СТРУКТУРНАЯ
- ИНТЕРПРЕТИРУЮЩАЯ СИСТЕМА
- ИНТУИЦИОНИЗМ
- ИНФОРМАТИВНОСТЬ ПРИЗНАКОВ
- ИНФОРМАТИКА
- ИНФОРМАЦИИ КОЛИЧЕСТВО
- ИНФОРМАЦИИ ПЕРЕДАЧА
- ИНФОРМАЦИИ ТЕОРИЯ
- ИНФОРМАЦИИ ХРАНЕНИЕ
- ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР ПРЕДПРИЯТИЯ
- ИНФОРМАЦИОННО-ЛОГИЧЕСКАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ ЯЗЫК
- ИНФОРМАЦИОННО-ПЛАНИРУЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ФАКТОГРАФИЧЕСКАЯ
- ИНФОРМАЦИОННО-ПОИСКОВОЕ УСТРОЙСТВО
- ИНФОРМАЦИОННО-ПОИСКОВЫЙ ЯЗЫК
- ИНФОРМАЦИОННО-СПРАВОЧНАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩИХ СИСТЕМ ТЕХНИЧЕСКОЕ ОСНАЩЕНИЕ
- ИНФОРМАЦИОННЫЕ ПОТОКИ НАУКИ
- ИНФОРМАЦИОННЫХ РАБОТ АВТОМАТИЗАЦИЯ
- ИНФОРМАЦИЯ (лат. informatio — разъяснение, изложение, осведомленность)
- ИНФОРМАЦИЯ ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИЯ НАУЧНАЯ
- ИНФОРМАЦИЯ СЕМАНТИЧЕСКАЯ
- ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН
- «ИСКРА»
- ИСКУССТВЕННАЯ МЫШЦА
- ИСКУССТВЕННЫЙ РАЗУМ
- ИСПОЛНИТЕЛЬНЫЙ МЕХАНИЗМ
- ИСТОЧНИК ОПОРНОГО НАПРЯЖЕНИЯ
- ИСТОЧНИК СООБЩЕНИЙ
- ИСЧИСЛЕНИЕ, дедуктивная система
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ, пропозициональное исчисление
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ МИНИМАЛЬНОЕ, логика минимальная
- ИСЧИСЛЕНИЕ ЗАДАЧ, теория задач
- ИСЧИСЛЕНИЕ ПРЕДИКАТОВ УЗКОЕ, исчисление предикатов первой ступени
- ИСЧИСЛЕНИЕ ПРОПОЗИЦИОНАЛЬНОЕ
- «ИТЕРАТОР»
- ИТЕРАЦИОННЫЕ МЕТОДЫ
- ИТЕРАЦИЯ СОБЫТИЯ
- ИФАК (International Federation of Automatic Control)
- ИФИП (International Federation for Information Processing)
- КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ
- КАНАЛ МАШИННЫЙ
- КАНАЛОВ СВЯЗИ ПРОПУСКНАЯ СПОСОБНОСТЬ
- КАНАЛЫ СВЯЗИ
- КАРДИНАЛЬНЫЕ ЧИСЛА
- КАРНАУ КАРТА, Вейча диаграмма
- КАРТА МАГНИТНАЯ
- КАСКАДОВ МЕТОД
- КАТАЛОГ
- КАТЕГОРИЙ ТЕОРИЯ
- КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ
- КВАДРАТУРНЫЕ ФОРМУЛЫ
- КВАЗИАНАЛОГОВАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- КВАЗИАНАЛОГОВАЯ МОДЕЛЬ
- КВАЗИАНАЛОГОВОЕ МОДЕЛИРОВАНИЕ
- КВАЗИРЕЗИСТОР
- КВАЙНА МЕТОД МИНИМИЗАЦИИ
- КВАНТОВАНИЕ
- КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- КВАНТОРЫ
- КИБЕРНЕТИКА
- «КИБЕРНЕТИКА»
- «КИБЕРНЕТИКА» — реферативный журнал,
- КИБЕРНЕТИКА БИОЛОГИЧЕСКАЯ
- КИБЕРНЕТИКА В ВОЕННОМ ДЕЛЕ
- КИБЕРНЕТИКА МЕДИЦИНСКАЯ
- КИБЕРНЕТИКА ТЕХНИЧЕСКАЯ
- КИБЕРНЕТИКА ЭКОНОМИЧЕСКАЯ
- КЛАСС ЗАМКНУТЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ИНВАРИАНТНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ПРЕДПОЛНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАССИФИКАЦИИ ИЕРАРХИЧЕСКИЕ
- КЛАССИФИКАЦИЯ АВТОМАТИЧЕСКАЯ
- КЛЮЧЕВОЕ СЛОВО
- КОБОЛ
- КОД (от лат. codex)
- КОД СЕМАНТИЧЕСКИЙ
- КОДИРОВАНИЕ АВТОМАТНОЕ
- КОДИРОВАНИЕ СОСТОЯНИЙ АВТОМАТА
- КОДИРОВАНИЯ ТЕОРИЯ
- КОДЫ КОРРЕКТИРУЮЩИЕ
- КОЛЕБАНИЯ СКРЫТЫЕ
- КОЛМОГОРОВА УРАВНЕНИЯ
- КОМАНД МОДИФИКАЦИЯ
- КОМАНД СИСТЕМА
- КОМАНДА МАШИННАЯ
- КОМАНДЫ ФОРМАТ
- КОМБИНАТОРНЫЙ АНАЛИЗ
- КОМБИНАЦИОННАЯ СХЕМА
- КОМБИНИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- КОМБИНИРОВАННАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОМБИНИРОВАННЫЕ МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- КОМИТ
- КОММУНИКАЦИОННЫЙ ПРОЦЕССОР
- «КОМПАНИ ИНТЕРНАСЬОНАЛЬ ПУР Л’ИНФОРМАТИК» (Compagnie internationale pour l’informatique)
- КОМПАУНДИРУЮЩИЕ СВЯЗИ В АВТОМАТИЧЕСКИХ СИСТЕМАХ
- КОМПЕНСАЦИОННЫЙ СПОСОБ НАСТРОЙКИ И ИЗМЕРЕНИЯ РЕЗУЛЬТАТОВ РЕШЕНИЯ
- КОМПЛЕКСИРОВАНИЕ МАШИН
- КОМПЛЕКТ ПЕРФОРАЦИОННЫЙ ВЫЧИСЛИТЕЛЬНЫЙ
- КОМПЬЮТЕР
- КОНЕЧНОРАЗНОСТНЫЕ МЕТОДЫ, методы сеток
- КОНКУРЕНЦИИ МОДЕЛИ
- КОНСТРУКТИВНОЕ НАПРАВЛЕНИЕ В МАТЕМАТИКЕ, конструктивная математика
- КОНСТРУКТИВНЫЙ АНАЛИЗ, рекурсивный анализ, вычислимый анализ
- «КОНТРОЛ ДЕЙТА КОРПОРЁЙШЕН» (Control Data Corporation)
- КОНТРОЛЬ ABM
- КОНТРОЛЬ НАБОРА ЗАДАЧ В АВМ
- КОНТРОЛЬ ПРОГРАММНЫЙ
- КОНТРОЛЬ ЦВМ
- КОНТРОЛЬНИК
- КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
- КОНЪЮНКЦИЯ
- КООРДИНАЦИОННО — УПРАВЛЯЮЩИЙ ЦЕНТР ПРЕДПРИЯТИЯ
- КОРНЕВОГО ГОДОГРАФА МЕТОД
- КОРНЕЙ АЛГЕБРАИЧЕСКИХ МНОГОЧЛЕНОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРНЕЙ НЕПРЕРЫВНЫХ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- КОРРЕКЦИЯ ДРЕЙФА НУЛЯ
- КОРРЕКЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОРРЕЛЯТОР, коррелометр, коррелограф
- КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ ПОЛЯРНАЯ (знаковая)
- КОРРЕЛЯЦИОННАЯ ЭКСТРЕМАЛЬНАЯ СИСТЕМА
- КОРРЕЛЯЦИОННЫЙ АППАРАТУРНЫЙ АНАЛИЗ случайных процессов
- КОРРЕЛЯЦИОННЫЙ МЕТОД РАСПОЗНАВАНИЯ
- КОРРЕЛЯЦИОННЫЙ ЧИТАЮЩИЙ АВТОМАТ
- КОРРЕЛЯЦИЯ в теории вероятностей
- КОШИ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ СПОСОБЫ РЕШЕНИЯ.
- КОЭФФИЦИЕНТ ПЕРЕДАЧИ АВМ
- КОЭФФИЦИЕНТ ПОЛНОТЫ ПОИСКА
- КОЭФФИЦИЕНТ ТОЧНОСТИ ПОИСКА
- КРАЕВАЯ ЗАДАЧА
- КРАЕВЫЕ УСЛОВИЯ
- КРАЕВЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- КРАЙНЯЯ ТОЧКА
- КРАТНЫХ ИНТЕГРАЛОВ СПОСОБЫ ПРИБЛИЖЁННОГО ВЫЧИСЛЕНИЯ
- КРИОГЕННЫЕ ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КРИОТРОН
- КРИТЕРИИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КРИТЕРИЙ СЕМАНТИЧЕСКОГО СООТВЕТСТВИЯ
- КРИТИЧЕСКИЙ ПУТЬ
- КУБ ФЕРРИТОВЫЙ
- КУБАТУРНЫЕ ФОРМУЛЫ
- «КИIВ-67»
- ЛАГ И ТАГ СИСТЕМЫ
- ЛАГРАНЖА ЗАДАЧА
- ЛАГРАНЖА ПРАВИЛО МНОЖИТЕЛЕЙ
- ЛАПЛАСА ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЛАПЛАСА ПРЕОБРАЗОВАНИЯ
- ЛЕЖАНДРА—КЛЕБША УСЛОВИЕ
- ЛЕНТА МАГНИТНАЯ
- ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ
- ЛИНГВИСТИКА ПРИКЛАДНАЯ
- ЛИНГВИСТИЧЕСКАЯ СТАТИСТИКА
- ЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ЛИНЕЙНАЯ ФОРМА, линейный функционал, ковектор
- ЛИНЕЙНЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ
- ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ЛИСП
- ЛОГИКА КОНСТРУКТИВНАЯ
- ЛОГИКА МАЖОРИТАРНАЯ
- ЛОГИКА МАТЕМАТИЧЕСКАЯ, формальная логика
- ЛОГИКА МИНИМАЛЬНАЯ
- ЛОГИКА МНОГОЗНАЧНАЯ
- ЛОГИКА ПОРОГОВАЯ
- ЛОГИКА ПРЕДИКАТОВ ВЫСШИХ СТУПЕНЕЙ
- ЛОГИКИ НЕКЛАССИЧЕСКИЕ
- ЛОГИКО-МАТЕМАТИЧЕСКОЕ ИСЧИСЛЕНИЕ
- ЛОГИЧЕСКАЯ РАСПОЗНАЮЩАЯ СИСТЕМА
- ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- ЛОГИЧЕСКИЙ ЗАДЕРЖИВАЮЩИЙ ЭЛЕМЕНТ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ АВМ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ЦВМ
- ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ НОРМАЛЬНЫЕ ФОРМЫ
- ЛОКАЛИЗОВАННЫЕ ПЕРЕМЕННЫЕ
- ЛОКАЛЬНОГО КОДИРОВАНИЯ ПРИНЦИП
- ЛЯПАС
- ЛЯПУНОВА МЕТОДЫ
- «М-20»
- МАЖОРИТАРНЫЙ ЭЛЕМЕНТ
- МАЙЕРА ЗАДАЧА
- МАК-КЛАСКИ АЛГОРИТМ
- МАКРОКОМАНДА
- МАКРОМОДЕЛИ ЭКОНОМИЧЕСКИЕ
- МАКСИМИНА ПРИНЦИП
- МАКСИМУМА ПРАВДОПОДОБИЯ МЕТОД
- МАНИПУЛЯТОР
- «MARK-1»
- МАРКЕР
- МАРКОВА ЦЕПЬ
- МАРКОВСКИЙ ПРОЦЕСС
- МАССИВ
- МАССИВ ИНФОРМАЦИОННЫЙ
- МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА
- МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ, теория очередей
- МАТЕМАТИКА ВЫЧИСЛИТЕЛЬНАЯ
- МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА
- МАТЕМАТИЧЕСКИЕ МЁТОДЫ В ПОЭТИКЕ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ ВНУТРЕННЕЕ
- МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, среднее значение
- МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- МАТРИЦА
- МАТРИЦА ВТОРЫХ МОМЕНТОВ
- МАТРИЦА ЗАПОМИНАЮЩАЯ
- МАТРИЦА ОБУЧАЕМАЯ
- МАТРИЦА ФЕРРИТОВАЯ МНОГООТВЕРСТНАЯ
- МАТРИЦА ФЕРРИТОВАЯ СЛОИСТАЯ
- МАТРИЧНЫЕ ИГРЫ
- МАШИНА
- МАШИНА ЦЕНТРАЛИЗОВАННОГО КОНТРОЛЯ
- МАШИННАЯ ПЕРЕМЕННАЯ
- МАШИННОЕ ПРОЕКТИРОВАНИЕ ИНТЕГРАЛЬНЫХ СХЕМ
- МАШИННОЕ СЛОВО
- МАШИННЫЙ «ИНТЕЛЛЕКТ»
- МАШИННЫЙ ПЕРЕВОД, автоматический перевод
- МЕДИЦИНСКАЯ ИНФОРМАЦИОННАЯ СИСТЕМА
- МЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- МЕЖДУНАРОДНАЯ АССОЦИАЦИЯ ПО АНАЛОГОВЫМ ВЫЧИСЛЕНИЯМ
- МЕЖДУНАРОДНАЯ ОРГАНИЗАЦИЯ ПО СТАНДАРТИЗАЦИИ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО АВТОМАТИЧЕСКОМУ УПРАВЛЕНИЮ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО ОБРАБОТКЕ ИНФОРМАЦИИ
- МЕМИСТОР
- МЕРЫ СЛОЖНОСТИ в теории автоматов.
- МЕТАЛОГИКА
- МЕТАМАТЕМАТИКА
- МЕТАСИМВОЛЫ
- МЕТАТЕОРИЯ
- МЕТАТРАНСЛЯТОР
- МЕТАЯЗЫК
- МЕТКА
- МЕТОД ЗАМЕНЫ ЯДРА ВЫРОЖДЕННЫМ
- МЕТРИЧЕСКИЕ СВОЙСТВА ДИЗЪЮНКТИВНЫХ НОРМАЛЬНЫХ ФОРМ
- МИКРОКОМАНДА
- МИКРОМОДЕЛЬ ЭКОНОМИЧЕСКАЯ
- МИКРООПЕРАЦИЯ
- МИКРОПРОГРАММ ПРЕОБРАЗОВАНИЯ.
- МИКРОПРОГРАММА
- МИКРОПРОГРАММНАЯ АЛГЕБРА
- МИКРОПРОГРАММНОЕ УПРАВЛЕНИЕ
- МИКРОСХЕМА
- МИКРОЭЛЕКТРОННАЯ ЭЛЕМЕНТНАЯ БАЗА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- МИЛИ АВТОМАТ
- МИНИМАКС
- МИНИМАКСНОЕ РЕШАЮЩЕЕ ПРАВИЛО
- МИНИМАЛЬНО-ФАЗОВАЯ СИСТЕМА
- МИНИМИЗАЦИИ ФУНКЦИЙ МЕТОДЫ
- МИНИМИЗАЦИЯ НАБОРА ПРИЗНАКОВ
- МИНИМИЗАЦИЯ СХЕМ ЦВМ
- МИНИМИЗАЦИЯ ЧИСЛА СОСТОЯНИЙ АВТОМАТА
- «МИНСК»
- «МИР», машина для инженерных расчетов
- «МИР-2» (разработана в 1969)