| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. Операторы рождения и уничтожения
Операторы  были введены для упрощения решения задачи на собственные значения. Если оператор
были введены для упрощения решения задачи на собственные значения. Если оператор  является гамильтонианом одной частицы в одном измерении, то эти операторы не имеют непосредственного физического смысла.
является гамильтонианом одной частицы в одном измерении, то эти операторы не имеют непосредственного физического смысла.
Однако задача на собственные значения  допускает и другую интерпретацию. Ввиду того, что уровни энергии эквидистантны с промежутком
допускает и другую интерпретацию. Ввиду того, что уровни энергии эквидистантны с промежутком  можно рассматривать
можно рассматривать  как гамильтониан системы тождественных частиц, находящихся в одном энергетическом состоянии
как гамильтониан системы тождественных частиц, находящихся в одном энергетическом состоянии  число которых N может изменяться, так что каждое собственное состояние
число которых N может изменяться, так что каждое собственное состояние  соответствует определенному значению
соответствует определенному значению  , следовательно, определенному значению полной энергии. Тогда вектор
, следовательно, определенному значению полной энергии. Тогда вектор  представляет состояние, в котором присутствует
представляет состояние, в котором присутствует  частиц: вектор
частиц: вектор  представляет состояние без частиц (вакуум). При переходе от состояния
представляет состояние без частиц (вакуум). При переходе от состояния  к состоянию
к состоянию  число частиц увеличивается на единицу, а полная энергия системы возрастает на величину
число частиц увеличивается на единицу, а полная энергия системы возрастает на величину  Замечаем, однако, что энергия пустого состояния равна не нулю, а величине
Замечаем, однако, что энергия пустого состояния равна не нулю, а величине  этой аномалии можно избежать, если о качестве оператора энергии системы взять не
этой аномалии можно избежать, если о качестве оператора энергии системы взять не  , но
, но 
Согласно этой интерпретации, оператор N представляет число частиц, и его собственные значения суть целые числа от 0 до  . Оператор
. Оператор  преобразует состояние с
преобразует состояние с  частицами в состояние с
частицами в состояние с  частицей:
частицей:  есть оператор рождения. Оператор а наоборот уменьшает на единицу число присутствующих частиц: а есть оператор уничтожения.
есть оператор рождения. Оператор а наоборот уменьшает на единицу число присутствующих частиц: а есть оператор уничтожения.
Подобная интерпретация гармонического осциллятора широко используется в квантовой теории поля и в теории кристаллических и молекулярных колебаний. Электромагнитное поле, например, может быть представлено в виде суперпозиции плоских волн, характеризуемых вектором поляризации  и волновым вектором
и волновым вектором  соответствующая частота равна
соответствующая частота равна  Классически интенсивность каждой составляющей может изменяться непрерывно, но в квантовой теории эти изменения происходят скачкообразно целыми световыми квантами или фотонами с энергией
Классически интенсивность каждой составляющей может изменяться непрерывно, но в квантовой теории эти изменения происходят скачкообразно целыми световыми квантами или фотонами с энергией  Гамильтониан квантового электромагнитного поля выражается совокупностью членов, относящихся к фотонам определенного типа, который характеризуется
Гамильтониан квантового электромагнитного поля выражается совокупностью членов, относящихся к фотонам определенного типа, который характеризуется  и
и  (пусть индекс
(пусть индекс  обозначает комбинированный индекс
обозначает комбинированный индекс 

Каждый парциальный гамильтониан может быть записан в форме

Операторы  и эрмитово сопряжены друг другу и удовлетворяют коммутационным соотношениям
и эрмитово сопряжены друг другу и удовлетворяют коммутационным соотношениям

которые являются простым обобщением соотношения (10). При этом операторы и  интерпретируются соответственно, как операторы рождения и уничтожения фотона типа
интерпретируются соответственно, как операторы рождения и уничтожения фотона типа  (см. гл. XXI, т. II).
(см. гл. XXI, т. II).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ФОРМАЛИЗМ И ЕГО ИНТЕРПРЕТАЦИЯ
- ГЛАВА I. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- Раздел I. КОНЕЦ КЛАССИЧЕСКОГО ПЕРИОДА
- § 2. Классическая теоретическая физика
- § 3. Успехи в изучении микроскопических явлений и появление квантов в физике
- Раздел II. СВЕТОВЫЕ КВАНТЫ, ИЛИ ФОТОНЫ
- § 5. Эффект Комптона
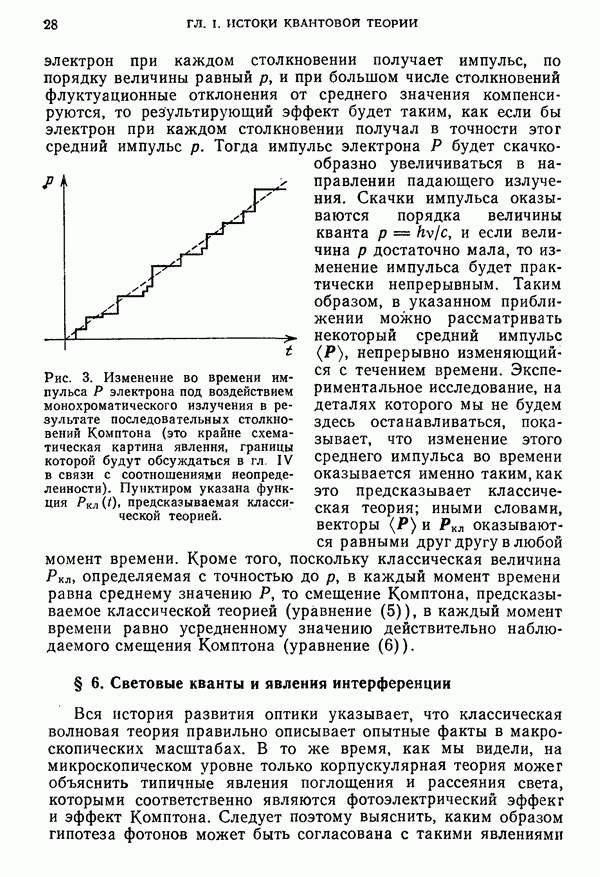
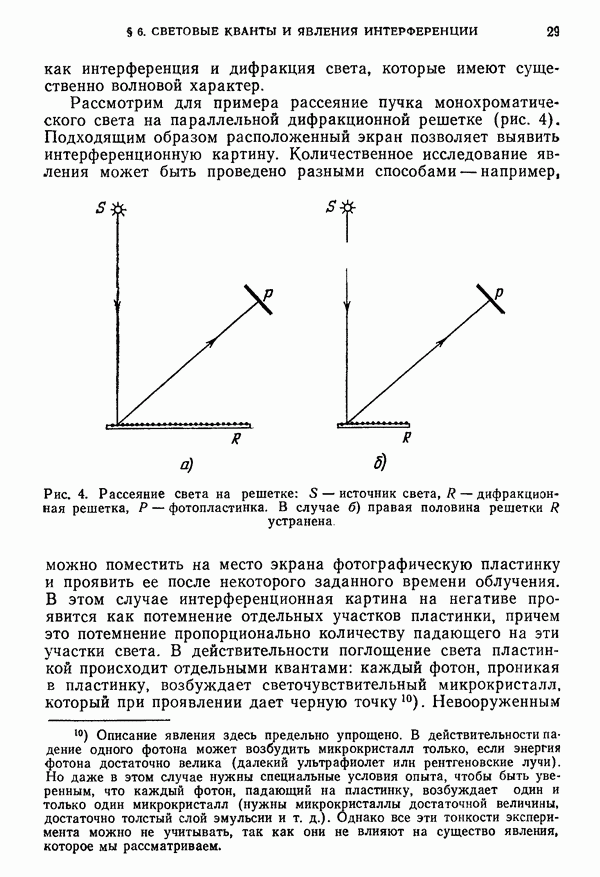
- § 6. Световые кванты и явления интерференции
- § 7. Заключение
- Раздел III. КВАНТОВАНИЕ В АТОМНЫХ СИСТЕМАХ
- § 8. Атомная спектроскопия и трудности классической модели Резерфорда
- § 9. Квантование энергетических уровней атомов
- § 10. Другие примеры квантования: пространственное квантование
- Раздел IV. ПРИНЦИП СООТВЕТСТВИЯ И СТАРАЯ КВАНТОВАЯ ТЕОРИЯ
- § 11. Недостаточность классической корпускулярной теории
- § 12. Принцип соответствия
- § 13. Применение принципа соответствия при вычислении постоянной Ридберга
- § 14. Лагранжева и гамильтонова формы уравнений к лассической механики
- § 15. Правила квантования Бора — Зоммерфельда
- § 16. Достижения и ограниченность старой теории квантов
- § 17. Заключение
- ГЛАВА II. ВОЛНЫ ВЕЩЕСТВА И УРАВНЕНИЕ ШРЕДИНГЕРА
- Раздел I. ВОЛНЫ ВЕЩЕСТВА
- § 3. Свободный волновой пакет. Фазовая и групповая скорости
- § 4. Волновой пакет в медленно меняющемся поле
- § 5. Квантование уровней энергии атомов
- § 6. Дифракция волн вещества
- § 7. Корпускулярная структура вещества
- § 8. Универсальный характер дуализма волна — частица
- Раздел II. УРАВНЕНИЕ ШРЕДИНГЕРА
- § 9. Закон сохранения числа частиц вещества
- § 10. Необходимость волнового уравнения и условия, которым оно должно удовлетворять
- § 11. Понятие оператора
- § 12. Волновое уравнение для свободной частицы
- § 13. Частица в области действия скалярного потенциала
- § 14. Заряженная частица в электромагнитном поле
- § 15. Общее правило построения уравнения Шредингера по принципу соответствия
- Раздел III. СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- § 16. Исследование стационарных состояний
- § 17. Общие свойства уравнения. Структура энергетического спектра
- ГЛАВА III. КВАНТОВЫЕ СИСТЕМЫ В ОДНОМ ИЗМЕРЕНИИ
- Раздел I. ПРЯМОУГОЛЬНЫЕ ПОТЕНЦИАЛЫ
- § 3. Скачок потенциала. Отражение и прохождение волн
- § 4. Бесконечно высокий потенциальный барьер
- § 5. Бесконечно глубокая потенциальная яма. Дискретный спектр
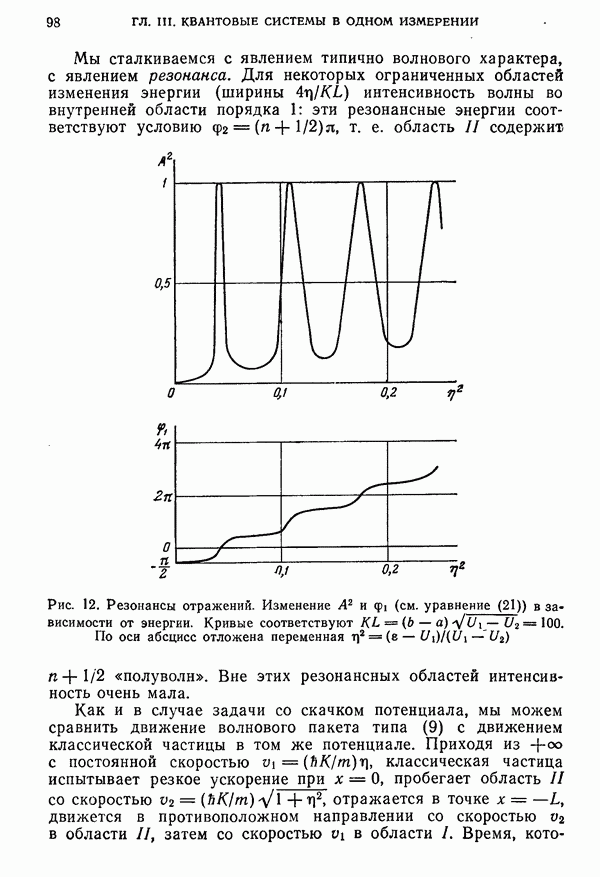
- § 6. Конечная потенциальная яма. Резонансы
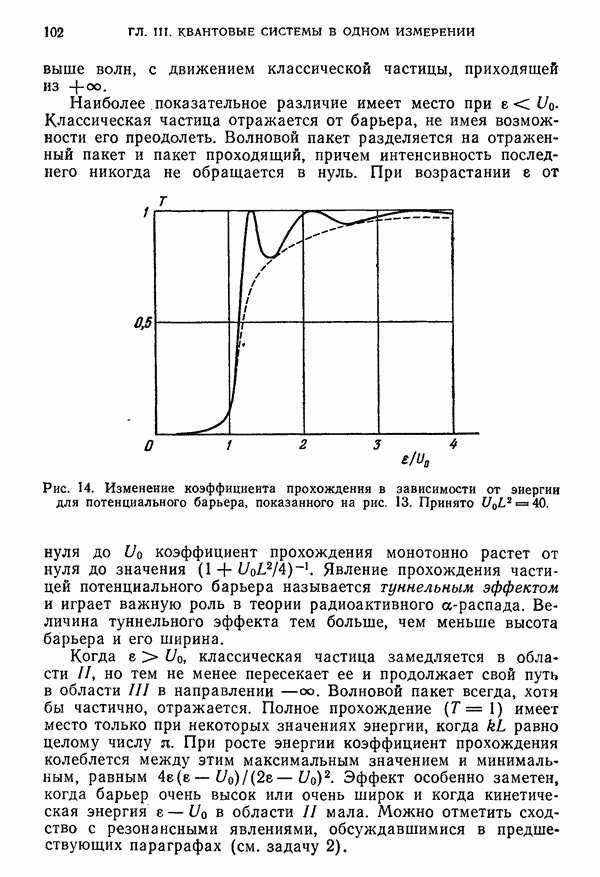
- § 7. Прохождение прямоугольного потенциального барьера. Туннельный эффект
- Раздел II. ОБЩИЕ СВОЙСТВА ОДНОМЕРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- § 8. Свойства вронскиана
- § 9. Асимптотическое поведение решений
- § 10. Структура спектра собственных значений
- § 11. Состояния непрерывного спектра: отражение и прохождение волн
- § 12. Число узлов связанных состояний
- § 13. Соотношения ортогональности
- § 14. Замечание по поводу четности
- ГЛАВА IV. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОРПУСКУЛЯРНО-ВОЛНОВОГО ДУАЛИЗМА И СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ
- Раздел I. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛНОВЫХ ФУНКЦИИ В ВОЛНОВОЙ МЕХАНИКЕ
- § 2. Вероятности результатов измерения координаты и импульса частицы
- § 3. Сохранение нормы во времени
- § 4. Понятие потока
- § 5. Средние значения функций от r и от p
- § 6. Системы многих частиц
- Раздел II. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- § 7. Соотношения неопределенности координата-импульс квантовой частицы
- § 8. Точное выражение соотношений неопределенности координата-импульс
- § 9. Обобщение: соотношения неопределенности для сопряженных переменных
- § 10. Соотношение неопределенности время-энергия
- § 11. Соотношения неопределенности для фотонов
- Раздел III. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ И МЕХАНИЗМ ИЗМЕРЕНИЯ
- § 12. Неконтролируемое возмущение в процессе измерения
- § 13. Измерения положения в пространстве
- § 14. Измерения импульса
- Раздел IV. ОПИСАНИЕ ЯВЛЕНИЙ В КВАНТОВОЙ ТЕОРИИ. ДОПОЛНИТЕЛЬНОСТЬ И ПРИЧИННОСТЬ
- § 16. Описание микроскопических явлений и дополнительность
- § 17. Дополнительные переменные. Совместные переменные
- § 18. Корпускулярно-волновой дуализм и дополнительность
- § 19. Дополнительность и причинность
- ГЛАВА V. ФОРМАЛИЗМ ВОЛНОВОЙ МЕХАНИКИ И ЕГО ИСТОЛКОВАНИЕ
- Раздел I. ЭРМИТОВЫ ОПЕРАТОРЫ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Пространство волновых функций
- § 3. Определение средних значений
- § 4. Отсутствие флуктуаций и проблема собственных значений
- Раздел II. ИССЛЕДОВАНИЕ ДИСКРЕТНОГО СПЕКТРА
- § 5. Собственные значения и собственные функции эрмитового оператора
- § 6. Разложение волновой функции в ряд по ортонормированным собственным функциям
- § 7. Статистическое распределение результатов измерений величины, оператор которой обладает полной системой собственных функций с конечной нормой
- Раздел III. СТАТИСТИКА ИЗМЕРЕНИЙ В ОБЩЕМ СЛУЧАЕ
- § 8. Трудности описания непрерывного спектра. Введение дельта-функции Дирака
- § 9. Разложение по собственным функциям в общем случае. Условие замкнутости
- § 10. Статистическое распределение результатов измерения в общем случае
- § 11. Другие методы исследования непрерывного спектра
- § 12. Комментарии и примеры
- Раздел IV. ОПРЕДЕЛЕНИЕ ВОЛНОВОЙ ФУНКЦИИ
- § 13. Операция измерения и редукция волнового пакета. Идеальные измерения
- § 14. Коммутирующие наблюдаемые и совместные переменные
- § 15. Полные наборы коммутирующих наблюдаемых
- § 16. Чистые и смешанные состояния
- Раздел V. АЛГЕБРА КОММУТАТОРОВ И ЕЕ ПРИЛОЖЕНИЯ
- § 17. Алгебра коммутаторов и основные свойства коммутаторов
- § 18. Соотношения коммутации для момента импульса
- § 19. Изменение статистического распределения во времени. Интегралы движения
- § 20. Примеры интегралов движения. Энергия. Четность
- ГЛАВА VI. КЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ И МЕТОД ВКБ
- Раздел I. КЛАССИЧЕСКИЙ ПРЕДЕЛ ВОЛНОВОЙ МЕХАНИКИ
- § 2. Теорема Эренфеста
- § 3. Движение и расплывание волновых пакетов
- § 4. Классический предел уравнения Шредингера
- § 5. Кулоновское рассеяние. Формула Резерфорда
- Раздел II. МЕТОД ВКБ
- § 7. Решения ВКБ в одном измерении
- § 8. Условия применимости приближения ВКБ
- § 9. Граничные точки и формулы согласования
- § 10. Прохождение потенциального барьера
- § 11. Уровни энергии в потенциальной яме
- ГЛАВА VII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ А. МАТЕМАТИЧЕСКИЙ АППАРАТ
- § 1. Принцип суперпозиции и представление динамических состояний векторами
- Раздел I. ВЕКТОРЫ И ОПЕРАТОРЫ
- § 2. Векторное пространство. Кет-векторы
- § 3. Дуальное пространство. Бра-векторы
- § 4. Скалярное произведение
- § 5. Линейные операторы
- § 6. Тензорное произведение двух векторных пространств
- Раздел II. ЭРМИТОВЫ ОПЕРАТОРЫ, ПРОЕКТОРЫ И НАБЛЮДАЕМЫЕ
- § 7. Сопряженные операторы и правила сопряжения
- § 8. Эрмитовы (самосопряженные) операторы, положительна определенные операторы, унитарные операторы
- § 9. Проблема собственных значений и наблюдаемые
- § 10. Проекторы (или операторы проектирования)
- § 11. Алгебра проекторов
- § 12. Наблюдаемые, обладающие только дискретным спектром
- § 13. Наблюдаемые в общем случае и обобщенное соотношение замкнутости
- § 14. Функции наблюдаемых
- § 15. Операторы, коммутирующие с наблюдаемой. Коммутирующие наблюдаемые
- Раздел III. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ
- § 16. Общее понятие о конечных матрицах
- § 17. Квадратные матрицы
- § 18. Бесконечные матрицы
- § 19. Представление векторов и операторов матрицами
- § 20. Преобразования матриц
- § 21. Смена представления
- § 22. Унитарные преобразования операторов и векторов
- ГЛАВА VIII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ Б. ОПИСАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
- Раздел I. ДИНАМИЧЕСКИЕ СОСТОЯНИЯ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
- § 2. Определение вероятностей. Постулаты измерения
- § 3. Наблюдаемые квантовой системы и соотношения коммутации
- § 4. Соотношения неопределенности Гейзенберга
- § 5. Определение состояний и построение пространства
- § 6. Квантовая одномерная система, обладающая классическим аналогом
- § 7. Построение пространства состояний путем тензорного умножения более простых пространств
- Раздел II. УРАВНЕНИЯ ДВИЖЕНИЯ
- § 8. Оператор эволюции и уравнение Шредингера
- § 9. «Представление» Шредингера
- § 10. «Представление» Гейзенберга
- § 11. «Представление» Гейзенберга и принцип соответствия
- § 12. Интегралы движения
- § 13. Уравнение эволюции средних значений и соотношение неопределенности время-энергия
- § 14. Промежуточные «представления»
- Раздел III. РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ ТЕОРИИ
- § 16. Волновая механика
- § 17. Представление {р}
- § 18. Пример: движение свободного волнового пакета
- § 19. Другие представления. Представление, в котором диагональна энергия
- Раздел IV. КВАНТОВАЯ СТАТИСТИКА
- § 20. Системы с неполной информацией и смешанные состояния
- § 21. Матрица плотности
- § 22. Эволюция смешанного состояния во времени
- § 23. Характеристические свойства матрицы плотности
- § 24. Чистые состояния
- § 25. Классическая статистика и квантовая статистика
- ЧАСТЬ II. ПРОСТЫЕ СИСТЕМЫ
- ГЛАВА IX. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПОТЕНЦИАЛ
- Раздел I. ЧАСТИЦА В ЦЕНТРАЛЬНО-СИММЕТРИЧНОМ ПОТЕНЦИАЛЬНОМ ПОЛЕ. ОБЩЕЕ РАССМОТРЕНИЕ ПРОБЛЕМЫ
- § 2. Гамильтониан частицы в сферических координатах
- § 3. Отделение угловых переменных. Сферические функции
- § 4. Радиальное уравнение
- § 5. Собственные решения радиального уравнения. Структура спектра.
- § 6. Заключение
- Раздел II. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПРЯМОУГОЛЬНЫЙ ПОТЕНЦИАЛ. СВОБОДНАЯ ЧАСТИЦА
- § 7. Сферические функции Бесселя
- § 8. Свободная частица. Свободные плоские и сферические волны
- § 9. Разложение плоской волны по сферическим функциям
- § 10. Сферическая прямоугольная яма
- Раздел III. ЗАДАЧА ДВУХ ТЕЛ. ОТДЕЛЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС
- § 11. Отделение движения центра масс в классической механике
- § 12. Отделение движения центра масс квантовой системы двух частиц
- § 13. Система многих частиц
- ГЛАВА X. ПРОБЛЕМА РАССЕЯНИЯ. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ И МЕТОД ФАЗОВЫХ СДВИГОВ
- Раздел I. ЭФФЕКТИВНЫЕ СЕЧЕНИЯ И АМПЛИТУДЫ РАССЕЯНИЯ
- § 3. Стационарная волна рассеяния
- § 4. Описание рассеяния при помощи пучка волновых пакетов
- § 5. Рассеяние волнового пакета на потенциале
- § 6. Вычисление эффективных сечений
- § 7. Столкновение двух частиц. Лабораторная система и система центра масс
- Раздел II. РАССЕЯНИЕ ЦЕНТРАЛЬНЫМ ПОТЕНЦИАЛОМ. ФАЗОВЫЕ СДВИГИ
- § 8. Разложение по парциальным волнам. Метод фазовых сдвигов
- § 9. Квазиклассическое представление рассеяния. Прицельный параметр
- Раздел III. ПОТЕНЦИАЛ ОГРАНИЧЕННОГО РАДИУСА ДЕЙСТВИЯ
- § 10. Сдвиг фазы и логарифмическая производная
- § 11. Сдвиги фаз при низких энергиях
- § 12. Парциальные волны более высокого порядка. Сходимость ряда
- § 13. Рассеяние на твердой сфере
- Раздел IV. РЕЗОНАНСНОЕ РАССЕЯНИЕ
- § 14. Рассеяние глубокой прямоугольной потенциальной ямой
- § 15. Общий закон резонансного рассеяния. Метастабильные состояния
- § 16. Наблюдение времени жизни метастабильных состояний
- Раздел V. РАЗЛИЧНЫЕ ФОРМУЛЫ И СВОЙСТВА
- § 17. Интегральные представления фазовых сдвигов
- § 18. Зависимость фазовых сдвигов от формы потенциала
- § 19. Приближение Борна
- § 20. Теория эффективного радиуса действия. Формула Бете
- ГЛАВА XI. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ
- Раздел I. АТОМ ВОДОРОДА
- § 2. Уравнение Шредингера для атома водорода
- § 3. Порядок величины энергии связи основного состояния
- § 4. Решение уравнения Шредингера в сферических координатах
- § 5. Спектр энергии. Вырождение
- § 6. Собственные функции связанных состояний
- Раздел II. КУЛОНОВСКОЕ РАССЕЯНИЕ
- § 7. Кулоновская функция рассеяния
- § 8. Формула Резерфорда
- § 9. Разложение по парциальным волнам
- § 10. Разложение по сферическим функциям
- § 11. Модификация кулоновского потенциала короткодействующим взаимодействием
- ГЛАВА XII. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- Раздел I. СОБСТВЕННЫЕ СОСТОЯНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ГАМИЛЬТОНИАНА
- § 3. Введение операторов
- § 4. Спектр и базисная система оператора N
- § 5. Представление [N]
- § 6. Операторы рождения и уничтожения
- § 7. Представление {Q}. Полиномы Эрмита
- Раздел II. ПРИЛОЖЕНИЯ И РАЗЛИЧНЫЕ СВОЙСТВА
- § 8. Производящая функция собственных функций
- § 9. Интегрирование уравнений Гейзенберга
- § 10. Классический и квантовый осцилляторы
- § 11. Движение минимизирующего волнового пакета и классический предел
- § 12. Гармонические осцилляторы в термодинамическом равновесии
- Раздел III. ИЗОТРОПНЫЕ МНОГОМЕРНЫЕ ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 13. Общее исследование изотропного осциллятора в р измерениях
- § 14. Изотропный осциллятор в двух измерениях
- § 15. Изотропный осциллятор в трех измерениях
- ДОПОЛНЕНИЕ А ОБОБЩЕННЫЕ ФУНКЦИИ, «ФУНКЦИЯ» ДЕЛЬТА И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Понятие функционала и строгий подход к проблеме непрерывного спектра
- § 2. Определение обобщенных функций
- § 3. Линейная комбинация обобщенных функций
- § 4. Произведение двух обобщенных функций
- § 5. Ряды и интегралы обобщенных функций
- § 6. Дифференцирование обобщенных функций
- Раздел II. СВОЙСТВА «ФУНКЦИИ» ДЕЛЬТА
- § 8. Представление в виде предела ядра интегрального оператора
- § 9. Основные свойства
- § 10. Производные
- Раздел III. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 11. Преобразование Фурье. Определение
- § 12. Абсолютно интегрируемые функции f(x)
- § 13. Функции «хи» (основные функции)
- § 14. Преобразование Фурье обобщенных функций. Определение
- § 15. Обобщенные функции медленного роста
- § 16. Квадратично интегрируемые функции
- § 17. Преобразование свертки
- ДОПОЛНЕНИЕ Б. СПЕЦИАЛЬНЫЕ ФУНКЦИИ И СВЯЗАННЫЕ С НИМИ ФОРМУЛЫ
- § 1. Уравнение Лапласа и вырожденная гипергеометрическая функция
- § 2. Полиномы Лагерра
- § 3. Собственные функции водородоподобных атомов (теория Шредингера)
- § 4. Чисто кулоновская волна
- § 5. Сферические кулоновские функции
- Раздел II. СФЕРИЧЕСКИЕ ФУНКЦИИ БЕССЕЛЯ
- § 6. Сферические функции Бесселя
- Раздел III. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР И ПОЛИНОМЫ ЭРМИТА
- § 7. Полиномы Эрмита
- § 8. Собственные функции гармонического осциллятора
- Раздел IV. ПОЛИНОМЫ И ФУНКЦИИ ЛЕЖАНДРА, СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 9. Полиномы и функции Лежандра
- § 10. Сферические функции
- Раздел V РАЗЛОЖЕНИЯ И РАЗЛИЧНЫЕ ФОРМУЛЫ