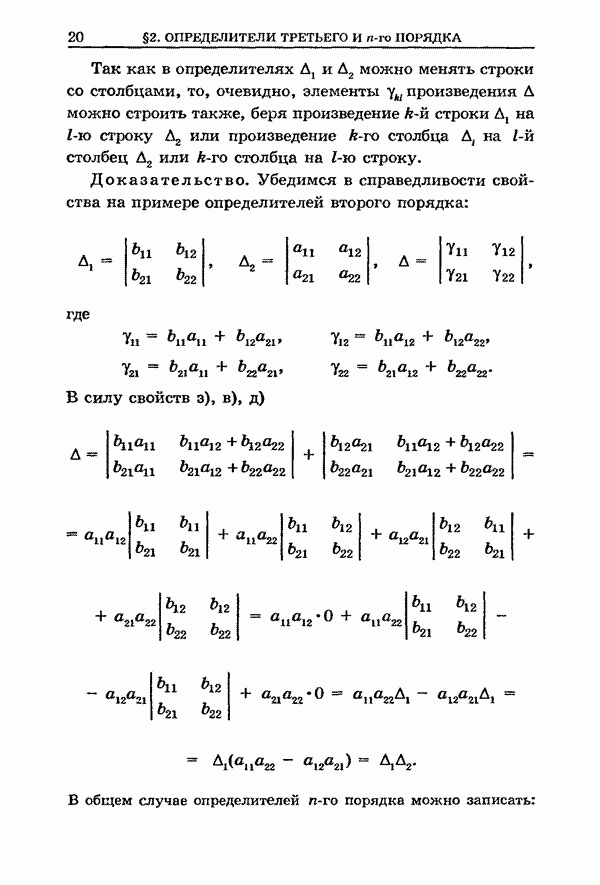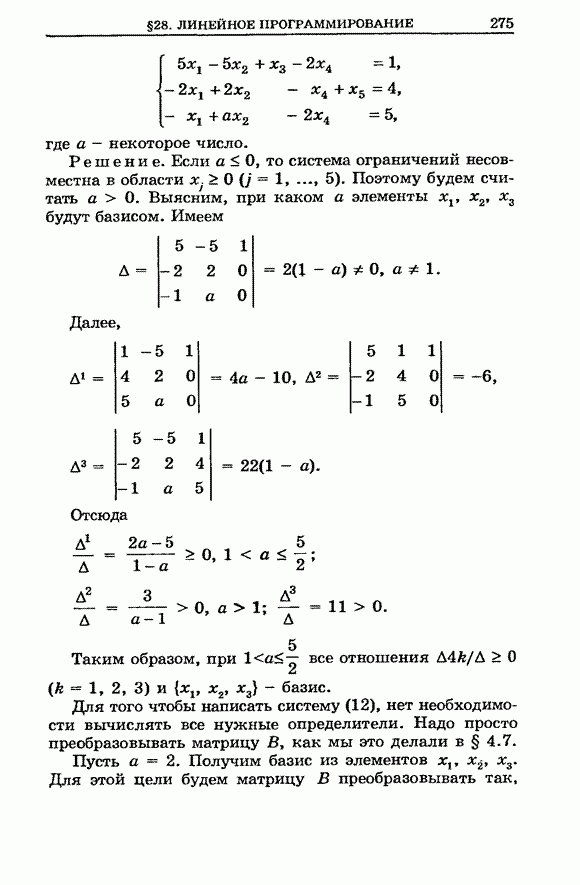| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 15. Линейные операторы
Зададим произвольную квадратную матрицу
 . (1)
. (1)
Матрицу ![]() можно рассматривать
как оператор, приводящий в соответствие каждому вектору
можно рассматривать
как оператор, приводящий в соответствие каждому вектору ![]() вектор
вектор ![]() , компоненты которого
вычисляются по формулам
, компоненты которого
вычисляются по формулам
 (2)
(2)
или, короче,
 . (2')
. (2')
Говорят, что ![]() -я координата вектора
-я координата вектора ![]() записывается с
помощью
записывается с
помощью ![]() -й
строки
-й
строки ![]() .
Этот оператор коротко будем записывать так:
.
Этот оператор коротко будем записывать так:
![]() (2'')
(2'')
Замечание 1.
Если ![]() и
далее
и
далее ![]() -комплексные
числа, то
-комплексные
числа, то ![]() надо
считать комплексным пространством. Если же
надо
считать комплексным пространством. Если же ![]() ,
, ![]() - действительные числа, то
- действительные числа, то ![]() может быть и
действительным и комплексным пространством.
может быть и
действительным и комплексным пространством.
В случае
одномерного пространства ![]() векторы
векторы ![]() и
и ![]() суть числа, и оператор (2")
превращается в функцию
суть числа, и оператор (2")
превращается в функцию
![]() .
.
Оператор (2") линейный. Это значит, что он удовлетворяет условию
![]()
для любых
векторов ![]() ,
, ![]() и чисел
и чисел ![]() ,
, ![]() . В самом деле,
. В самом деле,
 .
.
Если матрицы ![]() и
и ![]() равны, т. е. имеют
равные соответствующие элементы
равны, т. е. имеют
равные соответствующие элементы ![]() , то они определяют тождественно равные
операторы:
, то они определяют тождественно равные
операторы:
![]() . (3)
. (3)
Обратно, из равенства (3) вытекает, что
![]() ,
,
т. е. равенство
матриц ![]() и
и ![]()
![]() . В этом легко убедиться, если
положить в (3)
. В этом легко убедиться, если
положить в (3)
![]() ,
,
где 1 стоит на ![]() -м месте
-м месте ![]() .
.
Таким образом,
различным матрицам ![]() соответствуют
различные операторы - если две матрицы
соответствуют
различные операторы - если две матрицы ![]() , и
, и ![]() отличаются хотя бы одним элементом, то
обязательно существует вектор
отличаются хотя бы одним элементом, то
обязательно существует вектор ![]() , для которого
, для которого
![]() .
.
Пусть, кроме ![]() , задан еще другой
оператор
, задан еще другой
оператор ![]() ,
определяемый квадратной матрицей
,
определяемый квадратной матрицей ![]() -го порядка
-го порядка
![]() .
.
Каждому ![]() соответствует при
помощи оператора
соответствует при
помощи оператора ![]() вектор
вектор
![]() , которому
при помощи оператора
, которому
при помощи оператора ![]() соответствует вектор
соответствует вектор ![]() с компонентами,
вычисляемыми по формулам
с компонентами,
вычисляемыми по формулам
 .
.
В результате получим сложный линейный оператор
![]() (4)
(4)
где

с матрицей ![]() , называемой
произведением матриц
, называемой
произведением матриц ![]() и
и ![]() и обозначаемой так:
и обозначаемой так:
![]() , (5)
, (5)
где
 , (6)
, (6)
т.е. чтобы
получить элемент ![]() матрицы
матрицы
![]() (принадлежащий
к ее
(принадлежащий
к ее ![]() -й
строке и
-й
строке и ![]() -му
столбцу), надо элементы
-му
столбцу), надо элементы ![]() -й строки матрицы
-й строки матрицы ![]() умножить на соответствующие
элементы
умножить на соответствующие
элементы ![]() -того
столбца матрицы
-того
столбца матрицы ![]() и
результат сложить.
и
результат сложить.
Определитель
матрицы ![]() равен
произведению определителей матриц
равен
произведению определителей матриц ![]() и
и ![]() :
:
![]() (7)
(7)
Это свойство вытекает из формулы для произведения определителей (см. § 2, свойство к)).
Пусть матрица
оператора ![]() (см.
(1)) имеет определитель, не равный нулю:
(см.
(1)) имеет определитель, не равный нулю:
![]() .
.
В этом случае
(см. § 4, теорема 1) система уравнений (2), или, что все равно, операторное
уравнение ![]() имеет
единственное решение
имеет
единственное решение ![]() при любом заданном
при любом заданном ![]() . При этом формулы, по которым
находится
. При этом формулы, по которым
находится ![]() для
заданного
для
заданного ![]() ,
имеют вид
,
имеют вид
 . (8)
. (8)
Здесь
![]() (9)
(9)
(см. § 4, (З')),
где ![]() -
алгебраическое дополнение элемента
-
алгебраическое дополнение элемента ![]() в определителе
в определителе ![]() .
.
Впрочем, для нас
сейчас важно только отметить, что числа ![]() , являются элементами матрицы
, являются элементами матрицы
![]() ,
,
обладающей следующими замечательными свойствами:
![]() , (10)
, (10)
![]() . (11)
. (11)
В самом деле,
произвольный вектор ![]() переходит посредством оператора
переходит посредством оператора ![]() в некоторый вектор
в некоторый вектор ![]() , который переходит
посредством оператора
, который переходит
посредством оператора ![]() обратно в
обратно в ![]() . С другой стороны, каждому
. С другой стороны, каждому ![]() соответствует при
помощи оператора
соответствует при
помощи оператора ![]() (см.
(8)) некоторый
(см.
(8)) некоторый ![]() и
притом такой, что
и
притом такой, что ![]() .
.
В равенстве (11)
можно, очевидно, вместо ![]() поставить другую букву, поэтому мы
получили тождества
поставить другую букву, поэтому мы
получили тождества
![]() .
.
Оператор ![]() называется единичным
оператором. Матрица, ему соответствующая, имеет вид
называется единичным
оператором. Матрица, ему соответствующая, имеет вид

и называется единичной. Мы доказали, что
![]() .
.
Оператор ![]() , обладающий этим
свойством, называется обратным к оператору
, обладающий этим
свойством, называется обратным к оператору ![]() и обозначается через
и обозначается через ![]() . Соответственно его
матрица называется обратной матрицей к матрице
. Соответственно его
матрица называется обратной матрицей к матрице ![]() и обозначается тоже через
и обозначается тоже через ![]() . Элементы матрицы
. Элементы матрицы ![]() находятся по
элементам матрицы
находятся по
элементам матрицы ![]() с
помощью формул (9).
с
помощью формул (9).
Мы доказали, что
если определитель ![]() квадратной
матрицы
квадратной
матрицы ![]() не
равен нулю, то она имеет обратную матрицу
не
равен нулю, то она имеет обратную матрицу ![]() . Для
. Для ![]() , таким образом, выполняются свойства
, таким образом, выполняются свойства
![]() .
.
Если
определитель матрицы ![]() равен нулю
равен нулю ![]() , то она не имеет обратной
матрицы. Достаточно сказать, что уравнение
, то она не имеет обратной
матрицы. Достаточно сказать, что уравнение ![]() имеет решение не для всякого
имеет решение не для всякого ![]() . Между тем свойство
. Между тем свойство ![]() , если оно
выполняется, утверждает, что каждому
, если оно
выполняется, утверждает, что каждому ![]() соответствует (при помощи оператора
соответствует (при помощи оператора ![]() ) такой
) такой ![]() , что он есть решение
уравнения
, что он есть решение
уравнения ![]() .
.
Замечание.
Операцию умножения матриц можно распространить и на неквадратные матрицы ![]() и
и ![]() , лишь бы число
столбцов матрицы
, лишь бы число
столбцов матрицы ![]() совпадало
с числом строк матрицы
совпадало
с числом строк матрицы ![]() . Тогда умножение матриц производим по
формулам, подобным (6). Например, если
. Тогда умножение матриц производим по
формулам, подобным (6). Например, если
 ,
,  , то
, то  .
.
Произведение ![]() в данном случае
рассматривать нельзя, так как у матрицы
в данном случае
рассматривать нельзя, так как у матрицы ![]() два столбца, а у матрицы
два столбца, а у матрицы ![]() три строки.
три строки.
Для квадратных
матриц ![]() и
и
![]() произведения
произведения
![]() и
и ![]() имеют смысл, но
далеко не всегда
имеют смысл, но
далеко не всегда ![]() равно
равно
![]() . Например,
если
. Например,
если
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() ,
,
т.е. ![]() .
.
Легко проверить,
что ![]() .
.
Если ![]() -линейный оператор,
то запись
-линейный оператор,
то запись ![]() можно
рассматривать как произведение матрицы
можно
рассматривать как произведение матрицы ![]() на одностолбцовую матрицу
на одностолбцовую матрицу
 .
.
Пусть заданы
линейные операторы ![]() и
и
![]() . Суммой их
называется оператор
. Суммой их
называется оператор ![]() , определяемый равенством
, определяемый равенством
![]() .
.
Очевидно,
матрица оператора ![]() совпадает
с матрицей, равной сумме матриц операторов
совпадает
с матрицей, равной сумме матриц операторов ![]() и
и ![]() .
.
Легко проверить, что
![]()
![]() .
.
Пример 1. Найти матрицу, обратную матрице
 .
.
Матрица ![]() определяет линейный
оператор
определяет линейный
оператор ![]() ,
приводящий в соответствие каждому вектору
,
приводящий в соответствие каждому вектору ![]() вектор
вектор ![]() при помощи равенств
при помощи равенств
![]() ,
,
![]() ,
,
![]() ,
,
Эти равенства
можно рассматривать также как линейную систему трех уравнений относительно
неизвестных ![]() .
Определитель этой системы не равен пулю. Но тогда ее можно решить при любых
заданных
.
Определитель этой системы не равен пулю. Но тогда ее можно решить при любых
заданных ![]() . В
результате получим равенства
. В
результате получим равенства
![]() ,
,
![]() ,
,
![]() ,
,
определяющие
оператор ![]() , обратный
к оператору
, обратный
к оператору ![]() .
Матрица этого оператора
.
Матрица этого оператора
 .
.
Это и есть
матрица, обратная к матрице ![]() .
.
Элементы матрицы
![]() можно
получить путем вычислений по формулам (9). Обозначим элементы обратной матрицы
можно
получить путем вычислений по формулам (9). Обозначим элементы обратной матрицы ![]() через
через ![]() . Имеем
. Имеем ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Таким образом,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Итак,
![]()
 .
.
Пример 2.
Вычислить произведение матриц ![]() , где
, где
 ,
,  .
.
Вычисление можно произвести по формулам (5), (6), но можно рассуждать и следующим образом.
Матрица ![]() определяет оператор
определяет оператор ![]() , приводящий в
соответствие векторам
, приводящий в
соответствие векторам ![]() векторы
векторы ![]() при помощи равенств
при помощи равенств
![]() ,
,
![]() ,
,
![]() ,
,
Матрица же ![]() определяет оператор
определяет оператор ![]() , приводящий в
соответствие векторам
, приводящий в
соответствие векторам ![]() векторы
векторы ![]() при помощи равенств
при помощи равенств
![]() ,
,
![]() ,
,
![]() .
.
Но тогда оператор
![]()
определяется равенствами
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
произведение ![]() матриц
матриц
![]() и
и ![]() есть матрица
есть матрица
 .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
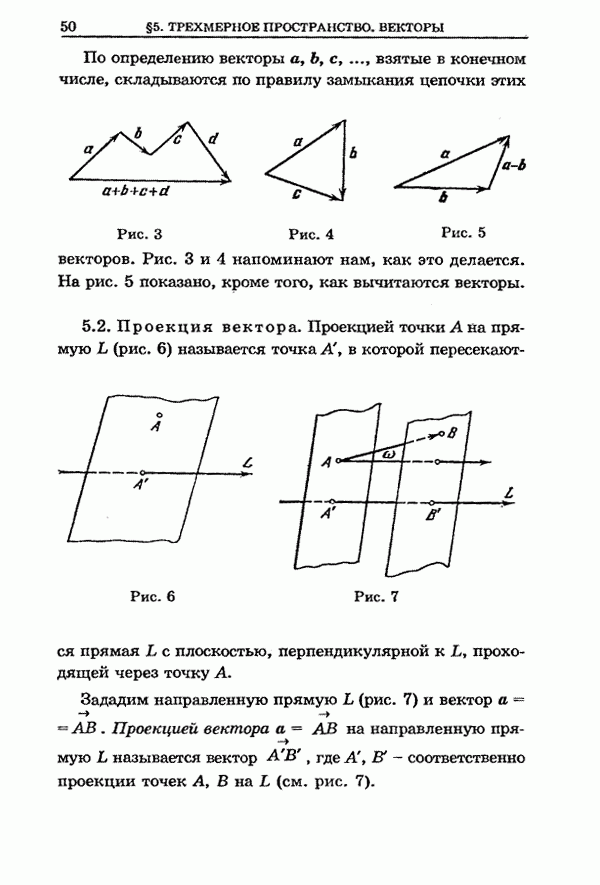
- 5.1. Понятие вектора
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
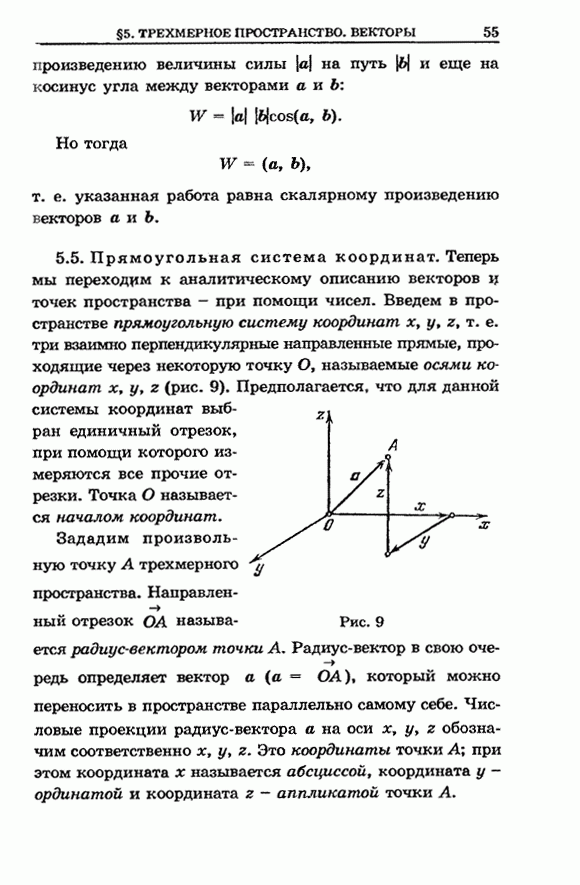
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
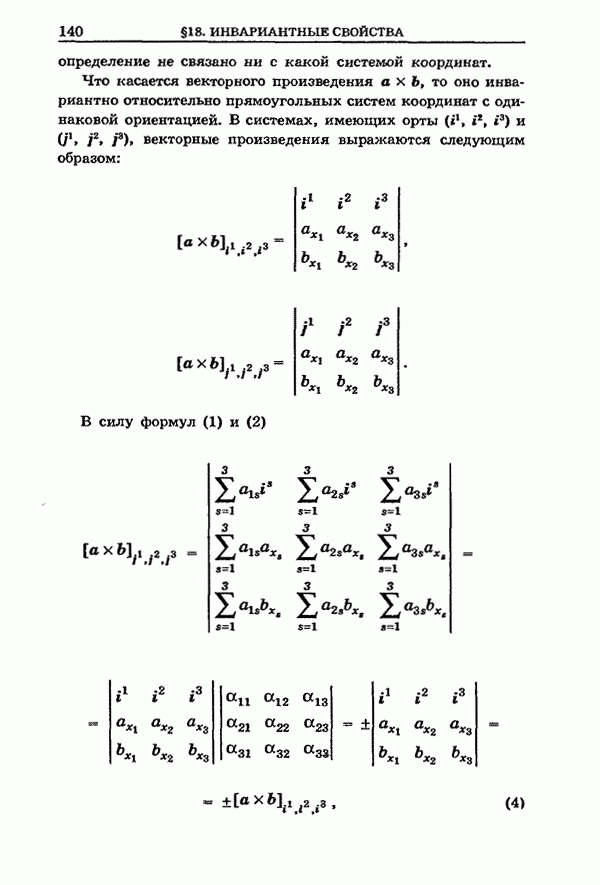
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
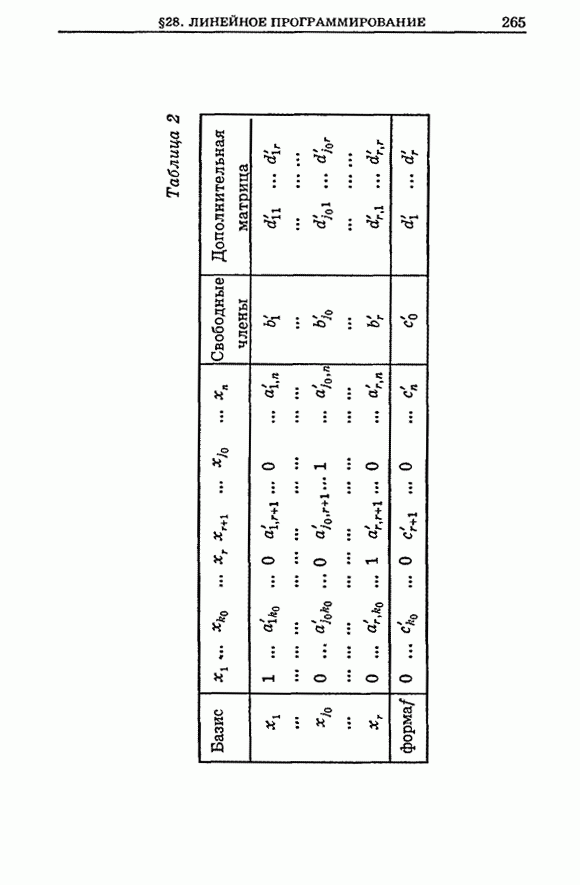
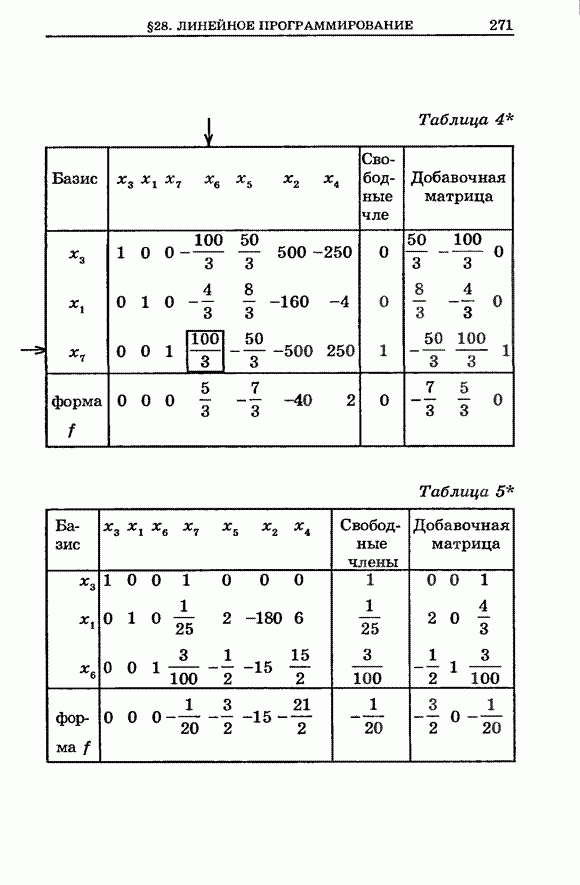
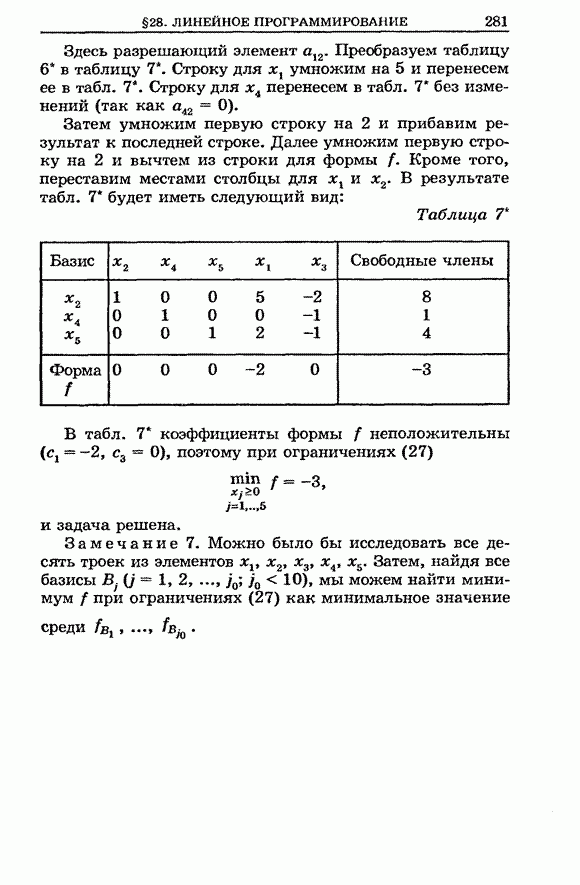
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса