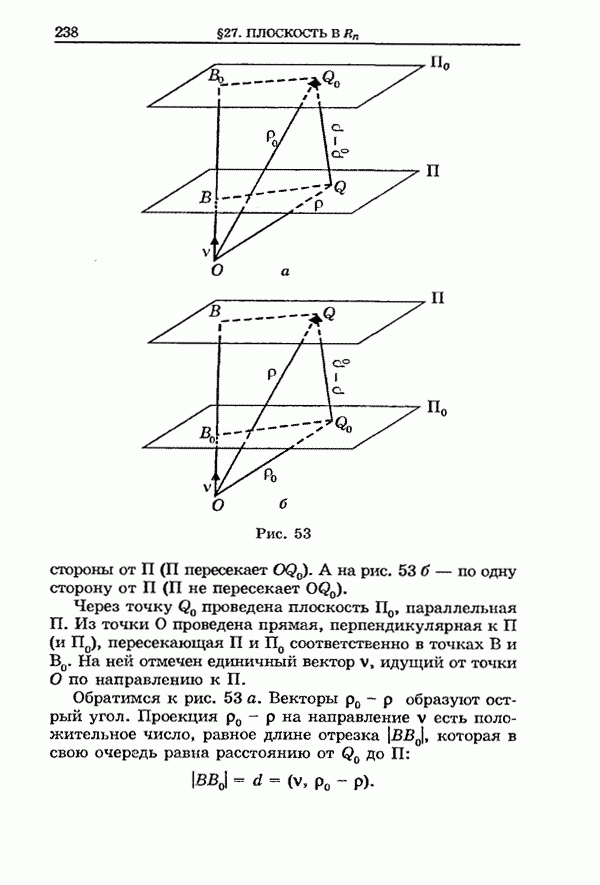
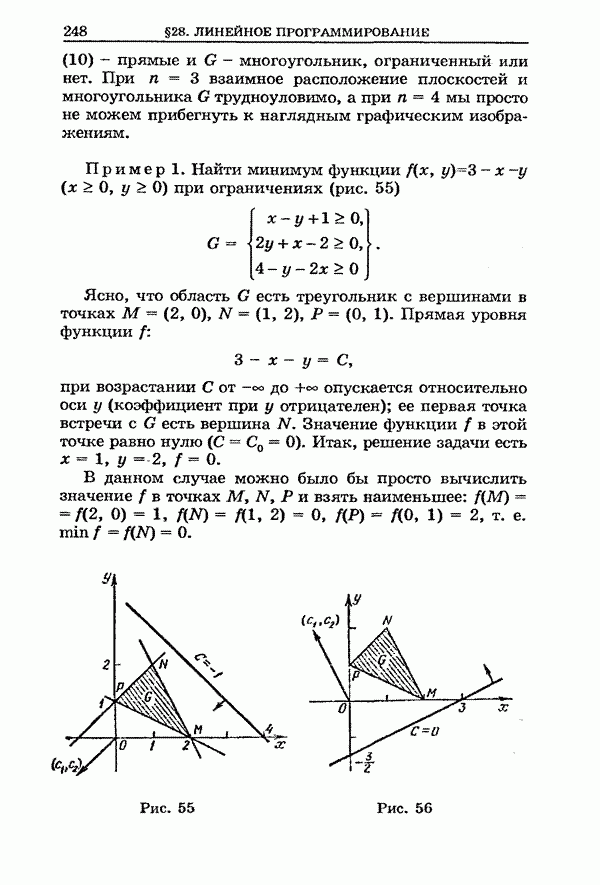
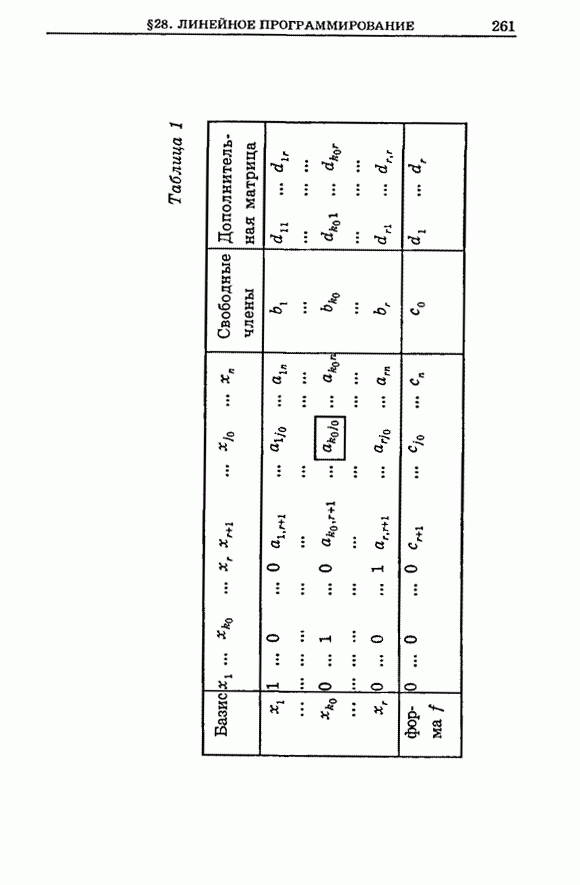
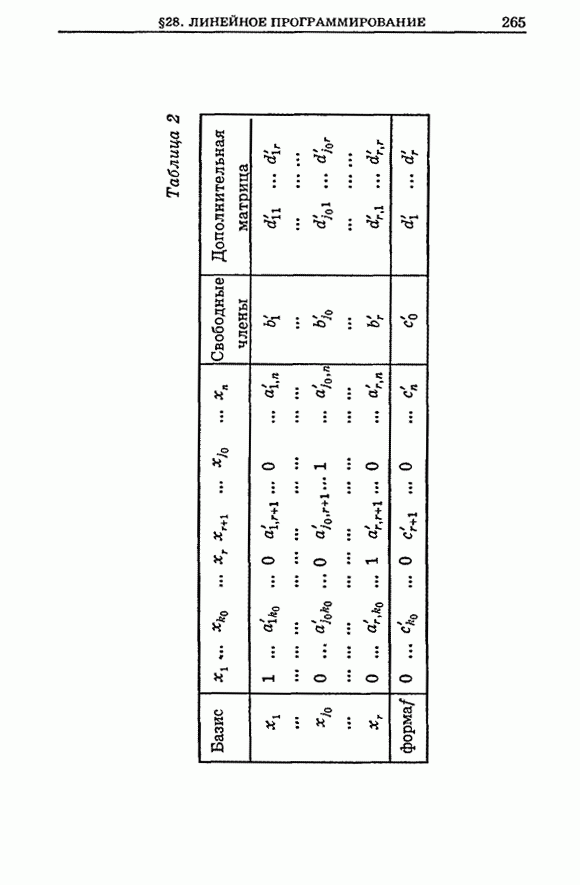
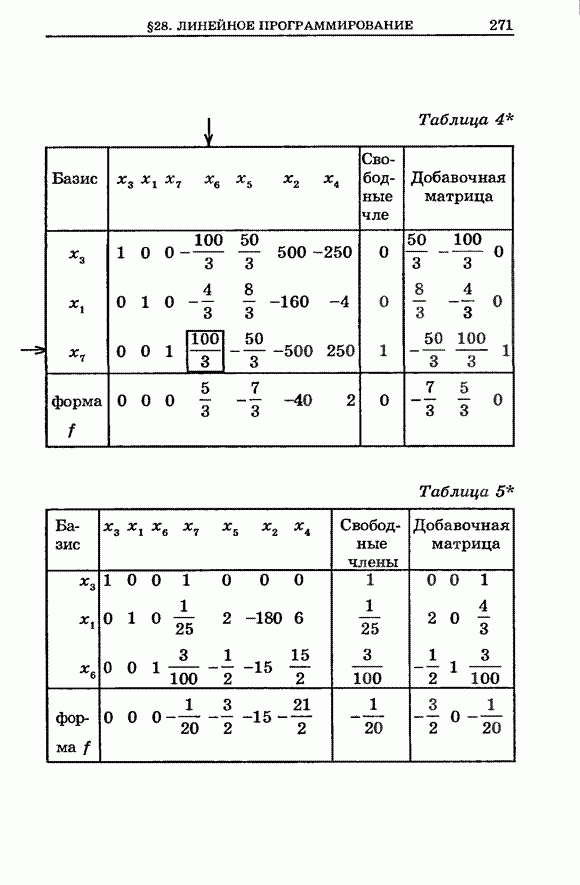
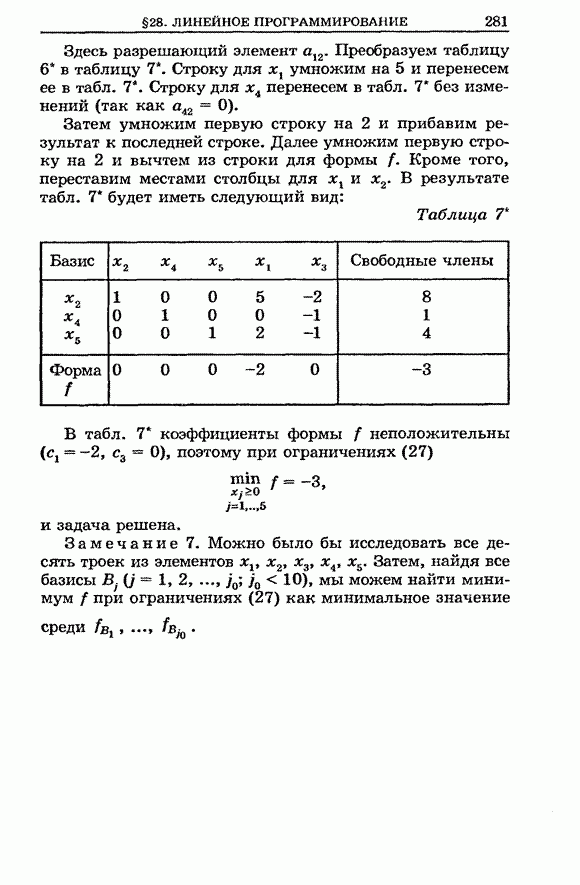
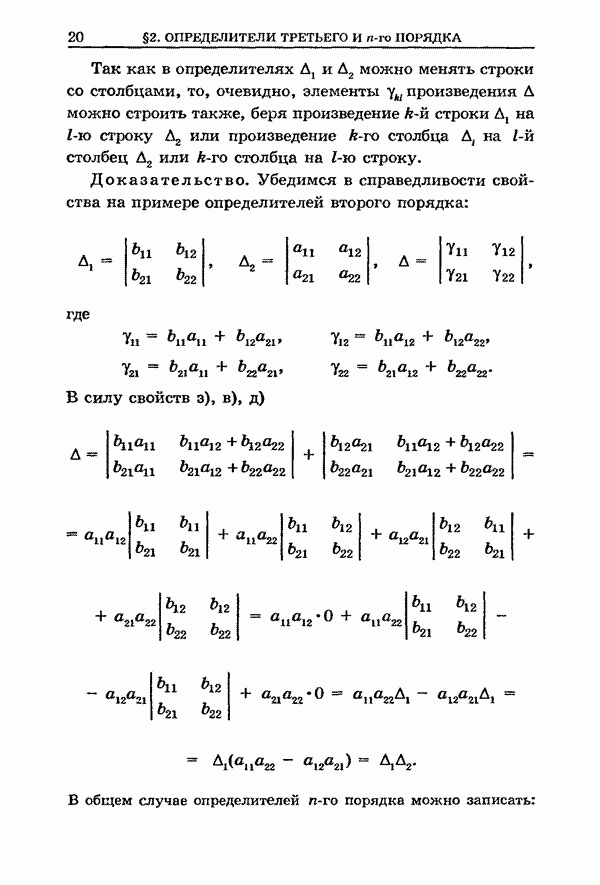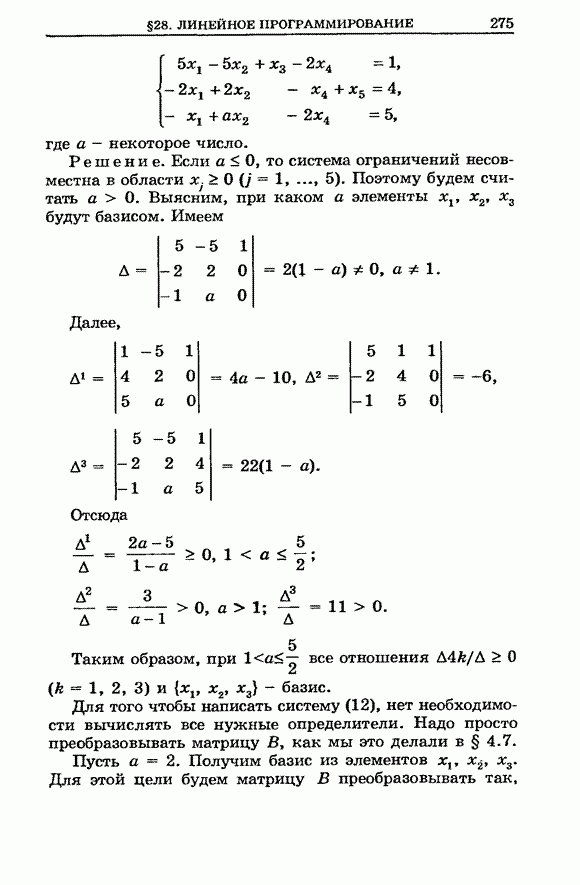| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Гипербола
![]() . (4)
. (4)
Положим
![]() и отметим
на оси
и отметим
на оси ![]() точки
точки
![]() и
и ![]() — фокусы гиперболы (4),
имеющие абсциссы
— фокусы гиперболы (4),
имеющие абсциссы ![]() и
и
![]() (рис.39).
(рис.39).

Рис.39
Гипербола
(4) может быть определена также как геометрическое место точек ![]() , разность расстояний
которых до фокусов
, разность расстояний
которых до фокусов ![]() и
и
![]() есть
величина постоянная равная
есть
величина постоянная равная ![]() .
.
Имеем (см. рис. 39)

откуда следует уравнение (4).
Мы получили правую ветвь гиперболы (см. рис. 39). Чтобы получить левую ветвь, надо исходить из равенства
![]() .
.
Рассуждениями,
проведенными в обратном порядке, можно заключить, отправляясь от уравнения (4),
что точки ![]() ему
удовлетворяющие, принадлежат к указанному выше геометрическому месту.
ему
удовлетворяющие, принадлежат к указанному выше геометрическому месту.
По
виду уравнения (4) заключаем, что гипербола (4) симметрична относительно оси ![]() и оси
и оси ![]() . Часть гиперболы
(4), находящаяся в первой четверти, имеет уравнение
. Часть гиперболы
(4), находящаяся в первой четверти, имеет уравнение
![]() . (5)
. (5)
Мы
видим, что наша гипербола проходит через точку ![]() и при возрастании
и при возрастании ![]() на полуинтервале
на полуинтервале ![]() ордината
ордината ![]() возрастает и
стремится к бесконечности. Точки
возрастает и
стремится к бесконечности. Точки ![]() и
и ![]() , в которых гипербола пересекает ось
, в которых гипербола пересекает ось ![]() , называются вершинами
гиперболы.
, называются вершинами
гиперболы.
На рис. 39 нарисованы две прямые:
![]() .
.
Это асимптоты нашей гиперболы.
Пусть на
полуинтервале ![]() (или
(или
![]() ) задана
кривая
) задана
кривая ![]() .
Говорят, что прямая
.
Говорят, что прямая ![]() есть асимптота этой кривой при
есть асимптота этой кривой при ![]() , если
, если
![]()
(соответственно ![]() ).
).
Рассмотрим кусок
нашей гиперболы, определяемый равенством (5), и сравним его с прямой ![]() . Предел
. Предел
![]() .
.
Это показывает,
что прямая ![]() есть
асимптота рассматриваемого куска гиперболы при
есть
асимптота рассматриваемого куска гиперболы при ![]() . Но тогда говорят, что прямая
. Но тогда говорят, что прямая ![]() есть асимптота
(всей!) гиперболы при
есть асимптота
(всей!) гиперболы при ![]() .
В силу симметрии нашей гиперболы относительно осей, так же как симметрии пары
прямых
.
В силу симметрии нашей гиперболы относительно осей, так же как симметрии пары
прямых ![]() относительно
осей, можно сказать, что обе эти прямые являются асимптотами нашей гиперболы и
притом как при
относительно
осей, можно сказать, что обе эти прямые являются асимптотами нашей гиперболы и
притом как при ![]() , так и
при
, так и
при ![]() .
.
Правая ветвь гиперболы (4) может быть записана в параметрическом виде
 (6)
(6)
В самом деле, так как
![]() , (7)
, (7)
то из уравнений (6) получим
![]() .
.
Верхняя половина
правой ветви гиперболы соответствует изменению ![]() , а нижняя – изменению
, а нижняя – изменению ![]() .
.
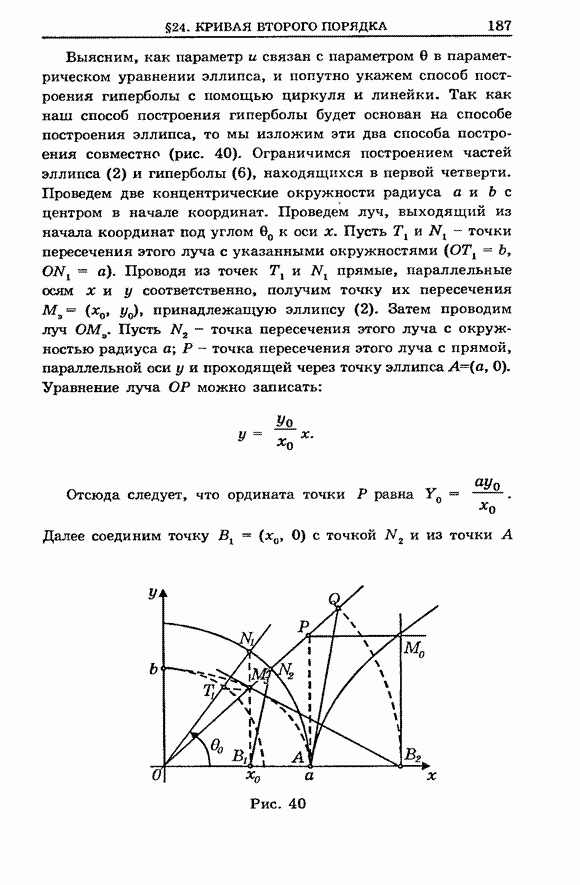
Выясним,
как параметр ![]() связан
с параметром
связан
с параметром ![]() в
параметрическом уравнении эллипса, и попутно укажем способ построения гиперболы
с помощью циркуля и линейки. Так как наш способ построения гиперболы будет
основан на способе построения эллипса, то мы изложим эти два способа построения
совместно (рис. 40). Ограничимся построением частей эллипса (2) и гиперболы
(6), находящихся в первой четверти. Проведем две концентрические окружности
радиуса
в
параметрическом уравнении эллипса, и попутно укажем способ построения гиперболы
с помощью циркуля и линейки. Так как наш способ построения гиперболы будет
основан на способе построения эллипса, то мы изложим эти два способа построения
совместно (рис. 40). Ограничимся построением частей эллипса (2) и гиперболы
(6), находящихся в первой четверти. Проведем две концентрические окружности
радиуса ![]() и
и ![]() с центром в начале координат.
Проведем луч, выходящий из начала координат под углом
с центром в начале координат.
Проведем луч, выходящий из начала координат под углом ![]() к оси
к оси ![]() . Пусть
. Пусть ![]() и
и ![]() - точки пересечения этого
луча с указанными окружностями
- точки пересечения этого
луча с указанными окружностями ![]() . Проводя из точек
. Проводя из точек ![]() и
и ![]() , прямые, параллельные осям
, прямые, параллельные осям ![]() и
и ![]() , получим точку их
пересечения
, получим точку их
пересечения ![]() ,
принадлежащую эллипсу (2). Затем проводим луч
,
принадлежащую эллипсу (2). Затем проводим луч ![]() . Пусть
. Пусть ![]() - точка пересечения этого луча с
окружностью радиуса
- точка пересечения этого луча с
окружностью радиуса ![]() ;
; ![]() - точка пересечения этого луча с
прямой, параллельной оси
- точка пересечения этого луча с
прямой, параллельной оси ![]() и проходящей через точку эллипса
и проходящей через точку эллипса ![]() . Уравнение луча
. Уравнение луча ![]() можно записать:
можно записать:
![]() .
.

Рис.40
Отсюда
следует, что ордината точки ![]() равна
равна ![]() . Далее соединим точку
. Далее соединим точку ![]() с точкой
с точкой ![]() и из точки
и из точки ![]() проведем прямую,
параллельную
проведем прямую,
параллельную ![]() ,
которая пересечет луч
,
которая пересечет луч ![]() в точке
в точке ![]() .
.
Из
подобия треугольников ![]() и
и ![]() получим, что
получим, что ![]() . Радиусом
. Радиусом ![]() на оси
на оси ![]() отмечаем точку
отмечаем точку ![]() .
.
Теперь
из точек ![]() и
и
![]() проводим
прямые, параллельные осям
проводим
прямые, параллельные осям ![]() и
и ![]() соответственно. Точка пересечения этих
прямых
соответственно. Точка пересечения этих
прямых ![]() ,
где
,
где ![]() принадлежит
гиперболе (4).
принадлежит
гиперболе (4).
В
самом деле, так как точка ![]() лежит на эллипсе (2), то
лежит на эллипсе (2), то
 ,
,
т.
е. точка ![]() , принадлежит
гиперболе (4).
, принадлежит
гиперболе (4).
Отметим,
что точка ![]() является
точкой пересечения касательной к эллипсу в точке
является
точкой пересечения касательной к эллипсу в точке ![]() с осью
с осью ![]() .
.
Таким
образом, каждой точке ![]() эллипса (2) соответствует вполне
определенная точка
эллипса (2) соответствует вполне
определенная точка ![]() гиперболы
(4) и обратно.
гиперболы
(4) и обратно.
Теперь, если эллипс (2) задан параметрически, то
![]() .
.
Поэтому
![]() .
.
Отсюда, учитывая (6), получаем
![]() .
.
Имеют место также следующие формулы:

т.е.
![]()
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
- 5.1. Понятие вектора
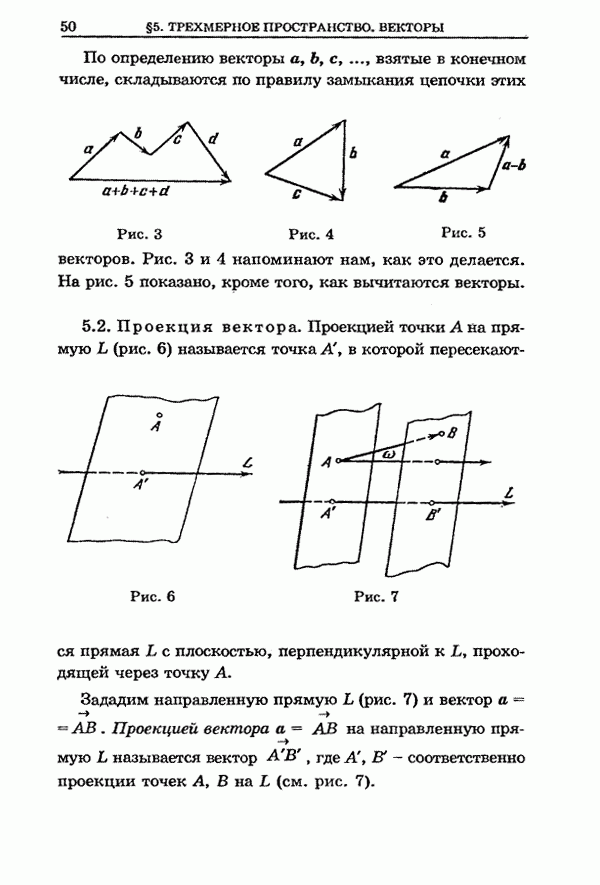
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
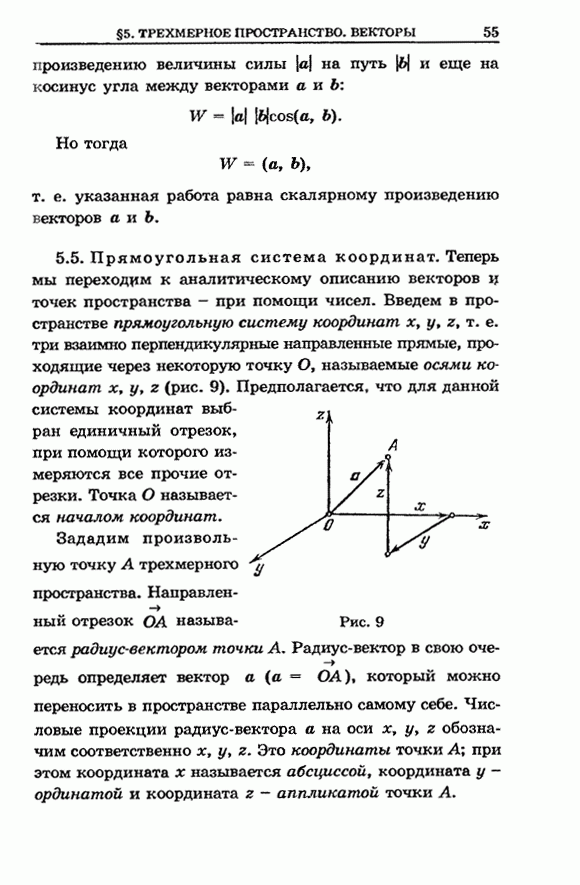
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
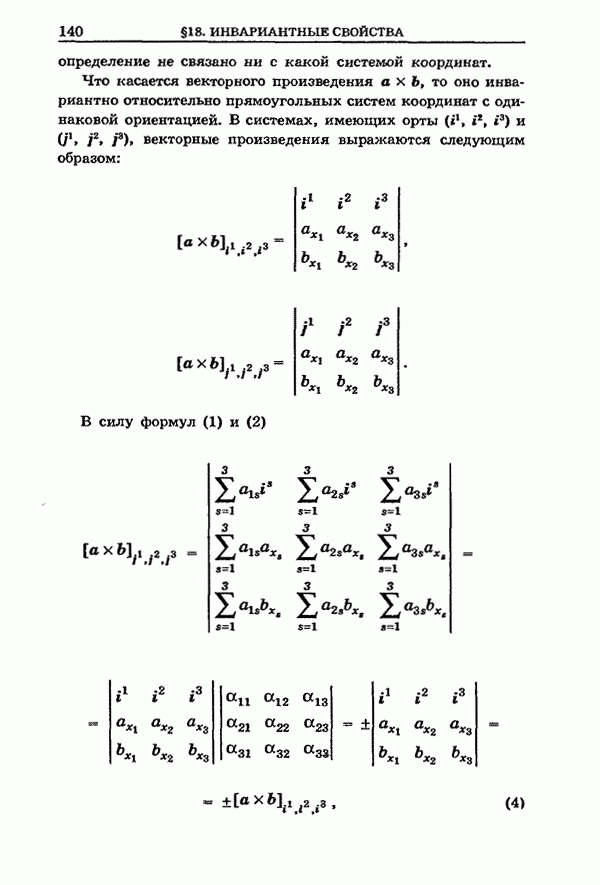
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса