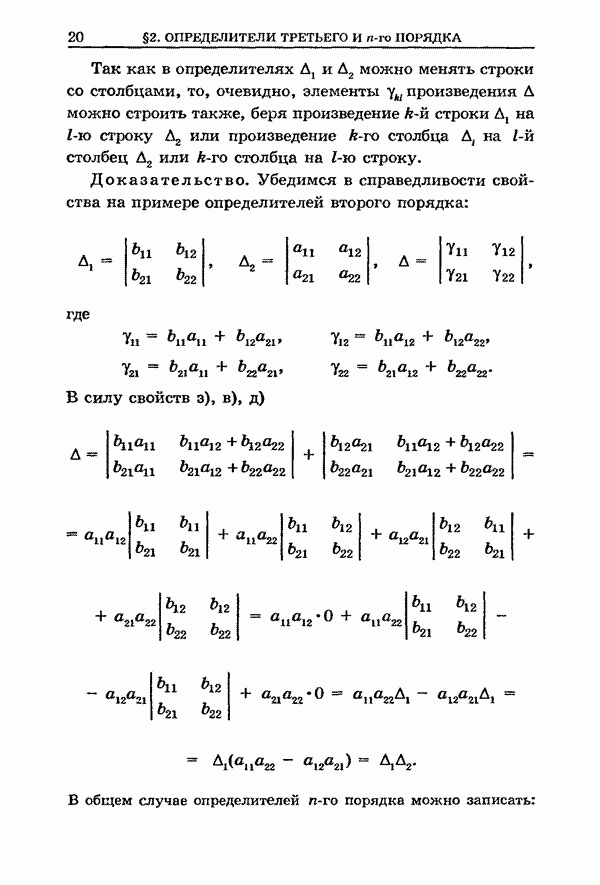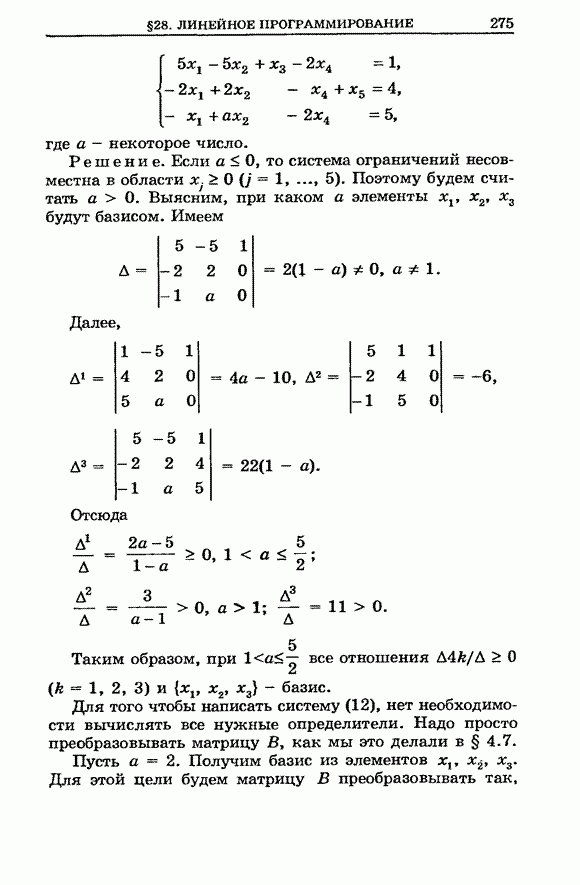| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. Линейные подпространства в Rn
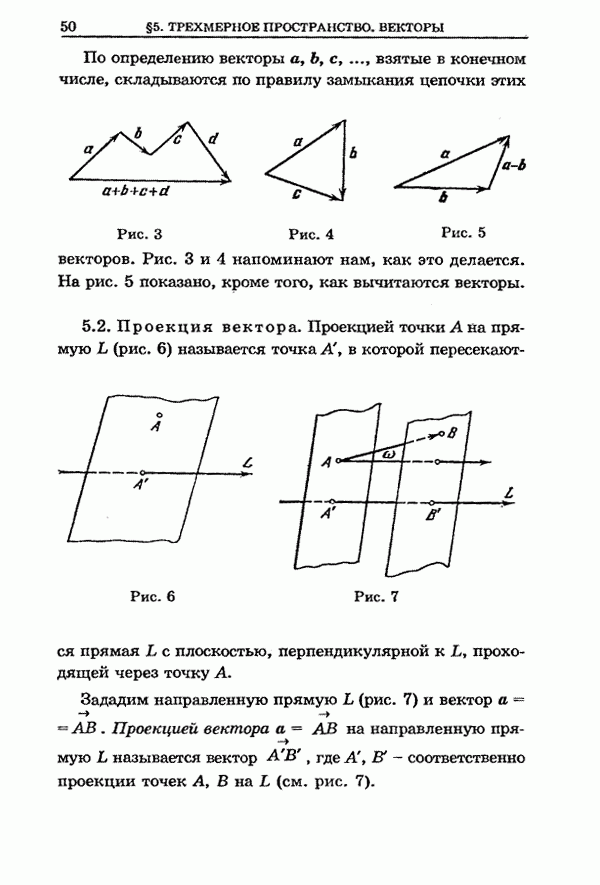
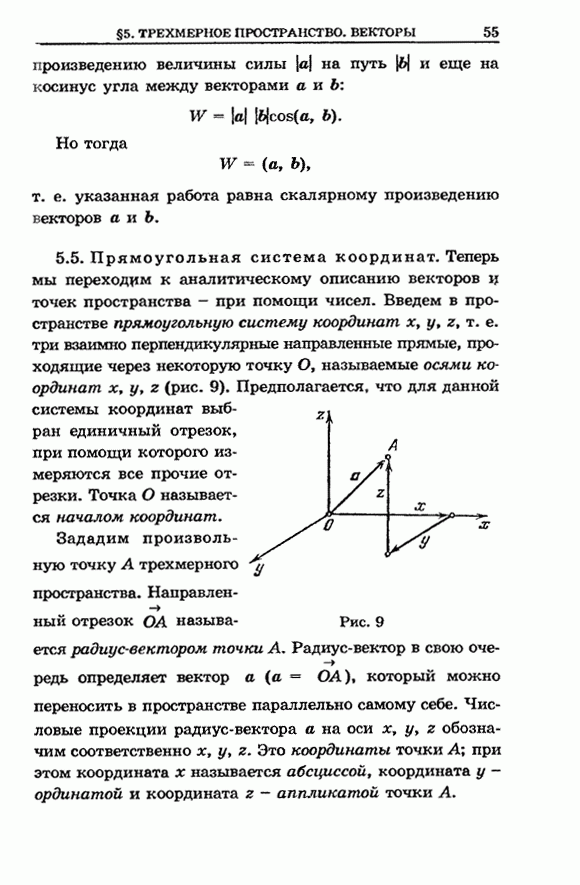
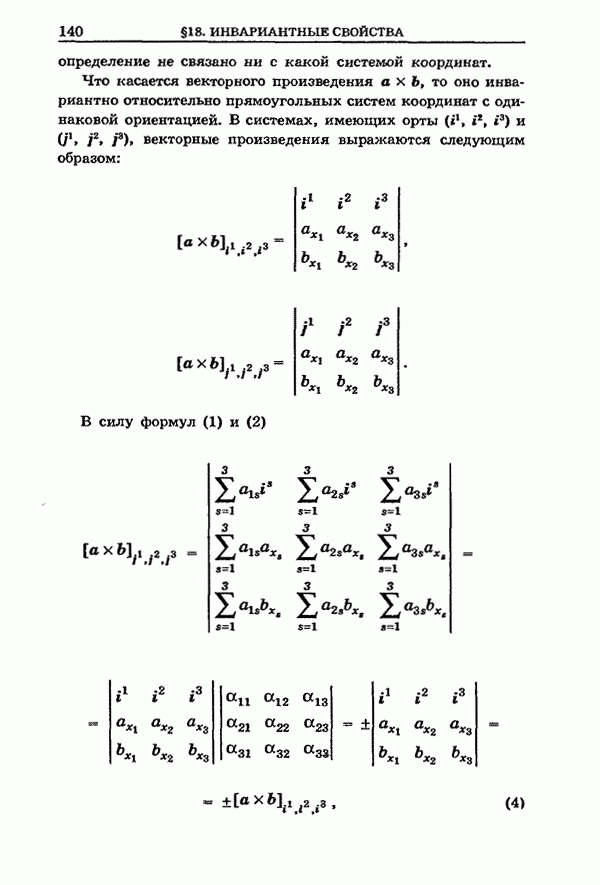
Множество ![]() в
в ![]() (
(![]() ) называется линейным подпространством
пространства
) называется линейным подпространством
пространства ![]() или, короче, подпространством в
или, короче, подпространством в ![]() , если из того, что
два каких-либо вектора
, если из того, что
два каких-либо вектора ![]() и
и ![]() принадлежат к
принадлежат к ![]() (
(![]() ), автоматически следует, что
вектор
), автоматически следует, что
вектор ![]() тоже
принадлежит к
тоже
принадлежит к ![]() (
(![]() ), где
), где ![]() ,
, ![]() - числа. Подпространство
- числа. Подпространство ![]() называется m-мерным, если в нем имеется линейно независимая система
называется m-мерным, если в нем имеется линейно независимая система ![]() , состоящая из m векторов, и нет системы, состоящей
из
, состоящая из m векторов, и нет системы, состоящей
из ![]() линейно
независимых векторов.
линейно
независимых векторов.
Таким образом,
если ![]() -
произвольный вектор в
-
произвольный вектор в ![]() (
(![]() ), то система
), то система ![]() , а линейно зависима, т.е.
существует нетривиальная система чисел
, а линейно зависима, т.е.
существует нетривиальная система чисел ![]() такая, что
такая, что
![]() . (1)
. (1)
Здесь ![]() , иначе было бы
, иначе было бы
![]() ,
,
и вследствие
линейной независимости системы ![]() было бы
было бы ![]() и вся система
и вся система ![]() была бы тривиальной. Тогда
уравнение (1) можно решить относительно
была бы тривиальной. Тогда
уравнение (1) можно решить относительно ![]() :
:
![]() ,
(2)
,
(2)
т.е. представить
в виде линейной комбинации из векторов ![]() . С другой стороны, линейная комбинация
вида (2) принадлежит к
. С другой стороны, линейная комбинация
вида (2) принадлежит к ![]() , потому что
, потому что ![]() - подпространство. В этом
смысле говорят, что система
- подпространство. В этом
смысле говорят, что система ![]() есть базис в
есть базис в ![]() . Очевидно, любая другая линейно
независимая система векторов
. Очевидно, любая другая линейно
независимая система векторов ![]() , принадлежащих к
, принадлежащих к ![]() , есть базис в
, есть базис в ![]() .
.
Если разложить
векторы ![]() по
векторам
по
векторам ![]() , то
получим
, то
получим
![]() .
.
По аналогии с
тем, как мы рассуждали в § 16 для ![]() (где теперь надо заменить
(где теперь надо заменить ![]() и
и ![]() соответственно на
соответственно на ![]() ,
, ![]() ), можно получить, что система
), можно получить, что система
![]() линейно
независима тогда и только тогда, когда определитель
линейно
независима тогда и только тогда, когда определитель ![]() , и что любая независимая система,
состоящая из
, и что любая независимая система,
состоящая из ![]() векторов,
уже не может быть базисом в
векторов,
уже не может быть базисом в ![]() .
.
Пространство ![]() можно рассматривать
как подпространство
можно рассматривать
как подпространство ![]() , имеющее
, имеющее ![]() измерений.
измерений.
Множество,
состоящее из одного нулевого вектора 0, есть линейное подпространство (![]() ). Про него говорят,
что оно имеет 0 измерений. Вектор 0 не образует линейно независимой системы -
из равенства
). Про него говорят,
что оно имеет 0 измерений. Вектор 0 не образует линейно независимой системы -
из равенства![]() ,
где
,
где ![]() -
число, не обязательно следует, что
-
число, не обязательно следует, что ![]() есть нуль.
есть нуль.
Если вектор ![]() , то множество
векторов вида
, то множество
векторов вида ![]() ,
где
,
где ![]() -
произвольное число, есть одномерное подпространство. В качестве базиса в нем
можно взять вектор
-
произвольное число, есть одномерное подпространство. В качестве базиса в нем
можно взять вектор ![]() .
.
Пусть ![]() есть линейное подпространство
в
есть линейное подпространство
в ![]() . Будем
говорить, что вектор
. Будем
говорить, что вектор ![]() ортогонален к
ортогонален к ![]() , если он ортогонален к любому
вектору
, если он ортогонален к любому
вектору ![]() . Обозначим
через
. Обозначим
через ![]() множество
всех векторов, ортогональных к
множество
всех векторов, ортогональных к ![]() .
. ![]() есть подпространство. В самом деле,
пусть
есть подпространство. В самом деле,
пусть ![]() , т.
е.
, т.
е.

Тогда для любых чисел ![]() ,
,![]()
![]()
т.е. ![]() .
.
По определению подпространство ![]() называется
ортогональным к данному подпространству
называется
ортогональным к данному подпространству ![]() , если
, если ![]() есть множество всех векторов, каждый из
которых ортогонален к
есть множество всех векторов, каждый из
которых ортогонален к ![]() .
.
Ниже
доказывается теорема, выясняющая структуру произвольного подпространства ![]() и ему ортогонального
подпространства
и ему ортогонального
подпространства ![]() .
В частности, из нее следует, что если
.
В частности, из нее следует, что если ![]() ортогонально к
ортогонально к ![]() , то и, обратно,
, то и, обратно, ![]() ортогонально к
ортогонально к ![]() .
.
Теорема 1. Пусть
![]() есть
линейное подпространство, отличное от
есть
линейное подпространство, отличное от ![]() и нулевого подпространства. Тогда:
и нулевого подпространства. Тогда:
а) существует
целое число ![]() ,
удовлетворяющее неравенствам
,
удовлетворяющее неравенствам
![]() , (3)
, (3)
и ортонормированный базис
![]() (4)
(4)
в ![]() ; если этот базис
продолжить любым способом до ортонормированного базиса в
; если этот базис
продолжить любым способом до ортонормированного базиса в ![]() :
:
![]() , (5)
, (5)
то линейное
подпространство ![]() с
базисом
с
базисом
![]() (6)
(6)
обладает следующими свойствами:
б) ![]() есть подпространство, ортогональное к
есть подпространство, ортогональное к ![]()
в) ![]() есть
подпространство, ортогональное к
есть
подпространство, ортогональное к ![]() ;
;
г)
любой вектор ![]() можно
представить в виде суммы
можно
представить в виде суммы
![]() ,
,
где ![]() ,
, ![]() и при этом единственным образом.
и при этом единственным образом.
Доказательство.
По условию ![]() отлично
от нулевого подпространства, следовательно, в
отлично
от нулевого подпространства, следовательно, в ![]() существует вектор
существует вектор ![]() , отличный от 0. Нормируя
, отличный от 0. Нормируя ![]() , получим нормальный
вектор
, получим нормальный
вектор
![]() .
.
Обозначим через ![]() любой, принадлежащий
к
любой, принадлежащий
к ![]() нормальный
вектор, ортогональный к
нормальный
вектор, ортогональный к ![]()
![]() , если такой существует. Далее, обозначим
через
, если такой существует. Далее, обозначим
через ![]() принадлежащий
к
принадлежащий
к ![]() нормальный
вектор, ортогональный к
нормальный
вектор, ортогональный к ![]() и
и ![]()
![]() , если такой существует. Этот процесс
закончится на некотором
, если такой существует. Этот процесс
закончится на некотором ![]() -м этапе, где
-м этапе, где ![]() удовлетворяет неравенствам
(3), т. е. найдется ортонормированная система векторов (4), принадлежащих к
удовлетворяет неравенствам
(3), т. е. найдется ортонормированная система векторов (4), принадлежащих к ![]() , но уже не будет в
, но уже не будет в ![]() единичного вектора,
ортогонального к векторам
единичного вектора,
ортогонального к векторам ![]() . В самом деле,
. В самом деле, ![]() , потому что заведомо
, потому что заведомо ![]() . С другой стороны,
. С другой стороны, ![]() не может быть равным
не может быть равным
![]() . В
противном случае векторы
. В
противном случае векторы ![]() принадлежали бы к
принадлежали бы к ![]() и вместе с ними принадлежали
бы к подпространству
и вместе с ними принадлежали
бы к подпространству ![]() все линейные комбинации
все линейные комбинации ![]() , и тогда получилось
бы, что
, и тогда получилось
бы, что ![]() совпадает
с
совпадает
с ![]() , но
, но ![]() отлично от
отлично от ![]() . Полученная
ортонормированная система
. Полученная
ортонормированная система ![]() есть
есть
базис в ![]() . В
самом деде, вместе с векторами
. В
самом деде, вместе с векторами ![]() принадлежат к
принадлежат к ![]() , и все их линейные комбинации
, и все их линейные комбинации
![]() . Но больше
в
. Но больше
в ![]() других
векторов нет, потому что, если допустить, что некоторый вектор
других
векторов нет, потому что, если допустить, что некоторый вектор ![]() не есть такая
линейная комбинация, то
не есть такая
линейная комбинация, то ![]() можно было бы записать в виде суммы
можно было бы записать в виде суммы
![]() ,
(7)
,
(7)
где ![]() . Так как векторы
. Так как векторы ![]() и
и ![]() принадлежат к подпространству
принадлежат к подпространству
![]() , то
пришлось бы заключить, что вектор
, то
пришлось бы заключить, что вектор
![]()
тоже принадлежит
к ![]() . Но
вектор
. Но
вектор ![]() ортогонален
ко всем
ортогонален
ко всем ![]() (см.
§ 17, (4)). Пронормированный вектор
(см.
§ 17, (4)). Пронормированный вектор
![]() (8)
(8)
тоже принадлежал
бы к ![]() и был
бы ортогональным ко всем
и был
бы ортогональным ко всем ![]() . Но это невозможно в силу максимального
свойства числа
. Но это невозможно в силу максимального
свойства числа ![]() .
Этим доказано утверждение а) теоремы.
.
Этим доказано утверждение а) теоремы.
Дополнение
ортонормированной системы (4) до ортонормированного базиса (5) осуществляется
на основании теоремы 1 § 17. Обозначим через ![]() подпространство всех линейных
комбинаций
подпространство всех линейных
комбинаций ![]() из
векторов системы (6). Каждый такой вектор, очевидно, ортогонален к любому
вектору
из
векторов системы (6). Каждый такой вектор, очевидно, ортогонален к любому
вектору ![]() , который
представляется в виде суммы
, который
представляется в виде суммы ![]() . С другой стороны, если
. С другой стороны, если ![]() , есть произвольный
вектор, ортогональный ко всем векторам
, есть произвольный
вектор, ортогональный ко всем векторам ![]() , в частности к
, в частности к ![]() , то его разложение по базису
(5) имеет вид
, то его разложение по базису
(5) имеет вид
![]() ,
,
т.е. ![]() . Мы доказали утверждение б)
теоремы.
. Мы доказали утверждение б)
теоремы.
Далее, любой
вектор ![]() ортогонален
ко всем векторам
ортогонален
ко всем векторам ![]() и,
если известно, что какой-либо вектор
и,
если известно, что какой-либо вектор ![]() ортогонален ко всем векторам из
ортогонален ко всем векторам из ![]() , в частности к
, в частности к ![]() , то
, то ![]() , т. е.
, т. е. ![]() . Мы доказали
утверждение в).
. Мы доказали
утверждение в).
Наконец, если ![]() - произвольный
вектор, то его единственным образом можно представить в виде суммы
- произвольный
вектор, то его единственным образом можно представить в виде суммы
![]() ,
,
где
![]() .
.
Этим теорема 1 доказана полностью.
Теорема 2. Пусть ![]() есть подпространство
есть подпространство
![]() измерений
в
измерений
в ![]() . Тогда
подпространство
. Тогда
подпространство ![]() ,
ортогональное к
,
ортогональное к ![]() ,
имеет
,
имеет ![]() измерений
и при этом
измерений
и при этом ![]() есть
в свою очередь подпространство, ортогональное к
есть
в свою очередь подпространство, ортогональное к ![]() .
.
Доказательство.
Если ![]() отлично
от
отлично
от ![]() и от
нулевого подпространства, то данная теорема содержится, очевидно, в теореме 1.
и от
нулевого подпространства, то данная теорема содержится, очевидно, в теореме 1.
Пусть ![]() есть нулевое
подпространство. Так как любой вектор
есть нулевое
подпространство. Так как любой вектор ![]() ортогонален к 0, то
ортогонален к 0, то ![]() и измерение
и измерение ![]() равно
равно ![]() . Обратно, вектор 0
ортогонален ко всем векторам
. Обратно, вектор 0
ортогонален ко всем векторам ![]() . Других векторов, ортогональных ко всем
векторам
. Других векторов, ортогональных ко всем
векторам ![]() ,
нет, потому что всякий отличный от 0 вектор уже не ортогонален к самому себе.
Мы доказали, что
,
нет, потому что всякий отличный от 0 вектор уже не ортогонален к самому себе.
Мы доказали, что ![]() ортогонально
к
ортогонально
к ![]() .
.
Если ![]() , то рассуждаем
подобным образом.
, то рассуждаем
подобным образом.
Следствие 1. Пусть задача система векторов
![]() , (9)
, (9)
и пусть ![]() есть подпространство
векторов
есть подпространство
векторов ![]() ,
каждый из которых ортогонален к векторам этой системы:
,
каждый из которых ортогонален к векторам этой системы:
![]() .
.
Пусть, далее,
дан вектор ![]() ,
ортогональный ко всем указанным векторам
,
ортогональный ко всем указанным векторам ![]() , т. е. ортогональный к подпространству
, т. е. ортогональный к подпространству ![]() . Тогда
. Тогда ![]() есть некоторая
линейная комбинация из векторов заданной системы (9)
есть некоторая
линейная комбинация из векторов заданной системы (9)
 .
.
Доказательство.
Рассмотрим подпространство ![]() , состоящее из всевозможных линейных
комбинаций векторов системы (9), т. е. всякий вектор
, состоящее из всевозможных линейных
комбинаций векторов системы (9), т. е. всякий вектор ![]() есть некоторая линейная
комбинация
есть некоторая линейная
комбинация
 .
.
В этом случае
будем также говорить, что подпространство ![]() натянуто на векторы системы (9).
натянуто на векторы системы (9).
Так как всякий
вектор ![]() ортогонален
к векторам системы (9), то он, очевидно, ортогонален к любому вектору
ортогонален
к векторам системы (9), то он, очевидно, ортогонален к любому вектору ![]() . Это показывает, что
подпространство
. Это показывает, что
подпространство ![]() ортогонально
к подпространству
ортогонально
к подпространству ![]() .
Но тогда по теореме 2 и
.
Но тогда по теореме 2 и ![]() ортогонально к
ортогонально к ![]() , т. е.
, т. е. ![]() состоит из всех векторов
состоит из всех векторов ![]() , ортогональных к
, ортогональных к ![]() . По условию
. По условию ![]() есть один из таких
векторов
есть один из таких
векторов ![]() , следовательно,
, следовательно,
![]() есть
некоторая линейная комбинация из векторов системы (9).
есть
некоторая линейная комбинация из векторов системы (9).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
- 5.1. Понятие вектора
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
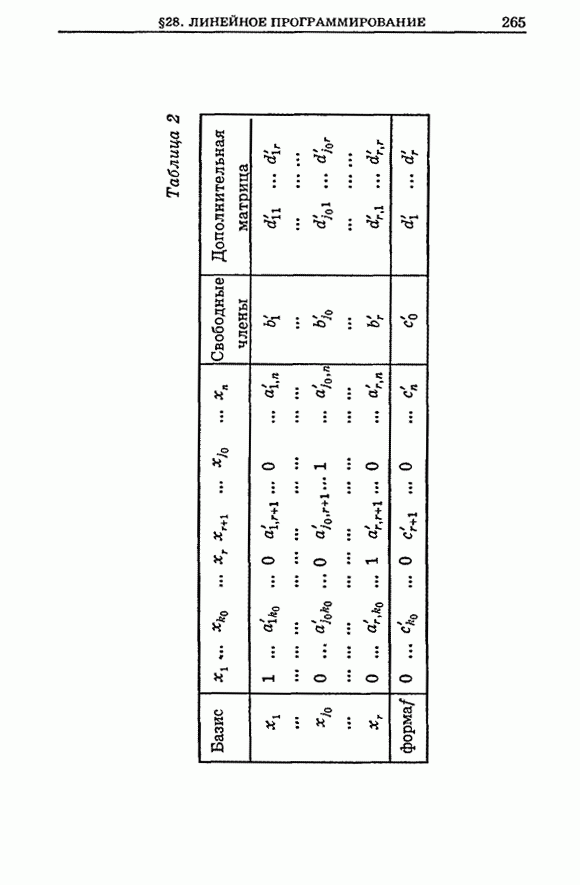
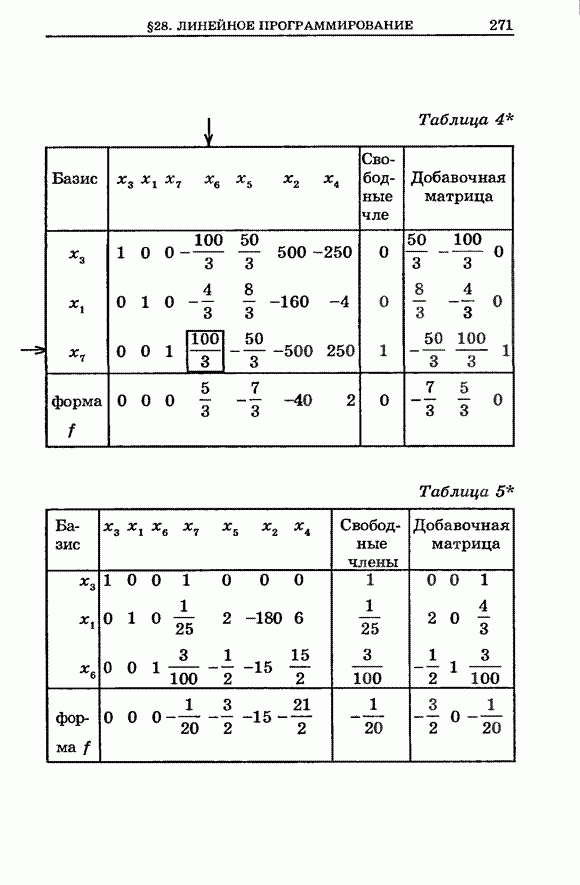
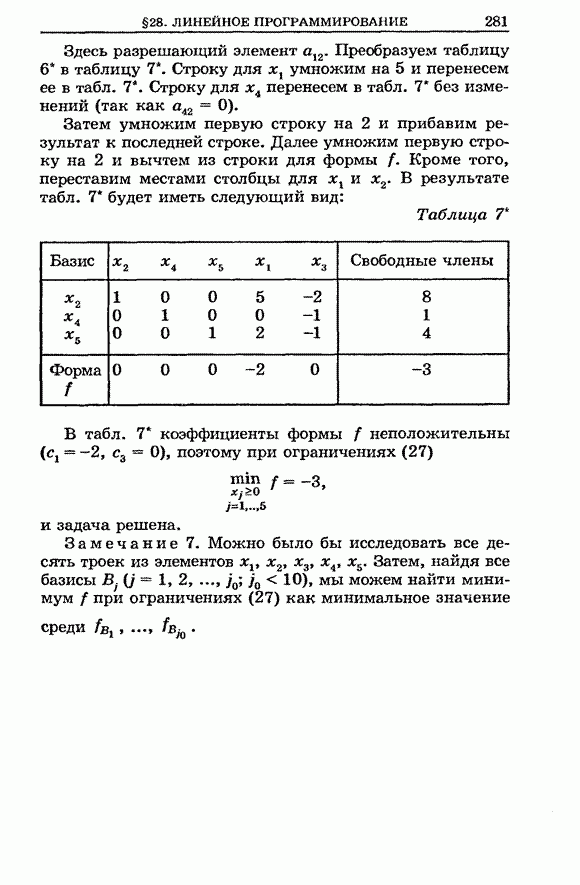
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса