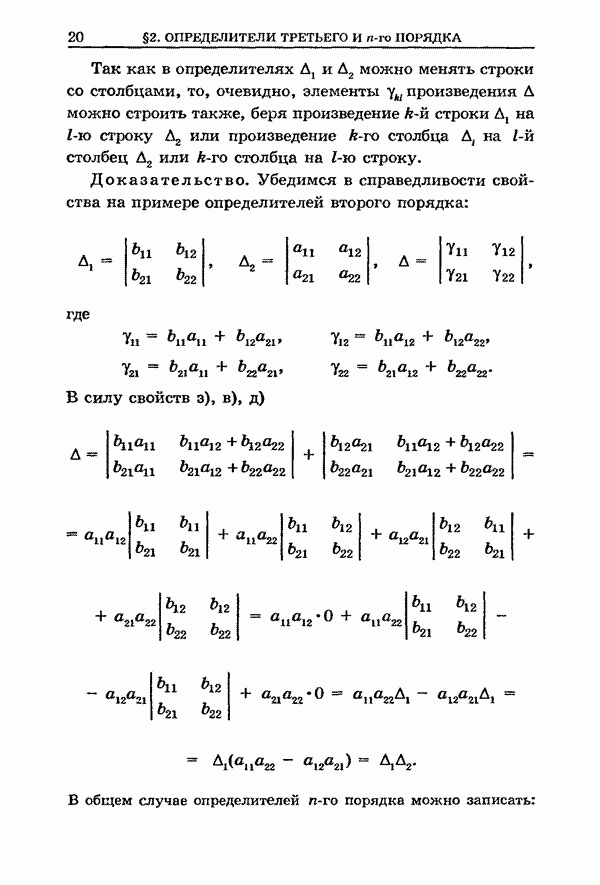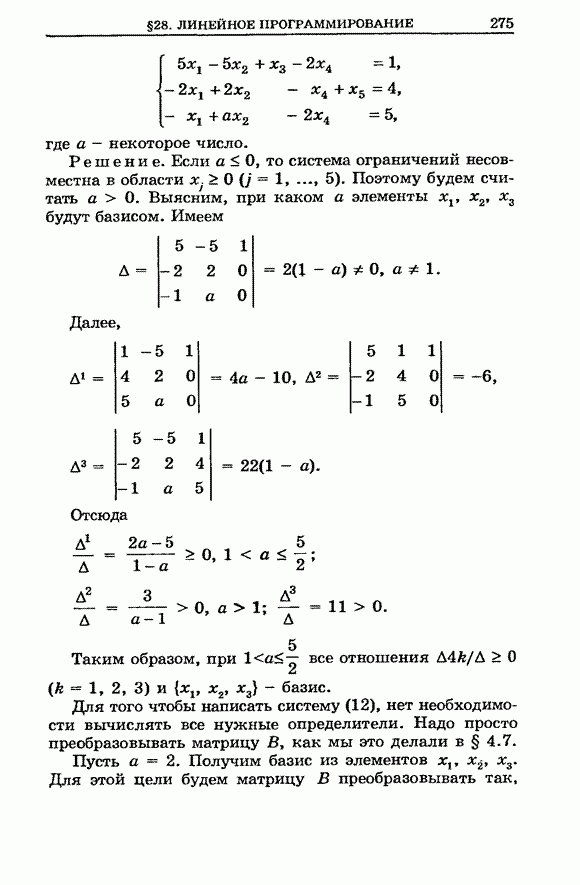| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 22. Самосопряженный оператор. Квадратичная форма
Линейный оператор
![]() (1)
(1)
или, коротко,
![]() (2)
(2)
называется самосопряженным,
если он равен своему сопряженному (![]() ), т.е. если
), т.е. если
![]() , (3)
, (3)
иначе говоря,
если матрица ![]() симметрическая:
симметрическая:
![]() (4)
(4)
(см. (3) и (3*)
§ 21). Мы считаем ![]() и
и
![]() действительными
(см. ниже замечание 1).
действительными
(см. ниже замечание 1).
Для самосопряженного оператора имеет место характерное равенство
![]()
(см. § 21, (4)). Очевидно,
![]() .
(4')
.
(4')
Выражение справа
в (4') называется квадратичной формой ![]() -го порядка. Это непрерывная функция от
вектора
-го порядка. Это непрерывная функция от
вектора ![]() или,
что все равно, от переменных
или,
что все равно, от переменных ![]()
Будем
рассматривать эту функцию на множестве ![]() значений
значений ![]() , имеющих единичную норму
, имеющих единичную норму ![]() . Множество
. Множество ![]() есть сфера в
есть сфера в ![]() радиуса 1 с центром в
точке 0.
радиуса 1 с центром в
точке 0. ![]() -ограниченное
множество. Кроме того, оно замкнуто: если точки последовательности
-ограниченное
множество. Кроме того, оно замкнуто: если точки последовательности ![]() принадлежат к
принадлежат к ![]() (т.е.
(т.е. ![]() ) и эта последовательность
стремится к некоторой точке
) и эта последовательность
стремится к некоторой точке ![]() , то неминуемо
, то неминуемо ![]() , т. е.
, т. е. ![]() , потому что
, потому что ![]() , откуда
, откуда ![]() .
.
Найдем максимум
квадратичной формы (4') на сфере ![]() . Так как форма (4') есть непрерывная
функция на замкнутом ограниченном множестве, то максимум ее на
. Так как форма (4') есть непрерывная
функция на замкнутом ограниченном множестве, то максимум ее на ![]() достигается для
некоторого единичного вектора
достигается для
некоторого единичного вектора ![]() . Обозначим этот максимум через
. Обозначим этот максимум через ![]() :
:
![]() . (5)
. (5)
Введем
подпространство ![]() ,
ортогональное к вектору
,
ортогональное к вектору ![]() , т. е. множество всех векторов
, т. е. множество всех векторов ![]() , каждый из которых
ортогонален к
, каждый из которых
ортогонален к ![]() .
В
.
В ![]() возьмем
произвольный единичный вектор
возьмем
произвольный единичный вектор ![]() . Вектор
. Вектор
![]()
зависит от ![]() и имеет единичную
норму
и имеет единичную
норму
![]() .
.
При ![]() этот вектор
обращается в
этот вектор
обращается в ![]() .
Но тогда функция
.
Но тогда функция
![]()
достигает своего
максимума в точке ![]() и
в силу необходимого условия экстремума
и
в силу необходимого условия экстремума
![]() .
.
Вычислим эту производную. Имеем
![]() .
.
Следовательно,
![]()
и
![]() .
.
Мы получили, что
вектор ![]() ортогонален
ко всем единичным векторам
ортогонален
ко всем единичным векторам ![]() , следовательно, и к любым векторам
, следовательно, и к любым векторам ![]() . Но тогда
. Но тогда ![]() отличается от
отличается от ![]() лишь множителем (см.
следствие 1 в конце § 20), т. е.
лишь множителем (см.
следствие 1 в конце § 20), т. е.
![]() ,
,
где ![]() - некоторое число.
- некоторое число.
Из первого
соотношения (равенства) в (5), учитывая, что ![]() , следует
, следует
![]() .
.
Таким образом,
мы доказали, что максимум квадратичной формы (4') на единичной сфере ![]() достигается в
некоторой точке
достигается в
некоторой точке ![]() ,
,
![]() .
.
При этом
![]() .
.
Мы видим, что
нетривиальный (не равный нулю) вектор ![]() отображается при помощи оператора
отображается при помощи оператора ![]() в вектор
в вектор ![]() , ему коллинеарный.
, ему коллинеарный.
Такой вектор
называется собственным вектором оператора ![]() , а число
, а число ![]() - принадлежащим этому вектору
собственным значением.
- принадлежащим этому вектору
собственным значением.
Будем теперь
рассматривать оператор ![]() на подпространстве
на подпространстве ![]() , определяемом как множество
векторов
, определяемом как множество
векторов ![]() ,
ортогональных к вектору
,
ортогональных к вектору ![]() (выше мы его обозначали через
(выше мы его обозначали через ![]() ).
). ![]() есть
есть ![]() -мерное
подпространство - в нем имеются ортонормированные базисы, состоящие из
-мерное
подпространство - в нем имеются ортонормированные базисы, состоящие из ![]() векторов. Цель наша
заключается в подыскании одного такого базиса, как мы увидим, естественно
связанного с оператором
векторов. Цель наша
заключается в подыскании одного такого базиса, как мы увидим, естественно
связанного с оператором ![]() .
.
Важно
подчеркнуть, что образ ![]() подпространства
подпространства ![]() при помощи оператора
при помощи оператора ![]() принадлежит к
принадлежит к ![]() , потому что, если
, потому что, если ![]() , то
, то
![]() ,
,
т. е. ![]() .
.
Самосопряженность
оператора ![]() на
на
![]() тривиальным
образом сохраняется, потому что равенство
тривиальным
образом сохраняется, потому что равенство
![]() ,
,
верное для всех ![]() , верно также для
всех
, верно также для
всех ![]() .
.
Итак, мы теперь
рассматриваем самосопряженный линейный оператор ![]() на линейном подпространстве
на линейном подпространстве ![]() измерения
измерения ![]() . К нему можно
применить приведенные выше рассуждения и обнаружить в
. К нему можно
применить приведенные выше рассуждения и обнаружить в ![]() существование единичного
вектора
существование единичного
вектора ![]() такого,
что
такого,
что

Дело в том, что
единичная сфера ![]() в
в
![]() определяется,
очевидно, как множество единичных векторов
определяется,
очевидно, как множество единичных векторов ![]() , ортогональных к
, ортогональных к ![]() . При этом
. При этом
![]() .
.
Мы нашли второй
собственный вектор оператора ![]() - вектор
- вектор ![]() и принадлежащее к нему собственное
значение
и принадлежащее к нему собственное
значение ![]() , очевидно,
не превышающее
, очевидно,
не превышающее ![]() (при
уменьшении области рассмотрения максимум может только уменьшиться). При этом
(при
уменьшении области рассмотрения максимум может только уменьшиться). При этом ![]() .
.
Подобным образом
можно ввести подпространство ![]() , измерения
, измерения ![]() , ортогональное к векторам
, ортогональное к векторам ![]() и
и ![]() , показать, что
оператор
, показать, что
оператор ![]() отображает
отображает
![]() в
в ![]() и определить третий
единичный вектор
и определить третий
единичный вектор ![]() ,
ортогональный к
,
ортогональный к ![]() и
к
и
к ![]() такой,
что для него имеет место
такой,
что для него имеет место

и
![]() .
.
Продолжив этот
процесс по индукции до ![]() -го вектора
-го вектора ![]() , мы получим ортонормированную
систему векторов
, мы получим ортонормированную
систему векторов
![]() (6)
(6)
и систему действительных чисел
![]() , (7)
, (7)
обладающих свойствами
 (8)
(8)
Мы получили полную
систему собственных векторов оператора ![]() и принадлежащих им собственных
значений. Так как ортонормированная система (6) принадлежит к
и принадлежащих им собственных
значений. Так как ортонормированная система (6) принадлежит к ![]() и состоит из
и состоит из ![]() векторов, то она
есть базис в
векторов, то она
есть базис в ![]() (см.
§ 17). Поэтому произвольный вектор
(см.
§ 17). Поэтому произвольный вектор ![]() можно разложить по этой системе:
можно разложить по этой системе:
![]() . (9)
. (9)
Тогда наш
самосопряженный оператор ![]() может быть записан следующим образом:
может быть записан следующим образом:
![]() .
(10)
.
(10)
Мы доказали теорему.
Теорема 1. Самосопряженному
оператору ![]() в
пространстве
в
пространстве ![]() соответствует
ортогональная система векторов
соответствует
ортогональная система векторов ![]() (базис
(базис ![]() ) и система действительных чисел
) и система действительных чисел ![]() такие, что
такие, что ![]() для любого
для любого ![]() представляется в виде суммы (10).
представляется в виде суммы (10).
Квадратичная форма (4') соответственно записывается следующим образом:
![]() . (4'')
. (4'')
На практике часто мы исходим из некоторой квадратичной формы
![]() . (4')
. (4')
Чтобы применить к ней полученные результаты, можно определить в связи с ней линейный оператор
![]() ,
,
определяемый равенствами
![]() .
.
В силу условия ![]() это самосопряженный
оператор, и к нему применима теорема 1. На языке квадратичной формы теорема 1
может быть переформулирована следующим образом.
это самосопряженный
оператор, и к нему применима теорема 1. На языке квадратичной формы теорема 1
может быть переформулирована следующим образом.
Теорема 2. Пусть
задана квадратичная форма (4') в ![]() -мерной системе координат
-мерной системе координат ![]() пространства
пространства ![]() с ортами
с ортами ![]() . Существует
прямоугольная система координат
. Существует
прямоугольная система координат ![]() с ортами
с ортами ![]() , образующими ортогональный базис
, образующими ортогональный базис ![]() , и система
действительных чисел
, и система
действительных чисел ![]() такие, что квадратичная форма (4') в
этой системе есть сумма квадратов координат
такие, что квадратичная форма (4') в
этой системе есть сумма квадратов координат ![]() вектора
вектора ![]() , помноженных соответственно на числа
, помноженных соответственно на числа ![]() :
:
![]() . (4''')
. (4''')
Переход от левой
части (4''') к правой можно осуществить, если известны разложения векторов ![]() по ортам
по ортам ![]() . Пусть
. Пусть
![]()
(см. § 17, (7),
где надо заменить ![]() ,
,
![]() соответственно
на
соответственно
на ![]() ). Так
как
). Так
как ![]() и
и ![]() - ортонормированные
базисы в
- ортонормированные
базисы в ![]() , то
матрица
, то
матрица
![]()
ортогональная.
Мы считаем, что она известна. Один и тот же вектор ![]() можно разложить по двум
базисам:
можно разложить по двум
базисам:
![]() .
.
Но тогда

и в силу
линейной независимости системы ![]() получим
получим
![]() (11)
(11)
Таким образом,
переход от координат ![]() к координатам
к координатам ![]() осуществляется посредством
матрицы
осуществляется посредством
матрицы ![]() ,
транспонированной к
,
транспонированной к ![]() (т. е. с помощью строк матрицы
(т. е. с помощью строк матрицы ![]() или столбцов матрицы
или столбцов матрицы
![]() ).
).
Если подставить
выражения (11) для ![]() в
левую часть (4'"), то должны получить правую. Запишем это равенство:
в
левую часть (4'"), то должны получить правую. Запишем это равенство:
![]() ,
,
где ![]() - символ Кронекера.
- символ Кронекера.
Если приравнять
коэффициенты при одинаковых ![]() , то получим равенства
, то получим равенства
![]() ,
,
которые можно трактовать следующим образом (см. § 15, (6)). Для матрицы
![]()
самосопряженного
оператора ![]() существует
ортогональная матрица
существует
ортогональная матрица
![]() ,
,
такая, что
![]() , (12)
, (12)
где ![]() - некоторая
диагональная матрица
- некоторая
диагональная матрица
 (13)
(13)
(![]() — действительные
числа), называемая канонической.
— действительные
числа), называемая канонической.
Отметим, что для
ортогональной действительной матрицы ![]()
![]() .
.
Так как
определители ортогональных матриц ![]() , то из (12) следует
, то из (12) следует
![]() .
(14)
.
(14)
Мы доказали, в частности, следующую теорему.
Теорема 3. Если определитель ![]() самосопряженной
матрицы
самосопряженной
матрицы ![]() неравен
нулю
неравен
нулю ![]() , то
все ее собственные числа
, то
все ее собственные числа ![]() не равны нулю
не равны нулю ![]() .
.
Из теоремы 2 следует, что
1) Если ![]() , то квадратичная
форма положительная для любых векторов
, то квадратичная
форма положительная для любых векторов ![]() , а следовательно, и любых векторов
, а следовательно, и любых векторов ![]() . В этом случае она
называется строго положительной.
. В этом случае она
называется строго положительной.
2) Если ![]() , то форма
отрицательная для любых
, то форма
отрицательная для любых ![]() , следовательно, и любых
, следовательно, и любых ![]() . В этом случае она
называется строго отрицательной.
. В этом случае она
называется строго отрицательной.
3) Если ![]() и
и ![]() , то форма неотрицательная. Существует
направление, (ось
, то форма неотрицательная. Существует
направление, (ось ![]() ),
вдоль которого она равна нулю. Это положительная форма, но не строго.
),
вдоль которого она равна нулю. Это положительная форма, но не строго.
4) Если ![]() , то форма отрицательная не строго.
, то форма отрицательная не строго.
5) Если ![]() , а
, а ![]() , то форма
неопределенна. Если исключить нулевую точку, то вдоль оси
, то форма
неопределенна. Если исключить нулевую точку, то вдоль оси ![]() она положительная, вдоль же
оси
она положительная, вдоль же
оси ![]() -
отрицательная.
-
отрицательная.
Оказывается, что
по виду матрицы ![]() ,
по знаку некоторых порождаемых ею определителей можно узнать, будут ли ее
собственные числа все положительные, все отрицательные или среди них есть как
положительные, так и отрицательные. В этом заключается теорема Сильвестра.
,
по знаку некоторых порождаемых ею определителей можно узнать, будут ли ее
собственные числа все положительные, все отрицательные или среди них есть как
положительные, так и отрицательные. В этом заключается теорема Сильвестра.
Составим ряд
главных миноров квадратичной формы ![]() :
:
 .
.
Согласно теореме Сильвестра, которую мы не доказываем, имеют место следующие утверждения:
1. Если ![]() , то форма строго положительна (случай
1)).
, то форма строго положительна (случай
1)).
2. Если ![]() , то форма строго отрицательная (случай
2)).
, то форма строго отрицательная (случай
2)).
3. Если ![]() или
или ![]() и имеется
и имеется ![]() , при котором
, при котором ![]() , то форма заведомо
не строго определенна.
, то форма заведомо
не строго определенна.
4. Во всех остальных случаях квадратическая форма неопределенна.
Замечание 1. Если ![]() - комплексное пространство, а
- комплексное пространство, а
![]() —
по-прежнему действительные числа, то рассуждения, приведенные выше, мало
отличаются. Формула (4') теперь записывается так
—
по-прежнему действительные числа, то рассуждения, приведенные выше, мало
отличаются. Формула (4') теперь записывается так
![]() .
.
Число ![]() остается
действительным, потому что
остается
действительным, потому что
![]() .
.
Это показывает,
что приведенные выше факты (формулы (4')-(10)) остаются неизменными. В
частности числа ![]() и
в случае комплексного
и
в случае комплексного ![]() действительны. Теорема 1 полностью
сохраняется для комплексного
действительны. Теорема 1 полностью
сохраняется для комплексного ![]() . Формула (4") теперь имеет вид
. Формула (4") теперь имеет вид
![]() ,
,
т. е. теперь уже
квадраты чисел ![]() надо
заменить на квадраты их модулей. Формула (4'") теперь уже выглядит
следующим образом:
надо
заменить на квадраты их модулей. Формула (4'") теперь уже выглядит
следующим образом:
![]() ,
,
а в остальном теорема 2 остается в силе.
Замечание 2.
Отметим, что действительность собственных значений самосопряженного линейного
оператора ![]() и
и
![]() (действительном
или комплексном) можно доказать следующим образом. Пусть
(действительном
или комплексном) можно доказать следующим образом. Пусть ![]() - собственное значение
оператора
- собственное значение
оператора ![]() и
и
![]() -
принадлежащий к нему собственный вектор. Так как
-
принадлежащий к нему собственный вектор. Так как ![]() , то
, то
![]() .
.
Ортогональность собственных векторов оператора, принадлежащих разным собственным значениям, тоже можно доказать непосредственно. В самом деле,

тогда
![]() .
.
Так как ![]() , то
, то ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
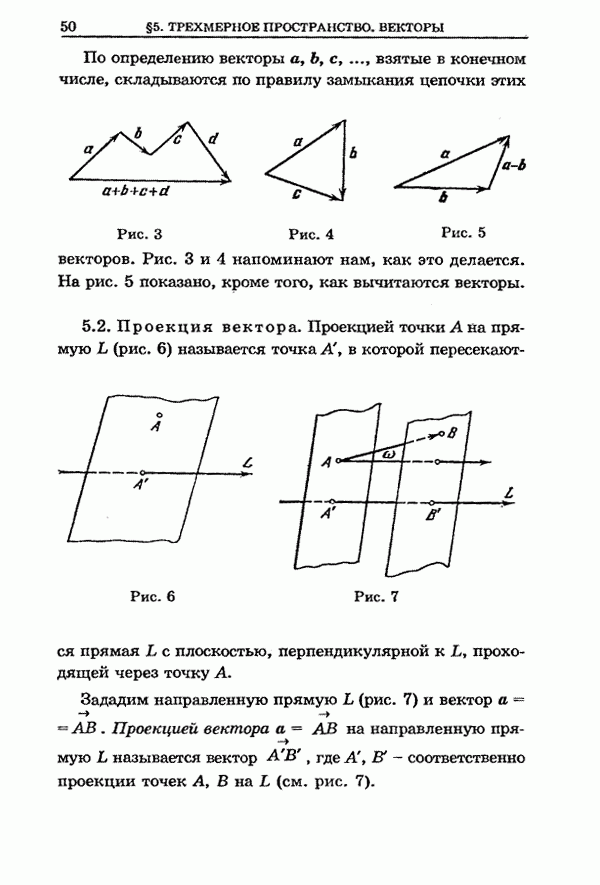
- 5.1. Понятие вектора
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
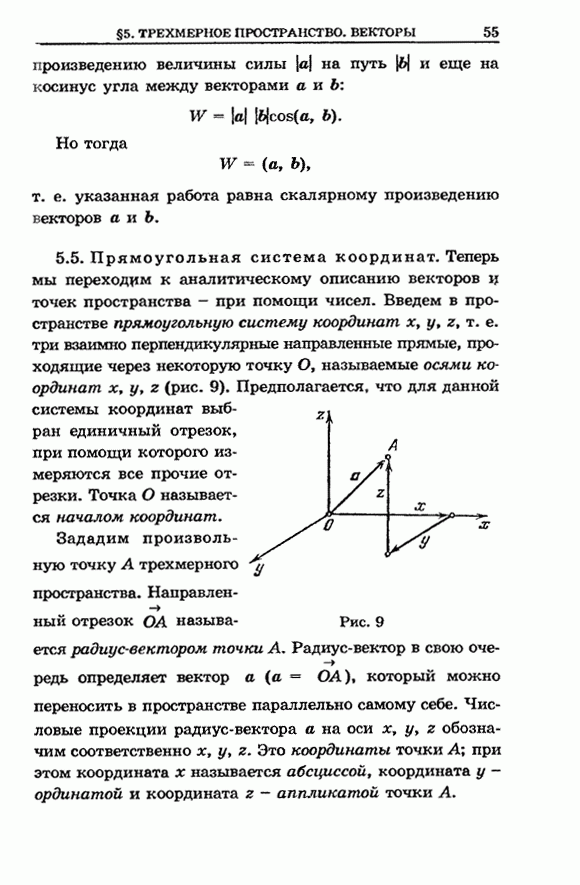
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
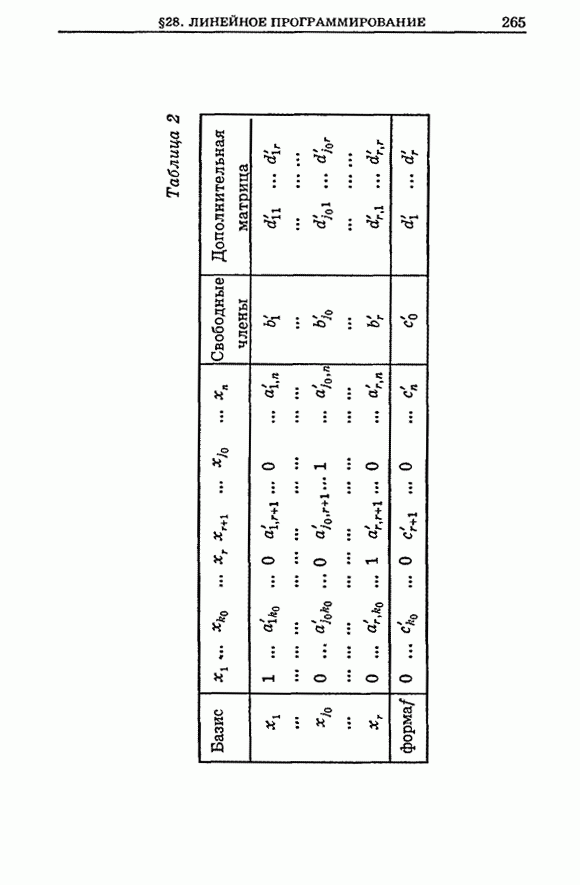
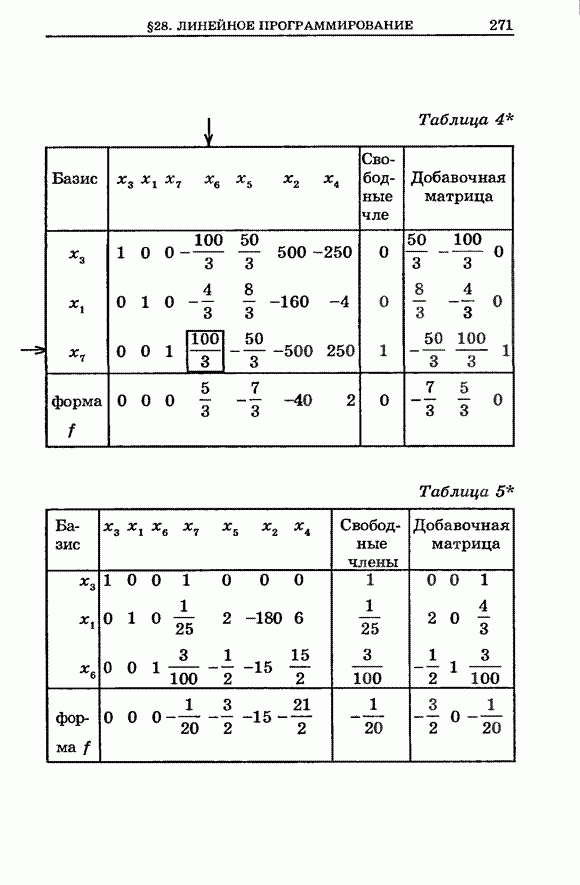
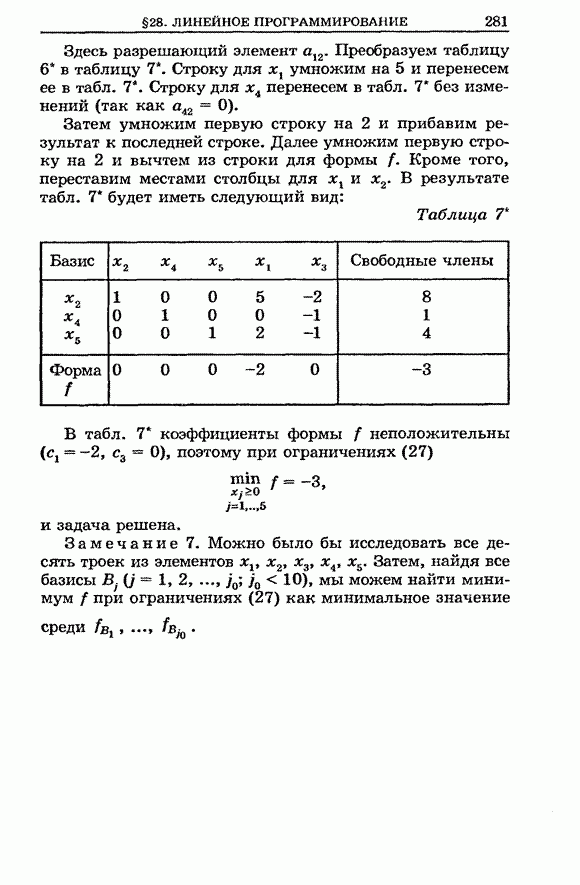
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса