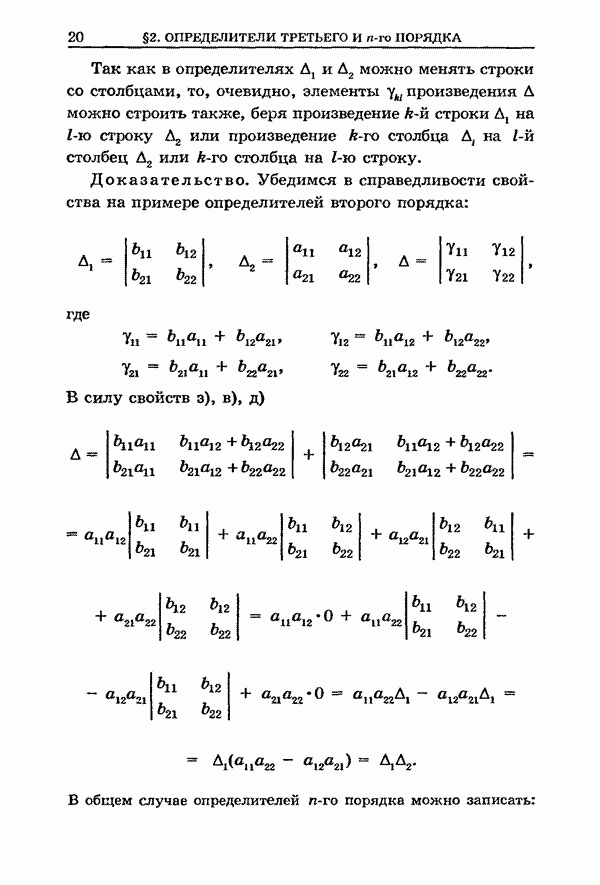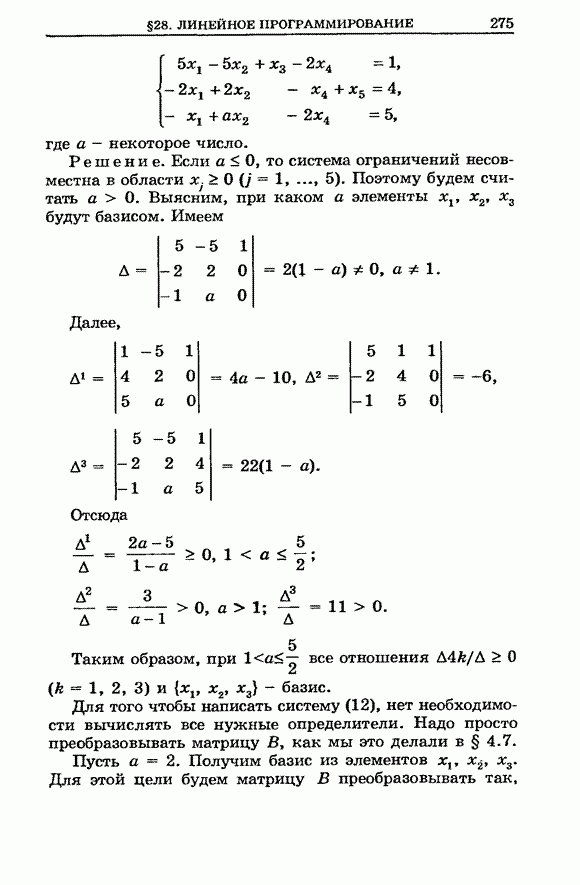| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 21. Теоремы фредгольмова типа
В этом параграфе излагается теория линейных уравнений, параллельная теории, изложенной в § 4.
Это бездетерминантная теория. В ее формулировки определитель системы уравнений явно не входит. Преимущество ее заключается в том, что она послужила основой и аналогом для многих обобщений в математическом анализе. Первые такие важные обобщения принадлежат Фредгольму.
Мы снова
рассматриваем линейный оператор (см. § 15) ![]() :
:
![]() ,
(1)
,
(1)
приводящий в
соответствие каждому вектору ![]() вектор
вектор ![]() при помощи равенств
при помощи равенств
 (2)
(2)
Здесь
 (3)
(3)
- заданная
квадратная матрица. Оператору ![]() соответствует сопряженный ему оператор
соответствует сопряженный ему оператор
![]() , (1*)
, (1*)
определяемый сопряженной к (3) матрицей
 (3*)
(3*)
При помощи
компонент векторов ![]() он
записывается в виде
он
записывается в виде
 (2*)
(2*)
т.е. компонента ![]() выражается через
координаты вектора
выражается через
координаты вектора ![]() с
помощью
с
помощью ![]() -й
строки матрицы
-й
строки матрицы ![]() или
или
![]() -го столбца
матрицы
-го столбца
матрицы ![]() .
.
Справедливо равенство
![]() , (4)
, (4)
верное для всех ![]() . В самом деле, для
действительных
. В самом деле, для
действительных ![]() и
и
![]()
 .
.
В комплексном случае
 .
.
Равенство (4)
характерно для сопряженного оператора, потому что, если для некоторого
линейного оператора ![]() выполняется равенство
выполняется равенство
![]() , (5)
, (5)
то необходимо ![]() . Действительно,
. Действительно, ![]() , для действительных
, для действительных ![]() ,
, ![]() ,
, ![]()
 ,
,
 .
.
Из (5) следует, что
 ,
(6)
,
(6)
откуда ![]() , в чем можно
убедиться, если положить в (6)
, в чем можно
убедиться, если положить в (6) ![]() и
и ![]() , где у
, где у ![]() единица стоит на
единица стоит на ![]() -м месте, а у
-м месте, а у ![]() на
на ![]() -м месте. В
комплексном случае
-м месте. В
комплексном случае
 ,
,
 ,
,
откуда ![]() или
или ![]() .
.
Таким образом, сопряженный
оператор ![]() к
линейному оператору
к
линейному оператору ![]() можно также определить как такой
линейный оператор, для которого выполняется равенство (4).
можно также определить как такой
линейный оператор, для которого выполняется равенство (4).
Равенства (1) и
(1*) можно рассматривать как уравнения - задан вектор ![]() , и мы ищем
, и мы ищем ![]() , для которого
выполняется равенство (1) или (1*).
, для которого
выполняется равенство (1) или (1*).
Соответствующие однородные уравнения имеют вид
![]() (10)
(10)
или
 (20)
(20)
и
![]() (10*)
(10*)
или
 . (20*)
. (20*)
Обозначим через ![]() образ пространства
образ пространства ![]() при помощи оператора
при помощи оператора
![]() :
:
![]()
- и через ![]() подпространство всех
векторов
подпространство всех
векторов ![]() , удовлетворяющих
однородному сопряженному уравнению (10*).
, удовлетворяющих
однородному сопряженному уравнению (10*).
Мы назвали ![]() подпространством,
потому что вместе с
подпространством,
потому что вместе с ![]() ,
, ![]() к нему принадлежат также
к нему принадлежат также ![]() , где
, где ![]() и
и ![]() - числа:
- числа:
![]() .
.
![]() есть тоже
подпространство, потому что, если
есть тоже
подпространство, потому что, если ![]() ,
, ![]() , то существуют векторы
, то существуют векторы ![]() ,
, ![]() такие, что
такие, что ![]() ,
, ![]() , и, следовательно,
, и, следовательно,
![]() ,
,
т.е. ![]() .
.
Справедлива лемма (см. § 20, теорема 2).
Лемма 1. Подпространства
![]() и
и ![]() взаимно ортогональны,
т. е.
взаимно ортогональны,
т. е. ![]() есть
множество всех векторов
есть
множество всех векторов ![]() , каждый из которых ортогонален к
, каждый из которых ортогонален к ![]() , а
, а ![]() в свою очередь есть
множество всех векторов
в свою очередь есть
множество всех векторов ![]() , каждый из которых ортогонален к
, каждый из которых ортогонален к ![]() . Если
. Если ![]() имеет
имеет ![]() измерений, то
измерений, то ![]() имеет
имеет ![]() измерений.
измерений.
Доказательство. Обратимся к равенству
![]() , (7)
, (7)
верному для всех
![]() . Пусть
. Пусть ![]() есть вектор,
ортогональный к
есть вектор,
ортогональный к ![]() ,
тогда для него левая часть (7) равна нулю для всех
,
тогда для него левая часть (7) равна нулю для всех ![]() , но тогда и правая часть
равна нулю для всех
, но тогда и правая часть
равна нулю для всех ![]() , в частности для
, в частности для ![]() :
:
![]() .
.
Следовательно, ![]() . Мы доказали, что
если вектор
. Мы доказали, что
если вектор ![]() ортогонален
к
ортогонален
к ![]() , то он
удовлетворяет уравнению
, то он
удовлетворяет уравнению ![]() (т.е.
(т.е. ![]() ).
).
Обратно, пусть
вектор ![]() удовлетворяет
уравнению
удовлетворяет
уравнению ![]() .
Для такого
.
Для такого ![]() правая
часть (7) равна нулю при любых
правая
часть (7) равна нулю при любых ![]() , но тогда и левая равна нулю, т. е.
, но тогда и левая равна нулю, т. е. ![]() ортогонален ко всем
векторам вида
ортогонален ко всем
векторам вида ![]() ,
т. е. ко всем векторам
,
т. е. ко всем векторам ![]() . Другими словами,
. Другими словами, ![]() ортогонален к
ортогонален к ![]() .
.
Мы доказали, что
![]() есть
множество всех векторов
есть
множество всех векторов ![]() , ортогональных к подпространству
, ортогональных к подпространству ![]() . Но тогда на
основании теоремы 2 § 20 и, обратно,
. Но тогда на
основании теоремы 2 § 20 и, обратно, ![]() есть множество всех векторов
есть множество всех векторов ![]() , ортогональных к
, ортогональных к ![]() , и сумма измерений
, и сумма измерений ![]() и
и ![]() равна
равна ![]() . Лемма доказана.
. Лемма доказана.
Справедлива теорема.
Теорема 1. Для того чтобы уравнение
![]() (1')
(1')
имело решение
для данного вектора ![]() , необходимо и достаточно, чтобы вектор
, необходимо и достаточно, чтобы вектор ![]() был ортогональным ко
всем векторам
был ортогональным ко
всем векторам ![]() ,
удовлетворяющим однородному сопряженному уравнению
,
удовлетворяющим однородному сопряженному уравнению
![]() .
(10*)
.
(10*)
Решение ![]() уравнения (1), если
оно существует, можно записать в виде суммы
уравнения (1), если
оно существует, можно записать в виде суммы
![]() ,
,
где ![]() - какое-либо частное
решение уравнения (1), а
- какое-либо частное
решение уравнения (1), а ![]() - произвольное решение однородного
уравнения
- произвольное решение однородного
уравнения
![]() . (10)
. (10)
Любая указанная сумма есть решение (1').
Доказательство.
В силу леммы 1, если ![]() , а
, а ![]() есть множество всех
есть множество всех ![]() , удовлетворяющих уравнению
, удовлетворяющих уравнению ![]() , то
, то ![]() и
и ![]() суть
подпространства, ортогональные взаимно. Но тогда, если для
суть
подпространства, ортогональные взаимно. Но тогда, если для ![]() существует решение уравнения
(1), то
существует решение уравнения
(1), то ![]() и
необходимо все
и
необходимо все ![]() ортогональны
к
ортогональны
к ![]() . Если же
вектор
. Если же
вектор ![]() ортогонален
ко всем
ортогонален
ко всем ![]() , то
, то
![]() , т. е.
существует
, т. е.
существует ![]() ,
для которого
,
для которого ![]() .
.
Пусть теперь для
вектора ![]() существует
решение уравнения (1'). Обозначим его через
существует
решение уравнения (1'). Обозначим его через ![]() :
:
![]() .
.
Тогда, очевидно,
сумма ![]() , где
, где
![]() , есть тоже
решение уравнения (1'):
, есть тоже
решение уравнения (1'):
![]() .
.
Обратно, если ![]() есть произвольное
решение уравнения (1'), а
есть произвольное
решение уравнения (1'), а ![]() - определенное
частное решение, то
- определенное
частное решение, то
![]() ,
,
и, следовательно,
![]() ,
,
где ![]() , т. е.
, т. е. ![]() , где
, где ![]() удовлетворяет
уравнению
удовлетворяет
уравнению ![]() .
.
Замечание.
Поясним на примере действительного пространства ![]() связь теоремы 1 с теорией
Кронекера-Капелли. Пусть вектор
связь теоремы 1 с теорией
Кронекера-Капелли. Пусть вектор ![]() ортогонален ко всем решениям системы
ортогонален ко всем решениям системы
 (8)
(8)
Покажем, что
тогда ранги матрицы ![]() и расширенной матрицы
и расширенной матрицы

равны между
собой. Если ранг ![]() ,
то, очевидно, ранг
,
то, очевидно, ранг ![]() .
Пусть ранг
.
Пусть ранг ![]() .
Всегда ранг
.
Всегда ранг ![]() ранг
ранг
![]() . Поэтому
нам необходимо доказать, что
. Поэтому
нам необходимо доказать, что
 .
.
В самом деле,
так как ![]() ортогонален
к решениям системы (8) (нетривиальным), то
ортогонален
к решениям системы (8) (нетривиальным), то ![]() . Поэтому, считая, что
. Поэтому, считая, что ![]() ,
,
![]() ,
,
![]() .
.
Отсюда следует,
что ранг ![]() =
ранг
=
ранг ![]() = 1.
= 1.
Обратно, пусть
вектор ![]() таков,
что ранг
таков,
что ранг ![]() =
ранг
=
ранг ![]() ,
тогда (1) имеет некоторое решение
,
тогда (1) имеет некоторое решение ![]() . Докажем, что
. Докажем, что ![]() ортогонален к решениям
ортогонален к решениям ![]() системы (8). В самом
деле,
системы (8). В самом
деле,

Теорема 2. Однородные уравнения
![]() (10)
(10)
и
![]() (10*)
(10*)
имеют одинаковое число линейно независимых решений.
В частности, если одно из этих уравнений имеет только тривиальное решение 0, т.е. имеет нуль независимых решений, то это верно и для другого.
Замечание. В последнем случае уравнение (1) имеет единственное решение.
Доказательство.
Матрицы ![]() и
и ![]() имеют один и тот же
ранг, который обозначим через
имеют один и тот же
ранг, который обозначим через ![]() . Они имеют также один и тот же
определитель
. Они имеют также один и тот же
определитель ![]() .
.
Если ![]() , то
, то ![]() и уравнения (10)
и (10*) имеют только тривиальные решения 0. В этом
случае, согласно теореме 1, уравнение (1) имеет единственное решение при любых
и уравнения (10)
и (10*) имеют только тривиальные решения 0. В этом
случае, согласно теореме 1, уравнение (1) имеет единственное решение при любых ![]() .
.
Пусть теперь ![]() . После
соответствующей перенумерации уравнений и компонент определитель
. После
соответствующей перенумерации уравнений и компонент определитель
 .
.
Первые ![]() уравнений (1°)
теперь запишем в виде
уравнений (1°)
теперь запишем в виде
 (9)
(9)
Ниже приводится
таблица ![]() векторов
векторов
 (10)
(10)
Чтобы получить первый вектор, подставляем в систему (9)
![]()
и решаем ее
относительно ![]() .
Единственные решения, которые здесь получаются, обозначим через
.
Единственные решения, которые здесь получаются, обозначим через ![]() . Чтобы получить
второй вектор, подставляем в (9)
. Чтобы получить
второй вектор, подставляем в (9)
![]()
и находим числа ![]() и т. д. Векторы (10)
обладают следующими свойствами.
и т. д. Векторы (10)
обладают следующими свойствами.
1) Система векторов (10) линейно независима, потому что ранг
матрицы этих векторов равен числу этих векторов ![]() .
.
2) Каждый вектор системы (10) есть решение (любых) уравнений
(![]() ) или
) или ![]() .
.
3) Всевозможные решения уравнения ![]() имеют вид
имеют вид
![]() ,
,
где ![]() - произвольные числа.
- произвольные числа.
Обычно эти три
утверждения заменяют словами: уравнение (![]() ) имеет
) имеет ![]() линейно независимых решений.
линейно независимых решений.
Подобными
рассуждениями, учитывая, что ранг ![]() ранг
ранг ![]() , доказываем, что уравнение
, доказываем, что уравнение ![]() тоже имеет
тоже имеет ![]() линейно независимых
решений. Теорема доказана.
линейно независимых
решений. Теорема доказана.
Теорема 3. Если одно из однородных
уравнений (![]() )
или (
)
или (![]() ) имеет
) имеет
![]() линейно
независимых решений, то и другое имеет
линейно
независимых решений, то и другое имеет ![]() линейно независимых решений; образы же
линейно независимых решений; образы же ![]() и
и ![]() пространства
пространства ![]() , получаемые при
помощи операторов
, получаемые при
помощи операторов ![]() и
и
![]() , суть
подпространства
, суть
подпространства ![]() измерений.
измерений.
Доказательство.
Первое утверждение теоремы о равенстве количеств линейно независимых решений
однородных уравнений (![]() ) и (
) и (![]() ) есть теорема 2, а второе - есть лемма
1, в силу которой измерение подпространства
) есть теорема 2, а второе - есть лемма
1, в силу которой измерение подпространства ![]() , равно
, равно ![]() , где
, где ![]() — измерение подпространства
— измерение подпространства ![]() векторов
векторов ![]() , удовлетворяющих
уравнению
, удовлетворяющих
уравнению ![]() .
Аналогично измерение
.
Аналогично измерение ![]() равно
равно ![]() , где
, где ![]() - количество измерений подпространства
векторов
- количество измерений подпространства
векторов ![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
- 5.1. Понятие вектора
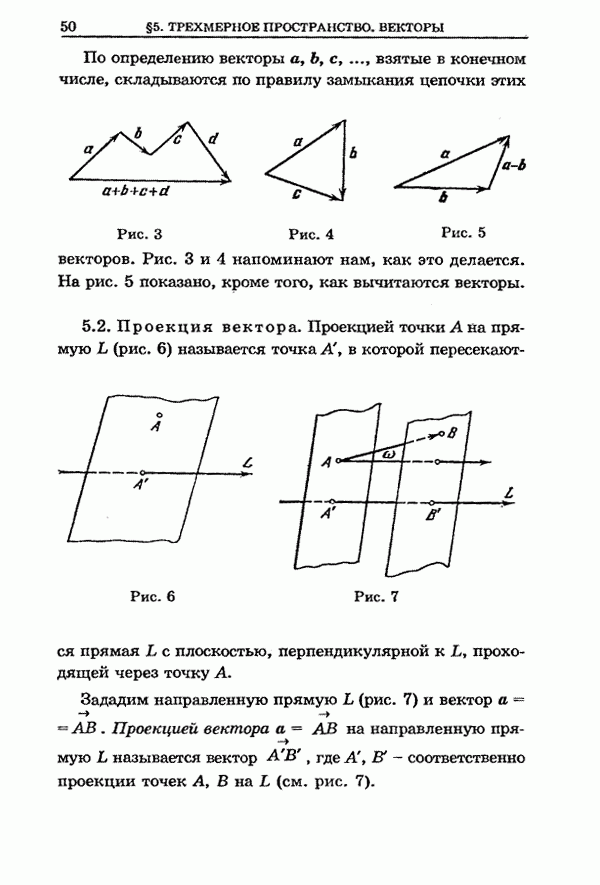
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
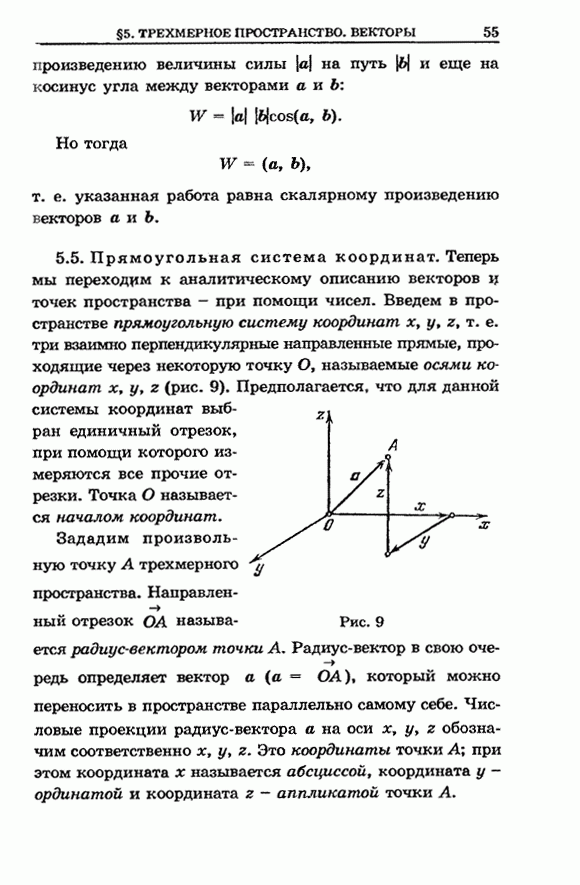
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
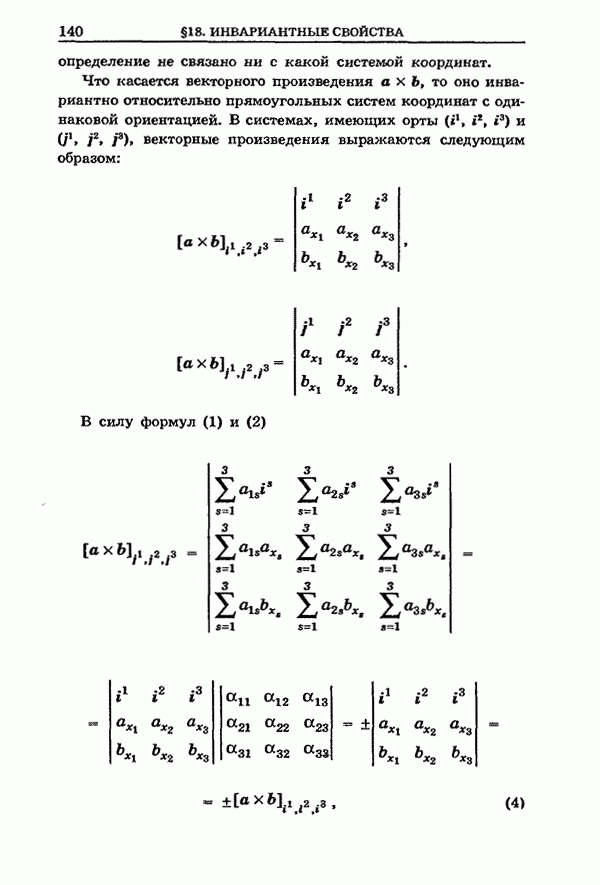
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
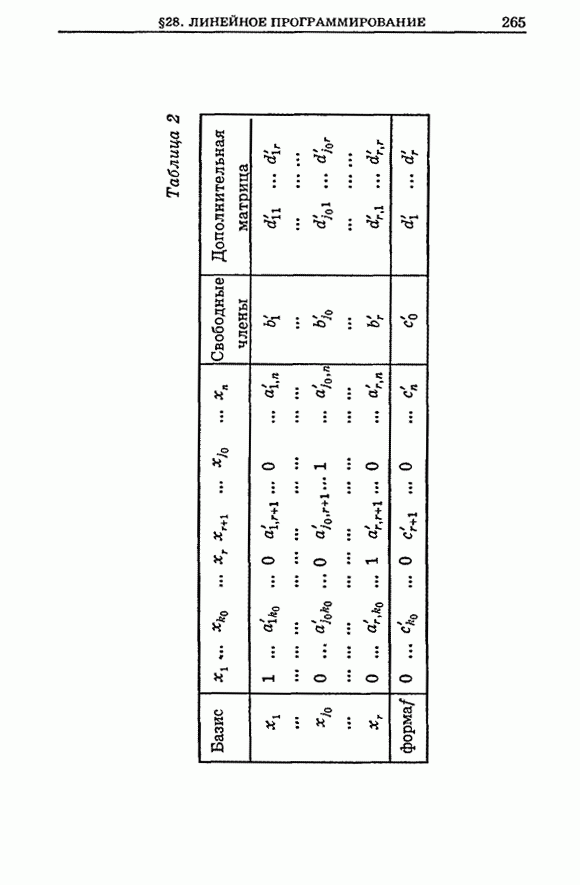
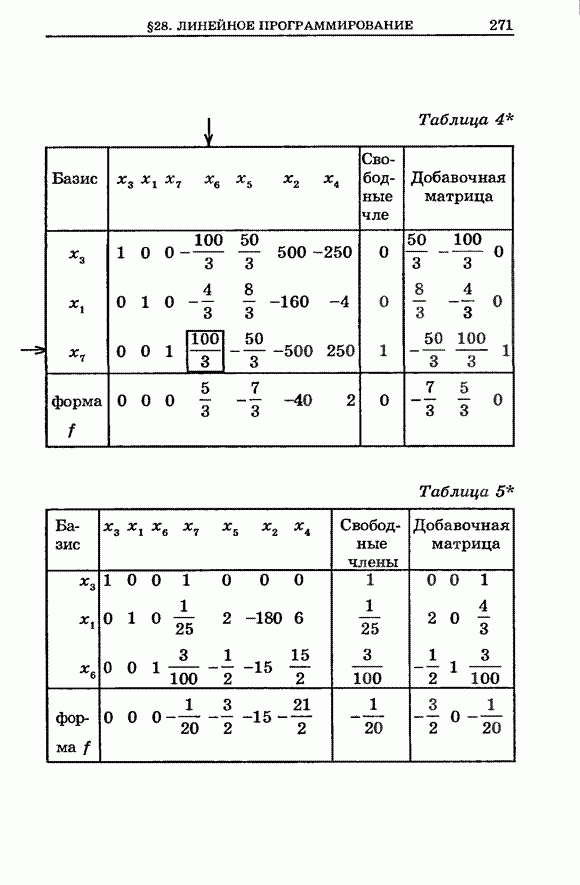
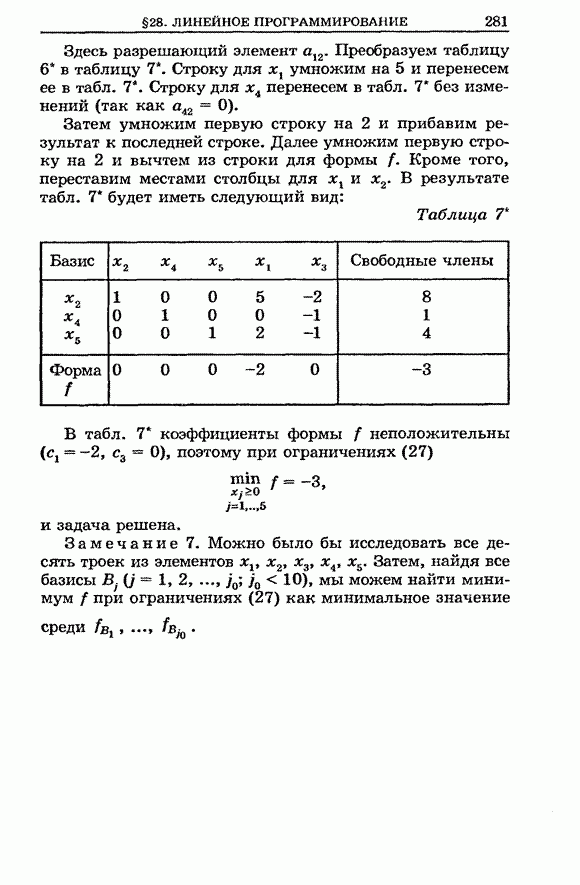
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса