| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
Пример 13. Определите температуру поверхности Солнца, если известно, что на границе земной атмосферы плотность потока солнечного излучения равна  Излучение Солица считайте близким к излучению черного тела.
Излучение Солица считайте близким к излучению черного тела.
Решение. Плотность потока теплового излучения, испускаемого единицей поверхности черного тела, определяется законом Стефана — Больцмана:

где  Отсюда:
Отсюда:

Для определения значения плотности потока до надо полную мощность  излучения Солнца разделить на площадь его поверхности:
излучения Солнца разделить на площадь его поверхности:

где  — радиус Солнца.
— радиус Солнца.
Полную мощность излучения Солнца определим из выражения:

где  — поверхность сферы, имеющей радиус
— поверхность сферы, имеющей радиус  равный расстоянию от Солнца до Земли. Так как
равный расстоянию от Солнца до Земли. Так как  то
то

Следовательно,

Подставляя значения входящих в эту формулу величин, получим:

Пример 14. Металлический шар радиусом 10 см облучают светом с длиной волны  Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна
Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна  Дж.
Дж.
Решение. Заряд на шаре будет установившимся при условии, что самые быстрые электроны, покидающие поверхность шара вследствие фотоэффекта, возвращаются на шар под действием электростатического поля. В этом случае выполняется
равенство:

Используя уравнение Эйнштейна

получим:

Подставив значения величин, найдем:

Пример 15. Две плоские заряженные металлические пластины расположены параллельно на расстоянии 1 см в вакууме. Напряжение между пластинами 10 В. Отрицательно заряженная пластина освещается узким пучком света, длина волны которого  Определите радиус окружности на поверхности положительно заряженной пластины, ограничивающей область попадания фотоэлектронов. Красная граница фотоэффекта с поверхности пластины равна
Определите радиус окружности на поверхности положительно заряженной пластины, ограничивающей область попадания фотоэлектронов. Красная граница фотоэффекта с поверхности пластины равна 
Решение. Выберем начало координат (точку О) на поверхности пластины, в которую попадает пучок света. Ось  направим перпендикулярно к плоскости пластины, а ось
направим перпендикулярно к плоскости пластины, а ось  пусть лежит в плоскости пластины.
пусть лежит в плоскости пластины.
В этом случае радиус  искомой окружности равен максимальному значению координаты у фотоэлектрона при достижении им положительно заряженной пластины:
искомой окружности равен максимальному значению координаты у фотоэлектрона при достижении им положительно заряженной пластины:

Двигаясь между пластинами, фотоэлектрон удаляется от оси  на максимальное расстояние в том случае, когда модуль составляющей скорости
на максимальное расстояние в том случае, когда модуль составляющей скорости  имеет максимальное значение, а модуль составляющей
имеет максимальное значение, а модуль составляющей  — минимальное (так как при этом время
— минимальное (так как при этом время  движения электрона между пластинами становится максимальным). Максимальное значение модуля составляющей скорости
движения электрона между пластинами становится максимальным). Максимальное значение модуля составляющей скорости  равно максимальному значению начальной скорости фотоэлектрона:
равно максимальному значению начальной скорости фотоэлектрона:

Максимальную скорость найдем из уравнения Эйнштейна:

Работу выхода определим по известной красной границе фотоэффекта:

Максимальное время движения фотоэлектрона между пластинами определится так:

Тогда для искомого радиуса окружности имеем:

Подставляя в это выражение значения величин, получим:

Пример 16. При бомбардировке быстрыми электронами металлического антикатода рентгеновской трубки возникает рентгеновское тормозное излучение.
Определите коротковолновую границу спектра рентгеновского излучения при скорости электронов 
Решение. Коротковолновая граница спектра рентгеновского излучения определяется условием равенства кинетической энергии электрона энергии фотона:

откуда получаем:

Так как скорость электрона  сравнима со скоростью света, то его кинетическую энергию следует рассчитывать по релятивистской формуле:
сравнима со скоростью света, то его кинетическую энергию следует рассчитывать по релятивистской формуле:

В этом случае выражение (1) можно записать:

При условии 

Пример 17. Неподвижный атом водорода излучил квант света, соответствующий головной линии серии Лаймана (серия Лаймана соответствует переходам на уровень  Определите относительное изменение частоты фотона вследствие отдачи атома. Какую скорость приобрел атом за счет энергии отдачи?
Определите относительное изменение частоты фотона вследствие отдачи атома. Какую скорость приобрел атом за счет энергии отдачи?
Решение. Для явления излучения фотона запишем законы сохранения энергии:

и импульса:

Из уравнений (1) и (2) следует:

Из выражений (1) и (2) следует и другое равенство:

Запишем выражение полной энергии для атома водорода:

Из второго закона Ньютона можно записать:

Из выражений (5) и (6) получим:

Из условия квантования орбит  и выражения (7) найдем радиус орбиты:
и выражения (7) найдем радиус орбиты:

и полную энергию:

где

На основании постулата Бора запишем:

Проведя преобразования выражений (4) и (8), получим:

Подставим полученное значение в выражение (3), найдем скорость:

Пример 18. Пользуясь соотношением неопределенностей, оцените размер атома водорода.
Решение. В устойчивом состоянии полная энергия атома минимальна. Энергия атома водорода складывается из потенциальной энергии системы «электрон — ядро»:

и кинетической энергии электрона:

где  — импульс электрона. В соответствии с соотношением неопределенности
— импульс электрона. В соответствии с соотношением неопределенности

где  — неопределенность в координате электрона, которую можно принять равной искомому радиусу
— неопределенность в координате электрона, которую можно принять равной искомому радиусу  атома водорода. Импульс электрона
атома водорода. Импульс электрона  можно принять равным его неопределенности
можно принять равным его неопределенности  . Тогда из соотношения неопределенностей следует:
. Тогда из соотношения неопределенностей следует:

а для кинетической энергии электрона имеем:

Полная энергия атома равна:

Так как в устойчивом состоянии полная энергия системы должна быть минимальной, для нахождения радиуса первой орбиты электрона найдем значение  , соответствующее минимуму энергии. Найдем производную энергии атома по его радиусу
, соответствующее минимуму энергии. Найдем производную энергии атома по его радиусу  и приравняем ее нулю:
и приравняем ее нулю:

отсюда находим искомый размер:

Подстановка числовых данных приводит к результату:

что соответствует действительному значению радиуса атома водорода в нормальном состоянии.
Пример 19. Пользуясь соотношением неопределенностей, докажите, что энергия ионизации обратно пропорциональна квадрату диаметра атома.
Решение. Считая неопределенность координаты  электрона в атоме равной его диаметру
электрона в атоме равной его диаметру  а неопределенность
а неопределенность
импульса  равной импульсу
равной импульсу  из соотношения неопределенностей получим:
из соотношения неопределенностей получим:

тогда:

Задачи для самостоятельного решения
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
Индивидуальные экспериментальные задания
1. Рассчитайте и измерьте периоды колебаний груза на двух пружинах, соединенных последовательно и параллельно.
2. Исследуйте зависимость периода колебаний линейки от расстояния между ее центром тяжести и осью качаний.
3. Исследуйте зависимость периода крутильных колебаний стержня, подвешенного за середину, от длины и диаметра лески. Дайте объяснение полученным результатам.
4. Рассчитайте, соберите и испытайте модели микроскопа и телескопа.
5. Изготовьте модель дифракционной решетки.
6. Изготовьте модель зонной пластинки.
7. Определите КПД солнечной батареи.
8. Рассчитайте и изготовьте действующую модель опыта Девиссона — Джермера, используя вместо пучка электронов электромагнитное излучение СВЧ ( см), а вместо кристаллической решетки — систему деревянных реек с упорядоченно забитыми в них гвоздями.
см), а вместо кристаллической решетки — систему деревянных реек с упорядоченно забитыми в них гвоздями.
Исследуйте зависимость амплитуды колебаний в отраженной электромагнитной волне от угла падения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
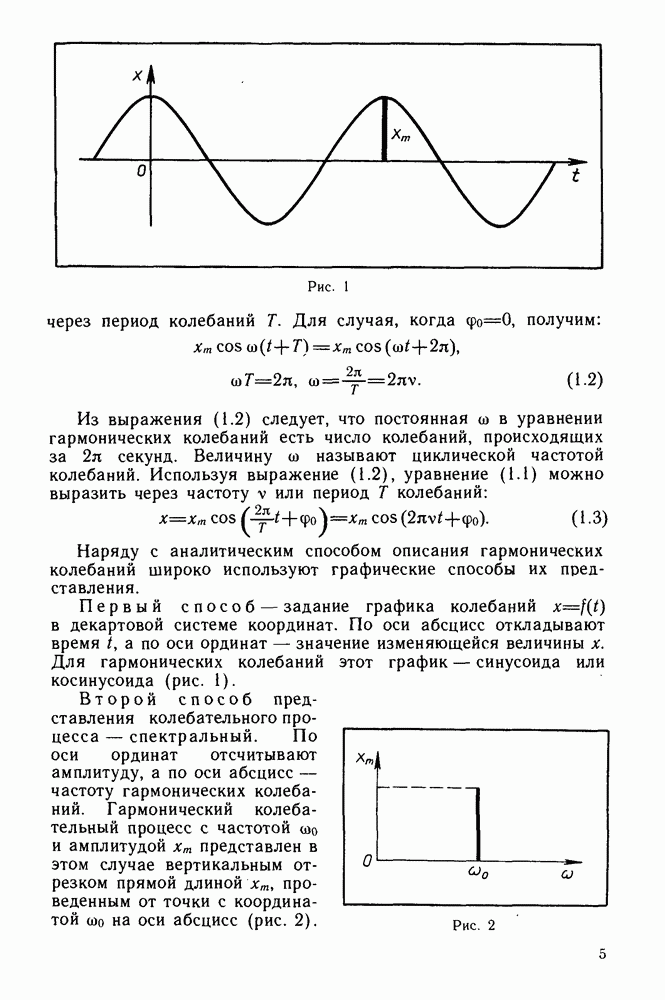
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
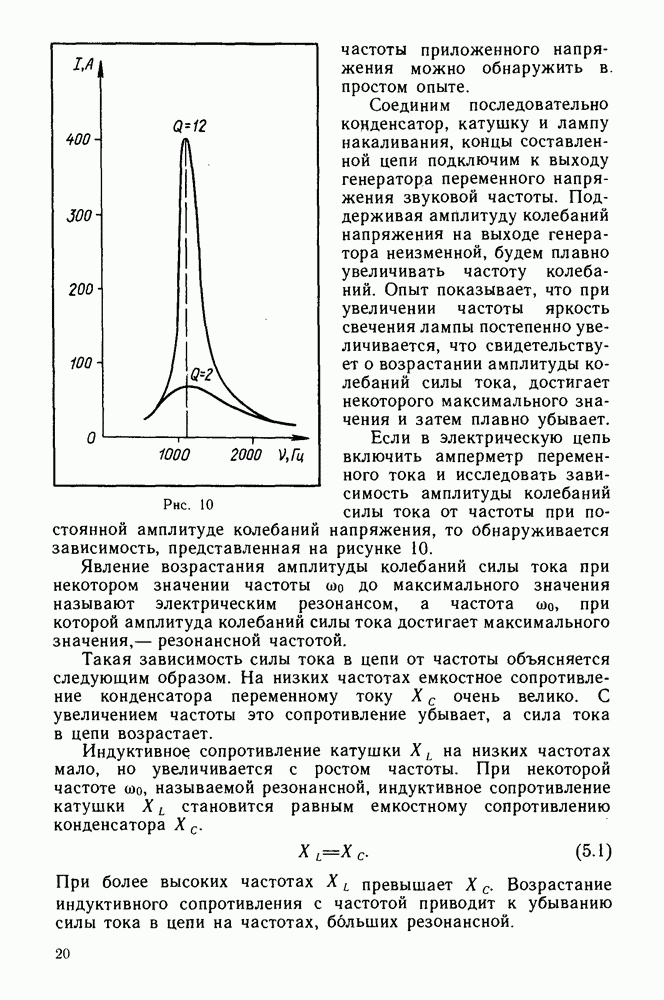
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
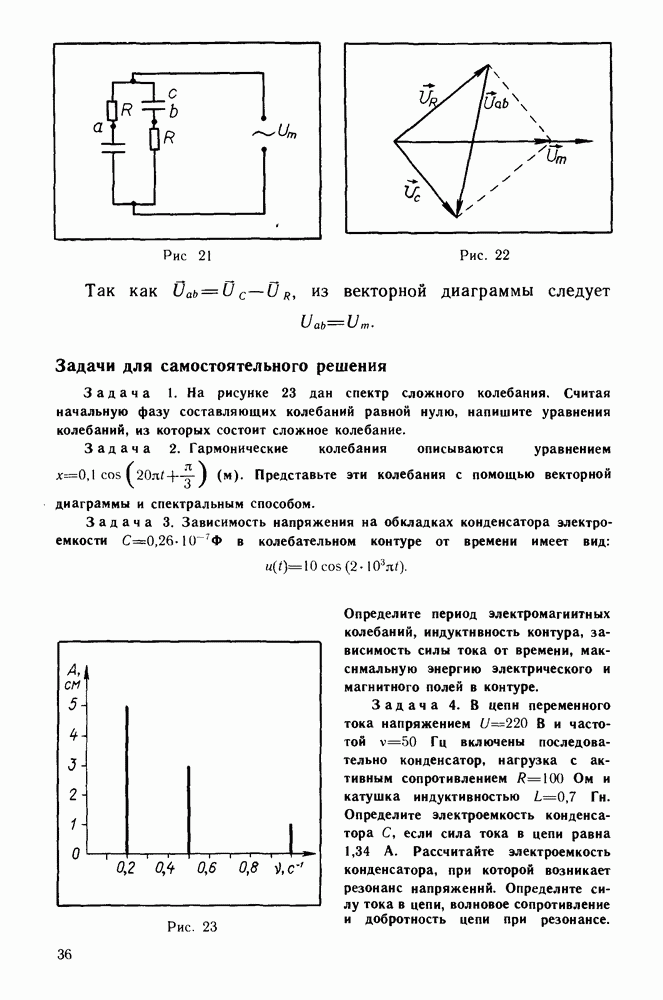
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
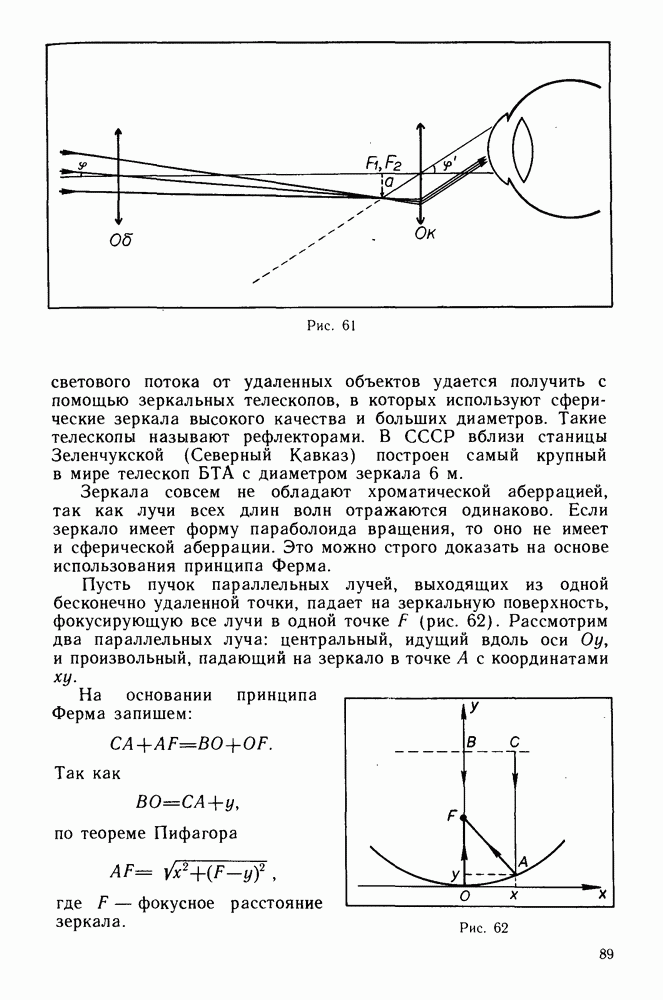
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
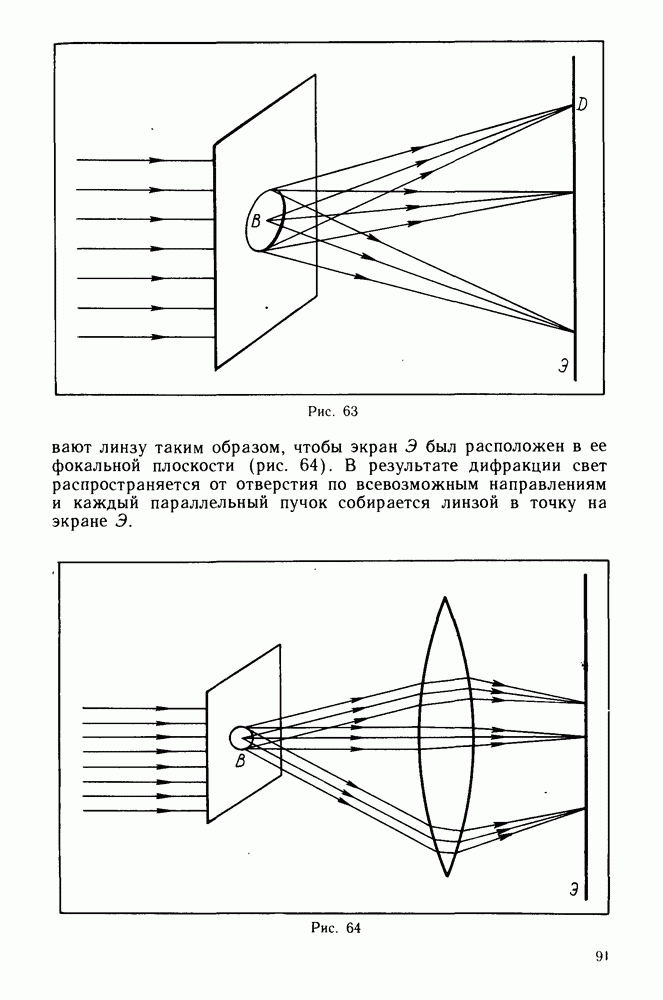
- Дифракция от круглого отверстия.
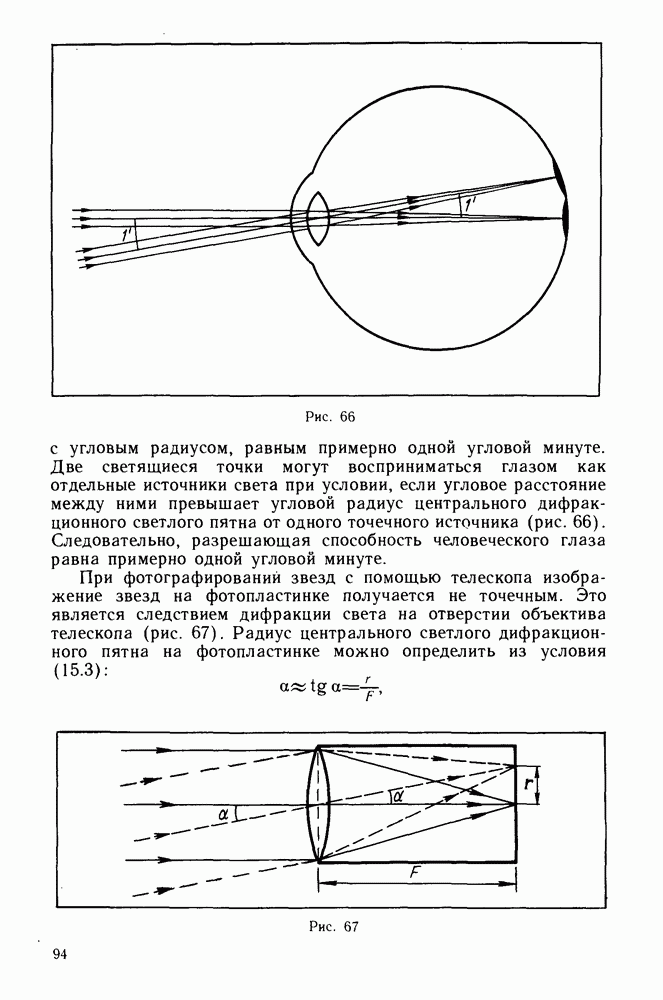
- Дифракция и разрешающая способность оптических приборов.
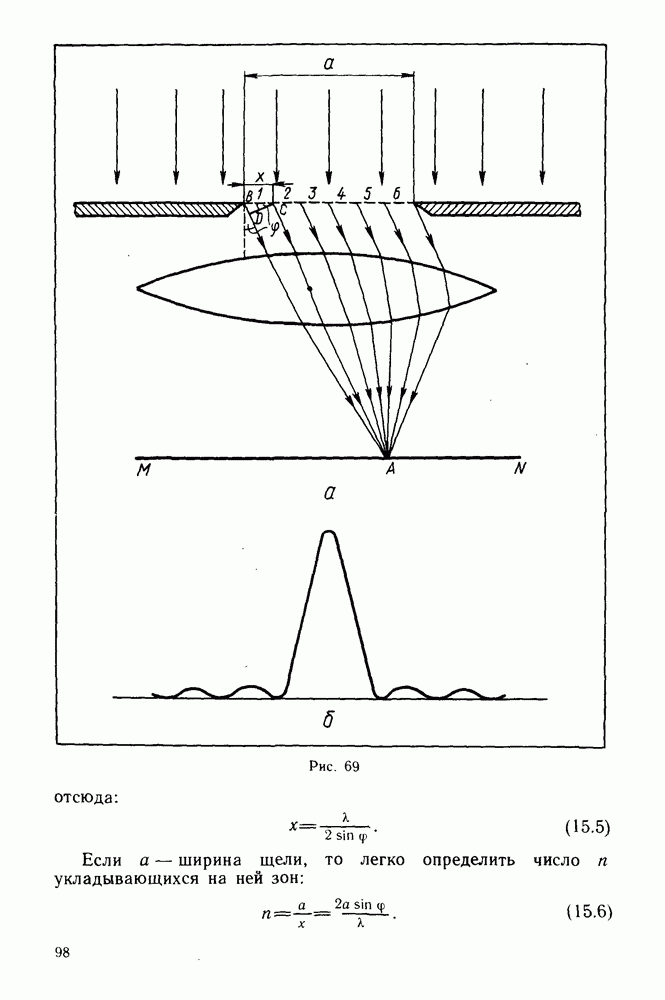
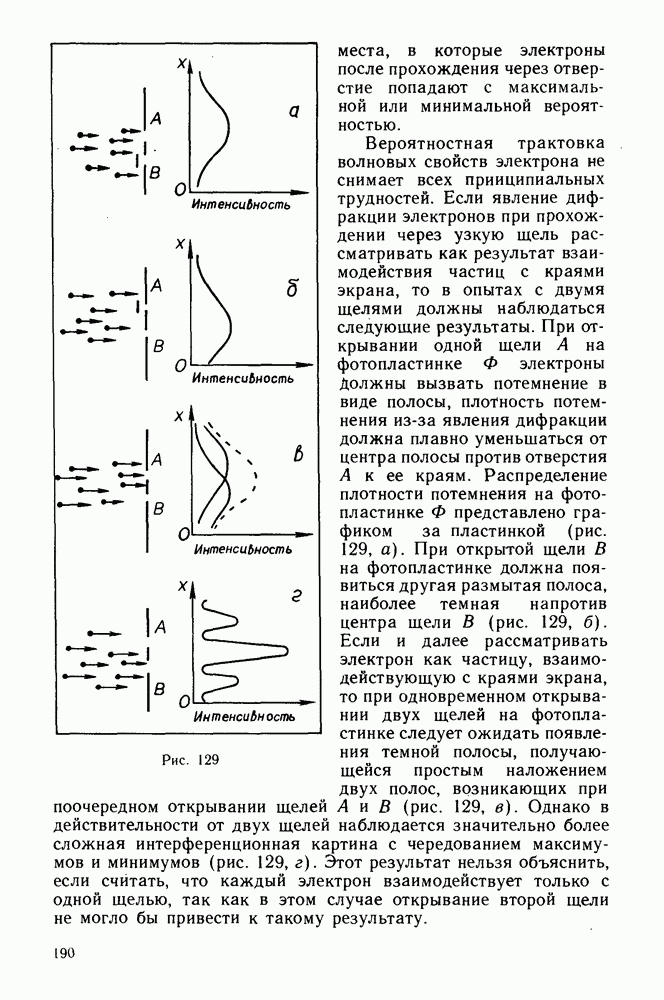
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
- Схема энергетических уровней.
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
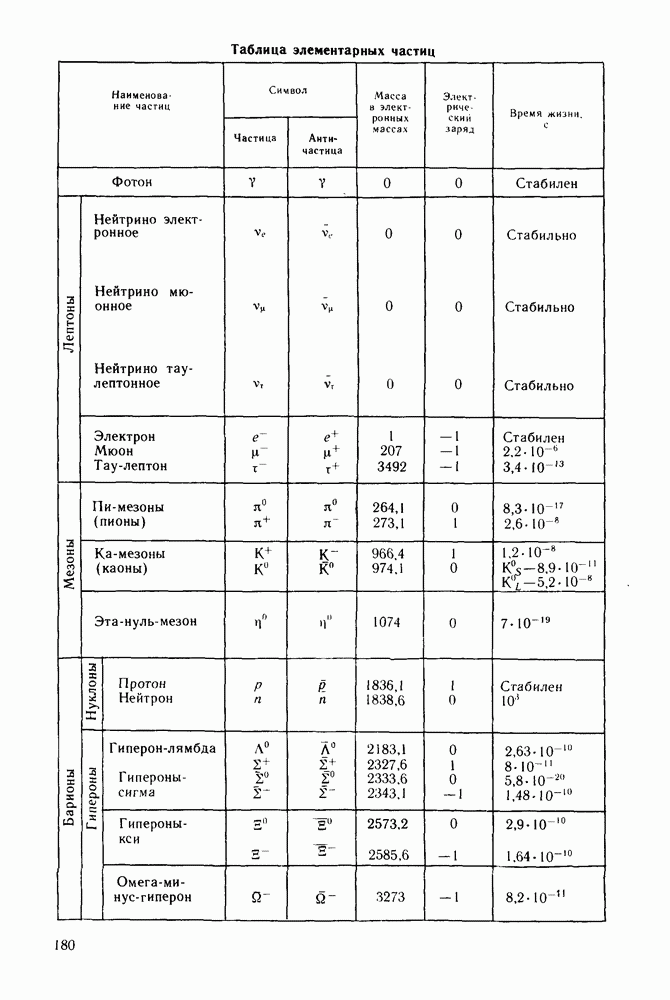
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
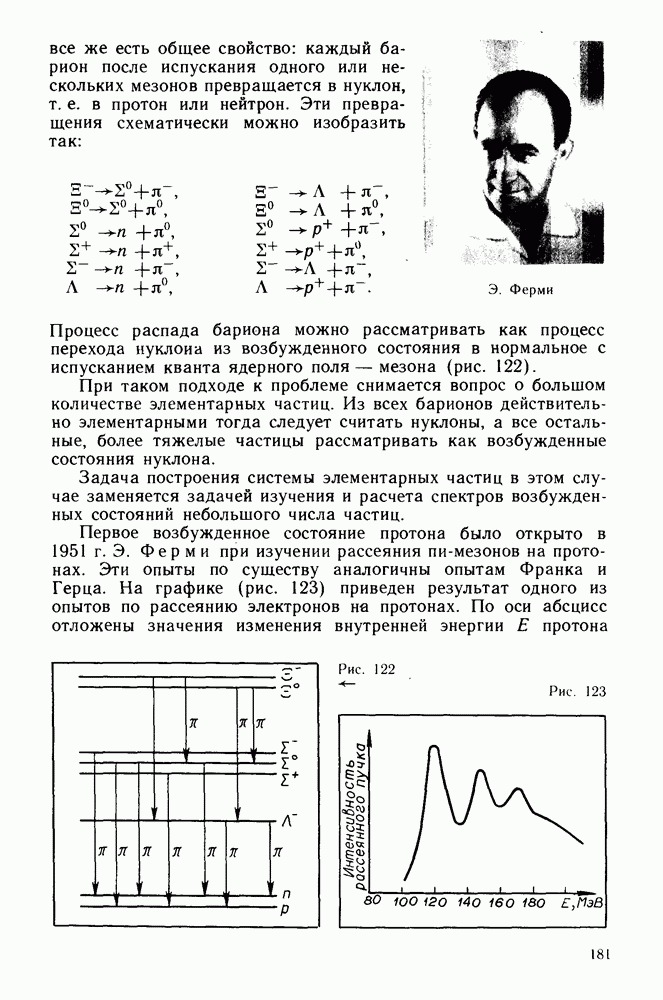
- Спектры элементарных частиц.
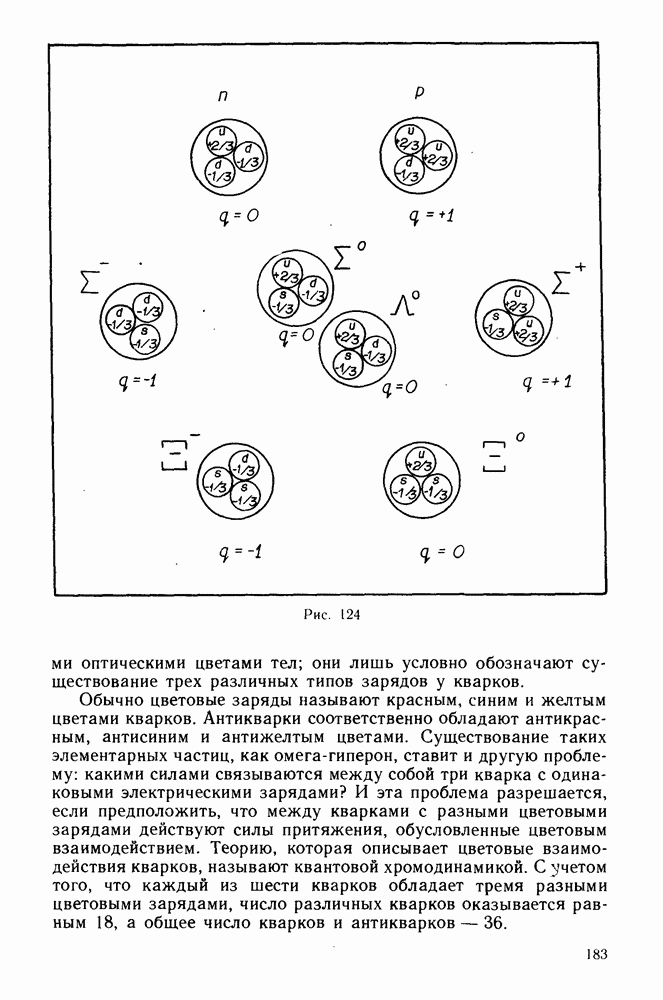
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ