| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
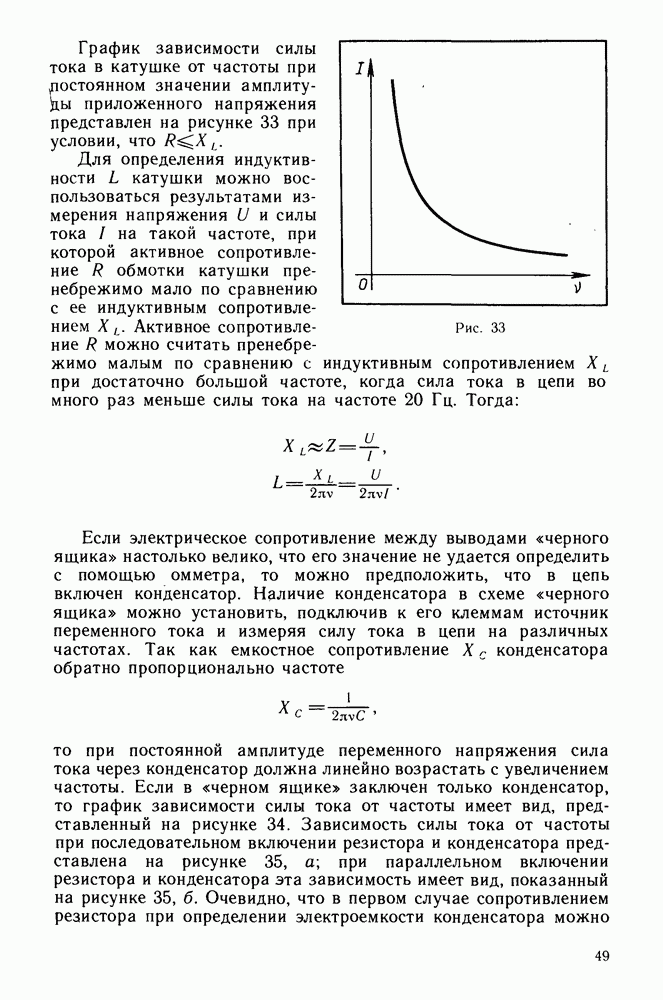
Гармонический анализ.
Сущность метода гармонического анализа заключается в том, что негармонический периодический колебательный процесс представляют как результат сложения некоторого числа гармонических колебаний. Возможность представления почти любой периодической функции в виде суммы бесконечного тригонометрического ряда была показана французским ученым Ж. Фурье в прошлом веке. Этот ряд для функции  с периодом Т имеет вид:
с периодом Т имеет вид:

или

Его называют рядом Фурье.
Первое слагаемое ряда Фурье  — постоянная составляющая
— постоянная составляющая  не зависящая от времени. Второе слагаемое
не зависящая от времени. Второе слагаемое  представляет собой первую, или основную, гармоническую составляющую разложения с периодом Т,
представляет собой первую, или основную, гармоническую составляющую разложения с периодом Т,
равным периоду функции  Третье слагаемое называют второй гармоникой. Период второй гармоники в два раза меньше периода функции
Третье слагаемое называют второй гармоникой. Период второй гармоники в два раза меньше периода функции  Период третьей гармоники в три раза меньше Т и т. д.
Период третьей гармоники в три раза меньше Т и т. д.
Если бы для анализа периодической функции  одинаково важны были все члены бесконечного тригонометрического ряда Фурье (2.1), гармонический анализ не имел бы никакой практической ценности, так как с его помощью невозможно было бы произвести никаких вычислений. Но в действительности амплитуда гармоник ряда Фурье с увеличением номера гармоники
одинаково важны были все члены бесконечного тригонометрического ряда Фурье (2.1), гармонический анализ не имел бы никакой практической ценности, так как с его помощью невозможно было бы произвести никаких вычислений. Но в действительности амплитуда гармоник ряда Фурье с увеличением номера гармоники  имеет тенденцию к убыванию. Поэтому для практических целей оказывается важным использовать вместо бесконечного ряда тригонометрических функций их конечное число. Количество членов ряда Фурье, которые необходимо использовать в расчетах, определяется видом функции
имеет тенденцию к убыванию. Поэтому для практических целей оказывается важным использовать вместо бесконечного ряда тригонометрических функций их конечное число. Количество членов ряда Фурье, которые необходимо использовать в расчетах, определяется видом функции  и заданной точностью вычислений. Определение амплитуд гармоник является сложной математической задачей, поэтому мы ограничимся лишь приведением без вывода нескольких примеров разложения периодических функций в ряд Фурье.
и заданной точностью вычислений. Определение амплитуд гармоник является сложной математической задачей, поэтому мы ограничимся лишь приведением без вывода нескольких примеров разложения периодических функций в ряд Фурье.
Примером негармонической периодической функции может служить функция, график которой представлен на рисунке 6. Периодический колебательный процесс, описываемый этой функцией, может быть получен, например, в электрической цепи, состоящей из источника тока напряжением  на выходных зажимах, ключа и резистора R. Если ключ замкнуть и через интервал времени
на выходных зажимах, ключа и резистора R. Если ключ замкнуть и через интервал времени  разомкнуть, а затем, спустя время Т после момента первого замыкания, вновь замкнуть на время
разомкнуть, а затем, спустя время Т после момента первого замыкания, вновь замкнуть на время  и таким образом повторять процесс включения и выключения, то график зависимости напряжения на резисторе R от времени будет иметь вид, представленный на рисунке 6. Переменное напряжение такого типа называют периодической последовательностью прямоугольных импульсов с периодом Т и длительностью т.
и таким образом повторять процесс включения и выключения, то график зависимости напряжения на резисторе R от времени будет иметь вид, представленный на рисунке 6. Переменное напряжение такого типа называют периодической последовательностью прямоугольных импульсов с периодом Т и длительностью т.
Амплитуда  гармоники спектрального расположения
гармоники спектрального расположения

Рис. 6

Рис. 7
периодической последовательности прямоугольных импульсов напряжения определяется выражением:

где  — амплитуда
— амплитуда  гармоники;
гармоники;  — амплитуда прямоугольного импульса;
— амплитуда прямоугольного импульса;  — длительность импульса; Т — период повторения импульса;
— длительность импульса; Т — период повторения импульса;  — порядковый номер гармоники.
— порядковый номер гармоники.
Постоянная составляющая определяется выражением:

Амплитудный спектр гармонических составляющих периодической последовательности прямоугольных импульсов, представленной на рисунке 6, показан на рисунке 7.
В импульсной технике гармонический анализ позволяет производить расчеты электрических цепей при прохождении через них электрических сигналов сложной формы, применяя простые правила расчета для гармонических составляющих.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
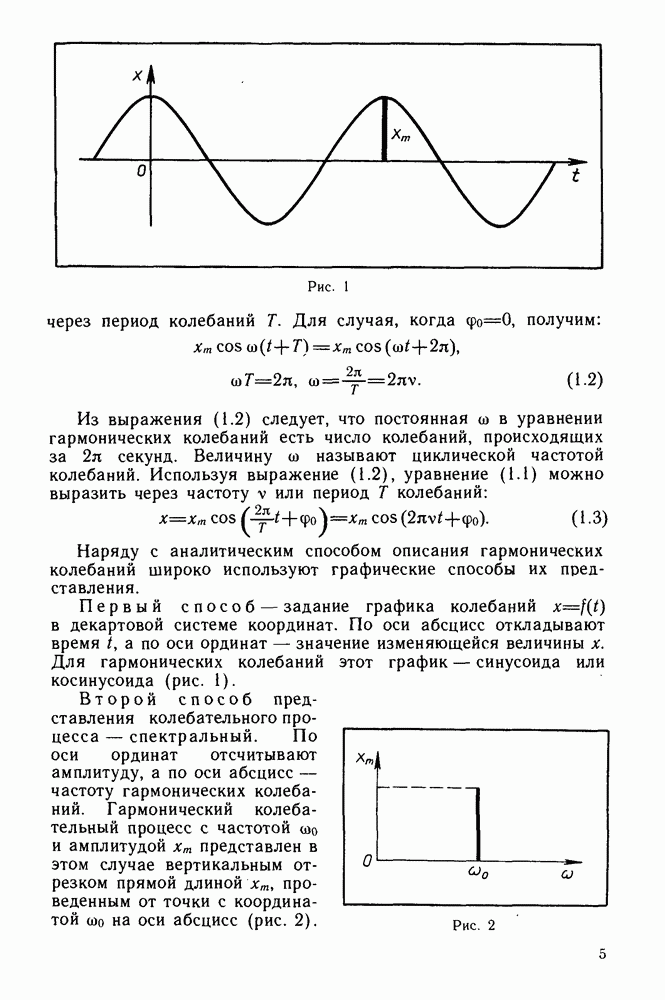
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
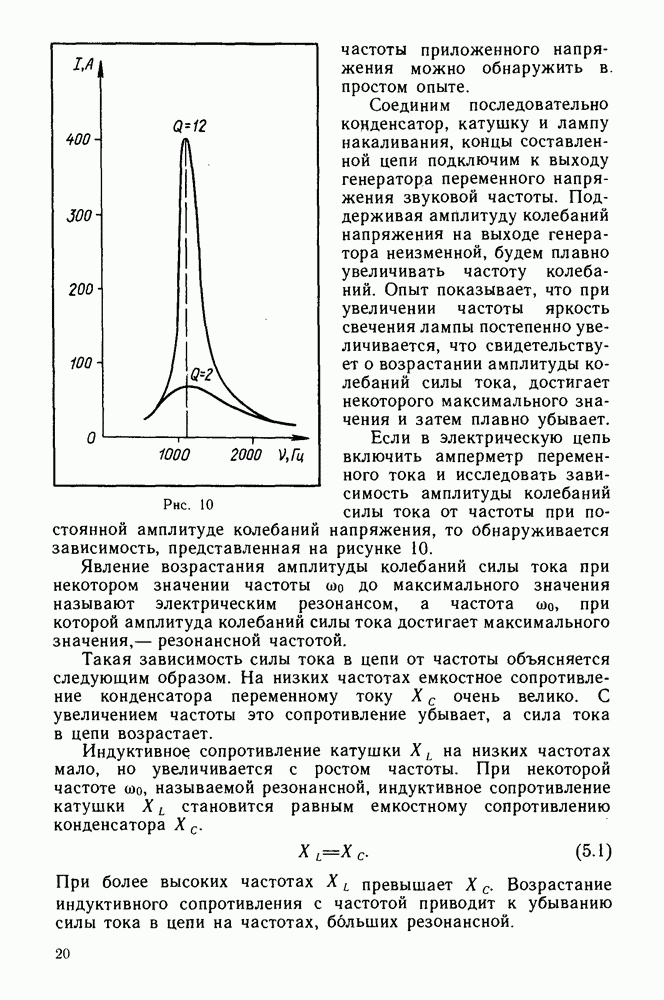
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
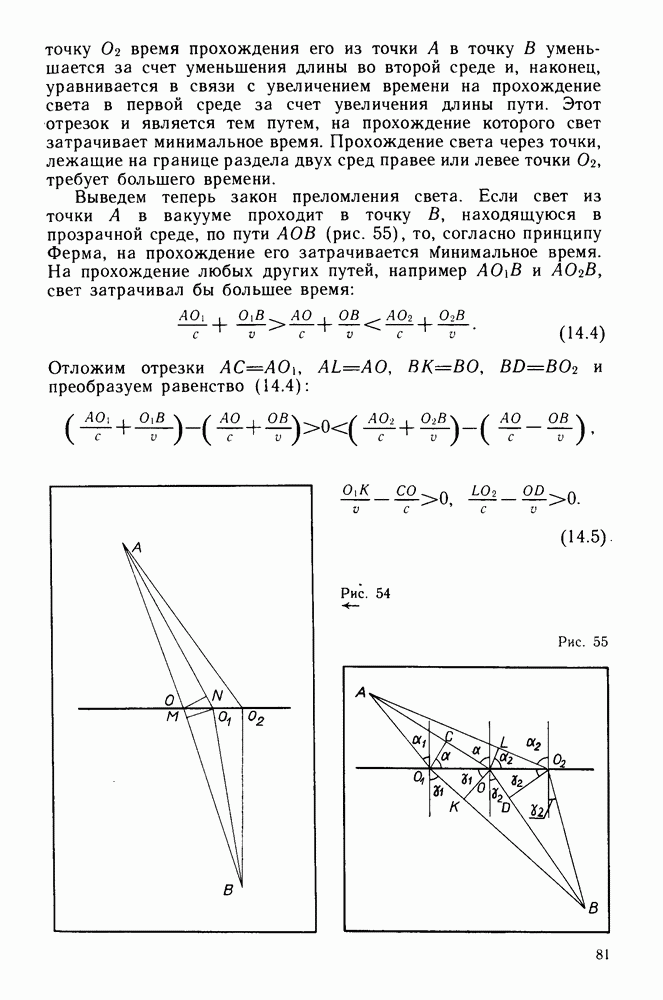
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
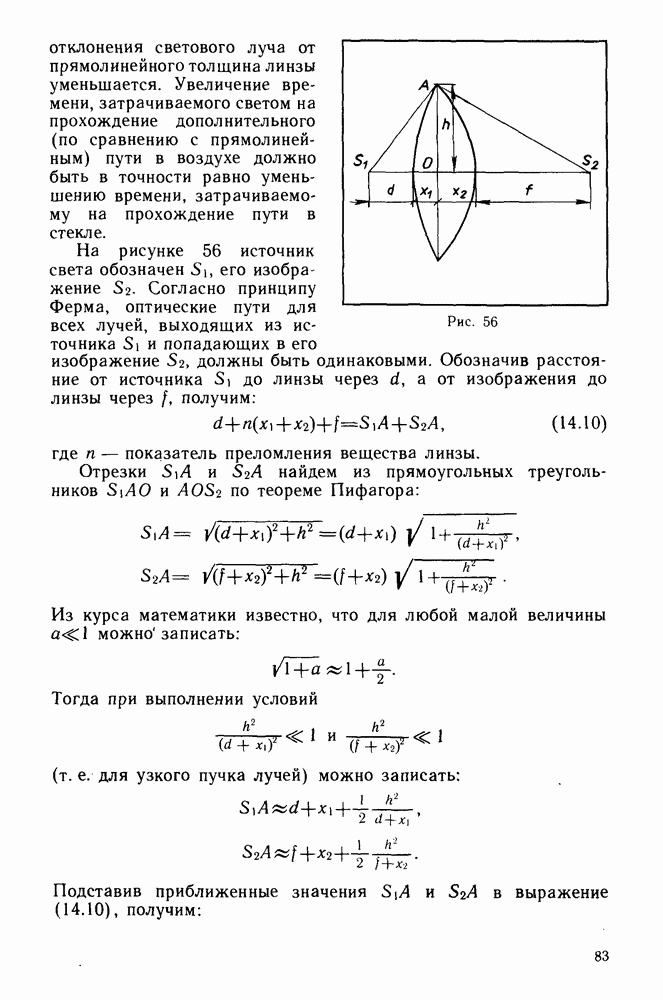
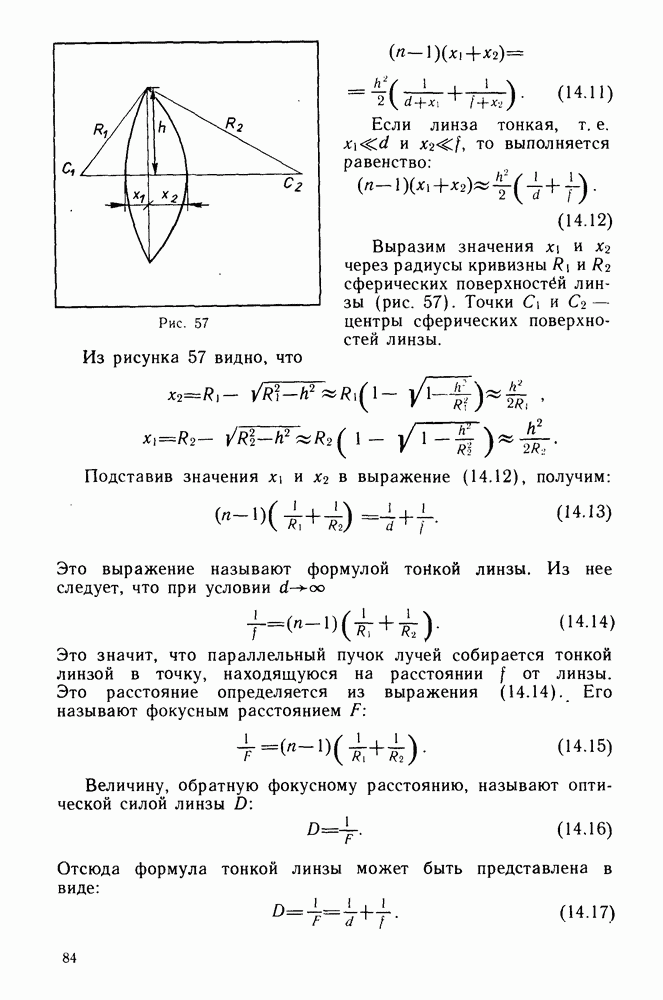
- Линзы.
- Аберрация линз.
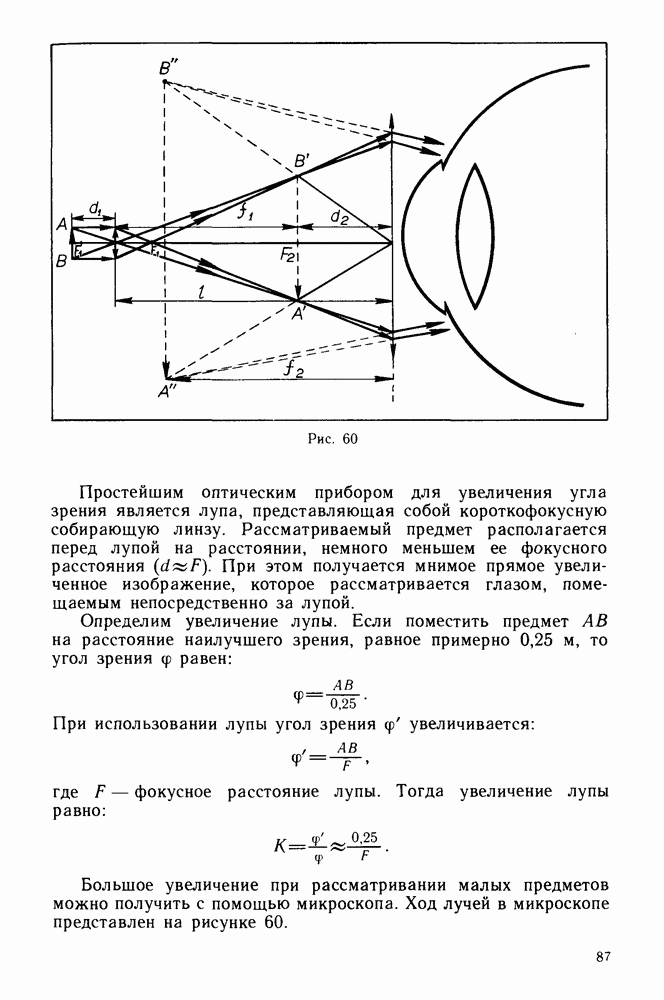
- Оптические приборы.
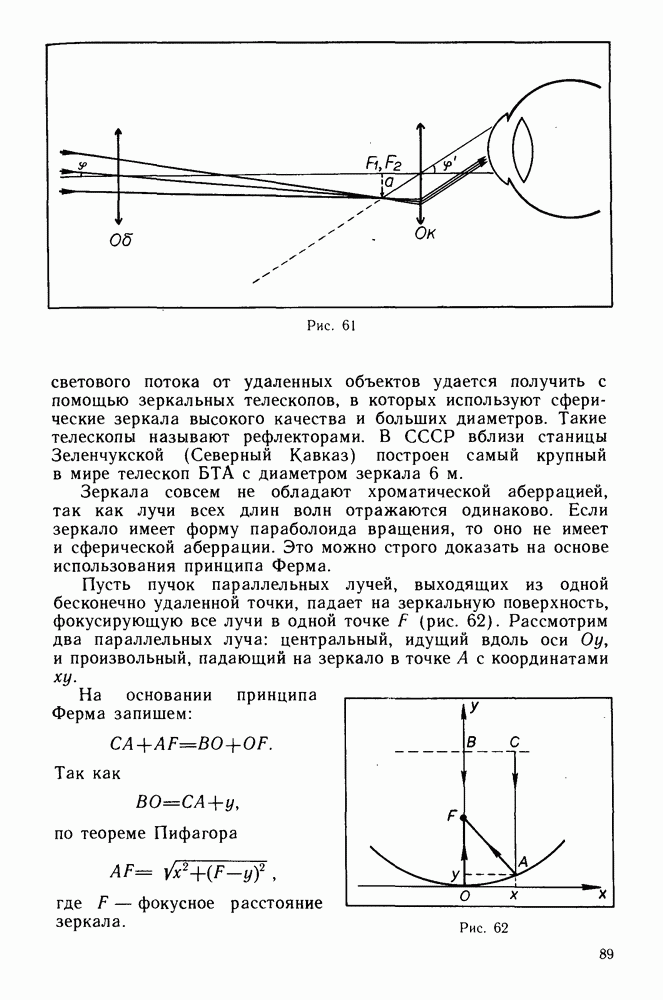
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
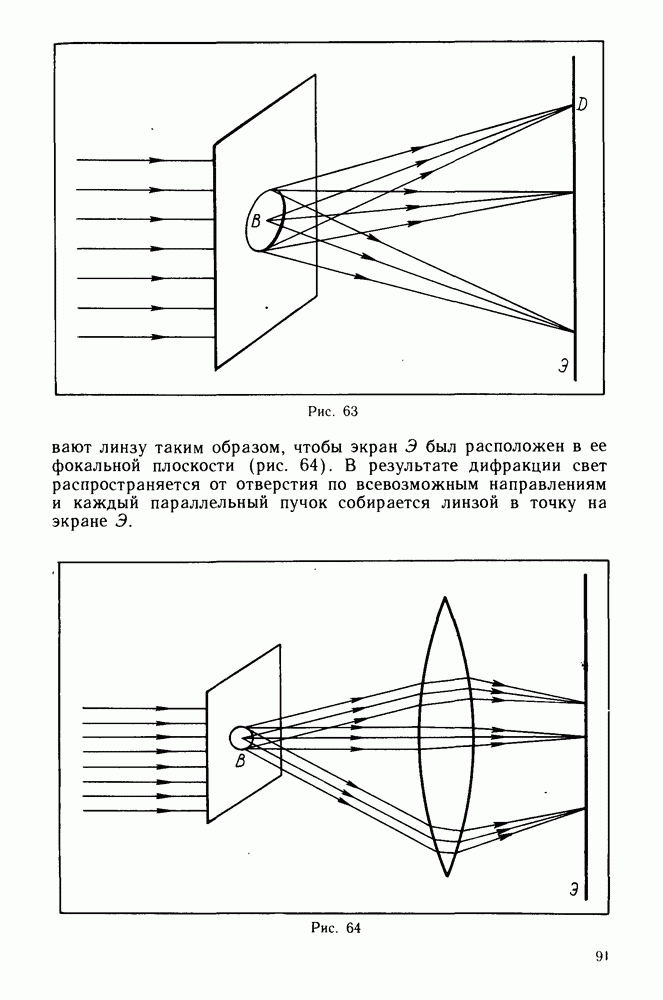
- Дифракция от круглого отверстия.
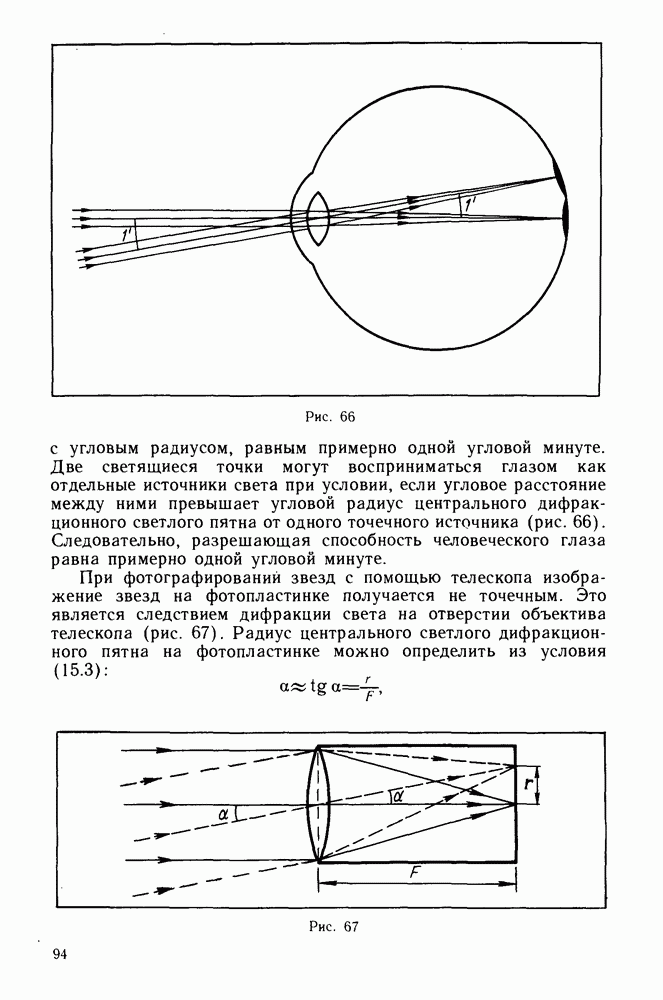
- Дифракция и разрешающая способность оптических приборов.
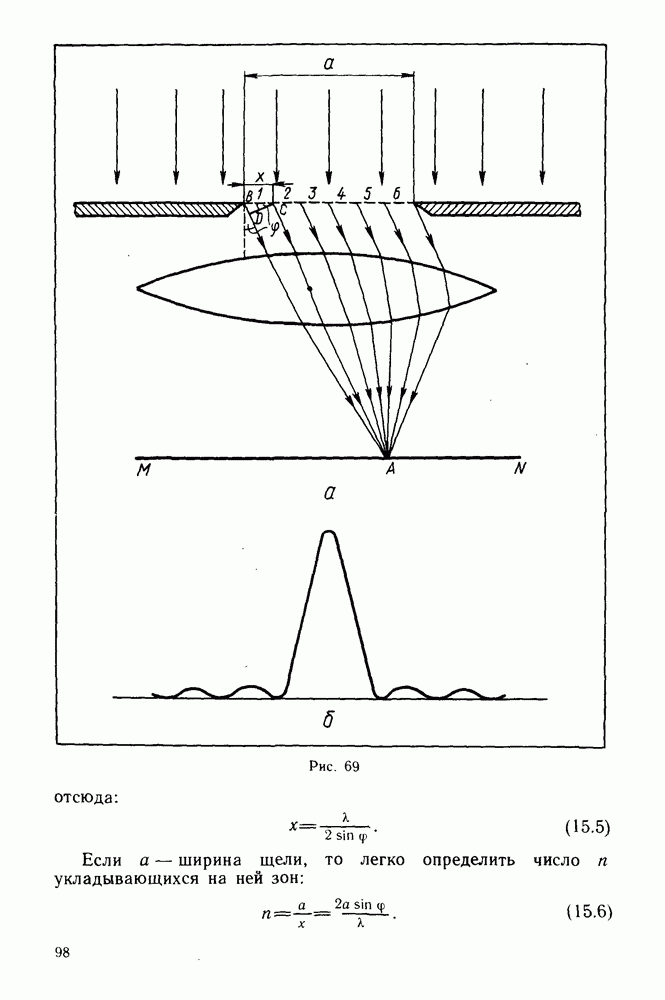
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
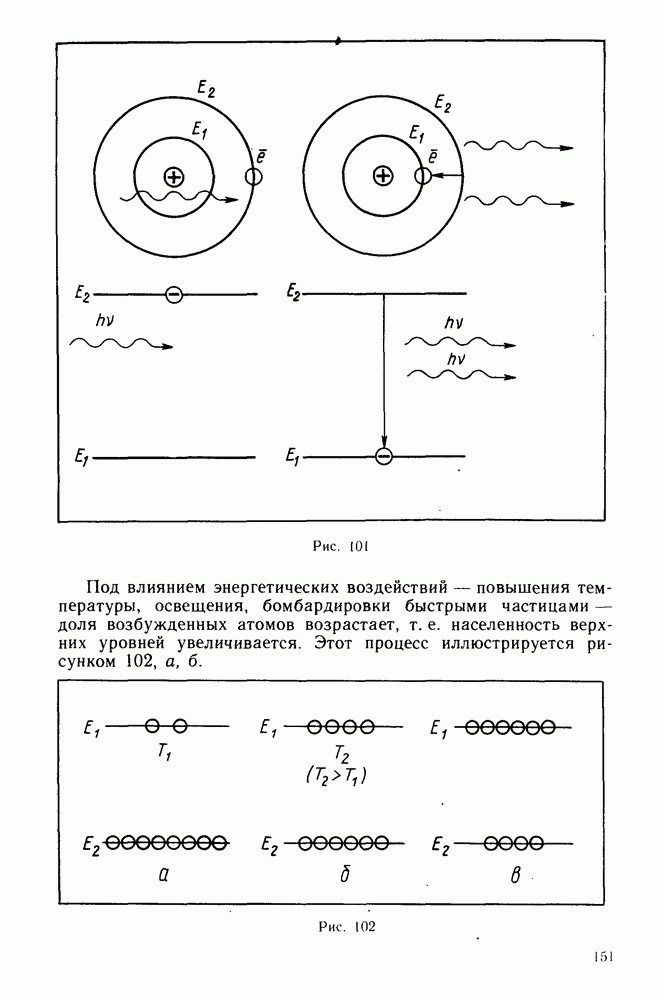
- Схема энергетических уровней.
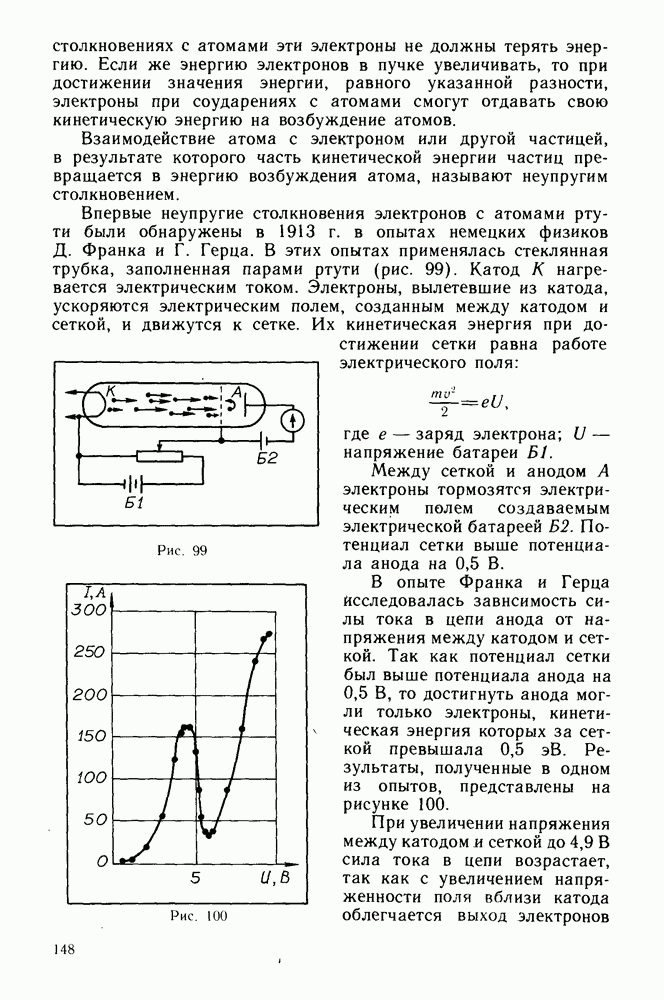
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
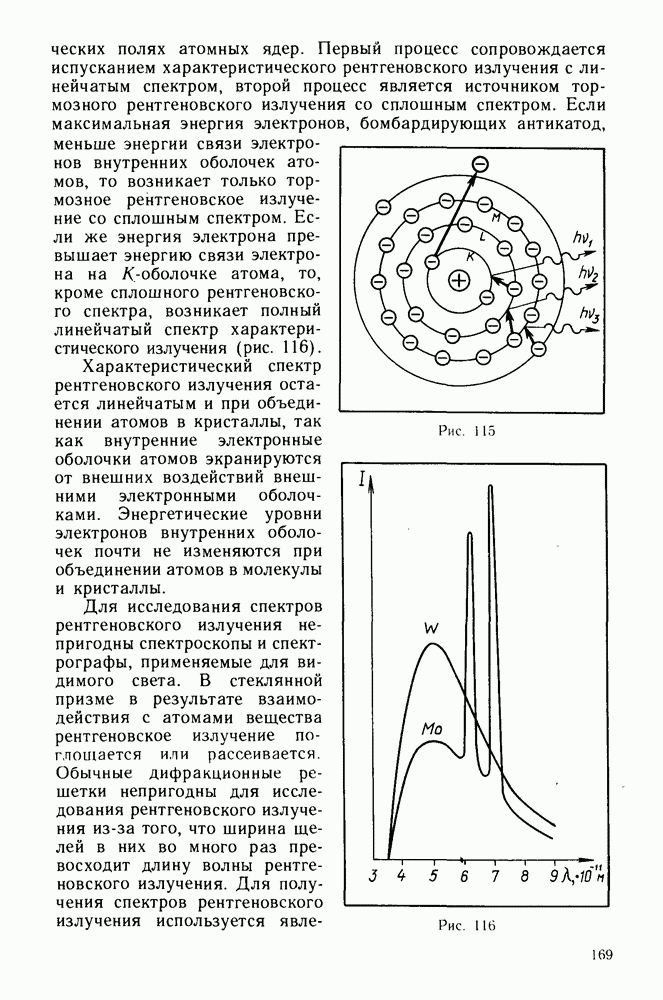
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
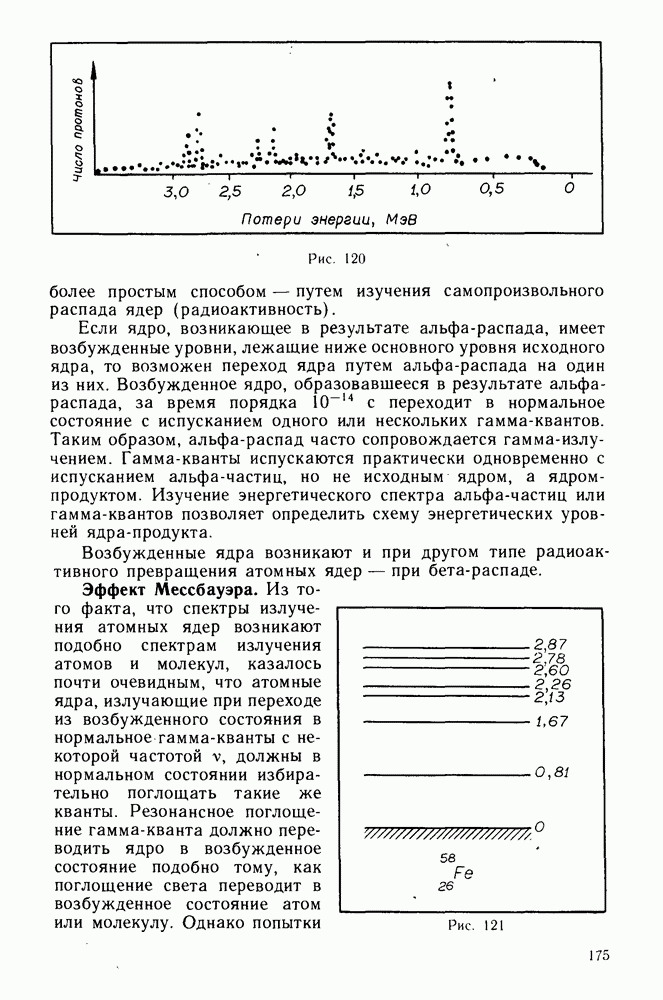
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
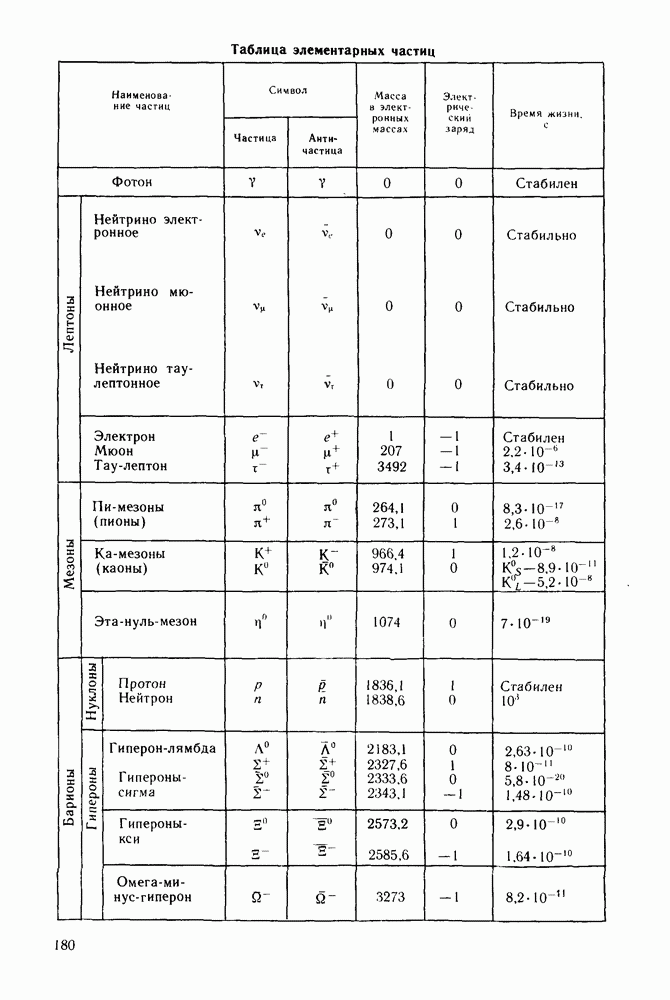
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
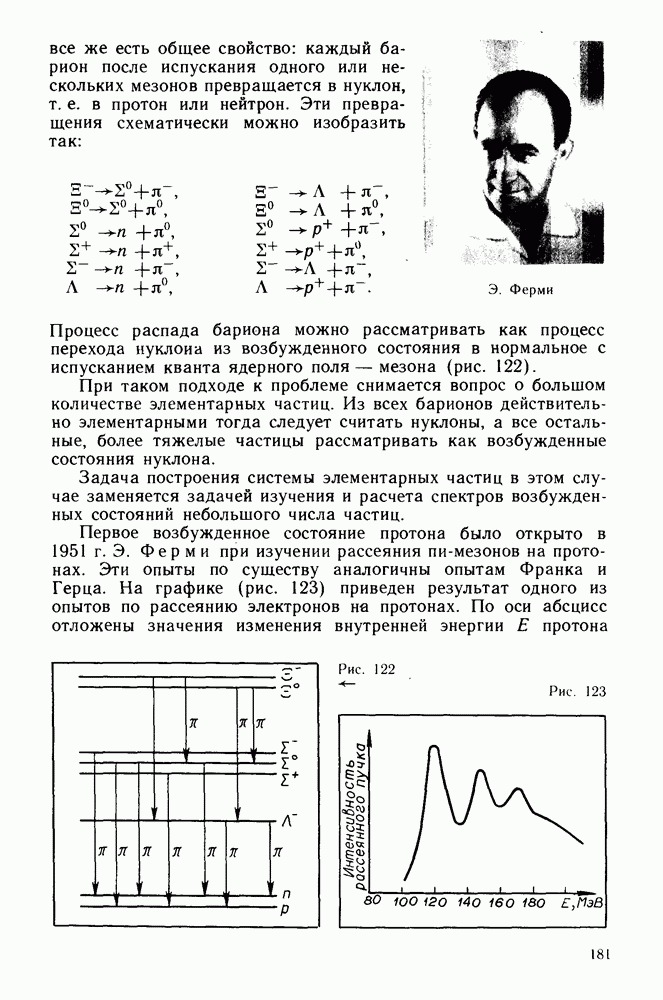
- Спектры элементарных частиц.
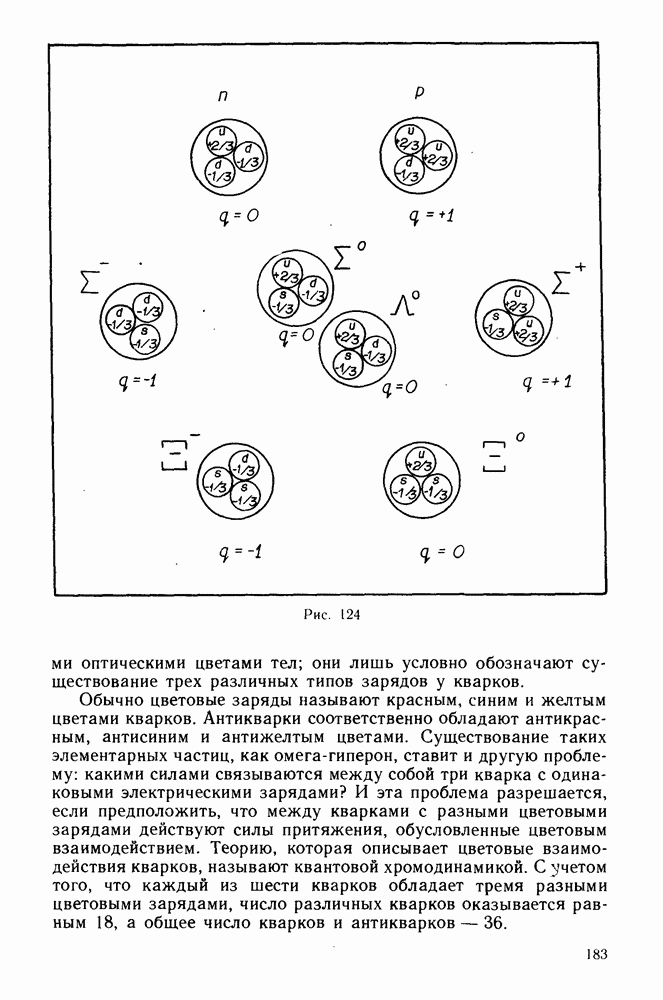
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
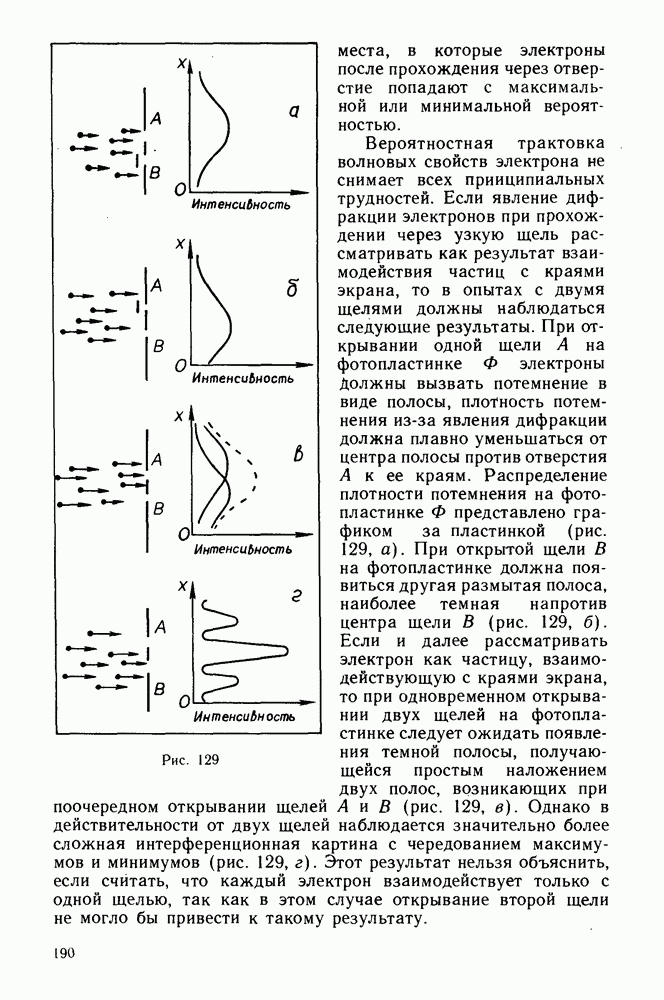
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ