| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Линзы.
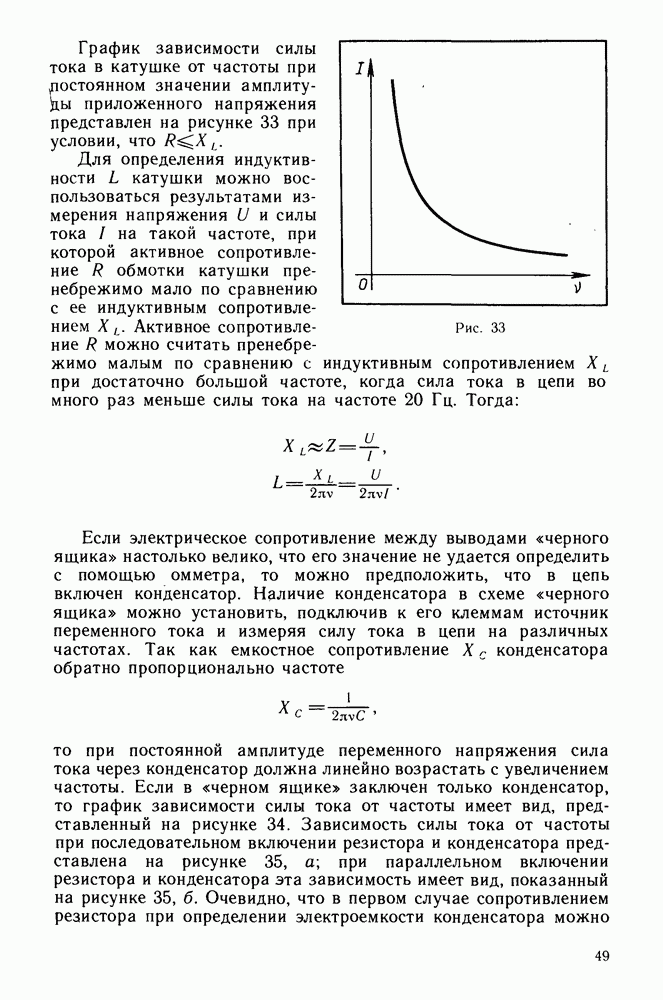
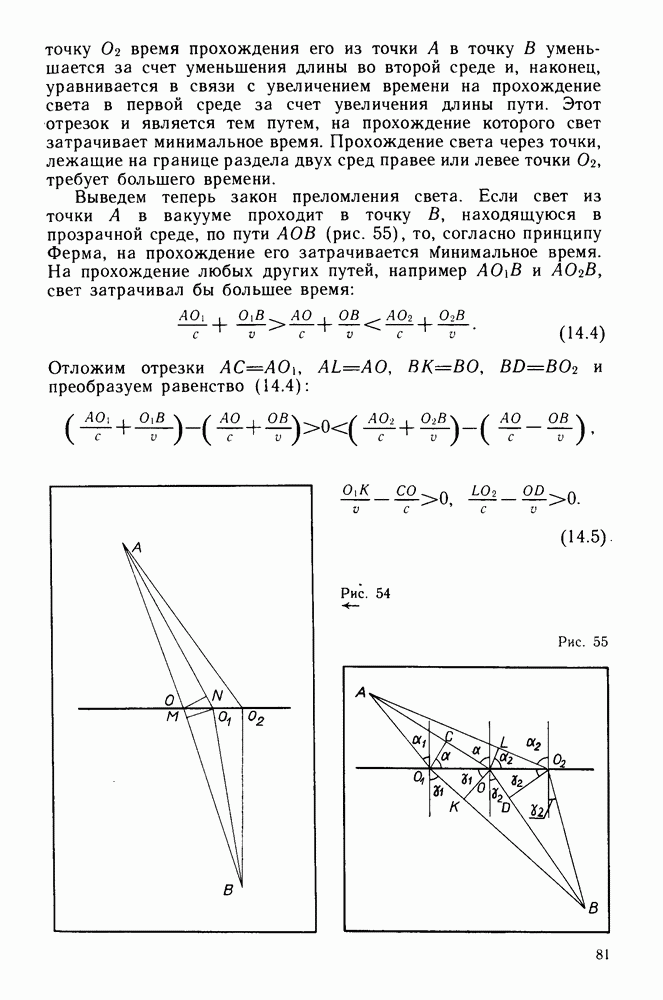
Используя принцип Ферма, можно вывести формулу линзы. Рассмотрим двояковыпуклую линзу. Согласно принципу Ферма, свет из одной точки в другую распространяется только по таким путям, на прохождение которых требуется экстремальное или одинаковое время. Поэтому лучи света, выходящие под различными углами из точки перед линзой и собирающиеся после прохождения линзы в другой точке, пройдя путь через линзу, должны затрачивать одно и то же время. Это условие может быть выполнено за счет того, что по мере

Рис. 56
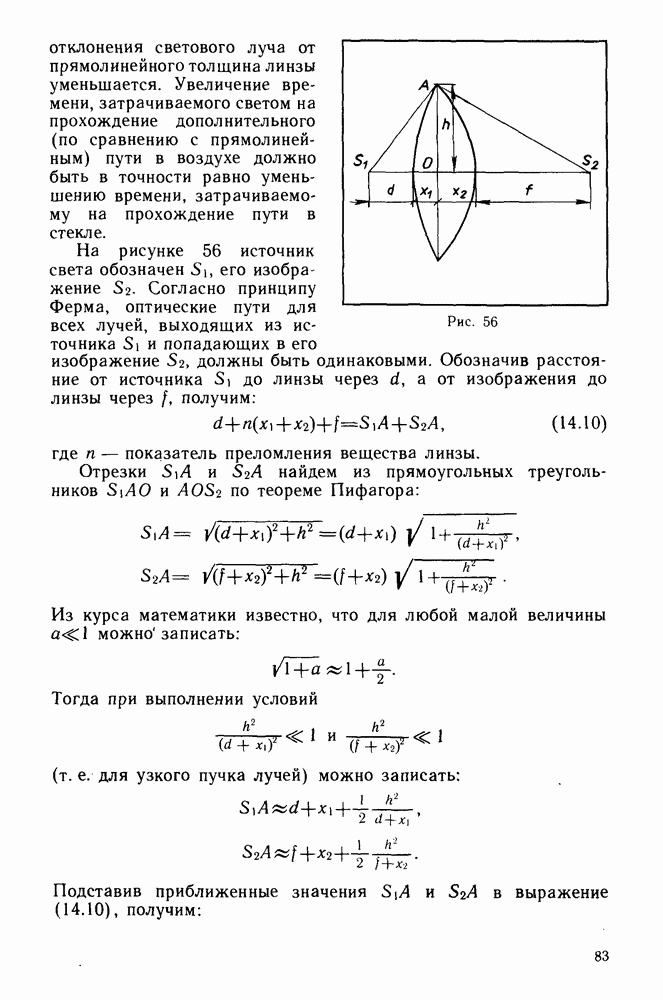
отклонения светового луча от прямолинейного толщина линзы уменьшается. Увеличение времени, затрачиваемого светом на прохождение дополнительного (по сравнению с прямолинейным) пути в воздухе должно быть в точности равно уменьшению времени, затрачиваемому на прохождение пути в стекле.
На рисунке 56 источник света обозначен  его изображение
его изображение  Согласно принципу Ферма, оптические пути для всех лучей, выходящих из источника
Согласно принципу Ферма, оптические пути для всех лучей, выходящих из источника  и попадающих в его изображение
и попадающих в его изображение  должны быть одинаковыми. Обозначив расстояние от источника
должны быть одинаковыми. Обозначив расстояние от источника  до линзы через
до линзы через  а от изображения до линзы через
а от изображения до линзы через  получим:
получим:

где  — показатель преломления вещества линзы.
— показатель преломления вещества линзы.
Отрезки  найдем из прямоугольных треугольников
найдем из прямоугольных треугольников  по теореме Пифагора:
по теореме Пифагора:

Из курса математики известно, что для любой малой величины  можно записать:
можно записать:

Тогда при выполнении условий

(т. е. для узкого пучка лучей) можно записать:

Подставив приближенные значения  и
и  в выражение (14.10), получим:
в выражение (14.10), получим:

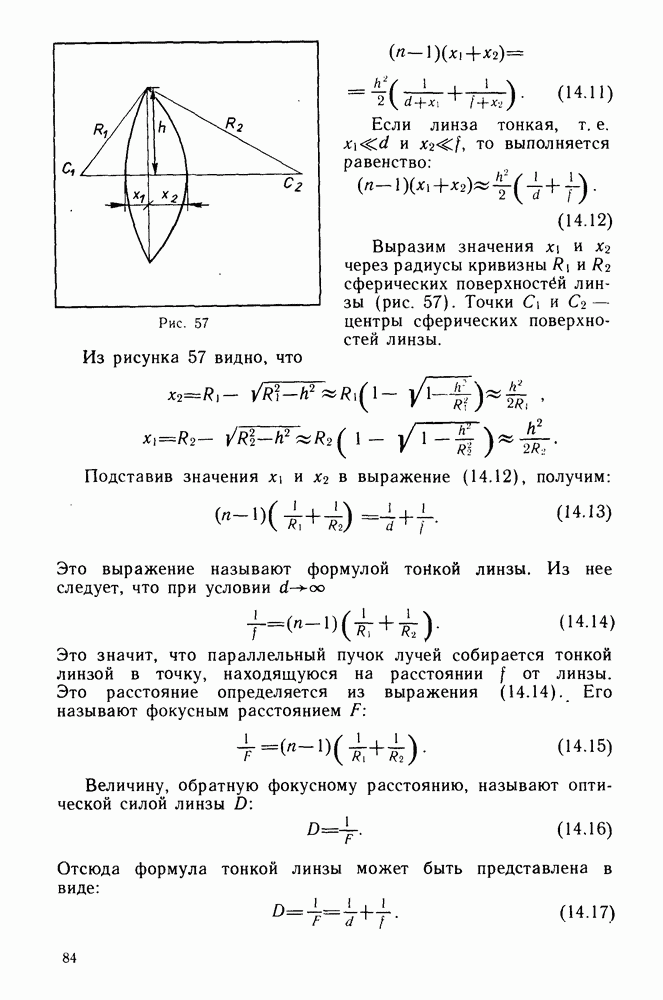
Рис. 57

Если линза тонкая, т. е.  то выполняется равенство:
то выполняется равенство:

Выразим значения  через радиусы кривизны
через радиусы кривизны  сферических поверхностёй линзы (рис. 57). Точки
сферических поверхностёй линзы (рис. 57). Точки  центры сферических поверхностей линзы.
центры сферических поверхностей линзы.
Из рисунка 57 видно, что

Подставив значения  в выражение (14.12), получим:
в выражение (14.12), получим:

Это выражение называют формулой тонкой линзы. Из нее следует, что при условии 

Это значит, что параллельный пучок лучей собирается тонкой линзой в точку, находящуюся на расстоянии  от линзы. Это расстояние определяется из выражения (14.14). Его называют фокусным расстоянием
от линзы. Это расстояние определяется из выражения (14.14). Его называют фокусным расстоянием 

Величину, обратную фокусному расстоянию, называют оптической силой линзы 

Отсюда формула тонкой линзы может быть представлена в виде:

Используя формулу линзы, нужно учитывать следующие правила знаков:
1) Считать для собирающей линзы фокусное расстояние F положительным, для рассеивающей — отрицательным.
2) Считать для действительных изображений расстояние  положительным, для мнимых — отрицательным.
положительным, для мнимых — отрицательным.
3) Расстояние  до предмета или его действительного изображения, находящегося перед линзой, считать положительным. Если лучи, падающие на линзу, не образуют перед ней действительного изображения, но образуют его на расстоянии
до предмета или его действительного изображения, находящегося перед линзой, считать положительным. Если лучи, падающие на линзу, не образуют перед ней действительного изображения, но образуют его на расстоянии  за линзой, то это расстояние считается отрицательным.
за линзой, то это расстояние считается отрицательным.
Формула тонкой линзы справедлива для случая, когда  т. е. утверждение о том, что тонкая линза фокусирует монохроматический пучок света в одной точке, справедливо лишь для узкого пучка лучей, близких к оптической оси.
т. е. утверждение о том, что тонкая линза фокусирует монохроматический пучок света в одной точке, справедливо лишь для узкого пучка лучей, близких к оптической оси.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
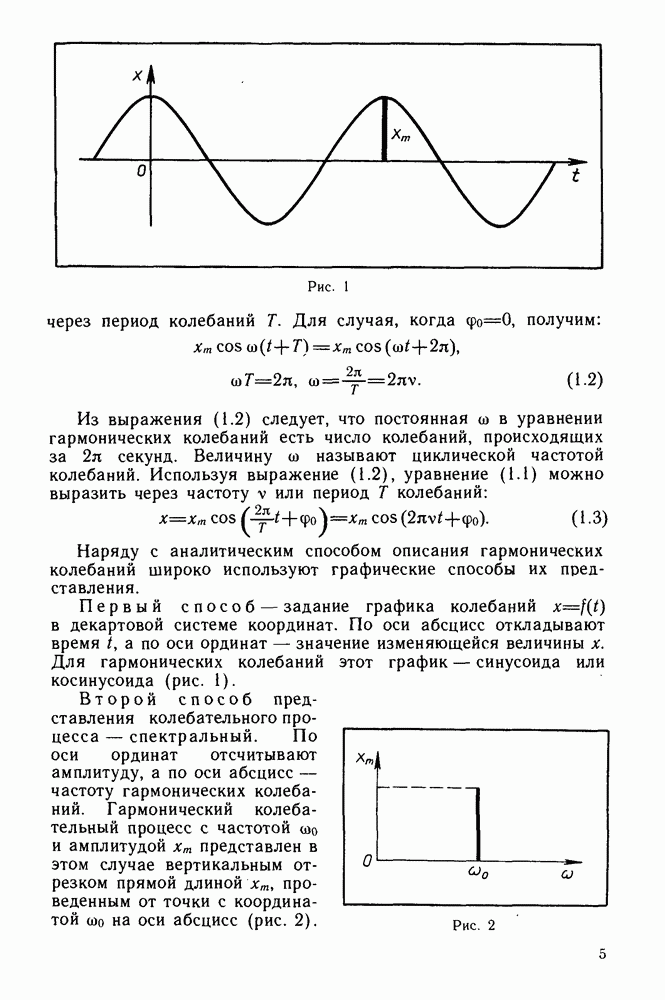
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
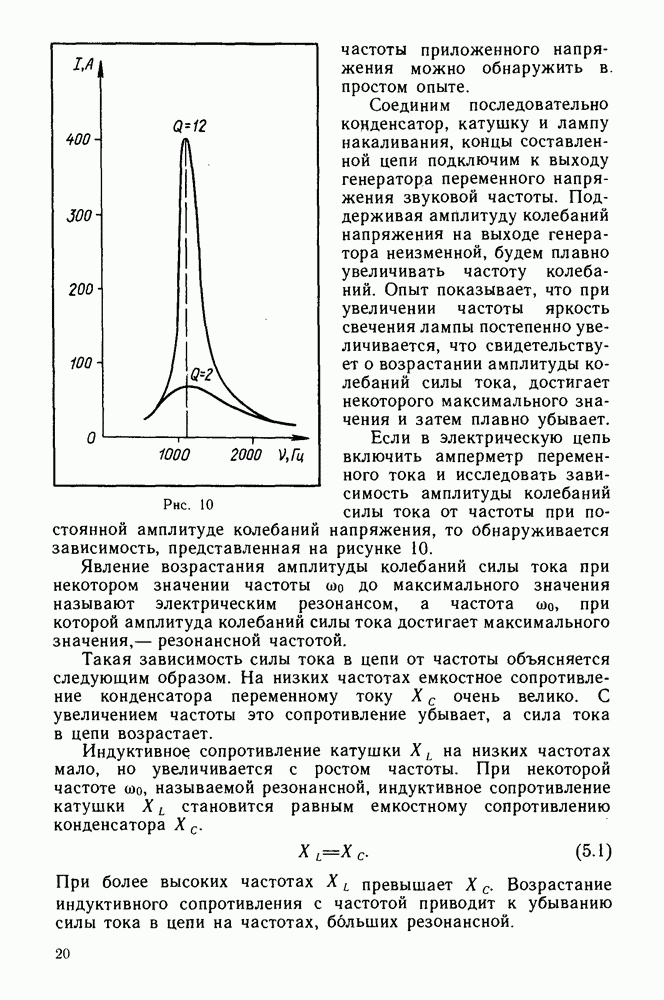
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
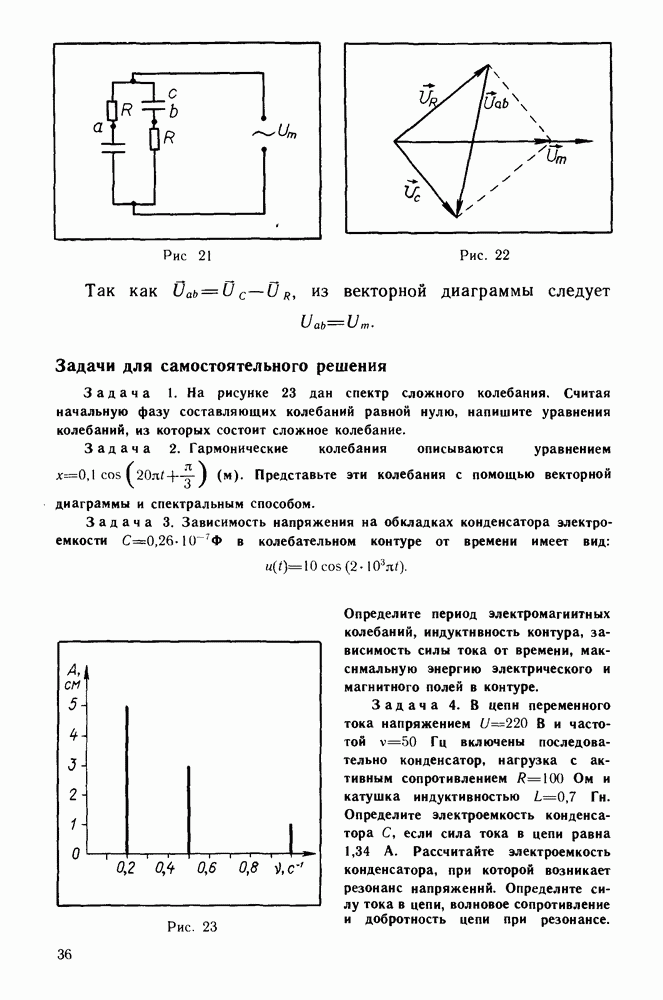
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
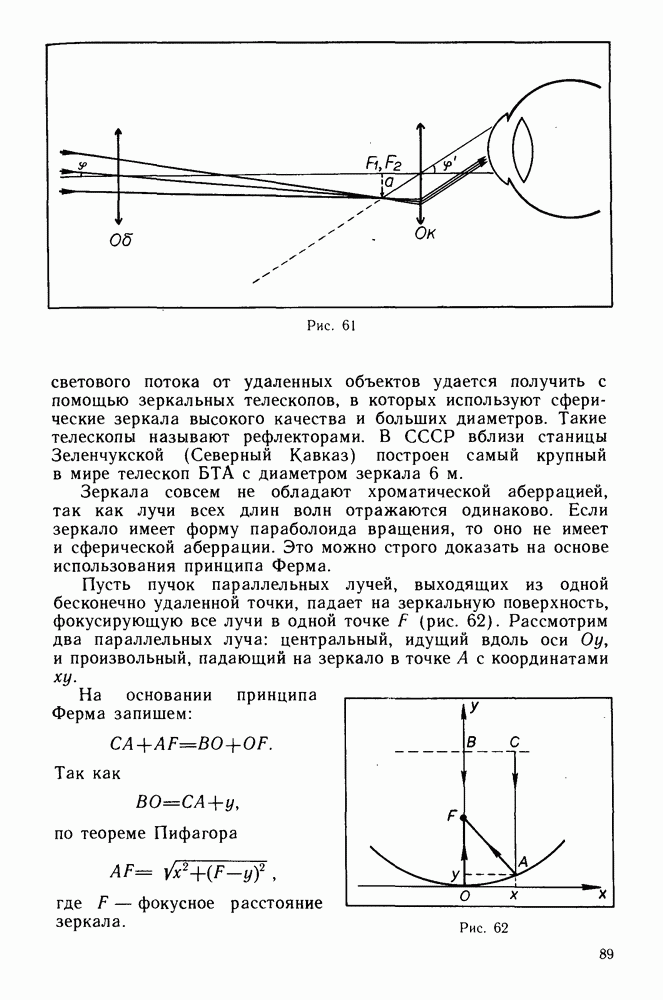
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
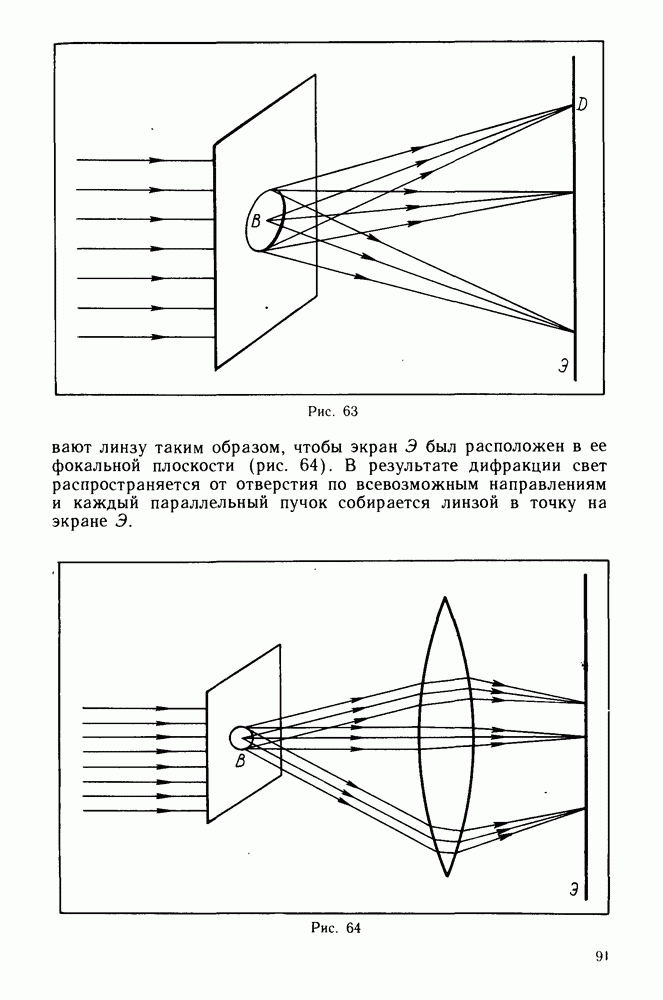
- Дифракция от круглого отверстия.
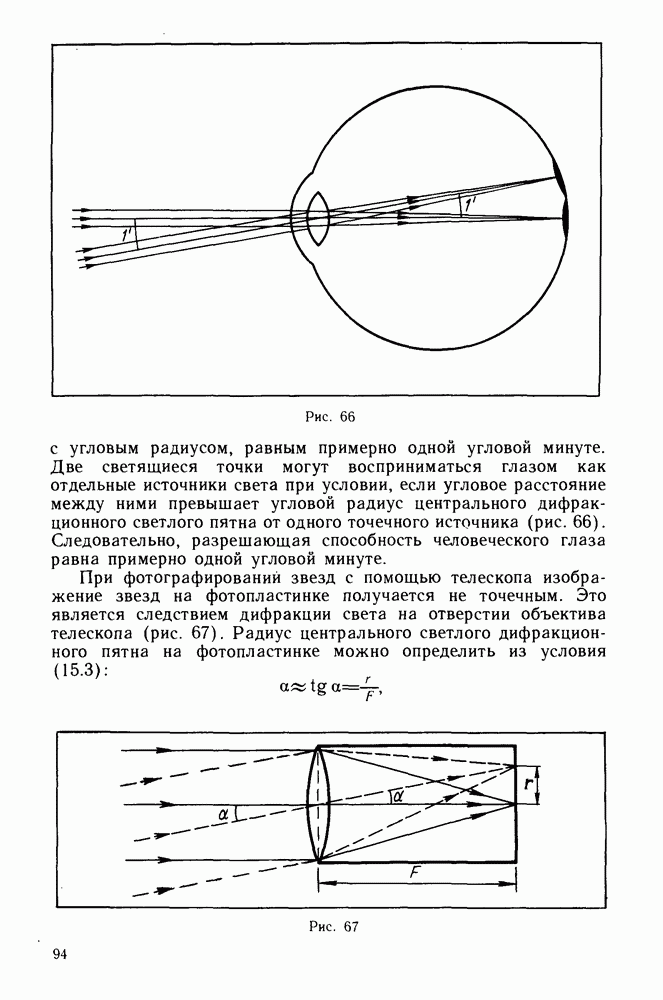
- Дифракция и разрешающая способность оптических приборов.
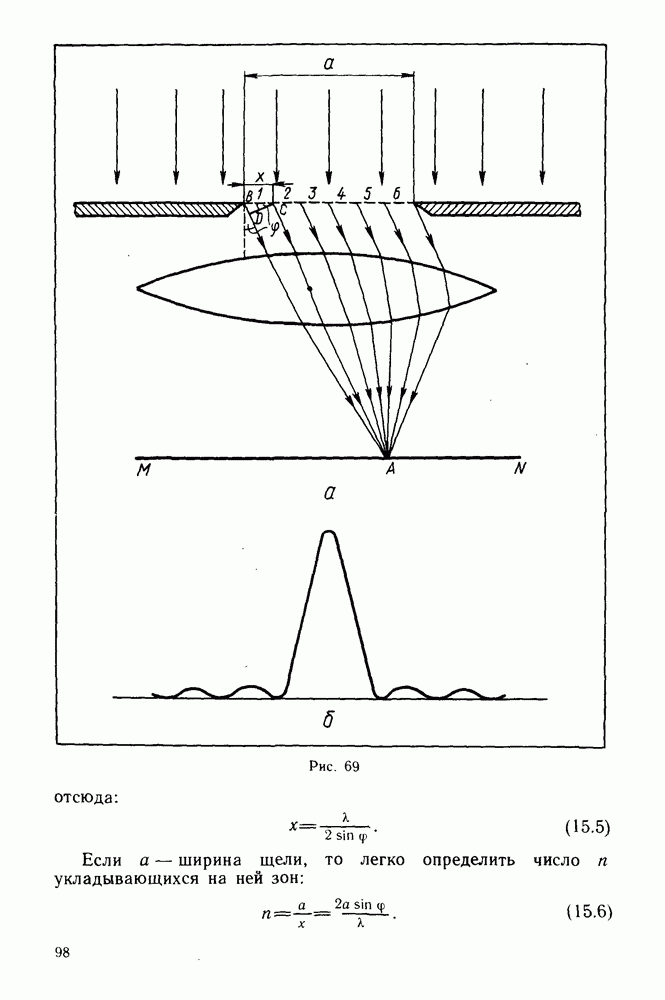
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
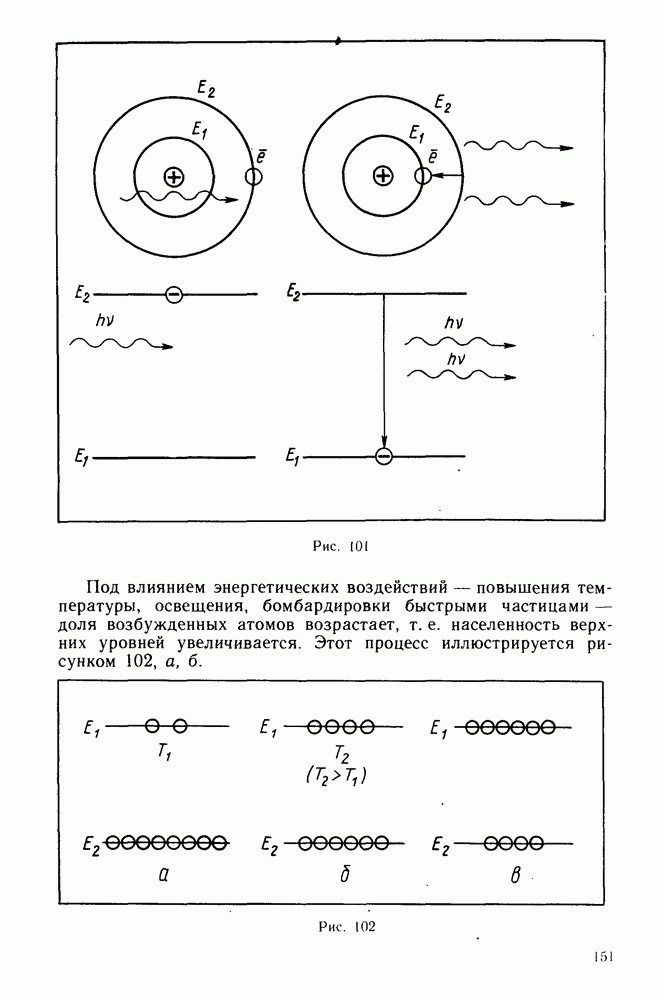
- Схема энергетических уровней.
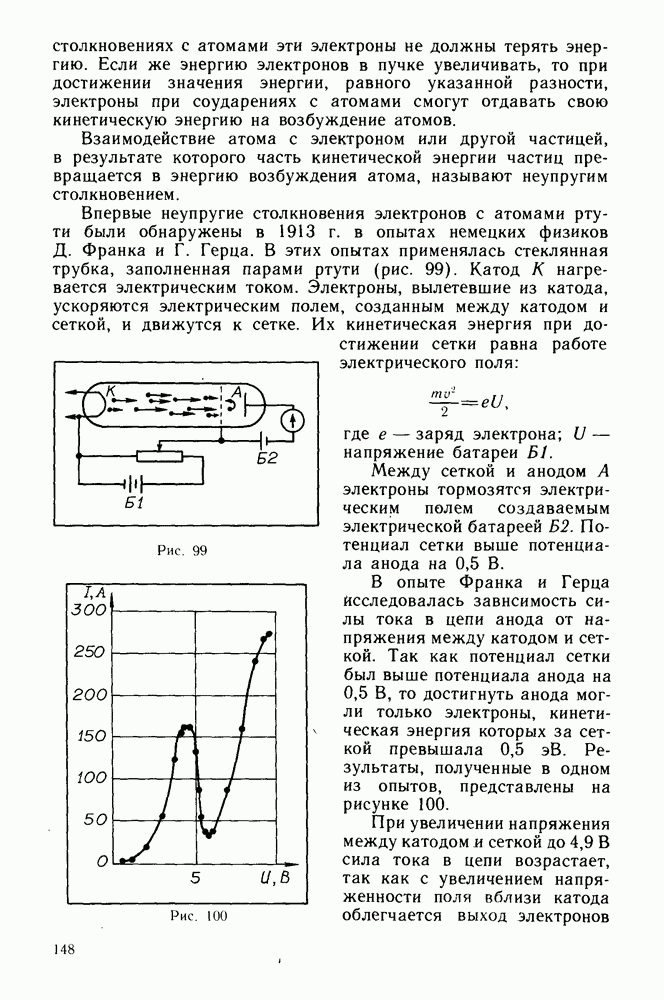
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
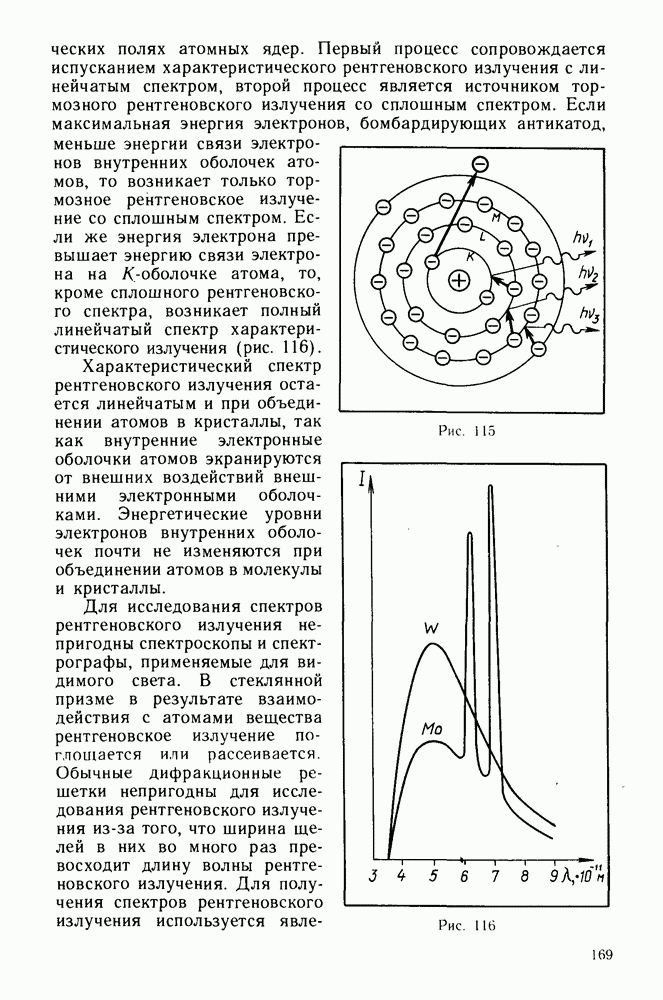
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
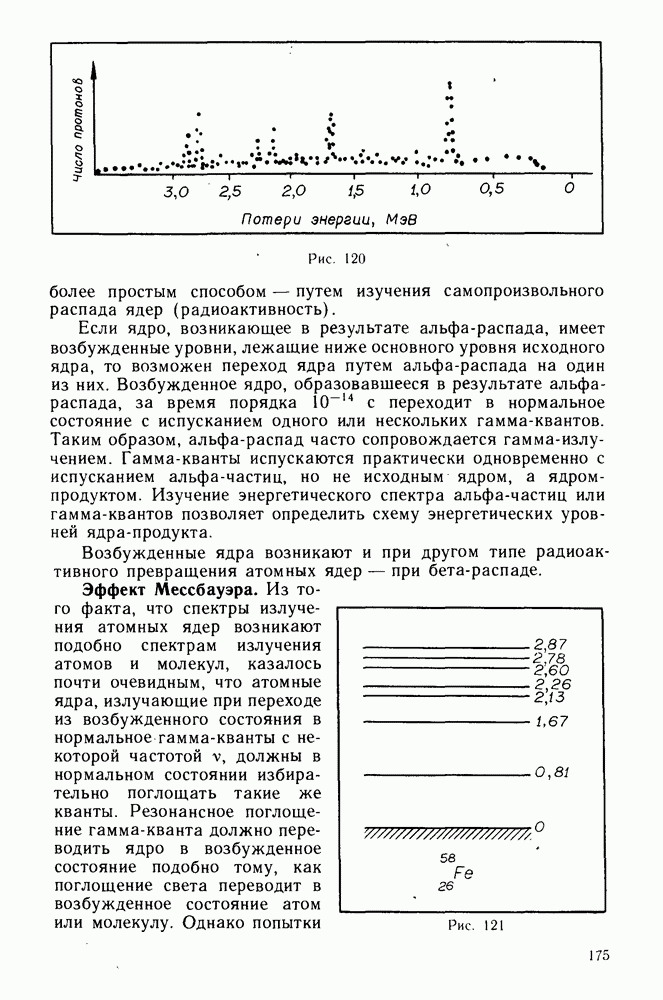
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
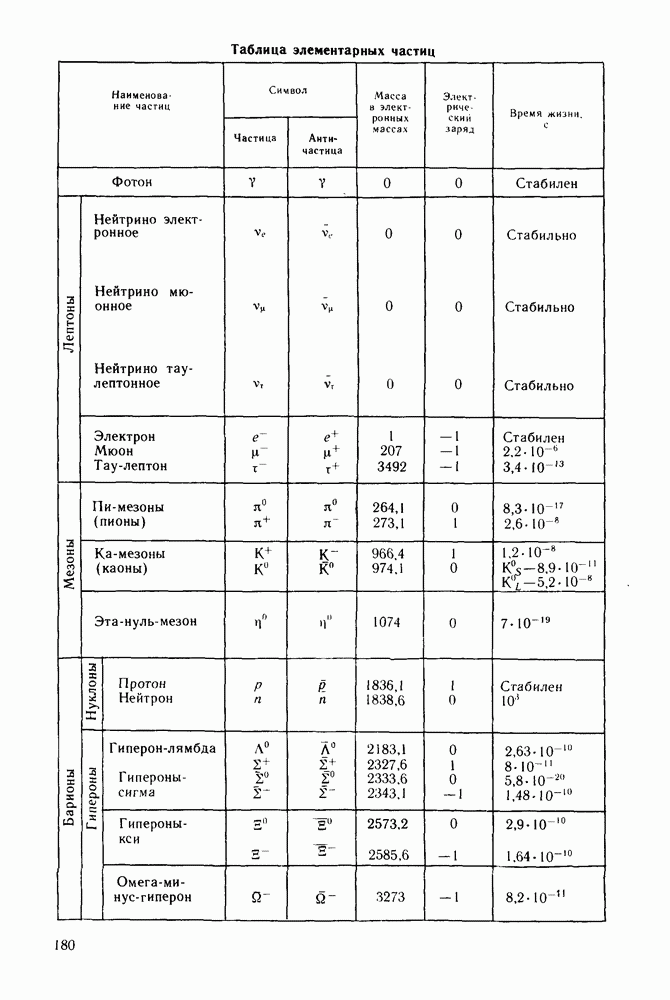
- Спектры элементарных частиц.
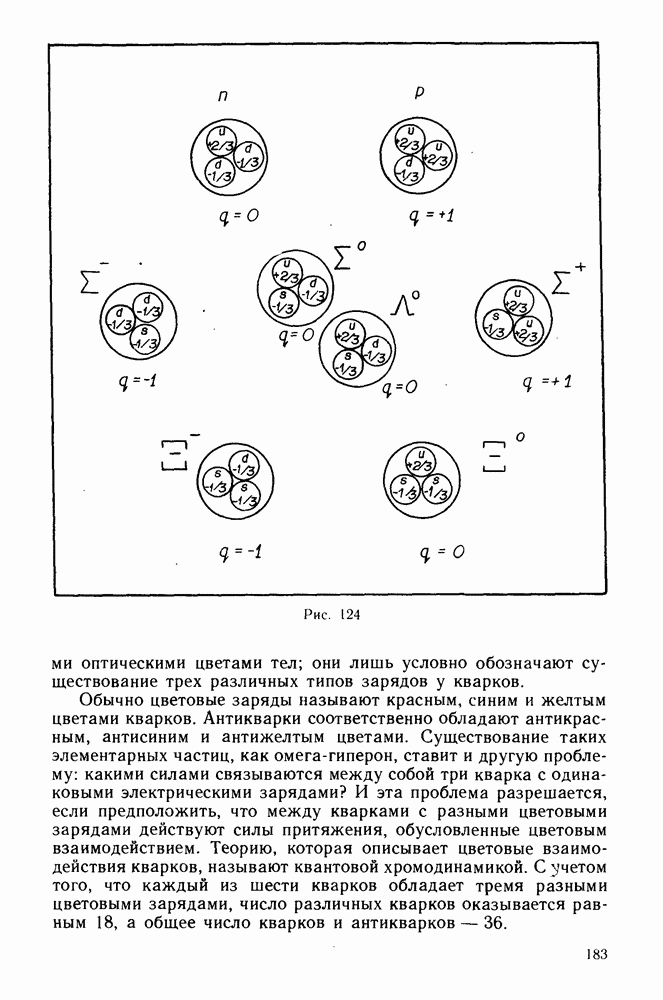
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
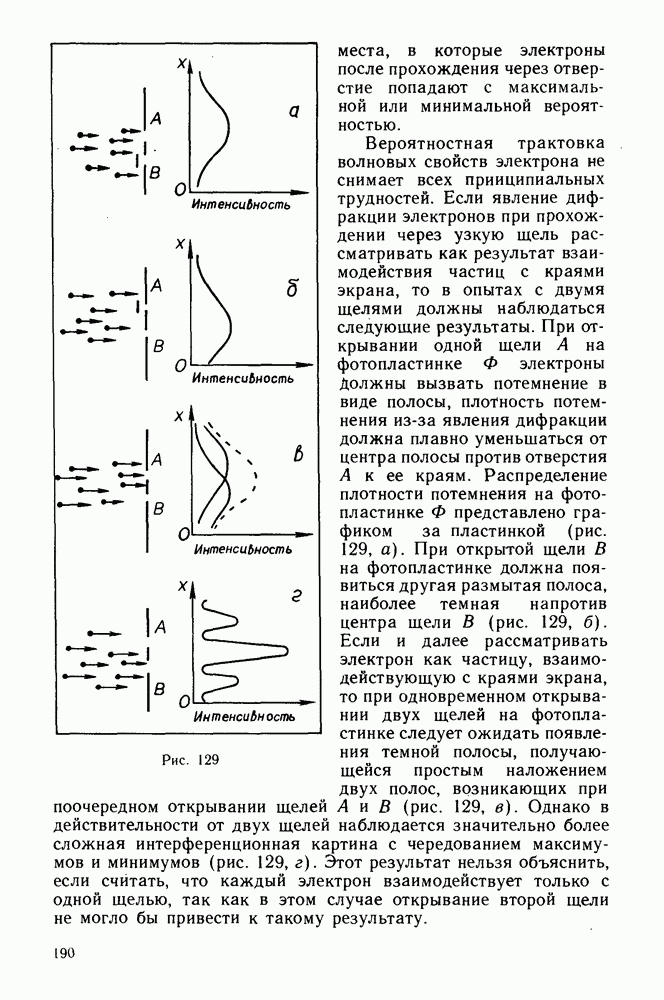
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ