| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
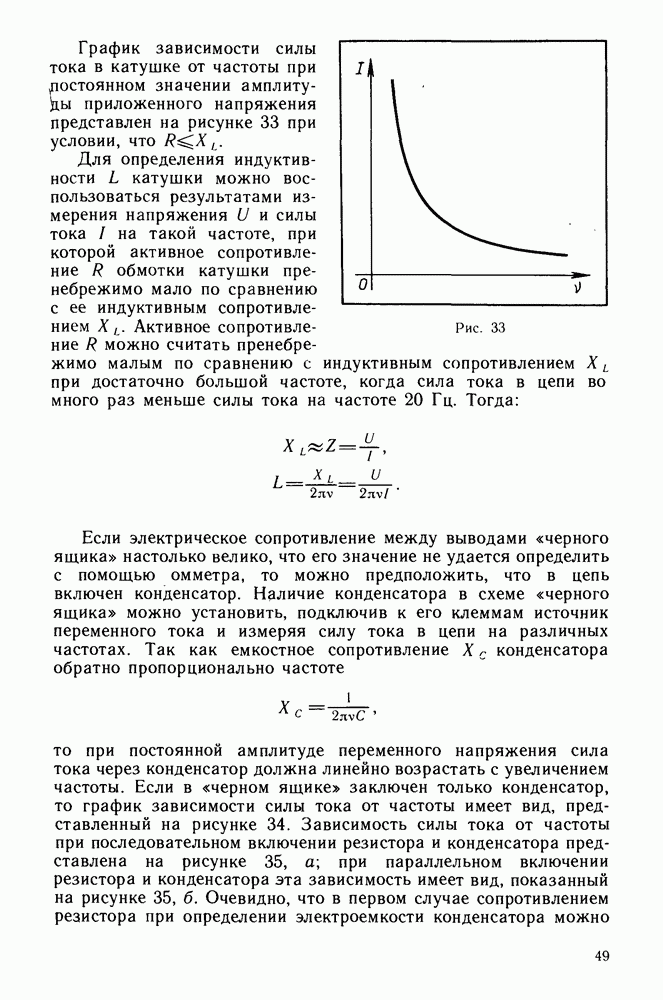
Среди различных примеров гармонических колебаний в природе и технике особого рассмотрения заслуживают электромагнитные колебания, возникающие в электрических цепях. Это колебания силы тока и напряжения в электрических цепях переменного тока, в антеннах радио- и телевизионных станций, в радиоприемниках, магнитофонах, телевизорах. Для анализа
процессов, протекающих в сложных электрических цепях переменного тока, прежде всего необходимо выяснить связь между колебаниями силы тока и напряжения на отдельных элементах цепи переменного тока.
Рассмотрим связь между амплитудами колебаний напряжения и силы тока при включении конденсатора и катушки в цепь переменного тока и найдем выражения для вычисления емкостного X с и индуктивного  сопротивлений.
сопротивлений.
Емкостное сопротивление.
Если конденсатор включен в цепь переменного тока и напряжение на его обкладках изменяется по гармоническому закону

то электрический заряд на его обкладках в момент времени  определяется выражением:
определяется выражением:

Вычислив первую производную от электрического заряда  по времени, найдем закон колебаний силы тока
по времени, найдем закон колебаний силы тока 

Таким образом, при изменении напряжения на обкладках конденсатора по гармоническому закону (3.2) сила тока изменяется по гармоническому закону (3.3). Амплитуда колебаний силы тока  связана с амплитудой колебаний напряжения
связана с амплитудой колебаний напряжения  выражением:
выражением:

колебания силы тока опережают по фазе колебания напряжения на обкладках конденсатора на 
Из выражений (3.1) и (3.3) следует, что отношение мгновенного значения напряжения  на конденсаторе к мгновенному значению силы тока
на конденсаторе к мгновенному значению силы тока  не является постоянной величиной и равно:
не является постоянной величиной и равно: 

Таким образом, связь между мгновенными значениями напряжения на конденсаторе и силы тока в цепи переменного тока оказывается более сложной, чем связь между напряжением на участке цепи постоянного тока и силой тока в цепи, выражаемая законом Ома. Однако для нахождения амплитуды  колебаний силы тока по известной амплитуде
колебаний силы тока по известной амплитуде  колебаний напряжения на конденсаторе можно воспользоваться выражением, совпадающим по форме с законом Ома для участка цепи постоянного тока. Действительно, обозначив
колебаний напряжения на конденсаторе можно воспользоваться выражением, совпадающим по форме с законом Ома для участка цепи постоянного тока. Действительно, обозначив

из выражения (3.4) получим:

Последнее выражение показывает, что амплитуда колебаний силы тока  цепи переменного тока прямо пропорциональна амплитуде колебаний напряжения на конденсаторе
цепи переменного тока прямо пропорциональна амплитуде колебаний напряжения на конденсаторе  и обратно пропорциональна величине X с, называемой емкостным сопротивлением конденсатора. Емкостное сопротивление X с обратно пропорционально частоте колебаний
и обратно пропорциональна величине X с, называемой емкостным сопротивлением конденсатора. Емкостное сопротивление X с обратно пропорционально частоте колебаний  и электроемкости С конденсатора.
и электроемкости С конденсатора.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
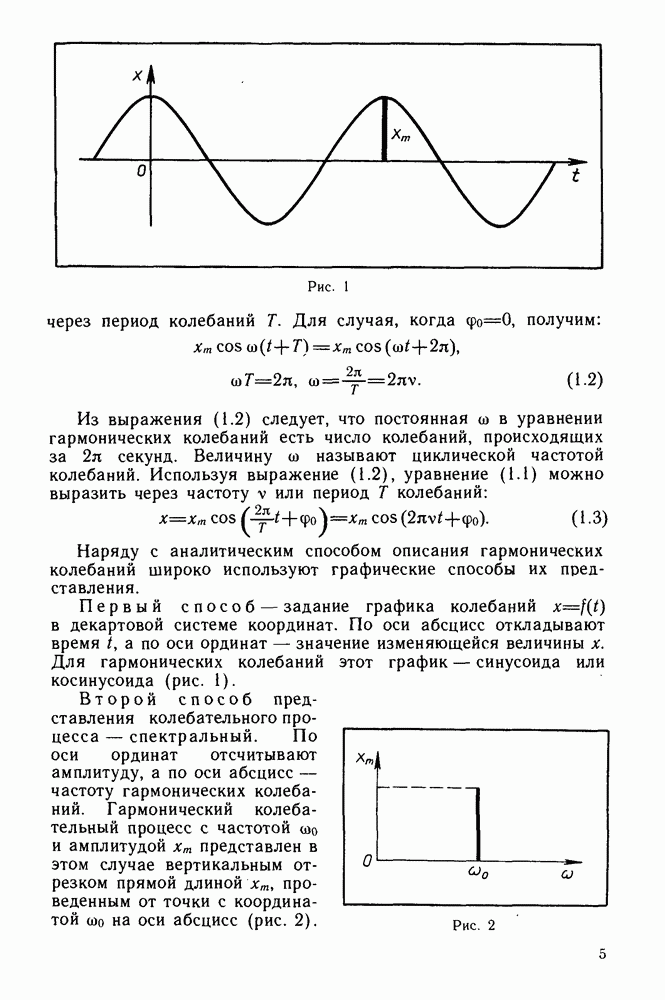
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
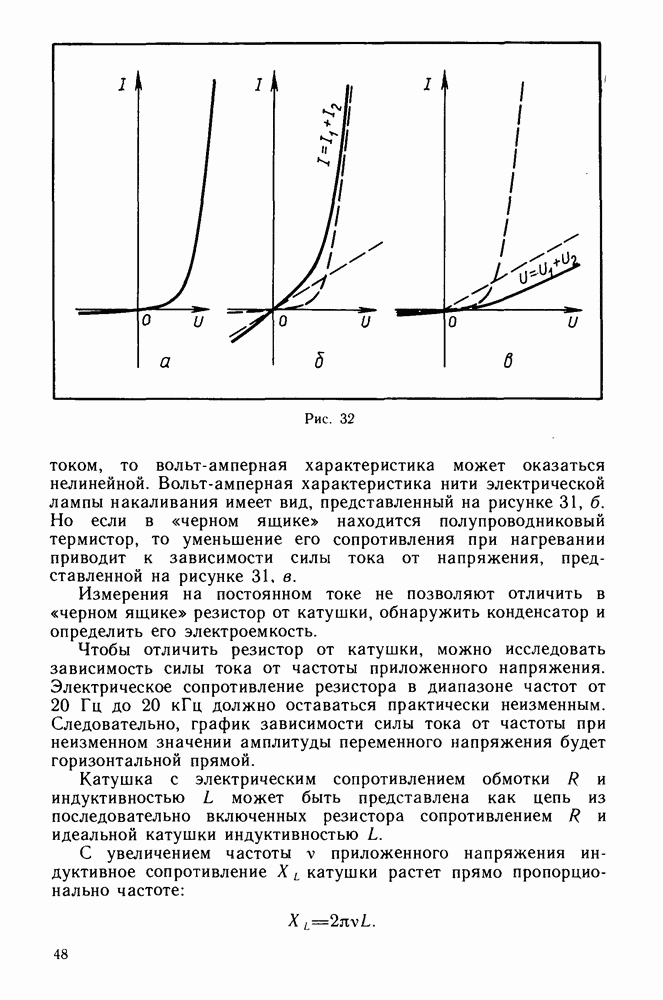
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
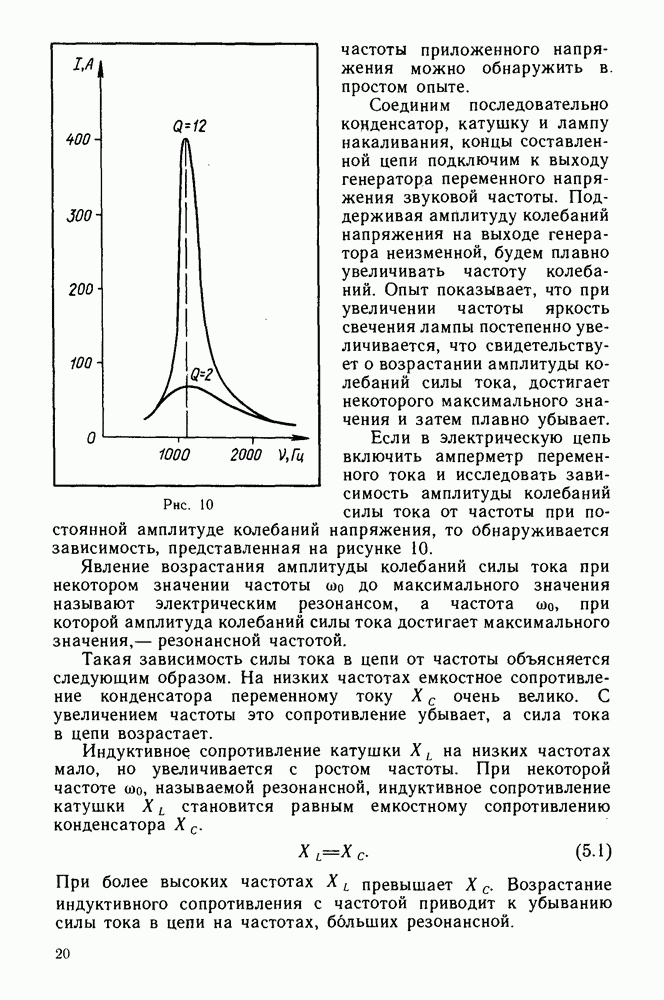
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
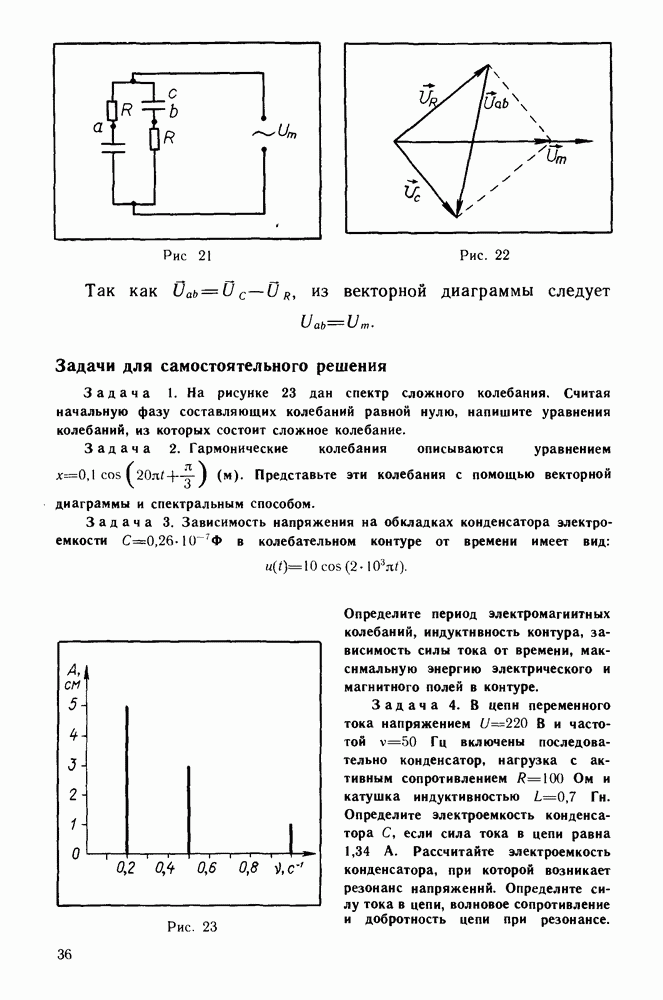
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
- Дифракция от круглого отверстия.
- Дифракция и разрешающая способность оптических приборов.
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
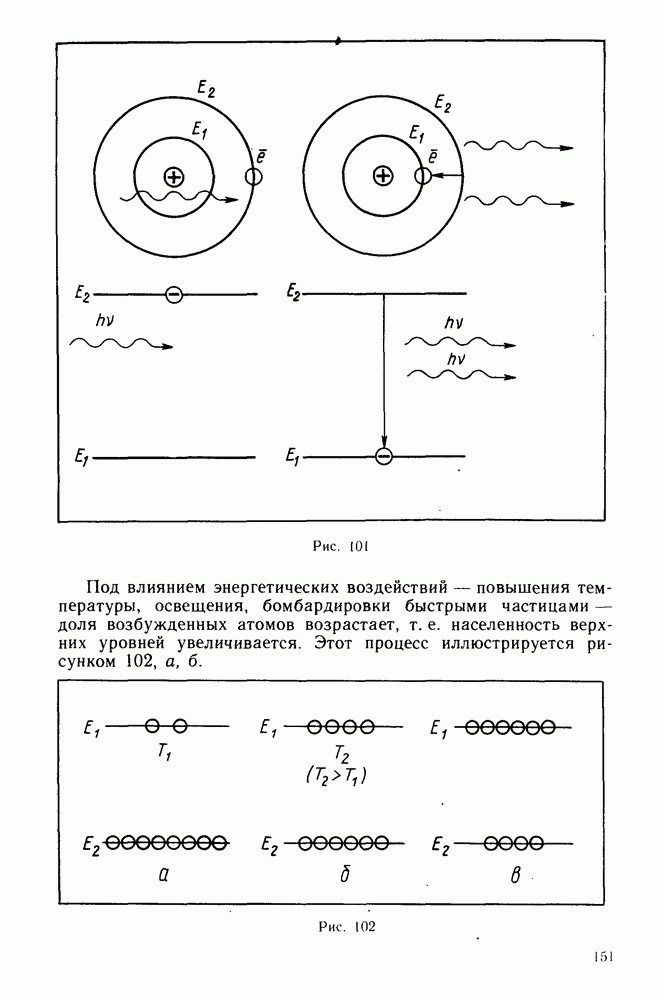
- Схема энергетических уровней.
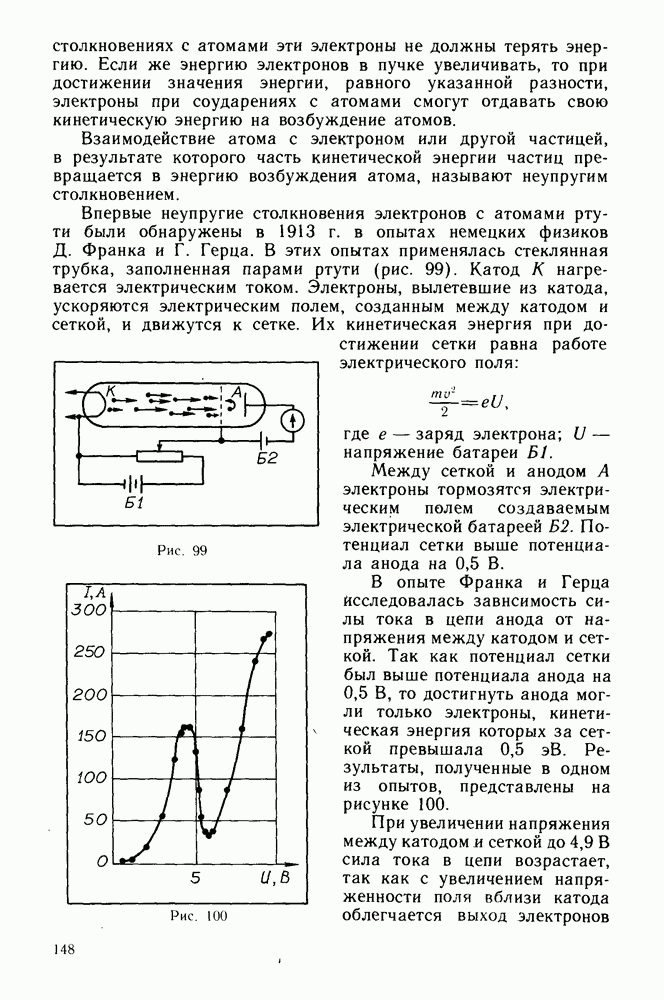
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
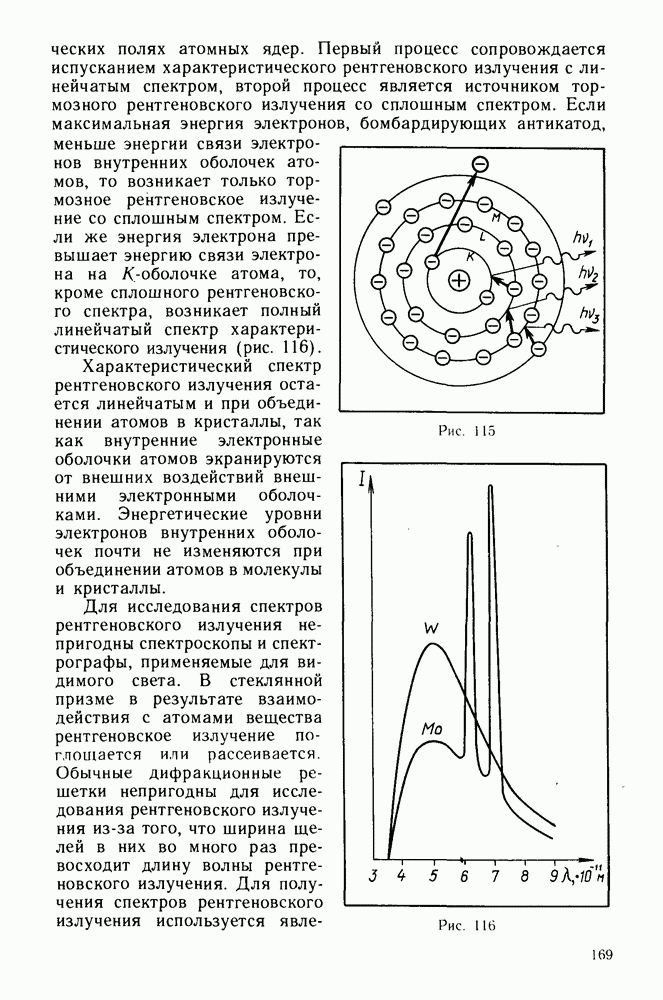
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
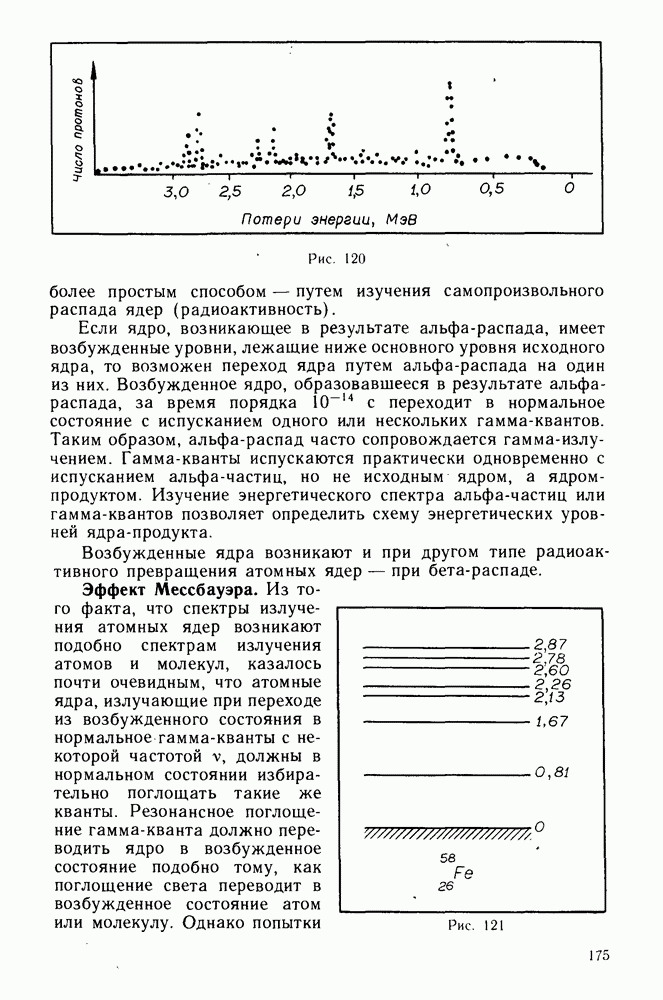
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
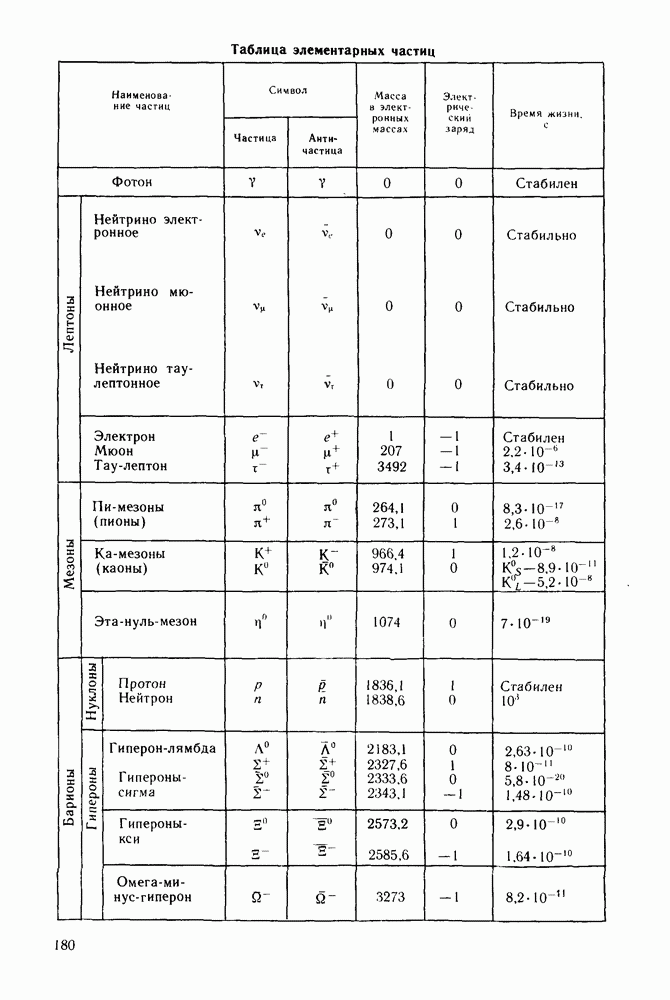
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
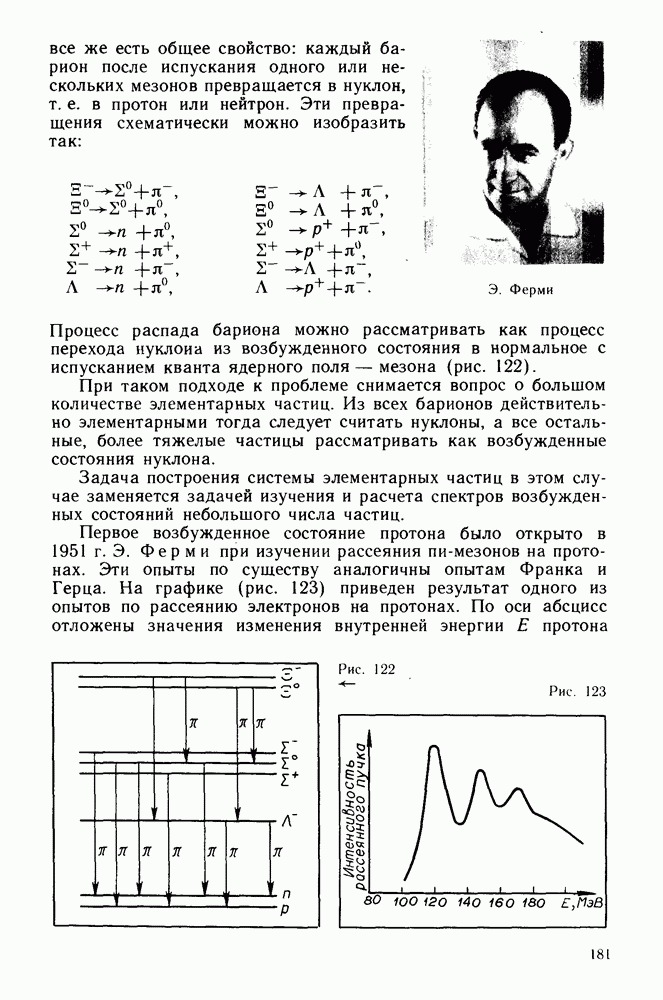
- Спектры элементарных частиц.
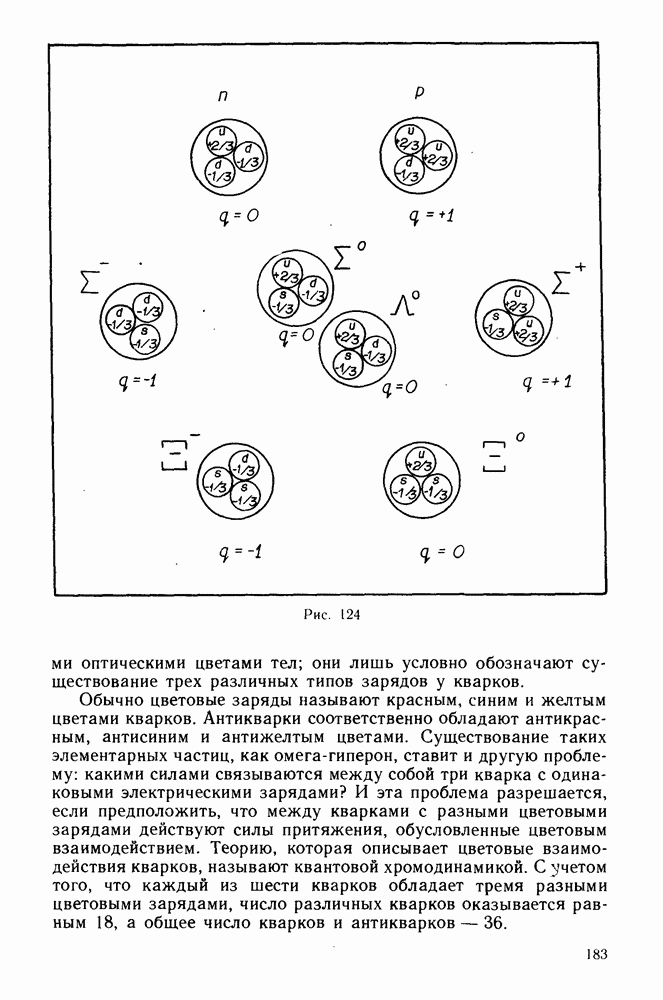
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
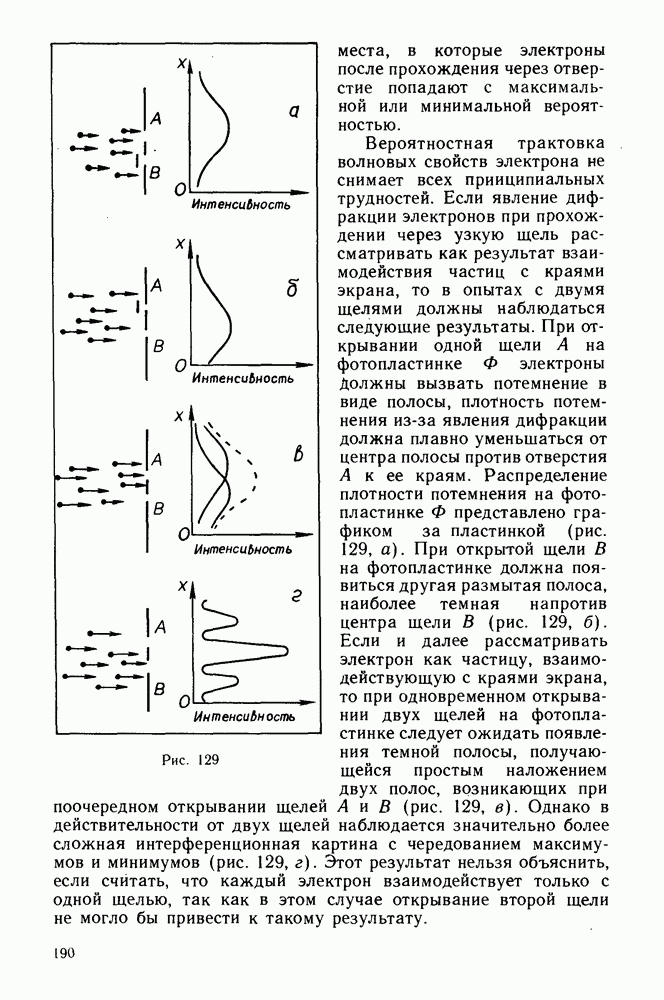
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ