| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава I. КОЛЕБАНИЯ
§ 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
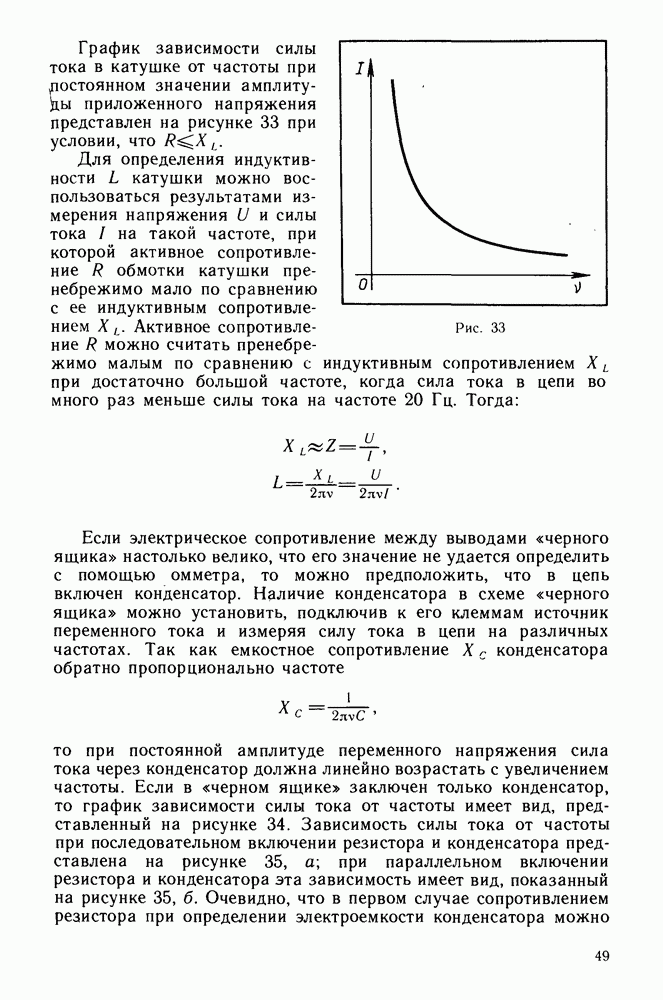
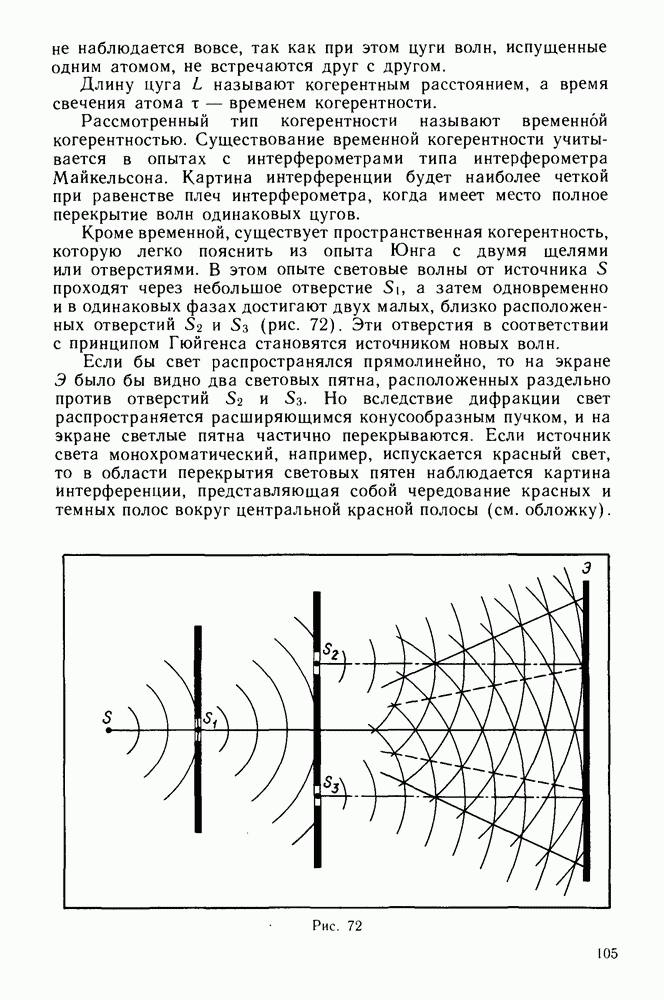
Движение маятника в часах, землетрясение, переменный ток в электрической цепи, процессы радиопередачи и радиоприема — это совершенно различные, не связанные друг с другом процессы. Каждый из них имеет свои особые причины, но их объединяет один признак — признак общности характера изменения физических величин с течением времени. Эти и многие другие процессы различной физической природы во многих случаях оказывается целесообразным рассматривать как один особый тип физических явлений — колебания.
Общий признак физических явлений, называемых колебаниями, — это их повторяемость во времени. При различной физической природе многие колебания происходят по одинаковым законам, что позволяет применять общие методы для их описания и анализа.
Гармонические колебания. Из большого числа различных колебаний в природе и технике особенно часто встречаются гармонические колебания. Гармоническими называют колебания, совершающиеся по закону косинуса или синуса:

где  — величина, испытывающая колебания;
— величина, испытывающая колебания;  — время;
— время;  — постоянная величина, смысл которой будет выяснен далее.
— постоянная величина, смысл которой будет выяснен далее.
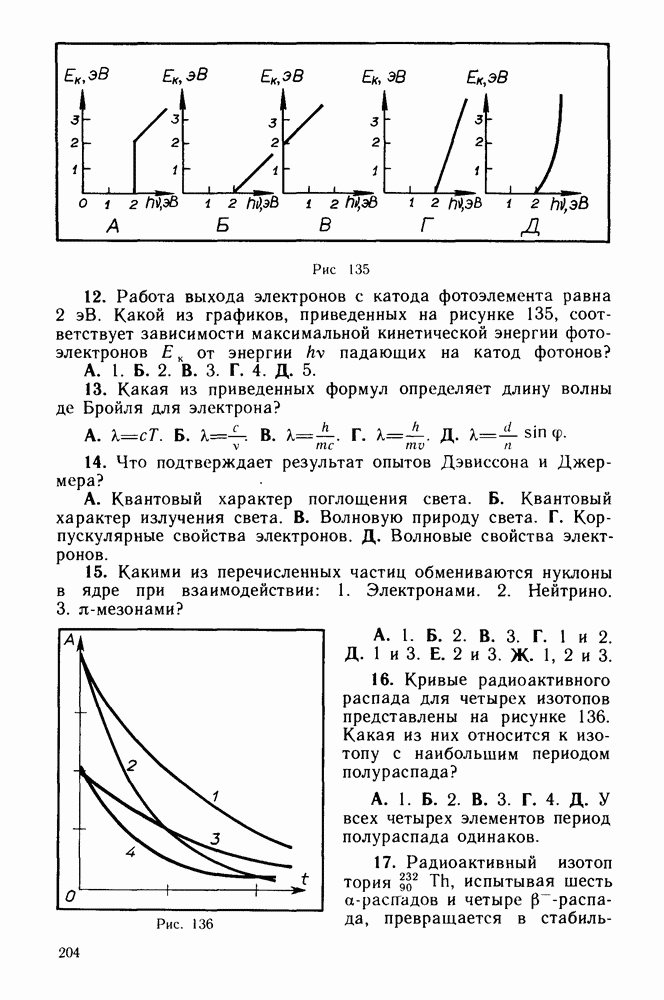
Максимальное значение  величины, изменяющейся по гармоническому закону, называют амплитудой колебаний. Аргумент косинуса или синуса при гармонических колебаниях называют фазой колебания
величины, изменяющейся по гармоническому закону, называют амплитудой колебаний. Аргумент косинуса или синуса при гармонических колебаниях называют фазой колебания 

Фазу колебания  в начальный момент времени называют начальной фазой. Начальная фаза определяет значение величины
в начальный момент времени называют начальной фазой. Начальная фаза определяет значение величины  в начальный момент времени
в начальный момент времени 
Значения функции синуса или косинуса при изменении аргумента функции на  повторяются, поэтому при гармонических колебаниях значения величины
повторяются, поэтому при гармонических колебаниях значения величины  повторяются при изменении фазы колебания на
повторяются при изменении фазы колебания на  . С другой стороны, при гармоническом колебании величина
. С другой стороны, при гармоническом колебании величина  должна принимать те же значения через интервал времени, называемый периодом колебаний Т. Следовательно, изменение фазы на
должна принимать те же значения через интервал времени, называемый периодом колебаний Т. Следовательно, изменение фазы на  происходит
происходит

Рис. 1
через период колебаний Т. Для случая, когда  получим:
получим:

Из выражения (1.2) следует, что постоянная  в уравнении гармонических колебаний есть число колебаний, происходящих за
в уравнении гармонических колебаний есть число колебаний, происходящих за  секунд. Величину
секунд. Величину  называют циклической частотой колебаний. Используя выражение (1.2), уравнение (1.1) можно выразить через частоту
называют циклической частотой колебаний. Используя выражение (1.2), уравнение (1.1) можно выразить через частоту  или период Т колебаний:
или период Т колебаний:

Наряду с аналитическим способом описания гармонических колебаний широко используют графические способы их представления.
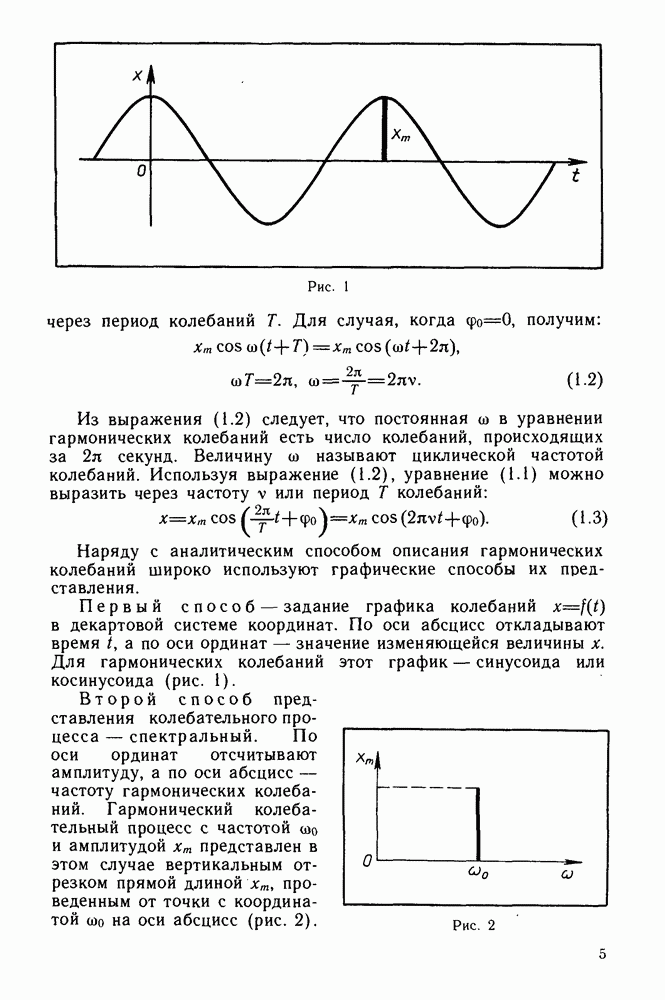
Первый способ — задание графика колебаний  в декартовой системе координат. По оси абсцисс откладывают время I, а по оси ординат — значение изменяющейся величины
в декартовой системе координат. По оси абсцисс откладывают время I, а по оси ординат — значение изменяющейся величины  Для гармонических колебаний этот график — синусоида или косинусоида (рис. 1).
Для гармонических колебаний этот график — синусоида или косинусоида (рис. 1).
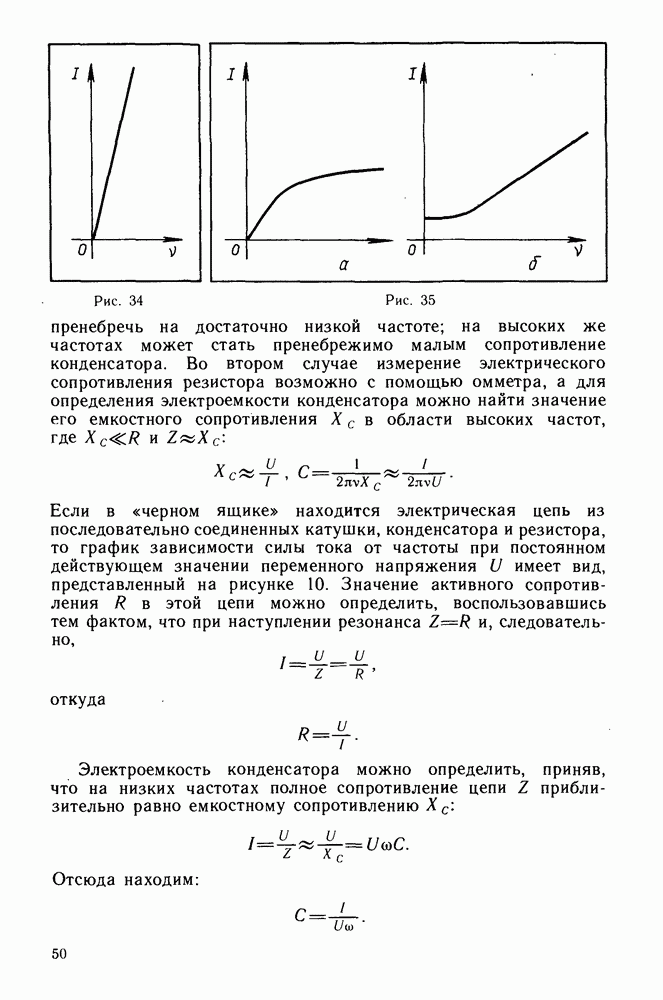
Второй способ представления колебательного процесса — спектральный. По оси ординат отсчитывают амплитуду, а по оси абсцисс — частоту гармонических колебаний. Гармонический колебательный процесс с частотой  и амплитудой
и амплитудой  представлен в этом случае вертикальным отрезком прямой длиной
представлен в этом случае вертикальным отрезком прямой длиной  проведенным от точки с координатой
проведенным от точки с координатой  на оси абсцисс (рис. 2).
на оси абсцисс (рис. 2).

Рис. 2

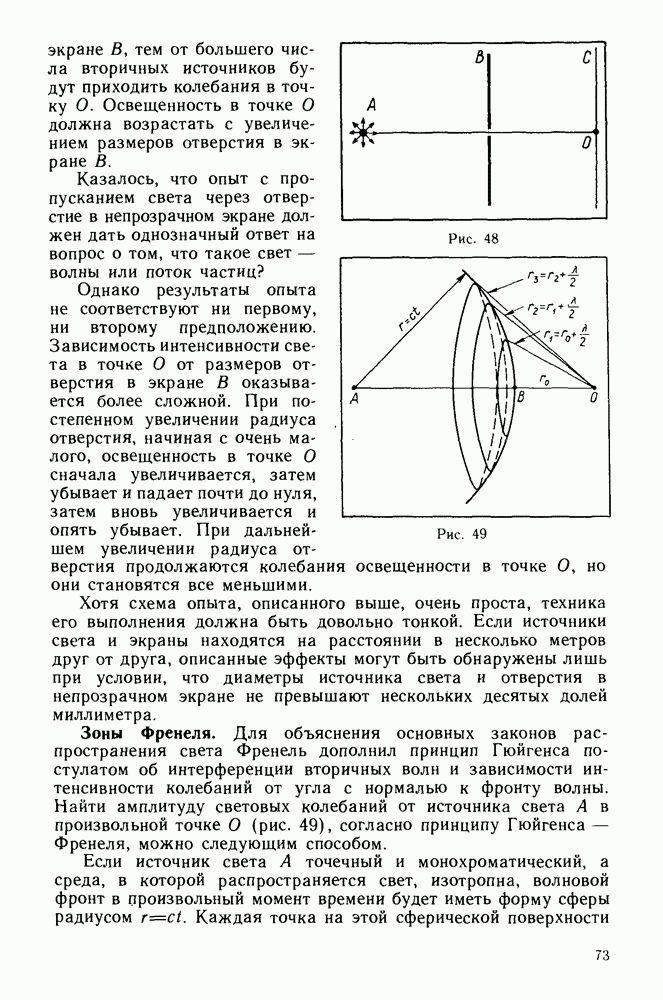
Рис. 3
Третий способ описания гармонических колебаний — метод векторных диаграмм. В этом способе используют следующий, чисто формальный прием для нахождения в любой момент времени  значения величины
значения величины  изменяющейся по гармоническому закону:
изменяющейся по гармоническому закону:

Выберем на плоскости произвольно направленную координатную ось  по которой будем отсчитывать интересующую нас величину
по которой будем отсчитывать интересующую нас величину  Из начала координат вдоль оси
Из начала координат вдоль оси  проведем вектор
проведем вектор  модуль которого равен амплитуде гармонического колебания хт. Если теперь представим себе, что вектор
модуль которого равен амплитуде гармонического колебания хт. Если теперь представим себе, что вектор  вращается вокруг начала координат в плоскости
вращается вокруг начала координат в плоскости  с постоянной угловой скоростью со против часовой стрелки, то угол а между вращающимся вектором и осью
с постоянной угловой скоростью со против часовой стрелки, то угол а между вращающимся вектором и осью  в любой момент времени определится выражением:
в любой момент времени определится выражением:

Проекция  вращающегося вектора
вращающегося вектора  на ось
на ось  (рис. 3) будет изменяться со временем по закону:
(рис. 3) будет изменяться со временем по закону:

Мы получили уравнение, тождественное по форме уравнению (1.4). Следовательно, значение величины  изменяющейся по гармоническому закону, можно найти в любой момент времени, определив проекцию на ось
изменяющейся по гармоническому закону, можно найти в любой момент времени, определив проекцию на ось  вектора
вектора  модуль которого равен амплитуде гармонического колебания
модуль которого равен амплитуде гармонического колебания  если начало этого вектора совпадает с началом координат, а сам он вращается в плоскости
если начало этого вектора совпадает с началом координат, а сам он вращается в плоскости  с угловой скоростью
с угловой скоростью  против часовой стрелки. В начальный момент времени
против часовой стрелки. В начальный момент времени  угол между вектором и осью
угол между вектором и осью  равен нулю.
равен нулю.
1. Что называют периодом колебаний?
2. Что такое частота колебаний?
3. Какие колебания называют гармоническими?
4. Что такое амплитуда колебаний?
5. Что называют фазой колебаний?
6. Что такое начальная фаза колебаний?
7. Что такое циклическая частота?
8. Какова связь циклической частоты с периодом колебаний?
9. Как описывается гармонический колебательный процесс спектральным методом?
10. Опишите способ задания гармонического колебания с помощью векторной диаграммы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
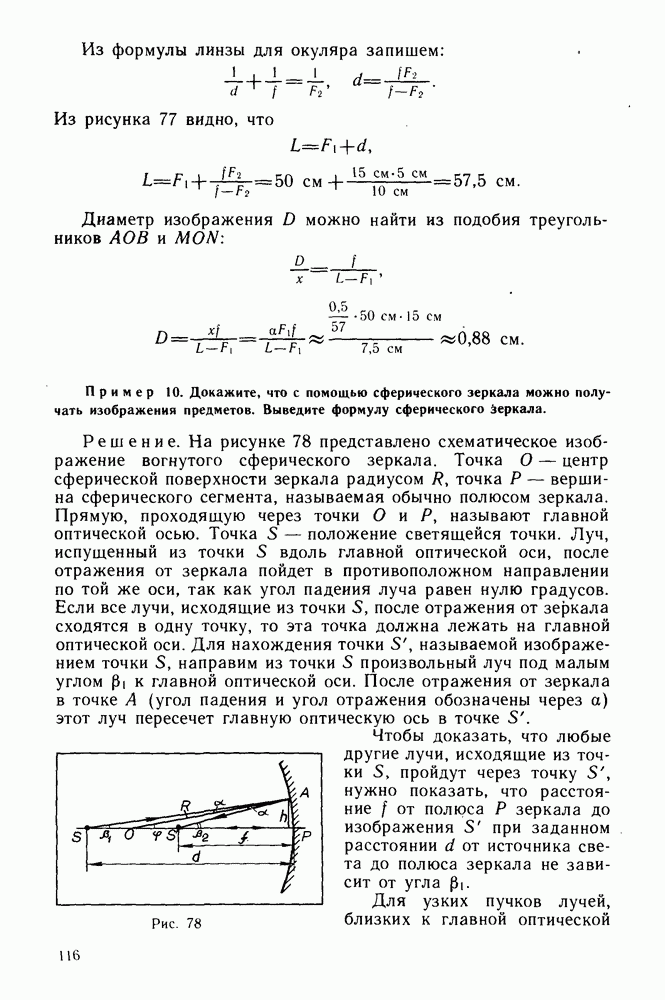
- Глава I. КОЛЕБАНИЯ
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
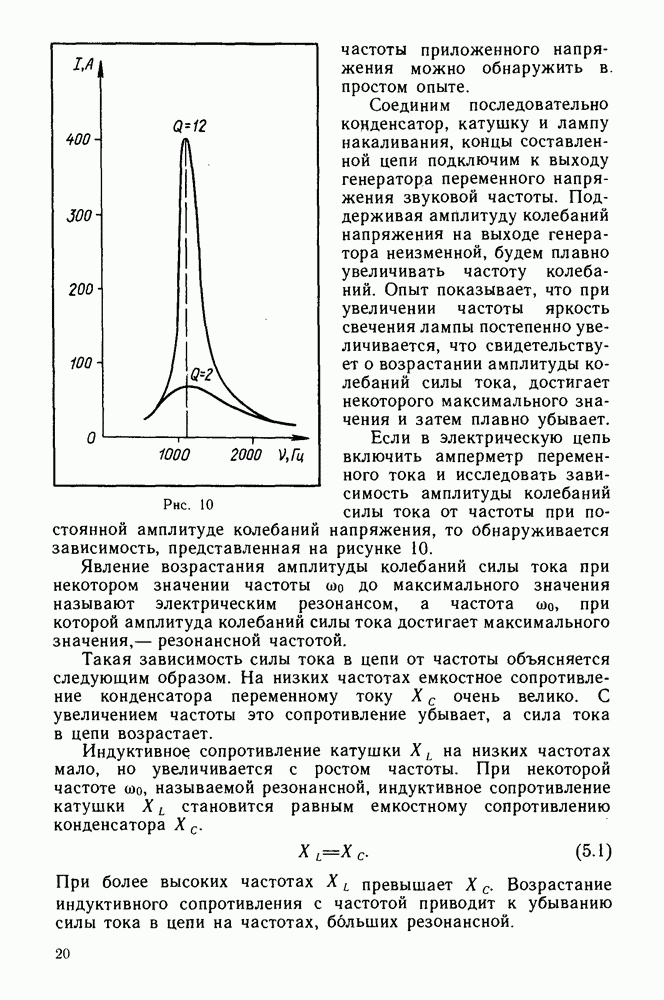
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
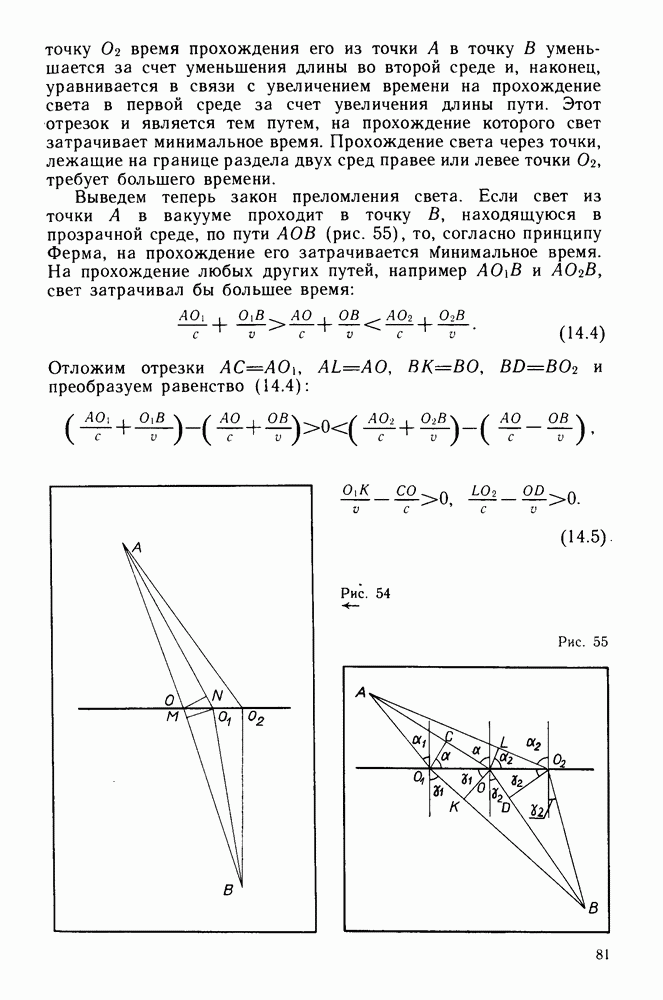
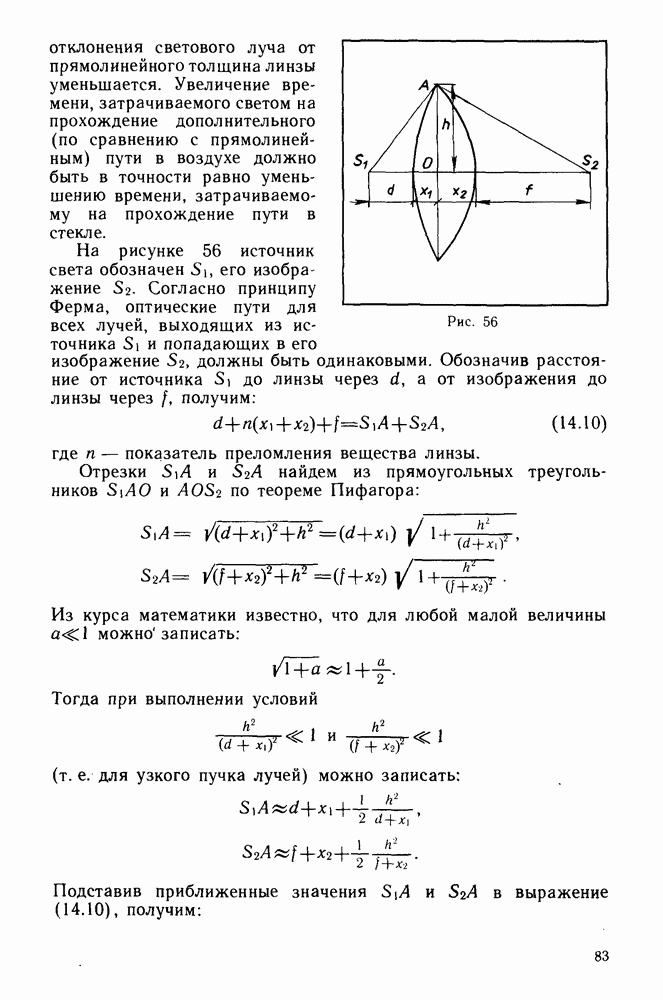
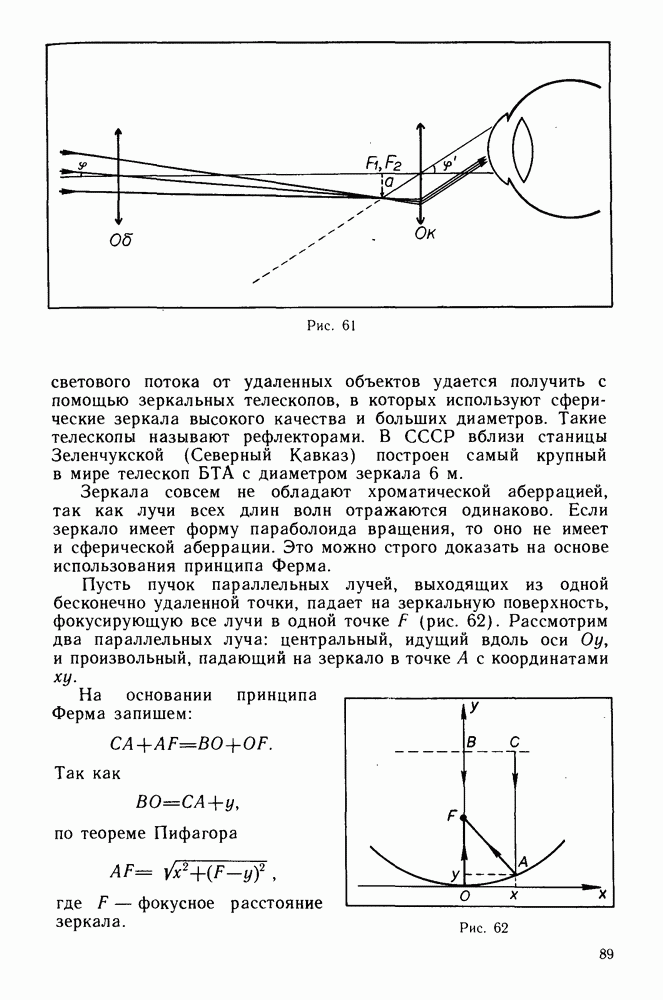
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
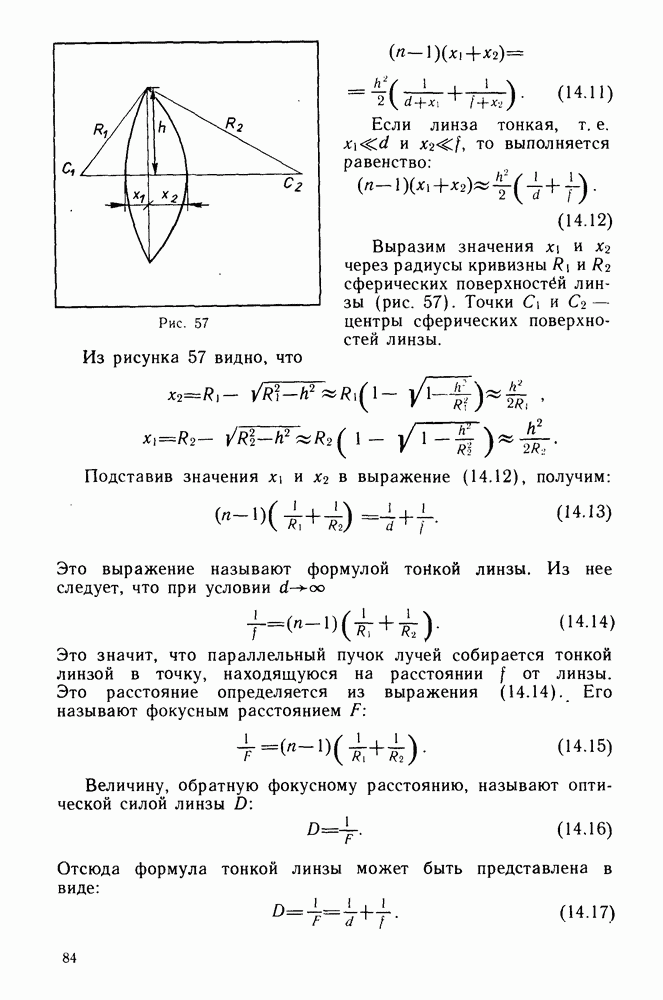
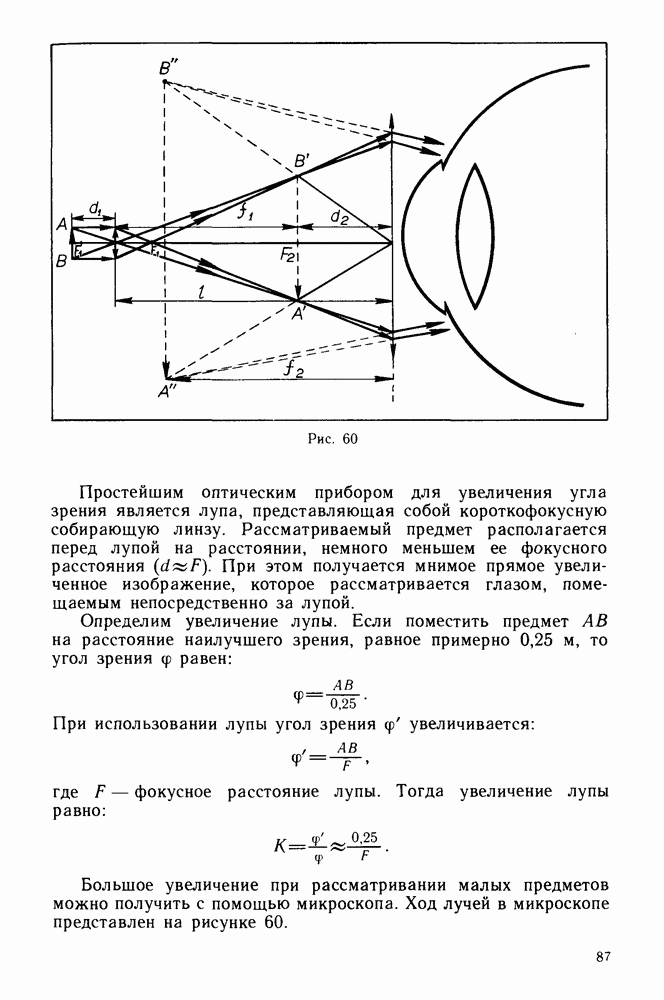
- Линзы.
- Аберрация линз.
- Оптические приборы.
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
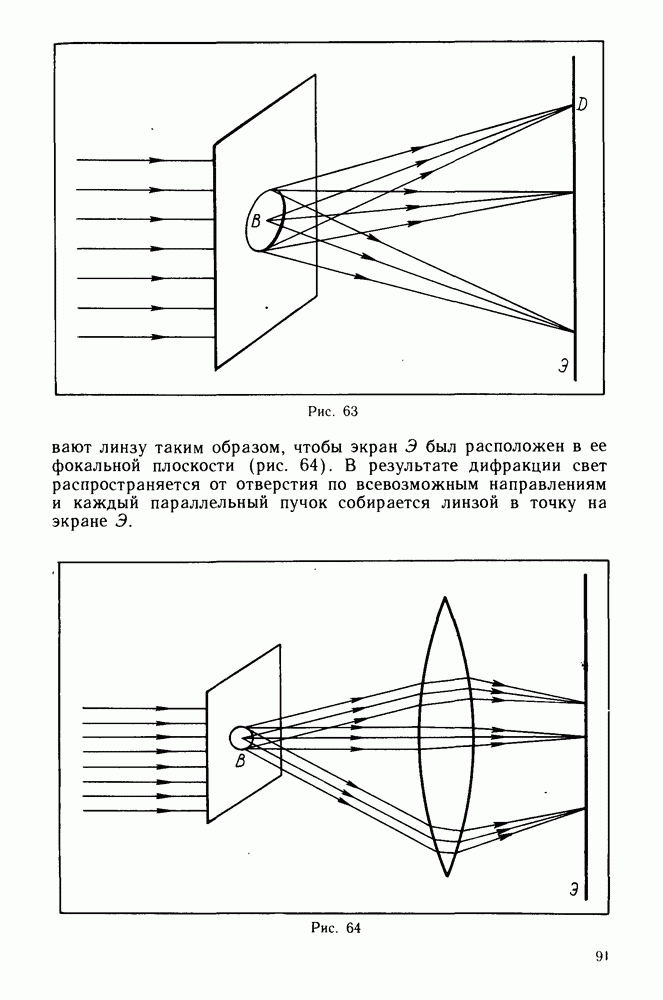
- Дифракция от круглого отверстия.
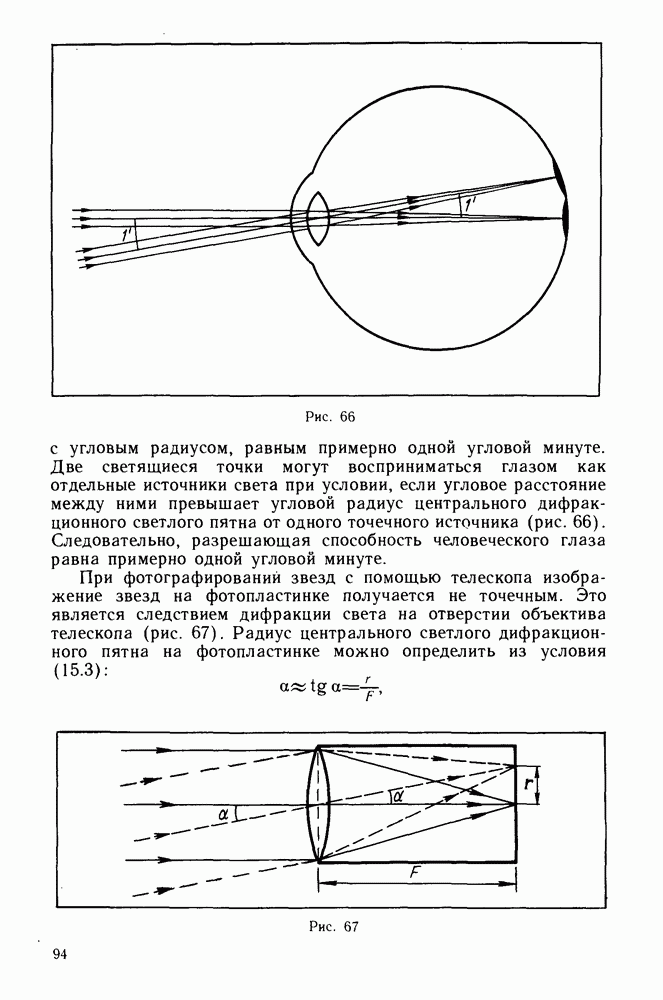
- Дифракция и разрешающая способность оптических приборов.
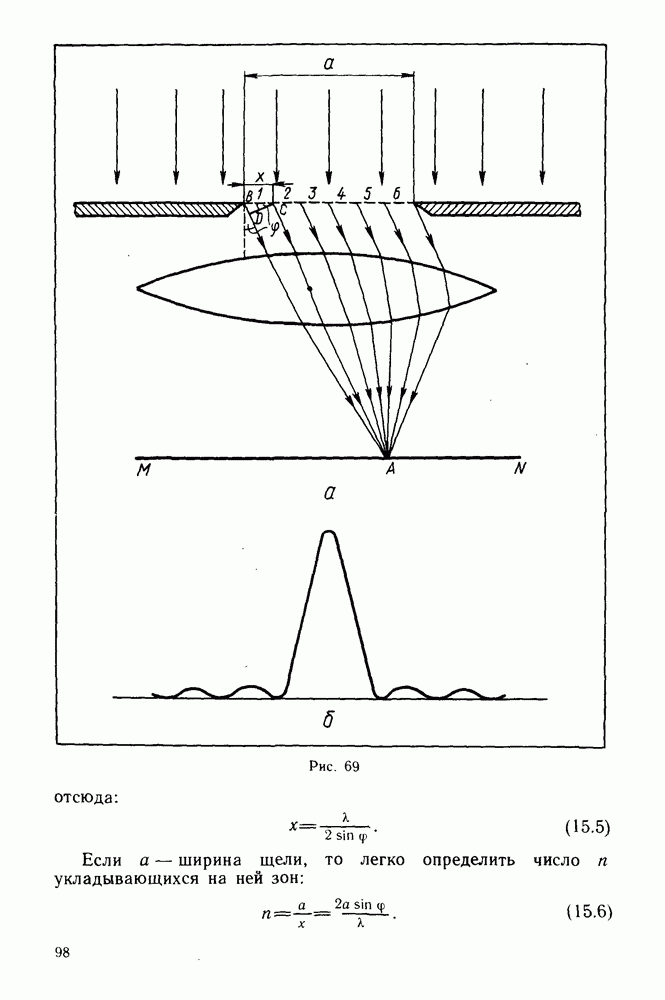
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
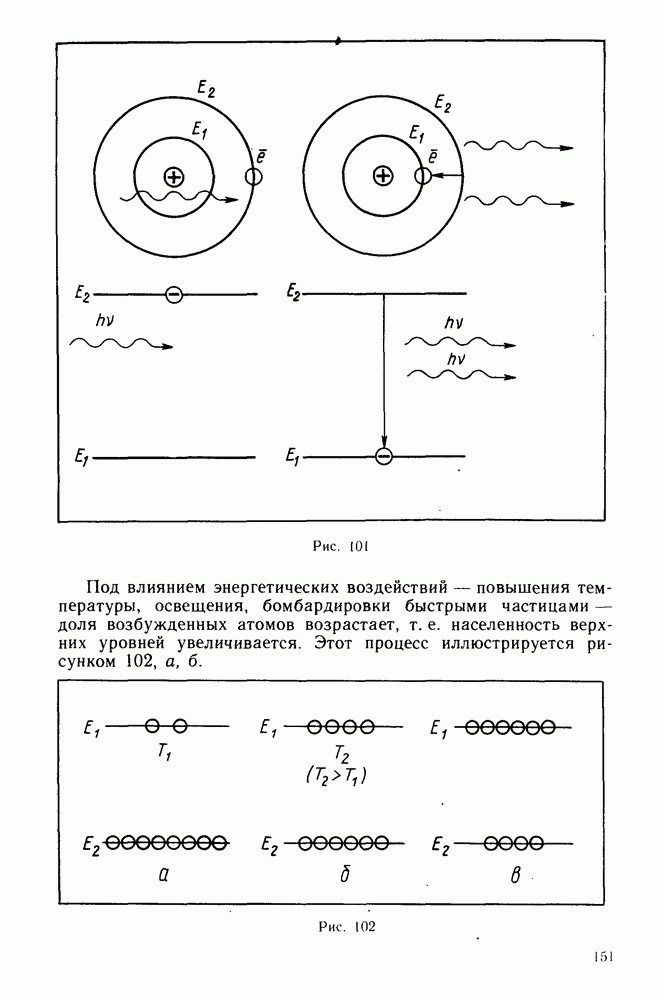
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
- Схема энергетических уровней.
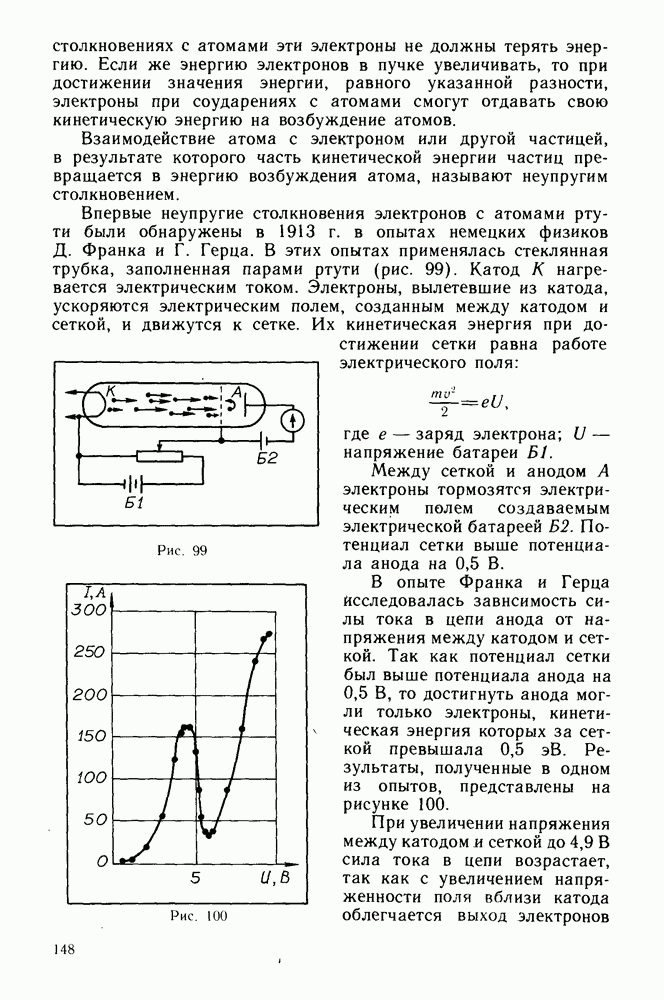
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
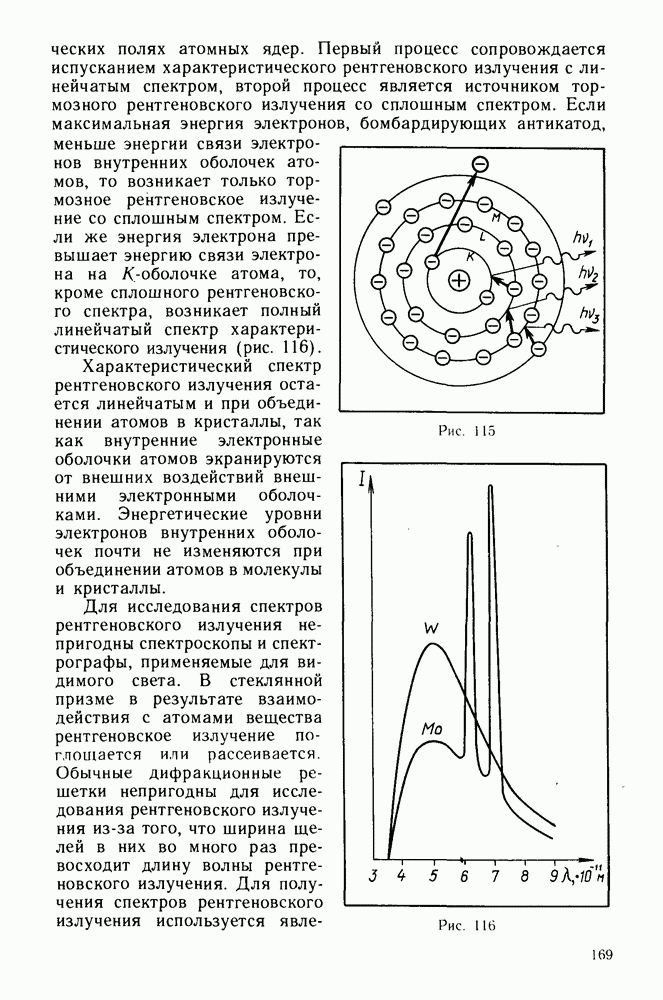
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
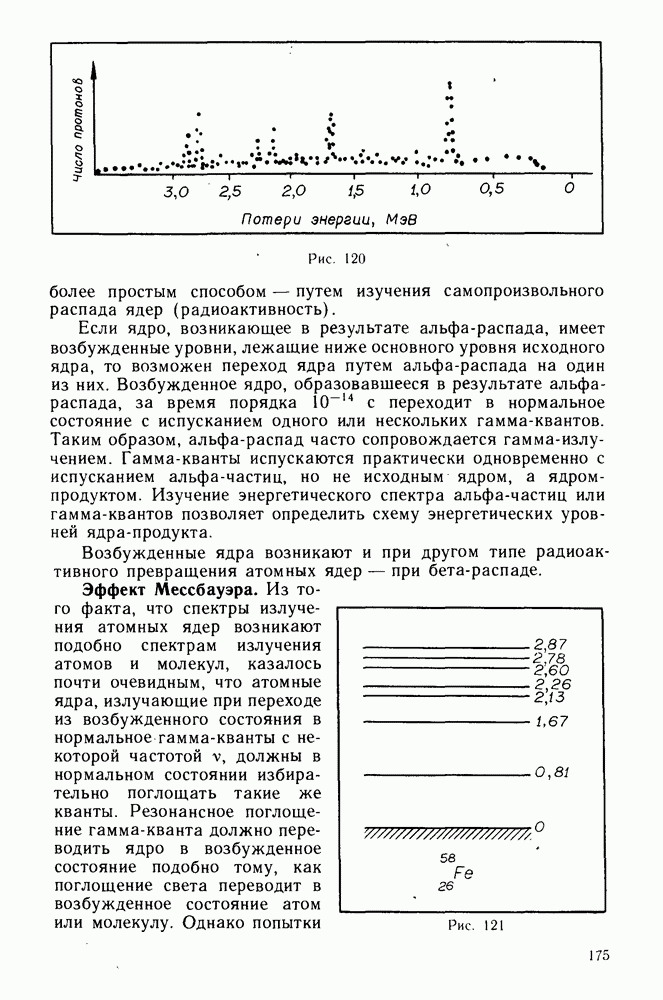
- Эффект Мессбауэра.
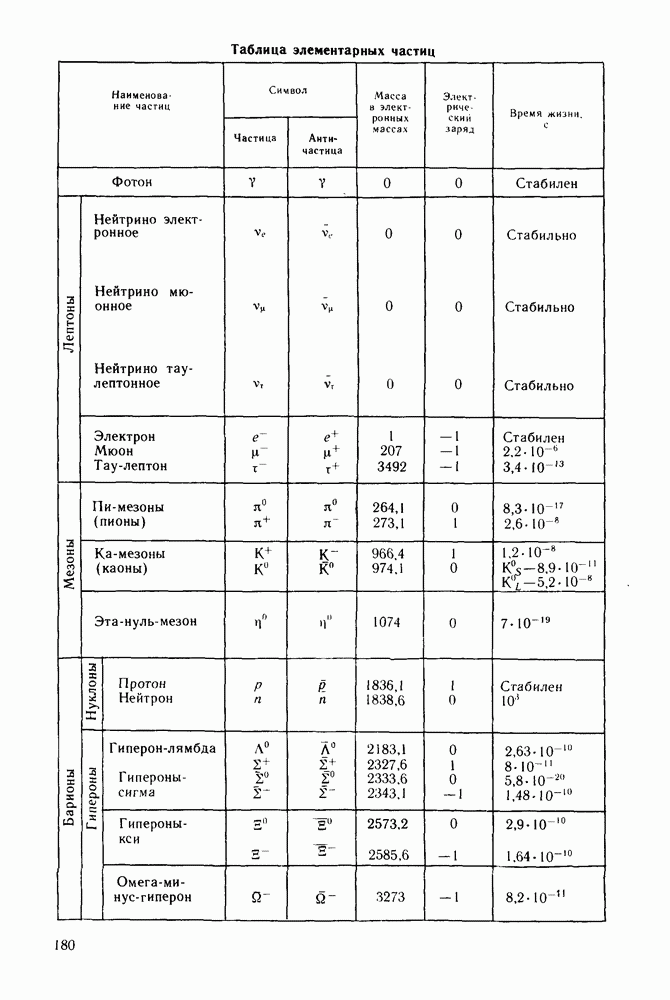
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
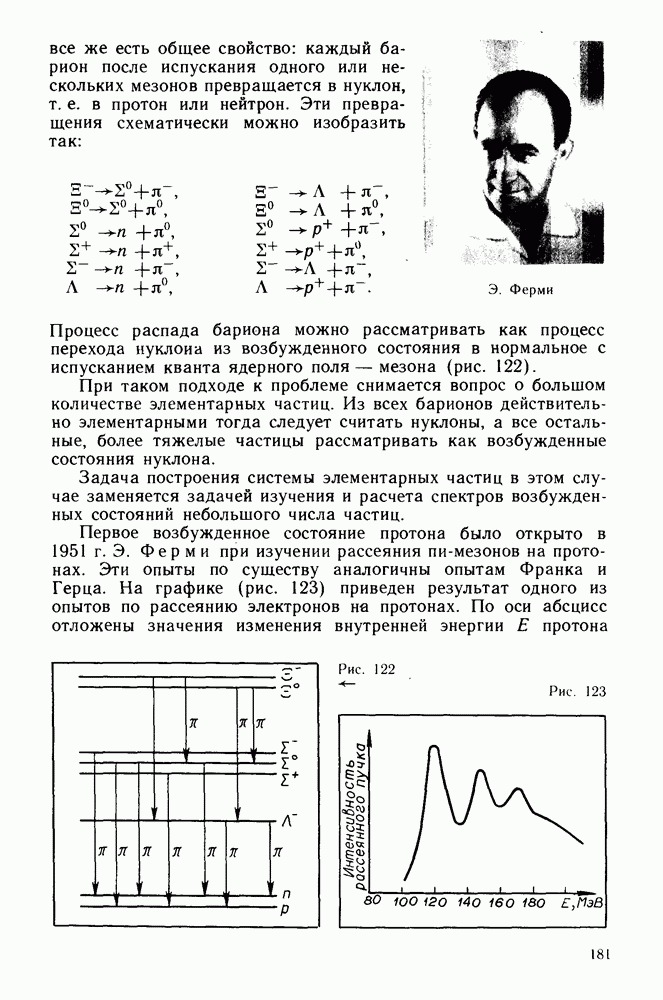
- Нуклоны.
- Спектры элементарных частиц.
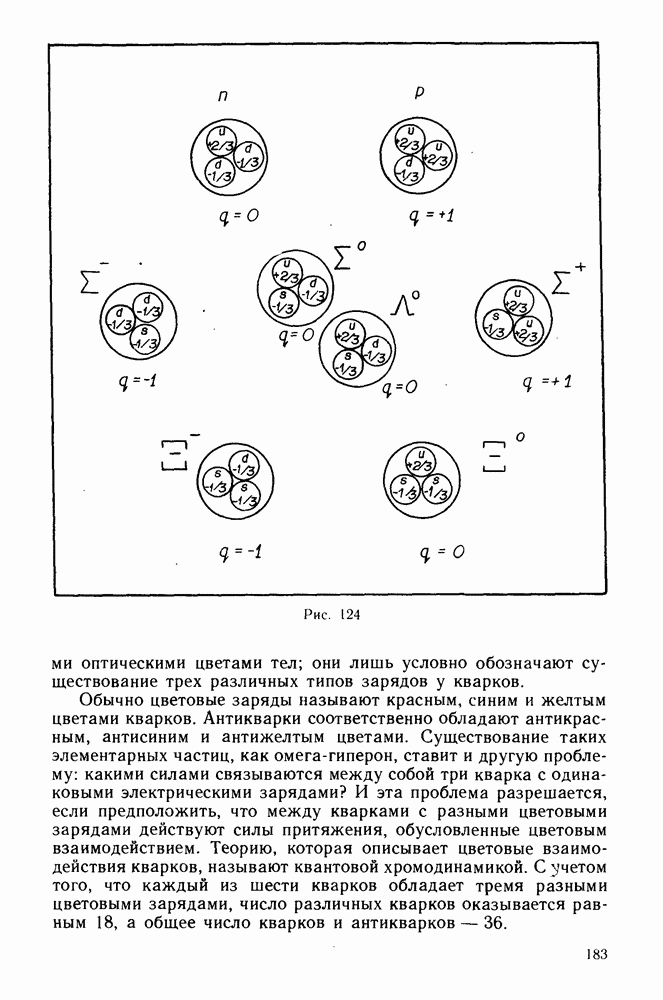
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
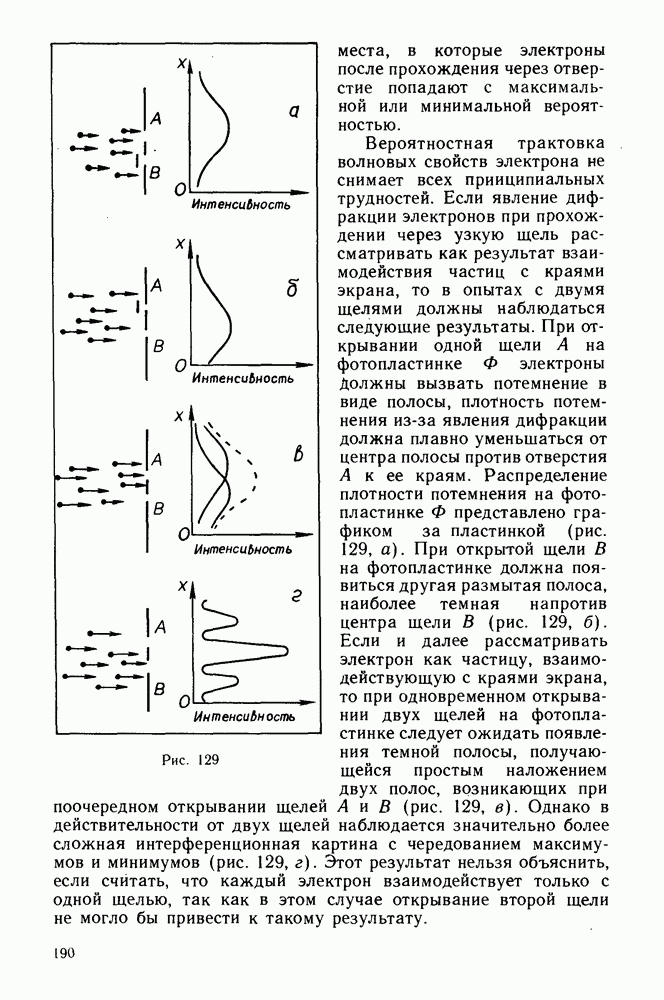
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ