| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
Пример 6. Определите фокусное расстояние объектива, необходимого для диапроекции в зале длиной L. Увеличение объектива равно К.
Решение. Из формулы линзы рассчитаем фокусное расстояние объектива:

Учитывая, что  после преобразований получим:
после преобразований получим:

Так как 


Рис. 76
Пример 7. Фотоаппаратом, сфокусированным на бесконечность, сделали фотоснимок. Фокусное расстояние объектива 5 см, отношение диаметра D объектива к фокусному расстоянию F равно  На каком минимальном расстоянии
На каком минимальном расстоянии  от фотоаппарата предметы на снимке будут достаточно резкими, если считать, что допустимое размытие изображения равно 0,1 мм?
от фотоаппарата предметы на снимке будут достаточно резкими, если считать, что допустимое размытие изображения равно 0,1 мм?
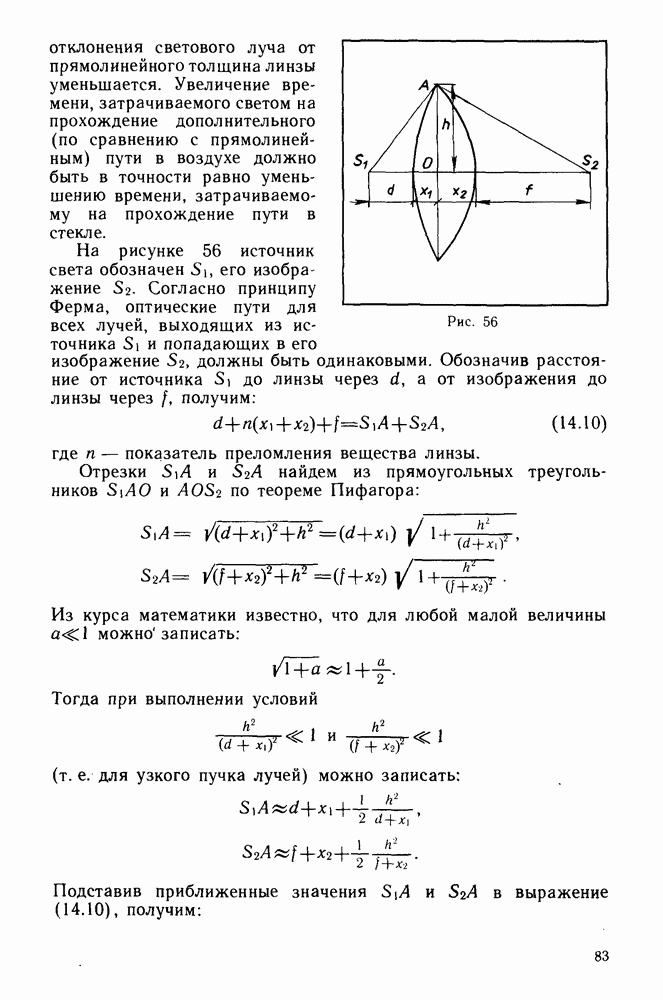
Решение. Если объектив фотоаппарата установлен на бесконечность, то фотопленку размещают в его фокальной плоскости (рис. 76).
Точечный источник света S на фотопленке будет изображаться в виде кружка диаметром 
Из подобия треугольников запишем:

Из условия задачи  и формулы линзы следует:
и формулы линзы следует:

Пример 8. Две собирающие тонкие линзы с фокусными расстояниями  имеют общую главную оптическую ось и находятся на расстоянии
имеют общую главную оптическую ось и находятся на расстоянии  друг от друга. Найдите связь между расстоянием
друг от друга. Найдите связь между расстоянием  от предмета до первой линзы и расстоянием
от предмета до первой линзы и расстоянием  от второй линзы до изображения, созданного системой линз. Найдите фокусное расстояние системы линз.
от второй линзы до изображения, созданного системой линз. Найдите фокусное расстояние системы линз.
Решение. Запишем формулу линзы для обеих линз:

Если свет падает сначала на первую линзу, то изображение, построенное первой линзой, является предметом для второй линзы. При этом выполняется равенство:

Из уравнений (1), (2) и (3) следует:

Если  — фокусное расстояние системы в том случае, когда свет падает на линзу с фокусным расстоянием
— фокусное расстояние системы в том случае, когда свет падает на линзу с фокусным расстоянием 

Если свет падает сначала на линзу с фокусным расстоянием  то фокусное расстояние
то фокусное расстояние  оптической системы определяется из уравнения:
оптической системы определяется из уравнения:

Из уравнений (5) и (6) следует, что  и лишь при
и лишь при  когда линзы находятся в контакте,
когда линзы находятся в контакте,

т. е.

Оптическая сила двух тонких линз, находящихся в контакте, равна сумме оптических сил каждой линзы.
Пример 9. Труба Кеплера наведена на Солнце. Фокусное расстояние объектива равно  см, окуляра
см, окуляра  см. На расстоянии
см. На расстоянии  см от окуляра расположен экран. При каком расстоянии
см от окуляра расположен экран. При каком расстоянии  между объективом и окуляром на экране получится четкое изображение Солнца? Чему равен диаметр
между объективом и окуляром на экране получится четкое изображение Солнца? Чему равен диаметр  этого изображения? Угловой диаметр Солнца
этого изображения? Угловой диаметр Солнца 
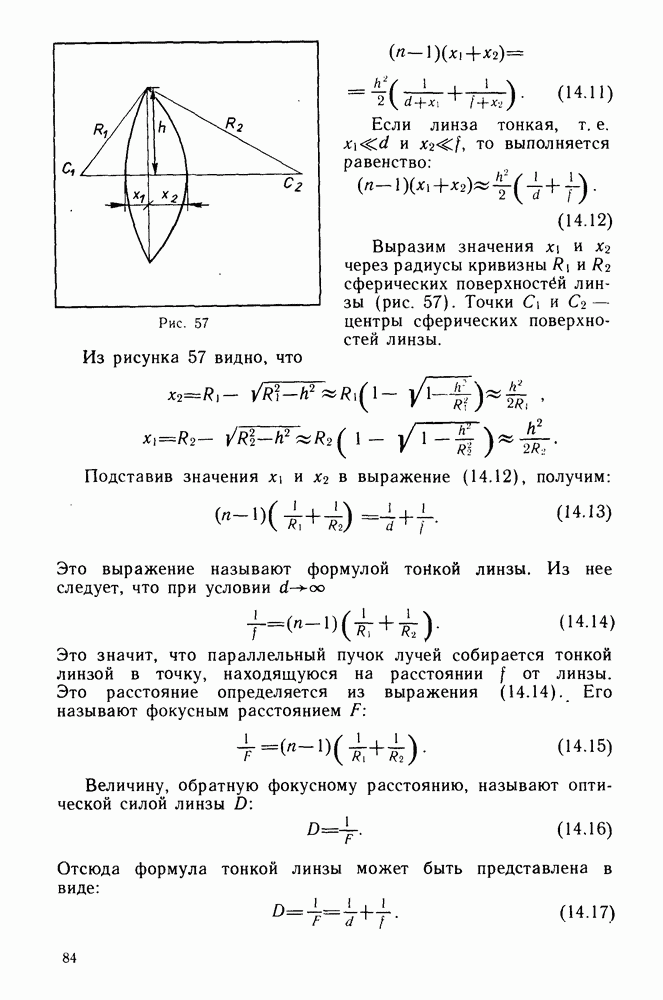
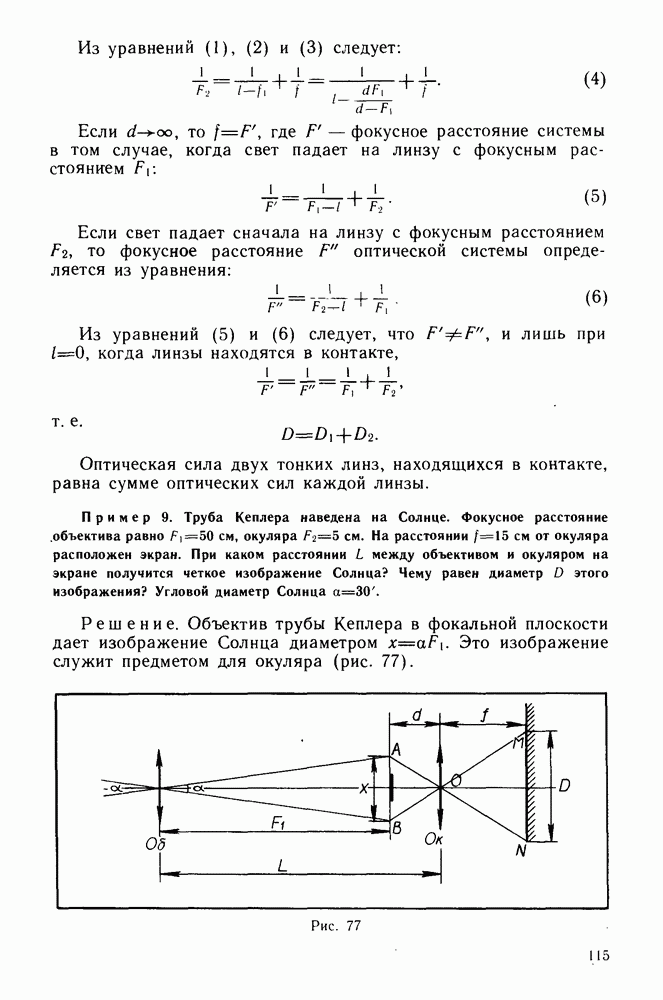
Решение. Объектив трубы Кеплера в фокальной плоскости дает изображение Солнца диаметром  Это изображение служит предметом для окуляра (рис. 77).
Это изображение служит предметом для окуляра (рис. 77).

Рис. 77
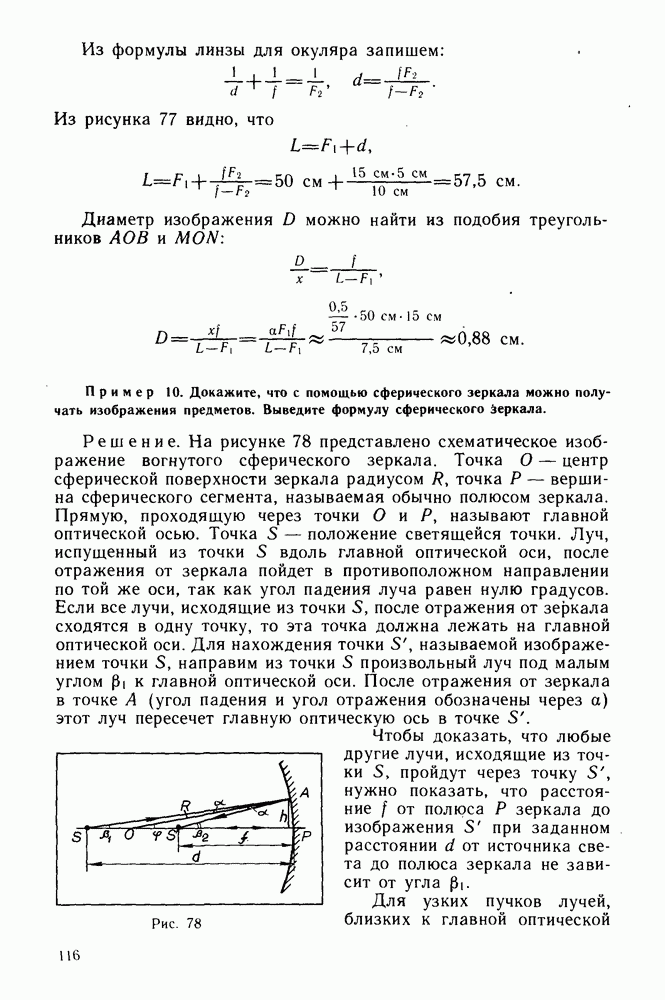
Из формулы линзы для окуляра запишем:

Из рисунка 77 видно, что

Диаметр изображения  можно найти из подобия треугольников
можно найти из подобия треугольников  и
и 

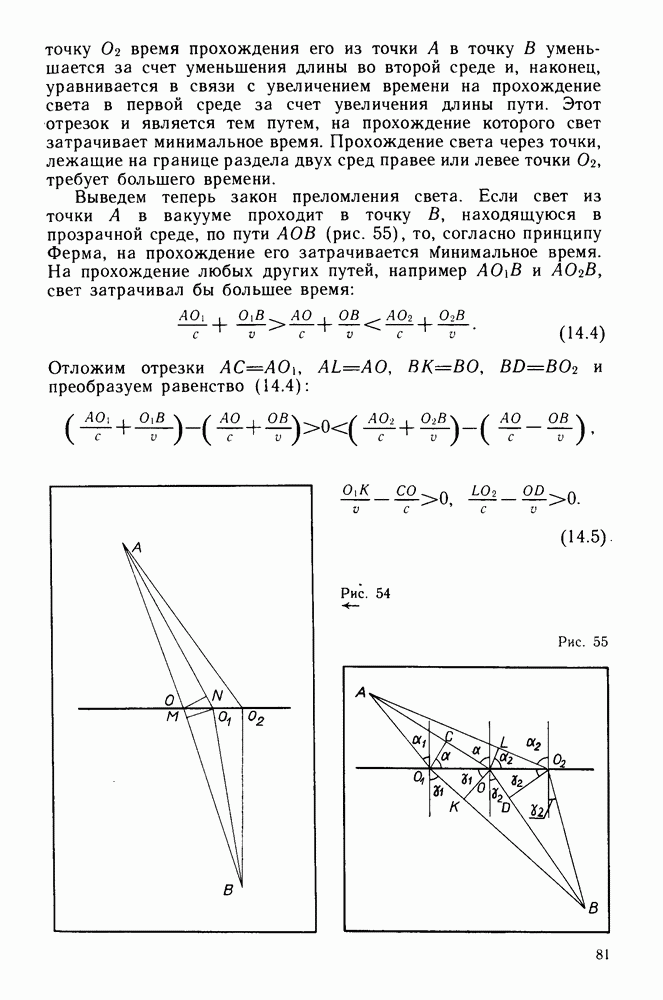
Пример 10. Докажите, что с помощью сферического зеркала можно получать изображения предметов. Выведите формулу сферического зеркала.
Решение. На рисунке 78 представлено схематическое изображение вогнутого сферического зеркала. Точка О — центр сферической поверхности зеркала радиусом  точка Р — вершина сферического сегмента, называемая обычно полюсом зеркала. Прямую, проходящую через точки О и Р, называют главной оптической осью. Точка
точка Р — вершина сферического сегмента, называемая обычно полюсом зеркала. Прямую, проходящую через точки О и Р, называют главной оптической осью. Точка  — положение светящейся точки. Луч, испущенный из точки
— положение светящейся точки. Луч, испущенный из точки  вдоль главной оптической оси, после отражения от зеркала пойдет в противоположном направлении по той же оси, так как угол падения луча равен нулю градусов. Если все лучи, исходящие из точки
вдоль главной оптической оси, после отражения от зеркала пойдет в противоположном направлении по той же оси, так как угол падения луча равен нулю градусов. Если все лучи, исходящие из точки  после отражения от зеркала сходятся в одну точку, то эта точка должна лежать на главной оптической оси. Для нахождения точки
после отражения от зеркала сходятся в одну точку, то эта точка должна лежать на главной оптической оси. Для нахождения точки  называемой изображением точки
называемой изображением точки  направим из точки
направим из точки  произвольный луч под малым углом
произвольный луч под малым углом  к главной оптической оси. После отражения от зеркала в точке А (угол падения и угол отражения обозначены через а) этот луч пересечет главную оптическую ось в точке
к главной оптической оси. После отражения от зеркала в точке А (угол падения и угол отражения обозначены через а) этот луч пересечет главную оптическую ось в точке 
Чтобы доказать, что любые другие лучи, исходящие из точки  пройдут через точку
пройдут через точку  нужно показать, что расстояние
нужно показать, что расстояние  от полюса Р зеркала до изображения
от полюса Р зеркала до изображения  при заданном расстоянии
при заданном расстоянии  от источника света до полюса зеркала не зависит от угла
от источника света до полюса зеркала не зависит от угла 
Для узких пучков лучей, близких к главной оптической

Рис. 78

Рис. 79

Рис. 80
оси, справедливо условие  Для них углы
Для них углы  достаточно малы, поэтому выполняются приближенные равенства:
достаточно малы, поэтому выполняются приближенные равенства:

Так как внешний угол любого треугольника равен сумме двух внутренних, не смежных с ним, то справедливы равенства:

Из условия (2) получаем:

С учетом выражения (1) находим:

Это выражение называют формулой сферического зеркала. Из полученной формулы следует, что величина  не зависит от угла
не зависит от угла  Следовательно, все лучи, испускаемые источником
Следовательно, все лучи, испускаемые источником  соберутся в точке
соберутся в точке 
Если источник света находится очень далеко от зеркала  то из формулы зеркала получаем:
то из формулы зеркала получаем:

т. е. при падении на вогнутое сферическое зеркало пучка лучей, параллельного главной оптической оси, все они собираются в одной точке  называемой фокусом зеркала. Фокусное расстояние
называемой фокусом зеркала. Фокусное расстояние  расстояние от полюса зеркала до его фокуса, равно половине радиуса кривизны зеркала:
расстояние от полюса зеркала до его фокуса, равно половине радиуса кривизны зеркала:  (Рис. 79).
(Рис. 79).
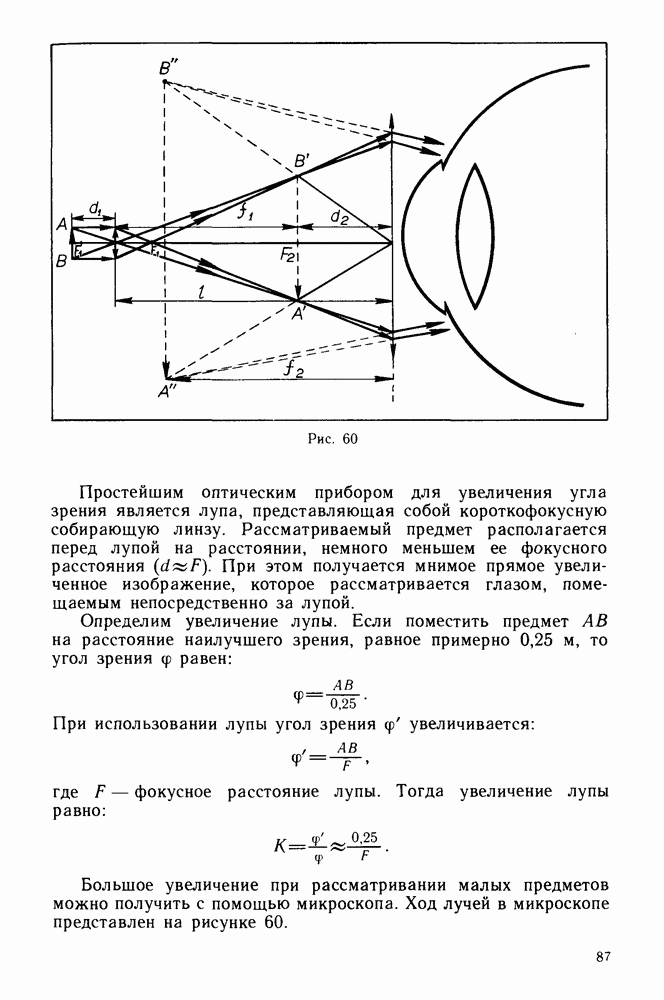
Используя свойство лучей, идущих параллельно главной оптической оси, можно построить изображение в сферическом зеркале от источника, находящегося в произвольном месте. После отражения от зеркала луч, идущий параллельно главной оптической оси, пересекает главную оптическую ось в фокусе зеркала (рис. 80). На основе принципа обратимости световых лучей
любой луч, проходящий через фокус, после отражения от зеркала пойдет параллельно главной оптической оси.
Примечание. При использовании формулы сферического зеркала следует учитывать правила знаков:
1. Фокусное расстояние вогнутого зеркала считают положительным, фокусное расстояние F выпуклого зеркала — отрицательным.
2. Расстояние  до действительного изображения считают положительным, до мнимого изображения — отрицательным.
до действительного изображения считают положительным, до мнимого изображения — отрицательным.
Пример 11. Постройте изображение предмета, находящегося на расстоянии  от сферического зеркала радиуса R.
от сферического зеркала радиуса R.
Решение. Для построения изображения используем любые из трех лучей, ход которых легко предсказать, исходя из основных свойств сферического зеркала, не проводя строгих геометрических построений:
1) луч, падающий на зеркало параллельно главной оптической оси, после отражения проходит через фокус, находящийся на расстоянии  от полюса зеркала;
от полюса зеркала;
2) луч, падающий на зеркало через главный фокус, вследствие принципа обратимости световых лучей после отражения идет параллельно главной оптической оси;
3) луч, проходящий через оптический центр зеркала, падает перпендикулярно поверхности зеркала и после отражения идет по этой же прямой.
В зависимости от соотношения между  и R, а также от вида зеркала (вогнутое или выпуклое) изменяются характер изображения и его размер. Например, построение изображения для вогнутого зеркала при условии
и R, а также от вида зеркала (вогнутое или выпуклое) изменяются характер изображения и его размер. Например, построение изображения для вогнутого зеркала при условии  представлено на рисунке 81. В этом случае изображение действительное, уменьшенное, перевернутое. Остальные случаи рассмотрите самостоятельно.
представлено на рисунке 81. В этом случае изображение действительное, уменьшенное, перевернутое. Остальные случаи рассмотрите самостоятельно.
Выпуклое зеркало всегда дает изображение мнимое, прямое, уменьшенное (рис. 82).

Рис. 81

Рис. 82

Рис. 83
Пример 12. Определите условия наблюдения интерференционных максимумов и минимумов при отражении монохроматического света с длиной волны X от тонкой плоскопараллельной пленки толщиной а. Показатель преломления пленки равен 
Решение. На рисунке 83 показан ход луча  падающего на тонкую плоскопараллельную пленку под углом а. В результате многократного отражения и преломления падающая на пленку световая волна разделится на ряд волн, отраженных и проходящих через пластинку.
падающего на тонкую плоскопараллельную пленку под углом а. В результате многократного отражения и преломления падающая на пленку световая волна разделится на ряд волн, отраженных и проходящих через пластинку.
Для расчета интерференционной картины при малом отражении достаточно ограничиться двумя лучами  так как энергия последующих отраженных волн будет мала по сравнению с энергией первых двух волн.
так как энергия последующих отраженных волн будет мала по сравнению с энергией первых двух волн.
Оптическая разность хода для этих двух волн равна:

Так как по закону преломления  то
то

При отражении волны в точке О от оптически более плотной среды происходит смена ее фазы на противоположную, при отражении волны в точке  от оптически менее плотной среды изменения фазы не происходит. Поэтому интерференционная картина будет определяться разностью хода
от оптически менее плотной среды изменения фазы не происходит. Поэтому интерференционная картина будет определяться разностью хода  с учетом потери
с учетом потери 

Из условия интерференционного максимума  следует:
следует:

а из условия интерференционного минимума 

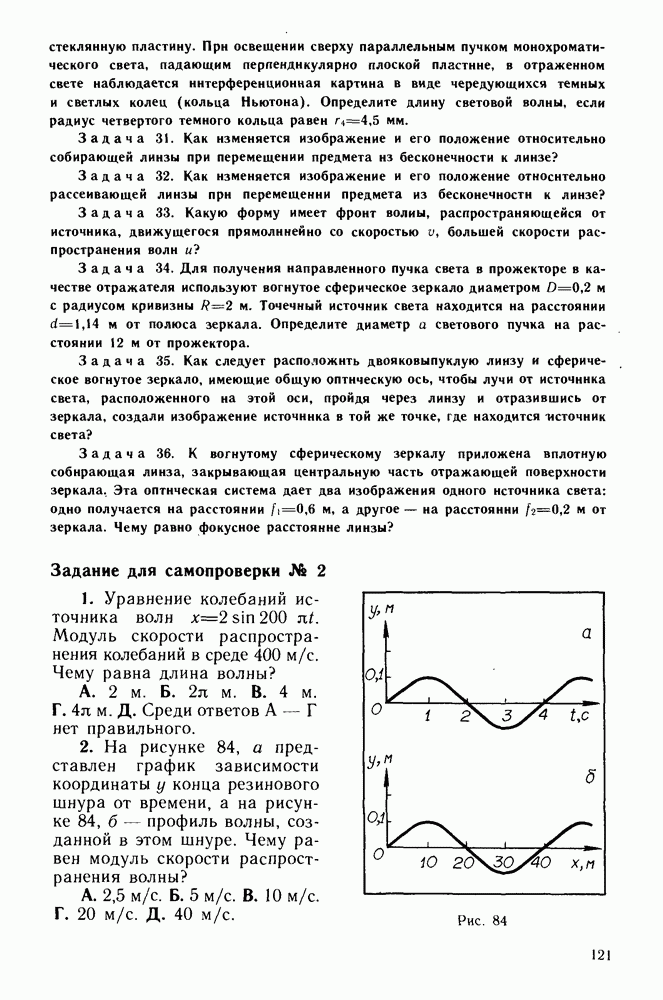
Задачи для самостоятельного решения
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
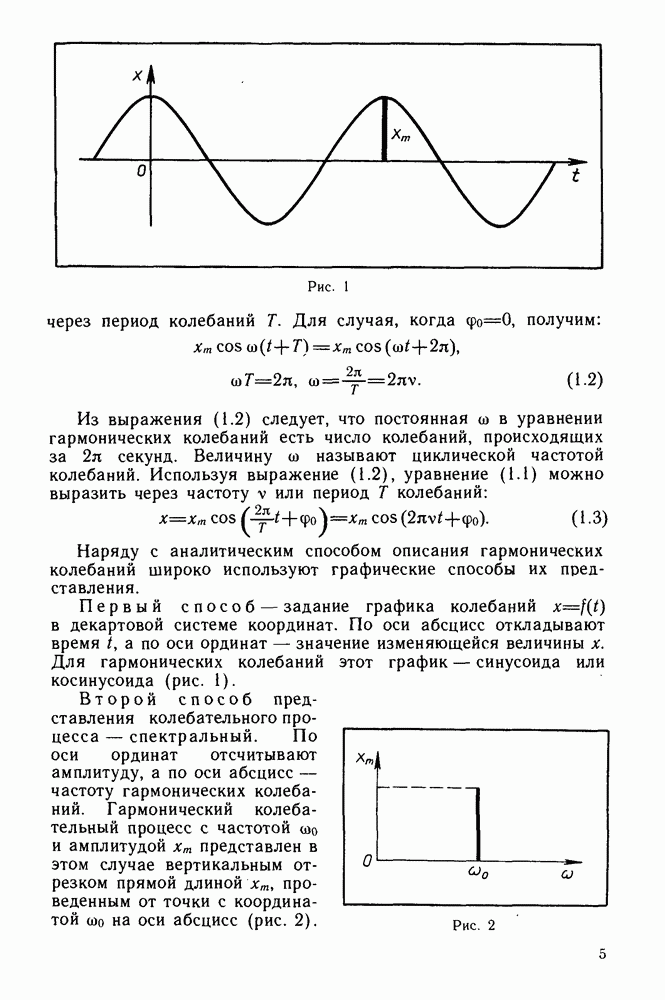
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
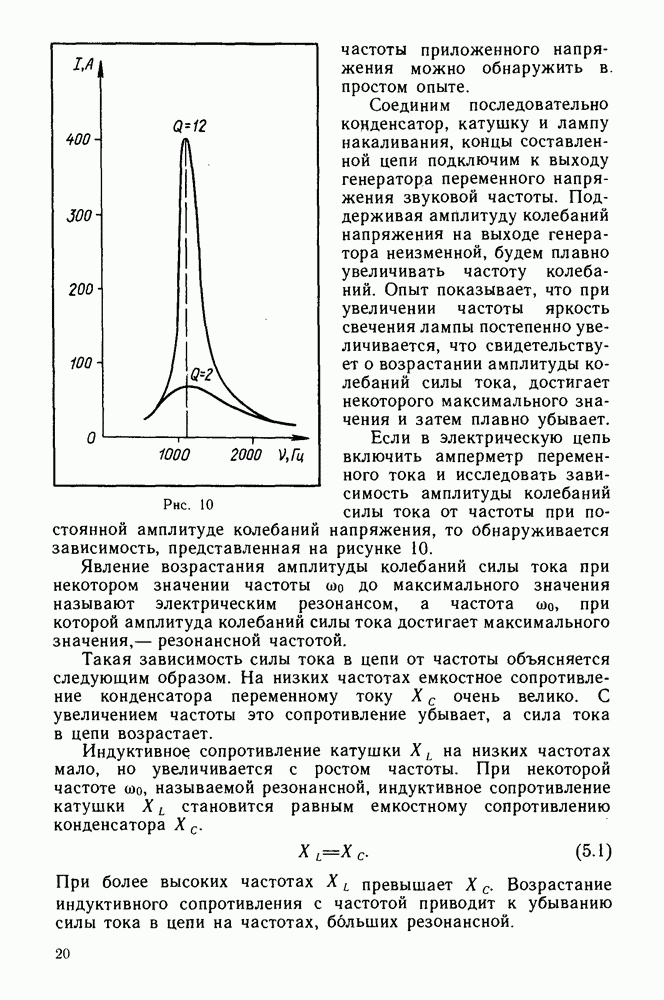
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
- Дифракция от круглого отверстия.
- Дифракция и разрешающая способность оптических приборов.
- Дифракция от одной щели.
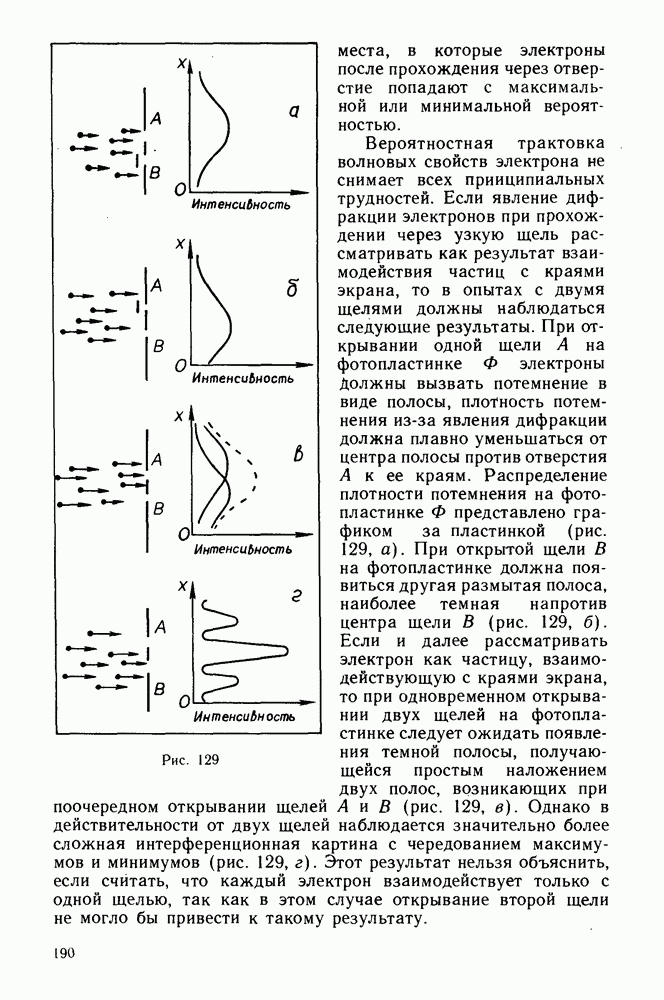
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
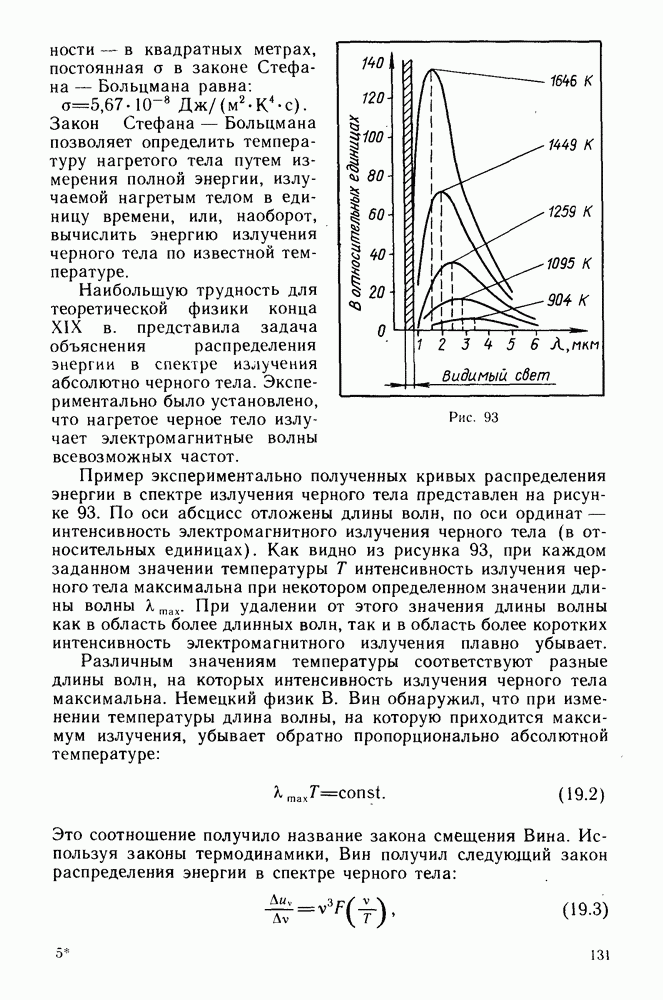
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
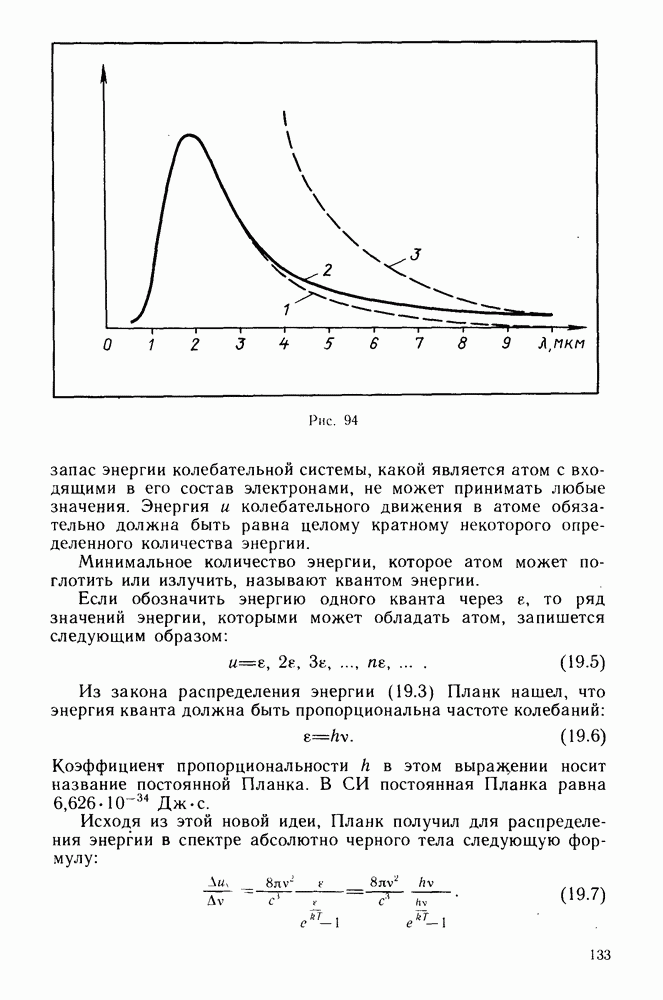
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
- Схема энергетических уровней.
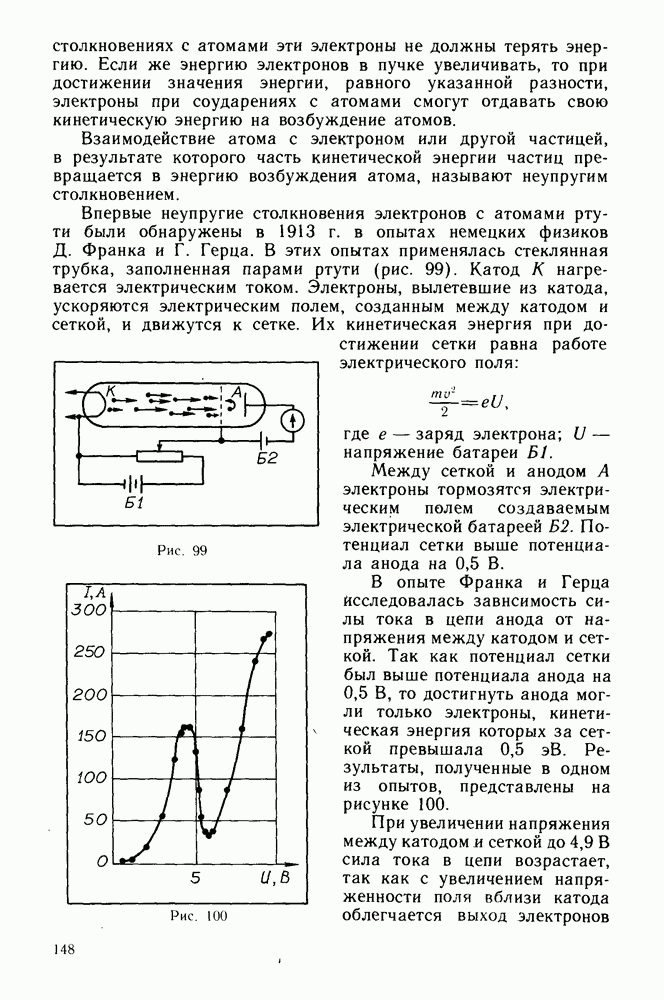
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
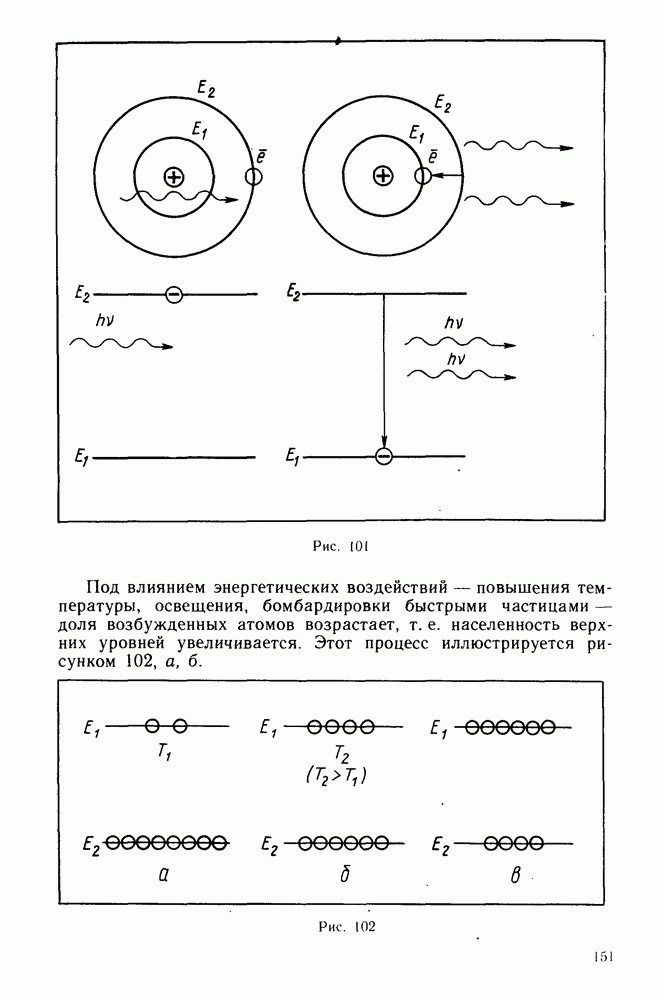
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
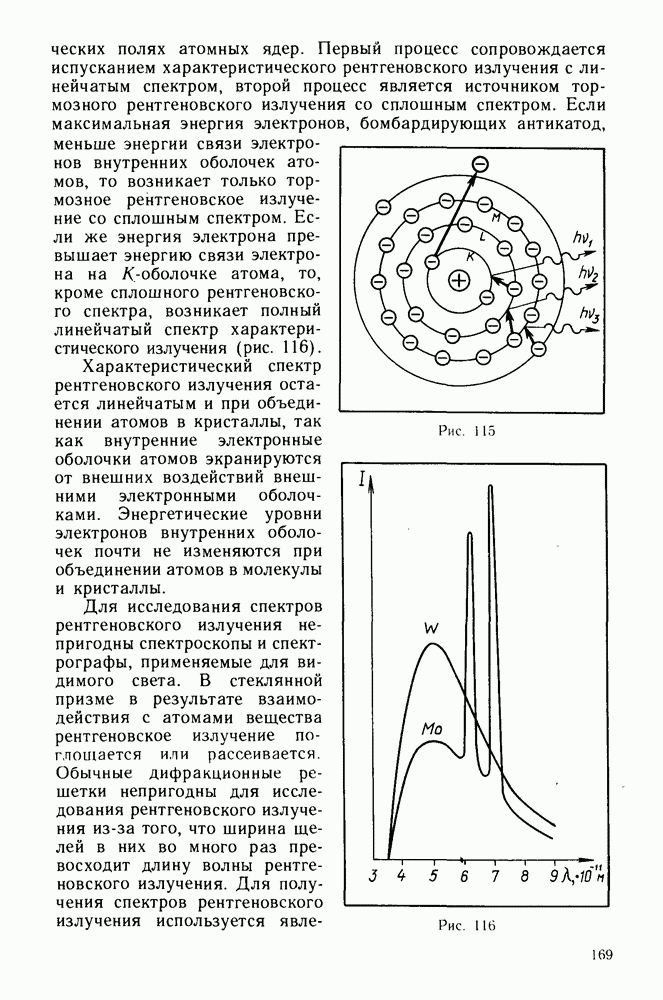
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
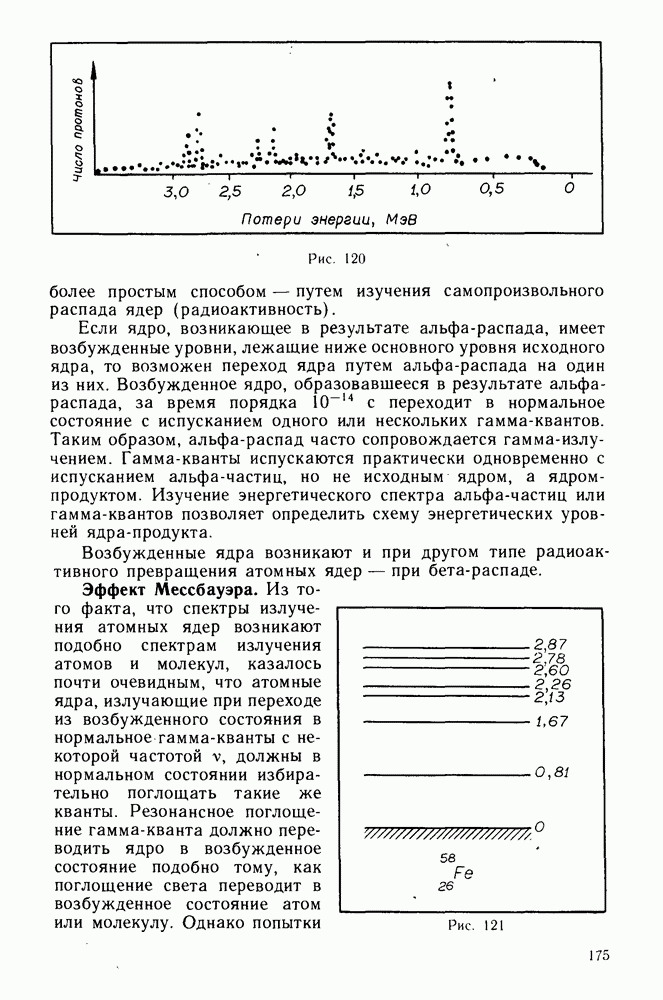
- Эффект Мессбауэра.
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
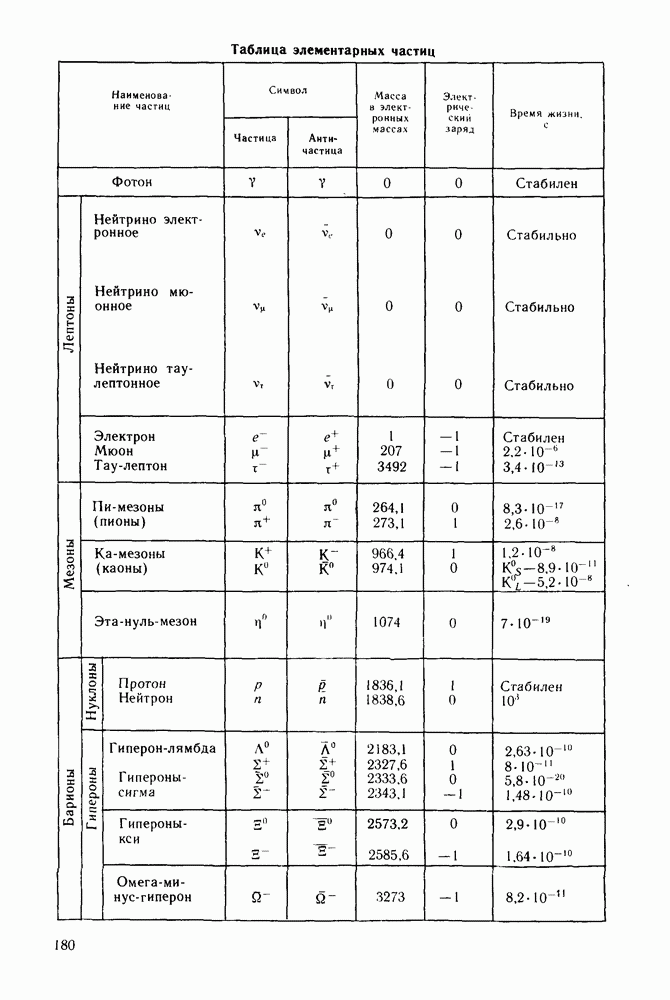
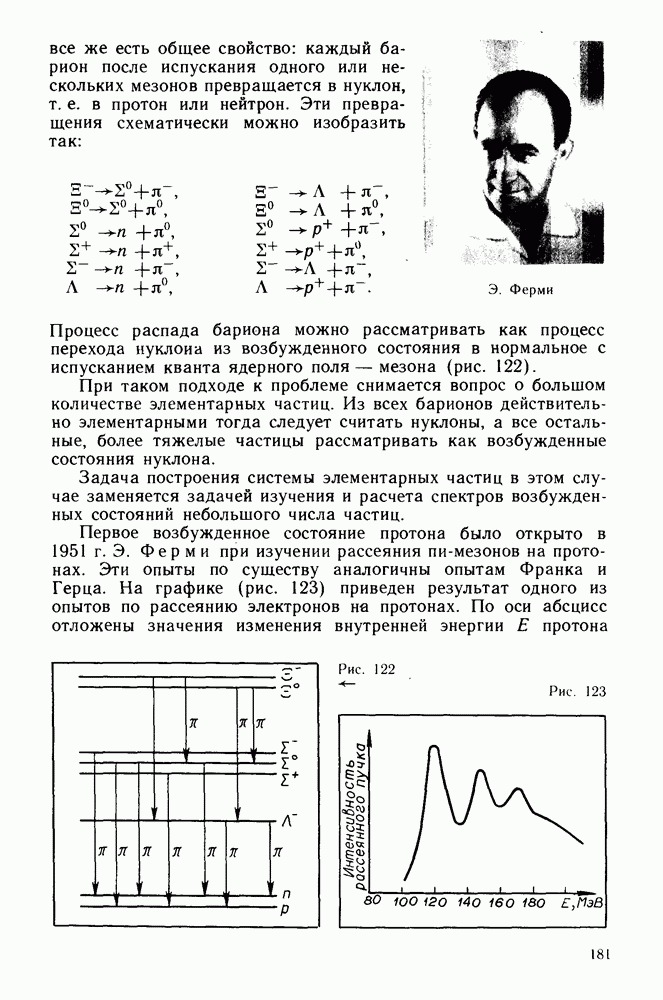
- Спектры элементарных частиц.
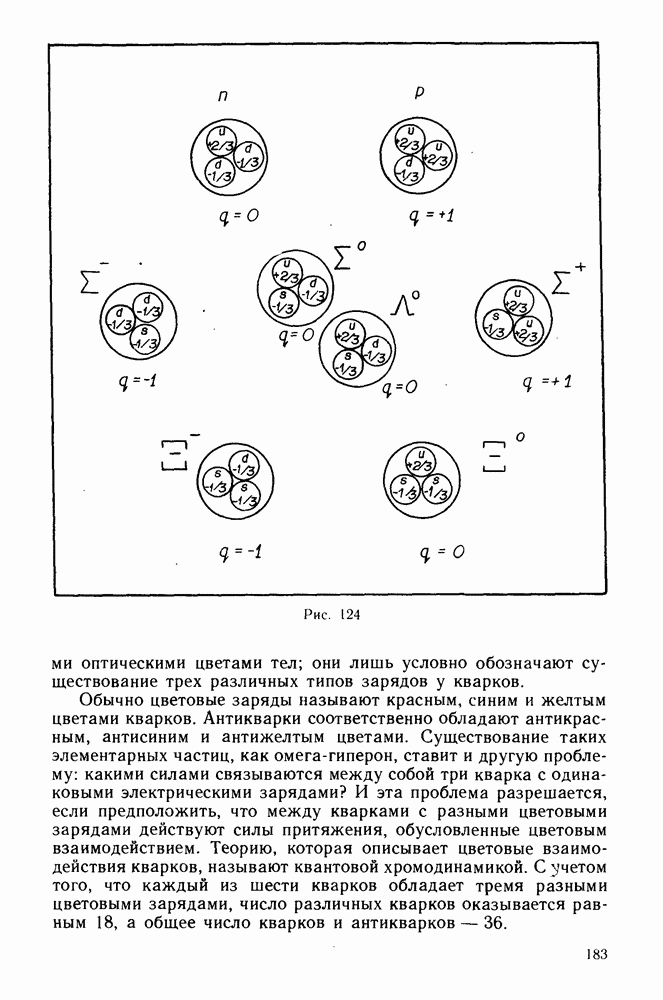
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ