| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
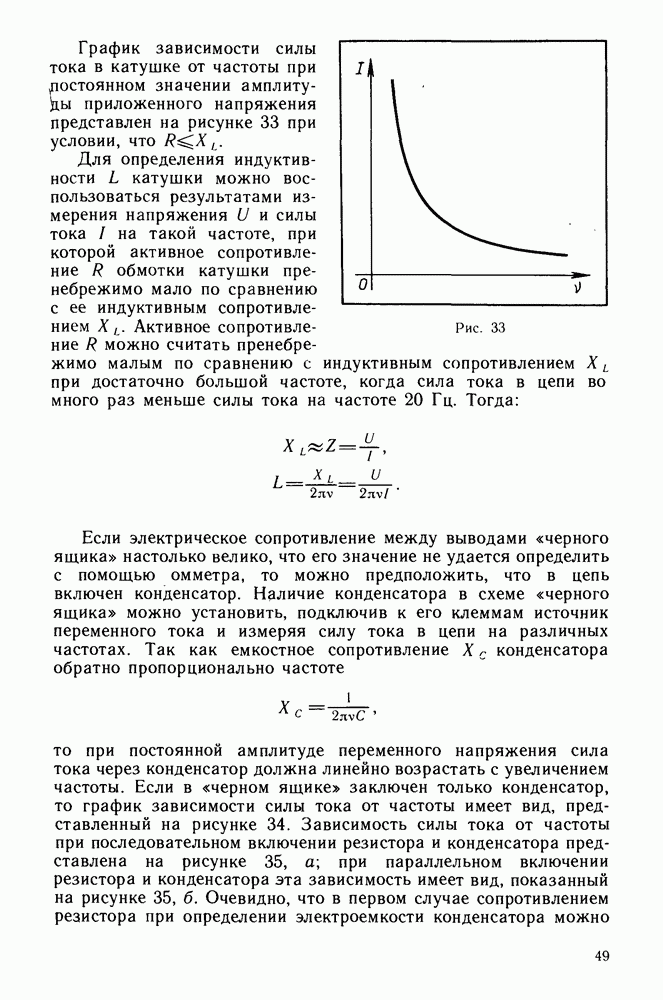
Волновые свойства электрона.
Полному отказу от волновых представлений о природе света препятствуют не только сила традиции, удобство волновой теории и трудность современной квантовой теории. Есть и более серьезная причина. В 1924 г. французский физик Луи де Бройль впервые высказал идею, согласно которой одновременное проявление корпускулярных и волновых свойств присуще не только свету, но и любому другому материальному объекту. Эта идея была лишь теоретической гипотезой, так как в то время наука не располагала экспериментальными фактами, которые бы подтверждали существование волновых свойств у элементарных частиц и атомов. В этом заключалось существенное отличие гипотезы де Бройля о волновых свойствах частиц от гипотезы Эйнштейна о существовании фотонов света, выдвинутой им после открытия явления фотоэффекта.
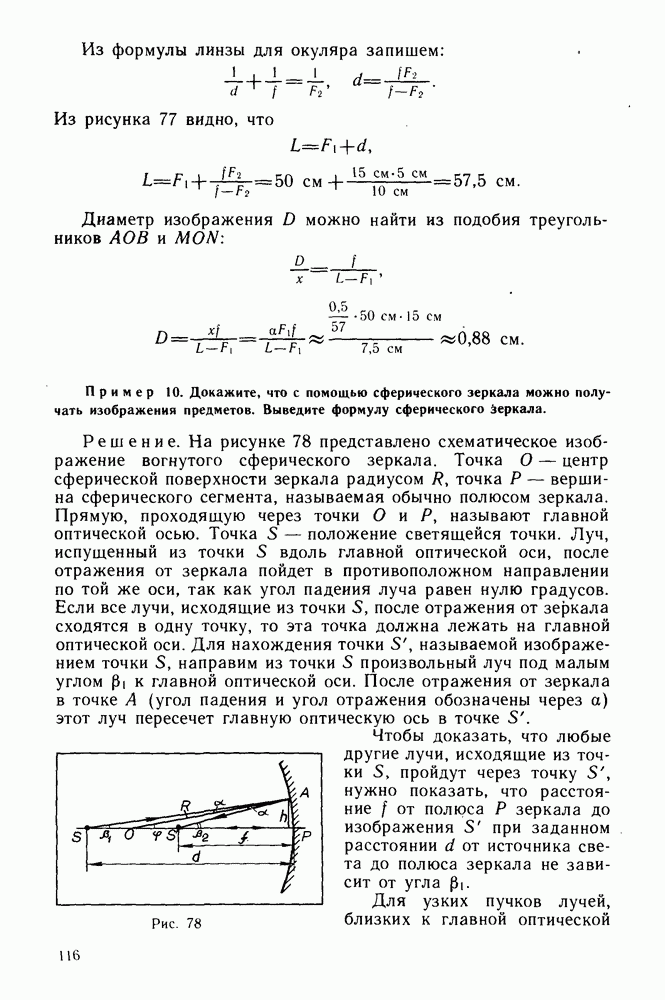
Гипотеза де Бройля о существовании волн материи была детально разработана, и полученные из нее следствия могли быть подвергнуты Экспериментальной проверке. Основное предположение де Бройля заключалось в том, что любой материальный объект обладает волновыми свойствами и длина волны связана с его импульсом таким же соотношением, каким связаны между собой длина световой волны и импульс фотона. Найдем выражение, связывающее импульс фотона  с длиной волны света К. Импульс фотона определяется формулой:
с длиной волны света К. Импульс фотона определяется формулой:


Рис. 125

Рис. 126
Из уравнения

можно определить массу фотона:

Учитывая это, можно формулу (27.1) преобразовать так:

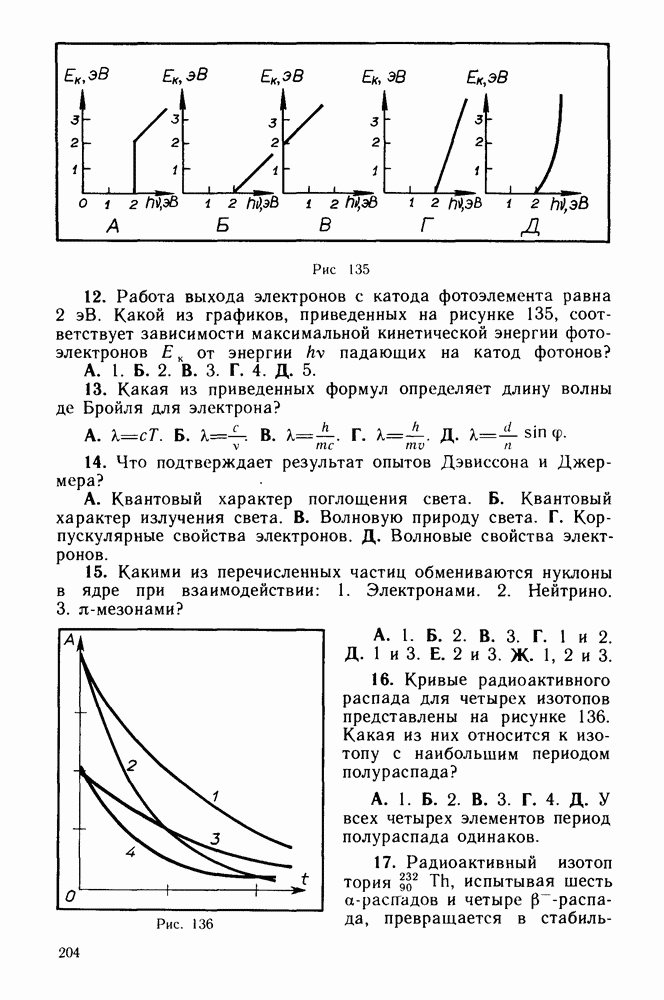
Отсюда получаем для длины световой волны формулу:

Если это выражение справедливо, как предположил де Бройль, для любого материального объекта, то длина волны тела массой  движущегося со скоростью
движущегося со скоростью  может быть найдена так:
может быть найдена так:

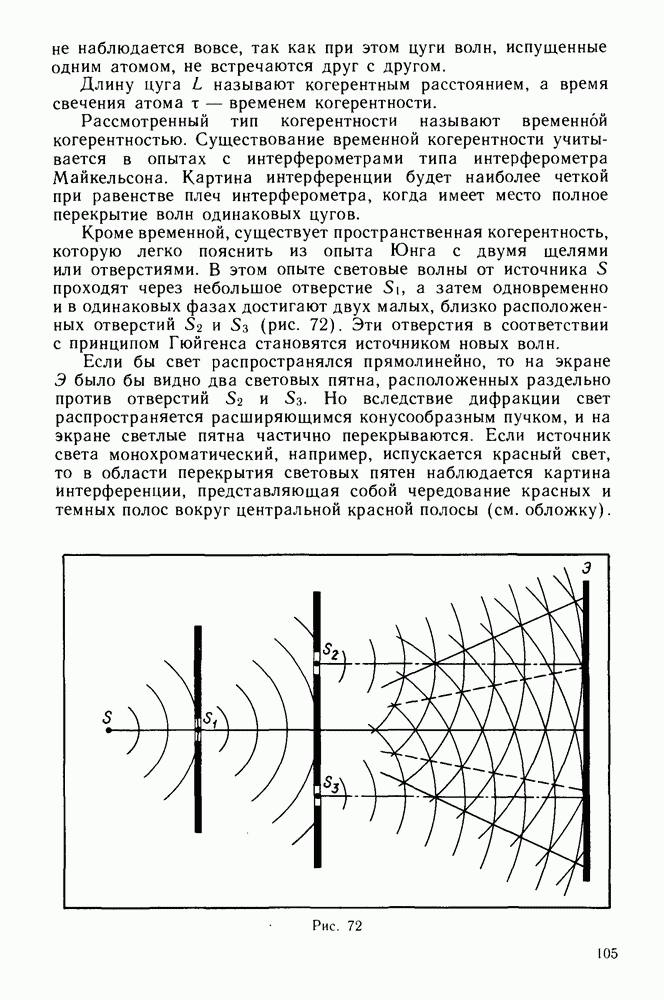
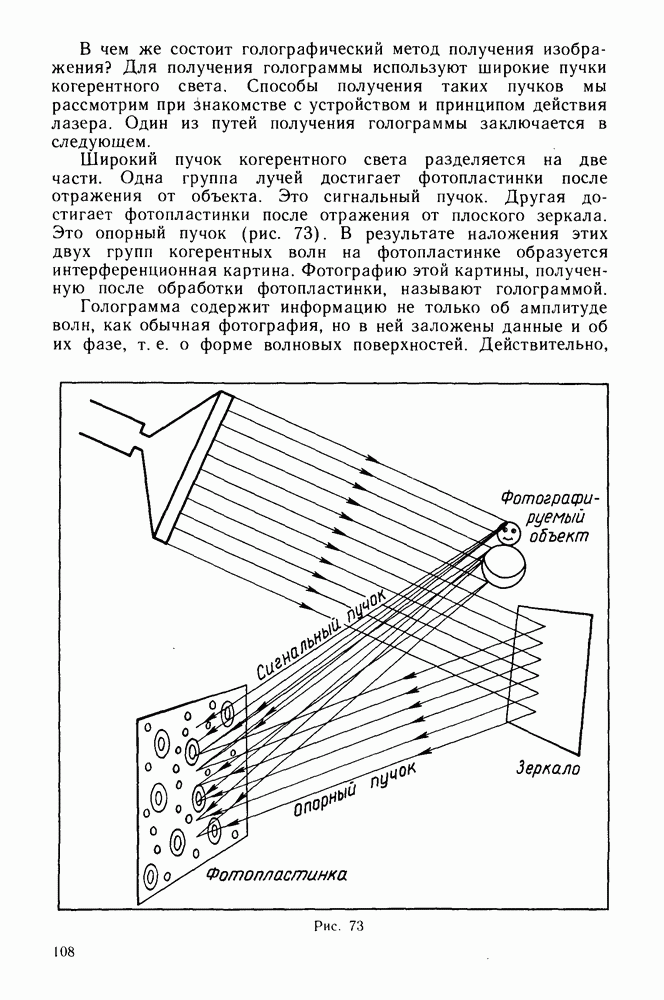
Первое экспериментальное подтверждение гипотезы де Бройля получили в 1927 г. независимо друг от друга американские физики К. Д. Дэвиссон и  . Джермер и английский физик Д. П. Томсон. Дэвиссон и Джермер изучали отражение электронных пучков от поверхности кристаллов на установке, схема которой изображена на рисунке 125. Перемещая приемник электронов по дуге окружности, центр которой находится в месте падения электронного пучка на кристалл, они обнаружили сложную зависимость интенсивности отраженного пучка от угла (рис. 126). Отражение излучения только под определенными углами означает, что это излучение представляет собой волновой процесс и его избирательное отражение есть результат дифракции на атомах кристаллической решетки. По известным значениям постоянной кристаллической решетки
. Джермер и английский физик Д. П. Томсон. Дэвиссон и Джермер изучали отражение электронных пучков от поверхности кристаллов на установке, схема которой изображена на рисунке 125. Перемещая приемник электронов по дуге окружности, центр которой находится в месте падения электронного пучка на кристалл, они обнаружили сложную зависимость интенсивности отраженного пучка от угла (рис. 126). Отражение излучения только под определенными углами означает, что это излучение представляет собой волновой процесс и его избирательное отражение есть результат дифракции на атомах кристаллической решетки. По известным значениям постоянной кристаллической решетки  и угла
и угла  дифракционного максимума можно по уравнению Вульфа — Брэггов
дифракционного максимума можно по уравнению Вульфа — Брэггов

вычислить длину волны дифрагировавшего излучения и сопоставить ее с дебройлевской длиной волны электронов  вычисленной по известному ускоряющему напряжению
вычисленной по известному ускоряющему напряжению 

Вычисленная таким образом из опытных данных длина волны совпала по значению с дебройлевской длиной волны.
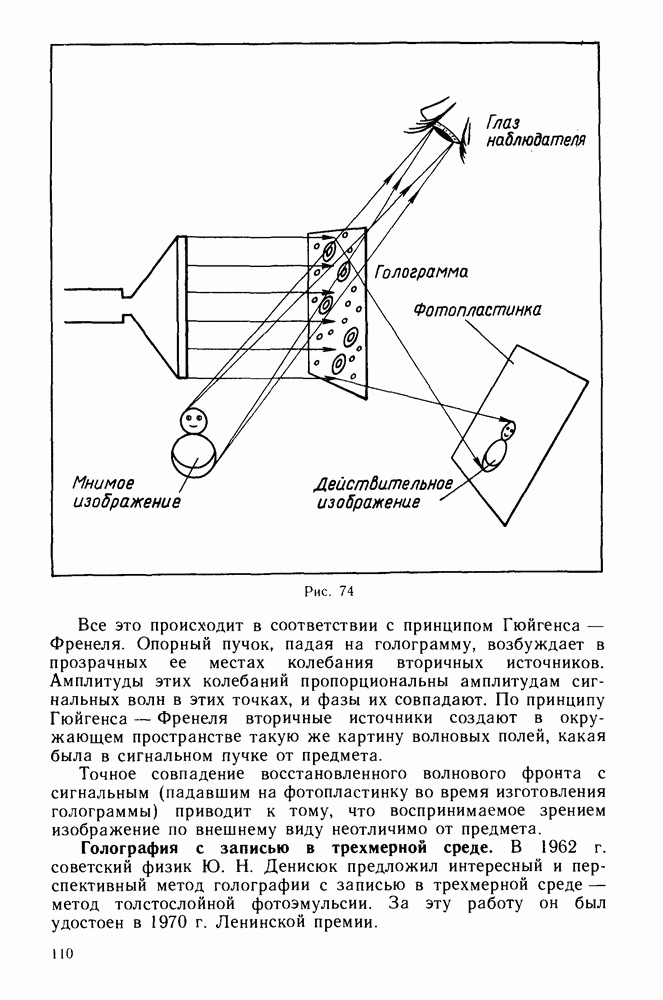
Интересны результаты другого опыта, в котором пучок электронов направлялся на монокристалл, но расположение приемника и кристалла не изменялось. При изменении ускоряющего напряжения, т. е. скорости электронов, зависимость силы тока через гальванометр от ускоряющего напряжения имела вид, представленный на рисунке 127. Электронный пучок испытывал наиболее эффективное отражение при скоростях частиц, удовлетворяющих условию дифракционного максимума.
Последующие эксперименты полностью подтвердили правильность гипотезы де Бройля и возможность использования уравнения (27.6) для расчета длины волны, связанной с любым материальным объектом. Обнаружена дифракция не только элементарных частиц (электрон, протон, нейтрон), но и атомов.
Выполнив расчеты длины дебройлевской волны для различных материальных объектов, можно понять, почему мы не замечаем в повседневной жизни волновых свойств окружающих нас тел. Их длины волн оказываются столь малыми, что проявление волновых свойств невозможно обнаружить. Так, для пули массой 10 г, движущейся со скоростью 660 м/с, длина дебройлевской волны равна:

Дифракция электронов на решетке кристалла никеля становится заметной лишь при таких скоростях движения электронов,

Рис. 127

Рис. 128
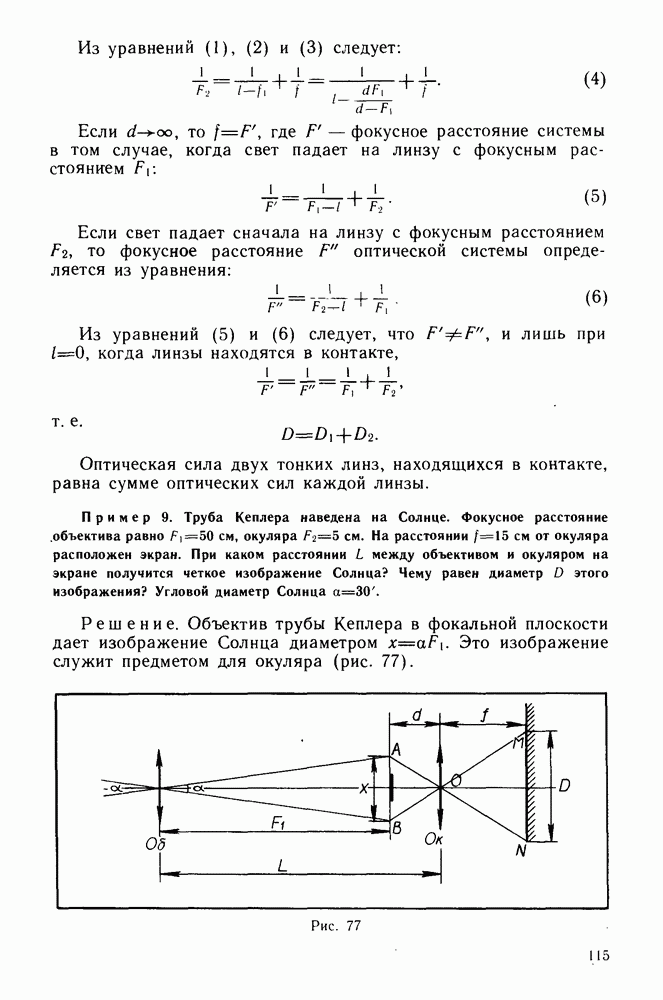
при которых их дебройлевская длина волны становится сравнимой с постоянной решетки. При этом условии дифракционная картина, получаемая от электронного пучка, становится подобной картине дифракции пучка рентгеновских лучей с такой же длиной волны. На рисунке 128 представлены фотографии дифракционных картин, наблюдающихся при прохождении пучка света (а) и пучка электронов (б) у края экрана.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
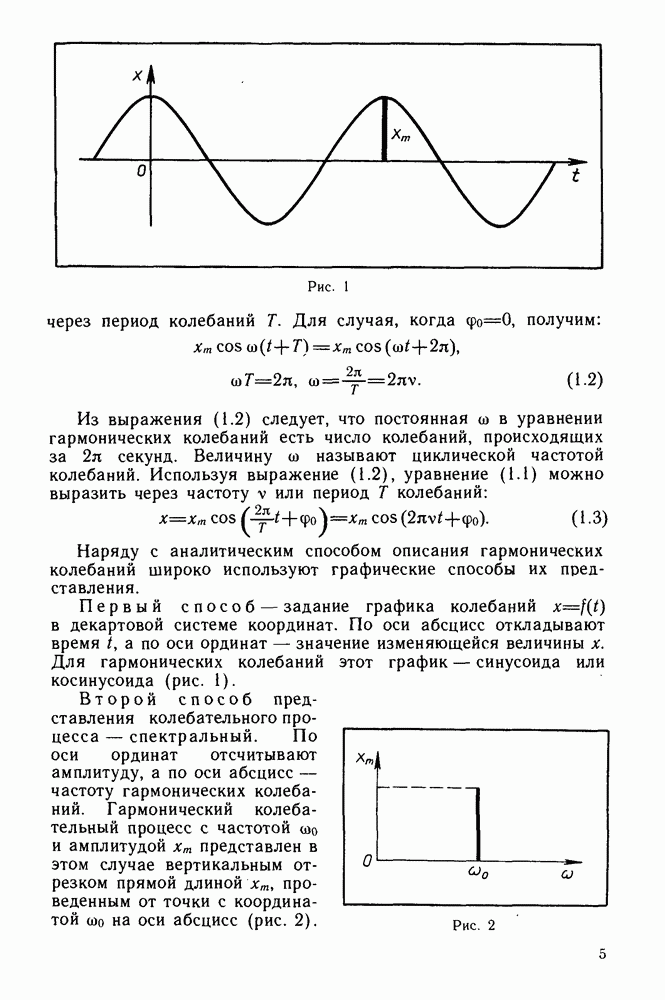
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
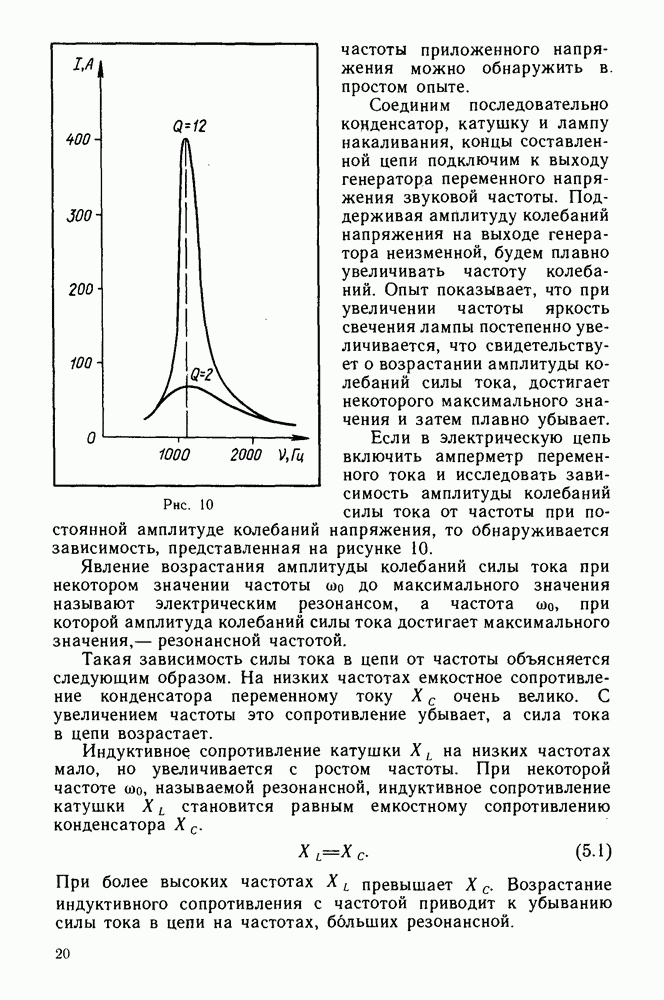
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- Принцип Ферма.
- Закон отражения света.
- Закон преломления.
- Линзы.
- Аберрация линз.
- Оптические приборы.
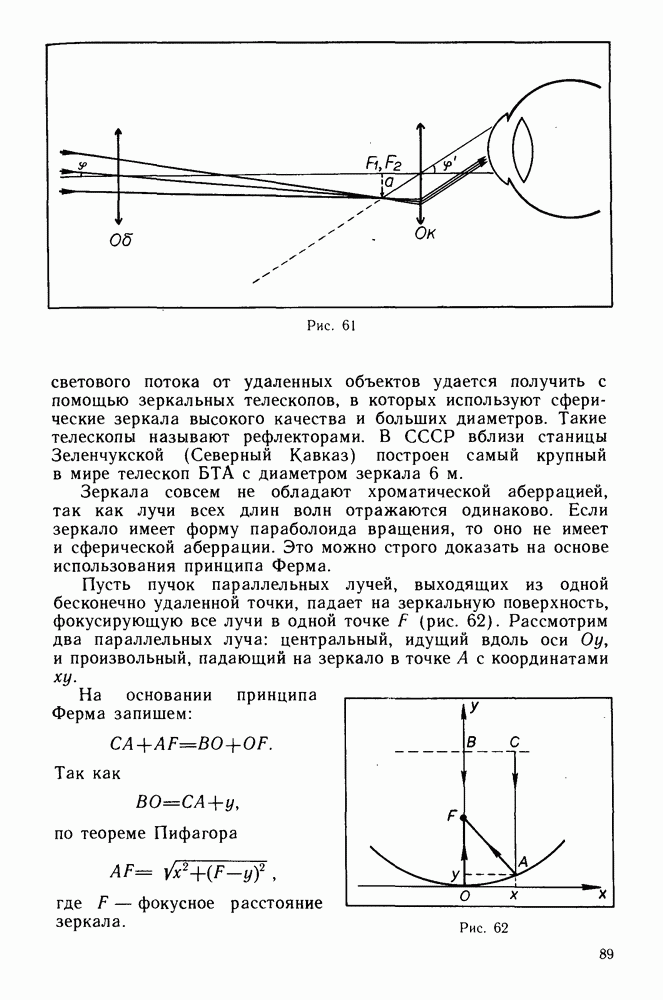
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
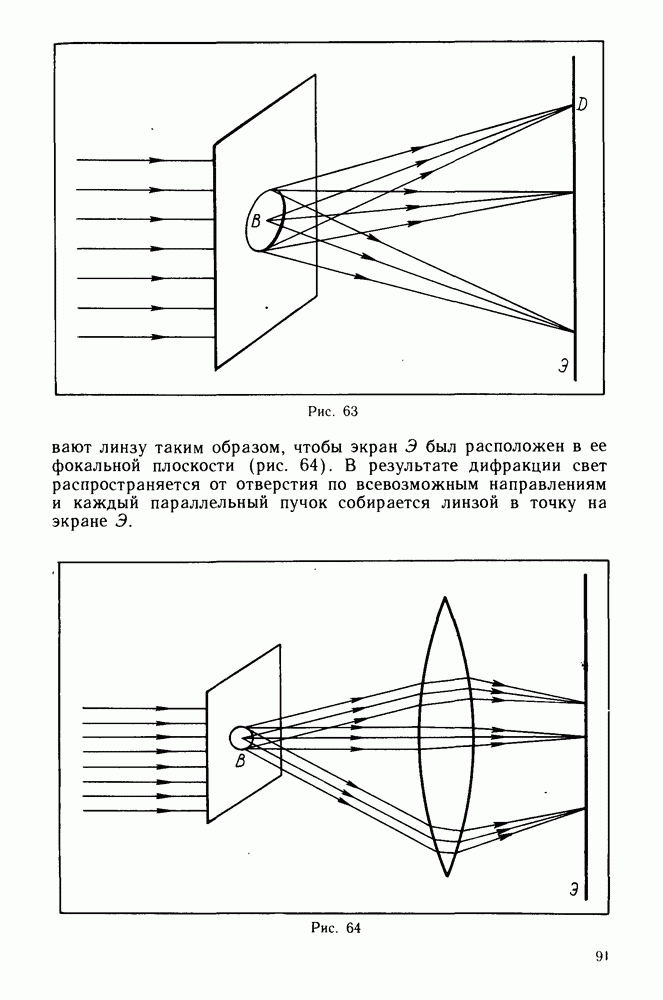
- Дифракция от круглого отверстия.
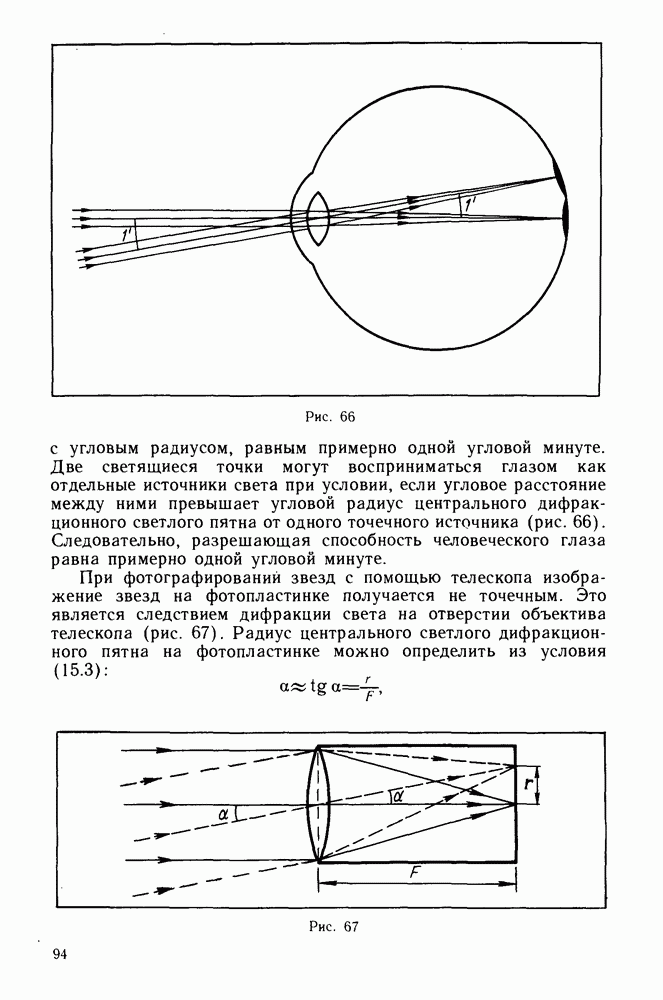
- Дифракция и разрешающая способность оптических приборов.
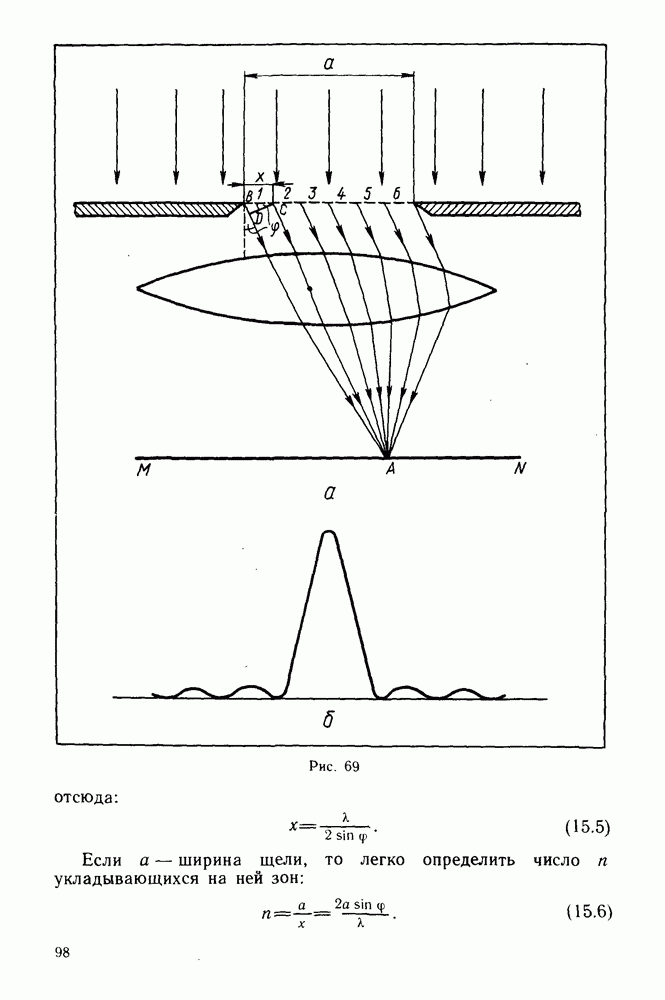
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
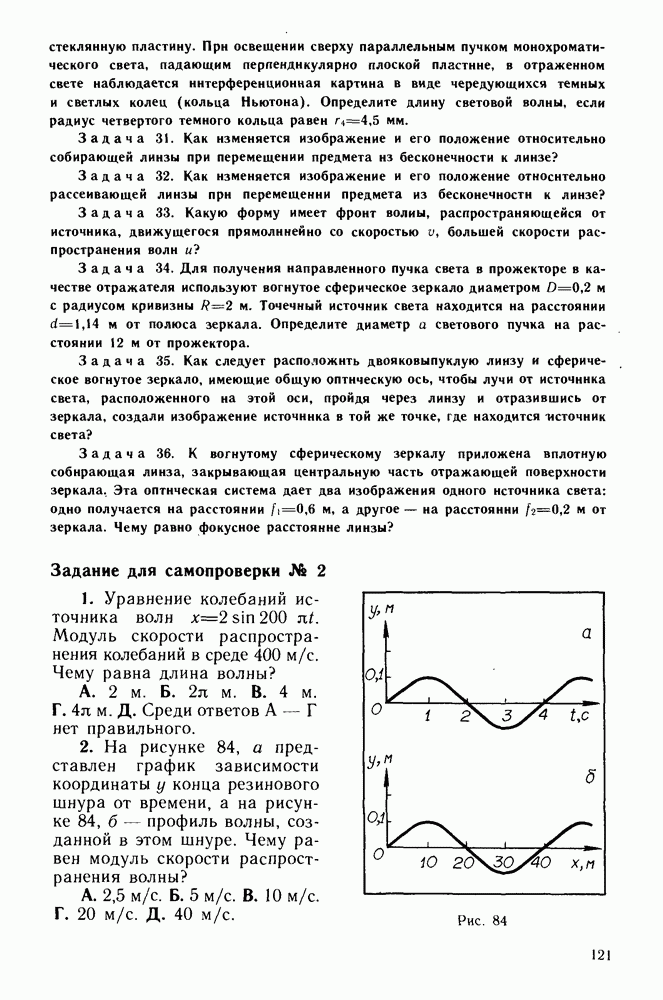
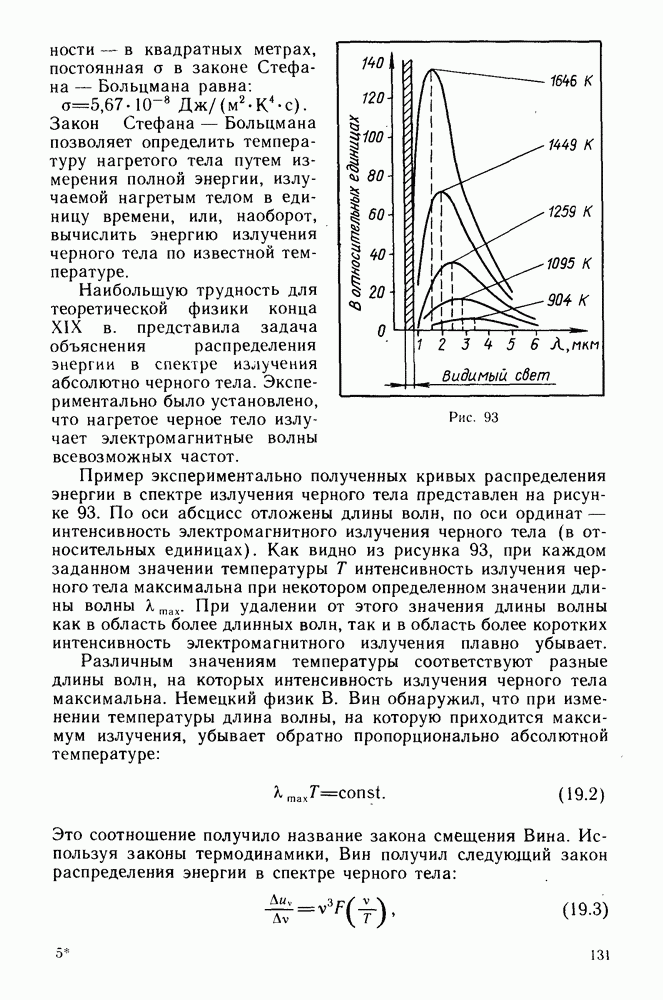
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
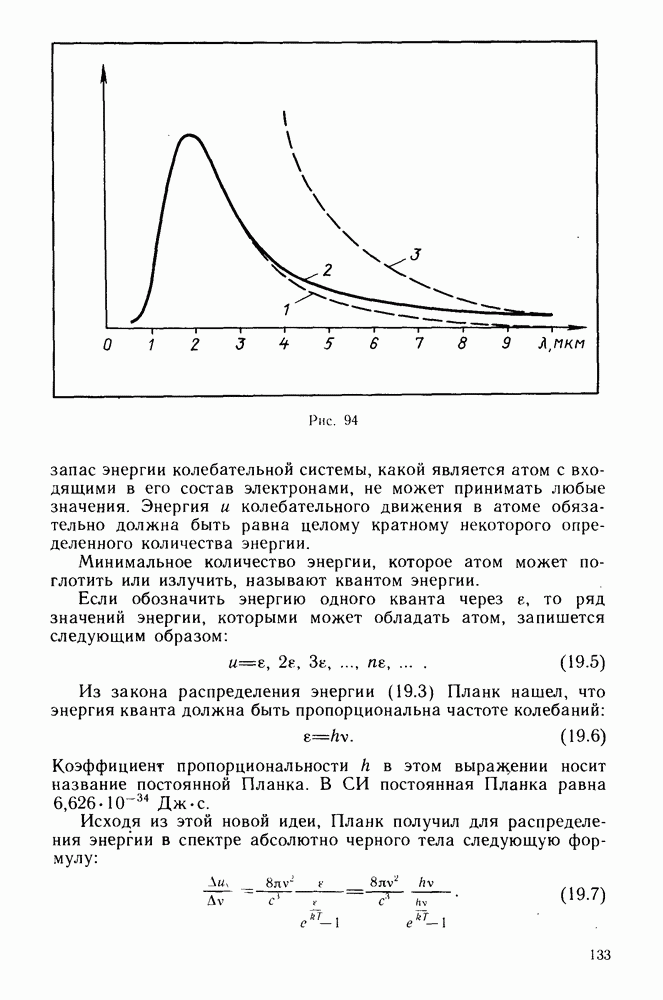
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
- Схема энергетических уровней.
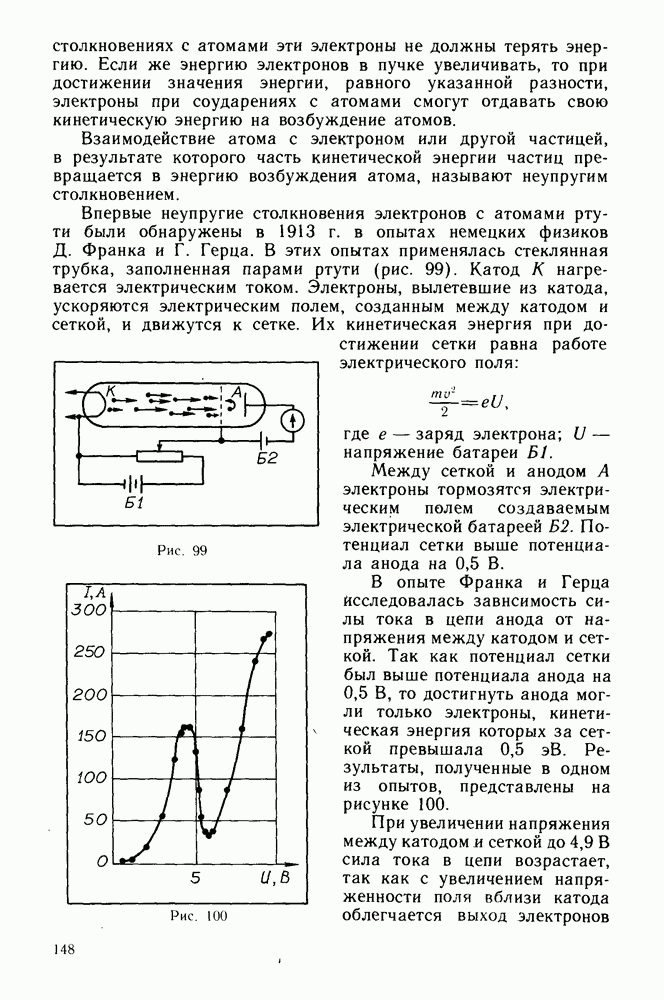
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
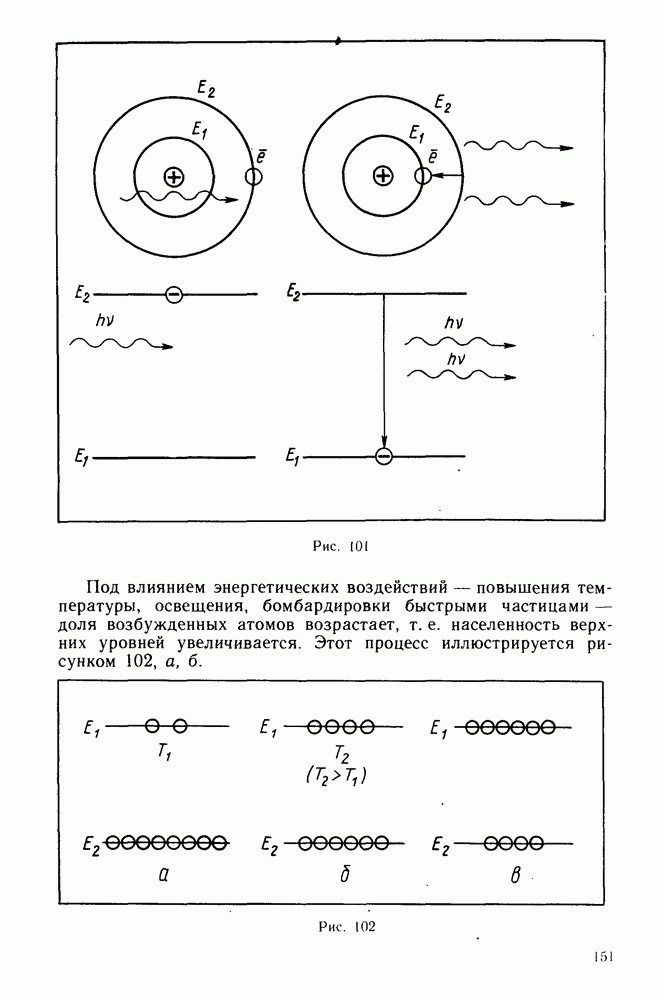
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
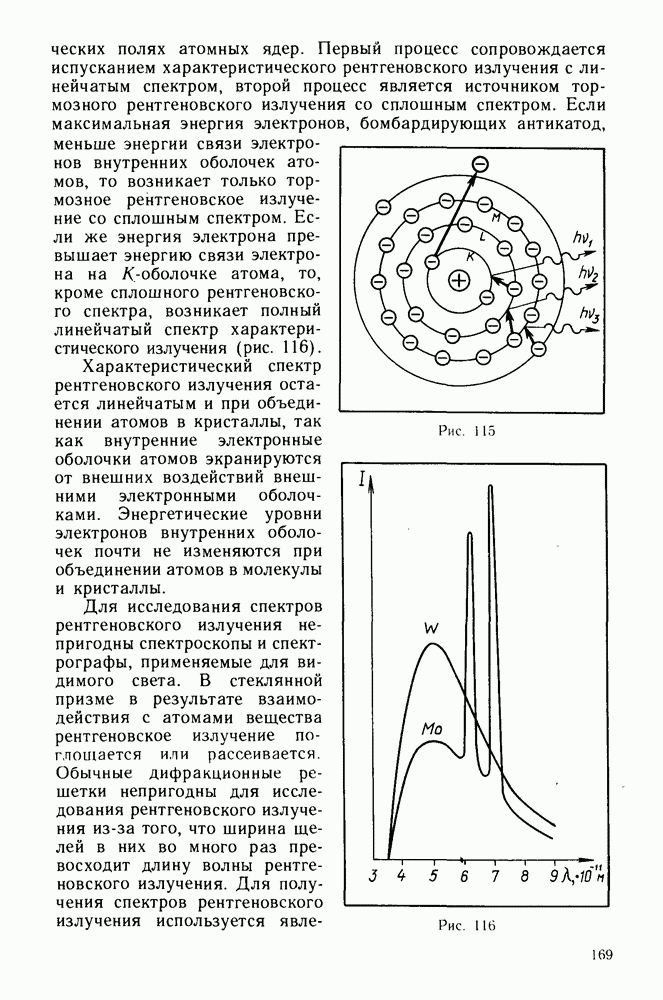
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
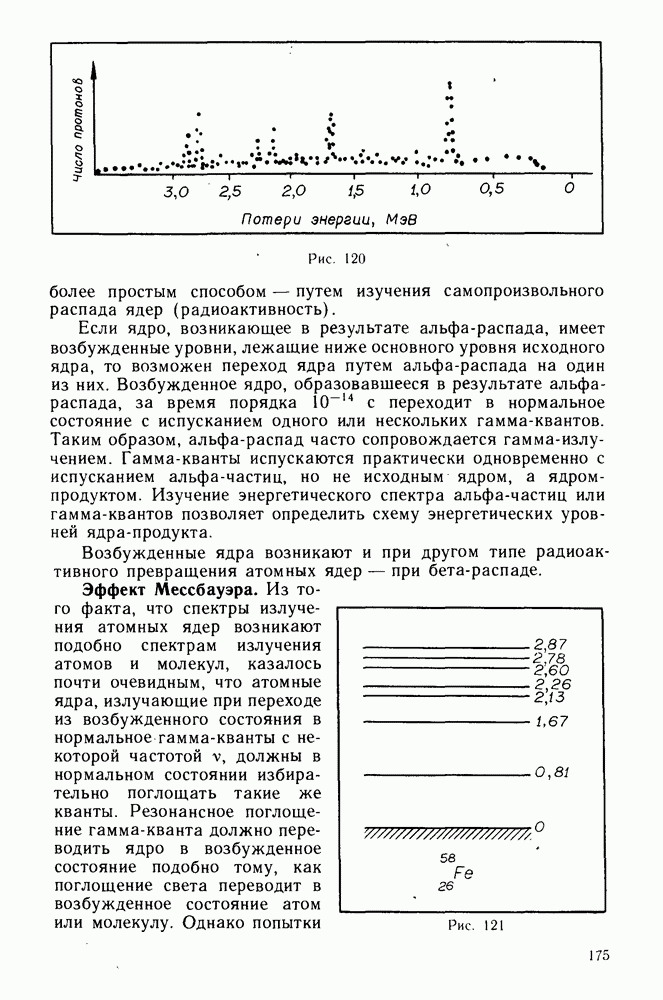
- Эффект Мессбауэра.
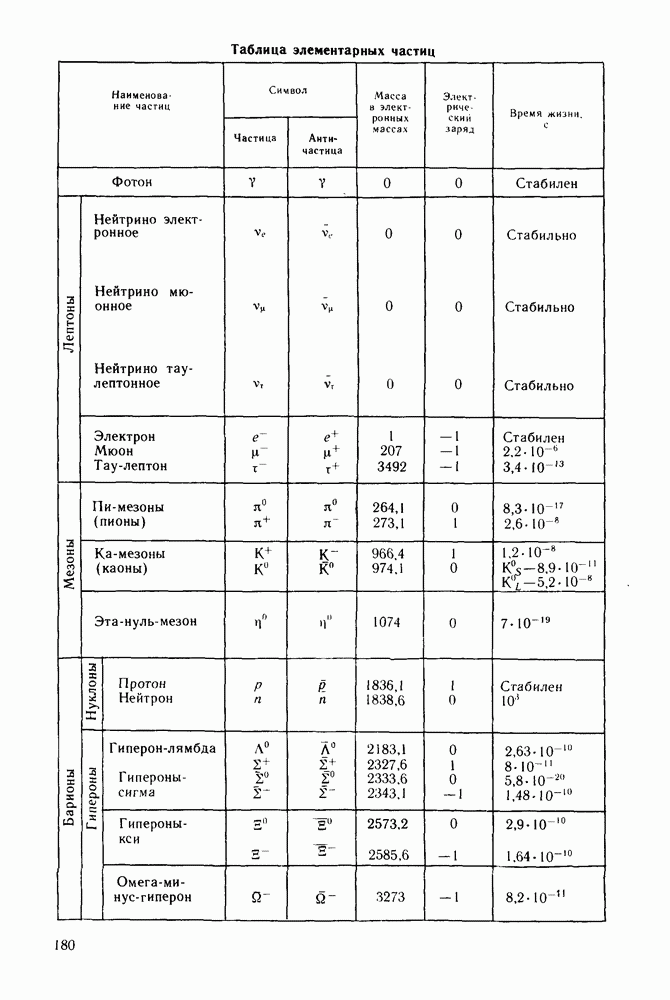
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
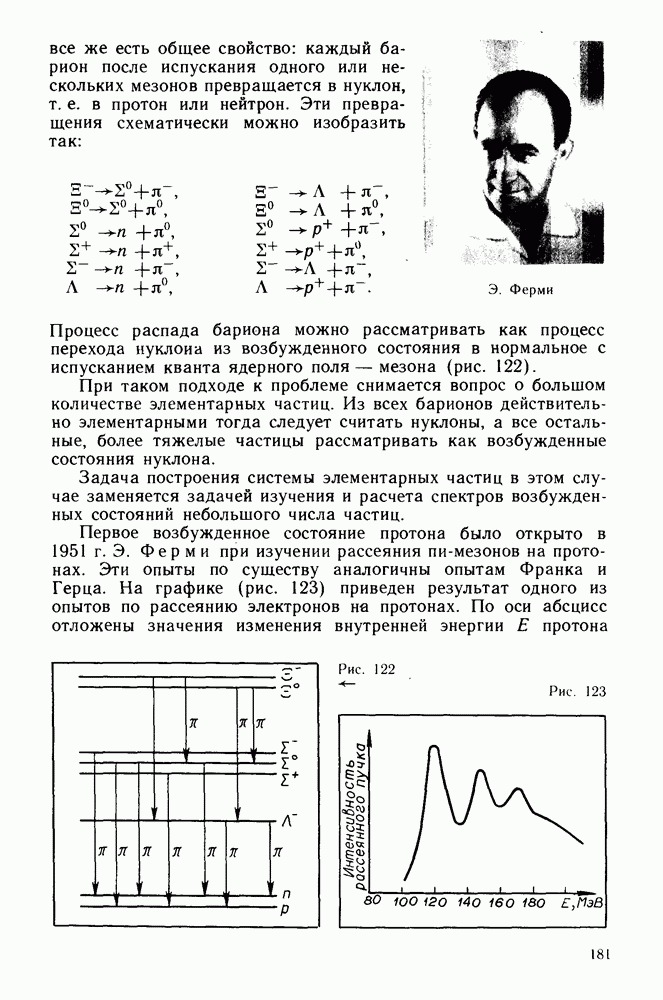
- Спектры элементарных частиц.
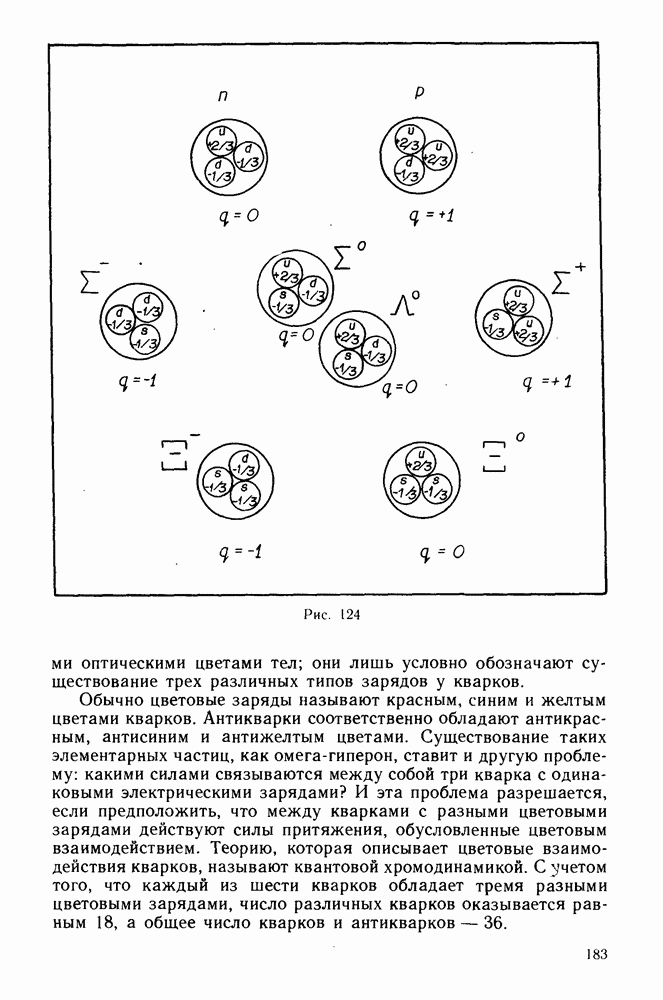
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
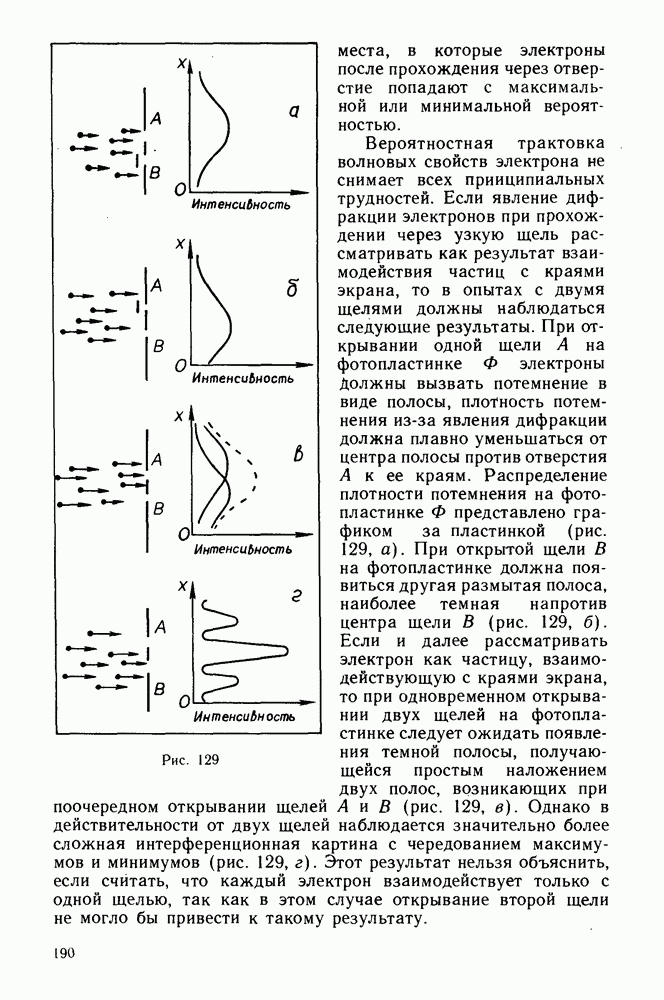
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ