| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Резонанс при последовательном включении элементов цепи.
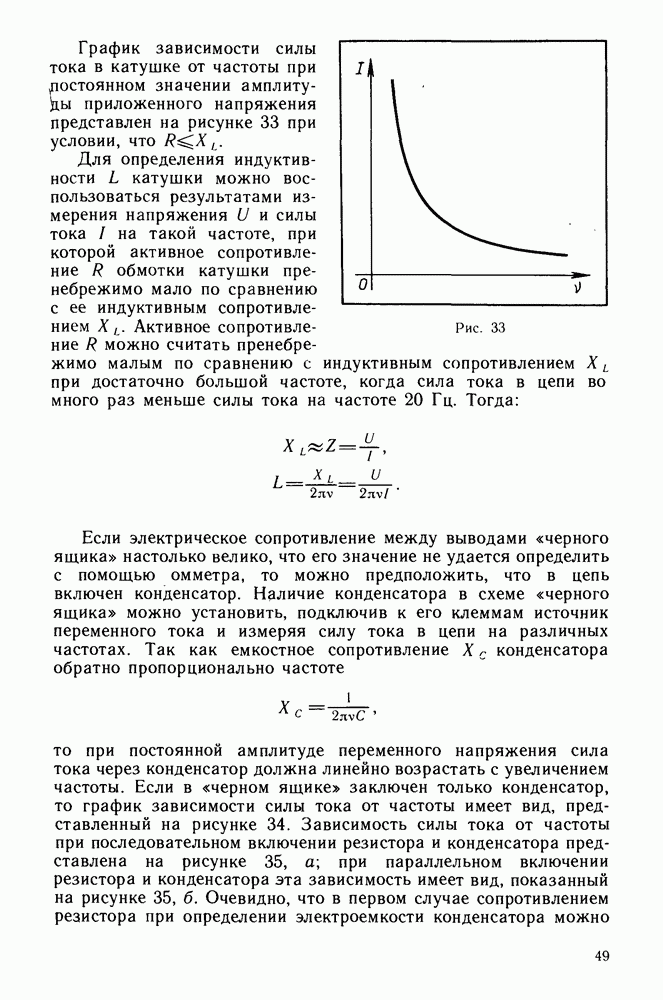
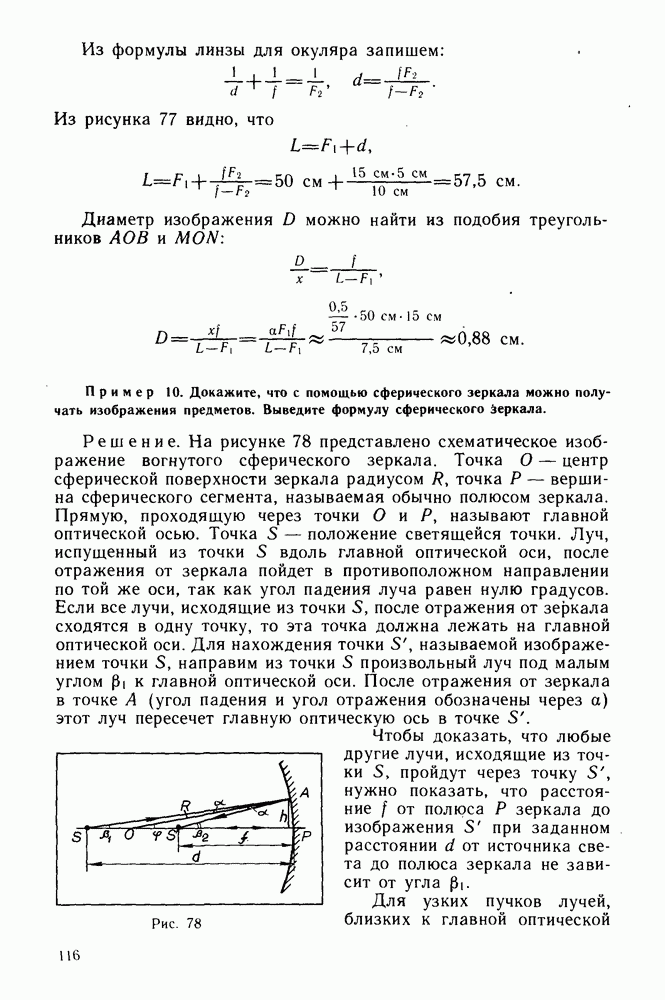
Полное сопротивление электрической цепи переменному току зависит не только от параметров цепи, но и от частоты переменного тока. Эта зависимость, выражаемая законом Ома (4.7) при последовательном включении элементов цепи переменного тока, имеет довольно сложный вид. Основные особенности зависимости полного сопротивления цепи из последовательно включенных конденсатора, катушки и лампы накаливания от

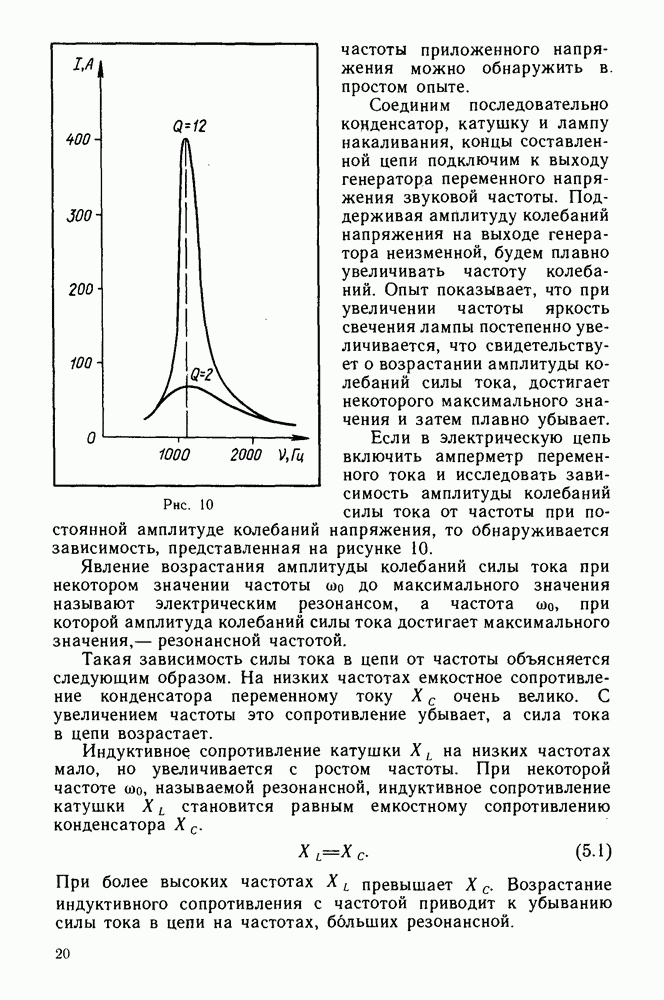
Рис. 10
частоты приложенного напряжения можно обнаружить в. простом опыте.
Соединим последовательно конденсатор, катушку и лампу накаливания, концы составленной цепи подключим к выходу генератора переменного напряжения звуковой частоты. Поддерживая амплитуду колебаний напряжения на выходе генератора неизменной, будем плавно увеличивать частоту колебаний. Опыт показывает, что при увеличении частоты яркость свечения лампы постепенно увеличивается, что свидетельствует о возрастании амплитуды колебаний силы тока, достигает некоторого максимального значения и затем плавно убывает.
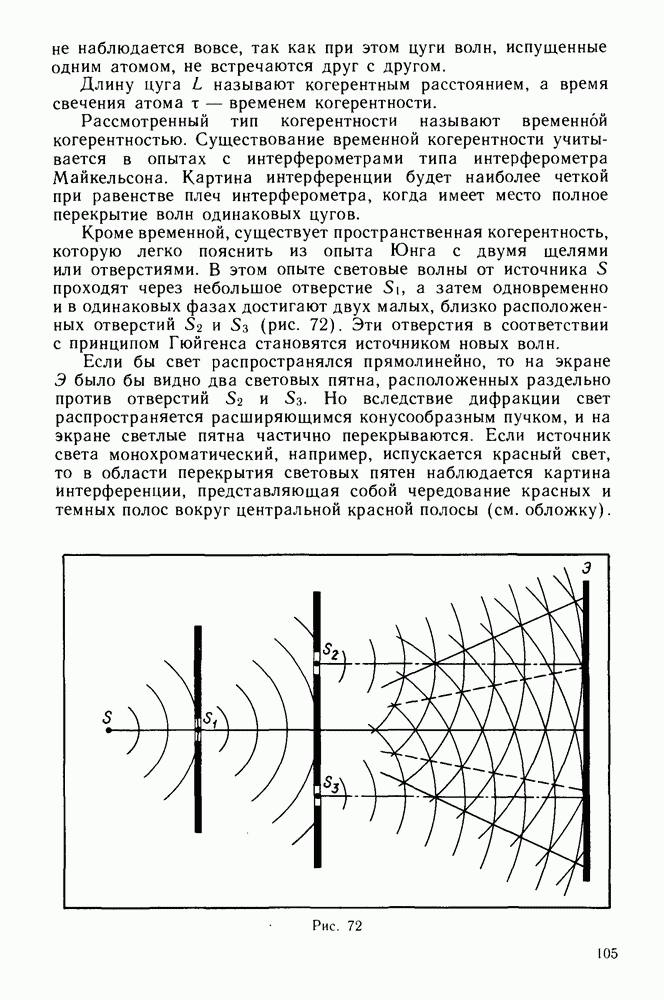
Если в электрическую цепь включить амперметр переменного тока и исследовать зависимость амплитуды колебаний силы тока от частоты при постоянной амплитуде колебаний напряжения, то обнаруживается зависимость, представленная на рисунке 10.
Явление возрастания амплитуды колебаний силы тока при некотором значении частоты  до максимального значения называют электрическим резонансом, а частота
до максимального значения называют электрическим резонансом, а частота  при которой амплитуда колебаний силы тока достигает максимального значения, — резонансной частотой.
при которой амплитуда колебаний силы тока достигает максимального значения, — резонансной частотой.
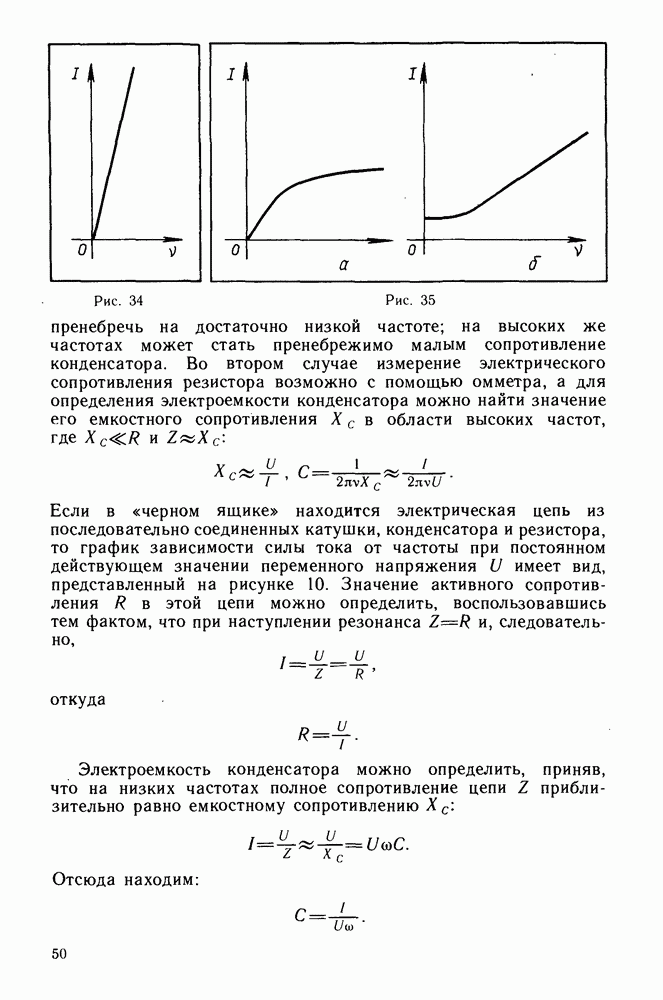
Такая зависимость силы тока в цепи от частоты объясняется следующим образом. На низких частотах емкостное сопротивление конденсатора переменному току X с очень велико. С увеличением частоты это сопротивление убывает, а сила тока в цепи возрастает.
Индуктивно сопротивление катушки  на низких частотах мало, но увеличивается с ростом частоты. При некоторой частоте
на низких частотах мало, но увеличивается с ростом частоты. При некоторой частоте  называемой резонансной, индуктивное сопротивление катушки
называемой резонансной, индуктивное сопротивление катушки  становится равным емкостному сопротивлению конденсатора X с.
становится равным емкостному сопротивлению конденсатора X с.

При более высоких частотах  превышает X с. Возрастание индуктивного сопротивления с частотой приводит к убыванию силы тока в цепи на частотах, больших резонансной.
превышает X с. Возрастание индуктивного сопротивления с частотой приводит к убыванию силы тока в цепи на частотах, больших резонансной.
Так как колебания напряжения на конденсаторе и катушке индуктивности при их последовательном включении происходят в противофазе, а ток через все элементы цепи протекает один и тот же, то при равенстве индуктивного и емкостного сопротивлений напряжения на них в любой момент времени одинаковы по модулю, но имеют противоположные знаки:

Такой вид резонанса в электрической цепи переменного тока называют резонансом напряжений.
При резонансе напряжение на активном сопротивлении оказывается равным напряжению на всех трех элементах цепи:

Отсюда можно найти мгновенные и действующие значения силы тока в цепи при наступлении резонанса:

Тот же результат можно получить из выражения (4.6), используя условия резонанса (5.1). Это условие позволяет определить резонансную частоту  по известным значениям индуктивности катушки
по известным значениям индуктивности катушки  и электроемкости конденсатора С:
и электроемкости конденсатора С:

Таким образом, резонанс наступает при совпадении частоты переменного тока  с частотой свободных колебаний в контуре. Индуктивное сопротивление катушки
с частотой свободных колебаний в контуре. Индуктивное сопротивление катушки  и емкостное сопротивление конденсатора Xс при резонансе можно выразить через величины
и емкостное сопротивление конденсатора Xс при резонансе можно выразить через величины  и С:
и С:

Величину называют волновым сопротивлением колебательного контура и обозначают буквой 

Определим амплитуду колебаний напряжения на катушке индуктивности  и на конденсаторе
и на конденсаторе  при наступлении резонанса:
при наступлении резонанса:

Выражение (5.7) показывает, что при наступлении резонанса амплитуды  колебаний напряжения на катушке и конденсаторе могут превосходить амплитуду колебаний приложенного напряжения
колебаний напряжения на катушке и конденсаторе могут превосходить амплитуду колебаний приложенного напряжения  Отношение амплитуды напряжения на катушке (или на конденсаторе) при наступлении резонанса к амплитуде приложенного напряжения равно отношению волнового сопротивления контура к его активному сопротивлению:
Отношение амплитуды напряжения на катушке (или на конденсаторе) при наступлении резонанса к амплитуде приложенного напряжения равно отношению волнового сопротивления контура к его активному сопротивлению:

Это отношение называют добротностью контура и обозначают буквой 

Добротность может достигать значений порядка 100 и даже более высокого.
Зная добротность контура, можно определить амплитуду вынужденных колебаний напряжения на катушке или конденсаторе при наступлении резонанса, если известна амплитуда напряжения, подведенного к контуру.
Если, например, в колебательный контур с добротностью  включен источник переменного напряжения с амплитудой, равной 1 В, то при наступлении резонанса амплитуда вынужденных колебаний напряжения на катушке и конденсаторе достигает 100 В!
включен источник переменного напряжения с амплитудой, равной 1 В, то при наступлении резонанса амплитуда вынужденных колебаний напряжения на катушке и конденсаторе достигает 100 В!
Явление увеличения амплитуды колебаний напряжения при настройке контура в резонанс с источником колебаний широко используют в радиотехнике: в схемах радиоприемников, усилителей, генераторов высокочастотных колебаний.
С увеличением добротности контура уменьшается ширина резонансного пика. Вид резонансных кривых, полученных при различных значениях добротности контура, представлен на рисунке 10.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. КОЛЕБАНИЯ
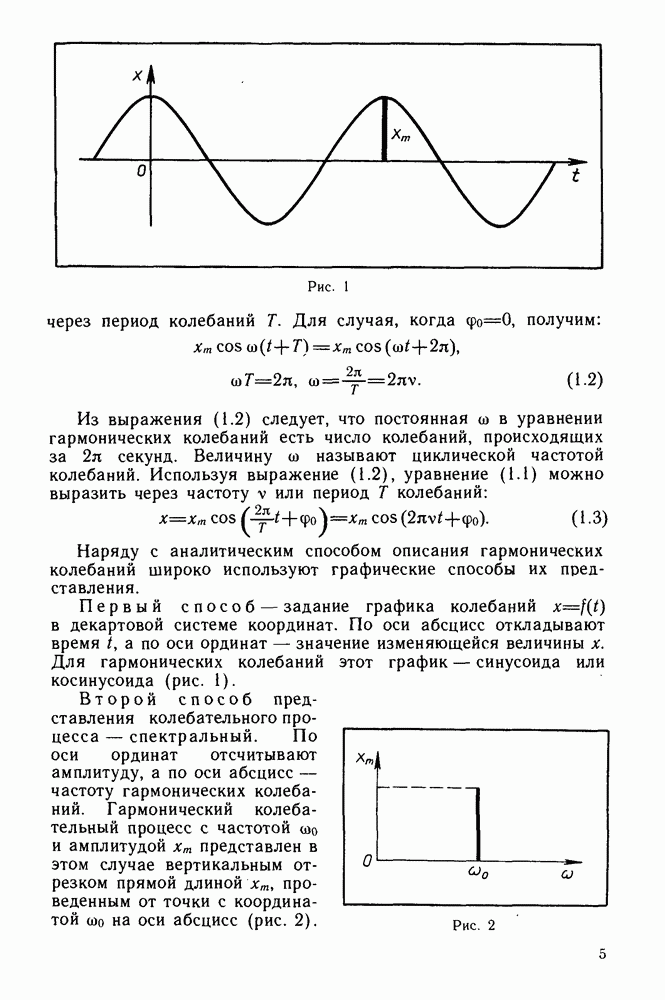
- § 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И СПОСОБЫ ИХ ОПИСАНИЯ
- § 2. ПОНЯТИЕ О ГАРМОНИЧЕСКОМ АНАЛИЗЕ ПЕРИОДИЧЕСКИХ ПРОЦЕССОВ
- Гармонический анализ.
- Анализ звука.
- § 3. ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Индуктивное сопротивление.
- Активное сопротивление.
- § 4. ЗАКОН ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- Мощность в цепи переменного тока.
- § 5. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- Резонанс при параллельном соединении элементов цепи переменного тока.
- § 6. ТРЕХФАЗНЫЙ ТОК
- Трехфазный генератор.
- Соединение фаз генератора звездой.
- Соединение нагрузки звездой.
- Соединение фазных обмоток генератора треугольником.
- Соединение нагрузки треугольником.
- Асинхронный трехфазный двигатель.
- § 7. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 8. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- 2. Измерение сопротивления конденсатора в цепи переменного тока
- 3. Измерение индуктивности катушки в цепи переменного тока
- 4. Исследование электрических схем с R-, L- и С-элементами и определение параметров этих элементов
- Глава II. ВОЛНЫ
- § 9. МЕХАНИЧЕСКИЕ ВОЛНЫ
- Зависимость скорости звука от свойств среды.
- Характеристики звука и слух человека.
- § 10. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- Изготовление граммофонных пластинок.
- Стереофоническая звукозапись.
- Магнитная запись звука.
- § 11. ЭФФЕКТ ДОПЛЕРА
- § 12. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- Излучение электромагнитных волн электрическим зарядом, совершающим гармонические колебания.
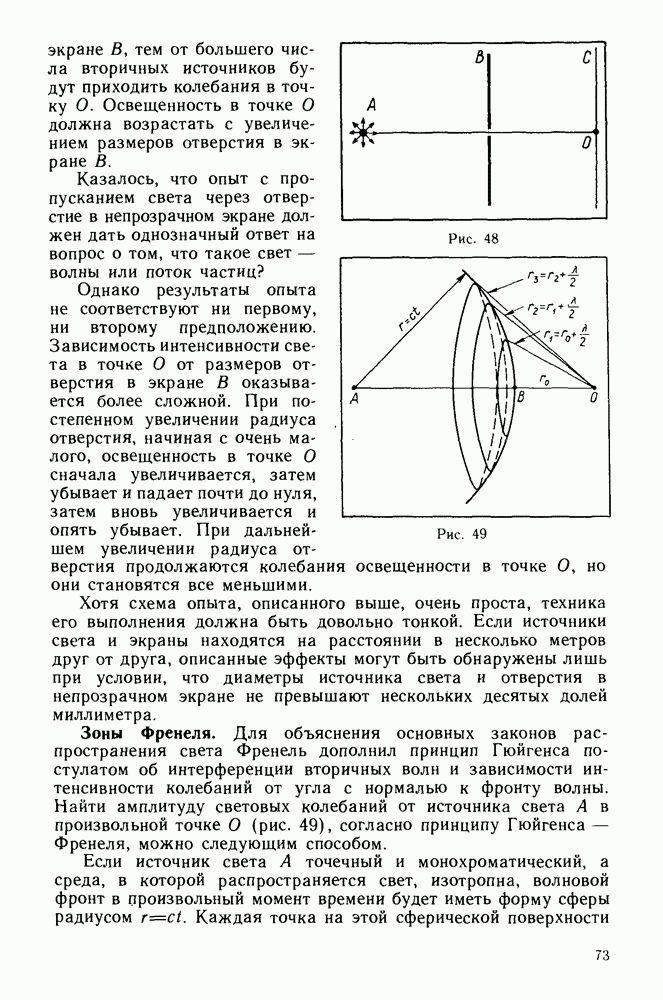
- § 13. ЗОНЫ ФРЕНЕЛЯ
- Зоны Френеля.
- Объяснение свойства прямолинейности распространения света.
- Пластинка зон.
- Дифракция от круглого экрана.
- § 14. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
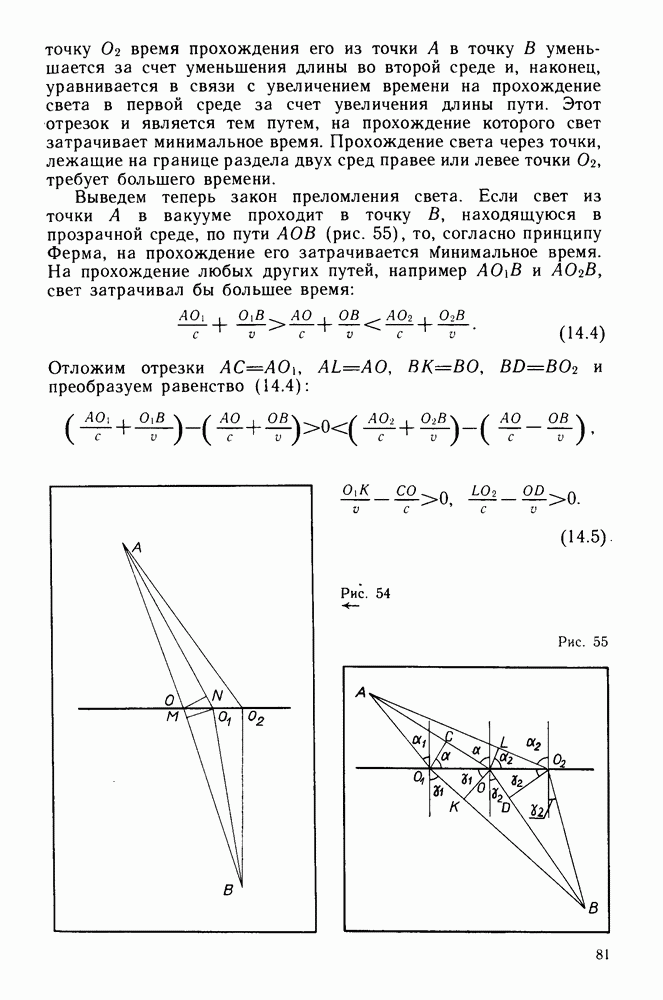
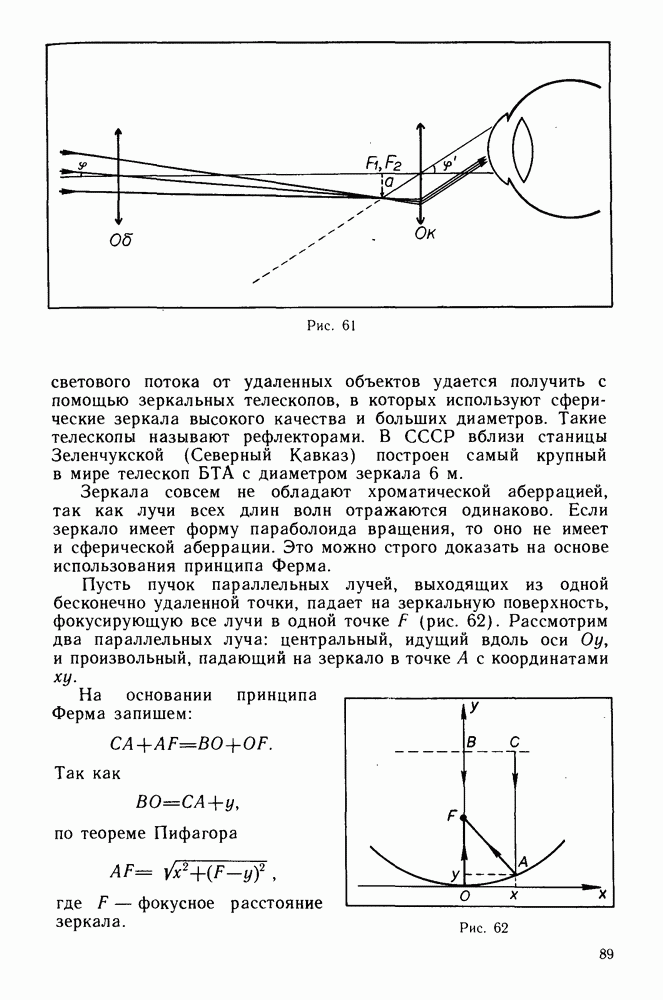
- Принцип Ферма.
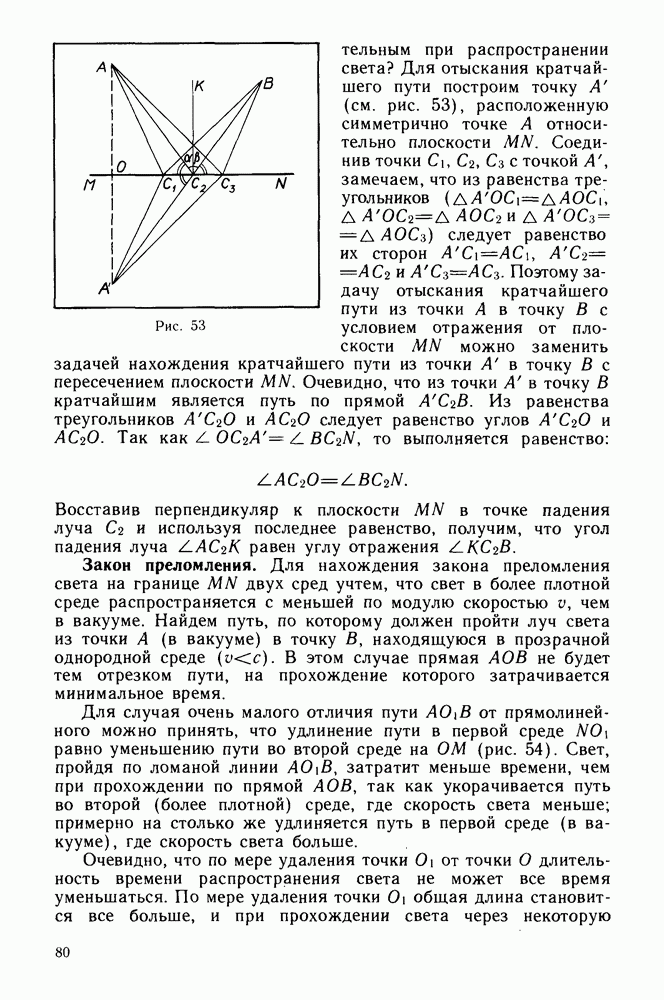
- Закон отражения света.
- Закон преломления.
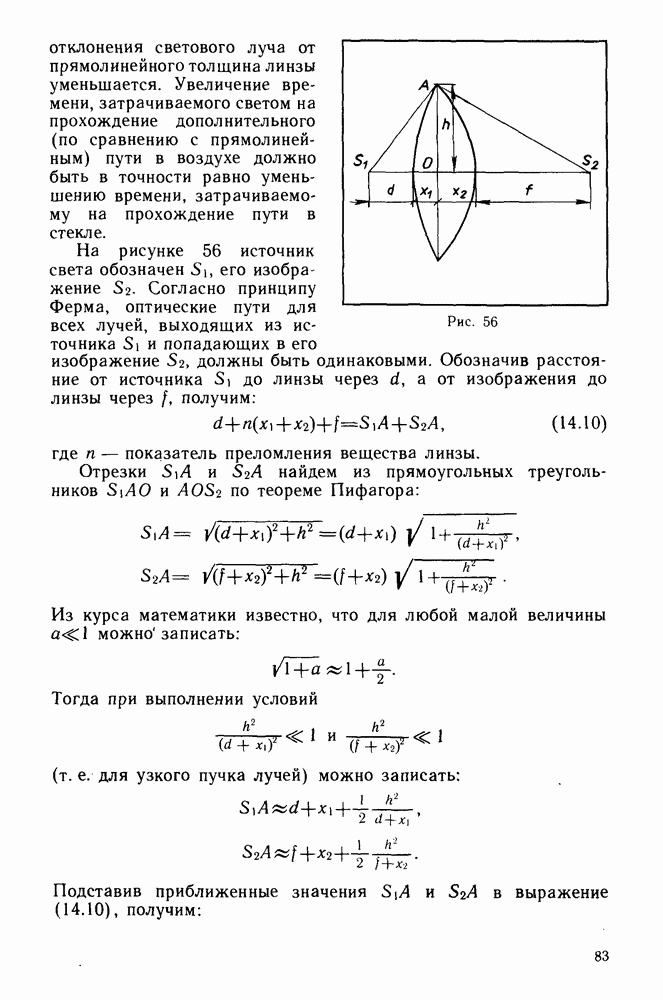
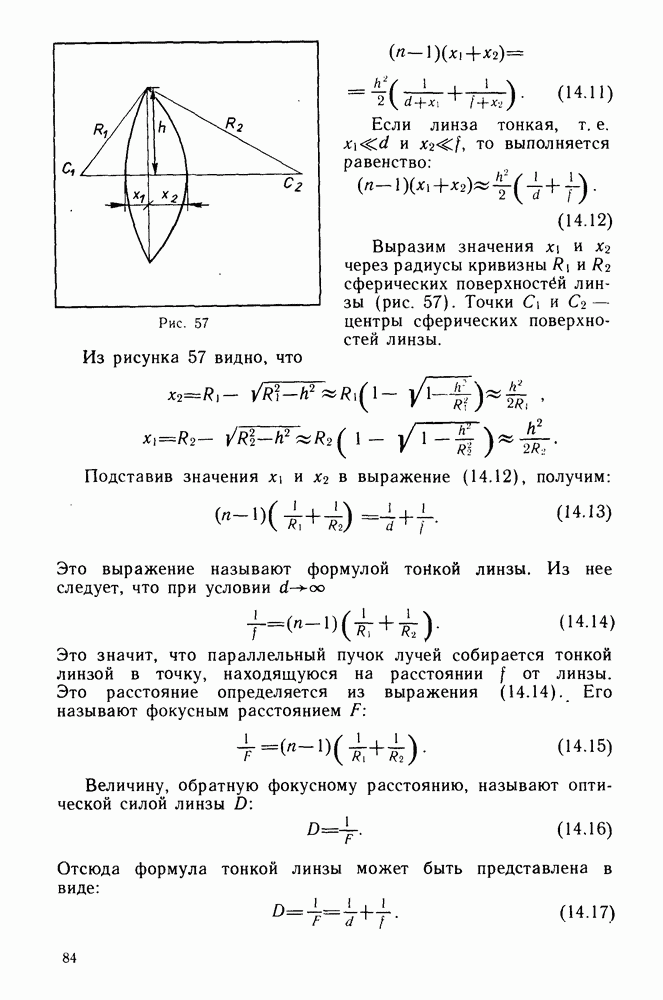
- Линзы.
- Аберрация линз.
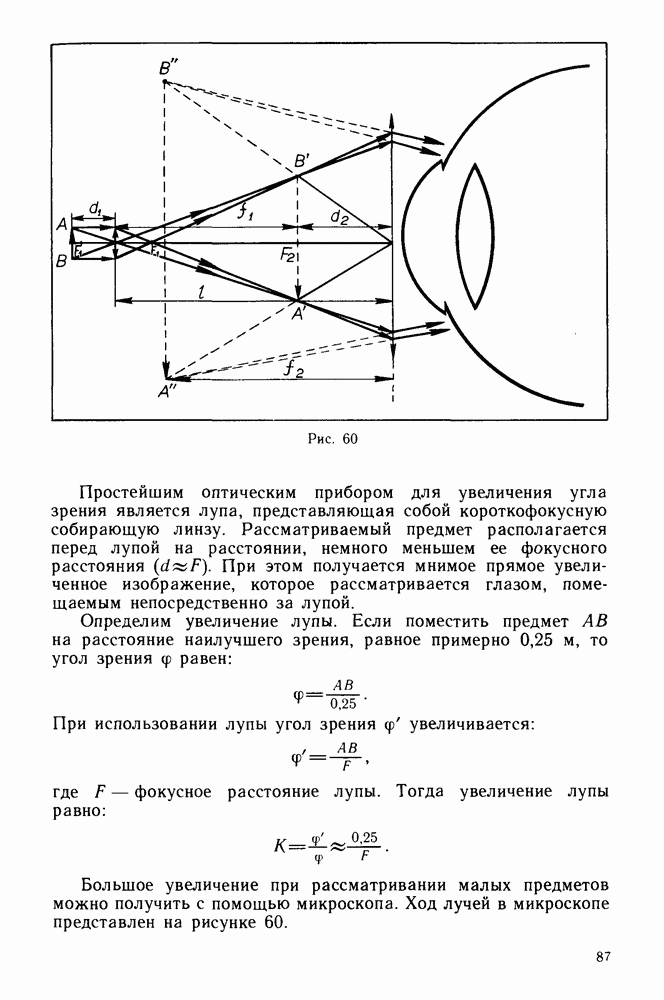
- Оптические приборы.
- Зрительная труба и телескоп.
- § 15. ДИФРАКЦИЯ СВЕТА
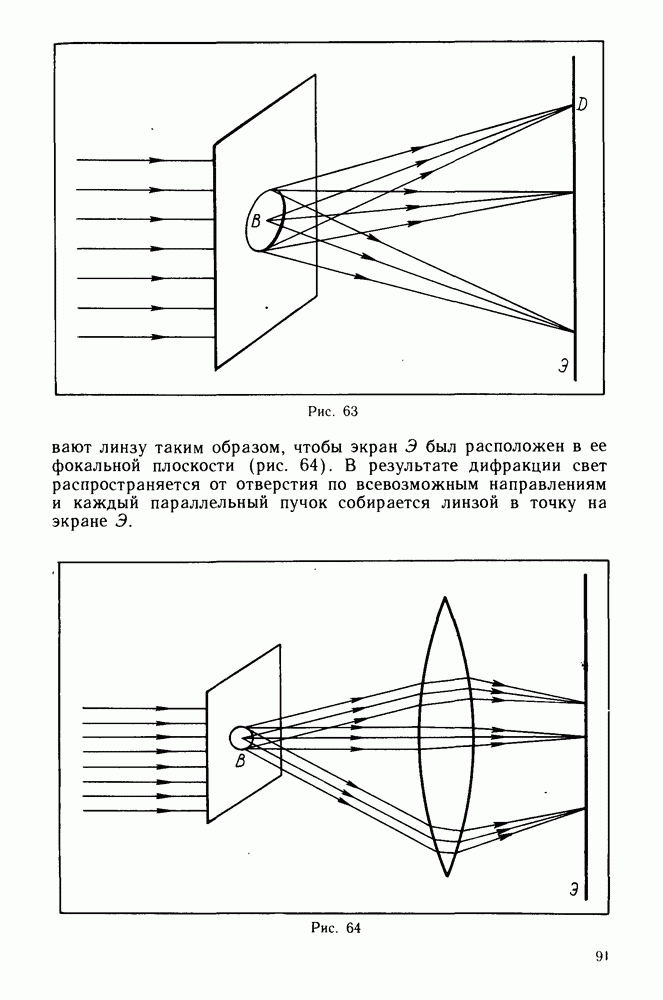
- Дифракция от круглого отверстия.
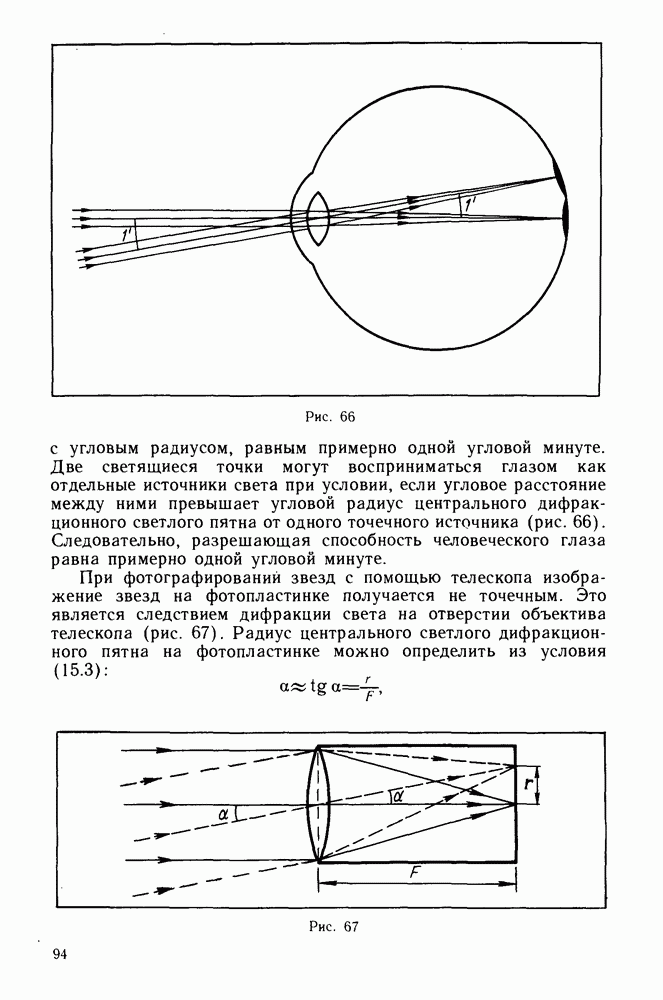
- Дифракция и разрешающая способность оптических приборов.
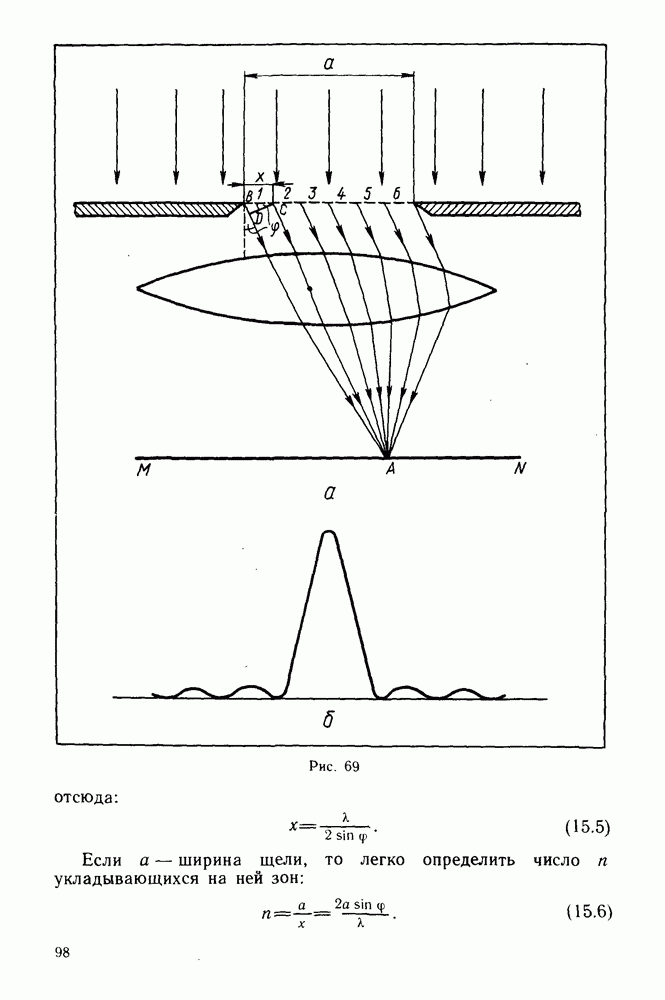
- Дифракция от одной щели.
- Дифракция от двух щелей.
- Дифракционная решетка.
- Применение и изготовление дифракционных решеток.
- § 16. ГОЛОГРАФИЯ
- Фотография.
- Голография.
- Голография с записью в трехмерной среде.
- Свойства и особенности голограмм. Применения голографии.
- § 17. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- § 18. ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава III. КВАНТЫ И ЧАСТИЦЫ
- § 19. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
- Гипотеза Планка.
- § 20. ФОТОН
- Затруднения волновой теории в объяснении фотоэффекта.
- Фотоны.
- Эффект Комптона.
- Опыт Боте.
- Дуализм свойств света.
- § 21. КВАНТЫ И АТОМЫ
- Квантовые постулаты Бора.
- Спектр атома водорода.
- Квантование момента импульса.
- Схема энергетических уровней.
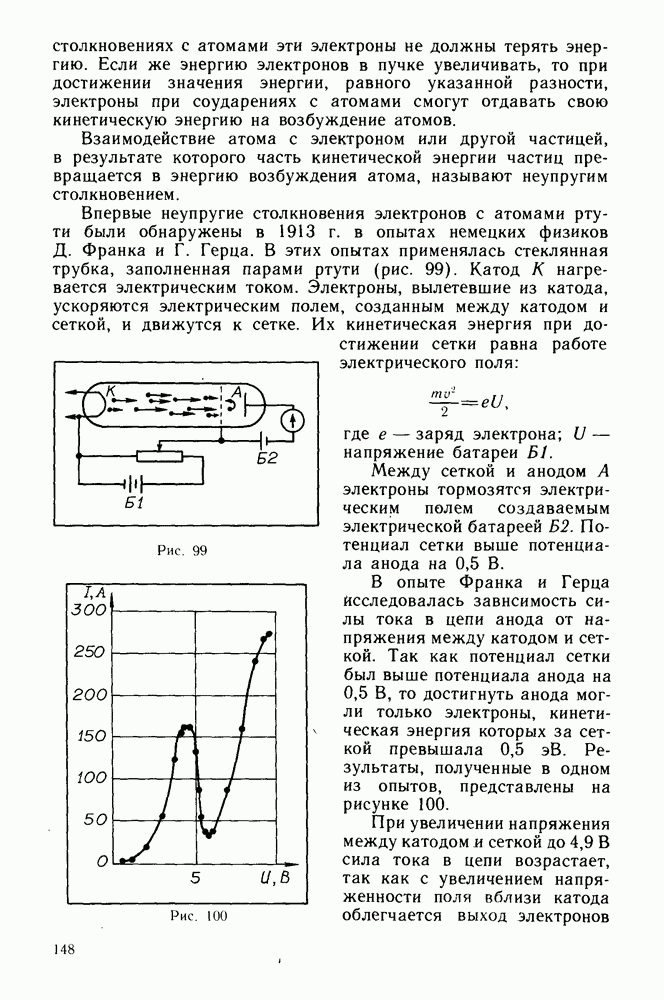
- Опыт Франка и Герца.
- § 22. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
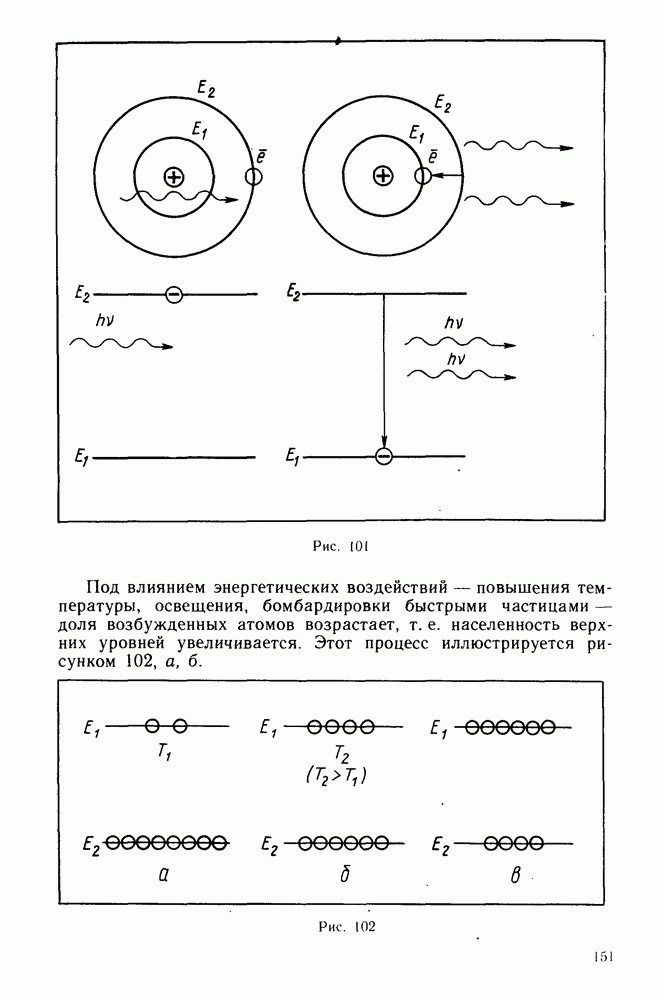
- Инверсная населенность уровней.
- Условия, необходимые для создания в веществе инверсной населенности энергетических уровней.
- Устройство рубинового лазера.
- Устройство газовых лазеров.
- Применения лазеров.
- § 23. НЕЛИНЕЙНАЯ ОПТИКА
- Явление просветления среды.
- Самофокусировка лазерного луча.
- Нарушение принципа суперпозиции световых пучков и преобразование частоты света.
- Многофотонные процессы.
- Механизм влияния света на оптические свойства среды.
- § 24. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
- Сплошной спектр излучения вещества в газообразном состоянии.
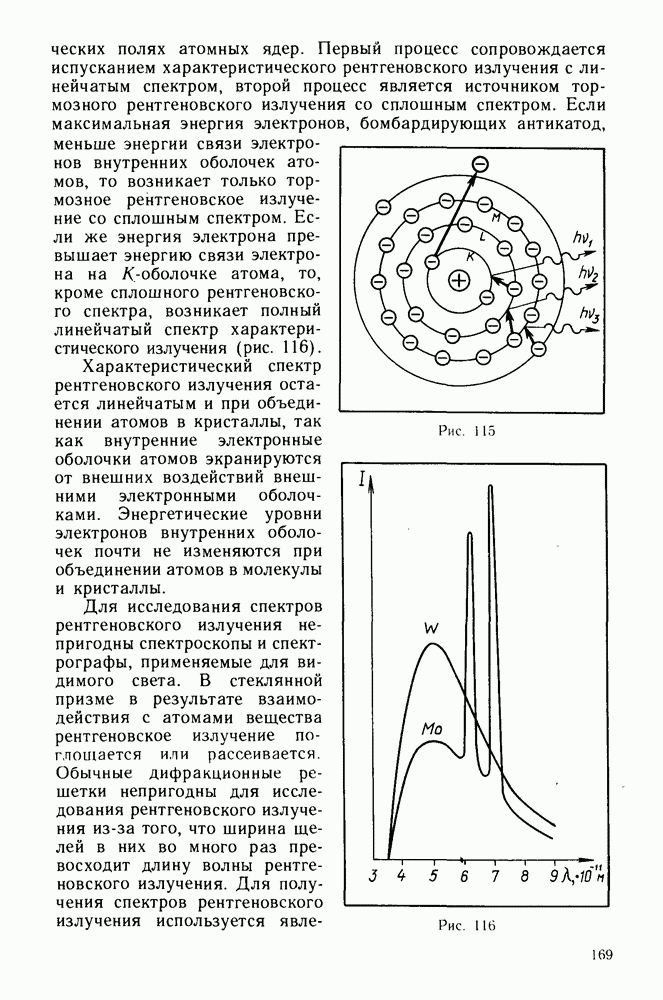
- Рентгеновские спектры.
- Молекулярные спектры.
- Радиоспектроскопия.
- Радиоволны космического происхождения.
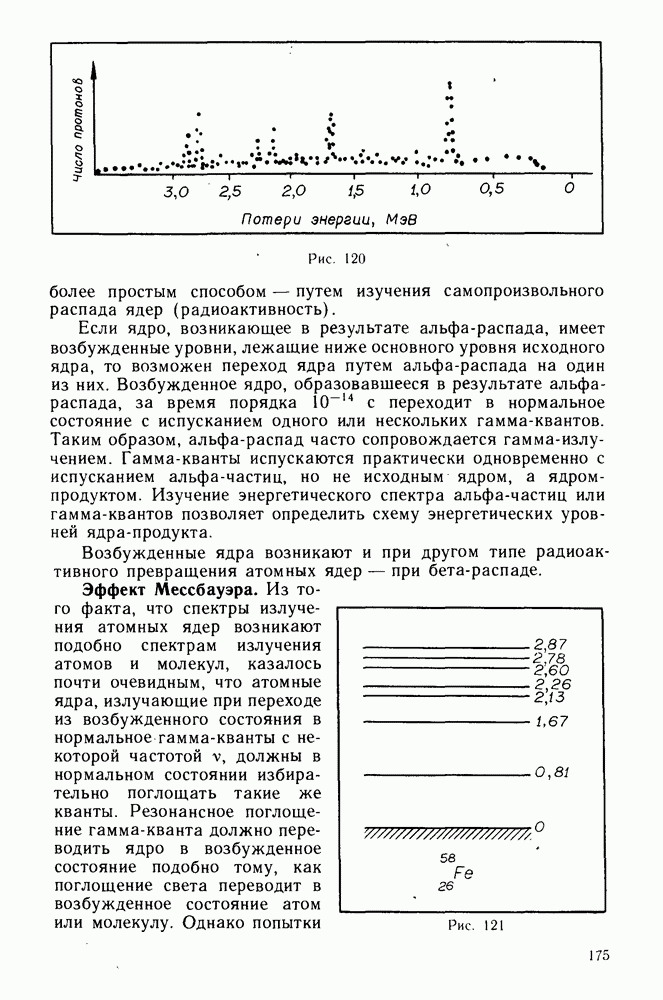
- § 25. ЯДЕРНЫЕ СПЕКТРЫ
- Эффект Мессбауэра.
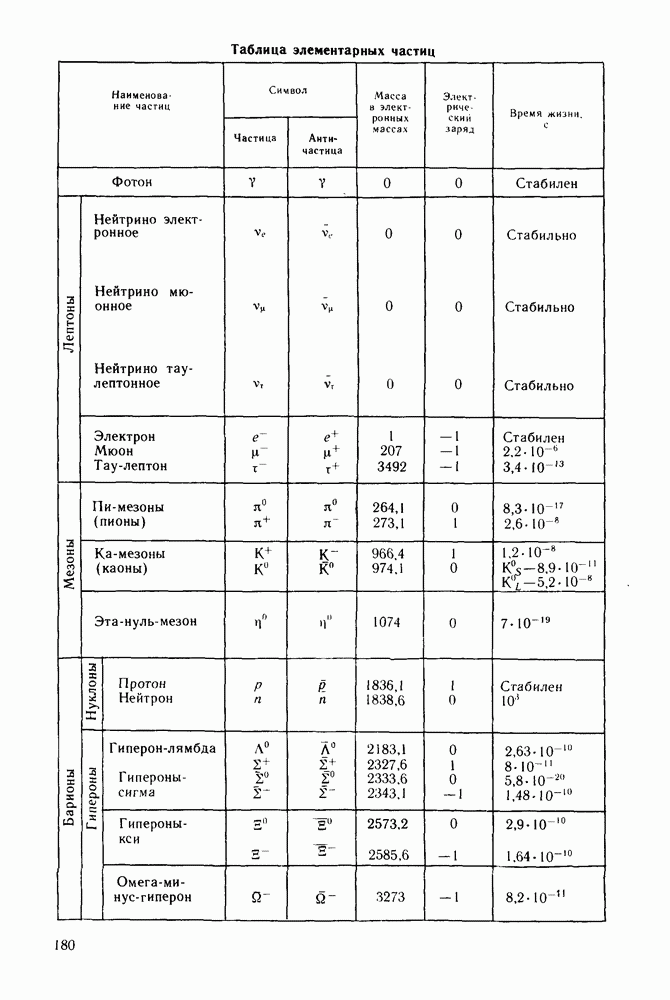
- § 26. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- Нуклоны.
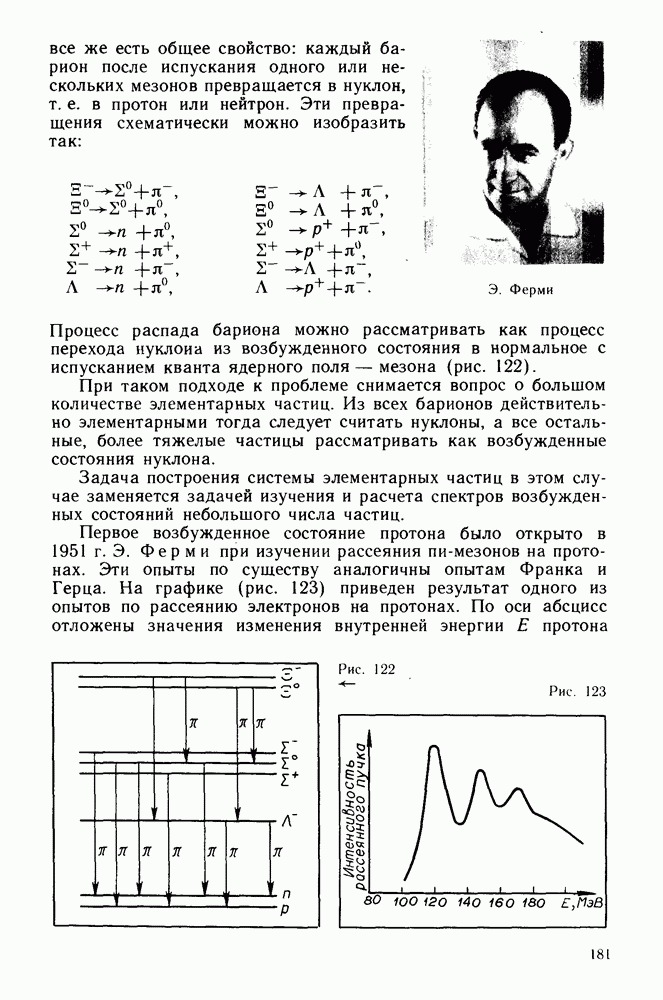
- Спектры элементарных частиц.
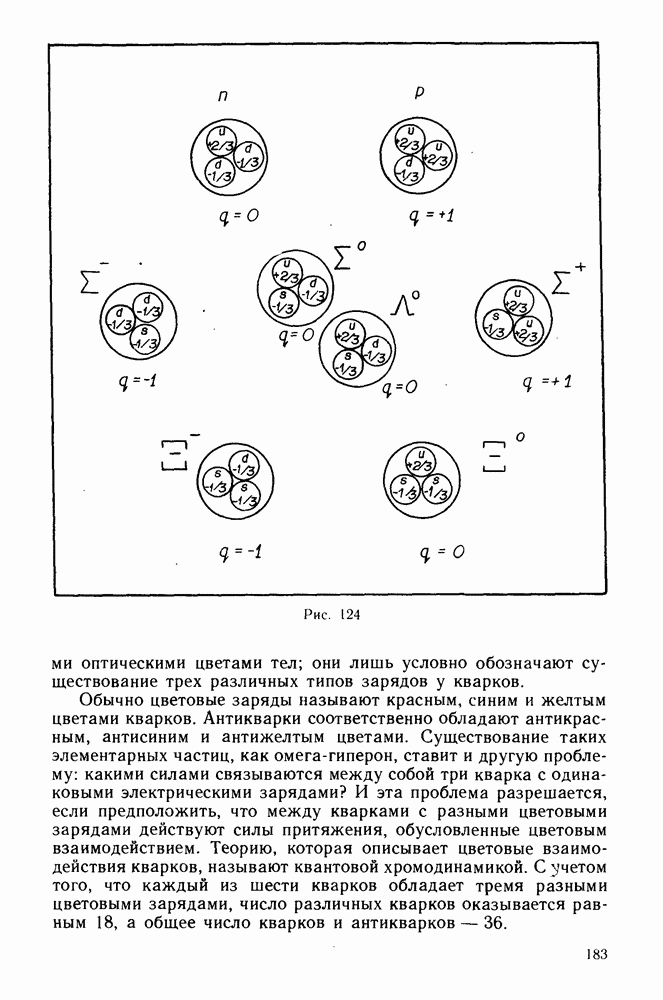
- Кварки.
- § 27. ЧАСТИЦЫ И ВОЛНЫ
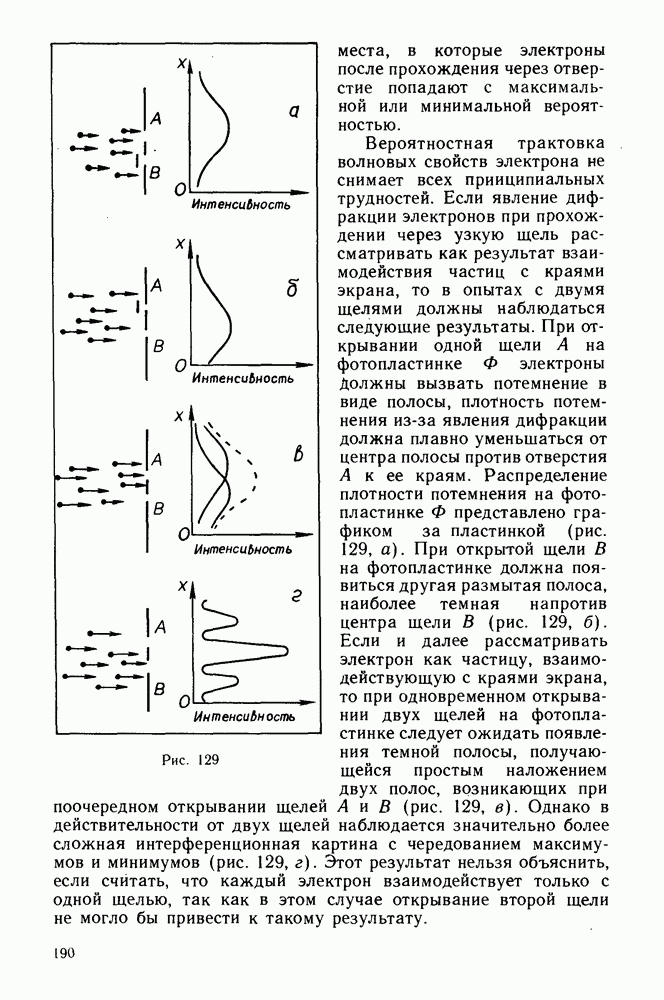
- Волновые свойства электрона.
- Гипотеза де Бройля и атом Бора.
- Интерференция волн де Бройля.
- Соотношение неопределенностей.
- Взаимные превращения света и вещества.
- § 28. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ОТВЕТЫ