| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
13.8. Центральная предельная теорема для одинаково распределенных слагаемых
Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых. Здесь мы сформулируем и докажем одну из самых простых форм центральной предельной теоремы, относящуюся к случаю одинаково распределенных слагаемых.
Теорема. Если ![]() - независимые
случайные величины, имеющие один и тот же закон распределения с математическим
ожиданием
- независимые
случайные величины, имеющие один и тот же закон распределения с математическим
ожиданием ![]() и
дисперсией
и
дисперсией ![]() ,
то при неограниченном увеличении
,
то при неограниченном увеличении ![]() закон распределения суммы
закон распределения суммы
 (13.8.1)
(13.8.1)
неограниченно приближается к нормальному.
Доказательство.
Проведем доказательство для
случая непрерывных случайных величин ![]() (для прерывных оно будет аналогичным).
(для прерывных оно будет аналогичным).
Согласно второму свойству
характеристических функций, доказанному в предыдущем ![]() , характеристическая функция
величины
, характеристическая функция
величины ![]() представляет
собой произведение характеристических функций слагаемых. Случайные величины
представляет
собой произведение характеристических функций слагаемых. Случайные величины ![]() имеют один и тот же
закон распределения с плотностью
имеют один и тот же
закон распределения с плотностью ![]() и, следовательно, одну и ту же характеристическую
функцию
и, следовательно, одну и ту же характеристическую
функцию
 . (13.8.2)
. (13.8.2)
Следовательно, характеристическая
функция случайной величины ![]() будет
будет
![]() . (13.8.3)
. (13.8.3)
Исследуем
более подробно функцию ![]() . Представим ее в окрестности точки
. Представим ее в окрестности точки ![]() по формуле Маклорена с
тремя членами:
по формуле Маклорена с
тремя членами:
![]() , (13.8.4)
, (13.8.4)
где
![]() при
при ![]() .
.
Найдем величины ![]() ,
, ![]() ,
, ![]() . Полагая в формуле (13.8.2)
. Полагая в формуле (13.8.2) ![]() имеем:
имеем:
 . (13.8.5)
. (13.8.5)
Продифференцируем
(13.8.2) по ![]() :
:
 . (13.8.6)
. (13.8.6)
Полагая
в (13.8.6) ![]() ,
получим:
,
получим:
 . (13.8.7)
. (13.8.7)
Очевидно,
не ограничивая общности, можно положить ![]() (для этого достаточно перенести начало
отсчета в точку
(для этого достаточно перенести начало
отсчета в точку ![]() ).
Тогда
).
Тогда
![]() .
.
Продифференцируем (13.8.6) еще раз:
 ,
,
отсюда
 . (13.8.8)
. (13.8.8)
При ![]() интеграл в выражении (13.8.8) есть не что
иное, как дисперсия величины
интеграл в выражении (13.8.8) есть не что
иное, как дисперсия величины ![]() с плотностью
с плотностью ![]() , следовательно
, следовательно
![]() . (13.8.9)
. (13.8.9)
Подставляя в (13.8.4) ![]() ,
, ![]() и
и ![]() , получим:
, получим:
 . (13.8.10)
. (13.8.10)
Обратимся к случайной величине ![]() . Мы хотим доказать,
что ее закон распределения при увеличении
. Мы хотим доказать,
что ее закон распределения при увеличении ![]() приближается к нормальному. Для этого
перейдем от величины
приближается к нормальному. Для этого
перейдем от величины ![]() к
другой («нормированной») случайной величине
к
другой («нормированной») случайной величине
![]() . (13.8.11)
. (13.8.11)
Эта величина удобна тем, что ее
дисперсия не зависит от ![]() и равна единице при любом
и равна единице при любом ![]() . В этом нетрудно
убедиться, рассматривая величину
. В этом нетрудно
убедиться, рассматривая величину ![]() как линейную функцию независимых
случайных величин
как линейную функцию независимых
случайных величин ![]() ,
каждая из которых имеет дисперсию
,
каждая из которых имеет дисперсию ![]() . Если мы докажем, что закон распределения
величины
. Если мы докажем, что закон распределения
величины ![]() приближается
к нормальному, то, очевидно, это будет справедливо и для величины
приближается
к нормальному, то, очевидно, это будет справедливо и для величины ![]() , связанной с
, связанной с ![]() линейной зависимостью
(13.8.11).
линейной зависимостью
(13.8.11).
Вместо того чтобы доказывать, что
закон распределения величины ![]() при увеличении
при увеличении ![]() приближается к нормальному,
покажем, что ее характеристическая функция приближается к характеристической
функции нормального закона.
приближается к нормальному,
покажем, что ее характеристическая функция приближается к характеристической
функции нормального закона.
Найдем характеристическую функцию
величины ![]() . Из
соотношения (13.8.11), согласно первому свойству характеристических функций
(13.7.8), получим
. Из
соотношения (13.8.11), согласно первому свойству характеристических функций
(13.7.8), получим
![]() , (13.8.12)
, (13.8.12)
где
![]() -
характеристическая функция случайной величины
-
характеристическая функция случайной величины ![]() .
.
Из формул (13.8.12) и (13.8.3) получим
 (13.8.13)
(13.8.13)
или, пользуясь формулой (13.8.10),
 . (13.8.14)
. (13.8.14)
Прологарифмируем выражение (13.8.14):
![]()
 .
.
Введем обозначение
 . (13.8.15)
. (13.8.15)
Тогда
![]() . (13.8.16)
. (13.8.16)
Будем неограниченно увеличивать ![]() . При этом величина
. При этом величина ![]() , согласно формуле
(13.8.15), стремится к нулю. При значительном
, согласно формуле
(13.8.15), стремится к нулю. При значительном ![]() ее можно считать весьма малой. Разложим,
ее можно считать весьма малой. Разложим, ![]() в ряд и ограничимся
одним членом разложения (остальные при
в ряд и ограничимся
одним членом разложения (остальные при ![]() станут пренебрежимо малыми):
станут пренебрежимо малыми):
![]() .
.
Тогда получим
![]()
 .
.
По
определению функция ![]() стремится
к нулю при
стремится
к нулю при ![]() ;
следовательно,
;
следовательно,
![]()
и
![]() ,
,
откуда
 . (13.8.17)
. (13.8.17)
Это есть не что иное, как
характеристическая функция нормального закона с параметрами ![]() ,
, ![]() (см. пример 2,
(см. пример 2, ![]() 13.7).
13.7).
Таким образом, доказано, что при
увеличении ![]() характеристическая
функция случайной величины
характеристическая
функция случайной величины ![]() неограниченно приближается к
характеристической функции нормального закона; отсюда заключаем что и закон
распределения величины
неограниченно приближается к
характеристической функции нормального закона; отсюда заключаем что и закон
распределения величины ![]() (а значит и величины
(а значит и величины ![]() ) неограниченно приближается к
нормальному закону. Теорема доказана.
) неограниченно приближается к
нормальному закону. Теорема доказана.
Мы доказали центральную предельную теорему для частного, но важного случая одинаково распределенных слагаемых. Однако в достаточно широком классе условий она справедлива и для неодинаково распределенных слагаемых. Например, А. М. Ляпунов доказал центральную предельную теорему для следующих условий:
 , (13.8.18)
, (13.8.18)
где
![]() - третий
абсолютный центральный момент величины
- третий
абсолютный центральный момент величины ![]() :
:
![]()
![]() .
.
![]() -
дисперсия величины
-
дисперсия величины ![]() .
.
Наиболее общим (необходимым и
достаточным) условием справедливости центральной предельной теоремы является
условие Линдеберга: при любом ![]()
 ,
,
где
![]() -
математическое ожидание,
-
математическое ожидание, ![]() - плотность распределения случайной
величины
- плотность распределения случайной
величины ![]() ,
,  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 1. Введение
- ПРЕДИСЛОВИЕ
- 1.1. Предмет теории вероятностей
- Теория вероятностей: 1.2. Краткие исторические сведения
- Глава 2. Основные понятия теории вероятностей
- 2.1. Событие. Вероятность события
- 2.2. Непосредственный подсчет вероятностей
- 2.3. Частота, или статистическая вероятность, события
- 2.4. Случайная величина
- 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности
- Глава 3. Основные теоремы теории вероятностей
- 3.1. Назначение основных теорем. Сумма и произведение событий
- 3.2. Теорема сложения вероятностей
- 3.3. Теорема умножения вероятностей
- 3.4. Формула полной вероятности
- 3.5. Теорема гипотез (формула Бейеса)
- Глава 4. Повторение опытов
- 4.1. Частная теорема о повторении опытов
- 4.2. Общая теорема о повторении опытов
- Глава 5. Случайные величины и их законы распределения
- 5.1. Ряд распределения. Многоугольник распределения
- 5.2. Функция распределения
- 5.3. Вероятность попадания случайной величины на заданный участок
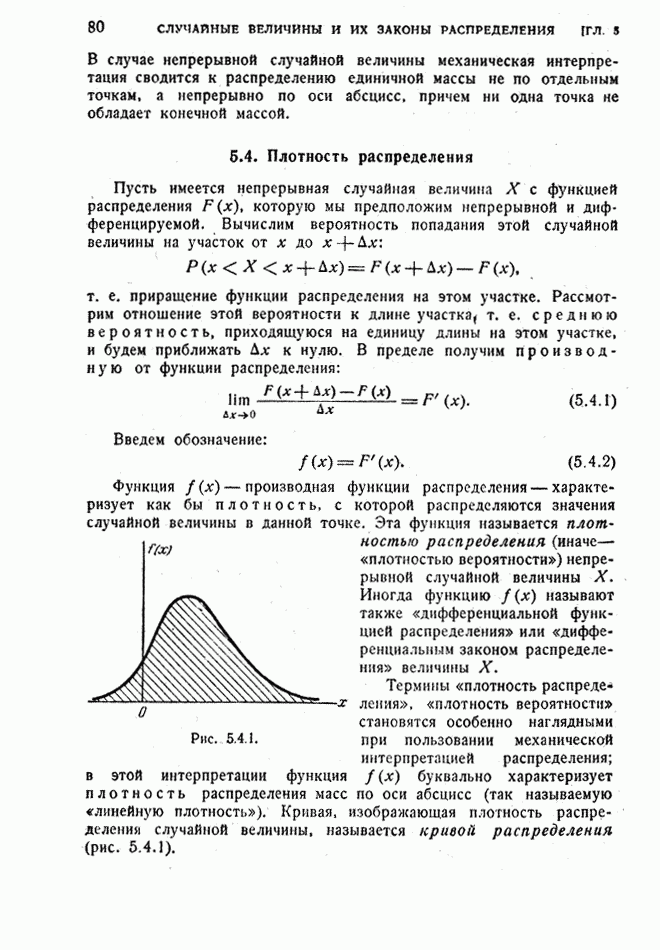
- 5.4. Плотность распределения
- 5.5. Числовые характеристики случайных величин. Их роль и назначение
- 5.6. Характеристики положения (математическое ожидание, мода, медиана)
- 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение
- 5.8. Закон равномерной плотности
- 5.9. Закон Пуассона
- Глава 6. Нормальный закон распределения
- 6.1. Нормальный закон распределения и его параметры
- 6.2. Моменты нормального распределения
- 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
- 6.4. Вероятное (срединное) отклонение
- Глава 7. Определение законов распределения случайных величин на основе опытных данных
- 7.1. Основные задачи математической статистики
- 7.2. Простая статистическая совокупность. Статистическая функция распределения
- 7.3. Статистический ряд. Гистограмма
- 7.4 Числовые характеристики статистического распределения
- 7.5. Выравнивание статистических рядов
- 7.6. Критерии согласия
- Глава 8. Системы случайных величин
- 8.1. Понятие о системе случайных величин
- 8.2. Функция распределения системы двух случайных величин
- 8.3. Плотность распределения системы двух случайных величин
- 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения
- 8.5 Зависимые и независимые случайные величины
- 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
- 8.7. Система произвольного числа случайных величин
- 8.8. Числовые характеристики системы нескольких случайных величин
- Глава 9. Нормальный закон распределении дли системы случайных величин
- 9.1. Нормальный закон на плоскости
- 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду
- 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания
- 9.4. Вероятность попадания в эллипс рассеивания
- 9.5. Вероятность попадания в область произвольной формы
- 9.6. Нормальный закон в пространстве трех измерений. Общая запись нормального закона для системы произвольного числа случайных величин
- Глава 10. Числовые характеристики функций случайных величин
- 10.1. Математическое ожидание функции. Дисперсия функции
- 10.2. Теоремы о числовых характеристиках
- 10.3. Применения теорем о числовых характеристиках
- Глава 11. Линеаризация функций
- 11.1. Метод линеаризации функций случайных аргументов
- 11.2. Линеаризация функции одного случайного аргумента
- 11.3. Линеаризация функции нескольких случайных аргументов
- 11.4. Уточнение результатов, полученных методом линеаризации
- Глава 12. Законы распределения функций случайных аргументов
- 12.1. Закон распределения монотонной функции одного случайного аргумента
- 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону
- 12.3. Закон распределения немонотонной функции одного случайного аргумента
- 12.4. Закон распределения функции двух случайных величин
- 12.5. Закон распределения суммы двух случайных величин. Композиция законов распределения
- 12.6. Композиция нормальных законов
- 12.7. Линейные функции от нормально распределенных аргументов
- 12.8. Композиция нормальных законов на плоскости
- Глава 13. Предельные теоремы теории вероятностей
- 13.1. Закон больших чисел и центральная предельная теорема
- 13.2. Неравенство Чебышева
- 13.3. Закон больших чисел (теорема Чебышева)
- 13.4. Обобщенная теорема Чебышева. Теорема Маркова
- 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона
- 13.6. Массовые случайные явления и центральная предельная теорема
- 13.7. Характеристические функции
- 13.8. Центральная предельная теорема для одинаково распределенных слагаемых
- 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении
- Глава 14. Обработка опытов
- 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения
- 14.2. Оценки для математического ожидания и дисперсии
- 14.3. Доверительный интервал. Доверительная вероятность
- 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону
- 14.5. Оценка вероятности по частоте
- 14.6. Оценки для числовых характеристик системы случайных величин
- 14.7. Обработка стрельб
- 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов
- Глава 15. Основные понятия теории случайных функций
- 15.1. Понятие о случайной функции
- 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции
- 15.3. Характеристики случайных функций
- 15.4. Определение характеристик случайной функции из опыта
- 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций
- 15.6. Линейные и нелинейные операторы. Оператор динамической системы
- 15.7. Линейные преобразования случайных функций
- 15.7.1. Интеграл от случайной функции
- 15.7.2. Производная от случайной функции
- 15.8. Сложение случайных функций
- 15.9. Комплексные случайные функции
- Глава 16. Канонические разложения случайных функций
- 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций
- 16.2. Каноническое разложение случайной функции
- 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями
- Глава 17. Стационарные случайные функции
- 17.1. Понятие о стационарном случайном процессе
- 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий
- 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции
- 17.4. Спектральное разложение случайной функции в комплексной форме
- 17.5. Преобразование стационарной случайной функции стационарной линейной системой
- 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем
- 17.7. Эргодическое свойство стационарных случайных функций
- 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации
- Глава 18. Основные понятия теории информации
- 18.1. Предмет и задачи теории информации
- 18.2. Энтропия как мера степени неопределенности состояния физической системы
- 18.3. Энтропия сложной системы. Теорема сложения энтропий
- 18.4. Условная энтропия. Объединение зависимых систем
- 18.5. Энтропия и информация
- 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии
- 18.7. Энтропия и информация для систем с непрерывным множеством состояний
- 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно
- 18.9. Передача информации с искажениями. Пропускная способность канала с помехами
- Глава 19. Элементы теории массового обслуживания
- 19.1. Предмет теории массового обслуживания
- 19.2. Случайный процесс со счетным множеством состояний
- 19.3. Поток событий. Простейший поток и его свойства
- 19.4 Нестационарный пуассоновский поток
- 19.5. Поток с ограниченным последействием (поток Пальма)
- 19.6. Время обслуживания
- 19.7. Марковский случайный процесс
- 19.8. Система массового обслуживания с отказами. Уравнения Эрланга
- 19.9. Установившийся режим обслуживания. Формулы Эрланга
- 19.10. Система массового обслуживания с ожиданием
- 19.11. Система смешанного типа с ограничением по длине очереди
- Приложения
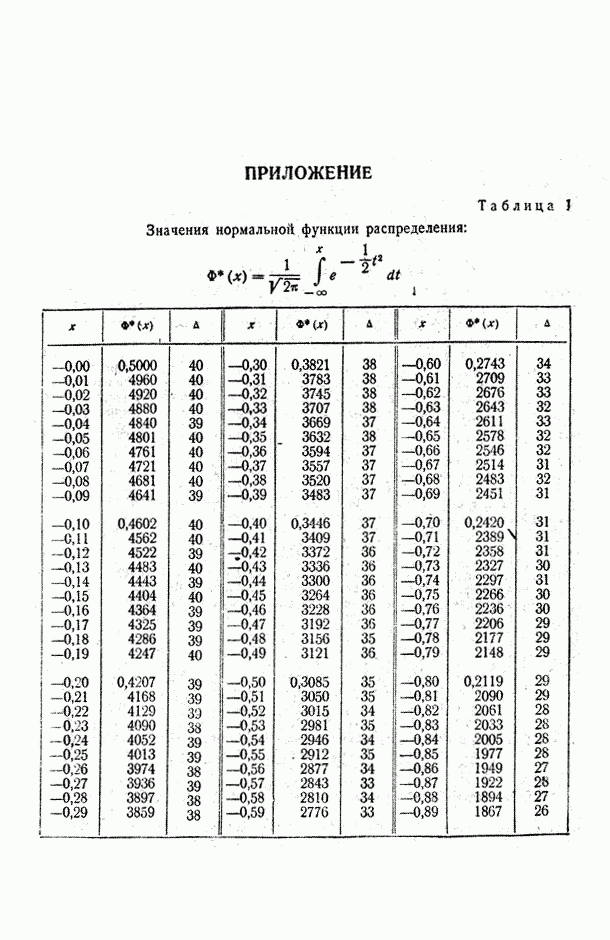
- Таблица 1 Значения нормальной функции распределения
- Таблица 2. Значения экспоненциальной функции
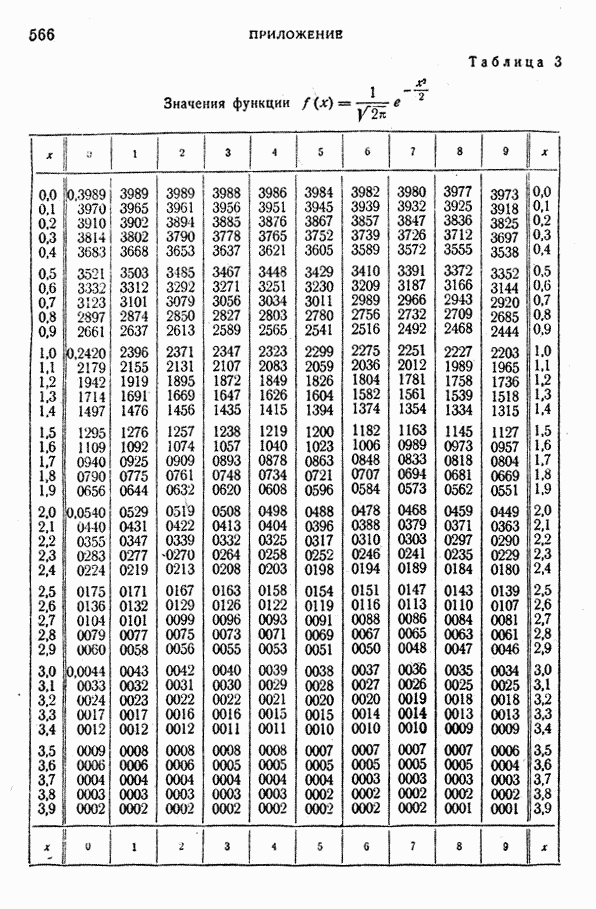
- Таблица 3. Значения нормальной функции
- Таблица 4. Значения «хи-квадрат» в зависимости от r и p
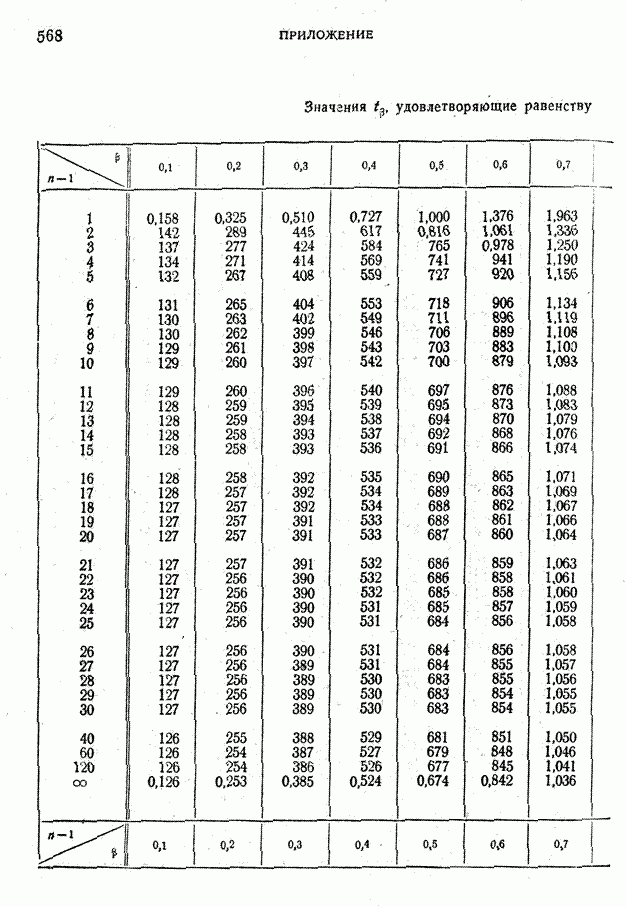
- Таблица 5. Значения удовлетворяющие равенству
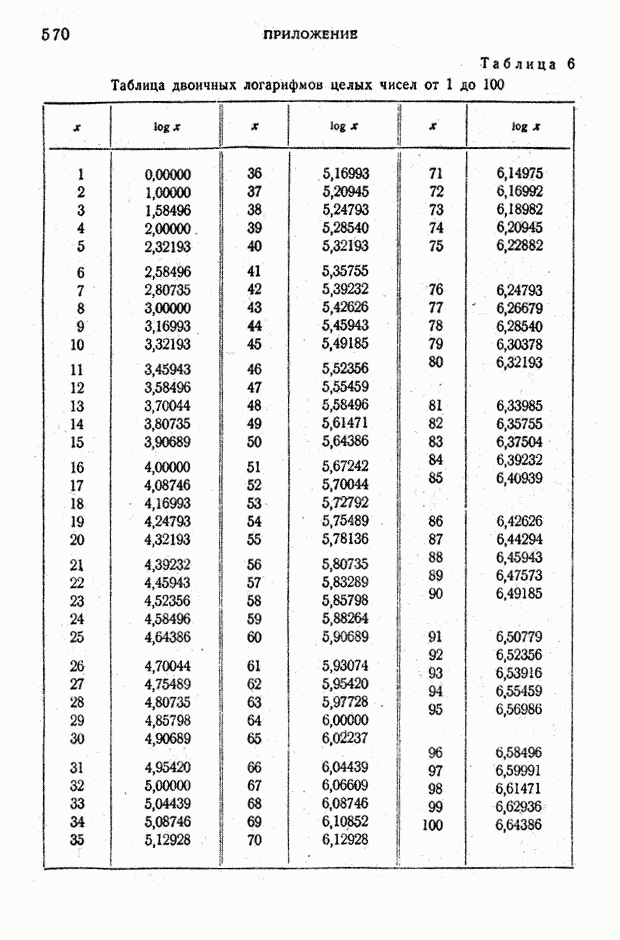
- Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100
- Таблица 7. Таблица значений функции
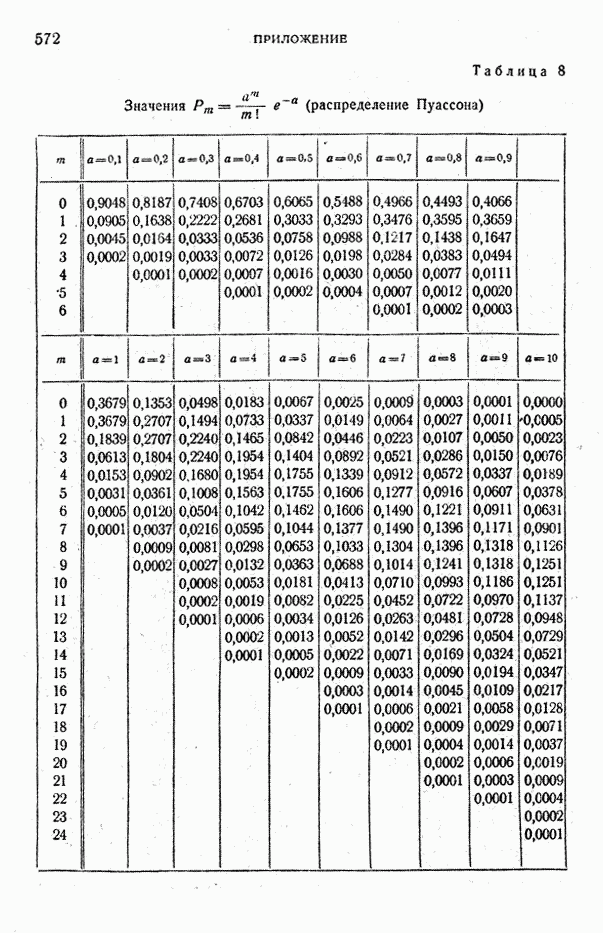
- Таблица 8. Значения распределение Пуассона