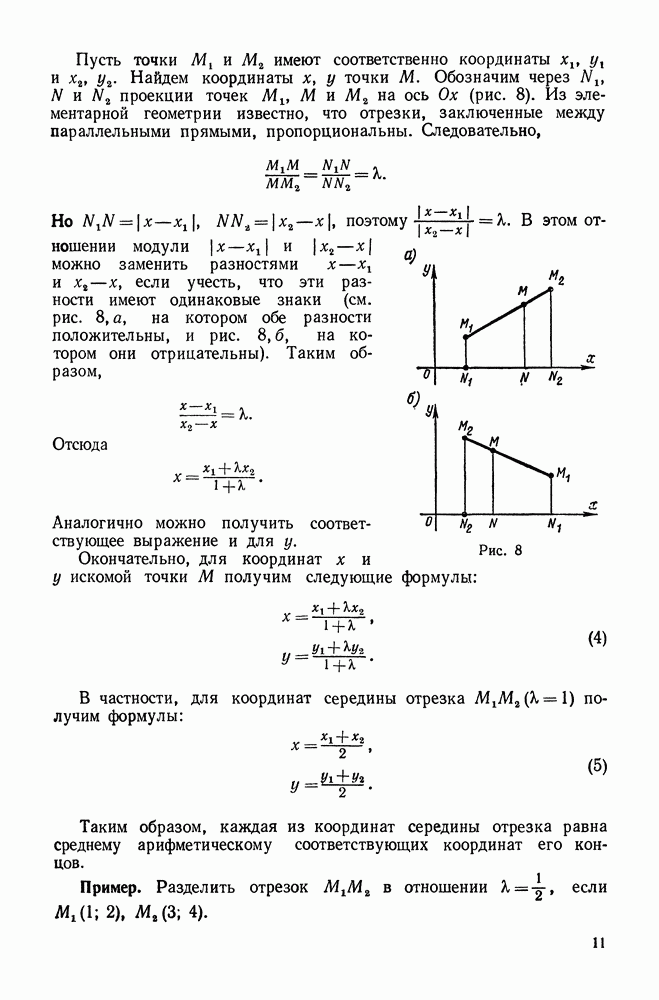
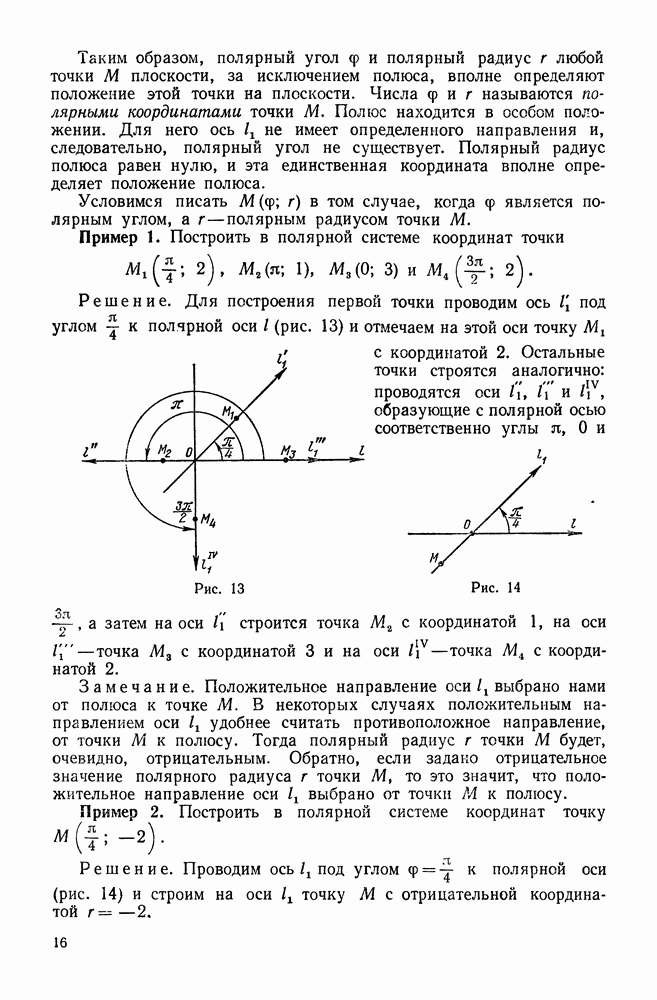
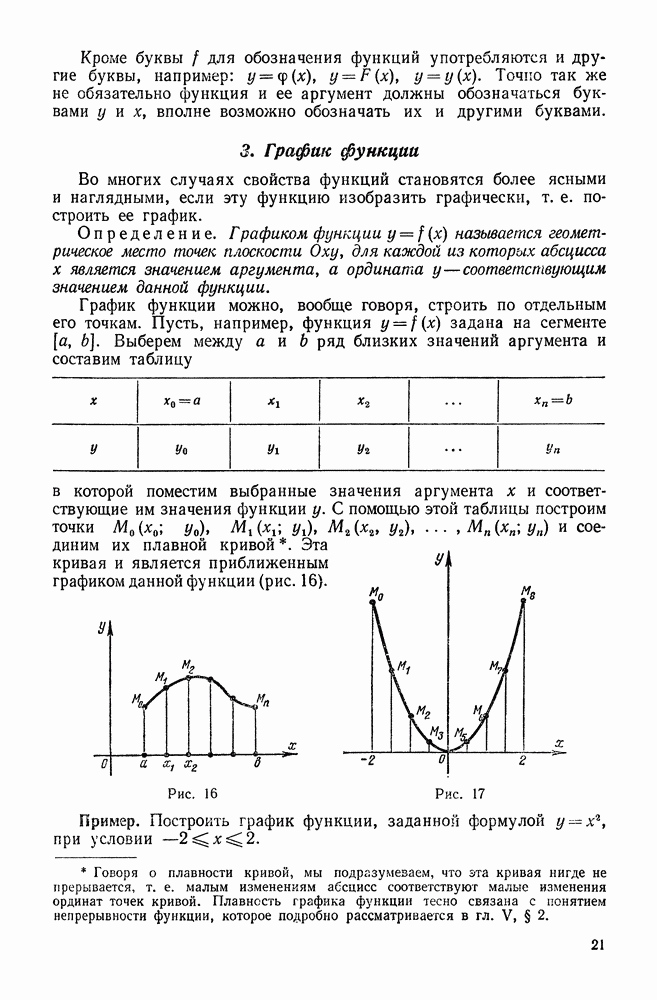
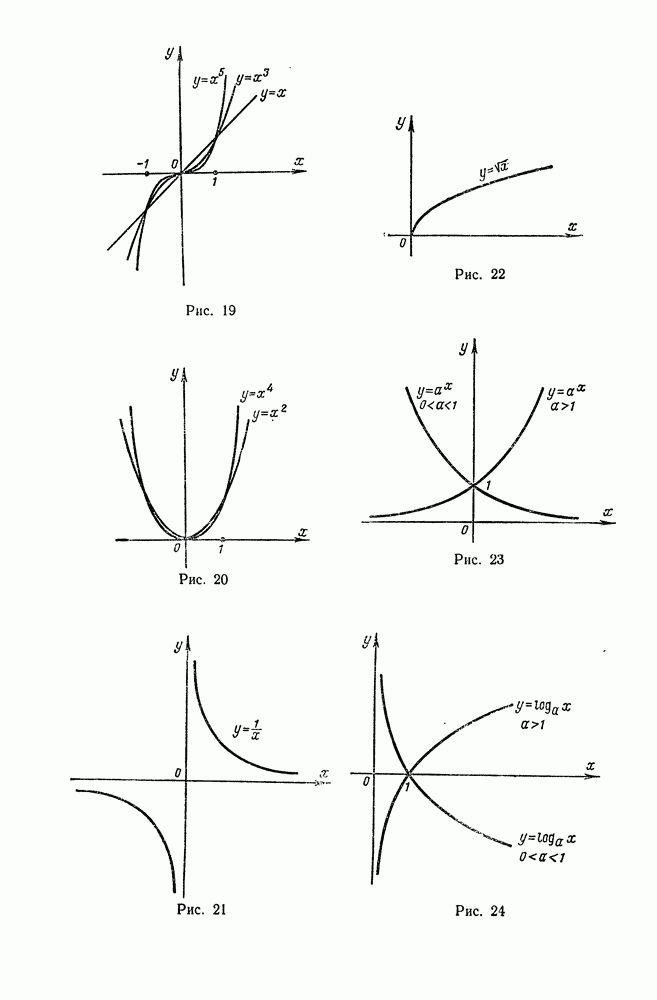
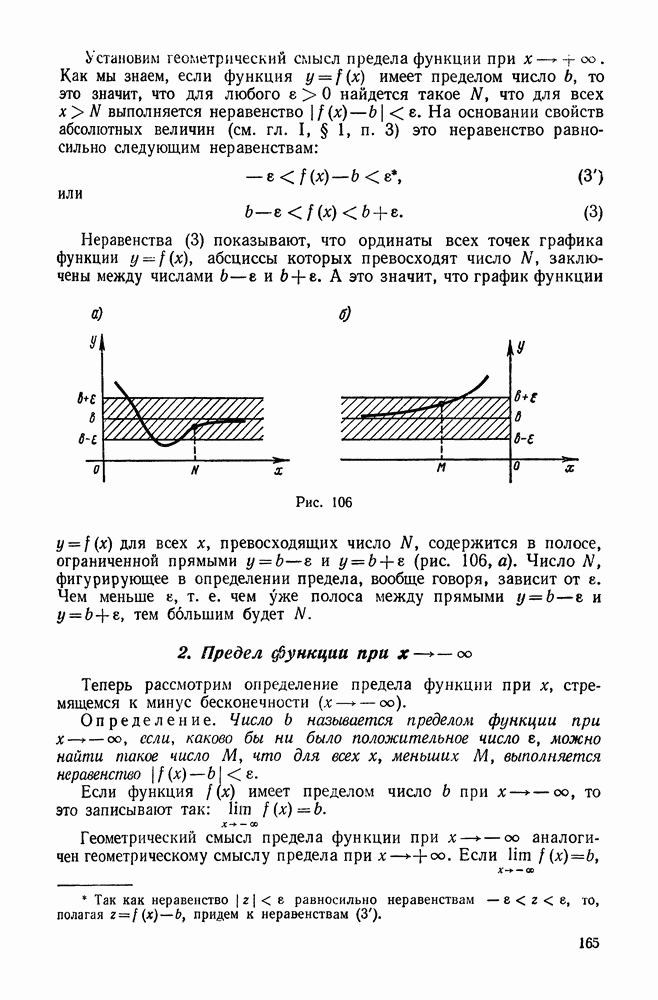
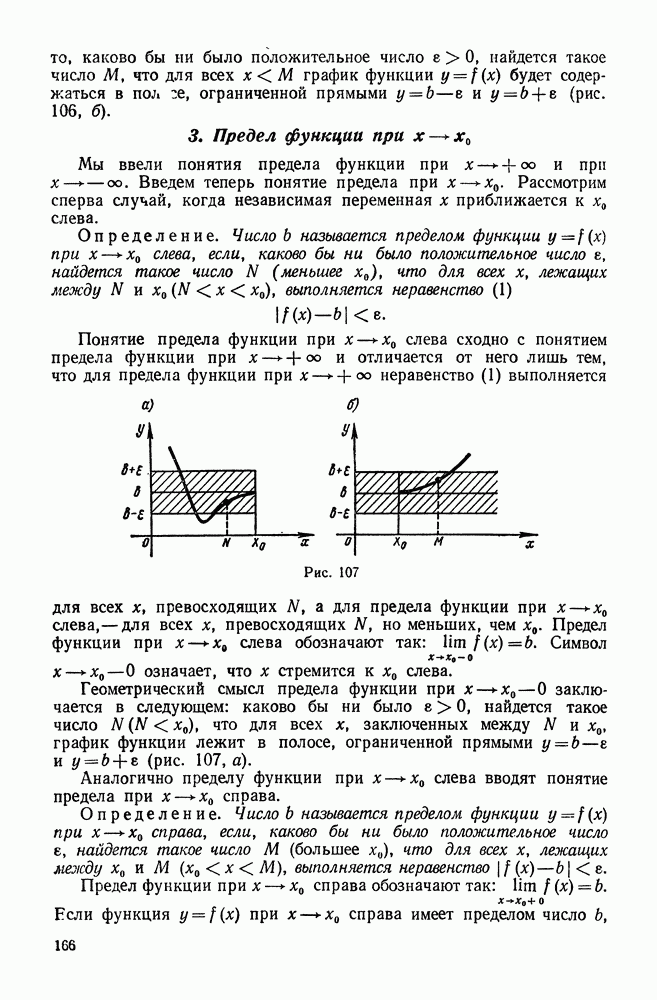
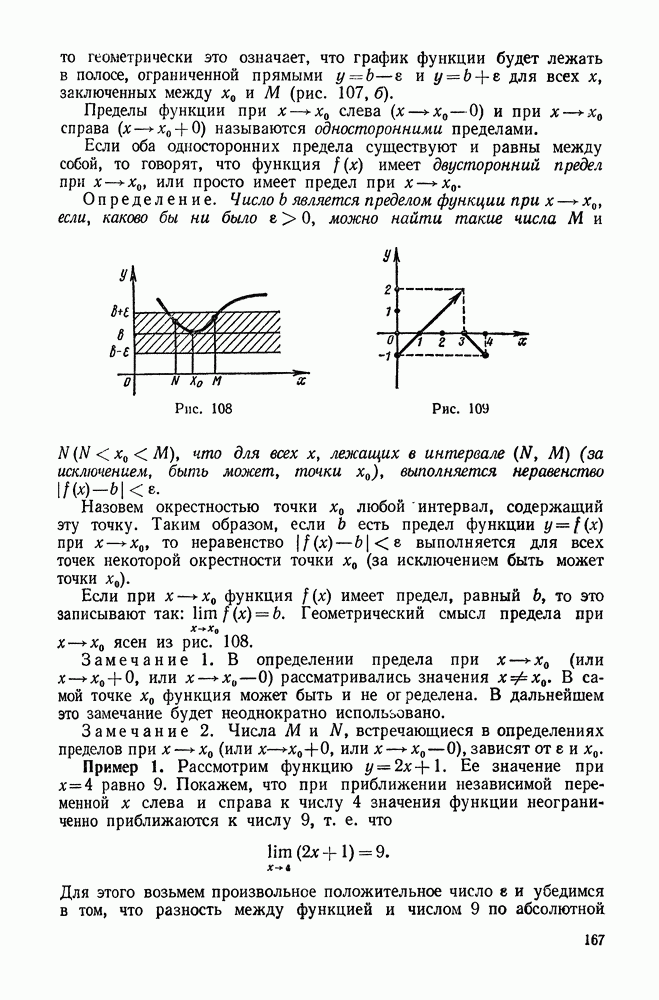
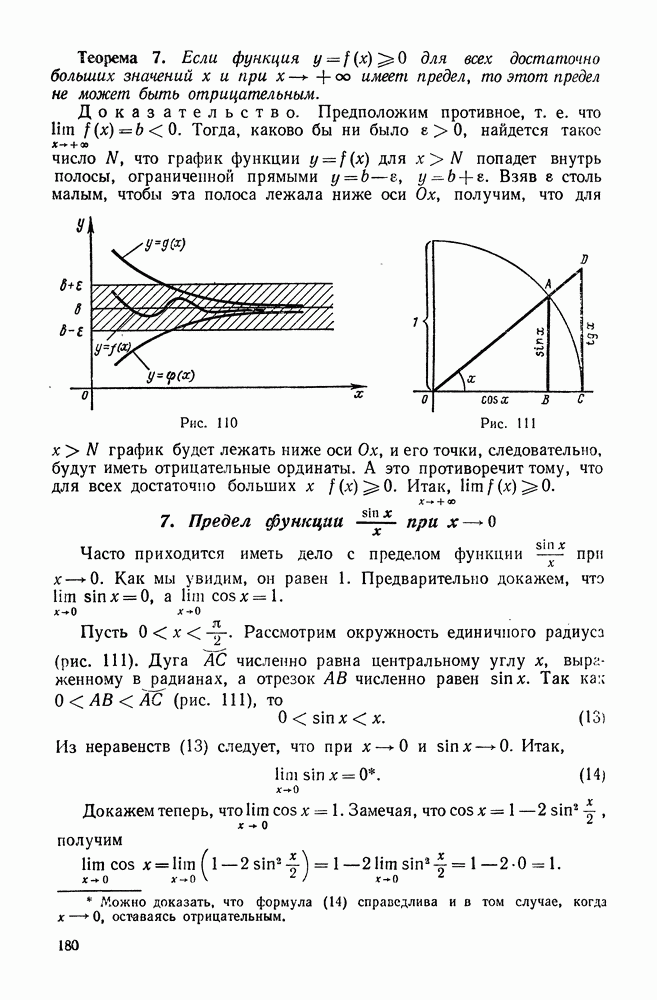
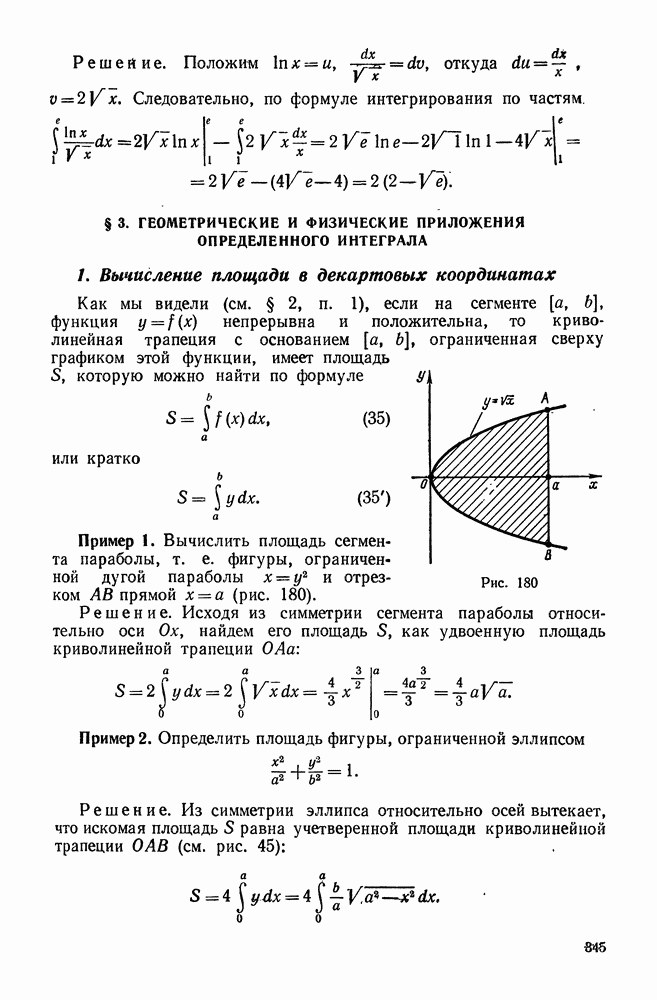
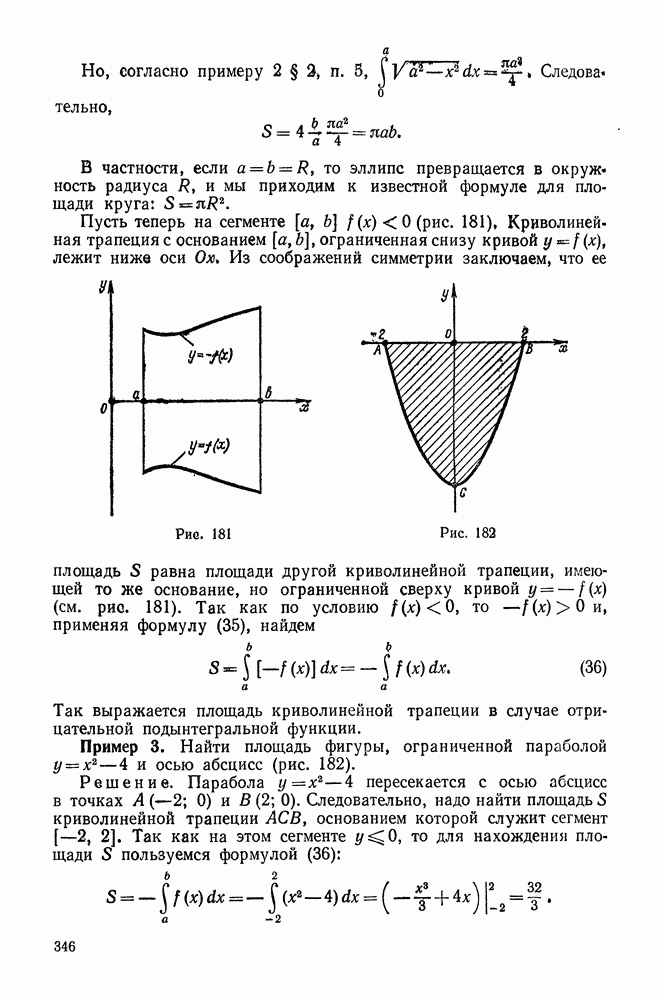
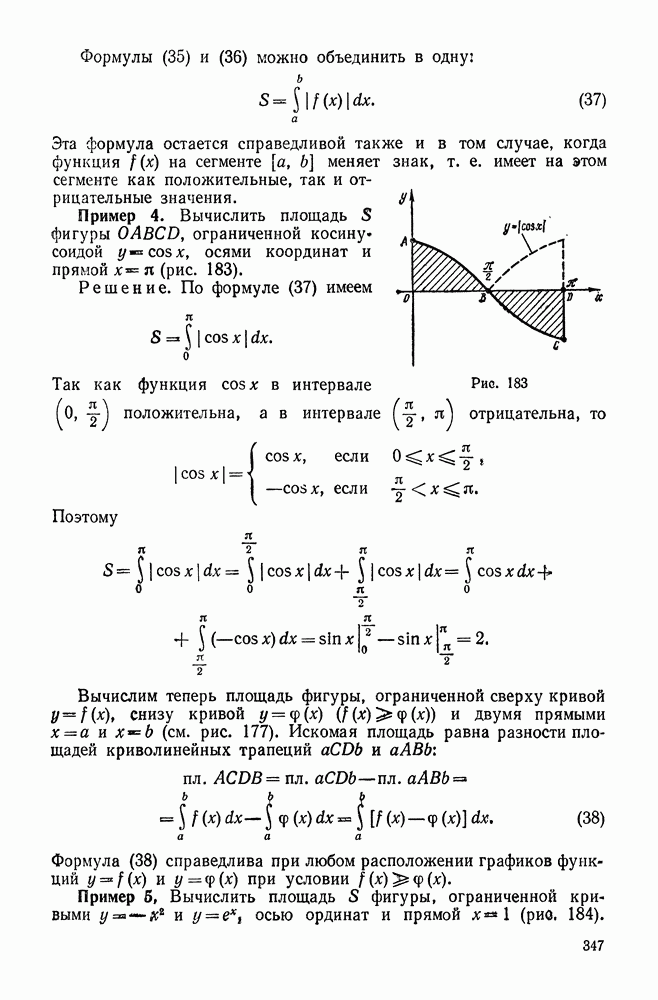
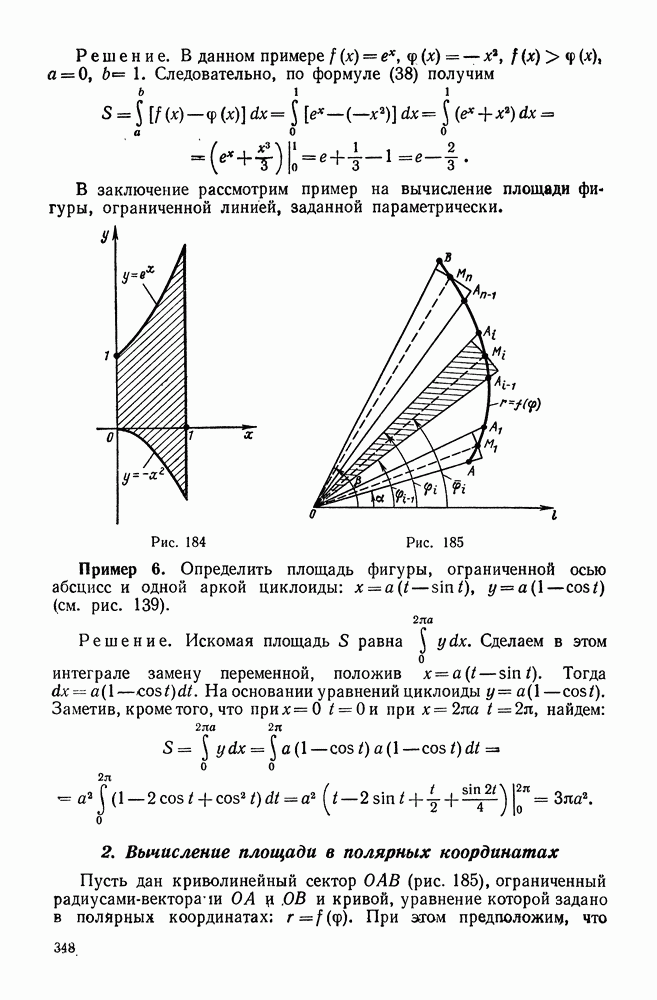
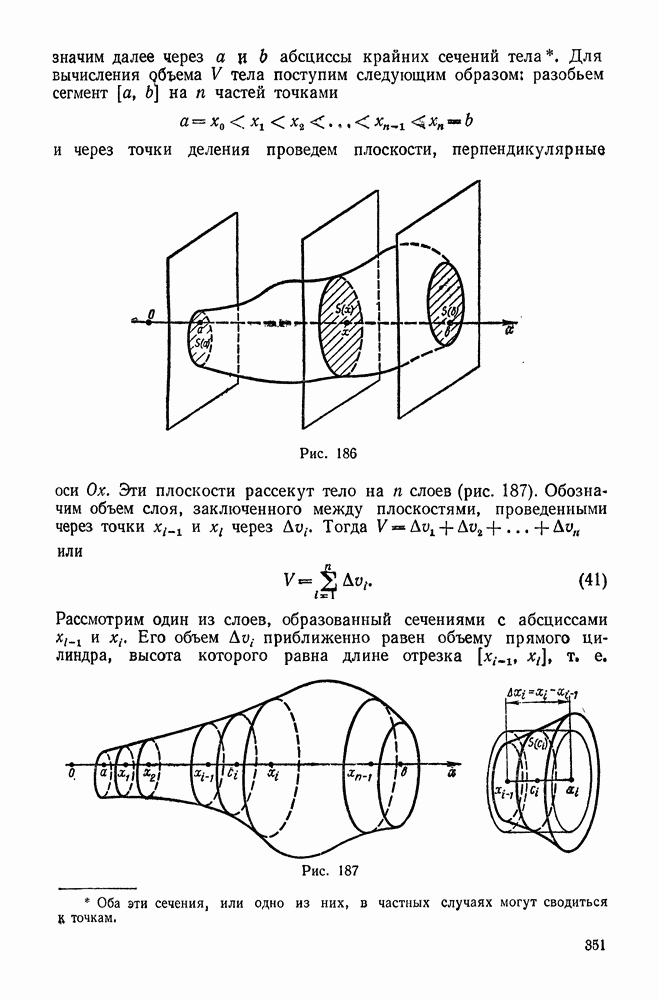
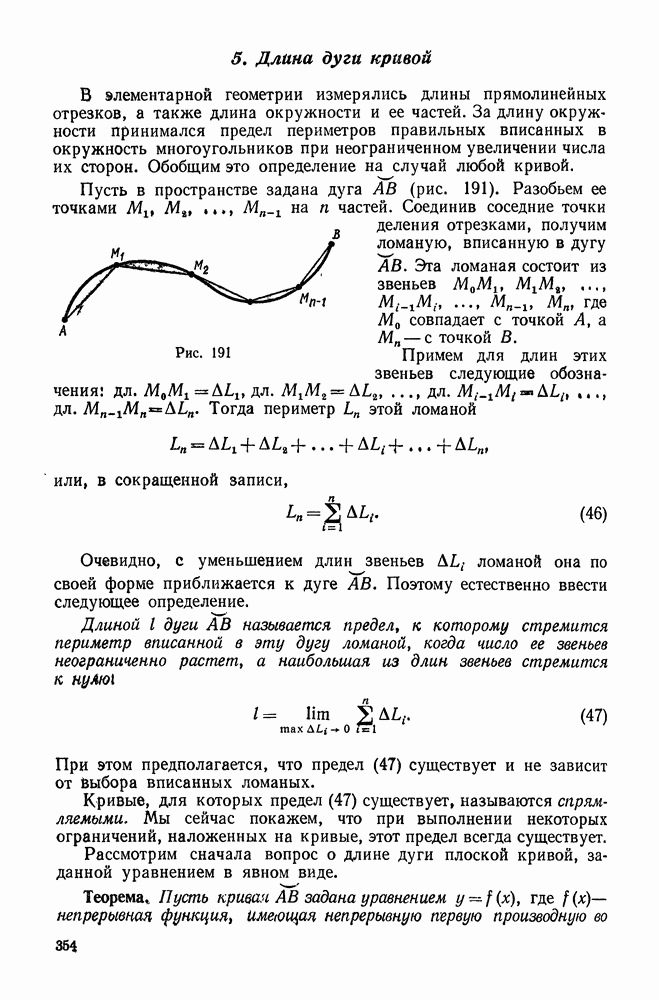
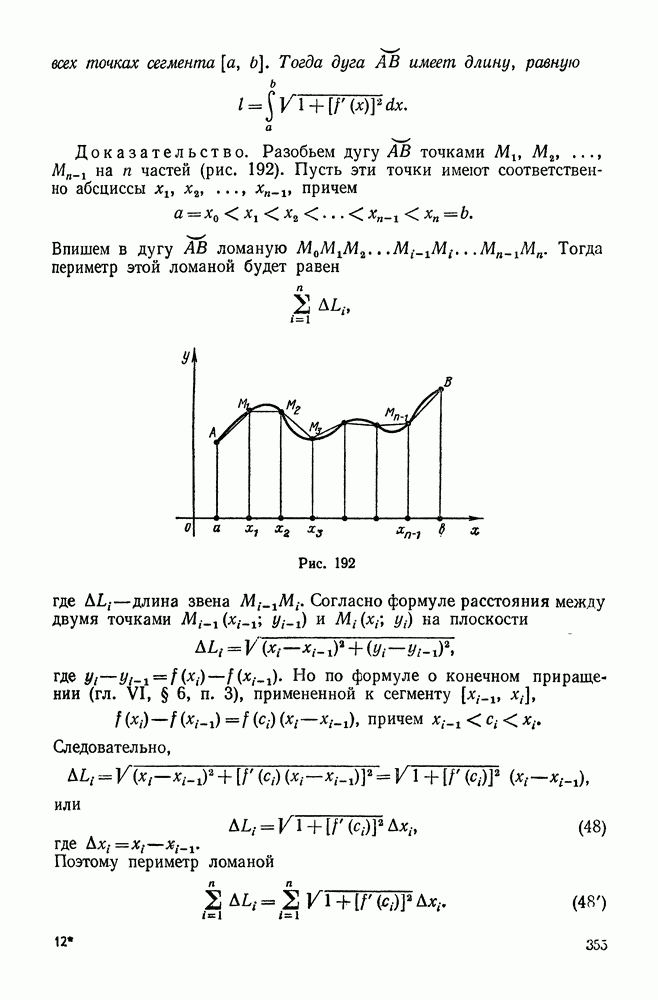
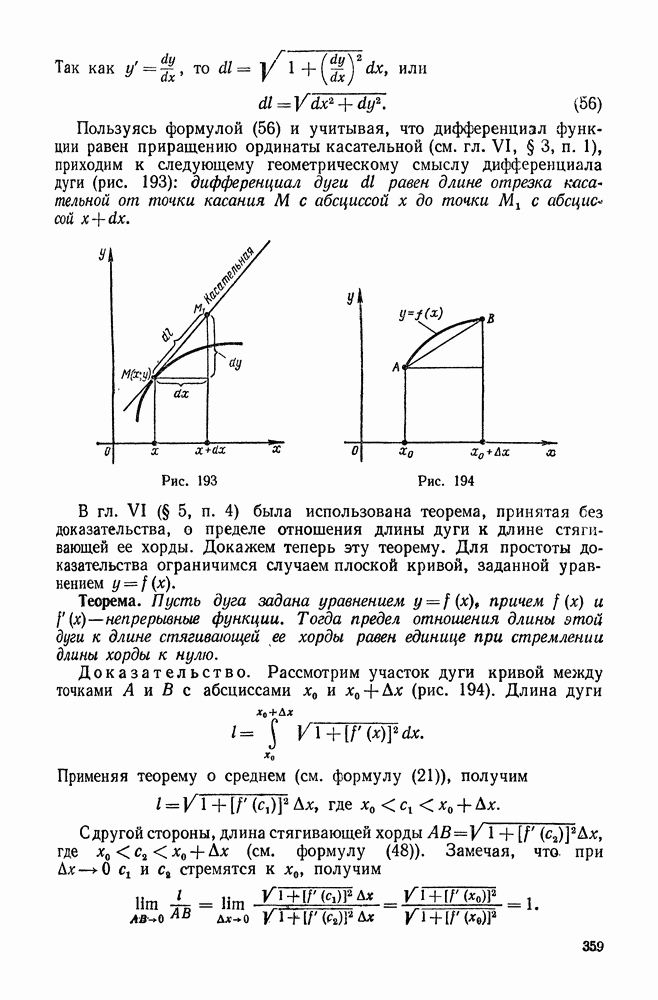
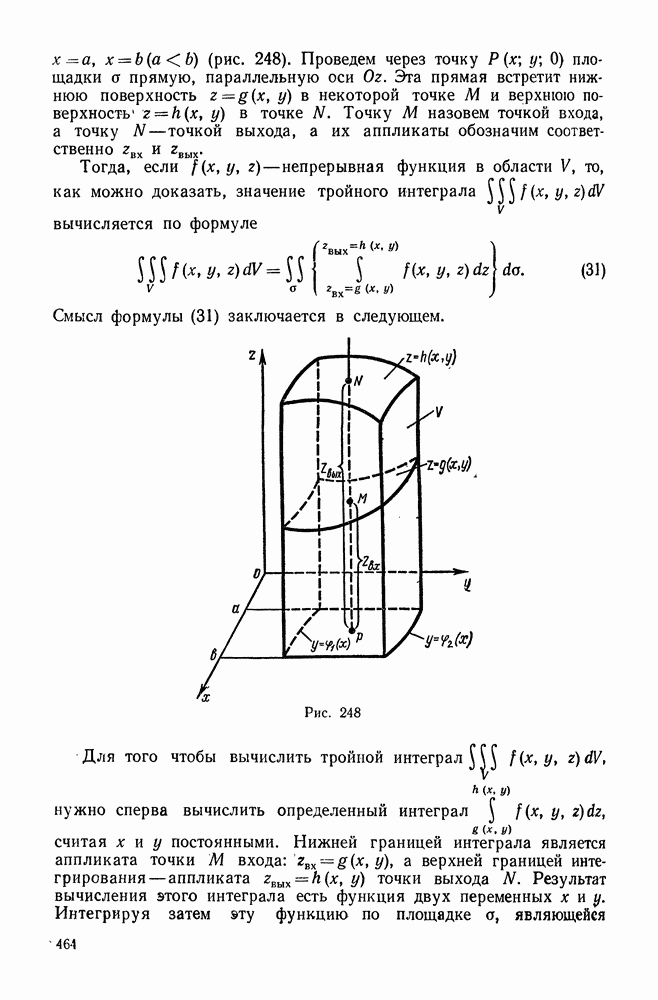
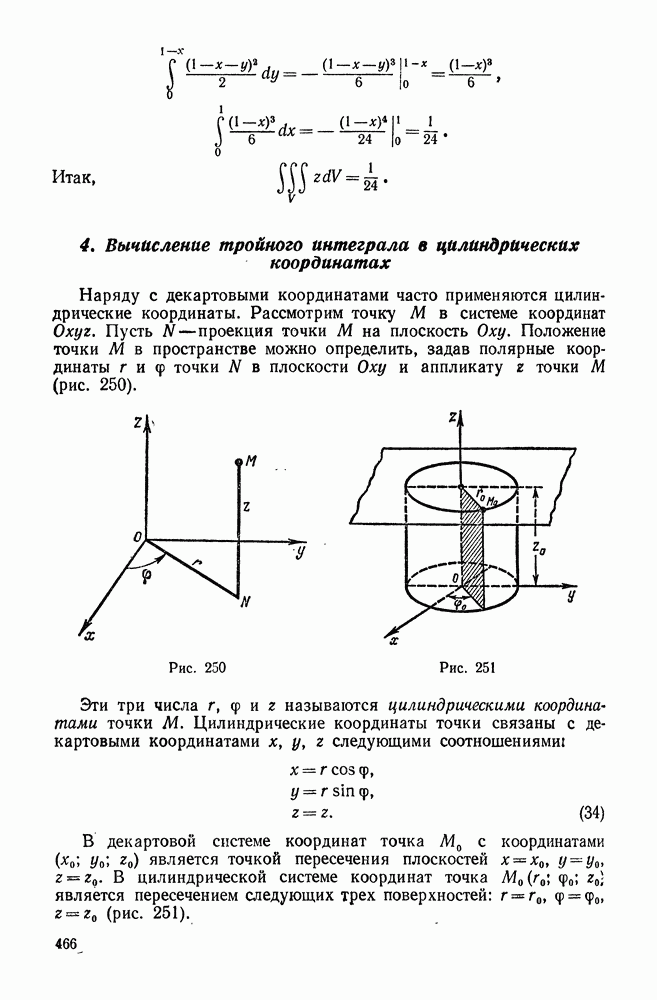
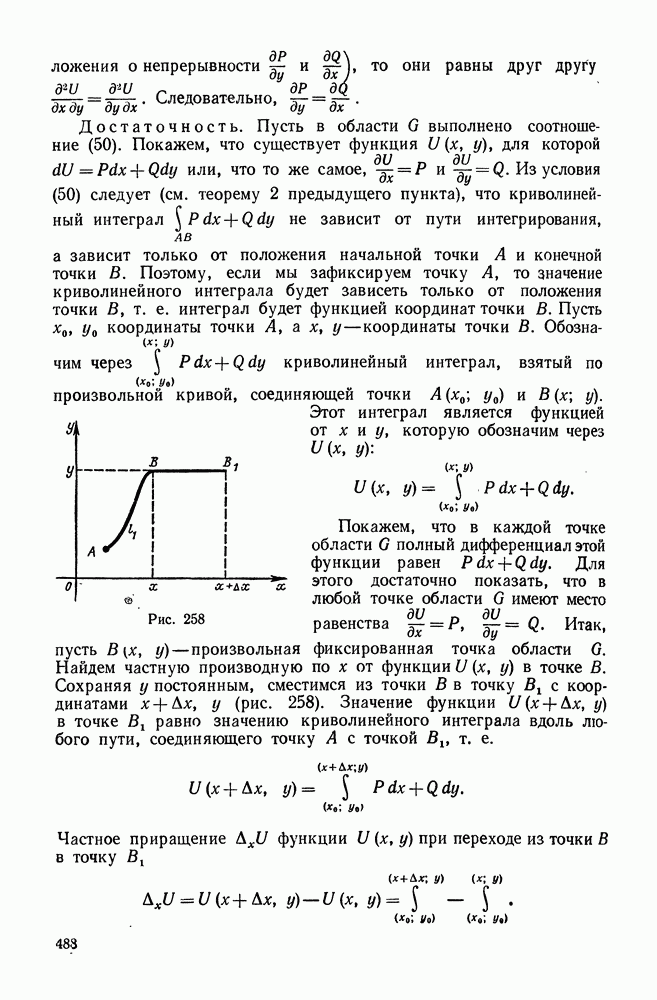
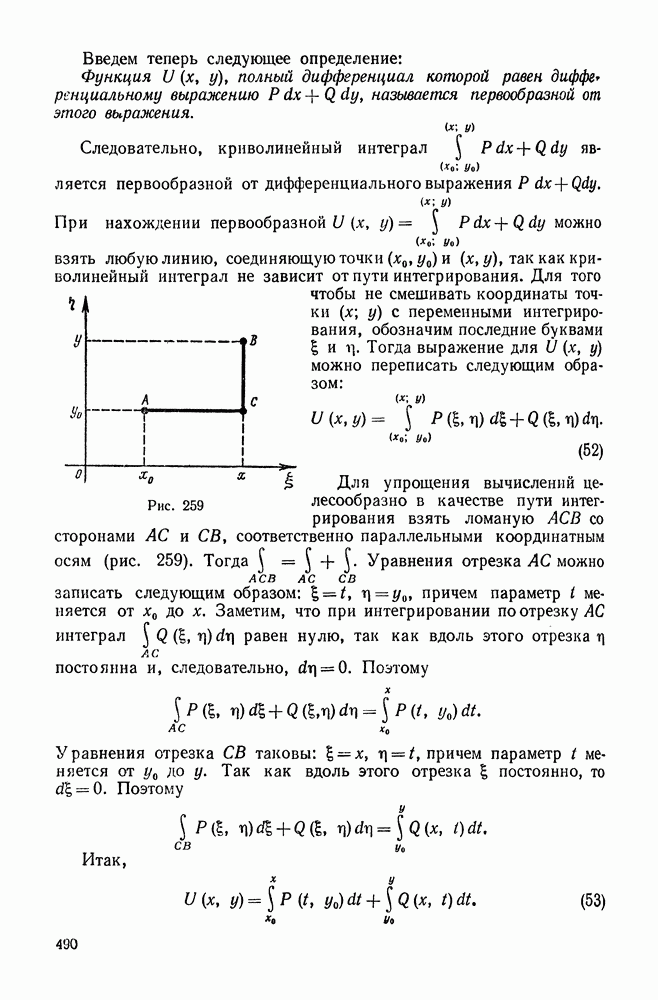
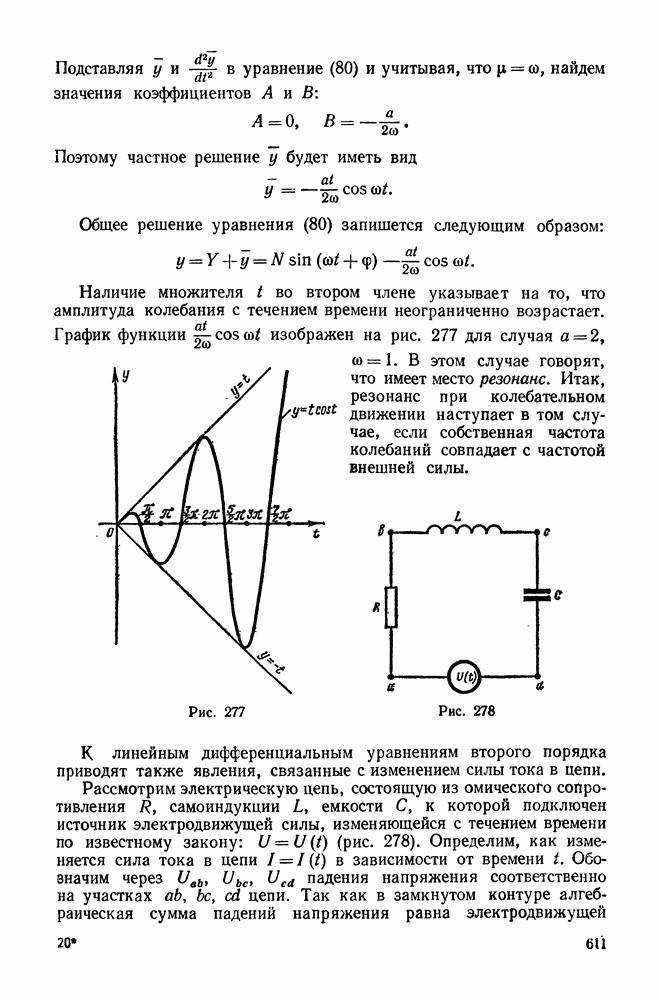
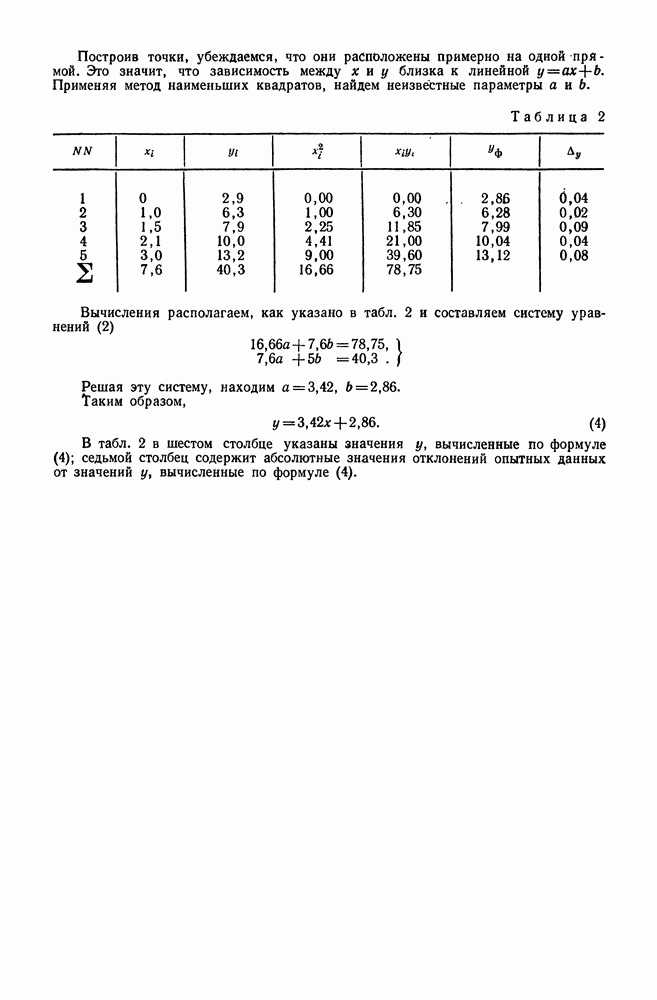
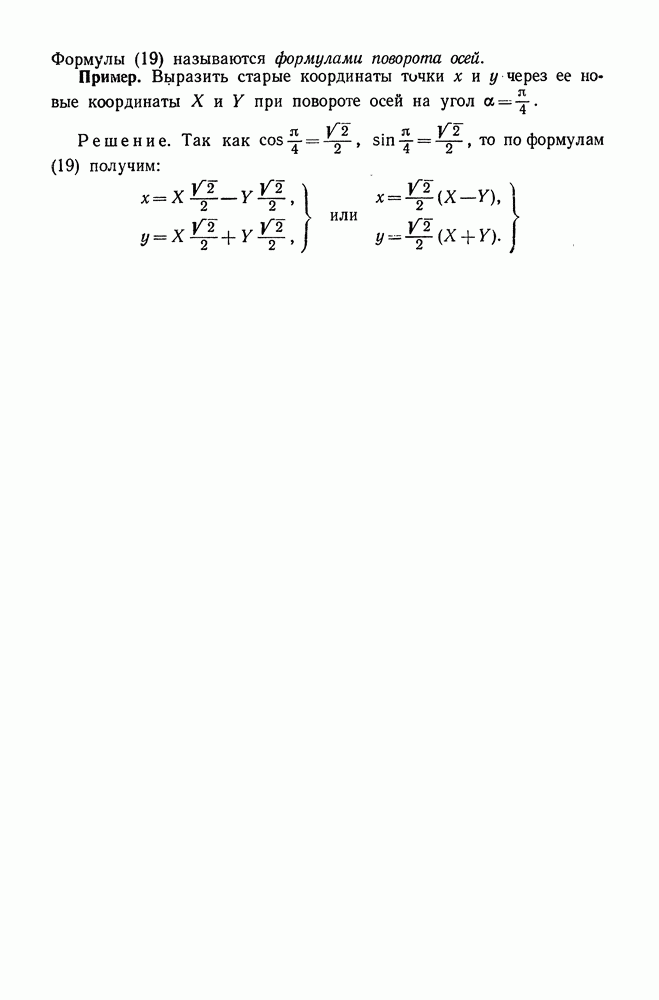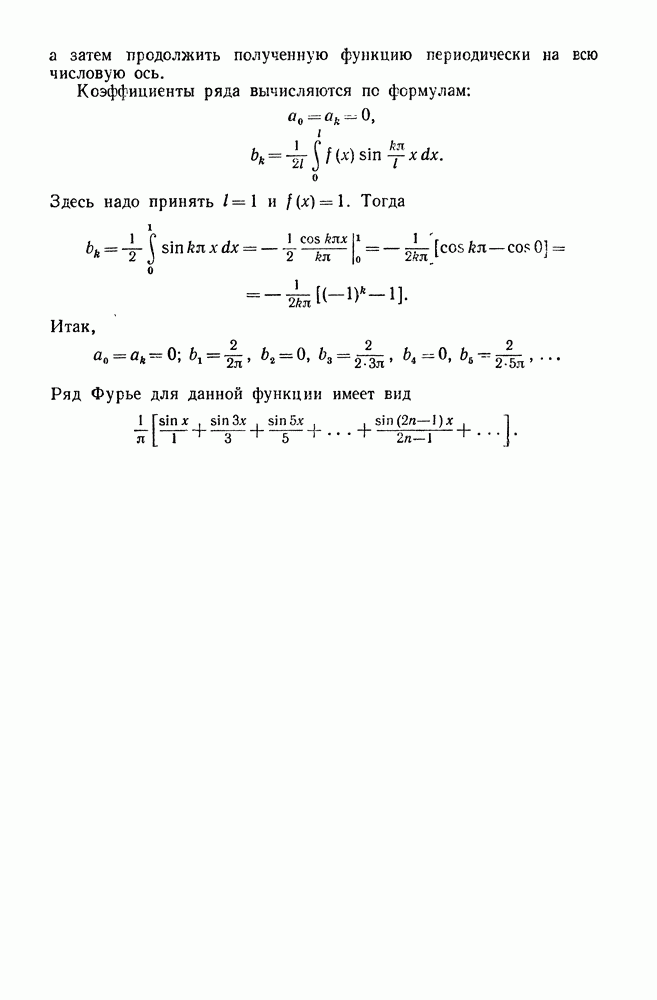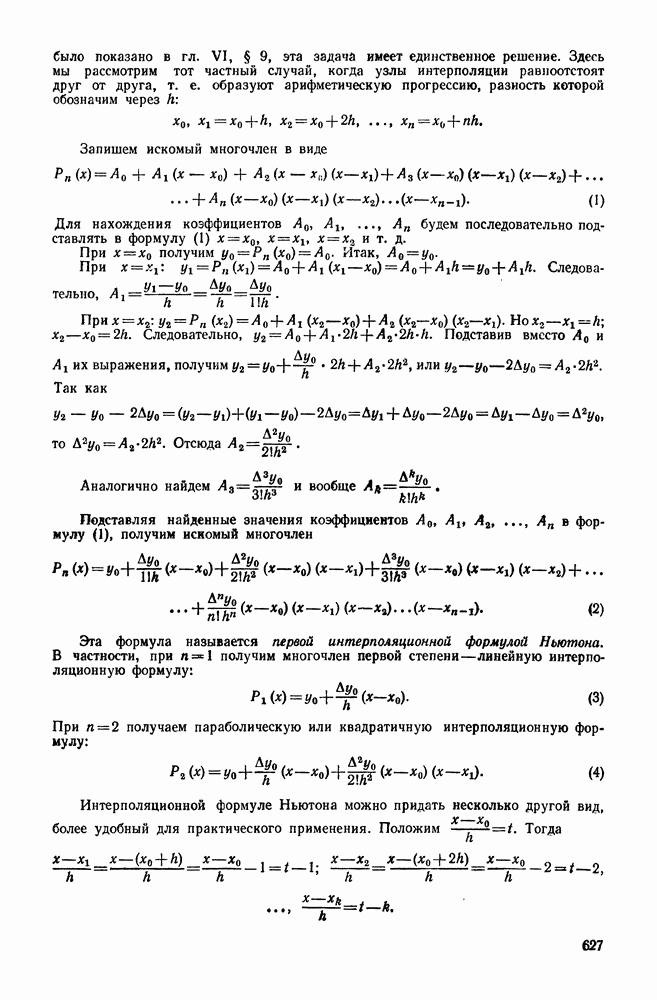| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
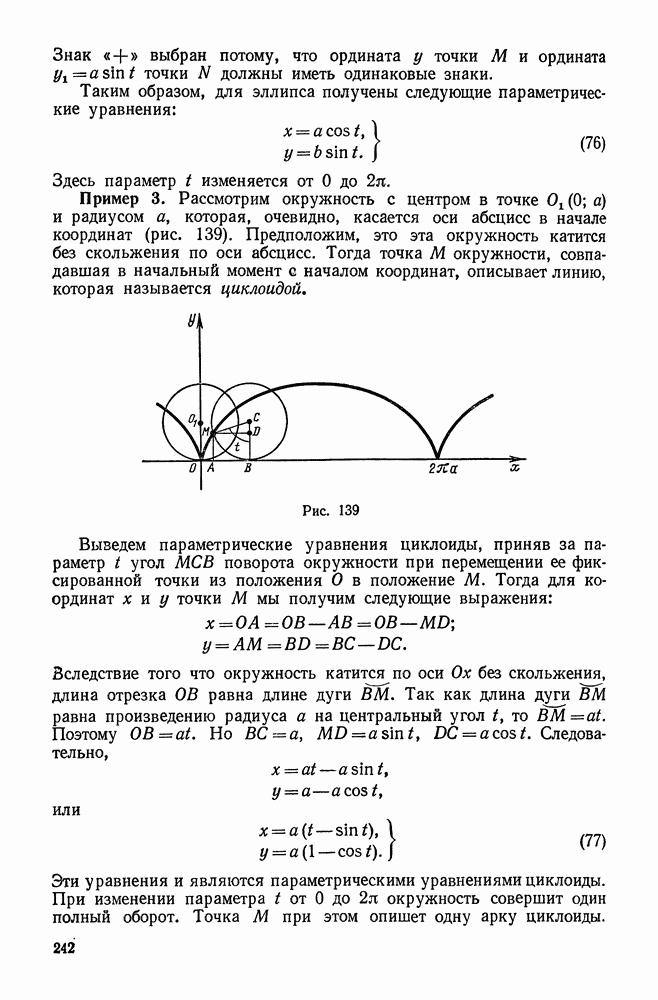
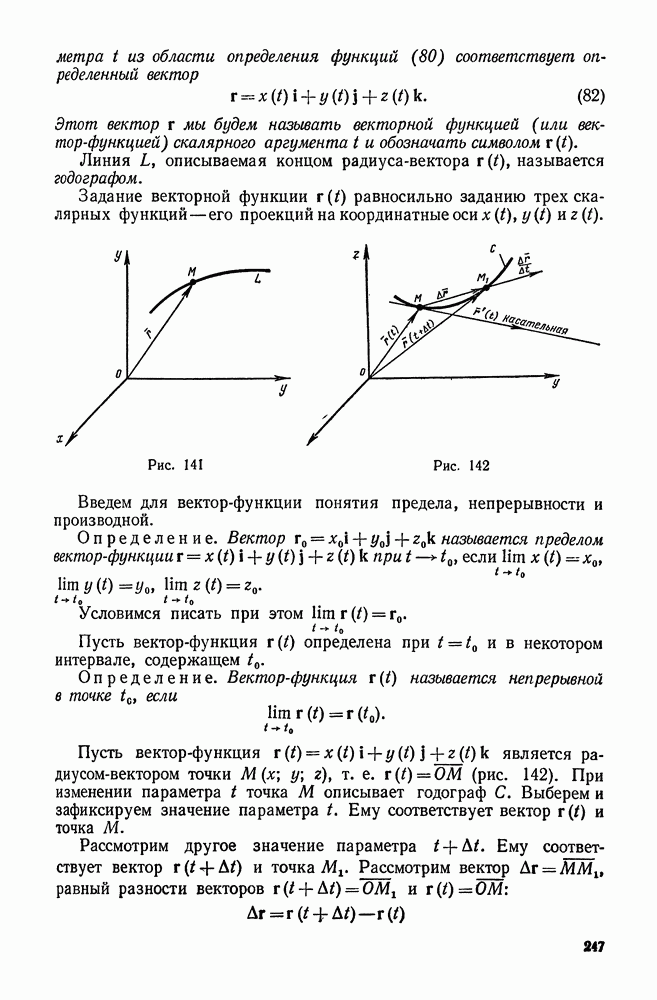
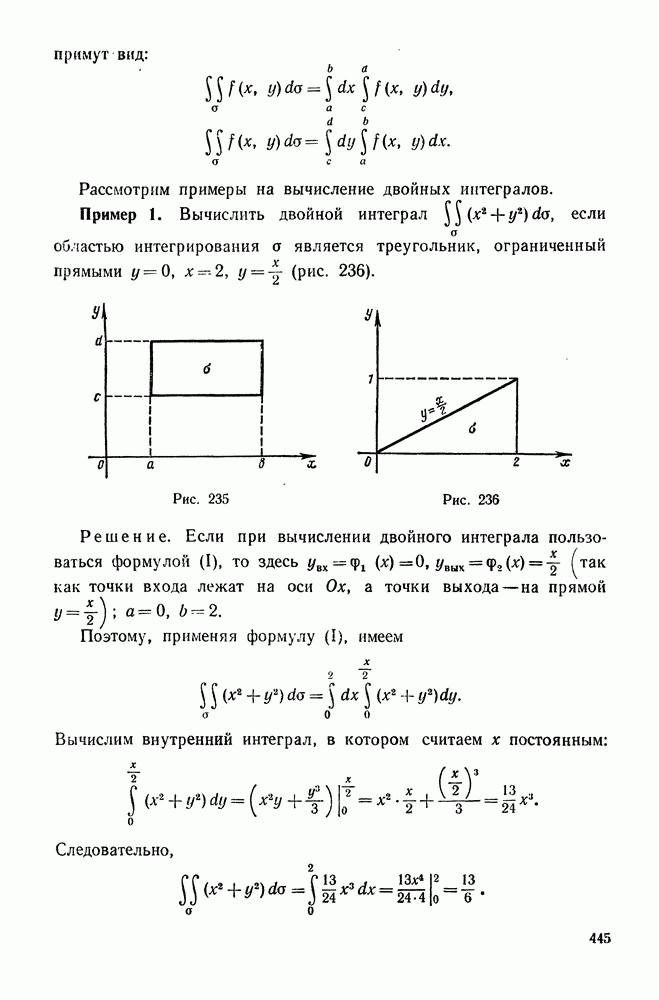
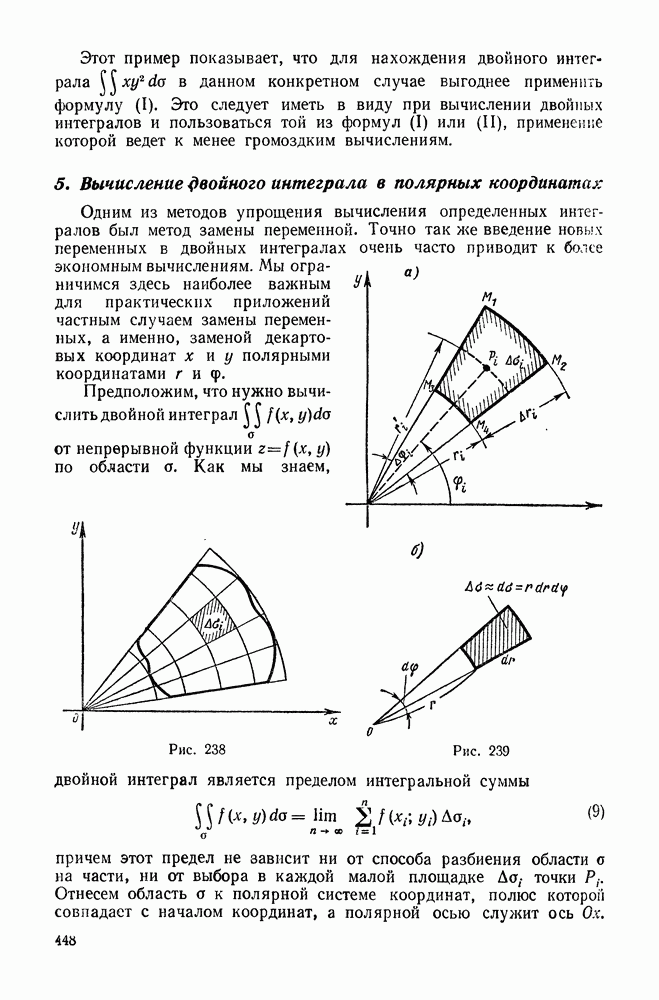
5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
Приведем примеры на разложение в степенные ряды некоторых элементарных функций.
1. Разложение в степенной ряд функции  . Находим производные:
. Находим производные:  . При
. При  имеем:
имеем:

Напишем ряд Маклорена для функции  воспользовавшись формулой (82):
воспользовавшись формулой (82):

Определим область сходимости этого ряда, применяя признак Даламбера:

Следовательно, для любого  , т. е. ряд (91) сходится абсолютно на всей числовой оси.
, т. е. ряд (91) сходится абсолютно на всей числовой оси.
Для того чтобы установить, что этот ряд имеет своей суммой функцию  , покажем, что для любого
, покажем, что для любого  стремится к нулю при
стремится к нулю при  . Напишем остаточный член ряда Маклорена.
. Напишем остаточный член ряда Маклорена.
Так как  то по формуле
то по формуле  имеет вид
имеет вид

где с заключено между 0 и  Функция
Функция  монотонно возрастает, поэтому так как
монотонно возрастает, поэтому так как  Таким образом,
Таким образом,

Мы только что видели, что ряд с общим членом сходится на всей числовой оси. Поэтому в силу необходимого признака сходимости при любом  Но тогда и также стремится к нулю при
Но тогда и также стремится к нулю при  Следовательно, на основании неравенства
Следовательно, на основании неравенства  Для любого значения
Для любого значения  и сумма ряда (91) совпадает с функцией е.
и сумма ряда (91) совпадает с функцией е.
Итак, на всей числовой оси имеет место разложение

2. Разложение в степенной ряд функции  . Находим производные:
. Находим производные: 
§ 2, п. 1, формула 
При  имеем:
имеем:

Принимая во внимание формулу (82), получим для функции  следующий ряд Маклорена:
следующий ряд Маклорена:

Как легко проверить, полученный ряд сходится на всей числовой оси. Исследуем его остаточный член  где с содержится между 0 и
где с содержится между 0 и  . Так как
. Так как  , то
, то  Принимая во внимание, что
Принимая во внимание, что  (см. предыдущий пример), заключаем, что
(см. предыдущий пример), заключаем, что 
Поэтому для функции  на всей числовой прямой имеет место разложение
на всей числовой прямой имеет место разложение

3. Разложение в степенной ряд функции  Разложение функции
Разложение функции  можно было бы получить приемом, аналогичным тому, с помощью которого было получено разложение в ряд функции
можно было бы получить приемом, аналогичным тому, с помощью которого было получено разложение в ряд функции  . Однако проще получить разложение функции
. Однако проще получить разложение функции  , если почленно продифференцировать разложение
, если почленно продифференцировать разложение  :
:

Следовательно,

Это разложение справедливо на всей числовой оси.
4. Биномиальный ряд. Разложим по степеням  функцию
функцию  где
где  — любое действительное число, отличное от нуля.
— любое действительное число, отличное от нуля.
Дифференцируя, имеем:

При 

Подставляя в формулу (82), получим ряд Маклорена для функции 

Этот ряд называется биномиальным. Найдем его интервал сходимости. Применяя признак Даламбера, получим

Мы видим, что ряд сходится при  т. е. в интервале —
т. е. в интервале —  Можно показать, что и в данном случае остаточный член
Можно показать, что и в данном случае остаточный член  для
для  при
при  стремится к нулю. Однако в связи со сложностью этого доказательства мы его опускаем.
стремится к нулю. Однако в связи со сложностью этого доказательства мы его опускаем.
Итак, в интервале  имеет место разложение
имеет место разложение

При  если только
если только  не является натуральным числом, ряд расходится. На границах интервала сходимости ряд будет сходиться или расходиться в зависимости от конкретных значений
не является натуральным числом, ряд расходится. На границах интервала сходимости ряд будет сходиться или расходиться в зависимости от конкретных значений  . Если
. Если  — натуральное число, то начиная с
— натуральное число, то начиная с  все коэффициенты обращаются в нуль, и получаем многочлен, называемый биномом Ньютона (см. в сноске на стр. 184 формулу бинома Ньютона, в которой следует положить
все коэффициенты обращаются в нуль, и получаем многочлен, называемый биномом Ньютона (см. в сноске на стр. 184 формулу бинома Ньютона, в которой следует положить 
Приведем несколько примеров биномиальных рядов для различных значений 
а)  . Здесь
. Здесь  Применяя формулу (96), получим
Применяя формулу (96), получим

или, после упрощений,

Это разложение имеет место во всяком случае для  Более подробные исследования показывают, что оно справедливо и при
Более подробные исследования показывают, что оно справедливо и при  и при
и при  (см. сноску.)
(см. сноску.)
б)  . Здесь
. Здесь  . По формуле (96) получим разложение
. По формуле (96) получим разложение

справедливое для  . Можно показать, что разложение (98) справедливо и для
. Можно показать, что разложение (98) справедливо и для  (см. сноску.)
(см. сноску.)
в)  . Здесь
. Здесь  Применяя формулу (96), получим после упрощений
Применяя формулу (96), получим после упрощений

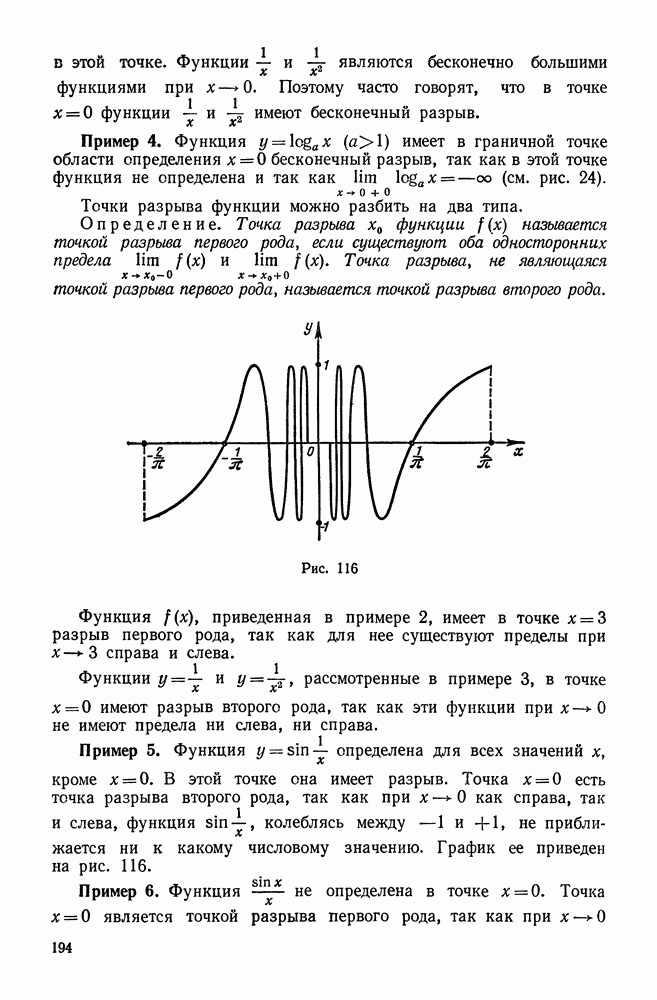
5. Разложение в степенной ряд функции  При функция
При функция  не определена, поэтому ее нельзя разложить по степеням
не определена, поэтому ее нельзя разложить по степеням  т. е. в ряд Маклорена. Разложим функцию
т. е. в ряд Маклорена. Разложим функцию  например, по степеням
например, по степеням 
Находим производные:

При  получим
получим

Применяя формулу (81), получим ряд Тейлора для функции 

или, после сокращений,

Применяя признак Даламбера и исследуя ряд на концах, найдем, что он сходится для всех значений  удовлетворяющих неравенствам
удовлетворяющих неравенствам  . Можно показать, что для всех значений
. Можно показать, что для всех значений  принадлежащих области сходимости,
принадлежащих области сходимости,  . Поэтому для
. Поэтому для  имеет место следующее разложение:
имеет место следующее разложение:

Разложение функций в степенной ряд по формулам (81) и (82) часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. Покажем некоторые приемы, позволяющие при разложении функции в степенной ряд, избежать этих трудностей. С одним из таких приемов, основанным на возможности почленного дифференцирования степенного ряда в интервале его сходимости, мы познакомились при разложении функции  .
.
Применение формулы суммы геометрической прогрессии. Рассмотрим функцию  Легко видеть, что эта функция является суммой геометрической прогрессии с первым членом, равным единице, и со знаменателем
Легко видеть, что эта функция является суммой геометрической прогрессии с первым членом, равным единице, и со знаменателем  Поэтому
Поэтому

Это разложение имеет место для  Заметим, что функцию
Заметим, что функцию  можно записать в виде
можно записать в виде  и, следовательно, ряд (99) является биномиальным и его можно было бы получить по формуле (96) при
и, следовательно, ряд (99) является биномиальным и его можно было бы получить по формуле (96) при 
Метод подстановки. Сущность этого метода ясна из следующих примеров.
Пример 1. Разложить в степенной ряд функцию  Решение. Положим
Решение. Положим  . Тогда
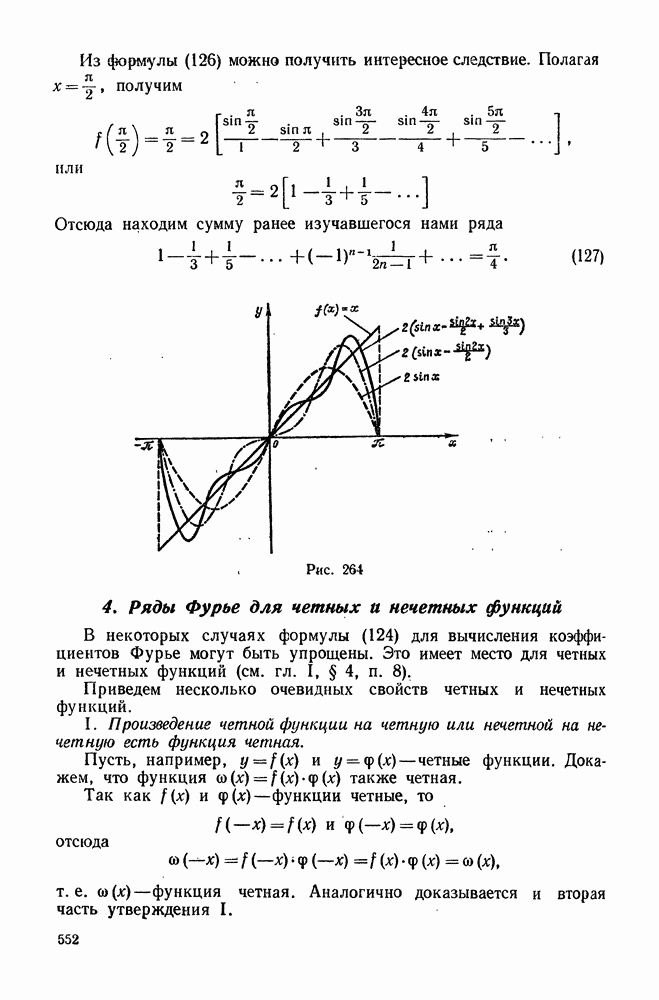
. Тогда  . Напишем разложение функции
. Напишем разложение функции  применив формулу (93):
применив формулу (93):

Это разложение имеет место для всех значений t. В частности, при  получим разложение
получим разложение

справедливое для всех значений 
Пример 2. Разложить по степеням  функцию
функцию 
Решение. Полагаем  Тогда
Тогда  Воспользовавшись формулой (98), получим разложение
Воспользовавшись формулой (98), получим разложение

справедливое для интервала 
Подставив в это разложение  вместо t, получим разложение, годное для всех значений
вместо t, получим разложение, годное для всех значений  из интервала
из интервала 

Пример 3. Разложить по степеням  функцию
функцию 
Решение. Полагая  получим
получим  . По формуле (99)
. По формуле (99)

Подставив в это разложение  вместо t, получим
вместо t, получим

справедливое для интервала 
Разложение в степенной ряд методом интегрирования. Сущность метода заключается в следующем. Допустим, что известно разложение в степенной ряд для производной от функции  . Тогда, интегрируя ряд почленно, получим разложение в ряд функции
. Тогда, интегрируя ряд почленно, получим разложение в ряд функции  Пример 4. Разложить по степеням
Пример 4. Разложить по степеням  функцию
функцию  .
.
Решение. Рассмотрим следующее тождество: 
Разложим подынтегральную функцию по формуле (99) в степенной ряд

который сходится для всех значений t из интервала  Так как в интервале сходимости степенной ряд можно почленно интегрировать, то для
Так как в интервале сходимости степенной ряд можно почленно интегрировать, то для  имеем
имеем

Таким образом, если  то
то

Можно показать, что это равенство справедливо и для  Пример 5. Разложить по степеням
Пример 5. Разложить по степеням  функцию
функцию  .
.
Решение. Рассмотрим тождество

Разложим подынтегральную функцию в степенной ряд, воспользовавшись формулой (102):

Этот ряд сходится для всех значений t, удовлетворяющих неравенствам —  Следовательно,
Следовательно,

Это разложение справедливо для всех значений  из интервала
из интервала  . Однако можно показать, что оно остается в силе и на концах интервала.
. Однако можно показать, что оно остается в силе и на концах интервала.
Итак, для всех  принадлежащих сегменту
принадлежащих сегменту  , имеет место равенство
, имеет место равенство

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
- § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
- 2. Геометрическое изображение действительных чисел. Координаты точки на прямой
- 3. Абсолютная величина действительного числа
- 4. Расстояние между двумя точками на прямой
- § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- 2. Расстояние между двумя точками на плоскости
- 3. Деление отрезка в данном отношении
- 4. Координаты точки в пространстве
- 5. Расстояние между двумя точками в пространстве
- § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
- 2. Полярные координаты
- 3. Зависимость между декартовыми и полярными координатами
- § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
- 2. Понятие функции
- 3. График функции
- 4. Способы задания функций
- 5. Основные элементарные функции и их графики
- 6. Сложные функции. Элементарные функции
- 7. Целые и дробно-рациональные функции
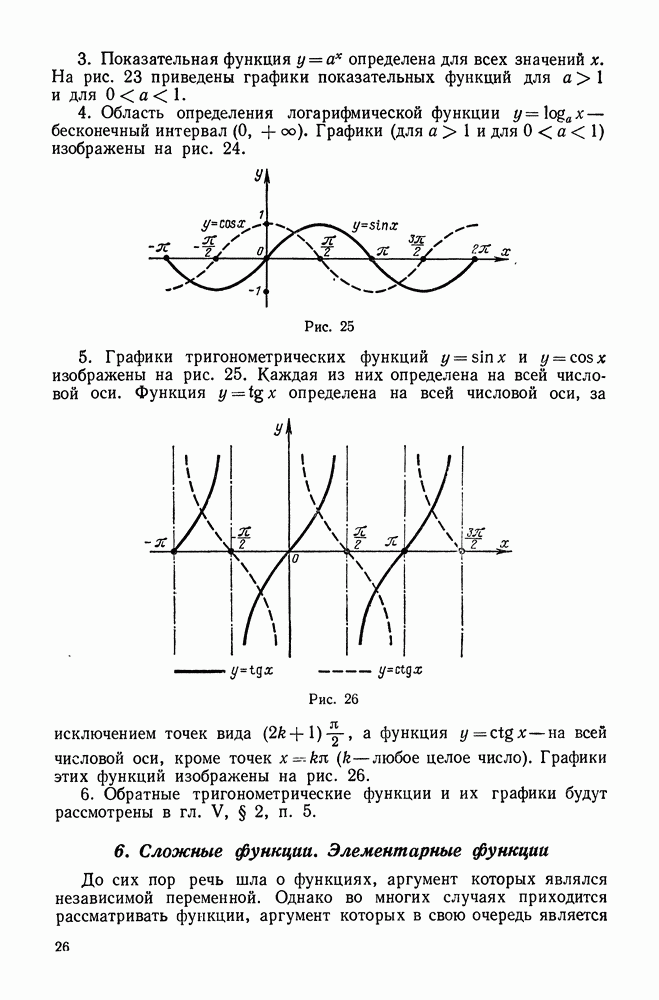
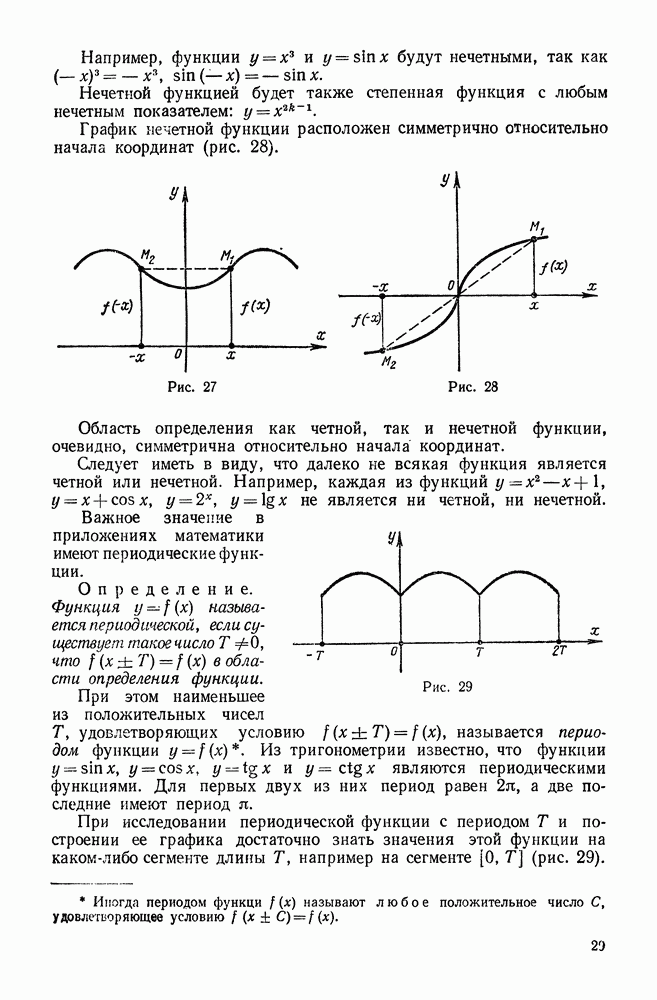
- 8. Функции четные и нечетные. Периодические функции
- § 5. УРАВНЕНИЕ ЛИНИИ
- 2. Нахождение уравнения линии по ее геометрическим свойствам
- § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 2. Поворот осей координат
- ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. ПРЯМАЯ
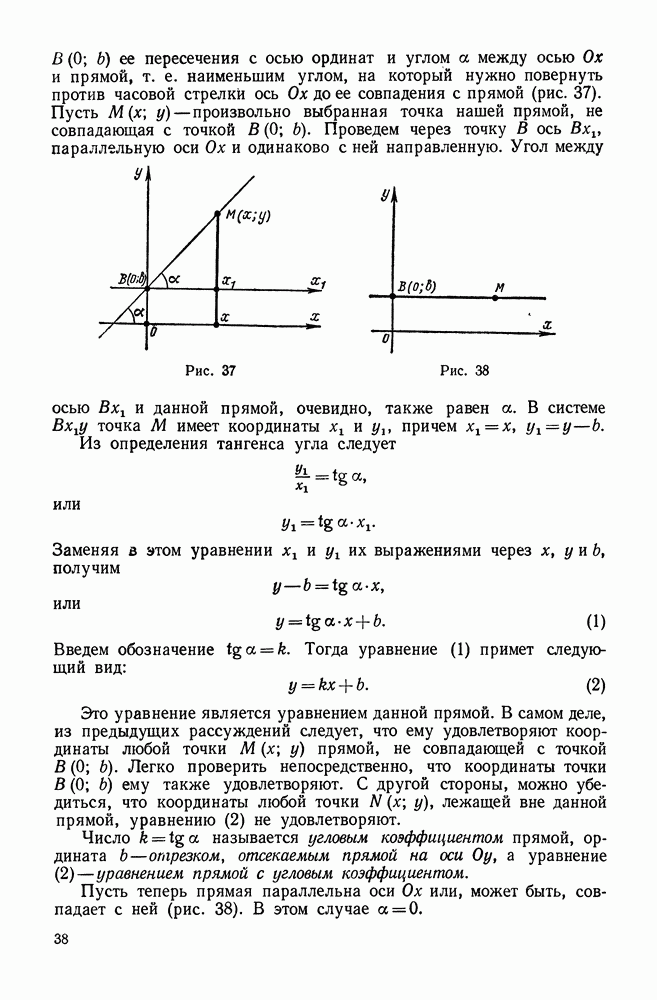
- 2. Уравнение прямой с угловым коэффициентом
- 3. Уравнение прямой, параллельной оси ординат
- 4. Общее уравнение прямой и его частные случаи
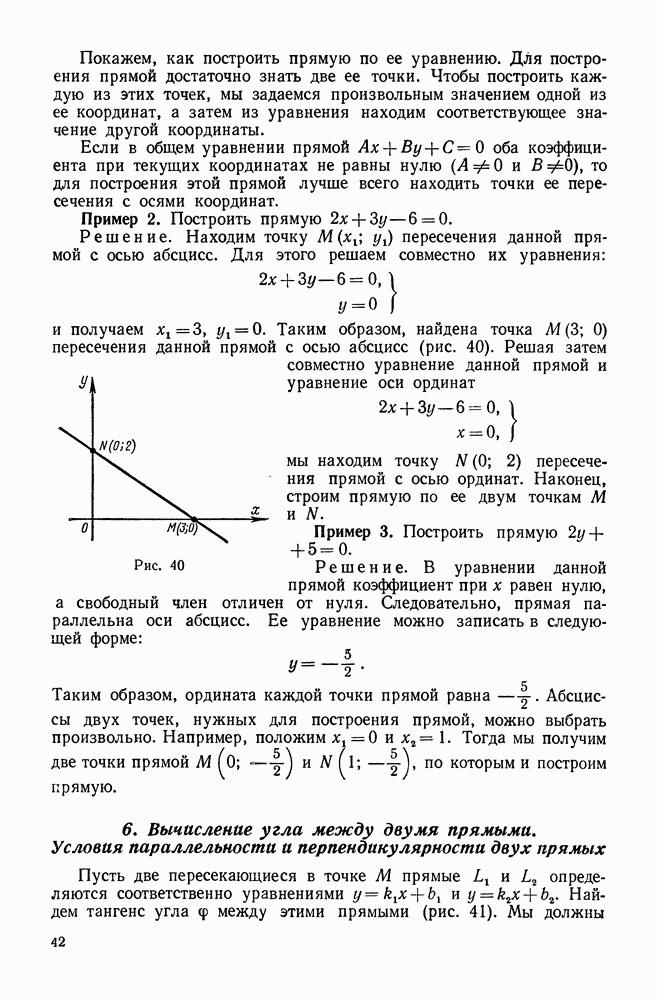
- 5. Точка пересечения прямых. Построение прямой по ее уравнению
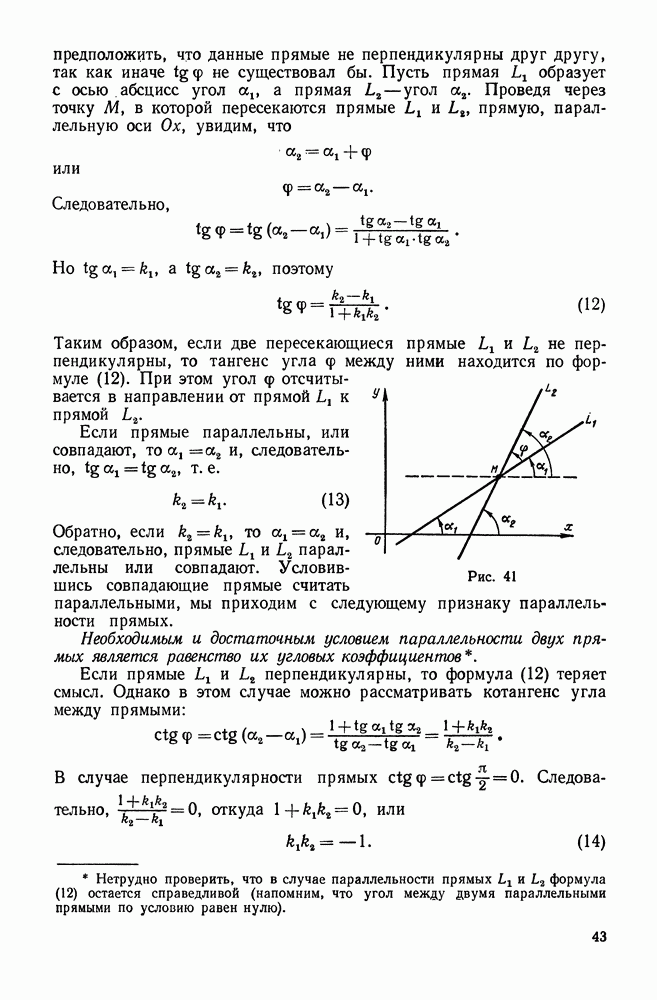
- 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
- 7. Уравнение прямой, проходящей через данную точку в заданном направлении
- 8. Пучок прямых
- 9. Уравнение прямой, проходящей через две данные точки
- 10. Расстояние от точки до прямой
- § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
- 2. Окружность
- 3. Эллипс
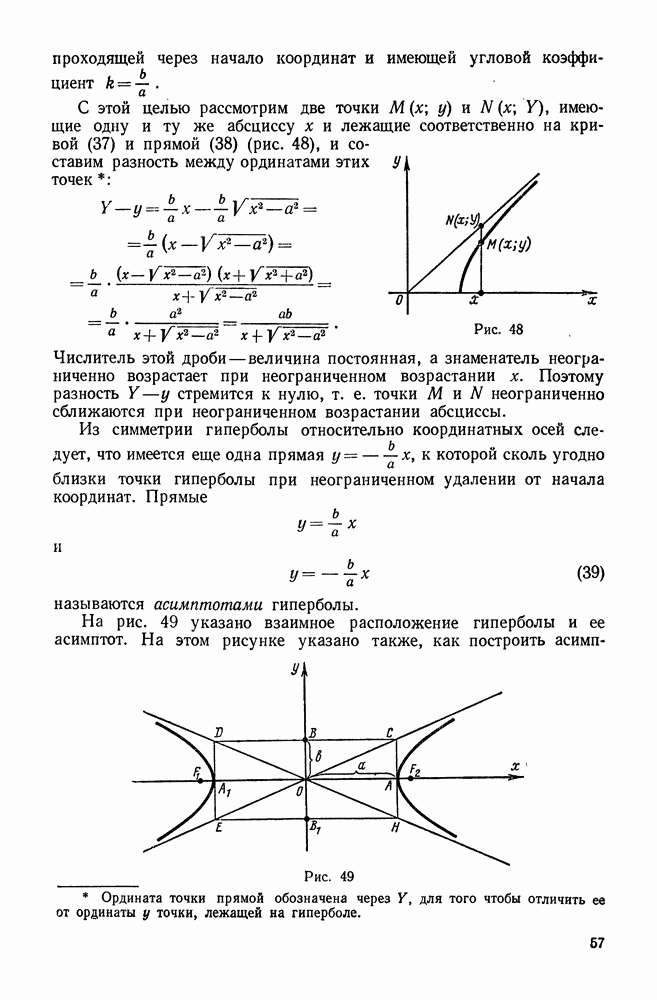
- 4. Гипербола
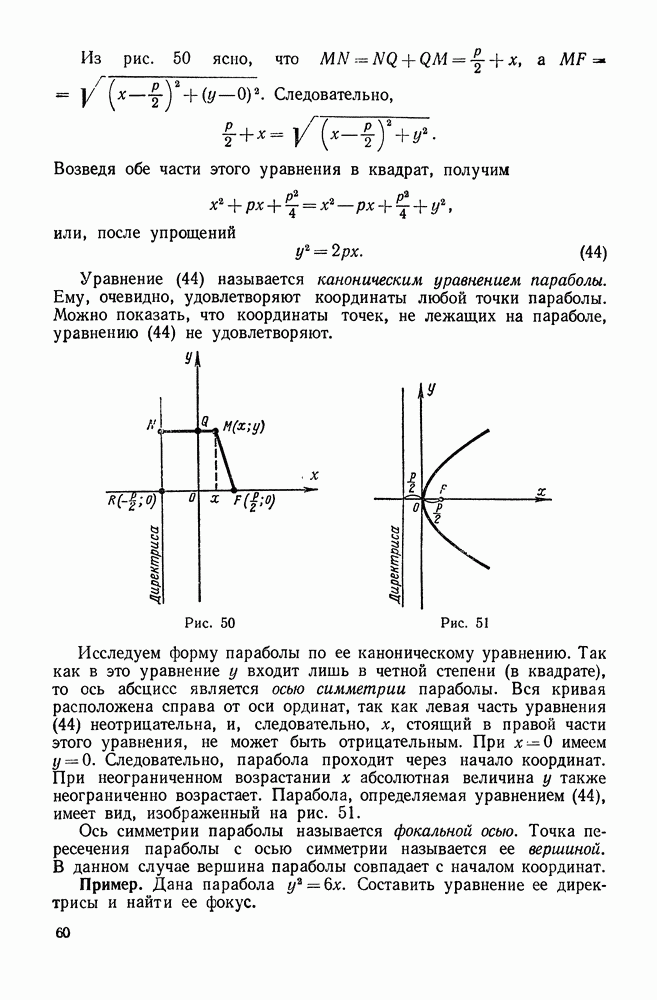
- 5. Парабола
- 6. Окружность, эллипс, гипербола и парабола как конические сечения
- 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена
- 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
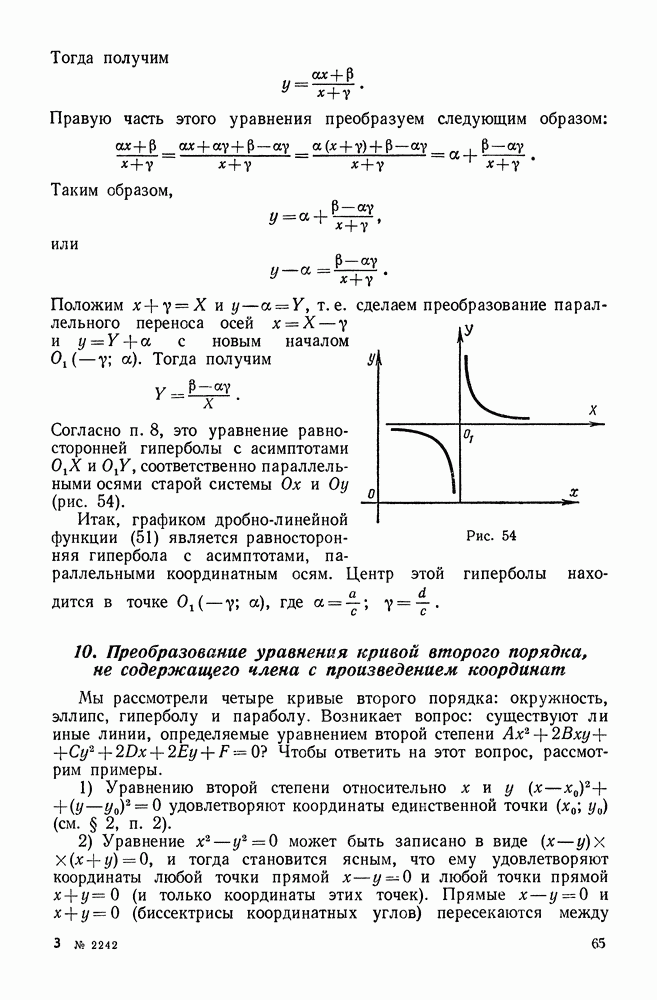
- 9. График дробно-линейной функции
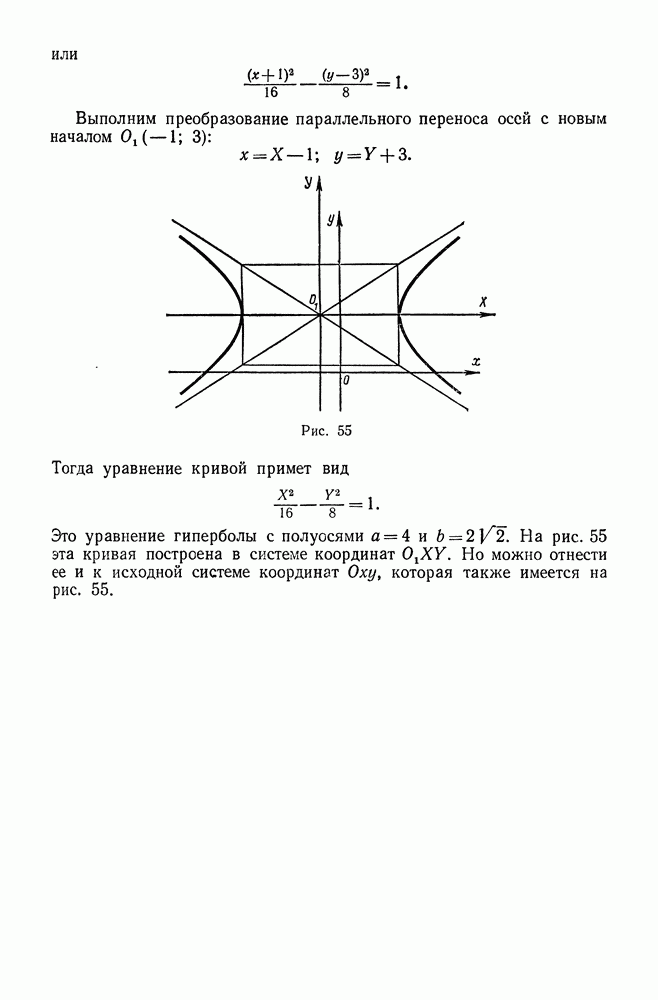
- 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
- ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
- § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
- 2. Определитель третьего порядка
- 3. Понятие об определителях высших порядков
- § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
- 2. Однородная система двух уравнений первой степени с тремя неизвестными
- 3. Система трех уравнений первой степени с тремя неизвестными
- 4. Однородная система трех уравнений первой степени с тремя неизвестными
- § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- 2. Линейные операции над векторами
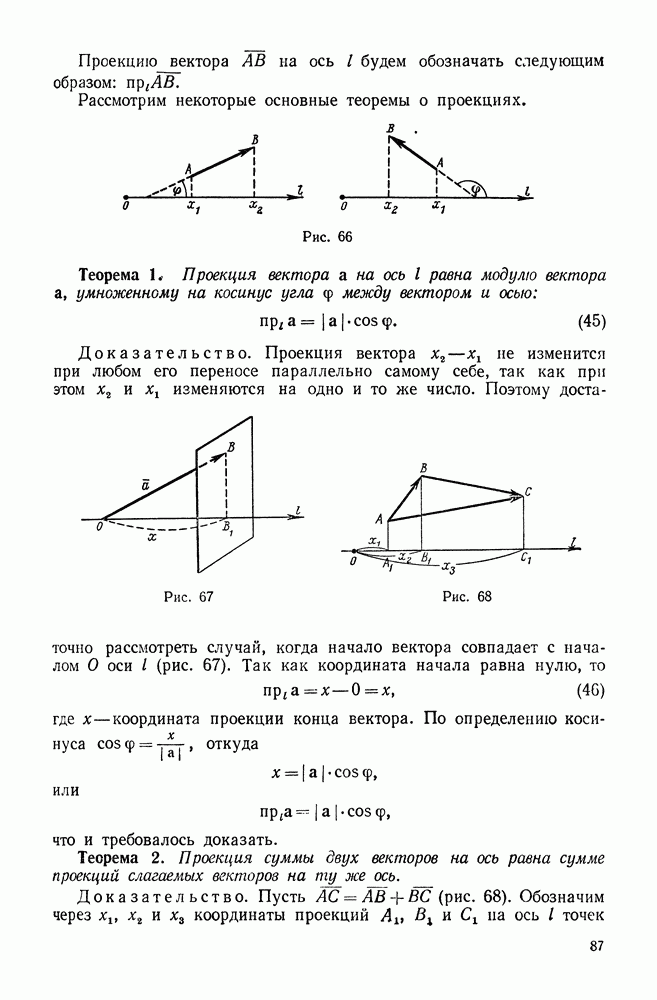
- 4. Проекция вектора на ось и составляются вектора по оси
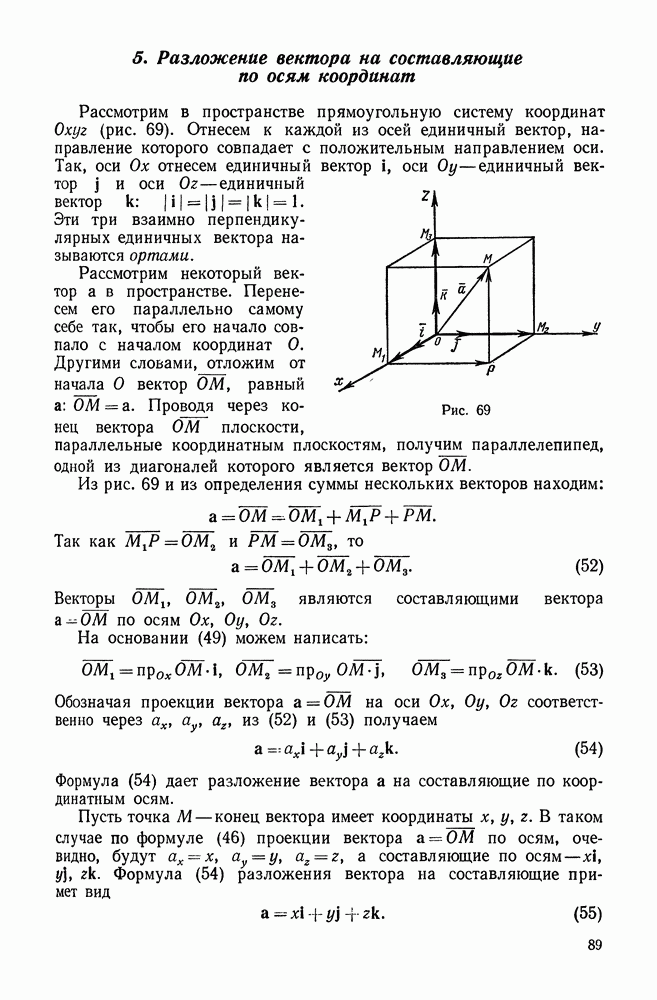
- 5. Разложение вектора на составляющие по осям координат
- 6. Направляющие косинусы вектора
- 7. Условие коллинеарности двух векторов
- 8. Скалярное произведение
- 9. Выражение скалярного произведения через проекции перемножаемых векторов
- 10. Косинус угла между двумя векторами
- 11. Векторное произведение
- 12. Выражение векторного произведения через проекции перемножаемых векторов
- 13. Смешанное произведение трех векторов
- 14. Геометрический смысл смешанного произведения
- 15. Условие компланарности трех векторов
- § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. Равенство матриц. Действия над матрицами
- 3. Обратная матрица
- 4. Матричная запись и матричное решение системы уравнений первой степени
- § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- 2. Преобразование координат
- 3. Приведение квадратичной формы к каноническому виду
- 4. Упрощение общего уравнения кривой второго порядка
- ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 1. ПЛОСКОСТЬ
- 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
- 3. Общее уравнение плоскости и его частные случаи
- 4. Построение плоскости по ее уравнению
- 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
- 6. Точка пересечения трех плоскостей
- § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
- 2. Общие уравнения прямой
- 3. Векторное уравнение прямой. Параметрические уравнения прямой
- 4. Канонические уравнения прямой
- 5. Уравнения прямой, проходящей через две точки
- 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
- § 3. Прямая и плоскость в пространстве
- 2. Точка пересечения прямой с плоскостью
- 3. Расстояние от точки до плоскости
- 4. Пучок плоскостей
- § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- 2. Цилиндрические поверхности
- 3. Конические поверхности
- 4. Поверхность вращения
- 6. Гиперболоиды
- 7. Параболоиды
- ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПРЕДЕЛ ФУНКЦИИ
- 2. Предел функции при х -> -оо
- 3. Предел функции при х->х0
- 4. Бесконечно малые функции. Ограниченные функции
- 5. Бесконечно большие функции и их связь с бесконечно малыми функциями
- 6. Основные теоремы о пределах
- 7. Предел функции при x -> 0
- 8. Последовательность. Число e
- 9. Натуральные логарифмы
- 10. Сравнение бесконечно малых функций
- § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Операции над непрерывными функциями. Непрерывность элементарных функций
- 3. Свойства функций, непрерывных на сегменте
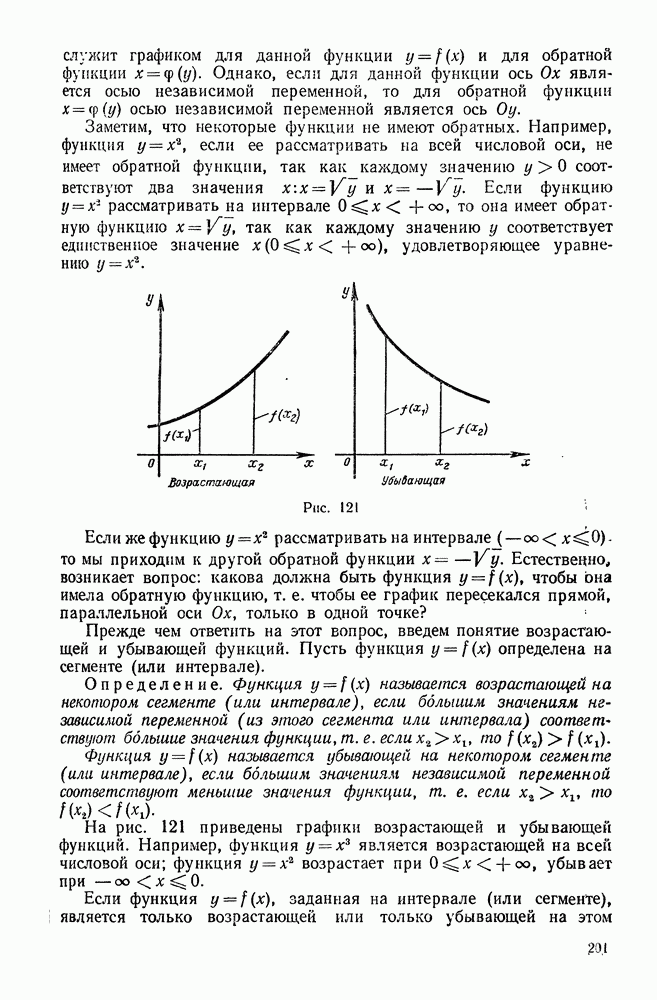
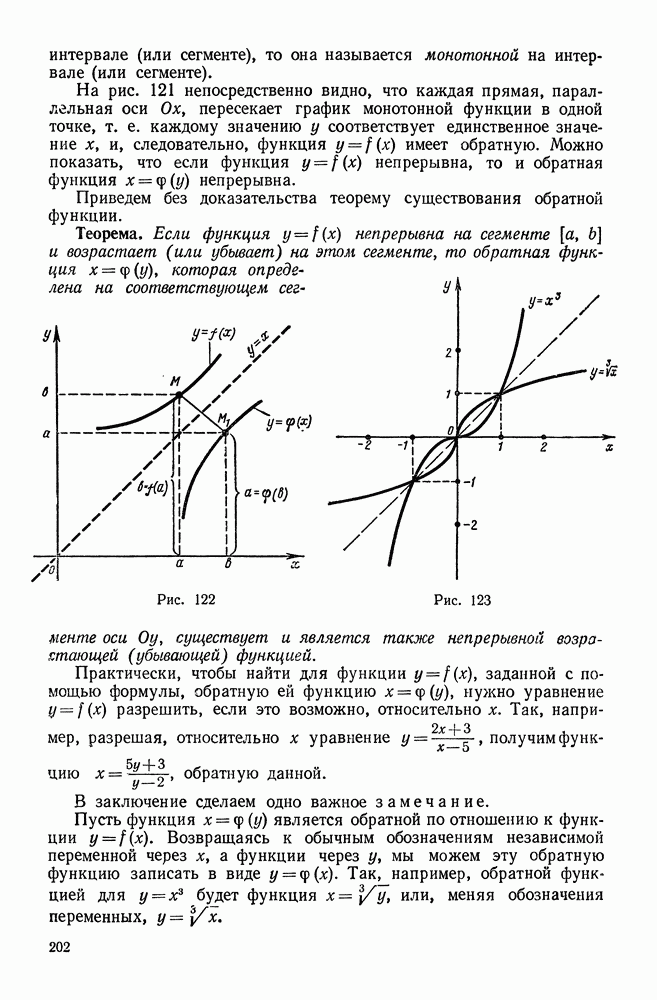
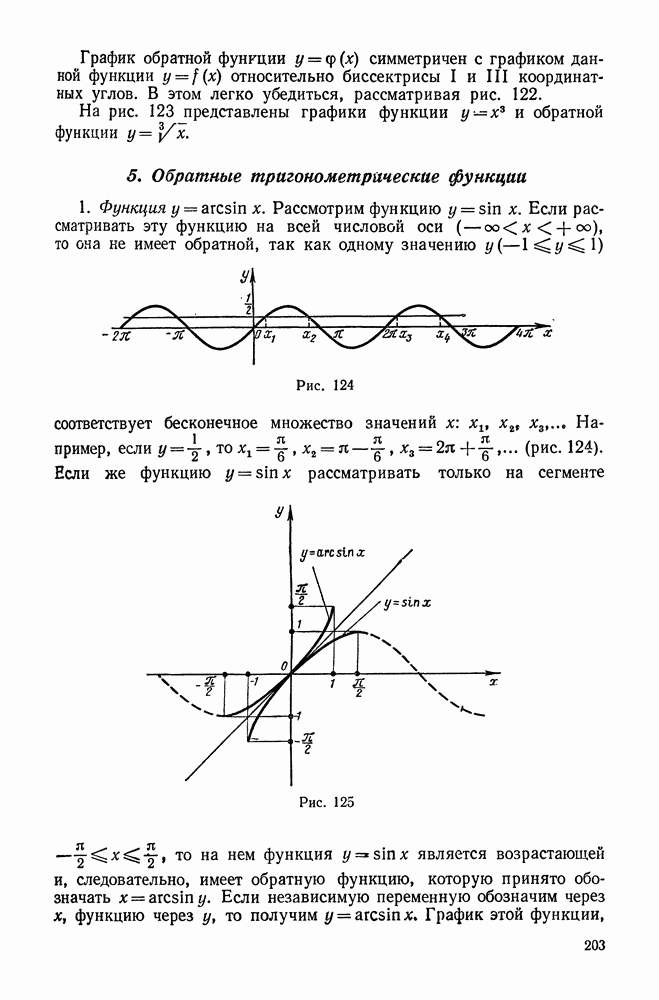
- 4. Понятие об обратной функции
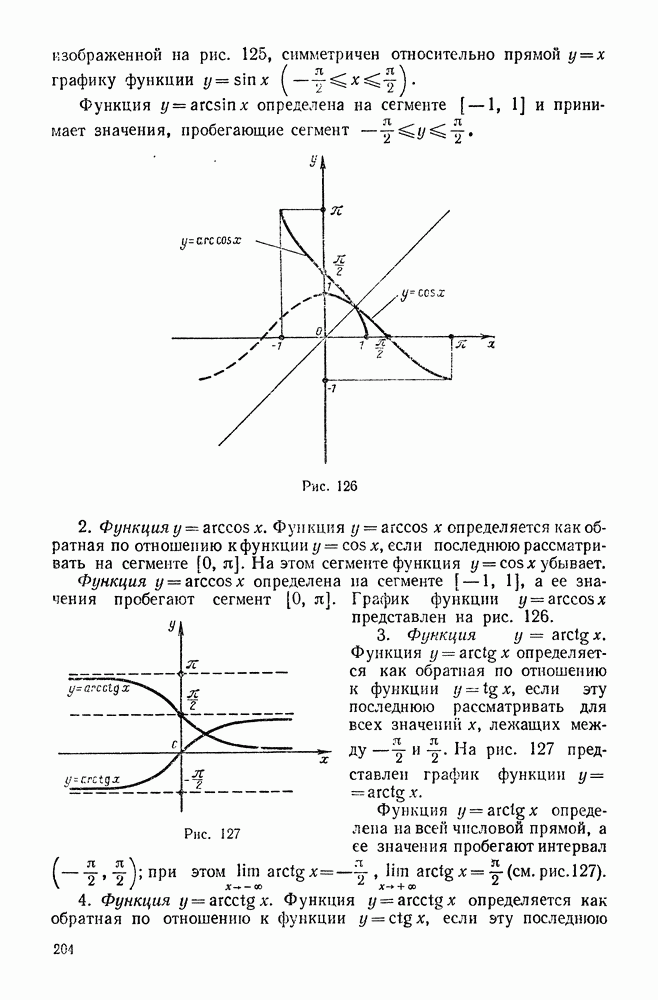
- 5. Обратные тригонометрические функции
- 6. Показательная и логарифмическая функции
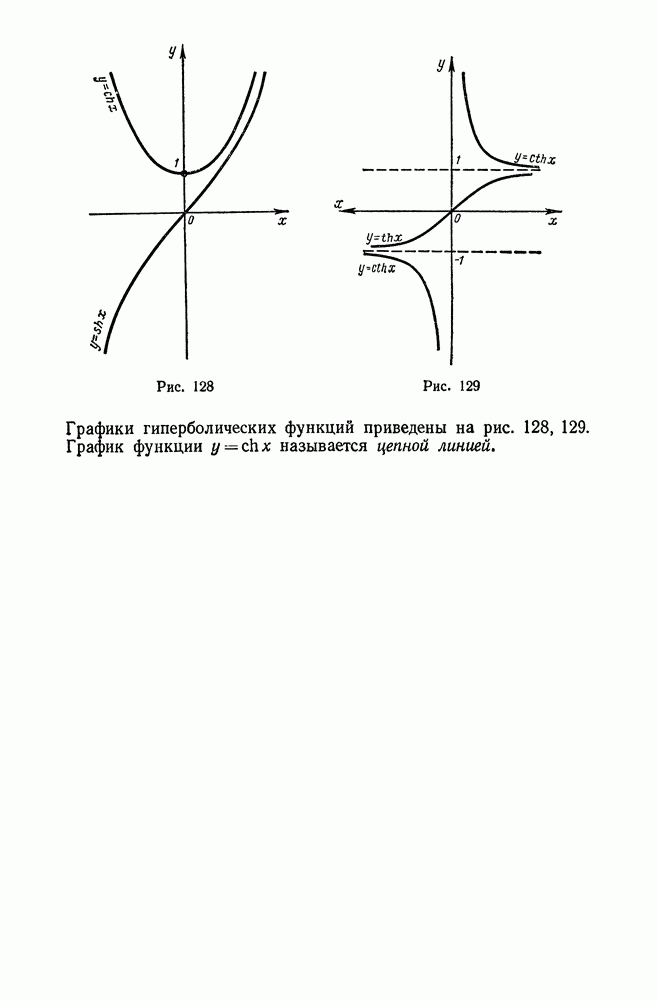
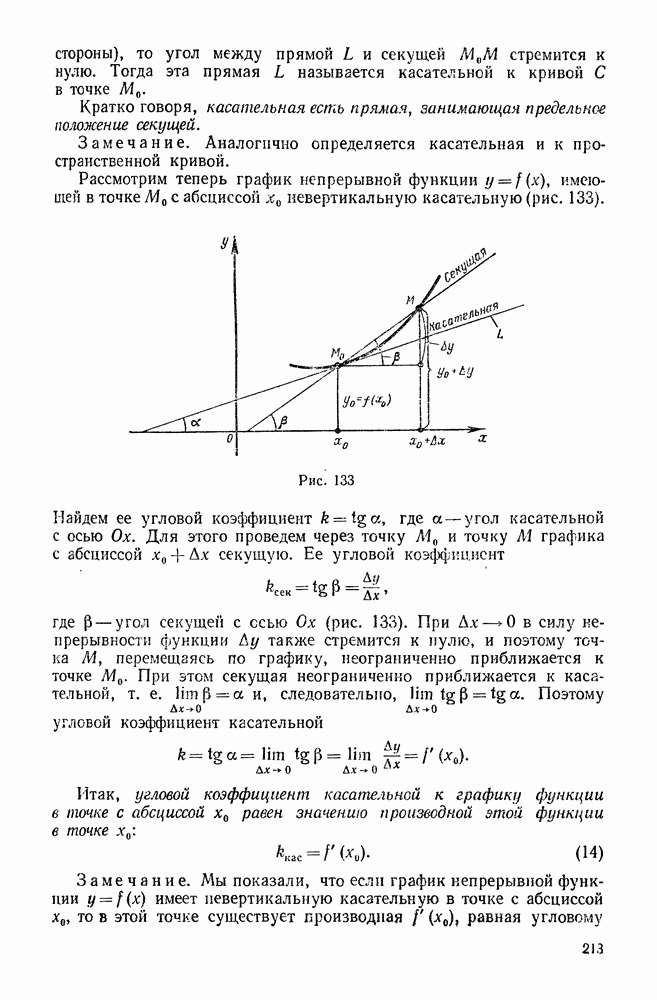
- 7. Понятие о гиперболических функциях
- ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- 1. Приращение аргумента и приращение функции
- 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
- 3. Задачи, приводящие к понятию производной
- 4. Определение производной и ее механический смысл
- 5. Дифференцируемость функции
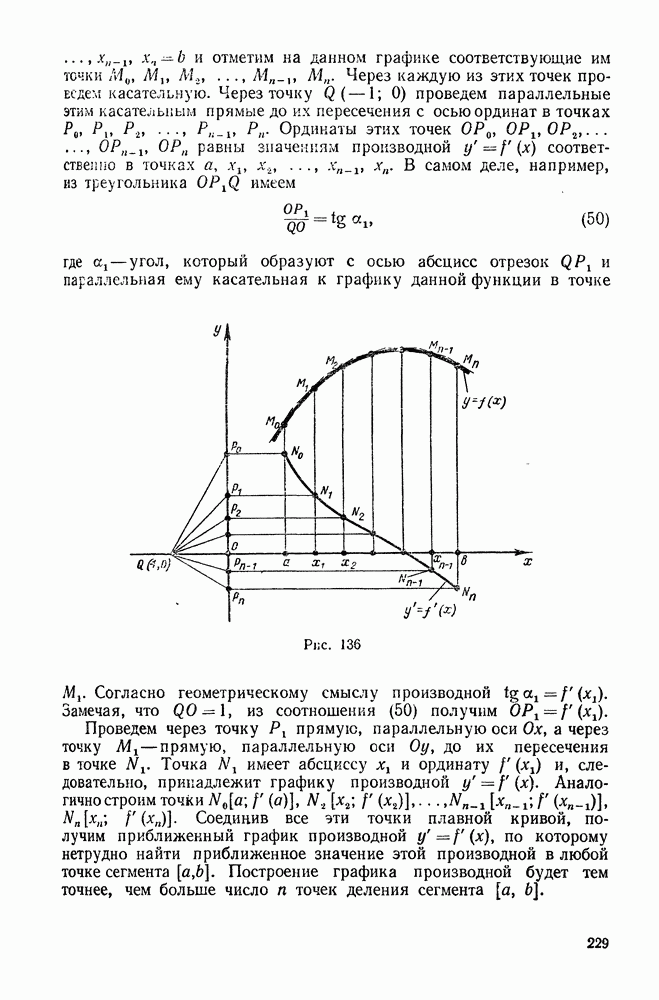
- 6. Геометрический смысл производной
- 7. Производные некоторых основных элементарных функций
- 8. Основные правила дифференцирования
- 9. Производная обратной функции
- 10. Производные обратных тригонометрических функций
- 11. Производная сложной функции
- § 12. Производные гиперболических функций
- 13. Производная степенной функции с любым показателем
- 14. Сводная таблица формул дифференцирования
- 15. Неявные функции и их дифференцирование
- 16. Уравнения касательной а нормали к кривой
- 17. Графическое дифференцирование
- § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- 1. Нахождение производных высших порядков
- 2. Механический смысл второй производной
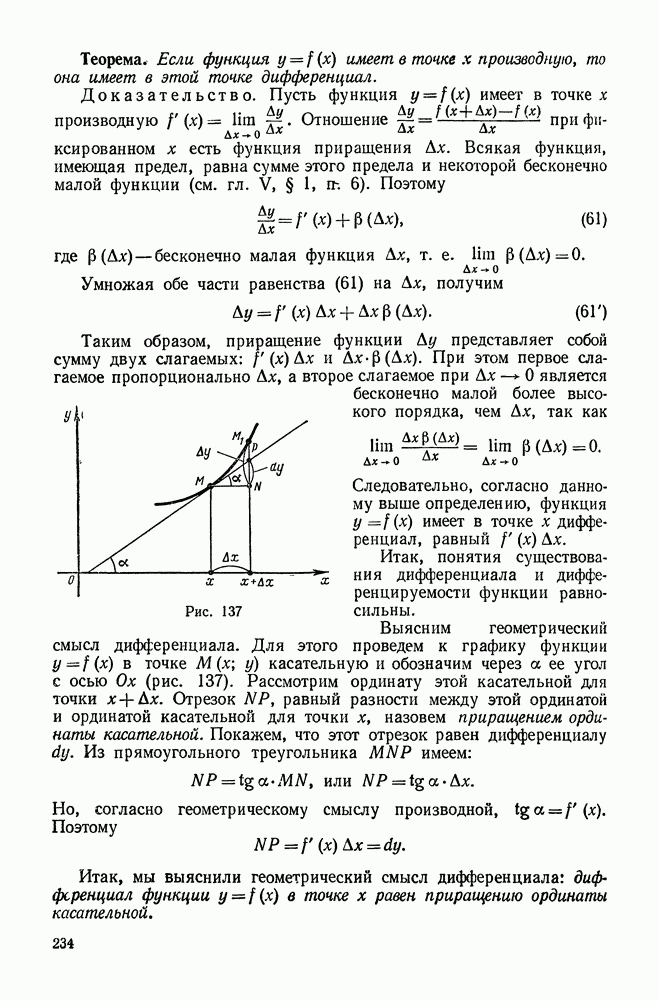
- § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- 2. Производная как отношение дифференциалов
- 3. Дифференциал суммы, произведения и частного функций
- 4. Дифференциал сложной функции. Инвариантность формы дифференциала
- 5. Применение дифференциала к приближенным вычислениям
- 6. Дифференциалы высших порядков
- § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
- 2. Дифференцирование функций, заданных параметрически
- § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
- 2. Векторная функция скалярного аргумента и ее производная
- 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой
- 4. Механический смысл первой и второй производных векторной функции скалярного аргумента
- § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
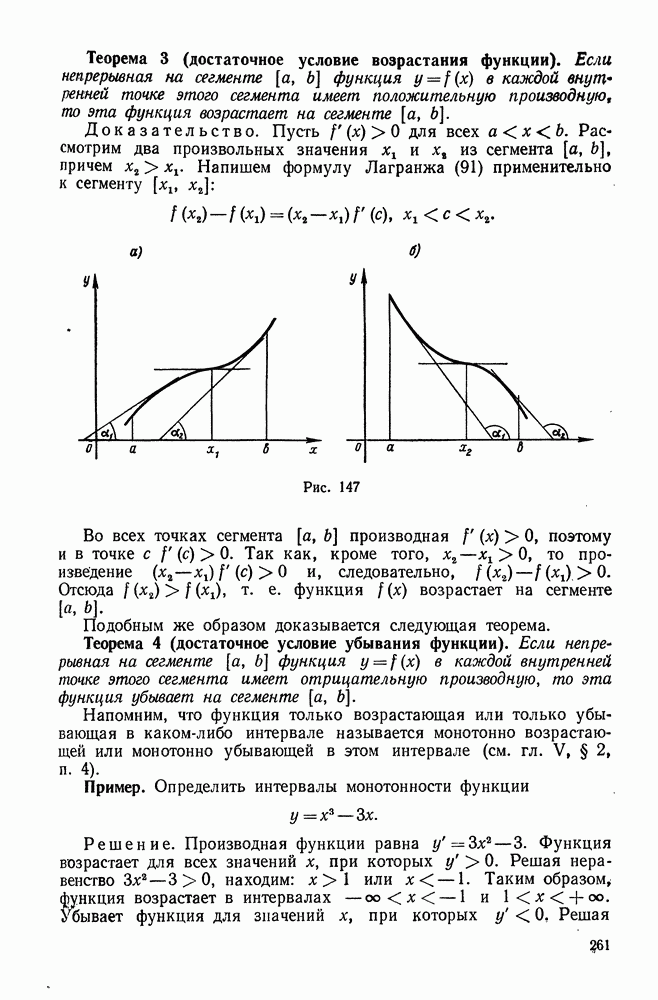
- 2. Теорема Ролля
- 3. Теорема Лагранжа
- 4. Правило Лопиталя
- § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
- 2. Максимум и минимум функции
- 3. Достаточный признак существования экстремума, основанный на знаке второй производной
- 4. Отыскание наибольшего и наименьшего значений функции
- 5. Применение теории максимума и минимума к решению задач
- 6. Выпуклость и вогнутость графика функции. Точки перегиба
- 7. Асимптоты графика функции
- 8. Общая схема исследования функции и построение ее графика
- § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
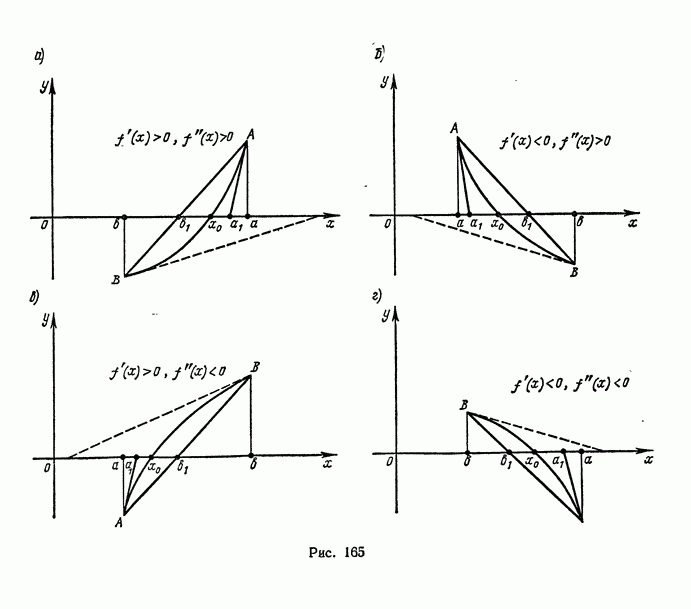
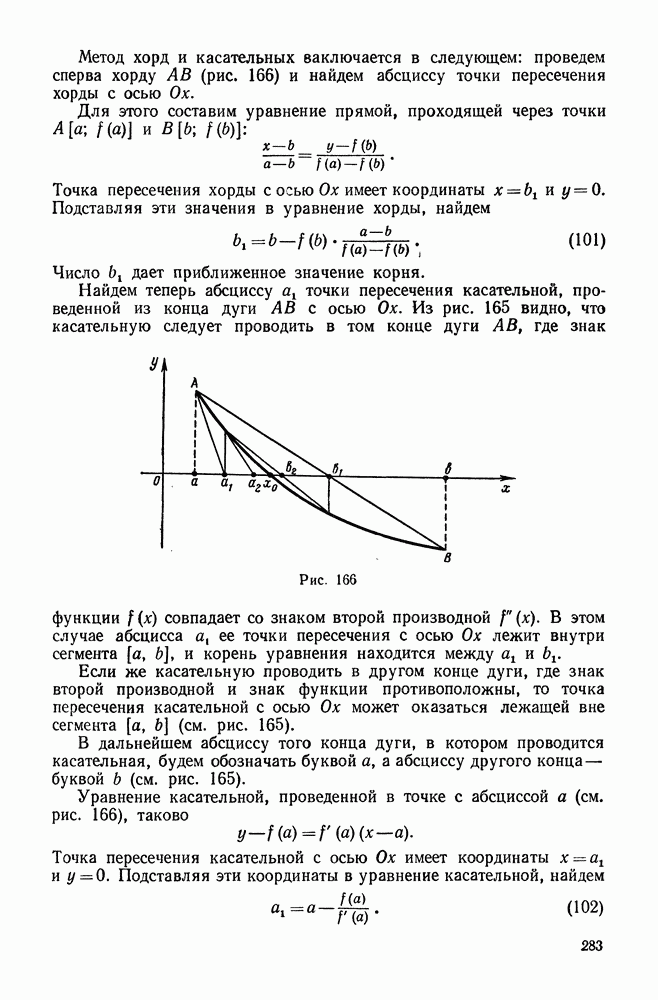
- 2. Уточнение найденных значений корней методом хорд и касательных
- § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
- ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
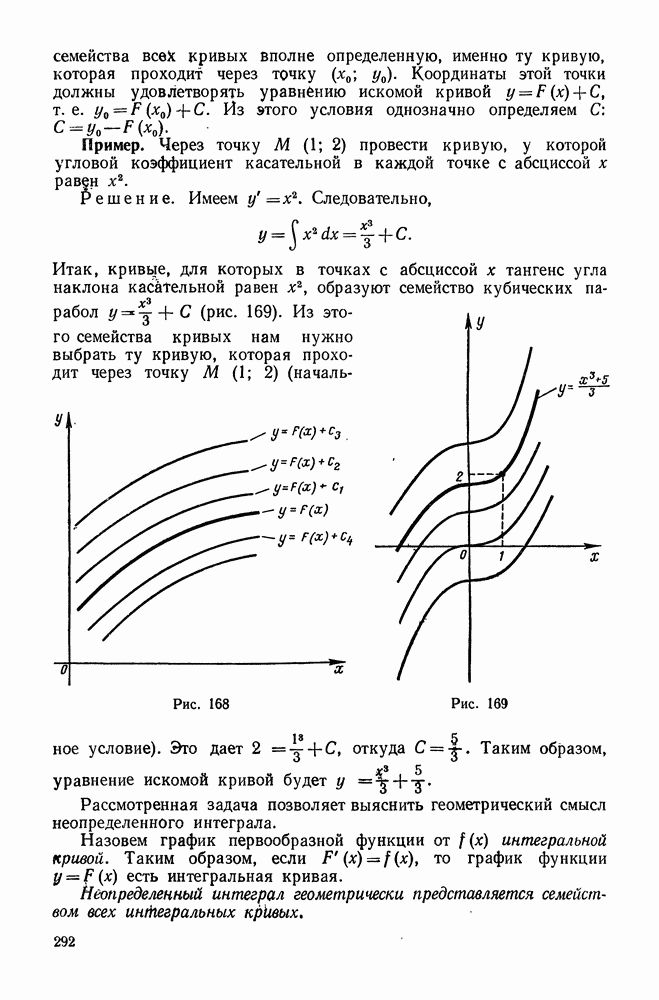
- 2. Геометрический смысл неопределенного интеграла
- 3. Таблица основных интегралов
- 4. Основные свойства неопределенного интеграла
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование методом замены переменной
- 3. Интегрирование по частям
- § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Рациональные дроби. Выделение правильной рациональной дроби
- 3. Интегрирование простейших рациональных дробей
- 4. Разложение правильной рациональной дроби на простейшие дроби
- 5. Метод неопределенных коэффициентов
- 6. Интегрирование рациональных дробей
- § 4. Интегрирование тригонометрических функций
- 2. Рациональные функции двух переменных
- 3. Интегралы вида
- § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Интеграл вида
- 3. Интегралы видов
- 4. Интегралы вида
- § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Понятие об интегралах, не берущихся в элементарных функциях
- ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
- 2. Задача о работе переменной силы
- § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- 2. Свойства определенного интеграла
- 3. Производная интеграла по переменной верхней границе
- 4. Формула Ньютона—Лейбница
- 5. Замена переменной в определенном интеграле
- 6. Интегрирование по частям в определенном интеграле
- § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Вычисление площади в полярных координатах
- 3. Вычисление объема тела по известным поперечным сечениям
- 4. Объем тела вращения
- 5. Длина дуги кривой
- 6. Дифференциал дуги
- 7. Площадь поверхности вращения
- 8. Общие замечания о решении задач методом интегральных сумм
- § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
- 2. Вычисление кривизны
- 3. Радиус кривизны. Круг кривизны. Центр кривизны
- 4. Эволюта и эвольвента
- § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
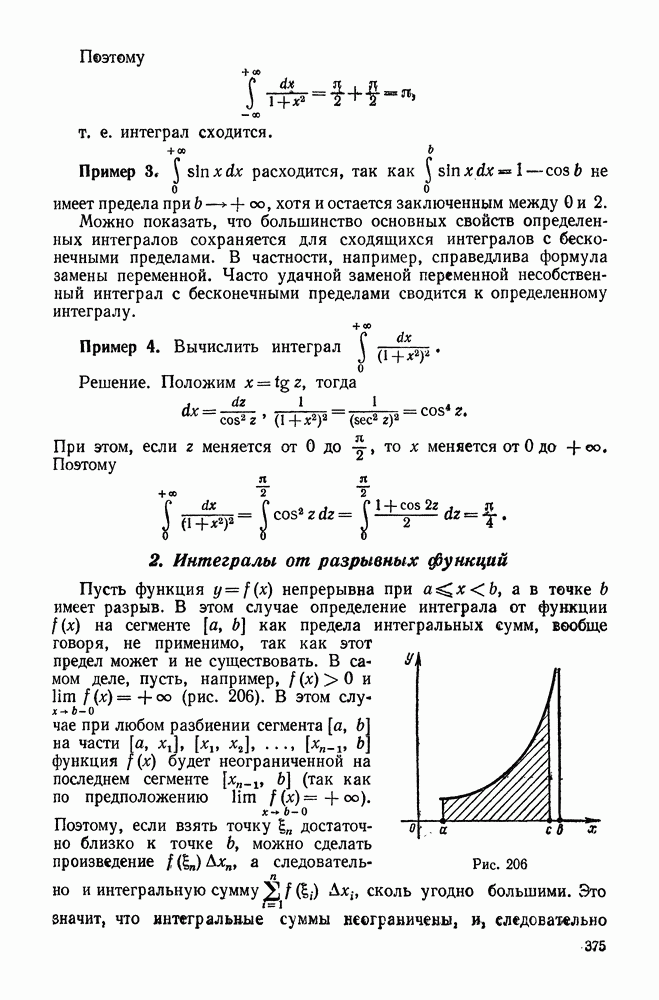
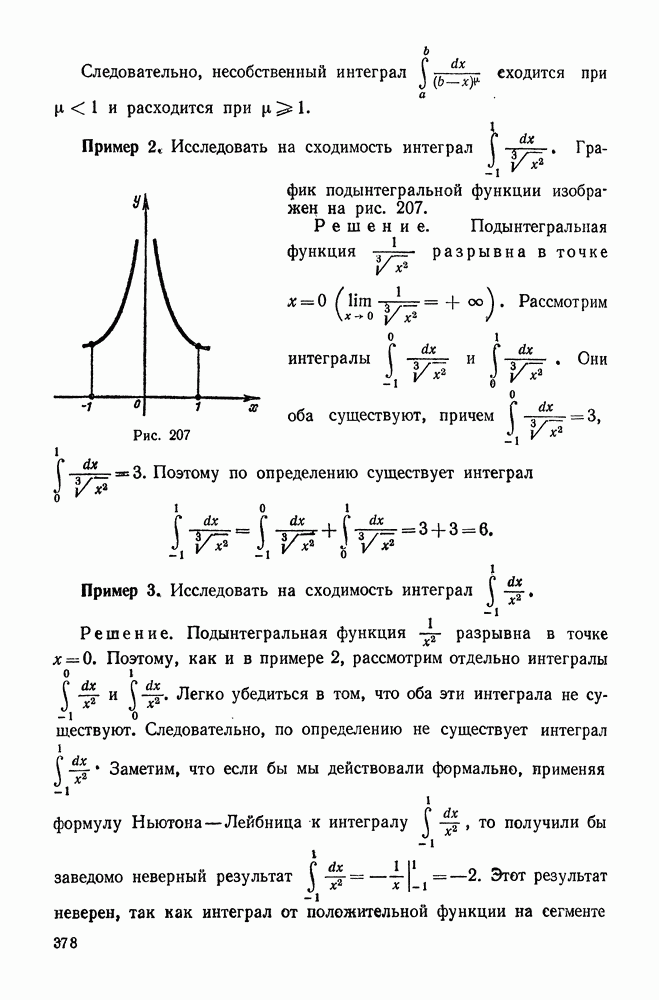
- 2. Интегралы от разрывных функций
- 3. Признаки сходимости несобственных интегралов
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
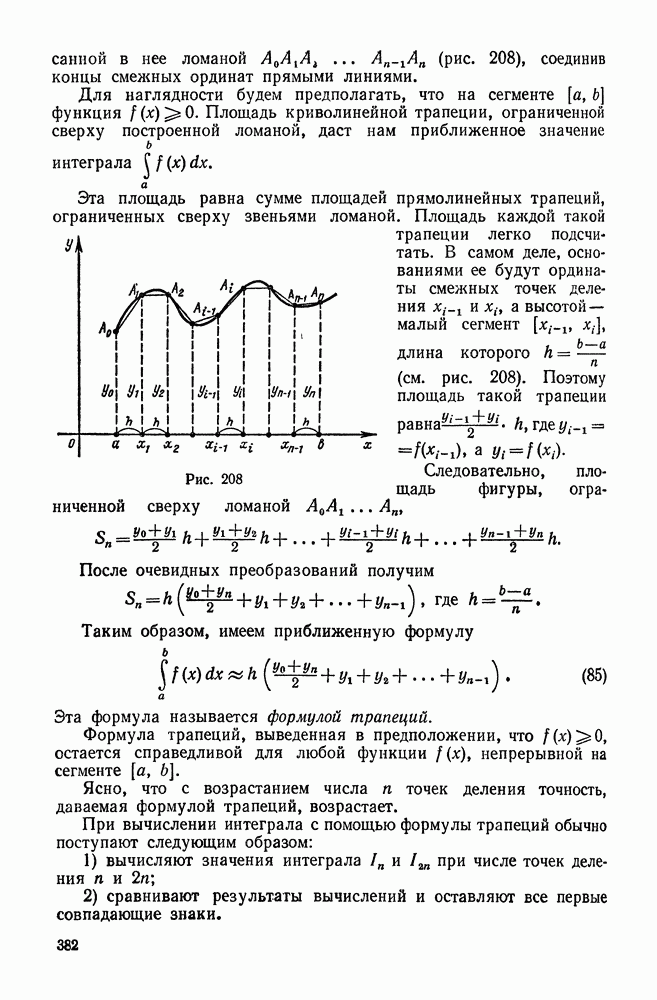
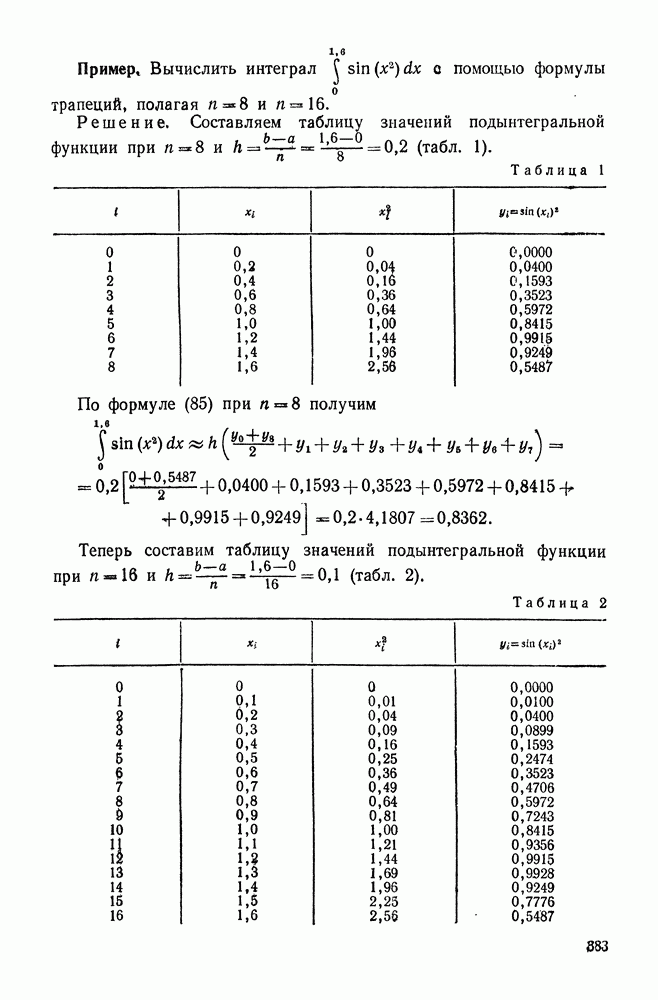
- 2. Метод трапеций
- 3. Метод параболических трапеций (метод Симпсона)
- ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. График функции двух переменных
- 3. Функции трех и большего числа переменных
- § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
- 2. Непрерывность функции нескольких переменных
- 3. Понятие области
- 4. Точки разрыва
- 5. Свойства функций, непрерывных в ограниченной замкнутой области
- § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
- 2. Геометрический смысл частных производных функции двух переменных
- 3. Частные производные высших порядков
- § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Полный дифференциал функции
- 3. Приложение полного дифференциала к приближенным вычислениям
- § 5. Дифференцирование сложных и неявных функций
- 2. Инвариантность формы полного дифференциала
- 3. Дифференцирование неявных функций
- § 6. СКАЛЯРНОЕ ПОЛЕ
- 2. Производная по направлению
- 3. Градиент
- 4. Касательная плоскость а нормаль к поверхности
- 5. Геометрический смысл полного дифференциала функции двух переменных
- § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- 2. Наибольшее и наименьшее значения функции двух переменных
- ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ДВОЙНОЙ ИНТЕГРАЛ
- 2. Двойной интеграл. Теорема существования
- 3. Свойства двойного интеграла
- 4. Вычисление двойного интеграла в декартовых координатах
- 5. Вычисление двойного интеграла в полярных координатах
- 6. Приложения двойного интеграла
- § 2. ТРОЙНОЙ ИНТЕГРАЛ
- 2. Тройной интеграл и его свойства
- 3. Вычисление тройного интеграла в декартовых координатах
- 4. Вычисление тройного интеграла в цилиндрических координатах
- 5. Приложения тройного интеграла
- § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
- 2. Задача о работе. Криволинейный интеграл
- 3. Вычисление криволинейного интеграла
- 4. Формула Остроградского — Грина
- 5. Независимость криволинейного интеграла от пути интегрирования
- 6. Отыскание первообразной по полному дифференциалу
- 7. Криволинейный интеграл по длине дуги
- ГЛАВА XI. РЯДЫ
- § 1. ЧИСЛОВЫЕ РЯДЫ
- 2. Геометрическая прогрессия
- 3. Простейшие свойства числовых рядов
- 4. Необходимый признак сходимости ряда
- 5. Достаточные признаки сходимости знакоположительных рядов
- 6. Знакопеременные ряды
- 7. Остаток ряда и его оценка
- § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- 2. Правильно сходящиеся функциональные ряды и их свойства
- § 3. СТЕПЕННЫЕ РЯДЫ
- 2. Свойства степенных рядов
- 3. Ряды по степеням разности х-а
- 4. Разложение функций в степенные ряды. Ряд Тейлора
- 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 2. Приближенное вычисление интегралов
- § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 2. Числовые ряды с комплексными членами
- 3. Степенные ряды в комплексной области
- § 6. РЯДЫ ФУРЬЕ
- 2. Ряд Фурье
- 3. Сходимость ряда Фурье
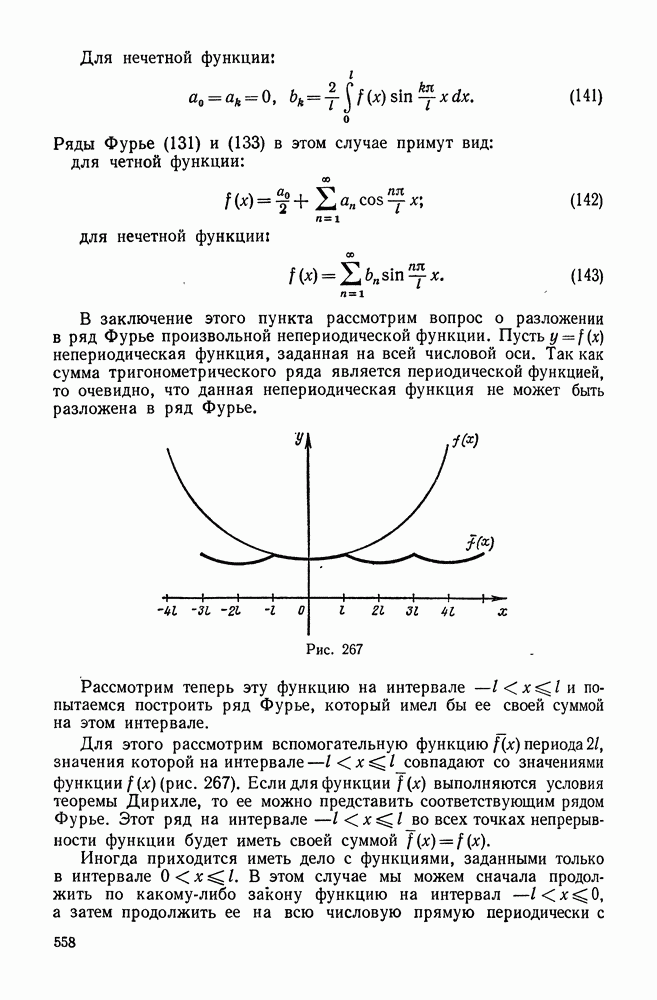
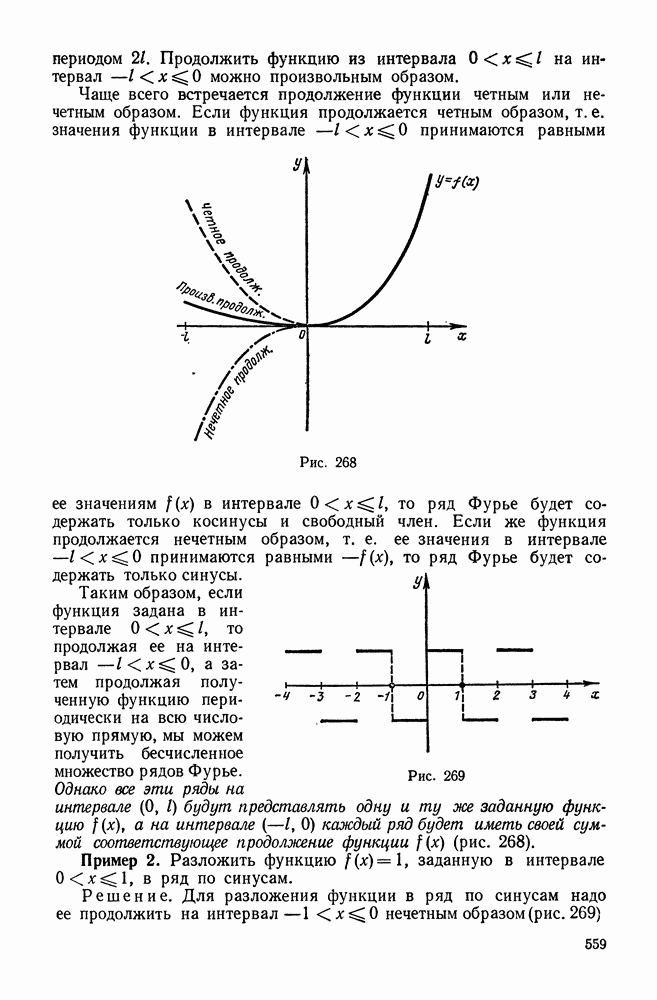
- 4. Ряды Фурье для четных и нечетных функций
- 5. Разложение в ряд Фурье функций с периодом 2l
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Дифференциальные уравнения первого порядка
- 3. Уравнения с разделяющимися переменными
- 4. Однородные уравнения
- 5. Линейные уравнения
- 6. Уравнение в полных дифференциалах
- 7. Особые решения
- 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Простейшие уравнения второго порядка, допускающие понижение порядка
- 3. Понятие о дифференциальных уравнениях высших порядков
- § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Линейные однородные дифференциальные уравнения второго порядка
- 3. Линейные неоднородные дифференциальные уравнения второго порядка
- 4. Метод вариации произвольных постоянных
- § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
- § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
- § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
- ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ