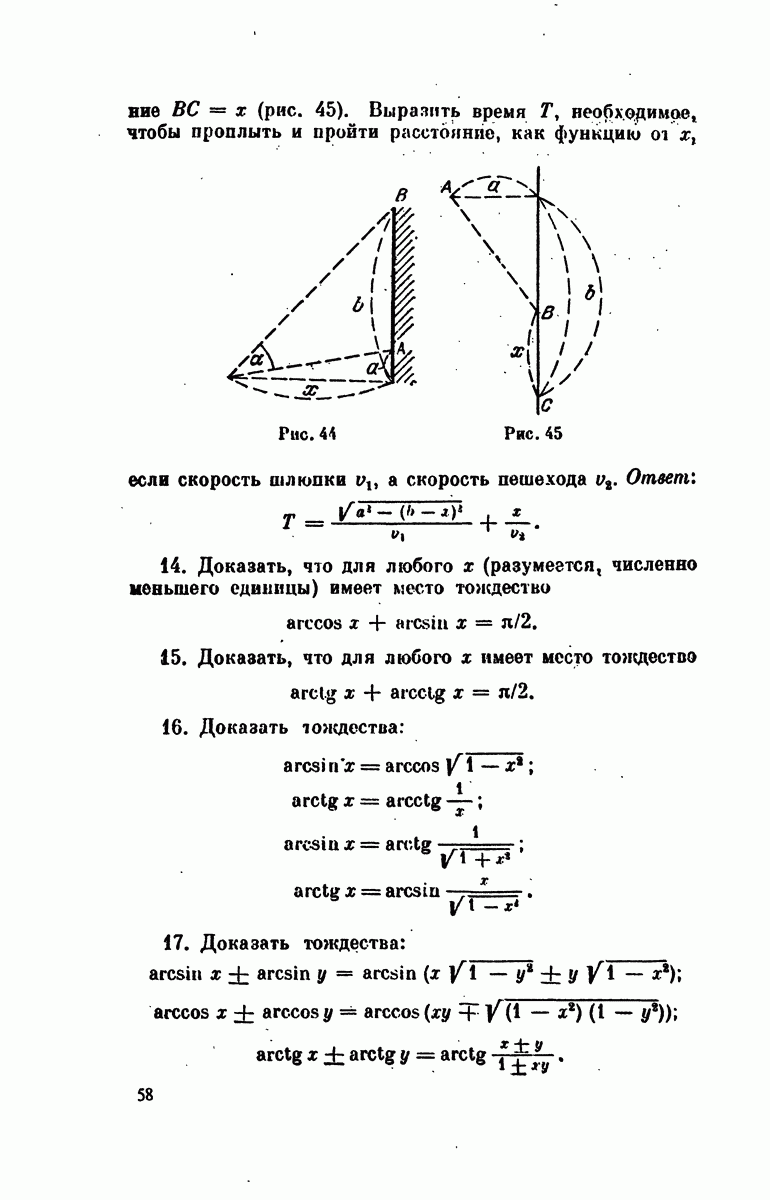
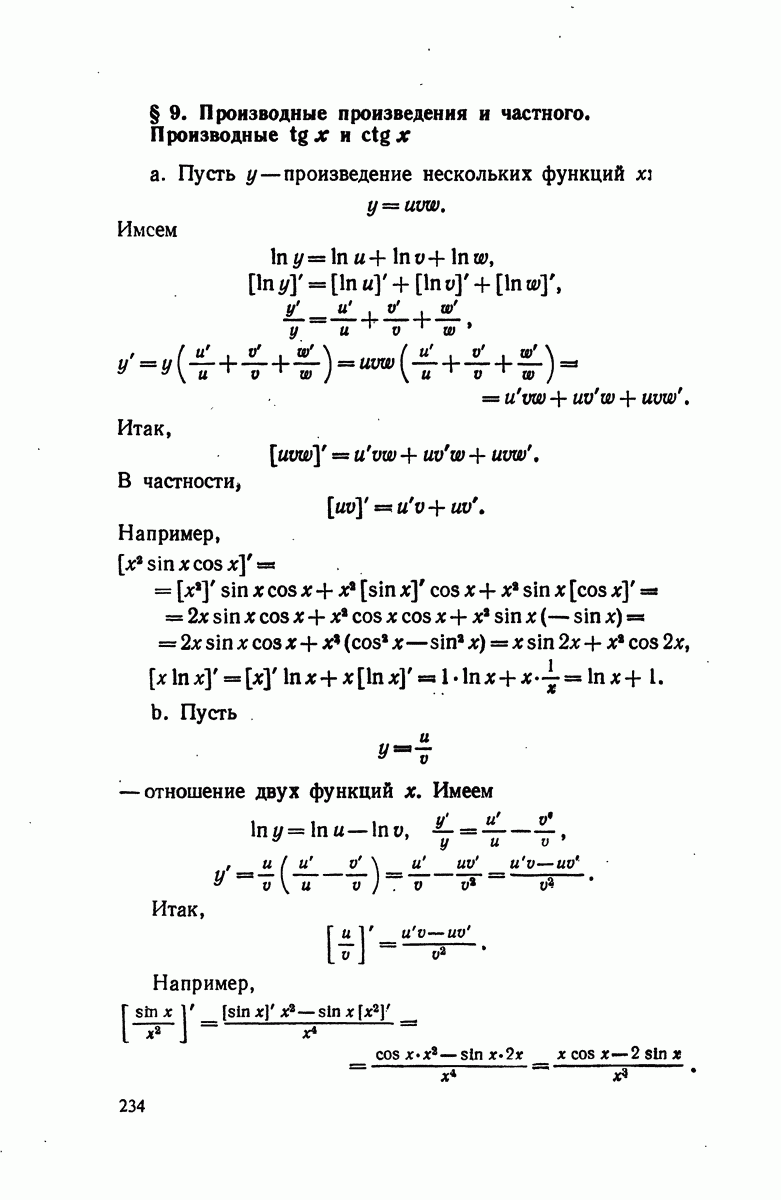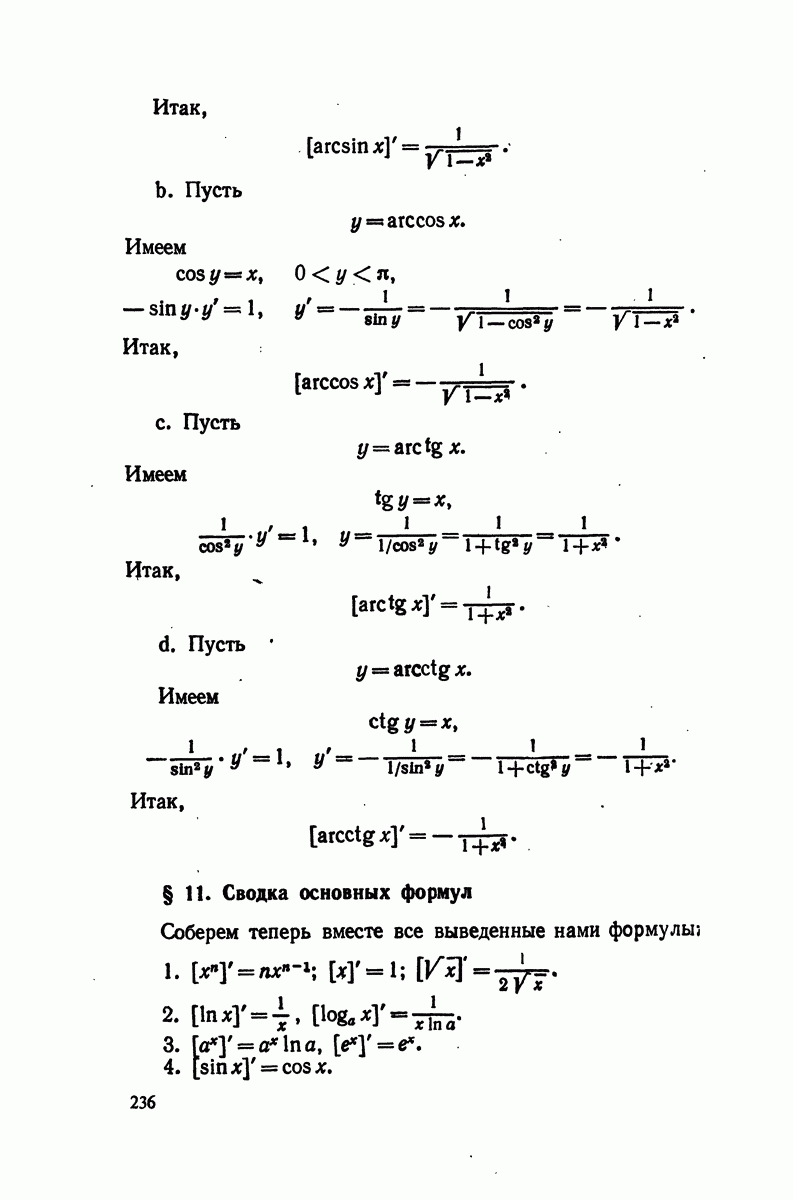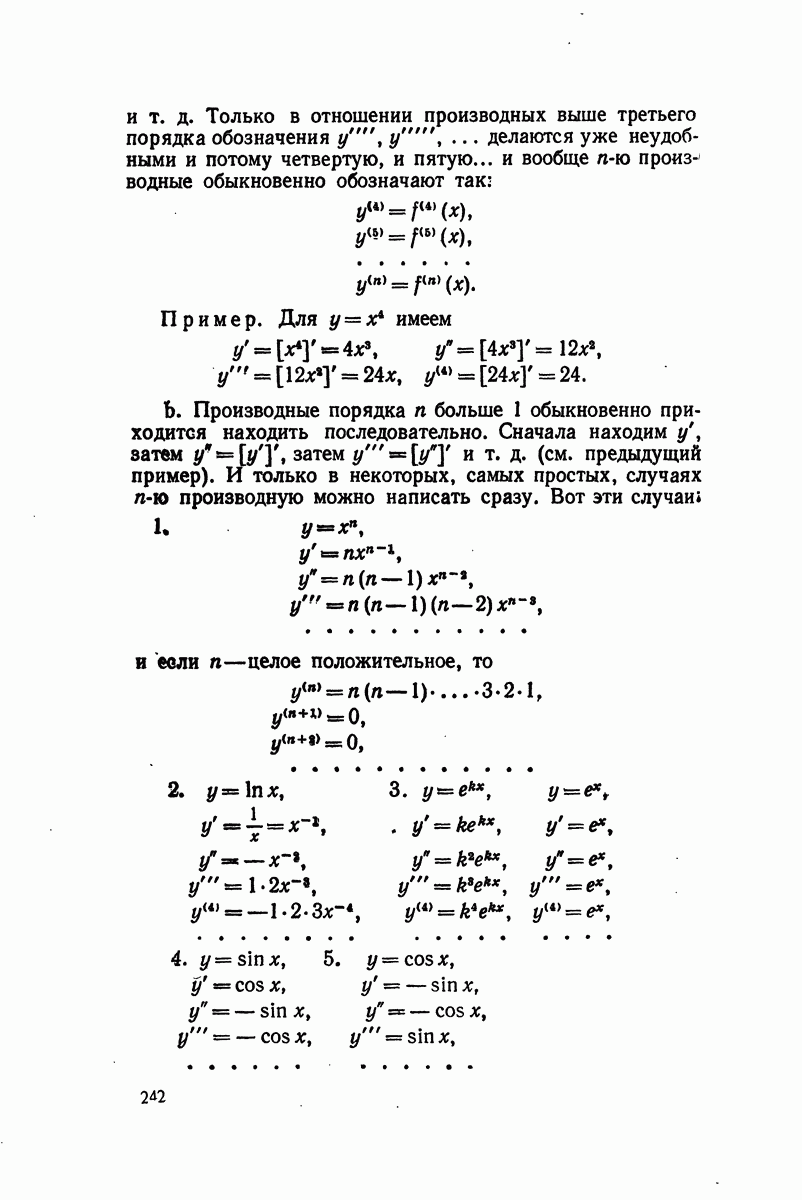| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Частные производные и полный дифференциал
а. Наиболее важным вопросом в теории функций является изучение характера изменения функции.
Займемся функцией двух переменных

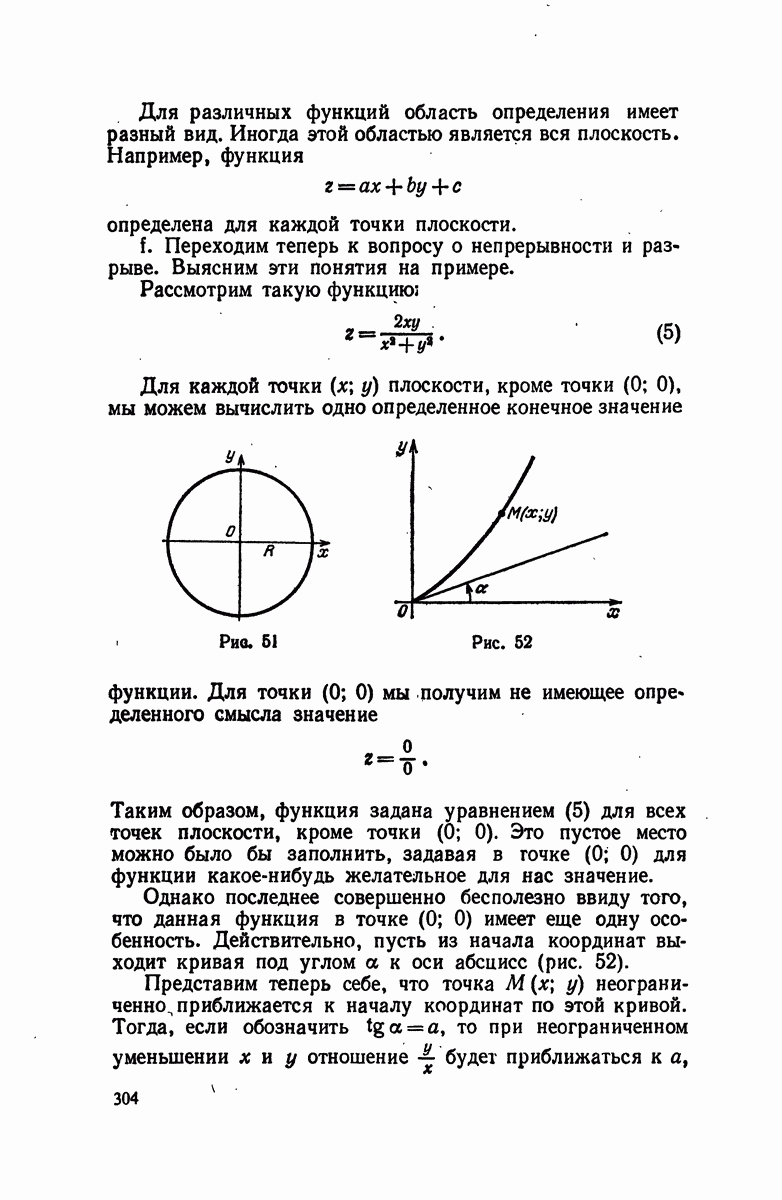
Пусть поверхность на рис. 53 изображает эту функцию.

Рис. 53
Если необходимо исследовать поведение функции (1) около какой-либо точки  , то наилучшим и простейшим способом является пересечение поверхности несколькими плоскостями, проходящими через эту точку.
, то наилучшим и простейшим способом является пересечение поверхности несколькими плоскостями, проходящими через эту точку.
Рассматривая все кривые, получившиеся на поверхности от этих сечений, мы можем изучить окрестность данной точки и притом тем точнее, чем больше сечений мы сделаем. Впрочем, для наших целей достаточно сделать только два сечения: плоскостями, проходящими через данную точку и параллельными вертикальным координатным плоскостям  При этом получаются кривая МА (назовем ее первой) и кривая MB (назовем ее второй).
При этом получаются кривая МА (назовем ее первой) и кривая MB (назовем ее второй).
Если точка будет двигаться по первой кривой, то у нее будут изменяться только х, а у будет постоянным числом ввиду того, что вся первая кривая лежит в плоскости, параллельной плоскости  . Поэтому можно получить уравнение первой кривой из уравнения поверхности, если, выходя из точки М, остановить у, а менять только х, так что
. Поэтому можно получить уравнение первой кривой из уравнения поверхности, если, выходя из точки М, остановить у, а менять только х, так что  будет функцией только
будет функцией только 
Таким образом, уравнение первой кривой будет

Дадим теперь  приращение
приращение  Тогда функция
Тогда функция  получит приращение, которое на рис. 53 изображено отрезком
получит приращение, которое на рис. 53 изображено отрезком 
Это приращение называется частным приращением функции  по
по  и обозначаете так:
и обозначаете так:

b. Найдем теперь предел отношения этого приращения к  при
при  Если этот предел существует, то он называется частной производной функции
Если этот предел существует, то он называется частной производной функции  по
по  и обозначается так!
и обозначается так!

Нетрудно видеть, что частная производная  по
по  равна тангенсу угла наклона касательной первой кривой, который эта касательная составляет с осью
равна тангенсу угла наклона касательной первой кривой, который эта касательная составляет с осью 
Совершенно так же уравнение второй кривой будет

Аналогично придем к понятию частного приращения функции  по у:
по у:

и к понятию частной производной  по
по 

Ясно, что последняя равна тангенсу угла  наклона касательной второй кривой к оси
наклона касательной второй кривой к оси  Для частных производных имеются еще такие обозначения:
Для частных производных имеются еще такие обозначения:

c. Если мы умножим частные производные на приращения соответствующих переменных, то получим произведения, называемые частными дифференциалами функции  и обозначаемые так:
и обозначаемые так:

Если  являются независимыми переменными, раз личия между
являются независимыми переменными, раз личия между  мы не делаем.
мы не делаем.
На рис. 53
 изображается приращением ага по касательной к первой кривой
изображается приращением ага по касательной к первой кривой
 изображается приращением ЬХЬ по касательной ко второй кривой.
изображается приращением ЬХЬ по касательной ко второй кривой.
Ясно, что частные дифференциалы отличаются от соответствующих частных приращений функции  на бесконечно малые высшего порядка по сравнению с
на бесконечно малые высшего порядка по сравнению с 
Важную роль в математике и прикладных науках играет сумма всех частных дифференциалов функции. Эта сумма называется полным дифференциалом функции и обозначается так же, как дифференциал функции одной переменной:

е. Полный дифференциал имеет простое геометрическое истолкование, которое мы сейчас покажем.
Допустим, что мы даем переменным  одновременно приращения
одновременно приращения  Тогда функция
Тогда функция  получит приращение, которое называется ее полным приращением и обозначается просто
получит приращение, которое называется ее полным приращением и обозначается просто  без знаков снизу. Это приращение равно
без знаков снизу. Это приращение равно


Рис. 54
Ниже на рис. 54 поверхность обозначена буквами так что  и, следовательно,
и, следовательно,  Построим плоскость, проходящую через касательные
Построим плоскость, проходящую через касательные  к первой и второй кривым.
к первой и второй кривым.
Эта плоскость называется касательной плоскостью к поверхности в точке М.
Последняя пересекается с продолжением боковой поверхности параллелепипеда с ребрами  и
и  так, что образуется параллелограмм
так, что образуется параллелограмм  Проведем еще прямую
Проведем еще прямую  параллельно
параллельно 
Треугольник  равен треугольнику
равен треугольнику  ввиду того, что
ввиду того, что  равны и параллельны как противоположные стороны параллелограмма,
равны и параллельны как противоположные стороны параллелограмма,  параллельна
параллельна  и
и  параллельна
параллельна 
Из равенства треугольников следует, что 
Следовательно,

Таким образом, полный дифференциал представляет собой приращение функции  , но взятое не по поверхности, а по ее касательной плоскости.
, но взятое не по поверхности, а по ее касательной плоскости.
f. Обозначим буквами X, Y, Z координаты точки с.
Тогда

Подставляя эти разности в полный дифференциал, получим

Это уравнение пригодно для любых численных значений  иными словами, оно остается верным, где бы на касательной плоскости ни находилась точка с.
иными словами, оно остается верным, где бы на касательной плоскости ни находилась точка с.
Поэтому X, Y, Z можно рассматривать как текущие координаты касательной плоскости. Следовательно, уравнение (13) есть уравнение касательной плоскости, причем  суть координаты точки касания.
суть координаты точки касания.
Итак, полный дифференциал представляет собой в замаскированном виде уравнение касательной плоскости.
g. Обратимся опять к чертежу. Мы видим, что приращение функции  отличается от полного дифференциала
отличается от полного дифференциала  на величину
на величину  . Чрезвычайно важным является то, что эта разность между ними представляет собой бесконечно малую высшего порядка. Доказать геометрически это нельзя. Поэтому сейчас мы будем вести чисто аналитические рассуждения.
. Чрезвычайно важным является то, что эта разность между ними представляет собой бесконечно малую высшего порядка. Доказать геометрически это нельзя. Поэтому сейчас мы будем вести чисто аналитические рассуждения.
h. Допустим, что функция

непрерывна и имеет непрерывные частные производные

Если мы дадим какой-либо переменной, например, у бесконечно малое приращение, то ввиду непрерывности каждая из частных производных получит также бесконечно малое приращение. Вместо (х, у) будем иметь  , но разность между ними будет бесконечно мала. Обозначим эту разность через а. Тогда получим
, но разность между ними будет бесконечно мала. Обозначим эту разность через а. Тогда получим

1. Займемся теперь исследованием полного приращения функции  , которое имеет вид
, которое имеет вид

Проделаем нижеследующие очевидные преобразования:

и рассмотрим те выражения, которые находятся в скобках, отдельно.
Возьмем сначала вторую дробь. Если бы мы устремили  к нулю, то эта дробь имела бы своим пределом
к нулю, то эта дробь имела бы своим пределом  . Но мы знаем, что если какая-либо величина имеет предел, то она отливается от своего предела на бесконечно малую величину. Обозначим эту бесконечно малую разность между нашей дробью и ее пределом через
. Но мы знаем, что если какая-либо величина имеет предел, то она отливается от своего предела на бесконечно малую величину. Обозначим эту бесконечно малую разность между нашей дробью и ее пределом через  , тогда
, тогда

Точно так же найдем, что

Подставляя (18) и (19) в (17), получим

Пользуясь еще равенством (15), найдем, что

Обозначая  и раскрывая скобки, получим
и раскрывая скобки, получим

или, иначе,

j. Выражение, находящееся в первых скобках, есть не что иное, как полный дифференциал  а сумма, стоящая во вторых скобках, по сравнению с
а сумма, стоящая во вторых скобках, по сравнению с  есть бесконечно малая высшего порядка ввиду того, что
есть бесконечно малая высшего порядка ввиду того, что  и
и  -бесконечно малые. Обозначая
-бесконечно малые. Обозначая

получим

Итак, доказано, что полное приращение функции отличается от ее полного дифференциала на бесконечно малую высшего порядка.
к. Основываясь на этом, можно приближенно заменять приращение функции ее полным дифференциалом и обратно, если, разумеется,  будут малыми величинами: при этом ошибка будет мала даже по сравнению с
будут малыми величинами: при этом ошибка будет мала даже по сравнению с 
1. Аналогичные рассуждения приведут нас к понятию частных производных и полного дифференциала функции трех и большего числа переменных. Но нужно помнить, что для функции, зависящей от более чем двух переменных, уместны только аналитические рассуждения, потому что такие функции не могут быть так хорошо и просто, как функции двух переменных, истолкованы геометрически.
m. Дадим определение частных производных и полного дифференциала для функций любого числа переменных.
Пусть имеется функция  переменных
переменных 

Частным приращением функции многих переменных по какой-либо переменной называется то приращение, которое получит функция, если мы дадим приращение этой переменной, принимая все остальные переменные за постоянные.
Например, частное приращение функции U по  будет
будет

Частной производной функции многих переменных по какой-либо переменной называется предел (если он существует) отношения частного приращения функции по этой переменной к приращению этой переменной при условии, что последнее стремится к нулю.
Например, частная производная V по  определяется так:
определяется так:

Частным дифференциалом функции многих переменных по какой-либо переменной называется произведение частной производной по этой переменной на бесконечно малое приращение этой переменной. Последнее называется дифференциалом этой независимой переменной.
Например, частный дифференциал U по  определяется так!
определяется так!

Заметим, что для независимых переменных мы считаем равносильными обозначения

Очевидно, частный дифференциал отличается от частного приращения на бесконечно малую высшего порядка.
Полным приращением функции многих переменных называется то ее приращение, которое она получит, когда мы всем независимым переменным дадим приращения, то есть

Полным дифференциалом функции многих переменных называется сумма всех ее частных дифференциалов, то есть

Так же как для функции двух переменных, можно доказать, что полный дифференциал отличается от полного ее приращения на бесконечно малую высшего порядка.
n. Частные производные и полный дифференциал часто встречаются в термодинамике, а так как современная физическая химия основана главным образом на термодинамике, то является совершенно необходимым, чтобы лица, имеющие дело с химией, в частности металлурги, могли свободно обращаться с частными производными.
о. Техника нахождения частных производных ничем не отличается от обычного дифференцирования, нужно только помнить, что при дифференцировании функции по какой-либо переменной все остальные переменные принимаются за постоянные.
Покажем это на примерах.
Пример 1. Найти частную производную по  функции
функции

Имеем

Ввиду того, что у мы здесь считаем постоянной, ее так же, как любую другую постоянную, можно выносить за знак частной производной; по той же причине частная производная  по
по  будет равна нулю.
будет равна нулю.
Следовательно,

Окончательно

Пример 2. Найти полный дифференциал той же функции. Нам не хватает еще частной производной по у. Поэтому находим ее:

Таким образом, полный дифференциал будет

Пример 3. Известно, что уравнение состояния идеального газа имеет вид

где  - постоянная,
- постоянная,  — абсолютная температура,
— абсолютная температура,  - объем,
- объем,  — давление.
— давление.
Найти увеличение давления, если температура изменилась на небольшую величину  а объем увеличился на
а объем увеличился на 
Здесь  является функцией двух независимых переменных
является функцией двух независимых переменных  . Следовательно, нам нужно найти полное приращение функции
. Следовательно, нам нужно найти полное приращение функции 
Так как приращения  по условию малы, то вместо полного приращения мы можем искать полный дифференциал
по условию малы, то вместо полного приращения мы можем искать полный дифференциал  ошибка будет малой высшего порядка, т. е. по сравнению с
ошибка будет малой высшего порядка, т. е. по сравнению с  ею можно пренебречь. Итак, имеем полный дифференциал, для чего сначала находим частные производные
ею можно пренебречь. Итак, имеем полный дифференциал, для чего сначала находим частные производные

Так как полный дифференциал имеет в данном случае выражение

то, подставляя сюда найденные частные производные, получим

Если необходимо, то, пользуясь начальным уравнением,  мы можем, заменяя у на
мы можем, заменяя у на  , упростить выражение для полного дифференциала, так что будем иметь
, упростить выражение для полного дифференциала, так что будем иметь

Пример 4. Идеальный газ имеет температуру  и объем
и объем  при давлении
при давлении  . Вычислить, насколько увеличится давление, если температура увеличится на 0,5 К, а объем уменьшится на
. Вычислить, насколько увеличится давление, если температура увеличится на 0,5 К, а объем уменьшится на  Очевидно, здесь
Очевидно, здесь  (Мы берем знак минус ввиду того, что объем не увеличился, а уменьшился.)
(Мы берем знак минус ввиду того, что объем не увеличился, а уменьшился.)
Подставляя все эти числа в выражение для полного дифференциала, которое мы уже получили в предыдущей задаче, будеил иметь

Итак, увеличение давления равно  .
.
p. Очень удобно использовать полный дифференциал в приближенных вычислениях для оценки погрешностей, что имеет большое значение для опытных наук. Допустим, что величины  и у мы измеряем непосредственно в результате эксперимента.
и у мы измеряем непосредственно в результате эксперимента.
Пусть на основании этих величин мы должны вычислить величину  по формуле
по формуле

Мы знаем, что всякое измерение сопряжено с теми или иными погрешностями. Поэтому и вычисленная величина  также будет неточной. Требуется оценить погрешность, которая получается при вычислении
также будет неточной. Требуется оценить погрешность, которая получается при вычислении  . Как мы уже выше сказали, значения х и у не являются точными. Обозначим точные значения этих величин через
. Как мы уже выше сказали, значения х и у не являются точными. Обозначим точные значения этих величин через

тогда  будет точным значением вычисленной величины. Погрешность при вычислении
будет точным значением вычисленной величины. Погрешность при вычислении  будет выражаться полным приращением функции
будет выражаться полным приращением функции

Так как  представляют собой погрешности измерения, а при хорошем эксперименте они должны быть малы, то можно полное приращение приближенно заменить полным дифференциалом:
представляют собой погрешности измерения, а при хорошем эксперименте они должны быть малы, то можно полное приращение приближенно заменить полным дифференциалом:

(Здесь мы, как часто делают экспериментаторы, приближенное равенство обозначим изогнутым знаком  ) Как видно, для того чтобы найти
) Как видно, для того чтобы найти  нужно знать
нужно знать  Однако точные величины погрешностей известными нам быть не могут. Кроме того, мы почти никогда не знаем, в какую сторону мы ошиблись при измерении, в сторону увеличения или в сторону уменьшения, иными словами, нам неизвестны ни величины
Однако точные величины погрешностей известными нам быть не могут. Кроме того, мы почти никогда не знаем, в какую сторону мы ошиблись при измерении, в сторону увеличения или в сторону уменьшения, иными словами, нам неизвестны ни величины  ни их знак. Нам может быть известно только, что при том или ином измерении мы делаем погрешность, не большую известной величины, т. е. мы можем гарантировать только верхнюю границу погрешности.
ни их знак. Нам может быть известно только, что при том или ином измерении мы делаем погрешность, не большую известной величины, т. е. мы можем гарантировать только верхнюю границу погрешности.
Но этого вполне достаточно, так как мы не ставим перед собой цель найти точную величину погрешности величины  , а намерены заняться ее оценкой, т. е. нахождением ее верхней границы. Допустим теперь, что
, а намерены заняться ее оценкой, т. е. нахождением ее верхней границы. Допустим теперь, что  — как раз максимальные возможные погрешности. Так как нам неизвестен знак погрешностей, то мы должны рассчитывать на самое худшее, а именно будем предполагать такой знак, чтобы величины
— как раз максимальные возможные погрешности. Так как нам неизвестен знак погрешностей, то мы должны рассчитывать на самое худшее, а именно будем предполагать такой знак, чтобы величины  были положительны. Чтобы не задумываться над знаком погрешностей, мы возьмем просто абсолютные величины
были положительны. Чтобы не задумываться над знаком погрешностей, мы возьмем просто абсолютные величины

Таким образом, для вычисления верхней границы погрешности величины  будем иметь формулу
будем иметь формулу

В экспериментальных науках бывает важно знать также относительную погрешность.
Относительной погрешностью называется отношение погрешности какой-либо величины к самой величине.
Иногда относительную погрешность выражают в процентах. Тогда, очевидно, относительную погрешность нужно умножить на 100. В этом случае будем иметь формулу

Таким же способом находится верхняя граница погрешности, если иметь дело с функциями трех или большего числа переменных.
Пример 1. Найти верхнюю границу погрешности алгебраической суммы

Так как полный дифференциал будет

то имеем

т. е. погрешность суммы не больше суммы погрешностей всех слагаемых.
Пример 2. Найти верхнюю границу относительной погрешности произведения

Так как полный дифференциал будет

то

т. е. относительная погрешность произведения не больше суммы относительных погрешностей всех множителей.
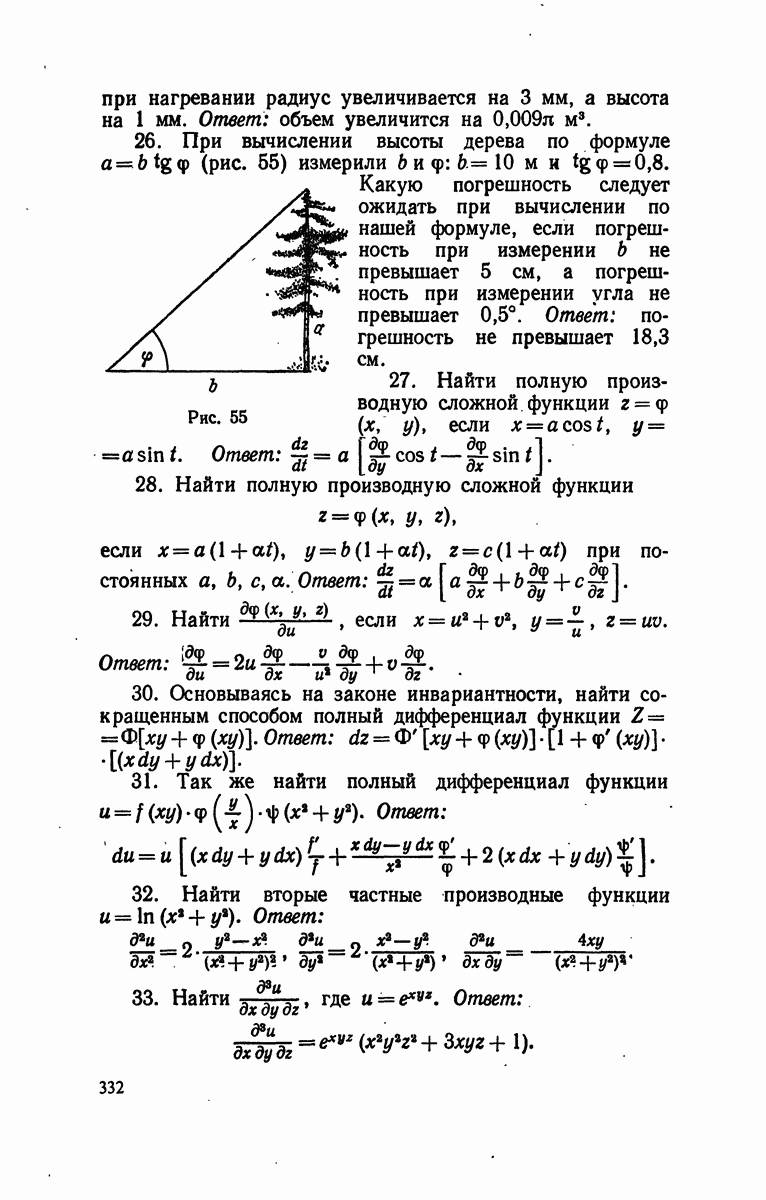
Пр и мер 3. Вычислить верхнюю границу погрешности, которая получается при вычислении площади треугольника по формуле

если при измерении стброн а  погрешность не превышает 0,5 мм, а при измерении угла
погрешность не превышает 0,5 мм, а при измерении угла  погрешность не превышает 0,5°.
погрешность не превышает 0,5°.
Так как

то

Далее,  см,
см,  (угол нужно выразить в радианной мере). Следовательно,
(угол нужно выразить в радианной мере). Следовательно,

Пример 4. Вычислить в процентах относительную погрешность, сохраняя все данные предыдущей задачи. Так как

то относительная погрешность будет

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- § 1. Ось
- § 2. Вектор
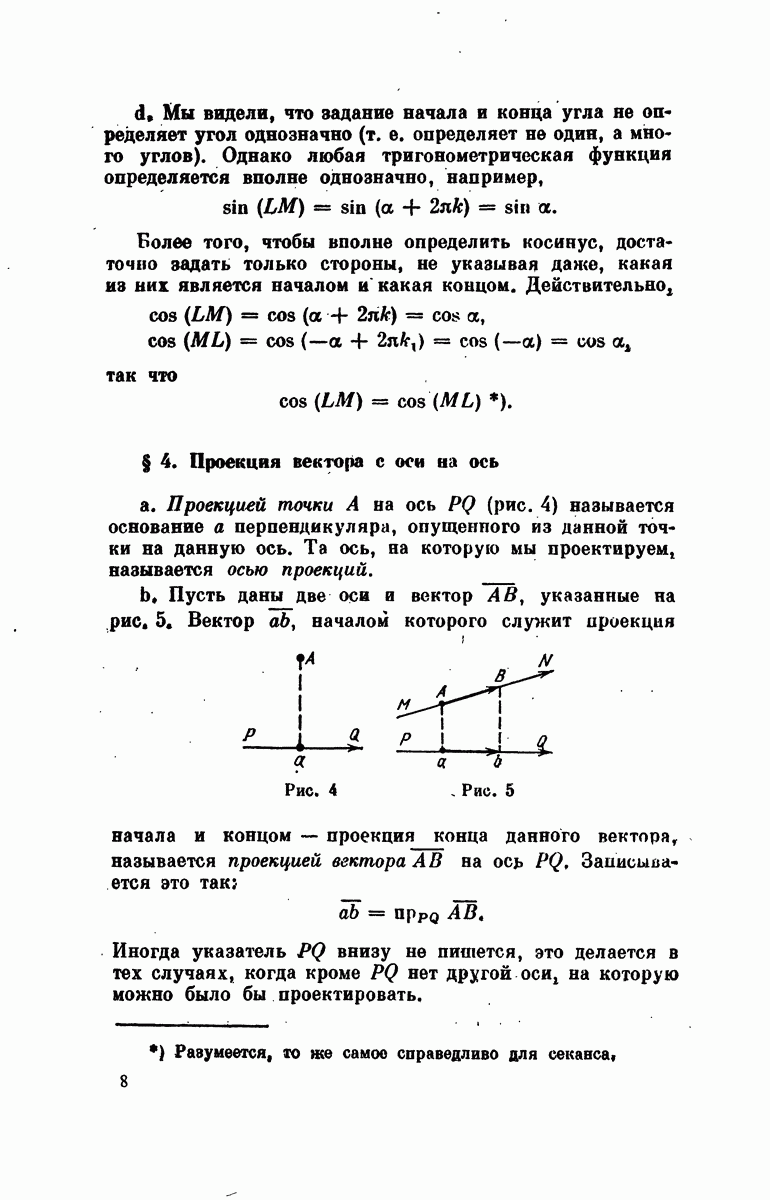
- § 3. Направленные углы
- § 4. Проекция вектора с оси на ось
- § 5. Векторные цепи
- § 6. Цепи углов
- § 7. Проекции вектора на две взаимно перпендикулярные оси
- § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности
- S 9. Упражнения и контрольные вопросы
- Глава 2. КООРДИНАТЫ
- § 1. Метод координат
- § 2. Основные задачи, решаемые методом координат
- § 3. Упражнения
- Глава 3. ФУНКЦИИ
- § 1. Переменные в постоянные
- § 2. Понятие о функциональной зависимости
- § 3. Классификация математических функций
- § 4. Обзор и графическое изображение простейших функции одного аргумента
- § 5. Обратные функции
- § 6. Понятие об уравнении линии
- § 7. Упражнения
- Глава 4. ПРЯМАЯ
- § 1. Уравнение прямой, проходящей через данную точку
- § 2. Общее уравнение прямой
- § 3. Частные случаи
- § 4. Переход к уравнению с угловым коэффициентом
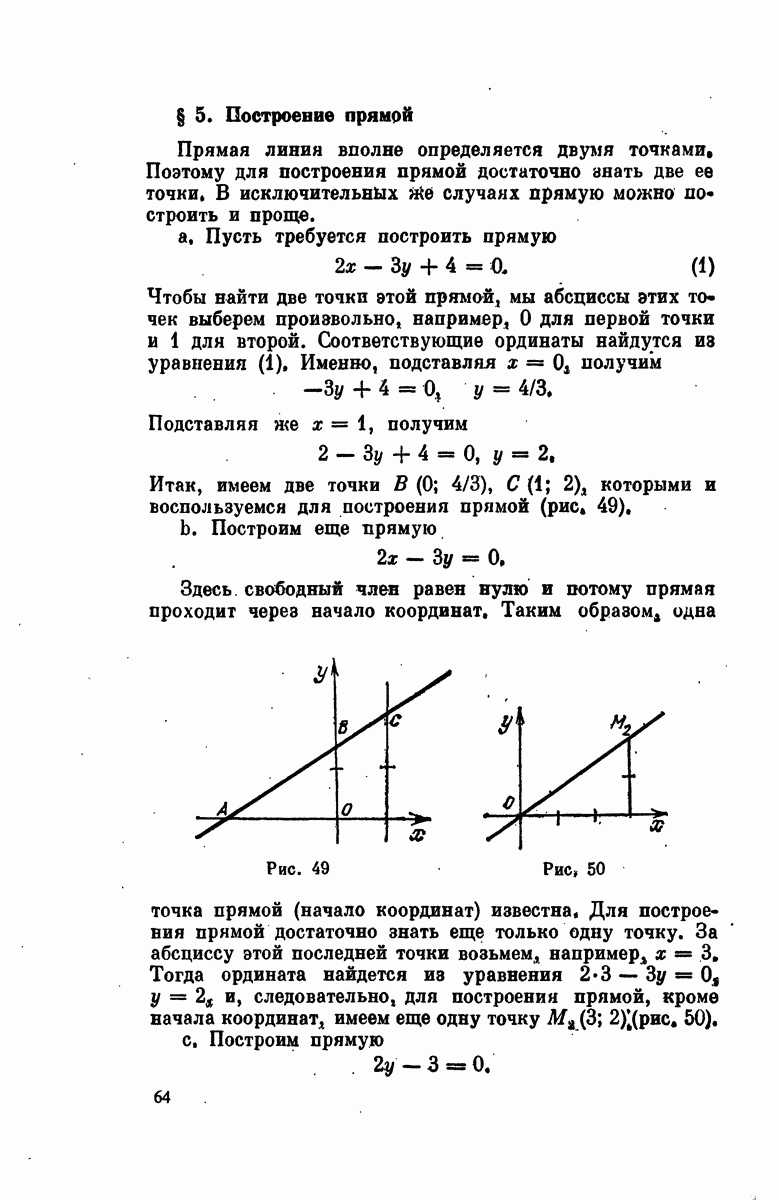
- § 5. Построение прямой
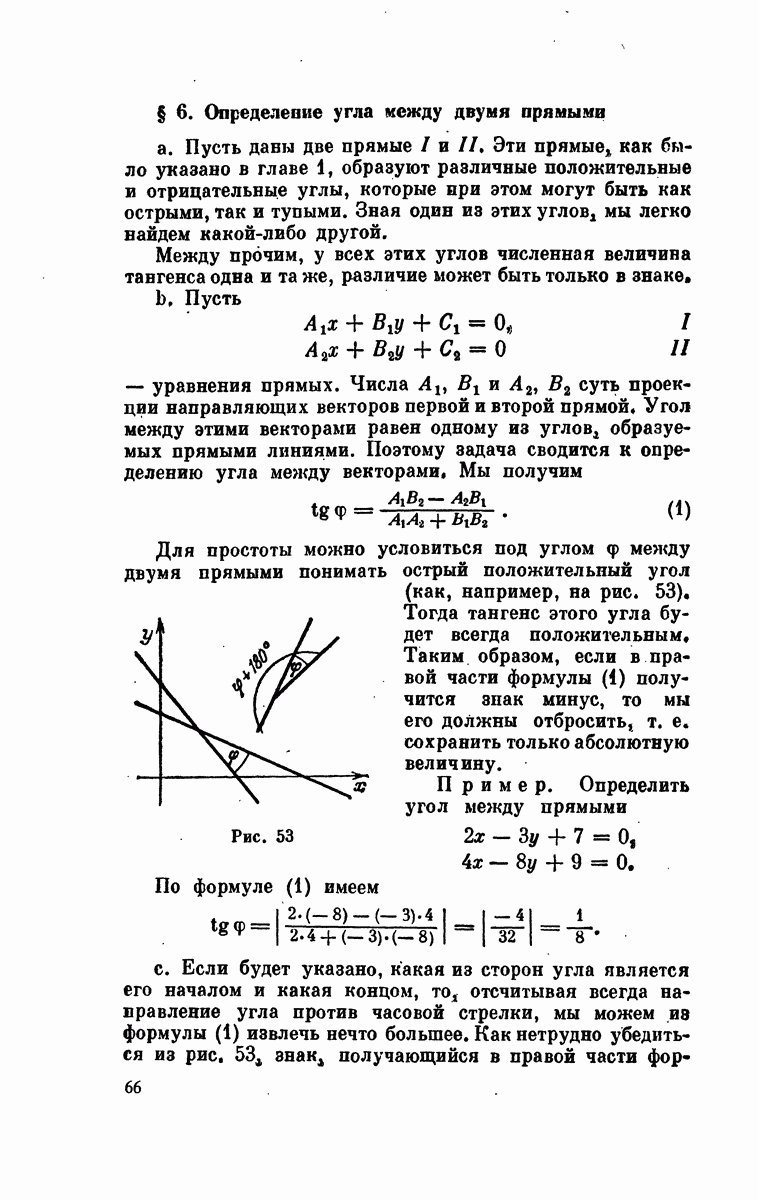
- § 6. Определение угла между двумя прямыми
- § 7. Условие совпадения прямых
- § 8 Пересечение прямых
- § 9. Расстояние от точки до прямой
- § 10. Другой подход к выводу уравнения прямой
- § 11. Прямая, проходящая через две точки
- § 12. Уравнение прямой в отрезках на осях
- § 13. Задачи на прямую линию
- Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- § 1. Окружность
- § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием
- § 3. Построение эллипса по точкам
- § 4. Уравнение эллипса
- § 5. Связь эллипса с окружностью
- § 6. Директрисы эллипса
- § 7. Гипербола. Построение посредством нити
- § 8. Построение гиперболы по точкам
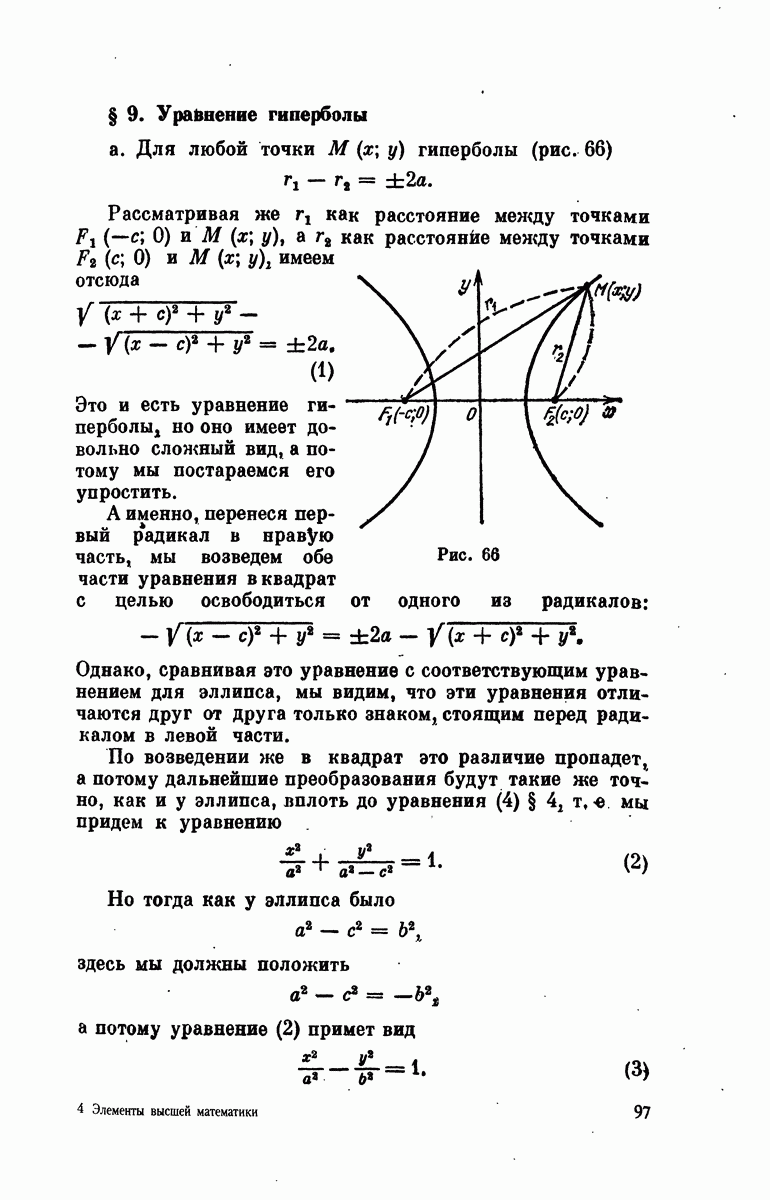
- § 9. Уравнение гиперболы
- § 10. Асимптоты. Геометрическое значение b
- § 11. Директрисы гиперболы
- § 12. Парабола. Построение по точкам
- § 13. Уравнение параболы
- § 14. Преобразование координат
- § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей
- § 16. Поворот осей
- § 17. Общий случай
- § 18. Полярные координаты
- § 19. Спираль Архимеда
- § 20. Логарифмическая спираль
- § 21. Примеры на составление полярных уравнений кривых
- § 22. Выражение прямоугольных координат через полярные
- § 23. Уравнение лемнискаты
- § 24. Параметрическое задание линий
- § 25. Построение графика
- § 26. Циклоида
- § 27. Упражнения
- Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Оси, векторы, углы
- § 2. Проекции
- § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции
- § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы
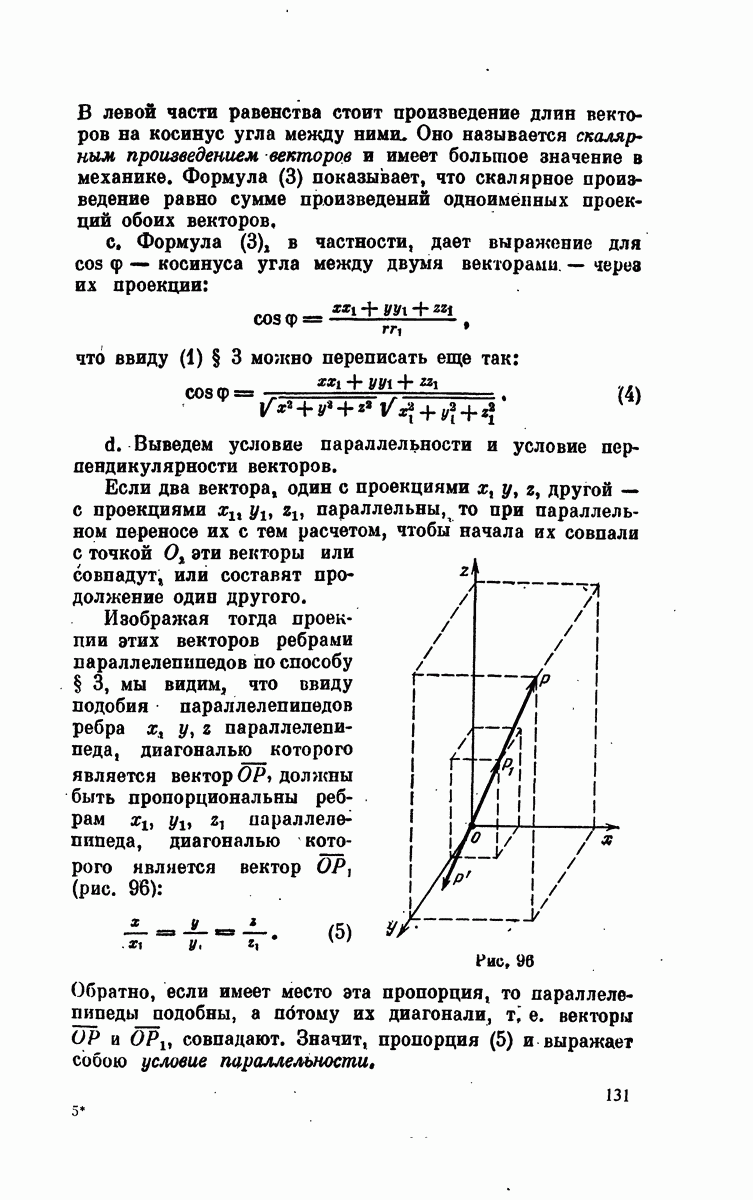
- § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов
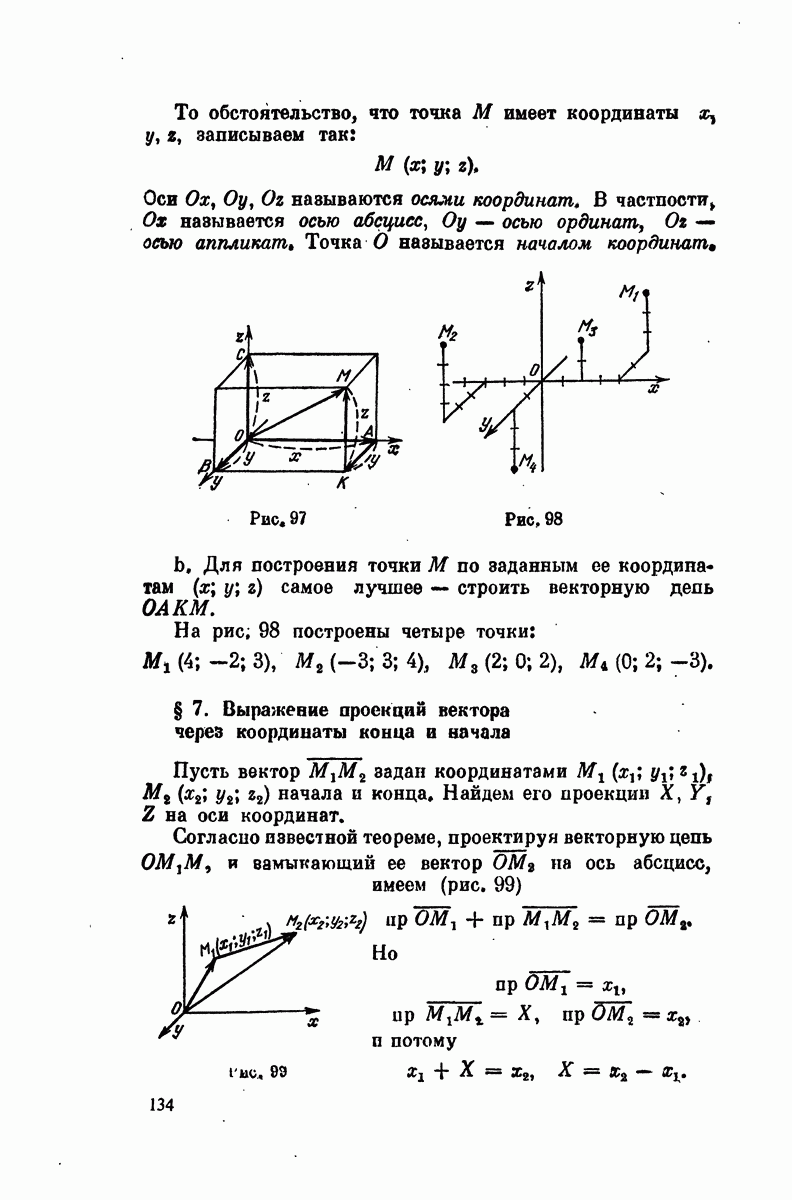
- § 6. Координаты
- § 7. Выражение проекций вектора через координаты конца и начала
- § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками
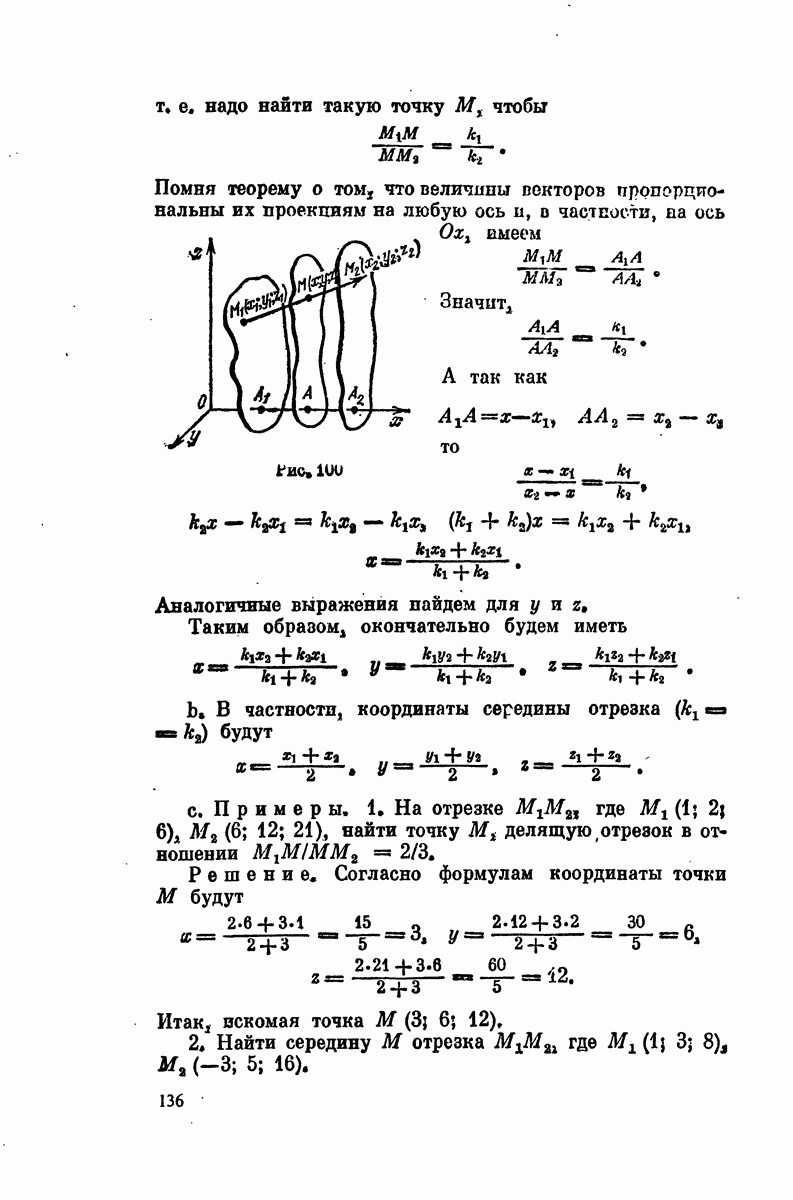
- § 9. Деление отрезка в данном отношении
- § 10. График уравнения с двумя переменными
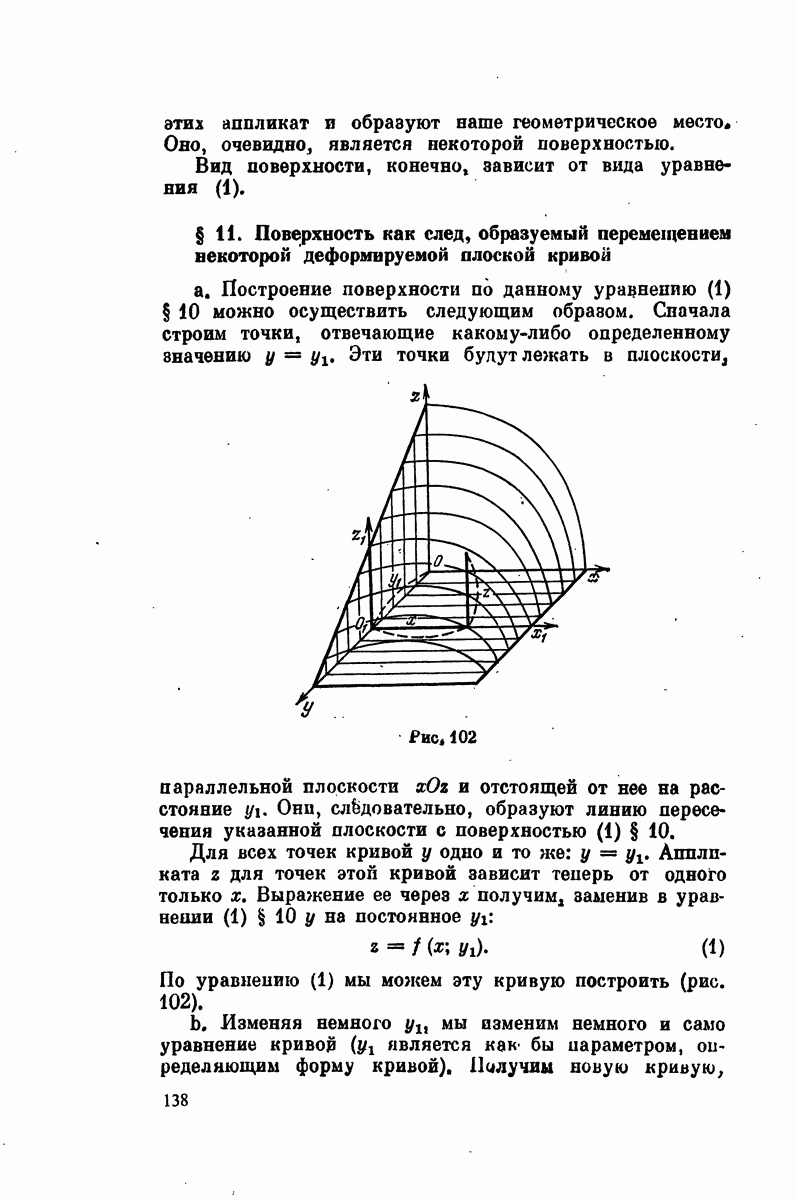
- § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой
- § 12. Цилиндрические поверхности
- § 13. Обратная задача. Уравнение шаровой поверхности
- § 14. Уравнение плоскости, проходящей через данную точку
- § 15. Общее уравнение плоскости
- § 16. Частные случаи
- § 17. Выяснение расположения плоскости относительно осей
- § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности
- § 19. Условие совпадения плоскостей
- § 20. Расстояние от точке до плоскости
- § 21. Прямая как пересечение двух плоскостей
- § 22. Прямая, проходящая через данную точку
- § 23. Прямая, проходящая через две точки
- § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций
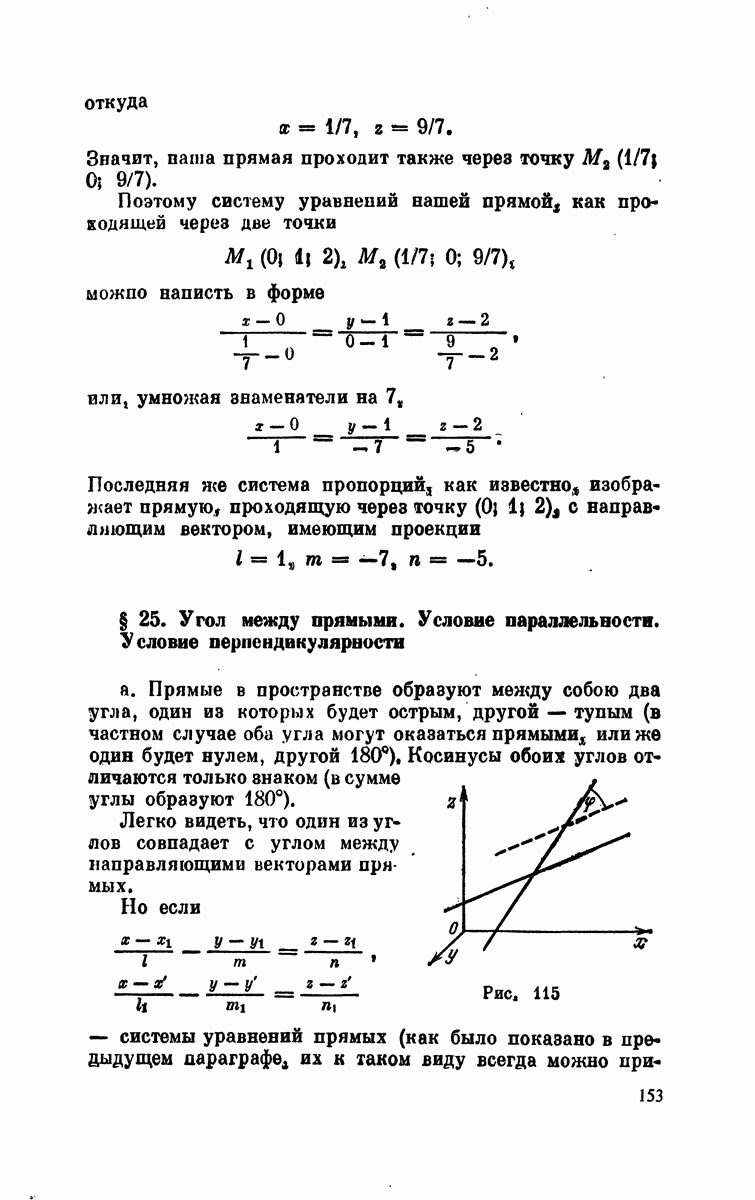
- § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности
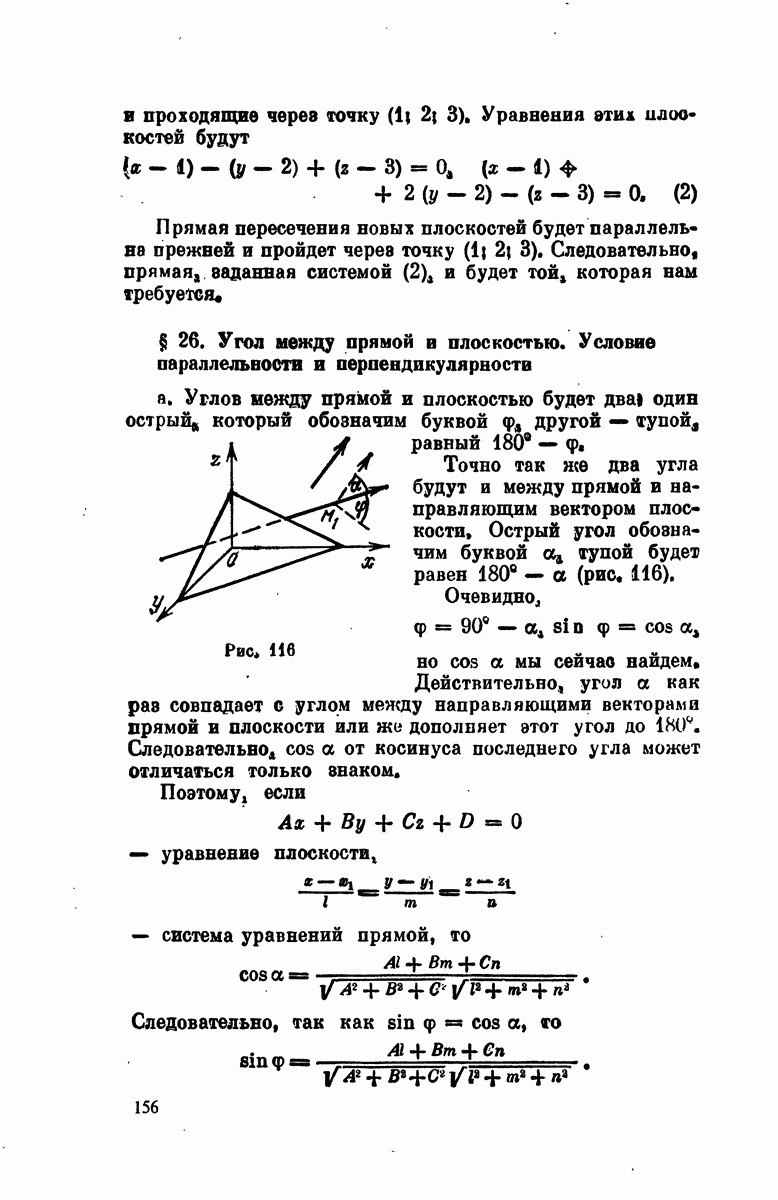
- § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности
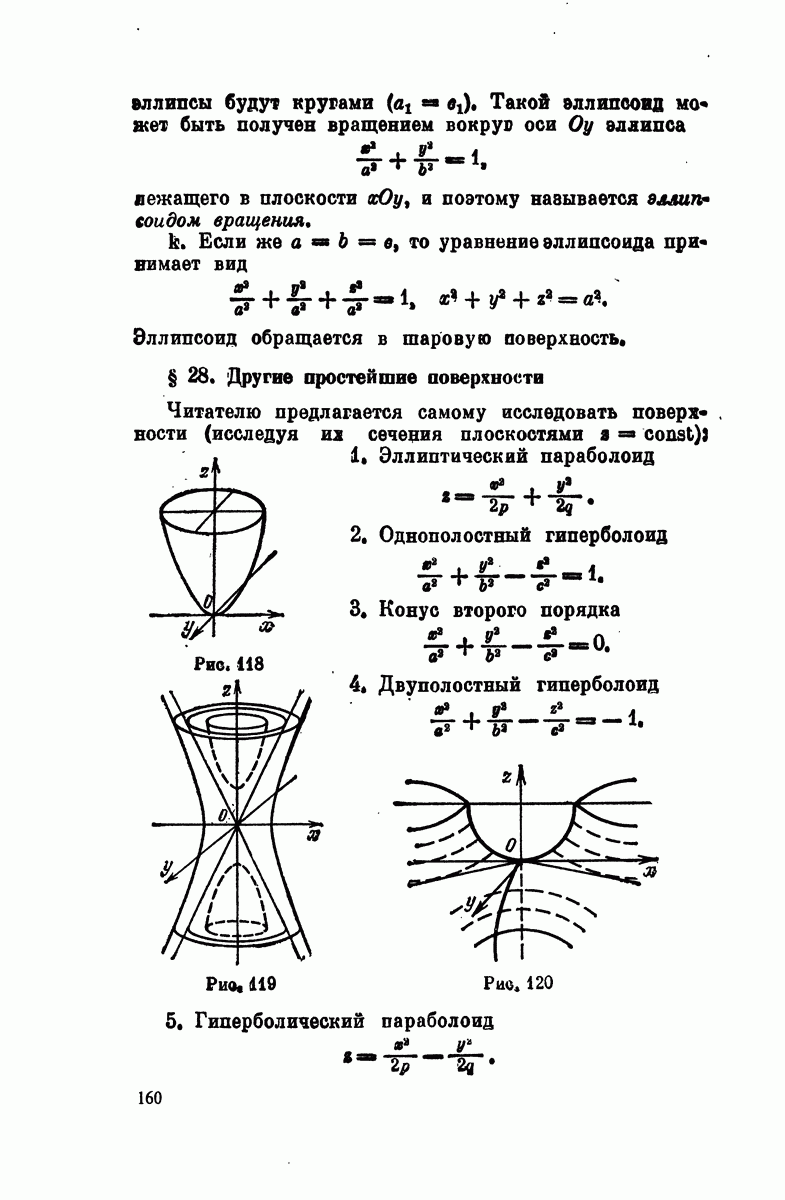
- § 27. Простейшие поверхности. Эллипсоид
- § 28. Другие простейшие поверхности
- § 29. Кривая в пространстве как пересечение двух поверхностей
- § 30. Параметрические уравнения
- § 31. Винтовая линия
- § 32. Параметрические уравнения в механике
- § 33. Переход от параметрического представления к общему и обратно
- § 34. Преобразование координат
- § 35. Упражнения
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. Бесконечно малые
- § 2. Понятие предела переменной величины
- § 3. Понятие бесконечно большой
- § 4. Свойства бесконечно малых
- § 5. Основные свойства пределов
- § 6. Предел непрерывной функции
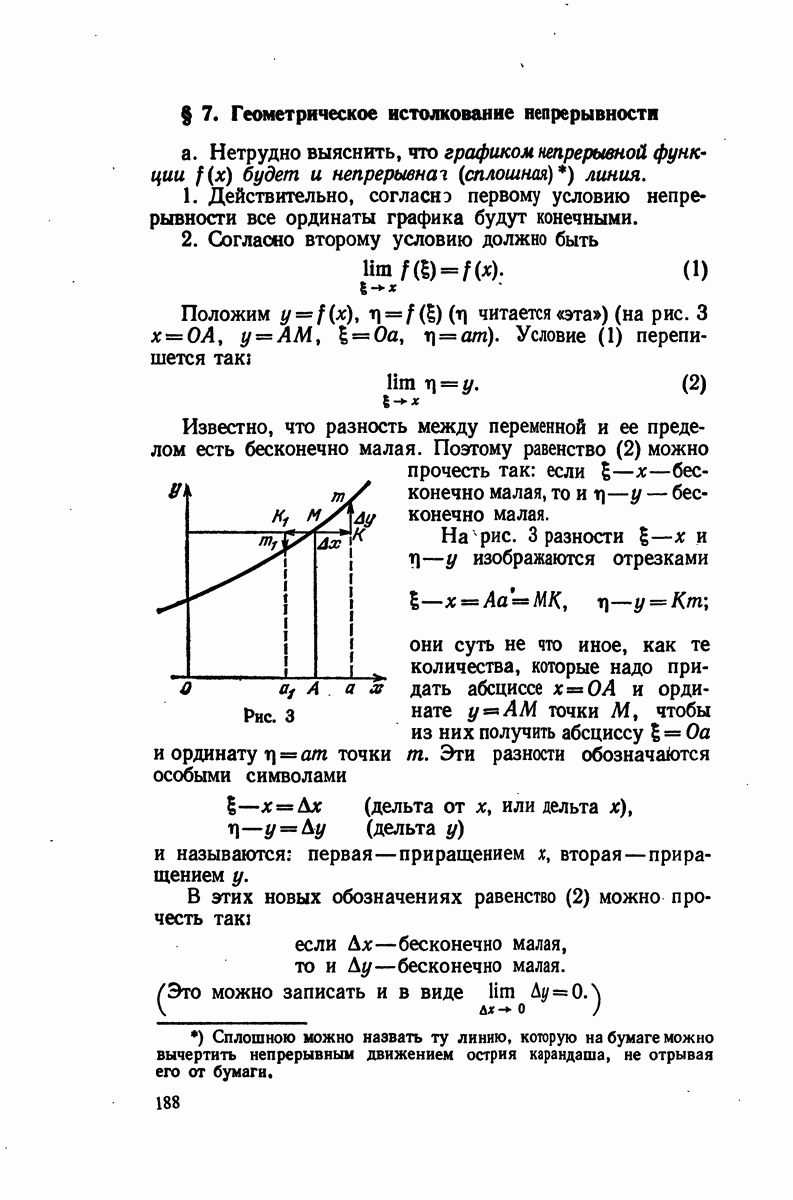
- § 7. Геометрическое истолкование непрерывности
- § 8. Свойство непрерывной функции
- § 9. Предел функции, зависящей от нескольких переменных
- § 10. Особые случаи разыскания предела
- § 11. Замечательный тригонометрический предел
- § 12. Признак существования предела
- § 13. Сходимость бесконечных рядов
- § 14. Простейшие признаки сходимости
- § 15. Основание натуральных логарифмов
- § 16. Порядок бесконечно малых
- § 17. Упражнения
- Глава 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная как угловой коэффициент касательной
- § 2. Производная как предел
- § 3. Пояснение общей теории на примере. Уравнения касательной и нормали
- § 4. Механическое значение производной
- § 5. Производные трех простейших функций
- § 6. Производная постоянного и суммы. Вынесение постоянного множителя за знак производной
- § 7. Производная сложной функции
- § 8. Разыскание производных путем логарифмирования. Производные функции х^n при любом n к функции а^x.
- § 9. Производные произведения и частного. Производные tg x и ctg x.
- § 10. Производные обратных тригонометрических функций
- § 11. Сводка основных формул
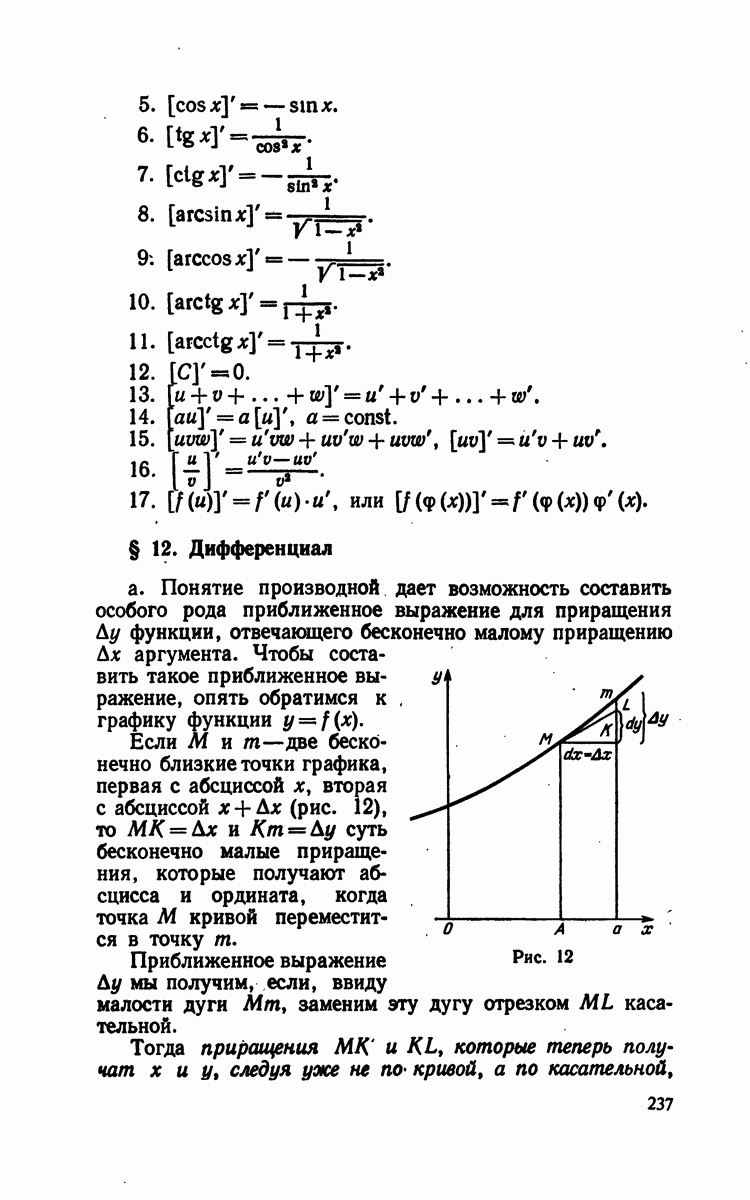
- § 12. Дифференциал
- § 13. Основные формулы для дифференциалов
- § 14. Высшие производные
- § 15. Высшие дифференциалы
- § 16. Дифференцирование неявных функций
- § 17. Дифференцирование функций, заданных параметрическим способом
- § 18. Преобразование дифференциалов к новой переменной
- § 19. Упражнения
- Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- § 1. Непрерывность первой производной
- § 2. Возрастание и убывание функций. Максимум и минимум
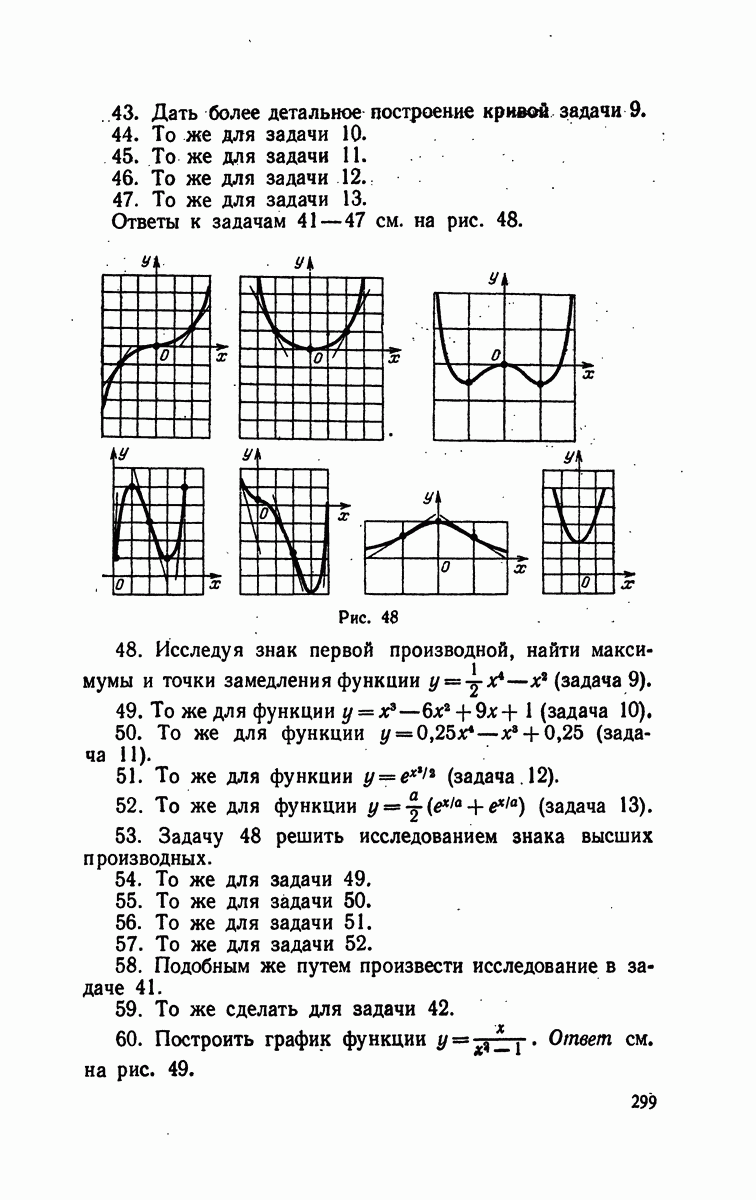
- § 3. Приложение к построению графиков
- § 4. Наибольшее и наименьшее значения функции
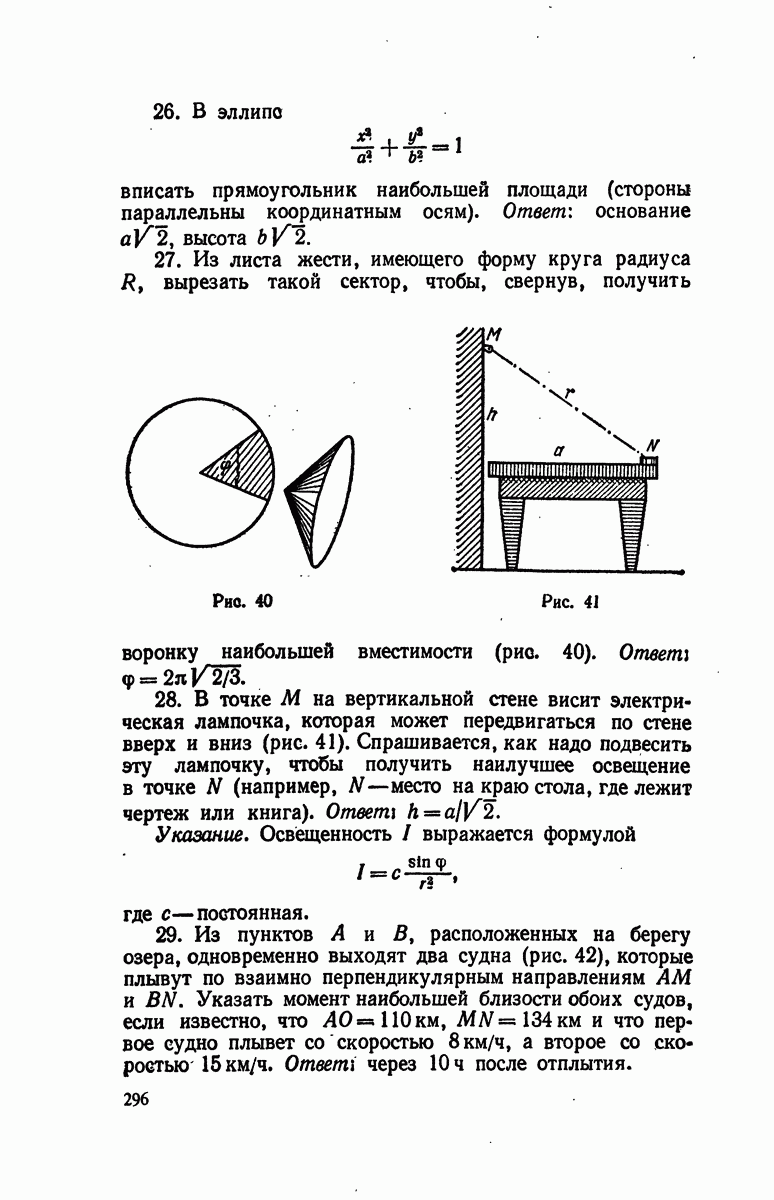
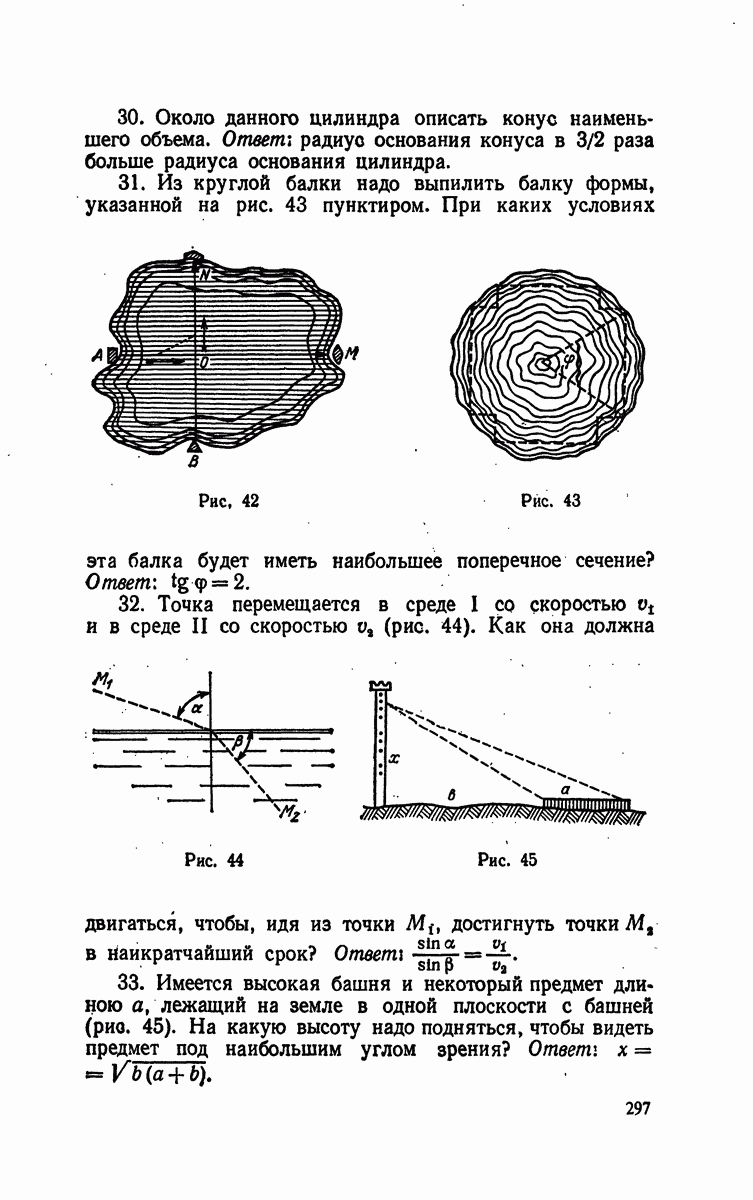
- § 5. Прикладные задачи на наибольшее и наименьшее значения
- § 6. Направление выпуклости, точки перегиба
- § 7. Приложение к построению графиков
- § 8. Построение графиков разрывных функций
- § 9. Признак максимума и минимума, основанный на исследовании знака первой производной
- § 10. Признак максимума и минимума, основанный на исследовании знака второй и высших производных
- § 11. Асимптоты
- § 12. Дифференциал дуги
- § 13. Направляющие косинусы касательной
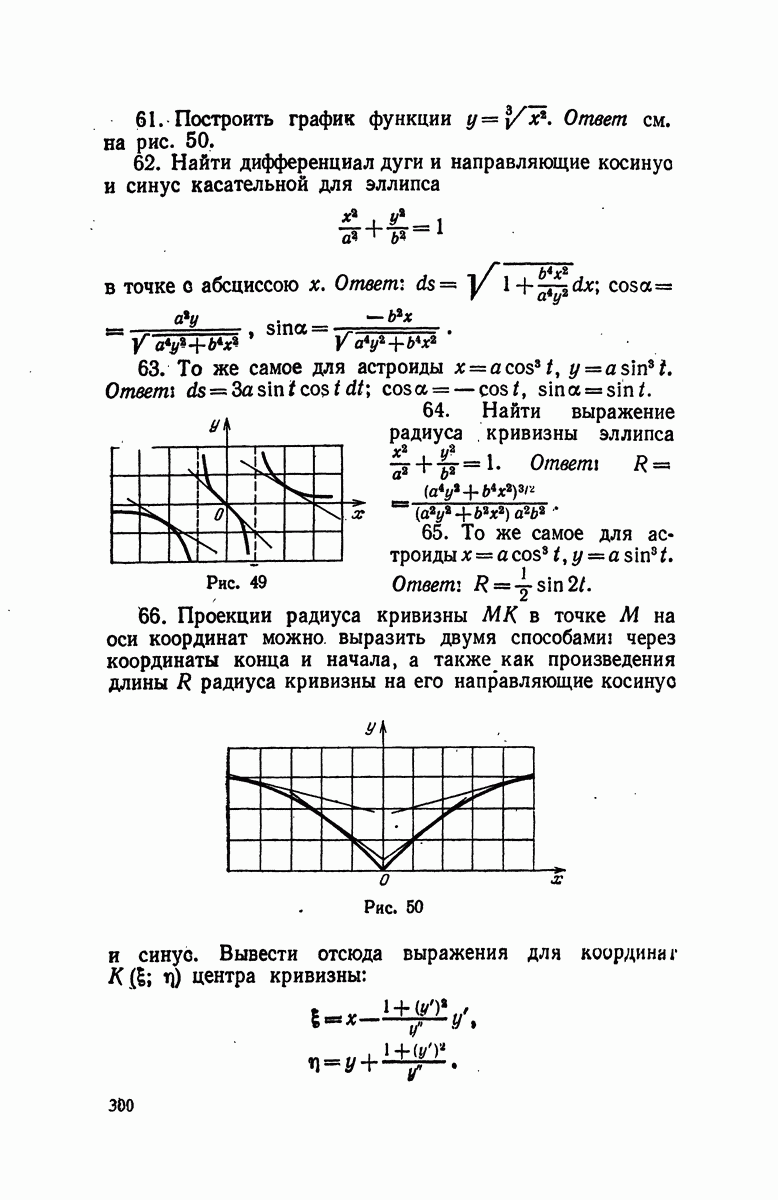
- § 14. Радиус кривизны, центр кривизны
- § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве
- § 16. Упражнения
- Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 1. Функции многих переменных. Область определения. Непрерывность
- § 2. Частные производные и полный дифференциал
- § 3. Частные производные и полный дифференциал сложной функции многих переменных
- § 4. Дифференцирование неявных функций
- § 5. Частные производные и полные дифференциалы высшего порядка
- § 6. Упражнения
- ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ
- Глава 1. ТЕОРИЯ ДЕЛИМОСТИ
- § 2. Общий наибольший делитель
- § 3. Общее наименьшее кратное
- § 4. Простые числа
- § 5. Единственность разложения на простые сомножители
- § 6. Непрерывные дроби и их связь с алгоритмом Евклида
- Вопросы к главе 1
- Глава 2. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
- § 1. Функции [x] и {x}
- § 2. Мультипликативные функции
- § 3. Число делителей и сумма делителей
- § 4. Функция Мёбиуса
- § 5. Функция Эйлера
- Вопросы к главе II
- Глава 3. СРАВНЕНИЯ
- § 2. Свойства сравнений, подобные свойствам равенств
- § 3. Дальнейшие свойства сравнений
- § 4. Полная система вычетов
- § 5. Приведенная система вычетов
- § 6. Теоремы Эйлера и Ферма
- Вопросы к главе 3
- Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
- § 2. Сравнения первой степени
- § 3. Система сравнений первой степени
- § 4. Сравнения любой степени по простому модулю
- § 5. Сравнения любой степени по составному модулю
- Вопросы к главе 4
- Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
- § 2. Символ Лежандра
- § 3. Символ Якоби
- § 4. Случай составного модуля
- Вопросы к главе 5
- Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- § 2. Первообразные корни по модулям
- § 3. Разыскание первообразных корней по модулям
- § 4. Индексы по модулям
- § 5. Следствия предыдущей теории
- § 6. Индексы по модулю 2^a
- § 7. Индексы по любому составному модулю
- Вопросы к главе 6
- Глава 7. ХАРАКТЕРЫ
- § 2. Важнейшие свойства характеров
- Вопросы к главе 7
- РЕШЕНИЯ ВОПРОСОВ
- Решения к главе 2
- Решения к главе 3
- Решения к главе 4
- Решения к главе 5
- Решения к главе 6
- ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ