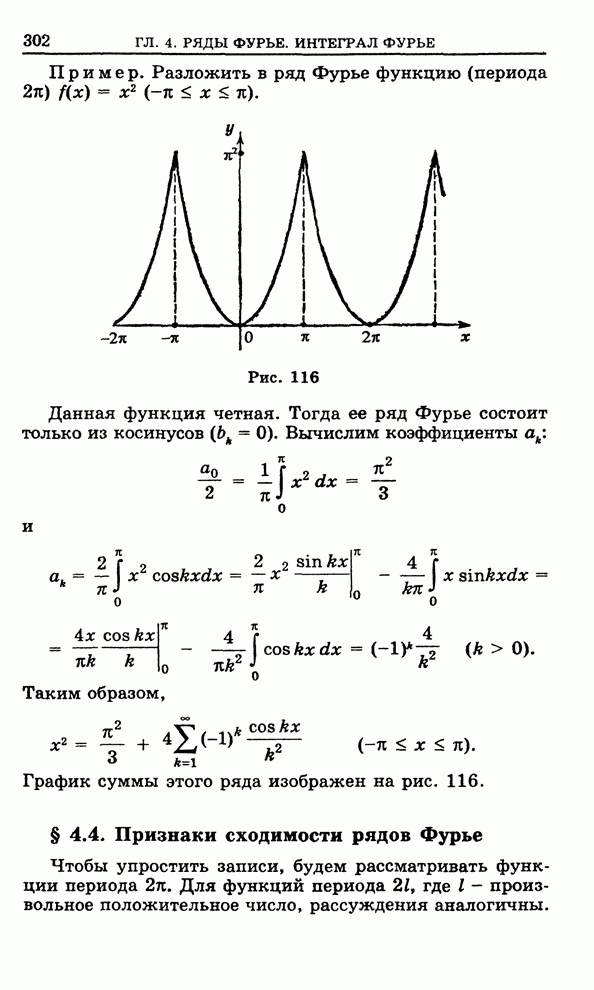
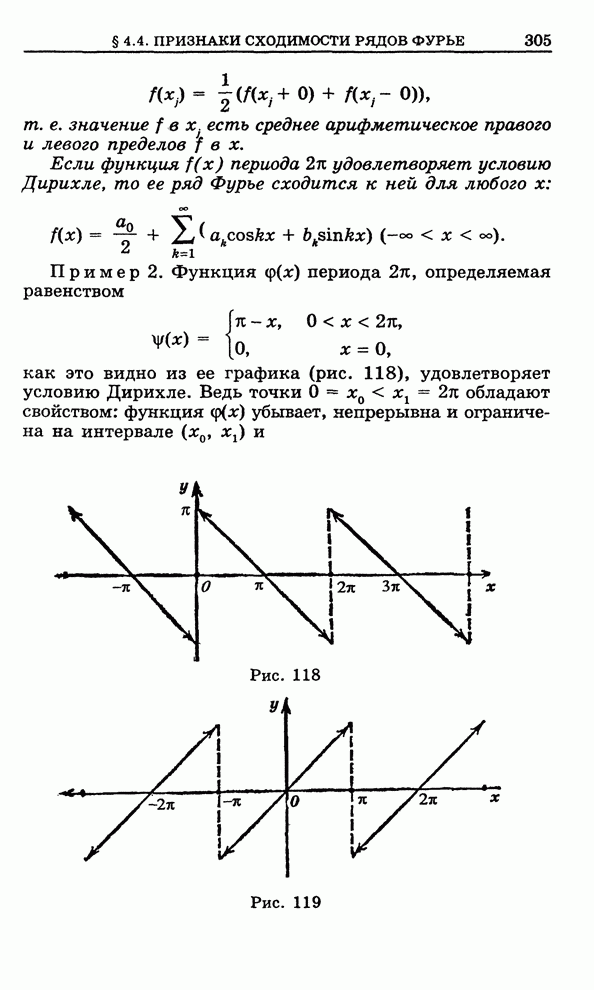
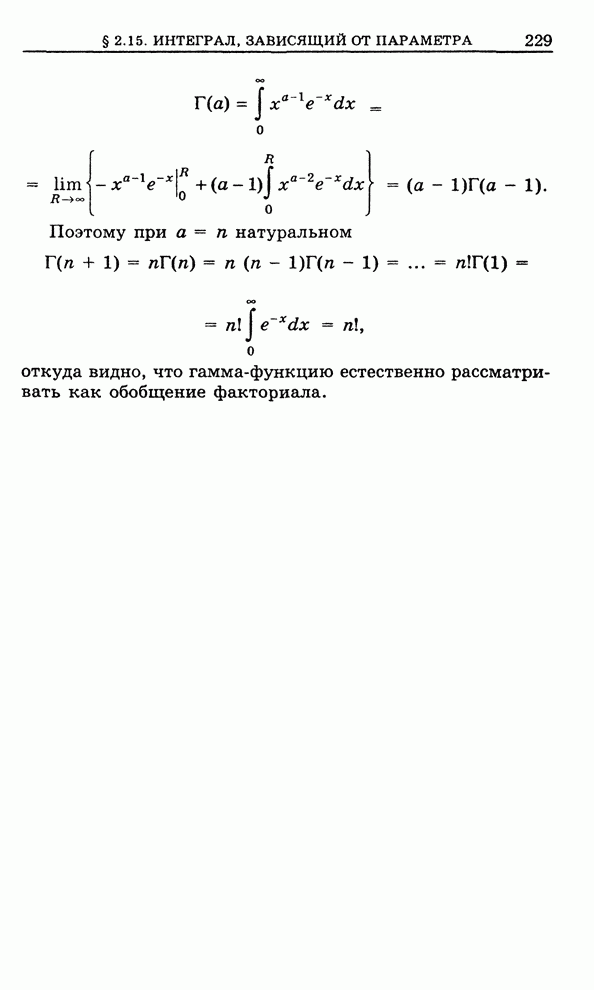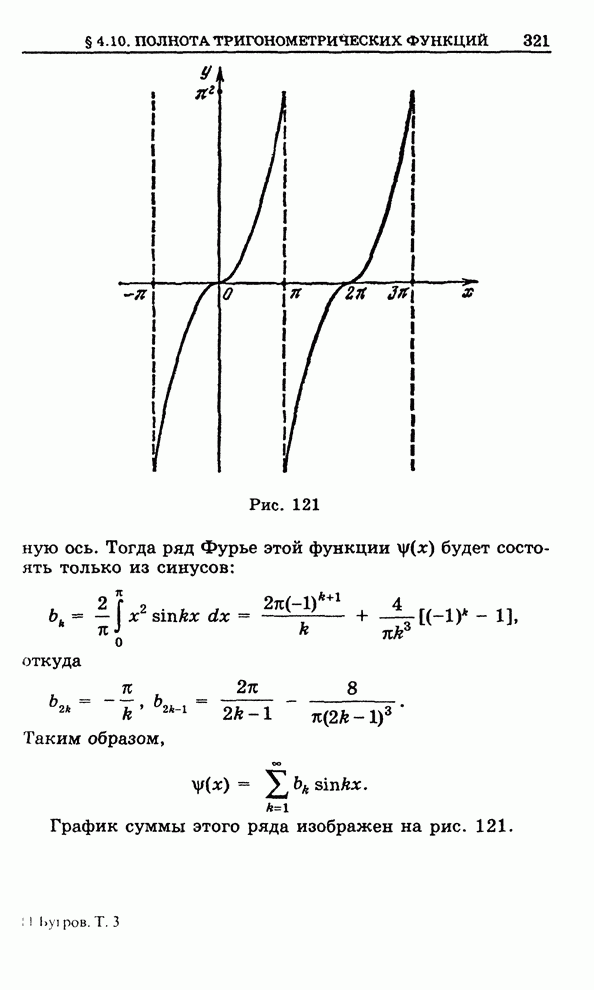| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.11. Дифференциальное уравнение второго порядка
Уравнение
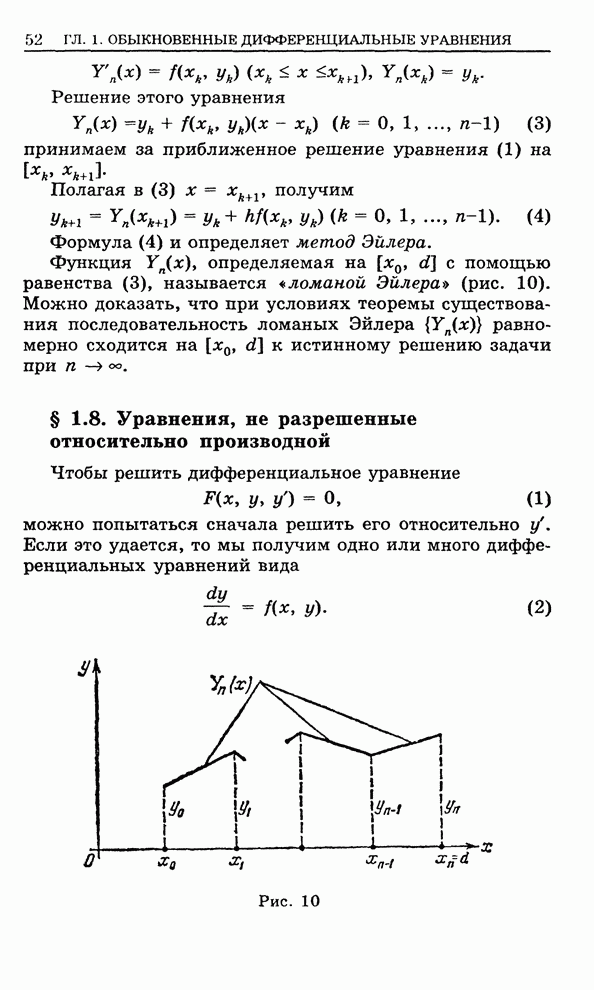
![]() (1)
(1)
называется дифференциальным уравнением второго порядка.
Предполагается, что ![]() - заданная непрерывно дифференцируемая
функция от точек
- заданная непрерывно дифференцируемая
функция от точек ![]() некоторой
области
некоторой
области ![]() четырехмерного
пространства.
четырехмерного
пространства.
Любая функция ![]() , имеющая на
некотором интервале непрерывную производную второго порядка и удовлетворяющая
уравнению (1), называется решением этого уравнения или его интегральной кривой.
, имеющая на
некотором интервале непрерывную производную второго порядка и удовлетворяющая
уравнению (1), называется решением этого уравнения или его интегральной кривой.
Каждое из них ![]() определено, вообще
говоря, на некотором своем интервале
определено, вообще
говоря, на некотором своем интервале ![]() . Конечно, для любого
. Конечно, для любого ![]() из этого интервала
точка
из этого интервала
точка
![]() .
.
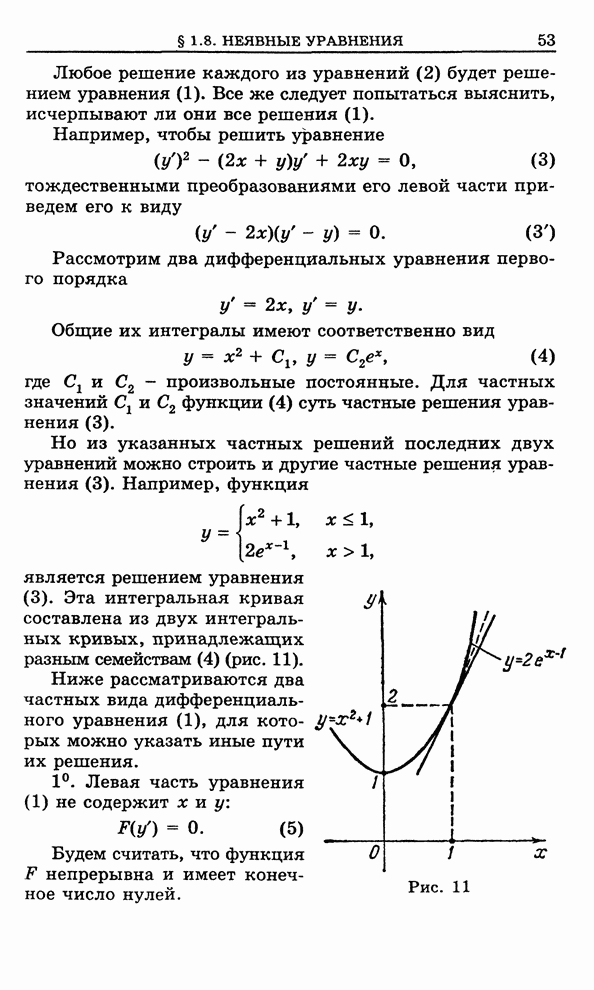
Нередко на решение, которое ищут, накладывают дополнительные условия. Особый интерес представляют такие условия, которые гарантируют единственное решение уравнения. Обычно эти условия имеют вид
![]() (2)
(2)
и называются начальными
условиями. Задача нахождения решения уравнения (1), удовлетворяющего начальным
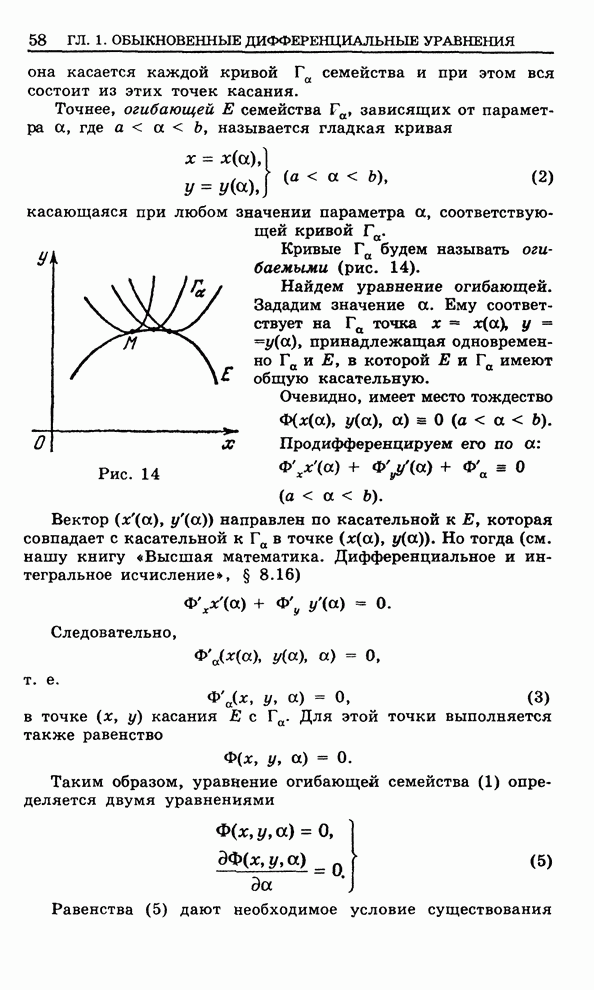
условиям (2), называется задачей Коши. С геометрической точки зрения условия (2) означают, что из семейства интегральных
кривых, проходящих через точку ![]() , мы
выделяем определенную интегральную кривую, имеющую заданный угол наклона
(
, мы
выделяем определенную интегральную кривую, имеющую заданный угол наклона
(![]() , рис.15).
, рис.15).

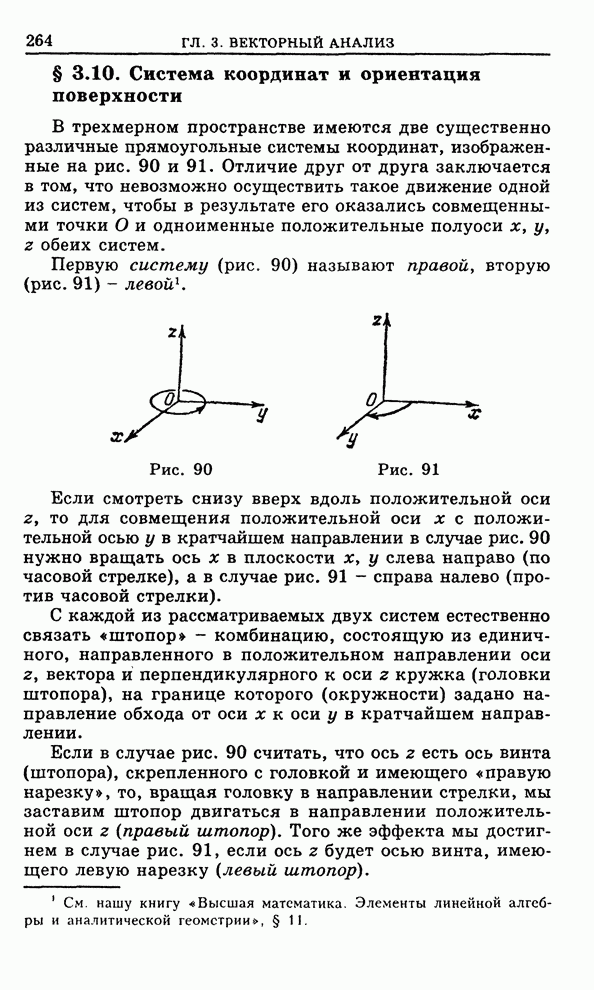
Рис.15
В уравнение (1)
могут не входить явно все переменные ![]() , но
, но ![]() должно входить, иначе это уравнение не
будет дифференциальным уравнением второго порядка, например,
должно входить, иначе это уравнение не
будет дифференциальным уравнением второго порядка, например, ![]() ,
, ![]() .
.
Разрешим
уравнение (1) относительно ![]() . Будем предполагать это возможным. Из
теории неявных функций известно, что если
функция
. Будем предполагать это возможным. Из
теории неявных функций известно, что если
функция ![]() равна
нулю в некоторой точке
равна
нулю в некоторой точке ![]() , имеет непрерывные
частные производные в окрестности этой точки и частная производная
, имеет непрерывные
частные производные в окрестности этой точки и частная производная ![]() в этой точке, то уравнение
в этой точке, то уравнение ![]() имеет
в некоторой окрестности указанной точки решение
имеет
в некоторой окрестности указанной точки решение ![]() и притом единственное.
и притом единственное.
Тогда уравнение (1) примет вид
![]() , (3)
, (3)
где функция ![]() задана на некоторой
области
задана на некоторой
области ![]() трехмерного
пространства точек
трехмерного
пространства точек ![]() , непрерывна на ней и имеет непрерывные
частные производные. Функция
, непрерывна на ней и имеет непрерывные
частные производные. Функция ![]() может и не зависеть явно от некоторых
из переменных
может и не зависеть явно от некоторых
из переменных ![]() .
Например, это имеет место для уравнений
.
Например, это имеет место для уравнений ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пусть некоторая
интегральная кривая ![]() проходит через точку
проходит через точку ![]() и имеет в этой
точке угловой коэффициент касательной,
равный заданному числу
и имеет в этой
точке угловой коэффициент касательной,
равный заданному числу ![]() (т. е.
(т. е. ![]() ).
).
Этим однозначно
определяется вторая производная от ![]() в точке
в точке ![]() , равная
, равная
![]() .
.
Однако возникает
вопрос, если мы зададим![]() и произвольные числа
и произвольные числа ![]() , то существует ли
на самом деле интегральная кривая
, то существует ли
на самом деле интегральная кривая ![]() уравнения (3), для которой
уравнения (3), для которой ![]() и
и ![]() , и как много таких интегральных кривых. Следующая теорема показывает, что
если функция
, и как много таких интегральных кривых. Следующая теорема показывает, что
если функция ![]() в окрестности точки
в окрестности точки ![]() достаточно гладкая,
то такая интегральная кривая существует и притом одна.
достаточно гладкая,
то такая интегральная кривая существует и притом одна.
Доказательство этой теоремы, так же как и теоремы 1 § 1.12 и теоремы 1 § 1.13, мы не приводим. Оно может быть проведено на основании принципа сжатых отображений.
Теорема 1. Пусть правая часть уравнения (3),
рассматриваемая как функция трех переменных ![]() , заданная на трехмерной области
, заданная на трехмерной области ![]() , непрерывна и имеет
на этой области непрерывные частные
производные
, непрерывна и имеет
на этой области непрерывные частные
производные ![]() .
.
Тогда, какова бы ни была точка ![]() , существует интервал
, существует интервал ![]() и определенная на нем дважды
непрерывно дифференцируемая функция
и определенная на нем дважды
непрерывно дифференцируемая функция ![]() , удовлетворяющая
дифференциальному уравнению (3) и
начальным условиям
, удовлетворяющая
дифференциальному уравнению (3) и
начальным условиям ![]() .
.
Функция, обладающая указанными свойствами, единственная.
Про функцию ![]() говорят, что она
есть решение (интегральная кривая) дифференциального уравнения (3),
удовлетворяющее начальным условиям (2). Или еще говорят, что она решает задачу
Коши для указанных начальных условий.
говорят, что она
есть решение (интегральная кривая) дифференциального уравнения (3),
удовлетворяющее начальным условиям (2). Или еще говорят, что она решает задачу
Коши для указанных начальных условий.
Каждое такое решение удобно записывать в виде
![]() ,
,
где ![]() - параметры
решения. Они независимы – их можно взять
какими угодно, лишь бы точка
- параметры
решения. Они независимы – их можно взять
какими угодно, лишь бы точка ![]() .
.
Если зафиксировать ![]() , то каждой системе чисел
, то каждой системе чисел ![]() ,
, ![]() ,
, ![]() , соответствует
решение дифференциального уравнения (3), которое можно записать (при
фиксированном
, соответствует
решение дифференциального уравнения (3), которое можно записать (при
фиксированном ![]() )
в виде
)
в виде
![]() ,
,
где ![]() - произвольные
постоянные - параметры.
- произвольные
постоянные - параметры.
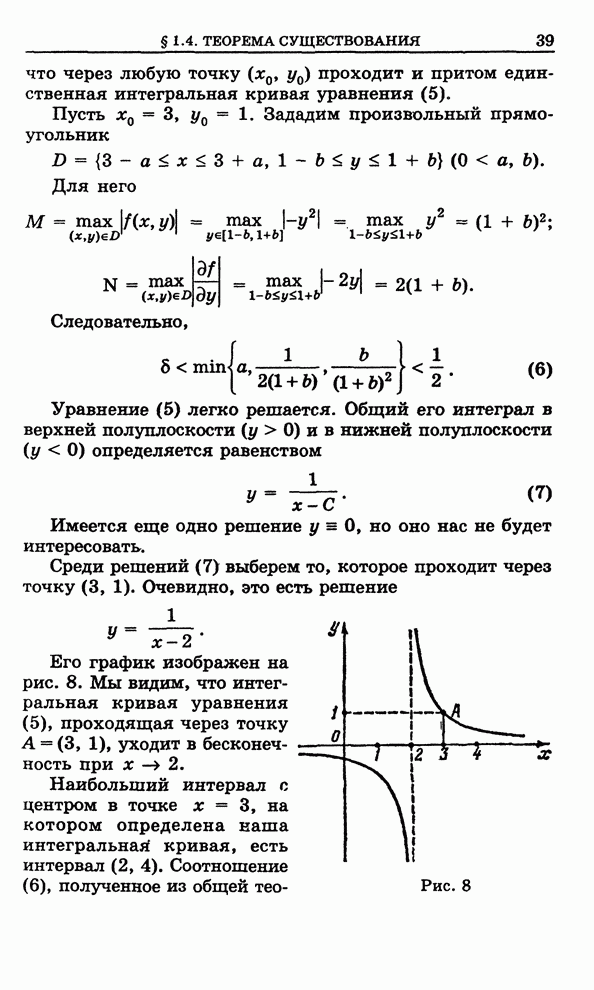
Пример. Найти
интегральную кривую уравнения ![]() , проходящую через точку
, проходящую через точку ![]() и имеющую в ней
угловой коэффициент касательной
и имеющую в ней
угловой коэффициент касательной ![]() .
.
Легко проверить,
что функция ![]() является
решением данного уравнения при любых постоянных
является
решением данного уравнения при любых постоянных ![]() и
и ![]() . Далее
. Далее ![]() . Чтобы высолнялись начальные условия,
необходимо положить
. Чтобы высолнялись начальные условия,
необходимо положить ![]() ,
, ![]() . Итак, искомая интегральная кривая
имеет вид:
. Итак, искомая интегральная кривая
имеет вид: ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
- 1.2.6. Поле направлений
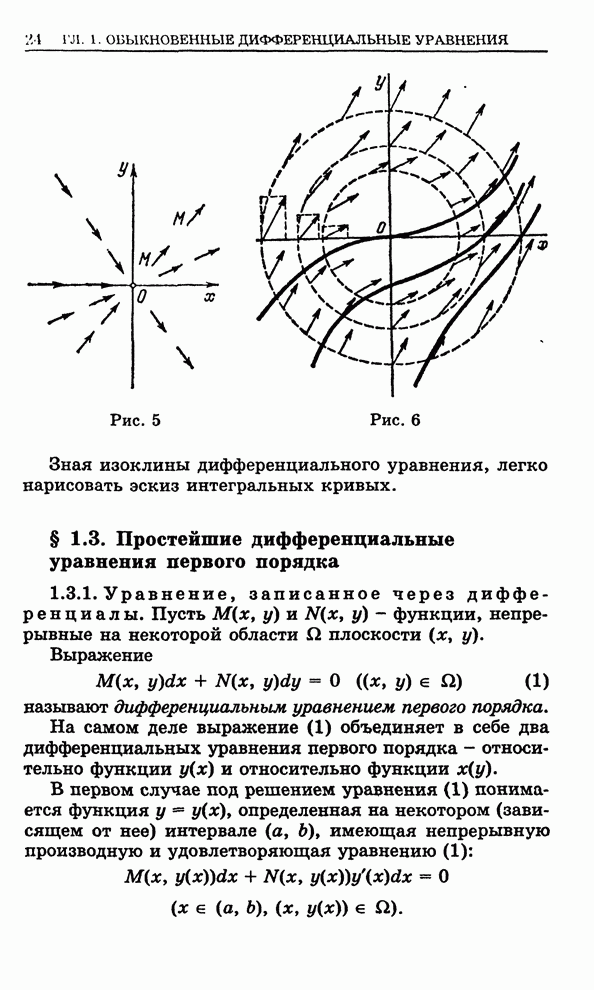
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
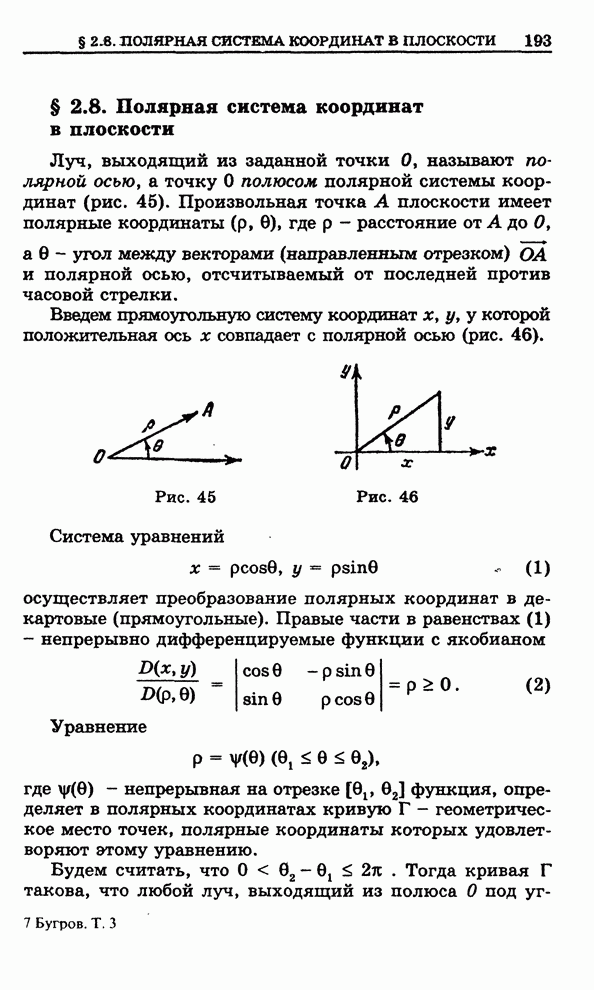
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
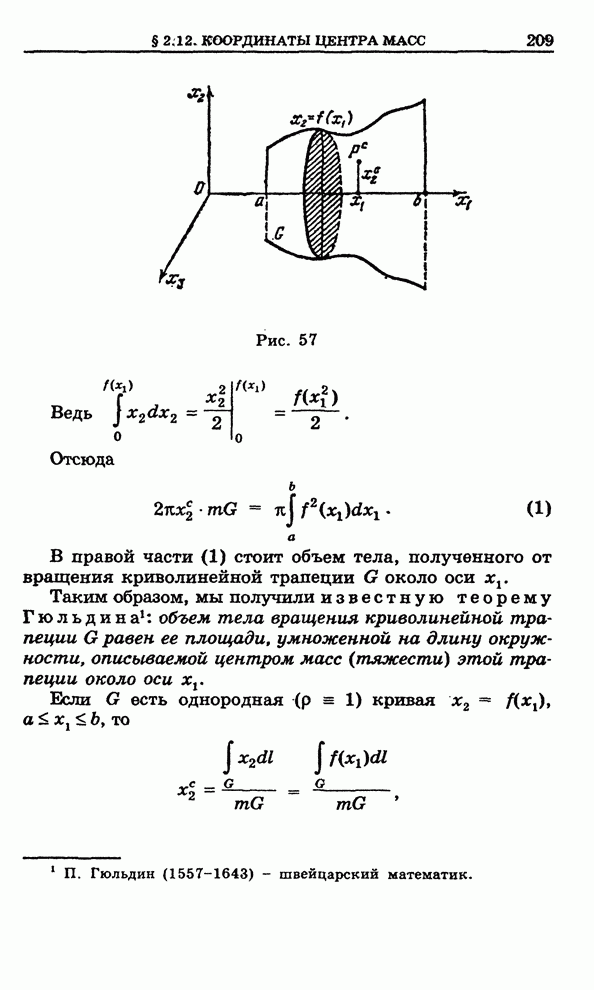
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
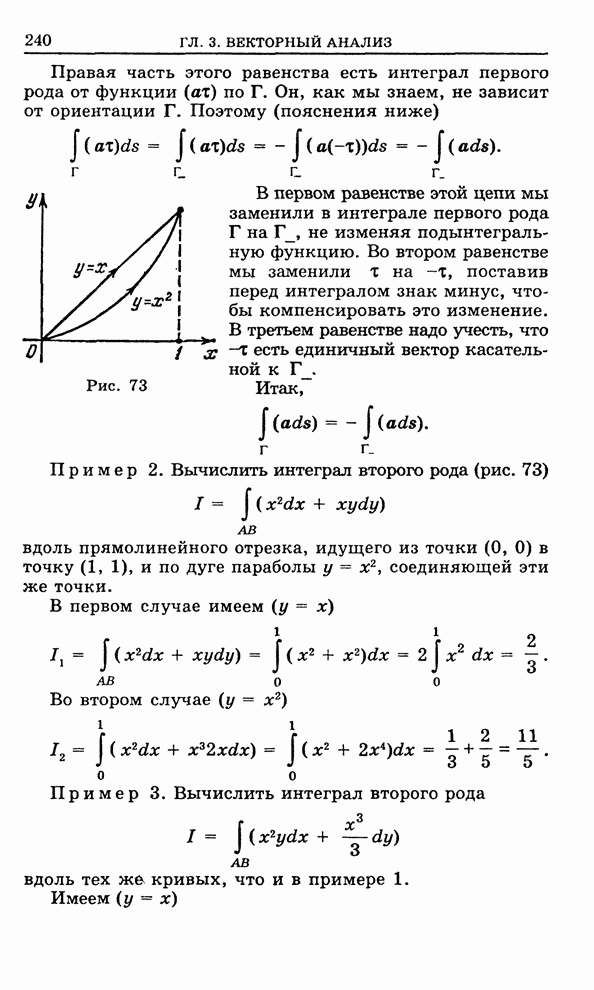
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций