| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
26. Прямоугольник. Ромб. Квадрат.
Прямоугольник — это параллелограмм, у которого все углы прямые. На рисунке 79, а изображен прямоугольник  .
.
Можно доказать теорему о свойстве прямоугольника.
Т. 1.33. Диагонали прямоугольника равны.
Ромб — это параллелограмм, у которого все стороны равны.
На рисунке  изображен ромб
изображен ромб 
Справедлива теорема о свойствах ромба.
Т. 1. 34. Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являютсй биссектрисами его углов.
Квадрат — это прямоугольник, у которого все стороны равны.



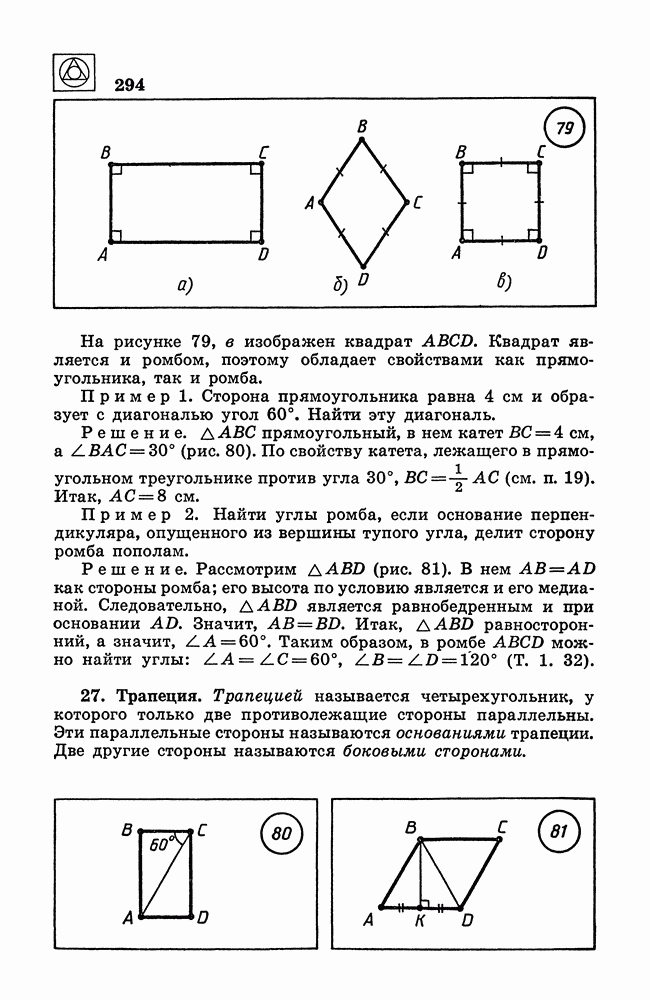
На рисунке 79, в изображен квадрат  Квадрат является и ромбом, поэтому обладает свойствами как прямоугольника, так и ромба.
Квадрат является и ромбом, поэтому обладает свойствами как прямоугольника, так и ромба.
Пример 1. Сторона прямоугольника равна 4 см и образует с диагональю угол 60°. Найти эту диагональ.
Решение.  прямоугольный, в нем катет
прямоугольный, в нем катет  (рис. 80). По свойству катета, лежащего в прямоугольном треугольнике против угла 30°,
(рис. 80). По свойству катета, лежащего в прямоугольном треугольнике против угла 30°,  (см. п. 19). Итак,
(см. п. 19). Итак,  см.
см.
Пример 2. Найти углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
Решение. Рассмотрим  (рис. 81). В нем
(рис. 81). В нем  как стороны ромба; его высота по условию является и его медианой. Следовательно,
как стороны ромба; его высота по условию является и его медианой. Следовательно,  является равнобедренным и при основании
является равнобедренным и при основании  Значит,
Значит,  Итак,
Итак,  равносторонний, а значит,
равносторонний, а значит,  60°. Таким образом, в ромбе
60°. Таким образом, в ромбе  можно найти углы:
можно найти углы:  (Т. 1. 32).
(Т. 1. 32).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- СЛОВО К УЧАЩИМСЯ
- ГЛАВА I. ЧИСЛА
- § 1. Натуральные числа
- 2. Арифметические действия над натуральными числами.
- 3. Деление с остатком.
- 4. Признаки делимости.
- 5. Разложение натурального числа на простые множители.
- 6. Наибольший общий делитель нескольких натуральных чисел.
- 7. Наименьшее общее кратное нескольких натуральных чисел.
- 8. Употребление букв в алгебре. Переменные.
- § 2. Рациональные числа
- 10. Равенство дробей. Основное свойство дроби. Сокращение дробей.
- 11. Приведение дробей к общему знаменателю.
- 12. Арифметические действия над обыкновенными дробями.
- 13. Десятичные дроби.
- 14. Арифметические действия над десятичными дробями.
- 15. Проценты.
- 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь.
- 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь.
- 18. Координатная прямая.
- 19. Множество рациональных чисел.
- § 3. Действительные числа
- 21. Действительные числа. Числовая прямая.
- 22 Обозначения некоторых числовых множеств.
- 23. Сравнение действительных чисел.
- 25. Числовые промежутки.
- 26. Модуль действительного числа.
- 27. Формула расстояния между двумя точками координатной прямой.
- 28. Правила действий над действительными числами.
- 29. Свойства арифметических действий над действительными числами.
- 30. Пропорции.
- 31. Целая часть числа. Дробная часть числа.
- 32. Степень с натуральным показателем.
- 33. Степень с нулевым показателем. Степень с отрицательным целым показателем.
- 34. Стандартный вид положительного действительного числа.
- 35. Определение арифметического корня.
- 36. Корень нечетной степени из отрицательного числа.
- 37. Степень с дробным показателем.
- 38. Свойства степеней с рациональными показателями.
- 39. Приближенные значения чисел. Абсолютная и относительная погрешности.
- 40. Десятичные приближения действительного числа по недостатку и по избытку.
- 41. Правило извлечения квадратного корня из натурального числа.
- 42. Понятие о степени с иррациональным показателем.
- 43. Свойства степеней с действительными показателями.
- § 4. Комплексные числа
- 45. Арифметические операции над комплексными числами.
- 46. Алгебраическая форма комплексного числа.
- 47. Отыскание комплексных корней уравнений.
- ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
- 49. Допустимые значения переменных.
- 50. Понятие тождественного преобразования выражения. Тождество.
- § 6. Целые рациональные выражения
- 52. Многочлены. Приведение многочленов к стандартному виду.
- 53. Формулы сокращенного умножения.
- 54. Разложение многочленов на множители.
- 55. Многочлены от одной переменной.
- 56. Разложение квадратного трехчлена на линейные множители.
- 57. Разложение на множители двучлена x^n-a^n.
- 58. Возведение двучлена в натуральную степень (бином Ньютона).
- § 7. Дробные рациональные выражения
- 60. Сокращение рациональных дробей.
- 61. Приведение рациональных дробей к общему знамена телю.
- 62. Сложение и вычитание рациональных дробей.
- 63. Умножение и деление рациональных дробей.
- 64. Возведение рациональной дроби в целую степень.
- 65. Преобразование рациональных выражений.
- § 8. Иррациональные выражения
- 67. Тождество sqrt(a^2)=|a|
- 68. Преобразование иррациональных выражений.
- Глава III. ФУНКЦИИ И ГРАФИКИ
- 70. Аналитическое задание функции.
- 71. Табличное задание функции.
- 72. Числовая плоскость. Координатная плоскость, оси координат.
- 73. График функции, заданной аналитически.
- 74. Четные и нечетные функции.
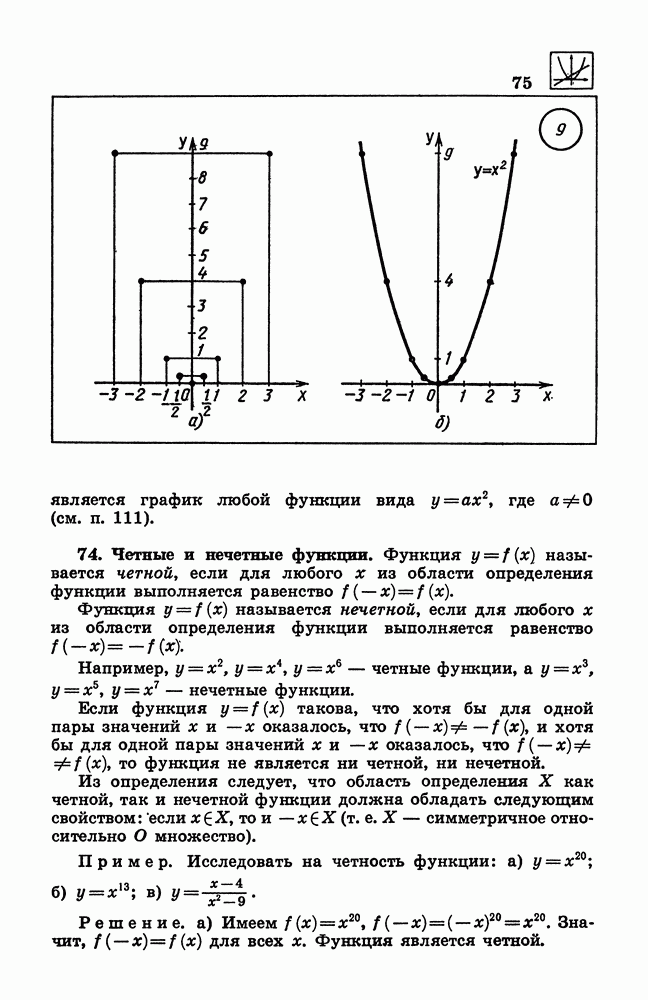
- 75. График четной функции. График нечетной функции.
- 76. Периодические функции.
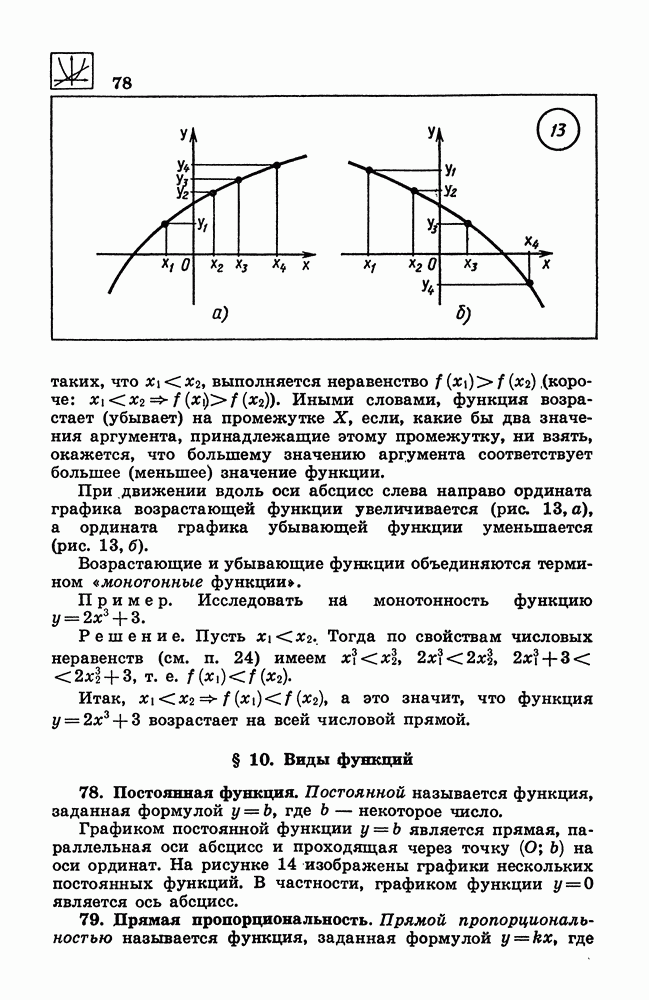
- 77. Монотонные функции.
- § 10. Виды функций
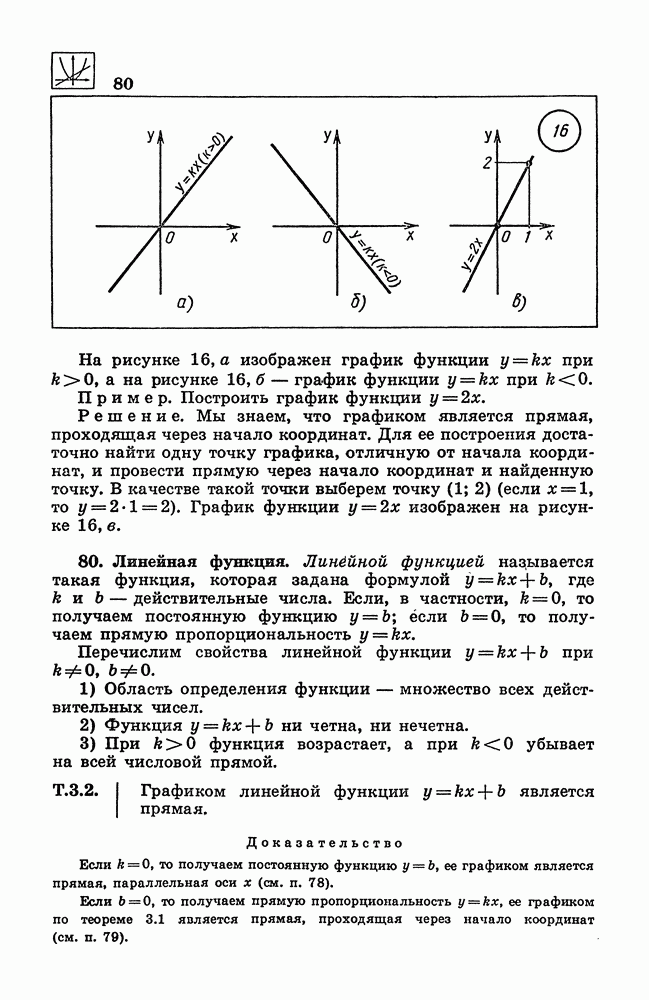
- 79. Прямая пропорциональность.
- 80. Линейная функция.
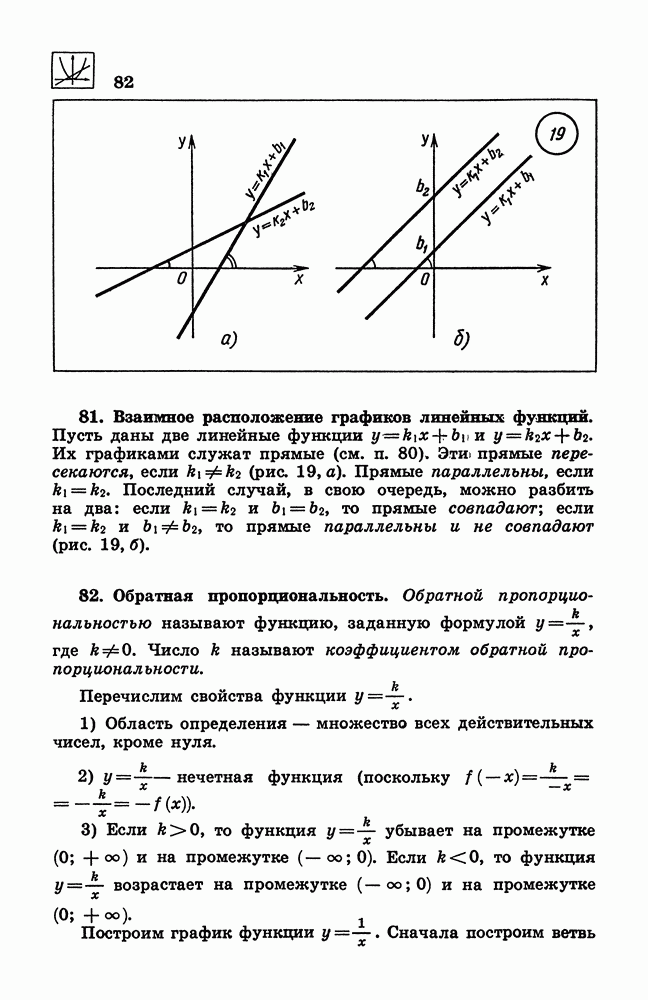
- 81. Взаимное расположение графиков линейных функций.
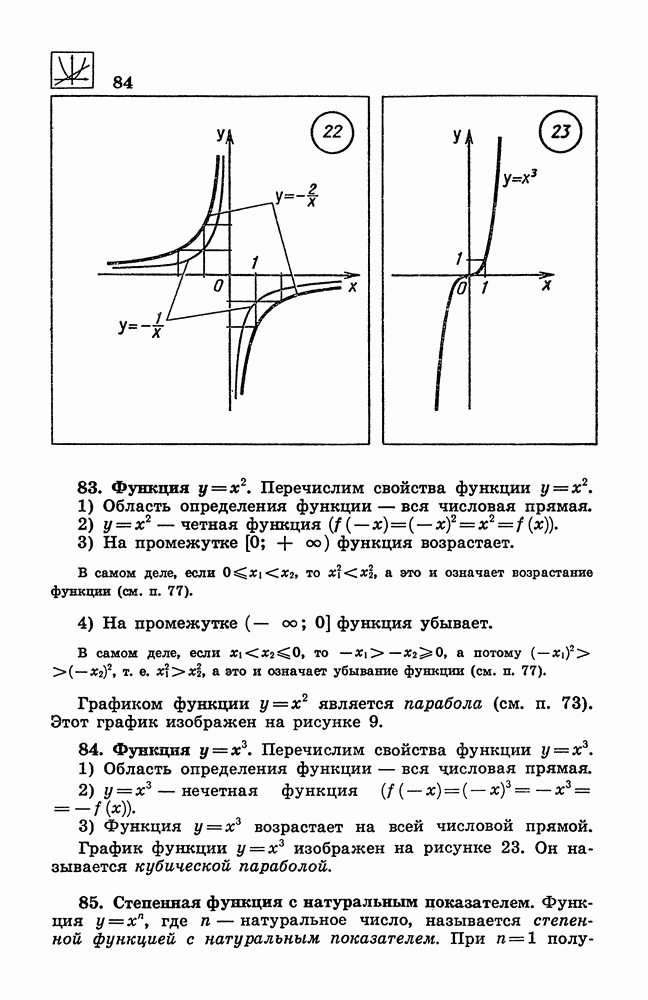
- 82. Обратная пропорциональность.
- 83. Функция у = x^2.
- 84. Функция y = x^3.
- 85. Степенная функция с натуральным показателем.
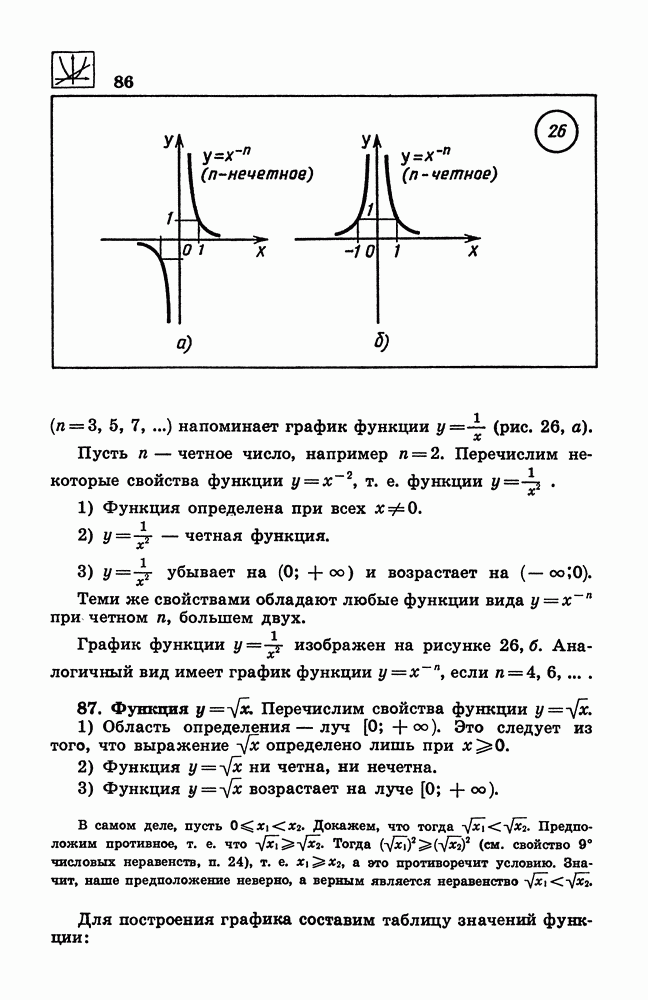
- 86. Степенная функция с целым отрицательным показателем.
- 87. Функция y = sqrt(x)
- 88. Функция y = x^(1/3)
- 89. Функция y = x^(1/n)
- 90. Степенная функция с положительным дробным показателем.
- 91. Степенная функция с отрицательным дробным показателем.
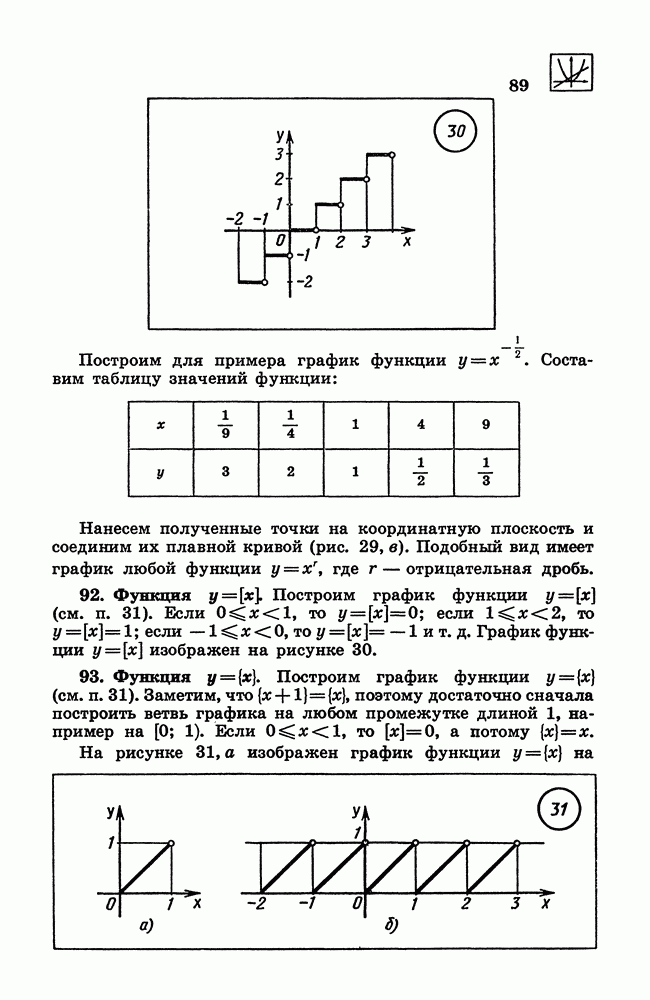
- 92. Функция у = [x].
- 93. Функция у = {х}.
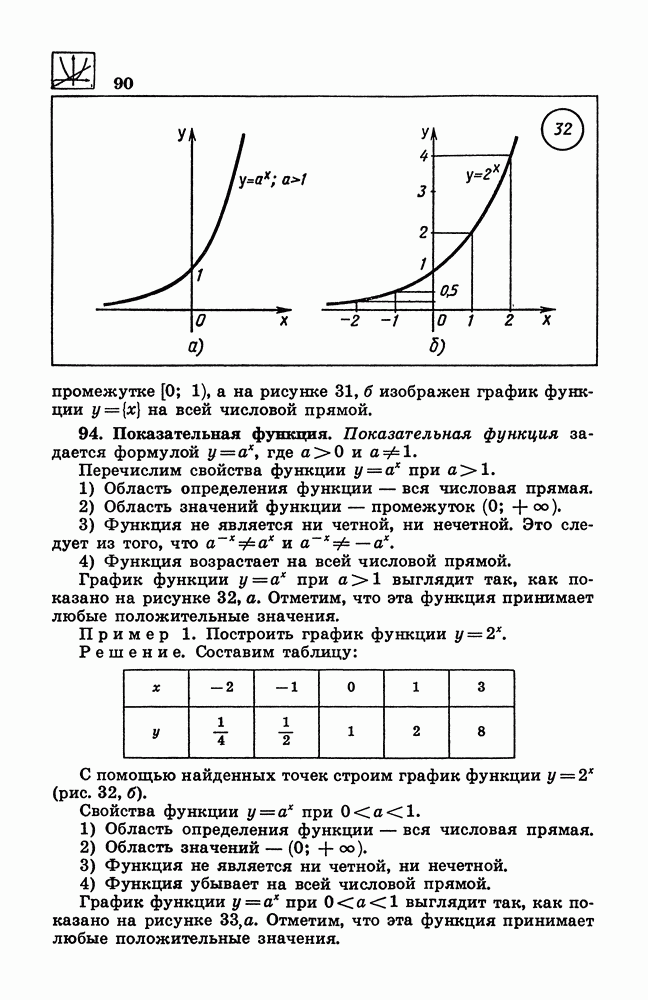
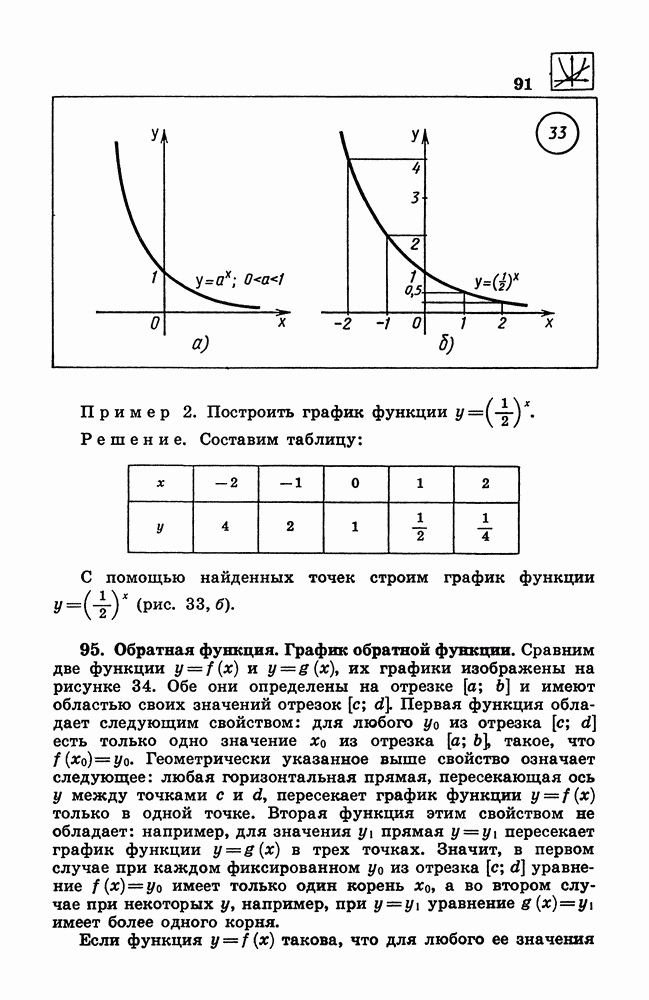
- 94. Показательная функция.
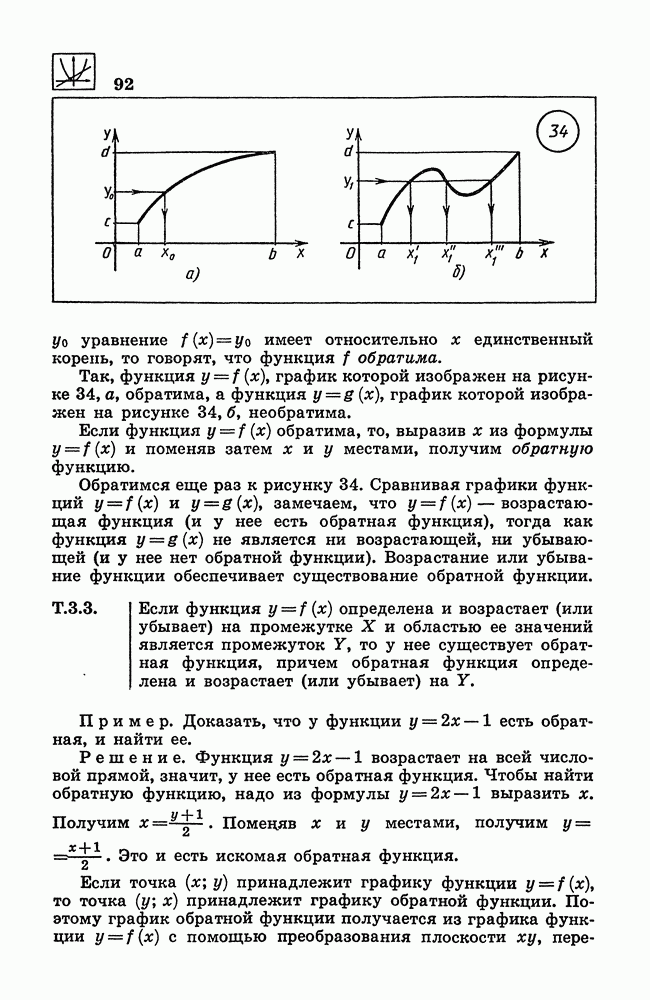
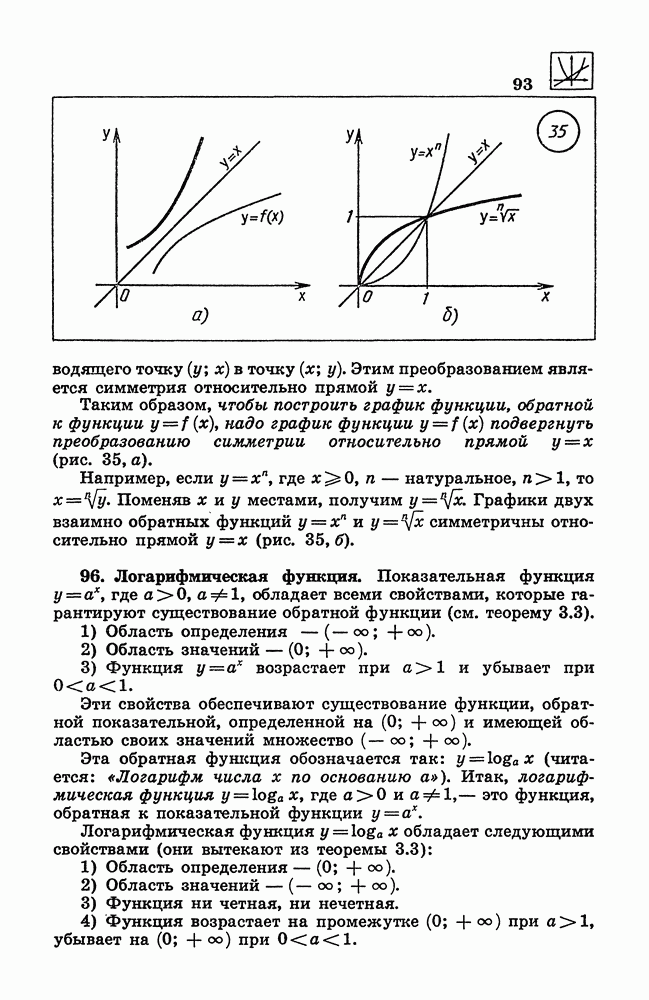
- 95. Обратная функция. График обратной функции.
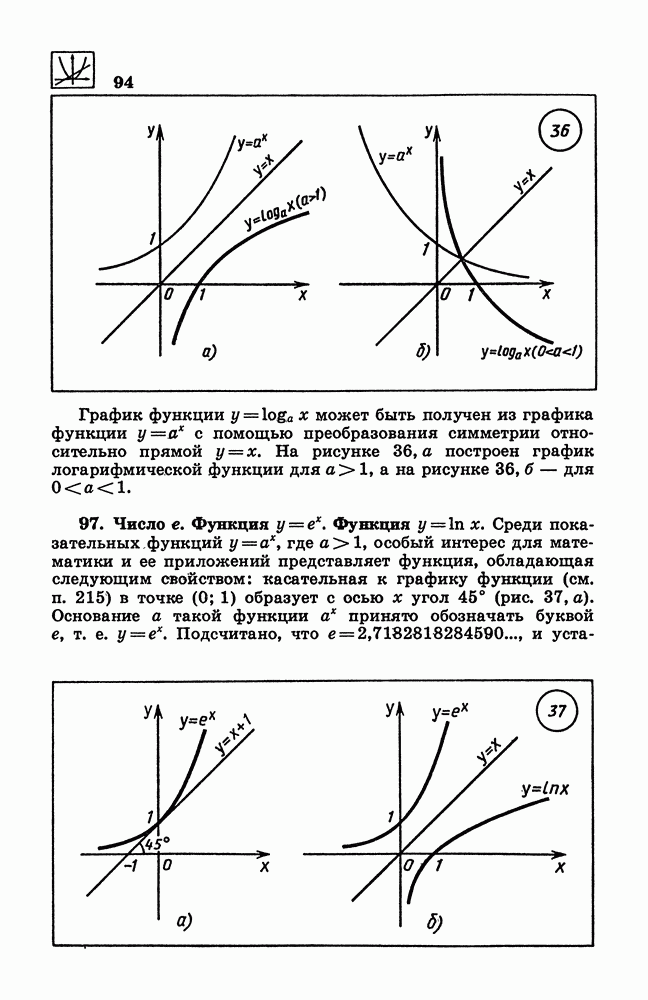
- 96. Логарифмическая функция.
- 97. Число е. Функция у = е^x. Функция у = ln х.
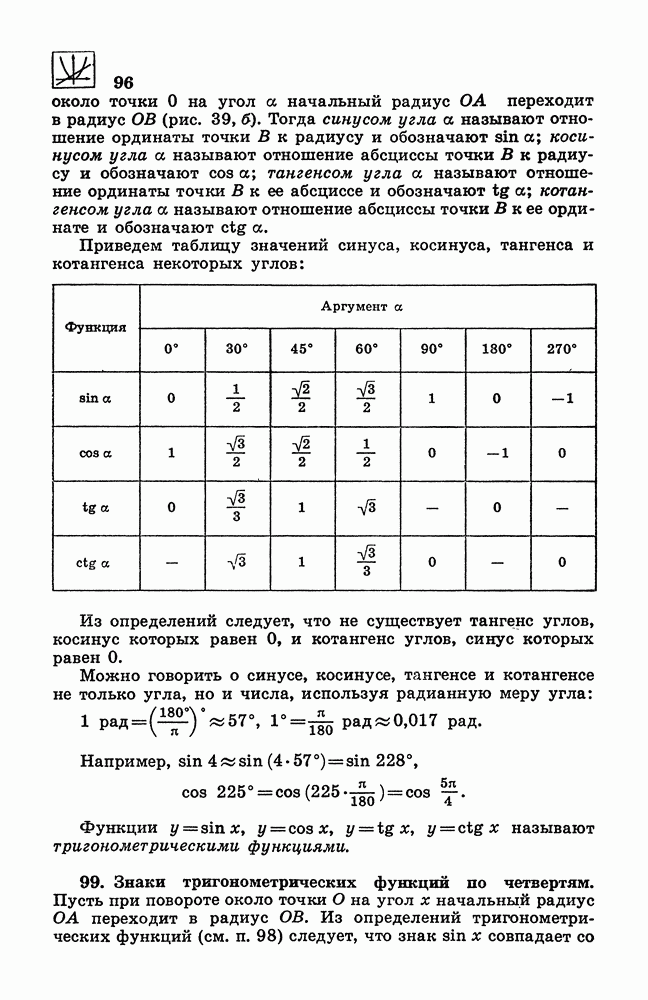
- 98. Определение тригонометрических функций.
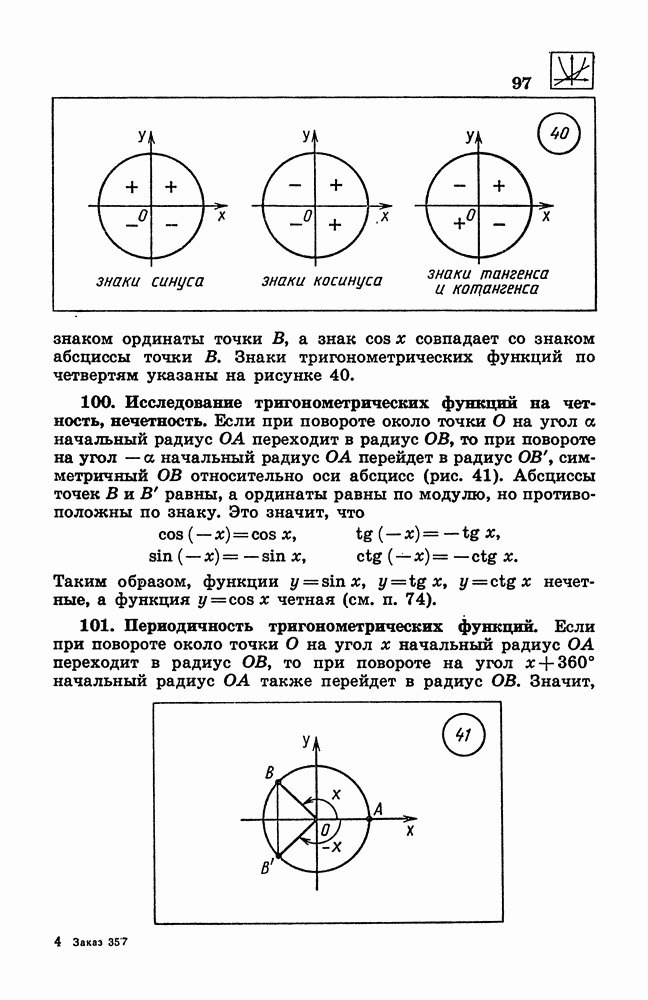
- 99. Знаки тригонометрических функций по четвертям.
- 100. Исследование тригонометрических функций на четность, нечетность.
- 101. Периодичность тригонометрических функций.
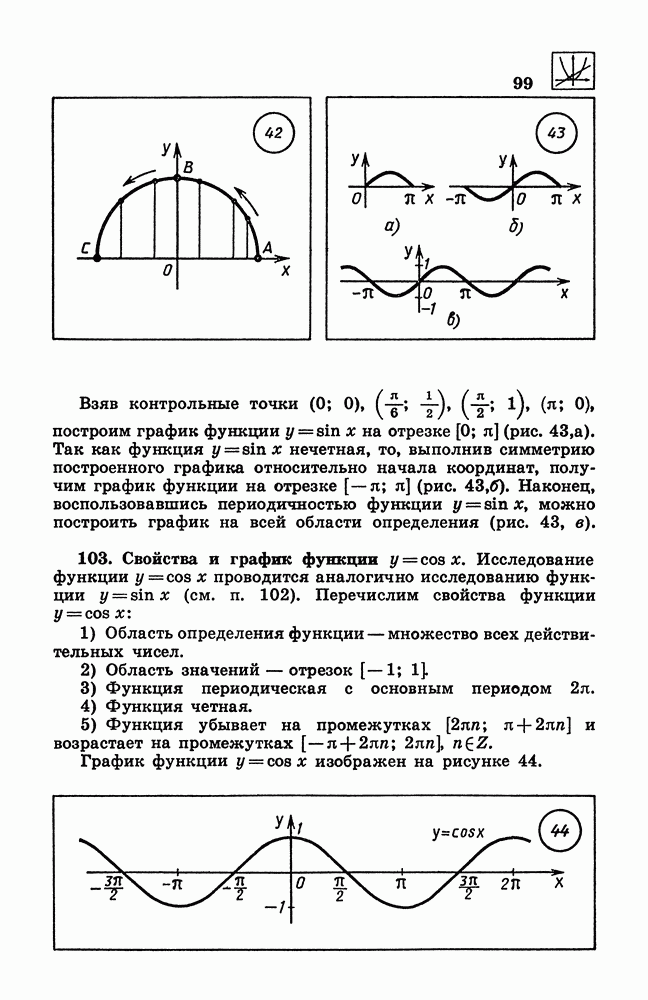
- 102. Свойства и график функции y = sin x.
- 103. Свойства и график функции у = cos x.
- 104. Свойства и график функции у = tg х.
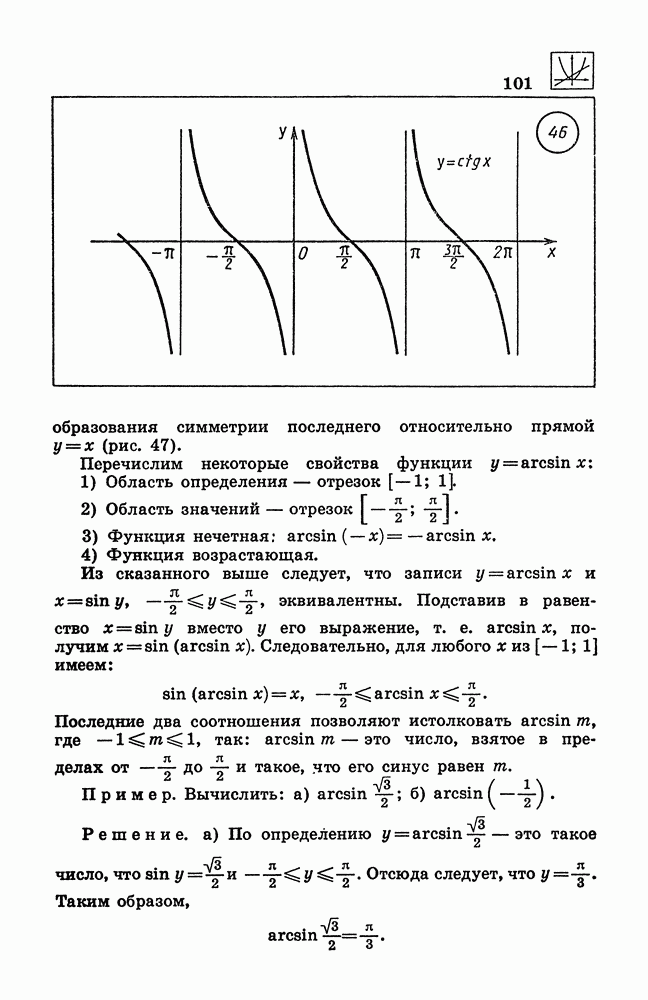
- 105. Свойства и график функции y = ctg x.
- 106. Функция у = arcsin х.
- 107. Функция y = arccos x.
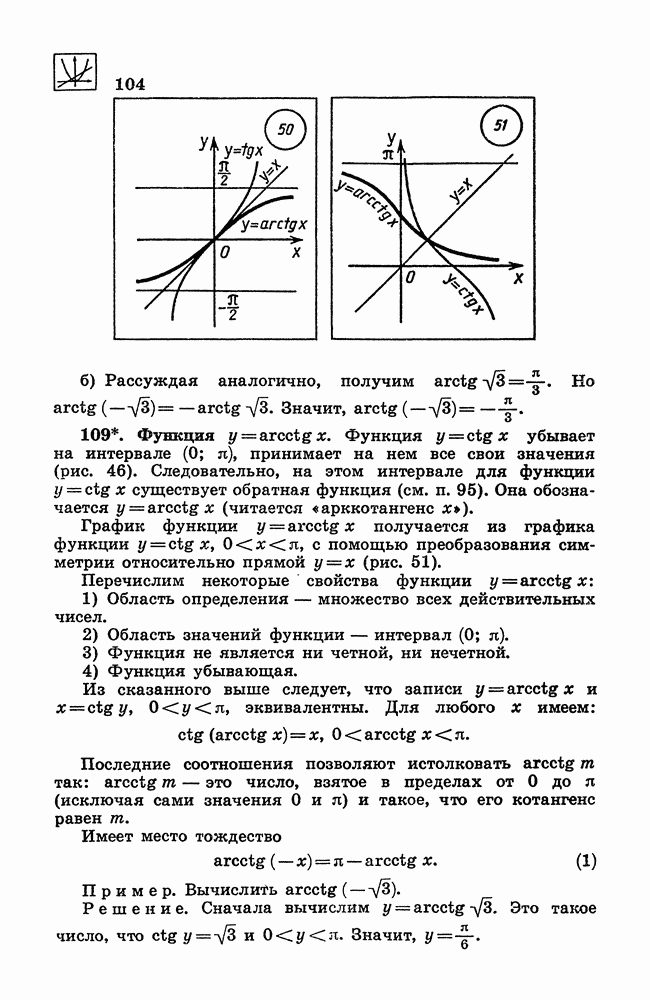
- 108. Функция у = arctg x.
- 109. Функция y = arcctg х.
- § 11. Преобразования графиков
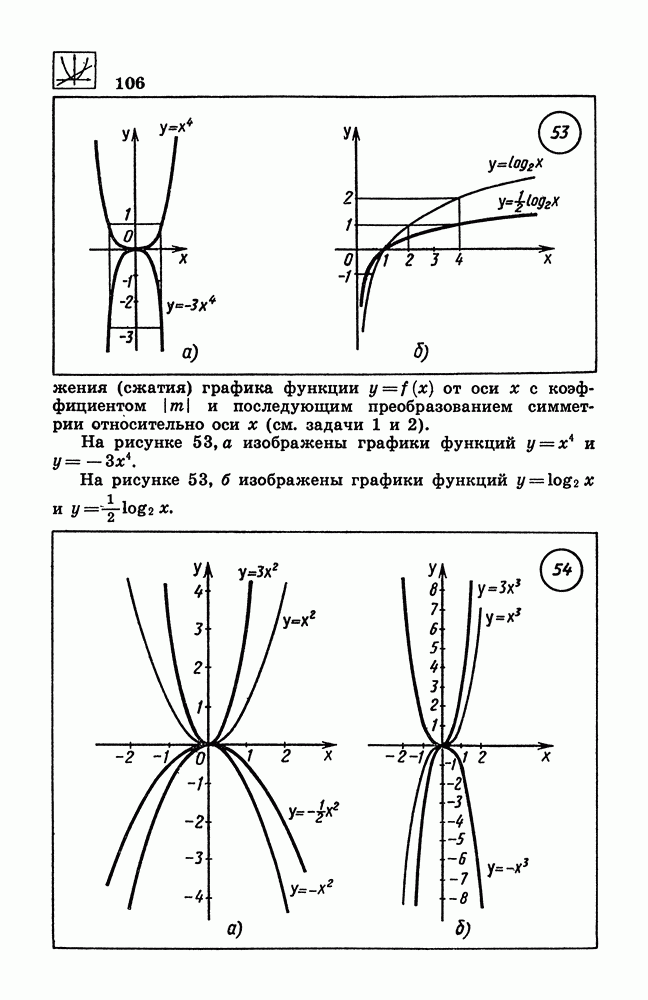
- 111. Графики функций y = ax^2, y = ax^3.
- 112. Построение графика функции y = f(x-m)+n
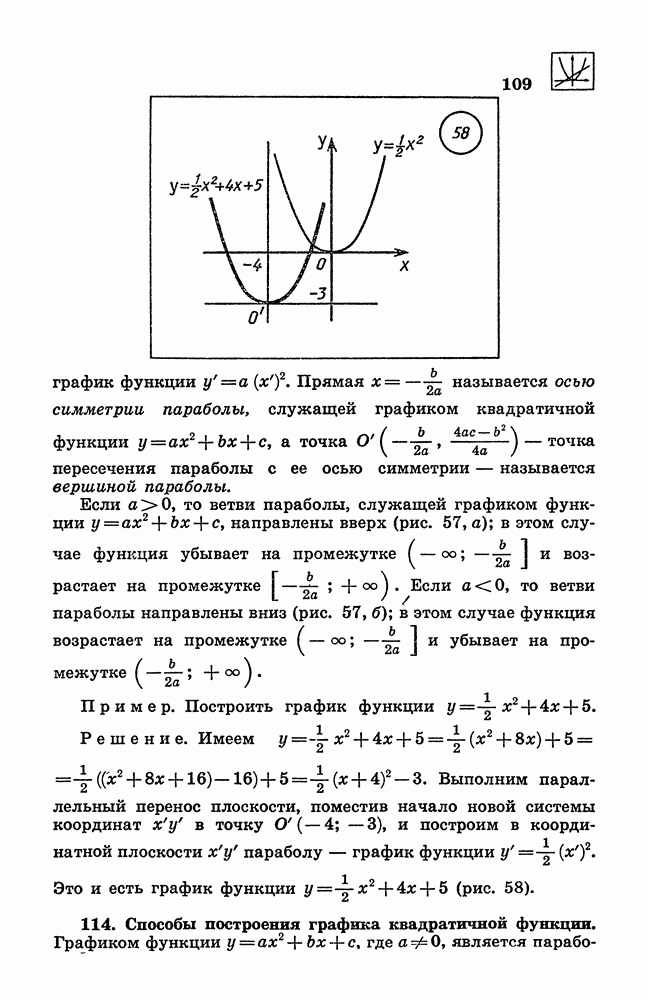
- 113. График квадратичной функции.
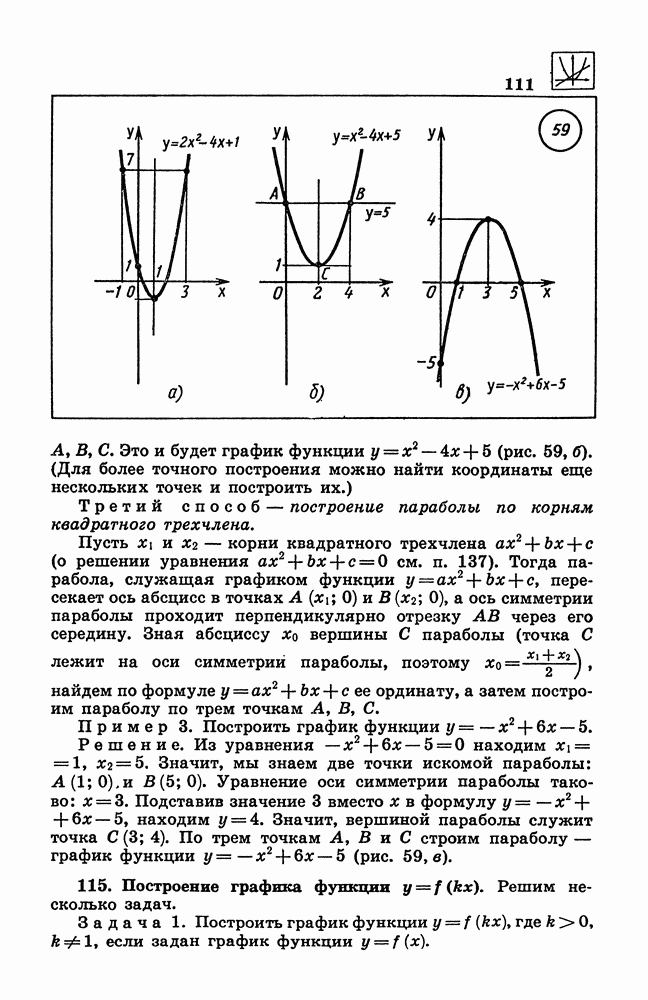
- 114. Способы построения графика квадратичной функции
- 115. Построение графика функции y = f(kx).
- 116. Сжатие и растяжение графиков тригонометрических функций.
- 117. График гармонического колебания
- ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
- § 12. Преобразование выражений, содержащих переменную под знаком логарифма
- 119. Определение логарифма положительного числа по данному основанию.
- 120. Свойства логарифмов.
- 121. Переход к новому основанию логарифма.
- 122. Логарифмирование и потенцирование.
- 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.
- § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
- 125. Формулы сложения и вычитания аргументов.
- 126. Формулы приведения.
- 127. Соотношения между тригонометрическими функциями одного и того же аргумента.
- 128. Формулы двойного угла.
- 129. Формулы понижения степени.
- 130. Преобразование суммы тригонометрических функций в произведение.
- 131. Преобразование произведения тригонометрических функций в сумму.
- 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a).
- 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции.
- ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
- § 14. Уравнения с одной переменной
- 135. Равносильность уравнений.
- 136. Линейные уравнения.
- 137. Квадратные уравнения.
- 138. Неполные квадратные уравнения.
- 139. Теорема Виета.
- 140. Системы и совокупности уравнений.
- 141. Уравнения, содержащие переменную под знаком модуля.
- 142. Понятие следствия уравнения. Посторонние корни.
- 143. Уравнения с переменной в знаменателе.
- 144. Область определения уравнения.
- 145. Рациональные уравнения.
- 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители.
- 147. Решение уравнений методом введения новой переменной.
- 148. Биквадратные уравнения.
- 149. Решение задач с помощью составления уравнений.
- 150. Иррациональные уравнения.
- 151. Показательные уравнения.
- 152. Логарифмические уравнения.
- 153. Примеры решения показательно-логарифмических уравнений.
- 154. Простейшие тригонометрические уравнения.
- 155. Методы решения тригонометрических уравнений.
- 156. Универсальная подстановка (для тригонометрических уравнений).
- 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений).
- 158. Графическое решение уравнений.
- 159. Уравнения с параметром.
- § 15. Уравнения с двумя переменными
- 161. График уравнения с двумя переменными.
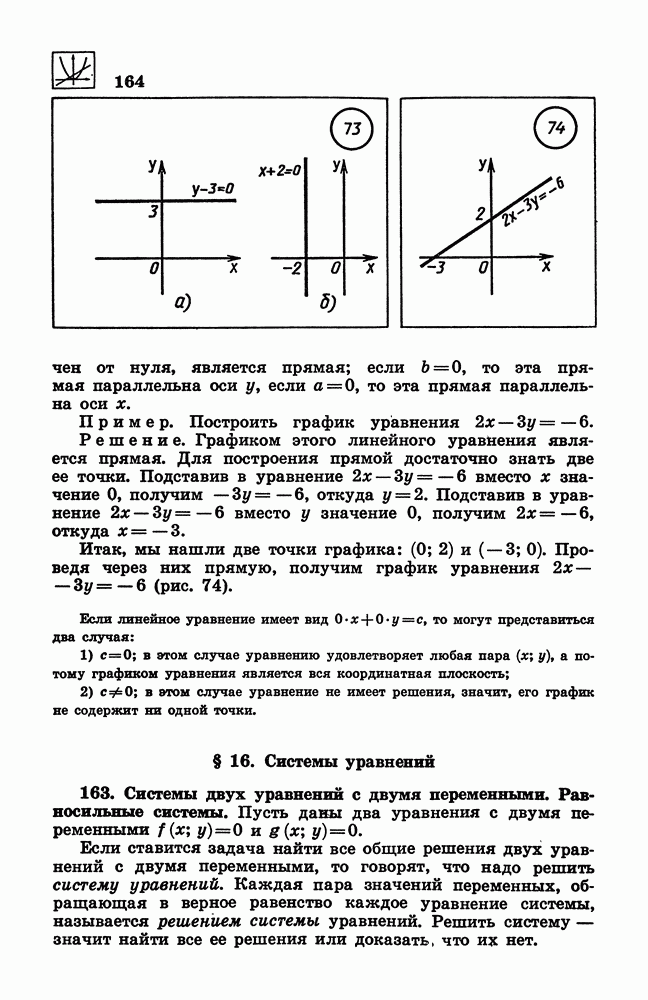
- 162. Линейное уравнение с двумя переменными и его график.
- § 16. Системы уравнений
- 164. Решение систем двух уравнений с двумя переменными методом подстановки.
- 165. Решение систем двух уравнений с двумя переменными методом сложения.
- 167. Графическое решение систем двух уравнений с двумя переменными.
- 168. Исследование системы двух линейных уравнений с двумя переменными.
- 169. Решение систем двух уравнений с двумя переменными методами умножения и деления.
- 170. Системы показательных и логарифмических уравнений.
- 171. Системы тригонометрических уравнений с двумя переменными.
- 172. Системы трех уравнений с тремя переменными.
- 173. Решение задач с помощью составления систем уравнений.
- Глава VI. НЕРАВЕНСТВА
- § 17. Решение неравенств с переменной
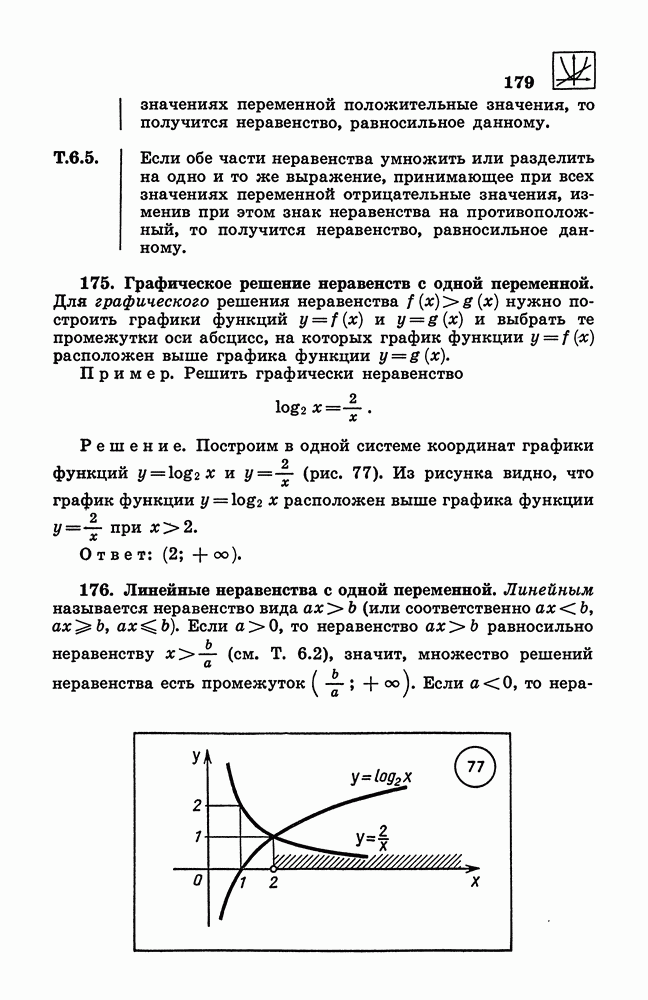
- 175. Графическое решение неравенств с одной переменной.
- 176. Линейные неравенства с одной переменной.
- 177. Системы неравенств с одной переменной.
- 178. Совокупность неравенств с одной переменной.
- 179. Дробно-линейные неравенства.
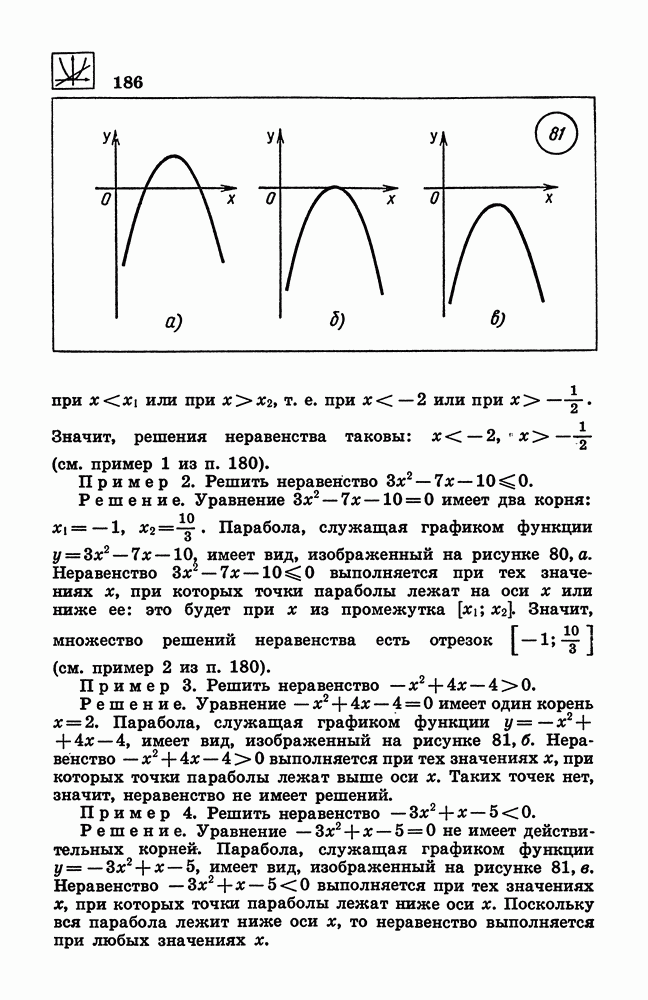
- 180. Неравенства второй степени.
- 181. Графическое решение неравенств второй степени.
- 182. Неравенства с модулями.
- 183. Решение рациональных неравенств методом промежутков.
- 184. Показательные неравенства.
- 185. Логарифмические неравенства.
- 186. Иррациональные неравенства.
- 187. Решение тригонометрических неравенств.
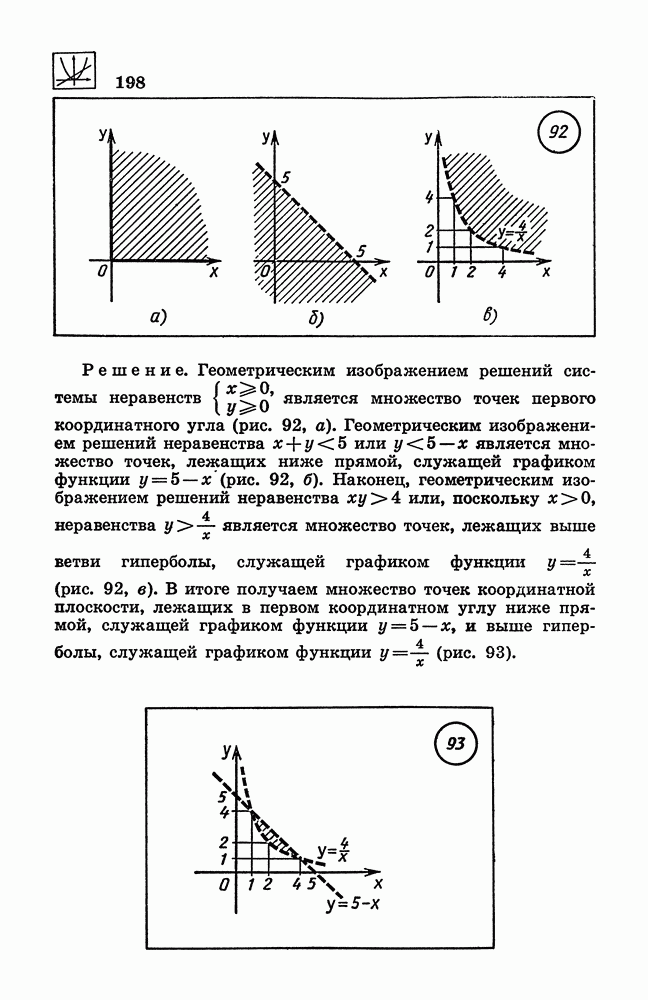
- 188. Неравенства и системы неравенств с двумя переменными.
- § 18. Доказательство неравенств
- 190. Синтетический метод доказательства неравенств.
- 191. Доказательство неравенств методом от противного.
- 192. Использование неравенств при решении уравнений.
- ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 19. Числовые последовательности
- 194. Способы задания последовательности.
- 195. Возрастание и убывание последовательности.
- 196. Определение арифметической прогрессии.
- 197. Свойства арифметической прогрессии
- 198. Определение геометрической прогрессии.
- 199. Свойства геометрической прогрессии.
- 200. Понятие о пределе последовательности.
- 201. Вычисление пределов последовательностей.
- 202. Сумма бесконечной геометрической прогрессии при |q| < 1.
- § 20. Предел функции
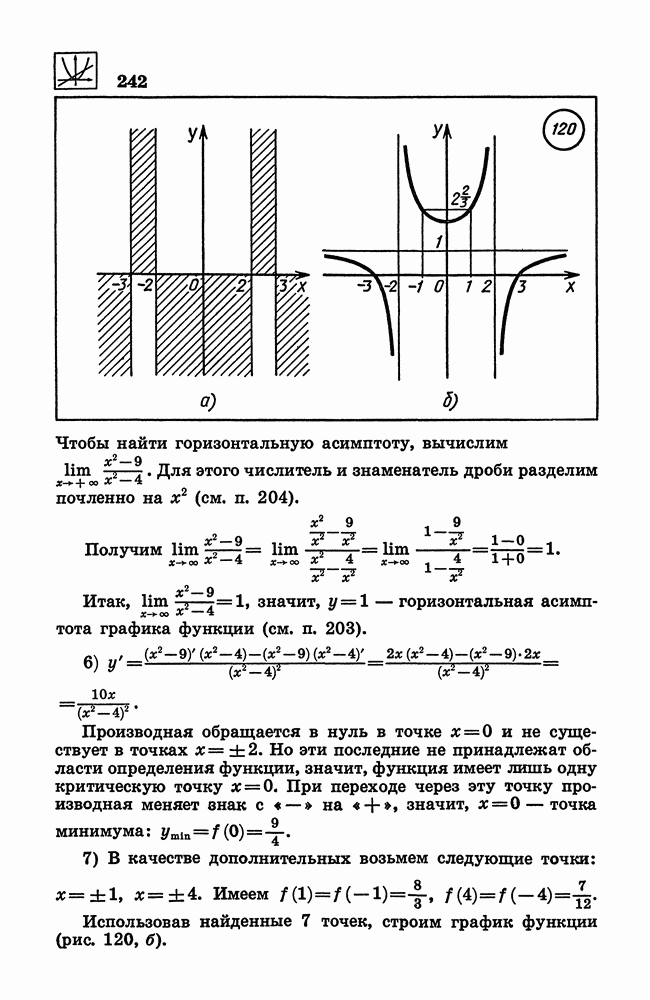
- 204. Вычисление пределов функции при х->оо.
- 205. Предел функции в точке. Непрерывные функции.
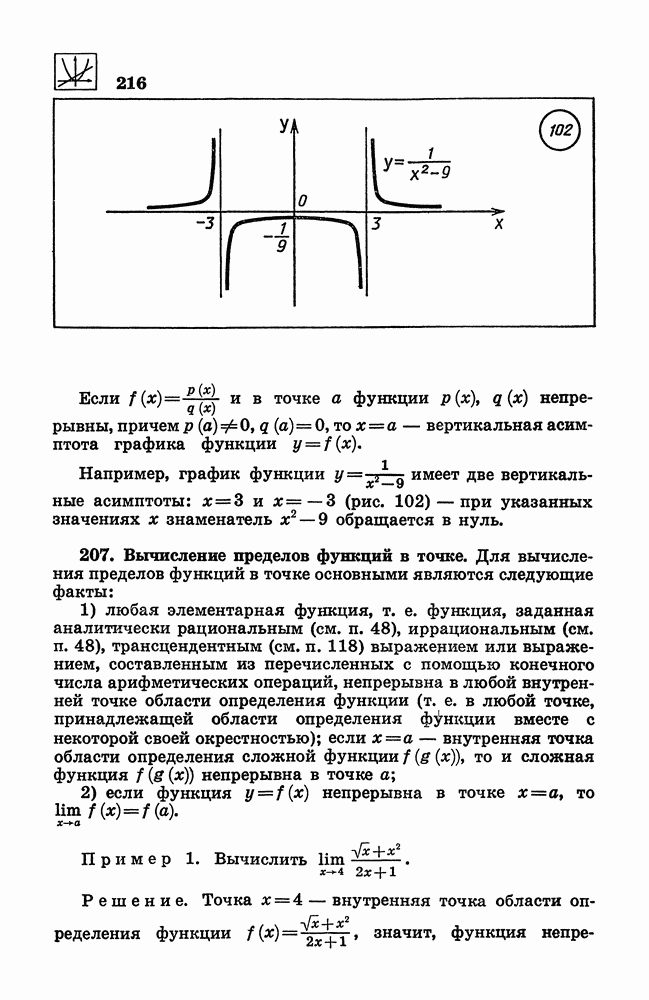
- 206. Вертикальная асимптота.
- 207. Вычисление пределов функций в точке.
- § 21. Производная и ее применения
- 209. Определение производной.
- 210. Формулы дифференцирования. Таблица производных.
- 211. Дифференцирование суммы, произведения, частного.
- 212. Сложная функция и ее дифференцирование.
- 213. Физический смысл производной.
- 214. Вторая производная и ее физический смысл.
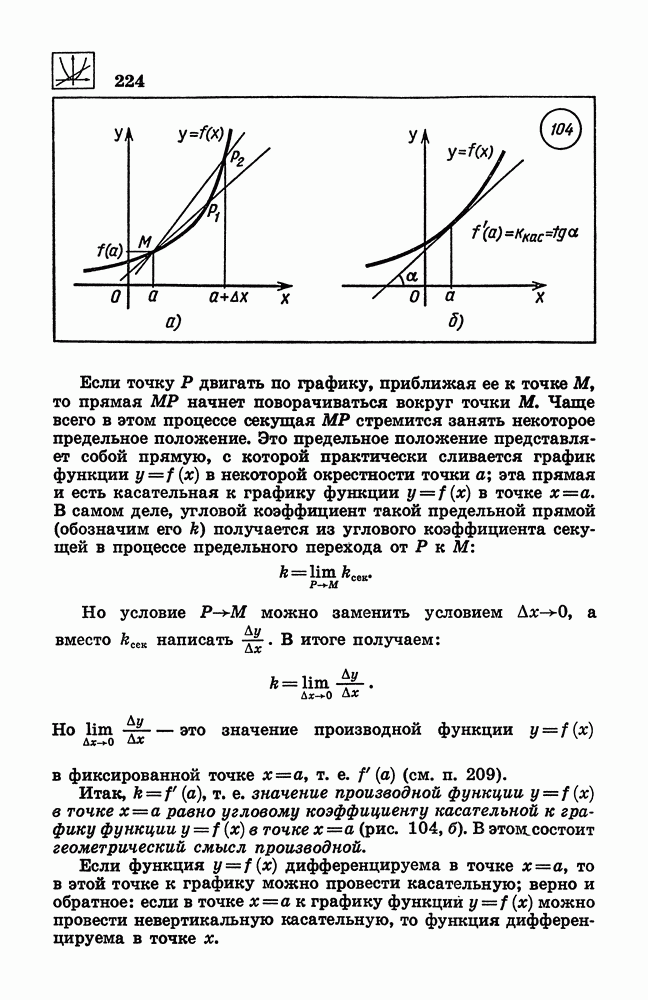
- 215. Касательная к графику функции.
- 216. Применение производной к исследованию функций на монотонность.
- 217. Применение производной к исследованию функций на экстремум.
- 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
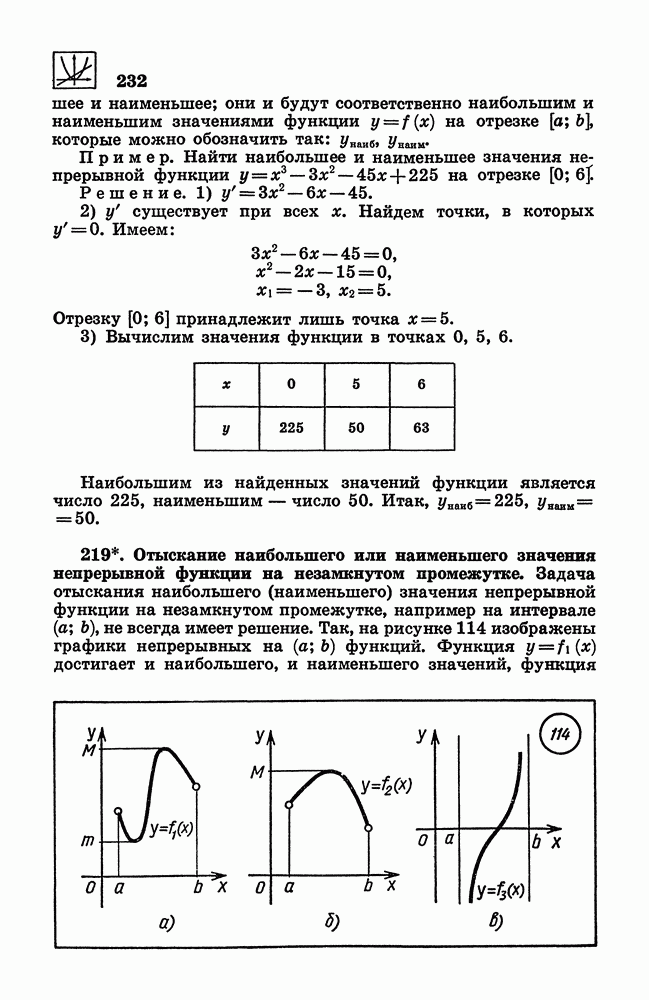
- 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке.
- 220. Задачи на отыскание наибольших или наименьших значений величин.
- 221. Применение производной для доказательства тождеств.
- 222. Применение производной для доказательства неравенств.
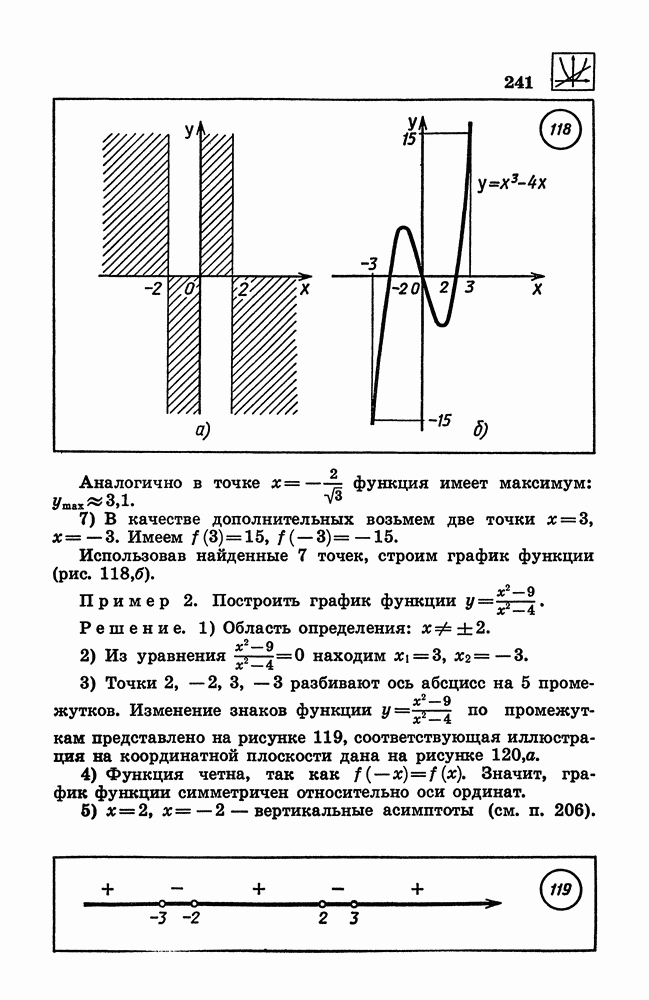
- 223. Общая схема построения графика функции.
- § 22. Первообразная и интеграл
- 225. Таблица первообразных.
- 226. Правила вычисления первообразных.
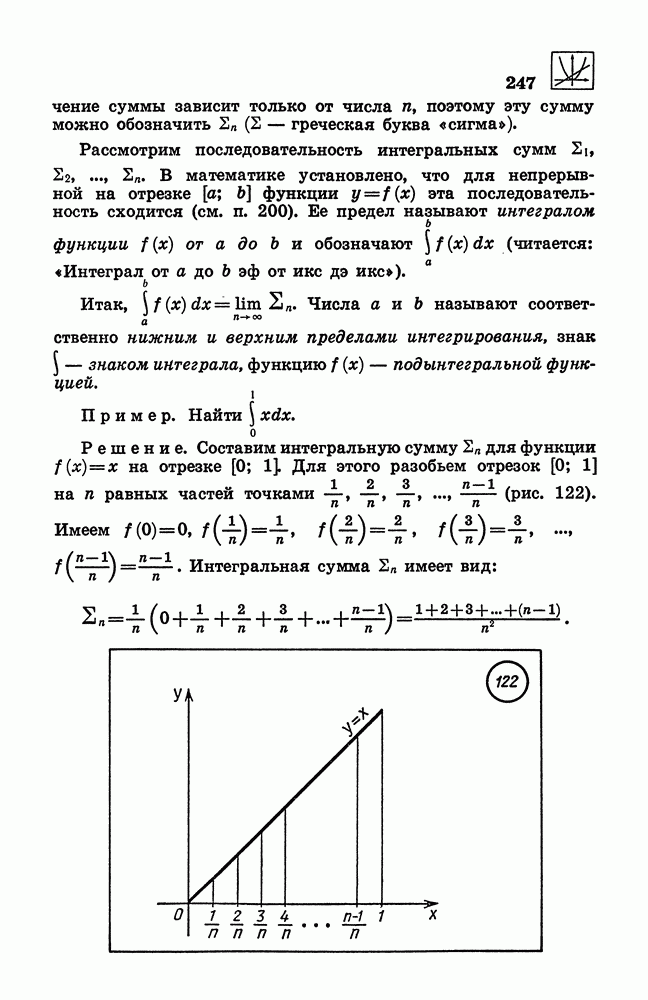
- 227. Интеграл.
- 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница).
- 229. Правила вычисления интегралов.
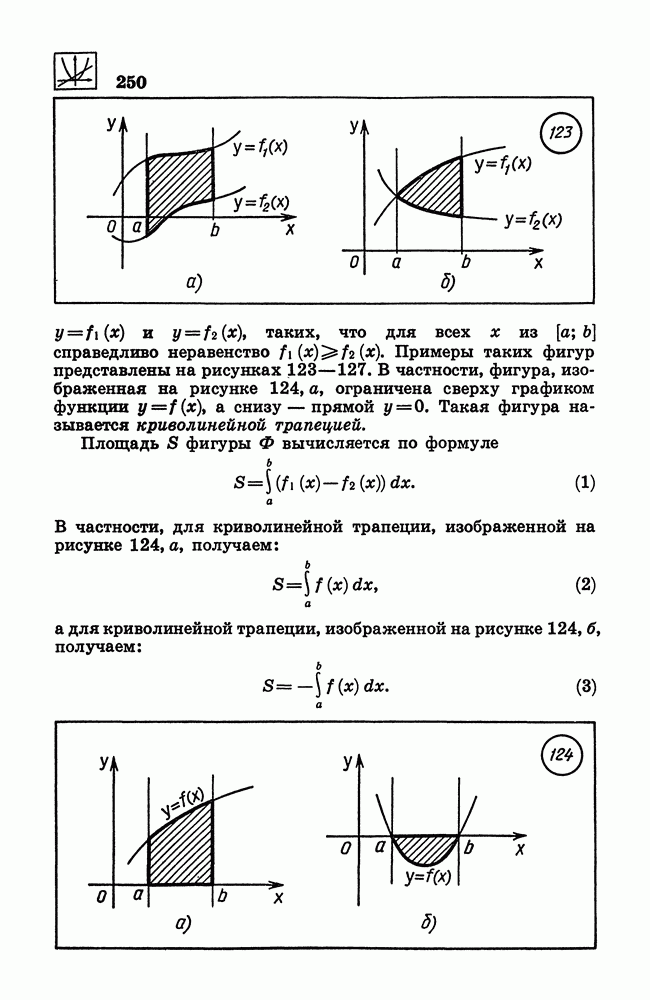
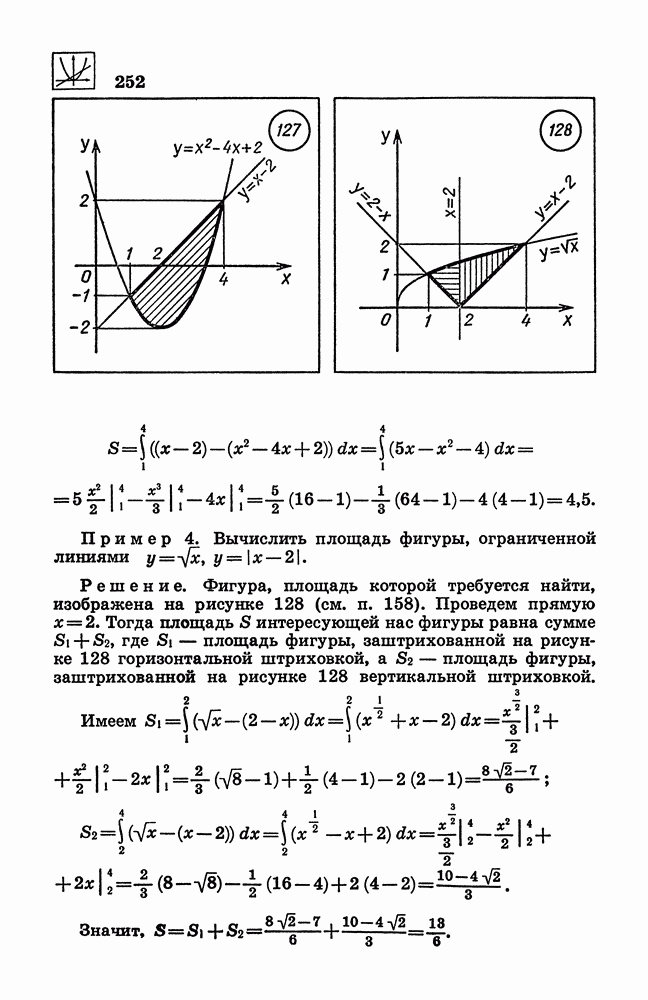
- 230. Использование интеграла для вычисления площадей плоских фигур.
- ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
- 2. Точка. Прямая.
- 3. Определения. Аксиомы. Теоремы.
- § 2. Основные свойства простейших геометрических фигур
- 5. Луч.
- 6. Окружность. Круг.
- 7. Полуплоскость.
- 8. Угол. Градусная мера угла.
- 9. Смежные и вертикальные углы.
- 10. Центральные и вписанные углы.
- 11. Параллельные прямые.
- 12. Признаки параллельности прямых.
- 13. Перпендикулярные прямые.
- 14. Касательная к окружности.
- 15. Треугольники.
- 16. Равенство треугольников.
- 17. Равнобедренный треугольник.
- 18. Сумма углов треугольника.
- 19. Прямоугольный треугольник. Теорема Пифагора.
- 20. Окружности, вписанные в треугольник и описанные около треугольника.
- § 3. Геометрические построения на плоскости
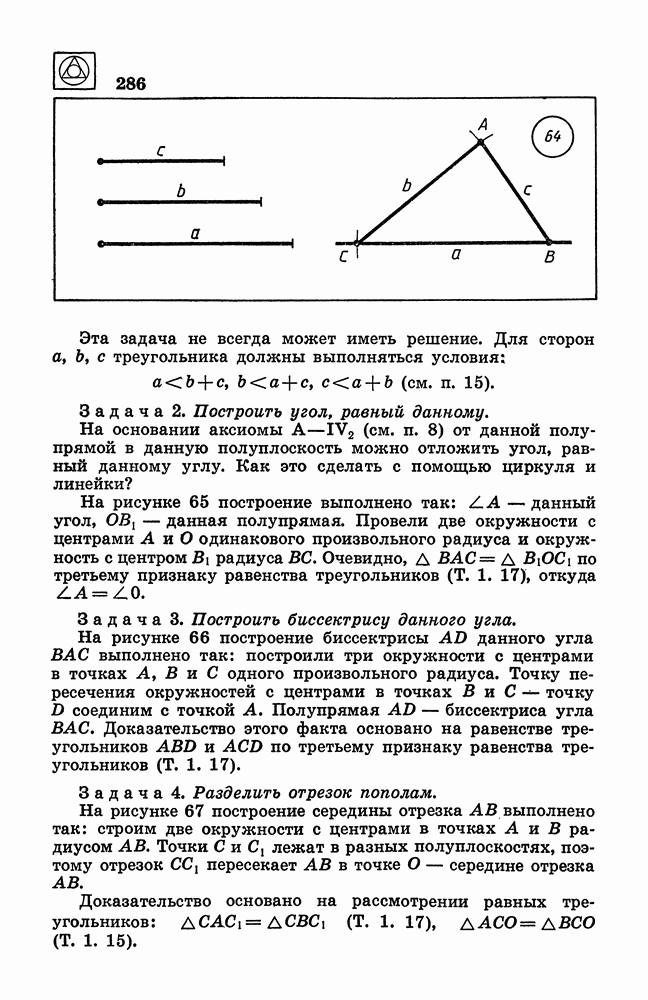
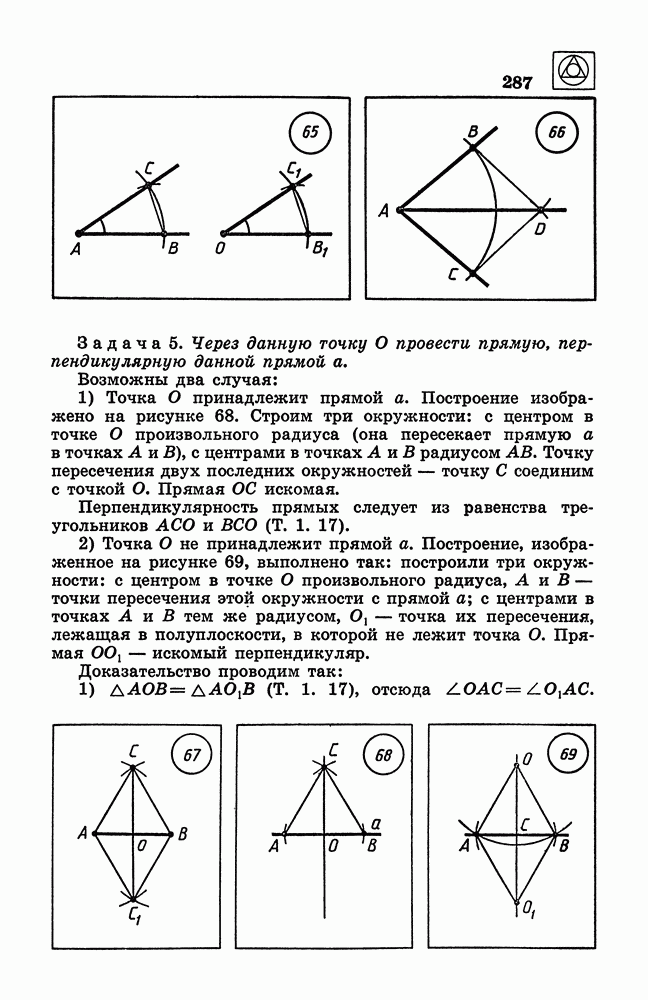
- 22. Простейшие задачи на построение.
- 23. Геометрическое место точек на плоскости.
- § 4. Четырехугольники
- 25. Параллелограмм.
- 26. Прямоугольник. Ромб. Квадрат.
- 27. Трапеция.
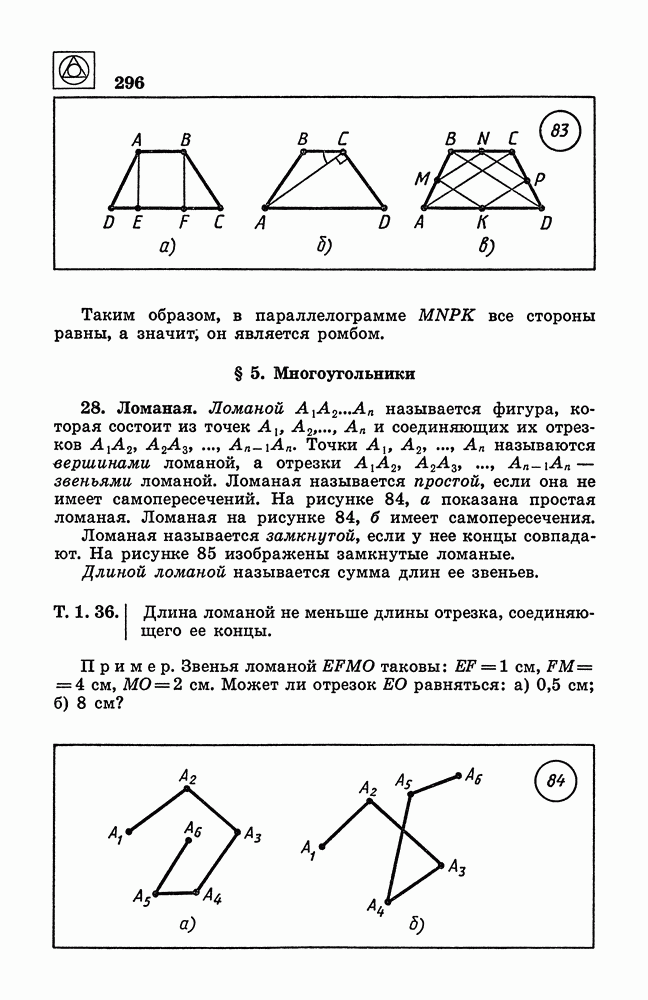
- § 5. Многоугольники
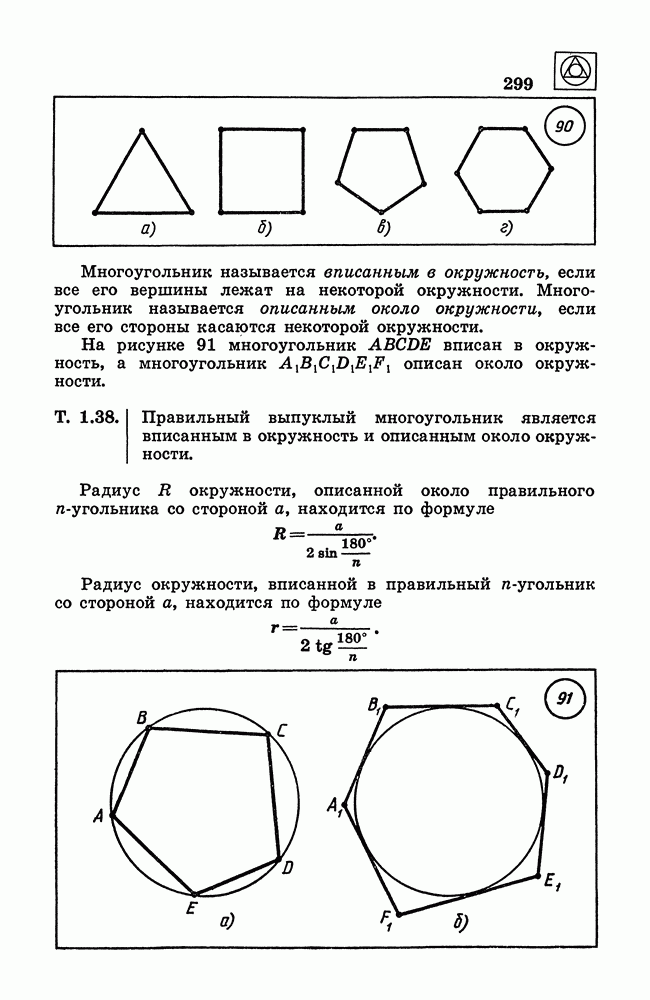
- 29. Выпуклые многоугольники.
- 30. Правильные многоугольники.
- 31. Длина окружности.
- § 6. Решение треугольников
- 33. Соотношения между сторонами и углами в прямоугольном треугольнике.
- 34. Теорема косинусов. Теорема синусов.
- 35. Решение треугольников.
- § 7. Площади плоских фигур
- 37. Площади многоугольников.
- 38. Площади подобных фигур.
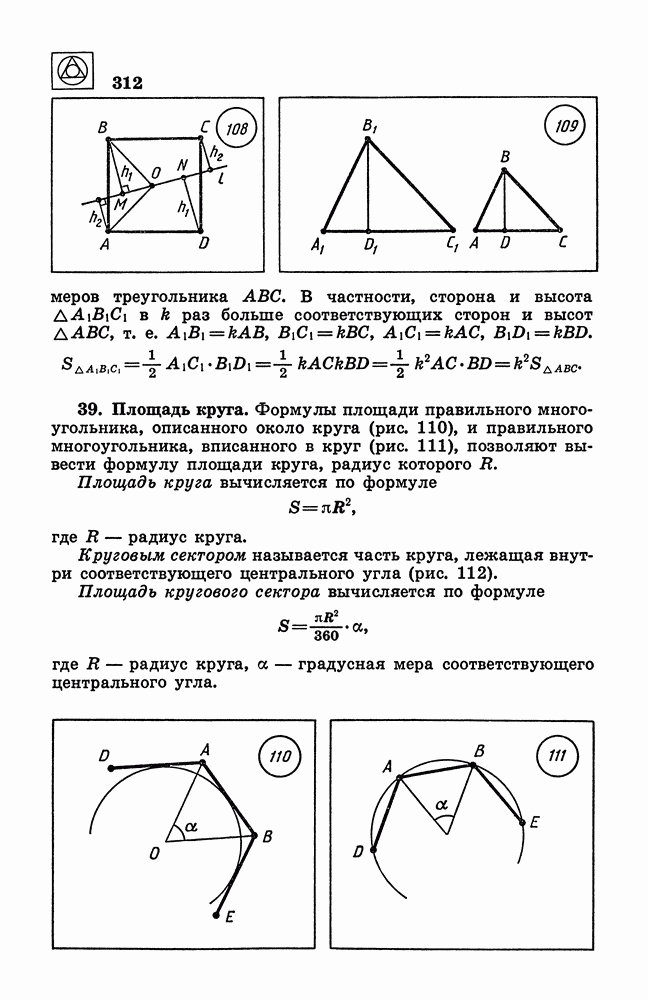
- 39. Площадь круга.
- ГЛАВА II. Прямые и плоскости в пространстве
- § 9. Параллельность прямых и плоскостей
- 42. Параллельность прямой и плоскости.
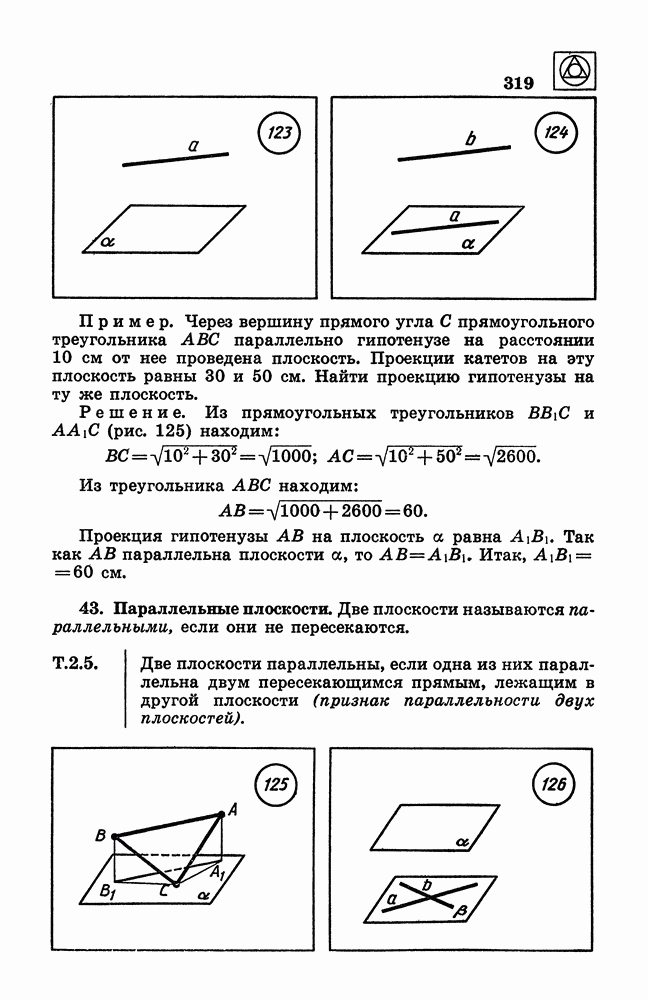
- 43. Параллельные плоскости.
- § 10. Перпендикулярность прямых и плоскостей
- 45. Перпендикуляр и наклонная к плоскости.
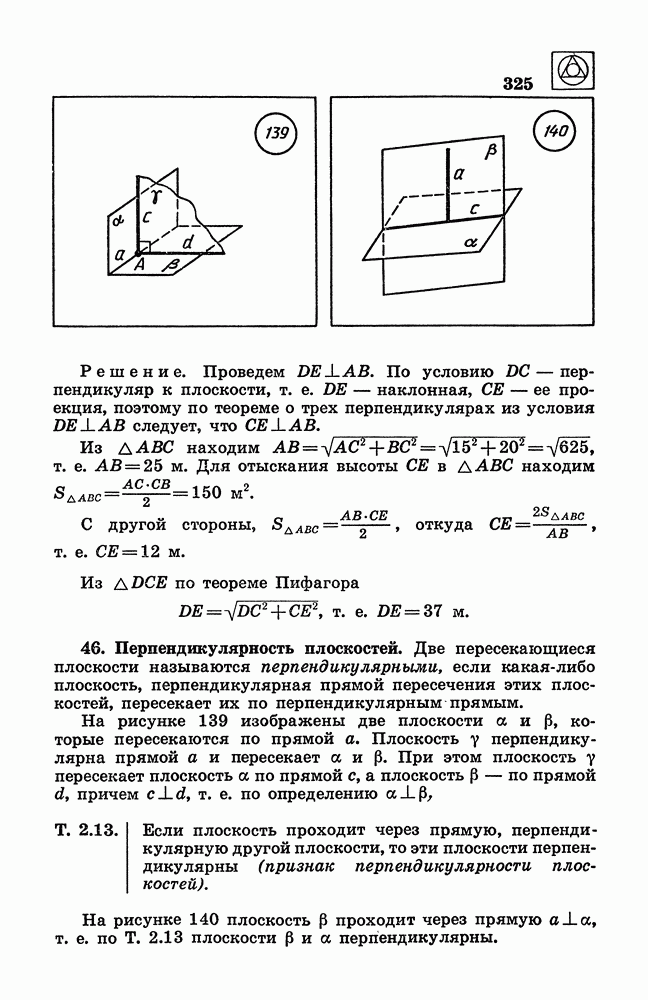
- 46. Перпендикулярность плоскостей.
- ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
- § 11. Многогранники
- 48. Многогранные углы. Многогранники.
- 49. Призма. Параллелепипед. Куб.
- 50. Пираприда.
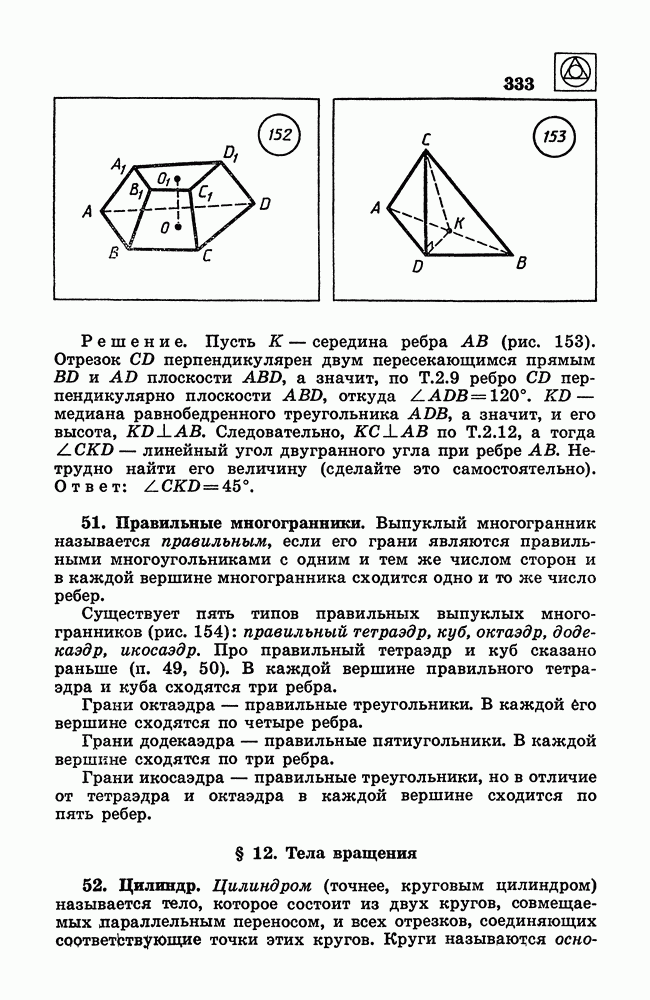
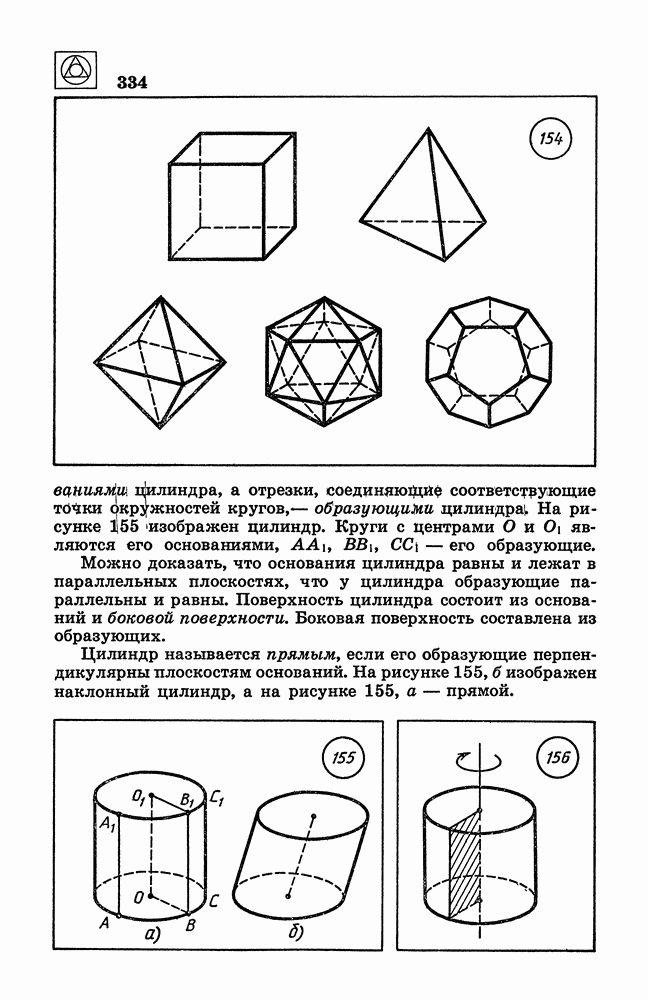
- 51. Правильные многогранники.
- § 12. Тела вращения
- 53. Конус.
- 54. Шар.
- § 13. Изображение пространственных фигур на плоскости
- 56. Ортогональное проектирование.
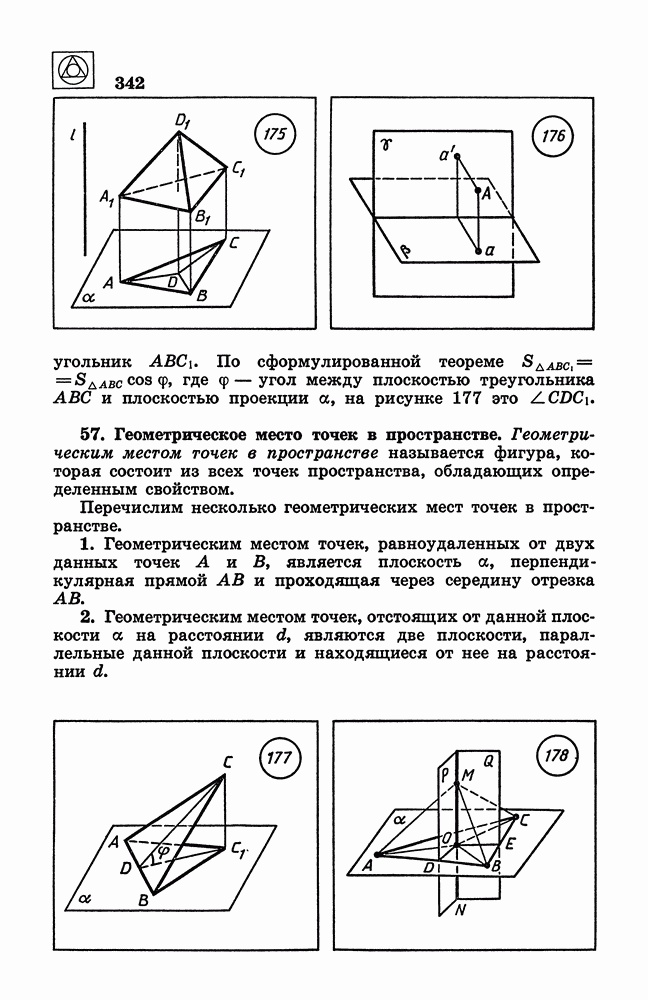
- 57. Геометрическое место точек в пространстве.
- § 14. Объемы тел
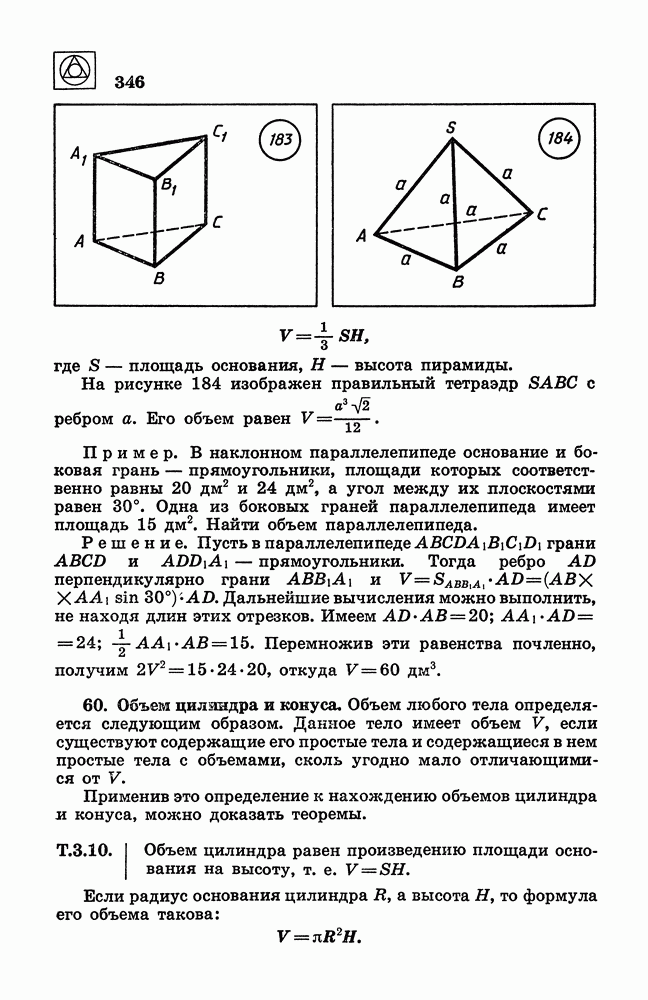
- 59. Объем параллелепипеда, призмы и пирамиды.
- 60. Объем цилиндра и конуса.
- 61. Общая формула объемов тел вращения.
- § 15. Площади поверхностей тел
- 63. Понятие площади поверхности.
- 64. Площади поверхностей тел вращения.
- ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ
- § 16. Координаты на плоскости и в пространстве
- 66. Координаты середины отрезка.
- § 17. Уравнения фигур на плоскости
- 68. Пересечение двух окружностей.
- 69. Уравнение прямой.
- 70. Пересечение прямой и окружности.
- § 18. Уравнения фигур в пространстве
- 72. Уравнение сферы.
- 73. Взаимное расположение сферы и плоскости.
- 74. Пересечение двух сфер.
- ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР
- 76. Понятие движения.
- § 20. Подобие фигур
- 78. Подобные фигуры.
- ГЛАВА VI. ВЕКТОРЫ
- 80. Понятие вектора.
- 81. Координаты вектора.
- § 22. Операции над векторами
- 83. Умножение вектора на число. Коллинеарные векторы.
- 84. Скалярное произведение векторов.
- ПРИЛОЖЕНИЯ
- ГЕОМЕТРИЯ