| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2. Теоремы о числовых характеристиках
В предыдущем ![]() мы привели ряд формул,
позволяющих находить числовые характеристики функций, когда известны законы
распределения аргументов. Однако во многих случаях для нахождения числовых
характеристик функций не требуется знать даже законов распределения аргументов,
а достаточно знать только некоторые их числовые характеристики; при этом мы
вообще обходимся без каких бы то ни было законов распределения. Определение
числовых характеристик функций по заданным числовым характеристикам аргументов
широко применяется в теории вероятностей и позволяет значительно упрощать
решение ряда задач. По преимуществу такие упрощенные методы относятся к
линейным функциям; однако некоторые элементарные нелинейные функции также
допускают подобный подход.
мы привели ряд формул,
позволяющих находить числовые характеристики функций, когда известны законы
распределения аргументов. Однако во многих случаях для нахождения числовых
характеристик функций не требуется знать даже законов распределения аргументов,
а достаточно знать только некоторые их числовые характеристики; при этом мы
вообще обходимся без каких бы то ни было законов распределения. Определение
числовых характеристик функций по заданным числовым характеристикам аргументов
широко применяется в теории вероятностей и позволяет значительно упрощать
решение ряда задач. По преимуществу такие упрощенные методы относятся к
линейным функциям; однако некоторые элементарные нелинейные функции также
допускают подобный подход.
В настоящем ![]() мы изложим ряд теорем о
числовых характеристиках функций, представляющих в своей совокупности весьма
простой аппарат вычисления этих характеристик, применимый в широком круге
условий.
мы изложим ряд теорем о
числовых характеристиках функций, представляющих в своей совокупности весьма
простой аппарат вычисления этих характеристик, применимый в широком круге
условий.
1. Математическое ожидание неслучайной величины
Если ![]() - неслучайная величина, то
- неслучайная величина, то
![]() .
.
Сформулированное свойство
является достаточно очевидным; доказать его можно, рассматривая неслучайную
величину ![]() как
частный вид случайной, при одном возможном значении с вероятностью единица;
тогда по общей формуле для математического ожидания:
как
частный вид случайной, при одном возможном значении с вероятностью единица;
тогда по общей формуле для математического ожидания:
![]() .
.
2. Дисперсия неслучайной величины
Если ![]() - неслучайная величина, то
- неслучайная величина, то
![]() .
.
Доказательство. По определению дисперсии
![]() .
.
3. Вынесение неслучайной величины за знак математического ожидания
Если ![]() - неслучайная величина, а
- неслучайная величина, а ![]() - случайная, то
- случайная, то
![]() , (10.2.1)
, (10.2.1)
т. е. неслучайную величину можно выносить за знак математического ожидания.
Доказательство.
а) Для прерывных величин
![]() .
.
б) Для непрерывных величин
 .
.
4. Вынесение неслучайной величины за знак дисперсии и среднего квадратического отклонения
Если ![]() - неслучайная величина, а
- неслучайная величина, а ![]() - случайная, то
- случайная, то
![]() , (10.2.2)
, (10.2.2)
т. е. неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.
Доказательство. По определению дисперсии
![]() .
.
Следствие
![]() ,
,
т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением. Доказательство получим, извлекая корень квадратный из формулы (10.2.2) и учитывая, что с.к.о. - существенно положительная величина.
5. Математическое ожидание суммы случайных величин
Докажем, что для любых двух
случайных величин ![]() и
и
![]()
![]() , (10.2.3)
, (10.2.3)
т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Это свойство известно под названием теоремы сложения математических ожиданий.
Доказательство.
а) Пусть ![]() - система прерывных случайных
величин. Применим к сумме случайных величин общую формулу (10.1.6) для математического
ожидания функции двух аргументов:
- система прерывных случайных
величин. Применим к сумме случайных величин общую формулу (10.1.6) для математического
ожидания функции двух аргументов:
![]()
![]() .
.
Ho ![]() представляет собой не что иное, как
полную вероятность того, что величина
представляет собой не что иное, как
полную вероятность того, что величина ![]() примет значение
примет значение ![]() :
:
![]() ;
;
следовательно,
![]() .
.
Аналогично докажем, что
![]() ,
,
и теорема доказана.
б) Пусть ![]() - система непрерывных случайных
величин. По формуле (10.1.7)
- система непрерывных случайных
величин. По формуле (10.1.7)

 . (10.2.4)
. (10.2.4)
Преобразуем первый из интегралов (10.2.4):

 ;
;
аналогично
 ,
,
и теорема доказана.
Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин - как зависимых, так и независимых.
Теорема сложения математических ожиданий обобщается на произвольное число слагаемых:
 , (10.2.5)
, (10.2.5)
т. е. математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.
Для доказательства достаточно применить метод полной индукции.
6. Математическое ожидание линейной функции
Рассмотрим линейную функцию
нескольких случайных аргументов ![]() :
:
 ,
,
где
![]() -
неслучайные коэффициенты. Докажем, что
-
неслучайные коэффициенты. Докажем, что
 , (10.2.6)
, (10.2.6)
т. е. математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов.
Доказательство. Пользуясь теоремой сложения м. о. и правилом вынесения неслучайной величины за знак м. о., получим:

 .
.
7. Диспepсия суммы случайных величин
Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:
![]() . (10.2.7)
. (10.2.7)
Доказательство. Обозначим
![]() . (10.2.8)
. (10.2.8)
По теореме сложения математических ожиданий
![]() . (10.2.9)
. (10.2.9)
Перейдем от случайных величин ![]() к соответствующим центрированным
величинам
к соответствующим центрированным
величинам ![]() .
Вычитая почленно из равенства (10.2.8) равенство (10.2.9), имеем:
.
Вычитая почленно из равенства (10.2.8) равенство (10.2.9), имеем:
![]() .
.
По определению дисперсии
![]()
![]() ,
,
что и требовалось доказать.
Формула (10.2.7) для дисперсии суммы может быть обобщена на любое число слагаемых:
 ,
(10.2.10)
,
(10.2.10)
где
![]() -
корреляционный момент величин
-
корреляционный момент величин ![]() ,
, ![]() знак
знак ![]() под суммой обозначает, что суммирование
распространяется на все возможные попарные сочетания случайных величин
под суммой обозначает, что суммирование
распространяется на все возможные попарные сочетания случайных величин ![]() .
.
Доказательство аналогично предыдущему и вытекает из формулы для квадрата многочлена.
Формула (10.2.10) может быть записана еще в другом виде:
 , (10.2.11)
, (10.2.11)
где
двойная сумма распространяется на все элементы корреляционной матрицы системы
величин ![]() ,
содержащей как корреляционные моменты, так и дисперсии.
,
содержащей как корреляционные моменты, так и дисперсии.
Если все случайные величины ![]() , входящие в систему,
некоррелированы (т. е.
, входящие в систему,
некоррелированы (т. е. ![]() при
при ![]() ), формула (10.2.10) принимает вид:
), формула (10.2.10) принимает вид:
 , (10.2.12)
, (10.2.12)
т. е. дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых.
Это положение известно под названием теоремы сложения дисперсий.
8. Дисперсия линейной функции
Рассмотрим линейную функцию нескольких случайных величин.
 ,
,
где
![]() -
неслучайные величины.
-
неслучайные величины.
Докажем, что дисперсия этой линейной функции выражается формулой
 , (10.2.13)
, (10.2.13)
где
![]() -
корреляционный момент величин
-
корреляционный момент величин ![]() ,
, ![]() .
.
Доказательство. Введем обозначение:
![]() .
.
Тогда
 . (10.2.14)
. (10.2.14)
Применяя к правой части выражения
(10.2.14) формулу (10.2.10) для дисперсии суммы и учитывая, что ![]() , получим:
, получим:
 ,
(10.2.15)
,
(10.2.15)
где
![]() -
корреляционный момент величин
-
корреляционный момент величин ![]() :
:
![]() .
.
Вычислим этот момент. Имеем:
![]() ;
;
аналогично
![]() .
.
Отсюда
![]() .
.
Подставляя это выражение в (10.2.15), приходим к формуле (10.2.13).
В частном случае, когда все
величины ![]() некоррелированны,
формула (10.2.13) принимает вид:
некоррелированны,
формула (10.2.13) принимает вид:
 , (10.2.16)
, (10.2.16)
т. е. дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициентов на дисперсии соответствующих аргументов.
9. Математическое ожидание произведения случайных величин
Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
![]() . (10.2.17)
. (10.2.17)
Доказательство. Будем исходить из определения корреляционного момента:
![]() ,
,
где
![]() ;
;
![]() .
.
Преобразуем это выражение, пользуясь свойствами математического ожидания:
![]()
![]() ,
,
что, очевидно, равносильно формуле (10.2.17).
Если случайные величины ![]() некоррелированны
некоррелированны ![]() , то формула (10.2.17)
принимает вид:
, то формула (10.2.17)
принимает вид:
![]() , (10.2.18)
, (10.2.18)
т. е. математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
Это положение известно под названием теоремы умножения математических ожиданий.
Формула (10.2.17) представляет собой не что иное, как выражение второго смешанного центрального момента системы через второй смешанный начальный момент и математические ожидания:
![]() . (10.2.19)
. (10.2.19)
Это выражение часто применяется на практике при вычислении корреляционного момента аналогично тому, как для одной случайной величины дисперсия часто вычисляется через второй начальный момент и математическое ожидание.
Теорема умножения математических ожиданий обобщается и на произвольное число сомножителей, только в этом случае для ее применения недостаточно того, чтобы величины были некоррелированны, а требуется, чтобы обращались в нуль и некоторые высшие смешанные моменты, число которых зависит от числа членов в произведении. Эти условия заведомо выполнены при независимости случайных величин, входящих в произведение. В этом случае
 , (10.2.20)
, (10.2.20)
т. е. математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
Это положение легко доказывается методом полной индукции.
10. Дисперсия произведения независимых случайных величин
Докажем, что для независимых
величин ![]()
![]() . (10.2.21)
. (10.2.21)
Доказательство. Обозначим ![]() . По определению
дисперсии
. По определению
дисперсии
![]() .
.
Так как величины ![]() независимы,
независимы, ![]() и
и
![]() .
.
При независимых ![]() величины
величины ![]() тоже независимы;
следовательно,
тоже независимы;
следовательно,
![]() ,
,
![]()
и
![]() . (10.2.22)
. (10.2.22)
Но ![]() есть не что иное, как второй начальный
момент величины
есть не что иное, как второй начальный
момент величины ![]() ,
и, следовательно, выражается через дисперсию:
,
и, следовательно, выражается через дисперсию:
![]() ;
;
аналогично
![]() .
.
Подставляя эти выражения в формулу (10.2.22) и приводя подобные члены, приходим к формуле (10.2.21).
В случае, когда перемножаются центрированные случайные величины (величины с математическими ожиданиями, равными нулю), формула (10.2.21) принимает вид:
![]() , (10.2.23)
, (10.2.23)
т. е. дисперсия произведения независимых центрированных случайных величин равна произведению их дисперсий.
11. Высшие моменты суммы случайных величин
В некоторых случаях приходится вычислять высшие моменты суммы независимых случайных величин. Докажем некоторые относящиеся сюда соотношения.
1) Если величины ![]() независимы, то
независимы, то
![]() . (10.2.24)
. (10.2.24)
Доказательство.
![]()
![]()
![]()
![]() ,
,
откуда по теореме умножения математических ожиданий
![]() .
.
Но первый центральный момент ![]() для любой величины равен нулю; два
средних члена обращаются в нуль, и формула (10.2.24) доказана.
для любой величины равен нулю; два
средних члена обращаются в нуль, и формула (10.2.24) доказана.
Соотношение (10.2.24) методом индукции легко обобщается на произвольное число независимых слагаемых:
 . (10.2.25)
. (10.2.25)
2) Четвертый центральный момент суммы двух независимых случайных величин выражается формулой
![]() . (10.2.26)
. (10.2.26)
где
![]() - дисперсии
величин
- дисперсии
величин ![]() и
и ![]() .
.
Доказательство совершенно аналогично предыдущему.
Методом полной индукции легко доказать обобщение формулы (10.2.26) на произвольное число независимых слагаемых:
 . (10.2.27)
. (10.2.27)
Аналогичные соотношения в случае необходимости легко вывести и для моментов более высоких порядков.
12. Сложение некоррелированных случайных векторов
Рассмотрим на плоскости ![]() два некоррелированных
случайных вектора: вектор
два некоррелированных
случайных вектора: вектор ![]() с составляющими
с составляющими ![]() и вектор
и вектор ![]() с составляющими
с составляющими ![]() (рис. 10.2.1).
(рис. 10.2.1).

Рис. 10.2.1
Рассмотрим их векторную сумму:
![]() ,
,
т. е. вектор с составляющими:
![]() ,
,
![]() .
.
Требуется определить числовые
характеристики случайного вектора ![]() - математические ожидания
- математические ожидания ![]() , дисперсии и корреляционный
момент составляющих:
, дисперсии и корреляционный
момент составляющих: ![]() .
.
По теореме сложения математических ожиданий:
![]() ;
;
![]() .
.
По теореме сложения дисперсий
![]() ;
;
![]() .
.
Докажем, что корреляционные моменты также складываются:
![]() , (10.2.28)
, (10.2.28)
где
![]() -
корреляционные моменты составляющих каждого из векторов
-
корреляционные моменты составляющих каждого из векторов ![]() и
и ![]() .
.
Доказательство. По определению корреляционного момента:
![]()
![]() . (10.2.29)
. (10.2.29)
Так как векторы ![]() и
и ![]() некоррелированны, то два
средних члена в формуле (10.2.29) равны нулю; два оставшихся члена представляют
собой
некоррелированны, то два
средних члена в формуле (10.2.29) равны нулю; два оставшихся члена представляют
собой ![]() и
и ![]() ; формула (10.2.28)
доказана.
; формула (10.2.28)
доказана.
Формулу (10.2.28) иногда называют «теоремой сложения корреляционных моментов».
Теорема легко обобщается на
произвольное число слагаемых. Если имеется две некоррелированные системы
случайных величин, т. е. два ![]() -мерных случайных вектора:
-мерных случайных вектора:
![]() с
составляющими
с
составляющими ![]() ,
,
![]() с
составляющими
с
составляющими ![]() ,
,
то их векторная сумма
![]()
имеет корреляционную матрицу, элементы которой получаются суммированием элементов корреляционных матриц слагаемых:
![]() , (10.2.30)
, (10.2.30)
где
![]() обозначают
соответственно корреляционные моменты величин
обозначают
соответственно корреляционные моменты величин ![]() ;
;![]() ;
; ![]() .
.
Формула (10.2.30) справедлива как
при ![]() , так и
при
, так и
при ![]() .
Действительно, составляющие вектора
.
Действительно, составляющие вектора ![]() равны:
равны:

По теореме сложения дисперсий
![]() ,
,
или в других обозначениях
![]() .
.
По теореме сложения
корреляционных моментов при ![]()
![]() .
.
В математике суммой двух матриц называется матрица, элементы которой получены сложением соответствующих элементов этих матриц. Пользуясь этой терминологией, можно сказать, что корреляционная матрица суммы двух некоррелированных случайных векторов равна сумме корреляционных матриц слагаемых:
![]() . (10.2.31)
. (10.2.31)
Это правило по аналогии с предыдущими можно назвать «теоремой сложения корреляционных матриц».
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Введение
- ПРЕДИСЛОВИЕ
- 1.1. Предмет теории вероятностей
- Теория вероятностей: 1.2. Краткие исторические сведения
- Глава 2. Основные понятия теории вероятностей
- 2.1. Событие. Вероятность события
- 2.2. Непосредственный подсчет вероятностей
- 2.3. Частота, или статистическая вероятность, события
- 2.4. Случайная величина
- 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности
- Глава 3. Основные теоремы теории вероятностей
- 3.1. Назначение основных теорем. Сумма и произведение событий
- 3.2. Теорема сложения вероятностей
- 3.3. Теорема умножения вероятностей
- 3.4. Формула полной вероятности
- 3.5. Теорема гипотез (формула Бейеса)
- Глава 4. Повторение опытов
- 4.1. Частная теорема о повторении опытов
- 4.2. Общая теорема о повторении опытов
- Глава 5. Случайные величины и их законы распределения
- 5.1. Ряд распределения. Многоугольник распределения
- 5.2. Функция распределения
- 5.3. Вероятность попадания случайной величины на заданный участок
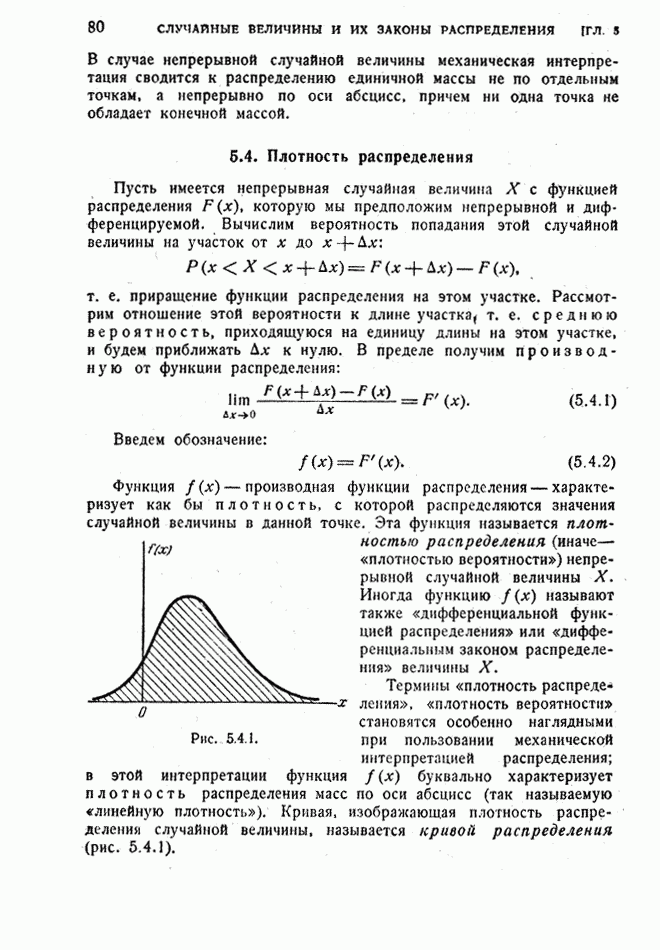
- 5.4. Плотность распределения
- 5.5. Числовые характеристики случайных величин. Их роль и назначение
- 5.6. Характеристики положения (математическое ожидание, мода, медиана)
- 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение
- 5.8. Закон равномерной плотности
- 5.9. Закон Пуассона
- Глава 6. Нормальный закон распределения
- 6.1. Нормальный закон распределения и его параметры
- 6.2. Моменты нормального распределения
- 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
- 6.4. Вероятное (срединное) отклонение
- Глава 7. Определение законов распределения случайных величин на основе опытных данных
- 7.1. Основные задачи математической статистики
- 7.2. Простая статистическая совокупность. Статистическая функция распределения
- 7.3. Статистический ряд. Гистограмма
- 7.4 Числовые характеристики статистического распределения
- 7.5. Выравнивание статистических рядов
- 7.6. Критерии согласия
- Глава 8. Системы случайных величин
- 8.1. Понятие о системе случайных величин
- 8.2. Функция распределения системы двух случайных величин
- 8.3. Плотность распределения системы двух случайных величин
- 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения
- 8.5 Зависимые и независимые случайные величины
- 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
- 8.7. Система произвольного числа случайных величин
- 8.8. Числовые характеристики системы нескольких случайных величин
- Глава 9. Нормальный закон распределении дли системы случайных величин
- 9.1. Нормальный закон на плоскости
- 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду
- 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания
- 9.4. Вероятность попадания в эллипс рассеивания
- 9.5. Вероятность попадания в область произвольной формы
- 9.6. Нормальный закон в пространстве трех измерений. Общая запись нормального закона для системы произвольного числа случайных величин
- Глава 10. Числовые характеристики функций случайных величин
- 10.1. Математическое ожидание функции. Дисперсия функции
- 10.2. Теоремы о числовых характеристиках
- 10.3. Применения теорем о числовых характеристиках
- Глава 11. Линеаризация функций
- 11.1. Метод линеаризации функций случайных аргументов
- 11.2. Линеаризация функции одного случайного аргумента
- 11.3. Линеаризация функции нескольких случайных аргументов
- 11.4. Уточнение результатов, полученных методом линеаризации
- Глава 12. Законы распределения функций случайных аргументов
- 12.1. Закон распределения монотонной функции одного случайного аргумента
- 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону
- 12.3. Закон распределения немонотонной функции одного случайного аргумента
- 12.4. Закон распределения функции двух случайных величин
- 12.5. Закон распределения суммы двух случайных величин. Композиция законов распределения
- 12.6. Композиция нормальных законов
- 12.7. Линейные функции от нормально распределенных аргументов
- 12.8. Композиция нормальных законов на плоскости
- Глава 13. Предельные теоремы теории вероятностей
- 13.1. Закон больших чисел и центральная предельная теорема
- 13.2. Неравенство Чебышева
- 13.3. Закон больших чисел (теорема Чебышева)
- 13.4. Обобщенная теорема Чебышева. Теорема Маркова
- 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона
- 13.6. Массовые случайные явления и центральная предельная теорема
- 13.7. Характеристические функции
- 13.8. Центральная предельная теорема для одинаково распределенных слагаемых
- 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении
- Глава 14. Обработка опытов
- 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения
- 14.2. Оценки для математического ожидания и дисперсии
- 14.3. Доверительный интервал. Доверительная вероятность
- 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону
- 14.5. Оценка вероятности по частоте
- 14.6. Оценки для числовых характеристик системы случайных величин
- 14.7. Обработка стрельб
- 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов
- Глава 15. Основные понятия теории случайных функций
- 15.1. Понятие о случайной функции
- 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции
- 15.3. Характеристики случайных функций
- 15.4. Определение характеристик случайной функции из опыта
- 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций
- 15.6. Линейные и нелинейные операторы. Оператор динамической системы
- 15.7. Линейные преобразования случайных функций
- 15.7.1. Интеграл от случайной функции
- 15.7.2. Производная от случайной функции
- 15.8. Сложение случайных функций
- 15.9. Комплексные случайные функции
- Глава 16. Канонические разложения случайных функций
- 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций
- 16.2. Каноническое разложение случайной функции
- 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями
- Глава 17. Стационарные случайные функции
- 17.1. Понятие о стационарном случайном процессе
- 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий
- 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции
- 17.4. Спектральное разложение случайной функции в комплексной форме
- 17.5. Преобразование стационарной случайной функции стационарной линейной системой
- 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем
- 17.7. Эргодическое свойство стационарных случайных функций
- 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации
- Глава 18. Основные понятия теории информации
- 18.1. Предмет и задачи теории информации
- 18.2. Энтропия как мера степени неопределенности состояния физической системы
- 18.3. Энтропия сложной системы. Теорема сложения энтропий
- 18.4. Условная энтропия. Объединение зависимых систем
- 18.5. Энтропия и информация
- 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии
- 18.7. Энтропия и информация для систем с непрерывным множеством состояний
- 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно
- 18.9. Передача информации с искажениями. Пропускная способность канала с помехами
- Глава 19. Элементы теории массового обслуживания
- 19.1. Предмет теории массового обслуживания
- 19.2. Случайный процесс со счетным множеством состояний
- 19.3. Поток событий. Простейший поток и его свойства
- 19.4 Нестационарный пуассоновский поток
- 19.5. Поток с ограниченным последействием (поток Пальма)
- 19.6. Время обслуживания
- 19.7. Марковский случайный процесс
- 19.8. Система массового обслуживания с отказами. Уравнения Эрланга
- 19.9. Установившийся режим обслуживания. Формулы Эрланга
- 19.10. Система массового обслуживания с ожиданием
- 19.11. Система смешанного типа с ограничением по длине очереди
- Приложения
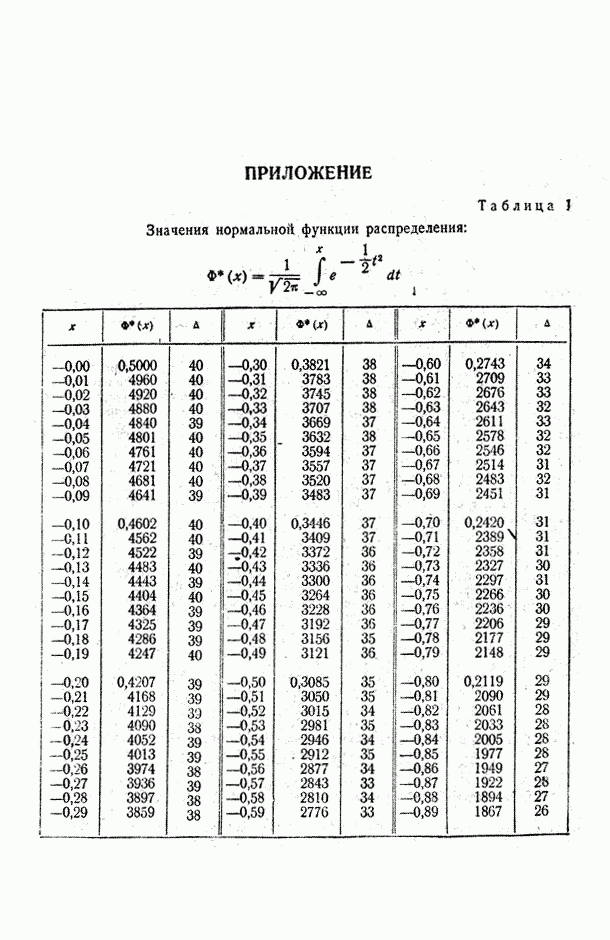
- Таблица 1 Значения нормальной функции распределения
- Таблица 2. Значения экспоненциальной функции
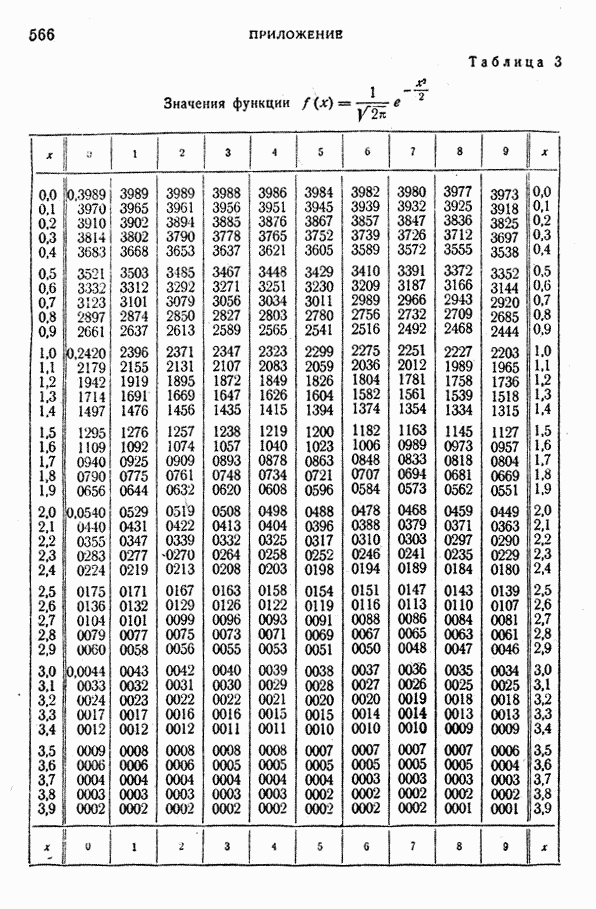
- Таблица 3. Значения нормальной функции
- Таблица 4. Значения «хи-квадрат» в зависимости от r и p
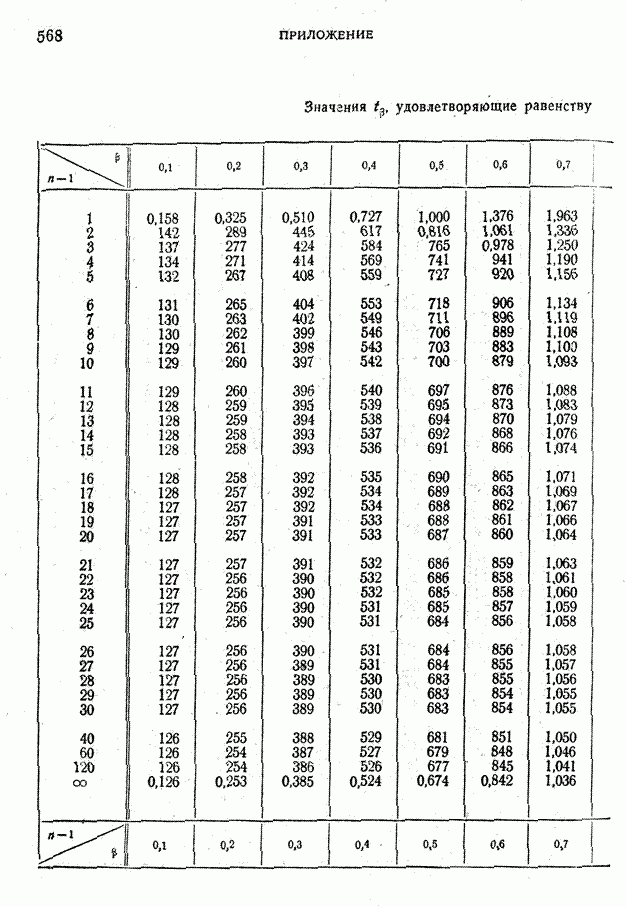
- Таблица 5. Значения удовлетворяющие равенству
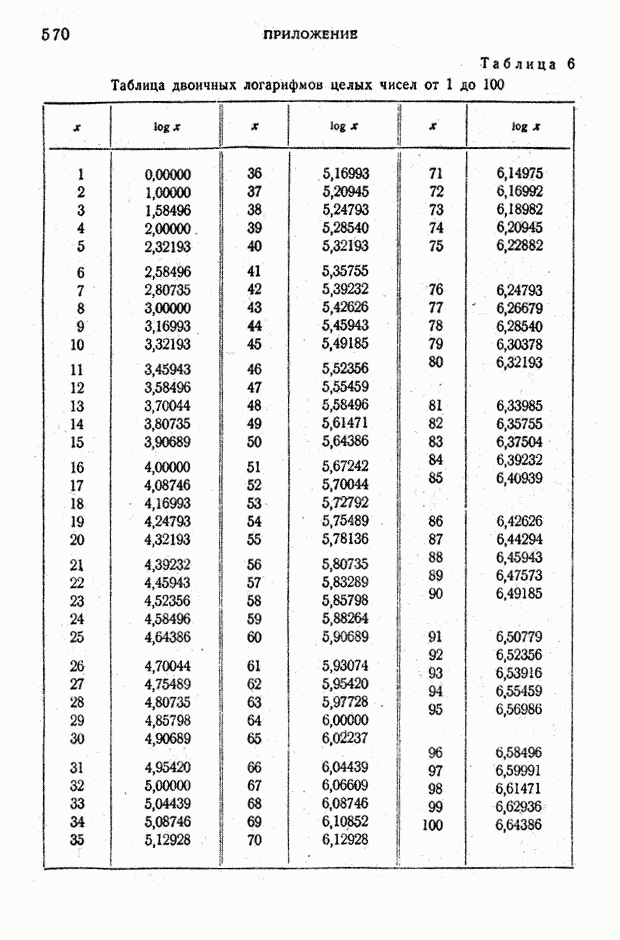
- Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100
- Таблица 7. Таблица значений функции
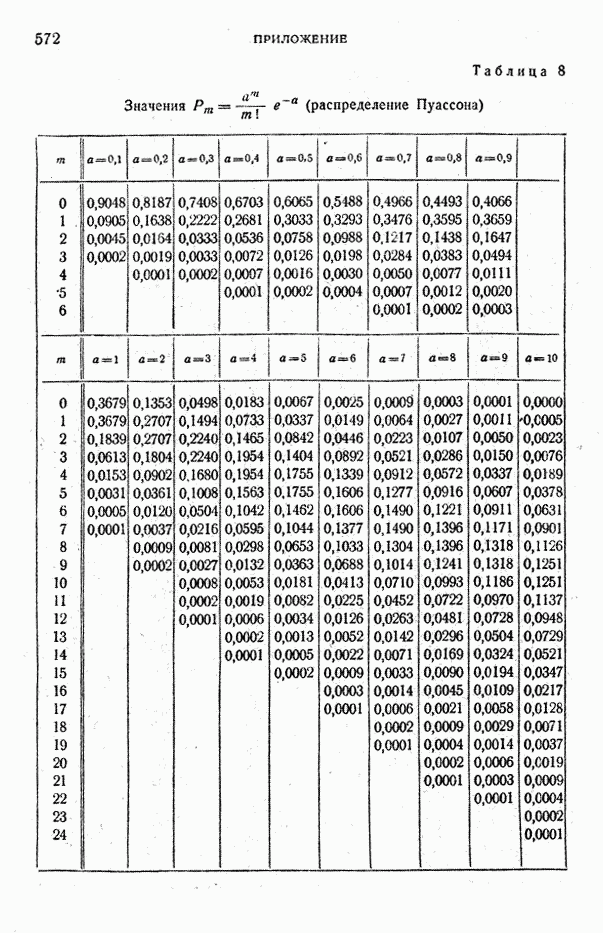
- Таблица 8. Значения распределение Пуассона