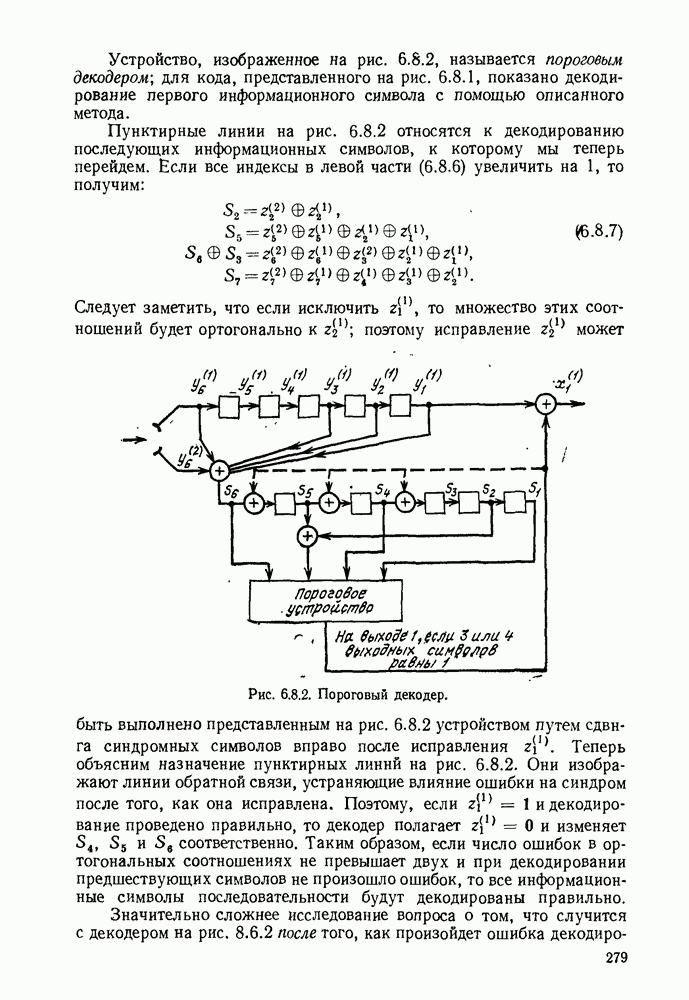
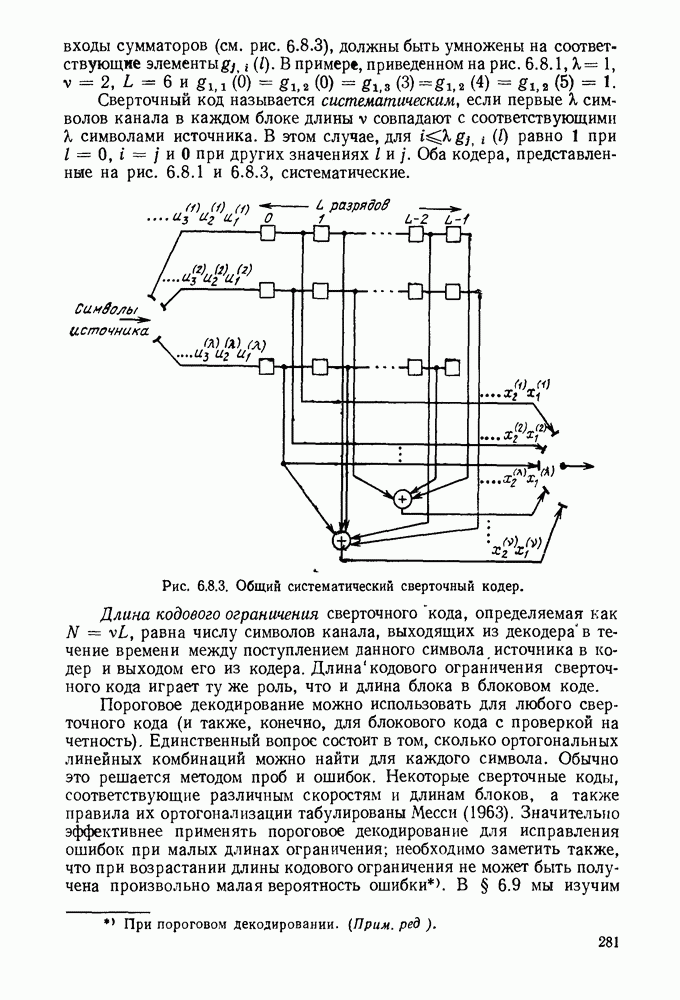
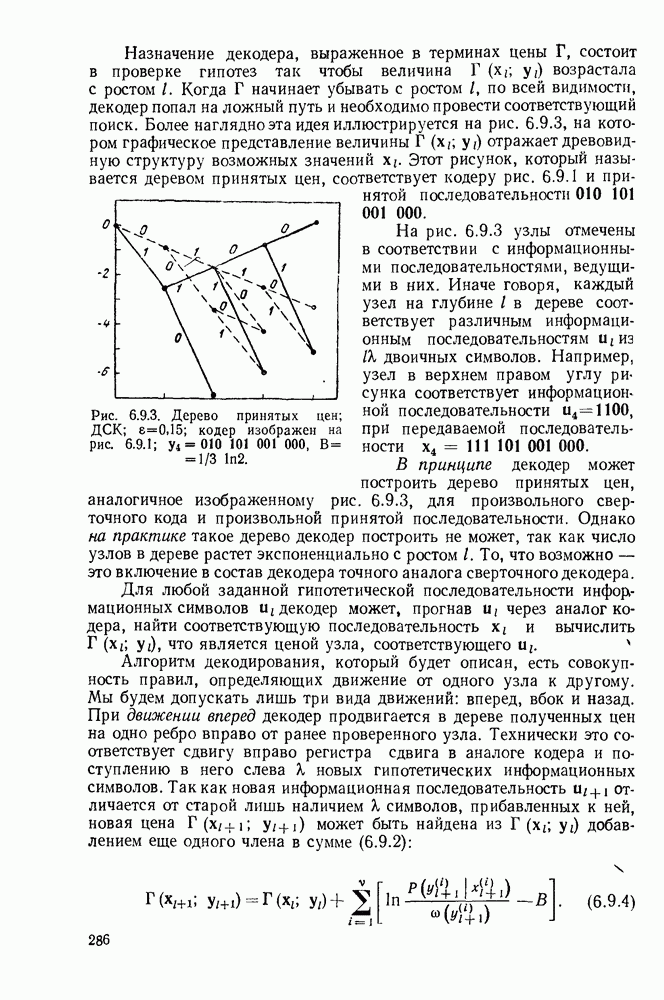
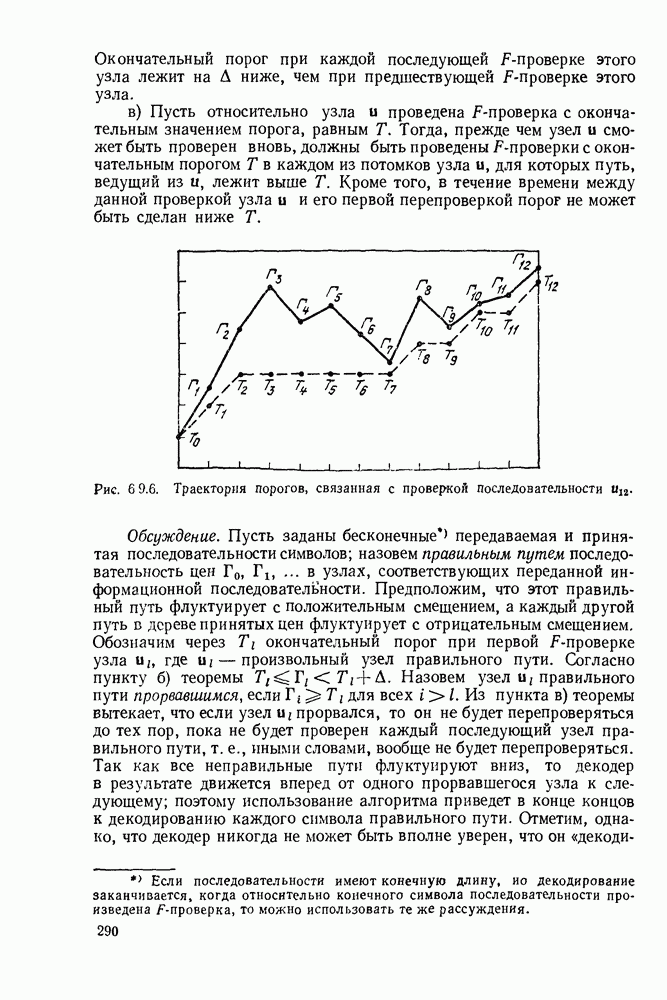
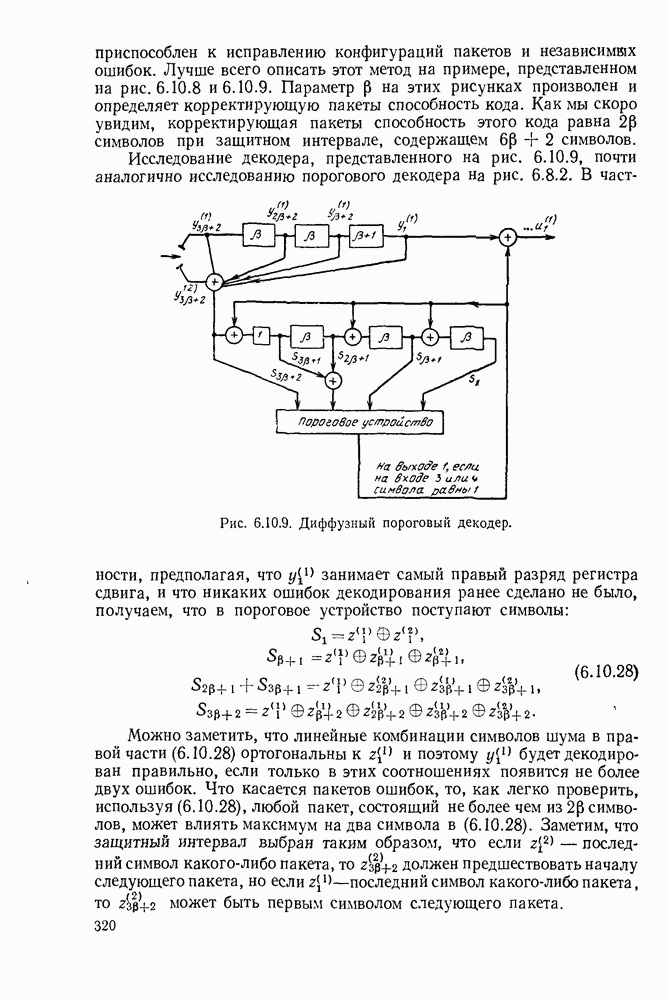
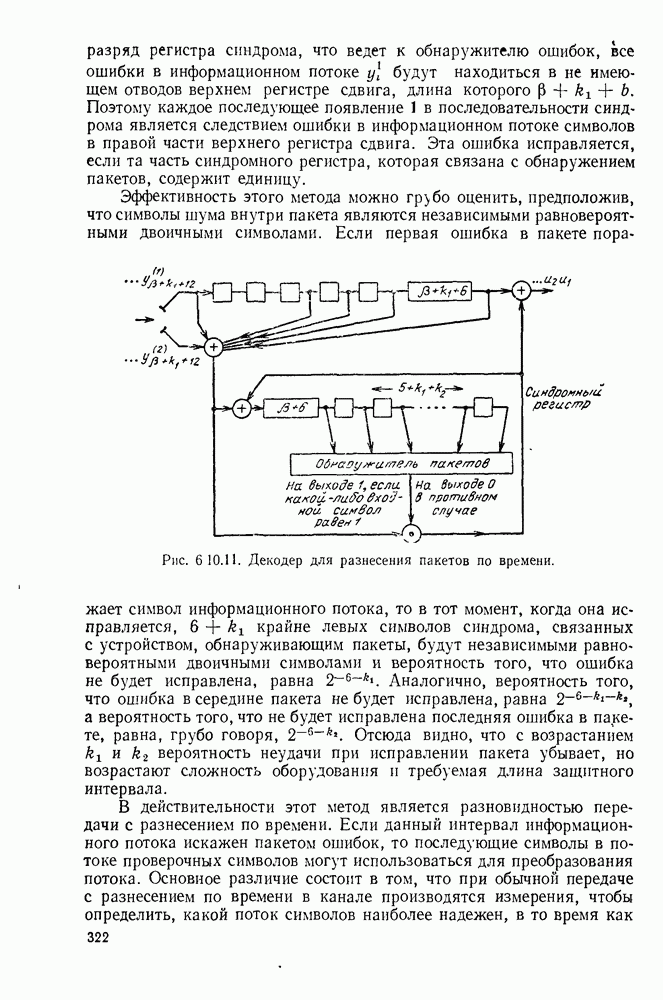
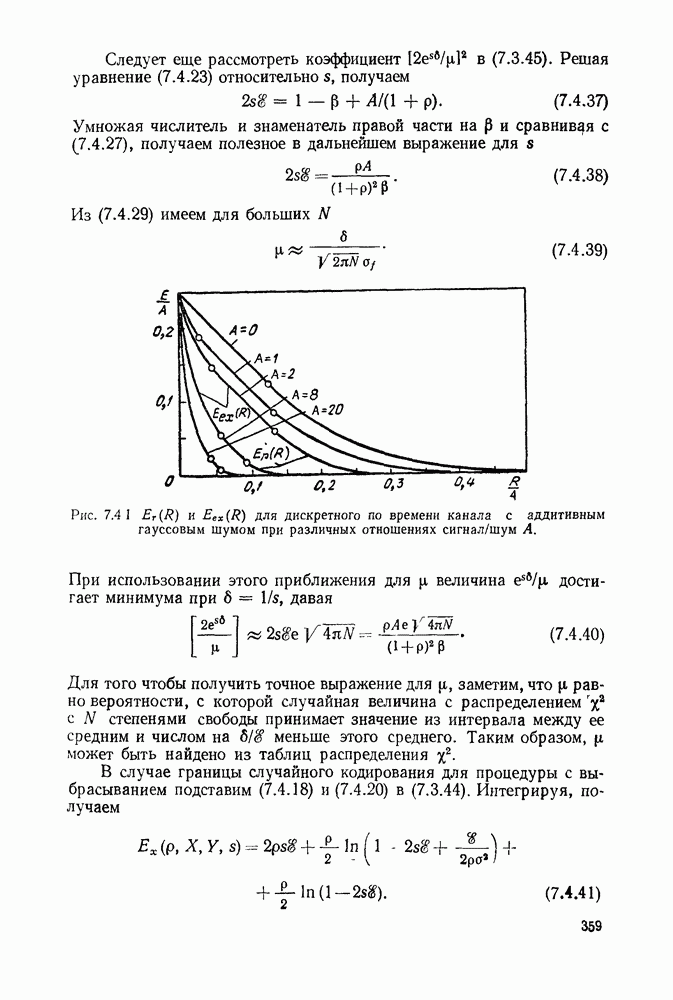
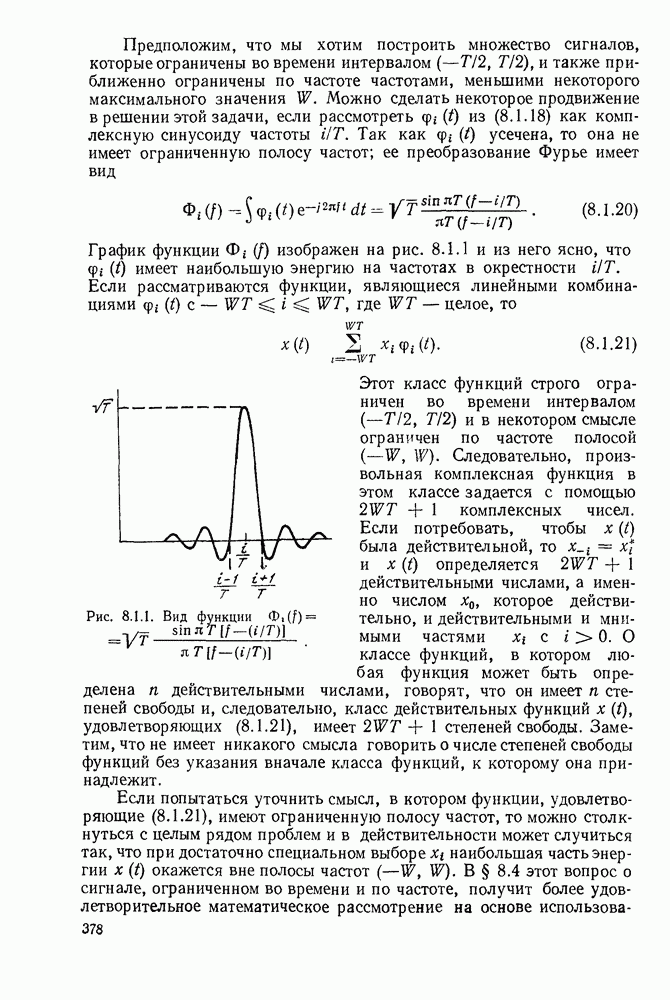
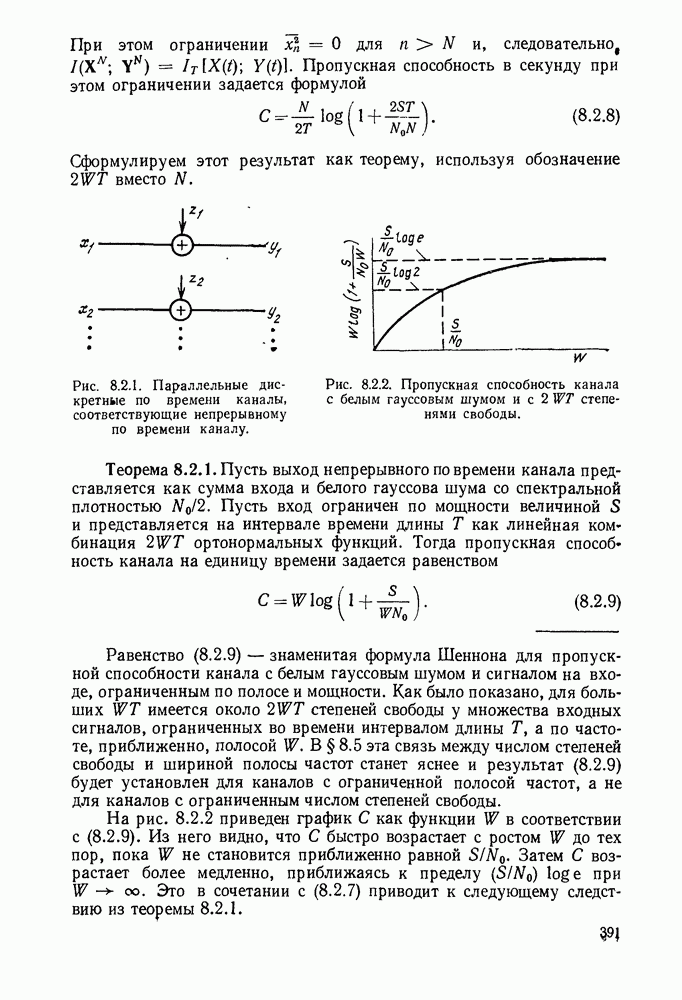
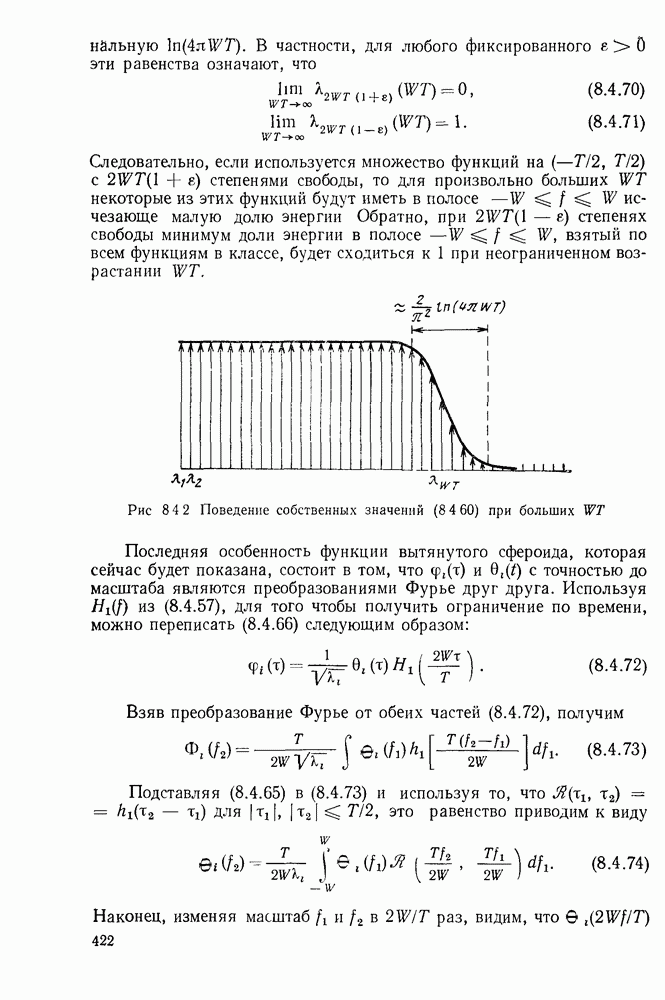
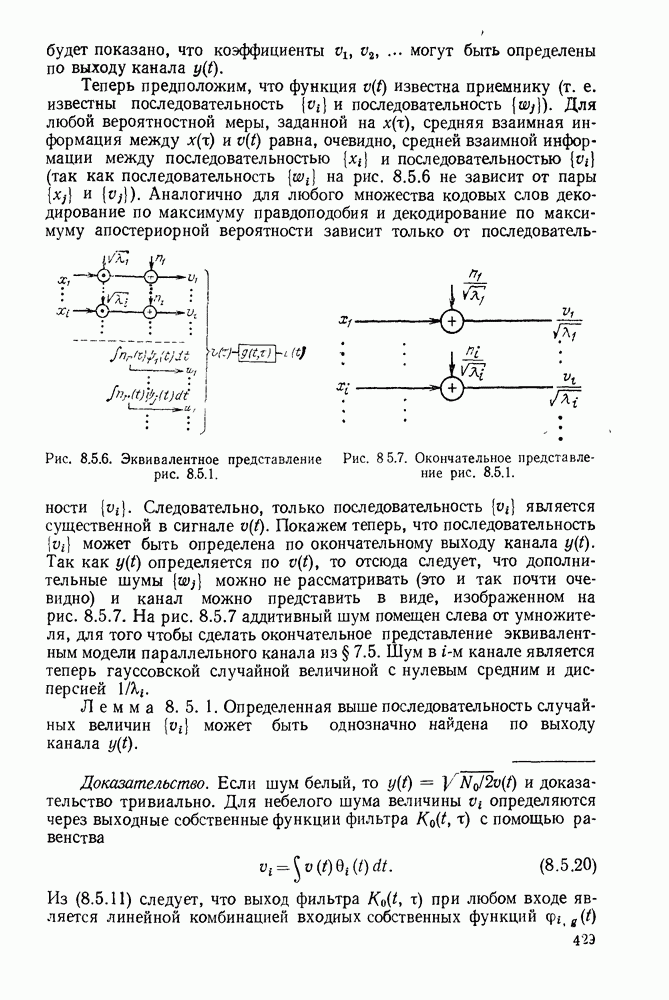
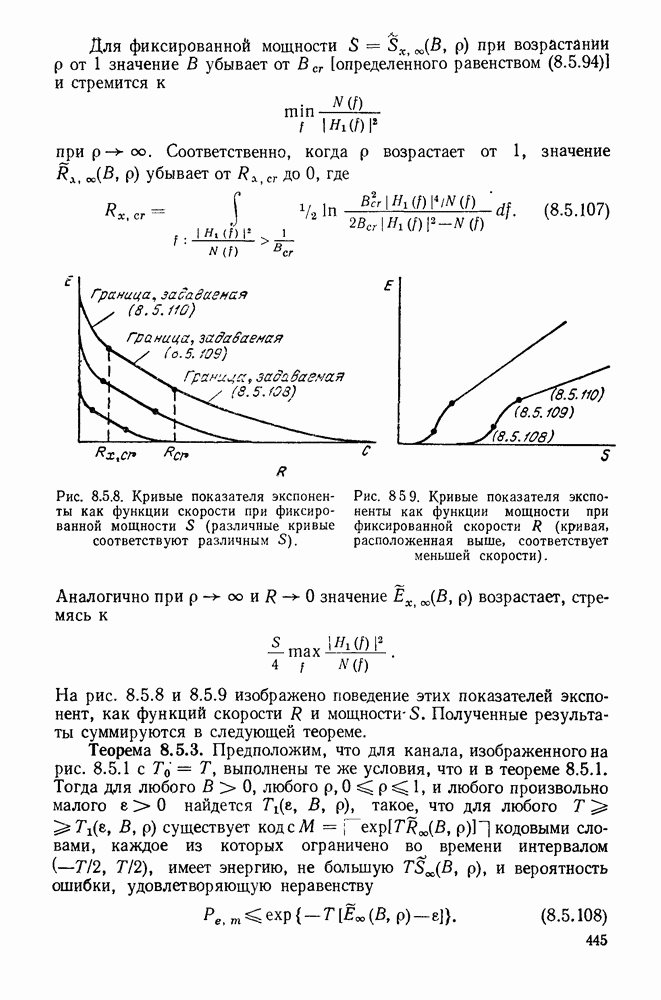
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3. ТЕОРИЯ ГРУПП
В предыдущих двух параграфах было широко использовано сложение по модулю 2. Для этого вначале было введено множество элементов 0 и 1, а затем определена операция  над этими элементами. Под операцией здесь будем понимать правило, ставящее что-то в соответствие комбинации двух элементов множества. Ниже также будет рассматриваться ряд других множеств элементов и операций. Так как все они будут иметь одну и ту же математическую природу (образовывать группу), то полезно здесь прервать изложение и привести некоторые элементарные результаты теории групп, которые потребуются в дальнейшем.
над этими элементами. Под операцией здесь будем понимать правило, ставящее что-то в соответствие комбинации двух элементов множества. Ниже также будет рассматриваться ряд других множеств элементов и операций. Так как все они будут иметь одну и ту же математическую природу (образовывать группу), то полезно здесь прервать изложение и привести некоторые элементарные результаты теории групп, которые потребуются в дальнейшем.
Группой называется множество элементов  с операцией, обозначаемой символом, обладающей следующими свойствами.
с операцией, обозначаемой символом, обладающей следующими свойствами.
1. Для любых элементов  принадлежащих множеству,
принадлежащих множеству,  также принадлежит множеству.
также принадлежит множеству.
2. Выполняется ассоциативный закон, т. е. для любых  принадлежащих множеству,
принадлежащих множеству,

3. В множестве имеется нейтральный элемент  такой, что а
такой, что а  для всех а, принадлежащих множеству.
для всех а, принадлежащих множеству.
4. Для любого элемента а из множества существует принадлежащий множеству обратный элемент  удовлетворяющий соотношениям
удовлетворяющий соотношениям

Абелева (или коммутативная) группа определяется как группа, для которой также выполняется коммутативный закон:

Ниже наибольший интерес будут представлять абелевы группы.
Введенная выше операция во многом подобна обычному умножению, и нетрудно убедиться, что множество обычных ненулевых действительных чисел с операцией обычного умножения удовлетворяет всем аксиомам группы. С равным успехом, однако, операцией в группе может быть сложение или любая другая произвольным образом введенная операция. Например, целые числа с операцией сложения образуют группу. В этом случае О является нейтральным элементом, а обратным элементом для а служит —а. Аналогично, элементы О и 1 образуют группу, в которой операцией является сложение по модулю 2. Во всех случаях, когда операция в группе обозначается знаком  или 0, условимся обозначать нейтральный элемент знаком О, а элемент, обратный для элемента а, через —а.
или 0, условимся обозначать нейтральный элемент знаком О, а элемент, обратный для элемента а, через —а.
Следующие свойства полезно знать при работе с группами. Пусть  нейтральный элемент, определяемый соотношением (6.3.2), а — произвольный элемент группы и
нейтральный элемент, определяемый соотношением (6.3.2), а — произвольный элемент группы и  обратный элемент для элемента а [см. (6.3.3)]. Первые два приведенных ниже свойства утверждают единственность элементов
обратный элемент для элемента а [см. (6.3.3)]. Первые два приведенных ниже свойства утверждают единственность элементов 
1. Единственным элементом х, для которого  является
является 
2. Единственным х, для которого а  является
является 
3. Если  то
то  с.
с.
4. Уравнение а  имеет единственное решение
имеет единственное решение

Чтобы проверить свойство 1, умножим обе части равенства  на
на  получим
получим  или
или  или
или  Свойства 2, 3 и 4 доказываются аналогично.
Свойства 2, 3 и 4 доказываются аналогично.
Подгруппы
Подмножество  элементов группы
элементов группы  удовлетворяющее аксиомам группы при том же определении операции, что и в группе
удовлетворяющее аксиомам группы при том же определении операции, что и в группе  называется подгруппой группы
называется подгруппой группы  В качестве примера рассмотрим множество всех двоичных последовательностей длины
В качестве примера рассмотрим множество всех двоичных последовательностей длины  Это множество с операцией сложения последовательностей по модулю 2 образует группу. Последовательность 0 является нейтральным элементом и каждая последовательность является обратным элементом для самой себя
Это множество с операцией сложения последовательностей по модулю 2 образует группу. Последовательность 0 является нейтральным элементом и каждая последовательность является обратным элементом для самой себя
Кодовые слова любого кода с проверкой на четность, имеющего длину блока  образуют подгруппу этой группы. Чтобы показать это, заметим, что 0 всегда является кодовым словом, обратным элементом для кодового слова служит само это слово, а сумма по модулю 2 любых двух кодовых слов также является кодовым словом.
образуют подгруппу этой группы. Чтобы показать это, заметим, что 0 всегда является кодовым словом, обратным элементом для кодового слова служит само это слово, а сумма по модулю 2 любых двух кодовых слов также является кодовым словом.
Порядком группы или подгруппы называется число элементов в группе или подгруппе. Следующая теорема Лагранжа содержит важный результат.
Теорема 6.3.1. (Лагранж.) Порядок группы, если он конечен, кратен порядку каждой подгруппы.
Нам потребуется несколько вспомогательных результатов. Правым смежным классом (левым смежным классом) группы  по подгруппе
по подгруппе  называется подмножество
называется подмножество  элементов
элементов  где а — произвольный заданный элемент группы
где а — произвольный заданный элемент группы  все элементы
все элементы  Непосредственно можно убедиться, что для подгруппы конечного порядка число элементов в смежном классе равно числу элементов в подгруппе, так как если
Непосредственно можно убедиться, что для подгруппы конечного порядка число элементов в смежном классе равно числу элементов в подгруппе, так как если  то
то  Кроме того, если два правых смежных класса (левых смежных класса) одной и той же подгруппы имеют какой-либо общий элемент, то эти два подмножества совпадают. Чтобы доказать это, предположим, что одно подмножество порождается элементом а, а другое — элементом
Кроме того, если два правых смежных класса (левых смежных класса) одной и той же подгруппы имеют какой-либо общий элемент, то эти два подмножества совпадают. Чтобы доказать это, предположим, что одно подмножество порождается элементом а, а другое — элементом  Если
Если  то
то  принадлежит смежному классу, порождаемому а. Поэтому для любого
принадлежит смежному классу, порождаемому а. Поэтому для любого  принадлежащего
принадлежащего  а и любой элемент смежного класса, порождаемого
а и любой элемент смежного класса, порождаемого  принадлежит смежному классу, порождаемому а.
принадлежит смежному классу, порождаемому а.
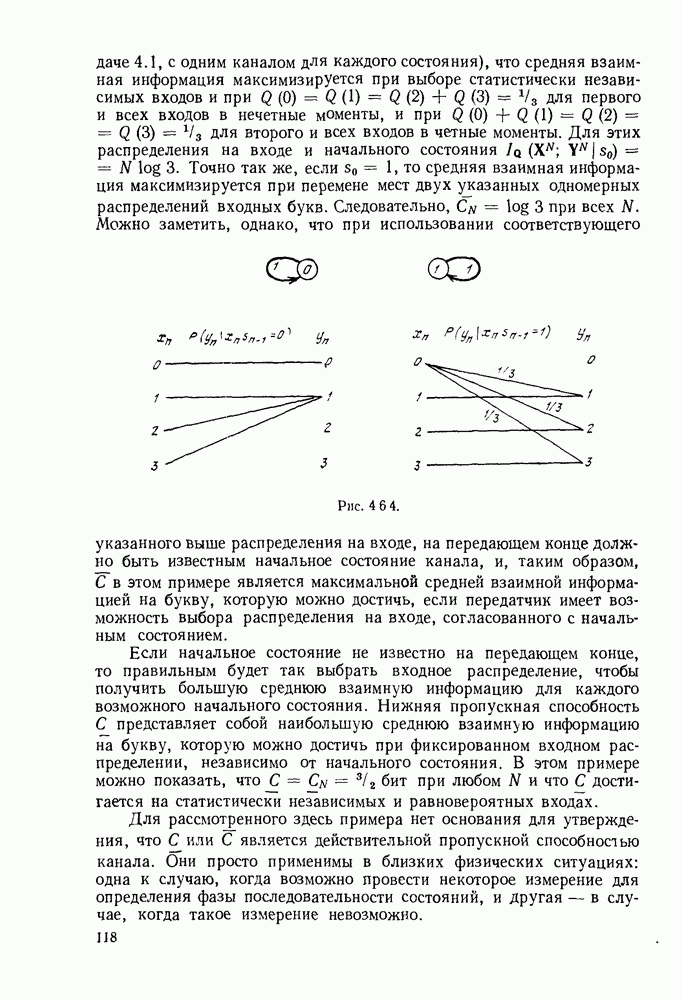
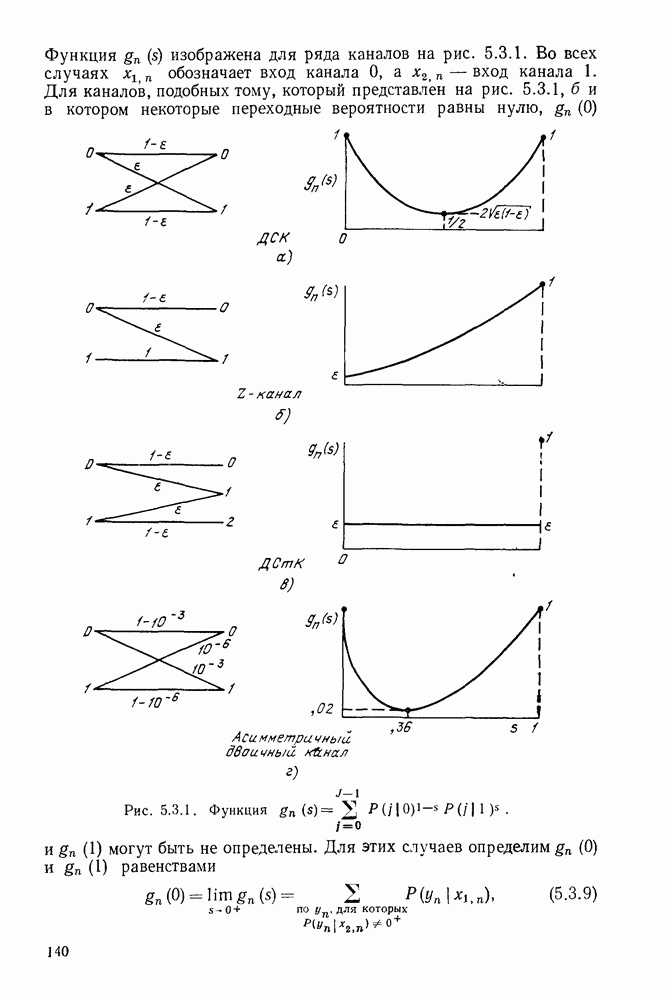
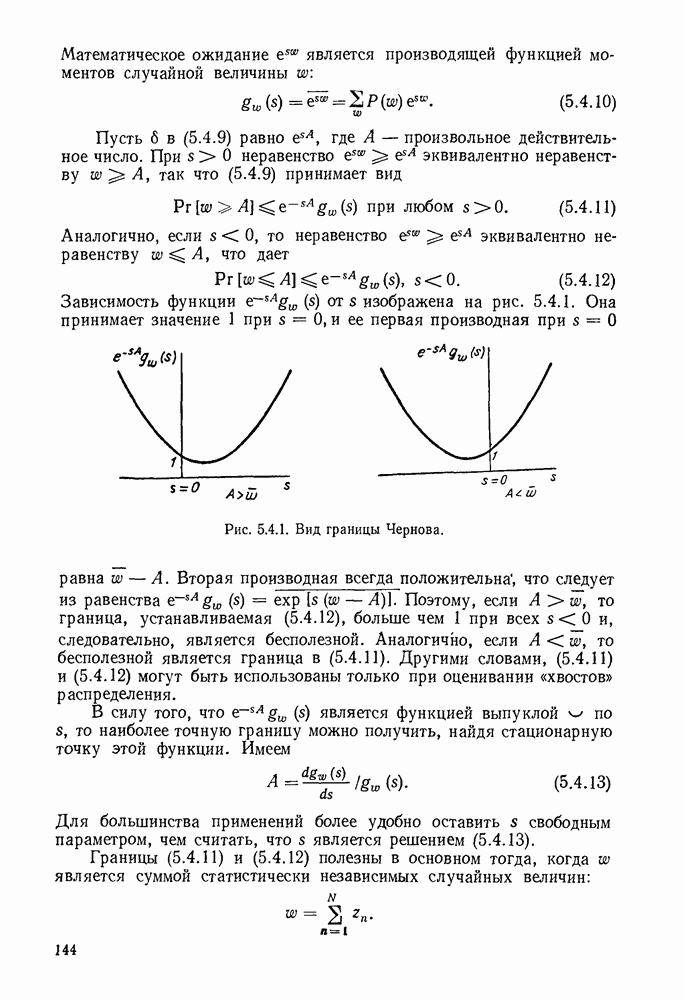
В коде с проверкой на четность, как было показано, для любой фиксированной последовательности у сумма  имеет тот же самый синдром, что и кодовое слово
имеет тот же самый синдром, что и кодовое слово  Поэтому множество последовательностей с данным синдромом является смежным классом по подгруппе, образуемой кодовыми словами. Тогда правило декодирования по максимуму правдоподобия в двоичном симметричном канале может быть переформулировано следующим образом: по заданному у найти шумовую последовательность
Поэтому множество последовательностей с данным синдромом является смежным классом по подгруппе, образуемой кодовыми словами. Тогда правило декодирования по максимуму правдоподобия в двоичном симметричном канале может быть переформулировано следующим образом: по заданному у найти шумовую последовательность  полагая, что она является последовательностью минимального веса в смежном классе, которому принадлежит у.
полагая, что она является последовательностью минимального веса в смежном классе, которому принадлежит у.
Теперь можно доказать теорему 6.3.1. Предположим, что группа  порядка
порядка  содержит подгруппу
содержит подгруппу  порядка
порядка  Если
Если  то выберем элемент группы
то выберем элемент группы  не принадлежащий
не принадлежащий  и образуем правый смежный класс. Подгруппа и смежный класс вместе содержат
и образуем правый смежный класс. Подгруппа и смежный класс вместе содержат  элементов; если
элементов; если  то можно выбрать другой элемент в
то можно выбрать другой элемент в  не принадлежащий ни подгруппе, ни смежному классу, и образовать новый правый смежный класс, что даст нам в совокупности
не принадлежащий ни подгруппе, ни смежному классу, и образовать новый правый смежный класс, что даст нам в совокупности  элементов. Продолжая таким образом, в конце концов достигнем того, что все элементы
элементов. Продолжая таким образом, в конце концов достигнем того, что все элементы  будут принадлежать либо
будут принадлежать либо  либо одному из смежных классов; если кроме подгруппы существуют и смежных классов, то получим
либо одному из смежных классов; если кроме подгруппы существуют и смежных классов, то получим  что завершает доказательство,
что завершает доказательство,
Циклические подгруппы
Пусть а — элемент конечной группы  Рассмотрим последовательность элементов
Рассмотрим последовательность элементов

где  означает а
означает а  означает
означает  а и т. д. Так как группа конечна, должны существовать два значения показателя степени
а и т. д. Так как группа конечна, должны существовать два значения показателя степени  для которых
для которых

Согласно (6.3.5) отсюда следует, что  Порядком элемента а группы называется наименьшее положительное целое число
Порядком элемента а группы называется наименьшее положительное целое число  для которого
для которого  Приведенные выше рассуждения показывают, что каждый элемент конечной группы имеет конечный порядок. Более
Приведенные выше рассуждения показывают, что каждый элемент конечной группы имеет конечный порядок. Более  того, элементы
того, элементы  должны быть различными, поскольку равенство
должны быть различными, поскольку равенство  где
где  может выполняться лишь при
может выполняться лишь при  Поэтому последовательность (6.3.9) степеней элемента а имеет следующее циклическое свойство:
Поэтому последовательность (6.3.9) степеней элемента а имеет следующее циклическое свойство:

Из (6.3.11) следует, что  тогда и только тогда, когда
тогда и только тогда, когда  кратно
кратно 
Теорема 6.3.2. Пусть элемент а конечной группы  имеет порядок
имеет порядок  Тогда элементы
Тогда элементы  образуют подгруппу группы
образуют подгруппу группы  является делителем для порядка группы
является делителем для порядка группы 
Доказательство. Подмножество  содержит нейтральный элемент
содержит нейтральный элемент  Тогда для любого
Тогда для любого  принадлежащего этому подмножеству,
принадлежащего этому подмножеству,  откуда следует, что каждый элемент подмножества имеет обратный элемент в том же подмножестве. Для завершения доказательства необходимо показать, что если
откуда следует, что каждый элемент подмножества имеет обратный элемент в том же подмножестве. Для завершения доказательства необходимо показать, что если  принадлежат подмножеству, то этому подмножеству принадлежит и
принадлежат подмножеству, то этому подмножеству принадлежит и  Имеем
Имеем  и при
и при  произведение
произведение  принадлежит подмножеству. Если
принадлежит подмножеству. Если  то имеем
то имеем  Так как
Так как  то
то  принадлежит подмножеству. Поэтому это подмножество образует подгруппу порядка
принадлежит подмножеству. Поэтому это подмножество образует подгруппу порядка  Из теоремы 6.3.1 следует, что
Из теоремы 6.3.1 следует, что  является делителем порядка группы
является делителем порядка группы 
Группа или подгруппа называется циклической, если в этой группе или подгруппе существует элемент, степени которого образуют всю группу или подгруппу. Поэтому подгруппы, входящие в формулировку теоремы 6.3.2, являются циклическими.
Следующие результаты, касающиеся порядка элементов конечной абелевой группы, будут использоваться в § 6.6.
Лемма. Пусть а — элемент порядка  элемент порядка
элемент порядка  в абелевой группе. Тогда, если тип взаимно простые, то порядок элемента а
в абелевой группе. Тогда, если тип взаимно простые, то порядок элемента а  равен
равен 
Доказательство. Имеем

Поэтому, обозначив порядок элемента а  через
через  получим
получим  Кроме того,
Кроме того,

Отсюда следует, что  кратно порядку
кратно порядку  элемента а. Так как тип взаимно простые, то
элемента а. Так как тип взаимно простые, то  кратно
кратно  Поменяв ролями
Поменяв ролями  в приведенных выше рассуждениях, получим, что
в приведенных выше рассуждениях, получим, что  также кратно пив силу того, что тип взаимно простые,
также кратно пив силу того, что тип взаимно простые,  что завершает доказательство.
что завершает доказательство.
Теорема 6.3.3. Пусть  максимальный порядок элементов конечной абелевой группы. Тогда
максимальный порядок элементов конечной абелевой группы. Тогда  кратно порядку каждого элемента группы.
кратно порядку каждого элемента группы.
Доказательство. Пусть а — элемент максимального порядка  и пусть
и пусть  порядок какого-либо другого элемента
порядок какого-либо другого элемента  Обозначим через
Обозначим через  все простые числа, которые служат делителями либо для
все простые числа, которые служат делителями либо для  либо для
либо для  и представим
и представим  в виде
в виде

где  целые неотрицательные числа. Если
целые неотрицательные числа. Если  не кратно
не кратно  то для некоторого
то для некоторого  должно выполняться
должно выполняться  Пусть далее для любого
Пусть далее для любого  через
через  обозначен элемент порядка
обозначен элемент порядка  (такой элемент равен а в степени
(такой элемент равен а в степени  Аналогично, пусть
Аналогично, пусть  есть элемент порядка
есть элемент порядка  Рассмотрим теперь элемент
Рассмотрим теперь элемент  Последовательно применяя предыдущую лемму при каждом включении нового сомножителя в это произведение, убеждаемся, что с имеет порядок
Последовательно применяя предыдущую лемму при каждом включении нового сомножителя в это произведение, убеждаемся, что с имеет порядок  Это привело к противоречию, поскольку
Это привело к противоречию, поскольку  равно наибольшему порядку элементов; поэтому
равно наибольшему порядку элементов; поэтому  кратно
кратно  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ РУССКОГО ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. СИСТЕМЫ СВЯЗИ И ТЕОРИЯ ИНФОРМАЦИИ
- 1.2. МОДЕЛИ ИСТОЧНИКОВ И КОДИРОВАНИЕ ДЛЯ ИСТОЧНИКОВ
- 1.3. МОДЕЛИ КАНАЛОВ И КОДИРОВАНИЕ ДЛЯ КАНАЛОВ
- 2. МЕРА ИНФОРМАЦИИ
- 2.2. ОПРЕДЕЛЕНИЕ ВЗАИМНОЙ ИНФОРМАЦИИ
- 2.3. СРЕДНЯЯ ВЗАИМНАЯ ИНФОРМАЦИЯ И ЭНТРОПИЯ
- 2.4. ВЕРОЯТНОСТЬ И ВЗАИМНАЯ ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ АНСАМБЛЕЙ
- 2.5. ВЗАИМНАЯ ИНФОРМАЦИЯ ДЛЯ ПРОИЗВОЛЬНЫХ АНСАМБЛЕЙ
- 3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.1. КОДЫ С ФИКСИРОВАННОЙ ДЛИНОЙ
- 3.2. НЕРАВНОМЕРНЫЕ КОДОВЫЕ СЛОВА
- 3.3. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ ИСТОЧНИКА
- 3.4. ПРОЦЕДУРА ВЫБОРА ОПТИМАЛЬНОГО НЕРАВНОМЕРНОГО КОДА
- 3.5. ДИСКРЕТНЫЕ СТАЦИОНАРНЫЕ ИСТОЧНИКИ
- 3.6. МАРКОВСКИЕ ИСТОЧНИКИ
- 4. ДИСКРЕТНЫЕ КАНАЛЫ БЕЗ ПАМЯТИ И ПРОПУСКНАЯ СПОСОБНОСТЬ
- 4.2. ДИСКРЕТНЫЕ КАНАЛЫ БЕЗ ПАМЯТИ
- 4.3. ОБРАЩЕНИЕ ТЕОРЕМЫ КОДИРОВАНИЯ
- 4.4. ВЫПУКЛЫЕ ФУНКЦИИ
- 4.5. НАХОЖДЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ ДИСКРЕТНОГО КАНАЛА БЕЗ ПАМЯТИ
- 4.6. ДИСКРЕТНЫЕ КАНАЛЫ С ПАМЯТЬЮ
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 4А
- 5. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КАНАЛА С ШУМАМИ
- 5.2. ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 5.3. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ДВУХ КОДОВЫХ СЛОВ
- 5.4. ОБОБЩЕННОЕ НЕРАВЕНСТВО ЧЕБЫШЕВА И ГРАНИЦА ЧЕРНОВА
- 5.5. СЛУЧАЙНЫЕ КОДОВЫЕ СЛОВА
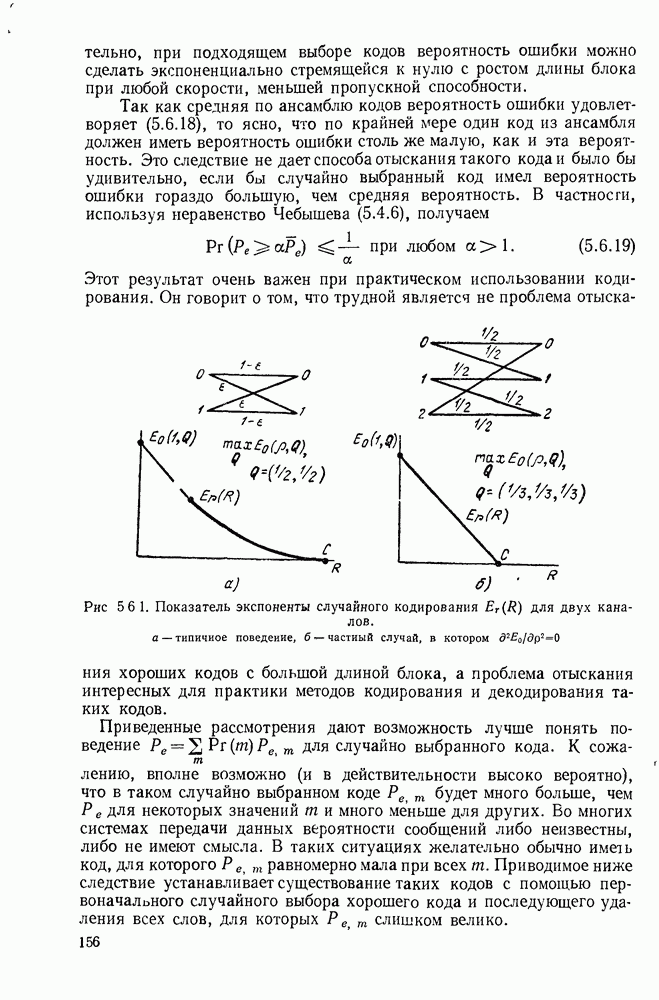
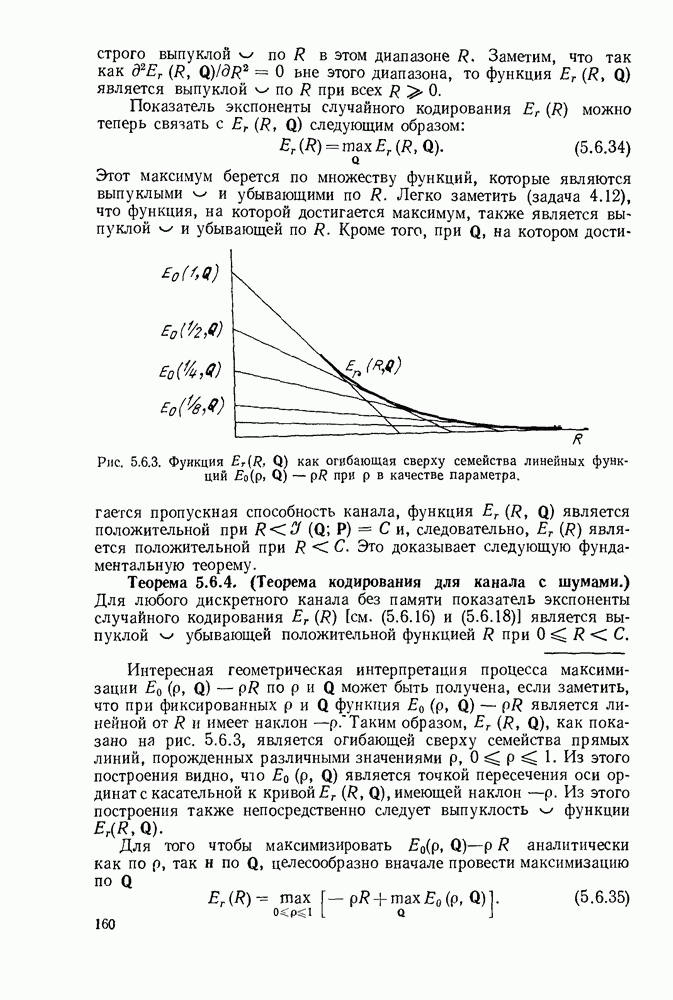
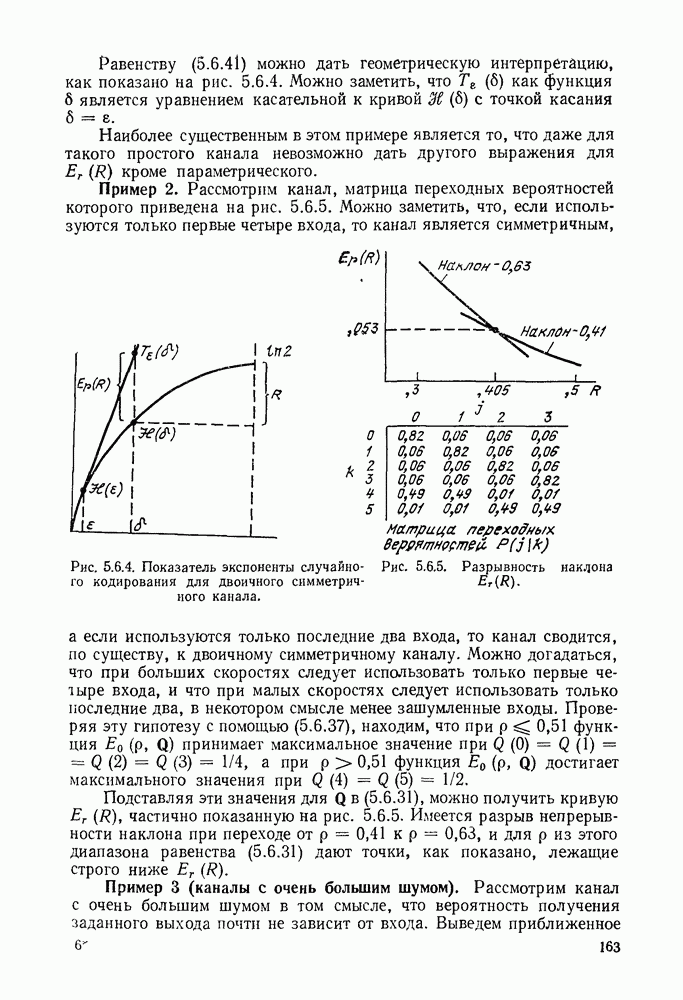
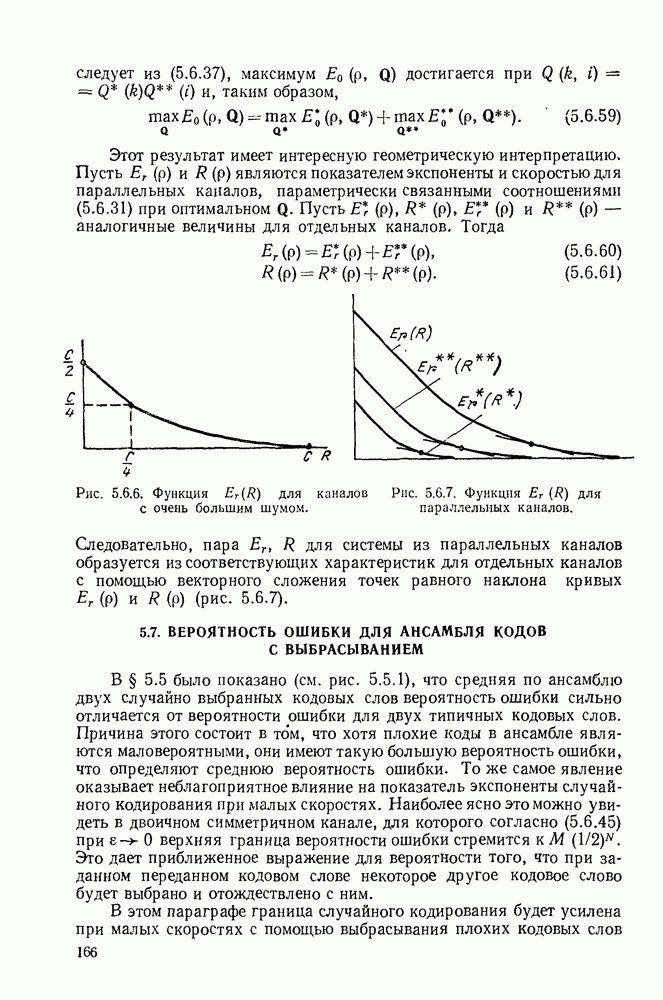
- 5.6. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КОДА С ЧИСЛОМ СЛОВ, БОЛЬШИМ ДВУХ
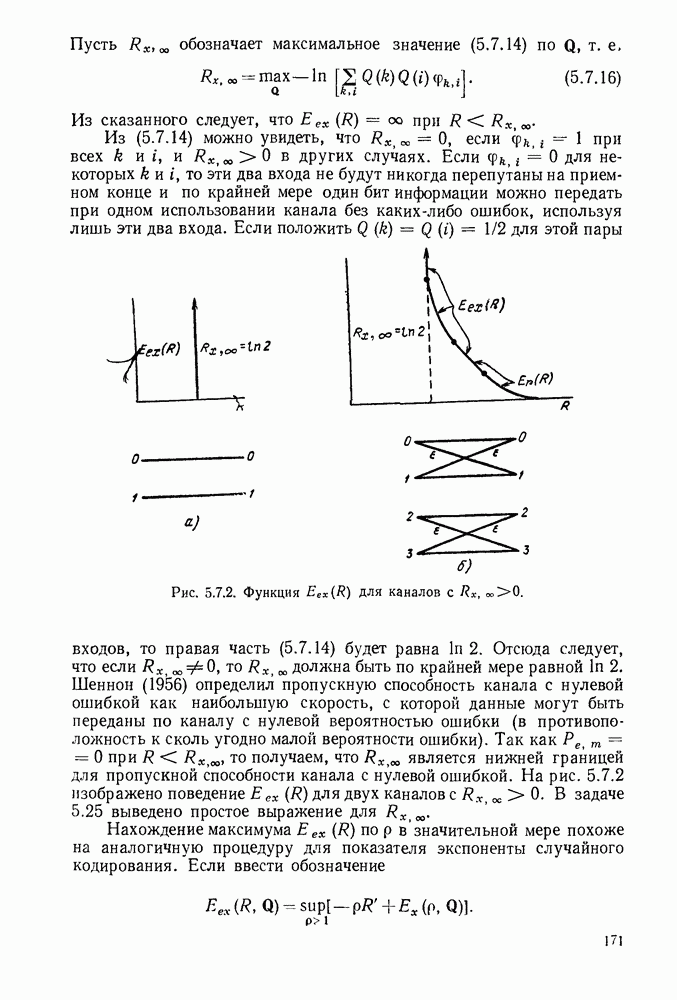
- 5.7. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ АНСАМБЛЯ КОДОВ С ВЫБРАСЫВАНИЕМ
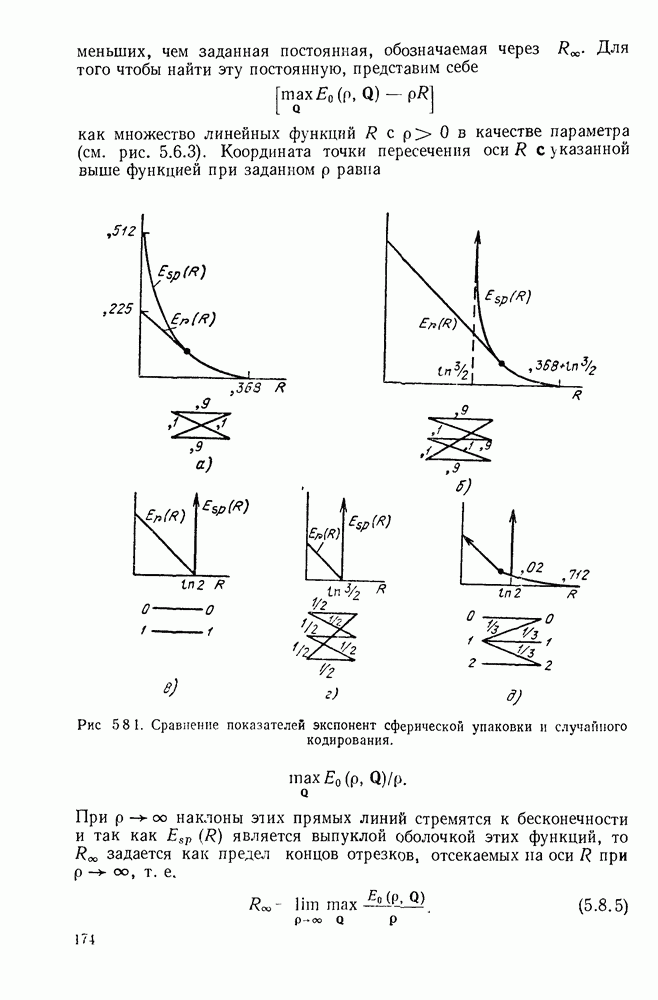
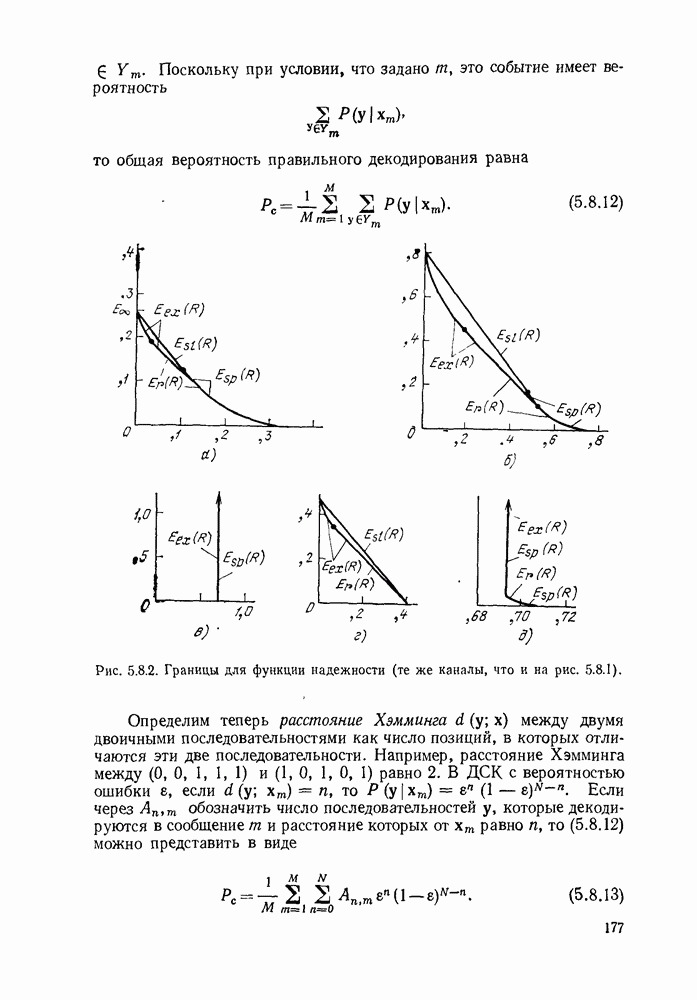
- 5.8. НИЖНИЕ ГРАНИЦЫ ДЛЯ ВЕРОЯТНОСТИ ОШИБКИ
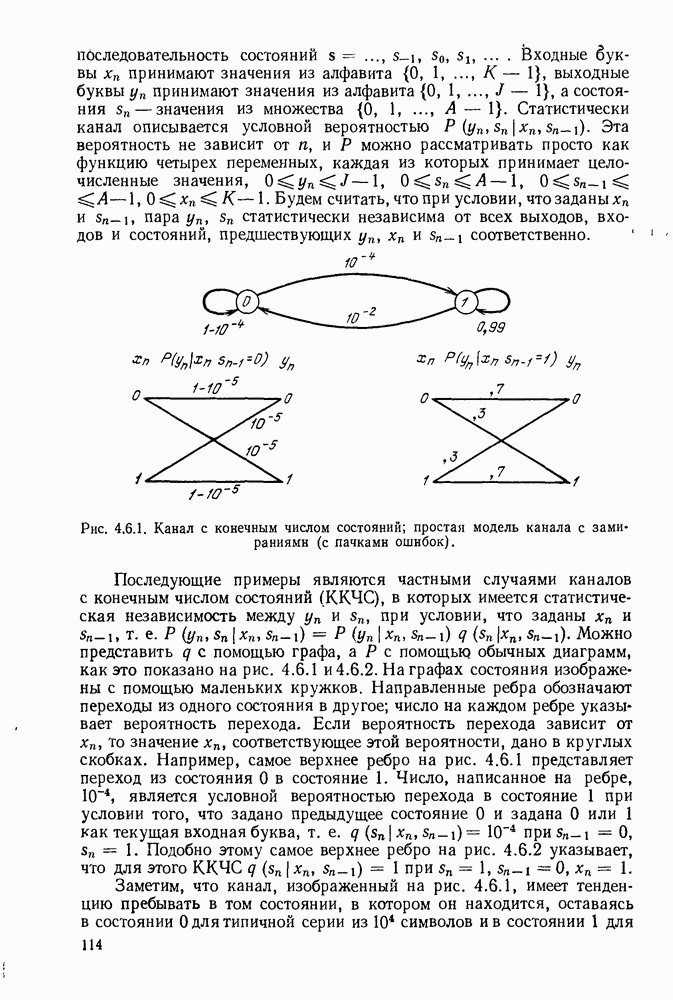
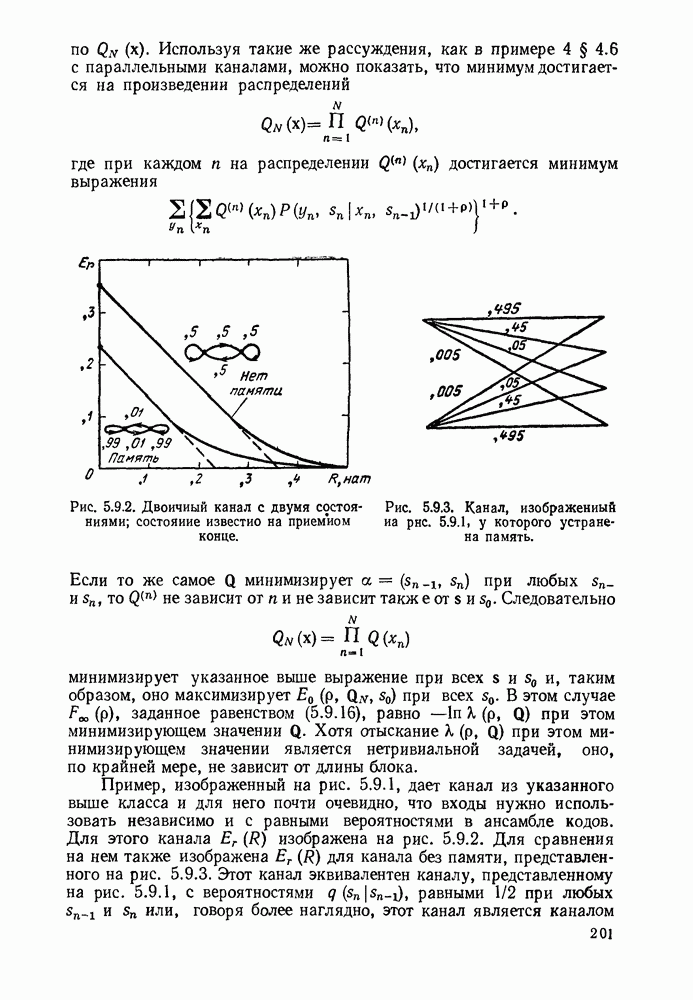
- 5.9. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЯ
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 5А
- ПРИЛОЖЕНИЕ 5Б
- 6. МЕТОДЫ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ
- 6.1. КОДЫ С ПРОВЕРКОЙ НА ЧЕТНОСТЬ
- 6.2. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КОДОВ С ПРОВЕРКОЙ НА ЧЕТНОСТЬ
- 6.3. ТЕОРИЯ ГРУПП
- 6.4. ПОЛЯ И МНОГОЧЛЕНЫ
- 6.5. ЦИКЛИЧЕСКИЕ КОДЫ
- 6.6. ПОЛЯ ГАЛУА
- Коды максимальной длины и коды Хэмминга
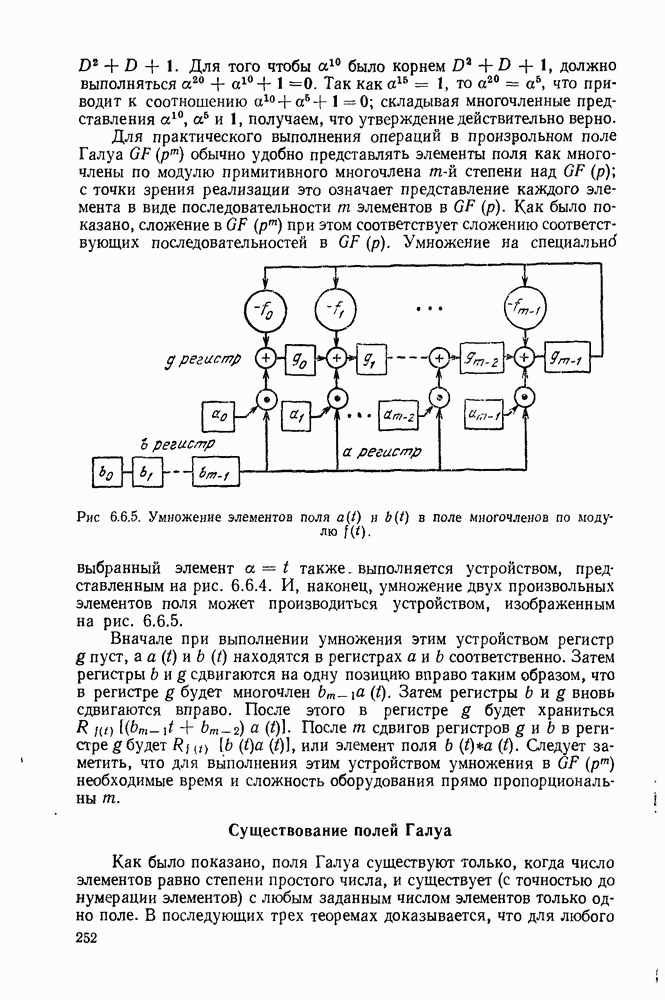
- Существование полей Галуа
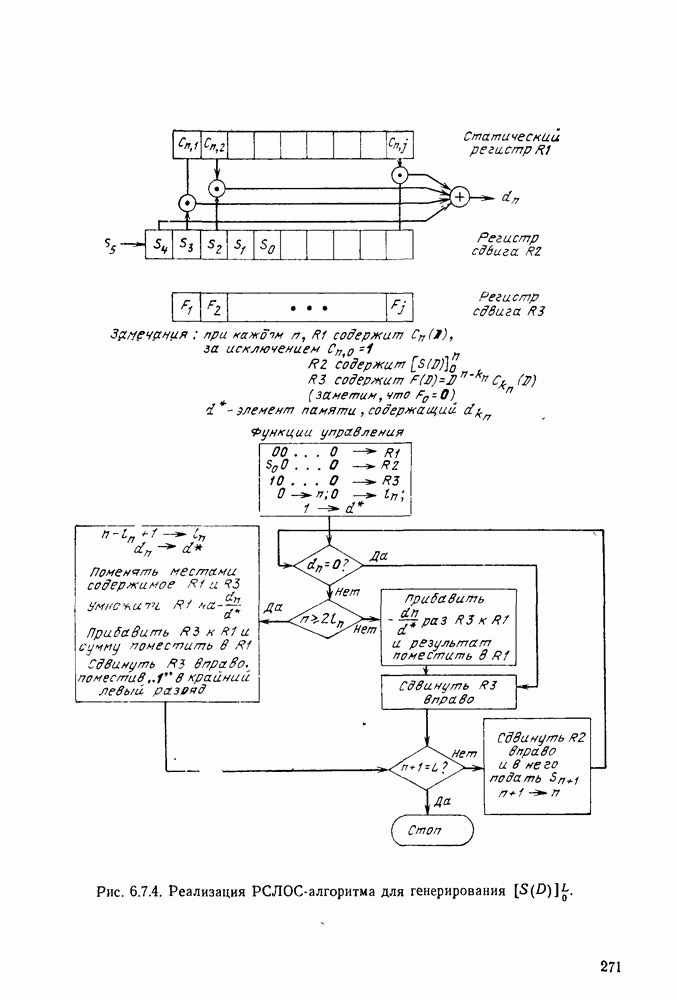
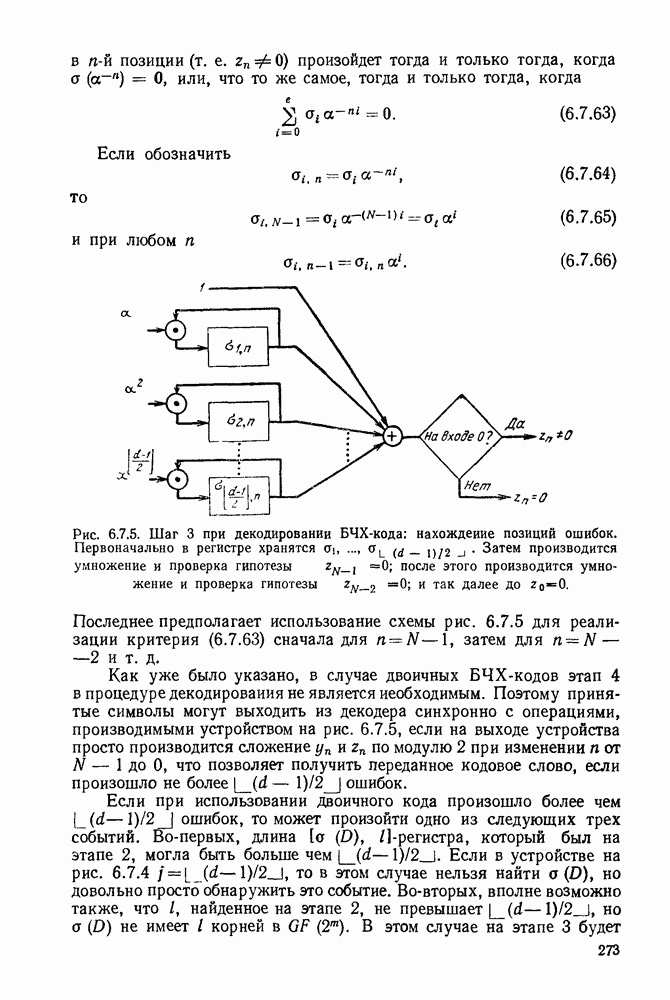
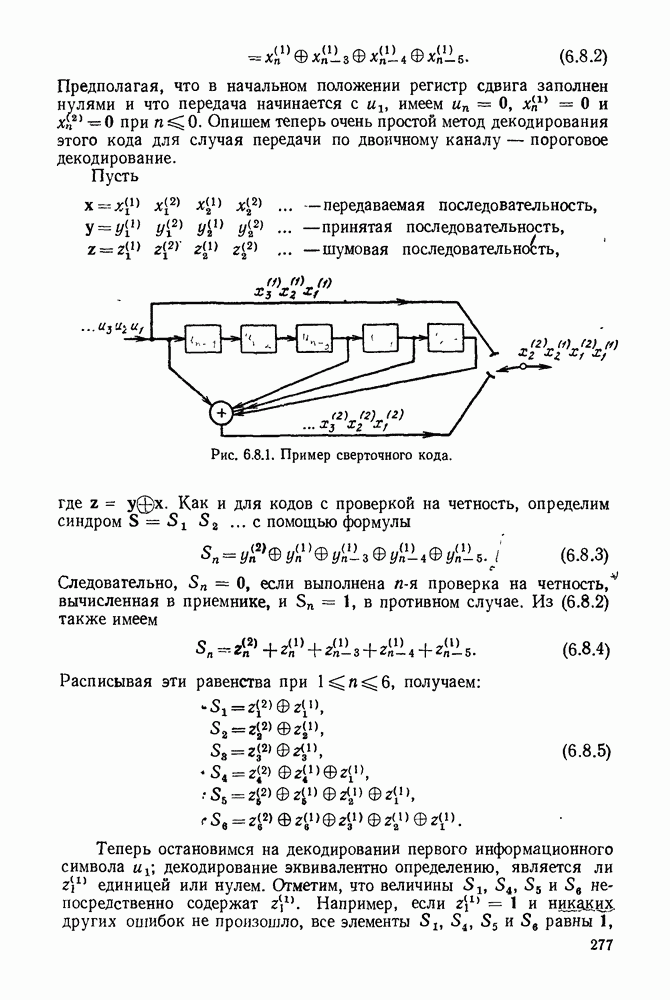
- 6.7. БЧХ-КОДЫ
- 6.8. СВЕРТОЧНЫЕ КОДЫ И ПОРОГОВОЕ ДЕКОДИРОВАНИЕ
- 6.9. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- 6.10. КОДИРОВАНИЕ В КАНАЛАХ С ПАКЕТАМИ ОШИБОК
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 6А
- ПРИЛОЖЕНИЕ 6Б
- 7. ДИСКРЕТНЫЕ ПО ВРЕМЕНИ КАНАЛЫ БЕЗ ПАМЯТИ
- 7.2. ОТСУТСТВИЕ ОГРАНИЧЕНИЙ НА ВХОДЕ
- 7.4. АДДИТИВНЫЙ ШУМ И АДДИТИВНЫЙ ГАУССОВ ШУМ
- 7.5. ПАРАЛЛЕЛЬНЫЕ КАНАЛЫ С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ
- ИТОГИ И ВЫВОДЫ
- 8. НЕПРЕРЫВНЫЕ КАНАЛЫ
- 8.1. ОРТОНОРМАЛЬНЫЕ РАЗЛОЖЕНИЯ СИГНАЛОВ И БЕЛЫЙ ГАУССОВ ШУМ
- Гауссовские случайные процессы
- Взаимная информация для каналов с непрерывным временем
- 8.2. БЕЛЫЙ ГАУССОВ ШУМ И ОРТОГОНАЛЬНЫЕ СИГНАЛЫ
- Вероятность ошибки для двух кодовых слов
- Вероятность ошибки для ортогональных кодовых слов
- 8.3. ЭВРИСТИЧЕСКОЕ ИЗУЧЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ КАНАЛА С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ И ОГРАНИЧЕНИЯМИ НА ПОЛОСУ ЧАСТОТ
- 8.4. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ФИЛЬТРОВ И НЕБЕЛЫЙ ШУМ
- Профильтрованный шум и разложение Карунена — Лоэва
- Идеальные фильтры нижних частот
- 8.5. КАНАЛЫ С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ И СИГНАЛАМИ НА ВХОДЕ, ОГРАНИЧЕННЫМИ ПО МОЩНОСТИ И ПО ЧАСТОТЕ
- 8.6. ДИСПЕРГИРУЮЩИЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- ИТОГИ И ВЫВОДЫ
- 9. КОДИРОВАНИЕ ИСТОЧНИКА С ЗАДАННЫМ КРИТЕРИЕМ ВЕРНОСТИ
- 9.2. ДИСКРЕТНЫЕ ИСТОЧНИКИ БЕЗ ПАМЯТИ И МЕРЫ ИСКАЖЕНИЯ ОТДЕЛЬНОЙ БУКВЫ
- 9.3. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ ИСТОЧНИКОВ ПРИ ЗАДАННОМ КРИТЕРИИ ВЕРНОСТИ
- 9.4. ВЫЧИСЛЕНИЕ R(d)
- 9.5. МОДИФИКАЦИЯ ОБРАЩЕНИЯ ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ КАНАЛА С ШУМАМИ
- 9.6. ДИСКРЕТНЫЕ ПО ВРЕМЕНИ ИСТОЧНИКИ С НЕПРЕРЫВНЫМИ АМПЛИТУДАМИ
- 9.7. ГАУССОВСКИЕ ИСТОЧНИКИ С КВАДРАТИЧНО-РАЗНОСТНЫМ ИСКАЖЕНИЕМ
- Источники, порождающие гауссовские случайные процессы
- 9.8. ДИСКРЕТНЫЕ ЭРГОДИЧЕСКИЕ ИСТОЧНИКИ
- ИТОГИ И ВЫВОДЫ
- ПРИМЕЧАНИЯ РЕДАКТОРОВ