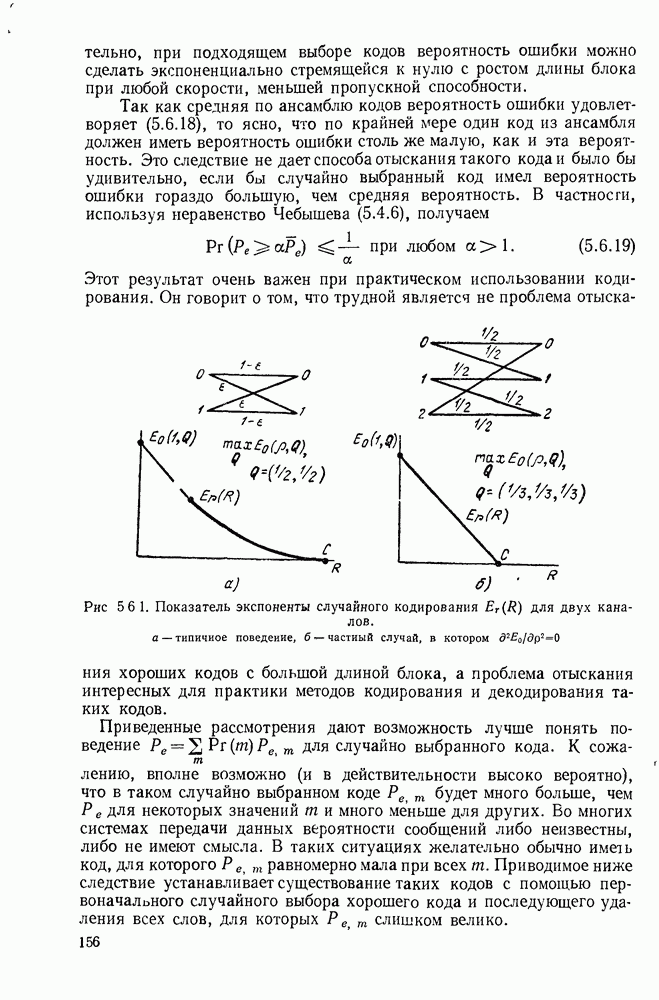
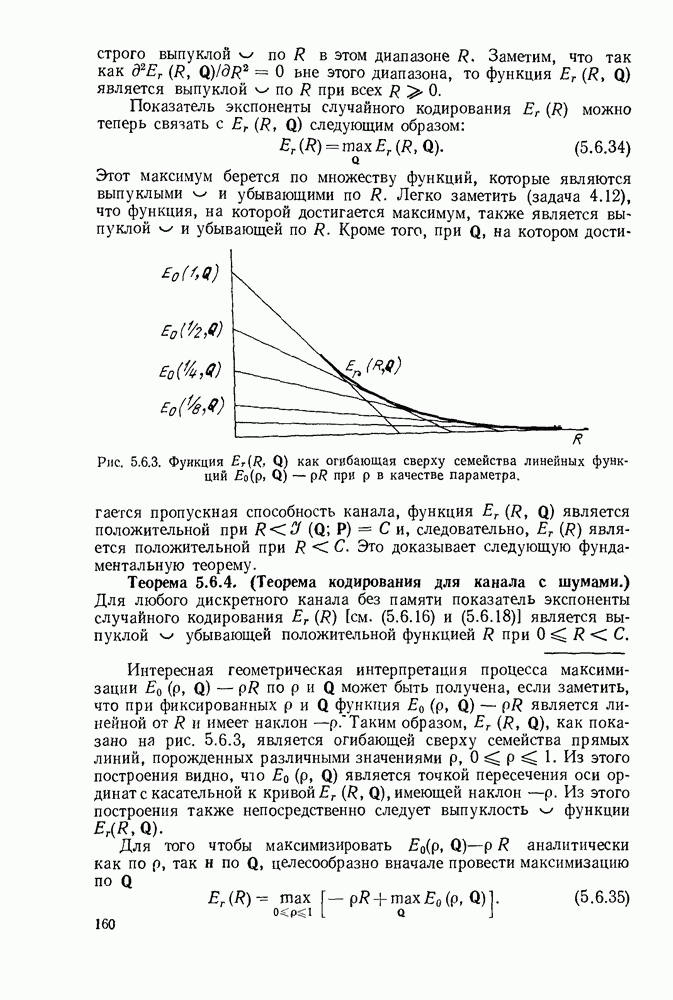
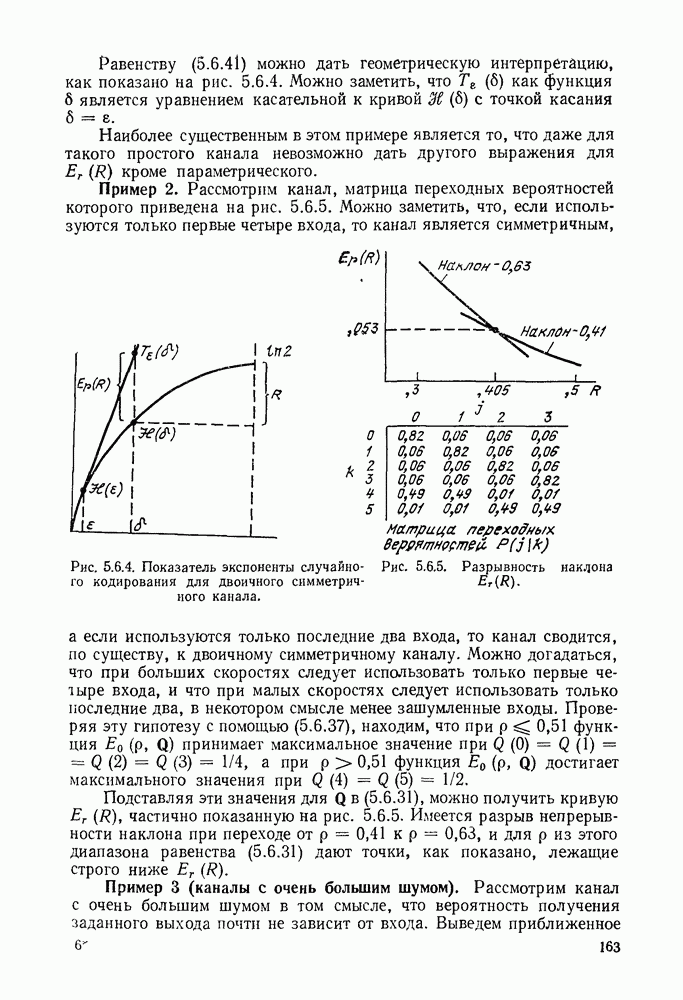
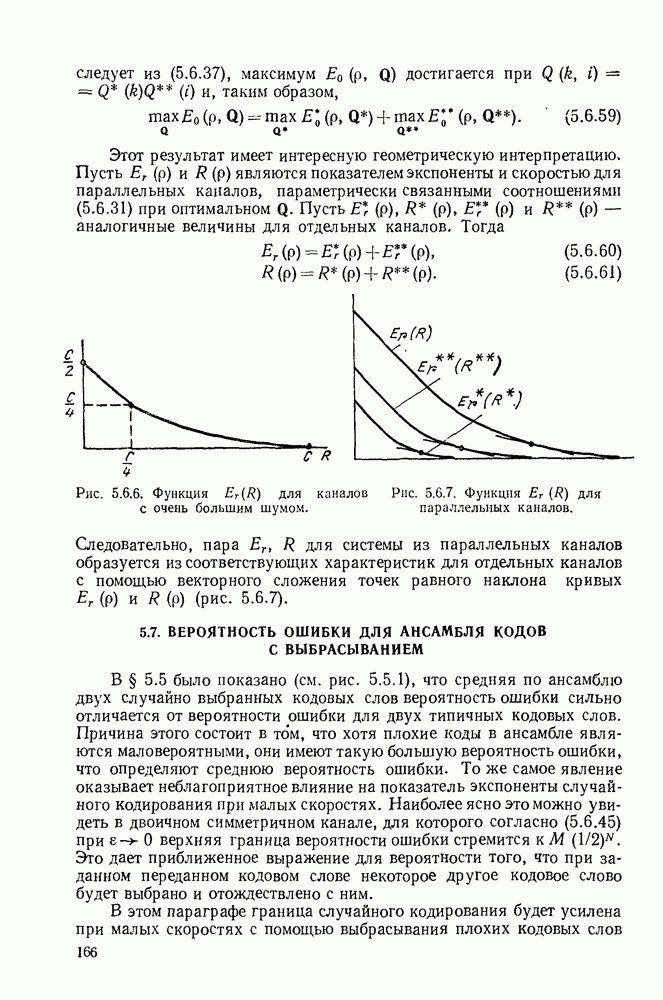
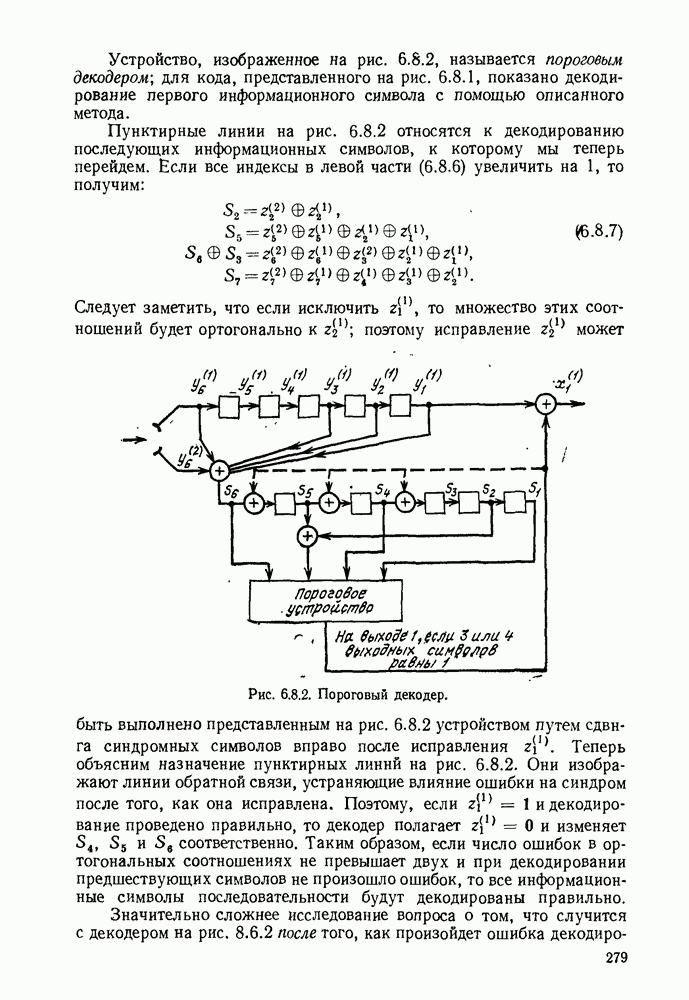
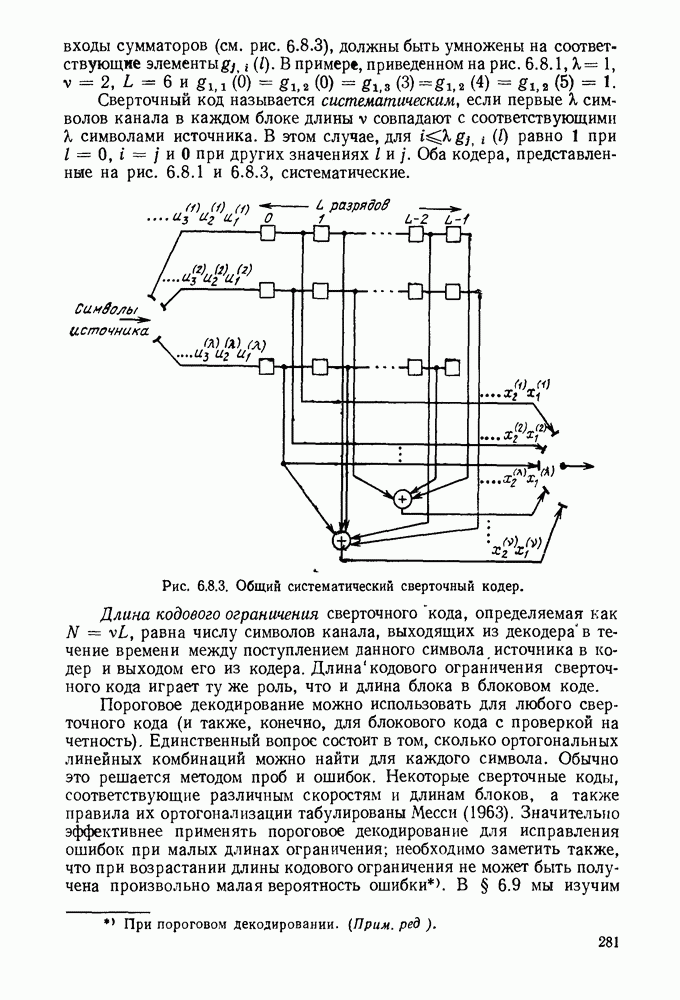
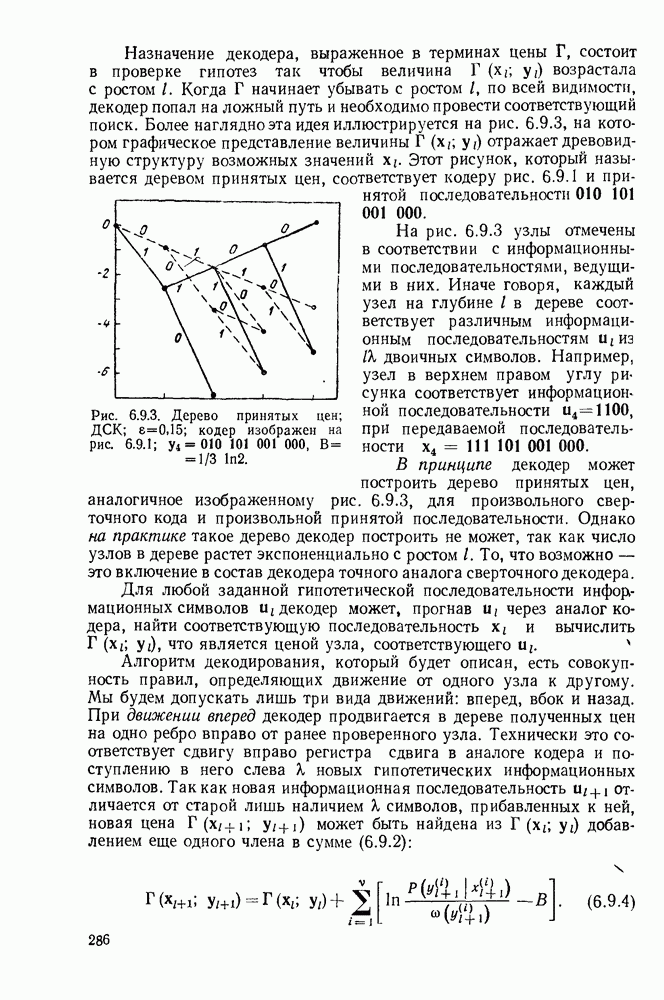
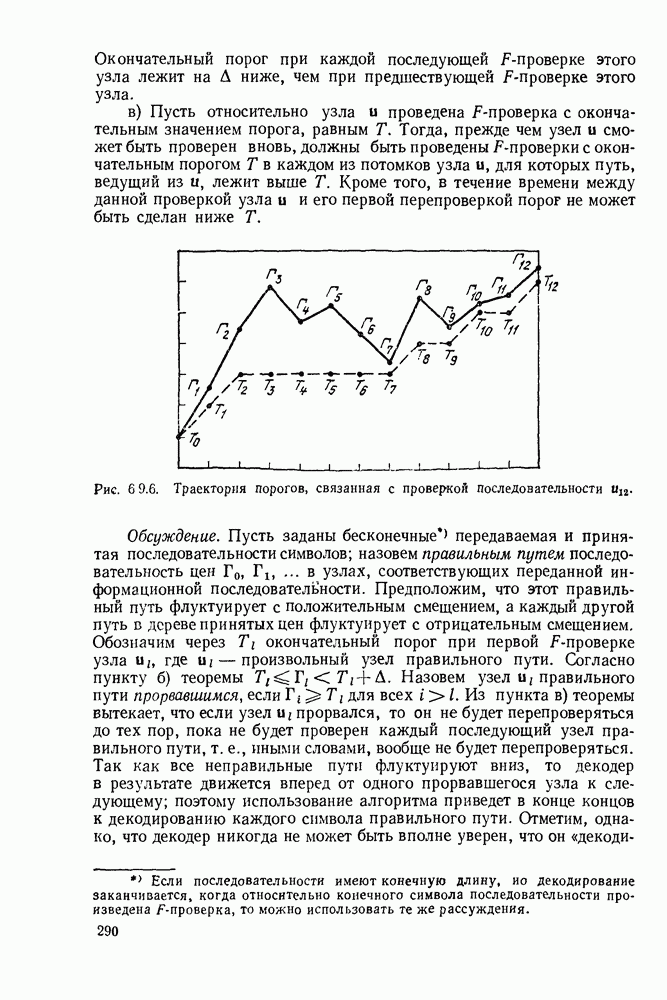
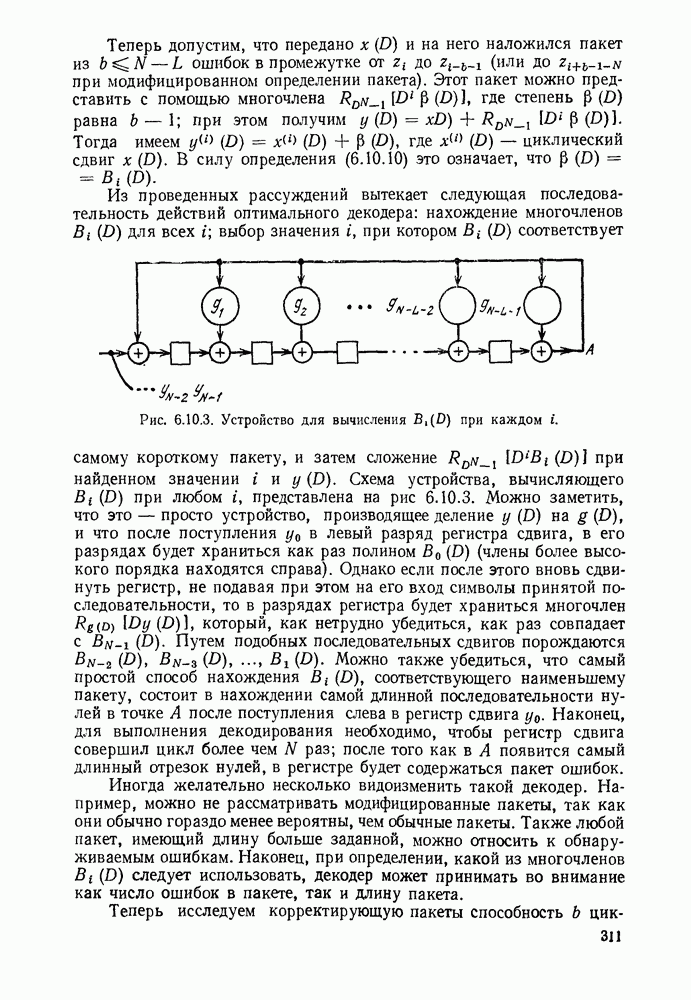
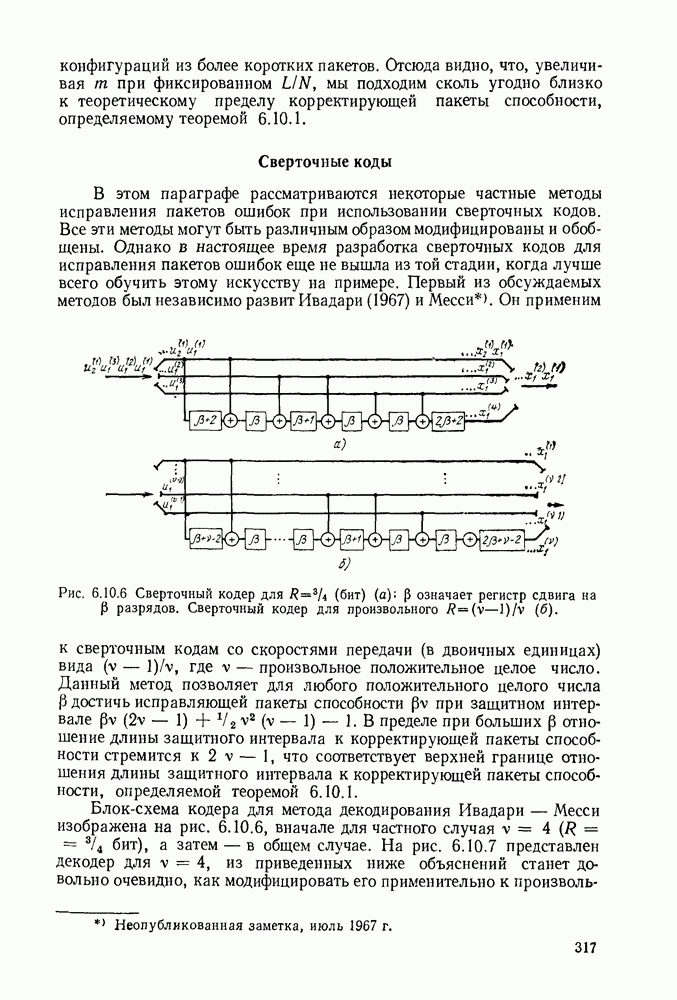
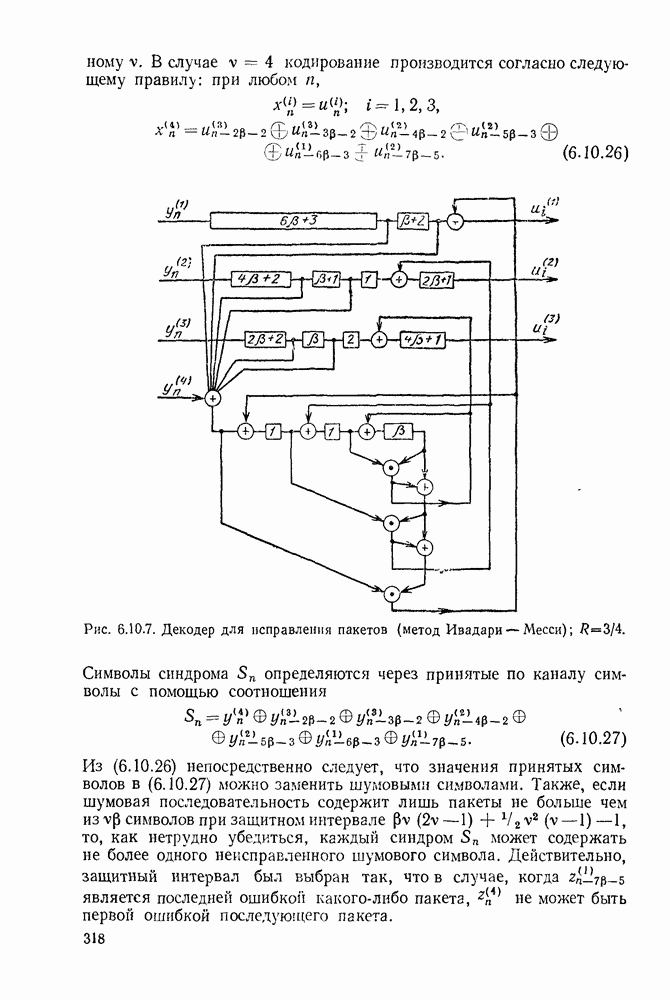
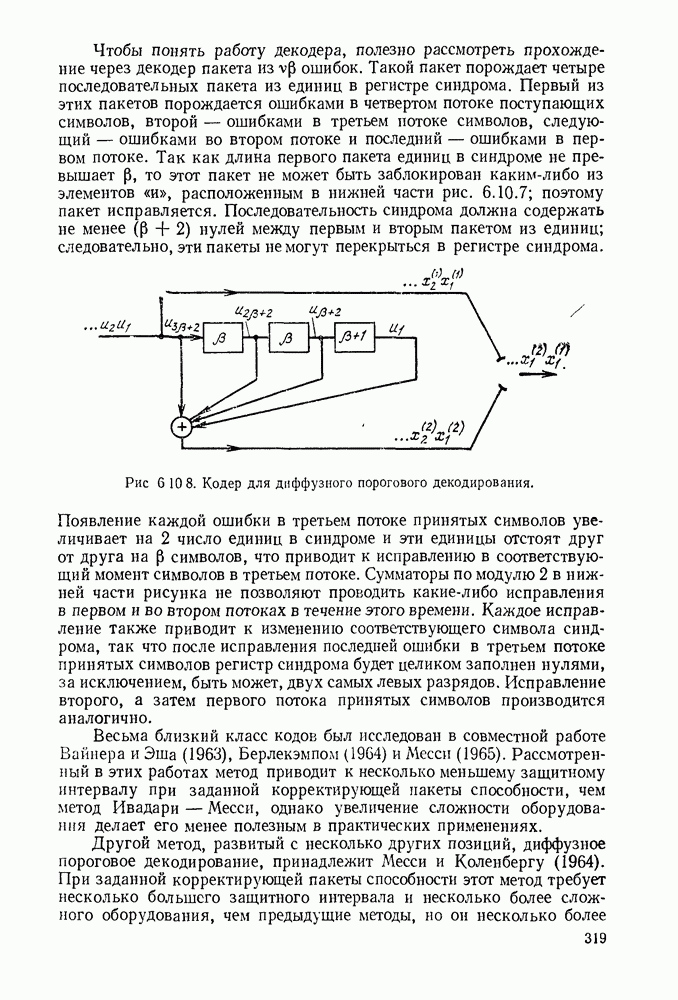
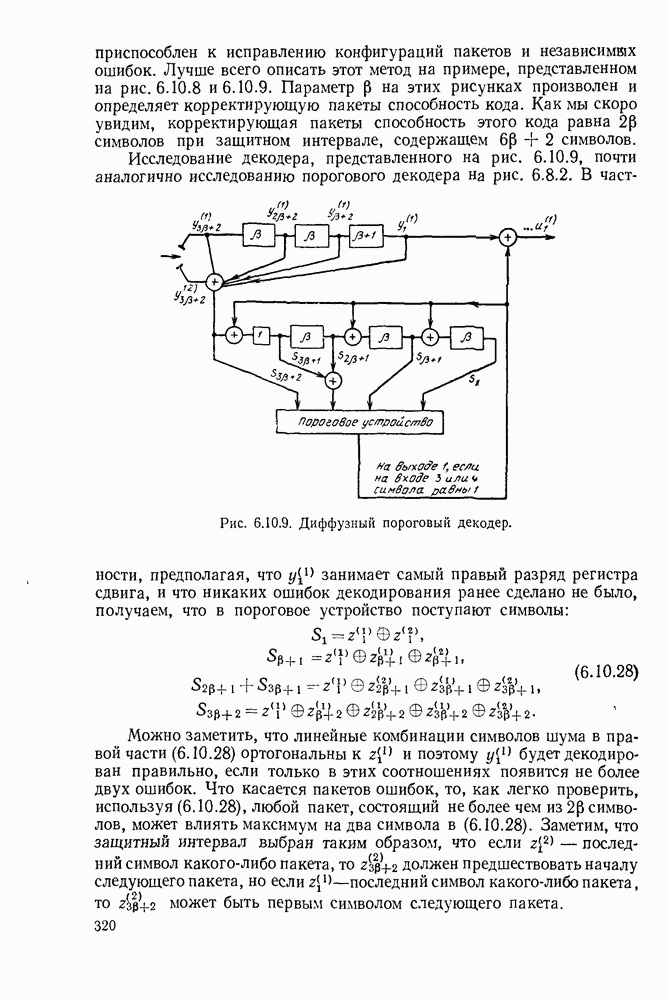
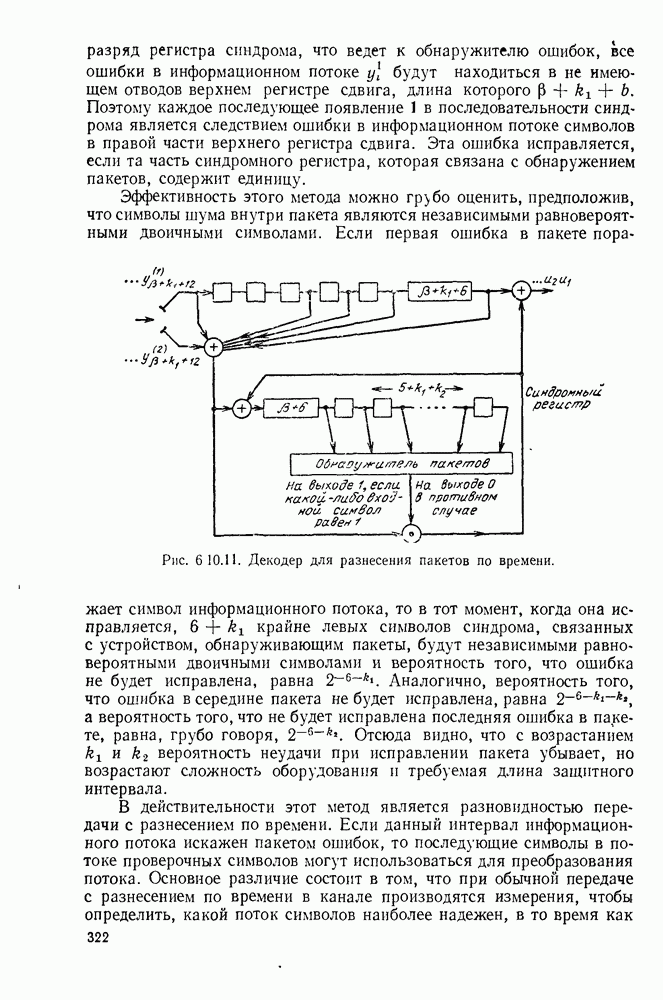
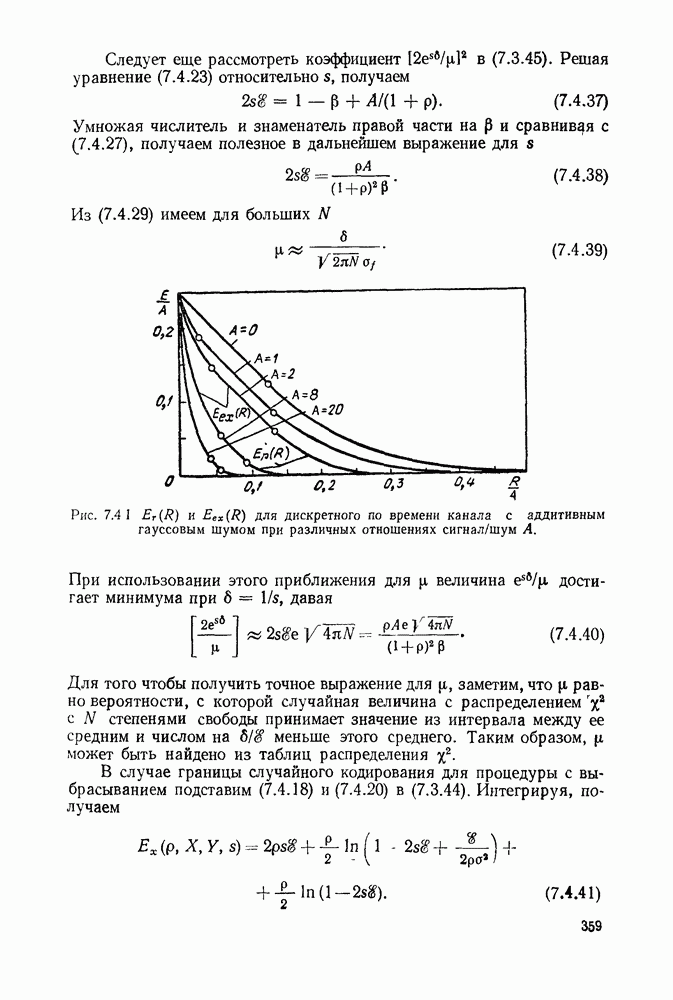
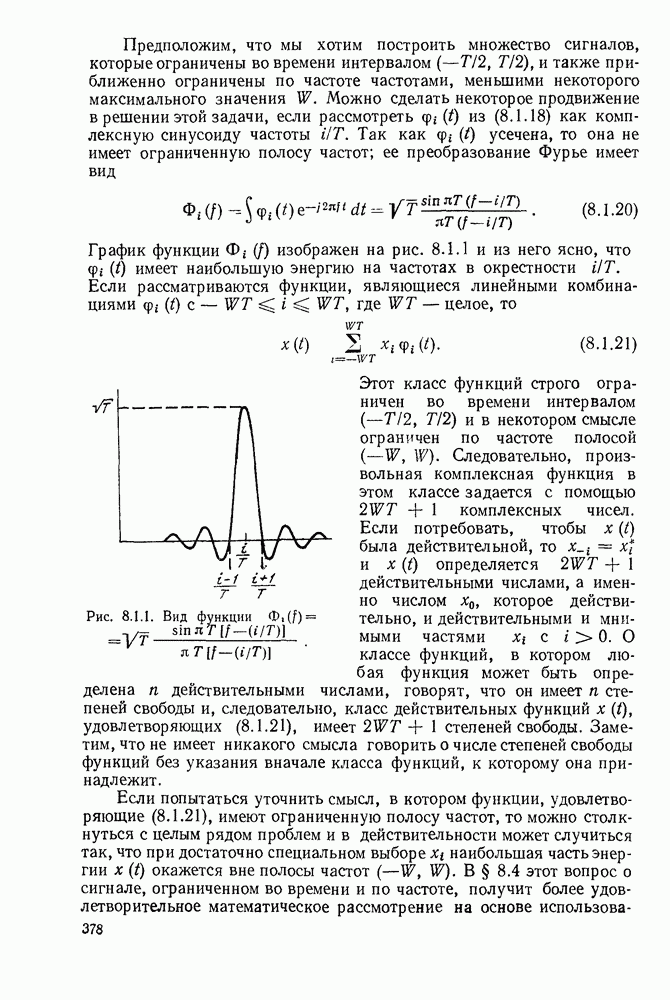
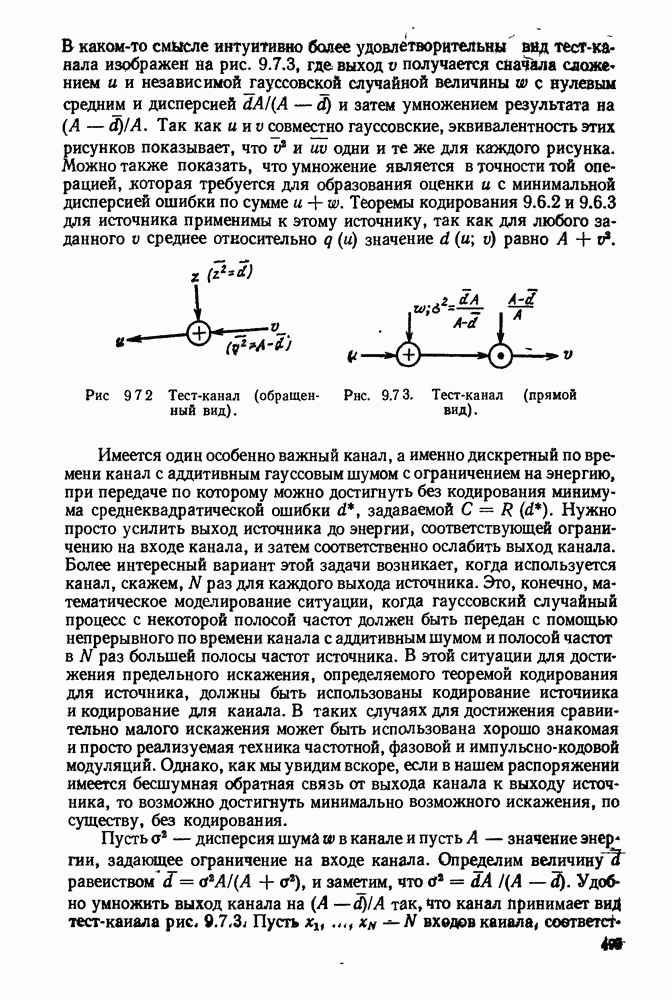
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
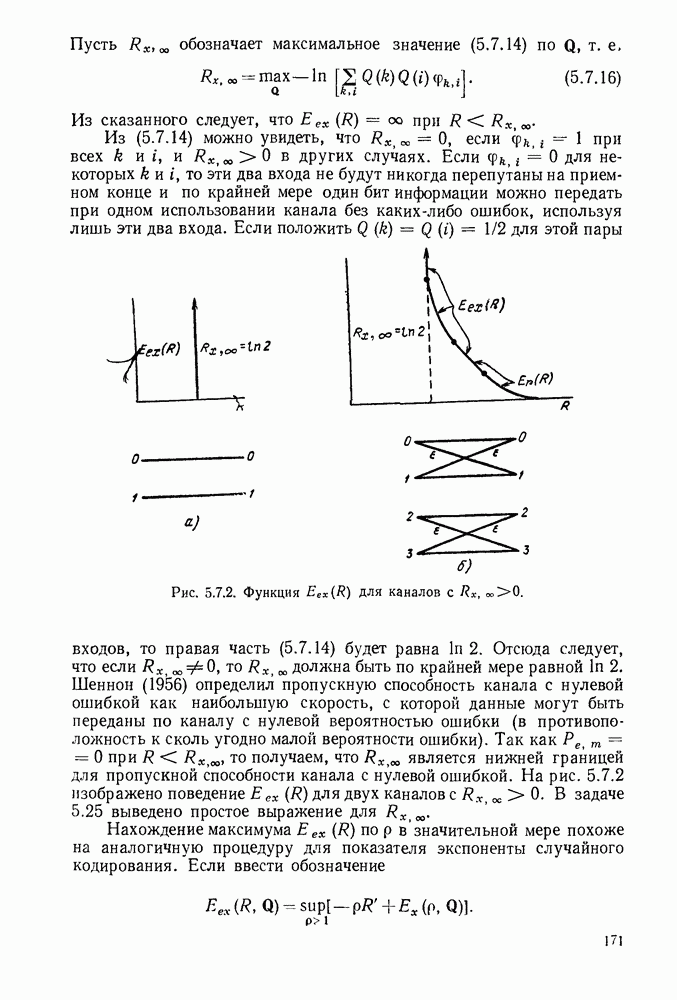
9.5. МОДИФИКАЦИЯ ОБРАЩЕНИЯ ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ КАНАЛА С ШУМАМИ
Как было уже отмечено, функция искажения

при  является приемлемой мерой искажения для изучения ошибок при воспроизведении выхода источника. Действительно, средняя вероятность ошибки на букву источника
является приемлемой мерой искажения для изучения ошибок при воспроизведении выхода источника. Действительно, средняя вероятность ошибки на букву источника  которая изучалась в гл. 4, является просто средним искажением на букву для указанной выше меры искажения. В этом параграфе вычисляется
которая изучалась в гл. 4, является просто средним искажением на букву для указанной выше меры искажения. В этом параграфе вычисляется  для произвольного дискретного источника без памяти и этой меры искажения и, таким образом, отыскивается минимальная вероятность ошибки на букву источника, которая может быть достигнута для скоростей источника, больших пропускной способности. Будет показано, что нижняя граница
для произвольного дискретного источника без памяти и этой меры искажения и, таким образом, отыскивается минимальная вероятность ошибки на букву источника, которая может быть достигнута для скоростей источника, больших пропускной способности. Будет показано, что нижняя граница  приведенная в гл. 4, равна фактически минимуму вероятности ошибки для некоторого диапазона пропускных способностей каналов, меньших энтропии источника. Это вычисление будет иметь некоторый дополнительный смысл, так как будет показывать, как
приведенная в гл. 4, равна фактически минимуму вероятности ошибки для некоторого диапазона пропускных способностей каналов, меньших энтропии источника. Это вычисление будет иметь некоторый дополнительный смысл, так как будет показывать, как
результаты последней главы могут быть применены. Неравенства, задающие ограничения

упрощаются для этой меры искажения и имеют вид

Из симметрии следует, что все эти неравенства могут быть удовлетворены с равенством, если положить все  равными одному и тому же значению, скажем
равными одному и тому же значению, скажем  Тогда
Тогда

Используя это  в нижней границе (9.4.10), получаем
в нижней границе (9.4.10), получаем

Тогда для всех  имеем
имеем

Правая часть максимизируется по  в результате давая точную границу при
в результате давая точную границу при  удовлетворяющем равенству
удовлетворяющем равенству

Подставляя (9.5.7) в (9.5.5) и производя преобразования, выводим

где

В соединении с теоремой 9.2.2 результат (9.5.8) эквивалентен для дискретных источников без памяти обращению теоремы кодирования для канала с шумом, т. е. теореме 4.3.4. Для того чтобы достигнуть вероятность ошибки на символ источника, равную  канал должен иметь пропускную способность, по крайней мере, равную правой части (9.5.8), или, что эквивалентно, для канала такой пропускной способности,
канал должен иметь пропускную способность, по крайней мере, равную правой части (9.5.8), или, что эквивалентно, для канала такой пропускной способности,  нижняя граница вероятности ошибки на символ.
нижняя граница вероятности ошибки на символ.
Теперь найдем условия, при выполнении которых (9.5.8) удовлетворяется и переходит в равенство. Из теоремы 9.4.1 следует, что (9.5.4) удовлетворяется с равенством, если для (9.5.7) существует решение с  которое для этой меры искажения принимает вид
которое для этой меры искажения принимает вид

Для 

Все со  неотрицательны, если
неотрицательны, если

Следовательно, (9.5.4) удовлетворяется с равенством для всех достаточно больших  Так как для каждого
Так как для каждого 

имеет с кривой  по крайней мере, одну общую точку, и так как эта точка задается (9.5.6) для всех
по крайней мере, одну общую точку, и так как эта точка задается (9.5.6) для всех  удовлетворяющих (9.5.12), то имеем
удовлетворяющих (9.5.12), то имеем

для

где (9.5.14) вытекает из (9.5.12) и (9.5.7) и где  наименьшее значение
наименьшее значение  Из этого результата и теорем 9.2.2 и 9.3.1 получаем следующую теорему.
Из этого результата и теорем 9.2.2 и 9.3.1 получаем следующую теорему.
Теорема 9.5.1. Пусть задан дискретный источник без памяти с энтропией  нат, с алфавитом объема К и минимальной вероятностью буквы
нат, с алфавитом объема К и минимальной вероятностью буквы  и пусть задано, что источник связан с адресатом дискретным каналом без памяти с пропускной способностью С (в натах на символ источника), тогда для любого
и пусть задано, что источник связан с адресатом дискретным каналом без памяти с пропускной способностью С (в натах на символ источника), тогда для любого  вероятность ошибки на символ источника
вероятность ошибки на символ источника  может быть всегда достигнута с помощью соответствующего кодирования, если
может быть всегда достигнута с помощью соответствующего кодирования, если

и никакими способами не может быть достигнута, если

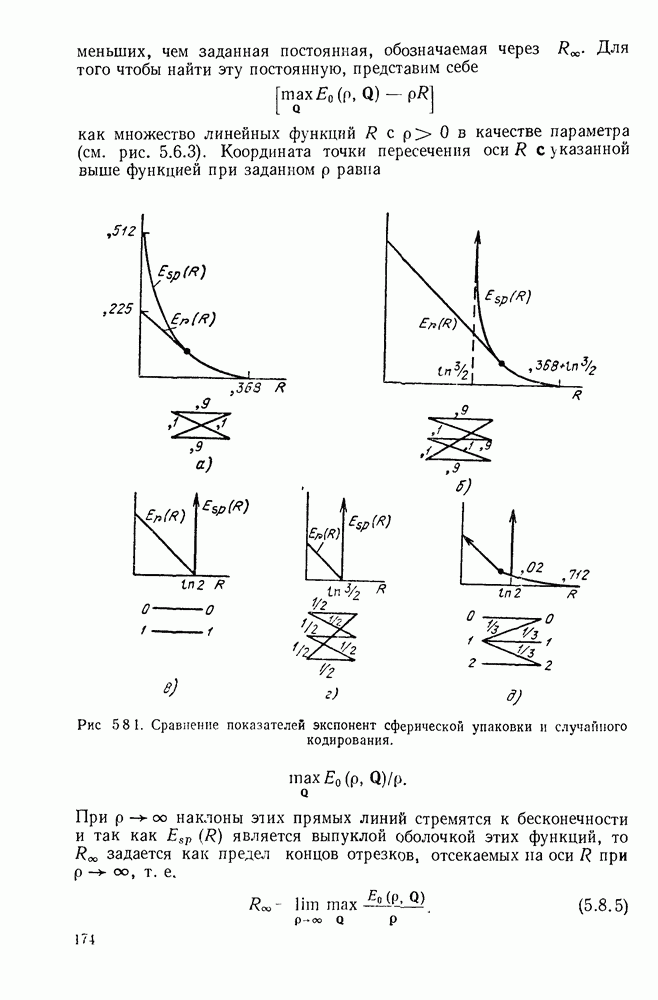
Для простоты в теореме рассматриваются лишь дискретные каналы без памяти. Она, очевидно, остается справедливой всегда, когда С может быть выражена как максимум средней взаимной информации и вместе с тем интерпретирована с помощью теоремы кодирования. Весьма примечательно, что этот минимум вероятности ошибки может быть однозначно определен с помощью столь малого числа параметров.
Теперь вычислим  для больших значений
для больших значений  Для простоты обозначений предположим, что вероятности букв упорядочены
Для простоты обозначений предположим, что вероятности букв упорядочены

Как из физических соображений, так и из рассмотрения выражения (9.5.11) можно предположить, что если какая-либо из выходных вероятностей равна 0, то она должна относиться к тем буквам, которые соответствуют наименее вероятным входам. Таким образом, мы принимаем, что для некоторого  которое будет выбрано позднее, со
которое будет выбрано позднее, со  при
при  и
и  при
при  Для
Для  равенство (9.5.10) принимает вид
равенство (9.5.10) принимает вид

Неравенство  задающее ограничение, должно удовлетворяться с равенством при —1. Следовательно, все
задающее ограничение, должно удовлетворяться с равенством при —1. Следовательно, все  должны быть одни и те же, скажем
должны быть одни и те же, скажем  при
при  при
при  Находя выражение, задающее ограничение для
Находя выражение, задающее ограничение для  и используя (9.5.18), получаем
и используя (9.5.18), получаем

где 
Из (9 5.18) видим, что  и ограничение
и ограничение  имеет место для
имеет место для  если
если

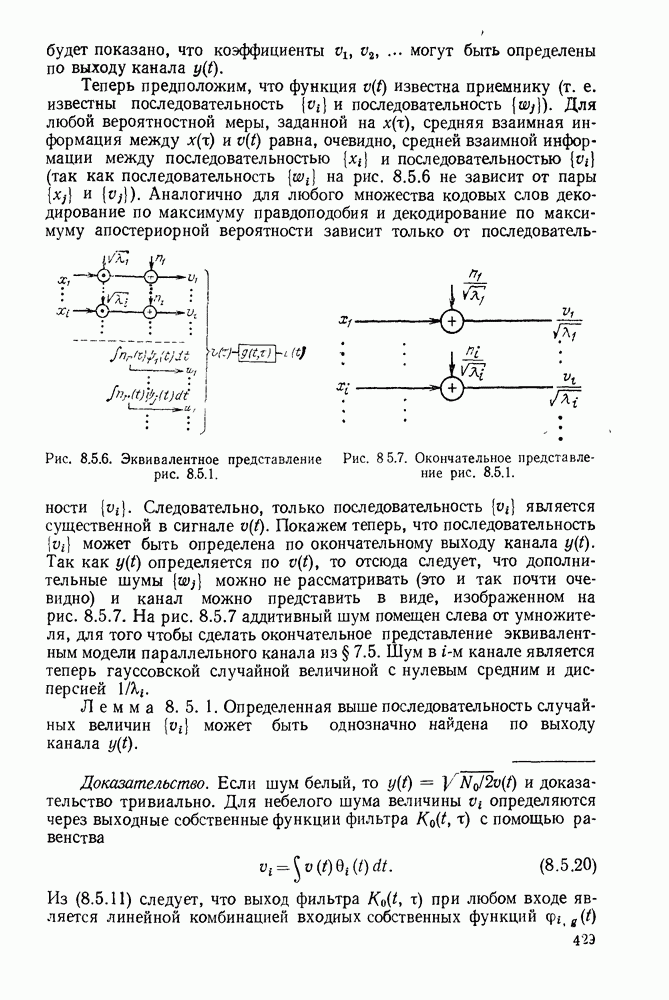
Вектор  задаваемый (9 5 18) и (9.5 20), максимизирует выражение
задаваемый (9 5 18) и (9.5 20), максимизирует выражение  если все
если все  определяемые (9.5.10), неотрицательны. Так как
определяемые (9.5.10), неотрицательны. Так как  то это требует только, чтобы
то это требует только, чтобы

Следовательно, для области  где (9 5 21) и (9.5 22) удовлетворяются, заданное
где (9 5 21) и (9.5 22) удовлетворяются, заданное  приводит к соотношению
приводит к соотношению

Теперь, зная  в некоторой области
в некоторой области  определяем
определяем  в соответствующей области наклонов Параметр
в соответствующей области наклонов Параметр  связан с
связан с  соотношением
соотношением

Для  , связанных (9.5.24), имеем
, связанных (9.5.24), имеем

После некоторых преобразований это выражение приводится к виду

где  энтропия редуцированного ансамбля с йераятйостймй
энтропия редуцированного ансамбля с йераятйостймй  определяется равенством
определяется равенством

Подставляя (9.5.24) в (9.5.21) и (9.5.22), находим, что это решение справедливо для заданного  если
если

Заметим, что для  нижняя граница для
нижняя граница для  совпадает с верхней границей для
совпадает с верхней границей для  если
если  удовлетворяет (9.5.13). Также верхняя граница для
удовлетворяет (9.5.13). Также верхняя граница для  при каком-либо значении
при каком-либо значении  (отличном от К— 1) совпадает с нижней границей при соседнем значении, меньшем
(отличном от К— 1) совпадает с нижней границей при соседнем значении, меньшем 
Наконец, верхняя граница для  при
при  равна
равна  так что для любого
так что для любого  большего чем то значение, для которого (9.5.13) задает
большего чем то значение, для которого (9.5.13) задает  определяет
определяет  для которого (9.5.25) задает
для которого (9.5.25) задает 
Имеется простое физическое истолкование (9.5.25). Для заданного  мы пытаемся представить источник, используя только буквы адресата от 0 до
мы пытаемся представить источник, используя только буквы адресата от 0 до  вероятностью
вероятностью  источник порождает одну из букв от
источник порождает одну из букв от  до
до  при этом искажение равно единице и нет никакого смысла в затрате какой-либо информации на эти буквы. Следовательно, минимум средней взаимной информации равняется умноженному на
при этом искажение равно единице и нет никакого смысла в затрате какой-либо информации на эти буквы. Следовательно, минимум средней взаимной информации равняется умноженному на  минимуму при условии появления какой-либо из букв от 0 до
минимуму при условии появления какой-либо из букв от 0 до  Из (9.5.26) следует, что
Из (9.5.26) следует, что  можно интерпретировать как минимум среднего искажения при условии появления одной из букв от 0 до
можно интерпретировать как минимум среднего искажения при условии появления одной из букв от 0 до  Для этого условного искажения член в скобках равен как раз минимуму условной средней взаимной информации, что можно было ожидать из (9.5.13).
Для этого условного искажения член в скобках равен как раз минимуму условной средней взаимной информации, что можно было ожидать из (9.5.13).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ РУССКОГО ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. СИСТЕМЫ СВЯЗИ И ТЕОРИЯ ИНФОРМАЦИИ
- 1.2. МОДЕЛИ ИСТОЧНИКОВ И КОДИРОВАНИЕ ДЛЯ ИСТОЧНИКОВ
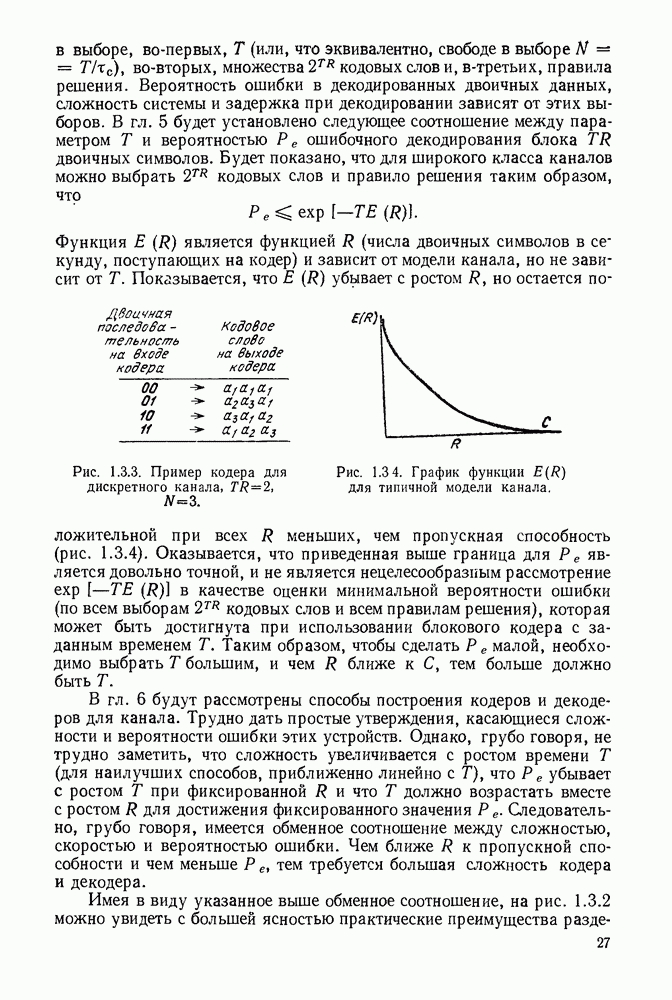
- 1.3. МОДЕЛИ КАНАЛОВ И КОДИРОВАНИЕ ДЛЯ КАНАЛОВ
- 2. МЕРА ИНФОРМАЦИИ
- 2.2. ОПРЕДЕЛЕНИЕ ВЗАИМНОЙ ИНФОРМАЦИИ
- 2.3. СРЕДНЯЯ ВЗАИМНАЯ ИНФОРМАЦИЯ И ЭНТРОПИЯ
- 2.4. ВЕРОЯТНОСТЬ И ВЗАИМНАЯ ИНФОРМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ АНСАМБЛЕЙ
- 2.5. ВЗАИМНАЯ ИНФОРМАЦИЯ ДЛЯ ПРОИЗВОЛЬНЫХ АНСАМБЛЕЙ
- 3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.1. КОДЫ С ФИКСИРОВАННОЙ ДЛИНОЙ
- 3.2. НЕРАВНОМЕРНЫЕ КОДОВЫЕ СЛОВА
- 3.3. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ ИСТОЧНИКА
- 3.4. ПРОЦЕДУРА ВЫБОРА ОПТИМАЛЬНОГО НЕРАВНОМЕРНОГО КОДА
- 3.5. ДИСКРЕТНЫЕ СТАЦИОНАРНЫЕ ИСТОЧНИКИ
- 3.6. МАРКОВСКИЕ ИСТОЧНИКИ
- 4. ДИСКРЕТНЫЕ КАНАЛЫ БЕЗ ПАМЯТИ И ПРОПУСКНАЯ СПОСОБНОСТЬ
- 4.2. ДИСКРЕТНЫЕ КАНАЛЫ БЕЗ ПАМЯТИ
- 4.3. ОБРАЩЕНИЕ ТЕОРЕМЫ КОДИРОВАНИЯ
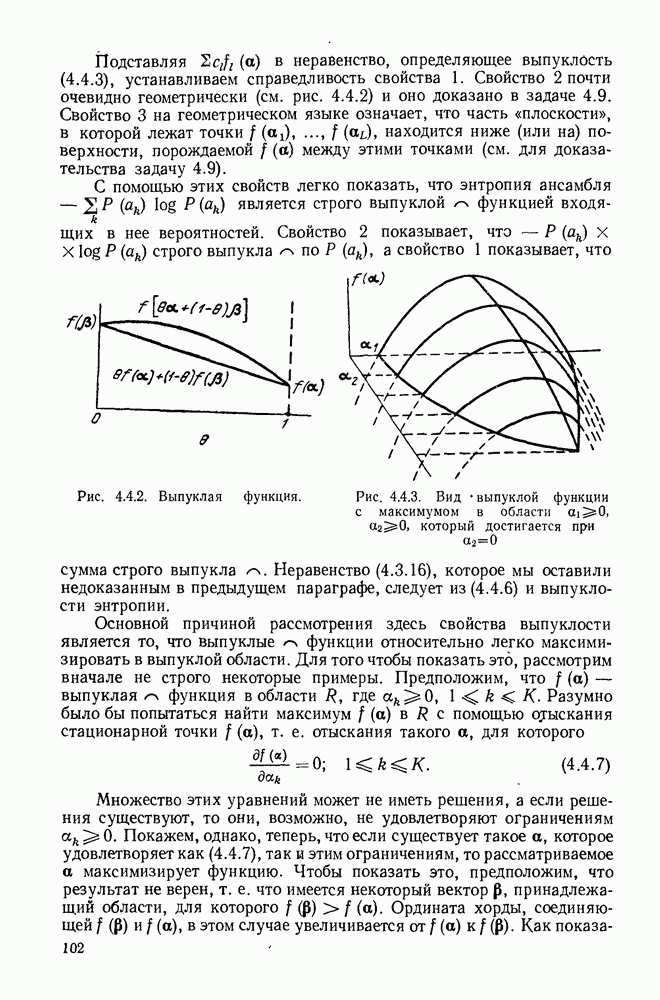
- 4.4. ВЫПУКЛЫЕ ФУНКЦИИ
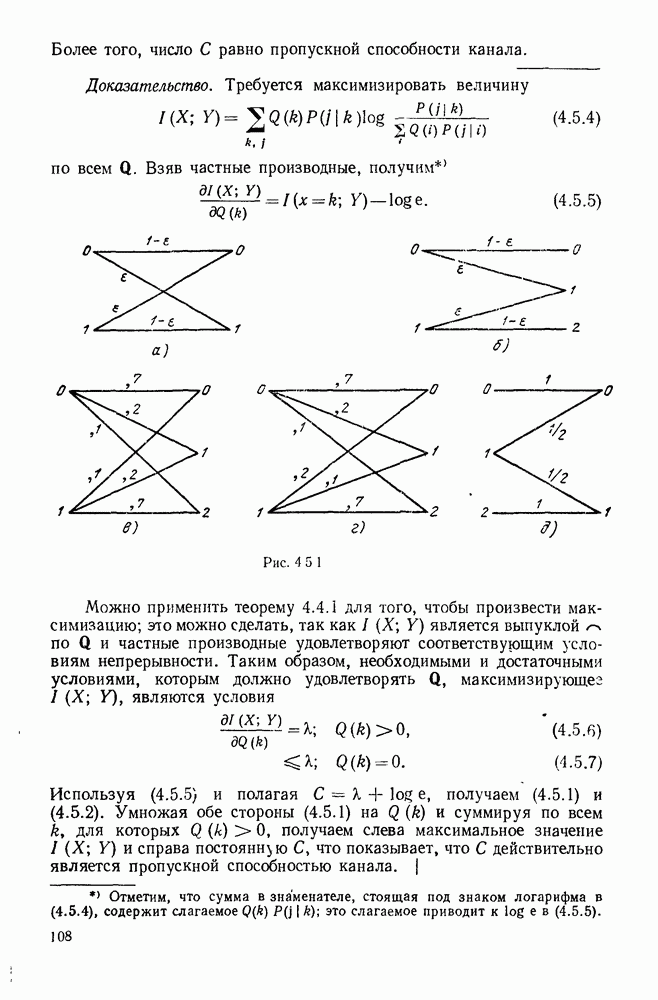
- 4.5. НАХОЖДЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ ДИСКРЕТНОГО КАНАЛА БЕЗ ПАМЯТИ
- 4.6. ДИСКРЕТНЫЕ КАНАЛЫ С ПАМЯТЬЮ
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 4А
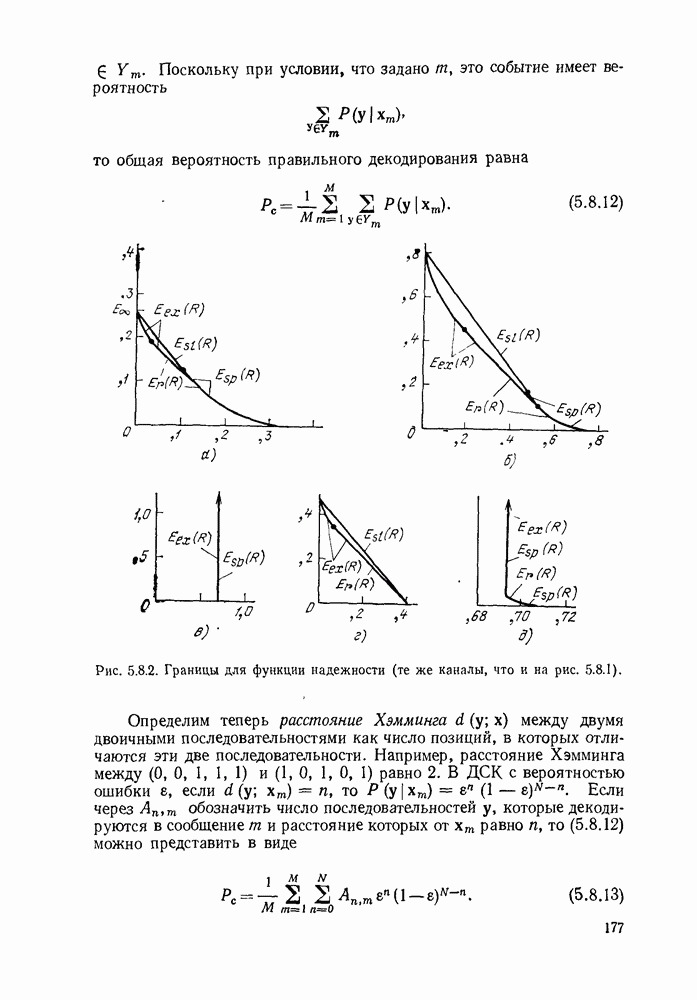
- 5. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КАНАЛА С ШУМАМИ
- 5.2. ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 5.3. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ ДВУХ КОДОВЫХ СЛОВ
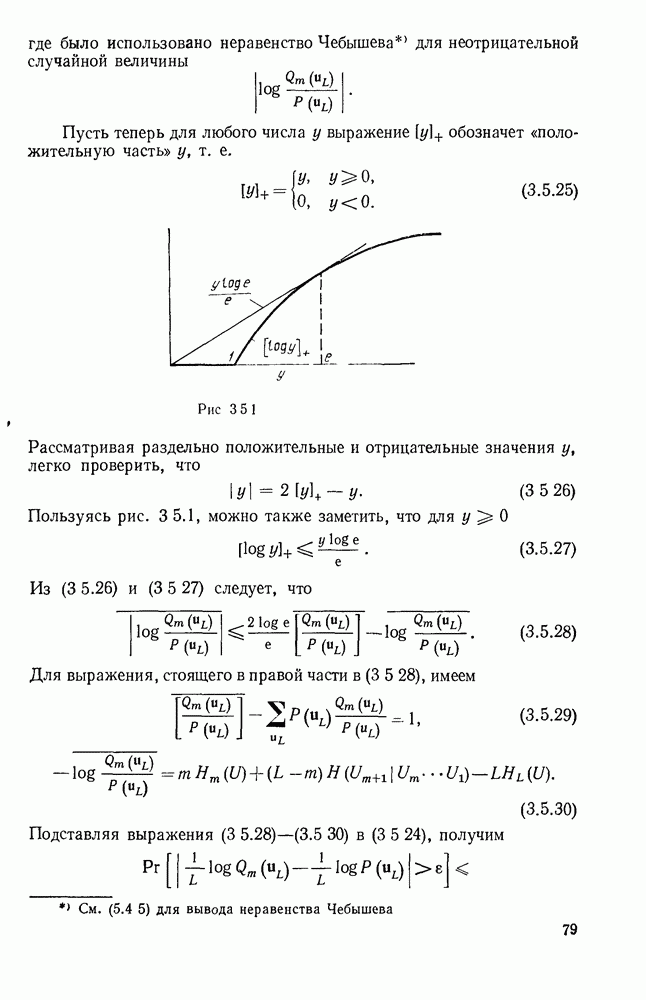
- 5.4. ОБОБЩЕННОЕ НЕРАВЕНСТВО ЧЕБЫШЕВА И ГРАНИЦА ЧЕРНОВА
- 5.5. СЛУЧАЙНЫЕ КОДОВЫЕ СЛОВА
- 5.6. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КОДА С ЧИСЛОМ СЛОВ, БОЛЬШИМ ДВУХ
- 5.7. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ АНСАМБЛЯ КОДОВ С ВЫБРАСЫВАНИЕМ
- 5.8. НИЖНИЕ ГРАНИЦЫ ДЛЯ ВЕРОЯТНОСТИ ОШИБКИ
- 5.9. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КАНАЛОВ С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЯ
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 5А
- ПРИЛОЖЕНИЕ 5Б
- 6. МЕТОДЫ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ
- 6.1. КОДЫ С ПРОВЕРКОЙ НА ЧЕТНОСТЬ
- 6.2. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ КОДОВ С ПРОВЕРКОЙ НА ЧЕТНОСТЬ
- 6.3. ТЕОРИЯ ГРУПП
- 6.4. ПОЛЯ И МНОГОЧЛЕНЫ
- 6.5. ЦИКЛИЧЕСКИЕ КОДЫ
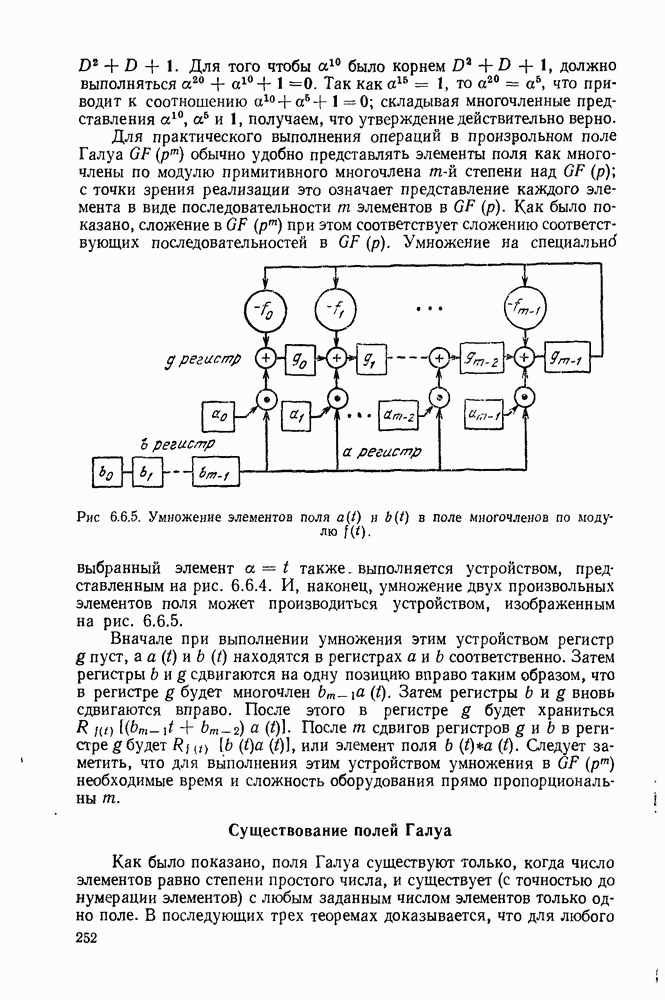
- 6.6. ПОЛЯ ГАЛУА
- Коды максимальной длины и коды Хэмминга
- Существование полей Галуа
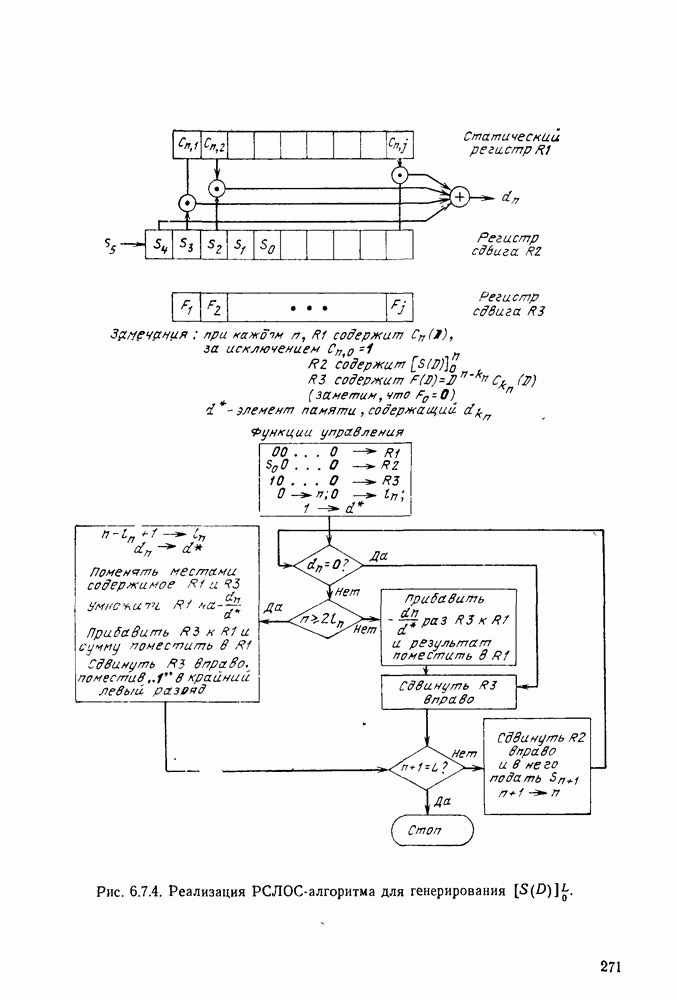
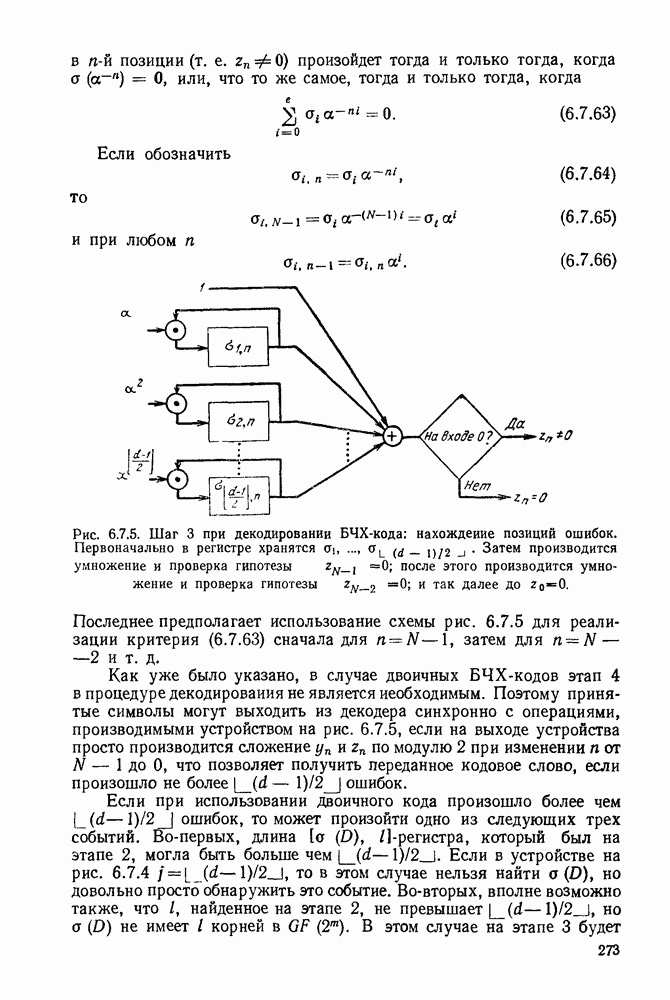
- 6.7. БЧХ-КОДЫ
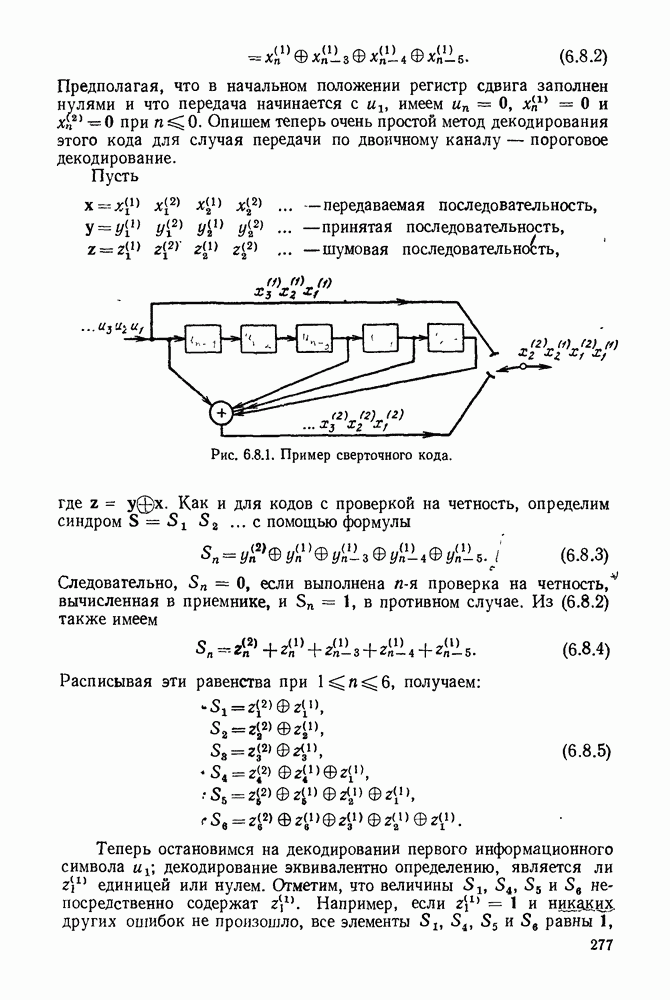
- 6.8. СВЕРТОЧНЫЕ КОДЫ И ПОРОГОВОЕ ДЕКОДИРОВАНИЕ
- 6.9. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- 6.10. КОДИРОВАНИЕ В КАНАЛАХ С ПАКЕТАМИ ОШИБОК
- ИТОГИ И ВЫВОДЫ
- ПРИЛОЖЕНИЕ 6А
- ПРИЛОЖЕНИЕ 6Б
- 7. ДИСКРЕТНЫЕ ПО ВРЕМЕНИ КАНАЛЫ БЕЗ ПАМЯТИ
- 7.2. ОТСУТСТВИЕ ОГРАНИЧЕНИЙ НА ВХОДЕ
- 7.4. АДДИТИВНЫЙ ШУМ И АДДИТИВНЫЙ ГАУССОВ ШУМ
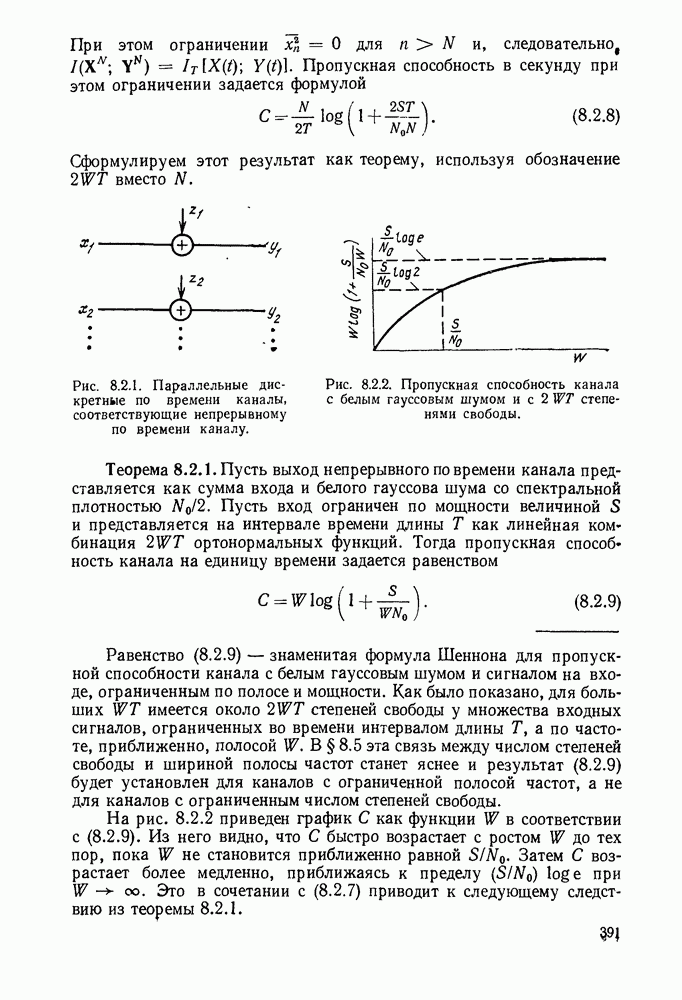
- 7.5. ПАРАЛЛЕЛЬНЫЕ КАНАЛЫ С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ
- ИТОГИ И ВЫВОДЫ
- 8. НЕПРЕРЫВНЫЕ КАНАЛЫ
- 8.1. ОРТОНОРМАЛЬНЫЕ РАЗЛОЖЕНИЯ СИГНАЛОВ И БЕЛЫЙ ГАУССОВ ШУМ
- Гауссовские случайные процессы
- Взаимная информация для каналов с непрерывным временем
- 8.2. БЕЛЫЙ ГАУССОВ ШУМ И ОРТОГОНАЛЬНЫЕ СИГНАЛЫ
- Вероятность ошибки для двух кодовых слов
- Вероятность ошибки для ортогональных кодовых слов
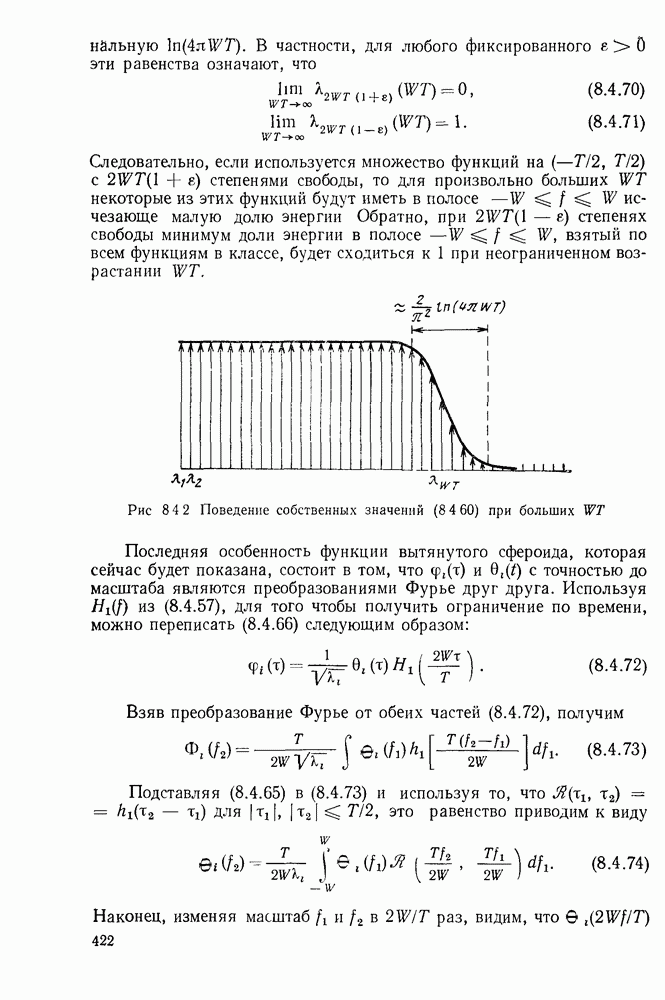
- 8.3. ЭВРИСТИЧЕСКОЕ ИЗУЧЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ КАНАЛА С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ И ОГРАНИЧЕНИЯМИ НА ПОЛОСУ ЧАСТОТ
- 8.4. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ФИЛЬТРОВ И НЕБЕЛЫЙ ШУМ
- Профильтрованный шум и разложение Карунена — Лоэва
- Идеальные фильтры нижних частот
- 8.5. КАНАЛЫ С АДДИТИВНЫМ ГАУССОВЫМ ШУМОМ И СИГНАЛАМИ НА ВХОДЕ, ОГРАНИЧЕННЫМИ ПО МОЩНОСТИ И ПО ЧАСТОТЕ
- 8.6. ДИСПЕРГИРУЮЩИЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- ИТОГИ И ВЫВОДЫ
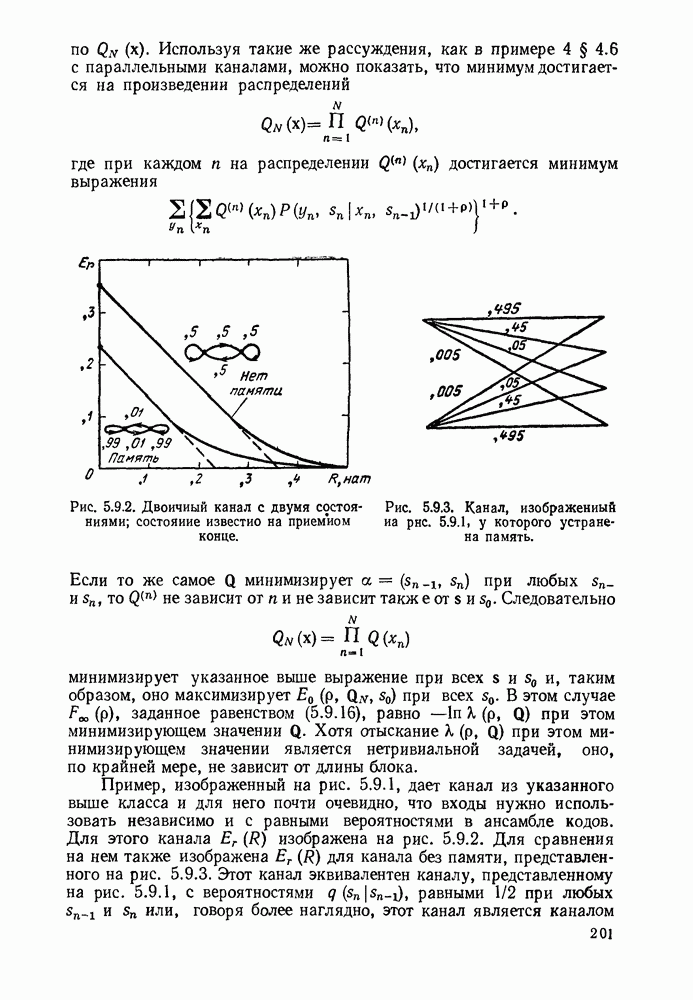
- 9. КОДИРОВАНИЕ ИСТОЧНИКА С ЗАДАННЫМ КРИТЕРИЕМ ВЕРНОСТИ
- 9.2. ДИСКРЕТНЫЕ ИСТОЧНИКИ БЕЗ ПАМЯТИ И МЕРЫ ИСКАЖЕНИЯ ОТДЕЛЬНОЙ БУКВЫ
- 9.3. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ ИСТОЧНИКОВ ПРИ ЗАДАННОМ КРИТЕРИИ ВЕРНОСТИ
- 9.4. ВЫЧИСЛЕНИЕ R(d)
- 9.5. МОДИФИКАЦИЯ ОБРАЩЕНИЯ ТЕОРЕМЫ КОДИРОВАНИЯ ДЛЯ КАНАЛА С ШУМАМИ
- 9.6. ДИСКРЕТНЫЕ ПО ВРЕМЕНИ ИСТОЧНИКИ С НЕПРЕРЫВНЫМИ АМПЛИТУДАМИ
- 9.7. ГАУССОВСКИЕ ИСТОЧНИКИ С КВАДРАТИЧНО-РАЗНОСТНЫМ ИСКАЖЕНИЕМ
- Источники, порождающие гауссовские случайные процессы
- 9.8. ДИСКРЕТНЫЕ ЭРГОДИЧЕСКИЕ ИСТОЧНИКИ
- ИТОГИ И ВЫВОДЫ
- ПРИМЕЧАНИЯ РЕДАКТОРОВ